Thông tin
Quiz

Lời giải bài toán bất đẳng thức, cực trị trong đề tuyển sinh lớp 10 môn Toán

Bài toán bất đẳng thức, cực trị (tìm giá trị lớn nhất – giá trị nhỏ nhất) luôn là bài toán khó nhất trong đề thi tuyển sinh vào lớp 10 môn Toán, đây là bài toán nhằm chọn lọc học sinh giỏi – xuất sắc môn Toán vào các lớp chuyên Toán tại các trường THPT chuyên.

Chủ đề:

Tài liệu ôn thi vào 10 môn Toán 110 tài liệu

Môn:

Môn Toán 1.3 K tài liệu

Thông tin:

177 trang 1 năm trước

Tác giả:

Nguyễn Vân

docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Lời giải bài toán bất đẳng thức, cực trị trong đề tuyển sinh lớp 10 môn Toán

133 67 lượt tải Tải xuống

THCS.TOANMATH.com

FB TRỊNH BÌNH

ĐÁP ÁN CÁC BÀI TOÁN BẤT ĐẲNG THỨC, CỰC TRỊ

TRONG ĐỀ CHUYÊN MÔN TOÁN GIAI ĐOẠN 2009-2019

NĂM HỌC 2019-2020

Câu 1: [TS10 Chuyên KHTN Hà Ni, 2019-2020]

Cho x, y là các s tha mãn:

4x 4y 17xy 5x 5y 1    

Tìm giá tr nh nht ca biu thc:

P 17x 17y 16xy  

Lời giải

Ta có:

   

4x 4y 17xy 5x 5y 1 4 x y 9xy 5 x y 1          

t

t x y, t 0  

, theo bng thc AM-GM, ta có:

 

xy .







9 2 2 2

4t t 5t 1 t



    

hay

2 2 2

x y .





Ta có:

 

P 17x 17y 16xy 17 x y 18xy     

 

25 25 2 2 2

17 x y 18 x y 6 4 2

4 4 4 5







       





Dy ra khi





Vy giá tr nh nht ca P là

6 4 2

Câu 2: [TS10 m Hà Ni, 2019-2020]

Cho các s thi, hãy tìm giá tr nh nht ca biu thc:

  

P xy x 2 y 6 13x 4y 26x 24y 46       

Lời giải

Ta có:

  

      

       

2 2 2 2

P xy x 2 y 6 13x 4y 26x 24y 46

x 2x y 6y 13 x 2x 4 y 6y 46

x 1 1 y 3 9 13 x 1 1 4 y 3 9 46

       

       

       

           

       

       

t

a x 1, b y 3   



      

2 2 2 2

2 2 2 2 2 2

P a 1 b 9 13 a 1 4 b 9 46

a b 9a b 9 13a 13 4b 36 46

       

        

THCS.TOANMATH.com

FB TRỊNH BÌNH

2 2 2 2

4a 3b a b 6

   



Dy ra khi

a 0 x 1 0

x 1,y 3

b 0 y 3 0

    

    



  



Vy giá tr nh nht ca P là 6.

Câu 3: [TS10 Chuyên Tin Hà Ni, 2019-2020]

a mãn:

ab bc ca abc 4   

1) Chng minh rng:

1 1 1

a 2 b 2 c 2

  

  

2) Tìm giá tr nh nht:

     

2 2 2 2 2 2

1 1 1

2 a b 4 2 b c 4 2 c a 4

  

     

Lời giải

1) Ta có:

            

     

1 1 1

a 2 b 2 c 2

b 2 c 2 a 2 c 2 b 2 a 2 a 2 b 2 c 2

ab bc ca 4 a b c 12 abc 2 ab bc ca 4 a b c 8

4 ab bc ca.

  

  

            

              

   

ng thc cu thit, các phép bi

ng thc chng minh.

2) Vng thc:

 

2 x y x y  

(*)

1 1 1 1

x y 4 x y











(**)

Tht vy:

   

* x y 0  



     

* * x y 4xy x y 0

4xy x y



       





Các bng thc (*), (**) xy ra d

Ln t áp dng (*) và (**) ta có:

 

   

1 1 1 1 1 1

a b 4 4 a 2 b 2

a 2 b 2

2 a b 4



   



   

  





:

   

2 2 2 2

1 1 1 1 1 1 1 1

;;

4 b 2 c 2 4 c 2 a 2

2 b c 4 2 c a 4

   

   

   

   

   

   

Cng theo v c:

THCS.TOANMATH.com

FB TRỊNH BÌNH

1 1 1 1 1 1

P .1 .

2 a 2 b 2 c 2 2 2



    



  



y ra khi a = b = c

Vy giá tr nh nht ca P là

Câu 4: [TS10 Chuyên Toán Hà Ni, 2019-2020]

Cho

K ab 4ac 4bc  

vi

a,b,c 0

và a + b + 2c = 1.

1) Chng minh rng:



2) Tìm giá tr ln nht ca K.

Lời giải

1) S dng bng thc AM-GM ta có:

b 2c a b 2c 1 1

4bc 2 2 4bc

2 2 2 2

      

      

   

   

Mt khác:

a,b,c 0 K ab 4ac 4bc 4bc

        

Dy ra khi

a 0,b ,c .

  

Cách khác:

Ta có:

    

 

K ab 4c a b ab 2 1 a b a b

ab 2 a b 2 a b

2b a 2 b 2a 2a

       

    

    



   

2b a 2 b 2a 2a K 0 *     

 tn ti có 2 nghim:

 

0 a 2 4.2. 2a 2a K 0

8K 20a 17a 4.

        

   

Vì

a,b,c 0

và

a b 2c 1 0 a 1     



   

2a 17a a 20 17a a 20 17.1 3a 0      



8K 4 K

    

Dy ra khi

a 0,b ,c .

  

2) S dng bng thc AM-GM ta có:

 

a b 2c 1

a b 2c .

   

  





THCS.TOANMATH.com

FB TRỊNH BÌNH

Mt khác:

 

a b 2c

a,b,c 0 K ab 4ac 4bc ab 4ac 2ab 4ac 2a b 2c .



            

Dy ra khi:

a b 2c,a b 2c 1,bc 0,ab 0 a ,b 0,c

          

Vy giá tr ln nht ca K là

Câu 5: [TS10 Chuyên Thái Bình, 2019-2020]

Cho các s thc a, b, c tha mãn

0 a,b,c

2a 3b 4c 3











  



. Tìm giá tr nh nht ca biu

thc

     

2 9 8

a 3b 4c 2 b 4a 8c 3 c 2a 3b 1

  

     

Lời giải

Ta có:

     

   

 

2 2 2

2 9 8

a 3b 4c 2 b 4a 8c 3 c 2a 3b 1

2 9 8

a 3 2a 2 b 6 6b 3 c 3 4c 1

2 3 4

a 1 2a b 1 2b c 1 2c

2a 3b 4c

a 1 2a b 1 2b

c 1 2c

  

     

  

     

  

  

  





Áp dng bng thc AM-GM ta có:

 

a a 1 2a 1

a 1 2a

3 27

    

  





:

 

b 1 2b



;

 

c 1 2c



Suy ra:

 

27 2a 3b 4c 81   

Dy ra khi

a b c

  

Vy giá tr nh nht ca P là 81.

Câu 6: [TS10 Chuyên Hòa Bình, 2019-2020]

Cho hai s a mãn: a + b = 4ab. Chng minh rng:

a b 1

4b 1 4a 1





Lời giải

THCS.TOANMATH.com

FB TRỊNH BÌNH

Ta có:

     

a b 4ab a b a b a b 1 0 a b 1 a b 0               



Li có:

a 4ab 4ab

a a a ab

4b 1 4b 1

     



b 4a b 4a b

b b a ab

4a 1 4a 1

     





     

a b a b 1 1

a b 2ab a b a b

2 2 2

4b 1 4a 1



         



Dy ra khi



Câu 7: [TS10 , 2019-2020]

Cho các s thc không âm x, y, z tha mãn:

2 2 2

x y z 3y  

Tìm giá tr nh nht ca biu thc:

     

2 2 2

1 4 8

x 1 y 2 z 3

  

  

Lời giải

S dng bng thc Cauchy-Schwarz ta có:

 

2 2 2

1 1 1 1 1 8

2 a b



   







(*)

Áp dng bng thc:

     

2 2 2 2 2 2

1 1 8 8 8 64

x 1 z 3 z 3

y y y

1 x 2 x z 5

2 2 2

     

  

     

     

     

     

Mt khác:

   

2 2 2

2 3y y

x z 2 x z 2 3y y .



     

 

64 64

6 2y y 8 y 2

  

   

   





   

Dy ra khi

   

,y,z 1,2,1 .

Vy giá tr nh nht ca P là 1.

Câu 8: [TS10 Chuyên Hà Nam, 2019-2020]

Cho các s tha mãn:

1 1 1

a 1 b 1 c 1

  

  

Tìm giá tr nh

nht ca biu thc:

3 3 3

2 2 2 2 2 2

a b c

a ab b b bc c c ca a

  

     

THCS.TOANMATH.com

FB TRỊNH BÌNH

Lời giải

Ta d dàng chng minh bng thc:

1 1 1 9

x y z x y z

  



(vi

x,y,z 0

) (*)

Tht vy:

 

1 1 1

(*) a b c 9

a b c



     





Áp dng AM  c:

 

1 1 1 3

a b c 3 abc. 9

a b c

abc



     





Vy bng thc chng minh, dy ra khi x = y = z.

S dng bng thc:

1 1 1 9

1 a b c 3 9 a b c 6

a 1 b 1 c 1 a b c 3

            

     

t

3 3 3

2 2 2 2 2 2

b c a

a ab b b bc c c ca a

  

     

Ta có:

 

     

3 3 3 3 3 3

2 2 2 2 2 2

a b b c c a

a ab b b bc c c ca a

a b a ab b b c b bc c c a c ca a

a ab b b bc c c ca a

a b b c c a

  

   

     

        

  

     

     





Mt khác:

 

2 2 2 2

x xy y x xy y * *

    

Tht vy:

 

2 2 2 2 2 2 2 2

x xy y x xy y 3x 3xy 3y x xy y 2 x y 0

             

S dc:

 

3 3 3 3 3 3

2 2 2 2 2 2

a b b c c a

a ab b b bc c c ca a

a b a ab b b c b bc c c a c ca a

a ab b b bc c c ca a

  

   

     

        

  

     

     

1 1 1

a b b c c a

3 3 3

     

 

a b c .6 4

    

Mà

P Q P 2  

Dy ra khi a = b = c = 2

THCS.TOANMATH.com

FB TRỊNH BÌNH

Vy giá tr nh nht ca P là 2.

Câu 9: [TS10 Chuyên Phan Bi Châu, 2019-2020]

Cho các s a mãn

abc a b c 2   

. Tìm giá tr ln nht

ca biu thc

2 2 2 2 2 2

1 1 1

a b b c c a

  

  

Lời giải.

T

abc a b c 2   

            

a b b 1 c 1 a 1 b 1 b 1 c 1 c 1 a 1

1 1 1

a 1 b 1 c 1

            

   

  

t

x,y,z 0

1 1 1

x, y, z

x y z 1.

a 1 b 1 c 1



   



  

  





y z x y

1 x z x

a ; b ;c

x x y z





   

Nên

2 2 2 2 2 2

1 1 1 1 1 1 1

2 ab bc ca

a b b c c a



     



  



1 x z z x

. . .

y z z x z x x y x y y z



  



     



1 x z x z

. . .

y z z x z x x y x y y z



  



     



1 x z x z

y z z x z x x y x y y z



     

     



     

     



     



1 x z z x 3 2

x y x y y z y z z x z x 4



   



      



   



     





   



Dy ra khi

x y z

hay

a b c

Vy giá tr ln nht ca biu thc P là

khi a = b = c = 2.

Câu 10: [TS10 Chuyên , 2019-2020]

Cho x, y, z là các s tha mãn

 

2 2 2

5 x y z 9x y z 18yz 0.     

Tìm giá tr ln nht ca biu thc:

2x y z







Lời giải

Ta có:

 

   

2 2 2

5 x y z 9x y z 18yz 0

5x 9x y z 5 y z 28yz 0

     

      

THCS.TOANMATH.com

FB TRỊNH BÌNH

     

   

5x 9x y z 5 y z 7.4yz 7 y z

5x 9x y z 2 y z 0

5 9. 2 0

y z y z

       

     



   







t:

 

t t 0







  

 

5t 9t 2 0 5t 1 t 2 0

t 2 do 5t 1 0

      

   





Ta có:

2x y z

Q 2. 1 2.2 1 3

y z y z



     



Dy ra khi

y z .



Vy giá tr ln nht ca Q là 3.

Câu 11: [TS10 Chuyên Bc Ninh, 2019-2020]

Cho x, y, z không âm tha mãn

x y z 3.  

Tìm GTLN. GTNN ca biu thc

2 2 2

M x 6x 25 y 6y 25 z 6z 25        

Lời giải

Ta có:

     

2 2 2

M x 6x 25 y 6y 25 z 6z 25

3 x 16 3 y 16 3 z 16

        

t

a 3 x,b 3 y,c 3 z,     



a b c 6

0 a,b,c 3

   







2 2 2

M a 16 b 16 c 16     

Tìm GTNN:

Theo bng thc Minkowski ta có:

   

2 2 2

M a 16 b 16 c 16 a b c 4 4 4 6 5            

ng thc xy ra khi a = b = c = 2

Tìm GTLN

S du kin

0 a 3

c

 

a 12

a 16 *





Tht vy:

 

   

* 9 a 16 a 12 8a 24a 0 a a 3 0         



THCS.TOANMATH.com

FB TRỊNH BÌNH

 và suy ra:

M 14

ng thc xy ra khi

   

,b,c 0,3,3

và các hóa v.

Câu 12: [TS10 Chuyên KHTN, 2019-2020]

Cho x, y,z là các s a mãn

xy yz zx 1

. Chng minh rng:

2 2 2

1 1 1 2 x z

1 x 1 y 1 z





    



  



(1)

Lời giải

Ta có:

  

1 x xy yz zx x x y x z       

:

     

1 y x y y z ; 1 z x z y z       



 

        

 

   

2 x y z

1 1 1

x y x z x y y z x z z y x y y z z x



   

        

Áp dng bng thc Cauchy-Schwarz, ta có:

 

        

  

   

 

   

2 2 2

x z x z

x y z

1 x 1 y 1 z

x y z

x y y z x y y z x z z y

2 x y z xy yz zx

x y y z z x

2 x y z

x y y z z x





      



  





    



     





   



  





  

Suy ra:

 

   

2 2 2

4 x y z

VP .

3 x y y z z x

1 x 1 y 1 z







  



  



  chng minh bng th cn chng minh:

 

2 2 2

x z 3

1 x 1 y 1 z

  

  

S dng bng thc AM-GM ta có:

  

x x 1 x x

2 x y x z

x y x z



  









:

y y y

1 z 1 z z

;

2 x y y z 2 z x y z

1 y 1 z

   

   

   

   



   

THCS.TOANMATH.com

FB TRỊNH BÌNH

Cng theo v 3 b nng thc bng thc

chng minh.

Dy ra khi

x y z

  

Câu 13: [TS10 Chuyên TP. H Chí Minh, 2019-2020]

Cho x, y, z là các s thc thun

0;2



thu kin:

x y z 3.  

a) Chng minh rng:

2 2 2

x y z 6  

b) Tìm giá tr ln nht ca biu thc:

3 3 3

P x y z 3xyz   

Lời giải

a) Ta có:

       

   

2 2 2 2 2 2

2 x 2 y 2 z 0 8 4 x y z 2 xy yz zx xyz 0

x y z x y z 8 4 x y z 2 xy yz zx xyz

x y z 4 x y z 8 xyz

9 4.3 8 xyz 5 xyz 5 6

            

             

       

       

b) Ta có:

 

   

 

3 3 3 2 2 2

2 2 2 2 2 2

2 2 2

P x y z 3xyz x y z x y z xy yz zx

3 x y z x y z 2xy yz zx

3 x y z x y z

3.5 9

           



        







     





   





Dy ra khi

   

,y,z 2,1,0

và các hoán v.

Câu 14: [TS10 Chuyên Hòa Bình, 2019-2020]

Cho x, y, z là các s tha mãn:

xy yz 4zx 32  

Tìm giá tr nh nht ca biu thc:

2 2 2

P x 16y 16z  

Lời giải.

Áp dng bng thc AM-GM ta có:

8y 4xy

8z 4xz

8y 8z 16yz



Cng theo v c:

 

2 2 2

P x 16y 16z 4 xy xz 4yz 128      

THCS.TOANMATH.com

FB TRỊNH BÌNH

Du kic:

8 6 2 6

x ;y z

  

Câu 15: [TS10 Chuyên Quc Hc Hu, 2019-2020]

Cho ba s a mãn xyz = 2. Chng minh rng:

2 2 2 2 2 2

x 4z 1

2x y 5 6y z 6 3z 4x 16

  

     

Lời giải

Ta có:

2 2 2 2 2

2x y 5 x y x 1 4 2xy 2x 4         

 

x x x

2xy 2x 4

2 xy x 2

2x y 5

  



 

2 2 2 2 2

) 6y z 6 4y z 2y 2 4 4yz 4y 4

2y 2y y

4yz 4y 4

2 yz y 1

6y z 6

          

  





   

     

 

zx 2z 2

2 xy x 2 2 yz y 1

y yz

xyz 2yz 2y

2 xy x xyz 2 yz y 1

y yz

2 yz y 1 2 yz y 1 2 yz y 1

yz y 1

2 yz y 1

  



   

  



   

  

     









Dy ra x = y = 1, z = 2.

Câu 16: [TS10 Chuyên Tin Hòa Bình, 2019-2020]

Cho các s tha mãn:

x y 1.

Tìm giá tr nh nht ca biu thc:

P 1 x y



  





Lời giải

Theo AM-GM ta có:

1 1 1

1 x y 2 xy xy xy 4

2 4 xy

        



THCS.TOANMATH.com

FB TRỊNH BÌNH

2 2 2 2

1 1 2 1

P 1 x y 1 x y 2 xy

x y xy



      





Suy ra:

1 1 15 1 15

P 2 xy 2 xy 2 2 .xy

xy 16xy 16xy 16xy 16xy

1 15

P 2 .4 17

2 16

      

   

Dy ra khi



Vy giá tr nh nht ca P là

Câu 17: [TS10 Chuyên Tin Giang, 2019-2020]

Cho hai s a mãn

 

     

2 x y 6xy x y 2 x y xy 4      

Tìm giá tr nh nht ca biu thc:

2 y x



  





Lời giải

Ta có:

 

     

2 x y 6xy x y 2 x y xy 4

2 x y 12xy x y xy 4

      

     

t

 

x y,b xy a,b 0   



 

3 2 2 3 2

2a 12b a b 4 b a 12 2a 4a      

Do VT > 0 nên

 

3 2 2

2a 4a 0 2a a 2 0 a 2      

Ta có:

2 2 4 2

y x y xy

1 x 1 1 a a 1 a 12a 1

T 1 1

2 y x 2 xy 2 b 2b 2 2

4a 8a







         







Ta s chng minh:



Tht vy:

 

3 2 2

a 6 a

5 a 12a

T 3 0

4a 8a 4a a 2





    





a2

)

Dy ra khi a = 6, b = 6

hay

x 3 3,y 3 3   

hoc

x 3 3,y 3 3   

Vy giá tr nh nht ca T là

Câu 18: [TS10 Chuyên Bà R, 2019-2020]

Cho các s th nh nht ca biu thc:

THCS.TOANMATH.com

FB TRỊNH BÌNH

   



Lời giải

Ta có:

 

2 4 2 2 4

2 2 2 2

xy xy

y x 2x y y

x y x y

y x x y

xy xy

x y x y

xy x y xy x y

xy xy

P 2 2 2

xy x y xy x y



     







   













       







t





.Theo AM  GM thì:

1 1 1

x y 2 xy t 2

x y 2 2 t

       





2 2 2

1 t t 1 15

P t 2 2

t 16t 16t

t t 1 15

3 . . .2 2

2 2 16

16t

1 15

3. 2



       





  

  



Dy ra khi x = y

Vy giá tr nh nht ca P là

Câu 19: [TS10 Chuyên KHTN Hà Ni, 2019-2020]

Vi x, y là các s thc tha mãn

1 y 2

và

xy 2 2y

. Tìm giá tr nh nht ca

biu thc







Lời giải.

Theo gii thit ta có:

4xy 8 8y.

S dng bng thc AM  GM ta có:

4x y 4xy.

Suy ra:

4x y 8 4xy 8 8y.    



   

  

 

2 2 2 2

4 x 4 8 8y y 4 y 1 5y 2 2 y 4 y 1 .          

Suy ra:

x 4 y 1 M 1



     



Dy ra khi x = 2, y = 1.

THCS.TOANMATH.com

FB TRỊNH BÌNH

Vy giá tr nh nht ca M là 1.

Câu 20: [TS10 , 2019-2020]

Vi x, y là cá s thc tha mãn

  

2 x y 1 .

  

Tìm giá tr nh nht ca biu

thc:

4 3 2 4 3 2

A x 4x 6x 4x 2 y 8y 24y 32y 17.         

Lời giải

Ta có:

   

4 3 2 4 3 2

A x 4x 6x 4x 2 y 8y 24y 32y 17

1 x 1 1 y 2

         

     

t

a x 1, b y 2   

c

A 1 a 1 b   

T gi thic:

  

a 1 b 1 a b ab

      

Theo AM  GM ta có:

4a 1 4a

a b a b

4b 1 4b







    









(1)

 

2 2 2 2

a b 2ab a b ab 2

    

Cng theo v c:

 

2 2 2 2

3 1 5 1 3 1

a b a b ab a b

2 2 4 2 4 2

          

Áp dng bng thc Minicopski ta c:

 

   

4 4 2 2 2 2

A 1 a 1 b 1 1 a b a b 4

1 17

          



  





Dy ra khi

1 1 5

a b x ,y

2 2 2

     

Vy giá tr nh nht ca A là

Câu 21: [TS10 Chuyên Bình Thun, 2019-2020]

Cho các s a

xyz .



Chng minh rng:

     

2 2 2

yz xy

xy yz zx.

x y z y z x z x y

    

  

Dy ra khi nào:

Lời giải

Ta có:

THCS.TOANMATH.com

FB TRỊNH BÌNH

     

2 2 2

yz xy

xy yz zx

x y z y z x z x y

1 1 1 1

1 1 1 1 1 1

2 x y z

y z x z x y

    

  



     







t

1 1 1

a ,b ,c abc 2

x y z

    

n chng minh:

2 2 2

a b c a b c

b c a c a b 2



  



Tht vy, s dng bng thc Cauchy-Schwarz c:

 

2 2 2

a b c

a b c a b c

VT VP

b c a c a b 2

2 a b c



     







Dy ra khi x = y = z.

Câu 22: [TS10 Chuyên Hi Phòng, 2019-2020]

Cho

x;y;z

là ba s tha mãn

x(x z) y(y z) 0.   

Tìm giá tr nh

nht ca biu thc

3 2 2

2 2 2 2

y x y 4

x z y z



  





Lời giải

Áp dng bng thc Côsi

3 2 2

2 2 2 2

x xz xz z

x x x

2xz 2

x z x z

     









. Suy ra

x y 4

P x y z



   



Theo gt







P x y 4

    



Vy

min

P 4 x y z 1    

Câu 23: [TS10 Chuyên Qung Nam, 2019-2020]

Cho ba s tha mãn abc = 1. Tìm giá tr nh nht ca biu

thc:

     

2 2 2

1 a b 5 1 b c 5 1 c a 5

ab a 4 bc b 4 ca c 4

        

  

     

Lời giải

Ta có:

   

1 a b 5 2 ab a 4 2

a b 2a 6 2ab 2a 6 2

ab a 4 ab a 4 ab a 4 ab a 4 ab a 4

     

    

    

         

THCS.TOANMATH.com

FB TRỊNH BÌNH

:

   

1 b c 5 1 c a 5

2 ; 2

bc b 4 bc b 4 ca c 4 ca c 4

     

   

       



1 1 1

P 6 2 6 2Q

ab a 4 bc 4 4 ca c 4



     



     



V

   

1 1 1 1 1

x y 0 x y 4xy

x y 4xy x y 4 x y





         







(*)

Dy ra khi x = y.

Áp dc:

 

1 1 1 1 1

ab a 4 4 ab a 1 3

ab a 1 3



  



   

  



:

1 1 1 1 1 1 1 1

;

bc b 4 4 bc b 1 3 ca c 4 4 ca c 1 3

   

   

   

       

   



1 1 1 1 1 1 1 1

Q 1 2Q 1

4 ab a 1 bc b 1 ca c 1 2 ab a 1 bc b 1 ca c 1

1 1 1 1

P 6 1

2 ab a 1 bc b 1 ca c 1

1 c ac 1

2 abc ac c bc.ac abc 1 ca c 1

1 c ac 1

2 ca c 1 ca c 1 ca c 1

6 .2

   

        

   

           

   



     



     





    



     





    



     







Dy ra khi a = b = c = 1.

Vy giá tr nh nht ca P là 5.

Câu 24: [TS10 Chuyên Lai Châu, 2019-2020]

Cho các s thng minh rng:

 

ab bc ca 1

a b c

a b 2c b c 2a c a 2b 4

    

     

Lời giải

V

   

1 1 1 1 1

x y 0 x y 4xy

x y 4xy x y 4 x y





         







(*)

Dy ra khi x = y.

S dc:

   

ab ab ab 1 1

a b 2c 4 a c b c

a c b c



  



   

  



THCS.TOANMATH.com

FB TRỊNH BÌNH

:

bc bc 1 1 ca ca 1 1

;

b c 2a 4 b a a c c a 2b 4 c b b a

   

   

   

       

   

Cng 3 bng thc trên theo v c:

ab bc ca

a b 2c b c 2a c a 2b

ab 1 1 bc 1 1 ca 1 1

4 a c b c 4 b a a c 4 c b b a



     

     

     

     

     

     

     

   

1 ab bc ab ca bc ca

4 c a b c a b

b a c a b c c a b

4 a c b c a b

a b c dpcm

    

  



  





  

  



  





  

ng thc xy ra khi a = b = c

Câu 25: [TS10 , 2019-2020]

Cho các s a mãn:

abc 1.

Chng minh rng:

a b c 3

b ac c ab a bc

  

  

Lời giải

Ta có:

 

a c a 2b c a 2b c

b ac b b ac

2 2 2

1 2 a a 2 2 2a 4 2a

a 2b c 4

a 2b c a 2b c

4 a 2b c

b ac b ac

    

      

     

  

   



Mt khác:

 

4 4 2a 12 2a

a b c 3 abc 3 a b c 4

3 a 2b c 4 7a 10b 7c

         

    



 

2 2 2

a b c

VT 12 2

7a 10b 7c 7b 10c 7a 10a 7b 7c

a b c

12 2

7 a b c 17 ab bc ca



  



     







    

Mt khác:

 

   

 

2 2 2 2 2 2

2 2 2

a b c ab bc ca 7 a b c 17 ab bc ca 8 a b c

12 2 a b c 12 2 a b c

dpcm

7 a b c 17 ab bc ca

8 a b c

             

   

  

    



Dy ra khi a = b = c = 1.

THCS.TOANMATH.com

FB TRỊNH BÌNH

Câu 26: [TS10 Chuyên Tuyên Quang, 2019-2020]

Cho các s a mãn

a b c 4  

.Tìm giá tr nh nht ca biu

thc:

a a b b c c

a 3 b b 3 c c 3 a

  

  

Lời giải

Ta có:

2 2 2

a a b b c c

a 3 b b 3 c c 3 a

a b c

a 3 ab b 3 bc c 3 ac

  

  

  

  

Áp dng bng thc Cauchy-Schwarz c:

 

2 2 2

a b c

a 3 ab b 3 bc c 3 ac

a b c

a b c 3 ab bc ca

  

  





    

Mt khác theo AM-GM:

a b b c c a

ab bc ca a b c

2 2 2

  

       



 

a b c

a b c 3 a b c



  

    

Dy ra khi

a b c

  

Vy giá tr nh nht ca P là 1.

Câu 27: [TS10 Chuyên Hà Nam, 2019-2020]

Cho các s ng minh:

2 2 2

a b c a b c

b c a

3. a b c



   



Lời giải

Áp dng bng thc Cauchy-Schwarz c:

 

   

2 2 2

2 2 2 2 2 2

2 2 2

2 2 2 2 2 2

a b c

a b c a b c ab bc ca

ab bc ca ab bc ca

3. a b c a b c

a b c ab bc ca

ab bc ca

a b c

a b c 1 ab bc ca 1 ab bc ca a b c

2 ab bc ca 2 ab bc ca

a b c a b c



   

     



   

  





       

    



   



THCS.TOANMATH.com

FB TRỊNH BÌNH

Áp dng bng thc AM-GM cho 3 s c:

 

2 2 2

2 2 2 2 2 2

a b c 1 ab bc ca 1 ab bc ca 1

VT 3 . . 2

2 2 2

2 ab bc ca

a b c a b c

2 4 dpcm

     

  



   

   

ng thc xy ra khi a = b = c.

Câu 28: [TS10 Chuyên Phú Yên, 2019-2020]

Cho a, b, c là các s tha mãn

ab bc ca 1.

Chng minh rng:

2 2 2

a b 1 b c 1 c a 1 2     

Dy ra khi nào?

Lời giải

S dng bng thc:

     

       

 

2 2 2

2 2 2 2 2 2

2 2 2

a b 1 b c 1 c a 1 ab a bc b ca c

ab bc ca a b c ab bc ca 3 ab bc ca

1 3 2 dpcm

          

           

  

Dy ra khi

a b c

  

Câu 29: [TS10 Chuyên Cao Bng, 2019-2020]

Cho a, b, c là các s u kin a+ b + c = 3. Tìm giá tr nh nht

ca biu thc:

2 2 2

a b c

1 b 1 c 1 a

  

  

Lời giải

Áp dng bng thc AM-c:

a ab ab ab

a a a

2b 2

1 b 1 b

     



:

b bc c ca

b ; c

1 c 1 a

   



Cng theo v 3 bc:

 

2 2 2

a b c ab bc ca

R a b c

1 b 1 c 1 a

a b c

a b c 3

6 6 2



      

  



      

Dy ra khi

a b c

  

Vy giá tr nh nht ca R là

Câu 30: [TS10 nh, 2019-2020]

THCS.TOANMATH.com

FB TRỊNH BÌNH

Cho x, y, z là s thc không âm thu kin

x y z

  

. Chng minh

rng:

x 2xy 4xyz 2  

Lời giải

S dng bng thc AM-c:

   

 

  

x 2xy 4xyz x x.4y z

1 3 1

x x. y z x x x

2 2 2

x x 2 x x 2 x 2 x 2

x 2 1 x 2x 2

x 2 x 1 2



    





   

       

   

   

       

    

   

x y z 0 x 2 x 2 0

        

. Vì th:

  

x 2xy 4xyz x 2 x 1 2 2      



Dy ra khi

x 1,y ,z 0

  

Câu 31: [TS10 nh, 2019-2020]

Cho a, b, c là các s tha mãn

   

b b c c a 8   

. Tìm giá tr

nh nht ca biu thc:

1 1 1 1

a 2b b 2c c 2a

abc

   

  

Lời giải.

c ht ta chng minh bng thc ph sau:

      

a b b c c a a b c ab bc ca

       

Tht vy:

      

b b c c a a b c ab bc ca abc        

L-GM ta có:

         

a b b c c a a b b c c a

abc ab. bc. ca . .

2 2 2 8

     

  

Suy ra:

      

b b c c a a b c ab bc ca abc        

  

   

a b b c c a

a b c ab bc ca

  

     



      

a b b c c a a b c ab bc ca

       

ab bc ca

a b c

   



Áp dng bng thc AM-GM dng cng mu s ta có:

THCS.TOANMATH.com

FB TRỊNH BÌNH

 

1 1 1 9 3 ab bc ca

a 2b b 2c c 2a a b c 3

3 a b c



    

    



Li có:

 

2 2 2

ab bc ca 3 ab c a bc abc 3abc a b c       

 

a b c

9 1 1 a b c

3abc a b c

abc 27 3

abc

a b c



       



Suy ra:

1 1 1 1 a b c 3

a 2b b 2c c 2a 3 a b c

abc



      

    

Dy ra khi:

   

a b b c c a 8

a b c a b c 1

3 a b c

a b c 3





   



     















Vy giá tr nh nht ca P là 2 khi a = b = c = 1.

Câu 32: [TS10 Chuyên Bà R, 2019-2020]

Cho các s a mãn

1 1 1

a b c

  

. Tìm giá tr nh nht ca biu

thc:

2 2 2 2 2 2

1 1 1

a ab 3b 1 b bc 3c 1 c ca 3a 1

  

        

Lời giải

Ta có:

   

 

2 2 2 2 2 2

2 2 2

a ab 3b 1 a 2ab b ab b 1 b

a b ab b 1 b b ab 2b b a b 2

         

           

 

a ab 3b 1 b a b 1

b a b 1

a ab 3b 1

       



  

:

   

2 2 2 2

1 1 1 1

;

c b c 2 a c a 2

b bc 3c 1 c ac 3a 1



   

     

V

   

1 1 1 1 1

x y 0 x y 4xy

x y 4xy x y 4 x y





         







(*)

Dy ra khi x = y.

Cng theo v và s dng bng thc AM-GM c:

THCS.TOANMATH.com

FB TRỊNH BÌNH

     

AM GM

1 1 1

b a b 2 c b c 2 a c a 2

2 2 2

4b a b 2 4c b c 2 4a c a 2

1 1 1 1 1 1

4b a b 2 4c b c 2 4a c a 2

1 1 1 1 1 1 1

4 a b c a b 2 b c 2 c a 2



  

     

  

     

     

     

     

     

     

   

     

   

     

   

S dng bng thc:

1 1 1 1 1 1 1 1 1 1 1 1 1

4 a b c 4 a b 2 4 b c 2 4 c a 2

3 1 1 1 1 1 1 1 1 1 1 1 1

4 8 8 8 16 a b 16 b c 16 c a

3 3 1 1 1 1

4 8 8 a b c

3 3 3 3

4 8 8 2



       

        



       

  

       





     

         



     

     







    









   

Dy ra khi a = b = c = 1.

Vy giá tr nh là P là

Câu 33: [TS10 Chuyên Tây Ninh, 2019-2020]

Chng minh

    

a b c 9abc 4 a b c ab bc ca       

vi x, y, z là các s thc

ng thc xy ra khi nào?

Lời giải

Theo bng thc Schur vi a, b, c là s thc không âm thì:

        

a b a c b b c b a c c a c b 0        

Bic h qu:

     

3 3 3 2 2 2

a b c 3abc a b c b c a c a b        

Mng thc:

     

3 3 3

a b c a b c 3 a b b c c a        



     

3 3 3

a b c 9abc a b c 9abc 3 a b b c c a          



         

2 2 2

VT a b c b c a c a b 9abc 3 a b b c c a          

ng thc:

        

      

2 2 2

) a b c b c a c a b 9abc a b c ab bc ca

) abc a b b c c a a b c ab bc ca

           

         

THCS.TOANMATH.com

FB TRỊNH BÌNH



            

2 2 2

a b c b c a c a b 9abc 3 a b b c c a 4 a b c ab bc ca              

Vy bng thc chng minh.

Dy ra khi a = b = c.

Câu 34: [TS10 Chuyên Qung Nam, 2019-2020]

Cho 3 s  nh nht ca biu thc:

        

xy yz

2x z 2y z 2y x 2z x 2z y 2x y

  

     

Lời giải

S dng bng thc:

     

 

2x z 2y z x x z y z y xy zx yz         



  

 

xy xy xy

2x z 2y z

xy yz zx

2x z 2y z

xy yz zx

  



:

     

zx zx

;

2y x 2z x 2z y 2x y

xy zx yz xy zx yz



   

Cng 3 bng thc trên theo v c:

xy zx yz







ng thc xy ra khi x = y = z.

Vy giá tr ln nht ca P là 1.

Câu 35: [TS10 c, 2019-2020]

1) Cho x, y là các s a mãn

xy 1.

Chng minh rng:

1 1 2

1 x 1 y

1 xy







2) Cho x, y là các s thu kin:

 

x y 4xy 12  

Tìm giá tr ln nht ca biu thc:

P 2018xy

1 x 1 y

  



Lời giải

1) Ta có:

THCS.TOANMATH.com

FB TRỊNH BÌNH

 

  

 

1 1 2 1 1 1 1

1 x 1 y 1 x 1 y

1 xy 1 xy 1 xy

1 xy 1 x 1 xy 1 y

1 x 1 xy 1 y 1 xy

xy x 1 y xy y 1 x

1 x 1 y 1 xy

   

   

      

   

   

  

   

     

  

   

    



  

 

  

 

x y x 1 y y x y 1 x

1 x 1 y 1 xy

    



  

 

  

 

     

  

 

    

  

 

y x x y x y x y

1 x 1 y 1 xy

y x x y xy y x

1 x 1 y 1 xy

y x y x xy 1

1 x 1 y 1 xy



   





  



   







  



  







  

   

  

 

y x xy 1

1 x 1 y 1 xy





  



xy 1

) (1)

Dy ra khi x = y = 1.

Bc

chng minh.

2) S dng AM-GM ta có:

 

12 x y 4xy 2 xy 4xy 8xy xy 4xy      

t

 

y t t 0



      

 

3 2 3 2 3 2 2

8t 4t 12 0 2t t 3 0 2t 2t 3t 3 0

2t t 1 3 t 1 t 1 0 t 1 2t 3t 3 0

           

          



Áp dng bng thc  ý 1 ta có:

1 1 2 2

P 2018xy 2018xy 2018t

1 x 1 y 1 t

1 xy

      

  



Ta s chng minh:

 

2018t 2019 *





Tht vy:

THCS.TOANMATH.com

FB TRỊNH BÌNH

 

  

* 1 2018 t 1 0

2018 t 1 t 1 0



    









    



   

1 t 2018 t 1 0



    









0 t 1

)

Dy ra khi x = y = 1.

Vy giá tr ln nht ca P là 2019.

Câu 36: [TS10 Chuyên c Lc, 2019-2020]

Cho 3 s tha mãn

2 2 2

a b c 3.  

Chng minh rng:

3 3 3 3 3 3

a b b c c a

a 2b b 2c c 2a

  

  

  

Lời giải.

S dng bng thc Cauchy-Schwarz c:

   

 

3 3 3 4 4 4

2 2 2

2 2 2 2 2 2

2 2 2

2 2 2 2 2 2

2 2 2

a b c a b c

)

a 2b b 2c c 2a

a 2ab b 2bc c 2ca

a b c a b c

a b c 2ab 2bc 2ca

a b c 2 a b c

a b c 3

     

  

   



    





 

3 3 3 4 4 4

2 2 2

2 2 2 2 2 2

2 2 2 2 2 2 2 2 2

b c a b c a

)

a 2b b 2c c 2a

ab 2b bc 2c ca 2a

a b c a b c

ab bc ca 2 a b c a b c 2 a b c

     

  

   



         

2 2 2

a b c 3





Cng theo v c:

3 3 3 3 3 3

a b b c c a

a 2b b 2c c 2a

  

  

  



Dy ra khi

a b c

  

Câu 37: [TS10 Chuyên Qung Nam, 2019-2020]

Cho hai s thc x, y tha mãn

x 3;y 3.

Tìm giá tr nh nht ca biu thc:

T 21 x 3 y .



   





Lời giải

Áp dng bng thc AM  GM ta có:

THCS.TOANMATH.com

FB TRỊNH BÌNH

1 1 x 3 21 62 2

T 21 x 3 y x y

y x 3 x 3 y 3 3

x 3 21 62 2

2 . 2 . .3 .3

3 x 3 y 3 3

2 2.7 62 2

   

         

   

   

   

   



Dy ra khi x = y = 3.

Vy giá tr nh nht ca T là 80.

NĂM HỌC 2018-2019

Câu 38: [TS10 Chuyên Thái Bình, 2018-2019]

Cho a, b, c là ba s thu kin :

2 2 2

1 1 1

a b c

  

Tìm giá tr ln nht ca biu thc

2 2 2 2 2 2

1 1 1

5a 2ab 2b 5b 2bc 2c 5c 2ca 2a

  

     

Lời giải

Ta có:

 

1 1 2

5a 2ab 2b

27. 5a 2ab 2b

1 27 1 1

2 27

5a 2ab 2b







  









Ch ta có:

2 2 2 2

1 27 1 1 1 27 1 1

;

2 27 2 27

5b 2bc 2c 5c 2ca 2c

5b 2bc 2c 5c 2ca 2a

   

   

   

   

   

   

     

2 2 2 2 2 2

27 1 1 1 1

5a 2ab 2b 5b 2bc 2c 5c 2ca 2a





    



     



S d

1 1 1 1 1

x y z 9 x y z



  







ta có:

     

2 2 2 2

2 2 2 2 2 2

1 1 1 1 1 1

3a 2ab a a 2b

5a 2ab 2b 3a 2ab a a 2b



   





     



THCS.TOANMATH.com

FB TRỊNH BÌNH

2 2 2 2 2 2 2

1 1 1 1 1 1 1 1 1 1 1 5 2 2

9 9 ab ab 9 9 9ab

3a a a b b 9a 9b



     

         



     

     



Ta li có :

AM GM

2 1 1 1

9ab 9











2 2 2 2 2 2 2 2

1 1 5 1 1 2 1 2 1

5a 2ab 2b 9a 9a 9a 9b 3a 3b

   

      

   



   

Ch:

2 2 2 2 2 2 2 2

1 1 2 1 1 1 2 1

;

5b 2bc 2c 3b 3c 5c 2ca 2a 3c 3a

   

   

   

   

   

2 2 2 2 2 2

2 2 2 2 2 2 2 2 2

1 1 1

5a 2ab b 5b 2bc 2c 5c 2ca 2a

1 2 1 1 2 1 1 2 1 1 1 1 1 1

. . .

9 9 9 9 9

3a 3b 3b 3c 3c 3a a b c

27 1 1 3

2 9 9 3

  

     

       

         

       

       



   





Du

""

xy ra

2 2 2

a b c

a b c 3

1 1 1

a b c







    



  





Vy

max



Câu 39: [TS10 Chuyên Trà Vinh, 2018-2019]

Cho

x,y,z

là ba s tha mãn:

2 2 2

x y z 2  

Chng minh:

3 3 3

2 2 2 2 2 2

x y z

2 2 2

2xyz

x y y z z x



   

  

Lời giải

Vì

2 2 2

x,y,z 0; x y z 2   

nên:

3 3 3

2 2 2 2 2 2

2 2 2 2 2 2 2 2 2 2

2 2 2 2 2 2

2 2 2 2

2 2 2 2 2 2

2 2 2 2 2

x y z

2 2 2

3 (1)

2xyz

x y y z z x

x y z x y z x y z y

2yz 2zx 2xy

x y y z z x

z x x z

1 1 1 3

2yz 2zx 2xy

x y y z z x

y z z x x



   

  

     

      

  

         

  

  



(2)

2yz 2zx 2xy

  



THCS.TOANMATH.com

FB TRỊNH BÌNH

Li có:

2 2 2

(x y) 0 x y 2xy

2xy

      



, ta có:

2 2 2 2

;

2zx 2xy

z x x y













Câu 40: c, 2018-2019]

a) Cho

x;y

là hai s th

  

b) Xét các s thc

a; b;c

vi

b a c



ax bx c 0  

có 2

nghim thc

m;n

tha mãn

0 m,n 1

. Tìm GTLN và GTNN ca biu thc

  

a b 2a c

a(a b c)







Lời giải

a) Vi

x,y 0

ta có:

 

3 3 2 2

x y x y xy(x y) (x y)(x xy y ) xy x y

            

 

2 2 2 2

x xy y xy x 2xy y 0 x y 0 x,y           

Vc chng minh, du

""

xy ra

x,y 0











b)  

ax bx c 0  

có hai nghim

m,n

 

m,n 1 a 0   

Áp dnh lý Vi-et ta có:



  













     

a b 2a c 1 m n 2 mn

a 1 m n mn

  



  

    

  

   

  



Vì

 

1 m n .2

2 mn 2; mn 0 M 2

1 m n



     



Vy

MaxM 2 mn 0 c 0    

Ta li có:

     

0 m,n 1 m n 1 n m 1 mn 1 0 mn m n 1

            

 

m n 1 3

1 m n 1 m n



  

    

THCS.TOANMATH.com

FB TRỊNH BÌNH

Vy

a b c 0

MinM m n 1

   

    







Câu 41: [TS10 Chuyên Hà Nam, 2018-2019]

Cho các s th

x,y,z



xy yz zx x y z.    

Chng minh rng

3 3 3

x 8 y 8 z 8

  

  

Lời giải

Ta có:

 

x 2 x 2x 4 x x 6

x 8 x 2 x 2x 4

     

      

:

y y 6





;

z z 6

z 8 .





Suy ra:

2 2 2 2

2 2 2

3 3 3

x z x z

2. .

x x 6 y y 6 z z 6

x 8 y 8 z 8



    



     

  



(*)

Chng minh rng

 

2 2 2

a b c

a,b,c,u,v,w 0 1

u v w u v w



    



Áp dc:

 

2 2 2

3 3 3

2 x y z

x y z x y z 18

x 8 y 8 z 8



  

     

  

(2)

Ta cn chng minh:

 

   

2 2 2

2 x y z

x y z x y z 18

x y z 4 xy yz zx 18 x y z





     

         

     

x y z x y z 2 xy yz zx 18 0          

. (3)

Li do:

xy yz zx x y z    

m tra

   

x y z 3 x y z 18 0      

  

y z 3 x y z 6 0       

. (4)

Tht vy ta có quan h:

     

x y z 3 xy yz zx 3 x y z       

nên

x y z 3  

t 

T u phi chng minh.

THCS.TOANMATH.com

FB TRỊNH BÌNH

D

x y z 1   

Câu 42: [TS10 Chuyên Lào Cai, 2018-2019]

Cho các s th

a,b,c

thu kin

1 1 1

a b c

    

Chng minh rng

 

2 2 2

3 a b c 8a 1 8b 1 8c 1       

Lời giải

Ta có:

       

2 2 2

18 a b c 8 a b c a b c 9 a b c

1 1 1

8a 9a 8b 9b 8c 9c

a b c

8a 1 8b 1 8c 1

9a 9b 9c

a b c

          

     

        

     

     

  

     

Áp dng bng thc Cosi ta có:

 

2 2 2

8a 1 8b 1 8c 1

9a 9b 9c 6 8a 1 6 8b 1 6 8c 1

a b c

18 a b c 6 8a 1 6 8b 1 6 8c 1

  

          

        

 

2 2 2

3 a b c 8a 1 8b 1 8c 1        



Dy ra khi và ch khi

a b c

Câu 43: [TS10 Chuyên Bn Tre, 2018-2019]

Cho hai s th

a,b

tha

a b 1

Tìm giá tr nh nht ca biu thc

  

Lời giải



a 1 a





 

4 1 a

a 1 a



  



Áp dAM-GM cho hai s 

 

4 1 a



;

1a

c:

 

4 1 a

T 2 . 5 9

a 1 a



  



ng thc xy ra



 

4 1 a

4 1 a a 3a 8a 4 0

a 1 a



       



 

a 2 loai

a nhan

















Vy

minT 9



và



THCS.TOANMATH.com

FB TRỊNH BÌNH

Câu 44: nh, 2018-2019]

Cho các s tha mãn

a b 1

Chng minh rng:

      

3 a b a b 4ab a 3b b 3a

      

Lời giải

Ta có:

  

AM GM

1 a 3b b 3a

a 3b b 3a a b



  

    

T gi thit ta có:

 

a b 1 a b 2 ab 1 2 ab 1 a b 4ab 1 a b             

        

3(a b) (a b) 4ab a 3b b 3a 3 a b a b 1 a b a b

               

2 2 2 2

3a 6ab 3b 2a 2b a b 1 2a 2b 2ab 0

4a 4b 1 8ab 4a 4b 0

           

      

 

1 2a 2b 0   



Vng thc chng minh.

Câu 45: [TS10 Chuyên Bà R-2019]

Cho các

a,b,c 3

a mãn

 

bc a b c 3  

a) Chng minh rng:

ab ac bc 3  

b) Tìm GTNN ca biu thc:

222

a b c

9 b 9 c 9 c

  

  

Lời giải

Áp dAM-GM ta có:

     

ab ac bc 3 ab.ac bc.ac ab.bc 3abc a b c 9

ab bc ca 3

        

   

Tip tc áp dAM-GM ta có:

     

 

2 2 2

a a 2 2a 2 2a 2 2a

6 2b 3 b 9 b

3 b 3 b 2 6 2b 3 b

2 2 a b c

2 2a 2 2b 2 2c 2 2a 2 2b 2 2c

9 b 9 c 9 a 9a ab 9b bc 9c ca

9 a b c ab ac bc

   

   

   





       

     

    

t

 

t a b c 3 ab ac bc 3      

THCS.TOANMATH.com

FB TRỊNH BÌNH

  

     

 

   

t 3 8t 3 0

8t 27t 9

8 a b c 27 a b c 3 ab ac bc

a b c

9. a b c ab ac bc

   

  

        





    



Vy

GTNN

ca P là

t ti

a b c 1  

Câu 46: [TS10 Chuyên Qung Nam, 2018-2019]

Cho ba s th

a, b, c

. Chng minh rng

2 2 2 2 2 2 2 2 2

a b b c c a 3(a b c )

a b b c c a a b c

    

  

    

Lời giải

Vi ba s th

a, b, c

ta có

2 2 2 2 2 2 2 2 2

a b b c c a 3(a b c )

a b b c c a a b c

    

  

    

. (1)

 

     

2 2 2 2 2 2

2 2 2

2 2 2 2 2 2

2 2 2

a b b c c a

a b c 3(a b c )

a b b c c a

c a b a b c b c a

a b c

a b b c c a



  

       



  



  

     

  

     

           

2 2 2 2 2 2

2 2 2

c a b a b c b c a

c a b 0

a b b c c a

ac c a bc c b ab b a bc b c ab a b ac a c

a b a b c a c a b c b c

  

      

  

     

      

     

 

  

 

  

 

  

2 2 2

ac c a bc c b ab b a

0. (2)

a b b c a b a c a c b c

  

   

     

Vi ba s th

a, b, c



Câu 47: [TS10 Chuyên Bc Giang, 2018-2019]

Cho

x,y,z

là các s thc tha mãn

2 2 2

x y z 8  

. Tìm giá tr ln nht ca biu thc

3 3 3 3 3 3

M x y y z z x     

Lời giải

Áp dng tính cht

a b a b  

ng thc xy ra khi và ch khi

ab 0

THCS.TOANMATH.com

FB TRỊNH BÌNH







3 3 3

M 2 x y z  

Mt khác

2 2 2

x y z 8  



2 3 2

x 2 2x

x 2 2

y 8 y 2 2 y 2 2y

z 2 2

z 2 2z













    

  

  









Vy





 

3 3 3

2 2 2

M 2 x y z 4 2 x y z     

32 2

ng thc xy ra khi

 

x;y;z 2 2;0;0

hoc

 

x;y;z 2 2;0;0

và các hoán

v ca nó. Vy giá tr ln nht ca

bng

32 2

Câu 48: [TS10 Chuyên TP. H Chí Minh, 2018-2019]

Chng minh rng

x x 0

  

vi mi s thc

Cho

x,y

là các s thc thu kin

x xy y 3  

. Tìm giá tr ln nht và

nh nht ca biu thc

P x y

Lời giải

a) Ta có

4 4 2 2 2

1 1 1 1 1

x x x x x x x x 0

2 4 4 2 2

   

            

   

   

Du bng xy ra

x 0 x



  















  







u bng không xy ra

Vy

x x 0

  

vi mi s thc

Ta có:

x xy y 3 P xy 3 xy P 3        

Áp dAM-GM cho hai s

x ; y

ta có:

2 2 2 2

x y 2 x y 2 xy xy



    

2 2 2 2

x y x y

xy xy

2 2 2 2



       

    

THCS.TOANMATH.com

FB TRỊNH BÌNH

P 3P

P 3 3

2 P 6

P 3 3



   



    





  





Du bng xy ra

x y x y   

222

2 2 2

x y 1

x x x 3

x y 3







  







  









Vy

max min

P 6 x y 3;P 2 x y 1       

Câu 49: -2019]

Cho

a,b,c

là các s ng minh rng:





3 3 3

2 2 2 2 2 2

a b c a b c

a ab b b bc c c ca a



  

     

Lời giải

a) Ta có :

3 2 2 2 2 2

2 2 2 2

a a(a b ) ab ab ab b

a a a

2ab 2

a b a b



      





 theo câu a), ta có:









Cng v theo v ba bng thc trên ta có:

3 3 3

2 2 2 2 2 2

a b c a b c

a b b c c a



  

  

Ta có:

3 3 3

2 2 2 2 2 2

a a 2 a

a ab b a b a b



   



Và

3 3 3

2 2 2 2 2 2

b b 2 b

b bc c b c b c



   



3 3 3

2 2 2 2 2 2

c c 2 c

c ac a c a c a



   



Cng v theo v ba bng thc trên ta có:

3 3 3 3 3 3

2 2 2 2 2 2 2 2 2 2 2 2

a b c 2 a b c a b c

a ab b b bc c c ca a a b b c c a





     



        



Câu 50: [TS10 Chuyên Khánh Hòa, 2018-2019]

Vi

a, b, c

là các s thu kin

a b c abc  

Chng minh rng

1 a 1 b

1 c 1



   

Lời giải

THCS.TOANMATH.com

FB TRỊNH BÌNH

Ta có

111

a b c abc 1

bc ca ab

      

t





x,y,z 0

và

xy yz zx 1

. Vì vy

















2 2 2

2 2 2 2

2 2 2

1 a 1 b 1 z

1 c 1 1 x 1 y 1

a b z

1 x 1 1 y 1 1 x 1 y 0

1 z z 1 x 1 y

1 x 1 1 y 1 0 (4)

  

         



         

   

      

Ta có:

     

2 2 2 2 2 2 2

1 x 1 y 1 x y x y 1 xy x y x y 1 z            

 









 









 

1 z z x y 1 z

4 1 x 1 1 y 1 0

1 z xz yz 1 z

1 x 1 1 y 1 0

   

      

   

      









 









1 z 1 xy 1 z

1 x 1 1 y 1 0

xy 1 z

1 x 1 1 y 1 0, x,y,z 0.

   

      



        

u phi chng minh.

Câu 51: [TS10 Chuyên Tha Thiên Hu, 2018-2019]

a) Cho

x,y,z

là các s thng bng 1.

Chng minh rng

1 1 1 49

16x 4y z 16

  

b) Cho s t nhiên

và các s nguyên

x,y

tha mãn

x y xy 1.  

Tìm giá tr

ca

x,y,z

sao cho

  

z 1 2 2 2 2

2 42 x y 1 x y



   

là s n nht.

Lời giải

a) Ta có

1 1 1 49 1 4 16

49.

16x 4y z 16 x y z

      

Vi hai s thc không âm

a,b

ta có

 

a b 0 a b 2 ab.    

Du "=" xy ra khi

a b a b.  

Áp dng kt qu trên, ta có:

1 1 1

49x 2 .49x 49x 14.

x x x

    

(1)

THCS.TOANMATH.com

FB TRỊNH BÌNH

Du "=" xy ra khi

49x x .

  

T

49y 28.



(2)

Du "=" xy ra khi

49y y .

  

Và

49z 56.



(3)

Du "=" xy ra khi

16 4

49z z .

  

Cng (1), (2), (3) theo v c:

 

1 4 16

49 x y z 98

x y z

     

1 4 16

49.

x y z

   

Du "=" xy ra khi

1 2 4

x ;y ;z .

7 7 7

  

Vy bng thc chng minh.

b) Ta có:

      

z 1 2 2 2 2 z 2 2

2 42 x y 1 x y 2 2 21 1 x 1 y .



       

Vi:

  

1 x x y xy x x y 1 x ,       

  

1 y x y xy y x y 1 y ,       

  

1 1 1 x y xy 1 x 1 y .        

Suy ra

    

     

2 2 2

z 1 2 2 2 2 z

2 42 x y 1 x y 2 21 x y 1 x 1 y .



        



  

z 1 2 2 2 2

2 42 x y 1 x y



   

là s  khi

2 21

là s



n ti s t nhiên

sao cho

2 21 n .

Ta có

     

2 1 mod3 2 1 mod3 .    

Nu

l thì

   

2 1 mod3 2 mod3 .  



 

n 2 mod3

vô lí (vì s chính

 c 1).

T 

là s chn.

t

 

2k, k .





Ta có

    

2 2k 2 k k k

n 21 2 n 2 21 n 2 n 2 21.        

Vì

21 1.21 3.7

và

n 2 n 2  

ng hp sau:

ng hp 1:

n 2 1

2 10,

n 2 21

















không có giá tr ca

thng hp

này.

THCS.TOANMATH.com

FB TRỊNH BÌNH

ng hp 2:

n 2 3

2 2 k 1.

n 2 7







   









T gi thit, ta có

  

1 x 1 y .  

Không mt tng quát, gi s

x 1 y 1 ,  

suy

x 1 1

y 1 2















Gii h c









hoc

  







Nu

x 0,y 1

thì

  

z 1 2 2 2 2 2

2 42 x y 1 x y 100 10 .



     

Nu

x 2,y 3   

thì

  

z 1 2 2 2 2 2

2 42 x y 1 x y 2500 50 .



     

Vy

x 2,y 3,z 2.    

Câu 52: [TS10 Chuyên Kiên Giang, 2018-2019]

Cho ba s 

x,y,z

thu kin

x y z 2  

Chng minh rng:

y z z x x y

  

  

Lời giải

Áp dng bng thc Bunyakoski vi b ba s có:

     

 

2 2 2 2

2 2 2

A B C A B C

a b c . a. b. c. A B C

a b c a b c



       





         

       





       



 

2 2 2

A B C

a b c a b c



   



Áp dng bng thc trên ta có:

 

     

 

x y z x y z

y x y z

y z z x x y 2(x y z) 2

y z z x x y

   



     

    

Dy ra khi:

x y z

  

Vu cn chng minh.

Câu 53:

[TS10 Chuyên Bc Ninh, 2018-2019]

Cho các s thc

a,b,c

tha mãn

0 a,b,c 2,a b c 3    

Tìm GTLN và GTNN ca

2 2 2

a b c

ab bc ca







Lời giải

THCS.TOANMATH.com

FB TRỊNH BÌNH

Áp dAM-GM ta có:

a b 2ab

b c 2bc

c a 2ca

















 

2 2 2 2 2 2 2 2 2

2 2 2

a b c a b a c b c 2ab 2ac 2bc

a b c ab ac bc

a b c

ab bc ca

           

     



  



Dy ra

a b c

a b c 1

a b c 3

  

    



  



Vy

MinP 1

khi

a b c 1  

 bài ta có:

   

   

 

2 2 2

0 a,b,c 2 a 2 b 2 c 2 0

abc 2 ab ac bc 4 a b c 8 0

abc 2 ab ac bc 12 8 0

2 ab ac bc 4 abc 4

ab bc ca 2

a b c 2ab 2ac 2bc

ab ac bc

a b c

P 2 2

ab ac bc 2 2

      

        

      

     

   

    

  



     



Du

""

xy ra

b c 3

abc 0

a c 3

a b c 3

a b 3

0 a,b,c 2

































  

























Vy

MaxP



khi

abc 0,a b c 3,0 a,b,c 2     

Câu 54: [TS10 Chuyên Thái Nguyên, 2018-2019]

Cho

x,y,z

là các s thng minh rng

2 2 2 2 2 2

y x y z

8x 3y 14xy 8y 3z 14yz 8z 3x 14xz



  

     

Lời giải

Áp dAM-GM ta có:

x y 2xy

THCS.TOANMATH.com

FB TRỊNH BÌNH

 

2 2 2 2 2 2 2 2

2 2 2 2

8x 3y 14xy 8x 3y 12xy 2xy 8x 3y 12xy x y

8x 3y 14xy 9x 12xy 4y 3x 2y 3x 2y

           

         

Ch ta có:

8y 3z 14yz 3y 2z

8z 3x 14xz 3z 2x



   





   





Áp dAM-GM Schawz:

 

2 2 2

a b c

x y z x y z



  



c:

 

x y z

y x y z

3x 2y 3y 2z 3z 2x 3x 2y 3y 2z 3z 2x 5



     

       

Vu phi chng minh

Du

""

xy ra khi và ch khi

x y z

Câu 55: [TS10 Chuyên Tuyên Quang, 2018-2019]

Cho các s th

a,b,c

tha mãn

a b c 3  

Tìm giá tr nh nht ca biu thc:

2 2 2

a 4a 1 b 4b 1 c 4c 1

a a b b c c

     

  

  

Lời giải

Áp dAM-GM c :

1 1 1 9

x y z x y z

  



 

2 2 2

AM GM

a 4a 1 b 4b 1 c 4c 1

a a b b c c

a 1 4a b 1 4b c 1 4c

c(c 1)

a a 1 b b 1

2a 4a 2b 4b 2c 4c 1 1 1 6.9 54

a(a 1) b(b 1) c(c 1) a 1 b 1 c 1 a b c 3 6



     

  

  

     

  





    

        



        



Vy giá tr nh nht ca M là 9, du bng xy ra khi và ch khi

a b c 1  

Câu 56: [TS10 Chuyên H-2019]

Cho

a,b,c

a mãn

ab bc ca 1

. Tìm giá tr ln nht ca biu thc

2 2 2

2a b c

P a 28b 28c

1 a 1 b 1 c

     

  

Lời giải

 bài ta có:

ab bc ca 1

Áp dAM-GM vào biu thc bài toán ta có:

THCS.TOANMATH.com

FB TRỊNH BÌNH

  

2a 2a 2a a a

a b a c

1 a ab bc ca a

b b b b b

4(b c) a b

b c b a

b 1 b ab ac bc

c c c c c

4(b c) a c

a c c b

c 1 c ab ac bc

   



   

   



   

   



   

Cng v theo v c:

2 2 2

2a b c a a b b c c

a b a c 4(b c) a b 4(b c) a c

1 a b 1 c 1

       

     

  

a b a c b c 1 9

a b a c 4(b c) 4 4

  

      

  

Mt khác:

2 2 2 2

a 49b a .49b

2 7ab

2 2 4

a 49c a .49c

2 7ac

2 2 4

  

 

2 2 2

b c 7bc

a 28b 28c 7 ab ac bc 7

9 19



      



   

Du

""

xy ra

7 15

a 7b 7c

ab bc ca 1







  



















Vy

MaxP



khi

7 15

















Câu 57: [TS10 Chuyên Qung Nam, 2018-2019]







a b ab



A a b

  



Lời giải







a b ab





A a b

  



THCS.TOANMATH.com

FB TRỊNH BÌNH

Ta có:

2 a b a b ab ab 4    

Dng thc xy ra

a b 4

ab 4







   









 

3 a b

ab a b ab 3 ab 5 ab

A a b ab 10

a b 4 4 a b 2 2



         



Suy ra:

A 10

ng th

a b 4

a b ab

4 a b

  



  













A

a b 4

Câu 58: ng Nai, 2018-2019]

Cho các s thc

a,b,c

. Chng minh rng

     

3 3 3 3 3 3

2 2 2 2 2 2

a b b c c a 1 1 1

a b c

ab a b bc b c ac c a

  

    

  

Lời giải

Ta có:

 

2 2 2

2 a b a ab b

a b 1 1 a b

2a 2b 2ab

ab(a b )

2ab a b

2 a ab b b 0 a b 0

  



   



       

u bng xy ra

ab

Ch ta có:

 

c b 1 1

2c 2b

cb c b

c a 1 1

2c 2a

ca c a



























Cng v theo v ta có:

     

3 3 3 3 3 3

2 2 2 2 2 2

a b b c c a 1 1 1 1 1 1 1 1 1

2a 2b 2c 2c 2a 2b a b c

ab a b bc b c ac c a

  

          

  

Dy ra khi

a b c

Vu phi chng minh

Câu 59: ng, 2018-2019]

Cho

a,b,c 0

và

a 2b 3c 20.  

Tìm giá tr nh nht ca biu thc:

3 9 4

S a b c

a 2b c

     

Lời giải

THCS.TOANMATH.com

FB TRỊNH BÌNH

Ta có:

 

3 9 4 a b 3c 3a 3 b 9 c 4

S a b c

a 2b c 4 2 4 4 a 2 2b 4 c

1 3a 3 b 9 c 4

a 2b 3c

4 4 a 2 2b 4 c

     

              

     

     

     

        

     

     

Áp dng bng thc AM-GM cho hai s không âm ta có:

 

3a 3 3a 3

) 2 . 3

4 a 4 a

b 9 b 9

) 2 . 3

2 2b 2 2b

c 4 c 4

) 2 . 2

4 c 4 c

1 3a 3 b 9 c 4 1

S a 2b 3c .20 3 3 2 13

4 4 a 2 2b 4 c 4

   

     

              

     

     

Dy ra khi và ch khi :

a 2b 3c 20

3a 3

b 3(a,b,c 0

2 2b

   











  



















Vy

MinS 13

khi

a 2;b 3;c 4  

Câu 60:

[TS10 Chuyên Thái Bình, 2018-2019]

Cho

x,y,z

l:

12x 10y 15z 60  

 .

Lời giải

x,y,z



12x 10y 15z 60  

Ta có

x,y,z 0



















(*)



2 2 2

T x y z 4x 4y z     

x(x 5) y(y 6) z(z 4) x 2y 3z

12x 60

x 2y 3z 2y 3z 12

        

       

2 2 2

44T x y z x y z     

THCS.TOANMATH.com

FB TRỊNH BÌNH

Vy GTLN ca T bc khi

x 0 x 0

y 6 or y 0

z 0 z 4

   













Câu 61: i Hc Vinh, 2018-2019]

Cho các s thc không âm

a,b

tha mãn:

 

a b a b 2   

Chng minh rng:

   

1 1 9

b 1 a 1

  

  

  

  



  

Lời giải

Ta có:

 

   

 

a b a b 2

a 2ab b a b 2

a b a b 2 2ab

a a b b 2 ab a b 1

   

     

     

       

      

   

  

a a 1 b b 1 2 a 1 b 1

a a 1 b b 1

a 1 b 1

b 1 a 1

      

  





  



t

x ;y x y 2

b 1 a 1

    



Ta có:

  

 

     

1 x 1 y 9

1 xy x y 9

xy x y x y 3xy 8

  

    



     





 

xy x y 6 0  

(do

 

0 xy 1



  

)

Du

""

xy ra khi và ch khi:

xy 0 a 0; b 2

x y 2 a 2; b 0

    







   



Câu 62: [TS10 Chuyên Hà Nam, 2018-2019]

Cho các s th

x,y,z

tha mãn

xy yz xz x y z    

Chng minh rng:

3 3 3

x 8 y 8 z 8

  

  

THCS.TOANMATH.com

FB TRỊNH BÌNH

Lời giải

Áp dAM-GM ta có:

     

xy yz xz x y z 3 xy xz yz xy xz yz 3           

Áp dAM-GM-Schwwarz ta có:

 

   

2 2 2

x y z

x 2 x 2x 4 y 2 y 2y 4 z 2 z 2 4

x y z

y z 6 x y z 2 x y z 12





          







        



 

   

 

   

2 2 2

x y z

2xy 2xz 2yz 3 x y z 2 x y z 12

2 x y z

x y z 2 x y z 15 2 xy yz xz







        







        

 

   

2 x y z

x y z 2 x y z 15





     



Ta cn chng minh:

 

   

  

2 x y z

x y z 2 x y z 15

x y z 2 x y z 15 0

x y z 5 x y z 3 0





     

       



 

x y z 3 xy yz xz 3     

Dy ra

x y z 1   

Vy

3 3 3

x 8 y 8 z 8

  

  

Câu 63: c Lc, 2018-2019]

1) Cho các s thc

x,y

không âm, chng minh rng

3 3 2 2

x y x y xy  

2) Cho các s th

a,b,c

tha mãn

abc 1

. Chng minh rng:

5 5 5 5 5 5

ab bc ca

a b ab b c bc c a ca

  

     

Lời giải

1) Cho các s thc

x,y

không âm, chng minh rng

3 3 2 2

x y x y xy  

Bng thc:

3 3 2 2

x y x y xy  

THCS.TOANMATH.com

FB TRỊNH BÌNH

x (x y) y (x y) 0    

(x y) (x y) 0   



x,y 0

2) Cho các s th

a,b,c

tha mãn

abc 1

. Chng minh rng:

5 5 5 5 5 5

ab bc ca

a b ab b c bc c a ca

  

     

Chng minh

5 5 2 3 3 2

a b a b a b  

3 2 2 3 2 2

a (a b ) b (a b ) 0    

2 2 2

(a b) (a b)(a ab b ) 0, a,b 0 (*)       

Áp dng (*):

5 5 2 2 5 5

a b c

a b a b (a b) a b ab ab.



      

ab c

(1)

a b c

a b ab







bc a

(2)

a b c

b c bc





;

ca b

(3)

a b c

c a ca





Cng c bng thc cn chng minh.

Du bng xy ra khi

a b c

Câu 64: [TS10 Chuyên Bn Tre, 2018-2019]

Cho hai s th

a,b

tha

a b 1

Tìm giá tr nh nht ca biu thc



Lời giải

Ta có:

4 1 4(a b) a b 4b a 4b a

T 5 5 2 . 5 4 9

a b a b a b a b



           

Áp dng bng thc AM-GM cho hai s th

4b a 4b a

2 . 4

a b a b

  

4b a

T 5 5 4 9

      

Dy ra

4b a

a (tm)

a b 1

a 4b

a 2b 1

a b 1

b (tm)









  



  

   

   





















Vy

MinT 9 khi a ;b

  

Câu 65: -2019]

Cho các s th

a,b,c

. Chng minh rng:

2 2 2

2 2 2 2 2 2

a b c

a ab b b bc c c ac a

  

     

THCS.TOANMATH.com

FB TRỊNH BÌNH

Lời giải

Ta có : Áp dng bng thc AM-GM  Schaw thì:

 

   

2 2 2 2 2

2 2 2 2 2 2

c a b c

a ab b a b c ab ac bc

b(a b c)

c ac a a b c ab ac bc

a(a b c)

b bc c a b c ab ac bc

a b c a b c

b(a b c) c(a b c)

a a b c

a ab b b bc c c ac a

a c b c







      







      







      

     

   



     

  



 

     

2 2 2

2 2 2 2 2 2 2 2 2

a b c ab ac bc

a c b c a b

a b c a b c

a b c

a ab b b bc c c ac a a b c ab ac bc



    



    



          

 

2 2 2

2 2 2 2 2 2 2 2 2

2 2 2

2 2 2 2 2 2

2 a b c ab ac bc

a c b

a ab b c ac a b bc c a b c ab ac bc

a c b

a ab b c ac a b bc c

    

    

          

    

     

2 2 2

2 2 2 2 2 2

a c b

a ab b c ac a b bc c

   

     



Du bng xy ra khi và ch khi a = b = c.

Câu 66: -2019]

Cho các s 

x,y,z

tha

xy yz zx 3xyz

Chng minh rng

2 2 2

x z 1 1 1 1

2 x y z

z x x y y z



    



  



Lời giải

 bài ta có:

xy yz zx 3xyz

xy yz

zx 1 1 1

xyz xyz xyz z x y

       

Li có:

 

AM GM

3xyz xy yz xz 3 xyz xyz 1 x y z 3



         

Ta có

AM GM

x xz xz z z 1

x x x x

z x z x

2 zx

z 1 z z 1 z z 1

(Do z 1 2 z z )

2 2 2 2 2





       



  

        

THCS.TOANMATH.com

FB TRỊNH BÌNH

 ta có:

y y 1

x 1 z

y ; z

x y y z



   



Cng v vi v ca 3 bng thc:

2 2 2

y x y z 3

x z 6 3 1 1 1 1

x y z 3

4 4 2 2 x y z

z x x y y z



  

           



  





Câu 67: -2019]

Cho a, b là hai s i thu kin

a0

và

a b 1

Tìm giá tr nh nht ca biu thc

8a b





Lời giải

Theo gi thit ta có:

a b 1 b 1 a    

2 2 2

8a 1 a 1 1 1 1

A b 2a b a a b

4a 4a 4 4a 4



           

2 2 2

1 1 1 3 1 1 1

a a a 2a 1 a a a a a a

4a 4 4a 4 4a 4 2

                 

AM GM

1 1 1 1 3

2 a. a 1

4a 2 2 2 2





      





Du bng xy ra

a ;a 0

a b (tm)

4a 2

b 1 a



  



   









Vy

MinA a b

   

Câu 68: nh, 2018-2019]

Cho hai s a mãn



. Chng minh rng:

1 1 25

a b 2

   

   

   

   

Lời giải

Ta có:



1 a ab 1 b

     

v(a > 0, b > 0)

L

2 2 2 2 2 2

(x y)

2(x y ) (x y) (x y) x y



       

(1) , d

và ch khi x= y



2 2 2

(x y) (x y) 4xy (x y) 4xy      

(2), d khi x= y

THCS.TOANMATH.com

FB TRỊNH BÌNH

Áp dng (1), ta có:

2 2 2

ab 1

1 1 1 b

a b 1 b 1

a b a a

a b 2 2 2 2

  

     



     



     

   

       

      

   

   



d khi:

  

và



Áp dng (2), ta có:

1 a a b

a 4 1 4 4

b b b a



     







d khi:



và



T 

1 1 (1 4)

a b 2

    

   

   

   

. Dy ra khi và ch khi:



hay



Vy

1 1 25

a b 2

   

   

   

   

, d khi: a =

và b = 2.

Câu 69: -2019]

Cho

x,y,z 0

tha mãn

x y z 1  

. Chng minh rng

xy yz

xz 3

xy z yz x xz y 2

  

  

Lời giải

Áp dng bng thc Cô si ta có:

    

xy xy xy y

xy z 2 x z y z

xy z x y z z x y z



   



  

    



Ch ta có:

yz y

1 z xz 1 z x

yz x 2 x y z x xz y 2 y z x y

   

   

   

     

   

1 x z z x

2 x z x y x z y z x y y z

1 x z x z

2 x z x z x y x y y z y z

P .3



      



     





   



      



   



     





   



  

Dy ra khi

x y z

  

THCS.TOANMATH.com

FB TRỊNH BÌNH

Vy giá tr nh nht ca P là

Câu 70: nh, 2018-2019]

Cho

x,y,z

là các s thc tha mãn

  

y x z 1; y z.   

Chng minh

     

2 2 2

1 1 1

x y y z z x

  

  

Lời giải

t

x y a; x z b   

c

ab 1; a b.

Bng thc cn chng minh tr thành:

 

2 2 2 2 2 2 2

1 1 1 a b 1

a b a b a b 2ab



     





a b 4

a b 2

   



a b 2 2.

a b 2

    



ab 1; a b

nên

a b 2ab

hay

a b 2 0.  

Mt khác

   

 

2 2 2 2

a b 2 2 a b 2 .

a b 2

     



tc là

a b 2 2

a b 2

   



Vy

     

2 2 2

1 1 1

x y y z z x

  

  

Câu 71: [TS10 Chuyên KHTN Hà Ni, 2018-2019]

Cho

a,b,c

là các s thng minh rng

ab bc 1 1

a b b c



  







Lời giải

Áp dCauchy-Schwarz ta có:

ab bc 1 1 ab bc 1 1

2. . 2

a b b c a b b c a b b c

a b b c

a c b b a c b b

a b b c a b b c a b b c a b b c

a b c b

a b a b b c b c



   

    



   



     



   



      

      

      

       

      

   

    

   

   

   

Vu phi chng minh

Du

""

xy ra khi và ch khi

a b c

THCS.TOANMATH.com

FB TRỊNH BÌNH

Câu 72: nh, 2018-2019]

Cho các s th

a,b

tha mãn

a b 1

Chng minh rng

      

3 a b a b 4ab a 3b b 3a .

      

Lời giải

Bng th

a 3b b 3a





Áp d-GM cho 2 s 

a a a b 1 a a b

. (1)

a b a 3b 2 a b a 3b

a 3b

   

  



   





và

b 1 2b 1 1 2b

. . (2)

2 a 3b 2 2 a 3b

a 3b



  









T (1) và (2) suy ra

a b 1 3 a 1 1 3 a

. (3)

2 2 a b 2 2 a b

a 3b a 3b

    

    

   



   

Ch 

1 1 3 b

. (4)

2 2 a b

b 3a











T (3) và (4) suy ra

a 3b b 3a





u phi chng minh)

Du

""

xy ra khi

a b .



Câu 73: [TS10 Chuyên Khánh Hòa, 2018-2019]

Cho a, b,c là các s thu kin

a b c abc  

. Chng minh

rng

1 a 1 b

1 c 1



   

Lời giải

Ta có:

111

a b c abc 1

ab ac bc

      

t

1 1 1

x ; y ;z

a b c



thì bng th thành :

xy xz yz 1  

2 2 2

1 a 1 b

1 c 1

1 1 1

1 1 c 1 1

a b c



   

      

1 x 1 y 1



     

THCS.TOANMATH.com

FB TRỊNH BÌNH

1 1 x 1 y 0



      









2 2 2 2

1 x 1 1 y 1 1 x . 1 y 0



         









2 2 2

1 z z 1 x 1 y

1 x 1 1 y 1 0

   

      

Ta li có:

   

 

   

































2 2 2 2 2 2

2 2 2

1 x 1 y 1 x y x y 1 xy x y

xz yz x y z 1 x y x y 1 z

1 z z(x y) 1 z

bdt 1 x 1 1 y 1 0

1 z (xz yz) 1 z

1 x 1 1 y 1 0

1 z (1 xy) 1 z

1 x 1 1 y 1 0

xy 1 z

1 x 1 1 y 1 0

         

         

   

       

   

      

   

      



      

T u phi chng minh.

Câu 74: [TS10 Chuyên Phan Bi Châu, 2018-2019]

Cho

a,b,c

tha mãn

abc 1.

Chng minh rng:

4 3 4 3 4 3

1 1 1

a a ab 2 b b bc 2 c c ac 2

  

        

Lời giải

Ta có:

 

    

2 2 2

4 3 4 3

a 1 a a 1 0 a 2a 1 a a 1 0

a a a 1 0 a a 1 a

a a ab 2 ab a 1

ab a 1

a a ab 2

         

        

      





  

Ch ta có:

4 3 4 3

1 1 1 1

;

bc b 1 ac c 1

b b bc 2 c c ac 2



   

     

y

1 1 1 1 1 1

VT 3.

ab a 1 bc b 1 ac c 1



     



     



(Áp d Bunyakovski cho 3 s)

THCS.TOANMATH.com

FB TRỊNH BÌNH

Li có

1 1 1 1 a ab

3. 3.

ab a 1 bc b 1 ac c 1 ab a 1 abc ab a

a bc abc ab

   

    

   

         



   

1 a ab

3. 3

ab a 1 1 ab a a ab 1



   



     



Vu phi chng minh

Dy ra khi và ch khi

a b c 1  

Câu 75: [TS10 Chuyên Hà Nam, 2018-2019]

Cho a là s bt kì,chng minh rng:

2010

a 2010

a 2009







Lời giải

Ta có:

2010 2010 2010 2010

a 2010 2 a 2009 a 2009 1 2 a 2009       





2010 2010

a 2009 2 a 2009 1 0     





2010

a 2009 1 0   

i mi a

Câu 76: [TS10 Chuyên nh, 2018-2019]

Cho các s tha mãn

a b 1

Chng minh rng:

      

3 a b a b 4ab a 3b b 3a

      

Lời giải

Ta có:

  

AM GM

1 a 3b b 3a

a 3b b 3a a b



  

    

T gi thit ta có:

 

a b 1 a b 2 ab 1 2 ab 1 a b 4ab 1 a b             

        

3(a b) (a b) 4ab a 3b b 3a 3 a b a b 1 a b a b

               

2 2 2 2

3a 6ab 3b 2a 2b a b 1 2a 2b 2ab 0

4a 4b 1 8ab 4a 4b 0

           

      

 

1 2a 2b 0   

Vng thc chng minh.

NĂM HỌC 2017-2018

THCS.TOANMATH.com

FB TRỊNH BÌNH

Câu 77: [TS10 Chuyên TP. H Chí Minh, 2017-2018]

Cho x, y là hai s thGTNN ca biu thc:

16 xy

x y xy







Lời giải

Áp d GM cho ba s không âm ta có:

16 xy

x y xy







16 xy

(x y)

x y xy







8 xy 8 xy

(x y)

x y x y xy



  



8 xy 8 xy

(x y)

3. . . 2 10

x y x y xy



  



ng thc xy ra khi

8 xy

(x y)

x y xy







⇔ x = y

Vy giá tr nh nht ca P là 10

Câu 78: [TS10 Chuyên , 2017-2018]

 dài ca ba cnh tam giác. Chng minh rng:

2 2 2 2 2 2 2 2 2

a b c b c a a c b

2ab 2bc 2ca

     

  

Lời giải

Ta có:

2 2 2 2 2 2 2 2 2

a b c b c a a c b

2ab 2bc 2ca

     

  

2 2 2 2 2 2 2 2 2

c(a b c ) a(b c a ) b(a c b ) 2abc

2abc

        



2 2 2 2 2 2 2 2 2

c(a b c ) a(b c a ) b(a c b ) 2abc 0          

2 2 2 2 2 2 2 2 2

c(a b c 2ab) a(b c a 2bc) b(a c b 2ca) 0            

2 2 2 2 2 2

c((a b) c ) a((b c) a ) b((c a) b ) 0         

c(a b c)(a b c) a(b c a)(b a c) b(c a b)(c b a) 0               

     

2 2 2

(a b c) c a b c a b c a b a c b >0

(a b c)(c a 2ab b ) 0

(a b c)[c (a b) ] 0

(a b c)(c a b)(c a b) 0



          



      

     

       



a b c 0

c b a 0

c a b 0

   



  





  



Suy ra:

(a b c)(c a b)(c a b) 0      

⇔ x = y 

Vy ta chu.

THCS.TOANMATH.com

FB TRỊNH BÌNH

Câu 79: [TS10 Chuyên KHTN Hà Ni vòng 1, 2017-2018]

Cho a, b là s các s th ln nht ca biu thc:

1 1 1

M (a b)( )

a b a b

   



Lời giải

Ta có:

3 2 3 2

(a b)( b) (a b) ;(b a)( a) (a b) .

       



3 3 2

a b a b (a b)

  



  

⇔ VT 

1 1 1

1 1.

a b ab ab ab

  

    



ng thc xy ra khi a = b = 1

Vy giá tr ln nht ca M là 1 khi a = b = 1.

Câu 80: [TS10 Chuyên KHTN Hà Ni vòng 2, 2017-2018]

Vi a, b, c là các s tha mãn: ab + bc + ca + abc = 2.

Tìm giá tr ln nht ca biu thc:

2 2 2

a 1 b 1 c 1

a 2a 2 b 2b 2 c 2x 2

  

  

     

Lời giải

Vng thc thc:

 

1 1 1 1

x y 4 x y











Tht vy:

     

* x y 4xy x y 0

4xy x y



       





Bng thc (*) xy ra d

Quay tr li bài toán ta có:

abc ab bc ca 2

abc ab ac bc a b c 1 a b c 3

(a 1)(b 1)(c 1) (a 1)(b 1)(c 1)

(a 1) (b 1) (c 1)

(a 1)(b 1)(c 1)

1 1 1

(a 1)(b 1) (b 1)(c 1) (c 1)(a 1)



           

       

    



  

   

     

t

3 3 3

a 1 ,b 1 ,c 1

x y z

     

 thit bài toán tr thành: xy + yz + zx = 3 và

THCS.TOANMATH.com

FB TRỊNH BÌNH

2 2 2

a 1 b 1 c 1

a 2a 2 b 2b 2 c 2x 2

a 1 b 1 c 1

(a 1) 1 (b 1) 1 (c 1) 1

1 1 1

a 1 b 1 c 1

111

3 x 3 3 z

xyz

333

3( )

x 1 y 1 z 1

3( )

(x y)(x z) (y z)(y x) (z x)(z y)

  

  

     

  

  

     

  

     

  

  



  

  

  

     

3 x x z z 3 3

( ) .

4 x y x z y z y x z x z y 4

      

     

(Áp dng bng thc (*))

ng thc xy ra khi x = y = z =

31

Vy giá tr ln nht ca M là

Câu 81: [TS10 Chuyên , 2017-2018]

Cho x, y 







Lời giải

Ta có :

2 2 2 2 2

x y x 4y 3y 4xy 3y

M 4 .

xy xy xy xy x 2 2



       



x 4y

x 2y



















khi x = 2y.

Câu 82: [TS10 Chuyên nh, 2017-2018]





P (a b)(4 5c).

a bc b ac

    



Lời giải

 :

1 1 1

( x,y 0)

x y x y

   



THCS.TOANMATH.com

FB TRỊNH BÌNH

Ta có :

1 1 4

P (a b)(5c 4) (a b)(5c 4)

a bc b ac (a b)(c 1)

4 5c 4 c

(1 c)(5c 4) 4 4 4 8

(1 c)(1 c) c 1 c 1

        

   



       

   

 = 

c 0,a b .

  



Câu 83: [TS10 Chuyên Bà R, 2017-2018]

 :

P ( ) 2(x y ).

   



Lời giải

Ta có : x

+ y

 : 2(x

+ y



.  :

2 2 2 2 2 2

2 2 2 2

2 2 2 2 2 2

xy xy xy x y

1 1 1 1

P ( ) 2(x y ) ( )(x y) 2

x y x y xy

x y x y x y

4xy x y 3xy 3(x y )

2 2 4 2

x y x y 2(x y )



          

  



      

  

  

 = 

x y 2xy

x y.

4xy x y























Câu 84: [TS10 Chuyên B, 2017-2018]



a 1;b 4;c 9  

 :

bc a 1 ac b 4 ab c 9

abc

    



Lời giải

Ta có :

a 1 b 4 c 9

a b c

  

  

a 1;b 4;c 9  

 :

THCS.TOANMATH.com

FB TRỊNH BÌNH

a 1 1

a (a 1) 1 2 a 1

b 4 1

b (b 4) 4 4 b 4

c (c 9) 9 6 c 9

c 9 1













    







      





    













 :

1 1 1 11

2 4 6 12

   

 = 

a 1 1 a 2

b 4 4 b 8

c 9 9 c 18

    



   





  



Câu 85: [TS10 Chuyên c Lc, 2017-2018]

1) Cho các s ng minh rng:

a b 4c

b c c a a b

  

  

2) Cho các s u kin:

2 2 2

a b c 11

ab bc ca 7



  











Chng minh:

a,b,c 3.



Lời giải

t

y z x

x a b

x y z

y b c b

z c a

x y z

  





  







   



















Ta có:

y z x x y z x y z

a b 4c

b c c a a b 2x 2y 2z

     

    

  

AM GM

y 2y

x z 2x z

2x 2y z 2y z 2x

y 2y

x z 2x z

2 . 2 . 2 . 3

2x 2y z 2y z 2x

1 2 2 3



   



      

   





   

   

   



Dy ra nên

a b 4c

b c c a a b

  

  



Cách khác:

S dng bng thc AM-GM-Schwars ta có:

THCS.TOANMATH.com

FB TRỊNH BÌNH

 

2 2 2

a b 2c

a b 4c a b 4c

b c c a a b ab ac bc ab ac bc

2 ab bc ca



     

     



Ta li có:

 

a b 2c

2 ab bc ca







Tht vy:

       

* a b 2c 4 ab bc ca 0 a b 4c 0          



Vy bng thc chng minh.

b) Ta có:

   

2 2 2

a b 5 c

a b c 11

ab 7 c a b 7 c 5 c

ab bc ca 7



  



  







     







Do:

       

2 2 2 2

a b 0 a b 4ab 5 c 4 7 5c c         

3c 10c 3 0 c 3

      

Ch c:

a 3, b 3

   

Vy

a,b,c 3



Câu 86: [TS10 Chuyên Bc Giang, 2017-2018]

Cho 2 s tha mãn

2 xy 1



Tìm giá tr nh nht biu thc:

x 4x

P 15xy.

y 3y

  

Lời giải

Tách và áp d-c:

x x 4 4

P 3xy 12xy

x y 3y 3 3

x x 4 4

2 . 2. .3xy 2 12xy.

x y 3y 3 3

      

   

2 2x 8 xy 2x 8 xy

2 2x. 8 xy 4 8 xy 4

      

    

Dy ra khi



Câu 87: [TS10 Chuyên , 2017-2018]

Cho các s a mãn:

1 2017 2018

1 a 2017 b 2018 c

  

  

Tìm giá tr nh nht ca biu thc:

P abc.

Lời giải

THCS.TOANMATH.com

FB TRỊNH BÌNH

Ta có:

AM GM

1 2017 2018 2018 1 2017

1 a 2017 b 2018 c 2018 c 1 a 2017 b

c 1 2017 1 2017

2018 c 1 a 2017 b 1 a 2017 b



      

     

  

    



:

b 1 2018 a 2017 2018

2 . ; 2 .

2017 b 1 a 2018 c 1 a 2017 b 2018 c



     

Nhân theo v c:

       

abc 2017.2018

8 abc 8.2017.2018

a 1 2017 b 2018 c a 1 2017 b 2018 c

  

     

Dy ra khi

a 1,b 2017,c 2018  

Vy giá tr ln nht ca P là 8.2017.2018

Câu 88: c, 2017-2018]

a) Cho ba s

a,b,c

tha mãn

a b c 0  

và

a 1, b 1, c 1.  

Chng minh rng

4 6 8

a b c 2.  

b) Tìm giá tr nh nht ca biu thc

   

  

3 3 2 2

x y x y

x 1 y 1

  





vi

x,y

là các s thc ln



Lời giải

a) T gi thit

a 1, b 1, c 1  

, ta có

4 2 6 2 8 2

a a ,b b ,c c  

. T 

4 6 8 2 2 2

a b c a b c    

Li có

   

1 b 1 c 1 0   

và

   

1 b 1 c 1 0   

nên

       

1 b 1 c 1 a 1 b 1 c 1 0       

 

ab 2bc 2ca 2 0 2 ab bc ca 2         

a

 

2 2 2

a b c 0 a b c ab bc ca 2          

. Vy

4 6 8

a b c 2  

b) Ta có

   

  

   

  

3 3 2 2

x y x y

x x 1 y y 1

y 1 x 1

x 1 y 1 x 1 y 1

  

  

   



   

x 1,y 1

nên

x 1 0,y 1 0   

Áp dng bng thc AM-GM cho 2 s 

y 1 x 1

, ta có :

 

x 1 1 2 x 1 x 1 1 0 x 2 x 1 0 2

             



THCS.TOANMATH.com

FB TRỊNH BÌNH

 

y 1 1 2 y 1 y 1 1 0 y 2 y 1 0 2

             





y 2xy

y 1 x 1

x 1. y 1

   



D



y ra khi

y 1 x 1

x 1 1

y 1 1















  















(thu kin)

Vy giá tr nh nht ca biu thc

T8

khi

x y 2.

Câu 89: [TS10 Chuyên Qung Ninh, 2017-2018]

Cho

;ab

tho mãn

a 2; b 2

. Chng minh rng:

(a 1)(b 1) (a b)(ab 1) 5     

Lời giải

Xét hiu

M (a 1)(b 1) (a b)(ab 1) 5      

2 2 2 2 2 2

(a b a b ab ab) (a b a b ab) 4         

ab(a 1)(b 1) (a b) a(a 2) b(b 2) 4



         



Ch ra vi

a2

thì

a(a 1) 2

và

a(a 2) 0

b2

thì

b(b 1) 2

và

b(b 2) 0

nên

ab(a 1)(b 1) 4  

;

(a b) a(a 2) b(b 2) 0



     



M0

hay

(a 1)(b 1) (a b)(ab 1) 5     

Câu 90: [TS10 Chuyên , 2017-2018]

Cho

a,b,c

là các s th mãn

a b c 3  

. Chng minh rng

   

2 2 2 3 3 3

4 a b c a b c 9.     

Lời giải

Bng thc cn ch

 

   

2 2 2 3 3 3

4 a b c a b c 3 a b c 27       

 

   

 

   

 

2 2 2 3 3 3

3 3 3 2 2 2 2 2 2

4 a b c a b c 3 a b c a b c

a b c 4 a b b c c a ab bc ca a b c (1)

          

           

THCS.TOANMATH.com

FB TRỊNH BÌNH

ng thc

 

   

3 3 3 2 2 2 2 2 2

a b c a b c 3 a b b c c a ab bc ca 6abc           

i

2 2 2 2 2 2

a b b c c a a c b a c b 6abc.     

Áp dng bng thc AM-GM, ta có

     

2 2 2 2 2 2 2 2 2

a b b c c a a c b a c b a b c b c a c a b          

 

2 2 2 2 2 2

2a bc 2b ca 2c ab 2 a bc b ca c ab 6abc.      

Vc chng thc xy ra khi và ch khi

a b c 1.  

Câu 91: [TS10 Chuyên m Hà Ni, 2017-2018]



1 2 3 9

x ,x ,x ,....,x



1 2 3 9

x x x ... x 10

x 2x 3x ... 9x 18

     



    



:

1 2 3 9

1.19x 2.18x 3.17x ... 9.11x 270    

Lời giải.

Ta có :

 

2 3 9

9 x x x ... x 90    

, suy ra :

 

1 2 3 9

9 x x x ... x 90

19x 29x 39x ... 99x 270

10 x 2x 3x ... 9x 180



    



     



    







1 2 3 9

1.19x 2.18x 3.17x ... 9.11x   

   

2 3 9 2 3 4 8

19x 29x 39x ... 99x 7x 12x 15x ... 7x 270          





2 3 8

x x ... x 0











   



Câu 92: [TS10 Chuyên H, 2017-2018]

Cho x, y, z là các s a mãn

2 2 2 2 2 2

x y y z z x 6     

Tìm giá tr nh nht ca biu thc:

y z z x x y

  

  

Lời giải

Ta có:

   

2 2 2 2 2 2

2 2 2 2 2 2 2 2 2

2 2 2

6 x y y z z x

3 x y y z z x 6 x y z

x y z 6

     

        

   



THCS.TOANMATH.com

FB TRỊNH BÌNH

     

2 2 2 2

2 2 2 2 2 2

x z x z

y z z x x y

2 y z 2 z x 2 x y

     

  

 

2 2 2 2 2 2

6 y z 6 z x 6 x y

2 y z 2 z x 2 x y

     

  

  





2 2 2 2 2 2

6 1 1 1 1

x y y z z x

y z z x x y





        



  



2 2 2 2 2 2

6 9 6

x y y z z x

6 9 6



    





Dy ra khi

a b c 2  

Vy giá tr nh nht ca M là

Câu 93: [TS10 Chuyên m Hà Ni vòng 2, 2017-2018]



2 2 2 2

1 1 1 1 1 1 1 1

a ; b ;c ;d

b c c d c d a b

       



Lời giải



2 2 2 2

1 1 1 1 1 1 1 1

P a b c d 3

b c c d c d a b

            



2 2 2 2 2 2 2 2

1 1 1 1 1 1 1 1 1 1 1 1

P a b c d a b c d 2

b c c d c d a b a b c d



                   





 

2 2 2 2

1 1 1 1 4

4 a b c d a b c d ;

a b c d a b c d

          

  

   

a b c d a b c d

16 16 16 16

P . . 12

4 a b c d a b c d 4 a b c d a b c d

     

     

           



Câu 94: [TS10 Chuyên , 2017-2018]

Cho 3 s 

4 4 4 4 4 4 4 4 4

a b b c c a 3a b c  

. Chng minh:

3 2 3 2 3 2

1 1 1 3

a b 2c 1 b c 2a 1 c a 2b 1

  

     

Lời giải

THCS.TOANMATH.com

FB TRỊNH BÌNH

Ta có:

4 4 4 4 4 4 4 4 4

4 4 4

1 1 1

a b b c c a 3a b c 4

a b c

      

(1)

S dng AM-GM ta có:

4 4 4 4 12 4 3

1 1 1 1 1 1 4

a a a b a b a b

    

 và cng theo v c:

4 4 4 3 3 3

1 1 1 1 1 1

a b c a b b c c a

    

(2)

Mt khác:

AM GM







 và cng lc:

2 2 2 4 4 4

1 1 1 1 1 1 1 3

a b c a b c



     





(3)

V

1 1 1 1 1 1

x y z t 16 x y z t



   



  



(*)

Tht vy, s dng AM-GM ta có:

 

1 1 1 1 4

x y z t 4 xyzt. 16

x y z t

xyzt

1 1 1 1 1 1

x y z t 16 x y z t



       







    



  



ng thc xy ra khi x = y = z = t.

Áp dc:

3 2 3 2 2 3 2 2

1 1 1 1 1 1

a b 2c 1 a b c c 1 a b c c



    



    



:

3 2 3 2 3 2 3 2

1 1 1 2 1 1 1 2

1 ; 1

16 16

b c 2a 1 b c a c a 2b 1 b c a

   

     

   

   

   

Cng theo v c:

3 2 3 2 3 2 3 3 3 2 2 2

1 1 1 1 1 1 1 1 1 1 1 3

16 8 16

a b 2c 1 b c 2a 1 c a 2b 1 a b b c c a a b c

   

        

   

     

   

Theo (1), (2) và (3) ta có th suy ra:

3 2 3 2 3 2 3 3 3 2 2 2

4 4 4 4 4 4

1 1 1 1 1 1 1 1 1 1 1 3

16 8 16

a b 2c 1 b c 2a 1 c a 2b 1 a b b c c a a b c

1 1 1 1 1 1 1 1 3

16 16 16

a b c a b c

   

        

   

     

   

   

       

   

   

3 6 3 3

16 16 16 4

   

THCS.TOANMATH.com

FB TRỊNH BÌNH

Dy ra khi a = b = c = 1.

Câu 95: [TS10 Chuyên Bà R, 2017-2018]

Cho a, b, c là các s th ln nht ca biu thc:

 

2 2 2

a b b c c a 1

P a b c .

a b c



   



Lời giải

V

 

   

2 2 2 2 2 2

a b c a b c 3 a b b c c a      

(1)

Tht vy:

 

       

 

2 2 2 3 2 2 2 2 2 3 2 2

2 2 2 3 2 3 2 3 2

AM GM

2 2 2 2 2 2

VT a b c a b c a ab ac b ba bc c ca cb

a b b c c a a ab b bc c ca

a b b c c a 2a b 2b c 2c a



             

        

    



 

2 2 2

3 a b b c c a  

=VP



2 2 2

a b b c c a a b c

a b c

   





   

2 2 2

2 2 2 2 2 2

2 2 2

a b b c c a 1 a b c 1

P a b c a b c

3 3 3

a b c

a b c 1 1 1 1 1

a b c a b c

3 9 4 3 2 4

   

       



   

         





Dy ra khi

a b c

  

Vy giá tr ln nht ca P là

Câu 96: [TS10 Chuyên Tây Ninh, 2017-2018]

Cho x, y là s th nh  ln nht ca biu thc:

 

   

xy 1 x y

x y 1 x 1 y





  

Lời giải

Ta có:

   

 

  

 

x y 1 x 1 y x y 1 x y xy

x y x y x y x y

Q xy 1 x y xy

xy 1 x y xy 1 x y 1 x y

      

   

     



     

c:

 

   

4 x y

x y x y x y x y

1 4 4 t

Q xy x y t 1 t

1 x y 1 x y 1 x y



   

       



     



S dng bng thc Cauchy-Schwarz c:

THCS.TOANMATH.com

FB TRỊNH BÌNH

 

1 4 t 2 1 9 1

1 1 1 8 Q

Q t 1 t t 1 t t 1 t 1 8



           

   

Dy ra khi



Vy giá tr ln nht ca Q là

Câu 97: [TS10 Chuyên Ninh Bình, 2017-2018]

u kin

a b c 2018  

. Tìm giá tr ln nht ca

biu thc:

a b c

a 2018a bc b 2018b ca c 2018c ab

  

     

Lời giải

Ta có:

 

a a a

a 2018a bc

a a b c a bc

a ab a bc ac

a a a

a b c

a ab 2a bc ac

a ab ac





   

  



  



:

b b c c

;

b 2018b ca a b c c 2018c ab a b c



       

Cng theo v c:

a b c







Dy ra khi

2018

a b c

  

Vy giá tr ln nht ca P là 1.

Câu 98: [TS10 Chuyên ng Tháp, 2018-2019]

Cho 3 s u kin

3 3 3

x y z 1.  

Chng minh bng

thc sau:

2 2 2

1 x 1 y 1 z

  

  

Lời giải

S d-c:

 

2 2 2 3

2 2 3

x 1 x 1 x x

x 1 x 2x

x 1 x



     



:

2y ; 2z

1 y 1 z





Cng theo v c:

 

3 3 3

2 2 2

2 x y z 2

1 x 1 y 1 z

     

  



THCS.TOANMATH.com

FB TRỊNH BÌNH

Câu 99: [TS10 Chuyên Tha Thiên Hu, 2018-2019]

Cho a, b, c là s i thu kiên:

ab bc ca 1.

Tìm giá

tr biu thc:

2 2 2

a b c

a b b c c a

  

  

Lời giải

S dng bng thc Cauchy-Schwarz c:

 

2 2 2

a b c

a b c a b c

E ab bc ca 1

a b b c c a 2

2 a b c



        

  



Dy ra khi a = b = c = 1.

Vy giá tr nh nht ca E là 1.

Câu 100: [TS10 Chuyên Bc Ninh, 2018-2019]

Cho các s thc a, b, c tha mãn

a b c 3.  

Tìm giá tr nh nht ca biu thc:

2 2 2

a 6a 3 b 6b 3 c 6c 3

a a b b c c

     

  

  

Lời giải

Ta có:

 

2 2 2

AM GM

2 2 2 2

3a 3 6a 2a

a 6a 3 6a 6a 2a 12a 2a 14

a a a a a a a a



  

    

   



   



:

b 6b 3 14 c 6c 3 14

2 ; 2

b 1 c 1

b b c c

   

   



Cng theo v và s dng bng thc AM-GM dng cng mu s c:

2 2 2

a 6a 3 b 6b 3 c 6c 3 1 1 1

M 14 6

a 1 b 1 c 1

a a b b c c

14. 6 14. 6 15

a b c 3 3 3

       

      



  



    

   

Dy ra khi a = b = c = 1.

Câu 101: [TS10 Chuyên , 2018-2019]

a mãn

x y z 4  

. Chng minh rng:

xy xz



Lời giải

Ta có:

 

1 1 1 1 1 1 4 4 16

xy xz x y z x y z

x y z



      











Dy ra khi x = 2, y = z = 1.

THCS.TOANMATH.com

FB TRỊNH BÌNH

NĂM HỌC 2016-2017

Câu 102: [TS10 Chuyên , 2016-2017]

Cho a, b, c là các s a mãn:

a b c 2016  

. Tìm giá tr ln nht ca

biu thc:

a b c

a 2016a bc b 2016b ac c 2016c ab

  

     

Lời giải

Ta có

    

a 2016a bc a a b c a bc a a b a c          

Áp dBunyakoskicopski ta có:

  

         

2 2 2 2 2

a b a c a b . c a ac ab

   

      

   

   

Suy ra

  

 

a a b a c a ac ab a a b c        

Suy ra

a 2016a bc a b c



   



b 2016b ac a b c



   

;

c 2016c ab a b c



   

Suy ra

a b c







, Du = xy ra khi

a b c 672  

Câu 103: [TS10 Chuyên Bà R, 2016-2017]

Cho a, b, c là 3 s a mãn ab + bc + ca = 3abc. Chng minh rng:

2 2 2

a b c 3

a bc b ca c ab

  

  

Lời giải

T u ki bài ta có

ab bc ca 1 1 1

abc a b c



    

Áp dng hai ln bng thc Côsi cho hai s 

a 2 1

a bc 2 a .bc 2a bc

a bc

2a bc 2 bc

     



1 1 1 1 1 a 1 1 1

2 b c 4 b c

a bc

   

    

   



   

 ta có:

b 1 1 1 c 1 1 1

;

4 c a 4 a b

b ca c ab

   

   

   



   

THCS.TOANMATH.com

FB TRỊNH BÌNH

Suy ra

2 2 2

a b c 1 1 1 1 3

2 a b c 2

a bc b ca c ab



     



  



Câu 104: [TS10 Chuyên Bà R, 2016-2017]

Cho hai s thc a, b u lng minh rng:

6 11

3ab 4 .

a b 1 b a 1

  

  

Lời giải

Ta có:

b 1 1 ab

a b 1 a. .



  

:

a 1 1 ab 6 6

b a 1 b. .

2 2 ab

a b 1 b a 1



    

  

Dy ra khi

a b 2.

6 6 18

Q 3ab 4 3ab 4 3ab 4.

ab 3ab

a b 1 b a 1

        

  

t

y 3ab 4 3ab y 4.    



AM GM

18 18 3 1 3 1 11

Q y (y 2) (y 2) 1 3 18. . 1 .

(y 2)(y 2) 4 4 4 4 2



          





Dy ra khi y = 2 hay

a b 2.

Câu 105: [TS10 Chuyên Bà R, 2016-2017]

Cho x, y, z là 3 s a mãn

2 2 2

x y z 3xyz  

. Chng minh :

y 2 z 2 x 2

  

  

Lời giải

Ta có

 , .

t v trái ca (*) là P. Cng các bng thc trên theo v c:

2 2 2

2 2 2 6 2

2 9 2 9 3 2 9

x y x y x x y

y y y

   

    

  

y y z







z z x







 

x y z

  



THCS.TOANMATH.com

FB TRỊNH BÌNH

Li có .

T gi thit suy ra .

 .

Câu 106: [TS10 Chuyên m Hà Ni, 2016-2017]

Cho a, b, c là ba s thc không âm và tha mãn: a + b + c = 1. Chng minh rng

5a 4 5b 4 5c 4 7     

Lời giải

Vì a, b, c không âm và có tng bng 1 nên

a(1 a) 0

0 a,b,c 1 b(1 b) 0 b b

c(1 c) 0





  



      











Suy ra

5a 4 a 4a 4 (a 2) a 2       



5b 4 b 2; 5c 4 c 2     



5a 4 5b 4 5c 4 (a b c) 6 7         



Câu 107: [TS10 , 2016-2017]

Cho hai s a mãn:

a b 2 2

. Tìm GTNN ca biu thc:



Lời giải

Vi mi a, b ta luôn có: (a - b)

 0

2 2 2 2 2 2 2

a b 2ab 0 a b 2ab a b 2ab 4ab (a b) 4ab             

(*)

ng thc (*) tr thành:

a b 4 1 1 4 4

ab a b a b a b a b



      

  

mà a+b

22

   



Dy ra

(a b) 0

a b 2

a b 2 2







   









Vy min P=

Câu 108: [TS10 Chuyên Bình Thun, 2016-2017]

 

2 2 2

x y z

xyz x y z x y z



     

 

x y z

x y z x y z



      

1P 

THCS.TOANMATH.com

FB TRỊNH BÌNH

Cho các s ng minh rng:

2 2 2

xy yz x y z

xy yz zx

x yz zx y zx xy z xy yz



  



     

Lời giải

Áp dng bng thc AM-GM-Schwar ta có:

 

  

 

xy y yz zx xy y yz zx

x yz zx

x yz zx y yz zx

xy yz zx

   





   



:

 

2 2 2 2

yz z zx xy zx x xy yz

;

y zx xy z xy yz

xy yz zx xy yz zx

   



   

Suy ra

 

2 2 2

2 2 2 2

x y z xy yz zx

xy yz x y z

xy yz zx

x yz zx y zx xy z xy yz

xy yz zx

   



   



     



Vy bng thc chng thc xy ra khi x = y = z.

Câu 109: [TS10 Chuyên Tha Thiên Hu, 2016-2017]

Cho x, y > 0 và

x y 3

. Tìm giá tr nh nht ca:

M 6x 4y 10xy 2016

     

Lời giải

S dng bng thc AM-c:

xy 4x



;

3xy 6y





 

2 2 2 2

A 6x 6xy 4y 4x 6y 6x x y 4y 6y 4x 6x.3 4y 6y 4x             

   

2x 4y 6y 22x 4 4y 4 6y 22 x y 16 50          

Suy ra:

M 50 2016 2066  

Dy ra khi x = 1; y = 2.

Vy giá tr nh nht ca M là 2066.

Câu 110: [TS10 Chuyên Thái Nguyên, 2016-2017]

Tìm giá tr nh nht ca biu thc:

P x 6 x 9 x 6 x 9     

Lời giải

u kin:

x9

Ta có:

P x 6 x 9 x 6 x 9 x 9 6 x 9 9 x 9 6 x 9 9               

   

x 9 3 x 9 3 x 9 3 3 x 9 x 9 3 3 x 9

                 



THCS.TOANMATH.com

FB TRỊNH BÌNH

Dy ra khi

9 x 18.

3 x 9 0





  



  





Vy giá tr nh nht ca P là 6.

Câu 111: [TS10 Chuyên Thái Bình, 2016-2017]

Cho x, y, z



1 và tha mãn

2 2 2

3x 4y 5z 52  

. Tìm giá tr nh nht ca biu

thc:

F x y z  

Dự đoán: u bng xy ra khi x = y = 1, z = 3.

Lời giải

Do x, y, z



1 nên:

  

1 y 1 0 xy x y 1      

 và cng theo v c:

 

y yz zx 2 x y z 3     



 

   

2 2 2 2 2

5 x y z 5 x y z 10 xy yz zx 52 2x y 10 2 x y z 3



              



 

2 2 1 20 x y z 30      

Suy ra:

x y z 5  

Dy ra khi x = y = 1, z = 3.

Vy giá tr nh nht ca F là 5.

Câu 112: [TS10 Chuyên Qung Bình, 2016-2017]

Cho a, b, c là các s tha mãn

ab bc ca 3abc.

Chng minh:

3 3 3

1 1 1 3

a b b c c a

  

  

Lời giải

Áp d-c:

1 1 1 1 3 1

a b 2. a .b

2 a .b



   







:

1 1 3 1 1 1 3 1

;

b c c a

4 2 4 2

b c c a

   

   

   

   



Cng theo v c:

3 3 3

1 1 1 1 4 4 4 1 ab bc ca 3

a b c abc

4 2 2 2

a b b c c a

   

      





  



Dy ra khi a = b = c = 1.

Câu 113: [TS10 Chuyên Phú Th, 2016-2017]

Cho các s  nh nht ca biu thc:

   

  

 

2x y x 2y

2 2 8

3 x y

2x y 1 1 x 2y 1 1



   



     

Lời giải

THCS.TOANMATH.com

FB TRỊNH BÌNH

t

2x y a, x 2y b   

và s dng bng thc AM-c:

 

2 2 2 2

2 2 ab 8

4 a b

a 1 1 b 1 1

2 2 ab 8

4 a b

a 1 a a 1 1 b 1 b a 1 1

2 2 ab 4 4 4 ab 4

a 1 a a 1 b 1 b a 1 a b

ab ab

   



   

   



       

       

       



8 ab 4

ab 4

  

t

t ab

. Ta s chng minh:

8 t 4

  

(*)

Tht vy:

   

 

* t 2 t 4t 8 0    

Vy

P1

. Dy ra khi



Vy giá tr nh nht ca P là 1.

Câu 114: [TS10 Chuyên TP. H Chí Minh, 2016-2017]

Cho x, y là hai s ng minh rng:

x y y x

x y 2 4







Lời giải

S dng bng thc AM-GM ta có:

 

x x 1 ;

y y 2 ;

x y 2 xy 3 .



Cng theo v (1) và (2):

 

x y x y 4

   

Nhân theo v (3) và (4):

   

 

x y x y 2 xy x y 5

    

Chia ca 2 v ca (5) cho

 

x y

c:

x y x y y x

x y x y

2 4 x y x y 2 4



    





Dy ra khi



Câu 115: [TS10 Chuyên Ninh Bình, 2016-2017]

Cho a, b, c là s tha mãn abc = 1. Chng minh rng:

THCS.TOANMATH.com

FB TRỊNH BÌNH

1 1 1 3

ab a 2 bc b 2 ca c 2 4

  

     

Lời giải

Vng thc thc:

 

1 1 1 1

x y 4 x y











Tht vy:

     

* x y 4xy x y 0

4xy x y



       





Bng thc (*) xy ra d

Áp dc:

1 c 1 c 1

ab a 2 1 ac 2c 4 c 1 a 1



  



     



Ch c:

1 1 a 1 1 1 b 1

;

bc b 2 4 a 1 b 1 ca c 2 4 b 1 c 1

   

   

   

       

   

Cng theo v 3 bng thc:

1 1 1 1 a 1 b 1 c 1 3

ab a 2 bc b 2 ca c 2 4 a 1 a 1 b 1 b 1 c 1 c 4



        



          





Dy ra khi a = b = c = 1.

Câu 116: [TS10 nh, 2016-2017]

Cho x, y, z là các s thc thu kin

  

y x z 1  

và

yz

. Chng

minh:

     

2 2 2

1 1 1

x y y z z x

  

  

Lời giải

Ta có:

   

    

   

2 2 2

2 2 2 2 2 2

x y x z y z 2 x y x z

x y z x x y x z x y x z

      

  

     

 

   

  

x y x z







S dng bng thc AM-c:

     

 

   

  

 

2 2 2 2 2 2

1 1 1 1 1

x y x z

x y y z z x x y x z z x



    



     

  

AM GM

x y x z









Câu 117: [TS10 Chuyên Ninh Thun, 2016-2017]

THCS.TOANMATH.com

FB TRỊNH BÌNH

Cho ba s a, b, c thu kin:

ab bc ca 3.

Tìm giá tr nh nht ca

biu thc:

 

2 2 2

P a b c 6 a b c 2017      

Lời giải

Ta có:

     

       

 

2 2 2 2 2 2

P a b c 6 a b c 2017 a b c 2 ab bc ca 6 6 a b c 2017

a b c 6 a b c 2011 a b c 6 a b c 9 2002

a b c 3 2002

2002

                 

              

    



Dy ra khi a = b = c = 1

Vy giá tr nh nht ca P là 2002.

Câu 118: [TS10 Chuyên Bc Ninh, 2016-2017]

Cho a, b, c > 0. Tìm giá tr nh nht ca

 

4 4 3

3a 3b c 2

a b c

  





Lời giải

S dng AM-c:

4 4 4 4 12 3 4 4 4 4 12 3

3a 1 a a a 1 4 a 4a ; 3b 1 b b b 1 4 b 4b             



   

4 4 3 3 3 3

3a 3b c 2 4a 4b c

a b c a b c

    



   

Ta d dàng ch:

 

   

4 a b a b *  

Tht vy:

      

* a b ab a b a b a b 0       



Vc chng minh. Dy ra khi a = b.

Áp dc:

 

3 3 3

a b c a b c

4a 4b c 1

a b c a b c 4 a b c

   



   

     

Dy ra khi a = b = 1, c = 2.

Vy giá tr nh nht ca M là

Câu 119: [TS10 Chuyên Ninh Thun, 2016-2017]

Cho các s a mãn

1 1 1

x y y z z x



  

Chng minh rng:

111

2x 3y 3z 3x 2y 3z 3x 3y 2z

  

     

ng thc xy ra khi nào?

Lời giải

THCS.TOANMATH.com

FB TRỊNH BÌNH

V

1 1 1 1

a b 4 a b











(*)

Thy vy:

 

1 1 2 1 1 1 1

a b 2 ab. 4

a b a b 4 a b

   

      

   



   

Vy (*) c chng minh, dy ra khi a = b .

S dc:

           

 

1 1 1 1 1

2x 3y 3z 4

x y x z 2 y z x y x z 2 y z

1 1 1 1 1 1 1 1 2

4 4 x y x z 16 x y x z y z

2 y z



  





        





   

     



   

    





   



:

1 1 1 1 2 1 1 1 1 2

3x 2y 3z 16 x y y z x z 3x 3y 2z 16 x z y z x y

   

     

   

         

   

C c:

1 1 1 1 1 1 1

2x 3y 3z 3x 2y 3z 3x 3y 2z 4 x y y z z x



     



        





Dy ra khi x = y = z.

Câu 120: [TS10 ng Tháp, 2016-2017]

Cho a, b, c là các s a mãn

2 2 2

a b c 1  

. Tìm giá tr nh nht ca

biu thc

2 2 2 2 2 2

a b c

b c c a a b

  

  

Lời giải

Ta có:

2 2 2 2 2 2 2 2 2

a b c a b c

b c c a a b 1 a 1 b 1 c

     

     



2 2 2 2

a b c 1 0 a 1 0 a 1        

Áp dng AM-c:

    

   

2 2 2

2 2 2 2 2

2x 1 x 2 x

1 1 4

a 1 a .2x . 1 x 1 x

2 2 3 27



   



     





 

2 1 3 3 a 3 3

a 1 a a

a 1 a

      



Ch c:

b 3 3 c 3 3

b ; c

1 b 1 c





Cng 3 bng thc trên theo v c:

 

2 2 2

a b c 3 3 3 3

P a b c

1 a 1 b 1 c

      

  



THCS.TOANMATH.com

FB TRỊNH BÌNH

ng thc xy ra khi

a b c

  

Câu 121: [TS10 Chuyên TP. H Chí Minh, 2016-2017]

Bit

x y z,x y z 0    

và

2 2 2

x y z 6.  

1) Tính

      

S x y x y y z y z      

2) Tìm giá tr ln nht ca biu thc

   

P x y y z z x   

Lời giải

1) Ta có:

 

2 2 2

x y z x y z

S x y z xy yz zx 6 6 9

    



          

2) t

a x y,b y z.   



a 0,b 0

và

a ab b 9  

 

a b 9 ab a b 2 3



       

t

t a b.



 

P t t 9

Ta s chng minh:

 

t t 9 6 3 *

Tht vy:

 

  

* t 2 3 t 3 0   





P 6 3

Dy ra khi

x 3,y 0,z 3   

Vy giá tr ln nht ca P là

Câu 122: [TS10 Chuyên KHTN, 2016-2017]

Vi x, y là s thc thu kin

0 x x y 2,2x y 2xy     

. Tìm giá tr

ln nht ca biu thc:

   

2 2 2 2

P x x 1 y y 1   

Lời giải

4 4 2 2

P x y x y   

Ta có bng thc:

   

a b a b *

  

Ta có:

2x y 2xy 2

    



Áp dng (*) suy ra:

 

2 2 2 2

1 4 1 1 2 1 4

2 2 1

2 x y

x y x y



      





Áp dng tip (*) ta có:

 

4 4 2 2 4

1 16 1 1 4 1 16

2 2 2

x y x y x



      





THCS.TOANMATH.com

FB TRỊNH BÌNH

Có

 

2 2 2

x 4x

x y 2 1 y 4 0 y 4 x



         





2 2 2 2 2

4x 4 1

x y 4 2x 4 x 2 4 x . 5



          





(do (1))

:

 

4 4 4

x 16x

1 y 4 0 y 16 x



      





4 4 4 4

16 1

y x 16 2 .x 16 .x 17



       





(do (2))

P 17 5 22  

Dy ra khi x = 1, y = 2.

Vy gí tr ln nht ca P là 22.

Câu 123: [TS10 nh, 2016-2017]

Cho hai s a, b không âm tha mãn

a b 3.

Chng minh rng:

2 2a 1 4b 8

1 2a 1 4b 15







Lời giải

Bng thc cn chi:

2 2a 1 4b 1 1 4b 1 2

1 2a 1 4b 1 2a 1 4b 1 2a 1 4b

  

      

     

S dng bng thc AM-c:

1 2a 1 4b





1 2 1 1 1

1 2a 1 4b 1 2a

(1 2a)( 2 b)

   

  





(1)

1 2a 2b

1 15

(1 2a)( 2 b)

2 2 4

  

   



(1 2a)( 2b)





(2)

T (1) và (2) suy ra:

2 2a 1 4b 8

1 2a 1 4b 15







Vy bng thc chng minh.

Dy ra ch khi : 1 + 2a =

+ 2b và a + b = 3 

11 13

a ; b



Cách khác:

THCS.TOANMATH.com

FB TRỊNH BÌNH

Ta có:

2 2a 1 4b 1 1 4b 1 2 1 1

P 1 2

1 2a 1 4b 1 2a 1 4b 1 2a 1 4b 2 4a 1 4b

    

        



       



V

1 1 4

a b a b





(*)

Thy vy:

 

1 1 2 1 1 4

a b 2 ab. 4

a b a b a b



      







Vc chng minh, dy ra khi a = b .

Áp dc:

 

1 1 4 8 8 8

P 2 2.

2 4a 1 4b 2 4a 1 4b 3 4.3 15

3 4 a b



     



     







Dy ra khi

a b 3

11 13

a ; b

2 4a 1 4b

  

  



  



Câu 124: [TS10 nh, 2016-2017]

a mãn

xy yz zx 1

. Tìm giá tr nh nht ca biu

thc :

2 2 2

1 1 1

4x yz 2 4y zx 2 4z xy 2

  

     

Lời giải

Ta có

  

2 2 2

1 1 1 1

2x y 2x z

4x yz 2 4x yz 2(xy yz zx) 4x 2xy yz 2zx

  



        

, ta có

        

1 1 1

2x y 2x z 2y z 2y x 2z x 2z y

  

     

        

yz xy

2xz yz 2xy yz 2xy xz 2yz xz 2yz xy 2xz xy

   

     

Vi mi

a,b

ta có

   

 

a b 0 a b 4ab ab .



      

Áp dng bng thc:

     

222

yz xy

2xy 2yz 2zx 2xy 2yz 2zx 2xy 2yz 2zx

444

  

     

 

xy yz zx

2xy 2yz 2zx



   



THCS.TOANMATH.com

FB TRỊNH BÌNH

ng thc xy ra khi

x y z

  

Vy giá tr nh nht ca

bng 1.

Cách khác:

t

a xy,b yz,c zx  



a b c 1  

và

2 2 2

ac ab bc

x ;y ,z

b c a

  

Ta có:

 

  

   

2 2 2

1 1 1

4ac 4ac

4x yz 2

b 2 a b c 2a b 2c

b b 4b a

2a b 2c b

4ac 2ab b 2bc

2a 2b 2c a b c





      

   



  

   

:

   

2 2 2 2

1 c 1 a

;

4y zx 2 4z xy 2

a b c a b c



   

   

Cng 3 bng trên theo v c:

 

a b c 1

a b c



  



Dy ra khi

x y z

  

Vy giá tr nh nht ca P là 1.

Câu 125: [TS10 , 2016-2017]

Cho 3 s tha mãn

x y z

  

. Tìm giá tr nh nht ca biu

thc:

 

2 2 2

x yz 1 y zx 1 z xy 1

z zx 1 x xy 1 y yz 1

  

  

  

Lời giải

Ta có:

 

2 2 2

xy 1

yz 1

zx 1

x yz 1 y zx 1 z xy 1

zx 1 yz 1

z zx 1 x xy 1 y yz 1

xy 1





  



  

     

     

       

  



     



THCS.TOANMATH.com

FB TRỊNH BÌNH

1 1 1

z x y

x y z



   







   

     

   

  

Áp dng bng thc AM-GM-Schwar ta có:

 

   

 

AM GM

1 1 1 1

x x y z

y x y z

1 1 1 1 1 1

z x y x y z

x y z x y z

1 1 1 9 9 27

x y z x y z x y z

x y z x y z

4 x y z 4 x y z

9 9 15

2 x y z .

4 x y z



   

     



   

       

   

       

              



   

    



Dy ra khi

x y z

  

Vy giá tr nh nht ca P là

Câu 126: [TS10 Chuyên Lam , 2016-2017]

Chng minh rng:

1 1 1 1931

...

1975

2 1 3 2 2016 2015

   

Lời giải

Ta có:

1 1 1 1 1 1 1 1 1 1 1

... ... 1 ...

1.2 2.3 2015.2016 2 2 3 2015 2016

2 1 3 2 2016 2015

             

1 2015 1931

2016 2016 1975

   



Câu 127: [TS10 Chuyên Hi Phòng, 2016-2017]

Cho

a,b,c 0; a b c 9   

, tìm giá tr nh nht ca:

b c 1 9 25

A 2 a 3

3 5 a b c

     

Lời giải

Áp dng bng thc AM-GM-Schwar c:

   

 

2 2 2 2

2 a b c

b c b c

a 1 3 5 a b c 2 a

3 5 3 5 3





          





 

1 3 5

1 9 25 81 1 9 25 27

a b c a b c a b c a b c

a b c



       

   



THCS.TOANMATH.com

FB TRỊNH BÌNH



 

2 a b c

b c 1 9 25 27

A 2 a 3

3 5 a b c 3

a b c



       



a b c a b c 27 27 9 a b c 27 27

3 . .

6 2 6 2

2 a b c 2 a b c 2 a b c 2 a b c

9 9 3 27

3. 15

6 2 2 2

     

     

       

    

Dy ra khi a = 1, b = 3, c = 5.

Vy giá tr nh nht ca A là 15.

Câu 128: [TS10 Chuyên Tin Giang, 2016-2017]

a mãn

a b c 3.  

Tìm giá tr nh nht ca biu thc:

2 2 2

1 2018

ab bc ca

a b c





Lời giải

Áp dng bng thc Cô si cho 3 s 

1 1 1 1

a b c abc; 3

a b c

abc

     

Suy ra

 

1 1 1

a b c 9(*)

a b c



    





Bng thc chng minh. Dng thc xy ra khi và ch khi

a b c

Ta có

 

2 2 2

a b c

ab bc ca a b c ab bc ca 3



         

Suy ra

2016 2016

672

ab bc ca 3





Áp dng bng thc (*) , ta có

 

2 2 2

1 1 1

a b c 2ab 2bc 2ca 9

ab bc ca ab bc ca

a b c



       



   





Suy ra

 

2 2 2 2

1 2 9

ab bc ca

a b c

  



c

2 2 2

1 2018

P 673

ab bc ca

a b c

  



Dng thc xy ra khi và ch khi

a b c 1  

Vy giá tr nh nht ca P là 673.

Câu 129: [TS10 Chuyên Lào Cai, 2016-2017]

THCS.TOANMATH.com

FB TRỊNH BÌNH

Cho a, b, c là s a mãn:

1 1 1

a 1 b 1 c 1

  

  

Chng minh rng:

2 2 2

1 1 1

8a 1 8b 1 8c 1

  

  

Lời giải

Ta có:

1 1 1 1 1 1 a b c

2 3 1 1

a 1 b 1 c 1 a 1 b 1 c 1 a 1 b 1 c 1



           



        



Mt khác:

2 2 2 2 2 2

1 1 1 1 1 1

1 3 2

8a 1 8b 1 8c 1 8a 1 8b 1 8c 1

8a 8b 8c 4a 4b 4c

8a 1 8b 1 8c 1 8a 1 8b 1 8c 1



       



     



       

     

Ta chng minh:

4a a

8a 1





(*)

Tht vy:

3 2 3 3 2

4a a

4a 4a 8a a 4a 4a a 0

8a 1

        



 

4a 4a 1 0 2a 1 0      



:

4b b 4c c

;

b 1 c 1

8b 1 8c 1





Cng 2 bng thc theo v c:

2 2 2

4a 4b 4c a b c

a 1 b 1 c 1

8a 1 8b 1 8c 1

     

  



Dy ra khi

a b c

  

Câu 130: [TS10 Chuyên C, 2016-2017]

Cho a, b, c l dài 3 cnh ca tam giác và

2ab 3bc 4ca 5abc  

Tìm giá tr nh nht ca biu thc:

7 6 5

a b c b c a c a b

  

     

Lời giải

Ta có:

 

2 3 4

2ab 3bc 4ca 5abc 5 do a,b,c 0

c a b

       

S dAM-GM-Schwar c:

 

2 2 2

2 3 4

2 3 4 2 3 4 81

5 3a 4b 2c

c a b 2c 3a 4b 3a 4b 2c 5



          



     

222

7 6 5 7 6 5

a b c b c a c a b

7 a b c 6 b c a 5 c a b

     

     

THCS.TOANMATH.com

FB TRỊNH BÌNH

 

       

7 6 5

7 a b c 6 b c a 5 c a b 2 3a 4b 2c



  

         

Dy ra khi

a b c

  

Vy giá tr nh nht ca P là 10.

Câu 131: [TS10 ng Nai, 2016-2017]

Cho a, b, c là s thc không âm tha mãn

a b c 3  

1) Chng minh rng:

ab bc ca 3  

2) Chng minh rng:

2 2 2

a b b c c a 4  

Lời giải

1) Ta có:

 

a b c

ab bc ca 3



   



Dy ra khi a = b = c =1.

2) Gi s b nm gia a và c ta có:

  

2 2 2 2 2

b a b c 0 b ac ab bc b c ac b c ac          

Áp dng AM-GM ta có:

    

 

2 2 2 2 2

4 a b c

a b b c c a a b b c 2abc b a c b a c a c 4



           

Câu 132: [TS10 nh, 2016-2017]

i tha mãn

2 2 2

x y z 1.  

Tìm GTLN ca biu thc:

     

222

2 2 2

P xy yz xz x y z y x z z x y



        





Lời giải

Ta chng minh:

     

 

222

2 2 2

2 2 2 2 2 2 2 2 2 2 2 2

P xy yz xz x y z y x z z x y 1

xy yz zx x y z x y y z z x xyz x y z x y z



         





             

 

2 2 2

2 2 2 2 2 2

x y x y y z y z z x x z 0



         







Dy ra khi

x y z

  

Vy giá tr ln nht ca P là 1.

Câu 133: [TS10 , 2016-2017]

Cho a, b, c là các s tha mãn:

a b c 3.  

Chng minh r

   

2 2 2 3 3 3

4 a b c a b c 9     

Lời giải

THCS.TOANMATH.com

FB TRỊNH BÌNH

Ta có:

   

   

2 2 2 3 3 3

3 3 3 2 2 2

2 2 2 2 2 2

4 a b c a b c 9

3 a b c 27 12 a b c

6abc a b b c c a ab bc ca

8abc a b b c c a

     

      

      

    

Bng thc cu-GM, vc chng minh.

Dy ra khi a = b = c.

Câu 134: [TS10 Chuyên Thái Bình, 2016-2017]

Cho các s thc x, y, z

1

và tha mãn

2 2 2

3x 4y 5z 52.  

Tìm giá tr nh nht

ca biu thc:

F x y z  

Lời giải

*) Bài này muốn giải được trước tiên ta phải dự đoán giá trị lớn nhất của F đạt

được khi x = y = 1, z = 3

Ta có:

 

2 2 2 2 2 2 2 2

5 x y z 52 2x y 52 2 1 55 x y z 11 1            

Li có:

  

1 y 1 0 xy 1 x y      

:

yz 1 y z ; zx 1 z x     

Cng theo v:

     

y yz zx 3 2 x y z 2 xy yz zx 6 4 x y z            

(2)

Ly (1) cng (2) theo v c:

   

x y z 5 4 x y z x y z 5         

Dy ra khi x = y = 1, z = 3.

Vy giá tr ln nht ca F là 5.

Câu 135: [TS10 Chuyên Tha Thiên Hu, 2016-2017]

Cho

x,y 0

và

x y 3

. Tìm giá tr nh nht ca

M 6x 4y 10xy 2016

     

Lời giải

Ta có:

  

   

4 x y 3 y x

M 6x 4y 10xy 2016 x y 6x 4y 2009

y x y x



           

 

3 4 3 4

x y 6x 4y 2009 3 6x 4y 2009

x y x y

   

          

   

   

THCS.TOANMATH.com

FB TRỊNH BÌNH

 

3 3x y 3 x y 2009

3 2 3x. 2 y. 3.3 2009 2066





      













    





Dy ra khi x = 1, y = 2.

Vy giá tr nh nht ca M là 2066.

Câu 136: [TS10 Chuyên Phan Bi Châu, 2016-2017]

Cho a, b, c là các s thi. Tìm GTNN ca biu thc:

   

a b c

a b b c

  



Lời giải

Vng thn sau (bc t chng minh):

   

 

2 2 2

x y 4xy 1

x y z x y z 2

x z 3

y z z x x y 2



    

  

  

Áp dng các bng thc:

             

2 2 2 2 2 2 2 2

2 2 2 2 2 2 2

a b c a b c a b c

4a 4ac

a b b c a b b c a b b c a c

1 a b c 1 3 3

3 b c b c a c 3 2 4

        

      

   

    

   

  

   

Dy ra kho a = b = c.

Vy giá tr ln nht ca P là

Câu 137: [TS10 Chuyên Qung Nam, 2016-2017]

Cho 2 s thc x, y tha mãn

0 x 1, 0 y 1   

và x + y = 3xy.

Tìm GTLN và GTNN ca biu thc:

P x y 4xy  

Lời giải

Ta có:

   

2 2 2 2

P x y 4xy x y 6xy 9x y 6xy 3xy 1 1          

  

x,y (0;1] 1 x 1 y 0 1 xy x y 3xy xy

           

Mt khác

AM GM

x,y (0;1] 3xy x y 2 xy xy



      

THCS.TOANMATH.com

FB TRỊNH BÌNH

Vy

 

4 1 1 1 1 1

xy 3xy 1 3xy 1

9 2 3 2 9 4

         



 

8 3 8 3

3xy 1 1 P

9 4 9 4

          

Vy: GTLN ca P là



khi

 

x,y 1; , ;1

   



   

   

GTNN ca P là



khi



Câu 138: [TS10 Chuyên Qung Nam, 2016-2017]

Cho 3 s thc a, b, c sao cho

0 a 1,0 b 1,0 c 1     

. Chng minh:

 

b c 3abc 2 ab bc ca     

Lời giải

Ta có:

    

a,b 1 1 a 1 b 0 1 ab a b c abc ac bc do 0 c 1               

Ch c:

b abc ab bc; a abc ab ac     

Cng 3 bng thc trên theo v c:

 

b c 3abc 2 ab bc ca     



Dy ra khi (a, b, c) = (1, 1, 0) và các hoán v.

Câu 139: [TS10 Chuyên Hà Ni, 2016-2017]

Cho các s tha mãn

2 2 2

a b c 3.  

Chng minh:

2 2 2

2a 2b 2c

a b c

a b b c c a

    

  

Lời giải

Áp dng AM-c:

 

2 2 2

2a a b 2ab

2a 2ab b ab

2a 2a b.ab 2a

a b a b a b





      

  

 và cng theo v ca bng thc:

 

2 2 2

2a 2b 2c 3 ab bc ca

a b c

a b b c c a



     

  

Mt khác ta có:

 

2 2 2

a b c a b c 3 ab bc ca a b c ab bc ca            



 

2 2 2

2a 2b 2c 3 ab bc ca

a b c a b c

a b b c c a



        

  



Dy ra khi

a b c

  

Câu 140: [TS10 Chuyên Long An, 2016-2017]

Cho a, b, c là ba cnh ca tam giác. Tìm giá tr nh nht ca biu thc:

THCS.TOANMATH.com

FB TRỊNH BÌNH

   

abc

b c a c a b a b c



     

Lời giải

Do a, b, c là 3 cnh ca tam giác nên

     

c a 0, c a b 0, a b c 0        

S dng AM-c:

  

b c a c a b

b c a c a b c

      

     





:

     

c a b a b c a ; b c a a b c b         

Nhân 3 bng thc trên theo v c:

         

222

2 2 2

b c a c a b a b c a b c b c a c a b a b c abc              

   

abc

b c a c a b a b c

  

     

Dy ra khi a = b = c

Vy giá tr nh nht ca Q là 1.

Câu 141: [TS10 Chuyên Phan B Châu, 2016-2017]

Cho a, b, c là các s thi tha mãn

a b c 1.  

Tìm giá tr nh

nht ca biu thc:

 

2 2 2

ab bc ca

Q 14 a b c

a b b c c a



   



Lời giải

V

 

   

2 2 2 2 2 2

a b c a b c 3 a b b c c a      

(1)

Tht vy:

 

       

 

2 2 2 3 2 2 2 2 2 3 2 2

2 2 2 3 2 3 2 3 2

AM GM

2 2 2 2 2 2

VT a b c a b c a ab ac b ba bc c ca cb

a b b c c a a ab b bc c ca

a b b c c a 2a b 2b c 2c a



             

        

    



 

2 2 2

3 a b b c c a  

=VP

Dy ra khi a = b = c.

S dc:

 

2 2 2

2 2 2 2 2 2

2 2 2

3 1 a b c

3 ab bc ca

Q 14 a b c 14 a b c

a b c

2 a b c

14 a b c

2 a b c

  



       



    



Ta có:

 

2 2 2

a b c a b c

     

S dng AM-c:

THCS.TOANMATH.com

FB TRỊNH BÌNH

 

2 2 2

2 2 2 2 2 2

2 2 2

Q 14 a b c

2 a b c

27 3 1 3

a b c a b c

2 2 2

2 a b c

    







       







 

2 2 2

27 3 1 3

2 a b c .

2 3 2

2 a b c

9 1 3

2 3 2

    



  



Dy ra khi

a b c .

  

Vy giá tr nh nht ca P là

NĂM HỌC 2015-2016

Câu 142: [TS10 Chuyên Hòa Bình, 2015-2016]

Cho

x 0,y 0,z 0

xyz 1

   







.Chng minh rng:

1 1 1

x y 1 y z 1 z x 1

  

     

Lời giải

t

















, vì

x,y,z 0 a,b,c 0

xyz 1 abc 1

   









Ta có

3 3 2 2

a b c

x y 1 a b 1 (a b)(a ab b ) 1 (a b)ab 1 ab(a b c)



                



x y 1 a b c



   

 ta có

1 a 1 b

;

y z 1 a b c z x 1 a b c



       

Cng 3 bng thc trên theo v ta có:

 

1 1 1 a b c

1 dpcm

x y 1 y z 1 z x 1 a b c



   

       

THCS.TOANMATH.com

FB TRỊNH BÌNH

Dy ra khi x = y = z.

Câu 143:

[TS10 Chuyên H-2016]

Cho

a,b

là các s u kin

(a b) 4ab 12.  

Chng minh bng thc

2015ab 2016.

1 a 1 b

  



Lời giải

Ta có

 

12 (a b) 4ab 2 ab 4ab    

t

t ab,t 0

thì

3 2 3 2 2

12 8t 4t 2t t 3 0 (t 1)(2t 3t 3) 0          

2t 3t 3 0, t   

nên

t 1 0 t 1   

. Vy

0 ab 1

Chc

1 1 2

, a,b 0

1 a 1 b

1 ab

   





tha mãn

ab 1

Tht v

1 1 1 1

1 a 1 b

1 ab 1 ab

   



ab a ab b b a a b

1 a 1 b

(1 a)(1 ab) (1 b)(1 ab) 1 ab

  

  

   

  



    

  

( b a) ( ab 1)

(1 ab)(1 a)(1 b)





  

0 ab 1



Tip theo ta s CM:

2015ab 2016, a,b 0

1 ab

   



tha mãn

ab 1

t

t ab,0 t t  

c

2015t 2016





2015t 2015t 2016t 2014 0   

(t 1)(2015t 4030t 2014) 0.    



t : 0 t 1  

ng thc xy ra a = b = 1

Vy

2015ab 2016.

1 a 1 b

  



Câu 144: [TS10 Chuyên Qung Nam, 2015-2016]

Cho ba s thc x; y; z tha mãn: x

+ y

+ z



Tìm giá tr ln nht ca biu thc P = x + y + z  (xy + yz + zx)

THCS.TOANMATH.com

FB TRỊNH BÌNH

Lời giải

Ta có

2 2 2 2

(x y z) (x y z )

xy yz xz

    





2 2 2 2

(x y z) (x y z )

P x y z

    

   

2 2 2 2 2 2 2 2

1 1 1

P 2(x y z) (x y z) (x y z ) (x y z 1) (x y z 1)

2 2 2



                 



Suy ra

2 2 2

P (x y z 1) (9 1) 5

      

Vy Pmax = 5 khi và ch khi

2 2 2

x y z 1 0

x y z 9

    



  



(chng hn

x 2;y 2;z 1   

)

Câu 145: [TS10 Chuyên Phú Th, 2015-2016]

Cho 3 s thx, y, z tha mãn:

2 2 2

1 1 1

x y z

  

Tìm giá tr nh nht ca biu thc:

2 2 2 2

2 2 2 2 2 2

y z x y

x(y z ) y(z x ) z(x y )

  

  

Lời giải

Ta có:

2 2 2 2 2 2

111

1 1 1 1 1 1

x( ) y( ) z( )

z y z x x y

  

  

t

1 1 1

a; b; c

x y z



thì a,b,c>0 và a

2 2 2

2 2 2 2 2 2 2 2 2

a b c a b c

b c c a a b a(1 a ) b(1 b ) c(1 c )

     

     

Áp dng bng thc Côsi cho 3 s 

222

2 2 2 2 2 2

1 1 2a 1 a 1 a 4

a (1 a ) .2a (1 a )(1 a )

2 2 3 27

2 a 3 3

a(1 a ) a (1)

a(1 a )



   

     





    



:

b 3 3 c 3 3

b (2); c (3)

b(1 b ) c(1 c )





T (1); (2); (3) ta có

2 2 2

3 3 3 3

P (a b c )

   

ng thc xy ra khi

a b c

  

hay

x y z 3  

THCS.TOANMATH.com

FB TRỊNH BÌNH

Vy giá tr nh nht ca P là

Câu 146: [TS10 Chuyên Ninh Bình, 2015-2016]

Cho a, b, c là các s u kin

1 1 1

a b c

  

. Chng minh rng:

2 2 2

a b c 1

(ab bc ca) 3

1 b 1 c 1 a

     

  

Lời giải

Ta ch

1 1 1

(a b c)( ) 9(*)

a b c

a b b c c a

(*) 3 ( ) ( ) ( ) 9

b a c b a c

    

       

Áp dAM-GM cho hai s có:

a b b c c a

2; 2; 2

b a c b a c

     

=> 

9 1 1 1

3 a b c 3

a b c a b c

        



Tr li bài toán: Áp dAM-GM cho hai s 

1 b 2b

Ta có:

a ab ab ab

a a a (1)

2b 2

1 b 1 b

     



 ta có:

b bc c ca

b (2); c (3)

1 c 1 a

   



Cng tng v ca (1), (2) và (3) ta có:

2 2 2

a b c 1

a b c (ab bc ca)

1 b 1 c 1 a

a b c 1

(ab bc ca) a b c 3

1 b 1 c 1 a

       

  

         

  



Du bng xy ra khi a = b = c = 1.

Câu 147: [TS10 Chuyên TP. H Chí Minh, 2015-2016]

Cho hai s a , b thu kin: a + b  1. Chng minh rng:

3 a 9

4a b 4



  

Lời giải

Bng thi:

3 4a

4a 9

  

Ta có:

a b 1 a 1 b    



0a1

THCS.TOANMATH.com

FB TRỊNH BÌNH



3 4a 3 4a 3 4a

4a 9

a b a 1 a a b

      



Vì th ch cn chng minh:

3 4a

4a 9

a 1 a

  



(*)

Tht vy:

 

a 3 2a 1

a 1 a









Dy ra khi



Vc chng minh.

Câu 148: [TS10 Chuyên c, 2015-2016]

1) Cho a, b là các s thng minh rng:

(1 a)(1 b) 1 ab   

2) Cho a, b là các s tha mãn

a b ab

. Tìm giá tr nh nht ca

biu thc

P (1 a )(1 b )

a 2a b 2b

    



Lời giải

a) Ta có

  

(1 a)(1 b) 1 ab 1 a 1 b 1 ab 2 ab

1 a b ab 1 ab 2 ab a b 2 ab 0

         

          

 

a b 0  



b) S d ý a)

(1 x)(1 y) 1 xy   

và 

1 1 4

x y x y





c:

2 2 2 2 2

4 4 4

P 1 ab 1 ab ab 1

a 2a b 2b (a b) 2ab 2(a b) a b

        

      

4 ab ab 7ab 1 1 7ab 7 7ab

1 3. 4. . 1

16 16 8 16 16 8 4 8



         





Mt khác: t gi thit, ta có:

ab a b 2 ab ab 4    



7 7.4 21

4 8 4

  

. Vy giá tr nh nht ca P bng

khi

a b 2

Câu 149: [TS10 Chuyên Qung Bình, 2015-2016]

THCS.TOANMATH.com

FB TRỊNH BÌNH

Cho a, b là các s a mãn

a 2b

1 a 1 b





. Chng minh



Lời giải

T gi thit

a 2b

1 a 1 b





t

x ; y

1 a 1 b





Suy ra

a ; b

1 x 1 y





c

x 2y 1

và bng thc cn chc vit li thành

  

1 x 1 y





T gi thit ta suy ra

1 x 2y; 1 y x y    

nên li vit bng thc cn chng

minh thành

 

4xy x y

2y x y

   



i cùng là mt bng thc chng minh

ng thc xy ra khi và ch khi

ab

Câu 150: [TS10 Chuyên Bc Giang, 2015-2016]

Cho a, b, c > 0 tha mãn: a + b + c = 3. Chng minh rng:

4 4 4

a b c 1

(a 2)(b 2) (b 2)(c 2) (c 2)(a 2) 3

  

     

Lời giải

Áp dAM-GM cho 4 s không âm, ta có:

4 4 4

a a 2 b 2 1 a a 2 b 2 1 a 4a

4 . . . 4

(a 2)(b 2) 27 27 9 (a 2)(b 2) 27 27 9 9

   

     

   

a 11a b 7

(1)

(a 2)(b 2) 27 27 27

   



 ta có:

b 11b c 7

(2)

(b 2)(c 2) 27 27 27

  



c 11c a 7

(3)

(c 2)(a 2) 27 27 27

  



Cng tng v ca (1), (2) và (3) ta có:

THCS.TOANMATH.com

FB TRỊNH BÌNH

4 4 4

a b c 11(a b c) a b c 21

(a 2)(b 2) (b 2)(c 2) (c 2)(a 2) 27 27 27

   

    

     

u kic:

4 4 4

a b c 1

(a 2)(b 2) (b 2)(c 2) (c 2)(a 2) 3

  

     

Du bng xy ra khi a = b = c = 1.

Câu 151: [TS10 Chuyên B, 2015-2016]

Cho a, b, c > 0 và a + b + c = 3. Chng minh rng a

+ b

+ c

1 1 1

a b c

  

Lời giải

Áp dng bng thc AM-GM:

a 2a



;

b 2b



;

c 2c



Suy ra a

+ b

+ c

2 2 2

1 1 1

2(a b c )

a b c

    

Mt khác

a 1 2a; b 1 2b; c² 1 2c     

Suy ra

 

2 2 2

a b c 2 a b c 3 3      



Dy ra khi a = b = c = 1.

Câu 152: [TS10 Chuyên i hc Vinh, 2015-2016]

Cho các s thc không âm a, b, c tha mãn a + b + c = 3. Tìm giá tr nh nht ca

biu thc:

2 2 2

a b c

1 b 1 c 1 a

  

  

Lời giải

Ta có:

a ab

1 b 1 b





(1)

Áp dAM-GM cho hai s không âm, ta có

1 b 2b

c:

a ab ab ab

a a a

2b 2

1 b 1 b

     



(2)

, ta có:

b bc





(3);

c ca





(4)

Cng tng v c:

2 2 2

a b c ab bc ca

a b c

1 b 1 c 1 a

   

     



  



(5)

Mt khác:

   

2 2 2

a b c 3 ab bc ca (a b) (b c) (c a) 0



           



THCS.TOANMATH.com

FB TRỊNH BÌNH

(a b c)

ab bc ca 3



    

(6)

u ki:

2 2 2

a b c 3

1 b 1 c 1 a

   

  

Du bng xy ra khi a = b = c = 1.

Vy giá tr nh nht ca P là

c khi a = b = c = 1.

Câu 153: [TS10 Chuyên Hà Giang, 2015-2016]

Tìm giá tr ln nht ca

A x 1 y 2   

, bit x + y = 4

Lời giải

Áp dng bng thc Bunyakoskicopxki cho 2 b s (1;1) và

 

x 1; y 2

ta có

 

   

2 2 2

A 1. x 1 1. y 2 1 1 x 1 y 2 2 x y 3 2 A 2              

Du bng xy ra khi và ch khi

1 x 1

x 1 y 2

x y 4 5

x y 4











   







  

















Vy GTLN ca A là

Câu 154: [TS10 Chuyên , 2015-2016]

Cho ba s tha mãn: x + y + z = 3.

Tìm giá tr nh nht ca biu thc:

2 2 2

1 y 1 z 1 x

  

  

Lời giải

S dng bng thc AM-c:

xy xy xy

x x x

2y 2

1 y 1 y

     



T :

y yz

z zx

y ; z

1 z 1 x

   



Cng theo v c:

 

2 2 2

y xy yz zx

S x y z

1 y 1 z 1 x

x y z

x y z 3 .

6 6 2



      

  



      

THCS.TOANMATH.com

FB TRỊNH BÌNH

Dy ra khi x = y = z = 1.

Vy giá tr nh nht ca S là :

Câu 155: [TS10 Chuyên nh, 2015-2016]

Cho ba s ng minh bng thc

2 2 2 2 2 2

2 2 2 2 2 2 2 2 2

4a (b c) 4b (c a) 4c (a b)

2a b c 2b c a 2c a b

     

  

     

Lời giải

Ta có:

2 2 2 2 2 2 2

2 2 2 2 2 2 2 2 2

4a (b c) 2(2a b c ) (b c) (b c)

2a b c 2a b c 2a b c

      

  

     

 và cng lc bng thi:

2 2 2

2 2 2 2 2 2 2 2 2

(b c) (c a) (a b)

2a b c 2b c a 2c a b

  

  

     

Áp dAM-GM  Schwarz cho 4 s 

 

m n m n







ta có:

2 2 2

2 2 2 2 2 2 2

(b c) b c

2a b c a b a c





   

, cng tng v ta có:

2 2 2

2 2 2 2 2 2 2 2 2

2 2 2 2 2 2

2 2 2 2 2 2 2 2 2 2 2 2

2 2 2 2 2 2

2 2 2 2 2 2 2 2 2 2 2 2

(b c) (c a) (a b)

2a b c 2b c a 2c a b

b c c a a b

a b a c b c a b c a c b

b a c b a c

a b a b b c c b a c a c

  



     

     

     

     

     

     

     

     

     

     

     

= 3

⇒ c chng minh

Du bng xy ra khi a = b = c.

Câu 156: [TS10 Chuyên nh, 2015-2016]

Xét các s tha, b, c tha mãn abc 1.Tìm giá tr ln nht ca biu thc

4 4 4 4 4 4

a b c

b c a a c b a b c

  

     

Lời giải

Ta có:

4 4 2 2

a b ab(a b ) a; b R    

THCS.TOANMATH.com

FB TRỊNH BÌNH

Tht vy:

4 4 2 2

4 4 3 3

a b ab(a b )

a b a b ab

(a b)(a b ) 0

  

   

   

2 2 2

(a b) (a ab b ) 0    



a;b R

)

4 4 2 2 4 4 2 2 2

a b c ab(a b ) c a b c ab(a b ) abc          

( vì a;b;c > 0 và abc = 1)

4 4 2 2 2 4 4 2 2 2

c c c c

(Vi c>0)<=>

a b c ab(a b ) abc a b c ab(a b c )

c c c c

(1)

a b c abc(a b c ) a b c a b c

  

       

   

       

:

4 4 2 2 2

(2)

a c b a b c

(3)

b c a a b c



   



   

Cng theo v các bng thc (1),(2) và (3) ta có:

2 2 2

4 4 4 4 4 4 2 2 2

a b c a b c

b c a a c b a b c a b c



   

       

Vy T



a;b;c 0

tha mãn abc = 1

Vi a = b = c = 1 thì T = 1

Vy GTLN ca T là 1

Câu 157: [TS10 Chuyên Ninh Bình, 2015-2016]

Cho a, b, c là các s u kin

1 1 1

a b c

  

. Chng minh rng:

2 2 2

a b c 1

(ab bc ca) 3

1 b 1 c 1 a

     

  

Lời giải

Ta ch

1 1 1

(a b c)( ) 9 (*)

a b c

a b b c c a

(*) 3 ( ) ( ) ( ) 9

b a c b a c

    

       

Áp dAM-GM cho hai s 

a b b c c a

2; 2; 2

b a c b a c

     



9 1 1 1

3 a b c 3

a b c a b c

        



Tr li bài toán: Áp dAM-GM cho hai s 

1 b 2b

THCS.TOANMATH.com

FB TRỊNH BÌNH

Ta có:

a ab ab ab

a a a (1)

2b 2

1 b 1 b

     



 ta có:

b bc c ca

b (2); c (3)

1 c 1 a

   



Cng tng v ca (1), (2) và (3) ta có:

2 2 2

a b c 1

a b c (ab bc ca)

1 b 1 c 1 a

a b c 1

(ab bc ca) a b c 3

1 b 1 c 1 a

       

  

         

  



Du bng xy ra khi a = b = c = 1.

Câu 158: [TS10 Chuyên c Lc, 2015-2016]

Cho ba s u kin x + y + z = 1. Chng minh rng

2 2 2

350 386

2015

xy yz zx

x y z





Lời giải

Vi mi a, b > 0 và x, y, z thu ki bài, áp dng bng thcAM-GM cho

2 s 

 

     

 

2 2 2 2 2 2 2 2 2

2 2 2

1 1 1 1 1 1 4

a b 2 ab.2 . 4 (*)

a b a b a b a b

x y y z z x 2xy 2yz 2zx x y z xy yz zx

x y z

x y z 2xy 2yz 2zx 3 xy yz zx xy yz zx



      







             



             

Áp dng 2 bng thc trên ta có:

2 2 2 2 2 2

2 2 2

350 386 1 1 157

P 386

xy yz zx 2xy 2yz 2zx xy yz zx

x y z x y z

4 157

386.

xy yz zx

2xy 2yz 2zx x y z

1544 157 157 157

1544 1544 2015

xy yz zx xy yz zx

(x y z)



    



     

   







    

      

   



Du bng xy ra khi và ch khi:

THCS.TOANMATH.com

FB TRỊNH BÌNH

2 2 2

x y z

x y z 1

2xy 2yz 2zx x y z





  



   







    







(không xy ra)

V

Câu 159: [TS10 Chuyên Qung Bình, 2015-2016]

Cho các s tha mãn ab + bc + ca = 11. Tìm GTNN

2 2 2

5a 5b 2c

12(a 11) 12(b 11) c 11





    

Lời giải

Thay 11 = ab + bc + ca vào P, ta có:

2 2 2

5a 5b 2c

12(a 11) 12(b 11) c 11

5a 5b 5c

12(a ab bc ca) 12(b ab bc ca) c ab bc ca

5a 5b 5c

(*)

2 3(a b)(a c) 2 3(b a)(b c) (c a)(c b)





    





          





       

Áp dsi cho hai s không âm, ta có:

2 3(a b)(a c) 3(a b) (a c) 4a 3b c        

(1)

:

2 3(b a)(b c) 4b 3a c    

(2)

(c a)(c b) (a b 2c)

    

(3)

Cng tng v ca (1), (2) và (3) ta có

15 15

2 3(a b)(a c) 2 3(b a)(b c) (c a)(c b) a b 3c

          

(**)

T (*) và (**) ta có

5a 5b 2c 2

15 15

a b 3c







THCS.TOANMATH.com

FB TRỊNH BÌNH

100

Du bng xy ra ⇔

3(a b) a c

3(b a) b c a b 1

c a c b c 5

ab bc ca 11

   





     









   















Vy GTNN ca P là

c khi a = b = 1, c = 5.

Câu 160: [TS10 Chuyên m Hà Ni, 2015-2016]

Tìm các s thc không âm a và b tha mãn

3 3 1 1

(a b )(b a ) (2a )(2b )

4 4 2 2

      

Lời giải

Vi mi x, y không âm, ta có:

(x ) 0 x x (*)

    

Du bng xy ra ⇔x 

Mt khác:

2 2 2

(x y) 0 x 2xy y 0

x 2xy y 4xy

(x y) 4xy (**)

     

   

  

Du bng xy ra ⇔ x = y.

Áp dc

2 2 2

3 1 1 1

a b (a ) b a b 0

4 4 2 2

3 1 1 1

b a (b ) a b a 0

4 4 2 2

3 3 1

(a b )(b a ) (a b ) (1)

4 4 2



         







         





       

Áp dc:

1 1 1 1 1

(a b ) a b 4(a )(b )

2 4 4 4 4

(2a )(2 b )(2)



   

        



   



   



  

T (1) và (2) ta suy ra:

3 3 1 1

(a b )(b a ) (2a )(2b )

4 4 2 2

      

Du bng xy ra khi và ch khi

b a b







   





  





THCS.TOANMATH.com

FB TRỊNH BÌNH

101

Vy



là giá tr cn tìm.

Câu 161: [TS10 Chuyên Thái Bình, 2015-2016]

Cho các s a, b, c tha mãn ab + bc + ca = 3. Chng minh rng:

2 2 2

1 1 1 3

a 1 b 1 c 1

  

  

Lời giải

Gi s a  b  c , t gi thit suy ra ab 1. Ta có bng thc sau:

2 2 2 2

1 1 2 (a b) (ab 1)

1 ab

1 a 1 b (1 a )(1 b )(1 ab)



   



    



Vy ta cn chng minh:

2 1 3

1 ab 2





2 2 2 2

c 3 ab 3abc c ca bc 3abc a b c 3abc           

Bng thc hi

(a b c) 3(ab bc ca) 9

ab bc ca 3 (abc)



     





  





Hay a + b + c



3abc

Du bng xy ra khi a = b = c =1

Cho các s a,b,c tha mãn a+ b +c  3.Chng minh rng:

2 2 2

ab bc ca 3

c 3 a 3 b 3

  

  

Ta có:

(a b c)

ab bc ca ab bc ca 3



      

Ta có

ab ab ab ab 1 1

()

2 a c b c

(a c)(b c)

c 3 c ab bc ca

1 ab ab bc bc ca ca 1 3

VT ( ) (a b c)

2 a c b c c a b a c b a b 2 2

   



   

         

     

Du bng xy ra khi a = b = c = 1

Câu 162: [TS10 Chuyên KHTN, 2015-2016]



y z 4 z x 4 x y 4

  

     

Lời giải

Ta có

4x 4z

4 y z 4 4 z x 4 4 x y 4

  

     

Áp dng bng thc

 

4 y z 4 2 4 y z 4 y z 4 4 y z          

THCS.TOANMATH.com

FB TRỊNH BÌNH

102

Áp d c

4y y

4x 4z x z

y z x z x y

4 y z 4 4 z x 4 4 x y 4



     





     



D dàng chc

x z 3

y z x z x y 2

  



c

P6

. Vy giá tr nh nht ca P là 6.

ng thc xy ra khi và ch khi

x y z 4  

Câu 163: [TS10 Chuyên Ngh An, 2015-2016]

Cho

a,b,c

là các s thc bt k . Chng minh rng:

   

 

2 2 2

3 a b c

a 1 b 1 c 1



   

Lời giải

Bng thc cn chi

   

 

2 2 2

2a 2 2b 2 2c 2 3 2a 2b 2c     

t

x a 2; y b 2; z c 2.

Bng thc cn chng minh tr thành

   

 

2 2 2

x 2 y 2 z 2 3 x y z     

Ta có

  

2 2 2 2 2 2

x 2 y 2 x y 1 2x 2y 3      

Suy ra

  

 

2 2 2 2

x 2 y 2 2xy x y 3 x y 2





         





   

   

     

2 2 2 2 2

x 2 y 2 z 2 x y z 4 2 x y 2z

4 x y z 2 x y 2z 3 x y z



         







       





c

   

 

2 2 2

3 a b c

a 1 b 1 c 1



   

Vy b ng th c ch  ng thc xy ra khi và ch khi

a b c .

   

Câu 164: [TS10 Chuyên , 2015-2016]

THCS.TOANMATH.com

FB TRỊNH BÌNH

103

Cho a, b, c là các s tha mãn

1 1 1

a b c

    

Chng minh rng:

3 3 3

a) a b c 3abc

a b c 3

1 3bc 1 3ca 1 3ab 2

  

  

Lời giải

 

 

bc a b c ab bc ca    



 

a b c

ab bc ca



  



 

a b c

abc a b c 3abc a b c



      



a b c 1  

 

4 4 4

a b c 3

a 3abc b 3abc c 3abc 2

  

  



4 4 4 2 2 2

a b c a b c

a 3abc b 3abc c 3abc

2a b c a 2b c a b 2c

    

  

     



2 2 2

a b c 3

2a b c a 2b c a b 2c

  

     



 

2 2 2

a b c

2a b c a 2b c a b 2c 2a b c a 2b c a b 2c



  

             

 

 

2a b c a 2b c a b 2c 12 a b c          

Suy ra

   

 

a b c a b c a b c a b c

2a b c a 2b c a b 2c 2 3

2 3 a b c

       



       





1 1 1

a b c

    



1 1 1 9

a b c a b c 3

a b c a b c

         





 

a b c a b c

   



THCS.TOANMATH.com

FB TRỊNH BÌNH

104



2 2 2

a b c 3

2a b c a 2b c a b 2c

  

     



a b c 1  

Câu 165: [TS10 Chuyên , 2015-2016]

Cho a, b, c là các s tha mãn

a b c 3  

. Chng minh rng:

2 2 2

1 1 1

2 a b 2 b c 2 c a

  

  

Lời giải

Bng thc cn chi

2 2 2

a b b c c a

2 a b 2 b c 2 c a

  

  

Áp dng bng thc Cauchy ta có

2 2 2

2 a b 1 1 a b 3 a b    

c

2 2 2

a b a b a ab

2 a b

3 a b





 c

2 2 2 2 2

2 2 2

a b b c c a a ab b bc c ca

2 a b 2 b c 2 c a



  

  

ng thc

a b b a 2b

  



Suy ra

 

a a 2b

a 2ab

a ab





 c

 

a b c

a ab b bc c ca 3



   

T c

2 2 2

a b b c c a

2 a b 2 b c 2 c a

  

  

Vy bng thc chng thc xy ra khi và ch khi

a b c 1  

Câu 166: [TS10 Chuyên C, 2015-2016]

Cho x, y, z là các s tha mãn

xy yz zx 2xyz

. Tìm giá tr nh nht

ca biu thc:

     

z z x x x y x x z

  

  

THCS.TOANMATH.com

FB TRỊNH BÌNH

105

Lời giải

Bii gi thic

1 1 1

x y z

  

t

1 1 1

a ; b ; c

x y z

  

 thit tr

thành

a b c 2  

Ta vit li biu thc P là

2 2 2

a b c

a 2b c 2a

b 2c

  





Áp dng bng thc Bunhiacopxki dng phân thc

 

2 2 2

a b c

a b c a b c 2

a 2b c 2a 3 3

3 a b c

b 2c



     





Vy giá tr nh nht ca P là

ng thc xy ra khi và ch khi

x y z

  

Câu 167: [TS10 Chuyên Tin Giang, 2015-2016]

Cho ba s thc

x;y;z 1

. Chng minh rng:

   

 

y 1 z 1

  





Lời giải

ng minh bng thc: Vi

a1

thì

 

a 16 a 1

Tht vy

   

 

4 4 2 2

a 16 a 1 a 16a 32a 16 0 a 2 a 4a 4 0           

Vì

a1

nên

a 4a 4 0  

ng th

Áp dng bng thc

 

y 16 y 1



 

x 16x





 c

   

 

4 4 4 4

2 2 4 4 4

x z x z

16 48

y z x

y 1 z 1



     









Vì theo bng thc Cauchy thì

4 4 4

y z x

  

Vy bng thc chng minh.

THCS.TOANMATH.com

FB TRỊNH BÌNH

106

Câu 168: [TS10 Chuyên i hc Vinh, 2015-2016]

Cho a, b, c là các s thc không âm tha mãn

a b c 2  

. Tìm giá tr nh nht

ca biu thc:

2 2 2

ab bc ca 1

P a b c

a b c



    



Lời giải

T gi thit

a b c 2  

c

 

2 2 2

4 a b c

ab bc ca

  



u thc vit li thành

 

2 2 2

4 a b c

P a b c

a b c

  

    



t

2 2 2

t a b c t 2

     

c

  

t 1 2 1

1 t t t 1 3t t 3 3 9

P t 1 1

4 8 8 4 4 4 4 2 4

t 2t



             

Vy giá tr nh nht ca P là

ng thc xy ra khi và ch khi

a b 0; c 2  

và

các hoán v.

Câu 169: [TS10 Chuyên KHTN Hà Ni, 2015-2016]

Gi s a, b, c là các s tha mãn

ab bc ac abc 4   

. Chng minh

rng:

 

2 2 2

a b c a b c 2 ab bc ac       

Lời giải

Áp dng bng thc Cauchy 4 s ta có :

3 3 3 2 2 2

4 abc ab bc ac 4 a b c 1 abc a b c 3 abc 3 a b c           

 chng minh

 

2 2 2 2 2 2

a b c 3 a b c 2 ab bc ac     

t

 

3 3 3

2 2 2

a x, b y, c z x,y,z 0   

, bng thc vit li thành

3 3 3 3 3 3 3 3 3

x y z 3xyz 2 x y 2 z x 2 z y     

D dàng chc

     

3 3 3

x y z 3xyz xy x y yz y z xz x z        

     

3 3 3 3 3 3

xy x y yz y z xz x z 2 x y 2 z x 2 z y       

c

3 3 3 3 3 3 3 3 3

x y z 3xyz 2 x y 2 z x 2 z y     

Vy bng thc chng thc xy ra khi và ch khi

a b c 1  

THCS.TOANMATH.com

FB TRỊNH BÌNH

107

Câu 170: [TS10 Chuyên KHTN Bình Thun, 2015-2016]

Cho x, y, z là các s tha mãn

x y z 3 2  

. Chng minh rng:

     

1 1 1 3

x 3y 5z y 3z 5x z 3x 5y

  

  

Lời giải

Áp dng bng thc

 

2 8x 3y 5z 8x 3y 5z   

Suy ra

   

1 4 2 4 2

8x 3y 5z

x 3y 5z 2 8x 3y 5z





 c

   

1 4 2 1 4 2

;

8y 3z 5x 8z 3x 5y

y 3z 5x z 3x 5y



   



Cng theo v các bng thc

     

111

x 3y 5z y 3z 5x z 3x 5y

4 2 4 2 4 2

8x 3y 5z 8y 3z 5x 8z 3x 5y



  

  

     

Mà theo bng thc Cauchy ta có

 

4 2 4 2 4 2 9.4 2 36 2 3

8x 3y 5z 8y 3z 5x 8z 3x 5y 4

16 x y z

16.3 2

    

     



Suy ra

     

1 1 1 3

x 3y 5z y 3z 5x z 3x 5y

  

  

Vy bng thc chng thc xy ra khi và ch khi

x y z 2  

NĂM HỌC 2014-2015

Câu 171: [TS10 Chuyên Bc Ninh, 2014-2015]

Tìm giá tr nh nht ca biu thc P = a

+ ab + b

 3a  3b + 2014 .

THCS.TOANMATH.com

FB TRỊNH BÌNH

108

Lời giải

Giá tr nh nht ca P là 2011 khi a =b = 1

4P = a

- 2 ab + b

+ 3(a

+ b

+ 4 + 2ab  4a  4b ) + 4. 2014  12

= (a - b)

+ 3 (a + b  2)



Suy ra: P 

y ra khi

a b 1

a b 2 0



  



  



Vy giá tr nh nht ca P là 2011 khi và ch khi a = b = 1.

Câu 172: [TS10 Chuyên Bc Ninh, 2014-2015]

Cho các s thng minh rng:

2 2 2 2 2 2

a b c

b c c a a b

  

  

Lời giải

Áp dng bng thc

 

2 2 2

a a 2a

a b c







 c

2 2 2 2 2 2

2 2 2 2

b 2b c 2c

;

a b c a b c

c a a b



   



Cng theo v các bng thc

2 2 2 2 2 2

a b c

b c c a a b

  

  

ng thc không xy ra nên ta có bng thc

2 2 2 2 2 2

a b c

b c c a a b

  

  

c chng minh xong.

Câu 173: [TS10 Chuyên Bc Ninh, 2014-2015]

 dài ba cnh ca mt tam giác thu kin

2c b abc

. Tìm

giá tr nh nht ca biu thc:

3 4 5

b c a c a b a b c

  

     

Lời giải

T gi thit ta có

a b c 0; b c a 0; c a b 0        

Áp dng bng thc Cauchy dng

1 1 4

x y x y





c

THCS.TOANMATH.com

FB TRỊNH BÌNH

109

1 1 1 1 1 1

S 2 3

b c a c a b b c a a b c c a b a b c

2 4 6

c b a

     

     

     

           

     

  

Mà

2c b abc a

    

nên kt hp vi bng thc

S 2a 4 3

  

Vy giá tr nh nht ca S là

du bng xy ra khi và ch khi

a b c 3.  

Câu 174: [TS10 Chuyên c Lc, 2014-2015]

Gi s a, b, c là các s tha mãn

a b c 3  

. Tìm giá tr nh nht ca

biu thc:

     

b c a c a b a b c

2a 2b 2c

     

  

Lời giải



   

b c a 3 b c a

2a 1

2a 4 2 2

   

  

   

c a b 3 c a b

2b 1

2b 4 2 2

   

  

   

a b c 3 a b c

2c 1

2c 4 2 2

   

  



       

b c a c a b a b c 3 a b c

a b c 3

2a 2b 2c 2 2 2

       



    

Hay

     

b c a c a b a b c

a b c

2a 2b 2c 2 2

     

      





a b c 1  

Câu 175: [TS10 Chuyên , 2014-2015]

Bi

+ ax

+ bx

+ ax + 1= 0 có nghim.

Chng minh rng



Lời giải

D dàng nhn thy x = 0 không phi là nghim c

THCS.TOANMATH.com

FB TRỊNH BÌNH

110

Gi s

x0

là nghim c c

x0

c

(x ) a(x ) b 0

    

t



|t| 2;x t 2

    



t 2 at b   

Áp dBunyakoski c

2 2 2 2 2 2

4 2 3 2 4 2 2 2

2 2 2 2

(a b )(t 1) (at b) (t 2)

t 4t 4 t 4t 4 4 4 5t 24t 16 4 (5t 4)(t 4) 4 4

5 5 5 5 5

t 1 t 1 5(t 1) 5(t 1)

     

       

          

   

Vy



. Dy ra khi và ch khi

|t| 2

|x | 1

a bt













 

  















Câu 176: [TS10 Chuyên nh, 2014-2015]

Cho các s thx, y, z tha mãn

2 2 2

x y z 3xyz  

. Chng minh rng:

4 4 4

x z 3

x yz y xz z xy

  

  

Lời giải

Vì x, y, z -si ta có:

1 1 x 1

)2x yz x yz (1)

x yz x yz

2x yz 2 yz

2 1 1 1 1 1 1

) ( ) (2)

y z 4 y z

yz 2 yz

      



     

T (1) và (2) =>

x 1 1 1

()

4 y z

x yz





:

1 1 1 z 1 1 1

( ); ( )

4 x z 4 x y

y xz z xy

   



xy yz zx

1 1 1 1 1 1 1 1 1 1 1 1

A ( ) ( ) . (3)

4 y z x z x y 2 y z x 2 xyz



          

Mà li có :

2 2 2

xy yz zx x y z (4)    

T (3) và (4) có :

2 2 2

x y z 3xyz

1 1 3

A . .

2 xyz 2 xyz 2



  

()

Dy ra khi x = y = z = 1

THCS.TOANMATH.com

FB TRỊNH BÌNH

111

Câu 177: [TS10 Chuyên nh, 2014-2015]

Tìm giá tr nh nht ca hàm s:

1 x x





vi 0 < x< 1

Lời giải

Ta có:

2 1 2 1 2x 1 x

y 2 1 3 3

1 x x 1 x x 1 x x



         

  

2x 1 x

Vì 0 x 1 => 0; 0

1 x x



   



Ta có:

2x 1 x 2x 1 x

2 . 2 2

1 x x 1 x x



  



(Bng thc AM-GM)

Dy ra khi:

2 2 2

x 1 2(TM)

2x 1 x

2x x 2x 1 x 2x 1 0

1 x x

x 1 2(L)



  



         







  



y 2 2 3  

Dy ra khi

x 1 2  

Vy

min

y 2 2 3 khi x= -1+ 2

Câu 178: [TS10 Chuyên Ninh Bình, 2014-2015]

Cho a, b, c là các s u kin a + b + c = 3. Tìm giá tr ln nht ca

biu thc:

3 3 3 3 3 3

2 2 2

5b a 5c b 5a c

ab 3b bc 3c ca 3a

  

  

  

Lời giải

Ta s chng minh:

5b a

P 2b a

ab 3b



  



Tht vy:

3 3 3 3 2

5b a 5b a (ab 3b )(2b a)

(2b a)

ab 3b ab 3b

    

  



3 3 2 2 3 2 5 3 2 2

5b a (2ab a b 6b 3b a) b a a b b a

ab 3b ab 3b

(a b)(a b)

ab 3b

5b a

2b a

ab 3b

        





  







  



:

3 3 3 3

5c b 5a c

2c b; 2a c

bc 3c ca 3a



   



Cng tng v  c

P 2(a b c) (a b c) a b c 3         

Du bng xy ra

a b c

a b c 1

a b c 3

  

    



  



Vy giá tr ln nht ca P là 3 ⇔ a = b = c = 1.

THCS.TOANMATH.com

FB TRỊNH BÌNH

112

Câu 179: [TS10 Chuyên Ngoi ng Hà Ni, 2014-2015]

Chng minh rng:

2 3 2013 2014

2 3 4 2014 2015

1 .... 4

2 2 2 2

      

Lời giải

t S=

2 3 2013 2014

3 4 2014 2015

....

2 2 2 2

   

Ta có:

2 2012 2013

2 3 2013 2014

3 4 2014 2015

2S ....

2 2 2

3 4 3 5 4 2015 2014 2015

2S S ....

2 2 2 2

1 1 1 1 2015

S (1 .... )

2 2 2 2

    

  

       

       

Ta có:

2014

2 3 2013 2013

1 ( )

1 1 1 1 1

1 .... 2

2 2 2 2



       





2013 2014 2 3 2013 2014

1 2015 2 3 4 2014 2015

S 2 2 1 .... 4

2 2 2 2 2 2

           

Câu 180: [TS10 Chuyên H, 2014-2015]

Cho x; y là hai s i. Tìm giá tr nh nht ca biu thc:

(x y) (x y)







Lời giải

Ta có:

2 2 2 2

(x y) (x y) 2xy x y

S 1 2

xy xy

x y x y

  

     



2 2 2 2

2xy x y x y

3 ( )

2xy 2xy



   



Do x, y là các s 

2 2 2 2

AM GM

2 2 2 2

2xy x y x y

2 . 2

2xy 2xy

x y x y





  



Dy ra khi và ch khi:

2 2 2 2 2 2 2 2

2xy x y

(x y ) 4x y (x y ) 0

2xy

x y x y (x; y 0)

) x y 2xy 1

2xy



      



    



    

Cng các bng thc S  6

THCS.TOANMATH.com

FB TRỊNH BÌNH

113

Dy ra khi x = y.

Vy Min S = 6 khi và ch khi x = y

Câu 181: [TS10 Chuyên Phan Bi Châu, 2014-2015]

Cho các s a, b, c không âm. Chng minh rng

2 2 2 2

a b c 3 (abc) 2(ab bc ca)     

ng thc xy ra khi nào?

Lời giải

t

3 3 3

2 2 2

a x; b y; c z.  

2 3 2 3 2 3 3 3 3

a x ;b y ;c z ,a x ;b y ;c z ;x,y,z 0       

Bng th thành:

3 3 3 3 3 3 3 3 3

x y z 3xyz 2( x y y z z x )(1)     

Vì vai trò ca x; y ; z ng nên có th gi s x  y  z  0

:

x(x y) z(y x) (z x y)(x y)(y z) 0        

3 3 3

x y z 3xyz xy(z y) yz(y z) zx(z x) (2)         

Áp dng Bng thc Côsi ta có

xy(x y) 2xy xy 2 x y (3)  

 ta có:

3 3 3 3

yz(y z) 2 y z (4); zx(z x) 2 z x (5)   

Cng v theo v các bng thc

3 3 3 3 3 3

xy(x y) yz(y z) zx(z x) 2( x y y z z x ) (6)       

T (2) và (6) ta có:

3 3 2 3 3 3 3 3 3

x y z 3xyz 2( x y y z z x )     

ng thc xy ra khi x = y = z hay a = b = c.

Câu 182: [TS10 Chuyên Thái Bình, 2014-2015]

Cho các s i th

Tìm giá tr nh nht ca biu thc:

1 1 1

x y 1 y z 1 z x 1

  

     

Lời giải

Vi mi a, b, c > 0, ta có:

2 2 2 2 2 2

2 2 2

2 2 2 2 2 2

2 2 2 2

(a b) (b c) (c a) 0 2a 2b 2c 2ab 2bc 2ca 0

2(a b c ) 2ab 2bc 2ca

3(a b c ) a b c 2ab 2bc 2ca

3(a b c ) (a b c) (*)

            

     

       

     

Vi mi a, b, c > 0, áp dsi cho ba s 

THCS.TOANMATH.com

FB TRỊNH BÌNH

114

a b c 3 abc 0

1 1 1

(a b c) 9

1 1 1 1

a b c

a b c abc

1 1 1 9

(**)

a b c a b c



   





     







   





   



Áp di a = x, b = y, c = z và t u kin ca x, y, z ta có:

2 2 2

(x y z)

18 x y z x y z x y z

(x y z) 3(x y z) 54 0

(x y z 9)(x y z 6) 0



         

       

x y z 6   

(do x + y + z + 9 > 0) (***)

Áp di a = x + y + 1, b = y + z + 1, c = z + x + 1, ta có:

1 1 1 9 9

x y 1 y z 1 z x 1 x y 1 y z 1 z x 1 2(x y z) 3

    

                

Áp dng (***) ta có:

2.6 3 5





Du bng xy ra

x y z

x y 1 y z 1 z x 1 x y z 2

x y z 6

  



            





  



Vy giá tr nh nht ca B là

, xy ra khi và ch khi x = y = z = 2.

Câu 183: [TS10 Chuyên Thái Bình, 2014-2015]

Cho a, b, c là ba s thng bng 1.

Chng minh:

a bc b ca c ab 3

a bc b ca c ab 2

  

  

  

Lời giải

Thay 1 = a + b + c ta có:

A+bc = a(a+b+c)+bc = (a+b)(a+c)



a bc a bc 2bc 2bc 2bc

a bc a bc a bc (a b)(a c)

  

    

    

ng th:

b ca 2ca c ab 2ab

1 ; 1

b ca (b c)(b a) c ab (c a)(c b)



   

     

Cng tng v cng thc trên ta có:

THCS.TOANMATH.com

FB TRỊNH BÌNH

115

a bc b ca c ab bc ca ab

a bc b ca c ab (a b)(a c) (b c)(b a) (c a)(c b)



  

     



        





a bc b ca c ab 3 bc ca ab 3

a bc b ca c ab 2 (a b)(a c) (b c)(b a) (c a)(c b) 4

bc(b c) ca(c a) ab(a b) 3

(a b)(b c)(c a) 4



  

      



        



    

 

  

2 2 2 2 2 2 2 2 2 2 2 2

2 2 2 2 2 2

4(b c bc c a ca a b ab ) 3(a b ab b c bc c a ca 2abc)

b c bc c a ca a b ab 6abc(*)

            

      

Áp dAM-GM cho ba s 

2 2 2

b c c a a b 3abc

(*)

bc ca ab 3abc



  







  







Vc chng minh.

Du bng xy ra khi

a b c

  

Câu 184: [TS10 Chuyên TP. H Chí Minh, 2014-2015]

a) Cho x, y là 2 s thc khác 0. Chng minh rng:

  

b) Cho a, b là hai s  nh nht ca biu thc:

a 3ab b

ab(a b)







Lời giải

a) Ta có:

2 2 4 4 3 3

2 2 2 2 2 2

y y y y x y x y xy

x x x x

y x y x

y x y x x y

  

        

3 3 2 2 2

2 2 2 2

(x y)(x y ) (x y) (x xy y )

x y x y

    



(x y) x y





  













Bng thc cuc chng minh.

Dy ra khi x = y.

b) Ta có:

THCS.TOANMATH.com

FB TRỊNH BÌNH

116

2 2 2

(a b) ab (a b)

a 3ab b (a b) ab

ab(a b) ab(a b) ab(a b)

1 3 3

2 (a b) .ab

(a b) ab (a b) ab

4 4 4

ab(a b) ab ab(a b) ab

   

  

  



  

   



  

Dấu bằng xảy ra

(a b) ab







  









Câu 185: [TS10 Chuyên , 2014-2015]

Cho các s a mãn:

2 2 2 2 2 2

x y y z z x 2014     

Tìm giá tr nh nht ca biu thc

y z z x x y

  

  

Lời giải

t

2 2 2 2 2 2

a x y ; b y z ;c z x (*) a b c 2014(1)         

T (*) =>

2 2 2 2 2 2 2 2 2

2 2 2

a b c a b c a b c

x ; y ;z

2 2 2

      

  

Áp dta có:

y z 2(y z ) b 2

z x 2(z x ) c 2

x y 2(x y ) a 2

   

T 

2 2 2 2 2 2 2 2 2 2 2

x z 1 a b c a b c a b c

T ( )

y z z x x y b c a

      

     

  

2 2 2 2 2 2

1 a c a b b c

T ( a b c) (2)

b b c c a a

        

Áp dAM-GM ta li có:

2 2 2 2 2 2

a c a b b c

b 2a; b 2c; c 2a; c 2b; a 2b; a 2c

b b c c a a

a c a b b c

4(a b c) 2(a b c) 2(a b c) (3)

b b c c a a

           

              

T (2) và (3)=>

T (a b c) (4)

  

T (1) và (4) =>

T .2014.



THCS.TOANMATH.com

FB TRỊNH BÌNH

117

Vy

MIN

2014 2014

T khi x = y = z =

2 2 3 2



Câu 186: [TS10 Chuyên , 2014-2015]

Cho ba s thc x, y, z. Tìm giá tr ln nht biu thc:

2 2 2

xyz(x y z x y z )

(x y z )(xy yz zx)

    



   

Lời giải

Theo Bunyakoski:

2 2 2 2 2 2 2

(x y z) 3(x y z ) x y z 3 x y z          

2 2 2 2 2 2

2 2 2

xyz( 3 x y z x y z )

xyz( 3 1)

(x y z )(xy yz zx)

x y z (xy yz zx)

    



  

   

2 2 2 2 2 2

xyz( 3 1)

3 x y z x y z



  

=>Smax=



khi x = y = z

Câu 187: [TS10 Chuyên , 2014-2015]



 

ax bx c 0 a 0   

có hai nghim thun

0;2



. Tìm giá

tr ln nht ca biu thc:

8a 6ab b

4a 2ab ac







Lời giải

Gi

 

2 1 2

x ; x x x

là hai nghim cnh lí Vi-ét ta có

1 2 1 2

x x ; x x

   



   

 

1 2 1 2

8 6 x x x x

8a 6ab b

4 2 x x x x

4a 2ab ac







   





  

  



2 2 2 2

1 2 1 1 2 2 1 2 1 2

0 x x 2 x x x ; x 4 x x x x 4         

 

1 2 1 2

x x 3x x 4   

c

 

1 2 1 2

8 6 x x 3x x 4

4 2 x x x x

   



  

ng thc xy ra khi

x x 2

hoc

x 0; x 2

hay

c b 4a

b 2a; c 0

   



  



Vy giá tr ln nht ca P là 3.

THCS.TOANMATH.com

FB TRỊNH BÌNH

118

Câu 188: [TS10 Chuyên Hà Ni Amsterdam, 2014-2015]

Cho ba s tha mãn (a + b)(b + c)(c + a) = 1.

Ch

Lời giải

Áp dsi cho ba s không âm, kt hu kin (1) ta có:

(a b) (b c) (c a) 3 (a b)(b c)(c a) 3 a b c (2)

             

Áp dsi cho hai s không âm, kt hu kin (1) ta có:

a b 2 ab

b c 2 ac 1 (a b)(b c)(c a) 8abc abc (3)

c a 2 ca







         











Bic:

(a b)(b c)(c a) 1

(a b)(bc ba c ca) 1

(a b)(bc ba ca) ac bc 1

(a b)(ab bc ca) c(ab bc ca) abc 1

(a b c)(ab bc ca) abc 1

1 abc 3

ab bc ca

a b c 3 4

   

     

      

        

      



     



Du bng xy ra khi a = b = c =

Câu 189: [TS10 Chuyên Hà Ni Amsterdam, 2014-2015]

Chng minh tn ti các s nguyên a, b, c sao cho 0 <

a b 2 c 3

1000

Lời giải

Xét na khong A = (0;1]. Chia na khong này thành 1000 na khong

1 2 n 1000

1 1 2 n 1 n 999

A 0; ,A ; ,...,A ; ,...,A ;1

1000 1000 1000 1000 1000 1000

        

   

   

   

       

Xét b s

1 2 1001

x ;x ;...;x

vi

x 1 k 2 k 2(k *,k 1001)



    



THCS.TOANMATH.com

FB TRỊNH BÌNH

119

Vi mi k ta có

k 2 1 k 2 1 k 2



    



(tính cht phn nguyên) nên

0 1 k 2 k 2 1 x A



     



⇒ xk thuc mt trong các 1000 khong A1, A2,..., A1000

Có 1001 s xk mà có 1000 na khon ti 2 s

x ,x

thuc cùng mt na

khong Am 

0 |x x | .

1000

  

t

a 1 i 2 1 j 2 ,b i j x x a b 2 0. 3

   

          

   

Mà a là s nguyên,

là s vô t nên

a b 2 0 |x x | 0    



0 |x x | 0 a b 2 0. 3

1000 1000

       

Vy tn ti các s nguyên a, b, c tha mãn  bài.

Câu 190: [TS10 Chuyên Phú Th, 2014-2015]

Cho a, b, c là các s tha mãn

6a 3b 2c abc  

. Tìm giá tr ln nht ca

biu thc:

2 2 2

1 2 3

a 1 b 4 c 9

  

  

Lời giải

Gi thit cc vit li thành

6 3 2

bc ca ab

  

t

1 2 3

a ; b ; c

x y z

  

c

xy yz zx 1

Biu thc vit li thành

2 2 2

x 1 y 1 z 1

  

  

 n gi thit

xy yz zx 1

ta có

  

x 1 x xy yz zx x y z x       

c

  

x y z x







 c

        

x y x z x y y z z x y z

  

     

Áp dng bng thc

THCS.TOANMATH.com

FB TRỊNH BÌNH

120

  

x 1 x x

2 x y z x

x y z x

y y y

2 x y y z

x y y z

z 1 z z

2 z x y z

x z y z































Cng theo v các bng thc

        

x z 3

x y x z x y y z z x y z

   

     

Vy giá tr ln nht ca B là

ng thc xy ra khi và ch khi

a 3; b 2 3; c 3 3  

Câu 191: [TS10 Chuyên Hà Ni 2014-2015]

Cho x, y, z là ba s tha mãn

x y z 1  

. Chng minh rng:

1 x 1 z

x yz y zx z xy





  

  

Lời giải

Áp dng gi thic

  

     

  

1 x 1 x x y y z z x y z

x yz

x y z x x y z x

      







   

c

     

  

     

  

x z x y x z y z

y zx

x y y z

x y y z x y x z

z xy

y z z x

    









    









t

        

x y y z ; b y z z x ; c x y z x        

t lc bt

ng thc thành

a b b c c a

c a b

  

  

Áp dng bng thc

a b b c c c

2; 2; 2

b a c b a a

     

THCS.TOANMATH.com

FB TRỊNH BÌNH

121

Cng theo v các bng thc

a b b c c a

c a b

  

  

Vc chng minh xong.

Câu 192: [TS10 Chuyên TP. H Chí Minh 2014-2015]

Cho x, y, z là ba s tha mãn

xy yz zx 1

. Chng minh rng:

2 2 2

x z 3

x 1 y 1 z 1

  

  

Lời giải

Áp dng gi thic

  

x x x

x y x z

x 1 x xy yz zx





   

Áp dng bng thc

  

x x 1 x x

2 x y z x

x y x z



  







c

x 1 x x

2 x y z x













 c

y y y

1 z 1 z z

;

2 x y y z 2 z x y z

y 1 z 1

   

   

   

   



   

Cng theo v các bng thc

2 2 2

x 1 y 1 z 1

1 x x z z 3

2 x y z x x y y z z x y z 2



  



      



     



Vy bng thc chng thc xy ra khi và ch khi

x y z

  

Câu 193: [TS10 Chuyên Tin Giang 2014-2015]

1) Cho a, b, c là ba s thng minh rng:

 

a ab abc a b c

    

2) Cho a, b, c là ba s thng minh rng:

THCS.TOANMATH.com

FB TRỊNH BÌNH

122

2 2 2

bc ca ab

a 2bc b 2ca c 2ab

  

  

Lời giải

1) S dng bng thc Cauchy ta có:

b 4c

a a a

ab 2. .b b; abc .b.4c

4 4 4 3



    

T 

 

b 4c

4 a b c

a ab abc a b

4 3 3



      

c chng thc xy ra khi và ch khi

a 4b 16c

2) Bng thc cn chi

2 2 2

a b c

a 2bc b 2ca c 2ab

  

  

Áp dng bng thc Bunhiacopxki dng phân thc

 

2 2 2

2 2 2 2 2 2

a b c

a 2bc b 2ca c 2ab a b c 2ab 2bc 2ca



   

       

c chng thc xy ra khi và ch khi

a b c

Câu 194: [TS10 Chuyên Bc Giang 2014-2015]

Cho a, b, c là ba s tha mãn

a b c 3  

. Chng minh rng:

2 2 2

a b c 3

b 3 c 3 a 3

  

  

Lời giải

Áp dng bng thc

2 2 2 2 2 2 2 2 2

a b c 4a 4b 4c 4a 4b 4c

b 7 c 7 a 7

b 3 c 3 a 3 4 b 3 4 c 3 4 a 3

       

  

     

Áp dng tip bng thc Bunhiacopxki dng phân thc

 

2 2 2

4 a b c

4a 4b 4c 4.9 3

b 7 c 7 a 7 a b c 21 3 21 2



    

      

c

2 2 2

a b c 3

b 3 c 3 a 3

  

  

Vy bng thc chng thc xy ra khi và ch khi

a b c 1  

THCS.TOANMATH.com

FB TRỊNH BÌNH

123

Câu 195: [TS10 Chuyên i hc Vinh 2014-2015]

Cho ba s thc x, y, z không âm tha mãn

x y z xyz 4   

. Tìm giá tr ln nht

ca biu thc:

P xy yz zx  

Lời giải

Gi s x là s ln nht trong các s x, y, z.

c

x y z 3x; xyz x   

Suy ra

x 3x 4

hay

 

x 1 x x 4 0 x 1     

Ta có

   

 

P xy yz zx x x y z yz x x 4 xyz yz x

x 2 4 yz 1 x 4

           

      

Suy ra

P4

. Vy giá tr nh nht ca P là 4.

ng thc xy ra khi và ch khi

x 0; y z 2  

và các hoán v.

Câu 196: [TS10 Chuyên Yên Bái 2014-2015]

Cho ba s thc x, y, z tha mãn

x 1; y 2; z 3     

và

x y z 5   

Chng minh rng:

1 4 9

x 1 y 2 z 3

  

  

Lời giải

x 1; y 2; z 3     

nên

x 1 0; y 2 0; z 3 0     

ng bng

thc Bunhiacopxki dng phân thc

 

1 2 3

1 4 9

x 1 y 2 z 3 x y z 6



   

     

Bng thc chng thc xy ra khi và ch khi

x y z 5

1 2 3

x 1 y 2 z 3

    









  



Câu 197: [TS10 Chuyên Qung Tr 2014-2015]

Cho các s thng minh rng:

2 2 2 2 2 2

a b c

b c c a a b

  

  

THCS.TOANMATH.com

FB TRỊNH BÌNH

124

Lời giải

Áp dng bng thc

 

2 2 2

a a 2a

a b c







 c

2 2 2 2 2 2

2 2 2 2

b 2b c 2c

;

a b c a b c

c a a b



   



Cng theo v các bng thc

2 2 2 2 2 2

a b c

b c c a a b

  

  

ng thc không xy ra nên ta có bng thc

2 2 2 2 2 2

a b c

b c c a a b

  

  

c chng minh xong.

NĂM HỌC 2013-2014

Câu 198: [TS10 Chuyên Hải Dương, 2013-2014]

Cho tam giác ABC có chu vi bng 2. Ký hi dài ba cnh ca tam giác.

Tìm giá tr nh nht ca biu thc:

a 4b 9c

b c a c a b a b c

  

     

Lời giải

V dài ba cnh ca tam giác có chu vi bng 2 nên

a b c 2  

t

b c a x; c a b y; a b c z        

 dài ba cnh ca tam giác

nên

x;y;z 0

c

x y z 2  

và

y z x y

a ; b ; c

2 2 2





  



       

4 x z 9 x y 4 x z 9 x y

y z y z

2x 2y 2z 2 x y z

y 9y

1 4x z 9x 4z

2 x y x z y z



   



     







   



     



   







   



Ta có

THCS.TOANMATH.com

FB TRỊNH BÌNH

125

4x x

2 2 2

x y x y

z 9x z x

3 6 6

x z x z

9y y

4z z

2 3 12 12

y z y z



    







    







    







 

S 4 6 12 11

   

ng thc xy ra khi và ch khi

y 2x

z 3x

2 5 2 1

y a ; b ; c

2z 3y

3 6 3 2

x y z 2















     











  









2 2 2

a b c

. Vy giá tr nh nht ca S là 11 khi

ABC

vuông .

Câu 199: [TS10 Chuyên Hải Dương, 2013-2014]

Cho x, y, z là các s th nh nht ca biu thc:

2 2 2 2

x xy y y yz z

z zx x

x y 2z y z 2x z x 2y

   



  

     

Lời giải

Ta có

   

3 x y x y

x xy y x y 3xy x y



        

Suy ra

 

x xy y

x y 2z

2 x z y z









  

Áp d c

x y y z

1 z x

2 y z z x z x x y x y y z







  



        



t

a x y; b y z; c z x     

c

1 a b c 1 3 3

2 b c c a a b 2 2 4



    



  



Vì theo bng thc Neibizt thì

a b c 3

b c c a a b 2

  

  

THCS.TOANMATH.com

FB TRỊNH BÌNH

126

Vc giá tr nh nht ca S là

c ti

x y z

Câu 200: [TS10 Chuyên KHTN Hà Nội, 2013-2014]

Gi s a, b, c, d là các s tha mãn

abc bcd cda dab 1   

Tìm giá tr nh nht ca biu thc

 

3 3 3 3

P 4 a b c 9c   

Lời giải

Do vai trò c ng thc xy ra ti

a b c kd  

, vi k là s 

ng bng thc AM-GM cho ba s c

 

3 3 2

1 3abc

a b c

a b 3abd

k k k

b b 3bcd

k k k

c a 3cad

k k k

  

Cng theo v các bng thc

 

3 3 2 3

2 3 2 2

3 abc abd bcd cad

1 2 3

a b c 3d

k k k k





     





Hay

 

3 3 2 3

2 3 2

3 6 9

a b c 9d

k k k



    





Ta c

4 4k 3k 6 0

     

và ta chn k là s 

t









c

x 12x 1 0  

Gic

x 6 35

 ý là

  

6 35 6 35 1  

nên ta

c

6 35 6 35

  



c giá tr nh nht ca P là

6 35 6 35



  





THCS.TOANMATH.com

FB TRỊNH BÌNH

127

ng thc xy ra khi và ch khi

6 35 6 35

a b c .d

  

  

Câu 201: [TS10 Chuyên KHTN Hà Nội, 2013-2014]

Gi s dãy s thc có th t

1 2 3 192

x x x ... x   

thu kin:

1 2 3 n

1 2 3 192

x x x ... x 0

x x x ... x 2013

     





    





Chng minh rng:

192 1

2013



Lời giải

c ht ta chng minh bài toán ph sau: Vi

1 2 3 n

a a a ... a   

tha mãn

1 2 3 n

a a a ... a 0

a a a ... a 1

     





    





c



Tht vy, t u kin ca bài toán ta nhn thy tn ti s t 

1 2 3 k k 1 n

a a a ... a 0 a ... a



       



1 2 3 n

a a a ... a 0

a a a ... a 1

     





    





suy ra

   

k 1 n

1 2 3 k k 1 n

1 2 3 k

a ... a

a a a ... a a ... a 0

a a a ... a a ... a 1

a a a ... a





  





       







        





     







1 2 3 k k 1 n

a a a ... a 0 a ... a



       

c

 

1 2 3 k 1

k 1 n n

a a a ... a a

a ... a a

2 n k



      

   





   

 

1 1 n 2n 2

2k n

2 n k 2 n k n

n k n

     





c chng minh xong.

T gi thit ca bài toán trên ta vit l

THCS.TOANMATH.com

FB TRỊNH BÌNH

128

1 2 n

3 192

x x x

... 0

2013 2013 2013 2013

... 1

2013 2013 2013 2013



    







    





Áp dng kt qu ca bài toán ph c

192

192 1

2 2013

2013 2013 192 96

    

Vc chng minh xong.

Câu 202: [TS10 Chuyên Vĩnh Phúc, 2013-2014]

. 

2 2 2

a b c 1  



2 2 2

ab 2c bc 2a ac 2b

2 ab ba ca

1 ab c 1 bc a 1 ac b

  

     

     

Lời giải

2 2 2

a b c 1  

nên ta có

  

2 2 2 2

2 2 2 2 2 2 2

2 2 2

ab 2c ab 2c ab 2c ab 2c

1 ab c a b c ab c a b ab

ab 2c a b ab

   

  

       

  

Áp dng bng thc AM-GM ta có

  

 

2 2 2

2 2 2 2 2 2

2 a b c

2c a b 2ab

ab 2c a b ab a b c



  

       

Suy ra

  

2 2 2

2 2 2 2

2 2 2

ab 2c ab 2c ab 2c

ab 2c

1 ab c a b c

ab 2c a b ab

  

   

   

  

 c

bc 2a ca 2b

bc 2a ; ca 2b

1 bc a 1 ca b



   

   

Cng v theo v các bng thc trên kt hp

2 2 2

a b c 1  

ta có bng thc

cn chng thc xy ra khi và ch khi

a b c

  

Câu 203: [TS10 Chuyên Vĩnh Phúc, 2013-2014]

Cho a, b, c là các s tha mãn

abc 1

. Chng minh rng:

        

a b c 3

a 1 b 1 b 1 c 1 c 1 a 1

  

     

THCS.TOANMATH.com

FB TRỊNH BÌNH

129

Lời giải

Bng thc cn chi

         

       

4a c 1 4b a 1 4c b 1 3 a 1 b 1 c 1

4 ab bc ca 4 a b c 3abc 3 ab bc ca 3 a b c 3

ab bc ca a b c 6

        

             

      

Áp dng bng thc AM-GM cho các s c

 

ab bc ca 3. abc 3; a b c 3 abc 3       

Cng theo v hai bng thc

ab bc ca a b c 6     

Vy bng thc chng thc xy ra khi và ch khi

a b c 1  

Câu 204: [TS10 Chuyên TP. Hà Nội, 2013-2014]

Cho a, b, c là các s tha mãn

a b c ab bc ca 6abc     

Chng minh rng:

2 2 2

1 1 1

a b c

  

Lời giải

Gi thit cc vit li thành

1 1 1 1 1 1

ab bc ca a b c

     

Áp dng bng thc AM-GM c

2 2 2 2 2 2

2 2 2

1 1 2 1 1 2 1 1 2

;;

ab bc ca

a b b c c a

1 2 1 2 1 2

1 ; 1 ; 1

a b c

     

Cng theo v các bng thc

2 2 2

1 1 1 1 1 1 1 1 1

3 3 2 2.6 12

ab bc ca a b c

a b c

   

          

   

   

Hay

2 2 2

1 1 1

a b c

  

Vy bng thc chng thc xy ra khi

a b c 1  

Câu 205: [TS10 Chuyên Ninh Bình, 2013-2014]



   

2 2 2 2

x x 2y 3 y 2 1    





C x y

Lời giải

Ta có:

THCS.TOANMATH.com

FB TRỊNH BÌNH

130

  

 

   

2 2 2 2 4 2 2 2 4 2

4 2 2 4 2 2 2

2 2 2 2 2

x x 2y 3 y 2 1 x 2x y 3x y 4y 4 1

x 2x y y 4 x y x 3 0

x y 4 x y 3 x 0 x

          

       

        

 thì ta có

;

 và ; maxC = 3 khi và .

Câu 206: [TS10 Chuyên TP. Hà Nội, 2013-2014]

Cho a, b, c là các s tha mãn

abc 1

. Chng minh rng:

1 1 1 3

ab a 2 bc b 2 ca c 2 4

  

     

Lời giải

t

a ; b ; c

y z x

  

. Gi P là v c

1 1 1

ab a 2 bc b 2 ca c 2

yz xy

xy xz 2yz xy yz 2xz xz yz 2xy

  

     

  

     

Bic

 

yz xy

3 P 1 1 1

xy xz 2yz xy yz 2xz xz yz 2xy

1 1 1

3 P xy yz xz

xy xz 2yz xy yz 2xz xz yz 2xy

      

     



     



     



Áp dng bng thc AM-GM dng

1 1 1 1

A B C A B C

  



Ta có

 

9 9 9 3

3 P xy yz xz P 3

4xy 4yz 4xz 4 4 4

        



Vy bng thc chng thc xy ra khi và ch khi

a b c 1  

Câu 207: [TS10 Chuyên Phú Thọ, 2013-2014]

a) Chng minh rng:

 

a b ab a b  

, vi a, b là hai s 

x y C

 

C 4C 3 0 C 4C 4 1 C 2 1         

C 2 1 1 C 2 1 1 C 3          

x y 1





  









x y 3







  











x0

y1

x0

y3

THCS.TOANMATH.com

FB TRỊNH BÌNH

131

b) Cho a, b là hai s a mãn

a b 1

. Tìm giá tr nh nht ca biu thc:

   

3 3 2 2

F a b a b ab

    

Lời giải

a) Bng thc cn chi

 

  

a b a ab b ab a b 0

a b a 2ab b 0 a b a b 0

     

        

Ta thy vi a, b là hai s ng th

b) Ta có

 

F a b a b ab

    

Mà ta luôn có bng thc

 





, vi mi a, b > 0.

Áp dng bng thc trên ta có

 

4 16







  





Áp dng bng thc AM-GM ta có

 

   

a b 7 a b

1 1 1 7 15

F a b

16 8 16 8 16 8 16



        

Vy giá tr nh nht ca F là bng

c khi



Câu 208: [TS10 Chuyên Bình Phước, 2013-2014]

a. Chng minh rng:

a b ab(a b)  

, vi a, b là hai s 

b. Cho a, b là hai s a mãn

a b 1

Tìm giá tr nh nht ca biu thc:

   

3 3 2 2

F a b a b ab.

    

Lời giải

a) Ta có bng thc

2 2 2 2 2

(a b)(a ab b ) ab(a b) 0 (a b)(a 2ab b ) 0 (a b)(a b) 0              

Ta thy vi a, b là hai s ng th

Dy ra khi a = b.

THCS.TOANMATH.com

FB TRỊNH BÌNH

132

b) Áp dng bng thng minh  câu (a) ta có:

 

a b ab(a b)    



mà theo gi thit

a b 1



 

3 3 2

a b ab(a b) (ab)     



+) Mt khác ta có:

 

F a b a b 2ab 1 1ab      



     

2 2 2

3 ab 1 1 15 1 15 15

F ab 1 2ab ab ab 1 ab 2.ab. ab

2 2 4 16 16 4 16 16



              





+) Dy ra

a b 1

  



   









+) Vy giá tr nh nht ca F là bng

c khi



Câu 209: [TS10 Chuyên Phú Thọ, 2013-2014]

Cho ba s tha mãn

2 2 2

1 1 1 1 1 1

12 3

a b c



     





Chng minh rng:

1 1 1 1

4a b c a 4b c a b 4c 6

  

     

Lời giải

Theo mc ta có

2 2 2

1 1 1 1 1 1 1 1 1

4 12 3

a b c a b c

a b c

   

        

   

   

Suy ra

1 1 1 1 1 1

1 4 3 0

a b c a b c



   

      



   

   



c

1 1 1

a b c

  

và

a b c 9  

t

111

4a b c a 4b c a b 4c

  

     

Áp dng bng thc AM-GM dng

4 1 1

x y x y





c

THCS.TOANMATH.com

FB TRỊNH BÌNH

133

111

4a b c a 4b c a b 4c

1 1 1 1 1 1 1

4 3a a b c 3a a b c 3a a b c

1 1 1 1 3 1 1 1 1

4 3a 3b 3c a b c 4 3 3 6

  

     



     



     



   

      

   



   

Vy bng thc chng thc xy ra khi và ch khi

a b c

  

Câu 210: [TS10 Chuyên Nam Định, 2013-2014]

Cho các s tha mãn

2 2 2

x y z 3xyz  

. Chng minh rng:

4 4 4

x z 3

x yz y xz z xy

  

  

Lời giải

Áp dng bng thc AM-GM ta có

1 1 x 1

2x yz x yz

x yz x yz

2x yz 2 yz

     



2 1 1 1 1 1 1

y z 4 y z

yz 2 yz



    





T hai bng thc

x 1 1 1

4 y z

x yz











 ta có

1 1 1 z 1 1 1

;

4 x z 4 x y

y xz z xy



   







Cng theo v các bng thc

4 4 4

y xy yz zx

x z 1 1 1 1 1

2 y z x 2 xyz

x yz y xz z xy





      



  



Mt khác ta li có

2 2 2

xy yz zx x y z    

c

2 2 2

x y z 3xyz

xyz xyz





Suy ra

4 4 4

x z 3

x yz y xz z xy

  

  

Vy bng thc chng thc xy ra khi và ch khi

x y z 1  

THCS.TOANMATH.com

FB TRỊNH BÌNH

134

Câu 211: [TS10 Chuyên Quảng Nam, 2013-2014]

Cho hai s x và y tha mãn:

xy y

xy(2013 ) 2014

2 4 4

   

Tìm giá tr ln nht và giá tr nh nht ca tích xy.

Lời giải

Ta có:

xy y

xy(2013 ) 2014

2 4 4

   



2. . 2014



Si) (*)

(*)



(xy)

 2013xy  

t t = xy thì (*)



 2013t 



(t+1)(t





GTLN ca xy là 2014 khi x = y =

2014

GTNN ca xy là 1 Khi (x = 1 ; y =1) hoc ( x = 1; y = 1)

Câu 212: [TS10 Chuyên KHTN Hà Nội, 2013-2014]

Cho a, b, c là các s tha mãn

ab bc ca 1

. Chng minh rng:

 

4 2 4 2 4 2

2abc a b c a b b c c a

     

Lời giải

Áp dng bng thc dng

2 2 2

x y z xy yz zx    

c

 

4 2 4 2 4 2 2 2 2

a b b c c a abc a b b c c a    

Bài toán quy v chng minh

 

2 2 2

2abc a b c abc a b b c c a

     

Hay

 

2 2 2

2 a b c a b b c c a

9abc

     

Áp dng bng thc

2 2 2

1 2a 1 2b 1 2c

a b ; b c ; c a

9b 3 9c 3 9a 3

     

Cng theo v các bng thc

2 2 2

1 1 1 2a 2b 2c

a b b c c a

9a 9b 9c 3 3 3

       

Hay

 

2 2 2

ab bc ca 2

a b b c c a a b c

9abc 3



     

y ta cn ch c

   

2 a b c a b c

9abc 3

     

THCS.TOANMATH.com

FB TRỊNH BÌNH

135

Hay

 

4abc a b c

3abc a b c 1



    

i cùng là m

   

1 ab bc ca 3abc a b c     

Vy bng thc chng thc xy ra khi và ch khi

a b c

  

NĂM HỌC 2012-2013

Câu 213: [TS10 Chuyên Nghệ An, 2012-2013]

Cho ba s 

x,y,z

tho mãn

1 1 1

x y z

  

Chng minh rng:

x yz y zx z xy xyz x y z.        

Lời giải

Bng thi

a bc b ca c ab 1 ab bc ca,        

vi

1 1 1

a , b , c , a b c 1.

x y z

     

Ta có:

a bc a(a b c) bc    

a a(b c) bc a 2a bc bc a bc.        

:

b ca b ca; c ab c ab.     

T u bng xy ra khi

x y z 3.  

Câu 214: [TS10 Chuyên TP. Hồ Chí Minh, 2012-2013]

Cho ba s a mãn

a b c 1  

. Tìm giá tr nh nht ca:

 

2 2 2

ab bc ca

A 14 a b c

a b b c c a



   



Lời giải

D c

 

2 2 2

1 a b c

ab bc ca

  



. Li có

 

2 2 2 2 2 2 3 2 3 2 3 2 2 2 2

a b c a b c a b c a b a b bc c ca a b b c c a               

Áp dng bng thc Cauchy ta có

THCS.TOANMATH.com

FB TRỊNH BÌNH

136

3 2 2 3 2 2 3 2 2

a b a 2a b; b bc 2b c; c ca 2c a     



 

2 2 2 3 2 3 2 3 2 2 2 2 2 2 2

a b c a b a b bc c ca a b b c c a 3 a b b c c a             

T c

2 2 2 2 2 2

a b b c c a a b c



   

Hay

 

2 2 2

2 2 2 2 2 2

2 2 2

3 3 a b c

3 ab bc ca

ab bc ca

a b b c c a a b c

2 a b c

  





   



t

2 2 2

t a b c t

    

. Khi này biu thc vit li thành

3 3t 28t 3 3t 27t 3 t 3

A 14t

2t 2 2t 2t 2 2t 2 2



        

Áp dng bng thc Cauchy ta có

27t 3 27t 3

2 . 9

2 2t 2 2t

  

Mt khác

t 3 1 3 4

2 2 6 2 3

    

. Suy ra

4 23

  

Vy giá tr nh nht ca A là

ng thc xy ra khi và ch khi

a b c

  

Câu 215: [TS10 Chuyên KHTN, 2012-2013]

Cho a, b, c là các s tha mãn

a b 3 c; c b 1; a b c      

Tìm giá tr nh nht ca biu thc:

 

   

2ab a b c ab 1

a 1 b 1 c 1

   



  

Lời giải

Ta có

 

   

     

   

  

2ab a b c ab 1 a 1 b 1 ab 1 c 1

a 1 b 1 c 1 a 1 b 1 c 1

1 ab 1 1 ab 1

c 1 a b 1 ab a b 1

a 1 b 1

        



     



   

     



T gi thit

  

b c b 1 b a 1 a 1 b 1 0 ab a b 1 c 1 2                 

Suy ra

 

1 ab 1

ab 2

2 ab 1







THCS.TOANMATH.com

FB TRỊNH BÌNH

137

t

x ab x 2  

c

 

1 x 1

2 x 1







Suy ra

 

  

x 2 x 5

5 1 x 1 5

12 x 2 12

2 x 1 12 x 1 x 2





     



  





Vy giá tr nh nht ca Q là

ng thc xy ra khi và ch

khi

a 1; b 2;c 3  

Câu 216: [TS10 Chuyên Bình Phước, 2012-2013]

Cho a, b, c là các s tha mãn

ab bc ca 3abc

Tìm giá tr ln nht ca biu thc:

2 2 2

1 1 1

a 1 b 1 c 1

  

  

Lời giải

Áp dng bng thc

2 2 2

1 1 1 1 1 1 ab bc ca 3

2a 2b 2a 2abc 2

a 1 b 1 c 1



       

  

Vy giá tr ln nht ca P là

ng thc xy ra khi và ch khi

a b c 1  

Câu 217: [TS10 Chuyên Sư Phạm Hà Nội, 2012-2013]

Cho n s thc

1 2 n

x , x , ..., x

vi

n3

. Kí hiu



2 n

Max x , x , ..., x }

là s ln nht

trong các s

1 2 n

x , x , ..., x

.Chng minh rng:



1 2 2 3 n 1

1 2 n

x x x x ... x x

x x ... x

Max x , x , ..., x }

n 2n

     

  



Lời giải



Min{x,y} x,y Max{x,y}

và

x y x y

Max{x,y}

  





x y x y

Max{x,y}

  



, ta có:

1 2 2 3 n 1

1 2 n

x x x x ... x x

x x ... x

n 2n

     

  



1 2 1 2 2 2 2 3 n 1 n 1

1 2 2 n 1

1 2 n

x x x x x x x x x x x x

...

2n 2n 2n

Max{x , x } Max{x ,x} Max{x ,x }

Max{x ; x ;...; x }

        

   







1 2 n

x x ... x  

THCS.TOANMATH.com

FB TRỊNH BÌNH

138

Câu 218: [TS10 Chuyên Phú Thọ, 2012-2013]

Cho x, y, z là các s không âm tha mãn

x y z

  

Tìm giá tr nh nht:

3 3 3 2 2 2

S x y z x y z   

Lời giải

Áp dng bng thc Bunyakoskicopxki ta có





     

 

2 2 2

2 2 2 2 2 2

x y z x x y y z z x y z



      





Hay

     

3 3 3 2 2 2 3 3 3 2 2 2

x y z x y z x y z x y z (*)

          

Mt khác, d dàng chc

   

   

 

2 2 2

2 2 2 2 2 2

3 3 3

xyz x y z x z y y z x 2z 2x 2y

2 2 2

27 9

x y z 6 xy yz xz 8xyz

x y z

27 3

9xyz 3 x y z x y z

8 8 3

   

          

   

   

       





       





t

 

2 2 2

x y z

t x y z



    

c

2 2 2

2 3 t 2t t t 9 7t t 9 1 3 11 3 25

S t t t

3 8 3 3 9 4 64 9 4 64 6 4 8 64 64

   

              

   

   

Vy giá

tr nh nht ca S là

ng thc xy ra khi và ch khi

x y z

  

Câu 219: [TS10 Chuyên Phú Thọ, 2012-2013]

Cho a,b,c là các s a mãn

ab bc ca 3

. Chng minh rng:

2 2 2

1 3a 1 3b 1 3c

1 b 1 c 1 a

  

  

  

Lời giải

Ta vit li v trái thành

2 2 2 2 2 2 2 2 2

1 3a 1 3b 1 3c 1 1 1 3a 3b 3c

1 b 1 c 1 a 1 b 1 c 1 a 1 b 1 c 1 a

  

       

        

ng thc :

1 b b b

1 1 1

2b 2

b 1 b 1

     



THCS.TOANMATH.com

FB TRỊNH BÌNH

139

 c

1 c 1 a

1 ; 1

c 1 a 1

   



ng thc:

2 2 2

1 1 1 a b c

b 1 c 1 a 1



   

  

Mt khác ta li có

2 2 2

a b c ab bc ca 3

a b c a b c

b 1 c 1 a 1



         

  

c :

 

2 2 2 2 2 2

5 a b c

1 1 1 3a 3b 3c 9

1 b 1 c 1 a 1 b 1 c 1 a



        

     

Vy bng thc chng minh.

Câu 220: [TS10 Chuyên Hải Dương, 2012-2013]

Cho 2 s a mãn



. Tìm giá tr ln nht ca biu thc

4 2 2 4 2 2

a b 2ab b a 2ba



   

Lời giải

Vi

a 0;b 0

ta có:

2 2 4 2 2 4 2 2

(a b) 0 a 2a b b 0 a b 2a b        

4 2 2 2 2

a b 2ab 2a b 2ab    

 

4 2 2

(1)

2ab a b

a b 2ab







 có

 

4 2 2

(2)

2ab a b

b a 2a b







. T (1) và (2)

 

ab a b





Vì

2 a b 2ab

    

mà

a b 2 ab ab 1   

2(ab)

  

Khi a = b = 1 thì



. Vy giá tr ln nht ca biu thc là

Câu 221: [TS10 Chuyên Phú Thọ, 2012-2013]

Cho a, b, c là các s tha mãn

a b c 1  

. Tìm giá tr nh nht ca biu

thc:

 

abc

1 2 ab bc ca



  

Lời giải

 

2 2 2

a b c 1 1 2 ab bc ca a b c         

Suy ra

2 2 2 2 2 2

1 a b c 1 1 1 1

abc ab bc ca

a b c a b c



     

   

THCS.TOANMATH.com

FB TRỊNH BÌNH

140

D chng minh:

1 1 1 9

ab bc ca ab bc ca

  



ng thc

2 2 2 2 2 2

1 1 1 1 1 9

ab bc ca ab bc ca

a b c a b c

    



   

Áp dng tic

 

2 2 2

1 1 1

a b c 2ab 2bc 2ca 9

ab bc ca ab bc ca

a b c



       



   





Hay

2 2 2

ab bc ca

a b c





Mt khác ta li có

ab bc ca





Cng theo v các bng thc

2 2 2

1 1 1 1

ab bc ca

a b c

   



Vy bng thc chng minh.

Vy giá tr nh nht ca P là 30. ng thc xy ra khi và ch khi

a b c

  

Câu 222: [TS10 Chuyên Sư Phạm Hà Nội, 2012-2013]

Cho các s thu kin:

 

y x y x y  

. Tìm giá tr nh

nht ca biu thc

P x y

Lời giải.

T gi thit suy ra: x > y > 0, Áp dng bng thc Cauchy ta có:

     





 

2 2 2 4

4xy x y 4xy

1 1 1

x y xy x y .4xy x y 4xy x y .

4 4 2 16



  



        







x y 4

. Vy

min 4A 

khi

x 2 2 2;y 2 2.   

Câu 223: [TS10 Chuyên Vĩnh Phúc, 2012-2013]

Cho các s tha mãn

abc 1

.Chng minh rng:

3 3 3

a b c

b c a

    

Lời giải

THCS.TOANMATH.com

FB TRỊNH BÌNH

141

t

1 1 1

x ; y ; z xyz 1

a b c

    

ng thc vit li thành

x z 1 1 1

z x y x y z

    

Áp dng bng thc

 

2 2 2

x y z

z x y xx yz zx



     



Phép chng minh s hoàn tt nu ta ch c

2 2 2

1 1 1

x y z

    

Tht vy theo mc và gi thit

xyz 1

ta có

2 2 2

xy yz zx

1 1 1

x y z xy yz zx

xyz x y z



        

Vy bng thc chng thc xy ra khi và ch khi

a b c 1  

Câu 224: [TS10 Chuyên KHTN, 2012-2013]

Gi s a, b là các s thu kin:

  

x 1 y 1 4  

. Tìm giá

tr nh nht ca biu thc:



Lời giải.

Ta có:

  

x y y 1

x 1 y 1 4 4 xy x y 1 1 x y 2

2 2 2





              

Mt

khác:

y 2y, x 2x

   



P x y 2  

Vy giá tr nh nht ca P là 2 khi x = y = 1.

Câu 225: [TS10 Chuyên Bắc Ninh, 2012-2013]

Cho ba s a mãn

a b c 1  

. Chng minh rng:

       

a 1 b 1 c 8 1 a 1 b 1 c      

Lời giải

Vì a, b, c là các s 

a b c 1  

nên ta có

a,b,c 1

Áp dng bng thc

THCS.TOANMATH.com

FB TRỊNH BÌNH

142

  

1 a 1 b 1 c 2 1 b 1 c       

 ta có

     

1 b 2 1 c 1 a ; 1 c 2 1 a 1 b       

Nhân theo v ba bng thc

       

a 1 b 1 c 8 1 a 1 b 1 c      

Vy bng thc chng thc xy ra khi và ch khi

a b c

  

Câu 226: [TS10 Chuyên Hải Dương, 2012-2013]

Cho 3 s a, b, c tha mãn

0 a b c 1   

. Tìm giá tr ln nht ca biu thc:

 

1 1 1

A a b c 1

a 1 b 1 c 1



     



  



Lời giải

t

x 1 c, y 1 b, z 1 a     

. T

0 a b c 1   

c

1 x y z 2   

Ta vit li biu thc A là

 

1 1 1 x x z z

A x y z 3

x y z y z x z x y



           





y y x.y y

x x x x

1 1 0 1 0 1

y z y z y.z y z z



           





y y z.y y

z z z z

1 1 0 1 0 1

y x y x y.x y x x

y y y y

x z x z x x z z x z

2 2 2

y z y x z x y z x z x y z x



           







               





t

t t 1

   

c

  

2t 1 t 2

x z 1 t 1 2t 5t 2 5 5

z x t t 2t 2 2t 2



  

       



nên ta có

  

2t 1 t 2



suy ra

x z 5

z x 2



T c

A 3 2. 2 10

   

Vy giá tr ln nht cng thc xy ra khi và ch khi.

Câu 227: [TS10 Chuyên Hải Phòng, 2012-2013]

THCS.TOANMATH.com

FB TRỊNH BÌNH

143

Cho ba s ng minh rng:

a 4b 9c

b c c a a b

  

  

Lời giải

a 4b 9c

b c c a a b

  

  

1 4 9

(a b c)( ) 18

b c a c a b

     



Tht vy:

1 4 9 b c 4(a c) 9(a b)

[(b c) (a c) a b)]( ) ( ) 36

b c a c a b b c (a c) (a b)

  

          

     

1 4 9

(a b c)( ) 18

b c a c a b

     





Câu 228: [TS10 Chuyên Nam Định, 2012-2013]

Cho a, b, c ,d là các s thu kin

a b c d 3   

. Tìm giá tr

nh nht ca biu thc:

4 4 4 4

3 3 3 3

a b c d

  



  

Lời giải

Áp dng bng thc

   

    

4 4 4 4 2 2 2 2

4 4 4 4 2 2 2 2 3 3 3 3

4 a b c d a b c d ;

a b c d a b c d a b c d

      

         

Nhân theo v các bng thc

     

4 4 4 4 3 3 3 3 2 2 2 2

4 a b c d a b c d a b c d         

Hay

     

4 4 4 4 3 3 3 3 2 2 2 2

16 a b c d 4 a b c d a b c d         

Mng thc Bunhiacopxki ta có

 

2 2 2 2

4 a b c d a b c d 9       

Do vy

     

3 3 3 3 2 2 2 2 3 3 3 3

4 a b c d a b c d 9 a b c d         

c

   

4 4 4 4 3 3 3 3

16 a b c d 9 a b c d      

Hay

   

4 4 4 4 3 3 3 3

4 a b c d 3 a b c d      

c

4 4 4 4

3 3 3 3

a b c d 3

a b c d

  



  

THCS.TOANMATH.com

FB TRỊNH BÌNH

144

Suy ra giá tr nh nht ca P là

c khi

a b c d

   

NĂM HỌC 2011-2012

Câu 229: [TS10 Chuyên Bình Phước, 2011-2012]

Cho a, b, c là ba s u kin

a b c 3.  

Chng minh rng:

1 1 1 3

1 ab 1 bc 1 ca 2

  



Lời giải

Áp dng bng thc Cauchy ta có

1 ab ab ab

1 1 1

1 ab 1 ab 2

2 ab

     



 ta có

1 bc 1 ca

1 ; 1

1 bc 2 1 ca 2

   



Cng theo v theo v các bng thc trên và áp dng bng thc Cauchy ta

c:

 

1 1 1 1

3 ab bc ca

1 ab 1 bc 1 ca 2

1 a b b c c a a b c 3 3

3 3 3

2 2 2 2 2 2 2

     



      

        





c chng minh xong.

Câu 230: [TS10 Chuyên Sư Phạm Hà Nội, 2011-2012]

Chng minh bng thc:

1 1 1 1

... 4

1 2 3 4 5 6 79 80

    

   

Lời giải

D thy

1 1 1 1 1 1

; ;...

1 2 2 3 3 4 3 4 79 80 80 81

  

     

c

1 1 1 1 1 1

... ...

1 2 3 4 79 80 2 3 4 5 80 81

      

     

THCS.TOANMATH.com

FB TRỊNH BÌNH

145

Suy ra

1 1 1 1 1 1

2 ... ...

1 2 3 4 79 80 1 2 2 3 80 81



      



     



Hay

1 1 1

2 ... 2 1 3 2 ... 81 80

1 2 3 4 79 80



         



  



c

1 1 1

... 4

1 2 3 4 79 80

   

  

Vy bng thc chng minh.

Câu 231: [TS10 Chuyên Nghệ An, 2011-2012]

Cho a, b, c là các s thng minh rng:

      

2 2 2 2 2 2 3 3 3

a b b c c a ab bc ca abc a abc b abc c abc        

Lời giải

Bng thc cn chi

2 2 2

a b c b c a a b c

1 1 1 1

c a b c a b bc ca ab

   

  

        

   

  

  

   

t

a b c

x ; y ; z x; y; z 0; xyz 1

b c a

     

ng thc trên tr thành

  

   

       

xy yz zx x y z 1 1 1 1

z x y

x y y z z x

x y y z z x xyz 1

xyz

x y y z z x 1 1 x y y z z x



        





  

      

         

t

   

t x y y z z x   

suy ra

t2

t li bng thc cn chng

minh thành

  

3 3 2

t 1 1 t t 1 1 2t t t t 2 t 1 0           

Bng thc cu

t2

Vc chng thc xy ra khi và ch khi

a b c

THCS.TOANMATH.com

FB TRỊNH BÌNH

146

Câu 232: [TS10 Chuyên Thanh Hóa, 2011-2012]

Cho a, b, c là ba s tha mãn

a b c 2  

. Tính giá tr ln nht ca biu

thc:

ab bc ca

ab 2c bc 2a ca 2b



  

Lời giải

 n gi thit

a b c 2  

ta có

    

b 2c ab c a b c b c c a       

ng thc

  

ab ab 2ab 2ab

b c c a

ab 2c

b c c a

  







 c

bc 2bc 2bc ca 2ca 2ca

;

a b c a a b b c

bc 2a ca 2b

   

   



Cng theo v các bng thc

 

ab bc ca 2ab 2ab 2bc 2bc 2ca 2ca

b c c a a b c a a b b c

ab 2c bc 2a ca 2b

2 a b c 4

       

     

  

   

Hay

P4

. Vy giá tr ln nht ca P là 4.

ng thc xy ra khi và ch khi

a b c

  

Câu 233: [TS10 Chuyên Kiên Giang, 2011-2012]



21. a 3. b 31

   

   

   

   



a, b 0

Lời giải



1 1 21 3

21. a 3. b 21a 3b

b a b a

   

      

   

   



a, b 0



21a 2 21a 6 7

   

(1)

21 21

3b 2 3b 6 7

   

(2)



21 a 3 b 12 7

   

     

   

   

THCS.TOANMATH.com

FB TRỊNH BÌNH

147



12 7 144.7 1008

;

31 31 961

12 7 31



21 a 3 b > 31

   

    

   

   



Câu 234: [TS10 Chuyên Vĩnh Phúc, 2011-2012]

Cho a, b, c là các s tha mãn

abc



. Chng minh rng:

3 3 3

a b c a b c b a c c a b       

Lời giải

Áp dng bng thc Cauchy ta có

     

ab a b ab a b ab a b

a b a b

2 2 abc c







T 

a b a b

c c 2c a b



    

 ta có

a c a c

b b 2b a c

b c b c

a a 2a b c



    



    

Cng v theo v các bng thc:

3 3 3

a b c a b c b a c c a b       

c chng minh xong.

Câu 235: [TS10 Chuyên Vĩnh Phúc, 2011-2012]

Cho các s thng minh rng:

     

 

       

222

2 2 2 2 2 2 2 2 2

2 4 4 4

54 abc

c a b a b c b c a

a b c ab bc ca

     

   

Lời giải

Theo bng thc Cauchy ta có

THCS.TOANMATH.com

FB TRỊNH BÌNH

148

     

       

 

222

2 2 2

2 2 2 2 2 2 2 2 2 2 2 2

2 2 2

2 4 4 4

3 3 3

8 8 8 4 4 3 8 8 8

2 2 2

c a b a b c b c a c 2ab a 2bc b 2ca

12a b c 2 3abc

a b c ab bc ca 3 abc 3 a b c 9 3. a b c . a b c

9 3a b c

       



     



Nhân theo v hai bng thc

     

       

 

222

2 4 4 4

2 2 2 2 2 2 2 2 2

2 2 2

c a b a b c b c a a b c ab bc ca

2 3abc.9 3a b c 54 abc

        



Hay

     

 

       

222

2 2 2 2 2 2 2 2 2

2 4 4 4

54 abc

c a b a b c b c a

a b c ab bc ca

     

   

Vy bng thc chng thc xy ra khi và ch khi

a b c

Câu 236: [TS10 Chuyên Vũng Tàu, 2011-2012]

Cho các s i và thoã mãn

3a 4b 5c 12  

. Tìm giá tr ln nht

ca biu thc:

ab 2ac 3bc

ab a b ac a c bc b c

  

     

Lời giải

Ta vit li biu thc S thành

1 2 3

1 1 1 1 1 1

1 1 1

a b c a b c

  

     

Áp dng bng thc

1 1 1 1 1

x y z 9 x y z



  







ta có

   

2 c a 1 3 b c 1

1 2 3 a b 1

1 1 1 1 1 1

9 9 9

1 1 1

a b c a b c

6 3a 4b 5c 18

   



     

     

  

  

Vy giá tr ln nht ca biu thng thc xy ra khi và ch khi

a b c 1  

Câu 237: [TS10 Chuyên KHTN Hà Nội, 2011-2012]

Cho a, b là các s th nh nht ca biu thc:

THCS.TOANMATH.com

FB TRỊNH BÌNH

149

 

3 3 3

a 4b

a 8b

b a b







Lời giải

Biu thc vit li là













t



ng thc vit li là

 

1 4t

1 8t

t 1 t







Áp dng bng thc Cauchy ta có

 

3 2 2

2 4t

1 8t 1 2t 1 2t 4t 1 2t



       

Suy ra

 

3 2 2

1 1 1

1 8t 1 2t

1 2t







Ta s chng minh

 

4t 2t

1 2t

t 1 t







Tht vy, bng thi

 

   

 

2 4 2

4t 2t

1 2t t t 1 t t 1 2t t 1 0

1 2t

t 1 t



          









Bng thc cui mi t.

c

 

3 3 2 2

1 4t 1 2t

1 8t 1 2t 1 2t

t 1 t

    

  



Vy giá tr nh nht ca biu thng thc xy ra khi và ch khi

ab

Câu 238: [TS10 Chuyên KHTN Hà Nội, 2011-2012]

THCS.TOANMATH.com

FB TRỊNH BÌNH

150

Cho các s tha mãn

ab bc ca 5

. Tìm giá tr nh nht ca

biu thc:

   

2 2 2

3a 3b 2c

6 a 5 6 b 5 c 5





    

Lời giải

T gi thit

ab bc ca 5

ta có

  

a 5 a ab bc ca a b c a       

Áp dng bng thc Cauchy ta có

 

  

   

3 a b 2 c a

5a 3b 2c

6 a 5 6 a b c a

  



     

Ch c

 

3a 5b 2c a b 2c

6 b 5 ; c 5

   

   

Cng theo v các bng thc

   

2 2 2

9a 9b 6c

6 a 5 6 b 5 c 5



     

Suy ra

   

 

2 2 2

2 3a 3b 2c

3a 3b 2c 2

9a 9b 6c 3

6 a 5 6 b 5 c 5



  



    

Vy giá tr nh nht ca biu thc P là

ng thc xy ra khi và ch khi

a b 1; c 2  

Câu 239: [TS10 Chuyên , 2011-2012]

Cho hai s

x,y



x 2xy 7(x y) 2y 10 0     





S x y 1  

Lời giải



(x y 1) 5(x y 1) 4 y (*)       







S 5S 4 0  



S x y 1  

)

Suy ra:

(S 4)(S 1) 0 4 S 1       



min

S4

, khi

  







max

S1

, khi

  







THCS.TOANMATH.com

FB TRỊNH BÌNH

151

Câu 240: [TS10 Chuyên Bc Ninh, 2011-2012]

Cho a, b, c là các s tha mãn

a b c 1  

. Tìm giá tr ln nht ca

biu thc:

2 2 2

P a abc b abc c abc 9 abc      

Lời giải

Ta có

    

a abc a a b c abc a a b a c       

c

  

   

a a b a c a a 1

a abc a a b a c

   

     

Ch c

   

b b 1 c c 1

b abc ; c abc



   

c

     

2 2 2

a a 1 b b 1 c c 1

a abc b abc c abc

2 2 2

  

       

Mt khác theo bng thc Cauchy ta li có

 

a a 1

a 1 b c a b c 1

abc a a a

2 2 2 2



        

    

   

   

Ch c

   

b b 1 c c 1

abc b; abc c



   

y ta có

2 2 2

P a abc b abc c abc 9 abc a b c 6 abc          

Mà ta có

 

a b c 2

a b c 3 a b c 3; 6 abc 6

   

       





Nên ta suy ra

2 5 5 3

   

Vy giá tr ln nht ca P là

ng thc xy ra khi và ch khi

a b c

  

Câu 241: [TS10 Chuyên Phú Th, 2011-2012]

Cho a, b, c là s thng minh rng:

THCS.TOANMATH.com

FB TRỊNH BÌNH

152

2ab 3bc 3ca a 2b 3c

3a 8b 6c 3b 6c a 9c 4a 4b 9



  

     

Lời giải

Áp dng bng thc Bunhiacopxki dng phân thc ta có

 

6 2 1

xy xy xy

18 2 1

3x 4y 2z 81 81 x y z y x

2 x y z 2y x

2xy 2x y

9 x y z





   



   









 c

   

yz 2y z 2yz

zx 2z x 2zx

;

3y 4z 2x 81 3z 4x 2y 81

9 x y z 9 x y z



   

   

Cng theo v các bng thc

 

2 xy yz zx

xy yz x y z

3x 4y 2z 3y 4z 2x 3z 4x 2y 27

9 x y z



   

     



 

Câu 242: [TS10 Chuyên H, 2011-2012]

Gi s a, b, c là các s  mãn

abc 1

. Tìm giá tr ln nht ca biu thc:

2 2 2 2 2 2

a b c

b c a c a b a b c

  

     

Lời giải

Ta chng minh

M1

t

3 3 3

a x; b y; c z  



x; y; z 0

và

xyz 1

Bng thc cn chng minh tr thành

6 6 3 6 6 3 6 6 3

y z x z x y x y z

  

     

D thy

 

5 5 6 6 5 5

y z y z 0 y z y z yz      

Suy ra

 

6 6 4 4 4 4

y z x yz yz x y z    

T c

 

6 6 3

4 4 4

y z x

yz x y z





THCS.TOANMATH.com

FB TRỊNH BÌNH

153

Hay

6 6 3 4 4 4

x yz

y z x x y z



   

c

6 6 3 4 4 4

y z x x y z



   

 ta có

6 6 3 4 4 4 6 6 3 4 4 4

;

z x y x y z x y z x y z



       

Cng theo v ba bng thc

6 6 3 6 6 3 6 6 3

y z x z x y x y z

  

     

Vy giá tr ln nht cng thc xy ra khi và ch khi

a b c 1  

Câu 243: [TS10 Chuyên , 2011-2012]

Tìm giá tr nh nht ca biu thc:

1 4 x 2x

2x 1







Lời giải. u kin:

x0

1 4 x 2x 2( x 1) (x 1)

F 1 1 2 2 2.

2x 1 2x 1

x 1 x 1

  

         



Vy MinF = - 2 khi và ch khi x = 1.

Câu 244: [TS10 Chuyên Thái Bình, 2011-2012]

Cho a, b, c là các s  mãn

abc 1

. Chng minh rng:

     

3 3 3

a b c 3

b c a c a b a b c

  

  

Lời giải

Áp dng bng thc Cauchy cho các s c

     

3 3 3

a b c a 3 b c a b 3 c a b c 3

a; b; c

2 4 2 2 4 2 2 4 2

b c a c a b a b c

  

        

  

Cng theo v các bng thc

     

 

3 3 3

3 a b c

a b c

b c a c a b a b c



     

  

Hay

     

3 3 3

a b c a b c

b c a c a b a b c



  

  

THCS.TOANMATH.com

FB TRỊNH BÌNH

154

Mt khác theo bng thc Cauchy ta li có

a b c 3 abc 3   

c

     

3 3 3

a b c 3

b c a c a b a b c

  

  

Bng thc chng minh. Dng thc xy ra khi

a b c 1  

NĂM HỌC 2010-2011

Câu 245: [TS10 Chuyên KHTN, 2010-2011]

Gi s x, y, z là các s th u kin

x y z 1  

Chng minh rng:

xy z 2x 2y

1 xy

  





Lời giải

Ta s quy bài toán v vic chng minh bng thc cùng bc là

 

  

xy z x y z 2x 2y

x y z xy

x z y z 2x 2y x y z xy

    



  

        

S dng bng thc Cauchy ta có

2x 2y x y  

 cn chng minh

  

z x z y z xy   

Bng thi

 

z xy z x y z xy 2z xy z x y 0        

c chng thc xy ra khi

x y ; z 0

  

Câu 246: [TS10 Chuyên TP. H Chí Minh, 2010-2011]

Cho a , b là các s a

2 2 2

a 2b 3c

.Chng minh

1 2 3

a b c



Lời giải

Ta có:

    

1 2 9

1 a 2b b 2a 9ab

a b a 2b

     



 

2a 4ab 2b 0 2 a b 0      



a + 2b

 

   

 

2 2 2 2

3 a 2b 2 a 2b 3 a 2b     

THCS.TOANMATH.com

FB TRỊNH BÌNH

155

 

2a 4ab 2b 0 2 a b 0      



T (1) và (2) suy ra :

 

1 2 9 9 3

a b a 2b c

3 a 2b

   



( do

2 2 2

a 2b 3c



Câu 247: [TS10 Chuyên KHTN, 2010-2011]

Cho a, b, c là các s a mãn

a b c ab bc ca 6     

. Chng minh rng:

3 3 3

2 2 2

a b c

a b c 3

b c a

     

Lời giải

c ht ta chng minh bng thc

3 3 3

2 2 2

a b c

b c a

    

Tht vy, theo bng thc Bunhiacopxki dng phân thc

 

2 2 2

3 3 3

a b c

b c a ab bc ac



  



Theo mc ta có

2 2 2

a b c ab bc ca    

c

   

 

2 2 2 2 2 2

a b c a b c ab bc ca      

Nên ta có

 

2 2 2

a b c

ab bc ac



  





3 3 3

2 2 2

a b c

b c a

    

+ Chng minh

2 2 2

a b c 3  

Tht vy, áp dng bng thc Cauchy ta có

2 2 2 2 2 2 2 2 2

a b 2ab; b c 2bc; c a 2ca; a 1 2a;b 1 2b;c 1 2c           

Cng theo v các bng thc

 

2 2 2

3 a b c 3 2 ab bc ca a b c 12         

Hay

2 2 2

a b c 3  

Kt hp hai kt qu c

3 3 3

2 2 2

a b c

a b c 3

b c a

     

Vc chng thc xy ra khi và ch khi

a b c 1  

THCS.TOANMATH.com

FB TRỊNH BÌNH

156

Câu 248: [TS10 Chuyên Phú Th, 2010-2011]

Cho các s  mãn

a b c abc  

. Tìm giá tr ln nht ca biu thc:

     

2 2 2

a b c

bc 1 a ca 1 b ab 1 c

  

  

Lời giải

Kt hp vi gi thit ta có

 

    

bc 1 a bc a bc bc a a b c a b a c         

 c

 

  

 

  

ca 1 b a b b c ; ba 1 c a c b c       

;

Nên

        

a b c

a b a c a b b c a c b c

a a b b c c

. . .

a b a c b c b c c b a c



     

  

     

Áp dng bng thc

a a 1 a a

a b a c 2 a b a c



   

 c

1 a a b b c c 3

2 a b a c b c a b a c b c 2



      



     



Vy giá tr ln nht ca S là

ng thc xy ra khi và ch khi

a b c 3  

Câu 249: [TS10 Chuyên Phú Th, 2010-2011]

Cho các s  nh nht ca biu thc

 

2 2 2

c ab 1 a bc 1 b ca 1

b bc 1 c ca 1 a ab 1

  

  

  

Lời giải

Áp dng bng thc Cauchy dng

x y z 3 xyz  

c

THCS.TOANMATH.com

FB TRỊNH BÌNH

157

     

   

2 2 2

c ab 1 .a bc 1 .b ca 1 ab 1 bc 1 ac 1

S 3 3

abc

b bc 1 .c ac 1 .a ab 1

2 ab.2 bc.2 ca

abc

     



  



Vy giá tr nh nht cng thc xy ra khi và ch khi

a b c 1  

Câu 250: [TS10 Chuyên i Hc Vinh, 2010-2011]

Cho x, y, z là các s a mãn

x y z 18 2  

. Chng minh rng:

     

1 1 1 1

x y z y z x z x y

  

  

Lời giải

Bng thc cn chi

     

1 1 1 1

2x y z 2y z x 2z x y

  

  

Áp dng bng thc Cauchy ta có

 

2 2x y z 2x y z   

c

 

2x y z







 c bng thc

     

1 1 1 1 1 1

2x y z x 2y z x y 2z

2x y z 2y z x 2z x y



    



     

  



Phép chng minh s hoàn tt nu ta ch c

1 1 1 1

2x y z x 2y z x y 2z

  

     

Tht vy theo bng thc

 

1 1 1 9 9 1

2x y z x 2y z x y 2z

4 x y z

4.18 2 8 2

    

     



Vc chng thc xy ra khi và ch khi

x y z 6 2  

Câu 251: [TS10 Chuyên , 2010-2011]

Cho a, b, c là các s tha mãn

abc 1

. Chng minh rng:

THCS.TOANMATH.com

FB TRỊNH BÌNH

158

a b c ab bc ca



   

Lời giải

Bng th

      

b c ab bc ca 3 ab bc ca 6 a b c         

 ý rng

     

ab bc ca 3abc a b c 3 a b c       

Nên bài toán quy v chng minh

     

3 a b c 3 3 a b c 6 a b c       

Bng thi

 

3 a b c a b c 3 0     

Bng thc cui cùng là mt bng thc chng

minh.

ng thc xy ra khi và ch khi

a b c 1  

Câu 252: [TS10 Chuyên , 2010-2011]

Cho 3 s thc không âm a, b, c tha mãn

a b c 1.  

Chng minh rng:

b c 16abc.

ng thc xy ra khi nào?

Lời giải.

Ta có:

(a b c) (a (b c)) 4a(b c).      

a b c 1  

nên t bng thc trên suy ra:

1 4a(b c) b c 4a(b c) .     

Li có:

(b c) 4bc b c 16abc.    

ng thc xy ra khi

a ; b c .

  

Câu 253: [TS10 Chuyên Hi Phòng, 2010-2011]

Cho a, b, c là các s tha mãn

a b c 2  

. Chng minh rng:

2 2 2

1 1 1 97

a b c

b c a

     

Lời giải

Áp dng bng thc

THCS.TOANMATH.com

FB TRỊNH BÌNH

159

1 81 9 9

a 1 a a

16 4b 4b

    

     

    

    

Hay

97 1 9

4 4b

  

Ch c

97 1 9 97 1 9

b b ; c c

4 4c 4 4a

     

Cng theo v các bng thc

2 2 2

97 1 1 1 9 1 1 1

a b c a b c

4 4 a b c

b c a



          





Mà ta li có

1 1 1 9

a b c a b c

  



c

 

2 2 2

1 1 1 4 81

a b c a b c

4 a b c

b c a



        









Ta cn chng minh

 

4 81 97

a b c

4 a b c



   









Hay

 

81 97

a b c

4 a b c

   



Tht vy, áp dng bng thc

   

 

81 4 65

a b c a b c

a b c

4 a b c 4 a b c

4 65 65 97

2 a b c 4

a b c 4.2 8 8

       



   

      



Bng thc chng thc xy ra khi và ch khi

a b c

  

Câu 254: [TS10 Chuyên , 2010-2011]



a, b, c 1;2 



ng:

2 2 2 2 2 2

a b b c c a

ab bc ca

  

  

Lời giải

THCS.TOANMATH.com

FB TRỊNH BÌNH

160

Bng thc cn chi

   

 

      

2 2 2 2 2 2

2 2 2 2

2 2 2

a b ab b c bc c a ca 7abc

c ab ca b bc a ab ca b bc 5abc 2bc 2a b 0

ab ca b bc c a b 4ca 2c 2a ca 0

a b b c c a b 2a c 2c a 0

     

           

         

       

Vì vai trò ct tính tng quát ta gi s

2 a b c 1   

c

2a 2 c; 2c 2 a   

c

      

b b c c a 0; b 2a c 2c a 0      

Nên bng thc cuy bng thc chng minh.

ng thc xy ra khi và ch khi

a b 2; c 1  

và các hoán v.

Câu 255: [TS10 Chuyên nh, 2010-2011]

Cho a, b, c là các s tha mãn a + b + c  1. Chng minh rng:

2 2 2

1 1 1

a 2bc b 2ca c 2ab

  

  

Lời giải.

Vi x, y, z là các s th

1 1 1 9

(*)

x y z x y z

  



Tht vy, theo bng thc Cauchy ta có:

1 1 1 1 1 1 1 9

(x y z) 3 xyz.3 9 .

x y z xyz x y z x y z



         







Vc chng minh.

ng thc xy ra khi x = y = z.

Áp d

2 2 2 2 2 2 2

1 1 1 9 9 9

a 2bc b 2ca c 2ab a b c 2ab 2bc 2ca (a b c)

     

         

Bng thc chng minh.

ng thc xy ra khi a = b = c.

Câu 256: [TS10 Chuyên i hc Vinh, 2010-2011]

Tìm giá tr nh nht ca biu thc:

P x x 2x y y y 2y x 2010.      

THCS.TOANMATH.com

FB TRỊNH BÌNH

161

Lời giải.

Ta có:

P (x y) (y x) 2010 2010( x 0; y 0).        

ng thc xy ra khi và ch khi x = y = 1 hoc x = y = 0.

Câu 257: [TS10 Chuyên Ngh An, 2010-2011]

Cho a, b, c là các s tha mãn

a b c 3  

. Tìm giá tr ln

nht ca biu thc:

P a b b c c a abc   

Lời giải

t

x a; y b; z c

. T gi thic

2 2 2

x y z 3  

Khi này biu thc P tr thành

2 2 2

P x y y z z x xyz   

D thy

P0

theo bng thc Cauchy

Không mt tính tng quát ta gi s y là s nm gi

  

2 2 2

z y z y x 0 y z z x xyz z y      



 

2 2 2 2 2 2 2

P x y y z z x xyz x y z y y x z       

Mt khác theo bng thc Cauchy ta có

  

2 2 2

2 2 2 2 2

2x 2y 2z

2y x z x z 8





   





Suy ra

 

y x z 2

c

P2

ng thc xy ra khi và ch khi

x y z

x 2y

  























và các hoán v

a b c 1

a 2; b 1; c 0

   





  



và các hoán v

Vy giá tr ln nht ca biu thc P là 2.

ng thc xy ra khi và ch khi

a b c 1  

hoc

a 2; b 1; c 0  

và các hoán v.

Câu 258: [TS10 Chuyên Hòa Bình, 2010-2011]

Cho x, y là hai s không âm. Chng minh rng

3 3 2 2

x 8y 2x y 4xy  

Lời giải

Ta các

THCS.TOANMATH.com

FB TRỊNH BÌNH

162

3 3 2 2

x 8y 2x y 4xy

(x 2y)(x 2xy 4y ) 2xy(x 2y)

(x 2y)(x 4xy 4y ) 0

  

     

    

(x 2y)(x 2y) 0   

x 0,y 0  



Vy bng thc chng minh.

Câu 259: [TS10 Chuyên , 2010-2011]

Cho ba s a mãn

ab bc ca 1

. Chng minh rng:

2 2 2

a 1 a b 1 b c 1 c 1 1 1

bc ac ab a b c

     

    

Lời giải

 ý là

  

a 1 a ab bc ca a b c a       

c

  

a 1 a b c a   

Áp dng bng thc

  

2a b c

a b c a a

a 1 a b c 1 1 1

bc bc bc 2bc 2 b c





  

    

    





 c

b 1 b 1 1 1 c 1 c 1 1 1

;

ac 2 a c ab 2 a b

       

   

   

   

Cng theo v ba bng thc

2 2 2

a 1 a b 1 b c 1 c 1 1 1

bc ac ab a b c

     

    

Vc chng thc xy ra khi và ch khi

a b c

  

Câu 260: [TS10 Chuyên , 2010-2011]

Chng minh rng:

1 1 1 1 (a b c abc)

a b b c c a (a b)(b c)(c a)

2 abc

  

   

     

( , , 0)abc

Lời giải.

D thy:

2 2 2

(a b)(b c)(c a) c (a b) a (b c) b (c a) 2abc.         

Áp dng bng thc Cô-si và bng thc Bu-nhi-a-cp-c:

THCS.TOANMATH.com

FB TRỊNH BÌNH

163

 

2 2 2

1 1 1 1

(c (a b) a (b c) b (c a) 2abc).

a b b c c a

2 abc

1 1 1 1

c a b. a b c. b c a. 2abc. c a b abc .

c a b c c a 2 abc



        



  





          



  



u phi chng thc xy ra khi a = b = c.

Câu 261: [TS10 Chuyên Kiên Giang, 2010-2011]

 biu thc: X = 2a

+ 9b

+ 2a  18b  t giá tr nh nht.

Tìm giá tr nh nh

Lời giải

Ta có:

X = (3b)

-2.3b.(3 + a) + 9 + 6a + a

+ a

 4a + 4 + 1997

= (3b)

-2.3b.(3 + a) + (3 + a)

+ (a

 4a + 4) + 1997

= (3b  3  a)

+ (a  2)

+ 1997



1997

Dy ra khi

3b 3 a 0 3b 3 2 0

a 2 0 a 2



       







  

  









Vy vi a = 2 và b =

thì Xmax = 1997

Câu 262: [TS10 Chuyên Phú Yên, 2010-2011]

a) Cho 2 s ng minh rng :

1 1 1 1

a b 4 a b











b) Cho 3 s a mãn

1 1 1

2010.

x y z

  

Tìm GTLN ca biu thc:

111

2x y z x 2y z x y 2z

  

     

Lời giải

a) Bit ng th

   

1 1 1 1

4ab a b 0 a b

a b 4 a b



       







Bng thc cuc chng thc

xy ra khi và ch khi

ab

b) Áp dng bng thc

THCS.TOANMATH.com

FB TRỊNH BÌNH

164

1 1 1 1 1 2 1 1

2x y z 4 x y x z 16 x y z

   

    

   

   

   

 c

1 1 1 2 1 1 1 1 1 2

;

x 2y z 16 x y z x y 2z 16 x y z

   

     

   

   

   

Cng theo v các bng thc

1 1 1 1 1 1 1 2010 1005

2x y z x 2y z x y 2z 4 x y z 4 2



       



     



Vy giá tr ln nht ca P là

1005

ng thc xy ra khi và ch khi

x y z 670  

NĂM HỌC 2009-2010

Câu 263: [TS10 Chuyên Thái Bình, 2009-2010]

Gi

1 1 1 1

x 2x 3 4x 3 5x 6



  



  



Lời giải

Ta chng minh:

1 1 1 1 1 1

a b c a 2b b 2c c 2a



    



  



(*)

vi a > 0; b > 0; c > 0

+ Vi a > 0; b > 0 ta có:

 

a 2 b 3 a 2b  

(1)

+ Do

 

a 2 b 9



  





nên

1 2 9

a b a 2 b





(2)

+ T (1) và (2) ta có:

1 2 3 3

a b a 2b





(3) (Vi a > 0; b> 0; c > 0)

+ Áp dng (3) ta có:

1 1 1 1 1 1

a b c a 2b b 2c c 2a



    



  



vi a > 0; b> 0; c > 0



1 1 1 1

x 2x 3 4x 3 5x 6



  



  



 



Áp dng bng thc (*) vi a = x; b = x; c = 2x - 3 ta có:

1 1 1 1 1 1

x x 2x 3 3x 5x 6 4x 3



    



  



THCS.TOANMATH.com

FB TRỊNH BÌNH

165

1 1 1 1

x 2x 3 5x 6 4x 3



   



  



vi



Dy ra

x 2x 3 x 3    

Vm duy nht x = 3.

Câu 264: [TS10 Chuyên Hi Phòng, 2009-2010]

a) Cho các s ng minh rng:

 

1 1 1

a b c 9

a b c



    





b) Cho các s  mãn

a b c 3  

. Chng ming rng:

2 2 2

1 2009

670

ab bc ca

a b c





Lời giải

a) Áp dng bng thc Cô si cho 3 s 

1 1 1 1

a b c abc; 3

a b c

abc

     

Suy ra

 

1 1 1

a b c 9

a b c



    





Bng thc chng minh. Dng thc xy ra khi và ch khi

a b c

b) Ta có

 

2 2 2

a b c

ab bc ca a b c ab bc ca 3



         

Suy ra

2007

669

ab bc ca





Áp dng bng thc trong câu a, ta có

 

2 2 2

1 1 1

a b c 2ab 2bc 2ca 9

ab bc ca ab bc ca

a b c



       



   





Suy ra

 

2 2 2 2

1 1 9

ab bc ca

a b c

  



c

2 2 2

1 2009

670

ab bc ca

a b c





Vy bng thc chng minh. Dng thc xy ra khi và ch khi

a b c 1  

Câu 265: [TS10 Chuyên Phú Yên, 2009-2010]

a) Cho x, y, z, a, b, c là các s ng minh rng:

abc + xyz (a + x)(b + y)(c + z)

THCS.TOANMATH.com

FB TRỊNH BÌNH

166

b) T 

3 3 3

3 3 3 3 2 3   

Lời giải

a) Ta có:

abc xyz (a + x)(b + y)(c + z) (1)

L cc :

abc + xyz + 3 (abc) xyz +3 abc(xyz) (a + x)(b + y)(c + z)

abc + xyz+ 3 (abc) xyz +3 abc(xyz) abc + xyz + abz + ayc + ayz + xbc + xyc + xbz

3 (abc) xyz +3 abc(xyz) (abz + ayc + xbc) + (ayz + xbz + xyc)

(2)

Theo bng thc Cauchy, ta có :

(abz + ayc + xbc) 3 (abc) xyz

(3)

(ayz + xbz + xyc) 3 abc(xyz)

(4)

Cng hai bng thc bng thc chng

minh.

b) Áp di

a = 3+ 3, b = 1, c = 1, x = 3 - 3, y = 1, z = 1

Ta có : abc = 3 +

, xyz = 3-

, a + x = 6, b + y = 2, c + z = 2

T 

3 3 3 3

3+ 3 3- 3 6.2.2 2 3  



Câu 266: [TS10 Chuyên ng, 2009-2010]

Cho ba s thc không âm a, b, c thu kin a + b + c = 1. Chng minh

rng

2 2 2

a b c 4(ab bc ca) 1.     

Lời giải



+ b

 2ab ; b

+ c

 2bc ; c

+ a

 2ca

 a

+ b

+ c

 ab + bc + ca (1)



+ b

+ c

= a

+ b

+ c

+ (a + b + c)

 1

Hay a

+ b

+ c

= 2(a

+ b

+ c

) + 2(ab + bc + ca)  1 (2)

  a

+ b

+ c

 4(ab + bc + ca)  

Câu 267: [TS10 Chuyên nh, 2009-2010]

Vi s t nhiên

n3

. Chúng minh rng



THCS.TOANMATH.com

FB TRỊNH BÌNH

167

Vi

   

 

1 1 1

S ...

3 1 2 5 2 3 2n 1 n n 1

   

    

Lời giải

Vi

n3

, ta có

 

1 n 1 n n 1 n

2n 1

2n 1 n n 1

4n 4n 1

n 1 n 1 1 1

2 n 1. n n n 1

4n 4n

   





  







   









n +1 - n

c

1 1 1 1 1 1 1 1 1

S 1 ... 1

2 2 2

2 2 3 n n 1 n 1



         







Vy bng thc chng minh.

Câu 268: [TS10 Chuyên H, 2009-2010]

Tìm giá tr ln nht ca biu thc:

P x 4x 5 x 6x 13     

Lời giải

Ta có:

   

P x 2 1 x 3 2     

Trên mt phng t Oxy lm A(x-2; 1), B(x+3; 2)

Ta chc:

   

AB x 2 x 3 1 2 25 1 26        

 

OA x 2 1  

 

OB x 3 2  

Mt khác ta có:

OA OB AB

   

x 2 1 x 3 2 26      

Dy ra khi A thun OB hoc B thun OA

x 2 1

x 3 2



   



.Th li x = 7 thì A(5; 1); B(10; 2).

Câu 269: [TS10 Chuyên nh, 2009-2010]

Chng minh rng

 

n 3 2





, vi mi s nguyên m, n.

Lời giải

THCS.TOANMATH.com

FB TRỊNH BÌNH

168

Vì m, n là các s nguyên nên

là s hu t và

là s vô t nên



ng hp sau

 ng hp 1: Vi



c

2 2 2 2

m 2n m 2n 1   

hay

1

m 2n

T 

 

m 2n 1 1

2 2 2 2

n 3 2

n 2 2



     



  











 ng hp 2: Vi



c

2 2 2 2

m 2n m 2n 1   

hay

1

m 2n

T 

 

m m 2n 1 1

2 2 2 2 2

n n n

n 3 2

n 2 2





        















Vc chng minh.

Câu 270: [TS10 Chuyên , 2009-2010]

Cho ba s tht phân bit. Chng minh rng:

     

2 2 2

a b c

b c c a a b

  

  

Lời giải

Bng thc cn chi

THCS.TOANMATH.com

FB TRỊNH BÌNH

169

        

a b c ab bc ca

b c c a a b

b c c a c a a b a b b c



     



  

     



Mà ta li có

        

     

   

ab bc ca

b c c a c a a b a b b c

ab a b bc b c ca c a a b b c c a

a b b c c a a b b c c a



     

       

   

     

ng thc trên tr thành

a b c

b c c a a b



  



  



B ng thc cui cùng là mt b ng th     c chng

minh.

Câu 271: [TS10 Chuyên , 2009-2010]

Cho biu thc

2 2 2 2

P a b c d ac bd     



ad bc 1

Chng minh rng:

P3

Lời giải

Ta có

   

      

2 2 2 2 2 2 2 2

2 2 2 2 2 2 2 2 2 2

ac bd ad bc a c 2abcd b d a d 2abcd b c

a c d b d c a b c d

        

      

Vì

ad bc 1

nên

 

  

2 2 2 2

1 ac bd a b c d (1)    

Áp dng bng thc

  

2 2 2 2 2 2 2 2

P a b c d ac bd 2 a b c d ac bd          

Suy ta

 

P 2 1 ac bd ac bd    

. Rõ ràng

P0

vì

 

2 1 ac bd ac bd   

t

x ac bd

c

   

2 2 2 2 2 2 2 2

P 2 1 x x P 4 1 x 4x 1 x x 1 x 4x 1 x 4x 3              

THCS.TOANMATH.com

FB TRỊNH BÌNH

170

Hay





P 1 x 2x 3 3    

c

P3

. Vy bng thc

chng thc xy ra khi và ch khi

ad bc 1

2a 3d c

2b 3c d

  









  



Câu 272: [TS10 Chuyên Ngh An, 2009-2010]

Cho a, b, c là các s thi tha mãn

a b c 3  

. Tìm giá tr nh nht

ca biu thc:

2 2 2

ab bc ca

P a b c

a b b c c a



   



Lời giải

D c dng thc xy ra ti

a b c 1  

và giá tr nh nht ca P là 4.

Ta quy bài toán v chng minh bng thc

2 2 2

ab bc ca

a b c 4

a b b c c a



   



Tht vy, kt hp vi gi thit ta có

 

2 2 2 2 2 2

3 3 3 2 2 2 2 2 2

3 a b c a b c a b c

a b c a b b c c a ab bc ca

      

        

Áp dng bc Cauchy ta có

3 2 2 3 2 2 3 2 2

a ab 2a b;b bc 2b c; c ca 2c a     

Suy ra

   

2 2 2 2 2 2

3 a b c 3 a b b c c a 0     

c

2 2 2 2 2 2

ab bc ca ab bc ca

a b c a b c

a b b c c a a b c

   

      

   

Phép chng minh s hoàn tt nu ta ch c

2 2 2

ab bc ca

a b c 4

a b c



   



Hay

 

2 2 2

9 a b c

a b c 4

2 a b c

  

   



t

2 2 2

t a b c  

T gi thit

2 2 2

a b c 3 a b c 3      

c

t3

THCS.TOANMATH.com

FB TRỊNH BÌNH

171

Bng thc trên tr thành

  

t 4 2t 9 t 8t t 3 2t 3 0



         

Bng thc cu

t3

. Vc chng minh xong.

Câu 273: [TS10 Chuyên , 2009-2010]

G dài ba cnh ca mt tam giác có ba góc nhn. Chng minh rng vi

mi s thc x, y, z ta luôn có:

2 2 2 2

2 2 2 2 2 2

y 2x 2y 2z

a b c a b c



  



Lời giải

Bng thc cn chi

 

2 2 2 2

2 2 2 2 2 2 2 2 2 2 2 2

y 2y

x 2x z 2z

a a b c b a b c c a b c

x b c a y a c b z a b c

a a b c b a b c c a b c

     

     

     

   

     

 dài các cnh ca mt tam giác nhn nên

2 2 2 2 2 2 2 2 2

a b c ; b c a ; c a b     

c

2 2 2 2 2 2 2 2 2

b c a 0; a c b 0; a b c 0        

Do vy bng thc chng minh xong.

Câu 274: [TS10 Chuyên KHTN, 2009-2010]

Vi a, b, c là nhng s thng minh rng:

2 2 2

2 2 2 2 2 2

a b c a b c

3a 8b 14ab 3b 8c 14bc 3c 8a 14ca



  

     

Lời giải

Áp dng bng thc

 

2 2 2 2 2 2

3a 8b 14ab 3a 8b 12ab 2ab 4a 9b 12ab 2a 3b          

Suy ra

 

2 2 2

a a a

2a 3b

3a 8b 14ab

2a 3b









Áp d c

THCS.TOANMATH.com

FB TRỊNH BÌNH

172

2 2 2

2 2 2 2 2 2

2 2 2

a b c

3a 8b 14ab 3b 8c 14bc 3c 8a 14ca

a b c

2a 3b 2b 3c 2c 3a



     

  

  

Mt khác theo bng thc Bunhiacopxki dng phân thc

 

2 2 2

a b c

a b c a b c

2a 3b 2b 3c 2c 3a 5

5 a b c



   

  



c:

2 2 2

2 2 2 2 2 2

a b c a b c

3a 8b 14ab 3b 8c 14bc 3c 8a 14ca



  

     

Vc chng thc xy ra khi và ch khi

a b c

Câu 275: [TS10 Chuyên KHTN, 2009-2010]

Gi s x, y, z là nhng s thc tho u kin

0 x, y, z 2

và

x y z 3  

Tìm giá tr nh nht và ln nht ca biu thc:

   

4 4 4

M x y z 12 1 x 1 y 1 z      

Lời giải

t

a x 1; b y 1; c z 1     

c

1 a; b; c 1  

và

a b c 0  

. Biu

thc vit li thành

   

 

4 4 4 3 3 3 2 2 2

M a b c 4 a b c 6 a b c 4 a b c 3 12abc             

 ý là khi

a b c 0  

thì

3 3 3

a b c 3abc 0   

nên biu thc trên th thành

 

4 4 4 2 2 2

M a b c 6 a b c 3      

Theo mc thì

 

4 4 4

2 2 2

a b c abc a b c 0

a b c a b c 0

     



M3

hay giá tr nh nht ca M là 3.

ng thc xy ra khi và ch khi

a b c 0  

hay

x y z 1  

Mt khác do

1 a; b; c 1  

nên ta có

a ; b ; c 1

. T 

4 2 4 2 4 2

a a a ; b b b ; c c c     

Suy ra

 

4 4 4 2 2 2

M a b c 6 a b c 3 7 a b c 3          

THCS.TOANMATH.com

FB TRỊNH BÌNH

173

Mà ta li có

a b c 0  

nên trong ba s a, b, c có mt hoc hai s âm, tc là luôn tn

ti hai s cùng du. Không mt tính tng quát ta gi s hai s c

b c b c a   



M 14 a 3 17  

hay giá tr ln nht cng thc xy ra khi và

ch khi

a 1; b 1;c 0   

và các hoán v hay

x 2; y 0; z 1  

và các hoán v

Câu 276: [TS10 Chuyên Thái Bình, 2009-2010]

a) Cho k là s t kì. Chng minh bng thc sau:

 

1 1 1

k 1 k k k 1











b) Chng minh rng:

1 1 1 1 88

2 45

3 2 4 3 2010 2009

    

Lời giải

a) Bng thc cn chi

 

1 2 k 1 2 k

2k 1 2 k k 1 0 k 1 k 0

k 1 k k. k 1



         



Bng thc cui m

Vy bng thc chng minh.

b) Áp dng kt qu câu a ta có

1 1 1 1

2 1 3 2 4 3 2010 2009

1 1 1 1 1 1

2 2 2

1 2 2 3 2009 2010

1 1 88

2 1 2 1 VP

45 45

2010

    

   



      

   





   



     





Vy bng thc chng minh xong.

Câu 277: [TS10 Chuyên TP. H Chí Minh, 2009-2010]

a) Cho 3 s thc a, b, c bt kì. Chng minh rng:

     

2 2 2

a b b c c a

a b c ab bc ca

26 6 2009

  

       

b) Cho

a 0; b 0

. Chng minh rng

1 2 8

a b 2a b





THCS.TOANMATH.com

FB TRỊNH BÌNH

174

Lời giải

a) Bng thc cn chi

           

2 2 2 2 2 2

a b b c c a a b b c c a

2 2 2 26 6 2009

     

    

Hay

     

2 2 2

12 a b b c 2007 c a

13 3 2

  

  

Bng thc cu

Vc chng thc xy ra khi và ch khi

a b c

b) Bng thc cn chi

1 2 8

a b 2a b





t

cb

, do

b0

c

c0

ng thc vit li

thành

1 2 8

a c 2a c





Theo mc

1 2 2 2 2.4 8

a c 2a c 2a c 2a c

    



Vy bng thc chng thc xy ra khi và ch khi

2a b

Câu 278: [TS10 Chuyên Phú Th 2009-2010]

Cho x, y, z là các s th

xyz x y z 2   

. Chng minh rng:

1 1 1 3

xy yz zx

  

Lời giải

Gi thit cc vit li thành

1 1 1

x 1 y 1 z 1

  

  

t

1 1 1

a ; b ; c

x 1 y 1 z 1

  

  

c

a b c 1  

. T 

1 a b c 1 b c a 1 c a b

x ; y ; z

a a b b c a

     

     

Bng thc cn chc vit li thành:

THCS.TOANMATH.com

FB TRỊNH BÌNH

175

        

ab bc ca 3

b c c a c a a b a b b c

  

     

Áp dng bng thc:

  

ab 1 b a

2 b c c a

b c c a

bc 1 c b

2 c a a b

c a a b

ca 1 a c

2 a b b c

a b b c































Cng theo v các bng thc:

        

ab bc ca 3

b c c a c a a b a b b c

  

     

Vy bng thc chng thc xy ra khi và ch khi

a b c 2  

Câu 279: [TS10 Chuyên Phú Th 2009-2010]

Cho các s thc không âm a, b, c sao cho

ab bc ca 3

. Chng minh rng:

2 2 2

1 1 1

a 2 b 2 c 2

  

  

Lời giải

Bng thc cn chi

2 2 2

a b c

a 2 b 2 c 2

  

  

Áp dng bng thc Bunhiacopxki dng phân thc

   

 

2 2 2

2 2 2 2 2 2 2 2 2

a b c a b c

a b c

a 2 b 2 c 2 a b c 6 a b c 2 ab bc ca

   

    

          

Vy bng thc chng thc xy ra khi và ch khi

a b c 1  

Câu 280: [TS10 Chuyên i hc Vinh 2009-2010]

Cho x, y, z là các s a mãn

x 2y 3z 18  

. Chng minh rng:

2y 3z 5 x 2y 5

3z x 5 51

1 x 1 2y 1 3z 7

   



  

  

Lời giải

THCS.TOANMATH.com

FB TRỊNH BÌNH

176

t

a x; b 2y; c 3x  

 thit tr thành

a b c 18  

và bng thc

c vit li thành

b c 5 c a 5 a b 5 51

1 a 1 b 1 c 7

     

  

  

Bng thi

b c 5 c a 5 a b 5 51

1 1 1 3

1 a 1 b 1 c 7

     

      

  

Hay

 

1 1 1 72

a b c 6

1 a 1 b 1 c 7



     



  



Phép chng minh s hoàn tt nu ta ch c

1 1 1 3

1 a 1 b 1 c 7

  

  

Tht vy theo bng thc Cauchy ta có

1 1 1 9 9 3

1 a 1 b 1 c 3 a b c 21 7

    

     

Vc chng minh.

ng thc xy ra khi và ch khi

a b c 6  

hay

x 6; y 3; z 2  

Câu 281: [TS10 Chuyên i hc Vinh 2009-2010]

Cho các s thc x, y tha mãn:

8 0.xy

Hãy tìm giá tr nh nht ca biu thc:

( 8 )

y x y





Lời giải

S d 

( 8 ) 8 6.

( 8 )

P x y y

y x y

    



ng thc xy ra khi và ch khi

( 8 )

x y y

y x y









  



  



  





Vy minP =

khi và ch khi x = 4 và y =

THCS.TOANMATH.com

FB TRỊNH BÌNH

177

Bấm Tải xuống để xem toàn bộ.

| 1/177

| | Tải xuống

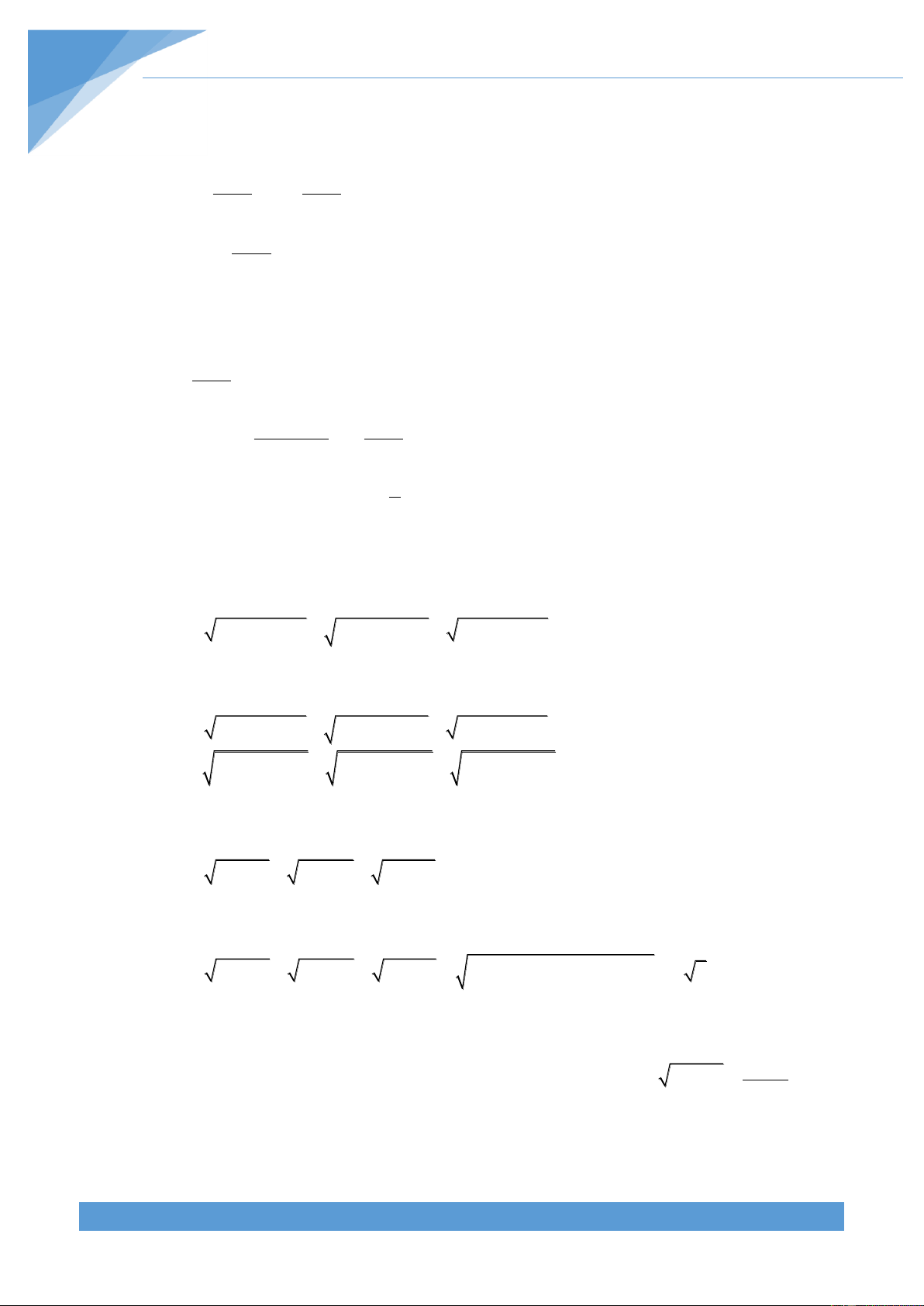
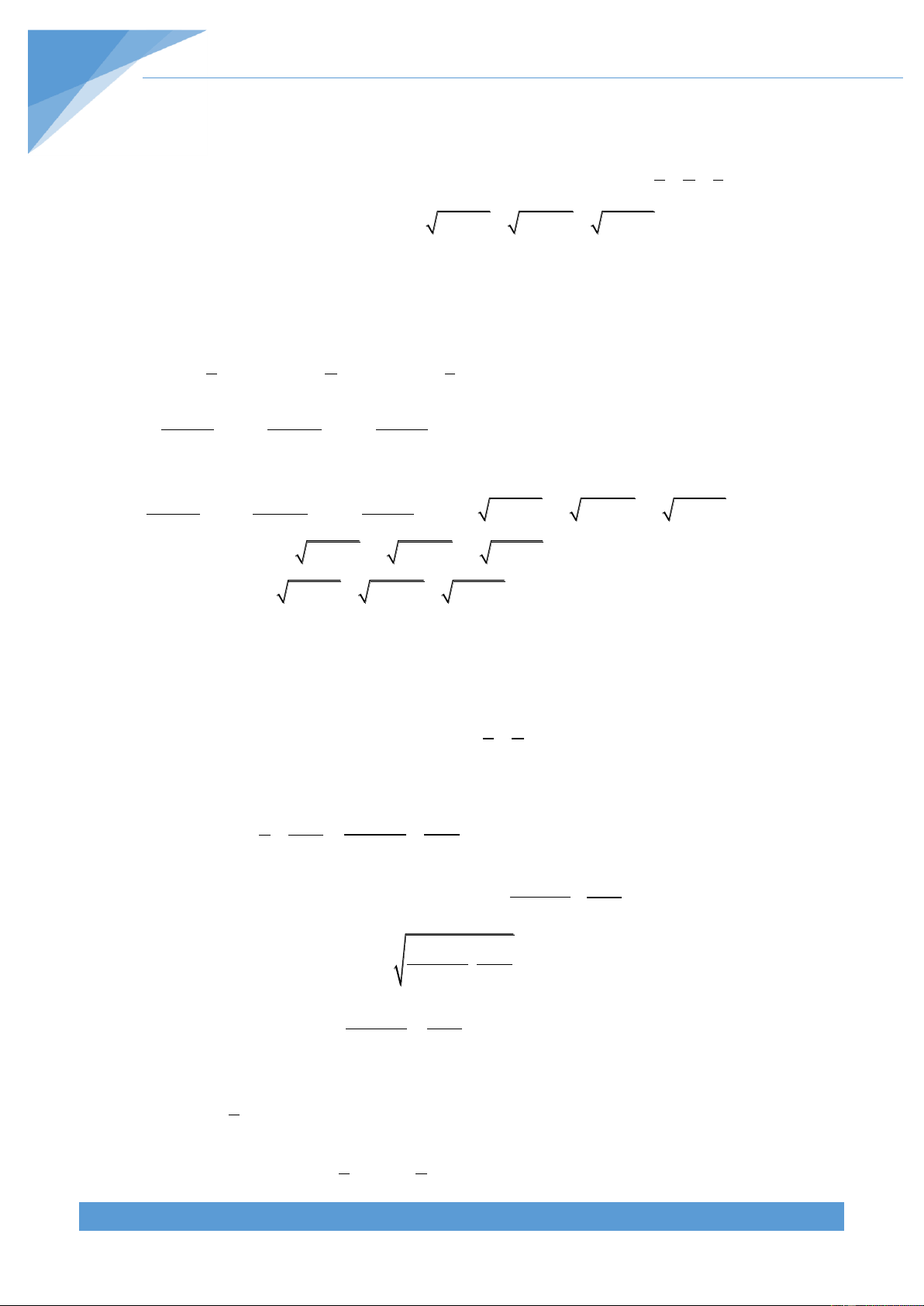
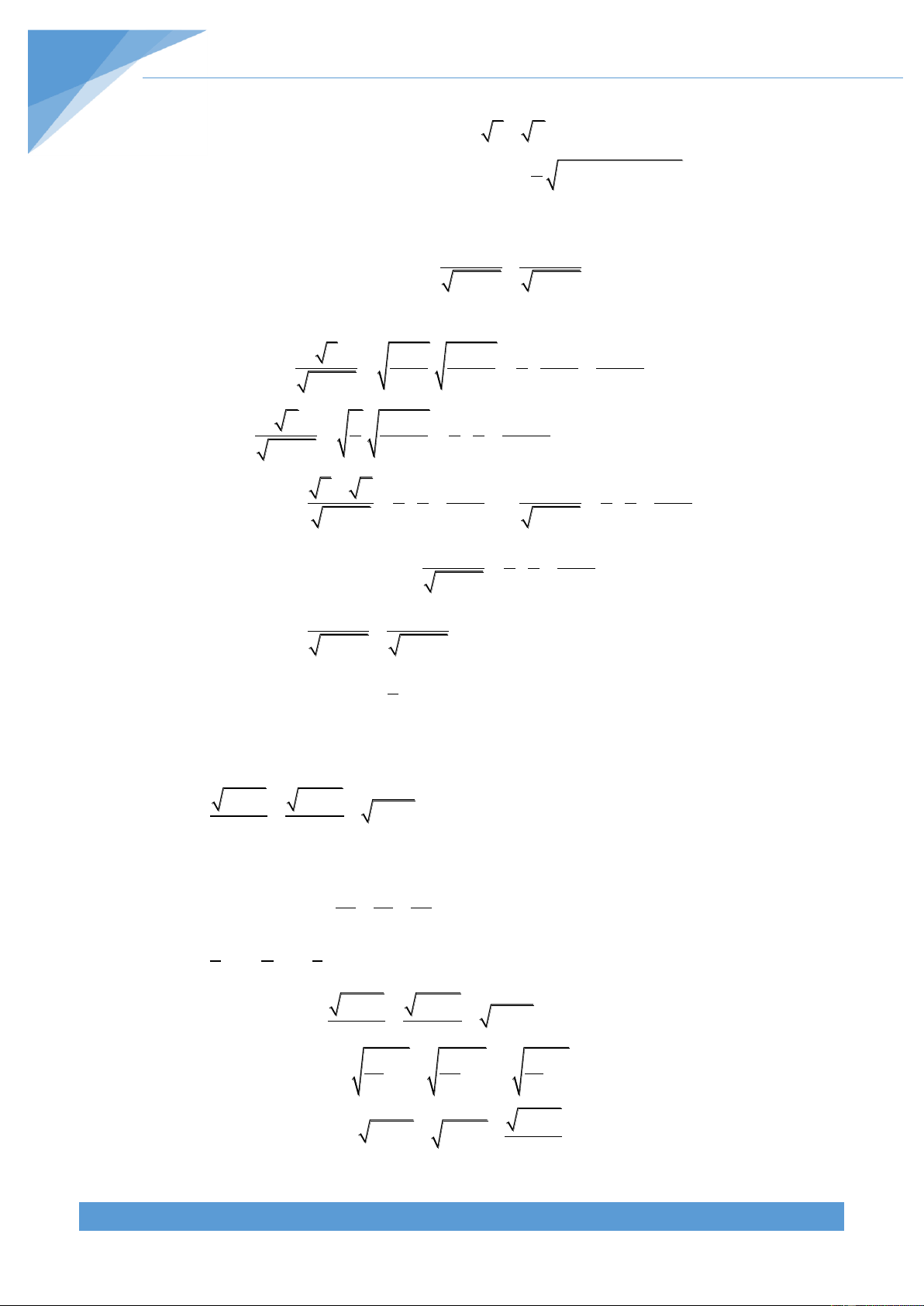
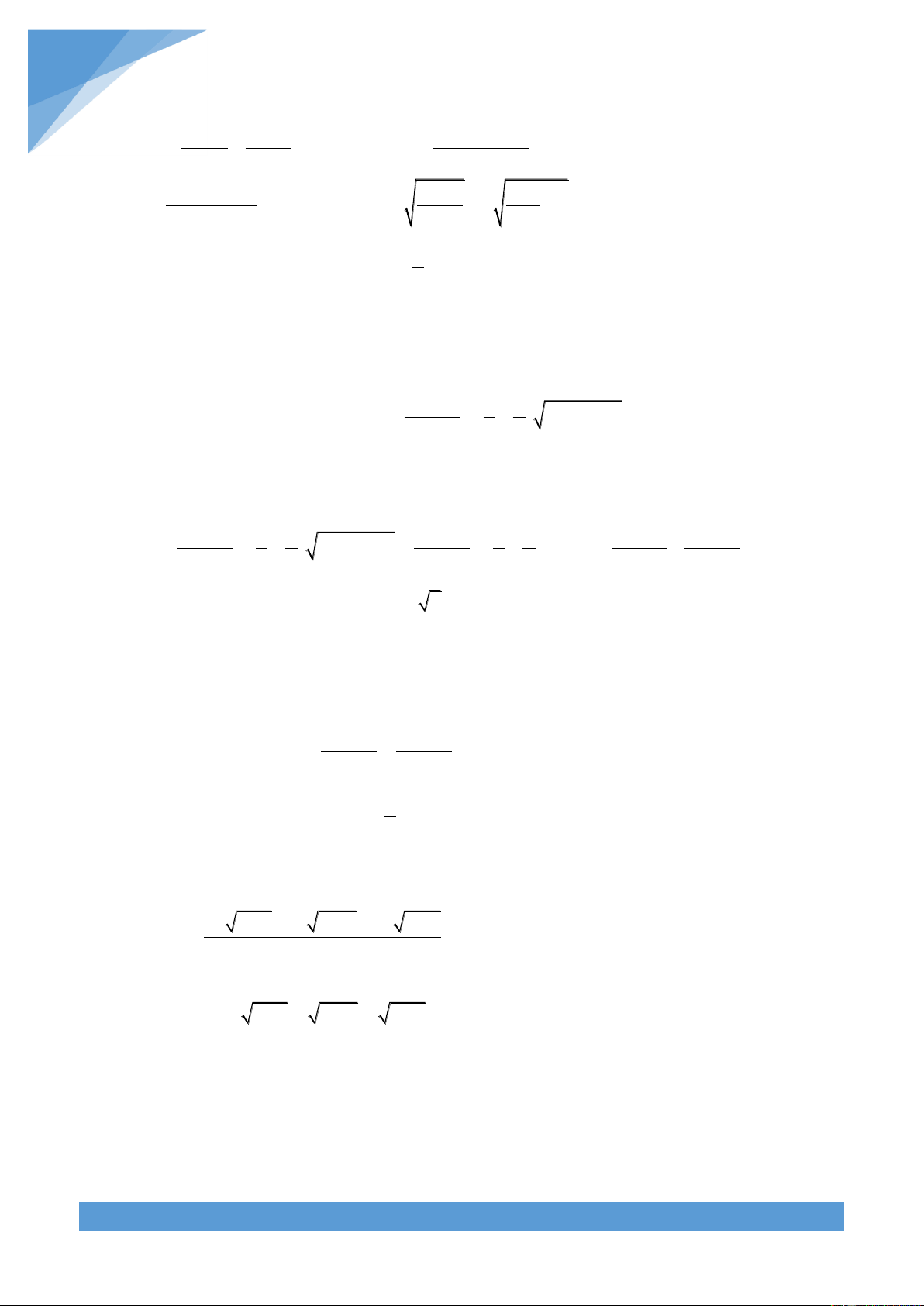
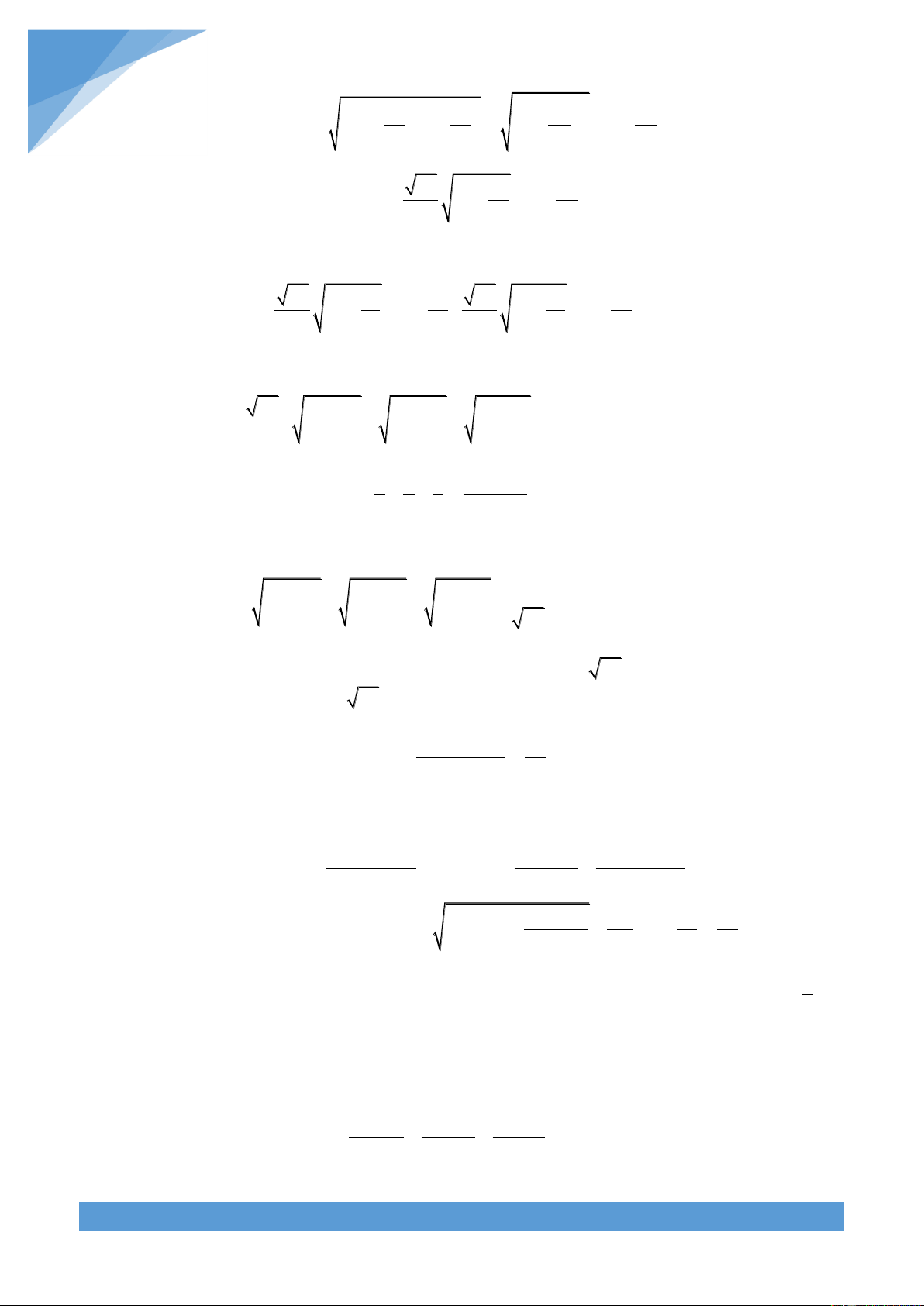
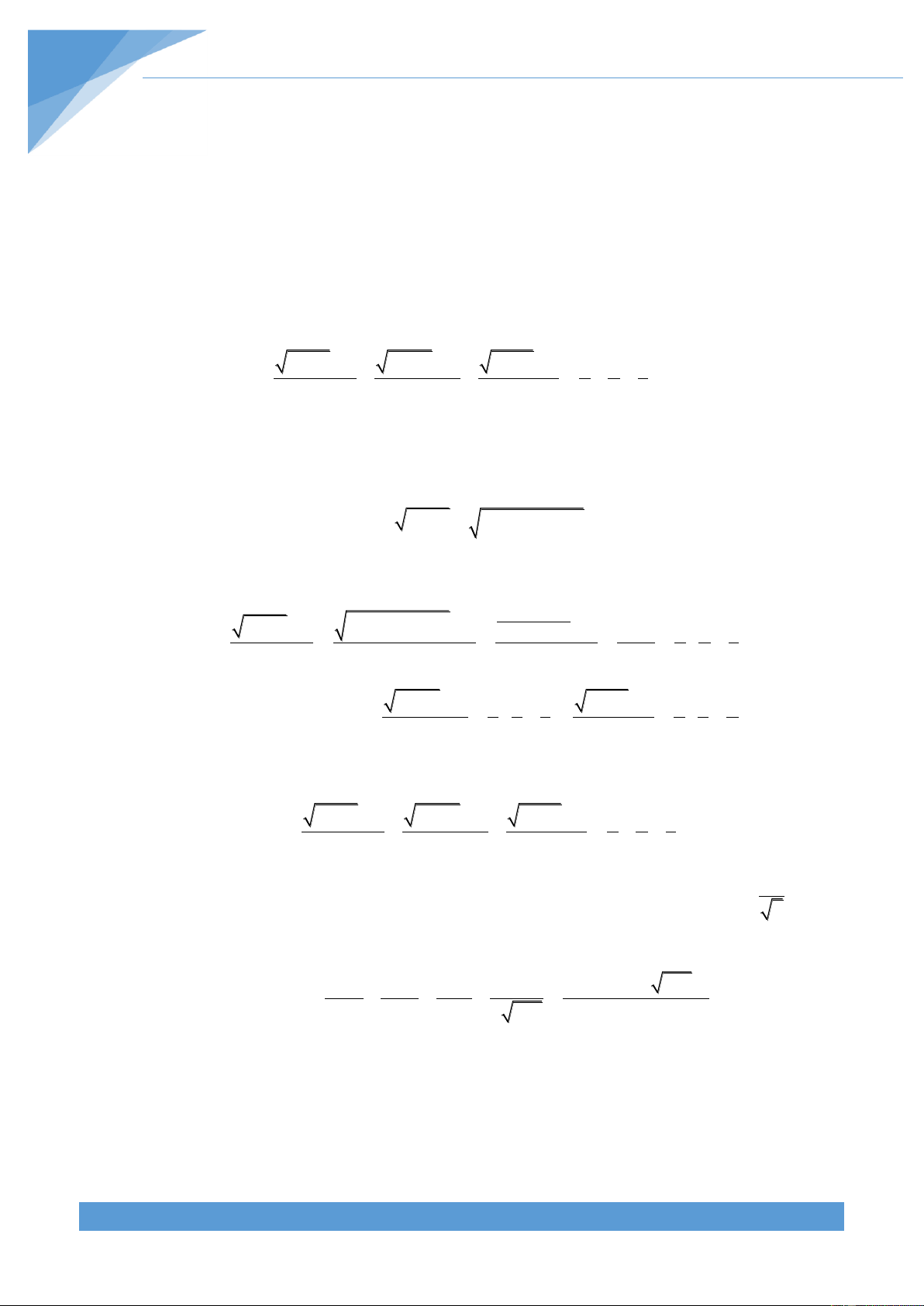
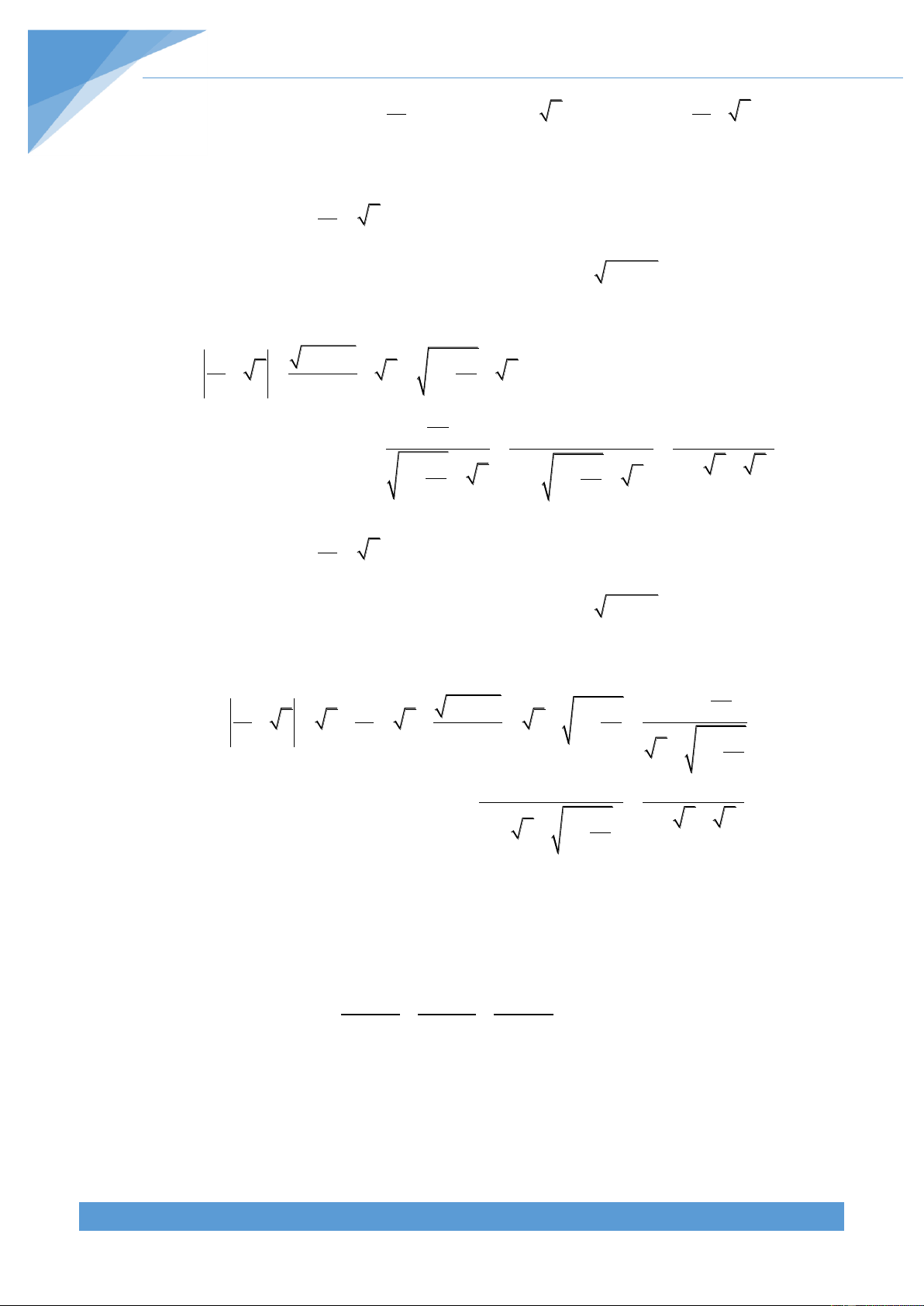
Preview text:

1
ĐÁP ÁN CÁC BÀI TOÁN BẤT ĐẲNG THỨC, CỰC TRỊ
TRONG ĐỀ CHUYÊN MÔN TOÁN GIAI ĐOẠN 2009-2019 NĂM HỌC 2019-2020
Câu 1: [TS10 Chuyên KHTN Hà Nội, 2019-2020]
Cho x, y là các số thực dương thỏa mãn: 2 2
4x  4y  17xy  5x  5y  1
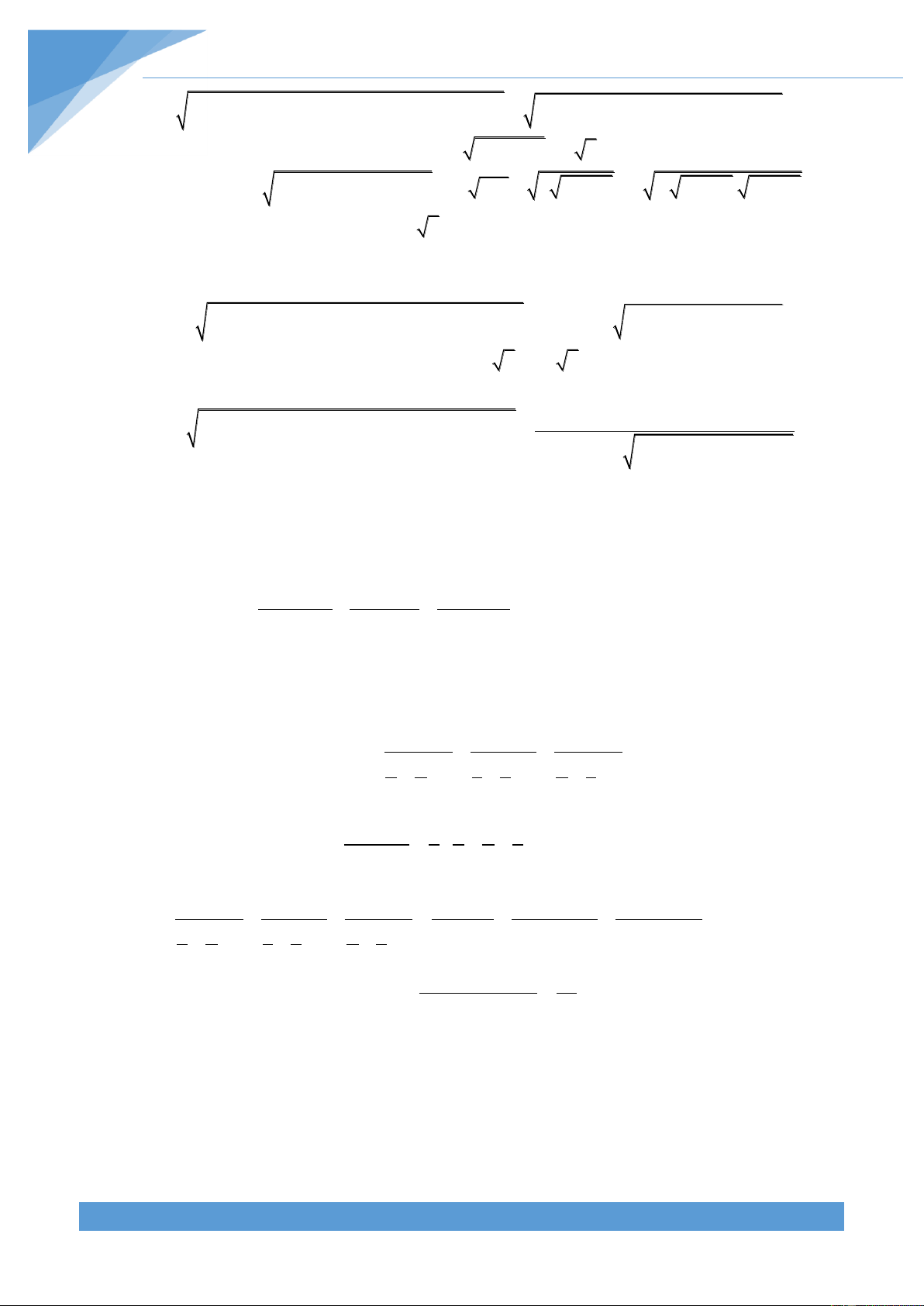
Tìm giá trị nhỏ nhất của biểu thức: 2 2 P  17x  17y  16xy Lời giải 2 Ta có: 2 2
4x  4y  17xy  5x  5y  1  4x  y  9xy  5x  y  1
Đặt t  x  y, t  0 , theo bất đẳng thức AM-GM, ta có:   2 2 x y t 9 2 2  2 2 2  2 xy   . Do đó: 2 2
4t  t  5t  1  t  hay x  y  . 4 4 4 5 5 Ta có:       2 2 2 P 17x 17y 16xy 17 x y 18xy 2 2         2 x y 25     2 25 2 2 2 17 x y 18 x y     6  4 2 4 4 4  5    2  1
Dấu “=” xảy ra khi x  y  5
Vậy giá trị nhỏ nhất của P là 6  4 2 Câu 2:
[TS10 Chuyên Sư Phạm Hà Nội, 2019-2020]
Cho các số thực x, y thay đổi, hãy tìm giá trị nhỏ nhất của biểu thức:       2 2
P xy x 2 y 6  13x  4y  26x  24y  46 Lời giải Ta có:
P  xy x  2y  6 2 2
 13x  4y  26x  24y  46   2 x  2x 2 y  6y  13 2 x  2x  4 2 y  6y  46 x 2 1
1 y 32 9 13 x 12 1 4 y 32 9             46        
Đặt a  x 1, b  y  3 , khi đó: P   2 a   1  2 b  9  13 2 a  1  4 2 b  9  46 2 2 2 2 2 2
 a b  9a  b  9 13a 13  4b  36  46
THCS.TOANMATH.com FB TRỊNH BÌNH 2 2 2 2 2  4a  3b  a b  6  6 a  0 x 1  0 Dấu “=” xảy ra khi     x  1,y  3  b  0 y  3    0
Vậy giá trị nhỏ nhất của P là 6. Câu 3:
[TS10 Chuyên Tin Hà Nội, 2019-2020]
Cho a, b, c dương thỏa mãn: ab  bc  ca  abc  4 1 1 1 1) Chứng minh rằng:    1 a  2 b  2 c  2 1 1 1
2) Tìm giá trị nhỏ nhất: P    2 . 2 2 a  b   4 2  2 2 b  c   4 2  2 2 c  a   4 Lời giải 1) Ta có: 1 1 1    1 a  2 b  2 c  2
 b  2c  2  a  2c  2  b  2a  2  a  2b  2c  2
 ab  bc  ca  4a  b  c 12  abc  2ab  bc  ca 4a  b  c 8  4  ab  bc  ca.
Đẳng thức cuối cùng đúng theo giả thiết, các phép biến đổi l| tương đương,
do đó đẳng thức đã cho được chứng minh.
2) Với x, y dương ta có bất đẳng thức:     2 2 2 2 x y x y (*) 1 1  1 1      (**) x  y 4  x y  Thật vậy:      2 * x y  0 (luôn đúng)   x y 1 * *  
 x  y2  4xy  x  y2  0 4xy x  (luôn đúng) y
Các bất đẳng thức (*), (**) xảy ra dấu “=” khi x = y.
Lần lượt áp dụng (*) và (**) ta có: 1 1 1 1  1 1         2 2   a  b  4  a2b2 2 a b 4  4 a2 b2  Tương tự: 1 1  1 1  1 1  1 1     ;      ; 2 2   4   b  2 c  2   2 2   4   c  2 a  2 2 b c 4 2 c a 4  Cộng theo vế ta được:
THCS.TOANMATH.com FB TRỊNH BÌNH 3 1  1 1 1  1 1 P     .1    .
2  a  2 b  2 c  2  2 2
D}u “=” xảy ra khi a = b = c 1
Vậy giá trị nhỏ nhất của P là 2 Câu 4:
[TS10 Chuyên Toán Hà Nội, 2019-2020]
Cho K  ab  4ac  4bc với a,b,c  0 và a + b + 2c = 1. 1
1) Chứng minh rằng: K  2
2) Tìm giá trị lớn nhất của K. Lời giải
1) Sử dụng bất đẳng thức AM-GM ta có: 2 2  b  2c   a  b  2c  1 1 4bc  2  2   4  bc        2   2  2 2 1
Mặt khác: a, b,c  0  K  ab  4ac  4bc  4  bc   2 1 1
Dấu “=” xảy ra khi a  0, b  ,c  . 2 4 Cách khác: Ta có:
K  ab  4c a  b  ab  21 a  ba  b
 ab  2a  b  2 2 2 a  b  2  2b  a  2 2 b  2a  2a Do đó: 2     2 2b
a 2 b  2a  2a  K  0 *
Để tồn tại K thì phương trình (*) Phải có 2 nghiệm:
   0  a  22  4.2. 2 2a  2a  K  0 2  8K  20a 17a  4.
Vì a, b,c  0 và a  b  2c  1  0  a  1 . Do đó: 2
2a 17a  a 20 17a  a20 17.  1  3a  0 1 Do đó 8K  4   K   2 1 1
Dấu “=” xảy ra khi a  0, b  ,c  . 2 4
2) Sử dụng bất đẳng thức AM-GM ta có: 2
   a b2c  1 a b 2c     .  2  4
THCS.TOANMATH.com FB TRỊNH BÌNH 4 Mặt khác:                 2 a b 2c 1 a, b,c 0
K ab 4ac 4bc ab 4ac 2ab 4ac 2a b 2c   . 2 2 Dấu “=” xảy ra khi: 1 1
a  b  2c,a  b  2c  1, bc  0,ab  0  a  , b  0,c  2 4 1
Vậy giá trị lớn nhất của K là 2 Câu 5:
[TS10 Chuyên Thái Bình, 2019-2020]  1  0  a, b,c 
Cho các số thực a, b, c thỏa mãn 
2 . Tìm giá trị nhỏ nhất của biểu 2a  3b  4c   3 2 9 8 thức P   
a 3b  4c  2 b 4a  8c  3 c 2a  3b 1 Lời giải Ta có: 2 9 8 P   
a 3b  4c  2 b4a  8c  3 c 2a  3b 1 2 9 8   
a 3  2a  2 b6  6b  3 c 3  4c 1 2 3 4   
a 1 2a b1 2b c 1  2c 2 2a 3b 4c    2 a 1 2a 2
b 1 2b c 1 2c2 2
Áp dụng bất đẳng thức AM-GM ta có: 2      2    a a 1 2a 1 a 1 2a      3  27 1 1 Tương tự: 2 b 1 2b  ; 2 c 1 2c  27 27
Suy ra: P  27 2a  3b  4c  81 1
Dấu “=” xảy ra khi a  b  c  3
Vậy giá trị nhỏ nhất của P là 81. Câu 6:
[TS10 Chuyên Hòa Bình, 2019-2020]
Cho hai số dương a, b thỏa mãn: a + b = 4ab. Chứng minh rằng: a b 1   2 2 4b  1 4a  1 2 Lời giải
THCS.TOANMATH.com FB TRỊNH BÌNH 5 Ta có:      2 a b 4ab a b
 a  ba  b1  0  a  b 1    a b  0 Lại có: 2 2 a 4ab 4ab  a   a   a ab 2 2 4b  1 4b  1 4b 2 2 b 4a b 4a b  b   b   a ab 2 2 4a  1 4a  1 4a a b a  b 1 1 Do đó: 
 a  b  2ab  a  b   a  b  2 2       4b  1 4a  1 2 2 2 1
Dấu “=” xảy ra khi a  b  2 Câu 7:
[TS10 Chuyên Hưng Yên, 2019-2020]
Cho các số thực không âm x, y, z thỏa mãn: 2 2 2 x  y  z  3y
Tìm giá trị nhỏ nhất của biểu thức: 1 4 8 P    x 2 1 y22 z32 Lời giải
Sử dụng bất đẳng thức Cauchy-Schwarz ta có: 2 1 1 1  1 1  8       (*) 2 2 a b 2  a b  a b2
Áp dụng bất đẳng thức (*) ta được: 1 1 8 8 8 64 P       x1 . 2 2  y  z32 2  y  z32 2  y   1 x   2 x   z       5  2   2   2  Mặt khác:  
x  z  2x  z   23y  y  2 2 3y y 2 2 2  . 2 64 64 P    1 2 2  1   1  6  2y  y 8   y   22 2   2   2 
Dấu “=” xẩy ra khi x, y,z  1,2,  1 .
Vậy giá trị nhỏ nhất của P là 1. Câu 8:
[TS10 Chuyên Hà Nam, 2019-2020] 1 1 1
Cho các số thực dương a, b, c thỏa mãn:    1. Tìm giá trị nhỏ a  1 b  1 c  1 3 3 3 a b c
nhất của biểu thức: P    2 2 2 2 2 2 a  ab  b b  bc  c c  ca  a
THCS.TOANMATH.com FB TRỊNH BÌNH 6 Lời giải
Ta dễ dàng chứng minh bất đẳng thức: 1 1 1 9    (với x, y,z  0 ) (*) x y z x  y  z   Thật vậy:      1 1 1 (*) a b c      9  a b c 
Áp dụng AM – GM ta được:     1 1 1 3 3 a b c    3 abc.    9 3  a b c  abc
Vậy bất đẳng thức (*) được chứng minh, dấu “=” xảy ra khi x = y = z.
Sử dụng bất đẳng thức (*) ta được: 1 1 1 9 1    
 a  b  c  3  9  a  b  c  6 a  1 b  1 c  1 a  b  c  3 3 3 3 b c a Đặt Q    2 2 2 2 2 2 a  ab  b b  bc  c c  ca  a Ta có: 3 3 3 3 3 3 a  b b  c c  a P  Q    2 2 2 2 2 2 a  ab  b b  bc  c c  ca  a a  b 2 2
a  ab  b  b  c 2 2
b  bc  c  c  a 2 2 c  ca  a     2 2 2 2 2 2 a  ab  b b  bc  c c  ca  a
 a  b  b  c  c a  0 Do đó: P = Q 1 Mặt khác: 2 2 x  xy  y   2 2 x  xy  y  * * 3 Thật vậy: 1
x  xy  y  x  xy  y   3x  3xy  3y  x  xy  y  2x  y2 2 2 2 2 2 2 2 2  0 3 Sử dụng (**) ta được: 3 3 3 3 3 3 a  b b  c c  a P  Q    2 2 2 2 2 2 a  ab  b b  bc  c c  ca  a a  b 2 2
a  ab  b  b  c 2 2
b  bc  c  c  a 2 2 c  ca  a     2 2 2 2 2 2 a  ab  b b  bc  c c  ca  a 1     1     1 a b b c  c  a 3 3 3 2      2 a b c  .6  4 3 3 Mà P  Q  P  2
Dấu “=” xảy ra khi a = b = c = 2
THCS.TOANMATH.com FB TRỊNH BÌNH 7
Vậy giá trị nhỏ nhất của P là 2. Câu 9:
[TS10 Chuyên Phan Bội Châu, 2019-2020]
Cho các số dương a, b, c dương thỏa mãn abc  a  b  c  2 . Tìm giá trị lớn nhất 1 1 1 của biểu thức P    2 2 2 2 2 2 a  b b  c c  a Lời giải.
Từ abc  a  b  c  2
 a  bb 1c 1  a 1b 1  b 1c 1  c 1a 1 1 1 1     1 a  1 b  1 c  1 1 1 1  x,y,z  0 Đặt  x,  y,  z   a  1 b  1 c  1 x  y  z  1. 1 x y  z z  x x  y Khi đó: a   ; b  ; c  x x y z 1 1 1 1  1 1 1  Nên P         2 2 2 2 2 2 a  b b  c c  a 2  ab bc ca  1  x y y z z x    .  .  .          2 y z z x z x x y x y y z   1  y x z y x z    .  .  .          2 y z z x z x x y x y y z   1  y x   z y   x z             
2 2  y  z z  x   z  x x  y   x  y y  z  1  x y   y z   z x  3 2             
2 2  x  y x  y   y  z y  z   z  x z  x  4 
Dấu “=” xảy ra khi x  y  z hay a  b  c 3 2
Vậy giá trị lớn nhất của biểu thức P là khi a = b = c = 2. 4
Câu 10: [TS10 Chuyên Vĩnh Phúc, 2019-2020]
Cho x, y, z là các số thực dương thỏa mãn  2 2 2
5 x  y  z   9xy  z 18yz  0. 2x  y  z
Tìm giá trị lớn nhất của biểu thức: Q  . y  z Lời giải Ta có: 5 2 2 2
x  y  z   9xy  z 18yz  0
 5x  9xy  z  5y  z2 2  28yz  0
THCS.TOANMATH.com FB TRỊNH BÌNH 8
 5x  9xy  z  5y  z2  7.4yz  7 y  z2 2
 5x  9xy  z  2y  z2 2  0 2  x  x  5   9.  2  0 y  z y    z x Đặt: t  t  0 khi đó: y  z 2
5t  9t  2  0  5t  1t  2  0  t  2 do 5t 1 0 x   2 y  z 2x  y  z x Ta có: Q   2. 1  2.2 1  3 y  z y  z x
Dấu “=” xảy ra khi y  z  . 4
Vậy giá trị lớn nhất của Q là 3.
Câu 11: [TS10 Chuyên Bắc Ninh, 2019-2020]
Cho x, y, z không âm thỏa mãn x  y  z  3. Tìm GTLN. GTNN của biểu thức 2 2 2
M  x  6x  25  y  6y  25  z  6z  25 Lời giải Ta có: 2 2 2
M  x  6x  25  y  6y  25  z  6z  25
 3  x2 16  3  y2 16  3  z2 16  a  b  c  6
Đặt a  3  x, b  3  y,c  3  z, Khi đó: 0  a,b,c   3 2 2 2
M  a  16  b  16  c  16 Tìm GTNN:
Theo bất đẳng thức Minkowski ta có:      
    2     2 2 2 2 M a 16 b 16 c 16 a b c 4 4 4  6 5
Đẳng thức xảy ra khi a = b = c = 2 Tìm GTLN 
Sử dụng phương ph{p UCT với điều kiện 0  a  3 ta được 2 a 12 a  16  * 3 Thật vậy:
       2 2 2 * 9 a 16 a 12
 8a  24a  0  aa 3  0 (đúng)
THCS.TOANMATH.com FB TRỊNH BÌNH 9
Ho|n to|n tương tự và suy ra: M  14
Đẳng thức xảy ra khi a, b,c  0,3,3 và các hóa vị.
Câu 12: [TS10 Chuyên KHTN, 2019-2020]
Cho x, y,z là các số dương thỏa mãn xy  yz  zx  1 . Chứng minh rằng: 3   1 1 1 2 x y z        (1) 2 2 2     2 2 2 1 x 1 y 1 z 3 1 x 1  y 1  z    Lời giải Ta có: 2 2
1 x  xy  yz  zx  x  x  yx  z Tương tự: 2        2 1 y
x y y z ; 1 z  x  zy  z Do đó: 1 1 1 2x  y  z  VT      1
x yxz x yyz xzzy xyyzzx
Áp dụng bất đẳng thức Cauchy-Schwarz, ta có: 2   x y z        x y z    x y z     2 2 2  2 2 2      1 x 1  y 1  z 1 x 1 y 1 z        x y z   x y z    
x  yy  z x  yy  z x  zz   y
2 x  y  zxy  yz  zx 
x yyzzx 2 x  y  z
       . x y y z z x Suy ra: 4x y z     x y z V       P  . 1
3x  yy  zz  x  2 2 2 1 x 1 y 1 z   
Như thế để chứng minh bất đẳng thức đã cho ta chỉ cần chứng minh: x y z 3    2 2 2 2    2 1 x 1 y 1 z
Sử dụng bất đẳng thức AM-GM ta có: x x 1  x x       2 1 x
     2 x y xz x y x z  y 1  y y  z 1  z z  Tương tự:    ;     2 2 2  x  y y  z  2  z  x y    z 1 y 1 z 
THCS.TOANMATH.com FB TRỊNH BÌNH 10
Cộng theo vế 3 bất đẳnng thức trên ta được bất đẳng thức (2). B|i to{n được chứng minh. 1
Dấu “=” xảy ra khi x  y  z  3 Câu 13:
[TS10 Chuyên TP. Hồ Chí Minh, 2019-2020]
Cho x, y, z là các số thực thuộc đoạn 0; 2 
 thỏa mãn điều kiện: x  y  z  3. a) Chứng minh rằng: 2 2 2 x  y  z  6
b) Tìm giá trị lớn nhất của biểu thức: 3 3 3 P  x  y  z  3xyz Lời giải a) Ta có:
2x2y2z  0  84x yz2xy yzzxxyz  0 2 2 2 2 2 2
 x  y  z  x  y  z  8  4x  y  z  2xy  yz  zx xyz
 x  y  z2  4x  y  z  8  xyz
 9  4.3  8  xyz  5  xyz  5  6 b) Ta có: 3 3 3
P  x  y  z  3xyz  x  y  z 2 2 2
x  y  z  xy  yz  zx  3     2 2 2    1 3 x y z   2 2 2
x  y  z  2xy  yz  zx 2 2  3 3  x y z  x y z2 2 2 2        2   3  3.5  9   2  9
Dấu “=” xảy ra khi x, y,z  2,1,0 và các hoán vị.
Câu 14: [TS10 Chuyên Hòa Bình, 2019-2020]
Cho x, y, z là các số thực dương thỏa mãn: xy  yz  4zx  32
Tìm giá trị nhỏ nhất của biểu thức: 2 2 2 P  x  16y  16z Lời giải.
Áp dụng bất đẳng thức AM-GM ta có: 2 x 2  8y  4xy 2 2 x 2  8z  4xz 2 2 2 8y  8z  16yz Cộng theo vế ta được: 2 2 2
P  x  16y  16z  4xy  xz  4yz  128
THCS.TOANMATH.com FB TRỊNH BÌNH 11 8 6 2 6
Dấu “=” xảy ra khi x = 4y = 4z , thay v| điều kiện ta được: x  ; y  z  3 3
Câu 15: [TS10 Chuyên Quốc Học Huế, 2019-2020]
Cho ba số dương x, y, z thỏa mãn xyz = 2. Chứng minh rằng: x 2y 4z 1    2 2 2 2 2 2 2x  y  5 6y  z  6 3z  4x  16 2 Lời giải Ta có: +) 2 2 2 2 2
2x  y  5  x  y  x 1 4  2xy  2x  4 x x x    2 2 2x  y  5 2xy  2x  4 2xy  x  2 2 2 2 2 2
) 6y  z  6  4y  z  2y  2  4  4yz  4y  4 2y 2y y    2 2 6y  z  6 4yz  4y  4 2 yz  y  1 Do đó: x y z VT   
2 xy  x  2 2yz  y  1 zx  2z  2 x y yz   
2 xy  x  xyz 2yz  y  1 xyz  2yz  2y 1 y yz   
2 yz  y  1 2yz  y  1 2 yz  y  1 yz  y  1  2yzy1 1  2
Dấu “=” xảy ra x = y = 1, z = 2.
Câu 16: [TS10 Chuyên Tin Hòa Bình, 2019-2020]
Cho các số thực dương x, y thỏa mãn: x  y  1.  1 1 
Tìm giá trị nhỏ nhất của biểu thức: 2 2 P     1 x y  x y  Lời giải Theo AM-GM ta có: 1 1 1
1  x  y  2 xy  xy   xy    4 2 4 xy Do đó:
THCS.TOANMATH.com FB TRỊNH BÌNH 12  1 1  2 2 2 2 2 1 P     1 x y  1 x y  2  xy  x y  xy xy Suy ra: 1 1 15 1 15 P  2  xy  2  xy   2 2 .xy  xy 16xy 16xy 16xy 16xy 1 15  P  2  .4  17 2 16 1
Dấu “=” xảy ra khi x  y  2
Vậy giá trị nhỏ nhất của P là 17
Câu 17: [TS10 Chuyên Tiền Giang, 2019-2020] 2
Cho hai số dương x, y thỏa mãn  3 3
2 x  y   6xyx  y  2  x  y xy  4 1  x y 
Tìm giá trị nhỏ nhất của biểu thức: T     1 2  y x  Lời giải Ta có:
2x  y   6xyx  y  2  x  y2 3 3 xy4
 2x  y3 12xy  x  y2 xy  4
Đặt a  x  y, b  xy a, b  0 khi đó: 3 2        2   3 2 2a 12b a b 4 b a 12  2a  4a Do VT > 0 nên 3 2 2
2a  4a  0  2a a  2  0  a  2 Ta có: 2 2 2 2 4 2 1  x y
 1  x  y  xy  1  a  a 1 a  12a 1 T     1      1     3 2 2 y x 2  xy  2 b 2b 2 4a      8a 2 5 Ta sẽ chứng minh: T  2 5 a  12a a62 2 4 2 a Thật vậy: T    3   0 (luôn đúng a   2 ) 3 2 2 2 4a  8a 4a a  2
Dấu “=” xảy ra khi a = 6, b = 6
hay x  3  3, y  3  3 hoặc x  3  3, y  3  3 5
Vậy giá trị nhỏ nhất của T là 2
Câu 18: [TS10 Chuyên Bà Rịa Vũng T|u, 2019-2020]
Cho các số thực dương x, y. Tìm gi{ trị nhỏ nhất của biểu thức:
THCS.TOANMATH.com FB TRỊNH BÌNH 13 2 2 x y xy P    2  2 2 y x x  y Lời giải Ta có: 2 2 4 2 2 4 x y xy x  2x y  y xy P    2    2 2 2 2 y x x  y x y x  y 2 2 2 2 2  x  y  xy x  y xy       xy x  y xy x    y  x  y  xy x y2 2 2 xy  P    2   2    2 xy x  y xy x    y xy xy 1 1 1 Đặt t 
.Theo AM – GM thì: x  y  2 xy    t    2 x  y x  y 2 2 t Khi đó: 1  t t 1  15 P   t  2        2 2 2 2 t  2 2 16t  16t t t 1 15 2  3 3 . .  .2  2 2 2 2 16t 16 1 15  3.   2 4 4 5  2
Dấu “=” xảy ra khi x = y 5
Vậy giá trị nhỏ nhất của P là 2
Câu 19: [TS10 Chuyên KHTN Hà Nội, 2019-2020]
Với x, y là các số thực thỏa mãn 1  y  2 và xy  2  2y . Tìm giá trị nhỏ nhất của 2 x  4 biểu thức M  2 y  1 Lời giải.
Theo giải thiết ta có: 4xy  8  8y.
Sử dụng bất đẳng thức AM – GM ta có: 2 2 4x  y  4xy. Suy ra: 2 2
4x  y  8  4xy  8  8y. Do đó:  2   2   
  2         2 4 x 4 8 8y y 4 y 1 5y 2 2 y 4 y   1 . 2 x  4 Suy ra: 2 2 x  4  y  1  M   1 2 y  1
Dấu “=” xảy ra khi x = 2, y = 1.
THCS.TOANMATH.com FB TRỊNH BÌNH 14
Vậy giá trị nhỏ nhất của M là 1.
Câu 20: [TS10 Chuyên Hưng Yên, 2019-2020]
Với x, y là cá số thực thỏa mãn      9
2 x y 1  . Tìm giá trị nhỏ nhất của biểu 4 thức: 4 3 2 4 3 2
A  x  4x  6x  4x  2  y  8y  24y  32y  17. Lời giải Ta có: 4 3 2 4 3 2
A  x  4x  6x  4x  2  y  8y  24y  32y  17  1 x  4 1  1 y  24
Đặt a  x  1, b  y  2 , ta được 4 4 A 1 a  1 b
Từ giả thiết ta được:      9 5 a 1 b 1   a  b  ab  4 4 Theo AM – GM ta có: 2 4a 1  4a 2 2 1 
 a  b  a  b  (1) 2 4b 1  4b 2 2 2 1 a  b  2ab   2 2 a  b   ab 2 2
Cộng theo vế (1) v| (2) ta được: 3  2 2   1 5 1 3 2 2 1 a b  a  b  ab      a  b  2 2 4 2 4 2
Áp dụng bất đẳng thức Minicopski ta được:
A 1  a  1  b  1 12 4 4   2 2 a  b 2   2 2 a  b 2  4 2  1  17   4     2  2 1 1 5
Dấu “=” xảy ra khi a  b   x   ,y  . 2 2 2 17
Vậy giá trị nhỏ nhất của A là 2
Câu 21: [TS10 Chuyên Bình Thuận, 2019-2020] 1
Cho các số dương x, y, z thỏa xyz  . Chứng minh rằng: 2 yz zx xy    xy  yz  zx. 2 x y  z 2 y z  x 2 z x  y
Dấu “=” xảy ra khi nào: Lời giải Ta có:
THCS.TOANMATH.com FB TRỊNH BÌNH 15 yz zx xy    xy  yz  zx 2 x y  z 2 y z  x 2 z x  y 1 1 1 2 2 2 y 1  1 1 1  x z         1 1 1 1 1 1 2  x y z     y z x z x y 1 1 1 Đặt a  , b  ,c   abc  2 x y z
Khi đó ta cần chứng minh: 2 2 2 a b c a  b  c    b  c a  c a  b 2
Thật vậy, sử dụng bất đẳng thức Cauchy-Schwarz ta được: a b c    2 2 2 2 a b c a  b  c VT          (đpcm) 2a  b  c VP b c a c a b 2
Dấu “=” xảy ra khi x = y = z.
Câu 22: [TS10 Chuyên Hải Phòng, 2019-2020]
Cho x; y; z là ba số thực dương thỏa mãn x(x  z)  y(y  z)  0. Tìm giá trị nhỏ 3 3 2 2 x y x  y  4
nhất của biểu thức P    2 2 2 2 x  z y  z x  y Lời giải 3 2 2 x xz xz z
Áp dụng bất đẳng thức Côsi  x   x   x  . 2 2 2 2 x  z x  z 2xz 2 3 y z 2 2 x  y  4 Tương tự
 y  . Suy ra P  x  y  z  . 2 2 y  z 2 x  y 2 2 x  y 4 Theo gt z   P  x  y   4 . x  y x  y Vậy P
 4  x  y  z  1. min
Câu 23: [TS10 Chuyên Quảng Nam, 2019-2020]
Cho ba số thực dương a, b, c thỏa mãn abc = 1. Tìm giá trị nhỏ nhất của biểu
  2     2     2 2 2 2 1 a b 5 1 b c 5 1 c  a  5 thức: P    ab  a  4 bc  b  4 ca  c  4 Lời giải Ta có:   2 2 2 2 1 a  b  5 a  b  2a  6 2ab  2a  6 2 ab  a  4  2 2     2  ab  a  4 ab  a  4 ab  a  4 ab  a  4 ab  a  4
THCS.TOANMATH.com FB TRỊNH BÌNH 16   2   2   2 2 2 1 b c 5 1 c  a  5 2 Tương tự:  2  ;  2  bc  b  4 bc  b  4 ca  c  4 ca  c  4  1 1 1  Do đó: P  6  2    6    2Q
 ab  a  4 bc  4  4 ca  c  4  Với x, y dương ta có:       2     2 1 x y 1 1 1 1 x y 0 x y  4xy        (*) x  y 4xy x  y 4  x y 
Dấu “=” xảy ra khi x = y. 1 1 1  1 1  Áp dụng (*) ta được:         ab  a   . ab a 4 1  3 4  ab  a  1 3  1 1  1 1  1 1  1 1  Tương tự:   ;       bc  b  4
4  bc  b  1 3  ca  c  4 4  ca  c  1 3  Do đó: 1  1 1 1  1  1 1 1  Q     1  2Q        1
4  ab  a  1 bc  b  1 ca  c  1 
2  ab  a  1 bc  b  1 ca  c  1  1  1 1 1   P  6      1
2  ab  a  1 bc  b  1 ca  c  1  1  c ac 1   6      1
2  abc  ac  c bc.ac  abc  1 ca  c  1  1  c ac 1   6      1
2  ca  c  1 ca  c  1 ca  c  1  1  6  .2 2  5
Dấu “=” xảy ra khi a = b = c = 1.
Vậy giá trị nhỏ nhất của P là 5.
Câu 24: [TS10 Chuyên Lai Châu, 2019-2020]
Cho các số thực dương a, b, c. Chứng minh rằng: ab bc ca 1    a  b  c a  b  2c b  c  2a c  a  2b 4 Lời giải Với x, y dương ta có:       2     2 1 x y 1 1 1 1 x y 0 x y  4xy        (*) x  y 4xy x  y 4  x y 
Dấu “=” xảy ra khi x = y. ab ab ab  1 1  Sử dụng (*) ta được:      a  b  2c
acbc 4 ac bc 
THCS.TOANMATH.com FB TRỊNH BÌNH 17 bc bc  1 1  ca ca  1 1  Tương tự:   ;       b  c  2a
4  b  a a  c  c  a  2b 4  c  b b  a 
Cộng 3 bất đẳng thức trên theo vế ta được: ab bc ca   a  b  2c b  c  2a c  a  2b ab  1 1  bc  1 1  ca  1 1              4  a  c b  c  4  b  a a  c  4  c  b b  a  1  ab  bc ab  ca bc  ca       4  c  a b  c a  b 
1  b a  c a b  c c a  b      4 a  c b  c a   b   1
 a  b  c dpcm 4
Đẳng thức xảy ra khi a = b = c
Câu 25: [TS10 Chuyên Vĩnh Phúc, 2019-2020]
Cho các số dương a, b, c thỏa mãn: abc  1. Chứng minh rằng: a b c 3       2 b ac c ab a bc Lời giải Ta có: a  c a  2b  c a  2b  c b  ac  b    b  ac  2 2 2 1 2 a a 2 2 2a 4 2a        a  2b  c  a  2b  c      b ac b ac 4 a 2b c a 2b c 4 Mặt khác: 3 4          4 2a 12 2a a b c 3 abc 3 a b c  4   3 a  2b  c  4 7a  10b  7c  a b c  VT  12 2    
 7a  10b  7c 7b  10c  7a 10a  7b  7c  Do đó: a bc2  12 2 7 2 2 2
a  b  c   17 ab  bc  ca Mặt khác:
a  b  c  ab  bc  ca  7 a  b  c   17 ab  bc  ca  8a  b  c2 2 2 2 2 2 2 12 2 a  b  c2 12 2 a  b  c2 3    7  dpcm 2 2 2
a  b  c   17 ab  bc  ca 2   8 a  b  c 2
Dấu “=” xảy ra khi a = b = c = 1.
THCS.TOANMATH.com FB TRỊNH BÌNH 18
Câu 26: [TS10 Chuyên Tuyên Quang, 2019-2020]
Cho các số dương a, b, c thỏa mãn a  b  c  4 .Tìm giá trị nhỏ nhất của biểu a a b b c c thức: P    . a  3 b b  3 c c  3 a Lời giải Ta có: a a b b c c P    a  3 b b  3 c c  3 a 2 2 2 a b c    a  3 ab b  3 bc c  3 ac
Áp dụng bất đẳng thức Cauchy-Schwarz ta được: 2 2 2 a b c P    a  3 ab b  3 bc c  3 ac a  bc2 
a  b  c  3 ab  bc  ca  a  b b  c c  a
Mặt khác theo AM-GM: ab  bc  ca     a  b  c 2 2 2    2 a b c a  b  c Do đó: P   
a  b  c  3a  b  c 1 4 4
Dấu “=” xảy ra khi a  b  c  3
Vậy giá trị nhỏ nhất của P là 1.
Câu 27: [TS10 Chuyên Hà Nam, 2019-2020] a b c a  b  c
Cho các số dương a, b, c. Chứng minh:     4 . 2 2 2 b c a 3. a  b  c Lời giải
Áp dụng bất đẳng thức Cauchy-Schwarz ta được: a b c a  b  c a  bc2 2 2 2 ab  bc  ca VT       2 2 2 2 2 2 ab bc ca ab  bc    ca 3. a b c a  b  c 2 2 2 a  b  c ab  bc  ca   2  2 2 2 ab  bc  ca a  b  c 2 2 2 2 2 2  a  b  c 1 ab  bc  ca 1 ab  bc  ca  a  b  c         2  ab  bc  ca 2 2 2 2 2 2 2 2 a  b  c 2 a  b  c  2  ab bcca
THCS.TOANMATH.com FB TRỊNH BÌNH 19
Áp dụng bất đẳng thức AM-GM cho 3 số ta được: 2 2 2 a  b  c
1 ab  bc  ca 1 ab  bc  ca 1 VT  33   2 ab  bc  ca . . 2 2 2 2 2 2 2 2 a  b  c 2 a  b  c 2 3 1    2  4 dpcm 2 2
Đẳng thức xảy ra khi a = b = c.
Câu 28: [TS10 Chuyên Phú Yên, 2019-2020]
Cho a, b, c là các số thực dương thỏa mãn ab  bc  ca  1. Chứng minh rằng: 2 2 2
a b  1  b c  1  c a 1  2
Dấu “=” xảy ra khi nào? Lời giải
Sử dụng bất đẳng thức Minicopski ta được:
a b  1  b c  1  c a  1  ab2  a  bc2  b  ca2 2 2 2 2 2 2  c
 ab  bc  ca2  a  b  c2  ab  bc  ca2  3ab  bc  ca  1 3  2 dpcm 1
Dấu “=” xảy ra khi a  b  c  3
Câu 29: [TS10 Chuyên Cao Bằng, 2019-2020]
Cho a, b, c là các số dương thỏa mãn điều kiện a+ b + c = 3. Tìm giá trị nhỏ nhất a b c của biểu thức: R    2 2 2 1 b 1 c 1  a Lời giải
Áp dụng bất đẳng thức AM-GM ta được: 2 2 a ab ab ab  a   a   a  2 2 1 b 1 b 2b 2 b bc c ca Tương tự:  b  ;  c  2 2 1 c 2 1 a 2
Cộng theo vế 3 bất đẳng trên ta được: a b c ab  bc  ca R     a  b  c  2 2 2   1  b 1  c 1  a 2 2
     a  b  c 2 3 3 a b c   3   6 6 2 1
Dấu “=” xảy ra khi a  b  c  3 3
Vậy giá trị nhỏ nhất của R là 2 Câu 30:
[TS10 Chuyên Nam Định, 2019-2020]
THCS.TOANMATH.com FB TRỊNH BÌNH 20 3
Cho x, y, z là số thực không âm thỏa mãn điều kiện x  y  z  . Chứng minh 2
rằng: x  2xy  4xyz  2 Lời giải
Sử dụng bất đẳng thức AM-GM ta được:  1 
x  2xy  4xyz  x  x.4y z     2  2 2  1   3 1   x  x. y  z   x  x  x       2   2 2 
 x  x2  x2  x  2  x2  x2  2  x  2 2 1  x  2x  2
 x  2x 12  2 3 Do x  y  z 
 0  x  2  x  2  0 . Vì thế: 2        2 x 2xy 4xyz x 2 x 1  2  2 (đpcm) 1
Dấu “=” xảy ra khi x  1, y  , z  0 2 Câu 31:
[TS10 Chuyên Bình Định, 2019-2020]
Cho a, b, c là các số thực dương thỏa mãn a  bb  cc  a  8 . Tìm giá trị 1 1 1 1
nhỏ nhất của biểu thức: P    
3 abc a  2b b  2c c  2a Lời giải.
Trước hết ta chứng minh bất đẳng thức phụ sau:
       8
a b b c c a  a  b  cab  bc  ca 9
Thật vậy: a  bb  cc  a  a  b  cab  bc  ca abc Lại theo BĐT AM-GM ta có:
a b bc ca a bbcca abc  ab. bc. ca  . .  2 2 2 8
Suy ra: a  bb  cc  a  a  b  cab  bc  ca abc    
 a  b  cab  bc  ca a bb cc a  8 8
Suy ra đpcm: a  bb  cc  a  a  b  cab  bc  ca 9 9
 ab  bc  ca  abc
Áp dụng bất đẳng thức AM-GM dạng cộng mẫu số ta có:
THCS.TOANMATH.com FB TRỊNH BÌNH 21 1 1 1 9 3 ab  bc  ca      a  2b b  2c c  2a
3a  b  c a  b  c 3 2 Lại có:       2 2 2 ab bc ca
3 ab c  a bc  abc   3abca  b  c 9 1 a  b  c 1 a  b  c   3abc a  b  c     2    2 2 a bc 3 abc 27 abc 3 1 1 1 1 a  b  c 3 Suy ra: P        2
3 abc a  2b b  2c c  2a 3 a  b  c
a  bbcca  8 
Dấu “=” xảy ra khi:  a  b  c  a  b  c  1  3 a  b  c    a  b  c 3
Vậy giá trị nhỏ nhất của P là 2 khi a = b = c = 1.
Câu 32: [TS10 Chuyên Bà Rịa Vũng T|u, 2019-2020] 1 1 1
Cho các số dương a, b, c thỏa mãn
   3 . Tìm giá trị nhỏ nhất của biểu a b c 1 1 1 thức: P    2 2 2 2 2 2 a  ab  3b  1 b  bc  3c  1 c  ca  3a  1 Lời giải Ta có: 2 2
a  ab  3b  1   2 2
a  2ab  b   ab   2 b  1 2  b
 a  b2 ab   2 b  1 2 2
 b  b  ab  2b  ba  b  2 2 2         1 1 a ab 3b 1 b a b 1   2 2 a  ab  3b  1 ba  b   1 1 1 1 1 Tương tự:  ;  2 2 b  bc  3c  1 c b  c  2 2 2 c  ac  3a  1 a c  a  2 Với x, y dương ta có:       2     2 1 x y 1 1 1 1 x y 0 x y  4xy        (*) x  y 4xy x  y 4  x y 
Dấu “=” xảy ra khi x = y.
Cộng theo vế và sử dụng bất đẳng thức AM-GM ta được:
THCS.TOANMATH.com FB TRỊNH BÌNH 22 1 1 1 P    b a  b  2 c b  c  2 a c  a  2 2 2 2    4b a  b  2 4c b  c  2 4a c  a  2 AMGM  1 1   1 1   1 1             
 4b a  b  2   4c b  c  2   4a c  a  2  1  1 1 1   1 1 1           
4  a b c   a  b  2 b  c  2 c  a  2 
Sử dụng bất đẳng thức (*) ta được: 1  1 1 1   1  1 1  1  1 1  1  1 1  P                  
4  a b c  4  a  b 2  4  b  c 2  4  c  a 2  3  1 1 1 1  1 1  1  1 1  1  1 1                  
4 8 8 8 16  a b  16  b c  16  c a  3  3 1  1 1 1          4 8 8  a b c  3 3 3 3     4 8 8 2
Dấu “=” xảy ra khi a = b = c = 1. 3
Vậy giá trị nhỏ là P là . 2 Câu 33:
[TS10 Chuyên Tây Ninh, 2019-2020] 3
Chứng minh a  b  c  9abc  4a  b  cab  bc  ca với x, y, z là các số thực
không }m. Đẳng thức xảy ra khi nào? Lời giải
Theo bất đẳng thức Schur với a, b, c là số thực không âm thì:
a a  ba  c  bb  cb a  cc ac  b  0
Biến đổi ta được hệ quả: 3 3 3 2        2     2 a b c 3abc a b c b c a  c a  b 3
Mặt kh{c ta có đẳng thức:     3 3 3 a b c
 a  b  c  3a  bb cc a 3
Khi đó ta có:     3 3 3
a b c  9abc  a  b  c  9abc  3a  bb  cc  a Do đó: 2     2     2 VT a b c
b c a  c a  b  9abc  3a  bb  cc  a Ta l| có 2 đẳng thức: 2     2     2 ) a b c
b c a  c a  b  9abc  a  b  cab  bc  ca
) abc  a  bb  cc a  a  b  cab  bc  ca
THCS.TOANMATH.com FB TRỊNH BÌNH 23 Do đó: 2    2     2 a b c
b c a  c a  b  9abc  3a  bb  cc  a  4a  b  cab  bc  ca
Vậy bất đẳng thức được chứng minh.
Dấu “=” xảy ra khi a = b = c.
Câu 34: [TS10 Chuyên Quảng Nam, 2019-2020]
Cho 3 số dương x, y, z. Tìm gi{ trị nhỏ nhất của biểu thức: xy yz zx P     2x  z2y  z
2yx2zx 2zy2xy Lời giải
Sử dụng bất đẳng thức Bunyakovski ta được:
                 2 2x z 2y z x x z y z y xy zx yz Do đó: xy xy xy xy     2x  z2y  z 2xz2yz    xy  yz  zx 2 xy yz zx yz yz zx zx Tương tự:       ;  2y x 2z x xy  zx  yz 2z y2x y xy  zx  yz xy  zx  yz
Cộng 3 bất đẳng thức trên theo vế ta được: P   1 xy  zx  yz
Đẳng thức xảy ra khi x = y = z.
Vậy giá trị lớn nhất của P là 1.
Câu 35: [TS10 Chuyên Bình Phước, 2019-2020]
1) Cho x, y là các số dương thỏa mãn xy  1. Chứng minh rằng: 1 1 2   1 x 1 y 1 xy
2) Cho x, y là các số thực dương thỏa mãn điều kiện:   3 x y  4xy  12 1 1
Tìm giá trị lớn nhất của biểu thức: P    2018xy 1 x 1  y Lời giải 1) Ta có:
THCS.TOANMATH.com FB TRỊNH BÌNH 24 1 1 2  1 1   1 1             0 1  x 1  y 1  xy
 1 x 1 xy   1 y 1 xy      1  xy  1  x 1  xy  1  y              0 1 x 1 xy 1 y 1 xy
 xy x1y xy y1x          0 1 x 1 y 1 xy
x  y  x 1 y  y  x  y 1 x          0 1 x 1 y 1 xy
 y  x x y x  y x y            0 1 x 1 y 1 xy
 y x x y xy y x                0 1 x 1 y 1 xy
 y x y x xy 1               0 1 x 1 y 1 xy   2 y x  xy 1      (đúng xy 1 ) (1)       0 1 x 1 y 1 xy
Dấu “=” xảy ra khi x = y = 1.
Bất đẳng thưc (1) đúng c{c phép biến đổi l| tương đương nên b|i to{n được chứng minh. 2) Sử dụng AM-GM ta có:        3 3 12 x y 4xy 2 xy  4xy  8xy xy  4xy
Đặt xy  t t  0 , khi đó: 3 2 3 2 3 2 2
8t  4t  12  0  2t  t  3  0  2t  2t  3t  3  0 2
 2t t 1  3t 1t 1  0  t 1 2 2t  3t  3  0  t  1
Áp dụng bất đẳng thức ở ý 1 ta có: 1 1 2 2 2 P    2018xy   2018xy   2018t 1 x 1 y 1 xy 1 t 2 Ta sẽ chứng minh: 2  2018t  2019 * 1 t Thật vậy:
THCS.TOANMATH.com FB TRỊNH BÌNH 25    2  * 
1  2018 2t 1    0  1 t  1  t 
 2018t 1t 1  0 1  t    1   1 t  2018t   1  
 0 (đúng do 0  t  1 )  1 t 
Dấu “=” xảy ra khi x = y = 1.
Vậy giá trị lớn nhất của P là 2019.
Câu 36: [TS10 Chuyên Đắc Lắc, 2019-2020]
Cho 3 số thực dương a, b, c thỏa mãn 2 2 2
a  b  c  3. Chứng minh rằng: 3 3 3 3 3 3 a  b b  c c  a    2 a  2b b  2c c  2a Lời giải.
Sử dụng bất đẳng thức Cauchy-Schwarz ta được: 3 3 3 4 4 4 a b c a b c )      2 2 2 a  2b b  2c c  2a a  2ab b  2bc c  2ca a b c 2 a b c 2 2 2 2 2 2 2   2 2 2 2 2 2
a  b  c  2ab  2bc  2ca a  b  c  2  2 2 2 a  b  c  2 2 2 a  b  c 3   3 2 3 3 3 4 4 4 b c a b c a )      2 2 2 a  2b b  2c c  2a ab  2b bc  2c ca  2a a b c 2 a b c 2 2 2 2 2 2 2   ab  bc  ca  2  2 2 2 a  b  c  2 2 2 a  b  c  2  2 2 2 a  b  c  2 2 2 a  b  c 3   3 2 3 3 3 3 3 3 a  b b  c c  a Cộng theo vế ta được:    2 a  2b b  2c c  (đpcm) 2a 2
Dấu “=” xảy ra khi a  b  c  3
Câu 37: [TS10 Chuyên Quảng Nam, 2019-2020]
Cho hai số thực x, y thỏa mãn x  3; y  3.  1   1 
Tìm giá trị nhỏ nhất của biểu thức: T  21 x    3 y  .  y   x  Lời giải
Áp dụng bất đẳng thức AM – GM ta có:
THCS.TOANMATH.com FB TRỊNH BÌNH 26  1   1   x 3   7y 21  62 2
T  21 x    3 y            x  y  y   x   3 x   3 y  3 3 x 3 7y 21 62 2  2 .  2 .  .3  .3 3 x 3 y 3 3  2  2.7  62  2  80
Dấu “=” xảy ra khi x = y = 3.
Vậy giá trị nhỏ nhất của T là 80. NĂM HỌC 2018-2019
Câu 38: [TS10 Chuyên Thái Bình, 2018-2019] 1 1 1
Cho a, b, c là ba số thức dương thỏa mãn điều kiện :    1 2 2 2 a b c
Tìm giá trị lớn nhất của biểu thức 1 1 1 P    2 2 2 2 2 2 5a  2ab  2b 5b  2bc  2c 5c  2ca  2a Lời giải Ta có: 1 1 2    2 2 5a  2ab  2b  27 27. 2 2 5a  2ab  2b  1 27  1 1    .    2 2 2 2   2  5a  2ab  2b 27 5a 2ab 2b 
Chứng minh tương tự ta có: 1 27  1 1  1 27  1 1    ;       2 2 2 2 2 2 2 2   2  5b  2bc  2c 27    2  5c  2ca  2c 27 5b 2bc 2c 5c 2ca 2a    27 1 1 1 1  P  .     2    2 2 5a  2ab  2b   2 2 5b  2bc  2c   2 2 5c  2ca  2a  9  1 1  1 1 1  Sử dụng BĐT      ta có: x  y  z 9  x y z  1 1 1  1 1 1         2 2 5a  2ab  2b  2 3a   2 2ab  a    2 2 a  2b  2 2 2 2 9  3a 2ab  a a  2b 
THCS.TOANMATH.com FB TR ỊNH BÌNH 27 1  1 1  1 1 1  1  1 1 1  1  5 2 2     .      .          2 2 2 2 2 2 2 9  3a 9  ab ab a  9  a b b  9  9a 9ab 9b  AMGM 2 1  1 1  Ta lại có :     2 2 9ab 9  a b  1 1  5 1 1 2  1  2 1    .     .      2 2 2 2 2 2 2 2 5a  2ab  2b 9  9a 9a 9a 9b  9  3a 3b  Chứng minh tương tự: 1 1  2 1  1 1  2 1    ;       2 2 2 2 2 2 2 2 5b  2bc  2c 9  3b 3c  5c  2ca  2a 9  3c 3a  1 1 1    2 2 2 2 2 2 5a  2ab  b 5b  2bc  2c 5c  2ca  2a 1  2 1  1  2 1  1  2 1  1  1 1 1  1  .   .     .            2 2 2 2 2 2 2 2 2 9  3a 3b  9  3b 3c  9  3c 3a  9  a b c  9 27  1 1  3  P  .     2  9 9  3 a   b  c 
Dấu "  " xảy ra   1 1 1  a  b  c  3     1 2 2 2 a b c 3 Vậy P  max 3
Câu 39: [TS10 Chuyên Trà Vinh, 2018-2019]
Cho x, y,z là ba số thực dương thỏa mãn: 2 2 2 x  y  z  2 . 3 3 3 2 2 2 x  y  z Chứng minh:     3 . 2 2 2 2 2 2 x  y y  z z  x 2xyz Lời giải Vì 2 2 2
x, y,z  0; x  y  z  2 nên: 3 3 3 2 2 2 x  y  z     3 (1) 2 2 2 2 2 2 x  y y  z z  x 2xyz 2 2 2 2 2 2 2 2 2 2 2 2 x  y  z x  y  z x  y  z x y z        3 2 2 2 2 2 2 x  y y  z z  x 2yz 2zx 2xy 2 2 2 2 2 2 z x y x y z  1  1  1     3 2 2 2 2 2 2 x  y y  z z  x 2yz 2zx 2xy 2 2 2 x y z 2 2 2    x y z    (2) 2 2 2 2 2 y  z z  x x 2  y 2yz 2zx 2xy
THCS.TOANMATH.com FB TRỊNH BÌNH 28 2 2 z z Lại có: 2 2 2
(x  y)  0  x  y  2xy   2 2 x  y 2xy 2 2 2 2 y y z z Tương tự, ta có:  ;  2 2 2 2 z  x 2zx x  y 2xy
 (2) đúng  (1) đúng (đpcm)
Câu 40: *TS10 Chuyên Bình Phước, 2018-2019] 2 2 x y
a) Cho x; y là hai số thực dương. CMR:   x  y y x
b) Xét các số thực a; b; c với b  a  c sao cho phương trình 2 ax  bx  c  0 có 2
nghiệm thực m; n thỏa mãn 0  m,n  1. Tìm GTLN và GTNN của biểu thức ab2ac M  a(a bc) Lời giải a) Với x, y  0 ta có: 2 2 x y 3 3 2 2 
 x  y  x  y  xy(x  y)  (x  y)(x  xy  y )  xyx  y y x            2 2 2 2 2 x xy y xy x 2xy y 0 x y  0 x  ,y x  y
Vậy BĐT được chứng minh, dấu "  " xảy ra  x,y   0
b) Theo đề b|i ta có phương trình 2
ax  bx  c  0 có hai nghiệm m,n
0  m,n  1a  0  b m  n   
Áp dụng định lý Vi-et ta có: a  c mn   a  b  c     1 2 a b 2a c     a 
a  1 m  n2  mn  M    a b c 1  m  n  mn 1   a a 1mn.2 Vì 2  mn  2; mn  0  M   2 1 m  n
Vậy MaxM  2  mn  0  c  0 1
Ta lại có: 0  m,n  1  m n  
1  n m 1  mn 1  0  mn  m  n  1 3 m  n  1 3  M   1        4 1 m n 1 m n 3
THCS.TOANMATH.com FB TRỊNH BÌNH 29 3 a   b  c  0 Vậy MinM   m  n  1   4 a   c
Câu 41: [TS10 Chuyên Hà Nam, 2018-2019]
Cho các số thực dương x, y,z sao cho phương trình xy  yz  zx  x  y  z. 2 2 2 x y z Chứng minh rằng    1. 3 3 3 x  8 y  8 z  8 Lời giải       Ta có:
        2 2 3 2 x 2 x 2x 4 x x 6 x 8 x 2 x 2x 4   2 2 2 y  y  6 2   Tương tự: 3 y  8  ; 3 z z 6 z  8  . 2 2 Suy ra: 2 2 2 2 2 2 x y z  x y z     2.   . (*) 2 2 2 3 3 3   
 x  x  6 y  y  6 z  z  6 x 8 y 8 z 8  a b c    2 2 2 2 a b c Chứng minh rằng    a,b,c,u,v,w  0 1 u v w u  v  w
Áp dụng (1) v| (*) ta thu được: 2 2 x y z 2x  y  z2 2    (2) 2 2 2 3 3 3   
x  y  z  x  y  z  18 x 8 y 8 z 8 Ta cần chứng minh: 2 x  y  z2  1 2 2 2
x  y  z  x  y  z  18 2 2 2
 x  y  z  4xy  yz  zx  18 x  y  z     2
x y z  x  y  z  2xy  yz  zx 18  0 . (3)
Lại do: xy  yz  zx  x  y  z nên ta đi kiểm tra    2
x y z  3x  y  z 18  0
 x  y  z  3x  y  z  6  0. (4) 2
Thật vậy ta có quan hệ: x  y  z  3xy  yz  zx  3x  y  z nên x  y  z  3 , từ đó (4) đúng.
Từ (2), (3), (4) suy ra điều phải chứng minh.
THCS.TOANMATH.com FB TRỊNH BÌNH 30
Dấu “=”  x  y  z  1
Câu 42: [TS10 Chuyên Lào Cai, 2018-2019] 1 1 1
Cho các số thực dương a, b,c thỏa mãn điều kiện a  b  c    . a b c
Chứng minh rằng     2 2 2
3 a b c  8a  1  8b  1  8c  1 Lời giải Ta có:
18 a  b  c  8a  b  c  a  b  c  9 a  b  c  1   1   1 
 8a   9a  8b   9b  8c        9c   a   b   c  2 2 2 8a  1 8b  1 8c  1   9a   9b   9c a b c
Áp dụng bất đẳng thức Cosi ta có: 2 2 2 8a  1 8b  1 8c  1 2 2 2  9a   9b 
 9c  6 8a  1  6 8b  1  6 8c  1 a b c  18a  b  c 2 2 2
 6 8a 1  6 8b 1  6 8c 1      2 2 2
3 a b c  8a  1  8b  1  8c  1 (đpcm)
Dấu “=” xảy ra khi và chỉ khi a  b  c .
Câu 43: [TS10 Chuyên Bến Tre, 2018-2019]
Cho hai số thực dương a, b thỏa a  b  1. 4 1
Tìm giá trị nhỏ nhất của biểu thức T    a b Lời giải 4 1 4 1 a a Khi đó T      5 a 1  a a 1  a 4 1 a a
Áp dụng BĐT AM-GM cho hai số dương ; ta được: a 1  a 41 a a T  2 .  5  9 a 1  a 41 a a Đẳng thức xảy ra    41a2 2 2
 a  3a  8a  4  0 a 1 a a  2 loai    2 a  nhan  3 1 Vậy min T  9  2 a  và b  3 3
THCS.TOANMATH.com FB TRỊNH BÌNH 31
Câu 44: *TS10 Chuyên Nam Định, 2018-2019]
Cho các số thực dương thỏa mãn a  b  1 2 1
Chứng minh rằng: 3a  b  a  b  4ab  a3bb3a 2 Lời giải     Ta có:      AM GM 1 a 3b b 3a a 3b b 3a   a  b 2 4 Từ giả thiết ta có:                2 a b 1 a b 2 ab 1 2 ab 1 a b 4ab 1 a b     
        2      2 2 1 3(a b) (a b) 4ab a 3b b 3a 3 a b a b 1 a b  a  b 2 2 2 2 2
 3a  6ab  3b  2a  2b  a  b 1 2a  2b  2ab  0 2 2
 4a  4b 1 8ab  4a  4b  0     2 1 2a 2b  0 (luôn đúng).
Vậy đẳng thức được chứng minh.
Câu 45: [TS10 Chuyên Bà Rịa Vũng T|u, 2018-2019]
Cho các a, b,c  3 dương thỏa mãn abca  b  c  3
a) Chứng minh rằng: ab  ac  bc  3 : a b c
b) Tìm GTNN của biểu thức: P    2 2 2 9  b 9  c 9  c Lời giải Áp dụng BĐT AM-GM ta có:    2 ab ac bc
 3ab.ac  bc.ac  ab.bc  3abca  b  c  9  ab  bc  ca  3
Tiếp tục áp dụng BĐT AM-GM ta có: a a 2 2a 2 2a 2 2a     2 9  b     
     62b3 b 9b 3 b 3 b 2 6 2b 3 b 2 2a 2 2b 2 2c 2 2a 2 2b 2 2c 2 2 a  b  c2 2 2 2  P        9  b 9  c 9  a 9a  ab 9b  bc 9c  ca
9 a  b  c  ab  ac  bc
Đặt t  a  b  c  3ab  ac  bc  3
THCS.TOANMATH.com FB TRỊNH BÌNH 32
 t  38t  3  0 2  8t  27t  9
 8a  b  c2  27 a  b  c  3ab ac  bc 8 a  bc2
 .        1 3 9. a b c ab ac bc 3 2  P  4 3 2 Vậy GTNN của P là
. Đạt tại a  b  c  1 4 Câu 46:
[TS10 Chuyên Quảng Nam, 2018-2019]
Cho ba số thực dương a, b, c . Chứng minh rằng 2 2 2 2 2 2 2 2 2 a  b b  c c  a 3(a  b  c )    a  b b  c c  a a  b  c Lời giải 2 2 2 2 2 2 2 2 2 a  b b  c c  a 3(a  b  c )
Với ba số thực dương a, b, c ta có    a  b b  c c  a a  b  . (1) c        a  b  c 2 2 2 2 2 2 a b b c c a 2 2 2      3(a  b  c ) a  b b  c c   a  c  2 2 a  b  a 2 2 b  c  b 2 2 c  a  2 2 2     a  b  c a  b b  c c  a c  2 2 a  b  a  2 2 b  c  b  2 2 c  a 2 2 2   c   a   b   0 a  b b  c c  a
ac c  a bcc  b abb  a bc b  c aba  b ac a  c        0 a  b a  b c  a c  a b  c b  c   2   2   2 ac c a bc c b ab b a
                   0. (2) a b b c a b a c a c b c
Với ba số thực dương a, b, c ta có (2) luôn đúng. Vậy (1) luôn đúng. (đpcm)
Câu 47: [TS10 Chuyên Bắc Giang, 2018-2019]
Cho x, y,z là các số thực thỏa mãn 2 2 2
x  y  z  8 . Tìm giá trị lớn nhất của biểu thức 3 3 3 3 3 3
M  x  y  y  z  z  x . Lời giải
Áp dụng tính chất a  b  a  b . Đẳng thức xảy ra khi và chỉ khi ab  0 .
THCS.TOANMATH.com FB TRỊNH BÌNH 33 3 3 3
Khi đó M  2 x  y  z  3 2   2   x  2 2 x  2 2x x 8      Mặt khác 2 2 2 x  y  z  8  2 3 2
y  8   y  2 2   y  2 2y  2    3 2 z 8   z  2 2  z  2 2z   3 3 3 Vậy        2 2 2 M 2 x y z
4 2 x  y  z  = 32 2 .
Đẳng thức xảy ra khi x; y; z  2 2;0;0 hoặc x; y;z   2  2;0;0 và các hoán
vị của nó. Vậy giá trị lớn nhất của M bằng 32 2 .
Câu 48: [TS10 Chuyên TP. Hồ Chí Minh, 2018-2019] Chứng minh rằng 4 1 x  x 
 0 với mọi số thực x 2
Cho x, y là các số thực thỏa mãn điều kiện 2 2
x  xy  y  3 . Tìm giá trị lớn nhất và
nhỏ nhất của biểu thức 2 2 P  x  y Lời giải a) Ta có 2     4 1 4 2 1 2 1 2 1 1 x  x 
 x  x   x  x   x   x       0 2 4 4  2   2    2 1 2 1 x   0 x     Dấu bằng xảy ra 2 2    
(vô lý), do đó dấu bằng không xảy ra 1   1 x   0 x   2  2 Vậy 4 1 x  x 
 0 với mọi số thực x 2 Ta có: 2 2
x  xy  y  3  P  xy  3  xy  P  3
Áp dụng BĐT AM-GM cho hai số 2 2 x ; y ta có: 2 2 x  y 2 2 2 2 x  y  2 x y  2 xy   xy 2 2 2 2 2 x  y x  y P P    xy     xy  2 2 2 2 P P    P  3  2 2
THCS.TOANMATH.com FB TRỊNH BÌNH 34  P  3P   P  3 3     2  2      2  P  6 P P P 3     3  2  2 Dấu bằng xảy ra 2 2  x  y  x  y 2 2 2 x  x  x  3  x  y  1     2 2 2 x  x  x  3  x  y  3  Vậy P
 6  x  y  3;P  2  x  y  1 max min
Câu 49: *TS10 Chuyên Vĩnh Long, 2018-2019]
Cho a, b,c là các số dương. Chứng minh rằng: 3 a b a)  a  . 2 2 a  b 2 3 3 3 a b c a  b  c b)    . 2 2 2 2 2 2 a  ab  b b  bc  c c  ca  a 3 Lời giải 3 2 2 2 2 2 a a(a  b )  ab ab ab b a) Ta có :   a   a   a  2 2 2 2 2 2 a  b a  b a  b 2ab 2 3 b c 3 c a
b) Tương tự theo câu a), ta có:  b  ,  c  2 2 b  c 2 2 2 c  a 2
Cộng vế theo vế ba bất đẳng thức trên ta có: 3 3 3 a b c a  b  c    2 2 2 2 2 2 a  b b  c c  a 2 3 3 3 a a 2 a Ta có:   . 2 2 2 2 2 2 a  ab  b   2 a b 2 3 a b a   b 2 3 3 3 b b 2 b 3 3 3 c c 2 c Và   .   . 2 2 2 2 2 2 b  bc  c   2 2 2 2 2 2     2 b c 2 3 b c c ac a c a 3 c a b   c 2 2 c   a 2 2
Cộng vế theo vế ba bất đẳng thức trên ta có: 3 3 3 3 3 3 a b c 2  a b c  a  b  c         2 2 2 2 2 2 2 2 2 2 2 2 a  ab  b b  bc  c c  ca  a 3 a  b b  c c   a  3
Câu 50: [TS10 Chuyên Khánh Hòa, 2018-2019]
Với a, b, c là các số thực dương thỏa mãn điều kiện a  b  c  abc . 2 2 1 a 1 b Chứng minh rằng 2   1 c  1. a b Lời giải
THCS.TOANMATH.com FB TRỊNH BÌNH 35 1 1 1 1 1 1
Ta có a  b  c  abc     1. Đặt  x ,  y ,  z bc ca ab a b c
Khi đó x, y,z  0 và xy  yz  zx  1 . Vì vậy 2 2 2 1  a 1  b  2 2 2 1 z 
 1 c  1  1 x  1 y   1 a b z
        2  2 2 2 2 1 z 1 x 1 1 y 1  1  x 1  y   0 z      
1  x  1 1 y 1 2 2 2 1 z z 1 x 1 y 2 2   0 (4) z 2 2 Ta có: 2 2 2 2 2 2      
            2 1 x 1 y 1 x y x y 1 xy x y x y 1 z .     
4   1 x 1 1 y 1 2 1 z z x y 2 1 z 2 2   0 z      
1 x  1 1 y 1 2 1 z xz yz 2 1 z 2 2   0 z      
1  x  1 1 y 1 2 1 z 1 xy 2 1 z 2 2   0 z   
1  x  1 1 y 1 2 xy 1 z 2 2   0, x  ,y,z  0. z
Ta có điều phải chứng minh.
Câu 51: [TS10 Chuyên Thừa Thiên Huế, 2018-2019]
a) Cho x, y,z là các số thực dương có tổng bằng 1. 1 1 1 49 Chứng minh rằng    . 16x 4y z 16
b) Cho số tự nhiên z và các số nguyên x, y thỏa mãn x  y  xy  1. Tìm giá trị
của x, y,z sao cho  z1   2 2 2 2 2
42 x  y  1 x y  là số chính phương lớn nhất. Lời giải a) Ta có 1 1 1 49 1 4 16        49. 16x 4y z 16 x y z
Với hai số thực không âm a, b ta có   2 a b  0  a  b  2 ab.
Dấu "=" xảy ra khi a  b  a  b.
Áp dụng kết quả trên, ta có: 1 1 1  49x  2 .49x   49x  14. (1) x x x
THCS.TOANMATH.com FB TRỊNH BÌNH 36 1 1 Dấu "=" xảy ra khi  49x  x  . x 7 4 Tương tư, ta có:  49y  28. (2) y 4 2 Dấu "=" xảy ra khi  49y  y  . y 7 16 Và  49z  56. (3) z 16 4 Dấu "=" xảy ra khi  49z  z  . z 7 1 4 16
Cộng (1), (2), (3) theo vế ta được:  
 49x  y  z  98 x y z 1 4 16     1 2 4
49. Dấu "=" xảy ra khi x  ; y  ; z  . x y z 7 7 7
Vậy bất đẳng thức đã cho được chứng minh. b) Ta có:  z1   2 2 2 2       z   2   2 2 42 x y 1 x y 2 2 21 1 x 1 y . Với: 2 2
1 x  x  y  xy  x  x  y1 x , 2 2
1 y  x  y  xy  y  x  y1 y ,
2  1 1  1 x  y  xy  1 x1 y. 2 2 2 Suy ra  z1   2 2 2 2     z 2 42 x y 1 x y 2  2 
1 x  y 1 x 1 y .
Do đó,  z1   2 2 2 2 2
42 x  y  1 x y  là số chính phương khi v| chỉ khi z 2  21 là số chính phương.
Nghĩa l| tồn tại số tự nhiên n sao cho z 2 2  21  n . z Ta có     z 2 1 mod 3  2    1 mod 3. Nếu z lẻ thì z 2  1
 mod3  2mod3. Khi đó 2
n  2mod 3 vô lí (vì số chính
phương khi chia cho 3 chỉ dư 0 hoặc 1).
Từ đó suy ra z là số chẵn. 2 Đặt z 2k,k    . Ta có 2 2k 2      k     k   k n 21 2 n 2 21 n 2 n  2   21. Vì 21  1.21  3.7 và k k
n  2  n  2 nên ta có hai trường hợp sau: k n  2  1 Trường hợp 1: k 
 2  10, không có giá trị của k thỏa mãn trường hợp k n  2  21 này.
THCS.TOANMATH.com FB TRỊNH BÌNH 37 k n  2  3 Trường hợp 2: k   2  2  k  1. k n  2  7
Từ giả thiết, ta có 2  1 x1 y. Không mất tổng quát, giả sử x  1  y  1 , suy  x 1   1 ra  . y  1   2  x  0 x  2  Giải hệ ta được  hoặc  . y   1 y  3  
Nếu x  0, y  1 thì  z1   2 2 2 2     2 2 42 x y 1 x y  100  10 . Nếu x  2  ,y  3
 thì  z1   2 2 2 2     2 2 42 x y 1 x y  2500  50 . Vậy x  2  ,y  3  ,z  2.
Câu 52: [TS10 Chuyên Kiên Giang, 2018-2019]
Cho ba số dương x, y,z thỏa mãn điều kiện x  y  z  2 . 2 2 2 x y z Chứng minh rằng:    1. y  z z  x x  y Lời giải
Áp dụng bất đẳng thức Bunyakoski với bộ ba số có:         2 2 2 2   2 2 2   A   B   C   A B C  a b c .           a.  b.  c.   A  B  C2 
  a   b   c    a b c    A B C    2 2 2 2 A B C     a b c a  b  c
Áp dụng bất đẳng thức trên ta có: 2 2 x y z x yz2 x yz2 2 x  y  z          
y  z  z  x  x  y 1 y z z x x y 2(x  y  z) 2 2
Dấu “=” xảy ra khi: x  y  z  . 3
Vậy ta có điều cần chứng minh.
Câu 53: [TS10 Chuyên Bắc Ninh, 2018-2019]
Cho các số thực a, b,c thỏa mãn 0  a, b,c  2,a  b  c  3 . 2 2 2 a  b  c
Tìm GTLN và GTNN của P  ab bcca Lời giải
THCS.TOANMATH.com FB TRỊNH BÌNH 38 2 2 a   b  2ab  Áp dụng BĐT AM-GM ta có: 2 2 b  c  2bc  2 2 c  a  2ca  2 2 2 1      2 2 2 2 2 2       1 a b c a b a c b c  2ab  2ac  2bc 2 2 2 2 2
 a  b  c  ab  ac  bc 2 2 2 a  b  c  P   1 ab  bc  ca a   b  c Dấu “=” xảy ra    a  b  c  1 a  b  c   3
Vậy MinP  1khi a  b  c  1 Theo đề bài ta có:
0  a, b,c  2  a  2b  2c  2  0
 abc  2ab  ac  bc  4a  b  c  8  0
 abc  2ab  ac  bc 12  8  0
 2ab  ac  bc  4  abc  4  ab  bc  ca  2 2 2 2
a  b  c  2ab  2ac  2bc  P   2 ab  ac  bc a  bc2 9 5  P   2   2  ab  ac  bc 2 2  a   0 bc   3 b  0 ab  c  0  Dấu "  " xảy ra     a   c  3 a   b  c  3 c  0   a  b   3  0  a,b,c  2 5 Vậy MaxP 
khi abc  0,a  b  c  3,0  a, b,c  2 2 Câu 54:
[TS10 Chuyên Thái Nguyên, 2018-2019]
Cho x, y,z là các số thực dương. Chứng minh rằng 2 2 2 x y z x  y  z    2 2 2 2 2 2       5 8x 3y 14xy 8y 3z 14yz 8z 3x 14xz Lời giải
Áp dụng BĐT AM-GM ta có: 2 2 x  y  2xy
THCS.TOANMATH.com FB TRỊNH BÌNH 39 2 2 2 2 2 2 2 2
 8x  3y 14xy  8x  3y 12xy  2xy  8x  3y 12xy  x  y
 8x  3y 14xy  9x 12xy  4y  3x  2y2 2 2 2 2  3x  2y  2 2
 8y  3z  14yz  3y  2z
Chứng minh ho|n to|n tương tự ta có:  2 2
 8z  3x 14xz  3z  2x a b c    2 2 2 2 a b c Áp dụng BĐT AM-GM Schawz:    ta được: x y z x  y  z 2 2 x y z x yz2 2 x  y  z  VT      3x  2y 3y  2z 3z  2x
3x  2y  3y  2z  3z  2x 5
Vậy ta có điều phải chứng minh
Dấu "  " xảy ra khi và chỉ khi x  y  z
Câu 55: [TS10 Chuyên Tuyên Quang, 2018-2019]
Cho các số thực dương a, b,c thỏa mãn a  b  c  3 . 2 2 2
a  4a  1 b  4b  1 c  4c  1
Tìm giá trị nhỏ nhất của biểu thức: M    2 2 2 a  a b  b c  c Lời giải 1 1 1 9
Áp dụng BĐT AM-GM v| BĐT quen thuộc :    x y z x  y  z 2 2 2
a  4a  1 b  4b  1 c  4c  1 M    2 2 2 a  a b  b c  c
 2a 14a  2b 14b  2c 14c    a a  1 b b  1 c(c  1) AMGM 2a  4a 2b  4b 2c  4c  1 1 1  6.9 54     6        9 a(a  1) b(b  1) c(c  1)
 a  1 b  1 c  1  a  b  c  3 6
Vậy giá trị nhỏ nhất của M là 9, dấu bằng xảy ra khi và chỉ khi a  b  c  1
Câu 56: [TS10 Chuyên Hải Dương, 2018-2019]
Cho a, b,c dương thỏa mãn ab  bc  ca  1. Tìm giá trị lớn nhất của biểu thức 2a b c 2 2 2 P     a  28b  28c 2 2 2 1 a 1 b 1 c Lời giải
Theo đề bài ta có: ab  bc  ca  1
Áp dụng BĐT AM-GM vào biểu thức bài toán ta có:
THCS.TOANMATH.com FB TRỊNH BÌNH 40 2a 2a 2a a a     2 2 1  a ab  bc  ca  a
     a  b a c a b a c b b b b b     2 2 b  1 b  ab  ac  bc
     4(bc) a  b b c b a c c c c c     2 2 c  1 c  ab  ac  bc
     4(bc) a c a c c b
Cộng vế theo vế ta được: 2a b c a a b b c c         2 2 2 a  b a  c 4(b  c) a  b 4(b  c) a     c 1 a b 1 c 1 a  b a  c b  c 1 9     1 1  a  b a  c 4(b  c) 4 4 Mặt khác: 2 2 2 2 a 49b a .49b   2  7ab 2 2 4 2 2 2 2 a 49c a .49c   2  7ac 2 2 4 7  2 2 b  c   7bc 2 2 2 2
 a  28b  28c  7 ab  ac  bc  7 9 1  9  P   7  4 4  7 15 a   a   7b  7c  Dấu "  " xảy ra 15     ab  bc  ca   1  15 b  c   15  7 15 a   19  Vậy MaxP   khi 15  4  15 b  c   15 Câu 57:
[TS10 Chuyên Quảng Nam, 2018-2019]
Cho hai số thực dương a v| b thỏa mãn a  b  ab . ab
Tìm gi{ trị nhỏ nhất của biểu thức A  a  b  a  b Lời giải
Cho hai số thực dương a v| b thỏa mãn a  b  ab . Tìm gi{ trị nhỏ nhất của ab
biểu thức A  a  b  . a  b
THCS.TOANMATH.com FB TRỊNH BÌNH 41 Ta có: 2
a b  a  b  ab  ab  4 .  a  b
Dấu đẳng thức xảy ra    a  b  4 .  ab  4 ab 3a  b a  b ab 3 ab 5 ab A  a  b       ab   10 . a  b 4 4 a  b 2 2 Suy ra: A  10 . a   b  4 
Đẳng thức xảy ra khi    a  b  4 a b ab .   4 a  b
Vậy gi{ trị nhỏ nhất của A bằng 10 khi a  b  4 .
Câu 58: *TS10 Chuyên Đồng Nai, 2018-2019]
Cho các số thực a, b,c . Chứng minh rằng 3 3 3 3 3 3 a  b b  c c  a 1 1 1      ab 2 2 a  b  bc 2 2 b  c  ac 2 2 c  a  a b c Lời giải Ta có: 2 a  b 2 2 3 3 a  ab   b a b 1 1  ab     2 2 ab(a  b ) 2a 2b 2ab 2 2 a  b  2ab
 2a ab  b   b  0  a  b2 2 2 2  0
Điều n|y luôn đúng, dấu bằng xảy ra  a  b 3 3  c  b 1 1    cb  2 2 c   b  2c 2b
Chứng minh ho|n to|n tương tự ta có:  3 3 c   a 1 1   ca   2 2 c  a  2c 2a Cộng vế theo vế ta có: 3 3 3 3 3 3 a  b b  c c  a 1 1 1 1 1 1 1 1 1            ab 2 2 a  b  bc 2 2 b  c  ac 2 2
c  a  2a 2b 2c 2c 2a 2b a b c
Dấu “=” xảy ra khi a  b  c
Vậy ta có điều phải chứng minh
Câu 59: *TS10 Chuyên L}m Đồng, 2018-2019]
Cho a, b,c  0 và a  2b  3c  20. 3 9 4
Tìm giá trị nhỏ nhất của biểu thức: S  a  b  c    a 2b c Lời giải
THCS.TOANMATH.com FB TRỊNH BÌNH 42 Ta có: 3 9 4 a b 3c  3a 3   b 9   c 4  S  a  b  c                   a 2b c 4 2 4  4 a   2 2b   4 c 
1      3a 3  b 9   c 4   a 2b 3c             4  4 a   2 2b   4 c 
Áp dụng bất đẳng thức AM-GM cho hai số không âm ta có: 3a 3 3a 3 )   2 .  3 4 a 4 a b 9 b 9 )   2 .  3 2 2b 2 2b c 4 c 4 )   2 .  2 4 c 4 c 1    
   3a 3   b 9   c 4  1 S a 2b 3c        .20  3  3  2        13 4  4
a   2 2b   4 c  4 a   2b  3c  20 3a 3   a   2  4 a  
Dấu “ = “ xảy ra khi và chỉ khi :   b  3(a,b,c  0 b 9    2 2b c  4   c 4  4 c
Vậy MinS  13khi a  2; b  3; c  4
Câu 60: [TS10 Chuyên Thái Bình, 2018-2019]
Cho x, y,z l| ba số thực không }m thỏa mãn: 12x  10y  15z  60 .
Tìm gi{ trị lớn nhất của 2 2 2
T  x  y  z  4x  4y  z . Lời giải
Do x, y,z l| ba số thực không }m thỏa mãn : 12x  10y  15z  60 . x,y,z  0  x  5 Ta có  (*) y  6  z   4
Từ điều kiện trên ta có 2 2 2
T  x  y  z  4x  4y  z
 x(x  5)  y(y  6)  z(z  4)  x  2y  3z 12x 60  x  2y  3z   2y  3z   12 5 5
THCS.TOANMATH.com FB TRỊNH BÌNH 43 x  0 x  0  
Vậy GTLN của T bằng 12 đạt được khi y  6 or y  0   z  0 z  4  
Câu 61: *TS10 Chuyên Đại Học Vinh, 2018-2019]
Cho các số thực không âm a, b thỏa mãn:   2 a b  a  b  2 .    3 3 a b Chứng minh rằng: 1       b  1 9 3 1  a 13       Lời giải Ta có: a b2  a  b2 2 2
 a  2ab  b  a  b  2 2 2
 a  b  a  b  2  2ab   2 a  a   2
b  b  2ab  a  b  1
 aa 1  bb 1  2a 1b 1
a a  1  bb  1        2 a 1 b 1 a b    2 b  1 a  1 a b Đặt x  ; y   x  y  2 b  1 a  1 Ta có:  3 1  x  3 1  y   9  1 xy3 3 3  x  y  9
xy3 x yx y2 3xy       8     2 2 xy x y  6  0   2 x y (do 0  xy   1) 4 xy  0 a  0; b  2
Dấu "  " xảy ra khi và chỉ khi:    x  y  2 a  2; b    0
Câu 62: [TS10 Chuyên Hà Nam, 2018-2019]
Cho các số thực dương x, y,z thỏa mãn xy  yz  xz  x  y  z 2 2 2 x y z Chứng minh rằng:    1 3 3 3 x  8 y  8 z  8
THCS.TOANMATH.com FB TRỊNH BÌNH 44 Lời giải Áp dụng BĐT AM-GM ta có:
   2    2 xy yz xz
x y z  3xy  xz  yz  xy  xz  yz  3
Áp dụng BĐT AM-GM-Schwwarz ta có: x yz2
VT  x2 2x 2x4 y2 2y 2y4 z2 2z 24 x yz2
 VT  yz6 2 2 2 x  y  z  2  x yz12 x y z2
 VT  2xy2xz2yz3 2 2 2 x  y  z  2  x y z12 2 x  y  z2  VT  2 2 2
x  y  z  2 x  y  z  15  2xy  yz  xz 2x  y  z2
 VT  xyz2 2xyz15 Ta cần chứng minh: 2 x  y  z2  x yz 1
2  2x  y  z15
 x  y  z2  2x  y  z 15  0
 x  y  z  5x  y  z  3  0
Điều n|y l| luôn đúng do: x  y  z  3xy  yz  xz  3
Dấu “=” xảy ra  x  y  z  1 2 2 2 x y z Vậy    1 3 3 3 x  8 y  8 z  8
Câu 63: *TS10 Chuyên Đắc Lắc, 2018-2019]
1) Cho các số thực x, y không âm, chứng minh rằng 3 3 2 2 x  y  x y  xy .
2) Cho các số thực dương a, b,c thỏa mãn abc  1. Chứng minh rằng: ab bc ca    1. 5 5 5 5 5 5 a  b  ab b  c  bc c  a  ca Lời giải
1) Cho các số thực x, y không âm, chứng minh rằng 3 3 2 2 x  y  x y  xy . Bất đẳng thức: 3 3 2 2 x  y  x y  xy
THCS.TOANMATH.com FB TRỊNH BÌNH 45 2 2
 x (x  y) y (x  y)  0 2
 (x  y) (x  y)  0, đúng x  ,y  0 .
2) Cho các số thực dương a, b,c thỏa mãn abc  1. Chứng minh rằng: ab bc ca    1. 5 5 5 5 5 5 a  b  ab b  c  bc c  a  ca Chứng minh 5 5 2 3 3 2 a  b  a b  a b 3 2 2 3 2 2
 a (a  b )  b (a  b )  0 2 2 2
 (a  b) (a  b)(a ab  b )  0, a  ,b  0 (*)   Áp dụng (*): 5 5 2 2 5 5 a b c
a  b  a b (a  b)  a  b  ab  ab. c ab c   (1) 5 5 a  b  ab a  b  c bc a ca b Tương tự  (2) ;  (3) 5 5 b  c  bc a  b  c 5 5 c  a  ca a  b  c
Cộng (1), (2), (3) ta được bất đẳng thức cần chứng minh.
Dấu bằng xảy ra khi a  b  c .
Câu 64: [TS10 Chuyên Bến Tre, 2018-2019]
Cho hai số thực dương a, b thỏa a  b  1. 4 1
Tìm giá trị nhỏ nhất của biểu thức T   a b Lời giải 4 1 4(a  b) a  b 4b a 4b a Ta có: T      5    5  2 .  5  4  9 a b a b a b a b 4b a 4b a
Áp dụng bất đẳng thức AM-GM cho hai số thực dương ta có:   2 .  4 a b a b 4b a  T  5    5  4  9 a b  2 4b a  2 2 a (tm)   a   4b a   b  1  Dấu “=” xảy ra 3   a b        a      b  1 a   2b 1 a  b 1 b  (tm)  3 2 1 Vậy MinT  9 khi a  ; b  3 3
Câu 65: *TS10 Chuyên Vĩnh Phúc, 2018-2019]
Cho các số thực dương a, b,c . Chứng minh rằng: 2 2 2 a b c    1 2 2 2 2 2 2 a  ab  b b  bc  c c  ac  a
THCS.TOANMATH.com FB TRỊNH BÌNH 46 Lời giải
Ta có : Áp dụng bất đẳng thức AM-GM – Schaw thì: a c a c2 2 2   2 2 a  ab  b c a  b  c 2 2 2
a  b  c  ab  ac  bc b c bc2 2 2   2 2 2 2 2 b(a  b  c) c  ac  a
a  b  c  ab  ac  bc a b a  b2 2 2   2 2 2 2 2 a(a  b  c) b  bc  c
a  b  c  ab  ac  bc 2 2 2 2 2 2 a b c a b c       2 2 2 2 2 2 a  ab  b b  bc  c c  ac  a
a a  b  c b(a  b  c) c(a  b  c)  2 2
a  c2  b  c  a  b  2 2 2
a  b  c  ab  ac  bc a b c a  b  c
a c2 bc2 a  b2 2 2 2      2 2 2 2 2 2 2 2 2 a  ab  b b  bc  c c  ac  a a  b  c
a  b  c  ab  ac  bc 2  2 2 2 2 2 2
a  b  c  ab  ac  bc a c b      1  2 2 2 2 2 2 2 2 2 a  ab  b c  ac  a b  bc  c
a  b  c  ab  ac  bc 2 2 2 a c b     1  2 2 2 2 2 2 2 a  ab  b c  ac  a b  bc  c 2 2 2 a c b     1 (đpcm) 2 2 2 2 2 2 a  ab  b c  ac  a b  bc  c
Dấu bằng xảy ra khi và chỉ khi a = b = c.
Câu 66: *TS10 Chuyên Hưng Yên, 2018-2019]
Cho các số dương x, y,z thỏa xy  yz  zx  3xyz . 3 3 3 x y z 1  1 1 1  Chứng minh rằng    .    2 2 2 z  x x  y y  z 2  x y z  Lời giải
Theo đề bài ta có: xy  yz  zx  3xyz xy yz zx 1 1 1     3     3 xyz xyz xyz z x y AMGM 3 Lại có: 3 3xyz  xy  yz  xz 
3 xyz  xyz  1  x  y  z  3 Ta có 3 AMGM x xz xz z z  1  x   x   x   x  2 2 2 z  x z  x 2 4 2 zx z  1 z z  1 z z  1 (Do z  1  2 z  z       ) 2 2 2 2 2
THCS.TOANMATH.com FB TRỊNH BÌNH 47 3 3 y x  1 z y  1 Tương tự ta có:  y  ;  z  3 2 x  y 4 y  z 4
Cộng vế với vế của 3 bất đẳng thức trên ta được: 3 3 3 x y z x  y  z  3 6 3 1  1 1 1     x  y  z 
 3       (đpcm) 2 2 2 z  x x  y y  z 4 4 2 2  x y z 
Câu 67: *TS10 Chuyên Hưng Yên, 2018-2019]
Cho a, b là hai số thay đổi thỏa mãn c{c điều kiện a  0 và a  b  1 2 8a  b
Tìm giá trị nhỏ nhất của biểu thức 2 A   b 4a Lời giải
Theo giả thiết ta có: a  b  1  b  1 a 2 8a  1 a 2 1 1 2 1 2 1  A   b  2a    b  a   a  b  4a 4a 4 4a 4 1 2 1 1 2 3 1 2 1 1  a 
 a  a  2a 1  a   a a   a   a a   4a 4 4a 4 4a 4 2 2 AMGM 1  1  1 1 3  2 a.  a    1    4a  2  2 2 2  1 1 a   ; a   0 1 Dấu bằng xảy ra   4a 2  a  b  (tm) 2 b  1  a 3 1 Vậy MinA   a  b  2 2
Câu 68: *TS10 Chuyên Bình Định, 2018-2019] 1
Cho hai số dương a, b thỏa mãn a   1. Chứng minh rằng: b 2 2  1   1  25 a   b        a   b  2 Lời giải 1 Ta có: a   1 1 
 1a  ab  1  b v(a > 0, b > 0) b b 2 (x  y) Lại có HĐT: 2 2 2 2 2 2
2(x  y )  (x  y)  (x  y)  x  y  (1) , dấu”=” xãy ra khi 2 và chỉ khi x= y v| có HĐT: 2 2 2
(x  y) (x  y)  4xy  (x  y)  4xy (2), dấu”=” xãy ra khi v| chỉ khi x= y
THCS.TOANMATH.com FB TRỊNH BÌNH 48 Áp dụng (1), ta có: 2 2 2 2  1 1   1   ab 1   b               2 2 a b 1 b 1 1   1   1   a b   a   a   a  a   b          (1’),  a   b  2 2 2 2 1 1 1
dấu “=” xãy ra khi v| chỉ khi: a   b  và a   1 a b b Áp dụng (2), ta có: 2  1  a a b a   4  1  4     4 (2’),  b  b b a 1 1
dấu “=” xãy ra khi v| chỉ khi: a  và a   1 b b Từ (1’) v| (2’) suy ra: 2 2 2  1   1  (1 4) 1 1 a   b      
. Dấu “=” xảy ra khi và chỉ khi: a  hay b   a   b  2 b a 2 2  1   1  25 1 Vậy a   b      
, dấu “=” xãy ra khi v| chỉ khi: a = và b = 2.  a   b  2 2
Câu 69: *TS10 Chuyên H| Tĩnh, 2018-2019]
Cho x, y,z  0 thỏa mãn x  y  z  1 . Chứng minh rằng xy yz xz 3    xy  z yz  x xz  y 2 Lời giải
Áp dụng bất đẳng thức Cô si ta có: xy xy xy 1  x y        xy  z xy  zx  y  z
zxyz 2 xz yz 
Chứng minh ho|n to|n tương tự ta có: yz 1  y z  xz 1  z x   .  ;     yz  x 2 x  y z  x xz  y 2 y  z x     y  1  x y z z x y   P         2 x  z x  y x  z y  z x  y y   z  1  x z   y x   z y   P             
2  x  z x  z   x  y x  y   y  z y  z  1 3  P  .3  2 2 1
Dấu “=” xảy ra khi x  y  z  3
THCS.TOANMATH.com FB TRỊNH BÌNH 49 3
Vậy giá trị nhỏ nhất của P là . 2
Câu 70: *TS10 Chuyên Nam Định, 2018-2019]
Cho x, y,z là các số thực thỏa mãn x  yx  z  1; y  z. Chứng minh 1 1 1    xy 4. 2 yz2 zx2 Lời giải
Đặt x  y  a; x  z  b ta được ab  1; a  b.
Bất đẳng thức cần chứng minh trở thành: 2 2 1 1 1 a  b 1    1 4    4 2 2  a  b   4 2 2 a b   2 2 2 2 2 a b a  b  2ab 2 2 a b a  b  2 2 2 1  a  b  2   2. 2 2 a  b  2 Do ab  1; a  b nên 2 2 a  b  2ab hay 2 2 a  b  2  0. 1 1 Mặt khác  2 2 a  b  2   2  2 2 a  b  2 . tức là 2 2  a  b  2  2 2 a  b  2 2 2 1 a  b  2   2 . 2 2 a  b  2 1 1 1 Vậy    xy 4. 2 yz2 zx2
Câu 71: [TS10 Chuyên KHTN Hà Nội, 2018-2019]
Cho a, b,c là các số thực dương. Chứng minh rằng  ab bc  1 1        2  a  b b  c    a  b b  c  Lời giải
Áp dụng BĐT Cauchy-Schwarz ta có:  ab bc  1 1   ab bc   1 1        2.   . 2     a  b b  c    a  b b  c   a  b b  c   a  b b  c   a c  b b   a c   b b   2             
 a  b b  c  a  b b  c   a  b b  c   a  b b  c   a b   c b           2
 a  b a  b   b  c b  c 
Vậy ta có điều phải chứng minh
Dấu "  " xảy ra khi và chỉ khi a  b  c
THCS.TOANMATH.com FB TRỊNH BÌNH 50
Câu 72: *TS10 Chuyên Nam Định, 2018-2019]
Cho các số thực dương a, b thỏa mãn a  b  1. 2 1
Chứng minh rằng 3a  b  a  b  4ab  a3bb3a. 2 Lời giải 1 1
Bất đẳng thức đã cho tương đương   2. a  3b b  3a
Áp dụng BĐT AM-GM cho 2 số dương ta có a a a  b 1  a a  b   .     (1) a  3b a  b a  3b 2  a  b a  3b  b 1 2b 1  1 2b  và  .    . (2) a  3b 2 a  3b 2  2 a  3b  a  b 1  3 a  1 1  3 a  Từ (1) và (2) suy ra         . (3) a  3b 2  2 a  b  a  3b 2  2 a  b  1 1  3 b 
Chứng minh tương tự ta cũng có    . (4) b  3a 2  2 a  b  1 1 Từ (3) và (4) suy ra 
 2. (điều phải chứng minh) a  3b b  3a 1
Dấu "  " xảy ra khi a  b  . 4
Câu 73: [TS10 Chuyên Khánh Hòa, 2018-2019]
Cho a, b,c là các số thực dương thỏa mãn điều kiện a  b  c  abc. Chứng minh 2 2 1 a 1 b rằng 2   1 c  1 a b Lời giải 1 1 1
Ta có: a  b  c  abc     1 ab ac bc 1 1 1 Đặt x  ; y 
; z  thì bất đẳng thức đã cho trở thành : xy  xz  yz  1 a b c 2 2 1  a 1  b 2   1 c  1 a b 1 1 1   1   1  c  1  1 2 2 2 a b c 2  2 2 1 z  1 x  1 y   1 z
THCS.TOANMATH.com FB TRỊNH BÌNH 51 2  2 2 1 z  1 1 x  1 y   0 z
        2  2 2 2 2 1 z 1 x 1 1 y 1  1 x . 1 y   0 z       1 x   1  1 y   2 2 2 1 z z 1 x 1 y 2 2 1   0 z Ta lại có: 1  x
1  y  1  x  y  x y  1 xy2  x  y2 2 2 2 2 2 2
 xz  yz2  x  y2  z 1x  y2 2  x  y 2 1  z    
 bdt   1 x 1 1 y 1 2 2 1 z z(x y) 1 z 2 2   0 z      
1  x  1 1 y 1 2 2 1 z (xz yz) 1 z 2 2   0 z      
1  x  1 1 y 1 2 2 1 z (1 xy) 1 z 2 2   0 z   
1  x  1 1 y 1 2 xy 1 z 2 2   0 z
Từ đó ta có điều phải chứng minh.
Câu 74: [TS10 Chuyên Phan Bội Châu, 2018-2019]
Cho a, b,c thực dương thỏa mãn abc  1. Chứng minh rằng: 1 1 1    3 4 3 4 3 4 3 a  a  ab  2 b  b  bc  2 c  c  ac  2 Lời giải Ta có:
a 12  2a a1  0   2a 2a1 2a a1  0 4 3 4 3
 a  a  a  1  0  a  a  1  a 4 3
 a  a  ab  2  ab  a  1 1 1   4 3 a  a  ab  2 ab  a  1
Chứng minh ho|n to|n tương tự ta có: 1 1 1 1  ;  4 3 4 3 b  b  bc  2 bc  b  1 c  c  ac  2 ac  c  1 Như vậy 1 1 1  1 1 1  VT     3.     ab  a  1 bc  b  1 ac  c  1
 ab  a  1 bc  b  1 ac  c  1 
(Áp dụng BĐT Bunyakovski cho 3 số)
THCS.TOANMATH.com FB TRỊNH BÌNH 52 Lại có  1 1 1   1 a ab  3.    3.       2
 ab  a  1 bc  b  1 ac  c  1 
 ab  a  1 abc  ab  a a bc  abc  ab   1 a ab   3.      3
 ab  a  1 1 ab  a a  ab  1 
Vậy ta có điều phải chứng minh
Dấu “=” xảy ra khi và chỉ khi a  b  c  1.
Câu 75: [TS10 Chuyên Hà Nam, 2018-2019] 2010 a  2010
Cho a là số bất kì,chứng minh rằng:  2 2010 a  2009 Lời giải Ta có: 2010 2010 2010 2010 a  2010  2 a  2009  a  2009 1  2 a  2009    2 2010 2010 a 2009  2 a  2009 1  0     2 2010 a
2009 1  0 luôn đúng với mọi a
Câu 76: [TS10 Chuyên Nam Định, 2018-2019]
Cho các số thực dương thỏa mãn a  b  1 2 1
Chứng minh rằng: 3a  b  a  b  4ab  a3bb3a 2 Lời giải     Ta có:      AM GM 1 a 3b b 3a a 3b b 3a   a  b 2 4 Từ giả thiết ta có:                2 a b 1 a b 2 ab 1 2 ab 1 a b 4ab 1 a b     
        2      2 2 1 3(a b) (a b) 4ab a 3b b 3a 3 a b a b 1 a b  a  b 2 2 2 2 2
 3a  6ab  3b  2a  2b  a  b 1 2a  2b  2ab  0 2 2
 4a  4b 1 8ab  4a  4b  0     2 1 2a 2b  0
Vậy đẳng thức được chứng minh. NĂM HỌC 2017-2018
THCS.TOANMATH.com FB TRỊNH BÌNH 53
Câu 77: [TS10 Chuyên TP. Hồ Chí Minh, 2017-2018] 2 2 16 xy x  y
Cho x, y là hai số thực dương. Tìm GTNN của biểu thức: P   x  y xy Lời giải
Áp dụng BĐT AM – GM cho ba số không âm ta có: 2 2 16 xy x  y 2 16 xy (x  y) 2 8 xy 8 xy (x  y) P   =   2 =    2 x  y xy x  y xy x  y x  y xy 2 8 xy 8 xy (x  y)  3 3. . .  2  10 x  y x  y xy 2 8 xy (x  y) Đẳng thức xảy ra khi  ⇔ x = y x  y xy
Vậy giá trị nhỏ nhất của P là 10
Câu 78: [TS10 Chuyên Lam Sơn, 2017-2018]
Cho a, b, c l| độ dài của ba cạnh tam giác. Chứng minh rằng: 2 2 2 2 2 2 2 2 2 a  b  c b  c  a a  c  b    1 2ab 2bc 2ca Lời giải 2 2 2 2 2 2 2 2 2 a  b  c b  c  a a  c  b Ta có:    1 2ab 2bc 2ca 2 2 2 2 2 2 2 2 2
c(a  b  c )  a(b  c  a )  b(a  c  b )  2abc   0 2abc 2 2 2 2 2 2 2 2 2
 c(a  b c ) a(b  c a )  b(a  c  b )  2abc  0 2 2 2 2 2 2 2 2 2
 c(a  b c  2ab) a(b  c a  2bc)  b(a  c  b  2ca)  0 2 2 2 2 2 2
 c((a  b)  c ) a((b c) a )  b((c a)  b )  0
 c(a  b  c)(a  b c)a(b c a)(b a c) b(c a  b)(c  b a)  0  (a  b  c) c
 a  b  c  a b  c  a  ba  c  b >0  2 2 2
 (a  b  c)(c a  2ab  b )  0 2 2
 (a  b  c)[c (a  b) ]  0
 (a  b  c)(c  a  b)(c  a  b)  0 a   b  c  0 
Do a, b, c l| ba cạnh của tam gi{c nên c  b  a  0 c a  b  0 
Suy ra: (a  b  c)(c  a  b)(c  a  b)  0 ⇔ x = y (luôn đúng)
Vậy ta chứng minh được BĐT ban đầu.
THCS.TOANMATH.com FB TRỊNH BÌNH 54
Câu 79: [TS10 Chuyên KHTN Hà Nội vòng 1, 2017-2018]
Cho a, b là số các số thực dương. Tìm gi{ trị lớn nhất của biểu thức: 1 1 1 M  (a  b)(  )  3 3 a  b a  b ab Lời giải 1 1 Ta có: 3 2 3 2
(a  b)(  b)  (a  b) ;(b  a)(  a)  (a  b) . a b 1 1 1 1 a  b      1 1 a b 1 1 1 Khi đó a b   a b   1   1. 3 3 2 a  b a  b (a  b) ⇔ VT ≤ a  b ab ab ab
Đẳng thức xảy ra khi a = b = 1
Vậy giá trị lớn nhất của M là 1 khi a = b = 1.
Câu 80: [TS10 Chuyên KHTN Hà Nội vòng 2, 2017-2018]
Với a, b, c là các số thực dương thỏa mãn: ab + bc + ca + abc = 2. a  1 b  1 c  1
Tìm giá trị lớn nhất của biểu thức: M    . 2 2 2 a  2a  2 b  2b  2 c  2x  2 Lời giải 1 1  1 1 
Với x, y dương ta có bất đẳng thức thức:     *: x  y 4  x y  x  y 1 2 2 Thật vậy: *  
 x  y  4xy  x  y  0 (luôn đúng) 4xy x  y
Bất đẳng thức (*) xảy ra dấu “=” khi x = y.
Quay trở lại bài toán ta có: abc  ab  bc  ca  2
 abc  ab  ac  bc  a  b  c  1  a  b  c  3
 (a  1)(b  1)(c  1)  (a  1)(b  1)(c  1)
(a  1)  (b  1)  (c  1)   1 (a  1)(b  1)(c  1) 1 1 1     1
(a  1)(b  1) (b  1)(c  1) (c  1)(a  1) 3 3 3 Đặt a  1  , b  1  ,c  1  x y z
Khi đó giả thiết bài toán trở thành: xy + yz + zx = 3 và
THCS.TOANMATH.com FB TRỊNH BÌNH 55 a  1 b  1 c  1 M    2 2 2 a  2a  2 b  2b  2 c  2x  2 a  1 b  1 c  1    2 2 2
(a  1)  1 (b  1)  1 (c  1)  1 1 1 1    1 1 1 a  1  b  1  c  1  a  1 b  1 c  1 1 1 1    3 x 3 y 3 z    x 3 y 3 z 3 x y z  3(   ) 2 2 2 x  1 y  1 z  1 x y z  3(   )
(x  y)(x  z) (y  z)(y  x) (z  x)(z  y) 3 x x y y z z 3 3  (      )  . 4 x  y x  z y  z y  x z  x z 
(Áp dụng bất đẳng thức (*)) y 4
Đẳng thức xảy ra khi x = y = z = 3  1 3 3
Vậy giá trị lớn nhất của M là 4
Câu 81: [TS10 Chuyên Bình Dương, 2017-2018]
Cho x, y l| số thực dương thỏa mãn x ≥ 2y. 2 2 x  y
Tìm GTNN của biểu thức M  . xy Lời giải 2 2 2 2 2 x  y x  4y 3y 4xy 3y 3 5 Ta có : M       4   . xy xy xy xy x 2 2 2 2 x  4y
Đẳng thức xảy ra khi   x  2y  x  2y 5
Vậy gi{ trị nhỏ nhất của M l| khi x = 2y. 2
Câu 82: [TS10 Chuyên Nam Định, 2017-2018]
Xét c{c số thực a, b, c không }m, kh{c 1 thỏa mãn a + b + c = 1. 1 1
Tìm gi{ trị nhỏ nhất cảu biểu thức P    (a  b)(4  5c). a  bc b  ac Lời giải 1 1 1 Áp dụng BĐT :   ( x  ,y  0) x y x  y
THCS.TOANMATH.com FB TRỊNH BÌNH 56 Ta có : 1 1 4 P    (a  b)(5c  4)   (a  b)(5c  4) a  bc b  ac (a  b)(c  1) 4 5c  4 c   (1 c)(5c  4)  4  4  4  8 (1 c)(1 c) c  1 c  1 1
Dấu « = » xảy ra khi c  0,a  b  . 2
Vậy gi{ trị nhỉ nhất của P l| 8
Câu 83: [TS10 Chuyên Bà Rịa Vũng T|u, 2017-2018]
Cho x, y l| c{c số thực dương. Tìm gi{ trị nhỏ nhất của biểu thức : xy 1 1 2 2 P   (  ) 2(x  y ). 2 2 x  y x y Lời giải
Ta có : x2 + y2 ≥ 2xy nên : 2(x2 + y2) ≥ (x + y)2. Do đó : 2 2 xy 1 1 xy 1 1 xy x  y 2 2 P   (  ) 2(x  y )   (  )(x  y)    2 2 2 2 2 2 2 x  y x y x  y x y x  y xy 2 2 2 2 4xy x  y 3xy 3(x  y )    2   2 4  2  2 2 2 2 2 2 x  y xy x  y 2(x  y ) 3 9  6   . 2 2 2 2  x  y  2xy  Dấu « = » xảy ra khi 2 2  4xy x  y  x  y.   2 2 x   y xy 9
Vậy gi{ trị nhỏ nhất của P l| . 2
Câu 84: [TS10 Chuyên Bạc Lưu, 2017-2018]
Cho a, b, c thỏa mãn a  1; b  4; c  9 . Tìm gi{ trị nhỏ nhất của biểu thức :
bc a  1  ac b  4  ab c  9 M  . abc Lời giải a  1 b  4 c  9 Ta có : M    . a b c
Do a  1; b  4; c  9 . Áp dụng BĐT AM –GM cho c{c cặp số không }m, ta có :
THCS.TOANMATH.com FB TRỊNH BÌNH 57  a 1 1          a 2 a (a 1) 1 2 a 1   b  4 1 1 1 1 11
b  (b  4)  4  4 b  4  
 . Do đó : M     . b 4   2 4 6 12
c  (c  9)  9  6 c  9   c  9 1    c 6   a 1  1  a  2  
Dấu « = » xảy ra khi b  4  4   b  8   c  9  9 c  18  
Câu 85: [TS10 Chuyên Đắc Lắc, 2017-2018] a b 4c
1) Cho các số dương a, b, c. Chứng minh rằng:    2 b  c c  a a  b 2 2 2 a   b  c  11
2) Cho các số dương a, b, c thỏa mãn điều kiện: abbcca 7 1 Chứng minh:  a,b,c  3. 3 Lời giải  y  z  x a   2 x  a  b    x  y  z
Đặt y  b  c  b  2   z  c  a   x  y  z c   2 Ta có: a b 4c y  z  x x  y  z x  y  z      4 b  c c  a a  b 2x 2y 2z  y x   2y z   2x z               3  2x 2y   z 2y   z 2x  AMGM y x 2y z 2x z  2 .  2 .  2 .  3 2x 2y z 2y z 2x  1 2  2  3  2 a b 4c
Dấu “=” không xảy ra nên    2 b  c c  a a  (đpcm) b Cách khác:
Sử dụng bất đẳng thức AM-GM-Schwars ta có:
THCS.TOANMATH.com FB TRỊNH BÌNH 58 a b 4c a b 4c    2 2 2 2 a b 2c       b  c c  a a  b ab  ac bc  ab ac  bc 2ab  bc  ca    2 a b 2c Ta lại có: 
2ab  bc  ca 2 * 2 2
Thật vậy:      
           2 * a b 2c 4 ab bc ca 0 a b  4c  0 (đúng)
Vậy bất đẳng thức đã cho được chứng minh. 2 2 2 a
  b  c  11  a  b  5  c b) Ta có:    ab  bc  ca  7 a  b  7  c 
a b  7 c5c 2 2 2 2 Do:
ab  0  ab  4ab  5c  47 5cc 2 1
 3c 10c  3  0   c  3 3 1 1
Chứng minh tương tự ta được:  a  3,  b  3 3 3 1 Vậy  a, b,c  3 3
Câu 86: [TS10 Chuyên Bắc Giang, 2017-2018] x
Cho 2 số thực dương x, y thỏa mãn 2 xy   1 . 3 x 4x
Tìm giá trị nhỏ nhất biểu thức: P    15xy. y 3y Lời giải
Tách và áp dụng BĐT AM-GM ta được: y x x 4 4 P     3xy  12xy   x y 3y 3 3 y x x 4 4  2 .  2. .3xy  2 12xy.  x y 3y 3 3 4 2
 2  2x  8 xy   2x   8 xy 3 3 2 x  2 2x.  8 xy  4  8 xy  4 3 3 1
Dấu “=” xảy ra khi x  y  3 Câu 87:
[TS10 Chuyên H| Tĩnh, 2017-2018] 1 2017 2018
Cho các số dương a, b, c thỏa mãn:    1 1 a 2017  b 2018  c
Tìm giá trị nhỏ nhất của biểu thức: P  abc. Lời giải
THCS.TOANMATH.com FB TRỊNH BÌNH 59 Ta có: 1 2017 2018 2018 1 2017    1  1   1  a 2017  b 2018  c 2018  c 1  a 2017  b AMGM c 1 2017 1 2017    2 .  2018  c 1  a 2017  b 1  a 2017  b b 1 2018 a 2017 2018 Tương tự:  2 . ;  2 . 2017  b 1 a 2018  c 1 a 2017  b 2018  c Nhân theo vế ta được: abc 2017.2018         8     
   abc  8.2017.2018 a 1 2017 b 2018 c a 1 2017 b 2018 c
Dấu “=” xảy ra khi a  1, b  2017,c  2018
Vậy giá trị lớn nhất của P là 8.2017.2018
Câu 88: *TS10 Chuyên Bình Phước, 2017-2018]
a) Cho ba số a, b,c thỏa mãn a  b  c  0 và a  1, b  1, c  1. Chứng minh rằng 4 6 8 a  b  c  2.  3 3   2 2 x y x  y 
b) Tìm giá trị nhỏ nhất của biểu thức T  
với x, y là các số thực lớn x  1y 1 hơn 1. Lời giải
a) Từ giả thiết a  1, b  1, c  1, ta có 4 2 6 2 8 2
a  a , b  b ,c  c . Từ đó 4 6 8 2 2 2
a  b  c  a  b  c Lại có a   1 b   1 c   1  0 và a   1 b   1 c   1  0 nên
a 1b 1c 1a 1b 1c 1  0
 2ab  2bc  2ca  2  0  2
 ab  bc  ca  2 . Hơn nữa 2 2 2
a  b  c  0  a  b  c  ab  bc  ca  2 . Vậy 4 6 8 a  b  c  2 .  3 3 x  y    2 2 x  y  2 x x   2 1  y y 1 2 2 x y b) Ta có T      x   1 y   1 x1y1 y  1 x  1
Do x  1, y  1 nên x 1  0, y 1  0 2 2 x y
Áp dụng bất đẳng thức AM-GM cho 2 số dương , y  1 x  , ta có : 1          2 x x 1 1 2 x 1
x 1 1  0  x  2 x  1  0   2 x  1
THCS.TOANMATH.com FB TRỊNH BÌNH 60          2 x y 1 1 2 y 1
y 1 1  0  y  2 y  1  0   2 y  1 2 2 x y 2xy Do đó T     8 y  1 x  1 x  1. y  1 2 2  x y   y  1 x  1  x  2
Dấu “  ” xẩy ra khi x  1  1   (thỏa mãn điều kiện) y    2 y  1  1  
Vậy giá trị nhỏ nhất của biểu thức T  8 khi x  y  2.
Câu 89: [TS10 Chuyên Quảng Ninh, 2017-2018] Cho ;
a b thoả mãn a  2; b  2 . Chứng minh rằng: 2 2
(a  1)(b  1)  (a  b)(ab  1)  5 . Lời giải Xét hiệu 2 2
M  (a  1)(b  1) (a  b)(ab  1)  5 2 2 2 2 2 2
 (a b a b ab ab) (a  b a  b ab)  4 1 2  ab(a 1)(b1)  (a
  b) a(a  2)  b(b  2)  4   . 2
Chỉ ra với a  2 thì a(a 1)  2 và a(a  2)  0
b  2 thì b(b 1)  2 và b(b  2)  0 1
nên ab(a 1)(b1)  4 ; 2 (a
  b) a(a  2)  b(b  2)  0   2  M  0hay 2 2
(a  1)(b  1)  (a  b)(ab  1)  5 .
Câu 90: [TS10 Chuyên Vĩnh Phúc, 2017-2018]
Cho a, b,c là các số thực dương thoả mãn a  b  c  3. Chứng minh rằng  2 2 2    3 3 3 4 a b c a  b  c   9. Lời giải
Bất đẳng thức cần chứng minh tương đương:     2 2 2     3 3 3 4 a b c a b c 3 a  b  c   27
 4a  b  ca  b  c  3a  b  c   a  b  c3 2 2 2 3 3 3
 a  b  c  4a b  b c  c a ab  bc  ca   a  b  c3 3 3 3 2 2 2 2 2 2 (1)
THCS.TOANMATH.com FB TRỊNH BÌNH 61 3
Ta có đẳng thức       3 3 3     2 2 2 2 2 2 a b c a b c
3 a b  b c  c a  ab  bc  ca   6abc .
Do đó (1) tương đương với 2 2 2 2 2 2
a b  b c  c a a c  b a c b  6abc.
Áp dụng bất đẳng thức AM-GM, ta có 2 2 2 2 2 2 2          2     2 a b b c c a a c b a c b a b c b c a  c a  b 2 2 2      2 2 2 2a bc 2b ca 2c ab 2 a bc  b ca  c ab   6abc.
Vậy BĐT (1) được chứng minh. Đẳng thức xảy ra khi và chỉ khi a  b  c  1.
Câu 91: [TS10 Chuyên Sư Phạm Hà Nội, 2017-2018]
 x  x  x ... x  10
C{c số thực không }m x ,x ,x ,....,x thỏa mãn 1 2 3 9  1 2 3 9
x  2x  3x  ...  9x  18  1 2 3 9
Chứng minh rằng: 1.19x  2.18x  3.17x  ...  9.11x  270 1 2 3 9 Lời giải.
Ta có : 9x  x  x ...  x  90 , suy ra : 1 2 3 9 
 9x  x  x ... x  90 1 2 3 9         10
 x  2x  3x ...  9x  19x 29x 39x ... 99x 270 1 2 3 9   180 1 2 3 9 Mặt kh{c:
1.19x  2.18x  3.17x  ...  9.11x 1 2 3 9
 19x  29x  39x ... 99x  7x 12x 15x ...7x  270 (đpcm) 1 2 3 9   2 3 4 8   x  9 1  Dấu “=” xảy ra khi  x  1 9 x  x  ...  x  0  2 3 8
Câu 92: [TS10 Chuyên Hải Dương, 2017-2018]
Cho x, y, z là các số dương thỏa mãn 2 2 2 2 2 2
x  y  y  z  z  x  6 2 2 2 x y z
Tìm giá trị nhỏ nhất của biểu thức: M    y  z z  x x  y Lời giải Ta có: 2 2 2 2 2 2
6  x  y  y  z  z  x  3 2 2 2 2 2 2
x  y  y  z  z  x   6 2 2 2 x  y  z  2 2 2  x  y  z  6 Do đó:
THCS.TOANMATH.com FB TRỊNH BÌNH 62 2 2 2 2 2 2 x y z x y z M       y  z z  x x  y 2 2 2 y  z  2 2 2 z  x  2  2 2 x  y  6   2 2 y  z  6   2 2 z  x  6   2 2 x  y     2  2 2 y  z  2  2 2 z  x  2  2 2 x  y    6 1 1 1 1          2 2 2 2 2 2
x  y  y  z  z  x 2 2 2 2 2 2  2 y  z z  x x  y 2   6 9 6  .  2 2 2 2 2 2 2
x  y  y  z  z  x 2 6 9 6  .  2 6 2 3 2  2
Dấu “=” xảy ra khi a  b  c  2 3 2
Vậy giá trị nhỏ nhất của M là 2
Câu 93: [TS10 Chuyên Sư Phạm Hà Nội vòng 2, 2017-2018]
Cho c{c số dương a,b,c,d . Chứng minh rằng trong 4 số 1 1 1 1 1 1 1 1 2 2 2 2 a 
 ; b   ;c   ;d   Có ít nhất một số không nhỏ hơn 3. b c c d c d a b Lời giải
Giả sử cả bốn số đều nhỏ hơn 3 thì 2 1 1 2 1 1 2 1 1 2 1 1 P  a 
  b    c    d    3 b c c d c d a b Mặt kh{c :   2 1 1 2 1 1 2 1 1 2 1 1 2 2 2 2 1 1 1 1 P  a 
  b    c    d    a  b  c  d  2      b c c d c d a b  a b c d  Do         2 2 2 2 2 1 1 1 1 4 4 a b c d a b c d ;     a b c d a  b  c  d a bcd2 16 16 a bcd2 16 16 3  P     . .  12 4
a  b  c  d a  b  c  d 4
a  b  c  d a  b  c  d
Tr{i điều giả sử suy ra có ít nhất một số không nhỏ hơn 3.
Câu 94: [TS10 Chuyên Hưng Yên, 2017-2018]
Cho 3 số a, b, c dương v| 4 4 4 4 4 4 4 4 4
a b  b c  c a  3a b c . Chứng minh: 1 1 1 3    . 3 2 3 2 3 2
a b  2c  1 b c  2a  1 c a  2b  1 4 Lời giải
THCS.TOANMATH.com FB TRỊNH BÌNH 63 Ta có: 4 4 4 4 4 4 4 4 4 1 1 1
a b  b c  c a  3a b c     4 (1) 4 4 4 a b c Sử dụng AM-GM ta có: 1 1 1 1 1 1 4     4 4 .  4 4 4 4 12 4 3 a a a b a b a b 1 1 1 1 1 1
L| tương tự và cộng theo vế ta được:      (2) 4 4 4 3 3 3 a b c a b b c c a AMGM 1 2 Mặt khác:  1  4 2 a a 1 1 1 1  1 1 1  3
L|m tương tự và cộng lại ta được:         (3) 2 2 2 4 4 4 a b c 2  a b c  2 1 1  1 1 1 1 
Với x, y, z, t dương ta có:       (*) x  y  z  t 16  x y z t 
Thật vậy, sử dụng AM-GM ta có:    x  y  z  t 1 1 1 1 4 4
      4 xyzt.  16 4  x y z t  xyzt 1 1  1 1 1 1         x  y  z  t 16  x y z t 
Đẳng thức xảy ra khi x = y = z = t. 1 1 1  1 1 1  Áp dụng (*) ta được:       1 3 2 3 2 2 3 2 2 a b  2c  1 a b  c  c  1 4  a b c c  Tương tự: 1 1  1 2  1 1  1 2     1 ;       1 3 2 3 2 3 2 3 2 b c  2a  1 16  b c a
 c a  2b 1 16  b c a  Cộng theo vế ta được: 1 1 1 1  1 1 1  1  1 1 1  3              3 2 3 2 3 2 3 3 3 2 2 2
a b  2c  1 b c  2a  1 c a  2b  1 16  a b b c c a  8  a b c  16
Theo (1), (2) và (3) ta có thể suy ra: 1 1 1 1  1 1 1  1  1 1 1  3              3 2 3 2 3 2 3 3 3 2 2 2
a b  2c  1 b c  2a  1 c a  2b  1 16  a b b c c a  8  a b c  16 1  1 1 1  1  1 1 1  3        3      4 4 4 4 4 4 16  a b c  16  a b c  16 3 6 3 3     16 16 16 4
THCS.TOANMATH.com FB TRỊNH BÌNH 64
Dấu “=” xảy ra khi a = b = c = 1.
Câu 95: [TS10 Chuyên Bà Rịa Vũng T|u, 2017-2018]
Cho a, b, c là các số thực dương.Tìm gi{ trị lớn nhất của biểu thức: 2 2 2 a b  b c  c a 1 P    2 2 2 a  b  c . 2 2 2  a  b  c 3 Lời giải
Với a, b, c dương ta có:     2 2 2      2 2 2 a b c a b c 3 a b  b c  c a (1) Thật vậy:
VT  a  b  c 2 2 2 a  b  c  3 2 2 2 2 2 3 2 2
 a  ab  ac  b  ba  bc  c  ca  cb   2 2 2
a b  b c  c a   3 2 a  ab    3 2 b  bc    3 2 c  ca  AMGM   2 2 2 a b  b c  c a 2 2 2  2a b  2b c  2c a   2 2 2 3 a b  b c  c a =VP 2 2 2 a b  b c  c a a  b  c Do đó:  2 2 2 a  b  c 3 2 2 2 a b  b c  c a 1      2 2 2    a b c 1 P a b c    2 2 2 a  b  c 2 2 2  a  b  c 3 3 3 2 a  b  c 1      2 1 1       1 1 a b c a b c     3 9 4 3 2  4 1
Dấu “=” xảy ra khi a  b  c  2 1
Vậy giá trị lớn nhất của P là 4 Câu 96:
[TS10 Chuyên Tây Ninh, 2017-2018]
Cho x, y là số thực dương nhỏ hơn 1.Tìm gi{ trị lớn nhất của biểu thức: xy 1 x  y
Q  xy1x1y Lời giải Ta có: 1
x y1x1y x y1xyxy x y x y x y x  y       Q xy 1 x  y xy 1 x  y xy 1  x  y xy 1  x  y
Đặt t = x + y, ta được: 1 x  y x  y 4x  y x  y 4 x  y 4 t         Q xy 1 x  y
  2 1x y x y 1x y x y  t 1t
Sử dụng bất đẳng thức Cauchy-Schwarz ta được:
THCS.TOANMATH.com FB TRỊNH BÌNH 65 1 4 t 2 1   2 2 2 1 9 1     1  1  1  8  Q  Q t 1 t t 1 t t  1 t 1 8 1
Dấu “=” xảy ra khi x  y  3 1
Vậy giá trị lớn nhất của Q là 8
Câu 97: [TS10 Chuyên Ninh Bình, 2017-2018]
Cho a, b, c dương thỏa mãn điều kiện a  b  c  2018 . Tìm giá trị lớn nhất của a b c biểu thức: P    a  2018a  bc b  2018b  ca c  2018c  ab Lời giải Ta có: a a a   a  2018a  bc
a  a  b  ca  bc a  ab   2 a  bc  ac a a a          2 a  b  c a ab 2a bc ac a ab ac b b c c Tương tự:  ;  b  2018b  ca a  b  c c  2018c  ab a  b  c a  b  c
Cộng theo vế ta được: P   1 a  b  c 2018
Dấu “=” xảy ra khi a  b  c  3
Vậy giá trị lớn nhất của P là 1.
Câu 98: [TS10 Chuyên Đồng Tháp, 2018-2019]
Cho 3 số dương x, y, z thỏa mãn điều kiện 3 3 3
x  y  z  1. Chứng minh bất đẳng 2 2 2 x y z thức sau:    2 2 2 2 1 x 1 y 1 z Lời giải
Sử dụng BĐT AM-GM ta được:   x 1 x  2 2 2 3 2 2 x 1 x 1 x x 3      2x 2 2 2 2 1 x x  2 1  x  2 2 y x Tương tự: 3 3  2y ;  2z 2 2 1 y 1  z 2 2 2 x y z Cộng theo vế ta được:    2 3 3 3
x  y  z   2 (đpcm) 2 2 2 1 x 1 y 1 z
THCS.TOANMATH.com FB TRỊNH BÌNH 66
Câu 99: [TS10 Chuyên Thừa Thiên Huế, 2018-2019]
Cho a, b, c là số dương thay đổi thỏa mãn điều kiên: ab  bc  ca  1. Tìm giá 2 2 2 a b c trị biểu thức: E    a  b b  c c  a Lời giải
Sử dụng bất đẳng thức Cauchy-Schwarz ta được: a b c    2 2 2 2 a b c a  b  c E             2a  b  c ab bc ca 1 a b b c c a 2
Dấu “=” xảy ra khi a = b = c = 1.
Vậy giá trị nhỏ nhất của E là 1.
Câu 100: [TS10 Chuyên Bắc Ninh, 2018-2019]
Cho các số thực a, b, c thỏa mãn a  b  c  3. Tìm giá trị nhỏ nhất của biểu thức: 2 2 2 a  6a  3 b  6b  3 c  6c  3 M    2 2 2 a  a b  b c  c Lời giải Ta có:    2 3a  3 2 2   AMGM 2 2 6a 2a a 6a 3 6a  6a  2a 12a  2a 14     2  2 2 2 2 a  a a  a a  a a  a a  1 2 2 b  6b  3 14 c  6c  3 14 Tương tự:   2 ;   2 2 2 b  b b  1 c  c c  1
Cộng theo vế và sử dụng bất đẳng thức AM-GM dạng cộng mẫu số ta được: 2 2 2 a  6a  3 b  6b  3 c  6c  3  1 1 1  M     14      6 2 2 2 a  a b  b c  c
 a  1 b  1 c  1  9 9  14.  6  14.  6  15 a  b  c  3 3  3
Dấu “=” xảy ra khi a = b = c = 1.
Câu 101: [TS10 Chuyên Vĩnh Long, 2018-2019] 1 1
Cho x, y, z dương thỏa mãn x  y  z  4 . Chứng minh rằng:   1 xy xz Lời giải Ta có: 1 1 1  1 1  1 4 4 16       .    (đpcm) xy xz
x  y z  x y  z xy  z x  y  z 1 2
Dấu “=” xảy ra khi x = 2, y = z = 1.
THCS.TOANMATH.com FB TRỊNH BÌNH 67 NĂM HỌC 2016-2017
Câu 102: [TS10 Chuyên H| Tĩnh, 2016-2017]
Cho a, b, c là các số dương thỏa mãn: a  b  c  2016 . Tìm giá trị lớn nhất của a b c biểu thức: P    . a  2016a  bc b  2016b  ac c  2016c  ab Lời giải
Ta có a  2016a  bc  a  a  b  ca  bc  a  a  ba  c
Áp dụng bđt Bunyakoskicopski ta có:  
  2  2  2  2             2 a b a c a b . c a ac ab    
Suy ra a  a  ba  c  a  ac  ab  a  a  b  c  a a Suy ra  a  2016a  bc a  b  c b b c c Tương tự  ;  b  2016b  ac a  b  c c  2016c  ab a  b  c a  b  c Suy ra P 
 1 , Dấu = xảy ra khi a  b  c  672 a  b  c
Câu 103: [TS10 Chuyên Bà Rịa Vũng T|u, 2016-2017]
Cho a, b, c là 3 số dương thỏa mãn ab + bc + ca = 3abc. Chứng minh rằng: a b c 3    2 2 2 a  bc b  ca c  ab 2 Lời giải ab  bc  ca 1 1 1
Từ điều kiện đề bài ta có  3     3 abc a b c
Áp dụng hai lần bất đẳng thức Côsi cho hai số dương, ta có: 2 2 a 2 1
a  bc  2 a .bc  2a bc    2 a  bc 2a bc 2 bc 1 1 1  1 1  a 1  1 1  .          2 b c 2  b c  a  bc 4  b c  b 1  1 1  c 1  1 1  Tương tự ta có:   ;       2 2 b  ca
4  c a  c  ab 4  a b 
THCS.TOANMATH.com FB TRỊNH BÌNH 68 a b c 1  1 1 1  3 Suy ra         . 2 2 2 a  bc b  ca c  ab 2  a b c  2
Câu 104: [TS10 Chuyên Bà Rịa Vũng T|u, 2016-2017]
Cho hai số thực a, b đều lớn hơn 1. Chứng minh rằng: 6 11  3ab  4  . a b  1  b a  1 2 Lời giải b  1 1 ab Ta có: a b  1  a.  . 2 2 a  1 1 ab 6 6 Tương tự: b a  1  b.    . 2 2 a b  1  b a  1 ab
Dấu “=” xảy ra khi a  b  2. 6 6 18 Q   3ab  4   3ab  4   3ab  4. a b  1  b a  1 ab 3ab Đặt 2
y  3ab  4  3ab  y  4. Khi đó: AMGM 18 18 3 1 3 1 11 3 Q   y 
 (y  2)  (y  2) 1  3 18. . 1  . 2 y  4 (y  2)(y  2) 4 4 4 4 2
Dấu “=” xảy ra khi y = 2 hay a  b  2.
Câu 105: [TS10 Chuyên Bà Rịa Vũng T|u, 2016-2017]
Cho x, y, z là 3 số dương thỏa mãn 2 2 2
x  y  z  3xyz . Chứng minh : 2 2 2 x y z    1. y  2 z  2 x  2 Lời giải 2 2 2 x y  2 x y  2 2 x 6x  y  2 Ta có   2 .  x   y  2 9 y  2 9 3 y  2 9 2 y 6 y  z  2 2 z 6z  x  2 Tương tự  ,  . z  2 9 x  2 9
Đặt vế trái của (*) là P. Cộng các bất đẳng thức trên theo vế ta được:
5 x  y  z  6 P  9
THCS.TOANMATH.com FB TRỊNH BÌNH 69
x  y  z3 1 2 Lại có 2 2 2
 3xyz, x  y  z  x  y  z . 9 3
x  y  z3 1 2 Từ giả thiết suy ra
 x  y  z  x  y  z  3 . 9 3 Do đó P  1.
Câu 106: [TS10 Chuyên Sư Phạm Hà Nội, 2016-2017]
Cho a, b, c là ba số thực không âm và thỏa mãn: a + b + c = 1. Chứng minh rằng
5a  4  5b  4  5c  4  7 Lời giải 2 a  (1 a)  0 a   a  
Vì a, b, c không âm và có tổng bằng 1 nên 2
0  a, b,c  1  b(1 b)  0  b  b   2 c(1  c)  0 c   c  Suy ra 2 2
5a  4  a  4a  4  (a  2)  a  2
Tương tự 5b  4  b  2; 5c  4  c  2
Do đó 5a  4  5b  4  5c  4  (a  b  c)  6  7 (đpcm)
Câu 107: [TS10 Chuyên Sơn La, 2016-2017] 1 1
Cho hai số dương a, b thỏa mãn: a  b  2 2 . Tìm GTNN của biểu thức: P   a b Lời giải
Với mọi a, b ta luôn có: (a - b)2  0 2 2 2 2 2 2 2
 a  b  2ab  0  a  b  2ab  a  b  2ab  4ab  (a  b)  4ab (*)
Vì a, b đều dương nên ab v| a+ b cũng dương bất đẳng thức (*) trở thành: a  b 4 1 1 4 4       P  mà a+b  2 2 ab a  b a b a  b a  b 4 4    P  2 a  b 2 2 2 (  a  b)  0
Dấu “ = ” xảy ra    a  b  2 a    b  2 2 Vậy min P= 2
Câu 108: [TS10 Chuyên Bình Thuận, 2016-2017]
THCS.TOANMATH.com FB TRỊNH BÌNH 70
Cho các số dương x, y, z. Chứng minh rằng: 2 2 2 xy yz zx x  y  z    2 2 2 x  yz  zx y  zx  xy z  xy  yz xy  yz  zx Lời giải
Áp dụng bất đẳng thức AM-GM-Schwar ta có: xy  2 y  yz  zx xy  2 y  yz  zx xy    2 x  yz  zx
 2x yzzx 2y yzzx xyyzzx2 yz 2 z  zx  xy zx 2 x  xy  yz yz zx  Tương tự:  ;  2 y  zx  xy    2 2 z  xy  yz xy yz zx xy yzzx2 Suy ra zx  2 2 2
x  y  z xy  yz  zx xy yz  2 2 2 x  y  z     2 2 2 x  yz  zx y  zx  xy z  xy  yz xy yzzx2 xy  yz  zx
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi x = y = z.
Câu 109: [TS10 Chuyên Thừa Thiên Huế, 2016-2017]
Cho x, y > 0 và x  y  3 . Tìm giá trị nhỏ nhất của: 4x 3y 2 2 M  6x  4y  10xy    2016 y x Lời giải
Sử dụng bất đẳng thức AM-GM ta được: 4x 3y xy   4x ; 3xy   6y y x Do đó: 2 2          2 2 A 6x 6xy 4y
4x 6y 6x x y  4y  6y  4x  6x.3  4y  6y  4x 2
 2x  4y  6y  22x  44y 46y  22x  y16  50
Suy ra: M  50  2016  2066
Dấu “=” xảy ra khi x = 1; y = 2.
Vậy giá trị nhỏ nhất của M là 2066.
Câu 110: [TS10 Chuyên Thái Nguyên, 2016-2017]
Tìm giá trị nhỏ nhất của biểu thức: P  x  6 x  9  x  6 x  9 Lời giải Điều kiện: x  9
Ta có: P  x  6 x  9  x  6 x  9  x  9  6 x  9  9  x  9  6 x  9  9
  x9  32   x9 32             x 9 3 3 x 9 x 9 3 3 x 9  6
THCS.TOANMATH.com FB TRỊNH BÌNH 71  x   9 Dấu “=” xảy ra khi   9  x  18. 3  x  9  0
Vậy giá trị nhỏ nhất của P là 6.
Câu 111: [TS10 Chuyên Thái Bình, 2016-2017]
Cho x, y, z  1 và thỏa mãn 2 2 2
3x  4y  5z  52 . Tìm giá trị nhỏ nhất của biểu thức: F  x  y  z
Dự đoán: Ta đo{n dấu bằng xảy ra khi x = y = 1, z = 3. Lời giải
Do x, y, z  1 nên: x   1 y  
1  0  xy  x  y 1
L|m tương tự và cộng theo vế ta được: xy  yz  zx  2x  y  z  3 Do đó:    2   2 2 2        2 2 5 x y z 5 x y z
10 xy yz zx  52  2x  y  10 2
 x  y  z  3
 52  2 1 20x  y  z 30 Suy ra: x  y  z  5
Dấu “=” xảy ra khi x = y = 1, z = 3.
Vậy giá trị nhỏ nhất của F là 5.
Câu 112: [TS10 Chuyên Quảng Bình, 2016-2017]
Cho a, b, c là các số thực dương thỏa mãn ab  bc  ca  3abc. 1 1 1 3 Chứng minh:    3 3 3 a  b b  c c  a 2 Lời giải
Áp dụng BĐT AM-GM ta được: 1 1 1 1  3 1        3 4 3 3 a  b 2. a .b 4 2  a b 2 a .b  1 1  3 1  1 1  3 1  Tương tự:   ;       3 3 b  c 4 2  b c  c  a 4 2  c a  Cộng theo vế ta được: 1 1 1 1  4 4 4  1 ab  bc  ca 3       .    (đpcm) 3 3 3 a  b b  c c  a 4 2  a b c  2 abc 2
Dấu “=” xảy ra khi a = b = c = 1.
Câu 113: [TS10 Chuyên Phú Thọ, 2016-2017]
Cho các số x, y dương. Tìm gi{ trị nhỏ nhất của biểu thức: 2 2 2x yx2y 8 P       2x  y3  1 1 x2y2 4 3x y  1 1 Lời giải
THCS.TOANMATH.com FB TRỊNH BÌNH 72
Đặt 2x  y  a, x  2y  b và sử dụng bất đẳng thức AM-GM ta được: 2 2 ab 8 P     3 3 4 a      b a 1 1 b 1 1 2 2 ab 8    
   2        2    4 a  b a 1 a a 1 1 b 1 b a 1  1 2 2 ab 4 4 4 ab 4         2 2 2 2 a  1  a  a  1 b  1  b  a  1 4 ab a b 4 ab 1 1 2 2 8 ab 4    ab 4 ab 2 8 t 4
Đặt t  ab . Ta sẽ chứng minh:    1 (*) 2 t 4 t 2
Thật vậy:        2 * t 2 t  4t  8  0 2
Vậy P  1 . Dấu “=” xảy ra khi x  y  3
Vậy giá trị nhỏ nhất của P là 1.
Câu 114: [TS10 Chuyên TP. Hồ Chí Minh, 2016-2017] x y  y x x  y 1
Cho x, y là hai số dương. Chứng minh rằng:   x  y 2 4 Lời giải
Sử dụng bất đẳng thức AM-GM ta có: 1 x   x 1; 4 1 y   y 2; 4 x  y  2 xy 3. 1
Cộng theo vế (1) và (2): x  y   x  y 4 2 Nhân theo vế (3) và (4):   2 1
x y  x  y  2 xy  x  y  5 2
Chia của 2 vế của (5) cho 2x  y được: x  y 1 x  y x y  y x x  y 1      (đpcm) 2 4 x  y x  y 2 4 1
Dấu “=” xảy ra khi x  y  . 4
Câu 115: [TS10 Chuyên Ninh Bình, 2016-2017]
Cho a, b, c là số thực dương thỏa mãn abc = 1. Chứng minh rằng:
THCS.TOANMATH.com FB TRỊNH BÌNH 73 1 1 1 3    ab  a  2 bc  b  2 ca  c  2 4 Lời giải 1 1  1 1 
Với x, y dương ta có bất đẳng thức thức:     *: x  y 4  x y  x  y 1 2 2 Thật vậy: *  
 x  y  4xy  x  y  0 (luôn đúng) 4xy x  y
Bất đẳng thức (*) xảy ra dấu “=” khi x = y. 1 c 1  c 1 
Áp dụng BĐT (*) ta được:      ab  a  2 1 ac  2c 4  c  1 a  1 
Chứng minh tương tự ta được: 1 1  a 1  1 1  b 1    ;       bc  b  2 4  a  1 b  1  ca  c  2 4  b  1 c  1 
Cộng theo vế 3 bất đẳng thức trên ta được: 1 1 1 1  a 1 b 1 c 1  3            (đpcm) ab  a  2 bc  b  2 ca  c  2
4  a  1 a  1 b  1 b  1 c  1 c  4
Dấu “=” xảy ra khi a = b = c = 1.
Câu 116: [TS10 Chuyên Nam Định, 2016-2017]
Cho x, y, z là các số thực thỏa mãn điều kiện x  yx  z  1 và y  z . Chứng 1 1 1 minh:    xy 4 2 yz2 zx2 Lời giải 1 1
xy2 xz2 yz2 2xyxz Ta có:   
xy2 zx2 xy2 xz2 xy2 xz2 yz2 1     2. 2  2 xyx   z x y x z 
Sử dụng bất đẳng thức AM-GM ta được: 1 1 1 yz2 1 1        2. 2  2  2  2  2 xyx      z x y y z z x x y x z  zx2 AMGM 4
      4 x y x z
Câu 117: [TS10 Chuyên Ninh Thuận, 2016-2017]
THCS.TOANMATH.com FB TRỊNH BÌNH 74
Cho ba số a, b, c thỏa mãn điều kiện: ab  bc  ca  3. Tìm giá trị nhỏ nhất của biểu thức: 2 2 2
P  a  b  c  6a  b  c  2017 Lời giải Ta có: 2 2 2
P  a  b  c  6 a  b  c 2 2 2
 2017  a  b  c  2ab  bc  ca 6  6a  b  c 2017
 a  b  c2  6a  b  c  2011  a  b  c2  6a  b  c 9  2002
 a  b  c  32  2002  2002
Dấu “=” xảy ra khi a = b = c = 1
Vậy giá trị nhỏ nhất của P là 2002.
Câu 118: [TS10 Chuyên Bắc Ninh, 2016-2017] 4 4 3 3a  3b  c  2
Cho a, b, c > 0. Tìm giá trị nhỏ nhất của M  a bc3 Lời giải
Sử dụng AM-GM ta được: 4 4 4 4 4 12 3 4 4 4 4 4 12 3
3a  1  a  a  a  1  4 a  4a ;
3b  1  b  b  b  1  4 b  4b Do đó: 4 4 3 3 3 3 3a  3b  c  2 4a  4b  c M   a bc3 a bc3 3
Ta dễ dàng chứng minh được BĐT với a, b dương thì:  3 3
4 a  b   a  b * Thật vậy:     
        2 3 3 * a b ab a b a b a b  0 (đúng)
Vậy (*) được chứng minh. Dấu “=” xảy ra khi a = b. Áp dụng (*) ta được: 4a  4b  c a b3 c a bc3 3 3 3 3 1 M        3    3    3 4 a b c a b c 4 a b c
Dấu “=” xảy ra khi a = b = 1, c = 2. 1
Vậy giá trị nhỏ nhất của M là 4
Câu 119: [TS10 Chuyên Ninh Thuận, 2016-2017] 1 1 1
Cho các số dương x, y, z thỏa mãn    12 x  y y  z z  x 1 1 1 Chứng minh rằng:    3. 2x  3y  3z 3x  2y  3z 3x  3y  2z
Đẳng thức xảy ra khi nào? Lời giải
THCS.TOANMATH.com FB TRỊNH BÌNH 75 1 1  1 1  Với a, b, c dương ta có:     (*) a  b 4  a b      Thậy vậy:    1 1 2 1 1 1 1 a b   2 ab.  4         a b  ab a  b 4  a b 
Vậy (*) được chứng minh, dấu “=” xảy ra khi a = b . Sử dụng (*) ta được: 1 1 1  1 1       2x  3y  3z
x yxz2yz 4 xyxz 2yz 1  1  1 1  1  1  1 1 2              4 4
  x  y x  z  2y   z 16 
 x  y x  z y  z  Tương tự: 1 1  1 1 2  1 1  1 1 2      ;     . 3x  2y  3z 16 x  y y  z x  z 3x  3y  2z 16 x  z y  z x     y 
Cộng 3 BĐT trên theo vế được: 1 1 1 1  1 1 1          3 (đpcm) 2x  3y  3z 3x  2y  3z 3x  3y  2z 4 x  y y  z z   x 
Dấu “=” xảy ra khi x = y = z.
Câu 120: [TS10 Chuyên Đồng Tháp, 2016-2017]
Cho a, b, c là các số dương thỏa mãn 2 2 2
a  b  c  1 . Tìm giá trị nhỏ nhất của a b c biểu thức P    2 2 2 2 2 2 b  c c  a a  b Lời giải Ta có: a b c a b c P       2 2 2 2 2 2 2 2 2 b  c c  a a  b 1 a 1 b 1 c Do a dương v| 2 2 2 2
a  b  c  1  0  a  1  0  a  1 Áp dụng AM-GM ta được:    
     2x 1x 2x  1 1  3 2 2 2 2 2 2 2 2 2 4 a 1 a .2x . 1 x 1 x     2 2  3  27     2   2 1 3 3 a 3 3 a 1 a      3 3 a  a 2 1 a  2 2 2 1 a 2 b 3 3 c 3 3
Chứng minh tương tự ta được: 2 2  b ;  c 2 2 1 b 2 1 c 2
Cộng 3 bất đẳng thức trên theo vế ta được: a b c 3 3      2 2 2 3 3 P a  b  c  (đpcm) 2 2 2  1 a 1 b 1 c 2 2
THCS.TOANMATH.com FB TRỊNH BÌNH 76 1
Đẳng thức xảy ra khi a  b  c  3
Câu 121: [TS10 Chuyên TP. Hồ Chí Minh, 2016-2017]
Biết x  y  z,x  y  z  0 và 2 2 2 x  y  z  6. 2 2
1) Tính S  x  y  x  yy  z  y  z
2) Tìm giá trị lớn nhất của biểu thức P  x  yy  zz  x Lời giải 1) Ta có: x yz2  2 2 2 x  y  z  2  2 2 2 0 6
S  x  y  z  xy  yz  zx  6   6   9 2 2
2) Đặt a  x  y, b  y  z. Khi đó ta có a  0, b  0 và 2 2 a  ab  b  9       2 2 a b a b  9  ab   a  b  2 3 4
Đặt t  a  b. Khi đó:   2 P t t  9 Ta sẽ chứng minh:  2 t t  9  6 3 *
Thật vậy: *  t  2 3t  3  0 (đúng) Do đó: P  6 3 .
Dấu “=” xảy ra khi x  3, y  0,z   3 .
Vậy giá trị lớn nhất của P là 6 3
Câu 122: [TS10 Chuyên KHTN, 2016-2017]
Với x, y là số thực thỏa mãn điều kiện 0  x  x  y  2,2x  y  2xy . Tìm giá trị
lớn nhất của biểu thức: 2   2   2   2 P x x 1 y y   1 Lời giải 4 4 2 2 P  x  y  x  y 2 Ta có bất đẳng thức: 2 2 1 a  b  a  b * 2 1 2 Ta có: 2x  y  2xy    2 (vì x, y dương) x y 2 1 4 1  1 2  1 4 Áp dụng (*) suy ra:       2   2  1 2 2 2 2   x y 2  x y  x y 2 1 16 1  1 4  1 16 Áp dụng tiếp (*) ta có:       2   2  2 4 4 4 2 2 4   x y 2  x y  x y
THCS.TOANMATH.com FB TRỊNH BÌNH 77 2 2  x  4x Có x  y  2  1  2 y  4 2 2  0  y  4  x  2 2  y  y 2   2 2 2 4x 2 4 2 1  x  y  4  2x   4  x 2    4  x .  5 (do (1)) 2 2 y  y  x 4 4  x  16x Tương tự: 1  4 y  4 4 4  0  y  16  x  4 4  y  y   4 4 16 4 1 4
 y  x  16  2  .x  16  .x  17 (do (2)) 4 4  y  x P  17  5  22
Dấu “=” xảy ra khi x = 1, y = 2.
Vậy gí trị lớn nhất của P là 22.
Câu 123: [TS10 Chuyên Nam Định, 2016-2017]
Cho hai số a, b không âm thỏa mãn a  b  3. Chứng minh rằng: 2  2a 1 4b 8   1 2a 1  4b 15 Lời giải
Bất đẳng thức cần chứng minh tương đương với: 2  2a 1 4b 1 1 4b 1 2 P     1   1 2a 1 4b 1 2a 1 4b 1 2a 1 4b
Sử dụng bất đẳng thức AM-GM ta được: 1 2  1 2 1 1 1 =     2 (1) 1 2a 1 4b 1 2a 1  4b 1  2a 1 1  2b (1 2a)(  2 b) 2 2 1 1 2a   2b 1 15 2 (1  2a)(  2 b)   2 2 4 1 8  2  (2) 1 15 (1  2 a)(  2 b) 2 2  2a 1 4b 8 Từ (1) và (2) suy ra:   1 2a 1  4b 15
Vậy bất đẳng thức được chứng minh. 1 11 13
Dấu “=” xảy ra chỉ khi : 1 + 2a = + 2b và a + b = 3  a  ; b  2 8 8 Cách khác:
THCS.TOANMATH.com FB TRỊNH BÌNH 78 Ta có: 2  2a 1 4b 1 1 4b 1 2  1 1  P     1    2    1 2a 1 4b 1 2a 1 4b 1  2a 1  4b  2  4a 1 4b  1 1 4
Với a, b, c dương ta có:   (*) a b a  b   Thậy vậy:    1 1 2 1 1 4 a b   2 ab.  4       a b  ab a b a  b
Vậy (*) được chứng minh, dấu “=” xảy ra khi a = b . Áp dụng (*) ta được:  1 1  4 8 8 8 P  2   2.      (đpcm)  2  4a 1 4b  2  4a  1 4b
3  4a  b 3  4.3 15  a  b  3 11 13 Dấu “=” xảy ra khi   a  ; b  2  4a  1  4b 8 8
Câu 124: [TS10 Chuyên Nam Định, 2016-2017]
Cho a, b, c dương v| thỏa mãn xy  yz  zx  1 . Tìm giá trị nhỏ nhất của biểu 1 1 1 thức : P    2 2 2 4x  yz  2 4y  zx  2 4z  xy  2 Lời giải Ta có 1 1 1 1    . 2 2 2 4x  yz  2
4x  yz  2(xy  yz  zx) 4x  2xy  yz  2zx 2x y2xz 1 1 1
Tương tự, ta có S    
2x  y2x  z 2y  z2y  x 2z  x2z  y yz xz xy  S    
2xz  yz2xy  yz 2xy  xz2yz  xz 2yz  xy2xz  xy 
Với mọi a, b ta có          2 2 2 a b a b 0 a b  4ab  ab  . 4
Áp dụng bất đẳng thức trên ta được: yz xz xy S   
2xy2yz2zx2 2xy2yz2zx2 2xy2yz2zx2 4 4 4 xy  yz  zx 1  S      1. 2 xy  yz    zx 2xy 2yz 2zx 4
THCS.TOANMATH.com FB TRỊNH BÌNH 79 1
Đẳng thức xảy ra khi x  y  z  . 3
Vậy giá trị nhỏ nhất của S bằng 1. Cách khác: ac ab bc
Đặt a  xy, b  yz,c  zx khi đó a  b  c  1 và 2 2 2 x  ; y  , z  b c a Ta có: 1 1 1   2 4x  yz  2
4ac  b 2a  bc 4ac  2a  b 2c b b b b 4b a     2 4ac  2ab  b  2bc
2a  b2c b 2a2b2c2 abc2 1 c 1 a Tương tự:  ;  2 4y  zx  2    2 2 4z  xy  2 a b c a bc2
Cộng 3 bất đẳng trên theo vế ta được: a  b  c 1 P      1 2 a  b    c a b c 1
Dấu “=” xảy ra khi x  y  z  3
Vậy giá trị nhỏ nhất của P là 1.
Câu 125: [TS10 Chuyên Lam Sơn, 2016-2017] 3
Cho 3 số thực dương x, y, z thỏa mãn x  y  z 
. Tìm giá trị nhỏ nhất của biểu 2 xyz  2 1 y zx  12 z xy  12 thức: P    2 z zx   2 1 x xy  1 2 y yz  1 Lời giải Ta có: 2 2 2  yz  1  zx  1  xy 1       x yz  12 y zx  12 z xy  12  z   x   y  P       2 z zx  1 2 x xy  1 2 y yz  1  zx  1  xy 1  yz  1        x   y   z 
THCS.TOANMATH.com FB TRỊNH BÌNH 80 2 2 2  1   1   1   y    z    x    z   x   y   P    1 1 1 z  x  y  x y z
Áp dụng bất đẳng thức AM-GM-Sc hwar ta có: 2 2 2 2  1   1   1   1 1 1   y    z    x  
 x  y  z      z   x   y   x y z  P     1 1 1 1 1 1 z  x  y  x  y  z    x y z x y z 1 1 1 9
               9 27 x y z x y z x y z   x y z x  y  z
4 x  y  z 4x  y  z AMGM      9 9 15 2 x y z .   4 x  y  z 3 2 4. 2 1
Dấu “=” xảy ra khi x  y  z  2 15
Vậy giá trị nhỏ nhất của P là 2
Câu 126: [TS10 Chuyên Lam Sơn vòng 2, 2016-2017] 1 1 1 1931 Chứng minh rằng:   ...  2 1 3 2 2016 2015 1975 Lời giải Ta có: 1 1 1 1 1 1 1 1 1 1 1   ...    ...  1   ...  2 1 3 2 2016 2015 1.2 2.3 2015.2016 2 2 3 2015 2016 1 2015 1931  1   (đpcm) 2016 2016 1975
Câu 127: [TS10 Chuyên Hải Phòng, 2016-2017]
Cho a, b,c  0; a  b  c  9 , tìm giá trị nhỏ nhất của: 2 2 2 b c 1 9 25 A  2 a    3   3 5 a b c Lời giải
Áp dụng bất đẳng thức AM-GM-Schwar ta được: 2 2  b c    a  
1 3  5  a  b  c 2 2 2 b c 2 a b c 2 2    2 a     3 5  3 5 3 1 9 25    2 1 3 5 81 1 9 25 27      3    a b c a  b  c a  b  c a b c a  b  c
THCS.TOANMATH.com FB TRỊNH BÌNH 81 Do đó: 2 2 b c 1 9 25 2 a  b  c 2   27 A  2 a    3     3 5 a b c 3 a  b  c = a  b  c a  b  c 27 27 9 a  b  c 27 27       33 . . 6 2 2 a  b  c 2 a  b  c 6 2
2 a  b  c 2 a  b  c 9 9 3 27   3.    15 6 2 2 2
Dấu “=” xảy ra khi a = 1, b = 3, c = 5.
Vậy giá trị nhỏ nhất của A là 15.
Câu 128: [TS10 Chuyên Tiền Giang, 2016-2017]
Cho a, b, c dương thỏa mãn a  b  c  3. Tìm giá trị nhỏ nhất của biểu thức: 1 2018 P   2 2 2 a  b  c ab  bc  ca Lời giải 1 1 1 1
Áp dụng bất đẳng thức Cô si cho 3 số dương 3 a  b  c  abc;    3 3 a b c abc   Suy ra     1 1 1 a b c      9 (*)  a b c 
Bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi và chỉ khi a  b  c a  b  c 2 2 2  2
Ta có ab  bc  ca  a  b  c  ab  bc  ca   3 3 2016 2016 Suy ra   672 ab  bc  ca 3
Áp dụng bất đẳng thức (*) , ta có  1 1 1     2 2 2
a  b  c  2ab  2bc  2ca    9 2 2 2   a  b  c ab  bc  ca ab  bc  ca  1 2 9 Suy ra    1 2 2 2 a  b  c ab  bc  ca a bc2 1 2018 Do đó ta được P    673 . 2 2 2 a  b  c ab  bc  ca
Dấu đẳng thức xẩy ra khi và chỉ khi a  b  c  1.
Vậy giá trị nhỏ nhất của P là 673.
Câu 129: [TS10 Chuyên Lào Cai, 2016-2017]
THCS.TOANMATH.com FB TRỊNH BÌNH 82 1 1 1
Cho a, b, c là số dương thỏa mãn:    2. Chứng minh rằng: a  1 b  1 c  1 1 1 1    1 2 2 2 8a  1 8b  1 8c  1 Lời giải Ta có: 1 1 1  1 1 1  a b c    2  3     1      1 a  1 b  1 c  1  a 1 b 1 c 1  a  1 b  1 c  1 Mặt khác: 1 1 1  1 1 1     1  3       2 2 2 2 2 2 2 8a  1 8b  1 8c  1
 8a  1 8b  1 8c  1  2 2 2 2 2 2 8a 8b 8c 4a 4b 4c     2     1 2 2 2 2 2 2 8a  1 8b  1 8c  1 8a  1 8b  1 8c  1 2 4a a Ta chứng minh:  (*) 2 8a  1 a  1 2 4a a Thật vậy: 3 2 3 3 2 
 4a  4a  8a  a  4a  4a  a  0 2 8a  1 a  1        2 2 4a 4a 1 0 2a 1  0 (đúng) 2 2 4b b 4c c Tương tự:  ;  2 2 8b  1 b  1 8c  1 c  1
Cộng 2 bất đẳng thức theo vế ta được: 2 2 2 4a 4b 4c a b c       1(đpcm) 2 2 2 8a  1 8b  1 8c  1 a  1 b  1 c  1 1
Dấu “=” xảy ra khi a  b  c  2
Câu 130: [TS10 Chuyên Cần Thơ, 2016-2017]
Cho a, b, c lần lượt l| độ dài 3 cạnh của tam giác và 2ab  3bc  4ca  5abc . 7 6 5
Tìm giá trị nhỏ nhất của biểu thức: P    a  b  c b  c  a c  a  b Lời giải 2 3 4
Ta có: 2ab  3bc  4ca  5abc 
   5 do a,b,c  0 c a b
Sử dụng BĐT AM-GM-Schwar ta được: 2 3 4 2 3 4    2 2 2 2 2 3 4 81 5         3a  4b  2c  c a b 2c 3a 4b 3a  4b  2c 5 2 2 2 7 6 5 7 6 5 P       a  b  c b  c  a c  a  b
7 a  b  c 6b  c  a 5c  a  b
THCS.TOANMATH.com
FB TRỊNH BÌNH 83    2 2 7 6 5 18
                  10 7 a b c 6 b c a 5 c a b 2 3a 4b 2c 9
Dấu “=” xảy ra khi a  b  c  5
Vậy giá trị nhỏ nhất của P là 10.
Câu 131: [TS10 Chuyên Đồng Nai, 2016-2017]
Cho a, b, c là số thực không âm thỏa mãn a  b  c  3
1) Chứng minh rằng: ab  bc  ca  3 2) Chứng minh rằng: 2 2 2 a b  b c  c a  4 Lời giải 1) Ta có:    2 a b c ab  bc  ca   3(đpcm) 3
Dấu “=” xảy ra khi a = b = c =1.
2) Giả sử b nằm giữa a và c ta có:      2 2 2 2 2
b a b c  0  b  ac  ab  bc  b c  ac  b c  ac Áp dụng AM-GM ta có:  
a b  b c  c a  a b  b c  2abc  ba  c  ba  ca  c 4a b c3 2 2 2 2 2 2   4 27
Câu 132: [TS10 Chuyên Bình Định, 2016-2017]
Cho x, y, z thay đổi thỏa mãn 2 2 2
x  y  z  1. Tìm GTLN của biểu thức: 1 P xy yz xz
x y z2 y x z2 z x y2 2 2 2           2   Lời giải Ta chứng minh: 1 P xy yz xz
x y z2 y x z2 z x y2 2 2 2            1 2  
 xy  yz  zxx  y  z  x y  y z  z x  xyzx  y  z  x  y  z 2 2 2 2 2 2 2 2 2 2 2 2 2 1 x y 
x y2 y z y z2 z x x z2 2 2 2 2 2 2            0 2   (đúng) 1
Dấu “=” xảy ra khi x  y  z  3
Vậy giá trị lớn nhất của P là 1.
Câu 133: [TS10 Chuyên Vĩnh Phúc, 2016-2017]
Cho a, b, c là các số thực dương thỏa mãn: a  b  c  3. Chứng minh rằng”  2 2 2    3 3 3 4 a b c a  b  c   9 Lời giải
THCS.TOANMATH.com FB TRỊNH BÌNH 84 Ta có: 4  2 2 2 a  b  c    3 3 3 a  b  c   9  3 3 3 3
a  b  c   27  12 2 2 2 a  b  c  2 2 2 2 2 2
 6abc  a b  b c  c a  ab  bc  ca
 8abc  a  bb  cc  a
Bất đẳng thức cuối cùng đúng theo AM-GM, vậy b|i to{n được chứng minh.
Dấu “=” xảy ra khi a = b = c.
Câu 134: [TS10 Chuyên Thái Bình, 2016-2017]
Cho các số thực x, y, z  1 và thỏa mãn 2 2 2
3x  4y  5z  52. Tìm giá trị nhỏ nhất
của biểu thức: F  x  y  z Lời giải
*) Bài này muốn giải được trước tiên ta phải dự đoán giá trị lớn nhất của F đạt
được khi x = y = 1, z = 3 Ta có:  2 2 2    2 2 2 2 2 5 x y z
 52  2x  y  52  2 1  55  x  y  z  11 1 Lại có: x   1 y  
1  0  xy  1  x  y
Tương tự: yz  1  y  z ; zx  1  z  x
Cộng theo vế: xy  yz  zx  3  2x  y  z  2xy  yz  zx  6  4x  y  z (2) 2
Lấy (1) cộng (2) theo vế ta được: x  y  z  5  4x  y  z  x  y  z  5
Dấu “=” xảy ra khi x = y = 1, z = 3.
Vậy giá trị lớn nhất của F là 5.
Câu 135: [TS10 Chuyên Thừa Thiên Huế, 2016-2017]
Cho x, y  0 và x  y  3 . Tìm giá trị nhỏ nhất của 4x 3y 2 2 M  6x  4y  10xy    2016 y x Lời giải Ta có: 4x 3y 4 x  y 3 y  x 2 2 M  6x  4y  10xy  
 2016  x  y6x  4y        2009 y x y x    3 4   3 4 
 x y 6x  4y     2009  36x  4y     2009  x y   x y 
THCS.TOANMATH.com FB TRỊNH BÌNH 85  3   4    3 3x  
  y    3x  y  2009  x   y    3 4 
 3 2 3x.  2 y.  3.3  2009  2066  x y  
Dấu “=” xảy ra khi x = 1, y = 2.
Vậy giá trị nhỏ nhất của M là 2066.
Câu 136: [TS10 Chuyên Phan Bội Châu, 2016-2017]
Cho a, b, c là các số thực dương thay đổi. Tìm GTNN của biểu thức: 2 2 a b c P      2   2 4a a b b c Lời giải
Với x, y dương ta có c{c bất đẳng thức cơ bản sau (bạn đọc tự chứng minh): x y2  4xy 1 1
x  y  z  x  y  z2 2 2 2 2 3 x y z 3    3 y  z z  x x  y 2
Áp dụng các bất đẳng thức (1), (2), (3) ta được: 2 2 2 2 2 2 2 2 a b c a b c a b c P         
  2   2 4a   2   2 4ac a b b c a b b c
a  b2 bc2 a c2 2 2 1  a b c  1  3  3     .     
3  b  c b  c a  c  3  2  4
Dấu “=” xảy ra kho a = b = c. 3
Vậy giá trị lớn nhất của P là 4
Câu 137: [TS10 Chuyên Quảng Nam, 2016-2017]
Cho 2 số thực x, y thỏa mãn 0  x  1, 0  y  1 và x + y = 3xy.
Tìm GTLN và GTNN của biểu thức: 2 2 P  x  y  4xy Lời giải Ta có:       2       2 2 2 2 2 P x y 4xy x y 6xy 9x y 6xy 3xy 1 1 Do        1 x, y (0;1]
1 x 1 y  0  1 xy  x  y  3xy  xy  2 AMGM 4
Mặt khác x, y (0;1]  3 xy  x y  2 xy  xy  9
THCS.TOANMATH.com FB TRỊNH BÌNH 86 4 1 1 1 1 1 Vậy
 xy    3xy 1    3xy  2 1  9 2 3 2 9 4  8     2 3 8 3
3xy 1  1      P   9 4 9 4 3     Vậy: GTLN của P là  khi   1 1 x, y  1;  , ;1 4  2   2  8 2 GTNN của P là  khi x  y  9 3
Câu 138: [TS10 Chuyên Quảng Nam, 2016-2017]
Cho 3 số thực a, b, c sao cho 0  a  1,0  b  1,0  c  1 . Chứng minh:
a  b  c  3abc  2ab  bc  ca Lời giải Ta có:
0  a, b  1  1a1 b  0  1 ab  a  b  c  abc  ac  bc do 0  c  1
Chứng minh tương tự được: b  abc  ab  bc ; a  abc  ab  ac
Cộng 3 bất đẳng thức trên theo vế được: a  b  c  3abc  2ab  bc  ca (đpcm)
Dấu “=” xảy ra khi (a, b, c) = (1, 1, 0) và các hoán vị.
Câu 139: [TS10 Chuyên Hà Nội, 2016-2017]
Cho các số thực dương a, b, c thỏa mãn 2 2 2
a  b  c  3. Chứng minh: 2 2 2 2a 2b 2c    a  b  c 2 2 2 a  b b  c c  a Lời giải Áp dụng AM-GM ta được: 2a  2 a  b  2 2  2 2ab 2a 2ab b  ab   2a   2a  b.ab  2a  2 2 2 a  b a  b a  b 2
L|m tương tự và cộng theo vế của bất đẳng thức ta được: 2 2 2 2a 2b 2c 3 ab  bc  ca    a  b  c  2 2 2   a  b b  c c  a 2 2
Mặt khác ta có:            2 2 2 2 a b c a b c 3 ab bc ca
 a  b  c  ab  bc  ca 2 2 2 2a 2b 2c 3 ab  bc  ca Do đó:    a  b  c   a  b  c (đpcm) 2 2 2   a  b b  c c  a 2 2 1
Dấu “=” xảy ra khi a  b  c  3
Câu 140: [TS10 Chuyên Long An, 2016-2017]
Cho a, b, c là ba cạnh của tam giác. Tìm giá trị nhỏ nhất của biểu thức:
THCS.TOANMATH.com FB TRỊNH BÌNH 87 abc
Q  bcacababc Lời giải
Do a, b, c là 3 cạnh của tam giác nên b  c  a  0,c  a  b  0,a  b  c  0
Sử dụng AM-GM ta được: 2        
b  c  ac  a  b b c a c a b 2     c  2 
Tương tự:        2 
       2 c a b a b c a ; b c a a b c  b
Nhân 3 bất đẳng thức trên theo vế ta được:
   2    2    2 2 2 2 b c a c a b a b c
 a b c  b c ac a  ba  b c  abc abc
 Q            1 b c a c a b a b c
Dấu “=” xảy ra khi a = b = c
Vậy giá trị nhỏ nhất của Q là 1.
Câu 141: [TS10 Chuyên Phan Bộ Châu, 2016-2017]
Cho a, b, c là các số thực dương thay đổi thỏa mãn a  b  c  1. Tìm giá trị nhỏ ab  bc  ca
nhất của biểu thức: Q  14 2 2 2 a  b  c   2 2 2 a b  b c  c a Lời giải
Với a, b, c dương ta có:     2 2 2      2 2 2 a b c a b c 3 a b  b c  c a (1) Thật vậy:
VT  a  b  c 2 2 2 a  b  c  3 2 2 2 2 2 3 2 2
 a  ab  ac  b  ba  bc  c  ca  cb   2 2 2
a b  b c  c a   3 2 a  ab    3 2 b  bc    3 2 c  ca  AMGM   2 2 2 a b  b c  c a 2 2 2  2a b  2b c  2c a   2 2 2 3 a b  b c  c a =VP
Dấu “=” xảy ra khi a = b = c. Sử dụng (1) ta được:     
Q  14 a  b  c  3ab bc ca 3 1 a b c   14 a  b  c  2 2 2    2 2 2 2 2 2 2 2 2  a  b  c 2 2 2 2 a  b  c    2 2 2    3 3 14 a b c   2  2 2 2 a  b  c  2 Ta có:       2 2 2 2 1 1 a b c a b c  3 3
Sử dụng AM-GM ta được:
THCS.TOANMATH.com FB TRỊNH BÌNH 88   2 2 2    3 3 Q 14 a b c   2  2 2 2 a  b  c  2   27    2 2 2    3 1 3 a b c        2 2  a b c   2 2 2 a b c 2 2 2   2 2  27   2 2 2    3 1 3 2 a b c .   2 2  2 2 2 a  b  c  3 2 9 1 3  2.   2 3 2 23  3 1
Dấu “=” xảy ra khi a  b  c  . 3 23
Vậy giá trị nhỏ nhất của P là 3 NĂM HỌC 2015-2016
Câu 142: [TS10 Chuyên Hòa Bình, 2015-2016] x  0,y  0,z  0 1 1 1 Cho  .Chứng minh rằng:    1 xyz   1
x  y  1 y  z  1 z  x  1 Lời giải 3 x  a  x,y,z  0 a  ,b,c  0 Đặt 3 y  b , vì     xyz  1 abc    1 3 z  c  Ta có   3 3 2 2 a b c
x  y  1  a  b  1  (a  b)(a  ab  b )  1  (a  b)ab  1  ab(a  b  c)  c Do đó 1 c  x  y  1 a  b  c Tương tự ta có 1 a 1 b  ;  y  z  1 a  b  c z  x  1 a  b  c
Cộng 3 bất đẳng thức trên theo vế ta có: 1 1 1 a  b  c     1 dpcm
x  y  1 y  z  1 z  x  1 a  b  c
THCS.TOANMATH.com FB TRỊNH BÌNH 89
Dấu “=” xảy ra khi x = y = z.
Câu 143: [TS10 Chuyên Hải Dương, 2015-2016]
Cho a, b là các số dương thỏa mãn điều kiện 3 (a  b)  4ab  12. 1 1
Chứng minh bất đẳng thức   2015ab  2016. 1 a 1 b Lời giải Ta có      3 3 12 (a b) 4ab 2 ab
 4ab . Đặt t  ab,t  0 thì 3 2 3 2 2
12  8t  4t  2t  t  3  0  (t 1)(2t  3t  3)  0 Do 2 2t  3t  3  0, t
 nên t 1 0  t  1 . Vậy 0  ab  1 1 1 2 Chứng minh được   , a
 ,b  0 thỏa mãn ab  1 1 a 1 b 1 ab 1 1 1 1 Thật vậy, BĐT     0 1 a 1 ab 1 b 1 ab ab  a ab  b  b  a  a b    0                (1 a)(1 ab) (1 b)(1 ab)  1 ab 1 a 1 b   2 ( b  a) ( ab  1) 
 0. Do 0  ab  1 nên BĐT n|y đúng (1 ab)(1 a)(1  b) 2 Tiếp theo ta sẽ CM:  2015ab  2016, a
 ,b  0 thỏa mãnab  1 1 ab 2
Đặt t  ab,0  t  t ta được 2  2015t  2016 1 t 3 2
2015t  2015t  2016t  2014  0 2
 (t 1)(2015t  4030t  2014)  0. BĐT n|y đúng t  : 0  t  1
Đẳng thức xảy ra a = b = 1 1 1 Vậy   2015ab  2016. 1 a 1 b
Câu 144: [TS10 Chuyên Quảng Nam, 2015-2016]
Cho ba số thực x; y; z thỏa mãn: x2 + y2 + z2 ≤ 9
Tìm giá trị lớn nhất của biểu thức P = x + y + z  (xy + yz + zx)
THCS.TOANMATH.com FB TRỊNH BÌNH 90 Lời giải 2 2 2 2
(x  y  z)  (x  y  z ) Ta có xy  yz  xz  2 2 2 2 2
(x  y  z)  (x  y  z )
Do đó P  x  y  z  2 1 2 2 2 2 1 2 1 2 2 2 P 
2(x  y  z) (x  y  z) (x  y  z )   (x  y  z 1)  (x  y  z 1)   2 2 2 1 1 Suy ra 2 2 2
P  (x  y  z  1)  (9  1)  5 2 2 x  y  z 1  0
Vậy Pmax = 5 khi và chỉ khi 
(chẳng hạn x  2; y  2  ;z  1 ) 2 2 2 x  y  z   9
Câu 145: [TS10 Chuyên Phú Thọ, 2015-2016] 1 1 1
Cho 3 số thực dương x, y, z thỏa mãn:    1 . 2 2 2 x y z 2 2 2 2 2 2 y z z x x y
Tìm giá trị nhỏ nhất của biểu thức: P    2 2 2 2 2 2 x(y  z ) y(z  x ) z(x  y ) Lời giải 1 1 1 Ta có: P    1 1 1 1 1 1 x(  ) y(  ) z(  ) 2 2 2 2 2 2 z y z x x y 1 1 1 Đặt
 a;  b;  c thì a,b,c>0 và a2+b2+c2=1 x y z 2 2 2 a b c a b c P       2 2 2 2 2 2 2 2 2 b  c c  a a  b a(1  a ) b(1  b ) c(1  c )
Áp dụng bất đẳng thức Côsi cho 3 số dương ta có: 2 2 2       2 2 2 1 2 2 2 1 2a 1 a 1 a 4
a (1  a )  .2a (1  a )(1  a )     2 2  3  27 2 2 2 a 3 3 2  a(1 a )    a (1) 2 3 3 a(1  a ) 2 2 2 b 3 3 c 3 3 Tương tự: 2 2  b (2);  c (3) 2 2 b(1 b ) 2 c(1  c ) 2 3 3 3 3 Từ (1); (2); (3) ta có 2 2 2 P  (a  b  c )  2 2 1
Đẳng thức xảy ra khi a  b  c  hay x  y  z  3 3
THCS.TOANMATH.com FB TRỊNH BÌNH 91 3 3
Vậy giá trị nhỏ nhất của P là 2
Câu 146: [TS10 Chuyên Ninh Bình, 2015-2016] 1 1 1
Cho a, b, c là các số dương thỏa mãn điều kiện 
  3 . Chứng minh rằng: a b c a b c 1    (ab  bc  ca)  3 2 2 2 1 b 1 c 1 a 2 Lời giải Ta chứng minh BĐT 1 1 1 (a  b  c)(   )  9(*) a b c a b b c c a
(*)  3  (  )  (  )  (  )  9 b a c b a c
Áp dụng BĐT AM-GM cho hai số dương ta có: a b b c c a   2;   2;   2 b a c b a c => (*) đúng 9 1 1 1 
    3  a  b  c  3 a  b  c a b c
Trở lại bài toán: Áp dụng BĐT AM-GM cho hai số dương ta có 2 1 b  2b 2 2 a ab ab ab Ta có:  a   a   a  (1) 2 2 1 b 1  b 2b 2 b bc c ca Tương tự ta có:  b  (2);  c  (3) 2 2 1 c 2 1 a 2
Cộng từng vế của (1), (2) và (3) ta có: a b c 1  
 a  b  c  (ab  bc  ca) 2 2 2 1  b 1  c 1  a 2 a b c 1   
 (ab  bc  ca)  a  b  c  3 2 2 2 1  b 1  c 1  a 2 =>đpcm
Dấu bằng xảy ra khi a = b = c = 1.
Câu 147: [TS10 Chuyên TP. Hồ Chí Minh, 2015-2016]
Cho hai số dương a , b thỏa mãn điều kiện: a + b  1. Chứng minh rằng:  2 3 a 9 a    4a b 4 Lời giải
Bất đẳng thức tương đương với: 2 3 4a 4a  9   a b
Ta có: a  b  1  a  1 b m| a, b dương nên 0  a  1
THCS.TOANMATH.com FB TRỊNH BÌNH 92 Do đó: 2 3 4a 3 4a 3 4a 4a  9       a b a 1 a a b
Vì thế chỉ cần chứng minh: 2 3 4a 4a  9   (*) a 1  a     2 2 a 3 2a 1 Thật vậy: *   (đúng)    0 a 1 a 1
Dấu “=” xảy ra khi x  y  2
Vậy b|i to{n được chứng minh.
Câu 148: [TS10 Chuyên Bình Phước, 2015-2016]
1) Cho a, b là các số thực dương. Chứng minh rằng: (1 a)(1 b)  1 ab
2) Cho a, b là các số thực dương thỏa mãn a  b  ab . Tìm giá trị nhỏ nhất của biểu thức 1 1 2 2 P    (1 a )(1 b ) 2 2 a  2a b  2b Lời giải a) Ta có
(1 a)(1  b)  1  ab  1 a1 b  1 ab  2 ab
 1 a  b  ab  1 ab  2 ab  a  b  2 ab  0    2 a b  0 (luôn đúng) 1 1 4 b) Sử dụng BĐT ở ý a)
(1 x)(1 y)  1 xy và BĐT   ta được: x y x  y 4 4 4 P   1 ab   1 ab   ab 1 2 2 2 2 2 a  2a  b  2b
(a  b)  2ab  2(a  b) a b  4 ab ab  7ab 1 1 7ab 7 7ab 3      1  3. 4. .   1     2 2  a b 16 16  8 16 16 8 4 8
Mặt khác: từ giả thiết, ta có: ab  a  b  2 ab  ab  4 7 7.4 21 21 Do đó P   
. Vậy giá trị nhỏ nhất của P bằng khi a  b  2 4 8 4 4
Câu 149: [TS10 Chuyên Quảng Bình, 2015-2016]
THCS.TOANMATH.com FB TRỊNH BÌNH 93 a 2b
Cho a, b là các số dương thỏa mãn   1. Chứng minh 2 1 ab  . 1 a 1 b 8 Lời giải a 2b a b x y Từ giả thiết   1. Đặt x  ; y  Suy ra a  ; b  . 1 a 1 b 1 a 1 b 1 x 1 y
Khi đó ta được x  2y  1 và bất đẳng thức cần chứng minh được viết lại thành 2 xy 1      2 8 1 x 1 y
Từ giả thiết ta suy ra 1 x  2y; 1 y  x  y nên lại viết bất đẳng thức cần chứng minh thành 2 xy 1   4xy  x  y 2  2    8 2y x y
Đ{nh gi{ cuối cùng là một bất đẳng thức đúng. Vậy b|i to{n được chứng minh
xong. Đẳng thức xẩy ra khi và chỉ khi a  b .
Câu 150: [TS10 Chuyên Bắc Giang, 2015-2016]
Cho a, b, c > 0 thỏa mãn: a + b + c = 3. Chứng minh rằng: 4 4 4 a b c 1   
(a  2)(b  2) (b  2)(c  2) (c  2)(a  2) 3 Lời giải
Áp dụng BĐT AM-GM cho 4 số không âm, ta có: 4 4 4 a a  2 b  2 1 a a  2 b  2 1 a 4a     4 4 4 . . .  4  4 (a  2)(b  2) 27 27 9 (a  2)(b  2) 27 27 9 9 9 4 a 11a b 7     (1) (a  2)(b  2) 27 27 27 Tương tự ta có: 4 b 11b c 7    (2) (b  2)(c  2) 27 27 27 4 c 11c a 7    (3) (c  2)(a  2) 27 27 27
Cộng từng vế của (1), (2) và (3) ta có:
THCS.TOANMATH.com FB TRỊNH BÌNH 94 4 4 4 a b c
11(a  b  c) a  b  c 21     
(a  2)(b  2) (b  2)(c  2) (c  2)(a  2) 27 27 27
Thay điều kiện a + b + c = 3 ta được: 4 4 4 a b c 1   
(a  2)(b  2) (b  2)(c  2) (c  2)(a  2) 3
Dấu bằng xảy ra khi a = b = c = 1.
Câu 151: [TS10 Chuyên Bạc Lưu, 2015-2016] 1 1 1
Cho a, b, c > 0 và a + b + c = 3. Chứng minh rằng a5 + b5 + c5 +    6 a b c Lời giải 1 1 1
Áp dụng bất đẳng thức AM-GM: 5 2 a   2a ; 5 2 b   2b ; 5 2 c   2c a b c 1 1 1 Suy ra a5 + b5 + c5 + 2 2 2    2(a  b  c ) a b c Mặt khác 2 2
a  1  2a; b  1  2b; c²  1  2c Suy ra 2 2 2
a  b  c  2a  b  c  3  3 (đpcm)
Dấu “=” xảy ra khi a = b = c = 1.
Câu 152: [TS10 Chuyên Đại học Vinh, 2015-2016]
Cho các số thực không âm a, b, c thỏa mãn a + b + c = 3. Tìm giá trị nhỏ nhất của a b c biểu thức: P    . 2 2 2 1 b 1 c 1 a Lời giải 2 a ab Ta có:  a  (1) 2 2 1 b 1  b
Áp dụng BĐT AM-GM cho hai số không âm, ta có 2 1 b  2b 2 2 a ab ab ab Thay v|o (1) ta được:  a   a   a  (2) 2 2 1 b 1 b 2b 2 b bc c ca Tương tự, ta có:  b  (3);  c  (4) 2 1 c 2 2 1 a 2
Cộng từng vế ba BĐT (2), (3), (4) ta được: a b c  ab  bc  ca     a  b  c    (5) 2 2 2 1 b 1 c 1 a  2  2 1 Mặt khác:
a bc 3ab bcca 2 2 2  (a
  b) (b c) (c a)   0   2
THCS.TOANMATH.com FB TRỊNH BÌNH 95 2 (a  b  c)  ab  bc  ca   3 (6) 3 a b c 3
Thay điều kiện a + b + c = 3 v| BĐT (6) v|o (5) ta có: P     2 2 2 1 b 1 c 1 a 2
Dấu bằng xảy ra khi a = b = c = 1. 3
Vậy giá trị nhỏ nhất của P là
, đạt được khi a = b = c = 1. 2
Câu 153: [TS10 Chuyên Hà Giang, 2015-2016]
Tìm giá trị lớn nhất của A  x  1  y  2 , biết x + y = 4 Lời giải
Áp dụng bất đẳng thức Bunyakoskicopxki cho 2 bộ số (1;1) và  x 1; y  2 ta có      2 2   2 2 A 1. x 1 1. y 2
1  1 x 1 y  2  2x  y  3  2  A  2   3 1 x  1 x    x 1  y  2 
Dấu bằng xảy ra khi và chỉ khi 2 1 y  2     x  y    4 5 y x y 4      2 Vậy GTLN của A là 2
Câu 154: [TS10 Chuyên Lam Sơn, 2015-2016]
Cho ba số thực dương x, y, z thỏa mãn: x + y + z = 3. x y z
Tìm giá trị nhỏ nhất của biểu thức: S    2 2 2 1 y 1 z 1 x Lời giải
Sử dụng bất đẳng thức AM-GM ta được: 2 2 x xy xy xy  x   x   x  2 2 1 y 1 y 2y 2 y yz z zx Tương tự :  y  ;  z  2 2 1 z 2 1 x 2 Cộng theo vế ta được: x y z xy  yz  zx S     x  y  z  2 2 2   1  y 1  z 1  x 2 2
     x  y  z 2 3 3 x y z   3   . 6 6 2
THCS.TOANMATH.com FB TRỊNH BÌNH 96
Dấu “=” xảy ra khi x = y = z = 1. 3
Vậy giá trị nhỏ nhất của S là : 2
Câu 155: [TS10 Chuyên Nam Định, 2015-2016]
Cho ba số dương a, b, c . Chứng minh bất đẳng thức 2 2 2 2 2 2 4a  (b  c) 4b  (c  a) 4c  (a  b)    3. 2 2 2 2 2 2 2 2 2 2a  b  c 2b  c  a 2c  a  b Lời giải 2 2 2 2 2 2 2 4a  (b  c)
2(2a  b  c )  (b  c) (b  c) Ta có:   2  2 2 2 2 2 2 2 2 2 2a  b  c 2a  b  c 2a  b  c
L|m tương tự và cộng lại ta được bất đẳng thức tương đương với: 2 2 2 (b  c) (c  a) (a  b)    3. 2 2 2 2 2 2 2 2 2 2a  b  c 2b  c  a 2c  a  b 2 x y x y2 2
Áp dụng BĐT AM-GM – Schwarz cho 4 số dương   , m n m  ta có: n 2 2 2 (b  c) b c   2 2 2 2 2 2 2 2a  b  c a  b a  c
Ta có hai BĐT tương tự, cộng từng vế ta có: 2 2 2 (b  c) (c  a) (a  b)   2 2 2 2 2 2 2 2 2 2a  b  c 2b  c  a 2c  a  b 2 2 2 2 2 2  b c   c a   a b              2 2 2 2 2 2 2 2 2 2 2 2 a  b a  c b  c a  b c  a c       b  2 2 2 2 2 2  b a   c b   a c              2 2 2 2 2 2 2 2 2 2 2 2 a  b a  b b  c c  b a  c a       c  = 3
⇒ BĐT đã cho được chứng minh
Dấu bằng xảy ra khi a = b = c.
Câu 156: [TS10 Chuyên Nam Định, 2015-2016]
Xét các số thực dương a, b, c thỏa mãn abc 1.Tìm giá trị lớn nhất của biểu thức a b c T    4 4 4 4 4 4 b  c  a a  c  b a  b  c Lời giải Ta có: 4 4 2 2 a  b  ab(a  b ) a  ; bR
THCS.TOANMATH.com FB TRỊNH BÌNH 97 Thật vậy: 4 4 2 2 a  b  ab(a  b ) 4 4 3 3
 a  b  a b  ab 3 3
 (a  b)(a  b )  0 2 2 2
 (a  b) (a  ab  b )  0 (luôn đúng a  ; bR ) => 4 4 2 2 4 4 2 2 2
a  b  c  ab(a  b )  c  a  b  c  ab(a  b )  abc ( vì a;b;c > 0 và abc = 1) c c c c   (Vi c>0)<=>  4 4 2 2 2 4 4 2 2 2 a  b  c ab(a  b )  abc a  b  c ab(a  b  c ) 2 2 c c c c     (1) 4 4 2 2 2 4 4 2 2 2 a  b  c abc(a  b  c ) a  b  c a  b  c Tương tự: 2 b b  (2) 4 4 2 2 2 a  c  b a  b  c 2 a c  (3) 4 4 2 2 2 b  c  a a  b  c
Cộng theo vế các bất đẳng thức (1),(2) và (3) ta có: 2 2 2 a b c a  b  c     1 4 4 4 4 4 4 2 2 2 b  c  a a  c  b a  b  c a  b  c Vậy T  1 a
 ; b;c  0 thỏa mãn abc = 1
Với a = b = c = 1 thì T = 1 Vậy GTLN của T là 1
Câu 157: [TS10 Chuyên Ninh Bình, 2015-2016] 1 1 1
Cho a, b, c là các số dương thỏa mãn điều kiện 
  3 . Chứng minh rằng: a b c a b c 1    (ab  bc  ca)  3 2 2 2 1 b 1 c 1 a 2 Lời giải Ta chứng minh BĐT 1 1 1 (a  b  c)(   )  9 (*) a b c a b b c c a
(*)  3  (  )  (  )  (  )  9 b a c b a c
Áp dụng BĐT AM-GM cho hai số dương ta có: a b b c c a   2;   2;   2 b a c b a c =>(*) đúng 9 1 1 1 
    3  a  b  c  3 a  b  c a b c
Trở lại bài toán: Áp dụng BĐT AM-GM cho hai số dương ta có 2 1 b  2b
THCS.TOANMATH.com FB TRỊNH BÌNH 98 2 2 a ab ab ab Ta có:  a   a   a  (1) 2 2 1 b 1  b 2b 2 Tương tự ta có: b bc c ca  b  (2);  c  (3) 2 2 1 c 2 1 a 2
Cộng từng vế của (1), (2) và (3) ta có: a b c 1  
 a  b  c  (ab  bc  ca) 2 2 2 1  b 1  c 1  a 2 a b c 1   
 (ab  bc  ca)  a  b  c  3 2 2 2 1  b 1  c 1  a 2 =>đpcm
Dấu bằng xảy ra khi a = b = c = 1.
Câu 158: [TS10 Chuyên Đắc Lắc, 2015-2016]
Cho ba số dương x, y, z thỏa mãn điều kiện x + y + z = 1. Chứng minh rằng 350 386   2015 2 2 2 xy  yz  zx x  y  z Lời giải
Với mọi a, b > 0 và x, y, z thỏa điều kiện đề bài, áp dụng bất đẳng thứcAM-GM cho 2 số dương:    1 1  1 1 1 1 4 a b   2 ab.2 .  4      (*)  a b  a b a b a  b  2 2 x  y    2 2 y  z    2 2 z  x  2 2 2
 2xy  2yz  2zx  x  y  z  xy  yz  zx 2 x  y  z 2 2 2              1 x y z
2xy 2yz 2zx 3 xy yz zx  xy  yz  zx   3 3
Áp dụng 2 bất đẳng thức trên ta có: 350 386  1 1  157 P    386    2 2 2 2 2 2 xy  yz  zx x  y  z 2xy  2yz  2zx x  y   z  xy  yz  zx 4 157  386.  2 2 2
2xy  2yz  2zx  x  y  z xy  yz  zx 1544 157 157 157    1544   1544   2015 2 (x  y  z) xy  yz  zx xy  yz  zx 1 3
Dấu bằng xảy ra khi và chỉ khi:
THCS.TOANMATH.com FB TRỊNH BÌNH 99   1 x  y  z x  y  z     3 x  y  z  1   (không xảy ra) 2 1  2 2 2 
2xy  2yz  2zx  x  y   z  3 3 Vậy P > 2015 (đpcm)
Câu 159: [TS10 Chuyên Quảng Bình, 2015-2016]
Cho các số thực dương a, b, c thỏa mãn ab + bc + ca = 11. Tìm GTNN 5a  5b  2c P  2 2 2
12(a  11)  12(b  11)  c  11 Lời giải
Thay 11 = ab + bc + ca vào P, ta có: 5a  5b  2c P  2 2 2
12(a  11)  12(b  11)  c  11 5a  5b  5c  2 2 2
12(a  ab  bc  ca)  12(b  ab  bc  ca)  c  ab  bc  ca 5a  5b  5c  (*)
2 3(a  b)(a  c)  2 3(b  a)(b  c)  (c  a)(c  b)
Áp dụng BĐT Cô–si cho hai số không âm, ta có:
2 3(a  b)(a  c)  3(a  b)  (a  c)  4a  3b  c (1) Tương tự:
2 3(b  a)(b  c)  4b  3a  c (2) 1
(c  a)(c  b)  (a  b  2c) (3) 2
Cộng từng vế của (1), (2) và (3) ta có 15 15
2 3(a  b)(a  c)  2 3(b  a)(b  c)  (c  a)(c  b)  a  b  3c (**) 2 2 Từ (*) và (**) ta có 5a  5b  2c 2 P   15 15 3 a  b  3c 2 2
THCS.TOANMATH.com FB TRỊNH BÌNH 100 3(a  b)  a  c   c 3(b  a)  b  c a   b  a   b  1 Dấu bằng xảy ra ⇔    5   c  a  c  b c     5 ab  bc  ca   11 a  b  bc  ca   11 2 Vậy GTNN của P là
,đạt được khi a = b = 1, c = 5. 3
Câu 160: [TS10 Chuyên Sư Phạm Hà Nội, 2015-2016]
Tìm các số thực không âm a và b thỏa mãn 2 3 2 3 1 1
(a  b  )(b  a  )  (2a  )(2b  ) 4 4 2 2 Lời giải
Với mọi x, y không âm, ta có: 1 2 2 1 (x )  0  x 
 x (*) Dấu bằng xảy ra ⇔x  1 . 2 4 2 Mặt khác: 2 2 2
(x  y)  0  x  2xy  y  0 2 2
 x  2xy  y  4xy 2  (x  y)  4xy (**)
Dấu bằng xảy ra ⇔ x = y.
Áp dụng BĐT (*) với x = a v| x = b ta được  2 3 2 1 1 1 a  b 
 (a  )  b   a  b   0  4 4 2 2   2 3 2 1 1 1 b  a 
 (b  )  a   b  a   0  4 4 2 2 2 3 2 3 1 2
 (a  b  )(b  a  )  (a  b  ) (1) 4 4 2
Áp dụng BĐT (**) ta được: 2 2 1       2 1 1 1 1 (a  b  )  a     b     4(a  )(b  ) 2  4   4   4 4   1 1  (2a  )(2 b )(2) 2 2 3 3 1 1 Từ (1) và (2) ta suy ra: 2 2
(a  b  )(b  a  )  (2a )(2b  ) 4 4 2 2  1 a   2   1 1
Dấu bằng xảy ra khi và chỉ khi b   a  b  2 2   1 1 a   b   4 4
THCS.TOANMATH.com FB TRỊNH BÌNH 101 1 Vậy a  b  là giá trị cần tìm. 2
Câu 161: [TS10 Chuyên Thái Bình, 2015-2016]
Cho các số dương a, b, c thỏa mãn ab + bc + ca = 3. Chứng minh rằng: 1 1 1 3    2 2 2 a  1 b  1 c  1 2 Lời giải
Giả sử a  b  c , từ giả thiết suy ra ab 1. Ta có bất đẳng thức sau: 2 1 1 2 (a b) (ab 1)     0 (luôn đúng). 2 2 2 2 1 a 1 b 1 ab (1 a )(1  b )(1  ab) 2 1 3 Vậy ta cần chứng minh:   2 1 ab 1 c 2 2 2 2 2
 c  3ab  3abc  c  ca  bc  3abc  a  b  c  3abc 2 (
 a  b  c)  3(ab  bc  ca)   9
Bất đẳng thức hiển nhiên đúng vì  3 2 a
 b  bc  ca  3 (abc) Hay a + b + c  3  3abc
Dấu bằng xảy ra khi a = b = c =1
Cho các số dương a,b,c thỏa mãn a+ b +c  3.Chứng minh rằng: ab bc ca 3    2 2 2    2 c 3 a 3 b 3 2 (a  b  c) Ta có:
 ab  bc  ca  ab  bc  ca  3 3 Ta có ab ab ab ab 1 1    (  ) 2 2 c  3 c  ab  bc  ca (a  c)(b  c) 2 a  c b  c 1 ab ab bc bc ca ca 1 3 VT  (      )  (a  b  c)  2 a  c b  c c  a b  a c  b a  b 2 2
Dấu bằng xảy ra khi a = b = c = 1
Câu 162: [TS10 Chuyên KHTN, 2015-2016]
Giả sử x, y, z l| c{c số thực lớn hơn 2. Tìm gi{ trị nhỏ nhất của biểu thức: x y z P    y  z  4 z  x  4 x  y  4 Lời giải 4x 4y 4z Ta có P    4 y  z  4 4 z  x  4 4 x  y  4
Áp dụng bất đẳng thức Cauchy ta được
4 y  z  4  2 4y  z  4  y  z  4  4  y  z
THCS.TOANMATH.com FB TRỊNH BÌNH 102
Áp dụng tương tự thì ta được 4x 4y 4z  x y z  P     4    4 y  z  4 4 z  x  4 4 x  y  4
 y  z x  z x  y  x y z 3
Dễ dàng chứng minh được    y  z x  z x  y 2
Do đó ta được P  6 . Vậy giá trị nhỏ nhất của P là 6.
Đẳng thức xẩy ra khi và chỉ khi x  y  z  4 .
Câu 163: [TS10 Chuyên Nghệ An, 2015-2016]
Cho a, b,c là các số thực bất kỳ . Chứng minh rằng:    a   1 b   1 c   3a b c2 2 2 2 1  4 Lời giải
Bất đẳng thức cần chứng minh tương đương với
          2 2 2 2 2a 2 2b 2 2c 2 3 2a 2b 2c
Đặt x  a 2; y  b 2; z  c 2. Bất đẳng thức cần chứng minh trở thành
          2 2 2 2 x 2 y 2 z 2 3 x y z
Ta có  2   2   2 2 2 2 x 2 y
2  x y  1 2x  2y  3 2 x  y 3 2 Suy ra  2 x 2 2 y 2 2 2   2xy x y 3 x y 2           2 2       3 x 2 y 2 z 2 x y2 z 4 2x y2 2 2 2 2 2 2z            2  
3 4x yz 2x y2 2z        3x  y  z2 2 2   3 a  b  c
Do đó ta được a 1b 1c 1  2 2 2 2  4
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi 1 a  b  c   . 2
Câu 164: [TS10 Chuyên Vũng T|u, 2015-2016]
THCS.TOANMATH.com FB TRỊNH BÌNH 103 1 1 1
Cho a, b, c là các số thực dương thỏa mãn a  b  c    a b c Chứng minh rằng: a) a  b  c  3abc 3 3 3 a b c 3 b)    1  3bc 1  3ca 1  3ab 2 Lời giải
a) Giả thiết của b|i to{n được viết lại th|nh
abc a  b  c  ab  bc  ca    2 a b c M| ta lại có ab  bc  ca  3   Do đó ta được      2 a b c abc a b c   3abc  a  b  c 3
Bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi v| chỉ khi a  b  c  1.
b) Bất đẳng thức cần chứng minh được viết lại th|nh 4 4 4 a b c 3    a  3abc b  3abc c  3abc 2
Áp dụng kết quả c}u a ta được 4 4 4 2 2 2 a b c a b c      a  3abc b  3abc c  3abc 2a  b  c a  2b  c a  b  2c Ta cần chỉ ra được 2 2 2 a b c 3    2a  b  c a  2b  c a  b  2c 2
Áp dụng bất đẳng thức Bunhiacopxki dạng ph}n thức ta được a b c    2 2 2 2 a b c    2a  b  c a  2b  c a  b  2c
2a  b  c  a  2b  c  a  b  2c
M| theo bất đẳng thức Bunhiacopxki ta được
2a  b  c  a  2b  c  a  b  2c  12a  b  c Suy ra    2    2 a b c a b c a bc a bc  
2a  b  c  a  2b  c  a  b  2c 2 3a  b  c 2 3 1 1 1
Cũng từ giả thiết a  b  c    ta suy ra được a b c 1 1 1 9 a  b  c      a  b  c  3 a b c a  b  c a bc a bc 3 Do đó  . 2 3 2
THCS.TOANMATH.com FB TRỊNH BÌNH 104 2 2 2 a b c 3
Từ c{c kết quả trên ta được    2a  b  c a  2b  c a  b  2c 2
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi v| chỉ khi a  b  c  1.
Câu 165: [TS10 Chuyên Vĩnh Phúc, 2015-2016]
Cho a, b, c là các số thực dương thỏa mãn a  b  c  3. Chứng minh rằng: 1 1 1    1 2 2 2 2  a b 2  b c 2  c a Lời giải
Bất đẳng thức cần chứng minh tương đương với 2 2 2 a b b c c a    1 2 2 2 2  a b 2  b c 2  c a
Áp dụng bất đẳng thức Cauchy ta có 2 2 3 2
2  a b  1 1 a b  3 a b 2 2 3 2 a b a b a ab Do đó ta được   2 3 2 2  a b 3 3 a b
Ho|n to|n tương tự ta được 2 2 2 3 2 3 2 3 a b b c c a a ab  b bc  c ca    2 2 2 2  a b 2  b c 2  c a 3   
Cũng theo bất đẳng thức Cauchy ta được 3 2 a b b a 2b ab   3 3 a a  2b  3 2   2a 2ab Suy ra a ab   3 3 a  b  c 3 2 3 2 3  2
Ho|n to|n tương tự ta được a ab  b bc  c ca   3 3 2 2 2 a b b c c a Từ đó ta được    1 2 2 2 2  a b 2  b c 2  c a
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi a  b  c  1.
Câu 166: [TS10 Chuyên Cần Thơ, 2015-2016]
Cho x, y, z là các số thực dương thỏa mãn xy  yz  zx  2xyz . Tìm giá trị nhỏ nhất của biểu thức: x y z P   
zz  x xx  y xx  z
THCS.TOANMATH.com FB TRỊNH BÌNH 105 Lời giải 1 1 1 1 1 1
Biến đổi giả thiết ta được 
  2 . Đặt a  ; b  ; c  , khi đó giả thiết trở x y z x y z thành a  b  c  2 . 2 2 2 a b c
Ta viết lại biểu thức P là P    2 a  2b b  2c c  2a
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được a b c a bc2 2 2 2 a  b  c 2 P       2 a  2b b  2c c  2a 3a  b  c 3 3 2 3
Vậy giá trị nhỏ nhất của P là
. Đẳng thức xẩy ra khi và chỉ khi x  y  z  3 2
Câu 167: [TS10 Chuyên Tiền Giang, 2015-2016]
Cho ba số thực x; y; z  1 . Chứng minh rằng: 4 4 4 x y z      48 2  2 x   1 y 1 z 1 Lời giải
Ta đi chứng minh bất đẳng thức: Với a  1 thì    2 4 a 16 a 1 Thật vậy    2         2 4 4 2  2 a 16 a 1 a 16a 32a 16 0 a 2 a  4a  4  0 Vì a  1 nên 2
a  4a  4  0 , do đó bất đẳng thức trên đúng. 4 4 x 16x
Áp dụng bất đẳng thức trên ta được    2 4 y 16 y 1 do đó   .  2 4 y y 1
Ho|n ta tương tự ta được 4 4 4 4 4 4 x y z  x y z             16 48 2   2 x  4 4 4 1  y z x y 1 z 1  4 4 4 x y z
Vì theo bất đẳng thức Cauchy thì    3 4 4 4 y z x
Vậy bất đẳng thức được chứng minh.
THCS.TOANMATH.com FB TRỊNH BÌNH 106
Câu 168: [TS10 Chuyên Đại học Vinh, 2015-2016]
Cho a, b, c là các số thực không âm thỏa mãn a  b  c  2 . Tìm giá trị nhỏ nhất ab  bc  ca 1 của biểu thức: 2 2 2 P  a  b  c   2 2 2 2 a  b  c Lời giải   2 2 2 4 a  b  c 
Từ giả thiết a  b  c  2 ta được ab  bc  ca  2
Do đó biểu thức P được viết lại thành 4   2 2 2 a  b  c 2 2 2  1 P  a  b  c   2 2 2 4 a  b  c Đặt 2 2 2 2 t  a  b  c 
 t  2. Khi đó ta được 3 2 2 1 t t t 1 3t t 3 t 12 1 3 9 P  t    1       1     2 2 t 4 8 8 2t 4 4 4 4 2 4 9
Vậy giá trị nhỏ nhất của P là
. Đẳng thức xẩy ra khi và chỉ khi a  b  0; c  2 và 4 các hoán vị.
Câu 169: [TS10 Chuyên KHTN Hà Nội, 2015-2016]
Giả sử a, b, c là các số thực dương thỏa mãn ab  bc  ac  abc  4 . Chứng minh rằng: 2 2 2
a  b  c  a  b  c  2ab  bc  ac Lời giải
Áp dụng bất đẳng thức Cauchy 4 số ta có : 4 3 3 3 3 3 2 2 2
4  abc  ab  bc  ac  4 a b c  1  abc  a  b  c  3 abc  3 a b c
Khi đó ta quy b|i to{n về chứng minh 2 2 2 3 2 2 2
a  b  c  3 a b c  2ab  bc  ac Đặt 3 2 3 2 3 2
a  x, b  y, c  z x, y,z  0 , bất đẳng thức được viết lại thành 3 3 3 3 3 3 3 3 3
x  y  z  3xyz  2 x y  2 z x  2 z y
Dễ dàng chứng minh được 3 3 3
x  y  z  3xyz  xyx  y  yzy  z  xzx  z
         3 3 3 3 3 3 xy x y yz y z
xz x z  2 x y  2 z x  2 z y Khi đó ta được 3 3 3 3 3 3 3 3 3
x  y  z  3xyz  2 x y  2 z x  2 z y
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi a  b  c  1
THCS.TOANMATH.com FB TRỊNH BÌNH 107
Câu 170: [TS10 Chuyên KHTN Bình Thuận, 2015-2016]
Cho x, y, z là các số thực dương thỏa mãn x  y  z  3 2 . Chứng minh rằng: 1 1 1 3             4 x 3y 5z y 3z 5x z 3x 5y Lời giải
Áp dụng bất đẳng thức Cauchy ta được
2 8x3y  5z  8x  3y  5z 1 4 2 4 2 Suy ra         8x3y5z x 3y 5z 2 8x 3y 5z
Ho|n to|n tương tự ta được 1 4 2 1 4 2      ; 8y  3z  5x    8z3x5y y 3z 5x z 3x 5y
Cộng theo vế các bất đẳng thức trên ta được 1 1 1   x 3y  5z y 3z  5x z 3x  5y 4 2 4 2 4 2    8x  3y  5z 8y  3z  5x 8z  3x  5y
Mà theo bất đẳng thức Cauchy ta có 4 2 4 2 4 2 9.4 2 36 2 3      8x  3y  5z 8y  3z  5x 8z  3x  5y 16x  y  z 16.3 2 4 1 1 1 3 Suy ra             4 x 3y 5z y 3z 5x z 3x 5y
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi x  y  z  2 . NĂM HỌC 2014-2015
Câu 171: [TS10 Chuyên Bắc Ninh, 2014-2015]
Tìm giá trị nhỏ nhất của biểu thức P = a2 + ab + b2 – 3a – 3b + 2014 .
THCS.TOANMATH.com FB TRỊNH BÌNH 108 Lời giải
Giá trị nhỏ nhất của P là 2011 khi a =b = 1
4P = a2 - 2 ab + b2 + 3(a2 + b2 + 4 + 2ab – 4a – 4b ) + 4. 2014 – 12
= (a - b)2 + 3 (a + b – 2)2 +8044 ≥ 8044 Suy ra: P ≥ 2011 a   b D}u “=” xảy ra khi   a  b  1 a  b  2   0
Vậy giá trị nhỏ nhất của P là 2011 khi và chỉ khi a = b = 1.
Câu 172: [TS10 Chuyên Bắc Ninh, 2014-2015] a b c
Cho các số thực a, b, c dương. Chứng minh rằng:    2 2 2 2 2 2 2 b  c c  a a  b Lời giải 2 2 a a 2a
Áp dụng bất đẳng thức Cauchy ta được       2 2 2 2 2 2 2 2 a  b  c b c a b c 2 2 b 2b c 2c
Ho|n to|n tương tự ta được  ;  2 2 2 2 2 2 2 2 2 2  a  b  c  a  b  c c a a b a b c
Cộng theo vế các bất đẳng thức trên ta được    2 2 2 2 2 2 2 b  c c  a a  b
Vì đẳng thức không xẩy ra nên ta có bất đẳng thức a b c    2 2 2 2 2 2 2 b  c c  a a  b
B|i to{n được chứng minh xong.
Câu 173: [TS10 Chuyên Bắc Ninh, 2014-2015]
Cho a, b, c l| độ dài ba cạnh của một tam giác thỏa mãn điều kiện 2c  b  abc . Tìm 3 4 5
giá trị nhỏ nhất của biểu thức: S    b  c  a c  a  b a  b  c Lời giải
Từ giả thiết ta có a  b  c  0; b  c  a  0; c  a  b  0 . 1 1 4
Áp dụng bất đẳng thức Cauchy dạng   x y x  ta được y
THCS.TOANMATH.com FB TRỊNH BÌNH 109  1 1   1 1   1 1  S    2   3       
 b  c  a c  a  b 
 b  c  a a  b  c 
 c  a  b a  b  c  2 4 6    c b a 2 1 Mà 2c  b  abc 
  a nên kết hợp với bất đẳng thức Cauchy ta được b c 6 S  2a   4 3 a
Vậy giá trị nhỏ nhất của S là 4 3 dấu bằng xảy ra khi và chỉ khi a  b  c  3.
Câu 174: [TS10 Chuyên Đắc Lắc, 2014-2015]
Giả sử a, b, c là các số thực dương thỏa mãn a  b  c  3. Tìm giá trị nhỏ nhất của biểu thức:
   3    3 b c a c a b a bc A    2a 2b 2c Lời giải
Áp dụng bất đẳng thức Cauchy ta được    3 b c a 2a 1 3b  c  a    2a 4 2 2    3 c a b 2b 1 3c  a  b    2b 4 2 2    3 a b c 2c 1 3a  b  c    2c 4 2 2
Cộng theo vế c{c bất đẳng thức trên ta được
   3    3 b c a c a b
a bc a bc 3 3a bc      2a 2b 2c 2 2 2
   3    3 b c a c a b a bc 3 3 Hay    a  b  c   2a 2b 2c 2 2 3
Vậy gi{ trị nhỏ nhất của A l|
. Đẳng thức xẩy ra khi v| chỉ khi a  b  c  1. 2
Câu 175: [TS10 Chuyên H| Tĩnh, 2014-2015]
Biết phương trình x4 + ax3 + bx2 + ax + 1= 0 có nghiệm. Chứng minh rằng 2 2 4 a  b  5 Lời giải
Dễ dàng nhận thấy x = 0 không phải là nghiệm của phương trình
THCS.TOANMATH.com FB TRỊNH BÌNH 110
Giả sử x  0 là nghiệm của phương trình đã cho. Chia 2 vế của phương trình cho 0 2 x  0 được 0 2 1 1 (x  )  a(x  )  b  0 0 2 0 x x 0 0 1 1 Đặt t  x  2 2  |  t| 2; x   t  2 0 x o 2 x 0 0
Do đó ta có phương trình: 2 t  2  a  t  b
Áp dụng BĐT Bunyakoski được 2 2 2 2 2 2
(a  b )(t  1)  (at  b)  (t  2) 4 2 3 2 4 2 2 2         2 2 t 4t 4 t 4t 4 4 4 5t 24t 16 4 (5t 4)(t 4) 4 4  a  b          2 2 2 2 t  1 t  1 5 5 5(t  1) 5 5(t  1) 5 5  2 |  t| 2 b    |  x | 1  Vậy 2 2 4 a  b 
. Dấu “=” xảy ra khi và chỉ khi 0 5 a b     5  a    bt 4  a  t t    5
Câu 176: [TS10 Chuyên Nam Định, 2014-2015]
Cho các số thực dương x, y, z thỏa mãn 2 2 2
x  y  z  3xyz . Chứng minh rằng: 2 2 2 x y z 3    4 4 4 x  yz y  xz z  xy 2 Lời giải
Vì x, y, z dương, {p dụng BĐT Cô-si ta có: 2 2 4 1 1 x 1
)2x yz  x  yz     (1) 4 4 2 2x yz x  yz x  yz 2 yz 2 1 1 1 1 1 1 )     (  ) (2) yz y z 2 yz 4 y z 2 x 1 1 1 Từ (1) và (2) =>  (  ) 4 x  yz 4 y z Tương tự: 2 2 y 1 1 1 z 1 1 1  (  );  (  ) 4 4 y  xz 4 x z z  xy 4 x y 1 1 1 1 1 1 1 1 1 1 1 1 xy  yz  zx
 A  (      )  (   )  . (3) 4 y z x z x y 2 y z x 2 xyz Mà lại có : 2 2 2
xy  yz  zx  x  y  z (4) 2 2 2 1 x  y  z 1 3xyz 3 Từ (3) và (4) có : A  .  .  (đpcm) 2 xyz 2 xyz 2
Dấu “=” xảy ra khi x = y = z = 1
THCS.TOANMATH.com FB TRỊNH BÌNH 111
Câu 177: [TS10 Chuyên Bình Định, 2014-2015] 2 1
Tìm giá trị nhỏ nhất của hàm số: y   1 với 0 < x< 1 x x Lời giải 2 1 2 1 2x 1  x Ta có: y     2  1 3    3 1 x x 1 x x 1 x x 2x 1 x Vì 0  x  1 =>  0;  0 1 x x 2x 1 x 2x 1  x Ta có:   2 .  2 2 1 x x 1  (Bất đẳng thức AM-GM) x x Dấu “=” xảy ra khi: 2x 1  x x  1   2(TM) 2 2 2 
 2x  x  2x 1  x  2x 1  0   1  x x x  1    2(L)  y  2 2  3
Dấu “=” xảy ra khi x  1   2 Vậy y  2 2  3 khi x= -1+ 2 min
Câu 178: [TS10 Chuyên Ninh Bình, 2014-2015]
Cho a, b, c là các số dương thỏa mãn điều kiện a + b + c = 3. Tìm giá trị lớn nhất của 3 3 3 3 3 3 5b  a 5c  b 5a  c biểu thức: P    2 2 2 ab  3b bc  3c ca  3a Lời giải 3 3 5b  a Ta sẽ chứng minh: P   2b a 2 ab  3b 3 3 3 3 2 5b  a
5b  a  (ab  3b )(2b  a) Thật vậy: (2b a)  2 2 ab  3b ab  3b 3 3 2 2 3 2 5 3 2 2
5b  a  (2ab  a b  6b  3b a) b a  a b  b a   2 2 ab  3b ab  3b 2 (  a  b)(a  b)   0 2 ab  3b 3 3 5b  a   2b  a 2 ab  3b Ta có 2 BĐT tương tự: 3 3 3 3 5c  b 5a  c  2c  b;  2a  c 2 2 bc  3c ca  3a
Cộng từng vế 3 BĐT trên ta được
P  2(a  b  c) (a  b  c)  a  b  c  3 a   b  c
Dấu bằng xảy ra    a  b  c  1 a  b  c   3
Vậy giá trị lớn nhất của P là 3 ⇔ a = b = c = 1.
THCS.TOANMATH.com FB TRỊNH BÌNH 112
Câu 179: [TS10 Chuyên Ngoại ngữ Hà Nội, 2014-2015] 2 3 4 2014 2015 Chứng minh rằng: 1    ....   4 2 3 2013 2014 2 2 2 2 2 Lời giải 3 4 2014 2015 Đặt S=   ....  2 3 2013 2014 2 2 2 2 Ta có: 3 4 2014 2015 2S    ....  2 2012 2013 2 2 2 2 3 4  3 5  4 2015  2014 2015  2S  S     ....  2 3 2013 2014 2 2 2 2 2 1 1 1 1 2015  S  (1    .... )  2 3 2013 2014 2 2 2 2 2 2014 1 1  ( ) 1 1 1 1 1 Ta có: 2 1     ....   2  2 3 2013 2013 2 2 2 2 1 2 1  2 1 2015 2 3 4 2014 2015 Do đó: S  2    2  1    ....   4 2013 2014 2 3 2013 2014 2 2 2 2 2 2 2
Câu 180: [TS10 Chuyên Hải Dương, 2014-2015]
Cho x; y là hai số dương thay đổi. Tìm giá trị nhỏ nhất của biểu thức: 2 2 (x  y) (x  y) S   2 2 x  y xy Lời giải 2 2 2 2 (x  y) (x y) 2xy x  y Ta có: S    1   2 2 2 2 2 x  y xy x  y xy 2 2 2 2 2xy x  y x  y  3 (  )  2 2 x  y 2xy 2xy
Do x, y là các số dương nên ta có: 2 2 AMGM 2 2 2xy x  y 2x x  y   2 .  2 2 2 2 2 x  y 2xy x  y 2xy
Dấu “=” xảy ra khi và chỉ khi: 2 2 2xy x  y 2 2 2 2 2 2 2 2 
 (x  y )  4x y  (x  y )  0 2 2 x  y 2xy 2 2
 x  y  x  y (x; y  0) 2 2 x  y 2 2 ) x  y  2xy   1 2xy
Cộng các bất đẳng thức ta được S  6
THCS.TOANMATH.com FB TRỊNH BÌNH 113
Dấu “=” xảy ra khi x = y.
Vậy Min S = 6 khi và chỉ khi x = y
Câu 181: [TS10 Chuyên Phan Bội Châu, 2014-2015]
Cho các số a, b, c không âm. Chứng minh rằng 2 2 2 3 2
a  b  c  3 (abc)  2(ab  bc  ca)
Đẳng thức xảy ra khi nào? Lời giải Đặt 3 2 3 2 3 2 a  x; b  y; c  z. 2 3 2 3 2 3 3 3 3
 a  x ; b  y ;c  z ,a  x ; b  y ;c  z ;x,y,z  0
Bất đẳng thức đã cho trở thành: 3 3 3 3 3 3 3 3 3
x  y  z  3xyz  2( x y  y z  z x )(1)
Vì vai trò của x; y ; z bình đẳng nên có thể giả sử x  y  z  0 Khi đó: 2 2
x(x  y)  z(y  x)  (z  x  y)(x y)(y  z)  0 3 3 3
 x  y  z  3xyz  xy(z y) yz(y z) zx(z x) (2)
Áp dụng Bất đẳng thức Côsi ta có 3 3
xy(x  y)  2 xy xy  2 x y (3) Tương tự ta có: 3 3 3 3 yz(y z)  2 y z (4); zx(z x)  2 z x (5)
Cộng vế theo vế các bất đẳng thức (3), (4), (5) ta được 3 3 3 3 3 3
xy(x y)  yz(y z)  zx(z x)  2( x y  y z  z x ) (6) Từ (2) và (6) ta có: 3 3 2 3 3 3 3 3 3
x  y  z  3xyz  2( x y  y z  z x )
Đẳng thức xảy ra khi x = y = z hay a = b = c.
Câu 182: [TS10 Chuyên Thái Bình, 2014-2015]
Cho các số dương x, y, z thay đổi thỏa mãn: x( x + 1) + y( y + 1) + z( z + 1) ≤ 18. 1 1 1
Tìm giá trị nhỏ nhất của biểu thức: B   
x  y  1 y  z  1 z  x  1 Lời giải
Với mọi a, b, c > 0, ta có: 2 2 2 2 2 2
(a  b)  (b  c)  (c  a)  0  2a  2b  2c  2ab  2bc  2ca  0 2 2 2
 2(a  b  c )  2ab  2bc  2ca 2 2 2 2 2 2
 3(a  b  c )  a  b  c 2ab  2bc  2ca 2 2 2 2
 3(a  b  c )  (a  b  c) (*)
Với mọi a, b, c > 0, áp dụng BĐT Cô–si cho ba số dương, ta có:
THCS.TOANMATH.com FB TRỊNH BÌNH 114 3 a
  b  c  3 abc  0   1 1 1    (a  b  c)      9 1 1 1 1 3       a b c 3 0  a b c abc 1 1 1 9     (**) a b c a  b  c
Áp dụng BĐT (*) với a = x, b = y, c = z và từ điều kiện của x, y, z ta có: 2 (x  y  z) 2 2 2
18  x  y  z  x  y  z   x  y  z 3 2
 (x  y  z)  3(x  y  z)  54  0
 (x  y  z  9)(x  y  z  6)  0
 x  y  z  6 (do x + y + z + 9 > 0) (***)
Áp dụng BĐT (**) với a = x + y + 1, b = y + z + 1, c = z + x + 1, ta có: 1 1 1 9 9 B     
x  y  1 y  z  1 z  x  1
x  y  1  y  z  1  z  x  1 2(x  y  z)  3 9 3 Áp dụng (***) ta có: B   2.6  3 5 x  y  z 
Dấu bằng xảy ra  x  y  1  y  z  1  z  x  1  x  y  z  2 x  y  z  6  3
Vậy giá trị nhỏ nhất của B là
, xảy ra khi và chỉ khi x = y = z = 2. 5
Câu 183: [TS10 Chuyên Thái Bình, 2014-2015]
Cho a, b, c là ba số thực dương v| có tổng bằng 1. a  bc b  ca c  ab 3 Chứng minh:    a  bc b  ca c  ab 2 Lời giải Thay 1 = a + b + c ta có:
A+bc = a(a+b+c)+bc = (a+b)(a+c) Do đó: a  bc a  bc  2bc 2bc 2bc   1  1 a  bc a  bc a  bc (a  b)(a  c)
Ta có 2 đẳng thức tương tự: b  ca 2ca c  ab 2ab  1 ;  1 b  ca (b  c)(b  a) c  ab (c a)(c b)
Cộng từng vế của 3 đẳng thức trên ta có:
THCS.TOANMATH.com FB TRỊNH BÌNH 115 a  bc b  ca c  ab  bc ca ab     3  2     a  bc b  ca c  ab
(a b)(a c) (b  c)(b  a) (c a)(c b) Do đó: a  bc b  ca c  ab 3  bc ca ab  3          a  bc b  ca c  ab 2
(a b)(a c) (b  c)(b  a) (c a)(c b)  4
bc(b  c)  ca(c  a)  ab(a  b) 3   (a  b)(b  c)(c  a) 4 2 2 2 2 2 2 2 2 2 2 2 2
 4(b c  bc  c a  ca  a b  ab )  3(a b  ab  b c  bc  c a  ca  2abc) 2 2 2 2 2 2
 b c  bc  c a  ca  a b  ab  6abc(*)
Áp dụng BĐT AM-GM cho ba số dương ta có: 2 2 2
b c  c a a b  3abc   (*) đúng 2 2 2
bc  ca  ab  3abc
Vậy BĐT đã cho được chứng minh. 1
Dấu bằng xảy ra khi a  b  c  3
Câu 184: [TS10 Chuyên TP. Hồ Chí Minh, 2014-2015] 2 2 x y x y
a) Cho x, y là 2 số thực khác 0. Chứng minh rằng:    2 2 y x y x 2 2 a  3ab  b
b) Cho a, b là hai số dương. Tìm gi{ trị nhỏ nhất của biểu thức: P  ab(a  b) Lời giải a) Ta có: 2 2 2 2 4 4 3 3 x y x y x y x y x  y  x y  xy          0 2 2 2 2 2 2 y x y x y x y x x y 3 3 2 2 2 (x  y)(x  y ) (x  y) (x  xy  y )   2 2 2 2 x y x y 2     2 1 3 2 (x  y)  x   y     2  4      0 2 2 x y
Bất đẳng thức cuối cùng đúng vậy b|i to{n được chứng minh.
Dấu “=” xảy ra khi x = y. b) Ta có:
THCS.TOANMATH.com FB TRỊNH BÌNH 116 1 2 3 2     2 2 2 (a b) ab (a b) a  3ab  b (a  b)  ab 4 4 P    ab(a  b) ab(a b) ab(a  b) 1 3 1 2 2 3 (a  b)  ab (a  b) 2 (a  b) .ab ab 4 4 4 4     ab(a  b) ab ab(a  b) ab 3 5  1  2 2 1 2  (a  b)  ab
Dấu bằng xảy ra  4  a  b a    b
Câu 185: [TS10 Chuyên Lam Sơn, 2014-2015]
Cho các số dương x, y, z thỏa mãn: 2 2 2 2 2 2
x  y  y  z  z  x  2014 2 2 2 x y z
Tìm giá trị nhỏ nhất của biểu thức T    y  z z  x x  y Lời giải Đặt 2 2 2 2 2 2
a  x  y ; b  y  z ; c  z  x (*)  a  b  c  2014(1) 2 2 2 2 2 2 2 2 2 a  b  c a  b  c a   b  c Từ (*) => 2 2 2 x  ; y  ; z  2 2 2
Áp dụng BĐT Cau chy ta có: 2 2
y  z  2(y  z )  b 2 2 2
z  x  2(z  x )  c 2 2 2
x  y  2(x  y )  a 2 Từ đó ta có: 2 2 2 2 2 2 2 2 2 2 2 2 x y z 1 a  b  c a  b  c a   b  c T     (   ) y  z z  x x  y 2 2 b c a 2 2 2 2 2 2 1 a c a b b c T  (       a  b  c) (2) 2 2 b b c c a a
Áp dụng BĐT AM-GM ta lại có: 2 2 2 2 2 2 a c a b b c  b  2a;  b  2c;  c  2a;  c  2b;  a  2b;  a  2c b b c c a a 2 2 2 2 2 2 a c a b b c      
 4(a  b  c)  2(a  b  c)  2(a  b  c) (3) b b c c a a 1 Từ (2) và (3)=> T  (a b c) (4) 2 2 1 Từ (1) và (4) => T  .2014. 2 2
THCS.TOANMATH.com FB TRỊNH BÌNH 117 2014 2014 Vậy T  khi x = y = z = MIN 2 2 3 2
Câu 186: [TS10 Chuyên Lam Sơn, 2014-2015] 2 2 2
xyz(x  y  z  x  y  z )
Cho ba số thực x, y, z. Tìm giá trị lớn nhất biểu thức: S  2 2 2
(x  y  z )(xy  yz  zx) Lời giải Theo Bunyakoski: 2 2 2 2 2 2 2
(x  y  z)  3(x  y  z )  x  y  z  3 x  y  z 2 2 2 2 2 2
xyz( 3 x  y  z  x  y  z ) xyz( 3  1)  S   2 2 2 2 2 2
(x  y  z )(xy  yz  zx)
x  y  z (xy  yz  zx) xyz( 3  1) 3  1  S   2 2 2 2 2 2 6 3 3 x y z x y z 3 3 3  1 =>Smax= khi x = y = z 3 3
Câu 187: [TS10 Chuyên Vĩnh Phúc, 2014-2015] Cho phương trình 2
ax  bx  c  0 a  0 có hai nghiệm thuộc đoạn 0; 2   . Tìm giá 2 2 8a  6ab  b
trị lớn nhất của biểu thức: P  2 4a  2ab  ac Lời giải Gọi x ; x x  x
là hai nghiệm của phương trình đã cho. Theo định lí Vi-ét ta có 1 2  1 2  b c x  x   ; x x  1 2 1 2 a a 2 b  b  8  6    8a  6ab  b a  a 8  6  x x  x  x 1 2   1 22 2 2 Khi đó P    2 4a  2ab  ac b c 4  2 x  x  x x 1 2  1 2 4  2  a a Do 2 2 2 2
0  x  x  2  x  x x ; x  4  x  x  x x  4 1 2 1 1 2 2 1 2 1 2
 x  x 2  3x x  4 1 2 1 2
8  6 x  x  3x x  4 1 2  Do đó ta được 1 2 P     3 4 2 x  x  x x 1 2  1 2 c  b  4a
Đẳng thức xảy ra khi x  x  2 hoặc x  0; x  2 hay  1 2 1 2 b  2  a; c   0
Vậy giá trị lớn nhất của P là 3.
THCS.TOANMATH.com FB TRỊNH BÌNH 118
Câu 188: [TS10 Chuyên Hà Nội Amsterdam, 2014-2015]
Cho ba số thực dương a, b, c thỏa mãn (a + b)(b + c)(c + a) = 1. 3
Chứng minh ab + ac + bc ≤ 4 Lời giải
Áp dụng BĐT Cô–si cho ba số không âm, kết hợp điều kiện (1) ta có: 3 3
(a  b)  (b  c)  (c  a)  3 (a  b)(b  c)(c  a)  3  a  b  c  (2) 2
Áp dụng BĐT Cô–si cho hai số không âm, kết hợp điều kiện (1) ta có: a   b  2 ab  1
b  c  2 ac  1  (a  b)(b  c)(c  a)  8abc  abc  (3) 8 ca  2 ca 
Biến đổi (1), chú ý 2 BĐT (2) v| (3), ta được:
(a  b)(b  c)(c  a)  1 2
 (a  b)(bc  ba  c  ca)  1 2 2
 (a  b)(bc  ba  ca)  ac  bc  1
 (a  b)(ab  bc  ca)  c(ab  bc  ca) abc  1
 (a  b  c)(ab  bc  ca)  abc  1 1 1  1  abc 3 8  ab  bc  ca    a  b  c 3 4 1
Dấu bằng xảy ra khi a = b = c = . 2
Câu 189: [TS10 Chuyên Hà Nội Amsterdam, 2014-2015] 1
Chứng minh tồn tại các số nguyên a, b, c sao cho 0 < a  b 2  c 3 < 1000 Lời giải
Xét nửa khoảng A = (0;1]. Chia nửa khoảng này thành 1000 nửa khoảng  1   1 2   n 1 n   999  A  0; ,A  ; ,...,A  ; ,...,A         ;1 1 2 n 1000   1000  1000 1000  1000 1000  1000  Xét bộ số x ; x ;...; x với x  1
  k 2  k 2(k *,k  1001) 1 2 1001 k  
THCS.TOANMATH.com FB TRỊNH BÌNH 119
Với mọi k ta có k 2  1   k 2  1 k 2  
(tính chất phần nguyên) nên 0  1
  k 2  k 2  1 x A k  
⇒ xk thuộc một trong các 1000 khoảng A1, A2,..., A1000
Có 1001 số xk mà có 1000 nửa khoảng, do đó tồn tại 2 số x , x thuộc cùng một nửa i j 1 khoảng Am n|o đó 0 |  x  x | . i j 1000 Đặt a  1  i 2  1
  j 2 ,b  i  j  x  x  a  b 2 0. 3 i j    
Mà a là số nguyên, b 2 là số vô tỷ nên a  b 2  0 |  x  x | 0 i j 1 1 Do đó 0 |  x  x |
 0  a  b 2  0. 3  i j 1000 1000
Vậy tồn tại các số nguyên a, b, c thỏa mãn đề bài.
Câu 190: [TS10 Chuyên Phú Thọ, 2014-2015]
Cho a, b, c là các số thực dương thỏa mãn 6a  3b  2c  abc . Tìm giá trị lớn nhất của 1 2 3 biểu thức: B    2 2 2 a  1 b  4 c  9 Lời giải 6 3 2 1 2 3
Giả thiết của b|i to{n được viết lại thành  
 1. Đặt a  ; b  ; c  , bc ca ab x y z
khi đó ta được xy  yz  zx  1 x y z
Biểu thức B được viết lại thành B    2 2 2 x  1 y  1 z  1
Để ý đến giả thiết xy  yz  zx  1 ta có 2 2
x  1  x  xy  yz  zx  x  yz  x x x Khi đó ta được  2 x  1 x yzx x y z
Ho|n to|n tương tự ta được B   
x yxz x yyz zxyz
Áp dụng bất đẳng thức Cauchy ta được
THCS.TOANMATH.com FB TRỊNH BÌNH 120 x 1  x x           2  x  y z  x x y z x  y 1  y y           2  x  y y  z x y y z  z 1  z z           2  z  x y  z x z y z 
Cộng theo vế các bất đẳng thức trên ta được x y z 3 B    
               2 x y x z x y y z z x y z 3
Vậy giá trị lớn nhất của B là . 2
Đẳng thức xẩy ra khi và chỉ khi a  3; b  2 3; c  3 3
Câu 191: [TS10 Chuyên Hà Nội 2014-2015]
Cho x, y, z là ba số thực dương thỏa mãn x  y  z  1 . Chứng minh rẳng: 2 2 2 1 x 1 y 1  z    6 x  yz y  zx z  xy Lời giải
Áp dụng giả thiết ta được 2 1 x
1x1x x yyzzxyz   x  yz x yzx x yzx
Ho|n to|n tương tưh ta được 2 1  y
xzx yxzyz  y  zx x yyz 2 1  z
x yyzx yxz  z  xy y zzx
Đặt a  x  yy  z; b  y  zz  x ; c  x  y z  
x , khi đó ta viết lại được bất đẳng thức thành a  b b  c c  a    6 c a b a b b c c c
Áp dụng bất đẳng thức Cauchy ta được
  2;   2;   2 b a c b a a
THCS.TOANMATH.com FB TRỊNH BÌNH 121 a  b b  c c  a
Cộng theo vế các bất đẳng thức trên ta được    6 c a b
Vậy b|i to{n được chứng minh xong.
Câu 192: [TS10 Chuyên TP. Hồ Chí Minh 2014-2015]
Cho x, y, z là ba số thực dương thỏa mãn xy  yz  zx  1 . Chứng minh rẳng: x y z 3    2 2 2    2 x 1 y 1 z 1 Lời giải x x x
Áp dụng giả thiết ta được   2 2 x  1 x  xy  yz  zx x yxz
Áp dụng bất đẳng thức Cauchy ta được 2 x x 1  x x             x  yx  z x y x z  2 x y zx x 1  x x  Do đó ta được     2 2 x  y z    x x 1 
Ho|n to|n tương tự ta được y 1  y y  z 1  z z     ;     2 2 2  x  y y  z  2  z  x y    z y 1 z 1 
Cộng theo vế các bất đẳng thức trên ta được x y z   2 2 2 x  1 y  1 z  1 1  x x y y z z  3          2 x  y z  x x  y y  z z  x y   z  2
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi 1 x  y  z  3
Câu 193: [TS10 Chuyên Tiền Giang 2014-2015]
1) Cho a, b, c là ba số thực dương tùy ý. Chứng minh rẳng: 3 3
a  ab  abc  a  b  c 4
2) Cho a, b, c là ba số thực dương tùy ý. Chứng minh rẳng:
THCS.TOANMATH.com FB TRỊNH BÌNH 122 bc ca ab    1 2 2 2 a  2bc b  2ca c  2ab Lời giải
1) Sử dụng bất đẳng thức Cauchy ta có: a  b 4c a a 3 a 3 4 ab  2. .b   b; abc  .b.4c  4 4 4 3 a  b 4c a 4 a  b  c 3   Từ đó ta có 4
a  ab  abc  a   b   . 4 3 3
B|i to{n được chứng minh xong. Đẳng thức xảy ra khi và chỉ khi a  4b  16c
2) Bất đẳng thức cần chứng minh tương đương với 2 2 2 a b c    1 2 2 2 a  2bc b  2ca c  2ab
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được a b c a bc2 2 2 2     1 2 2 2 2 2 2 a  2bc b  2ca c  2ab
a  b  c  2ab  2bc  2ca
B|i to{n được chứng minh xong. Đẳng thức xảy ra khi và chỉ khi a  b  c
Câu 194: [TS10 Chuyên Bắc Giang 2014-2015]
Cho a, b, c là ba số thực dương thỏa mãn a  b  c  3. Chứng minh rẳng: 2 2 2 a b c 3    b  3 c  3 a  3 2 Lời giải
Áp dụng bất đẳng thức Cauchy ta được 2 2 2 2 2 2 2 2 2 a b c 4a 4b 4c 4a 4b 4c         b  3 c  3 a  3 4 b  3 4 c  3 4 a  3 b  7 c  7 a  7
Áp dụng tiếp bất đẳng thức Bunhiacopxki dạng phân thức ta được 4a 4b 4c    2 2 2 2 4 a b c 4.9 3      b  7 c  7 a  7 a  b  c  21 3  21 2 2 2 2 a b c 3 Suy ra ta được    b  3 c  3 a  3 2
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi a  b  c  1
THCS.TOANMATH.com FB TRỊNH BÌNH 123
Câu 195: [TS10 Chuyên Đại học Vinh 2014-2015]
Cho ba số thực x, y, z không âm thỏa mãn x  y  z  xyz  4 . Tìm giá trị lớn nhất của biểu thức: P  xy  yz  zx Lời giải
Giả sử x là số lớn nhất trong các số x, y, z. Khi đó ta được 3
x  y  z  3x; xyz  x Suy ra 3
x  3x  4 hay    2
x 1 x  x  4  0  x  1 . Ta có
P  xy  yz  zx  x x  y  z 2
 yz  x  x4  xyz 2  yz  x
 x  22  4  yz 2 1 x   4
Suy ra P  4 . Vậy giá trị nhỏ nhất của P là 4.
Đẳng thức xẩy ra khi và chỉ khi x  0; y  z  2 và các hoán vị.
Câu 196: [TS10 Chuyên Yên Bái 2014-2015]
Cho ba số thực x, y, z thỏa mãn x  1  ; y  2  ; z  3  và x  y  z  5  . 1 4 9 Chứng minh rằng:    36 x  1 y  2 z  3 Lời giải Do x  1  ; y  2  ; z  3
 nên x 1  0; y  2  0; z  3  0. Khi đó {p dụng bất đẳng
thức Bunhiacopxki dạng phân thức ta được 1 4 9    2 1 2 3     36 x  1 y  2 z  3 x  y  z  6
Bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi x  y  z  5    1 2 3   x 1 y  2 z   3
Câu 197: [TS10 Chuyên Quảng Trị 2014-2015]
Cho các số thực a, b, c dương. Chứng minh rằng: a b c    2 2 2 2 2 2 2 b  c c  a a  b
THCS.TOANMATH.com FB TRỊNH BÌNH 124 Lời giải 2 2 a a 2a
Áp dụng bất đẳng thức Cauchy ta được       2 2 2 2 2 2 2 2 a  b  c b c a b c 2 2 b 2b c 2c
Ho|n to|n tương tự ta được  ;  2 2 2 2 2 2 2 2 2 2  a  b  c  a  b  c c a a b a b c
Cộng theo vế các bất đẳng thức trên ta được    2 2 2 2 2 2 2 b  c c  a a  b
Vì đẳng thức không xẩy ra nên ta có bất đẳng thức a b c    2 2 2 2 2 2 2 b  c c  a a  b
B|i to{n được chứng minh xong. NĂM HỌC 2013-2014
Câu 198: [TS10 Chuyên Hải Dương, 2013-2014]
Cho tam giác ABC có chu vi bằng 2. Ký hiệu a, b, c l| độ dài ba cạnh của tam giác.
Tìm giá trị nhỏ nhất của biểu thức: a 4b 9c S    b  c  a c  a  b a  b  c Lời giải
Với a, b, c l| độ dài ba cạnh của tam giác có chu vi bằng 2 nên a  b  c  2 .
Đặt b  c  a  x; c  a  b  y; a  b  c  z , do a, b, c l| độ dài ba cạnh của tam giác y  z x  z x  y
nên x; y; z  0 . Khi đó ta được x  y  z  2 và a  ; b  ; c  . 2 2 2 Khi đó y  z 4 x  z 9x  y 1  y  z
4 x  z 9x  y S         2x 2y 2z 2  x y z   1  y 4x   z 9x   4z 9y              2  x y   x z   y z  Ta có
THCS.TOANMATH.com FB TRỊNH BÌNH 125 2 y 4x  y x      2   2  2 x y  x y    2 z 9x  z x      3   6  6 x z  x z    2 4z 9y  z y     2  3   12  12 y z  y z    1
Do đó S  4  6  12  11 . Đẳng thức xẩy ra khi và chỉ khi 2  1 x  y  2x  3   z  3x  2 5 2 1 
 y   a  ; b  ; c  2z  3y 3 6 3 2        z  1  x y z 2  Khi đó 2 2 2
a  b  c . Vậy giá trị nhỏ nhất của S là 11 khi A  BCvuông .
Câu 199: [TS10 Chuyên Hải Dương, 2013-2014]
Cho x, y, z là các số thực dương. Tìm gi{ trị nhỏ nhất của biểu thức: 2 2 2 2 2 2 x  xy  y y  yz  z z  zx  x S    x  y  2z y  z  2x z  x  2y Lời giải 2 2   2 2 3 x y x y Ta có 2 2
x  xy  y  x  y  3xy  x  y       4 4 2 2 x  xy  y x  y Suy ra  x  y  2z 2x  z  y  z
Áp dụng tương tự ta được 1  x  y y  z z  x  S      2 y  z  z  x z  x  x  y x  y  y   z 
Đặt a  x  y; b  y  z; c  z  x, khi đó ta được 1  a b c  1 3 3 S     .   
2  b  c c  a a  b  2 2 4 a b c 3
Vì theo bất đẳng thức Neibizt thì    b  c c  a a  . b 2
THCS.TOANMATH.com FB TRỊNH BÌNH 126 3
Vậy ta được giá trị nhỏ nhất của S là
đạt được tại x  y  z . 4
Câu 200: [TS10 Chuyên KHTN Hà Nội, 2013-2014]
Giả sử a, b, c, d là các số thực dương thỏa mãn abc  bcd  cda  dab  1
Tìm giá trị nhỏ nhất của biểu thức   3 3 3    3 P 4 a b c  9c Lời giải
Do vai trò của a, b, c như nhau nên ta dự đo{n dấu đẳng thức xẩy ra tại
a  b  c  kd, với k là số dương.
Khi đó {p dụng bất đẳng thức AM-GM cho ba số dương ta được 1  3 3 2 3abc a  b  c  2  2 k k 3 3 a b 3 3abd   d  3 3 2 k k k 3 3 b b 3 3bcd   d  3 3 2 k k k 3 3 c a 3 3cad   d  3 3 2 k k k
Cộng theo vế các bất đẳng thức trên ta được  1 2  3 abc  abd  bcd  cad 3  a  b  c  3d     2 3  3 3 2 3   2 2  k k  k k  3 6  9 Hay   3 3 2 a  b  c  3  9d    2 3 2  k k  k 3 6 Ta cần tìm k để 3 
 4  4k  3k  6  0 và ta chọn k là số dương. 2 3 k k 2 1  1  Đặt k  x  
 thay v|o phương trình trên v| biến đổi ta thu được 2  x  6 3 x 12x  1  0
Giải phương trình n|y ta được 3
x  6  35 , để ý là 6  356  35  1 nên ta 3 3 6  35  6  35 tính được k  2 36
Do đó ta tính được giá trị nhỏ nhất của P là . 2  3 3   6  35  6  35   
THCS.TOANMATH.com FB TRỊNH BÌNH 127 3 3 6  35  6  35
Đẳng thức xẩy ra khi và chỉ khi a  b  c  .d 2
Câu 201: [TS10 Chuyên KHTN Hà Nội, 2013-2014]
Giả sử dãy số thực có thứ tự x  x  x  ...  x thỏa mãn điều kiện: 1 2 3 192
x  x  x ... x   0 1 2 3 n
 x  x  x ... x   2013  1 2 3 192 2013 Chứng minh rằng: x  x  192 1 96 Lời giải
Trước hết ta chứng minh bài toán phụ sau: Với a  a  a  ...  a thỏa mãn 1 2 3 n a
  a  a  ... a   0 1 2 3 n
 a  a  a ... a   1  1 2 3 n 2
Khi đó ta được a  a  . n 1 n
Thật vậy, từ điều kiện của bài toán ta nhận thấy tồn tại số tự nhiên k để
a  a  a  ...  a  0  a  ...  a 1 2 3 k k 1  n a
  a  a  ... a   0 Khi đó từ 1 2 3 n  suy ra
a  a  a  ...  a   1  1 2 3 n                   1 a ... a a a a ... a a ... a 0 k1 n  1 2 3 k k 1 n 2     
 a  a  a  ... a  a ... a   1 1 1 2 3 k   k1 n  a
 a a ...a   1 2 3 k  2
Cũng từ a  a  a  ...  a  0  a  ...  a ta được 1 2 3 k k 1  n 1
a  a  a  ...  a  a   1 2 3 k 1 2k 1 a  ...  a  a  k1 n n 2 n  k 1 1 n 2n 2 Do đó a  a      n 1 2n  k 2k
2 n  kn n  k  n2 n
Như vậy b|i to{n được chứng minh xong.
Từ giả thiết của bài toán trên ta viết lại như sau
THCS.TOANMATH.com FB TRỊNH BÌNH 128  x x x x 1 2 3 n    ...   0 2013 2013 2013 2013  x x x x  1 2 3 192    ...  1  2013 2013 2013 2013 
Áp dụng kết quả của bài toán phụ ta được x x 2 2013 192 1    x  x  192 1 2013 2013 192 96
Vậy b|i to{n được chứng minh xong.
Câu 202: [TS10 Chuyên Vĩnh Phúc, 2013-2014] .
Cho c{c số thực dương a, b, c thỏa mãn 2 2 2
a  b  c  1. Chứng minh: 2 2 2 ab  2c bc  2a ac  2b    2  ab  ba  ca 2 2 2 1 ab  c 1 bc  a 1 ac  b Lời giải Do 2 2 2
a  b  c  1 nên ta có 2 2 2 2 ab  2c ab  2c ab  2c ab  2c    2 2 2 2 2 2 2 1 ab  c a  b  c  ab  c a  b  ab  2 ab  2c  2 2 a  b  ab
Áp dụng bất đẳng thức AM-GM ta có      
ab  2c a  b  ab 2 2c a b 2ab  2 2 2 2 2 2 a b c 2 2 2  2 2 2    a  b  c 2 2 2 2 2 ab  2c ab  2c ab  2c Suy ra 2    ab  2c 2 1 ab  c    2 2 2 2 2 2 a  b     c ab 2c a b ab 2 2 bc  2a ca  2b Tương tự ta được 2 2  bc  2a ;  ca  2b 2 2 1 bc  a 1 ca  b
Cộng vế theo vế các bất đẳng thức trên kết hợp 2 2 2
a  b  c  1 ta có bất đẳng thức 1
cần chứng minh. Đẳng thức xẩy ra khi và chỉ khi a  b  c  . 3
Câu 203: [TS10 Chuyên Vĩnh Phúc, 2013-2014]
Cho a, b, c là các số thực dương thỏa mãn abc  1. Chứng minh rằng: a b c 3     a   1 b   1
b 1c 1 c 1a 1 4
THCS.TOANMATH.com FB TRỊNH BÌNH 129 Lời giải
Bất đẳng thức cần chứng minh tương đương với 4a c  
1  4ba  1  4c b  1  3a  1b  1c  1
 4ab  bc  ca  4a  b  c  3abc  3ab  bc  ca 3a  b  c 3
 ab  bc  ca  a  b  c  6
Áp dụng bất đẳng thức AM-GM cho các số dương ta được     2 3 3 ab bc ca 3. abc
 3; a  b  c  3 abc  3
Cộng theo vế hai bất đẳng thức trên ta được ab  bc  ca a  b  c  6
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi a  b  c  1
Câu 204: [TS10 Chuyên TP. Hà Nội, 2013-2014]
Cho a, b, c là các số thực dương thỏa mãn a  b  c  ab  bc  ca  6abc . 1 1 1 Chứng minh rằng:    3 2 2 2 a b c Lời giải
Giả thiết của b|i to{n được viết lại thành 1 1 1 1 1 1       6 ab bc ca a b c
Áp dụng bất đẳng thức AM-GM ta được 1 1 2 1 1 2 1 1 2   ;   ;   2 2 2 2 2 2 a b ab b c bc c a ca 1 2 1 2 1 2  1  ;  1  ;  1  2 2 2 a a b b c c
Cộng theo vế các bất đẳng thức trên ta được  1 1 1   1 1 1 1 1 1  3    3  2       2.6      12 2 2 2  a b c   ab bc ca a b c  1 1 1 Hay    3 2 2 2 a b c
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi a  b  c  1
Câu 205: [TS10 Chuyên Ninh Bình, 2013-2014]
Cho x, y l| c{c số thực thoả mãn      2 2 2 2 2 x x 2y 3 y 2
 1 . Tìm gi{ trị lớn nhất
v| gi{ trị nhỏ nhất của biểu thức 2 2 C  x  y . Lời giải Ta có:
THCS.TOANMATH.com FB TRỊNH BÌNH 130
x x  2y  3y  22 2 2 2 2 4 2 2 2 4 2
 1  x  2x y  3x  y  4y  4  1 4 2 2 4
 x  2x y  y  4 2 2 x  y  2  x  3  0  x  y 2 2 2  4 2 2 x  y  2  3  x  0 x  Với 2 2 x  y  C thì ta có           2 2 2 C 4C 3 0 C 4C 4 1 C 2 1  C  2 1 1
  C  2 11 C  3 x  0 x  0 x  0 x  0  C  1     ; C  3     2 2 x  y 1 y  1  2 2 x  y  3 y   3
Vậy minC = 1 khi x  0 và y  1
 ; maxC = 3 khi x  0 và y   3 .
Câu 206: [TS10 Chuyên TP. Hà Nội, 2013-2014]
Cho a, b, c là các số thực dương thỏa mãn abc  1. Chứng minh rằng: 1 1 1 3    ab  a  2 bc  b  2 ca  c  2 4 Lời giải x y z Đặt a  ; b  ; c 
. Gọi P là vế tr{i, khi đó ta được y z x 1 1 1 P    ab  a  2 bc  b  2 ca  c  2 yz zx xy    xy  xz  2yz xy  yz  2xz xz  yz  2xy
Biến đổi tương đương ta được yz zx xy 3  P  1  1  1 xy  xz  2yz xy  yz  2xz xz  yz  2xy       1 1 1  3 P xy yz xz     xy  xz  2yz xy  yz  2xz xz  yz   2xy  1 1 1 1
Áp dụng bất đẳng thức AM-GM dạng    A B C A  B  C Ta có       9 9 9 3 3 P xy yz xz   P  3   4xy  4yz  4xz 4 4 4
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi a  b  c  1
Câu 207: [TS10 Chuyên Phú Thọ, 2013-2014] a) Chứng minh rằng: 3 3
a  b  aba  b , với a, b là hai số dương.
THCS.TOANMATH.com FB TRỊNH BÌNH 131
b) Cho a, b là hai số dương thỏa mãn a  b  1. Tìm giá trị nhỏ nhất của biểu thức:    2 3 3   2 2   3 F a b a b  ab 2 Lời giải
a) Bất đẳng thức cần chứng minh tương đương với a b 2 2
a  ab  b   aba  b  0
 a  ba  2ab  b   0  a  ba  b2 2 2  0
Ta thấy với a, b là hai số dương nên bất đẳng thức đã cho luôn đúng. 2 2 1 b) Ta có F   3 3
a  b   a  b  ab 2 a  b 3 3  3
Mà ta luôn có bất đẳng thức a  b  , với mọi a, b > 0. 4  a b   1
Áp dụng bất đẳng thức trên ta có a  b    2 3 2 3 3     .  4  16  
Áp dụng bất đẳng thức AM-GM ta có 2 2 1        2 a b 1 7a b 1 7 15 F a b       16 8 16 8 16 8 16 15 1
Vậy giá trị nhỏ nhất của F là bằng
, đạt được khi a  b  . 16 2
Câu 208: [TS10 Chuyên Bình Phước, 2013-2014] a. Chứng minh rằng: 3 3
a  b  ab(a  b) , với a, b là hai số dương.
b. Cho a, b là hai số dương thỏa mãn a  b  1. 2 3
Tìm giá trị nhỏ nhất của biểu thức: F   3 3 a  b    2 2 a  b   ab. 2 Lời giải a) Ta có bất đẳng thức 2 2 2 2 2
(a  b)(a ab  b ) ab(a  b)  0  (a  b)(a 2ab  b )  0 (a  b)(a b)  0
Ta thấy với a, b là hai số dương nên bất đẳng thức đã cho luôn đúng.
Dấu “=” xảy ra khi a = b.
THCS.TOANMATH.com FB TRỊNH BÌNH 132 b)
Áp dụng bất đẳng thức đã chứng minh ở câu (a) ta có:   2 2 3 3 a b  ab(a  b) 
 mà theo giả thiết a  b  1 Do đó   2 2 3 3 2 a b  ab(a  b)  (ab)   +) Mặt khác ta có:      2 2 2 F a b a b  2ab  11ab +) Do đó 2   2 3      2 ab     2 1 1 15  1  15 15 F ab 1 2ab ab ab 1 ab  2.ab.    ab      2 2 4 16 16  4  16 16 a   b  1  1
+) Dấu “=” xảy ra    a  b 1  ab  2  4 15 1
+) Vậy giá trị nhỏ nhất của F là bằng
, đạt được khi a  b  . 16 2
Câu 209: [TS10 Chuyên Phú Thọ, 2013-2014]  1 1 1  1 1 1
Cho ba số thực dương a, b, c thỏa mãn 12    3      2 2 2  a b c  a b c 1 1 1 1 Chứng minh rằng:    4a  b  c a  4b  c a  b  4c 6 Lời giải
Theo một đ{nh gi{ quen thuộc ta có 2  1 1 1   1 1 1  1 1 1 4    12    3        2 2 2  a b c   a b c  a b c  1 1 1    1 1 1   Suy ra     1 4      3    0  a b c    a b c   1 1 1 Do đó ta được
   1 và a  b  c  9 a b c 1 1 1 Đặt P    4a  b  c a  4b  c a  b  4c 4 1 1
Áp dụng bất đẳng thức AM-GM dạng   x  ta được y x y
THCS.TOANMATH.com FB TRỊNH BÌNH 133 1 1 1 P    4a  b  c a  4b  c a  b  4c 1  1 1 1 1 1 1         
4  3a a  b  c 3a a  b  c 3a a  b  c  1  1 1 1 3  1  1 1  1           
4  3a 3b 3c a  b  c  4  3 3  6 1
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi a  b  c  3
Câu 210: [TS10 Chuyên Nam Định, 2013-2014]
Cho các số thực dương x, y, z thỏa mãn 2 2 2
x  y  z  3xyz . Chứng minh rằng: 2 2 2 x y z 3    4 4 4 x  yz y  xz z  xy 2 Lời giải
Áp dụng bất đẳng thức AM-GM ta có 2 2 4 1 1 x 1 2x yz  x  yz     4 4 2 2x yz x  yz x  yz 2 yz 2 1 1 1 1  1 1         yz y z 2 yz 4  y z  2 x 1  1 1 
Từ hai bất đẳng thức trên ta được     4 x  yz 4  y z  2 2 y 1  1 1  z 1  1 1  Ho|n to|n tương tự ta có    ;     4 4 y  xz 4  x z  z  xy 4  x y 
Cộng theo vế các bất đẳng thức trên ta được 2 2 2 x y z 1  1 1 1  1 xy  yz  zx          4 4 4 x  yz y  xz z  xy 2  y z x  2 xyz Mặt khác ta lại có 2 2 2
xy  yz  zx  x  y  z 2 2 2 x  y  z 3xyz Do đó ta được   3 xyz xyz 2 2 2 x y z 3 Suy ra    4 4 4 x  yz y  xz z  xy 2
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi x  y  z  1
THCS.TOANMATH.com FB TRỊNH BÌNH 134
Câu 211: [TS10 Chuyên Quảng Nam, 2013-2014] 4 4 xy x y
Cho hai số x và y thỏa mãn: xy(2013  )    2014 . 2 4 4
Tìm giá trị lớn nhất và giá trị nhỏ nhất của tích xy. Lời giải 4 4 xy x y 4 4 x y Ta có: xy(2013  )    2014 ≥ 2. .
 2014 ( theo BĐT CôSi) (*) 2 4 4 4 4
(*)  (xy)2  2013xy  2014 ≤ 0
Đặt t = xy thì (*)  t2  2013t 2014 ≤ 0  (t+1)(t2014) ≤ 0  1 ≤ t ≤ 2014
GTLN của xy là 2014 khi x = y =  2014
GTNN của xy là 1 Khi (x = 1 ; y =1) hoặc ( x = 1; y = 1)
Câu 212: [TS10 Chuyên KHTN Hà Nội, 2013-2014]
Cho a, b, c là các số thực dương thỏa mãn ab  bc  ca  1. Chứng minh rằng: 2abc a  b  c 5 4 2 4 2 4 2   a b  b c  c a 9 Lời giải
Áp dụng bất đẳng thức dạng 2 2 2
x  y  z  xy  yz  zx ta được 4 2 4 2 4 2     2 2 2 a b b c c a abc a b  b c  c a 5
Bài toán quy về chứng minh 2abc a  b  c   abc 2 2 2 a b  b c  c a 9 5 Hay 2a  b  c    2 2 2 a b  b c  c a 9abc 1 2a 1 2b 1 2c
Áp dụng bất đẳng thức Cauchy ta được 2 2 2 a b   ; b c   ; c a   9b 3 9c 3 9a 3
Cộng theo vế các bất đẳng thức trên ta được 2 2 2 1 1 1 2a 2b 2c a b  b c  c a       9a 9b 9c 3 3 3   Hay 2 2 2 ab bc ca 2 a b  b c  c a   a  b  c 9abc 3 4 2
Như vậy ta cần chỉ ra được 2a  b  c   a  b  c 9abc 3
THCS.TOANMATH.com FB TRỊNH BÌNH 135 4abc a  b  c 4 Hay
  3abca  b  c  1 3 9 2
Đ{nh gi{ cuối cùng là một đ{nh gi{ đúng vì 1  ab  bc  ca  3abca  b  c 1
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi a  b  c  . 3 NĂM HỌC 2012-2013
Câu 213: [TS10 Chuyên Nghệ An, 2012-2013] 1 1 1
Cho ba số dương x, y,z thoả mãn 
  1. Chứng minh rằng: x y z
x  yz  y  zx  z  xy  xyz  x  y  z. Lời giải
Bất đẳng thức đã cho tương đương với
a  bc  b  ca  c ab  1  ab  bc  ca , 1 1 1 với a  , b  , c  , a  b  c  1. x y z
Ta có: a  bc  a(a  b  c)  bc 2 2
 a  a(b  c)  bc  a  2a bc  bc  a  bc.
Tương tự: b  ca  b  ca; c  ab  c  ab.
Từ đó ta có đpcm. Dấu bằng xảy ra khi x  y  z  3.
Câu 214: [TS10 Chuyên TP. Hồ Chí Minh, 2012-2013]
Cho ba số dương a, b, c thỏa mãn a  b  c  1. Tìm giá trị nhỏ nhất của:     2 2 2    ab bc ca A 14 a b c  2 2 2 a b  b c  c a Lời giải   2 2 2 1 a  b  c 
Dễ d|ng tính được ab  bc  ca  . Lại có 2 2 2 2        2 2 2    3 2 3 2 3 2 2 2 2 a b c a b c a b c
 a  b a  b  bc  c  ca  a b  b c  c a
Áp dụng bất đẳng thức Cauchy ta có
THCS.TOANMATH.com FB TRỊNH BÌNH 136 3 2 2 3 2 2 3 2 2
a  b a  2a b; b  bc  2b c; c  ca  2c a Do đó suy ra 2 2 2 3 2 3 2 3 2 2 2 2              2 2 2 a b c a b a b bc c ca
a b b c c a 3 a b  b c  c a 1 3 Từ đó ta được  2 2 2 2 2 2 a b  b c  c a a  b  c ab  bc  ca
3ab  bc  ca 3  3 2 2 2 a  b  c  Hay   2 2 2 2 2 2 a b  b c  c a a  b  c 2 2 2 2 a  b  c  Đặt 2 2 2 1
t  a  b  c  t  . Khi này biểu thức được viết lại thành 3 3  3t 28t 3 3t 27t 3 t 3 A  14t         2t 2 2t 2t 2 2t 2 2 27t 3 27t 3
Áp dụng bất đẳng thức Cauchy ta có   2 .  9 2 2t 2 2t t 3 1 3 4 4 23 Mặt khác 
    . Suy ra A  9   . 2 2 6 2 3 3 3 23 1
Vậy giá trị nhỏ nhất của A là
. Đẳng thức xẩy ra khi và chỉ khi a  b  c  3 3
Câu 215: [TS10 Chuyên KHTN, 2012-2013]
Cho a, b, c là các số thực dương thỏa mãn a  b  3  c; c  b  1; a  b  c
2ab  a  b  c ab   1
Tìm giá trị nhỏ nhất của biểu thức: Q  a 1b 1c 1 Lời giải Ta có
2ab  a  b  c ab 1 a  1b  1  ab  1c  1 Q    a   1 b  1c  1
a 1b1c1 1 ab  1 1 ab  1     c  1 a  
1 b  1 a  b  1 ab  a  b  1 Từ giả thiết
a  b  c  b  1  b  a  1  a   1 b  
1  0  ab  a  b 1  c 1  2 1 ab  1 Suy ra Q   ab  2 2ab   1
THCS.TOANMATH.com FB TRỊNH BÌNH 137 1 x  1
Đặt x  ab  x  2 , khi đó ta được Q   x  2 2x   1 5 1 x  1 5 x2x5 Suy ra Q        2x   1
12 x  1x  2 0 12 x 2 12 5 5 Do đó ta có Q 
. Vậy giá trị nhỏ nhất của Q là
. Đẳng thức xẩy ra khi và chỉ 12 12 khi a  1; b  2; c  3
Câu 216: [TS10 Chuyên Bình Phước, 2012-2013]
Cho a, b, c là các số thực dương thỏa mãn ab  bc  ca  3abc . 1 1 1
Tìm giá trị lớn nhất của biểu thức: P    2 2 2 a  1 b  1 c  1 Lời giải
Áp dụng bất đẳng thức Cauchy ta được 1 1 1 1 1 1 ab  bc  ca 3 P         2 2 2 a  1 b  1 c  1 2a 2b 2a 2abc 2 3
Vậy giá trị lớn nhất của P là
. Đẳng thức xẩy ra khi và chỉ khi a  b  c  1 2
Câu 217: [TS10 Chuyên Sư Phạm Hà Nội, 2012-2013]
Cho n số thực x , x , ..., x với n  3 . Kí hiệu Maxx , x , ..., x } là số lớn nhất 1 2 n 1 2 n
trong các số x , x , ..., x .Chứng minh rằng: 1 2 n          Max x x ... x x x x x ... x x 1 2 2 3 n 1 1 2 n x , x , ..., x }   1 2 n n 2n Lời giải
Để ý l| trong hai số thực x, y bất kì ta luôn có x  y  x  y
Min{x, y}  x, y  Max{x, y} và Max{x, y}  2 x  y  x  y
Sử dụng đẳng thức Max{x, y}  , ta có: 2 x  x ...  x
x  x  x  x  ...  x  x 1 2 2 3 n 1 1 2 n  n 2n x  x  x  x x  x  x  x x  x  x  x 1 2 1 2 2 2 2 3 n 1 n 1    ... 2n 2n 2n
Max{x , x }  Max{x , x}  Max{x , x } 1 2 2 n 1   Max{x ; x ;...; x } 1 2 n n
Vậy b|i to{n được chứng minh. Đẳng thức xẩy ra khi v| chỉ khi x  x ...  x 1 2 n
THCS.TOANMATH.com FB TRỊNH BÌNH 138
Câu 218: [TS10 Chuyên Phú Thọ, 2012-2013] 3
Cho x, y, z là các số không âm thỏa mãn x  y  z  . 2 Tìm giá trị nhỏ nhất: 3 3 3 2 2 2 S  x  y  z  x y z Lời giải
Áp dụng bất đẳng thức Bunyakoskicopxki ta có 
 2  2  2           2 2 2 2 2 2 2 x y z x x y y z z x y z   2 2 3 2 Hay  3 3 3 x  y  z    2 2 2 x  y  z  3 3 3  x  y  z   2 2 2 x  y  z  (*) 2 3
Mặt khác, dễ dàng chứng minh được
            3  3  3  xyz x y z x z y y z x   2z  2x     2y   2  2  2  27 9 
 x  y  z  6xy  yz  xz  8xyz 8 2 2 27      9xyz   3x  y  z  2 2 2 3 x y z 2 2 2 2 2 2  x y z     8  8 3  x  y  z 2 2 2  2 3 Đặt t  x  y  z   . Khi đó ta được 3 4 2 2 2 2 2 2     2 3 t 2t t t 9 7t t 9 1 3 11 2 3 25 S  t           t   t       Vậy giá 3  8 3  3 9 4 64 9 4 64 6  4  8 64 64 25 1
trị nhỏ nhất của S là
. Đẳng thức xẩy ra khi và chỉ khi x  y  z  64 2
Câu 219: [TS10 Chuyên Phú Thọ, 2012-2013]
Cho a,b,c là các số dương thỏa mãn ab  bc  ca  3. Chứng minh rằng: 1 3a 1 3b 1 3c    6 2 2 2 1 b 1 c 1 a Lời giải
Ta viết lại vế trái thành 1 3a 1 3b 1 3c 1 1 1 3a 3b 3c         2 2 2 2 2 2 2 2 2 1 b 1 c 1 a 1 b 1 c 1 a 1  b 1  c 1  a 2 2 1 b b b
Khi đó {p dụng ta đẳng thức Cauchy ta được :  1  1  1 2 2 b  1 b  1 2b 2
THCS.TOANMATH.com FB TRỊNH BÌNH 139 1 c 1 a
Ho|n to|n tương tự ta được  1 ;  1 2 2 c  1 2 a  1 2 1 1 1 a  b  c
Khi đó ta có bất đẳng thức:    3  2 2 2 b  1 c  1 a  1 2 a b c ab  bc  ca 3 Mặt khác ta lại có    a  b  c   a  b  c  2 2 2 b  1 c  1 a  1 2 2 1 1 1 3a 3b 3c 5a  b  c 9 Do đó ta được :       3    6 2 2 2 2 2 2 1 b 1 c 1 a 1  b 1  c 1  a 2 2
Vậy bất đẳng thức được chứng minh.
Câu 220: [TS10 Chuyên Hải Dương, 2012-2013] 1 1
Cho 2 số dương a, b thỏa mãn 
 2 . Tìm giá trị lớn nhất của biểu thức a b 1 1 Q   . 4 2 2 4 2 2 a  b  2ab b  a  2ba Lời giải
Với a  0; b  0 ta có: 2 2 4 2 2 4 2 2
(a  b)  0  a  2a b  b  0  a  b  2a b 4 2 2 2 2  1 1
a  b  2ab  2a b  2ab   (1) 4 2 2 a  b  2ab 2aba  b 1 1 1 Tương tự có 
(2) . Từ (1) và (2)  Q  4 2 2 b  a  2a b 2aba  b aba  b 1 1 1 1 Vì 
 2  a  b  2ab mà a  b  2 ab  ab  1  Q   . a b 2 2(ab) 2 1 1 Khi a = b = 1 thì  Q 
. Vậy giá trị lớn nhất của biểu thức là 2 2
Câu 221: [TS10 Chuyên Phú Thọ, 2012-2013]
Cho a, b, c là các số thực dương thỏa mãn a  b  c  1. Tìm giá trị nhỏ nhất của biểu 1 1 thức: P  
abc 1 2ab  bc  ca Lời giải Do          2 2 2 a b c 1 1 2 ab bc ca  a  b  c 1 a  b  c 1 1 1 1 Suy ra P       2 2 2 2 2 2 a  b  c abc a  b  c ab bc ca
THCS.TOANMATH.com FB TRỊNH BÌNH 140 1 1 1 9 Dễ chứng minh:    ab bc ca ab  bc  ca
Do đó ta có bất đẳng thức 1 1 1 1 1 9      2 2 2 2 2 2 a  b  c ab bc ca a  b  c ab  bc  ca
Áp dụng tiếp đ{nh gi{ trên ta được  1 1 1     2 2 2
a  b  c  2ab  2bc  2ca    9 2 2 2   a  b  c ab  bc  ca ab  bc  ca  1 2 Hay   9 2 2 2 a  b  c ab  bc  ca 7 Mặt khác ta lại có  21 ab  bc  ca 1 1 1 1
Cộng theo vế các bất đẳng thức trên ta được     30 . 2 2 2 a  b  c ab bc ca
Vậy bất đẳng thức được chứng minh. 1
Vậy giá trị nhỏ nhất của P là 30. Đẳng thức xẩy ra khi và chỉ khi a  b  c  . 3
Câu 222: [TS10 Chuyên Sư Phạm Hà Nội, 2012-2013]
Cho các số thực dương x, y thỏa mãn điều kiện: xy x  y  x  y . Tìm giá trị nhỏ
nhất của biểu thức P  x  y Lời giải.
Từ giả thiết suy ra: x > y > 0, Áp dụng bất đẳng thức Cauchy ta có: 2 2         2    2 1 
  2   1 4xy x y 4xy 1 x y xy x y .4xy x y 4xy     x y4. 4 4  2  16  
Do đó x  y  4 . Vậy min A  4 khi x  2  2 2; y  2  2.
Câu 223: [TS10 Chuyên Vĩnh Phúc, 2012-2013]
Cho các số thực dương a, b, c thỏa mãn abc  1.Chứng minh rằng: a b c    a  b  c 3 3 3 b c a Lời giải
THCS.TOANMATH.com FB TRỊNH BÌNH 141 1 1 1 Đặt x  ; y  ; z 
 xyz  1. Khi đó bất đẳng thức được viết lại thành a b c 3 3 3 x y z 1 1 1      z x y x y z
Áp dụng bất đẳng thức Binhiacopcxki ta được 3 3 x z x y z y 2 2 2 2 3 2 2 2     x  y  z z x y xx  yz  zx
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được 2 2 2 1 1 1 x  y  z    x y z
Thật vậy theo một đ{nh gi{ quen thuộc và giả thiết xyz  1 ta có xy  yz  zx 2 2 2 1 1 1
x  y  z  xy  yz  zx     xyz x y z
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi a  b  c  1
Câu 224: [TS10 Chuyên KHTN, 2012-2013]
Giả sử a, b là các số thực dương thỏa mãn điều kiện:  x   1  y   1  4 . Tìm giá 2 2 x y
trị nhỏ nhất của biểu thức: P   . y x Lời giải. Ta có:     x   1  y   x y x 1 y 1
1  4  4  xy  x  y  1     1  x  y  2 Mặt 2 2 2 2 2 x y khác:  y  2y,  x  2x y x Do đó P  x  y  2
Vậy giá trị nhỏ nhất của P là 2 khi x = y = 1.
Câu 225: [TS10 Chuyên Bắc Ninh, 2012-2013]
Cho ba số dương a, b, c thỏa mãn a  b  c  1. Chứng minh rằng:
1a1b1c  81a1b1c Lời giải
Vì a, b, c là các số dương v| a  b  c  1 nên ta có a, b,c  1.
Áp dụng bất đẳng thức Cauchy ta được
THCS.TOANMATH.com FB TRỊNH BÌNH 142
1 a  1 b  1 c  2 1 b1 c
Tương tự ta có 1 b  2 1 c1a; 1 c  2 1a1 b
Nhân theo vế ba bất đẳng thức trên ta được
1a1b1c  81a1b1c 1
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi a  b  c  3
Câu 226: [TS10 Chuyên Hải Dương, 2012-2013]
Cho 3 số a, b, c thỏa mãn 0  a  b  c  1. Tìm giá trị lớn nhất của biểu thức:       1 1 1  A a b c 1      a  1 b  1 c  1 Lời giải
Đặt x  1 c, y  1 b, z  1 a . Từ 0  a  b  c  1 ta được 1  x  y  z  2  1 1 1  x x z z
Ta viết lại biểu thức A là A  x  y  z y y
     3        x y z  y z x z x y  x  y  x y x.y x y x 1 1   0  1    0     1  y  z  y z y.z y z z  z  y  z y z.y z y z 1 1   0  1    0     1  y  x  y x y.x y x x x y z y x z x x y y z z  x z 
       2        2     2 y z y x z x y z x z x y  z x  x 1 Đặt t 
  t  1. Do đó ta được z 2 2 2 x z 1 t  1 2t  5t  2 5 2t  1t 2 5   t       z x t t 2t 2 2t 2 1 2t 1t 2 x z 5 Do  t  1 nên ta có suy ra   2 2t z x 2 5
Từ đó ta được A  3  2.  2  10 2
Vậy giá trị lớn nhất của A l| 10. Đẳng thức xẩy ra khi và chỉ khi.
Câu 227: [TS10 Chuyên Hải Phòng, 2012-2013]
THCS.TOANMATH.com FB TRỊNH BÌNH 143 a 4b 9c
Cho ba số dương a,b,c .Chứng minh rằng:    4 b  c c  a a  b Lời giải a 4b 9c    1 4 9 4  (a  b  c)(   )  18 b  c c  a a  b b  c a  c a  b Thật vậy: 1 4 9 b  c 4(a  c) 9(a  b) 2
[(b  c)  (a  c)  a  b)](   )  (   )  36 b  c a  c a  b b  c (a  c) (a  b) 1 4 9  (a  b  c)(   )  18 (đpcm) b  c a  c a  b
Câu 228: [TS10 Chuyên Nam Định, 2012-2013]
Cho a, b, c ,d là các số thực dương thỏa mãn điều kiện a  b  c  d  3. Tìm giá trị 4 4 4 4 a  b  c  d
nhỏ nhất của biểu thức: P  3 3 3 3 a  b  c  d Lời giải
Áp dụng bất đẳng thức Bunhiacopxki ta được
4 a  b  c  d   a  b  c  d 2 4 4 4 4 2 2 2 2 ;
a b c d a b c d a b c d 2 4 4 4 4 2 2 2 2 3 3 3 3
Nhân theo vế các bất đẳng thức trên ta được
    2     2 4 4 4 4 3 3 3 3  2 2 2 2 4 a b c d a b c d a  b  c  d  2 2 Hay  4 4 4 4       3 3 3 3      2 2 2 2 16 a b c d 4 a b c d a  b  c  d 
Mặt kh{c cũng theo bất đẳng thức Bunhiacopxki ta có
        2 2 2 2 2 4 a b c d a b c d  9 2 2 Do vậy  3 3 3 3      2 2 2 2      3 3 3 3 4 a b c d a b c d 9 a  b  c  d  2 2 Suy ra ta được  4 4 4 4       3 3 3 3 16 a b c d 9 a  b  c  d  Hay  4 4 4 4      3 3 3 3 4 a b c d 3 a  b  c  d  4 4 4 4 a  b  c  d 3 Do đó ta được P   3 3 3 3 a  b  c  d 4
THCS.TOANMATH.com FB TRỊNH BÌNH 144 3 3
Suy ra giá trị nhỏ nhất của P là
, đạt được khi a  b  c  d  4 4 NĂM HỌC 2011-2012
Câu 229: [TS10 Chuyên Bình Phước, 2011-2012]
Cho a, b, c là ba số dương thỏa mãn điều kiện a  b  c  3. Chứng minh rằng: 1 1 1 3    1 ab 1 bc 1  ca 2 Lời giải
Áp dụng bất đẳng thức Cauchy ta có 1 ab ab ab  1  1  1 1 ab 1  ab 2 ab 2 1 bc 1 ca Tương tự ta có  1 ;  1 1 bc 2 1 ca 2
Cộng theo vế theo vế các bất đẳng thức trên và áp dụng bất đẳng thức Cauchy ta được: 1 1 1 1  
 3   ab  bc  ca 1  ab 1  bc 1  ca 2 1  a  b b  c c  a  a  b  c 3 3  3     3   3     2  2 2 2  2 2 2
B|i to{n được chứng minh xong.
Câu 230: [TS10 Chuyên Sư Phạm Hà Nội, 2011-2012]
Chứng minh bất đẳng thức: 1 1 1 1    ...  4 1  2 3  4 5  6 79  80 Lời giải 1 1 1 1 1 1 Dễ thấy  ;  ;...  1  2 2  3 3  4 3  4 79  80 80  81 Do đó ta được 1 1 1 1 1 1   ...    ... 1  2 3  4 79  80 2  3 4  5 80  81
THCS.TOANMATH.com FB TRỊNH BÌNH 145 Suy ra  1 1 1  1 1 1 2   ...     ...  1  2 3  4 79  80  1  2 2  3 80  81  1 1 1  Hay 2   ...
  2 1 3  2  ... 81  80  1  2 3  4 79  80  1 1 1 Nên ta được   ...  4 1  2 3  4 79  80
Vậy bất đẳng thức được chứng minh.
Câu 231: [TS10 Chuyên Nghệ An, 2011-2012]
Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:  2 2 2    2 2 2  
    3   3   3 3 a b b c c a ab bc ca abc a abc b abc c  abc Lời giải
Bất đẳng thức cần chứng minh tương đương với 2 2 2  a b c  b c a   a  b  c          1 3   1  1  1  c a b  c a b   bc  ca  ab  a b c Đặt x  ; y 
; z   x; y; z  0; xyz  1 b c a
Khi đó bất đẳng thức trên trở thành         x  y  z  xy yz zx x y z  1  3   1   1  1  z  x  y      
x  yy  zz  x x yy zz x    3 xyz 1 xyz
 x  yy  zz  x 3
 1  1 x  yy  zz  x Đặt 3
t  x  yy  zz  x suy ra t  2 . Khi đó ta viết lại bất đẳng thức cần chứng minh thành 3 3 2
t  1  1 t  t  1  1 2t  t  t t  2t 1  0
Bất đẳng thức cuối cùng luôn đúng do t  2 .
Vậy b|i to{n được chứng minh xong. Đẳng thức xẩy ra khi và chỉ khi a  b  c
THCS.TOANMATH.com FB TRỊNH BÌNH 146
Câu 232: [TS10 Chuyên Thanh Hóa, 2011-2012]
Cho a, b, c là ba số thực dương thỏa mãn a  b  c  2 . Tính giá trị lớn nhất của biểu ab bc ca thức: P    ab  2c bc  2a ca  2b Lời giải
Để ý đến giả thiết a  b  c  2 ta có ab  2c  ab  ca  b  c  b  cc  a
Do đó theo bất đẳng thức Cauchy ta được ab ab 2ab 2ab    ab  2c
bcca bc ca bc 2bc 2bc ca 2ca 2ca
Ho|n to|n tương tự ta được   ;   bc  2a a  b c  a ca  2b a  b b  c
Cộng theo vế các bất đẳng thức trên ta được ab bc ca 2ab 2ab 2bc 2bc 2ca 2ca         ab  2c bc  2a ca  2b b  c c  a a  b c  a a  b b  c  2a  b  c  4
Hay P  4 . Vậy giá trị lớn nhất của P là 4. 2
Đẳng thức xẩy ra khi và chỉ khi a  b  c  3
Câu 233: [TS10 Chuyên Kiên Giang, 2011-2012]  1   1  Chứng minh rằng: 21. a   3. b       31 , với a, b  0  b   a  Lời giải  1   1  21 3 *Ta có: 21. a   3. b   21a   3b       b   a  b a
Với a, b  0 . Áp dụng bất đẳng thức Côsi, ta được: 3 3 21a   2 21a  6 7 (1) a a 21 21 3b   2 3b  6 7 (2) b b  1   1 
Cộng từng vế của (1) v| (2) ta được: 21 a   3 b       12 7  a   b 
THCS.TOANMATH.com FB TRỊNH BÌNH 147 M|: 12 7  144.7  1008 ; 2
31  31  961  12 7  31   1   1  21 a   3 b      > 31 (đpcm)  a   b 
Câu 234: [TS10 Chuyên Vĩnh Phúc, 2011-2012] 9
Cho a, b, c là các số thực dương thỏa mãn abc  . Chứng minh rằng: 4 3 3 3
a  b  c  a b  c  b a  c  c a  b Lời giải
Áp dụng bất đẳng thức Cauchy ta có 3 3 a  b
aba  b aba  b aba  b a  b     2 2 9 abc c 4 3 3 a  b a  b Từ đó ta có 3 3 c   c   2c a  b 2 c Tương tự ta có 3 3   3 a c 3 a c b   b   2b a  c 2 b 3 3   3 b c 3 b c a   a   2a b  c 2 a
Cộng vế theo vế các bất đẳng thức trên ta được: 3 3 3
a  b  c  a b  c  b a  c  c a  b
B|i to{n được chứng minh xong.
Câu 235: [TS10 Chuyên Vĩnh Phúc, 2011-2012]
Cho các số thực dương a, b, c. Chứng minh rằng: 3
c a  b 2  a b  c 2  b c  a 2 54 abc 2 2 2 2 2 2 2 2 2  
 abc2 ab4 bc4 ca4 Lời giải
Theo bất đẳng thức Cauchy ta có
THCS.TOANMATH.com FB TRỊNH BÌNH 148
c a  b 2  a b  c 2  b c  a 2  c 2ab2  a 2bc2  b 2ca2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2  12a b c  2 3abc
a  bc ab bc ca   33 abc2 2 4 4 4 3 8 8 8 3 4 4 3 3 8 8 8 3 a b c  9 3. a b c . a b c 2 2 2  9 3a b c
Nhân theo vế hai bất đẳng thức trên ta được
c a  b 2  a b  c 2  b c  a 2 a  b  c2 ab4  bc4  ca4 2 2 2 2 2 2 2 2 2
 2 3abc.9 3a b c  54abc3 2 2 2 3 2 2 2 54 abc Hay 2 c  2 2 a  b  2  a  2 2 b  c  2  b  2 2 c  a   
 abc2 ab4 bc4 ca4
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi a  b  c .
Câu 236: [TS10 Chuyên Vũng Tàu, 2011-2012]
Cho các số dương a,b,c thay đổi và thoã mãn 3a  4b  5c  12 . Tìm giá trị lớn nhất ab 2ac 3bc của biểu thức: S    ab  a  b ac  a  c bc  b  c Lời giải
Ta viết lại biểu thức S thành 1 2 3 S    1 1 1 1 1 1   1   1   1 a b c a b c 1 1  1 1 1 
Áp dụng bất đẳng thức      ta có x  y  z 9  x y z  1 2 3
a  b  1 2 c  a  1 3b  c  1 S       1 1 1 1 1 1 9 9 9   1   1   1 a b c a b c 6  3a  4b  5c 18    2 9 9
Vậy giá trị lớn nhất của biểu thức S l| 2. Đẳng thức xẩy ra khi và chỉ khi a  b  c  1.
Câu 237: [TS10 Chuyên KHTN Hà Nội, 2011-2012]
Cho a, b là các số thực dương. Tìm gi{ trị nhỏ nhất của biểu thức:
THCS.TOANMATH.com FB TRỊNH BÌNH 149 3 3 a 4b P   3 3 a  8b b  a  b3 3 Lời giải 3 4b 3 1
Biểu thức P được viết lại là a P   3 3 3 8b b  b  1    3 1  3 a a  a  b Đặt t 
 0 . Khi đó bất đẳng thức được viết lại là a 3 1 4t P   3 1  8t t  1 t3 3
Áp dụng bất đẳng thức Cauchy ta có 2 2 
1 8t  1 2t1 2t  4t  2 4t    1 2t 2 3 2 2 2 1 1 1 Suy ra   3 1 8t   2 2 2 1  2t 1 2t 3 2 4t 2t Ta sẽ chứng minh     3 2 3 1  2t t 1 t
Thật vậy, bất đẳng thức trên tương đương với 2 3 2 4t  2t   
  1 2t 2  t  t1 t3  t 12 2 4  2 2t  t  1  0 3 2  3      1 2t t 1 t 
Bất đẳng thức cuối cùng đúng với mọi t. Do đó ta được 3 2 1 4t 1 2t P      1 3 1 8t    3 2 2 3 1  2t 1  2t t 1 t
Vậy giá trị nhỏ nhất của biểu thức P l| 1. Đẳng thức xẩy ra khi và chỉ khi a  b
Câu 238: [TS10 Chuyên KHTN Hà Nội, 2011-2012]
THCS.TOANMATH.com FB TRỊNH BÌNH 150
Cho các số thực dương a, b, c thỏa mãn ab  bc  ca  5. Tìm giá trị nhỏ nhất của 3a  3b  2c biểu thức: P  6 2 a  5  6 2 b  5 2  c  5 Lời giải
Từ giả thiết ab  bc  ca  5 ta có 2 2
a  5  a  ab  bc  ca  a  bc  a
Áp dụng bất đẳng thức Cauchy ta có  3 a  b  2 c  a   2             5a 3b 2c 6 a 5 6 a b c a   2 4
Chứng minh tương tự ta được      2   3a 5b 2c 2 a b 2c 6 b 5  ; c  5  2 2
Cộng theo vế các bất đẳng thức trên ta được    2     2   2 9a 9b 6c 6 a 5 6 b 5  c  5  2 3a  3b  2c 23a  3b  2c 2 Suy ra P     2     2   2 9a  9b  6c 3 6 a 5 6 b 5  c  5 2
Vậy giá trị nhỏ nhất của biểu thức P là . 3
Đẳng thức xẩy ra khi và chỉ khi a  b  1; c  2 .
Câu 239: [TS10 Chuyên Vĩnh Phúc, 2011-2012]
Cho hai số x, y liên hệ với nhau bởi đẳng thức 2 2
x  2xy  7(x  y)  2y  10  0 . Tìm
gi{ trị lớn nhất v| gi{ trị nhỏ nhất của biểu thức S  x  y  1 . Lời giải
Viết lại biểu thức đã cho th|nh 2 2
(x  y  1)  5(x  y  1)  4  y (*) .
Như vậy với mọi x v| mọi y ta luôn có 2
S  5S  4  0 (với S  x  y  1 )
Suy ra: (S  4)(S  1)  0  4   S  1  . x  5  Từ đó có: S  4  , khi  min y   0 x  2  S  1  , khi  . max y   0
THCS.TOANMATH.com FB TRỊNH BÌNH 151
Câu 240: [TS10 Chuyên Bắc Ninh, 2011-2012]
Cho a, b, c là các số thực dương thỏa mãn a  b  c  1. Tìm giá trị lớn nhất của biểu thức: 2 2 2
P  a  abc  b  abc  c  abc  9 abc Lời giải Ta có 2 2
a  abc  a a  b  c  abc  a a  ba  c a a  b  a  c a a 1 Do đó ta được 2
a  abc  a a  ba  c       2 2
Chứng minh tương tự ta được b b  1 c c  1 2   2   b  abc  ; c  abc  2 2 Do đó ta được a a  1 b b  1 c c  1 2 2 2      
a  abc  b  abc  c  abc    2 2 2
Mặt khác theo bất đẳng thức Cauchy ta lại có a a   1  a 1 b  c   a  b  c  1  abc  a   a      a 2  2 2   2 
Chứng minh tương tự ta được b b   1 c c   1  abc  b;  abc  c 2 2 Như vậy ta có 2 2 2
P  a  abc  b  abc  c  abc  9 abc  a  b  c  6 abc Mà ta có 3         a  b  c  2 a b c 3 a b c  3; 6 abc  6     3  3 2 5 5 3 Nên ta suy ra P  3    . 3 3 3 5 3 1
Vậy giá trị lớn nhất của P là
. Đẳng thức xẩy ra khi và chỉ khi a  b  c  . 3 3
Câu 241: [TS10 Chuyên Phú Thọ, 2011-2012]
Cho a, b, c là số thực dương. Chứng minh rằng:
THCS.TOANMATH.com FB TRỊNH BÌNH 152 2ab 3bc 3ca a  2b  3c    3a  8b  6c 3b  6c  a 9c  4a  4b 9 Lời giải
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta có xy xy    2 6 2 1 xy  18 2 1   .      3x  4y  2z
81 2 x  y  z  2y  x 81  x  y  z y x  2xy 2x  y   9 x  y  z 81
Ho|n to|n tương tự ta được yz 2y  z 2yz zx 2z  x 2zx       9x  y  z ; 3y 4z 2x 81 3z  4x  2y 81 9x  y  z
Cộng theo vế các bất đẳng thức trên ta được xy yz zx x  y  z 2xy  yz  zx     3x  4y  2z 3y  4z  2x 3z  4x  2y 27 9x  y  z
Đến đ}y chứng minh ho|n to|n tương tự như trên.
Câu 242: [TS10 Chuyên Hải Dương, 2011-2012]
Giả sử a, b, c là các số dương thoả mãn abc  1. Tìm giá trị lớn nhất của biểu thức: a b c M    2 2 2 2 2 2 b  c  a c  a  b a  b  c Lời giải Ta chứng minh M  1 Đặt 3 3 3
a  x; b  y; c  z , khi đó x; y; z  0 và xyz  1
Bất đẳng thức cần chứng minh trở thành 3 3 3 x y z    1 6 6 3 6 6 3 6 6 3 y  z  x z  x  y x  y  z Dễ thấy    5 5   6 6 5 5 y z y
z  0  y  z  y z  yz Suy ra 6 6 4     4 4 4 y z x yz yz x  y  z  1 1 Từ đó ta được  6 6 3 y  z  x yz 4 4 4 x  y  z 
THCS.TOANMATH.com FB TRỊNH BÌNH 153 4 4 x yz x Hay  6 6 3 4 4 4 y  z  x x  y  z 3 4 x x Do đó ta được  6 6 3 4 4 4 y  z  x x  y  z 3 4 3 4 y y z z Tương tự ta có  ;  6 6 3 4 4 4 6 6 3 4 4 4 z  x  y x  y  z x  y  z x  y  z
Cộng theo vế ba bất đẳng thức trên ta được 3 3 3 x y z    1 6 6 3 6 6 3 6 6 3 y  z  x z  x  y x  y  z
Vậy giá trị lớn nhất của M l| 1. Đẳng thức xẩy ra khi và chỉ khi a  b  c  1.
Câu 243: [TS10 Chuyên H| Tĩnh, 2011-2012] 1 4 x 2x
Tìm giá trị nhỏ nhất của biểu thức: F   . 2 2x  1 x  1
Lời giải. Điều kiện: x  0 2 2 1 4 x 2x 2( x  1) (x 1) F   1  1 2    2  2  . 2 2 2x  1 x  1 2x  1 x  1
Vậy MinF = - 2 khi và chỉ khi x = 1.
Câu 244: [TS10 Chuyên Thái Bình, 2011-2012]
Cho a, b, c là các số dương thoả mãn abc  1. Chứng minh rằng: 3 3 3 a b c 3   
bc  a ca  b a b  c 2 Lời giải
Áp dụng bất đẳng thức Cauchy cho các số dương ta được 3 3 3 a b c  a 3 b c a  b 3 c a b  c 3          bc  a a; cab b; abc c 2 4 2 2 4 2 2 4 2
Cộng theo vế các bất đẳng thức trên ta được 3 3 3 a b c 3a  b  c      
bc  a ca  b a b  c a b c 2 3 3 3 a b c a  b  c Hay   
bc  a ca  b ab  c 2
THCS.TOANMATH.com FB TRỊNH BÌNH 154
Mặt khác theo bất đẳng thức Cauchy ta lại có 3 a  b  c  3 abc  3 3 3 3 a b c 3 Nên ta được   
bc  a ca  b a b  c 2
Bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi a  b  c  1. NĂM HỌC 2010-2011
Câu 245: [TS10 Chuyên KHTN, 2010-2011]
Giả sử x, y, z là các số thực dương thoả mãn điều kiện x  y  z  1 . 2 2 xy  z  2x  2y Chứng minh rằng:  1 1  xy Lời giải
Ta sẽ quy bài toán về việc chứng minh bất đẳng thức cùng bậc là xy  z x  y  z 2 2  2x  2y 1 x  y  z  xy  x  zy  z 2 2
 2x  2y  x  y  z  xy
Sử dụng bất đẳng thức Cauchy ta có 2 2 2x  2y  x  y
Do đó ta chỉ cần chứng minh z  xz  y  z  xy
Bất đẳng thức trên tương đương với            2 2 2 z xy z x y z xy 2z xy z x y  0 1
B|i to{n được chứng minh ho|n to|n. Đẳng thức xảy ra khi x  y  ; z  0 . 2
Câu 246: [TS10 Chuyên TP. Hồ Chí Minh, 2010-2011] 1 2 3
Cho a , b là các số dương thỏa 2 2 2 a  2b  3c .Chứng minh   a b c Lời giải 1 2 9 Ta có:  
 1  a2bb2a  9ab a b a  2b 2 2
 2a  4ab  2b  0  2a  b  0 ( đúng) 2 a + 2b   2 2 
       2 2 3 a 2b 2 a 2b 3 a  2b 
THCS.TOANMATH.com FB TRỊNH BÌNH 155        2 2 2 2a 4ab 2b 0 2 a b  0 ( đúng) 1 2 9 9 3 Từ (1) và (2) suy ra :     ( do 2 2 2 a  2b  3c ) (đpcm) a b a  2b  2 2   c 3 a 2b
Câu 247: [TS10 Chuyên KHTN, 2010-2011]
Cho a, b, c là các số dương thỏa mãn a  b  c  ab  bc  ca  6 . Chứng minh rằng: 3 3 3 a b c 2 2 2    a  b  c  3 b c a Lời giải 3 3 3 a b c
Trước hết ta chứng minh bất đẳng thức 2 2 2    a  b  c b c a
Thật vậy, theo bất đẳng thức Bunhiacopxki dạng phân thức ta được    2 2 2 2 3 3 3 a b c a b c    b c a ab  bc  ac
Theo một đ{nh gi{ quen thuộc ta có 2 2 2
a  b  c  ab  bc  ca 2 Do đó ta được  2 2 2      2 2 2 a b c
a  b  c ab  bc  ca a b c 2 2 2 2 Nên ta có 2 2 2  a  b  c ab  bc  ac 3 3 3 a b c Do đó ta suy ra 2 2 2    a  b  c b c a + Chứng minh 2 2 2 a  b  c  3 .
Thật vậy, áp dụng bất đẳng thức Cauchy ta có 2 2 2 2 2 2 2 2 2
a  b  2ab; b  c  2bc; c  a  2ca; a  1  2a; b  1  2b; c 1  2c
Cộng theo vế các bất đẳng thức trên ta được  2 2 2
3 a  b  c   3  2ab  bc  ca  a  b  c  12 Hay 2 2 2 a  b  c  3 3 3 3 a b c
Kết hợp hai kết quả trên ta được 2 2 2    a  b  c  3 b c a
Vậy b|i to{n được chứng minh xong. Đẳng thức xẩy ra khi và chỉ khi a  b  c  1.
THCS.TOANMATH.com FB TRỊNH BÌNH 156
Câu 248: [TS10 Chuyên Phú Thọ, 2010-2011]
Cho các số dương a, b, c thoả mãn a  b  c  abc . Tìm giá trị lớn nhất của biểu thức: a b c S    bc  2 1 a  ca  2 1 b  ab 2 1  c  Lời giải
Kết hợp với giả thiết ta có  2   2 bc 1 a
 bc  a bc  bc  aa  b  c  a  ba  c
Ho|n to|n tương tự ta được  2          2 ca 1 b
a b b c ; ba 1 c   a  cb  c ; Nên a b c S  
a ba c a  bbc a cbc a a b b c c  .  .  . a  b a  c b  c b  c c  b a  c
Áp dụng bất đẳng thức Cauchy ta được a a 1 a a .   a  b a  c 2 a  b a  c
Ho|n to|n tương tự ta được 1  a a b b c c  3 S         
2  a  b a  c b  c a  b a  c b  c  2 3
Vậy giá trị lớn nhất của S là
. Đẳng thức xẩy ra khi và chỉ khi a  b  c  3 . 2
Câu 249: [TS10 Chuyên Phú Thọ, 2010-2011]
Cho các số dương a, b c .Tìm gi{ trị nhỏ nhất của biểu thức c ab  2 1 a bc  2 1 bca  2 1 S    2 b bc   2 1 c ca  1 2 a ab  1 Lời giải
Áp dụng bất đẳng thức Cauchy dạng 3
x  y  z  3 xyz ta được
THCS.TOANMATH.com FB TRỊNH BÌNH 157
c ab  12 .a bc  12 .bca  12
ab1bc1ac1 S  3 
b bc  1.c ac  1.a ab  1 3 3 3 2 2 2 abc 2 ab.2 bc.2 ca 3  3  6 abc
Vậy giá trị nhỏ nhất của S l| 6, đẳng thức xẩy ra khi và chỉ khi a  b  c  1
Câu 250: [TS10 Chuyên Đại Học Vinh, 2010-2011]
Cho x, y, z là các số dương thỏa mãn x  y  z  18 2 . Chứng minh rằng: 1 1 1 1             4 x y z y z x z x y Lời giải
Bất đẳng thức cần chứng minh tương đương với 1 1 1 1    2xy  z 2y z  x 2z x  y 4 2
Áp dụng bất đẳng thức Cauchy ta có 2 2xy  z  2x  y  z , do đó ta được 1 2     2x yz 2x y z
Ho|n to|n tương tự ta được bất đẳng thức 1 1 1  1 1 1                 2 
 2x  y  z x  2y  z x  y  2z 2x y z 2y z x 2z x y 
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được 1 1 1 1    2x  y  z x  2y  z x  y  2z 8 2
Thật vậy theo bất đẳng thức Cauchy ta được 1 1 1 9 9 1      2x  y  z x  2y  z x  y  2z 4x  y  z 4.18 2 8 2
Vậy b|i to{n được chứng minh xong. Đẳng thức xẩy ra khi và chỉ khi x  y  z  6 2
Câu 251: [TS10 Chuyên Vĩnh Phúc, 2010-2011]
Cho a, b, c là các số thực dương thỏa mãn abc  1. Chứng minh rằng:
THCS.TOANMATH.com FB TRỊNH BÌNH 158 3 6 1  a  b  c ab  bc  ca Lời giải
Bất đẳng thức đã cho tương đương:
abcabbcca3abbcca  6abc 2
Để ý rằng ab  bc  ca  3abca  b  c  3a  b  c 3
Nên bài toán quy về chứng minh 3a  b  c  3 3a  b  c  6a  b  c
Bất đẳng thức trên tương đương với
       2 3 a b c a b c 3  0
Bất đẳng thức cuối cùng là một bất đẳng thức đúng. Vậy b|i to{n được chứng minh.
Đẳng thức xẩy ra khi và chỉ khi a  b  c  1
Câu 252: [TS10 Chuyên Lam Sơn, 2010-2011]
Cho 3 số thực không âm a, b, c thỏa mãn a  b  c  1. Chứng minh rằng: b  c  16abc.
Đẳng thức xảy ra khi nào? Lời giải. Ta có: 2 2
(a  b  c)  (a  (b  c))  4a(b  c).
Do a  b  c  1 nên từ bất đẳng thức trên suy ra: 2
1  4a(b  c)  b  c  4a(b  c) . Lại có: 2
(b  c)  4bc  b  c  16abc. 1 1
Đẳng thức xảy ra khi a  ; b  c  . 2 4
Câu 253: [TS10 Chuyên Hải Phòng, 2010-2011]
Cho a, b, c là các số thực dương thỏa mãn a  b  c  2 . Chứng minh rằng: 2 1 2 1 2 1 97 a   b   c   2 2 2 b c a 2 Lời giải
Áp dụng bất đẳng thức Bunhiacopxki ta được
THCS.TOANMATH.com FB TRỊNH BÌNH 159 2      2 1 81 9 9 a  1  a   a       2  b  16   4b  4b 97 1 9 Hay 2 a   a  2 4 b 4b
Chứng minh tương tự ta được 97 2 1 9 97 2 1 9 b   b  ; c   c  2 2 4 c 4c 4 a 4a
Cộng theo vế các bất đẳng thức trên ta được 97     2 1 2 1 2 1 9 1 1 1  a   b   c    a  b  c      2 2 2 4  b c a  4    a b c  1 1 1 9 Mà ta lại có    a b c a  b  c Do đó ta được   2 1 2 1 2 1 4 81 a   b   c   a   b  c   2 2 2 b c a 97 4  a b  c 4  81  97 Ta cần chứng minh a  b  c    97 4  a b  c 2  81 97 Hay a  b  c   4a  b  c 8
Thật vậy, áp dụng bất đẳng thức Cauchy ta được 81 4 65 a  b  c      
4 a  b  c a b c a  b  c 4a  b  c      4 65 65 97 2 a b c   4   a  b  c 4.2 8 8 2
Bất đẳng thức đã được chứng minh. Đẳng thức xảy ra khi và chỉ khi a  b  c  3
Câu 254: [TS10 Chuyên H| Tĩnh, 2010-2011] Cho c{c số a, b, c  1  ; 2   . Chứng minhrằng: 2 2 2 2 2 2 a  b b  c c  a    7 ab bc ca Lời giải
THCS.TOANMATH.com FB TRỊNH BÌNH 160
Bất đẳng thức cần chứng minh tương đương với 2 2 2 2 2 2
a b  ab  b c  bc  c a  ca  7abc  c 2
ab  ca  b  bc  a 2 ab  ca  b  bc 2 2
 5abc  2bc  2a b  0   2
ab  ca  b  bcc  a  b 2 2
4ca  2c  2a  ca  0
 a  bb  cc  a  b2a  c2c a  0
Vì vai trò của a, b, c như nhau nên không mất tính tổng quát ta giả sử
2  a  b  c  1 khi đó ta được 2a  2  c; 2c  2  a . Do đó ta được
abbcca  0; b2ac2ca  0
Nên bất đẳng thức cuối cùng luôn đúng. Vậy bất đẳng thức được chứng minh.
Đẳng thức xẩy ra khi và chỉ khi a  b  2; c  1 và các hoán vị.
Câu 255: [TS10 Chuyên Bình Định, 2010-2011]
Cho a, b, c là các số thực dương thỏa mãn a + b + c ≤ 1. Chứng minh rằng: 1 1 1    9. 2 2 2 a  2bc b  2ca c  2ab Lời giải. 1 1 1 9
Với x, y, z là các số thực dương ta có:    (*) x y z x  y  z
Thật vậy, theo bất đẳng thức Cauchy ta có:  1 1 1  1 1 1 1 9 3
(x  y  z)     3 xyz.33  9     . x y z xyz x y z x  y    z
Vậy (*) được chứng minh.
Đẳng thức xảy ra khi x = y = z. Áp dụng BĐT (*) ta có: 1 1 1 9 9 9       9 2 2 2 2 2 2 2 a  2bc b  2ca c  2ab
a  b  c  2ab  2bc  2ca (a  b  c) 1
Bất đẳng thức đã cho được chứng minh.
Đẳng thức xảy ra khi a = b = c.
Câu 256: [TS10 Chuyên Đại học Vinh, 2010-2011]
Tìm giá trị nhỏ nhất của biểu thức: 2 2
P  x  x  2x y  y  y  2y x  2010.
THCS.TOANMATH.com FB TRỊNH BÌNH 161 Lời giải. Ta có: 2 2
P  (x  y)  (y  x)  2010  2010 ( x   0; y  0).
Đẳng thức xảy ra khi và chỉ khi x = y = 1 hoặc x = y = 0.
Câu 257: [TS10 Chuyên Nghệ An, 2010-2011]
Cho a, b, c là các số thực dương không }m thỏa mãn a  b  c  3. Tìm giá trị lớn
nhất của biểu thức: P  a b  b c  c a  abc Lời giải
Đặt x  a; y  b; z  c . Từ giả thiết ta được 2 2 2 x  y  z  3 .
Khi này biểu thức P trở thành 2 2 2
P  x y  y z  z x  xyz
Dễ thấy P  0 theo bất đẳng thức Cauchy
Không mất tính tổng quát ta giả sử y là số nằm giữa x, z. Khi đó ta có      2 2 2
z y z y x  0  y z  z x  xyz  z y Do đó ta có 2 2 2 2 2         2 2 P x y y z z x xyz x y z y y x  z 
Mặt khác theo bất đẳng thức Cauchy ta có 3    
2y x  z x  z  2 2 2 2x 2y 2z 2 2 2 2 2     8  3  Suy ra  2 2
y x  z   2 nên ta được P  2 . Đẳng thức xẩy ra khi và chỉ khi x  y  z       a b c 1 z  0 và các hoán vị   và các hoán vị   a  2; b  1; c   0 2 2 x  2y
Vậy giá trị lớn nhất của biểu thức P là 2.
Đẳng thức xẩy ra khi và chỉ khi a  b  c  1 hoặc a  2; b  1; c  0 và các hoán vị.
Câu 258: [TS10 Chuyên Hòa Bình, 2010-2011]
Cho x, y là hai số không âm. Chứng minh rằng 3 3 2 2 x  8y  2x y  4xy Lời giải Ta các
THCS.TOANMATH.com FB TRỊNH BÌNH 162 3 3 2 2 x  8y  2x y  4xy 2 2
 (x  2y)(x  2xy  4y )  2xy(x  2y) 2 2
 (x  2y)(x  4xy  4y )  0 2
 (x  2y)(x  2y)  0 x  0,y  0 (đúng)
Vậy bất đẳng thức được chứng minh.
Câu 259: [TS10 Chuyên Hưng Yên, 2010-2011]
Cho ba số dương a, b, c thỏa mãn ab  bc  ca  1. Chứng minh rằng: 2 2 2 a  1  a b  1  b c  1  c 1 1 1      bc ac ab a b c Lời giải Để ý là 2 2
a  1  a  ab  bc  ca  a  bc  a , do đó ta được 2
a  1  a  bc  a
Áp dụng bất đẳng thức Cauchy ta được 2a  b  c  2         a a b c a a a 1 a b  c 1  1 1 2         bc bc bc 2bc 2  b c  2 2 b  1  b 1  1 1  c  1  c 1  1 1 
Ho|n to|n tương tự ta được   ;       ac 2  a c  ab 2  a b 
Cộng theo vế ba bất đẳng thức trên ta được 2 2 2 a  1  a b  1  b c  1  c 1 1 1      bc ac ab a b c 1
Vậy b|i to{n được chứng minh. Đẳng thức xẩy ra khi và chỉ khi a  b  c  3
Câu 260: [TS10 Chuyên Vĩnh Phúc, 2010-2011] 3 2 1 1 1 1 (a  b  c  abc) Chứng minh rằng:     a  b c  3 a  b b  c c  a 2 abc (a  b)(b  c)(c  ( , , 0) a) Lời giải. Dễ thấy: 2 2 2
(a  b)(b  c)(c  a)  c (a  b)  a (b  c)  b (c  a)  2abc.
Áp dụng bất đẳng thức Cô-si và bất đẳng thức Bu-nhi-a-cốp-xki ta được:
THCS.TOANMATH.com FB TRỊNH BÌNH 163   2 2 2 1 1 1 1
(c (a  b)  a (b  c)  b (c  a)  2abc).     3 a  b b  c c   a 2 abc  2  1 1 1 1   c a  b.  a b  c.  b c  a.  2abc.     cab abc2 3 . 3 c  a b  c c   a 2 abc 
Suy ra điều phải chứng minh, đẳng thức xảy ra khi a = b = c.
Câu 261: [TS10 Chuyên Kiên Giang, 2010-2011]
Tìm a, b để biểu thức: X = 2a2 + 9b2 + 2a – 18b – 6ab + 2010 đạt giá trị nhỏ nhất.
Tìm giá trị nhỏ nhất đó. Lời giải Ta có:
X = (3b)2 -2.3b.(3 + a) + 9 + 6a + a2 + a2 – 4a + 4 + 1997
= (3b)2 -2.3b.(3 + a) + (3 + a)2 + (a2 – 4a + 4) + 1997
= (3b – 3 – a)2 + (a – 2)2 + 1997  1997  5 3b  3 a  0 3b  3  2  0 b  Dấu “=” xảy ra khi      3 a  2  0 a    2 a   2 5 Vậy với a = 2 và b = thì Xmax = 1997 3
Câu 262: [TS10 Chuyên Phú Yên, 2010-2011] 1 1  1 1 
a) Cho 2 số dương a v| b. Chứng minh rằng :     a  b 4  a b  1 1 1
b) Cho 3 số dương x, y, z thỏa mãn
   2010. Tìm GTLN của biểu thức: x y z 1 1 1 P    2x  y  z x  2y  z x  y  2z Lời giải
a) Biến đổi tương đương bất đẳng thức trên như sau 1 1  1 1   
 4ab  a  b2  0  a    b2 a  b 4  a b 
Bất đẳng thức cuối cùng luôn đúng. Vậy b|i to{n được chứng minh. Đẳng thức
xẩy ra khi và chỉ khi a  b
b) Áp dụng bất đẳng thức trên ta được
THCS.TOANMATH.com FB TRỊNH BÌNH 164 1 1  1 1  1  2 1 1           2x  y  z 4 x  y x   z  16  x y z 
Ho|n to|n tương tự ta được 1 1  1 2 1  1 1  1 1 2      ;      x  2y  z 16 x y z x  y    2z 16  x y z 
Cộng theo vế các bất đẳng thức trên ta được 1 1 1 1  1 1 1  2010 1005 P           2x  y  z x  2y  z x  y  2z 4  x y z  4 2 1005
Vậy giá trị lớn nhất của P là
. Đẳng thức xẩy ra khi và chỉ khi x  y  z  670 2 NĂM HỌC 2009-2010
Câu 263: [TS10 Chuyên Thái Bình, 2009-2010] 1 1  1 1  Giải phương trình:   3    . x 2x  3  4x  3 5x  6  Lời giải 1 1 1  1 1 1  Ta chứng minh:    3     (*) a b c  a  2b b  2c c  2a 
với a > 0; b > 0; c > 0
+ Với a > 0; b > 0 ta có:
a  2 b  3a  2b (1)  1 2  1 2 9 + Do  
 a  2 b  9 nên   (2)  a b  a b a  2 b 1 2 3 3 + Từ (1) và (2) ta có:  
(3) (Với a > 0; b> 0; c > 0) a b a  2b + Áp dụng (3) ta có: 1 1 1  1 1 1     3   
 với a > 0; b> 0; c > 0 a b c  a  2b b  2c c  2a  1 1  1 1  3 Phương trình   3    có ĐK: x  x 2x  3  4x  3 5x  6  2
Áp dụng bất đẳng thức (*) với a = x; b = x; c = 2x - 3 ta có: 1 1 1  1 1 1     3     x x 2x  3  3x 5x  6 4x  3 
THCS.TOANMATH.com FB TRỊNH BÌNH 165 1 1  1 1     3 3    với x  x 2x  3  5x  6 4x  3  2
Dấu “ = ” xảy ra  x  2x  3  x  3
Vậy phương trình có nghiệm duy nhất x = 3.
Câu 264: [TS10 Chuyên Hải Phòng, 2009-2010]  
a) Cho các số dương a, b, c tùy ý. Chứng minh rằng:     1 1 1 a b c      9  a b c 
b) Cho các số dương a, b, c thoả mãn a  b  c  3 . Chứng ming rằng: 1 2009   670 2 2 2 a  b  c ab  bc  ca Lời giải 1 1 1 1
a) Áp dụng bất đẳng thức Cô si cho 3 số dương 3 a  b  c  abc;    3 3 a b c abc   Suy ra     1 1 1 a b c      9  a b c 
Bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi và chỉ khi a  b  c a  b  c 2 2 2  2
b) Ta có ab  bc  ca  a  b  c  ab  bc  ca   3 3 2007 Suy ra  669 ab  bc  ca
Áp dụng bất đẳng thức trong câu a, ta có  1 1 1     2 2 2
a  b  c  2ab  2bc  2ca    9 2 2 2   a  b  c ab  bc  ca ab  bc  ca  1 1 9 Suy ra    1 2 2 2 a  b  c ab  bc  ca a bc2 1 2009 Do đó ta được   670 . 2 2 2 a  b  c ab  bc  ca
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi và chỉ khi a  b  c  1.
Câu 265: [TS10 Chuyên Phú Yên, 2009-2010]
a) Cho x, y, z, a, b, c là các số dương. Chứng minh rằng: 3 3 3
abc + xyz  (a + x)(b + y)(c + z) .
THCS.TOANMATH.com FB TRỊNH BÌNH 166 b) Từ đó suy ra : 3 3 3 3 3 3  3  3  3  2 3 Lời giải a) Ta có: 3 3 3 abc  xyz  (a + x)(b + y)(c + z) (1)
Lập phương 2 vế của (1) ta được : 2 2 3 3
abc + xyz + 3 (abc) xyz + 3 abc(xyz)  (a + x)(b + y)(c + z) 2 2 3 3
 abc + xyz+ 3 (abc) xyz + 3 abc(xyz)  abc + xyz + abz + ayc + ayz + xbc + xyc + xbz 2 2 3 3
 3 (abc) xyz + 3 abc(xyz)  (abz + ayc + xbc) + (ayz + xbz + xyc) (2)
Theo bất đẳng thức Cauchy, ta có : 2 3
(abz + ayc + xbc)  3 (abc) xyz (3) 2 3
(ayz + xbz + xyc)  3 abc(xyz) (4)
Cộng hai bất đẳng thức (3) v| (4) ta được bất đẳng thức (2), do đó (1) được chứng minh. b) Áp dụng BĐT (1) với 3 3
a = 3+ 3, b = 1, c = 1, x = 3 - 3, y = 1, z = 1
Ta có : abc = 3 + 3 3 , xyz = 3- 3 3 , a + x = 6, b + y = 2, c + z = 2 Từ đó : 3 3 3 3 3 3
3+ 3  3- 3  6.2.2  2 3 (đpcm).
Câu 266: [TS10 Chuyên Đ| Nẵng, 2009-2010]
Cho ba số thực không âm a, b, c thỏa mãn điều kiện a + b + c = 1. Chứng minh rằng 2 2 2
a  b  c  4(ab  bc  ca) 1. Lời giải
Ta có: a2 + b2  2ab ; b2 + c2  2bc ; c2 + a2  2ca
 a2 + b2 + c2  ab + bc + ca (1)
Lại có: a2 + b2 + c2 = a2 + b2 + c2 + (a + b + c)2  1
Hay a2 + b2 + c2 = 2(a2 + b2 + c2) + 2(ab + bc + ca)  1 (2)
(1) v| (2)  a2 + b2 + c2  4(ab + bc + ca)  1 đpcm
Câu 267: [TS10 Chuyên Bình Định, 2009-2010] 1
Với số tự nhiên n  3 . Chúng minh rằng S  . n 2
THCS.TOANMATH.com FB TRỊNH BÌNH 167 1 1 1 Với S    ... n 31 2  5 2  3 2n1 n  n1 Lời giải Với n  3 , ta có 1 n  1  n n  1  n         2 2n  1 2n 1 n n 1 4n  4n  1 n  1  n n +1 - n 1  1 1        2 4n  4n 2 n  1. n 2  n n  1  Do đó ta được 1  1 1 1 1 1  1  1  1 S  1    ...    1   n 2  2 2 3 n n  1  2  n  1  2
Vậy bất đẳng thức được chứng minh.
Câu 268: [TS10 Chuyên Hải Dương, 2009-2010]
Tìm giá trị lớn nhất của biểu thức: 2 2 P 
x  4x  5  x  6x  13 Lời giải 2 2 Ta có:     2      2 P x 2 1 x 3  2
Trên mặt phẳng tọa độ Oxy lấy c{c điểm A(x-2; 1), B(x+3; 2) 2 2
Ta chứng minh được: AB  x  2  x  3  1 2  25  1  26    2 2 OA x 2  1 ,    2 2 OB x 3  2 2 2
Mặt khác ta có: OA  OB  AB     2      2 x 2 1 x 3  2  26
Dấu “=” xảy ra khi A thuộc đoạn OB hoặc B thuộc đoạn OA x  2 1 
  x  7 .Thử lại x = 7 thì A(5; 1); B(10; 2). x  3 2
Câu 269: [TS10 Chuyên Bình Định, 2009-2010] m 1 Chứng minh rằng  2 
, với mọi số nguyên m, n. 2 n n  3  2  Lời giải
THCS.TOANMATH.com FB TRỊNH BÌNH 168 m m
Vì m, n là các số nguyên nên
là số hữu tỉ và 2 là số vô tỉ nên  2  0 . n n
Ta xét hai trường hợp sau m + Trường hợp 1: Với  2 , khi đó ta được n 2 2 2 2
m  2n  m  2n 1 hay  2 m 2n  1 Từ đó suy ra 2 m 2n  1 1  2   2  2   2 2 n n n 1 2   2 2 1 1 n    2 1    2 1 n       3 2 2 2  n 2 2  2 2 n  n    m + Trường hợp 2: Với  2 , khi đó ta được n 2 2 2 2
m  2n  m  2n 1 hay  2 m 2n  1 Từ đó suy ra 1   2 2 2  2 m m 2n 1 1 n  2  2   2   2  2   2 n n n n 1 2  2  2 n 1 1   2    2 1 n     3 2 n 2 2  2  n   
Vậy b|i to{n được chứng minh.
Câu 270: [TS10 Chuyên Vĩnh Phúc, 2009-2010]
Cho ba số thực a, b, c đôi một phân biệt. Chứng minh rằng: 2 2 2 a b c    bc 2 2 ca2 ab2 Lời giải
Bất đẳng thức cần chứng minh tương đương với
THCS.TOANMATH.com FB TRỊNH BÌNH 169 2  a b c   ab bc ca       2  2     b  c c  a a  b  
 b  cc  a c  aa  b a  bb  c  Mà ta lại có ab bc ca   
b  cc  a c  aa  b a  bb  c
aba  b  bcb  c  ca c  a a  bb  cc  a 
      
         1 a b b c c a a b b c c a 2  a b c 
Do đó bất đẳng thức trên trở thành      0 .
 b  c c  a a  b 
Bất đẳng thức cuối cùng là một bất đẳng thức đúng. Vậy b|i to{n được chứng minh.
Câu 271: [TS10 Chuyên Lam Sơn, 2009-2010] Cho biểu thức 2 2 2 2
P  a  b  c  d  ac  bd , trong đó ad  bc  1 . Chứng minh rằng: P  3 Lời giải Ta có
ac bd2 adbc2 2 2 2 2 2 2 2 2
 a c  2abcd  b d  a d  2abcd  b c 2  a  2 2 c  d  2  b  2 2 d  c    2 2 a  b  2 2 c  d  2
Vì ad  bc  1 nên       2 2   2 2 1 ac bd a b c  d  (1)
Áp dụng bất đẳng thức Cauchy ta được 2 2 2 2         2 2   2 2 P a b c d ac bd 2 a b c  d   ac  bd 2 Suy ta     2 P 2 1 ac bd
 ac  bd. Rõ ràng P  0 vì 2 1 ac  bd 2  ac  bd
Đặt x  ac  bd, khi đó ta được 2 2       2   2 2      2   2 2 P 2 1 x x P 4 1 x 4x 1 x x 1 x  4x 1 x  4x  3
THCS.TOANMATH.com FB TRỊNH BÌNH 170 Hay     2 2 2 P 1 x
2x  3  3 . Do đó ta được P  3 . Vậy bất đẳng thức được ad   bc  1 
chứng minh. Đẳng thức xẩy ra khi và chỉ khi 2a  3d  c 2b   3cd 
Câu 272: [TS10 Chuyên Nghệ An, 2009-2010]
Cho a, b, c là các số thực dương thay đổi thỏa mãn a  b  c  3. Tìm giá trị nhỏ nhất của biểu thức:   2 2 2 ab bc ca P  a  b  c  2 2 2 a b  b c  c a Lời giải
Dự đo{n được dấu đẳng thức xẩy ra tại a  b  c  1 và giá trị nhỏ nhất của P là 4.
Ta quy bài toán về chứng minh bất đẳng thức   2 2 2 ab bc ca a  b  c   4 2 2 2 a b  b c  c a
Thật vậy, kết hợp với giả thiết ta có 3 2 2 2
a  b  c   a  b  c 2 2 2 a  b  c  3 3 3 2 2 2 2 2 2
 a  b  c  a b  b c  c a  ab  bc  ca
Áp dụng bất đăngr thức Cauchy ta có 3 2 2 3 2 2 3 2 2
a  ab  2a b; b  bc  2b c; c  ca  2c a Suy ra  2 2 2      2 2 2 3 a b c
3 a b  b c  c a  0 ab  bc  ca ab  bc  ca Do đó ta được 2 2 2 2 2 2 a  b  c   a  b  c  2 2 2 2 2 2 a b  b c  c a a  b  c
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được   2 2 2 ab bc ca a  b  c   4 2 2 2 a  b  c 9   2 2 2 a  b  c 2 2 2  Hay a  b  c   2 4 2 2 2 a  b  c  Đặt 2 2 2 t  a  b  c . Từ giả thiết 2 2 2
a  b  c  3  a  b  c  3 , do đó ta được t  3
THCS.TOANMATH.com FB TRỊNH BÌNH 171
Bất đẳng thức trên trở thành 9  t 2 t 
 4  2t  9  t  8t  t  32t  3  0 2t
Bất đẳng thức cuối cùng luôn đúng do t  3 . Vậy b|i to{n được chứng minh xong.
Câu 273: [TS10 Chuyên Lam Sơn, 2009-2010]
Gọi a, b, c l| độ dài ba cạnh của một tam giác có ba góc nhọn. Chứng minh rằng với
mọi số thực x, y, z ta luôn có: 2 2 2 2 2 2 x y z 2x  2y  2z    2 2 2 2 2 2 a b c a  b  c Lời giải
Bất đẳng thức cần chứng minh tương đương với 2 2 2 2 2 2 x 2x y 2y z 2z       0 2 2 2 2 2 2 2 2 2 2 2 2 a a  b  c b a  b  c c a  b  c 2 x  2 2 2 b  c  a  2 y  2 2 2 a  c  b  2 z  2 2 2 a  b  c      0 2 a  2 2 2 a  b  c  2 b  2 2 2 a  b  c  2 c  2 2 2 a  b  c 
Do a, b, c l| độ dài các cạnh của một tam giác nhọn nên 2 2 2 2 2 2 2 2 2
a  b  c ; b  c  a ; c  a  b Nên ta được 2 2 2 2 2 2 2 2 2
b  c  a  0; a  c  b  0; a  b  c  0
Do vậy bất đẳng thức trên luôn đúng. B|i to{n được chứng minh xong.
Câu 274: [TS10 Chuyên KHTN, 2009-2010]
Với a, b, c là những số thực dương. Chứng minh rằng: 2 2 2 a b c a  b  c    2 2 2 2 2 2       5 3a 8b 14ab 3b 8c 14bc 3c 8a 14ca Lời giải
Áp dụng bất đẳng thức Cauchy ta được             2 2 2 2 2 2 2 3a 8b 14ab 3a 8b 12ab 2ab 4a 9b 12ab 2a 3b 2 2 2 a a a Suy ra    2 2 2 2a     3b 3a 8b 14ab 2a 3b
Áp dụng tương tự ta thu được
THCS.TOANMATH.com FB TRỊNH BÌNH 172 2 2 2 a b c   2 2 2 2 2 2 3a  8b  14ab 3b  8c  14bc 3c  8a  14ca 2 2 2 a b c    2a  3b 2b  3c 2c  3a
Mặt khác theo bất đẳng thức Bunhiacopxki dạng phân thức ta được a b c    2 2 2 2 a b c a  b  c     2a  3b 2b  3c 2c  3a 5a  b  c 5 2 2 2 a b c a  b  c Do đó ta được:    2 2 2 2 2 2       5 3a 8b 14ab 3b 8c 14bc 3c 8a 14ca
Vậy b|i to{n được chứng minh xong. Đẳng thức xẩy ra khi và chỉ khi a  b  c
Câu 275: [TS10 Chuyên KHTN, 2009-2010]
Giả sử x, y, z là những số thực thoả mãn điều kiện 0  x, y, z  2 và x  y  z  3 .
Tìm giá trị nhỏ nhất và lớn nhất của biểu thức: 4 4 4
M  x  y  z  121 x1 y1 z Lời giải
Đặt a  x 1; b  y  1; c  z  1, ta được 1
  a; b; c  1 và a  b c  0. Biểu
thức M được viết lại thành 4 4 4      3 3 3     2 2 2 M a b c 4 a b c
6 a  b  c   4a  b  c  3 12abc
Để ý là khi a  b  c  0 thì 3 3 3
a  b  c  3abc  0 nên biểu thức trên thử thành 4 4 4      2 2 2 M a b c 6 a  b  c   3
Theo một đ{nh gi{ quen thuộc thì 4 4 4
a  b  c  abc a  b  c  0 1
a  b  c  a  b  c2 2 2 2  0 3
Do đó suy ra M  3 hay giá trị nhỏ nhất của M là 3.
Đẳng thức xẩy ra khi và chỉ khi a  b  c  0 hay x  y  z  1. Mặt khác do 1
  a; b; c  1 nên ta có a ; b ; c  1. Từ đó ta có 4 2 4 2 4 2
a  a  a ; b  b  b ; c  c  c Suy ra 4 4 4      2 2 2 M a b c
6 a  b  c   3  7  a  b  c   3
THCS.TOANMATH.com FB TRỊNH BÌNH 173
Mà ta lại có a  b  c  0 nên trong ba số a, b, c có một hoặc hai số âm, tức là luôn tồn
tại hai số cùng dấu. Không mất tính tổng quát ta giả sử hai số đó l| b v| c. Khi đó ta được b  c  b  c  a
Đến đ}y ta có M  14 a  3  17 hay giá trị lớn nhất của M l| 17. Đẳng thức xẩy ra khi và chỉ khi a  1; b  1
 ;c  0 và các hoán vị hay x  2; y  0; z  1 và các hoán vị
Câu 276: [TS10 Chuyên Thái Bình, 2009-2010]
a) Cho k là số nguyên dương bất kì. Chứng minh bất đẳng thức sau: 1  1 1      2   k 1 k  k k  1  1 1 1 1 88 b) Chứng minh rằng:      2 3 2 4 3 2010 2009 45 Lời giải
a) Bất đẳng thức cần chứng minh tương đương với     2k 1 2 kk  
1  0   k 1  k 2 1 2 k 1 2 k     0 k 1 k k. k  1
Bất đẳng thức cuối cùng luôn đúng với mọi k nguyên dương.
Vậy bất đẳng thức được chứng minh.
b) Áp dụng kết quả câu a ta có 1 1 1 1 VT      2 1 3 2 4 3 2010 2009  1 1   1 1   1 1   2    2     2    1 2   2 3   2009 2010   1   1  88  21   21    VP  2010   45  45
Vậy bất đẳng thức được chứng minh xong.
Câu 277: [TS10 Chuyên TP. Hồ Chí Minh, 2009-2010]
a) Cho 3 số thực a, b, c bất kì. Chứng minh rằng:
ab2 bc2 ca2 2 2 2
a  b  c  ab  bc  ca    26 6 2009 1 2 8
b) Cho a  0; b  0 . Chứng minh rằng   a b 2a  b
THCS.TOANMATH.com FB TRỊNH BÌNH 174 Lời giải
a) Bất đẳng thức cần chứng minh tương đương với
  2   2   2   2   2   2 a b b c c a a b b c c a      2 2 2 26 6 2009   2   2   2 12 a b b c 2007 c a Hay    0 13 3 2
Bất đẳng thức cuối cùng luôn đúng.
Vậy b|i to{n được chứng minh. Đẳng thức xẩy ra khi và chỉ khi a  b  c .
b) Bất đẳng thức cần chứng minh tương đương với 1 2 8   a b 2a  b
Đặt c  b , do b  0 nên ta được c  0 , khi đó bất đẳng thức trên được viết lại thành 1 2 8   a c 2a  c
Theo một đ{nh gi{ quen thuộc ta được 1 2 2 2 2.4 8      a c 2a c 2a  c 2a  c
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi 2a  b .
Câu 278: [TS10 Chuyên Phú Thọ 2009-2010]
Cho x, y, z là các số thực dương sao cho xyz  x  y  z  2 . Chứng minh rằng: 1 1 1 3    xy yz zx 2 Lời giải 1 1 1
Giả thiết của b|i to{n được viết lại thành    1 x  1 y  1 z  . 1 1 1 1 Đặt a  ; b  ; c 
   . Từ đó suy ra x  1 y  1
z  . Khi đó ta được a b c 1 1 1 a b  c 1 b c  a 1 c a  b x   ; y   ; z   a a b b c a
Bất đẳng thức cần chứng minh được viết lại thành:
THCS.TOANMATH.com FB TRỊNH BÌNH 175 ab bc ca 3     b  cc  a
caa b a bbc 2
Áp dụng bất đẳng thức Cauchy ta được: ab 1  b a       b  cc  a 2  b  c c  a  bc 1  c b       c  aa  b 2  c  a a  b  ca 1  a c       a  bb  c 2  a  b b  c 
Cộng theo vế các bất đẳng thức trên ta được: ab bc ca 3     b  cc  a
caa b a bbc 2
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi a  b  c  2
Câu 279: [TS10 Chuyên Phú Thọ 2009-2010]
Cho các số thực không âm a, b, c sao cho ab  bc  ca  3. Chứng minh rằng: 1 1 1    1 2 2 2 a  2 b  2 c  2 Lời giải
Bất đẳng thức cần chứng minh tương đương với 2 2 2 a b c    1 2 2 2 a  2 b  2 c  2
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được a b c a bc2 a bc2 2 2 2      1 2 2 2 2 2 2 2 2 2 a  2 b  2 c  2 a  b  c  6
a  b  c  2 ab  bc  ca
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi a  b  c  1.
Câu 280: [TS10 Chuyên Đại học Vinh 2009-2010]
Cho x, y, z là các số dương thỏa mãn x  2y  3z  18 . Chứng minh rằng: 2y  3z  5 3z  x  5 x  2y  5 51    1 x 1 2y 1  3z 7 Lời giải
THCS.TOANMATH.com FB TRỊNH BÌNH 176
Đặt a  x; b  2y; c  3x, khi đó giả thiết trở thành a  b  c  18 và bất đẳng thức được viết lại thành
b  c  5 c  a  5 a  b  5 51    1 a 1 b 1 c 7
Bất đẳng thức trên tương đương với b  c  5 c  a  5 a  b  5 51 1  1  1   3 1 a 1 b 1 c 7   Hay      1 1 1 72 a b c 6       1 a 1 b 1 c  7
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được 1 1 1 3    1 a 1 b 1 c 7
Thật vậy theo bất đẳng thức Cauchy ta có 1 1 1 9 9 3      1 a 1 b 1 c 3  a  b  c 21 7
Vậy b|i to{n được chứng minh.
Đẳng thức xẩy ra khi và chỉ khi a  b  c  6 hay x  6; y  3; z  2 .
Câu 281: [TS10 Chuyên Đại học Vinh 2009-2010]
Cho các số thực x, y thỏa mãn: x  8y  0. Hãy tìm giá trị nhỏ nhất của biểu thức: 1 P  x  .
y(x  8y) Lời giải
Sử dụng BĐT Cauchy cho ba số dương ta có: 1
P  (x  8y)  8y   6.
y(x  8y)
 x 8y  8y  x 16y  x  4   
Đẳng thức xảy ra khi và chỉ khi  1   1   1 3 8y  y  y  .    
y(x  8y)  64  4 1
Vậy minP = 6. khi và chỉ khi x = 4 và y = . 4
THCS.TOANMATH.com FB TRỊNH BÌNH 177
THCS.TOANMATH.com FB TRỊNH BÌNH