lOMoAR cPSD| 49831834 Chương I :
MA TRẬN VÀ ĐỊNH THỨC
A. Tóm tắt lý thuyết :
I. ĐỊNH NGHĨA MA TRẬN & CÁC PHÉP TOÁN CƠ BẢN CỦA MA TRẬN.
1. Định nghĩa ma trận :
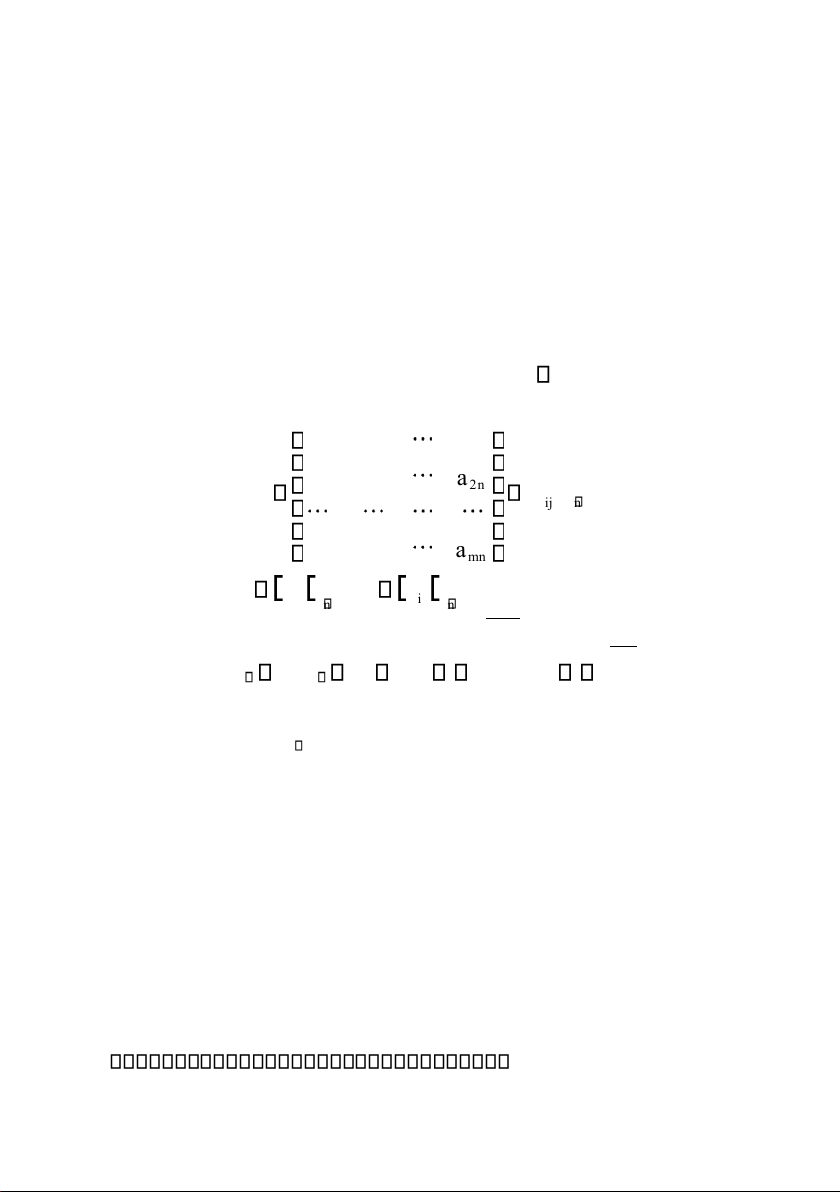
Ma trận A có cấp (còn gọi là kích thước) m n là một bảng số các
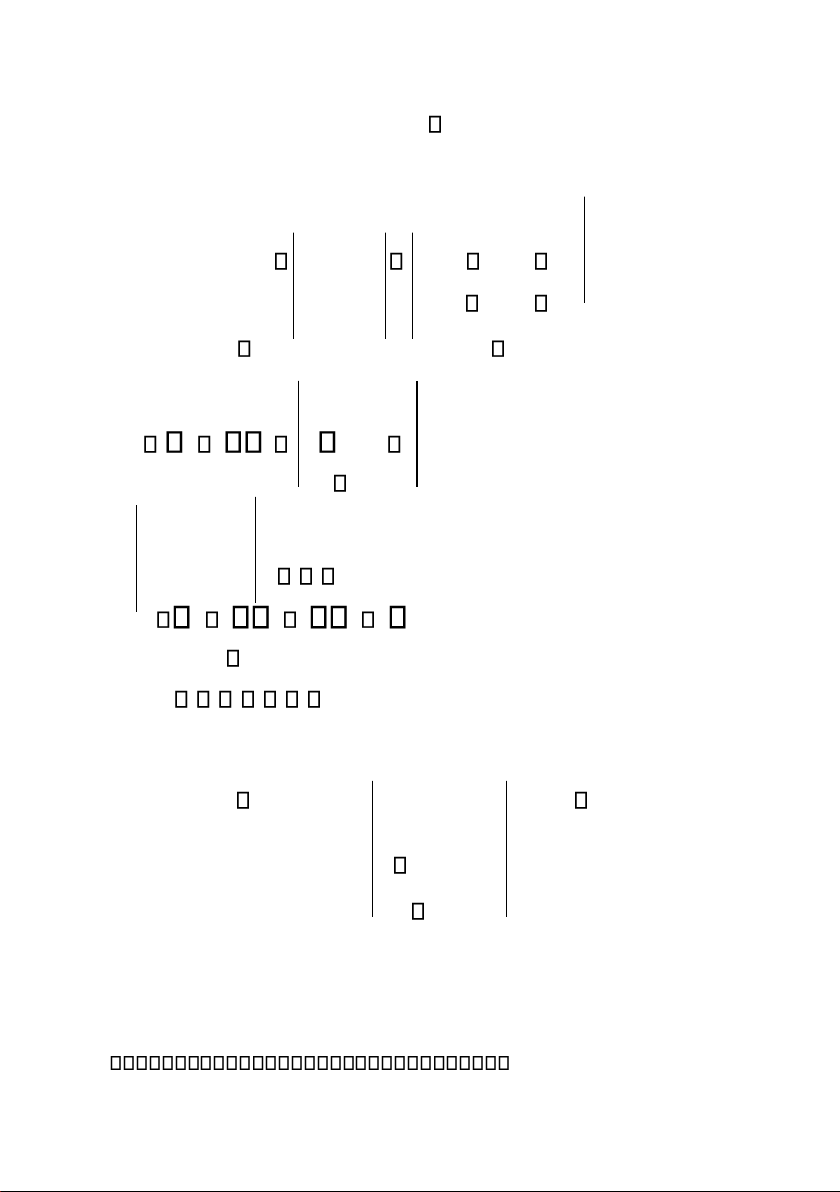
số thực, xếp thành m dòng và n cột có dạng a a a 11 12 1 n a a a 21 22 2 n A ( a ) ij mn a a a m1 m2 mn Cho ma trận A a , B b ij ij . Khi ó: mn mn
Am n Bm n aij bij , i 1,m và j 1,n
2. Các loại ma trận :
- Ma trận Om n là ma trận gồm toàn số 0 .
- Ma trận vuông : là ma trận mà số dòng bằng số cột. Ta
thường gọi số dòng của ma trận vuông là cấp của ma trận
ấy. Khi ó, ường chéo nối các phần tử a11 , a22 , …, ann ược
gọi là ường chéo chính của ma trận vuông. Khi ó, vết của
ma trận vuông là tổng của tất cả các phần tử của ường chéo chính.
- Ma trận tam giác trên : là ma trận vuông mà các phần tử ở
dưới ường chéo chính ều bằng 0 .
Bài tập Toán Cao cấp dành cho khối ngành Trang 1
Thương Mại, Kinh tế lOMoAR cPSD| 49831834
- Ma trận tam giác dưới : là ma trận vuông mà các phần tử ở
trên ường chéo chính ều bằng 0 .
- Ma trận ường chéo : là ma trận vuông mà các phần tử
không thuộc ường chéo chính ều bằng 0 .
- Ma trận ơn vị : là ma trận ường chéo mà các phần tử thuộc
ường chéo chính ều bằng 1. - Ma trận chuyển vị của A aij m n là AT a ji n m
3. Phép cộng hai ma trận : A aij , B bij m n m n A Baij bij m n
4. Phép nhân ma trận với một số thực : ) k.A k.aij m n (k
Tính chất. Cho A, B, C là các ma trận cấp m n và , . Khi ó : i. A B B A ii. (A B) C A (B C) iii. A O O A với O (0)m n iv.
A ( A) O với A ( aij m n) (còn gọi là ma trận ối của A ) v. (A B) A B
Bài tập Toán Cao cấp dành cho khối ngành Trang 2 lOMoAR cPSD| 49831834 vi. ( )A A A vii. ( )A ( A) viii. 1.A A ix. A B T AT BT
5. Phép nhân hai ma trận : Cho các ma trận A aij m p , B bij p n Thì : A.B c p ijm n với cij a b , iikkj 1,m, j 1,n . k 1
Tính chất : Cho Dk m , Am n , Bm n , Cn p . Khi ó i. (DB)C D(BC) ii. (A B)C AC BC iii. D(A B) DA DB iv. I Am m n A v. Am n n I A vi. (BC)T C BT T
Bài tập Toán Cao cấp dành cho khối ngành Trang 3
Thương Mại, Kinh tế lOMoAR cPSD| 49831834
II. ĐỊ NH TH Ứ C.
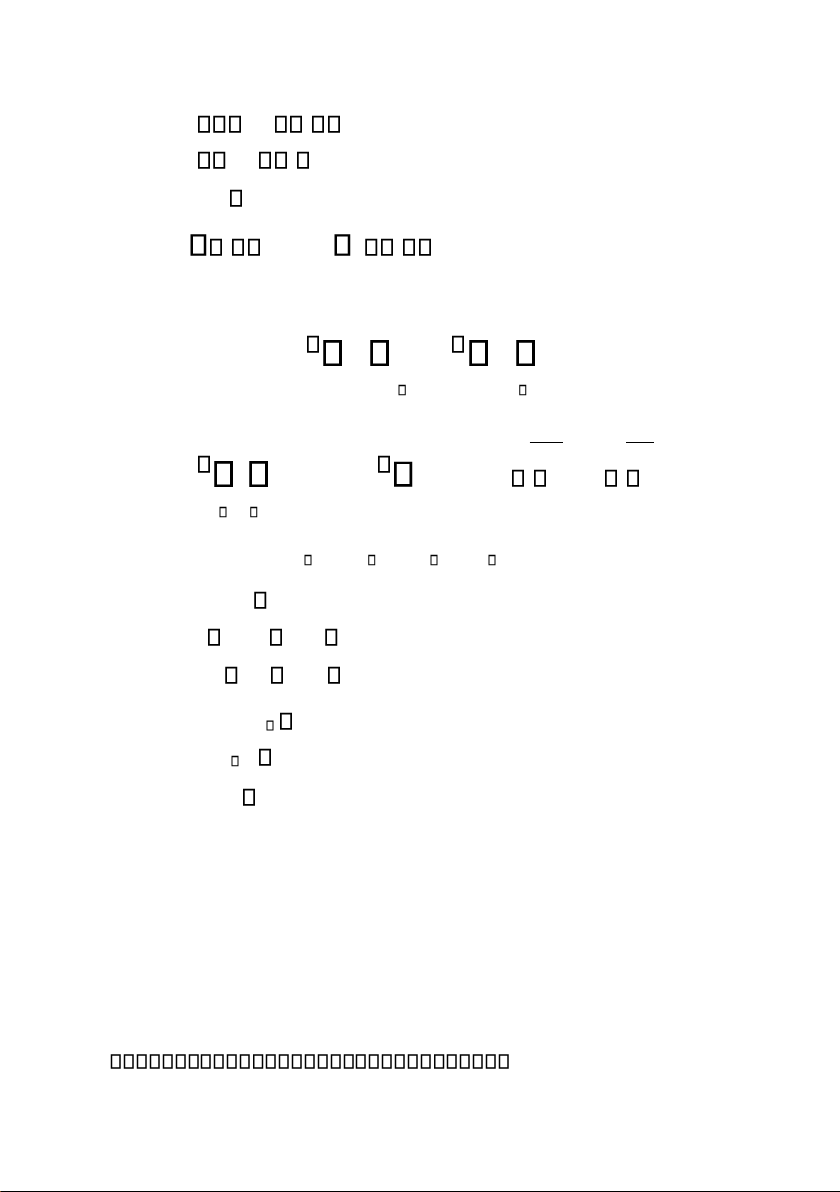
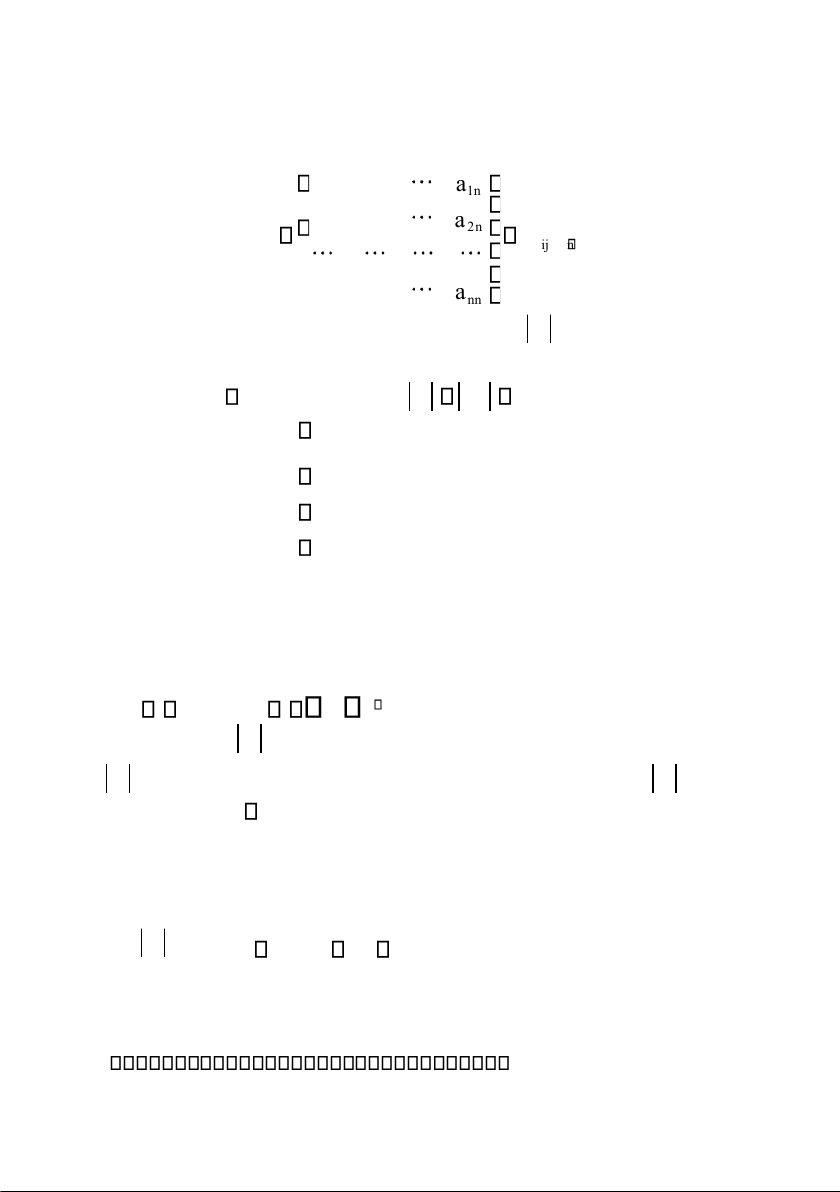
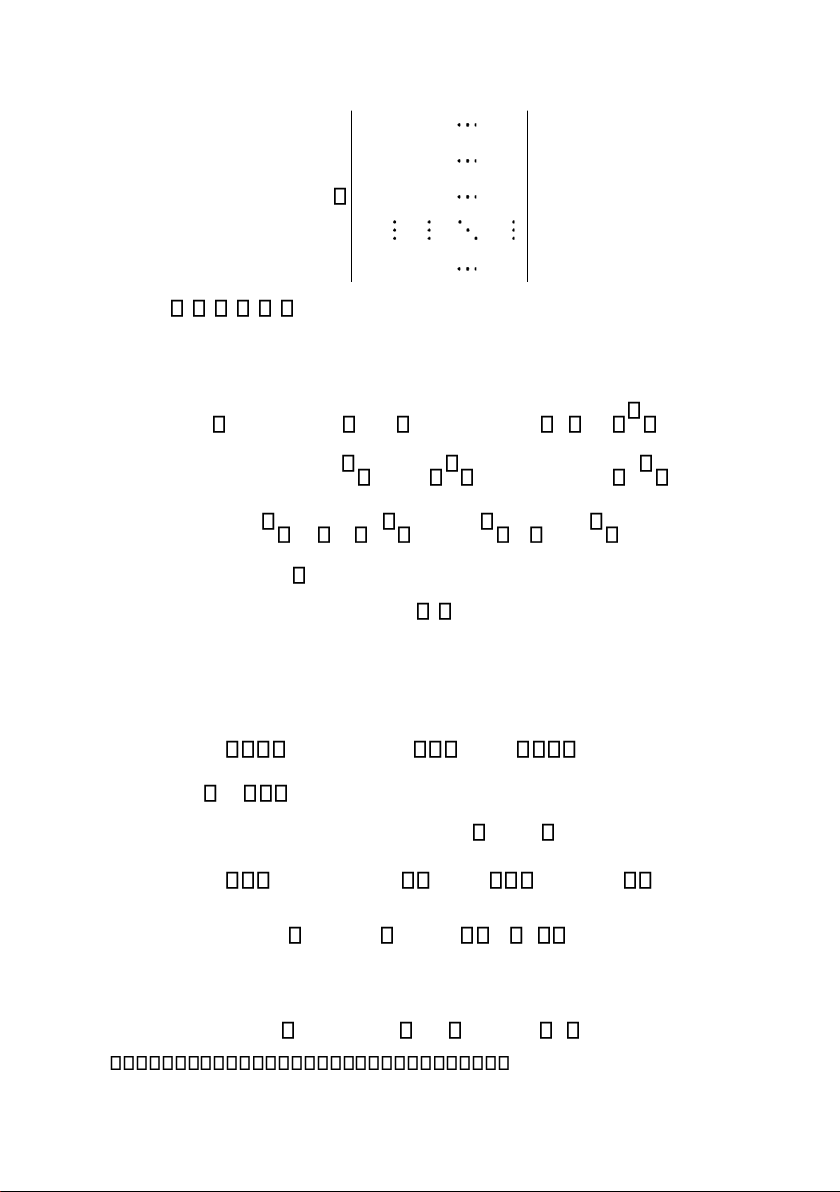
Cho ma trận vuông cấp n : a a a 11 12 1 n a a a 21 22 2 n A ( a ) ij nn a a a n1 n2 nn
Định thức của ma trận A ược ký hiệu là A hay det(A) ược xác ịnh như sau : i) ( n1 , ta ịnh nghĩa: A a a 11 11 (ii) n 2, ặt Aij
1 i j .Mij , gọi là phần bù ại số của aij trong
A , trong ó Mij là ịnh thức con bù của aij trong A (chú ý rằng Mij là
ịnh thức cấp n 1 có ược từ A bằng cách bỏ i dòng thứ i và cột thứ j của A ). Khi ó : A = a Ai1 i1 a Ai2 i2
a Ain in (khai triển theo dòng i)
Bài tập Toán Cao cấp dành cho khối ngành Trang 4 lOMoAR cPSD| 49831834 = a A1j 1j a A2j 2j a Anj nj (khai triển theo
cột j) Một số tính chất thường dùng : i.
A AT với A là ma trận vuông ii.
Định thức sẽ ổi dấu nếu ổi chỗ hai dòng với nhau trong ịnh thức. iii.
Nếu các phần tử của một dòng ều có thừa số chung là số
thì ta có thể rút ra ngoài khỏi dấu ịnh thức. iv.
Định thức có giá trị bằng không nếu có hai dòng tỷ lệ nhau. v.
Định thức sẽ không ổi nếu biến ổi dòng i thành dòng i cộng với k lần dòng j (với k , i j) vi.
Định thức của ma trận tam giác bằng tích các phần tử nằm trên ường chéo chính.
vii. AB A . B với A , B là các ma trận vuông cùng cấp Chú
ý : Các tính chất ii, iii, iv, v vẫn còn úng khi ta thay dòng bằng cột.
Quy tắc SARIUS (tính ịnh thức cấp 3) :
ường chéo chính ường chéo phụ a a11 a12 13 A a 21 a22 a23 (+) ( ) a a 31 a32 33 Hình 1.a Hình 1.b
a a a11 22 33 a a a12 23 31 a a a13 21 32 a a a31 22 13 a a a11 23 32 a a a21
12 33 Giá trị của ịnh thức cấp 3 bằng tổng ại số của hai nhóm:
Bài tập Toán Cao cấp dành cho khối ngành Trang 5
Thương Mại, Kinh tế lOMoAR cPSD| 49831834
✓ Nhóm thứ nhất mang dấu + là : Tích của các phần tử nằm
trên ường chéo chính, tích các phần tử song song với ường
chéo chính với phần tử ở góc ối diện. (hình 1.a)
✓ Nhóm thứ hai mang dấu là : Tích của các phần tử nằm
trên ường chéo phụ, tích các phần tử song song với ường
chéo phụ với phần tử ở góc ối diện. (hình 1.b)
III. MA TRẬN NGHỊCH ĐẢO : Cho A
aij n n . Ma trận B là ma trận nghịch ảo của A nếu : AB = BA = In
và B ược ký hiệu là A 1 . Khi ó A ược gọi là ma trận khả nghịch hay
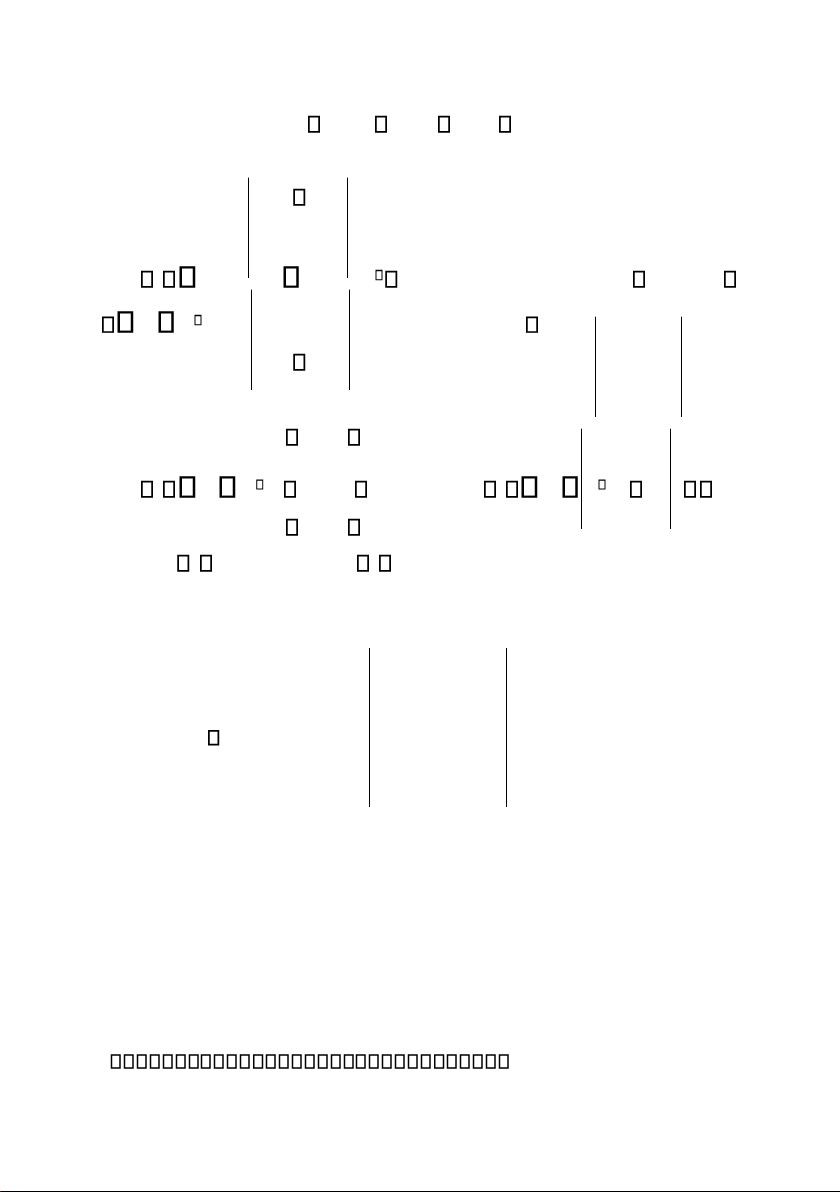
ma trận không suy biến. A A 11 21 n1 A A A 12 22 n2 A A 1 n 2 n nn Ta ký hiệu A A * với Ai j 1 i j .Mi j và A
Mij là ịnh thức con bù của aij trong A (là ịnh thức con của
Bài tập Toán Cao cấp dành cho khối ngành Trang 6 lOMoAR cPSD| 49831834
A sau khi bỏ i dòng i cột j), ta thường gọi A* là ma trận phụ hợp
của ma trận A ( ôi khi A* còn ược ký hiệu là A hoặc PA ) 1. Mệnh ề
: Với ma trận An n , ta có A.A* A .A* A .In
2. Mệnh ề : A 0 An n có ma trận nghịch ảo. Khi ó A 1 1 A* A
3. Tìm ma trận nghịch ảo bằng phép biến ổi theo dòng :
(thường dùng cho ma trận có cấp khá lớn) Các
phép biến ổi sơ cấp trên dòng :
i. Đổi chỗ hai dòng cho nhau.
ii. Lấy một dòng nhân với một số khác 0. iii. Thay một dòng
bằng dòng ó cộng với k lần dòng khác.
Biến ổi cùng một lúc hai ma trận A và I (ma trận ơn vị) cùng cấp
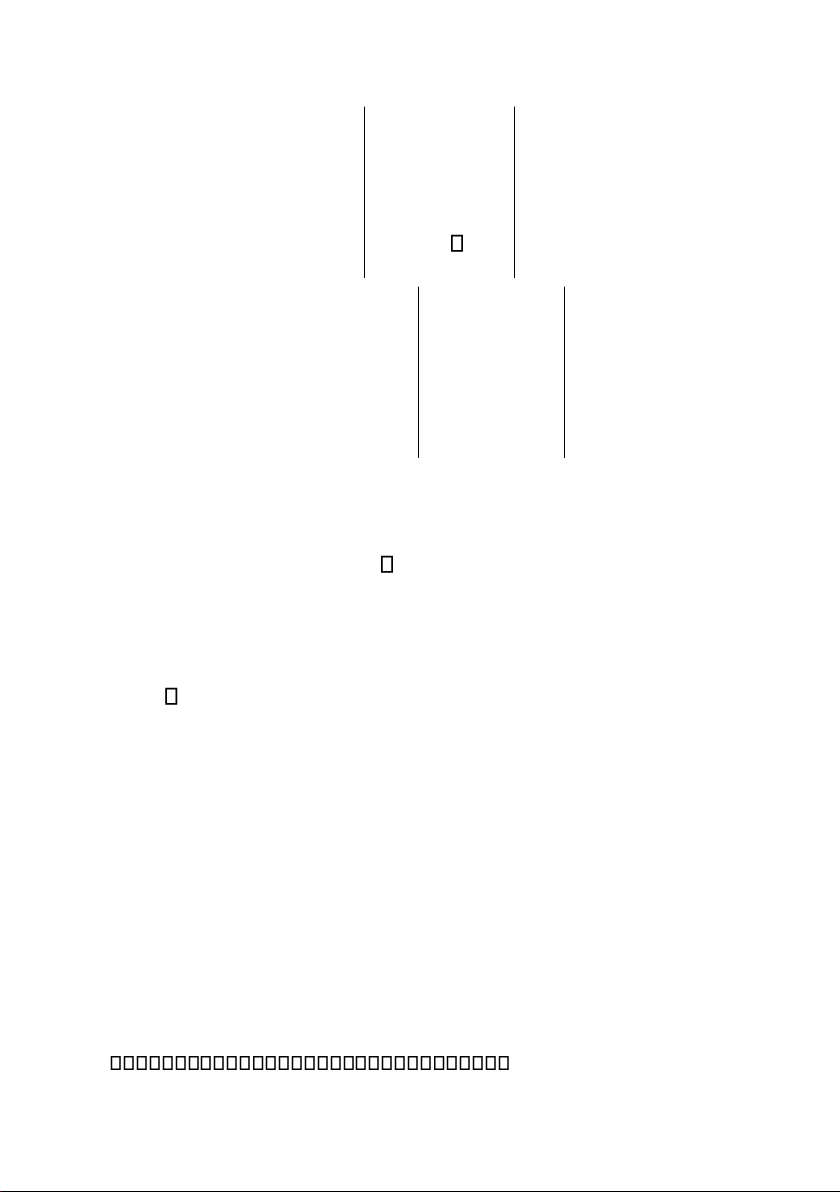
bằng các phép biến ổi sơ cấp trên dòng, theo sơ ồ như sau : A I I A 1
Chú ý: Trong quá trình biến ổi, nếu xuất hiện một dòng có các
phần tử ều bằng 0 thì ta kết luận không có ma trận nghịch ảo.
Tính chất : Cho A , B là các ma trận vuông khả nghịch và cùng cấp. Khi ó : i. A 1 là duy nhất. ii. AT 1 A 1 T iii. AB 1 B .A 1
Bài tập Toán Cao cấp dành cho khối ngành Trang 7
Thương Mại, Kinh tế lOMoAR cPSD| 49831834 1 iv. A 1 1 A 1 với 0
4. Giải phương trình ma trận :
Xét phương trình ma trận Am n .X Bm p (1)
• Cách 1 : Dựa vào kích thước của các ma trận A và B , ta ặt ma trận : X xij n p
với n là số cột của ma trận A và p là số cột của ma trận B . Dùng
phép nhân ma trận và cho hai ma trận bằng nhau ta ược một hệ
phương trình tuyến tính. Giải hệ phương trình ó, ta sẽ tìm ược các phần tử xij .
• Cách 2 (chỉ ược áp dụng khi A là một ma trận vuông) i.
Nếu A 0 , khi ó phương trình (1) có nghiệm duy nhất là X A B 1 ii.
Nếu A 0, B là ma trận vuông và B 0 không có ma
trận X (theo ịnh lý về phép nhân ịnh thức). iii.
Nếu A 0, B là ma trận vuông và B 0 thì sử dụng cách 1.
IV. HẠNG CỦA MA TRẬN : Cho A aij m n . Ma trận A có : ▪ m dòng A ,A ,...,A d d 1 d2 m
Bài tập Toán Cao cấp dành cho khối ngành Trang 8 lOMoAR cPSD| 49831834 ▪ n cột A ,A ,...,A c c 1 c2 n
Hơn nữa : Rank A ,A ,...,A1d d2dm = Rank A ,A ,...,A1c c2 cn .
Hạng của m dòng trong ma trận A ược gọi là hạng của ma trận A
và ược ký hiệu là R(A) hay r(A) hay Rank(A). Mệnh ề : Cho ma trận A
aij m n có ít nhất một ịnh thức con
cấp k khác 0 và mọi ịnh thức con cấp k 1 ều bằng 0 thì hạng của ma trận A bằng k .
Mệnh ề : Nếu dùng các phép biến ổi sơ cấp theo dòng (hay theo
cột) thì hạng của ma trận sẽ không thay ổi. Nhắc lại các phép biến
ổi sơ cấp theo dòng :
- Đổi chỗ hai dòng cho nhau.
- Nhân một dòng với một số khác 0.
- Thay dòng i bằng dòng i cộng với k lần dòng j với k và i j.
Chú ý : Ta dùng các phép biến ổi sơ cấp trong mệnh ề trên ể biến
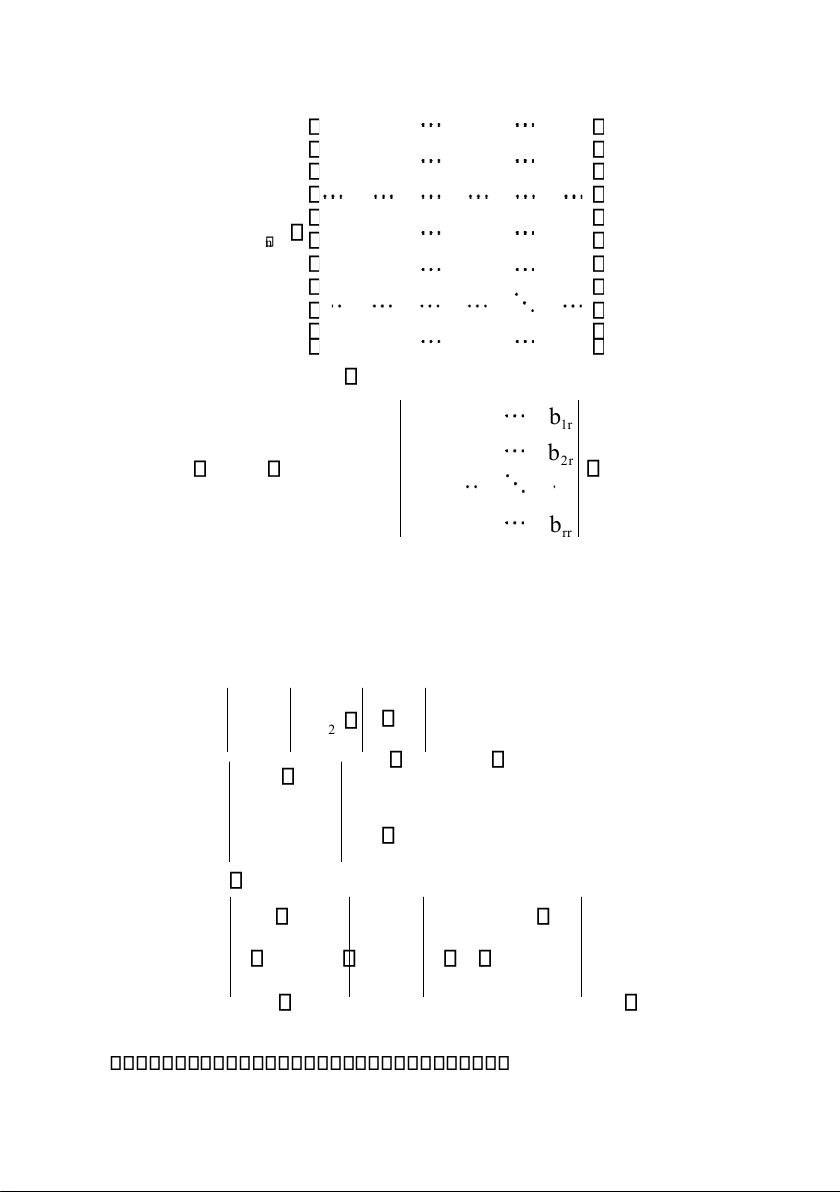
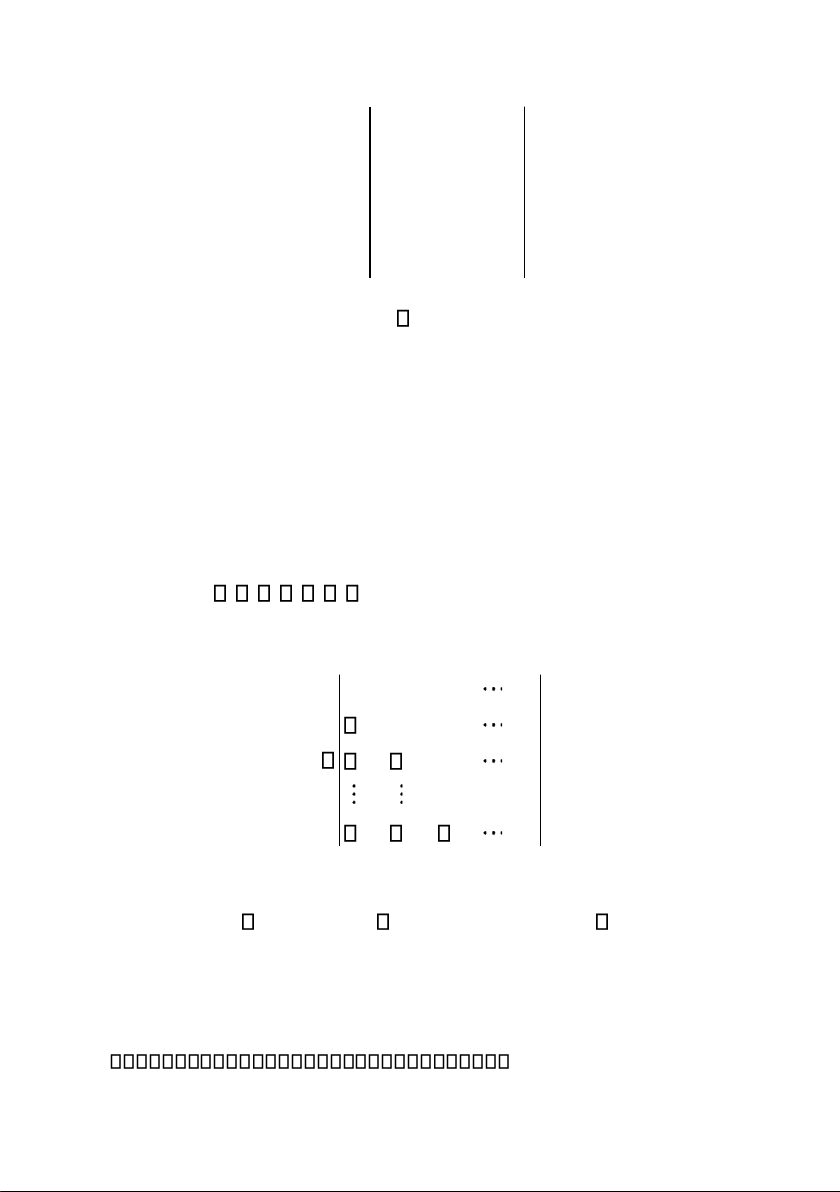
ổi ma trận A ban ầu về ma trận B có dạng bậc thang như sau
Bài tập Toán Cao cấp dành cho khối ngành Trang 9
Thương Mại, Kinh tế lOMoAR cPSD| 49831834 b b b b 11 12 1 r 1 n 0 b b b 22 2 r 2 n B mn 0 0 b b rr rn 0 0 0 0 0 0 0 0 trong ó b , b , ..., b . 11 22 rr 0 b b b 11 12 1 r 0 b và b R(A) 22 2 r R (B) r vì tồn tại 0 0 0 brr B. BÀI TẬP
Bài 1 : Tính các ịnh thức sau: a. D1 , D 1 22 3 2 1 31 1 2 1 3 1 2 b. D3 3 3 1 2 m 1 1m 1 1 c. D4 1 m 1, D5 m 1 1 0 1 1 m1 1 m 2
Bài tập Toán Cao cấp dành cho khối ngành Trang 10 lOMoAR cPSD| 49831834 Giải : a. D1 5, D2 5 b. D3 42 c. D4 m3 3m và D5 4 a b c 1
Bài 2 : Tính ịnh thức D b c a 1 c a b 1
Giải : Cộng cột 2 vào cột 1, ta có : a b c c 1 D a b c a 1 a b c b 1
Rút thừa số chung (a b c) ở cột 1 thì 1 c 1 D a b a 1 b 1 c 1 1
Vì cột 1 và cột 3 giống nhau nên ta có : D 0
Bài 3 : Chứng minh rằng 1 a a2 D 1 b b2 b a c a c b 1 c c2
Bài tập Toán Cao cấp dành cho khối ngành Trang 11
Thương Mại, Kinh tế lOMoAR cPSD| 49831834
Từ ó tìm iều kiện của a , b , c ể D 0
Giải : Thay dòng 2 bằng cách lấy dòng 2 trừ dòng 1 và thay dòng
3 bằng cách lấy dòng 3 trừ dòng 1 thì 1 a a21 a a2 D 1 b b2 0 b a b2 a2 1 c c20 c a c2 a2
Rút thừa số (b a) ở dòng 2 và thừa số (c a) ở dòng 3 thì 1 a a2 = D b a c a 0 1 b a 0 1 a c 1 a a2 Vì 0 1b a c b nên = D b a c a c b 0 1 a c Vậy, D 0 a b b c a c
Bài 4 : Tính ịnh thức sau ây bằng cách khai triển theo dòng 3 2 3 4 1 4 2 3 2 D a b c d 3 1 4 3 Giải :
Khai triển ịnh thức D theo dòng 3 ta có:
Bài tập Toán Cao cấp dành cho khối ngành Trang 12 lOMoAR cPSD| 49831834 D aA31 bA32 cA33 dA34
Ta tính các phần bù ại số : 3 4 12 4 1 A31 1 3 1 2 3 2 8 A32 1 3 2 4 3 2 15 1 4 33 4 3 2 3 12 3 4 A33 1 3 3 4 2 2 12 A34 1 3 4 4 2 3 19 3 1 33 1 4 Vậy: D 8a15b 12c 19d
Bài 5 : Tính ịnh thức sau ây 5 1 1 1 1 1 5 1 1 1 D 1 1 5 1 1 1 1 1 5 1 1 1 1 1 5 Giải :
Cộng cột 2, 3, 4, 5 vào cột 1, ta có
Bài tập Toán Cao cấp dành cho khối ngành Trang 13
Thương Mại, Kinh tế lOMoAR cPSD| 49831834 9 1 1 1 1 1 9 5 1 1 1 D 9 1 9 9 1 5 1 1 1 1 1 1 1 5 1 1 1 1 5 1 1 5 1 1 5 1 1 1 5 1
Rút thừa số 9 ở cột 1, thì : D 91 1 5 1 1 1 1 1 1
Áp dụng tính chất thay dòng k bằng cách lấy dòng k trừ dòng 1 (với k 2,3,4,5) ta có
Bài tập Toán Cao cấp dành cho khối ngành Trang 14 lOMoAR cPSD| 49831834 1 1 1 1 1 0 4 0 0 0 D 90 0 4 0 0 0 0 0 4 0 0 0 0 0 4 Như vậy D 9 1 4 4 4 4 2304
Bài 6 : Tính ịnh thức cấp n sau ây 1 2 3 n 1 0 3 n D 1 2 0 n n 1 2 3 0
Giải : Ký hiệu di là dòng thứ i .
Thay d2 bởi d1 d2 , d3 bởi d1 d3 ,…, dòng dn bởi d1 dn thì ta có :
Bài tập Toán Cao cấp dành cho khối ngành Trang 15
Thương Mại, Kinh tế lOMoAR cPSD| 49831834 1 2 3 n 0 2 6 2 n D 0 0 3 2 n 0 0 0 n Nên D 1 2 3 ... n n!
Bài 7 : Cho các ma trận sau 2 5 7 1 2 3 A 6 3 4 và B 3 2 4 5 2 3 3 1 0 a. Hãy tính 3A 2B.
b. Tìm ma trận X sao cho A X B. c. Tính A.B và B.A .
d. Kiểm tra lại ba câu hỏi trên với i. A 62 53 72 và B 13 22 34 1 2 ii. A 2 5 7 và B 3 2 6 3 4 3 1 Giải : 2 5 7 1 2 3
Bài tập Toán Cao cấp dành cho khối ngành Trang 16 lOMoAR cPSD| 49831834 a. 3A 2B = 3 6 3 4 +2 3 2 4 5 2 3 3 1 0 6 15 21 2 4 6 9 4 12 6 = 18 6 2 8 9 15 6 0 8 19 15 = 24 13 4 21 8 9 b. Từ phương trình A X B X B A 1 2 3 2 5 7 1 3 10 2 3 4 Nên X 3 1 4 3 1 8 6 2 3 3 2 1 3 0 5 2 5 7 1 2 3 38 7 26 3 2 6 2 4 3 1 4 27 14 c. A.B 5 3 3 30
Bài tập Toán Cao cấp dành cho khối ngành Trang 17
Thương Mại, Kinh tế lOMoAR cPSD| 49831834 0 10 9 7 1 2 3 2 5 7 1 17 24 3 B.A 2 3 4 6 2 29 41 3 1 2 4 0 5 3 0 12 17 d. Hướng dẫn : i.
Câu c không thực hiện ược.
ii. Chỉ thực hiện ược A.B và B.A 2 1
Bài 8 : Cho các ma trận A 121 và B 12 2 0 1 0 1
a. Tính AT , BT , AB T và B AT T .
b. Hãy kiểm tra AB T B AT T Giải : 1 2 a. AT 12 10 và BT 21 21 10
Bài tập Toán Cao cấp dành cho khối ngành Trang 18 lOMoAR cPSD| 49831834 2 1 A.B 21 02 11 1 2 44 61 0 1 A.B T 64 41 1 2 B AT T 21 21 10 12 10 64 41
b. Theo câu a, ta có: A.B T B AT T x 1 n Bài 9 : Tính An với x và n là số tự nhiên 0 x Giải :
Bài tập Toán Cao cấp dành cho khối ngành Trang 19
Thương Mại, Kinh tế lOMoAR cPSD| 49831834
Bằng phương pháp quy nạp : + Với n 1, ta có: A x 1 1 . 0 x + Với n 2, ta có : A2 x 1 2 x1 x1 x22x2 0 x 0 x 0 x 0 x
+ Giả sử An úng với n k , tức là : A k x 1 k xkkxk 1k 0 x 0 x
Ta phải chứng minh An úng với n k 1, nghĩa là: Ak 1 x1 k 1 xk 1 k k 11 xk (1) 0 x 0 x
Bài tập Toán Cao cấp dành cho khối ngành Trang 20