lOMoAR cPSD| 49831834 BÀI 5 1 lOMoAR cPSD| 49831834
§5: Hệ phương trình tuyến tính
5.1 Dạng tổng quát và dạng ma trận của hệ
phương trình tuyến tính.
5.1.1. Định nghĩa: Hệ phương trình tuyến tính m phương trình, n ẩn số có dạng:
a x a x11 1 12 2 ... a x b1n n 1
a x a x21 1 22 2 ... a x b2n n 2 (*) ...
a x a xm1 1 m2 2 ... a x bmn n m lOMoAR cPSD| 49831834
trong ó aij là hệ số của pt thứ i của ẩn xj , bi là hệ số tự do
của phương trình thứ i, xj là các ẩn số (i=1,..,m, j=1,..,n).
§5: Hệ phương trình tuyến tính
- Nếu bi = 0 với mọi i=1,2,…,m thì hệ ược gọi là hệ tuyến tính thuần nhất.
4x2 2x3 7x4 9
→Hệ 4 phương trình 4 ẩn
Ví dụ 2x1 3x2 5x3 x4 2 →Là hệ không thuần nhất x
1 2x2 3x3 4x4 0
3x1 8x2 5x3 3x4 2 3 lOMoAR cPSD| 49831834
§5: Hệ phương trình tuyến tính
+ Ma trận gọi là ma trận hệ số của hệ phương trình A [ ]aij m n (*). b1 lOMoAR cPSD| 49831834
+ Ma trận gọi là ma trận hệ số tự do của hệ
phương trình b b2 (*). ... bm x1 5 lOMoAR cPSD| 49831834
+ Ma trận gọi là ma trận ẩn số của hệ phương trình (*). x
x2 ... xn
§5: Hệ phương trình tuyến tính
◼ Ví dụ: Cho hệ phương trình lOMoAR cPSD| 49831834 2x 2
1 3x2 5x3 x4 0
x1 2x2 3x3 4x4 2 9
4x2 2x3 7x4
3x1 8x2 5x3 3x4 2 7 lOMoAR cPSD| 49831834 0 2 3 5 1 x1 A 1 2 3 4 ,b , x x2 2 3 8 5 3 x3 9 0 4 2 7 x4
§5: Hệ phương trình tuyến tính
Ma trận bổ sung của hệ (*): A bs A A | b lOMoAR cPSD| 49831834
◼ Ví dụ: Cho hệ phương trình 2 2 3 5 2 1
2x1 3x2 5x x3 4 0 3 4 0 3 2 1 2 3 5 2 9 2 9 7 3 8 0 4 xx11 482xxx222 523xxx333 374xxx 444 bs A A [A|b] 9 lOMoAR cPSD| 49831834
Nhận xét: Các hệ số của phương trình thứ i là các phần tử ở
hàng thứ i của Abs và ngược lại.
§5: Hệ phương trình tuyến tính
Với các kí hiệu ó, hệ (*) ược ưa về dạng Ax b (**)
gọi là dạng ma trận của hệ (*). ◼ Ví dụ: 2x 7y z 9 2 7 1 x 9 lOMoAR cPSD| 49831834 35x yx 9y 42zz 05 5 9 23 1 4 yz 05
§5: Hệ phương trình tuyến tính 5.2. Hệ Cramer 11 lOMoAR cPSD| 49831834
Định nghĩa: Hệ phương trình tuyến tính n pt,
n ẩn số mà ma trận hệ số không suy biến ược gọi là hệ Cramer
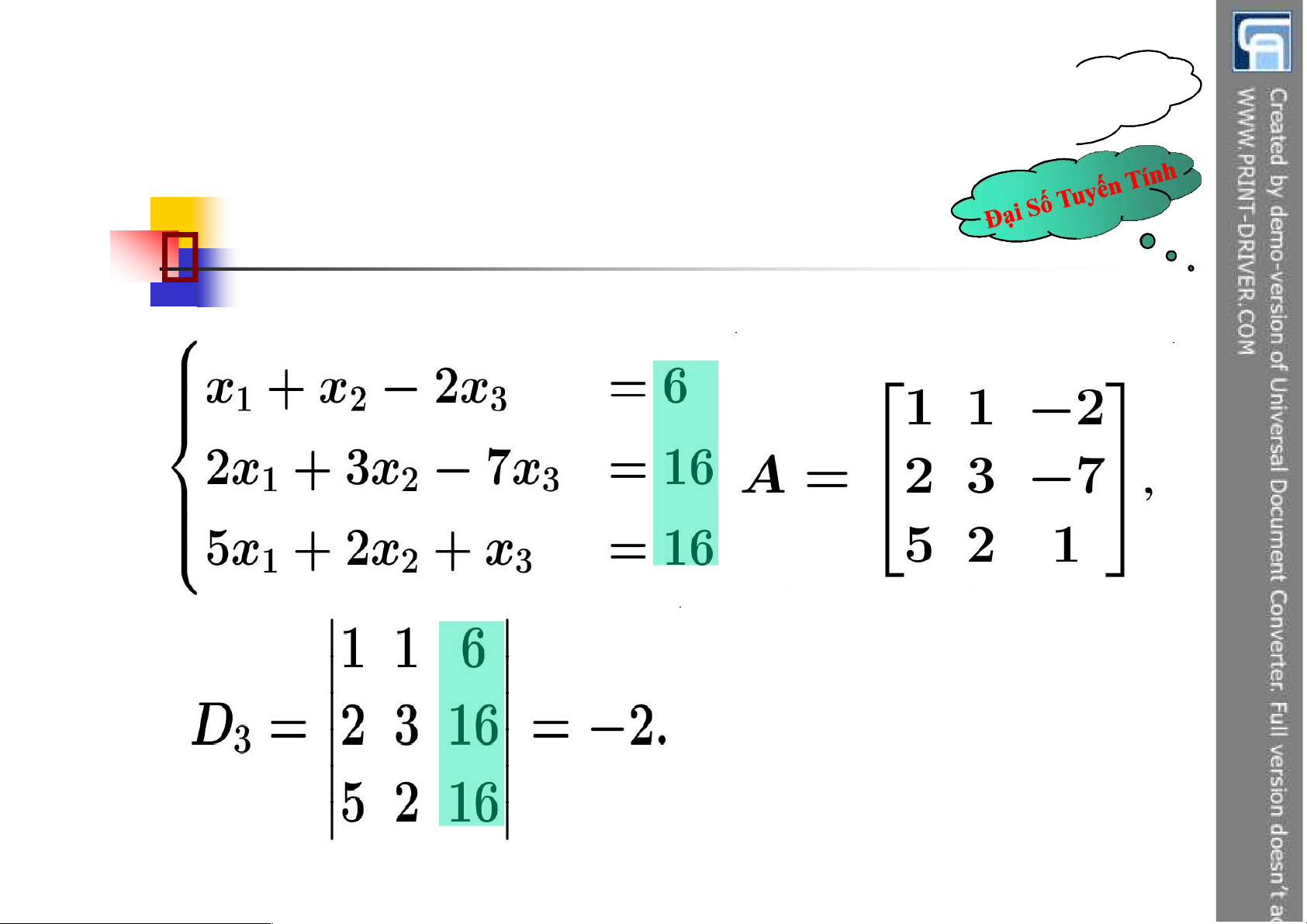
Ví dụ: Giải hệ phương trình tuyến tính sau: 5.2 Hệ Crame lOMoAR cPSD| 49831834
Định lý: Mọi hệ Cramer n pt ều có nghiệm
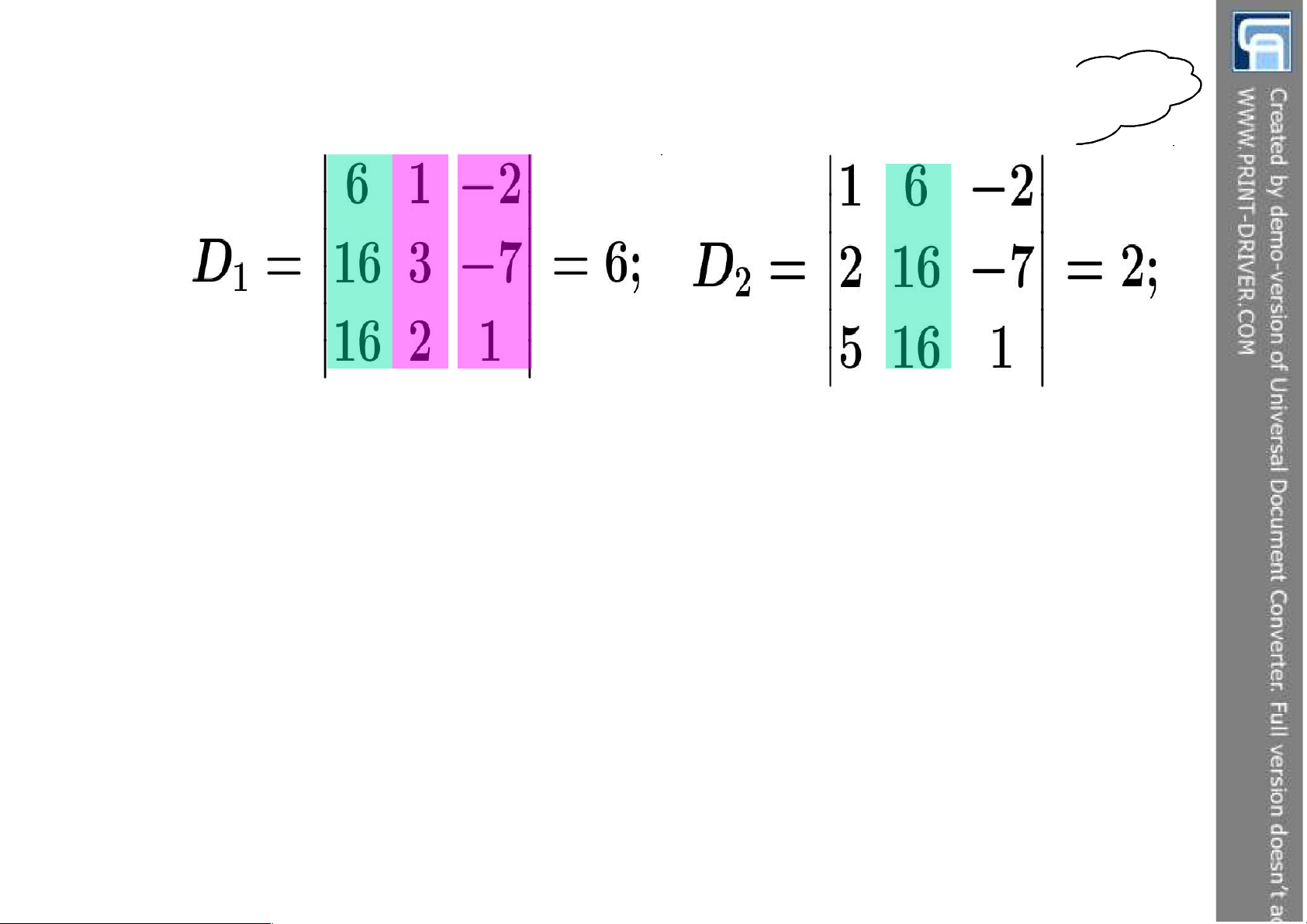
duy nhất (x1, x2, …,xn) ược xác ịnh bởi công thức x D j j D 13 lOMoAR cPSD| 49831834 5.2 Hệ Crame lOMoAR cPSD| 49831834 5.2 Hệ Crame
Ví dụ: Giải hệ phương trình tuyến tính sau: 15 lOMoAR cPSD| 49831834 5.2 Hệ Crame lOMoAR cPSD| 49831834 17 lOMoAR cPSD| 49831834 5.2 Hệ Crame lOMoAR cPSD| 49831834 5.2 Hệ Crame 19 lOMoAR cPSD| 49831834 5.2 Hệ Crame
◼ Bài tập: Giải hệ phương trình sau: x x 1 2 2x3 1 1 1 2 2x x 1 2 3x3 5 D1 1 2 15 1 3 = -19 3x 1 2x x2 3 1 1 1 2 D2 2 5 3 = -29