lOMoAR cPSD| 49831834
Chương 1. Ma Trận và Định thức 1.1. Ma trận 1.1.1. Khái niệm
Định nghĩa 1.1. Ma trận là một bảng số xếp theo dòng và theo cột. Một ma trận có m
dòng và n cột ược gọi là ma trận cỡ m n. Khi cho một ma trận ta viết bảng số bên trong
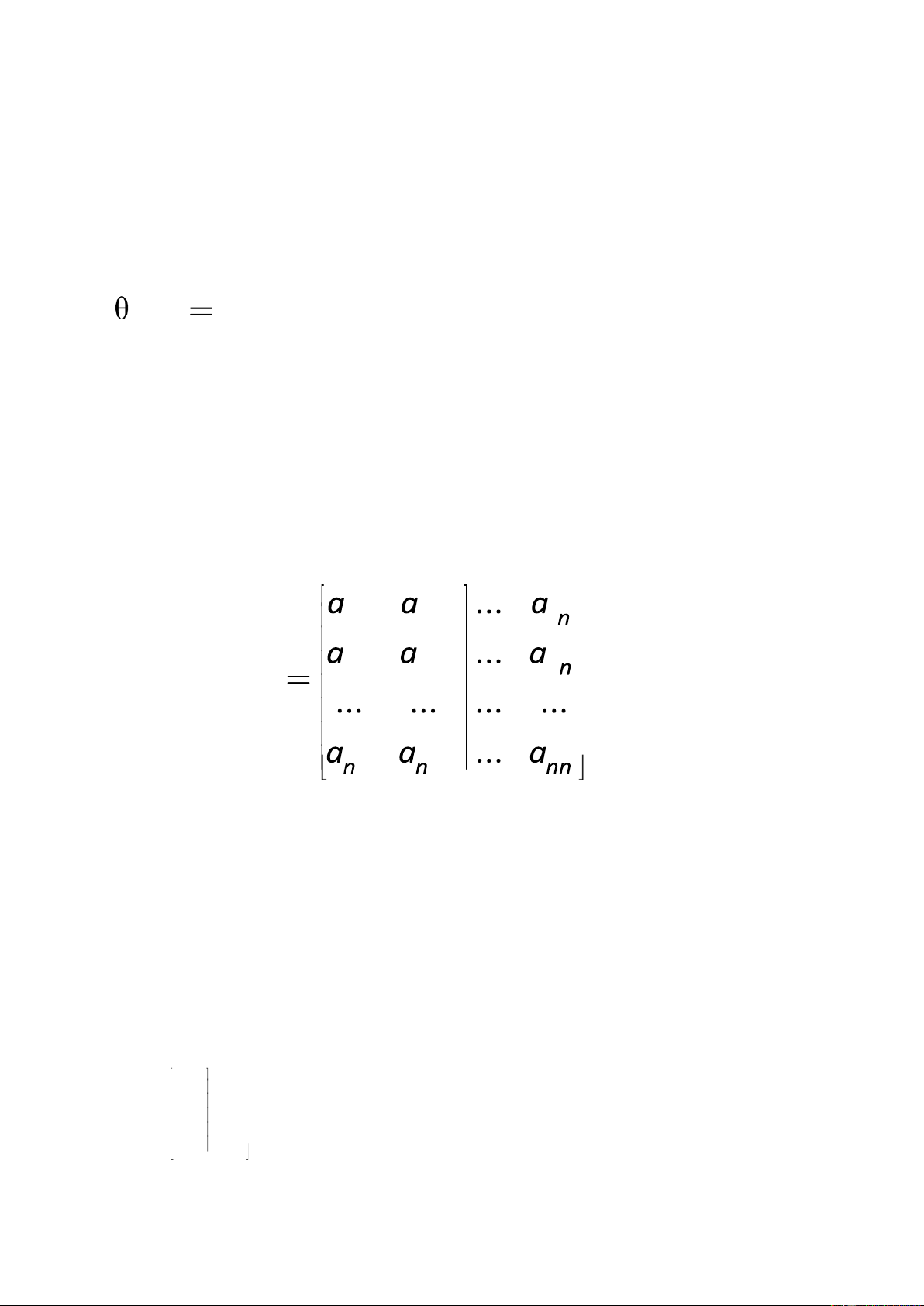
dấu ngoặc tròn hoặc ngoặc vuông. Ma trận cấp m n có dạng tổng quát như sau: a a ... 11 12 a1n ... a a 21 22 ... a2n ... ... am2 ... A= ... a a m1 mn
Viết tắt là A = (aij)mxn hoặc A = [aij]mxn Một số. •
Hai ma trận ược coi là bằng nhau khi và chỉ khi chúng cùng cấp và các
phần tử ở vị trí tương ứng của chúng ôi một bằng nhau.
Cho A = [aij]mxn B = [bij]mxn ta nói A=B nếu aij = bij với mọi i,j 1 −2 4 1 −2 4 VD A = 0 1 3 , B = 0 1 3 suy ra A=B •
Ma trận chuyển vị của A là AT với AT = [aji]nxm 1 0 AT 2 1 4 3 lOMoAR cPSD| 49831834 •
Ma trận ối của ma trận A = [aij]mxn là – A = [- aij]m x n •
Ma trận có số cột bằng 1 gọi là ma trận cột, ma trận có số dòng bằng 1 gọi là ma trận dòng. •
Ma trận không cấp m x n là ma trận mà mọi phần tử ểu bằng 0 : m nx [ ]0mxn • •
Ma trận vuông là ma trận có m=n, ược gọi là ma trận vuông cấp n. 11 12 1 21 22 2 1 2 A •
Đường chéo i qua các phần tử aii gọi là ường chéo chính,
+) Ma trận tam giác dưới là ma trận vuông có các phần tử nằm phía trên ường chéo chính bằng 0. 1 0 0 5 0 0 1 0 2 lOMoAR cPSD| 49831834
+) Ma trận tam giác trên là ma trận vuông có các phần tử nằm phía dưới ường chéo chính bằng 0. 1 0 0 0 0 7 0 0 2 • •
Ma trận chéo là ma trận mà có tất cả các phần tử nằm ngoài ường chéo chính bằng 0 1 0 0 • 0 0 0 0 0 2 •
Ma trận ường chéo có tất cả các phần tử thuộc ường chéo chính bằng 1 ược gọi
là ma trận ơn vị, ký hiệu E. Ma trận ơn vị cấp n ký hiệu là En. 1 0 0 • E 0 1 0 0 0 1
1.1.2. Phép toán tuyến tính
Định nghĩa 2.3. Phép cộng hai ma trận
Cho hai ma trận cùng cỡ m n: A
Tổng của hai ma trận A và B là một ma trận cỡ m n, kí hiệu A + B và ược xác ịnh như sau: lOMoAR cPSD| 49831834 1 2 4 1 2 5
Ví dụ 2.10. Cho hai ma trận A = ; B = 0 1 3 2 1 2 2 0 9 Tính A+B=? A B 2 0 1
Hiệu của A trừ B: A – B = A + (-B)
Định nghĩa 1.2. Phép nhân 1 số thực với 1 ma trận
Tích của một số thực với ma trận A cỡ m n, kí hiệu A và ược xác ịnh như sau: 1 −2 4
Ví dụ 1.10. Cho hai ma trận A = 0 1 3 . Tính 3.A=? 3 6 12 3A 0 3 9 −1 1 ; B =
Ví dụ 1.11. Cho hai ma trận A = 10 1 3−2 4 0 2 2 3 lOMoAR cPSD| 49831834
Tính: a) C=2A-3BT b) A B c) B A d) phép nhân A và B có giao hoán không? Giải: a) Ta có: C=2A – 3 B T = 2 10 1 3−2 4 −3 −1 2 31 0 2 2 −4 8 −3 0 6 5 −4 2 = 0 2 6 − 3 6 9 = −3 −4 −3 −1 1 c) BA= 0 22 3 10 1 3−2 4 3x2 * 2x3 = 3x3
Các tính chất cơ bản của phép toán tuyến tính
Gọi A, B, C là các ma trận bất kì cấp m n,
; là các số bất kì ta luôn có: 1) A + B = B + A 2) (A + B) +C = A + (B + C) 3) A + 0 = A 4) A + (-A) = 0 5) 1.A = A 6) (A + B) = A + B, 7) ( + )A = A + A 8) ( )A = ( A) lOMoAR cPSD| 49831834
1.2.3. Phép nhân ma trận và ma trận nghịch ảo
Phép nhân ma trận a b b
11 a12 ... a1n 11 12 ... b1p a a ... a b b ... b Cho hai ma trận : A = 21 22 2n ; B = 21 22 2p ... ... ... ... ... ... ... ... am1 am2 ... a b b
mn n1 n2 ... bnp
Trong ó, ma trận A có số cột bằng số dòng của ma trận B.
Định nghĩa 2.4.
Tích của ma trận A =[aij]mxn với ma trận B=[bij]nxp là một ma trận cấp C = [cij]mxp, kí hiệu
là AB và ược xác ịnh như sau: n = )
cij = a bi1 1j +a bi2 2 j + +... a bin a b nj
ik kj ;(i =1,2,...,m j; =1,2,..., p k=1
b) Nhân lần lượt các dòng của A với các cột của B, ta ược: −1 1 1 −2 4 0 2 (2x3 *3x2 = 2x2) ; B =
Ví dụ 2.10. Cho hai ma trận A = 0 1 3 2 3 lOMoAR cPSD| 49831834 c11 c12 1 1.( ) ( 2 0 42 11). . . ( 2 2 43). . 7 9 A B = c21 c22 0 1 10 32.( ) . . 01 12 33. . . 6 11 Tính BxA=? (3x2 * 2x3= 3x3) ( 1 1 10).. ( 1).( 2 11) . ( 1 4 13)..
BA. 01 20. . 0 2 21.( ) . 04 23. . 21 30. . 2 2 31.( ) . 24 33. . 13 1 0 2 6 2 117 BA.
(3x2 * 2x4= 3x4 2x4* 3x2 không có BA) Chú ý 2.3.
• Tích AB tồn tại khi và chỉ khi số cột của ma trận ứng trước bằng số dòng của ma trận ứng sau.
• Cấp của ma trận AB: Ma trận AB có số dòng bằng số dòng của ma trận ứng trước
và số cột bằng số cột của ma trận ứng sau.
• Các phần tử của AB ược tính theo quy tắc: Phần tử cij là tích vô hướng của dòng
thứ i của ma trận ứng trước và cột thứ j của ma trận ứng sau.
Các tính chất cơ bản của phép nhân ma trận
Phép nhân ma trận không có tính chất giao hoán 1)
Tính chất kết hợp: (AB)C = A(BC) 2)
Tính chất phân phối ối với phép cộng:
A(B+C) = AB+AC; (B+C)D =BD +CD lOMoAR cPSD| 49831834 3)
Với A,B là hai ma trận sao cho tích AB có nghĩa và là một số bất kì, ta luôn có: (AB) = ( A)B = A( B) 4)
Mọi ma trận vuông A, B cấp n ều không thay ổi khi nhân với ma trận ơn
vị E cấp n (nếu phép nhân tồn tại): A.E = A; E.B =B
Đặc biệt trong tập hợp các ma trận vuông cùng cấp n ta luôn có: AE = EA = A
, Am = A.A...A (tích của m ma trận A). A0 = E 5)
Ma trận chuyển vị của ma trận AB (khi tích AB có nghĩa) bằng tích
của ma trận chuyển vị B với ma trận chuyển vị A: (AB)T = BTAT.
Chú ý: A, B vuông cấp n: (A+B)2 =A2+2AB+B2
(A+B)(A+B)= (A+B).A+(A+B).B=A2+BA+AB+B2
• Nếu AB=BA thì các hằng ẳng thức ã biết với số thực cũng úng với 2 ma trận A và B. 1 2
Ví dụ 1. Cho ma trận A = , tìm các ma trận B giao hoán với A qua phép nhân. 3 4 a b lOMoAR cPSD| 49831834 B c d
X a b 2 a2 bc ab bd 0 0 c d X 2 0 0 ca dc cb d Ví dụ 2. X2
(Có ma trận X nào khác không mà bình phương lại ra ma trân 0 hay không?)
Không suy ra ược, vì
Ví dụ 3. X E2 Ví dụ 4. AB
( có 2 ma trận nào cùng khác 0 mà nhân với nhau
ra ma trận 0 hay không?)