











Preview text:
lOMoAR cPSD| 47207194
CHÖÔNG 3 BAØI TOAÙN VAÄN TAÛI
3.1. NOÄI DUNG VAØ ÑAËC ÑIEÅM CUÛA BAØI TOAÙN VAÄN TAÛI
3.1.1. PHAÙT BIEÅU BAØI TOAÙN VAÄN TAÛI COÅ ÑIEÅN Baøi toaùn:
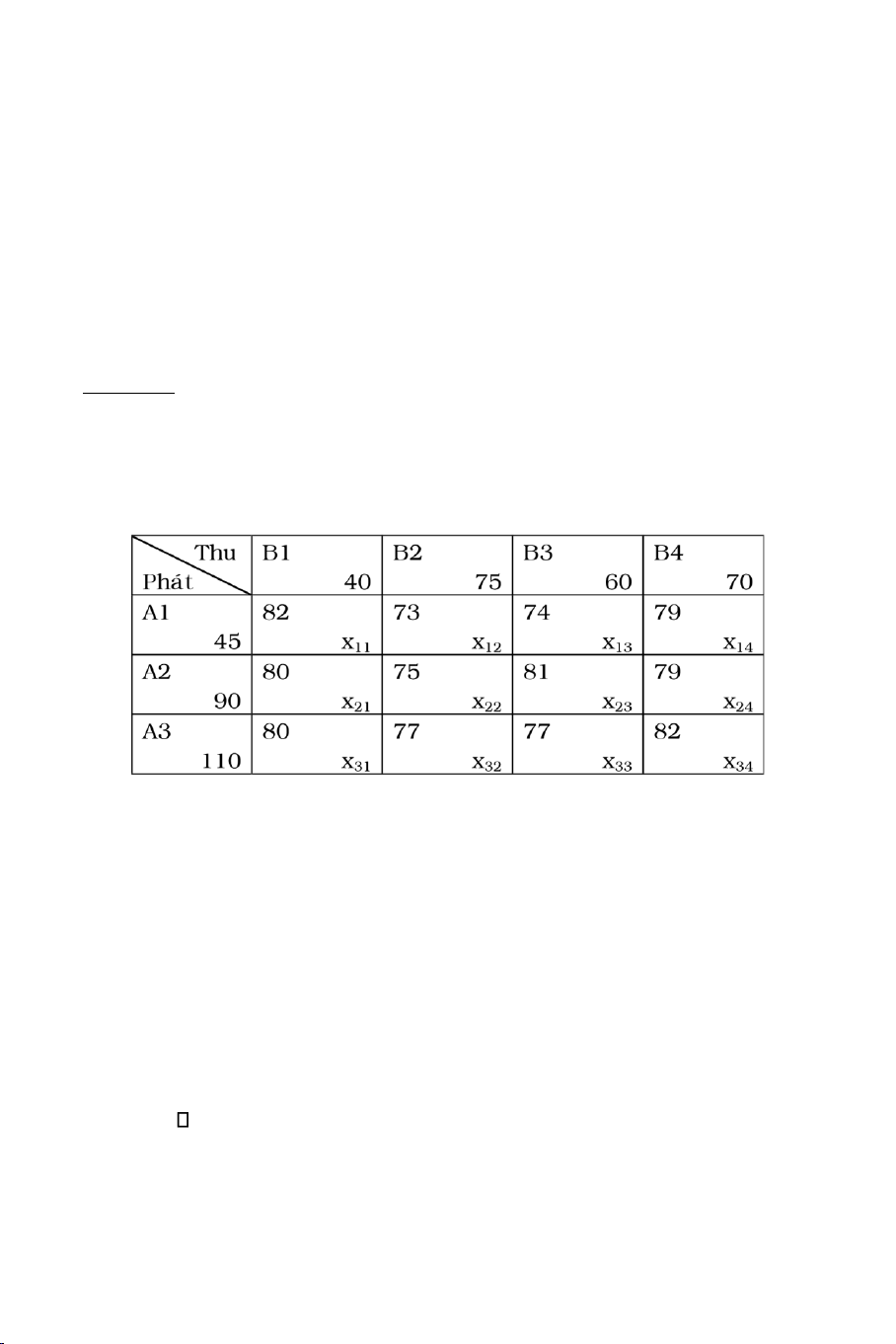
Moät coâng ty baùch hoùa coù 4 cöûa haøng B1, B2, B3, B4 coù nhu caàu veà moät loaïi
haøng töông öùng laø 40, 75, 60, 70 (taán). Coâng ty ñaõ ñaët mua loaïi haøng ñoù ôû 3 xí
nghieäp A1, A2, A3 vôùi khoái löôïng töông öùng laø 45, 90, 110 (taán). Giaù cöôùc vaän
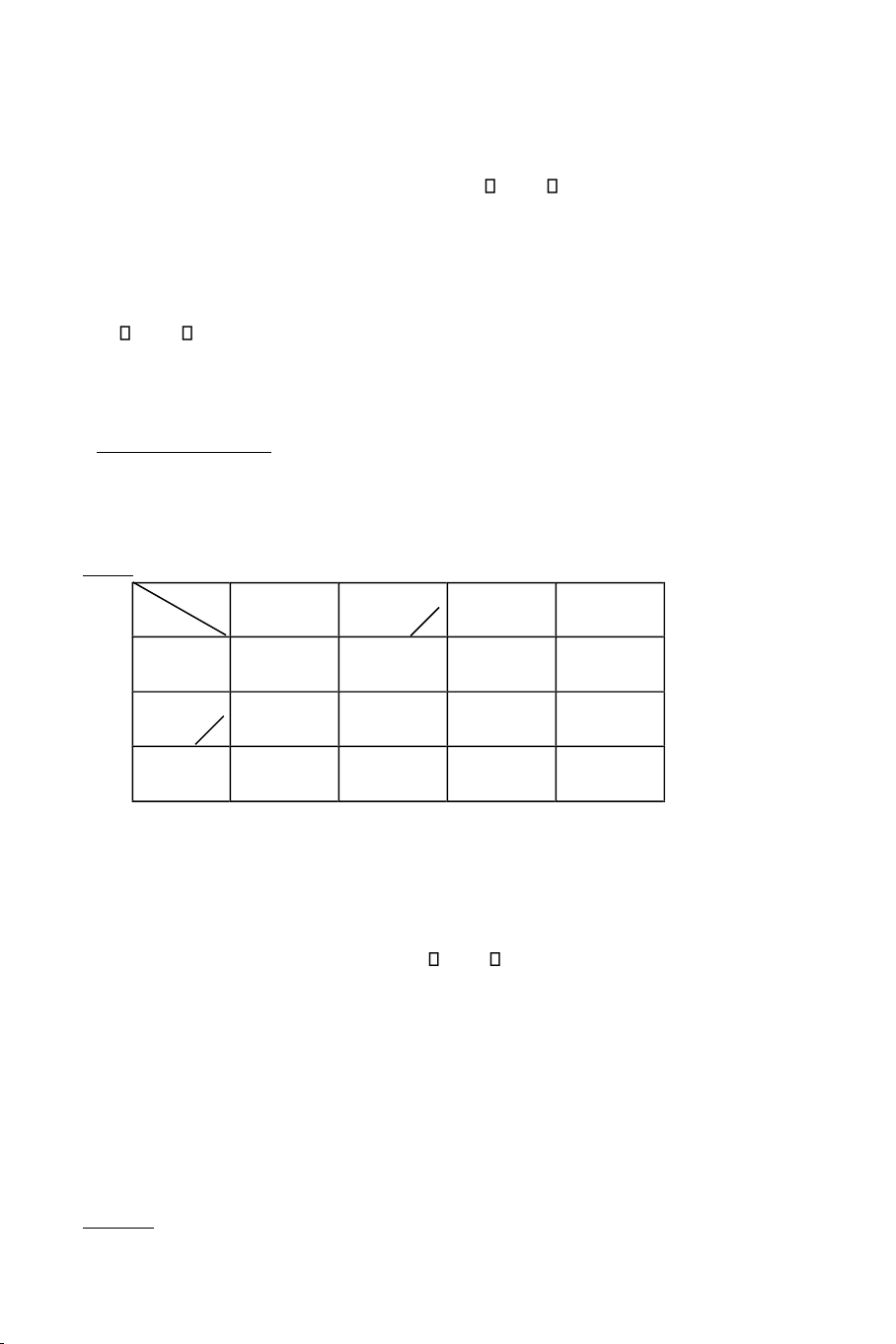
chuyeån haøng (ngaøn ñoàng/taán) töø moät xí nghieäp ñeán moät cöûa haøng cho trong baûng sau:
Vaán ñeà ñaët ra laø phaûi laäp keá hoaïch vaän chuyeån haøng töø caùc xí nghieäp ñeán
caùc cöûa haøng sao cho löôïng haøng ñaët mua ôû caùc xí nghieäp phaûi ñöôïc laáy ñi heát,
löôïng haøng maø caùc cöûa haøng yeâu caàu phaûi ñöôïc ñaùp öùng ñaày ñuû vaø toång
chi phí vaän taûi laø thaáp nhaát.
Ta chuù yù laø coâng ty baùch hoùa ñaët mua haøng treân cô sôû yeâu caàu cuûa caùc
cöûa haøng, do ñoù coù söï caân baèng giöõa toång soá löôïng haøng ñaët mua ôû caùc xí
nghieäp (Toång phaùt) vôùi toång soá löôïng haøng maø caùc cöûa haøng yeâu caàu (Toång thu).
Toång phaùt = 45 + 90 + 110 = 245 T
Toång thu = 40 + 75 + 60 + 70 = 245 T Toång phaùt = Toång thu
Baøi toaùn vaän taûi coù ñieàu kieän naøy ñöôïc goïi laø baøi toaùn vaän taûi coå ñieån
hay baøi toaùn vaän taûi caân baèng thu – phaùt. lOMoAR cPSD| 47207194
BAØI TOAÙN VAÄN TAÛI 141 Moâ hình
Goïi xij laø soá taán haøng vaän chuyeån töø Ai ñeán Bj, i=1,2,3; j=1,2,3,4.
Ta coù: xij 0, i=1,2,3; j=1,2,3,4.
Löôïng haøng ñöôïc laáy töø caùc xí nghieäp (Traïm phaùt) A1: x11 + x12 + x13 + x14 = 45
A2: x21 + x22 + x23 + x24 = 90 A3: x31 + x32 + x33 + x34 = 110
Löôïng haøng thu ñöôïc ôû caùc cöûa haøng (Traïm thu) B1: x11 + x21 + x31 = 40 B2: x12 + x22 + x32 = 75 B3: x13 + x23 + x33 = 60
B4: x14 + x24 + x34 = 70 Toång chi phí vaän chuyeån:
f = 82x11 + 73x12 + 74x13 + 79x14 + 80x21 + 75x22 + 81x23 + 79x24 + 80x31 + 77x32 + 77x33 + 82x34 min TOÅNG QUAÙT
Baøi toaùn vaän taûi coå ñieån cho döôùi daïng baûng sau ñaây: Trong ñoù:
ai > 0 laø soá ñôn vò haøng caàn chôû ñi töø traïm phaùt Ai, i=1,2,…,m.
(ai ñöôïc goïi laø yeâu caàu cuûa traïm phaùt Ai) bj > 0 laø soá ñôn vò
haøng yeâu caàu ôû traïm thu Bj, j=1,2,…,n.
(bj ñöôïc goïi laø yeâu caàu cuûa traïm thu Bj) lOMoAR cPSD| 47207194
142 BAØI TOAÙN VAÄN TAÛI
cij 0 laø chi phí vaän chuyeån 1 ñôn vò haøng (giaù cöôùc; khoaûng caùch;… ) töø Ai ñeán Bj, i=1,2,…,m; j=1,2,…,n.
Ñieàu kieän cuûa baøi toaùn: *
Haøng ôû moãi traïm phaùt coù theå chôû ñeán moät traïm thu baát kyø (Haøng
thuaàn nhaát). *
Ñieàu kieän caân baèng thu - phaùt: m n a i bj i 1 j 1
Yeâu caàu laäp keá hoaïch vaän taûi sao cho caùc traïm phaùt phaûi phaùt heát haøng,
caùc traïm thu phaûi thu ñuû haøng vaø toång chi phí vaän taûi laø thaáp nhaát. Moâ hình
Goïi xij laø soá ñôn vò haøng vaän chuyeån töø Ai ñeán Bj, i=1,2,…,m; j=1,2,…,n. Ta coù
moâ hình nhö sau: Cöïc tieåu toång chi phí vaän taûi : m n f c x ij ij min i 1 j 1
Vôùi heä raøng buoäc: Ai phaûi phaùt heát haøng: n x ij a , ii 1,2,...,m j 1 Bj phaûi thu ñuû haøng: m x ij b , jj 1,2,...,n i 1
Khoái löôïng haøng caàn vaän chuyeån phaûi khoâng aâm:
xij 0, i=1,2,…,m; j=1,2,…,n 3.1.2. ÑÒNH NGHÓA *
OÂ naèm treân doøng i vaø coät j ñöôïc kyù hieäu laø (i,j). *
Daây chuyeàn laø moät daõy oâ lieân tieáp nhau sao cho chæ soá doøng cuûa oâ
ñöùng tröôùc gioáng chæ soá doøng cuûa oâ ñöùng sau, hoaëc chæ soá coät cuûa oâ ñöùng
tröôùc gioáng chæ soá coät cuûa oâ ñöùng sau, vaø vieäc gioáng nhau naøy cuûa caùc chæ soá laø xen keõ nhau. *
Voøng (Chu trình) laø moät daây chuyeàn kheùp kín. lOMoAR cPSD| 47207194
BAØI TOAÙN VAÄN TAÛI 143 *
Vôùi moät phöông aùn cöïc bieân naøo ñoù cuûa baøi toaùn vaän taûi, (i,j) ñöôïc
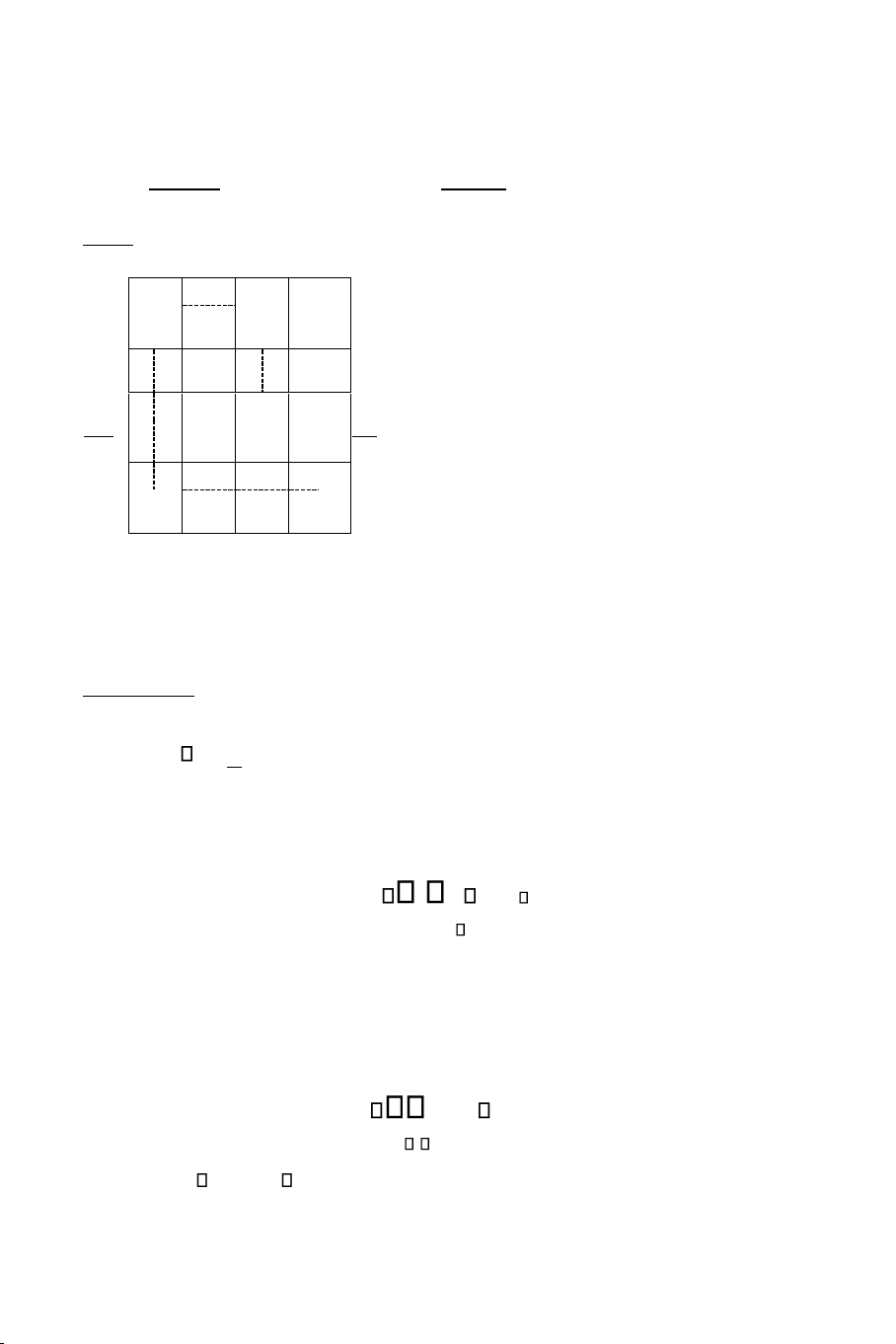
goïi laø oâ choïn neáu xij laø bieán cô sôû. OÂ loaïi laø oâ töông öùng vôùi bieán töï do (bieán phi cô sôû). Ví duï: 1 2 3 4 1 X X
Caùc oâ (1,1) (1,3) (3,3) (3,4) (4,4) 2 taïo thaønh moät daây chuyeàn. 3
Caùc oâ (1,1) (1,3) (3,3) (3,4) (4,4) (4,1) 4 taïo thaønh moät voøng. X X Löu
yù: Soá oâ treân moät voøng luoân luoân laø soá chaün. X
X 3.1.3. CAÙC TÍNH CHAÁT CUÛA BAØI TOAÙN VAÄN TAÛI
Kyù hieäu (VT) laø baøi toaùn vaän taûi caân baèng thu –
phaùt toång quaùt. Ta coù caùc tính chaát cuûa (VT) ñöôïc theå hieän thoâng qua caùc ñònh
lyù vaø heä quaû sau ñaây. Ñònh lyù 3.1.
Baøi toaùn vaän taûi caân baèng thu – phaùt luoân luoân coù phöông aùn toái öu. Chöùng minh: 0
a bi j , i=1,2,…,m; j=1,2,…,n. Trong ñoù: x * Ñaët: ij d m n d a i bj i 1 j 1
Roõ raøng ((x0ij))mxn laø phöông aùn cuûa (VT).
* Ngoaøi ra, laáy ((xij))mxn laø phöông aùn tuøy yù cuûa (VT). Ta coù: m n f c x ij ij 0 i 1 j 1
Vì cij 0 vaø xij 0, i=1,2,…,m; j=1,2,…,n.
Nhö vaäy, (VT) coù phöông aùn vaø haøm muïc tieâu bò chaän döôùi treân taäp phöông
aùn, do ñoù noù phaûi coù phöông aùn toái öu. lOMoAR cPSD| 47207194
144 BAØI TOAÙN VAÄN TAÛI Ñònh lyù 3.2.
Heä raøng buoäc chung cuûa (VT) coù haïng laø m+n-1 Chöùng minh:
Goïi Aij laø veùctô coät öùng vôùi bieán xij. Ta coù Aij laø veùctô coät coù m+n thaønh
phaàn vôùi thaønh phaàn thöù i vaø thaønh phaàn thöù m+j coù giaù trò laø 1, coøn taát
caû caùc thaønh phaàn khaùc ñeàu = 0.
Ta phaûi tìm rank(A) vôùi A = ((A11. . .A1n A21. . .A2n Am1. . .Amn))
Xeùt m+n-1 veùctô: A1n, A2n, . . . , Amn, A11, A12, . . . , A1(n-1). Ma traän taïo neân
bôûi caùc veùctô treân coù daïng sau: A1n A2n . . . Amn A11 A12 . . . A1(n-1) 1 0 . . . 0 1 1 . . . 1 1
0 1 . . . 0 0 0 . . . 0 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0 0 . . . 1 0 0 . . . 0 m 0 0 . . . 0 1 0 . . . 0 m+1
0 0 . . . 0 0 1 . . . 0 m+2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0 0 . . . 0 0 0 . . . 1 m+n-1 1 1 . . . 1 0 0 . . . 0 m+n
Ta chuù yù m+n-1 doøng ñaàu tieân cuûa ma traän treân taïo thaønh ma traän vuoâng
caáp m+n-1 khoâng suy bieán (coù ñònh thöùc = 1) vaø vì ma traän treân laø ma traän con
cuûa A neân: rank(A) m+n-1 (1)
Ngoaøi ra, giaû söû ta coù m+n-1 raøng buoäc ñaàu: n x ij a , ii 1,2,...,m j 1 m x ij b , jj 1,2,...,(n 1) i 1 Khi ñoù suy ra: m m n 1 m m n 1 m n 1 m xin ai xij ai xij ai xij lOMoAR cPSD| 47207194
BAØI TOAÙN VAÄN TAÛI 145 i 1 i 1 j 1 i 1 i 1 j 1 i 1 j 1i 1 m n 1 a i bj bn i 1 j 1
Nhö vaäy, raøng buoäc cuoái cuøng phuï thuoäc tuyeán tính vaøo m+n-1 raøng buoäc
ñaàu. Do ñoù: rank(A) m+n-1 (2) Töø (1) vaø (2) ta keát luaän: rank(A) = m+n-1.
Nhö vaäy, trong m+n raøng buoäc cuûa (VT) ta coù theå boû ñi 1 raøng buoäc maø khoâng
laøm thay ñoåi heä. Tuy nhieân do tính ñoái xöùng cuûa heä raøng buoäc neân ta vaãn giöõ
caùch trình baøy nhö cuõ. Heä quaû:
Soá oâ choïn trong 1 phöông aùn cöïc bieân cuûa (VT) laø m+n-1.
m+n-1 laø haïng cuûa heä raøng buoäc chung m+n-1 laø soá bieán cô sôû trong moãi
phöông aùn cöïc bieân, hay soá oâ choïn laø m+n-1. Ñònh lyù 3.3.
Ñieàu kieän caàn vaø ñuû ñeå heä caùc veùctô coät cuûa ma traän caùc heä soá cuûa
(VT) ñoäc laäp tuyeán tính laø caùc oâ töông öùng khoâng taïo thaønh voøng. Chöùng minh:
Ta chuù yù laø oâ (i,j) töông öùng vôùi bieán xij vaø töông öùng vôùi veùctô coät Aij.
* Ñieàu kieän caàn:
Giaû söû heä Aij, (i,j) S laø ñoäc laäp tuyeán tính. Ta phaûi chöùng minh S khoâng taïo thaønh voøng.
Giaû söû ngöôïc laïi: Trong S coù voøng:
(i1,j1) (i1,j2) (i2,j2) (i2,j3) . . . (ik-1,jk)(ik,jk)(ik,j1) Ta coù:
Ai j1 1 Ai j1 2 Ai j2 2 Ai j2 3 ... Aik 1 k 1 j Aik 1 k j Ai jk k Ai jk 1 0
Suy ra heä veùctô Aij, (i,j) S laø phuï thuoäc tuyeán tính. Voâ lyù.
* Ñieàu kieän ñuû:
Giaû söû S khoâng taïo thaønh voøng vaø: k A ij ij 0 (*) (i,j) S lOMoAR cPSD| 47207194
146 BAØI TOAÙN VAÄN TAÛI
Ta phaûi chöùng minh: kij = 0, vôùi moïi (i,j) S.
Vì S khoâng taïo thaønh voøng neân toàn taïi moät doøng hay moät coät naøo ñoù chæ
coù moät oâ thuoäc S (oâ treo), ta coù 2 tröôøng hôïp sau ñaây:
+ Neáu doøng i chæ coù (i,j) S, khi ñoù veá traùi cuûa (*) coù thaønh phaàn thöù i laø kij.
+ Neáu coät j chæ coù (i,j) S, khi ñoù veá traùi cuûa (*) coù thaønh phaàn thöù m+j laø kij.
Trong caû 2 tröôøng hôïp ta ñeàu suy ra ñöôïc kij = 0.
Ñaët S’ laø S tröø ñi oâ treo. Ta coù S’ khoâng taïo thaønh voøng vaø: k Aij ij 0 (i,j) S
Laëp laïi quaù trình treân, sau moät soá höõu haïn böôùc thöïc hieän ta ñöôïc ñieàu phaûi chöùng minh. Heä quaû:
Moät phöông aùn cuûa (VT) laø phöông aùn cöïc bieân khi vaø chæ khi caùc oâ töông
öùng vôùi caùc thaønh phaàn döông (> 0) khoâng taïo thaønh voøng. BAØI TAÄP 3.1.
1. Chöùng minh raèng baøi toaùn daïng vaän taûi caân baèng thu – phaùt vôùi haøm muïc
tieâu cöïc ñaïi luoân luoân coù phöông aùn toái öu.
2. Cho baøi toaùn vaän taûi caân baèng thu – phaùt, chöùng minh raèng: Neáu thöïc hieän
pheùp bieán ñoåi: c’ij = cij + di + ej, (i,j) thì ta ñöôïc baøi toaùn töông ñöông.
3. Xeùt xem caùc phöông aùn sau ñaây coù phaûi laø phöông aùn cöïc bieân cuûa baøi
toaùn vaän taûi caân baèng thu – phaùt hay khoâng ? Trong tröôøng hôïp khoâng phaûi
laø phöông aùn cöïc bieân, haõy bieán ñoåi phöông aùn ñoù ñeå thu ñöôïc moät phöông aùn cöïc bieân. 0 50 0 0 45 0 5 0 a) x 55 0 0 20 b) x 0 0 35 40 15 0 10 0 0 25 0 0 0 0 30 20 25 25 0 0 lOMoAR cPSD| 47207194
BAØI TOAÙN VAÄN TAÛI 147 35 0 0 15 0 30 0 20 c) x 35 0 40 0 d) x 55 20 0 0 0 0 0 25 15 0 10 0 0 50 0 0 0 0 30 20
3.2. PHÖÔNG PHAÙP THEÁ VÒ
3.2.1. TIEÂU CHUAÅN TOÁI ÖU CUÛA BAØI TOAÙN VAÄN TAÛI Baøi
toaùn vaän taûi caân baèng thu – phaùt (VT) coù daïng: m n f c x ij ij min i 1 j 1 n ( u x i tu øy yù) ij ai , i 1, 2 , ..., m j 1 m ( v j tu øy yù) x ij b j , j 1, 2 , ..., n i 1 x ij 0, i 1,2, ,m; j 1,2, ,n
Baøi toaùn ñoái ngaãu (VTD) coù daïng: m n f i 1 a u i i j 1 b vj j max ui vj c , iij 1,2,...,m; j 1,2,...,n lOMoAR cPSD| 47207194
148 BAØI TOAÙN VAÄN TAÛI
Theo ñònh lyù ñoä leäch buø yeáu ta coù: Phöông aùn ((xij)) laø phöông aùn toái öu cuûa
(VT) khi vaø chæ khi toàn taïi (ui,vj) laø phöông aùn cuûa (VTD) sao cho: xij(ui + vj – cij) = 0, i=1,2,…,m; j=1,2,…,n.
Noùi caùch khaùc: Phöông aùn ((xij)) laø phöông aùn toái öu cuûa (VT) khi vaø chæ khi
toàn taïi caùc giaù trò (ui,vj) sao cho: ui + vj cij, i=1,2,…,m; j=1,2,…,n.
xij(ui + vj – cij) = 0, i=1,2,…,m; j=1,2,…,n. Hoaëc:
ui u i v j v j c ijc ,, ijneáu (xi, jij ) 0
3.2.2. THUAÄT TOAÙN THEÁ VÒ
Thöïc chaát laø thuaät toaùn ñôn hình ñöôïc caûi bieân trong ñieàu kieän cuûa baøi toaùn vaän taûi.
Böôùc 1. Tìm phöông aùn cöïc bieân xuaát phaùt
Khi tieán haønh tìm phöông aùn cöïc bieân xuaát phaùt ta thöïc hieän theo nguyeân taéc
phaân phoái toái ña:
Giaû söû phaân phoái cho oâ (i,j). Ta coù löôïng haøng toái ña coù theå phaân phoái ñöôïc laø: xij = min ai , bj .
Sau ñoù ñieàu chænh laïi caùc yeâu caàu: a i ai xij b j bj xij Neáu
a i 0 (khi ai < bj ): Ta loaïi doøng i. Neáu b j 0
(khi ai > bj ): Ta loaïi coät j. Neáu a i
b j 0 (khi ai = bj ): Ta loaïi caû doøng i vaø coät j. lOMoAR cPSD| 47207194
BAØI TOAÙN VAÄN TAÛI 149
Trong thöïc haønh ta ñaùnh daáu ( ) vaøo caùc oâ naèm treân doøng vaø coät coù yeâu
caàu = 0 ñeå xaùc ñònh loaïi caùc doøng vaø coät naøy.
Nhö vaäy, kích thöôùc cuûa baûng seõ thu heïp laïi vaø trong phaàn baûng coøn laïi ta laïi
tieán haønh choïn oâ phaân phoái, vaø ñieàu chænh caùc yeâu caàu töông öùng,… cho ñeán
khi taát caû caùc yeâu caàu doøng vaø coät ñeàu = 0 (töùc laø, caùc khoái löôïng haøng ñaõ
ñöôïc laáy ñi heát ôû caùc traïm phaùt vaø thu ñuû theo yeâu caàu ôû caùc traïm thu. Caùc
oâ khoâng ñöôïc phaân phoái laø caùc oâ loaïi, coù xij = 0). Do ñoù, ta coù moät phöông aùn
vaän taûi, ñoàng thôøi ñaây cuõng laø moät phöông aùn cöïc bieân.
Thaät vaäy, giaû söû phöông aùn thu ñöôïc khoâng phaûi laø phöông aùn cöïc bieân, töùc
laø trong soá caùc oâ choïn toàn taïi voøng:
(i1,j1) (i1,j2) (i2,j2) (i2,j3) . . . (ik-1,jk)(ik,jk)(ik,j1) Xeùt (i 1,j1). Vì xi j1 1
0 laø keát quaû cuûa nguyeân taéc phaân phoái toái ña, neân ta coù: • Neáu a i1
bj1, ta coù doøng i1 bò loaïi, do ñoù khoâng theå phaân phoái vaøo (i1,j2). Hay x i j1 2 0. Voâ lyù. • Neáu a i1
bj1, ta coù coät j1 bò loaïi, do ñoù khoâng theå phaân phoái vaøo (ik,j1). Hay x i jk 1 0. Voâ lyù. • Neáu a i1
bj1, ta coù doøng i1 vaø coät j1 bò loaïi, do ñoù khoâng theå phaân phoái vaøo (i
1,j2) vaø (ik,j1). Hay xi j1 2 xi jk 1 0. Voâ lyù.
Toùm laïi, trong moïi tröôøng hôïp ta ñeàu coù ñieàu maâu thuaãn. Do ñoù coù ñieàu phaûi chöùng minh.
Döïa theo nguyeân taéc phaân phoái toái ña vaø caùch thöùc xaùc ñònh caùc oâ öu tieân
phaân phoái, ta coù caùc phöông phaùp phaân phoái sau ñaây:
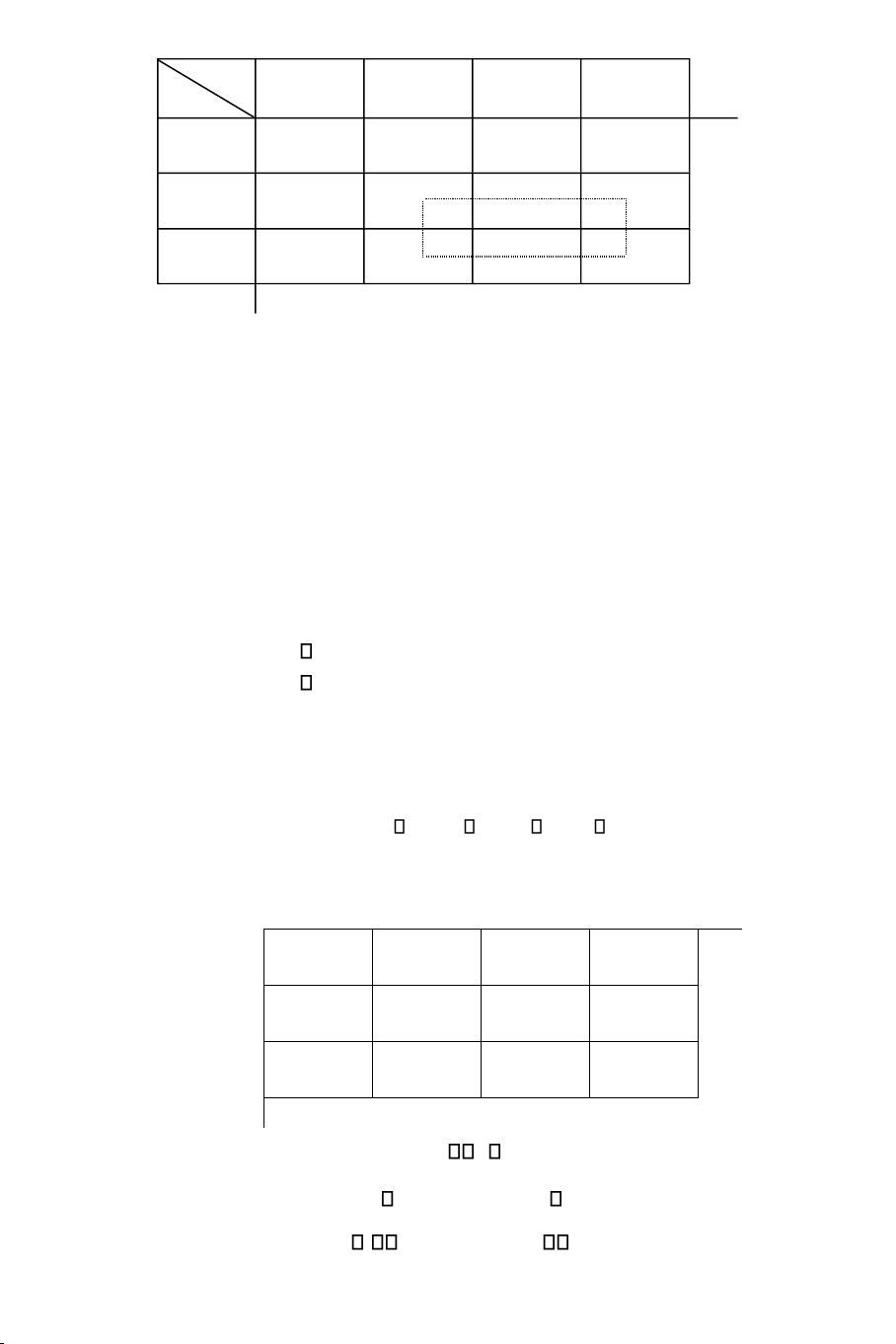
* Phöông phaùp goùc taây – baéc:
Öu tieân phaân phoái vaøo oâ ôû goùc phía treân vaø beân traùi (goùc taây – baéc) cuûa baûng. Ví duï: lOMoAR cPSD| 47207194
150 BAØI TOAÙN VAÄN TAÛI
Ñaàu tieân ta coù (1,1) laø goùc taây – baéc, ta phaân phoái: x11 =
min 45, 40 = 40. Vaø ñieàu chænh laïi caùc yeâu caàu:
a1 = 45 – 40 = 5, b1 = 40 – 40 = 0
Khoâng chuù yù ñeán coät coù yeâu caàu = 0 (coät 1): Ñaùnh daáu (-) vaøo caùc oâ naèm treân coät naøy.
Trong phaàn baûng coøn laïi (phaàn baûng chæ goàm caùc oâ troáng), ta coù goùc taây –
baéc laø: (1,2), ta xaùc ñònh: x12 = min 5, 75 = 5.
Ñaùnh daáu (-) vaøo caùc oâ naèm treân doøng coù yeâu caàu = 0 (doøng 1). Sau ñoù
laëp laïi quaù trình nhö treân, … Cuoái cuøng, ta coù phöông aùn cöïc bieân ñöôïc xaùc ñònh nhö treân.
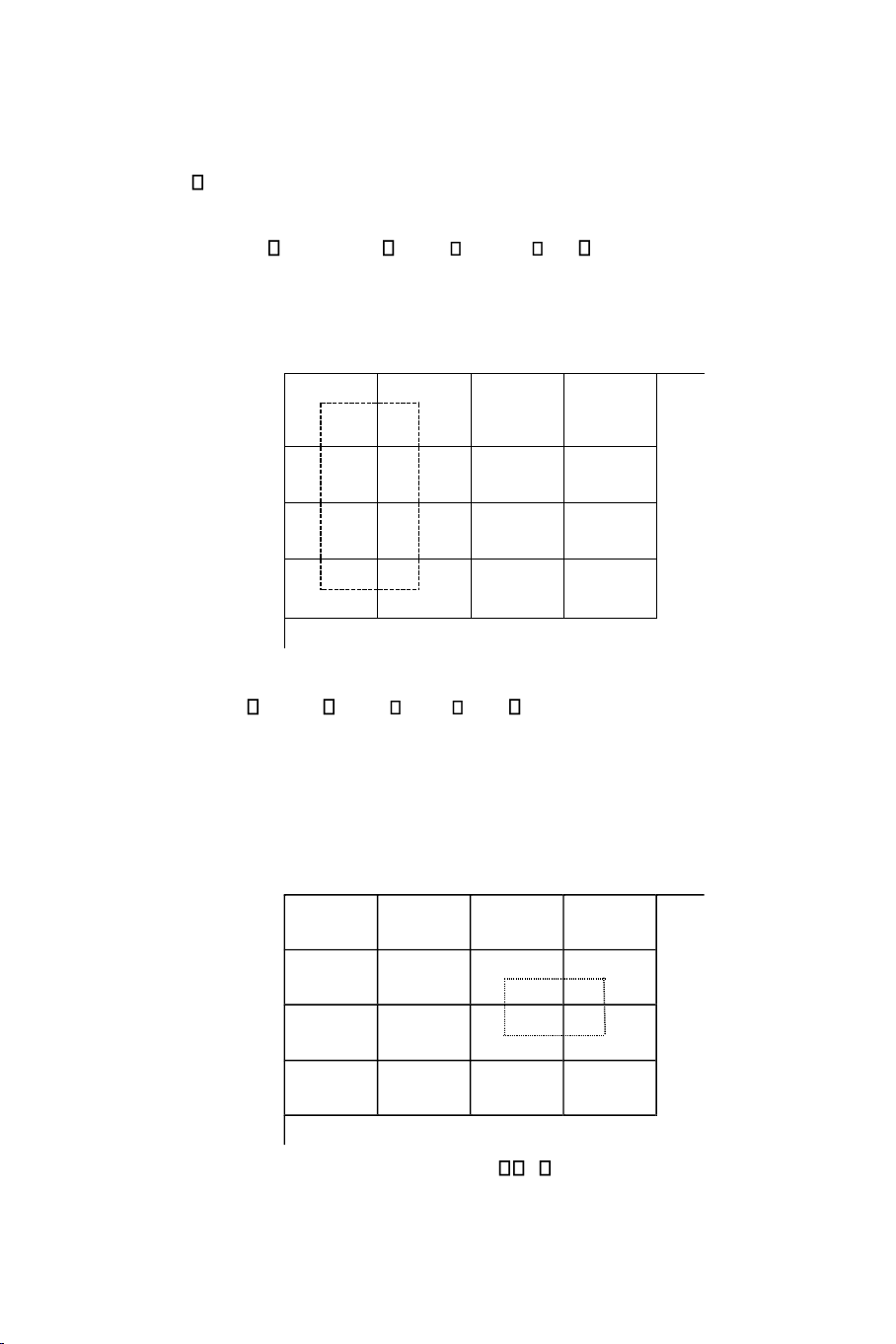
* Phöông phaùp phaân phoái theo giaù cöôùc thaáp nhaát (Cmin):
Quaù trình phaân phoái ñöôïc öu tieân cho oâ coù giaù cöôùc nhoû nhaát. Ví duï: lOMoAR cPSD| 47207194
BAØI TOAÙN VAÄN TAÛI 151
Ñaàu tieân ta coù giaù cöôùc nhoû nhaát laø 73, öùng vôùi (1,2).
Ta xaùc ñònh: x12 = min 45, 75 = 45.
Ñieàu chænh laïi caùc yeâu caàu töông öùng vôùi oâ ñöôïc phaân phoái: a1 = 45 – 45 = 0, b2 = 75 – 45 = 30
Ñaùnh daáu (-) vaøo caùc oâ naèm treân doøng coù yeâu caàu = 0 (doøng 1). Trong phaàn
baûng coøn laïi, ta coù giaù cöôùc nhoû nhaát laø 75, öùng vôùi (2,2), ta phaân phoái: x22 = min 90, 30 = 30.
Ñaùnh daáu (-) vaøo caùc oâ naèm treân coät coù yeâu caàu = 0 (coät 2). Sau ñoù laëp
laïi quaù trình nhö treân… Cuoái cuøng ta coù phöông aùn cöïc bieân xuaát phaùt ñöôïc xaùc ñònh trong baûng treân.
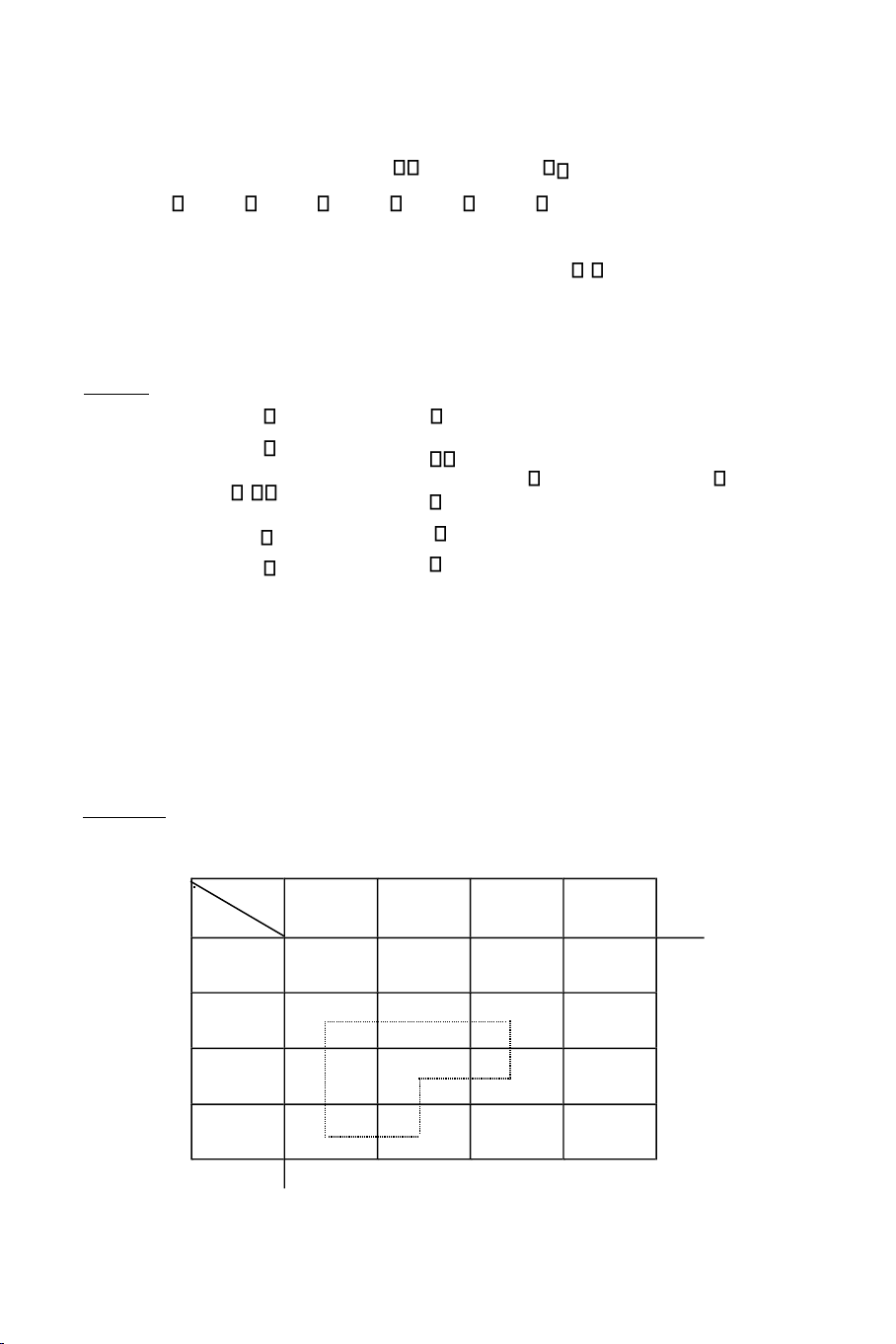
* Phöông phaùp Vogel:
Öu tieân phaân phoái cho oâ coù giaù cöôùc nhoû nhaát, naèm treân doøng hay coät
coù cheânh leäch giöõa giaù cöôùc nhoû nhì vaø giaù cöôùc nhoû nhaát, laø lôùn nhaát. Ví duï: Thu Phaùt 40 0 75 60 70 82 73 74 79 1, 5 45 - (45) 80 75 81 79 4, 1, 1 15 90 (75) (15) 80 77 77 82 3, 3, 2 110 (40) - (15) (55) 2, 0 2 3, 4 3, 3
Ñaàu tieân ta tính cheânh leäch giöõa giaù cöôùc nhoû nhì vaø giaù cöôùc nhoû nhaát
cho taát caû caùc doøng vaø taát caû caùc coät (caùc soá ghi ôû coät phía beân phaûi vaø
doøng phía döôùi cuûa baûng). Cheânh leäch lôùn nhaát laø 4 öùng vôùi doøng 2, ta phaân
phoái cho oâ (2,2) laø oâ coù giaù cöôùc nhoû nhaát naèm treân doøng naøy: x22 = min 90, 75 = 75
Sau ñoù ñieàu chænh laïi caùc yeâu caàu töông öùng:
a2 = 90 – 75 = 15, b2 = 75 – 75 = 0
Ñaùnh daáu (-) cho caùc oâ naèm treân coät coù yeâu caàu = 0 (coät 2). Sau ñoù laëp
laïi quaù trình tính caùc cheânh leäch cho caùc doøng vaø coät trong phaàn baûng coøn laïi
(thöïc teá chæ caàn tính laïi caùc cheânh leäch theo doøng), ta coù cheânh leäch nhieàu
nhaát laø 5, töông öùng vôùi doøng 1, ta tieán haønh phaân phoái vaøo oâ (1,3)… Cuoái
cuøng ta ñöôïc phöông aùn cöïc bieân xuaát phaùt nhö treân.
Böôùc 2. Tìm heä thoáng theá vò (ui ,vj) lOMoAR cPSD| 47207194
152 BAØI TOAÙN VAÄN TAÛI
Heä thoáng theá vò (ui , vj) phaûi thoûa ñieàu kieän:
ui + vj = cij , vôùi moïi (i,j) laø oâ choïn.
Vôùi phöông aùn cöïc bieân coù m+n-1 oâ choïn, ñaây laø heä m+n-1 phöông trình ñoäc
laäp tuyeán tính vaø m+n bieán. Ñeå giaûi heä naøy, tìm ra moät nghieäm cuï theå, ta phaûi
cho moät bieán baát kyø nhaän moät giaù trò naøo ñoù.
Ta coù thuaät toaùn tìm heä thoáng theá vò nhö sau:
Ñaàu tieân cho moät doøng hay moät coät baát kyø moät giaù trò theá vò ban ñaàu tuøy
yù naøo ñoù (chaúng haïn cho doøng 1 theá vò baèng 0 - töùc laø cho u1 = 0 - Hoaëc cho
doøng hay coät coù nhieàu oâ choïn nhaát theá vò = 0).
Caùc theá vò doøng vaø coät khaùc ñöôïc tính nhö sau: •
Treân doøng i ñaõ coù theá vò, neáu coù oâ choïn (i,j) naèm treân coät j chöa coù theá
vò, ta tính theá vò cho coät j naøy theo coâng thöùc: vj = cij – ui •
Treân coät j ñaõ coù theá vò, neáu coù oâ choïn (i,j) naèm treân doøng i chöa coù theá
vò, ta tính theá vò cho doøng i naøy theo coâng thöùc: ui = cij – vj
Quaù trình treân ñöôïc tieáp dieãn cho ñeán khi taát caû caùc doøng vaø caùc coät ñeàu coù theá vò. Chuù yù:
Tröôøng hôïp khoâng theå tính tieáp ñöôïc caùc theá vò (do soá oâ ñöôïc choïn khoâng
ñuû m+n-1), ta phaûi boå sung theâm oâ choïn. (i,j) ñöôïc laáy laøm oâ choïn boå sung
phaûi coù xij = 0 vaø vieäc boå sung theâm oâ choïn phaûi baûo ñaûm tính tieáp ñöôïc
caùc theá vò theo caùch treân ñaây (oâ choïn boå sung phaûi naèm treân doøng ñaõ coù
theá vò vaø coät chöa coù theá vò hoaëc naèm treân coät ñaõ coù theá vò vaø doøng chöa
coù theá vò, noùi caùch khaùc laø oâ choïn boå sung phaûi khoâng taïo thaønh voøng vôùi
caùc oâ ñaõ choïn) vaø neân laáy oâ choïn boå sung laø oâ coù giaù cöôùc thaáp nhaát
coù theå ñöôïc.
Böôùc 3. Kieåm tra daáu hieäu toái öu
Ta tính caùc heä soá öôùc löôïng: ij = ui + vj – cij
Löu yù: Theo caùch thöùc thöïc hieän ôû böôùc 2 ta luoân coù ij = 0, vôùi (i,j) laø oâ
choïn. Do ñoù chæ phaûi tính heä soá öôùc löôïng cho caùc oâ loaïi.
Ta coù 2 tröôøng hôïp sau ñaây: •
Tröôøng hôïp taát caû ij 0: Ta coù phöông aùn cöïc bieân töông öùng laø phöông aùn
toái öu. Thuaät toaùn keát thuùc. •
Ngöôïc laïi, neáu coù ij > 0: Ta chöa coù phöông aùn toái öu vaø phaûi chuyeån sang böôùc sau. lOMoAR cPSD| 47207194
BAØI TOAÙN VAÄN TAÛI 153
Böôùc 4. Caûi tieán phöông aùn (Tìm phöông aùn cöïc bieân môùi toát hôn)
Giaû söû (i0,j0) laø oâ vi phaïm daáu hieäu toái öu. Thöôøng choïn: i j 0 0 max ij / ij 0
(i0,j0) seõ laø oâ choïn trong baûng môùi. Ta xaùc ñònh voøng taïo bôûi (i0,j0) vôùi caùc
oâ choïn vaø ñaùnh daáu +, – lieân tieáp nhau cho caùc oâ naèm treân voøng naøy, baét
ñaàu töø (i0,j0) mang daáu +.
Löu yù: Voøng taïo bôûi (i0,j0) vôùi caùc oâ choïn luoân luoân toàn taïi vaø duy nhaát.
Thaät vaäy, heä veùctô coät töông öùng vôùi caùc oâ choïn (keå caû oâ choïn boå sung)
laø heä m+n-1 veùctô coät ñoäc laäp tuyeán tính cöïc ñaïi trong heä m n veùctô coät cuûa
ma traän caùc heä soá cuûa caùc raøng buoäc chung. Do ñoù moät veùctô coät baát kyø
khoâng thuoäc heä ñoäc laäp tuyeán tính cöïc ñaïi (töùc laø veùctô coät töông öùng vôùi
moät oâ loaïi) seõ phuï thuoäc tuyeán tính vaøo heä caùc veùctô ñoäc laäp tuyeán tính cöïc
ñaïi. Hay moät oâ loaïi baát kyø seõ taïo thaønh voøng vôùi caùc oâ choïn. Ngoaøi ra, do söï
bieåu dieãn cuûa veùctô phuï thuoäc tuyeán tính vaøo caùc veùctô ñoäc laäp tuyeán tính
laø duy nhaát, neân voøng taïo bôûi moät oâ loaïi vôùi caùc oâ choïn laø duy nhaát.
Sau ñoù ta xaùc ñònh löôïng ñieàu chænh theo coâng thöùc:
q = min xij / vôùi moïi (i,j) mang daáu –
Löôïng ñieàu chænh q ñöôïc xaùc ñònh seõ töông öùng vôùi moät oâ (r,s) naøo ñoù. Töùc
laø: q x rs. Khi ñoù (r,s) seõ laø oâ loaïi trong baûng môùi. Phöông aùn cöïc bieân môùi
ñöôïc xaùc ñònh nhö sau: x ij
xij+ q, vôùi (i,j) mang daáu + x ij
xij q, vôùi (i,j) mang daáu x ij
xij, vôùi (i,j) khoâng mang daáu
Heä thoáng oâ choïn môùi = Heä thoáng oâ choïn cuõ (i0,j0) \ (r,s)
Sau ñoù quay trôû laïi böôùc 2. Sau moät soá höõu haïn böôùc thöïc hieän ta seõ tìm
ñöôïc phöông aùn toái öu.
Ví duï 1: Thöïc hieän caùc böôùc coøn laïi cuûa thuaät toaùn theá vò cho baûng nhaän ñöôïc
töø phöông phaùp Cmin treân ñaây. Thu Phaùt 40 75 60 70 ui 82 73 74 79 lOMoAR cPSD| 47207194
154 BAØI TOAÙN VAÄN TAÛI 45 -7 (45) -2 -2 -5 80 75 ─ 81 79 + 90 -3 (30) -7 (60) -3 80 77 77 82 ─
110 (40) +1 (60) * (10) 0 vj 80 78 77 82
Ñaàu tieân cho u3 = 0 (Doøng coù nhieàu oâ choïn nhaát). Ta thaáy (3,1) laø oâ choïn
naèm treân doøng 3 ñaõ coù theá vò vaø coät 1 chöa coù theá vò, neân: v1 = c31 – u3 = 80 – 0 = 80
(3,3) laø oâ choïn naèm treân doøng 3 ñaõ coù theá vò vaø coät 3 chöa coù theá vò, neân:
v3 = c33 – u3 = 77 – 0 = 77.
Töông töï ta coù: v4 = c34 – u3 = 82 – 0 = 82. … Cuoái cuøng
ta coù heä thoáng theá vò nhö treân.
Vôùi heä thoáng theá vò vöøa tìm, ta tieán haønh tính caùc heä soá öôùc löôïng: laø caùc
soá ñöôïc ghi vaøo goùc phía döôùi, beân phaûi cuûa moãi oâ loaïi (khoâng tính heä soá
öôùc löôïng ôû caùc oâ choïn, maëc ñònh chuùng = 0).
11 = u1 + v1 – c11 = -5 + 80 – 82 = -7
13 = u1 + v3 – c13 = -5 + 77 – 74 = -2 . . .
Ta coù daáu hieäu toái öu bò vi phaïm ôû (3,2). Xeùt oâ vi phaïm (3,2): oâ naøy seõ laø oâ
choïn trong baûng sau. Ta xaùc ñònh voøng laäp bôûi (3,2) vôùi caùc oâ choïn vaø ñaùnh
daáu +, - lieân tieáp nhau cho caùc oâ naèm treân voøng, baét ñaàu töø (3,2) mang daáu +.
Löôïng ñieàu chænh: q = min x22, x34 = min 30, 10 = 10. Töông öùng vôùi
(1,4): ñaây laø oâ loaïi trong baûng môùi (ta ñaùnh daáu * vaøo oâ naøy). Töø ñoù ta coù baûng môùi nhö sau: ui 82 -6 73 74 -1 79 -2 (45) -4 80 -2 75 81 -6 79 (20) (70) -2 80 (40) 77 77 (60) 82 -1 (10) 0 v 80 77 77 81 j
ÔÛ baûng naøy ta coù daáu hieäu toái öu:
ij 0. Phöông aùn toái öu phaûi tìm laø: 0 45 0 0 x* 0 20 0 70 lOMoAR cPSD| 47207194
BAØI TOAÙN VAÄN TAÛI 155 40 10 60 0
fmin = 73 45 + 75 20 + 79 70 + 80 40 + 77 10 + 77 60 = 18.905 (ngaøn ñoàng).
ÔÛ baûng toái öu ta thaáy taát caû caùc oâ loaïi ñeàu coù ij 0, neân baøi toaùn
coù phöông aùn toái öu duy nhaát.
Ví duï 2. Giaûi baøi toaùn vaän taûi vôùi soá lieäu cho nhö sau: 7 10 16 11 8 13 9 10 12 9 (a ((c i ) (50, 40, 50,60) (bj ) ij )) 10 14 10 12 (50,75, 50, 25) 9 15 Baøi giaûi:
Tìm phöông aùn cöïc bieân xuaát phaùt baèng phöông phaùp Cmin. Ta coù baûng sau: bj ai 50 75 50 25 ui 7 10 16 11 50 (50) +1 -1 8 ─ 13 9 + 10 40 * (0) (40) 0 10 12 + 9 ─ 10 50 (15) (10) (25) 0 9 14 ─ 12 15
60 + 1 (60) 2 vj 8 12 9 10
ÔÛ baûng treân ta phaûi boå sung theâm 1 oâ choïn laø: (2,1). lOMoAR cPSD| 47207194
156 BAØI TOAÙN VAÄN TAÛI
Ta coù 2 oâ vi phaïm laø (1,2) vaø (4,1). ÔÛ ñaây ta xeùt oâ vi phaïm (4,1) (oâ töông öùng
vôùi cij nhoû) (4,1) laø oâ choïn trong baûng sau. Xaùc ñònh voøng ñieàu chænh nhö treân,
ta coù löôïng ñieàu chænh laø:
q = min x21 , x23 , x42 = min 0, 10, 60 = 0 (2,1): oâ loaïi trong baûng sau.
Thöïc hieän tìm phöông aùn cöïc bieân môùi, ta coù baûng sau: ui 7 ─ 10 16 11 * (50) + 2 0 8 13 9 9 0 (40) 10 12 9 10 0 (15) (10) (25) 9 + 14 ─ 12 15 2 (60) (0) v j 7 12 9 10
Xeùt oâ vi phaïm (1,2): oâ choïn trong baûng sau. Löôïng ñieàu chænh: q = min
x11 , x42 = min 50, 60 = 50 (1,1): oâ loaïi trong baûng sau.
Thöïc hieän tìm PACB môùi, ta coù baûng sau: ui 7 10 16 11 -2 (50) -9 -3 -2 8 13 9 ─ 10 -1 -1 (40) + 0 0 10 12 9 + 10 ─
-3 (15) (10) * (25) 0 9 14 12 15 (50) (10) -1 -3 2 vj 7 12 9 10
ÔÛ baûng treân ta thaáy coù daáu hieäu toái öu: ij 0 Do ñoù
baøi toaùn coù phöông aùn toái öu: lOMoAR cPSD| 47207194
BAØI TOAÙN VAÄN TAÛI 157 0 50 0 0 x* 0 0 40 0 vôùi f min 10 50 9 40 12 15 9 10 0 15 10 25 10 25 9 50 14 10 1.970 50 10 0 0
ÔÛ baûng toái öu, do oâ loaïi (2,4) coù 24
0, neân baøi toaùn coù theå coù phöông
aùn cöïc bieân toái öu khaùc. Laáy (2,4) laøm oâ choïn trong baûng sau vaø xaùc ñònh voøng
laäp bôûi (2,4) vôùi caùc oâ choïn, ta coù löôïng ñieàu chænh: q = min x23 , x34 = min
40, 25 = 25 (3,4): oâ loaïi trong baûng sau.
Thöïc hieän ñieàu chænh treân voøng ñaõ tìm, ta coù phöông aùn cöïc bieân toái öu khaùc: 0 50 0 0 x 0 0 15 25 0 15 35 0 50 10 0 0
Phöông aùn toái öu toång quaùt coù daïng: 0 50 0 0 x x* (1 )x 0 0 15 25 25 25 [0,1] 0 15 35 25 25 50 10 0 0 BAØI TAÄP 3.2.
1. Cho phöông aùn cöïc bieân x, xeùt voøng taïo bôûi oâ loaïi (i,j) vôùi caùc oâ choïn vaø
ñaùnh daáu +, lieân tieáp nhau cho caùc oâ naèm treân voøng baét ñaàu töø (i,j)
mang daáu +. Chöùng minh raèng: cij cij ij lOMoAR cPSD| 47207194
158 BAØI TOAÙN VAÄN TAÛI
( i , j )coù d aáu (i , j )coù d aáu
2. Giaûi caùc baøi toaùn vaän taûi ñöôïc cho bôûi caùc soá lieäu sau ñaây, tìm toång chi
phí vaän taûi thaáp nhaát. 1 2 4 3 a) ((cij )) (ai ) (60,70, 20) (bj ) (30,40,30,50) 2 3 2 7 3 5 6 4 1 2 4 3 b) ((cij )) (ai ) (80,70,100) (bj ) (40,100,60,50) 2 4 5 1 4 1 2 5
7 6 9 8 c) ((cij )) (ai ) (100,80, 20) (bj ) (60,70,40,30) 10 8 7 11 11 7 6 10 7 4 8 6 ((c (a ij )) 84 59 5378 i ) (100, 50, 80, 20) (bj ) d) (70, 30, 80,70) 5 9 7 5 6 6 9 9 4 6 4 6 e) ((cij )) 54 65 58 49 (a i ) (80,70, 50, 50) (bj ) (100, 50, 30,70) lOMoAR cPSD| 47207194
BAØI TOAÙN VAÄN TAÛI 159 8 7 5 5 9 f) ((cij )) 53 54 43 64 65 (b(ja)i ) (40, 30(50, 80,60,, 40,60)50, 50) 9 8 7 6 4 5 16 16 7 9 g) ((cij )) 178 89 1213 64 137 (b(ja)i ) (35, 30 (42,60, 45,, 28, 45)40, 25) 10 19 19 8 6




