











Preview text:
lOMoAR cPSD| 47207194
CHÖÔNG 7 QUY HOAÏCH ÑA MUÏC TIEÂU TUYEÁN TÍNH 7.1. ÑAËT VAÁN ÑEÀ
Caùc baøi toaùn QHTT maø ta ñaõ xem xeùt tröôùc ñaây ñeàu ôû daïng coù duy nhaát
moät haøm muïc tieâu. Tuy nhieân trong thöïc teá, chaúng haïn trong hoaït ñoäng saûn
xuaát, ngoaøi heä raøng buoäc bieåu hieän haïn cheá veà nguoàn nguyeân, vaät lieäu ñöôïc
söû duïng,… ngöôøi ta coøn xem xeùt ñoàng thôøi nhieàu muïc tieâu nhö: cöïc ñaïi lôïi
nhuaän thu ñöôïc, cöïc tieåu chi phí söû duïng lao ñoäng, cöïc ñaïi soá khaùch haøng bieát
ñeán saûn phaåm, cöïc tieåu voán ñaàu tö,… Caùc muïc tieâu treân thöôøng xung ñoät vôùi
nhau vaø vaán ñeà ñaët ra laø phaûi tìm PATÖ thoûa maõn taát caû caùc muïc tieâu ñoù.
Quy hoaïch ña muïc tieâu seõ giaûi quyeát vaán ñeà naøy. Tuy nhieân ôû ñaây ta chæ giôùi
haïn vieäc xem xeùt baøi toaùn quy hoaïch ña muïc tieâu tuyeán tính, töùc laø baøi toaùn
maø caùc haøm muïc tieâu vaø caùc raøng buoäc ñeàu ôû daïng tuyeán tính.
Sau ñaây ta seõ xeùt 2 caùch tieáp caän chính cho caùc baøi toaùn toái öu ña muïc tieâu
tuyeán tính: Tieáp caän theo muïc tieâu cöïc tieåu haøm phaït vaø tieáp caän theo toái öu Pareto.
7.2. CAÙCH TIEÁP CAÄN THEO MUÏC TIEÂU CÖÏC TIEÅU HAØM PHAÏT
Ta quy ñònh cho moãi muïc tieâu moät möùc laø moät con soá cuï theå, sau ñoù xaùc
ñònh caùc heä soá phaït do vi phaïm möùc quy ñònh naøy vaø cuoái cuøng laø tìm PATÖ ñaït
cöïc tieåu haøm toång ñoä leäch cuûa caùc giaù trò muïc tieâu vôùi möùc ñaõ quy ñònh cho
töøng muïc tieâu. Haøm toång caùc ñoä leäch naøy ñöôïc tính vôùi troïng soá laø caùc heä
soá phaït ñaõ ñöôïc xaùc ñònh (Haøm phaït).
7.2.1. QUY HOAÏCH NHIEÀU MUÏC TIEÂU KHOÂNG ÖU TIEÂN
Caùc muïc tieâu ñöôïc xem xeùt ñeàu coù taàm quan troïng nhö nhau. Ví duï:
Moät xí nghieäp döï ñònh saûn xuaát 3 loaïi saûn phaåm A, B, C. Giaùm ñoác xí nghieäp
chuù yù ñeán 3 muïc tieâu: Lôïi nhuaän, Lao ñoäng vaø Voán ñaàu tö.
Cuï theå trong kyø keá hoaïch caàn ñaït ñöôïc caùc möùc: •
Lôïi nhuaän toái thieåu laø 250 trieäu ñoàng. •
Ñoäi nguõ lao ñoäng ñöôïc duy trì laø 300 ngöôøi. •
Voán ñaàu tö khoâng vöôït quaù 350 trieäu ñoàng.
Giaùm ñoác xí nghieäp ñöa ra caùc heä soá phaït khi caùc muïc tieâu bò vi phaïm nhö sau: lOMoAR cPSD| 47207194
QUY HOAÏCH ÑA MUÏC TIEÂU TUYEÁN TÍNH 225 •
Heä soá 6 khi lôïi nhuaän ñaït thaáp hôn möùc quy ñònh 1 trieäu ñoàng. •
Heä soá 2 khi söû duïng theâm 10 lao ñoäng. •
Heä soá 5 khi khoâng söû duïng 10 lao ñoäng. •
Heä soá 4 khi voán ñaàu tö vöôït quaù möùc quy ñònh 1 trieäu ñoàng.
Caùc soá lieäu ñònh möùc cho moãi ñôn vò saûn phaåm, cuøng vôùi caùc möùc muïc
tieâu quy ñònh vaø caùc heä soá phaït cho trong baûng sau: Ñònh möùc cho 1 ñv SP Heä soá phaït Muïc tieâu A B C Möùc muïc tieâu Lôïi nhuaän 9 10 8 ≥ 250 (tr. ñoàng) 6 Lao ñoäng 0,8 1,2 0,6 = 30 ( 10 ngöôøi) 2 (+), 5 (─) Voán ñaàu tö 12 15 10 ≤ 350 (tr. ñoàng) 4 Baøi giaûi:
Goïi x1, x2, x3 töông öùng laø soá saûn phaåm A, B, C caàn ñöôïc saûn xuaát.
Ta coù heä raøng buoäc veà möùc quy ñònh cuûa caùc muïc tieâu:
Lôïi nhuaän: 9x1 + 10x2 + 8x3 ≥ 250 (trieäu ñoàng)
Lao ñoäng: 0,8x1 + 1,2x2 + 0,6x3 = 30 (chuïc ngöôøi)
Voán ñaàu tö: 12x1 + 15x2 + 10x3 ≤ 350 (trieäu ñoàng) Ñaët:
y1 = 9x1 + 10x2 + 8x3 - 250 (Lôïi nhuaän tröø möùc quy ñònh) y2 = 0,8x1 +
1,2x2 + 0,6x3 - 30 (Lao ñoäng tröø möùc quy ñònh) y3 = 12x1 + 15x2 + 10x3 -
350 (Voán ñaàu tö tröø möùc quy ñònh) Do y
j, j=1,2,3 coù theå nhaän giaù trò döông hay aâm, neân ta ñaët: y j y j y j , vôùi y j 0, y j 0, j 1, 2, 3.
Quan heä giöõa caùc bieán treân nhö sau: y j j y0j,,neáuneáu yyj 00y j 0y,j neáu, neáuyy jj 00 lOMoAR cPSD| 47207194
226 QUY HOAÏCH ÑA MUÏC TIEÂU TUYEÁN TÍNH
Ta coù baøi toaùn quy hoaïch tuyeán tính sau ñaây:
Cöïc tieåu haøm phaït do vi phaïm caùc möùc quy ñònh cuûa caùc muïc tieâu: f 6y1 2y2 5y2 4y3 min Vôùi heä raøngbu oäc: 9x1 10x2 8x3 y1 y1 250 y 2 30 0,8x 1
1,2x2 0,6x3 y2 12x1 15x2 10x3 y3 y 3 350 xj 0, yk 0, yk 0, j 1,2,3; k 1,2,3
Neáu baøi toaùn ñaõ cho coù theâm caùc raøng buoäc khaùc nöõa, nhö raøng buoäc veà
tieâu hao caùc loaïi nguyeân vaät lieäu, ñieàu kieän nguyeân cuûa caùc bieán,… thì ta phaûi
ñöa caùc raøng buoäc ñoù vaøo moâ hình treân.
Giaûi baøi toaùn quy hoaïch tuyeán tính treân baèng phöông phaùp ñôn hình, ta coù
phöông aùn toái öu: x* (0,15, 25/ 2)T y 1 0, y1 0, y2 0, y2 9/ 2, y3 0, y3 0, f * 45/ 2
y1* y1 y1 0, y2* y2 y2 9/ 2, y3* y3 y3 0
Töùc laø muïc tieâu veà lôïi nhuaän vaø voán ñaàu tö ñöôïc thoûa maõn, nhöng löôïng lao
ñoäng khoâng ñöôïc söû duïng heát (dö (9/2)( 10) = 45 ngöôøi). Löôïng phaït do vi phaïm
muïc tieâu veà lao ñoäng laø f* = 45/2.
7.2.2. QUY HOAÏCH NHIEÀU MUÏC TIEÂU COÙ ÖU TIEÂN
Tröôøng hôïp caùc muïc tieâu coù taàm quan troïng khaùc nhau ta seõ nhaân heä soá
phaït vôùi caùc nhaân töû M1, M2, …, MP. Trong ñoù: M1 laø nhaân töû öùng vôùi muïc
tieâu (hay nhoùm muïc tieâu) quan troïng nhaát, M2 laø nhaân töû öùng vôùi muïc tieâu
(hay nhoùm muïc tieâu) quan troïng thöù 2, …, MP laø nhaân töû öùng vôùi muïc tieâu (hay
nhoùm muïc tieâu) keùm quan troïng nhaát. Ta quy ñònh:
M1 laø soá raát lôùn so vôùi M2, M2
laø soá raát lôùn so vôùi M3, lOMoAR cPSD| 47207194
QUY HOAÏCH ÑA MUÏC TIEÂU TUYEÁN TÍNH 227
MP-1 laø soá raát lôùn so vôùi MP = 1. Ví duï:
Giaû söû giaùm ñoác xí nghieäp cho raèng muïc tieâu lôïi nhuaän toái thieåu caàn ñaït
ñöôïc laø 250 trieäu ñoàng vaø muïc tieâu lao ñoäng hieän coù phaûi ñöôïc söû duïng heát
(≥ 300 ngöôøi) thuoäc nhoùm muïc tieâu coù möùc öu tieân soá 1, coøn muïc tieâu voán
ñaàu tö khoâng vöôït quaù 350 trieäu ñoàng vaø muïc tieâu khoâng ñöôïc taêng theâm lao
ñoäng (≤ 300 ngöôøi) thuoäc nhoùm muïc tieâu coù möùc öu tieân 2. Vôùi 2 nhoùm muïc
tieâu coù möùc öu tieân khaùc nhau nhö treân, ta coù baûng vôùi heä soá phaït nhö sau: (M > 0 raát lôùn) Möùc öu Ñònh möùc cho 1 ñv SP Möùc muïc Heä soá tieân Muïc tieâu A B C tieâu phaït Möùc 1 Lôïi nhuaän Lao 9 10 1,2 8 ≥ 250 (tr.ñ) ≥ 30 6M ñoäng 0,8 0,6 ( 10ng) 5M Möùc 2 Voán ñaàu tö 12 0,8
15 1,2 10 0,6 ≤ 350 (tr.ñ) ≤ 30 4 Lao ñoäng ( 10ng) 2
Thöïc hieän caùch ñaët bieán gioáng nhö treân ñaây, ta coù moâ hình baøi toaùn quy hoaïch tuyeán tính: f 6My 1 2y2 5My2 4y3 min 9x1 10x2 8x3 y1 y1 250 0,8x 1 1,2x2 0,6x3 y2 y2 30 12x1 15x2 10x 3 y3 y3 350 xj 0, yk 0, yk 0, j 1,2,3; k 1,2,3 Vôùi M 0 raát lôùn.
Giaûi baøi toaùn treân baèng phöông phaùp ñôn hình, ta coù phöông aùn toái öu: x* = (0, 25, 0)T, (y * 1 0, y*2 0, y*3 25) vaø fmin 100
Nhö vaäy, muïc tieâu lôïi nhuaän vaø muïc tieâu söû duïng lao ñoäng ñöôïc thoûa maõn
nhöng muïc tieâu voán ñaàu tö bò vi phaïm (söû duïng vöôït 25 trieäu ñoàng). Möùc phaït laø 100. lOMoAR cPSD| 47207194
228 QUY HOAÏCH ÑA MUÏC TIEÂU TUYEÁN TÍNH BAØI TAÄP 7.1.
1. Coù baûng soá lieäu sau ñaây veà caùc möùc muïc tieâu ñöôïc quy ñònh, heä soá phaït
vaø ñònh möùc cho moãi ñôn vò saûn phaåm: Ñònh möùc cho 1 ñv SP Möùc muïc Heä soá Muïc tieâu A B C D tieâu phaït Lôïi nhuaän 12 6 10 4 11 5 13 7 ≥ 300 (tr. ñ) 8 Lao ñoäng 20 18 19 21 = 100 (ngöôøi) 3(+),5(─) Voán ñaàu tö ≤ 500 (tr. ñ) 6
Haõy xaùc ñònh phöông aùn toái öu.
2. Giaû söû phaûi xeùt theâm raøng buoäc veà nguyeân lieäu N bò tieâu hao: 3x1 + x2 + 2x3 + 4x4 ≤ 50
Haõy tìm phöông aùn toái öu.
3. Trong Baøi taäp 1. giaû söû muïc tieâu voán ñaàu tö khoâng vöôït quaù 500 trieäu ñoàng
vaø muïc tieâu lao ñoäng khoâng ñöôïc söû duïng hôn 100 ngöôøi thuoäc nhoùm öu tieân
1, coøn muïc tieâu lôïi nhuaän toái thieåu laø 300 trieäu ñoàng vaø muïc tieâu lao ñoäng
phaûi ñöôïc söû duïng heát thuoäc nhoùm öu tieân 2. Haõy giaûi baøi toaùn, tìm phöông aùn toái öu.
4. Trong Baøi taäp 2. giaû söû muïc tieâu lôïi nhuaän laø öu tieân soá 1, coøn caùc muïc
tieâu coøn laïi laø öu tieân soá 2. Haõy tìm phöông aùn toái öu. lOMoAR cPSD| 47207194
QUY HOAÏCH ÑA MUÏC TIEÂU TUYEÁN TÍNH 229
7.3. CAÙCH TIEÁP CAÄN THEO TOÁI ÖU PARETO
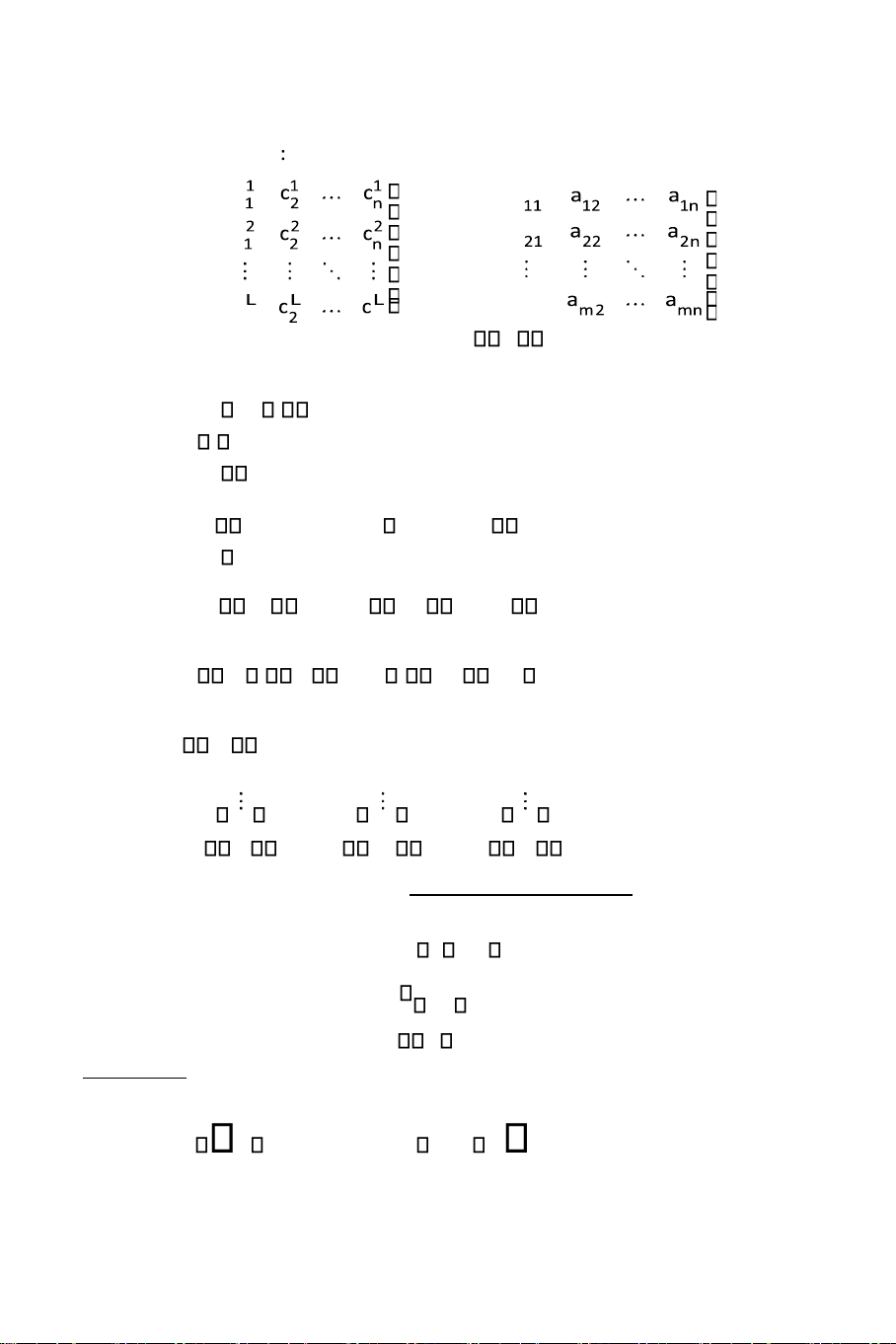
Xeùt baøi toaùn quy hoaïch ña muïc tieâu: n f 1 c x1j j min (max) j 1 n f 2 c x2j j min (max) j 1 n f L c xLj j min (max) j 1 Vôùi heä raøng bu oäc : n a x ij j b , ii 1,m j 1 x j 0, j 1,n Daïng ma traän: f Cx min (max) Ax b x 0 lOMoAR cPSD| 47207194
230 QUY HOAÏCH ÑA MUÏC TIEÂU TUYEÁN TÍNH T rong ñ où c a cA a C c1 n am1 x1 b1 f1 x x2 b b2 f f2 xn bm fL
Baøi toaùn treân coøn ñöôïc goïi laø Baøi toaùn toái öu veùctô. Khoâng
maát toång quaùt, ta xeùt daïng baøi toaùn: f Cx max (P) Ax b x 0 Ñònh nghóa: Kyù hieäu X x R / Axn
b, x 0 : Taäp phöông aùn cuûa baøi toaùn (P). lOMoAR cPSD| 47207194
QUY HOAÏCH ÑA MUÏC TIEÂU TUYEÁN TÍNH 231
x0 X ñöôïc goïi laø Ñieåm toái öu Pareto hay Ñieåm höõu hieäu cuûa baøi toaùn (P) neáu
khoâng toàn taïi x X sao cho: Cx ≥ Cx0 vaø Cx ≠ Cx0. Töùc laø: ≥ , k
1,L vaø > vôùi ít nhaát moät k
1,2,...,L . Trong ñoù: ck (c , c , k k 1 2 , c ) k T n
Ta thaáy ñieåm toái öu Pareto laø traïng thaùi taïi ñoù khoâng coù moät muïc tieâu
naøo thu ñöôïc giaù trò lôùn hôn maø laïi khoâng laøm giaûm giaù trò cuûa ít nhaát moät
muïc tieâu khaùc. (Noùi noâm na laø traïng thaùi laøm toát moät muïc tieâu nhöng khoâng
laøm xaáu hôn taát caû caùc muïc tieâu coøn laïi) Ñònh lyù 7.1.
Neáu x* laø phöông aùn toái öu duy nhaát cuûa baøi toaùn: (Pk) fAxk bc ,xk max (k 1 2, , ,L ) x 0
thì x* laø moät ñieåm höõu hieäu cuûa baøi toaùn (P). Chöùng minh:
Giaû söû x* khoâng laø ñieåm höõu hieäu cuûa (P). Töùc laø: x X sao cho : c ,k x c ,xk * , k 1,L (*) k , x ck *, x , vôùi ít nhaát moät k 1, 2 , , L (**) vaø c
Do x* laø phöông aùn toái öu cuûa (Pk) neân theo (*) ta coù x cuõng laø phöông aùn toái öu cuûa (Pk).
Maët khaùc, theo (**) ta phaûi coù: x x*
Nhö vaäy, ta coù x laø moät phöông aùn toái öu khaùc cuûa (Pk). Voâ lyù. lOMoAR cPSD| 47207194
232 QUY HOAÏCH ÑA MUÏC TIEÂU TUYEÁN TÍNH
Cho x0 X. Xeùt baøi toaùn quy hoaïch tuyeán tính: y 0 y1 y2 yL max Vôùiheä raøngbu oäc : (Py) CxAx yb Cx0 x 0 y ( y , y ,1 2 ,y )L T 0 Ñònh lyù 7.2.
1. x0 laø ñieåm höõu hieäu cuûa baøi toaùn (P) max y0 = 0.
2. (x*,y*) laø phöông aùn toái öu cuûa baøi toaùn (Py) vôùi max y0 ≥ 0 x* laø moät
ñieåm höõu hieäu cuûa baøi toaùn (P).
3. Neáu (Py) khoâng coù phöông aùn toái öu (do y0 → +∞) thì baøi toaùn (P) khoâng
coù ñieåm höõu hieäu. Chöùng minh:
1. Theo ñònh nghóa, x0 khoâng phaûi laø ñieåm höõu hieäu cuûa baøi toaùn (P) x X : Cx Cx0 vaø Cx Cx0
(x,y) laø moät phöông aùn cuûa (Py), vôùi y = Cx – Cx0 ≥ 0 vaø y ≠ 0.
max y0 > 0. Vaäy ta coù ñieàu phaûi chöùng minh.
2. Giaû söû x* khoâng phaûi laø moät ñieåm höõu hieäu cuûa baøi toaùn (P) x X : Cx Cx* vaø Cx Cx* Ñaët: y Cx Cx0 ,
ta coù : y Cx* Cx0 y* 0 vaø y y* L L y 0 yk y*k y*0 max y0 . Voâ lyù. k 1 k 1 lOMoAR cPSD| 47207194
QUY HOAÏCH ÑA MUÏC TIEÂU TUYEÁN TÍNH 233 3. Ñaët: D x X / Cx Cx0 L L Do: y 0 yk ( c ,xk c ,xk 0 ) k 1 k 1 L
Neân toàn taïi tia voâ haïn x( ) D : c , x( )k k 1 L k 0,x laø moät haèngsoá c k 1
Giaû söû baøi toaùn (P) coù ñieåm höõu hieäu laø x*
khoâng toàn taïi x X : Cx Cx , Cx* Cx*
Töùc laø ta coù: Cx ≤ Cx*, x X L c ,xk
bò chaën treân bôûi Cx*, x X. k 1
Ñieàu naøy maâu thuaãn vôùi vieäc x( ) D X : L c ,x( )k k 1
Nhö vaäy ta coù ñieàu phaûi chöùng minh.
THUAÄT TOAÙN TÌM MOÄT ÑIEÅM HÖÕU HIEÄU
(ÑIEÅM TOÁI ÖU PARETO)
Döïa treân caùc lyù thuyeát ñaõ ñöôïc xem xeùt treân ñaây, ta coù thuaät toaùn tìm moät
ñieåm höõu hieäu (ñieåm toái öu Pareto) cuûa baøi toaùn (P) nhö sau:
Böôùc 1. Giaûi baøi toaùn: (P 1) fAx1 bc ,x1 max lOMoAR cPSD| 47207194
234 QUY HOAÏCH ÑA MUÏC TIEÂU TUYEÁN TÍNH x 0
(Coù theå choïn baøi toaùn (Pk) baát kyø, k 1,2,...,L ) * Neáu
(P1) khoâng coù phöông aùn (P) khoâng coù ñieåm höõu hieäu.
* Neáu (P1) coù phöông aùn toái öu x0 :
+ Tröôøng hôïp x0 laø phöông aùn toái öu duy nhaát cuûa (P1) thì x0 laø ñieåm höõu hieäu.
+ Tröôøng hôïp x0 khoâng laø phöông aùn toái öu duy nhaát cuûa (P1) → Böôùc 2.
Böôùc 2. Thaønh laäp baøi toaùn (Py) vôùi x0 ñaõ bieát. •
Neáu (Py) khoâng coù phöông aùn toái öu (y0 → +∞) thì (P) khoâng coù ñieåm höõu hieäu. •
Neáu (Py) coù phöông aùn toái öu (x*, y*) thì x* laø ñieåm höõu hieäu cuûa (P).
Ví duï 1. Giaûi baøi toaùn quy hoaïch ña muïc tieâu sau ñaây: f 1 2x1 x2 f f2 2x1 5x2 max f3 6x1 9x2 Vôùi heä raøng buoäc : x 1 3x2 12 2x 1 x2 15 x j 0, j 1,2 Baøi giaûi: Xeùt baøi toaùn (P1): f 1 2x1 x2 max 2x1x 1 3xx22 1215 lOMoAR cPSD| 47207194
QUY HOAÏCH ÑA MUÏC TIEÂU TUYEÁN TÍNH 235 x j 0, j 1,2
(P1) coù PATÖ x0 = (15/2, 0)T, nhöng x0 khoâng phaûi laø phöông aùn toái öu duy nhaát
neân noù khoâng phaûi laø ñieåm höõu hieäu. Ta laäp baøi toaùn (Py): y 0 y1 y2 y3 max Vôùi heä raøng buoäc : 2x 0 0 1 x2 y1 2x1 x2 15 2x 0 0 1 5x2 y2 2x1 5x2 15 6x 0 0 1 9x2 y3 6x1 9x2 45 x1 3x 2 12 2x1 x2 15 xj 0, j 1,2 y k 0, k 1,2,3 (P
y) coù phöông aùn toái öu: x* = (33/5, 9/5)T, y* = (0, 36/5, 54/5)T, y*0 18.
(P) coù ñieåm höõu hieäu (ñieåm toái öu Pareto) laø: x* = (33/5, 9/5)T.
Ví duï 2. Giaûi baøi toaùn quy hoaïch ña muïc tieâu sau ñaây: f ff1 1 2 4xx1 33xx22 max Vôùi heä raøng buoäc : x 1 2x2 2 4x 1 3x2 15 x j 0, j 1,2 Baøi giaûi: lOMoAR cPSD| 47207194
236 QUY HOAÏCH ÑA MUÏC TIEÂU TUYEÁN TÍNH Xeùt baøi toaùn (P1): f 1 4x1 3x2 max x14x 12 x23x 22 15 x j 0, j 1,2
(P1) coù phöông aùn toái öu x0 = (0, 5)T, nhöng x0 khoâng phaûi laø phöông aùn toái öu
duy nhaát neân noù khoâng phaûi laø ñieåm höõu hieäu. Ta laäp baøi toaùn (Py): y 0 y1 y2 max Vôùi heä raøng buoäc : 4x 0 0 1 3x2 y1 4x1 3x2 15 x1 3x2 y2 x10 3x20 15 x 1 2x2 2 4x 1 3x2 15 xj 0, j 1,2 y k 0, k 1,2
(Py) khoâng coù phöông aùn toái öu (do y0 → + ∞) neân (P) khoâng coù ñieåm höõu
hieäu (ñieåm toái öu Pareto). BAØI TAÄP 7.2.
Tìm ñieåm höõu hieäu (ñieåm toái öu Pareto) cuûa caùc baøi toaùn quy hoaïch ña muïc
tieâu tuyeán tính sau ñaây: 1. lOMoAR cPSD| 47207194
QUY HOAÏCH ÑA MUÏC TIEÂU TUYEÁN TÍNH 237 f ff12 x51x1 8x42x2 411x3x3 max Vôùi heä raøng buoäc : 2x 1 2x2 x3 18 x 1 x2 2x3 12 x1 2x 2 x3 15 x j 0, j 1,2,3 2. f 1 32x1 30x2 22x3 25x4 f f2 24x 1 30x2 34x3 25x4 max f3 16x1 6x 2 18x3 5x4 Vôùi heä raøng buoäc : 2x 1 3x2 x3 x4 40 2x 1 x2 3x3 2x4 20 x 1 2x2 x3 2x4 24 x j 0, j 1,4 3. f ff12 x21x1 6x32x2 x23x3 max Vôùi heä raøng buoäc : x 1 4x2 x3 4 2x 1 4x2 2x3 4 x1 3x 2 2x3 6 lOMoAR cPSD| 47207194
238 QUY HOAÏCH ÑA MUÏC TIEÂU TUYEÁN TÍNH x j 0, j 1,2,3




