Lý thuyết và một số bài tập cơ bản về thể tích khối đa diện – Lê Bá Bảo Toán 12

Tài liệu gồm 32 trang tổng hợp lý thuyết, công thức giải và một số bài tập thể tích khối đa diện có lời giải chi tiết tương tự các bài toán trong đề minh họa lần 3 của Bộ GD và ĐT.Mời các bạn đón xem.

105 53 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Khối đa diện

Môn: Toán 12

Thông tin:

32 trang 8 tháng trước

Tác giả:

Profile Lan Tường
G
G
i
i
á
á
o
o
v
v
i
i
ê
ê
n
n
:
:
L
L
Ê
Ê
B
B
Á
Á
B
B
Ả
Ả
O
O
_
_
T
T
r
r
ư
ư
ờ
ờ
n
n
g
g
T
T
H
H
P
P
T
T
Đ
Đ
ặ
ặ
n
n
g
g
H
H
u
u
y
y
T
T
r
r
ứ
ứ
,
,
H
H
u
u
ế
ế
S
S
Đ
Đ
T
T
:
:
0
0
9
9
3
3
5
5
.
.
7
7
8
8
5
5
.
.
1
1
1
1
5
5
Đ
Đ
ị
ị
a
a
c
c
h
h
ỉ
ỉ
:
:
1
1
1
1
6
6
/
/
0
0
4
4
N
N
g
g
u
u
y
y
ễ
ễ
n
n
L
L
ộ
ộ
T
T
r
r
ạ
ạ
c
c
h
h
,
,
T
T
P
P
H
H
u
u
ế
ế
Chuyªn ®Ò:
THÓ TÝCH KhèI §A DIÖN
Mét sè bµi tËp c¬ b¶n
LuyÖn thi THPT 2017_2018
HuÕ, th¸ng 5/2017
[...Chuyªn ®Ò Tr¾c nghiÖm To¸n 12...]
LuyÖn thi THPT Quèc gia 2018
Gi¸o viªn:
Lª B¸ B¶o... 0935.785.115... 1
CLB Gi¸o viªn trÎ TP HuÕ
TỔNG QUAN CÁC ĐIỂM LÝ THUYẾT CẦN LƯU Ý
Giáo viên: LÊ BÁ BẢO Trường THPT Đặng Huy Trứ, Huế
SĐT: 0935.785.115 Địa chỉ: 116/04 Nguyễn Lộ Trạch, TP Huế
Phần 1: C¸C KhèI §A DIÖN, TÝNH CHÊT Vµ C¸CH DùNG
H×nh ®a diÖn
Dùng h×nh
TÝnh chÊt
Tø diÖn
D
C
A
+) Có 4 mặt là các tam giác.
+) Không quy định đỉnh nào nằm trên
(tùy thuộc giả thiết để dựng cho phù hợp).
*
§Æc biÖt:
Tứ diện đều có tất cả các cạnh đều bằng
nhau (các mặt là các tam giác đều).
H×nh chãp
A
S
B
C
Hình chóp
.:S ABC
+) Điểm
S
gọi là đỉnh của hình chóp.
+) Các cạnh bên
, , .SA SB SC
Đường
thẳng chứa
SA
có thể gọi tắt là cạnh bên.
+) Các mặt bên
, , .SAB SAC SBC
Mặt
phẳng
SAB
gọi là mặt phẳng bên (gọi
tắt là mặt bên).
+) Mặt đáy là đa giác
.ABC
Mặt phẳng
ABC
gọi là mặt phẳng đáy. (gọi tắt là
mặt đáy).
H×nh l¨ng
trô
A
B
C
B'
C'
A'
Hình lăng trụ
.:ABC A B C
+) Hai đa giác
,ABC A B C
bằng nhau và
/ / .ABC A B C
+) Các cạnh bên
,,AA BB CC
thỏa
/ / / /AA BB CC
và
.AA BB CC

+) Các mặt bên
,,ABB A BCC B ACC A
là các hình bình hành.
* Chó ý:
Các cạnh bên đều hợp với đáy một góc
bằng nhau (có nghĩa là ta có thể dùng cạnh
bên nào và mặt đáy nào phù hợp).
[...Chuyªn ®Ò Tr¾c nghiÖm To¸n 12...]
LuyÖn thi THPT Quèc gia 2018
Gi¸o viªn:
Lª B¸ B¶o... 0935.785.115... 2
CLB Gi¸o viªn trÎ TP HuÕ
H×nh hép
A'
B'
C'
D'
A
D
B
C
Hình hộp là hình lăng trụ có đáy là hình
bình hành.
H×nh chãp
tam gi¸c ®Òu
G
M
C
B
S
A
Hình chóp tam giác đều
.:S ABC
+) Đường cao của hình chóp là
,SG
G
là
tâm (trọng tâm) của đáy.
+) Đa giác đáy
ABC
là tam giác đều.
+) Các cạnh bên
,,SA SB SC
bằng nhau
và hợp với đáy một góc bằng nhau.
Cụ thể:
;SA ABC SAG
+) Các mặt bên
,,SAB SBC SAC
là các
tam giác cân tại
S
, bằng nhau và hợp với
đáy một góc bằng nhau.
Cụ thể:
;SBC ABC SMG
với
M
là
trung điểm
.BC
H×nh chãp tø
gi¸c ®Òu
M
S
D
A
O
C
B
Hình chóp tứ giác đều
.:S ABCD
+) Đường cao của hình chóp là
,SO
O
là
tâm của đáy.
+) Đa giác đáy
ABCD
là hình vuông.
+) Các cạnh bên
, , ,SA SB SC SD
bằng
nhau và hợp với đáy một góc bằng nhau
Cụ thể:
;SA ABCD SAO
+) Các mặt bên
, , ,SAB SBC SCD SAD
là
các tam giác cân tại
S
, bằng nhau và hợp
với đáy một góc bằng nhau.
Cụ thể:
;SBC ABCD SMO
với
M
là trung điểm
.BC
[...Chuyªn ®Ò Tr¾c nghiÖm To¸n 12...]
LuyÖn thi THPT Quèc gia 2018
Gi¸o viªn:
Lª B¸ B¶o... 0935.785.115... 3
CLB Gi¸o viªn trÎ TP HuÕ
H×nh l¨ng
trô ®øng
A
B
C
B'
C'
A'
Hình lăng trụ đứng
.:ABC A B C
+) Đường cao của lăng trụ là
, , .AA BB CC
+) Các mặt bên
,,ABB A ACC A BCC B
là các hình chữ nhật.
H×nh hép
®øng
C
B
D
A
D'
C'
B'
A'
Hình hộp đứng
.:ABCD A B C D
+) Đường cao của hình hộp là
, , , .AA BB CC DD
+) Các mặt bên
,,ABB A ADD A
,BCC B CDD C
là các hình chữ nhật.
H×nh hép
ch÷ nhËt
A'
B'
C'
D'
A
D
B
C
Hình hộp chữ nhật
.:ABCD A B C D
+) Đường cao của hình hộp là
, , , .AA BB CC DD
+) Các mặt bên
,,ABB A ADD A
,BCC B CDD A
là các hình chữ nhật.
+) Đáy là hình chữ nhật.
H×nh lËp
ph-¬ng
a
D'
C'
B'
A'
D
C
B
A
a
a
Hình lập phương
.:ABCD A B C D
+) Đường cao của hình lập phương là
, , , ,...AA BB CC DD
+) Tất cả 6 mặt đều là hình vuông.
[...Chuyªn ®Ò Tr¾c nghiÖm To¸n 12...]
LuyÖn thi THPT Quèc gia 2018
Gi¸o viªn:
Lª B¸ B¶o... 0935.785.115... 4
CLB Gi¸o viªn trÎ TP HuÕ
Phần 2: Kü N¡NG GãC Vµ KHO¶NG C¸CH
Kü n¨ng
C¸ch dùng
Tr×nh bµy
Gãc gi÷a
hai ®-êng
th¼ng
α
I
Δ
2
d
Δ
1
+) Với
1
và
2
chéo nhau.
2
1 2 2
1
; ; .
: / /
I
d
I d d

Gọi
12
;
là góc giữa
1
và
2
.
+)
00
0 90 .

+)
12
12
//
0
12
;0
+)
12
0
12
; 90 .
Gãc gi÷a
®-êng
th¼ng vµ
mÆt ph¼ng
d'
d
α
P
H
I
A
Xét
,d P I
ta thực hiện chiếu vuông
góc đường thẳng
d
lên mặt phẳng
P
được đường thẳng
; ; .d d P d d


Cụ
thể:
+) Chiếu vuông góc
A A d
xuống
P
được điểm
,H
chỉ rõ
.AH P
+)
;.d P AIH
Gọi
;dP
là góc giữa
d
và
.P
+)
00
0 90 .

+)
0
//
0.
dP
dP

+)
0
90 .dP
Trình bày:
Do
AH P HI
là hình chiếu của
AI
trên
;.P AI P AIH
Gãc gi÷a
hai mÆt
ph¼ng
I
Δ
d'
α
d
Q
P
Xét
,PQ
chọn điểm
I 
sao cho:
Gọi
;PQ
là góc giữa
P
và
.Q
+)
00
0 90 .

+)
0
//
0.
PQ
PQ

+)
0
90 .PQ
[...Chuyªn ®Ò Tr¾c nghiÖm To¸n 12...]
LuyÖn thi THPT Quèc gia 2018
Gi¸o viªn:
Lª B¸ B¶o... 0935.785.115... 5
CLB Gi¸o viªn trÎ TP HuÕ
;I d P I d Q
d
d


; ; .P Q d d

Kho¶ng
c¸ch tõ
®iÓm ®Õn
®-êng
th¼ng
Δ
H
A
; : .
H
d A AH
AH


§Æc biÖt:
1 2 1 2 2
/ / ; ;d d A
với
1
.A
Δ
1
A
H
Δ
2
Kho¶ng
c¸ch tõ
®iÓm mÆt
ph¼ng
A
H
P
; : .
HP
d A P AH
AH P
§Æc biÖt:
/ / ; ;P Q d P Q d A Q
với
.AP
P
A
H
Q
Kho¶ng
c¸ch gi÷a
hai ®-êng
th¼ng
chÐo nhau
I
Δ
Δ
2
Δ
1
H
P
A
Cho hai đường thẳng
1
và
2
chéo
nhau.
+) Chọn
21
: / / .PP
Dựng
trong
P
sao cho
1
/ / .
+)
1 2 1
;;d d P
[...Chuyªn ®Ò Tr¾c nghiÖm To¸n 12...]
LuyÖn thi THPT Quèc gia 2018
Gi¸o viªn:
Lª B¸ B¶o... 0935.785.115... 6
CLB Gi¸o viªn trÎ TP HuÕ
Phần 3: C¸C KÕT QU¶ QUAN TRäNG CÇN L¦U ý
KÕt qu¶ 1
KÕt qu¶ 2
KÕt qu¶ 3
Tam giác đều cạnh
.m
m
A
G
M
B
C
2
3
4
ABC
m
S
và
3
.
2
m
AM
Hình vuông cạnh
.m
O
D
A
B
C
m
2
ABCD
Sm
và
2
.
2
m
OD
Tam giác vuông cân
H
C
B
A
m
m
2
2
ABC
m
S
và
2
.
2
m
AH
KÕt qu¶ 4
KÕt qu¶ 5
KÕt qu¶ 6
Tam giác bất kì
α
c
b
a
A
B
C
1
sin
2
ABC
S ab
p p a p b p c
và
2 2 2
2 cosa b c bc
Hình chữ nhật
a
b
H
A
B
C
D
ABCD
S ab
và
2 2 2
1 1 1
.
DH DA DC

Hình thoi
a
A
D
C
B
a
1
.
2
ABCD
S AC BD
KÕt qu¶ 7
KÕt qu¶ 8
KÕt qu¶ 9
Hình thoi có
0
60BAD
60
0
H
a
B
C
D
A
a
Tam giác
ABD
đều
2
3
2
2
ABCD ABD
a
SS
Hình thoi có
0
120ADC
60
0
a
A
D
C
B
a
H
60
0
Tam giác
ABD
đều
2
3
2
2
ABCD ABD
a
SS
Hình thoi có
0
30BAC
30
0
H
a
B
C
D
A
a
Tam giác
ABD
đều
2
3
2
2
ABCD ABD
a
SS
[...Chuyªn ®Ò Tr¾c nghiÖm To¸n 12...]
LuyÖn thi THPT Quèc gia 2018
Gi¸o viªn:
Lª B¸ B¶o... 0935.785.115... 7
CLB Gi¸o viªn trÎ TP HuÕ
và
3
,.
2
a
BD a BH
và
3
,.
2
a
BD a BH
và
3
,.
2
a
BD a BH
KÕt qu¶ 10
KÕt qu¶ 11
KÕt qu¶ 12
Hình thang
H
A
B
C
D
a
a
a
a
2
ABCD
AB DC AD
S
và
,2BD BC BC a
Hình ngũ giác đều cạnh
a
a
36
0
A
B
C
O
D
E
H
2
0
5
5.
4tan 36
ABCDEF OBC
a
SS

Hình lục giác đều cạnh
a
a
60
0
O
F
E
D
C
B
A
2
33
6.
2
ABCDEF OBC
a
SS

TÝnh chÊt quan träng
TÝnh chÊt 1
TÝnh chÊt 2
TÝnh chÊt 3
b
a
I
P
Δ
;
;;
ab
P
a b P a b I

Δ
2
Δ
1
P
12
12
12
;
//
PP
Q
Δ
P
;
//
PQ
PQ
PQ
TÝnh chÊt 4
TÝnh chÊt 5
TÝnh chÊt 6
Q
Δ
P
P
PQ
Q



d
Q
P
H
A
;
:,
P Q P Q d
A P AH d H d
AH Q
R
Q
Δ
P
QP
R P P
QR
Cố gắng lên các em học sinh thân yêu của tôi! Thầy tin mọi việc rồi sẽ tốt đẹp thôi!
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 1 CLB Giáo viên trẻ TP Huế
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
Một số bài tập tương tự từ:
§Ò MINH HäA Sè 3
¤N THI THPT QuèC GIA
Giáo viên: LÊ BÁ BẢO Trường THPT Đặng Huy Trứ, Huế
SĐT: 0935.785.115 Địa chỉ: 116/04 Nguyễn Lộ Trạch, TP Huế
Câu 1: (Đề minh họa số 3 2017) Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a
SA
vuông
góc với đáy,
SD
tạo với mặt phẳng
SAB
một góc bằng
0
30 .
Tính thể tích
V
của khối chóp
..S ABCD
A.
3
6
.
18
a
V
B.
3
3.Va
C.
3
6
.
3
a
V
D.
3
3
.
3
a
V
Lời giải
Ta có:
;.
AD AB
AD SAB SD SAB DSA
AD SA

Xét tam giác
SAD
vuông tại
:A
tan
AD
DSA
SA
3
tan
AD
SA a
DSA
và
2
.
ABCD
Sa
Vậy
3
.
13
..
33
S ABCD ABCD
a
V SA S
Chọn đáp án D.
a
30
0
S
D
C
B
A
Chúng ta xét tiếp các bài tập tương tự
Câu 2: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a
hai mặt phẳng
SAB
và
SAD
cùng vuông góc với đáy,
SC
tạo với mặt phẳng
SAB
một góc bằng
0
30 .
Tính thể tích
V
của khối
chóp
..S ABCD
A.
3
6
.
3
a
V
B.
3
2
.
3
a
V
C.
3
6
.
6
a
V
D.
3
2.Va
Lời giải
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 2 CLB Giáo viên trẻ TP Huế
Ta có:
.
SAB ABCD
SA ABCD
SAD ABCD

và
;.
BC AB
BC SAB SC SAB BSC
BC SA

Xét tam giác
SBC
vuông tại
:B
tan
BC
BSC
SB
22
3 2.
tan
BC
SB a SA SB AB a
BSC
và
2
.
ABCD
Sa
Vậy
3
.
12
..
33
S ABCD ABCD
a
V SA S
Chọn đáp án B.
a
30
0
A
B
C
D
S
Câu 3: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a
SA
vuông góc với đáy,
SD
tạo với
mặt phẳng
SAC
một góc bằng
0
30 .
Tính thể tích
V
của khối chóp
..S ABCD
A.
3
.
3
a
V
B.
3
3.Va
C.
3
3
.
3
a
V
D.
3
23
.
3
a
V
Lời giải
Gọi
O
là tâm hình vuông
,ABCD
ta có:
;.
DO AC
DO SAC SD SAC DSO
DO SA

Xét tam giác
SOD
vuông tại
:O
sin 2
sin
OD OD
DSO SD a SA a
SD
DSO
và
2
.
ABCD
Sa
Vậy
3
.
1
..
33
S ABCD ABCD
a
V SA S
Chọn đáp án A.
O
a
30
0
A
B
C
D
S
Câu 4: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a
SA
vuông góc với đáy,
AC
tạo với
mặt phẳng
SBD
một góc bằng
0
45 .
Tính thể tích
V
của khối chóp
..S ABCD
A.
3
2
.
6
a
V
B.
3
2
.
2
a
V
C.
3
6
.
6
a
V
D.
3
2.Va
Lời giải
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 3 CLB Giáo viên trẻ TP Huế
Ta có:
BD AC
BD SAC
BD SA


SAC SBD
.
Dựng
AH SO AH SBD
0
; 45AC SBD AOH SOA
suy ra
SAO
vuông cân tại
2
2
a
A SA OA
và
2
.
ABCD
Sa
Vậy
3
.
12
..
36
S ABCD ABCD
a
V SA S
Chọn đáp án A.
H
45
0
O
S
D
C
B
A
a
Câu 5: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a
mặt bên
SAB
là tam giác cân tại
S
và nằm trong mặt vuông góc với đáy,
SC
tạo với mặt đáy một góc bằng
0
60 .
Tính thể tích
V
của
khối chóp
..S ABCD
A.
3
15
.
2
a
V
B.
3
3.Va
C.
3
15
.
6
a
V
D.
3
3
.
3
a
V
Lời giải
Dựng
SH AB H
là trung điểm
.AB
Do
.SAB ABCD SH ABCD
Vậy
0
; 60 .SC ABCD SCH
Xét tam giác
SHC
vuông tại
15
: tan
2
SH a
H SCH SH
HC
và
2
.
ABCD
Sa
Vậy
3
.
1 15
..
36
S ABCD ABCD
a
V SH S
Chọn đáp án C.
A
B
C
D
S
H
60
0
a
Câu 6: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a
mặt bên
SAB
là tam giác cân tại
S
và nằm trong mặt vuông góc với đáy,
SC
tạo với mặt phẳng
SAB
một góc
0
45 .
Tính thể tích
V
của khối chóp
..S ABCD
A.
3
3
.
2
a
V
B.
3
3
.
6
a
V
C.
3
6
.
3
a
V
D.
3
3
.
3
a
V
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 4 CLB Giáo viên trẻ TP Huế
Lời giải
Ta có:
;.
BC AB
BC SAB SC SAB BSC
BC SH

Xét tam giác
BSC
vuông cân tại
.B SB BC a
Vậy tam giác
SAB
đều cạnh
3
2
a
a SH
và
2
.
ABCD
Sa
Vậy
3
.
13
..
36
S ABCD ABCD
a
V SH S
Chọn đáp án B.
45
0
a
H
S
D
C
B
A
Câu 7: Cho hình chóp
.S ABCD
có đáy là hình thoi cạnh
,a
0
60ABC
,
SA
vuông góc với đáy,
SD
tạo với mặt phẳng
SAC
một góc bằng
0
45 .
Tính thể tích
V
của khối chóp
..S ABCD
A.
3
6
.
18
a
V
B.
3
3.Va
C.
3
6
.
3
a
V
D.
3
6
.
12
a
V
Lời giải
Do
ABCD
là hình thoi cạnh
a
và
0
60ABC
nên tam giác
ABC
đều. Vậy
22
33
2 2. .
42
ABCD ABC
aa
SS
Ta có:
BD AC
BD SAC
BD SA


0
; 45 .SD SAC DSO
Vậy tam giác
SOD
vuông cân tại
3
.
2
a
O SO DO
Xét tam giác
SAO
vuông tại
:A
22
2
2
a
SA SO AO
3
.
16
..
3 12
S ABCD ABCD
a
V SA S
Chọn đáp án D.
O
A
B
C
D
S
45
0
a
Câu 8: Cho hình chóp
.S ABCD
có đáy là hình thoi cạnh
,a
0
60ABC
,
SA
vuông góc với đáy,
SC
tạo với mặt phẳng
SAB
một góc bằng
0
45 .
Tính thể tích
V
của khối chóp
..S ABCD
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 5 CLB Giáo viên trẻ TP Huế
A.
3
6
.
4
a
V
B.
3
6
.
12
a
V
C.
3
6
.
3
a
V
D.
3
3
.
2
a
V
Lời giải
Do
ABCD
là hình thoi cạnh
a
và
0
60ABC
nên tam giác
ABC
đều. Vậy
22
33
2 2. .
42
ABCD ABC
aa
SS
Dựng
CH AB H
là trung điểm
.AB
Ta có:
CH AB
CH SAB
CH SA


0
; 45 .SC SAB HSC
Vậy tam giác
SHC
vuông cân tại
3
.
2
a
H SH HC
Xét tam giác
SAH
vuông tại
22
2
:.
2
a
A SA SH AH
Vậy
3
.
16
..
3 12
S ABCD ABCD
a
V SA S
Chọn đáp án B.
45
0
a
S
D
C
B
A
H
Câu 9: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật có
,2AB a BC a
và
,SA SC SB SD
,
SC
tạo với mặt đáy một góc bằng
0
60 .
Tính thể tích
V
của khối chóp
..S ABCD
A.
3
15
.
3
a
V
B.
3
15
.
4
a
V
C.
3
15
.
2
a
V
D.
3
4 15
.
3
a
V
Lời giải
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 6 CLB Giáo viên trẻ TP Huế
Gọi
O
là tâm đáy, ta có:
SO AC
SO BD

;.SO ABCD SC ABCD SCO
Xét tam giác
SCO
vuông tại
15
: tan tan
2
SO a
O SCO SO OC SCO
OC
và
2
2.
ABCD
Sa
Vậy
3
.
1 15
..
33
S ABCD ABCD
a
V SO S
Chọn đáp án A.
a
2a
60
0
S
D
C
B
A
O
Câu 10: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật có
,2AB a BC a
và
,SA SC SB SD
, mặt phẳng
SBC
tạo với mặt đáy một góc bằng
0
30 .
Tính thể tích
V
của khối
chóp
..S ABCD
A.
3
3
.
9
a
V
B.
3
3
.
3
a
V
C.
3
3
.
4
a
V
D.
3
23
.
3
a
V
Lời giải
Gọi
O
là tâm đáy, ta có:
SO AC
SO BD

;.SO ABCD SC ABCD SCO
Dựng
OH BC BC SOH BC SH
vậy
0
; 60 .SBC ABCD SHO
Xét tam giác
SHO
vuông tại
3
: tan tan
6
SO a
O SHO SO OH SHO
OH
và
2
2.
ABCD
Sa
Vậy
3
.
13
..
39
S ABCD ABCD
a
V SO S
Chọn đáp án A.
H
O
A
B
C
D
S
60
0
2a
a
Câu 11: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật
ABCD
có
2 2 ,CD BC a
SA
vuông góc với đáy,
SD
tạo với mặt phẳng
SAC
một góc bằng
0
45 .
Tính thể tích
V
của khối chóp
..S ABCD
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 7 CLB Giáo viên trẻ TP Huế
A.
3
15
.
15
a
V
B.
3
2 15
.
15
a
V
C.
3
2 15
.
5
a
V
D.
3
15
.
3
a
V
Lời giải
Dựng
DH AC DH SAC
0
; 45 .SD ABCD DSH
Vậy
SHD
vuông cân tại
.H SH HD
Tam giác
ACD
vuông tại
D
:
2 2 2 2
1 1 1 5 2 5
5
4
a
DH
DH DA DC a
22
5
.
5
a
AH AD DH
Suy ra:
22
15
5
a
SA SH AH
và
2
2.
ABCD
Sa
Vậy
3
.
1 2 15
..
3 15
S ABCD ABCD
a
V SA S
Chọn đáp án B.
a
45
0
H
2a
S
D
C
B
A
O
NHÓM HAI MẶT PHẲNG VUÔNG GÓC
Câu 12: Cho tứ diện
ABCD
có
ABC
là tam giác đều cạnh
,a
tam giác
BCD
vuông cân tại
D
và nằm trong mặt phẳng vuông góc với
.AB C
Tính thể tích
V
của khối tứ diện
.ABCD
A.
3
3
.
6
a
V
B.
3
.
12
a
V
C.
3
3
.
8
a
V
D.
3
3
.
24
a
V
Lời giải
Dựng
,AH BC
do
.ABC BCD AH BCD
Ta có, do
ABC
đều
3
2
a
AH
và
2
1
..
24
BCD
a
S DH BC
Vậy
3
13
..
3 24
ABCD BCD
a
V AH S
Chọn đáp án D.
a
H
D
C
B
A
a
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 8 CLB Giáo viên trẻ TP Huế
Câu 13: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a
mặt bên
SAB
là tam giác đều
và nằm trong mặt phẳng vuông góc với
.A B CD
Tính thể tích
V
của khối chóp
..S ABCD
A.
3
3
.
6
a
V
B.
3
.
12
a
V
C.
3
3
.
8
a
V
D.
3
3
.
24
a
V
Lời giải
Dựng
,SH AB
do
.SAB ABCD SH ABCD
Ta có, do
SAB
đều
3
2
a
SH
và
2
.
ABCD
Sa
Vậy
3
.
13
..
36
S ABCD ABCD
a
V SH S
Chọn đáp án A.
A
B
C
D
S
H
a
Câu 14: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a
mặt bên
SAB
nằm trong mặt
phẳng vuông góc với
0
, 30 , 2 .ABCD SAB SA a
Tính thể tích
V
của khối chóp
..S ABCD
A.
3
3
.
6
a
V
B.
3
.
3
a
V
C.
3
.
9
a
V
D.
3
.Va
Lời giải
Dựng
,SH AB
do
.SAB ABCD SH ABCD
Ta có, do
SHA
vuông tại
H
:
sin .sin
SH
SAH SH SA SAH a
SA
và
2
.
ABCD
Sa
Vậy
3
.
1
..
33
S ABCD ABCD
a
V SH S
Chọn đáp án B.
30
0
a
H
S
D
C
B
A
Câu 15: Cho tứ diện
ABCD
có
ABC
là tam giác đều cạnh
,a
tam giác
BCD
cân tại
D
và nằm
trong mặt phẳng vuông góc với
.AB C
Biết
AD
hợp với mặt phẳng
ABC
một góc
0
60 .
Tính thể
tích
V
của khối tứ diện
.ABCD
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 9 CLB Giáo viên trẻ TP Huế
A.
3
3
.
6
a
V
B.
3
.
12
a
V
C.
3
3
.
8
a
V
D.
3
3
.
24
a
V
Lời giải
Dựng
,AH BC
do
.ABC BCD AH BCD
Ta có, do
ABC
đều
3
2
a
AH
và
DH BC DH ABC
0
; 60 .AD ABC HAD
Xét tam giác
AHD
vuông tại
: tan
HD
H HAD
AH
3
.tan
2
a
HD AH HAD
.
Vậy
3
13
..
38
ABCD ABC
a
V HD S
Chọn đáp án C.
60
0
a
A
B
C
D
H
a
Câu 16: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a
mặt bên
SAB
nằm trong mặt
phẳng vuông góc với
0
, 60 , 2 .ABCD SAB SA a
Tính thể tích
V
của khối chóp
..S ABCD
A.
3
3
.
3
a
V
B.
3
.
3
a
V
C.
3
23
.
3
a
V
D.
3
.Va
Lời giải
Dựng
,SH AB
do
.SAB ABCD SH ABCD
Ta có, do
SHA
vuông tại
H
:
sin .sin 3.
SH
SAH SH SA SAH a
SA
và
2
.
ABCD
Sa
Vậy
3
.
13
..
33
S ABCD ABCD
a
V SH S
Chọn đáp án A.
A
B
C
D
S
H
a
60
0
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 10 CLB Giáo viên trẻ TP Huế
Câu 17: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật
, 2 2 ,ABCD BC AB a
tam giác
SAC
nằm trong mặt phẳng vuông góc với
0
, 60 , 2 .ABCD SAB SA a
Tính thể tích
V
của khối
chóp
..S ABCD
A.
3
3
.
3
a
V
B.
3
.
3
a
V
C.
3
23
.
3
a
V
D.
3
.Va
Lời giải
Dựng
,SH AC
do
.SAC ABCD SH ABCD
Ta có, do
SHA
vuông tại
H
:
sin .sin 3.
SH
SAH SH SA SAH a
SA
và
2
2.
ABCD
Sa
Vậy
3
.
1 2 3
..
33
S ABCD ABCD
a
V SH S
Chọn đáp án C.
60
0
2a
a
H
S
D
C
B
A
Câu 18: Cho hình chóp
.S ABCD
có đáy là hình thoi cạnh
,a
0
30CAD
, tam giác
SAB
đều và
nằm trong mặt phẳng vuông góc với
0
, 60 , 2 .ABCD SAB SA a
Tính thể tích
V
của khối chóp
..S ABCD
A.
3
.
12
a
V
B.
3
.
4
a
V
C.
3
23
.
3
a
V
D.
3
.Va
Lời giải
Dựng
,SH AB
do
.SAB ABCD SH ABCD
Ta có, do
SAB
là tam giác đều nên
3
2
a
SH
. Do
ABCD
là hình thoi cạnh
a
và
0
30CAD
nên
BAD
đều. Suy ra
22
33
2. .
42
ABCD
aa
S 
Vậy
3
.
1
..
34
S ABCD ABCD
a
V SH S
Chọn đáp án B.
60
0
2a
a
H
S
D
C
B
A
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 11 CLB Giáo viên trẻ TP Huế
NHÓM HÌNH CHIẾU VUÔNG GÓC
Câu 19: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
,a
hình chiếu vuông góc của
S
trên mặt phẳng
ABC
là trung điểm của
BC
và
2.SB a
Tính thể tích
V
của khối chóp
..S ABC
A.
3
35
.
8
a
V
B.
3
3
.
24
a
V
C.
3
5
.
8
a
V
D.
3
3
.
12
a
V
Lời giải
Xét tam giác
SBH
vuông tại
22
15
:
2
a
H SH SB BH
và
2
3
.
4
ABC
a
S
Vậy
3
.
15
..
38
S ABC ABC
a
V SH S
Chọn đáp án C.
a
H
A
C
B
S
2a
Câu 20: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
,a
hình chiếu vuông góc của
S
trên mặt phẳng
ABC
là trung điểm của
BC
và
SA
hợp với đáy một góc
0
60 .
Tính thể tích
V
của
khối chóp
..S ABC
A.
3
3
.
8
a
V
B.
3
3
.
24
a
V
C.
3
5
.
8
a
V
D.
3
3
.
12
a
V
Lời giải
Do
0
; 60 .SH ABC SA ABC SAH
Xét tam giác
SAH
vuông tại
3
: .tan
2
a
H SH AH SAH
và
2
3
.
4
ABC
a
S
Vậy
3
.
13
..
38
S ABC ABC
a
V SH S
Chọn đáp án A.
60
0
S
B
C
A
H
a
Câu 21: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
,a
hình chiếu vuông góc của
S
trên mặt phẳng
ABC
là trung điểm của
BC
và
SB
hợp với đáy một góc
0
60 .
Tính thể tích
V
của
khối chóp
..S ABC
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 12 CLB Giáo viên trẻ TP Huế
A.
3
3
.
8
a
V
B.
3
3
.
24
a
V
C.
3
.
8
a
V
D.
3
3
.
12
a
V
Lời giải
Do
0
; 60 .SH ABC SB ABC SBH
Xét tam giác
SBH
vuông tại
3
: .tan
2
a
H SH BH SBH
và
2
3
.
4
ABC
a
S
Vậy
3
.
1
..
38
S ABC ABC
a
V SH S
Chọn đáp án C.
60
0
S
B
C
A
H
a
Câu 22: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
,a
hình chiếu vuông góc của
S
trên mặt phẳng
ABC
là trung điểm của
BC
và
SAB
hợp với đáy một góc
0
45 .
Tính thể tích
V
của khối chóp
..S ABC
A.
3
3
.
16
a
V
B.
3
.
16
a
V
C.
3
.
8
a
V
D.
3
3
.
12
a
V
Lời giải
Do
HK AB AB SHK AB SK
0
; 45 .SAB ABC SKH
Gọi
M
là trung điểm
13
,
24
a
AB HK CM
do tam giác
SHK
vuông cân tại
3
4
a
H SH HK
và
2
3
.
4
ABC
a
S
Vậy
3
.
1
..
3 16
S ABC ABC
a
V SH S
Chọn đáp án B.
45
0
M
K
a
H
A
C
B
S
Câu 23: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
,a
hình chiếu vuông góc của
S
trên mặt phẳng
ABC
là điểm
H
trên cạnh
BC
sao cho
2,CH HB SB
hợp với đáy một góc
0
60 .
Tính thể tích
V
của khối chóp
..S ABC
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 13 CLB Giáo viên trẻ TP Huế
A.
3
.
12
a
V
B.
3
.
6
a
V
C.
3
.
4
a
V
D.
3
3
.
12
a
V
Lời giải
Do
0
; 60 .SH ABC SB ABC SBH
Xét tam giác
SBH
vuông tại
3
: .tan
3
a
H SH BH SBH
và
2
3
.
4
ABC
a
S
Vậy
3
.
1
..
3 12
S ABC ABC
a
V SH S
Chọn đáp án A.
60
0
S
B
C
A
H
a
Câu 24: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
,a
hình chiếu vuông góc của
S
trên mặt phẳng
ABC
là điểm
H
trên cạnh
BC
sao cho
2,HC BH SA
hợp với đáy một góc
0
60 .
Tính thể tích
V
của khối chóp
..S ABC
A.
3
.
12
a
V
B.
3
7
.
12
a
V
C.
3
.
4
a
V
D.
3
3
.
8
a
V
Lời giải
Do
0
; 60 .SH ABC SA ABC SAH
Xét tam giác
:AHB
2
2 2 2
7
2 . .cos .
9
a
AH AB BH AB BH ABH
7
.
3
a
AH
Xét tam giác
SAH
vuông tại
21
: .tan
3
a
H SH AH SBH
và
2
3
.
4
ABC
a
S
Vậy
3
.
17
..
3 12
S ABC ABC
a
V SH S
Chọn đáp án B.
60
0
a
H
A
C
B
S
A
B
C
H
a
60
0
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 14 CLB Giáo viên trẻ TP Huế
Câu 25: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
,a
hình chiếu vuông góc của
S
trên mặt phẳng
ABC
là điểm
H
trên cạnh
BC
sao cho
2,HC BH
và tam giác
SAH
vuông cân.
Tính thể tích
V
của khối chóp
..S ABC
A.
3
21
.
36
a
V
B.
3
7
.
12
a
V
C.
3
.
4
a
V
D.
3
3
.
8
a
V
Lời giải
Do
0
; 60 .SH ABC SA ABC SAH
Xét tam giác
:AHB
2
2 2 2
7
2 . .cos .
9
a
AH AB BH AB BH ABH
7
.
3
a
AH
Do tam giác
SAH
vuông cân tại
H
nên
SH AH
và
2
3
.
4
ABC
a
S
Vậy
3
.
1 21
..
3 36
S ABC ABC
a
V SH S
Chọn đáp án A.
60
0
a
H
A
C
B
S
A
B
C
H
a
60
0
Câu 26: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
,a
hình chiếu vuông góc của
S
trên mặt phẳng
ABC
là điểm
H
trên cạnh
BC
sao cho
2,HC BH SAB
hợp với đáy một góc
0
60 .
Tính thể tích
V
của khối chóp
..S ABC
A.
3
3
.
24
a
V
B.
3
3
.
12
a
V
C.
3
3
.
4
a
V
D.
3
3
.
6
a
V
Lời giải
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 15 CLB Giáo viên trẻ TP Huế
Gọi
M
là trung điểm
.AB
Dựng
//HK AB HK CM
và
13
.
36
a
HK CM
Ta có
AB SHK AB SK
0
; 60 .SAB ABC SKH
Xét tam giác
SKH
vuông tại
: .tan
2
a
H SH KH SKH
và
2
3
.
4
ABC
a
S
Vậy
3
.
13
..
3 24
S ABC ABC
a
V SH S
Chọn đáp án A.
K
M
S
B
C
A
H
a
60
0
K
M
a
H
C
B
A
SẼ CÒN UPDATE RẤT NHIỀU TRONG THỜI GIAN TỚI....
CÁC EM HỌC SINH THÂN YÊU CỐ GẮNG LÊN NHÉ! Huế 19.5.2017
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 1 CLB Giáo viên trẻ TP Huế
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
Một số bài tập tương tự từ:
§Ò MINH HäA Sè 3
¤N THI THPT QuèC GIA
Giáo viên: LÊ BÁ BẢO Trường THPT Đặng Huy Trứ, Huế
SĐT: 0935.785.115 Địa chỉ: 116/04 Nguyễn Lộ Trạch, TP Huế
DẠNG TOÁN 1: ThÓ tÝch khèi l¨ng trô
Nhóm giả thiết 1: CẠNH BÊN VUÔNG GÓC VỚI ĐÁY
Câu 1: Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông cân tại
, , 2 .A AB a BB a

Tính thể tích
V
của khối lăng trụ
.ABC A B C
A.
3
2
.
3
a
V
B.
3
.Va
C.
3
.
3
a
V
D.
3
2.Va
Lời giải
Ta có:
2
1
..
22
A B C
a
S A B A C

Vậy
3
..
A B C
V BB S a

Chọn đáp án B.
a
a
A'
C'
C
B
A
Câu 2: Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác đều cạnh
,a
mặt bên
ABB A

là hình vuông. Tính thể tích
V
của khối lăng trụ
.ABC A B C
A.
3
3
.
12
a
V
B.
3
3
.
4
a
V
C.
3
3
.
3
a
V
D.
3
2.Va
Lời giải
Ta có:
2
3
.
4
A B C
a
S
Do
ABB A

là hình vuông nên
.BB A B a

Vậy
3
3
..
4
A B C
a
V BB S

Chọn đáp án B.
a
A
B
C
B'
C'
A'
Câu 3: Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác đều cạnh
,a
tam giác
A B A

cân. Tính thể tích
V
của khối lăng trụ
.ABC A B C
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 2 CLB Giáo viên trẻ TP Huế
A.
3
3
.
12
a
V
B.
3
3
.
4
a
V
C.
3
3
.
3
a
V
D.
3
2.Va
Lời giải
Ta có:
2
3
.
4
A B C
a
S
Do
A B A

vuông cân tại
.A A A A B a
Vậy
3
3
..
4
A B C
a
V BB S

Chọn đáp án B.
a
A
B
C
B'
C'
A'
Câu 4: Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác đều cạnh
, 2 .a AB a
Tính
thể tích
V
của khối lăng trụ
.ABC A B C
A.
3
.
4
a
V
B.
3
3
.
2
a
V
C.
3
3
.
4
a
V
D.
3
2.Va
Lời giải
Ta có:
2
3
.
4
A B C
a
S
Do
A B A

vuông tại
22
3.A A A B A A B a
Vậy
3
3
..
4
A B C
a
V A A S

Chọn đáp án C.
2a
a
A
B
C
B'
C'
A'
Câu 5: Tính thể tích
V
của khối lăng trụ tam giác đều
.ABC A B C
có tất cả các cạnh đều bằng
2.a
A.
3
2 3 .Va
B.
3
23
.
3
a
V
C.
3
3
.
4
a
V
D.
3
2 3 .Va
Lời giải
Do
.ABC A B C
là lăng trụ đều nên đường cao của lăng trụ
là
2BB a
và
2
2
32
3.
4
A B C
a
Sa

Vậy
3
. 2 3 .
A B C
V BB S a

Chọn đáp án A.
a
a
A
B
C
B'
C'
A'
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 3 CLB Giáo viên trẻ TP Huế
Câu 6: Tính thể tích
V
của khối lăng trụ tứ giác đều
.ABCD A B C D
có tất cả các cạnh đều bằng
2.a
A.
3
8
.
3
a
V
B.
3
2
.
3
a
V
C.
3
8.Va
D.
3
2 3 .Va
Lời giải
Do
.ABCD A B C D
là lăng trụ đều nên đường cao của
lăng trụ là
2BB a
và
2
2
2 4 .
A B C D
S a a

Vậy
3
. 8 .
A B C
V BB S a

Chọn đáp án C.
2a
A'
D'
B'
C'
2a
D
A
B
C
2a
Câu 7: Cho hình lăng trụ ngũ giác đều
.ABCDE A B C D E
có cạnh đáy bằng
2,
cạnh bên bằng
4.
Thể tích
V
của khối lăng trụ đã cho gần bằng giá trị nào sau đây?
A.
22,02.V
B.
7,34.V
C.
32,02.V
D.
27,53.V
Lời giải
Do
.ABCDE A B C D E
là lăng trụ đều nên đường cao của
lăng trụ là
4.BB
Tính diện tích ngũ giác đều
.A B C D E
Ta có:
00
0
1
72 36 .
tan36
tan
HB
B OC HOB OH
HOB
Vậy
0
15
5 5. . .
2
tan 36
A B C D E OB C
S S OH B C

0
20
'. 27,53.
tan 36
A B C D E
V BB S
H
E'
D'
O
C'
B'
A'
36
0
2
Chọn đáp án D.
O
72
0
4
2
A
B
C
D
E
E'
A'
D'
B'
C'
Câu 8: Cho hình lăng trụ lục giác đều
.ABCDEF A B C D E F
có cạnh đáy bằng
,a
cạnh bên bằng
2.a
Tính thể tích
V
của khối lăng trụ
..ABCDEF A B C D E F
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 4 CLB Giáo viên trẻ TP Huế
A.
3
33
.
2
a
V
B.
3
3 3 .Va
C.
3
6 3 .Va
D.
3
43
.
3
a
V
Lời giải
Do
.ABCDEF A B C D E F
là lăng trụ đều nên đường
cao của lăng trụ là
2.BB a
Tính diện tích lục giác
đều
.A B C D E F
Ta có:
0
60B OC OB C

là tam giác đều.
Vậy
22
3 3 3
6 6. .
42
A B C D E F OB C
aa
SS
3
'. 3 3 .
A B C D E F
V BB S a
A'
B'
C'
D'
E'
F'
O
60
0
a
Chọn đáp án B.
A
B
C
D
E
F
2a
a
F'
E'
A'
B'
C'
O
D'
60
0
Câu 9: Tính thể tích
V
của khối lập phương
.ABCD A B C D
có diện tích một mặt bằng
2
4.a
A.
3
8
.
3
a
V
B.
3
2
.
3
a
V
C.
3
8.Va
D.
3
2 3 .Va
Lời giải
Gọi cạnh hình lập phương là
0,mm
theo giả thiết
22
4 2 .m a m a
Vậy
3
3
2 8 .V a a
Chọn đáp án C.
m
m
A
B
C
D
A'
B'
C'
D'
Câu 10: Tính thể tích
V
của khối lập phương
.ABCD A B C D
có diện tích tất cả các mặt bằng
2
24 .cm
A.
3
8.V cm
B.
3
16 .V cm
C.
3
24 .V cm
D.
3
12 .V cm
Lời giải
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 5 CLB Giáo viên trẻ TP Huế
Gọi cạnh hình lập phương là
0,mm
suy ra diện tích
một mặt bằng
2
.m
Theo giả thiết
2
6 24 2.mm
Vậy
3
3
2 8 .V cm
Chọn đáp án A.
m
m
A
B
C
D
A'
B'
C'
D'
Câu 11: Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông cân tại
,,A AB a AB
hợp với đáy một góc
0
60 .
Tính thể tích
V
của khối lăng trụ
.ABC A B C
A.
3
3
.
6
a
V
B.
3
3.Va
C.
3
.
3
a
V
D.
3
3
.
2
a
V
Lời giải
Ta có:
2
1
..
22
A B C
a
S A B A C

Do
AA A B C
0
; 60 .AB A B C AB A
Xét tam giác
AB A

vuông tại
:A
tan 3.A A A B AB A a

Vậy
3
3
..
2
A B C
a
V AA S

Chọn đáp án D.
60
0
A
B
C
B'
C'
A'
a
a
Câu 12: Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông cân tại
,,A AB a AB
hợp với mặt phẳng
ACC A

một góc
0
60 .
Tính thể tích
V
của khối lăng trụ
.ABC A B C
A.
3
23
.
3
a
V
B.
3
3
.
6
a
V
C.
3
.
3
a
V
D.
3
3
.
2
a
V
Lời giải
Ta có:
2
1
..
22
A B C
a
S A B A C

Do
AA A B
và
A B A C
A B ACC A

0
; 60 .AB A B C B AA
Xét tam giác
AB A

vuông tại
:A
3
tan .
3
tan
A B A B a
B AA A A
AA
B AA

Vậy
3
3
..
6
A B C
a
V AA S

Chọn đáp án B.
60
0
a
a
A'
C'
B'
C
B
A
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 6 CLB Giáo viên trẻ TP Huế
Câu 13: Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông cân tại
,,A AB a AB C

hợp với mặt đáy một góc
0
30 .
Tính thể tích
V
của khối lăng trụ
.ABC A B C
A.
3
6
.
6
a
V
B.
3
6
.
36
a
V
C.
3
6
.
12
a
V
D.
3
6
.
4
a
V
Lời giải
Ta có:
2
1
..
22
A B C
a
S A B A C

Dựng
,A M B C
do
AA B C
B C AMA B C AM
0
; 30 .AB C A B C AMA
Xét tam giác
AMA
vuông tại
:A
6
tan .
6
a
A A A M AMA

Vậy
3
6
..
12
A B C
a
V AA S

Chọn đáp án C.
M
A
B
C
B'
C'
A'
a
a
30
0
Câu 14: Cho hình lăng trụ tam giác đều
.ABC A B C
có cạnh đáy bằng
,a AB
hợp với mặt
đáy một góc
0
60 .
Tính thể tích
V
của khối lăng trụ
.ABC A B C
A.
3
3
.
4
a
V
B.
3
.
4
a
V
C.
3
3
.
12
a
V
D.
3
3
.
4
a
V
Lời giải
Ta có:
2
3
.
4
A B C
a
S
Do
A A A B C
0
; 60 .AB A B C AB A
Xét tam giác
AB A

vuông tại
:A
tan 3.A A A B AB A a

Vậy
3
3
..
4
A B C
a
V AA S

Chọn đáp án A.
a
a
a
A'
C'
B'
C
B
A
60
0
Câu 15: Cho hình lăng trụ tam giác đều
.ABC A B C
có cạnh đáy bằng
,a AC
hợp với mặt
phẳng
ABB A

một góc
0
45 .
Tính thể tích
V
của khối lăng trụ
.ABC A B C
A.
3
6
.
24
a
V
B.
3
3
.
4
a
V
C.
3
6
.
8
a
V
D.
3
6
.
4
a
V
Lời giải
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 7 CLB Giáo viên trẻ TP Huế
Ta có:
2
3
.
4
A B C
a
S
Dựng
C H A B C H ABB A
0
; 45 .AC ABB A C AH
Suy ra
AHC
vuông cân
tại
3
.
2
a
H HC AH
Xét tam giác
A AH
vuông tại
22
2
:.
2
a
A A A AH A H
Vậy
3
6
..
8
A B C
a
V AA S

Chọn đáp án C.
H
45
0
A
B
C
B'
C'
A'
a
a
a
Câu 16: Cho hình lăng trụ tam giác đều
.ABC A B C
có cạnh đáy bằng
,a AB C

hợp với
mặt đáy một góc
0
60 .
Tính thể tích
V
của khối lăng trụ
..ABC A B C
A.
3
3
.
24
a
V
B.
3
3
.
4
a
V
C.
3
3
.
8
a
V
D.
3
33
.
8
a
V
Lời giải
Ta có:
2
3
.
4
A B C
a
S
Dựng
,A M B C
do
AA B C
B C AMA B C AM
0
; 60 .AB C A B C AMA
Xét tam giác
AMA
vuông tại
:A
3
tan .
2
a
A A A M AMA

Vậy
3
33
..
8
A B C
a
V AA S

Chọn đáp án D.
60
0
a
a
A'
C'
B'
C
B
A
M
Câu 17: Cho hình lăng trụ đứng
.ABCD A B C D
có đáy
ABCD
là hình thoi cạnh
0
, 30 , 2 .a BAC AB a

Tính thể tích
V
của khối lăng trụ
..ABCD A B C D
A.
3
3
.
6
a
V
B.
3
3
.
2
a
V
C.
3
3
.
8
a
V
D.
3
33
.
8
a
V
Lời giải
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 8 CLB Giáo viên trẻ TP Huế
Do
A B C D
là hình thoi cạnh
a
và
0
30B A D
nên
A B D
là tam giác đều cạnh
2
3
2.
2
A B C D A B D
a
a S S
Xét tam giác
A AB

vuông tại
22
:.A A A B A A B a
Vậy
3
3
..
2
A B C D
a
V AA S

Chọn đáp án B.
a
a
C
B
A
D
D'
C'
B'
A'
30
0
Câu 18: Cho hình lăng trụ đứng
.ABCD A B C D
có đáy
ABCD
là hình thoi cạnh
0
, 120 ,a ADC AC
hợp với đáy một góc
0
45 .
Tính thể tích
V
của khối lăng trụ
..ABCD A B C D
A.
3
.
2
a
V
B.
3
3
.
2
a
V
C.
3
3
.
8
a
V
D.
3
3
.
2
a
V
Lời giải
Do
A B C D
là hình thoi cạnh
a
và
0
120A D C
nên
A B D
là tam giác đều cạnh
2
3
2.
2
A B C D A B D
a
a S S
Do
0
; 45 .A A A B C D AC A B C D AC A
Suy ra
A AC

vuông cân tại
A
2 3 .A A A C A O a
Vậy
3
3
..
2
A B C D
a
V AA S

Chọn đáp án D.
O
45
0
60
0
A'
B'
C'
D'
D
A
B
C
a
a
Câu 19: Cho hình lăng trụ đứng
.ABCD A B C D
có đáy
ABCD
là hình thoi cạnh
0
, 120 ,a ADC ADC B

hợp với đáy một góc
0
45 .
Tính thể tích
V
của khối lăng trụ
..ABCD A B C D
A.
3
.
4
a
V
B.
3
3
.
2
a
V
C.
3
3
.
4
a
V
D.
3
3
.
2
a
V
Lời giải
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Giáo viên: LÊ BÁ BẢO...0935.785.115... 9 CLB Giáo viên trẻ TP Huế
Do
A B C D
là hình thoi cạnh
a
và
0
120A D C
nên
A B D
là tam giác đều cạnh
2
3
2.
2
A B C D A B D
a
a S S
Dựng
D M B C B C D DM B C DM
0
; 45 .ADC B A B C D DMD
Suy ra
D MD
vuông cân tại
D
3
.
2
a
D D D M

Vậy
3
3
..
4
A B C D
a
V DD S

Chọn đáp án C.
M
45
0
a
a
C
B
A
D
D'
C'
B'
A'
60
0
O
Câu 20: Cho hình lăng trụ đứng
.ABCD A B C D
có đáy
ABCD
là hình thoi tâm
O
cạnh
0
, 120 .a ADC
Biết
OC
hợp với
DBB D

một góc
0
60 .
Tính thể tích
V
của khối lăng trụ
..ABCD A B C D
A.
3
3
.
4
a
V
B.
3
3
.
2
a
V
C.
3
3
.
4
a
V
D.
3
3
.
12
a
V
Lời giải
Do
A B C D
là hình thoi cạnh
a
và
0
120A D C
nên
A B D
là tam giác đều cạnh
2
3
2.
2
A B C D A B D
a
a S S
Gọi
O
là tâm
C O B D
A B C D C O DBB D
C O DD

0
; 60 .OC DBB D C OO
Xét
O OC

vuông tại
: tan
OC
O O OC
OO

.
2
tan
O C a
OO
O OC


Vậy
3
3
..
4
A B C D
a
V O O S

Chọn đáp án A.
O'
60
0
a
a
C
B
A
D
D'
C'
B'
A'
60
0
O
| 1/32
| | Tải xuống

Có thể bạn quan tâm:

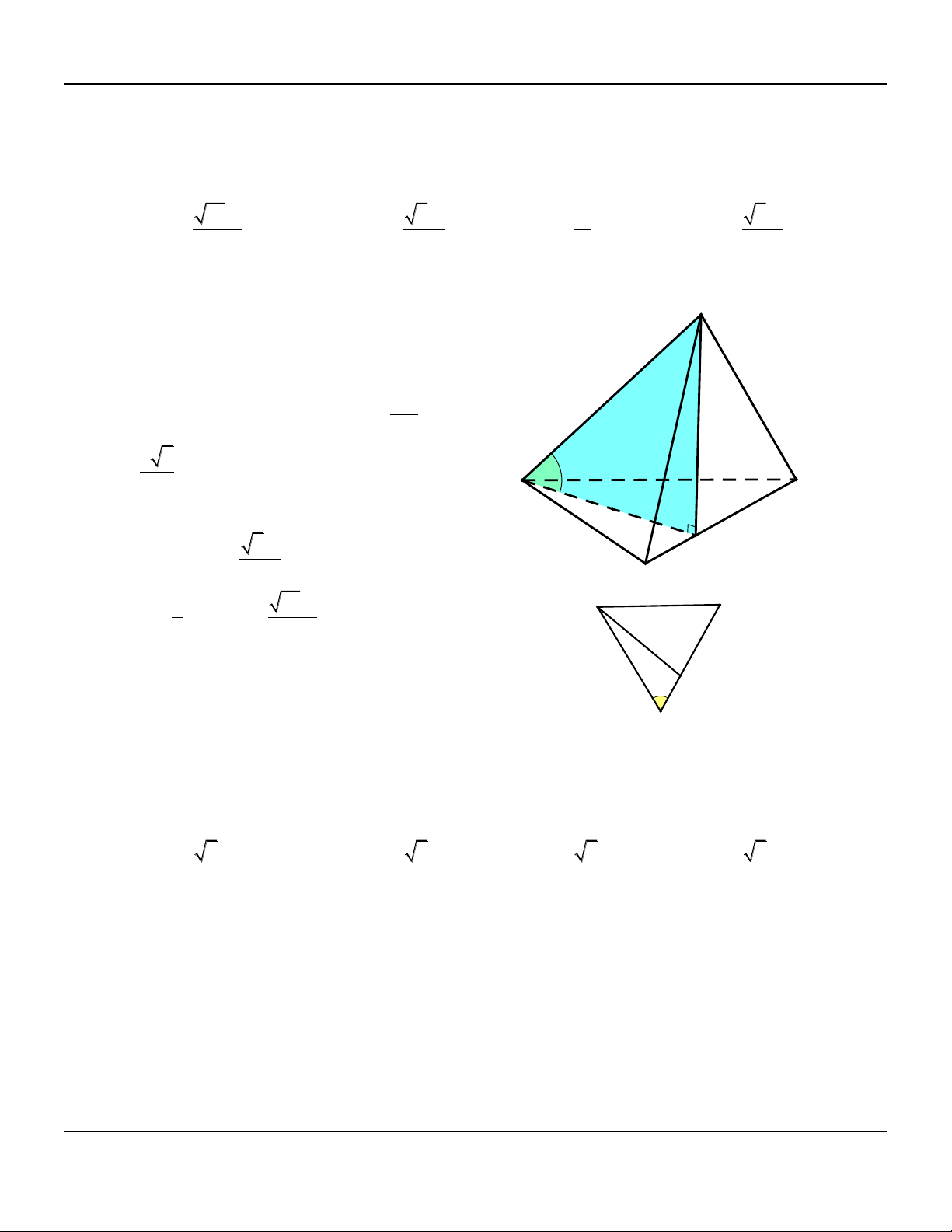
Preview text:


Giáo viên: LÊ BÁ BẢO_ Trường THPT Đặng Huy Trứ, Huế
SĐT: 0935.785.115 Địa chỉ: 116/04 Nguyễn Lộ Trạch, TP Huế Chuyªn ®Ò: THÓ TÝCH KhèI §A DIÖN Mét sè bµi tËp c¬ b¶n LuyÖn thi THPT 2017_2018 HuÕ, th¸ng 5/2017
[...Chuyªn ®Ò Tr¾c nghiÖm To¸n 12...] LuyÖn thi THPT Quèc gia 2018
TỔNG QUAN CÁC ĐIỂM LÝ THUYẾT CẦN LƯU Ý
Giáo viên: LÊ BÁ BẢO Trường THPT Đặng Huy Trứ, Huế
SĐT: 0935.785.115 Địa chỉ: 116/04 Nguyễn Lộ Trạch, TP Huế
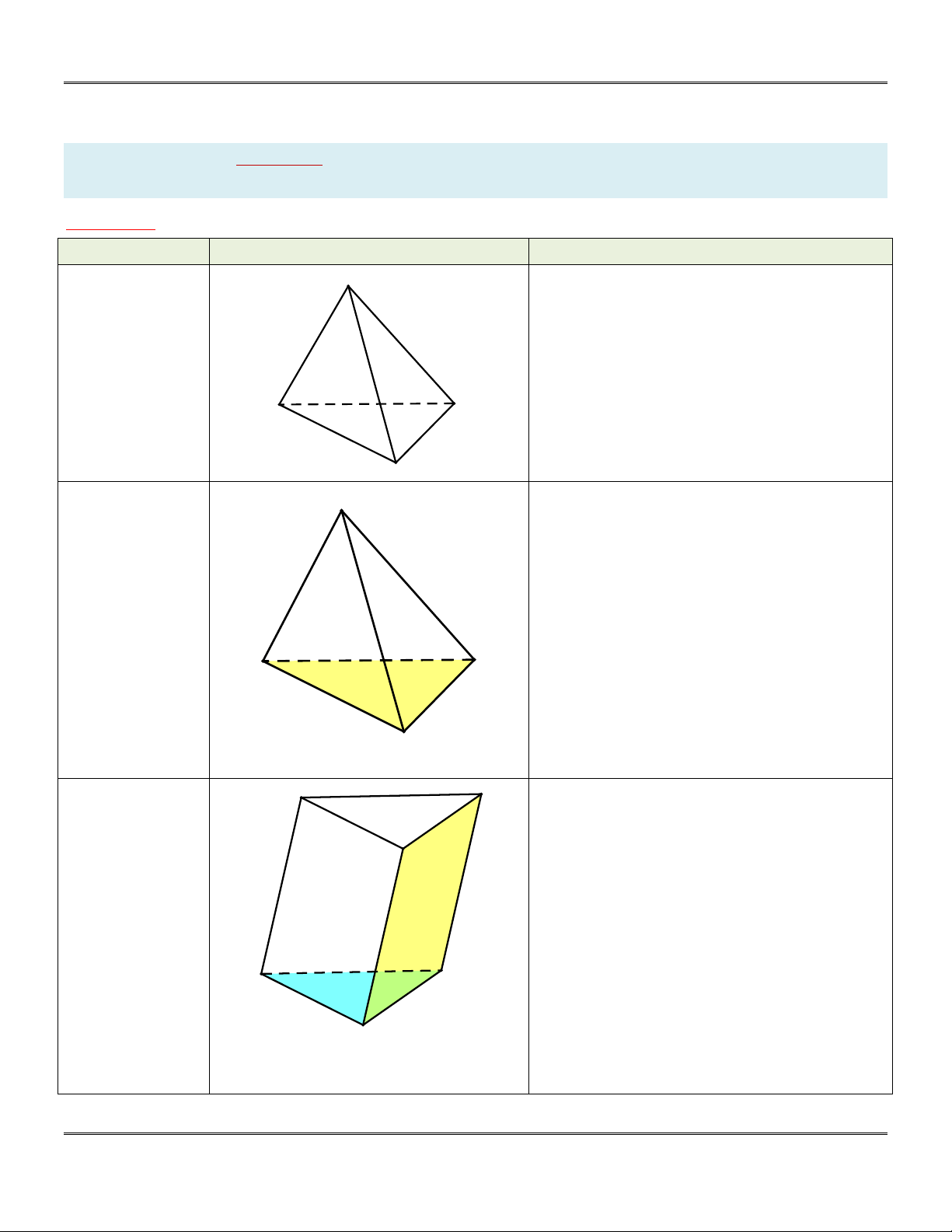
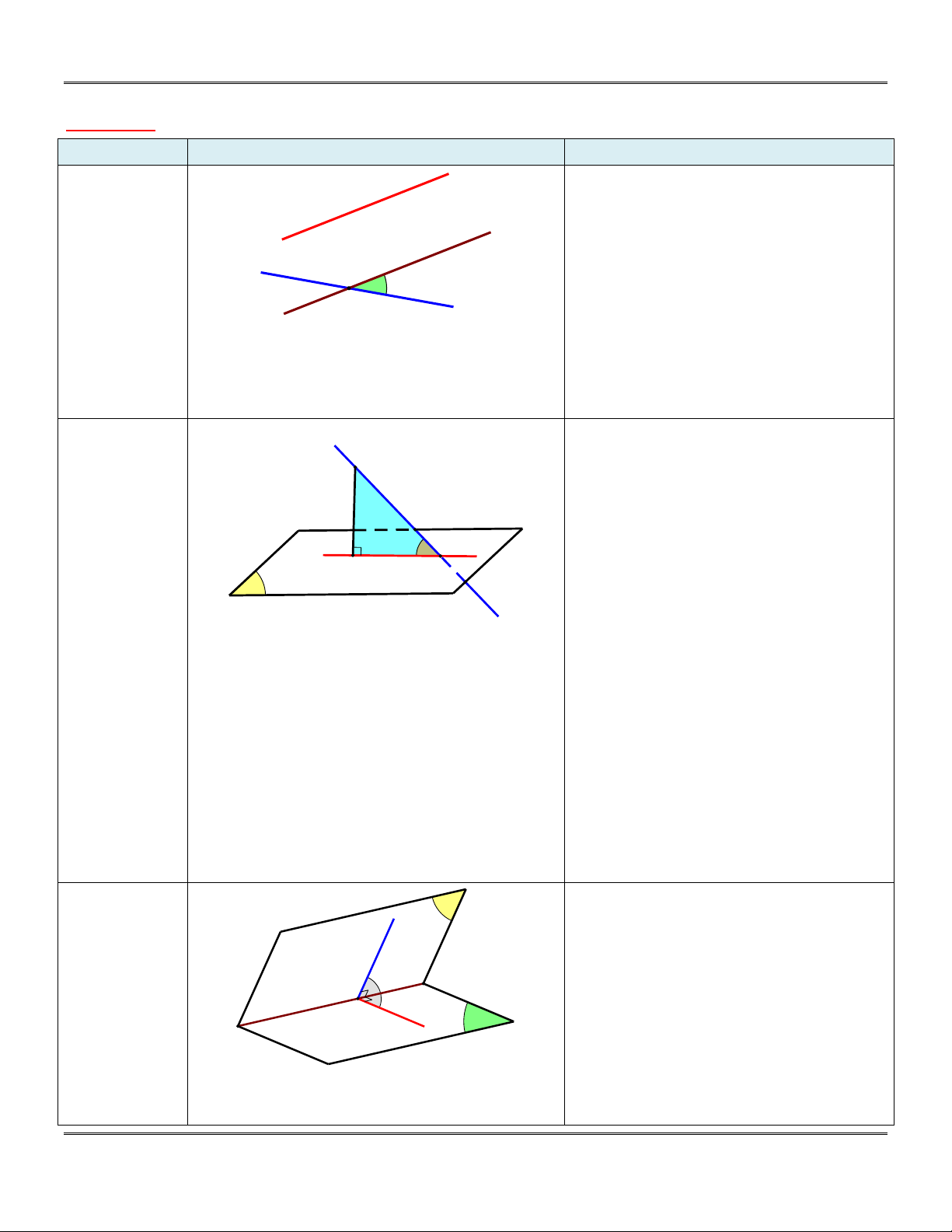
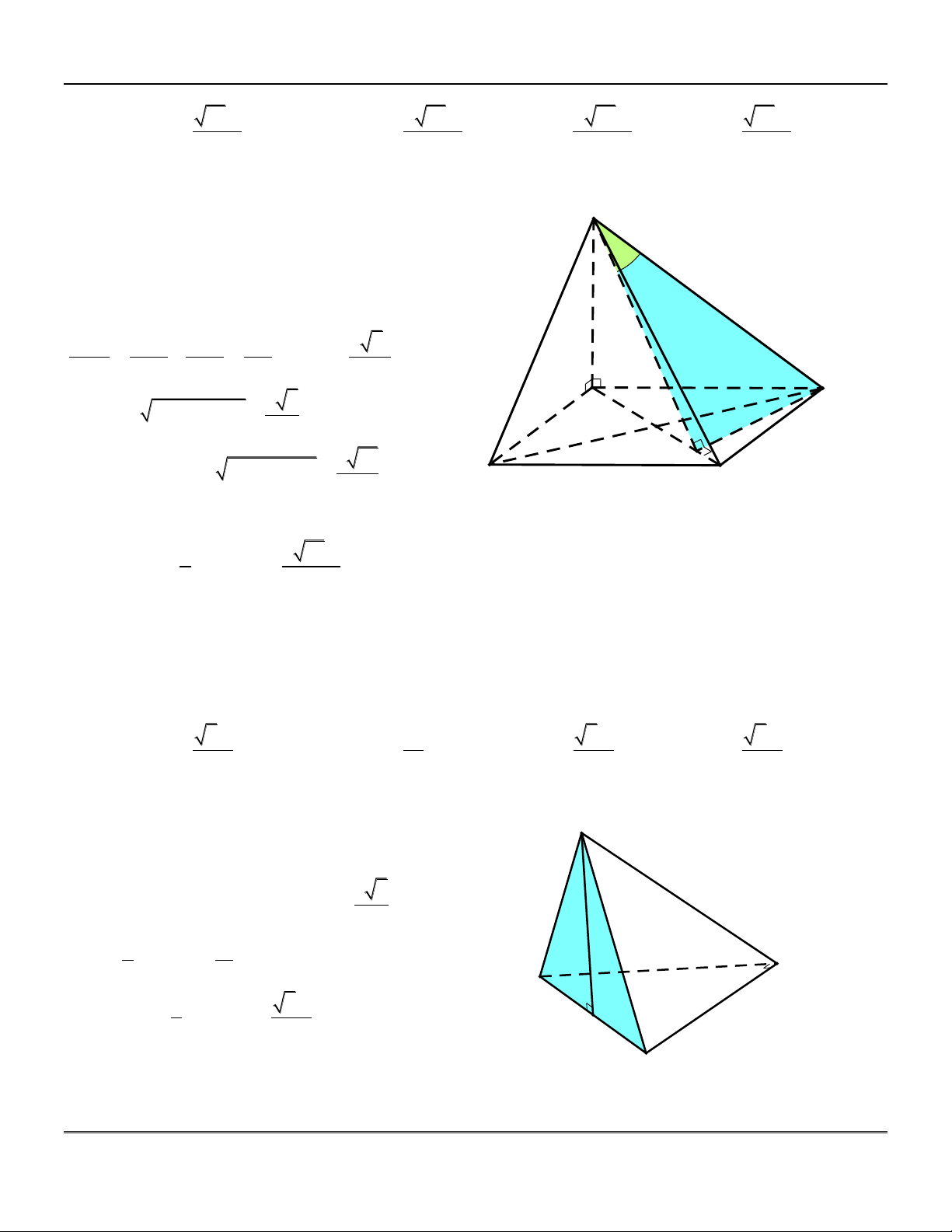
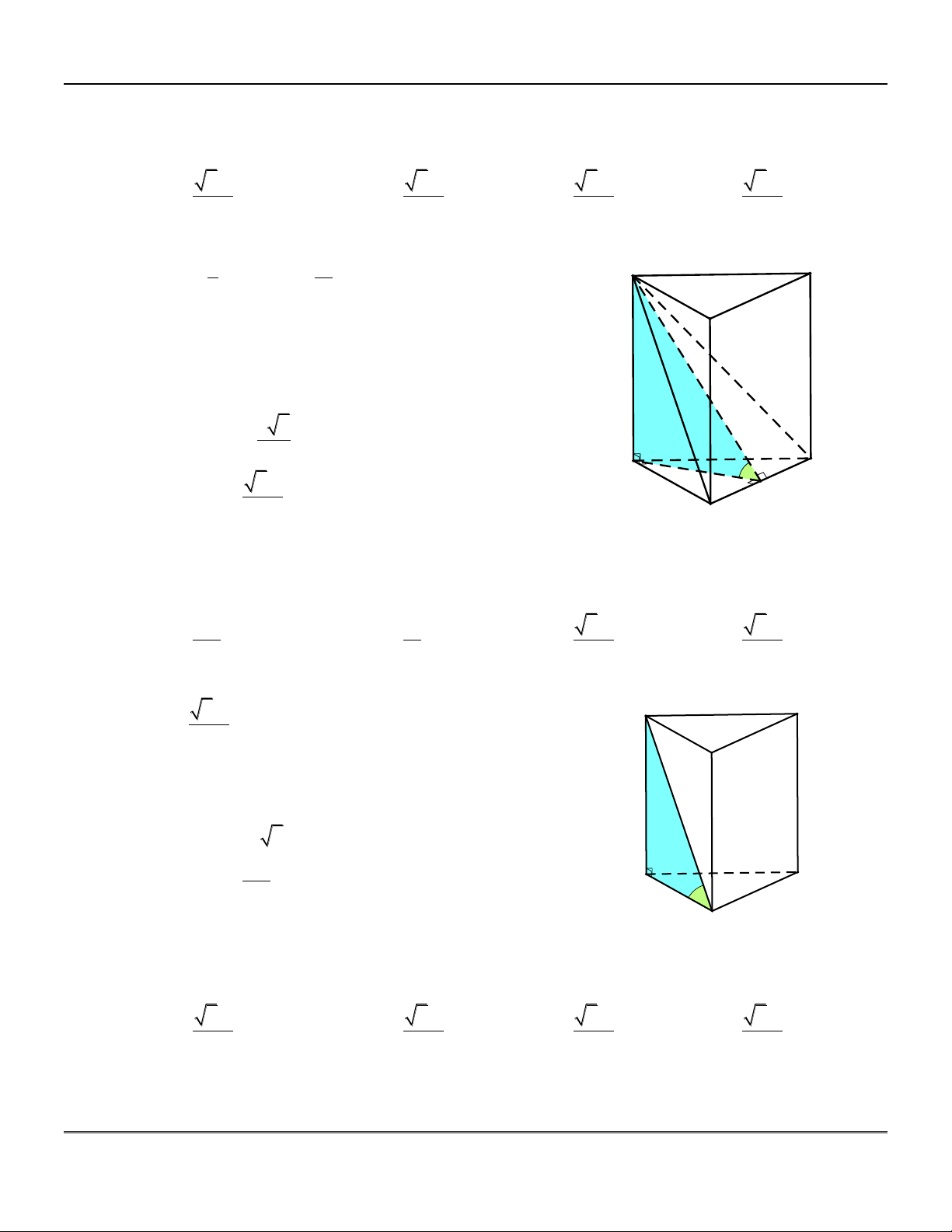
Phần 1: C¸C KhèI §A DIÖN, TÝNH CHÊT Vµ C¸CH DùNG H×nh ®a diÖn Dùng h×nh TÝnh chÊt Tø diÖn A
+) Có 4 mặt là các tam giác.
+) Không quy định đỉnh nào nằm trên
(tùy thuộc giả thiết để dựng cho phù hợp). * §Æc biÖt:
Tứ diện đều có tất cả các cạnh đều bằng B D
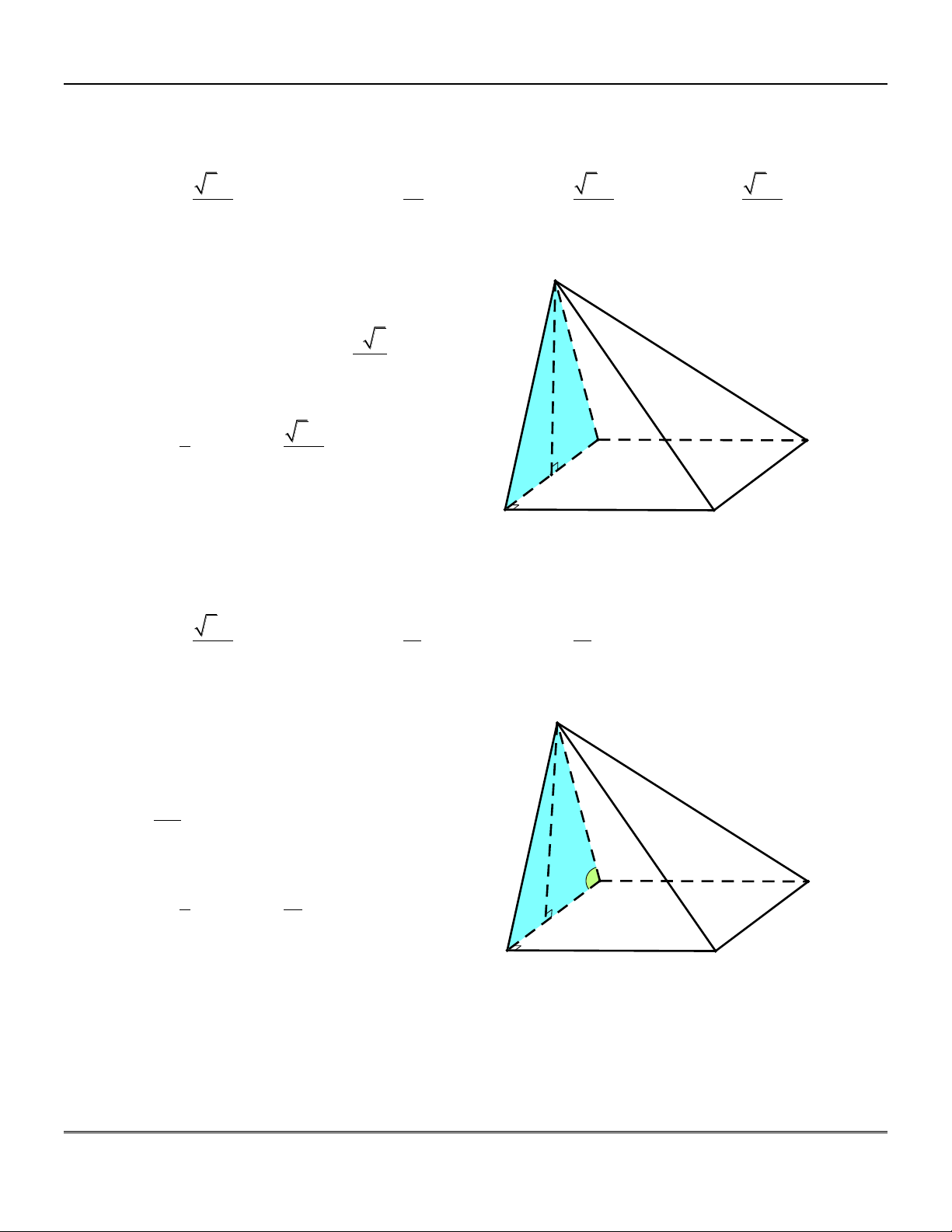
nhau (các mặt là các tam giác đều). C H×nh chãp S Hình chóp . S ABC :
+) Điểm S gọi là đỉnh của hình chóp.
+) Các cạnh bên SA, S , B S . C Đường
thẳng chứa SA có thể gọi tắt là cạnh bên. +) Các mặt bên SA ,
B SAC, SB . C Mặt
phẳng SAB gọi là mặt phẳng bên (gọi A C tắt là mặt bên).
+) Mặt đáy là đa giác AB . C Mặt phẳng ABCB
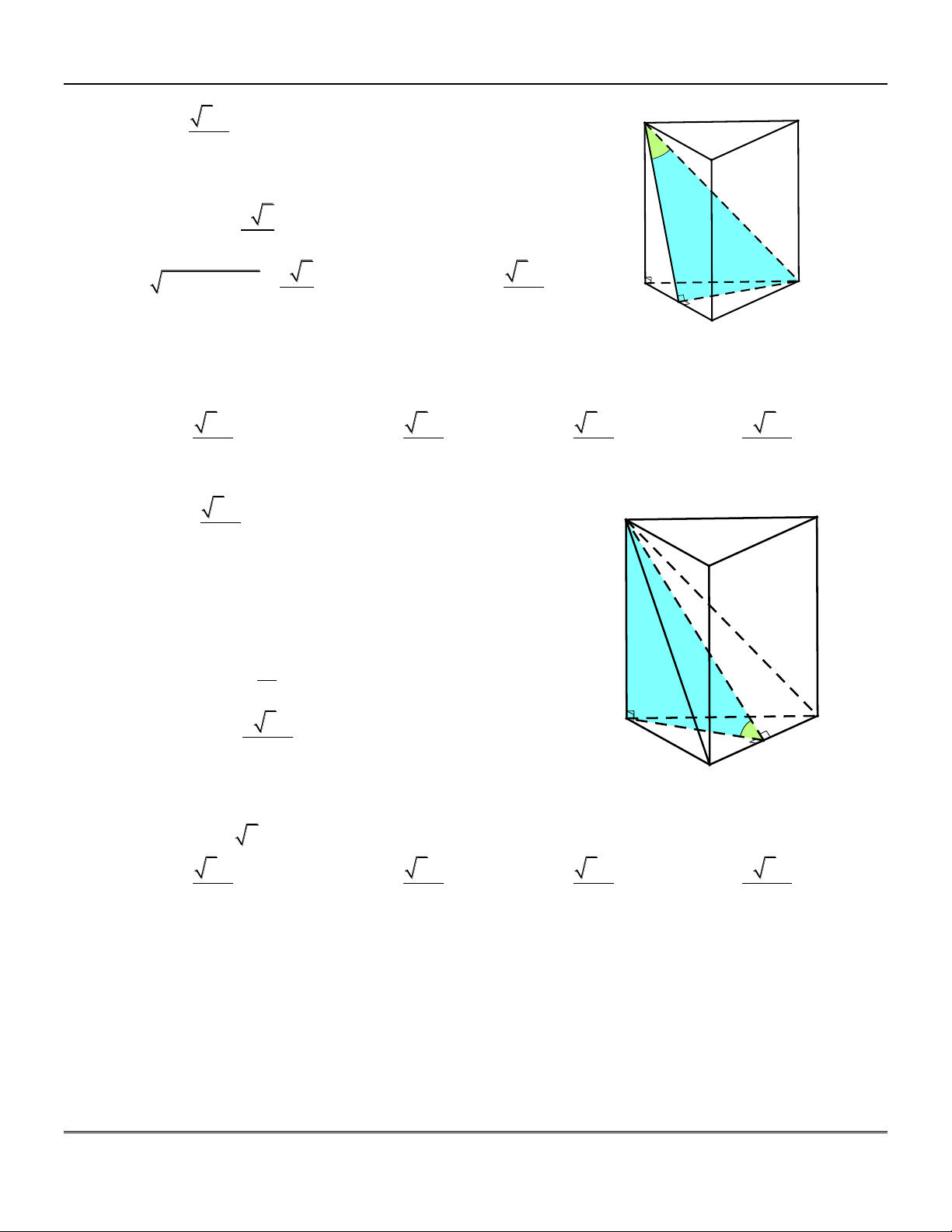
gọi là mặt phẳng đáy. (gọi tắt là mặt đáy). H×nh l¨ng A    C Hình lăng trụ AB . C A B C : trô
+) Hai đa giác ABC, A BC   bằng nhau và
ABC/ /A BC   B .
+) Các cạnh bên AA, BB, CC thỏa
AA / /BB / /CC và AA  BB  CC .
+) Các mặt bên ABB A  , BCC B  , ACC A   A' C' là các hình bình hành. * Chó ý:
Các cạnh bên đều hợp với đáy một góc B'
bằng nhau (có nghĩa là ta có thể dùng cạnh
bên nào và mặt đáy nào phù hợp).
Gi¸o viªn: Lª B¸ B¶o... 0935.785.115... 1 CLB Gi¸o viªn trÎ TP HuÕ
[...Chuyªn ®Ò Tr¾c nghiÖm To¸n 12...] LuyÖn thi THPT Quèc gia 2018 H×nh hép D
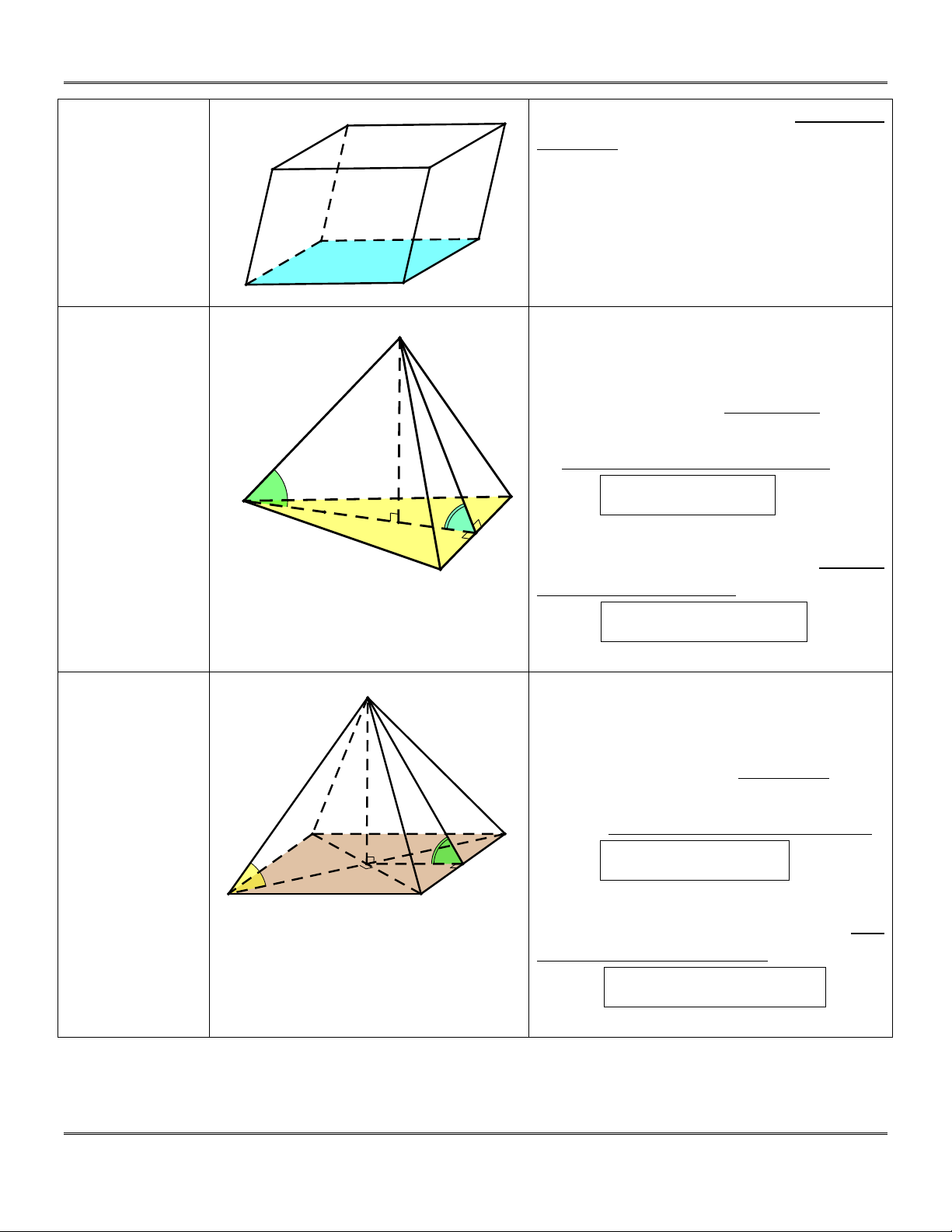
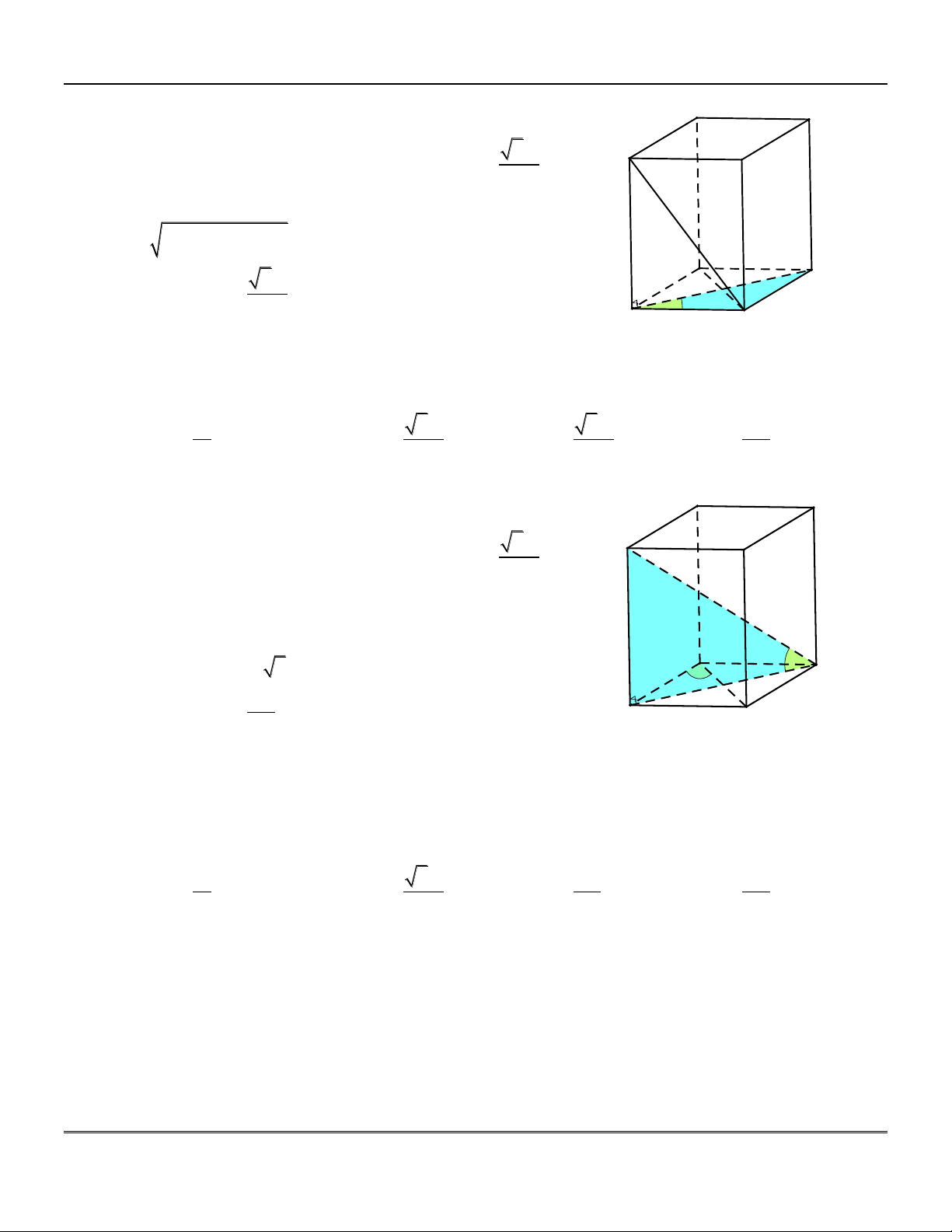
Hình hộp là hình lăng trụ có đáy là hình C bình hành. A B D' C' A' B' H×nh chãp S
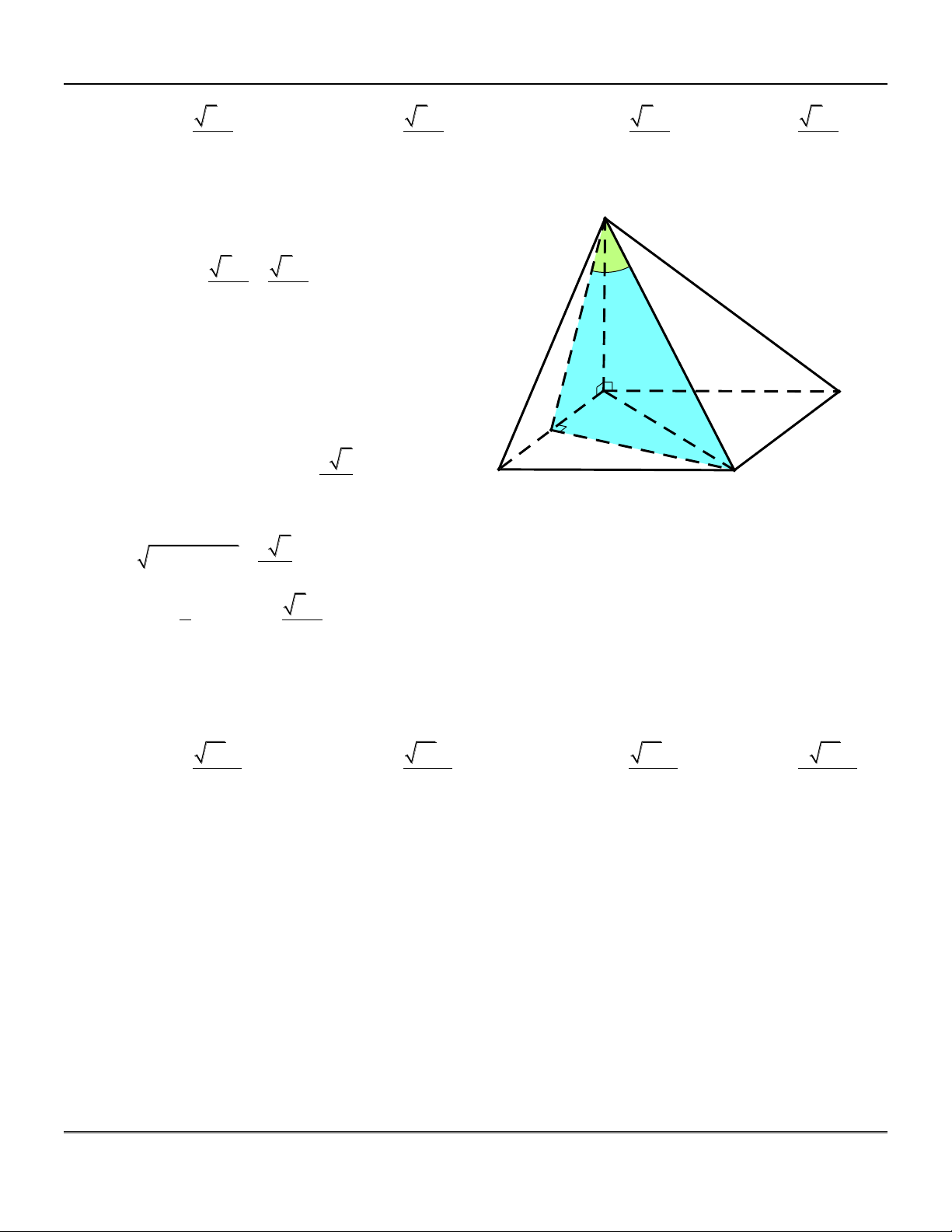
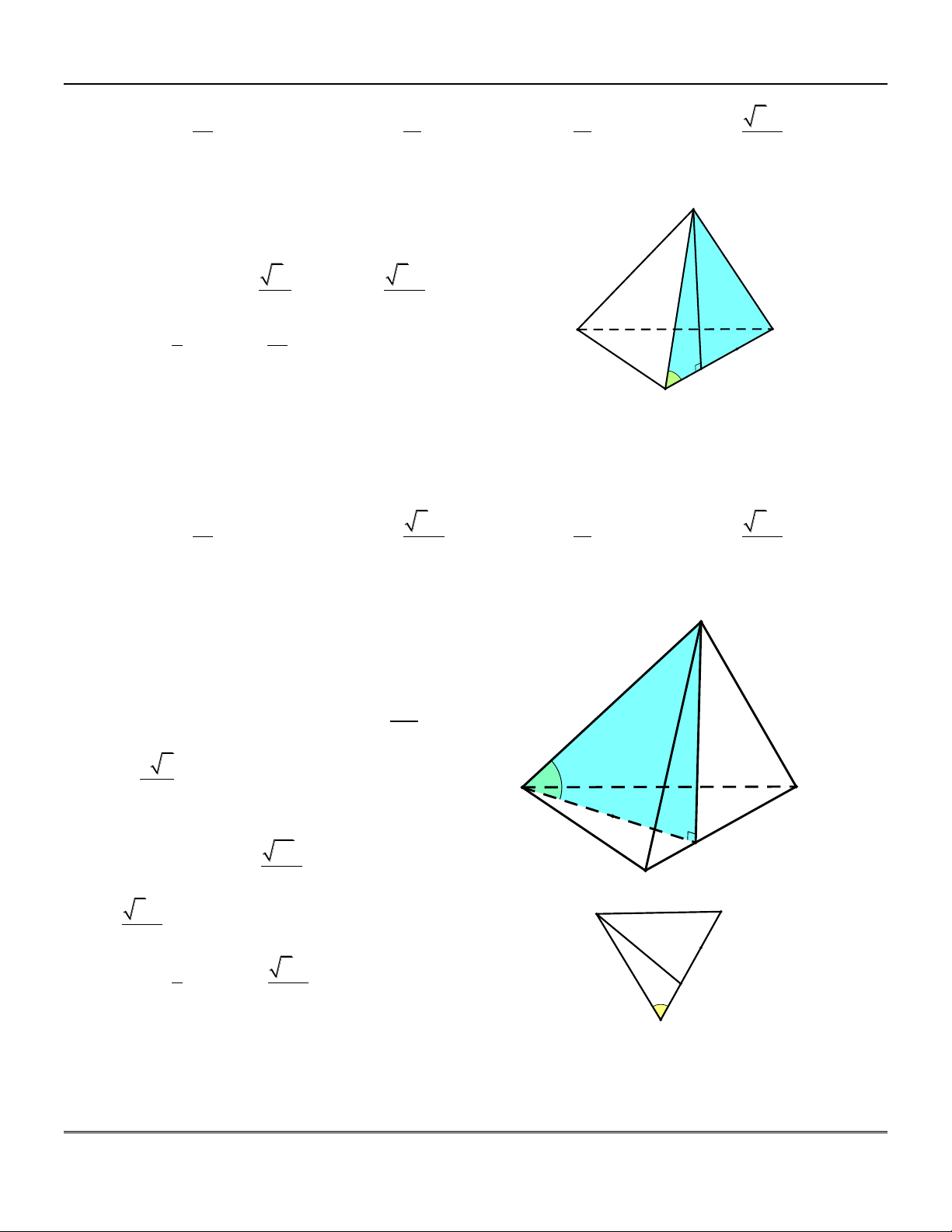
Hình chóp tam giác đều . S ABC : tam gi¸c ®Òu
+) Đường cao của hình chóp là SG, G là
tâm (trọng tâm) của đáy.
+) Đa giác đáy ABC là tam giác đều.
+) Các cạnh bên SA, S ,
B SC bằng nhau
và hợp với đáy một góc bằng nhau. C
S ;A ABC    SAG A Cụ thể:   G +) Các mặt bên SA ,
B SBC, SAC là các M
tam giác cân tại S , bằng nhau và hợp với B
đáy một góc bằng nhau.
Cụ thể: SBC;ABC 
SMG với M là trung điểm BC. H×nh chãp tø S
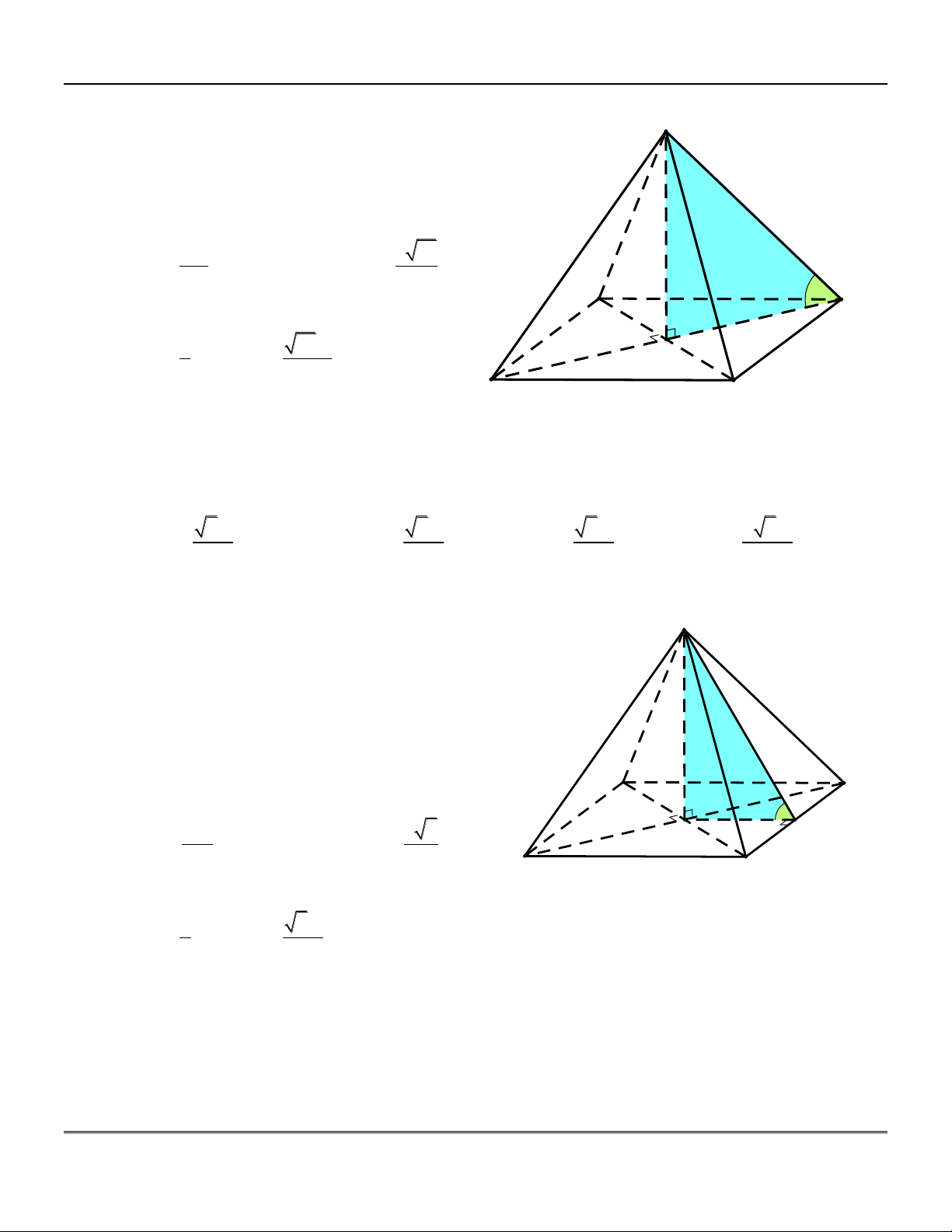
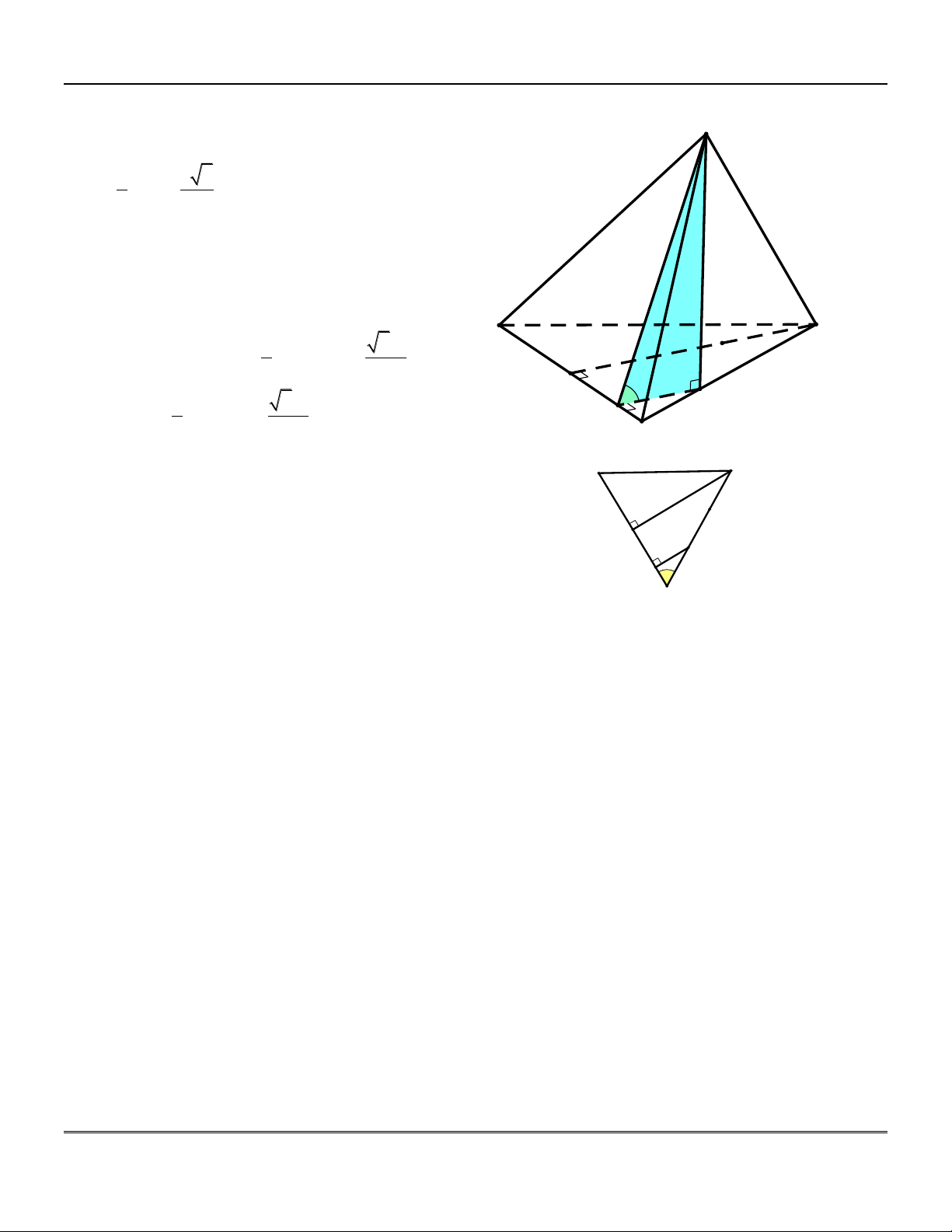
Hình chóp tứ giác đều . S ABCD : gi¸c ®Òu
+) Đường cao của hình chóp là SO, O là tâm của đáy.
+) Đa giác đáy ABCD là hình vuông.
+) Các cạnh bên SA, S ,
B SC, SD bằng D
nhau và hợp với đáy một góc bằng nhau C O
Cụ thể: S ;
A ABCD   SAO M +) Các mặt bên SA ,
B SBC, SCD, SAD là A B
các tam giác cân tại S , bằng nhau và hợp
với đáy một góc bằng nhau.
Cụ thể:SBC; ABCD 
SMO với M là trung điểm BC.
Gi¸o viªn: Lª B¸ B¶o... 0935.785.115... 2 CLB Gi¸o viªn trÎ TP HuÕ
[...Chuyªn ®Ò Tr¾c nghiÖm To¸n 12...] LuyÖn thi THPT Quèc gia 2018 H×nh l¨ng    A C
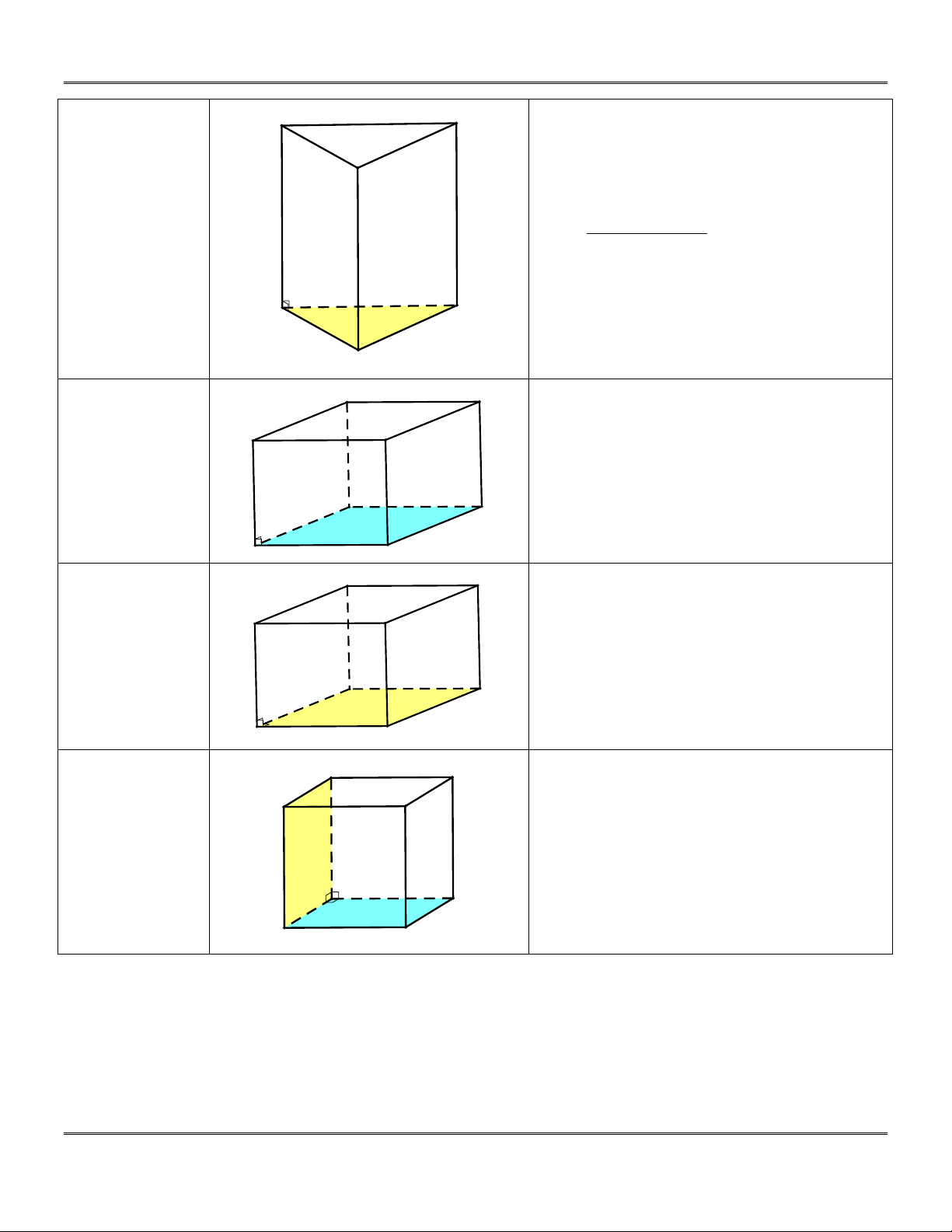
Hình lăng trụ đứng AB . C A B C : trô ®øng
+) Đường cao của lăng trụ là B
AA, BB, CC .
+) Các mặt bên ABB A  , ACC A  , BCC B   là các hình chữ nhật. A' C' B' H×nh hép D
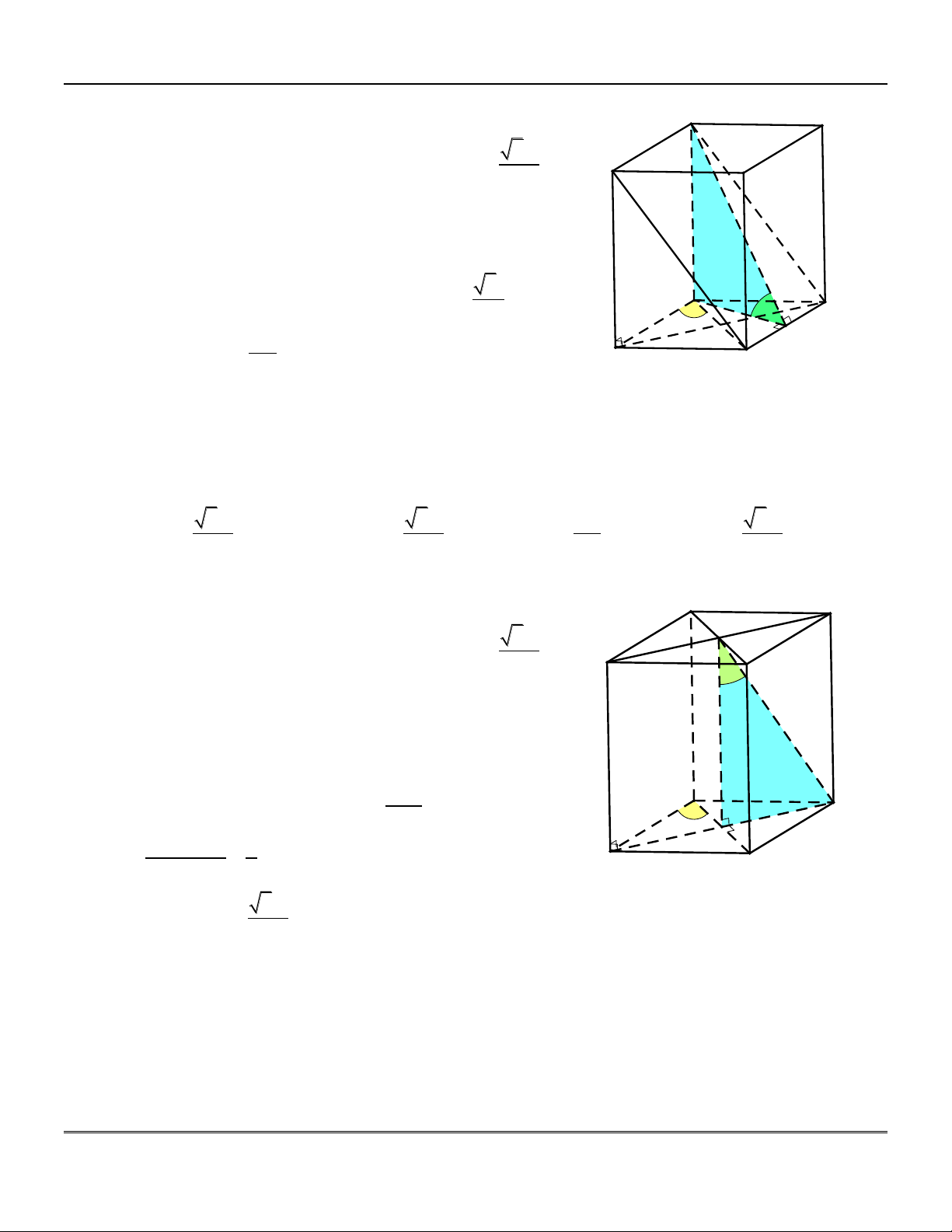
Hình hộp đứng ABC . D A BCD   : C ®øng
+) Đường cao của hình hộp là A B
AA, BB, CC, DD .
+) Các mặt bên ABB A  , ADD A  , D' BCC B  , CDD C
  là các hình chữ nhật. C' A' B' H×nh hép D
Hình hộp chữ nhật ABC . D A BCD   : C ch÷ nhËt
+) Đường cao của hình hộp là A B
AA, BB, CC, DD .
+) Các mặt bên ABB A  , ADD A  , D'     C'
BCC B , CDD A là các hình chữ nhật.
+) Đáy là hình chữ nhật. A' B' H×nh lËp     D
Hình lập phương ABC . D A B C D : C ph-¬ng
+) Đường cao của hình lập phương là A B
AA, BB, CC, DD,...
+) Tất cả 6 mặt đều là hình vuông. a D' a C' A' a B'
Gi¸o viªn: Lª B¸ B¶o... 0935.785.115... 3 CLB Gi¸o viªn trÎ TP HuÕ
[...Chuyªn ®Ò Tr¾c nghiÖm To¸n 12...] LuyÖn thi THPT Quèc gia 2018 Phần 2:
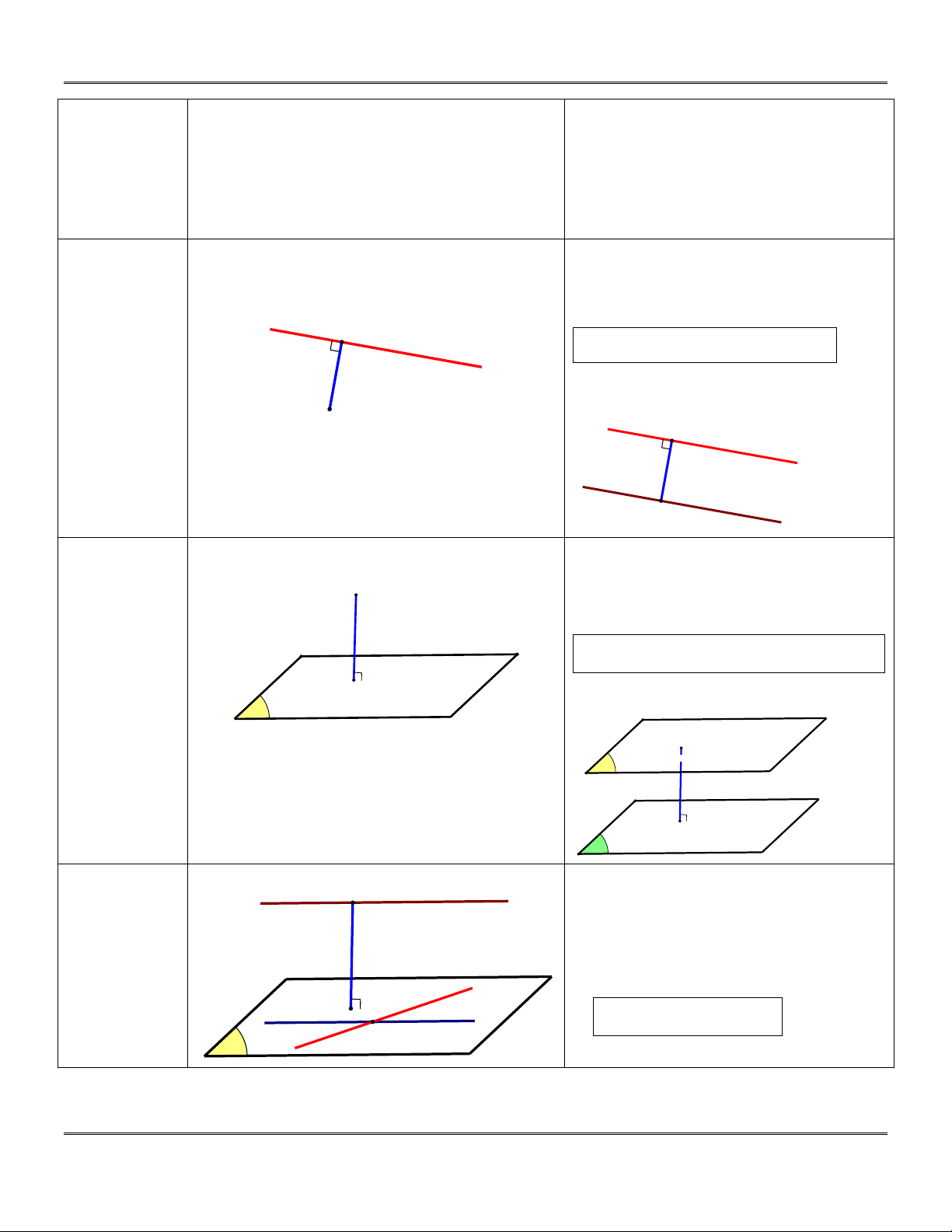
Kü N¡NG GãC Vµ KHO¶NG C¸CH Kü n¨ng C¸ch dùng Tr×nh bµy Gãc gi÷a
Gọi  ;    là góc giữa  và 1 2  1 hai ®-êng Δ1  . th¼ng d 2 +) 0 0 0    90 . I α  / / Δ2 +) 1 2          ;  00 1 2  1 2
+) Với  và  chéo nhau.        1 2 +)  ; 90 . 1 2  0 1 2 I 2 
  ;  d; . 1 2   2
I d : d / /  1 Gãc gi÷a d
Gọi d;P   là góc giữa d và P. ®-êng A    th¼ng vµ +) 0 0 0 90 . mÆt ph¼ng d / / P +) 0   0   d   P. d' α H I +) 0
  90  d  P. P
Xét d P  I, ta thực hiện chiếu vuông
góc đường thẳng d lên mặt phẳng PTrình bày:
được đường thẳng d   ;
d P  d;d. Cụ Do AH  P  HI là hình chiếu của thể:
AI trên P  AI P  ;  AIH.
+) Chiếu vuông góc AAd xuống P
được điểm H, chỉ rõ AH  P.
+) d P  ;  AIH. Gãc gi÷a
P ; Q   P Gọi    
là góc giữa P và hai mÆt d Q ph¼ng . α +) 0 0 0    90 . I Δ
P / /Q d' Q +) 0   0  
P  Q . +) 0
  90  P  Q.
Xét P Q  , chọn điểm I  sao cho:
Gi¸o viªn: Lª B¸ B¶o... 0935.785.115... 4 CLB Gi¸o viªn trÎ TP HuÕ
[...Chuyªn ®Ò Tr¾c nghiÖm To¸n 12...] LuyÖn thi THPT Quèc gia 2018
I d  P; I d  Q  d   d   
  P;Q  d;d. Kho¶ng  H 
d A;   AH :  . c¸ch tõ AH    ®iÓm ®Õn Δ §Æc biÖt: ®-êng H
 / /  d  ;   d ; A  với 1 2  1 2  2  th¼ng A  . 1 A Δ2 H Δ1 A Kho¶ng  H   P d A; P   c¸ch tõ  AH :  . A AH   P ®iÓm mÆt ph¼ng §Æc biÖt:
P / / Q  dP;Q  d ; A Q H
với A P. P A P H Q Kho¶ng
Cho hai đường thẳng  và  chéo Δ A 1 2 c¸ch gi÷a 1 nhau. hai ®-êng
+) Chọn P   :  / / P . Dựng  2 1   th¼ng chÐo nhau
trong P sao cho  / / . Δ 1 2 H Δ
+) d ;    d ;P 1 2 1 I P
Gi¸o viªn: Lª B¸ B¶o... 0935.785.115... 5 CLB Gi¸o viªn trÎ TP HuÕ
[...Chuyªn ®Ò Tr¾c nghiÖm To¸n 12...] LuyÖn thi THPT Quèc gia 2018
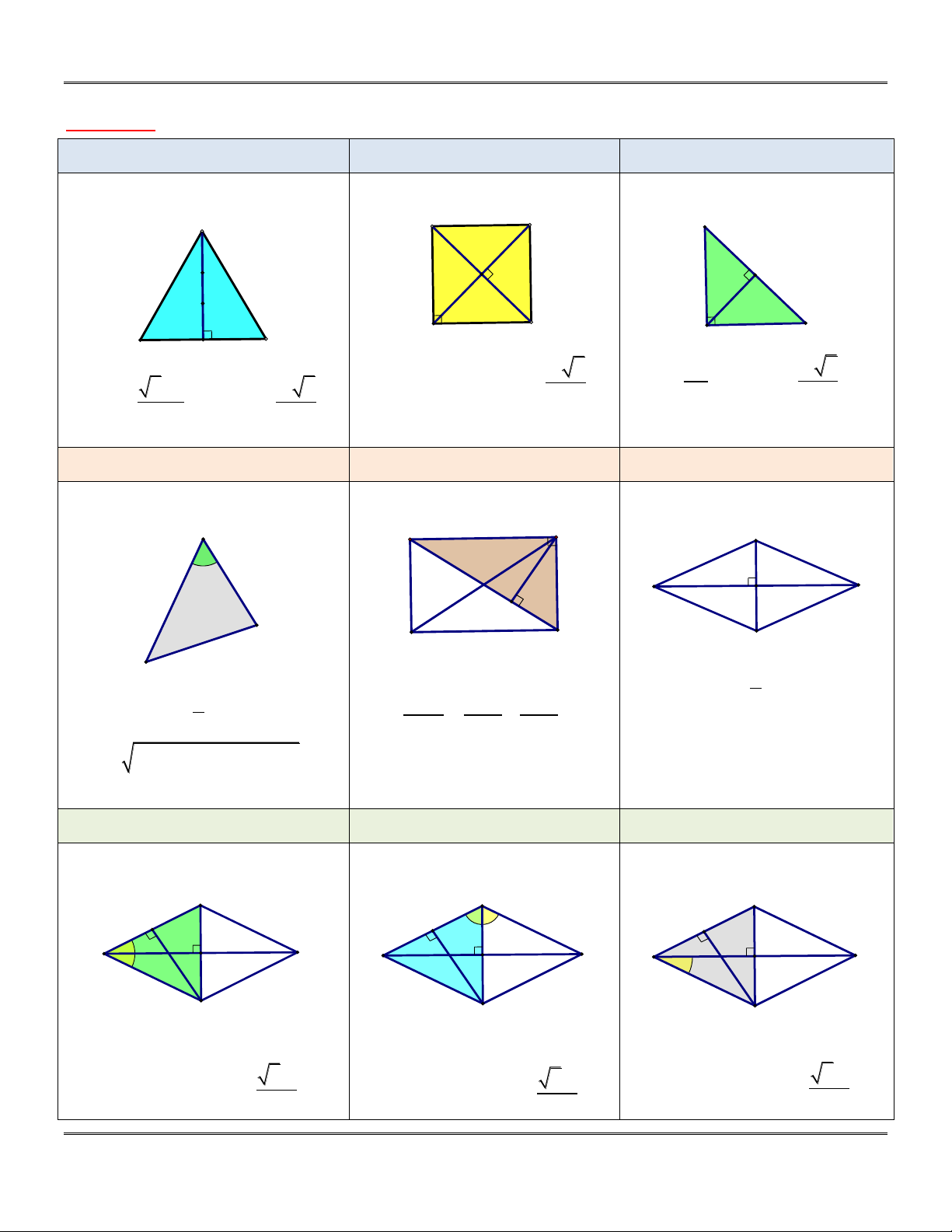
Phần 3: C¸C KÕT QU¶ QUAN TRäNG CÇN L¦U ý KÕt qu¶ 1 KÕt qu¶ 2 KÕt qu¶ 3 Tam giác đều cạnh . m Hình vuông cạnh . m Tam giác vuông cân A A D B O m H m m G B C C A m B M C 2 m m 2 2 m 2 2  3m m 3 S m và OD  . S  và AH  . ABCD ABC S  và AM  . 2 2 2 ABC 4 2 KÕt qu¶ 4 KÕt qu¶ 5 KÕt qu¶ 6 Tam giác bất kì Hình chữ nhật Hình thoi A a D A D a α b b A C c H a C B C B a BS ab và ABCD 1 SAC.BD 1 ABCD 2 Sabsin 1 1 1   ABC . 2 2 2 2 DH DA DC
pp ap bp c và 2 2 2
a b c  2bc cos KÕt qu¶ 7 KÕt qu¶ 8 KÕt qu¶ 9    Hình thoi có 0 BAD  60 Hình thoi có 0 ADC  120 Hình thoi có 0 BAC  30 D D D H H H 600 600 A C 600 A C A C 300 a a a a a a B B B Tam giác ABD đều Tam giác ABD đều Tam giác ABD đều 2 3a 2 2  3a S  2S  3a     S  2SABCD ABD S 2S 2 ABCD ABD ABCD ABD 2 2
Gi¸o viªn: Lª B¸ B¶o... 0935.785.115... 6 CLB Gi¸o viªn trÎ TP HuÕ
[...Chuyªn ®Ò Tr¾c nghiÖm To¸n 12...] LuyÖn thi THPT Quèc gia 2018 a 3 a 3 a 3
và BD a, BH  .
và BD a, BH  .
và BD a, BH  . 2 2 2 KÕt qu¶ 10 KÕt qu¶ 11 KÕt qu¶ 12 Hình thang
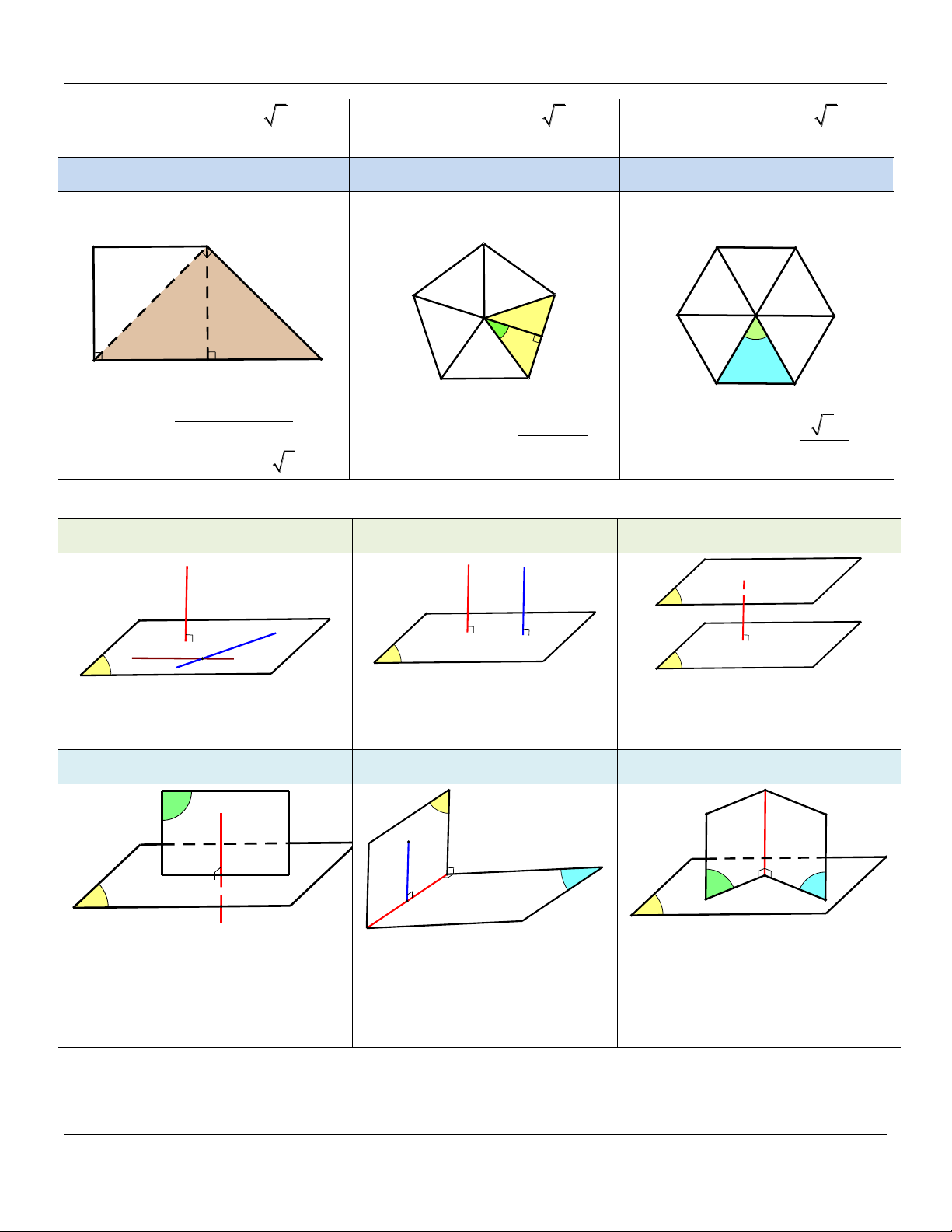
Hình ngũ giác đều cạnh a
Hình lục giác đều cạnh a A a B D F E E a C O O D A 360 C H 600 D H a a  a A B B a C
AB DCAD S  2 2 ABCD 5a 2 S  5S  . 3 3a ABCDEF OBC   0 S 6S . 4 tan 36 ABCDEF OBC 2
và BD BC, BC a 2 TÝnh chÊt quan träng TÝnh chÊt 1 TÝnh chÊt 2 TÝnh chÊt 3 Δ Δ1 Δ2 Δ Q b a I P P P  
  P;   P
  P;    Q 1 2   a;    b         / / P 1 2        P / / Q
a; b  P; a b   I   
PQ     1 2    TÝnh chÊt 4 TÝnh chÊt 5 TÝnh chÊt 6 Q P Δ Δ A d Q Q R P H P  
Q  P  P
P  Q;PQ   d    
R  P    P      Q P QA  
P: AH d, H  d
QR   
AH  Q
Cố gắng lên các em học sinh thân yêu của tôi! Thầy tin mọi việc rồi sẽ tốt đẹp thôi!
Gi¸o viªn: Lª B¸ B¶o... 0935.785.115... 7 CLB Gi¸o viªn trÎ TP HuÕ
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Page: CLB GIÁO VIÊN TRẺ TP HUẾ Một số bài tập tương tự từ: §Ò MINH HäA Sè 3 ¤N THI THPT QuèC GIA
Giáo viên: LÊ BÁ BẢO Trường THPT Đặng Huy Trứ, Huế
SĐT: 0935.785.115 Địa chỉ: 116/04 Nguyễn Lộ Trạch, TP Huế
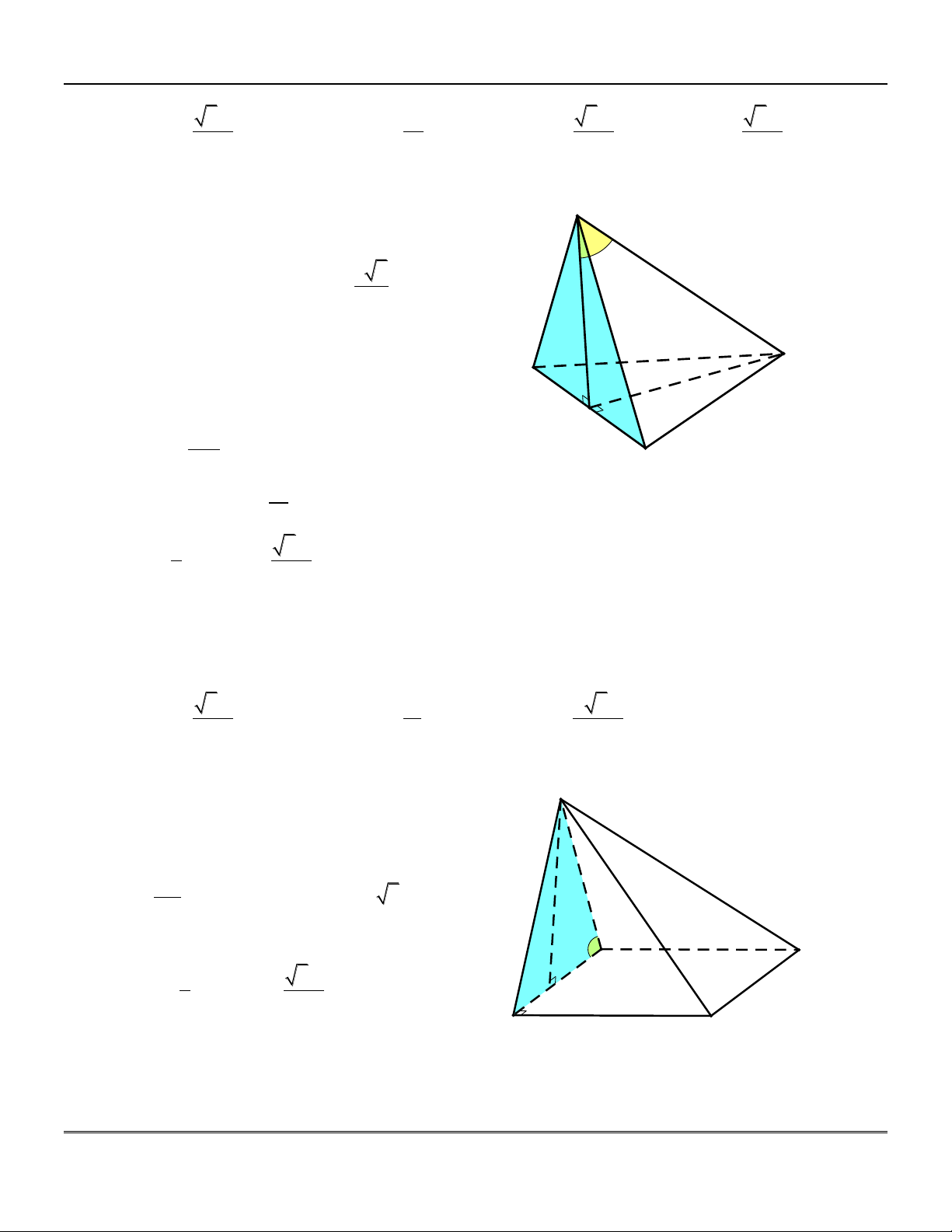
Câu 1: (Đề minh họa số 3 2017) Cho hình chóp .
S ABCD có đáy là hình vuông cạnh a, SA vuông
góc với đáy, SD tạo với mặt phẳng SAB một góc bằng 0
30 . Tính thể tích V của khối chóp . S ABC . D 3 6a 3 6a 3 3a A. V  . B. 3 V  3a . C. V  . D. V  . 18 3 3 Lời giải Ta có: SAD AB
AD  SAB  SD SAB  ;  DS . A AD   SA 300  AD
Xét tam giác SAD vuông tại A : tan DSA SA ADSA     a 3 và 2 S a . ABCD D tan DSA a A 3 1 3a Vậy VS . A S  . S.ABCD 3 ABCD 3  B
Chọn đáp án D. C
Chúng ta xét tiếp các bài tập tương tự
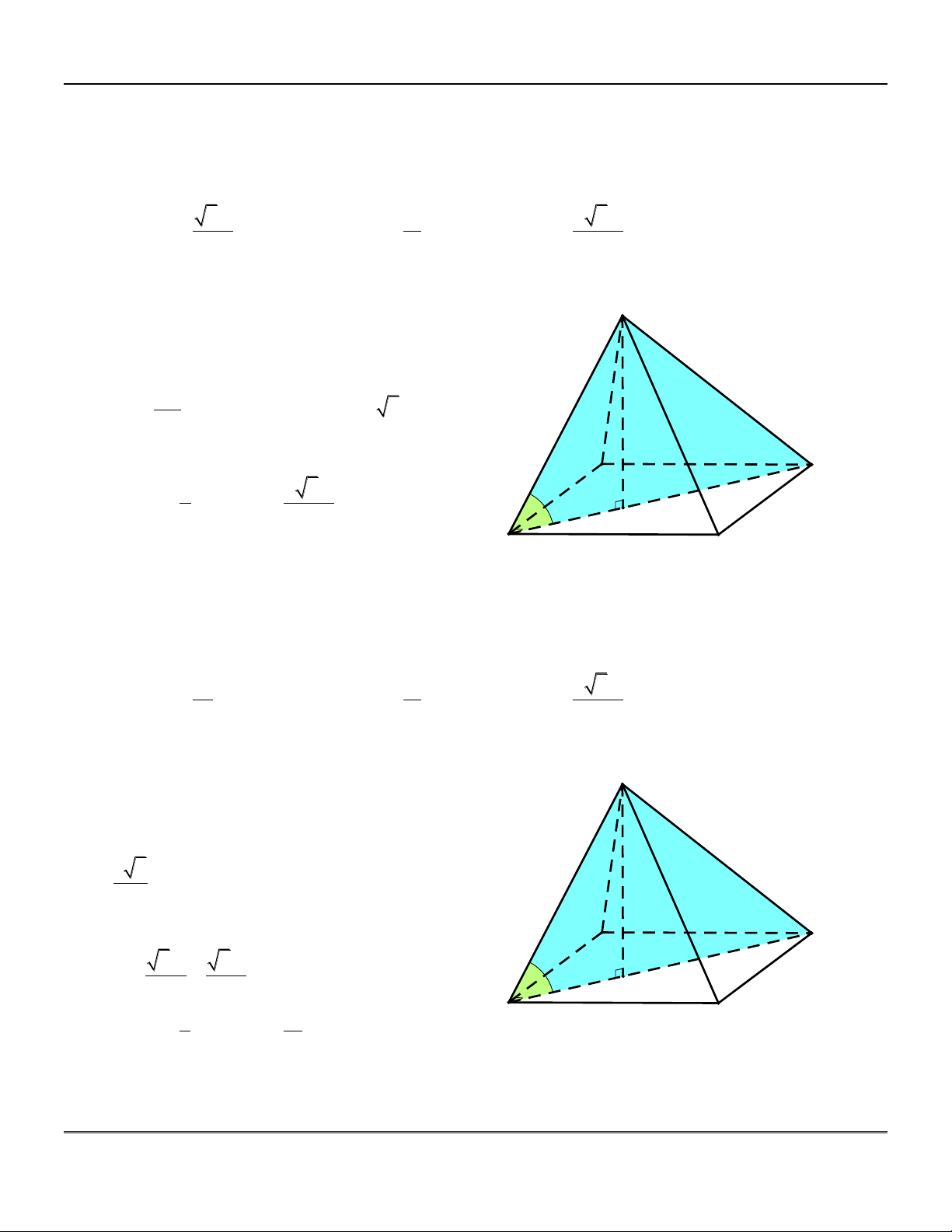
Câu 2: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh a, hai mặt phẳng SAB và SAD
cùng vuông góc với đáy, SC tạo với mặt phẳng SAB một góc bằng 0
30 . Tính thể tích V của khối chóp . S ABC . D 3 6a 3 2a 3 6a A. V  . B. V  . C. V  . D. 3 V  2a . 3 3 6 Lời giải
Giáo viên: LÊ BÁ BẢO...0935.785.115... 1 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018 SAB   ABCDS Ta có:    SAD  
ABCDSA ABCD. 300 BC AB và 
BC  SAB  SC SAB  ;  BSC. BC   SABC
Xét tam giác SBC vuông tại B : tan BSC D SB A BC 2 2  SB        a 3 SA SB AB a 2. tan BSC B a C và 2 Sa . ABCD 3 1 2a Vậy VS . A S  . S.ABCD 3 ABCD 3
Chọn đáp án B.
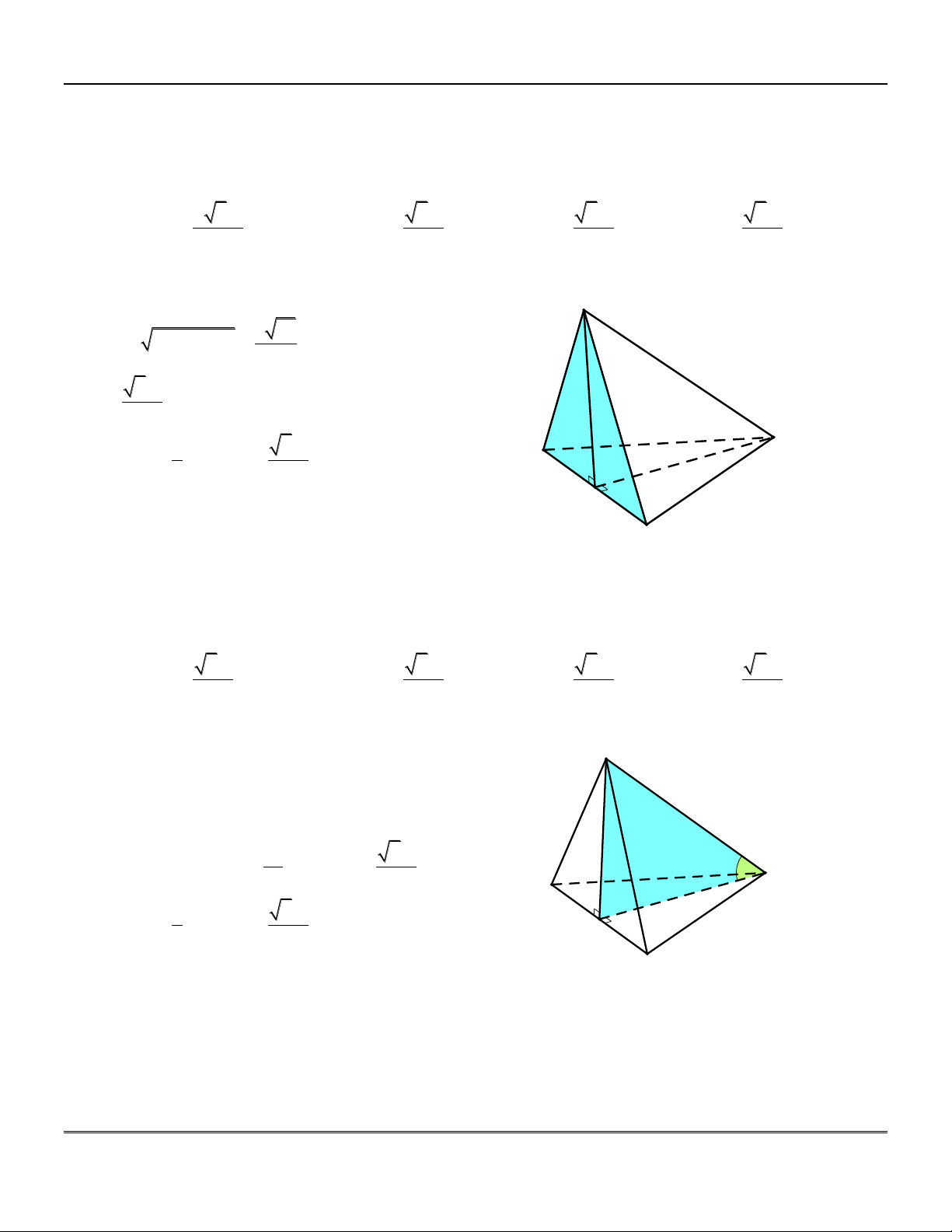
Câu 3: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy, SD tạo với
mặt phẳng SAC một góc bằng 0
30 . Tính thể tích V của khối chóp . S ABC . D 3 a 3 3a 3 2 3a A. V  . B. 3 V  3a . C. V  . D. V  . 3 3 3 Lời giải
Gọi O là tâm hình vuông ABCD, ta có: SDO AC
DO  SAC  SD SAC  ;  DS . O DO   SA 300 Xét tam giác SOD vuông tại O :  OD OD sin DSO   SD      2a SA a và SD sin DSO A D 2 Sa . ABCD a 3 1 a O Vậy VS . A S  . S.ABCD 3 ABCD 3 B C
Chọn đáp án A.
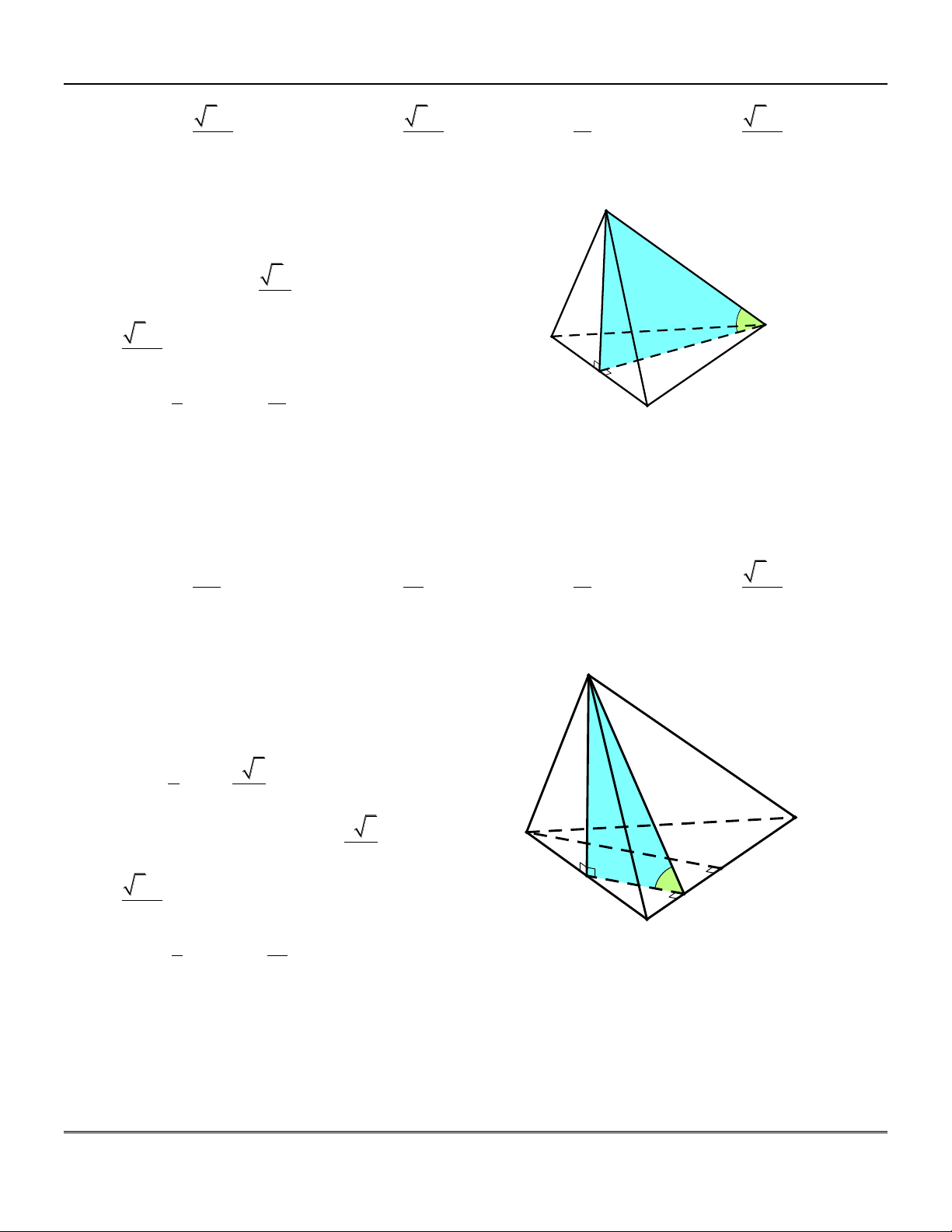
Câu 4: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy, AC tạo với
mặt phẳng SBD một góc bằng 0
45 . Tính thể tích V của khối chóp . S ABC . D 3 2a 3 2a 3 6a A. V  . B. V  . C. V  . D. 3 V  2a . 6 2 6 Lời giải
Giáo viên: LÊ BÁ BẢO...0935.785.115... 2 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018 BD AC Ta có: 
BD  SACS BD   SA
 SAC  SBD.
Dựng AH SO AH  SBD
 AC SBD   0 ;
AOH SOA  45 suy ra H a 2 A D S
AO vuông cân tại A SA OA  450 2 a và 2 Sa . Vậy O ABCD B 3 1 2a C VS . A S  . S.ABCD 3 ABCD 6
Chọn đáp án A.
Câu 5: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S
và nằm trong mặt vuông góc với đáy, SC tạo với mặt đáy một góc bằng 0
60 . Tính thể tích V của khối chóp . S ABC . D 3 15a 3 15a 3 3a A. V  . B. 3 V  3a . C. V  . D. V  . 2 6 3 Lời giải
Dựng SH AB H là trung điểm . AB Do S
SAB ABCDSH ABCD. Vậy
SC ABCD  0 ;  SCH  60 . Xét tam giác SHC vuông tại  SH 15a H : tanSCH   SH  và HC 2 A 3 D 2 1 15a Sa . Vậy VSH.S  . ABCD S.ABCD 3 ABCD 6 H 600
Chọn đáp án C. B a C
Câu 6: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S
và nằm trong mặt vuông góc với đáy, SC tạo với mặt phẳng SAB một góc 0
45 . Tính thể tích V của khối chóp . S ABC . D 3 3a 3 3a 3 6a 3 3a A. V  . B. V  . C. V  . D. V  . 2 6 3 3
Giáo viên: LÊ BÁ BẢO...0935.785.115... 3 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018 Lời giải Ta có: SBC AB
BC  SAB  SC SAB  ;  BSC. BC   SH 450
Xét tam giác BSC vuông cân tại B SB BC  . a a 3
Vậy tam giác SAB đều cạnh a SH  và 2 A D 3 2 1 3a Sa . Vậy VSH.S  . ABCD S.ABCD 3 ABCD 6 H
Chọn đáp án B. B a C
Câu 7: Cho hình chóp .
S ABCD có đáy là hình thoi cạnh a, 0
ABC  60 , SA vuông góc với đáy,
SD tạo với mặt phẳng SAC một góc bằng 0
45 . Tính thể tích V của khối chóp . S ABC . D 3 6a 3 6a 3 6a A. V  . B. 3 V  3a . C. V  . D. V  . 18 3 12 Lời giải
Do ABCD là hình thoi cạnh a và 0 ABC  60 S nên tam giác ABC đều. Vậy 2 2 3a 3a 450 S  2S  2.  . ABCD ABC 4 2 BD AC Ta có: 
BD  SACBD   SA A D
 SD SAC  0 ;
DSO  45 . Vậy tam giác a a 3 O
SOD vuông cân tại O SO DO  . 2 B C Xét tam giác SAO vuông tại A : 2 2 a 2
SA SO AO  2 3 1 6aVS . A S  . S.ABCD 3 ABCD 12
Chọn đáp án D.
Câu 8: Cho hình chóp .
S ABCD có đáy là hình thoi cạnh a, 0
ABC  60 , SA vuông góc với đáy,
SC tạo với mặt phẳng SAB một góc bằng 0
45 . Tính thể tích V của khối chóp . S ABC . D
Giáo viên: LÊ BÁ BẢO...0935.785.115... 4 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018 3 6a 3 6a 3 6a 3 3a A. V  . B. V  . C. V  . D. V  . 4 12 3 2 Lời giải
Do ABCD là hình thoi cạnh a và 0 ABC  60 S nên tam giác ABC đều. Vậy 2 2 3a 3a S  2S  2.  . Dựng ABCD ABC 450 4 2
CH AB H là trung điểm . AB CH AB Ta có: 
CH  SABCH   SA A D
 SC SAB  0 ;
HSC  45 . Vậy tam giác SHC H a 3
vuông cân tại H SH HC  . B 2 a C Xét tam giác SAH vuông tại 2 2 a 2
A : SA SH AH  . 2 3 1 6a Vậy VS . A S  . S.ABCD 3 ABCD 12
Chọn đáp án B.
Câu 9: Cho hình chóp .
S ABCD có đáy ABCD là hình chữ nhật có AB a, BC  2a và
SA SC, SB SD , SC tạo với mặt đáy một góc bằng 0
60 . Tính thể tích V của khối chóp . S ABC . D 3 15a 3 15a 3 15a 3 4 15a A. V  . B. V  . C. V  . D. V  . 3 4 2 3 Lời giải
Giáo viên: LÊ BÁ BẢO...0935.785.115... 5 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018 SO   AC
Gọi O là tâm đáy, ta có:  S SO   BD
SO  ABCD  SC ABCD  ;  SC . O Xét tam giác SCO vuông tại  SOa 15 O : tanSCO
SO OC tanSCO OC 2 600 D C và 2 S  2a . ABCD 3 1 15a Vậy VS . O S  . 2a O S.ABCD 3 ABCD 3 AB
Chọn đáp án A. a Câu 10: Cho hình chóp .
S ABCD có đáy ABCD là hình chữ nhật có AB a, BC  2a và
SA SC, SB SD , mặt phẳng SBC tạo với mặt đáy một góc bằng 0
30 . Tính thể tích V của khối chóp . S ABC . D 3 3a 3 3a 3 3a 3 2 3a A. V  . B. V  . C. V  . D. V  . 9 3 4 3 Lời giải SO   AC Gọi S
O là tâm đáy, ta có:  SO   BD
SO  ABCD  SC ABCD  ;  SC . O
Dựng OH BC BC  SOH  BC SH
vậy  SBC ABCD  0 ;  SHO  60 . D C Xét tam giác SHO vuông tại 600 2a  SOa 3 H O : tanSHO
SO OH tanSHO  và O OH 6 A B a 2 S  2a . ABCD 3 1 3a Vậy VS . O S  . S.ABCD 3 ABCD 9
Chọn đáp án A. Câu 11: Cho hình chóp .
S ABCD có đáy là hình chữ nhật ABCD có CD  2BC  2a, SA
vuông góc với đáy, SD tạo với mặt phẳng SAC một góc bằng 0
45 . Tính thể tích V của khối chóp . S ABC . D
Giáo viên: LÊ BÁ BẢO...0935.785.115... 6 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018 3 15a 3 2 15a 3 2 15a 3 15a A. V  . B. V  . C. V  . D. V  . 15 15 5 3 Lời giải
Dựng DH AC DH  SACS
 SD ABCD  0 ;
DSH  45 . Vậy SHD
vuông cân tại H SH H . D 450
Tam giác ACD vuông tại D : 1 1 1 5 2 5a     DH  2 2 2 2 DH DA DC 4a 5 A D 2 2 a 5
AH AD DH  . 5 O 2a a H Suy ra: 2 2 15
SA SH AH  và B a C 5 2 S  2a . ABCD 3 1 2 15a Vậy VS . A S  . S.ABCD 3 ABCD 15
Chọn đáp án B.
NHÓM HAI MẶT PHẲNG VUÔNG GÓC Câu 12:
Cho tứ diện ABCD có ABC là tam giác đều cạnh a, tam giác BCD vuông cân tại D
và nằm trong mặt phẳng vuông góc với  ABC. Tính thể tích V của khối tứ diện ABC . D 3 3a 3 a 3 3a 3 3a A. V  . B. V  . C. V  . D. V  . 6 12 8 24 Lời giải Dựng AH BC, do A
ABC BCD AH BCD. a 3 a Ta có, do A
BC đều AH  và 2 2 1 a a SDH.BC  . D BCD 2 4 B 3 1 3a Vậy VAH.S  . ABCD H 3 BCD 24
Chọn đáp án D. C
Giáo viên: LÊ BÁ BẢO...0935.785.115... 7 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018 Câu 13: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác đều
và nằm trong mặt phẳng vuông góc với  ABCD. Tính thể tích V của khối chóp . S ABC . D 3 3a 3 a 3 3a 3 3a A. V  . B. V  . C. V  . D. V  . 6 12 8 24 Lời giải Dựng SH AB, do S
SAB ABCDSH ABCD. a 3 Ta có, do S
AB đều  SH  và 2 2 Sa . ABCD 3 1 3a A D Vậy VSH.S  . S.ABCD 3 ABCD 6
Chọn đáp án A. H B a C Câu 14: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh a, mặt bên SAB nằm trong mặt
phẳng vuông góc với  ABCD  0
, SAB  30 , SA  2 .
a Tính thể tích V của khối chóp . S ABC . D 3 3a 3 a 3 a A. V  . B. V  . C. V  . D. 3 V a . 6 3 9 Lời giải Dựng SH AB, do S
SAB ABCDSH ABCD. Ta có, do S
HA vuông tại H :  SH  sinSAH   SH S .
A sinSAH a và SA 2 Sa . ABCD 300 A D 3 1 a Vậy VSH.S  . S.ABCD 3 ABCD 3 H
Chọn đáp án B. B a C Câu 15:
Cho tứ diện ABCD có ABC là tam giác đều cạnh a, tam giác BCD cân tại D và nằm
trong mặt phẳng vuông góc với  ABC. Biết AD hợp với mặt phẳng  ABC một góc 0 60 . Tính thể
tích V của khối tứ diện ABC . D
Giáo viên: LÊ BÁ BẢO...0935.785.115... 8 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018 3 3a 3 a 3 3a 3 3a A. V  . B. V  . C. V  . D. V  . 6 12 8 24 Lời giải Dựng AH BC, do A
ABC BCD AH BCD. 600 a 3 Ta có, do A
BC đều AH  và a 2
DH BC DH  ABC a D
 AD ABC  0 ;  HAD  60 . B Xét tam giác AHD vuông tại HHD H : tan HAD AH C  3a
HD AH.tan HAD  . 2 3 1 3a Vậy VH . D S  . ABCD 3 ABC 8
Chọn đáp án C. Câu 16: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh a, mặt bên SAB nằm trong mặt
phẳng vuông góc với  ABCD  0
, SAB  60 , SA  2 .
a Tính thể tích V của khối chóp . S ABC . D 3 3a 3 a 3 2 3a A. V  . B. V  . C. V  . D. 3 V a . 3 3 3 Lời giải Dựng SH AB, do S
SAB ABCDSH ABCD. Ta có, do S
HA vuông tại H :  SH  sinSAH   SH S .
A sinSAH a 3. SA và 2 Sa . 600 A ABCD D 3 1 3a Vậy VSH.S  . S.ABCD 3 ABCD 3 HB
Chọn đáp án A. a C
Giáo viên: LÊ BÁ BẢO...0935.785.115... 9 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018 Câu 17: Cho hình chóp .
S ABCD có đáy là hình chữ nhật ABC ,
D BC  2AB  2 , a tam giác
SAC nằm trong mặt phẳng vuông góc với  ABCD  0
, SAB  60 , SA  2 .
a Tính thể tích V của khối chóp . S ABC . D 3 3a 3 a 3 2 3a A. V  . B. V  . C. V  . D. 3 V a . 3 3 3 Lời giải Dựng SH AC, do S
SAC ABCDSH ABCD. Ta có, do S
HA vuông tại H :  SH  sinSAH   SH S .
A sinSAH a 3. SA và 2 S  2a . ABCD B C 3 1 2 3a Vậy VSH.S  . S.ABCD 3 ABCD 3 600 2a H
Chọn đáp án C. A a DCâu 18: Cho hình chóp .
S ABCD có đáy là hình thoi cạnh a, 0
CAD  30 , tam giác SAB đều và
nằm trong mặt phẳng vuông góc với  ABCD  0
, SAB  60 , SA  2 .
a Tính thể tích V của khối chóp . S ABC . D 3 a 3 a 3 2 3a A. V  . B. V  . C. V  . D. 3 V a . 12 4 3 Lời giải Dựng SH AB, do S
SAB ABCDSH ABCD. Ta có, do S
AB là tam giác đều nên a 3 SH
. Do ABCD là hình thoi cạnh a 2  và 0
CAD  30 nên BAD đều. Suy ra B C 2 2 3a 3a S  2.  . ABCD 600 2a 4 2 H 3 A 1 a a D Vậy VSH.S  . S.ABCD 3 ABCD 4
Chọn đáp án B.
Giáo viên: LÊ BÁ BẢO...0935.785.115... 10 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
NHÓM HÌNH CHIẾU VUÔNG GÓC Câu 19: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh a, hình chiếu vuông góc của S
trên mặt phẳng  ABC là trung điểm của BC và SB  2 .
a Tính thể tích V của khối chóp . S AB . C 3 3 5a 3 3a 3 5a 3 3a A. V  . B. V  . C. V  . D. V  . 8 24 8 12 Lời giải Xét tam giác SBH vuông tại S 2 2 a 15
H : SH SB BH  và 2 2 2a 3a S  . ABC 4 A 3 1 5a Vậy VSH.S  . B S.ABC 3 ABC 8  a
Chọn đáp án C. H C Câu 20: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh a, hình chiếu vuông góc của S
trên mặt phẳng  ABC là trung điểm của BC và SA hợp với đáy một góc 0
60 . Tính thể tích V của khối chóp . S AB . C 3 3a 3 3a 3 5a 3 3a A. V  . B. V  . C. V  . D. V  . 8 24 8 12 Lời giải Do S
SH   ABC  SA ABC  0 ;  SAH  60 . Xét tam giác SAH vuông tại  3a 2 3a
H : SH AH.tanSAH  và S  . 600 A 2 ABC 4 B 3 1 3a Vậy VSH.S  . H a S.ABC 3 ABC 8
Chọn đáp án A. C Câu 21: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh a, hình chiếu vuông góc của S
trên mặt phẳng  ABC là trung điểm của BC và SB hợp với đáy một góc 0
60 . Tính thể tích V của khối chóp . S AB . C
Giáo viên: LÊ BÁ BẢO...0935.785.115... 11 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018 3 3a 3 3a 3 a 3 3a A. V  . B. V  . C. V  . D. V  . 8 24 8 12 Lời giải
Do SH   ABC  SB ABC  0 ;  SBH  60 . S Xét tam giác SBH vuông tại  3a
H : SH BH.tanSBH  và 2 600 A 2 3a S  . B ABC 4 H a 3 1 a Vậy VSH.S  . S.ABC 3 ABC 8 C
Chọn đáp án C. Câu 22: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh a, hình chiếu vuông góc của S
trên mặt phẳng  ABC là trung điểm của BC và SAB hợp với đáy một góc 0
45 . Tính thể tích V của khối chóp . S AB . C 3 3a 3 a 3 a 3 3a A. V  . B. V  . C. V  . D. V  . 16 16 8 12 Lời giải
Do HK AB AB  SHK  AB SK S
  SAB ABC  0 ;  SKH  45 . Gọi M là trung điểm 1 a 3
AB HK CM  , do tam giác SHK 2 4 a A a 3 C
vuông cân tại H SH HK  và 4 450 2 3a M H S  . ABC K 4 3 B 1 a Vậy VSH.S  . S.ABC 3 ABC 16
Chọn đáp án B. Câu 23: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh a, hình chiếu vuông góc của S  
trên mặt phẳng  ABC là điểm H trên cạnh BC sao cho CH  2HB, SB hợp với đáy một góc 0 60 .
Tính thể tích V của khối chóp . S AB . C
Giáo viên: LÊ BÁ BẢO...0935.785.115... 12 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018 3 a 3 a 3 a 3 3a A. V  . B. V  . C. V  . D. V  . 12 6 4 12 Lời giải
Do SH   ABC  SB ABC  0 ;  SBH  60 . S Xét tam giác SBH vuông tại  3a 2 3a
H : SH BH.tanSBH  và S  . 3 ABC 4 3 C 1 a A Vậy VSH.S  . S.ABC 3 ABC 12 600 a
Chọn đáp án A. H B Câu 24: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh a, hình chiếu vuông góc của S  
trên mặt phẳng  ABC là điểm H trên cạnh BC sao cho HC  2BH, SA hợp với đáy một góc 0 60 .
Tính thể tích V của khối chóp . S AB . C 3 a 3 7a 3 a 3 3a A. V  . B. V  . C. V  . D. V  . 12 12 4 8 Lời giải Do S
SH   ABC  SA ABC  0 ;  SAH  60 . Xét tam giác AHB :  2 2 2 2 7a
AH AB BH  2A . B BH.cos ABH  . 9 a 7  600 AH  . C 3 A Xét tam giác SAH vuông tại a  21a
H : SH AH.tanSBH  và H 3 B 2 3a A C S  . ABC 4 3 1 7a Vậy VSH.S  . a S.ABC H 3 ABC 12 600
Chọn đáp án B. B
Giáo viên: LÊ BÁ BẢO...0935.785.115... 13 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018 Câu 25: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh a, hình chiếu vuông góc của S  
trên mặt phẳng  ABC là điểm H trên cạnh BC sao cho HC  2BH, và tam giác SAH vuông cân.
Tính thể tích V của khối chóp . S AB . C 3 21a 3 7a 3 a 3 3a A. V  . B. V  . C. V  . D. V  . 36 12 4 8 Lời giải Do S
SH   ABC  SA ABC  0 ;  SAH  60 . Xét tam giác AHB :  2 2 2 2 7a
AH AB BH  2A . B BH.cos ABH  . 9 a 7  600 AH  . C 3 A
Do tam giác SAH vuông cân tại H nên a 2 3a
SH AH và S  . H ABC 4 B 3 1 21a A C Vậy VSH.S  . S.ABC 3 ABC 36
Chọn đáp án A. a H 600 B Câu 26: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh a, hình chiếu vuông góc của S  
trên mặt phẳng  ABC là điểm H trên cạnh BC sao cho HC  2BH, SAB hợp với đáy một góc 0
60 . Tính thể tích V của khối chóp . S AB . C 3 3a 3 3a 3 3a 3 3a A. V  . B. V  . C. V  . D. V  . 24 12 4 6 Lời giải
Giáo viên: LÊ BÁ BẢO...0935.785.115... 14 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018 Gọi M là trung điểm . AB Dựng S
HK AB HK / /CM và 1 a 3 HK CM  . Ta có 3 6
AB  SHK  AB SK
  SAB ABC  0 ;  SKH  60 . Xét tam giác SKH vuông tại a A Ca 2 3a
H : SH KH.tanSKH  và S  . 2 ABC 4 M 600 3 1 3a H Vậy VSH.S  . K S.ABC 3 ABC 24 B
Chọn đáp án A. A a C M H K B
SẼ CÒN UPDATE RẤT NHIỀU TRONG THỜI GIAN TỚI....
CÁC EM HỌC SINH THÂN YÊU CỐ GẮNG LÊN NHÉ! Huế 19.5.2017
Giáo viên: LÊ BÁ BẢO...0935.785.115... 15 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Page: CLB GIÁO VIÊN TRẺ TP HUẾ Một số bài tập tương tự từ: §Ò MINH HäA Sè 3 ¤N THI THPT QuèC GIA
Giáo viên: LÊ BÁ BẢO Trường THPT Đặng Huy Trứ, Huế
SĐT: 0935.785.115 Địa chỉ: 116/04 Nguyễn Lộ Trạch, TP Huế DẠNG TOÁN 1: ThÓ tÝch khèi l¨ng trô
Nhóm giả thiết 1:
CẠNH BÊN VUÔNG GÓC VỚI ĐÁY
Câu 1: Cho hình lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác vuông cân tại
A, AB a, BB  2 .
a Tính thể tích V của khối lăng trụ AB . C A BC   3 2a 3 a A. V  . B. 3 V a . C. V  . D. 3 V  2a . 3 3 Lời giải 2 1 a A C Ta có: S           A B .A C . A B C 2 2 B Vậy 3
V BB .S      a . A B C
Chọn đáp án B. a A' C' a
Câu 2: Cho hình lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác đều cạnh a, mặt bên ABB A  
là hình vuông. Tính thể tích V của khối lăng trụ AB . C A BC   3 3a 3 3a 3 3a A. V  . B. V  . C. V  . D. 3 V  2a . 12 4 3 Lời giải 2 3a A C Ta có: S      . Do ABB A   là hình vuông nên A B C 4 B BB  A B    . a 3 3a
Vậy V BB .S      . A B C 4
Chọn đáp án B. A' C' a B'
Câu 3: Cho hình lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác đều cạnh a, tam giác A BA
cân. Tính thể tích V của khối lăng trụ AB . C A BC  
Giáo viên: LÊ BÁ BẢO...0935.785.115... 1 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018 3 3a 3 3a 3 3a A. V  . B. V  . C. V  . D. 3 V  2a . 12 4 3 Lời giải 2 3a A C Ta có: S        . Do
A B A vuông cân tại A B C 4 B A  A A   A B    . a 3 3a
Vậy V BB .S      . A B C 4
Chọn đáp án B. A' C' a B'
Câu 4: Cho hình lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác đều cạnh a, AB  2 . a Tính
thể tích V của khối lăng trụ AB . C A BC   3 a 3 3a 3 3a A. V  . B. V  . C. V  . D. 3 V  2a . 4 2 4 Lời giải 2 3a A C Ta có: S        . Do A B A vuông tại A B C 4 B A  A A   B A  2 A B  2  a 3. 2a 3 3a
Vậy V A . A S      . A B C 4  A'
Chọn đáp án C. C' a B'
Câu 5: Tính thể tích V của khối lăng trụ tam giác đều AB . C A BC
  có tất cả các cạnh đều bằng 2 . a 3 2 3a 3 3a A. 3 V  2 3a . B. V  . C. V  . D. 3 V  2 3a . 3 4 Lời giải Do AB . C A BC
  là lăng trụ đều nên đường cao của lăng trụ A C 3 2a2 B
là BB  2a và 2 S       3a . A B C 4 a Vậy 3
V BB .S      2 3a . A B C
Chọn đáp án A. A' C' a B'
Giáo viên: LÊ BÁ BẢO...0935.785.115... 2 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Câu 6: Tính thể tích V của khối lăng trụ tứ giác đều ABC . D A BCD
  có tất cả các cạnh đều bằng 2 . a 3 8a 3 2a A. V  . B. V  . C. 3 V  8a . D. 3 V  2 3a . 3 3 Lời giải Do ABC . D A BCD
  là lăng trụ đều nên đường cao của D C
lăng trụ là BB  2a và S        a2 2 2 4a . A B C D A B Vậy 3
V BB .S      8a . A B C
Chọn đáp án C. 2a D' C' 2a A' 2a B'
Câu 7: Cho hình lăng trụ ngũ giác đều ABCD . E A B  C DE
  có cạnh đáy bằng 2, cạnh bên bằng 4.
Thể tích V của khối lăng trụ đã cho gần bằng giá trị nào sau đây? A. V  22,02. B. V  7,34. C. V  32,02. D. V  27,53. Lời giải Do ABCD . E A BCDE
  là lăng trụ đều nên đường cao của D
lăng trụ là BB  4. Tính diện tích ngũ giác đều A BCDE  . C E Ta có: A B   0  0 HB 1 B O
C  72  HOB  36  OH    . 0 tan HOB tan 36 1 5 4 Vậy S          
5S   5. .OH.B C A B C D E OB C 0 2 tan 36 20
V BB'.S        27, 53. A B C D E 0 tan 36 D' D' E' C' O 720 2 A' B' E' C' O 360 H A' 2 B'
Chọn đáp án D.
Câu 8: Cho hình lăng trụ lục giác đều ABCDEF.A BCDEF
  có cạnh đáy bằng a, cạnh bên bằng 2 .
a Tính thể tích V của khối lăng trụ ABCDE . F A BCDEF  .
Giáo viên: LÊ BÁ BẢO...0935.785.115... 3 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018 3 3 3a 3 4 3a A. V  . B. 3 V  3 3a . C. 3 V  6 3a . D. V  . 2 3 Lời giải Do ABCDE . F A BCDEF
  là lăng trụ đều nên đường F E
cao của lăng trụ là BB  2 .
a Tính diện tích lục giác D A đều A BCDEF  . B C  Ta có: 0 B O
C  60  OB C   là tam giác đều. 2 2 3a 3 3a Vậy S          6S   6. . A B C D E F OB C 4 2 3
V BB'.S        3 3a . A B C D E F 2a F' E' F' E' O O D' A' D' A' 600 600 a B' C' B' a C'
Chọn đáp án B.
Câu 9: Tính thể tích V của khối lập phương ABC . D A BCD
  có diện tích một mặt bằng 2 4a . 3 8a 3 2a A. V  . B. V  . C. 3 V  8a . D. 3 V  2 3a . 3 3 Lời giải
Gọi cạnh hình lập phương là mm  0 , theo giả thiết D C 2 2
m  4a m  2 . a A B
Vậy V   a3 3 2  8a .
Chọn đáp án C. m D' C' m A' B' Câu 10:
Tính thể tích V của khối lập phương ABC . D A BCD
  có diện tích tất cả các mặt bằng 2 24 cm . A. V   3
8 cm . B. V   3
16 cm . C. V   3
24 cm . D. V   3 12 cm . Lời giải
Giáo viên: LÊ BÁ BẢO...0935.785.115... 4 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018
Gọi cạnh hình lập phương là mm  0 , suy ra diện tích D C một mặt bằng 2 m . Theo giả thiết 2
6m  24  m  2. A B 3
Vậy V      3 2 8 cm . m D'
Chọn đáp án A. C' m A' B' Câu 11:
Cho hình lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác vuông cân tại
A, AB a, AB hợp với đáy một góc 0
60 . Tính thể tích V của khối lăng trụ AB . C A BC   3 3a 3 a 3 3a A. V  . B. 3 V  3a . C. V  . D. V  . 6 3 2 Lời giải 2 1 a A C Ta có: S                A B .A C . Do AAA B C A B C 2 2 B
 AB A BC    0 ;  AB A    60 . Xét tam giác AB A
  vuông tại A :  A A   A B  tan AB A    a 3. a 3 3a A' C'
Vậy V AA .S  600     . A B C a 2  B'
Chọn đáp án D. Câu 12:
Cho hình lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác vuông cân tại
A, AB a, AB hợp với mặt phẳng  ACC A   một góc 0
60 . Tính thể tích V của khối lăng trụ AB . C A BC   3 2 3a 3 3a 3 a 3 3a A. V  . B. V  . C. V  . D. V  . 3 6 3 2 Lời giải 2 1 a A C Ta có: S               A B .A C . Do AA A B và A B C 2 2 B A B    A C    A B    ACC A   600
 AB A BC    0 ;  B AA  60 . Xét tam giác AB A
  vuông tại A :  A B   A B   a 3 a tan B AA   A A    A' C'   . A A   3 tan B AA a 3 B' 3a
Vậy V AA .S      . A B C 6
Chọn đáp án B.
Giáo viên: LÊ BÁ BẢO...0935.785.115... 5 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018 Câu 13:
Cho hình lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác vuông cân tại
A, AB a, AB C
  hợp với mặt đáy một góc 0
30 . Tính thể tích V của khối lăng trụ AB . C A BC   3 6a 3 6a 3 6a 3 6a A. V  . B. V  . C. V  . D. V  . 6 36 12 4 Lời giải 2 1 a A Ta có: S           C     A B .A C . Dựng A M B C , do A B C 2 2 B AA  B C    B C
   AMA  B C    AM   AB C   A BC    0 ;  AMA  30 .
Xét tam giác AMA vuông tại A :  a 6 A A   A M  tan AMA  . 6 a A' 300 C' 3 6a
Vậy V AA .S  a M     . A B C 12 B'
Chọn đáp án C. Câu 14:
Cho hình lăng trụ tam giác đều AB . C A BC
  có cạnh đáy bằng a, AB hợp với mặt đáy một góc 0
60 . Tính thể tích V của khối lăng trụ AB . C A BC   3 3a 3 a 3 3a 3 3a A. V  . B. V  . C. V  . D. V  . 4 4 12 4 Lời giải 2 3a A C Ta có: S      . A B C 4 B Do A A   A BC
   AB A BC    0 ;  AB A    60 . Xét tam giác AB A
  vuông tại A :  A A   A B  tan AB A    a 3. 3 3a a
Vậy V AA .SA' C'     . A B C 600 4 a a
Chọn đáp án A. B' Câu 15:
Cho hình lăng trụ tam giác đều AB . C A BC
  có cạnh đáy bằng a, AC hợp với mặt phẳng  ABB A   một góc 0
45 . Tính thể tích V của khối lăng trụ AB . C A BC   3 6a 3 3a 3 6a 3 6a A. V  . B. V  . C. V  . D. V  . 24 4 8 4 Lời giải
Giáo viên: LÊ BÁ BẢO...0935.785.115... 6 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018 2 3a A C Ta có: S               . Dựng C H A B C HABB A A B C 4 B   450 AC  ABB A    0 ;  C A
H  45 . Suy ra AHC vuông cân a 3
tại H HC  AH  . Xét tam giác A AH vuông tại 2 3 a 2 2 a 2 6a A : A A
  AH A H  
. Vậy V AA .SA'     . C' 2 A B C 8 a H a
Chọn đáp án C. B' Câu 16:
Cho hình lăng trụ tam giác đều AB . C A BC
  có cạnh đáy bằng a, AB C   hợp với mặt đáy một góc 0
60 . Tính thể tích V của khối lăng trụ AB . C A BC  . 3 3a 3 3a 3 3a 3 3 3a A. V  . B. V  . C. V  . D. V  . 24 4 8 8 Lời giải 2 3a A C Ta có: S              . Dựng A M B C , do AA B C A B C 4  B C
   AMA  B C    AM B   AB C   A BC    0 ;  AMA  60 .
Xét tam giác AMA vuông tại A :  3a A A   A M  tan AMA  . 2 a 3 3 3a A' 600 C'
Vậy V AA .S      . A B C 8 a M
Chọn đáp án D. B' Câu 17:
Cho hình lăng trụ đứng ABC . D A BCD
  có đáy ABCD là hình thoi cạnh  a 0
, BAC  30 , AB  2 .
a Tính thể tích V của khối lăng trụ ABC . D A BCD  . 3 3a 3 3a 3 3a 3 3 3a A. V  . B. V  . C. V  . D. V  . 6 2 8 8 Lời giải
Giáo viên: LÊ BÁ BẢO...0935.785.115... 7 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018  Do A BCD
  là hình thoi cạnh a và 0 B AD    30 nên D C 2 3a ABD
  là tam giác đều cạnh a S   A     2S    . B A B C D A B D 2 Xét tam giác A AB vuông tại AA A   B A  2 A B  2 :  . a D' 3 C' 3a a
Vậy V AA .S      . A B C D 2 300 A' a B'
Chọn đáp án B. Câu 18:
Cho hình lăng trụ đứng ABC . D A BCD
  có đáy ABCD là hình thoi cạnh  a 0
, ADC  120 , AC hợp với đáy một góc 0
45 . Tính thể tích V của khối lăng trụ ABC . D A BCD  . 3 a 3 3a 3 3a 3 3a A. V  . B. V  . C. V  . D. V  . 2 2 8 2 Lời giải D Do A BCD
  là hình thoi cạnh a và 0 A DC    120 nên C 2 3a A ABD
  là tam giác đều cạnh a S       2S    . B A B C D A B D 2 Do A A   A BCD
   AC A BCD    0 ;  AC A    45 . Suy ra AA
C vuông cân tại A 450 D'A A   A C    2A O   3 . a C' a 600 3 3a O
Vậy V AA .SA'     . a B' A B C D 2
Chọn đáp án D. Câu 19:
Cho hình lăng trụ đứng ABC . D A BCD
  có đáy ABCD là hình thoi cạnh  a 0
, ADC  120 ,  ADC B
  hợp với đáy một góc 0
45 . Tính thể tích V của khối lăng trụ ABC . D A BCD  . 3 a 3 3a 3 3a 3 3a A. V  . B. V  . C. V  . D. V  . 4 2 4 2 Lời giải
Giáo viên: LÊ BÁ BẢO...0935.785.115... 8 CLB Giáo viên trẻ TP Huế
[...Chuyên đề Trắc nghiệm Toán 12...] Luyện thi THPT Quốc gia 2018  Do A BCD
  là hình thoi cạnh a và 0 A DC    120 nên D C 2 3a ABD
  là tam giác đều cạnh a S       2S    . A B C D A B D 2 A B Dựng D M   B C    B C    D DM  B C    DM   ADC B   A BCD    0 ;  DMD  45 . a Suy ra DM
D vuông cân tại D 3  D D   D M   . 450 D' 2 C' a 600 3 3a O M
Vậy V DD .S      . A' A B C D B' 4 a
Chọn đáp án C. Câu 20:
Cho hình lăng trụ đứng ABC . D A BCD
  có đáy ABCD là hình thoi tâm O cạnh  a 0
, ADC  120 . Biết OC hợp với DBB D   một góc 0
60 . Tính thể tích V của khối lăng trụ ABC . D A BCD  . 3 3a 3 3a 3 3a 3 3a A. V  . B. V  . C. V  . D. V  . 4 2 4 12 Lời giải  Do A BCD
  là hình thoi cạnh a và 0 A DC    120 nên D C 2 O 3a ABD
  là tam giác đều cạnh a S       2S    . A B C D A B D 2 A B CO    B D   600
Gọi O là tâm A BCD      C O    DBB D   C O     DD
 OC DBB D    0 ;  C OO  60 .  O C   Xét OO
C vuông tại O : tanO OC  D' C' O O  a 600 O C   a O'O O     . A' a B' tanO OC 2 3 3a
Vậy V O . O S      . A B C D 4
Chọn đáp án A.
Giáo viên: LÊ BÁ BẢO...0935.785.115... 9 CLB Giáo viên trẻ TP Huế