




















Preview text:
Mục lục AN
1 Hình học không gian (cổ điển) ĂN 1 I.
Một số vấn đề cơ bản về quan hệ song song . . . . . . . . . . . . . . . . . V 1 1.
Việc xác định giao tuyến của hai mặt phẳng . . . . . . . . . . . 1 2.
Việc xác định giao điểm của đường thẳng và mặt phẳng . . . 1 3.
Một số định lý về nhận dạng quan hệ song song . . . . . . . . . 2 II.
Một số vấn đề cơ bản về quan hệ vuông góc . . . . . . . . . . . . . . . . . CHU 2 1.
Phương pháp chứng minh đường thẳng vuông góc với mặt
phẳng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 2.
Phương pháp chứng minh hai đường thẳng vuông góc . . . . . 2 3.
Phương pháp chứng minh hai mặt phẳng vuông góc . . . . . . 2 III.
Phương pháp xác định các loại góc trong không gian . . . . . . . . . . . 3 1.
Góc giữa hai đường thẳng . . . . . . . . . . . . . . . . . . . . . . . THPT 3 2.
Góc giữa đường thẳng và mặt phẳng (cắt nhau nhưng không
vuông góc) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . - 3 3.
Góc giữa hai mặt phẳng (cắt nhau) . . . . . . . . . . . . . . . . . G 3 IV.
Phương pháp xác định khoảng cách . . . . . . . . . . . . . . . . . . . . . . 4 1.
Khoảng cách từ một điểm đến một mặt phẳng . . . . . . . . . . 4 2.
Khoảng cách giữa 2 đối tượng song song nhau . . . . . . . . . . 4 3.
Khoảng cách giữa 2 đường thẳng a và b chéo nhau . . . . . . . SAN 4 V.
Một số vấn đề về khối đa diện lồi, khối đa diện đều . . . . . . . . . . . . 5 1.
Tính chất của một hình đa diện, khối đa diện . . . . . . . . . . 5 2.
Bảng tổng hợp tính chất của các đa diện đều . . . . . . . . . . . 5 VI.
Một số công thức tính toán hình học . . . . . . . . . . . . . . . . . . . . . . 6 1.
Công thức tính toán hình học liên quan đến tam giác . . . . . 6 2.
Công thức tính toán hình học liên quan đến tứ giác . . . . . . 7 3.
Công thức thể tính thể tích khối chóp và khối lăng trụ . . . . 8 4.
Công thức tính toán với các khối nón - trụ - cầu . . . . . . . . . PHƯỚC 8 5.
Phương pháp dựng tâm I của mặt cầu ngoại tiếp hình chóp . 9 VII.
Một số khối đa diện thường gặp trong các đề thi . . . . . . . . . . . . . . G 10 1.
Hình chóp tam giác đều . . . . . . . . . . . . . . . . . . . . . . . . 10 2.
Hình tam diện vuông O.ABC (vuông tại O) . . . . . . . . . . . . 10 3.
Hình chóp S.ABC có đường cao SA, AB vuông góc với BC . . . 10 4.
Hình chóp S.ABC có cạnh bên SA “thẳng đứng”, mặt đáy là
tam giác “thường” . . . . . . . . . . . . . . . . . . . . . . . . . . . . DƯƠN 11 5.
Hình chóp S.ABC có 1 mặt bên b “cân tại S” và “dựng đứng” 11 6.
Hình chóp tứ giác đều . . . . . . . . . . . . . . . . . . . . . . . . . 11 7.
Hình chóp S.ABCD có cạnh bên SA “thẳng đứng”, mặt đáy là
“hình chữ nhật” . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 8.
Hình chóp S.ABCD có 1 mặt bên “cân tại S” và “dựng đứng” . 12 9.
Hình hộp chữ nhật . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 0 MỤC LỤC
? Công thức tính nhanh một số khối tứ diện đặc biệt . . . . . . . . . . 13
? Một số công thức biệt liên quan khối tròn xoay . . . . . . . . . . . . . 14 VIII.
Ví dụ giải toán điển hình . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15 AN ĂN V CHU THPT - G SAN PHƯỚC G DƯƠN Chương 1 AN
Hình học không gian (cổ điển) ĂN
I. Một số vấn đề cơ bản về quan hệ song song V
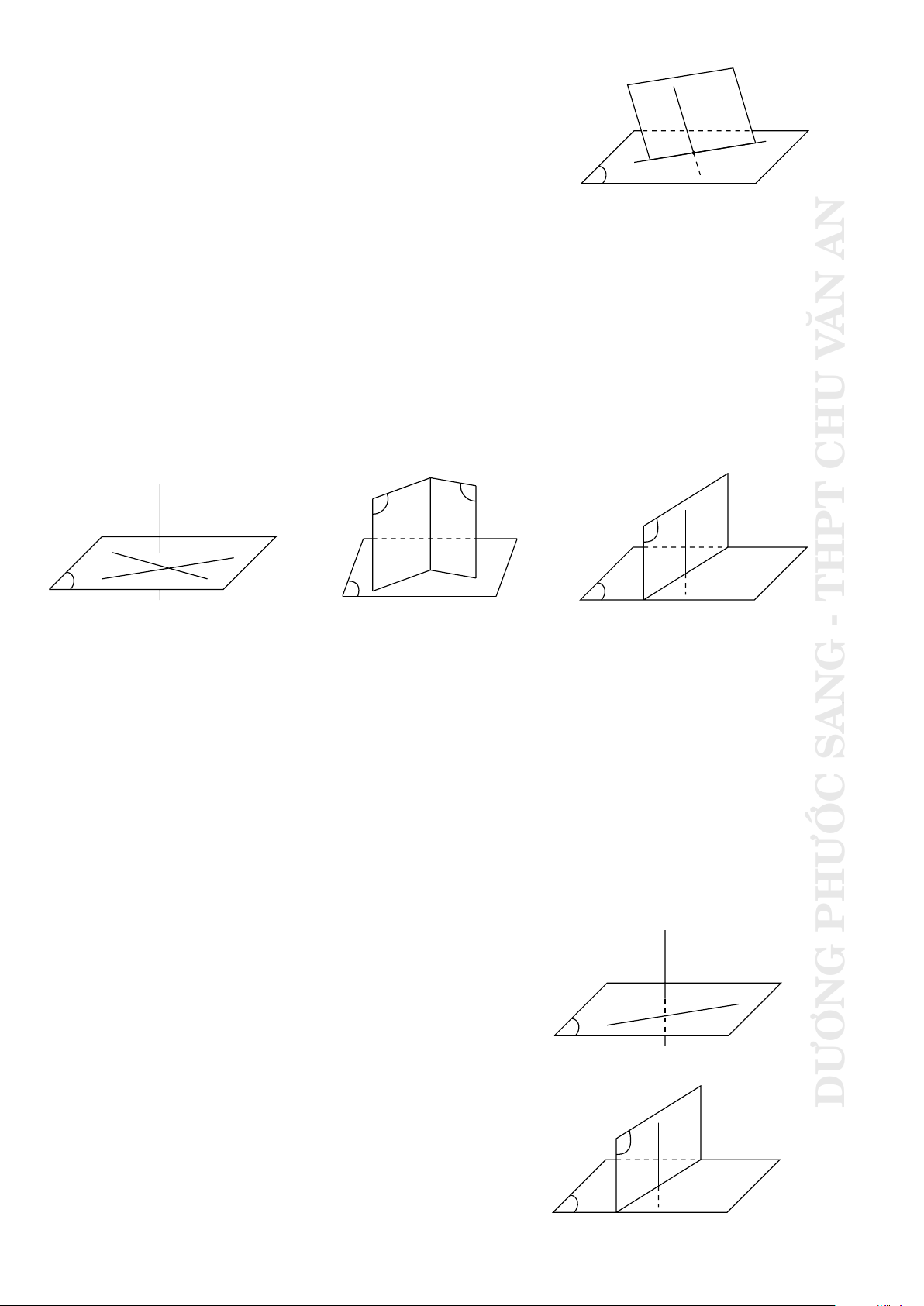
1. Việc xác định giao tuyến của hai mặt phẳng α α α a a CHU A B ∆ ∆ β β b β
Nếu 2 mặt phẳng phân biệt (α) và (β) có 2 điểm chung phân biệt A và B thì đường
thẳng AB là giao tuyến của chúng. THPT
Hai mặt phẳng phân biệt lần lượt qua 2 đường thẳng song song thì giao tuyến - của
chúng song song với cả hai đường thẳng đó hoặc trùng với 1 trong 2 đường thẳng Gđó.
Hai mặt phẳng phân biệt nếu thoả mãn tính chất “mặt phẳng này chứa đường thẳng
a, còn mặt phẳng kia song song với a” thì giao tuyến của chúng song song với a. γ c β γ β SAN α α a b b α b a c a β γ PHƯỚC
Ba mặt phẳng đôi một cắt nhau tạo thành 3 giao tuyến phân biệt thì ba giao tuyến ấy
hoặc đồng quy hoặc đôi một song song với nhau. G
Cho hai mặt phẳng song song với nhau. Nếu có mặt phẳng thứ ba cắt mặt phẳng thứ
nhất thì mặt phẳng thứ ba đó cắt luôn mặt phẳng thứ hai, đồng thời hai đường giao
tuyến tạo thành song song với nhau.
2. Việc xác định giao điểm của đường thẳng và mặt phẳng DƯƠN
PP cơ bản: muốn tìm giao điểm của đường thẳng d với d
mặt phẳng (α) ta tìm giao điểm của đường thẳng d đó
với 1 đường thẳng ∆ (hợp lý) trong mặt phẳng (α). I ∆
Nếu chưa tìm được đường thẳng ∆ trong (α) như trong α
PP cơ bản đã nêu, ta thực hiện 3 bước giải như sau: 1 2
CHƯƠNG 1. HÌNH HỌC KHÔNG GIAN (CỔ ĐIỂN) d
+o Bước 1: chọn mặt phẳng phụ (β) chứa đường thẳng d.
+o Bước 2: tìm giao tuyến ∆ của (β) và mp(α) đã cho. I ∆
+o Bước 3: tìm giao điểm I của ∆ và đường thẳng d. α
3. Một số định lý về nhận dạng quan hệ song song
Muốn chứng minh một đường thẳng song song với một mặt phẳng ta chứng minh AN
đường thẳng đó nằm ngoài mặt phẳng đồng thời song song với 1 đường thẳng nào đó nằm trong mặt phẳng.
Muốn chứng minh hai mặt phẳng song song với nhau ta chứng minh mặt phẳng này ĂN
chứa 2 đường thẳng cắt nhau cùng song song với mặt phẳng kia. V
II. Một số vấn đề cơ bản về quan hệ vuông góc
1. Phương pháp chứng minh đường thẳng vuông góc với mặt phẳng CHU d β α d d Q a P b ∆ P P THPT d ⊥ a ⊂ (P) (α) ⊥ (P) (P) ⊥ (Q) - d ⊥ b ⊂ (P) ⇒ d ⊥ (P) (β) ⊥ (P) ⇒ d ⊥ (P) d ⊂ (Q) ⇒ d ⊥ (P) G a ∩ b = I
d = (α) ∩ (β) d ⊥ ∆ = (P) ∩ (Q)
Muốn chứng minh một đường thẳng vuông góc với một mặt phẳng ta chứng minh
đường thẳng đó vuông góc với 2 đường thẳng cắt nhau nằm trong mặt phẳng. SAN
Nếu hai mặt phẳng phân biệt cùng vuông góc với mặt phẳng thứ ba thì giao tuyến
của chúng (nếu có) vuông góc với mặt phẳng thứ ba đó.
Xét 2 mặt phẳng vuông góc với nhau: nếu trong mặt phẳng này có 1 đường thẳng
vuông góc với giao tuyến của chúng thì đường thẳng đó vuông góc với mặt phẳng kia.
2. Phương pháp chứng minh hai đường thẳng vuông góc
Muốn chứng minh hai đường thẳng vuông góc với d PHƯỚC
nhau ta chứng minh đường thẳng này vuông góc với
một mặt phẳng chứa đường thẳng kia G (d ⊥ (P) ∆ ∆ ⇒ d ⊥ ∆ ⊂ (P) P
3. Phương pháp chứng minh hai mặt phẳng vuông góc
Muốn chứng minh hai mặt phẳng vuông góc với nhau DƯƠN
ta chứng minh mặt phẳng này chứa đường thẳng d
vuông góc với mặt phẳng kia. Q (d ⊥ (P) ⇒(P)⊥(Q) d ⊂ (Q) P 3
III. Phương pháp xác định các loại góc trong không gian
1. Góc giữa hai đường thẳng
Góc giữa hai đường thẳng a và b là góc giữa hai đường thẳng a0 và b0 cắt nhau lần
lượt song song hoặc trùng với hai đường thẳng a, b đó.
2. Góc giữa đường thẳng và mặt phẳng (cắt nhau nhưng không vuông góc)
Bước 1: Xác định giao điểm I của d và (α) AN
(góc cần vẽ có đỉnh đặt tại đây) d A
Bước 2: Tìm hình chiếu vuông góc d0 của d lên (α) ĂN
+o Trên d, lấy điểm A khác I. V ϕ
+o Tìm hình chiếu A0 của A trên (α) I A0 +o α
Kẻ đường thẳng nối I và A0, đó chính là d0
Bước 3: Xác định góc ϕ = à (d, (α)) = (d, d0). CHU d
? Lưu ý: Nếu đường thẳng d nằm trong mặt phẳng
(β) vuông góc với (α) thì góc hợp bởi d và (α) bằng ϕ I
góc hợp bởi d với giao tuyến của (α) và (β).
(giao tuyến của (α) và (β) trong trường hợp này α THPT
chính là hình chiếu vuông góc của d lên (α)) -
3. Góc giữa hai mặt phẳng (cắt nhau) G
Bước 1: xác định giao tuyến c của hai mặt phẳng (α) và (β). β
Bước 2: tìm 2 đường thẳng a, b cắt nhau, cùng c
vuông góc với giao tuyến c, lần lượt nằm trong 2 SAN a
mặt phẳng (α) và (β). I
Bước 3: xác định góc giữa 2 mặt phẳng (α) và (β): α góc đó chính là góc (a, b) 6 90◦.
? Lưu ý: góc giữa 2 mặt phẳng được định nghĩa là b
góc giữa hai đường thẳng lần lượt vuông góc với 2 mặt phẳng đó. PHƯỚC α α M M G d ∆ d ϕ I N β N β DƯƠN ? Đặc biệt:
Nếu có đường thẳng ∆ vuông góc với giao tuyến của 2 mặt phẳng (α) và (β) mà đường
thẳng ∆ đó đi qua 2 điểm ¡M ∈ (α) và N ∈ (β)¢, để xác định góc giữa 2 mặt phẳng (α) và
(β), từ điểm N ta vẽ N I ⊥ d tại I ∈ d. Khi đó á
((α),(β)) = M I N. 4
CHƯƠNG 1. HÌNH HỌC KHÔNG GIAN (CỔ ĐIỂN)
IV. Phương pháp xác định khoảng cách
1. Khoảng cách từ một điểm đến một mặt phẳng
Bài toán cơ bản 1:
Cho M là hình chiếu vuông góc của điểm S ∉ (β) lên α
mặt phẳng (β). Để tính khoảng cách từ điểm M đến mặt S
phẳng nằm nghiêng (α) ¡qua S và cắt (β)¢ ta làm như sau: H AN +o d
Bước 1: Xác định giao tuyến d của (α) và (β).
+o Bước 2: Từ M, vẽ M I ⊥ d tại I ∈ d. I +o Bước 3: Vẽ MH M
⊥ SI tại H ∈ SI thì d¡M, (α)¢ = MH. β ĂN V Bài toán cơ bản 2:
Cho hai mặt phẳng (α) và (β) vuông góc với nhau, điểm
M ∈ (β). Để tính khoảng cách từ điểm M đến mặt phẳng (α) ta làm như sau: α
+o Bước 1: Xác định giao tuyến d của (α) và (β). H CHU M d
+o Bước 2: vẽ MH ⊥ d tại H ∈ d thì d¡M,(α)¢ = MH. β Một số lưu ý: A M A B B THPT A C - I A0 B0 A0 B0 α α α B G d¡A, (α)¢ A I 3.VMABC =
d¡A, (α)¢ = d¡B,(α)¢ d¡M, (ABC)¢ = d¡B, (α)¢ BI S4ABC
2. Khoảng cách giữa 2 đối tượng song song nhau SAN
Khoảng cách giữa d và d0 (song song nhau) là khoảng cách từ điểm M ∈ d đến d0.
Khoảng cách giữa d và (α) (song song nhau) là khoảng cách từ điểm M ∈ d đến (α).
Khoảng cách giữa (α) và (β) (song song nhau) là khoảng cách từ điểm M ∈ (α) đến (β).
3. Khoảng cách giữa 2 đường thẳng a và b chéo nhau PHƯỚC a A a M A α G b B β b B P
Khoảng cách giữa 2 đường thẳng chéo nhau (a và b) bằng độ dài đoạn vuông góc chung DƯƠN
của chúng (tức đoạn thẳng AB có A ∈ a, B ∈ b và AB ⊥ a, AB ⊥ b).
Khoảng cách giữa 2 đường thẳng chéo nhau bằng khoảng cách giữa đường thẳng này
và một mặt phẳng song song với nó đồng thời chứa đường thẳng kia.
Khoảng cách giữa 2 đường thẳng chéo nhau bằng khoảng cách giữa 2 mặt phẳng song
song với nhau lần lượt chứa 2 đường thẳng đó. 5
V. Một số vấn đề về khối đa diện lồi, khối đa diện đều
1. Tính chất của một hình đa diện, khối đa diện
Hai đa giác phân biệt chỉ có thể: hoặc là không có điểm chung, hoặc chỉ có 1 đỉnh
chung, hoặc chỉ có 1 cạnh chung. Mỗi đỉnh là đỉnh chung của ít nhất 3 đa giác.
Mỗi cạnh của bất kỳ đa giác nào cũng đều là cạnh chung của đúng 2 đa giác.
Bất cứ hình đa diện nào cũng có thể phân chia thành nhiều khối tứ diện. AN
Bất cứ hình đa diện nào cũng có ít nhất 4 đỉnh, ít nhất 4 mặt và ít nhất 6 cạnh.
Hình chóp có mặt đáy là n-giác thì có (n + 1) đỉnh, (2n) cạnh và (n + 1) mặt.
Hình lăng trụ có mặt đáy là n-giác thì có (2n) đỉnh, (3n) cạnh và (n + 2) mặt. ĂN M p
Một hình đa diện có M mặt, mỗi mặt có p cạnh thì có cạnh. V 2
Với một đa diện lồi bất kỳ có Đ đỉnh, C cạnh và M mặt thì M +C−Đ = 2 (định lý Euler).
Khối đa diện là phần không gian giới hạn bởi một hình đa diện, kể cả hình đa diện đó.
Khối đa diện lồi là một khối đa diện mà đoạn thẳng nối 2 điểm bất kỳ của CHU khối đa
diện đó luôn thuộc vào chính nó.
2. Bảng tổng hợp tính chất của các đa diện đều THPT - G Tứ diện đều H.lập phương Bát diện đều 12 mặt đều 20 mặt đều Số Số Số Số mặt Số trục Bán SAN kính Tên đa diện Loại Thể tích
đỉnh cạnh mặt đ.xứng đ.xứng mc ng.tiếp p p 2c3 6c Tứ diện đều {3;3} 4 6 4 6 3 V = R = 12 4 p3c H.lập phương {4;3} 8 12 6 9 9 V = c3 R = 2 p p 2c3 2c Bát diện đều {3;4} 6 12 8 9 V = R = 3 2 PHƯỚC 12 mặt đều {5;3} 20 30 12 15 20 mặt đều {3;5} 12 30 20 15 G
Ký hiệu {p; q} cho biết p là số cạnh của mỗi mặt, q là số mặt đi qua mỗi đỉnh DƯƠN 6
CHƯƠNG 1. HÌNH HỌC KHÔNG GIAN (CỔ ĐIỂN)
VI. Một số công thức tính toán hình học
1. Công thức tính toán hình học liên quan đến tam giác Đối với tam giác đều A p (cạnh) × 3
+o Độ dài đường cao: h = 2 p (cạnh) × 3 O
+o Bán kính đường tròn ngoại tiếp: R = AN 3p (cạnh) × 3
+o Bán kính đường tròn nội tiếp: r = B H C 6 ĂN
Đối với tam giác vuông cân A V p
+o Độ dài cạnh huyền: cạnh huyền = (cạnh góc vuông) × 2 cạnh huyền
+o Độ dài cạnh góc vuông: cạnh góc vuông = p2 B C
Hệ thức lượng trong tam giác vuông CHU +o a2 = b2 + c2 +o ah = bc A +o b2 = b0.a +o c2 = c0.a b bc 1 1 1 c +o h = p +o = + h m b2 + c2 h2 b2 c2 a +o a THPT +o h2 = b0.c0 = 2.ma c0 b0 B H M C - b0 b2 c0 c2 +o = +o = a a a2 a a2 G
Hệ thức lượng trong mọi tam giác
+o Định lý côsin: a2 = b2 + c2 − 2bc cos A A b2 SAN + c2 − a2
+o Công thức tính góc: cos A = 2bc c a b c b +o Định lý sin: = = = 2R ma sin A sin B sin C b2 + c2 a2
+o Định lý trung tuyến: m2a = − 2 4 B a M C
Công thức tính diện tích tam giác PHƯỚC p (cạnh)2 × 3
+o Diện tích của tam giác đều: S4đều = G 4
+o Diện tích tam giác vuông bằng nửa tích của hai cạnh góc vuông.
+o Diện tích của mọi tam giác (bất kỳ): 1 1 abc p S4ABC = a.ha = bc sin A = = pr = p(p − a)(p − b)(p − c) 2 2 4R DƯƠN a * h + b + c
a: đường cao ứng với cạnh đáy a. * p = : nửa chu vi 2
* R: bán kính đường tròn ngoại tiếp
* r: bán kính đường tròn nội tiếp S AB0 AC0
+o Công thức tỉ số diện tích: 4AB0C0 = ·
, trong đó B0 ∈ AB, C0 ∈ AC. S4ABC AB AC 7 Định lý Menelaus Định lý Ceva A A M A K B NC N M × × = 1 N MB K C N A M K B C B K ANC (M, N, K thẳng hàng) (AK, BN, CM đồng quy)
2. Công thức tính toán hình học liên quan đến tứ giác ĂN V Đối với hình vuông A D p
+o Độ dài đường chéo: đường chéo = (cạnh) × 2 đường chéo +o Độ dài cạnh: cạnh = p2 2 CHU (đường chéo)
+o Diện tích hình vuông: Shv = (cạnh)2 = 2 B C
Đối với hình chữ nhật A D
+o Độ dài đường chéo hình chữ nhật: q 2 2 THPT đường chéo =
(chiều dài) + (chiều rộng) -
+o Diện tích: Shcn = (chiều dài) × (chiều rộng) B G C Đối với hình thang A D
+o Diện tích hình thang bằng nửa tổng hai đáy nhân với chiều cao: SAN (đáy lớn) + (đáy bé) Sh.thang = × (đường cao) 2 B C H
Đối với hình bình hành A D
+o Diện tích h.bình hành bằng cạnh nhân với đường cao
Sh.bình hành = (cạnh BC) × (đường cao AH)
+o Diện tích hình bình hành bằng tích của 2 cạnh kề PHƯỚC
nhân với sin của một góc B C H G
Sh.bình hành = (cạnh AB) × (cạnh BC) × sin ABC Đối với hình thoi A
+o Diện tích hình thoi bằng nửa tích hai đường chéo
(đường chéo 1) × (đường chéo 2) O S B D h.thoi = DƯƠN 2
? Đặc biệt: hình thoi có góc 60◦ hoặc 120◦ có diện tích p (cạnh)2 × 3 C Sh.thoi (ĐB) = 2
Với tứ giác lồi có 2 đường chéo vuông góc: diện tích bằng nửa tích của 2 đường chéo. 8
CHƯƠNG 1. HÌNH HỌC KHÔNG GIAN (CỔ ĐIỂN)
3. Công thức thể tính thể tích khối chóp và khối lăng trụ
Vlăng trụ = Smặt đáy × h 1 h h V S khối chóp = mặt đáy × h 3 AN
Công thức dùng để tính tỉ số thể tích: S S S A ĂN a = SA0 V A0 C0 C0 D0 SB B0 b = SB0 A0 SC B0 A A C D c = SC0 CHU SD B C d B = SD0 VS.A0B0C0 S A0 SB0 SC0 VS.A0B0C0D0 a + b + c + d = · · = VS.ABC S A SB SC VS.ABCD 4abcd A0 C0 A0 D0 THPT P - M M B0 B0 C0 Q G N A C A D P N SAN B B C V µ ¶ µ ¶ M N P.A0B0C0 1 A0M B0N C0P VMNPQ.A0B0C0D0 1 A0M C0P = + + = + VABC.A0B0C0 3 A A0 BB0 CC0 VABCD.A0B0C0D0 2 A A0 CC0
4. Công thức tính toán với các khối nón - trụ - cầu O
Đối với hình nón - hình nón cụt
+o Diện tích mặt đáy: Sđáy = πr2 PHƯỚC h0 l0
+o Diện tích xung quanh: Sxq = πrl G l
+o Diện tích toàn phần: S h tp = Sđáy + Sxq r0 1 1 I0
+o Thể tích: Vnón = Sđáy.h = πr2h A0 3 3
+o Chu vi đường tròn đáy: C = 2πr
+o Góc ở đỉnh nón: 2β = 2 I r IO A DƯƠN V 0 µ r0 ¶3 µ h0 ¶3 µ l0 ¶3 A +o (O,I0,r0) Tỉ số thể tích: = = = V(O,I,r) r h l 1 ³
+o Thể tích hình nón cụt có hai đáy (I, r) và (I0, r0) là: Vnón cụt = πh r2 + rr0 + r02´ 3
+o Diện tích xung quan hình nón cụt nêu trên là: Sxq (nón cụt) = π¡r + r0¢ l 9 Đối với hình trụ
+o Diện tích mặt đáy: Sđáy = πr2 I0 r0 A0
+o Diện tích xung quanh: Sxq = 2πrl
+o Diện tích toàn phần: Stp = 2Sđáy + Sxq I r
+o Thể tích: Vtrụ = Sđáy.h = πr2h A
+o Chu vi đường tròn đáy: C = 2πr AN Đối với hình cầu +o Diện tích mặt cầu: S I R mặt cầu = 4πR2 ĂN 4 +o Thể tích khối cầu: V πR3 M V khối cầu = 3
5. Phương pháp dựng tâm I của mặt cầu ngoại tiếp hình chóp S S S d d CHU H H K I I I A A A O O O B THPT - r 1 b2 r 1 Rmc = R2 + h2 R R R2 + R2 − (gt)2 d mc = 4 mc = 2h d b 4 G ? Một số lưu ý:
+o Một hình chóp nội tiếp được một mặt cầu khi và chỉ khi mặt đáy của nó là SAN một đa
giác nội tiếp được đường tròn.
+o Tâm của mặt cầu ngoại tiếp hình chóp luôn nằm trên trục của đường tròn ngoại
tiếp mặt đáy hình chóp.
Với hình chóp có cạnh bên (S A chẳng hạn) vuông góc với mặt đáy
+o Gọi d là trục của đường tròn ngoại tiếp mặt đáy thì d chứa tâm I.
+o Gọi H là trung điểm của cạnh bên (vuông với đáy). Khi đó PHƯỚC
I H ∥ AO và IH là 1 đường trung trực của cạnh bên S A. G Với hình chóp đều
+o Gọi SO là đường cao của hình chóp đều thì SO chứa tâm I.
+o Gọi H là trung điểm của cạnh bên S A. Khi đó
I H là 1 đường trung trực của cạnh bên S A. DƯƠN
Với hình chóp có 1 mặt bên vuông góc với mặt đáy
+o Gọi d là trục của đường tròn ngoại tiếp mặt đáy thì d chứa tâm I.
+o Gọi K tâm của đường tròn ngoại tiếp mặt bên (vuông với đáy). Khi đó
I K là trục của đường tròn ngoại tiếp mặt bên đó. 10
CHƯƠNG 1. HÌNH HỌC KHÔNG GIAN (CỔ ĐIỂN)
VII. Một số khối đa diện thường gặp trong các đề thi
1. Hình chóp tam giác đều S S S b AN I α A C A A C ϕ C O d M O O ĂN B B B V
Góc giữa cạnh bên và mặt đáy: α = S AO = SBO = SCO
Góc giữa mặt bên và mặt đáy: ϕ = SMO r 1 b tan ϕ
Công thức tính độ dài đường cao: h = b2 − d2 = 3 q tan2 ϕ CHU + 4 p d2 3b2 − d2 d3 tan ϕ d3 tan α
Công thức thể tích khối chóp tam giác đều: V = = = 12 24 12 b2
Công thức tính bán kính mặt cầu ngoại tiếp: R = 2h
Khoảng cách giữa 2 cạnh đối diện nhau: d(S A, BC) = d(M, SA) THPT
Tâm mặt cầu ngoại tiếp luôn thuộc SO đồng thời cách đều 2 điểm S và A. -
2. Hình tam diện vuông O.ABC (vuông tại O) G OH ⊥ (ABC) tại H A A
⇔ H là trực tâm của 4ABC E SAN 1 1 1 1 I = + + OH2 O A2 OB2 OC2 H G
Bán kính mặt cầu ngoại tiếp O C O C 1 p M R = O A2 + OB2 + OC2 B B 2
Đặt a = OA, b = OB, c = OC và S1 = S4OAB; S2 = S4OBC; S3 = S4OAC thì abc p2S1S2S3 PHƯỚC VO.ABC = = 6 3 G
3. Hình chóp S.ABC có đường cao SA, AB vuông góc với BC AH ⊥ (SBC), BC ⊥ (SAB), S S SC ⊥ (AHK), SC ⊥ (BMN), K BM ⊥ (S AC). I N DƯƠN ((S á BC), (S AC)) = AK H = BN M H O M ((S A C A C á BC), (ABC)) = SB A.
d¡A, (SBC)¢ = AH, d¡M,(SAC)¢ = BM B B 11
Tâm mặt cầu ngoại tiếp S.ABC (trường hợp này) là trung điểm I của cạnh bên SC.
Tâm mặt cầu ngoại tiếp đa diện lồi HK.ABC là trung điểm O của cạnh đáy AC.
Tâm mặt cầu ngoại tiếp tứ diện BCMN là trung điểm của cạnh đáy BC.
Tâm mặt cầu ngoại tiếp hình chóp B.S AMN là trung điểm của cạnh bên SB.
4. Hình chóp S.ABC có cạnh bên SA “thẳng đứng”, mặt đáy là tam giác “thường” S S ((S á BC), (ABC)) AN = SM A d¡A, (SBC)¢ = AH. d¡A, (S AC)¢ = d¡B, AC¢ ĂN H V
Nếu mặt đáy ABC cân tại A T A C C
(hoặc mặt đáy ABC đều) thì A
M là trung điểm của cạnh M ∆ B K B CHU BC, ngoài ra SB = SC.
Khoảng cách giữa 2 cạnh đối diện SB và AC: d¡SB, AC¢ = d¡AC,(SBK)¢ = AT r 1
Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là R = R2 + h2 d 4
(trong đó đường cao h = S A và Rd là bán kính đường tròn ngoại tiếp mặt đáy ABC)THPT
5. Hình chóp S.ABC có 1 mặt bên b “cân tại S” và “dựng đứng” - S S
Nếu 4ABC vuông tại A thì G M là trung điểm cạnh AB N là trung điểm cạnh AC ((S á AB), (ABC)) = SMH P Q SAN T ((S B C B C á AC), (ABC)) = SN H H H N d¡A, (SBC)¢ = d¡A, BC¢ M
d¡H, (S AB)¢ = HP,d¡H,(SAC)¢ = HQ A A K
Khoảng cách giữa hai cạnh S A và BC là d¡S A, BC¢ = d¡BC,(SAK)¢ = AT q
Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là R = R2 + R2 − 1(gt)2 PHƯỚC d b 4
(Rd, Rb: bán kính đ.tròn ngoại tiếp mặt đáy và mặt bên, gt: giao tuyến của c G húng)
6. Hình chóp tứ giác đều S S S DƯƠN A I H A A D D D B O E B O O B C C C 12
CHƯƠNG 1. HÌNH HỌC KHÔNG GIAN (CỔ ĐIỂN)
Góc giữa cạnh bên và mặt đáy: α = S AO = SBO = SCO = SCO
Góc giữa mặt bên và mặt đáy: ϕ = SEO r 1 b tan ϕ
Công thức tính độ dài đường cao: h = b2 − d2 = 2 q tan2 ϕ + 2 p d2 4b2 − 2d2 d3 tan ϕ Công thức thể tích: V = = 6 6 b2
Công thức tính bán kính mặt cầu ngoại tiếp (mọi hình chóp đều): R = AN 2h
Tâm mặt cầu ngoại tiếp luôn thuộc SO đồng thời cách đều 2 điểm S và A.
7. Hình chóp S.ABCD có cạnh bên SA “thẳng đứng”, mặt đáy là “hình chữ nhật” ĂN V BC ⊥ (SAB), S S AH ⊥ (SBC), K P CD ⊥ (S AD), CHU I AK ⊥ (SCD), H N T SC ⊥ (AHPK), D D A A O BD ⊥ (S AE), O M E AT ⊥ (SBD) B C B C THPT - ((SB á C), (ABCD)) = SB A; ((SC á D), (ABCD)) = SD A; ((SB á D), (ABCD)) = SE A
d¡A, (SBC)¢ = AH; d¡A,(SCD)¢ = AK; d¡A,(SBD)¢ = AT;d¡SB, AC¢ = AN G 1 1 1 1 = + + AT2 S A2 AB2 AD2
? Chú ý: nếu ABCD là hình vuông thì E ≡ O; AM ∥ OB; AH = AK; HK ∥ BD s µ ¶2 SAN h
Bán kính mặt cầu ngoại tiếp hình chóp S.ABCD là R = R2 + d 2
Mặt cầu ngoại tiếp hình chóp S.ABCD có tâm là trung điểm I của cạnh bên SC
Mặt cầu ngoại tiếp đa diện lồi HPK.ABCD có tâm là tr.điểm O của mặt đáy ABCD
Mặt cầu ngoại tiếp hình chóp S.AHPK có tâm là trung điểm của đường cao S A
8. Hình chóp S.ABCD có 1 mặt bên “cân tại S” và “dựng đứng” PHƯỚC CD ⊥ (SHE), S S G HK ⊥ (SCD), N AM ⊥ (SBC), K BN ⊥ (S AD), M A A D D T DƯƠN HT ⊥ (SBD) E H H d¡A, (SBC)¢ = AM M B C B C d¡B, (S AD)¢ = BN ((SB á C), (ABCD)) = SB A; ((SC á D), (ABCD)) = SEH; ((SB á D), (ABCD)) = SMH 13 q
Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là R = R2 + R2 − 1(gt)2 d b 4
(Rd, Rb: bán kính đ.tròn ngoại tiếp mặt đáy và mặt bên, gt: giao tuyến của chúng)
9. Hình hộp chữ nhật
Độ dài đường chéo của hình hộp chữ nhật: A b D p O AC0 a2 a AN = + b2 + c2 1 G
Bán kính mặt cầu ngoại tiếp: R = AC0 B C c 2 I
Thể tích hình hộp chữ nhật: V p hhcn = ab c = S1S2S3 ĂN A0 V D0
(S1, S2, S3 là diện tích của 3 mặt chung 1 đỉnh của hhcn) 1
Thể tích khối chóp BD A0C0: VBDA0C0 = Vhình hộp B0 C0 3 CHU
Công thức tính nhanh thể tích của một số khối tứ diện đặc biệt Điều kiện
Công thức tính thể tích abc ( p S A = a, SB = b, SC = c V =
1 − cos2 α − cos2 β − cos2 γ + 2cosαcosβcosγ THPT 6 ASB - = α, BSC = β, CS A = γ
(biết 3 cạnh chung đỉnh và 3 góc tại đỉnh đó) 1 G (S A = a,BC = b V = abd.sinα 6 d(S A, BC) = d;( á S A, BC) = α
(biết 2 cạnh đối diện; khoảng cách và góc giữa chúng) 2S1S2 sin ϕ SAN (S A = a, SSAB = S1, SSAC = S2 V = 3a ((S á AB), (S AC)) = ϕ
(biết 1 cạnh; diện tích và góc giữa 2 mặt kề với nó) S A = a, SB = b, SC = c 1
V = .abc.sinαsinβsinϕ 6 ASB = α, ASC = β ((S
(biết 3 cạnh chứa đỉnh, 2 góc ở đỉnh và 1 góc nhị diện) á AB), (S AC)) = ϕ p PHƯỚC S A = BC = a 2 p V (a2 =
+ b2 − c2)(b2 + c2 − a2)(a2 + c2 − b2) SB = AC = b 12 G SC = AB = c
(biết các cặp cạnh đối diện bằng nhau) 1
M = a2x2(b2 + c2 + y2 + z2 − a2 − x2)
N = b2 y2(a2 + c2 + x2 + z2 − b2 − y2) (S A = x,SB = y,SC = z
P = c2 z2(a2 + b2 + x2 + y2 − c2 − z2) DƯƠN BC = a, AC = b, AB = c
Q = (abc)2 + (a yz)2 + (x yc)2 + (xbz)2 1 V p = M + N + P − Q 12 14
CHƯƠNG 1. HÌNH HỌC KHÔNG GIAN (CỔ ĐIỂN)
Một số công thức về hình, khối đặc biệt liên quan khối tròn xoay Công thức Hình minh hoạ S h
xq = 2πR h = π(r2 + h2) µ ¶ AN h πh H V R (h2 chỏm cầu = πh2 − = + 3r2) r 3 6 R O ĂN V Sxq = πr(h1 + h2) h2 µ h ¶ 1 + h2 V = πr2 h1 2 O r CHU 2 2 h
Vhình nêm = r3 tanϕ = r2h 3 3 r ϕ O r r THPT - s 3 r r 4 S0 h0 µ r0 ¶3 G Sparabol = rh ; = = 3 S h r h h 1 r0 Vparabolic = πr2h h0 2 SAN B Selip = πab b 4 a Vquay quanh 2a = πab2 A0 A 3 O 4 Vquay quanh 2b = πa2b 3 B0 PHƯỚC A A Quay mọi tam giác ABC G xung quanh cạnh AB
ta sẽ được hình tròn xoay có 4π S2 B V = · 4ABC H 3 AB µ AC + BC ¶ C Sxq = 2πS4ABC DƯƠN AB H B C 15
VIII. Ví dụ giải toán điển hình
| Ví dụ 1. Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên bằng 2a. Gọi M
là trung điểm của cạnh BC.Tính góc hợp bởi hai đường thẳng dưới đây: a) AM và SC. b) SM và NC. $ Lời giải AN
? Phương pháp cổ điển S S
Để tính được góc giữa hai đường thẳng chéo nhau ĂN 2a N
thường ta dựng thêm một V
đường thẳng song song với
1 trong 2 đường thẳng đó và A C A C
cắt đường thẳng còn lại. a M a M
Góc giữa AM & SC dễ dựng CHU hơn góc giữa SM & NC! B B
Câu a. Gọi K là trung điểm cạnh SB thì MK ∥ SC, do đó ( á AM, SC) = ( á AM, MK ) p S A2 + AB2 SB2 3a2 1 a 3 Ta có AK2 = − = ; MK = SC = a ; AM = 2 4 2 2 2 p AM2 + MK2 − AK2 3 4AMK có cos AMK = = ⇒ ( á AM, SC) = AMK ≈ 81◦420. THPT 2.AM.MK 12 -
Câu b. Gọi I là trung điểm đoạn thẳng AM thì N I ∥ SM, do đó ( á SM, NC) = ( á N I, NC) p p p a 6 1 1 p a 15 p a 7 Ta có NC ; N I SM SC2 ; IC I M2 G = AK = = = − MC2 = = + CM2 = 2 2 2 4 4 p N I2 + NC2 − IC2 4 10 4I NC có cos I NC = = ⇒ ( á SM, NC) = I NC ≈ 32◦300. 2.N I.NC 15 S S S z SAN N 2a 2a K x A C A C C A I H a a M a M M PHƯỚC B B y B G
? Phương pháp toạ độ p p p a 3 a 3 r 1 r 1 a 33 Ta có AM = ; AH = ; SH = b2 − d2 = (2a)2 − a2 = . 2 6 3 3 3
Gắn hệ trục Mx yz (như hình vẽ) với toạ độ các điểm như sau: Ã p ! Ã p ! Ã p p ! Ã p p ! 3 µ 1 ¶ 3 3 33 3 33 M(0; 0; 0) ; A ; 0; 0 ; C 0; − ;0 ; H ; 0; 0 ⇒ S ; 0; ⇒ N ; 0; DƯƠN 2 2 6 6 3 3 6
Đến đây dùng công thức tính góc giữa hai đường thẳng ta giải được cả 2 câu a và b. # » # » # » # » ¯ ¯ ¯ A M .S C¯ ¯ ¯S M .N C¯ ¯ cos ( á SM, SC) = ; cos ( á SM, NC) = AM.SC SM.NC 16
CHƯƠNG 1. HÌNH HỌC KHÔNG GIAN (CỔ ĐIỂN)
| Ví dụ 2. Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB = a, AD = 2a, p
S A = a 3 và S A vuông góc với mặt đáy. Tính góc giữa các cặp đường thẳng và mặt phẳng sau đây: a) SC và (S AB) b) AC và (SCD) $ Lời giải
Câu a. Ta có SC ∩ (S AB) = S (BC ⊥ AB AN Do
nên BC ⊥ (S AB) tại B. Do đó S BC ⊥ S A (S á C, (S AB)) = (á SC, SB) = BSC E 3 ĂN p
4S AB vuông tại A có SB = S A2 + AB2 = 2a p a V BC 4SBC vuông tại B có tan BSC = = 1 ⇒ BSC = 45◦ SB 2a A D Vậy (S á C, (S AB)) = 45◦ a
Câu b. Ta có AC ∩ (SCD) = C CHU Vẽ AE B
⊥ SD tại E ∈ SD thì ... AE ⊥ (SCD) C Như vậy (A á C, (SCD)) = ( á AC, CE) = ACE p p S A.AD 2a 3 p p AE 2 105 Ta có AE = p = p ; AC = AB2 + BC2 = a 5 ; sin ACE = = S A2 + AD2 7 AC 135 THPT Vậy (A á C, (SCD)) ≈ 35◦500. -
| Ví dụ 3. Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB = 2a, BD = 3a, G
mặt bên S AB là tam giác cân tại S đồng thời nằm trong mặt phẳng vuông góc với mặt p
đáy. Biết SB = a 5, hãy tính góc hợp bởi các cặp mặt phẳng sau đây: a) (SCD) và (ABCD) b) (SBD) và (ABCD) c) (SBC) và (S AD) SAN $ Lời giải
Gọi H là trung điểm của cạnh AB thì SH ⊥ AB (do 4S AB cân tại S) (S AB) ⊥ (ABCD) Mà SH ⊂ (S AB) nên SH ⊥ (ABCD). S AB = (S AB) ∩ (ABCD) p PHƯỚC
4SHB vuông tại H có SH = SB2 − HB2 = 2a. p p
4ABD vuông tại A có AD = BD2 − AB2 = a 5 A G
Câu a. Gọi K là trung điểm cạnh CD ta có D ( H CD ⊥ HK K ⇒ CD ⊥ (SHK) ⇒ CD ⊥ SK I CD ⊥ SH B C CD = (SCD) ∩ (ABCD) DƯƠN Do CD ⊥ HK ⊂ (ABCD) nên ((SC á D), (ABCD)) = ( á SK , HK ) CD ⊥ SK ⊂ (SCD) SH 2a 2 4SHK vuông tại H có tan SK H = = p = p ⇒ SK H ≈ 41◦480 HK a 5 5 Vậy ((SC á D), (ABCD)) ≈ 41◦480. 17
Câu b. Vẽ H I ⊥ BD tại I ∈ BD, ta sẽ chứng minh được BD ⊥ (SHI) và BD ⊥ SI.
Với kết quả đó ta tiếp tục chứng minh được ((SB á D), (ABCD)) = á (S I, H I) p p H I BH AD.BH a 5.a a 5 Ta có 4BIH v 4BAD nên = ⇒ H I = = = AD BD BD 3a 3 SH 6 Cuối cùng tan S I H = = p , do đó ((SB á D), (ABCD)) = S I H ≈ 69◦330. I H AN 5
Câu c. Do (SBC) và (S AD) có chung điểm S và có BC ∥ AD nên giao tuyến ∆ của c ĂN húng
đi qua đỉnh S và song song với hai cạnh BC, AD. V
Hình chóp S.ABCD này có tính chất SB ⊥ BC và S A ⊥ AD vì thế SB ⊥ ∆ và S A ⊥ ∆ Như vậy ((S á BC), (S AD)) = (á SB, SC) = 2. BSH ≈ 53◦80. CHU
| Ví dụ 4. Cho hình chóp S.ABCD có đáy là hình vuông tâm O cạnh bằng a, cạnh
bên S A vuông góc với mặt đáy, cạnh bên SC tạo với mặt đáy một góc bằng 60◦.
a) Tính theo a thể tích của khối chóp S.ABCD
b) Tính khoảng cách từ điểm A đến mặt phẳng (SCD) THPT - $ Lời giải G
Câu a. Do SC ∩ (ABCD) = C và S A ⊥ (ABCD) nên (S á C, (ABCD)) = ( á SC, AC) ⇒ SC A = 60◦ S A
Tam giác S AC vuông tại C có tan S SC A = AC p p ⇒ S A = AC. tan SC A = a 2.tan60◦ = a 6 H SAN p 1 1 p a3 6
Vậy VS.ABCD = SABCD.S A = .a2.a 6 = 3 3 3
Câu b. Vẽ AH ⊥ SD tại H ∈ SD ta sẽ chứng minh được A D AH ⊥ (SCD) tại H ∈ (SCD) p S A.AD a 42 B C Suy ra d(A, (SCD)) = AH = p = . S A2 + AD2 7 PHƯỚC G
| Ví dụ 5. Cho hình chóp S.ABCD có mặt đáy ABCD là hình thang vuông tại A và
D với CD = a, AB = AD = 2a, mặt bên S AD cân tại S đồng thời nằm trong mặt phẳng
vuông góc với mặt đáy. Biết góc giữa (SBC) và (ABCD) bằng 60◦. Tính theo a
a) Thể tích của khối chóp S.ABCD
b) Khoảng cách từ điểm A đến mặt phẳng (SBC) DƯƠN $ Lời giải
Câu a. Gọi H là trung điểm cạnh AD thì SH ⊥ (ABCD)
Vẽ H I ⊥ BC tại I ∈ BC ta được BC ⊥ SI, từ đó ((SB á C), (ABCD)) = S I H = 60◦ . 18
CHƯƠNG 1. HÌNH HỌC KHÔNG GIAN (CỔ ĐIỂN) 1
Hình thang ABCD có SABCD = (AB + CD).AD = 3a2 S 2 3a2
Suy ra S4HBC = SABCD − S4HAB − S4HCD = 2 p 2S 3a2 3a 5 Từ đó I H = 4HBC = p = BC a 5 5p p A 3a 5 3a 15 B M SHI có SH = IH.tan S I H = tan 60◦ = 5 5 H p p AN 3a2 3a 15 3a3 15 Vậy V = · = I 3 5 5 D C p 1 a3 15
Câu b. S4ABC = SABCD − S4ACD = 2a2 ⇒ VS.ABC = S 3 4ABC.SH = 5 ĂN p p 6a 5 1 V 4SIH có SI = SH2 + IH2 = ⇒ S BC.S I = 3a2 5 4SBC = 2 p 3VS.ABC a 15 Như vậy d(A, (SBC)) = = S4SBC 5
| Ví dụ 6. Cho hình lăng trụ đứng ABC.A0B0C0 có đáy ABC là tam giác vuông tại CHU p
B, BC = a, mp(A0BC) tạo với đáy một góc 30◦ và ∆A0BC có diện tích bằng a2 3. Tính
thể tích khối lăng trụ. $ Lời giải (BC ⊥ AB A0 C0 THPT Do nên BC ⊥ A0B BC ⊥ A A0 - BC ⊥ AB ⊂ (ABC) G Do BC ⊥ AB ⊂ (A0BC) nên ((A0 á BC), (ABC)) = AB A0 BC = (ABC) ∩ (A0BC) B0 p 2.S 2a2 3 p A Ta có A0B = 4A0BC = = 2a 3. BC a C SAN p 30 4ABA0 có AB = A0B · cos ◦ AB A0 = 2a 3 · cos30◦ = 3a p p A A0 = A0B · sin AB A0 = 2a 3 · sin30◦ = a 3 B p 1 1 p 3a3 3
Vậy VABC.A0B0C0 = B · h = SABC · A A0 = AB · BC · A A0 = · 3a · a · a 3 = . 2 2 2
| Ví dụ 7. Cho hình chóp S.ABC có đường cao S A = a, AB vuông góc với BC, các p PHƯỚC
cạnh AB = a 3 và AC = 2a. Một mặt phẳng (α) đi qua điểm A vuông góc với cạnh SB,
cắt SB và SC lần lượt tại M và N. Tính theo a thể tích của khối chóp A.BCN M. G $ Lời giải S
Dễ dàng chứng minh được BC ⊥ (S AB) và BC ⊥ SB
Do SB ⊥ (AMN) nên SB ⊥ AM và SB ⊥ MN N M (BC ⊥ SB SM SN Xét trong (AMN), DƯƠN ⇒ MN ∥ BC ⇒ = M N ⊥ SB SB SC SM SN Do A C VS.AMN = . .VS.ABC nên SB SC µ SM2 ¶ VA.BCNM = 1 − VS.ABC SB2 B 19 p 4ABC vuông tại B có BC = AC2 − AB2 = a p p 1 a2 3 1 a3 3 ⇒ S4ABC = AB.BC = và VS.ABC = .S 2 2 3 4ABC.S A = 6 SM S A2 S A2 1 4S AB vuông tại A có = = = . SB SB2 S A2 + AB2 4 p p µ 1 ¶ a3 3 5a3 3 Vậy VA.BCNM = 1 − . = . 42 6 32 AN Chú ý ĂN
Giả thiết 2 đường thẳng phân biệt cùng vuông góc với đường thẳng thứ 3 không đủ Vđể
kết luận hai đường thẳng đó song song với nhau. Chỉ khi cả 3 đường thẳng cùng nằm
trên một mặt phẳng thì kết luận đó mới đúng. | Ví dụ 8. S CHU
Cho hình chóp S.ABCD có đáy là hình bình hành và
có thể tích là V . Gọi M là trung điểm của cạnh SB; P
là điểm thuộc cạnh SD sao cho SP = 2DP. Mặt phẳng
(AMP) cắt cạnh SC tại điểm N. Tính thể tích của khối P chóp S.AMNP theo V . M Nhận xét: THPTD A
Nếu không dựng được thiết diện của hình chóp cắt -
bởi (AMP) thì không thể giải được bài toán này! B C G $ Lời giải Dựng giao điểm N SAN
= SC ∩(AMP) (và tạo nên thiết diện của hình chóp cắt bởi (AMP))
+ Vẽ giao điểm O = AC ∩ BD S + Nối SO cắt MP tại I
+ Kéo dài AI cắt SD tại N S I N Tính tỉ số
(dựa vào tỉ số diện tích các tam giác): SO M P 1 2 1 I + 4SMP có S . .S .S PHƯỚC 4SMP = 2 3 4SBD = 3 4SBD (1) D µ 1 S I 2 S I ¶ 1 A + S4SMP = S4SMI + S4SPI = . + . . S4SBD (2) G 2 SO 3 SO 2 O S I 4
+ Từ (1) và (2) ta tính được = . B C SO 7 SN Tính tỉ số
(dựa vào tỉ số diện tích các tam giác): SC SN 2 DƯƠN
+ Dùng tỉ số giữa S4SAN và SSAC 2 lần tương tự như trên ta tính được = . SC 5
Dùng tỉ số thể tích giữa hai khối chóp tam giác để tính VS.AMNP µ SM SN SN SP ¶ 1 7
+ Ta có VS.AMNP = VS.AMN + VS.ANP = . + . . VS.ABCD = V . SB SC SC SD 2 30 20
CHƯƠNG 1. HÌNH HỌC KHÔNG GIAN (CỔ ĐIỂN)
| Ví dụ 9. Cho hình chóp S.ABC có đáy là tam giác ABC đều cạnh a, tam giác S AB
vuông tại B, tam giác S AC vuông tại C. Biết góc giữa hai mặt phẳng (S AB) và (ABC)
bằng 60◦. Tính thể tích khối chóp S.ABC theo a. $ Lời giải
Gọi I, M tương ứng là trung điểm của các cạnh S A, AB. S
Do 4S AB vuông tại B, 4S AC vuông tại C nên I A = IB = IC = SI AN
Gọi O là tâm của mặt đáy ABC thì IO ⊥ (ABC) I ( IM ⊥ AB Ngoài ra, ⇒ ((S á AB), (ABC)) = I MO ⇒ I MO = 60◦ ĂN OM ⊥ AB p V a 3 a 4I MO có IO = OM. tan M . tan 60◦ c = = 6 2 A C p p 2 2 a2 3 a a3 3 Suy ra V M S.ABC = 2VI.ABC = .S . . = . O 3 4ABC.IO = 3 4 2 12 B CHU ? d3 tan ϕ
Ghi nhớ: Vhình chóp đều S.ABC = 24
? Chú ý: nếu thuộc được công thức tính thể tích khối chóp tam giác đều khi biết trước
cạnh đáy và góc hợp bởi mặt bên với mặt đáy thì bài toán sẽ được giải nhanh hơn THPT
| Ví dụ 10. Cho hình lăng trụ đứng ABC.A0B0C0 có mặt đáy ABC là tam giác vuông p -
tại A. Biết AB = a 3, AC = a, A A0 = 2a, hãy tính khoảng cách giữa: a) B và (ACB0) b) A0B0 và AC0. c) BC và AC0. G $ Lời giải B0 C0 B0 C0 B0 C0 SAN A0 A0 K A0 I H B C B C B C PHƯỚC A A A
Chú ý: Với giả thiết của bài toán ta chứng minh được A0C0 G
⊥ (ABB0 A0) và A0B0 ⊥ (ACC0 A0).
Câu a. Từ B, ta vẽ BH ⊥ AB0 tại H ∈ AB0 thì sẽ chứng minh được BH ⊥ (ACB0) tại H. p B A.BB0 2a 21
Từ đó d(B, (ACB0)) = BH = p = . B A2 + BB02 7
Câu a có thể giải bằng phương pháp thể tích như sau (nếu không vẽ được hình) DƯƠN 3V V B0.ABC lăng trụ d(B, (ACB0)) = =
(có thể dùng CT. Hê-rông để tính S S 4ACB0 ) 4ACB0 S4ACB0
Câu b. Từ A0, ta vẽ A0K ⊥ AC0 sẽ chứng minh được A0K ⊥ A0B0. p A0C0.A A0 2a 5
Kết hợp A0K ⊥ AC0 ta suy ra được d(A0B0, AC0) = A0K = p = . A0C02 + A A02 5 21
Câu c. Ta có BC ∥ (AB0C0) nên d(BC, AC0) = d(BC,(AB0C0)) = d(C,(AB0C0))
Do C A0 cắt (AB0C0) tại điểm I là trung điểm của C A0 nên d(C, (AB0C0)) = d(A0,(AB0C0))
A0.AB0C0 là một tam diện vuông tại A0 nên nếu đặt h = d(A0,(AB0C0)) thì p 1 1 1 1 19 2a 57 = + + = ⇒ d(A0, (AB0C0)) = h = . h2 A0B02 A0C02 A A02 12a2 19
| Ví dụ 11. Cho hai hình vuông ABCD và ABEF có cạnh bằng 1, lần lượt nằm AN trên
hai mặt phẳng vuông góc với nhau. Gọi S là điểm đối xứng với B qua đường thẳng
DE. Tính thể tích của khối đa diện ABCDSEF. ĂN $ Lời giải V
Cắt khối đa diện ABCDSEF bởi mặt phẳng (CDFE) ta được
khối lăng trụ ABC.A0B0C0 và khối chóp S.CDFE. A F µ 1 ¶ 1 1 Ta có VABC.A0B0C0 = .BC.BE .AB = .1.1.1 = . 2 2 2 CHU D (BS ∩ (CDFE) = I
Gọi I = DE ∩ BS ta có IB = IS S I
⇒ d (S, (CDFE)) = d (B, (CDFE)) p BC.BE 2 = d (B, CE) = = . B CE 2 1 E THPT p p 1 1 p 2 1 1 2 -
⇒ VS.CDFE = .SCDFE.d (S, (CDFE)) = . 2. = 3 3 2 3 C 1 1 5 G
Vậy VABCDSEF = VABC.A0B0C0 + VS.CDFE = + = . 2 3 6
| Ví dụ 12. Cho hình chóp đều S.ABC có cạnh đáy bằng a và cạnh bên bằng 3a. SAN Một
mặt phẳng thay đổi luôn song song với hai cạnh SB và AC, cắt hình chóp theo thiết
diện là một đa giác (H). Tính diện tích lớn nhất của (H). $ Lời giải
Gọi (P) là mặt phẳng song song với SB và AC, (P) cắt AB tại M. S
Khi đó thiết diện của hình chóp S.ABC cắt bởi N P
(P) là hình hình hành M NPQ (như hình vẽ) PHƯỚC
Do S.ABC là hình chóp đều nên SB ⊥ AC, từ đó G M N PQ là hình chữ nhật. A C N A M N x
Đặt MN = x (0 < x < 3a), ta có = = S A SB 3a M Q SN 3a − x N P SN 3a − x 3a − x Suy ra = ⇒ = = ⇒ NP = B S A 3a AC S A 3a 3 DƯƠN x(3a − x) 1 µ x + (3a − x)¶2 3a2
Diện tích thiết diện: SMNPQ = MN.NP = 6 = (*) 3 3 2 4 3a
Dấu "=" của (*) xảy ra khi và chỉ khi x = 3a − x ⇔ x = ∈ (0; 3a). 2 3a2
Vậy diện tích lớn nhất của thiết diện (H) là Smax = . 4 22
CHƯƠNG 1. HÌNH HỌC KHÔNG GIAN (CỔ ĐIỂN)
| Ví dụ 13. Cho một hình nón có độ dài đường sinh bằng 5, bán kính đáy bằng 3.
a) Tính diện tích toàn phần và thể tích của hình nón đó.
b) Một mặt phẳng (α) qua đỉnh của hình nón, cách tâm của mặt đáy một đoạn bằng
2. Tính diện tích của thiết diện tạo bởi hình nón và mặt phẳng (α) đó. $ Lời giải p AN
Xét hình nón đỉnh S có l = 5, r = 3. Khi đó h = l2 − r2 = 4 S 1
Câu a. Stp = Sxq + Sđ = πrl + πr2 = π.3.5 + π.32 = 24π ; V = π.r2h = 12π. 3 ĂN
Câu b. Xét thiết diện S AB thoả đề bài (như hình vẽ) V
Gọi I là trung điểm dây cung AC
và H là hình chiếu vuông góc của O lên đoạn thẳng SI. A H O
Khi đó ta chứng minh được OH ⊥ (S AB) tại H. I B Suy ra OH = d(O,(S AB)) = 2 CHU 1 1 1 3 4 p 8 4SOI vuông tại O có = − = ⇒ OI = p ⇒ SI = SO2 + OI2 = p OI2 OH2 SO2 16 3 3 p p p 33 2 33
4IOB vuông tại I có IB = OB2 − OI2 = ⇒ AB = 2IB = 3 3 p 1 8 11
Vậy diện tích thiết diện S AB là S4SAB = .SI.AB = 2 3 THPT -
| Ví dụ 14. Cho tam giác ABC vuông tại A có AB = 3, AC = 4. Quay tam giác ABC
lần lượt quanh các cạnh của nó để tạo ra các khối tròn xoay. Tính tổng thể tích của G các khối tròn xoay đó. $ C Lời giải C B SAN H A A A B C B PHƯỚC
Xét khối nón có trục là cạnh AC. 1 1 G
Khối nón này có h1 = AC = 4, r1 = AB = 3 ⇒ V1 = π.r2h1 = π32.4 = 12π. 3 1 3
Xét khối nón có trục là cạnh AB. 1 1
Khối nón này có h2 = AB = 4, r2 = AC = 3 ⇒ V1 = π.r2h2 = π42.3 = 16π. 3 2 3
Xét khối tròn xoay (T) do 4ABC quay quanh cạnh BC tạo ra. DƯƠN 12
Khi đó (T) là hợp của hai khối nón (như hình vẽ), bán kính đáy chung r3 = AH = 5 1 1 1 48
Thể tích khối này là V3 = π.r2.AH + π.r2.BH = π.r2.AB = pi. 3 3 3 3 3 3 5 188
Vậy tổng thể tích của 3 khối là V1 + V2 + V3 = π. 5 23
| Ví dụ 15. Một khối nón tròn xoay có thiết diện qua trục là một tam giác đều cạnh
bằng 3. Một mặt phẳng qua đường kính AB của mặt đáy đồng thời hợp với mặt đáy
một góc bằng 60◦ cắt khối nón theo thiết diện là một hình parabol. Tính diện tích của thiết diện đó. $ Lời giải
Gọi SMN là thiết diện qua trục vuông góc với AB của hình nón. S AN
Gọi (T) là thiết diện cần tìm diện tích (với đỉnh I) 1 Từ giả thiết ta có I ION =
SM N = 60◦ ⇒ IO ∥ SM và IO = SM 2 ĂN 3 AB 3
Theo giả thiết SM = 3 ⇒ OI = , ngoài ra OA = OB = = A V 2 2 2 N
Do thiết diện là một hình parabol nên có diện tích 4 O Sth.diện = .OA.OI = 3. M 3 B CHU
| Ví dụ 16. Một hình trụ có bán kính đáy bằng 5, khoảng cách giữa hai đáy bằng 7.
a) Tính thể tích và diện tích toàn phần của hình trụ.
b) Cắt khối trụ bởi mặt phẳng song song với trục và cách trục một đoạn bằng 3. Tính
diện tích thiết diện được tạo thành. THPT $ Lời giải -
Câu a. Theo giả thiết r = 5; h = l = 7 nên
Stp = 2Sđ + Sxq = 2π.r2 + 2π.rl = 2π.52 + 2π.5.7 = 120π. G Q O0 V H
= π.r2h = π.52.7 = 175π. M
Câu b. Giả sử hình trụ (T) có trục OO0, thiết diện song song với trục
là hình chữ nhật MNPQ (N, P ∈ (O) và M,Q ∈ (O0)). SAN
Gọi H là trung điểm MQ khi đó O0H ⊥ MQ ⇒ O0H ⊥ (MNPQ).
Do đó d ¡OO0, (MNPQ)¢ = d ¡O0,(MNPQ)¢ = O0H = 3. P p O
Ta có MH = O0M2 − O0H2 = 4 cm ⇒ MQ = 2 · MH = 8. N
Diện tích thiết diện: S = MH · MN = 56. | Ví dụ 17. PHƯỚC
Cho hình trụ có thiết diện qua trục là hình vuông ABCD cạnh A B p
2 3 cm với AB là đường kính của đường tròn đáy. Gọi M là _ M G
điểm thuộc cung AB của đường tròn đáy sao cho ABM = 60◦.
Tính thể tích của khối tứ diện ACDM. D C $ Lời giải DƯƠN p p Ta có AMB = 90◦ nên AM = AB.sin ABM = 2 3.sin30◦ = 3cm. p
d(AM, CD) = AD = 2 3cm và ( á AM, CD) = ( á AM, AB) = M AB = 30◦. 1 1 p p p p
VACDM = .AM.CD.d(AM, CD).sin( á
AM, CD) = . 3.2 3.2 3.sin30◦ = 3cm2. 6 6 24
CHƯƠNG 1. HÌNH HỌC KHÔNG GIAN (CỔ ĐIỂN)
| Ví dụ 18. Một hình trụ có bán kính đáy r = 5 và chiều cao h = 6. Gọi (α) là mặt
phẳng không song song với trục của hình trụ, cắt hai đáy của hình trụ theo 2 dây
cung có chiều dài cùng bằng 5. Tính khoảng cách từ tâm O của mặt đáy đến mặt
phẳng (α) và diện tích của thiết diện tạo nên bởi khối trụ và (α). $ Lời giải
Câu a. Gọi MN và PQ là hai dây cung do (α) cắt hai đường tròn đáy tạo nên AN N Khi đó MN = PQ = 5. O0 E
Gọi E, F lần lượt là trung điểm của MN, PQ ĂN
Gọi I = EF ∩ OO0 thì I là trung điểm của EF lẫn OO0. M V
Vẽ OI ⊥ PQ tại F ∈ PQ và OT ⊥ EF tại T ∈ EF thì OT ⊥ (α) s p µ 5 ¶2 5 3 I p 4OFQ vuông tại F có OF = OQ2 − FQ2 = 52 − = 2 2 p p 111 P T CHU
4OIF vuông tại O có IF = OI2 + OF2 = 2 O OI.OF 15 F
Như vậy d(O, (α)) = OT = = p . I F 37 Q
Câu b. Gọi K là giao điểm của EF với mặt trụ (mở rộng) K H
Gọi H là hình chiếu của K lên trục OO0 (kéo dài) THPT I K HK HK .IF p Ta có OF ∥ HK nên = ⇒ IK = = 37 y - I F OF OF 5
Thiết diện của khối trụ cắt bởi (α) là một hình G p
elip cụt có trục lớn bằng 2 37, trục nhỏ bằng 10. p x2 y2 37 Phương trình của elip: + = 1 p 37 25 K F 111 x I p 2 SAN 111 Z 2 5 p
Diện tích thiết diện: S = 4 p 37 − x2 dx 0 37 p111 p p 20 µ x p 37 x ¶ ¯ 2 5 111 10π 37 = ¯ p 37 − x2 + arcsin p ¯ = + . 37 2 2 37 ¯ 2 3 0 | Ví dụ 19. A B PHƯỚC
Cho hình lập phương ABCD.A0B0C0D0 cạnh a. Tính bán kính I
của mặt cầu trong các trường hợp sau đây: D G C
a) Đi qua 8 đỉnh của hình lập phương; O H
b) Tiếp xúc với 12 cạnh của hình lập phương; A0 B0
c) Tiếp xúc với 6 mặt bên của hình lập phương. D0 C0 DƯƠN $ Lời giải
Gọi O là trung điểm của đường chéo AC0 thì O cách đều 8 đỉnh của hình lập phương,
O cách đều 12 cạnh của hình lập phương và O cách đều 6 mặt của hình lập phương. 25 p 1 a 3
a) Bán kính mặt cầu qua 8 đỉnh của hình lập phương là r1 = AC0 = . 2 2 p 1 a 2
b) Bán kính mặt cầu tiếp xúc 12 cạnh của hình lập phương là r2 = d(O, DD0) = BD = . 2 2 1 a
c) Bán kính mặt cầu tiếp xúc 6 mặt của hình lập phương là r3 = d(O,(ABCD)) = CC0 = . 2 2
| Ví dụ 20. Cho hình lăng trụ tam giác đều ABC.A0B0C0 có 9 cạnh đều bằng a. T ANính
diện tích của mặt cầu ngoại tiếp hình lăng trụ. $ Lời giải ĂN
Gọi I và I0 lần lượt là tâm của 4ABC và 4A0B0C0 A V C I
Ta có I I0 ⊥ (ABC) và I I0 ⊥ (A0B0C0). B
Gọi O là trung điểm của I I0 thì
O cách đều các đỉnh của hình lăng trụ ABC.A0B0C0. O CHU
⇒ O là tâm mặt cầu ngoại tiếp lăng trụ ABC.A0B0C0. A0 C0 a2 a2 7a2
4OI A vuông tại I nên O A2 = AI2 + IO2 = + = . 3 4 12 I0 7a2 7πa2
Diện tích mặt cầu là S = 4π.OA2 = 4π. = . B0 12 3 THPT
| Ví dụ 21. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, mặt bên tạo v -ới
đáy một góc α (0◦ < α < 90◦). Xác định tâm và tính theo a và α bán kính r của mặt G cầu nội tiếp hình chóp đó. $ Lời giải
Gọi H là tâm của tam giác đều ABC, ta có SH ⊥ (ABC). SAN BC = (SBC) ∩ (ABC)
Gọi M là trung điểm của BC, ta có BC ⊥ SM ⊂ (SBC) S BC ⊥ AM ⊂ (ABC) ⇒ ((S á BC), (ABC)) = SM A. Do đó SM A = α.
Gọi I là tâm của mặt cầu nội tiếp S.ABC thì I ∈ SH.
Vì I là tâm của mặt cầu nội tiếp hình chóp S.ABC nên I PHƯỚC
M I là đường phân giác trong của góc A C SM A. G
Khi đó,bán kính của mặt cầu nội tiếp S.ABC là r = IH. H p M α a 3 α
4IHM vuông tại H có IH = MH tan = × tan . 2 6 2 B DƯƠN
Document Outline
- Hình học không gian (cổ điển)
- Một số vấn đề cơ bản về quan hệ song song
- Việc xác định giao tuyến của hai mặt phẳng
- Việc xác định giao điểm của đường thẳng và mặt phẳng
- Một số định lý về nhận dạng quan hệ song song
- Một số vấn đề cơ bản về quan hệ vuông góc
- Phương pháp chứng minh đường thẳng vuông góc với mặt phẳng
- Phương pháp chứng minh hai đường thẳng vuông góc
- Phương pháp chứng minh hai mặt phẳng vuông góc
- Phương pháp xác định các loại góc trong không gian
- Góc giữa hai đường thẳng
- Góc giữa đường thẳng và mặt phẳng (cắt nhau nhưng không vuông góc)
- Góc giữa hai mặt phẳng (cắt nhau)
- Phương pháp xác định khoảng cách
- Khoảng cách từ một điểm đến một mặt phẳng
- Khoảng cách giữa 2 đối tượng song song nhau
- Khoảng cách giữa 2 đường thẳng a và b chéo nhau
- Một số vấn đề về khối đa diện lồi, khối đa diện đều
- Tính chất của một hình đa diện, khối đa diện
- Bảng tổng hợp tính chất của các đa diện đều
- Một số công thức tính toán hình học
- Công thức tính toán hình học liên quan đến tam giác
- Công thức tính toán hình học liên quan đến tứ giác
- Công thức thể tính thể tích khối chóp và khối lăng trụ
- Công thức tính toán với các khối nón - trụ - cầu
- Phương pháp dựng tâm I của mặt cầu ngoại tiếp hình chóp
- Một số khối đa diện thường gặp trong các đề thi
- Hình chóp tam giác đều
- Hình tam diện vuông O.ABC (vuông tại O)
- Hình chóp S.ABC có đường cao SA, AB vuông góc với BC
- Hình chóp S.ABC có cạnh bên SA “thẳng đứng”, mặt đáy là tam giác “thường”
- Hình chóp S.ABC có 1 mặt bên b “cân tại S” và “dựng đứng”
- Hình chóp tứ giác đều
- Hình chóp S.ABCD có cạnh bên SA “thẳng đứng”, mặt đáy là “hình chữ nhật”
- Hình chóp S.ABCD có 1 mặt bên “cân tại S” và “dựng đứng”
- Hình hộp chữ nhật
- '077 Công thức tính nhanh một số khối tứ diện đặc biệt
- '077 Một số công thức biệt liên quan khối tròn xoay
- Ví dụ giải toán điển hình
- Việc xác định giao tuyến của hai mặt phẳng
- Một số vấn đề cơ bản về quan hệ song song





