Midterm 19-20 - Calculus 1 | Trường Đại học Quốc tế, Đại học Quốc gia Thành phố HCM
Midterm 19-20 - Calculus 1 | Trường Đại học Quốc tế, Đại học Quốc gia Thành phố HCM được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Môn: Calculus 1 (MA001IU)
Trường: Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh
Thông tin:
Tác giả:
Thông tin :
Môn:
Trường:
Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh
Tác giả:
Tài liệu liên quan:
Preview text:
CALCULUS 1 – MIDTERM EXAMINATION
Semester 1, 2019-20 • Thu 14 Nov 2019 • Total duration: 85 minutes Student’s name: Student ID:
Chair of Mathematics Department Lecturers Proctor
INSTRUCTIONS: Each student is allowed one double-sided sheet of reference material (size A4 or sim-
ilar) marked with their name and ID. Calculators are allowed in Part 2 only, not in Part 1. All other
documents and electronic devices are forbidden.
PART 1: MULTIPLE CHOICE QUESTIONS – 45 Minutes – 60 points
1. The figure below shows the graphs of two functions, f and g. The relationship between them is:
(A) f (x) = g(2x)
(B) g(x) = f (2x)
(C) f (x) = 2g(x)
(D) g(x) = 2 f (x) Ans: (A)
2. The figure below shows the graph of a piecewise function h. What is the value of limh(x)? x→2 (A) 0 (B) 1 (C) 2 (D) does not exist Ans: (D) ex
3. Consider the function f (x) =
. The asymptote(s) of the graph of f are ex − 1 (A) x = 0 only
(C) x = 0 and y = 1 only (B) y = 1 only
(D) x = 0, y = 0 and y = 1 Ans: (D) x − 2 4. The value of lim √ is x→2 4x + 1 − 3 (A) 0 (B) 2 (C) 3 3 (D) does not exist 2 Ans: (C)
5. A particle is moving such that its height h at time t is given by h(t) = 10 − 8t + 3t2 − 1t3. At which 3
of the following time is the particle moving upwards? (A) t = 1 (B) t = 3 (C) t = 5 (D) t = 7 Ans: (B)
6. Let f (x) = x2 + 2x − 1 and g(x) = 2x − 3. Find (g ◦ f )(1). (A) 1 (B) 2 (C) −1 (D) 0 Ans: (A)
7. Let f 1 = 1 . Which of the following points belongs to the graph of f −1? 2 5 1 1 1 1 (D) 1 (A) , (B) , 5 (C) 5, , 1 5 2 2 5 2 2 Ans: (D)
8. Which of the following functions is the inverse of the function f (x) = ex3? √ 3 √ (A) y = ln(x3) (B) y = 3 ln x (C) y = 3 ln x (D) e x Ans: (C) 1
9. Let f (x) = √ . Then f 0(4) is 2x + 1 −1 −1 −1 −2 (A) (B) (C) (D) 27 36 45 27 Ans: (A) 1 lnx
10. The derivative of the function f (x) = is x 1lnx+1 1lnx+3
−2 ln x 1 lnx 1lnx−1 (A) ln x (B) (C) (D) ln x x x x x x Ans: (C)
11. Consider the curve with equation y + x sin(y) = x2. The slope of the tangent line to the curve at the point x = 0 is (A) 0 (B) 1 (C) doesn’t exist (D) ∞ Ans: (A) sin x − sin(π/4)
12. The value of I = lim is x→π/4 x − π/4 √ √ (A) I = 2/2 (B) I = 1 (C) I = 3/2 (D) I = 1/2 Ans: (A)
13. Let f (x) = 2x3 + 3 and g(x) = [ f −1(x)]2. Then the value of g0(5) is (A) doesn’t exist (B) 3 1 150 (C) (D) − 3 253 Ans: (C) √
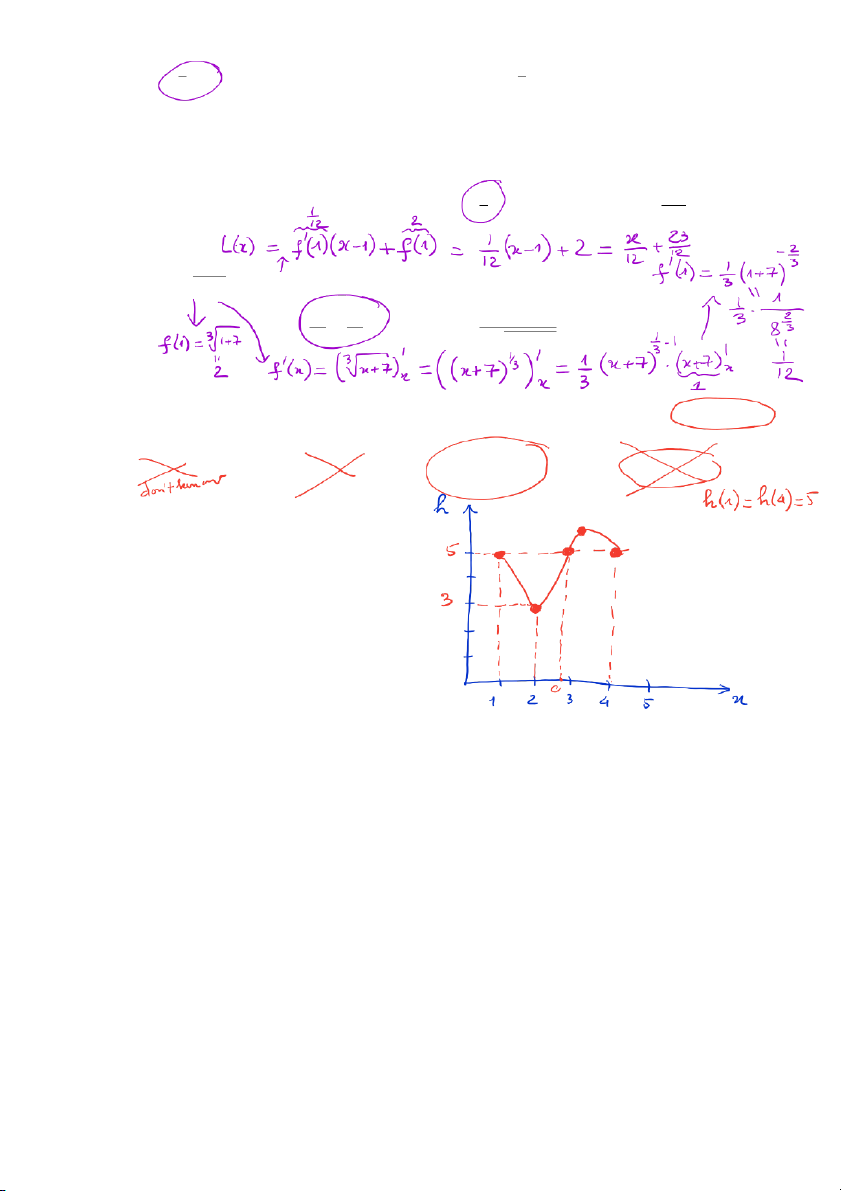
14. Let f (x) = 3 x + 7. The linear approximation of f near the point x = 1 is (A) 2x + 2 x 23 1 (B) + (C) (D) x2 + 3 12 12 3 3 p(x + 7)2 Answer: (B)
15. Suppose that h is a continuous function on [1, 5]. Given that the equation h(x) = 5 has only two
solutions x = 1 and x = 4, and h(2) = 3, then (A) h(3) = 4 (B) h(3) > 5 (C) h(3) < 5 (D) h(3) = 5 Ans: (C) – END OF PART 1 –
THE INTERNATIONAL UNIVERSITY(IU) - VIETNAM NATIONAL UNIVERSITY - HCMC
CALCULUS 1 – MIDTERM EXAMINATION
Semester 1, 2019-20 • Thu 14 Nov 2019 • Total duration: 85 minutes Student’s name: Student ID: Score
Chair of Mathematics Department Lecturers Proctor
PART 2: WRITTEN ANSWERS • 40 Minutes • 40 points
Write your answers on this paper. Ask for extra paper if you need more space. You must explain your
answers in detail; no points will be given for the answer alone.
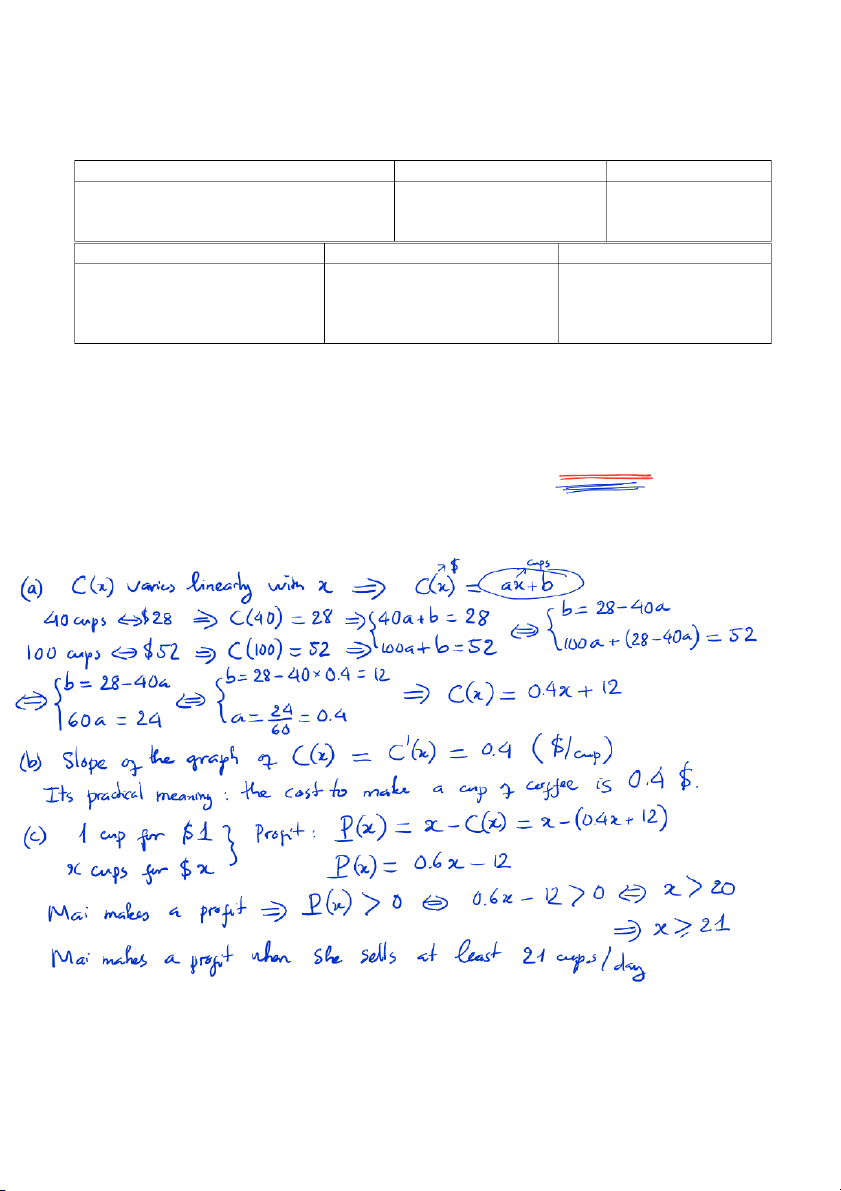
1. Mai plans to sell coffee. She calculates that the total cost of producing 40 cups will be $28 and the
total cost of producing 100 cups will $52. Assume the total cost, C, varies linearly with the number of cups, x.
a) [10 points] Find an equation for C(x).
b) [5 points] State the slope of the graph of C(x) (including its units) and explain its practical meaning.
c) [5 points] If a cup of coffee is sold for $1, how many cups must Mai sell in order to make a profit?
2. (10 points) The length of an edge of a cube is measured and found to be 15 cm with a possible error
in measurement of at most 0.03 cm. If this length is used to calculate the volume of the cube, what
is the maximum possible error in the volume? What is the corresponding percentage error in the volume?
3. (10 points) Find all the points on the curve
x2y2 + xy = 2 (1)
where the slope of the tangent line is −1. END Outline solutions
1.a) We have (x1,C1) = (40, 28) and (x2,C2) = (100, 52). Using C −C1 C = 2 −C1 x − x1 x2 − x1
gives C(x) = 0.4x + 12.
b) The slope is 0.4 $/cup. This means that for every extra cup produced, the cost increases by $0.4.
c) If x cups are sold the revenue is x. To make a profit, the revenue must be greater than the cost, that
is, Mai needs x > 0.4x + 12 which gives x > 20. So she must sell more than 20 cups.
2. Let the side’s lenght to be x, then volume V = x3. Using differential:
dV = 3x2 dx
where dx = 0.03, x = 15, then max error dV = 20.25 cm3. Percentage error: dV 3x2dx dx = = 3 = 0.006 = 0.6% V x3 x
3. Differentiate both sides of the equation (1) (implicit differentiation) we have
2yx2y0 + 2xy2 + xy0 + y = 0.
When y0 = 1 we get from the last equation that:
−2yx2 + 2xy2 − x + y = 0 or,
2xy(y − x) + (y − x) = 0, or (y − x)[2xy + 1] = 0.
This equation gives x = y or xy = −1/2.
• If x = y then from (1) we get
x4 + x2 − 2 = 0
which gives x2 = 1 (and hence, x = ±1) and x2 = −2 (excluded). In this case, we get two points (1,1)
and (−1,−1) where the slopes of the tangent lines to the given curve is -1.
• xy = −1/2. Substitute to (1) we get 1/4 − 1/2 = 2, impossible. So the case where xy = −1/2 is excluded.
In conclusion, there are only 2 points (1, 1) and (−1,−1) on the curve x2y2 + xy = 2 whose slop of the tangent line is −1. END