Midterm Exam - Calculus 1 | Trường Đại học Quốc tế, Đại học Quốc gia Thành phố HCM
Midterm Exam - Calculus 1 | Trường Đại học Quốc tế, Đại học Quốc gia Thành phố HCM được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Môn: Calculus 1 (MA001IU)
Trường: Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh
Thông tin:
Tác giả:
Thông tin :
Môn:
Trường:
Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh
Tác giả:
Tài liệu liên quan:
Preview text:
THE INTERNATIONAL UNIVERSITY(IU) - VIETNAM NATIONAL UNIVERSITY - HCMC MIDTERM EXAMINATION
Fall 2013 • Duration: 90 minutes SUBJECT: CALCULUS I
Department of Mathematics Lecturers: Chair:
T.T. Duong , N.N. Hai, J.C. Harris, Assoc. Prof. Dr P.H.A. Ngoc and N.M. Quan Instructions:
• Each student is allowed a scientific calculator and a maximum of two
double-sided sheets of reference material (size A4 or similar), stapled together
and marked with their name and ID. All other documents and electronic de- vices are forbidden.
• Answer any FIVE of the six questions. DO NOT answer more than five questions.
1. A rare species of monkey is introduced to a nature reserve. The popula-
tion p of these monkeys after t years can be modelled by the equation 120 p(t) = , ∀t ≥ 0 1 + 4e−0.5t (a) [7 marks] Find p0(t).
(b) [8 marks] When will the population growth rate be less than 1 monkey per year?
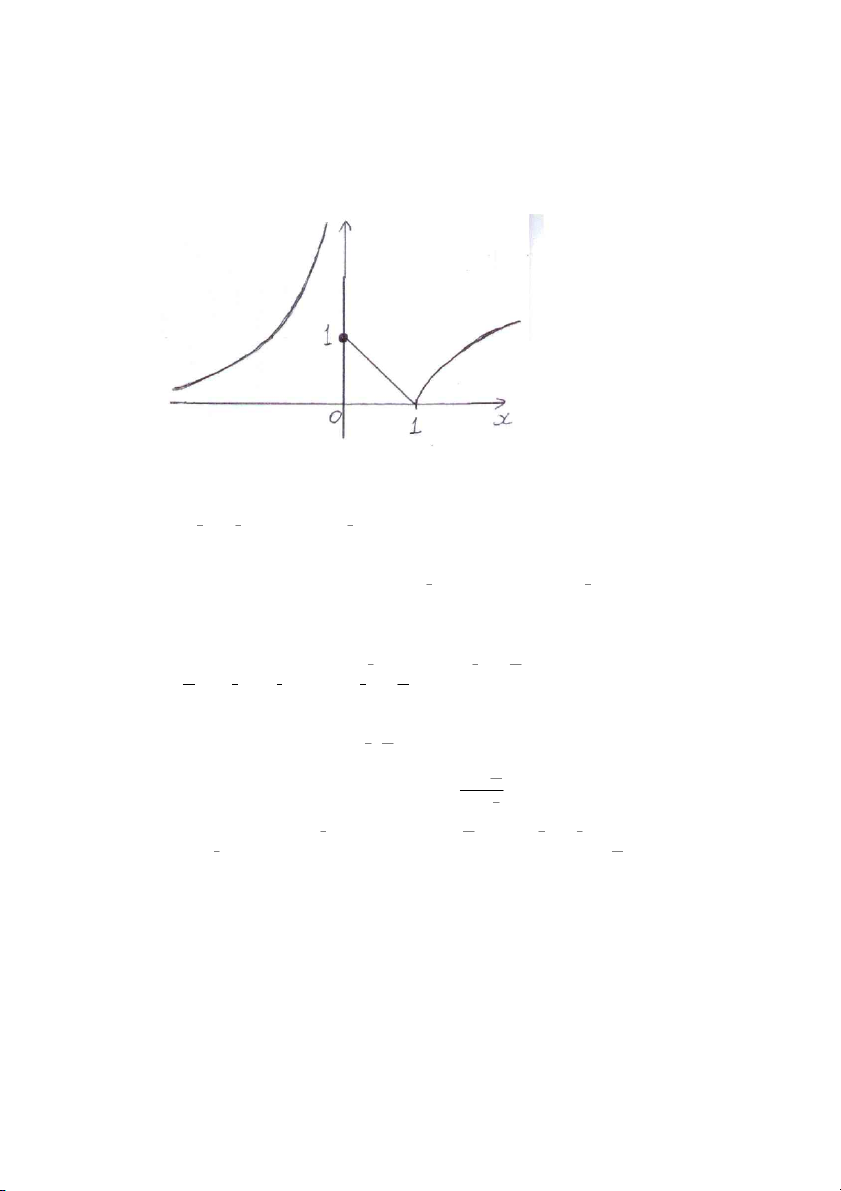
(c) [5 marks] Show that the population will never exceed a certain number. 2. Consider the function − 1 if x < 0 x f (x) = 1 − x if 0 ≤ x ≤ 1 √ x − 1 if x > 1
(a) [5 marks] Find the limits lim f (x) and lim f (x). x→0− x→0+
(b) [5 marks] Is f (x) continuous at x = 0? at x = 1? Explain your answers.
(c) [5 marks] Find all the vertical and horizontal asymptotes.
(d) [5 marks] Sketch the graph of f (x).
----- continued on next page ----- 3. Let f (x) = x2 − x + 3
(a) [5 marks] Find the slope m of the line 3x + 2y = 7.
(b) [5 marks] Find x ∈ R such that f0(x) = m.
(c) [5 marks] Find an equation of the straight line that is a tangent to the
graph of f and parallel to the line 3x + 2y = 7.
(d) [5 marks] Find the straight lines that are tangents to the graph of f and
pass through the point ( 3, 11 ). 4 4 √ 4.
(a) [6 marks] Find f 0(π ) where f(x) = 1 + 2 tan x. 4
(b) [7 marks] Show that lim xecos2(π ) x = 0. x→0
(c) [7 marks] A differentiable function y(x) is defined near x = 0 and is such that x3 + y3 = 1 + 5xy2 Find y(0) and y0(0).
5. An object is thrown upward and then falls to the ground. The object’s
height h (in feet) above ground level is given by the function h(t) = −16t2 + bt + c
where t is the time (in seconds) after the object is released. The object
is released at an initial height of 6 feet and it lands on the ground after 6 seconds.
(a) [10 marks] Find the initial speed of the object.
(b) [10 marks] Find the maximum height reached by the object.
6. Let f (x) = 5e3x − 3e−2x, then f is a one-to-one function from R onto R.
Let g be the inverse function of f , and evaluate the following:
(a) [5 marks] f (0), f 0(0), f 00(0). (b) [10 marks] g0(2). (c) [5 marks] g00(2). ----- END ----- ANSWERS
Instructions: In the case that the student answered all 6 questions,
grade questions 1 through 5. For any part that is worth 5 marks, if there is
anything wrong in the final answer, at most 4 marks will be given. 1. 120 p(t) = 1 + 4e−0.5t (a) [7 marks] 240e−0.5t p0(t) = (1 + 4e−0.5t)2
(b) [8 marks] Solve the inequality 240e−0.5t p0(t) = < 1 (1 + 4e−0.5t)2
which is equivalent to 16X2 − 232X + 1 > 0 where X = e−0.5t.
Since t > 0, we choose the solution t > 10.89.
(c) [5 marks] Since e−0.5t > 0, 1 + 4e−0.5t > 1 and therefore p(t) < 120. 2. Consider the function − 1 if x < 0 x f (x) = 1 − x if 0 ≤ x ≤ 1 √ x − 1 if x > 1
(a) [5 marks] Find the limits lim f (x) and lim f (x). x→0− x→0+ −1 lim f (x) = lim
= ∞ and lim f(x) = lim (1 − x) = 1. x→0− x→0− x x→0+ x→0+
(b) [5 marks] Is f (x) continuous at x = 0? at x = 1? Explain your answers.
f is not continuous at 0 because lim f (x) 6= lim f(x) and f is continuous x→0− x→0+ √
at 1 because lim f (x) = lim (1 − x) = 0 = lim f(x) = lim x − 1 x→1− x→1− x→1+ x→1+
(c) [5 marks] Find all the vertical and horizontal asymptotes.
The horizontal asymptote is the x-axis y = 0 and the vertical asymptote is the y-axis x = 0.
(d) [5 marks] Sketch the graph of f (x). 3. Let f (x) = x2 − x + 3
(a) [5 marks] Find the slope m of the line 3x + 2y = 7. y = −3x + 7 , hence m = −3 2 2 2
(b) [5 marks] Find x ∈ R such that f0(x) = m.
Solve the equation f 0(x) = 2x − 1 = −3 which implies x = −1 2 4
(c) [5 marks] Find an equation of the straight line that is tangent to the
graph of f and parallel to the line 3x + 2y = 7.
It is the tangent line at x = −1 and y = f(−1) = 53 and an equation is 4 4 16
y − 53 = −3(x + 1) or y = −3 x + 47 16 2 4 2 16
(d) [5 marks] Find the straight lines that are tangent to the graph of f
and going through the point ( 3 , 11 ) 4 4 Find x such that y − 11 f 0(x) = 2x − 1 = 4 x − 34
Therefore (2x − 1)(x − 3) = (x2 − x + 3) − 11 or x2 − 3x + 1 = 0. 4 4 2 2
For x = 1, the slope m = 2x − 1 = 0 and the tangent line is y = 11 2 4
For x = 1, the slope m = 2x − 1 = 1 and the tangent line is y = x + 2. 4. Evaluate the following: √
(a) [6 marks] f 0(π ) where f (x) = 1 + 2 tan x 4 1 π 2 f 0(x) = √ , f 0( ) = √ cos2 x 1 + 2 tan x 4 3
(b) [7 marks] Since −e|x| ≤ xecos2(π) x
≤ e|x|, we can apply the Sandwich theorem and get lim xecos2(π ) x = lim e|x| = 0 x→0 x→0
(c) [7 marks] For x = 0, the equation is y = 1, therefore y(0) = 1.
Differentiate the equation at x = 0, we have
3(0)2 + 3y(0)2y0(0) = 5(y(0))2 + 5(0)2y(0)y0(0) or y0(0) = 5. 3 5. h(t) = −16t2 + bt + c.
(a) [10 marks] Find the initial speed of the object.
c = h(0) = 6, h(6) = −16(36) + 6b + 6 = 0 which implies b = 95. Therefore
the initial speed is h0(0) = b = 95(ft/sec)
(b) [10 marks] Find the maximum height of the object.
The maximum height is at the vertex of the parabola where t = − b = 95. 2(−16) 32
Hence, the maximum height is h(95) = 952 + 6 ≈ 147(ft) 32 64
6. Let f (x) = 5e3x − 3e−2x, then f is an increasing bijection from R onto
R. Let g be the inverse function of f , and evaluate the following:
(a) [5 marks] f (0), f 0(0), f 00(0).
f (0) = 5 − 3 = 2, f0(0) = 15 + 6 = 21, f00(0) = 45 − 12 = 33 (b) [10 marks] g0(2). g0(2) = g0(f (0)) = 1 = 1 f 0(0) 21 (c) [5 marks] g00(2).
Let F (x) = g0(f (x)) = 1 , then F 0(0) = g00(f (0))f 0(0) = −f00(0) . f 0(x) (f 0(0))2
Hence g00(2) = g00(f (0)) = − 33 = − 11 . 213 3087