Midterm - practice material | Môn Data Mining - Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh

lOMoAR cPSD| 23136115
Student Name: ____________________________ Midterm Exam Text Data Mining (INLS 613)
Answer all of the following questions. Each answer should be thorough, complete, and relevant. Points
will be deducted for irrelevant details. Use the back of the pages if you need more room for your answer.
The points are a clue about how much time you should spend on each question. Plan your time accordingly. Good luck! Question Points 1 15 2 15 3 20 4 10 5 20 6 10 7 10 Total 100 lOMoAR cPSD| 23136115 1 0 9 8 8 7 6 5 5 4 4 3 3 2 2 1 1 0 0 0 - 4 9 5 0 -5 9 6 0 -6 9 7 0 -7 9 8 0 - 8 9 9 0 -9 9 1 0 0 lOMoAR cPSD| 23136115
1. Inter-annotator Agreement [15 points]
Predictive analysis of text often requires annotating data. In doing so, one important step is verifying
whether human annotators can reliably detect the phenomenon of interest (e.g., whether a product
review is positive or negative).
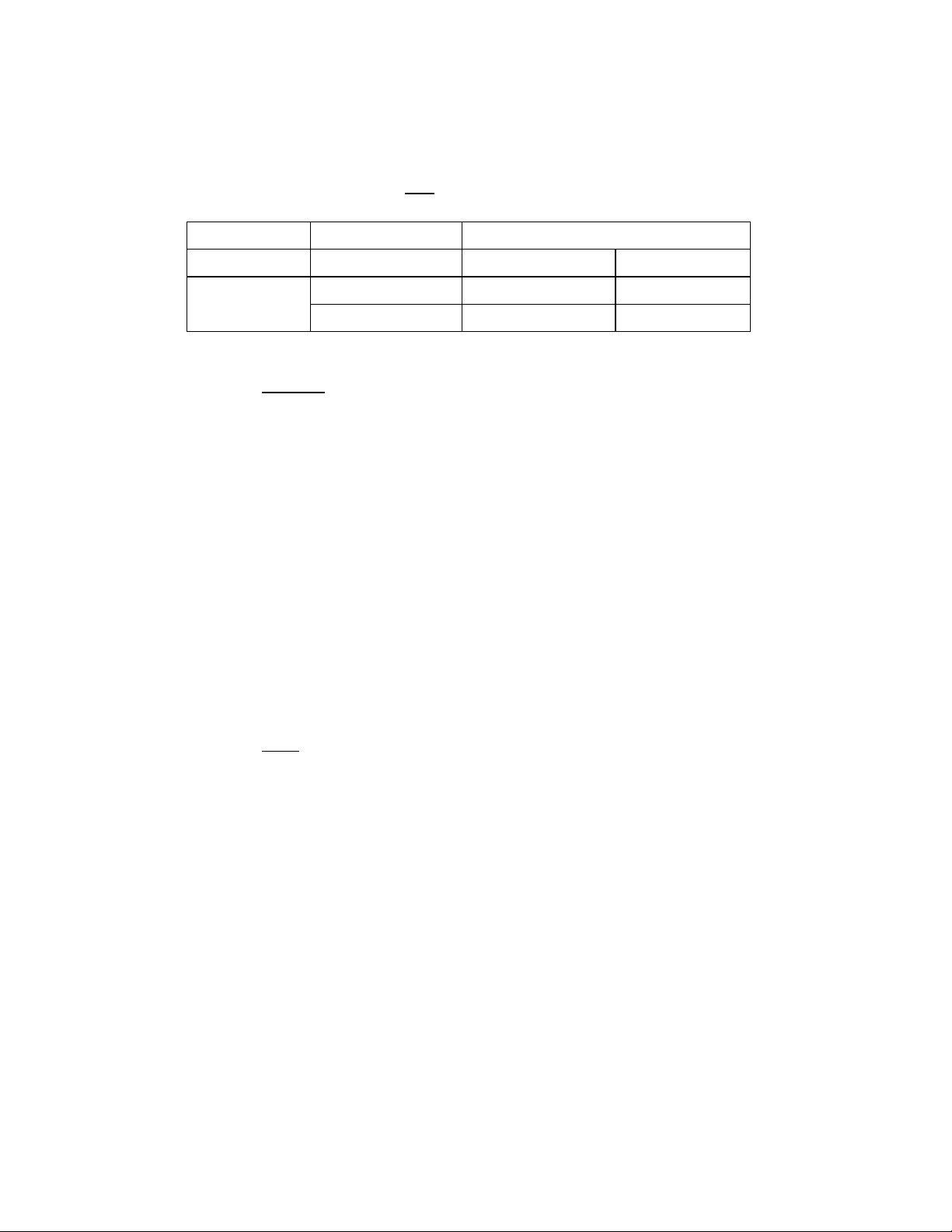
Suppose that two annotators (A and B) independently annotate 100 product reviews and produce
the following contingency matrix. Answer the following questions. Annotator B Positive Negative Positive 40 10 Annotator A Negative 10 40
(a) What is the inter-annotator agreement between A and B based on accuracy (i.e., the percentage
of times both annotators agreed)? [5 points]
(b) What is the inter-annotator agreement between A and B based on Cohen’s Kappa assuming
unbiased annotators (i.e., each annotator has a 50/50 chance of saying the review is
positive/negative) [10 points]
2. Training and Testing [15 points]
The goal in predictive analysis is to train a model that can make accurate predictions on new data.
When a model fails to do well on new data, it is often because it “catches on” to regularities in the
training data that do not hold true in general.
(a) Suppose we increased the size of the training set. Would this likely improve or deteriorate the
performance of the model on new data? Why? [5 points] lOMoAR cPSD| 23136115
(b) Suppose we decide to omit all features that appear only once in the training set. Would this
likely improve or deteriorate the performance of the model on new data? Why? [5 points]
(c) Suppose we are doing binary classification (positive vs. negative). Let POS(w) denote the
number of positive training set instances containing word w, and Let NEG(w) denote the number
of negative instances containing word w. Suppose we decide to omit from the feature
representation all words w where POS(w) = NEG(w). Would this likely improve or deteriorate the
performance of the model on new data? Why? [5 points] lOMoAR cPSD| 23136115
3. Evaluation Metrics [20 points]
Suppose we train a model to predict whether an email is Spam or Not Spam. After training the
model, we apply it to a test set of 200 new email messages (also labeled) and the model produces the contingency table below. True Class Spam Not Spam Spam 90 60 Predicted Class Not Spam 10 40
(a) Compute the precision of this model with respect to the Spam class. [5 points]
(b) Compute the recall of this model with respect to the Spam class. [5 points]
(c) Suppose we have two users (Emily and Simon) with the following preferences.
Emily hates seeing spam messages in her inbox! However, she doesn’t mind periodically
checking the “Junk” directory for messages incorrectly marked as spam. lOMoAR cPSD| 23136115
Simon doesn’t even know where the “Junk” directory is. He would much prefer to see
spam messages in his inbox than to miss genuine messages without knowing!
Would Emily like this classifier? Justify your answer based on the precision and recall values of
this classifier with respect to the Spam class. [5 points]
(d) Would Simon like this classifier? Justify your answer based on the precision and recall values of
this classifier with respect to the Spam class. [5 points]
4. Instance-Based Classification and Parameter Tuning [10 points]
Given a new instance, a KNN classifier predicts the majority class associated with the K nearest
neighbors. K is a parameter that needs to be set using training data.
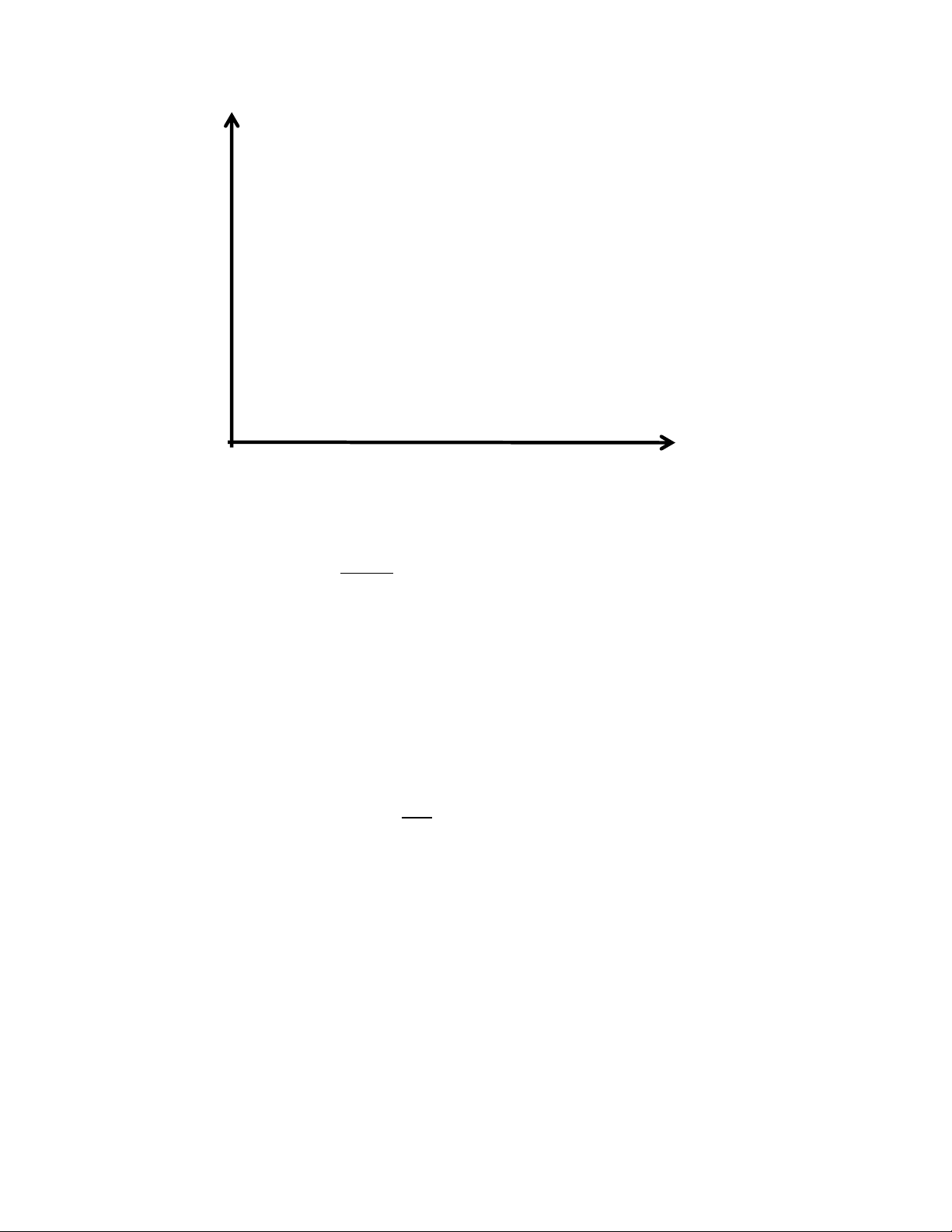
Suppose we have the following training set of positive (+) and negative (-) movie reviews.
All instances are projected onto a vector space of two real-valued features (X and Y) and distance
between instances is computed using Euclidean distance. lOMoAR cPSD| 23136115 - + - + Y - + - + X
(a) What value of K would maximize accuracy on this training set? What is the training set accuracy
of the classifier with this optimal value of K? [5 points]
(b) Is the training set accuracy of the classifier with the optimal value of K a good indicator of how
the classifier will perform on new test data? Why or why not? [5 points] lOMoAR cPSD| 23136115 lOMoAR cPSD| 23136115
5. Naïve Bayes [20 points]
Suppose you have the following training set of positive (+) and negative (-) movie reviews. There are
only 5 training instances and 3 features. great fine terrible class 1 0 0 + 0 1 1 -- 0 1 1 -- 0 0 0 + 1 0 1 --
Suppose we train a Naïve Bayes classifier on this training set without doing any sort of smoothing.
Answer the following questions.
(a) What is the prior probability of positive, denoted as P(+)? [5 points]
(b) What is the prior probability of negative, denoted as P(-)? [5 points]
(a) What class (positive or negative) would the model predict for a movie review that just says “terrible!”
and what would be the confidence value associated with the predicted class? lOMoAR cPSD| 23136115 [10 points]
Hint: notice that this test instance would have the following feature values: great=0, fine=0, and terrible=1. lOMoAR cPSD| 23136115
6. Prediction Confidence and Precision vs. Recall [10 points]
Suppose we train a Naïve Bayes Classifier to predict whether a movie review is positive or negative.
At test time, a Naïve Bayes Classifier produces a confidence value that the review is positive.
By default, a Naïve Bayes Classifier will predict positive if this confidence value is greater than 0.5.
While this is the default behavior of a Naive Bayes Classifier, we could also apply a threshold
to this confidence value to favor precision over recall, or vice versa.
(a) Suppose that we want high precision, even if it means low recall. Would you set this
threshold to greater than 0.5 or less than 0.5? Please explain. [5 points]
(b) Suppose that we want high recall, even if it means low precision. Would you set this
threshold to greater than 0.5 or less than 0.5? Please explain. [5 points]
7. Linear Regression [10 points] lOMoAR cPSD| 23136115
Linear regression is used to predict a real-valued output (𝑦) based on a real-valued input (𝑥).
The model is essentially a line with parameters 𝑤 to denote the slope of the line and 𝑏 to
denote the 𝑦-intercept of the line: 𝑦 = 𝑤𝑥 + 𝑏
The gradient descent algorithm can be used to set parameters 𝑤 and 𝑏. The gradient
descent algorithm looks at the 𝑚 training examples (i.e., pairs of 𝑥 and 𝑦 values) and
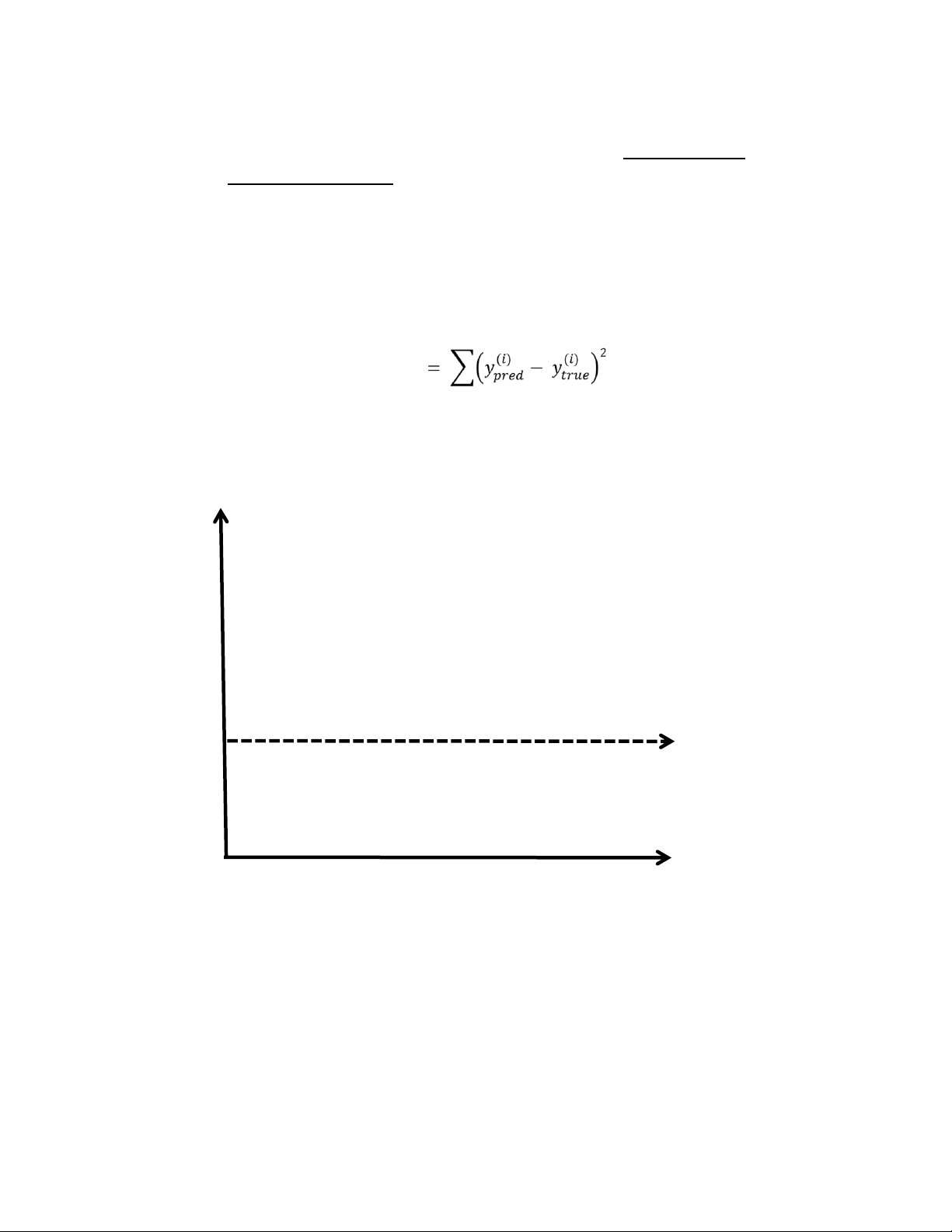
iteratively “adjusts” parameters 𝑤 and 𝑏 to minimize the following error: 𝑚 𝑒𝑟𝑟𝑜𝑟 𝑖=1
Suppose you have the following training set and suppose that the linear regression line after
1000 training iterations is given by 𝑦 = 0𝑥 + 0.5 (shown by the dashed line below). 𝒚
+ + + + + + + 0.5 + x lOMoAR cPSD| 23136115
(a) After 2000 iterations, do you expect the value of 𝑤 to greater than zero or less than
zero? Provide a brief explanation [5 points]
(b) After 2000 iterations, do you expect the value of 𝑏 to be greater than 0.5 or less than
0.5? Provide a brief explanation [5 points]