THE INTERNATIONAL UNIVERSITY (IU) - VIETNAM NATIONAL UNIVERSITY - HCMC MIDTERM EXAMINATION
Semester 1, 2016-17 • 8th Nov 2016 • 90 minutes CALCULUS I Head of Dept. of Mathematics: Lecturers: Assoc. Prof. Nguyen Dinh
TT Duong, JC Harris, HB Minh, NM Quan, MD Thanh
INSTRUCTIONS: Each student is allowed a scientific calculator and a maximum of two
double-sided sheets of reference material (size A4 or similar), stapled together and marked
with their name and ID. All other documents and electronic devices are forbidden. Question 1. (10 marks)
Find a formula for the inverse of the function f (x) = x2 + 2x, x ≥ −1. Question 2.
a) (10 marks) Evaluate the limit √6 − x − 2 lim √ . x→2 3 − x − 1
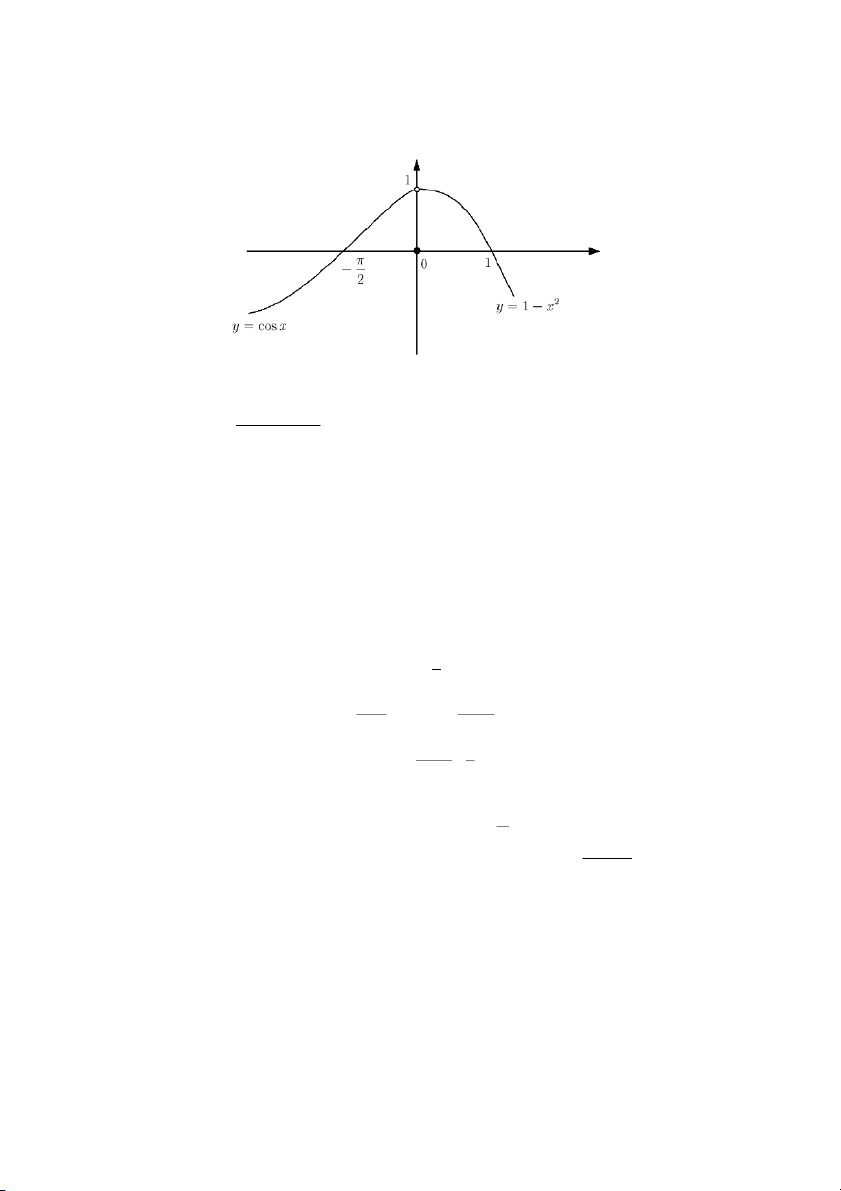
b) (10 marks) By using the Squeeze Theorem, or otherwise, evaluate the limit π lim (x − π) sin . x→π x − π Question 3.  cos x, if x < 0  Let g(x) = 0, if x = 0  1 − x2, if x > 0
a) (5 marks) Explain why g(x) is discontinuous at x = 0.
b) (5 marks) Sketch the graph of g(x).
Question 4. Let C be a circle with radius 2 centred at the point (2, 0).
a) (5 marks) Write an equation for the circle C.
b) (5 marks) Is curve C the graph of a function of x? Explain your answer.
c) (5 marks) Write parametric equations to traverse C once, in a clockwise direction, starting from the origin.
—– Continued on next page —– Question 5. 2
a) (5 marks) Differentiate the function h(x) = e−x sin(2x).  1ln x
b) (10 marks) Use logarithmic differentiation to differentiate the function y = . x Question 6. (15 marks) dy d2y Evaluate and
at the point (0, −2) on the curve 4x2 + y2 = 4. dx dx2 Question 7.
A particle is moving along an x-axis. Its x-coordinate (in meters) at time t seconds is given by x(t) = t3 − 3t + 1, t ≥ 0.
a) (5 marks) Find the velocity of the particle at time t.
b) (5 marks) When is the particle at rest?
c) (5 marks) Find the total distance traveled by the particle during the first 3 seconds. —– END —– SOLUTIONS Question 1.
Let y = f (x) = x2 + 2x, x ≥ −1. √
Then y = (x + 1)2 − 1, x + 1 ≥ 0, hence x = y + 1 − 1. √ Hence f −1(x) = x + 1 − 1. Question 2. a) √ √ √ √ 6 − x − 2
 ( 6 − x − 2)( 6 − x + 2) 3 − x + 1 lim √ = lim √ √ × √ x→2 3 − x − 1 x→2 ( 3 − x − 1)( 3 − x + 1) 6 − x + 2 √  (6 − x − 22) 3 − x + 1 = lim × √ x→2 (3 − x − 12) 6 − x + 2 √3 − x + 1 = lim √ x→2 6 − x + 2 √3 − 2 + 1 2 1 = √ = = 6 − 2 + 2 4 2 b) We have   (x − π) sin π  6 |x − π|. Therefore, x−π π
− |x − π| 6 (x − π) sin 6 |x − π| x − π
Since lim |x − π| = 0 = − lim |x − π|, by using the the Squeeze Theorem, we obtain x→π x→π π lim (x − π) sin = 0. x→π x − π Question 3.
a) The left-hand limit of g(x) at x = 0 is lim g(x) = lim cos x = 1 x→0− x→0− The right-hand limit is lim g(x) = lim (1 − x2) = 1 x→0+ x→0+ Therefore, lim g(x) = 1. x→0 We have lim g(x) = 1 6= 0 = g(0) x→0
therefore g(x) is not continuous at x = 0.
b) The graph of function y = f (x): Question 4. a) (x − 2)2 + y2 = 4
b) No. y = ±p4 − (x − 2)2 so one value of x can correspond to two values of y. (The
graph fails the vertical line test.)
c) The circle is commonly parameterised by x = 2 + 2 cos t, y = 2 sin t, where increasing
t corresponds to anti-clockwise motion. To travel clockwise we can replace t with −t,
giving x = 2 + 2 cos t, y = −2 sin t − π ≤ t ≤ π. Question 5. a) By product and chain rules, 2 2 2
h′(x) = e−x (2 cos 2x) − 2xe−x sin 2x = 2e−x (cos 2x − x sin 2x).
b) By logarithmic differentiation,  1  ln y = ln x ln = − ln2 x x 1 2 ln x y′(x) = − y(x) x 2 ln x 1 ln x y′(x) = − x x Question 6.
By implicit differentiation, 8x + 2yy′ = 0 so y′ = −4x. y y − xy′
Differentiating both sides with respect to x again gives: y′′ = −4 . y2
So at (0, −2) we have y′ = 0 and y′′ = 2. Question 7. a) The velocity is
x′(t) = 3 (t2 − 1) , t ≥ 0
b) It is at rest when x′ = 3 (t2 − 1) = 0, t ≥ 0, that is t = 1.
c) It changes direction at time t = 1 so the total distance traveled is
|x (1) − x (0)| + |x (3) − x (1)| = |−1 − 1| + |19 − (−1)| = 22 m.