Một số bài toán cực trị hình học trong không gian

Tuyển chọn một số bài toán cực trị hình học trong không gian có đáp án và lời giải chi tiết; tài liệu hỗ trợ học sinh lớp 12 trong quá trình học thêm chương trình Toán 12 phần Hình học chương 1: Khối đa diện và thể tích của chúng.Mời bạn đọc đón xem.

47 24 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Khối đa diện

Môn: Toán 12

Thông tin:

53 trang 8 tháng trước

Tác giả:

Profile Lan Tường
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 1 -
MỘT SỐ BÀI TOÁN CỰC TRỊ HÌNH HỌC TRONG KHÔNG GIAN
Câu 1. Một khối gỗ hình hộp chữ nhật có kích thước thoả mãn: Tổng của chiều dài và chiều
rộng bằng
12 cm
; tổng của chiều rộng và chiều cao là
24 cm
. Hỏi thể tích lớn nhất mà
khối hộp có thể đạt được là bao nhiêu?
A.
3
288cm
. B.
3
384 3 cm
. C.
3
1782cm
. D.
3
864cm
.
Câu 2. Trong không gian cho bốn mặt cầu có bán kính lần lượt là
2;3;3; 2
đôi một tiếp xúc
nhau. Mặt cầu nhỏ tiếp xúc ngoài với cả bốn mặt cầu nói trên có bán kính bằng
A.
7
15
. B.
3
7
. C.
6
11
. D.
.
Câu 3. Cho hình chóp
.
S ABC
có
SA ABC
,
2SB a
, hai mặt phẳng
SAB
và
SBC
vuông góc với nhau. Góc giữa
SC
và
SAB
bằng
0
45
, góc giữa
SB
và mặt đáy bằng
0
0 90
. Xác định
để thể tích khối chóp
.
S ABC
đạt giá trị lớn nhất.
A.
0
60
. B.
0
30
. C.
0
45
. D.
0
70
.
Câu 4. Cho hình chóp
.
S ABC
có
SA ABC
,
2SB a
, hai mặt phẳng
SAB
và
SBC
vuông góc với nhau. Góc giữa
SC
và
SAB
bằng
45
o
, góc giữa
SB
và mặt đáy bằng
, 0 90
o o
. Xác định
để thể tích khối chóp
.
S ABC
lớn nhất.
A.
60
o
. B.
30
o
. C.
45
o
. D.
70
o
.
Câu 5. Cho hình chóp
. DS ABC
có đáy
DABC
là hình thang cân đáy
AB
, nội tiếp đường
tròn tâm
O
, bán kính
R
. Biết rằng
AC BD
tại
I
, đồng thời
I
là hình chiếu của
lên
ABCD
và
SAC
vuông tại
. Thể tích lớn nhất của khối chóp
.
S ABCD
theo
R
là
A.
3
R
. B.
3
2
3
R
. C.
3
1
2
R
. D.
3
3
4
R
Câu 6. Trong không gian
Oxyz
cho mặt phẳng
: 4 0
x y
, mặt cầu
2
2 2
1
: 1 1
S x y z
và mặt cầu
2 2
2
2
: 4 5 4.
S x y z
Điểm
A
thuộc mặt
phẳng
,
điểm
M
thuộc mặt cầu
1
S
, điểm
N
thuộc mặt cầu
2
S
. Khi dó
AM AN
nhỏ nhất bằng
A.
5
. B.
8
. C.
11
. D.
3 2
.
Câu 7. Cho lăng trụ đứng
.
ABC A B C
có
0
6; 12; 60
AB BC ABC
. Thể tích khối chóp
.
C ABB A
bằng 216. Gọi
M
là điểm nằm trong tam giác
A B C
sao cho tổng diện tích
các mặt bên của hình chóp
.
M ABC
đạt giá trị nhỏ nhất. Tính cosin góc giữa 2 đường
thẳng
B M
,
AC
?
A.
2
2
. B.
2
3
. C.
2
4
. D.
1
2
.
Câu 8. Trong không gian
Oxyz
cho hai mặt cầu
2
2 2
1
: 4 16
S x y z
,
2
2 2
2
: 4 36
S x y z
và điểm
4; 0;0
A
.Đường thẳng
di động và luôn tiếp xúc
với
1
S
đồng thời cắt
2
S
tại hai điểm
,B C
. Tam giác
ABC
có thể có diện tích lớn
nhất là
A.
28 5
. B.
72
. C.
48
. D.
24 5
.
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 2 -
Câu 9. Cho hình chóp
.
S ABCD
, có đáy là hình bình hành,
M
là trung điểm của cạnh
SC
.
Mặt phẳng
( )P
chứa
AM
lần lượt cắt các cạnh
,SB SD
tại
' '
,B D
. Giá trị lớn nhất của
' '
SB SD
u
SB SD
là
a
b
,
*
( , )a b N
tối giản. Tích
.a b
bằng:
A.
3
. B.
12
. C.
15
. D.
6
.
Câu 10. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành tâm
O
. Gọi
I
là điểm
thuộc đoạn
SO
sao cho
1
3
SI SO
. Mặt phẳng
thay đổi đi qua
B
và
I
.
cắt các
cạnh
SA
,
SC
,
SD
lần lượt tại
M
,
N
,
P
. Gọi
m
,
n
lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của
.
.
S MBNP
S ABCD
V
V
. Giá trị của
m n
là
A.
4
15
. B.
6
75
. C.
14
75
. D.
.
Câu 11. Cho hình chóp
SABC
có đáy là tam giác đều cạnh bằng
6
biết các mặt bên của
hình chóp có diện tích bằng nhau và một trong các cạnh bên bằng
3 2
. Tính thể tích
nhỏ nhất của khối chóp
SABC
.
A.
3
. B.
2 2
. C.
2 3
. D.
4
.
Câu 12. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
4;0;0 , 0;4;0 , 0;0;A B S c
và
đường thẳng
1 1 1
:
1 1 2
x y z
d
. Gọi
,A B
lần lượt là hình chiếu vuông góc của
O
lên
,SA SB
. Khi góc giữa đường thẳng
d
và mặt phẳng
OA B
lớn nhất,mệnh đề
nào sau đây đúng?
A.
8; 6
c
. B.
9; 8
c
. C.
0;3
c
. D.
17 15
;
2 2
c
.
Câu 13. Cho hình lập phương
. ' ' ' 'ABCD A B C D
. Điểm
M
nằm trên cạnh
'AA
sao cho góc
'BMD
lớn nhất, đặt góc lớn nhất đó là
. Biết
cos ; , ; , 1; 0
a
a b a b b
b
. Mệnh
đề nào sau đây đúng?
A.
1
a b
. B.
2
a b
. C.
3
a b
. D.
4
a b
.
Câu 14. Cho khối chóp
.
S ABC
có
SA
vuông góc với đáy, tam giác
ABC
vuông tại
B
. Biết rằng
thể tích của khối chóp là
5
24
và giá trị nhỏ nhất diện tích toàn phần chóp
.
S ABC
là
5
p q
trong đó
,p q
. Tính giá trị biểu thức:
2 2
?
p q
A.
2 2
37
36
p q
. B.
2 2
37
9
p q
. C.
2 2
25
4
p q
. D.
2 2
16
p q
.
Câu 15. Cho hình chóp
SABCD
có đáy là hình bình hành tâm
O
. Gọi
I
là điểm thuộc đoạn
SO
sao cho
1
3
SI SO
. Mặt phẳng
thay đổi đi qua
B
và
I
.
cắt các cạnh
, ,SA SC SD
lần lượt tại
, ,M N P
. Gọi
,m n
lần lượt là GTLN, GTNN của
.
.
S BMPN
S ABCD
V
V
. Tính
m
n
?
A.
2
. B.
7
5
. C.
14
75
. D.
.
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 3 -
Câu 16. Trong không gian cho bốn mặt cầu có bán kính lần lượt là 2;3;3;2 đôi một tiếp xúc
nhau. Mặt cầu nhỏ tiếp xúc ngoài với cả bốn mặt cầu nói trên có bán kính bằng
A.
7
15
. B.
3
7
. C.
6
11
. D.
.
Câu 17. Cho tứ diện
SABC
và
G
là trọng tâm của tứ diện. Một mặt phẳng
quay quanh
AG
cắt các cạnh
,SB SC
lần lượt tại
M
và
N
(
,M N
không trùng
). Gọi
V
là thể tích
tứ diện
SABC
,
1
V
là thể tích tứ diện
SAMN
và gọi
,m n
lần lượt là giá trị lớn nhất và
giá trị nhỏ nhất của
1
V
V
. Hãy tính
m n
.
A.
1m n
. B.
17
18
m n
. C.
18
19
m n
. D.
19
20
m n
.
Câu 18. Cho hình nón
( )H
có đỉnh
, chiều cao là
h
và mặt phẳng
( )P
song song với mặt
phẳng đáy của khối nón. Một khối nón
( )T
có đỉnh là tâm của đường tròn đáy của
( )H
và đáy của
( )T
là thiết diện của
( )P
với hình nón. Thể tích lớn nhất của
( )T
là
bao nhiêu?
A.
2
4
81
R h
. B.
2
4
27
R h
. C.
2
24
R h
. D.
2 2
3
R h
.
Câu 19. Cho hình chóp đều
.
S ABC
có
0
1, 30
AB ASB
. Lấy các điểm
', 'B C
lần lượt thuộc
các cạnh
,SB SC
sao cho chu vi tam giác
' 'AB C
nhỏ nhất. Tính chu vi đó.
A.
1
1 3
. B.
3 1
. C.
3
. D.
1 3
.
Câu 20. Trong mặt phẳng
P
cho tam giác
ABC
đều cạnh bằng
8cm
và một điểm
S
di động
ngoài mặt phẳng
P
sao cho tam giác
MAB
luôn có diện tích bằng
2
16 3
cm
, với
M
là trung điểm của
SC
. Gọi
S
là mặt cầu đi qua bốn đỉnh
M
,
A
,
B
,
C
. Khi thể tích
hình chóp
.
S ABC
lớn nhất, tính bán kính nhỏ nhất của
S
:
A.
16 6
9
cm
. B.
4 3
3
cm
. C.
4 15
3
cm
. D.
4 39
3
cm
.
Câu 21. Cho hình chóp
.
S ABCD
có đáy
ABCD
đáy là hình vuông cạnh
a
,
3SA a
. Và
SA
vuông góc với đáy.
M
và
N
là hai điểm thay đổi lần lượt thuộc hai cạnh
BC
và
CD
sao cho
0
45
MAN
. Tính tỉ số giữa giá trị lớn nhất và giá trị nhỏ nhất của thể tích khối
chóp
.
S AMN
A.
2 2 2
. B.
1 2
6
. C.
2 2 1
. D.
1 2
2
.
Câu 22. Cho hình hộp chữ nhật
.
ABCD A B C D
có tổng diện tích tất cả các mặt là
36
, độ dài
đường chéo
AC
bằng
6
. Hỏi thể tích của khối hộp chữ nhật lớn nhất là bao nhiêu?
A.
8 2
. B.
6 6
. C.
24 3
. D.
16 2
.
Câu 23. Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
a
và đường cao
2SA a
.
MNPQ
là thiết diện song song với đáy,
M SA
và
AM x
. Xét hình trụ có đáy là đường tròn
ngoại tiếp tứ giác
MNPQ
và đường sinh
MA
. Giá trị của
x
để thể tích khối trụ lớn
nhất là
A.
3
a
x
. B.
2
3
a
x
. C.
2
a
x
. D.
3
4
a
x
.
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 4 -
Câu 24. Cho tứ diện
ABCD
có tam giác
ABC
đều cạnh
2a
và tam giác
ABD
vuông tại
D
,
2
a
AD
. Khoảng cách lớn nhất từ
B
đến mặt phẳng
ACD
là?
A.
2 2
2
a
. B.
3a
. C.
3
3
a
. D.
2 3a
.
Câu 25. Cho khối chóp tứ giác đều
.
S ABCD
mà khoảng cách từ
A
đến mặt phẳng
SCD
bằng
2a
. Gọi
là góc giữa mặt bên của hình chóp với đáy của hình chóp đó. Với giá
trị nào của
thì thể tích của khối chóp
.
S ABCD
đạt giá trị nhỏ nhất?
A.
2
arcsin
3
. B.
0
45
. C.
2
arccos
3
. D.
0
60
.
Câu 26. Cho hình chóp
SABCD
, có đáy
ABCD
là hình thoi cạnh
a
,
SA SB SC a
.Đặt
0 3
x SD x a
Tìm
x
theo a để tích
.SD
AC
đạt giá trị lớn nhất.
A.
3
2
a
x
. B.
3
3
a
x
. C.
6
2
a
x
. D. Đáp án khác.
Câu 27. Cho tứ diện
. DS ABC
và
M
là một điểm di động, nằm bên trong tam giác
ABC
.
Qua
M
kẻ các đường thẳng song song với
, ,SA SB SC
cắt các mặt phẳng tương ứng
,SBC
,SAC
SAB
lần lượt tại
', ', 'A B C
. Khi đó giá trị lớn nhất của biểu thức
' ' ' ' ' '
. .
MA MB MC MA MB MC
T
SA SB SC SA SB SC
là
A.
. B.
28
27
. C.
62
27
. D.
13
8
Câu 28. Trong không gian với hệ trục tọa độ
.O xyz
, cho điểm
; ;A a b c
với
; ;a b c
là các số
thực dương thỏa mãn
2 2 2
5 9 2
a b c ab bc ca
và
3
2 2
1a
Q
b c
a b c
có
giá trị lớn nhất. Gọi
, ,M N P
lần lượt là hình chiếu vuông góc của
A
lên các tia
; ;Ox Oy Oz
. Phương trình mặt phẳng
MNP
là
A.
4 4 12 0
x y z
. B.
3 12 12 1 0
x y z
.
C.
4 4 0
x y z
. D.
3 12 12 1 0
x y z
.
Câu 29. Trong mặt phẳng
cho đường tròn
T
đường kính
2AB R
. Gọi
C
là một diểm
di động trên
T
. Trên đường thẳng
đi qua
A
và vuông góc với mặt phẳng
lấy
điểm
sao cho
SA R
. Hạ
AH SB
tại
H
,
AK SC
tại
K
. Tìm giá trị lớn nhất
max
V
của thể tích tứ diện
SAHK
.
A.
3
max
5
75
R
V
. B.
3
max
5
25
R
V
. C.
3
max
3
27
R
V
. D.
3
max
3
9
R
V
.
.Câu 30. Cho tứ diện đều
ABCD
có cạnh bằng
1
. Hai điểm
,M N
di động trên các cạnh
,
AB AC
sao cho mặt phẳng
DMN
vuông góc mặt phẳng
ABC
. Gọi
1 2
,S S
lần lượt
là diện tích lớn nhất và nhỏ nhất của tam giác
AMN
. Tính
1
2
S
T
S
.
A.
8
9
T
. B.
9
8
T
. C.
8
7
T
. D.
9
7
T
.
Câu 31. Cho lăng trụ tam giác đều
. ' ' 'ABC A B C
với độ dài tất cả các cạnh đều bằng
a
. Xét tất
cả các đoạn thẳng song song với mặt phẳng
' 'ABB A
và có một đầu
E
nằm trên
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 5 -
đường chéo
'A C
của mặt bên
' 'AA C C
, còn đầu kia
F
nằm trên đường chéo
'BC
của
mặt bên
' 'BB C C
. Hãy tìm độ dài ngắn nhất của các đoạn thẳng này.
A.
2
5
a
. B.
5
a
. C.
5
a
. D.
2
5
a
.
Câu 32. Cho hình chóp tứ giác đều
.
S ABCD
mà khoảng cách từ
A
đến mặt phẳng
SBC
bằng
b
. Góc giữa mặt bên và mặt đáy của hình chóp bằng
. Tìm
để thể tích của
khối chóp
.
S ABCD
nhỏ nhất.
A.
3
arccos
3
. B.
arccos 3
. C.
1
arccos
3
. D.
2
arccos
3
.
Câu 33. Cho hình lăng trụ đều
. ' ' ' 'ABCD A B C D
có cạnh đáy bằng a. Điểm M và N lần lượt
thay đổi trên các cạnh
'BB
và
'DD
sao cho
MAC NAC
và
,BM x
DN y
. Tìm
giá trị nhỏ nhất của thể tích khối tứ diện
ACMN
.
A.
3
3 2
a
. B.
3
2
a
. C.
3
2 2
a
. D.
3
2 3
a
.
Câu 34. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, cạnh bên
SA b
và
vuông góc với
ABCD
. Điểm
M
thay đổi trên cạnh
CD
với
0
CM x x a
.
H
là
hình chiếu vuông góc của
trên
BM
. Tìm giá trị lớn nhất của thể tích khối chóp
.
S ABH
theo
,a b
.
A.
2
12
a b
. B.
2
24
a b
. C.
2
8
a b
. D.
2
18
a b
.
Câu 35. Cho tứ diện đều
SABC
có
D
là điểm thuộc cạnh
AB
sao cho
2BD AD
,
I
là trung
điểm của
SD
. Một đường thẳng
thay đổi qua
I
cắt các cạnh
SA
,
SB
lần lượt tại
M
,
N
. Biết
2AB a
. Khi
thay đổi, thể tích khối chóp
.
S MNC
nhỏ nhất bằng
3
3
.
m a
n
m
,
với
,m n
,
, 1
m n
. Tính
m n
.
A.
4
m n
. B.
6
m n
. C.
7
m n
. D.
5
m n
.
Câu 36. Cắt một khối trụ tròn có chiều cao h bởi một mặt phẳng song song với hai mặt đáy ta
thu được hai khối tròn nhỏ. Một trong hai khối đó ngoại tiếp một lăng trụ đứng thể
tích V có đáy là tam giác có chu vi là p. Khối còn lại ngoại tiếp một khối nón có bán
kính là R . Tìm giá trị của R sao cho thể tích của khối nón là lớn nhất?
A.
3
162
p
R
V
. B.
3
162
hp
R
V
. C.
3
162
p
R
. D.
3
162
p
R
V
.
Câu 37. Người ta cần trang trí một kim tự tháp hình chóp tứ giác đều
.
S ABCD
cạnh bên
bằng
200 m
,
0
15
ASB
bằng đường gấp khúc dây đèn led vòng quanh kim tự tháp
AEFGHIJKLS
trong đó điểm
cố định và
40m
LS
.
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 6 -
Khi đó cần dùng ít nhất bao nhiêu mét dây đèn led để trang trí?
A.
40 67 40
mét. B.
20 111 40
mét.
C.
40 31 40
mét
.
D.
40 111 40
mét.
Câu 38. Chohình chóp
.S ABC
có các cạnh bên bằng
1
. Mặt phẳng
thay đổi luôn đi qua
trọng tâm của hình chóp, cắt ba cạnh bên
, ,SA SB SC
lần lượt tại
, ,D E F
. Tìm giá trị
lớn nhất
max
P
của
1 1 1
. . .
P
SD SE SE SF SF SD
.
A.
4
3
. B.
16
3
. C.
4
3
. D.
3
4
.
Câu 39. Cho hình lập phương
. ' ' ' 'ABCD A B C D
có cạnh bằng
a
.
G
là trung điểm của
'BD
,
mặt phẳng
P
thay đổi qua
G
cắt
', ', ' 'AD CD B D
tương ứng tại
, ,H I K
. Tìm giá trị
lớn nhất của biểu thức
1 1 1
' . ' ' . ' ' . '
T
D H D I D I D K D K D H
.
A.
2
8
3a
. B.
2
16
3
a
. C.
2
8
3
a
. D.
2
16
3a
.
Câu 40. Cho hình hộp chữ nhật
. ' ' ' 'ABCD A B C D
có
, ' , D 'AC a AD b C c
. Tìm thể tích lớn
nhất của hình chữ nhật đã cho
khi
, ,a b c
thay đổi, còn chu vi tam giác
D 'AC
không
đổi.
Câu 41. Cho tứ diện
, , ,ABCD AB x CD y
các cạnh còn lại của tứ diện bằng
2,a
,x y
thay
đổi sao cho
2 .x y a
Khi
ABCD
V
đạt giá trị nhỏ nhất, tính cosin của góc giữa
ABC
và
.ABD
Câu 42. Cho hình chóp
SABCD
có đáy là
ABCD
là hình vuông cạnh
a
, cạnh
SA a
và vuông
góc với mp
( ).ABCD
M
là điểm di động trên đoạn
BC
và
0BM x x a
,
K
là
hình chiếu của
S
trên
.DM
a) Tính độ dài đoạn
SK
theo
a
và
x
.
b) Tìm min của đoạn
.SK
Câu 43. Cho hình chóp
.S ABCD
có tứ giác
ABCD
là hình bình hành tâm
O
. Điểm
C
di động
trên cạnh
SC
(
C
khác điểm
S
và
C
). Mặt phẳng
R
chứa đường thẳng
AC
và
song song với
BD
. Mặt phẳng
R
cắt đường thẳng
SB
,
SD
lần lượt tại
,B D
.
1/ Gọi
F
là giao điểm của
AD
với
B C
. Chứng minh rằng
F
luôn di động trên một
đường thẳng cố định khi
C
di động trên
SC
.
2/ Xác định vị trí của điểm
C
sao cho tổng
5
3 .
2
SC BB SD
CC SB DD
đạt giá trị nhỏ nhất.
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 7 -
Câu 44. Trong mặt phẳng
cho hình chữ nhật
ABCD
có
; 2AB a BC a
. Các điểm
,M N
lần
lượt di chuyển trên các đường thẳng
,m n
vuông góc với mặt phẳng
tại
,A B
sao
cho
DM CN
. Tìm giá trị nhỏ nhất của khối tứ diện
CDMN
.
Câu 45. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thang cân,
AB
song song với
CD
,
2
AB CD
, các cạnh bên có độ dài bằng
1
. Gọi
O AC BD
,
I
là trung điểm của
SO
.
Mặt phẳng
thay đổi đi qua
I
và cắt các cạnh
, , ,SA SB SC SD
lần lượt tại
, , ,M N P Q
. Tìm giá trị nhỏ nhất của biểu thức
2 2 2 2
1 1 1 1
T
SM SN SP SQ
.
Câu 46. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành. Gọi
E
là trung điểm của
SC
. Mặt phẳng
thay đổi nhưng luôn chứa
AE
cắt
SB
,
SD
lần lượt tại
M
,
N
. Xác
định vị trí của
M
,
N
trên các cạnh
SB
,
SD
sao cho
SM SN
SB SD
đạt giá trị lớn nhất.
Câu 47. Cho tứ diện
OABC
có các cạnh
, ,OA OB OC
đôi một vuông góc. Gọi
M
là điểm thuộc
miền trong của tam giác
ABC
. Tìm giá trị nhỏ nhất của biểu thức
2 2 2
2 2 2
MA MB MC
T
OA OB OC
BẢNG ĐÁP ÁN
1.B 2.C 3.C 4.C 5.B 6.A 7.C 8.D 9.B 10.C
11.A 12.D 13.D 14.D 15.C 16.C 17.B 18.A 19.D 20.C
21.D 22.A 23.B 24.B 25.A 26.C 27.B 28.B 29.A 30.B
31.B 32.A 33.A 34.A 35.D 36.B 37.C 38.B 39.A
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 8 -
LỜI GIẢI THAM KHẢO
Câu 1. Một khối gỗ hình hộp chữ nhật có kích thước thoả mãn: Tổng của chiều dài và chiều
rộng bằng
12 cm
; tổng của chiều rộng và chiều cao là
24 cm
. Hỏi thể tích lớn nhất mà
khối hộp có thể đạt được là bao nhiêu?
A.
3
288cm
. B.
3
384 3 cm
. C.
3
1782cm
. D.
3
864cm
.
Lời giải
Gọi chiều dài, chiều rộng và chiều cao của khối hộp chữ nhật lần lượt là
x
,
y
,
z
, , 0x y z
.
Theo giả thiết ta có:
12
24
x y
y z
12
24
x y
z y
. Vì , 0x z nên
12
12
24
y
y
y
.
Thể tích của khối hộp là
3 2
12 24 36 288V xyz y y y y y y
.
Xét hàm số
3 2
36 288f y y y y
trên khoảng
0;12
.
2
3 72 288f y y y
;
12 4 3
0
12 4 3
y
f y
y
.
Bảng biến thiên:
Từ bảng biến thiên ta có:
0;12
max 384 3f y
.
Vậy thể tích lớn nhất mà khối hộp có thể đạt được là
3
384 3 cm
.
Câu 2. Trong không gian cho bốn mặt cầu có bán kính lần lượt là
2;3;3; 2
đôi một tiếp xúc
nhau. Mặt cầu nhỏ tiếp xúc ngoài với cả bốn mặt cầu nói trên có bán kính bằng
A.
7
15
. B.
3
7
. C.
6
11
. D.
5
9
.
Lời giải
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 9 -
Gọi
, , ,A B C D
lần lượt là tâm của bốn mặt cầu nói trên và
, ( 0)
I x
lần lượt là tâm, bán
kính mặt cầu cần tìm.
Mặt cầu
I
tiếp xúc ngoài với bốn mặt cầu nêu trên nên
2
3
IA IC x
IB ID x
. Do đó,
I
nằm
trên giao tuyến của hai măt phẳng trung trực của
,AC BD
.
Vì bốn mặt cầu đôi một tiếp xúc nên
DA DC BA BC
. Gọi
,M N
lần lượt là trung
điểm của
,BD AC
. Khi đó,
MN
là đoạn vuông góc chung của
AC
và
BD
nên
I
thuộc
đường thẳng
MN
.
Ta có,
2 2 2 2
25 4 21, 21 9 2 3
DN DC CN MN DN DM
.
Xét
AIN
vuông tại
N
và
2
2
2 2
IN x
.
Xét
BIM
vuông tại
M
có
2
2
3 3
IM x
.
Vì
IM IN MN
nên dấu ‘‘=’’ xảy ra khi và chỉ khi
I MN
.
Khi đó,
2 2
2 2
2 2 3 3 2 3
IM IN MN x x
2
6
11 60 36 0
11
x x x
.
Câu 3. Cho hình chóp
.
S ABC
có
SA ABC
,
2SB a
, hai mặt phẳng
SAB
và
SBC
vuông góc với nhau. Góc giữa
SC
và
SAB
bằng
0
45
, góc giữa
SB
và mặt đáy bằng
0
0 90
. Xác định
để thể tích khối chóp
.
S ABC
đạt giá trị lớn nhất.
A.
0
60
. B.
0
30
. C.
0
45
. D.
0
70
.
Lời giải
N
M
B
A
C
D
I
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 10 -
Ta thấy
SA ABC
1SAB ABC
Theo giả thiết thì
SAB
2SBC
Từ và ta có
( )BC SAB BC AB
và
BC SB
Góc giữa
SC
và
SAB
là góc
0
45BSC
. Trong tam giác vuông cân
SBC
có
2SB BC a
.
Tam giác vuông
SAB
cạnh
.cos 2 cosAB SB a
;
.sin 2.sinSA SB a
3 3
.
1 1 2
. . . 2. .sin 2 .
3 6 6
S ABC ABC
V S SA a a
3 0 0
max
2
. sin 2 1 0 90 45
6
V a
Câu 4. Cho hình chóp
.S ABC
có
SA ABC
,
2SB a
, hai mặt phẳng
SAB
và
SBC
vuông góc với nhau. Góc giữa
SC
và
SAB
bằng
45
o
, góc giữa
SB
và mặt đáy bằng
, 0 90
o o
. Xác định
để thể tích khối chóp
.S ABC
lớn nhất.
A.
60
o
. B.
30
o
. C.
45
o
. D.
70
o
.
Lời giải
Ta có:
SA ABC SAB ABC
Mà
SAB SBC
,
ABC SBC BC
Nên
BC SAB
BC AB
ABC
vuông tại
B
.
Góc giữa
SC
và
SAB
là
45
o
CSB
.
2BC SB a
.
Góc giữa
SB
và mặt đáy là
SBA
.cosAB SB
;
.sinSA SB
.
Thể tích khối chóp
.S ABC
là:
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 11 -
3
1 1 1
. . .BC .sin .cos
3 6 6
ABC
V SA S SA AB SB
3
3
1 2
2 sin 2
6 6
a
a
.
Dấu “=” xảy ra
sin 2 1 2 90 45
o o
.
Câu 5. Cho hình chóp
. DS ABC
có đáy
DABC
là hình thang cân đáy
AB
, nội tiếp đường
tròn tâm
O
, bán kính
R
. Biết rằng
AC BD
tại
I
, đồng thời
I
là hình chiếu của
lên
ABCD
và
SAC
vuông tại
. Thể tích lớn nhất của khối chóp
.
S ABCD
theo
R
là
A.
3
R
. B.
3
2
3
R
. C.
3
1
2
R
. D.
3
3
4
R
Lời giải
Ta có thể tích của khối chóp
.
S ABCD
là
.
1
. .
3
S ABCD ABCD
V SI S
2
1 1 1
. . . .
3 2 6
SI AC BD SI AC
Tam giác
SAC
vuông tại
, đường cao
SI
nên
2
.SI IA IC
, do đó
2
.
1
. .
6
S ABCD
V IA IC AC
2 3
1 1
. . .
6 2 12
IA IC
AC AC
3
3
1 2
. 2
12 3
R R
.
Dấu “=” xảy ra khi và chỉ khi
2
IA IC
AC R
ABCD
là hình vuông.
Vậy thể tích lớn nhất của khối chóp
.
S ABCD
bằng
3
2
3
R
.
Câu 6. Trong không gian
Oxyz
cho mặt phẳng
: 4 0
x y
, mặt cầu
2
2 2
1
: 1 1
S x y z
và mặt cầu
2 2
2
2
: 4 5 4.
S x y z
Điểm
A
thuộc mặt
phẳng
,
điểm
M
thuộc mặt cầu
1
S
, điểm
N
thuộc mặt cầu
2
S
. Khi dó
AM AN
nhỏ nhất bằng
A.
5
. B.
8
. C.
11
. D.
3 2
.
Lời giải
Mặt cầu
1
S
có tâm
1
1;0;0
I
, bán kính
1
1
R
.
Mặt cầu
2
S
có tâm
2
4;5;0
I
, bán kính
2
2.
R
1 1
3 2
,
2
d I R
2 2
5 2
,
2
d I R
I
A
B
D
S
C
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 12 -
Ta thấy
1
S
và
không có điểm chung,
2
S
và
không có điểm chung,
và
2
I
nằm cùng phía so với
Phép đối xứng qua mặt phẳng
biến mặt cầu
1
S
thành mặt cầu
1
'S
, biến điểm
M
thành điểm
'M
, biến điểm
thành điểm
1
'I
.
Ta có
' 'AM AN AM AN M N
Dấu bằng xảy ra khi
, ',A M N
thẳng hàng.
Đoạn thẳng
'M N
ngắn nhất khi
',M N
thuộc đoạn thẳng
'
1 2
I I
Khi đó giá trị nhỏ nhất của
AM AN
là
'
1 2 1 2
P I I R R
Đường thẳng
đi qua
và vuông góc với
là
1
0
x t
y t t
z
Giao điểm của đường thẳng
và
là
5 3
; ;0
2 2
B
B
là trung điểm của
' '
1 1 1
4; 3;0
I I I
Vậy
8 1 2 5.
P
Câu 7. Cho lăng trụ đứng
.
ABC A B C
có
0
6; 12; 60
AB BC ABC
. Thể tích khối chóp
.
C ABB A
bằng 216. Gọi
M
là điểm nằm trong tam giác
A B C
sao cho tổng diện tích
các mặt bên của hình chóp
.
M ABC
đạt giá trị nhỏ nhất. Tính cosin góc giữa 2 đường
thẳng
B M
,
AC
?
A.
2
2
. B.
2
3
. C.
2
4
. D.
1
2
.
Lời giải
M'
I'
1
I
1
I
2
M
N
A
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 13 -
Gọi
I
là hình chiếu của
M
trên
( )ABC
;
, ,D E F
lần lượt là hình chiếu của
I
trên
, , .AB BC CA
Đặt
, , 2 , 2 , 2 , 'x ID y IE a AB b BC c CA h AA MI
.
Khi đó
ABC IAB IAC IBC
S S S S ax by cz
Diện tích toàn phần của hình chóp
.M ABC
nhỏ nhất khi và chỉ khi
MAB MBC MCA
S S S S
nhỏ nhất.
Có
2 2
2 2 2 2 2 2
1
.
2
MAB
MD MI ID h x S AB MD a h x ah ax
.
Tương tự ta chứng minh được
2 2 2 2 2 2
S ah ax bh by ch cz
Sử dụng bất đẳng thức
u v w u v w
với
; , ( ; ), ( ; )u ah ax v bh by w ch cz
ta
được:
2 2 2 2 2
( ) ( ) ( ) o
ABC
S ah bh ch ax by cz a b c h S c nst
.
Dấu bằng xảy ra khi và chỉ khi
ax by cz
x y z
ah bh ch
.
Suy ra
I
là tâm đương tròn nội tiếp tam giác
ABC
, nên
M
là tâm đường tròn nội tiếp
tam giác
' ' 'A B C
.
Tính cosin góc giữa hai đường thẳng
'B M
và
'AC
.
' ' '
1
. .sin 18 3
2
A B C ABC
S S BA BC ABC
2 2 2 2 0
' ' 2 . cos 60 108 ' ' 6 3A C AC AB BC AB BC A C
Do
. . ' '
3 3
.216 324 '. 324 ' 6 3
2 2
ABC A B C C ABB A ABC
V V AA S AA
Gọi K là chân đường phân giác trong của tam giác
' ' 'A B C
kẻ từ
B
, từ
K
kẻ đường
thẳng song song với
'AC
cắt
'AA
tại
H
, khi đó:
( ' , ') ( ' , ) cos cos '
B M AC B K KH B KH
0
1 18
sin 30 18 3 4 3
2 4
A B C B KC A KB
S S S B K B A B C B K B K
Ta có
1 1
2 3
2 3
A K A B
A K A C
B K C B
Do
/ /KH AC
nên
1
2 3
3
A H A K
A H
A A C A
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 14 -
2 2 2 2
2 6, 4 3KH A H A K B H A B A H
Vậy
2 2 2
2
cos =cos
2 . 4
B K KH B H
B KH
B K KH
.
Câu 8. Trong không gian
Oxyz
cho hai mặt cầu
2
2 2
1
: 4 16S x y z
,
2
2 2
2
: 4 36S x y z
và điểm
4; 0; 0A
.Đường thẳng
di động và luôn tiếp xúc
với
1
S
đồng thời cắt
2
S
tại hai điểm
,B C
. Tam giác
ABC
có thể có diện tích lớn
nhất là
A.
28 5
. B.
72
. C.
48
. D.
24 5
.
Lời giải
Gọi
M
là tiếp điểm của
và
1
S
4; 0;0I
là tâm của hai mặt cầu
1
S
và
2
S
có bán kính lần lượt
1
4R
và
2
6R
Ta có
2 1
6, 4 2 5 4 5IC R IM R BM BC
4;0; 0 , 4;0;0 8I A IA
1 1 1 1
. , . ( ) .4 5.(4 8) 24 5
2 2 2 2
ABC
S CB d A BC BC AM BC IA IM
Câu 9. Cho hình chóp
.S ABCD
, có đáy là hình bình hành,
M
là trung điểm của cạnh
SC
.
Mặt phẳng
( )P
chứa
AM
lần lượt cắt các cạnh
,SB SD
tại
' '
,B D
. Giá trị lớn nhất của
' '
SB SD
u
SB SD
là
a
b
,
*
( , )a b N
tối giản. Tích
.a b
bằng:
A.
3
. B.
12
. C.
15
. D.
6
.
Lời giải
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 15 -
Lấy
' ' ;I AM B D O AC BD
Ta có
, ,S O I
là các điểm chung của hai mặt phẳng
( );( )SAC SBD
Suy ra
, ,S O I
thẳng hàng
Và
I
là trọng tâm các mặt chéo
2
3
SI
SAC
SO
Vẽ
/ / ' ; / / 'BP B I DN D I OP ON
. Đặt
;
' '
SD SB
x y
SD SB
2 3
2. 3
' ' 2
SB SD SP SN SO
x y
SB SD SI SI SI
2
1 1 3 2 4
, [1; 2] 3( )
3
x y
x y xy x y
3; 4 . 12a b a b
Câu 10. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành tâm
O
. Gọi
I
là điểm
thuộc đoạn
SO
sao cho
1
3
SI SO
. Mặt phẳng
thay đổi đi qua
B
và
I
.
cắt các
cạnh
SA
,
SC
,
SD
lần lượt tại
M
,
N
,
P
. Gọi
m
,
n
lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của
.
.
S MBNP
S ABCD
V
V
. Giá trị của
m n
là
A.
4
15
. B.
6
75
. C.
14
75
. D.
1
5
.
Lời giải
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 16 -
Đặt
SA
x
SM
SC
y
SN
với
x
,
1y
.
Có
2 2.3 6 5
SB SD SO SD
SB SP SI SP
.
Mà
2 6 6
SO
x y y x
SI
, với
1 5x
.
Khi đó
.
2
.
1 5 12 3 3 3
.1. .5 20 5 5 6
5 6
S BMNP
S ABCD
V
x y
V x y xy xy x x
x x
.
Xét hàm số
2
3
5 6
f x
x x
, với
1 5x
.
Ta có
2
2
3 2 6
.
5
6
x
f x
x x
. Cho
0 2 6 0 3 1;5f x x x
.
Khi đó
3
1
25
f
,
1
3
15
f
và
3
5
25
f
.
Suy ra
3
25
m
và
1
15
n
.
Vậy
14
75
m n
.
Câu 11. Cho hình chóp
SABC
có đáy là tam giác đều cạnh bằng
6
biết các mặt bên của
hình chóp có diện tích bằng nhau và một trong các cạnh bên bằng
3 2
. Tính thể tích
nhỏ nhất của khối chóp
SABC
.
A.
3
. B.
2 2
. C.
2 3
. D.
4
.
Lời giải
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 17 -
Gọi
H
là hình chiếu vuông góc của
S
lên
( )ABC
, Gọi
, ,M N P
lần lượt là hình chiếu
vuông góc của
H
trên
, ,AB BC CA
thì
, ,SM SN SP
lần lượt là chiều cao của các mặt
bên
, ,SAB SBC SAC
.
Vì các mặt bên của hình chóp có diện tích bằng nhau nên
SM SN SP
nên suy ra
HM HN HP H
là tâm đường tròn nội tiếp hoặc tâm đường tròn bàng tiếp của
tam giác
ABC
.
Trường hợp 1:
H
là tâm đường tròn nội tiếp của tam giác
ABC
.
Khi đó
2
2
2 2
6
3 2 4
3
SH SA AH
.
Vậy
2
1 1 3
. .4. 6 . 2 3
3 3 4
SABC ABC
V SH S
Trường hợp 2:
H
là tâm đường tròn bàng tiếp của tam giác
ABC
.
Do tam giác
ABC
đều nên giả sử H là tâm đường tròn bàng tiếp góc
A
. Khi đó
3 2, 6AH BH CH
Nếu
2 2
3 2 0SA SH SA AH
.
Do đó
2 2
2 2
3 2 3 2 6 2 3SB SC SH SB BH
Suy ra
2
1 1 3
. .2 3. 6 . 3
3 3 4
SABC ABC
V SH S
.
Ta có
3 2 3
Vậy
min
3V
Câu 12. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
4;0;0 , 0;4;0 , 0;0;A B S c
và
đường thẳng
1 1 1
:
1 1 2
x y z
d
. Gọi
,A B
lần lượt là hình chiếu vuông góc của
O
lên
,SA SB
. Khi góc giữa đường thẳng
d
và mặt phẳng
OA B
lớn nhất,mệnh đề
nào sau đây đúng?
A.
8; 6c
. B.
9; 8c
. C.
0;3c
. D.
17 15
;
2 2
c
.
Lời giải
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 18 -
Gọi
C
là đỉnh thứ tư của hình vuông
4; 4;0AOBC C
.
Ta có
OA SA
OA SAC
OA AC
mà
SC SAC
nên SC OA
.
Tương tự
SC OB
, từ đó suy ra
SC OA B
. Vậy
4;4;SC c
là vectơ pháp
tuyến của mặt phẳng
OA B
.
Để góc giữa đường thẳng
d
và mặt phẳng
OA B
lớn nhất thì
d OA B
hay
SC
cùng phương với
1;1;2
d
u
. Suy ra
8c
.
Câu 13. Cho hình lập phương
. ' ' ' 'ABCD A B C D
. Điểm
M
nằm trên cạnh
'AA
sao cho góc
'BMD
lớn nhất, đặt góc lớn nhất đó là
. Biết
cos ; , ; , 1; 0
a
a b a b b
b
. Mệnh
đề nào sau đây đúng?
A.
1a b
. B.
2a b
. C.
3a b
. D.
4a b
.
Lời giải
Không mất tính tổng quát, giả sử cạnh hình lập phương có độ dài là
1
và
, 0 1AM x x
. Khi đó, ta có
2
2 2 2 2
1 ; ' 1 1 ; ' 3BM x D M x BD
.
Vậy
2
2
2
cos '
1 1 1
x x
BMD
x x
B'
C'
D'
C
A
B
D
A'
M
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 19 -
2
2
2
2
2
2
2
1
1
cos '
1 1 1
1 1
1 1
1
x x
BMD
x x
x
x
Ta có
2
2 2 2
2
1 1 1 1 1
1 1 1.1 . 1 25
1 1
1
2
x x x x
x x
.
Vậy
2
1
cos '
25
BMD
, suy ra
1
cos '
5
BMD
.
Dấu bằng xảy ra khi và chỉ khi
1
2
x
, hay
M
là trung điểm của
'AA
, khi đó
cos 'BMD
nhỏ nhất nên góc
'BMD
lớn nhất.
Vậy
1; 5a b
.
Câu 14. Cho khối chóp
.S ABC
có
SA
vuông góc với đáy, tam giác
ABC
vuông tại
B
. Biết rằng
thể tích của khối chóp là
5
24
và giá trị nhỏ nhất diện tích toàn phần chóp
.S ABC
là
5p q
trong đó
,p q
. Tính giá trị biểu thức:
2 2
?p q
A.
2 2
37
36
p q
. B.
2 2
37
9
p q
. C.
2 2
25
4
p q
. D.
2 2
16p q
.
Lời giải
Đặt
AB a
,
BC b
,
SA c
,
, , 0a b c
, khi đó ta có
.
1 5 5
6 24 4
S ABC
V abc abc
.
Diện tích toàn phần chóp
tp ABC SAB SAC SBC
S S S S S
2 2 2 2
1
2 2
P
ab ac c a b b a c
.
Có
2 2 2 2 2 2
2 9 2 5 2 5
1
3 4 3 4 3 2
a b a b a b a b
.
Tương tự
2 2
2 5
3 2
a c a c
. Do đó
2 5 2 5
3 2 3 2
P ab ac c a b b a c
2
3
5 2 5 2 5
.3. 5
3 3 2
5 5
bc
ab ac abc
.
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 20 -
Dấu
" "
xảy ra khi và chỉ khi
1
5
2
a
b c
.
Khi đó
2 2
5
5 25
5
4
4 16
0
Min
tp
p
S p q
q
Câu 15. Cho hình chóp
SABCD
có đáy là hình bình hành tâm
O
. Gọi
I
là điểm thuộc đoạn
SO
sao cho
1
3
SI SO
. Mặt phẳng
thay đổi đi qua
B
và
I
.
cắt các cạnh
, ,SA SC SD
lần lượt tại
, ,M N P
. Gọi
,m n
lần lượt là GTLN, GTNN của
.
.
S BMPN
S ABCD
V
V
. Tính
m
n
?
A.
2
. B.
7
5
. C.
14
75
. D.
8
5
.
Lời giải
+) Đặt
SA
a
SM
,
1
SB
b
SB
,
SC
c
SN
,
SD
d
SP
.
+) Có
2. 6
SO
a c b d
SI
6
5
a c
d
6
5
c a
d
. Do
1
1 5
1
a
a
c
.
+) Có
.
2
.
12 3 3
4 4. .1. .5 5 6
5 6
S BMPN
S ABCD
V
a b c d
f a
V abcd a c a a
a a
+)
2
2
3 2 6
5 6
a
f a
a a
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 21 -
3 1 14
.
25 15 75
m n
Câu 16. Trong không gian cho bốn mặt cầu có bán kính lần lượt là 2;3;3;2 đôi một tiếp xúc
nhau. Mặt cầu nhỏ tiếp xúc ngoài với cả bốn mặt cầu nói trên có bán kính bằng
A.
7
15
. B.
3
7
. C.
6
11
. D.
5
9
.
Lời giải
Gọi tâm của mặt cầu bán kính bằng 2 lần lượt là
2 2
,A B
.
Gọi tâm của mặt cầu bán kính bằng 3 lần lượt là
3 3
,A B
.
Vì bốn mặt cầu đôi một tiếp xúc nhau nên ta có
2 2 2 3 2 3 2 3 2 3 3 3
4, 5, 6A B A A A B B A B B A B
.
Mặt cầu tiếp xúc ngoài với bốn mặt cầu đã cho có tâm
I
bán kính
R
. Khi đó ta có
2 2
3 3
2
3
IA IB R
IA IB R
Suy ra điểm
I
nằm trên hai mặt phẳng trung trực của đoạn
2 2
A B
và
3 3
A B
. Gọi
,M N
lần lượt là trung điểm của
2 2
A B
và
3 3
A B
. Dễ dàng chứng minh được
3 3 2 2
,MA B NA B
lần lượt là mặt phẳng trung trực của
2 2
A B
và
3 3
A B
. Từ đó ta suy ra
I MN
.
Ta có
2 3MN
, đặt
,IM x IN y
với
0, 0x y
.
Suy ra
2
2
2
2
2 3
2 4
3 9
x y
R x
R y
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 22 -
Từ đó rút ra được
3 6 3
6
R
y
.
Trên
3 3
,IA IB
lần lượt lấy
,K H
sao cho
2IH IK R
.
Giải tam giác
2 3
A IB
ta có
2
2
24.
3
R
A H
R
.
Gọi
G
là giao điểm của
KH
và
IN
.
Ta có
3 3
2 2
3.
3 3
GH IG IH R R
GH
NB IN IB R R
và
3 6 3
6 3
R
GN
R
.
Xét tam giác
2
MA H
vuông tại
M
, ta có
2 2 2
2 2
MH A H A M
.
Xét tam giác
MGH
vuông tại
G
, ta có
2
2 2 2 2 2
2 2
2 2
24. 4 9.
3 3
R R
MG MH GH A H A M GH
R R
.
Khi đó ta có
2
2 2 3 6 3
24. 4 9. 2 3
3 3 6 3
R R R
R R R
.
Kiểm tra đáp án ta được
6
11
R
thỏa mãn.
Câu 17. Cho tứ diện
SABC
và
G
là trọng tâm của tứ diện. Một mặt phẳng
quay quanh
AG
cắt các cạnh
,SB SC
lần lượt tại
M
và
N
(
,M N
không trùng
S
). Gọi
V
là thể tích
tứ diện
SABC
,
1
V
là thể tích tứ diện
SAMN
và gọi
,m n
lần lượt là giá trị lớn nhất và
giá trị nhỏ nhất của
1
V
V
. Hãy tính
m n
.
A.
1m n
. B.
17
18
m n
. C.
18
19
m n
. D.
19
20
m n
.
Lời giải
Gọi
A
là trọng tâm của tam giác
SBC
, khi đó
A AG
nên
, ,M N A
thẳng hàng.
Đặt
,
SM SN
x y
SB SC
với
0 , 1x y
.
Ta có
1
V
SM SN
xy
V SB SC
.
Vì
2
3
2
3
SMA
SBI
SNA
SCI
S
SM SA
x
S SB SI
S
SN SA
y
S SC SI
nên
1 1
2 3
SMA SNA SMA SNA
SBC SBC SBI SCI
S S S S
x y
S S S S
.
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 23 -
Mặt khác
SMA SNA SMA SNA SMN
SBC SBC SBC SBC
S S S S S
SM SN
xy
S S S S SB SC
nên
1
3
x y xy
.
Do đó
3 1
x
y
x
, suy ra
2
1
3 1
V x
V x
.
Do
0 , 1x y
nên từ
3 1
x
y
x
ta suy ra
1
1
2
x
.
Xét hàm số
2
3 1
x
f x
x
với
1
1
2
x
.
2
2
3 2
3 1
x x
f x
x
2
2
3 2
0 0 0
3 1
x x
f x x
x
hoặc
2
3
x
.
Vì
1 1 2 4 1
, , 1
2 2 3 9 2
f f f
nên ta được
1 4
,
2 9
m n
hay
1 4 17
2 9 18
m n
.
Câu 18. Cho hình nón
( )H
có đỉnh
S
, chiều cao là
h
và mặt phẳng
( )P
song song với mặt
phẳng đáy của khối nón. Một khối nón
( )T
có đỉnh là tâm của đường tròn đáy của
( )H
và đáy của
( )T
là thiết diện của
( )P
với hình nón. Thể tích lớn nhất của
( )T
là
bao nhiêu?
A.
2
4
81
R h
. B.
2
4
27
R h
. C.
2
24
R h
. D.
2 2
3
R h
.
Lời giải
Gọi
O
và
'O
lần lượt là tâm của đường tròn đáy của hình nón
( )H
và
( )T
.
,h R
là chiều cao và bán kính của hình nón
( )H
.
', 'h R
là chiều cao và bán kính của hình nón
( )T
0 'h h
.
Vì mặt phẳng
( )P
song song với mặt phẳng đáy của khối nón nên từ hình vẽ ta có:
+
' ' ' ' ' '
' . 1
SO CO R R h h h
R R
SO AO R R h h
.
+
2
2 2
( )
1 1 '
' ' 1 '
3 3
T
h
V R h R h
h
.
Xét hàm số
2
2
2
' ( )
' 4 ' 3 '
( ') 1 ' '( ') 1 0
' ( )
3
h h ktm
h h h
f h h f h
h
h h
h tm
h
.
Ta có bảng biến thiên:
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 24 -
Từ bảng biến thiên ta có hàm số
( ')f h
đạt giá trị lớn nhất là
4
3 27
h h
f
.
Vậy thể tích của khối nón
( )T
đạt giá trị lớn nhất
2
( )
4
81
T
R h
V
.
Câu 19. Cho hình chóp đều
.S ABC
có
0
1, 30 AB ASB
. Lấy các điểm
', 'B C
lần lượt thuộc
các cạnh
,SB SC
sao cho chu vi tam giác
' 'AB C
nhỏ nhất. Tính chu vi đó.
A.
1
1 3
. B.
3 1
. C.
3
. D.
1 3
.
Lời giải
Trải các mặt của hình chóp
.S ABC
ra mặt phẳng
SBC
thì chu vi tam giác
' 'AB C
bằng
' ' ' ' ' ' ' 'AB B C C A AB B C C D AD
.
Dấu
" "
xảy ra khi
' , 'B E C F
.
Ta có
0
0
1 6 2
1, 30
2 sin15 2
AB ASB SA SB
.
Lại có chóp
.S ABC
đều,
0 0
30 90 2 1 3 ASB ASD AD SA
.
Vậy chu vi tam giác
' 'AB C
đạt giá trị nhỏ nhất bằng
1 3
.
Câu 20. Trong mặt phẳng
P
cho tam giác
ABC
đều cạnh bằng
8cm
và một điểm
S
di động
ngoài mặt phẳng
P
sao cho tam giác
MAB
luôn có diện tích bằng
2
16 3cm
, với
M
là trung điểm của
SC
. Gọi
S
là mặt cầu đi qua bốn đỉnh
M
,
A
,
B
,
C
. Khi thể tích
hình chóp
.S ABC
lớn nhất, tính bán kính nhỏ nhất của
S
:
A.
16 6
9
cm
. B.
4 3
3
cm
. C.
4 15
3
cm
. D.
4 39
3
cm
.
Lời giải
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 25 -
Gọi
H
là trung điểm cạnh
AB
, ta có:
CH AB
.
Ta có:
, 2 , 2
SABC MABC
d S ABC d M ABC V V
Mà
1 1 1
. , .16 3. , .16 3.
3 3 3
MABC CMAB MAB
V V S d C MAB d C MAB CH
Do đó
SABC
V
lớn nhất khi và chỉ khi
,d C MAB CH
hay
CH MAB
.
Gọi
J
,
O
lần lượt là tâm hai đường tròn ngoại tiếp hai tam giác
MAB
và tam giác
ABC
. Dựng hai trục của hai đường tròn ngoại tiếp hai tam giác
MAB
và tam giác
ABC
cắt nhau tại
I
. Khi đó
I
chính là tâm mặt cầu ngoại tiếp đi qua
4
điểm
A
,
B
,
C
,
M
và bán kính mặt cầu đi qua bốn điểm
A
,
B
,
C
,
M
là
2
2 2 2
8 3
3
R OC OI JH
Do
16 3
MAB
S
,
8AB
, 4 3d M AB
Chọn hệ trục toạ độ
Oxy
như hình vẽ, ta có
0;0H
,
4;0A
,
4;0B
,
; 4 3M a
.
Đường trung trục của đoạn thẳng
AM
đi qua điểm
4
;2 3
2
a
N
và có một vectơ
pháp tuyến
4;4 3
AM a

nên có phương trình là
4
4 4 3 2 3 0
2
a
a x y
Suy ra
2 2
32 32 4 3
0;
3
8 3 8 3
a a
J JH
.
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 26 -
Do đó
2 2
min
8 3 4 3 4 15
3 3 3
R
.
Câu 21. Cho hình chóp
.S ABCD
có đáy
ABCD
đáy là hình vuông cạnh
a
,
3SA a
. Và
SA
vuông góc với đáy.
M
và
N
là hai điểm thay đổi lần lượt thuộc hai cạnh
BC
và
CD
sao cho
0
45MAN
. Tính tỉ số giữa giá trị lớn nhất và giá trị nhỏ nhất của thể tích khối
chóp
.S AMN
A.
2 2 2
. B.
1 2
6
. C.
2 2 1
. D.
1 2
2
.
Lời giải
Ta có
.
1 3
. .
3 3
S AMN AMN AMN
a
V SA S S
Do đó thể tích của khối chóp
.S AMN
phụ thuộc vào diện tích tam giác
AMN
Đặt
, ; , [0; ]BM x DN y x y a
.
CMN
vuông tại
C
nên
2 2 2
MN CM CN
hay
2 2 2
( ) ( )MN a x a y
Áp dụng định lý hàm số cosin cho
AMN
ta có:
2 2 2
2 . cosMN AM AN AM AM MAN
2 2 2 2 2 2 2
2 2( )( )a x y a x a y
Suy ra
2 2 2 2 2 2 2 2 2
( ) ( ) 2 2( )( )a x a y a x y a x a y
2
2 2 2 2
( ) ( )
a ax
ax ay a xy ax ay a xy y
a x
2 2
2
1
( ) .
2 2
AMN ABCD ABM ADN CMN
a a x
S S S S S a xy
x a
Xét hàm số
2 2
( )
x a
f x
x a
trên đoạn
[0; ]a
.
Ta có
2 2
' '
2
2
( ) ; ( ) 0 ( 2 1)
( )
x ax a
f x f x x a
x a
.
Ta lại có
(0) ( ) ; (( 2 1) ) 2( 2 1)f f a a f a a
Suy ra
2
2
[0; ]
[0; ]
max ( ) ; min ( ) 2( 2 1) ( 2 1)
2
AMN
a
a
a
f x a f x a a S
.
Vậy tỉ số giữa giá trị lớn nhất và giá trị nhỏ nhất của thể tích khối chóp
.S AMN
là
1 2
2
.
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 27 -
Câu 22. Cho hình hộp chữ nhật
.ABCD A B C D
có tổng diện tích tất cả các mặt là
36
, độ dài
đường chéo
AC
bằng
6
. Hỏi thể tích của khối hộp chữ nhật lớn nhất là bao nhiêu?
A.
8 2
. B.
6 6
. C.
24 3
. D.
16 2
.
Lời giải
Gọi độ dài các cạnh của khối hộp chữ nhật là
, , AAAB a AD b c
.
Vì tổng diện tích tất cả các mặt là
36
nên
2 2 2 36ab bc ca
hay
18 1ab bc ca
.
Lại có: độ dài đường chéo
AC
bằng
6
nên
2 2 2 2 2 2
6 36 2a b c a b c
.
Từ và suy ra:
2
2 2 2
18
18 18
18
36
72
6 2 6 2
ab bc ca
ab bc ca bc ab ca
ab bc ca
a b c
a b c
a b c b c a
Vì:
2
4b c bc
nên
2
2
6 2 4 18 6 2 4 2 0 0 4 2
a a a a a a
Thể tích khối hộp chữ nhật là:
2 3
18 18 6 2 18 6 2V abc a a b c a a a a a a
với
0 4 2a
Xét hàm số:
3 2
6 2 18f t t t t
, với
0 4 2a
.
2
3 12 2 18f t t t
,
3 2
0
2
t
f t
t
Bảng biến thiên:
Vậy
2 8 2
MaxV f
.
Câu 23. Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
a
và đường cao
2SA a
.
MNPQ
là thiết diện song song với đáy,
M SA
và
AM x
. Xét hình trụ có đáy là đường tròn
ngoại tiếp tứ giác
MNPQ
và đường sinh
MA
. Giá trị của
x
để thể tích khối trụ lớn
nhất là
A.
3
a
x
. B.
2
3
a
x
. C.
2
a
x
. D.
3
4
a
x
.
Lời giải
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 28 -
Ta có:
MNPQ
là thiết diện song song với đáy
MNPQ
là hình vuông.
Vì
//MN AB
2
.
2 2
a a x
MN SM AB SM x
MN a
AB SA SA a
.
Gọi
R
là bán kính hình trụ, ta có:
2
.
2 2
x
R a
Thể tích hình trụ
2
3 2 2
2
2
. . . . .
2 2 8 2 2
x x ax a x
V R x a x
Xét
3 2 2
8 2 2
x ax a x
f x
2 2
3
8 2
x a
f x ax
2
0
2
3
x a
f x
x a
0; 2x a
Bảng xét dấu
Vậy để thể tích khối trụ lớn nhất thì
2
3
a
x
Câu 24. Cho tứ diện
ABCD
có tam giác
ABC
đều cạnh
2a
và tam giác
ABD
vuông tại
D
,
2
a
AD
. Khoảng cách lớn nhất từ
B
đến mặt phẳng
ACD
là?
A.
2 2
2
a
. B.
3a
. C.
3
3
a
. D.
2 3a
.
Lời giải
Q'
P'
N'
Q
N
P
S
D
A
C
B
M
-
+
f(x)
f'(x)
x
0
0
2a
2a
3
0
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 29 -
Giả sử
E
là hình chiếu của
B
lên mặt phẳng
ACD
. Khi đó
,d B ACD BE
.
Gọi
H
là trung điểm của
AC
. Suy ra
BH AC
Vì
BE ACD BE EH
. Do đó
BE BH
mà
3BH a
. Suy ra
BE
lớn nhất bằng
3a
. Dấu
" "
xảy ra khi và chỉ khi
E H
.
Khi đó:
2
2 2 2
2
2 2 2 2 2 2 2
15 15 3
2 3
2 4 4 4
a a a a
BD AB AD a DH BD BH a
2
2
a
DH
Khi đó điểm
D
hoàn toàn được xác định như sau:
+) Dựng
ABC
đều cạnh
2a
. Lấy
H
là trung điểm của
AC
.
+) Dựng mặt phẳng
Q
đi qua
H
và
Q BH
, do
AC BH
tại
H
nên
AC Q
.
+) Trong mặt phẳng
Q
:
D
là giao của đường tròn đường kính
AH
và đường tròn
tâm
A
bán kính
2
a
.
+) Khi đó
AD DH
AD BD
AD BH
và
2
a
AD
.
Do đó, tồn tại điểm
D
thỏa mãn yêu cầu bài toán để
3BE a
. Vậy
,d B ACD
lớn
nhất là
3a
.
Câu 25. Cho khối chóp tứ giác đều
.S ABCD
mà khoảng cách từ
A
đến mặt phẳng
SCD
bằng
2a
. Gọi
là góc giữa mặt bên của hình chóp với đáy của hình chóp đó. Với giá
trị nào của
thì thể tích của khối chóp
.S ABCD
đạt giá trị nhỏ nhất?
A.
2
arcsin
3
. B.
0
45
. C.
2
arccos
3
. D.
0
60
.
Lời giải
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 30 -
Gọi
O
là chân đường cao của khối chóp tứ giác đều
.
S ABCD
. Khi đó ta có:
SO ABCD
.
Thể tích khối chóp
.
S ABCD
là:
1
. .
3
ABCD
V SO S
.
Gọi
M
là trung điểm của
CD
, ta có:
, ,
OM CD
SCD ABCD OM SM SMO
SM CD
Từ đó suy ra:
CD SOM
.
Từ
O
kẻ
OH SM
tại
H
.
Mà
OH CD
.
Do vậy:
OH SCD
nên
1
, ,
2
d O SCD OH d A SCD a
.
Gọi
, .tan . tan
2 2
x x
AD x OM SO OM
.
Xét tam giác
OSM
vuông tại
O
có
OH
là đường cao. Khi đó ta có:
2 2 2 2 2 2 2
1 1 1 1 4 4
.tanOH OM SO a x x
2
2 2 2 2
2 2 2
2 2 2 2 2 2
2
1 4.tan 4
.tan .4 1 tan
.tan
1 2
.tan .4. .sin .4
cos sin
x a
a x
a
x a x a x
Như vậy:
.tan .tan
2 sin cos
x a a
SO
;
2
2
2
4
sin
ABCD
a
S x
.
Vậy
2 3
2
2
1 1 4 4 1
. . . . .
3 3 cos sin 3
cos 1 cos
ABCD
a a a
V SO S
.
Thể tích đạt giá trị nhỏ nhất khi
2
1
cos 1 cos
đạt giá trị nhỏ nhất hay
2
cos 1 cosy
đạt giá trị lớn nhất.
Xét hàm số
2
cos 1 cosy
,
0 0
0 ;90
.
Đặt
cos , 0;1
t t
. Khi đó:
3
, 0;1
y t t t
.
α
H
M
O
D
C
B
A
S
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 31 -
Ta có:
2 2
1
' 1 3 ; ' 0 1 3 0 ( 0;1 )
3
y t y t t do t
.
Bảng biến thiên:
Dựa vào bảng biến thiên ta thấy
max
y
khi
1 1 2 2
cos sin arcsin
3
3 3 3
t
.
Câu 26. Cho hình chóp
SABCD
, có đáy
ABCD
là hình thoi cạnh
a
,
SA SB SC a
.Đặt
0 3
x SD x a
Tìm
x
theo a để tích
.SDAC
đạt giá trị lớn nhất.
A.
3
2
a
x
. B.
3
3
a
x
. C.
6
2
a
x
. D. Đáp án khác.
Lời giải
Gọi O là tâm hình thoi
ABCD
ta có
OB OC
Theo đề bài
SA SC
nên
SAC
cân tại S do đó
SO OC
Ta có
SOC BOC
do
OC
chung,
SC BC a
,
90
o
SOC BOC
nên
SO OB
Mà
OB OC
nên
OB OC SO
do đó
SBD
vuông tại S
Ta có
2 2 2 2
2 2 2
BD SB SD a x
OB
;
2 2
2 2 2 2 2
20 2 2 3
4
a x
AC C BC OB a a x
Suy ra
2 2
.SD 3AC a x x
Áp dụng bất đẳng thức Cô- si ta có
2 2 2 2
2 2
3 3
3
2 2
a x x a
a x x
Dấu
" "
xãy ra khi
2 2 2 2 2
6
3 3
2
a
a x x a x x x
D
A
B
C
S
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 32 -
Vậy
6
2
a
x
thì tích
.SDAC
đạt giá trị lớn nhất suy ra chọn C
Câu 27. Cho tứ diện
. DS ABC
và
M
là một điểm di động, nằm bên trong tam giác
ABC
.
Qua
M
kẻ các đường thẳng song song với
, ,SA SB SC
cắt các mặt phẳng tương ứng
,SBC
,SAC
SAB
lần lượt tại
', ', 'A B C
. Khi đó giá trị lớn nhất của biểu thức
' ' ' ' ' '
. .
MA MB MC MA MB MC
T
SA SB SC SA SB SC
là
A.
9
8
. B.
28
27
. C.
62
27
. D.
13
8
Lời giải
Do
'/ /MA SA
nên bốn điểm này cùng nằm trong một mặt phẳng. Giả sử
',E BC MA SA
. Khi đó
, ,A E M
thẳng hàng và ta có
'
A
MBC
ABC
S
MA EM
SA E S
.
Tương tự ta có:
' '
,
MAC MAB
ABC ABC
S
SMB MC
SB S SC S
.
Khi đó
' ' '
1
MBC MAC ABCMAB
ABC ABC ABC ABC
S S S
SMA MB MC
P
SA SB SC S S S S
.
Mặt khác, áp dụng bất đẳng thức Cauchy cho các số
' ' '
, ,
MA MB MC
SA SB SC
ta được:
3
3
3
' ' ' ' ' '
3 . .
' ' '
3 . .
' ' ' 1 1
. .
3 27
MA MB MC MA MB MC
SA SB SC SA SB SC
MA MB MC
P
SA SB SC
MA MB MC
SA SB SC
.
Suy ra
' ' ' ' ' ' 1 28
. . 1
27 27
MA MB MC MA MB MC
T T
SA SB SC SA SB SC
.
Vậy giá trị lớn nhất của
28
27
T
. Dấu “=” xảy ra khi
' ' 'MA MB MC
SA SB SC
.
Câu 28. Trong không gian với hệ trục tọa độ
.O xyz
, cho điểm
; ;A a b c
với
; ;a b c
là các số
thực dương thỏa mãn
2 2 2
5 9 2a b c ab bc ca
và
3
2 2
1a
Q
b c
a b c
có
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 33 -
giá trị lớn nhất. Gọi
, ,M N P
lần lượt là hình chiếu vuông góc của
A
lên các tia
; ;Ox Oy Oz
. Phương trình mặt phẳng
MNP
là
A.
4 4 12 0x y z
. B.
3 12 12 1 0x y z
.
C.
4 4 0x y z
. D.
3 12 12 1 0x y z
.
Lời giải
Đặt
t b c
0t
2
2 2
2
t
b c
;
2
4
t
bc
.
2 2 2
5 9 2a b c ab bc ca
2
2
5 5 9 28 a b c a b c bc
2 2 2
5 5 9 7 a t at t
5 2 0 a t a t
2 a t
.
Vậy
3
4 1
27
Q f t
t t
với
0t
.
Ta có
2 4
4 1
0
9
f t
t t
1
6
t
.
Ta có bảng biến thiên
Vậy
max
16Q
1
3
a
;
1
12
b c
.
Suy ra tọa độ điểm
1 1 1
; ;
3 12 12
A
; tọa độ các điểm
1
;0;0
3
M
;
1
0; ;0
12
N
;
1
0;0;
12
P
.
Phương trình mặt phẳng
MNP
1
1 1 1
3 12 12
x y z
3 12 12 1 0 x y z
.
Câu 29. Trong mặt phẳng
cho đường tròn
T
đường kính
2AB R
. Gọi
C
là một diểm
di động trên
T
. Trên đường thẳng
d
đi qua
A
và vuông góc với mặt phẳng
lấy
điểm
S
sao cho
SA R
. Hạ
AH SB
tại
H
, AK SC
tại
K
. Tìm giá trị lớn nhất
max
V
của thể tích tứ diện
SAHK
.
A.
3
max
5
75
R
V
. B.
3
max
5
25
R
V
. C.
3
max
3
27
R
V
. D.
3
max
3
9
R
V
.
.Lời giải
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 34 -
Ta có
,
BC AC
BC SA BC SAC
AC SA SAB
BC AK
.
Lại có
,
AK SB
AK BC AK SBC AK SB
SB BC SBC
1
.
Ta có
SB AH
2
.
Từ
1
,
2
suy ra
SB AHK
tại
H
nên suy ra
SH
đường cao của khối chóp
.
S AHK
.
Ta có:
.
1
.
3
SAHK S AHK AHK
V V SH S
.
Do
, ,S A B
cố định nên
SH
không đổi. Do đó thể tích của khối chóp
.
S AHK
đạt giá
trị lớn nhất khi và chỉ khi
AHK
S
đạt giá trị lớn nhất.
Ta có
BC SAC
BC AK
mà
AK SC
,
AK SBC KH SBC AK HK
.
Gọi
E
là trung điểm của
AH
,
F
là hình chiếu vuông góc của
K
xuống
AH
.
Ta có:
1
. .
2
AHK
S AH KF
.
Mặt khác do độ dài đoạn
AH
không đổi nên
AHK
S
đạt gái trị lớn nhất khi và chỉ khi
KF
là lớn nhất.
Ta có độ dài đoạn
KF
có giá trị lớn nhất khi và chỉ khi
F
trùng với trung điểm
E
của
AH
.
Hay
max
2
AH
KF KE
.
Xét
SAB
vuông tại
A
có:
2 2
2
5
.
5
5
SA R R
SA SH SB SH
SB
R
và
. .2 2 5
. .
5
5
SA AB R R R
AH SB SA AB AH
SB
R
.
Diện tích lớn nhất của
AHK
là
2 2
max
1
.
2 2 4 5
AH AH R
S AH
.
F
E
K
H
I
C
B
A
S
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 35 -
Vậy
2 3
max max
1 1 5 5
. . . .
3 3 5 5 75
R R R
V SH S
.
Câu 30. Cho tứ diện đều
ABCD
có cạnh bằng
1
. Hai điểm
,M N
di động trên các cạnh
,
AB AC
sao cho mặt phẳng
DMN
vuông góc mặt phẳng
ABC
. Gọi
1 2
,S S
lần lượt
là diện tích lớn nhất và nhỏ nhất của tam giác
AMN
. Tính
1
2
S
T
S
.
A.
8
9
T
. B.
9
8
T
. C.
8
7
T
. D.
9
7
T
.
Lời giải
Gọi
H
là hình chiếu của
D
trên
MN DH MN
.
DMN ABC MN
và
DMN ABC
. Do đó
DH ABC
.
Mà
ABCD
là tứ diện đều nên
H
là tâm đường tròn ngoại tiếp của tam giác đều
ABC
hay
H
là trọng tâm tam giác đều
ABC
.
Đặt
, 0 , 1
AM x AN y x y
.
Diện tích tam giác
AMN
là
0
1 1 3 3
. .sin 60 . . .
2 2 2 4
AMN
xy
S AM AN x y
.
Gọi
P
là trung điểm của
3 2 2 3 3
.
2 3 3 2 3
BC AP AH AP
.
Mà
0 0
1 1 1 3 1 1 3 1
. .sin 30 . .sin 30 . . . . . .
2 2 2 3 2 2 3 2
AMN AMH ANH
S S S AM AH AN AH x y
.
Suy ra
3 1 3 1 1 3 1
. . . . . . 3
4 2 3 2 2 3 2 3 3
xy x y
x y xy x y xy
.
Đặt
3 ,xy t x y t x y
là nghiệm của phương trình
2
3 0
a ta t
.
2
3 1 *a a t
, với
0;1
t
.
Nếu
1
, *
3
a
trở thành
1
0
9
.
Nếu
1
3
a
, thì
*
trở thành
2
**
3 1
a
t
a
2
2
0
3 2
0
2
3 1
3
a
a a
t t
a
a
.
BBT:
P
N
M
H
D
C
B
A
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 36 -
Để tồn tại hai điểm
,M N
thỏa mãn bài toán thì
**
có hai nghiệm thuộc tập
0;1
.
4 1
9 2
t
.
Vậy
1
max
2
D
t
khi
1a
hay
1
3
8
S
.
4
min
9
D
t
khi
2
3
a
hay
2
3
9
S
.
Vậy
1
2
9
8
S
S
.
Câu 31. Cho lăng trụ tam giác đều
. ' ' 'ABC A B C
với độ dài tất cả các cạnh đều bằng
a
. Xét tất
cả các đoạn thẳng song song với mặt phẳng
' 'ABB A
và có một đầu
E
nằm trên
đường chéo
'A C
của mặt bên
' 'AA C C
, còn đầu kia
F
nằm trên đường chéo
'BC
của
mặt bên
' 'BB C C
. Hãy tìm độ dài ngắn nhất của các đoạn thẳng này.
A.
2
5
a
. B.
5
a
. C.
5
a
. D.
2
5
a
.
Lời giải
Gọi
H
là trung điểm của
AC
. Chọn hệ trục tọa độ
Hxyz
như hình vẽ.
Ta có
0;0;0H
,
;0;0
2
a
A
,
;0;0
2
a
C
,
3
0; ;0
2
a
B
,
' ;0;
2
a
A a
,
3
' 0; ;
2
a
B a
' ;0;
2
a
C a
.
3
' ; ;
2 2 2
a a a
BC a u
, với
1; 3; 2u
. Phương trình tham số của đường
thẳng
'BC
đi qua điểm
'C
có vec tơ chỉ phương
1; 3; 2u
0
0
0
∞
+∞
+
1
2
4
9
0
1
2
3
1
3
t
t'
a
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 37 -
2
3
2
a
x t
y t
z a t
. Do
'F BC
nên
; 3 ; 2
2
a
F t t a t
' ;0; 'A C a a au
, với
' 1;0;1u
. Phương trình tham số của đường thẳng
'A C
đi qua điểm
C
có vec tơ chỉ phương
' 1;0;1u
'
2
0
'
a
x t
y
z t
. Do
'E A C
nên
';0; '
2
a
E t t
.
'; 3 ; 2 'EF t t t a t t
.
3
; ;0
2 2
a a
AB
,
' 0;0;AA a
,
', 'AB AA
2 2 2
3
; ;0
2 2 2
a a a
n
, với
3;1;0
n
.
suy ra vec tơ pháp tuyến của mặt phẳng
' 'ABB A
:
3;1;0n
 Do
' 'EF ABB A
nên
. 0EF n
' 2t t
suy ra
; 3 ; 4EF t t a t
Có
2 2 2
20 8EF t at a
f t
. Dễ thấy
f t
là một hàm số bậc hai nên
f t
đạt
giá trị nhỏ nhất tại
5
a
t
,
2
min
5
a
f t
.
 Vậy
min
5
a
EF
.
Câu 32. Cho hình chóp tứ giác đều
.S ABCD
mà khoảng cách từ
A
đến mặt phẳng
SBC
bằng
b
. Góc giữa mặt bên và mặt đáy của hình chóp bằng
. Tìm
để thể tích của
khối chóp
.S ABCD
nhỏ nhất.
A.
3
arccos
3
. B.
arccos 3
. C.
1
arccos
3
. D.
2
arccos
3
.
Lời giải
+ Gọi
O AC BD
và
M
là trung điểm của
BC
.
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 38 -
+ Có:
SM BC
OM BC
Góc giữa hai mặt phẳng
SBC
và
ABCD
bằng
0
2
SMO
+Trong mặt phẳng
SOM
vẽ
(1)OH SM
.
+ Ta có:
SM BC
BC SOM
OM BC
mà
OH SOM
(2)BC OH
+ Từ và suy ra
,OH SBC d O SBC OH
.
+ Ta có:
, 2 , 2
2
b
d A SBC d O SBC OH b OH
.
2
2
sin
sin 2sin sin
sin
ABCD
OH OH b b b
OM AB S
OM
tan tan tan .
2sin 2 cos
SO b b
SO OM
OM
2 3
.
2
3
1 1
.
3 3 2cos
sin
6 cos cos
S ABCD ABCD
b b b
V SO S
Thể tích của khối chóp
.S ABCD
nhỏ nhất
3
cos cos
lớn nhất.
Đặt
cos t
. Vì
0 0 1
2
t
.
+ Xét:
3
( ) 0 1f t t t t
2
3
( )
3
'( ) 1 3 0
3
3
t L
f t t
t
+ Bảng biến thiên
Vậy thể tích của khối chóp
.S ABCD
nhỏ nhất bằng
3
3
4
b
đạt được khi
3
arccos
3
.
Câu 33. Cho hình lăng trụ đều
. ' ' ' 'ABCD A B C D
có cạnh đáy bằng a. Điểm M và N lần lượt
thay đổi trên các cạnh
'BB
và
'DD
sao cho
MAC NAC
và
,BM x DN y
. Tìm
giá trị nhỏ nhất của thể tích khối tứ diện
ACMN
.
A.
3
3 2
a
. B.
3
2
a
. C.
3
2 2
a
. D.
3
2 3
a
.
Lời giải
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 39 -
Cách 1: Gọi I là trung điểm AC, đặt
' ,BB b
ta có:
' '
2
' '
1 1 1
. . .
3 3 3
1
2.
3
2 2
1 . 2 . 2
2. 2
3 2 4 4
1 . 2 . 2 1
2. .
3 4 4 6
ACMN AMNI CMNI IMN IMN IMN
MND B BIM IBDD B DN
V V V IC S IA S AC S
a S S S S
b x y a
x a y a
a ab
x a y a
a a x y
Vì
MAC NAC
nên
2 2 2
2
2 2 2 2 2 2
2 .
2 2 2
a a a
MI IN IM IN MN x y a x y xy
Do đó
3
2 2
1 1
.
6 3
3 2
ACMN
a
V a x y a xy
Vậy thể tích khối tứ diện
ACMN
đạt giá trị nhỏ nhất là
3
3 2
a
khi
x y
.
Cách 2: Gọi I là trung điểm AC.
Dễ thấy
Δ , ΔMAC NAC
lần lượt cân tại
, NM
nên
,MI AC NI AC AC MIN
.
Lại có
;AC MAC NAC MAC NAC MI NAC MI NI
Khi đó
2 2 2
2
2 2 2 2 2 2
2 .
2 2 2
a a a
MI IN MN x y a x y xy
1 1 1 1
. . . . . . . .
3 3 3 6
ACMN AMNI CMIN IMN IMN IMN
V V V AI S CI S AC S IM IN AC
2 2 2 4
2
2 2 2 2
1 2
. 2. . .
6 2 2 6 2 4
ACMN
a a a a a
V a x y xy x y
Mà
2
2
a
xy
nên
2 4 2
2
2
. 2 .
6 2 2 6
ACMN
a a a a
V x y xy x y
Do đó
3
2 2
1 1
.
6 3
3 2
ACMN
a
V a x y a xy
Vậy thể tích khối tứ diện
ACMN
đạt giá trị nhỏ nhất là
3
3 2
a
khi
x y
.
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 40 -
Câu 34. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, cạnh bên
SA b
và
vuông góc với
ABCD
. Điểm
M
thay đổi trên cạnh
CD
với
0CM x x a
.
H
là
hình chiếu vuông góc của
S
trên
BM
. Tìm giá trị lớn nhất của thể tích khối chóp
.S ABH
theo
,a b
.
A.
2
12
a b
. B.
2
24
a b
. C.
2
8
a b
. D.
2
18
a b
.
Lời giải
Ta có
2 2
1 1 1
. . . . . . . .
3 3 2 6 6 2
SABH ABH
b b AH BH
V SA S b AH BH AH BH
2
2
.
.
12 12
SABH SABH
b b a
V AB V
.
Dấu “=” xảy ra khi và chỉ khi
45 45
o o
AH BH ABH ABM M D
.
Câu 35. Cho tứ diện đều
SABC
có
D
là điểm thuộc cạnh
AB
sao cho
2BD AD
,
I
là trung
điểm của
SD
. Một đường thẳng
d
thay đổi qua
I
cắt các cạnh
SA
,
SB
lần lượt tại
M
,
N
. Biết
2AB a
. Khi
d
thay đổi, thể tích khối chóp
.S MNC
nhỏ nhất bằng
3
3
.
m a
n
m
,
với
,m n
,
, 1m n
. Tính
m n
.
A.
4m n
. B.
6m n
. C.
7m n
. D.
5m n
.
Lời giải
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 41 -
Gọi
H
là tâm đường tròn ngoại tiếp tam giác
ABC
. Vì
SABC
là tứ diện đều và
2AB a
nên suy ra
SH ABC
,
H
là trọng tâm tam giác đều
ABC
và
2 2 3 2 3
.
3 2 3
a a
AH
.
Từ đó suy ra
2
2
2 2
2 3 2 6
2
3 3
a a
SH SA AH a
.
Vậy
2
3
2 3
1 1 2 6 2 2
. . .
3 3 3 4 3
SABC ABC
a
a a
V SH S
1
.
Đặt
,
SM SN
k l
SA SB
,
0 , 1k l
.
Ta có:
.
SMN
SAB
S
SM SN
S SA SB
.
Mặt khác
2
1 2
. . . .
3 3 3 3
SMN SMI SNI
SAB SAD SBD
S S S
SM SI SN SI
S S S SA SD SB SD
Nên ta có
1 1 2 1
. . . . . 6 2
3 2 3 2 2 3 1
k
k l k l kl k l l
k
2
.
Vì
0 1
0 1
k
l
nên
0 1
2
1 3 1 0
0 1
5
2 3 1
k
k k
k
k
.
Ta có:
. . . . .
SMNC
SMNC SABC
SABC
V
SM SN SC
k l V k l V
V SA SB SC
3
.
Từ
1
,
2
,
3
ta có
3 3 2
.
2 2 2 9
. . .
2 3 1 3 27 3 1
S MNC
k a a k
V k
k k
3 3
.
2 1 2 1
. 3 1 . 3 1 2
27 3 1 27 3 1
S MNC
a a
V k k
k k
.
Áp dụng bất đẳng thức Cô-si với hai số dương, ta có:
3
3 3 3
.
2 1 4 2 2
. 2. 3 1 . 2 .
27 3 1 27 3
2
S MNC
a a a
V k
k
.
Dấu “=” xảy ra
2
1 2
3 1 3 1 1
3 1 3
k k k
k
.
Vậy
3
3
.
2
min .
3
2
S MNC
a
V
2
3
k
.
Theo đề bài, thể tích khối chóp
.
S MNC
nhỏ nhất bằng
3
3
.
m a
n
m
, với
,m n
,
, 1
m n
nên ta có
2, 3
m n
, suy ra
5
m n
.
Câu 36. Cắt một khối trụ tròn có chiều cao h bởi một mặt phẳng song song với hai mặt đáy ta
thu được hai khối tròn nhỏ. Một trong hai khối đó ngoại tiếp một lăng trụ đứng thể
tích V có đáy là tam giác có chu vi là p. Khối còn lại ngoại tiếp một khối nón có bán
kính là R . Tìm giá trị của R sao cho thể tích của khối nón là lớn nhất?
A.
3
162
p
R
V
. B.
3
162
hp
R
V
. C.
3
162
p
R
. D.
3
162
p
R
V
.
Lời giải
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 42 -
Hình lăng trụ có đáy là tam giác có độ dài 3 cạnh là a,b,c có chiều cao là x
Khi đó
4
abc
S
R
và thể tích của hình lăng trụ là
.
4
abc
V x
R
.Suy ra
.
4
abc
R x
V
Áp dụng bất đẳng thức Cauchy cho 3 số dương a,b,c ta có
3
3
. .
27.4 108.
a b c
p
R x x
V V
Mặt khác
2 6
2
2
1 1
. . . . . .
3 3
108
H
x p
V h x R h x
V
Xét hàm số
2
.f x h x x
với
0 x h
2
3 2f x x hx
Suy ra
2
2
0 3 2 0
3
h
f x x hx x
Bảng biến thiên
Từ đó
3
2 4
.
3 27
h
f x f h
Do đó
6
3
2
1 4
. . . .
3 27
108
H
p
V h
V
6
3
2
1 4
ax . . . .
3 27
108
H
p
V m h
V
khi
2
3
h
x
và
a b c
Khi đó
3 3
2
.
3 108. 162.
h p hp
R
V V
Câu 37. Người ta cần trang trí một kim tự tháp hình chóp tứ giác đều
.S ABCD
cạnh bên
bằng
200 m
,
0
15ASB
bằng đường gấp khúc dây đèn led vòng quanh kim tự tháp
AEFGHIJKLS
trong đó điểm
L
cố định và
40mLS
.
Khi đó cần dùng ít nhất bao nhiêu mét dây đèn led để trang trí?
A.
40 67 40
mét. B.
20 111 40
mét.
C.
40 31 40
mét
.
D.
40 111 40
mét.
Lời giải
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 43 -
Cắt hình chóp theo
SA
rồi trải phẳng (
H
trùng với
H
). Lấy điểm
L A
sao cho
SL SL
,
P
đối xứng với
L
qua
SA
.
Ta có:
AE EF FG GH H I IJ JK KL AH H L AH HL AH HP AP
.
Áp dụng định lí Cô-sin trong
ASP
ta được:
2 2 2 2 2 0
2. . .cos 200 40 2.200.40.cos120 49.600AP AS SP AS SP ASP
40 31AP
.
Vậy độ dài đèn led ngắn nhất là
40 31 40
Câu 38. Chohình chóp
.S ABC
có các cạnh bên bằng
1
. Mặt phẳng
thay đổi luôn đi qua
trọng tâm của hình chóp, cắt ba cạnh bên
, ,SA SB SC
lần lượt tại
, ,D E F
. Tìm giá trị
lớn nhất
max
P
của
1 1 1
. . .
P
SD SE SE SF SF SD
.
A.
4
3
. B.
16
3
. C.
4
3
. D.
3
4
.
Lời giải
Gọi
I
là trọng tâm
ABC
. Ta có:
Ta có:
3
; . ; .
SA SB SC SI
SA SB SC
SA SD SB SE SC SF
SD SE SF
.
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 44 -
Mà ta có
3 1
4 4
SG SI SA SB SC
4
SG SA SB SC
4 . .
SA SB SC
SG SD SE SF
SD SE SF
. .
4 4 4
SA SB SC
SG SD SE SF
SD SE SF
1 1 1
. .
4 4 4
SG SD SE SF
SD SE SF
Do
, , ,D E F G
đồng phẳng nên
1 1 1
1
4 4 4SD SE SF
1 1 1 1 1 1 1
1 4
4 SD SE SF SD SE SF
Ta lại có
2
1 1 1 1 1 1 1
. . . 3
P
SD SE SE SF SF SD SD SE SF
.
Dấu
" "
xảy ra khi
SD SE SF
.
Vậy
2
1 1 1 1 1 1 1 16
. . . 3 3
P
SD SE SE SF SF SD SD SE SF
Dấu
" "
xảy ra khi
3
4
SD SE SF SA
.
Vậy
16
3
Max
P
Câu 39. Cho hình lập phương
. ' ' ' 'ABCD A B C D
có cạnh bằng
a
.
G
là trung điểm của
'BD
,
mặt phẳng
P
thay đổi qua
G
cắt
', ', ' 'AD CD B D
tương ứng tại
, ,H I K
. Tìm giá trị
lớn nhất của biểu thức
1 1 1
' . ' ' . ' ' . '
T
D H D I D I D K D K D H
.
A.
2
8
3a
. B.
2
16
3
a
. C.
2
8
3
a
. D.
2
16
3a
.
Lời giải
Bổ đề: Cho tứ diện
SABC
có
SA SB SC a
. Một mặt phẳng
( )P
thay đổi qua trọng
tâm
G
của tứ diện lần lượt cắt
, ,SA SB SC
tại
, ,M N P
.
1 1 1 4
:CMR
SM SN SP a
.
Chứng minh:
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 45 -
Gọi
G
là trọng tâm
ABC
. Theo tính chất trọng tâm của tứ diện ta có
, ,S G G
thẳng
hàng và
3
4
SG
SG
.
Thêm nữa
1
3
SABG SBCG SG CA SABC
V V V V
.
Ta có:
2 2
3
3 . .
. . 1
4 4
SMNG SMNG SMNG
SABG SABC SABC
V V V
SM SN SG SM SN SM SN
V SA SB SG V a V a
.
Lập luận tương tự thu được
2
.
2
4
SNPG
SABC
V
SN SP
V a
và
2
.
3
4
SGPM
SG CA
V
SP SM
V a
.
Cộng theo vế các đẳng thức
1
,
2
,
3
ta được
2
. . .
4
SMNP
SABC
V
SM SN SN SP SP SM
V a
2
. . .
. .
4
SM SN SP SM SN SN SP SP SM
SA SB SC a
2 3
4 . . . . . . .a SM SN SP SM SN SN SP SP SM a
1 1 1 4
SM SN SP a
. .
Xét hình lập phương
. ' ' ' 'ABCD A B C D
. Ta có hình chiếu của
'D B
lên mặt phẳng
ABCD
là
DB
, trên
ABCD
ta có
DB AC
nên
'D B AC
.
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 46 -
Tương tự, ta có
' 'D B B C
. Từ đó suy ra
' 'D B B AC
.
Xét tứ diện
' 'D AB C
là tứ diện đều cạnh bằng
2a
. Vì
' 'D B B AC
nên
'D B
là
đường cao của tứ diện.
Gọi
'G
là giao điểm của
'D B
với
'B AC
, ta chứng minh được
3
' ' '
4
D G D G
Vì tứ diện
' 'D AB C
là tứ diện đều nên
G
là trọng tâm của tam giác
B AC
, suy ra
G
là trọng tâm của tứ diện
D AB C
.
Ta có:
2
1 1 1 1 1 1 1
1
' . ' ' . ' ' . ' 3 ' ' '
T
D H D I D I D K D K D H D H D I D K
ÁP DỤNG Bổ đề trên: Xét tứ diện
' 'D AB C
là tứ diện đều cạnh bằng
2a
, ta có
1 1 1 4
2
' ' '
2
D H D I D K
a
Từ
1 , 2
ta được
2
2
2
1 1 1 1 1 1 1 1 4 8
.
' . ' ' . ' ' . ' 3 ' ' ' 3 3
2
T
D H D I D I D K D K D H D H D I D K a
a
.
Câu 40. Cho hình hộp chữ nhật
. ' ' ' 'ABCD A B C D
có
, ' , D 'AC a AD b C c
. Tìm thể tích lớn
nhất của hình chữ nhật đã cho
khi
, ,a b c
thay đổi, còn chu vi tam giác
D 'AC
không
đổi.
Lời giải
Đặt
D , D , 'A d C r DD h
Ta có:
2 2 2
2 2 2
2 2 2
2 0
2 0
2 0
a d r dr
b d h dh
c h r hr
2 2 2 2 2 2
8 2 2 .
2 2
abc
a b c d h r abc dhr V
Mà
3
3
3 27
a b c k
abc
nên
3
max
2
.
108
k
V
Dấu
" "
xảy ra khi và chỉ khi
.
3 2
3
d r h
k
d r h
k
a b c
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 47 -
Câu 41. Cho tứ diện
, , ,ABCD AB x CD y
các cạnh còn lại của tứ diện bằng
2,a
,x y
thay
đổi sao cho
2 .x y a
Khi
ABCD
V
đạt giá trị nhỏ nhất, tính cosin của góc giữa
ABC
và
.ABD
Lời giải
-Gọi
,M N
lần lượt là trung điểm
, .AB CD
,MN AB CD
MCD AB
-Gọi
,ABC ABD
,MD MC
-Coi
1 2a x y
2 2
8
1 1 1
. 4 2 .
3 6 4 12
ABCD MCD
x
V
y
AB S xy xy xy
-Đặt
2
( )
0 1.
4
x y
t xy t
Xét hàm số
1
4 2 ,
12
t tf t
với
0 1.t
Ta có:
1 1 4 3
4 2 0, 0; 1 .
12 12
4 2 4 2
t
t
t
f t t
t t
6
.
12
1Maxf t f
6
.
12
ABCD
MaxV
2 2
2
7
" " 1 .
2
2 5 5
cos cos .
2 7 7
x y MC MD
MC CD
DMC
MC
Câu 42. Cho hình chóp
SABCD
có đáy là
ABCD
là hình vuông cạnh
a
, cạnh
SA a
và vuông
góc với mp
( ).ABCD
M
là điểm di động trên đoạn
BC
và
0BM x x a
,
K
là
hình chiếu của
S
trên
.DM
a) Tính độ dài đoạn
SK
theo
a
và
x
.
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 48 -
b) Tìm min của đoạn
.SK
Lời giải
a) Do
DM SA
và
DM SK
nên
.DM AK
Ta có:
sin cosADK MDC
AK DC
AD DM
2
2
AK a
a
a a x
2
2
2
a
AK
a a x
Suy ra
4 2
2 2 2
2 2
2 2
1
a a
SK SA AK a a
a a x a a x
b) Do
2
2
2
1
a
SK a
a a x
nên SK nhỏ nhất khi
2
a x
lớn nhất hay
0x
.
Vậy
6
2
a
minSK
khi
0.x
Câu 43. Cho hình chóp
.S ABCD
có tứ giác
ABCD
là hình bình hành tâm
O
. Điểm
C
di động
trên cạnh
SC
(
C
khác điểm
S
và
C
). Mặt phẳng
R
chứa đường thẳng
AC
và
song song với
BD
. Mặt phẳng
R
cắt đường thẳng
SB
,
SD
lần lượt tại
,B D
.
1/ Gọi
F
là giao điểm của
AD
với
B C
. Chứng minh rằng
F
luôn di động trên một
đường thẳng cố định khi
C
di động trên
SC
.
2/ Xác định vị trí của điểm
C
sao cho tổng
5
3 .
2
SC BB SD
CC SB DD
đạt giá trị nhỏ nhất.
Lời giải
1/ Qua
S
kẻ đường thẳng
//d AD SAD SBC d
.
Xét các mặt phẳng
, ,SAD SBC AB C D
có:
a-x
x
D
A
C
B
S
M
K
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 49 -
SAD SBC d
SAD AB C D AD
SBC AB C D B C
AD B C F
nên
, ,d AD B C
đồng quy tại
F
.
Khi đó
J d
cố định.
2/ Ta có:
SA SC SB SD
SA SC SB SD
1 2
SC SB
SC SB
.
Lại có:
i)
1 1 1 1 1 1
1 1 2 2 2
2 1
SC
CC SC SC SC SC SB
SB
CC
SC SC SC SC SB
SB
1
ii)
3 3 3 1
BB SB SB SB
SB SB SB
2
iii)
5 5 1 5 5 5
2
2 2
2 1 2 1
SD
DD
SD SD SD SB
DD
SD
SD SB
SD
3
Từ , , ta có:
5
3 .
2
SC BB SD
CC SB DD
1 5
3 1
2 1 2 1
SB
SB SB
SB
SB SB
3
3 1 6
1
SB
SB
SB
SB
Dấu bằng xảy ra
1 1 2 3
SB SB SC
SB SB SC
.
Vậy tổng nhỏ nhất khi
C
thuộc đoạn
SC
thỏa
3
SC
SC
.
Câu 44. Trong mặt phẳng
cho hình chữ nhật
ABCD
có
; 2AB a BC a
. Các điểm
,M N
lần
lượt di chuyển trên các đường thẳng
,m n
vuông góc với mặt phẳng
tại
,A B
sao
cho
DM CN
. Tìm giá trị nhỏ nhất của khối tứ diện
CDMN
.
Lời giải
Đặt hệ trục tọa độ như hình vẽ, coi
1a
.
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 50 -
Do đó
0;0;0 , B 1; 0;0 , C 1; 2;0 , 0;2;0A D
.
Đặt
, 0;0; x , 1; 0;AM x BN y M N y
suy ra
0; 2;x , 0; 2; yDM CN
.
Mà
DM CN
nên
. 0DM CN
.
4
0.0 2 . 2 0 4xy xy y
x
.
1;0;0 ; 1; 2;x ; 0; 2;CD CM CN y
.
, 0; ; 2 , . 2 2CD CM x CD CM CN x y

.
1 1
, . 2 2
6 6
CDMN
V CD CM CN x y
.
1 4 1 4 4
.2 .
3 3 3
CDMN
V x x
x x
.
Vậy
3
4
min
3
CDMN
a
V
.
Câu 45. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang cân,
AB
song song với
CD
,
2AB CD
, các cạnh bên có độ dài bằng
1
. Gọi
O AC BD
,
I
là trung điểm của
SO
.
Mặt phẳng
thay đổi đi qua
I
và cắt các cạnh
, , ,SA SB SC SD
lần lượt tại
, , ,M N P Q
. Tìm giá trị nhỏ nhất của biểu thức
2 2 2 2
1 1 1 1
T
SM SN SP SQ
.
Lời giải
Nhận xét:
I
thuộc đoạn
MP
thì với điểm
S
bất kỳ, ta có
mSI nSM pSP m n p
.
Đặt
;
SA SC
x y
SM SP
.
1 1 1 2 1 2 2
2 2 2 3 2 3 3
SI SO SA AO SA AC SA SC SA
1 1
6 3
SA SC
6 3
x y
SM SP
.
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 51 -
Vì
I
thuộc đoạn
MP
nên
1 2
1 2 6 2 6 6
6 3
x y SA SC
x y
SM SP SM SP
.
Chứng minh tương tự
1 2
6
SN SQ
.
Ta có
2
2
1 1 2 2 1 1 2 2
12 12
SM SN SP SQ SM SN SP SQ
2 2 2 2
2 2 2 2
1 1 1 1 144 72
1 1 2 2 10
10 5
T T
SM SN SP SQ
.
Vậy
min
72
5
T
, đạt được khi
1 1 1 1 1 1
3 ;
2 2 3 6
SM SN SP SQ
SM SN SP SQ
.
Câu 46. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành. Gọi
E
là trung điểm của
SC
. Mặt phẳng
thay đổi nhưng luôn chứa
AE
cắt
SB
,
SD
lần lượt tại
M
,
N
. Xác
định vị trí của
M
,
N
trên các cạnh
SB
,
SD
sao cho
SM SN
SB SD
đạt giá trị lớn nhất.
Lời giải
Trong
ABCD
gọi
O AC BD
, trong
mp
gọi
I AE MN
. Khi đó ta có
+
I AE SAC
I SO SAC SBD
I MN SBD
suy ra
I
là trọng tâm tam giác
SAC
.
+
. .
. .
1 1
2 2 4
S AME S AME
S ABCD S ABC
V V
SM SE SM
V V SB SC SB
+
. .
. .
1 1
2 2 4
S ANE S ANE
S ABCD S ACD
V V
SN SE SN
V V SD SC SD
Suy ra
. . .
. .
1
1
4
S AMEN S ANE S AME
S ABCD S ABCD
V V V
SN SM
V V SD SB
+
. .
. .
1
2 2
S AMN S AMN
S ABCD S ABD
V V
SM SN
V V SB SD
+
. .
. .
1 1
2 2 4
S MEN S MEN
S ABCD S BCD
V V
SM SN SE SM SN
V V SB SD SC SB SD
Suy ra
. . .
. .
3
2
4
S AMEN S AMN S MEN
S ABCD S ABCD
V V V
SN SM
V V SD SB
I
E
O
A
B
D
C
S
N
M
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 52 -
Từ
1
và
2
ta có
1 3
3
4 4
SN SM SN SM SN SM SN SM
SD SB SD SB SD SB SD SB
Đặt
0 , 1
SN
x
SD
x y
SM
y
SB
vậy ta có
3x y xy
suy ra
1 , 0
1
1
3 1 2
x y
x
y x
x
Ta có
1 1
3 1 3 3 3 1
SM SN x
x y x x f x
SB SD x x
Xét
1 1 1
, ;1
3 3 3 1 3
f x x x
x
1
;1
3
2
3 1 1
1 2
' 1 0
3 1 1
3
3 1
x
x
f x x
x
x

Bảng biến thiên
Vậy ta có
1
;1
2
3
max
2
SM SN
Max f x
SB SD
đạt được khi
1
1
2
1
1
2
x y
x y
Khi đó
N D
,
M
là trung điểm
SB
hoặc
M B
,
N
là trung điểm
SD
Câu 47. Cho tứ diện
OABC
có các cạnh
, ,OA OB OC
đôi một vuông góc. Gọi
M
là điểm thuộc
miền trong của tam giác
ABC
. Tìm giá trị nhỏ nhất của biểu thức
2 2 2
2 2 2
MA MB MC
T
OA OB OC
Lời giải
Gọi
N AM BC
, kẻ
1
MM / /
OA thì ta có
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc Lôùp Toaùn Thaày Nghieäp
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 53 -
1
1
OA (OBC)
MM (OBC)
MM / /OA
kẻ
1 1
MA OA,A OA
. Khi đó
2 2 2 2 2 2
1 1 1 1
AM AA MA AA MO OA
2
1 1 1 1
OM AA OA AA OA
2
1
OM OA OA 2OA
2 2
1
OM OA 2OA OA
Suy ra
2 2
1
2 2
AM OM 2OA
1 (1)
OA OA OA
.
Tương tự gọi
1 1
B ,C
là các điểm tương tự như
1
A
thì ta có
2 2
1
2 2
MB OM 2OB
1
OB OB OB
2 2
1
2 2
MC OM 2OC
1 (3)
OC OC OC
Từ
(1),(2),(3)
ta có
2
1 1 1
2 2 2
1 1 1 OA OB OC
T OM 2 3
OA OB OC OA OB OC
Gọi
H
là trực tâm của tam giác
ABC
thì ta dã biết kết quả quen thuộc
2 2 2 2
1 1 1 1
OA OB OC OH
nên
2
1 1 1
2
OM OA OB OC
T 2 3
OH OA OB OC
Mặt khác
MhC
1
ABC
S
OA NM
OA NA S
Tương tự
MAC
1 1 MAB
ABC
S
OB OC S
,
OB S OC S
ABC
nên
1 1 1
OA OB OC
1
OA OB OC
Do đó
2
2
OM
T 1 2
OH
do
OM OH
.
Vậy
min T 2
khi
M H
.
----------HẾT----------
| 1/53
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp
MỘT SỐ BÀI TOÁN CỰC TRỊ HÌNH HỌC TRONG KHÔNG GIAN Câu 1.
Một khối gỗ hình hộp chữ nhật có kích thước thoả mãn: Tổng của chiều dài và chiều
rộng bằng 12 cm ; tổng của chiều rộng và chiều cao là 24 cm . Hỏi thể tích lớn nhất mà
khối hộp có thể đạt được là bao nhiêu? A. 3 288cm . B. 3 384 3 cm . C. 3 1782cm . D. 3 864cm . Câu 2.
Trong không gian cho bốn mặt cầu có bán kính lần lượt là 2;3;3; 2 đôi một tiếp xúc
nhau. Mặt cầu nhỏ tiếp xúc ngoài với cả bốn mặt cầu nói trên có bán kính bằng 7 3 6 5 A. . B. . C. . D. . 15 7 11 9 Câu 3.
Cho hình chóp S.ABC có SA   ABC  , SB a 2 , hai mặt phẳng SAB và SBC
vuông góc với nhau. Góc giữa SC và SAB bằng 0
45 , góc giữa SB và mặt đáy bằng   0
0    90  . Xác định  để thể tích khối chóp S.ABC đạt giá trị lớn nhất. A. 0   60 . B. 0   30 . C. 0   45 . D. 0   70 . Câu 4.
Cho hình chóp S.ABC có SA   ABC  , SB a 2 , hai mặt phẳng SAB và SBC
vuông góc với nhau. Góc giữa SC và SAB bằng 45o , góc giữa SB và mặt đáy bằng
,0o   90o  
 . Xác định  để thể tích khối chóp S.ABC lớn nhất. A. 60o   . B. 30o   . C. 45o   . D. 70o   . Câu 5.
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân đáy AB , nội tiếp đường
tròn tâm O , bán kính R . Biết rằng AC BD tại I , đồng thời I là hình chiếu của S
lên ABCD và S
AC vuông tại S . Thể tích lớn nhất của khối chóp S.ABCD theo R là 2 1 3 A. 3 R . B. 3 R . C. 3 R . D. 3 R 3 2 4 Câu 6. Trong không gian
Oxyz cho mặt phẳng   :x y  4  0 , mặt cầu  2 2
S  :  x  2 2 2
1  y z  1 và mặt cầu S : x  4  y  5  z  4. Điểm A thuộc mặt 2      2 1
phẳng  , điểm M thuộc mặt cầu S , điểm N thuộc mặt cầu S . Khi dó 2  1 
AM AN nhỏ nhất bằng A. 5. B. 8 . C. 11. D. 3 2 . Câu 7.
Cho lăng trụ đứng ABC.A BC   có  0
AB  6; BC  12; ABC  60 . Thể tích khối chóp C .ABB A
  bằng 216. Gọi M là điểm nằm trong tam giác A BC
  sao cho tổng diện tích
các mặt bên của hình chóp M.ABC đạt giá trị nhỏ nhất. Tính cosin góc giữa 2 đường thẳng B M  , AC ? 2 2 2 1 A. . B. . C. . D. . 2 3 4 2 Câu 8. Trong không gian Oxyz cho hai mặt cầu
S  :  x  42 2 2
y z  16 , 1
S  :  x  42 2 2
y z  36 và điểm A4;0;0 .Đường thẳng  di động và luôn tiếp xúc 2
với S đồng thời cắt  S tại hai điểm B,C . Tam giác ABC có thể có diện tích lớn 2  1  nhất là A. 28 5 . B. 72 . C. 48 . D. 24 5 .
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 1 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp Câu 9.
Cho hình chóp S.ABCD , có đáy là hình bình hành, M là trung điểm của cạnh SC .
Mặt phẳng (P) chứa AM lần lượt cắt các cạnh SB, SD tại ' '
B , D . Giá trị lớn nhất của ' ' SB SD a u   * là , ( ,
a b N ) tối giản. Tích . a b bằng: SB SD b A. 3 . B. 12 . C. 15 . D. 6 .
Câu 10. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Gọi I là điểm 1
thuộc đoạn SO sao cho SI SO . Mặt phẳng   thay đổi đi qua B và I .   cắt các 3
cạnh SA , SC , SD lần lượt tại M , N , P . Gọi m , n lần lượt là giá trị lớn nhất và giá trị V
nhỏ nhất của S.MBNP . Giá trị của m n là VS.ABCD 4 6 14 1 A. . B. . C. . D. . 15 75 75 5
Câu 11. Cho hình chóp SABC có đáy là tam giác đều cạnh bằng 6 biết các mặt bên của
hình chóp có diện tích bằng nhau và một trong các cạnh bên bằng 3 2 . Tính thể tích
nhỏ nhất của khối chóp SABC . A. 3 . B. 2 2 . C. 2 3 . D. 4 .
Câu 12. Trong không gian với hệ tọa độ Oxyz , cho điểm A4;0;0, B 0;4;0, S 0;0;c và x 1 y 1 z 1 đường thẳng d :   . Gọi A ,
B lần lượt là hình chiếu vuông góc của 1 1 2 O lên S ,
A SB . Khi góc giữa đường thẳng d và mặt phẳng OAB lớn nhất,mệnh đề nào sau đây đúng?  17 15  A. c  8  ; 6   . B. c  9  ; 8   .
C. c 0;3 . D. c   ;    .  2 2 
Câu 13. Cho hình lập phương ABC .
D A ' B 'C ' D ' . Điểm M nằm trên cạnh AA ' sao cho góc  a
BMD' lớn nhất, đặt góc lớn nhất đó là  . Biết cos  ; , a b ;   ,
a b 1;b  0 . Mệnh b
đề nào sau đây đúng?
A. a b 1.
B. a b  2 .
C. a b  3 .
D. a b  4 .
Câu 14. Cho khối chóp S.ABC có SA vuông góc với đáy, tam giác ABC vuông tại B . Biết rằng 5
thể tích của khối chóp là
và giá trị nhỏ nhất diện tích toàn phần chóp S.ABC là 24
p 5  q trong đó p, q   . Tính giá trị biểu thức: 2 2
p q  ? 37 37 25 A. 2 2 p q  . B. 2 2 p q  . C. 2 2 p q  . D. 2 2
p q  16 . 36 9 4
Câu 15. Cho hình chóp SABCD có đáy là hình bình hành tâm O . Gọi I là điểm thuộc đoạn 1
SO sao cho SI SO . Mặt phẳng   thay đổi đi qua B và I .   cắt các cạnh 3 V ,
SA SC, SD lần lượt tại M , N , P . Gọi ,
m n lần lượt là GTLN, GTNN của S.BMPN . Tính VS.ABCD m ? n 7 14 8 A. 2 . B. . C. . D. . 5 75 5
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 2 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp
Câu 16. Trong không gian cho bốn mặt cầu có bán kính lần lượt là 2;3;3;2 đôi một tiếp xúc
nhau. Mặt cầu nhỏ tiếp xúc ngoài với cả bốn mặt cầu nói trên có bán kính bằng 7 3 6 5 A. . B. . C. . D. . 15 7 11 9
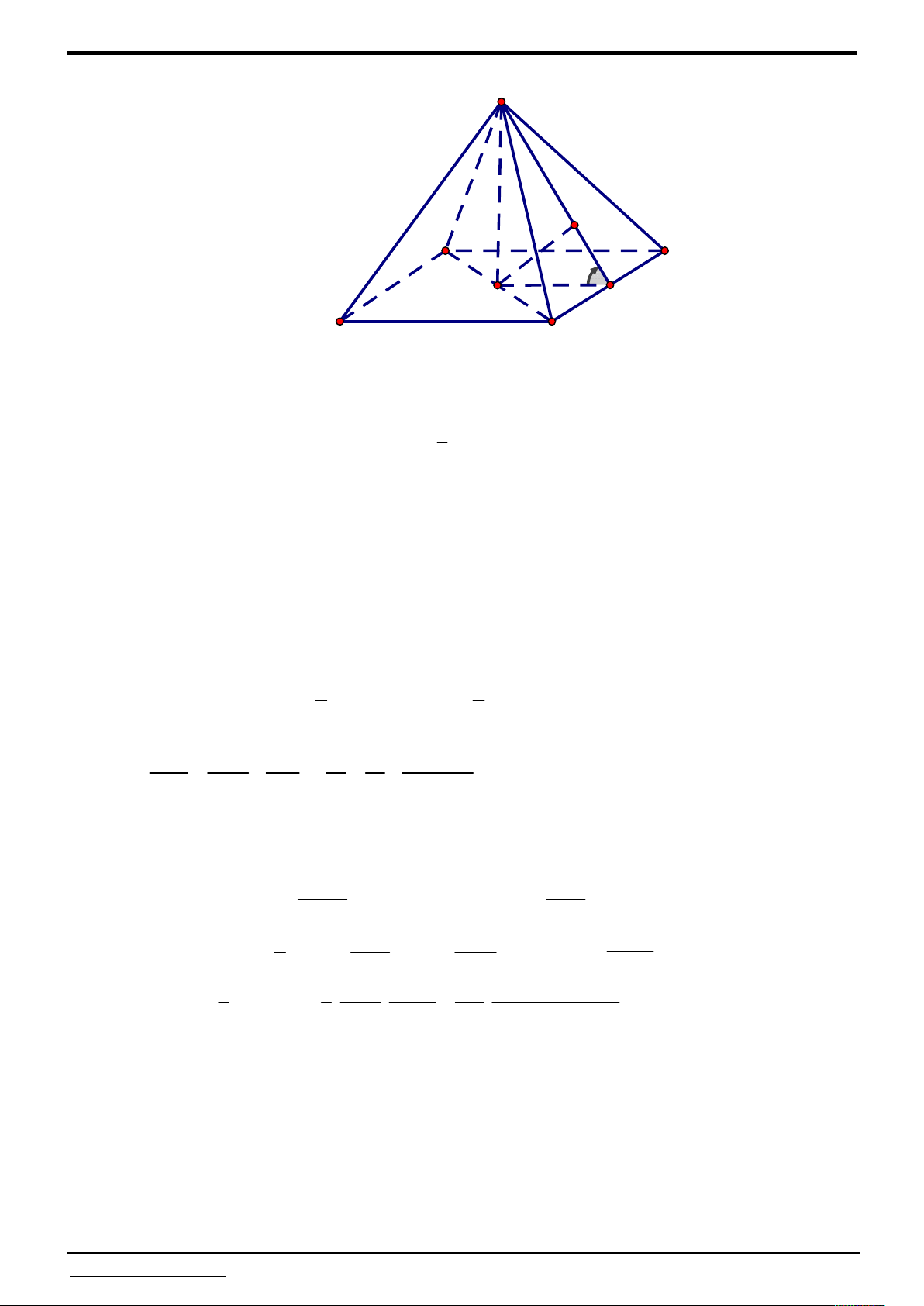
Câu 17. Cho tứ diện SABC và G là trọng tâm của tứ diện. Một mặt phẳng   quay quanh
AG cắt các cạnh SB, SC lần lượt tại M và N ( M , N không trùng S ). Gọi V là thể tích
tứ diện SABC , V là thể tích tứ diện SAMN và gọi m, n lần lượt là giá trị lớn nhất và 1 V
giá trị nhỏ nhất của 1 . Hãy tính m n . V 17 18 19
A. m n  1.
B. m n  .
C. m n  .
D. m n  . 18 19 20
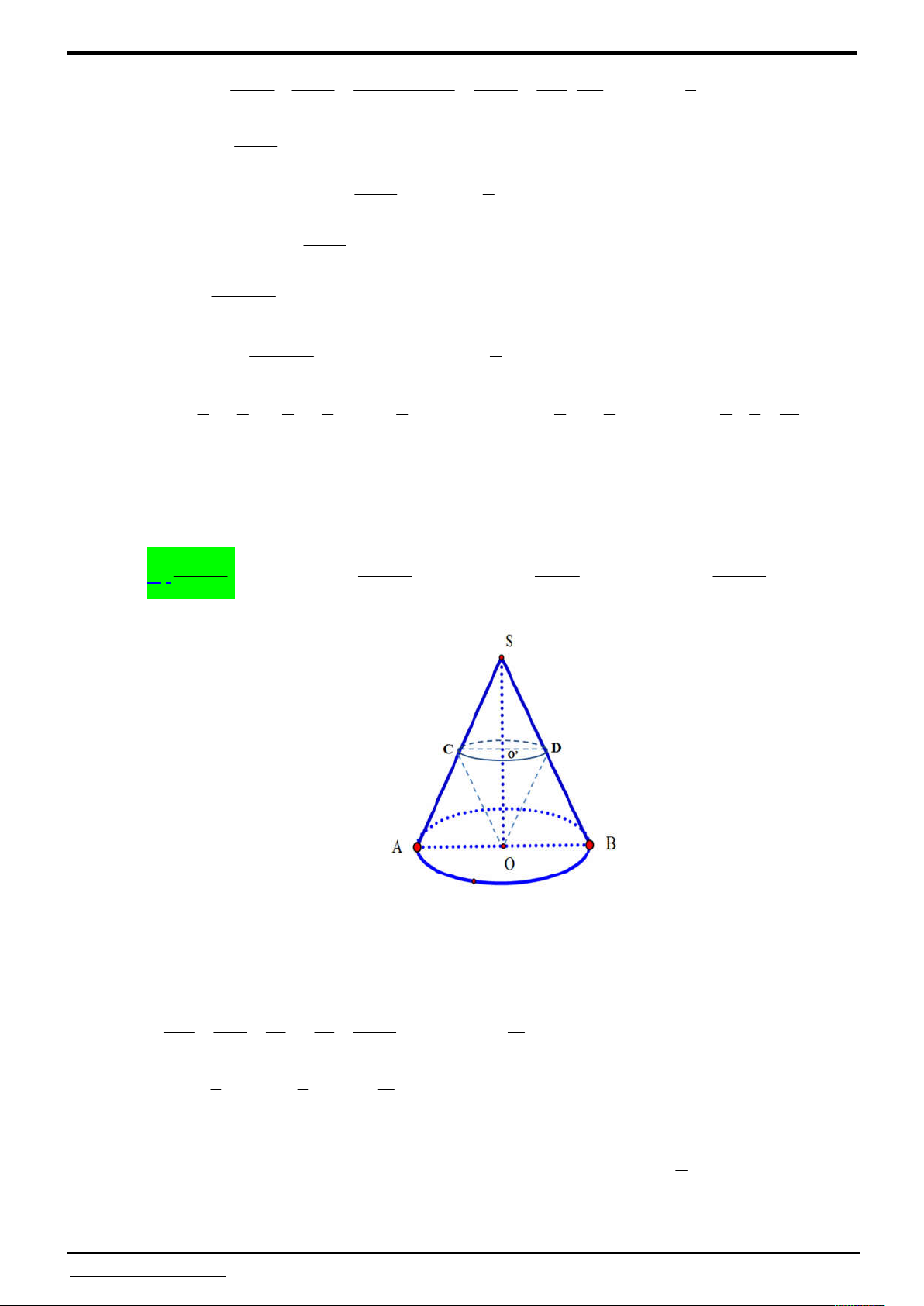
Câu 18. Cho hình nón (H ) có đỉnh S , chiều cao là h và mặt phẳng (P) song song với mặt
phẳng đáy của khối nón. Một khối nón (T ) có đỉnh là tâm của đường tròn đáy của
(H ) và đáy của (T ) là thiết diện của (P) với hình nón. Thể tích lớn nhất của (T ) là bao nhiêu? 2 4 R h 2 4 R h 2  R h 2 2  R h A. . B. . C. . D. . 81 27 24 3
Câu 19. Cho hình chóp đều S.ABC có  0
AB  1, ASB  30 . Lấy các điểm B ', C ' lần lượt thuộc
các cạnh SB, SC sao cho chu vi tam giác AB 'C ' nhỏ nhất. Tính chu vi đó. 1 A. . B. 3 1. C. 3 . D. 1 3 . 1 3
Câu 20. Trong mặt phẳng P cho tam giác ABC đều cạnh bằng 8cm và một điểm S di động
ngoài mặt phẳng P sao cho tam giác MAB luôn có diện tích bằng 2
16 3cm , với M
là trung điểm của SC . Gọi S  là mặt cầu đi qua bốn đỉnh M , A , B , C . Khi thể tích
hình chóp S.ABC lớn nhất, tính bán kính nhỏ nhất của S : 16 6 4 3 4 15 4 39 A. cm . B. cm . C. cm . D. cm . 9 3 3 3
Câu 21. Cho hình chóp S.ABCD có đáy ABCD đáy là hình vuông cạnh a , SA a 3 . Và SA
vuông góc với đáy. M và N là hai điểm thay đổi lần lượt thuộc hai cạnh BC và CD sao cho  0
MAN  45 . Tính tỉ số giữa giá trị lớn nhất và giá trị nhỏ nhất của thể tích khối chóp S.AMN 1 2 1 2 A. 2   2 2 . B. . C. 2 2 1. D. . 6 2
Câu 22. Cho hình hộp chữ nhật ABC . D A BCD
  có tổng diện tích tất cả các mặt là 36 , độ dài
đường chéo AC bằng 6 . Hỏi thể tích của khối hộp chữ nhật lớn nhất là bao nhiêu? A. 8 2 . B. 6 6 . C. 24 3 . D. 16 2 .
Câu 23. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và đường cao SA  2a . MNPQ
là thiết diện song song với đáy, M SA và AM x . Xét hình trụ có đáy là đường tròn
ngoại tiếp tứ giác MNPQ và đường sinh MA . Giá trị của x để thể tích khối trụ lớn nhất là a 2a a 3a A. x  . B. x  . C. x  . D. x  . 3 3 2 4
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 3 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp
Câu 24. Cho tứ diện ABCD có tam giác ABC đều cạnh 2a và tam giác ABD vuông tại D , a AD
. Khoảng cách lớn nhất từ B đến mặt phẳng  ACD là? 2 2a 2 a 3 A. . B. a 3 . C. . D. 2a 3 . 2 3
Câu 25. Cho khối chóp tứ giác đều S.ABCD mà khoảng cách từ A đến mặt phẳng SCD
bằng 2a . Gọi  là góc giữa mặt bên của hình chóp với đáy của hình chóp đó. Với giá
trị nào của  thì thể tích của khối chóp S.ABCD đạt giá trị nhỏ nhất? 2 2 A.   arcsin . B. 0   45 . C.   arccos . D. 0   60 . 3 3
Câu 26. Cho hình chóp SABCD , có đáy ABCD là hình thoi cạnh a , SA SB SC a .Đặt
x SD 0  x a 3 Tìm x theo a để tích A .
C SD đạt giá trị lớn nhất. a 3 a 3 a 6 A. x  . B. x  . C. x  . D. Đáp án khác. 2 3 2
Câu 27. Cho tứ diện S.AB D
C và M là một điểm di động, nằm bên trong tam giác ABC .
Qua M kẻ các đường thẳng song song với S ,
A SB, SC cắt các mặt phẳng tương ứng
SBC, SAC, SAB lần lượt tại A', B ',C '. Khi đó giá trị lớn nhất của biểu thức MA ' MB ' MC '
MA ' MB ' MC ' T     . . là SA SB SC SA SB SC 9 28 62 13 A. . B. . C. . D. 8 27 27 8
Câu 28. Trong không gian với hệ trục tọa độ .
O xyz , cho điểm A ; a ;
b c với a; ; b c là các số a 1
thực dương thỏa mãn  2 2 2
5 a b c   9ab  2bc ca và Q   có 2 2 b c
a b c3
giá trị lớn nhất. Gọi M , N , P lần lượt là hình chiếu vuông góc của A lên các tia
Ox; Oy; Oz . Phương trình mặt phẳng MNP là
A. x  4y  4z 12  0.
B. 3x 12y 1  2z 1   0.
C. x  4y  4z  0 .
D. 3x 12y 12z 1  0 .
Câu 29. Trong mặt phẳng   cho đường tròn T  đường kính AB  2R . Gọi C là một diểm
di động trên T  . Trên đường thẳng d đi qua A và vuông góc với mặt phẳng   lấy
điểm S sao cho SA R . Hạ AH SB tại H , AK SC tại K . Tìm giá trị lớn nhất Vmax
của thể tích tứ diện SAHK . 3 R 5 3 R 5 3 R 3 3 R 3 A. V  . B. V  . C. V  . D. V  . max 75 max 25 max 27 max 9
.Câu 30. Cho tứ diện đều ABCD có cạnh bằng 1. Hai điểm M , N di động trên các cạnh
AB , AC sao cho mặt phẳng  DMN  vuông góc mặt phẳng  ABC  . Gọi S , S lần lượt 1 2 S
là diện tích lớn nhất và nhỏ nhất của tam giác AMN . Tính 1 T  . S2 8 9 8 9 A. T  . B. T  . C. T  . D. T  . 9 8 7 7
Câu 31. Cho lăng trụ tam giác đều ABC.A' B 'C ' với độ dài tất cả các cạnh đều bằng a. Xét tất
cả các đoạn thẳng song song với mặt phẳng  ABB ' A' và có một đầu E nằm trên
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 4 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp
đường chéo A'C của mặt bên AA'C 'C , còn đầu kia F nằm trên đường chéo BC ' của
mặt bên BB 'C 'C . Hãy tìm độ dài ngắn nhất của các đoạn thẳng này. 2a a a 2a A. . B. . C. . D. . 5 5 5 5
Câu 32. Cho hình chóp tứ giác đều S.ABCD mà khoảng cách từ A đến mặt phẳng SBC
bằng b . Góc giữa mặt bên và mặt đáy của hình chóp bằng  . Tìm  để thể tích của
khối chóp S.ABCD nhỏ nhất.  3   1   2  A.   arccos    arccos 3   arccos   arccos  . B.  . C.   . D.   . 3     3   3 
Câu 33. Cho hình lăng trụ đều ABC .
D A ' B 'C ' D ' có cạnh đáy bằng a. Điểm M và N lần lượt
thay đổi trên các cạnh BB ' và DD ' sao cho MAC    NAC  và BM x, DN y . Tìm
giá trị nhỏ nhất của thể tích khối tứ diện ACMN . 3 a 3 a 3 a 3 a A. . B. . C. . D. . 3 2 2 2 2 2 3
Câu 34. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA b và
vuông góc với  ABCD . Điểm M thay đổi trên cạnh CD với CM x 0  x a . H là
hình chiếu vuông góc của S trên BM . Tìm giá trị lớn nhất của thể tích khối chóp
S.ABH theo a, b . 2 a b 2 2 2 a b a b a b A. . B. . C. . D. . 12 24 8 18
Câu 35. Cho tứ diện đều SABC có D là điểm thuộc cạnh AB sao cho BD  2 AD , I là trung
điểm của SD . Một đường thẳng d thay đổi qua I cắt các cạnh SA , SB lần lượt tại M , 3 3  m a
N . Biết AB  2a . Khi d thay đổi, thể tích khối chóp S.MNC nhỏ nhất bằng .   ,  n m với , m n  ,  ,
m n  1. Tính m n .
A. m n  4 .
B. m n  6 .
C. m n  7 .
D. m n  5 .
Câu 36. Cắt một khối trụ tròn có chiều cao h bởi một mặt phẳng song song với hai mặt đáy ta
thu được hai khối tròn nhỏ. Một trong hai khối đó ngoại tiếp một lăng trụ đứng thể
tích V có đáy là tam giác có chu vi là p. Khối còn lại ngoại tiếp một khối nón có bán
kính là R . Tìm giá trị của R sao cho thể tích của khối nón là lớn nhất? 3  p 3 hp 3  p 3 p A. R  . B. R  . C. R  . D. R  . 162V 162V 162 162V
Câu 37. Người ta cần trang trí một kim tự tháp hình chóp tứ giác đều S.ABCD cạnh bên bằng 200 m ,  0
ASB  15 bằng đường gấp khúc dây đèn led vòng quanh kim tự tháp
AEFGHIJKLS trong đó điểm L cố định và LS  40m .
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 5 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp
Khi đó cần dùng ít nhất bao nhiêu mét dây đèn led để trang trí?
A. 40 67  40 mét.
B. 20 111  40 mét. C. 40 31  40 mét. D. 40 111  40 mét.
Câu 38. Chohình chóp S.ABC có các cạnh bên bằng 1. Mặt phẳng   thay đổi luôn đi qua
trọng tâm của hình chóp, cắt ba cạnh bên S ,
A SB, SC lần lượt tại D, E, F . Tìm giá trị 1 1 1
lớn nhất P của P    . max S . D SE SE.SF SF.SD 4 16 4 3 A. . B. . C. . D. . 3 3 3 4
Câu 39. Cho hình lập phương ABC .
D A' B 'C ' D ' có cạnh bằng a . G là trung điểm của BD ' ,
mặt phẳng  P thay đổi qua G cắt AD ',CD ', B ' D ' tương ứng tại H , I, K . Tìm giá trị 1 1 1
lớn nhất của biểu thức T    .
D ' H . D ' I
D ' I. D ' K
D ' K. D ' H 8 2 16a 2 8a 16 A. . B. . C. . D. . 2 3a 3 3 2 3a
Câu 40. Cho hình hộp chữ nhật ABC .
D A' B 'C ' D ' có AC a, AD '  b, CD '  c . Tìm thể tích lớn
nhất của hình chữ nhật đã cho khi a,b,c thay đổi, còn chu vi tam giác ACD ' không đổi.
Câu 41. Cho tứ diện ABCD, AB  ,
x CD y, các cạnh còn lại của tứ diện bằng a 2, x, y thay
đổi sao cho x y  2 . a Khi V
đạt giá trị nhỏ nhất, tính cosin của góc giữa  ABCABCD và  ABD.
Câu 42. Cho hình chóp SABCD có đáy là ABCD là hình vuông cạnh a , cạnh SA a và vuông
góc với mp ( ABCD). M là điểm di động trên đoạn BC và BM x 0  x a , K là
hình chiếu của S trên DM.
a) Tính độ dài đoạn SK theo a và x .
b) Tìm min của đoạn SK.
Câu 43. Cho hình chóp S.ABCD có tứ giác ABCD là hình bình hành tâm O . Điểm C di động
trên cạnh SC ( C khác điểm S và C ). Mặt phẳng  R chứa đường thẳng AC và
song song với BD . Mặt phẳng  R cắt đường thẳng SB , SD lần lượt tại B, D .
1/ Gọi F là giao điểm của AD với B C
  . Chứng minh rằng F luôn di động trên một
đường thẳng cố định khi C di động trên SC . SCBB 5 SD
2/ Xác định vị trí của điểm C sao cho tổng  3  .
đạt giá trị nhỏ nhất. CCSB 2 DD
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 6 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp
Câu 44. Trong mặt phẳng  cho hình chữ nhật ABCD có AB a; BC  2a . Các điểm M , N lần
lượt di chuyển trên các đường thẳng m, n vuông góc với mặt phẳng   tại , A B sao
cho DM CN . Tìm giá trị nhỏ nhất của khối tứ diện CDMN .
Câu 45. Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AB song song với CD ,
AB  2CD , các cạnh bên có độ dài bằng 1. Gọi O AC BD , I là trung điểm của SO .
Mặt phẳng   thay đổi đi qua I và cắt các cạnh S ,
A SB, SC, SD lần lượt tại M , N , P,Q 1 1 1 1
. Tìm giá trị nhỏ nhất của biểu thức T     . 2 2 2 2 SM SN SP SQ
Câu 46. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi E là trung điểm của SC
. Mặt phẳng   thay đổi nhưng luôn chứa AE cắt SB , SD lần lượt tại M , N . Xác SM SN
định vị trí của M , N trên các cạnh SB , SD sao cho 
đạt giá trị lớn nhất. SB SD
Câu 47. Cho tứ diện OABC có các cạnh O ,
A OB, OC đôi một vuông góc. Gọi M là điểm thuộc
miền trong của tam giác ABC . Tìm giá trị nhỏ nhất của biểu thức 2 2 2 MA MB MC T    2 2 2 OA OB OC BẢNG ĐÁP ÁN 1.B 2.C 3.C 4.C 5.B 6.A 7.C 8.D 9.B 10.C 11.A 12.D 13.D 14.D 15.C 16.C 17.B 18.A 19.D 20.C 21.D 22.A 23.B 24.B 25.A 26.C 27.B 28.B 29.A 30.B 31.B 32.A 33.A 34.A 35.D 36.B 37.C 38.B 39.A
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 7 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp
LỜI GIẢI THAM KHẢO Câu 1.
Một khối gỗ hình hộp chữ nhật có kích thước thoả mãn: Tổng của chiều dài và chiều
rộng bằng 12 cm ; tổng của chiều rộng và chiều cao là 24 cm . Hỏi thể tích lớn nhất mà
khối hộp có thể đạt được là bao nhiêu? A. 3 288cm . B. 3 384 3 cm . C. 3 1782cm . D. 3 864cm . Lời giải
Gọi chiều dài, chiều rộng và chiều cao của khối hộp chữ nhật lần lượt là x , y , z
x, y, z  0 .
x y  12
x  12  yy  12 Theo giả thiết ta có:   
. Vì x, z  0 nên   y  12 . y z  24  z  24  yy  24 
Thể tích của khối hộp là V xyz    y y   y  3 2 12 24
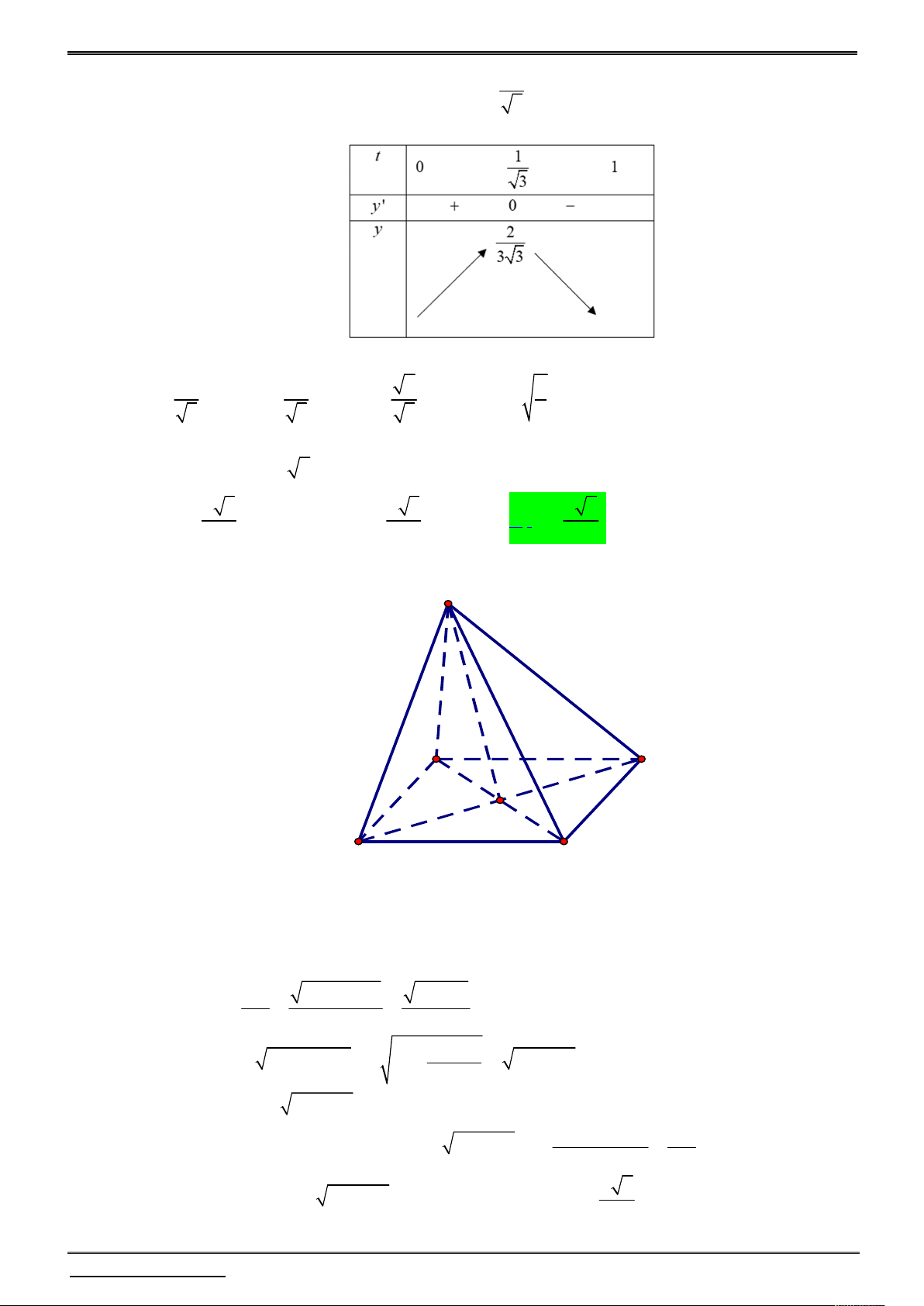
y  36 y  288 y .
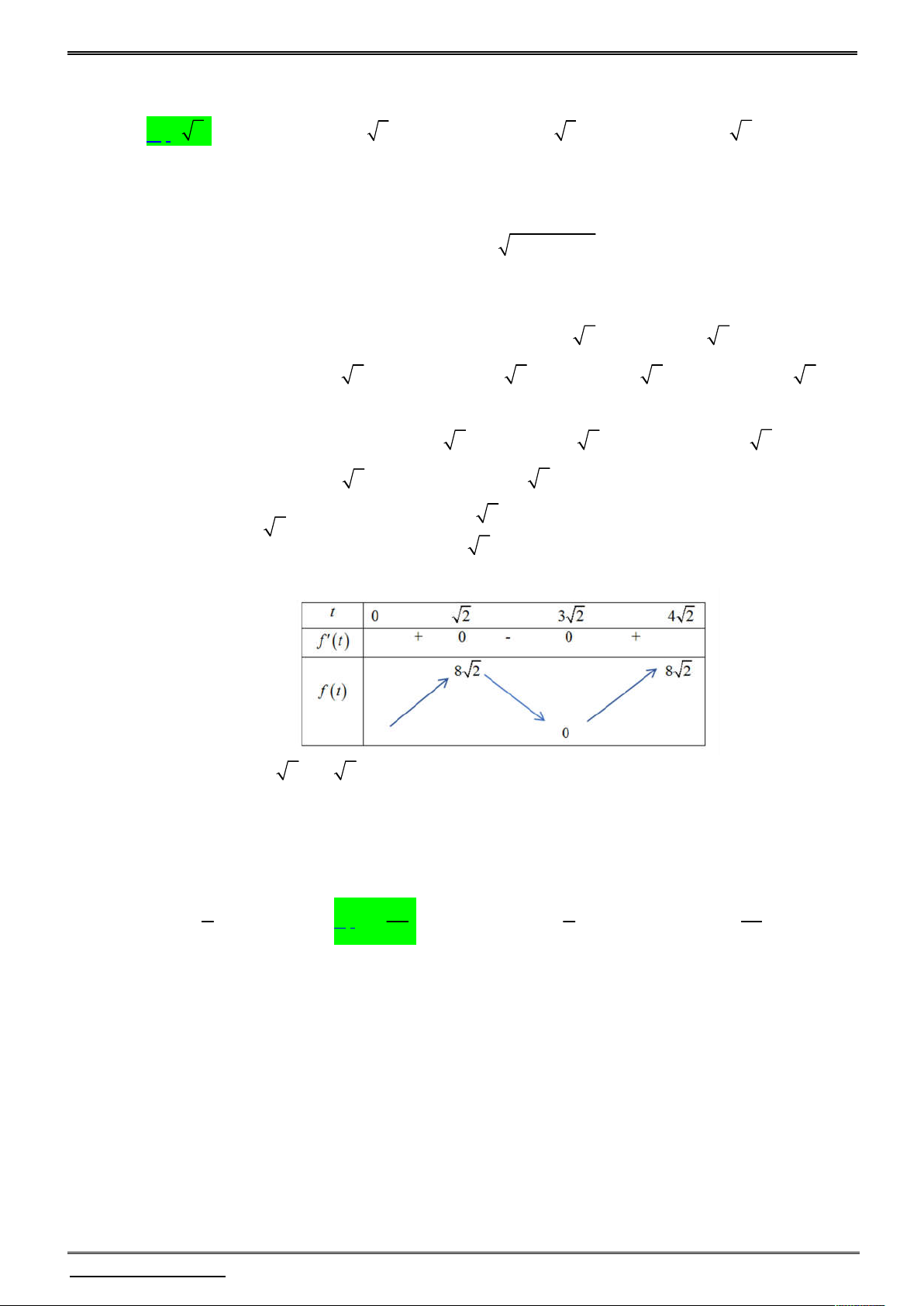
Xét hàm số f y 3 2
y  36 y  288 y trên khoảng 0;12 . f  y 2
 3y  72 y  288 ;  y  12  4 3
f  y  0   .  y  12  4 3  Bảng biến thiên:
Từ bảng biến thiên ta có: max f y  384 3 . 0;12
Vậy thể tích lớn nhất mà khối hộp có thể đạt được là 3 384 3 cm . Câu 2.
Trong không gian cho bốn mặt cầu có bán kính lần lượt là 2;3;3; 2 đôi một tiếp xúc
nhau. Mặt cầu nhỏ tiếp xúc ngoài với cả bốn mặt cầu nói trên có bán kính bằng 7 3 6 5 A. . B. . C. . D. . 15 7 11 9 Lời giải
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 8 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp B M I D A N C Gọi ,
A B, C, D lần lượt là tâm của bốn mặt cầu nói trên và I , x( 0) lần lượt là tâm, bán kính mặt cầu cần tìm.
IA IC x  2
Mặt cầu I tiếp xúc ngoài với bốn mặt cầu nêu trên nên  . Do đó, I nằm
IB ID x  3 
trên giao tuyến của hai măt phẳng trung trực của AC, BD .
Vì bốn mặt cầu đôi một tiếp xúc nên DA DC BA BC . Gọi M , N lần lượt là trung
điểm của BD, AC . Khi đó, MN là đoạn vuông góc chung của AC và BD nên I thuộc đường thẳng MN . Ta có, 2 2 2 2 DN
DC CN  25  4  21, MN
DN DM  21 9  2 3 . Xét AI
N vuông tại N và IN   x  2 2 2  2 .
Xét BIM vuông tại M có IM   x  2 2 3  3 .
Vì IM IN MN nên dấu ‘‘=’’ xảy ra khi và chỉ khi I MN . 2 2
Khi đó, IM IN MN   x   2    x   2 2 2 3  3  2 3 6 2
 11x  60x  36  0  x  . 11 Câu 3.
Cho hình chóp S.ABC có SA   ABC  , SB a 2 , hai mặt phẳng SAB và SBC
vuông góc với nhau. Góc giữa SC và SAB bằng 0
45 , góc giữa SB và mặt đáy bằng   0
0    90  . Xác định  để thể tích khối chóp S.ABC đạt giá trị lớn nhất. A. 0   60 . B. 0   30 . C. 0   45 . D. 0   70 . Lời giải
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 9 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp
Ta thấy SA   ABC   SAB   ABC   1
Theo giả thiết thì SAB  SBC 2
Từ và ta có BC  (SAB)  BC AB và BC SB
Góc giữa SC và SAB là góc  0
BSC  45 . Trong tam giác vuông cân SBC có
SB BC a 2 .
Tam giác vuông SAB cạnh AB S .
B cos   a 2 cos  ; SA S .
B sin   a 2.sin  1 1 2 3 3 V  .S .SA  . 2.a .sin 2  .a S . ABC 3 ABC 6 6 2 3 V
.a  sin 2  1 0 0    90  0    45 max 6 Câu 4.
Cho hình chóp S.ABC có SA   ABC  , SB a 2 , hai mặt phẳng SAB và SBC
vuông góc với nhau. Góc giữa SC và SAB bằng 45o , góc giữa SB và mặt đáy bằng
,0o   90o  
 . Xác định  để thể tích khối chóp S.ABC lớn nhất. A. 60o   . B. 30o   . C. 45o   . D. 70o   . Lời giải
Ta có: SA   ABC   SAB   ABC
Mà SAB  SBC  ,  ABC   SBC   BC
Nên BC  SAB  BC AB  ABC vuông tại B .
 Góc giữa SC và  SAB là  45o CSB  .
BC SB a 2 .
Góc giữa SB và mặt đáy là 
SBA    AB S .
B cos ; SA  . SB sin  .
Thể tích khối chóp S.ABC là:
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 10 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp 1 1 1 3 1 a 2 3 V  . SA S  . SA . AB BC  SB .sin .cos 3  a 2 sin 2  . 3 ABC 6 6 6 6
Dấu “=” xảy ra  sin 2  1  2  90o   45o    . Câu 5.
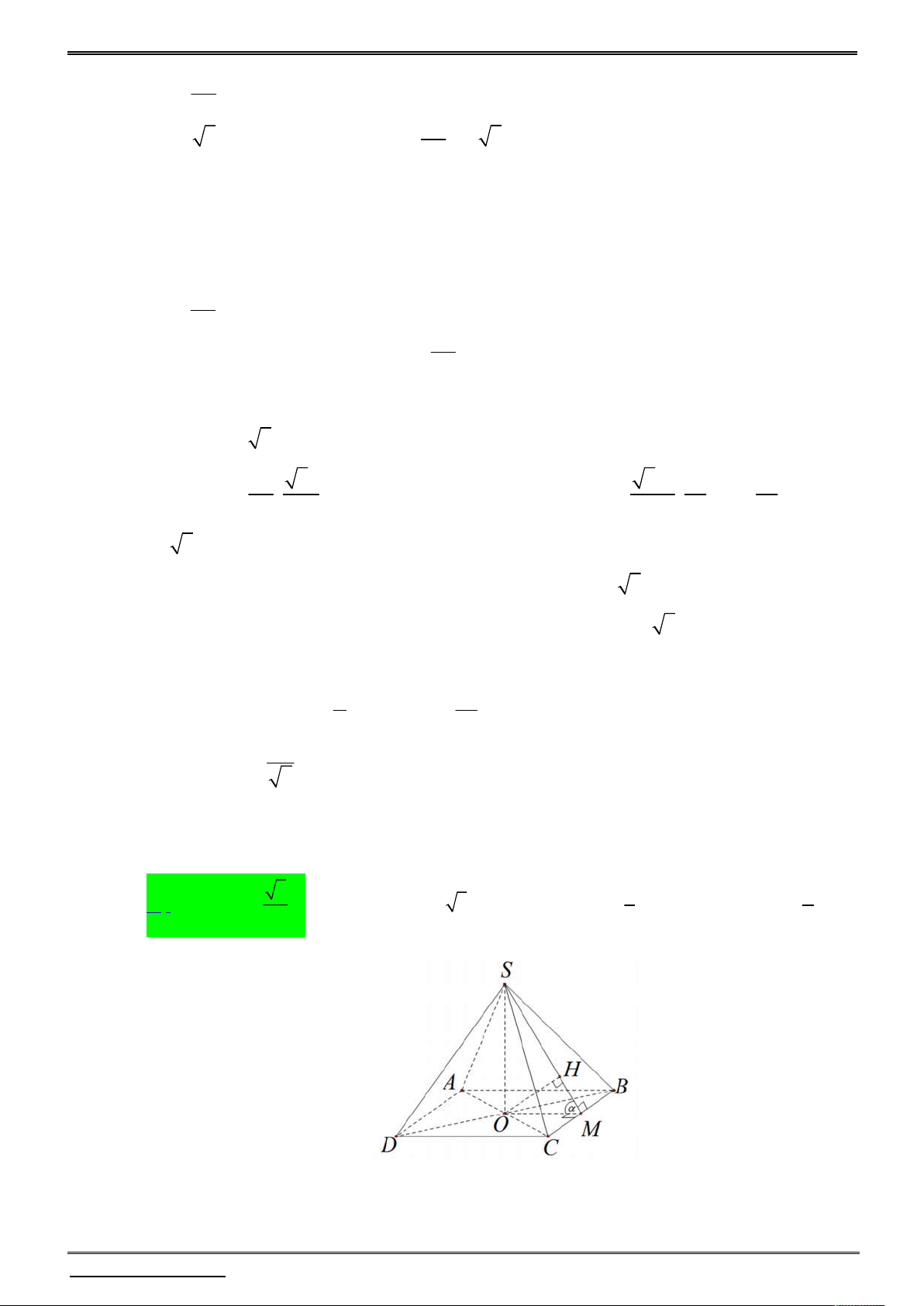
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân đáy AB , nội tiếp đường
tròn tâm O , bán kính R . Biết rằng AC BD tại I , đồng thời I là hình chiếu của S
lên ABCD và S
AC vuông tại S . Thể tích lớn nhất của khối chóp S.ABCD theo R là 2 1 3 A. 3 R . B. 3 R . C. 3 R . D. 3 R 3 2 4 Lời giải S A B I D C
Ta có thể tích của khối chóp S.ABCD là 1 1 1 1 V  .SI.S 2
 .SI. AC.BD SI.AC S . ABCD 3 ABCD 3 2 6
Tam giác S AC vuông tại S , đường cao SI nên 2 SI I . A IC , do đó 1 1 IA IC 1 1 2 2 VI . A IC .AC 2 3  . .AC  .AC  .2R3 3  R . S . ABCD 6 6 2 12 12 3
Dấu “=” xảy ra khi và chỉ khi IA IC   
ABCD là hình vuông. AC  2R  2
Vậy thể tích lớn nhất của khối chóp S.ABCD bằng 3 R . 3 Câu 6. Trong không gian
Oxyz cho mặt phẳng   :x y  4  0 , mặt cầu  2 2
S  :  x  2 2 2
1  y z  1 và mặt cầu S : x  4  y  5  z  4. Điểm A thuộc mặt 2      2 1
phẳng  , điểm M thuộc mặt cầu S , điểm N thuộc mặt cầu S . Khi dó 2  1 
AM AN nhỏ nhất bằng A. 5. B. 8 . C. 11. D. 3 2 . Lời giải
Mặt cầu S có tâm I 1;0;0 , bán kính R  1. 1   1  1
Mặt cầu S có tâm I 4;5;0 , bán kính R  2. 2   2  2 d  3 2 I ,    R 1   1 2 d  5 2 I ,    R 2   2 2
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 11 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp
Ta thấy S và   không có điểm chung, S và   không có điểm chung, I và I 2  1  1 2
nằm cùng phía so với   I2 I N 1 M A M' I'1
Phép đối xứng qua mặt phẳng   biến mặt cầu S thành mặt cầu S ' , biến điểm 1  1 
M thành điểm M ' , biến điểm I thành điểm I ' . 1 1
Ta có AM AN AM ' AN M ' N Dấu bằng xảy ra khi ,
A M ', N thẳng hàng.
Đoạn thẳng M ' N ngắn nhất khi M ', N thuộc đoạn thẳng ' I I 1 2
Khi đó giá trị nhỏ nhất của AM AN là '
P I I R R 1 2  1 2  x  1 t
Đường thẳng d đi qua I và vuông góc với   là  y t  t   1 z  0   5 3 
Giao điểm của đường thẳng d và   là B ;  ; 0    2 2 
B là trung điểm của ' ' I I I 4; 3  ; 0 1 1 1  
Vậy P  8  1 2  5. Câu 7.
Cho lăng trụ đứng ABC.A BC   có  0
AB  6; BC  12; ABC  60 . Thể tích khối chóp C .ABB A
  bằng 216. Gọi M là điểm nằm trong tam giác A BC
  sao cho tổng diện tích
các mặt bên của hình chóp M.ABC đạt giá trị nhỏ nhất. Tính cosin góc giữa 2 đường thẳng B M  , AC ? 2 2 2 1 A. . B. . C. . D. . 2 3 4 2 Lời giải
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 12 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp
Gọi I là hình chiếu của M trên ( ABC) ; ,
D E, F lần lượt là hình chiếu của I trên
AB, BC,C .
A Đặt x I ,
D y IE, 2a AB, 2b BC, 2c C ,
A h AA'  MI . Khi đó SSSS
ax by cz ABC IAB IAC IBC
Diện tích toàn phần của hình chóp M .ABC nhỏ nhất khi và chỉ khi S SSS nhỏ nhất. MAB MBC MCA 1 2 2 Có 2 2 2 2 2 2 MD
MI ID h x S  .
AB MD a h x ahax . MAB     2 2 2 2 2 2 2
Tương tự ta chứng minh được S  ah  ax  bh  by  ch  cz         
Sử dụng bất đẳng thức u v w u v w với u  a ;
h ax, v  (b ;
h by), w  (c ; h cz) ta được: 2 2 2 2 2
S  (ah bh ch)  (ax by cz)  (a b c) h S  o c nst . ABC ax by cz
Dấu bằng xảy ra khi và chỉ khi  
x y z . ah bh ch
Suy ra I là tâm đương tròn nội tiếp tam giác ABC , nên M là tâm đường tròn nội tiếp
tam giác A' B 'C ' .
Tính cosin góc giữa hai đường thẳng B ' M và AC ' . 1  SS  .
BA BC.sin ABC  18 3 A' B 'C ' ABC 2 2 2 2 2 0
A 'C '  AC AB BC  2 A .
B BC cos 60  108  A 'C '  6 3 3 3 Do VV
.216  324  AA '.S
 324  AA '  6 3
ABC. AB C  
C. ABB ' A' 2 2 ABC
Gọi K là chân đường phân giác trong của tam giác A' B 'C ' kẻ từ B , từ K kẻ đường
thẳng song song với AC ' cắt AA ' tại H , khi đó:   
  (B ' M , AC ')  (B ' K, KH )  cos  cos B ' KH 1 18 SSSB KB A    B C     B K   B K   AB C   B KC   A KB     0 sin 30 18 3 4 3 2 4 AK AB 1 1 Ta có    AK
AC  2 3 B KC B   2 3 AH AK 1
Do KH / / AC nên  
AH  2 3 AA C A   3
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 13 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp 2 2 2 2  KH
AH AK  2 6, B H  
AB  AH  4 3 B K   KH B H  Vậy  2 2 2 2 cos =cosB KH   . 2B K  .KH 4 Câu 8. Trong không gian Oxyz cho hai mặt cầu
S  :  x  42 2 2
y z  16 , 1
S  :  x  42 2 2
y z  36 và điểm A4;0;0 .Đường thẳng  di động và luôn tiếp xúc 2
với S đồng thời cắt S tại hai điểm B,C . Tam giác ABC có thể có diện tích lớn 2  1  nhất là A. 28 5 . B. 72 . C. 48 . D. 24 5 . Lời giải
Gọi M là tiếp điểm của  và S 1 
I 4;0;0 là tâm của hai mặt cầu S và S có bán kính lần lượt R  4 và R  6 2  1  1 2
Ta có IC R  6, IM R  4  BM  2 5  BC  4 5 2 1 I  4
 ;0; 0, A4;0;0  IA  8 1 1 1 1 SC . B d A BC BC AM BC IA IM    ABC  ,  . ( ) .4 5.(4 8) 24 5 2 2 2 2 Câu 9.
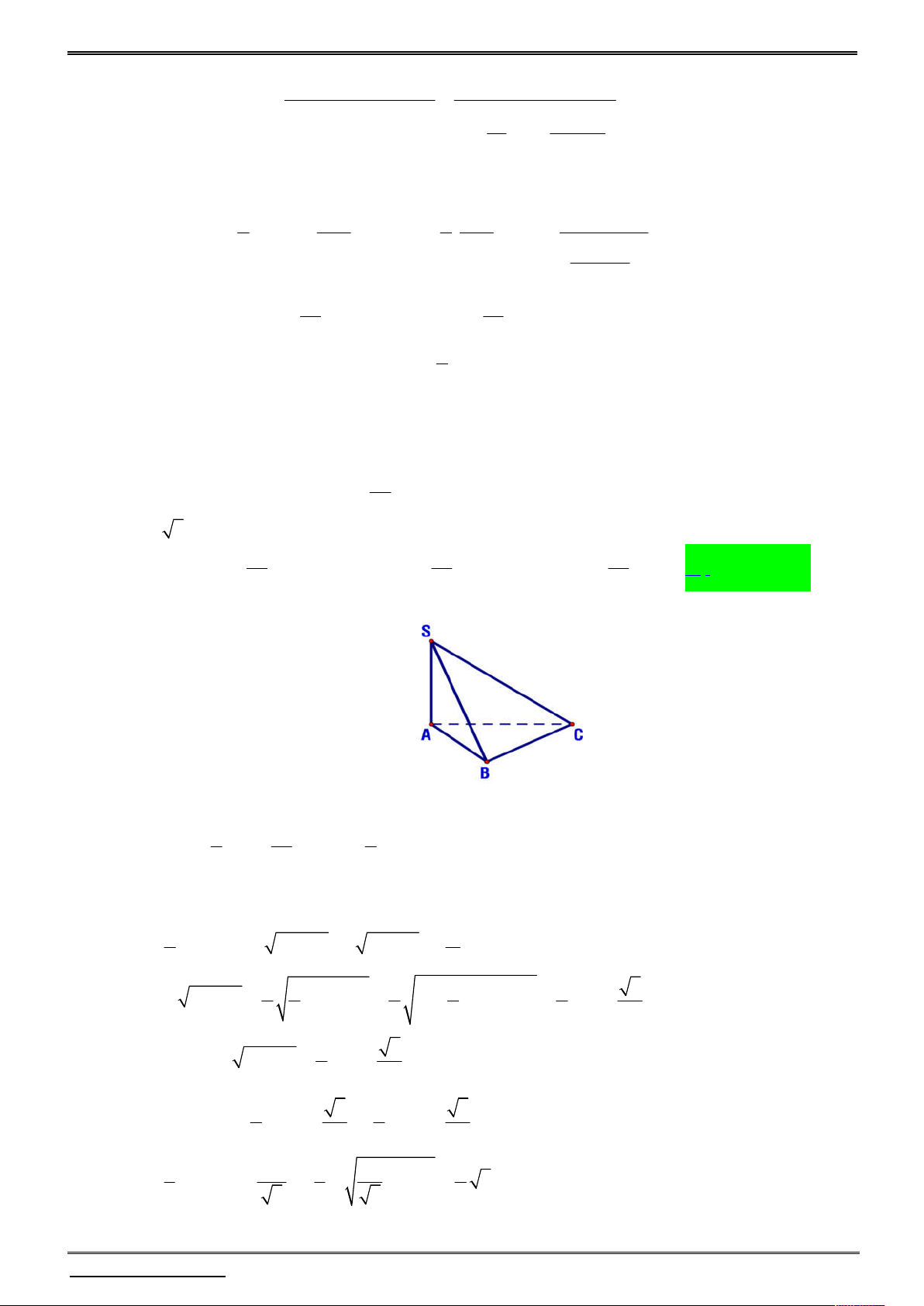
Cho hình chóp S.ABCD , có đáy là hình bình hành, M là trung điểm của cạnh SC .
Mặt phẳng (P) chứa AM lần lượt cắt các cạnh SB, SD tại ' '
B , D . Giá trị lớn nhất của ' ' SB SD a u   *
là , (a,b N ) tối giản. Tích a.b bằng: SB SD b A. 3 . B. 12 . C. 15 . D. 6 . Lời giải
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 14 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp
Lấy I AM B ' D ' ;O AC BD
Ta có S,O, I là các điểm chung của hai mặt phẳng (SAC);(SBD)
Suy ra S,O, I thẳng hàng SI 2
Và I là trọng tâm các mặt chéo SAC   SO 3 SD SB
Vẽ BP / /B ' I; DN / /D ' I OP ON . Đặt x  ; y SD ' SB ' SB SD SP SN 2SO 3  x y       2.  3 SB ' SD ' SI SI SI 2 1 1 3 2 4 2
x, y [1; 2]     3( ) 
a  3;b  4  . a b  12 x y xy x y 3
Câu 10. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Gọi I là điểm 1
thuộc đoạn SO sao cho SI SO . Mặt phẳng   thay đổi đi qua B và I .   cắt các 3
cạnh SA , SC , SD lần lượt tại M , N , P . Gọi m , n lần lượt là giá trị lớn nhất và giá trị V
nhỏ nhất của S.MBNP . Giá trị của m n là VS.ABCD 4 6 14 1 A. . B. . C. . D. . 15 75 75 5 Lời giải
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 15 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp SA x   SM Đặt 
với x , y  1. SC   y   SN SB SD SO SD Có   2  2.3  6   5 . SB SP SI SP SO
Mà x y  2
 6  y  6  x , với 1  x  5 . SI V
x 1 y  5 12 3 3 3
Khi đó S.BMNP      . V .1. x .5 y 20xy 5xy 5xx x x S ABCD 6  5 2 6 .  3
Xét hàm số f x 
, với 1  x  5 . 5 2 6x x  3 2x  6
Ta có f  x  .
. Cho f  x  0  2x  6  0  x  31;  5 .
5 6x x 2 2 3 1 3 Khi đó f   1  , f 3  và f 5  . 25 15 25 3 1 Suy ra m  và n  . 25 15 14
Vậy m n  . 75
Câu 11. Cho hình chóp SABC có đáy là tam giác đều cạnh bằng 6 biết các mặt bên của
hình chóp có diện tích bằng nhau và một trong các cạnh bên bằng 3 2 . Tính thể tích
nhỏ nhất của khối chóp SABC . A. 3 . B. 2 2 . C. 2 3 . D. 4 . Lời giải
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 16 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp
Gọi H là hình chiếu vuông góc của S lên ( ABC) , Gọi M , N, P lần lượt là hình chiếu
vuông góc của H trên AB, BC,CA thì SM , SN, SP lần lượt là chiều cao của các mặt
bên SAB, SBC, SAC .
Vì các mặt bên của hình chóp có diện tích bằng nhau nên SM SN SP nên suy ra
HM HN HP H là tâm đường tròn nội tiếp hoặc tâm đường tròn bàng tiếp của tam giác ABC .
Trường hợp 1: H là tâm đường tròn nội tiếp của tam giác ABC . 2 2  6  Khi đó 2 2 SH
SA AH  3 2      4 .  3    Vậy VSH S   SABC ABC  2 1 1 3 . .4. 6 . 2 3 3 3 4
Trường hợp 2: H là tâm đường tròn bàng tiếp của tam giác ABC .
Do tam giác ABC đều nên giả sử H là tâm đường tròn bàng tiếp góc A . Khi đó
AH  3 2, BH CH  6 Nếu 2 2
SA  3 2  SH SA AH  0 . 2 2 Do đó 2 2
SB SC  3 2  SH
SB BH  3 2    6   2 3 Suy ra VSH S   . SABC ABC  2 1 1 3 . .2 3. 6 . 3 3 3 4
Ta có 3  2 3 Vậy V  3 min
Câu 12. Trong không gian với hệ tọa độ Oxyz , cho điểm A4;0;0, B 0;4;0, S 0;0;c và x  1 y  1 z 1 đường thẳng d :   . Gọi A ,
B lần lượt là hình chiếu vuông góc của 1 1 2 O lên S ,
A SB . Khi góc giữa đường thẳng d và mặt phẳng OAB lớn nhất,mệnh đề nào sau đây đúng?  17 15  A. c  8  ; 6   . B. c  9  ; 8   .
C. c 0;3 . D. c   ;    .  2 2  Lời giải
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 17 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp
Gọi C là đỉnh thứ tư của hình vuông AOBC C 4;4;0 . OA  SA Ta có 
OA  SAC  mà SC  SAC  nên SC OA . OA  AC  
Tương tự SC OB , từ đó suy ra SC  OAB . Vậy SC  4;4; c   là vectơ pháp
tuyến của mặt phẳng OAB . 
Để góc giữa đường thẳng d và mặt phẳng OAB lớn nhất thì d  OAB hay SC 
cùng phương với u  1;1;2 . Suy ra c  8 . d
Câu 13. Cho hình lập phương ABC .
D A ' B 'C ' D ' . Điểm M nằm trên cạnh AA ' sao cho góc  a
BMD' lớn nhất, đặt góc lớn nhất đó là  . Biết cos  ; , a b ;   ,
a b 1;b  0 . Mệnh b
đề nào sau đây đúng?
A. a b 1.
B. a b  2 .
C. a b  3 .
D. a b  4 . Lời giải A' B' M D' C' A B D C
Không mất tính tổng quát, giả sử cạnh hình lập phương có độ dài là 1 và
AM x, 0  x 1 . Khi đó, ta có BM   x D M    x2 2 2 2 2 1 ; ' 1 1 ; BD '  3 .  2 x x Vậy cos BMD'  1  x  2 2 1 1 x
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 18 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp 2 2     BMD 2 x 1 x 1 cos '   1 x  1  1 x2 2  1  1         1 1   2  x  1 x2       2   2 2 2    1   1       1 1  1 Ta có 1     1     1.1 . 1          25   2 .   x     1 x     x 1 x     x 1 x         2    Vậy   BMD 2 1 cos '  , suy ra  1 cos BMD '  . 25 5 1
Dấu bằng xảy ra khi và chỉ khi x
, hay M là trung điểm của AA ' , khi đó  cos BMD ' 2 nhỏ nhất nên góc  BMD ' lớn nhất.
Vậy a  1;b  5 .
Câu 14. Cho khối chóp S.ABC có SA vuông góc với đáy, tam giác ABC vuông tại B . Biết rằng 5
thể tích của khối chóp là
và giá trị nhỏ nhất diện tích toàn phần chóp S.ABC là 24
p 5  q trong đó p, q   . Tính giá trị biểu thức: 2 2
p q  ? 37 37 25 A. 2 2 p q  . B. 2 2 p q  . C. 2 2 p q  . D. 2 2
p q  16 . 36 9 4 Lời giải
Đặt AB a , BC b , SA c , a, ,
b c  0 , khi đó ta có 1 5 5 Vabc   abc  . S . ABC 6 24 4
Diện tích toàn phần chóp S SSSS tp ABC SAB SAC SBC 1   P 2 2 2 2
ab ac c a b b a c   . 2 2 2 9 2 5 2  5    Có 2 2 a b   2 2 a b   1     2 2
a b    a b  . 3 4 3 4 3  2      2  5  Tương tự 2 2 a c   a c  . Do đó 3  2    2  5  2  5 
P ab ac
c a b  
b a c  3  2  3  2      5  2bc  5 2 5  ab ac   .3.   abc2 3  5 . 3  5  3 5 2
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 19 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp a  1 
Dấu "  " xảy ra khi và chỉ khi  5 . b c    2  5 5  p  25 Khi đó 2 2 S  5    p q tp 4 Min 4 16 q  0 
Câu 15. Cho hình chóp SABCD có đáy là hình bình hành tâm O . Gọi I là điểm thuộc đoạn 1
SO sao cho SI SO . Mặt phẳng   thay đổi đi qua B và I .   cắt các cạnh 3 V S ,
A SC, SD lần lượt tại M , N , P . Gọi ,
m n lần lượt là GTLN, GTNN của S.BMPN . Tính VS.ABCD m ? n 7 14 8 A. 2 . B. . C. . D. . 5 75 5 Lời giải SA SB SC SD +) Đặt a  , b   1, c  , d  . SM SB SN SP SOa c  6 c   6  aa  1
+) Có a c b d  2.  6     . Do   1  a  5 . SI d  5  d  5  c  1  V
a b c d 12 3 3
+) Có S.BMPN      f aV 4abcd 4. . a 1. . c 5 5aaa a S ABCD 6  5 2 6 .  32a  6
+) f a 
5a  6a2 2
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 20 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp 3 1 14  m n    . 25 15 75
Câu 16. Trong không gian cho bốn mặt cầu có bán kính lần lượt là 2;3;3;2 đôi một tiếp xúc
nhau. Mặt cầu nhỏ tiếp xúc ngoài với cả bốn mặt cầu nói trên có bán kính bằng 7 3 6 5 A. . B. . C. . D. . 15 7 11 9 Lời giải
Gọi tâm của mặt cầu bán kính bằng 2 lần lượt là A , B . 2 2
Gọi tâm của mặt cầu bán kính bằng 3 lần lượt là A , B . 3 3 Vì bốn mặt cầu đôi một tiếp xúc nhau nên ta có
A B  4, A A A B B A B B  5, A B  6 . 2 2 2 3 2 3 2 3 2 3 3 3
Mặt cầu tiếp xúc ngoài với bốn mặt cầu đã cho có tâm I bán kính R . Khi đó ta có
IA IB R  2 2 2 
IA IB R  3  3 3
Suy ra điểm I nằm trên hai mặt phẳng trung trực của đoạn A B và A B . Gọi M , N 2 2 3 3
lần lượt là trung điểm của A B và A B . Dễ dàng chứng minh được MA B , NA B 3 3   2 2  2 2 3 3
lần lượt là mặt phẳng trung trực của A B và A B . Từ đó ta suy ra I MN . 2 2 3 3
Ta có MN  2 3 , đặt IM x, IN y với x  0, y  0 .
x y  2 3   2
Suy ra  R  2 2  x  4   R  32 2  y  9 
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 21 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp R 3  6 3
Từ đó rút ra được y  . 6
Trên IA , IB lần lượt lấy K , H sao cho IH IK R  2 . 3 3 R  2
Giải tam giác A IB ta có A H  24. . 2 3 2 R  3
Gọi G là giao điểm của KH và IN . GH IG IH R  2 R  2 R 3  6 3 Ta có     GH  3. và GN  . NB IN IB R  3 R  3 6  R  3 3 3
Xét tam giác MA H vuông tại M , ta có 2 2 2
MH A H A M . 2 2 2 Xét tam giác MGH vuông tại G , ta có 2 R  2  R  2 2 2 2 2 2  MG MH GH
A H A M GH  24.  4  9. . 2 2   R  3  R  3  Khi đó ta có 2 R  2  R  2  R 3  6 3 24.  4  9.   2 3   . R  3  R  3  6  R  3 6
Kiểm tra đáp án ta được R  thỏa mãn. 11
Câu 17. Cho tứ diện SABC và G là trọng tâm của tứ diện. Một mặt phẳng   quay quanh
AG cắt các cạnh SB, SC lần lượt tại M và N ( M , N không trùng S ). Gọi V là thể tích
tứ diện SABC , V là thể tích tứ diện SAMN và gọi m, n lần lượt là giá trị lớn nhất và 1 V
giá trị nhỏ nhất của 1 . Hãy tính m n . V 17 18 19
A. m n  1.
B. m n  .
C. m n  .
D. m n  . 18 19 20 Lời giải
Gọi A là trọng tâm của tam giác SBC , khi đó A AG nên M , N , A thẳng hàng. SM SN Đặt  x,
y với 0  x, y  1. SB SC V SM SN Ta có 1    xy . V SB SCS SM SA 2 SMA    xS SB SI 3  S S 1  S S  1 Vì SBISMA SNASMA SNA  nên       
x y . S SN SA 2 S S 2 S S 3 SNA     y SBC SBCSBISCI   S SC SI 3  SCI
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 22 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp S S SS S SM SN 1 Mặt khác SMA SNA SMA SNA SMN     
xy nên  x y  xy . S S S S SB SC 3 SBCSBCSBCSBC x 2 V x Do đó y  , suy ra 1  . 3x 1 V 3x 1 x 1
Do 0  x, y  1 nên từ y
ta suy ra  x  1. 3x 1 2 2 x 1
Xét hàm số f x  với  x  1. 3x 1 2 2 3x  2x
f  x  3x  2 1 2 3x  2x 2
f  x  0 
 0  x  0 hoặc x  . 3x  2 1 3  1  1  2  4 1 1 4 1 4 17 Vì f  , f  , f   1     
nên ta được m  , n  hay m n    .  2  2  3  9 2 2 9 2 9 18
Câu 18. Cho hình nón (H ) có đỉnh S , chiều cao là h và mặt phẳng (P) song song với mặt
phẳng đáy của khối nón. Một khối nón (T ) có đỉnh là tâm của đường tròn đáy của
(H ) và đáy của (T ) là thiết diện của (P) với hình nón. Thể tích lớn nhất của (T ) là bao nhiêu? 2 4 R h 2 4 R h 2  R h 2 2  R h A. . B. . C. . D. . 81 27 24 3 Lời giải
Gọi O và O ' lần lượt là tâm của đường tròn đáy của hình nón (H ) và (T ) . ,
h R là chiều cao và bán kính của hình nón (H ) .
h ', R ' là chiều cao và bán kính của hình nón (T ) 0  h '  h .
Vì mặt phẳng (P) song song với mặt phẳng đáy của khối nón nên từ hình vẽ ta có: SO ' CO ' R ' R ' h h '  h '  +      R '  . R 1   . SO AO R R hh  2 1 1  h '  + 2 2 V
  R ' h '   R 1 h ' . (T )   3 3  h  2
h '  h (ktm) 2  h '  4h ' 3h '
Xét hàm số f (h ') 1 h ' f '(h ') 1 0            . 2 hh h hh '  (tm)  3 Ta có bảng biến thiên:
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 23 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp h  4h
Từ bảng biến thiên ta có hàm số f (h ') đạt giá trị lớn nhất là f    .  3  27 2 4 R h
Vậy thể tích của khối nón (T ) đạt giá trị lớn nhất V  . (T ) 81
Câu 19. Cho hình chóp đều S.ABC có  0
AB  1, ASB  30 . Lấy các điểm B ', C ' lần lượt thuộc
các cạnh SB, SC sao cho chu vi tam giác AB 'C ' nhỏ nhất. Tính chu vi đó. 1 A. . B. 3 1. C. 3 . D. 1 3 . 1 3 Lời giải
Trải các mặt của hình chóp S.ABC ra mặt phẳng  SBC  thì chu vi tam giác AB 'C '
bằng AB ' B 'C ' C ' A AB ' B 'C ' C ' D AD .
Dấu "  " xảy ra khi B '  E, C '  F . 1 6  2 Ta có  0
AB  1, ASB  30  SA SB   . 0 2 sin 15 2
Lại có chóp S.ABC đều,  0  0
ASB  30 ASD  90  AD SA 2  1  3 .
Vậy chu vi tam giác AB 'C ' đạt giá trị nhỏ nhất bằng 1 3 .
Câu 20. Trong mặt phẳng P cho tam giác ABC đều cạnh bằng 8cm và một điểm S di động
ngoài mặt phẳng P sao cho tam giác MAB luôn có diện tích bằng 2
16 3cm , với M
là trung điểm của SC . Gọi S  là mặt cầu đi qua bốn đỉnh M , A , B , C . Khi thể tích
hình chóp S.ABC lớn nhất, tính bán kính nhỏ nhất của S : 16 6 4 3 4 15 4 39 A. cm . B. cm . C. cm . D. cm . 9 3 3 3 Lời giải
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 24 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp
Gọi H là trung điểm cạnh AB , ta có: CH AB .
Ta có: d S,ABC  2d M ,ABC V  2V SABC MABC 1 1 1 Mà VVS .d C MAB d C MAB CH MABC CMABMAB  ,  .16 3.  ,  .16 3. 3 3 3 Do đó V
lớn nhất khi và chỉ khi d C,MAB  CH hay CH  MAB . SABC
Gọi J , O lần lượt là tâm hai đường tròn ngoại tiếp hai tam giác MAB và tam giác
ABC . Dựng hai trục của hai đường tròn ngoại tiếp hai tam giác MAB và tam giác
ABC cắt nhau tại I . Khi đó I chính là tâm mặt cầu ngoại tiếp đi qua 4 điểm A , B ,
C , M và bán kính mặt cầu đi qua bốn điểm
A , B , C , M là 2 8 3 2 2 2
R OC OI     JH     3  Do S 16 3
d M , AB  4 3  , AB  8   MAB
Chọn hệ trục toạ độ Oxy như hình vẽ, ta có H 0; 0 , A4; 0, B 4; 0, M a;4 3 . a4 
Đường trung trục của đoạn thẳng AM đi qua điểm N  ; 2 3  2  và có một vectơ  pháp
tuyến AM  a  4;4 3 nên có phương trình là    a   a 4 4 x    4 3   y2 30  2  2 2  a 32 a  32 4 3   Suy ra J 0;   JH      .  8 3  8 3 3
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 25 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp 2 2 8 3 4 3   4 15 Do đó R       . min        3   3  3
Câu 21. Cho hình chóp S.ABCD có đáy ABCD đáy là hình vuông cạnh a , SA a 3 . Và SA
vuông góc với đáy. M và N là hai điểm thay đổi lần lượt thuộc hai cạnh BC và CD sao cho  0
MAN  45 . Tính tỉ số giữa giá trị lớn nhất và giá trị nhỏ nhất của thể tích khối chóp S.AMN 1 2 1 2 A. 2   2 2 . B. . C. 2 2 1. D. . 6 2 Lời giải 1 a 3 Ta có VS . A SS . S.AMN 3 AMN 3 AMN
Do đó thể tích của khối chóp S.AMN phụ thuộc vào diện tích tam giác AMN
Đặt BM x, DN y; x, y [0; a] . CM
N vuông tại C nên 2 2 2
MN CM CN hay 2 2 2
MN  (a x)  (a y)
Áp dụng định lý hàm số cosin cho AMN ta có: 2 2 2 
MN AM AN  2AM .AM cos MAN 2 2 2 2 2 2 2
 2a x y  2(a x )(a y ) Suy ra 2 2 2 2 2 2 2 2 2
(a x)  (a y)  2a x y  2(a x )(a y ) 2 a ax 2 2 2 2
 (ax ay)  (a xy)  ax ay a xy y a x 2 2 1 a a x 2 SSSSS  (a xy)  . AMN ABCD ABM ADN CMN 2 2 x a 2 2 x a
Xét hàm số f (x) 
trên đoạn [0; a] . x a 2 2
x  2ax a Ta có ' ' f (x) 
; f (x)  0  x  ( 2 1)a . 2 (x a)
Ta lại có f (0)  f (a)  a; f (( 2 1)a)  2( 2 1)a 2 a Suy ra 2 max f (x)  ;
a min f (x)  2( 2 1)a a ( 2 1)  S  . AMN [0;a] [0;a] 2
Vậy tỉ số giữa giá trị lớn nhất và giá trị nhỏ nhất của thể tích khối chóp S.AMN là 1 2 . 2
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 26 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp
Câu 22. Cho hình hộp chữ nhật ABC . D A BCD
  có tổng diện tích tất cả các mặt là 36 , độ dài
đường chéo AC bằng 6 . Hỏi thể tích của khối hộp chữ nhật lớn nhất là bao nhiêu? A. 8 2 . B. 6 6 . C. 24 3 . D. 16 2 . Lời giải
Gọi độ dài các cạnh của khối hộp chữ nhật là AB a, AD b, AA  c .
Vì tổng diện tích tất cả các mặt là 36 nên 2ab  2bc  2ca  36 hay ab bc ca  18  1 .
Lại có: độ dài đường chéo AC bằng 6 nên 2 2 2 2 2 2
a b c  6  a b c  362 . Từ và suy ra:
ab bc ca  18
ab bc ca  18
ab bc ca  18 b
c  18  ab ca          
a b c  36 
a b c  2 2 2 2  72
a b c  6 2 b  
  c  6 2  a  2
Vì: b c2  4bc nên 
a    a   a 2 6 2 4 18 6 2
a  4 2a  0  0  a  4 2 Thể tích khối hộp chữ nhật là:
V abc a   ab c  a  a  a 2 3 18 18 6 2
 18a  6 2a a với 0  a  4 2
Xét hàm số: f t  3 2
t  6 2t 18t , với 0  a  4 2 . t  3 2 f t  2
 3t 12 2t 18 , f t   0   t  2  Bảng biến thiên:
Vậy MaxV f  2   8 2 .
Câu 23. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và đường cao SA  2a . MNPQ
là thiết diện song song với đáy, M SA và AM x . Xét hình trụ có đáy là đường tròn
ngoại tiếp tứ giác MNPQ và đường sinh MA . Giá trị của x để thể tích khối trụ lớn nhất là a 2a a 3a A. x  . B. x  . C. x  . D. x  . 3 3 2 4 Lời giải
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 27 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp S Q M N P Q' A D N' P' B C Ta có:
MNPQ là thiết diện song song với đáy  MNPQ là hình vuông. MN SM A . B SM
a 2a xx Vì MN //AB    MN    a  . AB SA SA 2a 2  x  2
Gọi R là bán kính hình trụ, ta có: R a  .    2  2 2 3 2 2  x  2   x ax a x  Thể tích hình trụ 2
V   .R .x   . a  . .x           2  2 8 2 2     3 2 2 x ax a x 2 2 3x a
Xét f x   
f  x   ax  8 2 2 8 2 x  2a
f x  0    2
x 0; 2a x a  3 Bảng xét dấu 2a x 0 2a 3 f'(x) + 0 - 0 f(x) 2a
Vậy để thể tích khối trụ lớn nhất thì x  3
Câu 24. Cho tứ diện ABCD có tam giác ABC đều cạnh 2a và tam giác ABD vuông tại D , a AD
. Khoảng cách lớn nhất từ B đến mặt phẳng  ACD là? 2 2a 2 a 3 A. . B. a 3 . C. . D. 2a 3 . 2 3 Lời giải
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 28 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp
Giả sử E là hình chiếu của B lên mặt phẳng  ACD . Khi đó d B, ACD  BE .
Gọi H là trung điểm của AC . Suy ra BH AC
Vì BE   ACD  BE EH . Do đó BE BH mà BH a 3 . Suy ra BE lớn nhất bằng
a 3 . Dấu "  " xảy ra khi và chỉ khi E H . 2 2 2 2  a  15a 15a 3a
Khi đó: BD AB AD  2a2 2 2 2 2 2 2 2  
DH BD BH   3a     2  4 4 4 a 2  DH  2
Khi đó điểm D hoàn toàn được xác định như sau: +) Dựng A
BC đều cạnh 2a . Lấy H là trung điểm của AC .
+) Dựng mặt phẳng Q đi qua H và Q  BH , do AC BH tại H nên AC  Q .
+) Trong mặt phẳng Q : D là giao của đường tròn đường kính AH và đường tròn a tâm A bán kính . 2  AD DH a +) Khi đó 
AD BD và AD  . AD BH  2
Do đó, tồn tại điểm D thỏa mãn yêu cầu bài toán để BE a 3 . Vậy d B, ACD lớn nhất là a 3 .
Câu 25. Cho khối chóp tứ giác đều S.ABCD mà khoảng cách từ A đến mặt phẳng SCD
bằng 2a . Gọi  là góc giữa mặt bên của hình chóp với đáy của hình chóp đó. Với giá
trị nào của  thì thể tích của khối chóp S.ABCD đạt giá trị nhỏ nhất? 2 2 A.   arcsin . B. 0   45 . C.   arccos . D. 0   60 . 3 3 Lời giải
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 29 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp S H D A α O M B C
Gọi O là chân đường cao của khối chóp tứ giác đều S.ABCD . Khi đó ta có:
SO   ABCD . 1
Thể tích khối chóp S.ABCD là: V  .S . O S . 3 ABCD Gọi M là trung điểm của CD , ta có: OM CD
 SCD  ABCD   OM SM    , ,  SMO   SM CD
Từ đó suy ra: CD  SOM  .
Từ O kẻ OH SM tại H . Mà OH CD . 1
Do vậy: OH  SCD nên d O,SCD  OH d  ,
A SCD  a . 2 x x
Gọi AD x OM  , SO OM .tan   . tan . 2 2
Xét tam giác OSM vuông tại O có OH là đường cao. Khi đó ta có: 1 1 1 1 4 4      2 2 2 2 2 2 2 OH OM SO a x x . tan  2 1 4.tan   4 2 2 2  
x . tan   a .4 2 1 tan  2 2 2  a x . tan  1 2a 2 2 2 2 2 2
x .tan   a .4.
x .sin   a .4  x  2 cos  sin x a a 2 4a
Như vậy: SO  .tan  . tan   ; 2 Sx  . 2 sin  cos ABCD 2 sin  2 3 1 1 a 4a 4a 1 Vậy V  . . SO S  . .  . . ABCD 2 3 3 cos sin  3 cos  2 1 cos   1
Thể tích đạt giá trị nhỏ nhất khi
đạt giá trị nhỏ nhất hay cos  2 1 cos   y    2 cos
1 cos   đạt giá trị lớn nhất. Xét hàm số y    2 cos 1 cos   , 0 0   0 ;90    .
Đặt t  cos,t 0  ;1 . Khi đó: 3
y t t , t 0  ;1 .
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 30 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp 1 Ta có: 2 2
y '  1 3t ;
y '  0  1 3t  0  t  (do t 0  ;1 ) . 3 Bảng biến thiên: Dựa vào bảng biến thiên ta thấy y khi max 1 1 2 2 t   cos   sin     arcsin . 3 3 3 3
Câu 26. Cho hình chóp SABCD , có đáy ABCD là hình thoi cạnh a , SA SB SC a .Đặt
x SD 0  x a 3 Tìm x theo a để tích AC.SD đạt giá trị lớn nhất. a 3 a 3 a 6 A. x  . B. x  . C. x  . D. Đáp án khác. 2 3 2 Lời giải S A D B C
Gọi O là tâm hình thoi ABCD ta có OB OC
Theo đề bài SA SC nên S
AC cân tại S do đó SO OC Ta có SOC B
OC do OC chung, SC BC a ,   90o SOC BOC
nên SO OB
Mà OB OC nên OB OC SO do đó SBD vuông tại S 2 2 2 2 BD SB SD a x Ta có OB    ; 2 2 2 2 2 a x 2 2 2 2 2
AC  20C  2 BC OB  2 a   3a x 4 Suy ra 2 2
AC.SD  3a x x 2 2 2 2
3a x x 3a
Áp dụng bất đẳng thức Cô- si ta có 2 2
3a x x   2 2 a 6 Dấu "  " xãy ra khi 2 2 2 2 2
3a x x  3a x x x  2
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 31 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp a 6 Vậy x  thì tích A .
C SD đạt giá trị lớn nhất suy ra chọn C 2
Câu 27. Cho tứ diện S.AB D
C và M là một điểm di động, nằm bên trong tam giác ABC .
Qua M kẻ các đường thẳng song song với ,
SA SB, SC cắt các mặt phẳng tương ứng
SBC, SAC, SAB lần lượt tại A', B ',C '. Khi đó giá trị lớn nhất của biểu thức MA ' MB ' MC '
MA ' MB ' MC ' T     . . là SA SB SC SA SB SC 9 28 62 13 A. . B. . C. . D. 8 27 27 8 Lời giải
Do MA'/ /SA nên bốn điểm này cùng nằm trong một mặt phẳng. Giả sử MA ' EM S
E BC  MA', SA . Khi đó ,
A E, M thẳng hàng và ta có MBC   . SA EA SABC MB ' S MC ' S Tương tự ta có: MAC  , MAB  . SB S SC S ABC ABC MA ' MB ' MC ' S S S S Khi đó MBC MAC MAB ABC P         1 . SA SB SC S S S S ABC ABC ABC ABC
MA ' MB ' MC '
Mặt khác, áp dụng bất đẳng thức Cauchy cho các số , , ta được: SA SB SC MA ' MB ' MC '
MA ' MB ' MC ' 3    3 . . SA SB SC SA SB SC
MA ' MB ' MC ' 3  P  3 . . . SA SB SC 3
MA ' MB ' MC '  1  1  . .     SA SB SC  3  27 MA ' MB ' MC '
MA ' MB ' MC ' 1 28 Suy ra T     . .  1  T  . SA SB SC SA SB SC 27 27 28 MA ' MB ' MC '
Vậy giá trị lớn nhất của T  . Dấu “=” xảy ra khi   . 27 SA SB SC
Câu 28. Trong không gian với hệ trục tọa độ .
O xyz , cho điểm A ; a ;
b c với a; ; b c là các số a 1
thực dương thỏa mãn  2 2 2
5 a b c   9ab  2bc ca và Q   có 2 2 b c
a b c3
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 32 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp
giá trị lớn nhất. Gọi M , N , P lần lượt là hình chiếu vuông góc của A lên các tia
Ox; Oy; Oz . Phương trình mặt phẳng MNP là
A. x  4y  4z 12  0.
B. 3x 12y 12z 1   0.
C. x  4y  4z  0 .
D. 3x 12y 12z 1  0 . Lời giải 2 t 2 t
Đặt t b c t  0 2 2  b c  ; bc  . 2 4  2 2 2 2
5 a b c   9ab  2bc ca 2
 5a  5b c  9a b c  28bc 2 2 2
 5a  5t  9at  7t
 5a ta  2t  0  a  2t . 4 1 Vậy Q  
f t với t  0. 3   t 27t 4 1 1
Ta có f t      0  t  . 2 4 t 9t 6 Ta có bảng biến thiên 1 1 Vậy Q  16  a  ; b c  . max 3 12  1 1 1   1   1   1 
Suy ra tọa độ điểm A ; ; 
 ; tọa độ các điểm M ; 0; 0   ; N 0; ; 0   ; P 0; 0;   .  3 12 12   3   12   12  x y z
Phương trình mặt phẳng MNP  
 1  3x 12 y 12z 1  0 . 1 1 1 3 12 12
Câu 29. Trong mặt phẳng   cho đường tròn T  đường kính AB  2R . Gọi C là một diểm
di động trên T  . Trên đường thẳng d đi qua A và vuông góc với mặt phẳng   lấy
điểm S sao cho SA R . Hạ AH SB tại H , AK SC tại K . Tìm giá trị lớn nhất Vmax
của thể tích tứ diện SAHK . 3 R 5 3 R 5 3 R 3 3 R 3 A. V  . B. V  . C. V  . D. V  . max 75 max 25 max 27 max 9 .Lời giải
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 33 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp S H F E K I B A C BC AC
Ta có BC SA
BC  SAC   BC AK .
AC,SA  SAB   AK SB
Lại có AK BC
AK  SBC  AK SB   1 . S ,
B BC  SBC 
Ta có SB AH 2 . Từ  
1 , 2 suy ra SB   AHK  tại H nên suy ra SH đường cao của khối chóp S.AHK . 1 Ta có: VVSH .S . SAHK S . AHK 3 AHK
Do S , A, B cố định nên SH không đổi. Do đó thể tích của khối chóp S.AHK đạt giá
trị lớn nhất khi và chỉ khi S
đạt giá trị lớn nhất. AHK
Ta có BC  SAC  BC AK mà AK SC AK  SBC , KH  SBC   AK HK .
Gọi E là trung điểm của AH , F là hình chiếu vuông góc của K xuống AH . 1 Ta có: S  .AH.KF . AHK 2
Mặt khác do độ dài đoạn AH không đổi nên S
đạt gái trị lớn nhất khi và chỉ khi AHK KF là lớn nhất.
Ta có độ dài đoạn KF có giá trị lớn nhất khi và chỉ khi F trùng với trung điểm E của AH . AH Hay KFKE  . max 2 2 2 SA R R 5
Xét SAB vuông tại A có: 2
SA SH .SB SH    SB R 5 5 . SA AB .2 R R 2 5R và AH.SB  . SA AB AH    . SB R 5 5 2 2 1 AH AH R
Diện tích lớn nhất của AHK là S  .AH   . max 2 2 4 5
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 34 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp 2 3 1 1 R 5 R R 5 Vậy V  .SH.S  . .  . max max 3 3 5 5 75
Câu 30. Cho tứ diện đều ABCD có cạnh bằng 1. Hai điểm M , N di động trên các cạnh
AB , AC sao cho mặt phẳng  DMN  vuông góc mặt phẳng  ABC  . Gọi S , S lần lượt 1 2 S
là diện tích lớn nhất và nhỏ nhất của tam giác AMN . Tính 1 T  . S2 8 9 8 9 A. T  . B. T  . C. T  . D. T  . 9 8 7 7 Lời giải D C P B N H M A
 Gọi H là hình chiếu của D trên MN DH MN .
DMN  ABC  MN và  DMN   ABC  . Do đó DH  ABC .
Mà ABCD là tứ diện đều nên H là tâm đường tròn ngoại tiếp của tam giác đều ABC
hay H là trọng tâm tam giác đều ABC .
 Đặt AM x , AN y 0  x, y   1 . 1 1 3 xy 3
Diện tích tam giác AMN là 0 S
AM .AN.sin 60  . . x y.  . AMN 2 2 2 4 3 2 2 3 3
 Gọi P là trung điểm của BC AP   AH AP  .  . 2 3 3 2 3 1 1 1 3 1 1 3 1 Mà 0 0 SSS
AM .AH .sin 30 
AN.AH .sin 30  . . x .  .y. . . AMNAMHANH 2 2 2 3 2 2 3 2 xy 3 1 3 1 1 3 1 x y Suy ra  . . x .  . . y .  xy  
x y  3xy . 4 2 3 2 2 3 2 3 3
 Đặt xy t x y  3t x , y là nghiệm của phương trình 2
a  3ta t  0 . 2
a  3a  
1 t * , với t 0  ;1 . 1 1
 Nếu a  , * trở thành  0 . 3 9 a  0 1 2 a 2 3a  2a
 Nếu a  , thì * trở thành t  *  *  t   t  0     2 . 3 2 3a 1 3a   1 a   3 BBT:
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 35 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp 1 2 a 0 1 3 3 t' 0 0 + 0 + ∞ 1 t 2 4 ∞ 9
 Để tồn tại hai điểm M , N thỏa mãn bài toán thì * 
* có hai nghiệm thuộc tập 0  ;1 . 4 1   t  . 9 2 1 3 Vậy max t
khi a  1 hay S  . 1 D 2 8 4 2 3 min t  khi a  hay S  . 2 D 9 3 9 S 9 Vậy 1  . S 8 2
Câu 31. Cho lăng trụ tam giác đều ABC.A' B 'C ' với độ dài tất cả các cạnh đều bằng a. Xét tất
cả các đoạn thẳng song song với mặt phẳng  ABB ' A' và có một đầu E nằm trên
đường chéo A'C của mặt bên AA'C 'C , còn đầu kia F nằm trên đường chéo BC ' của
mặt bên BB 'C 'C . Hãy tìm độ dài ngắn nhất của các đoạn thẳng này. 2a a a 2a A. . B. . C. . D. . 5 5 5 5 Lời giải
Gọi H là trung điểm của AC . Chọn hệ trục tọa độ Hxyz như hình vẽ.  a   a   3a   a   3a
Ta có H 0;0;0 , A ;0;0   , C ;0;0   , B  0; ;0  , A' ;0; a   , B ' 0; ; a   2   2  2    2  2    aC ' ;0; a   .  2    a 3aa   BC '    ;
; a    u , với u 1; 3; 2
  . Phương trình tham số của đường 2 2 2   
thẳng BC ' đi qua điểm C ' có vec tơ chỉ phương u 1; 3; 2  
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 36 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp  a x   t  2    a   y  3t
. Do F BC ' nên F
t; 3t; a  2t     2 
z a  2t      
A'C  a;0;a  au ', với u '1;0; 
1 . Phương trình tham số của đường thẳng 
A'C đi qua điểm C có vec tơ chỉ phương u '  1;0;  1  a x   t '  2   a   y  0
. Do E A'C nên Et ';0;t '   .   2  z t '   
EF  t t '; 3t;a  2t t ' .
  a 3a     2 2 2  3a aa AB   ;
; 0 , AA'  0;0;a ,
AB ', AA'   ; ;0   n , với 2 2     2 2 2   n 3;1;0. 
suy ra vec tơ pháp tuyến của mặt phẳng  ABB ' A' : n   3;1;0   
Do EF  ABB ' A' nên EF.n  0  t '  2t suy ra EF   t
 ; 3t; a  4t  Có 2 2 2
EF  20t  8at a f t  . Dễ thấy f t  là một hàm số bậc hai nên f t  đạt a 2 a
giá trị nhỏ nhất tại t
, min f t   . 5 5 a Vậy EF  . min 5
Câu 32. Cho hình chóp tứ giác đều S.ABCD mà khoảng cách từ A đến mặt phẳng SBC
bằng b . Góc giữa mặt bên và mặt đáy của hình chóp bằng  . Tìm  để thể tích của
khối chóp S.ABCD nhỏ nhất.  3   1   2  A.   arccos     arccos 3   arccos   arccos  . B.  . C.   . D.   . 3     3   3  Lời giải
+ Gọi O AC BD và M là trung điểm của BC .
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 37 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp SM BC + Có:   Góc giữa hai mặt phẳng SBC và  ABCD bằng OM BC     
SMO   0       2 
+Trong mặt phẳng SOM  vẽ OH SM (1) . SM BC + Ta có: 
BC  SOM  mà OH  SOM   BC OH (2) OM BC
+ Từ và suy ra OH  SBC   d O,SBC   OH . b + Ta có: d  ,
A SBC   2d O,SBC  2OH b OH  . 2 2 OH OH b b b sin   OM    AB   SABCD 2 OM sin 2sin sin sin  SO b b tan 
SO OM tan   tan   . OM 2sin  2 cos 2 3 1 1 b b bVS . O S   S.ABCD ABCD 2 3 3 2cos sin  6 3 cos  cos  
 Thể tích của khối chóp S.ABCD nhỏ nhất 3
 cos  cos  lớn nhất. 
Đặt cos  t . Vì 0     0  t  1 . 2  3 t   (L)  3 + Xét: 3
f (t)  t t 0  t   1 2
f '(t)  1 3t  0   3 t    3 + Bảng biến thiên 3 b 3  3 
Vậy thể tích của khối chóp S.ABCD nhỏ nhất bằng
đạt được khi   arccos   . 4  3   
Câu 33. Cho hình lăng trụ đều ABC .
D A ' B 'C ' D ' có cạnh đáy bằng a. Điểm M và N lần lượt
thay đổi trên các cạnh BB ' và DD ' sao cho MAC    NAC  và BM x, DN y . Tìm
giá trị nhỏ nhất của thể tích khối tứ diện ACMN . 3 a 3 a 3 a 3 a A. . B. . C. . D. . 3 2 2 2 2 2 3 Lời giải
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 38 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp
Cách 1: Gọi I là trung điểm AC, đặt BB '  , b ta có: 1 1 1 VVVIC.S  . IA SAC.S ACMN AMNI CMNI 3 IMN 3 IMN 3 IMN 1  a 2.SSSS BDD ' B ' MND ' B ' BIM IDN  3 1 
2b x ya 2 . x a 2 . y a 2   a 2. ab 2     3  2 4 4    1  . x a 2 . y a 2  1 2  a 2.   
a x y. 3  4 4  6  
Vì MAC    NAC  nên 2 2 2 a a a
MI IN IM IN MN x   y
a   x y2 2 2 2 2 2 2 2  xy  . 2 2 2 Do đó 3 1 1 a 2 Va x y a xy ACMN    2   . 6 3 3 2 3 a
Vậy thể tích khối tứ diện ACMN đạt giá trị nhỏ nhất là khi x y . 3 2
Cách 2: Gọi I là trung điểm AC.
Dễ thấy ΔMAC, ΔNAC lần lượt cân tại M , N nên MI AC, NI AC AC  MIN  .
Lại có AC  MAC    NAC ;MAC    NAC   MI   NAC   MI NI 2 2 2 a a 2 a Khi đó 2 2 2 2 2 2
MI IN MN x   y
 2a   x y  xy  . 2 2 2 1 1 1 1 VVV  .AI.SCI.S  .AC.S
.IM .IN.AC ACMN AMNI CMIN 3 IMN 3 IMN 3 IMN 6 2 2 2 4 1 a a a 2 a aV  .a 2. x  . y   . xyx yACMN  2 2 2  2 2  6 2 2 6 2 4 2 a 2 4 2 a 2 a 2 a a Mà xy  nên V .  x y xy      x y ACMN   2 .  2 6 2   2 6 Do đó 3 1 1 a 2 Va x y a xy ACMN    2   . 6 3 3 2 3 a
Vậy thể tích khối tứ diện ACMN đạt giá trị nhỏ nhất là khi x y . 3 2
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 39 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp
Câu 34. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA b và
vuông góc với  ABCD . Điểm M thay đổi trên cạnh CD với CM x 0  x a . H là
hình chiếu vuông góc của S trên BM . Tìm giá trị lớn nhất của thể tích khối chóp
S.ABH theo a, b . 2 a b 2 2 2 a b a b a b A. . B. . C. . D. . 12 24 8 18 Lời giải 2 2 1 1 1 b b AH BH Ta có V  .S . A S  . . b AH.BH  .AH.BH  . SABH 3 ABH 3 2 6 6 2 2 b . b a 2  V  .AB V  . SABH 12 SABH 12
Dấu “=” xảy ra khi và chỉ khi     45o    45o AH BH ABH ABMM D .
Câu 35. Cho tứ diện đều SABC có D là điểm thuộc cạnh AB sao cho BD  2 AD , I là trung
điểm của SD . Một đường thẳng d thay đổi qua I cắt các cạnh SA , SB lần lượt tại M , 3 3  m a
N . Biết AB  2a . Khi d thay đổi, thể tích khối chóp S.MNC nhỏ nhất bằng .   ,  n m với , m n  ,  ,
m n  1. Tính m n .
A. m n  4 .
B. m n  6 .
C. m n  7 .
D. m n  5 . Lời giải
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 40 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp
Gọi H là tâm đường tròn ngoại tiếp tam giác ABC . Vì SABC là tứ diện đều và
AB  2a nên suy ra SH   ABC , H là trọng tâm tam giác đều ABC và 2 2a 3 2a 3 AH  .  . 3 2 3 2  2a 3  2a 6
Từ đó suy ra SH SA AH  2a2 2 2     .  3  3   1 1 2a 6  a2 3 2 3 2a 2 Vậy VSH.S  . .    1 . SABC 3 ABC 3 3 4 3 SM SN Đặt  k,
l , 0  k, l  1. SA SB S SM SN Ta có: SMN  . . S SA SBSAB S S 2S 1 SM SI 2 SN SI Mặt khác SMNSMI SNI    . .  . . S 3S 3S 3 SA SD 3 SB SDSAB SAD SBD 1 1 2 1 k
Nên ta có k.l  .k.  .l.  6kl k  2l l  2 . 3 2 3 2 2 3k   1 0  k  1 0  k  1  2 Vì  nên  k
k  1  3k 1  0 . 0  l  1  0   1 5  23k   1  V SM SN SC Ta có: SMNC  . .
k.l Vk.l.V 3 . SMNC SABC V SA SB SC SABC 3 3 2 k 2a 2 a 2 9k Từ  
1 , 2 , 3 ta có Vk. .  . S.MNC 23k   1 3 27 3k 1 3 3 a 2  1  a 2  1   V  . 3k 1  . 3k 1  2 . S .MNC     27  3k 1  27  3k 1 
Áp dụng bất đẳng thức Cô-si với hai số dương, ta có: 3 3 3 3 a 2  1  4a 2  2  a V  . 2. 3k 1 .  2    . . S .MNC     27  3k 1   27  3  2   1 2
Dấu “=” xảy ra  3k 1   3k  2 1  1  k  . 3k 1 3 3 3  2  a 2 Vậy V min  .  k  . S .MNC    3  2 3 3 3  m a
Theo đề bài, thể tích khối chóp S.MNC nhỏ nhất bằng .   , với , m n  ,  n m  ,
m n  1 nên ta có m  2, n  3 , suy ra m n  5 .
Câu 36. Cắt một khối trụ tròn có chiều cao h bởi một mặt phẳng song song với hai mặt đáy ta
thu được hai khối tròn nhỏ. Một trong hai khối đó ngoại tiếp một lăng trụ đứng thể
tích V có đáy là tam giác có chu vi là p. Khối còn lại ngoại tiếp một khối nón có bán
kính là R . Tìm giá trị của R sao cho thể tích của khối nón là lớn nhất? 3  p 3 hp 3  p 3 p A. R  . B. R  . C. R  . D. R  . 162V 162V 162 162V Lời giải
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 41 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp
Hình lăng trụ có đáy là tam giác có độ dài 3 cạnh là a,b,c có chiều cao là x abc abc abc Khi đó S
và thể tích của hình lăng trụ làV  . x .Suy ra R  . x  4R 4R 4V
Áp dụng bất đẳng thức Cauchy cho 3 số dương a,b,c ta có
a b c3 3 p R  . x  . x 27.4V 108.V 2 6 1 1 x p Mặt khác 2 V
 . h x R h x H  . . . . .   3 3 108V 2
Xét hàm số f x  h x 2
.x với 0  x h 2h f   x 2
 3x  2hx Suy ra f x 2  0  3
x  2hx  0  x  3 Bảng biến thiên  2h  4
Từ đó f x 3  f  .h    3  27 6 1 4 p Do đó 3 V  . . .h . H  3 27 108V 2 6 1 4 p 2h V m   h khi x
và a b c H  ax  3 . . . .   3 27 108V 2 3 3 3 2h p hp Khi đó R  .  3 108.V 162.V
Câu 37. Người ta cần trang trí một kim tự tháp hình chóp tứ giác đều S.ABCD cạnh bên bằng 200 m ,  0
ASB  15 bằng đường gấp khúc dây đèn led vòng quanh kim tự tháp
AEFGHIJKLS trong đó điểm L cố định và LS  40m .
Khi đó cần dùng ít nhất bao nhiêu mét dây đèn led để trang trí?
A. 40 67  40 mét.
B. 20 111  40 mét. C. 40 31  40 mét. D. 40 111  40 mét. Lời giải
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 42 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp
Cắt hình chóp theo SA rồi trải phẳng ( H trùng với H  ). Lấy điểm L A  sao cho
SL  SL , P đối xứng với L qua SA . Ta có:
AE EF FG GH H I  IJ JK KL AH H L
  AH HL  AH HP AP .
Áp dụng định lí Cô-sin trong ASP ta được: 2 2 2  2 2 0
AP AS SP  2.AS.S .
P cos ASP  200  40  2.200.40.cos120  49.600  AP  40 31 .
Vậy độ dài đèn led ngắn nhất là 40 31  40
Câu 38. Chohình chóp S.ABC có các cạnh bên bằng 1. Mặt phẳng   thay đổi luôn đi qua
trọng tâm của hình chóp, cắt ba cạnh bên S ,
A SB, SC lần lượt tại D, E, F . Tìm giá trị 1 1 1
lớn nhất P của P    . max S . D SE SE.SF SF.SD 4 16 4 3 A. . B. . C. . D. . 3 3 3 4 Lời giải
Gọi I là trọng tâm ABC . Ta có:
    
SA SB SC  3SI  Ta có: 
SA  
SB   SC  . SA SD; SB  .SE ; SC  .SF   SD SE SF
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 43 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp  3  1    Mà ta có SG SI
SASB SC 4 4
   
 4SG SA SB SC  SA  SB  SC   4SG SD  .SE  .SF SD SE SF  SA  SB  SC   SG SD  .SE  .SF 4SD 4SE 4SF  1  1  1   SG SD  .SE  .SF 4SD 4SE 4SF 1 1 1 Do
D, E, F ,G đồng phẳng nên    1 4SD 4SE 4SF 1  1 1 1  1 1 1     1     4   4  SD SE SF SD SE SF 2 1 1 1 1  1 1 1  Ta lại có P         . S . D SE SE.SF SF.SD 3  SD SE SF
Dấu "  " xảy ra khi SD SE SF . 2 1 1 1 1  1 1 1  16 Vậy P          . SD SE SE.SF SF.SD 3  SD SE SF  3 3
Dấu "  " xảy ra khi SD SE SF SA . 4 16 Vậy PMax 3
Câu 39. Cho hình lập phương ABC .
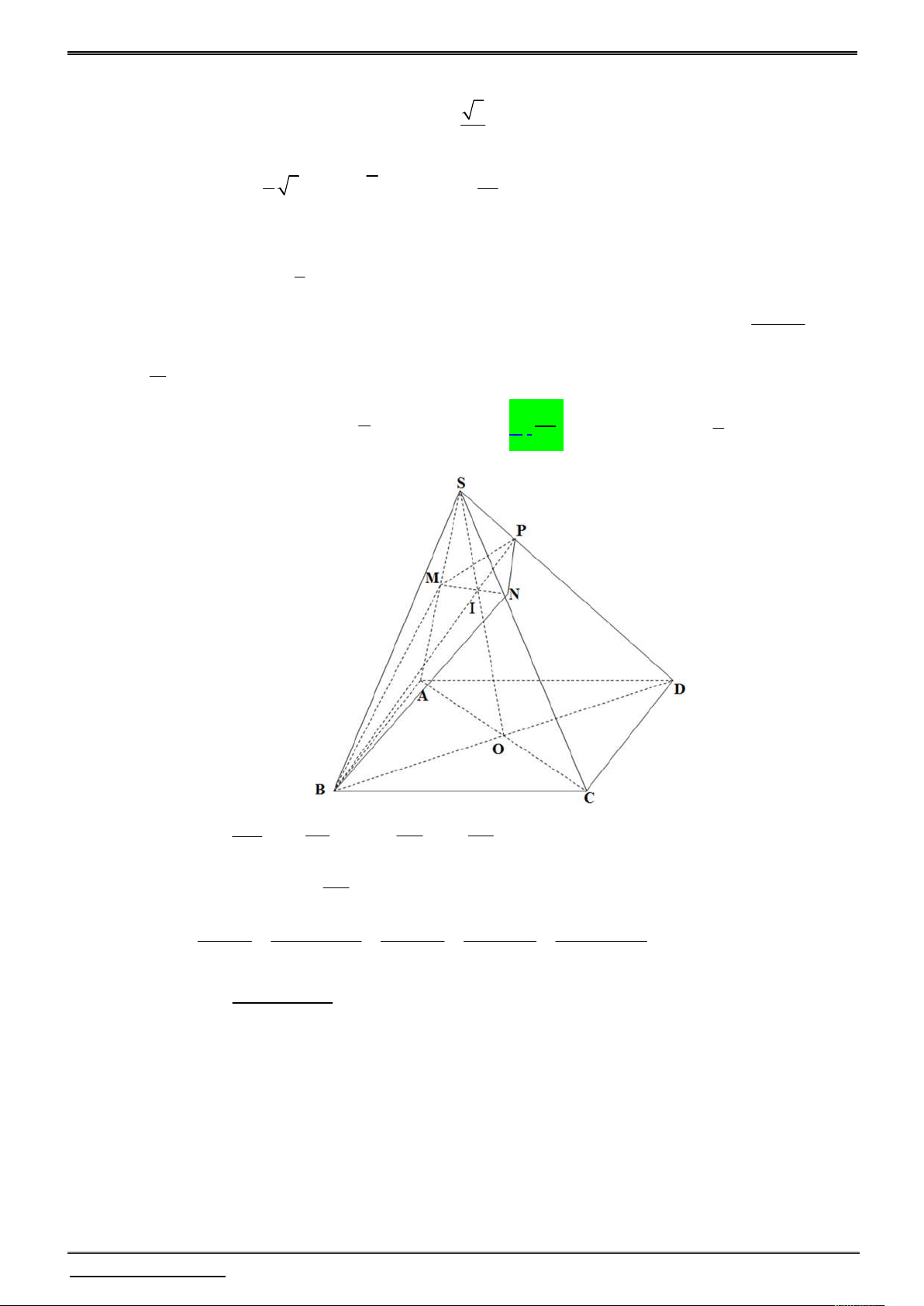
D A' B 'C ' D ' có cạnh bằng a . G là trung điểm của BD ' ,
mặt phẳng  P thay đổi qua G cắt AD ',CD ', B ' D ' tương ứng tại H , I, K . Tìm giá trị 1 1 1
lớn nhất của biểu thức T    .
D ' H . D ' I
D ' I. D ' K
D ' K. D ' H 8 2 16a 2 8a 16 A. . B. . C. . D. . 2 3a 3 3 2 3a Lời giải
Bổ đề: Cho tứ diện SABC có SA SB SC a . Một mặt phẳng (P) thay đổi qua trọng 1 1 1 4
tâm G của tứ diện lần lượt cắt ,
SA SB, SC tại M , N , P . CMR :    . SM SN SP a Chứng minh:
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 44 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp
Gọi G là trọng tâm A
BC . Theo tính chất trọng tâm của tứ diện ta có S , G, G thẳng SG 3 hàng và  . SG 4 1 Thêm nữa VVVV . SABGSBCGSG CA 3 SABC Ta có: V SM SN SG 3V 3SM .SN V SM .SN SMNG  . . SMNG SMNG       1 . 2 2 V SA SB SGV 4a V 4a SABGSABC SABC V SN.SP V S . P SM
Lập luận tương tự thu được SNPG  2 và SGPM  3 . 2 V 4a 2 V 4a SABC SG CA
Cộng theo vế các đẳng thức  
1 , 2 , 3 ta được V
SM .SN SN.SP S . P SM SM SN SP
SM .SN SN.SP S . P SM SMNP   . .  2 V 4a 2 SA SB SC 4a SABC 2 1 1 1 4
a SM SN SP  SM SN SN SP SP SM  3 4 . . . . . . .a     . . SM SN SP a
Xét hình lập phương ABC .
D A' B 'C ' D ' . Ta có hình chiếu của D ' B lên mặt phẳng
ABCD là DB , trên  ABCD ta có DB AC nên D ' B AC .
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 45 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp
Tương tự, ta có D ' B B 'C . Từ đó suy ra D ' B   B ' AC  .
Xét tứ diện D ' AB 'C là tứ diện đều cạnh bằng a 2 . Vì D ' B   B ' AC  nên D ' B là
đường cao của tứ diện. 3
Gọi G ' là giao điểm của D ' B với  B ' AC , ta chứng minh được D 'G D 'G ' 4
Vì tứ diện D ' AB 'C là tứ diện đều nên G là trọng tâm của tam giác B A
C , suy ra G
là trọng tâm của tứ diện D AB C  . 2 1 1 1 1  1 1 1  Ta có: T           1
D ' H. D ' I
D ' I. D ' K
D ' K. D ' H 3  D ' H D ' I D ' K
ÁP DỤNG Bổ đề trên: Xét tứ diện D ' AB 'C là tứ diện đều cạnh bằng a 2 , ta có 1 1 1 4    2 D ' H D ' I D ' K a 2 Từ   1 ,2 ta được 2 2 1 1 1 1  1 1 1  1  4  8 T        .      . 2
D ' H. D ' I
D ' I. D ' K
D ' K. D ' H 3  D ' H D ' I D ' K  3  a 2  3a
Câu 40. Cho hình hộp chữ nhật ABC .
D A' B 'C ' D ' có AC a, AD '  b, CD '  c . Tìm thể tích lớn
nhất của hình chữ nhật đã cho khi a,b,c thay đổi, còn chu vi tam giác ACD ' không đổi. Lời giải
Đặt AD  d ,CD  r, DD '  h Ta có: 2 2 2
a d r  2dr  0  2 2 2 abc b
  d h  2dh  0 2 2 2 2 2 2        a b c 8d h r abc 2 2dhr V .  2 2 2 2 2
c h r  2hr  0  3 3
a bck 3   k 2 Mà abc     V  . 3  nên 27 max 108
 d r h  k
Dấu "  " xảy ra khi và chỉ khi 
k d r h  . a
  b c   3 2  3
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 46 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp
Câu 41. Cho tứ diện ABCD, AB  ,
x CD y, các cạnh còn lại của tứ diện bằng a 2, x, y thay
đổi sao cho x y  2 . a Khi V
đạt giá trị nhỏ nhất, tính cosin của góc giữa  ABCABCD và  ABD. Lời giải
-Gọi M , N lần lượt là trung điểm AB, . CD
MN AB,CD
 MCD  AB -Gọi  
ABC ABD  ,
 MD MC  ,
-Coi a 1  x y  2  2 2 8 1 1 x y  1 V  . AB Sxyxy 4  2xy. ABCD 3 MCD 6 4 12 2 (x y) -Đặt t xy 0 t     1. 4
Xét hàm số f t 1 
t 4  2t , với 0  t 1. 12 1  t  1  4  3t      
Ta có: f t   4  2t      0, t  0;  1 .     12 4  2t 12 4  2t     
Maxf t f   6 1  . 12 6  MaxV  . ABCD 12 7
"  "  x y  1  MC MD  . 2  2 2 2MC CD 5 5 cos DMC    cos . 2 2MC 7 7
Câu 42. Cho hình chóp SABCD có đáy là ABCD là hình vuông cạnh a , cạnh SA a và vuông
góc với mp ( ABCD). M là điểm di động trên đoạn BC và BM x 0  x a , K là
hình chiếu của S trên DM.
a) Tính độ dài đoạn SK theo a và x .
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 47 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp
b) Tìm min của đoạn SK. Lời giải S A D K x M a-x C B
a) Do DM SA và DM SK nên DM AK. Ta có:   AK DC AK a 2 a
sin ADK  cos MDC      AK AD DM a 2
a  a x2 2 2
a  a x 4 2 a a Suy ra 2 2 2 SK SA AK a   a 1
a  a x2
a  a x2 2 2 2 a
b) Do SK a 1
nên SK nhỏ nhất khi   2 a
x lớn nhất hay x  0 .
a  a x2 2 a 6 Vậy minSK  khi x  0. 2
Câu 43. Cho hình chóp S.ABCD có tứ giác ABCD là hình bình hành tâm O . Điểm C di động
trên cạnh SC ( C khác điểm S và C ). Mặt phẳng  R chứa đường thẳng AC và
song song với BD . Mặt phẳng  R cắt đường thẳng SB , SD lần lượt tại B, D .
1/ Gọi F là giao điểm của AD với B C
  . Chứng minh rằng F luôn di động trên một
đường thẳng cố định khi C di động trên SC . SCBB 5 SD
2/ Xác định vị trí của điểm C sao cho tổng  3  .
đạt giá trị nhỏ nhất. CCSB 2 DD
Lời giải
1/ Qua S kẻ đường thẳng d //AD  SAD  SBC   d .
Xét các mặt phẳng SAD, SBC ,  AB CD   có:
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 48 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp
SAD  SBC   d
SADAB CD  AD 
nên d , AD , B C
  đồng quy tại F . SBC     AB CD    B C    AD B C    F
Khi đó J d cố định. SA SC SB SD SC SB 2/ Ta có:     1  2 . SA SCSBSDSCSB Lại có: SC 1 1 1 1 1 1 i)         1 CCCCSC SCSC SC SBSB  1 1 2 2  2 2 1 SC SC SC SC SB         SB  BBSB SB  SB  ii) 3  3  3 1   2 SBSB  SB  5 SD 5 1 5 5 5 iii)     3 2 DD 2 DD
2 SD SD  SD   SB  2 1 2 1 SD      SD  SD   SB  SCBB 5 SD 1  SB  5 Từ , , ta có:  3  .   3 1    CCSB 2 DD  SB   SB   SB  2 1 2 1     SBSB     3  SB    3 1  6  SB     SB 1      SB  SB SB SC Dấu bằng xảy ra  1  1   2   3 . SBSBSCSC
Vậy tổng nhỏ nhất khi C thuộc đoạn SC thỏa  3. SC
Câu 44. Trong mặt phẳng  cho hình chữ nhật ABCD có AB a; BC  2a . Các điểm M , N lần
lượt di chuyển trên các đường thẳng m, n vuông góc với mặt phẳng   tại , A B sao
cho DM CN . Tìm giá trị nhỏ nhất của khối tứ diện CDMN . Lời giải
Đặt hệ trục tọa độ như hình vẽ, coi a  1.
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 49 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp
Do đó A0;0;0, B1;0;0, C1; 2;0, D 0; 2;0 .  
Đặt AM x, BN y M 0;0; x, N 1;0; y suy ra DM 0; 2  ; x ,CN 0; 2  ; y .  
Mà DM CN nên DM .CN  0 . 4
 0.0  2.2  xy  0  xy  4  y  . x    CD  1  ;0; 0;CM  1  ; 2  ; x ;CN 0; 2  ; y .  
  
 CD, CM   0; x; 2  CD,CM .CN  2x  2 y .    
1    1  V
CD,CM  .CN  2x  2 y . CDMN 6   6 1 4 1 4 4  V  x   .2 . x  . CDMN 3 x 3 x 3 3 4a Vậy V min  . CDMN 3
Câu 45. Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AB song song với CD ,
AB  2CD , các cạnh bên có độ dài bằng 1. Gọi O AC BD , I là trung điểm của SO .
Mặt phẳng   thay đổi đi qua I và cắt các cạnh S ,
A SB, SC, SD lần lượt tại M , N , P, Q 1 1 1 1
. Tìm giá trị nhỏ nhất của biểu thức T     . 2 2 2 2 SM SN SP SQ Lời giải Nhận xét:    
I thuộc đoạn MP thì với điểm S bất kỳ, ta có mSI nSM pSP m n p . SA SC Đặt x  ; y  . SM SP
 1  1         
  1  1  SI SO  SAAO 1 2 1 2 2  SA AC SA SC SA      SA SC 2 2 2  3  2  3 3  6 3 x  y   SM SP . 6 3
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 50 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp x y SA SC 1 2
Vì I thuộc đoạn MP nên 1  
x  2 y  6   2  6    6 . 6 3 SM SP SM SP 1 2 Chứng minh tương tự   6 . SN SQ 2 1 1 2 2  1 1 2 2  Ta có 2     12  12       SM SN SP SQ SM SN SP SQ      1 1 1 1  144 72 2 2 2 2 1 1  2  2    
 10T T    . 2 2 2 2  SM SN SP SQ 10 5   72 1 1 1 1 1 1 Vậy T  , đạt được khi   
 3  SM SN  ; SP SQ  . min 5 SM SN 2SP 2SQ 3 6
Câu 46. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi E là trung điểm của SC
. Mặt phẳng   thay đổi nhưng luôn chứa AE cắt SB , SD lần lượt tại M , N . Xác SM SN
định vị trí của M , N trên các cạnh SB , SD sao cho 
đạt giá trị lớn nhất. SB SD Lời giải S M E I A B N O D C
Trong  ABCD gọi O AC BD , trong mp   gọi I AE MN . Khi đó ta có I AE   SAC + 
I SO  SAC    SBD suy ra I là trọng tâm tam giác SAC . I MN   SBD  V V 1 SM SE 1 SM + S.AME S . AME    V 2V 2 SB SC 4 SB S . ABCD S . ABC V V 1 SN SE 1 SN + S.ANE S . ANE    V 2V 2 SD SC 4 SD S . ABCD S . ACD V VV 1  SN SM  Suy ra S.AMEN S . ANE S. AME        1 V V 4  SD SB S .ABCD S . ABCDV V 1 SM SN + S.AMN S . AMN   V 2V 2 SB SD S . ABCD S . ABD V V 1 SM SN SE 1 SM SN + S.MEN S .MEN    V 2V 2 SB SD SC 4 SB SD S . ABCD S .BCD V VV 3 SN SM Suy ra S.AMEN S . AMN S .MEN   2 V V 4 SD SB S . ABCD S . ABCD
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 51 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp 1  SN SM  3 SN SM SN SM SN SM Từ   1 và 2 ta có      3   4  SD SB  4 SD SB SD SB SD SBSN x   SD xx y 1 Đặt 
0  x, y  
1 vậy ta có x y  3xy suy ra 1 , 0 y    x  1 SM  3x 1 2  y   SB SM SN x 1 1 Ta có 
x y x   x    f xSB SD 3x   1 3 33x   1 1 1 1 
Xét f x  x   , x  ;1 3 33x  1 3     1  x ;1 1 3x 1  1   2 f ' x 3  1  0    x   3x  2 1 3x 1  1 3  Bảng biến thiên  1
x  1  y   SM SN  3  Vậy ta có 2 Max
 max f x    đạt được khi   SB SD  1  1  2  ;1  x   y  1 2     2
Khi đó N D , M là trung điểm SB hoặc M B , N là trung điểm SD
Câu 47. Cho tứ diện OABC có các cạnh O ,
A OB, OC đôi một vuông góc. Gọi M là điểm thuộc
miền trong của tam giác ABC . Tìm giá trị nhỏ nhất của biểu thức 2 2 2 MA MB MC T    2 2 2 OA OB OC Lời giải
Gọi N  AM  BC , kẻ MM / / OA thì ta có 1
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 52 -
Taøi lieäu hoïc theâm moân Toaùn 12 – oân thi ñaïi hoïc
Lôùp Toaùn Thaày Nghieäp O  A  (OBC)   MM  (OBC) 1 MM / /OA  1
kẻ MA  OA, A  OA . Khi đó 1 1 2 2 2 2 2 2
AM  AA  MA  AA  MO  OA 1 1 1 1 2
 OM AA OA AA  OA 1 1  1 1  2  OM  OAOA 2OA 1  2 2  OM  OA  2OA  OA 1 2 2 AM OM 2OA Suy ra 1  1 (1) . 2 2 OA OA OA
Tương tự gọi B ,C là các điểm tương tự như A thì ta có 1 1 1 2 2 MB OM 2OB1  1 2 2 OB OB OB 2 2 MC OM 2OC1  1 (3) 2 2 OC OC OC  1 1 1  OA OB OC  Từ (1),(2),(3) ta có 2    1 1 1 T OM     2      3 2 2 2 OA OB OC   OA OB OC 
Gọi H là trực tâm của tam giác ABC thì ta dã biết kết quả quen thuộc 1 1 1 1 2      OM OA OB OC nên 1 1 1 T   2      3 2 2 2 2 OA OB OC OH 2 OH  OA OB OC  OA NM S Mặt khác 1 MhC   OA NA SABC OB S OC S OA OB OC Tương tự 1 MAC 1 MAB  ,  nên 1 1 1   1 OB S OC S OA OB OC ABC ABC 2 OM Do đó T  1 2 do OM  OH . 2 OH
Vậy min T  2 khi M  H .
----------HẾT----------
Giaùo vieân giaûng daïy: Phaïm Vaên Nghieäp Trang - 53 -