Một số bài toán liên quan đến tỷ số thể tích khối đa diện

Tài liệu gồm 45 trang, được biên soạn bởi thầy giáo Lê Bá Bảo, hướng dẫn phương pháp giải một số bài toán liên quan đến tỷ số thể tích khối đa diện trong chương trình môn Toán 12 phần Hình học..Mời bạn đọc đón xem.

97 49 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Khối đa diện

Môn: Toán 12

Thông tin:

45 trang 8 tháng trước

Tác giả:

Profile Lan Tường
THỂ TÍCH KHỐI ĐA DIỆN
TOÁN 12
LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ
TỶ SỐ THỂ TÍCH
LUYỆN THI THPT QUỐC GIA
CẬP NHẬT TỪ ĐỀ THI MỚI NHẤT
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <1 >
CHUY£N §Ò:
THÓ TÝCH KhèI §A DIÖN
Líp To¸n thÇy L£ B¸ B¶O
Trường THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10
Hương
Trµ
, HuÕ.
VÊn ®Ò 2:
Tû sè thÓ tÝch
CÁC KẾT QUẢ CẦN LƯU Ý
Hình
1) Tam giác
A'
B'
O
A
B
''
''
.
OA B
OAB
S
OA OB
S OA OB
2) Hình chóp tam giác
C'
C
S
A
B
A'
B'
.
. ' ' '
.
' ' '
.
S A B C
S ABC
V
SA SB SC
V SA SB SC
3) Hình chóp tứ giác có đáy là hình bình
hành
A'
B'
C'
D'
D
C
B
A
S
Tæng
TÝch
.
.
44
S A B C D
S ABCD
V
a b c d
V abcd

; ; ;
SA SB SC SD
a b c d
SA SB SC SD
, , ,A B C D
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <2 >
4) Hình lăng trụ tam giác
M
N
P
C'
B'
A'
A
B
C
.
.
1
3
ABC MNP
ABC A B C
V
AM BN CP
V AA BB CC



5) Hình hộp
Q
M
N
P
D'
A'
B'
C'
A
B
C
D
.
.
1
4
ABC MNP
ABC A B C
V
AM BN CP DQ
V AA BB CC DD



.
.
1
2
ABC MNP
ABC A B C
V
AM CP
V AA CC





, , ,M N P Q
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <3 >
MỘT SỐ BÀI TOÁN LIÊN QUAN ĐẾN TỶ SỐ THỂ TÍCH
Tặng các em học sinh thân yêu!
Dạng 1: Tỷ số liên quan đến diện tích đáy và đường cao
Mức 1: Cho hình chóp
.S ABC
có thể tích là
.V
Gọi
M
là trung điểm
.BC
(tham khảo hình vẽ)
M
C
B
A
S
Thể tích khối chóp
.S ABM
bằng
Đáp án:
Mức 2: Cho hình chóp
.S ABC
có thể tích là
.V
Gọi
,MN
là trung điểm
,.AB AC
(tham khảo hình vẽ)
N
M
S
A
B
C
Thể tích khối chóp
.S AMN
bằng
Đáp án:
Trình bày:
Mức 3: Cho hình chóp
.S ABC
có thể tích là
.V
Gọi
,,M N P
là trung điểm
, , .SA AB AC
(tham khảo
hình vẽ)
P
C
B
A
S
M
N
Thể tích khối chóp
.M ANP
bằng
Đáp án:
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <4 >
Mức 4: Cho hình chóp
.S ABCD
có đáy là hình bình
hành tâm
.O
Gọi
V
là thể tích khối chóp
..S ABCD
(tham khảo hình vẽ)
O
D
S
A
B
C
Thể tích khối chóp
.S ABO
bằng
Đáp án:
Trình bày:
Mức 5: Cho hình chóp
.S ABCD
có đáy là hình bình
hành tâm
.O
Gọi
V
là thể tích khối chóp
..S ABCD
M
là trung điểm
SA
(tham khảo hình vẽ)
M
C
B
A
S
D
O
Thể tích khối chóp
.M ABO
bằng
Đáp án:
Trình bày:
Dạng 2: Tỷ số thể tích khối chóp tam giác
Mức 1: Cho hình chóp
.S ABC
có thể tích là
.V
Gọi
,,M N P
lần lượt là trung điểm
,,SA SB SC
(tham
khảo hình vẽ)
P
N
S
A
B
C
M
Thể tích khối chóp
.S MNP
bằng
Đáp án:
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <5 >
Mức 2: Cho hình chóp
.S ABC
có thể tích là
.V
Gọi
,,M N P
lần lượt là trung điểm
,,SA SB SC
(tham
khảo hình vẽ)
P
N
S
A
B
C
M
Thể tích khối đa diện
MNPCBA
bằng
Đáp án:
Trình bày:
Mức 3: Cho hình chóp
.S ABC
có thể tích là
.V
Gọi
,MN
lần lượt là trung điểm
,SB SC
(tham khảo
hình vẽ)
M
C
B
A
S
N
Thể tích khối chóp
.S AMN
bằng
Đáp án:
Trình bày:
Mức 4: Cho hình chóp
.S ABC
có thể tích là
.V
Gọi
,MN
lần lượt là trung điểm
,SB SC
(tham khảo
hình vẽ)
M
C
B
A
S
N
Thể tích khối chóp
.A MNCB
bằng
Đáp án:
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <6 >
Dạng 3: Tỷ số thể tích khối chóp tứ giác
Mức 1: Cho hình chóp
.S ABCD
có đáy là hình
bình hành. Gọi
V
là thể tích khối chóp
..S ABCD
Gọi
, , ,M N P Q
lần lượt là trung điểm
, , ,SA SB SC SD
(tham khảo hình vẽ)
Q
P
N
M
C
B
A
S
D
Thể tích khối chóp
.S MNPQ
bằng
Đáp án:
Trình bày:
Mức 2: Cho hình chóp
.S ABCD
có đáy là hình
bình hành. Gọi
V
là thể tích khối chóp
..S ABCD
Gọi
,MN
lần lượt là trung điểm
,SA SB
(tham
khảo hình vẽ)
D
S
A
B
C
M
N
Thể tích khối chóp
.S MNCD
bằng
Đáp án:
Trình bày:
Dạng 4: Tỷ số thể tích khối lăng trụ
Mức 1: Cho hình lăng trụ
.ABC A B C
có thể tích là
.V
(tham khảo hình vẽ)
C
B
A
A'
B'
C'
Thể tích khối chóp
.A ABC
bằng
Đáp án:
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <7 >
Mức 2: Cho hình lăng trụ
.ABC A B C
có thể tích là
.V
(tham khảo hình vẽ)
C
B
A
A'
B'
C'
Thể tích khối chóp
.A B C CB
bằng
Đáp án:
Trình bày:
Mức 3: Cho hình lăng trụ
.ABC A B C
có thể tích là
.V
Gọi
,MN
lần lượt là trung điểm
,BB CC

(tham
khảo hình vẽ)
N
M
C'
B'
A'
A
B
C
Thể tích khối chóp
.A B C NM
bằng
Đáp án:
Trình bày:
Mức 4: Cho hình lăng trụ
.ABC A B C
có thể tích là
.V
Gọi
,,M N P
lần lượt là trung điểm
,,AA BB CC
(tham khảo hình vẽ)
P
C
A
A'
B'
C'
M
N
Thể tích khối
.A B C MNP
bằng
Đáp án:
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <8 >
Mức 5: Cho hình lăng trụ
.ABC A B C
có thể tích là
.V
Gọi
M
là trung điểm
BB
(tham khảo hình vẽ)
C
B
A
A'
B'
C'
M
Thể tích khối chóp
.M A B C
bằng
Đáp án:
Trình bày:
Mức 6: Cho hình hộp
.ABCD A B C D
có thể tích là
.V
(tham khảo hình vẽ)
D'
A'
B'
C'
D
A
B
C
Thể tích khối chóp
.A ABC
bằng
Đáp án:
Trình bày:
Mức 7: Cho hình hộp
.ABCD A B C D
có thể tích là
.V
(tham khảo hình vẽ)
C
B
A
D
C'
B'
A'
D'
Thể tích khối tứ diện
BDA C

bằng
Đáp án:
Trình bày:
Mức 8: Cho hình hộp
.ABCD A B C D
có thể tích là
.V
Gọi
, , ,M N P Q
lần lượt là trung điểm
, , ,AA BB CC DD
(tham khảo hình vẽ)
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <9 >
Q
P
N
M
C
B
A
D
C'
B'
A'
D'
Thể tích khối đa diện
.A B C D QMNP
bằng
Đáp án:
Mức 9: Cho hình hộp
.ABCD A B C D
có thể tích là
.V
Gọi
,MN
lần lượt là trung điểm
,AA BB

(tham
khảo hình vẽ)
D'
A'
B'
C'
D
A
B
C
M
N
Thể tích khối đa diện
A B NMDCC D
bằng
Đáp án:
Trình bày:
Dạng 5: Một số bài toán khác
Mức 1: Cho tam giác
ABC
đều có cạnh bằng
.a
Dựng
,,AA BB CC
vuông góc với
ABC
sao cho
3,AA a BM CN a
(tham khảo hình vẽ)
M
N
A'
A
B
C
Thể tích khối đa diện
A ABCNM
bằng
Đáp án:
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <10 >
Mức 2: Cho tam giác
ABC
đều có cạnh bằng
.a
Dựng
,,AA BB CC
vuông góc với
ABC
sao cho
4
4 , 2 ,
3
a
AA a BM a CN
(tham khảo hình vẽ)
M
N
A'
A
B
C
Thể tích khối đa diện
A ABCNM
bằng
Đáp án:
Trình bày:
LỜI GIẢI CHI TIẾT
Dạng 1: Tỷ số liên quan đến diện tích đáy và đường cao
Mức 1: Cho hình chóp
.S ABC
có thể tích là
.V
Gọi
M
là trung điểm
.BC
(tham khảo hình vẽ)
M
C
B
A
S
Thể tích khối chóp
.S ABM
bằng
Đáp án:
2
V
Trình bày:
Ta có:
1
.
2
ABM ABC
SS
Suy ra:
..
1
.
22
S ABM S ABC
V
VV
Mức 2: Cho hình chóp
.S ABC
có thể tích là
.V
Gọi
,MN
là trung điểm
,.AB AC
(tham khảo hình vẽ)
Trình bày:
Cách 1:
Ta có:
11
..
44
AMN
AMN ABC
ABC
S
AM AN
SS
S AB AC
Suy ra:
..
1
.
44
S AMN S ABC
V
VV
Cách 2:
..
..
1
..
4
S AMN A SMN
S ABC A SBC
VV
SA AM AN
V V SA AB AC
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <11 >
N
M
S
A
B
C
Thể tích khối chóp
.S AMN
bằng
Đáp án:
4
V
Suy ra:
..
1
.
44
S AMN S ABC
V
VV
Mức 3: Cho hình chóp
.S ABC
có thể tích là
.V
Gọi
,,M N P
là trung điểm
, , .SA AB AC
(tham khảo
hình vẽ)
P
C
B
A
S
M
N
Thể tích khối chóp
.M ANP
bằng
Đáp án:
8
V
Trình bày:
Cách 1:
Ta có:
11
.
44
ANP
ANP ABC
ABC
S
AP AN
SS
S AC AB
(1)
Mặt khác:
1
;;
2
d M APN d S ABC
(2)
Suy ra:
.
1
;.
3
M ANP APN
V d M ANP S
.
1 1 1 1
. ; . .
3 2 4 8 8
ABC S ABC
V
d S ABC S V
Cách 2:
Ta có:
11
. . .
8 8 8
AMNP
AMNP ASBC
ASBC
V
AM AN AP V
VV
V AS AB AC
Mức 4: Cho hình chóp
.S ABCD
có đáy là hình bình
hành tâm
.O
Gọi
V
là thể tích khối chóp
..S ABCD
(tham khảo hình vẽ)
O
D
S
A
B
C
Thể tích khối chóp
.S ABO
bằng
Đáp án:
4
V
Trình bày:
Ta có:
11
.
24
ABO ABC ABCD
S S S
Suy ra:
..
1
.
44
S ABO S ABCD
V
VV
Mức 5: Cho hình chóp
.S ABCD
có đáy là hình bình
hành tâm
.O
Gọi
V
là thể tích khối chóp
..S ABCD
M
là trung điểm
SA
(tham khảo hình vẽ)
Trình bày:
Ta có:
11
24
ABO ABC ABCD
S S S
(1)
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <12 >
M
C
B
A
S
D
O
Thể tích khối chóp
.M ABO
bằng
Đáp án:
8
V
Mặt khác:
1
;;
2
d M ABO d S ABCD
(2)
Từ (1), (2) suy ra:
..
1
.
88
M ABO S ABCD
V
VV
Dạng 2: Tỷ số thể tích khối chóp tam giác
Mức 1: Cho hình chóp
.S ABC
có thể tích là
.V
Gọi
,,M N P
lần lượt là trung điểm
,,SA SB SC
(tham
khảo hình vẽ)
P
N
S
A
B
C
M
Thể tích khối chóp
.S MNP
bằng
Đáp án:
8
V
Trình bày:
Ta có:
11
. . .
8 8 8
SMNP
SMNP SABC
SABC
V
SM SN SP V
VV
V SA SB SC
Mức 2: Cho hình chóp
.S ABC
có thể tích là
.V
Gọi
,,M N P
lần lượt là trung điểm
,,SA SB SC
(tham
khảo hình vẽ)
P
N
S
A
B
C
M
Thể tích khối đa diện
MNPCBA
bằng
Đáp án:
7
8
V
Trình bày:
Ta có:
11
. . .
8 8 8
SMNP
SMNP SABC
SABC
V
SM SN SP V
VV
V SA SB SC
Suy ra:
7
.
8
MNPCBA
V
V
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <13 >
Mức 3: Cho hình chóp
.S ABC
có thể tích là
.V
Gọi
,MN
lần lượt là trung điểm
,SB SC
(tham khảo
hình vẽ)
M
C
B
A
S
N
Thể tích khối chóp
.S AMN
bằng
Đáp án:
4
V
Trình bày:
Cách 1:
Ta có:
11
..
44
SMN
SMN SBC
SBC
S
SM SN
SS
S SB SC
Suy ra:
. . .
1
.
44
S AMN A SBC A SBC
V
V V V
Cách 2:
Ta có:
11
. . .
4 4 4
SAMN
SAMN SABC
SABC
V
SA SM SN V
VV
V SA SB SC
Mức 4: Cho hình chóp
.S ABC
có thể tích là
.V
Gọi
,MN
lần lượt là trung điểm
,SB SC
(tham khảo
hình vẽ)
M
C
B
A
S
N
Thể tích khối chóp
.A MNCB
bằng
Đáp án:
3
4
V
Trình bày:
Ta có:
11
. . .
4 4 4
SAMN
SAMN SABC
SABC
V
SA SM SN V
VV
V SA SB SC
Suy ra:
.
3
.
4
A MNCB
V
V
Dạng 3: Tỷ số thể tích khối chóp tứ giác
Mức 1: Cho hình chóp
.S ABCD
có đáy là hình
bình hành. Gọi
V
là thể tích khối chóp
..S ABCD
Gọi
, , ,M N P Q
lần lượt là trung điểm
, , ,SA SB SC SD
(tham khảo hình vẽ)
Trình bày:
Cách 1:
Ta có:
2; 2; 2; 2.
SA SB SC SD
a b c d
SM SN SP SQ
Suy ra:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <14 >
Q
P
N
M
C
B
A
S
D
Thể tích khối chóp
.S MNPQ
bằng
Đáp án:
8
V
.
..
.
11
.
4 8 8 8
S MNPQ
S MNPQ S ABCD
S ABCD
V
a b c d V
VV
V abcd
Cách 2:
.
. . .
.
1 1 1
8 8 16
S MNP
S MNP S ABC S ABCD
S ABC
V
V V V
V
.
. . .
.
1 1 1
8 8 16
S MQP
S MQP S ADC S ABCD
S ADC
V
V V V
V
. . . .
1
.
88
S MNPQ S MNP S MQP S ABCD
V
V V V V
Mức 2: Cho hình chóp
.S ABCD
có đáy là hình
bình hành. Gọi
V
là thể tích khối chóp
..S ABCD
Gọi
,MN
lần lượt là trung điểm
,SA SB
(tham
khảo hình vẽ)
D
S
A
B
C
M
N
Thể tích khối chóp
.S MNCD
bằng
Đáp án:
3
8
V
Trình bày:
Cách 1:
Ta có:
2; 2; 1; 1.
SA SB SC SD
a b c d
SM SN SC SD
Suy ra:
.
..
.
3 3 3
.
4 8 8 8
S MNCD
S MNCD S ABCD
S ABCD
V
a b c d V
VV
V abcd
Cách 2:
.
. . .
.
1 1 1
4 4 8
S MNC
S MNP S ABC S ABCD
S ABC
V
V V V
V
.
. . .
.
1 1 1
2 2 4
S MCD
S MCD S ACD S ABCD
S ACD
V
V V V
V
. . . .
33
.
88
S MNCD S MNC S MCD S ABCD
V
V V V V
Dạng 4: Tỷ số thể tích khối lăng trụ
Mức 1: Cho hình lăng trụ
.ABC A B C
có thể tích là
.V
(tham khảo hình vẽ)
C
B
A
A'
B'
C'
Thể tích khối chóp
.A ABC
bằng
Trình bày:
Ta có:
.
1
; . .
33
A ABC ABC
V
V d A ABC S

Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <15 >
Đáp án:
3
V
Mức 2: Cho hình lăng trụ
.ABC A B C
có thể tích là
.V
(tham khảo hình vẽ)
C
B
A
A'
B'
C'
Thể tích khối chóp
.A B C CB
bằng
Đáp án:
2
3
V
Trình bày:
Ta có:
.
1
; . .
33
A ABC ABC
V
V d A ABC S

Suy ra:
.
2
.
3
A B C CB
V
V
Mức 3: Cho hình lăng trụ
.ABC A B C
có thể tích là
.V
Gọi
,MN
lần lượt là trung điểm
,BB CC

(tham
khảo hình vẽ)
N
M
C'
B'
A'
A
B
C
Thể tích khối chóp
.A B C NM
bằng
Đáp án:
3
V
Trình bày:
Cách 1:
Ta có:
.
1
; . .
33
A ABC ABC
V
V d A ABC S

Suy ra:
. . .
21
.
3 2 3
A B C CB A B C NM A B C CB
VV
V V V
Cách 2:
Ta có:
.
.
11
.
33
A B C CB
A B C ABC
V
B M C N
V BB CC





Suy ra:
.
.
3
A B C NM
V
V
Mức 4: Cho hình lăng trụ
.ABC A B C
có thể tích là
.V
Gọi
,,M N P
lần lượt là trung điểm
,,AA BB CC
(tham khảo hình vẽ)
Trình bày:
Cách 1:
Ta có:
.
;.
A B C MNP A B C
V d M A B C S
1
; . .
22
A B C
V
d A A B C S

Cách 2:
Ta có:
.
.
11
.
32
A B C MNP
A B C ABC
V
A M B N C P
V A A BB CC



Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <16 >
P
C
A
A'
B'
C'
M
N
Thể tích khối
.A B C MNP
bằng
Đáp án:
2
V
Suy ra:
.
.
2
A B C MNP
V
V
Mức 5: Cho hình lăng trụ
.ABC A B C
có thể tích là
.V
Gọi
M
là trung điểm
BB
(tham khảo hình vẽ)
C
B
A
A'
B'
C'
M
Thể tích khối chóp
.M A B C
bằng
Đáp án:
6
V
Trình bày:
Cách 1:
Ta có:
.
1
;.
3
M A B C A B C
V d M A B C S
11
. ; . .
3 2 6
A B C
V
d B A B C S

Cách 2:
Ta có:
.
.
11
..
36
M A B C
A B C ABC
V
BM
V BB

Suy ra:
.
.
6
M A B C
V
V
V
Mức 6: Cho hình hộp
.ABCD A B C D
có thể tích là
.V
(tham khảo hình vẽ)
D'
A'
B'
C'
D
A
B
C
Thể tích khối chóp
.A ABC
bằng
Đáp án:
6
V
Trình bày:
Ta có:
.
1
;.
3
A ABC ABC
V d A ABC S
11
; . .
3 2 6
ABCD
V
d A ABC S

Mức 7: Cho hình hộp
.ABCD A B C D
có thể tích là
.V
(tham khảo hình vẽ)
Trình bày:
Ta có:
.
1
;.
3
A ABD ABD
V d A ABD S
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <17 >
C
B
A
D
C'
B'
A'
D'
Thể tích khối tứ diện
BDA C

bằng
Đáp án:
3
V
11
; . .
3 2 6
ABCD
V
d A ABD S

Tương tự:
. . .
.
6
C BCD B B A C D D A C
V
V V V
Suy ra:
4. .
63
BDA C
VV
VV

Mức 8: Cho hình hộp
.ABCD A B C D
có thể tích là
.V
Gọi
, , ,M N P Q
lần lượt là trung điểm
, , ,AA BB CC DD
(tham khảo hình vẽ)
Q
P
N
M
C
B
A
D
C'
B'
A'
D'
Thể tích khối đa diện
.A B C D QMNP
bằng
Đáp án:
2
V
Trình bày:
Cách 1:
Ta có:
.
;.
A B C D QMNP A B C D
V d M A B C D S
1
; . .
22
A B C D
V
d A A B C D S

Cách 2:
Ta có:
.
.
11
42
A B C D QMNP
ABCD A B C D
V
A M B N C P D Q
V A A B B C C D D



Suy ra:
..
1
.
22
A B C D QMNP ABCD A B C D
V
VV

Mức 9: Cho hình hộp
.ABCD A B C D
có thể tích là
.V
Gọi
,MN
lần lượt là trung điểm
,AA BB

(tham
khảo hình vẽ)
D'
A'
B'
C'
D
A
B
C
M
N
Thể tích khối đa diện
A B NMDCC D
bằng
Đáp án:
3
4
V
Trình bày:
Ta có:
.
13
44
A B NMDCC D
ABCD A B C D
V
A M B N C C D D
V A A B B C C D D



Suy ra:
.
33
.
44
A B NMDCC D ABCD A B C D
V
VV

Dạng 5: Một số bài toán khác
Mức 1: Cho tam giác
ABC
đều có cạnh bằng
.a
Dựng
,,AA BB CC
vuông góc với
ABC
sao cho
Trình bày:
Dựng lăng trụ đều
.ABC A B C
như hình vẽ:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <18 >
3,AA a BM CN a
(tham khảo hình vẽ)
M
N
A'
A
B
C
Thể tích khối đa diện
A ABCNM
bằng
Đáp án:
3
53
12
a
M
N
C
B
A
C'
B'
A'
Ta có:
3
2
.
3 3 3
. 3 . .
44
ABC A B C ABC
a
V V A A S a a
Ta có:
.
.
1 1 2 2 4
.
3 3 3 3 9
A B C NM
A B C ABC
V
B M C N
V BB CC


Suy ra:
3
.
4 5 5 3
.
9 9 12
A B C NM A ABCNM
V V a
VV
Cách khác:
Gọi
P
là điểm trên
AA
sao cho
.AP a
23
.
33
..
44
ABC MNP ABC
aa
V AP S a
23
.
1 1 3 3
. .2 .
3 3 4 6
A MNP MNP
aa
V A P S a
Suy ra:
3
. . .
53
.
12
A B C NM MNP ABC A MNP
a
V V V
Mức 2: Cho tam giác
ABC
đều có cạnh bằng
.a
Dựng
,,AA BB CC
vuông góc với
ABC
sao cho
4
4 , 2 ,
3
a
AA a BM a CN
(tham khảo hình vẽ)
M
N
A'
A
B
C
Trình bày:
Dựng lăng trụ đều
.ABC A B C
như hình vẽ:
M
N
C
B
A
C'
B'
A'
Ta có:
23
.
3
. 4 . 3 .
4
ABC A B C ABC
V V A A S a a a
Ta có:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <19 >
Thể tích khối đa diện
A ABCNM
bằng
Đáp án:
3
11 3
18
a
.
.
1 1 1 2 7
.
3 3 2 3 18
A B C NM
A B C ABC
V
B M C N
V BB CC


Suy ra:
3
.
7 11 11 3
.
18 18 18
A B C NM A ABCNM
V V a
VV
_________________HẾT_________________
Huế, 10h45’ Ngày 07 tháng 7 năm 2023
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <20 >
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
PHIẾU HỌC TẬP SỐ 01_TrNg 2023
CHUY£N §Ò TR¾C NGHIÖM
M«n:
To¸n 12
Chuyên đề: THỂ TÍCH KHỐI ĐA DIỆN
Tỷ số thể tích (CB)
Líp To¸n thÇy L£ B¸ B¶O
Tr-êng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10 H-¬ng Trµ
, HuÕ.
NỘI DUNG ĐỀ BÀI
Câu 1: Gọi
V
là thể tích khối chóp
..S ABC
Gọi
M
là trung điểm
.SA
Thể tích khối chóp
.M ABC
bằng
A.
.
4
V
B.
.
2
V
C.
.
3
V
D.
2
.
3
V
Câu 2: Gọi
V
là thể tích khối chóp
..S ABC
Gọi
M
là điểm trên cạnh
SA
sao cho
2.SM MA
Thể tích
khối chóp
.M ABC
bằng
A.
.
4
V
B.
.
2
V
C.
.
3
V
D.
2
.
3
V
Câu 3: Cho hình chóp
.S ABC
có thể tích là
.V
Gọi
G
là trọng tâm tam giác
.ABC
Thể tích khối chóp
.S ABG
bằng
A.
.
4
V
B.
.
2
V
C.
.
3
V
D.
2
.
3
V
Câu 4: Cho hình chóp
.S ABC
có thể tích là
.V
Gọi
,,M N P
lần lượt là trung điểm
, , .AB BC AC
Thể
tích khối chóp
.S MNP
bằng
A.
.
4
V
B.
.
8
V
C.
.
3
V
D.
2
.
3
V
Câu 5: Cho hình chóp
.S ABC
có thể tích là
.V
Gọi
G
là trọng tâm tam giác
,ABC M
là trung điểm
.SA
Thể tích khối chóp
.M ABG
bằng
A.
.
6
V
B.
.
2
V
C.
.
3
V
D.
2
.
3
V
Câu 6: Gọi
V
là thể tích khối chóp
.,S ABC
,MN
lần lượt là trung điểm
,.SC AB
Thể tích khối chóp
MNCB
bằng
A.
.
2
V
B.
3
.
8
V
C.
.
4
V
D.
3
.
4
V
Câu 7: Cho hình chóp
.S ABCD
có đáy là hình bình hành. Gọi thể tích khối chóp
.S ABCD
là
.V
Thể
tích khối chóp
.S ABC
bằng
A.
.
4
V
B.
.
2
V
C.
.
3
V
D.
2
.
3
V
Câu 8: Cho hình chóp
.S ABCD
có đáy là hình bình hành tâm
O
. Gọi thể tích khối chóp
.S ABCD
là
.V
Thể tích khối chóp
.S ABO
bằng
A.
.
4
V
B.
.
2
V
C.
.
3
V
D.
2
.
3
V
Câu 9: Cho hình chóp
.S ABCD
có đáy là hình bình hành tâm
O
. Gọi thể tích khối chóp
.S ABCD
là
.V
M
là trung điểm
.SD
Thể tích khối chóp
.M ABO
bằng
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <21 >
A.
.
4
V
B.
.
2
V
C.
.
3
V
D.
.
8
V
Câu 10: Gọi
V
là thể tích khối chóp
.,S ABC
,,M N P
lần lượt là trung điểm
, , .SA SB SC
Thể tích khối
chóp
.S MNP
bằng
A.
.
8
V
B.
7
.
8
V
C.
.
3
V
D.
2
.
3
V
Câu 11: Gọi
V
là thể tích khối chóp
.,S ABC
,,M N P
lần lượt là trung điểm
, , .SA SB SC
Thể tích khối
MNPCBA
bằng
A.
.
8
V
B.
7
.
8
V
C.
.
3
V
D.
2
.
3
V
Câu 12: Gọi
V
là thể tích khối chóp
.,S ABC
,MN
lần lượt là trung điểm
,.SB SC
Thể tích khối chóp
.S AMN
bằng
A.
.
8
V
B.
7
.
8
V
C.
.
4
V
D.
3
.
4
V
Câu 13: Gọi
V
là thể tích khối chóp
.,S ABC
,MN
lần lượt là trung điểm
,.SB SC
Thể tích khối
AMNCB
bằng
A.
.
8
V
B.
7
.
8
V
C.
.
4
V
D.
3
.
4
V
Câu 14: Gọi
V
là thể tích khối chóp
.,S ABC
M
là trung điểm
.SC
Thể tích khối chóp
.S ABM
bằng
A.
.
2
V
B.
3
.
8
V
C.
.
4
V
D.
3
.
4
V
Câu 15: Gọi
V
là thể tích khối chóp
.,S ABC
M
là trung điểm
.SC
Thể tích khối chóp
ABCM
bằng
A.
.
2
V
B.
3
.
8
V
C.
.
4
V
D.
3
.
4
V
Câu 16: Cho hình chóp
.S ABCD
có đáy là hình bình hành. Gọi thể tích khối chóp
.S ABCD
là
.V
, , ,M N P Q
lần lượt là trung điểm
, , , .SA SB SC SD
Thể tích khối chóp
.S MNPQ
bằng
A.
.
4
V
B.
.
16
V
C.
7
.
8
V
D.
.
8
V
Câu 17: Cho hình chóp
.S ABCD
có đáy là hình bình hành. Gọi thể tích khối chóp
.S ABCD
là
.V
, , ,M N P Q
lần lượt là trung điểm
, , , .SA SB SC SD
Thể tích khối
MNPQDABC
bằng
A.
15
.
16
V
B.
.
16
V
C.
7
.
8
V
D.
.
8
V
Câu 18: Cho hình chóp
.S ABCD
có đáy là hình bình hành. Gọi thể tích khối chóp
.S ABCD
là
.V
,MN
lần lượt là trung điểm
,.SA SB
Thể tích khối chóp
.S MNCD
bằng
A.
3
.
8
V
B.
5
.
8
V
C.
.
4
V
D.
3
.
4
V
Câu 19: Cho hình chóp
.S ABCD
có đáy là hình bình hành. Gọi thể tích khối chóp
.S ABCD
là
.V
,MN
lần lượt là trung điểm
,.SA SB
Thể tích khối
MNBADC
bằng
A.
3
.
8
V
B.
5
.
8
V
C.
.
4
V
D.
3
.
4
V
Câu 20: Gọi
V
là thể tích khối lăng trụ
..ABC A B C
Thể tích khối chóp
.A A B C
bằng
A.
.
3
V
B.
2
.
3
V
C.
.
2
V
D.
3
.
4
V
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <22 >
Câu 21: Gọi
V
là thể tích khối lăng trụ
.,ABC A B C M
là trung điểm
.AA
Thể tích khối chóp
.M A B C
bằng
A.
.
3
V
B.
2
.
3
V
C.
.
6
V
D.
3
.
4
V
Câu 22: Gọi
V
là thể tích khối lăng trụ
.,ABC A B C M
là điểm bất kì trên cạnh
.AB
Thể tích khối
chóp
.M A B C
bằng
A.
.
3
V
B.
2
.
3
V
C.
.
2
V
D.
3
.
4
V
Câu 23: Gọi
V
là thể tích khối lăng trụ
..ABC A B C
Thể tích khối chóp
.A BCC B

bằng
A.
.
3
V
B.
2
.
3
V
C.
.
2
V
D.
3
.
4
V
Câu 24: Gọi
V
là thể tích khối lăng trụ
.,ABC A B C M
là điểm bất kì trên
.AA
Thể tích khối chóp
.M BCC B

bằng
A.
.
3
V
B.
2
.
3
V
C.
.
2
V
D.
3
.
4
V
Câu 25: Gọi
V
là thể tích khối lăng trụ
. , , ,ABC A B C M N P
lần lượt là trung điểm
, , .AA BB CC
Thể
tích khối
.ABC MNP
bằng
A.
.
3
V
B.
2
.
3
V
C.
.
2
V
D.
3
.
4
V
Câu 26: Gọi
V
là thể tích khối lăng trụ
. , ,ABC A B C M N
lần lượt là trung điểm
,.AA BB

Thể tích
khối
ABCNM
bằng
A.
.
3
V
B.
2
.
3
V
C.
.
2
V
D.
3
.
4
V
Câu 27: Gọi
V
là thể tích khối lăng trụ
. , ,ABC A B C M N
lần lượt là trung điểm
,.AA BB

Thể tích
khối
CMNB C A
bằng
A.
.
3
V
B.
2
.
3
V
C.
.
2
V
D.
3
.
4
V
Câu 28: Gọi
V
là thể tích khối lăng trụ
.,ABC A B C M
là trung điểm
,AA N
trên cạnh
BB
sao cho
2.BN NB
Thể tích khối
ABCNM
bằng
A.
.
3
V
B.
2
.
3
V
C.
11
.
18
V
D.
7
.
18
V
Câu 29: Gọi
V
là thể tích khối hộp
. , , , ,ABCD A B C D M N P Q
lần lượt là trung điểm
, , , .AA BB CC DD
Thể tích khối
.ABCD MNPQ
bằng
A.
.
3
V
B.
2
.
3
V
C.
.
2
V
D.
3
.
4
V
Câu 30: Gọi
V
là thể tích khối hộp
. , ,ABCD A B C D M N
lần lượt là trung điểm
,.AA BB

Thể tích
khối
ABCDMNC D

bằng
A.
.
3
V
B.
2
.
3
V
C.
.
2
V
D.
3
.
4
V
Câu 31: Gọi
V
là thể tích khối hộp
..ABCD A B C D
Thể tích khối chóp
.B ABC
bằng
A.
.
6
V
B.
.
12
V
C.
.
24
V
D.
.
4
V
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <23 >
Câu 32: Gọi
V
là thể tích khối hộp
. , , ,ABCD A B C D M N P
lần lượt là trung điểm
, , .AB BC BB
Thể
tích khối
BMNP
bằng
A.
.
36
V
B.
.
12
V
C.
.
24
V
D.
.
48
V
Câu 33: Gọi
V
là thể tích khối lăng trụ
. , ,ABC A B C M N
lần lượt là trung điểm
,.AB AC
Thể tích khối
chóp
A AMN
bằng
A.
.
3
V
B.
.
12
V
C.
.
6
V
D.
11
.
12
V
Câu 34: Gọi
V
là thể tích khối lăng trụ
. , ,ABC A B C M N
lần lượt là trung điểm
,.AB AC
Thể tích khối
MNCBC A B
bằng
A.
5
.
6
V
B.
.
12
V
C.
.
6
V
D.
11
.
12
V
Câu 35: Gọi
V
là thể tích khối lăng trụ
. , ,ABC A B C M N
lần lượt là trung điểm
,.AB AC
Thể tích khối
MNCBB C

bằng
A.
3
.
4
V
B.
5
.
12
V
C.
.
4
V
D.
7
.
12
V
Câu 36: Gọi
V
là thể tích khối lăng trụ
. , ,ABC A B C M N
lần lượt là trung điểm
,.AB AC
Thể tích khối
AMNC B A
bằng
A.
3
.
4
V
B.
5
.
12
V
C.
.
4
V
D.
7
.
12
V
Câu 37: Cho lăng trụ
..ABC A B C
Gọi
12
,VV
lần lượt là thể tích các khối
.A A B C
và
.ABCC
Khẳng
định nào sau đây đúng?
A.
1
2
1.
V
V
B.
1
2
1
.
2
V
V
C.
1
2
1
.
3
V
V
D.
1
2
3
.
2
V
V
Câu 38: Cho khối chóp
.S ABC
có thể tích
V
. Gọi
,BC

lần lượt là trung điểm của
,AB AC
. Tính theo
V
thể tích khối chóp
.S AB C

.
A.
1
3
V
. B.
1
2
V
. C.
1
12
V
. D.
1
4
V
.
Câu 39: Cho khối tứ diện
SABC
có
,,M N P
lần lượt là trung điểm
,,SA SB SC
và
G
là trọng tâm tam
giác
ABC
. Gọi
V
là thể tích khối
SABC
,
V
là thể tích khối
GNMP
. Tỉ số
V
V
bằng
A.
1
6
V
V
. B.
1
8
V
V
. C.
1
4
V
V
. D.
2
7
V
V
.
Câu 40: Cho khối lăng trụ
.ABC A B C
. Gọi
,MN
lần lượt là trung điểm của đoạn thẳng
AA
và
'.BB
Tính tỉ số thể tích của khối tứ diện
'CMNC
với khối lăng trụ đã cho.
A.
1
3
. B.
1
2
. C.
2
3
. D.
3
4
.
___________________HẾT___________________
Huế, 10h5’ Ngày 25 tháng 10 năm 2021
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <24 >
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
PHIẾU HỌC TẬP SỐ 05_TrNg 2021
CHUY£N §Ò TR¾C NGHIÖM
M«n:
To¸n 12
Chuyên đề: THỂ TÍCH KHỐI ĐA DIỆN
Tỷ số thể tích (CB)
LỜI GIẢI CHI TIẾT
Câu 1: Gọi
V
là thể tích khối chóp
..S ABC
Gọi
M
là trung điểm
.SA
Thể tích khối chóp
.M ABC
bằng
A.
.
4
V
B.
.
2
V
C.
.
3
V
D.
2
.
3
V
Lời giải:
M
S
A
B
C
Do
M
là trung điểm
SA
nên
1
; ; .
2
d M ABC d S ABC
Vậy
.
.
2
M ABC
V
V
Chọn đáp án B.
Câu 2: Gọi
V
là thể tích khối chóp
..S ABC
Gọi
M
là điểm trên cạnh
SA
sao cho
2.SM MA
Thể tích
khối chóp
.M ABC
bằng
A.
.
4
V
B.
.
2
V
C.
.
3
V
D.
2
.
3
V
Lời giải:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <25 >
M
S
A
B
C
Do
1
3
AM
AS
nên
1
; ; .
3
d M ABC d S ABC
Vậy
.
.
3
M ABC
V
V
Chọn đáp án C.
Câu 3: Cho hình chóp
.S ABC
có thể tích là
.V
Gọi
G
là trọng tâm tam giác
.ABC
Thể tích khối chóp
.S ABG
bằng
A.
.
4
V
B.
.
2
V
C.
.
3
V
D.
2
.
3
V
Lời giải:
M
G
S
A
B
C
Gọi
M
là trung điểm
.BC
Ta có:
2 2 2 1 1
..
3 3 3 2 3
ABG
ABG ABM ABC ABC
ABM
S
AG
S S S S
S AM
Vậy
S.
.
3
ABG
V
V
Chọn đáp án C.
Câu 4: Cho hình chóp
.S ABC
có thể tích là
.V
Gọi
,,M N P
lần lượt là trung điểm
, , .AB BC AC
Thể
tích khối chóp
.S MNP
bằng
A.
.
4
V
B.
.
8
V
C.
.
3
V
D.
2
.
3
V
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <26 >
Lời giải:
P
N
M
S
A
B
C
Ta có:
11
.
44
MNP
MNP ABC
ABC
S
SS
S
Vậy
.
.
4
S MNP
V
V
Chọn đáp án A.
Câu 5: Cho hình chóp
.S ABC
có thể tích là
.V
Gọi
G
là trọng tâm tam giác
,ABC M
là trung điểm
.SA
Thể tích khối chóp
.M ABG
bằng
A.
.
6
V
B.
.
2
V
C.
.
3
V
D.
2
.
3
V
Lời giải:
M
C
B
A
S
G
M
Gọi
M
là trung điểm
.BC
Ta có:
2 2 2 1 1
..
3 3 3 2 3
ABG
ABG ABM ABC ABC
ABM
S
AG
S S S S
S AM
Mặt khác, do
M
là trung điểm
SA
nên
1
; ; .
2
d M ABC d S ABC
Vậy
S.
11
..
2 3 6
ABG
V
VV
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <27 >
Chọn đáp án A.
Câu 6: Gọi
V
là thể tích khối chóp
.,S ABC
,MN
lần lượt là trung điểm
,.SC AB
Thể tích khối chóp
MNCB
bằng
A.
.
2
V
B.
3
.
8
V
C.
.
4
V
D.
3
.
4
V
Lời giải:
N
M
S
A
B
C
Ta có:
11
.
22
CBN
CBN ABC
ABC
S
SS
S
Mặt khác, do
M
là trung điểm
SC
nên
1
; ; .
2
d M ABC d S ABC
Vậy
11
. . .
2 2 4
MNCB
V
VV
Chọn đáp án C.
Câu 7: Cho hình chóp
.S ABCD
có đáy là hình bình hành. Gọi thể tích khối chóp
.S ABCD
là
.V
Thể
tích khối chóp
.S ABC
bằng
A.
.
4
V
B.
.
2
V
C.
.
3
V
D.
2
.
3
V
Lời giải:
D
S
A
B
C
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <28 >
Ta có:
11
.
22
ABC
ABC ABCD
ABCD
S
SS
S
Vậy
S.
.
2
ABC
V
V
Chọn đáp án C.
Câu 8: Cho hình chóp
.S ABCD
có đáy là hình bình hành tâm
O
. Gọi thể tích khối chóp
.S ABCD
là
.V
Thể tích khối chóp
.S ABO
bằng
A.
.
4
V
B.
.
2
V
C.
.
3
V
D.
2
.
3
V
Lời giải:
O
C
B
A
S
D
Ta có:
11
.
44
ABO
ABO ABCD
ABCD
S
SS
S
Vậy
.
.
4
S ABO
V
V
Chọn đáp án A.
Câu 9: Cho hình chóp
.S ABCD
có đáy là hình bình hành tâm
O
. Gọi thể tích khối chóp
.S ABCD
là
.V
M
là trung điểm
.SD
Thể tích khối chóp
.M ABO
bằng
A.
.
4
V
B.
.
2
V
C.
.
3
V
D.
.
8
V
Lời giải:
M
O
D
S
A
B
C
Ta có:
11
.
44
ABO
ABO ABCD
ABCD
S
SS
S
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <29 >
Do
M
là trung điểm
SD
nên
1
; ; .
2
d M ABCD d S ABCD
Vậy
.
.
8
M ABO
V
V
Chọn đáp án D.
Câu 10: Gọi
V
là thể tích khối chóp
.,S ABC
,,M N P
lần lượt là trung điểm
, , .SA SB SC
Thể tích khối
chóp
.S MNP
bằng
A.
.
8
V
B.
7
.
8
V
C.
.
3
V
D.
2
.
3
V
Lời giải:
P
N
M
S
A
B
C
Ta có:
.
..
.
11
. . .
88
S MNP
S MNP S ABC
S ABC
V
SM SN SP
VV
V SA SB SC
Chọn đáp án A.
Câu 11: Gọi
V
là thể tích khối chóp
.,S ABC
,,M N P
lần lượt là trung điểm
, , .SA SB SC
Thể tích khối
MNPCBA
bằng
A.
.
8
V
B.
7
.
8
V
C.
.
3
V
D.
2
.
3
V
Lời giải:
P
N
M
S
A
B
C
Ta có:
.
. . .
.
1 1 7
. . .
8 8 8
S MNP
S MNP S ABC MNPCBA S ABC
S ABC
V
SM SN SP
V V V V
V SA SB SC
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <30 >
Chọn đáp án B.
Câu 12: Gọi
V
là thể tích khối chóp
.,S ABC
,MN
lần lượt là trung điểm
,.SB SC
Thể tích khối chóp
.S AMN
bằng
A.
.
8
V
B.
7
.
8
V
C.
.
4
V
D.
3
.
4
V
Lời giải:
C
B
A
S
M
N
Ta có:
.
..
.
11
. . .
44
S AMN
S AMN S ABC
S ABC
V
SA SM SN
VV
V SA SB SC
Chọn đáp án C.
Câu 13: Gọi
V
là thể tích khối chóp
.,S ABC
,MN
lần lượt là trung điểm
,.SB SC
Thể tích khối
AMNCB
bằng
A.
.
8
V
B.
7
.
8
V
C.
.
4
V
D.
3
.
4
V
Lời giải:
C
B
A
S
M
N
Ta có:
.
. . .
.
1 1 3
..
4 4 4
S AMN
S AMN S ABC AMNCB S ABC
S ABC
V
SA SM SN
V V V V
V SA SB SC
Chọn đáp án D.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <31 >
Câu 14: Gọi
V
là thể tích khối chóp
.,S ABC
M
là trung điểm
.SC
Thể tích khối chóp
.S ABM
bằng
A.
.
2
V
B.
3
.
8
V
C.
.
4
V
D.
3
.
4
V
Lời giải:
C
B
A
S
M
Ta có:
.
..
.
11
. . .
22
S ABM
S ABM S ABC
S ABC
V
SA SB SM
VV
V SA SB SC
Chọn đáp án A.
Câu 15: Gọi
V
là thể tích khối chóp
.,S ABC
M
là trung điểm
.SC
Thể tích khối chóp
ABCM
bằng
A.
.
2
V
B.
3
.
8
V
C.
.
4
V
D.
3
.
4
V
Lời giải:
C
B
A
S
M
Ta có:
.
. . .
.
1 1 1
..
2 2 2
S ABM
S ABM S ABC ABCM S ABC
S ABC
V
SA SB SM
V V V V
V SA SB SC
Chọn đáp án A.
Câu 16: Cho hình chóp
.S ABCD
có đáy là hình bình hành. Gọi thể tích khối chóp
.S ABCD
là
.V
, , ,M N P Q
lần lượt là trung điểm
, , , .SA SB SC SD
Thể tích khối chóp
.S MNPQ
bằng
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <32 >
A.
.
4
V
B.
.
16
V
C.
7
.
8
V
D.
.
8
V
Lời giải:
Q
P
N
M
C
B
A
S
D
Ta có:
2, 2, 2, 2.
SA SB SC SD
a b c d
AM SN SP SQ
Vậy
.
..
.
11
.
4 8 8
S MNPQ
S MNPQ S ABCD
S ABCD
V
a b c d
VV
V abcd
Cách khác:
Ta có:
11
44
MNPQ
MNPQ ABCD
ABCD
S
SS
S
và
1
; ; .
2
d S MNPQ d S ABCD
Vậy

S. .
11
..
4 2 8
MNPQ S ABCD
V
VV
Chọn đáp án D.
Câu 17: Cho hình chóp
.S ABCD
có đáy là hình bình hành. Gọi thể tích khối chóp
.S ABCD
là
.V
, , ,M N P Q
lần lượt là trung điểm
, , , .SA SB SC SD
Thể tích khối
MNPQDABC
bằng
A.
15
.
16
V
B.
.
16
V
C.
7
.
8
V
D.
.
8
V
Lời giải:
Q
P
N
M
C
B
A
S
D
Ta có:
2, 2, 2, 2.
SA SB SC SD
a b c d
SM SN SP SQ
Vậy
.
. . .
.
1 1 7
.
4 8 8 8
S MNPQ
S MNPQ S ABCD MNPQDABC S ABCD
S ABCD
V
a b c d
V V V V
V abcd
Chọn đáp án C.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <33 >
Câu 18: Cho hình chóp
.S ABCD
có đáy là hình bình hành. Gọi thể tích khối chóp
.S ABCD
là
.V
,MN
lần lượt là trung điểm
,.SA SB
Thể tích khối chóp
.S MNCD
bằng
A.
3
.
8
V
B.
5
.
8
V
C.
.
4
V
D.
3
.
4
V
Lời giải:
D
S
A
B
C
M
N
Ta có:
2, 2, 1, 1.
SA SB SC SD
a b c d
SM SN SC SD
Vậy
.
..
.
33
.
4 8 8
S MNCD
S MNCD S ABCD
S ABCD
V
a b c d
VV
V abcd
Chọn đáp án A.
Câu 19: Cho hình chóp
.S ABCD
có đáy là hình bình hành. Gọi thể tích khối chóp
.S ABCD
là
.V
,MN
lần lượt là trung điểm
,.SA SB
Thể tích khối
MNBADC
bằng
A.
3
.
8
V
B.
5
.
8
V
C.
.
4
V
D.
3
.
4
V
Lời giải:
D
S
A
B
C
M
N
Ta có:
2, 2, 1, 1.
SA SB SC SD
a b c d
SM SN SC SD
Vậy
.
. . .
.
3 3 5
.
4 8 8 8
S MNCD
S MNCD S ABCD MNBADC S ABCD
S ABCD
V
a b c d
V V V V
V abcd
Chọn đáp án B.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <34 >
Câu 20: Gọi
V
là thể tích khối lăng trụ
..ABC A B C
Thể tích khối chóp
.A A B C
bằng
A.
.
3
V
B.
2
.
3
V
C.
.
2
V
D.
3
.
4
V
Lời giải:
A
B
C
A'
B'
C'
Ta có:
.
1
; . .
33
A A B C A B C
V
V d A A B C S

Chọn đáp án A.
Câu 21: Gọi
V
là thể tích khối lăng trụ
.,ABC A B C M
là trung điểm
.AA
Thể tích khối chóp
.M A B C
bằng
A.
.
3
V
B.
2
.
3
V
C.
.
6
V
D.
3
.
4
V
Lời giải:
M
A
B
C
A'
B'
C'
Ta có:
.
1 1 1
; . . ; . .
3 3 2 6
A A B C A B C A B C
V
V d M A B C S d A A B C S
Chọn đáp án C.
Câu 22: Gọi
V
là thể tích khối lăng trụ
.,ABC A B C M
là điểm bất kì trên cạnh
.AB
Thể tích khối
chóp
.M A B C
bằng
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <35 >
A.
.
3
V
B.
2
.
3
V
C.
.
2
V
D.
3
.
4
V
Lời giải:
M
A
B
C
A'
B'
C'
Ta có:
.
1
; . .
33
M A B C A B C
V
V d M A B C S

Chọn đáp án A.
Câu 23: Gọi
V
là thể tích khối lăng trụ
..ABC A B C
Thể tích khối chóp
.A BCC B

bằng
A.
.
3
V
B.
2
.
3
V
C.
.
2
V
D.
3
.
4
V
Lời giải:
A
B
C
A'
B'
C'
Ta có:
..
12
; . .
3 3 3
A A B C A B C A BCC B
VV
V d A A B C S V
Chọn đáp án B.
Câu 24: Gọi
V
là thể tích khối lăng trụ
.,ABC A B C M
là điểm bất kì trên
.AA
Thể tích khối chóp
.M BCC B

bằng
A.
.
3
V
B.
2
.
3
V
C.
.
2
V
D.
3
.
4
V
Lời giải:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <36 >
M
A
B
C
A'
B'
C'
Ta có:
..
1 1 2
; . ; . .
3 3 3
M BCC B BCC B BCC B A BCC B
V
V d M BCC B S d A BCC B S V
Chọn đáp án B.
Câu 25: Gọi
V
là thể tích khối lăng trụ
. , , ,ABC A B C M N P
lần lượt là trung điểm
, , .AA BB CC
Thể
tích khối
.ABC MNP
bằng
A.
.
3
V
B.
2
.
3
V
C.
.
2
V
D.
3
.
4
V
Lời giải:
P
N
M
A
B
C
A'
B'
C'
Ta có:
.
.
1 1 1 1 1 1
3 3 2 2 2 2
ABC MNP
ABC A B C
V
AM BN CP
V AA BB CC
.
.
2
ABC MNP
V
V
Cách khác:
Khối
.ABC MNP
là khối lăng trụ, do đó
.
1
. ,( ) . ,( ) .
22
ABC MNP ABC ABC
V
V S d M ABC S d A ABC
Chọn đáp án C.
Câu 26: Gọi
V
là thể tích khối lăng trụ
. , ,ABC A B C M N
lần lượt là trung điểm
,.AA BB

Thể tích
khối
ABCNM
bằng
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <37 >
A.
.
3
V
B.
2
.
3
V
C.
.
2
V
D.
3
.
4
V
Lời giải:
C'
B'
A'
C
B
A
M
N
Ta có:
.
1 1 1 1 1
0.
3 3 2 2 3 3
ABCNM
ABCNM
ABC A B C
V
AM BN V
V
V AA BB

Cách khác:

..
1
33
C A B C ABC A B C
V
VV


.
2
3
C ABB A
V
V

..
1 1 2
..
2 2 3 3
C ABNM C ABB A
VV
VV
Chọn đáp án A.
Câu 27: Gọi
V
là thể tích khối lăng trụ
. , ,ABC A B C M N
lần lượt là trung điểm
,.AA BB

Thể tích
khối
CMNB C A
bằng
A.
.
3
V
B.
2
.
3
V
C.
.
2
V
D.
3
.
4
V
Lời giải:
C'
B'
A'
C
B
A
M
N
Cách 1:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <38 >
Ta có:
.
1 1 1 1 1
0.
3 3 2 2 3 3
ABCNM
ABCNM
ABC A B C
V
AM BN V
V
V AA BB

Vậy
2
.
3
CMNB C A
V
V
Cách 2:

..
1
33
C A B C ABC A B C
V
VV


.
2
3
C ABB A
V
V

..
1
.
23
C ABNM C ABB A
V
VV
Vậy
2
.
33
CMNB C A
VV
VV
Cách 3:

..
1
33
C A B C ABC A B C
V
VV
và

..C ABNM C MNB A
VV
, do đó:
. . .
3
C A B C C ABNM C MNB A
V
V V V
.
Vậy
2
.
3 3 3
CMNB C A
V V V
V
Chọn đáp án B.
Câu 28: Gọi
V
là thể tích khối lăng trụ
.,ABC A B C M
là trung điểm
,AA N
trên cạnh
BB
sao cho
2.BN NB
Thể tích khối
ABCNM
bằng
A.
.
3
V
B.
2
.
3
V
C.
11
.
18
V
D.
7
.
18
V
Lời giải:
N
M
A
B
C
A'
B'
C'
Ta có:
.
1 1 1 2 7 7
0.
3 3 2 3 18 18
ABCNM
ABCNM
ABC A B C
V
AM BN V
V
V AA BB

Chọn đáp án D.
Câu 29: Gọi
V
là thể tích khối hộp
. , , , ,ABCD A B C D M N P Q
lần lượt là trung điểm
, , , .AA BB CC DD
Thể tích khối
.ABCD MNPQ
bằng
A.
.
3
V
B.
2
.
3
V
C.
.
2
V
D.
3
.
4
V
Lời giải:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <39 >
Q
P
N
M
A
B
C
D
C'
B'
A'
D'
Ta có:
.
.
1 1 1 1 1 1 1
4 4 2 2 2 2 2
ABCD MNPQ
ABCD A B C D
V
AM BN CP DQ
V AA BB CC DD
.
.
2
ABCD MNPQ
V
V
Cách khác:
Khối
.ABCD MNPQ
là khối hộp, do đó:
.
1
. ,( ) . ,( ) .
22
ABCD MNPQ ABCD ABCD
V
V S d M ABCD S d A ABCD
Chọn đáp án C.
Câu 30: Gọi
V
là thể tích khối hộp
. , ,ABCD A B C D M N
lần lượt là trung điểm
,.AA BB

Thể tích
khối
ABCDMNC D

bằng
A.
.
3
V
B.
2
.
3
V
C.
.
2
V
D.
3
.
4
V
Lời giải:
D'
A'
B'
C'
D
C
B
A
M
N
Ta có:
.
1 1 1 1 3
1 1 1 1
4 4 2 2 4
ABCDMNC D
ABCD A B C D
V
AM BN
V AA BB


3
.
4
ABCDMNC D
V
V


Chọn đáp án D.
Câu 31: Gọi
V
là thể tích khối hộp
..ABCD A B C D
Thể tích khối chóp
.B ABC
bằng
A.
.
6
V
B.
.
12
V
C.
.
24
V
D.
.
4
V
Lời giải:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <40 >
A
B
C
D
C'
B'
A'
D'
Do
;;
1
2
BAC ABCD
d B BAC d B ABCD
SS

nên
.
1 1 1 1
; . .
3 3 2 6
B BAC BAC
V d B BAC S V V
Cách khác: Đặc biệt hóa, hình hộp là hình lập phương cạnh bằng 1
Suy ra:
.
.
1
.
1 1 1 1 1
6
. . . .1. .1.1
3 2 3 2 6
B BAC
B BAC
V
V
V
V BB BA BC

Chọn đáp án A.
Câu 32: Gọi
V
là thể tích khối hộp
. , , ,ABCD A B C D M N P
lần lượt là trung điểm
, , .AB BC BB
Thể
tích khối
BMNP
bằng
A.
.
36
V
B.
.
12
V
C.
.
24
V
D.
.
48
V
Lời giải:
P
N
M
D'
A'
B'
C'
D
C
B
A
Do
1
;;
2
1
8
BMN ABCD
d P BMM d B ABCD
SS
nên
.
1 1 1 1 1
; . . .
3 3 2 8 48
B BMN BMN
V d P BMM S V V
Cách khác: Đặc biệt hóa, hình hộp là hình lập phương cạnh bằng 1
Suy ra:
.
.
1
.
1 1 1 1 1 1 1 1
48
. . . . . . .
3 2 3 2 2 2 2 48
P BMN
P BMN
V
V
V
V PB BM BN

Chọn đáp án D.
Câu 33: Gọi
V
là thể tích khối lăng trụ
. , ,ABC A B C M N
lần lượt là trung điểm
,.AB AC
Thể tích khối
chóp
A AMN
bằng
A.
.
3
V
B.
.
12
V
C.
.
6
V
D.
11
.
12
V
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <41 >
Lời giải:
N
M
A
B
C
A'
B'
C'
Ta có:
.
1 1 1 1
; . . ; . .
4 3 3 4 12
AMN ABC A AMN AMN ABC
V
S S V d A ABC S d A ABC S

Chọn đáp án B.
Câu 34: Gọi
V
là thể tích khối lăng trụ
. , ,ABC A B C M N
lần lượt là trung điểm
,.AB AC
Thể tích khối
MNCBC A B
bằng
A.
5
.
6
V
B.
.
12
V
C.
.
6
V
D.
11
.
12
V
Lời giải:
N
M
A
B
C
A'
B'
C'
Ta có:
.
1 1 1 1
; . . ; . .
4 3 3 4 12
AMN ABC A AMN AMN ABC
V
S S V d A ABC S d A ABC S

11
.
12
MNCBC A B
V
V

Chọn đáp án D.
Câu 35: Gọi
V
là thể tích khối lăng trụ
. , ,ABC A B C M N
lần lượt là trung điểm
,.AB AC
Thể tích khối
MNCBB C

bằng
A.
3
.
4
V
B.
5
.
12
V
C.
.
4
V
D.
7
.
12
V
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <42 >
Lời giải:
M
N
C'
B'
A'
C
B
A
Ta có:
.
..
.
2 2 1 1 3 3
4 4.2.2.1.1 8 8
A MNC B
A MNC B A BCC B
A BCC B
V
a b c d
VV
V abcd


Vậy
.
5 5 2 5
..
8 8 3 12
MNCBB C A BCC B
V V V V
Chọn đáp án B.
Câu 36: Gọi
V
là thể tích khối lăng trụ
. , ,ABC A B C M N
lần lượt là trung điểm
,.AB AC
Thể tích khối
AMNC B A
bằng
A.
3
.
4
V
B.
5
.
12
V
C.
.
4
V
D.
7
.
12
V
Lời giải:
M
N
C'
B'
A'
C
B
A
Ta có:
.
..
.
2 2 1 1 3 3
4 4.2.2.1.1 8 8
A MNC B
A MNC B A BCC B
A BCC B
V
a b c d
VV
V abcd


Vậy
.
5 5 2 5 7
. ; .
8 8 3 12 12
MNCBB C A BCC B AMNC B A
V V V V V V
Chọn đáp án D.
Câu 37: Cho lăng trụ
..ABC A B C
Gọi
12
,VV
lần lượt là thể tích các khối
.A A B C
và
.ABCC
Khẳng
định nào sau đây đúng?
A.
1
2
1.
V
V
B.
1
2
1
.
2
V
V
C.
1
2
1
.
3
V
V
D.
1
2
3
.
2
V
V
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <43 >
Lời giải:
C'
B'
A'
C
B
A
Ta có:

1
12
2
1
;.
3
.
1
;.
3
A B C
ABC
V d A A B C S
VV
V d C ABC S
Chọn đáp án A.
Câu 38: Cho khối chóp
.S ABC
có thể tích
V
. Gọi
,BC

lần lượt là trung điểm của
,AB AC
. Tính theo
V
thể tích khối chóp
.S AB C

.
A.
1
3
V
. B.
1
2
V
. C.
1
12
V
. D.
1
4
V
.
Lời giải:
C'
B'
S
B
A
C
Ta có tỷ số thể tích
.
.
1 1 1
..
2 2 4
A SB C
A SBC
V
AB AC
V AB AC


. Do đó
..
1
4
A SB C A SBC
VV

hay
.
1
4
S AB C
VV

.
Chọn đáp án D.
Câu 39: Cho khối tứ diện
SABC
có
,,M N P
lần lượt là trung điểm
,,SA SB SC
và
G
là trọng tâm tam
giác
ABC
. Gọi
V
là thể tích khối
SABC
,
V
là thể tích khối
GNMP
. Tỉ số
V
V
bằng
A.
1
6
V
V
. B.
1
8
V
V
. C.
1
4
V
V
. D.
2
7
V
V
.
Lời giải:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <44 >
G
P
C
A
B
S
M
N
Ta có
,,d S MNP d G MNP
. Do đó

SNMP GMNP
V V V
.
Do đó
1 1 1 1
. . . .
2 2 2 8
SMNP
SABC
V
V SM SN SP
V V SA SB SC
.
Chọn đáp án B.
Câu 40: Cho khối lăng trụ
.ABC A B C
. Gọi
,MN
lần lượt là trung điểm của đoạn thẳng
AA
và
'.BB
Tính tỉ số thể tích của khối tứ diện
'CMNC
với khối lăng trụ đã cho.
A.
1
3
. B.
1
2
. C.
2
3
. D.
3
4
.
Lời giải:
C'
B'
A'
C
B
A
M
N
Ta có:
.
. . ' ' '
. ' ' '
1 1 1
3 ' ' ' 3 3
ABC MNC
ABC MNC ABC A B C
ABC A B C
V
AM BN CC
VV
V AA BB CC



.
Tương tự ta có:
' ' '. '
' ' '. ' ' ' '.
' ' '.
1 ' ' ' ' 1 1
3 ' ' ' 3 3
A B C MNC
A B C MNC A B C ABC
A B C ABC
V
A M B N C C
VV
V A A B B C C



.
'
' . ' ' '
. ' ' '
11
33
CMNC
CMNC ABC A B C
ABC A B C
V
VV
V
.
Chọn đáp án A.
_________________HẾT_________________
Huế, 10h45’ Ngày 07 tháng 7 năm 2023
| 1/45
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ TOÁN 12 THỂ TÍCH KHỐI ĐA DIỆN TỶ SỐ THỂ TÍCH
 LUYỆN THI THPT QUỐC GIA
 CẬP NHẬT TỪ ĐỀ THI MỚI NHẤT
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia CHUY£N §Ò: THÓ TÝCH KhèI §A DIÖN Líp To¸n thÇy L£ B¸ B¶O
Trường THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 Hương Trµ, HuÕ. VÊn ®Ò 2: Tû sè thÓ tÝch
CÁC KẾT QUẢ CẦN LƯU Ý Hình Kết quả
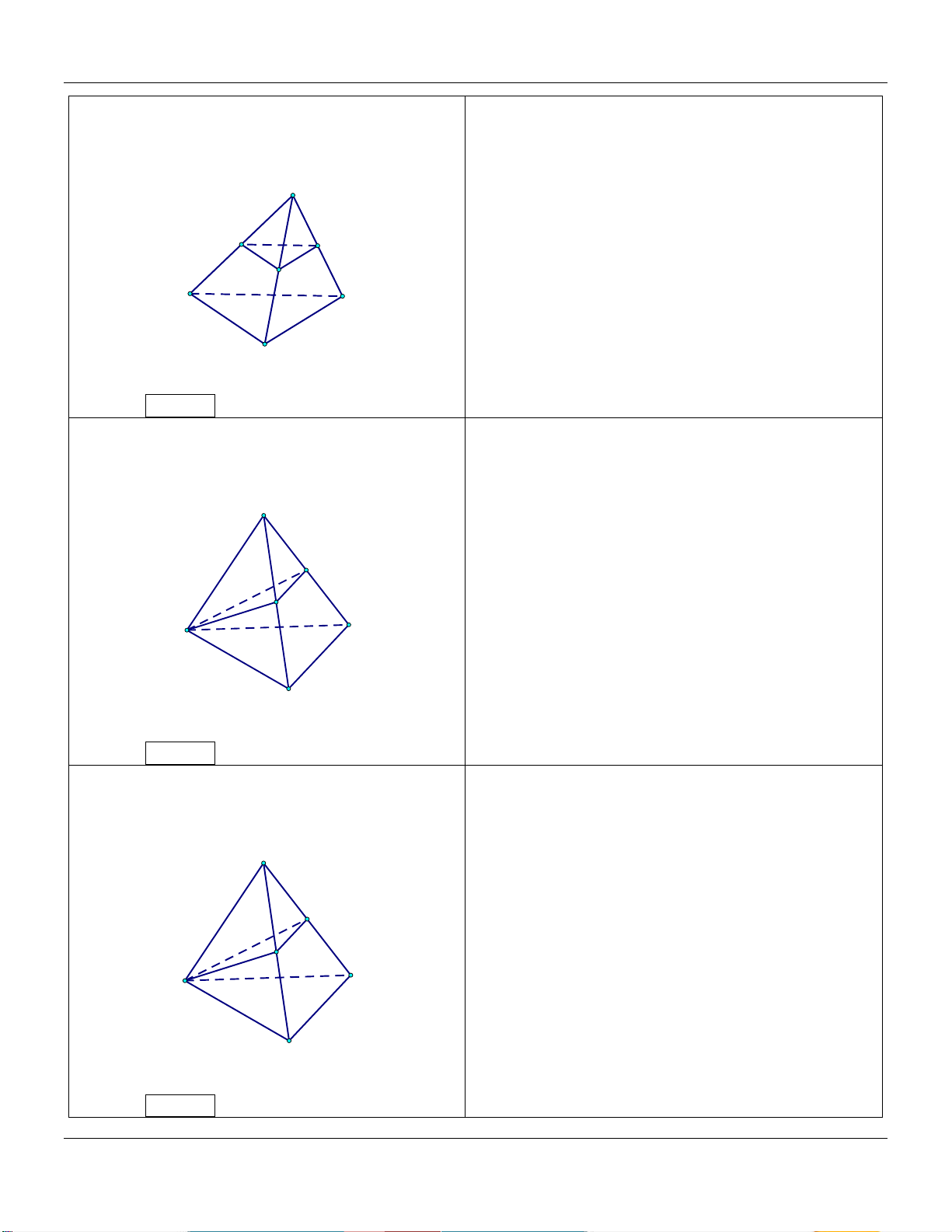
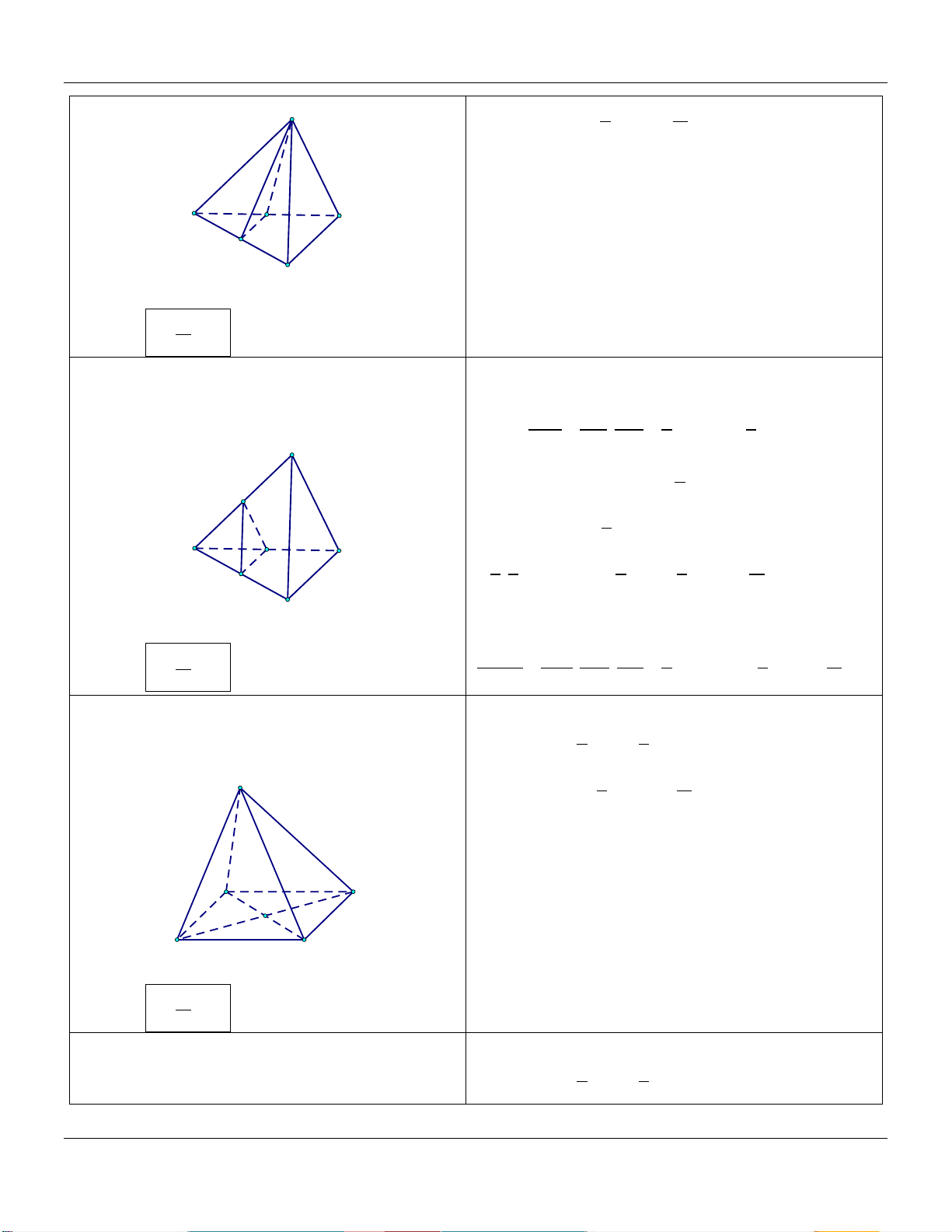
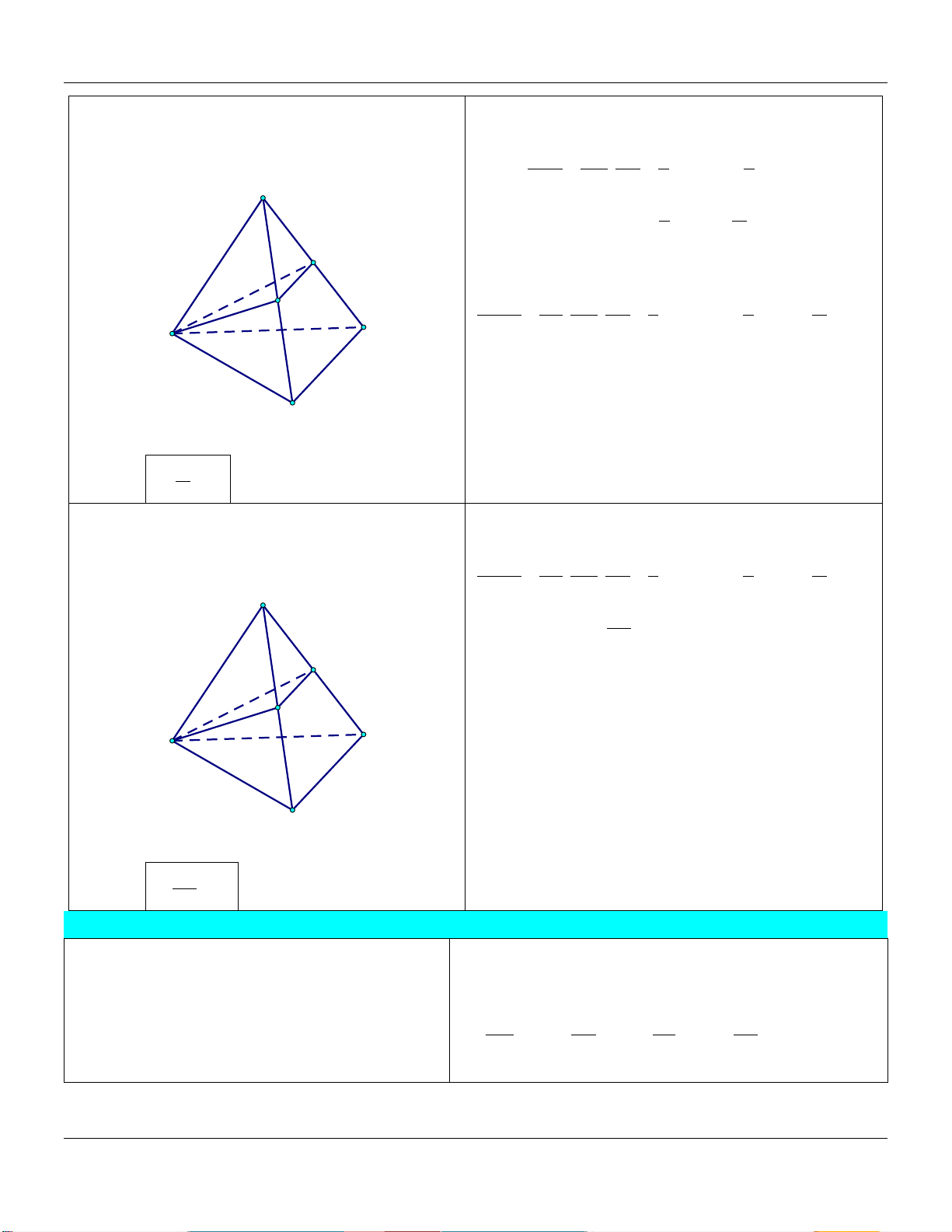
1) Tam giác O S OA' OB' OA' B'  A' . S OA OB OAB B' A B
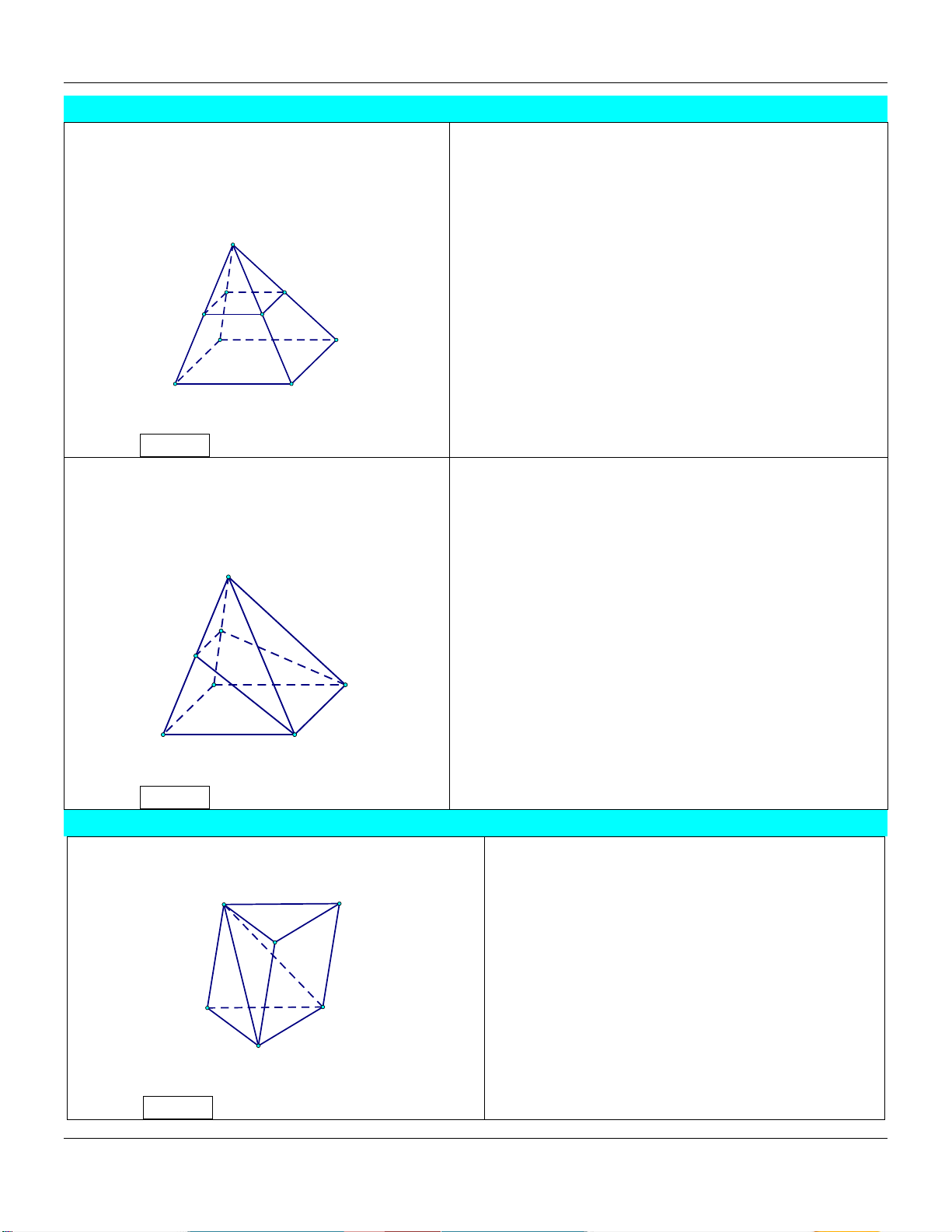
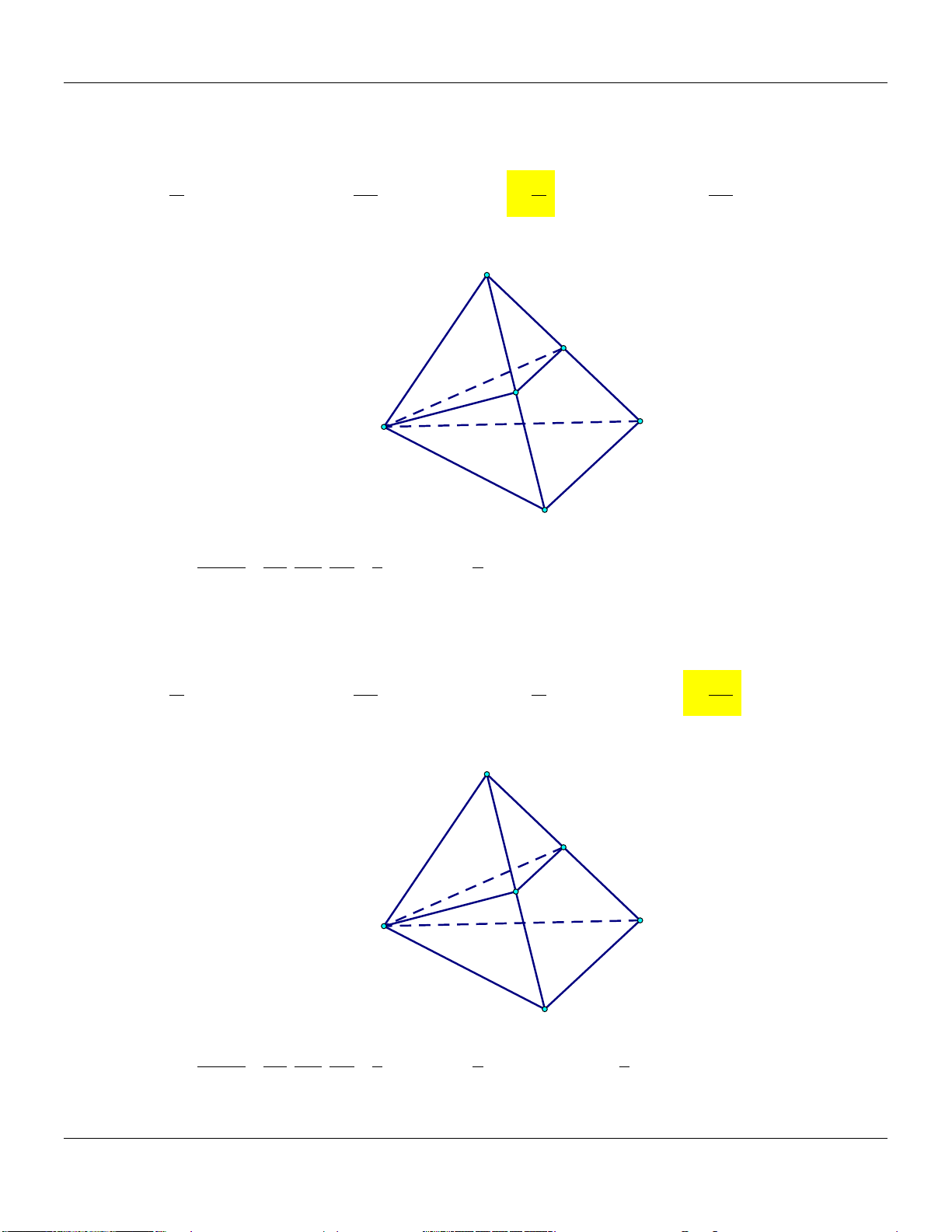
2) Hình chóp tam giác S V
SA' SB' SC ' A'
S.A'B'C'  . . C' V SA SB SC S.ABC B' C A B
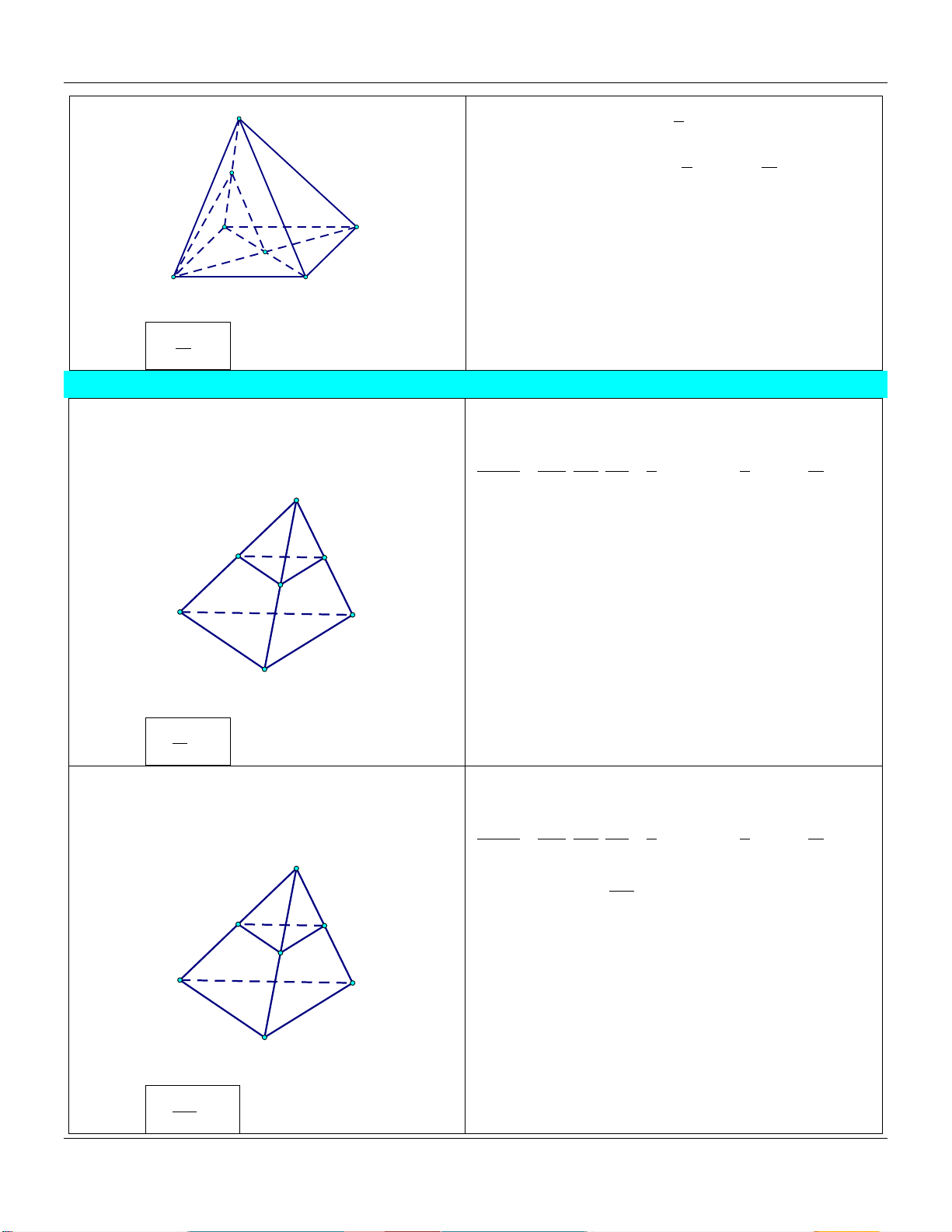
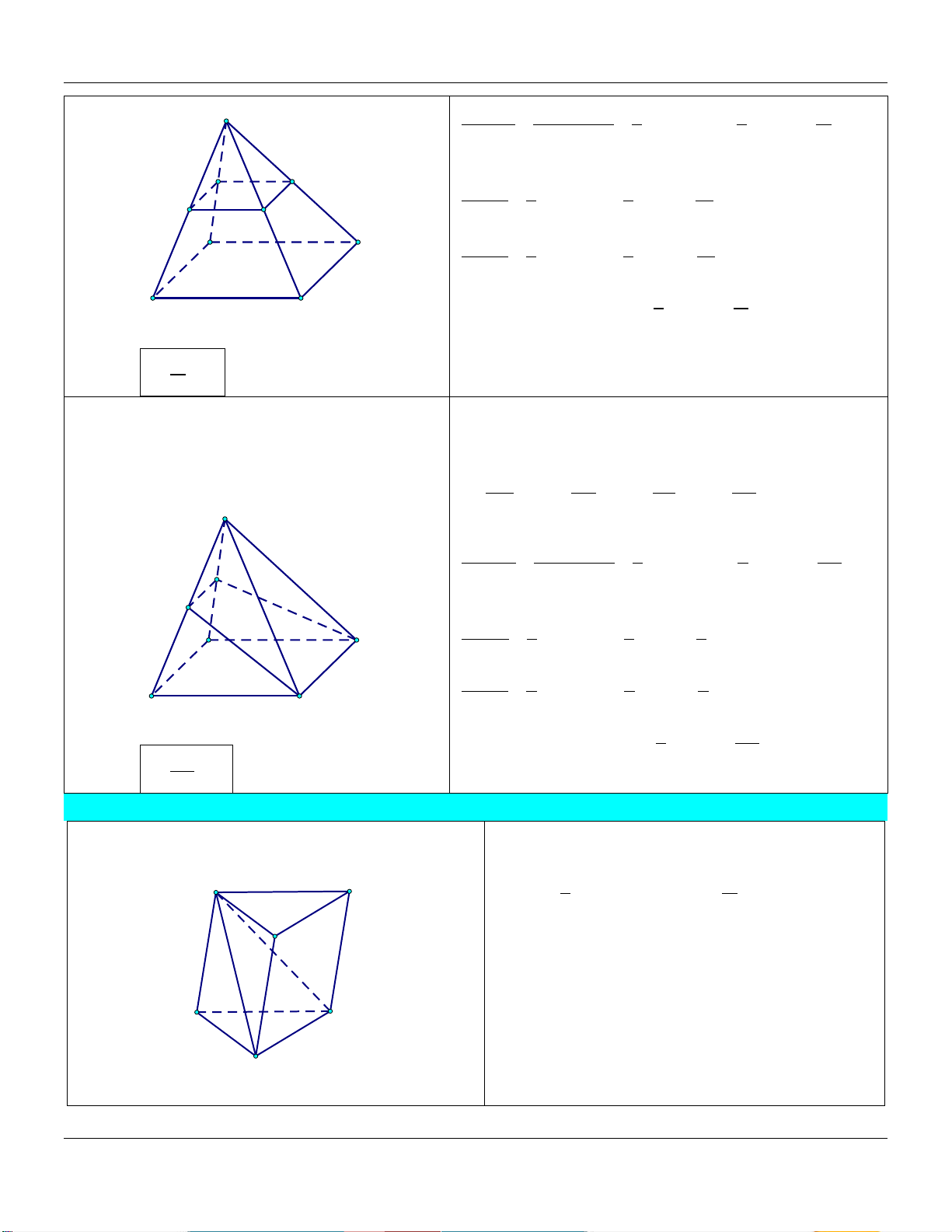
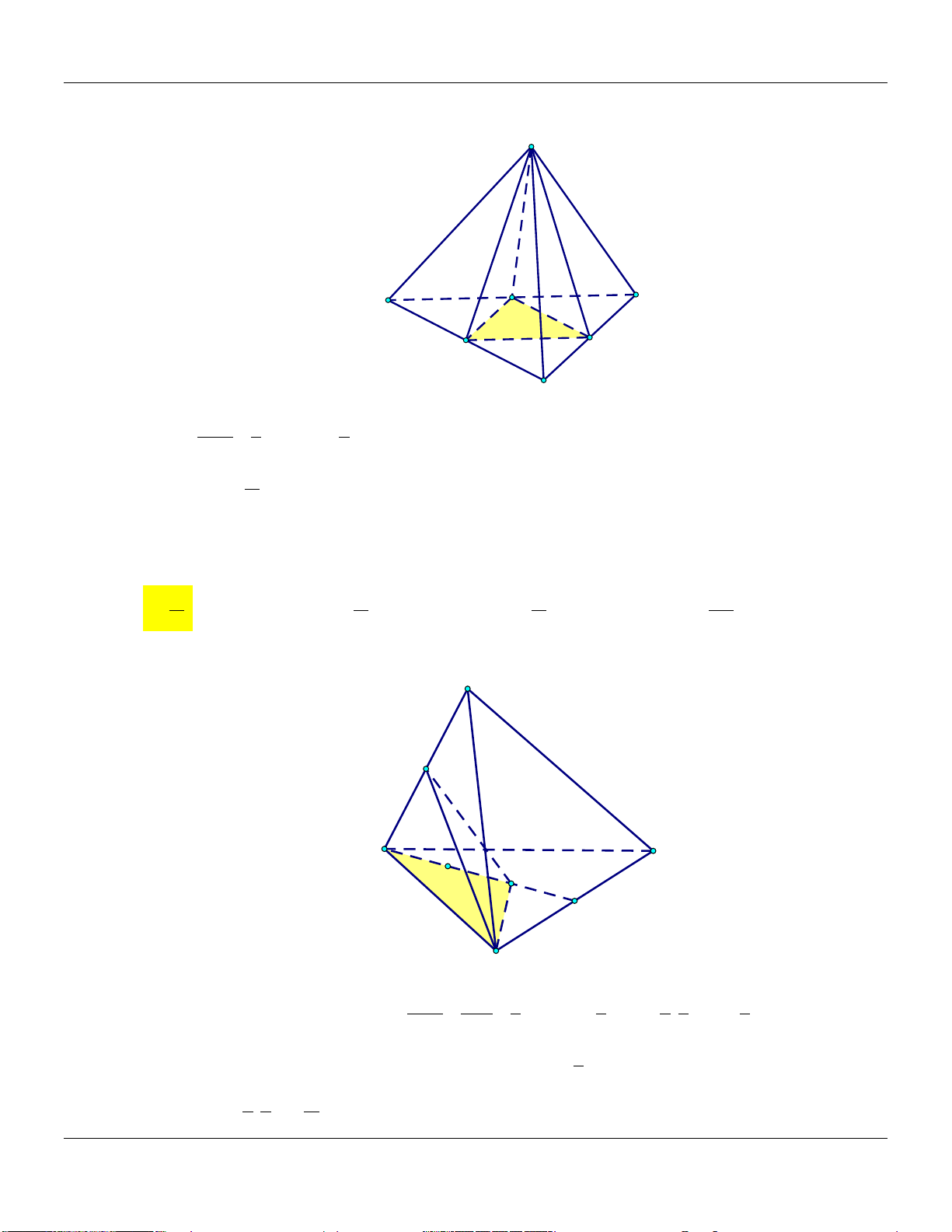
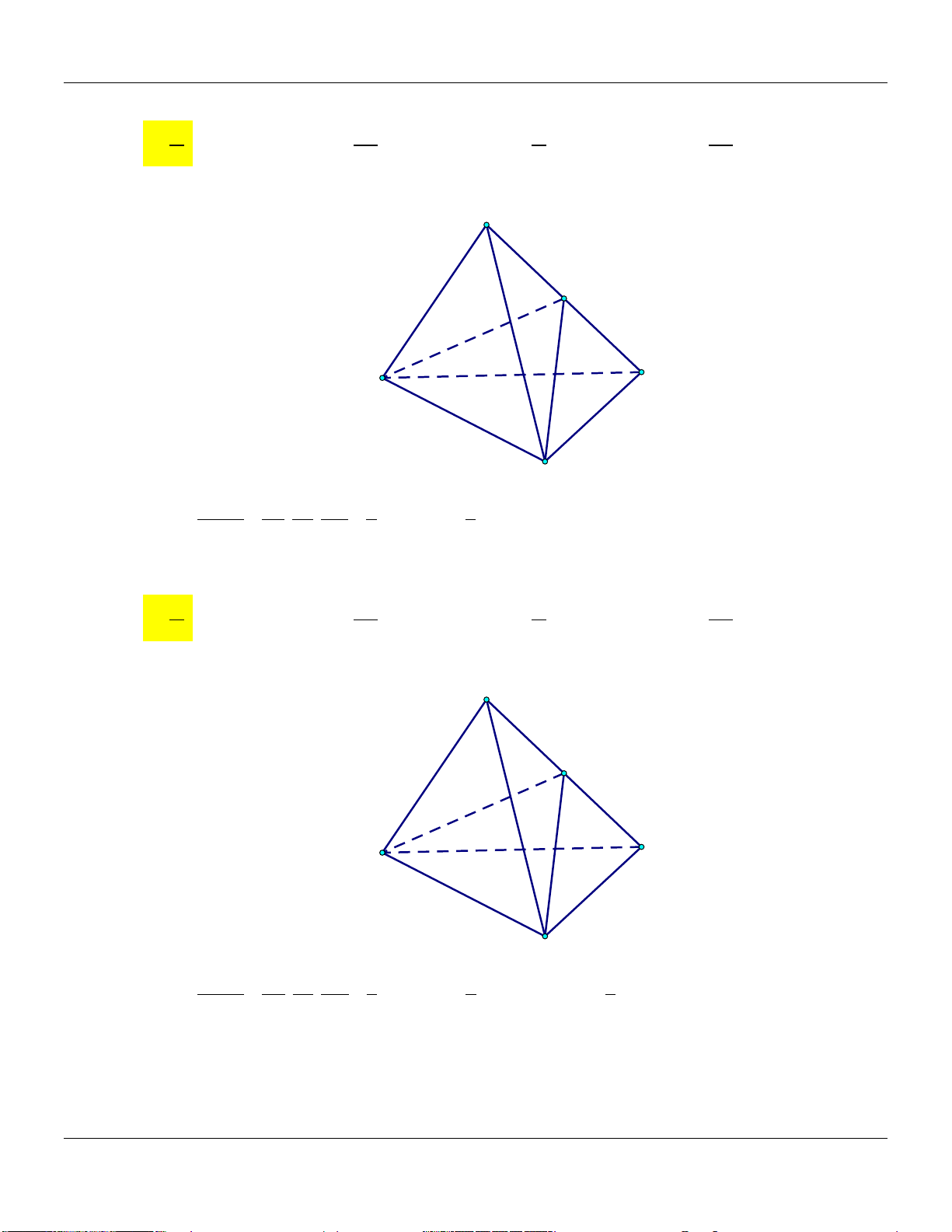
3) Hình chóp tứ giác có đáy là hình bình hành S V        a b c d Tæng S.A B C D   V 4abcd 4 TÝch S.ABCD C' SA SB SC SD D'     B' Trong đó: a ; b ; c ; d SASBSCSD ; A'
A, B, C, D đồng phẳng. D A B C
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <1 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
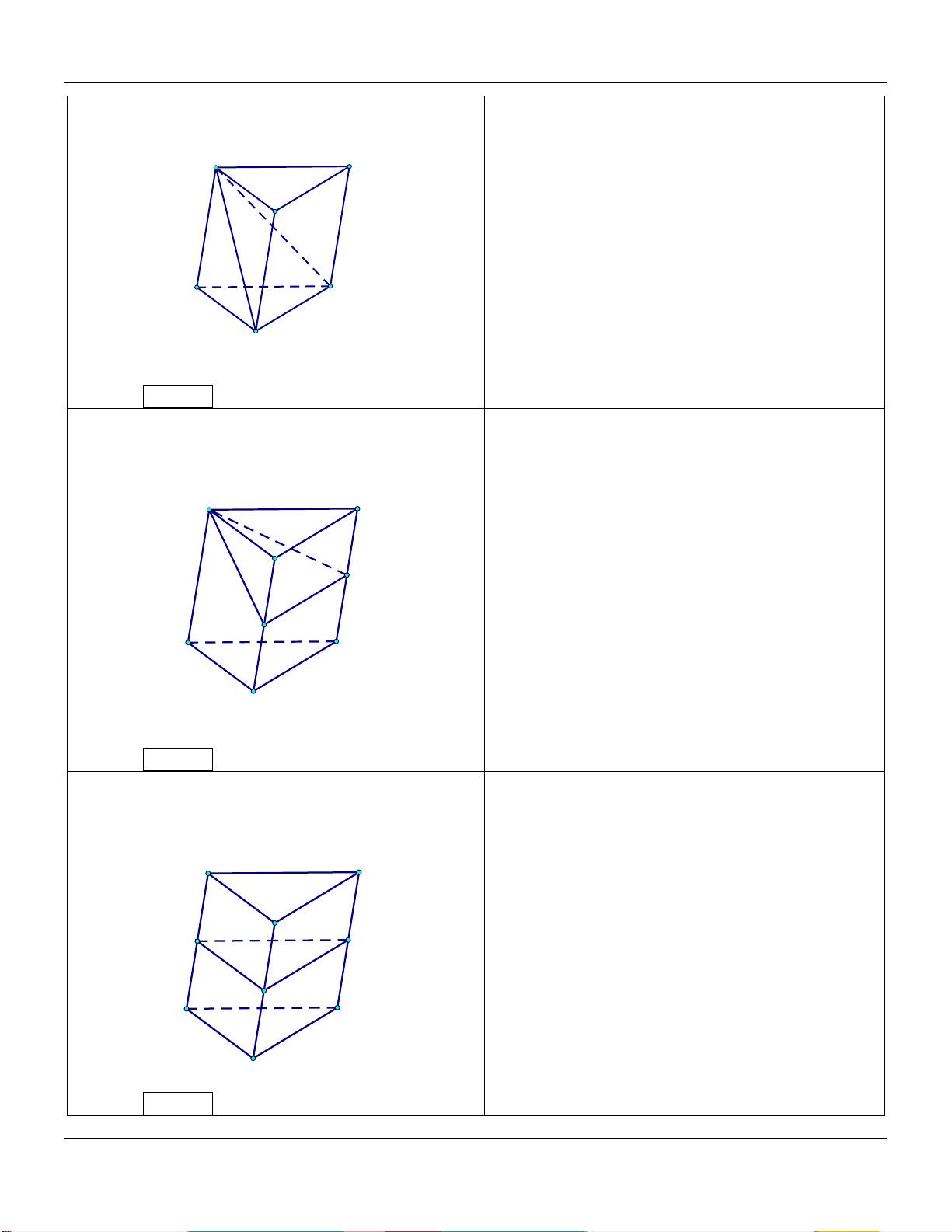
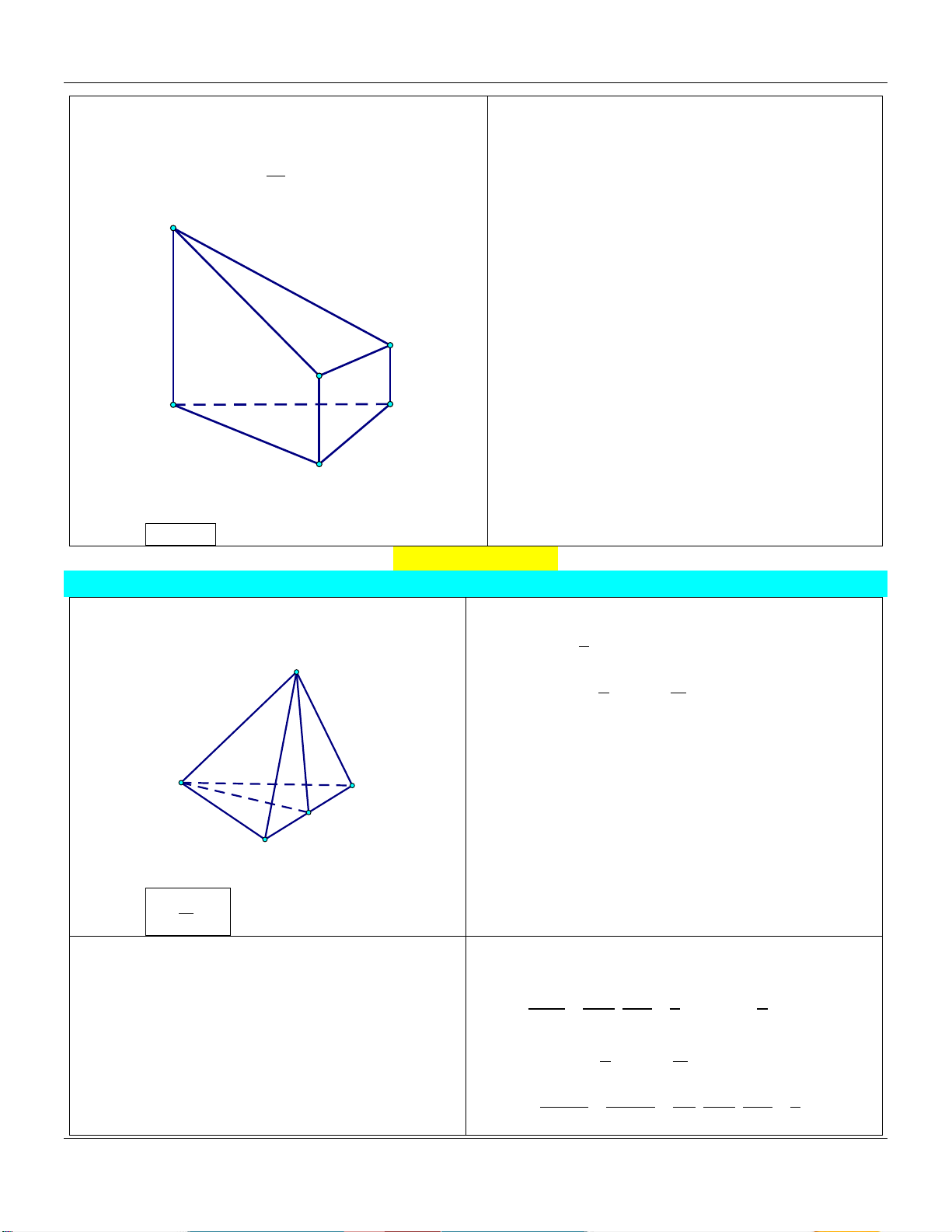
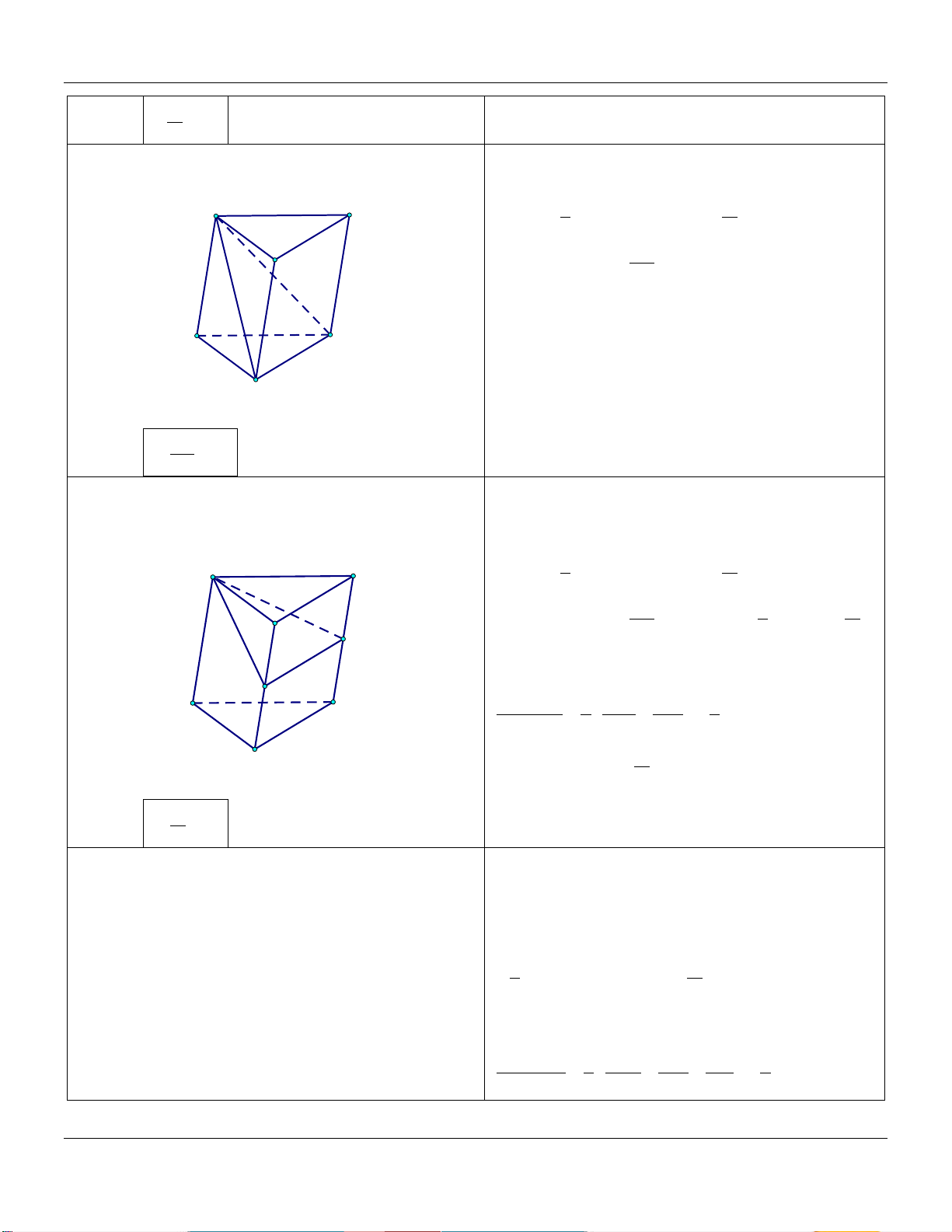
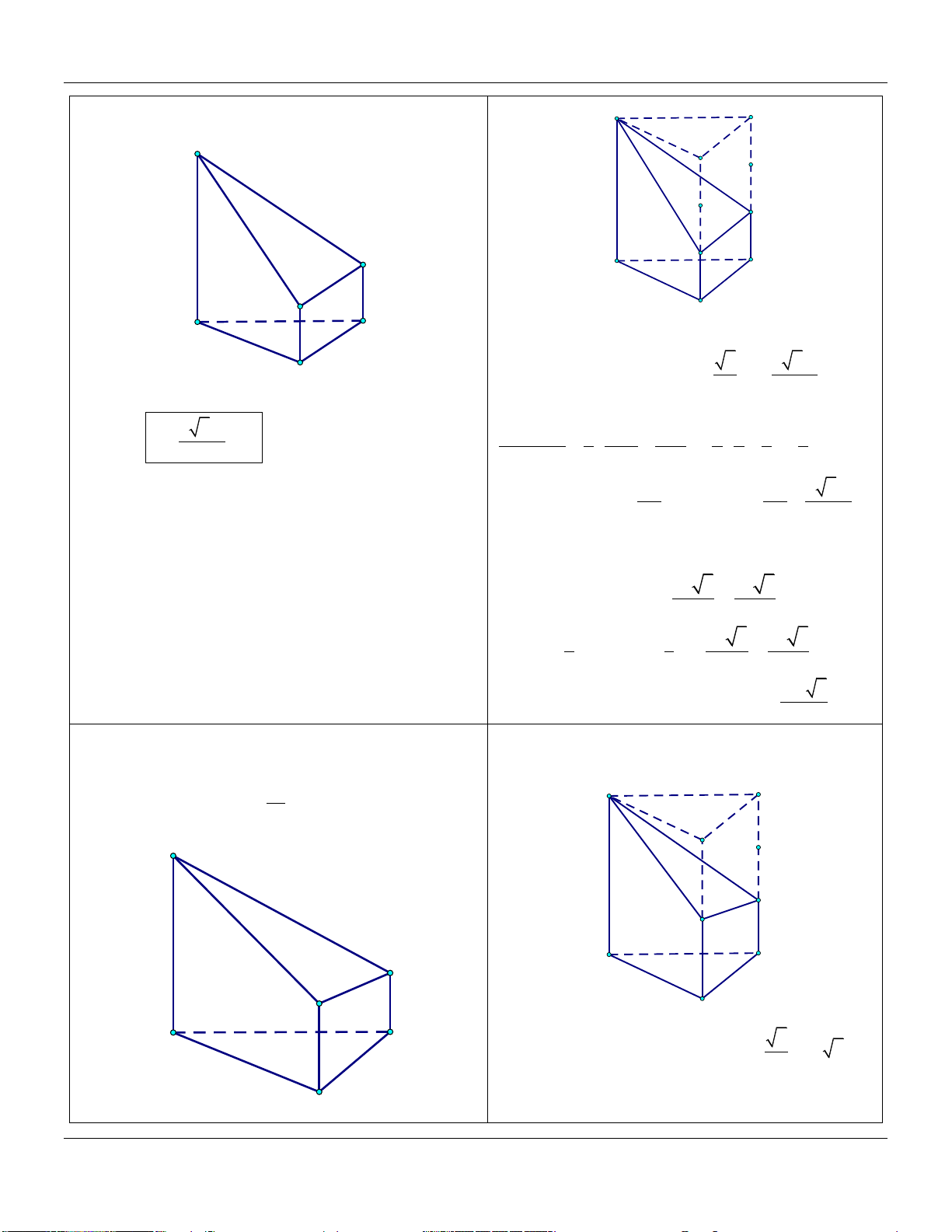
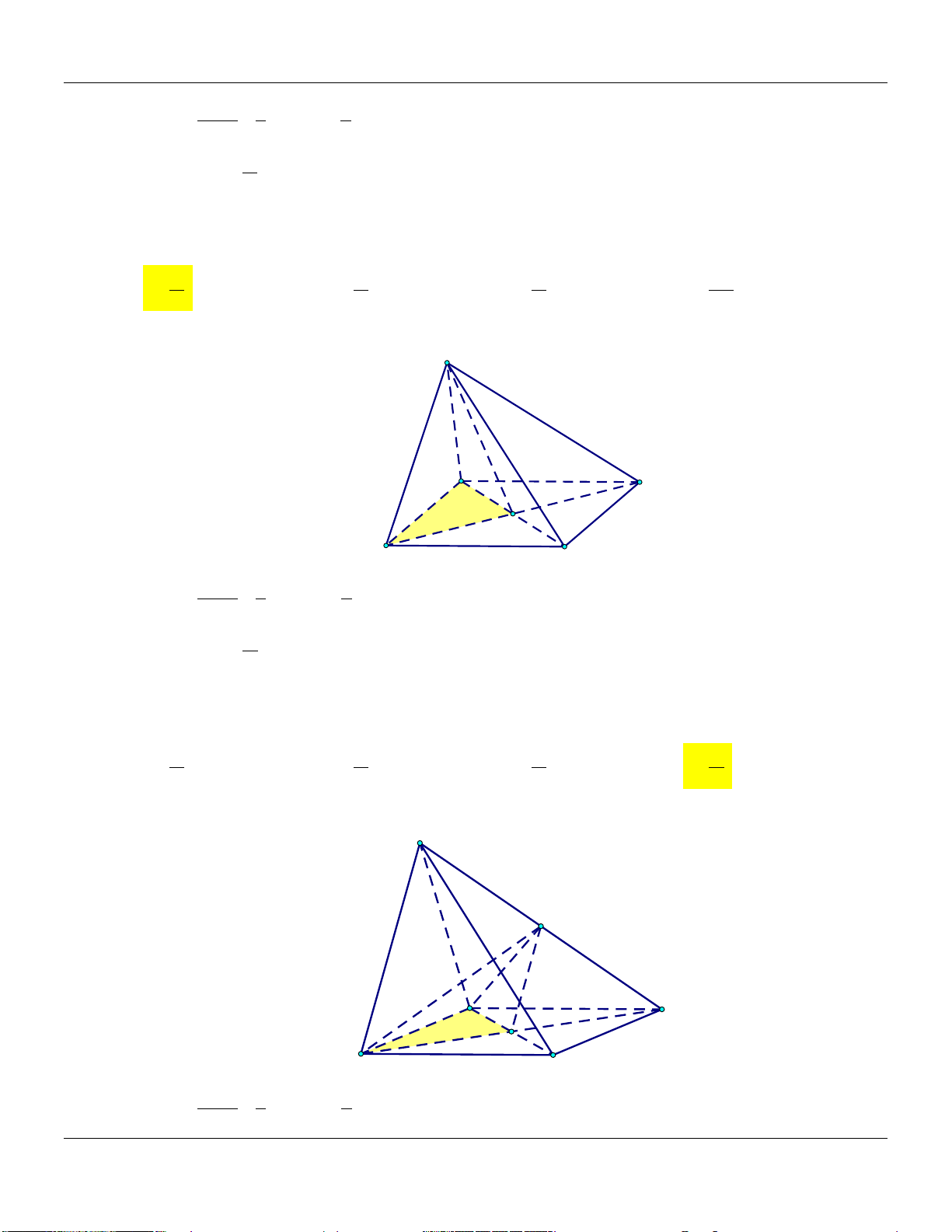
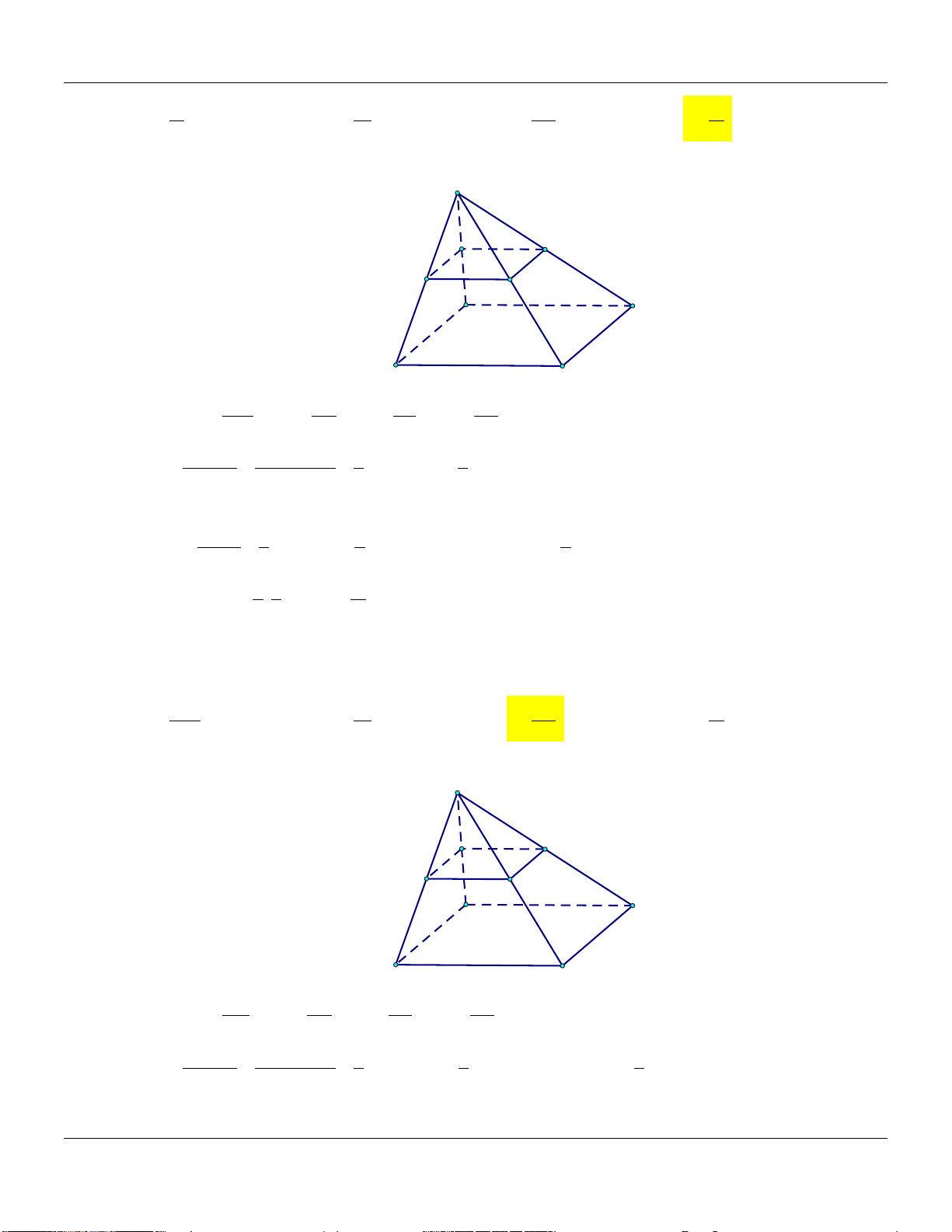
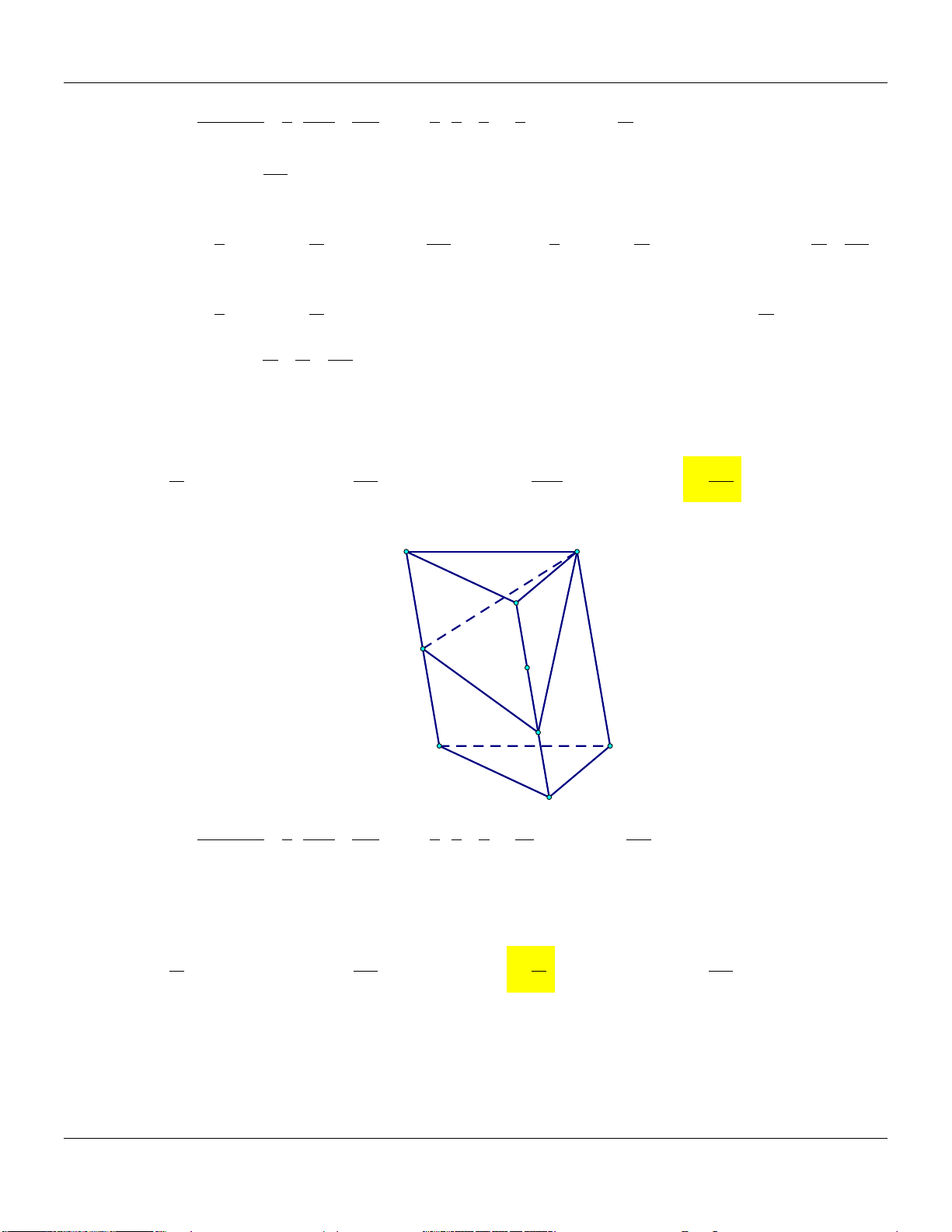
4) Hình lăng trụ tam giác A C V 1  AM BN CP ABC.MNP    M B   V       3  AA BB CC ABC.A B C P N C' A' B'
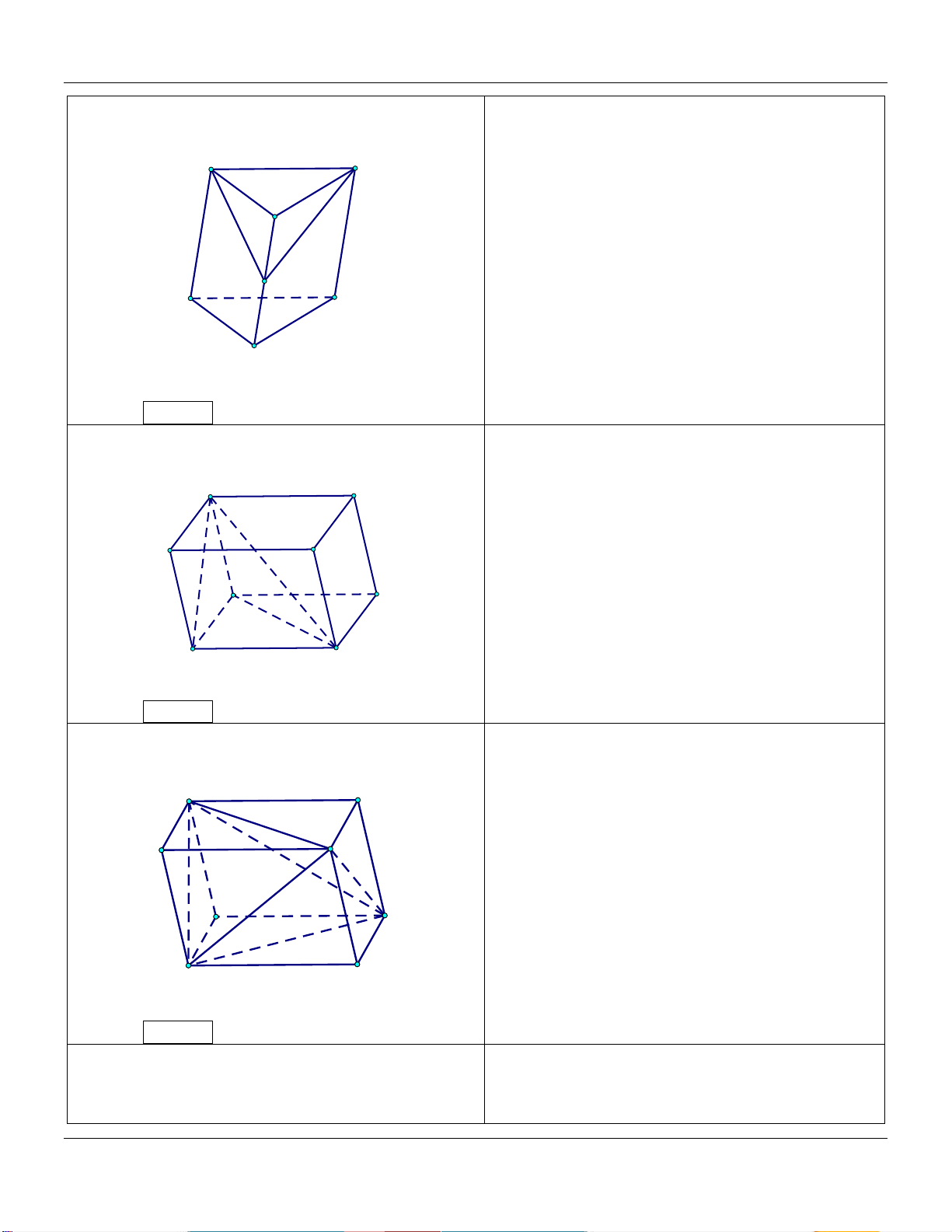
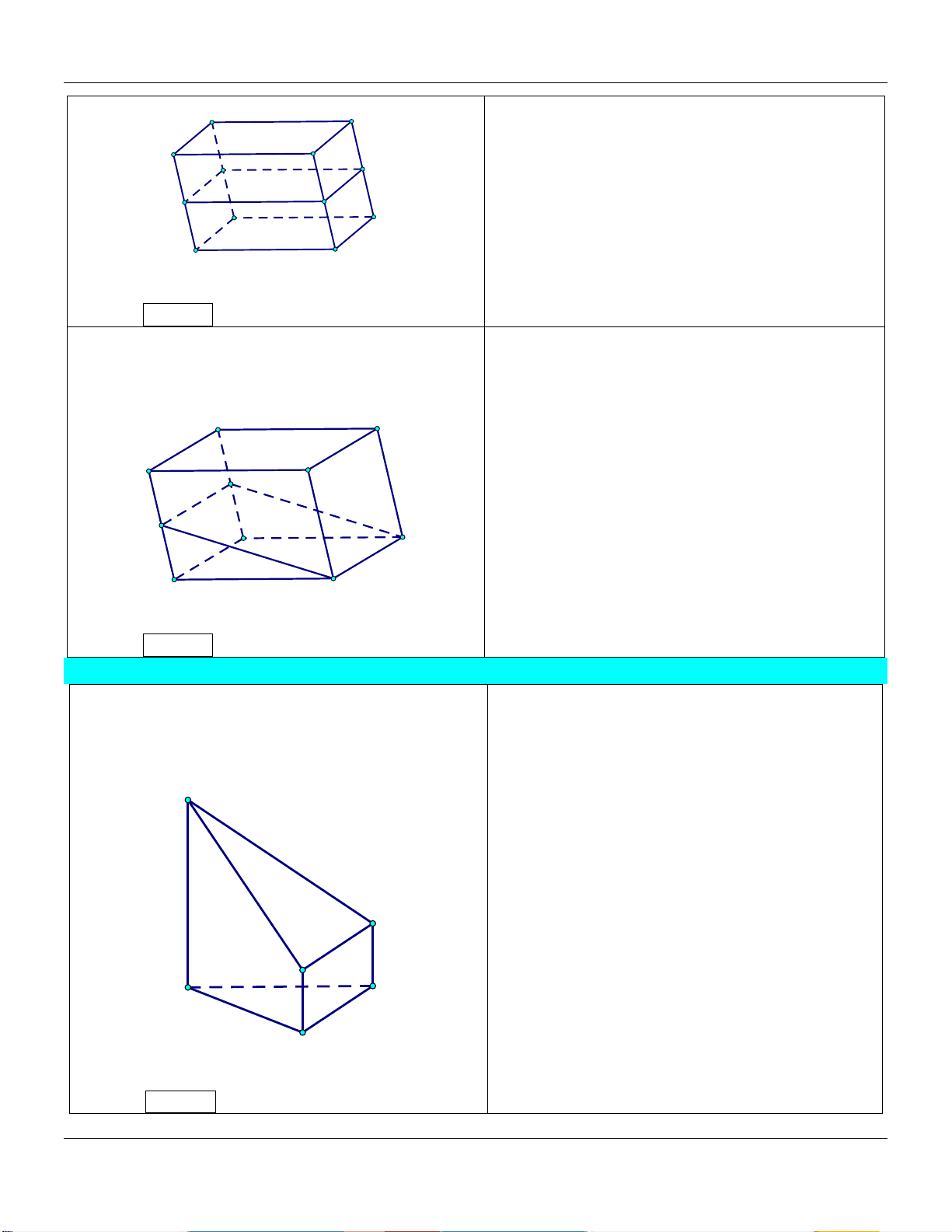
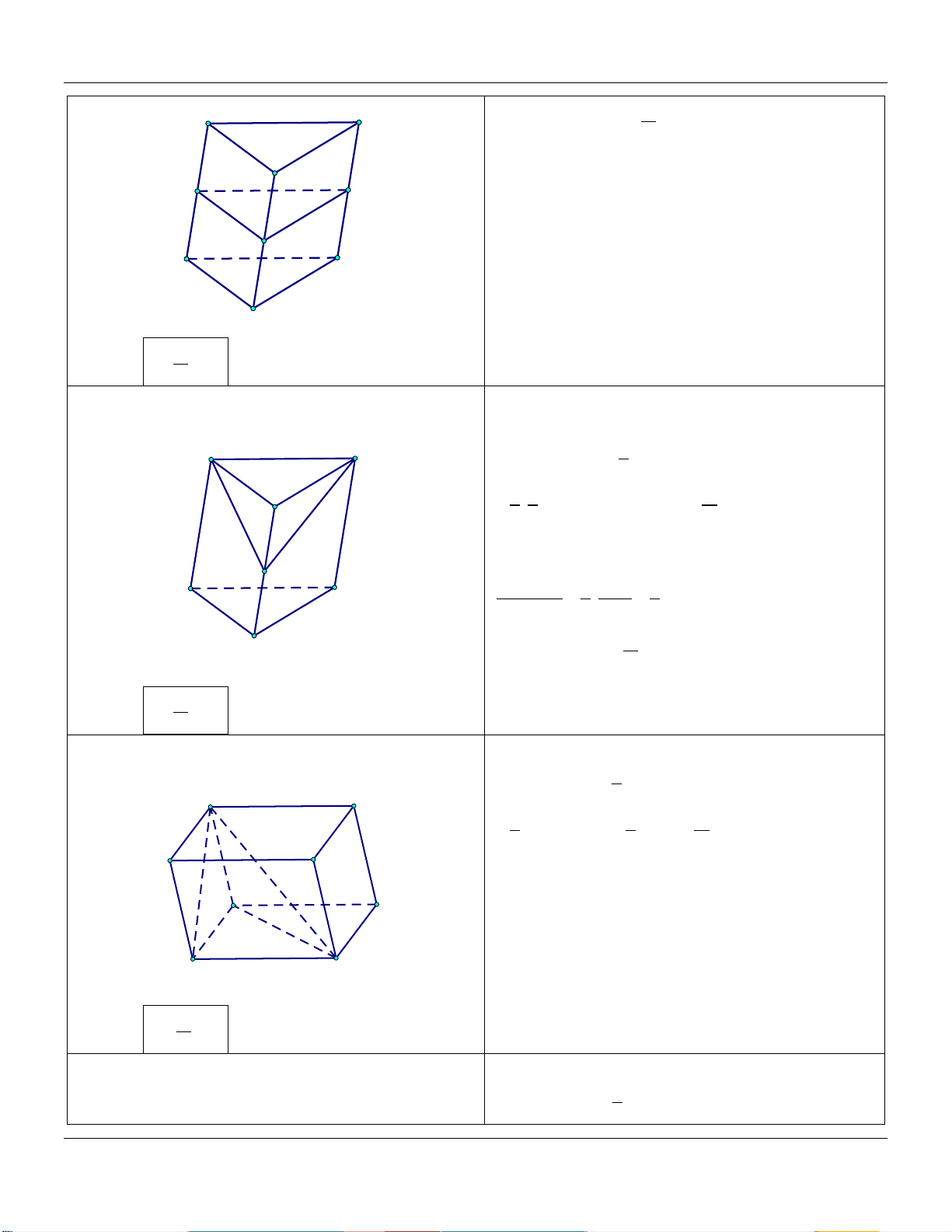
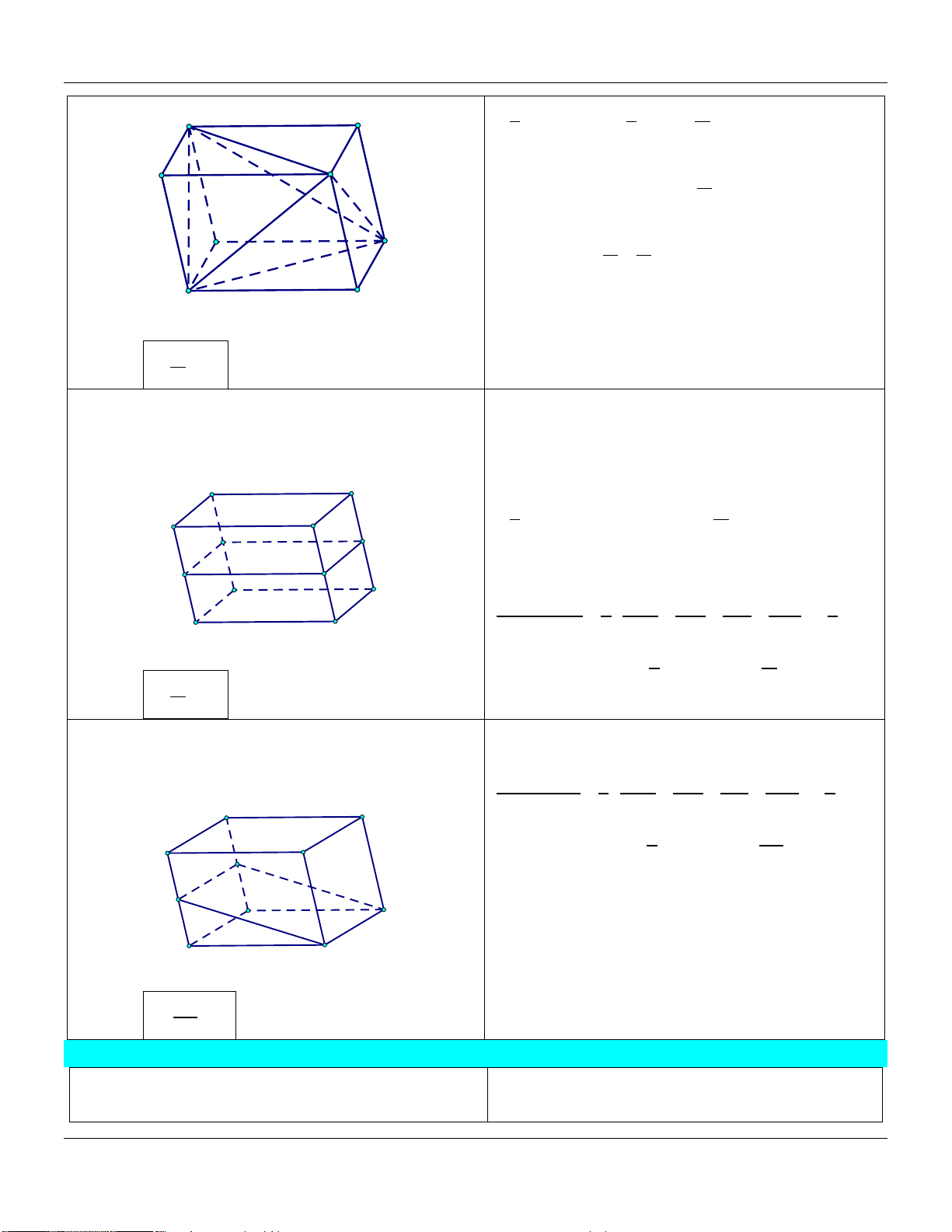
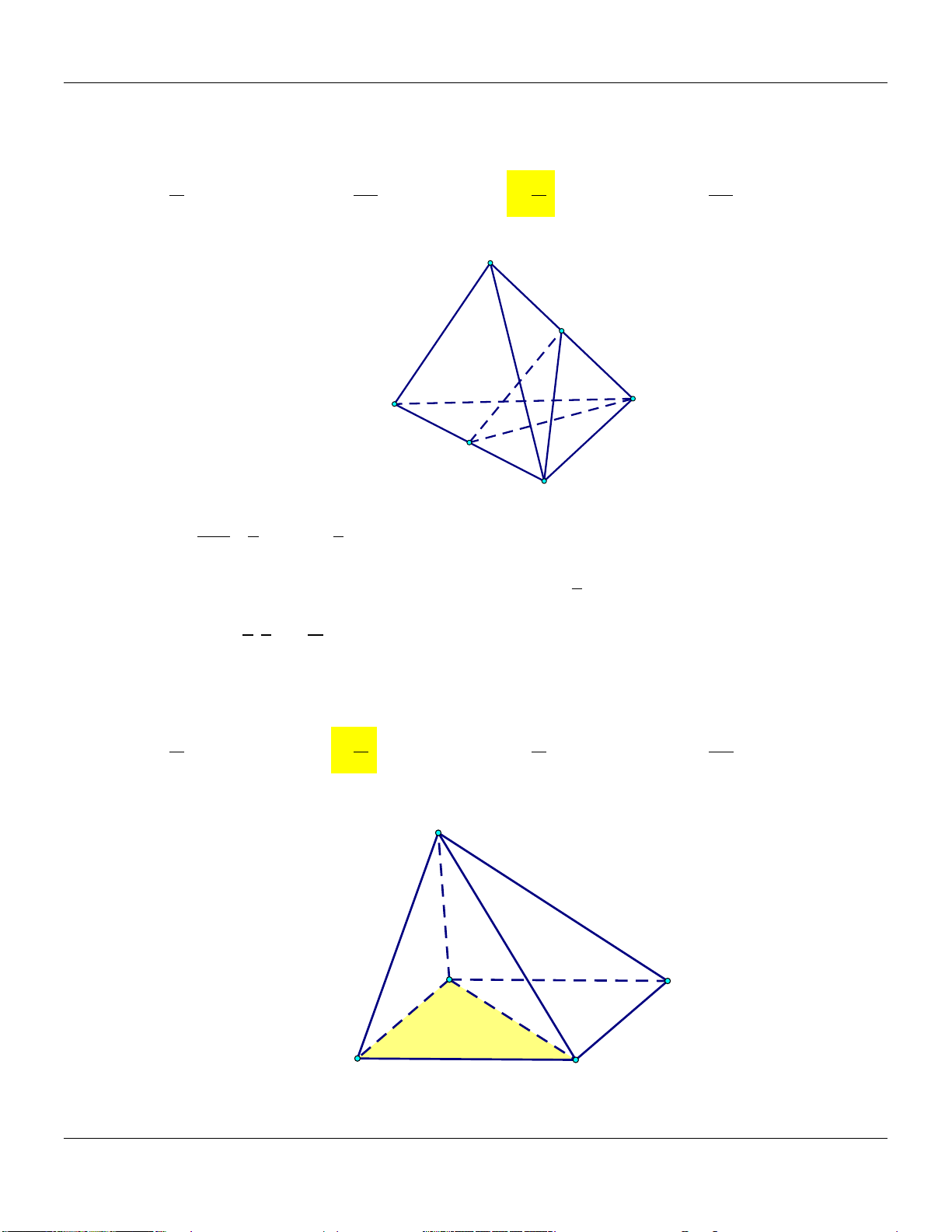
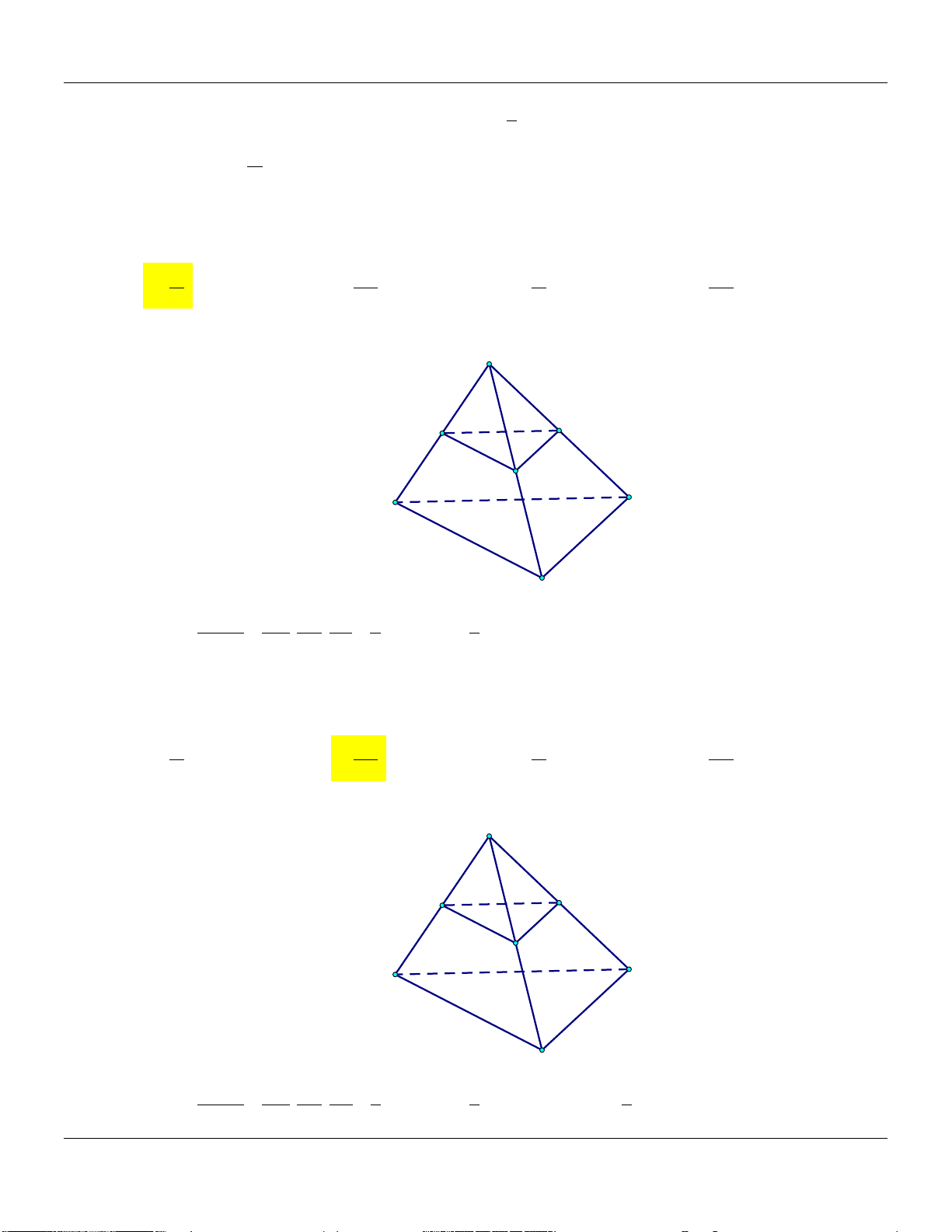
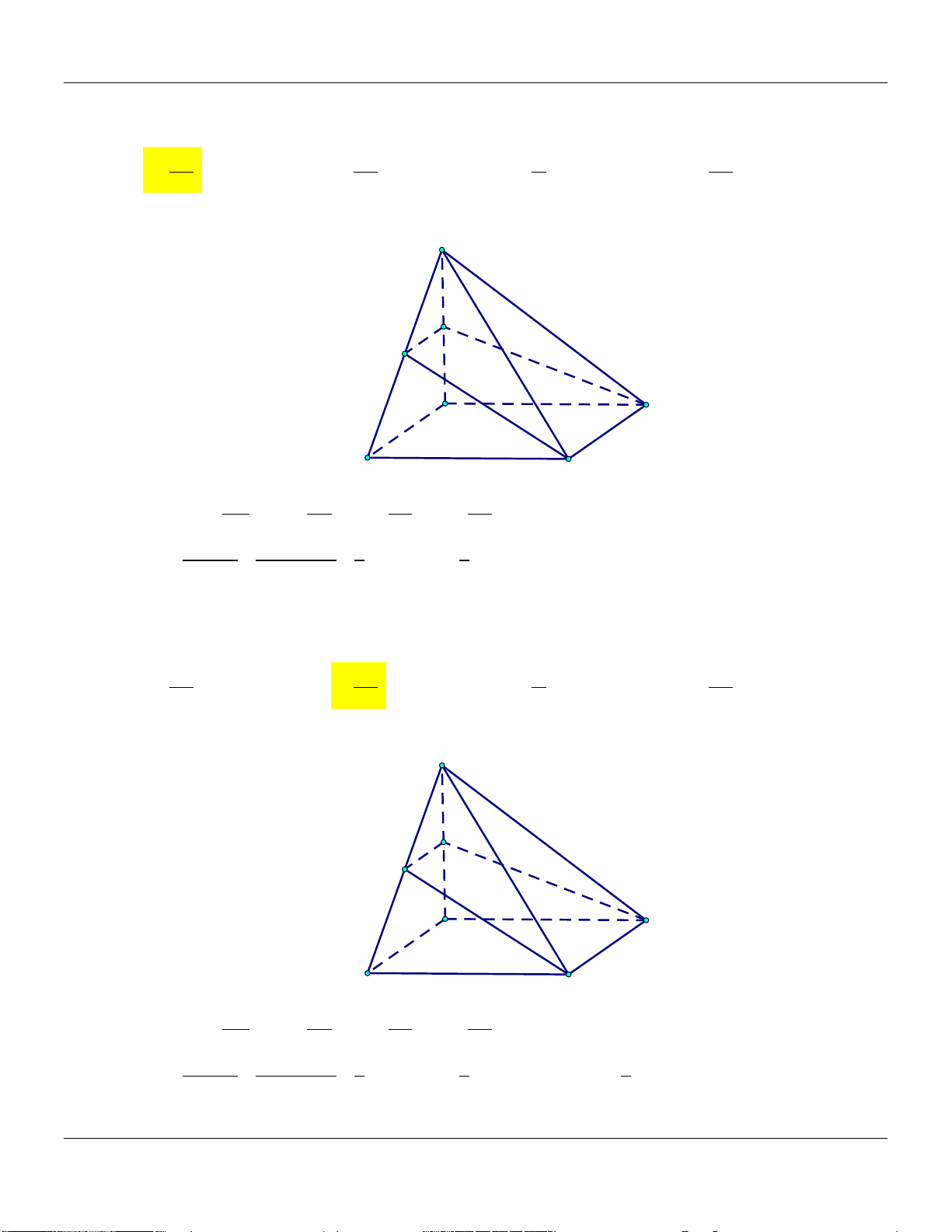
5) Hình hộp A D V 1  AM BN CP DQ ABC.MNP B     C   V        4  AA BB CC DD P ABC.A B C N Q V 1  AM CP  hay ABC.MNP     M V      2  AA CC ABC.A B C D' A'
M, N, P, Q đồng phẳng. B' C'
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <2 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
MỘT SỐ BÀI TOÁN LIÊN QUAN ĐẾN TỶ SỐ THỂ TÍCH
Tặng các em học sinh thân yêu! Dạng 1:
Tỷ số liên quan đến diện tích đáy và đường cao
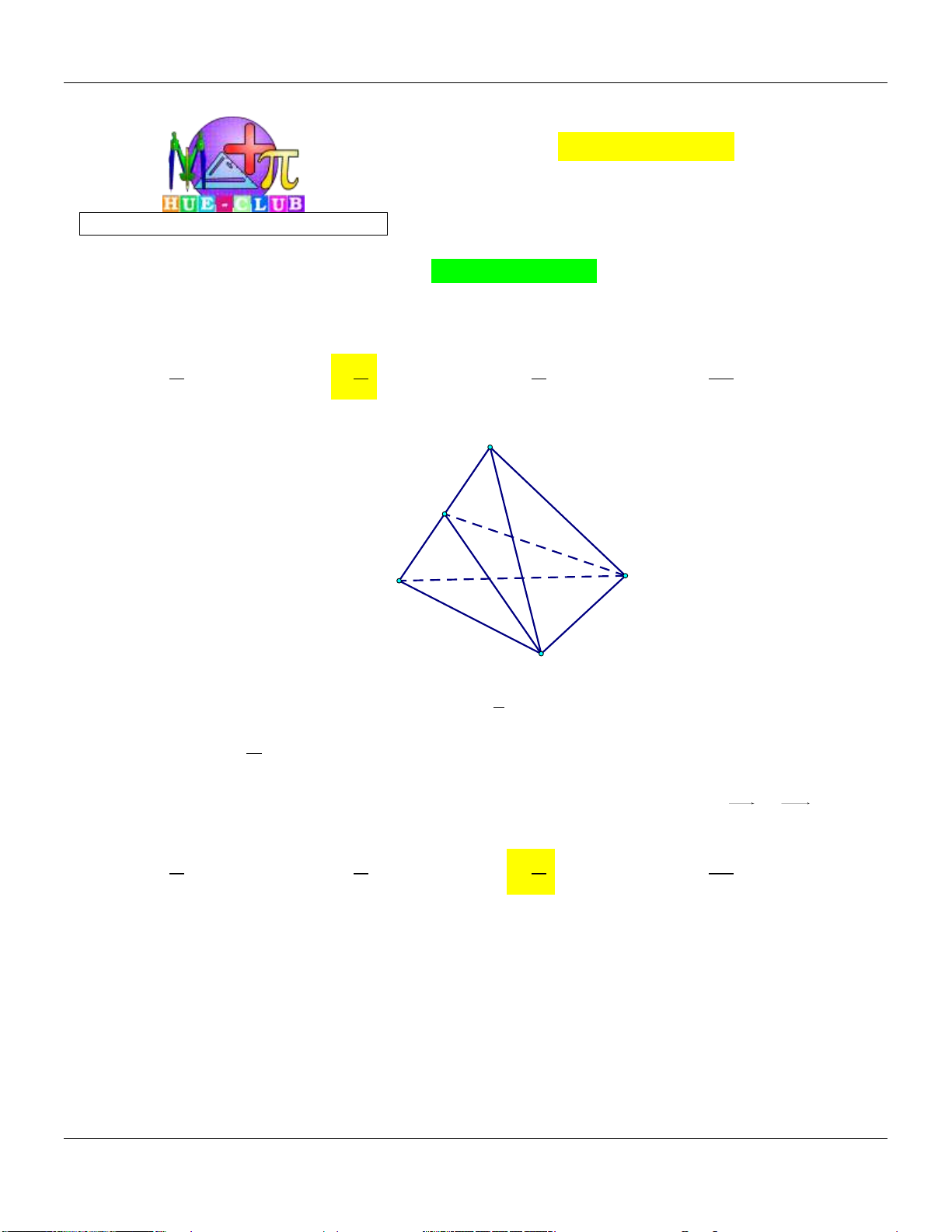
Mức 1: Cho hình chóp .
S ABC có thể tích là V . Gọi
M là trung điểm BC. (tham khảo hình vẽ) S A C M B
Thể tích khối chóp . S ABM bằng Đáp án:
Mức 2: Cho hình chóp .
S ABC có thể tích là V . Gọi Trình bày:
M , N là trung điểm AB, AC. (tham khảo hình vẽ) S N A C M B
Thể tích khối chóp . S AMN bằng Đáp án:
Mức 3: Cho hình chóp .
S ABC có thể tích là V . Gọi Trình bày:
M , N , P là trung điểm SA, AB, AC. (tham khảo hình vẽ) S M P A C N B
Thể tích khối chóp M.ANP bằng Đáp án:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <3 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
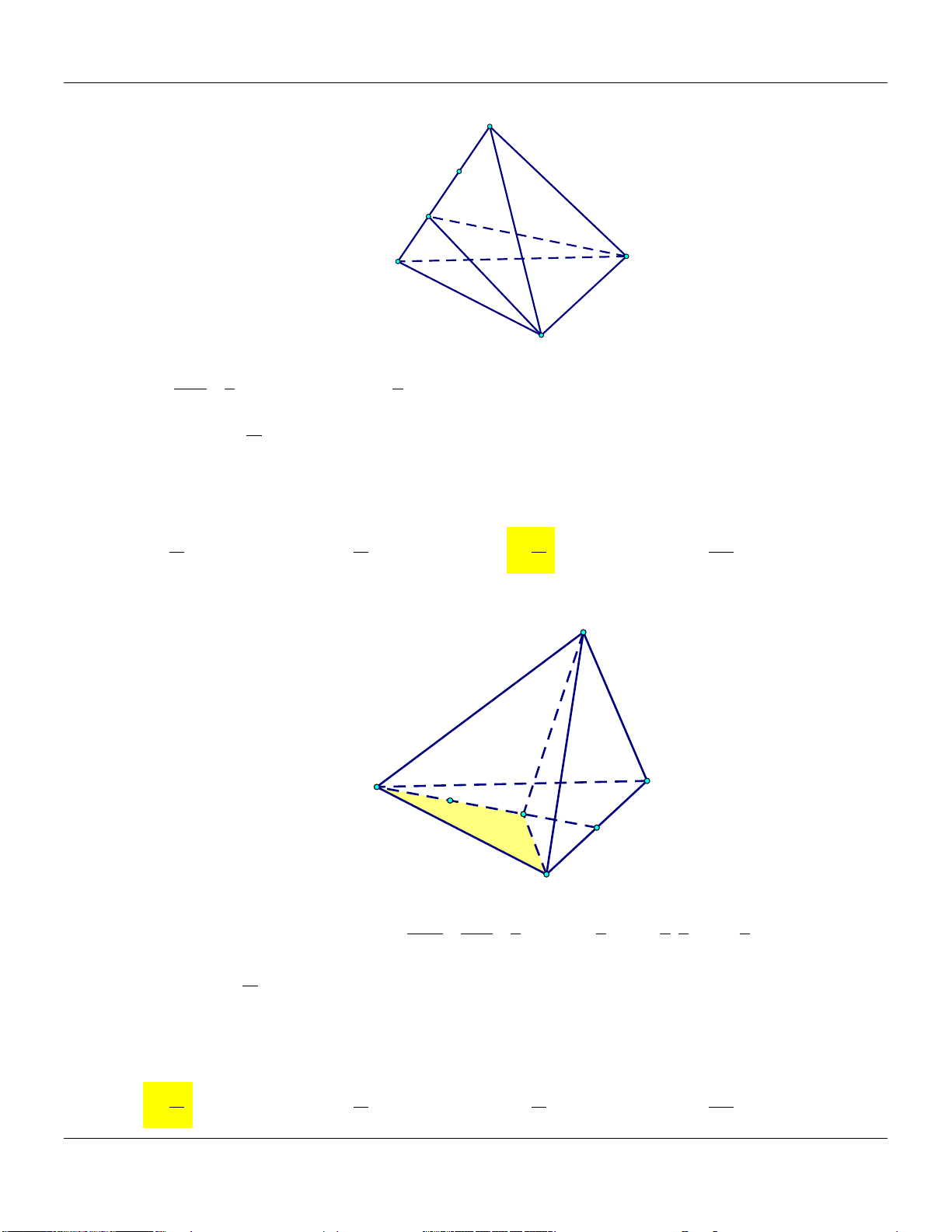
Mức 4: Cho hình chóp .
S ABCD có đáy là hình bình Trình bày:
hành tâm O. Gọi V là thể tích khối chóp . S ABCD.
(tham khảo hình vẽ) S A D O B C
Thể tích khối chóp . S ABO bằng Đáp án:
Mức 5: Cho hình chóp .
S ABCD có đáy là hình bình Trình bày:
hành tâm O. Gọi V là thể tích khối chóp . S ABCD.
M là trung điểm SA (tham khảo hình vẽ) S M A D O B C
Thể tích khối chóp M.ABO bằng Đáp án: Dạng 2:
Tỷ số thể tích khối chóp tam giác
Mức 1: Cho hình chóp .
S ABC có thể tích là V . Gọi Trình bày:
M , N , P lần lượt là trung điểm SA,SB,SC (tham khảo hình vẽ) S M P N A C B
Thể tích khối chóp . S MNP bằng Đáp án:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <4 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Mức 2: Cho hình chóp .
S ABC có thể tích là V . Gọi Trình bày:
M , N , P lần lượt là trung điểm SA,SB,SC (tham khảo hình vẽ) S M P N A C B
Thể tích khối đa diện MNPCBA bằng Đáp án:
Mức 3: Cho hình chóp .
S ABC có thể tích là V . Gọi Trình bày:
M , N lần lượt là trung điểm SB,SC (tham khảo hình vẽ) S N M C A B
Thể tích khối chóp . S AMN bằng Đáp án:
Mức 4: Cho hình chóp .
S ABC có thể tích là V . Gọi Trình bày:
M , N lần lượt là trung điểm SB,SC (tham khảo hình vẽ) S N M C A B
Thể tích khối chóp . A MNCB bằng Đáp án:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <5 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia Dạng 3:
Tỷ số thể tích khối chóp tứ giác
Mức 1: Cho hình chóp .
S ABCD có đáy là hình Trình bày:
bình hành. Gọi V là thể tích khối chóp . S ABCD. Gọi
M, N, P, Q lần lượt là trung điểm
SA,SB,SC,SD (tham khảo hình vẽ) S M Q N P D A B C
Thể tích khối chóp . S MNPQ bằng Đáp án:
Mức 2: Cho hình chóp .
S ABCD có đáy là hình Trình bày:
bình hành. Gọi V là thể tích khối chóp . S ABCD.
Gọi M, N lần lượt là trung điểm SA,SB (tham khảo hình vẽ) S M N D A B C
Thể tích khối chóp . S MNCD bằng Đáp án: Dạng 4:
Tỷ số thể tích khối lăng trụ
Mức 1: Cho hình lăng trụ ABC.A BC
  có thể tích là Trình bày:
V . (tham khảo hình vẽ) A' C' B' A C B
Thể tích khối chóp A .ABC bằng Đáp án:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <6 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Mức 2: Cho hình lăng trụ ABC.A BC
  có thể tích là Trình bày:
V . (tham khảo hình vẽ) A' C' B' A C B
Thể tích khối chóp A .B CCB bằng Đáp án:
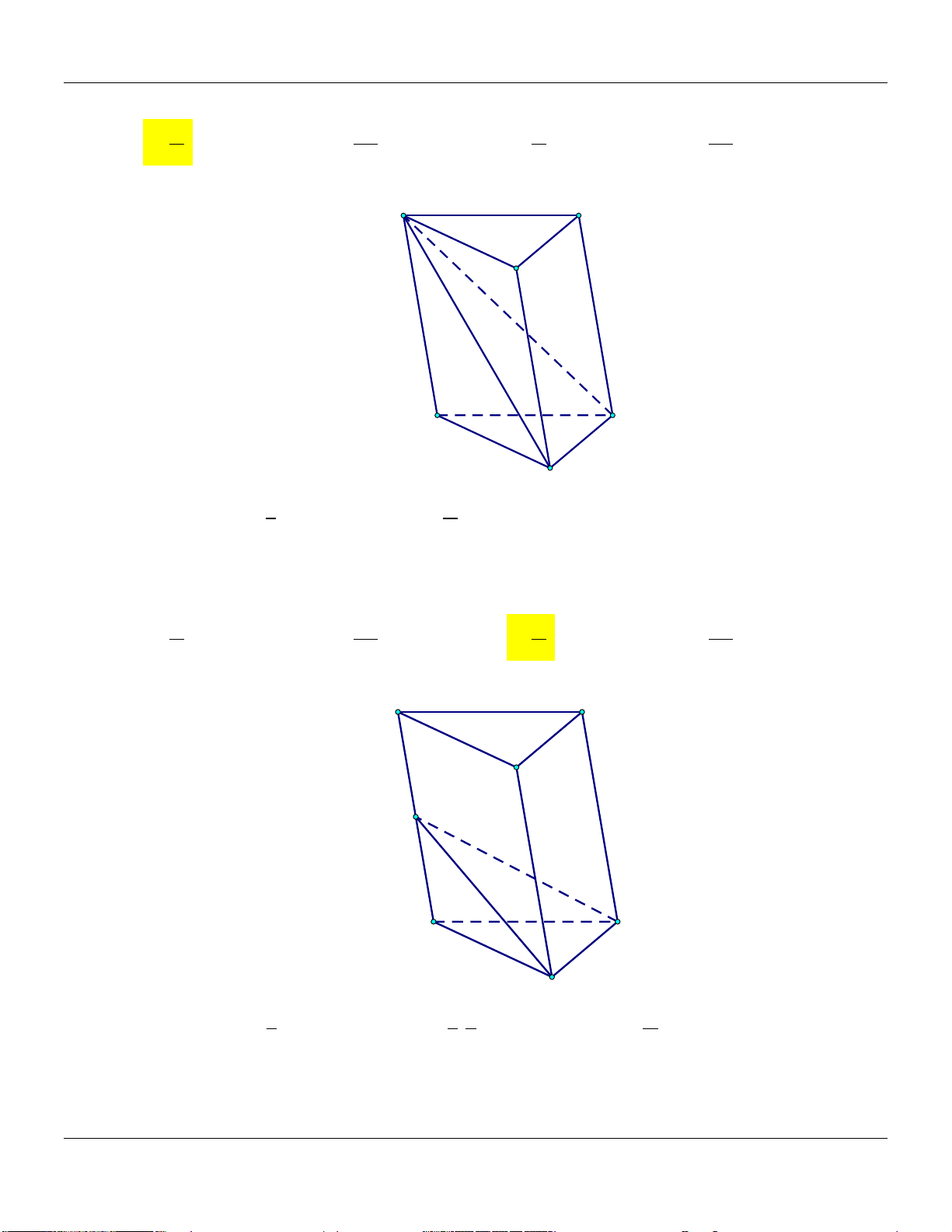
Mức 3: Cho hình lăng trụ ABC.A BC
  có thể tích là Trình bày:
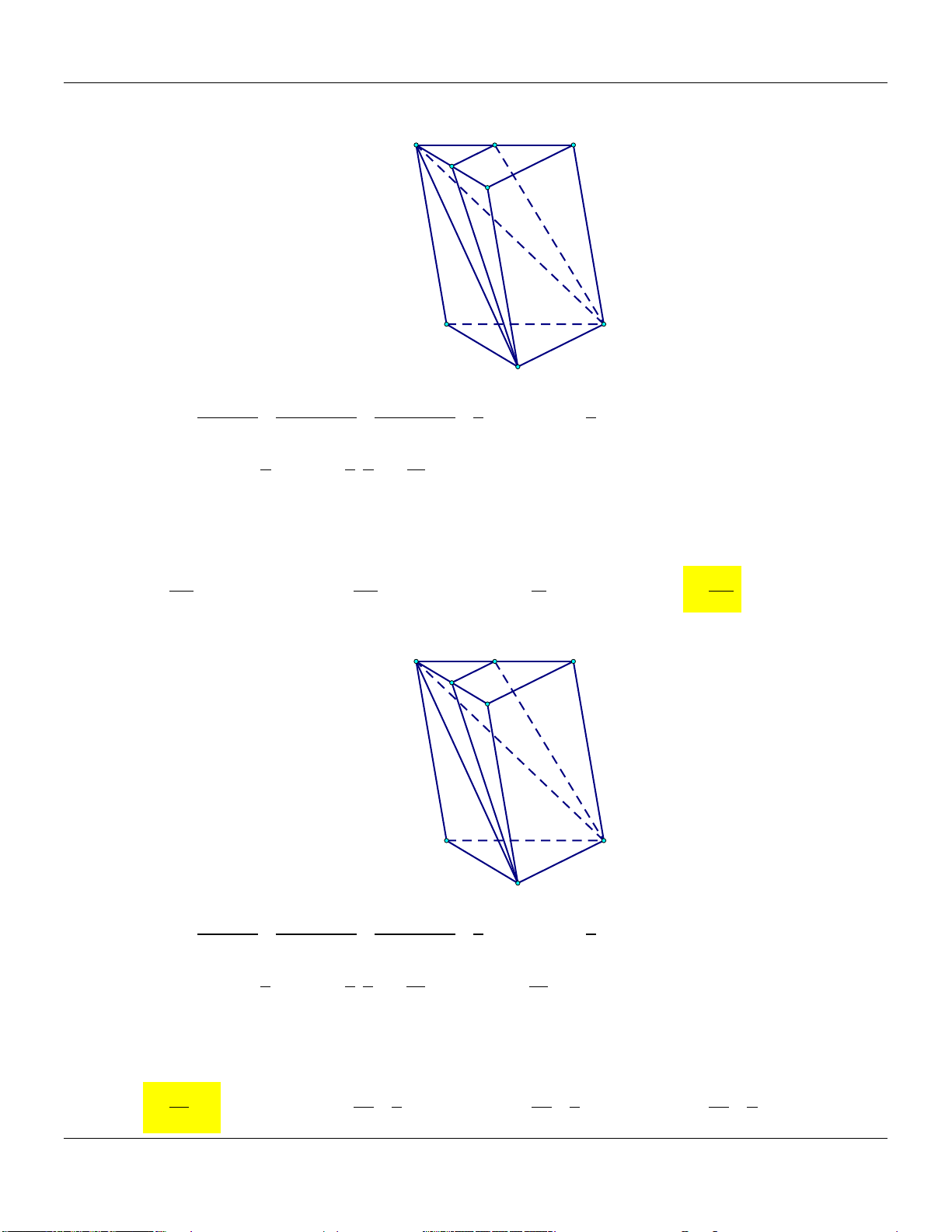
V . Gọi M, N lần lượt là trung điểm BB,CC (tham khảo hình vẽ) A' C' B' N M A C B
Thể tích khối chóp A .B CNM bằng Đáp án:
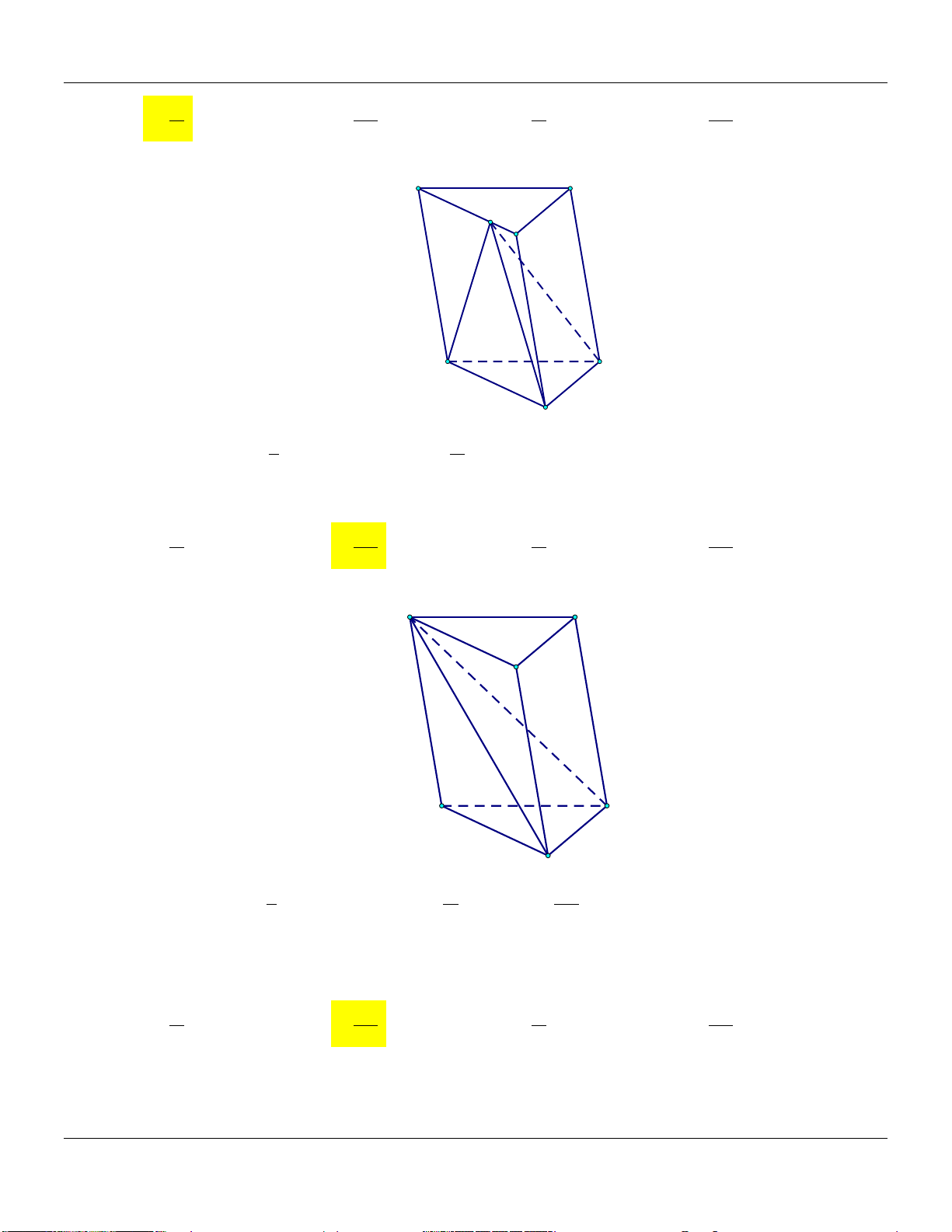
Mức 4: Cho hình lăng trụ ABC.A BC
  có thể tích là Trình bày:
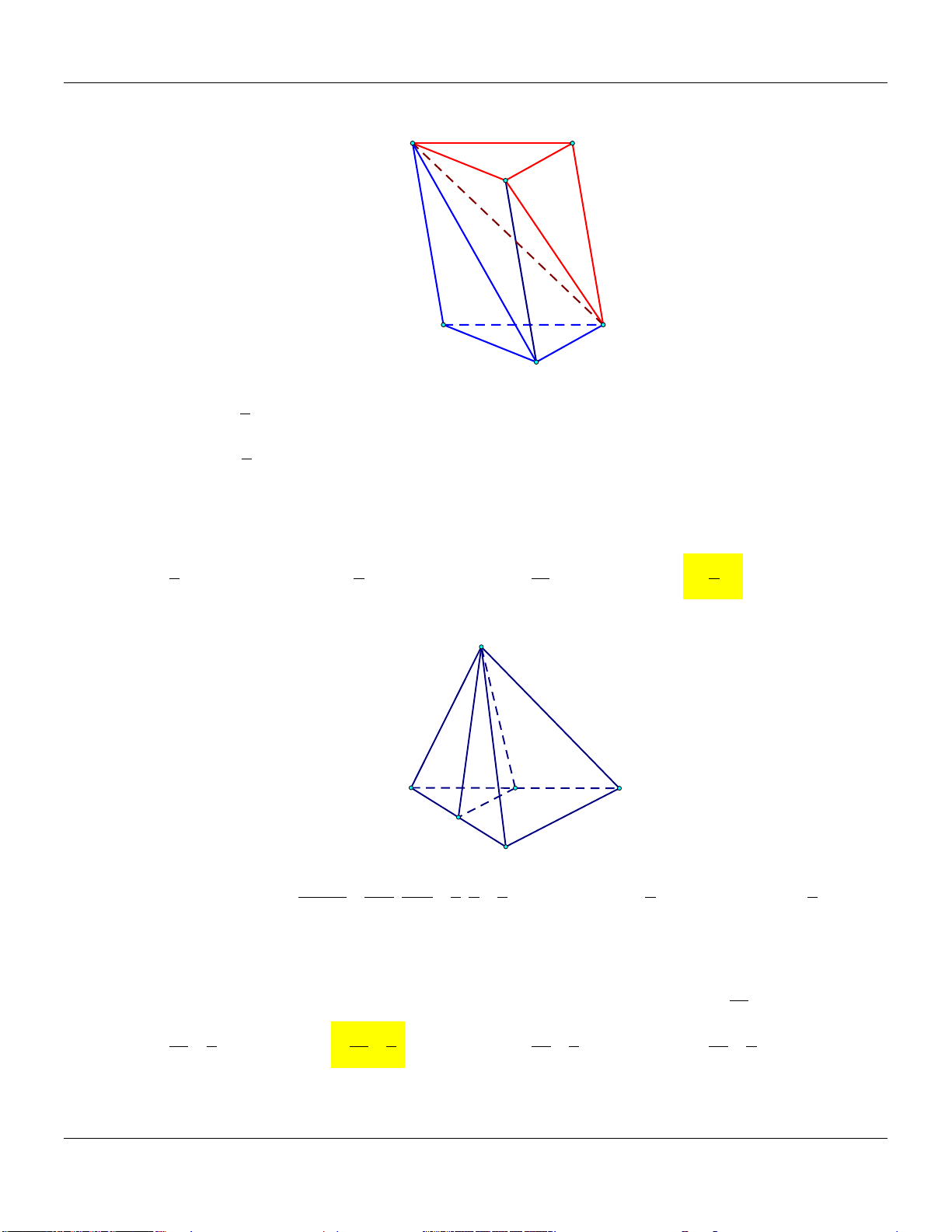
V . Gọi M, N , P lần lượt là trung điểm AA, BB,CC
(tham khảo hình vẽ) A' C' B' M P N A C Thể tích khối A BC  .MNP bằng Đáp án:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <7 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Mức 5: Cho hình lăng trụ ABC.A BC
  có thể tích là Trình bày:
V . Gọi M là trung điểm BB (tham khảo hình vẽ) A' C' B' M A C B
Thể tích khối chóp M.A BC   bằng Đáp án:
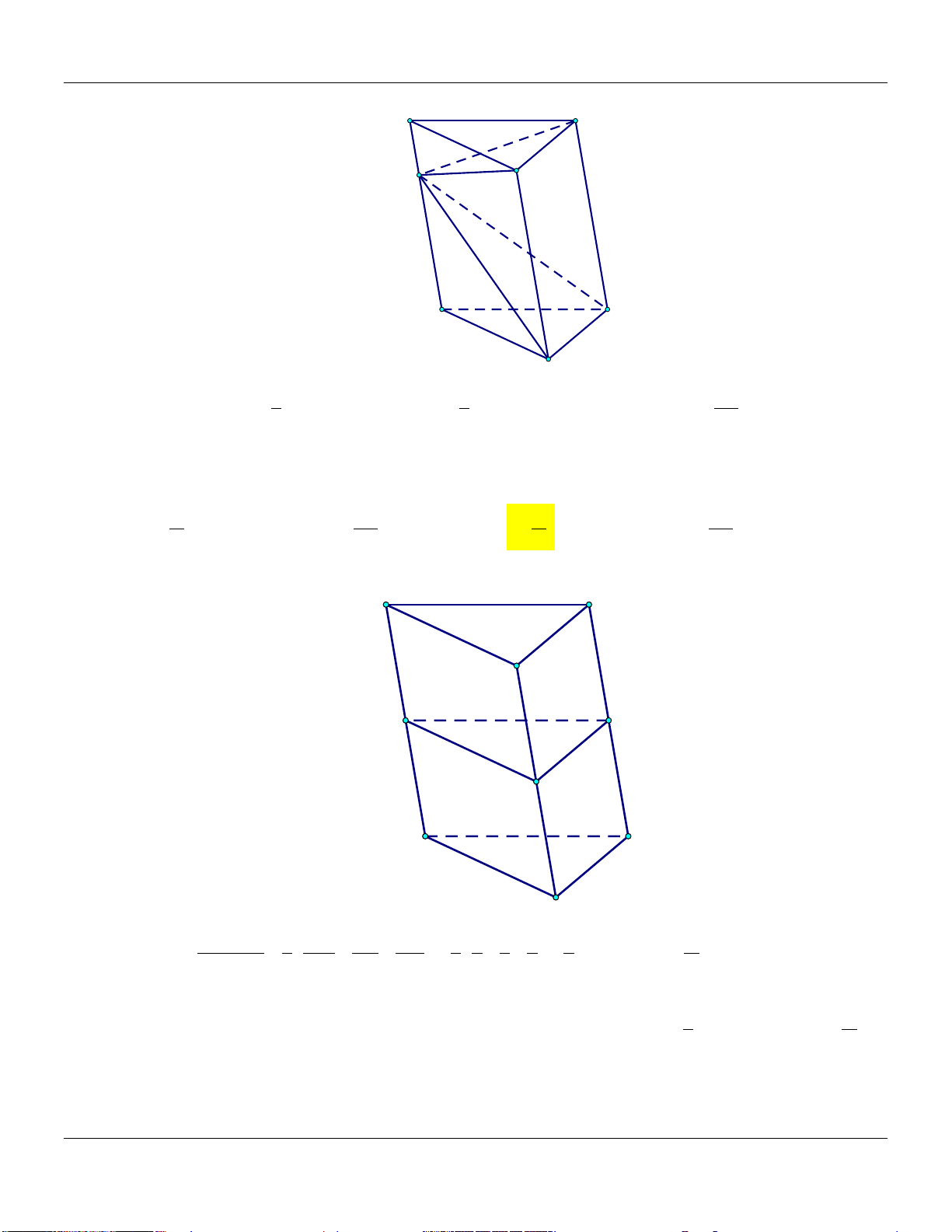
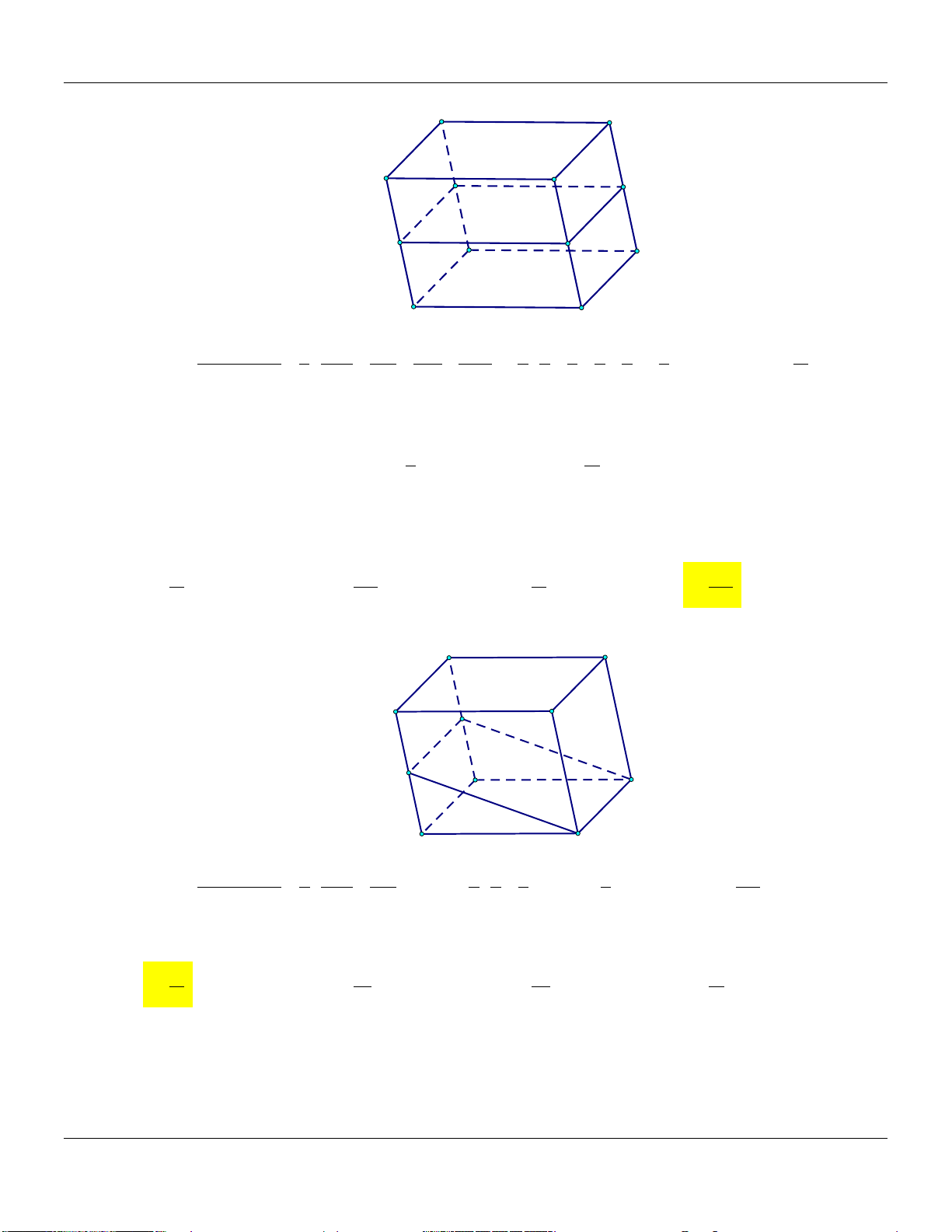
Mức 6: Cho hình hộp A . BCD A BCD
  có thể tích là Trình bày:
V . (tham khảo hình vẽ) A' D' B' C' A D B C
Thể tích khối chóp A .ABC bằng Đáp án:
Mức 7: Cho hình hộp A . BCD A BCD
  có thể tích là Trình bày:
V . (tham khảo hình vẽ) A' D' B' C' A D B C
Thể tích khối tứ diện BDA C   bằng Đáp án:
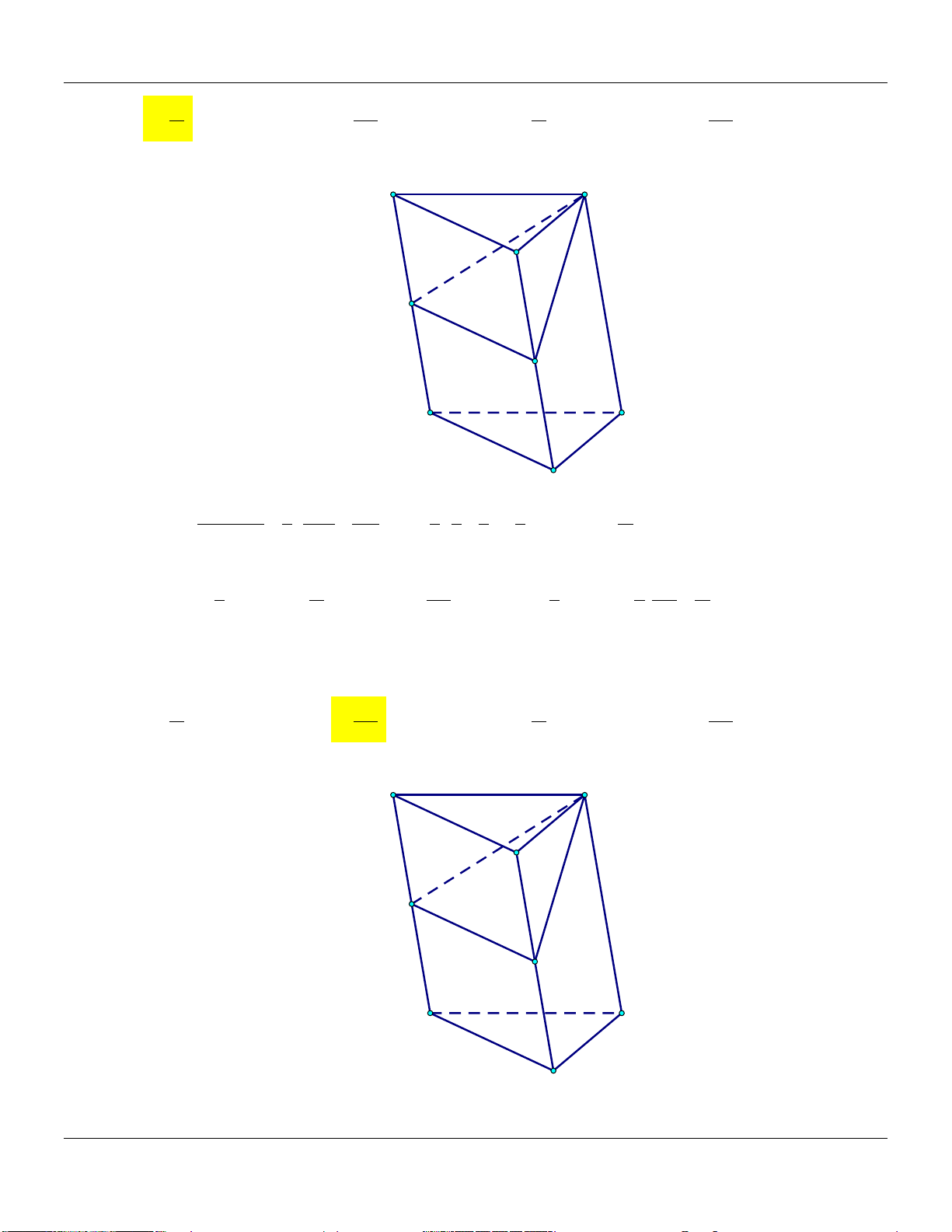
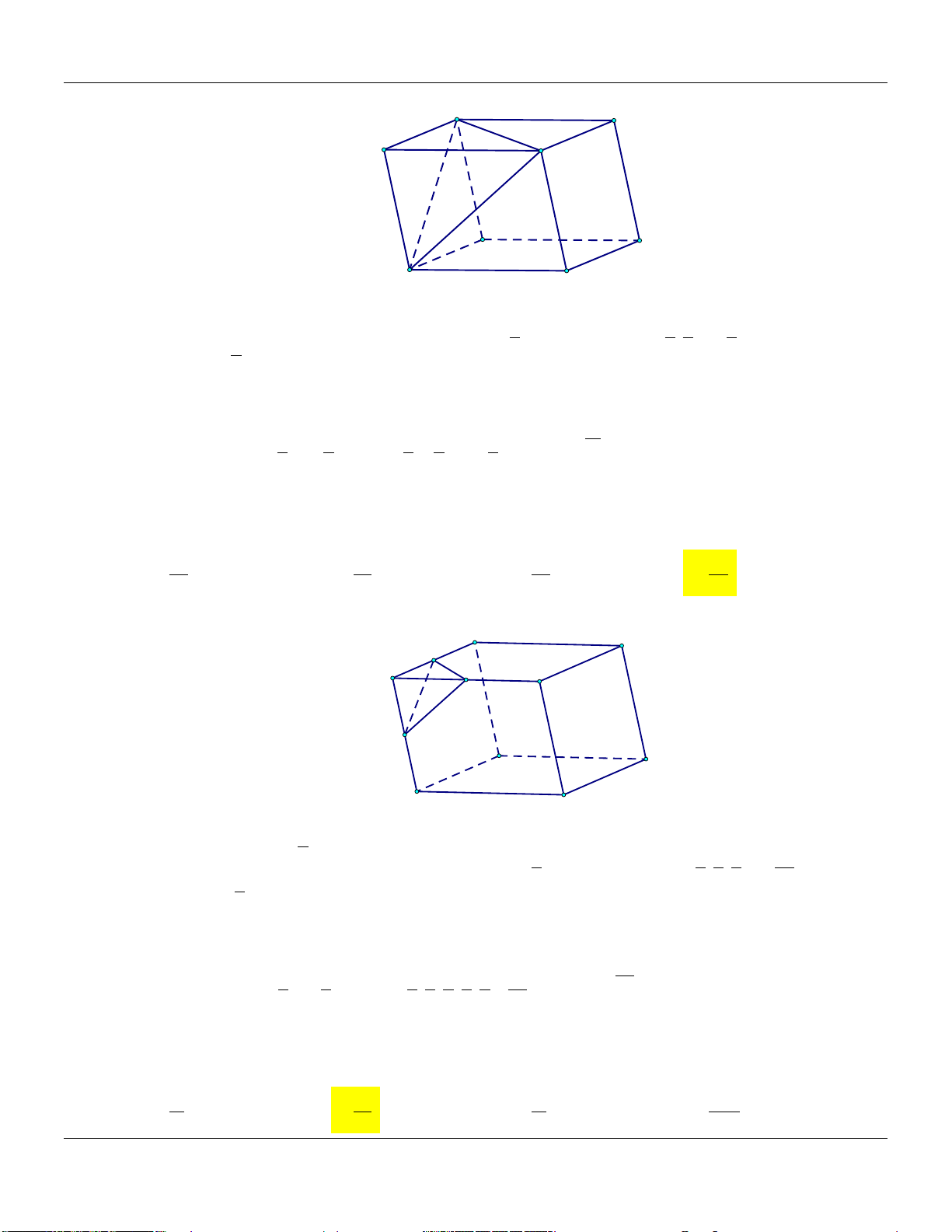
Mức 8: Cho hình hộp A . BCD A BCD
  có thể tích là Trình bày:
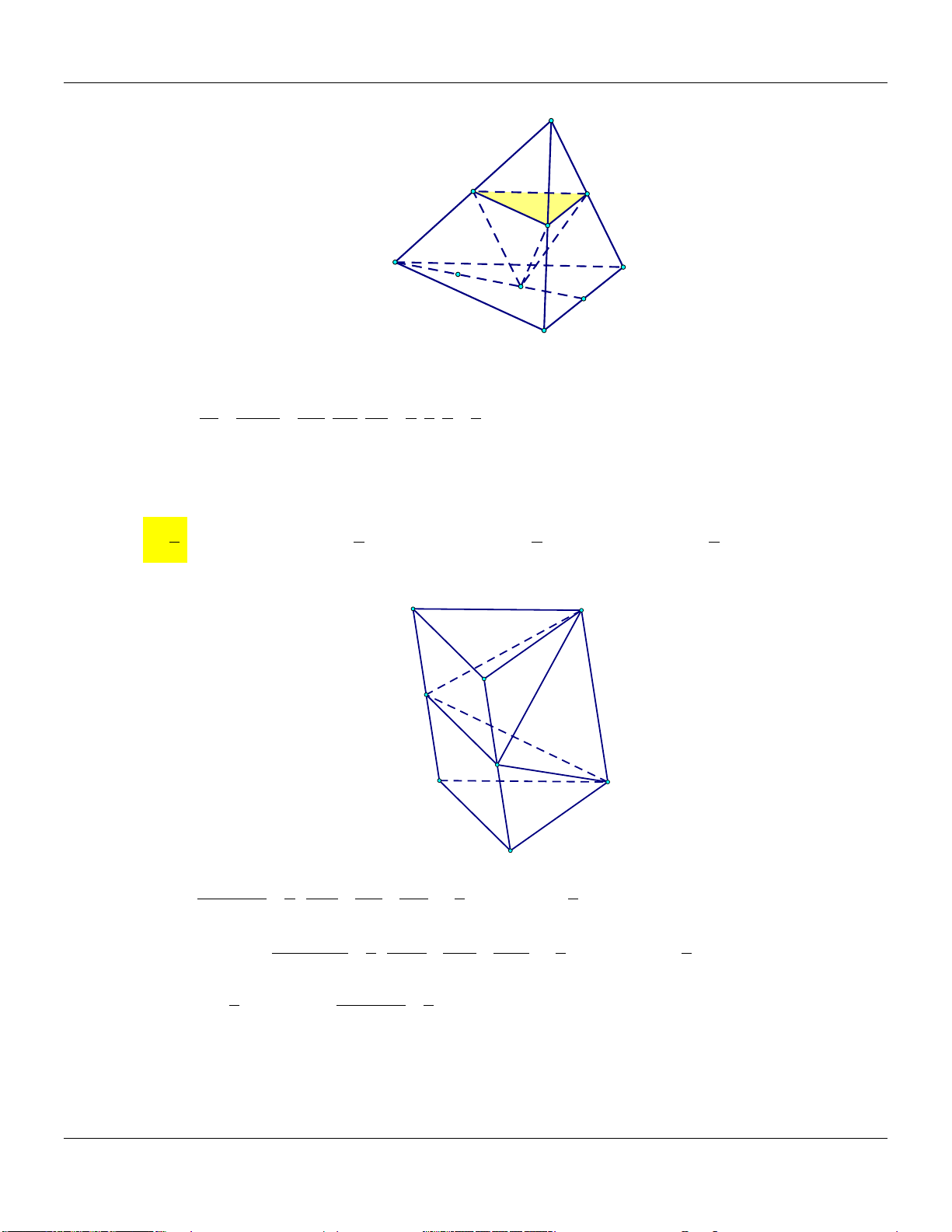
V . Gọi M, N, P,Q lần lượt là trung điểm
AA, BB,CC, DD (tham khảo hình vẽ)
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <8 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia A' D' B' C' Q M P N A D B C
Thể tích khối đa diện A BCD  .QMNP bằng Đáp án:
Mức 9: Cho hình hộp A . BCD A BCD
  có thể tích là Trình bày:
V . Gọi M, N lần lượt là trung điểm AA, BB (tham khảo hình vẽ) A' D' B' C' M A N D B C
Thể tích khối đa diện A BNMDCC D   bằng Đáp án: Dạng 5:
Một số bài toán khác
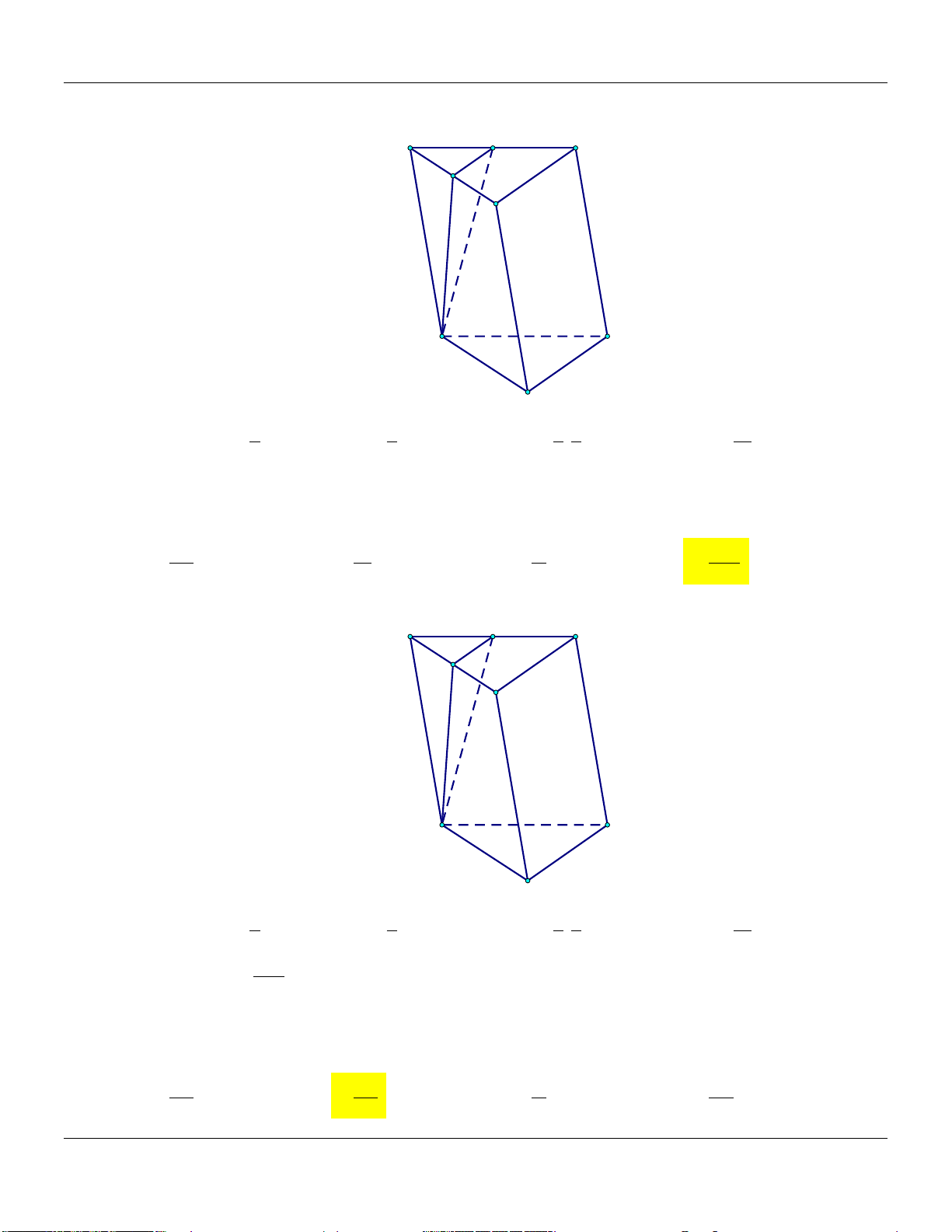
Mức 1: Cho tam giác ABC đều có cạnh bằng . a Dựng Trình bày:
AA, BB,CC vuông góc với ABC sao cho
AA  3a, BM CN a (tham khảo hình vẽ) A' N M A C B
Thể tích khối đa diện A ABCNM bằng Đáp án:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <9 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Mức 2: Cho tam giác ABC đều có cạnh bằng . a Dựng Trình bày:
AA, BB,CC vuông góc với ABC sao cho 4a
AA  4a, BM  2a, CN
(tham khảo hình vẽ) 3 A' N M A C B
Thể tích khối đa diện A ABCNM bằng Đáp án:
LỜI GIẢI CHI TIẾT Dạng 1:
Tỷ số liên quan đến diện tích đáy và đường cao
Mức 1: Cho hình chóp .
S ABC có thể tích là V . Gọi Trình bày:
M là trung điểm BC. (tham khảo hình vẽ) 1 Ta có: SS . ABM ABC S 2 1 V Suy ra: VV  . S.ABM S. 2 ABC 2 A C M B
Thể tích khối chóp . S ABM bằng V Đáp án: 2
Mức 2: Cho hình chóp .
S ABC có thể tích là V . Gọi Trình bày:
M , N là trung điểm AB, AC. (tham khảo hình vẽ) Cách 1: S AM AN 1 1 Ta có: AMN  .   SS . S AB AC 4 AMN 4 ABC ABC 1 V Suy ra: VV  . S.AMN S. 4 ABC 4 V V SA AM AN 1
Cách 2: S.AMN A.SMN  . .  V V SA AB AC 4 S.ABC A.SBC
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <10 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia S 1 V Suy ra: VV  . S.AMN S. 4 ABC 4 N A C M B
Thể tích khối chóp . S AMN bằng V Đáp án: 4
Mức 3: Cho hình chóp .
S ABC có thể tích là V . Gọi Trình bày:
M , N , P là trung điểm SA, AB, AC. (tham khảo Cách 1: hình vẽ) S AP AN 1 1 Ta có: ANP  .   SS (1) ANP ABC S S AC AB 4 4 ABC 1
Mặt khác: dM;APN  dS;ABC (2) M 2 1 Suy ra: V
d M; ANP .S M.ANP    APN P A 3 C 1 1 
dS ABC 1 1 V . ; . SV  . N ABC S. 3 2 4 8 ABC 8 B Cách 2:
Thể tích khối chóp M.ANP bằng Ta có: V V AM AN AP 1 1 V Đáp án: AMNP  . .   VV  . 8 V AS AB AC 8 AMNP 8 ASBC 8 ASBC
Mức 4: Cho hình chóp .
S ABCD có đáy là hình bình Trình bày:
hành tâm O. Gọi V là thể tích khối chóp . S ABCD. 1 1 Ta có: SSS .
(tham khảo hình vẽ) ABO 2 ABC 4 ABCD S 1 V Suy ra: VV  . S.ABO S. 4 ABCD 4 A D O B C
Thể tích khối chóp . S ABO bằng V Đáp án: 4
Mức 5: Cho hình chóp .
S ABCD có đáy là hình bình Trình bày:
hành tâm O. Gọi V là thể tích khối chóp . S ABCD. 1 1 Ta có: SSS (1)
M là trung điểm SA (tham khảo hình vẽ) ABO 2 ABC 4 ABCD
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <11 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia S 1
Mặt khác: dM;ABO  dS;ABCD (2) 2 1 V M Từ (1), (2) suy ra: VV  . M.ABO S. 8 ABCD 8 A D O B C
Thể tích khối chóp M.ABO bằng V Đáp án: 8 Dạng 2:
Tỷ số thể tích khối chóp tam giác
Mức 1: Cho hình chóp .
S ABC có thể tích là V . Gọi Trình bày:
M , N , P lần lượt là trung điểm SA,SB,SC (tham Ta có: khảo hình vẽ) V SM SN SP 1 1 V SMNP  . .   VV  . SMNP SABC S V SA SB SC 8 8 8 SABC M P N A C B
Thể tích khối chóp . S MNP bằng V Đáp án: 8
Mức 2: Cho hình chóp .
S ABC có thể tích là V . Gọi Trình bày:
M , N , P lần lượt là trung điểm SA,SB,SC (tham Ta có: khảo hình vẽ) V SM SN SP 1 1 V SMNP  . .   VV  . SMNP SABC S V SA SB SC 8 8 8 SABC 7V Suy ra: V  . MNPCBA 8 M P N A C B
Thể tích khối đa diện MNPCBA bằng 7V Đáp án: 8
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <12 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Mức 3: Cho hình chóp .
S ABC có thể tích là V . Gọi Trình bày:
M , N lần lượt là trung điểm SB,SC (tham khảo Cách 1: hình vẽ) S SM SN 1 1 Ta có: SMN  .   SS . SMN SBC S S SB SC 4 4 SBC 1 V Suy ra: VVV  . S.AMN A.SBC A. 4 SBC 4 N Cách 2: Ta có: M V SA SM SN 1 1 V SAMN  . .   VV  . C SAMN SABC A V SA SB SC 4 4 4 SABC B
Thể tích khối chóp . S AMN bằng V Đáp án: 4
Mức 4: Cho hình chóp .
S ABC có thể tích là V . Gọi Trình bày:
M , N lần lượt là trung điểm SB,SC (tham khảo Ta có: hình vẽ) V SA SM SN 1 1 V SAMN  . .   VV  . SAMN SABC S V SA SB SC 4 4 4 SABC 3V Suy ra: V  . A.MNCB 4 N M C A B
Thể tích khối chóp . A MNCB bằng 3V Đáp án: 4 Dạng 3:
Tỷ số thể tích khối chóp tứ giác
Mức 1: Cho hình chóp .
S ABCD có đáy là hình Trình bày:
bình hành. Gọi V là thể tích khối chóp .
S ABCD. Cách 1: Gọi
M, N, P, Q lần lượt là trung điểm Ta có:
SA,SB,SC,SD (tham khảo hình vẽ) SA SB SC SD a   2;b   2;c   2;d   2. SM SN SP SQ Suy ra:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <13 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia S V    S.MNPQ a b c d 1 1 V    VV  . S.MNPQ S. V 4abcd 8 8 ABCD 8 S.ABCD Cách 2: M Q V 1 1 1 S.MNP   VVV N S.MNP S.ABC S.ABCD P V 8 8 16 S.ABC D VS MQP 1 1 1 A .   VVV S.MQP S.ADC S. V 8 8 16 ABCD S.ADC 1 V B C VVVV  . S.MNPQ S.MNP S.MQP S. 8 ABCD 8
Thể tích khối chóp . S MNPQ bằng V Đáp án: 8
Mức 2: Cho hình chóp .
S ABCD có đáy là hình Trình bày:
bình hành. Gọi V là thể tích khối chóp .
S ABCD. Cách 1:
Gọi M, N lần lượt là trung điểm SA,SB (tham Ta có: khảo hình vẽ) SA SB SC SD a   2;b   2;c   1;d   1. S SM SN SC SD Suy ra: V
a b c d 3 3 3V S.MNCD    VV  . M S.MNCD S. V 4abcd 8 8 ABCD 8 S.ABCD Cách 2: N V 1 1 1 S.MNC     D V V V S.MNP S.ABC S.ABCD A V 4 4 8 S.ABC V 1 1 1 S.MCD   VVV S.MCD S.ACD S.ABCD B C V 2 2 4 S.ACD
Thể tích khối chóp . S MNCD bằng 3 3V VVVV  . S.MNCD S.MNC S.MCD S.ABCD 3V 8 8 Đáp án: 8 Dạng 4:
Tỷ số thể tích khối lăng trụ
Mức 1: Cho hình lăng trụ ABC.A BC
  có thể tích là Trình bày:
V . (tham khảo hình vẽ) Ta có: A' C' 1 V V    
d A ; ABC .S . A .ABC    3 ABC 3 B' A C B
Thể tích khối chóp A .ABC bằng
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <14 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia V Đáp án: 3
Mức 2: Cho hình lăng trụ ABC.A BC
  có thể tích là Trình bày:
V . (tham khảo hình vẽ) Ta có: A' C' 1 V V    
d A ; ABC .S . A .ABC    3 ABC 3 B' 2V Suy ra: V     . A .B C CB 3 A C B
Thể tích khối chóp A .B CCB bằng 2V Đáp án: 3
Mức 3: Cho hình lăng trụ ABC.A BC
  có thể tích là Trình bày:
V . Gọi M, N lần lượt là trung điểm BB,CC (tham Cách 1: khảo hình vẽ) Ta có: A' 1 V C' V    
d A ; ABC .S . A .ABC    3 ABC 3 2V 1 V Suy ra: V        V    V    . A .B C CB A .B C NM A .B C CB B' 3 2 3 N Cách 2: Ta có: M A C V        1 B M C N 1 A .B C CB      . V      3  BB CC  3 A B C .ABC V B Suy ra: V     . A .B C NM 3
Thể tích khối chóp A .B CNM bằng V Đáp án: 3
Mức 4: Cho hình lăng trụ ABC.A BC
  có thể tích là Trình bày:
V . Gọi M , N , P lần lượt là trung điểm AA, BB,CC Cách 1:
(tham khảo hình vẽ) Ta có: V        d M; A B C .S A B C .MNP  
 ABC 1   V d A; A BC  .S     . 2 A B C 2 Cách 2: Ta có: V         1 A M B N C P 1 A B C .MNP       . V       3  A A BB CC  2 A B C .ABC
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <15 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia A' C' V Suy ra: V     . A B C .MNP 2 B' M P N A C Thể tích khối A BC  .MNP bằng V Đáp án: 2
Mức 5: Cho hình lăng trụ ABC.A BC
  có thể tích là Trình bày:
V . Gọi M là trung điểm BB (tham khảo hình vẽ) Cách 1: A' C' 1 Ta có: V        d M; A B C .S M.A B C       3 A B C 1 1 V  . d ; B A BC  .S     . B' 3 2 A B C 6 Cách 2: Ta có: M AC V    1 B M 1 M.A B C  .  . V     3 BB 6 A B C .ABC V B Suy ra: V .
VM.A BC   6
Thể tích khối chóp M.A BC   bằng V Đáp án: 6
Mức 6: Cho hình hộp A . BCD A BCD
  có thể tích là Trình bày:
V . (tham khảo hình vẽ) 1 Ta có: V   
d A ; ABC .S A .ABC    ABC A' D' 3 1    ABC 1 V d A ; . S  . 3 2 ABCD 6 B' C' A D B C
Thể tích khối chóp A .ABC bằng V Đáp án: 6
Mức 7: Cho hình hộp A . BCD A BCD
  có thể tích là Trình bày:
V . (tham khảo hình vẽ) 1 Ta có: V   
d A ; ABD .S A .ABD    3 ABD
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <16 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia A' 1 1 V D'
dA ;ABD. S  . 3 2 ABCD 6 Tương tự: B' C' V V     V    V    . C .BCD B.B A C D.D A C 6 Suy ra: A D V V V      V 4. . BDA C 6 3 B C
Thể tích khối tứ diện BDA C   bằng V Đáp án: 3
Mức 8: Cho hình hộp A . BCD A BCD
  có thể tích là Trình bày:
V . Gọi M, N, P,Q lần lượt là trung điểm Cách 1:
AA, BB,CC, DD (tham khảo hình vẽ) Ta có: V          d M; A B C D .S A B C D .QMNP    A'     D' A B C D 1 V B'
dA;A BCD  .S      . C' 2 A B C D 2 Q M Cách 2: P N Ta có: A D V       A BCD  .QMNP 1 A M B N C P D Q 1            B C V     4  A A B B C C D D  2 ABCD.A B C D
Thể tích khối đa diện A BCD  .QMNP bằng 1 V Suy ra: V       V     . A B C D .QMNP ABCD.A B C D V 2 2 Đáp án: 2
Mức 9: Cho hình hộp A . BCD A BCD
  có thể tích là Trình bày:
V . Gọi M, N lần lượt là trung điểm AA, BB (tham Ta có: khảo hình vẽ) V           1 A M B N C C D D 3 A B NMDCC D        A'     D' V     4  A A B B C C D D  4 ABCD.A B C D 3 3V Suy ra:   B' V     V     . C' A B NMDCC D ABCD.A B C D M 4 4 A N D B C
Thể tích khối đa diện A BNMDCC D   bằng 3V Đáp án: 4 Dạng 5:
Một số bài toán khác
Mức 1: Cho tam giác ABC đều có cạnh bằng . a Dựng Trình bày:
AA, BB,CC vuông góc với ABC sao cho Dựng lăng trụ đều ABC.A BC   như hình vẽ:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <17 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
AA  3a, BM CN a (tham khảo hình vẽ) A' C' A' B' N M N C A M B A C Ta có: 3 3 3 3a B 2 V         V A . A S 3 . a a . ABC.A B C ABC 4 4
Thể tích khối đa diện A ABCNM bằng Ta có: 3 5 3a       Đáp án: V    1 B M C N 1 2 2 4 A .B C NM      12     . V      3  BB CC  3  3 3  9 A B C .ABC 3 4V 5V 5 3a Suy ra: V        V  . A .B C NM 9 A ABCNM 9 12 Cách khác:
Gọi P là điểm trên AA sao cho AP  . a 2 3 a 3 a 3 VA . P S  . aABC.MNP ABC 4 4 2 3 1 1 a 3 a 3 V      A . P S .2 . a A .MNP 3 MNP 3 4 6 3 5a 3 Suy ra: VVVA . .  B CNM MNP.ABC A.MNP 12
Mức 2: Cho tam giác ABC đều có cạnh bằng . a Dựng Trình bày:
AA, BB,CC vuông góc với ABC sao cho Dựng lăng trụ đều ABC.A BC   như hình vẽ: 4a A' C'
AA  4a, BM  2a, CN
(tham khảo hình vẽ) 3 B' A' N M C N A M B A C 3 Ta có: 2 3 V         V A . A S 4 . a a 3a . ABC.A B C ABC 4 Ta có: B
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <18 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Thể tích khối đa diện A ABCNM bằng V          1 B M C N 1 1 2 7 A .B C NM          . 3 11 3a V      3  BB CC  3  2 3  18 Đáp án: A B C .ABC 18 Suy ra: 3 7V 11V 11 3a V        V  . A .B C NM 18 A ABCNM 18 18
_________________HẾT_________________
Huế, 10h45’ Ngày 07 tháng 7 năm 2023
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <19 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TR¾C NGHIÖM M«n: To¸n 12
Chuyên đề: THỂ TÍCH KHỐI ĐA DIỆN
Tỷ số thể tích (CB)
PHIẾU HỌC TẬP SỐ 01_TrNg 2023 Líp To¸n thÇy L£ B¸ B¶O Tr-êng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ
Trung t©m KM 10 H-¬ng Trµ, HuÕ. NỘI DUNG ĐỀ BÀI
Câu 1: Gọi V là thể tích khối chóp .
S ABC. Gọi M là trung điểm .
SA Thể tích khối chóp M.ABC bằng V V V 2V A. . B. . C. . D. . 4 2 3 3
Câu 2: Gọi V là thể tích khối chóp .
S ABC. Gọi M là điểm trên cạnh SA sao cho SM  2M . A Thể tích
khối chóp M.ABC bằng V V V 2V A. . B. . C. . D. . 4 2 3 3
Câu 3: Cho hình chóp .
S ABC có thể tích là V . Gọi G là trọng tâm tam giác ABC. Thể tích khối chóp . S ABG bằng V V V 2V A. . B. . C. . D. . 4 2 3 3
Câu 4: Cho hình chóp .
S ABC có thể tích là V . Gọi M , N , P lần lượt là trung điểm AB, BC, AC. Thể tích khối chóp . S MNP bằng V V V 2V A. . B. . C. . D. . 4 8 3 3
Câu 5: Cho hình chóp .
S ABC có thể tích là V . Gọi G là trọng tâm tam giác ABC, M là trung điểm .
SA Thể tích khối chóp M.ABG bằng V V V 2V A. . B. . C. . D. . 6 2 3 3
Câu 6: Gọi V là thể tích khối chóp .
S ABC, M, N lần lượt là trung điểm SC, A .
B Thể tích khối chóp MNCB bằng V 3V V 3V A. . B. . C. . D. . 2 8 4 4
Câu 7: Cho hình chóp .
S ABCD có đáy là hình bình hành. Gọi thể tích khối chóp .
S ABCD là V . Thể tích khối chóp . S ABC bằng V V V 2V A. . B. . C. . D. . 4 2 3 3
Câu 8: Cho hình chóp .
S ABCD có đáy là hình bình hành tâm O . Gọi thể tích khối chóp . S ABCD là
V . Thể tích khối chóp . S ABO bằng V V V 2V A. . B. . C. . D. . 4 2 3 3
Câu 9: Cho hình chóp .
S ABCD có đáy là hình bình hành tâm O . Gọi thể tích khối chóp . S ABCD là
V . M là trung điểm .
SD Thể tích khối chóp M.ABO bằng
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <20 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia V V V V A. . B. . C. . D. . 4 2 3 8
Câu 10: Gọi V là thể tích khối chóp .
S ABC, M , N , P lần lượt là trung điểm SA,SB,SC. Thể tích khối chóp . S MNP bằng V 7V V 2V A. . B. . C. . D. . 8 8 3 3
Câu 11: Gọi V là thể tích khối chóp .
S ABC, M , N , P lần lượt là trung điểm SA,SB,SC. Thể tích khối MNPCBA bằng V 7V V 2V A. . B. . C. . D. . 8 8 3 3
Câu 12: Gọi V là thể tích khối chóp .
S ABC, M, N lần lượt là trung điểm SB,SC. Thể tích khối chóp . S AMN bằng V 7V V 3V A. . B. . C. . D. . 8 8 4 4
Câu 13: Gọi V là thể tích khối chóp .
S ABC, M, N lần lượt là trung điểm SB,SC. Thể tích khối AMNCB bằng V 7V V 3V A. . B. . C. . D. . 8 8 4 4
Câu 14: Gọi V là thể tích khối chóp .
S ABC, M là trung điểm SC. Thể tích khối chóp . S ABM bằng V 3V V 3V A. . B. . C. . D. . 2 8 4 4
Câu 15: Gọi V là thể tích khối chóp .
S ABC, M là trung điểm SC. Thể tích khối chóp ABCM bằng V 3V V 3V A. . B. . C. . D. . 2 8 4 4
Câu 16: Cho hình chóp .
S ABCD có đáy là hình bình hành. Gọi thể tích khối chóp . S ABCD là V .
M, N, P,Q lần lượt là trung điểm SA,SB,SC,S .
D Thể tích khối chóp . S MNPQ bằng V V 7V V A. . B. . C. . D. . 4 16 8 8
Câu 17: Cho hình chóp .
S ABCD có đáy là hình bình hành. Gọi thể tích khối chóp . S ABCD là V .
M, N, P,Q lần lượt là trung điểm SA,SB,SC,S .
D Thể tích khối MNPQDABC bằng 15V V 7V V A. . B. . C. . D. . 16 16 8 8
Câu 18: Cho hình chóp .
S ABCD có đáy là hình bình hành. Gọi thể tích khối chóp . S ABCD là V .
M, N lần lượt là trung điểm SA,S .
B Thể tích khối chóp . S MNCD bằng 3V 5V V 3V A. . B. . C. . D. . 8 8 4 4
Câu 19: Cho hình chóp .
S ABCD có đáy là hình bình hành. Gọi thể tích khối chóp . S ABCD là V .
M, N lần lượt là trung điểm SA,S .
B Thể tích khối MNBADC bằng 3V 5V V 3V A. . B. . C. . D. . 8 8 4 4
Câu 20: Gọi V là thể tích khối lăng trụ ABC.A BC
 . Thể tích khối chóp . A A BC   bằng V 2V V 3V A. . B. . C. . D. . 3 3 2 4
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <21 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Câu 21: Gọi V là thể tích khối lăng trụ ABC.A BC
 , M là trung điểm AA . Thể tích khối chóp M.A BC   bằng V 2V V 3V A. . B. . C. . D. . 3 3 6 4
Câu 22: Gọi V là thể tích khối lăng trụ ABC.A BC
 , M là điểm bất kì trên cạnh . AB Thể tích khối chóp M.A BC   bằng V 2V V 3V A. . B. . C. . D. . 3 3 2 4
Câu 23: Gọi V là thể tích khối lăng trụ ABC.A BC
 . Thể tích khối chóp . A BCC B   bằng V 2V V 3V A. . B. . C. . D. . 3 3 2 4
Câu 24: Gọi V là thể tích khối lăng trụ ABC.A BC
 ,M là điểm bất kì trên AA . Thể tích khối chóp M.BCC B   bằng V 2V V 3V A. . B. . C. . D. . 3 3 2 4
Câu 25: Gọi V là thể tích khối lăng trụ ABC.A BC
 , M,N,P lần lượt là trung điểm AA,BB,CC . Thể
tích khối ABC.MNP bằng V 2V V 3V A. . B. . C. . D. . 3 3 2 4
Câu 26: Gọi V là thể tích khối lăng trụ ABC.A BC
 , M,N lần lượt là trung điểm AA,BB . Thể tích khối ABCNM bằng V 2V V 3V A. . B. . C. . D. . 3 3 2 4
Câu 27: Gọi V là thể tích khối lăng trụ ABC.A BC
 , M,N lần lượt là trung điểm AA,BB . Thể tích khối CMNB CA   bằng V 2V V 3V A. . B. . C. . D. . 3 3 2 4
Câu 28: Gọi V là thể tích khối lăng trụ ABC.A BC
 , M là trung điểm AA,N trên cạnh BB sao cho
BN  2NB . Thể tích khối ABCNM bằng V 2V 11V 7V A. . B. . C. . D. . 3 3 18 18
Câu 29: Gọi V là thể tích khối hộp ABC . D A BCD
 , M,N,P,Q lần lượt là trung điểm
AA, BB,CC, DD . Thể tích khối ABC . D MNPQ bằng V 2V V 3V A. . B. . C. . D. . 3 3 2 4
Câu 30: Gọi V là thể tích khối hộp AB . CD A B  C D
 , M,N lần lượt là trung điểm AA,BB . Thể tích khối ABCDMNC D   bằng V 2V V 3V A. . B. . C. . D. . 3 3 2 4
Câu 31: Gọi V là thể tích khối hộp A . BCD A BCD
 . Thể tích khối chóp B .ABC bằng V V V V A. . B. . C. . D. . 6 12 24 4
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <22 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Câu 32: Gọi V là thể tích khối hộp AB . CD A B  C D
 , M,N,P lần lượt là trung điểm AB,BC,BB . Thể
tích khối BMNP bằng V V V V A. . B. . C. . D. . 36 12 24 48
Câu 33: Gọi V là thể tích khối lăng trụ ABC.A BC
 , M,N lần lượt là trung điểm AB, AC. Thể tích khối chóp A AMN bằng V V V 11V A. . B. . C. . D. . 3 12 6 12
Câu 34: Gọi V là thể tích khối lăng trụ ABC.A BC
 , M,N lần lượt là trung điểm AB, AC. Thể tích khối MNCBC AB   bằng 5V V V 11V A. . B. . C. . D. . 6 12 6 12
Câu 35: Gọi V là thể tích khối lăng trụ ABC.A BC
 , M,N lần lượt là trung điểm AB, AC. Thể tích khối MNCBB C   bằng 3V 5V V 7V A. . B. . C. . D. . 4 12 4 12
Câu 36: Gọi V là thể tích khối lăng trụ ABC.A BC
 , M,N lần lượt là trung điểm AB, AC. Thể tích khối AMNC BA   bằng 3V 5V V 7V A. . B. . C. . D. . 4 12 4 12
Câu 37: Cho lăng trụ ABC.A BC
 . Gọi V ,V lần lượt là thể tích các khối . A A BC
  và ABCC . Khẳng 1 2
định nào sau đây đúng? V V 1 V 1 V 3 A. 1  1. B. 1  . C. 1  . D. 1  . V V 2 V 3 V 2 2 2 2 2
Câu 38: Cho khối chóp .
S ABC có thể tích V . Gọi B,C lần lượt là trung điểm của AB, AC . Tính theo
V thể tích khối chóp . S AB C   . 1 1 1 1 A. V . B. V . C. V . D. V . 3 2 12 4
Câu 39: Cho khối tứ diện SABC có M, N , P lần lượt là trung điểm SA, SB, SC và G là trọng tâm tam V
giác ABC . Gọi V là thể tích khối SABC , V  là thể tích khối GNMP . Tỉ số bằng V V  1 V  1 V  1 V  2 A.  . B.  . C.  . D.  . V 6 V 8 V 4 V 7
Câu 40: Cho khối lăng trụ ABC.A BC
  . Gọi M,N lần lượt là trung điểm của đoạn thẳng AA và BB'.
Tính tỉ số thể tích của khối tứ diện CMNC ' với khối lăng trụ đã cho. 1 1 2 3 A. . B. . C. . D. . 3 2 3 4
___________________HẾT___________________
Huế, 10h5’ Ngày 25 tháng 10 năm 2021
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <23 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TR¾C NGHIÖM M«n: To¸n 12
Chuyên đề: THỂ TÍCH KHỐI ĐA DIỆN
Tỷ số thể tích (CB)
PHIẾU HỌC TẬP SỐ 05_TrNg 2021
LỜI GIẢI CHI TIẾT
Câu 1: Gọi V là thể tích khối chóp .
S ABC. Gọi M là trung điểm .
SA Thể tích khối chóp M.ABC bằng V V V 2V A. . B. . C. . D. . 4 2 3 3 Lời giải: S M A C B 1
Do M là trung điểm SA nên dM;ABC  dS;ABC. 2 V Vậy V  . M.ABC 2
Chọn đáp án B.
Câu 2: Gọi V là thể tích khối chóp .
S ABC. Gọi M là điểm trên cạnh SA sao cho SM  2M . A Thể tích
khối chóp M.ABC bằng V V V 2V A. . B. . C. . D. . 4 2 3 3 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <24 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia S M A C B AM 1 1 Do
 nên dM;ABC  dS;ABC. AS 3 3 V Vậy V  . M.ABC 3
Chọn đáp án C.
Câu 3: Cho hình chóp .
S ABC có thể tích là V . Gọi G là trọng tâm tam giác ABC. Thể tích khối chóp . S ABG bằng V V V 2V A. . B. . C. . D. . 4 2 3 3 Lời giải: S A C G M B S AG 2 2 2 1 1
Gọi M là trung điểm BC. Ta có: ABG    SS  . SS . S AM 3 ABG 3 ABM 3 2 ABC 3 ABC ABM V Vậy V  . S.ABG 3
Chọn đáp án C.
Câu 4: Cho hình chóp .
S ABC có thể tích là V . Gọi M, N , P lần lượt là trung điểm AB, BC, AC. Thể tích khối chóp . S MNP bằng V V V 2V A. . B. . C. . D. . 4 8 3 3
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <25 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia Lời giải: S P A C N M B S 1 1 Ta có: MNP   SS . S 4 MNP 4 ABC ABC V Vậy V  . S.MNP 4
Chọn đáp án A.
Câu 5: Cho hình chóp .
S ABC có thể tích là V . Gọi G là trọng tâm tam giác ABC, M là trung điểm .
SA Thể tích khối chóp M.ABG bằng V V V 2V A. . B. . C. . D. . 6 2 3 3 Lời giải: S M A C G M B S AG 2 2 2 1 1
Gọi M là trung điểm BC. Ta có: ABG    SS  . SS . S AM 3 ABG 3 ABM 3 2 ABC 3 ABC ABM 1
Mặt khác, do M là trung điểm SA nên dM;ABC  dS;ABC. 2 1 1 V Vậy V  . V  . S.ABG 2 3 6
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <26 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Chọn đáp án A.
Câu 6: Gọi V là thể tích khối chóp .
S ABC, M, N lần lượt là trung điểm SC, A .
B Thể tích khối chóp MNCB bằng V 3V V 3V A. . B. . C. . D. . 2 8 4 4 Lời giải: S M A C N B S 1 1 Ta có: CBN   SS . S 2 CBN 2 ABC ABC 1
Mặt khác, do M là trung điểm SC nên dM;ABC  dS;ABC. 2 1 1 V Vậy V  . .V  . MNCB 2 2 4
Chọn đáp án C.
Câu 7: Cho hình chóp .
S ABCD có đáy là hình bình hành. Gọi thể tích khối chóp .
S ABCD là V . Thể tích khối chóp . S ABC bằng V V V 2V A. . B. . C. . D. . 4 2 3 3 Lời giải: S A D B C
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <27 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia S 1 1 Ta có: ABC   SS . S 2 ABC 2 ABCD ABCD V Vậy V  . S.ABC 2
Chọn đáp án C.
Câu 8: Cho hình chóp .
S ABCD có đáy là hình bình hành tâm O . Gọi thể tích khối chóp . S ABCD là
V . Thể tích khối chóp . S ABO bằng V V V 2V A. . B. . C. . D. . 4 2 3 3 Lời giải: S A D O B C S 1 1 Ta có: ABO   SS . S 4 ABO 4 ABCD ABCD V Vậy V  . S.ABO 4
Chọn đáp án A.
Câu 9: Cho hình chóp .
S ABCD có đáy là hình bình hành tâm O . Gọi thể tích khối chóp . S ABCD là
V . M là trung điểm .
SD Thể tích khối chóp M.ABO bằng V V V V A. . B. . C. . D. . 4 2 3 8 Lời giải: S M A D O B C S 1 1 Ta có: ABO   SS . S 4 ABO 4 ABCD ABCD
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <28 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 1
Do M là trung điểm SD nên dM;ABCD  dS;ABCD. 2 V Vậy V  . M.ABO 8
Chọn đáp án D.
Câu 10: Gọi V là thể tích khối chóp .
S ABC, M , N , P lần lượt là trung điểm SA,SB,SC. Thể tích khối chóp . S MNP bằng V 7V V 2V A. . B. . C. . D. . 8 8 3 3 Lời giải: S M P N A C B V SM SN SP 1 1
Ta có: S.MNP  . .   VV . S.MNP S. V SA SB SC 8 8 ABC S.ABC
Chọn đáp án A.
Câu 11: Gọi V là thể tích khối chóp .
S ABC, M, N , P lần lượt là trung điểm SA,SB,SC. Thể tích khối MNPCBA bằng V 7V V 2V A. . B. . C. . D. . 8 8 3 3 Lời giải: S M P N A C B V SM SN SP 1 1 7
Ta có: S.MNP  . .   VVVV . S.MNP S.ABC MNPCBA S. V SA SB SC 8 8 8 ABC S.ABC
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <29 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Chọn đáp án B.
Câu 12: Gọi V là thể tích khối chóp .
S ABC, M, N lần lượt là trung điểm SB,SC. Thể tích khối chóp . S AMN bằng V 7V V 3V A. . B. . C. . D. . 8 8 4 4 Lời giải: S N M A C B V SA SM SN 1 1
Ta có: S.AMN  . .   VV . S.AMN S. V SA SB SC 4 4 ABC S.ABC
Chọn đáp án C.
Câu 13: Gọi V là thể tích khối chóp .
S ABC, M, N lần lượt là trung điểm SB,SC. Thể tích khối AMNCB bằng V 7V V 3V A. . B. . C. . D. . 8 8 4 4 Lời giải: S N M A C B V SA SM SN 1 1 3
Ta có: S.AMN  . .   VVVV S.AMN S.ABC AMNCB S. V SA SB SC 4 4 4 ABC S.ABC
Chọn đáp án D.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <30 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Câu 14: Gọi V là thể tích khối chóp .
S ABC, M là trung điểm SC. Thể tích khối chóp . S ABM bằng V 3V V 3V A. . B. . C. . D. . 2 8 4 4 Lời giải: S M A C B V SA SB SM 1 1
Ta có: S.ABM  . .   VV . S.ABM S. V SA SB SC 2 2 ABC S.ABC
Chọn đáp án A.
Câu 15: Gọi V là thể tích khối chóp .
S ABC, M là trung điểm SC. Thể tích khối chóp ABCM bằng V 3V V 3V A. . B. . C. . D. . 2 8 4 4 Lời giải: S M A C B V SA SB SM 1 1 1
Ta có: S.ABM  . .   VVVV S.ABM S.ABC ABCM S. V SA SB SC 2 2 2 ABC S.ABC
Chọn đáp án A.
Câu 16: Cho hình chóp .
S ABCD có đáy là hình bình hành. Gọi thể tích khối chóp . S ABCD là V .
M, N, P,Q lần lượt là trung điểm SA,SB,SC,S .
D Thể tích khối chóp . S MNPQ bằng
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <31 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia V V 7V V A. . B. . C. . D. . 4 16 8 8 Lời giải: S M Q N P A D B C SA SB SC SD Ta có: a   2,b   2,c   2,d   2. AM SN SP SQ V    S MNPQ a b c d 1 1 Vậy .    VV . S.MNPQ S. V 4abcd 8 8 ABCD S.ABCD Cách khác: SMNPQ 1 1 Ta có:   SS
và dS MNPQ  1 ;
dS;ABCD. S 4 MNPQ 4 ABCD 2 ABCD 1 1 V Vậy V  . V  . S.MNPQ S. 4 2 ABCD 8
Chọn đáp án D.
Câu 17: Cho hình chóp .
S ABCD có đáy là hình bình hành. Gọi thể tích khối chóp . S ABCD là V .
M, N, P,Q lần lượt là trung điểm SA,SB,SC,S .
D Thể tích khối MNPQDABC bằng 15V V 7V V A. . B. . C. . D. . 16 16 8 8 Lời giải: S M Q N P A D B C SA SB SC SD Ta có: a   2,b   2,c   2,d   2. SM SN SP SQ V    S MNPQ a b c d 1 1 7 Vậy .    VVVV . S.MNPQ S.ABCD MNPQDABC S . V 4abcd 8 8 8 ABCD S.ABCD
Chọn đáp án C.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <32 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Câu 18: Cho hình chóp .
S ABCD có đáy là hình bình hành. Gọi thể tích khối chóp . S ABCD là V .
M, N lần lượt là trung điểm SA,S .
B Thể tích khối chóp . S MNCD bằng 3V 5V V 3V A. . B. . C. . D. . 8 8 4 4 Lời giải: S M N D A B C SA SB SC SD Ta có: a   2,b   2,c   1,d   1. SM SN SC SD V
a b c d 3 3 Vậy S.MNCD    VV . S.MNCD S. V 4abcd 8 8 ABCD S.ABCD
Chọn đáp án A.
Câu 19: Cho hình chóp .
S ABCD có đáy là hình bình hành. Gọi thể tích khối chóp . S ABCD là V .
M, N lần lượt là trung điểm SA,S .
B Thể tích khối MNBADC bằng 3V 5V V 3V A. . B. . C. . D. . 8 8 4 4 Lời giải: S M N D A B C SA SB SC SD Ta có: a   2,b   2,c   1,d   1. SM SN SC SD V
a b c d 3 3 5 Vậy S.MNCD    VVVV . S.MNCD S.ABCD MNBADC S . V 4abcd 8 8 8 ABCD S.ABCD
Chọn đáp án B.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <33 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Câu 20: Gọi V là thể tích khối lăng trụ ABC.A BC
 . Thể tích khối chóp . A A BC   bằng V 2V V 3V A. . B. . C. . D. . 3 3 2 4 Lời giải: A C B C' A' B' 1 V Ta có: V         d A; A B C .S    . A.A B C    3 A B C 3
Chọn đáp án A.
Câu 21: Gọi V là thể tích khối lăng trụ ABC.A BC
 , M là trung điểm AA . Thể tích khối chóp M.A BC   bằng V 2V V 3V A. . B. . C. . D. . 3 3 6 4 Lời giải: A C B M C' A' B' 1 1 1 V Ta có: V             d M; A B C .S    . d A; A B C .S    . A.A B C    ABC    3 3 2 A B C 6
Chọn đáp án C.
Câu 22: Gọi V là thể tích khối lăng trụ ABC.A BC
 , M là điểm bất kì trên cạnh . AB Thể tích khối chóp M.A BC   bằng
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <34 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia V 2V V 3V A. . B. . C. . D. . 3 3 2 4 Lời giải: A C M B C' A' B' 1 V Ta có: V         d M; A B C .S    . M.A B C    3 A B C 3
Chọn đáp án A.
Câu 23: Gọi V là thể tích khối lăng trụ ABC.A BC
 . Thể tích khối chóp . A BCC B   bằng V 2V V 3V A. . B. . C. . D. . 3 3 2 4 Lời giải: A C B C' A' B' 1 V 2V Ta có: V           d A; A B C .S    V   . A.A B C    ABC A. 3 3 BCC B 3
Chọn đáp án B.
Câu 24: Gọi V là thể tích khối lăng trụ ABC.A BC
 ,M là điểm bất kì trên AA . Thể tích khối chóp M.BCC B   bằng V 2V V 3V A. . B. . C. . D. . 3 3 2 4 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <35 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia A C M B C' A' B' 1 1 2V Ta có: V           d M; BCC B .S   d A; BCC B .S   V   . M.BCC B    BCCB    BCCB A. 3 3 BCC B 3
Chọn đáp án B.
Câu 25: Gọi V là thể tích khối lăng trụ ABC.A BC
 , M,N,P lần lượt là trung điểm AA,BB,CC . Thể
tích khối ABC.MNP bằng V 2V V 3V A. . B. . C. . D. . 3 3 2 4 Lời giải: A C B P M N C' A' B' V 1  AM BN CP  1  1 1 1  1 V
Ta có: ABC.MNP             V  . V    ABC.MNP    3  AA BB
CC  3  2 2 2  2 2 ABC.A B C Cách khác: 1 V
Khối ABC.MNP là khối lăng trụ, do đó VS .d M ABC S d A ABC ABC MNP ABC  ,( )  . ABC  ,( )  . . 2 2
Chọn đáp án C.
Câu 26: Gọi V là thể tích khối lăng trụ ABC.A BC
 , M,N lần lượt là trung điểm AA,BB . Thể tích khối ABCNM bằng
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <36 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia V 2V V 3V A. . B. . C. . D. . 3 3 2 4 Lời giải: A C B M N C' A' B' V 1  AM BN  1  1 1  1 V Ta có: ABCNM    0     V      . V      3  AA BB  3  2 2  3 ABCNM 3 ABC.A B C Cách khác:  1  V 2V 1 1 2V V V VV   VV  .  . C.A  B CABC.A  B CC.AB B AC.ABNM C.AB B A 3 3 3 2 2 3 3
Chọn đáp án A.
Câu 27: Gọi V là thể tích khối lăng trụ ABC.A BC
 , M,N lần lượt là trung điểm AA,BB . Thể tích khối CMNB CA   bằng V 2V V 3V A. . B. . C. . D. . 3 3 2 4 Lời giải: A C B M N C' A' B' Cách 1:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <37 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia V 1  AM BN  1  1 1  1 V Ta có: ABCNM    0     V      . V      3  AA BB  3  2 2  3 ABCNM 3 ABC.A B C 2V Vậy V     . CMNB C A 3 Cách 2:  1  V 2V 1 V V V V VV   VV  . Vậy VV   2 . C.A  B CABC.A  B CC.AB B AC.ABNM
C.ABBACMN B C  3 3 3 2 3 A 3 3 Cách 3:  1  V V V V và VV , do đó: VVV  . C.A  B CABC.A  B CC.ABNM
C.MNBAC.A  B CC.ABNM C.MN B A 3 3 3 V V V Vậy V    2
CMNBCA . 3 3 3
Chọn đáp án B.
Câu 28: Gọi V là thể tích khối lăng trụ ABC.A BC
 , M là trung điểm AA,N trên cạnh BB sao cho
BN  2NB . Thể tích khối ABCNM bằng V 2V 11V 7V A. . B. . C. . D. . 3 3 18 18 Lời giải: A C B M N C' A' B' V 1  AM BN  1  1 2  7 7V Ta có: ABCNM    0     V      . V      3  AA BB  3  2 3  18 ABCNM 18 ABC.A B C
Chọn đáp án D.
Câu 29: Gọi V là thể tích khối hộp ABC . D A BCD
 , M,N,P,Q lần lượt là trung điểm
AA, BB,CC, DD . Thể tích khối ABC . D MNPQ bằng V 2V V 3V A. . B. . C. . D. . 3 3 2 4 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <38 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia A D B C Q M P N D' A' C' B' V     ABCD MNPQ 1 AM BN CP DQ 1 1 1 1 1 1 V Ta có: .               V  . V     ABCD.MNPQ     4  AA BB CC
DD  4  2 2 2 2  2 2 ABCD.A B C D Cách khác: Khối ABC .
D MNPQ là khối hộp, do đó:  V V S d M ABCD S d A ABCD ABCD MNPQ ABCD    1 . ,( ) . ABCD  ,( )  . . 2 2
Chọn đáp án C.
Câu 30: Gọi V là thể tích khối hộp AB . CD A B  C D
 , M,N lần lượt là trung điểm AA,BB . Thể tích khối ABCDMNC D   bằng V 2V V 3V A. . B. . C. . D. . 3 3 2 4 Lời giải: A D C B M A' N D' B' C' V       1 AM BN 1 1 1 3 3V Ta có: ABCDMNC D    1 1    1 1       V    . V   ABCDMNC D     4  AA BB  4  2 2  4 4 ABCD.A B C D
Chọn đáp án D.
Câu 31: Gọi V là thể tích khối hộp A . BCD A BCD
 . Thể tích khối chóp B .ABC bằng V V V V A. . B. . C. . D. . 6 12 24 4 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <39 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia A D B C A' D' C' B'
dB ;BAC  dB ;ABCD  1 1 1 1 Do  V      d B ; BAC S . V V . B .BAC   1 nên  BAC S   S 3 3 2 6 BAC  2 ABCD
Cách khác: Đặc biệt hóa, hình hộp là hình lập phương cạnh bằng 1V  1  V Suy ra:   V   . 1 1 1 1 1 B . V       .BB . B . A BC .1. .1.1 BAC 6 B .BAC  3 2 3 2 6
Chọn đáp án A.
Câu 32: Gọi V là thể tích khối hộp AB . CD A B  C D
 , M,N,P lần lượt là trung điểm AB,BC,BB . Thể
tích khối BMNP bằng V V V V A. . B. . C. . D. . 36 12 24 48 Lời giải: A D M B N C P A' D' B' C' d
 P BMM 1 ;
dB ;ABCD  1 1 1 1 1 Do 2  nên V     d P; BMM S . . V V . B .BMN    1 3 BMN 3 2 8 48 S   S BMN  8 ABCD
Cách khác: Đặc biệt hóa, hình hộp là hình lập phương cạnh bằng 1V  1  V Suy ra:   V  . 1 1 1 1 1 1 1 1 P. V  .P . B
BM.BN  . . . . BMN  48 P.BMN  3 2 3 2 2 2 2 48
Chọn đáp án D.
Câu 33: Gọi V là thể tích khối lăng trụ ABC.A BC
 , M,N lần lượt là trung điểm AB, AC. Thể tích khối chóp A AMN bằng V V V 11V A. . B. . C. . D. . 3 12 6 12
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <40 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia Lời giải: N A C M B A' C' B' 1 1 1 1 V Ta có: SSV      
d A ; ABC .S
. d A ; ABC .S . AMN ABC A .AMN    AMN    4 3 3 4 ABC 12
Chọn đáp án B.
Câu 34: Gọi V là thể tích khối lăng trụ ABC.A BC
 , M,N lần lượt là trung điểm AB, AC. Thể tích khối MNCBC AB   bằng 5V V V 11V A. . B. . C. . D. . 6 12 6 12 Lời giải: N A C M B A' C' B' 1 1 1 1 V Ta có: SSV      
d A ; ABC .S
. d A ; ABC .S . AMN ABC A .AMN    AMN    4 3 3 4 ABC 12 11VV     . MNCBC A B 12
Chọn đáp án D.
Câu 35: Gọi V là thể tích khối lăng trụ ABC.A BC
 , M,N lần lượt là trung điểm AB, AC. Thể tích khối MNCBB C   bằng 3V 5V V 7V A. . B. . C. . D. . 4 12 4 12
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <41 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia Lời giải: A N C M B C' A' B' V         a b c d 2 2 1 1 3 3
Ta có: A.MNC B     V    V A.MNC B A.   V   4abcd 4.2.2.1.1 8 8 BCC B A.BCC B 5 5 2 5 Vậy V      V   . V V . MNCBB C A. 8 BCC B 8 3 12
Chọn đáp án B.
Câu 36: Gọi V là thể tích khối lăng trụ ABC.A BC
 , M,N lần lượt là trung điểm AB, AC. Thể tích khối AMNC BA   bằng 3V 5V V 7V A. . B. . C. . D. . 4 12 4 12 Lời giải: A N C M B C' A' B' V         a b c d 2 2 1 1 3 3
Ta có: A.MNC B     V    V A.MNC B A.   V   4abcd 4.2.2.1.1 8 8 BCC B A.BCC B 5 5 2 5 7 Vậy V       V   . V V ;V    V . MNCBB C A. 8 BCC B 8 3 12 AMNC B A 12
Chọn đáp án D.
Câu 37: Cho lăng trụ ABC.A BC
 . Gọi V ,V lần lượt là thể tích các khối . A A BC
  và ABCC . Khẳng 1 2
định nào sau đây đúng? V V 1 V 1 V 3 A. 1  1. B. 1  . C. 1  . D. 1  . V V 2 V 3 V 2 2 2 2 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <42 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia Lời giải: A C B C' A' B' V  1  d A; A B C .S 1
     ABC  Ta có:  3  V V .  1 2
V  1 d C ; ABC .S 2      3 ABC
Chọn đáp án A.
Câu 38: Cho khối chóp .
S ABC có thể tích V . Gọi B,C lần lượt là trung điểm của AB, AC . Tính theo
V thể tích khối chóp . S AB C   . 1 1 1 1 A. V . B. V . C. V . D. V . 3 2 12 4 Lời giải: S C' A C B' B V     AB AC 1 1 1 1 1
Ta có tỷ số thể tích A.SB C  .  .  . Do đó V     V hay V   V . V AB AC 2 2 4 A.SB C A. 4 SBC S.AB C 4 A.SBC
Chọn đáp án D.
Câu 39: Cho khối tứ diện SABC có M, N , P lần lượt là trung điểm SA, SB, SC và G là trọng tâm tam V
giác ABC . Gọi V là thể tích khối SABC , V  là thể tích khối GNMP . Tỉ số bằng V V  1 V  1 V  1 V  2 A.  . B.  . C.  . D.  . V 6 V 8 V 4 V 7 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <43 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia S M P N A C G B
Ta có dS,MNP  dG,MNP . Do đó VVV  . SNMP GMNP V V SM SN SP 1 1 1 1 Do đó  SMNP  . .  . .  . V V SA SB SC 2 2 2 8 SABC
Chọn đáp án B.
Câu 40: Cho khối lăng trụ ABC.A BC
  . Gọi M,N lần lượt là trung điểm của đoạn thẳng AA và BB'.
Tính tỉ số thể tích của khối tứ diện CMNC ' với khối lăng trụ đã cho. 1 1 2 3 A. . B. . C. . D. . 3 2 3 4 Lời giải: A C B M N A' C' B' V 1  AM BN CC  1 1 Ta có: ABC.MNC      V    V . ABC.MNC
ABC.A' B'C ' V
3  AA' BB' CC'  3 3
ABC.A' B'C ' V 1  A' M B' N C'C'  1 1
Tương tự ta có: A'B'C'.MNC'      V    V .
A' B'C '.MNC ' A' B'C'. V 3  A' A B' B C 'C  3 3 ABC
A' B'C '.ABC 1 V 1 CMNC '  VV   . CMNC '
ABC.A' B'C ' 3 V 3
ABC.A' B'C '
Chọn đáp án A.
_________________HẾT_________________
Huế, 10h45’ Ngày 07 tháng 7 năm 2023
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <44 >