Một số công thức giải nhanh phần thể tích khối chóp – Nguyễn Chiến Toán 12

MỘT SỐ CÔNG THỨC GIẢI NHANH PHẦN THỂ TÍCH KHỐI CHÓP
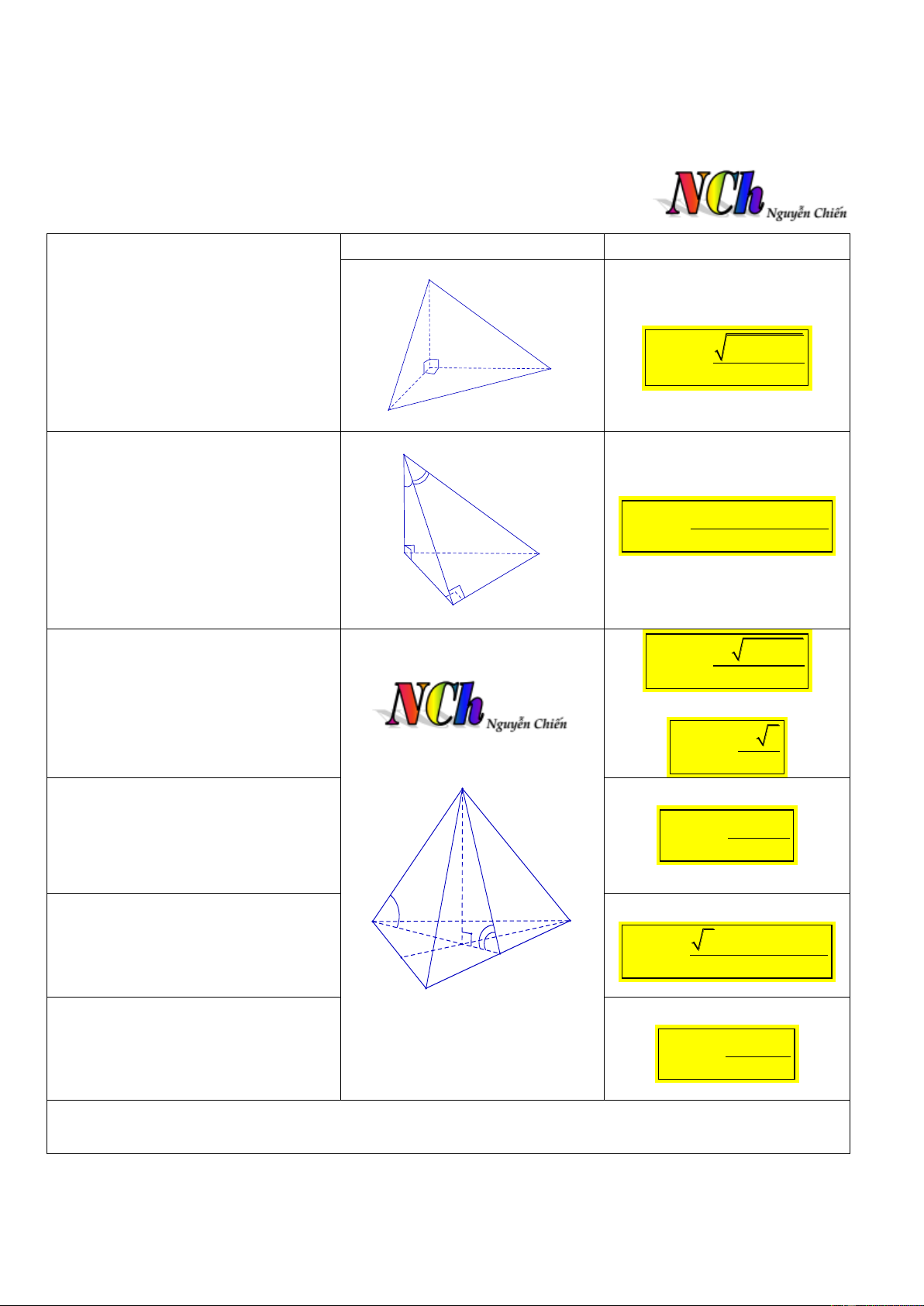
CT 1. Cho hình chóp SABC với Hình vẽ Thể tích
các mặt phẳng SAB , SBC A 
SAC vuông góc với nhau từng
đôi một, diện tích các tam giác 2S .S .S 1 2 3 SA , B SBC,SAC S V  lần lượt là C S.ABC 3 S ,S ,S . 1 2 3 B
CT 2. Cho hình chóp S.ABC có S
SA vuông góc với  ABC , hai
mặt phẳng SAB và SBC 3 SB .sin 2.tan . V 
vuông góc với nhau, BSC   , S.ABC 12 A C ASB   . B
CT 3. Cho hình chóp đều 2 2 2 a 3b  a
S.ABC có đáy ABC là tam giác V  S.ABC 12
đều cạnh bằng a, cạnh bên
Khi a  b được tứ diện đều bằng b . 3 a 2 V  S.ABC 12 S
CT 4. Cho hình chóp tam giác
đều S.ABC có cạnh đáy bằng a và 3 a tan
mặt bên tạo với mặt phẳng đáy V  S.ABC 24 góc  .
CT 5. Cho hình chóp tam giác
đều S.ABC có các cạnh bên bằng A C 3 2 3b .sin  cos 
b và cạnh bên tạo với mặt phẳng G V  S.ABC M 4 đáy góc  .
CT 6. Cho hình chóp tam giác B
đều S.ABC có các cạnh đáy bằng 3 a .tan 
a, cạnh bên tạo với mặt phẳng V  S.ABC 12 đáy góc  .
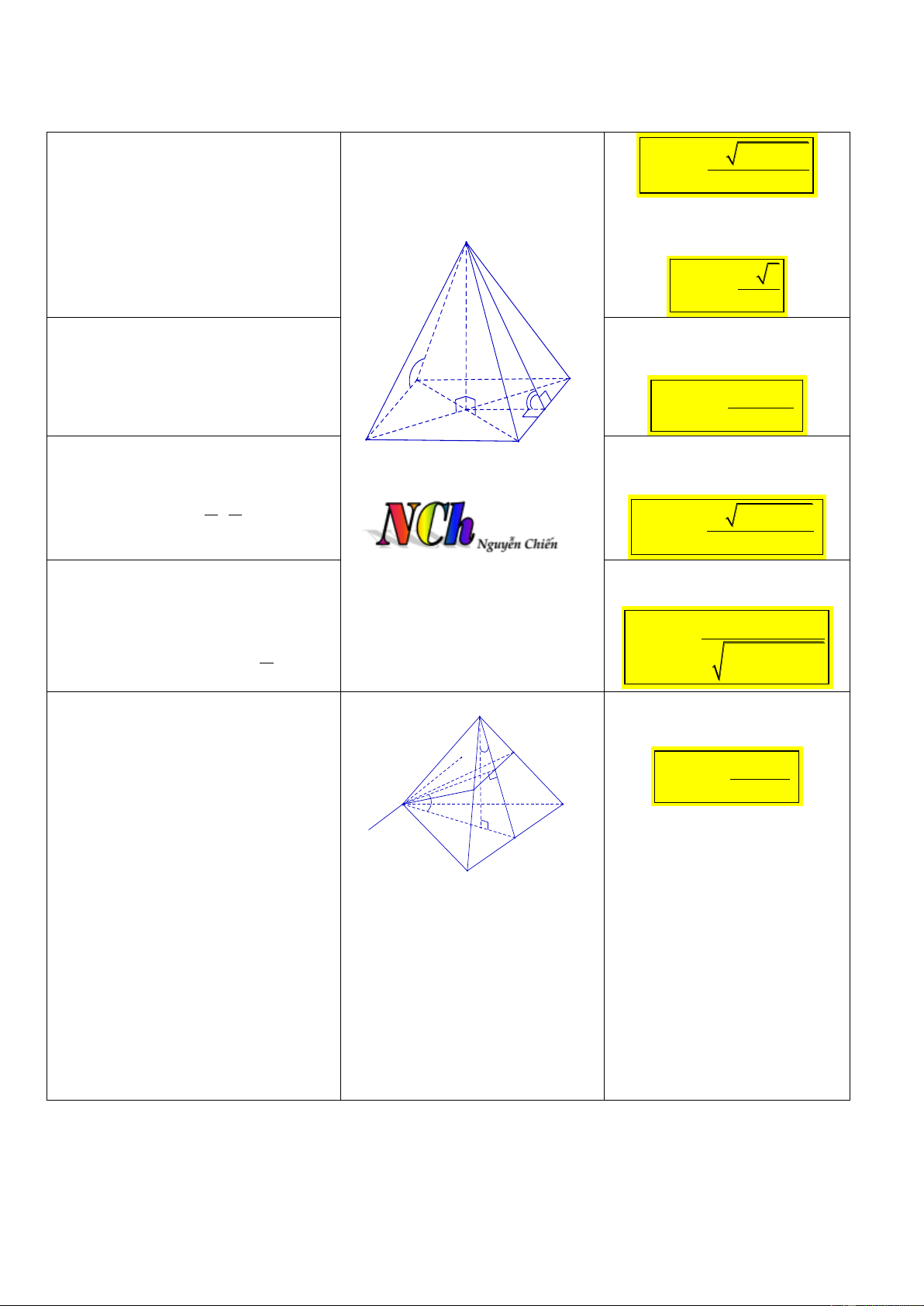
CT 7. Cho hình chóp tứ giác 2 2 2 a 4b  2a
đều S.ABCD có đáy ABCD là V  S.ABC 6
hình vuông cạnh bằng a, và
SA  SB  SC  SD  b.
Khi chóp tứ giác có tất cả S
các cạnh bằng a thì 3 a 2 V  S.ABC 6
CT 8. Cho hình chóp tứ giác
đều S.ABCD có cạnh đáy bằng a, A
góc tạo bởi mặt bên và mặt D 3 a .tan phẳng đáy là  V  . S.ABCD O M 6
CT 9. Cho hình chóp tứ giác đều B C
S.ABCD có cạnh đáy bằng a,  
SAB   , với    ; . 3 2    a tan 1 4 2  V  . S.ABCD 6
CT 10. Cho hình chóp tứ giác
đều S.ABCD có các cạnh bên
bằng a, góc tạo bởi mặt bên và 3 4a .tan   V S.ABCD 3 mặt đáy là  với    0; . 3  2 2  tan    2 
CT 11. Cho hình chóp tam giác S
đều S.ABC có cạnh đáy bằng a. F
Gọi P là mặt phẳng đi qua A 3 a cot N V  . S.ABCD A E 24
song song với BC và vuông góc C x
với SBC , góc giữa P với mặt G M phẳng đáy là  . B
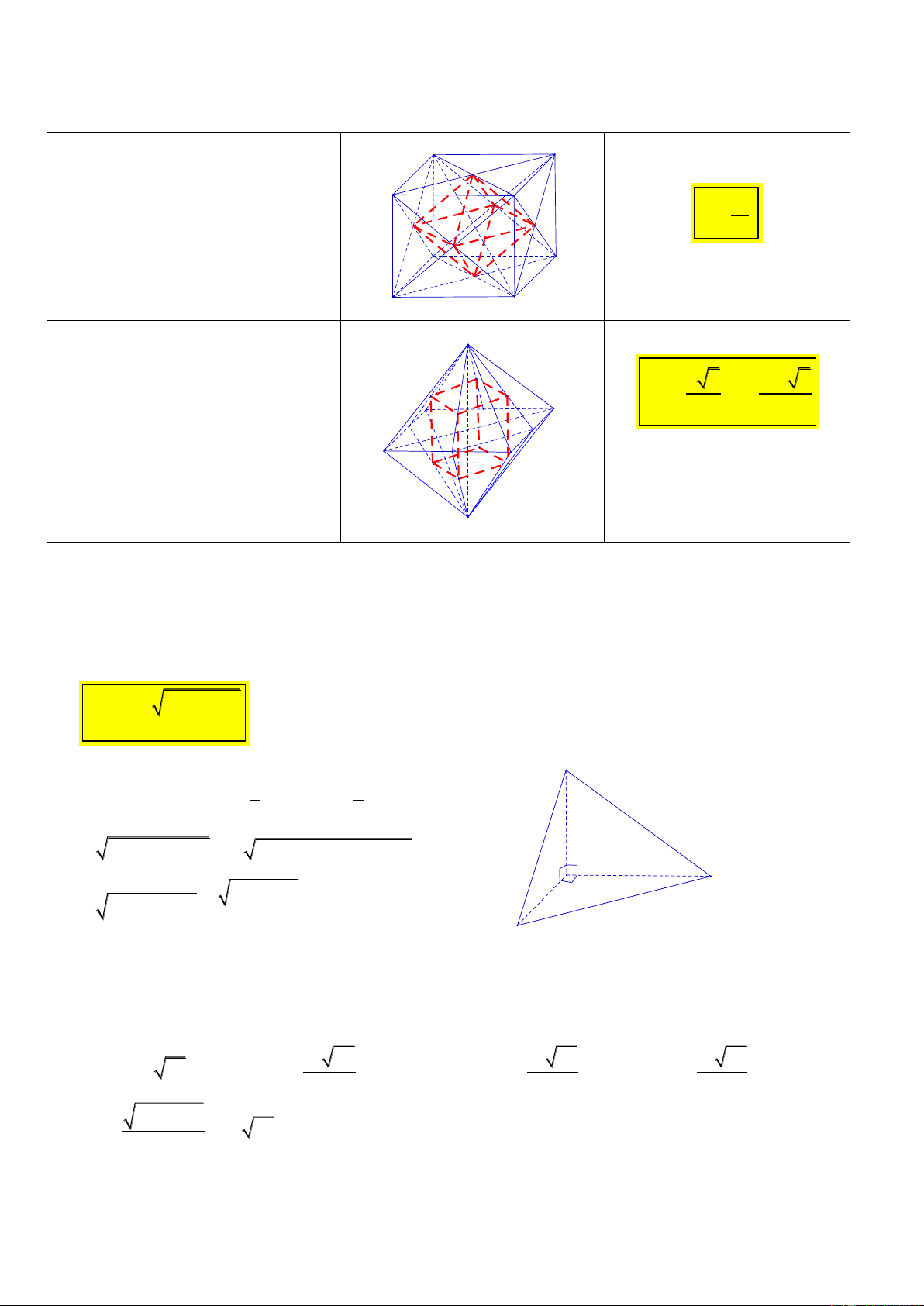
CT 12. Khối tám mặt đều có A' B'
đỉnh là tâm các mặt của hình lập O' phương cạnh a D' 3 O1 C' a V  . O4 O2 6 A O3 B O D C
CT 13. Cho khối tám mặt S
đều cạnh a. Nối tâm của các mặt 3 3   bên ta được khối lập a 2 2a 2 G2 V       phương D 3 27 G1   A N M B C S'
LỜI GIẢI CHI TIẾT
CT 1. Cho hình chóp SABC với các mặt phẳng SAB ,SBC ,SAC vuông góc với
nhau từng đôi một, diện tích các tam giác SA ,
B SBC,SAC lần lượt là S ,S ,S . Thể tích khối chóp SABC 1 2 3 2S .S .S là: 1 2 3 V  S.ABC 3 Lời giải A 1 1
AS  SBC  V  .S .SA  S . A S . B SC SABC 3 SBC 6 1 2 2 2 1 
SA .SB .SC  S . A S . B S . B SC.S . A SC 6 6 S C 1 2S .S .S 1 2 3 
2S .2S .2S  1 2 3 6 3 B
Áp dụng: Cho hình chóp SABC với các mặt phẳng SAB ,SBC ,SAC vuông góc với
nhau từng đôi một, diện tích các tam giác SA ,
B SBC,SAC lần lượt là 2 2 2
15cm ,20cm ,18cm Thể tích khối chóp SABC là 3 a 20 3 a 20 3 a 20 A. 3 a 20. B. . C. . D. . 3 2 6 2S .S .S 1 2 3 3 V 
 a 20 Chọn đáp án A. ABCD 3
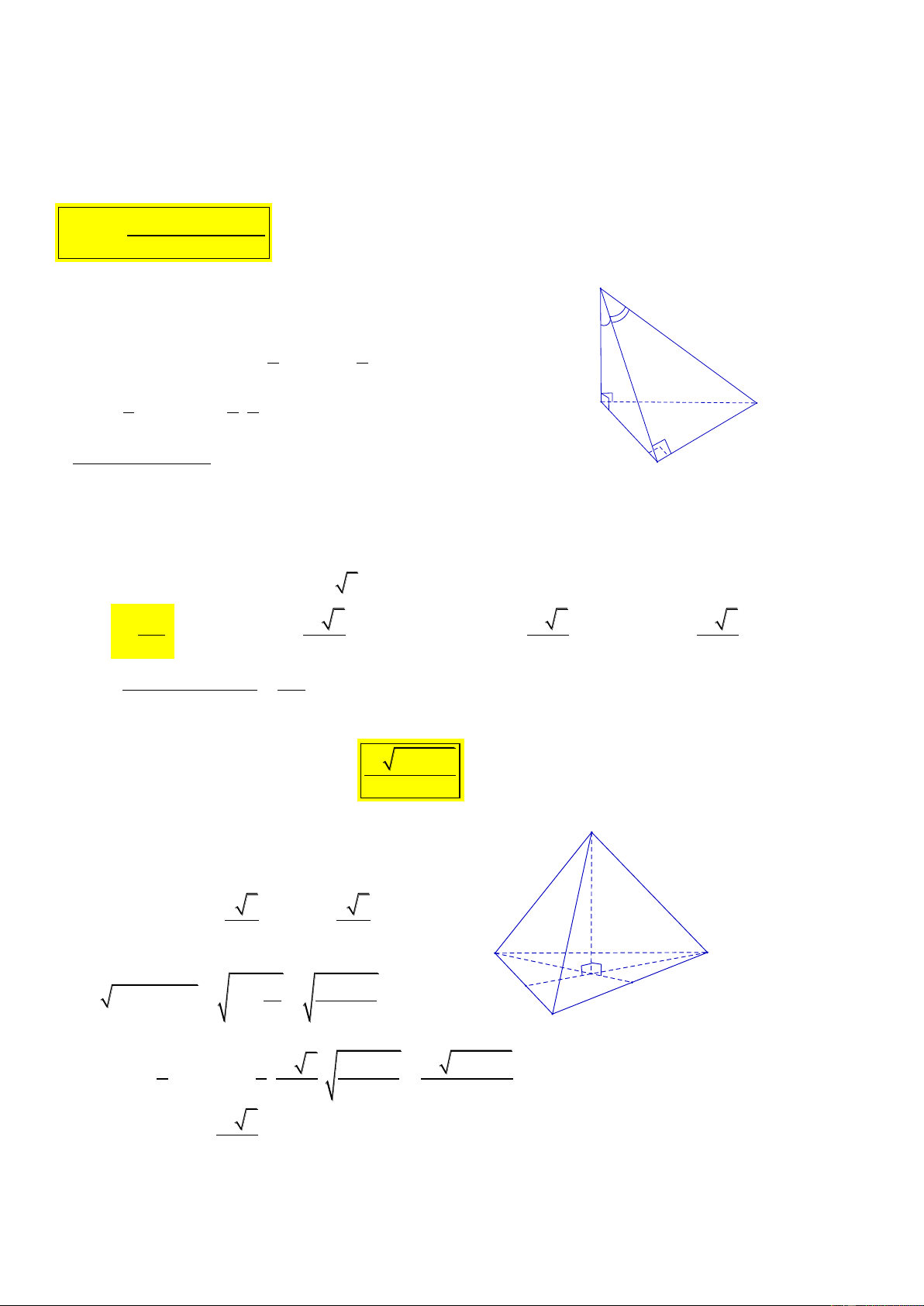
CT 2. Cho hình chóp SABC có SA vuông góc với mặt phẳng  ABC , hai mặt phẳng
SABvà SBCvuông góc với nhau, BSC  , ASB   . Thể tích khối chóp SABC là 3 SB .sin 2.tan .  V  S.ABC 12 Lời giải S
+ SAB vuông tại A có : AB  S .
B sin , SA  S . B cos
+ SBC vuông tại B có : 1 1 BC  S . B tan  2  S  A .
B BC  .SB .sin.tan   ABC 2 2 1 1 1 2 V  .S
.SA  . .SB .sin.tan .S . B cos A C S.ABC 3 A  BC 3 2 3 SB .sin 2.tan .  12 B
Áp dụng: Cho hình chóp SABC có SA vuông góc với mặt phẳng  ABC , hai mặt phẳng SAB và
SBCvuông góc với nhau, SB  a 3 ,  45o BSC ,  30o ASB
. Thể tích khối chóp SABC là 3 3a 3 a 6 3 a 2 3 a 3 A. . B. . C. . D. . 8 8 2 6 3 3 SB .sin 2.tan  3a V  
 Chọn đáp án A. S.ABC 12 8
CT 3. Cho hình chóp đều S.ABC có đáy ABC là tam giác đều cạnh bằng a, cạnh bên 2 2 2 a 3b  a
bằng b . Thể tích khối chóp S.ABC là 12 S Lời giải
Gọi G là trọng tâm A
 BC  SG  ABC a 3 a A
 BC đều  AM  3  AG  2 3 S
 GAvuông tại G có: C A 2 2 2  G 2 2 2 a 3b a
SG  SA  AG  b   M 3 3 B 2 2 2 2 2 2 1 1 a 3 3b  a a 3b  a Vậy V  .S .SG  . .  SABC 3 ABC 3 4 3 12 3 a 2
Khi a  b  V  SABC 12
Áp dụng: Cho hình chóp đều S.ABC có đáy ABC là tam giác đều cạnh bằng a, cạnh bên
bằng a . Thể tích khối chóp S.ABC là 3 3 a 3 a 2 3 a 2 3 a 3 A. . B. . C. . D. . 24 12 24 12
 Chọn đáp án B.
CT 4. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và mặt bên tạo với 3 a tan
mặt phẳng đáy góc  . Thể tích khối chóp S.ABC là 24 3 a 3 3 a 3 a 3 3 a A. . B. . C. . D. . 48 24 24 12 Lời giải S a2 3
+ ABC đều  S  A  BC 4
+ Gọi G là trọng tâm ABC  SG   ABC
  SBC,ABC  SMG  C A Xét S
 GM vuông tại G có : G 1 a 3.tan M
SG  GM.tanSMG  .AM tan  3 6 B 2 3 1 1 a 3 a 3.tan a tan Vậy V  .S .SG  . .  SABC 3 A  BC 3 4 6 24
Áp dụng: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và mặt bên tạo với
mặt phẳng đáy góc 600. Thể tích khối chóp S.ABC là 3 a 3 3 a 3 a 3 3 a A. . B. . C. . D. . 48 24 24 12 3 3 a tan a 3 V  
 Chọn đáp án C. SABC 24 24
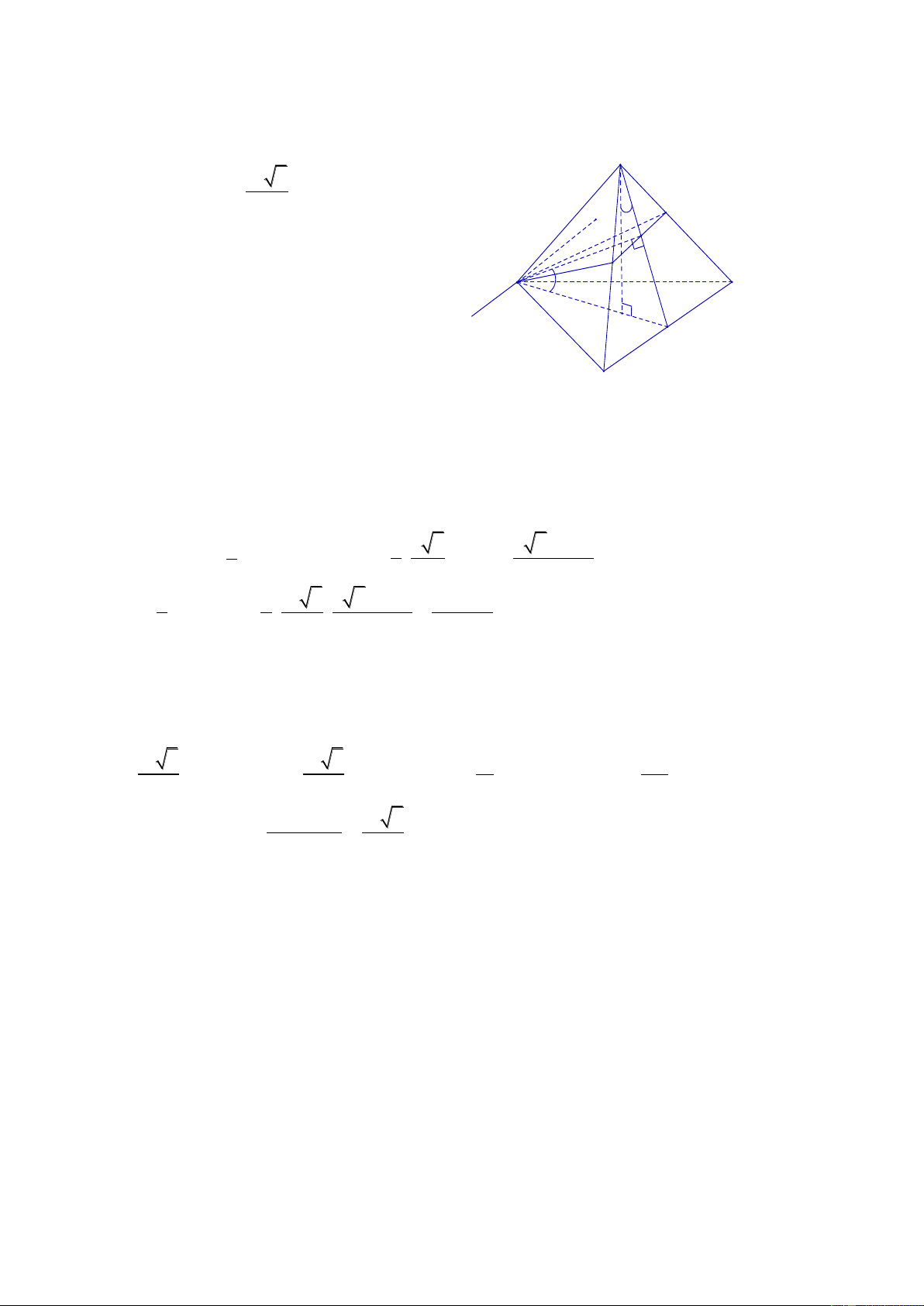
CT 5. Cho hình chóp tam giác đều S.ABC có các cạnh bên bằng b và tạo với mặt phẳng 3 2 3b .sin  cos 
đáy góc  . Thể tích khối chóp S.ABC là 4 Lời giải S
+ Gọi G là trọng tâm ABC  SG   ABC
Xét SGA vuông tại G có: SG  S . A sin   . b sin  b  AG  3 3 .cos S .
A cos   AM  AG  2 2 3 A C
+ ABC đều  AM  AB 2 G M 2  AB  AM  3 . b cos  B 3 2 AB b   S   b   A  BC   2 2 2 3 3 3 3 cos 3 .cos 4 4 4 3 2 1 3b .sin  cos  Vậy V  .S .SG  SABC 3 A  BC 4
CT 6. Cho hình chóp tam giác đều S.ABC có các cạnh đáy bằng a, cạnh bên tạo với 3 a .tan 
mặt phẳng đáy góc  . Thể tích khối chóp S.ABC là 12 Lời giải S
+ Gọi G là trọng tâm ABC  SG   ABC
Xét SGA vuông tại G có : 2  SG  A . G tan   AM.tan  3 3
+ ABC đều  AM  AB 2 A C 2 3 a 3.tan  G  SG  . A . B tan   M 3 2 3 B 2 3 1 1 a 3 a 3.tan  a .tan  Vậy V  .S .SG  .  SABC 3 A  BC 3 4 3 12
Áp dụng: Cho hình chóp tam giác đều S.ABC có các cạnh đáy bằng a, mặt bên tạo với mặt phẳng đáy góc 0
30 . Thể tích khối chóp S.ABC là 3 a 3 a 3 a 3 3 a 3 A. . B. . C. . D. . 48 24 24 36 3 3 a tan  a 3 V  
.  Chọn đáp án D. SABC 12 36
CT 7. Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh bằng a, 2 2 2 a 4b  2a
và SA  SB  SC  SD  b. Thể tích khối chóp S.ABCD là 6 Lời giải S
AC  BD   
O  SO  ABCD
Gọi M là trung điểm AB. 2 a 2 2 2 2
 SM  SA  AM  b  4 S
 OM vuông tại O có: D A 2 2 2 2  2 2 2 a a 4b 2a
SO  SM  OM  b    4 4 2 O M 2 2 2 1 a 4b  2a C Vậy V  .S .SO  B SABCD 3 ABCD 6 3 a 2
Khi SA  SB  SC  SD  a  V  . SABCD 6
Áp dụng: Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh bằng a,
và SA  SB  SC  SD  a . Thể tích khối chóp S.ABCD là 3 a 6 3 a 2 3 a 2 3 a 3 A. . B. . C. . D. . 6 2 6 3
 Chọn đáp án C.
CT 8. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc tạo bởi mặt 3 a .tan
bên và mặt phẳng đáy là  . Thể tích khối chóp S.ABCD là . 6 Lời giải S
AC  BD   
O  SO  ABCD
Gọi M là trung điểm CD
  SCD,ABCD  SMO 
+ Tam giác SOM vuông tại O có: A a D
SO  OM.tanSMO  .tan 2 O M 1 1 2 a a3 tan V  S . S . O  a . . .tan  SABCD ABCD 3 3 2 6 B C
Áp dụng: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc tạo bởi mặt bên và mặt phẳng đáy là 0
45 . Thể tích khối chóp S.ABCD là 3 a 3 a 3 3 a 6 3 a A. . B. . C. . D. . 12 6 2 6 3 3 a tan a V  
 Chọn đáp án D. SABCD 6 6
CT 9. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, SAB   , với   3 2       a tan 1
 ;  . Thể tích khối chóp S.ABCD là .  4 2  6 Lời giải S
AC  BD   
O  SO  ABCD
Gọi M là trung điểm AB. S
 MA vuông tại M có: .atan
 SM  AM.tanSAB  2 D S
 OM vuông tại O có: A 2 2      M 2 2 . a tan a
SO  SM  OM   O      2   2  C B a 2  tan   1 2 3 2 1 1  2 a 2 a tan 1 V .S .SO .a . tan     1  SABCD 3 ABCD 3 2 6
Áp dụng: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, 0
SAB  60 . Thể tích khối chóp S.ABCD là 3 a 2 3 a 2 3 a 6 3 a A. . B. . C. . D. . 12 6 2 6 3 2 3 a tan   1 a 2 V  
 Chọn đáp án B. SABCD 6 6
CT 10. Cho hình chóp tứ giác đều S.ABCD có các cạnh bên bằng a, góc tạo bởi mặt  3 4a .tan
bên và mặt đáy là  với   
0; . Thể tích khối chóp S.ABCD là  2  3 2  tan  3 2 Lời giải S
AC  BD   
O  SO  ABCD
Gọi M là trung điểm CD
  SCD ABCD  SMO  0 , 60
Gọi độ dài một cạnh hình vuông là x A
+ Tam giác SMC vuông tại M có: D 2 2 2 x2
SM  SC  CM  a  O M 4 B C
+ Tam giác SOM vuông tại O có: 1 2 2 2 x x x  x  2 x2
OM  SM.cosSMO  . a  2 2 2   cos. a    a  cos  2 4 2 4 2  4  1 2 2 4a2. 4a cos  2 1  2 2 tan  4a2  2a 4a x     x   S  1  2 cos  1 2  2 tan  ABCD 2  2 tan  1  2  2 tan  1  2 tan  x a.tan
Ta có: SO  OM.tanSMO  .tan  2 2  2 tan  1 1 4a2 a.tan 4a3.tan V  S . SO .  . .  SABCD ABCD 3 3 2  2 tan  2  2 tan  3 2  tan  3 2
CT 11. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a. Gọi P là mặt phẳng đi qua A song
song với BC và vuông góc với SBC , góc giữa P với mặt phẳng đáy là  . Thể tích khối chóp S.ABC 3 a cot là . 24 Lời giải S a2 3
+ ABC đều  S  A  BC 4 F
+ Gọi G là trọng tâm ABC  SG   ABC N
+ Gọi P SBC  EF  EF / /BC A E C
 PSBC  Ax với Ax / /EF / /BC x
+ Gọi M là trung điểm của BC, SM  EF  N G M
Ta có: AM  BC,SG  BC
 BC  SAM  AN  BC  AN  Ax B
Mà AM  BC, BC / /Ax  AM  Ax
  P,ABC  NAM 
Ta có: GSM  NAM   (cùng phụ với SMA ) Xét S
 GM vuông tại G có : 1 a 3 a 3.cot SG  GM GSM  1 .cot
.AM cot  SG  . .cot  3 3 2 6 a2 a  a3 1 1 3 3.cot cot Vậy V  S . S . G  . .  SABC ABC 3 3 4 6 24
Áp dụng: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a. Gọi P là mặt phẳng đi qua A song
song với BC và vuông góc với SBC , góc giữa P với mặt phẳng đáy là 0 30 . Thể tích khối chóp S.ABC là: a3 3 a3 3 a3 a3 3 A. B. C. D. 24 8 8 8 3 0 3 a cot 30 a 3 Áp dụng bài này: V  
 Chọn đáp án A SABC 24 24
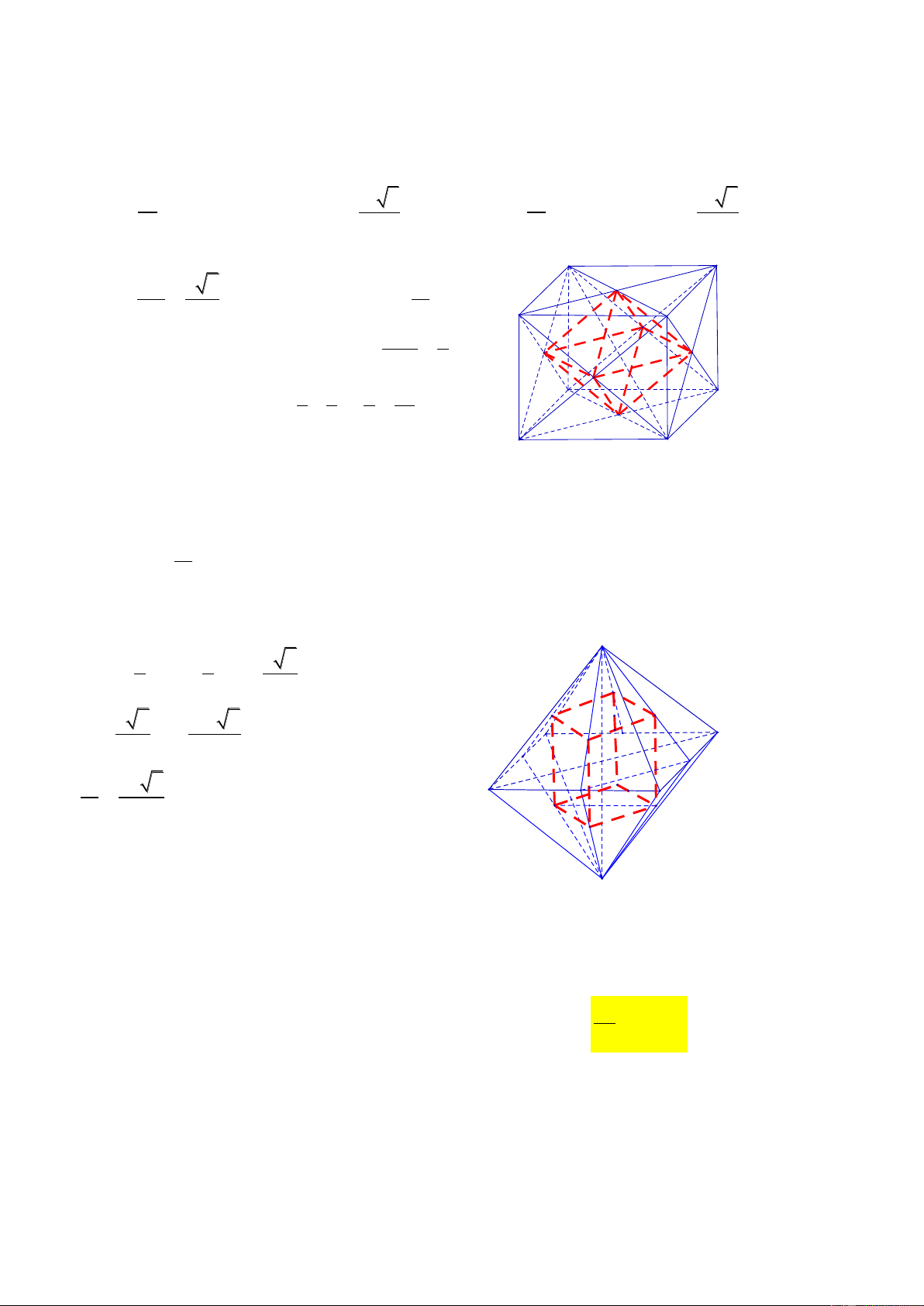
CT 12. Khối tám mặt đều có đỉnh là tâm các mặt của hình lập phương cạnh a có thể tích là 3 a 3 a 3 3 a 3 a 3 A. . B. . C. . D. . 12 4 6 2 Lời giải A' B' BD a 2 2 O' 2 a + O O    S  O O  . O O O O  2 3 2 3 2 2 1 2 3 4 2 D' O1 C' OO' a
Chiều cao khối chóp O O O O là h   1 2 3 4 2 2 O4 O2 2 3 1  a  a a A O3  B V  2V  2. .  .  OO O O O O' OO O O O 1 2 3 4 1 2 3 4 3  2  2 12 O
 Chọn đáp án C. D C
CT 13. Cho khối tám mặt đều cạnh a. Nối tâm của các mặt bên ta được khối lập phương có thể tích 3 a bằng V. Tỷ số
gần nhất giá trị nào trong các giá trị sau? V A. 9,5. B. 7,8. C. 15,6. D. 22,6. Lời giải S 2 1 a 2 + G G  MN  BD  1 2 3 3 3 3 3  G2 a 2  2a 2 + V      D 3  27   A G1 N 3 a 27 2    M
9, 5  Chọn đáp án A. C V 4 B S'
MỘT SỐ CÔNG THỨC GIẢI NHANH PHẦN TỈ LỆ THỂ TÍCH
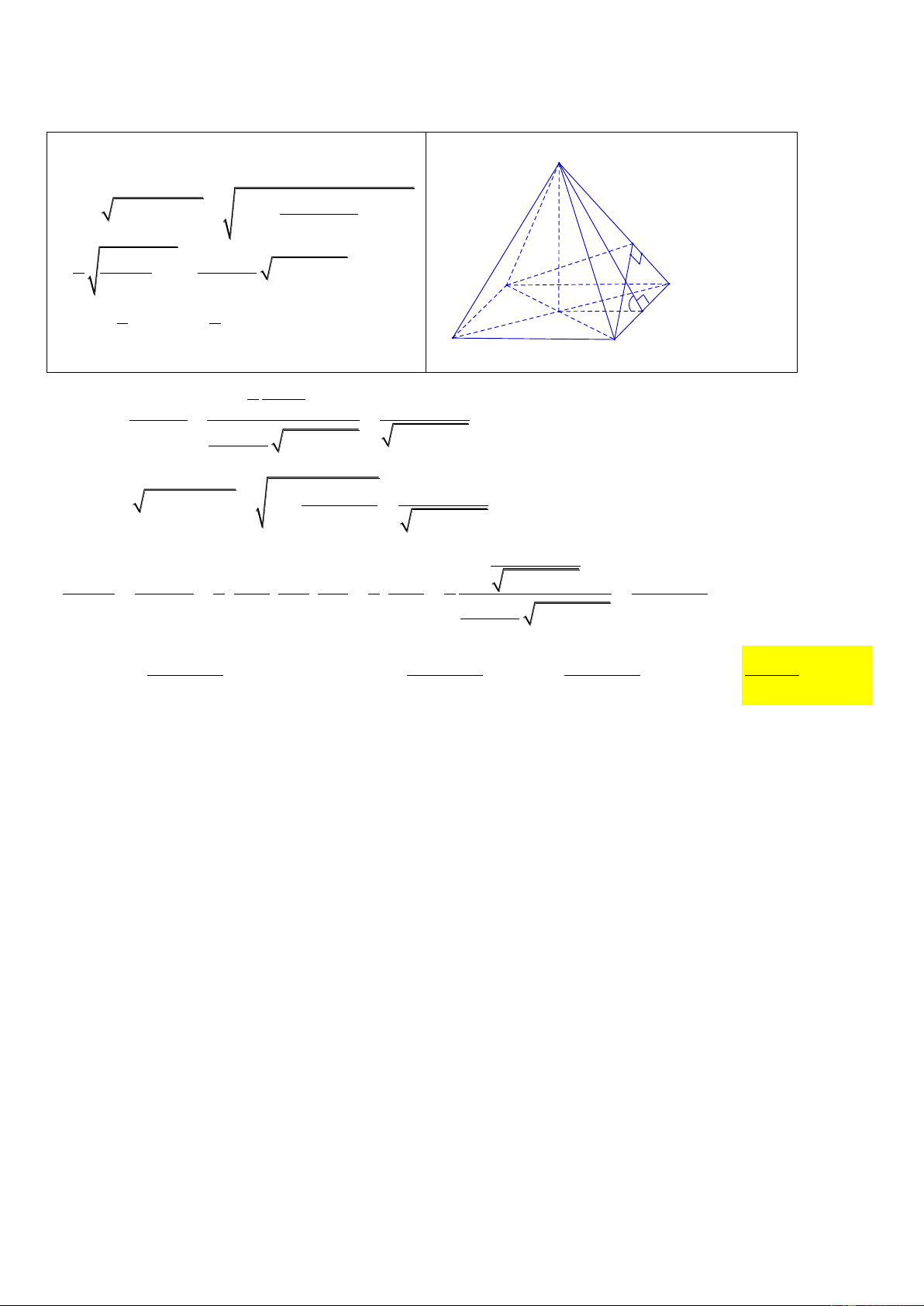
Câu 1. Cho hình chóp tứ giác đều .
S ABCDcó đáy là hình vuông ABCD cạnh a, góc giữa mặt bên và
mặt phẳng đáy là  . Mặt phẳng P qua AC và vuông góc với mặt phẳng SAD chia khối chóp V .
S ABCD thành hai khối đa diện. Tỉ lệ thể tích hai khối đa diện là 1 2  cos  V2 Lời giải: S Ta có: 2 2 2 1 2
SD  SN  ND  ON .  ND 2 cos SNO M a 1 a 2   1  cos   1 Ta có : 2 2 cos  2.cos A D 1 1 S
 CM.SD  SN. N  CD SCD O 2 2 B C a 1 .a SN.CD 2 cos      a CM 2 SD a 2 1   cos cos 1   2.cos 2  2 2 2 a . a cos
 DM  CD CM  a   2 2 1 cos  1 cos  .acos 2 2 V V 1 DM DA DC 1 DM 1    MACD MACD 1 cos cos   . . .  .   2 V 2.V 2 DS DA DC 2 DS 2 a   2 1 cos SABCD SACD 1  cos  2.cos 2 2 cos   cos   1  V V  V  V  V V Vậy MACD 2  cos  MACD SABCD SABCM 1   2 2 SABCD 2 1 cos  1 cos  1   cos SABCD  VSABCM