Một số dạng toán liên quan đến thể tích khối chóp

Tài liệu gồm 50 trang, được biên soạn bởi thầy giáo Lê Bá Bảo, hướng dẫn giải một số dạng toán liên quan đến thể tích khối chóp trong chuyên đề thể tích khối đa diện môn Toán 12..Mời bạn đọc đón xem.

68 34 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Khối đa diện

Môn: Toán 12

Thông tin:

50 trang 8 tháng trước

Tác giả:

Profile Lan Tường
THỂ TÍCH KHỐI ĐA DIỆN
TOÁN 12
LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ
THỂ TÍCH KHỐI CHÓP
LUYỆN THI THPT QUỐC GIA
CẬP NHẬT TỪ ĐỀ THI MỚI NHẤT
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
MỘT SỐ DẠNG TOÁN LIÊN QUAN ĐẾN
THỂ TÍCH KHỐI CHÓP
Dạng 1: Khối chóp có cạnh bên vuông góc với đáy
Phương pháp:
Cho hình chóp
.S ABCD
có
vuông góc với mặt phẳng đáy…
+) Đường cao:
.SA
+) Thể tích khối chóp:
1
.
3
ABCD
V SA S
Form hình vẽ:
D
C
B
A
S
BÀI TẬP TRẮC NGHIỆM MINH HỌA
Câu 1: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
,a SA
vuông góc với đáy. Biết
2,SA a
thể
tích của khối chóp
.S ABC
bằng
A.
3
2
.
12
a
B.
3
2
.
6
a
C.
3
3
.
3
a
D.
3
3
.
6
a
Câu 2: Cho tứ diện
.O ABC
có các cạnh
OA
,
OB
,
OC
đôi một vuông góc với nhau. Biết
2 cmOA
,
3 cmOB
,
6 cmOC
. Tính thể tích của khối tứ diện
.O ABC
.
A.
3
6 cm
. B.
3
36 cm
. C.
3
12 cm
. D.
3
18 cm
.
Câu 3: Cho hnh chóp
.S ABCD
có
SA
vuông góc với mt phng
,ABCD
đáy
ABCD
là hình thang
vuông tại
A
và
B
có
, 3 , .AB a AD a BC a
Biết
3,SA a
tnh thể tch khối chóp
.S BCD
theo
.a
A.
3
2 3 .a
B.
3
3
.
6
a
C.
3
23
.
3
a
D.
3
3
.
4
a
Câu 4: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
,a SA
vuông góc với đáy. Biết diện tích
tam giác
SAB
bằng
2
4,a
thể tích của khối chóp
.S ABC
bằng
A.
3
4 3 .a
B.
3
23
.
3
a
C.
3
3
.
3
a
D.
3
3
.
6
a
Câu 5: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông, cạnh bên
2SA a
và
SA
vuông
góc với mt phng đáy, tam giác
SBD
là tam giác đều. Thể tích của khối chóp
.S ABCD
bằng.
A.
3
22a
. B.
3
2
3
a
. C.
3
2a
. D.
3
22
3
a
.
Câu 6: Cho hình chóp
.S ABCD
có đáy là hnh vuông cạnh bằng
,a SA
vuông góc với đáy. Biết
SB
hợp với mt đáy một góc
o
60 ,
thể tích của khối chóp
.S ABCD
bằng
A.
3
2
.
3
a
B.
3
3
.
3
a
C.
3
2
.
3
a
D.
3
7
.
3
a
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Câu 7: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
,a SA
vuông góc với đáy. Biết
SB
hợp với
mt đáy một góc bằng
0
60 ,
thể tích của khối chóp
.S ABC
bằng
A.
3
2
.
12
a
B.
C.
3
3
.
3
a
D.
3
3
.
6
a
Câu 8: Cho khối chóp
.S ABCD
có đáy là hnh vuông cạnh
a
,
SA
vuông góc với đáy và khoảng
cách từ
A
đến mt phng
SBC
bằng
2
2
a
. Tính thể tích
V
của khối chóp đã cho.
A.
3
3
a
V
. B.
3
2
a
V
. C.
3
3
9
a
V
. D.
3
Va
.
Câu 9: Tính thể tích khối chóp
.S ABC
có
AB a
,
2AC a
,
120BAC 
,
SA ABC
, góc giữa
SBC
và
ABC
là
60
.
A.
3
21
14
a
. B.
3
7
14
a
. C.
3
3 21
14
a
. D.
3
7
7
a
.
Câu 10: Cho hình chóp
.S ABC
có đáy là tam giác vuông tại
, , 2 ,B AB a BC a SA
vuông góc với đáy.
Biết
SB
hợp với mt đáy một góc
0
60 ,
thể tích của khối chóp
.S ABC
bằng
A.
3
2
.
12
a
B.
C.
3
2
.
3
a
D.
3
3
.
3
a
Câu 11: Cho hình chóp
.S ABC
có đáy là tam giác vuông tại
, , 2 ,B AB a BC a SA
vuông góc với đáy.
Biết
SBC
hợp với mt đáy một góc
0
60 ,
thể tích của khối chóp
.S ABC
bằng
A.
3
15
.
3
a
B.
3
5
.
2
a
C.
3
2
.
3
a
D.
3
3
.
3
a
Câu 12: Cho hình chóp
.S ABCD
có đáy là hnh vuông cạnh bằng
,a SA
vuông góc với đáy. Biết
SBD
hợp với mt đáy một góc
0
60 ,
thể tích của khối chóp
.S ABCD
bằng
A.
3
6
.
3
a
B.
3
3
.
3
a
C.
3
2
.
3
a
D.
3
6
.
6
a
Câu 13: Cho hình chóp
.S ABC
có đáy là tam giác vuông tại
, , 2 ,B AB a BC a SA
vuông góc với đáy.
Biết
SC
hợp với
SAB
một góc
0
30 ,
thể tích của khối chóp
.S ABC
bằng
A.
3
15
.
3
a
B.
3
5
.
2
a
C.
3
11
.
3
a
D.
3
3
.
3
a
Câu 14: Cho hình chóp
.S ABCD
có đáy là hnh chữ nhật có
, 2 ,AB a BC a SA
vuông góc với đáy.
Biết
SBD
hợp với mt đáy một góc
o
60 ,
thể tích của khối chóp
.S ABCD
bằng
A.
3
2
.
5
a
B.
3
4 15
.
15
a
C.
3
2 15
.
3
a
D.
3
43
.
9
a
Câu 15: Cho hình chóp
.S ABCD
có đáy là hnh thoi cạnh bằng
o
, 60 ,a ABC SA
vuông góc với đáy.
Biết
2,SA a
thể tích của khối chóp
.S ABCD
bằng
A.
3
3
.
3
a
B.
3
6
.
6
a
C.
3
3
.
12
a
D.
3
3
.
4
a
Câu 16: Cho hình chóp
.S ABCD
có đáy là hnh thoi cạnh bằng
o
, 60 ,a ABC SA
vuông góc với đáy.
Biết
SB
hợp với đáy một góc
o
60 ,
thể tích của khối chóp
.S ABCD
bằng
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
A.
3
3
.
3
a
B.
3
6
.
6
a
C.
3
3
.
12
a
D.
Câu 17: Cho hình chóp
.S ABCD
có đáy là hnh thang vuông tại
,,AB
2 , ,AD a AB BC a SA
vuông góc với đáy. Biết
2,SC a
thể tích của khối chóp
.S ABCD
bằng
A.
3
3
.
2
a
B.
3
2
.
2
a
C.
3
6
.
2
a
D.
3
3
.
4
a
Câu 18: Cho hình chóp
.S ABCD
có đáy là hnh thang vuông tại
,,AB
2 , ,AD a AB BC a SA
vuông góc với đáy. Biết
SC
hợp với mt đáy một góc
0
60 ,
thể tích của khối chóp
.S ABCD
bằng
A.
3
3
.
2
a
B.
3
2
.
2
a
C.
3
6
.
2
a
D.
3
3
.
4
a
Câu 19: Cho hnh chóp
.S AB CD
có đáy
ABCD
là hnh vuông cạnh
a
, cạnh bên
SA
vuông góc với mt
phng đáy. Gi
M
là trung điểm của
CD
. Biết khoảng cách giữa hai đường thng
BC
và
SM
bằng
3
4
a
. Tnh thể tch của khối chóp đã cho theo
a
.
A.
3
3
4
a
B.
3
3
2
a
C.
3
3
6
a
D.
3
3
12
a
BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN
Câu 20: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
,a SA
vuông góc với đáy. Biết
2,SB a
thể
tích của khối chóp
.S ABC
bằng
A.
3
2
.
12
a
B.
C.
3
3
.
3
a
D.
3
3
.
6
a
Câu 21: Cho hình chóp
.S ABCD
có đáy là hnh vuông cạnh bằng
,a SA
vuông góc với đáy. Biết
2,SA a
thể tích của khối chóp
.S ABCD
bằng
A.
3
2
.
12
a
B.
C.
3
2
.
3
a
D.
3
.a
Câu 22: Cho hình chóp
.S ABCD
có đáy là hnh vuông cạnh bằng
,a SA
vuông góc với đáy. Biết
3,SC a
thể tích của khối chóp
.S ABCD
bằng
A.
3
2
.
3
a
B.
3
3
.
3
a
C.
3
2
.
3
a
D.
3
7
.
3
a
Câu 23: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
,a SA
vuông góc với đáy. Biết
SBC
hợp
với mt đáy một góc bằng
0
30 ,
thể tích của khối chóp
.S ABC
bằng
A.
3
2
.
12
a
B.
3
3
.
8
a
C.
3
3
.
24
a
D.
3
3
.
6
a
Câu 24: Cho hình chóp
.S ABCD
có đáy là hnh thang vuông ở
A
và
B
,
3AB a
,
22AD BC a
. SA vuông góc với đáy, mt phng
SCD
tạo với đáy một góc
45
. Thể
tích khối chóp
.S ABC
bằng
A.
3
3
2
a
. B.
3
3 10
10
a
. C.
3
8
10
a
. D.
3
43
3
a
Câu 25: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
,a SA
vuông góc với đáy. Biết
SC
hợp với
mt phng
SAB
một góc bằng
30 ,
thể tích của khối chóp
.S ABC
bằng
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
A.
3
6
.
12
a
B.
C.
3
3
.
3
a
D.
3
3
.
6
a
Câu 26: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật tâm
O
,
,AB a
3,AD a
SA ABCD
. Khoảng cách từ
O
đến mt phng
SCD
bằng
3
4
a
. Tính thể
tích
V
của khối chóp
.S ABCD
.
A.
3
15
10
a
V
. B.
3
3Va
. C.
3
3
3
a
V
. D.
3
3
6
a
V
.
Câu 27: Cho hình chóp
.S ABCD
có đáy là hnh vuông cạnh bằng
,a SA
vuông góc với đáy. Biết
SC
hợp với mt đáy một góc
45 ,
thể tích của khối chóp
.S ABCD
bằng
A.
3
2
.
3
a
B.
3
3
.
3
a
C.
3
2
.
3
a
D.
3
7
.
3
a
Câu 28: Cho hình chóp
.S ABCD
có đáy là hnh vuông cạnh bằng
,a SA
vuông góc với đáy. Biết
SBC
hợp với mt đáy một góc
60 ,
thể tích của khối chóp
.S ABCD
bằng
A.
3
2
.
3
a
B.
3
3
.
3
a
C.
3
2
.
3
a
D.
3
7
.
3
a
Câu 29: Cho hình chóp
.S ABC
có đáy là tam giác vuông tại
, , 2 ,B AB a BC a SA
vuông góc với đáy.
Biết
3,SA a
thể tích của khối chóp
.S ABC
bằng
A.
3
2
.
12
a
B.
C.
3
3
.
3
a
D.
3
.a
Câu 30: Cho hình chóp
.S ABCD
có đáy là hnh vuông cạnh bằng
,a SA
vuông góc với đáy. Biết
SC
hợp với
SAB
một góc
30 ,
thể tích của khối chóp
.S ABCD
bằng
A.
3
6
.
3
a
B.
3
3
.
3
a
C.
3
2
.
3
a
D.
3
6
.
6
a
Câu 31: Cho hình chóp
.S ABCD
có đáy là hnh chữ nhật có
, 2 ,AB a BC a SA
vuông góc với đáy.
Biết
3,SA a
thể tích của khối chóp
.S ABCD
bằng
A.
3
2.a
B.
3
25
.
3
a
C.
3
2 15
.
3
a
D.
3
43
.
9
a
Câu 32: Cho hình chóp
.S ABCD
có đáy là hnh chữ nhật có
, 2 ,AB a BC a SA
vuông góc với đáy.
Biết
3,SD a
thể tích của khối chóp
.S ABCD
bằng
A.
3
2.a
B.
3
25
.
3
a
C.
3
2 15
.
3
a
D.
3
43
.
9
a
Câu 33: Cho hình chóp
.S ABCD
có đáy là hnh chữ nhật có
, 2 ,AB a BC a SA
vuông góc với đáy.
Biết
SC
hợp với mt đáy một góc
60 ,
thể tích của khối chóp
.S ABCD
bằng
A.
3
2.a
B.
3
25
.
3
a
C.
3
2 15
.
3
a
D.
3
43
.
9
a
Câu 34: Cho hình chóp
.S ABC
có đáy là tam giác vuông tại
, , 2 ,B AB a BC a SA
vuông góc với đáy.
Biết
SC
hợp với mt đáy một góc
60 ,
thể tích của khối chóp
.S ABC
bằng
A.
3
15
.
3
a
B.
3
5
.
2
a
C.
3
2
.
3
a
D.
3
3
.
3
a
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Câu 35: Cho hình chóp
.S ABCD
có đáy là hnh chữ nhật có
, 2 ,AB a BC a SA
vuông góc với đáy.
Biết
SCD
hợp với mt đáy một góc
30 ,
thể tích của khối chóp
.S ABCD
bằng
A.
3
2.a
B.
3
25
.
3
a
C.
3
2 15
.
3
a
D.
3
43
.
9
a
Câu 36: Cho hình chóp
.S ABCD
có đáy là hnh chữ nhật có
, 2 ,AB a BC a SA
vuông góc với đáy.
Biết
SC
hợp với
SAB
một góc
30 ,
thể tích của khối chóp
.S ABCD
bằng
A.
3
2 11
.
3
a
B.
3
25
.
3
a
C.
3
2 15
.
3
a
D.
3
43
.
9
a
Câu 37: Cho hình chóp
.S ABCD
có đáy là hnh thoi cạnh bằng
, 60 ,a ABC SA
vuông góc với đáy.
Biết
SC
hợp với đáy một góc
60 ,
thể tích của khối chóp
.S ABCD
bằng
A.
3
3
.
3
a
B.
3
6
.
6
a
C.
3
3
.
12
a
D.
Câu 38: Cho hình chóp
.S ABCD
có đáy là hnh thoi cạnh bằng
, 60 ,a ABC SA
vuông góc với đáy.
Biết
SBC
hợp với đáy một góc
30 ,
thể tích của khối chóp
.S ABCD
bằng
A.
3
3
.
3
a
B.
3
6
.
6
a
C.
3
3
.
12
a
D.
Câu 39: Cho hình chóp
.S ABCD
có đáy là hnh thang vuông tại
,,AB
2 , ,AD a AB BC a SA
vuông
góc với đáy. Biết
2,SB a
thể tích của khối chóp
.S ABCD
bằng
A.
3
3
.
2
a
B.
3
2
.
2
a
C.
3
6
.
2
a
D.
3
3
.
4
a
Dạng 2: Khối chóp có mặt bên là tam giác cân tại S và vuông góc với đáy
Phương pháp:
Cho hình chóp
.S ABCD
có mặt bên
SAB
là tam giác cân tại
S
và nằm trong mặt phẳng vuông góc với
mặt phẳng đáy…
+) Đường cao:
,SH H
là trung điểm
.AB
+) Thể tích khối chóp:
1
.
3
ABCD
V SH S
Form hình vẽ:
S
A
B
C
D
H
BÀI TẬP TRẮC NGHIỆM MINH HỌA
Câu 40: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
.a
Biết mt bên
SAB
là tam giác đều và
nằm trong mt phng vuông góc với đáy, thể tích của khối chóp
.S ABC
bằng
A.
B.
3
3
.
24
a
C.
D.
3
15
.
6
a
Câu 41: Cho hình chóp
.S ABCD
có đáy là hnh vuông cạnh
.a
Biết mt bên
SAB
là tam giác vuông
cân tại
S
và nằm trong mt phng vuông góc với đáy, thể tích của khối chóp
.S ABCD
bằng
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
A.
B.
3
3
.
24
a
C.
3
3
.
6
a
D.
Câu 42: Cho hình chóp
.S ABC
có mt phng
SAC
vuông góc với mt phng
ABC
,
SAB
là
tam giác đều cạnh
3a
,
3BC a
đường thng
SC
tạo với mt phng
ABC
góc
60
.
Thể tích của khối chóp
.S ABC
bằng
A.
3
3
3
a
. B.
3
6
2
a
. C.
3
6
6
a
. D.
3
26a
.
BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN
Câu 43: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
.a
Biết mt bên
SAB
là tam giác vuông
cân tại
S
và nằm trong mt phng vuông góc với đáy, thể tích của khối chóp
.S ABC
bằng
A.
B.
3
3
.
24
a
C.
D.
3
15
.
6
a
Câu 44: Cho hình chóp
.S ABCD
có đáy là hnh vuông cạnh
.a
Biết mt bên
SAB
là tam giác đều và
nằm trong mt phng vuông góc với đáy, thể tích của khối chóp
.S ABCD
bằng
A.
B.
3
3
.
24
a
C.
3
3
.
6
a
D.
3
15
.
6
a
Câu 45: Cho hình chóp
.S ABCD
với
ABCD
là hình vuông cạnh
a
. Mt bên
SAB
là tam giác cân tại
S
và
nằm trên mt phng vuông góc với mt phng đáy. Cạnh bên
SC
tạo với đáy một góc
60
. Tính
thể tích khối chóp
.S ABCD
.
A.
3
15
2
a
. B.
3
15
6
a
. C.
3
6
3
a
. D.
3
3
6
a
.
Dạng 3: Khối chóp có hình chiếu của S trên mặt đáy là điểm H
Phương pháp:
Cho hình chóp
.S ABC
có điểm H là hình chiếu vuông góc của S trên mặt đáy…
+) Đường cao:
.SH
+) Thể tích khối chóp:
1
.
3
ABC
V SH S
Form hình vẽ:
H
S
A
B
C
BÀI TẬP TRẮC NGHIỆM MINH HỌA
Câu 46: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
.a
Biết hình chiếu vuông góc của
S
trên
mt đáy là trung điểm của
AB
và
2,SB a
thể tích của khối chóp
.S ABC
bằng
A.
3
5
.
8
a
B.
C.
3
3
.
8
a
D.
3
3
.
48
a
Câu 47: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
.a
Biết hình chiếu vuông góc của
S
trên
mt đáy là trung điểm của
AB
và
0
; 60 ,SC ABC
thể tích của khối chóp
.S ABC
bằng
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
A.
3
5
.
8
a
B.
C.
3
3
.
8
a
D.
3
3
.
48
a
Câu 48: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
.a
Biết hình chiếu vuông góc của
S
trên
mt đáy là trung điểm của
AB
và
0
; 30 ,SBC ABC
thể tích của khối chóp
.S ABC
bằng
A.
3
5
.
8
a
B.
C.
3
3
.
8
a
D.
3
3
.
48
a
Câu 49: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
.a
Biết hình chiếu vuông góc của
S
trên
mt đáy là điểm
H
trên cạnh
,2AB AH HB
và
0
; 30 ,SC ABC
thể tích của khối chóp
.S ABC
bằng
A.
3
3
.
24
a
B.
3
7
.
36
a
C.
3
.
12
a
D.
3
6
.
6
a
Câu 50: Cho hình chóp
.S ABCD
có đáy là hnh vuông cạnh
.a
Biết hình chiếu vuông góc của
S
trên
mt đáy là điểm
H
trên cạnh
,2AB BH HA
và
0
; 60 ,SD ABCD
thể tích của khối chóp
.S ABCD
bằng
A.
3
23
.
9
a
B.
3
30
.
9
a
C.
3
42
.
27
a
D.
3
3
.
3
a
Câu 51: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
.a
Biết hình chiếu vuông góc của
S
trên
mt đáy là điểm
H
trên cạnh
,2AB BH HA
và
0
; 60 ,SBD ABCD
thể tích của khối chóp
.S ABCD
bằng
A.
3
23
.
9
a
B.
3
30
.
9
a
C.
3
42
.
27
a
D.
3
6
.
9
a
BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN
Câu 52: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
.a
Biết hình chiếu vuông góc của
S
trên
mt đáy là trung điểm của
AB
và
; 60 ,SB ABC 
thể tích của khối chóp
.S ABC
bằng
A.
3
5
.
8
a
B.
C.
3
3
.
8
a
D.
3
3
.
48
a
Câu 53: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
.a
Biết hình chiếu vuông góc của
S
trên
mt đáy là điểm
H
trên cạnh
,2AB AH HB
và
2,SA a
thể tích của khối chóp
.S ABC
bằng
A.
3
3
.
24
a
B.
3
7
.
36
a
C.
3
6
.
9
a
D.
3
6
.
6
a
Câu 54: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
.a
Biết hình chiếu vuông góc của
S
trên
mt đáy là điểm
H
trên cạnh
,2AB AH HB
và
; 60 ,SB ABC 
thể tích của khối chóp
.S ABC
bằng
A.
3
3
.
24
a
B.
3
7
.
36
a
C.
3
.
12
a
D.
3
6
.
6
a
Câu 55: Cho hình chóp
.S ABCD
có đáy là hnh vuông cạnh
.a
Biết hình chiếu vuông góc của
S
trên
mt đáy là điểm
H
trên cạnh
,2AB BH HA
và
; 60 ,SB ABCD 
thể tích của khối chóp
.S ABCD
bằng
A.
3
23
.
9
a
B.
3
30
.
9
a
C.
3
42
.
27
a
D.
3
3
.
3
a
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Câu 56: Cho hình chóp
.S ABCD
có đáy là hnh vuông cạnh
.a
Biết hình chiếu vuông góc của
S
trên
mt đáy là điểm
H
trên cạnh
,2AB BH HA
và
; 30 ,SC ABCD 
thể tích của khối chóp
.S ABCD
bằng
A.
3
23
.
9
a
B.
3
30
.
9
a
C.
3
42
.
27
a
D.
3
39
.
27
a
Câu 57: Cho hình chóp
.S ABCD
có đáy là hnh vuông cạnh
.a
Biết hình chiếu vuông góc của
S
trên
mt đáy là điểm
H
trên cạnh
,2AB BH HA
và
; 60 ,SCD ABCD 
thể tích của khối chóp
.S ABCD
bằng
A.
3
23
.
9
a
B.
3
30
.
9
a
C.
3
42
.
27
a
D.
3
3
.
3
a
Dạng 4: Khối chóp có hai mặt bên cùng vuông góc với mặt đáy
Phương pháp:
Cho hình chóp
.S ABCD
có hai mặt
SAB
và
SBC
cùng vuông góc với mặt phẳng đáy…
+) Đường cao:
+) Thể tích khối chóp:
1
.
3
ABCD
V SBS
Form hình vẽ:
D
C
B
A
S
BÀI TẬP TRẮC NGHIỆM MINH HỌA
Câu 58: Cho hình chóp
.S A BC
là tam giác vuông tại
A
,
30ABC
,
BC a
. Hai mt bên
SAB
và
SAC
cùng vuông góc với đáy
ABC
, mt bên
SBC
tạo với đáy một góc
45
. Thể tích
của khối chóp
.S A BC
bằng
A.
3
64
a
. B.
3
16
a
. C.
3
9
a
. D.
3
32
a
.
Câu 59: Cho hình chóp
.S ABCD
, đáy
ABCD
là hình vuông cạnh
2a
. Hai mt phng
SAB
,
SAD
cùng vuông góc với đáy, góc giữa hai mt phng
SBC
và
ABC D
bằng
30
. Tính tỉ số
3
3V
a
biết
V
là thể tích của khối chóp
.S ABCD
.
A.
3
12
. B.
3
2
. C.
. D.
83
3
.
Câu 60: Cho hnh chóp
.S ABCD
có đáy
ABCD
là hnh vuông cạnh
a
, hai mt phng
SAB
và
SAD
cùng vuông góc với mt phng
ABC D
; góc giữa đường thng
SC
và mt phng
ABC D
bằng
60
. Tính theo
a
thể tch khối chóp
.S ABCD
.
A.
3
3a
. B.
3
6
9
a
. C.
3
6
3
a
. D.
3
32a
.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN
Câu 61: Cho khối chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
và hai mt bên
SAB
,
SAC
cng vuông góc với đáy. Tnh thể tch khối chóp
.S ABC
biết
3SC a
.
A.
3
a3
2
. B.
3
a3
4
. C.
3
2a 6
9
. D.
3
a6
12
.
Câu 62: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, hai mt phng
SAC
và
SAB
cùng vuông góc với
ABCD
. Góc giữa
SCD
và
ABCD
là
60
. Thể tích khối
chóp
.S ABCD
bằng
A.
3
6
3
a
. B.
3
3
3
a
. C.
3
3
6
a
. D.
3
6
6
a
.
Câu 63: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật. Hai mt phng
SAB
và
SAC
cùng vuông góc với mt phng
ABC D
. Biết rằng
AB a
,
3AD a
và
7SC a
. Tính thể
tích khối chóp
.S ABCD
.
A.
3
Va
. B.
3
2Va
. C.
3
3Va
. D.
3
4Va
Dạng 5: Khối chóp đều
Phương pháp:
Cho hình chóp tam giác đều
.S ABC
…
+) Đường cao:
,SG G
là trng tâm
.ABC
+) Thể tích khối chóp:
1
.
3
ABC
V SG S
C
B
A
S
G
M
Cho hình chóp tứ giác đều
.S ABCD
…
+) Đường cao:
,SO O
là tâm hình vuông
.ABCD
+) Thể tích khối chóp:
1
.
3
ABCD
V SO S
O
D
C
B
A
S
Đặc biệt:
+) Thể tích khối tứ diện đều cạnh bằng
t
là
3
2
12
t
V
+) Thể tích khối chóp tứ giác đều có tất cả các cạnh bằng
t
là
3
2
6
t
V
+) Thể tích khối bát diện đều cạnh bằng
t
là
3
2
3
t
V
BÀI TẬP TRẮC NGHIỆM MINH HỌA
Câu 64: Cho tứ diện đều
ABCD
có cạnh bằng
.t
Thể tích của khối tứ diện
ABCD
bằng
A.
3
2
.
12
t
B.
3
2
.
6
t
C.
3
2
.
3
t
D.
3
3
.
6
t
Câu 65: Cho hnh chóp tam giác đều
.S ABC
có cạnh đáy bằng
.a
Biết
2,SA a
thể tích của khối chóp
.S ABC
bằng
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
A.
3
3
.
12
a
B.
3
2
.
2
a
C.
3
11
.
12
a
D.
3
3
.
72
a
Câu 66: Cho hnh chóp tam giác đều
.S ABC
có cạnh đáy bằng
.a
Biết
SBC
hợp với đáy một góc
30 ,
thể tích của khối chóp
.S ABC
bằng
A.
3
3
.
12
a
B.
3
2
.
2
a
C.
3
11
.
12
a
D.
3
3
.
72
a
Câu 67: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
.a
Biết
hợp với mt đáy một góc
60 ,
thể tích của khối chóp
.S ABCD
bằng
A.
3
3
.
18
a
B.
3
6
.
6
a
C.
3
14
.
6
a
D.
3
15
.
6
a
Câu 68: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
.a
Biết
SBC
hợp với mt đáy một góc
30 ,
thể tích của khối chóp
.S ABCD
bằng
A.
3
3
.
18
a
B.
3
6
.
6
a
C.
3
14
.
6
a
D.
3
15
.
6
a
BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN
Câu 69: Cho hnh chóp tam giác đều
.S ABC
có cạnh đáy bằng
.a
Biết
hợp với đáy một góc
60 ,
thể tích của khối chóp
.S ABC
bằng
A.
3
3
.
12
a
B.
3
2
.
2
a
C.
3
11
.
12
a
D.
3
3
.
72
a
Câu 70: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
.a
Biết
2,SA a
thể tích của khối chóp
.S ABCD
bằng
A.
3
3
.
18
a
B.
3
6
.
6
a
C.
3
14
.
6
a
D.
3
15
.
6
a
Câu 71: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
.a
Biết diện tích một mt bên của hình
chóp đó có diện tích bằng
2
,a
thể tích của khối chóp
.S ABCD
bằng
A.
3
3
.
18
a
B.
3
6
.
6
a
C.
3
14
.
6
a
D.
3
15
.
6
a
_____________________HẾT_____________________
Huế, 10h20’ Ngày 18 tháng 5 năm 2022
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
LỜI GIẢI CHI TIẾT
Câu 1: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
,a SA
vuông góc với đáy. Biết
2,SA a
thể
tích của khối chóp
.S ABC
bằng
A.
3
2
.
12
a
B.
3
2
.
6
a
C.
3
3
.
3
a
D.
3
3
.
6
a
Lời giải:
S
C
B
A
Ta có:
2
3
.
4
ABC
a
S
Vậy
23
.
1 1 3 3
. .2 . .
3 3 4 6
S ABC ABC
aa
V SA S a
Chọn đáp án D.
Câu 2: Cho tứ diện
.O ABC
có các cạnh
OA
,
OB
,
OC
đôi một vuông góc với nhau. Biết
2 cmOA
,
3 cmOB
,
6 cmOC
. Tính thể tích của khối tứ diện
.O ABC
.
A.
3
6 cm
. B.
3
36 cm
. C.
3
12 cm
. D.
3
18 cm
.
Lời giải:
Ta có:
OA OB
OA OBC
OA OC

.
Do đó
.
1 1 1
. . . . . .2.3.6 6
3 6 6
O ABC OBC
V OAS OAOB OC
3
cm
.
Chọn đáp án A.
Câu 3: Cho hnh chóp
.S ABCD
có
SA
vuông góc với mt phng
,ABCD
đáy
ABCD
là hnh thang
vuông tại
A
và
B
có
, 3 , .AB a AD a BC a
Biết
3,SA a
tnh thể tch khối chóp
.S BCD
theo
.a
A.
3
2 3 .a
B.
3
3
.
6
a
C.
3
23
.
3
a
D.
3
3
.
4
a
Lời giải:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Ta có
.
1
..
3
S BCD BCD
V SAS
Lại có
BCD ABCD ABD
S S S
11
..
22
AB AD BC AB AD
2
11
..
22
AB BC a
Mà
23
.
13
3 3. .
3 2 6
S BCD
aa
SA a V a
Chọn đáp án B.
Câu 4: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
,a SA
vuông góc với đáy. Biết diện tích
tam giác
SAB
bằng
2
4,a
thể tích của khối chóp
.S ABC
bằng
A.
3
4 3 .a
B.
3
23
.
3
a
C.
3
3
.
3
a
D.
3
3
.
6
a
Lời giải:
S
C
B
A
Ta có:
2
3
.
4
ABC
a
S
Xét tam giác
SAB
vuông tại
2
1
: . 4 8 .
2
SAB
A S SA AB a SA a
Vậy
23
.
1 1 3 2 3
. .8 . .
3 3 4 3
S ABC ABC
aa
V SA S a
Chọn đáp án B.
Câu 5: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông, cạnh bên
2SA a
và
SA
vuông
góc với mt phng đáy, tam giác
SBD
là tam giác đều. Thể tích của khối chóp
.S ABCD
bằng.
A.
3
22a
. B.
3
2
3
a
. C.
3
2a
. D.
3
22
3
a
.
Lời giải:
S
A
B
C
D
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
.
Đt
AB x
,
ABD
vuông cân tại
2A BD x
.
Do
SBD
là tam giác đều nên
2SB SD BD x
.
Lại có
SAB
vuông tại
A
.
22
2 2 2 2
22SA AB SB a x x
22
22x a x a
.
3
2
.
1 1 2 2
. . . 2. 2
3 3 3
S ABCD ABCD
a
V SAS a a
.
Chọn đáp án D.
Câu 6: Cho hình chóp
.S ABCD
có đáy là hnh vuông cạnh bằng
,a SA
vuông góc với đáy. Biết
SB
hợp với mt đáy một góc
o
60 ,
thể tích của khối chóp
.S ABCD
bằng
A.
3
2
.
3
a
B.
3
3
.
3
a
C.
3
2
.
3
a
D.
3
7
.
3
a
Lời giải:
S
A
B
C
D
Ta có:
2
.
ABCD
Sa
Do
SA ABCD
nên
AB
là hình chiếu vuông góc của
SB
trên
.ABCD
Suy ra:
o
; ; 60 .SB ABCD SB AB SBA SBA
Xét tam giác
SAB
vuông tại
: tan 3.
SA
A SBA SA a
AB
Vậy
3
2
.
1 1 3
. . 3 . .
3 3 3
S ABCD ABCD
a
V SA S a a
Chọn đáp án B.
Câu 7: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
,a SA
vuông góc với đáy. Biết
SB
hợp với
mt đáy một góc bằng
0
60 ,
thể tích của khối chóp
.S ABC
bằng
A.
3
2
.
12
a
B.
C.
3
3
.
3
a
D.
3
3
.
6
a
Lời giải:
A
S
B
D
C
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
S
C
B
A
Ta có:
2
3
.
4
ABC
a
S
Do
SA ABC
nên
AB
là hình chiếu vuông góc của
SB
trên
.ABC
Suy ra:
; ; .SB ABC SB AB SBA
Xét tam giác
SAB
vuông tại
: tan .tan 3.
SA
A SBA SA AB SBA a
AB
Vậy
23
.
1 1 3
. . 3. .
3 3 4 4
S ABC ABC
aa
V SA S a
Chọn đáp án B.
Câu 8: Cho khối chóp
.S ABCD
có đáy là hnh vuông cạnh
a
,
SA
vuông góc với đáy và khoảng
cách từ
A
đến mt phng
SBC
bằng
2
2
a
. Tính thể tích
V
của khối chóp đã cho.
A.
3
3
a
V
. B.
3
2
a
V
. C.
3
3
9
a
V
. D.
3
Va
.
Lời giải:
H
D
C
B
A
S
Kẻ
AH
vuông góc
SB
.
Ta có
()AH SBC
nên
AH
chính là khoảng cách từ
A
đến mp
SBC
.
Ta có
2 2 2 2 2 2 2
1 1 1 1 1 1 1
AH SA AB SA AH AB a
.
Suy ra
SA a
. Thể tích cần tính là
3
1
..
33

a
V a a a
.
Chọn đáp án A.
Câu 9: Tính thể tích khối chóp
.S ABC
có
AB a
,
2A C a
,
120BAC 
,
SA ABC
, góc giữa
SBC
và
ABC
là
60
.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
A.
3
21
14
a
. B.
3
7
14
a
. C.
3
3 21
14
a
. D.
3
7
7
a
.
Lời giải:
60
o
120
o
2a
a
A
C
B
S
H
+ Diện tch đáy
1
. .sin120
2
ABC
S AB AC
13
. .2 .
22
aa
2
3
2
a
+ Tính chiều cao
SA
:
Dựng
AH BC
(với
H BC
) suy ra
SH BC
, do đó góc
, 60SBC ABC SHA
, suy
ra
.tan60SA AH
Tính
AH
: ta có diện tích
1
.
2
ABC
S AH BC
2.
ABC
S
AH
BC

mà theo định lý hàm côsin thì
2 2 2
2. . .cosBC AB AC AB AC A
22
1
4 2. .2 .
2
a a a a



2
7a
7.BC a
Suy ra
2
3
2.
21
2
7
7
a
AH a
a

.
+ Thể tích khối chóp
.S ABC
là
1
.
3
ABC
V S SA
2
1 3 21
..
3 2 7
aa
3
7
.
14
a
Chọn đáp án B.
Câu 10: Cho hình chóp
.S ABC
có đáy là tam giác vuông tại
, , 2 ,B AB a BC a SA
vuông góc với đáy.
Biết
SB
hợp với mt đáy một góc
0
60 ,
thể tích của khối chóp
.S ABC
bằng
A.
3
2
.
12
a
B.
C.
3
2
.
3
a
D.
3
3
.
3
a
Lời giải:
S
C
B
A
Ta có:
2
1
..
2
ABC
S AB BC a
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Do
SA ABC
nên
AB
là hình chiếu vuông góc của
SB
trên
.ABC
Suy ra:
0
; ; 60 .SB ABC SB AB SBA SBA
Xét tam giác
SAB
vuông tại
: tan .tan 3.
SA
A SBA SA AB SBA a
AB
Vậy
3
2
.
1 1 3
. . 3. .
3 3 3
S ABC ABC
a
V SA S a a
Chọn đáp án D.
Câu 11: Cho hình chóp
.S ABC
có đáy là tam giác vuông tại
, , 2 ,B AB a BC a SA
vuông góc với đáy.
Biết
SBC
hợp với mt đáy một góc
0
60 ,
thể tích của khối chóp
.S ABC
bằng
A.
3
15
.
3
a
B.
3
5
.
2
a
C.
3
2
.
3
a
D.
3
3
.
3
a
Lời giải:
S
C
B
A
Ta có:
2
1
..
2
ABC
S AB BC a
Ta có:
.
BC AB
BC SAB BC SB
BC SA
Suy ra:
0
; 60 .SBC ABC SBA SBA
Xét tam giác
SAB
vuông tại
: tan .tan 3.
SA
A SBA SA AB SBA a
AB
Vậy
3
2
.
1 1 3
. . 3. .
3 3 3
S ABC ABC
a
V SA S a a
Chọn đáp án D.
Câu 12: Cho hình chóp
.S ABCD
có đáy là hnh vuông cạnh bằng
,a SA
vuông góc với đáy. Biết
SBD
hợp với mt đáy một góc
0
60 ,
thể tích của khối chóp
.S ABCD
bằng
A.
3
6
.
3
a
B.
3
3
.
3
a
C.
3
2
.
3
a
D.
3
6
.
6
a
Lời giải:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
O
S
A
B
C
D
Ta có:
2
.
ABCD
Sa
Gi
O
là tâm hình vuông
.ABCD
Ta có:
.
BD AO
BD SAO BD SO
BD SA
Suy ra:
0
; 60 .SBD ABCD SOA SOA
Xét tam giác
SAO
vuông tại
o
26
: tan .tan60 .
22
SA a a
A SOA SA
AO
Vậy
3
2
.
1 1 6 6
. . . .
3 3 2 6
S ABCD ABCD
aa
V SA S a
Chọn đáp án D.
Câu 13: Cho hình chóp
.S ABC
có đáy là tam giác vuông tại
, , 2 ,B AB a BC a SA
vuông góc với đáy.
Biết
SC
hợp với
SAB
một góc
0
30 ,
thể tích của khối chóp
.S ABC
bằng
A.
3
15
.
3
a
B.
3
5
.
2
a
C.
3
11
.
3
a
D.
3
3
.
3
a
Lời giải:
S
C
B
A
Ta có:
2
1
..
2
ABC
S AB BC a
Ta có:
BC AB
BC SAB SB
BC SA
là hình chiếu vuông góc của
SC
trên
.SAB
Suy ra:
0
; ; 30 .SC SAB SC SB BSC BSC
Xét tam giác
SBC
vuông tại
: sin 4 .
sin
BC BC
B BSC SC a
SC
BSC
Xét tam giác
ABC
vuông tại
2 2 2 2
: 5 .B AC AB BC a
Xét tam giác
SAC
vuông tại
22
: 11.A SA SC AC a
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Vậy
3
2
.
1 1 11
. . 11. .
3 3 3
S ABC ABC
a
V SA S a a
Chọn đáp án C.
Câu 14: Cho hình chóp
.S ABCD
có đáy là hnh chữ nhật có
, 2 ,AB a BC a SA
vuông góc với đáy.
Biết
SBD
hợp với mt đáy một góc
o
60 ,
thể tích của khối chóp
.S ABCD
bằng
A.
3
2
.
5
a
B.
3
4 15
.
15
a
C.
3
2 15
.
3
a
D.
3
43
.
9
a
Lời giải:
H
S
A
B
C
D
Ta có:
2
. 2 .
ABCD
S AB BC a
Dựng
.AH BD
Ta có:
.
BD AH
BD SAH BD SH
BD SA
Suy ra:
;.SBD ABCD SHA
Xét tam giác
BAD
vuông tại
2 2 2 2
1 1 1 5 2 5
:.
5
4
a
A AH
AH AB AD a
Xét tam giác
SAH
vuông tại
2 15
: tan .
5
SA a
A SHA SA
AH
Vậy
3
2
.
1 1 2 15 4 15
. . .2 .
3 3 5 15
S ABCD ABCD
aa
V SA S a
Chọn đáp án B.
Câu 15: Cho hình chóp
.S ABCD
có đáy là hnh thoi cạnh bằng
o
, 60 ,a ABC SA
vuông góc với đáy.
Biết
2,SA a
thể tích của khối chóp
.S ABCD
bằng
A.
3
3
.
3
a
B.
3
6
.
6
a
C.
3
3
.
12
a
D.
3
3
.
4
a
Lời giải:
a
a
60
o
A
B
C
D
S
A
B
C
D
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Do
ABCD
là hình thoi cạnh bằng
o
, 60a ABC ABC
là tam giác đều cạnh
.a
Suy ra:
22
33
2 2. .
42
ABCD ABC
aa
SS
Vậy
23
.
1 1 3 3
. .2 . .
3 3 2 3
S ABCD ABCD
aa
V SA S a
Chọn đáp án A.
Câu 16: Cho hình chóp
.S ABCD
có đáy là hnh thoi cạnh bằng
o
, 60 ,a ABC SA
vuông góc với đáy.
Biết
SB
hợp với đáy một góc
o
60 ,
thể tích của khối chóp
.S ABCD
bằng
A.
3
3
.
3
a
B.
3
6
.
6
a
C.
3
3
.
12
a
D.
Lời giải:
D
C
B
A
S
D
C
B
A
60
o
a
a
Do
ABCD
là hình thoi cạnh bằng
o
, 60a ABC ABC
là tam giác đều cạnh
.a
Suy ra:
22
33
2 2. .
42
ABCD ABC
aa
SS
Do
SA ABCD
nên
AB
là hình chiếu vuông góc của
SB
trên
.ABCD
Suy ra:
; ; .SB ABCD SB AB SBA
Xét tam giác
SAB
vuông tại
: tan 3.
SA
A SBA SA a
AB
Vậy
23
.
1 1 3
. . 3. .
3 3 2 2
S ABCD ABCD
aa
V SA S a
Chọn đáp án D.
Câu 17: Cho hình chóp
.S ABCD
có đáy là hnh thang vuông tại
,,AB
2 , ,AD a AB BC a SA
vuông góc với đáy. Biết
2,SC a
thể tích của khối chóp
.S ABCD
bằng
A.
3
3
.
2
a
B.
3
2
.
2
a
C.
3
6
.
2
a
D.
3
3
.
4
a
Lời giải:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
D
C
B
A
S
Ta có:
2
3
.
22
ABCD
AB AD BC
a
S

Xét tam giác
SAC
vuông tại
2
2
22
: 2 2 2.A SA SC AC a a a
Vậy
23
.
1 1 3 2
. . 2. .
3 3 2 2
S ABCD ABCD
aa
V SA S a
Chọn đáp án B.
Câu 18: Cho hình chóp
.S ABCD
có đáy là hnh thang vuông tại
,,AB
2 , ,AD a AB BC a SA
vuông góc với đáy. Biết
SC
hợp với mt đáy một góc
0
60 ,
thể tích của khối chóp
.S ABCD
bằng
A.
3
3
.
2
a
B.
3
2
.
2
a
C.
3
6
.
2
a
D.
3
3
.
4
a
Lời giải:
S
A
B
C
D
Ta có:
2
3
.
22
ABCD
AB AD BC
a
S

Do
SA ABCD AC
là hình chiếu vuông góc của
SC
trên
.ABCD
Suy ra:
;.SC ABCD SCA
Xét tam giác
SAC
vuông tại
: tan .tan 2. 3 6.
SA
A SCA SA AC SCA a a
AC
Vậy
23
.
1 1 3 6
. . 6. .
3 3 2 2
S ABCD ABCD
aa
V SA S a
Chọn đáp án C.
Câu 19: Cho hnh chóp
.S ABCD
có đáy
ABCD
là hnh vuông cạnh
a
, cạnh bên
SA
vuông góc với mt
phng đáy. Gi
M
là trung điểm của
CD
. Biết khoảng cách giữa hai đường thng
BC
và
SM
bằng
3
4
a
. Tnh thể tch của khối chóp đã cho theo
a
.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
A.
3
3
4
a
B.
3
3
2
a
C.
3
3
6
a
D.
3
3
12
a
Lời giải:
S
O
N
M
A
B
C
D
H
Gi
N
là trung điểm của
AB
//BC SMN
.
, , , ,d BC SM d BC SMN d B SMN d A SMN
.
Dựng
AH
vuông góc với
SN
tại
H
AH SMN
.
Vậy
3
,
4
a
d A SMN AH
.
Lại có, trong tam giác vuông
SAN
:
2 2 2
1 1 1 3
2
a
SA
AH AN AS
.
Vậy
3
2
.
1 3 3
..
3 2 6
S ABCD
aa
Va
.
Chọn đáp án C.
Câu 20: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
,a SA
vuông góc với đáy. Biết
2,SB a
thể
tích của khối chóp
.S ABC
bằng
A.
3
2
.
12
a
B.
C.
3
3
.
3
a
D.
3
3
.
6
a
Lời giải:
S
C
B
A
Ta có:
2
3
.
4
ABC
a
S
Xét tam giác
SAB
vuông tại
22
: 3.A SA SB AB a
Vậy
23
.
1 1 3
. . 3. .
3 3 4 4
S ABC ABC
aa
V SA S a
Chọn đáp án B.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Câu 21: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh bằng
,a SA
vuông góc với đáy. Biết
2,SA a
thể tích của khối chóp
.S ABCD
bằng
A.
3
2
.
12
a
B.
C.
3
2
.
3
a
D.
3
.a
Lời giải:
D
C
B
A
S
Ta có:
2
.
ABCD
Sa
Vậy
3
2
.
1 1 2
. .2 . .
3 3 3
S ABCD ABCD
a
V SAS a a
Chọn đáp án C.
Câu 22: Cho hình chóp
.S ABCD
có đáy là hnh vuông cạnh bằng
,a SA
vuông góc với đáy. Biết
3,SC a
thể tích của khối chóp
.S ABCD
bằng
A.
3
2
.
3
a
B.
3
3
.
3
a
C.
3
2
.
3
a
D.
3
7
.
3
a
Lời giải:
D
C
B
A
S
Ta có:
2
.
ABCD
Sa
Xét tam giác
SAC
vuông tại
2 2 2 2
: 9 2 7.A SA SC AC a a a
Vậy
3
2
.
1 1 7
. . 7 . .
3 3 3
S ABCD ABCD
a
V SA S a a
Chọn đáp án D.
Câu 23: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
,a SA
vuông góc với đáy. Biết
SBC
hợp
với mt đáy một góc bằng
0
30 ,
thể tích của khối chóp
.S ABC
bằng
A.
3
2
.
12
a
B.
3
3
.
8
a
C.
3
3
.
24
a
D.
3
3
.
6
a
Lời giải:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
M
A
B
C
S
Ta có:
2
3
.
4
ABC
a
S
Dựng
,AM BC M
là trung điểm
.BC
Ta có:
.
BC AM
BC SAM BC SM
BC SA
Suy ra:
;.SBC ABC SMA
Xét tam giác
SAM
vuông tại
o
3
: tan .tan .tan30 .
22
SA a a
A SMA SA AM SMA
AM
Vậy
23
.
1 1 3 3
. . . .
3 3 2 4 24
S ABC ABC
a a a
V SA S
Chọn đáp án C.
Câu 24: Cho hình chóp
.S ABCD
có đáy là hnh thang vuông ở
A
và
B
,
3AB a
,
22AD BC a
. SA vuông góc với đáy, mt phng
SCD
tạo với đáy một góc
45
. Thể
tích khối chóp
.S ABC
bằng
A.
3
3
2
a
. B.
3
3 10
10
a
. C.
3
8
10
a
. D.
3
43
3
a
Lời giải:
Ta có
22
10AC AB BC a
Gi M là trung điểm AD
AM MD a
và
CM AD
;
22
3
10 sin
5
DC DM MC a ACD
Kẻ
AN DC
ta có
3 10
sin
5
AN AC ACN a
Góc giữa
SCD
với
ABCD
là
45SNA 
;
2
3 10 1 3
;.
5 2 2
ABC
a
SA AN a S AB BC
.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Vậy
3
.
1 3 10
.
3 10
S ABC A BC
V S SA a
.
Chọn đáp án B.
Câu 25: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
,a SA
vuông góc với đáy. Biết
SC
hợp với
mt phng
SAB
một góc bằng
30 ,
thể tích của khối chóp
.S ABC
bằng
A.
3
6
.
12
a
B.
C.
3
3
.
3
a
D.
3
3
.
6
a
Lời giải:
M
A
B
C
S
Ta có:
2
3
.
4
ABC
a
S
Dựng
,CM AB M
là trung điểm
.AB
Ta có:
.
CM AB
CM SAB
CM SA

Suy ra:
SM
là hình chiếu vuông góc của
SC
trên
;.SAB SC SAB CSM
Xét tam giác
SMC
vuông tại
0
33
: sin : sin30 3.
1
2
sin
2.
2
CM CM a a
M CSM SC a
SC
CSM
Xét tam giác
SAC
vuông tại
22
: 2.A SA SC AC a
Vậy
23
.
1 1 3 6
. . 2. .
3 3 4 12
S ABC ABC
aa
V SA S a
Chọn đáp án A.
Câu 26: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật tâm
O
,
,AB a
3,AD a
SA ABCD
. Khoảng cách từ
O
đến mt phng
SCD
bằng
3
4
a
. Tính thể
tích
V
của khối chóp
.S ABCD
.
A.
3
15
10
a
V
. B.
3
3Va
. C.
3
3
3
a
V
. D.
3
3
6
a
V
.
Lời giải:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
H
O
D
C
B
A
S
Gi
H
là hình chiếu của
A
lên
;d A S ASD CD H
.
3
2. ;
2
a
AH d O SCD
.
Xét
SAD
vuông ở
A
, đường cao
AH
, có:
2 2 2
1 1 1
SA a
AH AS AD
.
3
.
1 1 3
. . . .
2 2 3
S ABCD ABCD
a
V SA S SA AB AD
.
Chọn đáp án C.
Câu 27: Cho hình chóp
.S ABCD
có đáy là hnh vuông cạnh bằng
,a SA
vuông góc với đáy. Biết
SC
hợp với mt đáy một góc
45 ,
thể tích của khối chóp
.S ABCD
bằng
A.
3
2
.
3
a
B.
3
3
.
3
a
C.
3
2
.
3
a
D.
3
7
.
3
a
Lời giải:
S
A
B
C
D
Ta có:
2
.
ABCD
Sa
Do
SA ABCD
nên
AC
là hình chiếu vuông góc của
SC
trên
.ABCD
Suy ra:
0
; ; 45 .SC ABCD SC AC SCA SCA
Xét tam giác
SAC
vuông tại
: tan 2.
SA
A SCA SA AC a
AC
Vậy
3
2
.
1 1 2
. . 2 . .
3 3 3
S ABCD ABCD
a
V SA S a a
Chọn đáp án A.
Câu 28: Cho hình chóp
.S ABCD
có đáy là hnh vuông cạnh bằng
,a SA
vuông góc với đáy. Biết
SBC
hợp với mt đáy một góc
60 ,
thể tích của khối chóp
.S ABCD
bằng
A.
3
2
.
3
a
B.
3
3
.
3
a
C.
3
2
.
3
a
D.
3
7
.
3
a
Lời giải:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
S
A
B
C
D
Ta có:
2
.
ABCD
Sa
Ta có:
.
BC AB
BC SAB BC SB
BC SA
Suy ra:
0
; 60 .SBC ABCD SBA SBA
Xét tam giác
SAB
vuông tại
: tan 3.
SA
A SBA SA a
AB
Vậy
3
2
.
1 1 3
. . 3 . .
3 3 3
S ABCD ABCD
a
V SA S a a
Chọn đáp án B.
Câu 29: Cho hình chóp
.S ABC
có đáy là tam giác vuông tại
, , 2 ,B AB a BC a SA
vuông góc với đáy.
Biết
3,SA a
thể tích của khối chóp
.S ABC
bằng
A.
3
2
.
12
a
B.
C.
3
3
.
3
a
D.
3
.a
Lời giải:
A
B
C
S
Ta có:
2
1
..
2
ABC
S AB BC a
Vậy
23
.
11
. .3 . .
33
S ABC ABC
V SAS a a a
Chọn đáp án D.
Câu 30: Cho hình chóp
.S ABCD
có đáy là hnh vuông cạnh bằng
,a SA
vuông góc với đáy. Biết
SC
hợp với
SAB
một góc
30 ,
thể tích của khối chóp
.S ABCD
bằng
A.
3
6
.
3
a
B.
3
3
.
3
a
C.
3
2
.
3
a
D.
3
6
.
6
a
Lời giải:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
S
A
B
C
D
Ta có:
2
.
ABCD
Sa
Ta có:
BC AB
BC SAB SB
BC SA
là hình chiếu vuông góc của
SC
trên
.SAB
Suy ra:
0
; 30 .SC SAB BSC BSC
Xét tam giác
SBC
vuông tại
: tan 3.
BC
B BSC SB a
SB
Xét tam giác
SAB
vuông tại
22
: 2.A SA SB AB a
Vậy
3
2
.
1 1 2
. . 2. .
3 3 3
S ABCD ABCD
a
V SA S a a
Chọn đáp án C.
Câu 31: Cho hình chóp
.S ABCD
có đáy là hnh chữ nhật có
, 2 ,AB a BC a SA
vuông góc với đáy.
Biết
3,SA a
thể tích của khối chóp
.S ABCD
bằng
A.
3
2.a
B.
3
25
.
3
a
C.
3
2 15
.
3
a
D.
3
43
.
9
a
Lời giải:
D
C
B
A
S
Ta có:
2
. 2 .
ABCD
S AB BC a
Vậy
23
.
11
. .3 .2 2 .
33
S ABCD ABCD
V SA S a a a
Chọn đáp án A.
Câu 32: Cho hình chóp
.S ABCD
có đáy là hnh chữ nhật có
, 2 ,AB a BC a SA
vuông góc với đáy.
Biết
3,SD a
thể tích của khối chóp
.S ABCD
bằng
A.
3
2.a
B.
3
25
.
3
a
C.
3
2 15
.
3
a
D.
3
43
.
9
a
Lời giải:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
D
C
B
A
S
Ta có:
2
. 2 .
ABCD
S AB BC a
Xét tam giác
SAD
vuông tại
22
: 5.A SA SD AD a
Vậy
3
2
.
1 1 2 5
. . 5 .2 .
3 3 3
S ABCD ABCD
a
V SA S a a
Chọn đáp án B.
Câu 33: Cho hình chóp
.S ABCD
có đáy là hnh chữ nhật có
, 2 ,AB a BC a SA
vuông góc với đáy.
Biết
SC
hợp với mt đáy một góc
60 ,
thể tích của khối chóp
.S ABCD
bằng
A.
3
2.a
B.
3
25
.
3
a
C.
3
2 15
.
3
a
D.
3
43
.
9
a
Lời giải:
S
A
B
C
D
Ta có:
2
. 2 .
ABCD
S AB BC a
Do
SA ABCD
nên
AC
là hình chiếu vuông góc của
SC
trên
.ABCD
Suy ra:
; ; .SC ABCD SC AC SCA
Xét tam giác
SAC
vuông tại
: tan 15.
SA
A SCA SA a
AC
Vậy
3
2
.
1 1 2 15
. . 15.2 .
3 3 3
S ABCD ABCD
a
V SAS a a
Chọn đáp án C.
Câu 34: Cho hình chóp
.S ABC
có đáy là tam giác vuông tại
, , 2 ,B AB a BC a SA
vuông góc với đáy.
Biết
SC
hợp với mt đáy một góc
60 ,
thể tích của khối chóp
.S ABC
bằng
A.
3
15
.
3
a
B.
3
5
.
2
a
C.
3
2
.
3
a
D.
3
3
.
3
a
Lời giải:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
S
C
B
A
Ta có:
2
1
..
2
ABC
S AB BC a
Do
SA ABC
nên
AC
là hình chiếu vuông góc của
SC
trên
.ABC
Suy ra:
0
; ; 60 .SC ABC SC AB SCA SCA
Xét tam giác
ABC
vuông tại
22
: 5.B AC AB BC a
Xét tam giác
SAC
vuông tại
: tan .tan 15.
SA
A SCA SA AC SCA a
AC
Vậy
3
2
.
1 1 15
. . 15. .
3 3 3
S ABC ABC
a
V SA S a a
Chọn đáp án A.
Câu 35: Cho hình chóp
.S ABCD
có đáy là hnh chữ nhật có
, 2 ,AB a BC a SA
vuông góc với đáy.
Biết
SCD
hợp với mt đáy một góc
30 ,
thể tích của khối chóp
.S ABCD
bằng
A.
3
2.a
B.
3
25
.
3
a
C.
3
2 15
.
3
a
D.
3
43
.
9
a
Lời giải:
S
A
B
C
D
Ta có:
2
. 2 .
ABCD
S AB BC a
Ta có:
.
CD AD
CD SAD CD SD
CD SA
Suy ra:
;.SCD ABCD SDA
Xét tam giác
SAD
vuông tại
23
: tan .
3
SA a
A SDA SA
AD
Vậy
3
2
.
1 1 2 3 4 3
. . .2 .
3 3 3 9
S ABCD ABCD
aa
V SA S a
Chọn đáp án D.
Câu 36: Cho hình chóp
.S ABCD
có đáy là hnh chữ nhật có
, 2 ,AB a BC a SA
vuông góc với đáy.
Biết
SC
hợp với
SAB
một góc
30 ,
thể tích của khối chóp
.S ABCD
bằng
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
A.
3
2 11
.
3
a
B.
3
25
.
3
a
C.
3
2 15
.
3
a
D.
3
43
.
9
a
Lời giải:
S
A
B
C
D
Ta có:
2
. 2 .
ABCD
S AB BC a
Ta có:
BC AB
BC SAB SB
BC SA
là hình chiếu vuông góc của
SC
trên
.SAB
Suy ra:
;.SC SAB BSC
Xét tam giác
SBC
vuông tại
: tan 2 3.
BC
B BSC SB a
SB
Xét tam giác
SAB
vuông tại
22
: 11.A SA SB AB a
Vậy
3
2
.
1 1 2 11
. . 11.2 .
3 3 3
S ABCD ABCD
a
V SA S a a
Chọn đáp án A.
Câu 37: Cho hình chóp
.S ABCD
có đáy là hnh thoi cạnh bằng
, 60 ,a ABC SA
vuông góc với đáy.
Biết
SC
hợp với đáy một góc
60 ,
thể tích của khối chóp
.S ABCD
bằng
A.
3
3
.
3
a
B.
3
6
.
6
a
C.
3
3
.
12
a
D.
Lời giải:
D
C
B
A
S
D
C
B
A
60
o
a
a
Do
ABCD
là hình thoi cạnh bằng
o
, 60a ABC ABC
là tam giác đều cạnh
.a
Suy ra:
22
33
2 2. .
42
ABCD ABC
aa
SS
Do
SA ABCD
nên
AC
là hình chiếu vuông góc của
SC
trên
.ABCD
Suy ra:
; ; .SC ABCD SC AC SCA
Xét tam giác
SAC
vuông tại
: tan 3.
SA
A SCA SA a
AC
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Vậy
23
.
1 1 3
. . 3. .
3 3 2 2
S ABCD ABCD
aa
V SA S a
Chọn đáp án D.
Câu 38: Cho hình chóp
.S ABCD
có đáy là hnh thoi cạnh bằng
, 60 ,a ABC SA
vuông góc với đáy.
Biết
SBC
hợp với đáy một góc
30 ,
thể tích của khối chóp
.S ABCD
bằng
A.
3
3
.
3
a
B.
3
6
.
6
a
C.
3
3
.
12
a
D.
Lời giải:
H
H
D
C
B
A
S
D
C
B
A
60
o
a
a
Do
ABCD
là hình thoi cạnh bằng
o
, 60a ABC ABC
là tam giác đều cạnh
.a
Suy ra:
22
33
2 2. .
42
ABCD ABC
aa
SS
Dựng
,AH BC H
là trung điểm
.BC
Ta có:
.
BC AH
BC SAH BC SH
BC SA
Suy ra:
;.SBC ABCD SHA
Xét tam giác
SAH
vuông tại
o
33
: tan .tan30 . .
2 3 2
SA a a
A SHA SA AH
AH
Vậy
23
.
1 1 3 3
. . . .
3 3 2 2 12
S ABCD ABCD
a a a
V SA S
Chọn đáp án C.
Câu 39: Cho hình chóp
.S ABCD
có đáy là hnh thang vuông tại
,,AB
2 , ,AD a AB BC a SA
vuông
góc với đáy. Biết
2,SB a
thể tích của khối chóp
.S ABCD
bằng
A.
3
3
.
2
a
B.
3
2
.
2
a
C.
3
6
.
2
a
D.
3
3
.
4
a
Lời giải:
D
C
B
A
S
Ta có:
2
3
.
22
ABCD
AB AD BC
a
S

Xét tam giác
SAB
vuông tại
22
: 3.A SA SB AB a
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Vậy
23
.
1 1 3 3
. . 3. .
3 3 2 2
S ABCD ABCD
aa
V SA S a
Chọn đáp án A.
Câu 40: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
.a
Biết mt bên
SAB
là tam giác đều và
nằm trong mt phng vuông góc với đáy, thể tích của khối chóp
.S ABC
bằng
A.
B.
3
3
.
24
a
C.
D.
3
15
.
6
a
Lời giải:
H
B
A
C
S
Ta có:
2
3
.
4
ABC
a
S
Gi
H
là trung điểm
.AB
Ta có:

.
SAB ABC
SH ABC
SH AB
Vậy
23
.
1 1 3 3
. . . . .
3 3 2 4 8
S ABC ABC
a a a
V SH S
Chọn đáp án A.
Câu 41: Cho hình chóp
.S ABCD
có đáy là hnh vuông cạnh
.a
Biết mt bên
SAB
là tam giác vuông
cân tại
S
và nằm trong mt phng vuông góc với đáy, thể tích của khối chóp
.S ABCD
bằng
A.
B.
3
3
.
24
a
C.
3
3
.
6
a
D.
Lời giải:
H
S
A
B
C
D
Ta có:
2
.
ABCD
Sa
Gi
H
là trung điểm
.AB
Ta có:
.
SAB ABCD
SH ABCD
SH AB

Vậy
3
2
.
11
. . . . .
3 3 2 6
S ABCD ABCD
aa
V SH S a
Chọn đáp án D.
Câu 42: Cho hình chóp
.S ABC
có mt phng
SAC
vuông góc với mt phng
ABC
,
SAB
là
tam giác đều cạnh
3a
,
3BC a
đường thng
SC
tạo với mt phng
ABC
góc
60
.
Thể tích của khối chóp
.S ABC
bằng
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
A.
3
3
3
a
. B.
3
6
2
a
. C.
3
6
6
a
. D.
3
26a
.
Lời giải:
60
o
A
C
B
S
H
Ta thấy tam giác
ABC
cân tại
B
, gi
H
là trung điểm của
AB
suy ra
.BH AC
Do
SAC ABC
nên
BH SAC
.
Ta lại có
BA BC BS
nên
B
thuộc trục đường tròn ngoại tiếp tam giác
ABC
H
là tâm
đường tròn ngoại tiếp tam giác
SAC
SA SC
.
Do
AC
là hình chiếu của
SC
lên mt phng
ABC
0
60SCA
.
Ta có
0
.cot60SC SA a
,
0
2
sin60
SA
AC a
HC a
22
2BH BC HC a
.
.S ABC
V
1
.
3
SAC
BH S
1
..
6
BH SA SC
3
6
6
a
.
Chọn đáp án C.
Câu 43: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
.a
Biết mt bên
SAB
là tam giác vuông
cân tại
S
và nằm trong mt phng vuông góc với đáy, thể tích của khối chóp
.S ABC
bằng
A.
B.
3
3
.
24
a
C.
D.
3
15
.
6
a
Lời giải:
H
B
A
C
S
Ta có:
2
3
.
4
ABC
a
S
Gi
H
là trung điểm
.AB
Ta có:

.
SAB ABC
SH ABC
SH AB
Vậy
23
.
1 1 3 3
. . . . .
3 3 2 4 24
S ABC ABC
a a a
V SH S
Chọn đáp án B.
Câu 44: Cho hình chóp
.S ABCD
có đáy là hnh vuông cạnh
.a
Biết mt bên
SAB
là tam giác đều và
nằm trong mt phng vuông góc với đáy, thể tích của khối chóp
.S ABCD
bằng
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
A.
B.
3
3
.
24
a
C.
3
3
.
6
a
D.
3
15
.
6
a
Lời giải:
H
S
A
B
C
D
Ta có:
2
.
ABCD
Sa
Gi
H
là trung điểm
.AB
Ta có:
.
SAB ABCD
SH ABCD
SH AB

Vậy
3
2
.
1 1 3 3
. . . . .
3 3 2 6
S ABCD ABCD
aa
V SH S a
Chọn đáp án C.
Câu 45: Cho hình chóp
.S ABCD
với
ABCD
là hình vuông cạnh
a
. Mt bên
SAB
là tam giác cân tại
S
và
nằm trên mt phng vuông góc với mt phng đáy. Cạnh bên
SC
tạo với đáy một góc
60
. Tính
thể tích khối chóp
.S ABCD
.
A.
3
15
2
a
. B.
3
15
6
a
. C.
3
6
3
a
. D.
3
3
6
a
.
Lời giải:
A
a
a
I
D
C
B
S
Gi
I
là trung điểm của
AB
.
Ta có:
SAB
cân tại
S
SI AB
1
Mt khác:

SAB ABCD
SAB ABCD AB
2
Từ
1
và
2
, suy ra:
SI ABCD
SI
là chiều cao của hình chóp
.S ABCD
IC
là hình chiếu của
SC
lên mt phng
ABCD
, , 60SC ABCD SC IC SCI
Xét
IBC
vuông tại
B
, ta có:



2
2 2 2
5
22
aa
IC IB BC a
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Xét
SIC
vuông tại
I
, ta có:
5 15
.tan60 . 3
22
aa
SI IC
Vậy thể tích khối chóp
.S ABCD
là:
3
2
1 1 15 15
. . . .
3 3 2 6
ABCD
aa
V S SI a
.
Chọn đáp án B.
Câu 46: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
.a
Biết hình chiếu vuông góc của
S
trên
mt đáy là trung điểm của
AB
và
2,SB a
thể tích của khối chóp
.S ABC
bằng
A.
3
5
.
8
a
B.
C.
3
3
.
8
a
D.
3
3
.
48
a
Lời giải:
H
B
A
C
S
Ta có:
2
3
.
4
ABC
a
S
Gi
H
là trung điểm
.AB
Ta có:
.SH ABC
Xét tam giác
SHB
vuông tại
22
15
:.
2
a
H SH SB HB
Vậy
23
.
1 1 15 3 5
. . . . .
3 3 2 4 8
S ABC ABC
a a a
V SH S
Chọn đáp án A.
Câu 47: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
.a
Biết hình chiếu vuông góc của
S
trên
mt đáy là trung điểm của
AB
và
0
; 60 ,SC ABC
thể tích của khối chóp
.S ABC
bằng
A.
3
5
.
8
a
B.
C.
3
3
.
8
a
D.
3
3
.
48
a
Lời giải:
H
B
A
C
S
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Ta có:
2
3
.
4
ABC
a
S
Gi
H
là trung điểm
.AB
Ta có:
.SH ABC
Suy ra:
HC
là hình chiếu vuông góc của
SC
trên
;.ABC SC ABC SCH
Xét tam giác
SHC
vuông tại
3
: tan .
2
SH a
H SCH SH
HC
Vậy
23
.
1 1 3 3 3
. . . . .
3 3 2 4 8
S ABC ABC
a a a
V SH S
Chọn đáp án C.
Câu 48: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
.a
Biết hình chiếu vuông góc của
S
trên
mt đáy là trung điểm của
AB
và
0
; 30 ,SBC ABC
thể tích của khối chóp
.S ABC
bằng
A.
3
5
.
8
a
B.
C.
3
3
.
8
a
D.
3
3
.
48
a
Lời giải:
K
M
S
C
A
B
H
Ta có:
2
3
.
4
ABC
a
S
Gi
,HM
lần lượt là trung điểm
,.AB BC
Dựng
,HK BC K
là trung điểm
.BC
Ta có:
.
BC HK
BC SHK BC SK
BC SH
Suy ra:
;.SBC ABC SKH
Xét tam giác
SHK
vuông tại
o
1
: tan .tan .tan30 .
24
SH a
H SCH SH HK SCH AM
HK
Vậy
23
.
1 1 3 3
. . . . .
3 3 4 4 48
S ABC ABC
a a a
V SH S
Chọn đáp án D.
Câu 49: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
.a
Biết hình chiếu vuông góc của
S
trên
mt đáy là điểm
H
trên cạnh
,2AB AH HB
và
0
; 30 ,SC ABC
thể tích của khối chóp
.S ABC
bằng
A.
3
3
.
24
a
B.
3
7
.
36
a
C.
3
.
12
a
D.
3
6
.
6
a
Lời giải:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
A
B
C
H
S
Ta có:
2
3
.
4
ABC
a
S
Ta có:
.SH ABC
Suy ra:
HC
là hình chiếu vuông góc của
SC
trên
;.ABC SC ABC SCH
Xét tam giác
:HBC
2
2 2 2
77
2 . .cos .
93
aa
HC BH BC BH BC HBC HC
Xét tam giác
SHC
vuông tại
21
: tan .
9
SH a
H SCH SH
HC
Vậy
23
.
1 1 21 3 7
. . . . .
3 3 9 4 36
S ABC ABC
a a a
V SH S
Chọn đáp án B.
Câu 50: Cho hình chóp
.S ABCD
có đáy là hnh vuông cạnh
.a
Biết hình chiếu vuông góc của
S
trên
mt đáy là điểm
H
trên cạnh
,2AB BH HA
và
0
; 60 ,SD ABCD
thể tích của khối chóp
.S ABCD
bằng
A.
3
23
.
9
a
B.
3
30
.
9
a
C.
3
42
.
27
a
D.
3
3
.
3
a
Lời giải:
H
S
B
C
D
A
Ta có:
2
.
ABCD
Sa
Ta có:
22
10
.
3
a
HD AH AD
Ta có:
SH ABCD HD
là hình chiếu vuông góc của
trên
ABCD
;.SD ABCD SDH
Xét tam giác
SHD
vuông tại
30
: tan .
3
SH a
H SDH SH
HD
Vậy
3
2
.
1 1 30 30
. . . . .
3 3 3 9
S ABCD ABCD
aa
V SH S a
Chọn đáp án B.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Câu 51: Cho hình chóp
.S ABCD
có đáy là hnh vuông cạnh
.a
Biết hình chiếu vuông góc của
S
trên
mt đáy là điểm
H
trên cạnh
,2AB BH HA
và
0
; 60 ,SBD ABCD
thể tích của khối chóp
.S ABCD
bằng
A.
3
23
.
9
a
B.
3
30
.
9
a
C.
3
42
.
27
a
D.
3
6
.
9
a
Lời giải:
K
O
H
S
B
C
D
A
Ta có:
2
.
ABCD
Sa
Gi
O
là tâm hình vuông
.ABCD
Dựng
.
BD HK
HK AC BD SHK BD SK
BD SH
Suy ra:
;.SBD ABCD SKH
Xét tam giác
SHK
vuông tại
o
26
: tan .tan60 .
33
SH a
H SKH SH AO
HK
Vậy
3
2
.
1 1 6 6
. . . . .
3 3 3 9
S ABCD ABCD
aa
V SH S a
Chọn đáp án D.
Câu 52: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
.a
Biết hình chiếu vuông góc của
S
trên
mt đáy là trung điểm của
AB
và
; 60 ,SB ABC 
thể tích của khối chóp
.S ABC
bằng
A.
3
5
.
8
a
B.
C.
3
3
.
8
a
D.
3
3
.
48
a
Lời giải:
H
B
A
C
S
Ta có:
2
3
.
4
ABC
a
S
Gi
H
là trung điểm
.AB
Ta có:
.SH ABC
Suy ra:
HB
là hình chiếu vuông góc của
SB
trên
;.ABC SB ABC SBH
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Xét tam giác
SHB
vuông tại
3
: tan .
2
SH a
H SBH SH
HB
Vậy
23
.
1 1 3 3
. . . . .
3 3 2 4 8
S ABC ABC
a a a
V SH S
Chọn đáp án B.
Câu 53: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
.a
Biết hình chiếu vuông góc của
S
trên
mt đáy là điểm
H
trên cạnh
,2AB AH HB
và
2,SA a
thể tích của khối chóp
.S ABC
bằng
A.
3
3
.
24
a
B.
3
7
.
36
a
C.
3
6
.
9
a
D.
3
6
.
6
a
Lời giải:
S
H
C
B
A
Ta có:
2
3
.
4
ABC
a
S
Xét tam giác
SHA
vuông tại
22
42
:.
3
a
H SH SA HA
Vậy
23
.
1 1 4 2 3 6
. . . . .
3 3 3 4 9
S ABC ABC
a a a
V SH S
Chọn đáp án C.
Câu 54: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
.a
Biết hình chiếu vuông góc của
S
trên
mt đáy là điểm
H
trên cạnh
,2AB AH HB
và
; 60 ,SB ABC 
thể tích của khối chóp
.S ABC
bằng
A.
3
3
.
24
a
B.
3
7
.
36
a
C.
3
.
12
a
D.
3
6
.
6
a
Lời giải:
A
B
C
H
S
Ta có:
2
3
.
4
ABC
a
S
Ta có:
SH ABC HB
là hình chiếu vuông góc của
SB
trên
;.ABC SB ABC SBH
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Xét tam giác
SHB
vuông tại
3
: tan .
3
SH a
H SBH SH
HB
Vậy
23
.
1 1 3 3
. . . . .
3 3 3 4 12
S ABC ABC
a a a
V SH S
Chọn đáp án C.
Câu 55: Cho hình chóp
.S ABCD
có đáy là hnh vuông cạnh
.a
Biết hình chiếu vuông góc của
S
trên
mt đáy là điểm
H
trên cạnh
,2AB BH HA
và
; 60 ,SB ABCD 
thể tích của khối chóp
.S ABCD
bằng
A.
3
23
.
9
a
B.
3
30
.
9
a
C.
3
42
.
27
a
D.
3
3
.
3
a
Lời giải:
A
D
C
B
S
H
Ta có:
2
.
ABCD
Sa
Ta có:
SH ABCD HB
là hình chiếu vuông góc của
SB
trên
ABCD
;.SB ABCD SBH
Xét tam giác
SHB
vuông tại
23
: tan .
3
SH a
H SBH SH
HB
Vậy
3
2
.
1 1 2 3 2 3
. . . . .
3 3 3 9
S ABCD ABCD
aa
V SH S a
Chọn đáp án A.
Câu 56: Cho hình chóp
.S ABCD
có đáy là hnh vuông cạnh
.a
Biết hình chiếu vuông góc của
S
trên
mt đáy là điểm
H
trên cạnh
,2AB BH HA
và
; 30 ,SC ABCD 
thể tích của khối chóp
.S ABCD
bằng
A.
3
23
.
9
a
B.
3
30
.
9
a
C.
3
42
.
27
a
D.
3
39
.
27
a
Lời giải:
H
S
B
C
D
A
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Ta có:
2
.
ABCD
Sa
Ta có:
22
13
.
3
a
HC HB BC
Ta có:
SH ABCD HC
là hình chiếu vuông góc của
SC
trên
ABCD
;.SC ABCD SCH
Xét tam giác
SHC
vuông tại
39
: tan .
9
SH a
H SCH SH
HC
Vậy
3
2
.
1 1 39 39
. . . . .
3 3 9 27
S ABCD ABCD
aa
V SH S a
Chọn đáp án D.
Câu 57: Cho hình chóp
.S ABCD
có đáy là hnh vuông cạnh
.a
Biết hình chiếu vuông góc của
S
trên
mt đáy là điểm
H
trên cạnh
,2AB BH HA
và
; 60 ,SCD ABCD 
thể tích của khối chóp
.S ABCD
bằng
A.
3
23
.
9
a
B.
3
30
.
9
a
C.
3
42
.
27
a
D.
3
3
.
3
a
Lời giải:
K
H
S
B
C
D
A
Ta có:
2
.
ABCD
Sa
Dựng
.
CD HK
HK AD CD SHK CD SK
CD SH
Suy ra:
;.SCD ABCD SKH
Xét tam giác
SHK
vuông tại
: tan 3.
SH
H SKH SH a
HK
Vậy
3
2
.
1 1 3
. . . 3. .
3 3 3
S ABCD ABCD
a
V SH S a a
Chọn đáp án D.
Câu 58: Cho hình chóp
.S A BC
là tam giác vuông tại
A
,
30ABC
,
BC a
. Hai mt bên
SAB
và
SAC
cùng vuông góc với đáy
ABC
, mt bên
SBC
tạo với đáy một góc
45
. Thể tích
của khối chóp
.S A BC
bằng
A.
3
64
a
. B.
3
16
a
. C.
3
9
a
. D.
3
32
a
.
Lời giải:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Ta có:
SAB ABC
SAC ABC SA ABC
SAB SAC SA

.
Kẻ
AH BC SH BC
. Khi đó:
45
o
SBC ABC BC
BC AH SHA
BC SH

Mà
0
3
.cos30
2
a
AB BC
và
.sin30
2
o
a
AC BC
nên
0
3
.sin30
4
a
AH AB
Nên
3
.
4
a
SA
Do đó:
3
11
. . .
3 6 32
ABC
a
V S SA AB AC SA
.
Chọn đáp án D.
Câu 59: Cho hình chóp
.S ABCD
, đáy
ABCD
là hình vuông cạnh
2a
. Hai mt phng
SAB
,
SAD
cùng vuông góc với đáy, góc giữa hai mt phng
SBC
và
ABC D
bằng
30
. Tính tỉ số
3
3V
a
biết
V
là thể tích của khối chóp
.S ABCD
.
A.
3
12
. B.
3
2
. C.
. D.
83
3
.
Lời giải:
C
A
B
D
S
Do
SAB ABCD
SA ABCD
SAD ABCD

.
Góc giữa
SBC
và
ABC D
bằng góc
SBA
. Do đó
1
tan
3
SA
SBA
AB

2
3
a
SA
.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Suy ra
23
.
1 1 2 8
. .4
33
3 3 3
S ABCD ABCD
a
V SA S a a
.
Chọn đáp án D.
Câu 60: Cho hnh chóp
.S ABCD
có đáy
ABCD
là hnh vuông cạnh
a
, hai mt phng
SAB
và
SAD
cùng vuông góc với mt phng
ABC D
; góc giữa đường thng
SC
và mt phng
ABC D
bằng
60
. Tính theo
a
thể tch khối chóp
.S ABCD
.
A.
3
3a
. B.
3
6
9
a
. C.
3
6
3
a
. D.
3
32a
.
Lời giải:
Ta có
SAB ABCD
SAD ABCD SA ABCD
SAB SAD SA

AC
là hình chiếu vuông góc của
SC
lên
ABC D
, 60SC ABCD SCA
Tam giác
SAC
vuông tại
A
có
.tan60 6SA AC a
.
Khi đó
3
2
1 1 6
. . . 6.
3 3 3
SABCD ABCD
a
V SAS a a
.
Chọn đáp án C.
Câu 61: Cho khối chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
và hai mt bên
SAB
,
SAC
cng vuông góc với đáy. Tnh thể tch khối chóp
.S ABC
biết
3SC a
.
A.
3
a3
2
. B.
3
a3
4
. C.
3
2a 6
9
. D.
3
a6
12
.
Lời giải:
A
C
B
S
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Ta có:

( ) ( )
()
( ) ( )
SAB ABC
SA ABC
SAC ABC
.
Xt tam giác
SAC
vuông tại
A
nên
22
2SA SC AC a
;
2
3
.
4
ABC
a
S
Vậy

23
1 3 6
. . 2
3 4 12
SABC
aa
Va
.
Chọn đáp án D.
Câu 62: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, hai mt phng
SAC
và
SAB
cùng vuông góc với
ABCD
. Góc giữa
SCD
và
ABCD
là
60
. Thể tích khối
chóp
.S ABCD
bằng
A.
3
6
3
a
. B.
3
3
3
a
. C.
3
3
6
a
. D.
3
6
6
a
.
Lời giải:
Ta có
60SA ABCD SDA
3
2
13
3 3 3.
33
a
SA AD a V a a
.
Chọn đáp án B.
Câu 63: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật. Hai mt phng
SAB
và
SAC
cùng vuông góc với mt phng
ABCD
. Biết rằng
AB a
,
3AD a
và
7SC a
. Tính thể
tích khối chóp
.S AB CD
.
A.
3
Va
. B.
3
2Va
. C.
3
3Va
. D.
3
4Va
Lời giải:
D
B
C
A
S
Ta có:

SAB ABCD
SAC ABCD SA ABCD
SAB SAC SA
.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115

22
AC AB BC
2
2
32a a a
;

22
SA SC AC
2
2
7 2 3a a a
.
Vậy
.
1
.
3
S ABCD ABCD
V S SA
3
11
. . . . . 3. 3 .
33
AB ADSA a a a a
Chọn đáp án A.
Câu 64: Cho tứ diện đều
ABCD
có cạnh bằng
.t
Thể tích của khối tứ diện
ABCD
bằng
A.
3
2
.
12
t
B.
3
2
.
6
t
C.
3
2
.
3
t
D.
3
3
.
6
t
Lời giải:
M
G
D
A
B
C
Ta có:
2
3
.
4
BCD
a
S
Gi
M
là trung điểm
,CD G
là trng tâm tam giác
.BCD
Do
ABCD
là tứ diện đều nên
.AG BCD
Xét tam giác
ABG
vuông tại
2
2
2 2 2 2
2 2 3 6
: . .
3 3 2 3
t
G AG AB BG AB BM t t







Lúc đó:
2
3
1 1 6 3 2
. . . .
3 3 3 4 12
ABCD BCD
tt
V AG S t
Cách khác: Dùng công thức giải nhanh:
3
2
.
12
ABCD
Vt
Chọn đáp án A.
Câu 65: Cho hnh chóp tam giác đều
.S ABC
có cạnh đáy bằng
.a
Biết
2,SA a
thể tích của khối chóp
.S ABC
bằng
A.
3
3
.
12
a
B.
3
2
.
2
a
C.
3
11
.
12
a
D.
3
3
.
72
a
Lời giải:
M
G
C
B
A
S
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Ta có:
2
3
.
4
ABC
a
S
Gi
G
là trng tâm tam giác
,ABC M
là trung điểm
.BC
Do
.S ABC
là chóp tam giác đều nên
.SG ABC
Xét tam giác
SAG
vuông tại
:G
2
2
2
2 2 2
2 2 3 33
2 . .
3 3 2 3
aa
SG SA AG SA AM a







Vậy
23
.
1 1 33 3 11
. . . .
3 3 3 4 12
S ABC ABC
a a a
V SG S
Chọn đáp án C.
Câu 66: Cho hnh chóp tam giác đều
.S ABC
có cạnh đáy bằng
.a
Biết
SBC
hợp với đáy một góc
30 ,
thể tích của khối chóp
.S ABC
bằng
A.
3
3
.
12
a
B.
3
2
.
2
a
C.
3
11
.
12
a
D.
3
3
.
72
a
Lời giải:
S
A
B
C
G
M
Ta có:
2
3
.
4
ABC
a
S
Gi
G
là trng tâm tam giác
,ABC M
là trung điểm
.BC
Do
.S ABC
là chóp tam giác đều nên
.SG ABC
Ta có:
.
BC GM
BC SGM BC SM
BC SG
Suy ra:
;.SBC ABC SMG
Xét tam giác
SMG
vuông tại
o
1 3 3
: tan .tan60 . . .
3 2 3 6
SG a a
G SMG SG MG
MG
Vậy
23
.
1 1 3 3
. . . .
3 3 6 4 72
S ABC ABC
a a a
V SG S
Chọn đáp án D.
Câu 67: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
.a
Biết
hợp với mt đáy một góc
60 ,
thể tích của khối chóp
.S ABCD
bằng
A.
3
3
.
18
a
B.
3
6
.
6
a
C.
3
14
.
6
a
D.
3
15
.
6
a
Lời giải:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
S
A
B
C
D
O
Ta có:
2
.
ABCD
Sa
Gi
O
là tâm hình vuông
.ABCD
Do
.S ABCD
là chóp tứ giác đều nên
.SO ABCD
Suy ra:
AO
là hình chiếu vuông góc của
trên
;.ABCD SA ABCD SAO
Xét tam giác
SAO
vuông tại
:O
o
26
tan .tan60 . 3 .
22
SO a a
SAO SO AO
AO
Vậy
3
2
.
1 1 6 6
. . . .
3 3 2 6
S ABC ABCD
aa
V SO S a
Chọn đáp án B.
Câu 68: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
.a
Biết
SBC
hợp với mt đáy một góc
30 ,
thể tích của khối chóp
.S ABCD
bằng
A.
3
3
.
18
a
B.
3
6
.
6
a
C.
3
14
.
6
a
D.
3
15
.
6
a
Lời giải:
M
O
D
C
B
A
S
Ta có:
2
.
ABCD
Sa
Gi
O
là tâm hình vuông
,ABCD M
là trung điểm
.BC
Do
.S ABCD
là chóp tứ giác đều nên
.SO ABCD
Ta có:
.
BC OM
BC SOM BC SM
BC SO
Suy ra:
;.SBC ABCD SMO
Xét tam giác
SMO
vuông tại
o
33
: tan .tan30 . .
2 3 6
SO a a
O SMO SO OM
MO
Vậy
3
2
.
1 1 3 3
. . . .
3 3 6 18
S ABC ABCD
aa
V SO S a
Chọn đáp án A.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Câu 69: Cho hnh chóp tam giác đều
.S ABC
có cạnh đáy bằng
.a
Biết
hợp với đáy một góc
60 ,
thể tích của khối chóp
.S ABC
bằng
A.
3
3
.
12
a
B.
3
2
.
2
a
C.
3
11
.
12
a
D.
3
3
.
72
a
Lời giải:
S
A
B
C
G
M
Ta có:
2
3
.
4
ABC
a
S
Gi
G
là trng tâm tam giác
,ABC M
là trung điểm
.BC
Do
.S ABC
là chóp tam giác đều nên
.SG ABC
Suy ra:
AG
là hình chiếu vuông góc của
trên
;.ABC AA ABC SAG

Xét tam giác
SAG
vuông tại
o
23
: tan .tan60 . . 3 .
32
SG a
G SAG SG AG a
AG
Vậy
23
.
1 1 3 3
. . . .
3 3 4 12
S ABC ABC
aa
V SG S a
Chọn đáp án A.
Câu 70: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
.a
Biết
2,SA a
thể tích của khối chóp
.S ABCD
bằng
A.
3
3
.
18
a
B.
3
6
.
6
a
C.
3
14
.
6
a
D.
3
15
.
6
a
Lời giải:
O
D
C
B
A
S
Ta có:
2
.
ABCD
Sa
Gi
O
là tâm hình vuông
.ABCD
Do
.S ABCD
là chóp tứ giác đều nên
.SO ABCD
Xét tam giác
SAO
vuông tại
:O
2
2
2
2 2 2
1 2 14
2.
2 2 2
aa
SO SA AO SA AC a







Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Vậy
3
2
.
1 1 14 14
. . . .
3 3 2 6
S ABC ABCD
aa
V SO S a
Chọn đáp án C.
Câu 71: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
.a
Biết diện tích một mt bên của hình
chóp đó có diện tích bằng
2
,a
thể tích của khối chóp
.S ABCD
bằng
A.
3
3
.
18
a
B.
3
6
.
6
a
C.
3
14
.
6
a
D.
3
15
.
6
a
Lời giải:
M
S
A
B
C
D
O
Gi
M
là trung điểm
.BC
Ta có:
22
11
. . 2 .
22
SBC
S SM BC a SM a a SM a
Xét tam giác
SOM
vuông tại
2
2
22
15
: 2 .
22
aa
O SO SM OM a



Vậy
3
2
.
1 1 15 15
. . . .
3 3 2 6
S ABC ABCD
aa
V SO S a
Chọn đáp án D.
_____________________HẾT_____________________
Huế, 10h20’ Ngày 18 tháng 5 năm 2022
| 1/50
| | Tải xuống

Có thể bạn quan tâm:

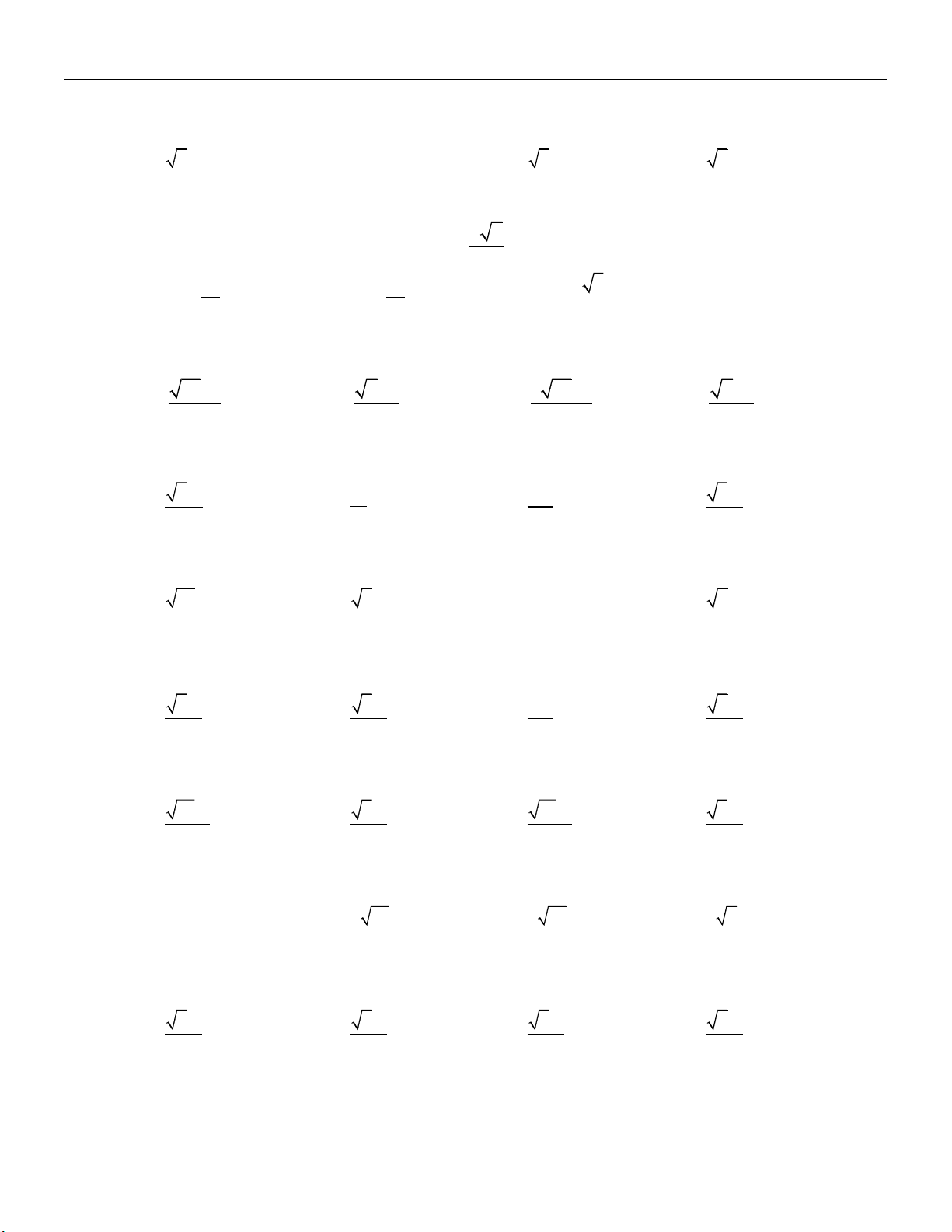
Preview text:

LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ TOÁN 12 THỂ TÍCH KHỐI ĐA DIỆN THỂ TÍCH KHỐI CHÓP
 LUYỆN THI THPT QUỐC GIA
 CẬP NHẬT TỪ ĐỀ THI MỚI NHẤT
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
MỘT SỐ DẠNG TOÁN LIÊN QUAN ĐẾN
THỂ TÍCH KHỐI CHÓP
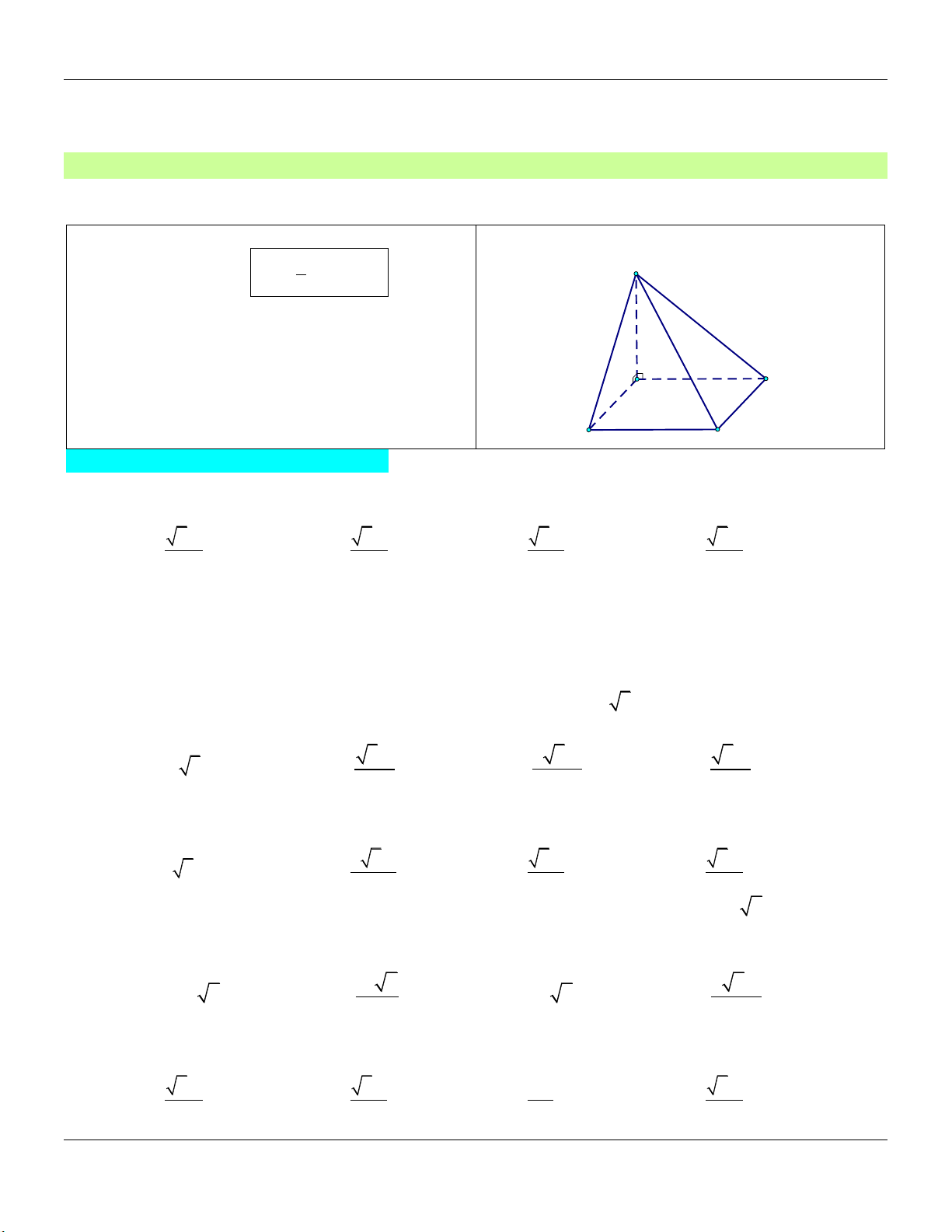
Dạng 1: Khối chóp có cạnh bên vuông góc với đáy Phương pháp: Cho hình chóp .
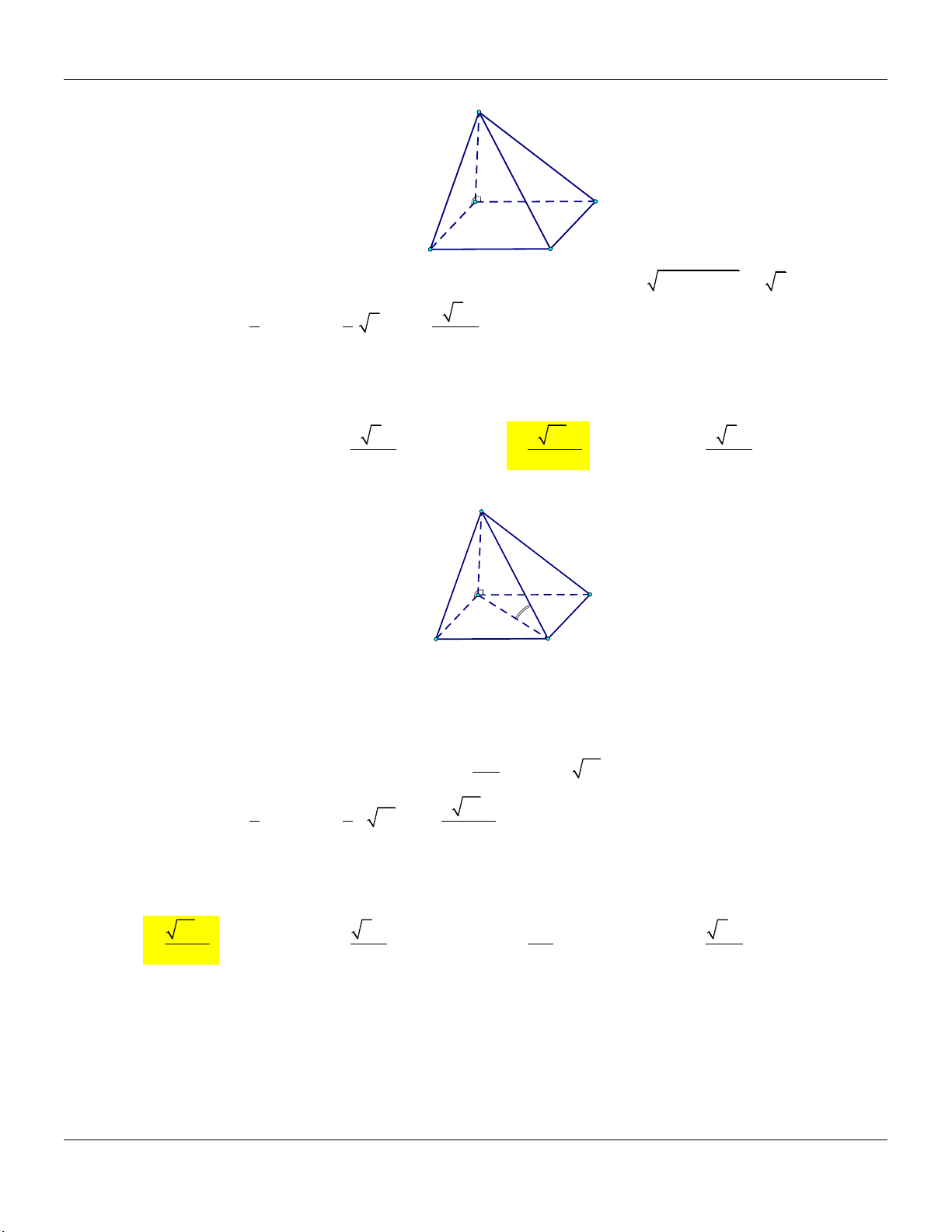
S ABCD có SA vuông góc với mặt phẳng đáy… +) Đường cao: . SA Form hình vẽ: S
+) Thể tích khối chóp: V  1 . SA S 3 ABCD A D B C
BÀI TẬP TRẮC NGHIỆM MINH HỌA Câu 1: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh a, SA vuông góc với đáy. Biết SA  2a, thể tích của khối chóp . S ABC bằng 3 2a 3 2a 3 3a 3 3a A. . B. . C. . D. . 12 6 3 6 Câu 2: Cho tứ diện .
O ABC có các cạnh OA , OB , OC đôi một vuông góc với nhau. Biết
OA  2 cm , OB  3cm , OC  6cm . Tính thể tích của khối tứ diện . O ABC . A.  3 6 cm . B.  3 36 cm  . C.  3 12 cm  . D.  3 18 cm  . Câu 3:
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng  ABCD, đáy ABCD là hình thang
vuông tại A và B có AB a, AD  3a, BC  .
a Biết SA a 3, tính thể tích khối chóp S.BCD theo . a 3 3a 3 2 3a 3 3a A. 3 2 3a . B. . C. . D. . 6 3 4 Câu 4: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh a, SA vuông góc với đáy. Biết diện tích tam giác SAB bằng 2
4a , thể tích của khối chóp . S ABC bằng 3 2 3a 3 3a 3 3a A. 3 4 3a . B. . C. . D. . 3 3 6 Câu 5:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA a 2 và SA vuông
góc với mặt phẳng đáy, tam giác SBD là tam giác đều. Thể tích của khối chóp S.ABCD bằng. 3 a 2 3 2 2a A. 3 2a 2 . B. . C. 3 a 2 . D. . 3 3 Câu 6: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh bằng a, SA vuông góc với đáy. Biết SB
hợp với mặt đáy một góc o
60 , thể tích của khối chóp . S ABCD bằng 3 2a 3 3a 3 2a 3 7a A. . B. . C. . D. . 3 3 3 3
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia Câu 7: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh a, SA vuông góc với đáy. Biết SB hợp với
mặt đáy một góc bằng 0
60 , thể tích của khối chóp . S ABC bằng 3 2a 3 a 3 3a 3 3a A. . B. . C. . D. . 12 4 3 6 Câu 8:
Cho khối chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với đáy và khoảng a 2
cách từ A đến mặt phẳng SBC  bằng
. Tính thể tích V của khối chóp đã cho. 2 3 3 3 3 A.a V . B.a V . C.a V . D. 3 V a . 3 2 9 Câu 9:
Tính thể tích khối chóp S.ABC có AB a , AC  2a , BAC  120 , SA   ABC  , góc giữa
SBC và  ABC là 60 . 3 21 a 3 7 a 3 3 21 a 3 7 a A. . B. . C. . D. . 14 14 14 7
Câu 10: Cho hình chóp .
S ABC có đáy là tam giác vuông tại B, AB a, BC  2a, SA vuông góc với đáy.
Biết SB hợp với mặt đáy một góc 0
60 , thể tích của khối chóp . S ABC bằng 3 2a 3 a 3 2a 3 3a A. . B. . C. . D. . 12 2 3 3
Câu 11: Cho hình chóp .
S ABC có đáy là tam giác vuông tại B, AB a, BC  2a, SA vuông góc với đáy.
Biết SBC hợp với mặt đáy một góc 0
60 , thể tích của khối chóp . S ABC bằng 3 15a 3 5a 3 2a 3 3a A. . B. . C. . D. . 3 2 3 3
Câu 12: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh bằng a, SA vuông góc với đáy. Biết
SBD hợp với mặt đáy một góc 0
60 , thể tích của khối chóp . S ABCD bằng 3 6a 3 3a 3 2a 3 6a A. . B. . C. . D. . 3 3 3 6
Câu 13: Cho hình chóp .
S ABC có đáy là tam giác vuông tại B, AB a, BC  2a, SA vuông góc với đáy.
Biết SC hợp với SAB một góc 0
30 , thể tích của khối chóp . S ABC bằng 3 15a 3 5a 3 11a 3 3a A. . B. . C. . D. . 3 2 3 3
Câu 14: Cho hình chóp .
S ABCD có đáy là hình chữ nhật có AB a, BC  2a, SA vuông góc với đáy.
Biết SBD hợp với mặt đáy một góc o
60 , thể tích của khối chóp . S ABCD bằng 3 2a 3 4 15a 3 2 15a 3 4 3a A. . B. . C. . D. . 5 15 3 9
Câu 15: Cho hình chóp .
S ABCD có đáy là hình thoi cạnh bằng o
a, ABC  60 , SA vuông góc với đáy.
Biết SA  2a, thể tích của khối chóp . S ABCD bằng 3 3a 3 6a 3 3a 3 3a A. . B. . C. . D. . 3 6 12 4
Câu 16: Cho hình chóp .
S ABCD có đáy là hình thoi cạnh bằng o
a, ABC  60 , SA vuông góc với đáy.
Biết SB hợp với đáy một góc o
60 , thể tích của khối chóp . S ABCD bằng
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 3 3a 3 6a 3 3a 3 a A. . B. . C. . D. . 3 6 12 2
Câu 17: Cho hình chóp .
S ABCD có đáy là hình thang vuông tại A, B, A D 2 ,a A BB C  , a S A
vuông góc với đáy. Biết SC  2a, thể tích của khối chóp . S ABCD bằng 3 3a 3 2a 3 6a 3 3a A. . B. . C. . D. . 2 2 2 4
Câu 18: Cho hình chóp .
S ABCD có đáy là hình thang vuông tại A, B, A D 2 ,a A BB C  , a S A
vuông góc với đáy. Biết SC hợp với mặt đáy một góc 0
60 , thể tích của khối chóp . S ABCD bằng 3 3a 3 2a 3 6a 3 3a A. . B. . C. . D. . 2 2 2 4
Câu 19: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc với mặt
phẳng đáy. Gọi M là trung điểm của CD . Biết khoảng cách giữa hai đường thẳng BC và SM a 3 bằng
. Tính thể tích của khối chóp đã cho theo a . 4 3 a 3 3 a 3 3 a 3 3 a 3 A. B. C. D. 4 2 6 12
BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN Câu 20: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh a, SA vuông góc với đáy. Biết SB  2a, thể tích của khối chóp . S ABC bằng 3 2a 3 a 3 3a 3 3a A. . B. . C. . D. . 12 4 3 6
Câu 21: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh bằng a, SA vuông góc với đáy. Biết
SA  2a, thể tích của khối chóp . S ABCD bằng 3 2a 3 a 3 2a A. . B. . C. . D. 3 a . 12 2 3
Câu 22: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh bằng a, SA vuông góc với đáy. Biết
SC  3a, thể tích của khối chóp . S ABCD bằng 3 2a 3 3a 3 2a 3 7a A. . B. . C. . D. . 3 3 3 3
Câu 23: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh a, SA vuông góc với đáy. Biết SBC hợp
với mặt đáy một góc bằng 0
30 , thể tích của khối chóp . S ABC bằng 3 2a 3 3a 3 3a 3 3a A. . B. . C. . D. . 12 8 24 6
Câu 24: Cho hình chóp S.ABCD có đáy là hình thang vuông ở A và B , AB  3a ,
AD  2BC  2a . SA vuông góc với đáy, mặt phẳng  SCD tạo với đáy một góc 45 . Thể
tích khối chóp S.ABC bằng 3 a 3 3 3a 10 3 8a 3 4 3a A. . B. . C. . D. 2 10 10 3
Câu 25: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh a, SA vuông góc với đáy. Biết SC hợp với
mặt phẳng SAB một góc bằng 30, thể tích của khối chóp . S ABC bằng
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 3 6a 3 a 3 3a 3 3a A. . B. . C. . D. . 12 4 3 6
Câu 26: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O , AB a, a 3
AD a 3, SA   ABCD . Khoảng cách từ O đến mặt phẳng  SCD bằng . Tính thể 4
tích V của khối chóp S.ABCD . 3 a 15 3 a 3 3 a 3 A. V  . B. 3 V a 3 . C. V  . D. V  . 10 3 6
Câu 27: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh bằng a, SA vuông góc với đáy. Biết SC
hợp với mặt đáy một góc 45, thể tích của khối chóp . S ABCD bằng 3 2a 3 3a 3 2a 3 7a A. . B. . C. . D. . 3 3 3 3
Câu 28: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh bằng a, SA vuông góc với đáy. Biết SBC
hợp với mặt đáy một góc 60, thể tích của khối chóp . S ABCD bằng 3 2a 3 3a 3 2a 3 7a A. . B. . C. . D. . 3 3 3 3
Câu 29: Cho hình chóp .
S ABC có đáy là tam giác vuông tại B, AB a, BC  2a, SA vuông góc với đáy.
Biết SA  3a, thể tích của khối chóp . S ABC bằng 3 2a 3 a 3 3a A. . B. . C. . D. 3 a . 12 2 3
Câu 30: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh bằng a, SA vuông góc với đáy. Biết SC
hợp với SAB một góc 30, thể tích của khối chóp . S ABCD bằng 3 6a 3 3a 3 2a 3 6a A. . B. . C. . D. . 3 3 3 6
Câu 31: Cho hình chóp .
S ABCD có đáy là hình chữ nhật có AB a, BC  2a, SA vuông góc với đáy.
Biết SA  3a, thể tích của khối chóp . S ABCD bằng 3 2 5a 3 2 15a 3 4 3a A. 3 2a . B. . C. . D. . 3 3 9
Câu 32: Cho hình chóp .
S ABCD có đáy là hình chữ nhật có AB a, BC  2a, SA vuông góc với đáy.
Biết SD  3a, thể tích của khối chóp . S ABCD bằng 3 2 5a 3 2 15a 3 4 3a A. 3 2a . B. . C. . D. . 3 3 9
Câu 33: Cho hình chóp .
S ABCD có đáy là hình chữ nhật có AB a, BC  2a, SA vuông góc với đáy.
Biết SC hợp với mặt đáy một góc 60, thể tích của khối chóp . S ABCD bằng 3 2 5a 3 2 15a 3 4 3a A. 3 2a . B. . C. . D. . 3 3 9
Câu 34: Cho hình chóp .
S ABC có đáy là tam giác vuông tại B, AB a, BC  2a, SA vuông góc với đáy.
Biết SC hợp với mặt đáy một góc 60, thể tích của khối chóp . S ABC bằng 3 15a 3 5a 3 2a 3 3a A. . B. . C. . D. . 3 2 3 3
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Câu 35: Cho hình chóp .
S ABCD có đáy là hình chữ nhật có AB a, BC  2a, SA vuông góc với đáy.
Biết SCD hợp với mặt đáy một góc 30, thể tích của khối chóp . S ABCD bằng 3 2 5a 3 2 15a 3 4 3a A. 3 2a . B. . C. . D. . 3 3 9
Câu 36: Cho hình chóp .
S ABCD có đáy là hình chữ nhật có AB a, BC  2a, SA vuông góc với đáy.
Biết SC hợp với SAB một góc 30, thể tích của khối chóp . S ABCD bằng 3 2 11a 3 2 5a 3 2 15a 3 4 3a A. . B. . C. . D. . 3 3 3 9
Câu 37: Cho hình chóp .
S ABCD có đáy là hình thoi cạnh bằng a, ABC  60, SA vuông góc với đáy.
Biết SC hợp với đáy một góc 60, thể tích của khối chóp . S ABCD bằng 3 3a 3 6a 3 3a 3 a A. . B. . C. . D. . 3 6 12 2
Câu 38: Cho hình chóp .
S ABCD có đáy là hình thoi cạnh bằng a, ABC  60, SA vuông góc với đáy.
Biết SBC hợp với đáy một góc 30, thể tích của khối chóp . S ABCD bằng 3 3a 3 6a 3 3a 3 a A. . B. . C. . D. . 3 6 12 2
Câu 39: Cho hình chóp .
S ABCD có đáy là hình thang vuông tại A, B, AD  2a, AB BC a, SA vuông
góc với đáy. Biết SB  2a, thể tích của khối chóp . S ABCD bằng 3 3a 3 2a 3 6a 3 3a A. . B. . C. . D. . 2 2 2 4
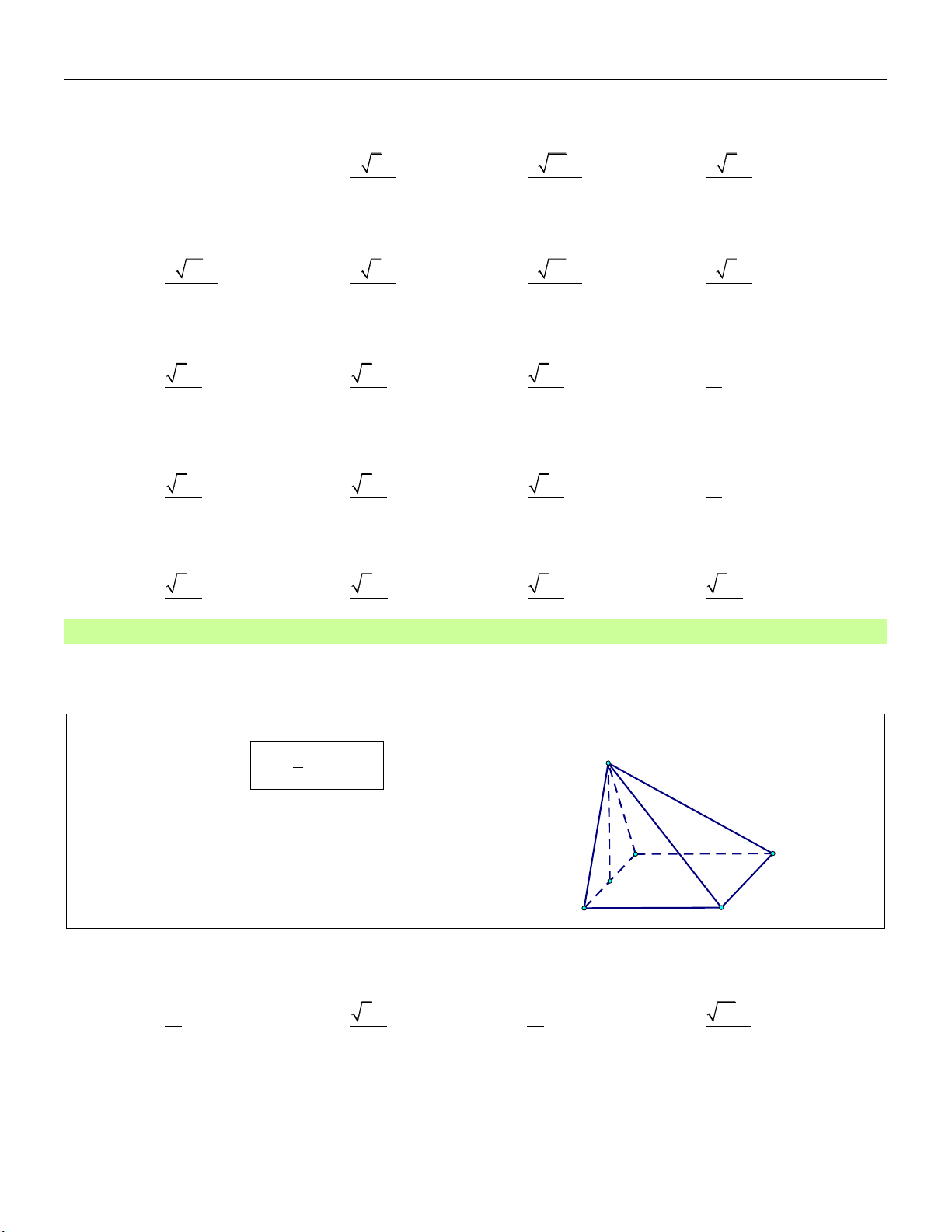
Dạng 2: Khối chóp có mặt bên là tam giác cân tại S và vuông góc với đáy Phương pháp: Cho hình chóp .
S ABCD có mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy…
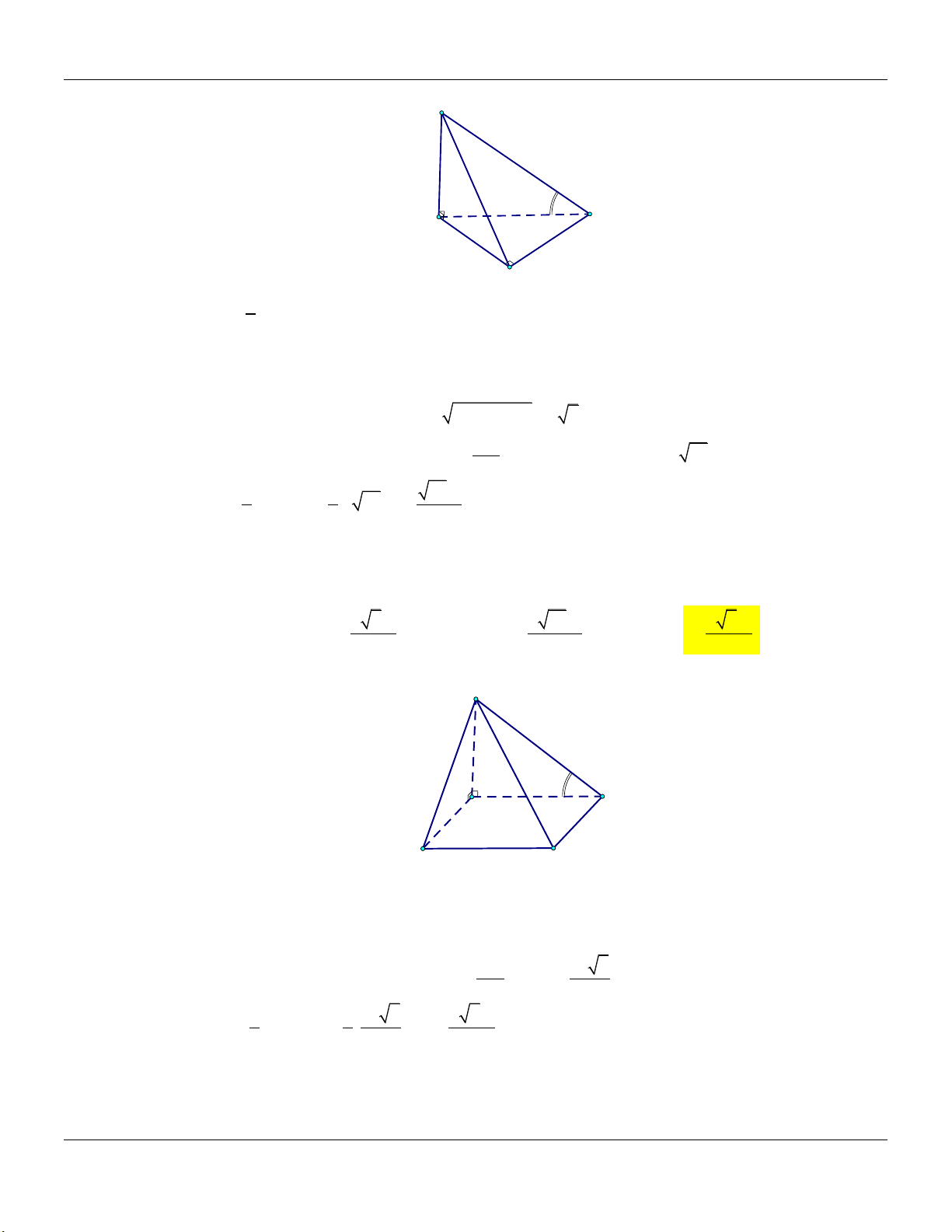
+) Đường cao: SH , H là trung điểm . AB Form hình vẽ: S
+) Thể tích khối chóp: V  1 SH.S 3 ABCD A D H B C
BÀI TẬP TRẮC NGHIỆM MINH HỌA Câu 40: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh .
a Biết mặt bên SAB là tam giác đều và
nằm trong mặt phẳng vuông góc với đáy, thể tích của khối chóp . S ABC bằng 3 a 3 3a 3 a 3 15a A. . B. . C. . D. . 8 24 6 6
Câu 41: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh .
a Biết mặt bên SAB là tam giác vuông
cân tại S và nằm trong mặt phẳng vuông góc với đáy, thể tích của khối chóp . S ABCD bằng
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 3 a 3 3a 3 3a 3 a A. . B. . C. . D. . 8 24 6 6
Câu 42: Cho hình chóp S.ABC có mặt phẳng  SAC  vuông góc với mặt phẳng  ABC  , SAB là
tam giác đều cạnh a 3 , BC a 3 đường thẳng SC tạo với mặt phẳng  ABC  góc 60 .
Thể tích của khối chóp S.ABC bằng 3 a 3 3 a 6 3 a 6 A. . B. . C. . D. 3 2a 6 . 3 2 6
BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN Câu 43: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh .
a Biết mặt bên SAB là tam giác vuông
cân tại S và nằm trong mặt phẳng vuông góc với đáy, thể tích của khối chóp . S ABC bằng 3 a 3 3a 3 a 3 15a A. . B. . C. . D. . 8 24 6 6
Câu 44: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh .
a Biết mặt bên SAB là tam giác đều và
nằm trong mặt phẳng vuông góc với đáy, thể tích của khối chóp . S ABCD bằng 3 a 3 3a 3 3a 3 15a A. . B. . C. . D. . 8 24 6 6
Câu 45: Cho hình chóp .
S ABCD với ABCD là hình vuông cạnh a . Mặt bên SAB là tam giác cân tại S và
nằm trên mặt phẳng vuông góc với mặt phẳng đáy. Cạnh bên SC tạo với đáy một góc 60 . Tính thể tích khối chóp . S ABCD . 3 a 15 3 a 15 3 a 6 3 a 3 A. . B. . C. . D. . 2 6 3 6
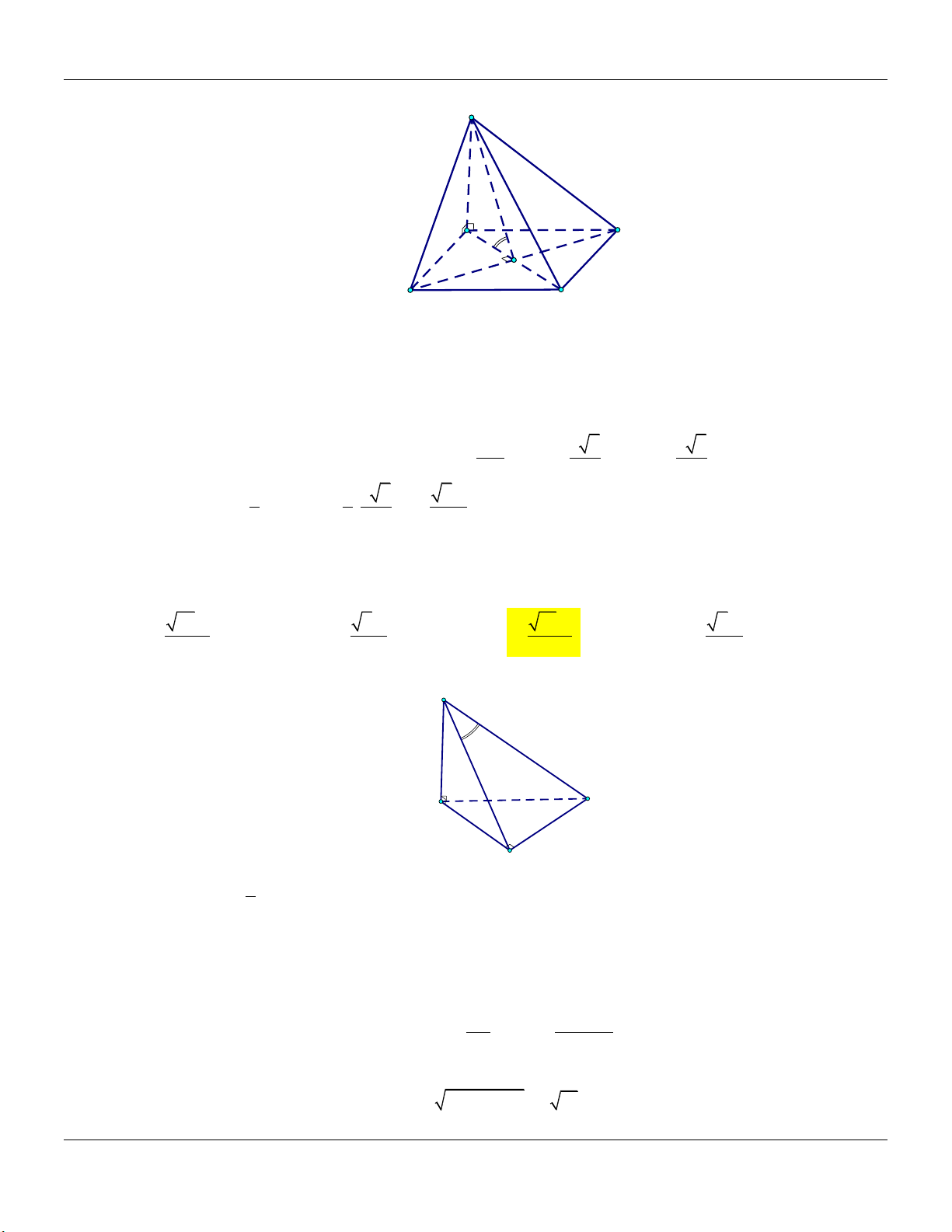
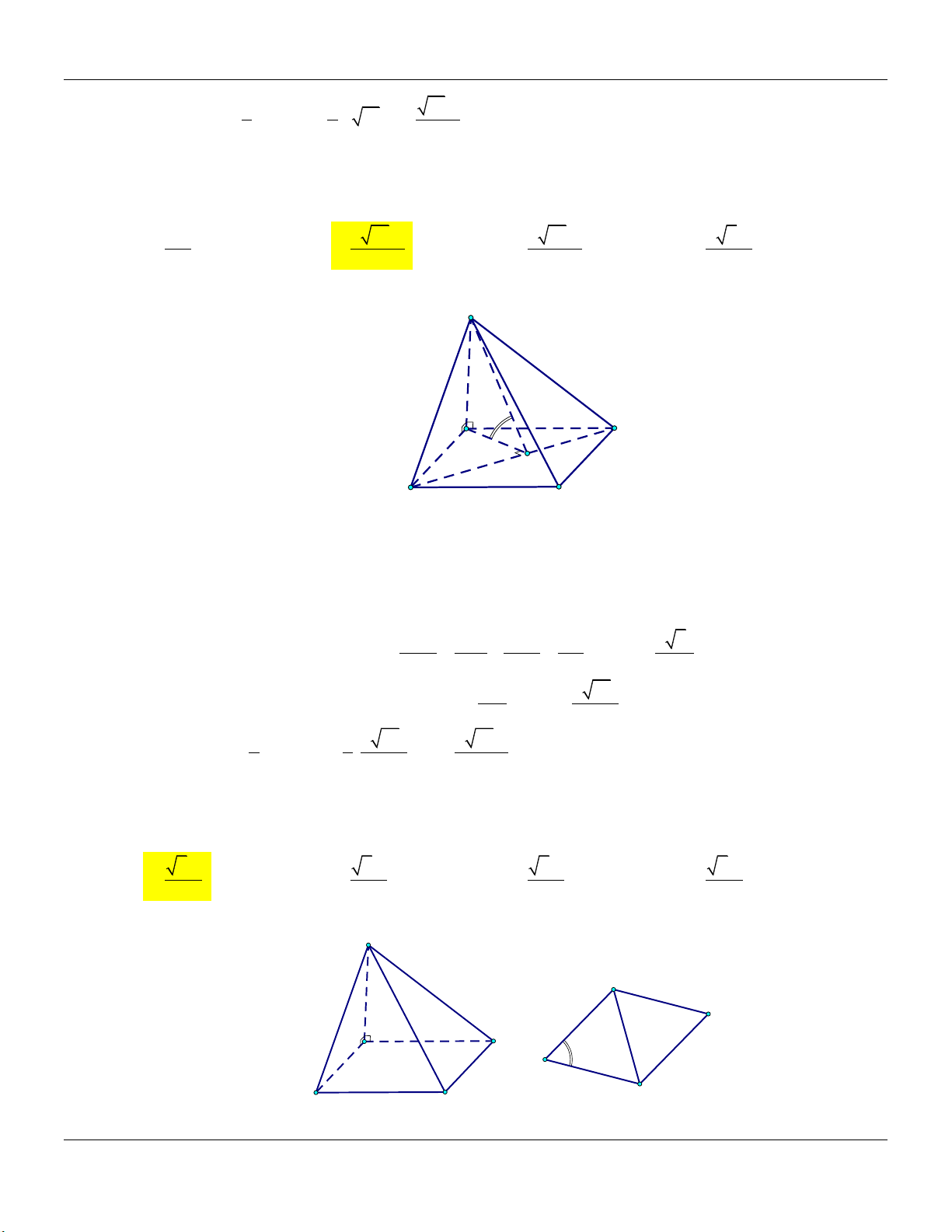
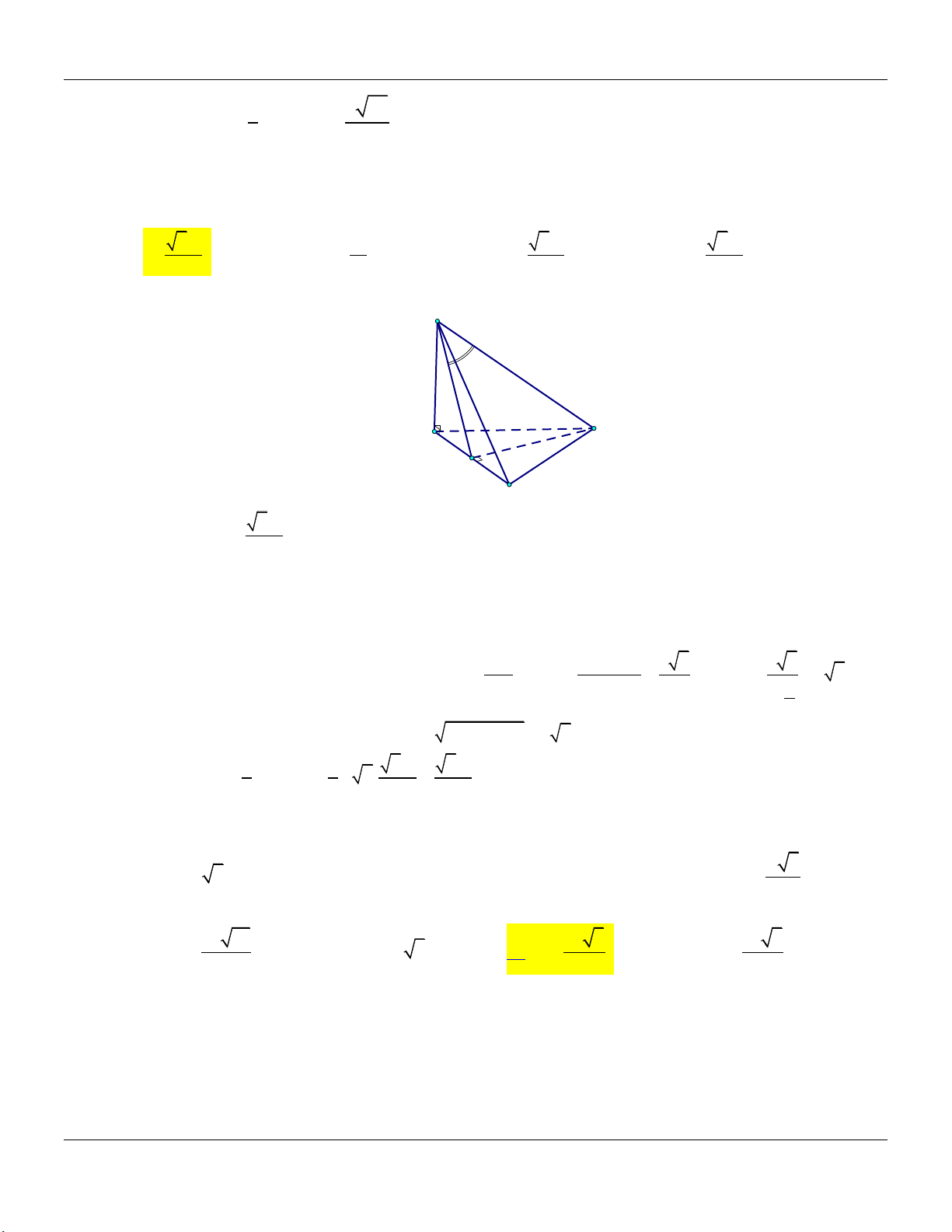
Dạng 3: Khối chóp có hình chiếu của S trên mặt đáy là điểm H Phương pháp: Cho hình chóp .
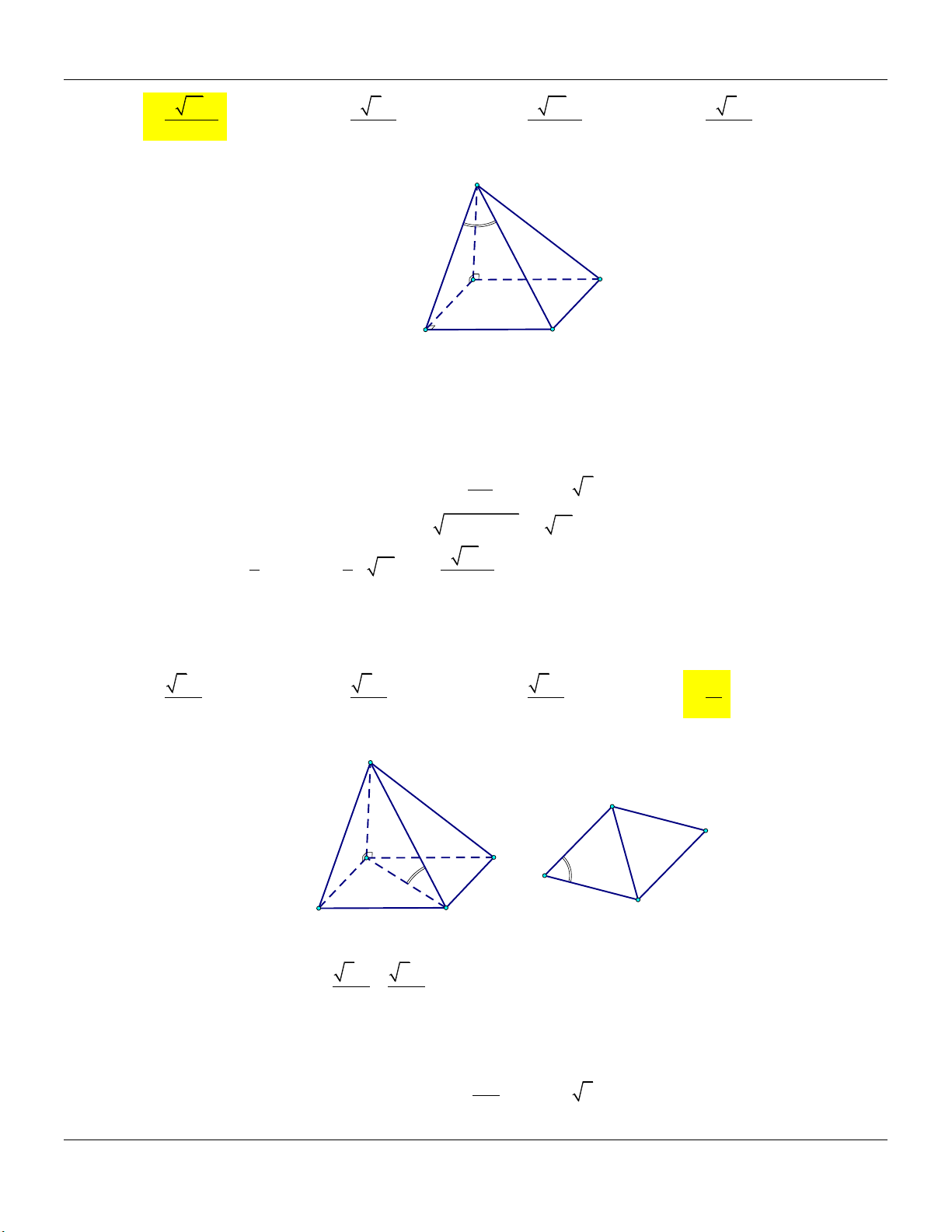
S ABC có điểm H là hình chiếu vuông góc của S trên mặt đáy… +) Đường cao: SH. Form hình vẽ: S
+) Thể tích khối chóp: V  1 SH.S 3 ABC A C H B
BÀI TẬP TRẮC NGHIỆM MINH HỌA Câu 46: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh .
a Biết hình chiếu vuông góc của S trên
mặt đáy là trung điểm của AB và SB  2a, thể tích của khối chóp . S ABC bằng 3 5a 3 a 3 3a 3 3a A. . B. . C. . D. . 8 8 8 48
Câu 47: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh .
a Biết hình chiếu vuông góc của S trên
mặt đáy là trung điểm của AB và SC ABC 0 ;
 60 , thể tích của khối chóp . S ABC bằng
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 3 5a 3 a 3 3a 3 3a A. . B. . C. . D. . 8 8 8 48
Câu 48: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh .
a Biết hình chiếu vuông góc của S trên
mặt đáy là trung điểm của AB và  SBC  ABC 0 ;
 30 , thể tích của khối chóp . S ABC bằng 3 5a 3 a 3 3a 3 3a A. . B. . C. . D. . 8 8 8 48
Câu 49: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh .
a Biết hình chiếu vuông góc của S trên
mặt đáy là điểm H trên cạnh AB, AH  2HB và SC ABC 0 ;
 30 , thể tích của khối chóp . S ABC bằng 3 3a 3 7a 3 a 3 6a A. . B. . C. . D. . 24 36 12 6
Câu 50: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh .
a Biết hình chiếu vuông góc của S trên
mặt đáy là điểm H trên cạnh AB, BH  2HA và SD ABCD 0 ;
 60 , thể tích của khối chóp . S ABCD bằng 3 2 3a 3 30a 3 42a 3 3a A. . B. . C. . D. . 9 9 27 3
Câu 51: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh .
a Biết hình chiếu vuông góc của S trên
mặt đáy là điểm H trên cạnh AB, BH  2HA và  SBD  ABCD 0 ;
 60 , thể tích của khối chóp . S ABCD bằng 3 2 3a 3 30a 3 42a 3 6a A. . B. . C. . D. . 9 9 27 9
BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN Câu 52: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh .
a Biết hình chiếu vuông góc của S trên
mặt đáy là trung điểm của AB và  ;
SB ABC  60, thể tích của khối chóp . S ABC bằng 3 5a 3 a 3 3a 3 3a A. . B. . C. . D. . 8 8 8 48
Câu 53: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh .
a Biết hình chiếu vuông góc của S trên
mặt đáy là điểm H trên cạnh AB, AH  2HB và SA  2a, thể tích của khối chóp . S ABC bằng 3 3a 3 7a 3 6a 3 6a A. . B. . C. . D. . 24 36 9 6
Câu 54: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh .
a Biết hình chiếu vuông góc của S trên
mặt đáy là điểm H trên cạnh AB, AH  2HB và  ;
SB ABC  60, thể tích của khối chóp . S ABC bằng 3 3a 3 7a 3 a 3 6a A. . B. . C. . D. . 24 36 12 6
Câu 55: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh .
a Biết hình chiếu vuông góc của S trên
mặt đáy là điểm H trên cạnh AB, BH  2HA và  ;
SB ABCD  60, thể tích của khối chóp . S ABCD bằng 3 2 3a 3 30a 3 42a 3 3a A. . B. . C. . D. . 9 9 27 3
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Câu 56: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh .
a Biết hình chiếu vuông góc của S trên
mặt đáy là điểm H trên cạnh AB, BH  2HA và SC;ABCD  30, thể tích của khối chóp . S ABCD bằng 3 2 3a 3 30a 3 42a 3 39a A. . B. . C. . D. . 9 9 27 27
Câu 57: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh .
a Biết hình chiếu vuông góc của S trên
mặt đáy là điểm H trên cạnh AB, BH  2HA và  SCD;ABCD  60, thể tích của khối chóp . S ABCD bằng 3 2 3a 3 30a 3 42a 3 3a A. . B. . C. . D. . 9 9 27 3
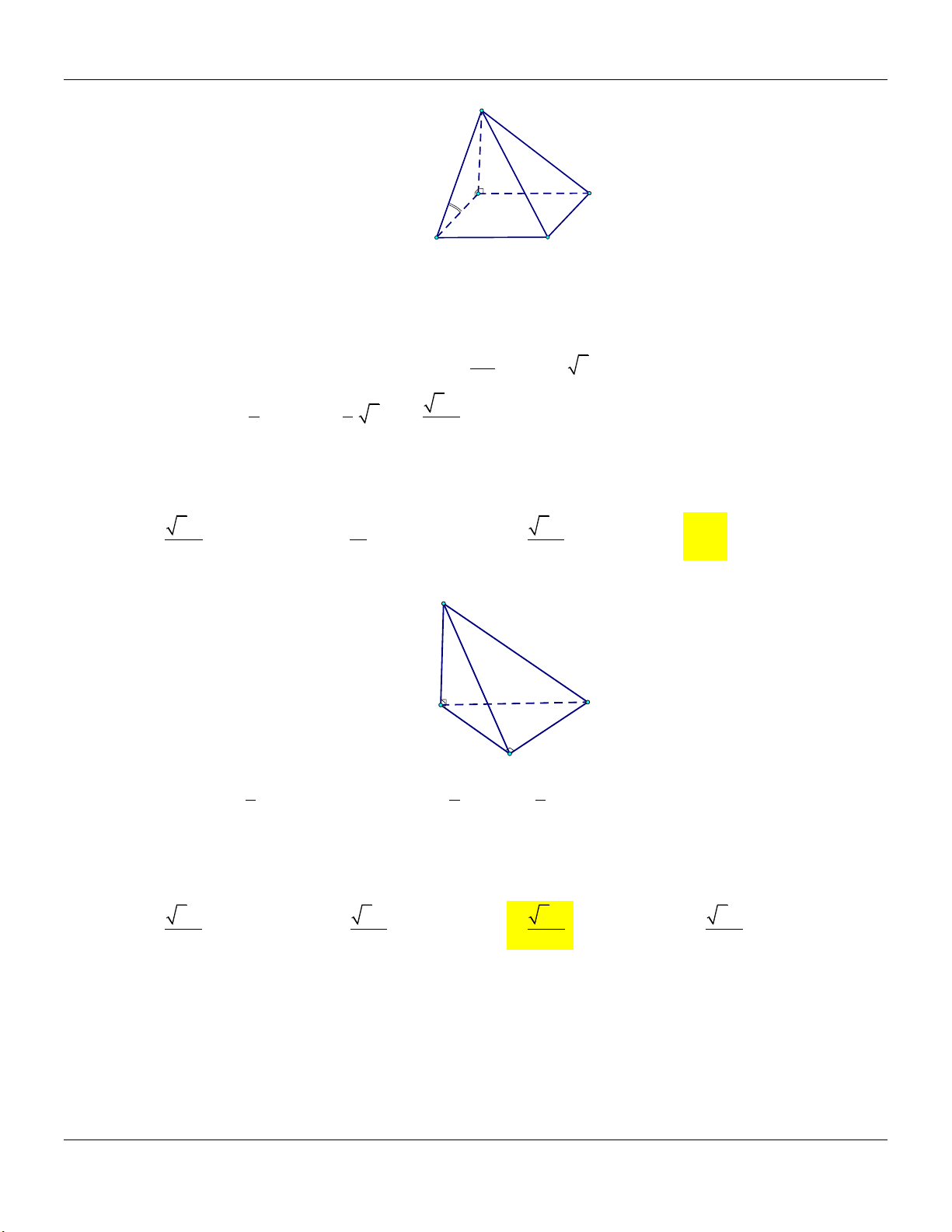
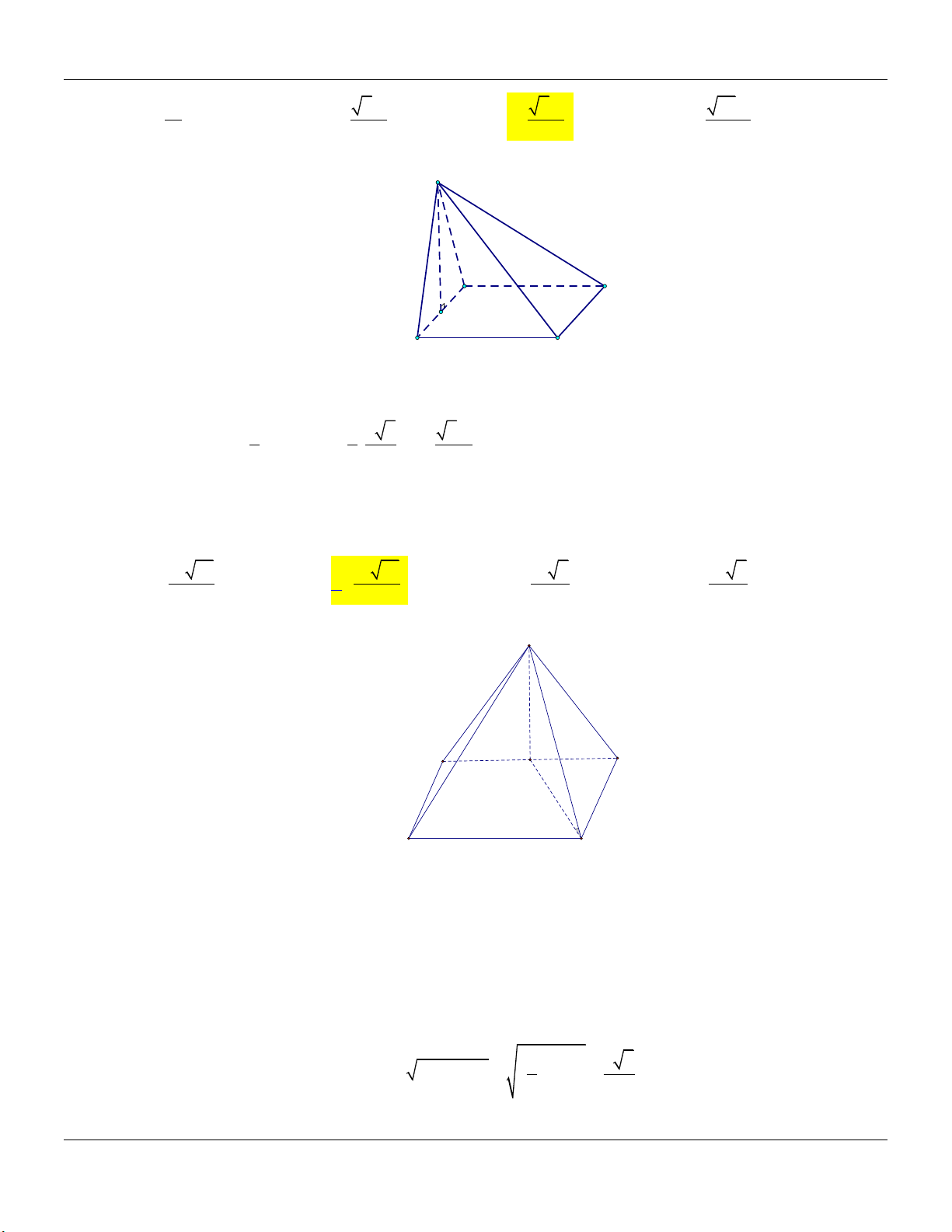
Dạng 4: Khối chóp có hai mặt bên cùng vuông góc với mặt đáy Phương pháp: Cho hình chóp .
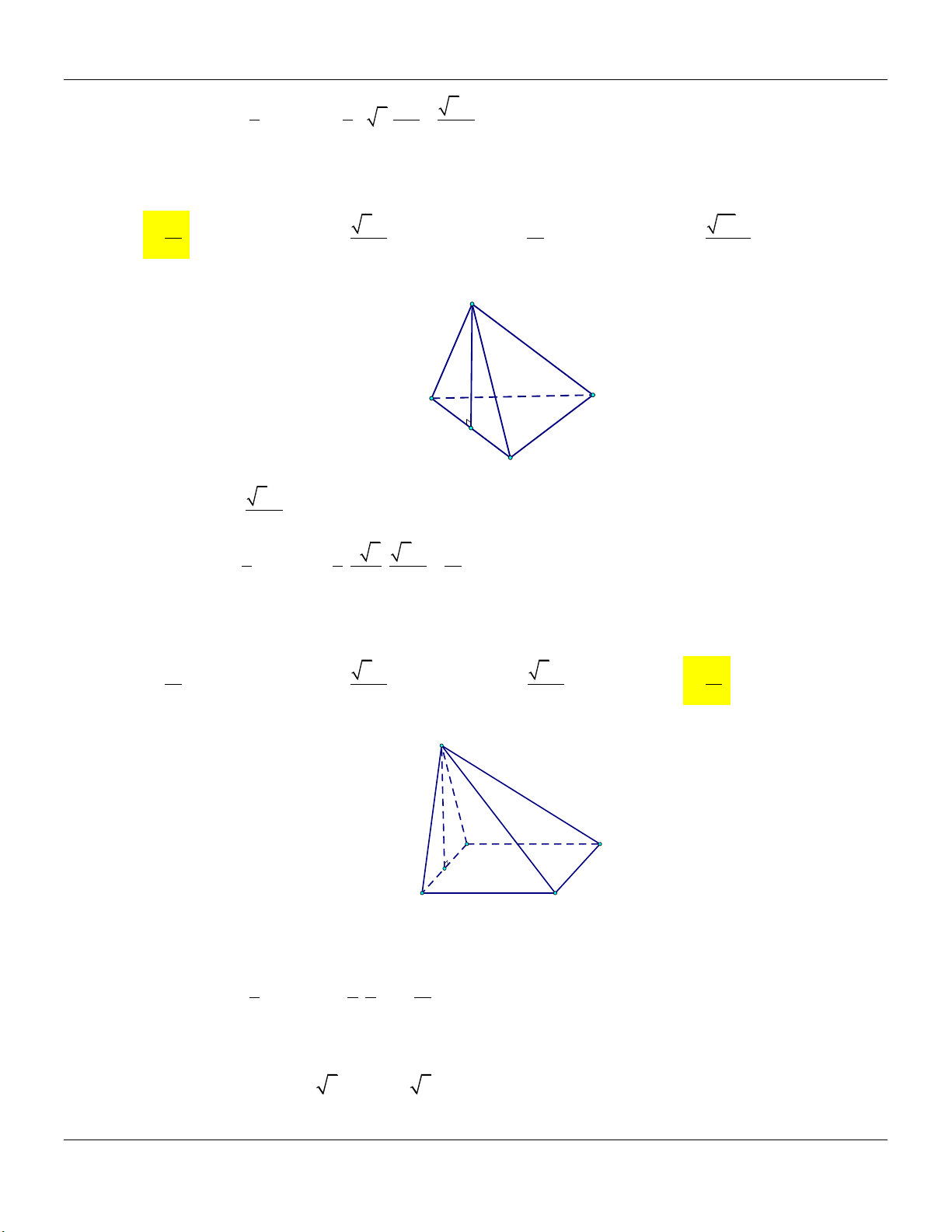
S ABCD có hai mặt SAB và SBC cùng vuông góc với mặt phẳng đáy… +) Đường cao: . SB Form hình vẽ: S
+) Thể tích khối chóp: V  1 S . B S 3 ABCD B A C D
BÀI TẬP TRẮC NGHIỆM MINH HỌA
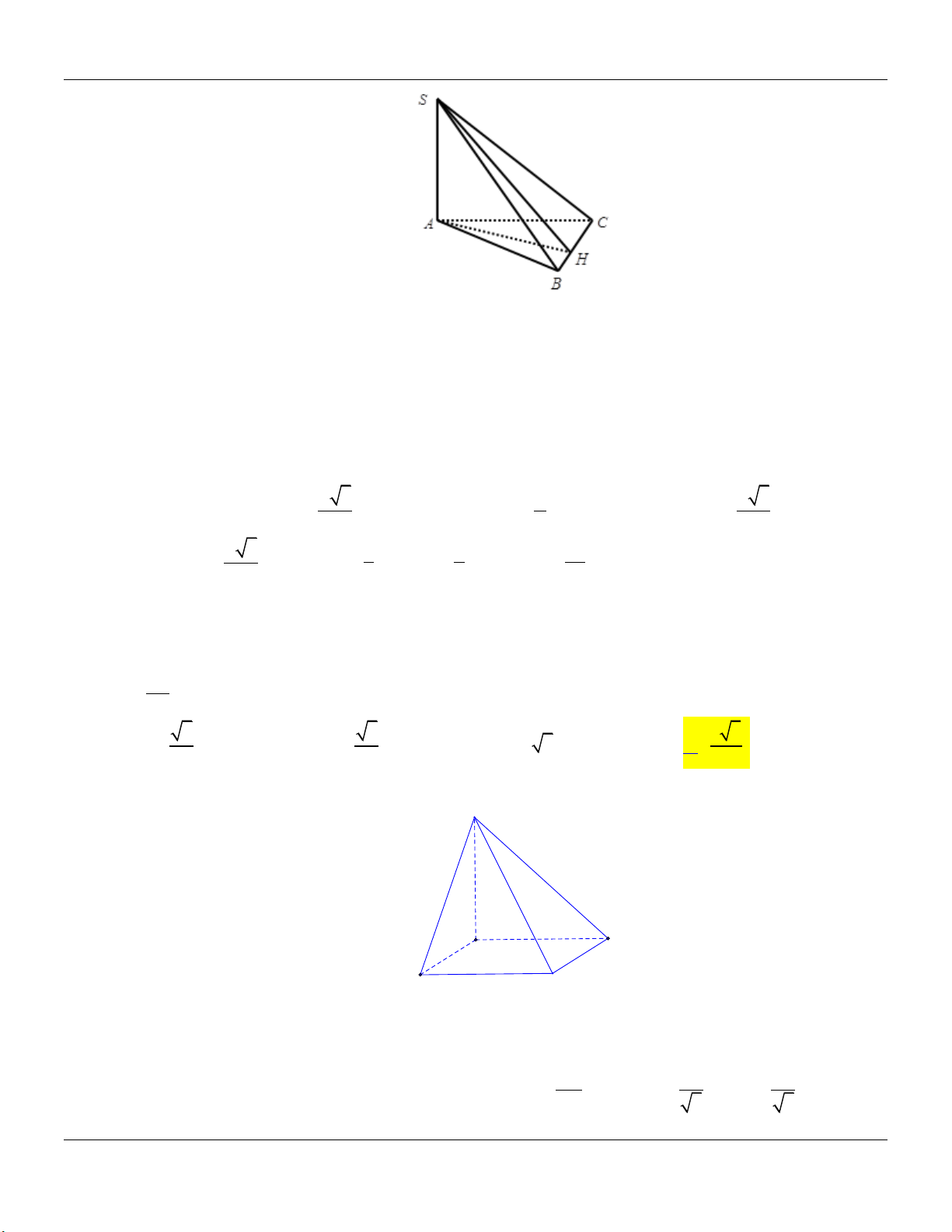
Câu 58: Cho hình chóp S.ABC là tam giác vuông tại A , ABC  30 , BC a . Hai mặt bên  SAB và
SAC cùng vuông góc với đáy  ABC, mặt bên SBC tạo với đáy một góc 45. Thể tích
của khối chóp S.ABC bằng 3 a 3 a 3 a 3 a A. . B. . C. . D. . 64 16 9 32
Câu 59: Cho hình chóp S.ABCD , đáy ABCD là hình vuông cạnh 2a . Hai mặt phẳng  SAB ,  SAD
cùng vuông góc với đáy, góc giữa hai mặt phẳng  SBC  và  ABCD bằng 30 . Tính tỉ số
3V biết V là thể tích của khối chóp S.ABCD . 3 a 3 3 8 3 A. . B. . C. 3 . D. . 12 2 3
Câu 60: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , hai mặt phẳng  SAB và
SAD cùng vuông góc với mặt phẳng  ABCD ; góc giữa đường thẳng SC và mặt phẳng
ABCD bằng 60. Tính theo a thể tích khối chóp S.ABCD . 3 a 6 3 a 6 A. 3 3a . B. . C. . D. 3 3 2a . 9 3
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN
Câu 61: Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a và hai mặt bên  SAB , SAC
cùng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết SC a 3 . 3 a 3 3 a 3 3 2a 6 3 a 6 A. . B. . C. . D. . 2 4 9 12
Câu 62: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , hai mặt phẳng  SAC  và
SAB cùng vuông góc với ABCD . Góc giữa SCD và ABCD là 60. Thể tích khối
chóp S.ABCD bằng 3 a 6 3 a 3 3 a 3 3 a 6 A. . B. . C. . D. . 3 3 6 6
Câu 63: Cho hình chóp .
S ABCD có đáy ABCD là hình chữ nhật. Hai mặt phẳng SAB và SAC
cùng vuông góc với mặt phẳng  ABCD. Biết rằng AB a , AD a 3 và SC  7a . Tính thể
tích khối chóp S.ABCD . A. 3 V a . B. 3 V  2a . C. V  3 3a . D. 3
V  4a
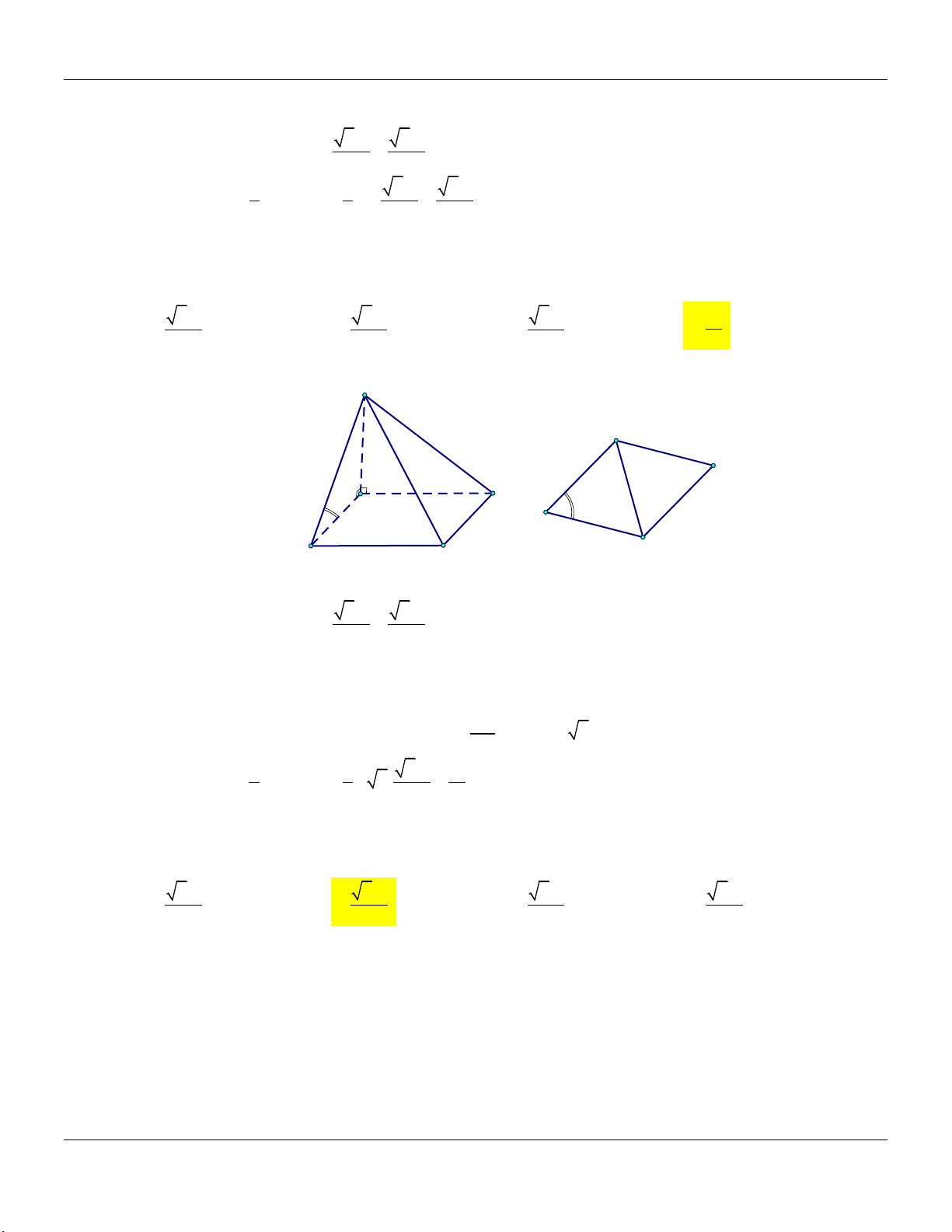
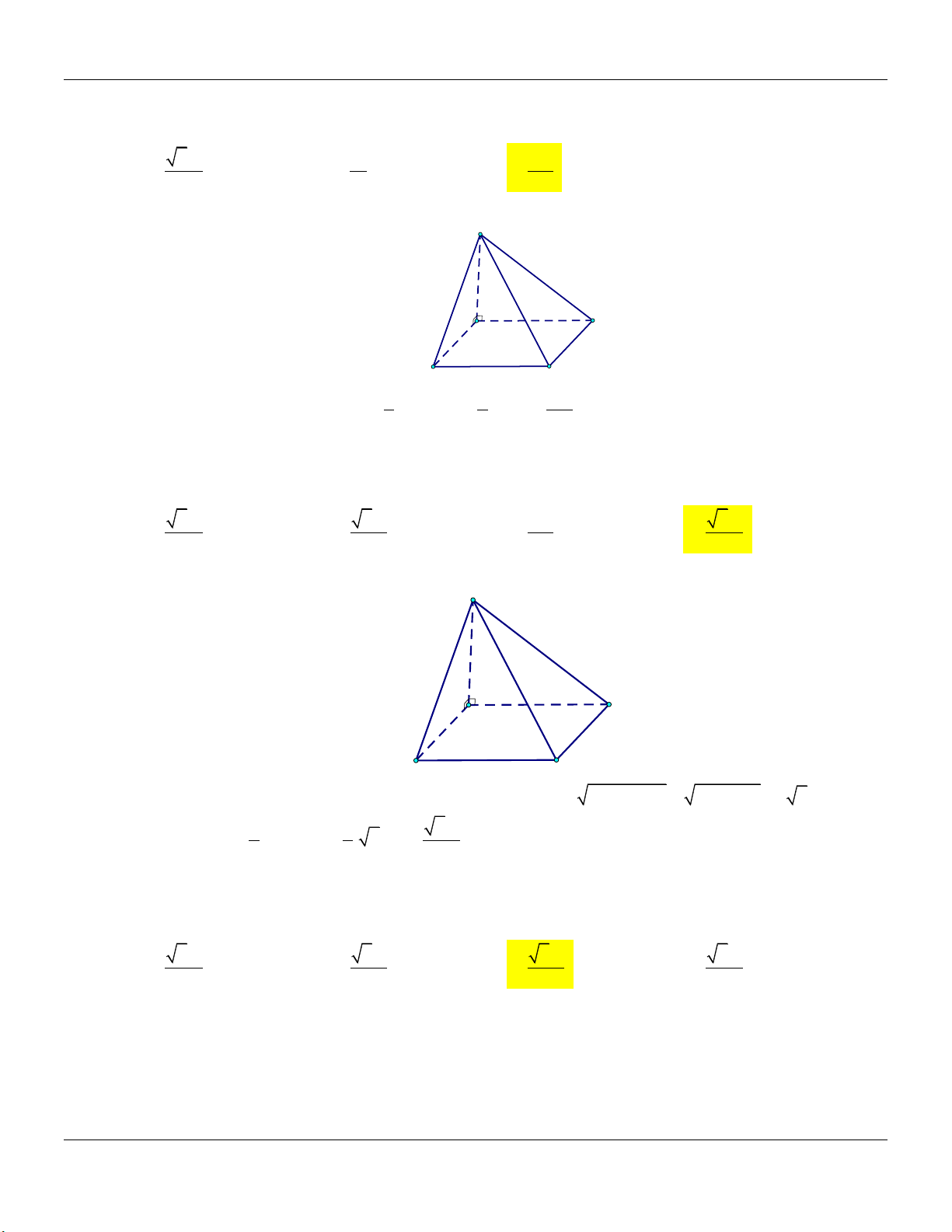
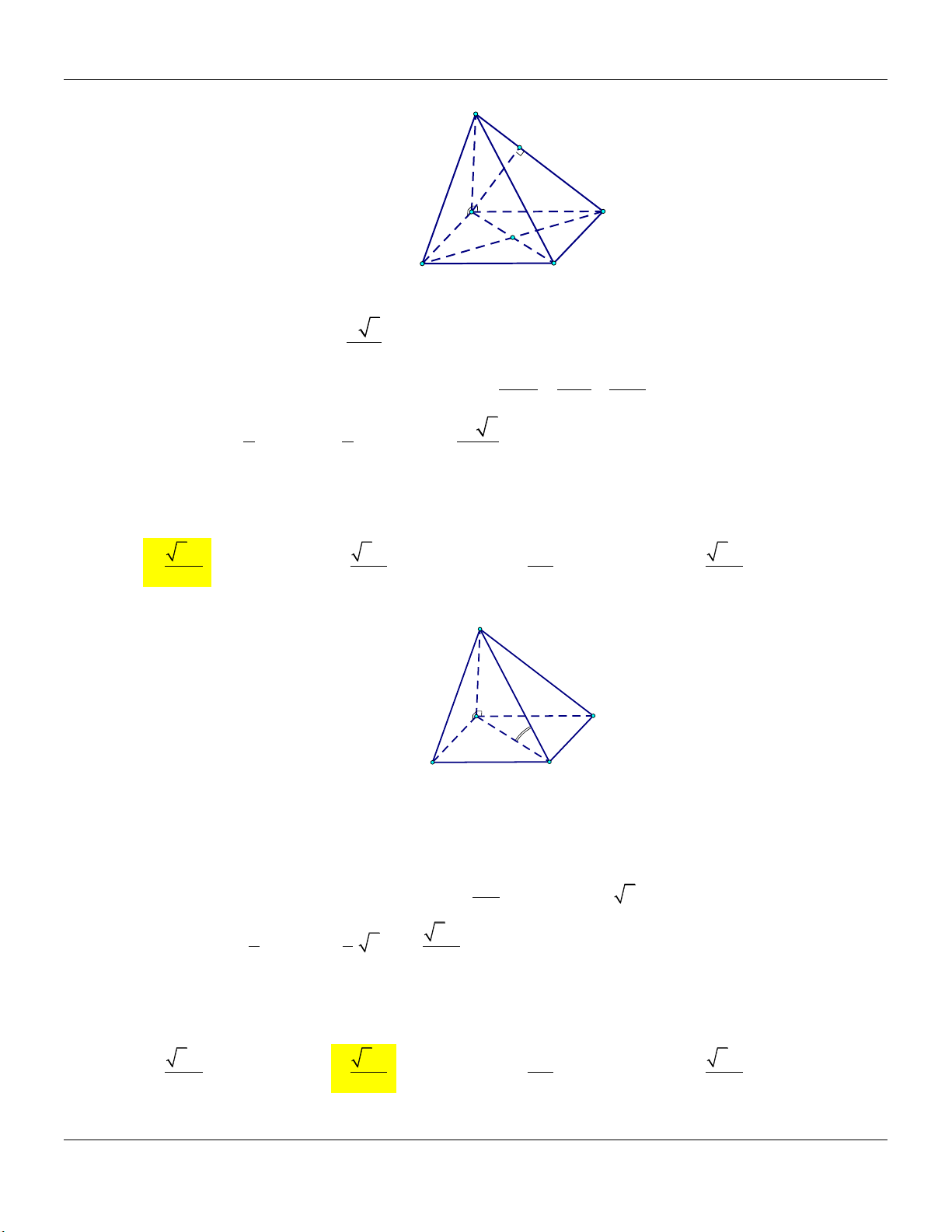
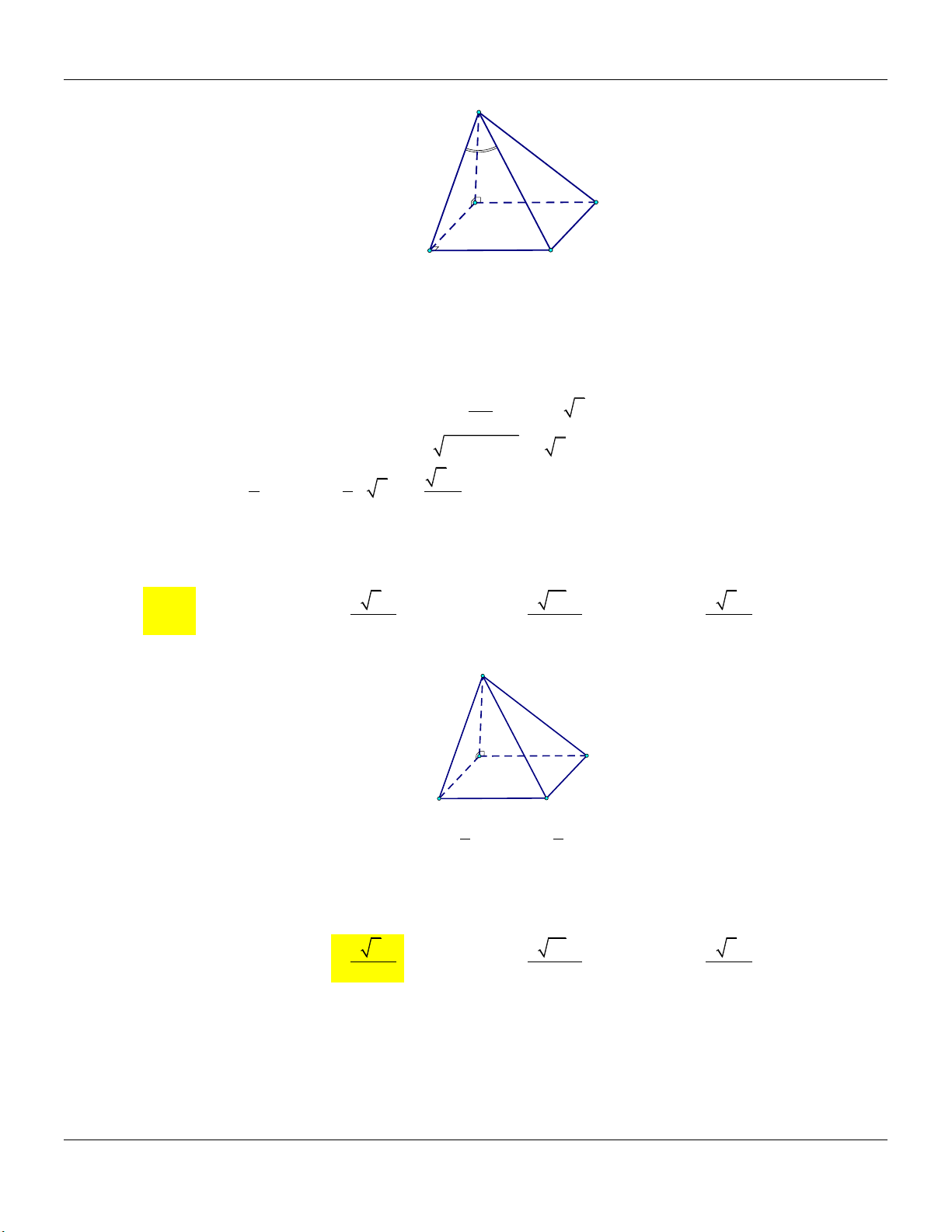
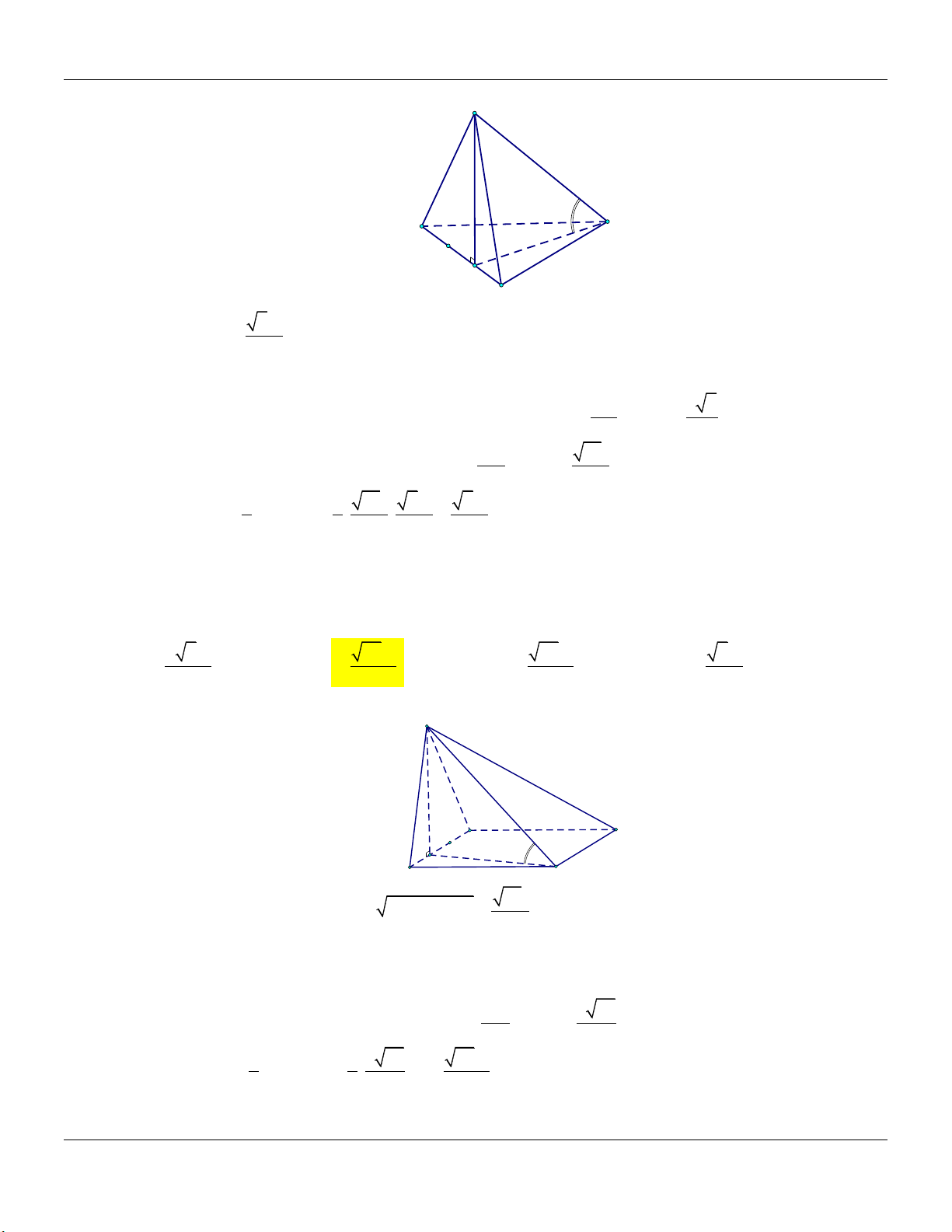
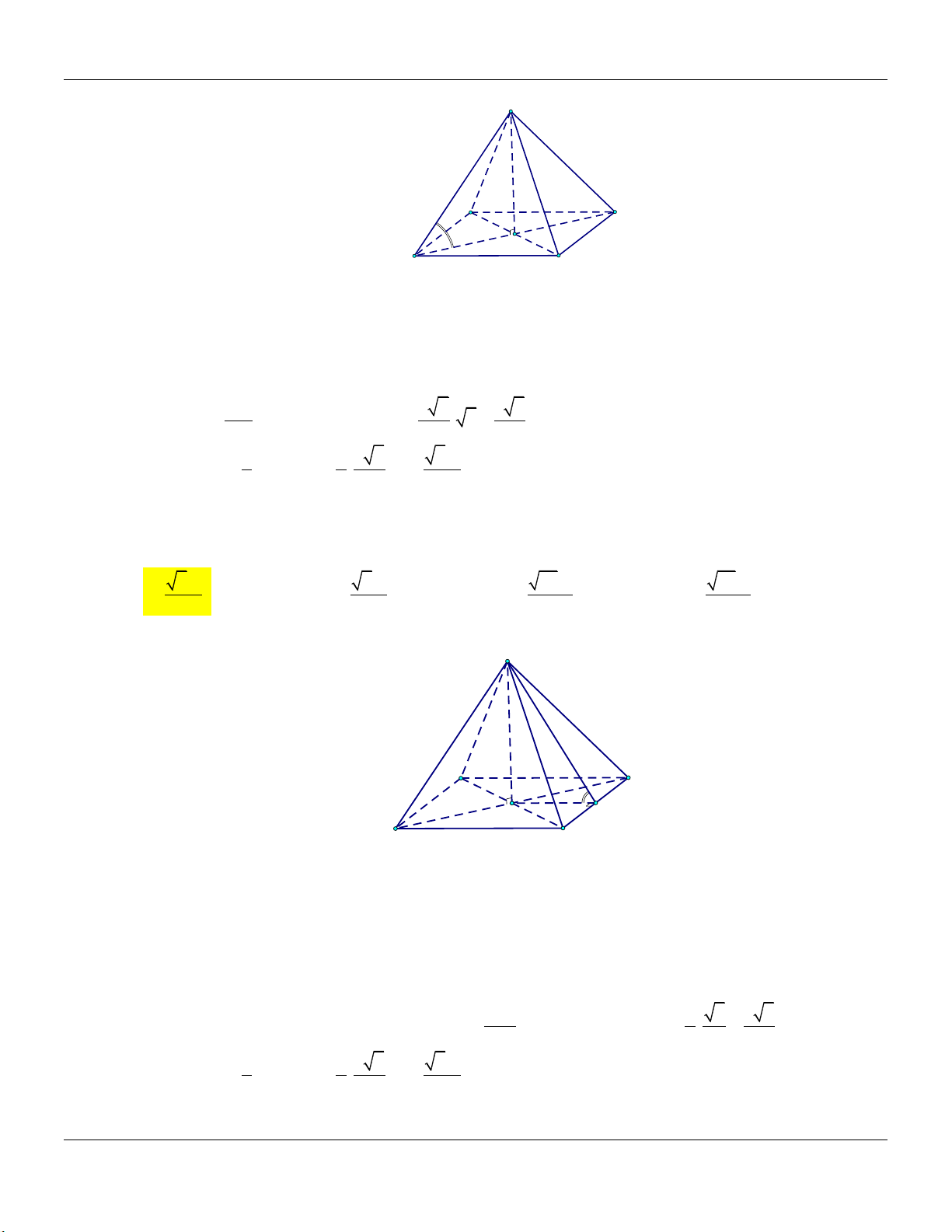
Dạng 5: Khối chóp đều Phương pháp:
Cho hình chóp tam giác đều . S ABC …
Cho hình chóp tứ giác đều . S ABCD …
+) Đường cao: SG,G là trọng tâm ABC.
+) Đường cao: SO,O là tâm hình vuông ABCD.
+) Thể tích khối chóp: V  1 S . G S
+) Thể tích khối chóp: V  1 S . O S 3 ABC 3 ABCD S S D A C C G O M A B B Đặc biệt: 3 2t
+) Thể tích khối tứ diện đều cạnh bằng t là V  12 3 2t
+) Thể tích khối chóp tứ giác đều có tất cả các cạnh bằng t là V  6 3 2t
+) Thể tích khối bát diện đều cạnh bằng t là V  3
BÀI TẬP TRẮC NGHIỆM MINH HỌA
Câu 64: Cho tứ diện đều ABCD có cạnh bằng t. Thể tích của khối tứ diện ABCD bằng 3 2t 3 2t 3 2t 3 3t A. . B. . C. . D. . 12 6 3 6
Câu 65: Cho hình chóp tam giác đều .
S ABC có cạnh đáy bằng .
a Biết SA  2a, thể tích của khối chóp . S ABC bằng
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 3 3a 3 2a 3 11a 3 3a A. . B. . C. . D. . 12 2 12 72
Câu 66: Cho hình chóp tam giác đều .
S ABC có cạnh đáy bằng .
a Biết SBC hợp với đáy một góc 30,
thể tích của khối chóp . S ABC bằng 3 3a 3 2a 3 11a 3 3a A. . B. . C. . D. . 12 2 12 72
Câu 67: Cho hình chóp tứ giác đều .
S ABCD có cạnh đáy bằng .
a Biết SA hợp với mặt đáy một góc
60, thể tích của khối chóp . S ABCD bằng 3 3a 3 6a 3 14a 3 15a A. . B. . C. . D. . 18 6 6 6
Câu 68: Cho hình chóp tứ giác đều .
S ABCD có cạnh đáy bằng .
a Biết SBC hợp với mặt đáy một góc
30, thể tích của khối chóp . S ABCD bằng 3 3a 3 6a 3 14a 3 15a A. . B. . C. . D. . 18 6 6 6
BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN
Câu 69: Cho hình chóp tam giác đều .
S ABC có cạnh đáy bằng .
a Biết SA hợp với đáy một góc 60,
thể tích của khối chóp . S ABC bằng 3 3a 3 2a 3 11a 3 3a A. . B. . C. . D. . 12 2 12 72
Câu 70: Cho hình chóp tứ giác đều .
S ABCD có cạnh đáy bằng .
a Biết SA  2a, thể tích của khối chóp . S ABCD bằng 3 3a 3 6a 3 14a 3 15a A. . B. . C. . D. . 18 6 6 6
Câu 71: Cho hình chóp tứ giác đều .
S ABCD có cạnh đáy bằng .
a Biết diện tích một mặt bên của hình
chóp đó có diện tích bằng 2
a , thể tích của khối chóp . S ABCD bằng 3 3a 3 6a 3 14a 3 15a A. . B. . C. . D. . 18 6 6 6
_____________________HẾT_____________________
Huế, 10h20’ Ngày 18 tháng 5 năm 2022
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
LỜI GIẢI CHI TIẾT Câu 1: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh a, SA vuông góc với đáy. Biết SA  2a, thể tích của khối chóp . S ABC bằng 3 2a 3 2a 3 3a 3 3a A. . B. . C. . D. . 12 6 3 6 Lời giải: S C A B 2 3a 2 3 1 1 3a 3a Ta có: S  . Vậy VS . A S  .2 . a  . ABC 4 S.ABC 3 ABC 3 4 6
Chọn đáp án D. Câu 2: Cho tứ diện .
O ABC có các cạnh OA , OB , OC đôi một vuông góc với nhau. Biết
OA  2 cm , OB  3cm , OC  6cm . Tính thể tích của khối tứ diện . O ABC . A.  3 6 cm . B.  3 36 cm  . C.  3 12 cm  . D.  3 18 cm  . Lời giải: OA OB Ta có: 
OA  OBC . OA OC 1 1 1 Do đó V  .O . A S  .O . A O . B OC  .2.3.6  6  3 cm  . O. ABC 3 OBC 6 6
Chọn đáp án A. Câu 3:
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng  ABCD, đáy ABCD là hình thang
vuông tại A và B có AB a, AD  3a, BC  .
a Biết SA a 3, tính thể tích khối chóp S.BCD theo . a 3 3a 3 2 3a 3 3a A. 3 2 3a . B. . C. . D. . 6 3 4 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia S A D B C 1 Ta có VS . A S . S .BCD 3 BCD 1 1 1 1 Lại có SSSA .
B AD BC   A . B AD 2  A . B BC a . BCD ABCD ABD 2 2 2 2 2 3 1 a a 3
Mà SA a 3  Va 3.  . S .BCD 3 2 6
Chọn đáp án B. Câu 4: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh a, SA vuông góc với đáy. Biết diện tích tam giác SAB bằng 2
4a , thể tích của khối chóp . S ABC bằng 3 2 3a 3 3a 3 3a A. 3 4 3a . B. . C. . D. . 3 3 6 Lời giải: S C A B 2 3a 1 Ta có: S
. Xét tam giác SAB vuông tại 2 A : S  .
SA AB  4a SA  8 . a ABC 4 SAB 2 2 3 1 1 3a 2 3a Vậy VS . A S  .8 . a  . S.ABC 3 ABC 3 4 3
Chọn đáp án B. Câu 5:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA a 2 và SA vuông
góc với mặt phẳng đáy, tam giác SBD là tam giác đều. Thể tích của khối chóp S.ABCD bằng. 3 a 2 3 2 2a A. 3 2a 2 . B. . C. 3 a 2 . D. . 3 3 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia S A D B C .
Đặt AB x , ABD vuông cân tại A BD x 2 .
Do SBD là tam giác đều nên  SB SD BD x 2 .
Lại có SAB vuông tại A .
SA AB SB  a 2  x  x 2 2 2 2 2 2 2 2 2
x  2a x a 2 . 1 1 aVSA Sa a  . S ABCD ABCD   3 2 2 2 . . . 2. 2 . 3 3 3
Chọn đáp án D. Câu 6: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh bằng a, SA vuông góc với đáy. Biết SB
hợp với mặt đáy một góc o
60 , thể tích của khối chóp . S ABCD bằng 3 2a 3 3a 3 2a 3 7a A. . B. . C. . D. . 3 3 3 3 Lời giải: S A D B C Ta có: 2 Sa . ABCD
Do SA   ABCD nên AB là hình chiếu vuông góc của SB trên  ABCD. Suy ra:  ;
SB ABCD  ; SB AB o 
SBA SBA  60 . SA
Xét tam giác SAB vuông tại A : tanSBA   SA a 3. AB 3 1 1 3a Vậy 2 VS . A S  . 3 . a a  . S.ABCD 3 ABCD 3 3
Chọn đáp án B. Câu 7: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh a, SA vuông góc với đáy. Biết SB hợp với
mặt đáy một góc bằng 0
60 , thể tích của khối chóp . S ABC bằng 3 2a 3 a 3 3a 3 3a A. . B. . C. . D. . 12 4 3 6 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia S C A B 2 3a Ta có: S
. Do SA   ABC nên AB là hình chiếu vuông góc của SB trên  ABC. ABC 4 Suy ra: S ;
B ABC  S ; B AB  SB . A SA
Xét tam giác SAB vuông tại A : tanSBA   SA A .
B tanSBA a 3. AB 2 3 1 1 3a a Vậy VS . A S  .a 3.  . S.ABC 3 ABC 3 4 4
Chọn đáp án B. Câu 8:
Cho khối chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với đáy và khoảng a 2
cách từ A đến mặt phẳng SBC  bằng
. Tính thể tích V của khối chóp đã cho. 2 3 3 3 3 A.a V . B.a V . C.a V . D. 3 V a . 3 2 9 Lời giải: S H A D B C
Kẻ AH vuông góc SB .
Ta có AH  (SBC) nên AH chính là khoảng cách từ A đến mp SBC  . 1 1 1 1 1 1 1 Ta có       . 2 2 2 2 2 2 2 AH SA AB SA AH AB a 3 1
Suy ra SA a . Thể tích cần tính là  . .  a V a a a . 3 3
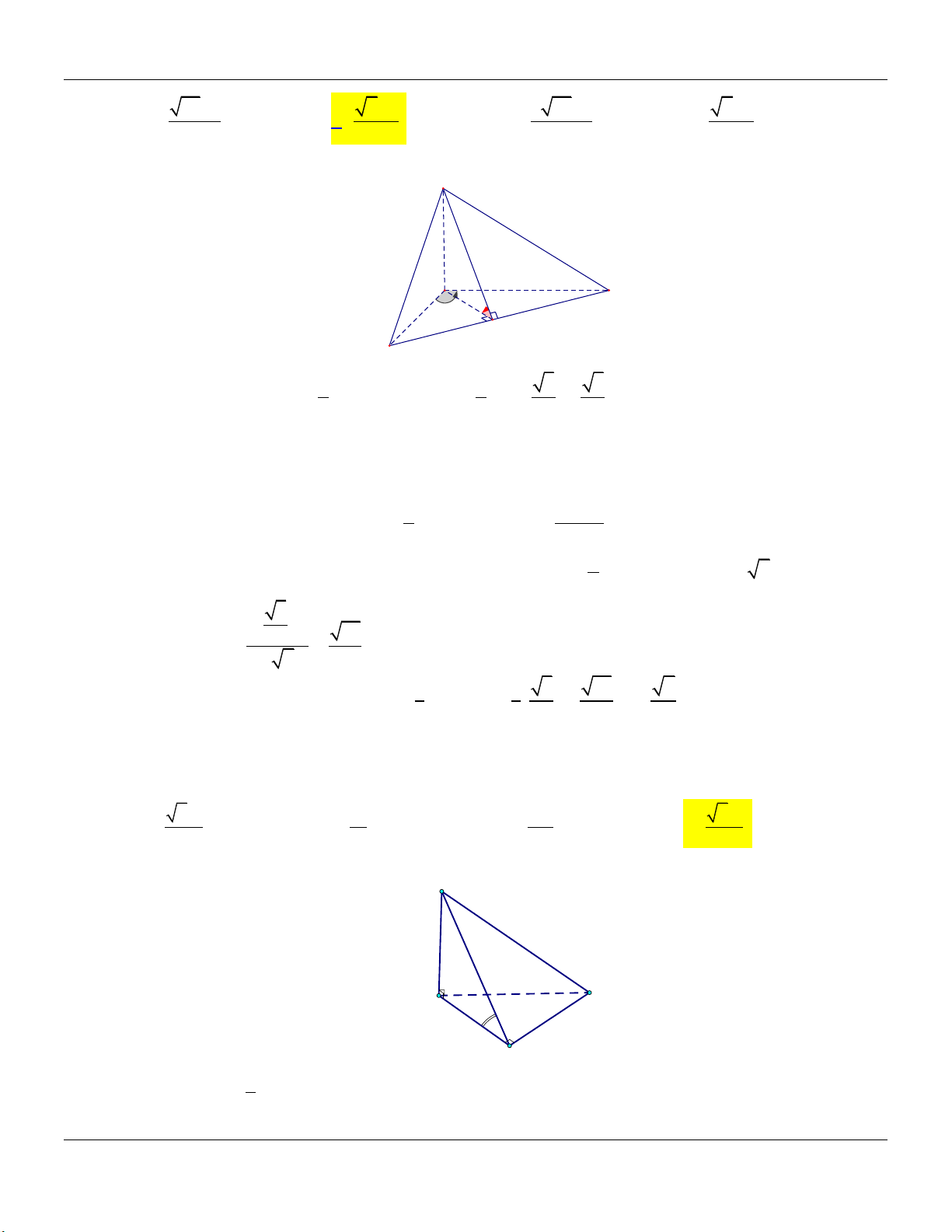
Chọn đáp án A. Câu 9:
Tính thể tích khối chóp S.ABC có AB a , AC  2a , BAC  120 , SA   ABC  , góc giữa
SBC và  ABC là 60 .
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 3 21 a 3 7 a 3 3 21 a 3 7 a A. . B. . C. . D. . 14 14 14 7 Lời giải: S A 2a 120o C 60o a H B 1 1 3 3 + Diện tích đáy SA . B AC.sin120  . .2 a . a 2  a ABC 2 2 2 2
+ Tính chiều cao SA : 
SBC , ABC
Dựng AH BC (với H BC ) suy ra SH BC , do đó góc   
  SHA  60 , suy
ra SA AH. tan 60  1 2.S
Tính AH : ta có diện tích SAH.BC ABCAH
mà theo định lý hàm côsin thì ABC 2 BC  1  2 2 2
BC AB AC  2. . AB AC.cos A 2 2
a  4a  2. . a 2 . a      BC a  7. 2  2 7a 3 2 2. a 21 Suy ra 2 AH   a . a 7 7 1 1 3 21 7
+ Thể tích khối chóp S.ABC là V S .SA 2  . a . a 3  a . 3 ABC 3 2 7 14
Chọn đáp án B.
Câu 10: Cho hình chóp .
S ABC có đáy là tam giác vuông tại B, AB a, BC  2a, SA vuông góc với đáy.
Biết SB hợp với mặt đáy một góc 0
60 , thể tích của khối chóp . S ABC bằng 3 2a 3 a 3 2a 3 3a A. . B. . C. . D. . 12 2 3 3 Lời giải: S C A B 1 Ta có: 2 SA . B BC a . ABC 2
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Do SA   ABC nên AB là hình chiếu vuông góc của SB trên  ABC.
Suy ra: SB ABC  SB AB  SBA SBA  0 ; ; 60 . SA
Xét tam giác SAB vuông tại A : tanSBA   SA A .
B tanSBA a 3. AB 3 1 1 3a Vậy 2 V  . SA S  .a 3.a  . S.ABC 3 ABC 3 3
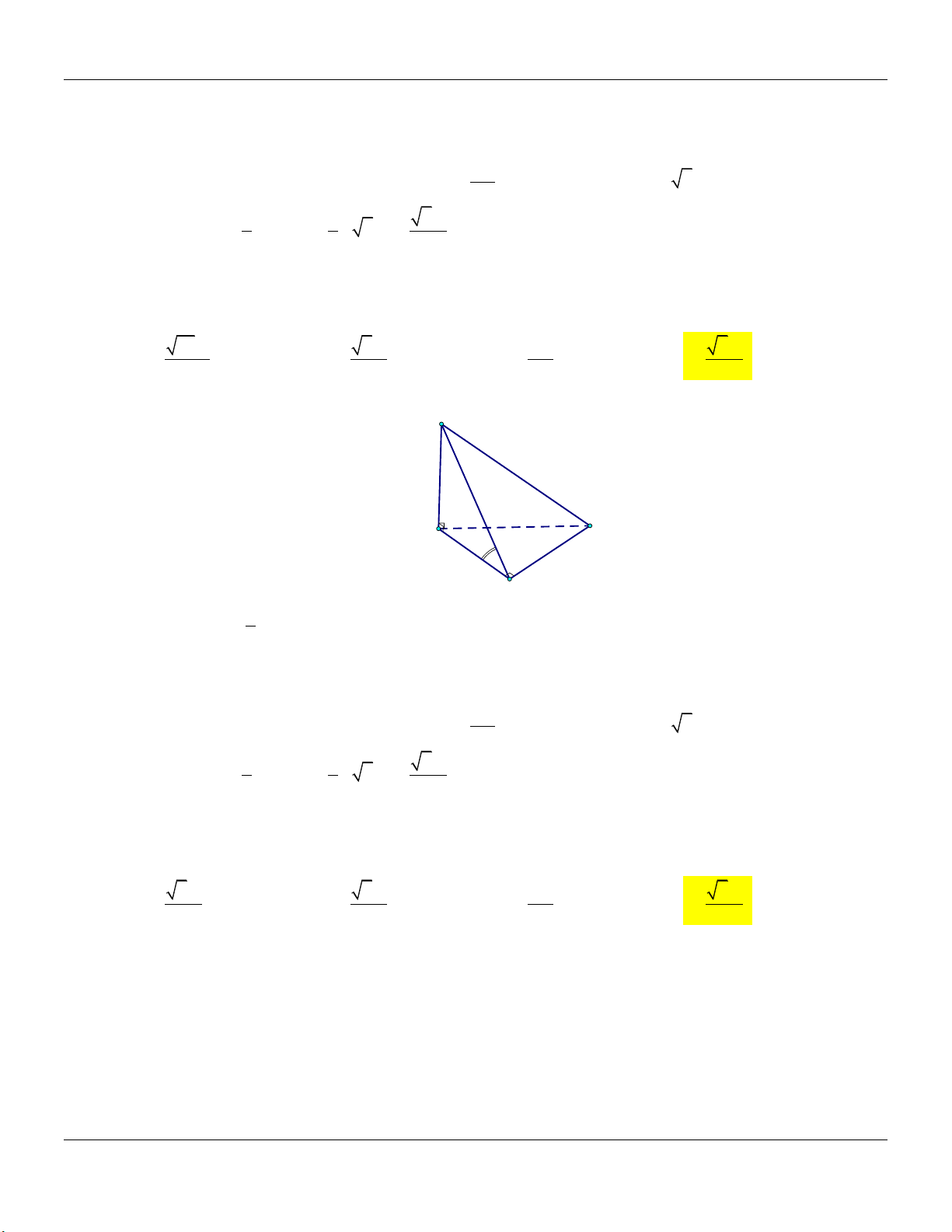
Chọn đáp án D.
Câu 11: Cho hình chóp .
S ABC có đáy là tam giác vuông tại B, AB a, BC  2a, SA vuông góc với đáy.
Biết SBC hợp với mặt đáy một góc 0
60 , thể tích của khối chóp . S ABC bằng 3 15a 3 5a 3 2a 3 3a A. . B. . C. . D. . 3 2 3 3 Lời giải: S C A B 1 Ta có: 2 SA . B BC a . ABC 2 BC AB Ta có: 
BC  SAB  BC S .
B Suy ra:  SBC  ABC  SBA SBA  0 ; 60 . BC   SA SA
Xét tam giác SAB vuông tại A : tanSBA   SA A .
B tanSBA a 3. AB 3 1 1 3a Vậy 2 V  . SA S  .a 3.a  . S.ABC 3 ABC 3 3
Chọn đáp án D.
Câu 12: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh bằng a, SA vuông góc với đáy. Biết
SBD hợp với mặt đáy một góc 0
60 , thể tích của khối chóp . S ABCD bằng 3 6a 3 3a 3 2a 3 6a A. . B. . C. . D. . 3 3 3 6 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia S A D O B C Ta có: 2 Sa . ABCDBD AO
Gọi O là tâm hình vuông ABCD. Ta có: 
BD  SAO  BD S . O BD   SA
Suy ra:  SBD ABCD  SOA SOA  0 ; 60 . SA a 2 a 6
Xét tam giác SAO vuông tại o A : tanSOA   SA  .tan 60  . AO 2 2 3 1 1 a 6 6a Vậy 2 VS . A S  . .a  . S.ABCD 3 ABCD 3 2 6
Chọn đáp án D.
Câu 13: Cho hình chóp .
S ABC có đáy là tam giác vuông tại B, AB a, BC  2a, SA vuông góc với đáy.
Biết SC hợp với SAB một góc 0
30 , thể tích của khối chóp . S ABC bằng 3 15a 3 5a 3 11a 3 3a A. . B. . C. . D. . 3 2 3 3 Lời giải: S C A B 1 Ta có: 2 SA . B BC a . ABC 2 BC AB Ta có: 
BC  SAB 
là hình chiếu vuông góc của SC trên SAB. BC SBSA
Suy ra: SC SAB  SC SB  BSC BSC  0 ; ; 30 . BC BC
Xét tam giác SBC vuông tại B : sin BSC   SC   4 . a SC sin BSC
Xét tam giác ABC vuông tại 2 B AC  2 AB  2 BC  2 : 5a .
Xét tam giác SAC vuông tại 2 2
A : SA SC AC a 11.
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 3 1 1 11a Vậy 2 VS . A S  .a 11.a  . S.ABC 3 ABC 3 3
Chọn đáp án C.
Câu 14: Cho hình chóp .
S ABCD có đáy là hình chữ nhật có AB a, BC  2a, SA vuông góc với đáy.
Biết SBD hợp với mặt đáy một góc o
60 , thể tích của khối chóp . S ABCD bằng 3 2a 3 4 15a 3 2 15a 3 4 3a A. . B. . C. . D. . 5 15 3 9 Lời giải: S A D H B C Ta có: 2 SA . B BC  2a . ABCDBD AH Dựng AH  . BD Ta có: 
BD  SAH  BD SH. BD   SA
Suy ra:  SBD;ABCD  . SHA 1 1 1 5 2 5a
Xét tam giác BAD vuông tại A :     AH  . 2 2 2 2 AH AB AD 4a 5 SA 2 15a
Xét tam giác SAH vuông tại A : tanSHA   SA  . AH 5 3 1 1 2 15a 4 15a Vậy 2 VS . A S  . .2a  . S.ABCD 3 ABCD 3 5 15
Chọn đáp án B.
Câu 15: Cho hình chóp .
S ABCD có đáy là hình thoi cạnh bằng o
a, ABC  60 , SA vuông góc với đáy.
Biết SA  2a, thể tích của khối chóp . S ABCD bằng 3 3a 3 6a 3 3a 3 3a A. . B. . C. . D. . 3 6 12 4 Lời giải: S A a D A D 60o B a B C C
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Do ABCD là hình thoi cạnh bằng o
a, ABC  60  ABC là tam giác đều cạnh . a 2 2 3a 3a Suy ra: S  2S  2.  . ABCD ABC 4 2 2 3 1 1 3a 3a Vậy V  . SA S  .2 . a  . S.ABCD 3 ABCD 3 2 3
Chọn đáp án A.
Câu 16: Cho hình chóp .
S ABCD có đáy là hình thoi cạnh bằng o
a, ABC  60 , SA vuông góc với đáy.
Biết SB hợp với đáy một góc o
60 , thể tích của khối chóp . S ABCD bằng 3 3a 3 6a 3 3a 3 a A. . B. . C. . D. . 3 6 12 2 Lời giải: S A a D A D 60o B a B C C
Do ABCD là hình thoi cạnh bằng o
a, ABC  60  ABC là tam giác đều cạnh . a 2 2 3a 3a Suy ra: S  2S  2.  . ABCD ABC 4 2
Do SA   ABCD nên AB là hình chiếu vuông góc của SB trên  ABCD. Suy ra:  ;
SB ABCD   ;
SB AB  SB . A SA
Xét tam giác SAB vuông tại A : tanSBA   SA a 3. AB 2 3 1 1 3a a Vậy VS . A S  .a 3.  . S.ABCD 3 ABCD 3 2 2
Chọn đáp án D.
Câu 17: Cho hình chóp .
S ABCD có đáy là hình thang vuông tại A, B, A D 2 ,a A BB C  , a S A
vuông góc với đáy. Biết SC  2a, thể tích của khối chóp . S ABCD bằng 3 3a 3 2a 3 6a 3 3a A. . B. . C. . D. . 2 2 2 4 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia S A D B C
ABAD BC 2 3a Ta có: S   . ABCD 2 2
Xét tam giác SAC vuông tại A SA SC AC   a  a 2 2 2 2 : 2 2 a 2. 2 3 1 1 3a 2a Vậy V  . SA S  .a 2.  . S.ABCD 3 ABCD 3 2 2
Chọn đáp án B.
Câu 18: Cho hình chóp .
S ABCD có đáy là hình thang vuông tại A, B, A D 2 ,a A BB C  , a S A
vuông góc với đáy. Biết SC hợp với mặt đáy một góc 0
60 , thể tích của khối chóp . S ABCD bằng 3 3a 3 2a 3 6a 3 3a A. . B. . C. . D. . 2 2 2 4 Lời giải: S A D B C
ABAD BC 2 3a Ta có: S   . ABCD 2 2
Do SA   ABCD  AC là hình chiếu vuông góc của SC trên  ABCD.
Suy ra: SC; ABCD  S . CA SA
Xét tam giác SAC vuông tại A : tanSCA
SA AC.tanSCA a 2. 3  a 6. AC 2 3 1 1 3a 6a Vậy V  . SA S  .a 6.  . S.ABCD 3 ABCD 3 2 2
Chọn đáp án C.
Câu 19: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc với mặt
phẳng đáy. Gọi M là trung điểm của CD . Biết khoảng cách giữa hai đường thẳng BC và SM a 3 bằng
. Tính thể tích của khối chóp đã cho theo a . 4
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 3 a 3 3 a 3 3 a 3 3 a 3 A. B. C. D. 4 2 6 12 Lời giải: S H A D N O M B C
Gọi N là trung điểm của AB BC// SMN  .
d BC, SM   d BC,SMN   d B,SMN   d  ,
A SMN  .
Dựng AH vuông góc với SN tại H AH  SMN  . a
Vậy d A SMN  3 ,  AH  . 4 1 1 1 a 3
Lại có, trong tam giác vuông SAN :    SA  . 2 2 2 AH AN AS 2 3 1 a 3 a 3 Vậy 2 V  .a .  . S . ABCD 3 2 6
Chọn đáp án C.
Câu 20: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh a, SA vuông góc với đáy. Biết SB  2a, thể tích của khối chóp . S ABC bằng 3 2a 3 a 3 3a 3 3a A. . B. . C. . D. . 12 4 3 6 Lời giải: S C A B 2 3a Ta có: S
. Xét tam giác SAB vuông tại 2 2
A : SA SB AB a 3. ABC 4 2 3 1 1 3a a Vậy VS . A S  .a 3.  . S.ABC 3 ABC 3 4 4
Chọn đáp án B.
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Câu 21: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh bằng a, SA vuông góc với đáy. Biết
SA  2a, thể tích của khối chóp . S ABCD bằng 3 2a 3 a 3 2a A. . B. . C. . D. 3 a . 12 2 3 Lời giải: S A D B C 3 1 1 2a Ta có: 2 Sa . Vậy 2 V  . SA S  .2 . a a  . ABCD S.ABCD 3 ABCD 3 3
Chọn đáp án C.
Câu 22: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh bằng a, SA vuông góc với đáy. Biết
SC  3a, thể tích của khối chóp . S ABCD bằng 3 2a 3 3a 3 2a 3 7a A. . B. . C. . D. . 3 3 3 3 Lời giải: S A D B C Ta có: S  2
a . Xét tam giác SAC vuông tại A SA  2 SC  2 AC  2 a  2 : 9 2a a 7. ABCD 3 1 1 7a Vậy 2 VS . A S  . 7 . a a  . S.ABCD 3 ABCD 3 3
Chọn đáp án D.
Câu 23: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh a, SA vuông góc với đáy. Biết SBC hợp
với mặt đáy một góc bằng 0
30 , thể tích của khối chóp . S ABC bằng 3 2a 3 3a 3 3a 3 3a A. . B. . C. . D. . 12 8 24 6 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia S A C M B 2 3a Ta có: S  . ABC 4 BC AM
Dựng AM BC, M là trung điểm BC. Ta có: 
BC  SAM  BC SM. BC   SA
Suy ra:  SBC;ABC  SM . A SA a 3 a
Xét tam giác SAM vuông tại o A : tanSMA
SA AM.tanSMA  .tan 30  . AM 2 2 2 3 1 1 a 3a 3a Vậy VS . A S  . .  . S.ABC 3 ABC 3 2 4 24
Chọn đáp án C.
Câu 24: Cho hình chóp S.ABCD có đáy là hình thang vuông ở A và B , AB  3a ,
AD  2BC  2a . SA vuông góc với đáy, mặt phẳng  SCD tạo với đáy một góc 45 . Thể
tích khối chóp S.ABC bằng 3 a 3 3 3a 10 3 8a 3 4 3a A. . B. . C. . D. 2 10 10 3 Lời giải: Ta có 2 2 AC
AB BC a 10
Gọi M là trung điểm AD  3
AM MD a và CM AD ; 2 2 DC
DM MC a 10  sin ACD  5 3 10
Kẻ AN DC ta có AN AC sin ACN a 5 2 3 10 1 3a
Góc giữa  SCD với  ABCD  là SNA  45 ; SA AN  ; a SA . B BC  . 5 ABC 2 2
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 1 3 10 Vậy 3 VS .SA a . S . ABC 3 ABC 10
Chọn đáp án B.
Câu 25: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh a, SA vuông góc với đáy. Biết SC hợp với
mặt phẳng SAB một góc bằng 30, thể tích của khối chóp . S ABC bằng 3 6a 3 a 3 3a 3 3a A. . B. . C. . D. . 12 4 3 6 Lời giải: S A C M B 2 3a Ta có: S  . ABC 4 CM AB
Dựng CM AB, M là trung điểm . AB Ta có: 
CM  SAB. CM   SA
Suy ra: SM là hình chiếu vuông góc của SC trên SAB  SC;SAB  CSM. CM CM a 3 a 3
Xét tam giác SMC vuông tại M : sinCSM   SC   0 : sin 30   a 3. SC 2 1 sinCSM 2. 2
Xét tam giác SAC vuông tại 2 2
A : SA SC AC a 2. 2 3 1 1 3a 6a Vậy V  . SA S  .a 2.  . S.ABC 3 ABC 3 4 12
Chọn đáp án A.
Câu 26: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O , AB a, a 3
AD a 3, SA   ABCD . Khoảng cách từ O đến mặt phẳng  SCD bằng . Tính thể 4
tích V của khối chóp S.ABCD . 3 a 15 3 a 3 3 a 3 A. V  . B. 3 V a 3 . C. V  . D. V  . 10 3 6 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia S H A D O B C
Gọi H là hình chiếu của A lên SD d  ;
A SCD  AH .
AH d O SCD a 3 2. ;  . 2 1 1 1
Xét SAD vuông ở A , đường cao AH , có:    SA a . 2 2 2 AH AS AD 3  1 1 a 3 VS . A S  .S . A A . B AD  . S . ABCD 2 ABCD 2 3
Chọn đáp án C.
Câu 27: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh bằng a, SA vuông góc với đáy. Biết SC
hợp với mặt đáy một góc 45, thể tích của khối chóp . S ABCD bằng 3 2a 3 3a 3 2a 3 7a A. . B. . C. . D. . 3 3 3 3 Lời giải: S A D B C Ta có: 2 Sa . ABCD
Do SA   ABCD nên AC là hình chiếu vuông góc của SC trên  ABCD.
Suy ra: SC ABCD  SC AC  SCA SCA  0 ; ; 45 . SA
Xét tam giác SAC vuông tại A : tanSCA
SA AC a 2. AC 3 1 1 2a Vậy 2 VS . A S  . 2 . a a  . S.ABCD 3 ABCD 3 3
Chọn đáp án A.
Câu 28: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh bằng a, SA vuông góc với đáy. Biết SBC
hợp với mặt đáy một góc 60, thể tích của khối chóp . S ABCD bằng 3 2a 3 3a 3 2a 3 7a A. . B. . C. . D. . 3 3 3 3 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia S A D B CBC AB Ta có: 2 Sa . Ta có: 
BC  SAB  BC S . B ABCD BC   SA
Suy ra:  SBC ABCD  SBA SBA  0 ; 60 . SA
Xét tam giác SAB vuông tại A : tanSBA   SA a 3. AB 3 1 1 3a Vậy 2 VS . A S  . 3 . a a  . S.ABCD 3 ABCD 3 3
Chọn đáp án B.
Câu 29: Cho hình chóp .
S ABC có đáy là tam giác vuông tại B, AB a, BC  2a, SA vuông góc với đáy.
Biết SA  3a, thể tích của khối chóp . S ABC bằng 3 2a 3 a 3 3a A. . B. . C. . D. 3 a . 12 2 3 Lời giải: S A C B 1 1 1 Ta có: 2 SA .
B BC a . Vậy 2 3 VS . A S  .3 . a a a . ABC 2 S.ABC 3 ABC 3
Chọn đáp án D.
Câu 30: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh bằng a, SA vuông góc với đáy. Biết SC
hợp với SAB một góc 30, thể tích của khối chóp . S ABCD bằng 3 6a 3 3a 3 2a 3 6a A. . B. . C. . D. . 3 3 3 6 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia S A D B C Ta có: 2 Sa . ABCDBC AB Ta có: 
BC  SAB  SB là hình chiếu vuông góc của SC trên SAB. BC   SA
Suy ra: SC SAB  BSC BSC  0 ; 30 . BC
Xét tam giác SBC vuông tại B : tan BSC   SB a 3. SB
Xét tam giác SAB vuông tại 2 2
A : SA SB AB a 2. 3 1 1 2a Vậy 2 VS . A S  .a 2.a  . S.ABCD 3 ABCD 3 3
Chọn đáp án C.
Câu 31: Cho hình chóp .
S ABCD có đáy là hình chữ nhật có AB a, BC  2a, SA vuông góc với đáy.
Biết SA  3a, thể tích của khối chóp . S ABCD bằng 3 2 5a 3 2 15a 3 4 3a A. 3 2a . B. . C. . D. . 3 3 9 Lời giải: S A D B C 1 1 Ta có: 2 SA .
B BC  2a . Vậy 2 3 V  . SA S  .3 .
a 2a  2a . ABCD S.ABCD 3 ABCD 3
Chọn đáp án A.
Câu 32: Cho hình chóp .
S ABCD có đáy là hình chữ nhật có AB a, BC  2a, SA vuông góc với đáy.
Biết SD  3a, thể tích của khối chóp . S ABCD bằng 3 2 5a 3 2 15a 3 4 3a A. 3 2a . B. . C. . D. . 3 3 9 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia S A D B C Ta có: 2 SA .
B BC  2a . Xét tam giác SAD vuông tại 2 2
A : SA SD AD a 5. ABCD 3 1 1 2 5a Vậy 2 V  . SA S  . 5 . a 2a  . S.ABCD 3 ABCD 3 3
Chọn đáp án B.
Câu 33: Cho hình chóp .
S ABCD có đáy là hình chữ nhật có AB a, BC  2a, SA vuông góc với đáy.
Biết SC hợp với mặt đáy một góc 60, thể tích của khối chóp . S ABCD bằng 3 2 5a 3 2 15a 3 4 3a A. 3 2a . B. . C. . D. . 3 3 9 Lời giải: S A D B C Ta có: 2 SA . B BC  2a . ABCD
Do SA   ABCD nên AC là hình chiếu vuông góc của SC trên  ABCD.
Suy ra: SC;ABCD  SC; AC  . SCA SA
Xét tam giác SAC vuông tại A : tanSCA
SA a 15. AC 3 1 1 2 15a Vậy 2 V  . SA S  .a 15.2a  . S.ABCD 3 ABCD 3 3
Chọn đáp án C.
Câu 34: Cho hình chóp .
S ABC có đáy là tam giác vuông tại B, AB a, BC  2a, SA vuông góc với đáy.
Biết SC hợp với mặt đáy một góc 60, thể tích của khối chóp . S ABC bằng 3 15a 3 5a 3 2a 3 3a A. . B. . C. . D. . 3 2 3 3 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia S C A B 1 Ta có: 2 SA . B BC a . ABC 2
Do SA   ABC nên AC là hình chiếu vuông góc của SC trên  ABC.
Suy ra: SC ABC  SC AB  SCA SCA  0 ; ; 60 .
Xét tam giác ABC vuông tại B AC  2 AB  2 : BC a 5. SA
Xét tam giác SAC vuông tại A : tanSCA
SA AC.tanSCA a 15. AC 3 1 1 15a Vậy 2 VS . A S  .a 15.a  . S.ABC 3 ABC 3 3
Chọn đáp án A.
Câu 35: Cho hình chóp .
S ABCD có đáy là hình chữ nhật có AB a, BC  2a, SA vuông góc với đáy.
Biết SCD hợp với mặt đáy một góc 30, thể tích của khối chóp . S ABCD bằng 3 2 5a 3 2 15a 3 4 3a A. 3 2a . B. . C. . D. . 3 3 9 Lời giải: S A D B C Ta có: 2 SA . B BC  2a . ABCD CD AD Ta có: 
CD  SAD  CD S .
D Suy ra:  SCD; ABCD  . SDA CD   SA SA 2a 3
Xét tam giác SAD vuông tại A : tanSDA   SA  . AD 3 3 1 1 2a 3 4 3a Vậy 2 V  . SA S  . .2a  . S.ABCD 3 ABCD 3 3 9
Chọn đáp án D.
Câu 36: Cho hình chóp .
S ABCD có đáy là hình chữ nhật có AB a, BC  2a, SA vuông góc với đáy.
Biết SC hợp với SAB một góc 30, thể tích của khối chóp . S ABCD bằng
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 3 2 11a 3 2 5a 3 2 15a 3 4 3a A. . B. . C. . D. . 3 3 3 9 Lời giải: S A D B C Ta có: 2 SA . B BC  2a . ABCDBC AB Ta có: 
BC  SAB  SB là hình chiếu vuông góc của SC trên SAB. BC   SA
Suy ra: SC;SAB  BSC. BC
Xét tam giác SBC vuông tại B : tan BSC
SB  2a 3. SB
Xét tam giác SAB vuông tại 2 2
A : SA SB AB a 11. 3 1 1 2 11a Vậy 2 V  . SA S  .a 11.2a  . S.ABCD 3 ABCD 3 3
Chọn đáp án A.
Câu 37: Cho hình chóp .
S ABCD có đáy là hình thoi cạnh bằng a, ABC  60, SA vuông góc với đáy.
Biết SC hợp với đáy một góc 60, thể tích của khối chóp . S ABCD bằng 3 3a 3 6a 3 3a 3 a A. . B. . C. . D. . 3 6 12 2 Lời giải: S A a D A D 60o B a B C C
Do ABCD là hình thoi cạnh bằng o
a, ABC  60  ABC là tam giác đều cạnh . a 2 2 3a 3a Suy ra: S  2S  2.  . ABCD ABC 4 2
Do SA   ABCD nên AC là hình chiếu vuông góc của SC trên  ABCD.
Suy ra: SC;ABCD  SC; AC  . SCA SA
Xét tam giác SAC vuông tại A : tanSCA   SA a 3. AC
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 2 3 1 1 3a a Vậy VS . A S  .a 3.  . S.ABCD 3 ABCD 3 2 2
Chọn đáp án D.
Câu 38: Cho hình chóp .
S ABCD có đáy là hình thoi cạnh bằng a, ABC  60, SA vuông góc với đáy.
Biết SBC hợp với đáy một góc 30, thể tích của khối chóp . S ABCD bằng 3 3a 3 6a 3 3a 3 a A. . B. . C. . D. . 3 6 12 2 Lời giải: S A a a D A D 60o B H B C H C
Do ABCD là hình thoi cạnh bằng o
a, ABC  60  ABC là tam giác đều cạnh . a 2 2 3a 3a Suy ra: S  2S  2.  . ABCD ABC 4 2 BC AH
Dựng AH BC, H là trung điểm BC. Ta có: 
BC  SAH  BC SH. BC   SA
Suy ra:  SBC;ABCD  SH . A SA a 3 3 a
Xét tam giác SAH vuông tại o A : tanSHA
SA AH.tan30  .  . AH 2 3 2 2 3 1 1 a 3a 3a Vậy V  . SA S  . .  . S.ABCD 3 ABCD 3 2 2 12
Chọn đáp án C.
Câu 39: Cho hình chóp .
S ABCD có đáy là hình thang vuông tại A, B, AD  2a, AB BC a, SA vuông
góc với đáy. Biết SB  2a, thể tích của khối chóp . S ABCD bằng 3 3a 3 2a 3 6a 3 3a A. . B. . C. . D. . 2 2 2 4 Lời giải: S A D B C
ABAD BC 2 3a Ta có: S  
. Xét tam giác SAB vuông tại 2 2
A : SA SB AB a 3. ABCD 2 2
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 2 3 1 1 3a 3a Vậy V  . SA S  .a 3.  . S.ABCD 3 ABCD 3 2 2
Chọn đáp án A.
Câu 40: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh .
a Biết mặt bên SAB là tam giác đều và
nằm trong mặt phẳng vuông góc với đáy, thể tích của khối chóp . S ABC bằng 3 a 3 3a 3 a 3 15a A. . B. . C. . D. . 8 24 6 6 Lời giải: S A C H B 2 3a
SAB  ABC Ta có: S
. Gọi H là trung điểm . AB Ta có: 
SH  ABC. ABC 4 SH   AB 2 3 1 1 a 3 3a a Vậy V  .SH.S  . .  . S.ABC 3 ABC 3 2 4 8
Chọn đáp án A.
Câu 41: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh .
a Biết mặt bên SAB là tam giác vuông
cân tại S và nằm trong mặt phẳng vuông góc với đáy, thể tích của khối chóp . S ABCD bằng 3 a 3 3a 3 3a 3 a A. . B. . C. . D. . 8 24 6 6 Lời giải: S A D H B C
SAB  ABCD Ta có: 2 S
a . Gọi H là trung điểm . AB Ta có: 
SH  ABCD. ABCD SH    AB 3 1 1 a a Vậy 2 V  .SH.S  . .a  . S.ABCD 3 ABCD 3 2 6
Chọn đáp án D.
Câu 42: Cho hình chóp S.ABC có mặt phẳng  SAC  vuông góc với mặt phẳng  ABC  , SAB là
tam giác đều cạnh a 3 , BC a 3 đường thẳng SC tạo với mặt phẳng  ABC  góc 60 .
Thể tích của khối chóp S.ABC bằng
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 3 a 3 3 a 6 3 a 6 A. . B. . C. . D. 3 2a 6 . 3 2 6 Lời giải: B A S 60o H C
Ta thấy tam giác ABC cân tại B , gọi H là trung điểm của AB suy ra BH AC.
Do SAC    ABC  nên BH  SAC  .
Ta lại có BA BC BS nên B thuộc trục đường tròn ngoại tiếp tam giác ABC H là tâm
đường tròn ngoại tiếp tam giác SAC SA SC .
Do AC là hình chiếu của SC lên mặt phẳng  ABC   0 SCA  60 . SA Ta có 0 SC  .
SA cot 60  a , AC
 2a HC a 2 2
BH BC HC a 2 . 0 sin 60 1 3 a 6 V  1 BH.SBH. . SA SC  . S . ABC 3 SAC 6 6
Chọn đáp án C.
Câu 43: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh .
a Biết mặt bên SAB là tam giác vuông
cân tại S và nằm trong mặt phẳng vuông góc với đáy, thể tích của khối chóp . S ABC bằng 3 a 3 3a 3 a 3 15a A. . B. . C. . D. . 8 24 6 6 Lời giải: S A C H B 2 3a
SAB  ABC Ta có: S
. Gọi H là trung điểm . AB Ta có: 
SH  ABC. ABC 4 SH   AB 2 3 1 1 a 3a 3a Vậy V  .SH.S  . .  . S.ABC 3 ABC 3 2 4 24
Chọn đáp án B.
Câu 44: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh .
a Biết mặt bên SAB là tam giác đều và
nằm trong mặt phẳng vuông góc với đáy, thể tích của khối chóp . S ABCD bằng
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 3 a 3 3a 3 3a 3 15a A. . B. . C. . D. . 8 24 6 6 Lời giải: S A D H B C
SAB  ABCD Ta có: 2 S
a . Gọi H là trung điểm . AB Ta có: 
SH  ABCD. ABCD SH    AB 3 1 1 a 3 3a Vậy 2 V  .SH.S  . .a  . S.ABCD 3 ABCD 3 2 6
Chọn đáp án C.
Câu 45: Cho hình chóp .
S ABCD với ABCD là hình vuông cạnh a . Mặt bên SAB là tam giác cân tại S và
nằm trên mặt phẳng vuông góc với mặt phẳng đáy. Cạnh bên SC tạo với đáy một góc 60 . Tính thể tích khối chóp . S ABCD . 3 a 15 3 a 15 3 a 6 3 a 3 A. . B. . C. . D. . 2 6 3 6 Lời giải: S A I B a D a C
Gọi I là trung điểm của AB .
Ta có: SAB cân tại S SI AB  1 SAB   ABCD Mặt khác:  2
SAB   ABCD   AB Từ  
1 và 2 , suy ra: SI   ABCD  SI là chiều cao của hình chóp . S ABCD
IC là hình chiếu của SC lên mặt phẳng ABCD  SC,ABCD  SC,IC SCI  6  0  a 2 a 5
Xét IBC vuông tại B , ta có: IC  2 IB  2 BC   2 a     2  2
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia a 5 a 15
Xét SIC vuông tại I , ta có: SI IC.tan 6  0  . 3  2 2 3 1 1 a 15 a 15
Vậy thể tích khối chóp .
S ABCD là: V  .S .SI  2 .a .  . 3 ABCD 3 2 6
Chọn đáp án B.
Câu 46: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh .
a Biết hình chiếu vuông góc của S trên
mặt đáy là trung điểm của AB và SB  2a, thể tích của khối chóp . S ABC bằng 3 5a 3 a 3 3a 3 3a A. . B. . C. . D. . 8 8 8 48 Lời giải: S A C H B 2 3a Ta có: S
. Gọi H là trung điểm .
AB Ta có: SH   ABC. ABC 4 a
Xét tam giác SHB vuông tại 2 2 15
H : SH SB HB  . 2 2 3 1 1 15a 3a 5a Vậy V  .SH.S  . .  . S.ABC 3 ABC 3 2 4 8
Chọn đáp án A.
Câu 47: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh .
a Biết hình chiếu vuông góc của S trên
mặt đáy là trung điểm của AB và SC ABC 0 ;
 60 , thể tích của khối chóp . S ABC bằng 3 5a 3 a 3 3a 3 3a A. . B. . C. . D. . 8 8 8 48 Lời giải: S A C H B
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 2 3a Ta có: S
. Gọi H là trung điểm .
AB Ta có: SH   ABC. ABC 4
Suy ra: HC là hình chiếu vuông góc của SC trên  ABC  SC;ABC  SCH. SH 3a
Xét tam giác SHC vuông tại H : tanSCH   SH  . HC 2 2 3 1 1 3a 3a 3a Vậy V  .SH.S  . .  . S.ABC 3 ABC 3 2 4 8
Chọn đáp án C.
Câu 48: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh .
a Biết hình chiếu vuông góc của S trên
mặt đáy là trung điểm của AB và  SBC  ABC 0 ;
 30 , thể tích của khối chóp . S ABC bằng 3 5a 3 a 3 3a 3 3a A. . B. . C. . D. . 8 8 8 48 Lời giải: S A C H M K B 2 3a Ta có: S
. Gọi H , M lần lượt là trung điểm AB, BC. ABC 4 BC HK
Dựng HK BC, K là trung điểm BC. Ta có: 
BC  SHK  BC SK. BC   SH
Suy ra:  SBC; ABC  SKH. SH 1 a
Xét tam giác SHK vuông tại o H : tanSCH
SH HK.tanSCH AM.tan30  . HK 2 4 2 3 1 1 a 3a 3a Vậy V  .SH.S  . .  . S.ABC 3 ABC 3 4 4 48
Chọn đáp án D.
Câu 49: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh .
a Biết hình chiếu vuông góc của S trên
mặt đáy là điểm H trên cạnh AB, AH  2HB và SC ABC 0 ;
 30 , thể tích của khối chóp . S ABC bằng 3 3a 3 7a 3 a 3 6a A. . B. . C. . D. . 24 36 12 6 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia S A C H B 2 3a Ta có: S
. Ta có: SH   ABC. ABC 4
Suy ra: HC là hình chiếu vuông góc của SC trên  ABC  SC;ABC  SCH. 2 a a Xét tam giác HBC : 2 2 2 7 7
HC BH BC  2BH.BC.cos HBC   HC  . 9 3 SH 21a
Xét tam giác SHC vuông tại H : tanSCH   SH  . HC 9 2 3 1 1 21a 3a 7a Vậy V  .SH.S  . .  . S.ABC 3 ABC 3 9 4 36
Chọn đáp án B.
Câu 50: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh .
a Biết hình chiếu vuông góc của S trên
mặt đáy là điểm H trên cạnh AB, BH  2HA và SD ABCD 0 ;
 60 , thể tích của khối chóp . S ABCD bằng 3 2 3a 3 30a 3 42a 3 3a A. . B. . C. . D. . 9 9 27 3 Lời giải: S B C H A D a Ta có: 2 Sa . Ta có: 2 2 10
HD AH AD  . ABCD 3
Ta có: SH   ABCD  HD là hình chiếu vuông góc của SD trên  ABCD
 SD;ABCD  SDH. SH a 30
Xét tam giác SHD vuông tại H : tanSDH   SH  . HD 3 3 1 1 a 30 30a Vậy 2 V  .SH.S  . .a  . S.ABCD 3 ABCD 3 3 9
Chọn đáp án B.
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Câu 51: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh .
a Biết hình chiếu vuông góc của S trên
mặt đáy là điểm H trên cạnh AB, BH  2HA và  SBD  ABCD 0 ;
 60 , thể tích của khối chóp . S ABCD bằng 3 2 3a 3 30a 3 42a 3 6a A. . B. . C. . D. . 9 9 27 9 Lời giải: S B C K H O A D Ta có: 2 S
a . Gọi O là tâm hình vuông ABCD. ABCDBD HK Dựng HK AC  
BD  SHK  BD SK. Suy ra:  SBD;ABCD  SKH. BD   SH SH 2 a 6
Xét tam giác SHK vuông tại o H : tanSKH   SH A . O tan 60  . HK 3 3 3 1 1 a 6 6a Vậy 2 V  .SH.S  . .a  . S.ABCD 3 ABCD 3 3 9
Chọn đáp án D.
Câu 52: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh .
a Biết hình chiếu vuông góc của S trên
mặt đáy là trung điểm của AB và  ;
SB ABC  60, thể tích của khối chóp . S ABC bằng 3 5a 3 a 3 3a 3 3a A. . B. . C. . D. . 8 8 8 48 Lời giải: S A C H B 2 3a Ta có: S
. Gọi H là trung điểm .
AB Ta có: SH   ABC. ABC 4
Suy ra: HB là hình chiếu vuông góc của SB trên  ABC  SB;ABC  SBH.
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia SH a 3
Xét tam giác SHB vuông tại H : tanSBH   SH  . HB 2 2 3 1 1 a 3 3a a Vậy V  .SH.S  . .  . S.ABC 3 ABC 3 2 4 8
Chọn đáp án B.
Câu 53: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh .
a Biết hình chiếu vuông góc của S trên
mặt đáy là điểm H trên cạnh AB, AH  2HB và SA  2a, thể tích của khối chóp . S ABC bằng 3 3a 3 7a 3 6a 3 6a A. . B. . C. . D. . 24 36 9 6 Lời giải: S A C H B 2 3a a Ta có: S
. Xét tam giác SHA vuông tại 2 2 4 2
H : SH SA HA  . ABC 4 3 2 3 1 1 4 2a 3a 6a Vậy V  .SH.S  . .  . S.ABC 3 ABC 3 3 4 9
Chọn đáp án C.
Câu 54: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh .
a Biết hình chiếu vuông góc của S trên
mặt đáy là điểm H trên cạnh AB, AH  2HB và  ;
SB ABC  60, thể tích của khối chóp . S ABC bằng 3 3a 3 7a 3 a 3 6a A. . B. . C. . D. . 24 36 12 6 Lời giải: S A C H B 2 3a Ta có: S  . ABC 4
Ta có: SH   ABC  HB là hình chiếu vuông góc của SB trên  ABC  SB;ABC  SBH.
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia SH a 3
Xét tam giác SHB vuông tại H : tanSBH   SH  . HB 3 2 3 1 1 a 3 3a a Vậy V  .SH.S  . .  . S.ABC 3 ABC 3 3 4 12
Chọn đáp án C.
Câu 55: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh .
a Biết hình chiếu vuông góc của S trên
mặt đáy là điểm H trên cạnh AB, BH  2HA và  ;
SB ABCD  60, thể tích của khối chóp . S ABCD bằng 3 2 3a 3 30a 3 42a 3 3a A. . B. . C. . D. . 9 9 27 3 Lời giải: S B C H A D Ta có: 2 Sa . ABCD
Ta có: SH   ABCD  HB là hình chiếu vuông góc của SB trên  ABCD   ;
SB ABCD  SBH. SH 2a 3
Xét tam giác SHB vuông tại H : tanSBH   SH  . HB 3 3 1 1 2a 3 2 3a Vậy 2 V  .SH.S  . .a  . S.ABCD 3 ABCD 3 3 9
Chọn đáp án A.
Câu 56: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh .
a Biết hình chiếu vuông góc của S trên
mặt đáy là điểm H trên cạnh AB, BH  2HA và SC; ABCD  30, thể tích của khối chóp . S ABCD bằng 3 2 3a 3 30a 3 42a 3 39a A. . B. . C. . D. . 9 9 27 27 Lời giải: S B C H A D
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia Ta có: 2 Sa . ABCD a Ta có: 2 2 13
HC HB BC  . 3
Ta có: SH   ABCD  HC là hình chiếu vuông góc của SC trên  ABCD
 SC;ABCD  SCH. SH a 39
Xét tam giác SHC vuông tại H : tanSCH   SH  . HC 9 3 1 1 a 39 39a Vậy 2 V  .SH.S  . .a  . S.ABCD 3 ABCD 3 9 27
Chọn đáp án D.
Câu 57: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh .
a Biết hình chiếu vuông góc của S trên
mặt đáy là điểm H trên cạnh AB, BH  2HA và  SCD;ABCD  60, thể tích của khối chóp . S ABCD bằng 3 2 3a 3 30a 3 42a 3 3a A. . B. . C. . D. . 9 9 27 3 Lời giải: S B C H K A D Ta có: 2 Sa . ABCD CD HK Dựng HK AD  
CD  SHK  CD SK. Suy ra:  SCD;ABCD  SKH. CD   SH SH
Xét tam giác SHK vuông tại H : tanSKH   SH a 3. HK 3 1 1 3a Vậy 2 V  .SH.S  .a 3.a  . S.ABCD 3 ABCD 3 3
Chọn đáp án D.
Câu 58: Cho hình chóp S.ABC là tam giác vuông tại A , ABC  30 , BC a . Hai mặt bên  SAB và
SAC cùng vuông góc với đáy  ABC, mặt bên SBC tạo với đáy một góc 45. Thể tích
của khối chóp S.ABC bằng 3 a 3 a 3 a 3 a A. . B. . C. . D. . 64 16 9 32 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
SAB   ABC  Ta có: 
SAC   ABC
SA   ABC .   SAB
SAC  SA
SBC  ABC  BC
Kẻ AH BC SH BC . Khi đó: BC AH
SHA  45o BC SHa 3 a a 3 Mà 0
AB BC.cos30 
và AC BC.sin 30o  nên 0 AH A . B sin 30  2 2 4 3 3 1 1 a Nên  a SA . Do đó: V S .SA A . B AC.SA  . ABC 4 3 6 32
Chọn đáp án D.
Câu 59: Cho hình chóp S.ABCD , đáy ABCD là hình vuông cạnh 2a . Hai mặt phẳng  SAB ,  SAD
cùng vuông góc với đáy, góc giữa hai mặt phẳng  SBC  và  ABCD bằng 30 . Tính tỉ số
3V biết V là thể tích của khối chóp S.ABCD . 3 a 3 3 8 3 A. . B. . C. 3 . D. . 12 2 3 Lời giải: S A B D C   SAB     ABCD Do 
SA   ABCD  .  SAD     ABCDSA 1 a
Góc giữa  SBC  và  ABCD bằng góc SBA . Do đó  tan SBA  2  SA  . AB 3 3
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 1 1 2a 8 Suy ra 2 3 VS . A S  .4a a . S . ABCD 3 ABCD 3 3 3 3
Chọn đáp án D.
Câu 60: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , hai mặt phẳng SAB và
SAD cùng vuông góc với mặt phẳng  ABCD ; góc giữa đường thẳng SC và mặt phẳng
ABCD bằng 60. Tính theo a thể tích khối chóp S.ABCD . 3 a 6 3 a 6 A. 3 3a . B. . C. . D. 3 3 2a . 9 3 Lời giải:
SAB   ABCD  Ta có 
SAD   ABCD
SA   ABCD   SAB
SAD  SA
AC là hình chiếu vuông góc của SC lên  ABCD  SC, ABCD  SCA  60
Tam giác SAC vuông tại A có SA AC.tan 60  a 6 . 3 1 1 a 6 Khi đó 2 V  .S . A S  .a 6.a  . SABCD 3 ABCD 3 3
Chọn đáp án C.
Câu 61: Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a và hai mặt bên  SAB , SAC
cùng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết SC a 3 . 3 a 3 3 a 3 3 2a 6 3 a 6 A. . B. . C. . D. . 2 4 9 12 Lời giải: S C A B
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia (SA ) B  (ABC) Ta có: 
SA ABC . (SAC)  ( )  (ABC) 2 a 3
Xét tam giác SAC vuông tại A nên SA  2 SC  2
AC a 2 ; S   . ABC 4 2 3 1 a 3 a 6 Vậy V  . .a 2  . SABC 3 4 12
Chọn đáp án D.
Câu 62: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , hai mặt phẳng  SAC  và
SAB cùng vuông góc với ABCD . Góc giữa SCD và ABCD là 60. Thể tích khối
chóp S.ABCD bằng 3 a 6 3 a 3 3 a 3 3 a 6 A. . B. . C. . D. . 3 3 6 6 Lời giải: 3 1 a 3
Ta có SA   ABCD  SDA  
60  SA AD 3  a 3  V  2 a 3.a  . 3 3
Chọn đáp án B.
Câu 63: Cho hình chóp .
S ABCD có đáy ABCD là hình chữ nhật. Hai mặt phẳng SAB và SAC
cùng vuông góc với mặt phẳng  ABCD. Biết rằng AB a , AD a 3 và SC  7a . Tính thể
tích khối chóp S.ABCD . A. 3 V a . B. 3 V  2a . C. V  3 3a . D. 3
V  4a Lời giải: S A D B C
SAB  ABCD 
Ta có: SAC   ABCD
  SA  ABCD .
SAB SAC    SA
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 2 2  2  2 2 AC AB BC  2
a  a 3  2a ;  2  2 SA SC
AC  a 7   2a  a 3 . 1 1 1 Vậy VS .SA  .A . B A . D SA  . . a a 3.a 3  3 a . S.ABCD 3 ABCD 3 3
Chọn đáp án A.
Câu 64: Cho tứ diện đều ABCD có cạnh bằng t. Thể tích của khối tứ diện ABCD bằng 3 2t 3 2t 3 2t 3 3t A. . B. . C. . D. . 12 6 3 6 Lời giải: A D B G M C 2 3a Ta có: S
. Gọi M là trung điểm CD, G là trọng tâm tam giác BCD. BCD 4
Do ABCD là tứ diện đều nên AG  BCD. 2 2  2   2 t 3  6
Xét tam giác ABG vuông tại 2 2 2 2
G : AG AB BG AB   BM   t   .   t. 3  3 2    3   2 1 1 6t 3t 2 Lúc đó: VA . G S  . .  3 t . ABCD 3 BCD 3 3 4 12 2
Cách khác: Dùng công thức giải nhanh: V  3 t . ABCD 12
Chọn đáp án A.
Câu 65: Cho hình chóp tam giác đều .
S ABC có cạnh đáy bằng .
a Biết SA  2a, thể tích của khối chóp . S ABC bằng 3 3a 3 2a 3 11a 3 3a A. . B. . C. . D. . 12 2 12 72 Lời giải: S C A G M B
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 2 3a Ta có: S
. Gọi G là trọng tâm tam giác ABC, M là trung điểm BC. ABC 4 Do .
S ABC là chóp tam giác đều nên SG   ABC.
Xét tam giác SAG vuông tại G : 2 2             a2 2 2 2 2 2 a 3 33a SG SA AG SA AM 2   .   . 3  3 2    3   2 3 1 1 33a 3a 11a Vậy V  . SG S  . .  . S.ABC 3 ABC 3 3 4 12
Chọn đáp án C.
Câu 66: Cho hình chóp tam giác đều .
S ABC có cạnh đáy bằng .
a Biết SBC hợp với đáy một góc 30,
thể tích của khối chóp . S ABC bằng 3 3a 3 2a 3 11a 3 3a A. . B. . C. . D. . 12 2 12 72 Lời giải: S A C G M B 2 3a Ta có: S
. Gọi G là trọng tâm tam giác ABC, M là trung điểm BC. ABC 4 Do .
S ABC là chóp tam giác đều nên SG   ABC. BC GM Ta có: 
BC  SGM  BC SM. Suy ra:  SBC;ABC  SM . G BC   SG SG 1 a 3 3 a
Xét tam giác SMG vuông tại o G : tanSMG   SG M . G tan 60  . .  . MG 3 2 3 6 2 3 1 1 a 3a 3a Vậy VS . G S  . .  . S.ABC 3 ABC 3 6 4 72
Chọn đáp án D.
Câu 67: Cho hình chóp tứ giác đều .
S ABCD có cạnh đáy bằng .
a Biết SA hợp với mặt đáy một góc
60, thể tích của khối chóp . S ABCD bằng 3 3a 3 6a 3 14a 3 15a A. . B. . C. . D. . 18 6 6 6 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia S D C O A B Ta có: 2 S
a . Gọi O là tâm hình vuông ABCD. ABCD Do .
S ABCD là chóp tứ giác đều nên SO   ABCD.
Suy ra: AO là hình chiếu vuông góc của SA trên  ABCD  SA;ABCD  SA . O
Xét tam giác SAO vuông tại O : SO a 2 a 6 o tanSAO   SO A . O tan 60  . 3  . AO 2 2 3 1 1 a 6 6a Vậy 2 VS . O S  . .a  . S.ABC 3 ABCD 3 2 6
Chọn đáp án B.
Câu 68: Cho hình chóp tứ giác đều .
S ABCD có cạnh đáy bằng .
a Biết SBC hợp với mặt đáy một góc
30, thể tích của khối chóp . S ABCD bằng 3 3a 3 6a 3 14a 3 15a A. . B. . C. . D. . 18 6 6 6 Lời giải: S D C M O A B Ta có: 2 S
a . Gọi O là tâm hình vuông ABCD,M là trung điểm BC. ABCD Do .
S ABCD là chóp tứ giác đều nên SO   ABCD. BC OM Ta có: 
BC  SOM  BC SM. BC   SO
Suy ra:  SBC; ABCD  SM . O SO a 3 a 3
Xét tam giác SMO vuông tại o O : tanSMO
SO OM.tan30  .  . MO 2 3 6 3 1 1 a 3 3a Vậy 2 VS . O S  . .a  . S.ABC 3 ABCD 3 6 18
Chọn đáp án A.
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Câu 69: Cho hình chóp tam giác đều .
S ABC có cạnh đáy bằng .
a Biết SA hợp với đáy một góc 60,
thể tích của khối chóp . S ABC bằng 3 3a 3 2a 3 11a 3 3a A. . B. . C. . D. . 12 2 12 72 Lời giải: S A C G M B 2 3a Ta có: S
. Gọi G là trọng tâm tam giác ABC, M là trung điểm BC. ABC 4 Do .
S ABC là chóp tam giác đều nên SG   ABC.
Suy ra: AG là hình chiếu vuông góc của SA trên  ABC  AA ;ABC  SA . G SG 2 a 3
Xét tam giác SAG vuông tại o G : tanSAG   SG A . G tan 60  . . 3  . a AG 3 2 2 3 1 1 3a 3a Vậy VS . G S  . . a  . S.ABC 3 ABC 3 4 12
Chọn đáp án A.
Câu 70: Cho hình chóp tứ giác đều .
S ABCD có cạnh đáy bằng .
a Biết SA  2a, thể tích của khối chóp . S ABCD bằng 3 3a 3 6a 3 14a 3 15a A. . B. . C. . D. . 18 6 6 6 Lời giải: S D C O A B Ta có: 2 S
a . Gọi O là tâm hình vuông ABCD. ABCD Do .
S ABCD là chóp tứ giác đều nên SO   ABCD.
Xét tam giác SAO vuông tại O : 2 2             a2 2 2 2 1 a 2 14a SO SA AO SA AC 2     . 2  2    2  
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 3 1 1 14a 14a Vậy 2 V  . SO S  . .a  . S.ABC 3 ABCD 3 2 6
Chọn đáp án C.
Câu 71: Cho hình chóp tứ giác đều .
S ABCD có cạnh đáy bằng .
a Biết diện tích một mặt bên của hình
chóp đó có diện tích bằng 2
a , thể tích của khối chóp . S ABCD bằng 3 3a 3 6a 3 14a 3 15a A. . B. . C. . D. . 18 6 6 6 Lời giải: S D C O M A B 1 1
Gọi M là trung điểm BC. Ta có: 2 2 S
SM.BC a SM.a a SM  2 . a SBC 2 2 2 2  a  15a
Xét tam giác SOM vuông tại 2 2
O : SO SM OM  2a     .  2  2 3 1 1 15a 15a Vậy 2 V  . SO S  . .a  . S.ABC 3 ABCD 3 2 6
Chọn đáp án D.
_____________________HẾT_____________________
Huế, 10h20’ Ngày 18 tháng 5 năm 2022
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115