Một số dạng toán liên quan đến thể tích khối lăng trụ

Tài liệu gồm 40 trang, được biên soạn bởi thầy giáo Lê Bá Bảo, hướng dẫn giải một số dạng toán liên quan đến thể tích khối lăng trụ trong chuyên đề thể tích khối đa diện môn Toán 12..Mời bạn đọc đón xem.

34 17 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Khối đa diện

Môn: Toán 12

Thông tin:

40 trang 8 tháng trước

Tác giả:

Profile Lan Tường
THỂ TÍCH KHỐI ĐA DIỆN
TOÁN 12
LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ
THỂ TÍCH KHỐI LĂNG TRỤ
LUYỆN THI THPT QUỐC GIA
CẬP NHẬT TỪ ĐỀ THI MỚI NHẤT
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
MỘT SỐ DẠNG TOÁN LIÊN QUAN ĐẾN
THỂ TÍCH KHỐI LĂNG TRỤ
Dạng 1: Khối lăng trụ có cạnh bên vuông góc với đáy
Phương pháp:
Cho hình lăng trụ đứng
.ABC A B C
…
AA
+) Thể tích khối lăng trụ:
.
ABC
V AA S
A
B
C
B'
A'
C'
BÀI TẬP TRẮC NGHIỆM MINH HỌA
Câu 1: Cho khối lăng trụ có thể tích bằng
3
24a
và chiều cao bằng
3a
. Diện tích một mặt đáy của khối
lăng trụ đã cho bằng
A.
2
16a
. B.
2
8a
. C.
2
6a
. D.
2
72a
.
Câu 2: Cho hnh lăng trụ đng
. ' ' 'ABC A B C
c đáy
ABC
l tam giác vuông cân ti
A
vi
BC a
v
mặt bên
''AA B B
l hnh vuông. Thể tch của khối lăng trụ
. ' ' 'ABC A B C
bằng
A.
3
2
.
8
a
B.
3
2
.
4
a
C.
3
.
4
a
D.
3
.
12
a
Câu 3: Cho lăng trụ đng
.ABC A B C
c đáy
ABC
là tam giác vuông cân ti
,B
.AB a
Biết
AC
hợp vi
ABC
một góc
60 ,
thể tích của khối lăng trụ
.ABC A B C
bằng
A.
3
3
.
4
a
B.
3
2
.
2
a
C.
3
3
.
2
a
D.
3
6
.
2
a
Câu 4: Cho hnh lăng trụ đng
.ABCD A B C D
c đáy
ABCD
là hình thoi cnh
, 30 , 2 .a BAC AB a
Thể tích của khối lăng trụ
.ABCD A B C D
bằng
A.
3
3
.
6
a
B.
3
3
.
2
a
C.
3
3
.
8
a
D.
3
33
.
8
a
Câu 5: Cho lăng trụ đng
.ABC A B C
c đáy
ABC
là tam giác vuông cân ti
,B
.AB a
Biết
AC
hợp vi
A B BA

một góc
30 ,
thể tích của khối lăng trụ
.ABC A B C
bằng
A.
3
3
.
4
a
B.
3
2
.
2
a
C.
3
3
.
2
a
D.
3
6
.
2
a
Câu 6: Cho hnh lăng trụ đng
. ' ' 'ABC A B C
c đáy
ABC
là tam giác vuông cân ti
A
. Biết
2BC a
và thể tch lăng trụ bằng
3
2,a
khoảng cách
d
từ
A
đến mặt phẳng
'A BC
bằng
A.
35
.
5
a
B.
5a
. C.
5
.
5
a
D.
25
.
5
a
Câu 7: Cho hình hộp đng
.ABCD A B C D
c đáy
ABCD
là hình thoi cnh
a
, góc
60BAD 
. Cho
biết góc giữa đường chéo
BD
và mặt đáy bằng
45
. Thể tích khối hộp đã cho l
A.
3
3
6
a
. B.
3
3
4
a
. C.
3
3
3
a
. D.
3
3
.
2
a
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Câu 8: Cho hình hộp đng
.ABCD A B C D
c đáy
ABCD
là hình thoi cnh
a
,
120BAD 
. Gọi
G
là trọng tâm tam giác
ABD
, góc to bởi
CG
và mặt đáy bằng
30
. Tính theo
a
thể tích khối
hộp
.ABCD A B C D
.
A.
3
a
. B.
3
3
a
. C.
3
12
a
. D.
3
6
a
.
Câu 9: Cho lăng trụ đng
.
ABC A B C
có cnh đáy
2BC a
, góc giữa hai mặt phẳng
ABC
và
A BC
bằng
60
. Biết diện tích tam giác
A BC
bằng
2
2a
. Tính thể tích của khối lăng trụ
.
ABC A B C
.
A.
3
3
3
a
V
. B.
3
3Va
. C.
3
3Va
. D.
3
2
3
a
V
.
BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN
Câu 10: Một khối lăng trụ đng tam giác có các cnh đáy lần lượt bằng
37;13;30
và diện tích xung
quanh bằng 480. Khi đ thể tích của khối lăng trụ bằng
A.
1170
. B.
2160
. C.
360
. D.
1080
.
Câu 11: Cho hnh lăng trụ đng
.ABC A B C
c đáy
ABC
là tam giác vuông cân ti
,.A AB a
Biết
diện tích t giác
ABB A

bằng
2
2,a
thể tích khối lăng trụ
.ABC A B C
bằng
A.
3
3
.
2
a
B.
3
3
.
6
a
C.
3
.a
D.
3
.
3
a
Câu 12: Cho hnh lăng trụ đng
.ABC A B C
có
2, , 2AA a AB a AC a
,
60BAC
. Thể tích
hnh lăng trụ đ bằng
A.
3
2a
. B.
3
33a
. C.
3
6
2
a
. D.
3
6
2
a
.
Câu 13: Cho hnh lăng trụ đng
.ABC A B C
c đáy
ABC
là tam giác vuông cân ti
,.A AB a
Biết góc
giữa
AB C

và
ABC
bằng
60 ,
thể tích khối lăng trụ
.ABC A B C
bằng
A.
3
3
.
2
a
B.
3
3
.
6
a
C.
3
.a
D.
3
6
.
4
a
Câu 14: Cho lăng trụ đng
.ABC A B C
c đáy
ABC
là tam giác vuông cân ti
,B
.AB a
Biết
AB C

hợp vi
ABC
một góc
60 ,
thể tích của khối lăng trụ
.ABC A B C
bằng
A.
3
3
.
4
a
B.
3
2
.
2
a
C.
3
3
.
2
a
D.
3
6
.
2
a
Câu 15: Cho khối lăng trụ đng
.ABCD A B C D
c đáy l hai hnh thoi cnh
a
,
3BD a
và
4AA a
(tham khảo hình vẽ dưi)
Thể tch của khối lăng trụ đã cho bằng
A.
3
23a
. B.
3
43
3
a
. C.
3
43a
. D.
3
23
3
a
.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Câu 16: Cho hnh lăng trụ đng
.ABCD A B C D
c đáy l hnh thoi
ABCD
cnh
a
,
60ABC
.
Đường chéo
AC
to vi mặt phẳng
ABCD
một góc
30
. Thể tích khối lăng trụ
.ABCD A B C D
tính theo
a
bằng
A.
3
1
.
4
a
B.
3
1
.
6
a
C.
3
1
.
2
a
D.
3
3
2
a
.
Dạng 2: Khối lăng trụ đều
Phương pháp:
.ABC A B C
A
B
C
B'
A'
C'
+) Đường cao:
AA
+) Thể tích khối lăng trụ:
.
ABC
V AA S
.ABC A B C
C'
A'
B'
D'
A
B
C
D
+) Đường cao:
AA
+) Thể tích khối lăng trụ:
.
ABCD
V AA S
BÀI TẬP TRẮC NGHIỆM MINH HỌA
Câu 17: Thể tích của khối lăng trụ tam giác đều có tất cả các cnh bằng
a
bằng
A.
3
3
12
a
. B.
3
3
6
a
. C.
3
3
2
a
. D.
3
3
4
a
.
Câu 18: Cho khối lăng trụ tam giác đều c độ dài cnh đáy bằng
a
và diện tích xung quanh bằng
2
6a
. Thể tích của khối lăng trụ đã cho l
A.
3
23
3
a
V
. B.
3
3
4
a
V
. C.
3
3
2
a
V
. D.
3
3
3
a
V
.
Câu 19: Cho lăng trụ tam giác đều
.ABC A B C
có cnh đáy bằng
.a
Biết
2,AB a
thể tích của khối
lăng trụ
.ABC A B C
bằng
A.
3
3
.
4
a
B.
3
3
.
8
a
C.
3
3
.
24
a
D.
3
.
4
a
Câu 20: Cho lăng trụ tam giác đều
.ABC A B C
có cnh đáy bằng
.a
Biết
AB C

hợp vi mặt đáy một
góc
30 ,
thể tích của khối lăng trụ
.ABC A B C
bằng
A.
3
3
.
4
a
B.
3
3
.
8
a
C.
3
3
.
24
a
D.
3
.
4
a
Câu 21: Cho hnh lăng trụ tam giác đều
.ABC A B C
có cnh đáy bằng
2a
, góc giữa hai đường thẳng
AB
và
BC
bằng
60
. Thể tích của khối lăng trụ đ l
A.
3
26Va
. B.
3
23
3
a
V
. C.
3
26
3
a
V
. D.
3
23Va
.
Câu 22: Cho hnh lăng trụ tam giác đều
.ABC A B C
có
AA a
. Khoảng cách giữa
'AB
và
'CC
bằng
3a
. Thể tích khối lăng trụ
. ' ' 'ABC A B C
.
A.
3
23
3
a
. B.
3
3a
. C.
3
3
2
a
. D.
3
3
3
a
.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Câu 23: Cho hnh lăng trụ đều
.ABC A B C
có cnh đáy bằng
23
3
a
. Đường thẳng
BC
to vi mặt
phẳng
ACC A

góc
thỏa mãn
cot 2
. Thể tích khối trụ
.ABC A B C
bằng
A.
3
4
11
3
a
. B.
3
1
11
9
a
. C.
3
1
11
3
a
. D.
3
2
11
3
a
.
BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN
Câu 24: Thể tích khối lăng trụ t giác đều
.ABCD A B C D
có
2AC AA a

là
A.
3
4a
. B.
3
2a
. C.
3
2a
. D.
3
22a
.
Câu 25: Cho hnh lăng trụ tam giác đều
. ' ' 'ABC A B C
cnh đáy
4a
, biết diện tích tam giác
'A BC
bằng 8. Thể tích khối lăng trụ
. ' ' 'ABC A B C
bằng
A.
10 3
. B.
23
. C.
83
. D.
43
.
Câu 26: Cho lăng trụ tam giác đều
.ABC A B C
có cnh đáy bằng
.a
Biết
AB
hợp vi mặt đáy một
góc
60 ,
thể tích của khối lăng trụ
.ABC A B C
bằng
A.
3
3
.
4
a
B.
3
3
.
8
a
C.
3
3
.
24
a
D.
3
.
4
a
Câu 27: Cho lăng trụ tam giác đều
.ABC A B C
có cnh đáy bằng
.a
Biết
AC
hợp vi
ABB A

một
góc
30 ,
thể tích của khối lăng trụ
.ABC A B C
bằng
A.
3
3
.
4
a
B.
3
3
.
8
a
C.
3
3
.
24
a
D.
3
6
.
4
a
Câu 28: Cho hnh lăng trụ tam giác đều
.ABC A B C
có cnh đáy bằng
,a AC
hợp vi mặt phẳng
ABB A

một góc
45 .
Thể tích của khối lăng trụ
.ABC A B C
bằng
A.
3
6
.
24
a
B.
3
3
.
4
a
C.
3
6
.
8
a
D.
3
6
.
4
a
Câu 29: Cho khối lăng trụ tam giác đều
.ABC A B C
có cnh đáy l
2a
và khoảng cách từ
A
đến mặt
phẳng
A BC
bằng
a
. Tính thể tích của khối lăng trụ
.ABC A B C
.
A.
3
22a
. B.
3
32
2
a
. C.
3
2
2
a
. D.
3
2
2
a
.
Câu 30: Cho hnh lăng trụ tam giác đều
.ABC A B C
có cnh đáy bằng
2a
, góc giữa hai đường thẳng
AB
và
B C
bằng
60
. Tính thể tích
V
của khối lăng trụ đ.
A.
3
26
3
a
V
. B.
3
23Va
. C.
3
23
3
a
V
. D.
3
26Va
.
Dạng 3: Khối hộp chữ nhật – Khối lập phương
Phương pháp:
.ABCD A B C D
c
b
a
C'
A'
B'
D'
A
B
C
D
+) Thể tích khối hộp:
V abc
.ABCD A B C D
a
a
a
C'
A'
B'
D'
A
B
C
D
+) Thể tích khối lập phương:
3
Va
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
BÀI TẬP TRẮC NGHIỆM MINH HỌA
Câu 31: Thể tích của khối lập phương cnh
3a
bằng
A.
3
9a
. B.
3
27a
. C.
3
18a
. D.
3
36 .a
Câu 32: Thể tích của khối hộp chữ nhật c ba kch thưc
2,3,7
bằng
A.
14.
B.
42.
C.
126.
D.
12.
Câu 33: Cho hình hộp chữ nhật
.ABCD A B C D
có
2 , .AB a BC a
Biết
3,AC a
thể tích của khối
hộp chữ nhật
.ABCD A B C D
bằng
A.
3
4.a
B.
3
4 3 .a
C.
3
2 15
.
3
a
D.
3
3
.
4
a
Câu 34: Cho hình lập phương
.ABCD A B C D
có diện tích mặt chéo
ACC A

bằng
2
22a
. Thể tích
của khối lập phương
.ABCD A B C D
là
A.
3
16 2a
. B.
3
22a
. C.
3
8a
. D.
3
a
.
Câu 35: Cho hình hộp chữ nhật
.ABCD A B C D
có
, 3,AB a AD a
góc giữa mặt phẳng
ABC D

và
ABCD
bằng
45 .
Thể tích khối hộp chữ nhật đã cho bằng
A.
3
3.a
B.
3
.a
C.
3
3.a
D.
3
2 3 .a
BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN
Câu 36: Thể tích của khối hộp chữ nhật
.ABCD A B C D
có
3, 5AB AC
,
8AA
bằng
A.
120
. B.
32
C.
96
. D.
60
.
Câu 37: Diện tích toàn phần của một hình lập phương bằng
2
96 cm
. Khối lập phương đã cho c thể
tích bằng
A.
3
84 cm
. B.
3
48 cm
. C.
3
64 cm
. D.
3
91 cm
.
Câu 38: Cho hình lập phương
.ABCD A B C D
có diện tích tam giác
ACD
bằng
2
3a
. Thể tích của
khối lập phương đã cho bằng:
A.
3
4 2 .a
B.
3
8a
. C.
3
a
. D.
3
22a
.
Câu 39: Cho hnh lăng trụ đng
.ABCD A B C D
c đáy l hnh vuông cnh bằng
6
, đường chéo
AB
của mặt bên
ABB A

c độ dài bằng
10
. Tính thể tích
V
của khối lăng trụ
.ABCD A B C D
.
A.
384V
. B.
180V
. C.
480V
. D.
288V
.
Câu 40: Cho hình hộp chữ nhật
.ABCD A B C D
có
2 , .AB a BC a
Biết
ADC B

hợp vi mặt đáy
một góc
60 ,
thể tích của khối hộp chữ nhật
.ABCD A B C D
bằng
A.
3
4.a
B.
3
4 3 .a
C.
3
2 15
.
3
a
D.
3
3
.
4
a
Câu 41: Cho hình hộp chữ nhật
.ABCD A B C D
có
2 , .AB a BC a
Biết
AC
hợp vi mặt đáy một góc
60 ,
thể tích của khối hộp chữ nhật
.ABCD A B C D
bằng
A.
3
2 15 .a
B.
3
4 3 .a
C.
3
2 15
.
3
a
D.
3
3
.
4
a
Câu 42: Cho hình hộp chữ nhật c đường chéo
21.d
Độ di ba kch thưc của hình hộp chữ nhật
lập thành một cấp số nhân vi công bội
2.q
Thể tích của khối hộp chữ nhật đã cho l
A.
8V
. B.
8
3
V
. C.
4
3
V
. D.
6V
.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Dạng 4: Khối lăng trụ xiên bất kì
Phương pháp:
Cho hình lăng trụ
.ABC A B C
…
,AH H
A
.ABC
+) Thể tích khối lăng trụ:
.
ABC
V AH S
H
M
A
B
C
A'
B'
C'
BÀI TẬP TRẮC NGHIỆM MINH HỌA
Câu 43: Cho lăng trụ
.ABC A B C
c đáy
ABC
l tam giác đều cnh
a
, cnh bên bằng
4a
và to vi
đáy gc
o
30
. Thể tích khối lăng trụ
.ABC A B C
bằng
A.
3
1
2
a
. B.
3
3
2
a
. C.
3
3a
. D.
3
3
2
a
.
Câu 44: Cho lăng trụ tam giác
.ABC A B C
c đáy l tam giác đều cnh
a
, góc giữa cnh bên và mặt
đáy bằng
30
. Hình chiếu của
A
lên
ABC
l trung điểm
I
của
BC
. Tính thể tích khối
lăng trụ
.ABC A B C
.
A.
3
3
8
a
. B.
3
13
12
a
. C.
3
3
6
a
. D.
3
3
2
a
.
Câu 45: Cho hnh lăng trụ
.ABC A B C
c đáy l tam giác đều cnh bằng
.a
Biết hình chiếu vuông
góc của
A
trên
ABC
là trọng tâm tam giác
, 2 ,ABC AA a
thể tích của khối lăng trụ
.ABC A B C
bằng
A.
3
11
.
4
a
B.
3
3
.
4
a
C.
3
3
.
8
a
D.
3
6
.
9
a
Câu 46: Cho hnh lăng trụ
.ABC A B C
c đáy l tam giác đều cnh bằng
.a
Biết hình chiếu vuông
góc của
A
trên
ABC
là trọng tâm tam giác
, ; 60 ,ABC AA ABC

thể tích của khối lăng
trụ
.ABC A B C
bằng
A.
3
11
.
4
a
B.
3
3
.
4
a
C.
3
3
.
8
a
D.
3
6
.
9
a
Câu 47: Cho lăng trụ
. ' ' 'ABC A B C
c đáy
ABC
là tam giác vuông ti
B
, đường cao
BH
. Biết
'A H ABC
và
1, 2, ' 2AB AC AA
. Thể tích của khối lăng trụ đã cho bằng
A.
21
12
. B.
7
4
. C.
21
4
. D.
37
4
.
Câu 48: Cho lăng trụ
.ABC A B C
c đáy
ABC
l tam giác vuông ti
B
và
A A A B A C

. Biết rằng
,3AB a BC a
v mặt phẳng
A BC
to vi mặt phẳng đáy một gc
60
. Thể tch khối
lăng trụ
.ABC A B C
bằng
A.
3
3
4
a
. B.
3
3
2
a
C.
3
a
. D.
3
4
a
Câu 49: Cho hnh lăng trụ
.ABCD A B C D
có
ABCD
là hình chữ nhật. Tính thể tích khối lăng trụ đã
cho biết
A A A B A D

và
, 3, 2AB a AD a AA a
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
A.
3
3a
. B.
3
a
. C.
3
3a
. D.
3
33a
.
Câu 50: Cho khối lăng trụ
.ABC A B C
c đáy l tam giác đều cnh
4 , 2 3a AA a
. Gọi
,MN
lần
lượt l trung điểm của
,BB CC

. Biết mặt bên
BCC B

là hình chữ nhật và mặt phẳng
ANM
vuông góc vi mặt phẳng
BCC B

. Thể tích khối lăng trụ đã cho bằng
A.
3
33a
. B.
3
24 3a
. C.
3
12 3a
. D.
3
43a
.
Câu 51: Cho hình hộp
. ' ' ' 'ABCD A B C D
c đáy l hnh chữ nhật,
3, 7AB AD
. Hai mặt
''ABB A
và
''ADD A
lần lượt to vi đáy gc
45
và
60
, biết cnh bên bằng 1. Tính thể
tích khối hộp
. ' ' ' 'ABCD A B C D
.
A.
3
. B.
33
4
. C.
3
4
. D.
3
.
BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN
Câu 52: Khối lăng trụ tam giác c độ di các cnh đáy lần lượt bằng
13,14,15.
Cnh bên to vi mặt
phẳng đáy một gc
30
v c chiều di bằng
8.
Thể tch khối lăng trụ đã cho bằng
A.
124 3
. B.
340
. C.
274 3
. D.
336
.
Câu 53: Cho lăng trụ
.ABC A B C
c đáy
ABC
l tam giác đều cnh
a
, độ dài cnh bên bằng
2
3
a
, hình
chiếu của đỉnh
A
trên mặt phẳng
ABC
trùng vi trọng tâm của tam giác
ABC
. Thể tích
khối lăng trụ
.ABC A B C
bằng
A.
3
3
36
a
. B.
3
3
6
a
. C.
3
3
12
a
. D.
3
3
24
a
.
Câu 54: Cho lăng trụ
.ABC A B C
c đáy
ABC
l tam giác đều cnh
a
,
3
2
a
AA
. Biết rằng hình chiếu
vuông góc của
A
lên
ABC
l trung điểm
BC
. Thể tích của khối lăng trụ
.ABC A B C
bằng
A.
3
2
8
a
. B.
3
32
8
a
. C.
3
6
2
a
. D.
3
2
3
a
.
Câu 55: Cho lăng trụ
.ABC A B C
c đáy
ABC
l tam giác đều,
4AA a
. Biết rằng hình chiếu vuông
góc của
A
lên
ABC
l trung điểm
M
của
BC
,
2A M a
. Thể tích của khối lăng trụ
.ABC A B C
bằng
A.
3
8 3a
. B.
3
8 3
3
a
. C.
3
16 3a
. D.
3
16 3
3
a
.
Câu 56: Cho lăng trụ
.ABC A B C
, c đáy
ABC
l tam giác đều cnh
a
. Cho biết hnh chiếu của đỉnh
A
lên mặt đáy
ABC
l điểm
H
trên cnh
AB
mà
2HA HB
v gc giữa mặt bên
A C CA

v mặt đáy
ABC
bằng
45
. Thể tch của khối lăng trụ đã cho l
A.
3
1
4
a
. B.
3
1
12
a
. C.
3
3
4
a
. D.
3
3
4
a
.
Câu 57: Cho hnh lăng trụ
.ABC A B C
c đáy l tam giác đều cnh bằng
.a
Biết hình chiếu vuông
góc của
A
trên
ABC
là trọng tâm tam giác
, ; 60 ,ABC AA B B ABC


thể tích của khối
lăng trụ
.ABC A B C
bằng
A.
3
3
.
24
a
B.
3
3
.
4
a
C.
3
3
.
8
a
D.
3
6
.
9
a
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Câu 58: Cho hnh lăng trụ tam giác
.ABC A B C
c đáy
ABC
là tam giác vuông ti
A
và
AB a
,
3AC a
. Tính thể tích khối lăng trụ
.ABC A B C
biết
2A A A B A C a
.
A.
3
3a
. B.
3
3
2
a
. C.
3
2
a
. D.
3
3
3
a
.
Câu 59: Cho khối lăng trụ
.ABC A B C
c đáy l tam giác vuông ti
, , 3A AB a AC a
. Hình chiếu
vuông góc của
A
trên mặt phẳng
ABC
l trung điểm
H
của
BC

. Khoảng cách từ
A
đến
mặt phẳng
BCC B

bằng
3
4
a
. Thế tích của khối lăng trụ đã cho bằng
A.
3
3
8
a
. B.
3
3
2
a
. C.
3
3
4
a
. D.
3
3
4
a
.
Câu 60: Cho khối lăng trụ
ABCA B C
c đáy l tam giác đều, góc giữa hai mặt phẳng
ABC
và
BCC B

bằng
60
, hình chiếu vuông góc của
B
lên mặt phẳng
ABC
trùng vi trọng tâm
tam giác
ABC
. Khoảng cách giữa hai đường thẳng
AA
và
BC
bằng
3a
. Thể tích khối lăng
trụ đã cho bằng
A.
3
83a
. B.
3
83
3
a
. C.
3
86
3
a
. D.
3
86a
.
_____________________HẾT_____________________
Huế, 15h20’ Ngày 18 tháng 5 năm 2022
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
LỜI GIẢI CHI TIẾT
Dạng 1: Khối lăng trụ có cạnh bên vuông góc với đáy
Phương pháp:
Cho hình lăng trụ đứng
.ABC A B C
…
AA
+) Thể tích khối lăng trụ:
.
ABC
V AA S
A
B
C
B'
A'
C'
BÀI TẬP TRẮC NGHIỆM MINH HỌA
Câu 1: Cho khối lăng trụ có thể tích bằng
3
24a
và chiều cao bằng
3a
. Diện tích một mặt đáy của khối
lăng trụ đã cho bằng
A.
2
16a
. B.
2
8a
. C.
2
6a
. D.
2
72a
.
Lời giải:
Ta có
3
2
24
.8
3
Va
V S h S a
ha
.
Vậy diện tích một mặt đáy của khối lăng trụ đã cho bằng
2
8a
.
Chọn đáp án B.
Câu 2: Cho hnh lăng trụ đng
. ' ' 'ABC A B C
c đáy
ABC
l tam giác vuông cân ti
A
vi
BC a
v
mặt bên
''AA B B
l hnh vuông. Thể tch của khối lăng trụ
. ' ' 'ABC A B C
bằng
A.
3
2
.
8
a
B.
3
2
.
4
a
C.
3
.
4
a
D.
3
.
12
a
Lời giải:
Tam giác
ABC
vuông cân ti
A
c
BC a
nên
2
a
AB AC
.
2
11
. . . .
2 2 4
22
ABC
a a a
S AB AC
.
Do mặt bên
''AA B B
l hnh vuông nên
'
2
a
AA AB
.
V
. ' ' 'ABC A B C
l lăng trụ đng nên
23
. ' ' '
2
. ' .
48
2
ABC A B C ABC
a a a
V S AA
.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chọn đáp án A.
Câu 3: Cho lăng trụ đng
.ABC A B C
c đáy
ABC
là tam giác vuông cân ti
,B
.AB a
Biết
AC
hợp vi
ABC
một góc
60 ,
thể tích của khối lăng trụ
.ABC A B C
bằng
A.
3
3
.
4
a
B.
3
2
.
2
a
C.
3
3
.
2
a
D.
3
6
.
2
a
Lời giải:
C'
A'
B'
C
B
A
Ta có:
2
1
..
22
ABC
a
S AB BC
Do
AA A B C A C

là hình chiếu vuông góc của
AC
trên
.ABC
Suy ra
;.AC A B C AC A
Xét tam giác
AC A

vuông ti
: tan 6.
AA
A AC A AA a
AC

Vậy
23
.
6
. 6. .
22
ABC A B C ABC
aa
V AA S a
Chọn đáp án D.
Câu 4: Cho hnh lăng trụ đng
.ABCD A B C D
c đáy
ABCD
là hình thoi cnh
, 30 , 2 .a BAC AB a
Thể tích của khối lăng trụ
.ABCD A B C D
bằng
A.
3
3
.
6
a
B.
3
3
.
2
a
C.
3
3
.
8
a
D.
3
33
.
8
a
Lời giải:
a
a
C
B
A
D
D'
C'
B'
A'
30
0
Do
A B C D
là hình thoi cnh
a
và
30 60B A C B A D
nên
A B D
l tam giác đều
cnh
2
3
2.
2
A B C D A B D
a
a S S
Xét tam giác
A AB

vuông ti
22
:.A A A B A A B a
Vậy
3
3
..
2
A B C D
a
V AA S

Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chọn đáp án B.
Câu 5: Cho lăng trụ đng
.ABC A B C
c đáy
ABC
là tam giác vuông cân ti
,B
.AB a
Biết
AC
hợp vi
A B BA

một góc
30 ,
thể tích của khối lăng trụ
.ABC A B C
bằng
A.
3
3
.
4
a
B.
3
2
.
2
a
C.
3
3
.
2
a
D.
3
6
.
2
a
Lời giải:
A
B
C
B'
A'
C'
Ta có:
2
1
..
22
ABC
a
S AB BC
Ta có:
B C A B
B C AA B AB
B C AA
là hình chiếu vuông góc của
AC
trên
.A B BA

Suy ra
;.AC A B BA C AB
Xét tam giác
AB C

vuông ti
: sin 2 .
BC
B C AB AC a
AC

Xét tam giác
AC A

vuông ti
22
: 2.A AA AC A C a
Vậy
23
.
2
. 2. .
22
ABC A B C ABC
aa
V AA S a
Chọn đáp án B.
Câu 6: Cho hnh lăng trụ đng
. ' ' 'ABC A B C
c đáy
ABC
là tam giác vuông cân ti
A
. Biết
2BC a
và thể tch lăng trụ bằng
3
2,a
khoảng cách
d
từ
A
đến mặt phẳng
'A BC
bằng
A.
35
.
5
a
B.
5a
. C.
5
.
5
a
D.
25
.
5
a
Lời giải:
H
K
A'
C'
B'
2a
A
B
C
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Do tam giác
ABC
là tam giác vuông cân ti
A
và
2BC a
nên suy ra
2AB AC a
,
2
1
.
2
ABC
S AB AC a
.
Lúc đ lăng trụ đã cho c thể tích là:
'.
ABC
V AA S
.
Theo giả thiết:
23
'. 2 ' 2 .AA a a AA a
Gọi H l trung điểm BC
.AH a
Ta có:
'.AH BC BC A AH
Dựng
''AK A H AK A BC
. Vậy
; ' .d A A BC AK
Xét
'A AH
vuông ti
A
:
2 2 2
1 1 1 2 5
.
5
'
a
AK
AK A A AH
Chọn đáp án D.
Câu 7: Cho hình hộp đng
.ABCD A B C D
c đáy
ABCD
là hình thoi cnh
a
, góc
60BAD 
. Cho
biết góc giữa đường chéo
BD
và mặt đáy bằng
45
. Thể tích khối hộp đã cho l
A.
3
3
6
a
. B.
3
3
4
a
. C.
3
3
3
a
. D.
3
3
.
2
a
Lời giải:
Ta có :
ABD
đều cnh
a
BD a
Ta có:
D D ABCD
BD
là hình chiếu của
BD
lên mặt phẳng
ABCD
.
Do đ:
, , 45BD ABCD BD BD D BD
.
Ta có:
D BD
vuông cân ti
D
DD BD a
.
Vậy
22
.
33
. .2 .2.
42
ABCD A B C D ABCD ABD
aa
V DD S DD S a

.
Chọn đáp án D.
Câu 8: Cho hình hộp đng
.ABCD A B C D
c đáy
ABCD
là hình thoi cnh
a
,
120BAD 
. Gọi
G
là trọng tâm tam giác
ABD
, góc to bởi
CG
và mặt đáy bằng
30
. Tính theo
a
thể tích khối
hộp
.ABCD A B C D
.
A.
3
a
. B.
3
3
a
. C.
3
12
a
. D.
3
6
a
.
Lời giải:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Tam giác
ABC
đều, suy ra
AC a
.
Suy ra
2
3
a
GC
;
2
.tan30
33
a
CC GC
.
Thể tích khối hộp đã cho l:
23
32
..
23
33
ABCD
a a a
V S CC
.
Chọn đáp án B.
Câu 9: Cho lăng trụ đng
.
ABC A B C
có cnh đáy
2BC a
, góc giữa hai mặt phẳng
ABC
và
A BC
bằng
60
. Biết diện tích tam giác
A BC
bằng
2
2a
. Tính thể tích của khối lăng trụ
.
ABC A B C
.
A.
3
3
3
a
V
. B.
3
3Va
. C.
3
3Va
. D.
3
2
3
a
V
.
Lời giải:
Gọi
H
là hình chiếu vuông góc của
A
lên
BC
, khi đ
0
, 60A BC ABC AHA


.
Áp dụng công thc diện tích hình chiếu ta có:
22
1
.cos60 2 .
2

ABC A BC
S S a a
Mặt khác:
2
2
12
.
22
ABC
ABC
S
a
S AH BC AH a
BC a
.
Khi đ
0
.tan60 3AA AH a

.
Vậy
23
.
. . 3 3
ABC A BC ABC
V S A A a a a
.
Chọn đáp án C.
BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN
Câu 10: Một khối lăng trụ đng tam giác có các cnh đáy lần lượt bằng
37;13;30
và diện tích xung
quanh bằng 480. Khi đ thể tích của khối lăng trụ bằng
A.
1170
. B.
2160
. C.
360
. D.
1080
.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Lời giải:
+) Chu vi đáy của khối lăng trụ l:
37 13 30 80P
.
Diện tch đáy của khối lăng trụ l:
37 13 30 180
2 2 2 2
P P P P
S
.
+) Khối lăng trụ c diện tch xung quanh
480
xq
S
.
Suy ra chiều cao khối lăng trụ:
480
6
80
xq
S
h
P
.
+) Thể tch khối lăng trụ:
. 180.6 1080V S h
.
Chọn đáp án D.
Câu 11: Cho hnh lăng trụ đng
.ABC A B C
c đáy
ABC
là tam giác vuông cân ti
,.A AB a
Biết
diện tích t giác
ABB A

bằng
2
2,a
thể tích khối lăng trụ
.ABC A B C
bằng
A.
3
3
.
2
a
B.
3
3
.
6
a
C.
3
.a
D.
3
.
3
a
Lời giải:
C'
B'
A'
C
B
A
Ta có:
2
; . 2 .
2
ABC ABB A
a
S S A A A B A A a

Suy ra:
3
.
..
ABC A B C ABC
V AA S a

Chọn đáp án C.
Câu 12: Cho hnh lăng trụ đng
.ABC A B C
có
2, , 2AA a AB a AC a
,
60BAC
. Thể tích
hnh lăng trụ đ bằng
A.
3
2a
. B.
3
33a
. C.
3
6
2
a
. D.
3
6
2
a
.
Lời giải:
Ta có
2
1 1 3
. .sin .2 .sin60
2 2 2
ABC
a
S AB AC BAC a a
.
Ta có
2
.
3
. . 2
2
ABC A B C ABC
a
V S AA a

3
6
2
a
.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chọn đáp án C.
Câu 13: Cho hnh lăng trụ đng
.ABC A B C
c đáy
ABC
là tam giác vuông cân ti
,.A AB a
Biết góc
giữa
AB C

và
ABC
bằng
60 ,
thể tích khối lăng trụ
.ABC A B C
bằng
A.
3
3
.
2
a
B.
3
3
.
6
a
C.
3
.a
D.
3
6
.
4
a
Lời giải:
H
A
B
C
A'
B'
C'
Ta có:
2
.
2
ABC
a
S
Gọi
H
l trung điểm
.
B C A H
B C B C A AH B C AH
B C A A
Vậy
; 60 .AB C A B C AHA
Suy ra:
3
.
6
..
4
ABC A B C ABC
a
V AA S

Chọn đáp án D.
Câu 14: Cho lăng trụ đng
.ABC A B C
c đáy
ABC
là tam giác vuông cân ti
,B
.AB a
Biết
AB C

hợp vi
ABC
một góc
60 ,
thể tích của khối lăng trụ
.ABC A B C
bằng
A.
3
3
.
4
a
B.
3
2
.
2
a
C.
3
3
.
2
a
D.
3
6
.
2
a
Lời giải:
C'
A'
B'
C
B
A
Ta có:
2
1
..
22
ABC
a
S AB BC
Ta có:
.
B C A B
B C AA B B C AB
B C AA
Suy ra
;.AB C A B C AB A
Xét tam giác
AB A

vuông ti
: tan 3.
AA
A AB A AA a
AB

Vậy
23
.
3
. 3. .
22
ABC A B C ABC
aa
V AA S a
Chọn đáp án C.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Câu 15: Cho khối lăng trụ đng
.ABCD A B C D
c đáy l hai hnh thoi cnh
a
,
3BD a
và
4AA a
(tham khảo hình vẽ dưi)
Thể tch của khối lăng trụ đã cho bằng
A.
3
23a
. B.
3
43
3
a
. C.
3
43a
. D.
3
23
3
a
.
Lời giải:
Tam giác
ABO
vuông ti
O
(
O
là tâm của hình thoi
ABCD
):
2
2 2 2
3
42
aa
AO AB BO a AC a
2
13
22
ABCD
a
S AC BD
.
Thể tích khối lăng trụ
.ABCD A B C D
là
2
3
3
4 2 3
2
ABCD
a
V S AA a a
.
Chọn đáp án A.
Câu 16: Cho hnh lăng trụ đng
.ABCD A B C D
c đáy l hnh thoi
ABCD
cnh
a
,
60ABC
.
Đường chéo
AC
to vi mặt phẳng
ABCD
một góc
30
. Thể tích khối lăng trụ
.ABCD A B C D
tính theo
a
bằng
A.
3
1
.
4
a
B.
3
1
.
6
a
C.
3
1
.
2
a
D.
3
3
2
a
.
Lời giải:
Góc giữa
AC
và
ABCD
là góc
ACA
.
Tam giác
ABC
cân ti
B
có
60ABC
nên tam giác
ABC
l đều
AC a
.
Diện tích hình thoi :
22
33
2 2.
42
ABCD ABC
aa
SS
.
Xét
A AC
vuông ti
3
.tan .tan30
3

a
A AA AC ACA a
.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Vậy thể tích khối lăng trụ
.ABCD A B C D
là
23
33
.
2 3 2
ABCD
a a a
V S AA
.
Chọn đáp án C.
Dạng 2: Khối lăng trụ đều
Phương pháp:
.ABC A B C
A
B
C
B'
A'
C'
+) Đường cao:
AA
+) Thể tích khối lăng trụ:
.
ABC
V AA S
.ABC A B C
C'
A'
B'
D'
A
B
C
D
+) Đường cao:
AA
+) Thể tích khối lăng trụ:
.
ABCD
V AA S
BÀI TẬP TRẮC NGHIỆM MINH HỌA
Câu 17: Thể tích của khối lăng trụ tam giác đều có tất cả các cnh bằng
a
bằng
A.
3
3
12
a
. B.
3
3
6
a
. C.
3
3
2
a
. D.
3
3
4
a
.
Lời giải:
Ta có
23
.
33
..
44
ABC A B C ABC
aa
V S AA a
.
Chọn đáp án D.
Câu 18: Cho khối lăng trụ tam giác đều c độ dài cnh đáy bằng
a
và diện tích xung quanh bằng
2
6a
. Thể tích của khối lăng trụ đã cho l
A.
3
23
3
a
V
. B.
3
3
4
a
V
. C.
3
3
2
a
V
. D.
3
3
3
a
V
.
Lời giải:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Giả sử lăng trụ tam giác đều
.ABC A B C
có độ di cnh đáy bằng
a
suy ra:
2
3
4
ABC
a
S
.
Lăng trụ tam giác đều
.ABC A B C
có diện tch xung quanh bằng
2
6a
suy ra:
2 2 2
6 :3 2 . 2 2
ABB A
S a a AB AA a AA a


.
Vậy
23
.
33
. .2
42
ABC A B C ABC
aa
V S AA a
.
Chọn đáp án C.
Câu 19: Cho lăng trụ tam giác đều
.ABC A B C
có cnh đáy bằng
.a
Biết
2,AB a
thể tích của khối
lăng trụ
.ABC A B C
bằng
A.
3
3
.
4
a
B.
3
3
.
8
a
C.
3
3
.
24
a
D.
3
.
4
a
Lời giải:
C'
A'
B'
C
B
A
Ta có:
2
3
.
4
ABC
a
S
Xét tam giác
AB A

vuông ti
22
: 3.A AA AB A B a
Vậy
23
.
33
. 3. .
44
ABC A B C ABC
aa
V AA S a
Chọn đáp án A.
Câu 20: Cho lăng trụ tam giác đều
.ABC A B C
có cnh đáy bằng
.a
Biết
AB C

hợp vi mặt đáy một
góc
30 ,
thể tích của khối lăng trụ
.ABC A B C
bằng
A.
3
3
.
4
a
B.
3
3
.
8
a
C.
3
3
.
24
a
D.
3
.
4
a
Lời giải:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
M
C'
A'
B'
C
B
A
Ta có:
2
3
.
4
ABC
a
S
Dựng
,A M B C M
l trung điểm
.BC

Ta có:
.
B C A M
B C AA M B C AM
B C AA
Suy ra
;.AB C A B C AMA
Xét tam giác
AMA
vuông ti
: tan .
2
AA a
A AMA AA
AM
Vậy
23
.
33
. . .
2 4 8
ABC A B C ABC
a a a
V AA S
Chọn đáp án B.
Câu 21: Cho hnh lăng trụ tam giác đều
.ABC A B C
có cnh đáy bằng
2a
, góc giữa hai đường thẳng
AB
và
BC
bằng
60
. Thể tích của khối lăng trụ đ l
A.
3
26Va
. B.
3
23
3
a
V
. C.
3
26
3
a
V
. D.
3
23Va
.
Lời giải:
D
C
B
B'
C'
A'
A
Dựng hình bình hành
B C BD

, suy ra
//BC DB

, do đ gc giữa hai đường thẳng
AB
và
BC
bằng góc giữa hai đường thẳng
AB
và
DB
.
Xét tam giác
ACD
có trung tuyến
AB
bằng nửa cnh đối diện
CD
nên
ACD
vuông ti
A
.
2 2 2 2
16 4 2 3AD DC AC a a a
.
Li do
.ABC A B C
l lăng trụ tam giác đều nên
AB BC

hay
AB DB

B DA
cân ti
B
,
mà
o
, 60AB DB

nên tam giác
B DA
đều cnh bằng
23a
.
2 2 2 2
12 4 2 2BB AB AB a a a

.
Tính thể tích
V
của khối lăng trụ đã cho:
2
3
23
. 2 2. 2 6
4
ABC
a
V BB S a a
.
Chọn đáp án A.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Câu 22: Cho hnh lăng trụ tam giác đều
.ABC A B C
có
AA a
. Khoảng cách giữa
'AB
và
'CC
bằng
3a
. Thể tích khối lăng trụ
. ' ' 'ABC A B C
.
A.
3
23
3
a
. B.
3
3a
. C.
3
3
2
a
. D.
3
3
3
a
.
Lời giải:
A
B
C
A'
B'
C'
H
Kẻ
'CH AB CH ABB
', ' 3d CC ABB CH a
Ta có
', ' ', ' 3d CC AB d CC ABB CH a
.
Do tam giác
ABC
đều c đường cao
3CH a
2
23
ABC
AB a S a
Khi đ
3
. ' ' '
'. 3
ABC A B C ABC
V AA S a
.
Chọn đáp án B.
Câu 23: Cho hnh lăng trụ đều
.ABC A B C
có cnh đáy bằng
23
3
a
. Đường thẳng
BC
to vi mặt
phẳng
ACC A

góc
thỏa mãn
cot 2
. Thể tích khối trụ
.ABC A B C
bằng
A.
3
4
11
3
a
. B.
3
1
11
9
a
. C.
3
1
11
3
a
. D.
3
2
11
3
a
.
Lời giải:
Gọi
I
l trung điểm của
AC BI AC BI ACC A

.
Ta có
,,BC ACC A BC C I BC I
.
Xét tam giác
ABC
có
23
.3
3
2
a
BI a
.
Xét tam giác vuông
BIC
ti
I
có
tan 2
tan
BI a
C I a
CI
.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Xét tam giác vuông
CC I
có
2
2
22
3 33
2
33
aa
CC C I IC a





.
Ta có
2
2
23
3
3
3
43
ABC
a
a
S




.
Ta có
23
.
3 33 11
..
3 3 3
ABC A B C ABC
a a a
V S CC
.
Chọn đáp án C.
BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN
Câu 24: Thể tích khối lăng trụ t giác đều
.ABCD A B C D
có
2AC AA a

là
A.
3
4a
. B.
3
2a
. C.
3
2a
. D.
3
22a
.
Lời giải:
Trong tam giác vuông
ABC
ta có
2 2 2
2AB BC AC AB BC a
.
Vậy
3
.
. . 2. 2.2 4
ABCD A B C D
V AB BC AA a a a a
.
Chọn đáp án A.
Câu 25: Cho hnh lăng trụ tam giác đều
. ' ' 'ABC A B C
cnh đáy
4a
, biết diện tích tam giác
'A BC
bằng 8. Thể tích khối lăng trụ
. ' ' 'ABC A B C
bằng
A.
10 3
. B.
23
. C.
83
. D.
43
.
Lời giải:
Gọi
M
l trung điểm
BC
. Khi đ,
'
2
'4
A BC
S
AM
BC

.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Ta có tam giác
ABC
đều
22
43
2 3 ' ' 2
2
1
.4.2 3 4 3.
2
ABC
AM AA A M AM
S

Vậy
. ' ' '
' 8 3
ABC A B C ABC
V AA S
.
Chọn đáp án C.
Câu 26: Cho lăng trụ tam giác đều
.ABC A B C
có cnh đáy bằng
.a
Biết
AB
hợp vi mặt đáy một
góc
60 ,
thể tích của khối lăng trụ
.ABC A B C
bằng
A.
3
3
.
4
a
B.
3
3
.
8
a
C.
3
3
.
24
a
D.
3
.
4
a
Lời giải:
C'
A'
B'
C
B
A
Ta có:
2
3
.
4
ABC
a
S
Do
AA A B C A B

là hình chiếu vuông góc của
AB
trên
.ABC
Suy ra
;.AB A B C AB A
Xét tam giác
AB A

vuông ti
: tan 3.
AA
A AB A AA a
AB

Vậy
23
.
33
. 3. .
44
ABC A B C ABC
aa
V AA S a
Chọn đáp án A.
Câu 27: Cho lăng trụ tam giác đều
.ABC A B C
có cnh đáy bằng
.a
Biết
AC
hợp vi
ABB A

một
góc
30 ,
thể tích của khối lăng trụ
.ABC A B C
bằng
A.
3
3
.
4
a
B.
3
3
.
8
a
C.
3
3
.
24
a
D.
3
6
.
4
a
Lời giải:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
M
C'
A'
B'
C
B
A
Ta có:
2
3
.
4
ABC
a
S
Dựng
,C M A B M
l trung điểm
.AB

Ta có:
C M A B
C M ABB A
C M AA

AM
là hình chiếu vuông góc của
AC
trên
.ABB A

Suy ra
;.AC ABB A MAC
Xét tam giác
MAC
vuông ti
: sin 3.
CM
M MAC AC a
AC

Xét tam giác
AA C

vuông ti
22
: 2.A AA AC A C a
Vậy
23
.
36
. 2. .
44
ABC A B C ABC
aa
V AA S a
Chọn đáp án D.
Câu 28: Cho hnh lăng trụ tam giác đều
.ABC A B C
có cnh đáy bằng
,a AC
hợp vi mặt phẳng
ABB A

một góc
45 .
Thể tích của khối lăng trụ
.ABC A B C
bằng
A.
3
6
.
24
a
B.
3
3
.
4
a
C.
3
6
.
8
a
D.
3
6
.
4
a
Lời giải:
H
45
0
A
B
C
B'
C'
A'
a
a
a
Ta có:
2
3
.
4
A B C
a
S
Dựng
C H A B C H ABB A
; 45 .AC ABB A C AH
Suy ra
AHC
vuông cân ti
3
.
2
a
H HC AH
Xét tam giác
A AH
vuông ti
22
2
:.
2
a
A A A AH A H
Vậy
3
6
..
8
A B C
a
V AA S

Chọn đáp án C.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Câu 29: Cho khối lăng trụ tam giác đều
.ABC A B C
có cnh đáy l
2a
và khoảng cách từ
A
đến mặt
phẳng
A BC
bằng
a
. Tính thể tích của khối lăng trụ
.ABC A B C
.
A.
3
22a
. B.
3
32
2
a
. C.
3
2
2
a
. D.
3
2
2
a
.
Lời giải:
Gọi
M
l trung điểm của
BC

Ta có
B C A M
, vì
ABC
đều v
B C AA
nên
B C AA M
.
Dựng
A E AM
, khi đ
A E AB C
, do đ
;d A AB C A E a

AA M
vuông ti
A
vi đường cao
AH
nên
2 2 2 2 2 2 2
2
1 1 1 1 1 1 1 1 6
2
( 3)
a
AA
A H AA AM AA A E A M a
a
Thể tch khối lăng trụ
.ABC A B C
là:
23
6 (2 ) 3 3 2
2 4 2
a a a
V
.
Chọn đáp án B.
Câu 30: Cho hnh lăng trụ tam giác đều
.ABC A B C
có cnh đáy bằng
2a
, góc giữa hai đường thẳng
AB
và
B C
bằng
60
. Tính thể tích
V
của khối lăng trụ đ.
A.
3
26
3
a
V
. B.
3
23Va
. C.
3
23
3
a
V
. D.
3
26Va
.
Lời giải:
Gọi
N
l giao điểm của
AB
và
AB
.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Gọi
M
l trung điểm của
AC

thì
MN
là trung bình tam giác
//A BC MN B C
.
Khi đ gc giữa
AB
và
B C
là góc giữa
BN
và
MN
(1).
Đặt:
AA x
. Khi đ:
2 2 2 2
1 1 1
4
2 2 2
B N AB AA A B x a
2 2 2 2
1 1 1
4
2 2 2
MN BC BB BC x a

.
Do đ :
BN MN B MN
cân ti
N
(2).
Từ (1) và (2) suy ra
B MN
đều. Suy ra:
23
3
2
a
MN B N B M a

.
Do đ :
22
1
4 3 2 2
2
MN x a a x a
.
Vậy thể tích khối lăng trụ là :
2
3
43
. 2 2. 2 6
4
ABC
a
V AA S a a
.
Chọn đáp án D.
Dạng 3: Khối hộp chữ nhật – Khối lập phương
Phương pháp:
.ABCD A B C D
c
b
a
C'
A'
B'
D'
A
B
C
D
+) Thể tích khối hộp:
V abc
.ABCD A B C D
a
a
a
C'
A'
B'
D'
A
B
C
D
+) Thể tích khối lập phương:
3
Va
BÀI TẬP TRẮC NGHIỆM MINH HỌA
Câu 31: Thể tích của khối lập phương cnh
3a
bằng
A.
3
9a
. B.
3
27a
. C.
3
18a
. D.
3
36 .a
Lời giải:
Thể tch của khối lập phương cnh
3a
bằng
3
3
3 27aa
.
Chọn đáp án B.
Câu 32: Thể tích của khối hộp chữ nhật c ba kch thưc
2,3,7
bằng
A.
14.
B.
42.
C.
126.
D.
12.
Lời giải:
Thể tích của khối hộp chữ nhật là:
2.3.7 42V 
.
Chọn đáp án B.
Câu 33: Cho hình hộp chữ nhật
.ABCD A B C D
có
2 , .AB a BC a
Biết
3,AC a
thể tích của khối
hộp chữ nhật
.ABCD A B C D
bằng
A.
3
4.a
B.
3
4 3 .a
C.
3
2 15
.
3
a
D.
3
3
.
4
a
Lời giải:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
D'
A'
B'
C'
D
C
B
A
Xét tam giác
AA C

vuông ti
2
2
22
: 3 5 2 .A AA AC A C a a a
Vậy
3
.
. . 4 .
ABCD A B C D
V AA AB AD a

Chọn đáp án A.
Câu 34: Cho hình lập phương
.ABCD A B C D
có diện tích mặt chéo
ACC A

bằng
2
22a
. Thể tích
của khối lập phương
.ABCD A B C D
là
A.
3
16 2a
. B.
3
22a
. C.
3
8a
. D.
3
a
.
Lời giải:
Giả sử độ dài cnh hình lập phương l
x
, khi đ
2AC x
và
2
2
ACC A
Sx

. Suy ra
2xa
. Vậy thể tích khối lập phương l
3
3
2 2 2aa
.
Chọn đáp án B.
Câu 35: Cho hình hộp chữ nhật
.ABCD A B C D
có
, 3,AB a AD a
góc giữa mặt phẳng
ABC D

và
ABCD
bằng
45 .
Thể tích khối hộp chữ nhật đã cho bằng
A.
3
3.a
B.
3
.a
C.
3
3.a
D.
3
2 3 .a
Lời giải:
Ta có góc giữa
ABC D

và
ABCD
bằng
0
45C BC
.tan 45 3CC BC a
3
.
. . . 3. 3 3
ABCD A B C D
V AB AD AA a a a a
.
Chọn đáp án A.
BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN
Câu 36: Thể tích của khối hộp chữ nhật
.ABCD A B C D
có
3, 5AB AC
,
8AA
bằng
A.
120
. B.
32
C.
96
. D.
60
.
Lời giải:
Tính
22
4BC AC AB
Thể tích khối hộp bằng
.
. . 3.4.8 96
ABCD A B C D
V AB BC AA
.
Chọn đáp án C.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Câu 37: Diện tích toàn phần của một hình lập phương bằng
2
96 cm
. Khối lập phương đã cho c thể
tích bằng
A.
3
84 cm
. B.
3
48 cm
. C.
3
64 cm
. D.
3
91 cm
.
Lời giải:
Gọi
x
0x
là cnh của hình lập phương
2
6 96 4
tp
S x x
.
Vậy
33
4 64V cm
.
Chọn đáp án C.
Câu 38: Cho hình lập phương
.ABCD A B C D
có diện tích tam giác
ACD
bằng
2
3a
. Thể tích của
khối lập phương đã cho bằng:
A.
3
4 2 .a
B.
3
8a
. C.
3
a
. D.
3
22a
.
Lời giải:
Đặt
0AB x x
. Do
ACD
l tam giác đều
2
2 2 2
3
3 4 2
4
x
a x a x a
.
Vậy
3
3
. ' ' ' '
28
ABCD A B C D
V a a
.
Chọn đáp án B.
Câu 39: Cho hnh lăng trụ đng
.ABCD A B C D
c đáy l hnh vuông cnh bằng
6
, đường chéo
AB
của mặt bên
ABB A

c độ dài bằng
10
. Tính thể tích
V
của khối lăng trụ
.ABCD A B C D
.
A.
384V
. B.
180V
. C.
480V
. D.
288V
.
Lời giải:
Diện tch của hnh vuông
ABCD
là
2
6 36S 
.
Xét tam giác
ABB
vuông ti
B
có
2 2 2 2
10 6 8B B B A AB

.
Vậy thể tch của hnh lăng trụ l
36.8 288V 
.
Chọn đáp án D.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Câu 40: Cho hình hộp chữ nhật
.ABCD A B C D
có
2 , .AB a BC a
Biết
ADC B

hợp vi mặt đáy
một góc
60 ,
thể tích của khối hộp chữ nhật
.ABCD A B C D
bằng
A.
3
4.a
B.
3
4 3 .a
C.
3
2 15
.
3
a
D.
3
3
.
4
a
Lời giải:
A
B
C
D
C'
B'
A'
D'
Ta có:
;.ADC B A B C D DC D
Xét tam giác
DC D

vuông ti
:tan 2 3.
DD
D DC D DD a
CD

Vậy
3
.
. . 4 3 .
ABCD A B C D
V AA AB AD a

Chọn đáp án B.
Câu 41: Cho hình hộp chữ nhật
.ABCD A B C D
có
2 , .AB a BC a
Biết
AC
hợp vi mặt đáy một góc
60 ,
thể tích của khối hộp chữ nhật
.ABCD A B C D
bằng
A.
3
2 15 .a
B.
3
4 3 .a
C.
3
2 15
.
3
a
D.
3
3
.
4
a
Lời giải:
D'
A'
B'
C'
D
C
B
A
Ta có:
AA A B C D A C

là hình chiếu vuông góc của
AC
trên
.A B C D
Suy ra:
;.AC A B C D AC A
Xét tam giác
AC A

vuông ti
:tan 15.
AA
A AC A AA a
AC

Vậy
3
.
. . 2 15 .
ABCD A B C D
V AA AB AD a

Chọn đáp án A.
Câu 42: Cho hình hộp chữ nhật c đường chéo
21.d
Độ di ba kch thưc của hình hộp chữ nhật
lập thành một cấp số nhân vi công bội
2.q
Thể tích của khối hộp chữ nhật đã cho l
A.
8V
. B.
8
3
V
. C.
4
3
V
. D.
6V
.
Lời giải:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Gọi ba kch thưc của hình hộp chữ nhật là
, , 0 .a b c a b c
Do
,,a b c
lập thành cấp số nhân
nên
2 ; 4 .b a c a
Theo giả thiết:
2 2 2 2
21 21 21 1.a b c a a
Vậy thể tích khối hộp chữ nhật là
1.2.4 8.V abc
Chọn đáp án A.
Dạng 4: Khối lăng trụ xiên bất kì
Phương pháp:
Cho hình lăng trụ
.ABC A B C
…
,AH H
A
.ABC
+) Thể tích khối lăng trụ:
.
ABC
V AH S
H
M
A
B
C
A'
B'
C'
BÀI TẬP TRẮC NGHIỆM MINH HỌA
Câu 43: Cho lăng trụ
.ABC A B C
c đáy
ABC
l tam giác đều cnh
a
, cnh bên bằng
4a
và to vi
đáy gc
o
30
. Thể tích khối lăng trụ
.ABC A B C
bằng
A.
3
1
2
a
. B.
3
3
2
a
. C.
3
3a
. D.
3
3
2
a
.
Lời giải:
C
B
A'
C'
B'
H
A
Tam giác
ABC
l tam giác đều cnh
a
nên
2
3
4
ABC
a
S
.
Gọi
H
l hnh chiếu vuông gc của
A
trên
ABC
, do đ
A H ABC
.
Ta có
,( ) 30A H ABC A AH


nên
1
.sin 4 . 2
2
A H AA A AH a a
.
Vậy
.
2
3
33
. 2 .
42
ABC A B CC AB
a
V A H S a a
.
Chọn đáp án D.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Câu 44: Cho lăng trụ tam giác
.ABC A B C
c đáy l tam giác đều cnh
a
, góc giữa cnh bên và mặt
đáy bằng
30
. Hình chiếu của
A
lên
ABC
l trung điểm
I
của
BC
. Tính thể tích khối
lăng trụ
.ABC A B C
.
A.
3
3
8
a
. B.
3
13
12
a
. C.
3
3
6
a
. D.
3
3
2
a
.
Lời giải:
I
A
C
B
B'
C'
A'
Vì
A I ABC
nên
AI
l hnh chiếu vuông gc của
AA
lên
ABC
.
Do đ
, , 30AA ABC AA AI AIA
Ta có
tan30 .
2
a
A I AI
23
.
33
..
2 4 8
ABC A B C ABC
a a a
V IA S
.
Chọn đáp án A.
Câu 45: Cho hnh lăng trụ
.ABC A B C
c đáy l tam giác đều cnh bằng
.a
Biết hình chiếu vuông
góc của
A
trên
ABC
là trọng tâm tam giác
, 2 ,ABC AA a
thể tích của khối lăng trụ
.ABC A B C
bằng
A.
3
11
.
4
a
B.
3
3
.
4
a
C.
3
3
.
8
a
D.
3
6
.
9
a
Lời giải:
M
G
C
B
A
C'
B'
A'
Ta có:
2
3
.
4
ABC
a
S
Gọi
G
là trọng tâm tam giác
.ABC
Xét tam giác
A AG
vuông ti
22
33
:.
3
a
G A G AA AG

Vậy
23
.
33 3 11
. . .
3 4 4
ABC A B C ABC
a a a
V A G S
Chọn đáp án A.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Câu 46: Cho hnh lăng trụ
.ABC A B C
c đáy l tam giác đều cnh bằng
.a
Biết hình chiếu vuông
góc của
A
trên
ABC
là trọng tâm tam giác
, ; 60 ,ABC AA ABC

thể tích của khối lăng
trụ
.ABC A B C
bằng
A.
3
11
.
4
a
B.
3
3
.
4
a
C.
3
3
.
8
a
D.
3
6
.
9
a
Lời giải:
M
G
C
B
A
C'
B'
A'
Ta có:
2
3
.
4
ABC
a
S
Gọi
G
là trọng tâm tam giác
.ABC
Do
A G ABC
nên
AG
là hình chiếu của
AA
trên
.ABC
Suy ra:
;.AA ABC A AG

Xét tam giác
A AG
vuông ti
o
2
:tan .tan60 .
3
AG
G A AG A G AM a
AG

Vậy
23
.
33
. . .
44
ABC A B C ABC
aa
V A G S a
Chọn đáp án B.
Câu 47: Cho lăng trụ
. ' ' 'ABC A B C
c đáy
ABC
là tam giác vuông ti
B
, đường cao
BH
. Biết
'A H ABC
và
1, 2, ' 2AB AC AA
. Thể tích của khối lăng trụ đã cho bằng
A.
21
12
. B.
7
4
. C.
21
4
. D.
37
4
.
Lời giải:
Độ dài của đường cao
BH
:
.3
2
AB BC
BH
AC

. Suy ra
31
:3
22
AH 
.
Khi đ độ di đường cao
'AH
của hnh lăng trụ bằng :
22
17
' ' 2
42
A H AA AH
.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Thể tích khối lăng trụ đã cho bằng :
1 1 7 21
. . ' .1. 3
2 2 2 4
V AB BC A H
.
Chọn đáp án B.
Câu 48: Cho lăng trụ
.ABC A B C
c đáy
ABC
l tam giác vuông ti
B
và
A A A B A C

. Biết rằng
,3AB a BC a
v mặt phẳng
A BC
to vi mặt phẳng đáy một gc
60
. Thể tch khối
lăng trụ
.ABC A B C
bằng
A.
3
3
4
a
. B.
3
3
2
a
C.
3
a
. D.
3
4
a
Lời giải:
Gọi
H
l trung điểm của
AC
, vì tam giác
ABC
vuông ti
B
nên
H
l tâm đường tròn ngoi
tiếp của tam giác
ABC
.
Ta có:
A A A B A C
HA HB HC


A H ABC

.
Kẻ
HM BC
; 60A BC ABC A MH

.
Diện tích tam giác
ABC
:
2
13
.
22
ABC
a
S AB BC
.
Xét tam giác vuông
A HM
có:
13
.tan60 .tan60
22
a
A H HM AB
.
Thể tích khối lăng trụ
.ABC A B C
:
23
3 3 3
..
2 2 4
ABC
a a a
V A H S
.
Chọn đáp án A.
Câu 49: Cho hnh lăng trụ
.ABCD A B C D
có
ABCD
là hình chữ nhật. Tính thể tích khối lăng trụ đã
cho biết
A A A B A D

và
, 3, 2AB a AD a AA a
A.
3
3a
. B.
3
a
. C.
3
3a
. D.
3
33a
.
Lời giải:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Gọi
H
l hnh chiếu của
A
trên
ABCD
. Vì
A A A B A D HA HB HD
H AC BD
22
2 2 2
3
4
AB AD
A H AA AH AA a
.
Vậy
23
.
. 3. 3 3
ABCD A B C D ABCD
V A H S a a a
.
Chọn đáp án A.
Câu 50: Cho khối lăng trụ
.ABC A B C
c đáy l tam giác đều cnh
4 , 2 3a AA a
. Gọi
,MN
lần
lượt l trung điểm của
,BB CC

. Biết mặt bên
BCC B

là hình chữ nhật và mặt phẳng
ANM
vuông góc vi mặt phẳng
BCC B

. Thể tích khối lăng trụ đã cho bằng
A.
3
33a
. B.
3
24 3a
. C.
3
12 3a
. D.
3
43a
.
Lời giải:
N
M
C'
A'
B
C
A
B'
H
Ta có
22
16 3 13CC MN CC AMN CC AN AN a a a
.
Tương tự
13AM a
, do đ tam giác
AMN
cân ti
A
. Gọi
H
l trung điểm
MN
.
Suy ra
AH MN AH BCC B

và
22
13 4 3AH a a a
.
Mặt khác
3
..
3 3 1 1
. . . .3 .4 .2 3 12 3
2 2 3 2
ABC A B C A BCC B BCC B
V V AH S a a a a
.
Chọn đáp án C.
Câu 51: Cho hình hộp
. ' ' ' 'ABCD A B C D
c đáy l hnh chữ nhật,
3, 7AB AD
. Hai mặt
''ABB A
và
''ADD A
lần lượt to vi đáy gc
45
và
60
, biết cnh bên bằng 1. Tính thể
tích khối hộp
. ' ' ' 'ABCD A B C D
.
A.
3
. B.
33
4
. C.
3
4
. D.
3
.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Lời giải:
K
J
C
D
B
C'
B'
A'
D'
I
A
Gọi
I
là hình chiếu của
A
trên
( ' ' ' ')A B C D
. Đặt
( 0)AI x x
Gọi
,JK
lần lượt là hình chiếu của
I
trên
''AB
và
''AD
.
Ta có
''
' ' ' ' ; ' ' ' ' 45
''
A B AI
A B AIJ ABB A A B C D AJI
A B IJ
JI AI x
.
Ta có
''
' ' ' ' ; ' ' ' ' 60
''
A D AI
A D AIK ADD A A B C D AKI
A D IK
3
tan60 3
AI x
IK
; Do
'A JIK
là hình chữ nhật
23
'
3
x
IA
Ta li có
2 2 2
3
''
7
AA AI A I x
. ' ' ' '
. . 3
ABCD A B C D
V AB AD AI
.
Chọn đáp án D.
BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN
Câu 52: Khối lăng trụ tam giác c độ di các cnh đáy lần lượt bằng
13,14,15.
Cnh bên to vi mặt
phẳng đáy một gc
30
v c chiều di bằng
8.
Thể tch khối lăng trụ đã cho bằng
A.
124 3
. B.
340
. C.
274 3
. D.
336
.
Lời giải:
Tam giác đáy của lăng trụ c diện tch
13 14 15 84S p p p p
vi
13 14 15
21.
2
p


Chiều cao lăng trụ:
8.sin30 4. h
Vậy thể tch khối lăng trụ l
. 336.V S h
Chọn đáp án D.
Câu 53: Cho lăng trụ
.ABC A B C
c đáy
ABC
l tam giác đều cnh
a
, độ dài cnh bên bằng
2
3
a
, hình
chiếu của đỉnh
A
trên mặt phẳng
ABC
trùng vi trọng tâm của tam giác
ABC
. Thể tích
khối lăng trụ
.ABC A B C
bằng
A.
3
3
36
a
. B.
3
3
6
a
. C.
3
3
12
a
. D.
3
3
24
a
.
Lời giải:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
a
a
a
2a/3
C'
B'
G
I
A
B
C
A'
Gọi
G
l trọng tâm của tam giác
ABC
. Ta có:
23
33
a
AG AI
;
2
2
2
2 2 2
23
.
3 3 9 3
a a a a
A G A A AG A G







Vậy
23
33
..
4 3 12
a a a
V B h
.
Chọn đáp án C.
Câu 54: Cho lăng trụ
.ABC A B C
c đáy
ABC
l tam giác đều cnh
a
,
3
2
a
AA
. Biết rằng hình chiếu
vuông góc của
A
lên
ABC
l trung điểm
BC
. Thể tích của khối lăng trụ
.ABC A B C
bằng
A.
3
2
8
a
. B.
3
32
8
a
. C.
3
6
2
a
. D.
3
2
3
a
.
Lời giải:
Gọi
M
l trung điểm
BC
, khi đ
A M ABC
. Tam giác
ABC
đều cnh
a
nên
AM BC
và
3
2
a
AM
.
Xét tam giác vuông
A AM
vuông ti
M
có
2 2 2
A M AM AA


.
2
2
22
3 3 6
2 2 2
a a a
A M AA AM








.
23
.
6 3 3 2
.S .
2 4 8
ABC A B C ABC
a a a
V A M
.
Chọn đáp án B.
Câu 55: Cho lăng trụ
.ABC A B C
c đáy
ABC
l tam giác đều,
4AA a
. Biết rằng hình chiếu vuông
góc của
A
lên
ABC
l trung điểm
M
của
BC
,
2A M a
. Thể tích của khối lăng trụ
.ABC A B C
bằng
A.
3
8 3a
. B.
3
8 3
3
a
. C.
3
16 3a
. D.
3
16 3
3
a
.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Lời giải:
Do
A M ABC
nên tam giác
A MA
vuông ti
M
.
Trong tam giác
A MA
vuông ti
M
:
22 22
23416AM A A A M aa a

.
Do
ABC
l tam giác đều nên
3 2. 2.
2
23
4
33
AAB
A
Ma
A aMB 
.
Vậy thể tch lăng trụ
.ABC A B C
là
2
3
43
. .2 8 3
4
ABC
a
V S A M a a
(đvtt).
Chọn đáp án A.
Câu 56: Cho lăng trụ
.ABC A B C
, c đáy
ABC
l tam giác đều cnh
a
. Cho biết hnh chiếu của đỉnh
A
lên mặt đáy
ABC
l điểm
H
trên cnh
AB
mà
2HA HB
v gc giữa mặt bên
A C CA

v mặt đáy
ABC
bằng
45
. Thể tch của khối lăng trụ đã cho l
A.
3
1
4
a
. B.
3
1
12
a
. C.
3
3
4
a
. D.
3
3
4
a
.
Lời giải:
+) Gọi
K
l trung điểm
AC
,
E
l điểm thuộc
AK
sao cho
2
3
AE
AK
.
+) Ta có:
ABC A C CA AC


.
1
+) Ta có:
AC HE
(vì
AC BK
và
//HE BK
) và
AC A H
(vì
A H ABC
)
AC HE ABC
AC A HE
AC A E A C CA


2
+) Từ
1
và
2
suy ra
, , 45A C CA ABC A E HE A EH
A HE
vuông cân ti
H
2 2 3 3
3 3 2 3
aa
A H HE BK
.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
+) Ta có:
23
.
33
.
4 3 4
ABC A B C ABC
a a a
V S A H
.
Chọn đáp án A.
Câu 57: Cho hnh lăng trụ
.ABC A B C
c đáy l tam giác đều cnh bằng
.a
Biết hình chiếu vuông
góc của
A
trên
ABC
là trọng tâm tam giác
, ; 60 ,ABC AA B B ABC


thể tích của khối
lăng trụ
.ABC A B C
bằng
A.
3
3
.
24
a
B.
3
3
.
4
a
C.
3
3
.
8
a
D.
3
6
.
9
a
Lời giải:
A'
B'
C'
A
B
C
G
M
Ta có:
2
3
.
4
ABC
a
S
Gọi
G
là trọng tâm tam giác
.ABC
Dựng
,GM AB M
l trung điểm
.
AB A G
AB AB A GM AB A M
AB GM

Suy ra:
;.AA B B ABC A MG
Xét tam giác
A MG
vuông ti
o
1
:tan .tan60 .
32
A G a
G A MG A G AM
GM

Vậy
23
.
33
. . .
2 4 8
ABC A B C ABC
a a a
V A G S
Chọn đáp án C.
Câu 58: Cho hnh lăng trụ tam giác
.ABC A B C
c đáy
ABC
là tam giác vuông ti
A
và
AB a
,
3AC a
. Tính thể tích khối lăng trụ
.ABC A B C
biết
2A A A B A C a
.
A.
3
3a
. B.
3
3
2
a
. C.
3
2
a
. D.
3
3
3
a
.
Lời giải:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
H
C
B
A
C'
B'
A'
Gọi
H
l chân đường cao h từ
A
xuống đáy
ABC
.
Vì
A A A B A C

và tam giác
ABC
vuông ti
A
nên
H
l trung điểm
BC
Ta có
2
3
2
BC
AH a A H A A AH a

.
Thể tích khối lăng trụ là
3
.
13
. 3. . 3
22
ABC A B C ABC
a
V A H S a a a



.
Chọn đáp án B.
Câu 59: Cho khối lăng trụ
.ABC A B C
c đáy l tam giác vuông ti
, , 3A AB a AC a
. Hình chiếu
vuông góc của
A
trên mặt phẳng
ABC
l trung điểm
H
của
BC

. Khoảng cách từ
A
đến
mặt phẳng
BCC B

bằng
3
4
a
. Thế tích của khối lăng trụ đã cho bằng
A.
3
3
8
a
. B.
3
3
2
a
. C.
3
3
4
a
. D.
3
3
4
a
.
Lời giải:
Kẻ
BC AH
AK BC BC AHK
BC AK
.
Do đ kẻ
BC AT
AT HK AT BCC B
HK AT

.
Có
22
.3
2
2
AB AC a
BC AB AC a AK
BC
và
3
,
4
a
AT d A BCC B


.
Tam giác vuông
AHK
có
2 2 2
1 1 1
2
a
AH
AT AK AH
.
Vậy
3
.
13
. . 3 .
2 2 4
ABC A B C ABC
aa
V S AH a a
.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chọn đáp án D.
Câu 60: Cho khối lăng trụ
ABCA B C
c đáy l tam giác đều, góc giữa hai mặt phẳng
ABC
và
BCC B

bằng
60
, hình chiếu vuông góc của
B
lên mặt phẳng
ABC
trùng vi trọng tâm
tam giác
ABC
. Khoảng cách giữa hai đường thẳng
AA
và
BC
bằng
3a
. Thể tích khối lăng
trụ đã cho bằng
A.
3
83a
. B.
3
83
3
a
. C.
3
86
3
a
. D.
3
86a
.
Lời giải:
Gọi
0x
l độ dài cnh
BC
. Gọi
M
là trung điểm của
BC
và kẻ
GH BCC B

.
Khi đ:
ABC BCC B BC


. Do
BC GM
BC BMG BC GHM
BC B G
.
Ta có:
; ; 3d AA B C d AA BCC B a HG a
Suy ra:
3
; 60 .sin60 . 4
2
23
x
ABC BCC B HMG GH GM a x a

.
Khi đ:
4
.tan60 . 3 2 .
23
a
B G GM a
Thể tch khối lăng trụ đã cho l
2
3
34
. .2 8 3
4
ABCA B C ABC
a
V S B G a a
.
Chọn đáp án A.
_____________________HẾT_____________________
Huế, 15h20’ Ngày 18 tháng 5 năm 2022
| 1/40
| | Tải xuống

Có thể bạn quan tâm:

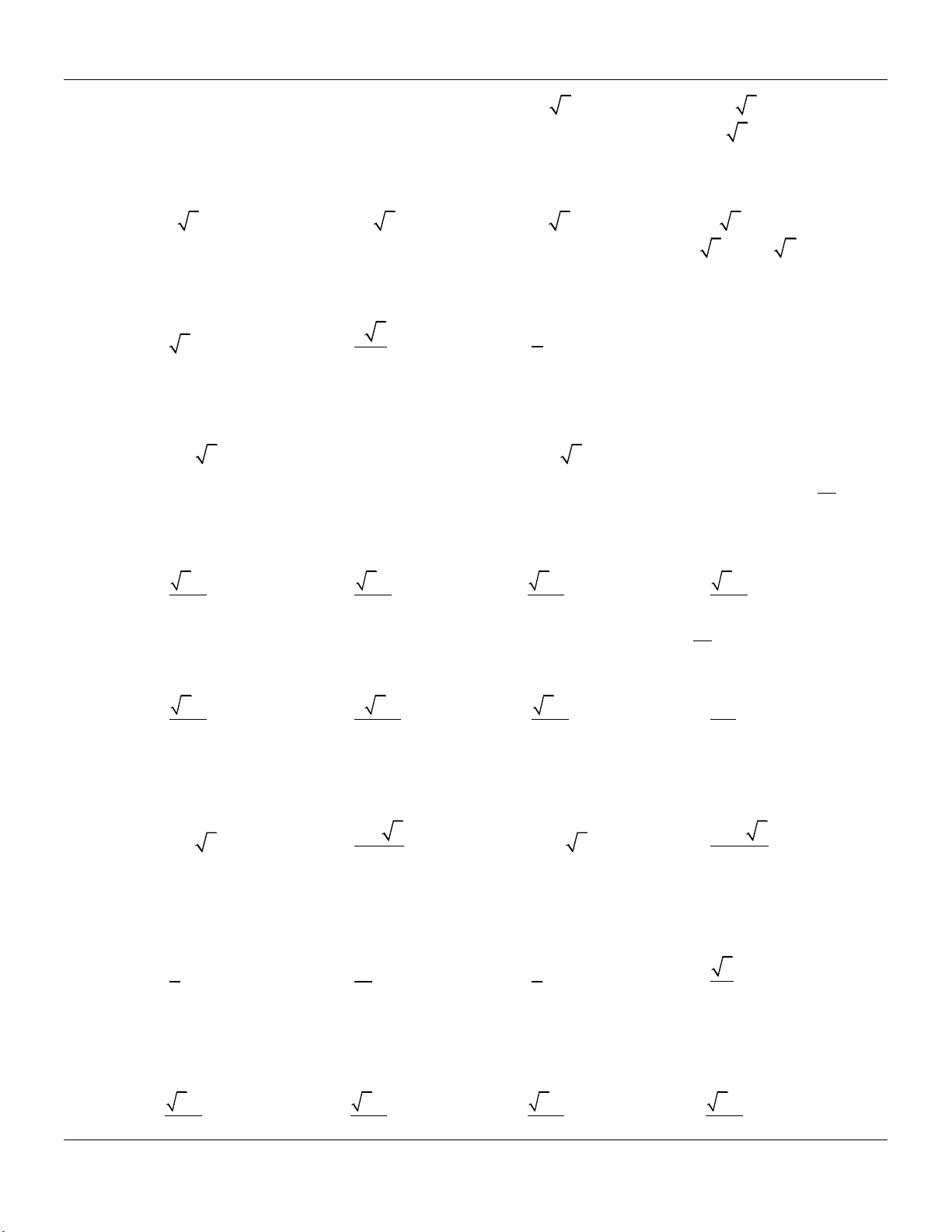
Preview text:

LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ TOÁN 12 THỂ TÍCH KHỐI ĐA DIỆN
THỂ TÍCH KHỐI LĂNG TRỤ
 LUYỆN THI THPT QUỐC GIA
 CẬP NHẬT TỪ ĐỀ THI MỚI NHẤT
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
MỘT SỐ DẠNG TOÁN LIÊN QUAN ĐẾN
THỂ TÍCH KHỐI LĂNG TRỤ
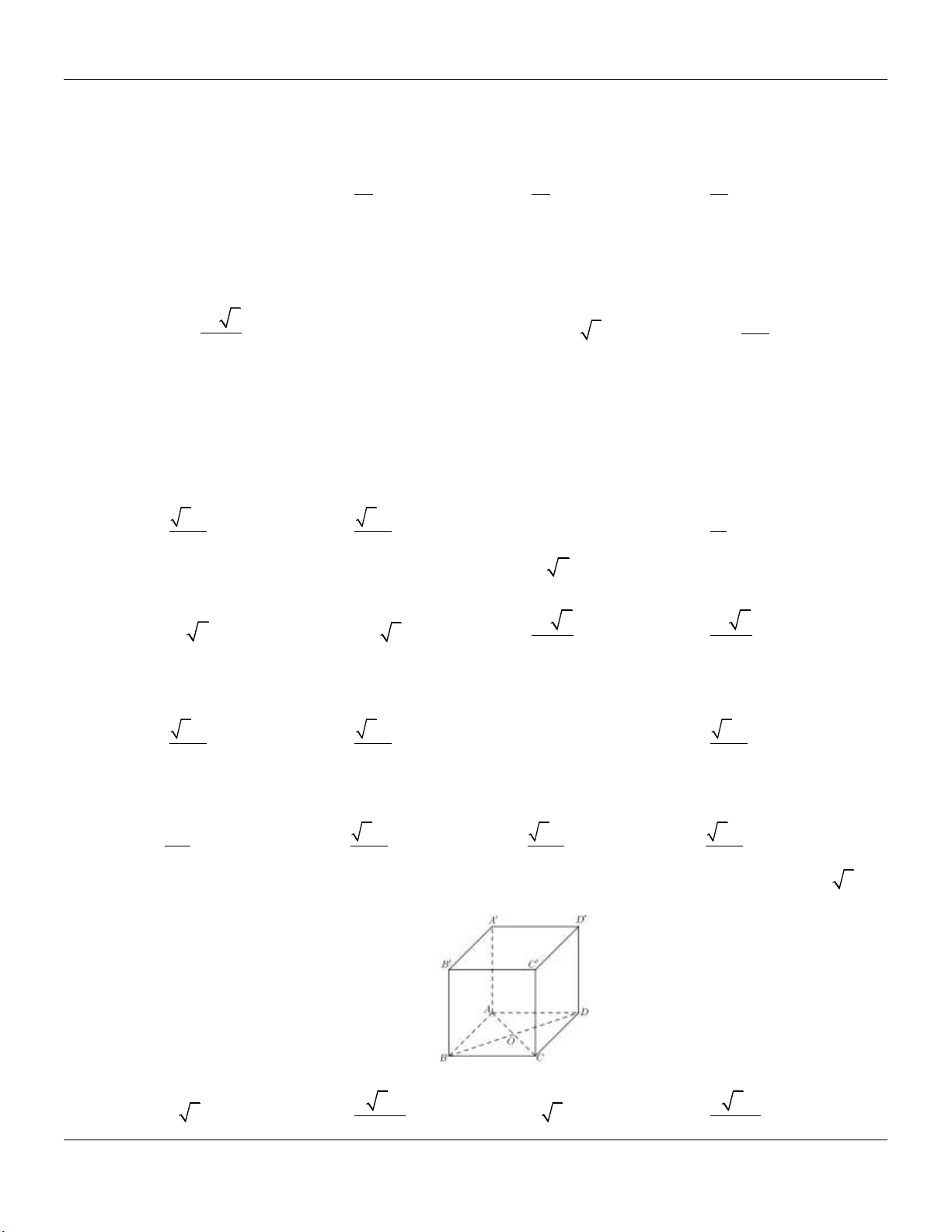
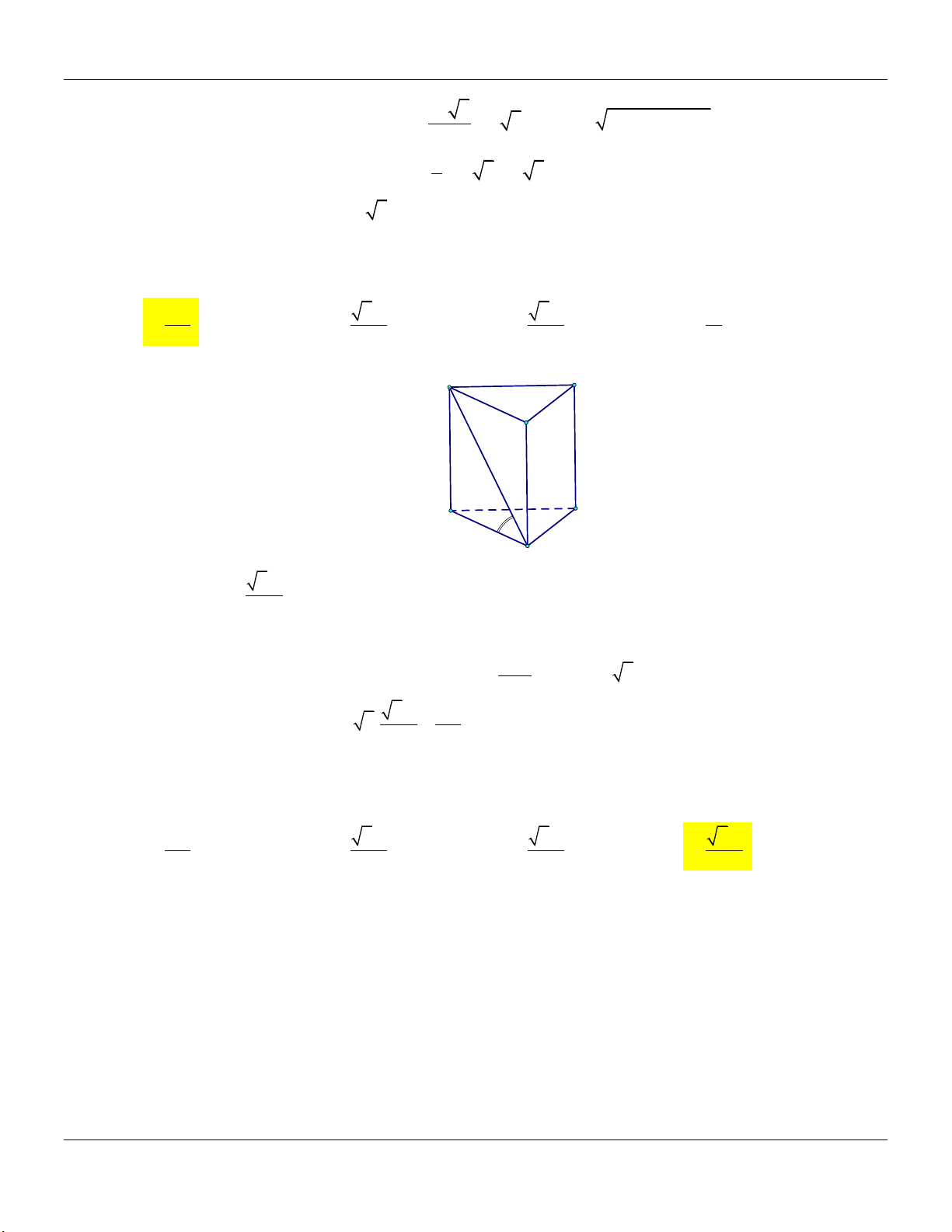
Dạng 1: Khối lăng trụ có cạnh bên vuông góc với đáy Phương pháp:
Cho hình lăng trụ đứng ABC.A BC   …
+) Đường cao: AAForm hình vẽ:
+) Thể tích khối lăng trụ: V AA .S A C ABC B C' A' B'
BÀI TẬP TRẮC NGHIỆM MINH HỌA Câu 1:
Cho khối lăng trụ có thể tích bằng 3
24a và chiều cao bằng 3a . Diện tích một mặt đáy của khối lăng trụ đã cho bằng A. 2 16a . B. 2 8a . C. 2 6a . D. 2 72a . Câu 2:
Cho hình lăng trụ đứng ABC.A' B'C ' có đáy ABC là tam giác vuông cân tại A với BC a và
mặt bên AA'B'B là hình vuông. Thể tích của khối lăng trụ ABC.A' B'C ' bằng 3 2a 3 2a 3 a 3 a A. . B. . C. . D. . 8 4 4 12 Câu 3:
Cho lăng trụ đứng ABC.A BC
  có đáy ABC là tam giác vuông cân tại B, AB  .a Biết AC hợp với  A BC
  một góc 60, thể tích của khối lăng trụ ABC.A BC   bằng 3 3a 3 2a 3 3a 3 6a A. . B. . C. . D. . 4 2 2 2 Câu 4:
Cho hình lăng trụ đứng A . BCD A BCD
  có đáy ABCD là hình thoi cạnh
a, BAC  30, AB  2 .
a Thể tích của khối lăng trụ A . BCD A BCD   bằng 3 3a 3 3a 3 3a 3 3 3a A. . B. . C. . D. . 6 2 8 8 Câu 5:
Cho lăng trụ đứng ABC.A BC
  có đáy ABC là tam giác vuông cân tại B, AB  .a Biết AC hợp với  A BB
A một góc 30, thể tích của khối lăng trụ ABC.A BC   bằng 3 3a 3 2a 3 3a 3 6a A. . B. . C. . D. . 4 2 2 2 Câu 6:
Cho hình lăng trụ đứng ABC.A' B'C ' có đáy ABC là tam giác vuông cân tại A . Biết BC  2a
và thể tích lăng trụ bằng 3
2a , khoảng cách d từ A đến mặt phẳng  A' BC bằng 3 5a 5a 2 5a A. .
B. a 5 . C. . D. . 5 5 5 Câu 7:
Cho hình hộp đứng ABC . D AB CD
  có đáy ABCD là hình thoi cạnh a , góc BAD  60 . Cho
biết góc giữa đường chéo BD và mặt đáy bằng 45 . Thể tích khối hộp đã cho là 3 3a 3 3a 3 3a 3 3a A. . B. . C. . D. . 6 4 3 2
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia Câu 8:
Cho hình hộp đứng ABC . D AB CD
  có đáy ABCD là hình thoi cạnh a , BAD 120 . Gọi G
là trọng tâm tam giác ABD , góc tạo bởi C G
 và mặt đáy bằng 30 . Tính theo a thể tích khối hộp ABC . D AB CD   . 3 a 3 a 3 a A. 3 a . B. . C. . D. . 3 12 6 Câu 9:
Cho lăng trụ đứng ABC. 
A BC có cạnh đáy BC  2a , góc giữa hai mặt phẳng  ABC  và
ABC bằng 60. Biết diện tích tam giác ABC bằng 2
2a . Tính thể tích của khối lăng trụ ABC.  A BC . 3 a 3 3 2a A. V  . B. 3 V  3a . C. 3 V a 3 . D. V  . 3 3
BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN
Câu 10: Một khối lăng trụ đứng tam giác có các cạnh đáy lần lượt bằng 37;13;30 và diện tích xung
quanh bằng 480. Khi đó thể tích của khối lăng trụ bằng A. 1170 . B. 2160 . C. 360 . D. 1080 .
Câu 11: Cho hình lăng trụ đứng ABC.A BC
  có đáy ABC là tam giác vuông cân tại A, AB  .a Biết
diện tích tứ giác ABB A   bằng 2
2a , thể tích khối lăng trụ ABC.A BC   bằng 3 3a 3 3a 3 a A. . B. . C. 3 a . D. . 2 6 3
Câu 12: Cho hình lăng trụ đứng ABC.AB C
  có AA  a 2, AB a, AC  2a , BAC  60 . Thể tích
hình lăng trụ đó bằng 3 a 6 3 a 6 A. 3 a 2 . B. 3 3a 3 . C. . D. . 2 2
Câu 13: Cho hình lăng trụ đứng ABC.A BC
  có đáy ABC là tam giác vuông cân tại A, AB  .a Biết góc giữa  AB C   và A BC
  bằng 60, thể tích khối lăng trụ ABC.A BC   bằng 3 3a 3 3a 3 6a A. . B. . C. 3 a . D. . 2 6 4
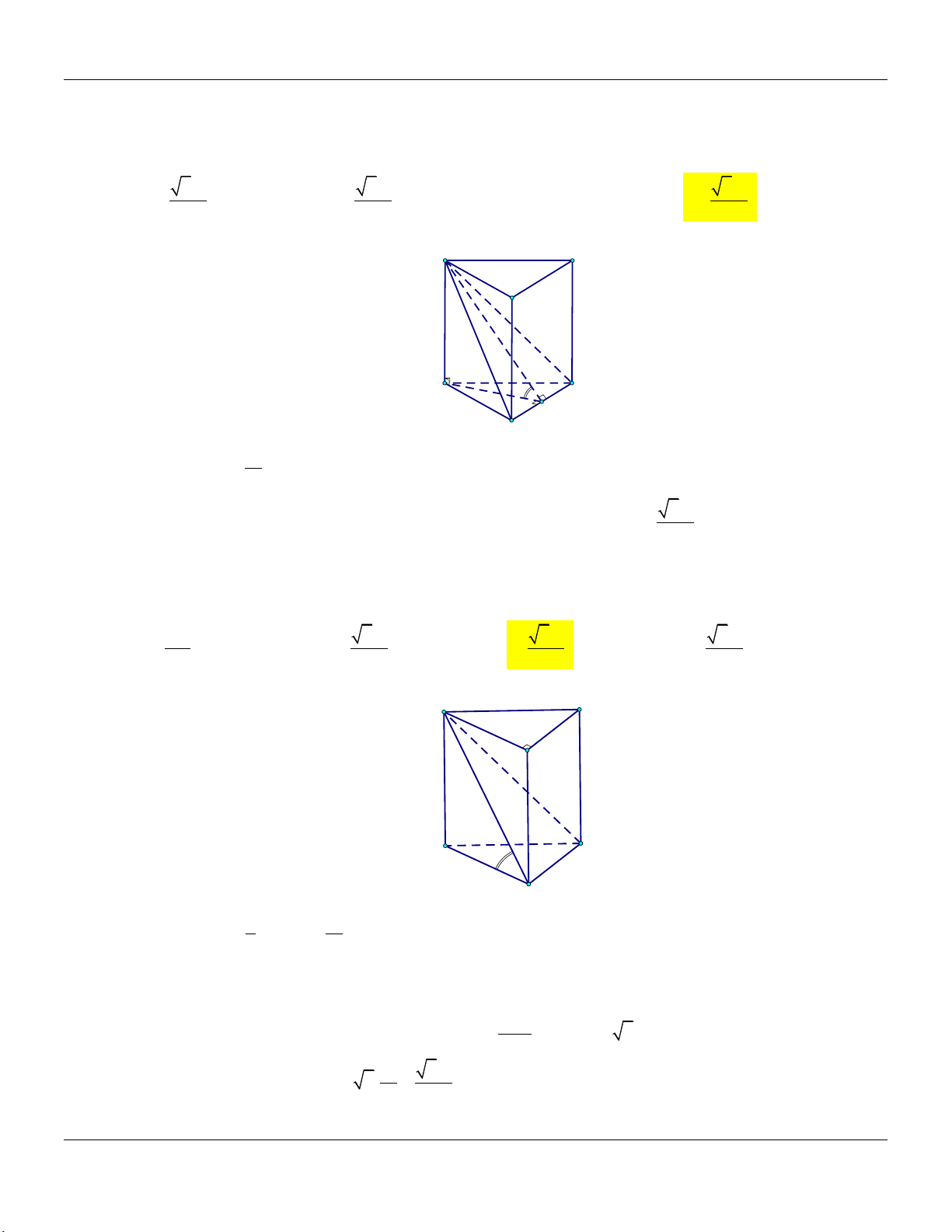
Câu 14: Cho lăng trụ đứng ABC.A BC
  có đáy ABC là tam giác vuông cân tại B, AB  .a Biết
ABC hợp với A BC một góc 60, thể tích của khối lăng trụ ABC.A BC bằng 3 3a 3 2a 3 3a 3 6a A. . B. . C. . D. . 4 2 2 2
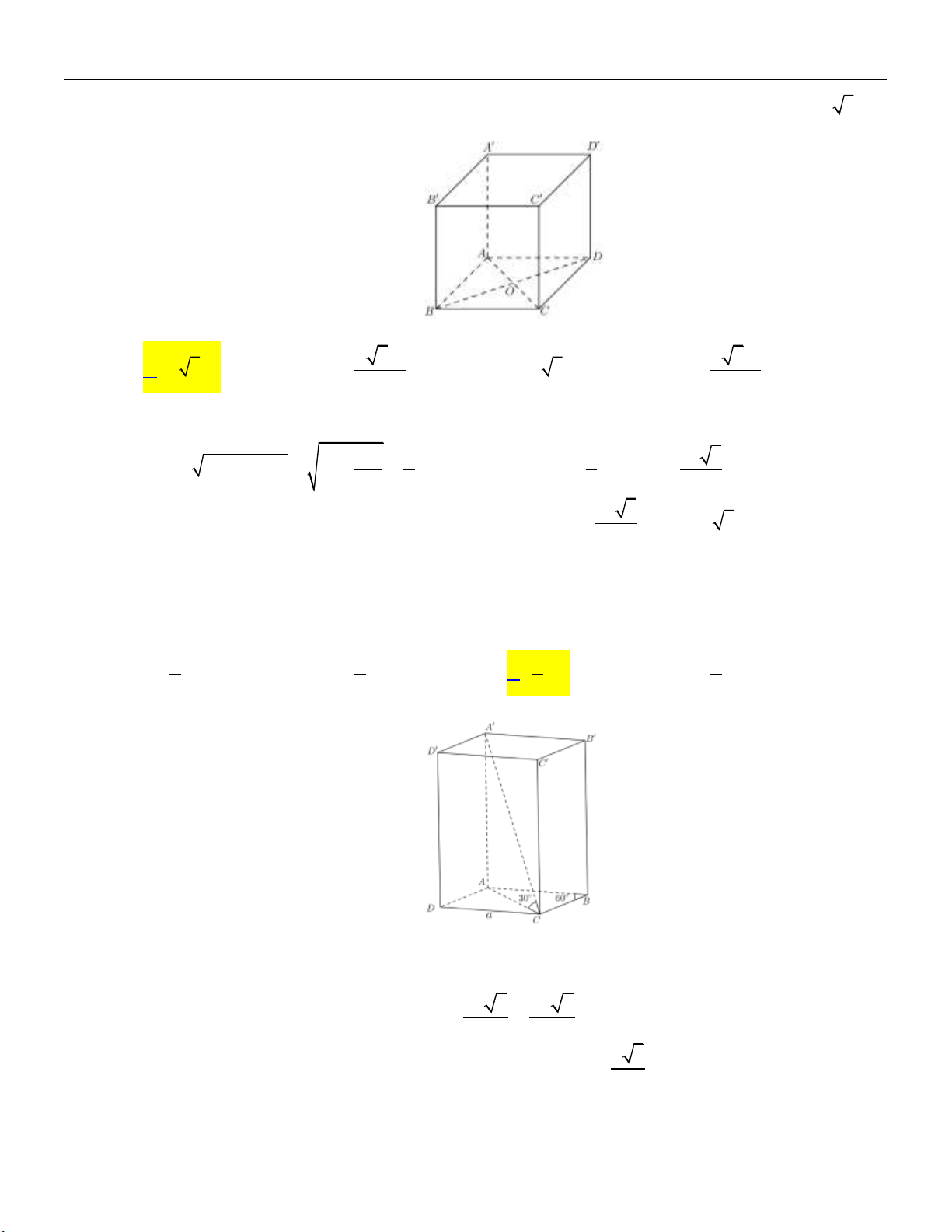
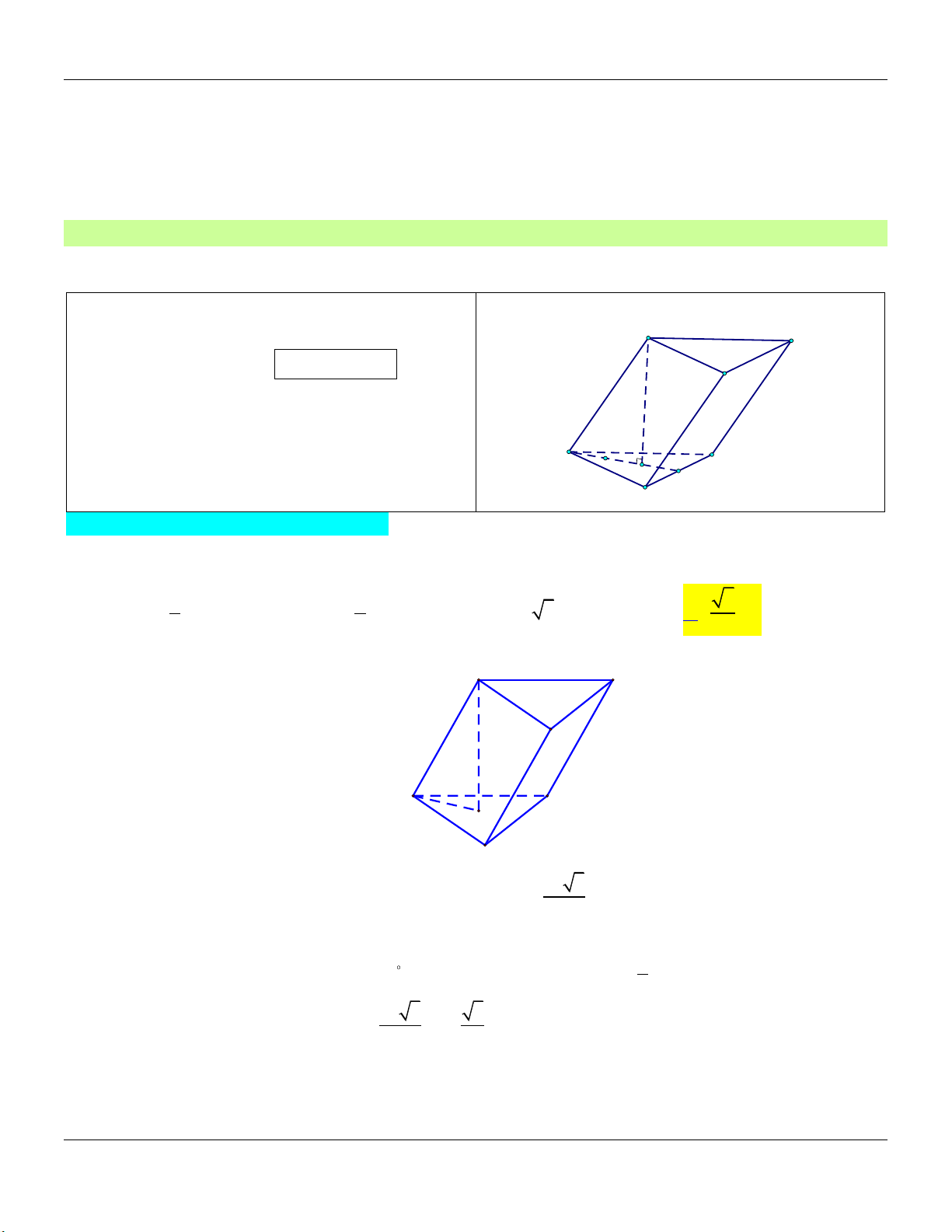
Câu 15: Cho khối lăng trụ đứng ABC . D AB CD
  có đáy là hai hình thoi cạnh a , BD a 3 và
AA  4a (tham khảo hình vẽ dưới)
Thể tích của khối lăng trụ đã cho bằng 3 4 3a 3 2 3a A. 3 2 3a . B. . C. 3 4 3a . D. . 3 3
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
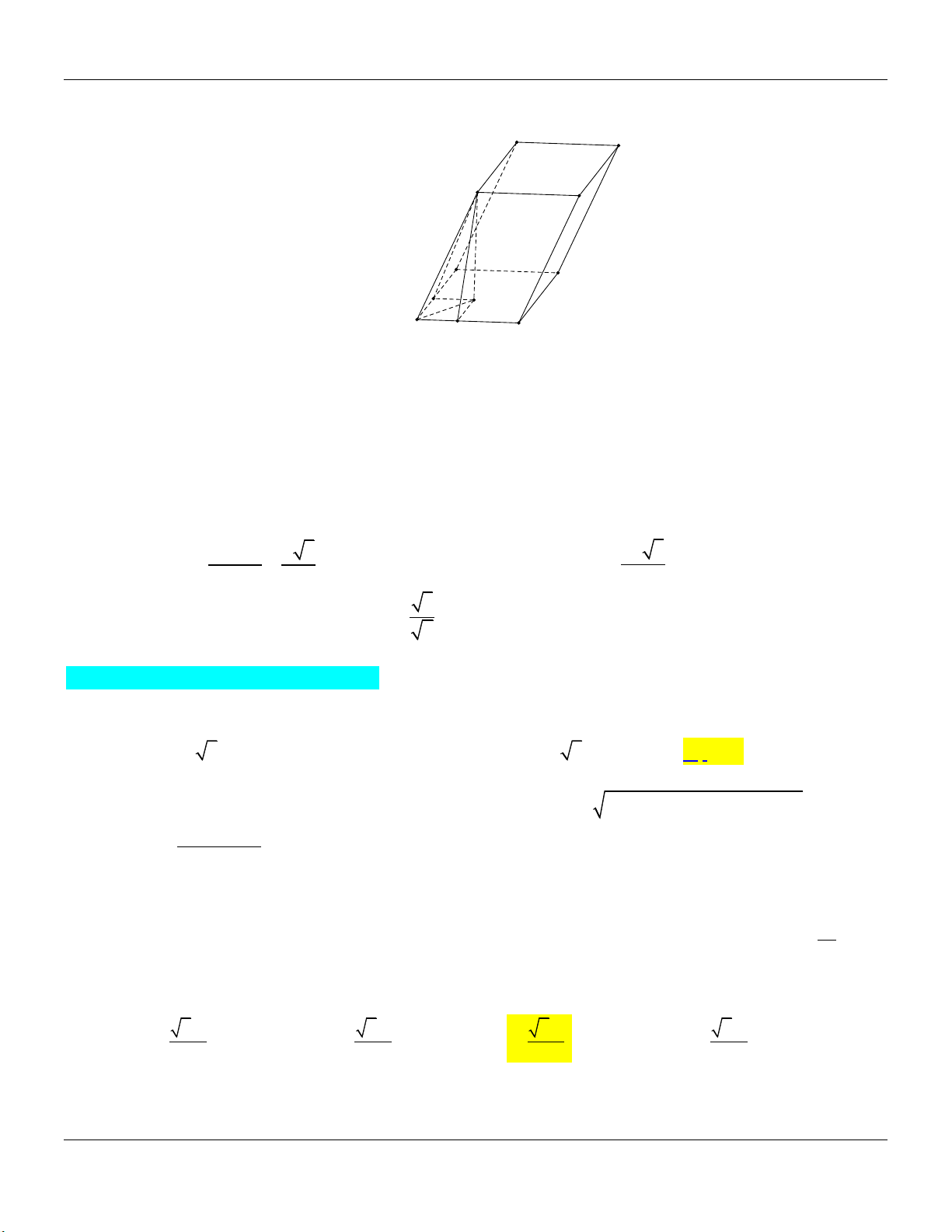
Câu 16: Cho hình lăng trụ đứng ABC . D AB CD
  có đáy là hình thoi ABCD cạnh a , ABC  60 .
Đường chéo AC tạo với mặt phẳng  ABCD một góc 30 . Thể tích khối lăng trụ ABC . D AB CD
  tính theo a bằng 1 1 1 3 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 4 6 2 2
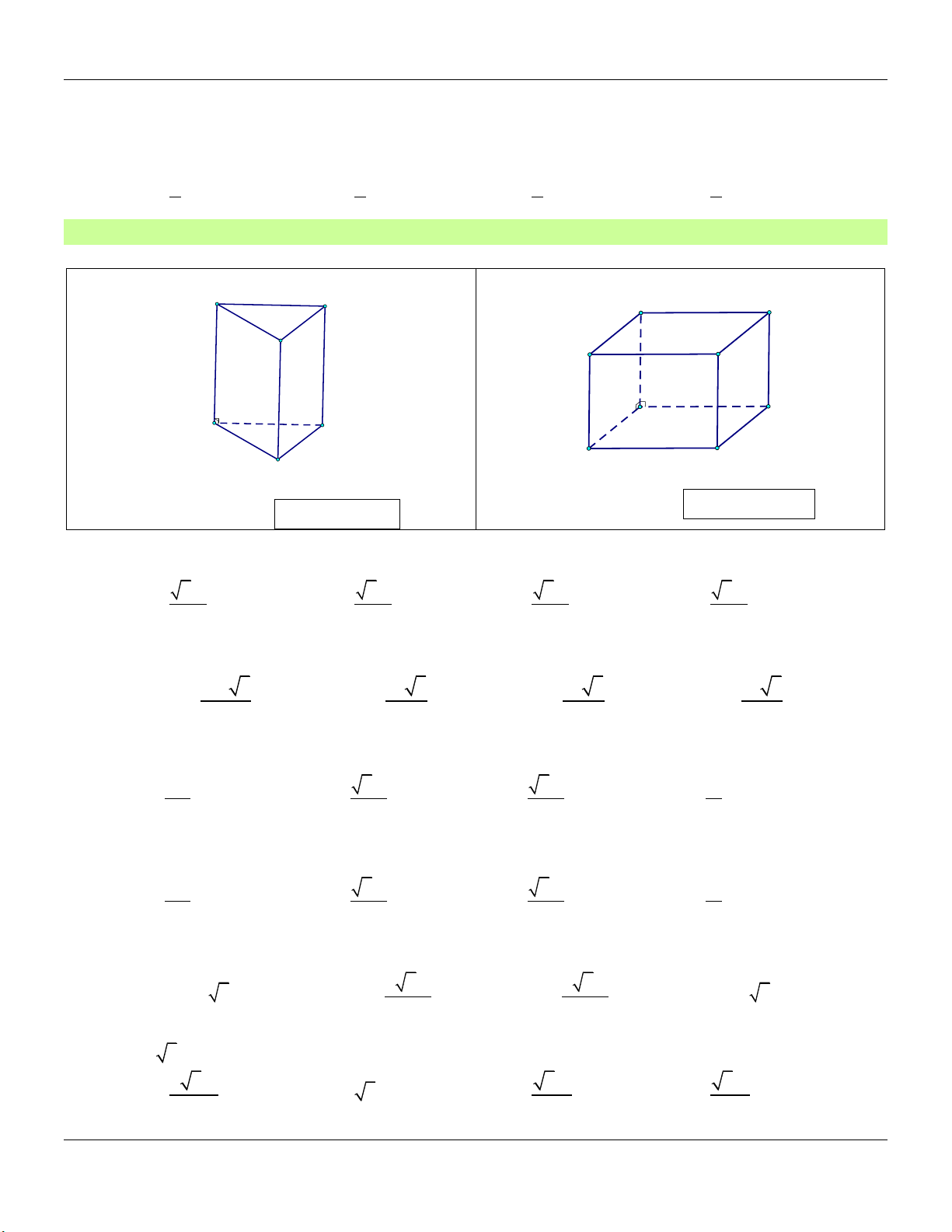
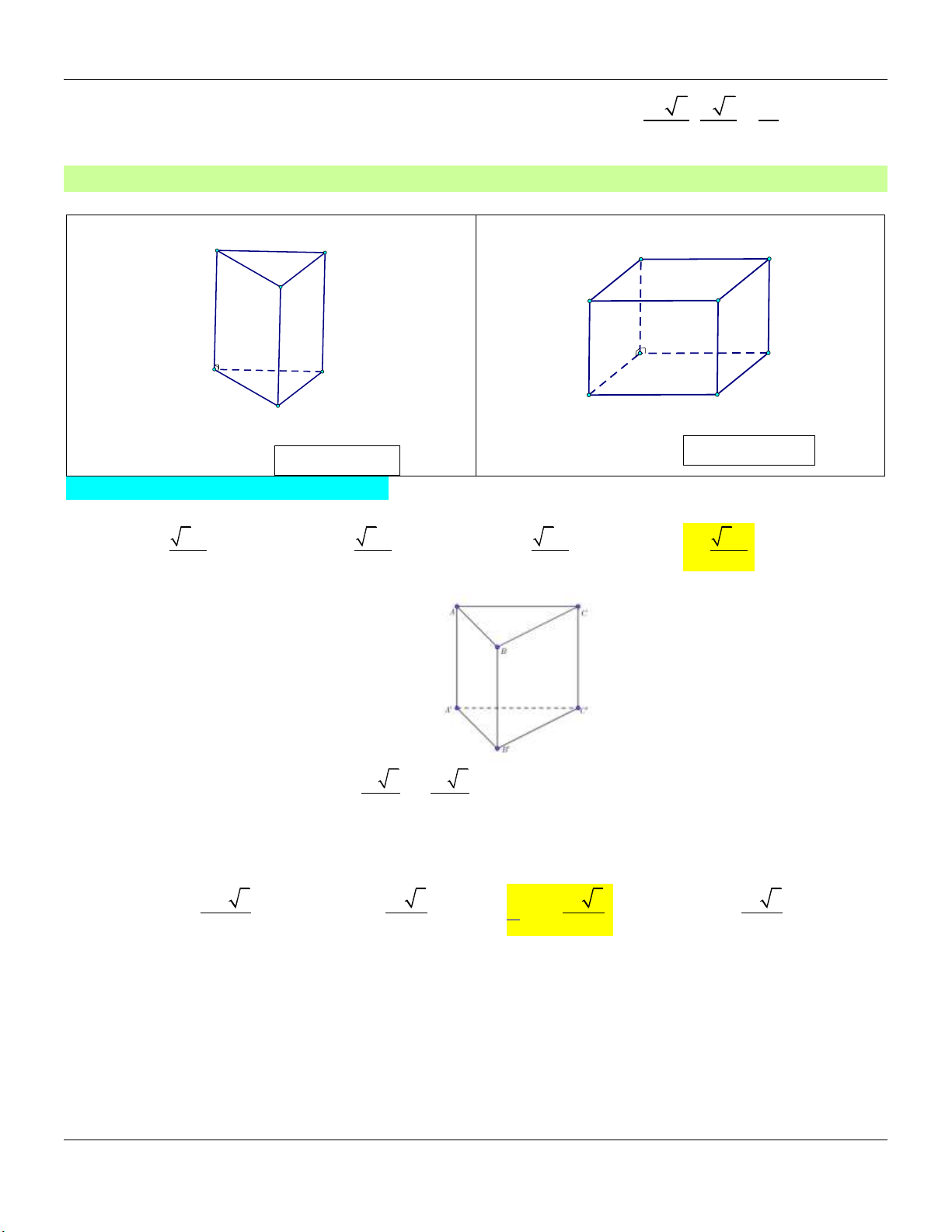
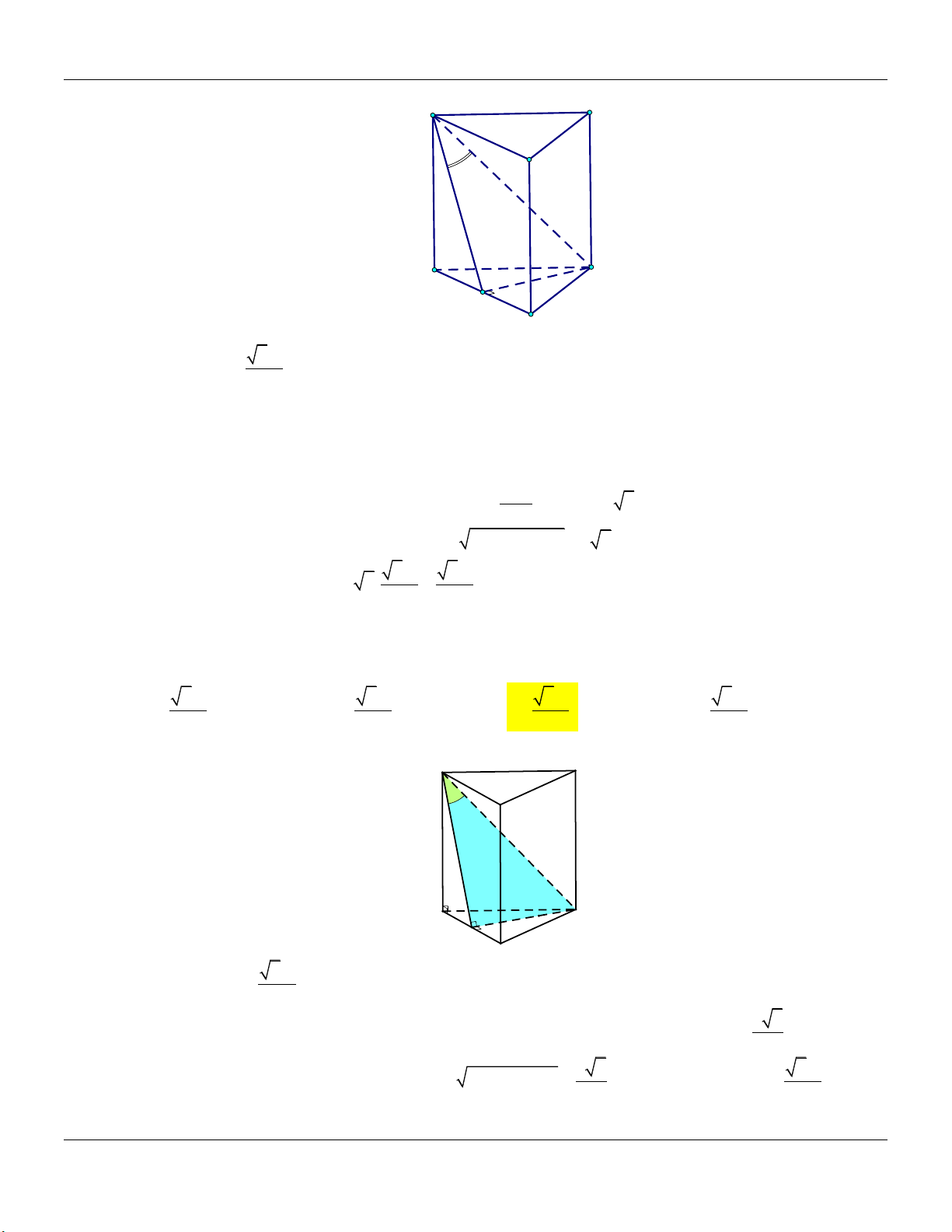
Dạng 2: Khối lăng trụ đều Phương pháp:
Cho hình lăng trụ tam giác đều ABC.A BC   …
Cho hình lăng trụ tứ giác đều ABC.A BC   … A C A D B B C A' D' C' A' B' C' B'
+) Đường cao: AA
+) Đường cao: AA
+) Thể tích khối lăng trụ: V AA .S
+) Thể tích khối lăng trụ: V AA .S ABCD ABC
BÀI TẬP TRẮC NGHIỆM MINH HỌA
Câu 17: Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng a bằng 3 3a 3 3a 3 3a 3 3a A. . B. . C. . D. . 12 6 2 4
Câu 18: Cho khối lăng trụ tam giác đều có độ dài cạnh đáy bằng a và diện tích xung quanh bằng 2
6a . Thể tích của khối lăng trụ đã cho là 3 2a 3 3 a 3 3 a 3 3 a 3 A. V  . B. V  . C. V  . D. V  . 3 4 2 3
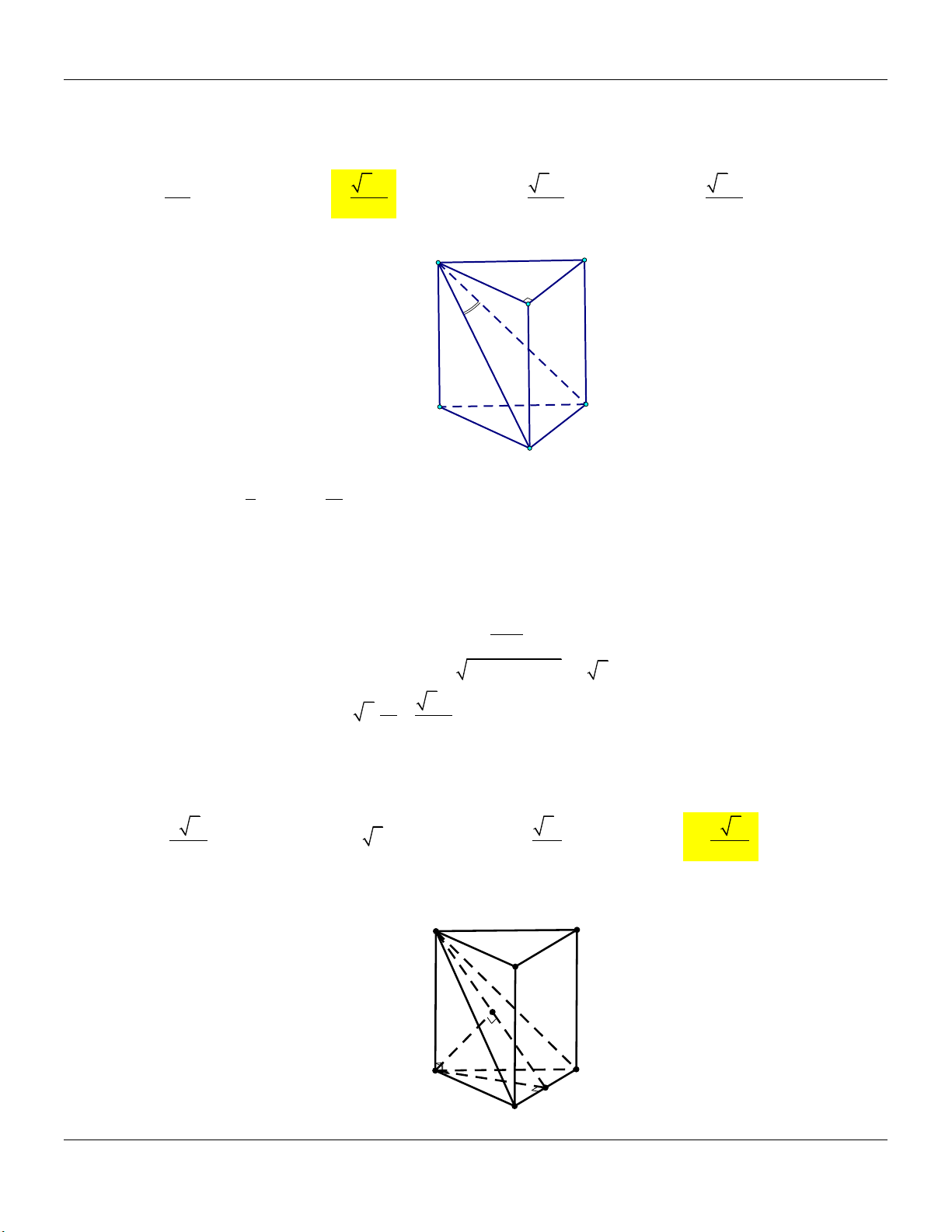
Câu 19: Cho lăng trụ tam giác đều ABC.A BC
  có cạnh đáy bằng .
a Biết AB  2a, thể tích của khối
lăng trụ ABC.A BC   bằng 3 3a 3 3a 3 3a 3 a A. . B. . C. . D. . 4 8 24 4
Câu 20: Cho lăng trụ tam giác đều ABC.A BC
  có cạnh đáy bằng .
a Biết  AB C
  hợp với mặt đáy một
góc 30, thể tích của khối lăng trụ ABC.A BC   bằng 3 3a 3 3a 3 3a 3 a A. . B. . C. . D. . 4 8 24 4
Câu 21: Cho hình lăng trụ tam giác đều ABC.A BC
  có cạnh đáy bằng 2a , góc giữa hai đường thẳng
AB và BC bằng 60 . Thể tích của khối lăng trụ đó là 3 2 3a 3 2 6a A. 3
V  2 6a . B. V . C. V . D. 3
V  2 3a . 3 3
Câu 22: Cho hình lăng trụ tam giác đều ABC.AB C
  có AA  a . Khoảng cách giữa AB ' và CC ' bằng
a 3 . Thể tích khối lăng trụ ABC.A ' B 'C ' . 3 2 3a 3 3a 3 3a A. . B. 3 3a . C. . D. . 3 2 3
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 2a 3
Câu 23: Cho hình lăng trụ đều ABC.AB C
  có cạnh đáy bằng
. Đường thẳng BC tạo với mặt 3 phẳng  ACC A
  góc  thỏa mãn cot  2 . Thể tích khối trụ ABC.AB C   bằng 4 1 1 2 A. 3 a 11 . B. 3 a 11 . C. 3 a 11 . D. 3 a 11 . 3 9 3 3
BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN
Câu 24: Thể tích khối lăng trụ tứ giác đều ABC . D AB CD
  có AC AA  2a là A. 3 4a . B. 3 2a . C. 3 2a . D. 3 2 2a .
Câu 25: Cho hình lăng trụ tam giác đều ABC.A' B 'C ' cạnh đáy a  4 , biết diện tích tam giác A ' BC
bằng 8. Thể tích khối lăng trụ ABC.A ' B 'C ' bằng A. 10 3 . B. 2 3 . C. 8 3 . D. 4 3 .
Câu 26: Cho lăng trụ tam giác đều ABC.A BC
  có cạnh đáy bằng .
a Biết AB hợp với mặt đáy một
góc 60, thể tích của khối lăng trụ ABC.A BC   bằng 3 3a 3 3a 3 3a 3 a A. . B. . C. . D. . 4 8 24 4
Câu 27: Cho lăng trụ tam giác đều ABC.A BC
  có cạnh đáy bằng .
a Biết AC hợp với  ABB A   một
góc 30, thể tích của khối lăng trụ ABC.A BC   bằng 3 3a 3 3a 3 3a 3 6a A. . B. . C. . D. . 4 8 24 4
Câu 28: Cho hình lăng trụ tam giác đều ABC.A BC
  có cạnh đáy bằng a, AC hợp với mặt phẳng ABB A
  một góc 45 . Thể tích của khối lăng trụ ABC.A BC   bằng 3 6a 3 3a 3 6a 3 6a A. . B. . C. . D. . 24 4 8 4
Câu 29: Cho khối lăng trụ tam giác đều ABC.AB C
  có cạnh đáy là 2a và khoảng cách từ A đến mặt
phẳng  ABC  bằng a . Tính thể tích của khối lăng trụ ABC.AB C  . 3 3a 2 3 a 2 3 2a A. 3 2 2a . B. . C. . D. . 2 2 2
Câu 30: Cho hình lăng trụ tam giác đều AB . C AB C
  có cạnh đáy bằng 2a , góc giữa hai đường thẳng
AB và B C bằng 60 . Tính thể tích V của khối lăng trụ đó. 3 2 6a 3 2 3a A. V  . B. 3 V  2 3a . C. V  . D. 3 V  2 6a . 3 3
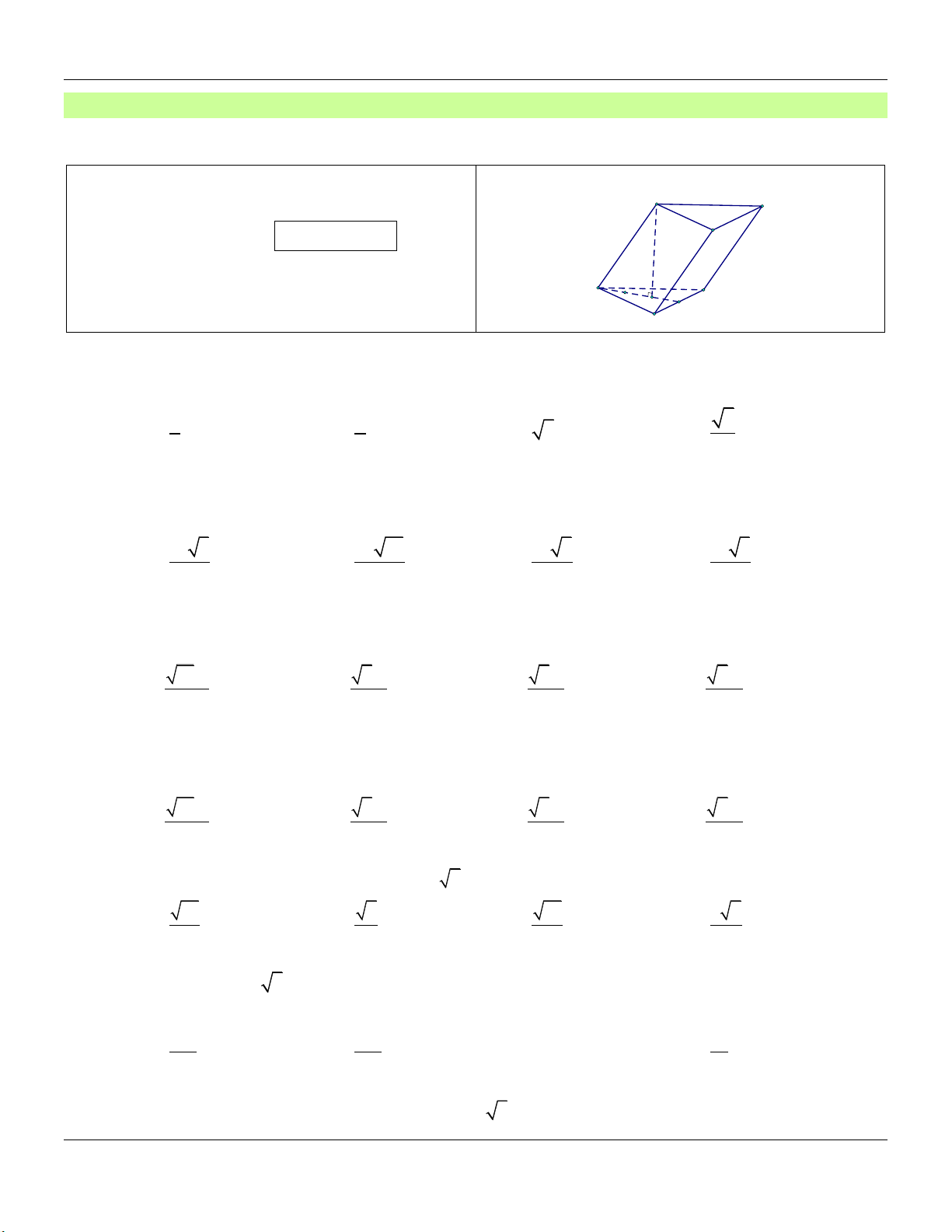
Dạng 3: Khối hộp chữ nhật – Khối lập phương Phương pháp:
Cho hình hộp chữ nhật A . BCD A BCD   …
Cho hình lập phương ABCD.A BCD … A c D A a D b a a a B B C C A' D' A' D' B' C' B' C'
+) Thể tích khối hộp: V abc
+) Thể tích khối lập phương: 3 V a
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
BÀI TẬP TRẮC NGHIỆM MINH HỌA
Câu 31: Thể tích của khối lập phương cạnh 3a bằng A. 3 9a . B. 3 27a . C. 3 18a . D. 3 36a .
Câu 32: Thể tích của khối hộp chữ nhật có ba kích thước 2,3,7 bằng A. 14. B. 42. C. 126. D. 12.
Câu 33: Cho hình hộp chữ nhật A .
BCD ABC D
  có AB  2a, BC  .a Biết AC  3a, thể tích của khối hộp chữ nhật A .
BCD ABC D   bằng 3 2 15a 3 3a A. 3 4a . B. 3 4 3a . C. . D. . 3 4
Câu 34: Cho hình lập phương ABC . D A BCD
  có diện tích mặt chéo ACC A   bằng 2 2 2a . Thể tích
của khối lập phương ABC . D A BCD   là A. 3 16 2a . B. 3 2 2a . C. 3 8a . D. 3 a .
Câu 35: Cho hình hộp chữ nhật ABC . D AB CD
  có AB a, AD a 3, góc giữa mặt phẳng  ABC D  
và  ABCD bằng 45 .
 Thể tích khối hộp chữ nhật đã cho bằng A. 3 3a . B. 3 a . C. 3 3a . D. 3 2 3a .
BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN
Câu 36: Thể tích của khối hộp chữ nhật ABC . D AB CD
  có AB  3, AC  5 , AA  8 bằng A. 120 . B. 32 C. 96 . D. 60 .
Câu 37: Diện tích toàn phần của một hình lập phương bằng  2
96 cm  . Khối lập phương đã cho có thể tích bằng 3 A.  3 84 cm  .
B. 48cm  . C.  3 64 cm  . D.  3 91 cm  .
Câu 38: Cho hình lập phương ABC . D A BCD
  có diện tích tam giác ACD bằng 2 a 3 . Thể tích của
khối lập phương đã cho bằng: A. 3 4 2a . B. 3 8a . C. 3 a . D. 3 2 2a .
Câu 39: Cho hình lăng trụ đứng ABC . D AB CD
  có đáy là hình vuông cạnh bằng 6 , đường chéo
AB của mặt bên  ABB A
  có độ dài bằng 10 . Tính thể tích V của khối lăng trụ ABC . D AB CD   . A. V  384 . B. V  180 . C. V  480 . D. V  288 .
Câu 40: Cho hình hộp chữ nhật A .
BCD ABC D
  có AB  2a, BC  .a Biết ADC B
  hợp với mặt đáy
một góc 60, thể tích của khối hộp chữ nhật A .
BCD ABC D   bằng 3 2 15a 3 3a A. 3 4a . B. 3 4 3a . C. . D. . 3 4
Câu 41: Cho hình hộp chữ nhật A .
BCD ABC D
  có AB  2a, BC  .a Biết AC hợp với mặt đáy một góc
60, thể tích của khối hộp chữ nhật A .
BCD ABC D   bằng 3 2 15a 3 3a A. 3 2 15a . B. 3 4 3a . C. . D. . 3 4
Câu 42: Cho hình hộp chữ nhật có đường chéo d  21. Độ dài ba kích thước của hình hộp chữ nhật
lập thành một cấp số nhân với công bội q  2. Thể tích của khối hộp chữ nhật đã cho là A. V  8 . B. V  8 . C. V  4 . D. V  6 . 3 3
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
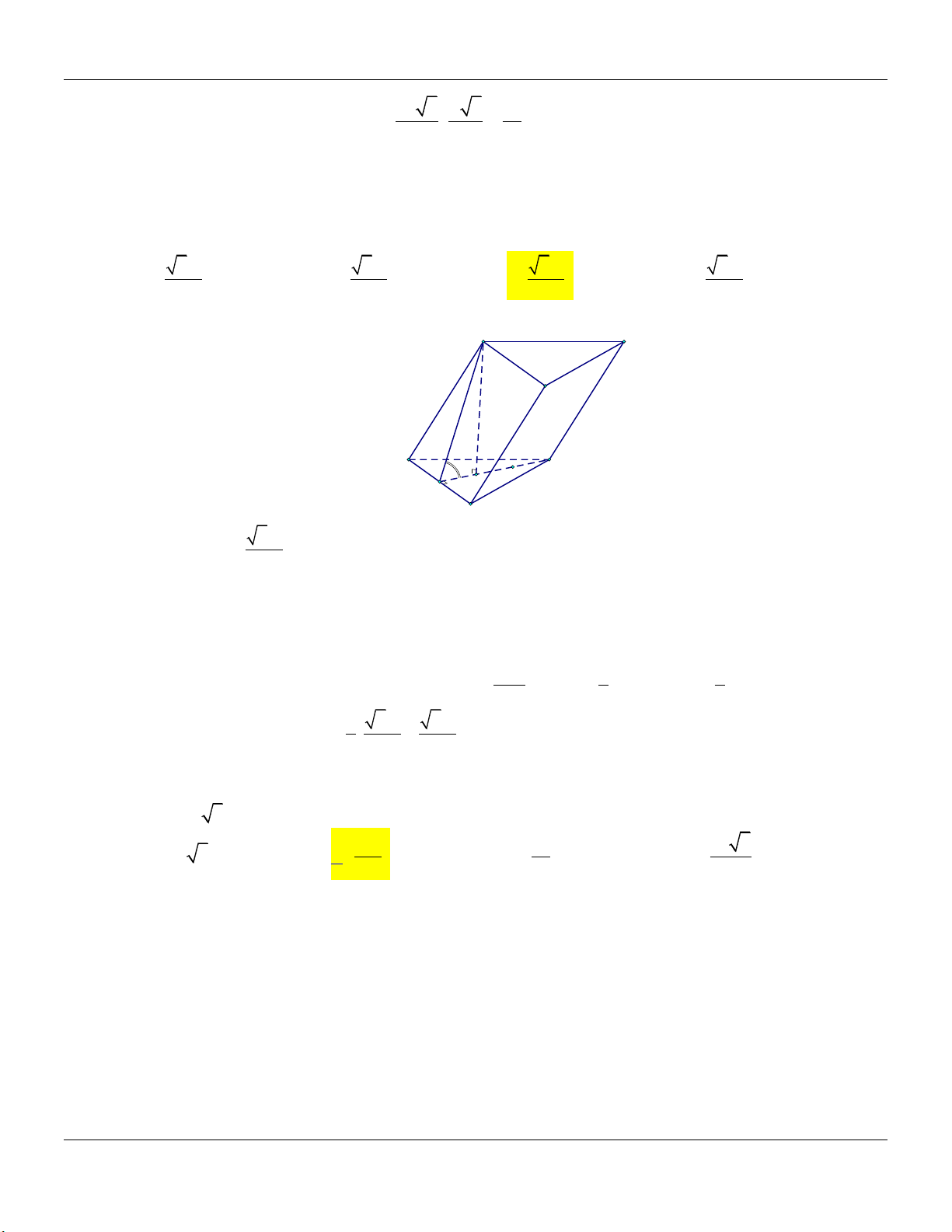
Dạng 4: Khối lăng trụ xiên bất kì Phương pháp:
Cho hình lăng trụ ABC.A BC   …
+) Đường cao: AH , H là hình chiếu vuông góc của Form hình vẽ: A A trên A BC  . C B
+) Thể tích khối lăng trụ: V AH.S ABC A' C' H M B'
BÀI TẬP TRẮC NGHIỆM MINH HỌA
Câu 43: Cho lăng trụ ABC.AB C
 có đáy ABC là tam giác đều cạnh a , cạnh bên bằng 4a và tạo với đáy góc o
30 . Thể tích khối lăng trụ ABC.AB C   bằng 1 3 3 A. 3 a . B. 3 a . C. 3 3a . D. 3 a . 2 2 2
Câu 44: Cho lăng trụ tam giác ABC.AB C
  có đáy là tam giác đều cạnh a , góc giữa cạnh bên và mặt
đáy bằng 30 . Hình chiếu của A lên  ABC  là trung điểm I của BC . Tính thể tích khối
lăng trụ ABC.AB C  . 3 a 3 3 a 13 3 a 3 3 a 3 A. . B. . C. . D. . 8 12 6 2
Câu 45: Cho hình lăng trụ ABC.A BC
  có đáy là tam giác đều cạnh bằng .
a Biết hình chiếu vuông
góc của A trên  ABC là trọng tâm tam giác ABC, AA  2a, thể tích của khối lăng trụ ABC.A BC   bằng 3 11a 3 3a 3 3a 3 6a A. . B. . C. . D. . 4 4 8 9
Câu 46: Cho hình lăng trụ ABC.A BC
  có đáy là tam giác đều cạnh bằng .
a Biết hình chiếu vuông
góc của A trên  ABC là trọng tâm tam giác ABC, AA ;ABC  60, thể tích của khối lăng trụ ABC.A BC   bằng 3 11a 3 3a 3 3a 3 6a A. . B. . C. . D. . 4 4 8 9
Câu 47: Cho lăng trụ ABC.A' B'C ' có đáy ABC là tam giác vuông tại B , đường cao BH . Biết
A' H   ABC  và AB  1, AC  2, AA'  2 . Thể tích của khối lăng trụ đã cho bằng 21 7 21 3 7 A. . B. . C. . D. . 12 4 4 4
Câu 48: Cho lăng trụ ABC.AB C
  có đáy ABC là tam giác vuông tại B và AA AB AC . Biết rằng
AB a, BC a 3 và mặt phẳng  ABC  tạo với mặt phẳng đáy một góc 60 . Thể tích khối
lăng trụ ABC.AB C   bằng 3 3a 3 3a 3 a A. . B. C. 3 a . D. 4 2 4
Câu 49: Cho hình lăng trụ ABC . D AB CD
  có ABCD là hình chữ nhật. Tính thể tích khối lăng trụ đã
cho biết AA AB AD và AB a, AD a 3, AA  2a
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia A. 3 3a . B. 3 a . C. 3 a 3 . D. 3 3a 3 .
Câu 50: Cho khối lăng trụ ABC.AB C
  có đáy là tam giác đều cạnh 4a, AA  2 3a . Gọi M , N lần
lượt là trung điểm của BB ,CC . Biết mặt bên BCC B
  là hình chữ nhật và mặt phẳng  ANM
vuông góc với mặt phẳng  BCC B
  . Thể tích khối lăng trụ đã cho bằng A. 3 3 3a . B. 3 24 3a . C. 3 12 3a . D. 3 4 3a .
Câu 51: Cho hình hộp ABC .
D A' B 'C ' D ' có đáy là hình chữ nhật, AB  3, AD  7 . Hai mặt
ABB' A' và  ADD' A' lần lượt tạo với đáy góc 45 và 60, biết cạnh bên bằng 1. Tính thể
tích khối hộp ABC .
D A' B 'C ' D ' . 3 3 3 A. 3 . B. . C. . D. 3 . 4 4
BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN
Câu 52: Khối lăng trụ tam giác có độ dài các cạnh đáy lần lượt bằng 13,14,15. Cạnh bên tạo với mặt
phẳng đáy một góc 30 và có chiều dài bằng 8. Thể tích khối lăng trụ đã cho bằng A. 124 3 . B. 340 . C. 274 3 . D. 336 . 2a
Câu 53: Cho lăng trụ ABC.A BC
  có đáy ABC là tam giác đều cạnh a , độ dài cạnh bên bằng , hình 3
chiếu của đỉnh A trên mặt phẳng  ABC trùng với trọng tâm của tam giác ABC . Thể tích
khối lăng trụ ABC.A BC   bằng 3 3a 3 3a 3 3a 3 3a A. . B. . C. . D. . 36 6 12 24 3a
Câu 54: Cho lăng trụ ABC.A BC
  có đáy ABC là tam giác đều cạnh a , AA  . Biết rằng hình chiếu 2
vuông góc của A lên  ABC là trung điểm BC . Thể tích của khối lăng trụ ABC.A BC   bằng 3 2a 3 3 2a 3 6a 3 2a A. . B. . C. . D. . 8 8 2 3
Câu 55: Cho lăng trụ ABC.AB C
 có đáy ABC là tam giác đều, AA  4a . Biết rằng hình chiếu vuông
góc của A lên  ABC  là trung điểm M của BC , AM  2a . Thể tích của khối lăng trụ
ABC.AB C   bằng 3 8a 3 3 16a 3 A. 3 8a 3 . B. . C. 3 16a 3 . D. . 3 3
Câu 56: Cho lăng trụ ABC.AB C
 , có đáy ABC là tam giác đều cạnh a . Cho biết hình chiếu của đỉnh
A lên mặt đáy  ABC  là điểm H trên cạnh AB mà HA  2HB và góc giữa mặt bên  AC CA
 và mặt đáy  ABC bằng 45. Thể tích của khối lăng trụ đã cho là 1 1 3 3 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 4 12 4 4
Câu 57: Cho hình lăng trụ ABC.A BC
  có đáy là tam giác đều cạnh bằng .
a Biết hình chiếu vuông
góc của A trên  ABC là trọng tâm tam giác ABC,  AA BB
 ;ABC  60, thể tích của khối
lăng trụ ABC.A BC   bằng 3 3a 3 3a 3 3a 3 6a A. . B. . C. . D. . 24 4 8 9
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Câu 58: Cho hình lăng trụ tam giác ABC.AB C
  có đáy ABC là tam giác vuông tại A và AB a ,
AC a 3 . Tính thể tích khối lăng trụ ABC.AB C
  biết AA AB AC  2a . 3 3a 3 a 3 a 3 A. 3 a 3 . B. . C. . D. . 2 2 3
Câu 59: Cho khối lăng trụ ABC.AB C
  có đáy là tam giác vuông tại ,
A AB a, AC  3a . Hình chiếu
vuông góc của A trên mặt phẳng  AB C
 là trung điểm H của B C
  . Khoảng cách từ A đến 3a mặt phẳng  BCC B   bằng
. Thế tích của khối lăng trụ đã cho bằng 4 3 3a 3 3a 3 3a 3 3a A. . B. . C. . D. . 8 2 4 4
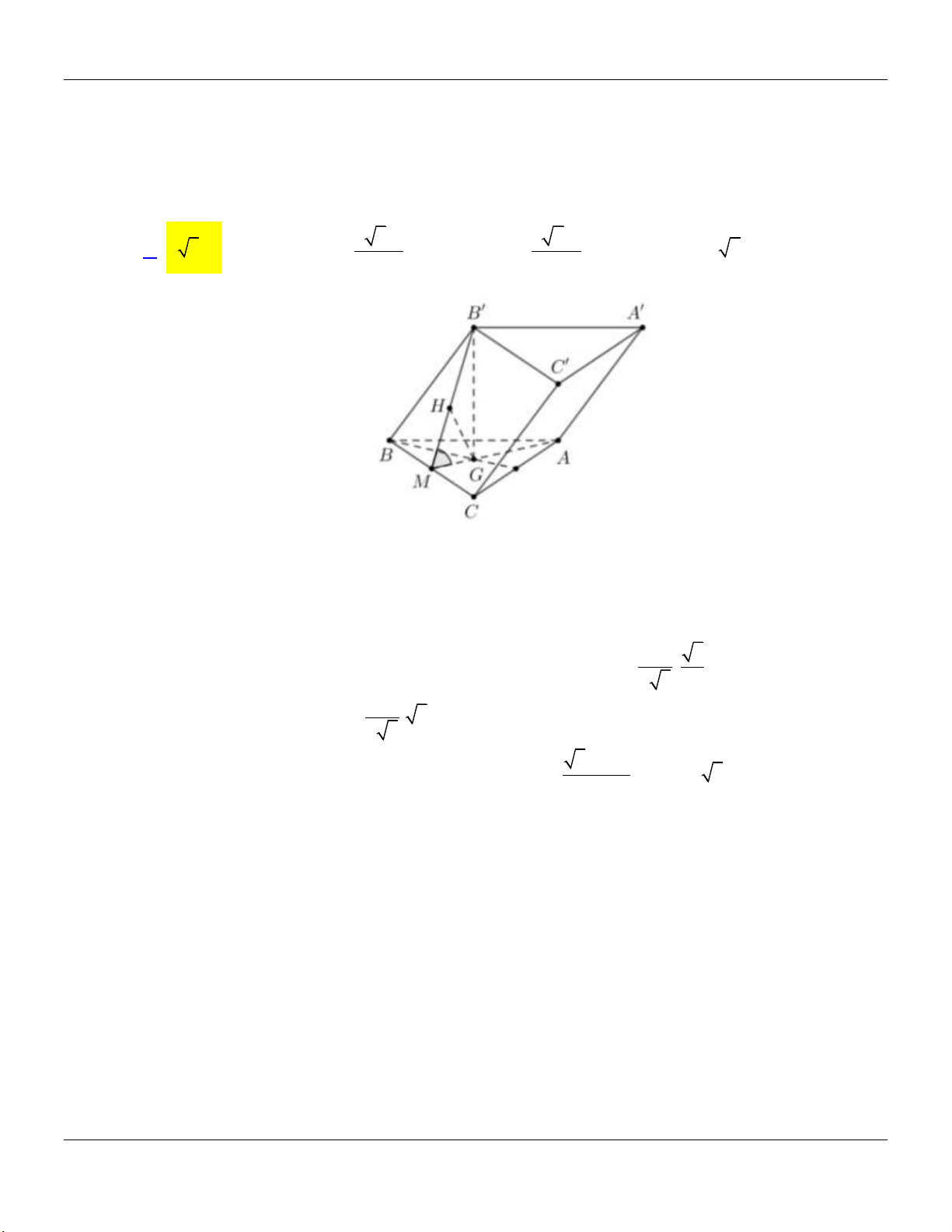
Câu 60: Cho khối lăng trụ ABCAB C
  có đáy là tam giác đều, góc giữa hai mặt phẳng  AB C   và
BCC B bằng 60, hình chiếu vuông góc của B lên mặt phẳng  ABC trùng với trọng tâm
tam giác ABC . Khoảng cách giữa hai đường thẳng AA và B C
 bằng 3a . Thể tích khối lăng trụ đã cho bằng 3 8 3a 3 8 6a A. 3 8 3a . B. . C. . D. 3 8 6a . 3 3
_____________________HẾT_____________________
Huế, 15h20’ Ngày 18 tháng 5 năm 2022
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
LỜI GIẢI CHI TIẾT
Dạng 1: Khối lăng trụ có cạnh bên vuông góc với đáy Phương pháp:
Cho hình lăng trụ đứng ABC.A BC   …
+) Đường cao: AAForm hình vẽ:
+) Thể tích khối lăng trụ: V AA .S A C ABC B C' A' B'
BÀI TẬP TRẮC NGHIỆM MINH HỌA Câu 1:
Cho khối lăng trụ có thể tích bằng 3
24a và chiều cao bằng 3a . Diện tích một mặt đáy của khối lăng trụ đã cho bằng A. 2 16a . B. 2 8a . C. 2 6a . D. 2 72a . Lời giải: 3 V 24a Ta có 2 V  . S h S    8a . h 3a
Vậy diện tích một mặt đáy của khối lăng trụ đã cho bằng 2 8a .
Chọn đáp án B. Câu 2:
Cho hình lăng trụ đứng ABC.A' B'C ' có đáy ABC là tam giác vuông cân tại A với BC a và
mặt bên AA'B'B là hình vuông. Thể tích của khối lăng trụ ABC.A' B'C ' bằng 3 2a 3 2a 3 a 3 a A. . B. . C. . D. . 8 4 4 12 Lời giải: a
Tam giác ABC vuông cân tại A có BC a nên AB AC  . 2 2 1 1 a a aS  .A . B AC  . .  . ABC 2 2 2 2 4 a
Do mặt bên AA'B'B là hình vuông nên AA'  AB  . 2 2 3 a a a 2
Vì ABC.A' B'C ' là lăng trụ đứng nên VS .AA'  .  .
ABC.A' B'C ' ABC 4 2 8
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Chọn đáp án A. Câu 3:
Cho lăng trụ đứng ABC.A BC
  có đáy ABC là tam giác vuông cân tại B, AB  .a Biết AC hợp với  A BC
  một góc 60, thể tích của khối lăng trụ ABC.A BC   bằng 3 3a 3 2a 3 3a 3 6a A. . B. . C. . D. . 4 2 2 2 Lời giải: A C B C' A' B' 2 1 a Ta có: SA . B BC  . ABC 2 2
Do AA   A BC    A C
  là hình chiếu vuông góc của AC trên A BC  . AA
Suy ra AC ;A BC    AC A
 . Xét tam giác AC A
  vuông tại A : tan AC A   
AA  a 6. A C   2 3 a 6a Vậy V        AA .S a 6. . ABC.A B C ABC 2 2
Chọn đáp án D. Câu 4:
Cho hình lăng trụ đứng A . BCD A BCD
  có đáy ABCD là hình thoi cạnh
a, BAC  30, AB  2 .
a Thể tích của khối lăng trụ A . BCD A BCD   bằng 3 3a 3 3a 3 3a 3 3 3a A. . B. . C. . D. . 6 2 8 8 Lời giải: D C A B D' C' a 300 A' a B' Do A BCD
  là hình thoi cạnh a và B AC
   30  B AD
   60 nên A BD   là tam giác đều 2 3a cạnh a S       2S    . A B C D A B D 2 2 2 Xét tam giác A A
B vuông tại A : A A   B A    A B    .a 3 3a
Vậy V AA .S      . A B C D 2
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Chọn đáp án B. Câu 5:
Cho lăng trụ đứng ABC.A BC
  có đáy ABC là tam giác vuông cân tại B, AB  .a Biết AC hợp với  A BB
A một góc 30, thể tích của khối lăng trụ ABC.A BC   bằng 3 3a 3 2a 3 3a 3 6a A. . B. . C. . D. . 4 2 2 2 Lời giải: A C B A' C' B' 2 1 a Ta có: SA . B BC  . ABC 2 2 B C    A B   Ta có:   B C    AA B
   AB là hình chiếu vuông góc của AC trên A BBA. B C     AA
Suy ra AC ;A BB
A  C AB . B C   Xét tam giác AB C
  vuông tại B : sinC AB   AC  2 . a AC Xét tam giác AC A   vuông tại 2 2
A : AA  AC  A C    a 2. 2 3 a 2a Vậy V        AA .S a 2. . ABC.A B C ABC 2 2
Chọn đáp án B. Câu 6:
Cho hình lăng trụ đứng ABC.A' B'C ' có đáy ABC là tam giác vuông cân tại A . Biết BC  2a
và thể tích lăng trụ bằng 3
2a , khoảng cách d từ A đến mặt phẳng  A' BC bằng 3 5a 5a 2 5a A. .
B. a 5 . C. . D. . 5 5 5 Lời giải: A' C' B' 2a K A C H B
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Do tam giác ABC là tam giác vuông cân tại A và BC  2a nên suy ra AB AC a 2 , 1 2 SA . B AC a . ABC 2
Lúc đó lăng trụ đã cho có thể tích là: V AA'.S . ABC Theo giả thiết: 2 3
AA'.a  2a AA'  2 . a
Gọi H là trung điểm BC AH  .
a Ta có: AH BC BC   A' AH .
Dựng AK A' H AK   A'BC . Vậy dA;A'BC  AK. 1 1 1 2a 5 Xét A
 ' AH vuông tại A :    AK  . 2 2 2 AK A' A AH 5
Chọn đáp án D. Câu 7:
Cho hình hộp đứng ABC . D AB CD
  có đáy ABCD là hình thoi cạnh a , góc BAD  60 . Cho
biết góc giữa đường chéo BD và mặt đáy bằng 45 . Thể tích khối hộp đã cho là 3 3a 3 3a 3 3a 3 3a A. . B. . C. . D. . 6 4 3 2 Lời giải:
Ta có : ABD đều cạnh a BD a Ta có: D D
   ABCD  BD là hình chiếu của BD lên mặt phẳng  ABCD .
Do đó: BD , ABCD   BD , BD  D BD  45. Ta có: D B
D vuông cân tại D DD  BD a . 2 2 Vậy a 3 a 3 V       .     DD .S DD .2S . a 2. ABCD. A B C D ABCD ABD 4 2
Chọn đáp án D. Câu 8:
Cho hình hộp đứng ABC . D AB CD
  có đáy ABCD là hình thoi cạnh a , BAD 120 . Gọi G
là trọng tâm tam giác ABD , góc tạo bởi C G
 và mặt đáy bằng 30 . Tính theo a thể tích khối hộp ABC . D AB CD   . 3 a 3 a 3 a A. 3 a . B. . C. . D. . 3 12 6 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Tam giác ABC đều, suy ra AC a . 2a 2a Suy ra GC
; CC  GC.tan 30  . 3 3 3 2 3 a 3 2a a
Thể tích khối hộp đã cho là: V S .CC  .  . ABCD 2 3 3 3
Chọn đáp án B. Câu 9:
Cho lăng trụ đứng ABC. 
A BC có cạnh đáy BC  2a , góc giữa hai mặt phẳng  ABC  và
ABC bằng 60. Biết diện tích tam giác ABC bằng 2
2a . Tính thể tích của khối lăng trụ ABC.  A BC . 3 a 3 3 2a A. V  . B. 3 V  3a . C. 3 V a 3 . D. V  . 3 3 Lời giải:
Gọi H là hình chiếu vuông góc của A lên BC , khi đó  A B
C  ABC 0 ,  AHA  60 . 1
Áp dụng công thức diện tích hình chiếu ta có: 2 2 SS   a   a ABC   .cos 60 2 . A BC 2 2 1 2S 2a Mặt khác: SAH. ABC BC AH     a . ABC  2 BC 2a Khi đó 0
AA  AH . tan 60  a 3 . Vậy 2 3 V      S .A A a .a 3 a 3 . ABC. A BC ABC
Chọn đáp án C.
BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN
Câu 10: Một khối lăng trụ đứng tam giác có các cạnh đáy lần lượt bằng 37;13;30 và diện tích xung
quanh bằng 480. Khi đó thể tích của khối lăng trụ bằng A. 1170 . B. 2160 . C. 360 . D. 1080 .
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia Lời giải:
+) Chu vi đáy của khối lăng trụ là: P  37 13  30  80 . P P  P  P
Diện tích đáy của khối lăng trụ là: S   37 13  30 180     . 2  2  2  2 
+) Khối lăng trụ có diện tích xung quanh S  480 . xq Sxq 480
Suy ra chiều cao khối lăng trụ: h    6 . P 80
+) Thể tích khối lăng trụ: V S.h  180.6  1080 .
Chọn đáp án D.
Câu 11: Cho hình lăng trụ đứng ABC.A BC
  có đáy ABC là tam giác vuông cân tại A, AB  .a Biết
diện tích tứ giác ABB A   bằng 2
2a , thể tích khối lăng trụ ABC.A BC   bằng 3 3a 3 3a 3 a A. . B. . C. 3 a . D. . 2 6 3 Lời giải: A C B C' A' B' 2 a Ta có: S  ; S             A . A A B A A 2 . a Suy ra: 3 V    AA .S a . ABC 2 ABB A ABC.A B C ABC
Chọn đáp án C.
Câu 12: Cho hình lăng trụ đứng ABC.AB C
  có AA  a 2, AB a, AC  2a , BAC  60 . Thể tích
hình lăng trụ đó bằng 3 a 6 3 a 6 A. 3 a 2 . B. 3 3a 3 . C. . D. . 2 2 Lời giải: 2 1 1 a 3 Ta có SA . B AC.sin BAC  . a 2 . a sin 60  . ABC  2 2 2 2 a 3 3 a 6 Ta có V        S .AA .a 2 . ABC.A B C ABC 2 2
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Chọn đáp án C.
Câu 13: Cho hình lăng trụ đứng ABC.A BC
  có đáy ABC là tam giác vuông cân tại A, AB  .a Biết góc giữa  AB C   và A BC
  bằng 60, thể tích khối lăng trụ ABC.A BC   bằng 3 3a 3 3a 3 6a A. . B. . C. 3 a . D. . 2 6 4 Lời giải: A C B C' A' H B' 2 aB C    A H  Ta có: S
. Gọi H là trung điểm B C      B C    A AH  B C    AH. ABC 2 B C     A A  3 6a Vậy  AB C  ;A BC
   AHA  60 . Suy ra: V       AA .S . ABC.A B C ABC 4
Chọn đáp án D.
Câu 14: Cho lăng trụ đứng ABC.A BC
  có đáy ABC là tam giác vuông cân tại B, AB  .a Biết
ABC hợp với A BC một góc 60, thể tích của khối lăng trụ ABC.A BC bằng 3 3a 3 2a 3 3a 3 6a A. . B. . C. . D. . 4 2 2 2 Lời giải: A C B C' A' B' 2 1 a Ta có: SA . B BC  . ABC 2 2 B C    A B   Ta có:   B C    AA B    B C
   AB . Suy ra  AB C  ;A BC    AB A  . B C     AAAA Xét tam giác AB A
  vuông tại A : tan AB A   
AA  a 3. A B   2 3 a 3a Vậy V        AA .S a 3. . ABC.A B C ABC 2 2
Chọn đáp án C.
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Câu 15: Cho khối lăng trụ đứng ABC . D AB CD
  có đáy là hai hình thoi cạnh a , BD a 3 và
AA  4a (tham khảo hình vẽ dưới)
Thể tích của khối lăng trụ đã cho bằng 3 4 3a 3 2 3a A. 3 2 3a . B. . C. 3 4 3a . D. . 3 3 Lời giải:
Tam giác ABO vuông tại O ( O là tâm của hình thoi ABCD ): 2 3a a 2 1 a 3 2 2 2 AO
AB BO a
  AC a S
AC BD  . 4 2 ABCD 2 2 2 a 3
Thể tích khối lăng trụ ABC . D AB CD   là 3 V SAA 
4a  2a 3 . ABCD 2
Chọn đáp án A.
Câu 16: Cho hình lăng trụ đứng ABC . D AB CD
  có đáy là hình thoi ABCD cạnh a , ABC  60 .
Đường chéo AC tạo với mặt phẳng  ABCD một góc 30 . Thể tích khối lăng trụ ABC . D AB CD
  tính theo a bằng 1 1 1 3 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 4 6 2 2 Lời giải:
Góc giữa AC và  ABCD là góc ACA .
Tam giác ABC cân tại B có ABC  60 nên tam giác ABC là đều  AC a . 2 2 a 3 a 3
Diện tích hình thoi : S  2S  2.  . ABCD ABC 4 2 3
Xét AAC vuông tại    .tan
  .tan 30  a A AA AC ACA a . 3
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 2 3 a 3 a 3 a
Vậy thể tích khối lăng trụ ABC . D AB CD
  là V S .AA    . ABCD 2 3 2
Chọn đáp án C.
Dạng 2: Khối lăng trụ đều Phương pháp:
Cho hình lăng trụ tam giác đều ABC.A BC   …
Cho hình lăng trụ tứ giác đều ABC.A BC   … A C A D B B C A' D' C' A' B' C' B'
+) Đường cao: AA
+) Đường cao: AA
+) Thể tích khối lăng trụ: V AA .S
+) Thể tích khối lăng trụ: V AA .S ABCD ABC
BÀI TẬP TRẮC NGHIỆM MINH HỌA
Câu 17: Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng a bằng 3 3a 3 3a 3 3a 3 3a A. . B. . C. . D. . 12 6 2 4 Lời giải: 2 3 a 3 a 3 Ta có V        S .AA .a . ABC.A B C ABC 4 4
Chọn đáp án D.
Câu 18: Cho khối lăng trụ tam giác đều có độ dài cạnh đáy bằng a và diện tích xung quanh bằng 2
6a . Thể tích của khối lăng trụ đã cho là 3 2a 3 3 a 3 3 a 3 3 a 3 A. V  . B. V  . C. V  . D. V  . 3 4 2 3 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 2 a 3
Giả sử lăng trụ tam giác đều ABC.AB C
  có độ dài cạnh đáy bằng a suy ra: S  . ABC  4
Lăng trụ tam giác đều ABC.AB C
  có diện tích xung quanh bằng 2 6a suy ra: 2 2 2 S           6a : 3 2a A . B AA 2a AA 2a . ABB A 2 3 a 3 a 3 Vậy V        S .AA .2a . ABC. A B C ABC 4 2
Chọn đáp án C.
Câu 19: Cho lăng trụ tam giác đều ABC.A BC
  có cạnh đáy bằng .
a Biết AB  2a, thể tích của khối
lăng trụ ABC.A BC   bằng 3 3a 3 3a 3 3a 3 a A. . B. . C. . D. . 4 8 24 4 Lời giải: A C B C' A' B' 2 3a Ta có: S  . Xét tam giác AB A   vuông tại 2 2
A : AA  AB  A B    a 3. ABC 4 2 3 3a 3a Vậy V        AA .S a 3. . ABC.A B C ABC 4 4
Chọn đáp án A.
Câu 20: Cho lăng trụ tam giác đều ABC.A BC
  có cạnh đáy bằng .
a Biết  AB C
  hợp với mặt đáy một
góc 30, thể tích của khối lăng trụ ABC.A BC   bằng 3 3a 3 3a 3 3a 3 a A. . B. . C. . D. . 4 8 24 4 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia A C B C' A' M B' 2 3a Ta có: S  . ABC 4 B C    A M  Dựng A M   B C
 ,M là trung điểm B C  . Ta có:   B C    AA M    B C    AM. B C     AA Suy ra  AB C  ;A BC
   AMA . AAa
Xét tam giác AMA vuông tại A : tan AMA   AA  . A M  2 2 3 a 3a 3a Vậy V        AA .S . . ABC.A B C ABC 2 4 8
Chọn đáp án B.
Câu 21: Cho hình lăng trụ tam giác đều ABC.A BC
  có cạnh đáy bằng 2a , góc giữa hai đường thẳng
AB và BC bằng 60 . Thể tích của khối lăng trụ đó là 3 2 3a 3 2 6a A. 3
V  2 6a . B. V . C. V . D. 3
V  2 3a . 3 3 Lời giải: B' C' A' D C B A
Dựng hình bình hành B CB
D , suy ra BC// DB , do đó góc giữa hai đường thẳng AB và BC
bằng góc giữa hai đường thẳng AB và DB .
Xét tam giác ACD có trung tuyến AB bằng nửa cạnh đối diện CD nên ACD vuông tại A . 2 2 2 2
AD DC AC  16a  4a  2a 3 . Lại do ABC.A BC
  là lăng trụ tam giác đều nên AB  BC hay AB  DB  B DA  cân tại B ,
mà  ABDB o ,
 60 nên tam giác B D
A đều cạnh bằng 2a 3 . 2 2 2 2
BB  AB  AB  12a  4a  2a 2 . 2a2 3
Tính thể tích V của khối lăng trụ đã cho: 3
V BB .S  2a 2.  2 6a . ABC 4
Chọn đáp án A.
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Câu 22: Cho hình lăng trụ tam giác đều ABC.AB C
  có AA  a . Khoảng cách giữa AB ' và CC ' bằng
a 3 . Thể tích khối lăng trụ ABC.A ' B 'C ' . 3 2 3a 3 3a 3 3a A. . B. 3 3a . C. . D. . 3 2 3 Lời giải: A C B H A' C' B'
Kẻ CH AB CH   ABB '  d CC ', ABB '  CH a 3
Ta có d CC ', AB '  d CC ', ABB '  CH a 3 .
Do tam giác ABC đều có đường cao CH a 3 2
AB  2a Sa 3 ABC Khi đó 3 VAA'.Sa 3 .
ABC. A' B 'C ' ABC
Chọn đáp án B. 2a 3
Câu 23: Cho hình lăng trụ đều ABC.AB C
  có cạnh đáy bằng
. Đường thẳng BC tạo với mặt 3 phẳng  ACC A
  góc  thỏa mãn cot  2 . Thể tích khối trụ ABC.AB C   bằng 4 1 1 2 A. 3 a 11 . B. 3 a 11 . C. 3 a 11 . D. 3 a 11 . 3 9 3 3 Lời giải:
Gọi I là trung điểm của AC BI AC BI   ACC A  .
Ta có BC , ACC A
   BC ,C I   BC I  . 2a 3 . 3
Xét tam giác ABC có 3 BI   a . 2 BI a
Xét tam giác vuông BIC tại I có tan   C I   2a C I  . tan
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 2   2 a 3 a 33
Xét tam giác vuông CC I  có 2 2 CC  C I
  IC  2a       . 3 3   2  2a 3    3 2 3   a 3 Ta có S   . ABC  4 3 2 3 a 3 a 33 a 11 Ta có V        S .CC . . ABC. A B C ABC 3 3 3
Chọn đáp án C.
BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN
Câu 24: Thể tích khối lăng trụ tứ giác đều ABC . D AB CD
  có AC AA  2a là A. 3 4a . B. 3 2a . C. 3 2a . D. 3 2 2a . Lời giải:
Trong tam giác vuông ABC ta có 2 2 2
AB BC AC AB BC a 2 . Vậy 3 V         A . B BC.AA
a 2.a 2.2a 4a . ABCD.A B C D
Chọn đáp án A.
Câu 25: Cho hình lăng trụ tam giác đều ABC.A' B 'C ' cạnh đáy a  4 , biết diện tích tam giác A ' BC
bằng 8. Thể tích khối lăng trụ ABC.A ' B 'C ' bằng A. 10 3 . B. 2 3 . C. 8 3 . D. 4 3 . Lời giải: 2  S
Gọi M là trung điểm BC . Khi đó, A' A' BC M   4 . BC
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia  4  3 2 2 AM
 2 3  AA'  A'M AM  2 
Ta có tam giác ABC đều 2   1
S  .4.2 3  4 3. ABC  2 Vậy VAA' S  8 3 .
ABC.A' B 'C ' ABC
Chọn đáp án C.
Câu 26: Cho lăng trụ tam giác đều ABC.A BC
  có cạnh đáy bằng .
a Biết AB hợp với mặt đáy một
góc 60, thể tích của khối lăng trụ ABC.A BC   bằng 3 3a 3 3a 3 3a 3 a A. . B. . C. . D. . 4 8 24 4 Lời giải: A C B C' A' B' 2 3a Ta có: S
. Do AA   A BC    A B
  là hình chiếu vuông góc của AB trên A BC  . ABC 4
Suy ra AB ;A BC    AB A  . AA Xét tam giác AB A
  vuông tại A : tan AB A   
AA  a 3. A B   2 3 3a 3a Vậy V        AA .S a 3. . ABC.A B C ABC 4 4
Chọn đáp án A.
Câu 27: Cho lăng trụ tam giác đều ABC.A BC
  có cạnh đáy bằng .
a Biết AC hợp với  ABB A   một
góc 30, thể tích của khối lăng trụ ABC.A BC   bằng 3 3a 3 3a 3 3a 3 6a A. . B. . C. . D. . 4 8 24 4 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia A C B C' A' M B' 2 3a Ta có: S  . Dựng C M   A B
 ,M là trung điểm A B  . ABC 4 CM   A B   Ta có:   C M   ABB A
   AM là hình chiếu vuông góc của AC trên ABB A  . C M    AA
Suy ra AC ;ABB A
   MAC . C M
Xét tam giác MAC vuông tại M : sin MAC 
AC  a 3. AC Xét tam giác AA C   vuông tại 2 2
A : AA  AC  A C    a 2. 2 3 3a 6a Vậy V        AA .S a 2. . ABC.A B C ABC 4 4
Chọn đáp án D.
Câu 28: Cho hình lăng trụ tam giác đều ABC.A BC
  có cạnh đáy bằng a, AC hợp với mặt phẳng ABB A
  một góc 45 . Thể tích của khối lăng trụ ABC.A BC   bằng 3 6a 3 3a 3 6a 3 6a A. . B. . C. . D. . 24 4 8 4 Lời giải: A C B 450 a A' C' a H a B' 2 3a Ta có: S               . Dựng C H A B C HABB A A B C 4   a 3 AC ; ABB A    C A
H  45 . Suy ra AHC vuông cân tại H HC  AH  . 2 a 3 6a Xét tam giác A AH vuông tại 2 2 2 A : A A
  AH A H  
. Vậy V AA .S      . 2 A B C 8
Chọn đáp án C.
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Câu 29: Cho khối lăng trụ tam giác đều ABC.AB C
  có cạnh đáy là 2a và khoảng cách từ A đến mặt
phẳng  ABC  bằng a . Tính thể tích của khối lăng trụ ABC.AB C  . 3 3a 2 3 a 2 3 2a A. 3 2 2a . B. . C. . D. . 2 2 2 Lời giải:
 Gọi M là trung điểm của B C    Ta có B C
   AM , vì ABC đều và B C
   AA nên B C
    AAM  .
 Dựng AE AM , khi đó AE   AB C
  , do đó d A ; AB C    A E   a
 AAM vuông tại A với đường cao AH nên 1 1 1 1 1 1 1 1  a 6         AA   2 2   2 2   2  2 2 2 A H AA A M AA A E A M a (a 3) 2 2 3  a 6 (2a) 3 3a 2
Thể tích khối lăng trụ ABC.AB C   là: V    . 2 4 2
Chọn đáp án B.
Câu 30: Cho hình lăng trụ tam giác đều AB . C AB C
  có cạnh đáy bằng 2a , góc giữa hai đường thẳng
AB và B C bằng 60 . Tính thể tích V của khối lăng trụ đó. 3 2 6a 3 2 3a A. V  . B. 3 V  2 3a . C. V  . D. 3 V  2 6a . 3 3 Lời giải:
 Gọi N là giao điểm của AB và AB .
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
 Gọi M là trung điểm của AC thì M N là trung bình tam giác ABC  MN // B C .
 Khi đó góc giữa AB và B C là góc giữa B N
 và M N (1). 1 1 1
 Đặt: AA  x . Khi đó: 2 2 2 2 B N   AB 
AA  AB  x  4a 2 2 2 1 1 1 2 2 2 2 MN BC  BB  BC x  4a . 2 2 2
 Do đó : BN M N BM
N cân tại N (2).  2a 3
Từ (1) và (2) suy ra B M
N đều. Suy ra: MN B N   B M    a 3 . 2 1  Do đó : 2 2 MN
x  4a a 3  x  2a 2 . 2 2 4a 3
 Vậy thể tích khối lăng trụ là : 3
V AA .S  2a 2.  2a 6 . ABC  4
Chọn đáp án D.
Dạng 3: Khối hộp chữ nhật – Khối lập phương Phương pháp:
Cho hình hộp chữ nhật A . BCD A BCD   …
Cho hình lập phương ABCD.A BCD … A c D A a D b a a a B C B C A' D' A' D' B' C' B' C'
+) Thể tích khối hộp: V abc
+) Thể tích khối lập phương: 3 V a
BÀI TẬP TRẮC NGHIỆM MINH HỌA
Câu 31: Thể tích của khối lập phương cạnh 3a bằng A. 3 9a . B. 3 27a . C. 3 18a . D. 3 36a . Lời giải:
Thể tích của khối lập phương cạnh 3a bằng  a3 3 3  27a .
Chọn đáp án B.
Câu 32: Thể tích của khối hộp chữ nhật có ba kích thước 2,3,7 bằng A. 14. B. 42. C. 126. D. 12. Lời giải:
Thể tích của khối hộp chữ nhật là: V  2.3.7  42 .
Chọn đáp án B.
Câu 33: Cho hình hộp chữ nhật A .
BCD ABC D
  có AB  2a, BC  .a Biết AC  3a, thể tích của khối hộp chữ nhật A .
BCD ABC D   bằng 3 2 15a 3 3a A. 3 4a . B. 3 4 3a . C. . D. . 3 4 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia A D B C A' D' B' C' Xét tam giác AA C
  vuông tại AAA  AC  A C
    a  a 2 2 2 2 : 3 5  2 . a Vậy 3 V        AA .A . B AD 4a . ABCD.A B C D
Chọn đáp án A.
Câu 34: Cho hình lập phương ABC . D A BCD
  có diện tích mặt chéo ACC A   bằng 2 2 2a . Thể tích
của khối lập phương ABC . D A BCD   là A. 3 16 2a . B. 3 2 2a . C. 3 8a . D. 3 a . Lời giải:
Giả sử độ dài cạnh hình lập phương là x , khi đó AC x 2 và 2 S    x 2 . Suy ra ACC A
x a 2 . Vậy thể tích khối lập phương là a 3 3 2  2 2a .
Chọn đáp án B.
Câu 35: Cho hình hộp chữ nhật ABC . D AB CD
  có AB a, AD a 3, góc giữa mặt phẳng  ABC D  
và  ABCD bằng 45 .
 Thể tích khối hộp chữ nhật đã cho bằng A. 3 3a . B. 3 a . C. 3 3a . D. 3 2 3a . Lời giải:
Ta có góc giữa  ABC D
  và ABCD bằng 0 C BC
45  CC  BC.tan 45  a 3 3  V         A . B A . D AA . a a 3.a 3 3a . ABCD.A B C D
Chọn đáp án A.
BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN
Câu 36: Thể tích của khối hộp chữ nhật ABC . D AB CD
  có AB  3, AC  5 , AA  8 bằng A. 120 . B. 32 C. 96 . D. 60 . Lời giải: Tính 2 2 BC AC AB  4
Thể tích khối hộp bằng V         A . B BC.AA 3.4.8 96 . ABCD. A B C D
Chọn đáp án C.
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Câu 37: Diện tích toàn phần của một hình lập phương bằng  2
96 cm  . Khối lập phương đã cho có thể tích bằng 3 A.  3 84 cm  .
B. 48cm  . C.  3 64 cm  . D.  3 91 cm  . Lời giải:
Gọi x x  0 là cạnh của hình lập phương 2
S  6x  96  x  4 . tp Vậy 3 V    3 4 64 cm  .
Chọn đáp án C.
Câu 38: Cho hình lập phương ABC . D A BCD
  có diện tích tam giác ACD bằng 2 a 3 . Thể tích của
khối lập phương đã cho bằng: A. 3 4 2a . B. 3 8a . C. 3 a . D. 3 2 2a . Lời giải: 2 x 3
Đặt AB xx  0 . Do ACD là tam giác đều 2 2 2 
a 3  x  4a x  2a . 4 Vậy Va a . A B C D 2 3 3 8 ABCD. ' ' ' '
Chọn đáp án B.
Câu 39: Cho hình lăng trụ đứng ABC . D AB CD
  có đáy là hình vuông cạnh bằng 6 , đường chéo
AB của mặt bên  ABB A
  có độ dài bằng 10 . Tính thể tích V của khối lăng trụ ABC . D AB CD   . A. V  384 . B. V  180 . C. V  480 . D. V  288 . Lời giải:
Diện tích của hình vuông ABCD 2 là S  6  36 . Xét tam giác ABB 2 2 2 2   
vuông tại B có B B
B A AB  10  6  8 .
Vậy thể tích của hình lăng trụ là V  36.8  288 .
Chọn đáp án D.
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Câu 40: Cho hình hộp chữ nhật A .
BCD ABC D
  có AB  2a, BC  .a Biết ADC B
  hợp với mặt đáy
một góc 60, thể tích của khối hộp chữ nhật A .
BCD ABC D   bằng 3 2 15a 3 3a A. 3 4a . B. 3 4 3a . C. . D. . 3 4 Lời giải: A D B C A' D' B' C' Ta có:  ADC B  ;A BCD    DC D  . DD Xét tam giác DC D
  vuông tại D :tan DC D   
DD  2a 3. C D   Vậy 3 V        AA .A . B AD 4 3a . ABCD.A B C D
Chọn đáp án B.
Câu 41: Cho hình hộp chữ nhật A .
BCD ABC D
  có AB  2a, BC  .a Biết AC hợp với mặt đáy một góc
60, thể tích của khối hộp chữ nhật A .
BCD ABC D   bằng 3 2 15a 3 3a A. 3 2 15a . B. 3 4 3a . C. . D. . 3 4 Lời giải: A D B C A' D' B' C'
Ta có: AA   A BCD    A C
  là hình chiếu vuông góc của AC trên A BCD  .
Suy ra: AC ;A BCD    AC A  . AA Xét tam giác AC A
  vuông tại A :tan AC A   
AA  a 15. A C   Vậy 3 V        AA .A . B AD 2 15a . ABCD.A B C D
Chọn đáp án A.
Câu 42: Cho hình hộp chữ nhật có đường chéo d  21. Độ dài ba kích thước của hình hộp chữ nhật
lập thành một cấp số nhân với công bội q  2. Thể tích của khối hộp chữ nhật đã cho là A. V  8 . B. V  8 . C. V  4 . D. V  6 . 3 3 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Gọi ba kích thước của hình hộp chữ nhật là a,b,c 0  a b c. Do a,b,c lập thành cấp số nhân
nên b  2a; c  4 . a Theo giả thiết: 2 2 2 2
a b c  21  21a  21  a  1.
Vậy thể tích khối hộp chữ nhật là V abc  1.2.4  8.
Chọn đáp án A.
Dạng 4: Khối lăng trụ xiên bất kì Phương pháp:
Cho hình lăng trụ ABC.A BC   …
+) Đường cao: AH , H là hình chiếu vuông góc của Form hình vẽ: A trên A BC  . A C
+) Thể tích khối lăng trụ: V AH.S B ABC A' C' H M B'
BÀI TẬP TRẮC NGHIỆM MINH HỌA
Câu 43: Cho lăng trụ ABC.AB C
 có đáy ABC là tam giác đều cạnh a , cạnh bên bằng 4a và tạo với đáy góc o
30 . Thể tích khối lăng trụ ABC.AB C   bằng 1 3 3 A. 3 a . B. 3 a . C. 3 3a . D. 3 a . 2 2 2 Lời giải: A' C' B' A C H B 2 a 3
Tam giác ABC là tam giác đều cạnh a nên S  . ABC 4
Gọi H là hình chiếu vuông góc của A trên  ABC  , do đó AH   ABC  . 1 Ta có  A H
 ,(ABC)  A A
H  30 nên A H
  AA .sin A AH  4 . a  2a . 2 2 a 3 3 Vậy 3 V        A H.S 2 . a a . ABC. A B C C AB 4 2
Chọn đáp án D.
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Câu 44: Cho lăng trụ tam giác ABC.AB C
  có đáy là tam giác đều cạnh a , góc giữa cạnh bên và mặt
đáy bằng 30 . Hình chiếu của A lên  ABC  là trung điểm I của BC . Tính thể tích khối
lăng trụ ABC.AB C  . 3 a 3 3 a 13 3 a 3 3 a 3 A. . B. . C. . D. . 8 12 6 2 Lời giải: A' C' B' A C I B
Vì AI   ABC  nên AI là hình chiếu vuông góc của AA lên  ABC  .
Do đó  AA , ABC   AA , AI   AIA  30 a 2 3 a a 3 a 3 Ta có  A I  tan 30 .  AI   V        IA .S .  . 2 ABC. A B C ABC 2 4 8
Chọn đáp án A.
Câu 45: Cho hình lăng trụ ABC.A BC
  có đáy là tam giác đều cạnh bằng .
a Biết hình chiếu vuông
góc của A trên  ABC là trọng tâm tam giác ABC, AA  2a, thể tích của khối lăng trụ ABC.A BC   bằng 3 11a 3 3a 3 3a 3 6a A. . B. . C. . D. . 4 4 8 9 Lời giải: A' C' B' A C G M B 2 3a Ta có: S
. Gọi G là trọng tâm tam giác ABC. ABC 4 a Xét tam giác A AG vuông tại 2 2 33 G : A G
  AA  AG  . 3 2 3 33a 3a 11a Vậy V        A . G S . . ABC.A B C ABC 3 4 4
Chọn đáp án A.
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Câu 46: Cho hình lăng trụ ABC.A BC
  có đáy là tam giác đều cạnh bằng .
a Biết hình chiếu vuông
góc của A trên  ABC là trọng tâm tam giác ABC, AA ;ABC  60, thể tích của khối lăng trụ ABC.A BC   bằng 3 11a 3 3a 3 3a 3 6a A. . B. . C. . D. . 4 4 8 9 Lời giải: A' C' B' A C G M B 2 3a Ta có: S
. Gọi G là trọng tâm tam giác ABC. ABC 4 Do A G
  ABC nên AG là hình chiếu của AA trên ABC.
Suy ra:  AA ; ABC  A A  . G A G  2 Xét tam giác A AG vuông tại o G :tan A AG   A G   AM.tan60  . a AG 3 2 3 3a 3a Vậy V        A . G S . a . ABC.A B C ABC 4 4
Chọn đáp án B.
Câu 47: Cho lăng trụ ABC.A' B'C ' có đáy ABC là tam giác vuông tại B , đường cao BH . Biết
A' H   ABC  và AB  1, AC  2, AA'  2 . Thể tích của khối lăng trụ đã cho bằng 21 7 21 3 7 A. . B. . C. . D. . 12 4 4 4 Lời giải: A . B BC 3 3 1
Độ dài của đường cao BH : BH   . Suy ra AH  : 3  . AC 2 2 2
Khi đó độ dài đường cao A'H của hình lăng trụ bằng : 2 2 1 7
A' H AA'  AH  2   . 4 2
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 1 1 7 21
Thể tích khối lăng trụ đã cho bằng : V A .
B BC.A' H  .1. 3  . 2 2 2 4
Chọn đáp án B.
Câu 48: Cho lăng trụ ABC.AB C
  có đáy ABC là tam giác vuông tại B và AA AB AC . Biết rằng
AB a, BC a 3 và mặt phẳng  ABC  tạo với mặt phẳng đáy một góc 60 . Thể tích khối
lăng trụ ABC.AB C   bằng 3 3a 3 3a 3 a A. . B. C. 3 a . D. 4 2 4 Lời giải:
Gọi H là trung điểm của AC , vì tam giác ABC vuông tại B nên H là tâm đường tròn ngoại
tiếp của tam giác ABC . A A   A B   A C  Ta có: 
AH   ABC .
HA HB HC
Kẻ HM BC   A B
C; ABC  A MH  60. 2 1 a 3
Diện tích tam giác ABC : SA . B BC  . ABC 2 2 1 3a
Xét tam giác vuông AHM có: A H
  HM.tan 60  A . B tan 60  . 2 2 2 3 3a 3a 3a
Thể tích khối lăng trụ ABC.AB C
 : V A H  .S  .  . ABC 2 2 4
Chọn đáp án A.
Câu 49: Cho hình lăng trụ ABC . D AB CD
  có ABCD là hình chữ nhật. Tính thể tích khối lăng trụ đã
cho biết AA AB AD và AB a, AD a 3, AA  2a A. 3 3a . B. 3 a . C. 3 a 3 . D. 3 3a 3 . Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
 Gọi H là hình chiếu của A trên  ABCD . Vì AA AB AD HA HB HD
H AC BD 2 2 AB AD  2 2 2 A H
  AA  AH AA   a 3 . 4  Vậy 2 3 V         A H.S a 3.a 3 3a . ABCD.A B C D ABCD
Chọn đáp án A.
Câu 50: Cho khối lăng trụ ABC.AB C
  có đáy là tam giác đều cạnh 4a, AA  2 3a . Gọi M , N lần
lượt là trung điểm của BB ,CC . Biết mặt bên BCC B
  là hình chữ nhật và mặt phẳng  ANM
vuông góc với mặt phẳng  BCC B
  . Thể tích khối lăng trụ đã cho bằng A. 3 3 3a . B. 3 24 3a . C. 3 12 3a . D. 3 4 3a . Lời giải: B' A' M C' H N B A C
Ta có CC  MN CC   AMN  2 2
CC  AN AN  16a  3a a 13 .
Tương tự AM a 13 , do đó tam giác AMN cân tại A . Gọi H là trung điểm MN .
Suy ra AH MN AH   BCC B   và 2 2
AH  13a  4a  3a . 3 3 1 1 Mặt khác 3 V        V   . .AH.S   .3 . a 4 . a 2a 3 12 3a . ABC. A B C . 2 A BCC B 2 3 BCC B 2
Chọn đáp án C.
Câu 51: Cho hình hộp ABC .
D A' B 'C ' D ' có đáy là hình chữ nhật, AB  3, AD  7 . Hai mặt
ABB' A' và  ADD' A' lần lượt tạo với đáy góc 45 và 60, biết cạnh bên bằng 1. Tính thể
tích khối hộp ABC .
D A' B 'C ' D ' . 3 3 3 A. 3 . B. . C. . D. 3 . 4 4
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia Lời giải: B C A D B' C' J A' I K D'
Gọi I là hình chiếu của A trên ( A' B 'C ' D ') . Đặt AI x(x  0)
Gọi J , K lần lượt là hình chiếu của I trên A' B ' và A' D ' .
A' B '  AI Ta có 
A' B '   AIJ   ABB' A';A'B'C'D'  AJI  45
A' B '  IJ
JI AI x .
A' D '  AI Ta có 
A' D '   AIK   ADD' A';A'B'C'D'  AKI  60
A' D '  IK AI x 3  2x 3 IK  
; Do A' JIK là hình chữ nhật  IA'  tan 60 3 3 3 Ta lại có 2 2 2
AA'  AI A' I x   VA . B A . D AI  3 .
ABCD. A' B 'C ' D ' 7
Chọn đáp án D.
BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN
Câu 52: Khối lăng trụ tam giác có độ dài các cạnh đáy lần lượt bằng 13,14,15. Cạnh bên tạo với mặt
phẳng đáy một góc 30 và có chiều dài bằng 8. Thể tích khối lăng trụ đã cho bằng A. 124 3 . B. 340 . C. 274 3 . D. 336 . Lời giải:
Tam giác đáy của lăng trụ có diện tích S
p p 13 p 14 p 15  84 với 13 14 15 p   21. 2
Chiều cao lăng trụ: h  8.sin 30  4. Vậy thể tích khối lăng trụ là V S.h  336.
Chọn đáp án D. 2a
Câu 53: Cho lăng trụ ABC.A BC
  có đáy ABC là tam giác đều cạnh a , độ dài cạnh bên bằng , hình 3
chiếu của đỉnh A trên mặt phẳng  ABC trùng với trọng tâm của tam giác ABC . Thể tích
khối lăng trụ ABC.A BC   bằng 3 3a 3 3a 3 3a 3 3a A. . B. . C. . D. . 36 6 12 24 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia A' C' 2a/3 B' a A C G a a I B
Gọi G là trọng tâm của tam giác ABC . Ta có: 2 2 2 a 3 2  a   a a a AG AI  ; 2 2 2 2 3 A G   A A   AG         A G   . 3 3 3  3    9 3   2 3 a 3 a a 3
Vậy V B.h  .  . 4 3 12
Chọn đáp án C. 3a
Câu 54: Cho lăng trụ ABC.A BC
  có đáy ABC là tam giác đều cạnh a , AA  . Biết rằng hình chiếu 2
vuông góc của A lên  ABC là trung điểm BC . Thể tích của khối lăng trụ ABC.A BC   bằng 3 2a 3 3 2a 3 6a 3 2a A. . B. . C. . D. . 8 8 2 3 Lời giải:
Gọi M là trung điểm BC , khi đó A M
  ABC . Tam giác ABC đều cạnh a nên AM BC và a 3 AM  . 2
Xét tam giác vuông A A
M vuông tại M có 2 2     2 2 2 a a a A M
AM AA . 2 2 3 3 6  A M
  AA  AM        . 2  2    2   2 3 a 6 a 3 3 2aV        A M.S . . ABC.A B C ABC 2 4 8
Chọn đáp án B.
Câu 55: Cho lăng trụ ABC.AB C
 có đáy ABC là tam giác đều, AA  4a . Biết rằng hình chiếu vuông
góc của A lên  ABC  là trung điểm M của BC , AM  2a . Thể tích của khối lăng trụ
ABC.AB C   bằng 3 8a 3 3 16a 3 A. 3 8a 3 . B. . C. 3 16a 3 . D. . 3 3
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia Lời giải: Do A M
   ABC nên tam giác AMA vuông tại M .
Trong tam giác AMA vuông tại M : 2 2 2 2 AM A A   A M
 16a  4a  2 3a . AB 3 2.AM 2.2 3a
Do ABC là tam giác đều nên AM   AB    4a . 2 3 3 4a2 3
Vậy thể tích lăng trụ ABC.AB C   là 3 V S .A M   .2a  8a 3 (đvtt). ABC 4
Chọn đáp án A.
Câu 56: Cho lăng trụ ABC.AB C
 , có đáy ABC là tam giác đều cạnh a . Cho biết hình chiếu của đỉnh
A lên mặt đáy  ABC  là điểm H trên cạnh AB mà HA  2HB và góc giữa mặt bên  AC CA
 và mặt đáy  ABC bằng 45. Thể tích của khối lăng trụ đã cho là 1 1 3 3 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 4 12 4 4 Lời giải: AE 2
+) Gọi K là trung điểm AC , E là điểm thuộc AK sao cho  . AK 3
+) Ta có:  ABC    A CCA    AC .   1
+) Ta có: AC HE (vì AC BK và HE //BK ) và AC AH (vì AH   ABC  ) AC HE    ABC
AC   AHE   2
AC AE    AC CA +) Từ  
1 và 2 suy ra  AC CA
, ABC  A E
 , HE  A EH  45   2 2 a 3 a 3
AHE vuông cân tại H A H
  HE BK    . 3 3 2 3
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 2 3 a 3 a 3 a +) Ta có: V         S .A H . ABC. A B C ABC 4 3 4
Chọn đáp án A.
Câu 57: Cho hình lăng trụ ABC.A BC
  có đáy là tam giác đều cạnh bằng .
a Biết hình chiếu vuông
góc của A trên  ABC là trọng tâm tam giác ABC,  AA BB
 ;ABC  60, thể tích của khối
lăng trụ ABC.A BC   bằng 3 3a 3 3a 3 3a 3 6a A. . B. . C. . D. . 24 4 8 9 Lời giải: A' C' B' A C G M B 2 3a Ta có: S
. Gọi G là trọng tâm tam giác ABC. ABC 4 AB A G
Dựng GM AB, M là trung điểm AB  
AB  A G
M  AB A . M AB   GM Suy ra:  AA BB
 ;ABC  A M  . G A G  1 a Xét tam giác A MG vuông tại o G :tan A MG   A G   AM.tan60  . GM 3 2 2 3 a 3a 3a Vậy V        A . G S . . ABC.A B C ABC 2 4 8
Chọn đáp án C.
Câu 58: Cho hình lăng trụ tam giác ABC.AB C
  có đáy ABC là tam giác vuông tại A và AB a ,
AC a 3 . Tính thể tích khối lăng trụ ABC.AB C
  biết AA AB AC  2a . 3 3a 3 a 3 a 3 A. 3 a 3 . B. . C. . D. . 2 2 3 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia A' C' B' A C H B
Gọi H là chân đường cao hạ từ A xuống đáy  ABC  .
Vì AA AB AC và tam giác ABC vuông tại A nên H là trung điểm BC BC Ta có 2 AH   a A H   A A
  AH a 3 . 2 3  1  3a
Thể tích khối lăng trụ là V        A H.S a 3. . a a 3 . ABC. A B C ABC    2  2
Chọn đáp án B.
Câu 59: Cho khối lăng trụ ABC.AB C
  có đáy là tam giác vuông tại ,
A AB a, AC  3a . Hình chiếu
vuông góc của A trên mặt phẳng  AB C
 là trung điểm H của B C
  . Khoảng cách từ A đến 3a mặt phẳng  BCC B   bằng
. Thế tích của khối lăng trụ đã cho bằng 4 3 3a 3 3a 3 3a 3 3a A. . B. . C. . D. . 8 2 4 4 Lời giải: BC AH
Kẻ AK BC  
BC   AHK  . BC AKBC AT
Do đó kẻ AT HK  
AT  BCC B   . HK AT A . B AC 3a a Có 2 2 BC
AB AC  2a AK  
và AT d A BCC B   3 ,  . BC 2 4 1 1 1 a
Tam giác vuông AHK có    AH  . 2 2 2 AT AK AH 2 3 1 a 3a Vậy V       S .AH . a 3 . a . ABC. A B C ABC 2 2 4
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Chọn đáp án D.
Câu 60: Cho khối lăng trụ ABCAB C
  có đáy là tam giác đều, góc giữa hai mặt phẳng  AB C   và
BCC B bằng 60, hình chiếu vuông góc của B lên mặt phẳng  ABC trùng với trọng tâm
tam giác ABC . Khoảng cách giữa hai đường thẳng AA và B C
 bằng 3a . Thể tích khối lăng trụ đã cho bằng 3 8 3a 3 8 6a A. 3 8 3a . B. . C. . D. 3 8 6a . 3 3 Lời giải:
Gọi x  0 là độ dài cạnh BC . Gọi M là trung điểm của BC và kẻ GH   BCC B   . BC GM
Khi đó:  ABC    BCC B
   BC . Do 
BC BMG  BC  GHM . BC B G
Ta có: d AA ; B C
   d AA ;BCC B
   3a HG a x
Suy ra:  ABC BCC B   3 ;
HMG  60  GH GM.sin 60  .
a x  4a . 2 3 2 4a Khi đó: B G
  GM.tan 60  . 3  2 . a 2 3 3 4a2
Thể tích khối lăng trụ đã cho là 3 V        S .B G .2a 8a 3 . ABCA B C ABC 4
Chọn đáp án A.
_____________________HẾT_____________________
Huế, 15h20’ Ngày 18 tháng 5 năm 2022
Lớp Toán thầy Lê Bá Bảo TP Huế Địa chỉ lớp: Trung tâm KM10 hoặc Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế 0935.785.115