Một số dạng toán về số phức ôn thi tốt nghiệp thpt có lời giải và đáp án

Một số dạng toán về số phức ôn thi tốt nghiệp THPT có lời giải và đáp án được soạn dưới dạng file PDF gồm 22 trang. Chuyên đề được phân dạng có phần tự luận và trắc nghiệm được biên soạn bởi thầy giáo Hà Trọng Đạt-Như Thụy–Sông Lô–Vĩnh Phúc. Các bạn xem và tải về ở dưới.

30 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung

Môn: Toán 12

Thông tin:

22 trang 7 tháng trước

Tác giả:

Profile ha phan
Trang1
MỘT SỐ DẠNG TOÁN VỀ SỐ PHỨC ÔN THI TỐT NGHIỆP THPTQG
A. KIẾN THỨC CƠ BẢN
1. Một số phức là một biểu thức có dạng a + bi, trong đó a, b là các số thực và số i thoả
mãn i
2
= -1. Ký hiệu số phức đó là z và viết z = a + bi .
i được gọi là đơn vị ảo
a được gọi là phần thực. Ký hiệu Re(z) = a
b được gọi là phần ảo của số phức z = a + bi , ký hiệu Im(z) = b
Tập hợp các số phức ký hiệu là C.
*) Một số lưu ý:
- Mỗi số thực a dương đều được xem như là số phức với phần ảo b = 0.
- Số phức z = a + bi có a = 0 được gọi là số thuần ảo hay là số ảo.
- Số 0 vừa là số thực vừa là số ảo.
2. Hai số phức bằng nhau.
Cho z = a + bi và z’ = a’ + b’i.
z = z’
'
'
aa
bb
3. Biểu diễn hình học của số phức.
Mỗi số phức được biểu diễn bởi một điểm M(a;b) trên mặt phẳng toạ độ Oxy.
Ngược lại, mỗi điểm M(a;b) biểu diễn một số phức là z = a + bi .
4. Phép cộng và phép trừ các số phức.
Cho hai số phức z = a + bi và z’ = a’ + b’i. Ta định nghĩa:
' ( ') ( ')
' ( ') ( ')
z z a a b b i
z z a a b b i
5. Phép nhân số phức.
Cho hai số phức z = a + bi và z’ = a’ + b’i. Ta định nghĩa:
' ' ' ( ' ' ) zz aa bb ab a b i
6. Số phức liên hợp.
Cho số phức z = a + bi. Số phức
z
= a – bi gọi là số phức liên hợp với số phức trên.
Vậy
z
=
a bi
= a - bi
Chú ý: 1
0
)
z
= z z và
z
gọi là hai số phức liên hợp với nhau.
2
0
) z.
z
= a
2
+ b
2
*) Tính chất của số phức liên hợp:
(1):
zz
(2):
'' z z z z
(3):
(4): z.
z
=
22
ab
(z = a + bi )
Trang2
7. Môđun của số phức.
Cho số phức z = a + bi . Ta ký hiệu
z
là môđun của số phư z, đó là số thực không
âm được xác định như sau:
- Nếu M(a;b) biểu diễn số phc z = a + bi, thì
z
=

OM
=
22
ab
- Nếu z = a + bi, thì
z
=
.zz
=
22
ab
8. Phép chia số phức khác 0.
Cho số phức z = a + bi ≠ 0 (tức là a
2
+b
2
> 0 )
Ta định nghĩa số nghịch đảo z
-1
của số phức z ≠ 0 là số
z
-1
=
2
22
11
zz
ab
z
Thương
'z
z
của phép chia số phức z’ cho số phức z ≠ 0 được xác định như sau:
1
2
' '.
.

z z z
zz
z
z
Với các phép tính cộng, trừ, nhân chia số phức nói trên nó cũng có đầy đủ tính chất
giao hoán, phân phối, kết hợp như các phép cộng, trừ, nhân, chia số thực thông thường.
9. Phƣơng trình bậc hai với hệ số thực.
* Cho phương trình bậc hai :
2
0 ax bx c
, có
2
4a bc
.
+ Nếu
> 0, PT có 2 nghiệm thực phân biệt
1,2
2
b
x
a
+ Nếu
= 0, PT có nghiệm kép x
1
= x
2
=
2
b
a
+ Nếu
< 0, PT có 2 nghiệm phức
1,2
||
2
bi
x
a
* Cho phương trình bậc hai :
2
0 ax bx c
.
Khi b chẵn có b’ = b/2 ;
'
=b’
2
– ac.
+ Nếu
'
> 0, PT có 2 nghiệm thực phân biệt
1,2
''
b
x
a
+ Nếu
'
= 0, PT có nghiệm kép x
1
= x
2
=
'b
a
+ Nếu
'
< 0, PT có 2 nghiệm phức
1,2
' | '|
bi
x
a
10. Một số kết quả cần nhớ
1) i
0
= 1
i
4n
= 1 2) i
1
= i
i
4n + 1
= i
3) i
2
= - 1
i
4n + 2
= - 1 4) i
3
= - i
i
4n + 3
= - i
5) (1 – i)
2
= - 2i 6) (1 + i)
2
= 2i
Trang3
B. MỘT SỐ DẠNG TOÁN THƢỜNG GẶP
DẠNGI. TÍNH TOÁN CÁC YẾU TỐ CỦA SỐ PHỨC
I. PHƢƠNG PHÁP: Sử dụng định nghĩa, các phép toán để tính toán các yếu tố có liên
quan.
II. CÁC VÍ DỤ
Ví dụ 1. (Mã đề 101 - QG – 2017) Cho hai số phức
1
57zi
và
2
23zi
. Tìm số phức
12
z z z
.
A.
74zi
B.
25zi
C.
25 zi
D.
3 10zi
Hƣớng dẫn giải
Ta có
12
5 7 2 3 7 4 z z z i i i
Đáp án: A
Ví dụ 2. (Mã đề 102 - QG – 2017) Cho số phức
3
1 z i i
. Tìm phần thực
a
và phần ảo
b
của
z
.
A.
0, 1ab
B.
2, 1 ab
C.
1, 0ab
D.
1, 2 ab
Hƣớng dẫn giải
Ta có
3
1 1 1 2 1, 2 z i i i i i a b
.
Đáp án: D
Ví dụ 3. (Mã đề 104 - QG – 2017) Tìm số phức z thỏa mãn
2 3 3 2 z i i
A.
15zi
B.
1zi
C.
55zi
D.
1zi
Hƣớng dẫn giải
Ta có
2 3 3 2 3 2 2 3 1 z i i z i i i
Đáp án: B
Ví dụ 4. (Mã đề 104 - QG – 2017) Cho số phức
2zi
. Tính
z
.
A.
3z
B.
5z
C.
2z
D.
5z
Hƣớng dẫn giải
Ta có
22
2 1 5 z
Đáp án: D
Ví dụ 5. (QG-2019) Số phức liên hợp của số phức là
A. . B. . C. . D. .
Hƣớng dẫn giải
Đáp án: C
III. BÀI TẬP
Câu 1. (Mã đề 101 - QG – 2017) Số phức nào dưới đây là số thuần ảo?
A.
23 zi
. B.
3zi
. C.
2z
. D.
3zi
.
Câu 2. (Mã đề 102 - QG – 2017) Cho hai số phức
1
43zi
và
2
73zi
. Tìm số phức
12
z z z
A.
11z
. B.
36zi
C.
1 10 zi
D.
36 zi
Câu 3. (Mã đề 103 - QG – 2017) Cho hai số phức
1
13zi
và
2
25 zi
. Tìm phần ảo b
của số phức
12
z z z
.
A.
2b
B.
2b
C.
3b
D.
3b
Câu 4. (Mã đề 103 - QG – 2017) Cho số phức
23zi
. Tìm phần thực a của z.
34i
34i
34i
34i
43i
Trang4
A.
2a
B.
3a
C.
3a
D.
2a
Câu 5. (QG – 2018) Số phức
37i
có phần ảo bằng
A.
3
. B.
7
. C.
3
. D.
7
.
Câu 6. (QG – 2018) Số phức có phần thực bằng
3
và phần ảo bằng
4
là
A.
34 i
. B.
43 i
. C.
34 i
. D.
43 i
.
Câu 7.(QG – 2018) Số phức
56 i
có phần thực bằng
A. – 5. B. 5. C. – 6. D. 6.
Câu 8. (QG – 2018) Số phức có phần thực bằng
1
và phần ảo bằng
3
là
A.
13i
. B.
13 i
. C.
13i
. D.
13 i
.
Câu 9. (QG-2019) Số phức liên hợp của số phức là
A. . B. . C. . D. .
Câu 10. (QG-2019) Số phức liên hợp của số phức là
A. . B. . C. . D. .
Câu 11. (QG-2019)Số phức liên hợp của số phức là
A. . B. . C. . D. .
Câu 12. Cho số phức
63 zi
. Tìm phần thực và phần ảo của số phức
z
.
A. Phần thực bằng
6
và phần ảo bằng
3 i
B. Phần thực bằng
6
và phần ảo bằng
3
C. Phần thực bằng
6
và phần ảo bằng
3
D. Phần thực bằng
6
và phần ảo bằng
3i
Câu 13. Cho 2 số phức z và z’. Các phát biểu nào sau đây sai ?
A.
'' z z z z
B.
2
. z z z
C.
zz
D.
.
' '.
z z z
z z z
Câu 14. Cho số phức z = 3- 4i. Phần thực và phần ảo số phức z là
A. Phần thực bằng 3 và phần ảo bằng - 4i;
B. Phần thực bằng 3 và phần ảo bằng 4;
C. Phần thực bằng 3 và phần ảo bằng 4i;
D. Phần thực bằng 3 và phần ảo bằng -4.
Câu 15. Tìm phần thực và phần ảo của số phức z = i
2020
.
A. 0 và 2020 B. 0 và 1 C. 1 và 0 D. 2020 và 0
Câu 16. Tìm phần thực, phần ảo của
4 2 3 5 z i i i
A. phần thực là 1, phần ảo là 1 B.phần thực là 11, phần ảo là 1
C. phần thực là 1, phần ảo là 3 D. phần thực là 11, phần ảo là 3
Câu 17. Cho số phức
11
11



ii
z
ii
. Trong các kết luận sau kết luận nào đúng?
A.
z
có phần thực và phần ảo
0
.
B.
z
là số thuần ảo.
C. Mô đun của
z
bằng 1
D.
z
có phần thực và phần ảo đều bằng 0.
Câu 18. Tính
zz
và
.zz
biết
23zi
A. 4 và 13 B. 4 và 5 C. 4 và 0 D. 13 và 5
Câu 19. Cho số phức
23zi
. Tìm số phức
w = 2iz - z
.
A.
87 wi
B.
8 wi
C.
47wi
D.
87 wi
Câu 20. Cho số phức
1
13zi
và
2
34zi
. Môđunsố phức
12
zz
là
A.
17
; B.
15
; C. 4; D. 8.
53 i
53i
35i
53i
53 i
32i
32i
32i
32i
23i
12i
12i
12i
2 i
12i
Trang5
Câu 21. Số phức nghịch đảo của số phức z = 1 -
3i
là:
A.
1
z
=
13
44
i
B.
1
z
=
13
22
i
C.
1
z
= 1 +
3i
D.
1
z
= -1 +
3i
Câu 22. Mô đun của số phức
3
5 2 1 z i i
là
A.
7
B.
3
C.
5
D.
2
Câu 23. Cho số phức z = a + bi (với a, b là các số thực). Xét các phát biểu sau
(1) z² –
z
² là số thực (2) z² +
z
² là số ảo
(3) z
z
là số thực (4) |z| – z là bằng 0
Số câu phát biểu đúng là
A. 0 B. 1 C. 2 D. 3
Câu 24. Giá trị của A = (1 + i)
20
bằng
A. 1024 B. 2
20
C. –1024 D. 1024 – 1024i
Câu 25. Cho
s
ố phức z thỏa mãn:
(1 2 ) 7 4 z i i
.Tìm mô đun
s
ố phức
2
zi
.
A
. 5
B.
17
C.
24
D.
4
Câu 26. Cho số phức z biết
2
1
i
zi
i
. Phần ảo của số phức z
2
là
A.
5
2
i
. B. -
5
2
i
. C.
5
2
. D.
5
2
.
Câu 27. Cho số phức z thỏa mãn:
3
13
1
i
z
i
. Tìm môđun của
z iz
.
A.
82
B.
42
C. 8 D. 4
Câu 28. Phần thực của số phức
z
thỏa mãn
2
1 2 8 1 2 i i z i i z
là
A.
6
B.
3
C.
2
D.
1
DẠNG II. PHƢƠNG TRÌNH TRÊN TẬP SỐ PHỨC
I. PHƢƠNG PHÁP : Sử dụng các phương pháp giải phương trình mẫu mực như phương
trình bậc nhất, phương trình bậc hai….với ẩn là số phức z.
II. CÁC VÍ DỤ
Ví dụ 1. (Mã đề 101 - QG – 2017) Phương trình nào dưới đây nhận hai số phức
12 i
và
12 i
là nghiệm ?
A.
2
2 3 0 zz
B.
2
2 3 0 zz
C.
2
2 3 0 zz
D.
2
2 3 0 zz
Hƣớng dẫn giải
Cách 1: Ta có
1 2 1 2 2 ii
;
1 2 1 2 2 ii
. Suy ra
12 i
và
12 i
là
nghiệm của phương trình
2
2 3 0 zz
.
Đáp án: C
Cách 2: Thử đáp án bằng MTBT
Ví dụ 2. (Mã đề 102 - QG – 2017) Kí hiệu
12
,zz
là hai nghiệm phức của phương trình
2
3 1 0 zz
. Tính
12
P z z
A.
3
3
P
. B.
23
3
P
C.
2
3
P
. D.
14
3
P
.
Hƣớng dẫn giải
Phương trình
2
3 1 0 zz
có hai nghiệm
1,2
1 11
6
i
z
.
Trang6
Khi đó
12
23
3
P z z
Đáp án: B
Ví dụ 3. Tìm số phức sau:
a) (1 + z)(2 + 3i) = 1 + i
b)
Giải
a) Ta có (1 + z)(2 + 3i) = 1 + i
1
1
23
5
1
13
81
13 13
i
z
i
i
z
zi
b) Ta có
2
2 1 3 ( 1 3 )(1 )
1 2 (2 )
2 4 (2 4 )(3 4 )
3 4 25
22 4
25 25
i i i i
zz
i i i
i i i
zz
i
zi
Ví dụ 4. Giải các phương trình sau trên trường số phức:
a)z
4
+ 2z
2
-3 = 0
b) z
4
– 4z
3
+7z
2
– 16z + 12 = 0 (1)
Giải
a) Ta có z
4
+ 2z
2
-3 = 0
2
2
1
1
3
3
z
z
zi
z




Vậy phương trình có 4 nghiệm
1
3
z
zi


b) Do tổng tất cả các hệ số của phương trình (1) bằng 0 nên (1) có nghiệm z = 1.
(1) (z – 1)(z
3
– 3z
2
+ 4z – 12) = 0
(z – 1) (z – 3) (z
2
+ 4) = 0
2
1
1
3
3
2
40
2
z
z
z
z
zi
z
zi



Vậy phương trình đã cho có 4 nghiệm:
z = 2i; z = −2i; z = 1; z = 3
III. BÀI TẬP
i
i
z
i
i
2
31
1
2
Trang7
Câu 1. (Mã đề 103 - QG – 2017) Kí hiệu
12
,zz
là hai nghiệm phức của phương trình
2
60 zz
. Tính
12
11
P
zz
A.
1
6
P
. B.
1
12
P
C.
1
6
P
. D.
6P
.
Câu 2. (QG-2019)Gọi là hai nghiệm phức phương trình . Giá trị
bằng
A.16. B. 56. C. 20. D. 26.
Câu 3. (QG-2019)Gọi là hai nghiệm phức của phương trình . Giá trị
của bằng
A. . B. . C. . D. .
Câu 4. (QG-2019)Gọi là hai nghiệm phức của phương trình . Gái trị của
bằng
A. . B. . C. . D. .
Câu 5. (QG-2019)Gọi là hai nghiệm phức của phương trình . Giá trị của
bằng
A. 10. B. 8. C. 16. D. 2.
Câu 6. Tìm mô đun của số phức z thoả
3 (3 i)(1 i) 2 iz
.
A.
22
3
z
B.
32
2
z
C.
33
2
z
D.
23
3
z
Câu 7. Cho số phức z thỏa mãn (1 + 2i)z – 5 – 5i = 0. Tìm số phức w =
10
z
z
A. 6 + 2i B. 2 + 6i C. –2 + 6i D. –6 + 2i
Câu 8.Giải phương trình
2 3 1. i z z
A.
13
.
10 10
zi
B.
13
.
10 10
zi
C.
13
.
10 10
zi
D.
13
.
10 10
zi
Câu 9.Giải phương trình
2 4 0 iz
.
A.
13
.
55
zi
B.
84
.
55
zi
C.
53
.
10 10
zi
D.
13
.
13 13
zi
Câu 10.Giải phương trình
2 1 3
.
12

ii
z
ii
A.
13
.
55
zi
B.
84
.
55
zi
C.
22 4
.
25 25
zi
D.
13
.
13 13
zi
Câu 11. Tìm nghiệm của phương trình
21
1

z
i
zi
A.
13
.
55
zi
B.
14
.
55
zi
C.
11
.
22
zi
D.
11
22
zi
Câu 12.Tìm nghiệm của phương trình
2
2 5 0 zz
.
A.
12
-1 2 ; -1-2 . z i z i
B.
12
-1 2 ; -1-2 . z i z i
12
,zz
2
6 10 0zz
22
12
zz
12
,zz
2
6 14 0zz
22
12
zz
36
8
28
18
12
,zz
2
4 5 0zz
22
12
zz
6
8
16
26
12
,zz
2
4 7 0zz
22
12
zz
Trang8
C.
12
1 2 ; -1 2 . z i z i
D.
12
-1 2 ; -1 2 . z i z i
Câu 13. Tìm các số thực b,c để phương trình (với ẩn z):
2
0 z bz c
nhận
1zi
làm một
nghiệm.
A.
2, 2. bc
B.
2, 3. bc
C.
1, 2. bc
D.
2, 2. bc
Câu 14. Gọi z
1
và z
2
lần lượt là nghiệm của phương trình:
2
2 10 0 zz
. Tính giá trị của
biểu thức
22
12
A z z
A.
15
B.
17
C.
20
D.
10
Câu 15. Gọi A, B là hai điểm biểu diễn cho các số phức là nghiệm của phương trình
2
2 3 0 zz
. Tính độ dài đoạn thẳng
AB
.
A.
22
B.
32
C.
23
D.
3
Câu 16. Cho số phức z có phần thực dương thỏa mãn
2
6 13 0 zz
. Tính
6
z
zi
.
A.
13
B.
17
C.
7
D.
73
DẠNG III. TÌM SỐ PHỨC THỎA MÃN ĐIỀU KIỆN
I. PHƢƠNG PHÁP: Để giải bài toán tìm số phức thỏa mãn điều kiện cho trước, ta thực
hiện theo các bước sau:
B1: Đặt
, z a bi a b
B2: Thay vào đk được hệ phương trình hai ẩn a,b.
B3: Giải tìm a,b
Chú ý:
Tìm số phức
, z a bi a b
thật ra là tìm phần thực a và phần ảo b của nó.
0
0
0
a
z a bi
b
,
1 1 1 2 2 2
; z a b i z a b i
. Khi đó:
12
12
12

aa
zz
bb
, z a bi a b
. Khi đó
z
là số ảo (thuần ảo) khi
0a
,
z
là số thực khi
0b
.
Ví dụ 1. (Mã đề 101 - QG – 2017) Có bao nhiêu số phức z thỏa mãn
35zi
và
4
z
z
là
số thuần ảo ?
A.
0
B. Vô số C.
1
D.
2
Hƣớng dẫn giải
Đặt
, z a bi a b
. Điều kiện
4z
.
Ta có
3 5 3 5 z i a b i
2
2
3 25 ab
22
6 16 0 1 a b b
Lại có
2
22
22
4
4
44
44

a a b
z a bi b
i
z a bi
a b a b
.
Trang9
Vì
4
z
z
là số thuần ảo nên
2
22
2
2
4
0 4 0 2
4


a a b
a b a
ab
.
Từ (1) + (2) suy ra
3
4 6 16 4
2
a b a b
. Thay vào (1), ta được:
2
2
0
3
6 16 0
24
2
13




b
a b b b
b
.
Với
0 4 4b a z loaïi
.
Với
24 16 16 24
13 13 13 13
b a z i thoûamaõn
.
Đáp án: C
Ví dụ 2. (Mã đề 101 - QG – 2017) Cho số phức
z a bi
( , ) ab
thỏa mãn
1 3 0 z i z i
. Tính
3S a b
A.
7
3
S
B.
5S
C.
5S
D.
7
3
S
Hƣớng dẫn giải
Theo giả thiết, ta có:
2
1 3 0 1 3 1 3 z i z i z z i z z
2
2
5
13
3
44
1 1; 3 5
33
z z z
z i a b S a b
Đáp án: B
Ví dụ 3. (Mã đề 103 - QG – 2017) Tìm tất cả các số thực x, y sao cho
2
1 1 2 x yi i
A.
2, 2 xy
B.
2, 2xy
C.
0, 2xy
D.
2, 2 xy
Hƣớng dẫn giải
Ta có
2
2
0
12
1 1 2
2
2

x
x
x yi i
y
y
Đáp án: C
Ví dụ 4. (Mã đề 103 - QG – 2017) Có bao nhiêu số phức z thỏa mãn
3 13zi
và
2
z
z
là số thuần ảo ?
A. Vô số B.
2
C.
0
D.
1
Hƣớng dẫn giải
Đặt
, z a bi a b
, ta có:
2
2 2 2
3 13 3 13 3 13 6 4 0 1 z i a b i a b a b b
.
Lại có
2
22
22
2
2
22
22

a a b
z a bi b
i
z a bi
a b a b
.
Vì
2
z
z
là số thuần ảo nên
2
2 2 2
2
2
2
0 2 0 2 0 2
2


a a b
a a b a b a
ab
.
Trang10
Từ (1)+(2) suy ra
2 6 4 3 2 a b a b
. Thay vào (1), ta được:
2
2
0
3 2 6 4 0
3
5
b
b b b
b
.
Với
0 2 2b a z loaïi
.
Với
3 1 1 3
5 5 5 5
b x z i thoûamaõn
.
Đáp án: D
Ví dụ 5. (Mã đề 104 - QG – 2017) Cho số phức z thỏa mãn
5z
và
3 3 10 z z i
.
Tìm số phức
43 w z i
.
A.
38 wi
B.
13wi
C.
17 wi
D.
48 zi
Hƣớng dẫn giải
Đặt
, z a bi a b
, ta có:
2
2
3 5 3 5 3 25 z a bi a b
Lại có
3 3 10 3 3 10 z z i a bi a b i
2 2 2 2
22
3 3 10 2 a b a b b b
5 0 5 4 8 b a z i w i
.
Đáp án: D
III. BÀI TẬP
Câu 1. (Mã đề 102 - QG – 2017) Cho số phức
( , ) z a bi a b
thoả mãn
2 z i z
.
Tính
4S a b
.
A.
4S
B.
2S
C.
2S
D.
4S
Câu 2. (QG – 2018) Có bao nhiêu số phức
z
thỏa mãn
3 2 4 z z i i i z
?
A.
1
. B.
3
. C.
2
. D.
4
.
Câu 3.(QG – 2018) Có bao nhiêu số phức
z
thỏa mãn
( 6 ) 2 (7 ) z z i i i z
?
A. 2. B. 3. C. 1. D. 4.
Câu 4. (QG – 2018) Có bao nhiêu số phức
z
thỏa mãn
5 2 6 z z i i i z
?
A.
1
. B.
3
. C.
4
. D.
2
.
Câu 5. (Mã đề 103 - QG – 2017) Cho số phức z thỏa mãn
35z
và
2 2 2 z i z i
.
Tìm số phức
z
.
A.
17.z
B.
17.z
C.
10.z
D.
10.z
Câu 6. (QG – 2018) Tìm hai số thực
x
và
y
thỏa mãn
2 3 1 3 6 x yi i x i
với
i
là
đơn vị ảo.
A.
1x
;
3y
. B.
1x
;
1y
. C.
1x
;
1y
. D.
1x
;
3y
.
Câu 7. (QG – 2018) Có bao nhiêu số phức
z
thỏa mãn
4 2 5 z z i i i z
?
A.
2
. B.
3
. C.
1
. D.
4
.
Câu 8. (QG – 2018) Tìm hai số thực
x
và
y
thỏa mãn
3 2 2 2 3 x yi i x i
với
i
là
đơn vị ảo.
Trang11
A.
2; 2 xy
. B.
2; 1 xy
. C.
2; 2 xy
. D.
2; 1 xy
Câu 9. (QG – 2018) Tìm hai số thực x và y thỏa mãn
(3 ) (4 2 ) 5 2 x yi i x i
với i là đơn
vị ảo.
A.
2; 4 xy
. B.
2; 4xy
. C.
2; 0 xy
. D.
2; 0xy
.
Câu 10. (QG – 2018) Tìm hai số
x
và
y
thỏa mãn
2 3 3 5 4 x yi i x i
với
i
là đơn
vị ảo.
A.
1x
;
1y
. B.
1x
;
1y
. C.
1x
;
1y
. D.
1x
;
1y
.
Câu 11. (QG-2019)Cho số phức thỏa mãn . Mô đun của bằng
A. . B. . C. . D. .
Câu 12. (QG-2019)Cho số phức thỏa mãn . Môđun của bằng
A. . B. . C. . D. .
Câu 13. (QG-2019)Cho số phức thỏa . Môđun của bằng
A. . B. . C. . D. .
Câu 14. (QG-2019)Cho số phức thỏa . Môđun của bằng
A. . B. . C. . D. .
Câu 15. Tìm số phức z, biết
A.
7
4
6
zi
B.
3z
C.
7
4
6
zi
D.
34 zi
Câu 16. Số phức z thỏa mãn:
(1 ) (2 ) 13 2 i z i z i
là
A. 3 + 2i ; B. 3-2i; C. -3 + 2i ; D. -3 -2i.
Câu 17. Cho số phức z thỏa mãn điều kiện 2z + 3(1 – i)
z
= 1 – 9i. Tìm modun của z.
A. |z| =
3
B. |z| = 3 C. |z| =
13
D. |z| = 13
Câu 18. Tìm phần thực và phần ảo của số phức z thỏa mãn (1 – i)z – (2 – i)
z
= 2 + 9i
A. 4 và –3 B. –4 và 3 C. 4 và 3 D. –4 và –3
Câu 19. Số số phức z thỏa mãn đẳng thức:
2
11
1
22
z z z z z i
.
A. 1
B.2
C.3
D.4
Câu 20. Sốsố phức z thỏa mãn
2
2
1 1 10 3 z z i z
.
A. 1
B.2
C.3
D.4
Câu 21. Tìm mô đun số phức z thỏa mãn
22
2
2 1 2



iz z i
z
ii
.
A.
1
B.
2
C.
2
D.
22
Câu 22. Biết
z
là số phức thỏa điều kiện
2
0z i z
. Tìm số phức
z
có phần ảo âm
A.
1
1
2
zi
B.
11
22
zi
C.
11
22
zi
D.
1
1
2
zi
DẠNG IV. BIỂU DIỄN HÌNH HỌC CỦA SỐ PHỨC
I. PHƢƠNG PHÁP: Giả sử z = x + yi (x, y R). Khi đó số phức z biểu diễn trên mặt
phẳng phức bởi điểm M(x;y).
z
3 2 3 10z i i z i
z
3
5
5
3
z
3 2 3 7 16z i i z i
z
5
5
3
3
z
(2 ) 4( ) 8 19i z z i i
z
13
5
13
5
z
(2 ) 3 16 2( )i z i z i
z
5
13
13
5
34z z i
Trang12
Sử dụng dữ kiện của đề bài để tìm mối liên hệ giữa x và y từ đó suy ra tập hợp điểm M.
Một số quỹ tích thường gặp:
Với z = x+yi (x, y là các số thực) khi đó nếu:
* x= a : Quỹ tích z là đường thẳng x = a (song song với Oy).
* y= b: Quỹ tích z là đường thẳng y = b (song song với Ox).
* (x-a)
2
+(y-b)
2
= R
2
Quỹ tích z là đường tròn tâm I(a.b) bán kính R.
* (x-a)
2
+(y-b)
2
R
2
Quỹ tích z là hình tròn tâm I(a.b) bán kính R ( kể cả biên).
* (x-a)
2
+(y-b)
2
> R
2
Quỹ tích z là các điểm nằm ngoài đường tròn tâm I(a.b) bán kính R.
II. CÁC VÍ DỤ
Ví dụ 1. (Mã đề 101- QG – 2017) Cho số phức
12zi
. Điểm nào dưới đây là điểm biểu
diễn của số phức
w iz
trên mặt phẳng tọa độ ?
A.
(1;2)Q
B.
(2;1)N
C.
(1; 2)M
D.
( 2;1)P
Hƣớng dẫn giải
Ta có
1 2 2 w iz i i i
. Suy ra điểm biểu diễn của số phức
w
là
(2;1)N
.
Đáp án: B
Ví dụ 2. (Mã đề 102 - QG – 2017) Số phức nào sau đây có điểm biểu diễn trên mặt phẳng
tọa độ là điểm M như hình bên ?
A.
4
2zi
B.
2
12zi
C.
3
2 zi
D.
1
12zi
Hƣớng dẫn giải
Đáp án: C
Ví dụ 3. (Mã đề 102 - QG – 2017) Có bao nhiêu số phức
z
thỏa mãn
| 2 | 2 2 zi
và
2
( 1)z
là số thuần ảo.
A.
0
B.
4
C.
3
D.
2
Hƣớng dẫn giải
Đặt
, z x yi x y
.
Theo giả thiết, ta có
| 2 | 2 2 2 1 2 2 z i x y i
22
2 1 8 x y C
.
Mặt khác,
2
22
2
1 1 1 2 1 z x yi x y x yi
.
Theo giả thiết
2
( 1)z
là số thuần ảo nên
22
22
10
1
1 0 1
1
10

x y d
yx
x y y x
yx
xy
.
Đường tròn (C) có tâm
2;1I
, bán kính
22R
.
Ta có
, 2 2d I d R
, suy ra d tiếp xúc (C).
Ta có
,2d I d R
, suy ra
cắt (C) tại hai điểm phân biệt.
Tập hợp các điểm biểu diễn cho số phức chính là các giao điểm của (C) với hai đường thẳng
d và
. Số giao điểm là 3.
x
y
O
2
1
Trang13
Đáp án: C
Ví dụ 4. (Mã đề 104 - QG – 2017) Cho số phức
12
1 2 , 3 z i z i
. Tìm điểm biểu diễn
của số phức
12
z z z
trên mặt phẳng tọa độ.
A.
(4; 3)N
B.
(2; 5)M
C.
( 2; 1)P
D.
( 1;7)Q
Hƣớng dẫn giải
Ta có
12
2 z z z i
.
Vậy điểm biểu diễn của số phức
z
là
( 2; 1)P
.
Đáp án: C
Ví dụ 5. (Mã đề 104 - QG – 2017) Kí hiệu
12
,zz
là hai nghiệm phức của phương trình
2
40z
. Gọi M, N lần lượt là các điểm biểu diễn của
12
,zz
trên mặt phẳng tọa độ. Tính
T OM ON
với O là gốc tọa độ.
A.
22T
. B.
2T
C.
8T
. D.
4T
.
Hƣớng dẫn giải
Ta có
1
2
2
2
40
2

zi
z
zi
.
Suy ra
0;2 , 0; 2 2 4. M N OM ON T OM ON
Đáp án: D
Ví dụ 6. (Mã đề 104 - QG – 2017) Gọi S là tập hợp tất cả các giá trị thực của tham số m để
tồn tại duy nhất số phức z thỏa mãn
.1zz
và
3 z i m
. Tìm số phần tử của S.
A.
2
B.
4
C. 1 D. 3.
Hƣớng dẫn giải
Điều kiện:
0m
.
Đặt
, z x yi x y
.
Theo giả thiết
2
22
1
. 1 1 1 z z z x y C
.
1
C
là đường tròn tâm
0;0O
, bán kính
1
1R
.
Mặt khác
2
2
2
2
3 3 1 3 1 z i m x y m x y m C
2
C
là đường tròn tâm
3; 1I
, bán kính
2
Rm
.
Để tồn tại duy nhất số phức zthì
1
C
và
2
C
tiếp xúc ngoài hoặc trong.
TH1:
1
C
và
2
C
tiếp xúc ngoài khi và chỉ khi
12
1 2 1 R R OI m m thoûamaõn
.
TH2
1
C
và
2
C
tiếp xúc trong khi và chỉ khi
12
21
1 2 3
2 1 1
R OI R m m thoûamaõn
OI R R m m loaïi
.
Vậy
1,3S
.
Đáp án: A
Ví dụ 7. (QG – 2018) Xét các số phức
z
thỏa mãn
2z i z
là số thuần ảo. Trên mặt
phẳng tọa độ, tập hợp tất cả các điểm biểu diễn số phức
z
là một đường tròn có bán kính
bằng
Trang14
A.
1
. B.
5
4
. C.
5
2
. D.
3
2
.
Hƣớng dẫn giải
Đặt
, z x yi x y
.
Ta có
22
2 2 2 2 2 z i z x yi i x yi x x y y x y i
Vì
2z i z
là số thuần ảo nên
2
2
22
15
2 0 1
24



x x y y x y
.
Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn số phức
z
là một đường tròn có
bán kính bằng
5
2
.
Đáp án: C
III. BÀI TẬP
Câu 1. (QG – 2018) Xét các số phức
z
thỏa mãn
33z i z
là số thuần ảo. Trên mặt
phẳng tọa độ, tập hợp tất cả các điểm biểu diễn các số phức
z
là một đường tròn có bán kính
bằng
A.
9
2
. B.
32
. C.
3
. D.
32
2
.
Câu 2.(QG – 2018) Xét các số phức z thỏa mãn
22z i z
là số thuần ảo. Trên mặt
phẳng tọa độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính
bằng
A. 2. B.
22
. C. 4. D.
2
.
Câu 3. (QG – 2018) Xét các số phức
z
thỏa mãn
22z i z
là số thuần ảo. Trên mặt
phẳng tọa độ, tập hợp tất cả các điểm biểu diễn các số phức
z
là một đường tròn có bán kính
bằng
A.
22
. B.
2
. C.
2
. D.
4
.
Câu 4. (QG-2019)Cho hai số phức và . Trên mặt phẳng toạ độ , điểm
biểu diễn số phức có toạ độ là
A. . B. . C. . D. .
Câu 5. (QG-2019)Xét các số phức thỏa mãn . Trên mặt phẳng tọa độ , tập
hợp điểm biểu diễn của các số phức là một đường tròn có bán kính bằng
A. B. C. D.
Câu 6. (QG-2019)Xét các số phức thỏa mãn . Trên mặt phẳng tọa độ , tập
hợp điểm biểu diễn các số phức là một đường tròn có bán kính bằng
A. B. C. D.
Câu 7. (QG-2019)Cho hai số phức và . Trên mặt phẳng tọa độ điểm
biểu diễn số phức có tọa độ là
1
1zi
2
12zi
Oxy
12
3zz
41;
14;
41;
14;
z
2z
Oxy
4
w
1
iz
z
34.
26.
34.
26.
z
2z
Oxy
3
1
iz
w
z
23
12
20
25
1
2zi
2
1zi
Oxy
12
2zz
Trang15
A. . B. . C. . D. .
Câu 8. (QG-2019)Cho hai số phức và . Trên mặt phẳng , điểm biểu
diễn số phức có tọa độ là
A. . B. . C. . D. .
Câu 9. (QG-2019)Cho số phức thỏa mãn . Trên mặt phẳng tọa độ , tập hợp
các điểm biểu diễn của số phức thỏa mãn là một đường tròn có bán kính bằng
A. . B. . C. . D. .
Câu 10. (QG-2019)Cho hai số phức . Trên mặt phẳng tọa độ Oxy, điểm
biểu diễn số phức có tọa độ là:
A. . B. . C. . D. .
Câu 11. (QG-2019)Cho số phức thỏa mãn . Trên mặt phẳng tọa độ , tập hợp
các điểm biểu diễn của số phức thỏa mãn là một đường tròn có bán kính bằng
A. . B. . C. . D. .
Câu 12. Giả sử M(z) là điểm trên mặt phẳng tọa độ biểu diễn số phức z. Tập hợp những
điểm M(z) thỏa mãn điều
2 z i z
là
A. Đường thẳng
4 2 3 0 xy
B. Đường thẳng
4 2 3 0 xy
A. Đường thẳng
2 3 0 xy
D. Đường thẳng
9 3 0 xy
Câu 13. Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức z thỏa mãn điều
kiện
21 z i z i
là
A. Đường thẳng
30 xy
B. Đường thẳng
2 3 0 xy
A. Đường thẳng
2 3 0 xy
D. Đường thẳng
10 xy
Câu 15.Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức z thỏa mãn điều kiện
12 zi
là
A. Đuờng thẳng
20 xy
B. Đường tròn
22
1 1 4 xy
C. Đường thẳng
20 xy
D. Đường tròn tâm
1; 1I
và bán kính
2.R
Câu 16. Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức z thỏa mãn điều
kiện
4 4 10 z i z i
là
A. Đuờng elip
22
1
9 16

xy
B. Đuờng elip
22
1
16 9

xy
C. Đuờng elip
22
1
43

xy
D. Đuờng elip
22
1
94

xy
3; 3
2; 3
3;3
3;2
1
1zi
2
2zi
Oxy
12
2zz
2;5
3;5
5;2
5;3
z
2z
Oxy
w
2
1
iz
w
z
10
2
2
10
12
2 , 1z i z i
12
2zz
5; 1
1;5
5;0
0;5
z
2z
Oxy
w
5
1
iz
w
z
52
2 13
2 11
44
Trang16
Câu 17. Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức z thỏa mãn điều
kiện
22 zz
là
A. Tập hợp các điểm là nửa mặt phẳng ở bên phải trục tung
B. Tập hợp các điểm là nửa mặt phẳng ở bên trái trục tung
C. Tập hợp các điểm là nửa mặt phẳng phía trên trục hoành
D. Tập hợp các điểm là nửa mặt phẳng phía dưới trục hoành
Câu 18. Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức z thỏa mãn điều
kiện
1 1 2 zi
là
A. Tập hợp các điểm là hình tròn có tâm
1; 1I
, bán kính 2
B. Tập hợp các điểm là hình vành khăn có tâm tại
1;1A
và các bán kính lớn và nhỏ lần
lượt là
2; 1
C. Tập hợp các điểm là hình tròn có tâm
1; 1I
, bán kính 1
D. Tập hợp các điểm là hình vành khăn có tâm tại
1; 1I
và các bán kính lớn và nhỏ lần
lượt là
2; 1
Câu 19.Tìm tập hợp các điểm biểu diễn số phức z sao cho
23
zi
u
zi
là một số thuần ảo.
A. Đường tròn tâm
1; 1I
bán kính
5R
B. Đường tròn tâm
1; 1I
bán kính
5R
trừ đi hai điểm
0;1 ; 2; 3AB
.
C. Đường tròn tâm
1;1I
bán kính
5R
D. Đường tròn tâm
1;1I
bán kính
5R
trừ đi hai điểm
0;1 ; 2; 3AB
.
Câu 20. Tìm tập hợp các điểm biểu diễn số phức
z x yi
thỏa mãn điều kiện
1xy
là
A. Ba cạnh của tam giác
B. Bốn cạnh của hình vuông
C. Bốn cạnh của hình chữ nhật
D. Bốn cạnh của hình thoi
DẠNG V. CỰC TRỊ CỦASỐ PHỨC
I. PHƢƠNG PHÁP: Sử dụng các kiến thức cơ bản như: Bất đẳng thức liên hệ giữa trung
bình cộng và trung bình nhân, bất đẳng thức Bunhia- Cốpxki, bất đẳng thức hình học và
một số bài toán công cụ sau:
BÀI TOÁN CÔNG CỤ 1:
Cho đường tròn
()T
cố định có tâm I bán kính R và điểm A cố định. Điểm M di
động trên đường tròn
()T
. Hãy xác định vị trí điểm M sao cho AM lớn nhất, nhỏ
nhất.
Hướng dẫn giải:
TH1: A thuộc đường tròn (T)
Ta có: AM đạt giá trị nhỏ nhất bằng 0 khi M trùng với A
Trang17
AM đạt giá trị lớn nhất bằng 2R khi M là điểm đối xứng với A qua I
TH2: A không thuộc đường tròn (T)
Gọi B, C là giao điểm của đường thẳng qua A,I và đường tròn (T);
Giả sử AB < AC.
+) Nếu A nằm ngoài đường tròn (T) thì với điểm M bất kì trên (T), ta có:
AM AI IM AI IB AB
.
Đẳng thức xảy ra khi
MB
AM AI IM AI IC AC
.
Đẳng thức xảy ra khi
MC
+) Nếu A nằm trong đường tròn (T) thì với điểm M bất kì trên (T), ta có:
AM IM IA IB IA AB
.
Đẳng thức xảy ra khi
MB
AM AI IM AI IC AC
.
Đẳng thức xảy ra khi
MC
Vậy khi M trùng với B thì AM đạt gía trị nhỏ nhất.
Vậy khi M trùng với C thì AM đạt gía trị lớn nhất.
BÀI TOÁN CÔNG CỤ 2:
Cho hai đường tròn
1
()T
có tâm I, bán kính R
1
;
đường tròn
2
()T
có tâm J, bán kính R
2
. Tìm vị trí
của điểm M trên
1
()T
, điểm N trên
2
()T
sao cho
MN đạt giá trị lớn nhất, nhỏ nhất.
Hướng dẫn giải:
Gọi d là đường thẳng đi qua I, J;
d cắt đường tròn
1
()T
tại hai điểm phân biệt A, B (giả sử JA > JB) ; d cắt
2
()T
tại hai điểm
phân biệt C, D ( giả sử ID > IC).
Với điểm M bất khì trên
1
()T
và điểm N bất kì trên
2
()T
.
Ta có:
12
MN IM IN IM IJ JN R R IJ AD
.
Đẳng thức xảy ra khi M trùng với A và N trùng với D
12
MN IM IN IJ IM JN IJ R R BC
.
Đẳng thức xảy ra khi M trùng với B và N
trùng với C.
Vậy khi M trùng với A và N trùng với D thì
MN đạt giá trị lớn nhất.
khi M trùng với B và N trùng với C thì
MN đạt giá trị nhỏ nhất.
BÀI TOÁN CÔNG CỤ 3:
Cho hai đường tròn
()T
có tâm I, bán kính R; đường thẳng
không có điểm chung
với
()T
. Tìm vị trí của điểm M trên
()T
, điểm N trên
sao cho MN đạt giá trị nhỏ
nhất.
Hướng dẫn giải:
Trang18
Gọi H là hình chiếu vuông góc của I trên d
Đoạn IH cắt đường tròn
()T
tại J
Với M thuộc đường thẳng
, N thuộc đường tròn
()T
, ta có:
MN IN IM IH IJ JH const
.
Đẳng thức xảy ra khi
;M H N I
Vậy khi M trùng với H; N trùng với J thì MN đạt giá trị nhỏ nhất.
II. CÁC VÍ DỤ
Ví dụ 1. Trong các số phức
z
thoả mãn
3 4 4 zi
. Tìm giá trị lớn nhất, giá trị nhỏ
nhất của
z
.
Hƣớng dẫn giải
Cách 1
Gọi
; Rz x yi x y
( ; )M x y
biểu diễn cho số phức
z
trong hệ toạ độ Oxy
2 2 2 2
3 4 4 ( 3) ( 4) 4 ( 3) ( 4) 16 z i x y x y
Vậy điểm M biểu diễn cho số phức z thuộc đường tròn (T) có tâm
(3; 4)I
, bán kính R = 4.
22
z x y OM
;
5OI R
nên O nằm ngoài đường tròn (T)
z
lớn nhất khi OM lớn nhất, nhỏ nhất khi OM nhỏ nhất.
(Bài toán qui về Bài toán công cụ 1- Trường hợp 2)
Đường thẳng OI cắt đường tròn (T) tại hai điểm phân biệt
3 4 27 36
; ; ; 1; 9
5 5 5 5
A B OA OB
Với M di động trên (T), ta có:
19 OA OM OB OM
19 z
OM nhỏ nhất khi M trùng với A; OM lớn nhất khi M trùng với B
Vậy
z
nhỏ nhất bằng 1 khi
34
55
zi
;
z
lớn nhất bằng 9 khi
27 36
55
zi
Cách 2
Gọi
; Rz x yi x y
( ; )M x y
biểu diễn cho số phức z trong hệ toạ độ Oxy
34
i
(3; 4)A
biểu diễn cho số phức
; 5

z OM OA z AM
;
Theo giả thiết
3 4 4 4 4
z i z AM
.
Ta có:
4 4 4 4 1 9 OM OA AM OM OA OA OM OA OM
19 z
;
1z
khi
34
55
zi
;
9z
khi
27 36
55
zi
Vậy
z
nhỏ nhất bằng 1 khi
34
55
zi
;
z
lớn nhất bằng 9 khi
27 36
55
zi
Nhận xét: Ngoài ra bài toán trên có thể Hướng dẫn giải bằng phương pháp sử dụng bất
đẳng thức Bunhia-Cốpxki hoặc phương pháp lượng giác hoá.
Ví dụ 2. Trong các số phức
z
thoả mãn điều kiện
( 2 4 )z z i
là một số ảo, tìm số
Trang19
phức
z
sao cho
1
zi
có môđun lớn nhất.
Hƣớng dẫn giải
Gọi
; Rz x yi x y
( ; )M x y
biểu diễn cho số phức z trong hệ toạ độ Oxy
( 2 4 ) ( ) ( 2) ( 4) ( 2) ( 4) ( 4) ( 2) z z i x yi x y i x x y y x y y x i
( 2 4 )z z i
là
một số ảo
2 2 2 2
( 2) ( 4) 0 2 4 0 ( 1) ( 2) 5 x x y y x y x y x y
M biểu diễn cho
z
thuộc đường tròn (T) có tâm
( 1;2)I
, bán kính
5R
22
1 ( 1) ( 1) ( 1) ( 1)
z i x y i x y AM
với
(1;1)A
5 ( ) IA A T
(Bài toán được qui về Bài toán công cụ 1 - trường hợp 1)
Vì M là điểm di động trên (T) nên AM lớn nhất
AM là đường kính của (T)
M đối xứng với A qua I
I là trung diểm của AM
( 3;3) 3 3 4 2
M z i i
Vậy
lớn nhất bằng
25
khi
33 zi
.
Ví dụ 3. Trong các số phức
z
có môđun bằng
22
. Tìm số phức
z
sao cho biểu thức
1 P z z i
đạt giá trị lớn nhất.
Hƣớng dẫn giải
Gọi
; Rz x yi x y
2 2 2 2
2 2 2 2 8 z x y x y
2 2 2 2
1 ( 1) ( 1) P z z i x y x y
Áp dụng bất đẳng thức Bunhia-côpxki cho hai bộ số
1;1 và
2 2 2 2
( 1) ; ( 1) x y x y
, ta có:
2 2 2 2 2
2 ( 1) ( 1) 4(9 )


P x y x y x y
Áp dụng bất đẳng thức Bunhia-cốpxki cho hai bộ số 1;1 và
;xy
, ta có:
22
24 x y x y
2
52 2 13 PP
. Đẳng thức xảy ra khi
2xy
Vậy P đạt giá trị lớn nhất bằng
2 13 khi 2 2zi
.
Ví dụ 4. Trong các số phức
z
có môđun bằng
2
. Tìm số phức
z
sao cho biểu thức
1 1 7 P z z i
đạt giá trị lớn nhất.
Hƣớng dẫn giải
Gọi
; Rz x yi x y
2 2 2 2
2 2 4 z x y x y
Trang20
2 2 2 2
1 1 7 ( 1) ( 1) ( 7) P z z i x y x y
Xét
1; , 1 ; 7 0; 7
u x y v x y u v
. Khi đó:
7
P u v u v
. Đẳng thức xảy ra khi
,
uv
cùng hướng
( 1)( 7 ) (1 ) 1 x y y x x
13 xy
Với
1; 3xy
thì
,
uv
ngược hướng (không thoả mãn)
Với
1; 3 xy
thì
,
uv
cùng hướng (thoả mãn)
Vậy
13zi
thì P đạt giá trị nhỏ nhất bằng 7.
Ví dụ 5. Trong các số phức z
1
, z
2
thoả mãn:
12
1 1 ; 6 6 6 z i z i
, tìm số phức
z
1
, z
2
sao cho
12
zz
đạt giá trị lớn nhất.
Hƣớng dẫn giải
Gọi
12
. ; . ; ( , , , z a bi z c d i a b c d
là những số thực);
1
z
được biểu diễn bởi điểm M(a; b);
2
z
được biểu diễn bởi điểm N(c; d) trong mặt phẳng toạ độ Oxy
2
22
11
1 1 1 1 ( 1) ( 1) 1 z i z i a b
suy ra M thuộc đường tròn tâm I(1; 1),
bán kính R = 1.
2
22
22
6 6 6 6 6 36 ( 6) ( 6) 36 z i z i c d
suy ra M thuộc đường tròn tâm
J(6; 6), bán kính R' = 6.
22
12
( ) ( ) z z c a d b MN
.
(Bài toán được qui về Bài toán công cụ 2)
Đường thẳng IJ có phương trình y = x. Đường thẳng IJ cắt đường tròn tâm I tại hai điểm
12
2 2 2 2 2 2 2 2
; ; ;
2 2 2 2
MM
Đường thẳng IJ cắt đường tròn tâm J tại hai điểm
12
6 3 2;6 3 2 ; 6 3 2;6 3 2 NN
.
2 1 1 2
M N MN M N
12
5 2 7 5 2 7 zz
1 2 1 2
max 5 2 7 , z z khi M M N N
.
Vậy
12
2 2 2 2
; 6 3 2 6 3 2
22

z i z i
thì
12
zz
đạt giá trị lớn nhất.
Ví dụ 6. Cho các số phức
12
;zz
thoả mãn:
1 2 2
1; (1 ) 6 2 z z z i i
là một số thực.
Tìm số phức
12
;zz
sao cho
2
2 1 2 1 2
P z z z z z
đạt giá trị nhỏ nhất.
Hƣớng dẫn giải
Gọi
12
; ; , , , Rz a bi z c di a b c d
( ; ), ( ; ) M a b N c d
lần lượt biểu diễn cho
12
;zz
trong hệ toạ độ Oxy
2 2 2 2
1
1 1 1 z a b a b
M thuộc đường tròn
()T
có tâm O, bán kính R = 1
Trang21
2
;
1 6 2 ( 1) ( 1) 2 6
( 1) ( 1) 2 ( 1) ( 1) 6



z c di
z z i i c di c d i i
c c d d c d d c i
là số thực
( 1) ( 1) 6 0 6 0 c d d c c d
N thuộc đường thẳng
: 6 0 xy
Ta có
( ; ) 1dO
nên
và
()T
không có điểm chung
12
1 2 1 2 1 2
( ) ;
( ) 2( )
z z ac bd bc ad i
z z ac bd bc ad i z z z z ac bd
2 2 2 2 2
2( ) ( ) ( ) 1 1 P c d ac bd c a b d MN
(vì
22
1ab
)
(Bài toán được qui về Bài toán công cụ 3)
Gọi H là hình chiếu vuông góc của O trên
: 6 0 (3;3) x y H
Đoạn OH cắt đường tròn
()T
tại
22
;
22




I
Với N thuộc đường thẳng
, M thuộc đường tròn
()T
, ta có:
3 2 1 MN ON OM OH OI IH
.
Đẳng thức xảy ra khi
;M I N H
2
3 2 1 1 18 6 2 P
.
Đẳng thức xảy ra khi
12
22
; 3 3
22
z i z i
Vậy P đạt giá trị nhỏ nhất bằng
18 3 2
khi
12
22
; 3 3
22
z i z i
.
Ví dụ 7. Trong các số phức
z
thoả mãn điều kiện
3 3 10 zz
. Tìm số phức z có
môđun lớn nhất.
Hƣớng dẫn giải
Gọi
; Rz x yi x y
( ; )M x y
biểu diễn cho số phức z trong hệ toạ độ Oxy
2 2 2 2
12
3 3 10 ( 3) ( 3) 10
10
z z x y x y
MF MF
;
(với
12
( 3;0); (3;0)FF
).
()ME
có tâm O, trục lớn bằng 10; tiêu cự bằng 6
22
( ): 1
25 9
xy
ME
;z OM OM
lớn nhất
5 (5;0) ( 5;0) OM a M M
Vậy
z
lớn nhất bằng 5 khi
55 zz
III. BÀI TẬP
Câu 1.Trong các số phức z thỏa mãn điều kiện
. 3 5 12 z z z z i
.Số phức nào có mô
đun lớn nhất?
Trang22
A.1+2i B.1-2i C.2+4i D.1/2-i
Câu 2. Trong các số phức z thỏa mãn điều kiện
22 zi
.Số phức nào có mô đun nhỏ
nhất?
A.2+i B.4-i C.
1 3 1i
D.
3 2 2i
Câu 3. Xét các số phức
z
thỏa mãn
2 4 7 6 2. z i z i
Gọi
, mM
lần lượt là giá trị
nhỏ nhất và giá trị lớn nhất của
1zi
. Tính
.P m M
A.
13 73P
. B.
5 2 2 73
2
P
.
C.
5 2 2 73P
. D.
5 2 73
2
P
.
Câu 4. Xét số phức
z
thỏa mãn
3 2 3 3 5. z i z i
Gọi
, Mm
lần lượt là giá trị lớn
nhất và giá trị nhỏ nhất của biểu thức
2 1 3 P z z i
.
A.
17 5, 3 2. Mm
B.
26 2 5, 3 2. Mm
C.
26 2 5, 2. Mm
D.
17 5, 2. Mm
Câu 5. Xét số phức
z
thỏa mãn
2 3 6 2 17. z i z i
Gọi
, Mm
lần lượt là giá trị lớn
nhất và giá trị nhỏ nhất của biểu thức
1 2 2 P z i z i
.
A.
3 2, 0.Mm
B.
3 2, 2.Mm
C.
3 2, 5 2 2 5. Mm
D.
2, 5 2 2 5. Mm
Câu 6. Xét số phức
z
thỏa mãn
2 2 1 3 34. z i z i
Tìm giá trị nhỏ nhất của biển
thức
1. P z i
A.
min
9
.
34
P
B.
min
3.P
C.
min
13.P
D.
min
4.P
Câu 7.Trong các số phức z thỏa mãn điều kiện
1 2 2 zi
, tìm số phức z có
môđun nhỏ nhất.
A.
24
12
55
zi
B.
24
12
55
zi
C.
24
12
55
zi
D.
24
12
55
zi
Câu 8. Cho số phức z thỏa mãn
2
2
1


zi
zi
. Tìm giá trị nhỏ nhất và giá trị lớn
nhất của
z
.
A.
min max
10 3; 10 3 zz
B.
min max
10 3; 10 3 zz
C.
min max
10 3; 10 3 zz
D.
min max
10 3; 10 3 zz
| 1/22
| | Tải xuống

Có thể bạn quan tâm:

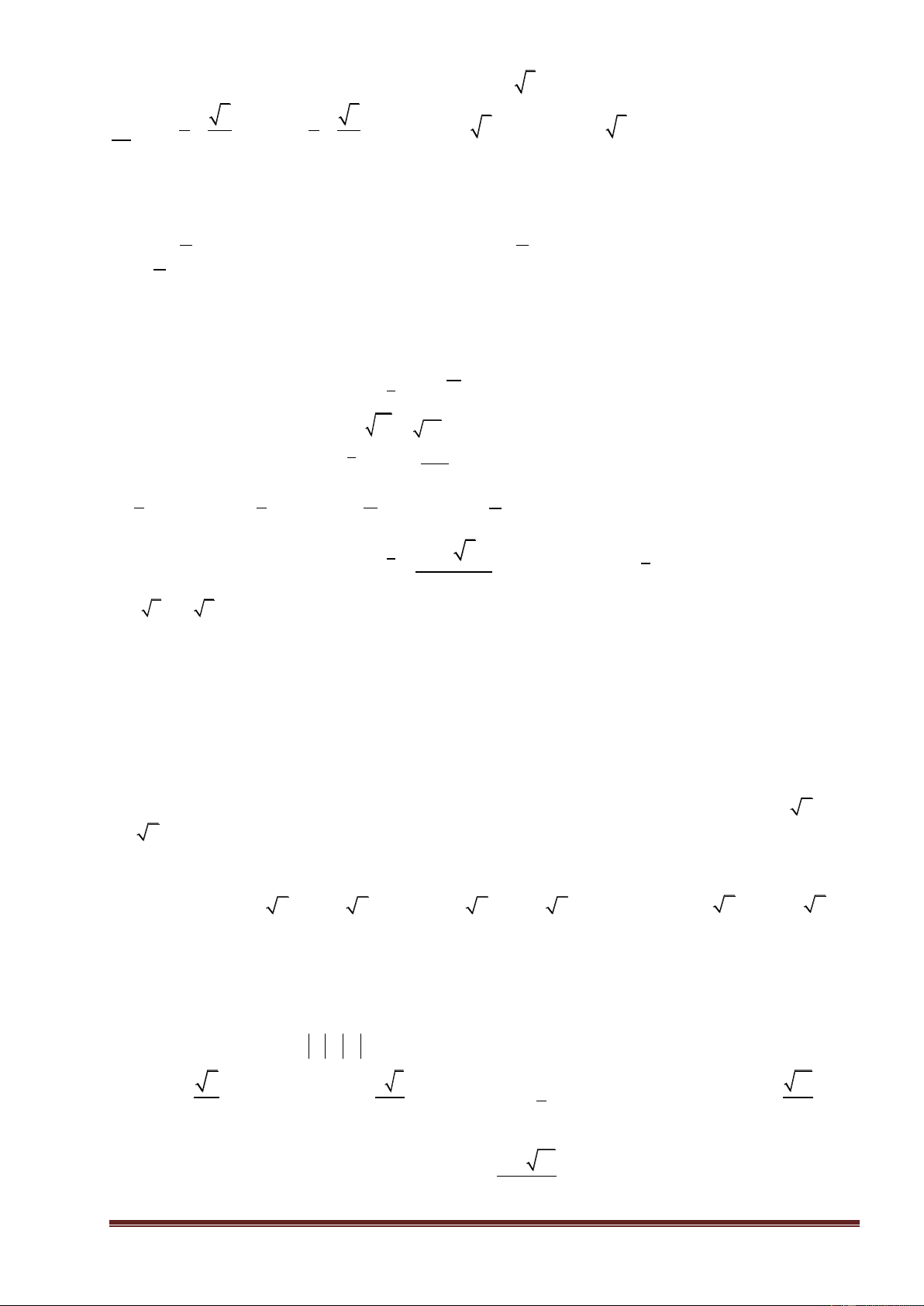
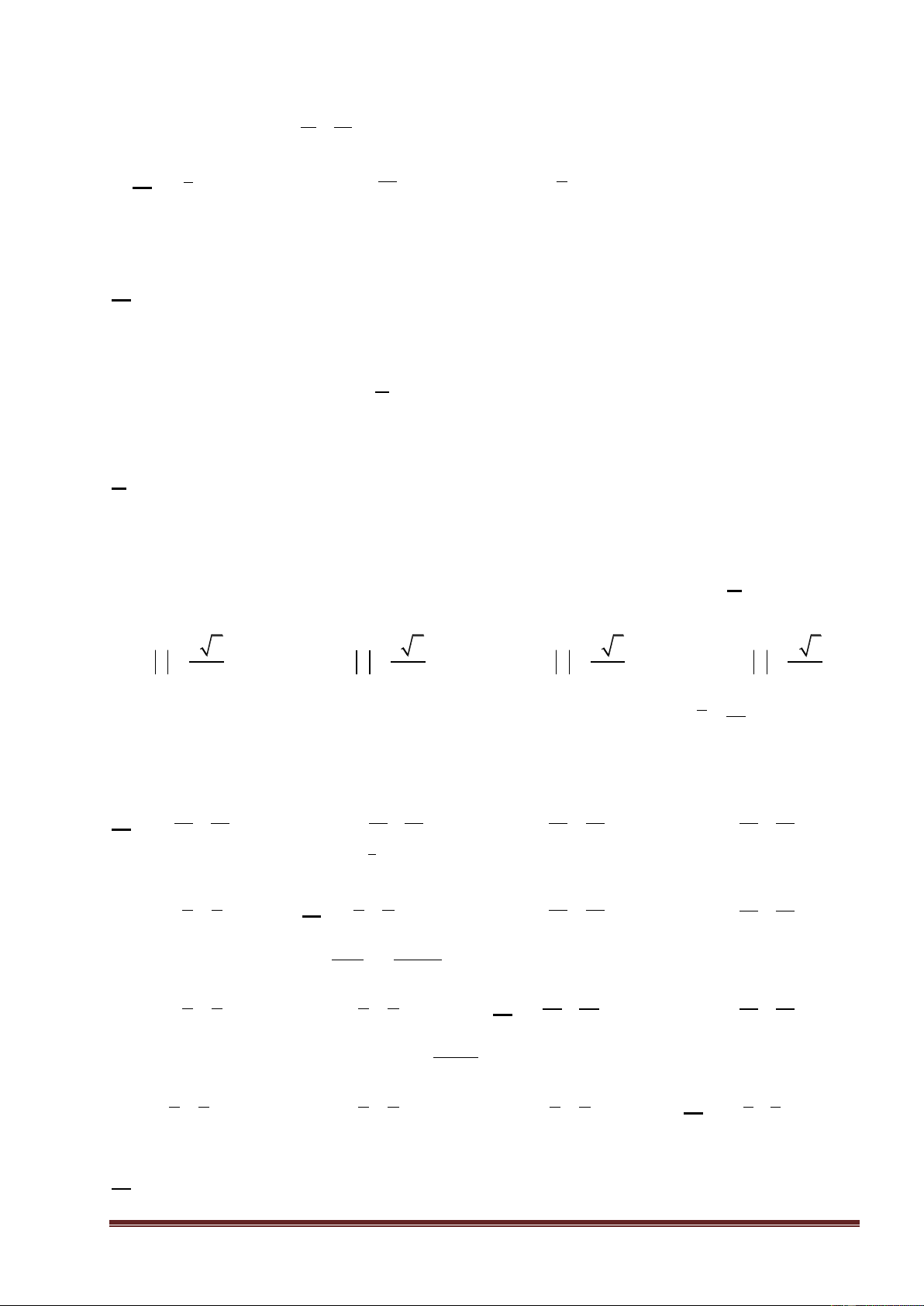
Preview text:


MỘT SỐ DẠNG TOÁN VỀ SỐ PHỨC ÔN THI TỐT NGHIỆP THPTQG
A. KIẾN THỨC CƠ BẢN
1. Một số phức là một biểu thức có dạng a + bi, trong đó a, b là các số thực và số i thoả
mãn i2 = -1. Ký hiệu số phức đó là z và viết z = a + bi .
i được gọi là đơn vị ảo
a được gọi là phần thực. Ký hiệu Re(z) = a
b được gọi là phần ảo của số phức z = a + bi , ký hiệu Im(z) = b
Tập hợp các số phức ký hiệu là C. *) Một số lưu ý:
- Mỗi số thực a dương đều được xem như là số phức với phần ảo b = 0.
- Số phức z = a + bi có a = 0 được gọi là số thuần ảo hay là số ảo.
- Số 0 vừa là số thực vừa là số ảo.
2. Hai số phức bằng nhau.
Cho z = a + bi và z’ = a’ + b’i. a a z = z’  '  b b'
3. Biểu diễn hình học của số phức.
Mỗi số phức được biểu diễn bởi một điểm M(a;b) trên mặt phẳng toạ độ Oxy.
Ngược lại, mỗi điểm M(a;b) biểu diễn một số phức là z = a + bi .
4. Phép cộng và phép trừ các số phức.
Cho hai số phức z = a + bi và z’ = a’ + b’i. Ta định nghĩa:
z z '  (a a ')  (b b')i
z z '  (a a')  (b b')i
5. Phép nhân số phức.
Cho hai số phức z = a + bi và z’ = a’ + b’i. Ta định nghĩa:
zz '  aa ' bb ' (ab ' a 'b)i
6. Số phức liên hợp.
Cho số phức z = a + bi. Số phức z = a – bi gọi là số phức liên hợp với số phức trên.
Vậy z = a bi = a - bi
Chú ý: 10) z = z  z và z gọi là hai số phức liên hợp với nhau. 20) z. z = a2 + b2
*) Tính chất của số phức liên hợp: (1): z z
(2): z z '  z z ' (3): . z z '  . z z ' (4): z. z = 2 2
a b (z = a + bi ) Trang1
7. Môđun của số phức.
Cho số phức z = a + bi . Ta ký hiệu z là môđun của số phư z, đó là số thực không
âm được xác định như sau: 
- Nếu M(a;b) biểu diễn số phc z = a + bi, thì z = OM = 2 2 a b
- Nếu z = a + bi, thì z = z.z = 2 2 a b
8. Phép chia số phức khác 0.
Cho số phức z = a + bi ≠ 0 (tức là a2+b2 > 0 )
Ta định nghĩa số nghịch đảo z-1 của số phức z ≠ 0 là số 1 1 z-1= z z 2 2 2 a b z
Thương z ' của phép chia số phức z’ cho số phức z ≠ 0 được xác định như sau: z z ' z '.z 1 .   z z 2 z z
Với các phép tính cộng, trừ, nhân chia số phức nói trên nó cũng có đầy đủ tính chất
giao hoán, phân phối, kết hợp như các phép cộng, trừ, nhân, chia số thực thông thường.
9. Phƣơng trình bậc hai với hệ số thực.
* Cho phương trình bậc hai : 2
ax bx c  0 , có 2
  b  4ac .   
+ Nếu  > 0, PT có 2 nghiệm thực phân biệt  b x 1,2 2ab
+ Nếu  = 0, PT có nghiệm kép x1 = x2 = 2a   |  |
+ Nếu  < 0, PT có 2 nghiệm phức  b i x 1,2 2a
* Cho phương trình bậc hai : 2
ax bx c  0 .
Khi b chẵn có b’ = b/2 ;  ' =b’2 – ac.  ' '
+ Nếu  ' > 0, PT có 2 nghiệm thực phân biệt  b x 1,2 ab '
+ Nếu  ' = 0, PT có nghiệm kép x1 = x2 = a  ' |  ' |
+ Nếu  ' < 0, PT có 2 nghiệm phức  b i x 1,2 a
10. Một số kết quả cần nhớ
1) i0 = 1  i4n = 1 2) i1 = i  i4n + 1 = i
3) i2 = - 1  i4n + 2 = - 1
4) i3 = - i  i4n + 3 = - i
5) (1 – i)2 = - 2i 6) (1 + i)2 = 2i Trang2
B. MỘT SỐ DẠNG TOÁN THƢỜNG GẶP
DẠNGI. TÍNH TOÁN CÁC YẾU TỐ CỦA SỐ PHỨC
I. PHƢƠNG PHÁP: Sử dụng định nghĩa, các phép toán để tính toán các yếu tố có liên quan. II. CÁC VÍ DỤ
Ví dụ 1. (Mã đề 101 - QG – 2017) Cho hai số phức z  5  7i và z  2  3i . Tìm số phức 1 2
z z z . 1 2
A. z  7  4i
B. z  2  5i C. z  2  5i
D. z  310i Hƣớng dẫn giải
Ta có z z z  5  7i  2  3i  7  4i 1 2     Đáp án: A
Ví dụ 2. (Mã đề 102 - QG – 2017) Cho số phức 3
z  1 i i . Tìm phần thực a và phần ảo b của z .
A. a  0,b  1 B. a  2  ,b  1
C. a  1,b  0
D. a  1,b  2  Hƣớng dẫn giải Ta có 3
z  1 i i  1 i i  1 2i a  1,b  2  . Đáp án: D
Ví dụ 3. (Mã đề 104 - QG – 2017) Tìm số phức z thỏa mãn z  2 3i  3 2i
A. z 15i
B. z 1 i
C. z  55i
D. z 1 i Hƣớng dẫn giải
Ta có z  2 3i  3 2i z  3 2i  2  3i 1 i Đáp án: B
Ví dụ 4. (Mã đề 104 - QG – 2017) Cho số phức z  2  i . Tính z . A. z  3 B. z  5 C. z  2
D. z  5 Hƣớng dẫn giải Ta có 2 2 z  2 1  5 Đáp án: D
Ví dụ 5. (QG-2019) Số phức liên hợp của số phức 3  4i là A. 3   4i . B. 3   4i . C. 3  4i . D. 4   3i . Hƣớng dẫn giải Đáp án: C III. BÀI TẬP
Câu 1. (Mã đề 101 - QG – 2017) Số phức nào dưới đây là số thuần ảo? A. z  2  3i .
B. z  3i .
C. z  2 .
D. z  3  i .
Câu 2. (Mã đề 102 - QG – 2017) Cho hai số phức z  4  3i và z  7  3i . Tìm số phức 1 2
z z z 1 2 A. z  11.
B. z  3 6i C. z  1  10i D. z  3  6i
Câu 3. (Mã đề 103 - QG – 2017) Cho hai số phức z 1 3i và z  2
  5i . Tìm phần ảo b 1 2
của số phức z z z . 1 2 A. b  2 
B. b  2
C. b  3 D. b  3 
Câu 4. (Mã đề 103 - QG – 2017) Cho số phức z  2 3i . Tìm phần thực a của z. Trang3
A. a  2
B. a  3 C. a  3  D. a  2 
Câu 5. (QG – 2018) Số phức 3
 7i có phần ảo bằng A. 3 . B. 7  . C. 3  . D. 7 .
Câu 6. (QG – 2018) Số phức có phần thực bằng 3 và phần ảo bằng 4 là A. 3  4i . B. 4  3i . C. 3  4i . D. 4  3i .
Câu 7.(QG – 2018) Số phức 5  6i có phần thực bằng A. – 5. B. 5. C. – 6. D. 6.
Câu 8. (QG – 2018) Số phức có phần thực bằng 1 và phần ảo bằng 3 là A. 1  3i . B.1 3i . C. 1  3i . D.1 3i .
Câu 9. (QG-2019) Số phức liên hợp của số phức 5  3i là A. 5   3i . B. 3   5i . C. 5   3i . D. 5  3i .
Câu 10. (QG-2019) Số phức liên hợp của số phức 3  2i là A. 3   2i . B. 3  2i . C. 3   2i . D. 2   3i .
Câu 11. (QG-2019)Số phức liên hợp của số phức 1  2i là A. 1   2i . B. 1  2i . C. 2   i . D. 1   2i .
Câu 12. Cho số phức z  6
 3i . Tìm phần thực và phần ảo của số phức z .
A. Phần thực bằng 6  và phần ảo bằng 3  i
B. Phần thực bằng 6  và phần ảo bằng 3
C. Phần thực bằng 6 và phần ảo bằng 3
D. Phần thực bằng 6 và phần ảo bằng 3i
Câu 13. Cho 2 số phức z và z’. Các phát biểu nào sau đây sai ? A. z z z
z z '  z z ' B. 2 .
z z z C. z z D. .  z ' z '.z
Câu 14. Cho số phức z = 3- 4i. Phần thực và phần ảo số phức z là
A. Phần thực bằng 3 và phần ảo bằng - 4i;
B. Phần thực bằng 3 và phần ảo bằng 4;
C. Phần thực bằng 3 và phần ảo bằng 4i;
D. Phần thực bằng 3 và phần ảo bằng -4.
Câu 15. Tìm phần thực và phần ảo của số phức z = i2020. A. 0 và 2020 B. 0 và 1 C. 1 và 0 D. 2020 và 0
Câu 16. Tìm phần thực, phần ảo của z  4  i  2  3i  5  i
A. phần thực là 1, phần ảo là 1 B.phần thực là 11, phần ảo là 1
C. phần thực là 1, phần ảo là 3 D. phần thực là 11, phần ảo là 3  i
Câu 17. Cho số phức 1 1   i z
. Trong các kết luận sau kết luận nào đúng? 1  i 1  i A.
z có phần thực và phần ảo 0 .
B. z là số thuần ảo.
C. Mô đun của z bằng 1
D. z có phần thực và phần ảo đều bằng 0.
Câu 18. Tính z z và z.z biết z  2  3i
A. 4 và 13 B. 4 và 5 C. 4 và 0 D. 13 và 5
Câu 19. Cho số phức z  2  3i . Tìm số phức w = 2iz - z . A. w  8
 7i B. w  8  i
C. w  4  7i D. w  8  7i
Câu 20. Cho số phức z  1 3i z  3  4i z z 1 và 2 . Môđunsố phức 1 2 là
A. 17 ; B. 15 ; C. 4; D. 8. Trang4
Câu 21. Số phức nghịch đảo của số phức z = 1 - 3i là: 1 3 1 3 A. 1 z =  i 1 z =  i 1 z = 1 + 3i 1
D. z = -1 + 3i 4 4 B. 2 2 C.
Câu 22. Mô đun của số phức z   i  i  3 5 2 1 là
A.7 B. 3C.5D. 2
Câu 23. Cho số phức z = a + bi (với a, b là các số thực). Xét các phát biểu sau
(1) z² – z ² là số thực
(2) z² + z ² là số ảo
(3) z z là số thực (4) |z| – z là bằng 0
Số câu phát biểu đúng là A. 0 B. 1 C. 2 D. 3
Câu 24. Giá trị của A = (1 + i)20 bằng A. 1024 B. 220 C. –1024 D. 1024 – 1024i
Câu 25. Cho số phức z thỏa mãn: z (1 2i)  7  4i .Tìm mô đun số phức   z  2i .
A. 5 B. 17 C. 24 D. 4
Câu 26. Cho số phức z biết  i z 2  i
. Phần ảo của số phức z2 là 1 i A. 5 i . B. - 5 i . C. 5 . D. 5  . 2 2 2 2  i 3 1 3
Câu 27. Cho số phức z thỏa mãn: z
. Tìm môđun của z iz . 1 i
A.8 2 B. 4 2 C. 8 D. 4
Câu 28. Phần thực của số phức 2
z thỏa mãn 1 i  2  i z  8  i  1 2i z là A. 6  B. 3  C.2D. 1
DẠNG II. PHƢƠNG TRÌNH TRÊN TẬP SỐ PHỨC
I. PHƢƠNG PHÁP : Sử dụng các phương pháp giải phương trình mẫu mực như phương
trình bậc nhất, phương trình bậc hai….với ẩn là số phức z. II. CÁC VÍ DỤ
Ví dụ 1. (Mã đề 101 - QG – 2017) Phương trình nào dưới đây nhận hai số phức 1 2i và 1 2i là nghiệm ? A. 2
z  2z  3  0 B. 2
z  2z  3  0 C. 2
z  2z  3  0 D. 2
z  2z  3  0 Hƣớng dẫn giải
Cách 1: Ta có 1 2i 1 2i  2 ; 1 2i 1 2i  2 . Suy ra 1 2i và 1 2i là
nghiệm của phương trình 2
z  2z  3  0 . Đáp án: C
Cách 2: Thử đáp án bằng MTBT
Ví dụ 2. (Mã đề 102 - QG – 2017) Kí hiệu z , z 1
2 là hai nghiệm phức của phương trình 2
3z z  1  0 . Tính P z z 1 2 3 2 3 14 A. P  . B. P C. 2 P  . D. P  . 3 3 3 3 Hƣớng dẫn giải  Phương trình 1 i 11 2
3z z  1  0 có hai nghiệm z  . 1,2 6 Trang5 2 3
Khi đó P z z  1 2 3 Đáp án: B
Ví dụ 3. Tìm số phức sau: a) (1 + z)(2 + 3i) = 1 + i 2  1 b) i i 3 z  1  i 2  i Giải
a) Ta có (1 + z)(2 + 3i) = 1 + i 1 i
 1 z  23i 5  i  1 z  13 8 1  z    i 13 13 b) Ta có 2  i 1   3i ( 1
  3i)(1 i) z   z  2 1 i 2  i (2  i) 2  4i
(2  4i)(3  4i)  z   z 3  4i 25 22 4  z   i 25 25
Ví dụ 4. Giải các phương trình sau trên trường số phức: a)z4 + 2z2 -3 = 0
b) z4 – 4z3 +7z2 – 16z + 12 = 0 (1) Giải 2 z 1 z  1 
a) Ta có z4 + 2z2 -3 = 0     2 z  3  z  i 3 z  1 
Vậy phương trình có 4 nghiệm  z  i 3
b) Do tổng tất cả các hệ số của phương trình (1) bằng 0 nên (1) có nghiệm z = 1.
(1)  (z – 1)(z3 – 3z2 + 4z – 12) = 0
 (z – 1) (z – 3) (z2 + 4) = 0 z  1 z 1   z  3  z  3     z  2i 2
z  4  0 z  2i
Vậy phương trình đã cho có 4 nghiệm:
z = 2i; z = −2i; z = 1; z = 3 III. BÀI TẬP Trang6
Câu 1. (Mã đề 103 - QG – 2017) Kí hiệu z , z là hai nghiệm phức của phương trình 1 2 1 1 2
z z  6  0 . Tính P   z z 1 2 A. 1 P  . B. 1 P C. 1 P   . D. P  6 . 6 12 6
Câu 2. (QG-2019)Gọi z , z là hai nghiệm phức phương trình 2
z  6z  10  0 . Giá trị 1 2 2 2 z z bằng 1 2 A.16. B. 56. C. 20. D. 26.
Câu 3. (QG-2019)Gọi z , z là hai nghiệm phức của phương trình 2
z  6z 14  0 . Giá trị 1 2 của 2 2
z z bằng 1 2 A. 36 . B. 8 . C. 28 . D. 18 . Câu 4. (QG-2019)Gọi 2
z , z là hai nghiệm phức của phương trình z  4z  5  0 . Gái trị của 1 2 2 2 z z bằng 1 2 A. 6 . B. 8 . C. 16 . D. 26 .
Câu 5. (QG-2019)Gọi z , z 2 1
2 là hai nghiệm phức của phương trình z  4z  7  0 . Giá trị của 2 2
z z bằng 1 2 A. 10. B. 8. C. 16. D. 2.
Câu 6. Tìm mô đun của số phức z thoả 3iz  (3  i)(1 i)  2 . 2 2 3 2 3 3 2 3 A. z B. z C. z D. z 3 2 2 3
Câu 7. Cho số phức z thỏa mãn (1 + 2i)z – 5 – 5i = 0. Tìm số phức w = 10 z z A. 6 + 2i B. 2 + 6i C. –2 + 6i D. –6 + 2i
Câu 8.Giải phương trình 2  3iz z 1. A. 1 3 z    . i B. 1 3 z    . i C. 1 3 z   . i D. 1 3 z   . i 10 10 10 10 10 10 10 10
Câu 9.Giải phương trình 2  iz  4  0 . A. 1 3 z    . i B. 8 4 z   . i C. 5 3 z   . i D. 1 3 z   . i 5 5 5 5 10 10 13 13  i  
Câu 10.Giải phương trình 2 1 3  i z . 1 i 2  i A. 1 3 z    . i B. 8 4 z   . i C. 22 4 z   . i D. 1 3 z   . i 5 5 5 5 25 25 13 13 z
Câu 11. Tìm nghiệm của phương trình 2 1 1 i z i A. 1 3 z   . i B. 1 4 z   . i C. 1 1 z   . i D. 1 1 z    i 5 5 5 5 2 2 2 2
Câu 12.Tìm nghiệm của phương trình 2
z  2z  5  0 .
A. z  -1 2 ; i z  -1- 2 . i z  -1 2 ; i z  -1- 2 . i 1 2 B. 1 2 Trang7
C. z  1 2 ; i
z  -1 2 .i
D. z  -1 2 ; i
z  -1 2 .i 1 2 1 2
Câu 13. Tìm các số thực b,c để phương trình (với ẩn z): 2
z bz c  0 nhận z 1 i làm một nghiệm. A. b  2  ,c  2. 
B. b  2, c  3. C. b  1  , c  2.
D. b  2, c  2. Câu 14. Gọi z z z  
1 và z2 lần lượt là nghiệm của phương trình: 2 2 10 0 . Tính giá trị của biểu thức 2 2 A zz 1 2 A. 15 B. 17 C. 20 D. 10
Câu 15. Gọi A, B là hai điểm biểu diễn cho các số phức là nghiệm của phương trình 2
z  2z  3  0 . Tính độ dài đoạn thẳng AB . A. 2 2 B. 3 2 C. 2 3 D. 3 6
Câu 16. Cho số phức z có phần thực dương thỏa mãn 2
z  6z 13  0 . Tính z  . z i A. 13 B. 17 C. 7 D. 7 3
DẠNG III. TÌM SỐ PHỨC THỎA MÃN ĐIỀU KIỆN
I. PHƢƠNG PHÁP: Để giải bài toán tìm số phức thỏa mãn điều kiện cho trước, ta thực hiện theo các bước sau:
B1: Đặt z a bia,b 
B2: Thay vào đk được hệ phương trình hai ẩn a,b. B3: Giải tìm a,b Chú ý:
 Tìm số phức z a bi ,
a b    thật ra là tìm phần thực a và phần ảo b của nó. a   0
z a bi  0   , b  0 a   a
z a b i; z a b i z z  1 1 1 2 2 2 . Khi đó: 1 2  1 2 b   b 1 2
z a bia,b  . Khi đó a b
z là số ảo (thuần ảo) khi
0 , z là số thực khi 0 .
Ví dụ 1. (Mã đề 101 - QG – 2017) Có bao nhiêu số phức z thỏa mãn z  3i  5 và z là z  4 số thuần ảo ? A.0 B. Vô số C.1 D. 2 Hƣớng dẫn giải
Đặt z a bia,b  . Điều kiện z  4 .
Ta có z  3i  5  a  b  3i  5
a  b  2 2 3  25 2 2
a b  6b 16  0  1 z a bi a a  4 2  b 4b Lại có    i . z  4
a 4bi a42 b a42 2 2  b Trang8 a a  4 2  b Vì z là số thuần ảo nên 2 2
 0  a b  4a  0 2 . 2   z  4 a 4 2  b Từ (1) + (2) suy ra 3
4a  6b  16  a  4 
b . Thay vào (1), ta được: 2 b  2 0  3  2  a b
b  6b 16  0    24 .  2  b    13
Với b  0  a  4  z  4loaïi  . Với 24 16 16 24 b    a   z  
i thoûamaõn. 13 13 13 13 Đáp án: C
Ví dụ 2. (Mã đề 101 - QG – 2017) Cho số phức z a bi (a, b   ) thỏa mãn
z 1 3i z i  0 . Tính S a 3b A. 7 S B. S  5  C. S  5 D. 7 S   3 3 Hƣớng dẫn giải Theo giả thiết, ta có:
z   i z i   z     z  i z    z  2 1 3 0 1 3 1 3 2
z    z  2 5 1 3  z  3 4 4  z  1
  i a  1
 ;b    S a  3b  5  3 3 Đáp án: B 2
Ví dụ 3. (Mã đề 103 - QG – 2017) Tìm tất cả các số thực x, y sao cho x 1 yi  1   2i
A. x   2, y  2
B. x  2, y  2
C. x  0, y  2 x y   D. 2, 2 Hƣớng dẫn giải 2 x 1  2  x  0 Ta có 2
x 1 yi  1   2i      y  2  y  2 Đáp án: C
Ví dụ 4. (Mã đề 103 - QG – 2017) Có bao nhiêu số phức z thỏa mãn z
z  3i  13 và z  2 là số thuần ảo ? A. Vô số B. 2 C. 0 D. 1 Hƣớng dẫn giải
Đặt z a bia,b  , ta có: z i
a  b  i
a  b  2 2 2 2 3 13 3 13 3
 13  a b  6b  4  0  1 . z a bi a a  2 2  b 2b Lại có    i . z  2
a  2bi a22 b a22 2 2  b a a  2 2  b Vì z là số thuần ảo nên
 0  aa  2 2 2 2
b  0  a b  2a  0 2 . 2   z  2 a  2 2  b Trang9
Từ (1)+(2) suy ra 2a  6b  4
  a  3b2. Thay vào (1), ta được: b  0   3b  22 2
b  6b  4  0  3 . b   5
Với b  0  a  2   z 2  loaïi . Với 3 1 1 3 b
x    z    i thoûamaõn . 5 5 5 5 Đáp án: D
Ví dụ 5. (Mã đề 104 - QG – 2017) Cho số phức z thỏa mãn z  5 và z  3  z  3 10i .
Tìm số phức w z  4  3i . A. w  3  8i
B. w 1 3i C. w  1  7i D. z  4  8i Hƣớng dẫn giải
Đặt z a bia,b  , ta có: z
  a    bi   a  2 2 3 5 3 5 3  b  25
Lại có z  3  z  3 10i  a  3  bi  a  3  b 10i
 a  2 b  a  2  b  2  b  b  2 2 2 3 3 10 2
b  5 a  0  z  5i w  4  8i . Đáp án: D III. BÀI TẬP
Câu 1. (Mã đề 102 - QG – 2017) Cho số phức z a bi ( ,
a b   ) thoả mãn z  2  i z .
Tính S  4a b . A. S  4 B. S  2 C. S  2  D. S  4 
Câu 2. (QG – 2018) Có bao nhiêu số phức
z z   i i   z thỏa mãn
 3  2 4 iz ? A. 1. B.3 . C. 2 . D. 4 .
Câu 3.(QG – 2018) Có bao nhiêu số phức
z z   i i   z thỏa mãn ( 6 ) 2 (7 i)z ? A. 2. B. 3. C. 1. D. 4.
Câu 4. (QG – 2018) Có bao nhiêu số phức
z z   i i   z thỏa mãn
 5  2 6 iz ? A.1. B.3 . C. 4 . D. 2 .
Câu 5. (Mã đề 103 - QG – 2017) Cho số phức z thỏa mãn z  3  5 và z  2i z  2  2i . Tìm số phức z .
A. z  17.
B. z  17.
C. z  10.
D. z  10.
Câu 6. (QG – 2018) Tìm hai số thực x và y thỏa mãn 2x  3yi  1 3i  x  6i với i là đơn vị ảo. A. x  1  ; y  3 . B. x  1
 ; y  1. C. x 1; y  1. D. x 1 ; y  3 .
Câu 7. (QG – 2018) Có bao nhiêu số phức
z z   i i   z thỏa mãn
 4  2 5 iz ? A. 2 . B.3 . C.1. D. 4 .
Câu 8. (QG – 2018) Tìm hai số thực x và y thỏa mãn 3x  2yi  2  i  2x  3i với i là đơn vị ảo. Trang10
A. x  2; y  2 .
B. x  2; y  1.
C. x  2; y  2 .
D. x  2; y  1 
Câu 9. (QG – 2018) Tìm hai số thực x và y thỏa mãn (3x yi)  (4  2i)  5x  2i với i là đơn vị ảo.
A. x  2; y  4 .
B. x  2; y  4 .
C. x  2; y  0 .
D. x  2; y  0 .
Câu 10. (QG – 2018) Tìm hai số x và y thỏa mãn 2x  3yi  3  i  5x  4i với i là đơn vị ảo. A. x  1
 ; y  1 . B. x  1  ; y 1 .
C. x 1; y  1 .
D. x 1 ; y  1 .
Câu 11. (QG-2019)Cho số phức 3 z iz thỏa mãn
 2  iz  310i . Mô đun của z bằng A. 3 . B. 5. C. 5 . D. 3 .
Câu 12. (QG-2019)Cho số phức z thỏa mãn 3 z i  2  3iz  7 16i . Môđun của z bằng A. 5 . B. 5 . C. 3 . D. 3 .
Câu 13. (QG-2019)Cho số phức       z thỏa (2
i)z 4(z i)
8 19i . Môđun của z bằng A. 13 . B. 5. C. 13 . D. 5 .
Câu 14. (QG-2019)Cho số phức      z thỏa (2
i)z 3 16i 2(z i) . Môđun của z bằng A. 5 . B. 13 . C. 13 . D. 5.
Câu 15. Tìm số phức z, biết z z  3  4i A. 7 z   4i B. z  3 C. 7 z    4i D. z  3   4i 6 6
Câu 16. Số phức z thỏa mãn: (1 i)z  (2  i)z 13 2i là A. 3 + 2i ; B. 3-2i;
C. -3 + 2i ; D. -3 -2i.
Câu 17. Cho số phức z thỏa mãn điều kiện 2z + 3(1 – i) z = 1 – 9i. Tìm modun của z. A. |z| = 3 B. |z| = 3 C. |z| = 13 D. |z| = 13
Câu 18. Tìm phần thực và phần ảo của số phức z thỏa mãn (1 – i)z – (2 – i) z = 2 + 9i A. 4 và –3 B. –4 và 3 C. 4 và 3 D. –4 và –3
Câu 19. Số số phức z thỏa mãn đẳng thức: 2 1 z  z z 1
 1 z zi . 2 2 A. 1 B.2 C.3 D.4
Câu 20. Sốsố phức z thỏa mãn  z  2 2
1  z 1 10i z  3 . A. 1 B.2 C.3 D.4 iz z
Câu 21. Tìm mô đun số phức z thỏa mãn 2 2  i  2z . 2  i 1 2i A. 1 B. 2 C. 2 D. 2 2 2 Câu 22. Biết z i z
z là số phức thỏa điều kiện
0 . Tìm số phức z có phần ảo âm 1 1 1 1 1 1 A. z  1   i B. z    i C. z   i D. z  1 i 2 2 2 2 2 2
DẠNG IV. BIỂU DIỄN HÌNH HỌC CỦA SỐ PHỨC
I. PHƢƠNG PHÁP: Giả sử z = x + yi (x, y  R). Khi đó số phức z biểu diễn trên mặt
phẳng phức bởi điểm M(x;y). Trang11
Sử dụng dữ kiện của đề bài để tìm mối liên hệ giữa x và y từ đó suy ra tập hợp điểm M.
Một số quỹ tích thường gặp:
Với z = x+yi (x, y là các số thực) khi đó nếu:
* x= a : Quỹ tích z là đường thẳng x = a (song song với Oy).
* y= b: Quỹ tích z là đường thẳng y = b (song song với Ox).
* (x-a)2 +(y-b)2= R2 Quỹ tích z là đường tròn tâm I(a.b) bán kính R.
* (x-a)2 +(y-b)2 R2 Quỹ tích z là hình tròn tâm I(a.b) bán kính R ( kể cả biên).
* (x-a)2 +(y-b)2> R2 Quỹ tích z là các điểm nằm ngoài đường tròn tâm I(a.b) bán kính R. II. CÁC VÍ DỤ
Ví dụ 1. (Mã đề 101- QG – 2017) Cho số phức z 1 2i . Điểm nào dưới đây là điểm biểu
diễn của số phức w iz trên mặt phẳng tọa độ ?
A. Q(1; 2)
B. N (2;1)
C. M (1; 2) D. P( 2  ;1) Hƣớng dẫn giải
Ta có w iz i 1 2i  2  i . Suy ra điểm biểu diễn của số phức w là N (2;1) . Đáp án: B
Ví dụ 2. (Mã đề 102 - QG – 2017) Số phức nào sau đây có điểm biểu diễn trên mặt phẳng y
tọa độ là điểm M như hình bên ? 1
A. z  2  i z  1 2i 4 B. 2 2  O x C. z  2   i z  1 2i 3 D. 1 Hƣớng dẫn giải Đáp án: C
Ví dụ 3. (Mã đề 102 - QG – 2017) Có bao nhiêu số phức z   i z thỏa mãn | 2 | 2 2 và 2
(z 1) là số thuần ảo. A. 0 B. 4 C. 3 D. 2 Hƣớng dẫn giải
Đặt z x yi x, y  .
Theo giả thiết, ta có | z  2  i | 2 2   x  2   y   1 i  2 2
 x  2   y  2 2 1  8C . 2 2
Mặt khác,  z     x    yi   x  2 2 1 1 1
y  2x   1 yi . 2
Theo giả thiết (z 1) là số thuần ảo nên  y x 1
x y 1  0 d 2 2   x   2 2
1  y  0  y   x   1     .
y  x 1
x y 1  0  
Đường tròn (C) có tâm I  2  ; 
1 , bán kính R  2 2 .
Ta có d I , d   2 2  R , suy ra d tiếp xúc (C).
Ta có d I, d   2  R , suy ra  cắt (C) tại hai điểm phân biệt.
Tập hợp các điểm biểu diễn cho số phức chính là các giao điểm của (C) với hai đường thẳng
d và  . Số giao điểm là 3. Trang12 Đáp án: C
Ví dụ 4. (Mã đề 104 - QG – 2017) Cho số phức z  1 2i, z  3
  i . Tìm điểm biểu diễn 1 2
của số phức z z z trên mặt phẳng tọa độ. 1 2 A. N (4; 3) B. M (2; 5)
C. P(2; 1) D. Q( 1  ;7) Hƣớng dẫn giải
Ta có z z z  2  i . 1 2
Vậy điểm biểu diễn của số phức z là P(2; 1) . Đáp án: C
Ví dụ 5. (Mã đề 104 - QG – 2017) Kí hiệu z , z là hai nghiệm phức của phương trình 1 2 2
z  4  0 . Gọi M, N lần lượt là các điểm biểu diễn của z , z trên mặt phẳng tọa độ. Tính 1 2
T OM ON với O là gốc tọa độ. A. T  2 2 . B. T  2 C. T  8. D. T  4 . Hƣớng dẫn giải z  2i Ta có 2 1 z  4  0   . z  2   i 2
Suy ra M 0;2, N 0; 2
   OM ON  2 T OM ON  4. Đáp án: D
Ví dụ 6. (Mã đề 104 - QG – 2017) Gọi S là tập hợp tất cả các giá trị thực của tham số m để
tồn tại duy nhất số phức z thỏa mãn .
z z  1 và z  3  i m . Tìm số phần tử của S. A. 2 B. 4 C. 1 D. 3. Hƣớng dẫn giải
Điều kiện: m  0.
Đặt z x yi x, y  . Theo giả thiết 2 2 2 .
z z  1  z  1  x y   1 C . 1 
C là đường tròn tâm O0;0, bán kính R 1. 1  1 2
Mặt khác z  3  i m  x  3  y  
1  m  x  3   y  2 2 1  m C 2 
C là đường tròn tâm R I  3; , bán kính m . 2  1  2
Để tồn tại duy nhất số phức zthì C và C tiếp xúc ngoài hoặc trong. 2  1 
TH1: C và C tiếp xúc ngoài khi và chỉ khi R R OI  1 m  2  m  1 thoûa maõn 1 2   2  1  .
R OI R 1 2  m m  3 thoûa maõn 1 2  
TH2 C và C tiếp xúc trong khi và chỉ khi  2  1 
OI R R m  2 1  m  1   loaïi 2 1   . Vậy S  1,  3 . Đáp án: A
Ví dụ 7. (QG – 2018) Xét các số phức z i z z thỏa mãn 
 2 là số thuần ảo. Trên mặt
phẳng tọa độ, tập hợp tất cả các điểm biểu diễn số phức z là một đường tròn có bán kính bằng Trang13 5 3 A.1. B. 5 . C. . D. . 4 2 2 Hƣớng dẫn giải
Đặt z x yi x, y  .
Ta có  z i z     x yi ix yi     2 2 2 2
x  2x y y   x  2y  2i 2  1  5
Vì  z i z  2 là số thuần ảo nên x  2x y y  0   x  2 2 2 1  y     .  2  4
Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn số phức z là một đường tròn có 5 bán kính bằng . 2 Đáp án: C III. BÀI TẬP
Câu 1. (QG – 2018) Xét các số phức z thỏa mãn z 3iz 3 là số thuần ảo. Trên mặt
phẳng tọa độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng 3 2 A. 9 . B. 3 2 . C.3 . D. . 2 2
Câu 2.(QG – 2018) Xét các số phức z thỏa mãn z  2iz  2 là số thuần ảo. Trên mặt
phẳng tọa độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng A. 2. B. 2 2 . C. 4. D. 2 .
Câu 3. (QG – 2018) Xét các số phức z i z z thỏa mãn  2 
2 là số thuần ảo. Trên mặt
phẳng tọa độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng A. 2 2 . B. 2 . C. 2 . D. 4 .
Câu 4. (QG-2019)Cho hai số phức z  1 i z  1 2i 1 và 2
. Trên mặt phẳng toạ độ Oxy , điểm
biểu diễn số phức 3z z 1 2 có toạ độ là 1;4 A. 4;  1 . B.  1  ;4 . C. 4  1 ; . D. .
Câu 5. (QG-2019)Xét các số phức z thỏa mãn z
2 . Trên mặt phẳng tọa độ Oxy , tập 
hợp điểm biểu diễn của các số phức 4 iz w 
là một đường tròn có bán kính bằng 1 z A. 34. B. 26. C. 34. D. 26.
Câu 6. (QG-2019)Xét các số phức z thỏa mãn z  2 . Trên mặt phẳng tọa độ Oxy , tập 3  iz
hợp điểm biểu diễn các số phức w
là một đường tròn có bán kính bằng 1 z A. 2 3 B. 12 C. 20 D. 2 5
Câu 7. (QG-2019)Cho hai số phức z  2
  i và z 1 i . Trên mặt phẳng tọa độ Oxy điểm 1 2
biểu diễn số phức 2z z có tọa độ là 1 2 Trang14 A. 3; 3 . B. 2;  3 . C.  3  ;3 . D.  3  ;2.
Câu 8. (QG-2019)Cho hai số phức z  1 i và z  2  i . Trên mặt phẳng Oxy , điểm biểu 1 2
diễn số phức z  2z có tọa độ là 1 2 A. 2;5 . B. 3;5 . C. 5;2 . D. 5;  3 .
Câu 9. (QG-2019)Cho số phức z thỏa mãn z
2 . Trên mặt phẳng tọa độ Oxy , tập hợp các điể 
m biểu diễn của số phức 2 iz
w thỏa mãn w
là một đường tròn có bán kính bằng 1 z A. 10 . B. 2 . C. 2 . D. 10 .
Câu 10. (QG-2019)Cho hai số phức z  2  i, z  1 i 1 2
. Trên mặt phẳng tọa độ Oxy, điểm
biểu diễn số phức 2z z 1 2 có tọa độ là: A. 5; 1  . B.  1  ;5. C. 5;0 . D. 0;5 .
Câu 11. (QG-2019)Cho số phức z thỏa mãn z
2 . Trên mặt phẳng tọa độ Oxy , tập hợp các điể 
m biểu diễn của số phức w thỏa mãn 5 iz w
là một đường tròn có bán kính bằng 1 z A. 52 . B. 2 13 . C. 2 11 . D. 44 .
Câu 12. Giả sử M(z) là điểm trên mặt phẳng tọa độ biểu diễn số phức z. Tập hợp những
điểm M(z) thỏa mãn điều 2  z i z là
A. Đường thẳng 4x  2 y  3  0
B. Đường thẳng 4x  2 y  3  0
A. Đường thẳng x  2 y  3  0
D. Đường thẳng x  9 y  3  0
Câu 13. Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức z thỏa mãn điều
kiện z  2i z 1 i là
A. Đường thẳng x y  3  0
B. Đường thẳng x  2 y  3  0
A. Đường thẳng x  2 y  3  0
D. Đường thẳng x y 1  0
Câu 15.Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức z thỏa mãn điều kiện
z 1 i  2 là
A. Đuờng thẳng x y  2  0
B. Đường tròn  x  2   y  2 1 1  4
C. Đường thẳng x y  2  0
D. Đường tròn tâm I 1; 1  và bán kính R  2.
Câu 16. Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức z thỏa mãn điều
kiện z  4i z  4i  10 là 2 2 x y 2 2 x y A. Đuờng elip  1 B. Đuờng elip  1 9 16 16 9 2 2 x y 2 2 x y C. Đuờng elip  1 D. Đuờng elip  1 4 3 9 4 Trang15
Câu 17. Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức z thỏa mãn điều
kiện 2  z z  2 là
A. Tập hợp các điểm là nửa mặt phẳng ở bên phải trục tung
B. Tập hợp các điểm là nửa mặt phẳng ở bên trái trục tung
C. Tập hợp các điểm là nửa mặt phẳng phía trên trục hoành
D. Tập hợp các điểm là nửa mặt phẳng phía dưới trục hoành
Câu 18. Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức z thỏa mãn điều
kiện 1  z 1 i  2 là
A. Tập hợp các điểm là hình tròn có tâm I 1; 1  , bán kính 2
B. Tập hợp các điểm là hình vành khăn có tâm tại A 1  
;1 và các bán kính lớn và nhỏ lần lượt là 2; 1
C. Tập hợp các điểm là hình tròn có tâm I 1; 1  , bán kính 1
D. Tập hợp các điểm là hình vành khăn có tâm tại I 1; 1
 và các bán kính lớn và nhỏ lần lượt là 2; 1 z  
Câu 19.Tìm tập hợp các điểm biểu diễn số phức z sao cho 2 3  i u là một số thuần ảo. z i
A. Đường tròn tâm I  1  ;  1 bán kính R  5
B. Đường tròn tâm I  1  ; 
1 bán kính R  5 trừ đi hai điểm A0;  1 ; B  2  ; 3  .
C. Đường tròn tâm I 1  ;1 bán kính R  5
D. Đường tròn tâm I 1 
;1 bán kính R  5 trừ đi hai điểm A0;  1 ; B  2  ; 3  .
Câu 20. Tìm tập hợp các điểm biểu diễn số phức z x yi thỏa mãn điều kiện x y  1 là
A. Ba cạnh của tam giác
B. Bốn cạnh của hình vuông
C. Bốn cạnh của hình chữ nhật
D. Bốn cạnh của hình thoi
DẠNG V. CỰC TRỊ CỦASỐ PHỨC
I. PHƢƠNG PHÁP: Sử dụng các kiến thức cơ bản như: Bất đẳng thức liên hệ giữa trung
bình cộng và trung bình nhân, bất đẳng thức Bunhia- Cốpxki, bất đẳng thức hình học và
một số bài toán công cụ sau:
BÀI TOÁN CÔNG CỤ 1:
Cho đường tròn (T ) cố định có tâm I bán kính R và điểm A cố định. Điểm M di
động trên đường tròn (T ) . Hãy xác định vị trí điểm M sao cho AM lớn nhất, nhỏ nhất. Hướng dẫn giải:
TH1: A thuộc đường tròn (T)
Ta có: AM đạt giá trị nhỏ nhất bằng 0 khi M trùng với A Trang16
AM đạt giá trị lớn nhất bằng 2R khi M là điểm đối xứng với A qua I
TH2: A không thuộc đường tròn (T)
Gọi B, C là giao điểm của đường thẳng qua A,I và đường tròn (T);
Giả sử AB < AC.
+) Nếu A nằm ngoài đường tròn (T) thì với điểm M bất kì trên (T), ta có:
AM AI IM AI IB AB .
Đẳng thức xảy ra khi M B
AM AI IM AI IC AC .
Đẳng thức xảy ra khi M C
+) Nếu A nằm trong đường tròn (T) thì với điểm M bất kì trên (T), ta có:
AM IM IA IB IA AB .
Đẳng thức xảy ra khi M B
AM AI IM AI IC AC .
Đẳng thức xảy ra khi M C
Vậy khi M trùng với B thì AM đạt gía trị nhỏ nhất.
Vậy khi M trùng với C thì AM đạt gía trị lớn nhất. BÀI TOÁN CÔNG CỤ 2:
Cho hai đường tròn (T ) 1 có tâm I, bán kính R1; đường tròn (T )
2 có tâm J, bán kính R2. Tìm vị trí
của điểm M trên (T ) , điể (T ) 1 m N trên 2 sao cho
MN đạt giá trị lớn nhất, nhỏ nhất. Hướng dẫn giải:
Gọi d là đường thẳng đi qua I, J;
d cắt đường tròn (T ) (T )
1 tại hai điểm phân biệt A, B (giả sử JA > JB) ; d cắt 2 tại hai điểm
phân biệt C, D ( giả sử ID > IC).
Với điểm M bất khì trên (T ) (T )
1 và điểm N bất kì trên 2 .
Ta có: MN IM IN IM IJ JN R R IJ AD 1 2 . Đẳng thức xảy ra khi M trùng với A và N trùng với D
MN IM IN IJ IM JN IJ R R BC . 1 2
Đẳng thức xảy ra khi M trùng với B và N trùng với C.
Vậy khi M trùng với A và N trùng với D thì
MN đạt giá trị lớn nhất.
khi M trùng với B và N trùng với C thì
MN đạt giá trị nhỏ nhất. BÀI TOÁN CÔNG CỤ 3:
Cho hai đường tròn (T ) có tâm I, bán kính R; đường thẳng  không có điểm chung
với (T ) . Tìm vị trí của điểm M trên (T ) , điểm N trên  sao cho MN đạt giá trị nhỏ nhất. Hướng dẫn giải: Trang17
Gọi H là hình chiếu vuông góc của I trên d
Đoạn IH cắt đường tròn (T ) tại J Với M thuộc đường thẳng
 , N thuộc đường tròn (T ) , ta có:
MN IN IM IH IJ JH const .
Đẳng thức xảy ra khi M H; N I
Vậy khi M trùng với H; N trùng với J thì MN đạt giá trị nhỏ nhất. II. CÁC VÍ DỤ
Ví dụ 1. Trong các số phức z   i z thoả mãn 3 4
4 . Tìm giá trị lớn nhất, giá trị nhỏ
nhất của z . Hƣớng dẫn giải Cách 1
Gọi z x yi  ;
x y  R   M (x; y) biểu diễn cho số phức z trong hệ toạ độ Oxy 2 2 2 2
z  3  4i  4 
(x  3)  ( y  4)  4  (x  3)  ( y  4)  16
Vậy điểm M biểu diễn cho số phức z thuộc đường tròn (T) có tâm I (3; 4) , bán kính R = 4. 2 2 z
x y OM ; OI  5  R nên O nằm ngoài đường tròn (T)
z lớn nhất khi OM lớn nhất, nhỏ nhất khi OM nhỏ nhất.
(Bài toán qui về Bài toán công cụ 1- Trường hợp 2) Đường thẳng OI cắt đường tròn (T) tại hai điểm phân biệt  3 4   27 36  A ;  ; B ; 
OA 1;OB  9      5 5   5 5 
Với M di động trên (T), ta có: OA OM OB 1 OM  9 1  z  9
 OM nhỏ nhất khi M trùng với A; OM lớn nhất khi M trùng với B
Vậy z nhỏ nhất bằng 1 khi 3 4 z
i ; z lớn nhất bằng 9 khi 27 36 z   i 5 5 5 5 Cách 2
Gọi z x yi  ; x y  R 
M (x; y) biểu diễn cho số phức z trong hệ toạ độ Oxy   34i  (3
A ; 4) biểu diễn cho số phức 
z OM ;   OA  5  z   AM ;
Theo giả thiết z  3  4i  4  z   4  AM  4 .
Ta có: OM OA AM  4
  OM OA  4  4
 OA OM  4OA 1 OM  9
1 z  9 ; z 1 khi 3 4 z
i ; z  9 khi 27 36 z   i 5 5 5 5
Vậy z nhỏ nhất bằng 1 khi 3 4 z
i ; z lớn nhất bằng 9 khi 27 36 z   i 5 5 5 5
Nhận xét: Ngoài ra bài toán trên có thể Hướng dẫn giải bằng phương pháp sử dụng bất
đẳng thức Bunhia-Cốpxki hoặc phương pháp lượng giác hoá.
Ví dụ 2. Trong các số phức z thoả mãn điều kiện z (z  2  4i) là một số ảo, tìm số Trang18 phức   z   z sao cho
1 i có môđun lớn nhất. Hƣớng dẫn giải
Gọi z x yi  ; x y  R 
M (x; y) biểu diễn cho số phức z trong hệ toạ độ Oxy
z (z  2  4i)  (x yi)(x  2)  (y  4)i  x(x  2)  y(y  4)  (
x y  4)  y(x  2)i z (z  2  4i) là một số ảo 2 2 2 2
x(x  2)  y(y  4)  0  x y  2x  4y  0  (x 1)  (y  2)  5  M biểu diễn cho R
z thuộc đường tròn (T) có tâm I (1; 2) , bán kính 5 2 2
  z 1 i  (x 1)  (y 1)i  (x 1)  (y 1)  AM với ( A 1;1)
IA  5  A(T) (Bài toán được qui về Bài toán công cụ 1 - trường hợp 1)
Vì M là điểm di động trên (T) nên AM lớn nhất
 AM là đường kính của (T)
 M đối xứng với A qua I
 I là trung diểm của AM M ( 3  ;3)  z  3
  3i    4  2i
Vậy  lớn nhất bằng 2 5 khi z  3  3i .
Ví dụ 3. Trong các số phức z có môđun bằng 2 2 . Tìm số phức z sao cho biểu thức
P z 1  z i đạt giá trị lớn nhất. Hƣớng dẫn giải
Gọi z x yi  ; x y  R  2 2 2 2 z  2 2 
x y  2 2  x y  8 2 2 2 2
P z 1  z i
(x 1)  y
x  ( y 1)
Áp dụng bất đẳng thức Bunhia-côpxki cho hai bộ số 1;1 và 2 2 2 2
(x 1)  y ; x  ( y 1) , ta có: 2 2 2 2 2
P  2 (x 1)  y x  ( y 1)   4(9  x y)  
Áp dụng bất đẳng thức Bunhia-cốpxki cho hai bộ số 1;1 và ; x y , ta có: x y   2 2
2 x y   4 2
P  52  P  2 13 . Đẳng thức xảy ra khi x y  2
Vậy P đạt giá trị lớn nhất bằng 2 13 khi z  2  2i .
Ví dụ 4. Trong các số phức z có môđun bằng 2 . Tìm số phức z sao cho biểu thức
P z 1  z 1 7i đạt giá trị lớn nhất. Hƣớng dẫn giải
Gọi z x yi  ; x y  R  2 2 2 2 z  2 
x y  2  x y  4 Trang19 2 2 2 2
P z 1  z 1 7i
(x 1)  y  (x 1)  ( y  7)    
Xét u x 1; y,v 1 ; x 7
  y  u v  0; 7  . Khi đó:      
P u v u v  7 . Đẳng thức xảy ra khi u , v cùng hướng  (x 1)( 7
  y)  y(1 x)  x  1
x 1 y   3  
Với x 1; y  3 thì u ,v ngược hướng (không thoả mãn)  
Với x 1; y   3 thì u ,v cùng hướng (thoả mãn)
Vậy z  1 i 3 thì P đạt giá trị nhỏ nhất bằng 7.
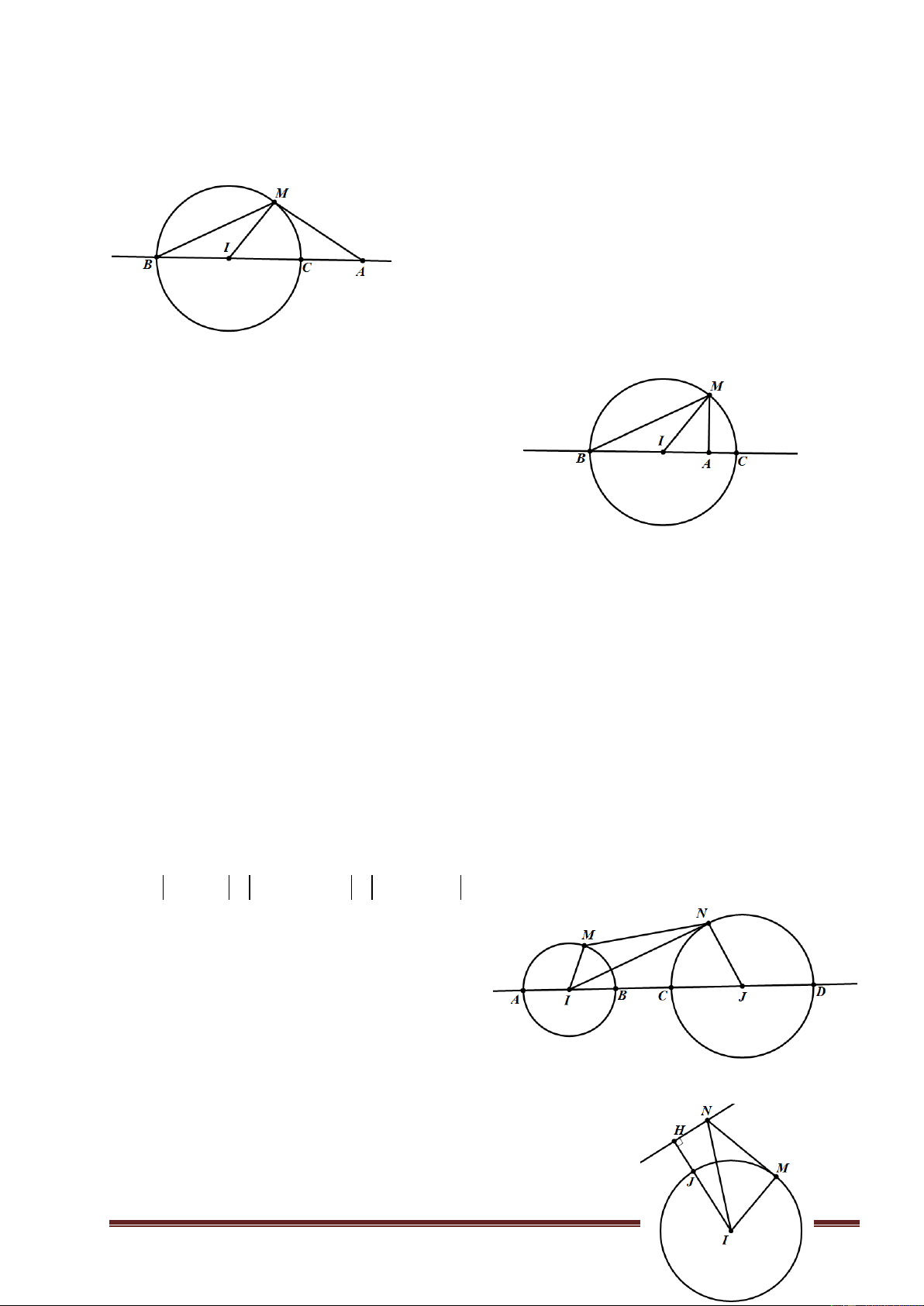
Ví dụ 5. Trong các số phức z
z 1 i 1 ; z  6  6i  6 1, z2 thoả mãn: , tìm số phức 1 2 z z z 1, z2 sao cho
đạt giá trị lớn nhất. 1 2 Hƣớng dẫn giải
Gọi z a  .
b i ; z c d.i ; (a, ,
b c, d là những số thực); z được biểu diễn bởi điểm M(a; b); 1 2 1 z đượ 2
c biểu diễn bởi điểm N(c; d) trong mặt phẳng toạ độ Oxy 2 2 2
z 1 i  1  z 1 i
1  (a 1)  (b 1) 1 suy ra M thuộc đường tròn tâm I(1; 1), 1 1 bán kính R = 1. 2 2 2
z  6  6i  6  z  6  6i
 36  (c  6)  (d  6)  36 suy ra M thuộc đường tròn tâm 2 2
J(6; 6), bán kính R' = 6. 2 2 z z
(c a)  (d b)  MN . 1 2
(Bài toán được qui về Bài toán công cụ 2)
Đường thẳng IJ có phương trình y = x. Đường thẳng IJ cắt đường tròn tâm I tại hai điểm  2  2 2  2   2  2 2  2  M  ; ;M  ;  1 2     2 2 2 2    
Đường thẳng IJ cắt đường tròn tâm J tại hai điểm N 6 3 2;6 3 2 ; N 6 3 2;6 3 2 . 1   2 
M N MN M N
  z z   2 1 1 2 5 2 7 5 2 7 1 2 max z z
 5 2  7 khi M M , N N . 1 2 1 2 2  2 2  2 Vậy z  
i ; z  6  3 2  6  3 2 i thì z z đạt giá trị lớn nhất. 1 2   2 2 1 2
Ví dụ 6. Cho các số phức z ; z
z 1 ; z z  (1 i)  6  2i 1 2 thoả mãn: là một số thực. 1 2  2 
Tìm số phức z ; z 2 P zz z  1 2 sao cho z z
đạt giá trị nhỏ nhất. 2  1 2 1 2  Hƣớng dẫn giải
Gọi z a bi ; z c di ; a, ,
b c, d  R 1 2  
M (a;b), N ( ;
c d ) lần lượt biểu diễn cho z ; z 1
2 trong hệ toạ độ Oxy 2 2 2 2 z  1 
a b  1  a b  1 1
 M thuộc đường tròn (T ) có tâm O, bán kính R = 1 Trang20
z c di; 2
  z z  
1i 6  2i  
c di(c 1)  (d 1)i 26i
c(c 1)  d(d 1)  2  c(d 1)  d(c 1)  6i
 là số thực  c(d 1)d(c 1)6  0  c d 6  0
 N thuộc đường thẳng  : x y  6  0 Ta có d ( ;
O )  1 nên  và (T ) không có điểm chung
z z ac bd  (bc ad )i; 1 2
z z ac bd  (bc ad )i z z z z  2(ac bd ) 1 2 1 2 1 2 2 2 2 2 2
P c d  2(ac bd)  (c a)  (b d) 1  MN 1 (vì 2 2
a b  1 )
(Bài toán được qui về Bài toán công cụ 3)
Gọi H là hình chiếu vuông góc của O trên  : x y  6  0  H (3;3)  2 2 
Đoạn OH cắt đường tròn (T ) tại I  ;    2 2  
Với N thuộc đường thẳng  , M thuộc đường tròn (T ) , ta có:
MN ON OM OH OI IH  3 2 1.
Đẳng thức xảy ra khi M I; N H P    2
3 2 1 1  18  6 2 . 2 2
Đẳng thức xảy ra khi z   ;
i z  3  3i 1 2 2 2 2 2
Vậy P đạt giá trị nhỏ nhất bằng 18  3 2 khi z   ;
i z  3  3i . 1 2 2 2
Ví dụ 7. Trong các số phức
z   z  
z thoả mãn điều kiện 3 3 10 . Tìm số phức z có môđun lớn nhất. Hƣớng dẫn giải
Gọi z x yi  ; x y  R 
M (x; y) biểu diễn cho số phức z trong hệ toạ độ Oxy 2 2 2 2
z  3  z  3  10  (x  3)  y  (x  3)  y  10 ;
MF MF  10 1 2 (với F ( 3  ;0); F (3;0) 1 2 ). 2 2 x y
M  (E) có tâm O, trục lớn bằng 10; tiêu cự bằng 6  M (E) :  1 25 9
z OM ;OM lớn nhất  OM a  5  M (5;0)  M ( 5  ;0)
Vậy z lớn nhất bằng 5 khi z  5 z  5  III. BÀI TẬP
Câu 1.Trong các số phức z thỏa mãn điều kiện .
z z  3z z  512i .Số phức nào có mô đun lớn nhất? Trang21 A.1+2i B.1-2i C.2+4i D.1/2-i
Câu 2. Trong các số phức z thỏa mãn điều kiện z  2  i  2 .Số phức nào có mô đun nhỏ nhất? A.2+i B.4-i C.1  3   1 i
D.  3  2  2i
Câu 3. Xét các số phức z thỏa mãn z  2  i z  4  7i  6 2. Gọi m, M lần lượt là giá trị
nhỏ nhất và giá trị lớn nhất của z 1 i . Tính P m M. 5 2  2 73
A. P  13  73 . B. P  . 2 5 2  73
C. P  5 2  2 73 . D. P  . 2
Câu 4. Xét số phức z thỏa mãn z  3  2i z  3  i  3 5. Gọi M , m lần lượt là giá trị lớn
nhất và giá trị nhỏ nhất của biểu thức P z  2  z 1 3i .
A. M  17  5, m  3 2.
B. M  26  2 5, m  3 2.
C. M  26  2 5, m  2.
D. M  17  5, m  2.
Câu 5. Xét số phức z thỏa mãn z  2  3i z  6  i  2 17. Gọi M , m lần lượt là giá trị lớn
nhất và giá trị nhỏ nhất của biểu thức P z 1 2i z  2  i .
A. M  3 2, m  0.
B. M  3 2, m  2.
C. M  3 2, m  5 2  2 5.
D. M  2, m  5 2  2 5.
Câu 6. Xét số phức z thỏa mãn z  2  2i z 1 3i  34. Tìm giá trị nhỏ nhất của biển
thức P z 1 i . 9 A. P  . B. P
 3. C. P  13. D. P  4. min min min min 34
Câu 7.Trong các số phức z thỏa mãn điều kiện z 1 2i  2 , tìm số phức z có môđun nhỏ nhất.  2   4   2   4  A. z  1  2     i B. z  1  2     i  5   5   5   5   2   4   2   4  C. z  1  2     i
D. z   1  2     i  5   5   5   5  z  2  i
Câu 8. Cho số phức z thỏa mãn
 2 . Tìm giá trị nhỏ nhất và giá trị lớn z 1 i nhất của z . z  10  3; z  10  3 z   10  3; z  10  3 A. min max B. min max C. z   10  3; z  10  3 z   10  3; z  10  3 min max D. min max Trang22