Một Số Dạng và Ứng Dụng của Định Lý Stolz | Đại học Điện lực

lOMoARcPSD| 59629529 ĐẠI HỌC THÁI NGUYÊN
TRƯỜNG ĐẠI HỌC KHOA HỌC
——————–o0o——————– NGUYỄN THỊ NGA
MỘT SỐ DẠNG CỦA ĐỊNH LÝ STOLZ-CESÀRO VÀ ỨNG DỤNG
LUẬN VĂN THẠC SĨ TOÁN HỌC THÁI NGUYÊN - 2018 lOMoAR cPSD| 59629529 ĐẠI HỌC THÁI NGUYÊN
TRƯỜNG ĐẠI HỌC KHOA HỌC
——————–o0o——————– NGUYỄN THỊ NGA
MỘT SỐ DẠNG CỦA ĐỊNH LÝ STOLZ-CESÀRO VÀ ỨNG DỤNG
Chuyên ngành: Phương pháp Toán sơ cấp Mã số: 84 60 113
LUẬN VĂN THẠC SĨ TOÁN HỌC
NGƯỜI HƯỚNG DẪN KHOA HỌC TS. Trần Văn Thắng THÁI NGUYÊN - 2018 lOMoARcPSD| 59629529 i Mục lục
MỞ ĐẦU .............................................................................................................................................. 1
Chương 1. Một số dạng của định lý Stolz-Cesàro .............................................................. 2
1.1 Một số kiến thức chuẩn bị ................................................................................................... 3
1.1.1 Dãy số ....................................................................................................................................... 3
1.1.2 Chuỗi số ................................................................................................................................... 5
1.1.3 Hàm số ..................................................................................................................................... 6
1.2 Một số dạng của định lý Stolz-Cesàro ............................................................................. 8
1.2.1 Một số dạng cổ điển của định lý Stolz-Cesàro ......................................................... 8
1.2.2 Một số dạng mở rộng của định lý Stolz-Cesàro .................................................... 15
1.2.3 Một số dạng mới của định lý Stolz-Cesàro.............................................................. 22
Chương 2. Một số ứng dụng của định lý Stolz-Cesàro .................................................. 26
2.1 Tính giới hạn của dãy số ..................................................................................................... 26
2.2 Tổng các lũy thừa với số mũ nguyên ............................................................................. 50
2.3 Bài toán 11174 của P. P. Dalyay ...................................................................................... 52
KẾT LUẬN .......................................................................................................................................... 55 TÀI LIỆU THAM KHẢO 52 lOMoARcPSD| 59629529 1 MỞ ĐẦU
Các định lý Stolz-Cesàro cổ điển được các nhà toán học Otto Stolz (1842-
1905) và Ernesto Cesàro (1859- 1906) đưa ra. Định lý đề cập tới sự tồn tại của các giới hạn và cùng các điều kiện
để các giới hạn này bằng nhau. Định lý được xuất bản lần đầu tiên trong [11]
và kể từ đó, đã được xuất bản lại trong nhiều tài liệu khác nhau có chủ đề về
dãy số và chuỗi số. Định lý được xem như là phiên bản rời
rạc của quy tắc L’Hopital trong giới hạn của hàm số và nó cho ta một ∞
phương pháp hữu hiệu để tính các giới hạn có dạng không xác định ∞
và trong các bài toán tính giới hạn, đặc biệt là trong các bài toán tính giới
hạn liên quan tới tổng. Gần đây, định lý được sử dụng tính hệ số của đa thức
được định nghĩa là tổng các lũy thừa của các số nguyên ([7]) và nghiên cứu
tính chất tuần hoàn của hàm số ([5]). Với những ứng dụng kể trên, định lý
Stolz-Cesàro ngày càng được các nhà toán học quan tâm mở rộng, phát biểu
ở những dạng khác nhau và có thêm được những ứng dụng mới, điển hình
là các kết quả của C. Mortici ([8]), G. Nagy ([9]) và S. Puspană ([10]).
Luận văn này sẽ tổng hợp và trình bày một số dạng cổ điển của định lý
Stolz-Cesàro; một số dạng mở rộng của G. Nagy và S. Puspană; và một số
dạng mới được đưa ra bởi C. Mortici. Tiếp theo, luận văn trình bày một số
ứng dụng của định lý Stolz-Cesàro trong việc tính giới hạn của dãy số, trong
đó có tính giới hạn của một tổng, đây là bài toán hay thường xuất hiện trong
các đề thi toán dành cho học sinh và sinh viên. Một ứng dụng khác của định
lý Stolz-Cesàro là tính tổng hữu hạn của các lũy thừa nguyên cũng được
chúng tôi trình bày trong luận văn này.
Cuối cùng, chúng tôi sẽ sử dụng một dạng mở rộng định lý Stolz-Cesàro của
G. Nagy để nghiên cứu tính chất tuần hoàn của hàm số trong bài toán 11147 của P. P. Dalyay. lOMoARcPSD| 59629529 2
Ngoài phần mở đầu và kết luận, luận văn gồm 2 chương:
Chương 1. Một số dạng của định lý Stolz-Cesàro.
Phần đầu của chương trình bày một số khái niệm cơ bản phục vụ cho các
mục sau của luận văn. Tiếp theo, chúng tôi trình bày các dạng cổ điển, một
số dạng mở rộng và mới của định lý Stolz-Cesàro.
Chương 2. Một số ứng dụng của định lý Stolz-Cesàro.
Chương này tìm hiểu một số ứng dụng của định lý Stolz-Cesàro trong việc
tính giới hạn của dãy số, tính tổng lũy thừa của các số nguyên và nghiên cứu
tính chất tuần hoàn của hàm số trong bài toán 11147 của P. P. Dalyay.
Luận văn được hoàn thành tại trường Đại học Khoa học, Đại học Thái
Nguyên. Lời đầu tiên tác giả xin được bày tỏ lòng biết ơn sâu sắc tới thầy giáo
TS. Trần Văn Thắng. Thầy đã dành nhiều thời gian hướng dẫn cũng như giải
đáp các thắc mắc của tôi trong suốt quá trình làm luận văn. Tôi xin bày tỏ
lòng biết ơn sâu sắc tới thầy.
Tác giả xin chân thành cảm ơn toàn thể các thầy cô trong Khoa Toán Tin,
trường Đại học Khoa học - Đại học Thái Nguyên đã tận tình hướng dẫn,
truyền đạt kiến thức trong suốt thời gian theo học, thực hiện và hoàn thành luận văn.
Xin cảm ơn bạn bè, đồng nghiệp tại trường THPT Tiên Du số 1 và gia đình
thân yêu đã tạo điều kiện về thời gian và luôn ủng hộ tôi trong suốt quá trình học tập.
Thái Nguyên, tháng 05 năm 2018 Người viết luận văn Nguyễn Thị Nga Chương 1
Một số dạng của định lý lOMoARcPSD| 59629529 3 Stolz-Cesàro
Chương này trình bày một số kiến thức cơ bản, dạng cổ điển và một số
dạng mở rộng của định lý Stolz-Cesàro. 1.1
Một số kiến thức chuẩn bị 1.1.1 Dãy số
Định nghĩa 1.1.1. Dãy số là một hàm số từ N vào một tập hợp số (N, Q, R).
Các số hạng của dãy số thường được ký hiệu là un,vn,xn,yn ...Dãy số được ký
hiệu là {un}, {vn}, {xn}, {yn}....
Nhận xét 1.1.2. Vì dãy số là một trường hợp đặc biệt của hàm số nên nó cũng
có các tính chất của một hàm số.
Định nghĩa 1.1.3. (i) Dãy số {xn} được gọi là dãy giảm nếu xn+1 ≤ xn với mọi n ∈ N∗.
(ii) Dãy số {xn} được gọi là dãy tăng nếu xn+1 ≥ xn với mọi n ∈ N∗.
(iii) Dãy số {xn} được gọi là dãy giảm ngặt nếu xn+1 < xn với mọi n ∈ N∗.
(vi) Dãy số {xn} được gọi là dãy tăng ngặt nếu xn+1 > xn với mọi n ∈ N∗. Dãy số
tăng hoặc dãy số giảm được gọi chung là dãy đơn điệu.
Định nghĩa 1.1.4. Dãy số {xn} được gọi là bị chặn trên nếu tồn tại số thực M
sao cho xn ≤ M với mọi n. Dãy số {xn} được gọi là bị chặn dưới nếu tồn tại số
thực m sao cho xn ≥ m với mọi n. Một dãy số vừa bị chặn trên, vừa bị chặn
dưới được gọi là dãy bị chặn. lOMoARcPSD| 59629529 4
Định nghĩa 1.1.5. (i) Ta nói dãy số {xn} có giới hạn hữu hạn a khi n dần đến vô cùng nếu với mọi
, tồn tại số tự nhiên N0 (phụ thuộc vào dãy số
) sao cho với mọi n > N0 ta có |xn − a| nhỏ hơn . Ta viết (ii)
Dãy số {xn} dần đến dương vô cùng khi n dần đến vô cùng nếu với mọi
số thực dương M lớn tuỳ ý, tồn tại số tự nhiên N0 (phụ thuộc vào dãy số {xn}
và M) sao cho với mọi n > N0 ta có |xn| lớn hơn M. Ta viết
lim→∞ xn = +∞ ⇔ ∀M > 0,∃N0 ∈ N : ∀n > N0,|xn| > M. n
(iii) Dãy số có giới hạn hữu hạn được gọi là dãy hội tụ. Dãy số không cógiới
hạn hoặc dần đến vô cùng khi n dần đến vô cùng gọi là dãy phân kỳ.
Giả sử {xn} là một dãy bị chặn. Với mỗi n ta đặt
un = sup{xn+1,xn+2,...} = sup xn+k,
k=1,2,...
vn = inf{xn+1,xn+2,...} =
inf xn+k. k=1,2,...
Dễ thấy un đơn điệu giảm và bị chặn dưới, nên tồn tại giới hạn. Giới hạn này
được gọi là giới hạn trên của dãy {xn} và ký hiệu là limsupxn. n→∞
Tương tự, dãy {vn} là dãy tăng và bị chặn trên, nên tồn tại giới hạn. Giới hạn
này được gọi là giới hạn dưới của dãy {xn} và ký hiệu là .
Định lý 1.1.6. Điều kiện cần và đủ để dãy hội tụ là giới hạn trên và giới hạn
dưới của dãy đó bằng nhau.
Định lý 1.1.7. (Sự hội tụ của dãy đơn điệu)
Dãy số tăng và bị chặn trên thì hội tụ. Dãy số giảm và bị chặn dưới thì hội tụ.
Định lý 1.1.8. Nếu {xn}, {yn} là các dãy hội tụ và có giới hạn tương lOMoARcPSD| 59629529 5
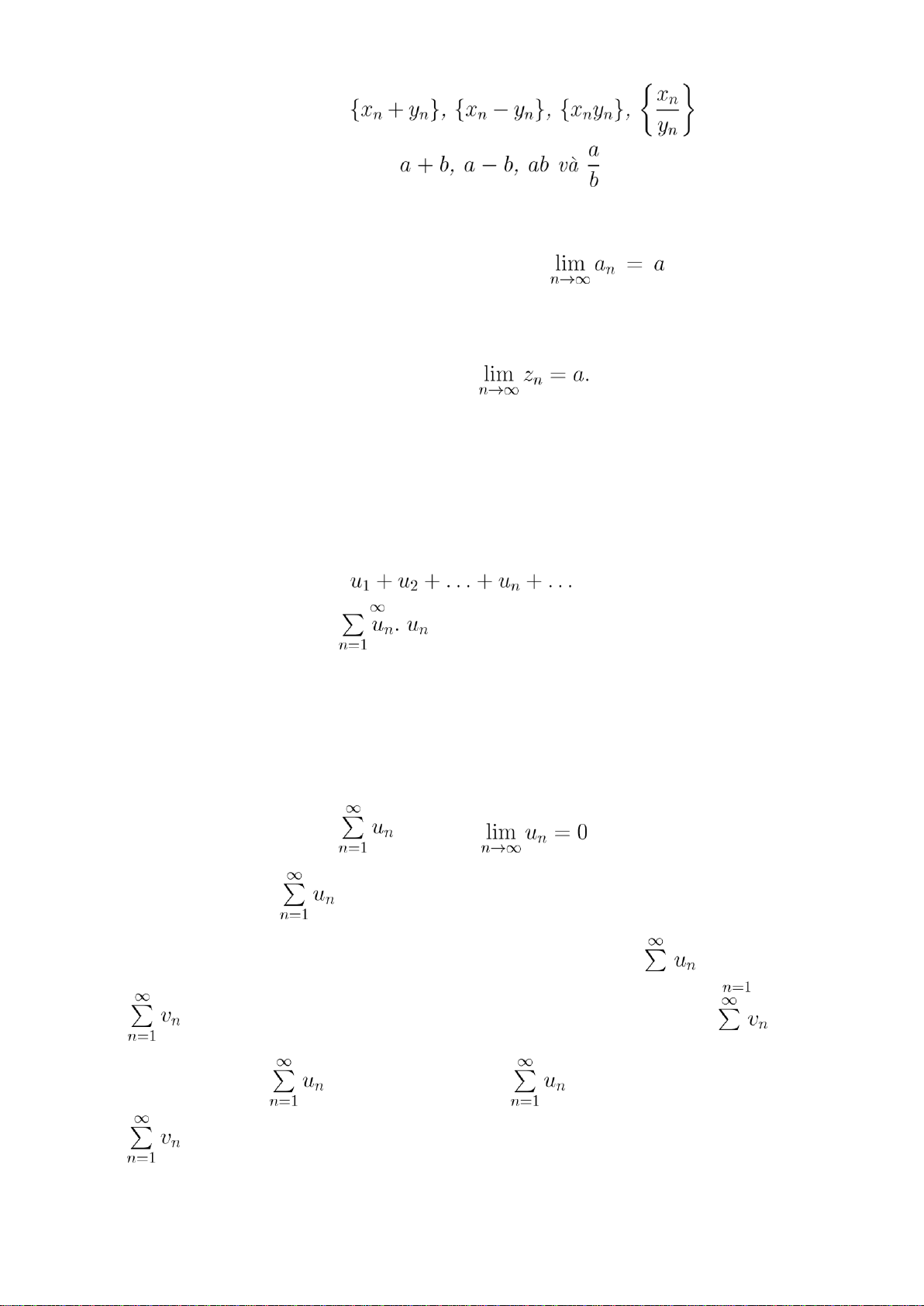
ứng là a,b thì các dãy số cũng hội
tụ và có giới hạn tương ứng là
(trong trường hợp dãy
số thương, ta giả sử yn và b khác không).
Định lý 1.1.9. Giả sử an ≤ bn ∀n ≥ N0, N0 ∈ N và
, lim bn = b. Khi
đó, ta có a ≤ b.
n→∞ Định lý 1.1.10 (Nguyên lý kẹp). Giả sử lim an = lim bn = a và n→∞ n→∞
an ≤ zn ≤ bn với mọi n ∈ N. Khi đó, ta có 1.1.2 Chuỗi số
Định nghĩa 1.1.11. Cho dãy số u1;u2;...;un;.... Khi đó gọi tổng vô hạn
là chuỗi số và ký hiệu là
là số hạng tổng quát; sn = u1 +u2 +
...+un được gọi là tổng riêng thứ n của chuỗi số; rn = un+1 +un+2 +... được gọi
là phần dư thứ n. Nếu lim sn = s (hữu hạn) thì chuỗi được gọi n→∞
là hội tụ và s là tổng của chuỗi. Nếu sn không dần tới một giá trị hữu hạn thì
chuỗi đó gọi là phân kỳ.
Định lý 1.1.12. Chuỗi số hội tụ thì . Chuỗi số
được gọi là chuỗi số dương nếu un > 0 với mọi n ∈ N.
Định lý 1.1.13. (Tiêu chuẩn so sánh) Cho 2 chuỗi số dương và
nếu un ≤ vn với ∀n ≥ n0(n0 ∈ N) thì từ sự hội tụ của suy n=1
ra sự hội tụ của
và từ sự phân kỳ của
suy ra sự phân kỳ của . lOMoARcPSD| 59629529 6
Định lý 1.1.14. (Tiêu chuẩn tương đương) Cho hai chuỗi số dương và . Khi đó, ta có: n=1 n
Nếu (0 < k < +∞) thì hai chuỗi đã cho cùng hội tụ hoặc cùng phân kỳ.
Nếu k = 0 thì từ sự hội tụ của
suy ra sự hội tụ của .
Nếu k = +∞ thì từ sự phân kỳ của
, ta suy ra sự phân kỳ của . 1.1.3 Hàm số
Cho hàm số thực f(x) xác định trên một miền trong R.
Định nghĩa 1.1.15. Cho hàm số y = f(x) có tập xác định D và (a;b) là một
khoảng con của D. Hàm số gọi là hàm số đồng biến trên khoảng (a;b) nếu
x1, x2 ∈ (a;b) : x1 ≤ x2 ⇒ f(x1) ≤ f(x2).
Hàm số nghịch biến trên khoảng (a;b) nếu
x1, x2 ∈ (a;b) : x1 ≤ x2 ⇒ f(x1) ≥ f(x2).
Hàm số đồng biến hoặc nghịch biến trên khoảng (a;b) gọi là đơn điệu trên khoảng (a;b).
Định nghĩa 1.1.16. Cho hàm số y = f(x) xác định trong một lân cận của a (có
thể trừ điểm a). Số thực l hữu hạn được gọi là giới hạn của hàm số f(x) khi x → a nếu: lOMoARcPSD| 59629529 7
Định nghĩa 1.1.17. Cho hàm số y = f(x) xác định trong một lân cận của a (có
thể trừ điểm a). Số thực l hữu hạn được gọi là giới hạn trái (phải) của hàm
số f(x) khi x → a nếu:
Định nghĩa 1.1.18. Cho hàm số y = f(x) xác định trong một lân cận của x0. Khi
đó hàm f(x) được gọi là liên tục tại x0 nếu lim f(x) = f(x0). x→x0
Định nghĩa 1.1.19. Hàm số y = f(x) được gọi là liên tục trái (phải) tại x0 nếu
hàm f(x) xác định trong một lân cận trái (phải) của x0 (kể cả x0) và
lim f(x) = f(x0)( lim f(x) = f(x0)). x→x−0 x→x0+
Định nghĩa 1.1.20. Hàm f(x) được gọi là liên tục trong khoảng (a;b) nếu f(x)
liên tục tại mọi x thuộc khoảng (a;b). Hàm f(x) được gọi là liên tục trên [a;b]
nếu f(x) liên tục trong khoảng (a;b), liên tục phải tại x = a và liên tục trái tại x = b.
Định nghĩa 1.1.21. Hàm f(x) được gọi là liên tục đều trên D nếu với mỗi ε >
0 tồn tại δ > 0 sao cho với mọi x,y ∈ D thỏa mãn |x − y| < δ ta có |f(x) − f(y)| < ε.
Định lý 1.1.22. Hàm f(x) liên tục trên tập compact D thì liên tục đều trên tập D.
Một hệ quả được suy ra từ định lý trên.
Hệ quả 1.1.23. Mọi hàm liên tục tuần hoàn trên R là liên tục đều.
Định lý 1.1.24 (Định lý giá trị trung gian). Cho f(x) là một hàm số liên tục trên
[a;b], f(a) 6= f(b). Khi đó f(x) đạt mọi giá trị trung gian giữa f(a) và f(b)
trên [a;b]. lOMoARcPSD| 59629529 8
Định nghĩa 1.1.25. Hàm f(x) được gọi là tuần hoàn với chu kỳ T > 0 trên miền
D nếu x ± T ∈ D với mọi x ∈ D và
f(x ± T) = f(x), ∀x ∈ D.
Định nghĩa 1.1.26. Cho hàm số y = f(x) xác định trong khoảng (a;b), x0 ∈
(a;b). Nếu giới hạn
tồn tại hữu hạn thì giá trị giới hạn đó được gọi là đạo hàm của hàm số y =
f(x) tại điểm x0, ký hiệu là f0(x0).
Định lý 1.1.27 (Định lý giá trị trung bình Cauchy). Cho các hàm số f và g cùng
liên tục trên [a;b] và khả vi trên (a,b). Khi đó tồn tại một điểm c ∈ (a;b) sao cho
(f(b) − f(a))g0(c) = (g(b) − g(a))f0(c). Nếu
g(a) 6= g(b) và g0(c) 6= 0, điều này tương đương với . 1.2
Một số dạng của định lý Stolz-Cesàro
Mục này trình bày một số dạng cổ điển, một số dạng mở rộng và một số
dạng mới của định lý Stolz-Cesàro. 1.2.1
Một số dạng cổ điển của định lý Stolz-Cesàro
Phần này, chúng tôi trình bày ba dạng cổ điển của định lý Stolz-Cesàro
được các nhà toán học Otto Stolz và Ernesto Cesàro đưa ra. lOMoARcPSD| 59629529 9
Định lý 1.2.1. Cho {an} và {bn} là hai dãy số thực, dãy {bn} tăng ngặt và không
bị chặn trên. Nếu tồn tại giới hạn , thì .
Chứng minh. Xét trường hợp l ∈ R và giả sử rằng {bn} là dãy tăng và lim bn =
∞. Cho V là một lân cận của l, khi đó tồn tại α > 0 sao cho n→∞
(l−α,l+α) ⊆ V . Cho β ∈ R sao cho 0 < β < α. Do nên tồn
tại k ∈ N∗ sao cho ∀n ≥ k thì , từ đó suy ra rằng:
(l − β)(bn+1 − bn) < an+1 − an < (l + β)(bn+1 − bn), ∀n ≥ k. Ta lại có:
(l − β)(bk+1 − bk) < ak+1 − ak < (l + β)(bk+1 − bk),
(l − β)(bk+2 − bk+1) < ak+2 − ak+1 < (l + β)(bk+2 − bk+1), ......
(l − β)(bn − bn−1) < an − an−1 < (l + β)(bn − bn−1).
Cộng từng vế các bất đẳng thức này ta được:
(l − β)(bn − bk) < an − ak < (l + β)(bn − bk).
Vì lim bn = ∞ nên bắt đầu từ một chỉ số n nào đó ta có bn > 0. Do đó n→∞ Do lOMoARcPSD| 59629529 10 ,
nên tồn tại một chỉ số p ∈ N∗ sao cho ∀n ≥ p chúng ta có: .
Do vậy chúng ta có các bất đẳng thức sau:
Chọn m = max{k,p}, khi đó, ∀n ≥ m chúng ta có: Điều này có nghĩa . Suy ra n
Trong trường hợp l = ±∞ ta có thể chứng minh tương tự khi ta chọn V =
(α,+∞) và V = (−∞,α).
Nhận xét 1.2.2. Dạng phát biểu đảo của định lý Stolz-Cesàro sẽ không còn
đúng, nghĩa là với giả thiết {bn} tăng, không bị chặn và thì chưa chắc có khẳng định
Để thấy điều này ta lấy an = 3n − (−1)n và bn = 3n + (−1)n, ta có và .
Dễ dàng chỉ ra rằng không tồn tại giới hạn .
Từ kết quả của định lý trên chúng ta thu được các hệ quả sau.
Hệ quả 1.2.3. Cho dãy số thực dương {un}. Nếu tồn tại giới hạn thì chúng ta có: lOMoARcPSD| 59629529 11 .
Chứng minh. Chúng ta có .
Đặt an = lnun và bn = n, áp dụng Định lý 1.2.1 cho hai dãy {an} và {bn} ta thu được Do đó √
lim √n u = lim eln √n un = enlim→∞ ln n un = elnl = l. n n→∞ n→∞
Nhận xét 1.2.4. Hệ quả trên còn được phát biểu dưới dạng tương đương sau:
Cho dãy số thực dương {un} với lim un = l. Khi đó chúng ta có n→∞ √
lim n u1u2 ...un = l. n→∞
Chứng minh. Đặt an = u1u2 ...un, ta có
Áp dụng Định lý trung bình nhân Stolz-Cesàro cho dãy {an} ta thu được
Từ đây về sau chúng ta gọi Hệ quả 1.2.3 và dạng phát biểu tương đương
của nó là Định lý trung bình nhân Stolz-Cesàro.
Hệ quả 1.2.5 (Định lý trung bình cộng Stolz-Cesàro). Cho dãy số {un},
. Khi đó chúng ta có lOMoARcPSD| 59629529 12
Chứng minh. Đặt an = u1 + u2 + ... + un và bn = n, ta có
Áp dụng Định lý 1.2.1 cho hai dãy {an} và {bn} ta thu được
Nhận xét 1.2.6. Bằng cách đặt vn = u1 + u2 + ... + un ta thu được phát biểu
dưới dạng tương đương với hệ quả trên như sau. Cho dãy số thực {vn}. Nếu
tồn tại giới hạn lim (vn+1 −vn) = l thì ta có n→∞ .
Từ đây về sau chúng ta gọi Hệ quả 1.2.5 và dạng phát biểu tương đương
của nó là Định lý trung bình cộng Stolz-Cesàro.
Tiếp theo chúng tôi trình bày một dạng khác của định lý Stolz-Cesàro.
Định lý 1.2.7 (Trường hợp ). Nếu {an} và {bn} là hai dãy số thực thỏa mãn
i. lim an = lim bn = 0, n→∞ n→∞
ii. {bn} là dãy số giảm, iii. , thì .
Chứng minh. Ta chia ba trường hợp sau: - Trường hợp 1:
. Khi đó, với bất kỳ , tồn
tại một chỉ số N sao cho
với mọi n ≥ N. Vì {bn} là dãy số giảm, nên bn+1 − bn < 0 với mọi n. Suy ra lOMoARcPSD| 59629529 13 ,
với mọi n ≥ N. Cố định số n, viết các bất đẳng thức trên tương ứng với n,n +
1,...,n + p, ta được ...... .
Cộng từng vế các bất đẳng thức trên ta nhận được .
Cho p → ∞, ta được .
Do vậy ta kết luận được rằng
với mọi n ≥ N. + Trường hợp 2: . Khi đó với , tồn tại một chỉ số N sao cho
với mọi n ≥ N.
Với m > n ≥ N ta có: , (1.1) và do đó
Giữ n cố định và cho
với mọi m > n ≥ N. Từ đó ta kết luận . lOMoARcPSD| 59629529 14 - Trường hợp 3:
. Trường hợp này được chứng minh
tương tự như ở Trường hợp 2.
Nhận xét 1.2.8. Dạng phát biểu đảo của Định lý 1.2.7 sẽ không còn đúng,
nghĩa là với giả thiết lim an = lim bn = 0, {bn} là dãy số giảm n→∞ n→∞ và
thì chưa chắc có khẳng định Thực vậy, chọn , ta có và .
Dễ dàng chỉ ra rằng không tồn tại giới hạn .
Dạng đảo của định lý Stolz-Cesàro được phát biểu như sau.
Định lý 1.2.9. Nếu {an} và {bn} là hai dãy số thực thỏa mãn
i. {bn} là dãy số dương, tăng ngặt và không bị chặn trên. ii. , iii. , Khi đó, .
Chứng minh. Chúng ta có
Lấy qua giới hạn hai vế của đẳng thức trên ta thu được: Suy ra . lOMoARcPSD| 59629529 15 1.2.2
Một số dạng mở rộng của định lý Stolz-Cesàro
Phần đầu của mục này chúng tôi trình bày một số mở rộng của định lý
Stolz-Cesàro được đưa ra bởi Gabriel Nagy ([9]).
Định lý mở rộng của Định lý 1.2.1 được phát biểu như sau.
Định lý 1.2.10. Nếu {bn} là dãy số thực dương sao cho , thì với
bất kì dãy {an} ⊂ R ta có các bất đẳng thức ; (1.2) . (1.3)
Đặc biệt, nếu dãy
có giới hạn, thì .
Chứng minh. Ta chỉ cần chứng minh (1.2), bất đẳng thức (1.3) được chứng
minh bằng cách thay thế an bởi −an.
Bất đẳng thức (1.2) là tầm thường, nếu vế phải là +∞. Giả sử rằng giá trị
là hữu hạn hoặc −∞. Lấy l > L, theo định nghĩa
của limsup, tồn tại một số chỉ số k ∈ N sao cho (1.4)
Sử dụng (1.4) ta có bất đẳng thức a1+a2+...+an ≤ a1+...+ak
+l(bk+1+bk+2+...+bn),∀n > k. (1.5)
Đặt a1 + a2 + ... + an = An và b1 + b2 + ... + bn = Bn, bất đẳng thức trên trở thành
An ≤ Ak + l(Bn − Bk),∀n > k. lOMoARcPSD| 59629529 16
Chia hai vế của bất đẳng thức trên cho Bn ta được . (1.6)
Vì Bn → ∞, cố định k lấy giới hạn cận trên trong (1.6) ta nhận được
. Nói cách khác, ta được bất đẳng thức suy ra
Để thấy rõ định lý trên là mở rộng của Định lý 1.2.1 chúng ta phát biểu lại
dưới dạng tương đương sau. Định lý 1.2.11. Nếu {yn} là dãy tăng ngặt với
lim yn = ∞, thì với bất n→∞
kì dãy {xn} có các bất đẳng thức sau ; (1.7) . (1.8)
Đặc biệt, nếu dãy có giới hạn thì .
Chứng minh. Do lim yn = ∞, không mất tính tổng quát ta giả sử tất cả n→∞
các yn đều dương. Xét các dãy {an} và {bn}, xác định bởi a1 = x1,b1 = y1 và an
= xn −xn−1,bn = yn −yn−1,∀n ≥ 2, khi đó ta có xn = a1 +...+an và yn = b1 + ... + bn.
Như vậy định lý được chứng minh.
Từ kết quả mở rộng trên chúng ta thu được các hệ quả sau.
Hệ quả 1.2.12. Bất kì dãy {an} ⊂ R ta có các bất đẳng thức sau