Một số phương pháp chứng minh bất đẳng thức

Tài liệu gồm 78 trang, hướng dẫn một số phương pháp chứng minh bất đẳng thức, đây thường là bài toán khó nhất trong các đề thi tuyển sinh vào lớp 10 môn Toán.

58 29 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

BẤT ĐẲNG THỨC

I. BẤT ĐẲNG THỨC CÔSI .............................................................................................................................. 2

DẠNG 1: DẠNG TỔNG SANG TÍCH ........................................................................................................... 2

DẠNG 2: DẠNG TÍCH SANG TỔNG, NHÂN BẰNG SỐ THÍCH HỢP. ................................................ 3

DẠNG 3: QUA MỘT BƢỚC BIẾN ĐỔI RỒI SỬ DỤNG BẤT ĐẲNG THỨC CÔSI .............................. 4

DẠNG 4: GHÉP CẶP ĐÔI ............................................................................................................................... 7

DẠNG 5: DỰ ĐOÁN KẾT QUẢ RỒI TÁCH THÍCH HỢP ........................................................................ 7

DẠNG 6: KẾT HỢP ĐẶT ẨN PHỤ VÀ DỰ ĐOÁN KÊT QUẢ ............................................................... 10

DẠNG 7: TÌM LẠI ĐIỀU KIỆN CỦA ẨN .................................................................................................... 13

II. BẤT ĐẲNG THỨC BUNHIA ................................................................................................................... 15

III. PHƢƠNG PHÁP BIẾN ĐỔI TƢƠNG ĐƢƠNG ................................................................................... 18

DẠNG 1: ĐƢA VỀ BÌNH PHƢƠNG ............................................................................................................ 18

DẠNG 2: TẠO RA BẬC HAI BẰNG CÁCH NHÂN HAI BẬC MỘT .................................................... 20

DẠNG 3: TẠO RA ab+bc+ca .......................................................................................................................... 22

DẠNG 4: SỬ DỤNG TÍNH CHẤT TRONG BA SỐ BẤT KÌ LUÔN TÒN TẠI HAI SỐ CÓ TÍCH

KHÔNG ÂM..................................................................................................................................................... 22

DẠNG 5: SỬ DỤNG TÍNH CHẤT CỦA MỘT SỐ BỊ CHẶN TỪ 0 ĐẾN 1 ............................................ 25

DẠNG 6 : DỰ ĐOÁN KẾT QUẢ RỒI XÉT HIỆU ...................................................................................... 27

HỆ THỐNG BÀI TẬP SỬ DỤNG TRONG CHỦ ĐỀ ................................................................................. 75

I. BẤT ĐẲNG THỨC CÔSI ....................................................................................................................... 75

II. BẤT ĐẲNG THỨC BUNHIA ............................................................................................................... 77

III. PHƢƠNG PHÁP BIẾN ĐỔI TƢƠNG ĐƢƠNG ................................................................................... 77

I. BẤT ĐẲNG THỨC CÔSI

1. Dạng hai số không âm

,xy

 Dạng tổng sang tích:

2x y xy

 Dạng tích sang tổng:





hay











 Dạng lũy thừa:

2x y xy

hay





Dấu

""

xảy ra

xy

 Dạng đặc biệt:





2. Dạng ba số không âm

,,x y z

 Dạng tổng sang tích:

3x y z xyz  

 Dạng tích sang tổng:

x y z

xyz





hay

x y z

xyz











 Dạng lũy thừa:

3 3 3

3x y z xyz  

hay

3 3 3

x y z

xyz





Dấu

""

xảy ra

x y z  

 Dạng đặc biệt:

.1.1





3. Dạng tổng quát với

số không âm

, ,...,

x x x

 Dạng tổng sang tích:

1 2 1 2

... ...

x x x n x x x   

 Dạng tích sang tổng:

...

x x x

  



hay

...

x x x

  









 Dạng lũy thừa:

1 2 1 2

... ...

n n n

x x x x x x   

hay

...

n n n

x x x

  



Dấu

""

xảy ra

...

x x x   

 Dạng đặc biệt:

.1.1...1







4. Bất đẳng thức trung gian



1 1 4

0, 0xy

x y x y

    



. Dấu

""

xảy ra

xy



1 1 1 9

0, 0, 0x y z

x y z x y z

      



. Dấu

""

xảy ra

x y z  

DẠNG 1: DẠNG TỔNG SANG TÍCH

Ví dụ 1. Cho

0x 

. Tìm giá trị nhỏ nhất của biểu thức

8 4 15

T x x

   

Lời giải

Có

 

4 4 1 4 14

T x x x



     





 

2 1 4 14 0 2 4 . 14 16

x x x



        





Vậy

16MinT 

khi

x 

Ví dụ 2. Cho

0x 

. Tìm giá trị nhỏ nhất của biểu thức

4 3 2011

M x x

   

Lời giải

Có

4 4 1 2010

M x x x

     

 

2 1 2010 0 2 . 2010 2011

x x x



        





Vậy

2011MinM 

khi

x 

Ví dụ 2. Cho

0xy

và

2xy 

. Tìm giá trị nhỏ nhất của biểu thức







Lời giải

Có

 

x y xy xy

x y x y



  





   

2 . 4x y x y

x y x y

     



Vậy

4MinH 

khi

2 3 1

2 2 0

x y x







   







  

   



  













DẠNG 2: DẠNG TÍCH SANG TỔNG, NHÂN BẰNG SỐ THÍCH HỢP.

Ví dụ 1: Cho a ≥ 1, b ≥ 1. Chứng minh :

11a b b a ab   

Lời giải

Có

1 ( 1)

1 1.( 1) 1 ;

2 2 2

b b ab

b b a b



       

V| tƣơng tự:

1 1 1

2 2 2

ab ab ab

b a a b b a ab         

đpcm

Dấu ‘=” xảy ra khi a = b = 2

Ví dụ 2: Cho a ≥ 9, b≥ 4, c≥ 1. Chứng minh:

1 9 4

abc

ab c bc a ca b     

Lời giải:

Có:

1 9 4 ( 1).1 . ( 9).9 . ( 4).4

( 1) 1 ( 9) 9 ( 4) 4 11

. . .

2 3 2 2 2 12

bc ca

ab c bc a ca b ab c a b

c bc a ca b abc

          

     

   

Dấu “=” xảy ra khi a = 18, b = 8, c = 2

Ví dụ 3: Cho a ≥ 0, b ≥ 0, a

+ b

≤ 2. Tìm gi{ trị lớn nhất của biểu thức: M =

( 2 ) ( 2 )a b a b b a b a  

Lời giải

Xét:

2 2 2 2

3 ( 2 ) 3 ( 2 )

. 3 . 3 ( 2 ) 3 ( 2 ) . . 5

2 2 2

5. 6 2 3

b a b a b a a b

M a b a b b a b a a b ab

a b a b

    

       



    

Vậy MaxM = 2

khi a = b = 1

Ví dụ 4. Cho

0x 

0y 

và

2xy

. Tìm giá trị lớn nhất của biểu thức

   

14 10 14 10P x x y y y x   

Lời giải

Xét:

   

. 24 24 14 10 24 14 10P x x y y y x   

   

 

24 14 10 24 14 10

24 .1 .1

x x y y y x

   

   

2 2 2 2

1 1 1 48

24 24 48 4 6

2 2 2

x y x y

   

   

       

   

   

Vậy

Max 4 6P 

khi

1xy

Ví dụ 5. Cho

0x 

0y 

và

 

xy x y x y  

. Tìm giá trị nhỏ nhất của

P x y

Lời giải

Từ

 

xy x y x y x y    

và

   

     

2 2 2 4

xy x y x y

x y xy x y xy x y

  

      

   

4 0 4x y x y x y       

Dấu "=" xảy ra khi

   

x y xy x y xy

x y x y







   





  



   









là hai nghiệm phƣơng trình

4 2 0 2 2t t t     

22x y x   

22y 

Vậy

4MinP 

khi

22x 

22y 

DẠNG 3: QUA MỘT BƯỚC BIẾN ĐỔI RỒI SỬ DỤNG BẤT ĐẲNG THỨC CÔSI

Ví dụ 1. Cho

0c 

và

1ab bc ac  

. Tìm giá trị lớn nhất của biểu thức:

2 2 2

1 1 1

abc

  

  

Lời giải

Thay

1 ab bc ac  

, ta đƣợc:

2 2 2

abc

a ab bc ac b ab bc ac c ab bc ac

  

        

        

abc

a b a c b a b c c a c b

  

     

. . .

a a b b c c

a b a c b a b c c a c b

  

     

2 2 2

a a b b c c

a b a c b a b c c a c b

  

     

  

a b a c b c

a b a b a c a c b c b c

     

    

     

     

     



Vậy

MaxP 

khi

abc  

Ví dụ 2. Cho các số dƣơng

thỏa mãn

1abc  

. Chứng minh:

ab bc ca

c ab a bc b ca

  

  

Lời giải

Ta có

.1 .1 .1

ab bc ca ab bc ca

c ab a bc b ca c ab a bc b ca

    

     

     

ab bc ca

c a b c ab a a b c bc b a b c ca

  

        

        

ab bc ac

a c b c a b a c b c b a

  

     

. . .

a b b c c a

a c c b a b a c b c b a

  

     

a b b c c a

c a c b a b a c b c a b



     

      

     



     

     



( đpcm).

Ví dụ 3. Cho

0a 

0b 

0c 

và

3ab bc ac abc  

. Tìm giá trị nhỏ nhất của

     

222

2 2 2 2 2 2

a b c

c c a a a b b b c

  

  

Lời giải

Có

     

222

2 2 2 2 2 2

a b c

c c a a a b b b c

  

  

     

2 2 2 2 2 2 2 2 2

2 2 2 2 2 2

a c c b a a c b b

c c a a a b b b c

     

  

  

2 2 2 2 2 2

1 1 1c a b

c c a a a b b b c

     

     

     

  

     

2 2 2 2 2 2

1 1 1

2 2 2

c a b

c a a b b c

     

     

     

     

1 1 1 1 1 1 1 1 1 1 3

2 2 2 2 2 2

ab bc ac

c a a b b c a b c abc



       

          

       

       

Vậy

MinP 

khi

1abc  

Ví dụ 4. Cho

0a 

0b 

0c 

và

1abc  

. Tìm giá trị nhỏ nhất của biểu thức

2 2 2

1 9 1 9 1 9

a b c

b c a

  

  

Lời giải

Có

     

2 2 2 2 2 2

2 2 2

1 9 9 1 9 9 1 9 9

1 9 1 9 1 9

a b ab b c bc c a ca

b c a

     

  

  

2 2 2

9 9 9

1 9 1 9 1 9

ab bc ca

a b c

b c a

     

     

     

  

     

2 2 2

9 9 9

2 1.9 2 1.9 2 1.9

ab bc ca

a b c

b c a

     

     

     

     

   

3 1 1

2 2 2

a b c ab bc ac a b c a b c            

 

do 1abc  

Vậy

MinT 

khi

abc  

Ví dụ 5. Cho

0c 

và

1 1 1

1 1 1abc

  

  

. Chứng minh:

abc 

Lời giải

Có

1 1 1

1 1 1abc

  

  

  

cos

1 1 1

1 1 2 . 2

1 1 1 1 1 1 1 1 1

b c b c bc

a b c b c b c b c

   

        

   

        

   

Tƣơng tự:

  

1 1 1

b a c



  

;

  

1 1 1

c a b



  

Nhân các bất đẳng thức dƣơng, cùng chiều ta đƣợc:

       

1 1 1 1 1 1

abc

a b c a b c



     

hay

abc 

(đpcm).

DẠNG 4: GHÉP CẶP ĐÔI

Tách

     

1 1 1

2 2 2

x y z x y y z z x       

..xyz xy yz zx

, , 0x y z

Ví dụ 1. Cho

0a 

0b 

0c 

và

2 2 2

1abc  

. Chứng minh:

ab bc ac

abc

c a b

    

; b)

bc ca ab

a b c

  

Lời giải

a) Có

1 1 1

2 2 2

ab bc ac bc ca ca ab ab bc

c a b a b b c c a

     

       

     

     

1 1 1

.2 . . . . .

2 2 2

bc ca ca ab ab bc

abc

a b b c c a

     

(đpcm).

b) Xét

 

2 2 2 2 2 2

2 2 2

bc ca ab b c c a a b

abc

a b c a b c



       





2 2 2 2 2 2 2 2 2 2 2 2

2 2 2 2 2 2

1 1 1

2 2 2

b c c a c a a b a b b c

a b b c c a

     

      

     

     

2 2 2 2 2 2 2 2 2 2 2 2

2 2 2 2 2 2

1 1 1

.2 . .2 . .2 .

2 2 2

b c c a c a a b a b b c

a b b c c a

  

2 2 2

23abc    

, do đó

bc ac ab

  

(đpcm).

Ví dụ 2. Cho

,,abc

l| độ d|i ba cạnh của

ABC

. Chứng minh

( )( )( )a b c b c a c a b abc      

Lời giải

Vì

,,abc

l| độ d|i ba cạnh của

ABC

nên

a b c 0,b c a 0,c a b 0        

Có

( ) ( )

0 ( )( )

a b c b c a

a b c b c a b

    

      

;

( ) ( )

0 ( )( )

b c a c a b

b c a c a b c

    

      

;

(c a b) (a b c)

0 (c a b)(a b c) a

    

      

;

Nh}n ba đẳng thức dƣơng cùng chiều ta đƣợc

( )( )( )a b c b c a c a b abc      

(điều phải chứng minh).

DẠNG 5: DỰ ĐOÁN KẾT QUẢ RỒI TÁCH THÍCH HỢP

Bước 1: Kẻ bảng dự đoán giái trị lớn nhất,nhỏ nhất và đạt tại giá trị nào của biến.

Bước 2: Kẻ bảng xác định số nào sẽ đi với nhau.

Bước 3: Tách ghép thích hợp số hạng và sử dụng bất đẳng thức Cô-si.

Ví dụ 1. Cho

2a 

. Tìm gi{ trị nhỏ nhất của biểu thức

2Pa



Lời giải

Phân tích bài toán

6,5



7,7



9,25



Từ bảng thứ nhất dự đo{n

min 2

Pa  

2a 

Từ bảng thứ hai, ta suy ra

sẽ đi với

nên

sẽ đi với

Trình bày lời giải

Có

5 5 3 5 5 3 3 3.2 13

2 5 5 ( do 2)

4 4 4 4 4 4 2

a a a a a



           





Vậy

min

P 

khi

















(thỏa mãn).

Ví dụ 2. Cho

0, 0xy

và

6xy

. Tìm gi{ trị nhỏ nhất của biểu thức

6 24

F x y

   

Lời giải

Phân tích bài toán

( ; )xy

(1 ; 5)

(2 ; 4)

(3 ; 3)

(4 ; 2)

(5 ; 1)

16,8



19,5



156

31,2



Từ bảng thứ nhất, ta dự đo{n

min 15F 

khi

2, 4xy

Từ bảng thứ hai, ta suy ra

sẽ đi với

nên

sẽ đi với



;

sẽ đi với

nên

sẽ đi với

24 3

16 4



Trình bày lời giải

Có

6 3 24 3

2 2 2 2

6 3 24 3 1 1

2 2 ( ) 18 ( )

2 2 2 2

18 6 15 (do 6).

x y x y



   

     



   

   



        

     

Vậy

6 3 24 3

min 15 khi ; ; 6

F x y





     







(thỏa mãn).

Ví dụ 3. Cho

0, 0xy

và

3xy

. Tìm gi{ trị nhỏ nhất của biểu thức

28 1

2P x y

   

Lời giải

Phân tích bài toán

 

;xy

 

1;2

 

2;1

34,5



Từ bảng thứ nhất, ta dự đo{n

min 24 khi 2, 1P x y  

2, 1xy

Từ bảng thứ hai, ta suy ra

sẽ đi với

nên

sẽ đi với

x

;

se đi với

Trình bày lời giải

Có

28 1

7 2 7

28 1

7 2( 2) ( 1) ( ) 9

28 1

2 7 2 0 0 3 9 24.

P x y x y x y

x y x y x y



       







          





        

Vậy

28 1

min 24 khi 7 ; ; 2 0; 1 0; 3 2, 1P x y x y x y x y

           

Ví dụ 4. Cho

2 3,4 6,4 6x y z     

và

12x y z  

. Tìm giá trị lớn nhất của biểu thức

P xyz

Lời giải

Nhận xét: Do

và

vai trò nhƣ nhau nên sử dụng bất đẳng thức Cô-si đối với tích

, ta đƣợc

( ) (12 )(12 )

P x yz x x x x





    





Đến đ}y ta kẻ bảng để dự đo{n gi{ trị lớn nhất của

243

60,75



Từ bảng thứ nhất dự đo{n

243

max

P 

khi

3x 

12 x

3x 

Từ bảng thứ hai, ta suy ra

sẽ đi với

12 x

nên ta biến đổi

1 1 24 1 3 24 243

[(3 )(12 )(12 )]

12 12 3 12 3 4

P x x x



   

     

   

   

Vậy

243 9

max khi 3,

P x y z   

DẠNG 6: KẾT HỢP ĐẶT ẨN PHỤ VÀ DỰ ĐOÁN KÊT QUẢ

 Khi đặt ẩn phụ ta cần tìm điều kiện của ẩn phụ.

 Một số bất đẳng thức trung gian thƣờng dùng:

 Với mọi

,ab

thì

 

2 2 2

2 ( ) 4a b a b ab   

. Dấu bằng xảy ra khi

ab

 Với mọi

,,abc

thì

 

2 2 2 2

3 ( ) 3( )a b c a b c ab bc ca       

. Dấu bằng xảy ra khi

abc

 Với mọi

,ab

thì

2 2 3 3

, ; 0

2 2 2 2

a b a b a b a b

a b a b

   

   

     

   

   

. Dấu bằng xảy ra khi

ab



1 1 4

0, 0ab

a b a b

    



. Dấu bằng xảy ra khi

ab



1 1 1 9

0, 0, 0abc

a b c a b c

      



. Dấu bằng xảy ra khi

abc

Ví dụ 1. Cho

0, 0xy

và



. Tìm giá trị nhỏ nhất của biểu thức

2xy



Lời giải

Đặt

, do

8 8 1 1

2 2 . 4 0

2 2 4 4

x x x x

y y y y

Có

2 2 2

32 31 2 .32 31

1 33 1

16 31 16 31. 0

4 4 4

K a a a a a

a a a

a do a

Vậy

33 1

2, 8.

MinK khia hay x y

Ví dụ 2. Cho

0, 0xy

. Tìm giá trị nhỏ nhất của biểu thức

xy x y

Đặt

xy x y

xy x y a

3( ) 1 3 3m n p mn np pm x y xy x y a

Vậy

MinA khia x y

Ví dụ 3. Cho

0, 0xy

. Tìm giá trị nhỏ nhất của

xy x y

Lời giải

Có

x y xy x y

xy xy xy

xy x y xy x y x y

Đặt

, 2 2 2

x y x y

t do x y xy t

xy xy

Ta đƣợc

Cos

2 2 2

1 1 7 1 7

2 2 2 . 2

8 8 8 8

A t t t

t t t

7 2 7 5

2 .2 2

2 8 2 8 2

(do

Vậy

MinA

khi

2t x y

Ví dụ 4. Cho

0, 0, 0abc

thỏa mãn

2 2 2

b c a

. Tìm giá trị nhỏ nhất của biểu thức

2 2 2

1 1 1

P b c a

a b c

Lời giải

Có

2 2 2

2 2 2 2 2

1 1 1 2 2

bc a bc a

P b c a

a b c a bc a bc

Dặt

2 2 2

a b c bc

bc bc bc

ta đƣợc

1 1 3 1 3

2 2 2 2 .

4 4 4 4

t t t t

t t t

3 3.2

2 1 2 1 5

(do

Vậy

5MinP

khi

2 2 2

b c a

Ví dụ 5. Cho

0, 0xy

và

1xy

. Tìm giá trị nhỏ nhất của biểu thức

.1P x y

Lời giải

Có

1 1 1

2 . . 1 2

P x y xy

x y x y

Đặt

a xy

, do

2 4 4

xy a

, ta đƣợc

1 1 1 1 1

2 2 16 15 2 2 .16 15 2 8 15 2. 8 15. 17 0

P a a a a a a do a

a a a

MinP khia hay x y

Ví dụ 6: Cho

0,y 0x

và

1xy

. Tìm giá trị nhỏ nhất của biểu thức

4P xy

x y xy

Lời giải

Có

1 1 1

P xy

x y xy xy

Sử dụng

1 1 4

,0ab

a b a b

, ta đƣợc

2 2 2 2 2 2

1 1 4 4 4

4( 0 1)

2 2 ( ) 1

do x y

x y xy x y xy x y

. Suy ra

4 4 .

P xy

Đặt a = xy,

2 4 4

do xy a

ta đƣợc

1 1 1 1 1

4 4 4 8 4 4 2 .8 4 8 4 8 4. 7( 0 )

2 2 2 4 4

P a a a a a a do a

a a a

MinP khi x y

Ví dụ 7: Cho x,y >0 và

1xy

. Tìm giá trị nhỏ nhất của biểu thức

K x y

Lời giải

Cách 1: Sử dụng

a b a b

và

1 1 4

, 0.ab

a b a b

ta đƣợc

2. 2.

2 2 2

K x y

Đặt

a x y

, điều kiện

01a

, ta đƣợc:

1 4 1 1 3 1 1 3

2 2 2

K a a a

a a a a a

1 3 1 3 25

2 . 2

2 2 1 2a

(do

01a

). Vậy,

MinK

khi

Cách 2:

1 1 1 1 1

4 2. 4.K x y x y xy

x y x y xy

Đặt

,a xy

2 4 4

xy a

Ta đƣợc:

1 15 1 15 25

2. 4 2. 4

2 4 2 2

0 .

do a

Vậy,

MinK

khi

Ví dụ 8: Cho

0, 0xy

và

1.xy

Tìm giá trị nhỏ nhất của biểu thức

11S x y

Lời giải

Sử dụng

a b a b





   





và

1 1 4

+ 0ab

a b a b

   



, ta đƣợc

2. 2



    













Đặt

a x y

, điều kiện

01a

, ta đƣợc

3 3 3

1 4 1 1 3 1 1 3 1 3 1 3 343

2 2 2 2 . 4 4

4 4 4 4 4 1 4

S a a a

a a a a a a



       

              



       



       



Vậy

343

MinS



khi

xy

DẠNG 7: TÌM LẠI ĐIỀU KIỆN CỦA ẨN

Ví dụ 1. Cho

,0xy

và

2 2 2 8x xy y x   

. Tìm giá trị nhỏ nhất của biểu thức

23P x y

   

Lời giải

Có

2 2 2 2 2

2 2 2 8 2 2 1 9x xy y x x xy y x x          

   

19x y x    

, mà

     

2 2 2

1x y x y x    

 

9 0 3x y x y      

Có

2 4 2 4

2 4 4 2 .2 2 . 4( )P x y x y x y x y

x y x y



         





8 4( ) 8 4.3 4xy      

(do

03xy  

). Vậy

MinP 4

khi

1, 2xy

Ví dụ 2: Cho

0, 0, 0abc

thỏa mãn

2 2 2

2 3 3b bc c a

. Tìm giá trị nhỏ nhất của biểu

thức

2 2 2

T a b c

a b c

Lời giải

Có

2 2 2 2 2 2

2 3 3 3 2 2 2 9b bc c a a b bc c

2 2 2

3 2 2 2 2 2 2 2 9a b bc ab ac c ab ac

2 2 2 2 2 2 2

2 2 2 2 2 9a b c ab bc ca a b ab a c ac

2 2 2 2

9 9 0 3a b c a b a c a b c a b c

Sử dụng

1 1 1 9

a b c a b c

ta đƣợc

T a b c

abc

Đặt

, 0 3x a b c x

, ta đƣợc

18 18 18

2 2 .2 12 12 3 9T x x x x x x

x x x

(do

03x

)

Vậy

9MinT

khi

hay

1abc

Ví dụ 3: Cho

0, 0ab

và

68a b ab

. Tìm giá trị nhỏ nhất của biểu thức:

P ab

a b ab

Lời giải

Có

3 3 3 3 2 2 2 2

6 8 3 3 3 3 6 8a b ab a b a b ab a b ab ab

3 2 8 2 3 2 0a b ab a b a b ab a b

2 2 4 3 2 0a b a b a b ab a b

2 2 2 4 0a b a b ab a b

2 2 2 2 4 4 8 0a b a b ab a b

2 2 2

2 2 2 0a b a b a b

02ab

Có

1 1 5

P ab

a b ab ab

Sử dụng

1 1 4

,0xy

x y x y

, ta đƣợc:

2 2 2 2 2

1 1 1 4 4

2 2 2a b ab a ab b

(do

02ab

)

Suy ra

P ab

Đặt

x ab

, do

1 0 1

ab x

, ta đƣợc:

5 5 5 3

2 2 2 2

5 5 3 3 3.1 9

1 2 . 6 6

2 2 2 2 2 2

x x x

(do

01x

)

Vậy

MinP

khi

1ab

Ví dụ 4: Cho

0, 0ab

và

a b a b

. Tìm giá trị nhỏ nhất của biểu thức

2020

P a b

Lời giải

Sử dụng

x y x y

, ta đƣợc

2. 2 1 0 2

2 2 2 2

a b a b a b

2 2 2

2020 2020 2020

2. 2

2 2 2

a b a b a b

Đặt

, ),0 4x a b x

, ta đƣợc:

2020 8 2012 8 2012

2 2 2

x x x

x x x x x

2012 2012

4 4 50

(do

04x

)

Vậy

507MinP

khi

hay

1ab

Ví dụ 5: Cho

0, 0xy

và

1 1 4xy

. Tìm giá trị nhỏ nhất của biểu thức

Lời giải

Có

1 1 4 3 3 .1 .1x y xy x y xy x y

Mà

.1 .1 1

2 2 2

x y x y

xy x y x y

, suy ra

2xy

Có

2 2 2 2

x y x y

P y x x y

y x y x

2 . 2 . 2

y x x y x y

Vậy

2MinP

khi

1xy

II. BẤT ĐẲNG THỨC BUNHIA

1. Dạng bộ hai số

;ab

và

;xy

bất kỳ



2 2 2 2

ax by a b x y

Dấu

xảy ra

 Đặc biệt

2 2 2 2

1. 1. 1 1x y x y x y

2. Dạng bộ ba số

;;abc

và

;y;zx

bất kì



2 2 2 2 2 2

ax by cz a b c x y z

Dấu

xảy ra

x y z

a b c

 Đặc biệt

2 2 2 2 2 2

1. 1. 1. 1 1 1x y z x y z x y z

3. Dạng tổng quát bộ n số

; ; ;

a a a

và

; ; ;

x x x



2 2 2 2 2 2

1 1 2 2 1 2 1 2n n n n

a x a x a x a a a x x x

Dấu

xảy ra

a a a

Quy ƣớc trong dấu

xảy ra, nếu mẫu nào bằng 0 thì tử tƣơng ứng bằng 0.

Ví dụ 1. Cho 4x + 9y = 13. Tìm giá trị nhỏ nhất của biểu thức A = 4x

+ 9y

Lời giải

Có 13

= (4x + 9y)

= (2.2x + 3.3y)

Bunhia



+ 3

)(4x

+ 9y

) = 13A

A 13

Ví dụ 2. Cho 4x + 3y = 1. Tìm giá trị nhỏ nhất của biểu thức A = 4x

+ 3y

Lời giải

Có 1

= (4x + 3y)

= (2.2x +

3 . 3

Bunhia



(4 + 3)(4x

+ 3y

) = 7A



Vậy MinA =

khi

2x 3x

x = y =

4x + 3y = 1













Ví dụ 3. Cho x ≥ 0; y ≥ 0; z ≥ 0 v| x + y + z = 2. Tìm giá trị nhỏ nhất của biểu thức A = x

+ y

+ z

Lời giải

Có 2

= (1.x + 1.y + 1.z)

Bunhia



+ 1

)( x

+ y

+ z

) = 3A



Vậy MinA =

khi

x = y =

1 1 1

x + y + z = 2















Ví dụ 4. Cho 3x

+ 2y

. Tìm giá trị nhỏ nhất của biểu thức A = 2x + 3y

Lời giải

Có S

= (2x + 3y)

. 3x + . 2y







Bunhia



   

2 2 2 2

4 9 35 35 6

+ 3x +2y = 3x +2y . =1 S 1

3 2 6 6 35



  





Vậy MaxS = 1

4y 4

3x 2

3x 2y

x = x =

9 35

8y 9

2x + 3y = 1

+ 3y = 1 y =

2x + 3y = 1

9 35











   

   

   

   











Ví dụ 5. Cho 4a

+ 25b

≤

. Tìm giá trị nhỏ nhất của biểu thức H = 6a – 5b

Lời giải

Có H

= (6a – 5b)

= (3.2a + (–1) .5b)

Bunhia



(9 + 1)(4a

+ 25b

) = 10(4a

+ 25b

) ≤ 10.

= 1



H ≤ 1

Vậy MaxH = 1

2a 5b

a =

2a + 15b = 0

3 -1

18a - 15b = 3 1

6a - 5b = 1

b = -









  

  











Ví dụ 6. Cho x

+ y

+ z

. Tìm giá trị lớn nhất của biểu thức P = x + y + z

Lời giải

Có P

= (1.x + 1.y + 1.z)

Bunhia



+ 1

)(x

+ y

+ z

) = 3.



P ≤

Vậy MaxP =

khi

1 1 1

x = y = z =

x + y + z =















Ví dụ 7. Tìm giá trị lớn nhất của biểu thức

P = x - 1 + 3 - x

khi 1 ≤ x ≤ 3

Lời giải

Có P

 

1. x - 1 + 1. 3 - x

Bunhia



 





x - 1 + 31 1 - x

= 4



P ≤ 2

Vậy MaxP = 2 khi

xx





x = 2 (thỏa mãn)

Ví dụ 8. Cho a ≥ 0, b ≥ 0, c ≥ 0 v| a + b + c = 3. Tìm gi{ trị lớn nhất của biểu thức

K = 4a + 5 + 4b + 5 + 4c + 5

Lời giải

Có K

 

1. 4a + 5 + 1. 4b + 5 + 1. 4c + 5

Bunhia



+ 1

)( 4a + 5 + 4b + 5 + 4c + 5)

= 3[4(a + b + c) + 15] = 3(4.3 + 15) = 81



K ≤ 9

Vậy MaxK = 9 khi

4a + 5 4b + 5 4c + 5

a = b = c = 1

111

a + b + c = 3













Ví dụ 9. Cho a ≥ 0, b ≥ 0, c ≥ 0 v| a + b + c = 1. Tìm gi{ trị lớn nhất của biểu thức

P = b + c + c + a + a + b

Lời giải

Có P

 

1. b + c + 1. c + a + 1. a + b

Bunhia



+ 1

)





2 2 2

b + c + c + a + a + b

= 6 (a +b + c) = 6



P 6

Vậy MaxP =

khi

a + b b + c c + a

a = b = c =

1 1 1

a + b + c = 1













Ví dụ 10. Cho a, b, c ≥ 0 v|

a + b + c = 3

. Tìm giá trị nhỏ nhất của biểu thức

a + b b + c c + a

M = + +

2 2 2

Lời giải

Ta có

   

 

   

 

   

 

   

Bunhia

a+ b = 1. a+1. b 1 +1 a+b =2 a+b

b+ c = 1. b+1. c 1 +1 b+c =2 b+c

c+ a = 1. c+1. a 1 +1 c+a =2 c+a



















Suy ra

a+ b 2(a+b), b+ c 2(b+c), c+ a 2(c+a)  

   

2 a+ b+ c 2 a+b+ b+c+ c+a

a+b b+c c+a

a+ b+ c + +

2 2 2



hay M ≥ 3

Vậy MinM = 3 khi a = b = c = 1

III. PHƯƠNG PHÁP BIẾN ĐỔI TƯƠNG ĐƯƠNG

DẠNG 1: ĐƯA VỀ BÌNH PHƯƠNG

 A

± m ≥ 0 ± m ; - A

± m ≤ 0 ± m

Dấu “=” xảy ra khi A = 0.

 A

+ B

± m ≥ 0 + 0 ± m; - A

- B

± m ≤ 0 + 0 ± m

Dấu “=” xảy ra khi A = 0, B = 0.

Ví dụ 1. Cho x ≥ - 2; y ≥ 1. Tìm gi{ trị nhỏ nhất của biểu thức

A = x + y - 2 x + 2 - 4 y - 1 + 24

Lời giải

Có

   

A = x + 2 - 2 x + 2 1 + y - 1 - 4 y - 1 4 + 18

   

= x + 2 - 1 + y - 1 - 2 +18 0 + 0 + 18 = 18

Vậy MinA = 18 khi

x + 2 = 1

x = -1

y = 5

y - 1 = 2















( thỏa mãn)

Ví dụ 2. Cho x ≥ -

. Tìm giá trị nhỏ nhất của biểu thức

E = 5x - 6 2x + 7 - 4 3x + 1 + 2

Lời giải

Có

   

E = 2x + 7 - 6 2x + 7 9 + 3x + 1 - 4 3x + 1 4 - 19

   

= 2x + 7 - 3 + 3x + 1 - 2 - 19 0 + 0 - 19 = - 19

Vậy MinA = - 19 khi

2x + 7 = 3 2x + 7 = 9

x = 1

3x + 1 = 4

3x + 1 = 2















( thỏa mãn)

Ví dụ 3. Cho

1.x 

Tìm giá trị nhỏ nhất của biểu thức

T =

1 3 7 28.x x x    

Lời giải

Xét 2T =

2 2 1 6 7 56x x x    

   

1 2 1 1 7 6 7 9 40

1 1 7 3 40 0 0 40 40 20

x x x x

x x T

          

            

Vậy Min

20T 

khi

1 1 1 1



   





  













(thỏa mãn)

Ví dụ 4. Cho

15.x 

Tìm giá trị nhỏ nhất của biểu thức

 

2 2 2

15 3 15 3 38.F x x x x x x         

Lời giải

Xét

 

2 2 2

2 2 2 2 15 3 2 15 3 76F x x x x x x         

 









 









 

2 2 2 2

15 3 2 15 3 15 2 15 1 3 2 3 1

15 3 15 1 3 1 42 0 0 42 42

x x x x x x x x

x x x x

                

               

  

Vậy Min

21F 

khi

15 3 1 4x x x     

(thỏa mãn)

Ví dụ 5. Cho

0, 0,c 0ab  

và

6.abc  

Tìm giá trị lớn nhất của biểu thức

2 2 2 2 2 2

4 4 4 .a ab b b ab c c ca a       

Lời giải

Chú ý: Với

0, 0,xy

ta có

     

 

2 2 2

6 2 6

x y x y x y

x xy y

   

   



   

Vận dụng vào bài toán, ta có

     

 

6 6 6

2 2 2

a b b c c a

abc

  

      

Vậy MaxT

66

khi a = b = c =2.

Ví dụ 6. Cho

0, 0,c 0ab  

1.x y z  

Tìm giá trị lớn nhất của biểu thức

S =

2 2 2 2 2 2

.x xy y y yz z z zx z       

Lời giải

Chú ý: Với

0, 0,xy

ta có

     

2 2 2

a b a b a b

a ab b

   

   



   

Vận dụng vào bài toán, ta có

2 2 2

x y y z z x

S x y z

  

      

Vậy MinS

1

khi

x y z  

DẠNG 2: TẠO RA BẬC HAI BẰNG CÁCH NHÂN HAI BẬC MỘT



  

0.m x n x m x n     



  

0.m x n x m x n     

Ví dụ 1.Cho

2 , , 3abc  

và

2 2 2

22.abc  

Tìm giá trị nhỏ nhất của biểu thức

.M a b c  

Lời giải

Vì

23a  

nên

2 0, 3 0.aa   

Suy ra

  

2 3 0 6 0 6.a a a a a a         

Tƣơng tự, ta cũng tìm đƣợc

6, 6b b c c   

Do đó

2 2 2

18 22 18 4.M a b c a b c         

Vậy MinM =4 khi

2, 3

3, 2

2,b 3

3, 2

2, 3

3, 2

a b c

a c b

b c a

abc

  



   





  





    





  





   





  



Ví dụ 2.Cho

x 0,y 0,z 0  

thỏa mãn

6.x y z  

Tìm giá trị nhỏ nhất của biểu thức

2 2 2

y z .Ax  

Lời giải

 Tìm MinA

Cách 1 (Sử dụng bất đẳng thức Bunhia)

Có

 

  

2 2 2 2 2 2 2

6 1. 1. 1. 1 1 1 3 12.

Bunhia

x y z x y z A A          

Vậy MinA = 12 khi

1 1 1

x y z







   





  



Cách 2 (Sử dụng bất đẳng thức Côsi – dự đo{n min đạt tại x=y=z=2)

Có

     

2 2 2 2 2 2

4 4 4 12A x y z x y z         

 

2 2 2

2 .4 2 .4 2 .4 12 4 12 4.6 12 12.x y z x y z          

Vậy MinA

12

Khi

2.x y z  

 Tìm MaxA

Có

, , 0x y z 

và

6x y z  

nên

0 , , 6.x y z

     

 

2 2 2

6 6 6 0

6 6.6 36 36.

x x y y z z

x y z x y z A

      

         

Vậy MaxA

36

khi

0,x 6

0,y 6

0,z 6

x y z

















  



hay

 

;;x y z

là hoán vị của

 

0;0;6 .

Ví dụ 3.Cho

0,b 0,c 0a   

thỏa mãn

3.abc  

Tìm giá trị nhỏ nhất của biểu thức

3 1 3 1 3 1.K a b c     

Lời giải

 Tìm MaxK

Cách 1 (Sử dụng bất đẳng thức Bunhia)

Xét

 

1. 3 1 1. 3 1 1. 3 1K a b c     

 

   

222

1 1 1 3 1 3 1 3 1 9 1 36 6.

Bunhia

a b c a b c K              

Vậy MaxK

6

khi

1.abc  

Cách 2 (Sử dụng bất đẳng thức Côsi – dự đo{n min đạt tại a=b=c=1)

     

3 1 3 1 3 1 3 1 .4 3 1 .4 3 1 .4

K a b c a b c



           



       

3 1 4 3 1 4 3 1 4 3 15

1 3.3 15

2 2 2 2 4 4

a b c a b c        





     





Vậy Max

6K 

khi

1.abc  

 Tìm MinA

Có

     

3 3 3 3 9 3 1 3 1 3 1 12.a b c a b c a b c             

Đặt

3 1, 3 1, 3 1 , , 1x a y b z c x y z       

và

12.x y z  

Từ

, , 1x y z 

và

12 1 , , 10x y z x y z     

    

1 10 0 10 1 10 0 .

10 1

x x x x x



          



Tƣơng tự

10 10

10 1 10 1







, suy ra

3 10 12 3 10

10 2.

10 1 10 1

x y z

x y z K

   

      



Vậy MinK

10 2

khi

 

,,x y z

là hoán vị của

 

1;1;10

nên

 

;;abc

hoán vị của

 

0;0;3 .

DẠNG 3: TẠO RA ab+bc+ca



   

0 , , 0a b c m m a m b m c      



        

0 , , 0a b c m m a m b m a m c m b m c           

Ví dụ 1. Cho

0 , , 2abc

và

3.abc  

Chứng minh

2.ab bc ca  

Lời giải

0 , , 2abc

nên

   

2 2 2 0abc   

   

8 4 2 0a b c ab bc ca abc        

 

8 4.3 2 0ab bc ca abc      

(do

3abc  

)

abc

ab bc ca    

, mà

abc



nên

2ab bc ca  

(đpcm).

Ví dụ 2: Cho a



1, b



1, c



1 và ab+bc+ca =9.

Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức: P =a

+ b

+ c

Lời giải:

* Tìm Min P

Có (a –b)

+(b- c)

+(c-a)



0 => a



ab +bc+ca => P



Vậy MinP =9 khi a = b= c =

* Tìm MãP

Do a



1, b



1, c



1 => (a-1)(b-1) +(b-1)(c-1) +(c-1)(a-1)



<=> (ab+ bc +ca) -2(a+b+c) +3



0 <=> a+ b+ c



<=> a

+ b

+2(ab+bc+ca)



36 <=> P



Vậy MaxP=18 khi (a,b,c) là hoán vị của (1;1;4)

DẠNG 4: SỬ DỤNG TÍNH CHẤT TRONG BA SỐ BẤT KÌ LUÔN TÒN TẠI HAI SỐ CÓ TÍCH

KHÔNG ÂM

Tính chất 1: Nếu -1



1 thì

a a n N*  

Dấu “=” xảy ra khi a=0 hoặc a=1 nếu n lẻ, khi a=0 hoặc a=



1 nếu n chẳn

Tính chất 2: Nếu hai số a và b có tích ab



0 thì

a b a b  

Tính chất 3: Với ba số x, y, z bất kỳ, luôn tồn tại hai số có tích không âm.

Bài toán cơ bản: Cho -1



x, y, z



1, x+ y+ z =0

Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức: T =

x y z

Lời giải:

Với ba số x, y, z bất kỳ, luôn tồn tại hai số có tích không âm.

Giả sử xy



0 =>

x y x y z z     

Nên

T 2 z 2

( do -1



1 ).

Vậy MaxT =2 khi (x;y;z) là hoán vị (-1;0;1).

Ví dụ 1. Cho -2



x, y, z



2, x+ y+ z =0. Chứng minh rằng a

32

Lời giải:

Có -2



x, y, z



2 =>

aaa

1 , , , 1

222

  

Đặt

a b c

x , y , z 1 x, y, z 1

2 2 2

      

và x+y+z=0.

Khi đó a

=16(x

)



 

16 x y z

Với ba số x, y, z bất kỳ, luôn tồn tại hai số có tích không âm.

Giả sử: xy



0 =>

x y x y z z     

nên

4 4 4

x y z 2 z 2 a b c 32       

( đpcm)

Ví dụ 2. Cho 0



x, y, z



1 và x+ y+ z =

Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức: P=x

Lời giải:

Tìm Min P

Cách 1( Sử dụng bất đẳng thúc Bunhia)

Có

Bunhia

2 2 2 2 2 2 2

(1.x 1.y 1.z) (1 1 1 )(x y z ) 3P P



          





Vậy MinP =

Khi

x y z

1 1 1

x y z







   





  





Cách 2( Sử dụng bất đẳng thức Côsi – dự đo{n min đạt tại x=y=z=

)

     

                

     

     

2 2 2 2 2 2 2 2 2

1 1 1 1 1 1 3 3

Cã P x y z x y z 2 x . 2 y . 2 z . x y z .

4 4 4 4 4 4 4 4

Vậy MinP =

Khi x = y = z =

Tìm MaxP

Có x + y + z =

 (2x – 1) + (2y – 1) + (2z – 1) = 0

Đặt a = 2x – 1, b = 2y – 1, c = 2z – 1.

Do (2x – 1) + (2y – 1) + (2z – 1) = 0 nên a + b + c = 0

Vì 0 ≤ x, y, z ≤ 1  - 1 ≤ 2x – 1, 2y – 1, 2z – 1 ≤ 1 nên – 1 ≤ a, b, c ≤ 1.

Có P =

2 2 2

1 1 1 2( ) 3

2 2 2 4

a b c a b c a b c        

     

  

     

     

2 2 2

( 1 , , 1)

abc

do a b c

  

   

Với ba số a, b, c bất kì, luôn tồn tại hai số có tích không âm.

Giả sử a.b ≥ 0 thì

a b a b c c     

nên

2 3 5

( 1)

4 4 4

P do c



   

Vậy MaxP =

khi (a; b; c) là hoán vị của (- 1; 0; 1) hay (x; y; z) là hoán vị của

0; ;







Ví dụ 3: Cho 0 ≤ x, y, z ≤ 2 v| x + y + z = 3. Tìm gi{ trị lớn nhất và nhỏ nhất của biểu thức

M = x

+ y

+ z

+ 12(1 – x)(1 – y)(1 – z).

Lời giải

Có x + y + z = 3  (x – 1) + (y – 1) + (z – 1) = 0

Đặt a = x – 1, b = y – 1, c = z – 1  - 1 ≤ a, b, c ≤ 1 v| a + b + c = 0

Với a + b + c = 0 thì a

+ b

+ c

= 3abc

Có M = (a + 1)

+ (b + 1)

+ (c + 1)

– 12abc

= (a

+ b

+ c

) + 4(a

+ b

+ c

) + 6(a

+ b

+ c

) + 4(a + b + c) – 12abc

= (a

+ b

+ c

) + 6(a

+ b

+ c

* Có M = (a

+ b

+ c

) + 6(a

+ b

+ c

) ≥ 0

Vậy Min M = 0 khi a = b = c = 0  x = y = z = 1

* Có M = (a

+ b

+ c

) + 6(a

+ b

+ c

) ≤

     

67a b c a b c a b c       

Với ba số a, b, c bất kì, luôn tồn tại hai số có tích không âm.

Giả sử ab ≥ 0 

a b a b c c     



2 2 14a b c c M     

Vậy MaxM = 14 khi (a; b; c) là hoán vị của (- 1; 0; 1) hay (x, y, z) là hoán vị của (0; 1; 2).

Ví dụ 4: Cho 0 ≤ a, b, c ≤ 4 v| a + b + c = 6.

Tìm giá trị lớn nhất của biểu thức P = a

+ b

+ c

+ ab + bc + ca.

Lời giải

Có P

 

2 2 2 2 2 2

18.

2 2 2

abc

a b c a b c



   

  

Do a + b + c = 6  (a – 2) + (b – 2) + (c – 2) = 0 

2 2 2

abc  

  

Đặt

2 2 2

a b c

x y z

  

  

 x + y + z = 0.

Vì 0 ≤ a, b, c ≤ 4  - 2 ≤ a – 2, b – 2, c – 2 ≤ 2  - 1

2 2 2

, , 1.

2 2 2

abc  



 - 1 ≤ x, y, z ≤ 1.

Có P

     

2 2 2

2 2 2 2 2 2

x y z    



= 2(x

+ y

+ z

) + 4(x + y + z) + 24

= 2(x

+ y

+ z

) + 24 ≤

 

2 24x y z  

Với ba số x, y, z bất kì, luôn tồn tại hai số có tích không âm.

Giả sử xy ≥ 0 

x y x y z z     

nên

4 24 4 24 28 ( 1 1).P z do z       

Vậy MaxP = 28 khi (x, y, z) là hoán vị của (- 1; 0; 1) nên (a, b, c) là hoán vị của

(0; 2; 4).

DẠNG 5: SỬ DỤNG TÍNH CHẤT CỦA MỘT SỐ BỊ CHẶN TỪ 0 ĐẾN 1

* Nếu

01x

thì

xx

. Dấu

“”

xảy ra khi

0x 

hoặc

1x 

* Nếu

01x

thì

x x n  

. Dấu

“”

xảy ra khi

0x 

hoặc

1x 

Ví dụ 1: Cho

0; 0; 0abc  

và

1abc  

. Tìm giá trị lớn nhất và nhỏ nhất của biểu thức

P b c c a a b     

Lời giải

* Tìm

MaxP

Cách 1: ( Sử dụng bất đẳng thức Bunhia)

Xét

(1. 1. 1. )P b c c a a b     

 





2 2 2

222

111

6( ) 6( 1) 6

Bunhia

b c c a a b

a b c doa b c P

       

        

Vậy

6Max P 

khi

abc  

Cách 2: ( Sử dụng bất đẳng thức Cosi - dự đo{n max đạt tại

abc  

)

Xét

2 2 2 2

. ( ) ( ) (a b)

3 3 3 3

P b c c a     

2 2 2

( ) ( ) (a )

3 3 3

2 2 2

1 2( 1) 2: 6

b c c a b

a b c doa b c P

     



          

Vậy

6Max P 

khi

abc  

* Tìm

MinP

Sử dụng tính chất:

01x

thì

xx

, , 0abc

và

1abc  

nên

0 , , 1a b b c c a    

Có

( ) ( ) ( ) 1P b c c a a b b c c a a b            

2( ) 2( 1).a b c doa b c      

Vậy

2MinP 

khi

( ; ; )abc

là hoán vị

(1;0;0)

Ví dụ 2: Cho

0; 0; 0abc  

và

3abc  

. Tìm giá trị lớn nhất và nhỏ nhất của biểu thức

T b c c a a b     

Lời giải

* Tìm

MaxP

Cách 1: ( Sử dụng bất đẳng thức Bunhia)

Xét

(1. 1. 1. )T b c c a a b     

 





2 2 2

222

111

6( ) 18( 3) 3 2

Bunhia

b c c a a b

a b c doa b c P

       

        

Vậy

32MaxT 

khi

1abc  

Cách 2: ( Sử dụng bất đẳng thức Cosi - dự đo{n max đạt tại

1abc  

)

Xét

T. 2 2( ) 2( ) 2(a b)b c c a     

2 ( ) 2 ( ) 2 (a )

2 2 2

3 6( 3) 6: 2 3 2

b c c a b

a b c doa b c P

     



          

Vậy

32MaxT 

khi

1abc  

* Tìm

MinP

Sử dụng tính chất:

01x

thì

xx

, , 0abc

và

abc



    

nên

0 ; ; 1

3 3 3

a b b c c a  



Có

3 3 3 3 3 3

b c c a a b b c c a a b



     



     





2( )

3 2 3( 3).

abc

doa b c



    

Vậy

23MinT 

khi

( ; ; )abc

là hoán vị

(3;0;0)

Ví dụ 3: Cho

0; 0; 0abc  

và

1abc  

. Tìm giá trị nhỏ nhất của biểu thức

3 1 3 1 3 1F a b c     

Lời giải:

Cách 1: Có

0; 0; 0; 1a b c a b c     

2 2 2

0 , , 1 , , .a b c a a b b c c      

Do đó :

2 2 2

3 1 3 1 3 1 2 1 2 1 2 1

2 1 2 1 2 1 3 4

F a b c a a b b c c

a a b b c c a b c

              

             

Vậy

4MinF 

khi

( ; ; )abc

là hoán vị

(0;0;1)

Cách 2: Có

     

1 3 3 3 3 3 1 3 1 3 1 6a b c a b c a b c             

Đặt

3 1; 3 1; 3 1.x a y b z c     

, , 1x y z

và

6x y z  

và

F x y z  

Từ

, , 1x y z 

và

6 1 , , 4x y z x y z     

  

1 4 0 3 2 0

x x x x x



         

Tƣơng tự:

;





, suy ra

x y z

x y z F

  

    

Vậy

4MinF 

khi

( ; ; )x y z

là hoán vị

(1;1;4)

nên

 

,,abc

là hoán vị

(0;0;1)

Ví dụ 4: Cho

0; 0; 0abc  

và

1abc  

. Tìm giá trị lớn nhất của biểu thức

2 2 2

2 3 4 2 3 4 2 3 4M a a b b c c        

Lời giải:

Có

0; 0; 0; 1a b c a b c     

2 2 2

0 , , 1 a, b, c.a b c a b c      

Do đó :

     

2 2 2 2 2 2

2 2 2

3 4 3 4 3 4

2 2 2 6 7

M a a a b b b c c c

a a a b b b c c c

a b c a b c

           

           

          

Vậy

7MinM 

khi

( ; ; )abc

là hoán vị

(0;0;1)

DẠNG 6 : DỰ ĐOÁN KẾT QUẢ RỒI XÉT HIỆU

Ví dụ 1: Cho

;0xy

thỏa mãn

10xy

. Tìm giá trị nhỏ nhất của biểu thức

  

11P x y  

Lời giải

Có

      

4 4 4 4 4 4 4 4 2 2 2 2

1 1 1 2 1P x y x y x y x y x y x y           

 

4 4 2 2 4 4 2 2

10 2 2 1 2 40 101.x y xy x y x y x y xy        

Đặt

0t xy

thì

10 5 5

2 2 2 2

xy t







     





Ta đƣợc

2 40 101; 0

P t t t t     

Đến đ}y ta kẻ bảng dự đo{n

MinP

2,5

101

52,5625

Từ bảng trên ta dự đo{n

45MinP 

khi

2t 

nên ta xét hiệu :

   

4 2 4 2 2

45 2 40 56 8 16 10 40 40P t t t t t t t          

 

4 4 2 0 45t t P      

Vậy

45MinP 

khi

2t 

















là hai nghiệm của phƣơng trình :

10 2 10 2 10 2

10. 2 0 ;

2 2 2

t t t x y



       

Ví dụ 2: Cho

4 4 4a b ab a b   

. Tìm giá trị lớn nhất của biểu thức

   

3 3 2 2

20 6 2013A a b a b    

Lời giải

Có :

 

4 4 4 4 4 2a b ab a b a b ab a b ab



         



   

12 4ab a b a b    

, mà

 

4ab a b

hay

 

12 3ab a b

Nên

         

2 2 2

4 3 0 0 1a b a b a b a b a b a b             

Đặt

x a b

thì

01x

và

12 4ab x x

Ta có

     

20 3 6 2 2013A a b ab a b a b ab

   

       

   

     

20 60 6 12 2013a b ab a b a b ab       

 

3 2 2 2 2

20 5 4 6 4 2013 3 2013x x x x x x x x x         

Đến đ}y ta kẻ bảng dự đo{n

MaxA

2013

2015

Từ bảng trên ta dự đo{n

2015MaxA

khi

1x 

nên ta xét hiệu

  

2015 3 2 1 3 2A x x x x      

. Do

01x

nên

  

1 3 2 0xx  

, suy ra

2015A

Vậy

2015MaxA

khi

1x 

hay

ab

CÁC BÀI TOÁN PHÂN LOẠI VÀO LỚP 10 CÁC TỈNH NĂM 2019-2020

Câu 1: [TS10 TP Hà Nội, 2019-2020]

Cho biểu thức

P a b ab  

, với a, b là các số thực thỏa mãn

a ab b 3.  

Tìm giá trị nhỏ nhất,

giá trị lớn nhất của biểu thức P

Lời giải

Ta có:

 

4 4 2 2 2 2 2 2

P a b ab a b 2a b ab 3 ab 2a b ab          

7 85



   





Ta có:

 

a b 2ab 3 ab 3 ab a b 0 ab 3           

3 ab a b 2ab ab 1     

Vì:

7 7 7 1 7 9 1 7 81

3 ab 1 ab a

2 2 2 2 2 2 4 2 4



             





81 7 1 7 85

a 1 a 21

4 2 4 2 4

   

             

   

   

1 P 21  

GTLN của P là 21 khi

a 3,b 3  

hoặc

a 3,b 3  

GTNN của P là 1 khi a = b = 1.

Câu 2: [TS10 Tỉnh Bắc Ninh, 2019-2020]

Cho hai số thực không âm a, b thỏa mã:

a b 2.

Tìm GTLN và GTNN của biểu thức

a b 4

ab 1







Lời giải

Tìm GTNN:

Ta có:

 

AM GM

3 3 3 3

a b 4 a b 1 3 3ab 3.



       

Dấu “=” xảy ra khi a = b = 1.

Vì a, b > 0 nên

 

3 ab 1

a b 4

ab 1 ab 1





  



Do đó giá trị nhỏ nhất của biểu thức M l| 3 đạt đƣợc khi a = b = 1.

Tìm GTLN:

Đặt

S a b,P ab  

Vì

 

2 2 2

a b 2 a b 2ab 2 S 2P 2 P .



          

Ta có:

 

a b a 2ab b 2 2ab 2 a b 2         

Do đó

S2

   

S 3. .S 4

a b 3ab a b 4

S 3PS 4

ab 1 P 1









   





  







S 6S 8 8 6 8 6

S 2 4 2.

  

        

Dấu “=” xảy ra khi

 

   

a b 0; 2 ; 2;0

ab 0







  









Vậy giá trị lớn nhất của M là

4 2 2

khi

   

0; 2 ; 2;0

Câu 3: [TS10 Tỉnh Nghệ An, 2019-2020]

Giải phƣơng trình:

5x 27x 25 5 x 1 x 4     

Lời giải

ĐKXĐ:

x2

 

   

 

   

2 2 2

5x 27x 25 5 x 1 x 4

5x 27x 25 25 x 1 x 4 10 x 4 x 1

2x x 2 5 x 4 x 1 0

2 x x 2 5 x x 2 x 2 3 x 2 0

     

         

      

         

Đặt

x x 2 a 0; x 2 b 2      

Phƣơng trình trở thành:

  

2a 5ab b 0 2a 3b a b 0

2a 3b



       







Với

 

x 1 5 TM

a b x x 2 x 2 x 2x 4

y 1 5 L







         







Với

 

1 3 65

x TM

2a 3b 4 x x 2 9 x 2 4x 13x 26 0

13 3 65









          











Vậy phƣơng trình có 2 nghiệm:

1 3 65

x 1 5;x



  

Câu 4: [TS10 Tỉnh Hải Phòng, 2019-2020]

a) Cho

,,x y z

là ba số dƣơng. Chứng minh

 

1 1 1

9x y z

x y z



     





b) Cho

,,abc

là ba số dƣơng thỏa mãn

6.abc  

Tìm giá trị lớn nhất của biểu thức

3 2 3 2 3 2

ab bc ca

a b c b c a c a b

   

     

Lời giải

a) Ta có

 

1 1 1

2 2 2 0

x y z

x x y y z z

y z x z x y

x y y z z x

y x z y x z

    

      

         







   





   



   

     

2 2 2

0 , , 0

x y y z z x

x y z

xy yz zx

  

     

Vậy

 

1 1 1

9x y z

x y z

    







b) Áp dụng bất đẳng thức ở câu a) ta có

   

9 1 1 1

3 2 9 2 9 2

(1)

3 2 9 2

ab ab ab

a b c a c b c b a c b c b

ab ab ab a

a b c a c b c

    

       

   

   















Chứng minh tƣơng tự ta có:

(2)

3 2 9 2

(3)

3 2 9 2

bc bc bc b

b c a a b a c

ca ac ac c

c a b b c a b



   



   





   



   



Cộng từng vế của các bất đẳng thức (1); (2) và (3) ta có

ac bc ab ac bc ab a b c

a b b c c a

    

   

  







     

 

1 1 3.6

9 2 9 2

c a b a b c b c a

abc

a b b c c a

abc

  



    

  



     







Dấu “=” xảy ra

2.abc   

Vậy giá trị lớn nhất của biểu thức

là

đạt đƣợc khi

2.abc  

Câu 5: [TS10 Tỉnh Thanh Hóa, 2019-2020]

Xét các số thực dƣơng a, b, c thỏa mãn abc 1.Chứng minh rằng:

4 4 4 4 4 4

ab bc ca

a b ab b c bc c a ca

  

     

Lời giải

Ta có:

4 4 2 2

a b ab(a b ) a;b R    

Thật vậy:

4 4 2 2

4 4 3 3

a b ab(a b )

a b a b ab

(a b)(a b ) 0

  

   

   

2 2 2

(a b) (a ab b ) 0    

(luôn đúng

a;b R

)

4 4 2 2 4 4 2 2

a b ab ab(a b ) ab a b ab ab(a b ) abc          

( vì a;b;c > 0 và abc = 1)

Do đó:

  

 

4 4 2 2 2 2 2

2 2 2

ab ab 1 1 1 c 2 c

a b ab ab(a b ) ab a b 1

a b 1 1 1 c

a b c

  

   

     

   



Tƣơng tự:

   

4 4 2 4 4 2

bc 1 a ca 1 b

(2); (3)

b c bc c a ca

a b c a b c





   

Mặt khác:

 

2 2 2

2 ab bc ca 2.3 a b c 6   

Cộng theo vế các bất đẳng thức (1),(2) và (3) ta có:

 

2 2 2

4 4 4 4 4 4 2 2

a b c 2 ab bc ca

a b c a b c 6

b c a a c b a b c

a b c a b c

    

  

    

     

   

Vậy b|i to{n đƣợc chứng minh

Dấu “=” xảy ra kh a = b = c = 1

Câu 6: [TS10 Tỉnh Quảng Ninh, 2019-2020]

Cho các số dƣơng a, b, c thoả mãn

a b c 1  

. Tìm giá trị nhỏ nhất của:

2 2 2

1 2019

ab bc ca

a b c





Lời giải

Áp dụng bất đẳng thức Cô si cho 3 số dƣơng

1 1 1 1

a b c abc; 3

a b c

abc

     

Suy ra

   

1 1 1

a b c 9 *

a b c



    





Bất đẳng thức đƣợc chứng minh. Dấu đẳng thức xẩy ra khi và chỉ khi

a b c

b) Ta có

 

2 2 2

a b c

ab bc ca a b c ab bc ca



         

Suy ra

2017

6051

ab bc ca





Áp dụng bất đẳng thức trong câu a, ta có

 

2 2 2

1 1 1

a b c 2ab 2bc 2ca 9

ab bc ca ab bc ca

a b c



       



   





Suy ra

 

2 2 2 2

1 2 9

ab bc ca

a b c

  



Do đó ta đƣợc

2 2 2

1 2019

P 6060

ab bc ca

a b c

  



Vậy giá trị nhỏ nhất của P là 6060

Dấu đẳng thức xẩy ra khi và chỉ khi

a b c

  

Câu 7: [TS10 Tỉnh Bắc Giang, 2019-2020]

Cho x, y là các số thực thỏa mãn

x y 1

. Tìm giá trị nhỏ nhất của biểu thức

  

P 3 x 3 y  

Lời giải

Ta có:

    

 

   

 

18 6 2

3 3 9 3

17 6 2

8 6 9

x y xy

P x y x y xy

x y x y xy

x y x y

  

       

    







Từ

1xy

chỉ ra đƣợc

 

2 2 2;x y x y     

Suy ra

2 3 3 2 3 0.xy       

 

19 6 2

2 2 2







     

Vậy gi{ trị nhỏ nhất của P là

19 6 2



khi

xy  

Câu 8: [TS10 Tỉnh Vũng T|u, 2019-2020]

Cho số thực dƣơng x, y thỏa mãn

x y 3

Tìm Giá trị nhỏ nhất của biểu thức

5xy x 2y 5





Lời giải

5 2 5

xy x y





1 5 1 5

5 ( ) 5 5 8xy x y y xy y

  

   

1 5 8 8

5 20 8 20 20

xy y xy y

xy y

  

     



Ta lại có:

 

8 ( 1) 8 3

20 20 20 5

xy y y x





   

  

Khi đó:

1 5 8 8

5 20 8 20 20

1 3 3

5 5 5

xy y xy y

xy y

   

  

    

   



   

     

Vậy

Min













Câu 9: [TS10 Tỉnh Bình Định, 2019-2020]

Cho

,xy

là hai số thực thỏa











. Tìm giá trị nhỏ nhất của biểu thức







Lời giải

Với

, 1x y xy

, ta có

2 2 2

( ) 2 2x y x y xy

P x y

x y x y x y

  

    

  

Vì

0; 0x y x y

    



và

1xy 

Áp dụng bất đẳng thức Cô-si cho hai số dƣơng

; xy



, ta có

2 2( )

2 2 2 2 2

x y x y



    



Suy ra

min 2 2P 

Dấu đẳng thức xảy ra

( ) 2 2 2x y x y x y x y

           



Mà

1 ( 2) 1 2 1 2 1 0

xy y y y y y y









           











Vậy

min 2 2P 

tại





















hoặc





















Câu 10: [TS10 Tỉnh Đắk Lắk, 2019-2020]

Cho ba số thực dƣơng

x,y,z

thỏa mãn:

x 2y 3z 2  

Tìm giá trị lớn nhất của biểu thức:

xy 3yz 3xz

xy 3z 3yz x 3xz 4y

  

  

Lời giải

Đặt

a x;b 2y;c 3z  

, ta đƣợc:

a,b,c 0; a b c 2   

Khi đó:

ab bc ac

ab 2c bc 2a ac 2b

  

  

Xét

    

ab ab ab 1 a b

ab 2c ab a b c c a c b c 2 a c b c



   



       



Dấu đẳng thức xảy ra khi và chỉ khi

a c b c





Tƣơng tự ta có:

bc 1 b c ac 1 a c

;

bc 2a 2 b a c a ac 2b 2 a b c b

   

   

   

     

   

Dấu đẳng thức xảy ra khi và chỉ khi

b a c a





;

a b c b





Cộng c{c vế ta đƣợc:

1 a b b c a c 3

2 a b b c a c 2

  



   



  



Vậy gi{ trị lớn nhất của

bằng

khi v| chỉ khi

a b c

  

hay gi{ trị lớn nhất của

bằng

khi và

chỉ khi

2 1 2

x ;y ;z

3 3 9

  

Câu 11: [TS10 Tỉnh Đắk Nông, 2019-2020]

Cho các số thực dƣơng

,,abc

thỏa mãn

abc

  

. Tìm giá trị nhỏ nhất của biểu thức

  

P a b a c  

Lời giải

Ta có:

abc

  

 

1abc a b c   

Theo bất đẳng thức côsi ta có:

  

P a b a c  

a ab ac bc   

 

2 . 2a a b c bc   

Đẳng thức xảy ra khi:

   

a a b c bc a a b c

bc bc

     















Ta thấy hệ có vô số nghiệm dƣơng chẳng hạn

1, 2 1b c a   

Vậy

min

2P 

Câu 12: [TS10 Tỉnh Đồng Nai, 2019-2020]

Cho ba số thực

,,a b c

. Chứng minh rằng:

         

3 3 3

2 2 2 2 2 2

3a bc b ca c ab a bc b ca c ab        

Lời giải

Phƣơng pháp:

- Đặt

2 2 2

,,x a bc y b ca z c ab

đƣa bất đẳng thức cần chứng minh về

3 3 3

3.x y z xyz

- Chứng minh đẳng thức

 

3 3 3 2 2 2

3x y z xyz x y z x y z xy yz zx          

- Từ đó đ{nh g{i hiệu

3 3 3

3x y z xyz

và kết luận.

Đặt

2 2 2

,,x a bc y b ca z c ab

Bất đẳng thức cần chứng minh trở thành :

3 3 3

3.x y z xyz

Ta có:

 

   

       

 

3 3 3 3 3 3

2 2 2

x y z xyz x y xyz z

x y xy x y xyz z

x y z xy x y z

x y z x y x y z z xy x y z

x y z x xy y xz yz z xy

x y z x y z xy yz zx

      

     

     



         





        



       

Dễ thấy:

 

     

2 2 2 2 2 2 2 2 2

2 2 2

0, , ,

x y z xy yz zx x xy y y yz z z zx x

x y y z z x x y z

             



       



Do đó ta đi xét dấu của

x y z

Ta có:

2 2 2

x y z a bc b ca c ab

     

2 2 2

0, ,b,c

a b c ab bc ca a b b c c a a



             



Suy ra

 

2 2 2

00x y z x y z x y z xy yz zx           

2 2 2

00x y z x y z x y z xy yz zx

3 3 3

3x y z xyz

hay

         

3 3 3

2 2 2 2 2 2

3a bc b ca c ab a bc b ca c ab        

(đpcm)

Dấu “ =” xảy ra khi

a b c

Câu 13: [TS10 Tỉnh Hà Nam, 2019-2020]

Cho

a,b,c

l| c{c số thực dƣơng v| thỏa mãn điều kiện

1abc

Chứng minh

1 1 1

2 2 2

  

  abc

Lời giải

Bất đẳng thức cần chứng minh

1 1 1

2 2 2

  

  abc

            

2 2 2 2 2 2 2 2 2            b c a c a b a b c

     

4 12 2 4 8              ab bc ca a b c abc ab bc ca a b c

     

4 12 1 2 4 8              ab bc ca a b c ab bc ca a b c

3   ab bc ca

Thật vậy {p dụng bất đẳng thức CauChy cho 3 số dƣơng ta có

 

33    ab bc ca abc

Dấu “=” xảy ra khi

1  abc

Ho|n tất chứng minh.

Câu 14: [TS10 Tỉnh H| Tĩnh, 2019-2020]

Cho hai số thực dƣơng

,ab

thỏa mãn:

31  a b ab

Tìm giá trị lớn nhất của biểu thức

  



P a b

Lời giải

Ta có:

2 2 2 2

(a ) 0 2 (a ) 4 ;       b a b ab b ab

(a )





Từ giả thiết

31  a b ab

 

1 3 1

      a b ab a b

   

 

 

3 4 4 0 2 3 2 0

              





a b a b a b a b a b

(vì

,b 0a

)

3 1 ( ) 1 3 1



     



ab a b

a b a b a b

 

2 2 2 2

2 9 9



       

a b a b

 

2 2 2 2

6 3 2 7

        



ab ab

P a b a b

a b a b

Vậy giá trị lớn nhất của P bằng

khi





  



  



a b ab

Câu 15: [TS10 Tỉnh Hải Dƣơng, 2019-2020]

Cho các số dƣơng

,,abc

thỏa mãn điều kiện:

2019  abc

Tìm giá trị nhỏ nhất của biểu thức:

2 2 2 2 2 2

2 2 2 2 2 2        P a ab b b bc c c ca a

Lời giải

Ta có:

     

 

2 2 2

5 3 5

4 4 4

       

    

a ab b a b a b a b

a ab b a b

Tƣơng tự:

   

2 2 2 2

2 2 ; 2 2

       b bc c b c c ca a c a

       

5 5 5

2 2 2

2019 5

         



P a b b c c a a b c

Dấu “=” xảy ra

2019

673

    abc

Vậy

min 2019 5 673    P a b c

Câu 16: [TS10 Tỉnh Hậu Giang, 2019-2020]

Với

x0

, tìm giá trị nhỏ nhất của biểu thức:

x 3x 2019





Lời giải

Điều kiện

x0

Ta có

x 3x 2019 3 2019

x x x



   

Đặt

 

t t 0



ta đƣợc:

A 1 3t 2019t 2019 t t 1

673



     





1 1 1

2019 t 2t 2019 1

1346 1346 1346



   

     



   

   





1 2689 2689

2019 t

1346 2692 2692



   





với mọi t thuộc R

Dấu “=” xảy ra khi

 

t tm

1346



. Vậy

2689

minA

2692



khi

 

t x 1346 tm

1346

  

Câu 17: [TS10 Tỉnh Hòa Bình, 2019-2020]

Cho hai số thực dƣơng a, b thỏa mãn a + b = 4ab

Chứng minh rằng:

4 1 4 1 2





Lời giải

Từ a + b = 4ab

ab ab ab   

Chứng minh đƣợc BĐT: Với x, y >0 ta có

 

x y x y







(*)

Áp dụng (*) ta có

 

2 2 2 2

4 1 4 1 4 4 4 ( ) ( )

a b a b

b a ab a a b b ab a b a b



   

      

4 1 1

4 1 4 1 4 1 2

a b ab

ab ab ab



   

  

Dấu đẳng thức xảy ra khi

ab

Câu 18: [TS10 Tỉnh Hƣng Yên, 2019-2020]

Cho các số thực dƣơng x, y, z thỏa mãn:

2 2 2

3x y z xyz  

Tìm giá trị lớn nhất của biểu thức

2 2 2

4 4 4

x y z

x yz y xz z xy

  

  

Lời giải

2 2 2

x y z

x y z xyz

yz xz xy

      

Áp dụng bất đẳng thức Cô-si cho hai số dƣơng

;

yz xz

ta có:

x y x y

yz xz yz x z

  

Tƣơng tự ta cũng có:

;

y z z x

xz xy x xy yz y

   

2 2 2x y y z z x

yz xz xz xy xy yz z x y

     

        

     

     

1 1 1 1 1 1

x y z

yz zx xy x y z x y z

         

Lại có:

4 4 2

1 1 1 1 1 1 1

2 2 .2. . ( )

x yz x yz x yz

x yz y z

yz y z

       



Tƣơng tự

1 1 1 1 1 1

( ); ( )

y xz x z z xy x y

   



Suy ra

2 2 2

4 4 4

1 2 2 2 1 1 1 1 3

( ) ( )

4 2 2

x y z

x yz y xz z xy x y z x y z

         

  

 

Vậy giá trị nhỏ nhất của P = 3/2 khi x = y = z = 1.

Câu 19: [TS10 Tỉnh Kon Tum, 2019-2020]

Chứng minh

1 1 1

... 38

2 3 400

Lời giải

1 1 1 1 1 1

... 2 ...

2 3 400 2 2 3 3 400 400

1 1 1

2 ...

2 1 3 2 400 399

Ta có :

1 1 1

2 ...

2 1 3 2 400 399

2 1 3 2 ... 400 399

2 1 400 38

Vậy

1 1 1

... 38

2 3 400

Câu 20: [TS10 Tỉnh Lai Châu, 2019-2020]

Cho c{c số thực dƣơng a, b, c. Chứng minh rằng:

()

2 2 2 4

ab bc ca

a b c

a b c b c a c a b

    

     

Lời giải

Ta chứng minh bất đẳng thức

1 1 1 1











x y x y

với x, y > 0.

Thậy vậy, với x, y > 0 thì:

2 2 2

1 1 1 1 1

( ) 4 2 4 0





           







x y xy x xy y xy

x y x y x y xy

2 2 2

2 0 ( ) 0      x xy y x y

(luôn đúng)

Do đó:

1 1 1 1











x y x y

với x, y > 0.

Áp dụng bất đẳng thức trên ta có:

1 1 1 1 1 1 1

()

2 ( ) ( ) 4 2 4

ab ab

a b c a c b c a c b c a b c a c b c



     



          



Tƣơng tự ta có:











   

  













   





bc bc

b c a b a c a

ca ca

c a b c b a b

Cộng vế với vế c{c bất đẳng thức với nhau ta đƣợc:

1 1 1 1 1 1

2 2 2 4 4 4

ab bc ca ab bc ca

a b c b c a c a b a c b c b a c a c b a b

     

       

     

           

     

1 1 ( ) ( ) ( ) 1

()

4 4 4

ab ab bc bc ca ca

a c b c b a c a c b a b

ab bc ab ca bc ca b a c a b c c b a

a b c

a c c b b a a c c b b a



     



     



   

     

        

   

     

   

Do đó

VT VP

(đpcm).

Dấu “=” xảy ra khi a = b = c.

Câu 21: [TS10 Tỉnh Lạng Sơn, 2019-2020]

Cho ba số thực không âm a, b, c và thỏa mãn a+b+c=1. Chứng minh rằng:

2 4(1 )(1 )(1 )a b c a b c     

Lời giải

Ta có

2 4(1 )(1 )(1 ) 2 4( )( )( )a b c a b c a b c b c a c a b            

Áp dụng bất đẳng thức cô si ta có

2 ( )( ) ( 2 ) 4( )( ) ( 2 ) ( ) 4( )( )( )a b b c a b b c a b c a b b c a b c a c a b b c a c                   

Áp

dụng bất đẳng thức cô si

2 2( )

( 2 )( ) ( 2 )( ) 1 ( 2 )( )

a b c a c a b c

a b c a c a b c a c a b c a c

     

             

1 ( 2 )( ) 2 ( 2 ) ( )a b c a c a b c a b c a c           

2 4( )( )( )a b c a b a c b c      

Câu 22: [TS10 Tỉnh Nam Định, 2019-2020]

Xét c{c số x, y, z thay đổi thoả mãn x

+ y

+ z

– 3xyz = 2.

Tìm gi{ trị nhỏ nhất của biểu thức

2 2 2 2

P (x y z) 4(x y z xy yz zx)

        

Lời giải

Ta có:

x³ + y³ + z³ - 3xyz = (x + y)³ - 3xy(x - y) + z³ - 3xyz = 2

 [(x + y)³ + z³] - 3xy(x + y +z ) = 2

 (x + y + z)³ - 3z(x + y)(x + y + z) - 3xy(x – y - z) = 2

 (x + y + z)[(x + y + z)² - 3z(x + y) - 3xy] = 2

 (x + y + z)(x² + y² + z² + 2xy + 2xz + 2yz - 3xz - 3yz - 3xy) = 2

 (x + y + z)(x² + y² + z² - xy - xz - yz) = 2

 x² + y² + z² - xy - xz – yz ≠ 0

Chứng minh: x² + y² + z² - xy - xz – yz ≥ 0 với mọi x, y, z

 x² + y² + z² - xy - xz – yz > 0  x + y + z

Đặt x + y + z = t (t > 0)  x² + y² + z² - xy - xz – yz



khi đó ta có

2 2 2 2

1 t 8 t 8

P (x y z) 4(x y z xy yz zx) 2 2

2 2 t 2 t



              





Áp dụng BĐT Cô si ta có:

2 2 .2 2t

  

(dấu bằng xảy ra  t = 2)

2t 2 2t. 8

  

(dấu bằng xảy ra  t = 2)

 P ≥ 8 – 2 = 6. Tồn tại x = y = 1, z = 0 thì P = 6

Vậy giá trị nhỏ nhất của P là 6.

Câu 23: [TS10 Tỉnh Ninh Bình, 2019-2020]

1. Tìm tất cả c{c số nguyên tố

sao cho tổng c{c ƣớc nguyên dƣơng của

l| một số chính phƣơng.

2. Cho

, , x y z

l| c{c số thực dƣơng thỏa mãn

2019x y z  

. Tìm gi{ trị nhỏ nhất của biểu thức

2 2 2

x y z

x yz y zx z xy

  

  

Lời giải

1. Ta có

là số nguyên tố (

p

)

 p

là số có c{c ƣớc dƣơng l|

1; ;pp

Theo đề bài ta có tổng c{c ƣớc nguyên dƣơng của

là một số chính phƣơng

 

2 2 *

1 ( )

4 4 4 4

4 2 1 3

    

   

   

   

p p k k

k p p

  

2 2 1 2 2 1 3     k p k p

(*)

Ta có

, 2 2 1 0; 2 2 1 2 2 1         k p k p k p k p

2 2 1 1 2 2 2 1 (

(*)

2 2 1 3 2 2 2 0 (

     

  

  

  

     

  

k p k p k

k p k p p

thoûa maõn)

khoâng thoûa maõn)

Vậy không có số nguyên tố

nào thỏa mãn đề bài

2. Ta chứng minh bất đẳng thức

 

2 2 2

a b c

x y z x y z



  



với

a,b,c,x,y,z 0

Áp dụng bất đẳng thức Bu – nhi – a - cốp – xki cho ba bộ số

a b c

; x , ; y , ; z

x y z



   



   



   



ta có

 

     

2 2 2

a b c a b c

x y z x y z

x y z





   





        



   









   





 

a b c

. x . y . z a b c

x y z



     





 

2 2 2

a b c

x y z x y z



   



(*)

Dấu “=” xảy khi khi

a b c

x y z



Áp dụng bất đẳng thức Cô si ta có

y z z x x y

yz ; zx ; xy

2 2 2

  

  

2 2 2

x y z

y z z x x y

x y z

2 2 2

   

  

2 2 2

2x 2y 2z

2x y z x 2y z x y 2z

  

     

2 2 2

x y z

2x y z x 2y z x y 2z



  



     



Áp dụng bất đẳng thức (*) ta có

 

x y z

x y z 2019

4 x y z 2 2



  



Dấu “=” xảy ra khi

x y z 673  

Vậy gi{ trị nhỏ nhất của biểu thức

2019

T

khi

x y z 673  

Câu 24: [TS10 Tỉnh Phú Thọ, 2019-2020]

Giải hệ phƣơng trình sau

















  







Lời giải

ĐKXĐ: x



- 1; y



Hệ phƣơng trình đã cho tƣơng đƣơng với hệ phƣơng trình:

1 1 1 1



   

   















   



    

  











Đặt





;





Hệ phƣơng trình đã cho trở th|nh:

a b a

a b b

  







   



+ Với a = 1 ta có:

1 ( 1) 1 1

1 1 1

1 1 0 ( / )

x x x

x x x x t m

  

   

  

      

+ Với b = 3 ta có:

1 ( 1) 1 3.( 1)

1 1 1

1 3 3 4 4 0 2 ( / )

y y y

y y y y y y t m

  

   

  

          

Vậy hệ phƣơng trình đã cho có nghiệm duy nhất (x; y) =(0; 2)

Câu 25: [TS10 Tỉnh Quảng Nam, 2019-2020]

Cho hai số thực

, xy

thỏa mãn

3; 3.xy

Tìm gi{ trị nhỏ nhất của biểu thức

21 3T x y



   





Lời giải

21 3 62 3 21 7 2

21 3

3 3 3 3

3 21 7 62 2

2 14 62 2 80

3 3 3 3

T x y x y y

y x x y

y x y

         



          





Dấu

“”

xảy ra













Vậy gi{ trị nhỏ nhất của

là 80 khi x = 3; y =3.

Câu 26: [TS10 Tỉnh Quảng Ngãi, 2019-2020]

Cho hình vuông ABCD. Gọi

là diện tích phần giao

của hai nửa đƣờng tròn đƣờng kính AB và AD.

là diện tích phần còn lại của hình vuông nằm

ngoài hai nửa đƣờng trong nói trên (như hình vẽ bên).Tính

Lời giải.

Gọi a l| cạnh hình vuông ABCD. Ta cm đƣợc:

360 2 2 4 4 2









   



     

   

   

2 2 2

1 3 4

1 1 1

4 4 2 4 4 2 2 4 2

a a a

S S S

  

     

       

     

     

1 1 3

2 2 4 2 2 2 4



   

    

   

   

Do đó

2 4 2

2 2 4



























Câu 27: [TS10 Tỉnh Quảng Ninh, 2019-2020]

Cho x, y, z l| c{c số thực dƣơng thỏa mãn       . Tìm gi{ trị nhỏ nhất của biểu thức

zxyzxy

zyx









222

Lời giải.

Ta có

 







zyx

zxyzxy

nên

6051

2017



 zxyzxy

Áp dụng BĐT

 

111

















zyx

, ta có:

 

111

222

111

222





















































zxyzxyzxyzxy

zyx

)zxyzxyzyx(

zxyzxyzxyzxy

zyx

)zxyzxy()zxyzxy()zyx(

Hay

222









zxyzxy

zyx

Từ đó ta có:

606060519

201721

222















zxyzxyzxyzxy

zyx

 







 











    





    

     

6060 P

Vậy GTNN của P là 6060 khi và chỉ khi

 zyx

     





Câu 28: [TS10 Tỉnh Sơn La, 2019-2020]

Giải phƣơng trình

33x x x  

Lời giải.

33x x x  

Điều kiện

09x

Bình phƣơng hai vế phƣơng trình đã cho, ta đƣợc:

3 .( 3 )

3. 3

x x x

  

   

2 3 3

1 1 1 1

3. . 3. . 3

3 3 3 3

1 10 10 3

3 3 3

1 10 3

x x x

     

     

     

     



   





  

10 3 3

x  

(thỏa mãn điều kiện)

Vậy phƣơng trình đã cho có 1 nghiệm

10 3 3

x 

Câu 29: [TS10 Tỉnh Vĩnh Long, 2019-2020]

Cho

,xy

là các số thực dƣơng thỏa

1.xy

Tìm giá trị nhỏ nhất của biểu thức

2 1.A x y x

    

Lời giải.

Ta có:

11x y y x    

thay v|o A ta đƣợc:

2 2 2 2

2 1 2 (1 ) 1A x y x x x x

          

 

2 2 2

2 2 1 1 2x x x x x x x

          

1 1 1 1 1 1

4 4 2 4

x x x x x

       

          

       

       

Dễ thấy



  





Áp dụng bất đẳng thức Cô-si ta có

4 2 4 . 4xx

  

Suy ra

1 1 1 1 15

4 0 4

2 4 4 4

   

       

   

   

Dấu "=" xảy ra khi

x 

Vậy

min

A 

khi

x 

Câu 30: [TS10 Tỉnh Thái Nguyên, 2019-2020]

Cho

là các số thực dƣơng thỏa mãn

6     a b c ab bc ac

. Chứng minh rằng:

3 3 3

3  

abc

b c a

Lời giải

Đặt

3 3 3

abc

b c a

  

Có

là các số thực dƣơng, theo bất đẳng thức AM-GM có:



















ab a

bc b

ac c

 

         

3 3 3

2 2 2

a b c

P a b c ab bc ac

b c a

, mà

6a b c ab bc ac     

 

       

2 2 2

26P a b c a b c

Có

     

     

222

0a b b c a c

 

     

2 2 2

22a b c ab bc ca

 

     

2 2 2

3 a b c a b c

Suy ra

   

      

P a b c a b c

Có

2 2 2

ab bc ca a b c    

   

3 ab bc ac a b c     

Do đó

 

           a b c ab bc ac a b c a b c

   

a b c a b c       

 

3a b c   

 

9a b c  

Suy ra

.9 3 6 3

P    

. Dấu đẳng thức xảy ra khi

a b c

Vậy

3 3 3

3  

abc

b c a

Câu 31: [TS10 Tỉnh Vĩnh Phúc, 2019-2020]

Cho ba số thực dƣơng a, b, c. Chứng minh:

 

2 6 3 6 2 16

2 2 2

2 2 3

a b bc

b a c

  





  

Lời giải

Theo bất đẳng thức AM-GM ta có:

Mặt kh{c theo BĐT Bu-nhi-a-cốp –xki thì:

         

2 2 1 1 1. 1.

b a c b a c b a c b a c VP

abc



             





  

Vậy ta chỉ cần chứng minh:

   

1 16

3 1 0 1

abc

a b c a b c

      

    

Ta có (1) đúng hiển nhiên do đó bất đẳng thức đƣợc chứng minh.

Dấu “=” bằng xảy ra khi:

ĐÁP ÁN CÁC CÂU PHÂN LOẠI CHYÊN NĂM 2019-2020

Câu 32: [TS10 Chuyên KHTN Hà Nội, 2019-2020]

Cho x, y là các số thực dƣơng thỏa mãn:

4x 4y 17xy 5x 5y 1    

Tìm giá trị nhỏ nhất của biểu thức:

P 17x 17y 16xy  

Lời giải

Ta có:

   

4x 4y 17xy 5x 5y 1 4 x y 9xy 5 x y 1          

Đặt

t x y, t 0  

, theo bất đẳng thức AM-GM, ta có:

2 2 1

2 2 2 3 3 3

2 2 2

a c bc VT

a b b c a b c

a b bc

a b c

b a c

 

xy .





Do đó:

9 2 2 2

4t t 5t 1 t



    

hay

2 2 2

x y .





Ta có:

 

P 17x 17y 16xy 17 x y 18xy     

 

25 25 2 2 2

17 x y 18 x y 6 4 2

4 4 4 5







       





Dấu “=” xảy ra khi





Vậy giá trị nhỏ nhất của P là

6 4 2

Câu 33: [TS10 Chuyên Sƣ Phạm Hà Nội, 2019-2020]

Cho các số thực x, y thay đổi, hãy tìm giá trị nhỏ nhất của biểu thức:

  

P xy x 2 y 6 13x 4y 26x 24y 46       

Lời giải

Ta có:

  

      

       

2 2 2 2

P xy x 2 y 6 13x 4y 26x 24y 46

x 2x y 6y 13 x 2x 4 y 6y 46

x 1 1 y 3 9 13 x 1 1 4 y 3 9 46

       

       

       

           

       

       

Đặt

a x 1, b y 3   

, khi đó:

      

2 2 2 2

2 2 2 2 2 2

P a 1 b 9 13 a 1 4 b 9 46

a b 9a b 9 13a 13 4b 36 46

       

        

2 2 2 2

4a 3b a b 6

   



Dấu “=” xảy ra khi

a 0 x 1 0

x 1,y 3

b 0 y 3 0

    

    



  



Vậy giá trị nhỏ nhất của P là 6.

Câu 34: [TS10 Chuyên Tin Hà Nội, 2019-2020]

Cho a, b, c dƣơng thỏa mãn:

ab bc ca abc 4   

1) Chứng minh rằng:

1 1 1

a 2 b 2 c 2

  

  

2) Tìm giá trị nhỏ nhất:

     

2 2 2 2 2 2

1 1 1

2 a b 4 2 b c 4 2 c a 4

  

     

Lời giải

1) Ta có:

            

     

1 1 1

a 2 b 2 c 2

b 2 c 2 a 2 c 2 b 2 a 2 a 2 b 2 c 2

ab bc ca 4 a b c 12 abc 2 ab bc ca 4 a b c 8

4 ab bc ca.

  

  

            

              

   

Đẳng thức cuối cùng đúng theo giả thiết, các phép biến đổi l| tƣơng đƣơng, do đó đẳng thức đã cho

đƣợc chứng minh.

2) Với x, y dƣơng ta có bất đẳng thức:

 

2 x y x y  

(*)

1 1 1 1

x y 4 x y











(**)

Thật vậy:

   

* x y 0  

(luôn đúng)

     

* * x y 4xy x y 0

4xy x y



       



(luôn đúng)

Các bất đẳng thức (*), (**) xảy ra dấu “=” khi x = y.

Lần lƣợt áp dụng (*) và (**) ta có:

 

   

1 1 1 1 1 1

a b 4 4 a 2 b 2

a 2 b 2

2 a b 4



   



   

  





Tƣơng tự:

   

2 2 2 2

1 1 1 1 1 1 1 1

;;

4 b 2 c 2 4 c 2 a 2

2 b c 4 2 c a 4

   

   

   

   

   

   

Cộng theo vế ta đƣợc:

1 1 1 1 1 1

P .1 .

2 a 2 b 2 c 2 2 2



    



  



D}u “=” xảy ra khi a = b = c

Vậy giá trị nhỏ nhất của P là

Câu 35: [TS10 Chuyên Toán Hà Nội, 2019-2020]

Cho

K ab 4ac 4bc  

với

a,b,c 0

và a + b + 2c = 1.

1) Chứng minh rằng:



2) Tìm giá trị lớn nhất của K.

Lời giải

1) Sử dụng bất đẳng thức AM-GM ta có:

b 2c a b 2c 1 1

4bc 2 2 4bc

2 2 2 2

      

      

   

   

Mặt khác:

a,b,c 0 K ab 4ac 4bc 4bc

        

Dấu “=” xảy ra khi

a 0,b ,c .

  

Cách khác:

Ta có:

    

 

K ab 4c a b ab 2 1 a b a b

ab 2 a b 2 a b

2b a 2 b 2a 2a

       

    

    

Do đó:

   

2b a 2 b 2a 2a K 0 *     

Để tồn tại K thì phƣơng trình (*) Phải có 2 nghiệm:

 

0 a 2 4.2. 2a 2a K 0

8K 20a 17a 4.

        

   

Vì

a,b,c 0

và

a b 2c 1 0 a 1     

. Do đó:

   

2a 17a a 20 17a a 20 17.1 3a 0      

Do đó

8K 4 K

    

Dấu “=” xảy ra khi

a 0,b ,c .

  

2) Sử dụng bất đẳng thức AM-GM ta có:

 

a b 2c 1

a b 2c .

   

  





Mặt khác:

 

a b 2c

a,b,c 0 K ab 4ac 4bc ab 4ac 2ab 4ac 2a b 2c .



            

Dấu “=”

xảy ra khi:

a b 2c,a b 2c 1,bc 0,ab 0 a ,b 0,c

          

Vậy giá trị lớn nhất của K là

Câu 36: [TS10 Chuyên Thái Bình, 2019-2020]

Cho các số thực a, b, c thỏa mãn

0 a,b,c

2a 3b 4c 3











  



. Tìm giá trị nhỏ nhất của biểu thức

     

2 9 8

a 3b 4c 2 b 4a 8c 3 c 2a 3b 1

  

     

Lời giải

Ta có:

     

   

 

2 2 2

2 9 8

a 3b 4c 2 b 4a 8c 3 c 2a 3b 1

2 9 8

a 3 2a 2 b 6 6b 3 c 3 4c 1

2 3 4

a 1 2a b 1 2b c 1 2c

2a 3b 4c

a 1 2a b 1 2b

c 1 2c

  

     

  

     

  

  

  





Áp dụng bất đẳng thức AM-GM ta có:

 

a a 1 2a 1

a 1 2a

3 27

    

  





Tƣơng tự:

 

b 1 2b



;

 

c 1 2c



Suy ra:

 

P 27 2a 3b 4c 81   

Dấu “=” xảy ra khi

a b c

  

Vậy giá trị nhỏ nhất của P là 81.

Câu 37: [TS10 Chuyên Hòa Bình, 2019-2020]

Cho hai số dƣơng a, b thỏa mãn: a + b = 4ab. Chứng minh rằng:

a b 1

4b 1 4a 1





Lời giải

Ta có:

     

a b 4ab a b a b a b 1 0 a b 1 a b 0               



Lại có:

a 4ab 4ab

a a a ab

4b 1 4b 1

     



b 4a b 4a b

b b a ab

4a 1 4a 1

     



Do đó:

     

a b a b 1 1

a b 2ab a b a b

2 2 2

4b 1 4a 1



         



Dấu “=” xảy ra khi



Câu 38: [TS10 Chuyên Hƣng Yên, 2019-2020]

Cho các số thực không âm x, y, z thỏa mãn:

2 2 2

x y z 3y  

Tìm giá trị nhỏ nhất của biểu thức:

     

2 2 2

1 4 8

x 1 y 2 z 3

  

  

Lời giải

Sử dụng bất đẳng thức Cauchy-Schwarz ta có:

 

2 2 2

1 1 1 1 1 8

2 a b



   







(*)

Áp dụng bất đẳng thức (*) ta đƣợc:

     

2 2 2 2 2 2

1 1 8 8 8 64

x 1 z 3 z 3

y y y

1 x 2 x z 5

2 2 2

     

  

     

     

     

     

Mặt khác:

   

2 2 2

2 3y y

x z 2 x z 2 3y y .



     

 

64 64

6 2y y 8 y 2

  

   

   





   

Dấu “=” xẩy ra khi

   

x,y,z 1,2,1 .

Vậy giá trị nhỏ nhất của P là 1.

Câu 39: [TS10 Chuyên Hà Nam, 2019-2020]

Cho các số thực dƣơng a, b, c thỏa mãn:

1 1 1

a 1 b 1 c 1

  

  

Tìm giá trị nhỏ nhất của biểu thức:

3 3 3

2 2 2 2 2 2

a b c

a ab b b bc c c ca a

  

     

Lời giải

Ta dễ dàng chứng minh bất đẳng thức:

1 1 1 9

x y z x y z

  



(với

x,y,z 0

) (*)

Thật vậy:

 

1 1 1

(*) a b c 9

a b c



     





Áp dụng AM – GM ta đƣợc:

 

1 1 1 3

a b c 3 abc. 9

a b c

abc



     





Vậy bất đẳng thức (*) đƣợc chứng minh, dấu “=” xảy ra khi x = y = z.

Sử dụng bất đẳng thức (*) ta đƣợc:

1 1 1 9

1 a b c 3 9 a b c 6

a 1 b 1 c 1 a b c 3

            

     

Đặt

3 3 3

2 2 2 2 2 2

b c a

a ab b b bc c c ca a

  

     

Ta có:

 

     

3 3 3 3 3 3

2 2 2 2 2 2

a b b c c a

a ab b b bc c c ca a

a b a ab b b c b bc c c a c ca a

a ab b b bc c c ca a

a b b c c a

  

   

     

        

  

     

     



Do đó: P = Q

Mặt khác:

 

2 2 2 2

x xy y x xy y * *

    

Thật vậy:

 

2 2 2 2 2 2 2 2

x xy y x xy y 3x 3xy 3y x xy y 2 x y 0

             

Sử dụng (**) ta đƣợc:

 

3 3 3 3 3 3

2 2 2 2 2 2

a b b c c a

a ab b b bc c c ca a

a b a ab b b c b bc c c a c ca a

a ab b b bc c c ca a

  

   

     

        

  

     

     

1 1 1

a b b c c a

3 3 3

     

 

a b c .6 4

    

Mà

P Q P 2  

Dấu “=” xảy ra khi a = b = c = 2

Vậy giá trị nhỏ nhất của P là 2.

Câu 40: [TS10 Chuyên Phan Bội Châu, 2019-2020]

Cho các số dƣơng a, b, c dƣơng thỏa mãn

abc a b c 2   

. Tìm giá trị lớn nhất của biểu thức

2 2 2 2 2 2

1 1 1

a b b c c a

  

  

Lời giải.

Từ

abc a b c 2   

            

a b b 1 c 1 a 1 b 1 b 1 c 1 c 1 a 1

1 1 1

a 1 b 1 c 1

            

   

  

Đặt

x,y,z 0

1 1 1

x, y, z

x y z 1.

a 1 b 1 c 1



   



  

  



Khi đó:

y z x y

1 x z x

a ;b ;c

x x y z





   

Nên

2 2 2 2 2 2

1 1 1 1 1 1 1

2 ab bc ca

a b b c c a



     



  



1 x z z x

. . .

y z z x z x x y x y y z



  



     



1 x z x z

. . .

y z z x z x x y x y y z



  



     



1 x z x z

y z z x z x x y x y y z



     

     



     

     



     



1 x z z x 3 2

x y x y y z y z z x z x 4



   



      



   



     





   



Dấu “=” xảy ra khi

x y z

hay

a b c

Vậy giá trị lớn nhất của biểu thức P là

khi a = b = c = 2.

Câu 41: [TS10 Chuyên Vĩnh Phúc, 2019-2020]

Cho x, y, z là các số thực dƣơng thỏa mãn

 

2 2 2

5 x y z 9x y z 18yz 0.     

Tìm giá trị lớn nhất

của biểu thức:

2x y z







Lời giải

Ta có:

 

   

2 2 2

5 x y z 9x y z 18yz 0

5x 9x y z 5 y z 28yz 0

     

      

     

   

5x 9x y z 5 y z 7.4yz 7 y z

5x 9x y z 2 y z 0

5 9. 2 0

y z y z

       

     



   







Đặt:

 

t t 0





khi đó:

  

 

5t 9t 2 0 5t 1 t 2 0

t 2 do 5t 1 0

      

   





Ta có:

2x y z

Q 2. 1 2.2 1 3

y z y z



     



Dấu “=” xảy ra khi

y z .



Vậy giá trị lớn nhất của Q là 3.

Câu 42: [TS10 Chuyên Bắc Ninh, 2019-2020]

Cho x, y, z không âm thỏa mãn

x y z 3.  

Tìm GTLN. GTNN của biểu thức

2 2 2

M x 6x 25 y 6y 25 z 6z 25        

Lời giải

Ta có:

     

2 2 2

M x 6x 25 y 6y 25 z 6z 25

3 x 16 3 y 16 3 z 16

        

Đặt

a 3 x,b 3 y,c 3 z,     

Khi đó:

a b c 6

0 a,b,c 3

   







2 2 2

M a 16 b 16 c 16     

Tìm GTNN:

Theo bất đẳng thức Minkowski ta có:

   

2 2 2

M a 16 b 16 c 16 a b c 4 4 4 6 5            

Đẳng thức xảy ra khi a = b = c = 2

Tìm GTLN

Sử dụng phƣơng ph{p UCT với điều kiện

0 a 3

ta đƣợc

 

a 12

a 16 *





Thật vậy:

 

   

* 9 a 16 a 12 8a 24a 0 a a 3 0         

(đúng)

Ho|n to|n tƣơng tự và suy ra:

M 14

Đẳng thức xảy ra khi

   

a,b,c 0,3,3

và các hóa vị.

Câu 43: [TS10 Chuyên KHTN, 2019-2020]

Cho x, y,z là các số dƣơng thỏa mãn

xy yz zx 1

. Chứng minh rằng:

2 2 2

1 1 1 2 x z

1 x 1 y 1 z





    



  



(1)

Lời giải

Ta có:

  

1 x xy yz zx x x y x z       

Tƣơng tự:

     

1 y x y y z ;1 z x z y z       

Do đó:

 

        

 

   

2 x y z

1 1 1

x y x z x y y z x z z y x y y z z x



   

        

Áp dụng bất đẳng thức Cauchy-Schwarz, ta có:

 

        

  

   

 

   

2 2 2

x z x z

x y z

1 x 1 y 1 z

x y z

x y y z x y y z x z z y

2 x y z xy yz zx

x y y z z x

2 x y z

x y y z z x





      



  





    



     





   



  





  

Suy ra:

 

   

2 2 2

4 x y z

VP .

3 x y y z z x

1 x 1 y 1 z







  



  



Nhƣ thế để chứng minh bất đẳng thức đã cho ta chỉ cần chứng minh:

 

2 2 2

x z 3

1 x 1 y 1 z

  

  

Sử dụng bất đẳng thức AM-GM ta có:

  

x x 1 x x

2 x y x z

x y x z



  









Tƣơng tự:

y y y

1 z 1 z z

;

2 x y y z 2 z x y z

1 y 1 z

   

   

   

   



   

Cộng theo vế 3 bất đẳnng thức trên ta đƣợc bất đẳng thức (2). B|i to{n đƣợc chứng minh.

Dấu “=” xảy ra khi

x y z

  

Câu 44: [TS10 Chuyên TP. Hồ Chí Minh, 2019-2020]

Cho x, y, z là các số thực thuộc đoạn

0;2



thỏa mãn điều kiện:

x y z 3.  

a) Chứng minh rằng:

2 2 2

x y z 6  

b) Tìm giá trị lớn nhất của biểu thức:

3 3 3

P x y z 3xyz   

Lời giải

a) Ta có:

       

   

2 2 2 2 2 2

2 x 2 y 2 z 0 8 4 x y z 2 xy yz zx xyz 0

x y z x y z 8 4 x y z 2 xy yz zx xyz

x y z 4 x y z 8 xyz

9 4.3 8 xyz 5 xyz 5 6

            

             

       

       

b) Ta có:

 

   

 

3 3 3 2 2 2

2 2 2 2 2 2

2 2 2

P x y z 3xyz x y z x y z xy yz zx

3 x y z x y z 2xy yz zx

3 x y z x y z

3.5 9

           



        







     





   





Dấu “=” xảy ra khi

   

x,y,z 2,1,0

và các hoán vị.

Câu 45: [TS10 Chuyên Hòa Bình, 2019-2020]

Cho x, y, z là các số thực dƣơng thỏa mãn:

xy yz 4zx 32  

Tìm giá trị nhỏ nhất của biểu thức:

2 2 2

P x 16y 16z  

Lời giải.

Áp dụng bất đẳng thức AM-GM ta có:

8y 4xy

8z 4xz

8y 8z 16yz



Cộng theo vế ta đƣợc:

 

2 2 2

P x 16y 16z 4 xy xz 4yz 128      

Dấu “=” xảy ra khi x = 4y = 4z , thay v| điều kiện ta đƣợc:

8 6 2 6

x ;y z

  

Câu 46: [TS10 Chuyên Quốc Học Huế, 2019-2020]

Cho ba số dƣơng x, y, z thỏa mãn xyz = 2. Chứng minh rằng:

2 2 2 2 2 2

x 4z 1

2x y 5 6y z 6 3z 4x 16

  

     

Lời giải

Ta có:

2 2 2 2 2

2x y 5 x y x 1 4 2xy 2x 4         

 

x x x

2xy 2x 4

2 xy x 2

2x y 5

  



 

2 2 2 2 2

) 6y z 6 4y z 2y 2 4 4yz 4y 4

2y 2y y

4yz 4y 4

2 yz y 1

6y z 6

          

  



Do đó:

   

     

 

zx 2z 2

2 xy x 2 2 yz y 1

y yz

xyz 2yz 2y

2 xy x xyz 2 yz y 1

y yz

2 yz y 1 2 yz y 1 2 yz y 1

yz y 1

2 yz y 1

  



   

  



   

  

     









Dấu “=” xảy ra x = y = 1, z = 2.

Câu 47: [TS10 Chuyên Tin Hòa Bình, 2019-2020]

Cho các số thực dƣơng x, y thỏa mãn:

x y 1.

Tìm giá trị nhỏ nhất của biểu thức:

P 1 x y



  





Lời giải

Theo AM-GM ta có:

1 1 1

1 x y 2 xy xy xy 4

2 4 xy

        

Do đó:

2 2 2 2

1 1 2 1

P 1 x y 1 x y 2 xy

x y xy



      





Suy ra:

1 1 15 1 15

P 2 xy 2 xy 2 2 .xy

xy 16xy 16xy 16xy 16xy

1 15

P 2 .4 17

2 16

      

   

Dấu “=” xảy ra khi



Vậy giá trị nhỏ nhất của P là

Câu 48: [TS10 Chuyên Tiền Giang, 2019-2020]

Cho hai số dƣơng x, y thỏa mãn

 

     

2 x y 6xy x y 2 x y xy 4      

Tìm giá trị nhỏ nhất của biểu thức:

2 y x



  





Lời giải

Ta có:

 

     

2 x y 6xy x y 2 x y xy 4

2 x y 12xy x y xy 4

      

     

Đặt

 

a x y,b xy a,b 0   

khi đó:

 

3 2 2 3 2

2a 12b a b 4 b a 12 2a 4a      

Do VT > 0 nên

 

3 2 2

2a 4a 0 2a a 2 0 a 2      

Ta có:

2 2 4 2

y x y xy

1 x 1 1 a a 1 a 12a 1

T 1 1

2 y x 2 xy 2 b 2b 2 2

4a 8a







         







Ta sẽ chứng minh:



Thật vậy:

 

3 2 2

a 6 a

5 a 12a

T 3 0

4a 8a 4a a 2





    



(luôn đúng

a2

)

Dấu “=” xảy ra khi a = 6, b = 6

hay

x 3 3,y 3 3   

hoặc

x 3 3,y 3 3   

Vậy giá trị nhỏ nhất của T là

Câu 49: [TS10 Chuyên Bà Rịa Vũng T|u, 2019-2020]

Cho các số thực dƣơng x, y. Tìm gi{ trị nhỏ nhất của biểu thức:

   



Lời giải

Ta có:

 

2 4 2 2 4

2 2 2 2

xy xy

y x 2x y y

x y x y

y x x y

xy xy

x y x y

xy x y xy x y

xy xy

P 2 2 2

xy x y xy x y



     







   













       







Đặt





.Theo AM – GM thì:

1 1 1

x y 2 xy t 2

x y 2 2 t

       



Khi đó:

2 2 2

1 t t 1 15

P t 2 2

t 16t 16t

t t 1 15

3 . . .2 2

2 2 16

16t

1 15

3. 2



       





  

  



Dấu “=” xảy ra khi x = y

Vậy giá trị nhỏ nhất của P là

Câu 50: [TS10 Chuyên KHTN Hà Nội, 2019-2020]

Với x, y là các số thực thỏa mãn

1 y 2

và

xy 2 2y

. Tìm giá trị nhỏ nhất của biểu thức







Lời giải.

Theo giải thiết ta có:

4xy 8 8y.

Sử dụng bất đẳng thức AM – GM ta có:

4x y 4xy.

Suy ra:

4x y 8 4xy 8 8y.    

Do đó:

   

  

 

2 2 2 2

4 x 4 8 8y y 4 y 1 5y 2 2 y 4 y 1 .          

Suy ra:

x 4 y 1 M 1



     



Dấu “=” xảy ra khi x = 2, y = 1.

Vậy giá trị nhỏ nhất của M là 1.

Câu 51: [TS10 Chuyên Hƣng Yên, 2019-2020]

Với x, y là cá số thực thỏa mãn

  

2 x y 1 .

  

Tìm giá trị nhỏ nhất của biểu thức:

4 3 2 4 3 2

A x 4x 6x 4x 2 y 8y 24y 32y 17.         

Lời giải

Ta có:

   

4 3 2 4 3 2

A x 4x 6x 4x 2 y 8y 24y 32y 17

1 x 1 1 y 2

         

     

Đặt

a x 1, b y 2   

, ta đƣợc

A 1 a 1 b   

Từ giả thiết ta đƣợc:

  

a 1 b 1 a b ab

      

Theo AM – GM ta có:

4a 1 4a

a b a b

4b 1 4b







    









(1)

 

2 2 2 2

a b 2ab a b ab 2

    

Cộng theo vế (1) v| (2) ta đƣợc:

 

2 2 2 2

3 1 5 1 3 1

a b a b ab a b

2 2 4 2 4 2

          

Áp dụng bất đẳng thức Minicopski ta đƣợc:

 

   

4 4 2 2 2 2

A 1 a 1 b 1 1 a b a b 4

1 17

          



  





Dấu “=” xảy ra khi

1 1 5

a b x ,y

2 2 2

     

Vậy giá trị nhỏ nhất của A là

Câu 52: [TS10 Chuyên Bình Thuận, 2019-2020]

Cho các số dƣơng x, y, z thỏa

xyz .



Chứng minh rằng:

     

2 2 2

yz xy

xy yz zx.

x y z y z x z x y

    

  

Dấu “=” xảy ra khi nào:

Lời giải

Ta có:

     

2 2 2

yz xy

xy yz zx

x y z y z x z x y

1 1 1 1

1 1 1 1 1 1

2 x y z

y z x z x y

    

  



     







Đặt

1 1 1

a ,b ,c abc 2

x y z

    

Khi đó ta cần chứng minh:

2 2 2

a b c a b c

b c a c a b 2



  



Thật vậy, sử dụng bất đẳng thức Cauchy-Schwarz ta đƣợc:

 

2 2 2

a b c

a b c a b c

VT VP

b c a c a b 2

2 a b c



     





(đpcm)

Dấu “=” xảy ra khi x = y = z.

Câu 53: [TS10 Chuyên Hải Phòng, 2019-2020]

Cho

x;y;z

là ba số thực dƣơng thỏa mãn

x(x z) y(y z) 0.   

Tìm giá trị nhỏ nhất của biểu thức

3 2 2

2 2 2 2

y x y 4

x z y z



  





Lời giải

Áp dụng bất đẳng thức Côsi

3 2 2

2 2 2 2

x xz xz z

x x x

2xz 2

x z x z

     



Tƣơng tự





. Suy ra

x y 4

P x y z



   



Theo gt







P x y 4

    



Vậy

min

P 4 x y z 1    

Câu 54: [TS10 Chuyên Quảng Nam, 2019-2020]

Cho ba số thực dƣơng a, b, c thỏa mãn abc = 1. Tìm giá trị nhỏ nhất của biểu thức:

     

2 2 2

1 a b 5 1 b c 5 1 c a 5

ab a 4 bc b 4 ca c 4

        

  

     

Lời giải

Với x, y dƣơng ta có:

   

1 1 1 1 1

x y 0 x y 4xy

x y 4xy x y 4 x y





         







(*)

Dấu “=” xảy ra khi x = y.

Ta có:

   

1 a b 5 2 ab a 4 2

a b 2a 6 2ab 2a 6 2

ab a 4 ab a 4 ab a 4 ab a 4 ab a 4

     

    

    

         

Tƣơng tự:

   

1 b c 5 1 c a 5

2 ; 2

bc b 4 bc b 4 ca c 4 ca c 4

     

   

       

Do đó:

1 1 1

P 6 2 6 2Q

ab a 4 bc 4 4 ca c 4



     



     



Áp dụng (*) ta đƣợc:

 

1 1 1 1 1

ab a 4 4 ab a 1 3

ab a 1 3



  



   

  



Tƣơng tự:

1 1 1 1 1 1 1 1

;

bc b 4 4 bc b 1 3 ca c 4 4 ca c 1 3

   

   

   

       

   

Do đó:

1 1 1 1 1 1 1 1

Q 1 2Q 1

4 ab a 1 bc b 1 ca c 1 2 ab a 1 bc b 1 ca c 1

1 1 1 1

P 6 1

2 ab a 1 bc b 1 ca c 1

1 c ac 1

2 abc ac c bc.ac abc 1 ca c 1

1 c ac 1

2 ca c 1 ca c 1 ca c 1

6 .2

   

        

   

           

   



     



     





    



     





    



     







Dấu “=” xảy ra khi a = b = c = 1.

Vậy giá trị nhỏ nhất của P là 5.

Câu 55: [TS10 Chuyên Lai Châu, 2019-2020]

Cho các số thực dƣơng a, b, c. Chứng minh rằng:

 

ab bc ca 1

a b c

a b 2c b c 2a c a 2b 4

    

     

Lời giải

Với x, y dƣơng ta có:

   

1 1 1 1 1

x y 0 x y 4xy

x y 4xy x y 4 x y





         







(*)

Dấu “=” xảy ra khi x = y.

Sử dụng (*) ta đƣợc:

   

ab ab ab 1 1

a b 2c 4 a c b c

a c b c



  



   

  



Tƣơng tự:

bc bc 1 1 ca ca 1 1

;

b c 2a 4 b a a c c a 2b 4 c b b a

   

   

   

       

   

Cộng 3 bất đẳng thức trên theo vế ta đƣợc:

ab bc ca

a b 2c b c 2a c a 2b

ab 1 1 bc 1 1 ca 1 1

4 a c b c 4 b a a c 4 c b b a



     

     

     

     

     

     

     

   

1 ab bc ab ca bc ca

4 c a b c a b

b a c a b c c a b

4 a c b c a b

a b c dpcm

    

  



  





  

  



  





  

Đẳng thức xảy ra khi a = b = c

Câu 56: [TS10 Chuyên Vĩnh Phúc, 2019-2020]

Cho các số dƣơng a, b, c thỏa mãn:

abc 1.

Chứng minh rằng:

a b c 3

b ac c ab a bc

  

  

Lời giải

Ta có:

 

a c a 2b c a 2b c

b ac b b ac

2 2 2

1 2 a a 2 2 2a 4 2a

a 2b c 4

a 2b c a 2b c

4 a 2b c

b ac b ac

    

      

     

  

   



Mặt khác:

 

4 4 2a 12 2a

a b c 3 abc 3 a b c 4

3 a 2b c 4 7a 10b 7c

         

    

Do đó:

 

2 2 2

a b c

VT 12 2

7a 10b 7c 7b 10c 7a 10a 7b 7c

a b c

12 2

7 a b c 17 ab bc ca



  



     







    

Mặt khác:

 

   

 

2 2 2 2 2 2

2 2 2

a b c ab bc ca 7 a b c 17 ab bc ca 8 a b c

12 2 a b c 12 2 a b c

dpcm

7 a b c 17 ab bc ca

8 a b c

             

   

  

    



Dấu “=” xảy ra khi a = b = c = 1.

Câu 57: [TS10 Chuyên Tuyên Quang, 2019-2020]

Cho các số dƣơng a, b, c thỏa mãn

a b c 4  

.Tìm giá trị nhỏ nhất của biểu thức:

a a b b c c

a 3 b b 3 c c 3 a

  

  

Lời giải

Ta có:

2 2 2

a a b b c c

a 3 b b 3 c c 3 a

a b c

a 3 ab b 3 bc c 3 ac

  

  

  

  

Áp dụng bất đẳng thức Cauchy-Schwarz ta đƣợc:

 

2 2 2

a b c

a 3 ab b 3 bc c 3 ac

a b c

a b c 3 ab bc ca

  

  





    

Mặt khác theo AM-GM:

a b b c c a

ab bc ca a b c

2 2 2

  

       

Do đó:

 

a b c

a b c 3 a b c



  

    

Dấu “=” xảy ra khi

a b c

  

Vậy giá trị nhỏ nhất của P là 1.

Câu 58: [TS10 Chuyên Hà Nam, 2019-2020]

Cho các số dƣơng a, b, c. Chứng minh:

2 2 2

a b c a b c

b c a

3. a b c



   



Lời giải

Áp dụng bất đẳng thức Cauchy-Schwarz ta đƣợc:

 

   

2 2 2

2 2 2 2 2 2

2 2 2

2 2 2 2 2 2

a b c

a b c a b c ab bc ca

ab bc ca ab bc ca

3. a b c a b c

a b c ab bc ca

ab bc ca

a b c

a b c 1 ab bc ca 1 ab bc ca a b c

2 ab bc ca 2 ab bc ca

a b c a b c



   

     



   

  





       

    



   



Áp dụng bất đẳng thức AM-GM cho 3 số ta đƣợc:

 

2 2 2

2 2 2 2 2 2

a b c 1 ab bc ca 1 ab bc ca 1

VT 3 . . 2

2 2 2

2 ab bc ca

a b c a b c

2 4 dpcm

     

  



   

   

Đẳng thức xảy ra khi a = b = c.

Câu 59: [TS10 Chuyên Phú Yên, 2019-2020]

Cho a, b, c là các số thực dƣơng thỏa mãn

ab bc ca 1.

Chứng minh rằng:

2 2 2

a b 1 b c 1 c a 1 2     

Dấu “=” xảy ra khi nào?

Lời giải

Sử dụng bất đẳng thức Minicopski ta đƣợc:

     

       

 

2 2 2

2 2 2 2 2 2

2 2 2

a b 1 b c 1 c a 1 ab a bc b ca c

ab bc ca a b c ab bc ca 3 ab bc ca

1 3 2 dpcm

          

           

  

Dấu “=” xảy ra khi

a b c

  

Câu 60: [TS10 Chuyên Cao Bằng, 2019-2020]

Cho a, b, c là các số dƣơng thỏa mãn điều kiện a+ b + c = 3. Tìm giá trị nhỏ nhất của biểu thức:

2 2 2

a b c

1 b 1 c 1 a

  

  

Lời giải

Áp dụng bất đẳng thức AM-GM ta đƣợc:

a ab ab ab

a a a

2b 2

1 b 1 b

     



Tƣơng tự:

b bc c ca

b ; c

1 c 1 a

   



Cộng theo vế 3 bất đẳng trên ta đƣợc:

 

2 2 2

a b c ab bc ca

R a b c

1 b 1 c 1 a

a b c

a b c 3

6 6 2



      

  



      

Dấu “=” xảy ra khi

a b c

  

Vậy giá trị nhỏ nhất của R là

Câu 61: [TS10 Chuyên Nam Định, 2019-2020]

Cho x, y, z là số thực không âm thỏa mãn điều kiện

x y z

  

. Chứng minh rằng:

x 2xy 4xyz 2  

Lời giải

Sử dụng bất đẳng thức AM-GM ta đƣợc:

   

 

  

x 2xy 4xyz x x.4y z

1 3 1

x x. y z x x x

2 2 2

x x 2 x x 2 x 2 x 2

x 2 1 x 2x 2

x 2 x 1 2



    





   

       

   

   

       

    

   

x y z 0 x 2 x 2 0

        

. Vì thế:

  

x 2xy 4xyz x 2 x 1 2 2      

(đpcm)

Dấu “=” xảy ra khi

x 1,y ,z 0

  

Câu 62: [TS10 Chuyên Bình Định, 2019-2020]

Cho a, b, c là các số thực dƣơng thỏa mãn

   

a b b c c a 8   

. Tìm giá trị nhỏ nhất của biểu

thức:

1 1 1 1

a 2b b 2c c 2a

abc

   

  

Lời giải.

Trƣớc hết ta chứng minh bất đẳng thức phụ sau:

      

a b b c c a a b c ab bc ca

       

Thật vậy:

      

a b b c c a a b c ab bc ca abc        

Lại theo BĐT AM-GM ta có:

         

a b b c c a a b b c c a

abc ab. bc. ca . .

2 2 2 8

     

  

Suy ra:

      

a b b c c a a b c ab bc ca abc        

  

   

a b b c c a

a b c ab bc ca

  

     

Suy ra đpcm:

      

a b b c c a a b c ab bc ca

       

ab bc ca

a b c

   



Áp dụng bất đẳng thức AM-GM dạng cộng mẫu số ta có:

 

1 1 1 9 3 ab bc ca

a 2b b 2c c 2a a b c 3

3 a b c



    

    



Lại có:

 

2 2 2

ab bc ca 3 ab c a bc abc 3abc a b c       

 

a b c

9 1 1 a b c

3abc a b c

abc 27 3

abc

a b c



       



Suy ra:

1 1 1 1 a b c 3

a 2b b 2c c 2a 3 a b c

abc



      

    

Dấu “=” xảy ra khi:

   

a b b c c a 8

a b c a b c 1

3 a b c

a b c 3





   



     















Vậy giá trị nhỏ nhất của P là 2 khi a = b = c = 1.

Câu 63: [TS10 Chuyên Bà Rịa Vũng T|u, 2019-2020]

Cho các số dƣơng a, b, c thỏa mãn

1 1 1

a b c

  

. Tìm giá trị nhỏ nhất của biểu thức:

2 2 2 2 2 2

1 1 1

a ab 3b 1 b bc 3c 1 c ca 3a 1

  

        

Lời giải

Ta có:

   

 

2 2 2 2 2 2

2 2 2

a ab 3b 1 a 2ab b ab b 1 b

a b ab b 1 b b ab 2b b a b 2

         

           

 

a ab 3b 1 b a b 1

b a b 1

a ab 3b 1

       



  

Tƣơng tự:

   

2 2 2 2

1 1 1 1

;

c b c 2 a c a 2

b bc 3c 1 c ac 3a 1



   

     

Với x, y dƣơng ta có:

   

1 1 1 1 1

x y 0 x y 4xy

x y 4xy x y 4 x y





         







(*)

Dấu “=” xảy ra khi x = y.

Cộng theo vế và sử dụng bất đẳng thức AM-GM ta đƣợc:

     

AM GM

1 1 1

b a b 2 c b c 2 a c a 2

2 2 2

4b a b 2 4c b c 2 4a c a 2

1 1 1 1 1 1

4b a b 2 4c b c 2 4a c a 2

1 1 1 1 1 1 1

4 a b c a b 2 b c 2 c a 2



  

     

  

     

     

     

     

     

     

   

     

   

     

   

Sử dụng bất đẳng thức (*) ta đƣợc:

1 1 1 1 1 1 1 1 1 1 1 1 1

4 a b c 4 a b 2 4 b c 2 4 c a 2

3 1 1 1 1 1 1 1 1 1 1 1 1

4 8 8 8 16 a b 16 b c 16 c a

3 3 1 1 1 1

4 8 8 a b c

3 3 3 3

4 8 8 2



       

        



       

  

       





     

         



     

     







    









   

Dấu “=” xảy ra khi a = b = c = 1.

Vậy giá trị nhỏ là P là

Câu 64: [TS10 Chuyên Tây Ninh, 2019-2020]

Chứng minh

    

a b c 9abc 4 a b c ab bc ca       

với x, y, z là các số thực không }m. Đẳng

thức xảy ra khi nào?

Lời giải

Theo bất đẳng thức Schur với a, b, c là số thực không âm thì:

        

a a b a c b b c b a c c a c b 0        

Biến đổi ta đƣợc hệ quả:

     

3 3 3 2 2 2

a b c 3abc a b c b c a c a b        

Mặt kh{c ta có đẳng thức:

     

3 3 3

a b c a b c 3 a b b c c a        

Khi đó ta có:

     

3 3 3

a b c 9abc a b c 9abc 3 a b b c c a          

Do đó:

         

2 2 2

VT a b c b c a c a b 9abc 3 a b b c c a          

Ta l| có 2 đẳng thức:

        

      

2 2 2

) a b c b c a c a b 9abc a b c ab bc ca

) abc a b b c c a a b c ab bc ca

           

         

Do đó:

            

2 2 2

a b c b c a c a b 9abc 3 a b b c c a 4 a b c ab bc ca              

Vậy bất đẳng thức đƣợc chứng minh.

Dấu “=” xảy ra khi a = b = c.

Câu 65: [TS10 Chuyên Quảng Nam, 2019-2020]

Cho 3 số dƣơng x, y, z. Tìm gi{ trị nhỏ nhất của biểu thức:

        

xy yz

2x z 2y z 2y x 2z x 2z y 2x y

  

     

Lời giải

Sử dụng bất đẳng thức Bunyakovski ta đƣợc:

     

 

2x z 2y z x x z y z y xy zx yz         

Do đó:

  

 

xy xy xy

2x z 2y z

xy yz zx

2x z 2y z

xy yz zx

  



Tƣơng tự:

     

zx zx

;

2y x 2z x 2z y 2x y

xy zx yz xy zx yz



   

Cộng 3 bất đẳng thức trên theo vế ta đƣợc:

xy zx yz







Đẳng thức xảy ra khi x = y = z.

Vậy giá trị lớn nhất của P là 1.

Câu 66: [TS10 Chuyên Bình Phƣớc, 2019-2020]

1) Cho x, y là các số dƣơng thỏa mãn

xy 1.

Chứng minh rằng:

1 1 2

1 x 1 y

1 xy







2) Cho x, y là các số thực dƣơng thỏa mãn điều kiện:

 

x y 4xy 12  

Tìm giá trị lớn nhất của biểu thức:

P 2018xy

1 x 1 y

  



Lời giải

1) Ta có:

 

  

 

1 1 2 1 1 1 1

1 x 1 y 1 x 1 y

1 xy 1 xy 1 xy

1 xy 1 x 1 xy 1 y

1 x 1 xy 1 y 1 xy

xy x 1 y xy y 1 x

1 x 1 y 1 xy

   

   

      

   

   

  

   

     

  

   

    



  

 

  

 

x y x 1 y y x y 1 x

1 x 1 y 1 xy

    



  

 

  

 

     

  

 

    

  

 

y x x y x y x y

1 x 1 y 1 xy

y x x y xy y x

1 x 1 y 1 xy

y x y x xy 1

1 x 1 y 1 xy



   





  



   







  



  







  

   

  

 

y x xy 1

1 x 1 y 1 xy





  

(đúng

xy 1

) (1)

Dấu “=” xảy ra khi x = y = 1.

Bất đẳng thƣc (1) đúng c{c phép biến đổi l| tƣơng đƣơng nên b|i to{n đƣợc chứng minh.

2) Sử dụng AM-GM ta có:

 

12 x y 4xy 2 xy 4xy 8xy xy 4xy      

Đặt

 

xy t t 0

, khi đó:

      

 

3 2 3 2 3 2 2

8t 4t 12 0 2t t 3 0 2t 2t 3t 3 0

2t t 1 3 t 1 t 1 0 t 1 2t 3t 3 0

           

          



Áp dụng bất đẳng thức ở ý 1 ta có:

1 1 2 2

P 2018xy 2018xy 2018t

1 x 1 y 1 t

1 xy

      

  



Ta sẽ chứng minh:

 

2018t 2019 *





Thật vậy:

 

  

* 1 2018 t 1 0

2018 t 1 t 1 0



    









    



   

1 t 2018 t 1 0



    







(đúng do

0 t 1

)

Dấu “=” xảy ra khi x = y = 1.

Vậy giá trị lớn nhất của P là 2019.

Câu 67: [TS10 Chuyên Đắc Lắc, 2019-2020]

Cho 3 số thực dƣơng a, b, c thỏa mãn

2 2 2

a b c 3.  

Chứng minh rằng:

3 3 3 3 3 3

a b b c c a

a 2b b 2c c 2a

  

  

  

Lời giải.

Sử dụng bất đẳng thức Cauchy-Schwarz ta đƣợc:

   

 

3 3 3 4 4 4

2 2 2

2 2 2 2 2 2

2 2 2

2 2 2 2 2 2

2 2 2

a b c a b c

)

a 2b b 2c c 2a

a 2ab b 2bc c 2ca

a b c a b c

a b c 2ab 2bc 2ca

a b c 2 a b c

a b c 3

     

  

   



    





 

3 3 3 4 4 4

2 2 2

2 2 2 2 2 2

2 2 2 2 2 2 2 2 2

b c a b c a

)

a 2b b 2c c 2a

ab 2b bc 2c ca 2a

a b c a b c

ab bc ca 2 a b c a b c 2 a b c

     

  

   



         

2 2 2

a b c 3





Cộng theo vế ta đƣợc:

3 3 3 3 3 3

a b b c c a

a 2b b 2c c 2a

  

  

  

(đpcm)

Dấu “=” xảy ra khi

a b c

  

Câu 68: [TS10 Chuyên Quảng Nam, 2019-2020]

Cho hai số thực x, y thỏa mãn

x 3;y 3.

Tìm giá trị nhỏ nhất của biểu thức:

T 21 x 3 y .



   





Lời giải

Áp dụng bất đẳng thức AM – GM ta có:

1 1 x 3 21 62 2

T 21 x 3 y x y

y x 3 x 3 y 3 3

x 3 21 62 2

2 . 2 . .3 .3

3 x 3 y 3 3

2 2.7 62 2

   

         

   

   

   

   



Dấu “=” xảy ra khi x = y = 3.

Vậy giá trị nhỏ nhất của T là 80.

HỆ THỐNG BÀI TẬP SỬ DỤNG TRONG CHỦ ĐỀ

I. BẤT ĐẲNG THỨC CÔSI

Bài 1. Cho

0x 

. Tìm giá trị nhỏ nhất của biểu thức

8 4 15

T x x

   

Bài 2. Cho

0x 

. Tìm giá trị nhỏ nhất của biểu thức

4 3 2011

M x x

   

Bài 3. Cho

0xy

và

2xy 

. Tìm giá trị nhỏ nhất của biểu thức







Bài 4. Cho

1; 1a b

. Chứng minh

11a b b a ab   

Bài 5. Cho

9; 4; 1a b c  

. Chứng minh

1 9 4

abc

ab c bc a ca b     

Bài 6. Cho

0; 0; 2a b a b   

Tìm giá trị lớn nhất của biểu thức

   

22M a b a b b a b a   

Bài 7. Cho

0; 0; 2x y x y   

Tìm giá trị lớn nhất của biểu thức

   

14 10 14 10P x x y y y x   

Bài 8. Cho

0; 0x y

và

 

xy x y x y  

. Tìm giá trị nhỏ nhất của biểu thức

P x y

Bài 9. Cho

, , 0abc

và

1ab bc ca  

Tính giá trị lớn nhất của biểu thức

2 2 2

1 1 1

abc

  

  

Bài 10. Cho các số dƣơng

,,a b c

thỏa mãn

1abc  

chứng minh

ab bc ca

c ab a bc b ca

  

  

Bài 11. Cho

0, 0, 0a b c  

và

3ab bc ca abc  

Tìm giá trị nhỏ nhất của

     

222

2 2 2 2 2 2

a b c

c c a a a b b b c

  

  

Bài 12. Cho

0, 0, 0a b c  

và

1abc  

Tìm giá trị nhỏ nhất của biểu thức

2 2 2

1 9 1 9 1 9

a b c

b c a

  

  

Bài 13. Cho

, , 0abc

và

1 1 1

1 1 1abc

  

  

. Chứng minh rằng

abc 

Bài 14. Cho

0, 0, 0a b c  

và

2 2 2

1abc  

. Chứng minh :

ab bc ca

abc

c a b

    

bc ca ab

a b c

  

Bài 15. Cho

,,a b c

l| độ dài ba cạnh của

ABC

Chứng minh

   

a b c b c a c a b abc      

Bài 16. Cho

2a 

. Tìm giá trị nhỏ nhất của biểu thức

2Pa



Bài 17. Cho

0, 0x y

và

6xy

. Tìm giá trị nhỏ nhất của biểu thức

6 24

F x y

   

Bài 18. Cho

0, 0x y

và

3xy

. Tìm giá trị nhỏ nhất của biểu thức

28 1

2P x y

   

Bài 19. Cho

2 3, 4 6, 4 6x y z     

và

12x y z  

. Tìm giá trị lớn nhất của biểu thức

P xyz

Bài 20. Cho

0, 0x y

và



. Tìm giá trị nhỏ nhất của biểu thức

2xy



Bài 21. Cho

0, 0x y

. Tìm giá trị nhỏ nhất của biểu thức

 

xy x y







Bài 22. Cho

0, 0x y

. Tìm giá trị nhỏ nhất của biểu thức

xy x y







Bài 23. Cho

0, 0, 0a b c  

thỏa mãn

2 2 2

b c a

Tìm giá trị nhỏ nhất của biểu thức

 

2 2 2

1 1 1

P b c a

a b c



   





Bài 24. Cho

0, 0x y

và

1xy

. Tìm giá trị nhỏ nhất của biểu thức

1P x y



  





Bài 25. Cho

0, 0x y

và

1xy

. Tìm giá trị nhỏ nhất của biểu thức

4P xy

x y xy

  



Bài 26. Cho

0, 0x y

và

1xy

. Tìm giá trị nhỏ nhất của biểu thức

K x y



   





Bài 27. Cho

0, 0x y

và

1xy

. Tìm giá trị nhỏ nhất của biểu thức

11S x y



     





Bài 28. Cho

0, 0x y

và

2 2 2 8x xy y x   

Tìm giá trị nhỏ nhất của biểu thức

23P x y

   

Bài 29. Cho

0, 0, 0a b c  

thỏa mãn

   

2 2 2

2 3 3b bc c a   

Tìm giá trị nhỏ nhất của biểu thức

2 2 2

T a b c

a b c

     

Bài 30. Cho

0, 0a b

và

68a b ab  

Tìm giá trị nhỏ nhất của biểu thức

P ab

a b ab

  



Bài 31. Cho

0, 0a b

và

a b a b  

Tìm giá trị nhỏ nhất của biểu thức

 

2020

P a b

  



Bài 32. Cho

0, 0x y

và

  

1 1 4xy  

Tìm giá trị nhỏ nhất của biểu thức



II. BẤT ĐẲNG THỨC BUNHIA

Bài 1. Cho

4 9 13xy

. Tìm giá trị nhỏ nhất của biểu thức

49A x y

Bài 2. Cho

4 3 1xy

. Tìm giá trị nhỏ nhất của biểu thức

43A x y

Bài 3. Cho

0, 0, 0x y z  

và

2x y z  

. Tìm giá trị nhỏ nhất của biểu thức

2 2 2

A x y z  

Bài 4. Cho

xy

. Tìm giá trị lớn nhất của biểu thức

23S x y

Bài 5. Cho

4 25

ab

. Tìm giá trị lớn nhất của biểu thức

65H a b

Bài 6. Cho

2 2 2

x y z  

. Tìm giá trị lớn nhất của biểu thức

P x y z  

Bài 7. Tìm giá trị lớn nhất của biểu thức

13P x x   

khi

13x

Bài 8. Cho

0, 0, 0a b c  

và

3abc  

Tìm giá trị lớn nhất của biểu thức

4 5 4 5 4 5K a b c     

Bài 9. Cho

0, 0, 0a b c  

và

1abc  

Tìm giá trị lớn nhất của biểu thức

P b c c a a b     

Bài 10. Cho

, , 0abc

và

3abc  

Tìm giá trị nhỏ nhất của biểu thức

2 2 2

a b b c c a

  

  

III. PHƯƠNG PHÁP BIẾN ĐỔI TƯƠNG ĐƯƠNG

Bài 1. Cho

x2

y1

. Tìm giá trị nhỏ nhất của biểu thức:

A x y 2 x 2 4 y 1 24      

Bài 2. Cho



. Tìm giá trị nhỏ nhất của biểu thức:

E 5x 6 2x 7 4 3x 1 2     

Bài 3. Cho

x1

. Tìm giá trị nhỏ nhất của biểu thức:

T x x 1 3 x 7 28     

Bài 4. Cho

x 15

. Tìm giá trị nhỏ nhất của biểu thức:

 

2 2 2

F x x x 15 x 3 x 15 x 3 38         

Bài 5. Cho

a 0,b 0,c 0  

và

a b c 6  

. Tìm giá trị lớn nhất của biểu thức:

2 2 2 2 2 2

T a 4ab b b 4bc c c 4ca a        

Bài 6. Cho

x 0,y 0,z 0,x y z 1     

. Tìm giá trị nhỏ nhất của biểu thức:

2 2 2 2 2 2

S x xy y y yz z z zx x        

Bài 7. Cho

2 a,b,c 3  

và

2 2 2

a b c 22  

. Tìm giá trị nhỏ nhất của biểu thức:

M a b c  

Bài 8. Cho

x 0,y 0,z 0  

thỏa mãn

x y z 6  

. Tìm giá trị lớn nhất và nhỏ nhất của biểu thức:

2 2 2

A x y z  

Bài 9. Cho

a,b,c 0

và

a b c 3  

. Tìm giá trị lớn nhất và nhỏ nhất của biểu thức:

K 3a 1 3b 1 3c 1     

Bài 10. Cho

0 a,b,c 2

và

a b c 3  

. Chứng minh:

ab bc ca 2  

Bài 11. Cho

a 1,b 1,c 1  

và

ab bc ca 9  

. Tìm giá trị lớn nhất và nhỏ nhất của biểu thức:

2 2 2

P a b c  

Bài 12. Cho

1 x,y,z 1  

x y z 0  

. Tìm giá trị lớn nhất của biểu thức:

T x y z  

Bài 13. Cho

2 a,b,c 2  

và

a b c 0  

. Chứng minh:

4 4 4

a b c 32  

Bài 14. Cho

0 x,y,z 1

và

x y z

  

Tìm giá trị lớn nhất và nhỏ nhất của biểu thức:

2 2 2

P x y z  

Bài 15. Cho

0 x,y,z 2

và

x y z 3  

Tìm giá trị lớn nhất và nhỏ nhất của biểu thức:

   

4 4 4

M x y z 12 1 x 1 y 1 z      

Bài 16. Cho

0 a,b,c 4

và

a b c 6  

Tìm giá trị lớn nhất của biểu thức:

2 2 2

P a b c ab bc ca     

Bài 17. Cho

a 0,b 0,c 0  

và

a b c 1  

. Tìm giá trị lớn nhất và nhỏ nhất của biểu thức:

P b c c a a b     

Bài 18. Cho

a 0,b 0,c 0  

và

a b c 3  

.Tìm giá trị lớn nhất và nhỏ nhất của biểu thức:

P b c c a a b     

Bài 19. Cho

a 0,b 0,c 0  

và

a b c 1  

.Tìm giá trị lớn nhất và nhỏ nhất của biểu thức:

F 3a 1 3b 1 3c 1     

Bài 20. Cho

a 0,b 0,c 0  

và

a b c 1  

. Tìm giá trị lớn nhất của biểu thức:

2 2 2

2a 3a 4 2b 3b 4 2c 3c 4       

Bài 21. Cho

x,y 0

thỏa mãn:

x y 10

Tìm giá trị nhỏ nhất của biểu thức:

  

P x 1 y 1  

Bài 22. Cho

a b 4ab 4a 4b   

Tìm giá trị lớn nhất của biểu thức:

   

3 3 2 2

A 20 a b 6 a b 2013    

--------Hết------

Bấm Tải xuống để xem toàn bộ.

| 1/78

| | Tải xuống

Preview text:

BẤT ĐẲNG THỨC
I. BẤT ĐẲNG THỨC CÔSI .............................................................................................................................. 2
DẠNG 1: DẠNG TỔNG SANG TÍCH ........................................................................................................... 2
DẠNG 2: DẠNG TÍCH SANG TỔNG, NHÂN BẰNG SỐ THÍCH HỢP. ................................................ 3
DẠNG 3: QUA MỘT BƢỚC BIẾN ĐỔI RỒI SỬ DỤNG BẤT ĐẲNG THỨC CÔSI .............................. 4
DẠNG 4: GHÉP CẶP ĐÔI ............................................................................................................................... 7
DẠNG 5: DỰ ĐOÁN KẾT QUẢ RỒI TÁCH THÍCH HỢP ........................................................................ 7
DẠNG 6: KẾT HỢP ĐẶT ẨN PHỤ VÀ DỰ ĐOÁN KÊT QUẢ ............................................................... 10
DẠNG 7: TÌM LẠI ĐIỀU KIỆN CỦA ẨN .................................................................................................... 13
II. BẤT ĐẲNG THỨC BUNHIA ................................................................................................................... 15
III. PHƢƠNG PHÁP BIẾN ĐỔI TƢƠNG ĐƢƠNG ................................................................................... 18
DẠNG 1: ĐƢA VỀ BÌNH PHƢƠNG ............................................................................................................ 18
DẠNG 2: TẠO RA BẬC HAI BẰNG CÁCH NHÂN HAI BẬC MỘT .................................................... 20
DẠNG 3: TẠO RA ab+bc+ca .......................................................................................................................... 22
DẠNG 4: SỬ DỤNG TÍNH CHẤT TRONG BA SỐ BẤT KÌ LUÔN TÒN TẠI HAI SỐ CÓ TÍCH
KHÔNG ÂM..................................................................................................................................................... 22
DẠNG 5: SỬ DỤNG TÍNH CHẤT CỦA MỘT SỐ BỊ CHẶN TỪ 0 ĐẾN 1 ............................................ 25
DẠNG 6 : DỰ ĐOÁN KẾT QUẢ RỒI XÉT HIỆU ...................................................................................... 27
HỆ THỐNG BÀI TẬP SỬ DỤNG TRONG CHỦ ĐỀ ................................................................................. 75 I.
BẤT ĐẲNG THỨC CÔSI ....................................................................................................................... 75
II. BẤT ĐẲNG THỨC BUNHIA ............................................................................................................... 77
III. PHƢƠNG PHÁP BIẾN ĐỔI TƢƠNG ĐƢƠNG ................................................................................... 77 1
I. BẤT ĐẲNG THỨC CÔSI
1. Dạng hai số không âm , x y 
Dạng tổng sang tích: x  y  2 xy . 2  x  y  x  y 
Dạng tích sang tổng: xy  hay xy    . 2  2  2 2   x y Dạng lũy thừa: 2 2
x  y  2xy hay xy  . 2
Dấu "  " xảy ra  x  y . 2   x 1
Dạng đặc biệt: x  .1 x  . 2
2. Dạng ba số không âm , x y, z  Dạng tổng sang tích: 3
x  y  z  3 xyz .   3  x y z
 x  y  z 
Dạng tích sang tổng: 3 xyz  hay xyz    . 3  3  3 3 3    x y z Dạng lũy thừa: 3 3 3
x  y  z  3xyz hay xyz  . 3
Dấu "  " xảy ra  x  y  z . 3    x 1 1
Dạng đặc biệt: x  . x 1.1  . 3
3. Dạng tổng quát với n số không âm x , x ,..., x 1 2 n 
Dạng tổng sang tích: x  x  ... n
 x  n x x ...x . 1 2 n 1 2 n    n      x x ... x x x ... x  Dạng tích sang tổng: 1 2 x x ... n n x  hay 1 2 x x ... n x  . 1 2 n   n 1 2 n  n  n n n     x x ... x Dạng lũy thừa: n n x  x  ... n
 x  x x ...x hay 1 2 x x ... n x  . 1 2 n 1 2 n 1 2 n n
Dấu "  " xảy ra  x  x  ...  x . 1 2 n n    x n 1
Dạng đặc biệt: x  . x 1.1...1  .  n n 1
4. Bất đẳng thức trung gian  1 1 4   x
  0, y  0 . Dấu "  " xảy ra  x  y . x y x  y  1 1 1 9    x
  0, y  0, z  0 . Dấu "  " xảy ra  x  y  z . x y z
x  y  z
DẠNG 1: DẠNG TỔNG SANG TÍCH 1
Ví dụ 1. Cho x  0 . Tìm giá trị nhỏ nhất của biểu thức 2
T  8x  4x  15 . 2 4x Lời giải 2  1  Có T   2
4x  4x   2 1  4x  14   2  4x      2x  2 1 1 2 2 1  4x  14  0  2 4x . 14 16   2 2  4x  4x 1
Vậy MinT 16 khi x  2 1
Ví dụ 2. Cho x  0 . Tìm giá trị nhỏ nhất của biểu thức 2
M  4x  3x   2011. 4x Lời giải 1 Có 2
M  4x  4x 1 x   2010 4x     x  2 1 1 2 1  x   2010  0  2 . x  2010  2011   .  4x  4x 1
Vậy MinM  2011 khi x  2 2 2 x  y
Ví dụ 2. Cho x  y  0 và xy  2 . Tìm giá trị nhỏ nhất của biểu thức H  x  . y Lời giải
x  y  2xy  2xy x  y2 2 2  4 Có H   x  y x  y
 x  y 4   x  y 4 2 .  4 . x  y x  y  4 x  y  x  y  2 y  2  x x  3 1
Vậy Min H  4 khi  x  y       . 2  xy  2
x  2x  2  0    y  3 1 xy 2
DẠNG 2: DẠNG TÍCH SANG TỔNG, NHÂN BẰNG SỐ THÍCH HỢP.
Ví dụ 1: Cho a ≥ 1, b ≥ 1. Chứng minh : a b 1  b a 1  ab Lời giải 1 (b 1) b ab
Có b 1  1.(b 1)    a b 1  ; 2 2 2 ab ab ab
V| tƣơng tự: b a 1 
 a b 1  b a 1    ab  đpcm 2 2 2
Dấu ‘=” xảy ra khi a = b = 2 11abc
Ví dụ 2: Cho a ≥ 9, b≥ 4, c≥ 1. Chứng minh: ab c 1  bc a  9  ca b  4  12 Lời giải: Có: 3 bc ca
ab c 1  bc a  9  ca b  4  ab (c 1).1  . (a  9).9  . (b  4).4 3 2 (c 1) 1
bc (a  9)  9
ca (b  4)  4 11abc  . ab  .  .  2 3 2 2 2 12
Dấu “=” xảy ra khi a = 18, b = 8, c = 2
Ví dụ 3: Cho a ≥ 0, b ≥ 0, a2 + b2 ≤ 2. Tìm gi{ trị lớn nhất của biểu thức: M = a ( b a  2 )
b  b a(b  2a) Lời giải Xét: 2 2
3b  (a  2b)
3a  (b  2a) a  b M . 3  .
a 3b(a  2b)  b 3a(b  2a)  . a  . b   5ab 2 2 2 2 2 2 2 a  b a  b   5.  6  M  2 3 2 2
Vậy MaxM = 2 3 khi a = b = 1
Ví dụ 4. Cho x  0 , y  0 và 2 2
x  y  2 . Tìm giá trị lớn nhất của biểu thức P 
x 14x 10y  y 14y 10x Lời giải Xét: .
P 24  24x 14x 10y  24y 14y 10x
24x  14x 10y 24y  14y 10x    24 .x1 . y  1 2 2 2 2 2 2
 x 1 y 1
 x  y 1 48  24    24   48  P   P  4 6 .  2 2   2  24
Vậy MaxP  4 6 khi x  y 1.
Ví dụ 5. Cho x  0 , y  0 và xy  x  y  x  y . Tìm giá trị nhỏ nhất của P  x  y . Lời giải
Từ xy  x  y  x  y  x  y 2 2    2 1 2 1 4xy x y x y
và x  y  xy  x  y 
4xy  x  y         2 2 2 4
 x  y2  4x  y  0  x  y  4. 
 x  y2  4xy 
 x  y2  8xy xy  2 Dấu "=" xảy ra khi            x  y  4 x y 4 x y 4
 x , y là hai nghiệm phƣơng trình 2
t  4t  2  0  t  2  2 .
Do x  y  x  2  2 , y  2  2 .
Vậy MinP  4 khi x  2  2 , y  2  2 .
DẠNG 3: QUA MỘT BƯỚC BIẾN ĐỔI RỒI SỬ DỤNG BẤT ĐẲNG THỨC CÔSI
Ví dụ 1. Cho a , b , c  0 và ab  bc  ac 1. Tìm giá trị lớn nhất của biểu thức: 4 a b c P    . 2 2 2 a 1 b 1 c 1 Lời giải
Thay 1  ab  bc  ac , ta đƣợc: a b c P    2 2 2
a  ab  bc  ac
b  ab  bc  ac
c  ab  bc  ac a b c    
a  ba  c
b  ab c
c  ac b a a b b c c  .  .  .
a  b a  c
b  a b  c c  a c  b a a b b c c          a b a c b a b c c a c b    2 2 2  a b   a c   b c            
 a  b a  b   a  c a  c   b  c b  c  3   2 2 3 1 Vậy MaxP 
khi a  b  c  . 2 3
Ví dụ 2. Cho các số dƣơng a , b , c thỏa mãn a  b  c 1. Chứng minh: ab bc ca 3    c  ab a  bc b  ca 2 Lời giải ab bc ca ab bc ca Ta có      c  ab a  bc b  ca . c 1 ab . a 1 bc . b 1 ca ab bc ca   
c a  b  c  ab
a a  b  c  bc
b a  b  c  ca ab bc ac    
a  cb  c
a ba c
b cb  a a b b c c a  .  .  .
a  c c  b
a  b a  c b  c b  a 1  a b   b c   c a  3              ( đpcm).
2  c  a c  b   a  b a  c   b  c a  b  2
Ví dụ 3. Cho a  0 , b  0 , c  0 và ab  bc  ac  3abc . Tìm giá trị nhỏ nhất của 2 2 2 a b c P    . c  2 2
c  a  a 2 2
a  b  b 2 2 b  c  Lời giải 2 2 2 a b c Có P    c  2 2
c  a  a 2 2
a  b  b 2 2 b  c  5 2 2 2 2 2 2 2 2 2
a  c  c
b  a  a
c  b  b    c  2 2 c  a  a  2 2 a  b  b  2 2 b  c   1 c   1 a   1 b              2 2 2 2 2 2
 c c  a   a a  b   b b  c   1 c   1 a   1 b              2 2 2 2 2 2 c  2 a   2 b c a a b   2 b c   1 1   1 1   1 1  1  1 1 1 
ab  bc  ac 3                    .
 c 2a   a 2b   b 2c  2  a b c  2abc 2 3 Vậy MinP 
khi a  b  c 1. 2
Ví dụ 4. Cho a  0 , b  0 , c  0 và a  b  c 1. Tìm giá trị nhỏ nhất của biểu thức a b c T    . 2 2 2 1 9b 1 9c 1 9a Lời giải a  2 1 9b  2 9ab b  2 1 9c  2 9bc c  2 1 9a  2 9ca Có T    2 2 2 1 9b 1 9c 1 9a 2 2 2  9ab   9bc   9ca    a    b    c   2 2 2  1 9b   1 9c   1 9a  2 2 2  9ab   9bc   9ca    a    b    c   2 2 2  2 1.9b   2 1.9c   2 1.9a  3 1 1
 a  b  c  ab  bc  ac  a  b  c  a  b  c2  do a  b  c   1 . 2 2 2 1 1
Vậy MinT  khi a  b  c  . 2 3 1 1 1 1
Ví dụ 5. Cho a , b , c  0 và  
 2 . Chứng minh: abc  . 1 a 1 b 1 c 8 Lời giải 1 1 1 Có    2 1 a 1 b 1 c cos 1  1   1 i  b c b c bc   1  1    2 .  2     . 1 a  1 b  
1 c  1 b 1 c 1 b 1 c
1b1 c 1 ac 1 ab Tƣơng tự:  2 ;  2 . 1 b
1 a1c 1 c
1 a1b
Nhân các bất đẳng thức dƣơng, cùng chiều ta đƣợc: 1 8abc 1   abc  (đpcm).
1 a1 b1 c
1 a1b1 hay c 8 6
DẠNG 4: GHÉP CẶP ĐÔI 1 1 1
Tách x  y  z   x  y   y  z   z  x . 2 2 2
xyz  xy. yz. zx  , x y, z  0 .
Ví dụ 1. Cho a  0 , b  0 , c  0 và 2 2 2
a  b  c  1. Chứng minh: ab bc ac bc ca ab a)  
 a  b  c ; b)    3 . c a b a b c Lời giải ab bc ac 1  bc ca  1  ca ab  1  ab bc  a) Có               c a b 2  a b  2  b c  2  c a  1 bc ca 1 ca ab 1 ab bc  .2 .  . .  . .
 a  b  c (đpcm). 2 a b 2 b c 2 c a 2 2 2 2 2 2 2  bc ca ab  b c c a a b b) Xét       2    2 2 2
a  b  c 2 2 2   a b c  a b c 2 2 2 2 2 2 2 2 2 2 2 2 1  b c c a  1  c a a b  1  a b b c               2 2 2 2 2 2 2 2  a b  2  b c  2  c a  2 2 2 2 2 2 2 2 2 2 2 2 1 b c c a 1 c a a b 1 a b b c  .2 .  .2 .  .2 . 2 2 2 2 2 2 2 a b 2 b c 2 c a bc ac ab 2 2 2
 a  b  c  2  3, do đó    3 (đpcm). a b 2
Ví dụ 2. Cho a, ,
b c l| độ d|i ba cạnh của ABC 
. Chứng minh (a  b  c)(b  c  a)(c  a  ) b  abc . Lời giải Vì a, ,
b c l| độ d|i ba cạnh của ABC  nên
a  b  c  0, b  c  a  0, c  a  b  0 .
(a  b  c)  (b  c  a)
Có 0  (a  b  c)(b  c  a)   b ; 2
(b  c  a)  (c  a  b)
0  (b  c  a)(c  a  b)   c ; 2
(c  a  b)  (a  b  c)
0  (c  a  b)(a  b  c)   a ; 2
Nh}n ba đẳng thức dƣơng cùng chiều ta đƣợc
(a  b  c)(b  c  a)(c  a  )
b  abc (điều phải chứng minh).
DẠNG 5: DỰ ĐOÁN KẾT QUẢ RỒI TÁCH THÍCH HỢP
Bước 1: Kẻ bảng dự đoán giái trị lớn nhất,nhỏ nhất và đạt tại giá trị nào của biến.
Bước 2: Kẻ bảng xác định số nào sẽ đi với nhau.
Bước 3: Tách ghép thích hợp số hạng và sử dụng bất đẳng thức Cô-si. 5
Ví dụ 1. Cho a  2 . Tìm gi{ trị nhỏ nhất của biểu thức P  2a  . a Lời giải
Phân tích bài toán 7 a 2 3 4 13 23 37 P  6,5  7,7  9,25 2 3 4 13
Từ bảng thứ nhất dự đo{n min P   a  2 . 2 1 a a 1 a  2 2 2 1 a 5 5a
Từ bảng thứ hai, ta suy ra sẽ đi với nên sẽ đi với . a 4 a 4
Trình bày lời giải  5 5a  3a 5 5a 3a 3a 3.2 13 Có P     2    5  5  ( do a  2)   .  a 4  4 a 4 4 4 4 2 5 5a 13   Vậy min P  khi a
4  a  2 (thỏa mãn). 2 a  2 6 24
Ví dụ 2. Cho x  0, y  0 và x  y  6 . Tìm gi{ trị nhỏ nhất của biểu thức F  x  y   . x y Lời giải
Phân tích bài toán (x ; y) (1 ; 5) (2 ; 4) (3 ; 3) (4 ; 2) (5 ; 1) 84 39 156 F 16,8 15 16 19,5  31,2 5 2 5
Từ bảng thứ nhất, ta dự đo{n min F 15 khi x  2, y  4 . 1 1 x y x y 1 1
x  2, y  4 2 4 2 4 1 x 6 6x 3x 1 y 24
Từ bảng thứ hai, ta suy ra sẽ đi với nên sẽ đi với  ; sẽ đi với nên sẽ đi với x 4 x 4 2 y 16 y 24 y 3y  . 16 4
Trình bày lời giải Có
 6 3x   24 3y   x y  F              x 2   y 2   2 2  6 3x 24 3y 1 1  2   2 
 (x  y)  18  (x  y) x 2 y 2 2 2 1
18  6 15 (do x  y  6). 2 8 6 3x 24 3y x  2 Vậy min F  15 khi  ; 
; x  y  6   (thỏa mãn). x 2 y 2 y  4 28 1
Ví dụ 3. Cho x  0, y  0 và x  y  3 . Tìm gi{ trị nhỏ nhất của biểu thức 2 2
P  2x  y   . x y Lời giải
Phân tích bài toán  ;x y 1;2 2  ;1 69 P  34,5 24 2
Từ bảng thứ nhất, ta dự đo{n min P  24 khi x  2, y 1. 1 1 x y x y 1
x  2, y  1 2 1 1 2 1 x 28 28x 1
Từ bảng thứ hai, ta suy ra sẽ đi với nên sẽ đi với
 7x ; se đi với y . x 4 x 4 y
Trình bày lời giải Có  28   1  2 2 P   7x 
 y  2x  y  7x  y      x   y   28   1  2 2   7x 
 y  2(x  2)  (y 1)  (x  y)  9      x   y  28 1  2 7x  2
 y  0  0  3 9  24. x y 28 1 Vậy min P  24 khi  7 ; x  ;
y x  2  0; y 1  0; x  y  3  x  2, y  1. x y
Ví dụ 4. Cho 2  x  3, 4  y  6, 4  z  6 và x  y  z  12 . Tìm giá trị lớn nhất của biểu thức P  xyz . Lời giải
Nhận xét: Do y và z vai trò nhƣ nhau nên sử dụng bất đẳng thức Cô-si đối với tích yz , ta đƣợc 2  y  z  1
P  x( yz)  x  x(12  ) x (12  ) x   .  2  4
Đến đ}y ta kẻ bảng để dự đo{n gi{ trị lớn nhất của P x 2 3 243 P 50  60,75 4 243
Từ bảng thứ nhất dự đo{n max P  khi x  3. 4 x 12  x x  3 3 9
Từ bảng thứ hai, ta suy ra 3x sẽ đi với 12  x nên ta biến đổi 9 3 3 1 1  x  24  1  3  24  243 P 
[(3x)(12  x)(12  x)]        . 12 12  3  12  3  4 243 9 Vậy max P 
khi x  3, y  z  . 4 2
DẠNG 6: KẾT HỢP ĐẶT ẨN PHỤ VÀ DỰ ĐOÁN KÊT QUẢ 
Khi đặt ẩn phụ ta cần tìm điều kiện của ẩn phụ. 
Một số bất đẳng thức trung gian thƣờng dùng: 
Với mọi a,b thì  2 2 a  b  2 2  (a  ) b
 4ab . Dấu bằng xảy ra khi a  b .  Với mọi a, , b c thì  2 2 2
a  b  c  2 3
 (a  b  c)  3(ab  bc  ca) . Dấu bằng xảy ra khi a  b  c . 2 3 2 2 3 3          a b a b a b a b
Với mọi a,b thì  a  , ; b  a   b  0    
. Dấu bằng xảy ra khi a  b . 2  2  2  2   1 1 4   a
  0,b  0 . Dấu bằng xảy ra khi a  b . a b a  b  1 1 1 9    a
  0,b  0,c  0. Dấu bằng xảy ra khi a  b  c . a b c
a  b  c x 8 x 2 y
Ví dụ 1. Cho x  0, y  0 và 
 2 . Tìm giá trị nhỏ nhất của biểu thức K   . 2 y y x Lời giải x x 8 x 8 x x 1 1 Đặt a , do 2 2 . 4 0 a y 2 y 2 y y y 4 4 2 2 2 K a 32a 31a 2 .32a 31a a a a Có 1 33 1 16 31a 16 31. do 0 a 4 4 4 33 1 Vậy MinK khi a hay x 2, y 8. 4 4 2 x y 1 xy x y
Ví dụ 2. Cho x 0, y
0 . Tìm giá trị nhỏ nhất của biểu thức A 2 xy x y x y 1 2 x y 1 xy x y 1 Đặt a 2 xy x y x y 1 a 2 2 Do m n p 3(mn np p ) m x y 1 3 xy x y a 3 10 Vậy MinA khi a 3 x y 1. 3 2 2 x y xy
Ví dụ 3. Cho x 0, y
0 . Tìm giá trị nhỏ nhất của A xy x y Lời giải 10 2 2 2 x y 2xy xy x y xy x y xy Có A 2 2 xy x y xy x y xy x y x y x y Đặt t , do x y 2 xy 2 t 2 xy xy 2 2 Cos 1 1 7 i t t 1 7 Ta đƣợc 2 2 2 A t 2 t 2 2 . t 2 t 8 t 8 8 t 8 t 7 2 7 5 2 2 t 2 .2 2 (do t 2 ). 2 8 2 8 2 5 Vậy MinA khi t 2 x y . 2
Ví dụ 4. Cho a 0,b 0, c 0 thỏa mãn 2 2 2 b c
a . Tìm giá trị nhỏ nhất của biểu thức 1 1 1 2 2 2 P b c a 2 2 2 a b c Lời giải 2 2 1 1 1 2bc 2a bc a Có 2 2 2 P b c a 2 2 2 2 2 2 a b c a bc a bc 2 2 2 a b c 2bc Dặt t 2 ta đƣợc bc bc bc 1 t 1 3t t 1 3t 3t 3.2 P 2 t 2 2 2 . 2 1 2 1 5 (do t 2 ). t 4 t 4 4 t 4 4 4 b c a Vậy MinP 5 khi b c 2 2 2 b c a 2 1 1
Ví dụ 5. Cho x 0, y 0 và x y
1. Tìm giá trị nhỏ nhất của biểu thức 2 2 P . 1 x y x y Lời giải 1 1 1 Có 2 2 P 2 . . 1 x y 2 xy x y . x y 2 x y 1 1 Đặt a xy , do xy 0 a , ta đƣợc 2 4 4 1 1 1 1 1 P 2 a 2 16a 15a 2 2 .16a 15a 2 8 15a 2. 8 15. 17 do 0 a a a a 4 4 1 1 MinP 17 khi a hay x y 4 2 1 1
Ví dụ 6: Cho x 0, y 0 và x y
1. Tìm giá trị nhỏ nhất của biểu thức P 4xy . 2 2 x y xy Lời giải 11 1 1 1 1 1 4 Có P 4xy . Sử dụng a,b 0 , ta đƣợc 2 2 x y 2xy 2xy a b a b 1 1 4 4 4 1 4 (do 0 x y 1) . Suy ra P 4 4xy . 2 2 2 2 2 2 x y 2xy x y 2xy (x y) 1 2xy 2 x y 1 1 Đặt a = xy, do xy 0 a ta đƣợc 2 4 4 1 1 1 1 1 P 4 4a 4 8a 4a 4 2 .8a 4a 8 4a 8 4. 7 (do 0 a ) 2a 2a 2a 4 4 1 MinP 7 khi x y 2 2 2 1 1
Ví dụ 7: Cho x,y >0 và x y
1. Tìm giá trị nhỏ nhất của biểu thức K x y x y Lời giải 2 2 2 a b a b 1 1 4 Cách 1: Sử dụng a,b và a,b 0. 2 c a b a b 2 2 2 1 1 1 1 x y x y 2 x y x y 1 4 ta đƣợc K 2. 2. x y 2 2 2 x y Đặt a x y , điều kiện 0 a 1, ta đƣợc: 2 2 2 1 4 1 1 3 1 1 3 K a a 2 . a 2 a 2 a a 2 a a 2 2 1 3 1 3 25 25 1 2 . 2 (do 0 a 1). Vậy, MinK khi x y . 2 a 2 1 2 2 2 2 2 1 1 1 1 1 Cách 2: 2 2 K x y x y 4 2. xy 4. 2 2 x y x y xy 2 x y 1 1 Đặt a x , y do xy 0 a . Ta đƣợc: 2 4 4 1 15 1 15 25 1 25 1 K 2. 4 2. 4 do 0 a . Vậy, MinK khi x y . 2 4a 2 1 2 4 2 2 4. 4 3 3 1 1
Ví dụ 8: Cho x 0, y 0 và x y
1. Tìm giá trị nhỏ nhất của biểu thức S 1 x 1 y x y Lời giải 3 3 3 a  b  a  b  1 1 4 Sử dụng  a   b  0   và +  a
  b  0 , ta đƣợc 2  2  a b a  b 12 3 3 3  1   1   1 1  1 x   1 y      1 x  1 y     x   y  x y S  2.  2  2  2     
Đặt a  x  y , điều kiện 0  a 1, ta đƣợc 3 3 3 3 3 1  4  1   1  3  1  1 3  1  3  1  3  343 S  2  a   2  a          2  2 . a    4   4       4  a  4   a  a  4 a a 4    a  4  1  4 343 1 Vậy MinS  khi x  y  4 2
DẠNG 7: TÌM LẠI ĐIỀU KIỆN CỦA ẨN 2 4
Ví dụ 1. Cho , x y  0 và 2 2
2x  2xy  y  2x  8 . Tìm giá trị nhỏ nhất của biểu thức P 
  2x  3y . x y Lời giải Có 2 2 2 2 2
2x  2xy  y 2
 x  8  x  2xy  y  x  2x 1 9   2 2 2
x  y2   x  2 1
 9, mà x  y  x  y  x  
1   x  y2  9  0  x  y  3  2   4  2 4 Có P   2x 
 y  4x  4y  2 .2x  2
.y  4(x  y)      x   y  x y
 8  4(x  y)  8  4.3  4
 (do 0  x  y  3). Vậy MinP  4
 khi x 1, y  2.
Ví dụ 2: Cho a 0, b 0, c 0 thỏa mãn 2 2 2 2 b bc c 3 3 a
. Tìm giá trị nhỏ nhất của biểu 2 2 2 thức T a b c a b c Lời giải Có 2 2 2 2 2 2 2 b bc c 3 3 a 3a 2b 2bc 2c 9 2 2 2 3a 2b 2bc 2ab 2ac 2c 2ab 2ac 9 2 2 2 2 2 2 2 a b c 2ab 2bc 2ca a b 2ab a c 2ac 9 2 2 2 2 a b c a b a c 9 a b c 9 0 a b c 3 1 1 1 9 18 Sử dụng ta đƣợc T a b c a b c a b c a b c Đặt x a b , c 0 x 3 , ta đƣợc 18 18 18 T x 2x x 2 .2x x 12 x 12 3 9 (do 0 x 3 ) x x x Vậy MinT 9 khi x 3 hay a b c 1
Ví dụ 3: Cho a 0, b 0 và 3 3 a b 6ab
8 . Tìm giá trị nhỏ nhất của biểu thức: 1 3 P ab 2 2 a b ab Lời giải 13 Có 3 3 3 3 2 2 2 2 a b 6ab 8 a b 3a b 3ab 3a b 3ab 6ab 8 3 3 3 a b 3ab a b 2 8 a b 2 3ab a b 2 0 2 a b 2 a b 2 a b 4 3ab a b 2 0 2 2 a b 2 a b ab 2a 2b 4 0 2 2 a b 2 2a 2b 2ab 4a 4b 8 0 2 2 2 a b 2 a b a 2 b 2 0 0 a b 2 1 1 5 Có P ab 2 2 a b 2ab 2ab 1 1 4 Sử dụng , x y 0 , ta đƣợc: x y x y 1 1 1 4 4 1 (do 0 a b 2 ) 2 2 2 2 2 2 a b 2ab a 2ab b a b 2 5 Suy ra P 1 ab 2ab 2 2 a b 2 Đặt x ab , do ab 1 0 x 1, ta đƣợc: 2 2 5 5 5x 3x P 1 x 1 2x 2x 2 2 5 5x 3x 3x 3.1 9 1 2 . 6 6 (do 0 x 1) 2x 2 2 2 2 2 9 Vậy MinP khi a b 1 2
Ví dụ 4: Cho a 0, b 0 và 2 2 a b a
b . Tìm giá trị nhỏ nhất của biểu thức 2020 4 4 P a b 2 a b Lời giải 2 2 2 x y x y Sử dụng , ta đƣợc 2 2 2 2 2 2 a b a b a b a b 2 2 a b a b 2. 2 1 0 a b 2 2 2 2 2 2 2 2 2 2 2 2 2 a b 2020 a b 2020 a b 2020 P 2. 2 2 2 2 2 a b 2 a b 2 a b Đặt 2 x a b , ), 0 x 4 , ta đƣợc: x 2020 x 8 2012 x 8 2012 P 2 . 2 x 2 x x 2 x x 14 2012 2012 4 4 50 (do 0 x 4 ) x 4 Vậy MinP 507 khi x 4 hay a b 1 2 2 x y
Ví dụ 5: Cho x 0, y 0 và x 1 y 1
4 . Tìm giá trị nhỏ nhất của biểu thức P y x Lời giải Có x 1 y 1 4 xy x y 3 3 xy . x 1 . y 1 x y x 1 y 1 Mà xy . x 1 . y 1 x y 1, suy ra x y 2 2 2 2 2 2 2 2 x y x y Có P y x x y y x y x 2 2 x y 2 .y 2 .x x y x y 2 y x Vậy MinP 2 khi x y 1 II.
BẤT ĐẲNG THỨC BUNHIA 1.
Dạng bộ hai số ; a b và ; x y bất kỳ  2 2 2 2 2 ax by a b x y x y Dấu " " xảy ra a b  2 2 Đặc biệt 2 2 2 2 x y 1.x 1.y 1 1 x y 2.
Dạng bộ ba số ; a ; b c và ;
x y; z bất kì  2 2 2 2 2 2 2 ax by cz a b c x y z x y z Dấu " " xảy ra a b c  2 2 Đặc biệt 2 2 2 2 2 2 x y z 1.x 1.y 1.z 1 1 1 x y z 3.
Dạng tổng quát bộ n số a ;a ; ; a và x ; x ; ; x 1 2 n 1 2 n  2 2 2 2 2 2 2 a x a x a x a a a x x x 1 1 2 2 n n 1 2 n 1 2 n x x x Dấu " " xảy ra 1 2 n a a a 1 2 n Quy ƣớc trong dấu "
" xảy ra, nếu mẫu nào bằng 0 thì tử tƣơng ứng bằng 0.
Ví dụ 1. Cho 4x + 9y = 13. Tìm giá trị nhỏ nhất của biểu thức A = 4x2 + 9y2 Lời giải 15 Bunhia
Có 132 = (4x + 9y)2 = (2.2x + 3.3y)2
 (22 + 32)(4x2 + 9y2) = 13A  A 13
Ví dụ 2. Cho 4x + 3y = 1. Tìm giá trị nhỏ nhất của biểu thức A = 4x2 + 3y2 Lời giải Bunhia 1
Có 12 = (4x + 3y)2 = (2.2x + 3 . 3 y)2
 (4 + 3)(4x2 + 3y2) = 7A  A  7 2x 3x 1  = 1 Vậy MinA = khi  3y 3  x = y = 7 7  4x + 3y = 1
Ví dụ 3. Cho x ≥ 0; y ≥ 0; z ≥ 0 v| x + y + z = 2. Tìm giá trị nhỏ nhất của biểu thức A = x2 + y2 + z2 Lời giải Bunhia 4 Có 22 = (1.x + 1.y + 1.z)2
 (12 + 12 + 12)( x2 + y2 + z2) = 3A  A  3 x y z 4  =  2 Vậy MinA = khi  1 1 1  x = y = 3 3 x + y + z = 2 6
Ví dụ 4. Cho 3x2 + 2y2 =
. Tìm giá trị nhỏ nhất của biểu thức A = 2x + 3y 35 Lời giải 2  2 3  Có S2 = (2x + 3y)2 = . 3x + . 2y    3 2  Bunhia  4 9  35 35 6  +   2 2 3x +2y  =  2 2 3x +2y   . =1  S  1  3 2  6 6 35  3x 2 y  4y  4  = 3x 2y x = x = 2 3 =      9  35 Vậy MaxS = 1     2 3     3 2 8y 9  2x + 3y = 1  + 3y = 1   y = 2x + 3y = 1  9  35 1
Ví dụ 5. Cho 4a2 + 25b2 ≤
. Tìm giá trị nhỏ nhất của biểu thức H = 6a – 5b 10 Lời giải
Có H2 = (6a – 5b)2 = (3.2a + (–1) .5b)2 Bunhia 1
 (9 + 1)(4a2 + 25b2) = 10(4a2 + 25b2) ≤ 10. = 1  H ≤ 1 10 16  3 2a 5b a =  = 2a + 15b = 0  20 Vậy MaxH = 1   3 -1     1   8a - 15b = 3 1 6a - 5b = 1   b = -  50 3
Ví dụ 6. Cho x2 + y2 + z2 = . Tìm giá trị lớn nhất của biểu thức P = x + y + z 4 Lời giải Bunhia 3 19 3 Có P2 = (1.x + 1.y + 1.z)2
 (12+ + 12 + 12)(x2 + y2 + z2) = 3. =  P ≤ 4 4 2 x y z =  3 1 1 1 1 Vậy MaxP = khi   x = y = z = 2 3 2 x + y + z =  2
Ví dụ 7. Tìm giá trị lớn nhất của biểu thức P = x - 1 + 3 - x khi 1 ≤ x ≤ 3 Lời giải Bunhia 2 2 Có P2 =  2 1. x - 1 + 1. 3 - x   2 2
1  1  x - 1 + 3 - x  = 4  P ≤ 2 x 1 3  x Vậy MaxP = 2 khi   x = 2 (thỏa mãn) 1 1
Ví dụ 8. Cho a ≥ 0, b ≥ 0, c ≥ 0 v| a + b + c = 3. Tìm gi{ trị lớn nhất của biểu thức K = 4a + 5 + 4b + 5 + 4c + 5 Lời giải Có K2 =  2
1. 4a + 5 + 1. 4b + 5 + 1. 4c + 5 Bunhia
 (12+ + 12 + 12)( 4a + 5 + 4b + 5 + 4c + 5)
= 3[4(a + b + c) + 15] = 3(4.3 + 15) = 81  K ≤ 9  4a + 5 4b + 5 4c + 5  = = Vậy MaxK = 9 khi   a = b = c = 1 1 1 1 a + b + c = 3
Ví dụ 9. Cho a ≥ 0, b ≥ 0, c ≥ 0 v| a + b + c = 1. Tìm gi{ trị lớn nhất của biểu thức P = b + c + c + a + a + b Lời giải Có P2 =  2 1. b + c + 1. c + a + 1. a + b Bunhia 2 2 2
 (12+ + 12 + 12) b + c + c + a + a + b 
= 6 (a +b + c) = 6  P  6 17  a + b b + c c + a  = = 1 Vậy MaxP = 6 khi   a = b = c = 1 1 1 3 a + b + c = 1
Ví dụ 10. Cho a, b, c ≥ 0 v| a + b + c = 3 . Tìm giá trị nhỏ nhất của biểu thức a + b b + c c + a M = + + 2 2 2 Lời giải
 a+ b2 =1. a+1. b2 Bunhia    2 2 1 +1 a+b =2 a+b  2 2 Bunhia  Ta có
 b+ c =1. b+1. c   2 2
1 +1 b+c =2 b+c
 c+ a2=1. c+1. a2 Bunhia 2 2
1 +1 c+a  =2 c+a   Suy ra a + b  2(a+b), b + c  2(b+c), c + a  2(c+a)
 2 a + b+ c   2  a+b+ b+c+ c+a  a+b b+c c+a  a + b + c  + + hay M ≥ 3 2 2 2
Vậy MinM = 3 khi a = b = c = 1
III. PHƯƠNG PHÁP BIẾN ĐỔI TƯƠNG ĐƯƠNG
DẠNG 1: ĐƯA VỀ BÌNH PHƯƠNG
 A2 ± m ≥ 0 ± m ; - A2 ± m ≤ 0 ± m
Dấu “=” xảy ra khi A = 0.
 A2 + B2 ± m ≥ 0 + 0 ± m; - A2 - B2 ± m ≤ 0 + 0 ± m
Dấu “=” xảy ra khi A = 0, B = 0.
Ví dụ 1. Cho x ≥ - 2; y ≥ 1. Tìm gi{ trị nhỏ nhất của biểu thức
A = x + y - 2 x + 2 - 4 y - 1 + 24 . Lời giải
Có A = x + 2 - 2 x + 2  
1 +  y - 1 - 4 y - 1  4 + 18 2 2 =  x + 2 - 
1 +  y - 1 - 2 +18  0 + 0 + 18 = 18  x + 2 = 1 x = -1 Vậy MinA = 18 khi    ( thỏa mãn)  y = 5 y - 1 = 2  1
Ví dụ 2. Cho x ≥ - . Tìm giá trị nhỏ nhất của biểu thức E = 5x - 6 2x + 7 - 4 3x + 1 + 2 . 3 18 Lời giải
Có E = 2x + 7 - 6 2x + 7 9 +  3x + 1 - 4 3x + 1  4 - 19 2 2
=  2x + 7 - 3 + 3x + 1 - 2 - 19  0 + 0 - 19 = - 19
 2x + 7 = 3 2x + 7 = 9 Vậy MinA = - 19 khi     x = 1 ( thỏa mãn) 3   x + 1 = 4 3x + 1 = 2
Ví dụ 3. Cho x  1. Tìm giá trị nhỏ nhất của biểu thức
T = x  x 1  3 x  7  28. Lời giải
Xét 2T = 2x  2 x 1  6 x  7  56
 x 1 2 x 1 
1  x  7  6 x  7  9  40   x 1 2
1   x  7  32  40  0  0  40  40  T  20  x 1 1 x 1 1
Vậy Min T  20 khi   
 x  2 (thỏa mãn)    x  7  9 x 7 3
Ví dụ 4. Cho x  15. Tìm giá trị nhỏ nhất của biểu thức 2
F  x  x   2 x  x  2 15
3  x 15  x  3  38. Lời giải Xét 2
F  x  x 
 2x  x  2 2 2 2 2 15
3  2 x 15  x  3  76
  2x 15 x32  2x 15x3 2 2
x 15  2 x 15  
1  x  3 2 x  3   1
  x 15  x 32  x 15  2
1   x  3  2 2 2
1  42  0  0  42  4  2  F  21  Vậy Min F  21  khi 2 x 15 
x  3  1  x  4 (thỏa mãn)
Ví dụ 5. Cho a  0,b  0,c  0 và a  b  c  6. Tìm giá trị lớn nhất của biểu thức T= 2 2 2 2 2 2
a  4ab  b  b  4ab  c  c  4ca  a . Lời giải
Chú ý: Với x  0, y  0, ta có
6 x  y2  2 x  y2
6  x  y2 2 2
x  4xy  y   4 4 x  y 6 2 2  
 x  4xy  y  . 2
Vận dụng vào bài toán, ta có
a b 6 bc 6 c  a 6 T   
 a  b  c 6  6 6 2 2 2 19
Vậy MaxT  6 6 khi a = b = c =2.
Ví dụ 6. Cho a  0,b  0,c  0 , x  y  z 1. Tìm giá trị lớn nhất của biểu thức S = 2 2 2 2 2 2
x  xy  y 
y  yz  z  z  zx  z . Lời giải
Chú ý: Với x  0, y  0, ta có
a b2 3a b2 a b2 2 2
a  ab  b   4 4 a  b 2 2
 a  ab  b  2 x  y y  z z  x
Vận dụng vào bài toán, ta có S   
 x  y  z 1. 2 2 2 1
Vậy MinS  1 khi x  y  z  . 3
DẠNG 2: TẠO RA BẬC HAI BẰNG CÁCH NHÂN HAI BẬC MỘT 
m  x  n   x  m x  n  0.  m 
x  n   x  m x  n  0. Ví dụ 1.Cho 2   , a , b c  3 và 2 2 2
a  b  c  22.
Tìm giá trị nhỏ nhất của biểu thức M  a  b  . c Lời giải Vì 2
  a  3 nên a  2  0,a 3  0.
Suy ra a  a   2 2 2
3  0  a  a  6  0  a  a  6.
Tƣơng tự, ta cũng tìm đƣợc 2 2
b  b  6, c  c  6 Do đó 2 2 2
M  a  b  c  a  b  c 18  22 18  4. a  2  ,a  3 
a  b  3,c  2  b   2  , b  3  Vậy MinM =4 khi 
 a  c  3,b  2  c 2, c 3     
b  c  3,a  2  
a b  c  4
Ví dụ 2.Cho x  0, y  0, z  0 thỏa mãn x  y  z  6.
Tìm giá trị nhỏ nhất của biểu thức 2 2 2
A  x  y  z . Lời giải  Tìm MinA
Cách 1 (Sử dụng bất đẳng thức Bunhia) Bunhia Có
  x  y  z2 2   2 2 2    2 2 2 6 1. 1. 1. 1 1 1
x  y  z   3A  A 12.  x y z    Vậy MinA = 12 khi 1 1 1
 x  y  z  2.
x  y  z  6
Cách 2 (Sử dụng bất đẳng thức Côsi – dự đo{n min đạt tại x=y=z=2) 20 Có 2 2 2
A  x  y  z   2 x     2 y     2 4 4 z  4 12 2 2 2
 2 x .4  2 y .4  2 z .4 12  4x  y  z 12  4.6 12 12.
Vậy MinA  12 Khi x  y  z  2.  Tìm MaxA Có ,
x y, z  0 và x  y  z  6 nên 0  , x y, z  6.
 xx  6  y y  6  zz  6  0 2 2 2
 x  y  z  6x  y  z  6.6  36  A  36. x  0, x  6  y  0, y  6 Vậy MaxA  36 khi  hay  ;
x y; z  là hoán vị của 0;0;6. z  0, z  6 
x  y  z  6
Ví dụ 3.Cho a  0, b  0,c  0 thỏa mãn a  b  c  3.
Tìm giá trị nhỏ nhất của biểu thức K  3a 1  3b 1  3c 1. Lời giải  Tìm MaxK
Cách 1 (Sử dụng bất đẳng thức Bunhia) Xét K   a   b   c  2 2 1. 3 1 1. 3 1 1. 3 1 Bunhia   2 2 2
1 1 1 3a 1 3b 1 3c  
1  9 a  b  c   1  36  K  6.
Vậy MaxK  6 khi a  b  c 1.
Cách 2 (Sử dụng bất đẳng thức Côsi – dự đo{n min đạt tại a=b=c=1) 1
K  3a 1  3b 1  3c 1   3a   1 .4  3b   1 .4  3c   1 .4  2   1 3a   1  4 3b   1  4 3c   1  4 
3a  b  c 15 3.3 15       6.   2 2 2 2 4 4  
Vậy Max K  6 khi a  b  c 1.  Tìm MinA
Có a  b  c  3  3a  3b  3c  9  3a   1  3b   1  3c   1  12.
Đặt x  3a 1, y  3b 1, z  3c 1 ,
x y, z  1 và x  y  z  12. Từ ,
x y, z  1 và x  y  z 12 1 , x , y z  10   
x   x 
  x   x 10 1 10 0 10 1 x  10  0  x  . 10 1 y  10 z  10 Tƣơng tự y  , z  , suy ra 10 1 10 1 21
x  y  z  3 10 12  3 10 x  y  z   K   10  2. 10 1 10 1
Vậy MinK  10  2 khi  ,
x y, z  là hoán vị của 1;1;10 nên  ; a ;
b c hoán vị của 0;0;3.
DẠNG 3: TẠO RA ab+bc+ca  0  , a ,
b c  m  m  am  bm  c  0  0  , a ,
b c  m  m  am  b  m  am  c  m  bm  c  0
Ví dụ 1. Cho 0  , a ,
b c  2 và a  b  c  3. Chứng minh ab  bc  ca  2. Lời giải Do 0  , a ,
b c  2 nên 2  a2  b2  c  0
 8  4a  b  c  2ab  bc  ca  abc  0
 8  4.3 2ab  bc  ca  abc  0 (do a  b  c  3 ) abc abc
 ab  bc  ca  2  , mà 2 
 2 nên ab bc  ca  2 (đpcm). 2 2
Ví dụ 2: Cho a  1, b  1, c  1 và ab+bc+ca =9.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức: P =a2 + b2 + c2 Lời giải: * Tìm Min P
Có (a –b)2 +(b- c)2 +(c-a)2  0 => a2 +b2 +c 2  ab +bc+ca => P  9.
Vậy MinP =9 khi a = b= c = 3 * Tìm MãP
Do a  1, b  1, c  1 => (a-1)(b-1) +(b-1)(c-1) +(c-1)(a-1)  0
<=> (ab+ bc +ca) -2(a+b+c) +3  0 <=> a+ b+ c  6
<=> a2 + b2 +c2 +2(ab+bc+ca)  36 <=> P  18
Vậy MaxP=18 khi (a,b,c) là hoán vị của (1;1;4)
DẠNG 4: SỬ DỤNG TÍNH CHẤT TRONG BA SỐ BẤT KÌ LUÔN TÒN TẠI HAI SỐ CÓ TÍCH KHÔNG ÂM
Tính chất 1: Nếu -1  a  1 thì n a  a n   N*
Dấu “=” xảy ra khi a=0 hoặc a=1 nếu n lẻ, khi a=0 hoặc a=  1 nếu n chẳn
Tính chất 2: Nếu hai số a và b có tích ab  0 thì a  b  a  b
Tính chất 3: Với ba số x, y, z bất kỳ, luôn tồn tại hai số có tích không âm.
Bài toán cơ bản: Cho -1  x, y, z  1, x+ y+ z =0
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức: T = x  y  z Lời giải:
Với ba số x, y, z bất kỳ, luôn tồn tại hai số có tích không âm.
Giả sử xy  0 => x  y  x  y  z  z
Nên T  2 z  2 ( do -1  z  1 ). 22
Vậy MaxT =2 khi (x;y;z) là hoán vị (-1;0;1).
Ví dụ 1. Cho -2  x, y, z  2, x+ y+ z =0. Chứng minh rằng a4 +b4 +c4  32 Lời giải: a a a
Có -2  x, y, z  2 => 1   , , ,1 2 2 2 a b c Đặt x  , y  , z   1
  x, y, z 1 và x+y+z=0. 2 2 2
Khi đó a4 +b4 +c4 =16(x4 +y4 +z4)  16 x  y  z  .
Với ba số x, y, z bất kỳ, luôn tồn tại hai số có tích không âm.
Giả sử: xy  0 => x  y  x  y  z  z nên 4 4 4
x  y  z  2 z  2  a  b  c  32 ( đpcm) 3
Ví dụ 2. Cho 0  x, y, z  1 và x+ y+ z = . 2
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức: P=x2 +y2 +z2 Lời giải: Tìm Min P
Cách 1( Sử dụng bất đẳng thúc Bunhia) 2 Bunhia  3  3 Có 2 2 2 2 2 2 2
 (1.x 1.y 1.z)  (1 1 1 )(x  y  z )  3P  P     2  4 x y z    3 1 1 1 1 Vậy MinP = Khi   x  y  z  4 3 2 x  y  z   2 1
Cách 2( Sử dụng bất đẳng thức Côsi – dự đo{n min đạt tại x=y=z= ) 2 1 1 1 1 1 1 3 3 2 2 2  2   2   2  Cã P  x  y  z  x   y   z   2 2 x .  2 2 y .  2 2 z .   x  y  z        .  4   4   4  4 4 4 4 4 3 1 Vậy MinP = Khi x = y = z = 4 2 Tìm MaxP 3
Có x + y + z =  (2x – 1) + (2y – 1) + (2z – 1) = 0 2
Đặt a = 2x – 1, b = 2y – 1, c = 2z – 1.
Do (2x – 1) + (2y – 1) + (2z – 1) = 0 nên a + b + c = 0
Vì 0 ≤ x, y, z ≤ 1  - 1 ≤ 2x – 1, 2y – 1, 2z – 1 ≤ 1 nên – 1 ≤ a, b, c ≤ 1. 2 2 2 2 2 2  a 1  b 1  c 1
a  b  c  2(a  b  c)  3 Có P =           2   2   2  4 2 2 2
a  b  c  3
a  b  c  3 = 
(do 1  a, , b c  1) 4 4 23
Với ba số a, b, c bất kì, luôn tồn tại hai số có tích không âm.
Giả sử a.b ≥ 0 thì a  b  a  b  c   c nên 2 c  3 2  3 5 P    (do c 1) . 4 4 4 5  1 3 
Vậy MaxP = khi (a; b; c) là hoán vị của (- 1; 0; 1) hay (x; y; z) là hoán vị của 0; ;   . 4  2 2 
Ví dụ 3: Cho 0 ≤ x, y, z ≤ 2 v| x + y + z = 3. Tìm gi{ trị lớn nhất và nhỏ nhất của biểu thức
M = x4 + y4 + z4 + 12(1 – x)(1 – y)(1 – z). Lời giải
Có x + y + z = 3  (x – 1) + (y – 1) + (z – 1) = 0
Đặt a = x – 1, b = y – 1, c = z – 1  - 1 ≤ a, b, c ≤ 1 v| a + b + c = 0
Với a + b + c = 0 thì a3 + b3 + c3 = 3abc
Có M = (a + 1)4 + (b + 1)4 + (c + 1)4 – 12abc
= (a4 + b4 + c4 ) + 4(a3 + b3 + c3) + 6(a2 + b2 + c2) + 4(a + b + c) – 12abc
= (a4 + b4 + c4) + 6(a2 + b2 + c2).
* Có M = (a4 + b4 + c4) + 6(a2 + b2 + c2) ≥ 0
Vậy Min M = 0 khi a = b = c = 0  x = y = z = 1
* Có M = (a4 + b4 + c4) + 6(a2 + b2 + c2) ≤  a  b  c   6 a  b  c   7 a  b  c .
Với ba số a, b, c bất kì, luôn tồn tại hai số có tích không âm.
Giả sử ab ≥ 0  a  b  a  b  c   c
 a  b  c  2 c  2  M 14 .
Vậy MaxM = 14 khi (a; b; c) là hoán vị của (- 1; 0; 1) hay (x, y, z) là hoán vị của (0; 1; 2).
Ví dụ 4: Cho 0 ≤ a, b, c ≤ 4 v| a + b + c = 6.
Tìm giá trị lớn nhất của biểu thức P = a2 + b2 + c2 + ab + bc + ca. Lời giải
a  b  c
a bc2 2 2 2 2 2 2
a  b  c Có P   18. 2 2 2 a  2 b  2 c  2
Do a + b + c = 6  (a – 2) + (b – 2) + (c – 2) = 0     0 2 2 2 a  2 b  2 c  2 Đặt x  , y  , z   x + y + z = 0. 2 2 2
a  2 b  2 c  2
Vì 0 ≤ a, b, c ≤ 4  - 2 ≤ a – 2, b – 2, c – 2 ≤ 2  - 1  , , 1. 2 2 2  - 1 ≤ x, y, z ≤ 1.
 x  2  y  2  z  2 2 2 2 2 2 2 Có P 
18 = 2(x2 + y2 + z2) + 4(x + y + z) + 24 2 24
= 2(x2 + y2 + z2) + 24 ≤ 2 x  y  z   24
Với ba số x, y, z bất kì, luôn tồn tại hai số có tích không âm.
Giả sử xy ≥ 0  x  y  x  y  z  z nên P  4 z  24  4  24  28 (do 1 z 1).
Vậy MaxP = 28 khi (x, y, z) là hoán vị của (- 1; 0; 1) nên (a, b, c) là hoán vị của (0; 2; 4).
DẠNG 5: SỬ DỤNG TÍNH CHẤT CỦA MỘT SỐ BỊ CHẶN TỪ 0 ĐẾN 1
* Nếu 0  x 1 thì x  x . Dấu “ ”
 xảy ra khi x  0 hoặc x  1
* Nếu 0  x 1 thì n * x  x n   . Dấu “ ”
 xảy ra khi x  0 hoặc x  1.
Ví dụ 1: Cho a  0;b  0;c  0 và a  b  c 1 . Tìm giá trị lớn nhất và nhỏ nhất của biểu thức
P  b  c  c  a  a  b . Lời giải * Tìm MaxP
Cách 1: ( Sử dụng bất đẳng thức Bunhia) Xét 2 2
P  (1. b  c 1. c  a 1. a  b) Bunhia      2 2 2 2 2 2 1 1 1
b  c  c  a  a  b 
 6(a  b  c)  6( do a  b  c 1)  P  6 1
Vậy Max P  6 khi a  b  c  3 1
Cách 2: ( Sử dụng bất đẳng thức Cosi - dự đo{n max đạt tại a  b  c  ) 3 2 2 2 2 Xét . P  (b  c)  (c  a)  (a b) 3 3 3 3 2 2 2  (b  c)  (c  a)  (a b) 3 3 3    2 2 2 2
1 a  b  c  2( do a  b  c 1)  P  2 :  6 3 1
Vậy Max P  6 khi a  b  c  3 * Tìm MinP
Sử dụng tính chất: 0  x 1 thì x  x Do , a ,
b c  0 và a  b  c  1 nên 0  a  , b b  , c c  a  1
Có P  b  c  c  a  a  b  (b  c)  (c  a)  (a  ) b  1
 2(a b  c)  2(doa b  c 1).
Vậy MinP  2 khi ( ; a ;
b c) là hoán vị (1;0;0) . 25
Ví dụ 2: Cho a  0;b  0;c  0 và a  b  c  3 . Tìm giá trị lớn nhất và nhỏ nhất của biểu thức
T  b  c  c  a  a  b . Lời giải * Tìm MaxP
Cách 1: ( Sử dụng bất đẳng thức Bunhia) Xét 2 2
T  (1. b  c 1. c  a 1. a  b) Bunhia      2 2 2 2 2 2 1 1 1
b  c  c  a  a  b 
 6(a  b  c) 18( do a  b  c  3)  P  3 2
Vậy MaxT  3 2 khi a  b  c 1
Cách 2: ( Sử dụng bất đẳng thức Cosi - dự đo{n max đạt tại a  b  c 1 )
Xét T. 2  2(b  c)  2(c  a)  2(a b) 2  (b  c) 2  (c  a) 2  (a b)    2 2 2
 3 a  b  c  6( do a  b  c  3)  P  6 : 2  3 2
Vậy MaxT  3 2 khi a  b  c 1 * Tìm MinP
Sử dụng tính chất: 0  x 1 thì x  x
a  b  c
a  b b  c c  a Do , a ,
b c  0 và a  b  c  3  1 nên 0  ; ; 1 3 3 3 3  b  c c  a a  b 
 b  c c  a a  b  Có T  3      3       3 3 3    3 3 3 
2(a  b  c)  3
 2 3 ( do a  b  c  3). 3
Vậy MinT  2 3 khi ( ; a ;
b c) là hoán vị (3;0;0) .
Ví dụ 3: Cho a  0;b  0;c  0 và a  b  c 1 . Tìm giá trị nhỏ nhất của biểu thức
F  3a 1  3b 1  3c 1 . Lời giải:
Cách 1: Có a  0; b  0; c  0; a  b  c 1 2 2 2  0  , a ,
b c  1 a  a ,b  b , c  c . Do đó :
F  3a 1  3b 1  3c 1  a  2a 1  b  2b 1  c  2c 1 . 2 2 2
 a  2a 1  b  2b 1  c  2c 1  a  b  c  3  4
Vậy MinF  4 khi ( ; a ;
b c) là hoán vị (0;0;1)
Cách 2: Có a  b  c 1  3a  3b  3c  3  3a   1  3b   1  3c   1  6 26
Đặt x  3a 1; y  3b 1; z  3c 1.  ,
x y, z  1 và x  y  z  6 và F  x  y  z Từ ,
x y, z  1 và x  y  z  6 1  , x y, z  4   
x   x   x 2 1
4  0  x  3 x  2  0  x  3 y  2 z  2
x  y  z  6 Tƣơng tự: y  ; z 
, suy ra x  y  z   F  4 3 3 3
Vậy MinF  4 khi ( ; x ;
y z) là hoán vị (1;1; 4) nên a, ,
b c là hoán vị (0;0;1) .
Ví dụ 4: Cho a  0;b  0;c  0 và a  b  c 1 . Tìm giá trị lớn nhất của biểu thức 2 2 2
M  2a  3a  4  2b  3b  4  2c  3c  4 . Lời giải:
Có a  0; b  0; c  0; a  b  c 1 2 2 2  0  , a ,
b c  1 a  a,b  b, c  c. Do đó : 2
M  a   2
a  3a  4 2  b   2
b  3b  4 2  c   2
c  3c  4 2
 a  a  3a  4 2
 b  b  3b  4 2
 c  c  3c  4 .
 a  22  b  22  c  22  a  b  c  6  7
Vậy MinM  7 khi ( ; a ;
b c) là hoán vị (0;0;1) .
DẠNG 6 : DỰ ĐOÁN KẾT QUẢ RỒI XÉT HIỆU
Ví dụ 1: Cho ;
x y  0 thỏa mãn x  y  10 . Tìm giá trị nhỏ nhất của biểu thức P   4 x   4 1 y   1 . Lời giải
Có P  x   y    x y  x  y    x y  x  y 2 4 4 4 4 4 4 4 4 2 2 2 2 1 1 1  2x y 1
 x y    xy2 4 4 2 2 4 4 2 2 10 2
 2x y 1 x y  2x y  40xy 101. 2 2  x  y   10  5 5
Đặt t  xy  0 thì xy         0  t     2  2 2 2   5 Ta đƣợc 4 2
P  t  2t  40t 101; 0  t  2
Đến đ}y ta kẻ bảng dự đo{n MinP t 0 1 2 2,5 P 101 64 45 52,5625
Từ bảng trên ta dự đo{n MinP  45 khi t  2 nên ta xét hiệu : 27 4 2 P 
 t  t  t    4 2 t  t   2 45 2 40 56 8 16
10t  40t  40
 t  2  t  2 2 4 4 2  0  P  45
x  y 
Vậy MinP  45 khi t  10 2  
 x, y là hai nghiệm của phƣơng trình : xy  2 10  2 10  2 10 2 2
t  10.t  2  0  t   x  ; y  . 2 2 2 Ví dụ 2: Cho 2 2
a  b  4ab  4a  4b . Tìm giá trị lớn nhất của biểu thức A   3 3
a  b    2 2 20
6 a  b   2013 . Lời giải
Có : a  b  ab  a  b  a  b  ab  a b2 2 2 4 4 4 4 4  2ab  
 ab  a b2 12 4
a b , mà    2 4ab a b hay
ab  a  b2 12 3 .
Nên a  b2  a  b  a  b2  a  b2 4 3
 a b  0  0  a b 1.
Đặt x  a  b thì 0  x 1 và 2
12ab  4x  x 3 2 Ta có A  20 
 a b 3aba b 6a b 2ab  2013     
a b3  aba b a b2 20 60 6 12ab  2013 3  x   2 x  x 2 2 2 20 5 4
x  6x  4x  x  2013  3x  x  2013
Đến đ}y ta kẻ bảng dự đo{n MaxA t 0 1 A 2013 2015
Từ bảng trên ta dự đo{n MaxA  2015 khi x  1 nên ta xét hiệu 2
A  2015  3x  x  2   x  
1 3x  2 . Do 0  x 1 nên  x  
1 3x  2  0 , suy ra A  2015 1
Vậy MaxA  2015 khi x  1 hay a  b  . 2
CÁC BÀI TOÁN PHÂN LOẠI VÀO LỚP 10 CÁC TỈNH NĂM 2019-2020 Câu 1:
[TS10 TP Hà Nội, 2019-2020] Cho biểu thức 4 4
P  a  b  ab , với a, b là các số thực thỏa mãn 2 2
a  ab  b  3. Tìm giá trị nhỏ nhất,
giá trị lớn nhất của biểu thức P Lời giải Ta có: 28       2      2 4 4 2 2 2 2 2 2 P a b ab a b 2a b ab 3 ab  2a b  ab 2  7  85   ab      2  4 Ta có:          2 2 3 a b 2ab 3 ab 3 ab a b  0  ab  3  2 2
3  ab  a  b  2ab  ab  1 2 7 7 7 1 7 9 1  7  81 Vì: 3
   ab   1   ab     a     2 2 2 2 2 2 4  2  4 2 2 81  7  1  7  85     a     1    a        21 4  2  4  2  4  1  P  21
GTLN của P là 21 khi a  3, b   3 hoặc a   3, b  3
GTNN của P là 1 khi a = b = 1. Câu 2:
[TS10 Tỉnh Bắc Ninh, 2019-2020]
Cho hai số thực không âm a, b thỏa mã: 2 2
a  b  2. Tìm GTLN và GTNN của biểu thức 3 3 a  b  4 M  ab  1 Lời giải Tìm GTNN:  Ta có:        AM GM 3 3 3 3 a b 4 a b 1  3  3ab  3.
Dấu “=” xảy ra khi a = b = 1. 3 3 a  b  4 3ab   1 Vì a, b > 0 nên M    3 ab  1 ab  1
Do đó giá trị nhỏ nhất của biểu thức M l| 3 đạt đƣợc khi a = b = 1. Tìm GTLN: Đặt S  a  b,P  ab  Vì       2 2 2 2 2 S 2 a b 2
a b  2ab  2  S  2P  2  P  . 2 Ta có:   2 2 2 a b
 a  2ab  b  2  2ab  2  a  b  2 Do đó S  2 29 2  S  2      
a  b  3aba  b 2 2 S 3. .S 4 2  4 S  3PS  4  2  M    2 ab  1 P  1 S  2 1 2 2 S  6S  8 8 6 8 6     S    2  4  2. 2 2 S S S 2 2 2 2 a   b Dấu “=” xảy ra khi 
 a  b  0; 2; 2;0  ab  0
Vậy giá trị lớn nhất của M là 4  2 2 khi 0; 2; 2;0 Câu 3:
[TS10 Tỉnh Nghệ An, 2019-2020] Giải phƣơng trình: 2 2
5x  27x  25  5 x  1  x  4 Lời giải ĐKXĐ: x  2 2 2
5x  27x  25  5 x  1  x  4 2
 5x  27x  25  25x 1   2 x  4  10  2 x  4x  1 2  2x  x  2  5  2 x  4x  1  0  2 2 x  x  2  5  2
x  x  2x  2  3x  2  0 Đặt 2
x  x  2  a  0; x  2  b  2 Phƣơng trình trở thành:  a  b 2 2
2a  5ab  b  0  2a  3ba  b  0   2a   3b x  1 5TM Với 2 2
a  b  x  x  2  x  2  x  2x  4    y  1 5  L  1  3 65 x  TM Với 
  2        2       8 2a 3b 4 x x 2 9 x 2 4x 13x 26 0  13  3 65  x  L  8 1 3 65
Vậy phƣơng trình có 2 nghiệm: x  1 5; x  8 Câu 4:
[TS10 Tỉnh Hải Phòng, 2019-2020]   a) Cho ,
x y, z là ba số dƣơng. Chứng minh  x  y  z 1 1 1    9    x y z  30 b) Cho a, ,
b c là ba số dƣơng thỏa mãn a  b  c  6. Tìm giá trị lớn nhất của biểu thức ab bc ca A    
a  3b  2c
b  3c  2a
c  3a  2b Lời giải a) Ta có   
x  y  z  1 1 1    9    x y z  x x y y z z        6 y z x z x y  x y   y z   z x     2    2    2  0        y x   z y   x z 
x  y2  y  z2 z  x2     0 x
 , y, z  0 xy yz zx  
Vậy  x  y  z 1 1 1    9    x y z  b)
Áp dụng bất đẳng thức ở câu a) ta có ab ab 9 ab  1 1 1        
a  3b  2c 9
a  c  b  c  2b 9  a  c b  c 2b  ab 1  ab ab a       (1)  
a  3b  2c 9  a  c b  c 2 
Chứng minh tƣơng tự ta có: bc 1  bc bc b      (2)  
b  3c  2a 9  a  b a  c 2  ca 1  ac ac c      (3)  
c  3a  2b 9  b  c a  b 2 
Cộng từng vế của các bất đẳng thức (1); (2) và (3) ta có 1  ac  bc ab  ac bc  ab
a  b  c  A       9  a  b b  c c  a 2 
1  c a  b
a b  c
b c  a
a  b  c   A       9 a  b b  c c  a 2  
1 3a  b  c 1 3.6  A      1. 9 2 9 2
Dấu “=” xảy ra  a  b  c  2.
Vậy giá trị lớn nhất của biểu thức A là 1 đạt đƣợc khi a  b  c  2. 31 Câu 5:
[TS10 Tỉnh Thanh Hóa, 2019-2020]
Xét các số thực dƣơng a, b, c thỏa mãn abc 1.Chứng minh rằng: ab bc ca    1 4 4 4 4 4 4 a  b  ab b  c  bc c  a  ca Lời giải 4 4 2 2      Ta có: a b ab(a b ) a; b R Thật vậy: 4 4 2 2 a  b  ab(a  b ) 4 4 3 3
 a  b  a b  ab 3 3
 (a  b)(a  b )  0 2 2 2
 (a  b) (a ab  b )  0 (luôn đúng a  ; bR ) => 4 4 2 2 4 4 2 2
a  b  ab  ab(a  b )  ab  a  b  ab  ab(a  b )  abc ( vì a;b;c > 0 và abc = 1) Do đó: 2 2 ab ab 1 1 1 c 2  c     4 4 2 2 2 2 a  b  ab ab(a  b )  ab a  b  1  2 2 a  b   1  2
1 1 c  a  b  c2 Tƣơng tự: 2 2 bc 1 a ca 1  b  (2);  (3) 4 4 b  c  bc    2 4 4 c  a  ca a b c a bc2 Mặt khác:     2 2 2 2
2 ab bc ca  2.3 a b c  6
Cộng theo vế các bất đẳng thức (1),(2) và (3) ta có: 2 2 2 2 2 2 a b c a  b  c  6
a  b  c  2ab  bc  ca      1 4 4 4 4 4 4 b  c  a a  c  b a  b  c a bc2 a bc2
Vậy b|i to{n đƣợc chứng minh
Dấu “=” xảy ra kh a = b = c = 1 Câu 6:
[TS10 Tỉnh Quảng Ninh, 2019-2020]
Cho các số dƣơng a, b, c thoả mãn a  b  c  1. Tìm giá trị nhỏ nhất của: 1 2019 P   2 2 2 a  b  c ab  bc  ca Lời giải 1 1 1 1
Áp dụng bất đẳng thức Cô si cho 3 số dƣơng 3 a  b  c  abc;    3 3 a b c abc 32  1 1 1  Suy ra a  b  c      9 *  a b c 
Bất đẳng thức đƣợc chứng minh. Dấu đẳng thức xẩy ra khi và chỉ khi a  b  c a  b  c 2 2 2  2 1
b) Ta có ab  bc  ca  a  b  c  ab  bc  ca   3 3 2017 Suy ra  6051 ab  bc  ca
Áp dụng bất đẳng thức trong câu a, ta có  1 1 1     2 2 2
a  b  c  2ab  2bc  2ca    9 2 2 2   a  b  c ab  bc  ca ab  bc  ca  1 2 9 Suy ra    9 2 2 2 a  b  c ab  bc  ca a bc2 1 2019 Do đó ta đƣợc P    6060. 2 2 2 a  b  c ab  bc  ca
Vậy giá trị nhỏ nhất của P là 6060 1
Dấu đẳng thức xẩy ra khi và chỉ khi a  b  c  . 3 Câu 7:
[TS10 Tỉnh Bắc Giang, 2019-2020]
Cho x, y là các số thực thỏa mãn 2 2
x  y  1 . Tìm giá trị nhỏ nhất của biểu thức
P  3  x3  y Lời giải Ta có:     
 x  y   x  y
18 6  x y 2xy P 3 3 9 3  xy  2 17   2 2
x  y   6 x  y  2xy
8   x  y2  6 x  y  9   2 2
x  y 32   4. 2 Từ 2 2
x  y  1chỉ ra đƣợc  x  y2  2  2  x  y  2;
Suy ra  2  3  x  y  3  2  3  0. 33
x  y     2 2 2 3 3 19  6 2 P   4   4   2 2 2 19  6 2 2
Vậy gi{ trị nhỏ nhất của P là khi x  y   2 2 Câu 8:
[TS10 Tỉnh Vũng T|u, 2019-2020]
Cho số thực dƣơng x, y thỏa mãn x  y  3
Tìm Giá trị nhỏ nhất của biểu thức 1 5 P   5xy x  2y  5 Lời giải 1 5 1 5 1 5 P      5xy x  2 y  = 5 5xy
(x  y)  y  5 5xy y  8 1 xy 5 y  8 xy  y  8  P      5xy 20 y  8 20 20
x  y  2 1  8 xy  y  8 y(x 1)  8 3 Ta lại có: 4    20 20 20 5 Khi đó:  1 xy   5 y  8  xy  y  8 P         
 5xy 20   y  8 20  20 1 3 3
 P  1  P  5 5 5 3 x 1 Vậy P    Min 5 y  2 Câu 9:
[TS10 Tỉnh Bình Định, 2019-2020] x  y 2 2 x  y Cho ,
x y là hai số thực thỏa 
. Tìm giá trị nhỏ nhất của biểu thức P  . xy 1 x  y Lời giải
Với x  y, xy 1, ta có 2 2 2 x  y
(x  y)  2xy 2 P    x  y  x  y x  y x  y 2
Vì x  y  x  y  0;  0 xy  . x  và 1 y 2
Áp dụng bất đẳng thức Cô-si cho hai số dƣơng x  y; x  , ta có y 34 2 2(x  y) x  y   2  2 2  2 2 x  y x  y Suy ra min P  2 2 . 2 Dấu đẳng thức xảy ra 2  x  y 
 (x  y)  2  x  y  2  x  y  2 . x  y  6  2  y  2 Mà 2 2
xy  1  ( y  2) y  1  y  2 y  1  y  2 y 1  0     6  2  y   2  2  6  2  6 x     x 2  2
Vậy min P  2 2 tại  hoặc    2  6   2  6 y   y  .   2  2
Câu 10: [TS10 Tỉnh Đắk Lắk, 2019-2020]
Cho ba số thực dƣơng x, y, z thỏa mãn: x  2y  3z  2 . xy 3yz 3xz
Tìm giá trị lớn nhất của biểu thức: S    xy  3z 3yz  x 3xz  . 4y Lời giải
Đặt a  x;b  2y;c  3z , ta đƣợc: a, b,c  0; a  b  c  2 . ab bc ac Khi đó: S    ab  2c bc  2a ac  . 2b ab ab ab 1  a b  Xét       ab  2c ab  a  b  cc
a cb c 2  a c b c  a b
Dấu đẳng thức xảy ra khi và chỉ khi  a  c b  . c bc 1  b c  ac 1  a c  Tƣơng tự ta có:   ;       . bc  2a 2  b  a c  a  ac  2b 2  a  b c  b  b c a c
Dấu đẳng thức xảy ra khi và chỉ khi   b  a c  ; a a  b c  . b 1  a  b b  c a  c  3
Cộng c{c vế ta đƣợc: S       . 2  a  b b  c a  c  2 35 3 2 3
Vậy gi{ trị lớn nhất của S bằng
khi v| chỉ khi a  b  c 
hay gi{ trị lớn nhất của S bằng khi và 2 3 2 2 1 2
chỉ khi x  ; y  ; z  . 3 3 9
Câu 11: [TS10 Tỉnh Đắk Nông, 2019-2020] 1
Cho các số thực dƣơng a, ,
b c thỏa mãn a  b  c 
. Tìm giá trị nhỏ nhất của biểu thức abc
P  a  ba  c . Lời giải 1
Ta có: a  b  c 
 abca b  c 1. abc
Theo bất đẳng thức côsi ta có:
P  a  ba  c 2
 a  ab  ac  bc  2 aa b  c.bc  2
aa  b  c  bc
aa  b  c 1
Đẳng thức xảy ra khi:    b  c 1 b  c 1
Ta thấy hệ có vô số nghiệm dƣơng chẳng hạn b  c 1, a  2 1. Vậy P  2 . min
Câu 12: [TS10 Tỉnh Đồng Nai, 2019-2020]
Cho ba số thực a, b,c . Chứng minh rằng:
a bc3 b ca3 c ab3 2 2 2   2 a  bc 2 b  ca 2 3 c  ab Lời giải Phƣơng pháp: - Đặt 2 2 2 x a bc, y b ca, z c
ab đƣa bất đẳng thức cần chứng minh về 3 3 3 x y z 3xy . z - Chứng minh đẳng thức 3 3 3
x  y  z  xyz   x  y  z 2 2 2 3
x  y  z  xy  yz  zx - Từ đó đ{nh g{i hiệu 3 3 3 x y z
3xyz và kết luận. Đặt 2 2 2 x a bc, y b ca, z c ab
Bất đẳng thức cần chứng minh trở thành : 3 3 3 x y z 3xy . z Ta có: 36 3 3 3
x  y  z  3xyz   3 3 x  y  3  3xyz  z
 x  y3 3xyx  y 3  3xyz  z
 x  y3 3
 z  3xy x  y  z
 x  y  z x  y2 x  y 2
z  z   3xy  x  y  z   
 x  y  z 2 2 2
x  2xy  y  xz  yz  z  3xy  
 x  y  z 2 2 2
x  y  z  xy  yz  zx Dễ thấy: 1 2 2 2
x  y  z  xy  yz  zx   2 2 2 2 2 2
x  2xy  y  y  2 yz  z  z  2zx  x  2 1
 x  y2   y  z2  z  x2   0, x  , y, z 2  
Do đó ta đi xét dấu của x y z Ta có: 2 2 2 x y z a bc b ca c ab 1
 a  b  c  ab bc  ca  a b2  b  c2  c  a2 2 2 2   0, a  ,b,c 2   Suy ra
x  y  z    x  y  z 2 2 2 0
x  y  z  xy  yz  zx  0 2 2 2 x y z 0 x y z x y z xy yz zx 0 3 3 3 x y z 3xyz hay
a bc3 b ca3 c ab3 2 2 2   2 a  bc 2 b  ca 2 3
c  ab (đpcm)
Dấu “ =” xảy ra khi a b c
Câu 13: [TS10 Tỉnh Hà Nam, 2019-2020]
Cho a, b, c l| c{c số thực dƣơng v| thỏa mãn điều kiện abc  1 1 1 1 Chứng minh    1. 2  a 2  b 2  c Lời giải 1 1 1
Bất đẳng thức cần chứng minh    1 2  a 2  b 2  c 37
 b  2c  2  a  2c  2  a  2b  2  a  2b  2c  2
 ab  bc  ca  4a  b  c 12  abc  2ab  bc  ca  4a  b  c  8
 ab  bc  ca  4a  b  c 12 1 2ab  bc  ca  4a  b  c  8
 ab  bc  ca  3
Thật vậy {p dụng bất đẳng thức CauChy cho 3 số dƣơng ta có  ab  bc  ca  abc2 3 3  3 .
Dấu “=” xảy ra khi a  b  c  1. Ho|n tất chứng minh.
Câu 14: [TS10 Tỉnh H| Tĩnh, 2019-2020]
Cho hai số thực dƣơng a,b thỏa mãn: a  b  3ab 1. 6ab
Tìm giá trị lớn nhất của biểu thức 2 2 P   a  b . a  b Lời giải 2 (a ) Ta có: 2 2 2 2 (a ) b
 0  a  b  2ab  (a ) b  4a ; b 2 2   b a b 2 3
Từ giả thiết a  b  3ab 1  a  b  1 3ab  1 a  b2 4
 a b2  a b    a b   a b 2 3 4 4 0 2 3
 2  0  a  b   (vì , a b  0 ) 3 3ab 1 (a  b) 1 3 1   1 1  a  b a  b a  b 2 2 a b2 2 2 2 2 a  b     2 2
a  b    2 9 9 6ab 3ab 2 7 2 2 P 
 a  b  2   2 2
a  b   1  a  b a  b 9 9 7 a  b 1
Vậy giá trị lớn nhất của P bằng khi 
 a  b  . 9
a  b  3ab 1 3 Câu 15:
[TS10 Tỉnh Hải Dƣơng, 2019-2020]
Cho các số dƣơng a, ,
b c thỏa mãn điều kiện: a  b  c  2019 .
Tìm giá trị nhỏ nhất của biểu thức: 2 2 2 2 2 2
P  2a  ab  2b  2b  bc  2c  2c  ca  2a Lời giải Ta có: 38 5
a  ab  b  a  b2 3
 a  b2 5 2 2
 a  b2 2 2 4 4 4 5 2 2
 2a  ab  2b  a  b 2 Tƣơng tự: 5 5 2 2
2b  bc  2c  b  c 2 2
; 2c  ca  2a  c  a 2 2 5  P  a b 5  b  c 5 
c  a  5a  b  c 2 2 2  P  2019 5 2019
Dấu “=” xảy ra  a  b  c   673 3
Vậy min P  2019 5  a  b  c  673 Câu 16:
[TS10 Tỉnh Hậu Giang, 2019-2020] 2 x  3x  2019
Với x  0 , tìm giá trị nhỏ nhất của biểu thức: A  2 x Lời giải Điều kiện x  0 2 x  3x  2019 3 2019 Ta có A  1  2 2 x x x 1 Đặt t  t  0 ta đƣợc: x  2 2 1   1 1     1  2 2
A  1 3t  2019t  2019 t  t 1   2  2019  t  2t      2019 1    673   1346 1346    1346   2  1  2689 2689  2019 t     
với mọi t thuộc R  1346  2692 2692 1 2689 1
Dấu “=” xảy ra khi t  tm . Vậy minA  khi t   x 1346tm 1346 2692 1346 Câu 17:
[TS10 Tỉnh Hòa Bình, 2019-2020]
Cho hai số thực dƣơng a, b thỏa mãn a + b = 4ab a b 1 Chứng minh rằng:   2 2 4b 1 4a 1 2 Lời giải 1
Từ a + b = 4ab  4ab  2 ab  ab  4 39 a b   2 2 2 a b
Chứng minh đƣợc BĐT: Với x, y >0 ta có   x y x  (*) y Áp dụng (*) ta có a b a b a b2 2 2     2 2 2 2 4b 1 4a 1 4ab  a 4a b  b 4a (
b a  b)  (a  b) a  b 4ab 1 1 =  1  4ab 1 4ab 1 4ab 1 2 1
Dấu đẳng thức xảy ra khi a  b  2 Câu 18:
[TS10 Tỉnh Hƣng Yên, 2019-2020]
Cho các số thực dƣơng x, y, z thỏa mãn: 2 2 2
x  y  z  3xyz 2 2 2 x y z
Tìm giá trị lớn nhất của biểu thức P    4 4 4 x  yz y  xz z  xy Lời giải x y z 2 2 2
x  y  z  3xyz     3 yz xz xy x y x y x y 2
Áp dụng bất đẳng thức Cô-si cho hai số dƣơng ; ta có:   2 .  yz xz yz xz yz x z y z 2 z x 2 Tƣơng tự ta cũng có:   ;   xz xy x xy yz y  x y   y z   z x  2 2 2               
 yz xz   xz xy   xy yz  z x y x y z 1 1 1 1 1 1           3 yz zx xy x y z x y z 2 x 1 1 1 1 1 1 1 Lại có: 4 4 2
x  yz  2 x yz  2x yz    .2. .  (  ) 4 x  yz 2 yz 4 y z 4 y z 2 2 y 1 1 1 z 1 1 1 Tƣơng tự  (  );  (  ) 4 4 y  xz 4 x z z  xy 4 x y Suy ra 2 2 2 x y z 1 2 2 2 1 1 1 1 3 P   
 (   )  (   )  4 4 4 x  yz y  xz z  xy 4 x y z 2 x y z 2 3  P  2
Vậy giá trị nhỏ nhất của P = 3/2 khi x = y = z = 1. Câu 19:
[TS10 Tỉnh Kon Tum, 2019-2020] 1 1 1 Chứng minh ... 38 . 2 3 400 40 Lời giải 1 1 1 1 1 1 ... 2 ... 2 3 400 2 2 3 3 400 400 1 1 1 2 ... 2 1 3 2 400 399 1 1 1 Ta có : 2 ... 2 1 3 2 400 399 2 1 3 2 ... 400 399 2 1 400 38 1 1 1 Vậy ... 38 2 3 400 Câu 20:
[TS10 Tỉnh Lai Châu, 2019-2020]
Cho c{c số thực dƣơng a, b, c. Chứng minh rằng: ab bc ca 1  
 (a  b  c) a
 b  2c b  c  2a c  a  2b 4 Lời giải 1 1  1 1 
Ta chứng minh bất đẳng thức     x  y 4  x
y  với x, y > 0.
Thậy vậy, với x, y > 0 thì: 1 1  1 1  1 x  y 2 2 2    
 (x  y)  4xy  x  2xy  y  4xy  0   x  y 4  x y  x  y 4xy 2 2 2
 x  2xy  y  0  (x  y)  0 (luôn đúng) 1 1  1 1  Do đó:     x  y 4  x
y  với x, y > 0.
Áp dụng bất đẳng thức trên ta có: 1 1 1 1 1 ab ab  1 1    (  )   
a b 2c (a c) (b c) 4 a c b c a b 2c 4   a c b c               bc bc  1 1      
b  c  2a 4  b  a c  a  Tƣơng tự ta có:   ca ca  1 1     
c  a  2b 4  c b a b 
Cộng vế với vế c{c bất đẳng thức với nhau ta đƣợc: ab bc ca ab  1 1  bc  1 1  ca  1 1         
a b 2c b c 2a c a 2b 4 
 a c b c  4  b a c a  4  c b a b               41 1  ab ab bc bc ca ca       
4 a c b c b a c a c b a b       
1 ab  bc ab  ca bc  ca 1  ( b a  c) ( a b  c) ( c b  a) 1      
 (a  b  c) 4  a c c b
b a  4  a c c b b a         4 1
Do đó VT  VP (đpcm). 4
Dấu “=” xảy ra khi a = b = c. Câu 21:
[TS10 Tỉnh Lạng Sơn, 2019-2020]
Cho ba số thực không âm a, b, c và thỏa mãn a+b+c=1. Chứng minh rằng:
a  2b  c  4(1 ) a (1 ) b (1 c) Lời giải
Ta có a  2b  c  4(1 ) a (1 ) b (1 )
c  a  2b  c  4(b  ) c (a  ) c (a  ) b
Áp dụng bất đẳng thức cô si ta có 2 2
a  b  b  c  2 (a  )
b (b  c)  (a  2b  c)  4(a  )
b (b  c)  (a  2b  c) (a  c)  4(a  b)(b  c)(a  c) Áp
dụng bất đẳng thức cô si
a  2b  c  a  c
2(a  b  c)
 (a  2b  c)(a  c) 
 (a  2b  c)(a  c) 1 (a  2b  c)(a  c) 2 2 2
1 (a  2b  c)(a  c)  a  2b  c  (a  2b  c) (a  c)
 a  2b  c  4(a  ) b (a  )
c (b  c) Câu 22:
[TS10 Tỉnh Nam Định, 2019-2020]
Xét c{c số x, y, z thay đổi thoả mãn x3 + y3 + z3 – 3xyz = 2. 1
Tìm gi{ trị nhỏ nhất của biểu thức 2 2 2 2 P 
(x  y  z)  4(x  y  z  xy yz zx) 2 Lời giải Ta có:
x³ + y³ + z³ - 3xyz = (x + y)³ - 3xy(x - y) + z³ - 3xyz = 2
 [(x + y)³ + z³] - 3xy(x + y +z ) = 2
 (x + y + z)³ - 3z(x + y)(x + y + z) - 3xy(x – y - z) = 2
 (x + y + z)[(x + y + z)² - 3z(x + y) - 3xy] = 2
 (x + y + z)(x² + y² + z² + 2xy + 2xz + 2yz - 3xz - 3yz - 3xy) = 2
 (x + y + z)(x² + y² + z² - xy - xz - yz) = 2
 x² + y² + z² - xy - xz – yz ≠ 0
Chứng minh: x² + y² + z² - xy - xz – yz ≥ 0 với mọi x, y, z
 x² + y² + z² - xy - xz – yz > 0  x + y + z t
Đặt x + y + z = t (t > 0)  x² + y² + z² - xy - xz – yz  khi đó ta có 2 2 2 1 t 8  t  8 2 2 2 2 P 
(x  y  z)  4(x  y  z  xy yz zx) 
    2   2 2 2 t 2 t   42 2 2 t t
Áp dụng BĐT Cô si ta có:  2  2
.2  2t (dấu bằng xảy ra  t = 2) 2 2 8 8 2t 
 2 2t.  8 (dấu bằng xảy ra  t = 2) t t
 P ≥ 8 – 2 = 6. Tồn tại x = y = 1, z = 0 thì P = 6
Vậy giá trị nhỏ nhất của P là 6. Câu 23:
[TS10 Tỉnh Ninh Bình, 2019-2020]
1. Tìm tất cả c{c số nguyên tố p sao cho tổng c{c ƣớc nguyên dƣơng của 2
p l| một số chính phƣơng. 2. Cho ,
x y, z l| c{c số thực dƣơng thỏa mãn x  y  z  2019 . Tìm gi{ trị nhỏ nhất của biểu thức 2 2 2 x y z T    . x  yz y  zx z  xy Lời giải 1.
Ta có p là số nguyên tố ( * p  ) 2
 p là số có c{c ƣớc dƣơng l| 2 1; ; p p
Theo đề bài ta có tổng c{c ƣớc nguyên dƣơng của p là một số chính phƣơng 2 2 *
1 p  p  k (k  ) 2 2
 4k  4  4 p  4 p
 4k  2 p  2 2 1  3
 4k  2 p  2 2 1  3
 2k  2p  
1 2k  2 p   1  3 (*) Ta có * k, p 
 2k  2p 1 0; 2k  2p 1 2k  2p 1
2k  2 p 1 1
2k  2 p  2
k 1 (thoûa maõn) (*)      
2k  2 p 1  3
2k  2 p  2
 p  0 (khoâng thoûa maõn)
Vậy không có số nguyên tố p nào thỏa mãn đề bài a b c    2 2 2 2 a b c 2.
Ta chứng minh bất đẳng thức     x y z x  y  với a,b,c, x, y,z 0 z  a   b   c 
Áp dụng bất đẳng thức Bu – nhi – a - cốp – xki cho ba bộ số ; x ,    ; y , ; z      x  y    z  2 2 2   2 2 2       2 2 2 a b c a b  c    ta có    x  y  z            
  x    y   z   x y z    x  y    z       2  a b c    . x  . y 
. z   a  b  c2   x y z   a b c    2 2 2 2 a b c     x y z x  y  (*) z 43 a b c Dấu “=” xảy khi khi   x y z y  z z  x x  y
Áp dụng bất đẳng thức Cô si ta có yz  ; zx  ; xy  2 2 2 2 2 2 x y z  T    y  z z  x x  y x  y  z  2 2 2 2 2 2 2x 2y 2z    2x  y  z x  2y  z x  y  2z 2 2 2  x y z   2   
 2x  y  z x  2y  z x  y  2z 
Áp dụng bất đẳng thức (*) ta có    2 x y z x  y  z 2019 T  2   4x  y  z 2 2
Dấu “=” xảy ra khi x  y  z  673 2019
Vậy gi{ trị nhỏ nhất của biểu thức T  khi x  y  z  673 2 Câu 24:
[TS10 Tỉnh Phú Thọ, 2019-2020] 2 2  x y   4
x 1 y 1
Giải hệ phƣơng trình sau  x  2 y  2    y  . x
 x 1 y 1 Lời giải ĐKXĐ: x  - 1; y  1
Hệ phƣơng trình đã cho tƣơng đƣơng với hệ phƣơng trình: 2 2       1 1 x 1 1 y 1 1   x   y   4 4      x 1 y 1 x 1 y 1     x 11 y 11 1  1      y  x x   y   2     x 1 y 1  x 1   y 1  1 1 Đặt x   a ; y   b x 1 y  1
Hệ phƣơng trình đã cho trở th|nh: a  b  4 a  1    a  b  2  b   3 + Với a = 1 ta có: 44 1 x(x 1) 1 x 1 x   1   x 1 x 1 x 1 2
 x  x 1  x 1  x  0 (t / m) + Với b = 3 ta có: 1 y( y 1) 1 3.( y 1) y   3   y 1 y 1 y 1 2 2
 y  y 1  3y  3  y  4y  4  0  y  2 (t / ) m
Vậy hệ phƣơng trình đã cho có nghiệm duy nhất (x; y) =(0; 2) Câu 25:
[TS10 Tỉnh Quảng Nam, 2019-2020] Cho hai số thực ,
x y thỏa mãn x  3; y  3.  1   1 
Tìm gi{ trị nhỏ nhất của biểu thức T  21 x   3 y       y   x  Lời giải 21 3 x 62 3 21 7 2 T  21x   3y    x    y  y y x 3 3 x y 3 3
 x 3   21 7  62 2     y  x 
y  2 14  62  2  80    
 3 x   y 3  3 3 x  3 Dấu “ ”  xảy ra   y  3
Vậy gi{ trị nhỏ nhất của T là 80 khi x = 3; y =3. Câu 26:
[TS10 Tỉnh Quảng Ngãi, 2019-2020]
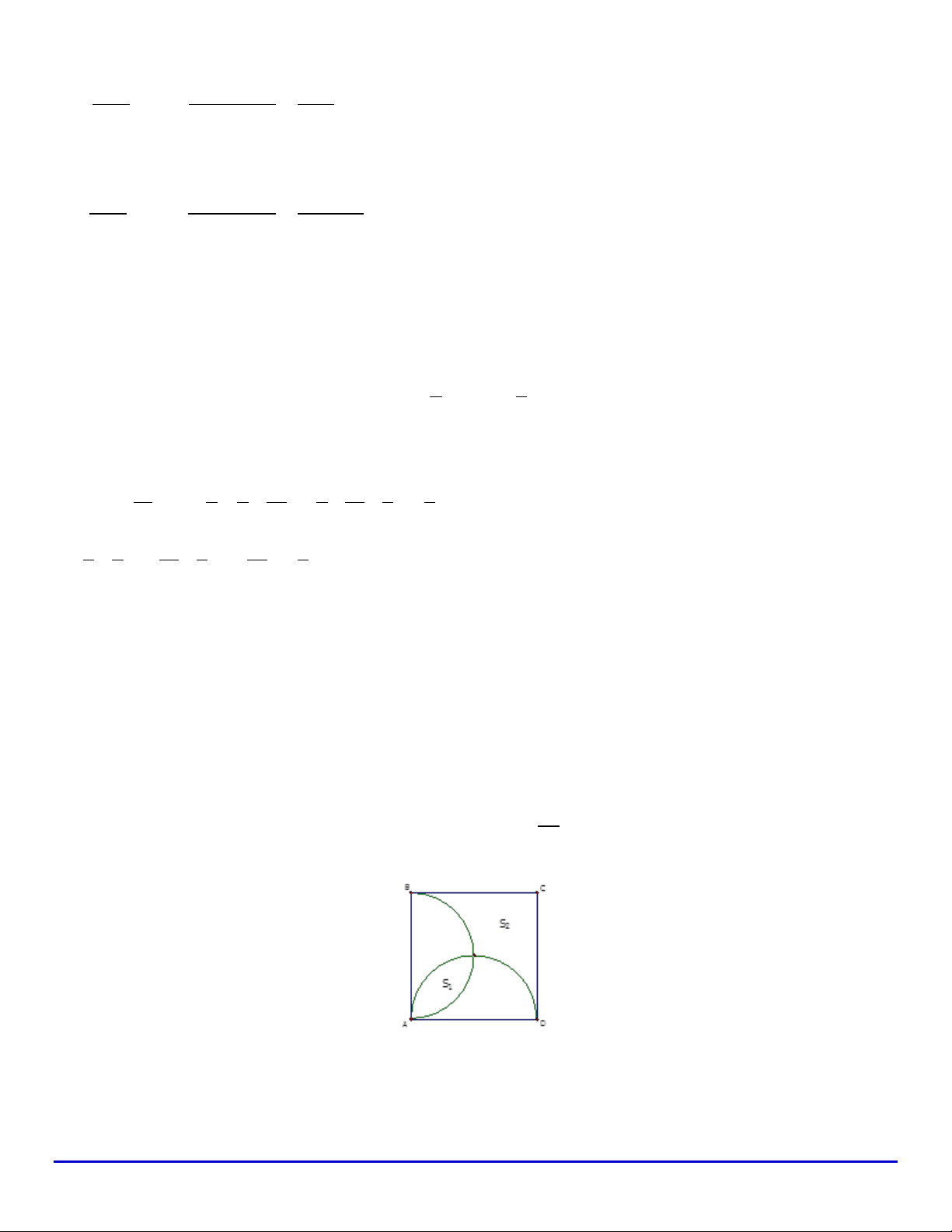
Cho hình vuông ABCD. Gọi S là diện tích phần giao 1
của hai nửa đƣờng tròn đƣờng kính AB và AD. S là diện tích phần còn lại của hình vuông nằm 2 S
ngoài hai nửa đƣờng trong nói trên (như hình vẽ bên).Tính 1 S2 Lời giải. 45 B C S3 S2 S S 4 1 A D
Gọi a l| cạnh hình vuông ABCD. Ta cm đƣợc: 2
 a  . 90 . 2   2  2  1  a  a   1  S  S      3 4     360 2  2  4  4 2  2 2 2 a   1  a   1  a   1 
S  S  S       1 3 4       4  4 2  4  4 2  2  4 2  2 2 1 a   1  a  3   2 S  a     2     2 2  4 2  2  2 4  2 a   1     S 2  4 2    2 Do đó 1   2 S a  3   6   2    2  2 4  Câu 27:
[TS10 Tỉnh Quảng Ninh, 2019-2020]
Cho x, y, z l| c{c số thực dƣơng thỏa mãn . Tìm gi{ trị nhỏ nhất của biểu thức 1 1 P  
x2  y 2  z 2
xy  yz  zx Lời giải.
x  y  z3 1 2017
Ta có xy  yz  zx   nên  6051 3 3
xy  yz  zx  1 1 1 
Áp dụng BĐT x  y  z    9   , ta có:  x y z     2 2 2
( x  y  z )  ( xy  yz  zx )  ( xy  yz  zx  1 1 1 )    9  2 2 2 
 x  y  z
xy  yz  zx
xy  yz  zx  Hay   2 2 2 1 1 1
 ( x  y  z  2xy  2yz  2zx )    9  2 2 2 
 x  y  z
xy  yz  zx
xy  yz  zx  1 2   9 2 2 2
x  y  z
xy  yz  zx 46 1 2 2017 Từ đó ta có: P     9  6051  6060 2 2 2
x  y  z
xy  yz  zx
xy  yz  zx  1
P  6060 Vậy GTNN của P là 6060 khi và chỉ khi x  y  z  3 Câu 28:
[TS10 Tỉnh Sơn La, 2019-2020] Giải phƣơng trình 3  x  x 3  x Lời giải. 3  x  x 3  x
Điều kiện 0  x  9
Bình phƣơng hai vế phƣơng trình đã cho, ta đƣợc: 2
3  x  x .( 3  x) 3 2
 x  3.x  x  3 2 3 3 1  1   1   1  3 2  x  3.x .  3. . x   3        3  3   3   3  3  1  10 10 3  x       3  3 3 9 1 10 3 3  x   3 9 10 3 3 3  x   (thỏa mãn điều kiện) 9 3 10 3 3
Vậy phƣơng trình đã cho có 1 nghiệm 3 x   9 3 Câu 29:
[TS10 Tỉnh Vĩnh Long, 2019-2020] Cho ,
x y là các số thực dƣơng thỏa x  y  1. 1
Tìm giá trị nhỏ nhất của biểu thức 2 2
A  2x  y  x  1. x Lời giải.
Ta có: x  y 1 y 1 x thay v|o A ta đƣợc: 1 1 2 2 2 2
A  2x  y  x 
1  2x  (1 x)  x  1 x x 1 1 2  2x   2 x  2x   2 1  x 
1  x  2x  x  x x 2  1   1  1  1   1  1 2  x  x   4x    x   4x            4   x  4  2   x  4 47 2  1  Dễ thấy x   0, x     2  1 1
Áp dụng bất đẳng thức Cô-si ta có 4x   2 4 . x  4 x x 2  1   1  1 1 15 Suy ra x   4x    0  4        2   x  4 4 4 1
Dấu "=" xảy ra khi x  2 15 1 Vậy A  khi x  . min 4 2 Câu 30:
[TS10 Tỉnh Thái Nguyên, 2019-2020]
Cho a , b , c là các số thực dƣơng thỏa mãn a  b  c  ab  bc  ac  6 . Chứng minh rằng: 3 3 3
a  b  c  3. b c a Lời giải 3 3 3 a b c Đặt P    . b c a
Có a , b , c là các số thực dƣơng, theo bất đẳng thức AM-GM có:  3 a   ab  2 2a  b  3 b 3 3 3 a b c   bc  2 2b . P      2 a  2 b  2 2
c ab bc  ac
a  b  c  ab  bc  ac  .  c b c a , mà 6  3 c ac   2 2c  a  P   2 a  2 b  2 2
c a bc6 . 2 2 2 2
Có a  b  b  c  a  c  0   2 a  2 b  2 2
c   2ab bc ca   2  2  2 3 a b
c   a bc . 2 2
Suy ra P  a  b  c  a  b  c  6 3 . Có 2 2 2
ab  bc  ca  a  b  c          2 3 ab bc ac a b c . 1 1 2
Do đó 6  a  b  c  ab  bc  ac  a  b  c  a  b  c2  a  b  c  a  b  c  6  0 . 3 3
 a  b  c  3 , a  b  c2  9 . 48 2
Suy ra P  .9  3  6  3   3
. Dấu đẳng thức xảy ra khi a b c . 3 3 3 a b c Vậy    3. b c a Câu 31:
[TS10 Tỉnh Vĩnh Phúc, 2019-2020]
Cho ba số thực dƣơng a, b, c. Chứng minh:
2  6a  3b  6 2bc 16 
2a  b  2 2bc
2b  2a  c2 2  3 Lời giải
Theo bất đẳng thức AM-GM ta có: 2 2 1
a 2c 2 2bc VT 3 3 3 2a b 2 2bc 2a b b 2c a b c
Mặt kh{c theo BĐT Bu-nhi-a-cốp –xki thì:
2b  2a  c2  1  1 b
  a  c2 16 2 2   1  .b 1.   
a c 2  b 
a c VP  abc 3
Vậy ta chỉ cần chứng minh: 1 16  3 
 a  b  c  2 1  0   1
a  b  c
a  b  c  3
Ta có (1) đúng hiển nhiên do đó bất đẳng thức đƣợc chứng minh. a b c 1 1 a c 4
Dấu “=” bằng xảy ra khi: b 2c 1 b a c b 2
ĐÁP ÁN CÁC CÂU PHÂN LOẠI CHYÊN NĂM 2019-2020
Câu 32: [TS10 Chuyên KHTN Hà Nội, 2019-2020]
Cho x, y là các số thực dƣơng thỏa mãn: 2 2
4x  4y  17xy  5x  5y  1
Tìm giá trị nhỏ nhất của biểu thức: 2 2 P  17x  17y  16xy Lời giải 2 Ta có: 2 2
4x  4y  17xy  5x  5y  1  4x  y  9xy  5x  y  1
Đặt t  x  y, t  0 , theo bất đẳng thức AM-GM, ta có: 49   2 2 x y t 9 2 2  2 2 2  2 xy   . Do đó: 2 2
4t  t  5t  1  t  hay x  y  . 4 4 4 5 5 Ta có:       2 2 2 P 17x 17y 16xy 17 x y 18xy 2 2         2 x y 25     2 25 2 2 2 17 x y 18 x y     6  4 2 4 4 4  5    2  1
Dấu “=” xảy ra khi x  y  5
Vậy giá trị nhỏ nhất của P là 6  4 2
Câu 33: [TS10 Chuyên Sƣ Phạm Hà Nội, 2019-2020]
Cho các số thực x, y thay đổi, hãy tìm giá trị nhỏ nhất của biểu thức:       2 2
P xy x 2 y 6  13x  4y  26x  24y  46 Lời giải Ta có:
P  xy x  2y  6 2 2
 13x  4y  26x  24y  46   2 x  2x 2 y  6y  13 2 x  2x  4 2 y  6y  46 x 2 1
1 y 32 9 13 x 12 1 4 y 32 9             46        
Đặt a  x 1, b  y  3 , khi đó: P   2 a   1  2 b  9  13 2 a  1  4 2 b  9  46 2 2 2 2 2 2
 a b  9a  b  9 13a 13  4b  36  46 2 2 2 2  4a  3b  a b  6  6 a  0 x 1  0 Dấu “=” xảy ra khi     x  1,y  3  b  0 y  3    0
Vậy giá trị nhỏ nhất của P là 6.
Câu 34: [TS10 Chuyên Tin Hà Nội, 2019-2020]
Cho a, b, c dƣơng thỏa mãn: ab  bc  ca  abc  4 1 1 1 1) Chứng minh rằng:    1 a  2 b  2 c  2 1 1 1 2)
Tìm giá trị nhỏ nhất: P    2 . 2 2 a  b   4 2  2 2 b  c   4 2  2 2 c  a   4 Lời giải 1) Ta có: 50 1 1 1    1 a  2 b  2 c  2
 b  2c  2  a  2c  2  b  2a  2  a  2b  2c  2
 ab  bc  ca  4a  b  c 12  abc  2ab  bc  ca 4a  b  c 8  4  ab  bc  ca.
Đẳng thức cuối cùng đúng theo giả thiết, các phép biến đổi l| tƣơng đƣơng, do đó đẳng thức đã cho đƣợc chứng minh. 2)
Với x, y dƣơng ta có bất đẳng thức:     2 2 2 2 x y x y (*) 1 1  1 1      (**) x  y 4  x y  Thật vậy:      2 * x y  0 (luôn đúng)   x y 1 * *  
 x  y2  4xy  x  y2  0 4xy x  (luôn đúng) y
Các bất đẳng thức (*), (**) xảy ra dấu “=” khi x = y.
Lần lƣợt áp dụng (*) và (**) ta có: 1 1 1 1  1 1         2 2   a  b  4  a2b2 2 a b 4  4 a 2 b2  Tƣơng tự: 1 1  1 1  1 1  1 1     ;      ; 2 2   4   b  2 c  2   2 2   4   c  2 a  2 2 b c 4 2 c a 4  Cộng theo vế ta đƣợc: 1  1 1 1  1 1 P     .1    .
2  a  2 b  2 c  2  2 2
D}u “=” xảy ra khi a = b = c 1
Vậy giá trị nhỏ nhất của P là 2
Câu 35: [TS10 Chuyên Toán Hà Nội, 2019-2020]
Cho K  ab  4ac  4bc với a,b,c  0 và a + b + 2c = 1. 1 1) Chứng minh rằng: K  2 2)
Tìm giá trị lớn nhất của K. Lời giải 1)
Sử dụng bất đẳng thức AM-GM ta có: 51 2 2  b  2c   a  b  2c  1 1 4bc  2  2   4  bc        2   2  2 2 1
Mặt khác: a, b,c  0  K  ab  4ac  4bc  4  bc   2 1 1
Dấu “=” xảy ra khi a  0, b  ,c  . 2 4 Cách khác: Ta có:
K  ab  4c a  b  ab  21 a  ba  b
 ab  2a  b  2 2 2 a  b  2  2b  a  2 2 b  2a  2a Do đó: 2     2 2b
a 2 b  2a  2a  K  0 *
Để tồn tại K thì phƣơng trình (*) Phải có 2 nghiệm:
   0  a  22  4.2. 2 2a  2a  K  0 2  8K  20a 17a  4.
Vì a, b,c  0 và a  b  2c  1  0  a  1 . Do đó: 2
2a 17a  a 20 17a  a20 17.  1  3a  0 1 Do đó 8K  4   K   2 1 1
Dấu “=” xảy ra khi a  0, b  ,c  . 2 4 2)
Sử dụng bất đẳng thức AM-GM ta có: 2
   a b2c  1 a b 2c     .  2  4   Mặt khác:               2 a b 2c 1 a, b,c 0 K ab 4ac 4bc ab 4ac 2ab 4ac 2a b 2c   . Dấu “=” 2 2 xảy ra khi: 1 1
a  b  2c,a  b  2c  1, bc  0,ab  0  a  , b  0,c  2 4 1
Vậy giá trị lớn nhất của K là 2
Câu 36: [TS10 Chuyên Thái Bình, 2019-2020] 52  1  0  a, b,c 
Cho các số thực a, b, c thỏa mãn 
2 . Tìm giá trị nhỏ nhất của biểu thức 2a  3b  4c   3 2 9 8 P   
a 3b  4c  2 b 4a  8c  3 c 2a  3b 1 Lời giải Ta có: 2 9 8 P   
a 3b  4c  2 b4a  8c  3 c 2a  3b 1 2 9 8   
a 3  2a  2 b6  6b  3 c 3  4c 1 2 3 4   
a 1 2a b1 2b c 1 2c 2 2a 3b 4c    2 a 1 2a 2
b 1 2b c 1 2c2 2
Áp dụng bất đẳng thức AM-GM ta có: 2      2    a a 1 2a 1 a 1 2a      3  27 1 1 Tƣơng tự: 2 b 1 2b  ; 2 c 1 2c  27 27
Suy ra: P  27 2a  3b  4c  81 1
Dấu “=” xảy ra khi a  b  c  3
Vậy giá trị nhỏ nhất của P là 81.
Câu 37: [TS10 Chuyên Hòa Bình, 2019-2020]
Cho hai số dƣơng a, b thỏa mãn: a + b = 4ab. Chứng minh rằng: a b 1   2 2 4b  1 4a  1 2 Lời giải Ta có:      2 a b 4ab a b
 a  ba  b1  0  a  b 1    a b  0 Lại có: 2 2 a 4ab 4ab  a   a   a ab 2 2 4b  1 4b  1 4b 2 2 b 4a b 4a b  b   b   a ab 2 2 4a  1 4a  1 4a 53 a b a  b 1 1 Do đó: 
 a  b  2ab  a  b   a  b  2 2       4b  1 4a  1 2 2 2 1
Dấu “=” xảy ra khi a  b  2
Câu 38: [TS10 Chuyên Hƣng Yên, 2019-2020]
Cho các số thực không âm x, y, z thỏa mãn: 2 2 2 x  y  z  3y
Tìm giá trị nhỏ nhất của biểu thức: 1 4 8 P     x  2 1 y22 z32 Lời giải
Sử dụng bất đẳng thức Cauchy-Schwarz ta có: 2 1 1 1  1 1  8       (*) 2 2 a b 2  a b  a b2
Áp dụng bất đẳng thức (*) ta đƣợc: 1 1 8 8 8 64 P        x  1 . 2 2  y  z32 2  y  z32 2  y   1 x   2 x   z       5  2   2   2  Mặt khác:  
x  z  2x  z   23y  y  2 2 3y y 2 2 2  . 2 64 64 P    1 2 2  1   1  6  2y  y 8   y   22 2   2   2 
Dấu “=” xẩy ra khi x, y,z  1,2,  1 .
Vậy giá trị nhỏ nhất của P là 1.
Câu 39: [TS10 Chuyên Hà Nam, 2019-2020] 1 1 1
Cho các số thực dƣơng a, b, c thỏa mãn:  
 1. Tìm giá trị nhỏ nhất của biểu thức: a  1 b  1 c  1 3 3 3 a b c P    2 2 2 2 2 2 a  ab  b b  bc  c c  ca  a Lời giải
Ta dễ dàng chứng minh bất đẳng thức: 1 1 1 9     ) (*) x y z x  y  (với x, y,z 0 z   Thật vậy:      1 1 1 (*) a b c      9  a b c  54
Áp dụng AM – GM ta đƣợc:     1 1 1 3 3 a b c    3 abc.    9 3  a b c  abc
Vậy bất đẳng thức (*) đƣợc chứng minh, dấu “=” xảy ra khi x = y = z.
Sử dụng bất đẳng thức (*) ta đƣợc: 1 1 1 9 1    
 a  b  c  3  9  a  b  c  6 a  1 b  1 c  1 a  b  c  3 3 3 3 b c a Đặt Q    2 2 2 2 2 2 a  ab  b b  bc  c c  ca  a Ta có: 3 3 3 3 3 3 a  b b  c c  a P  Q    2 2 2 2 2 2 a  ab  b b  bc  c c  ca  a a  b 2 2
a  ab  b  b  c 2 2
b  bc  c  c  a 2 2 c  ca  a     2 2 2 2 2 2 a  ab  b b  bc  c c  ca  a
 a  b  b  c  c a  0 Do đó: P = Q 1 Mặt khác: 2 2 x  xy  y   2 2 x  xy  y  * * 3 Thật vậy: 1
x  xy  y  x  xy  y   3x  3xy  3y  x  xy  y  2x  y2 2 2 2 2 2 2 2 2  0 3 Sử dụng (**) ta đƣợc: 3 3 3 3 3 3 a  b b  c c  a P  Q    2 2 2 2 2 2 a  ab  b b  bc  c c  ca  a a b 2 2
a  ab  b  b  c 2 2
b  bc  c  c  a 2 2 c  ca  a     2 2 2 2 2 2 a  ab  b b  bc  c c  ca  a 1     1     1 a b b c  c  a 3 3 3 2      2 a b c  .6  4 3 3 Mà P  Q  P  2
Dấu “=” xảy ra khi a = b = c = 2
Vậy giá trị nhỏ nhất của P là 2.
Câu 40: [TS10 Chuyên Phan Bội Châu, 2019-2020]
Cho các số dƣơng a, b, c dƣơng thỏa mãn abc  a  b  c  2 . Tìm giá trị lớn nhất của biểu thức 1 1 1 P    2 2 2 2 2 2 a  b b  c c  a 55 Lời giải.
Từ abc  a  b  c  2  a  bb  
1 c  1  a  1b  1  b  1c  1  c  1a  1 1 1 1     1 a  1 b  1 c  1 1 1 1  x,y,z  0 Đặt  x,  y,  z   a  1 b  1 c  1 x  y  z  1. 1 x y  z z  x x  y Khi đó: a   ; b  ; c  x x y z 1 1 1 1  1 1 1  Nên P         2 2 2 2 2 2 a  b b  c c  a 2  ab bc ca  1  x y y z z x    .  .  .          2 y z z x z x x y x y y z   1  y x z y x z    .  .  .          2 y z z x z x x y x y y z   1  y x   z y   x z             
2 2  y  z z  x   z  x x  y   x  y y  z  1  x y   y z   z x  3 2             
2 2  x  y x  y   y  z y  z   z  x z  x  4 
Dấu “=” xảy ra khi x  y  z hay a  b  c 3 2
Vậy giá trị lớn nhất của biểu thức P là khi a = b = c = 2. 4
Câu 41: [TS10 Chuyên Vĩnh Phúc, 2019-2020]
Cho x, y, z là các số thực dƣơng thỏa mãn  2 2 2
5 x  y  z   9xy  z 18yz  0. Tìm giá trị lớn nhất 2x  y  z của biểu thức: Q  . y  z Lời giải Ta có: 5 2 2 2
x  y  z   9xy  z 18yz  0
 5x  9xy  z  5y  z2 2  28yz  0 56
 5x  9xy  z  5y  z2  7.4yz  7 y  z2 2
 5x  9xy  z  2y  z2 2  0 2  x  x  5   9.  2  0 y  z y    z x Đặt: t  t  0 y  khi đó: z 2
5t  9t  2  0  5t  1t  2  0  t  2 do 5t 1 0 x   2 y  z 2x  y  z x Ta có: Q   2. 1  2.2 1  3 y  z y  z x
Dấu “=” xảy ra khi y  z  . 4
Vậy giá trị lớn nhất của Q là 3.
Câu 42: [TS10 Chuyên Bắc Ninh, 2019-2020]
Cho x, y, z không âm thỏa mãn x  y  z  3. Tìm GTLN. GTNN của biểu thức 2 2 2
M  x  6x  25  y  6y  25  z  6z  25 Lời giải Ta có: 2 2 2
M  x  6x  25  y  6y  25  z  6z  25
 3  x2 16  3  y2 16  3  z2 16  a  b  c  6
Đặt a  3  x, b  3  y,c  3  z, Khi đó:  0  a, b,c   3 2 2 2
M  a  16  b  16  c  16 Tìm GTNN:
Theo bất đẳng thức Minkowski ta có:      
    2     2 2 2 2 M a 16 b 16 c 16 a b c 4 4 4  6 5
Đẳng thức xảy ra khi a = b = c = 2 Tìm GTLN 
Sử dụng phƣơng ph{p UCT với điều kiện 0  a  3 ta đƣợc 2 a 12 a  16  * 3 Thật vậy: 57
        2 2 2 * 9 a 16 a 12
 8a  24a  0  aa  3  0 (đúng)
Ho|n to|n tƣơng tự và suy ra: M  14
Đẳng thức xảy ra khi a, b,c  0,3,3 và các hóa vị.
Câu 43: [TS10 Chuyên KHTN, 2019-2020]
Cho x, y,z là các số dƣơng thỏa mãn xy  yz  zx  1 . Chứng minh rằng: 3   1 1 1 2 x y z        (1) 2 2 2     2 2 2 1 x 1 y 1 z 3 1  x 1  y 1  z    Lời giải Ta có: 2 2
1 x  xy  yz  zx  x  x  yx  z Tƣơng tự: 2        2 1 y
x y y z ; 1 z  x  zy  z Do đó: 1 1 1 2x  y  z  VT      1
x yxz xyyz xzzy xyyzz x
Áp dụng bất đẳng thức Cauchy-Schwarz, ta có: 2   x y z        x y z    x y z     2 2 2  2 2 2      1 x 1  y 1  z 1 x 1 y 1 z        x y z   x y z    
x  yy  z x  yy  z x  zz   y
2 x  y  zxy  yz  zx 
x yyzzx 2 x  y  z
       . x y y z z x Suy ra: 4 x y z     x y z V       P  . 1
3x  yy  zz  x  2 2 2 1 x 1  y 1  z   
Nhƣ thế để chứng minh bất đẳng thức đã cho ta chỉ cần chứng minh: x y z 3    2 2 2 2    2 1 x 1 y 1 z
Sử dụng bất đẳng thức AM-GM ta có: x x 1  x x       2 1 x
     2 x y xz x y x z  58 y 1  y y  z 1  z z  Tƣơng tự:    ;     2 2 2  x  y y  z  2  z  x y    z 1 y 1 z 
Cộng theo vế 3 bất đẳnng thức trên ta đƣợc bất đẳng thức (2). B|i to{n đƣợc chứng minh. 1
Dấu “=” xảy ra khi x  y  z  3
Câu 44: [TS10 Chuyên TP. Hồ Chí Minh, 2019-2020]
Cho x, y, z là các số thực thuộc đoạn 0; 2 
 thỏa mãn điều kiện: x  y  z  3. a) Chứng minh rằng: 2 2 2 x  y  z  6 b)
Tìm giá trị lớn nhất của biểu thức: 3 3 3 P  x  y  z  3xyz Lời giải a) Ta có:
2x2y2z  0  84x yz2xy yzzxxyz  0 2 2 2 2 2 2
 x  y  z  x  y  z  8  4x  y  z 2xy  yz  zx xyz
 x  y  z2  4x  y  z  8  xyz
 9  4.3  8  xyz  5  xyz  5  6 b) Ta có: 3 3 3
P  x  y  z  3xyz  x  y  z 2 2 2
x  y  z  xy  yz  zx  3     2 2 2    1 3 x y z   2 2 2
x  y  z  2xy  yz  zx 2 2  3 3  x y z  x y z2 2 2 2        2   3  3.5  9   2  9
Dấu “=” xảy ra khi x, y,z  2,1,0 và các hoán vị.
Câu 45: [TS10 Chuyên Hòa Bình, 2019-2020]
Cho x, y, z là các số thực dƣơng thỏa mãn: xy  yz  4zx  32
Tìm giá trị nhỏ nhất của biểu thức: 2 2 2 P  x  16y  16z Lời giải.
Áp dụng bất đẳng thức AM-GM ta có: 2 x 2  8y  4xy 2 2 x 2  8z  4xz 2 2 2 8y  8z  16yz 59 Cộng theo vế ta đƣợc: 2 2 2
P  x  16y  16z  4xy  xz  4yz  128 8 6 2 6
Dấu “=” xảy ra khi x = 4y = 4z , thay v| điều kiện ta đƣợc: x  ; y  z  3 3
Câu 46: [TS10 Chuyên Quốc Học Huế, 2019-2020]
Cho ba số dƣơng x, y, z thỏa mãn xyz = 2. Chứng minh rằng: x 2y 4z 1    2 2 2 2 2 2 2x  y  5 6y  z  6 3z  4x  16 2 Lời giải Ta có: +) 2 2 2 2 2
2x  y  5  x  y  x 1 4  2xy  2x  4 x x x    2 2 2x  y  5 2xy  2x  4 2xy  x  2 2 2 2 2 2
) 6y  z  6  4y  z  2y  2  4  4yz  4y  4 2y 2y y    2 2 6y  z  6 4yz  4y  4 2 yz  y  1 Do đó: x y z VT   
2 xy  x  2 2yz  y  1 zx  2z  2 x y yz   
2 xy  x  xyz 2yz  y  1 xyz  2yz  2y 1 y yz   
2 yz  y  1 2yz  y  1 2 yz  y  1 yz  y  1  2yzy1 1  2
Dấu “=” xảy ra x = y = 1, z = 2.
Câu 47: [TS10 Chuyên Tin Hòa Bình, 2019-2020]
Cho các số thực dƣơng x, y thỏa mãn: x  y  1.  1 1 
Tìm giá trị nhỏ nhất của biểu thức: 2 2 P     1 x y  x y  Lời giải Theo AM-GM ta có: 1 1 1
1  x  y  2 xy  xy   xy    4 2 4 xy 60 Do đó:  1 1  2 2 2 2 2 1 P     1 x y  1 x y  2  xy  x y  xy xy Suy ra: 1 1 15 1 15 P  2  xy  2  xy   2 2 .xy  xy 16xy 16xy 16xy 16xy 1 15  P  2  .4  17 2 16 1
Dấu “=” xảy ra khi x  y  2
Vậy giá trị nhỏ nhất của P là 17
Câu 48: [TS10 Chuyên Tiền Giang, 2019-2020] 2
Cho hai số dƣơng x, y thỏa mãn  3 3
2 x  y   6xyx  y  2  x  y xy  4 1  x y 
Tìm giá trị nhỏ nhất của biểu thức: T     1 2  y x  Lời giải Ta có:
2x  y   6xyx  y  2  x  y2 3 3 xy4
 2x  y3 12xy  x  y2 xy  4
Đặt a  x  y, b  xy a, b  0 khi đó: 3 2        2   3 2 2a 12b a b 4 b a 12  2a  4a Do VT > 0 nên 3 2 2
2a  4a  0  2a a  2  0  a  2 Ta có: 2 2 2 2 4 2 1  x y
 1  x  y  xy  1  a  a 1 a  12a 1 T     1      1     3 2 2 y x 2  xy  2 b 2b 2 4a      8a 2 5 Ta sẽ chứng minh: T  2 5 a  12a a62 2 4 2 a Thật vậy: T    3   0 (luôn đúng a   2 ) 3 2 2 2 4a  8a 4a a  2
Dấu “=” xảy ra khi a = 6, b = 6
hay x  3  3, y  3  3 hoặc x  3  3, y  3  3 5
Vậy giá trị nhỏ nhất của T là 2 61
Câu 49: [TS10 Chuyên Bà Rịa Vũng T|u, 2019-2020]
Cho các số thực dƣơng x, y. Tìm gi{ trị nhỏ nhất của biểu thức: 2 2 x y xy P    2  2 2 y x x  y Lời giải Ta có: 2 2 4 2 2 4 x y xy x  2x y  y xy P    2    2 2 2 2 y x x  y x y x  y 2 2 2 2 2  x  y  xy x  y xy       xy x  y xy x    y  x  y  xy x y2 2 2 xy  P    2   2    2 xy x  y xy x    y xy xy 1 1 1 Đặt t 
.Theo AM – GM thì: x  y  2 xy    t    2 x  y x  y 2 2 t Khi đó: 1  t t 1  15 P   t  2        2 2 2 2 t  2 2 16t  16t t t 1 15 2  3 3 . .  .2  2 2 2 2 16t 16 1 15  3.   2 4 4 5  2
Dấu “=” xảy ra khi x = y 5
Vậy giá trị nhỏ nhất của P là 2
Câu 50: [TS10 Chuyên KHTN Hà Nội, 2019-2020]
Với x, y là các số thực thỏa mãn 1  y  2 và xy  2  2y . Tìm giá trị nhỏ nhất của biểu thức 2 x  4 M  2 y  1 Lời giải.
Theo giải thiết ta có: 4xy  8  8y.
Sử dụng bất đẳng thức AM – GM ta có: 2 2 4x  y  4xy. Suy ra: 2 2
4x  y  8  4xy  8  8y. Do đó:  2   2   
  2         2 4 x 4 8 8y y 4 y 1 5y 2 2 y 4 y   1 . 62 2 x  4 Suy ra: 2 2 x  4  y  1  M   1 2 y  1
Dấu “=” xảy ra khi x = 2, y = 1.
Vậy giá trị nhỏ nhất của M là 1.
Câu 51: [TS10 Chuyên Hƣng Yên, 2019-2020]
Với x, y là cá số thực thỏa mãn      9
2 x y 1  . Tìm giá trị nhỏ nhất của biểu thức: 4 4 3 2 4 3 2
A  x  4x  6x  4x  2  y  8y  24y  32y  17. Lời giải Ta có: 4 3 2 4 3 2
A  x  4x  6x  4x  2  y  8y  24y  32y  17  1 x  4 1  1 y  24
Đặt a  x  1, b  y  2 , ta đƣợc 4 4 A 1 a  1 b
Từ giả thiết ta đƣợc:      9 5 a 1 b 1   a  b  ab  4 4 Theo AM – GM ta có: 2 4a 1  4a 2 2 1 
 a  b  a  b  (1) 2 4b 1  4b 2 2 2 1 a  b  2ab   2 2 a  b   ab 2 2 3 1 5 1 3 1
Cộng theo vế (1) v| (2) ta đƣợc:  2 2 a  b  2 2
 a  b  ab      a  b  2 2 4 2 4 2
Áp dụng bất đẳng thức Minicopski ta đƣợc:
A 1  a  1  b  1 12 4 4   2 2 a  b 2   2 2 a  b 2  4 2  1  17   4     2  2 1 1 5
Dấu “=” xảy ra khi a  b   x   ,y  . 2 2 2 17
Vậy giá trị nhỏ nhất của A là 2
Câu 52: [TS10 Chuyên Bình Thuận, 2019-2020] 1
Cho các số dƣơng x, y, z thỏa xyz  . Chứng minh rằng: 2 yz zx xy    xy  yz  zx. 2 x y  z 2 y z  x 2 z x  y 63
Dấu “=” xảy ra khi nào: Lời giải Ta có: yz zx xy    xy  yz  zx 2 x y  z 2 y z  x 2 z x  y 1 1 1 2 2 2 y 1  1 1 1  x z         1 1 1 1 1 1 2  x y z     y z x z x y 1 1 1 Đặt a  , b  ,c   abc  2 x y z
Khi đó ta cần chứng minh: 2 2 2 a b c a  b  c    b  c a  c a  b 2
Thật vậy, sử dụng bất đẳng thức Cauchy-Schwarz ta đƣợc: a b c    2 2 2 2 a b c a  b  c VT          2a  b  (đpcm) c VP b c a c a b 2
Dấu “=” xảy ra khi x = y = z.
Câu 53: [TS10 Chuyên Hải Phòng, 2019-2020]
Cho x; y; z là ba số thực dƣơng thỏa mãn x(x  z)  y(y  z)  0. Tìm giá trị nhỏ nhất của biểu thức 3 3 2 2 x y x  y  4 P    2 2 2 2 x  z y  z x  y Lời giải 3 2 2 x xz xz z
Áp dụng bất đẳng thức Côsi  x   x   x  . 2 2 2 2 x  z x  z 2xz 2 3 y z 2 2 x  y  4 Tƣơng tự
 y  . Suy ra P  x  y  z  . 2 2 y  z 2 x  y 2 2 x  y 4 Theo gt z   P  x  y   4 x  y x  . y Vậy P
 4  x  y  z  1. min
Câu 54: [TS10 Chuyên Quảng Nam, 2019-2020]
Cho ba số thực dƣơng a, b, c thỏa mãn abc = 1. Tìm giá trị nhỏ nhất của biểu thức:
  2     2     2 2 2 2 1 a b 5 1 b c 5 1 c  a  5 P    ab  a  4 bc  b  4 ca  c  4 Lời giải 64    2 2 1 x y 1 1 1 1
Với x, y dƣơng ta có: x  y  0  x  y  4xy        (*) x  y 4xy x  y 4  x y 
Dấu “=” xảy ra khi x = y. Ta có:   2 2 2 2 1 a  b  5 a  b  2a  6 2ab  2a  6 2 ab  a  4  2 2     2  ab  a  4 ab  a  4 ab  a  4 ab  a  4 ab  a  4   2   2   2 2 2 1 b c 5 1 c  a  5 2 Tƣơng tự:  2  ;  2  bc  b  4 bc  b  4 ca  c  4 ca  c  4  1 1 1  Do đó: P  6  2    6    2Q
 ab  a  4 bc  4  4 ca  c  4  1 1 1  1 1  Áp dụng (*) ta đƣợc:         ab  a   . ab a 4 1  3 4  ab  a  1 3  1 1  1 1  1 1  1 1  Tƣơng tự:   ;       bc  b  4
4  bc  b  1 3  ca  c  4 4  ca  c  1 3  Do đó: 1  1 1 1  1  1 1 1  Q     1  2Q        1
4  ab  a  1 bc  b  1 ca  c  1 
2  ab  a  1 bc  b  1 ca  c  1  1  1 1 1   P  6      1
2  ab  a  1 bc  b  1 ca  c  1  1  c ac 1   6      1
2  abc  ac  c bc.ac  abc  1 ca  c  1  1  c ac 1   6      1
2  ca  c  1 ca  c  1 ca  c  1  1  6  .2 2  5
Dấu “=” xảy ra khi a = b = c = 1.
Vậy giá trị nhỏ nhất của P là 5.
Câu 55: [TS10 Chuyên Lai Châu, 2019-2020] ab bc ca 1
Cho các số thực dƣơng a, b, c. Chứng minh rằng:    a  b  c a  b  2c b  c  2a c  a  2b 4 Lời giải    2 2 1 x y 1 1 1 1
Với x, y dƣơng ta có: x  y  0  x  y  4xy        (*) x  y 4xy x  y 4  x y 
Dấu “=” xảy ra khi x = y. ab ab ab  1 1  Sử dụng (*) ta đƣợc:      a  b  2c
acbc 4 a c bc  65 bc bc  1 1  ca ca  1 1  Tƣơng tự:   ;       b  c  2a
4  b  a a  c  c  a  2b 4  c  b b  a 
Cộng 3 bất đẳng thức trên theo vế ta đƣợc: ab bc ca   a  b  2c b  c  2a c  a  2b ab  1 1  bc  1 1  ca  1 1              4  a  c b  c  4  b  a a  c  4  c  b b  a  1  ab  bc ab  ca bc  ca       4  c  a b  c a  b  1  b a  c
a b  c c a  b      4 a  c b  c a   b   1
 a  b  c dpcm 4
Đẳng thức xảy ra khi a = b = c
Câu 56: [TS10 Chuyên Vĩnh Phúc, 2019-2020]
Cho các số dƣơng a, b, c thỏa mãn: abc  1. Chứng minh rằng: a b c 3       2 b ac c ab a bc Lời giải Ta có: a  c a  2b  c a  2b  c b  ac  b    b  ac  2 2 2 Mặt khác: 1 2 a a 2 2 2a 4 2a        a  2b  c  a  2b  c      b ac b ac 4a 2b c a 2b c 4 3 4          4 2a 12 2a a b c 3 abc 3 a b c  4   3 a  2b  c  4 7a  10b  7c  a b c  VT  12 2    
 7a  10b  7c 7b  10c  7a 10a  7b  7c  Do đó:  a  b  c2  12 2 7 2 2 2
a  b  c   17 ab  bc  ca
a  b  c  ab  bc  ca  7 a  b  c   17 ab  bc  ca  8a  b  c2 2 2 2 2 2 2 Mặt khác: 12 2 a  b  c2 12 2 a  b  c2 3    7  dpcm 2 2 2
a  b  c   17 ab  bc  ca 2   8 a  b  c 2
Dấu “=” xảy ra khi a = b = c = 1. 66
Câu 57: [TS10 Chuyên Tuyên Quang, 2019-2020]
Cho các số dƣơng a, b, c thỏa mãn a  b  c  4 .Tìm giá trị nhỏ nhất của biểu thức: a a b b c c P    . a  3 b b  3 c c  3 a Lời giải Ta có: a a b b c c P       a 3 b b 3 c c 3 a 2 2 2 a b c    a  3 ab b  3 bc c  3 ac
Áp dụng bất đẳng thức Cauchy-Schwarz ta đƣợc: 2 2 2 a b c P    a  3 ab b  3 bc c  3 ac  a  b  c2 
a  b  c  3 ab  bc  ca  a  b b  c c  a
Mặt khác theo AM-GM: ab  bc  ca     a  b  c 2 2 2    2 a b c a  b  c Do đó: P   
a  b  c  3a  b  c 1 4 4
Dấu “=” xảy ra khi a  b  c  3
Vậy giá trị nhỏ nhất của P là 1. Câu 58:
[TS10 Chuyên Hà Nam, 2019-2020] a b c a  b  c
Cho các số dƣơng a, b, c. Chứng minh:     4 . 2 2 2 b c a 3. a  b  c Lời giải
Áp dụng bất đẳng thức Cauchy-Schwarz ta đƣợc: a b c a  b  c a  bc2 2 2 2 ab  bc  ca VT       2 2 2 2 2 2 ab bc ca ab  bc    ca 3. a b c a  b  c 2 2 2 a  b  c ab  bc  ca   2  2 2 2 ab  bc  ca a  b  c 2 2 2 2 2 2  a  b  c 1 ab  bc  ca 1 ab  bc  ca  a  b  c         2  ab  bc  ca 2 2 2 2 2 2 2 2 a  b  c 2 a  b  c  2  ab bcca
Áp dụng bất đẳng thức AM-GM cho 3 số ta đƣợc: 67 2 2 2 a  b  c
1 ab  bc  ca 1 ab  bc  ca 1 VT  33   2 ab  bc  ca . . 2 2 2 2 2 2 2 2 a  b  c 2 a  b  c 2 3 1    2  4 dpcm 2 2
Đẳng thức xảy ra khi a = b = c.
Câu 59: [TS10 Chuyên Phú Yên, 2019-2020]
Cho a, b, c là các số thực dƣơng thỏa mãn ab  bc  ca  1. Chứng minh rằng: 2 2 2
a b  1  b c  1  c a  1  2
Dấu “=” xảy ra khi nào? Lời giải
Sử dụng bất đẳng thức Minicopski ta đƣợc:
a b  1  b c  1  c a  1  ab2  a  bc2  b  ca2 2 2 2 2 2 2  c
 ab  bc  ca2  a  b  c2  ab  bc  ca2  3ab  bc  ca  1 3  2 dpcm 1
Dấu “=” xảy ra khi a  b  c  3
Câu 60: [TS10 Chuyên Cao Bằng, 2019-2020]
Cho a, b, c là các số dƣơng thỏa mãn điều kiện a+ b + c = 3. Tìm giá trị nhỏ nhất của biểu thức: a b c R    2 2 2 1 b 1 c 1  a Lời giải
Áp dụng bất đẳng thức AM-GM ta đƣợc: 2 2 a ab ab ab  a   a   a  2 2 1 b 1 b 2b 2 b bc c ca Tƣơng tự:  b  ;  c  2 2 1 c 2 1 a 2
Cộng theo vế 3 bất đẳng trên ta đƣợc: a b c ab  bc  ca R     a  b  c  2 2 2   1  b 1  c 1  a 2 2
     a  b  c 2 3 3 a b c   3   6 6 2 1
Dấu “=” xảy ra khi a  b  c  3 3
Vậy giá trị nhỏ nhất của R là 2 Câu 61:
[TS10 Chuyên Nam Định, 2019-2020] 68 3
Cho x, y, z là số thực không âm thỏa mãn điều kiện x  y  z  . Chứng minh rằng: 2 x  2xy  4xyz  2 Lời giải
Sử dụng bất đẳng thức AM-GM ta đƣợc:  1 
x  2xy  4xyz  x  x.4y z     2  2 2  1   3 1   x  x. y  z   x  x  x       2   2 2 
 x  x2  x2  x  2  x2  x2  2  x  2 2 1  x  2x  2
 x  2x 12  2 3 Do x  y  z 
 0  x  2  x  2  0 . Vì thế:        2 x 2xy 4xyz x 2 x 1  2  2 (đpcm) 2 1
Dấu “=” xảy ra khi x  1, y  , z  0 2
Câu 62: [TS10 Chuyên Bình Định, 2019-2020]
Cho a, b, c là các số thực dƣơng thỏa mãn a  bb  cc  a  8 . Tìm giá trị nhỏ nhất của biểu 1 1 1 1 thức: P     3 abc a  2b b  2c c  2a Lời giải.
Trƣớc hết ta chứng minh bất đẳng thức phụ sau:
       8
a b b c c a  a  b  cab  bc  ca 9
Thật vậy: a  bb  cc  a  a  b  cab  bc  ca abc
a b bc ca a bbcca
Lại theo BĐT AM-GM ta có: abc  ab. bc. ca  . .  2 2 2 8
Suy ra: a  bb  cc  a  a  b  cab  bc  ca abc a  b b  c c  a
 a  b  cab  bc  ca      8 8
Suy ra đpcm: a  bb  cc  a  a  b  cab  bc  ca 9 9  ab  bc  ca  a  b  c
Áp dụng bất đẳng thức AM-GM dạng cộng mẫu số ta có: 69 1 1 1 9 3 ab  bc  ca      a  2b b  2c c  2a
3a  b  c a  b  c 3 2 Lại có:       2 2 2 ab bc ca
3 ab c  a bc  abc   3abca  b  c 9 1 a  b  c 1 a  b  c   3abc a  b  c     2    2 2 a  bc 3 abc 27 abc 3 1 1 1 1 a  b  c 3 Suy ra: P        2
3 abc a  2b b  2c c  2a 3 a  b  c
a  bbcca  8 
Dấu “=” xảy ra khi:  a  b  c  a  b  c  1  3 a  b  c    a  b  c 3
Vậy giá trị nhỏ nhất của P là 2 khi a = b = c = 1. Câu 63:
[TS10 Chuyên Bà Rịa Vũng T|u, 2019-2020] 1 1 1
Cho các số dƣơng a, b, c thỏa mãn
   3 . Tìm giá trị nhỏ nhất của biểu thức: a b c 1 1 1 P    2 2 2 2 2 2 a  ab  3b  1 b  bc  3c  1 c  ca  3a  1 Lời giải Ta có: 2 2
a  ab  3b  1   2 2
a  2ab  b   ab   2 b  1 2  b
 a  b2  ab   2 b  1 2 2
 b  b  ab  2b  ba  b  2 2 2         1 1 a ab 3b 1 b a b 1   2 2 a  ab  3b  1 ba  b   1 1 1 1 1 Tƣơng tự:  ;  2 2 b  bc  3c  1 c b  c  2 2 2 c  ac  3a  1 a c  a  2    2 2 1 x y 1 1 1 1
Với x, y dƣơng ta có: x  y  0  x  y  4xy        (*) x  y 4xy x  y 4  x y 
Dấu “=” xảy ra khi x = y.
Cộng theo vế và sử dụng bất đẳng thức AM-GM ta đƣợc: 70 1 1 1 P    b a  b  2 c b  c  2 a c  a  2 2 2 2    4b a  b  2 4c b  c  2 4a c  a  2 AMGM  1 1   1 1   1 1             
 4b a  b  2   4c b  c  2   4a c  a  2  1  1 1 1   1 1 1           
4  a b c   a  b  2 b  c  2 c  a  2 
Sử dụng bất đẳng thức (*) ta đƣợc: 1  1 1 1   1  1 1  1  1 1  1  1 1  P                  
4  a b c  4  a  b 2  4  b  c 2  4  c  a 2  3  1 1 1 1  1 1  1  1 1  1  1 1                  
4 8 8 8 16  a b  16  b c  16  c a  3  3 1  1 1 1          4 8 8  a b c  3 3 3 3     4 8 8 2
Dấu “=” xảy ra khi a = b = c = 1. 3
Vậy giá trị nhỏ là P là . 2 Câu 64:
[TS10 Chuyên Tây Ninh, 2019-2020] 3
Chứng minh a  b  c  9abc  4a  b  cab  bc  ca với x, y, z là các số thực không }m. Đẳng thức xảy ra khi nào? Lời giải
Theo bất đẳng thức Schur với a, b, c là số thực không âm thì:
aa  ba  c  bb  cb a  cc ac  b  0
Biến đổi ta đƣợc hệ quả: 3 3 3 2        2     2 a b c 3abc a b c b c a  c a  b 3
Mặt kh{c ta có đẳng thức:     3 3 3 a b c
 a  b  c  3a  bb cc a 3
Khi đó ta có:     3 3 3
a b c  9abc  a  b  c  9abc  3a  bb  cc  a Do đó: 2     2     2 VT a b c
b c a  c a  b  9abc  3a  bb  cc  a Ta l| có 2 đẳng thức: 2     2     2 ) a b c
b c a  c a  b  9abc  a  b  cab  bc  ca
) abc  a  bb  cc a  a  b  cab  bc  ca 71 Do đó: 2    2     2 a b c
b c a  c a  b  9abc  3a  bb  cc  a  4a  b  cab  bc  ca
Vậy bất đẳng thức đƣợc chứng minh.
Dấu “=” xảy ra khi a = b = c.
Câu 65: [TS10 Chuyên Quảng Nam, 2019-2020]
Cho 3 số dƣơng x, y, z. Tìm gi{ trị nhỏ nhất của biểu thức: xy yz zx P     2x  z2y  z
2yx2zx 2z y2xy Lời giải
Sử dụng bất đẳng thức Bunyakovski ta đƣợc:
                 2 2x z 2y z x x z y z y xy zx yz Do đó: xy xy xy xy     2x  z2y  z 2xz2yz    xy  yz  zx 2 xy yz zx yz yz zx zx
Tƣơng tự:       ;  2y x 2z x xy  zx  yz 2zy2xy xy  zx  yz xy  zx  yz
Cộng 3 bất đẳng thức trên theo vế ta đƣợc: P   1 xy  zx  yz
Đẳng thức xảy ra khi x = y = z.
Vậy giá trị lớn nhất của P là 1. Câu 66:
[TS10 Chuyên Bình Phƣớc, 2019-2020] 1)
Cho x, y là các số dƣơng thỏa mãn xy  1. Chứng minh rằng: 1 1 2   1 x 1 y 1 xy 2)
Cho x, y là các số thực dƣơng thỏa mãn điều kiện:   3 x y  4xy  12 1 1
Tìm giá trị lớn nhất của biểu thức: P    2018xy 1 x 1  y Lời giải 1) Ta có: 72 1 1 2  1 1   1 1             0 1  x 1  y 1  xy
 1 x 1 xy   1 y 1 xy      1  xy  1  x 1  xy  1  y              0 1 x 1 xy 1 y 1 xy
 xy x1y xy y1x          0 1 x 1 y 1 xy
x  y  x 1 y  y  x  y 1 x          0 1 x 1 y 1 xy
 y  x x y x  y x y            0 1 x 1 y 1 xy
 y x x y xy y x                0 1 x 1 y 1 xy
 y x y x xy 1               0 1 x 1 y 1 xy   2 y x  xy 1      (đúng xy 1 ) (1)       0 1 x 1 y 1 xy
Dấu “=” xảy ra khi x = y = 1.
Bất đẳng thƣc (1) đúng c{c phép biến đổi l| tƣơng đƣơng nên b|i to{n đƣợc chứng minh. 2) Sử dụng AM-GM ta có:        3 3 12 x y 4xy 2 xy  4xy  8xy xy  4xy
Đặt xy  t t  0 , khi đó: 3 2 3 2 3 2 2
8t  4t  12  0  2t  t  3  0  2t  2t  3t  3  0 2
 2t t 1  3t 1t 1  0  t 1 2 2t  3t  3  0  t  1
Áp dụng bất đẳng thức ở ý 1 ta có: 1 1 2 2 2 P    2018xy   2018xy   2018t 1 x 1 y 1 xy 1 t 2 Ta sẽ chứng minh: 2  2018t  2019 * 1 t Thật vậy: 73    2  * 
1  2018 2t 1    0  1 t  1  t 
 2018t 1t 1  0 1  t    1   1 t  2018t   1  
 0 (đúng do 0  t  1 )  1 t 
Dấu “=” xảy ra khi x = y = 1.
Vậy giá trị lớn nhất của P là 2019.
Câu 67: [TS10 Chuyên Đắc Lắc, 2019-2020]
Cho 3 số thực dƣơng a, b, c thỏa mãn 2 2 2
a  b  c  3. Chứng minh rằng: 3 3 3 3 3 3 a  b b  c c  a    2 a  2b b  2c c  2a Lời giải.
Sử dụng bất đẳng thức Cauchy-Schwarz ta đƣợc: 3 3 3 4 4 4 a b c a b c )      2 2 2 a  2b b  2c c  2a a  2ab b  2bc c  2ca a b c 2 a b c 2 2 2 2 2 2 2   2 2 2 2 2 2
a  b  c  2ab  2bc  2ca a  b  c  2  2 2 2 a  b  c  2 2 2 a  b  c 3   3 2 3 3 3 4 4 4 b c a b c a )      2 2 2 a  2b b  2c c  2a ab  2b bc  2c ca  2a a b c 2 a b c 2 2 2 2 2 2 2   ab  bc  ca  2  2 2 2 a  b  c  2 2 2 a  b  c  2  2 2 2 a  b  c  2 2 2 a  b  c 3   3 2 3 3 3 3 3 3 a  b b  c c  a Cộng theo vế ta đƣợc:    2 (đpcm) a  2b b  2c c  2a 2
Dấu “=” xảy ra khi a  b  c  3
Câu 68: [TS10 Chuyên Quảng Nam, 2019-2020]
Cho hai số thực x, y thỏa mãn x  3; y  3.  1   1 
Tìm giá trị nhỏ nhất của biểu thức: T  21 x    3 y  .  y   x  Lời giải
Áp dụng bất đẳng thức AM – GM ta có: 74  1   1   x 3   7y 21  62 2
T  21 x    3 y            x  y  y   x   3 x   3 y  3 3 x 3 7y 21 62 2  2 .  2 .  .3  .3 3 x 3 y 3 3  2  2.7  62  2  80
Dấu “=” xảy ra khi x = y = 3.
Vậy giá trị nhỏ nhất của T là 80.
HỆ THỐNG BÀI TẬP SỬ DỤNG TRONG CHỦ ĐỀ I.
BẤT ĐẲNG THỨC CÔSI 1
Bài 1. Cho x  0 . Tìm giá trị nhỏ nhất của biểu thức 2
T  8x  4x  15 . 2 4x 1
Bài 2. Cho x  0 . Tìm giá trị nhỏ nhất của biểu thức 2
M  4x  3x   2011. 4x 2 2 x  y
Bài 3. Cho x  y  0 và xy  2 . Tìm giá trị nhỏ nhất của biểu thức H  x  . y
Bài 4. Cho a 1; b 1. Chứng minh a b 1  b a 1  ab . 11abc
Bài 5. Cho a  9; b  4; c 1. Chứng minh ab c 1  bc a  9  ca b  4  . 12 Bài 6. Cho 2 2
a  0; b  0; a  b  2 .
Tìm giá trị lớn nhất của biểu thức M  a ba  2b  b a b  2a . Bài 7. Cho 2 2
x  0; y  0; x  y  2 .
Tìm giá trị lớn nhất của biểu thức P  x 14x 10y  y 14y 10x .
Bài 8. Cho x  0; y  0 và xy  x  y  x  y . Tìm giá trị nhỏ nhất của biểu thức P  x  y . Bài 9. Cho , a ,
b c  0 và ab  bc  ca  1. a b c
Tính giá trị lớn nhất của biểu thức P    . 2 2 2 a 1 b 1 c 1
Bài 10. Cho các số dƣơng , a ,
b c thỏa mãn a  b  c  1 ab bc ca 3 chứng minh    c  ab a  bc b  ca 2
Bài 11. Cho a  0, b  0, c  0 và ab  bc  ca  3abc 2 2 2 a b c
Tìm giá trị nhỏ nhất của P    c  2 2
c  a  a 2 2
a  b  b 2 2 b  c 
Bài 12. Cho a  0, b  0, c  0 và a  b  c 1 a b c
Tìm giá trị nhỏ nhất của biểu thức T    2 2 2 1 9b 1 9c 1 9a 75 1 1 1 1 Bài 13. Cho , a , b c  0 và  
 2 . Chứng minh rằng abc  . 1 a 1 b 1 c 8
Bài 14. Cho a  0, b  0, c  0 và 2 2 2
a  b  c  1. Chứng minh : ab bc ca bc ca ab a)  
 a  b  c b)    3 c a b a b c Bài 15. Cho , a ,
b c l| độ dài ba cạnh của ABC  .
Chứng minh a  b  cb  c  ac  a  b  abc 5
Bài 16. Cho a  2 . Tìm giá trị nhỏ nhất của biểu thức P  2a  . a 6 24
Bài 17. Cho x  0, y  0 và x  y  6 . Tìm giá trị nhỏ nhất của biểu thức F  x  y   . x y 28 1
Bài 18. Cho x  0, y  0 và x  y  3 . Tìm giá trị nhỏ nhất của biểu thức 2 2
P  2x  y   . x y
Bài 19. Cho 2  x  3, 4  y  6, 4  z  6 và x  y  z  12 . Tìm giá trị lớn nhất của biểu thức P  xyz . x 8 x 2 y
Bài 20. Cho x  0, y  0 và 
 2 . Tìm giá trị nhỏ nhất của biểu thức K   . 2 y y x
x  y  2 1
xy  x  y
Bài 21. Cho x  0, y  0 . Tìm giá trị nhỏ nhất của biểu thức A   .
xy  x  y
x  y  2 1 2 2 x  y xy
Bài 22. Cho x  0, y  0 . Tìm giá trị nhỏ nhất của biểu thức A   . xy x  y
Bài 23. Cho a  0, b  0, c  0 thỏa mãn 2 2 2
b  c  a . 1  1 1 
Tìm giá trị nhỏ nhất của biểu thức P   2 2 b  c  2  a    . 2 2 2 a  b c   1 1 
Bài 24. Cho x  0, y  0 và x  y 1. Tìm giá trị nhỏ nhất của biểu thức 2 2 P   1 x y   .  x y  1 1
Bài 25. Cho x  0, y  0 và x  y 1. Tìm giá trị nhỏ nhất của biểu thức P    4xy . 2 2 x  y xy 2 2  1   1 
Bài 26. Cho x  0, y  0 và x  y 1. Tìm giá trị nhỏ nhất của biểu thức K  x   y      .  x   y  3 3  1   1 
Bài 27. Cho x  0, y  0 và x  y 1. Tìm giá trị nhỏ nhất của biểu thức S  1 x   1 y      .  x   y 
Bài 28. Cho x  0, y  0 và 2 2
2x  2xy  y  2x  8 . 2 4
Tìm giá trị nhỏ nhất của biểu thức P 
  2x  3y . x y
Bài 29. Cho a  0, b  0, c  0 thỏa mãn  2 2
b  bc  c    2 2 3 3  a  . 2 2 2
Tìm giá trị nhỏ nhất của biểu thức T  a  b  c    . a b c
Bài 30. Cho a  0, b  0 và 3 3
a  b  6ab  8 . 1 3
Tìm giá trị nhỏ nhất của biểu thức P    ab . 2 2 a  b ab 76
Bài 31. Cho a  0, b  0 và 2 2
a  b  a  b . 2020
Tìm giá trị nhỏ nhất của biểu thức 4 4
P  a  b   . a  b2
Bài 32. Cho x  0, y  0 và  x   1  y   1  4 . 2 2 x y
Tìm giá trị nhỏ nhất của biểu thức P   . y x
II. BẤT ĐẲNG THỨC BUNHIA
Bài 1. Cho 4x  9y 13 . Tìm giá trị nhỏ nhất của biểu thức 2 2
A  4x  9y .
Bài 2. Cho 4x  3y 1. Tìm giá trị nhỏ nhất của biểu thức 2 2
A  4x  3y .
Bài 3. Cho x  0, y  0, z  0 và x  y  z  2 . Tìm giá trị nhỏ nhất của biểu thức 2 2 2
A  x  y  z . 6 Bài 4. Cho 2 2 3x  2 y 
. Tìm giá trị lớn nhất của biểu thức S  2x  3y . 35 1 Bài 5. Cho 2 2 4a  25b 
. Tìm giá trị lớn nhất của biểu thức H  6a  5b . 10 3 Bài 6. Cho 2 2 2
x  y  z 
. Tìm giá trị lớn nhất của biểu thức P  x  y  z . 4
Bài 7. Tìm giá trị lớn nhất của biểu thức P  x 1  3 x khi 1 x  3 .
Bài 8. Cho a  0, b  0, c  0 và a  b  c  3.
Tìm giá trị lớn nhất của biểu thức K  4a  5  4b  5  4c  5 .
Bài 9. Cho a  0, b  0, c  0 và a  b  c 1.
Tìm giá trị lớn nhất của biểu thức P  b  c  c  a  a  b . Bài 10. Cho , a ,
b c  0 và a  b  c  3. a  b b  c c  a
Tìm giá trị nhỏ nhất của biểu thức M    . 2 2 2
III. PHƯƠNG PHÁP BIẾN ĐỔI TƯƠNG ĐƯƠNG Bài 1. Cho x  2
 , y 1. Tìm giá trị nhỏ nhất của biểu thức: A  x  y  2 x  2  4 y 1  24. 1
Bài 2. Cho x   . Tìm giá trị nhỏ nhất của biểu thức: E  5x  6 2x  7  4 3x 1  2 3
Bài 3. Cho x  1. Tìm giá trị nhỏ nhất của biểu thức: T  x  x 1  3 x  7  28 .
Bài 4. Cho x  15 . Tìm giá trị nhỏ nhất của biểu thức: 2 
   2     2 F x x x
15 x 3  x 15  x  3  38 .
Bài 5. Cho a  0, b  0,c  0 và a  b  c  6 . Tìm giá trị lớn nhất của biểu thức: 2 2 2 2 2 2
T  a  4ab  b  b  4bc  c  c  4ca  a .
Bài 6. Cho x  0, y  0, z  0, x  y  z 1 . Tìm giá trị nhỏ nhất của biểu thức: 2 2 2 2 2 2 S 
x  xy  y  y  yz  z  z  zx  x . Bài 7. Cho 2   a,b,c  3 và 2 2 2
a  b  c  22 . Tìm giá trị nhỏ nhất của biểu thức: M  a  b  c .
Bài 8. Cho x  0, y  0, z  0 thỏa mãn x  y  z  6 . Tìm giá trị lớn nhất và nhỏ nhất của biểu thức: 2 2 2 A  x  y  z . 77
Bài 9. Cho a, b,c  0 và a  b  c  3 . Tìm giá trị lớn nhất và nhỏ nhất của biểu thức:
K  3a 1  3b 1  3c 1 .
Bài 10. Cho 0  a, b,c  2 và a  b  c  3 . Chứng minh: ab  bc  ca  2 .
Bài 11. Cho a 1, b 1,c 1 và ab  bc  ca  9. Tìm giá trị lớn nhất và nhỏ nhất của biểu thức: 2 2 2 P  a  b  c . Bài 12. Cho 1
  x, y,z 1, x  y  z  0 . Tìm giá trị lớn nhất của biểu thức: T  x  y  z . Bài 13. Cho 2
  a,b,c  2 và a  b  c  0. Chứng minh: 4 4 4 a  b  c  32 . 3
Bài 14. Cho 0  x, y, z 1 và x  y  z  . 2
Tìm giá trị lớn nhất và nhỏ nhất của biểu thức: 2 2 2 P  x  y  z .
Bài 15. Cho 0  x, y, z  2 và x  y  z  3.
Tìm giá trị lớn nhất và nhỏ nhất của biểu thức: 4 4 4
M  x  y  z 121 x1 y1 z .
Bài 16. Cho 0  a, b,c  4 và a  b  c  6 .
Tìm giá trị lớn nhất của biểu thức: 2 2 2
P  a  b  c  ab  bc  ca .
Bài 17. Cho a  0, b  0,c  0 và a  b  c 1. Tìm giá trị lớn nhất và nhỏ nhất của biểu thức:
P  b  c  c  a  a  b .
Bài 18. Cho a  0, b  0,c  0 và a  b  c  3 .Tìm giá trị lớn nhất và nhỏ nhất của biểu thức:
P  b  c  c  a  a  b .
Bài 19. Cho a  0, b  0,c  0 và a  b  c 1.Tìm giá trị lớn nhất và nhỏ nhất của biểu thức:
F  3a 1  3b 1  3c 1 .
Bài 20. Cho a  0, b  0,c  0 và a  b  c 1. Tìm giá trị lớn nhất của biểu thức: 2 2 2
2a  3a  4  2b  3b  4  2c  3c  4 .
Bài 21. Cho x, y  0 thỏa mãn: x  y  10 .
Tìm giá trị nhỏ nhất của biểu thức:   4   4 P x 1 y   1 . Bài 22. Cho 2 2
a  b  4ab  4a  4b .
Tìm giá trị lớn nhất của biểu thức:   3 3     2 2 A 20 a b 6 a  b   2013 . --------Hết------ 78

Một số phương pháp chứng minh bất đẳng thức

Thông tin :

Tài liệu liên quan:

Tổng hợp kiến thức Đại số THCS

Cấu trúc đề thi vào 10 năm 2023 tỉnh Tỉnh Bà Rịa - Vũng Tàu

Cấu trúc đề thi tuyển sinh lớp 10 tỉnh Thái Nguyên năm 2023 - 2024

Cấu trúc đề thi vào lớp 10 năm 2023 - 2024 tỉnh Thanh Hóa

Cấu trúc đề thi vào 10 tỉnh Quãng Ngãi năm 2023 - 2024