Một số ứng dụng hay về tỷ số thể tích trong việc giải toán trắc nghiệm

Tài liệu gồm 105 trang, được biên soạn bởi thầy giáo Nguyễn Hoàng Việt, trình bày một số ứng dụng hay về tỷ số thể tích trong việc giải toán trắc nghiệm..Mời bạn đọc đón xem.

52 26 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Khối đa diện

Môn: Toán 12

Thông tin:

105 trang 8 tháng trước

Tác giả:

Profile Lan Tường
Chuyên đề: Tỉ số thể tích
Trang 1/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
MỘT SỐ ỨNG DỤNG HAY VỀ TỶ SỐ THỂ TÍCH TRONG VIỆC
GIẢI TOÁN TRẮC NGHIỆM
Từ khi Bộ Giáo Dục và Đào Tạo chuyển hướng sang thi trắc nghiệm, việc dạy và học môn
toán cũng có sự thay đổi để đáp ứng đối với kì thi. Giáo viên phải dạy học sinh hiểu rõ bản chất
và cách làm nhanh nhất để đi đến kết quả. Còn học sinh mong muốn mình giải quyết một bài
toán với con đường đơn giản nhất và đáp số chính xác nhất. Sau đây tôi xin biên soạn lại một
vấn đề rất hay gặp trong các kì thi thử và thi THPTQG, giúp các em học sinh giải quyết rất
nhanh các bài toán liên quan đến thể tích khối đa diện..
I. KIẾN THỨC CƠ SỞ.
+) Hai hình chóp có cùng diện tích đáy thì tỷ số thể tích của chúng chính là tỷ số của đường cao
và ngược lại.
+) Với khối chóp tam giác ta có tính chất quen thuộc sau.
Cho khối chóp tam giác
.S ABC
. Mặt phẳng
( )
P
cắt các đường thẳng
lần lượt
tại
', ', 'A B C
. Khi đó ta có
( )
. ' ' '
.
' ' '
. . * .
S A B C
S ABC
V SA SB SC
V SA SB SC
=
Chứng minh.
Gọi
,'HH
lần lượt là hình chiếu của
,'AA
trên
( )
mp SBC
.
..
1
. . .sin
6
S ABC A SBC
V V AH SB SC BSC==
và
'. ' '
1
' '. '. '.sin ' '
6
A SB C
V A H SB SC B SC=
. ' ' '
.
' ' '
..
S A B C
S ABC
V AH SB SC
V AH SB SC
=
Rõ ràng
' ' 'A H SA
AH SA
=
. ' ' '
.
' ' '
..
S A B C
S ABC
V SA SB SC
V SA SB SC
=
Đây là kết quả quen thuộc và nó là bài toán
mở đầu cho rất nhiều ứng dụng hay sau này.
\
II. MỘT SỐ TÍNH CHẤT .
1. Tính chất 1.
Cho hình chóp
.S ABCD
, đáy
ABCD
là hình bình hành. Mặt phẳng
( )
P
, , ,SA SB SC SD
lần
lượt tại
', ', ', 'A B C D
. Khi đó ta có
' ' ' '
SA SC SB SD
SA SC SB SD
+ = +
Chứng minh.
Đặt
. . . . .
2
S ABCD S ABC S ADC S BAD S BCD
V
V V V V V V= = = = =
S
A
C
B
A’
C’
B’
H’
H
Chuyên đề: Tỉ số thể tích
Trang 2/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Ta có
. ' ' ' . ' ' '
' ' '
..
2
S A B C S A B C
SABC
V SA SB SC V
V
V SA SB SC
==
. ' ' '
' ' '
..
2
S A D C
V SA SD SC
V
SA SD C
và
S
=
( )
. ' ' ' . ' ' ' . ' ' ' '
' ' ' ' ' '
. . . . 1
22
S A B C S A C D S A B C D
SA SB SC SA SC SD V V V
VV
SA SB SC SA SC SD
+
+ = =
Tượng tự ta có
( )
. ' ' ' . ' ' ' . ' ' ' '
' ' ' ' ' '
. . . . 2
22
S B A D S B C D S A B C D
SB SA SD SB SC SD V V V
VV
SB SA SD SB SC SD
+
+ = =
Từ (1), (2)
( )
' ' ' ' ' '
. . . .
' ' ' ' ' '
. . . . 3
SA SB SC SA SC SD
SA SB SC SA SC SD
SB SA SD SB SC SD
SB SA SD SB SC SD
+
=+
Nhân vào hai vế của (3) với
. . .
' ' ' '
SA SB SC SD
SA SB SC SD
ta được
' ' ' '
SA SC SB SD
SA SC SB SD
+ = +
Suy ra điều phải chứng minh.
Tính chất 1 ta chỉ áp dụng cho chóp có đáy là hình bình hành.
Việc chứng minh Tính chất 1 như trên là ta đã áp dụng tính chất (*). Tuy nhiên ta có thể chứng
minh Tính chất 1 nhanh gọn như sau :
Gọi
O
là tâm hình bình hành,
I
là giao điểm của
SO
và
( )
' ' ' 'A B C D
.
Ta có
' ' ' '
2 '. '. '. '
2.
. . .
SA I SC I SA C
SAO SCO SAC
S S S SA SI SC SI SA SC
S S S SASO SC SO SASC
+ = + =
. Nhân cả hai vế của đẳng thức sau
cho
..
'. '.
SA SC SO
SA SC SI
ta được
2.
''
SA SC SO
SA SC SI
+=
. Chứng minh tương tự ta có
2.
''
SB SD SO
SB SD SI
+=
.
Vậy ta có điều phải chứng minh.
*) Cách chứng minh này còn cho ta kết quả mạnh hơn là
S
A
B
C
D
O
I
A’
B’
C’
D’
Chuyên đề: Tỉ số thể tích
Trang 3/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Kết quả 1 : Cho hình chóp
.S ABCD
, đáy
ABCD
là hình bình hành. Mặt phẳng
( )
P
, , ,SA SB SC SD
lần lượt tại
', ', ', 'A B C D
. Khi đó ta có
2.
' ' ' '
SA SC SB SD SO
SA SC SB SD SI
+ = + =
.
Kết quả trên còn có thể được chứng minh bằng nhiều cách khác nữa. Nó là kết quả rất hay và
được ứng dụng nhiều trong hình học không gian.
Tính chất 1 được ứng dụng rất nhiều trong bài toán tìm thiết diện cũng như thể tích khối đa
diện.
Đặt
( )( )
; ; ; , , , 0 **
' ' ' '
SA SB SC SD
x y z t x y z t
SA SB SC SD
= = = =
Vận dụng Tính chất (*) và Tính chất 1 ta có
. ' ' ' ' . ' ' ' . ' ' '
. . .
1 ' ' ' ' ' '
. . . .
2 2 2
S A B C D S A B C S A D C
S ABCD S ABC S ADC
V V V SA SB SC SA SD SC
V V V SA SB SC SA SD SC

= + = +


1 1 1
2 2 4
y t x y z t
xyz xtz xyz xyz

+ + + +
= + = =


do
x z y t+ = +
. Ta có
Kết quả 2 :
. ' ' ' '
.
4
S A B C D
S ABCD
V x y z t
V xyzt
+ + +
=
với
, , ,x y z t
được xác định như
( )
** .
Chú ý : Nếu
', ', ', 'A B C D
lần lượt thuộc các cạnh
, , ,SA SB SC SD
thì
, , , 1x y z t
.
Kết quả 2 được áp dụng vào giải quyết các bài toán thể tích khối chóp có đáy là hình bình hành
một cách rất nhanh gọn và đơn giản thay cho việc phải chia khối chóp tứ giác loại này thành các
khối chóp tam giác để sử dụng Tính chất (*)
Ví dụ 1. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành. Gọi
M
là trung điểm
SB
,
điểm
P
thuộc cạnh
SD
sao cho
2SP PD=
. Mặt phẳng
( )
AMP
cắt
SC
tại
N
. Tỷ số
.
.
S AMNP
S ABCD
V
V
bằng
Giải.
Ta có
3
12
2
5
2
SA SC SB SD SC
SA SN SM SP SN
SC
SN
+ = + + = +
=
Vậy
.
.
53
12
7
22
53
30
4.1.2. .
22
S AMNP
S ABCD
V
V
+ + +
==
S
A
M
N
P
B
C
D
Chuyên đề: Tỉ số thể tích
Trang 4/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Ví dụ 2. Cho hình chóp
.S ABCD
có thể tích bằng
V
, đáy
ABCD
là hình vuông. Cạnh
( )
SA ABCD⊥
và
SC
hợp với đáy một góc bằng
30
. Mặt phẳng
( )
P
đi qua
A
và vuông góc
với
SC
, cắt các cạnh
,,SB SC SD
lần lượt tại
,,E F K
. Thể tích khối chóp
.S AEFK
bằng
Giải.
Ta có
22
2
22
.
SA SE SB SB
SA SE SB
SB SB SE SA
= = =
Tương tự
2
2
SD SD
SK SA
=
nên
SB SD
SE SK
=
Mà
2
2
4
SC SC
SF SA
==
( do
SCA
vuông tại
0
, 30A SCA =
)
nên
5
15
2
SC SB SD SB SD
SF SE SK SE SK
+ = + = = =
..
.
.
10 1
.
55
10 10 10
4.1.4. .
22
S AEFK S ABCD
S AEFK
S ABCD
V V V
V
V
= = = =
Ví dụ 3. Cho khối chóp
.S ABCD
có đáy
ABCD
là hình bình hành. Mặt phẳng
( )
P
chứa cạnh
AB
và đi qua điểm
M
trên
SC
chia khối chóp
.S ABCD
thành hai phần có thể tích bằng nhau.
Tính tỷ số
SM
k
SC
=
.
Giải.
Gọi
( )
N P SC=
ta có
( )
AB P
AB CD

nên
MN CD
.
Ta có
1SM SC SD
k
SC SM SN k
= = =
Khi đó
2
11
11
1
1
2
4.
SABMN
SABCD
V
kk
V
k
+ + +
==
2
1 1 1 1 5 5 1
10
22
k
k k k
+−
− − = = =
.
Ví dụ 4. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành. I nằm trên
SC
sao cho
2IS IC=
.
Mặt phẳng
( )
P
chứa cạnh
AI
cắt cạnh
,SB SD
lần lượt tại
,MN
. Gọi
',VV
lần lượt là thể tích
khối chóp
.S AMIN
và
.S ABCD
. Tính giá trị nhỏ nhất của tỉ số thể tích
'V
V
Giải.
Chuyên đề: Tỉ số thể tích
Trang 5/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Đặt
, , 1
SB SD
x y x y
SM SN
= =
.
Ta có
3 5 5
1
2 2 2
x y x y + = + = + =
Ta có
2
3
1
' 5 5 8
2
3
6 15
4 . .1.
6
2
2
xy
V
V xy
xy
xy
+ + +
= = =
+



Dấu bằng xảy ra khi
5
.
4
xy==
Ví dụ 5. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành tâm
O
. Mặt phẳng
( )
thay đổi luôn đi qua
B
, trung điểm
I
của
SO
và cắt các cạnh
,SA SC
và
SD
lần lượt tại
,MN
và
.P
Tính GTNN và GTLN cùa tỷ số
.
.
S BMPN
S ABCD
V
V
.
Giải.
Đặt
, , 1
SA SC
x y x y
SM SN
= =
.
Ta có
2. 4
SA SC SB SD SO
SM SN SB SP SI
+ = + = =
Nên
3; 4
SD
xy
SP
= + =
. Từ đó
( )
.
.
8 2 2
4. . .3.1 3 3 4
S BMPN
S ABCD
V
V x y xy x x
= = =
−
Từ
4 4 3x y x y+ = = −
vì
1.y
Xét
( )
( )
2
,1 3
34
f x x
xx
=
−
( )
( )
( )
2
2 4 2
' 0 2
34
x
f x x
xx
−
= = =
−


Ta có
( ) ( ) ( )
21
1 3 ; 2
96
f f f= = =
.
Vậy
.
.
S BMPN
S ABCD
V
V
đạt GTNN, GTLN lần lượt là
12
,
69
.
Nhận xét. Qua năm ví dụ trên ta thấy sự lợi hại của Kết quả 2 đem lại. Vừa nhanh, dễ sử dụng
mà hiệu quả thì cực tốt. Rất hợp cho học sinh trong việc làm bài trắc nghiệm.
Chuyên đề: Tỉ số thể tích
Trang 6/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
2. Tính chất 2. Cho lăng trụ
1 1 1
.ABC A B C
có các điểm
,,M N P
lần lượt thuộc các cạnh
1 1 1
,,AA BB CC
sao cho
1 1 1
,,
AM BN CP
x y z
AA BB CC
= = =
. Khi đó ta có tỷ số
1 1 1
.
3
ABCMNP
ABC A B C
V x y z
V
++
=
.
Chứng minh. Ta có
..ABCMNP M ABC M BCPN
V V V=+
, đặt
1 1 1
.ABC A B C
VV=
dễ thấy
11
.
2
3
A BCC B
V
V =
+ Ta có
.
1 1 1
1
( ;( )).
1 ( ;( )) 1 1
3
.
( ;( ). 3 ( ;( ) 3 3
ABC
M ABC
ABC
d M ABC S
V d M ABC AM
x
V d A ABC S d A ABC AA
= = = =
Suy ra
( )
.
.1
3
M ABC
x
VV=
.
Do
( )
1 1 . .
//
M BCPN A BCPN
AM BCC A V V=
Nên
( )
( )
( )
1 1 1 1 1 1
1
. . 1 1
11
. . 1 1 1
1
. ( ; )
2
. , 2 2
M BCPN A BCPN BCPN
A BCC B A BCC B BCC B
CP BN d P BB
V V S yBB zCC y z
BB CC
V V S BB d P BB BB
+
++
= = = = = =
( )
11
.
.
.
2
. . 2 .
2 2 3 3
M BCPN
M BCPN
A BCC B
V y z y z V y z
VV
V
+ + +
= = =
Vậy từ
( ) ( )
1 , 2
ta có
1 1 1
..
.
.
33
ABCMNP
ABCMNP M ABC M BCPN
ABC A B C
x y z V x y z
V V V V
V
+ + + +
= + = =
.
Đặc biệt:
1 1 1 1 1 1
..
..
,
33
A MNP M BCPN
ABC A B C ABC A B C
V x V y z
VV
+
==
.
Ví dụ 6. Cho khối lăng trụ
.ABC A B C
, có
,,M N P
lần lượt thuộc các cạnh
,,AA BB CC
sao
cho
, 3 , 3AM MA BN NB CP PC
= = =
. Đặt
1
V
là thể tích của khối đa diện
ABCMNP
,
2
V
là thể
tích của khối đa diện còn lại. Tính tỉ số
1
2
V
V
.
Chuyên đề: Tỉ số thể tích
Trang 7/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Giải. Ta có
13
; 3 ;
24
3
3
4
MA BN
MA MA BN NB
AA BB
CP
CP PC
CC

= = = =

= =
Đặt
.ABC A B C
VV
=
Suy ra
1
1 2 1
1
2
1 3 3
2 2 1
244
3 3 3 3
2
V
V V V V V V
V
V
V
++
= = = = − =
=
Ví dụ 7. Cho khối lăng trụ
.ABC A B C
có thể tích bằng
V
, các điểm
,,M N P
lần lượt thuộc
các cạnh
,,AA BB CC
sao cho
2 , 3 , .AM MA BN NB CP x PC
= = =
. Đặt
1
V
là thể tích của khối
đa diện
.ABC MNP
, tính giá trị của
x
để
1
3
5
V
V
=
.
Giải.
Ta có
23
2 ; 3 ;
34
1
AM BN
MA MA BN NB
AA BB
CP x
CP xPC
CC x

= = = =

= =
+
Suy ra
1
23
3 17 9
3 4 1
3 5 12 1 5
23 23
.
1 60 37
x
Vx
x
Vx
x
x
x
++
+
= = + =
+
= =
+
.
Ví dụ 8. Cho khối lăng trụ
.ABC A B C
có thể tích bằng
3
60cm
, các điểm
,,M N P
lần lượt
thuộc các cạnh
,,AA BB CC
sao cho
2 , 3 , 4 .AM MA BN NB CP PC
= = =
Thể tích của khối đa
diện
.BC MNP
.
Chuyên đề: Tỉ số thể tích
Trang 8/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Giải.
Ta có
23
2 ; 3 ;
34
4
4
5
AM BN
MA MA BN NB
AA BB
CP
CP PC
CC

= = = =

= =
Nên
' ' '
234
133
3 4 5
3 180
133 133
.60
180 3
ABCMNP
ABCA B C
ABCMNP
V
V
V
++
==
= =
Mà
( )
( )
( )
( )
. . ' ' '
1 1 2 2 40
; . . '; . .
3 3 3 9 3
M ABC ABC ABC ABC A B C
V d M ABC S d A ABC S V= = = =
.
Vậy
( )
3
133 40
31 .
33
BCMNP
V cm= − =
Nhận xét. Các bài toán dạng này sẽ xuất hiện nhiều khối không phải là các khối có công thức
tính thể tích như chóp hay lăng trụ.. Thay vì việc phải phân chia các khối này thành các khối có
công thức tính, nay ta có ngay một kết quả rất nhanh và chính xác.
Ví dụ 9.
Cho lăng trụ
. ' ' 'ABC A B C
có
,'GG
lần
lượt là trọng tâm của
, ' 'ABC A B C
.
Mặt phẳng
( )
cắt
AA', ', ', 'BB CC GG
lần lượt tại
, , ,M N P I
. Chứng minh
rằng
AM
3.
' ' ' '
BN CP GI
AA BB CC GG
+ + =
Chứng minh.
Đặt
AM
,,,
' ' ' '
BN CP GI
x y z t
AA BB CC GG
= = = =
;
. ' ' 'ABC A B C
VV=
Dễ thấy
. ' ' ' . ' ' ' . ' ' '
3
AGB A G B CGB C G B AGC A G C
V
V V V= = =
Ta có
. ' ' '
3
AGB A G B
AGBMIN
V
V x y t
V
++
=
. Tương tụ ta có
. ' ' ' . ' ' '
;
33
CGB C G B CGA C G A
CGBPIN CGAPIN
VV
V z y t V z y t
VV
+ + + +
==
Cộng vế với vế cả 3 đẳng thức trên ta được
( )
2
3
3 3 3 3
ABCMNBP
x y z
V x y t z y t z y t
t
V
++
+ + + + + +
= + + = +
A
B
C
G
A’
B’
C’
M
N
P
I
G’
Chuyên đề: Tỉ số thể tích
Trang 9/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Mà
3
3.
3
ABCMNBP
V x y z
x y z
V
++
= = + +
nên
3
x y z
t
++
=
. Ta được điều phải chứng minh.
Từ kết quả trên ta có
. ' ' '
.
'
ABCMNBP
ABC A B C
V GI
V GG
=
Nhận xét. Dựa vào kết quả trên ta thấy rẳng chỉ cần biết
( )
cắt
'GG
tại vị trí điểm
I
xác định
là ta đã biết
( )
chia lăng trụ thành hai phần với tỉ số bao nhiêu rồi.
3. Tính chất 3. Cho hình
hộp
. ' ' ' 'ABCD A B C D
. Mặt phẳng
( )
cắt
các cạnh
', ', ', 'AA BB CC DD
lần lượt tại
, , ,M N P Q
sao cho
' ' ' '
,,,
DD
AM BN CP DQ
x y z t
AA BB CC
= = = =
.
Khi đó ta có :
a.
.x z y t+ = +
b.
. ' ' ' '
4 2 2
ABCDMNQP
ABCD A B C D
V
x y z t x z y t
V
+ + + + +
= = =
Chứng minh.
a. Dễ thấy tứ giác
MNPQ
là hình bình hành. Gọi
,IO
lần lượt là tâm của hình bình hành
MNPQ
và hình vuông
ABCD
. Ta có
OI
là đường trung bình của hình thang
AMPC
nên
2
AM CP
OI
+
=
. Tương tự
2
BN DQ
OI
+
=
, do đó
AA'+zCC'=yBB'+tDD'AM CP BN DQ x x z y t+ = + + = +
b. Áp dụng Tính chất 2 ta có
. ' ' ' . ' ' ' ' . ' ' ' '
2
3 3 6
ABDMNQ ABDMNPQ ABDMNQ
ABD A B D ABCD A B C D ABCD A B C D
V V V
x y t x y t x y t
V V V
+ + + + + +
= = =
tương tự
. ' ' ' '
6
BCDNPQ
ABCD A B C D
V
y z t
V
++
=
Do đó,
. ' ' ' ' . ' ' ' ' . ' ' ' '
6 6 6
2
64
ABCDMNPQ ABDMNQ BCDNPQ
ABCD A B C D ABCD A B C D ABCD A B C D
V V V
x y t y z t x y z t y t
V V V
x y z t
x y z t
x y z t
+ + + + + + + + +
= + = + =
+ + +
+ + + +
+ + +
==
Chú ý :
. ' ' ' '
.
4'
ABCDMNQP
ABCD A B C D
V
x y z t OI
V OO
+ + +
==
Nhận xét. Một kết quả tương tự như Tính chất 2. Ở lăng trụ là tổng ba tỉ số chia ba, còn hình
hộp là chia bốn.
Chuyên đề: Tỉ số thể tích
Trang 10/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Và cũng chỉ cần biết
( )
cắt đoạn thẳng nối hai tâm đáy ở đâu là ta đã tìm được tỷ số hai khối
tạo thành do
( )
cắt hình hộp. Tuy nhiên, Tính chất 3 cũng khẳng định chỉ cần biết hai tỉ số ở
hai cạnh bên đối diện của hình hộp mà
( )
cắt là ta cũng tìm được tỉ số thể tích các khối.
Ví dụ 10. Cho khối hộp chữ nhật
.ABCD A B C D
có thể tích bằng
2110
. Biết
,3A M MA DN ND

==
và
2CP C P
=
. Mặt phẳng
( )
MNP
chia khối hộp đã cho thành hai khối
đa diện. Thể tích khối đa diện nhỏ hơn bằng bao nhiêu.
Giải.
( )
MNP
cắt
’BB
tại
Q
.
Từ giải thiết ta có
12
;
' 2 ' 3
AM CP
AA CC
==
.
Do đó
. ' ' ' '
12
7
' ' 2 3
2 2 12
7 7385
.2110
12 6
ABCDMNPQ
ABCD A B C D
ABCDMNPQ
AM CP
V
AA CC
V
V
++
= = =
= =
Vậy
' ' ' '
7385 5275
2110
66
A B C D MNPQ
V = − =
Ví dụ 11. Cho hình lập phương
.ABCD A B C D
có
N
là trung điểm
.CC
Mặt phẳng
( )
đi
qua
AN
, cắt các cạnh
',BB DD
lần lượt tại
,MP
.
( )
chia khối lập phương thành hai phần có
thể tích tương ứng bằng
1
V
và
( )
2 1 2
V V V
. Tính tỉ số
2
1
V
V
Từ giải thiết ta có
. ' ' ' '
1
0
1
''
2
2 2 4
ABCDPNM
ABCD A B C D
AA CN
V
AA CC
V
+
+
= = =
Nên
2
' ' ' ' 1
1
3
3
ABCDPNM
AMNPA B C D
VV
VV
= =
Kết luận. Việc áp dụng các tính chất trên vào lớp các bài toán thể tích tương ứng rất là hữu ích.
Nó làm cho việc giải toán trắc nghiệm của các em học sinh nhanh gọn và nhẹ nhàng hơn nhiều
so với việc giải truyền thống. Hy vọng nó sẽ giúp các em đạt kết quả cao nhất trong các kỳ thi
sắp tới.
III. MỘT SỐ BÀI TẬP ÁP DỤNG .
Chuyên đề: Tỉ số thể tích
Trang 11/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
TỶ SỐ THỂ TÍCH KHỐI ĐA DIỆN
(ĐỀ SỐ 01)
A. LÝ THUYẾT
1. Một số kiến thức cần biết
Kiến thức cần nhớ đối với khối lăng trụ tam giác và khối hộp
3
A ABC
V
V
=
,
'.
2
3
A BCC B
V
V

=
6
A ABD
V
V
=
,
3
BDA C
V
V

=
Tam giác
ABC
vuông tại
A
có đường cao
AH
có
22
,
BH AB CH AC
BC BC CB BC
==
Định lý menelaus: Ba điểm
,,D E F
lần lượt nằm trên
3
đường thẳng chứa
3
cạnh
,,BC CA AB
của
tam giác
ABC
, khi đó
,A B C
thẳng hàng khi và chỉ khi
. . 1
FA DB EC
FB DC EA
=
Công thức 1: Hai khối chóp có chung đỉnh và chung mặt đáy
11
22
VS
VS
=
Hai khối chóp
12
. ...
n
S A A A
và
12
. ...
n
S B B B
có chung đỉnh và hai mặt đáy cùng nằm trên một mặt phẳng,
ta có
1 2 1 2
1 2 1 2
. ... ...
. ... ...
nn
nn
S A A A A A A
S B B B B B B
VS
VS
=
Ví dụ 1: Cho khối chóp
.S ABC
có thể tích
V
. Gọi
,,M N P
lần lượt là trung điểm các cạnh
và
V
là thể tích khối chóp
.S MNP
. Tính tỉ số
V
V
.
A.
3
4
V
V
=
. B.
1
3
V
V
=
. C.
1
2
V
V
=
. D.
1
4
V
V
=
.
Lời giải
Chn D
Ta có:
2
11
24
MNP
ABC
S
V
VS

= = =


. Chọn đáp án D.
Chuyên đề: Tỉ số thể tích
Trang 12/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Ví dụ 2: Cho khối chóp
.S ABCD
có thể tích
V
. Gọi
, , ,M N P Q
lần lượt là trung điểm các cạnh
,AB BC
,
,CD DA
. Gọi
V
là thể tích khối chóp
.S MNPQ
. Tính tỉ số
V
V
.
A.
3
4
V
V
=
. B.
1
8
V
V
=
. C.
1
2
V
V
=
. D.
1
4
V
V
=
.
Lời giải
Chn D
Ta có:
1
2
MNPQ
ABCD
S
V
VS
==
. Chọn đáp án C.
Ví dụ 3: Cho khối chóp
.S ABCD
có thể tích
V
và đáy
ABCD
là hình vuông tâm
I
. Các điểm
,PQ
lần lượt
trên các cạnh
,AB AD
sao cho
90PIQ =
(
,PQ
không phải là đỉnh của hình vuông). Tính thể tích
của khối chóp tứ giác
.S APIQ
.
A.
2
V
. B.
3
V
. C.
4
V
. D.
6
V
.
Lời giải
Chn C
Ta có:
.
.
1
44
S APIQ APIQ
S APIQ
ABCD
VS
V
V
VS
= = =
. Chọn đáp án C.
Công thức 2 : Công thức Simson (tỷ số thể tích) Cho khối chóp tam giác
.S ABC
. Gọi
1 1 1
,,A B C
lần
lượt là các điểm nằm trên các cạnh
,,SA SB SC
ta có :
1 1 1
.
1 1 1
.
..
S A B C
S ABC
V
SA SB SC
V SA SB SC
=
.
Chuyên đề: Tỉ số thể tích
Trang 13/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Ví dụ 4: Cho khối tứ diện
ABCD
có thể tích
V
. Gọi
V
là thể tích của khối tám mặt có các đỉnh là trung điểm
các cạnh của khối tứ diện
ABCD
. Tính tỷ số
V
V
.
A.
3
4
V
V
=
. B.
1
8
V
V
=
. C.
1
2
V
V
=
. D.
1
4
V
V
=
.
Lời giải
Chn B
Ta có:
3
.
1
. . .
28
A MNP
AM AN AP V
V V V
AB AC AD

= = =


.
Tương tự ta có:
. . .
; ; .
8 8 8
B MSQ C NQR D PSR
V V V
V V V= = =
Do đó,
'
'
1
4.
8 2 2
V V V
VV
V
= − = =
.
Công thức 3: Cắt khối chóp bởi mặt phẳng song song với đáy sao cho
1
1
SB
k
SA
=
thì
12
12
...
3
...
n
n
SB B B
SA A A
V
k
V
=
(Đây
là trường hợp đặc biệt cho hai khối đa diện đồng dạng theo tỷ sồ
k
.
Công thức 4: Mặt phẳng cắt cắt các cạnh của khối lăng trụ tam giác
' ' '
ABCA B C
lần lượt tạ
;;M N P
sao cho
, , .
AM BN CP
x y z
AA BB CC
= = =
Ta có
..
3
ABC MNP ABC A B C
x y z
VV
++
=
.
Chuyên đề: Tỉ số thể tích
Trang 14/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Ví dụ 5: Cho khối lăng trụ tam giác
' ' '
ABCA B C
có thể tích
V
. Các điểm
;MN
lần lượt thuộc các cạnh
''
;BB CC
sao cho
'
11
,
24
MB NC
x
BB CC
==
. Thể tích của khối chóp tứ giác
.A BMNC
V
là?
A.
3
V
. B.
3
8
V
. C.
6
V
. D.
4
V
.
Lời giải
Chn D
Ta có
.
11
0
24
3 3 4
A BMNC
x y z V
V V V
++
++
= = =
. Chọn đáp án D.
Công thức 5: Mặt phẳng cắt các cạnh của khối hộp
.ABCD ABC D
lần lượt tại
, , ,M N P Q
sao cho
,,,
AM BN CP DQ
x y z t
AA BB CC DD
= = = =
ta có
..
4
ABCD MNPQ ABCD A B C D
x y z t
VV
+ + +
=
và
x z y t+ = +
.
Chứng minh: Xem bài giảng:
Chuyên đề: Tỉ số thể tích
Trang 15/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Ví dụ 6: Cho hình lập phương
.ABCD ABC D
cạnh
2a
, gọi
M
là trung điểm của
BB
và
P
thuộc cạnh
DD
sao cho
1
4
DP DD
=
. Mặt phẳng
( )
AMP
cắt
CC
tại
N
. Thể tích khối đa diện
AMNPQBCD
bằng.
A.
3
2a
. B.
3
3a
. C.
3
11
3
a
. D.
3
9
4
a
.
Lời giải
Chn B
Thể tích khối lập phương
3
0
8Va=
. Có
11
0, , ,
24
AA BM CN DP
x y z t
AA BB CC DD
= = = = = = =
và
1 1 3
0
2 4 4
x z y t z z+ = + + = + =
.
Khi đó
33
0
1 3 1
0
244
.8 3
44
AMNPBCD
x y z t
V V a a
+++
+ + +
= = =
. Chọn đáp án B.
Ví dụ 7: Người ta cần cắt một khối hộp lập phương thành hai khối đa diện bởi mặt phẳng đi qua
A
( như hình
vẽ ) sao cho phần thể tích của khối đa diện chứa đỉnh
B
bằng một nửa thể tích của khối đa diện còn
lại. Tính tỉ số
CN
k
CC
=
.
Chuyên đề: Tỉ số thể tích
Trang 16/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
A.
1
3
k =
. B.
2
3
k =
. C.
3
4
k =
.
D.
1
2
k =
.
Lời giải
Chn B
Gọi
V
là thể tích khối đa diện chứa đỉnh
B
và
V
là thể tích khối lập phương.
Theo giả thiết, ta có
1
3
VV
=
và
0 1 2
2 2 3 3
AA CN
k
AA CC
V V V V k
+
+

= = = =
.
Công thức 6: Mặt phẳng cắt các cạnh cử khối chóp tứ giác
.S ABCD
có đáy là hình bình hành lần lượt
tại
, , ,M N P Q
sao cho
; ; ;
SM SN SP SQ
x y z t
SA SB SC SD
= = = =
. Ta có
..
1 1 1 1
4
S MNPQ S ABCD
xyzt
VV
x y z t

= + + +


và
1 1 1 1
x z y t
+ = +
.
Chuyên đề: Tỉ số thể tích
Trang 17/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Công thức 7: Hai khối đa diện đồng dạng với tỷ số
k
có
3
1
2
V
k
V
=
.
Ví dụ 8: Cho khối tứ diện
ABCD
có thể tích
V
. Gọi
V
là thể tích của khối tứ diện có bốn đỉnh là trọng tâm
các mặt bên của khối tứ diện
ABCD
. Tính tỷ số
V
V
A.
8
27
V
V
=
. B.
1
27
V
V
=
. C.
4
27
V
V
=
.
D.
4
9
V
V
=
.
Lời giải
Chn B
Gọi
, , ,A B C D
lần lượt là trọng tâm các mặt
( ) ( ) ( ) ( )
, , ,BCD ACD ABD ABC
; Ta có
1
3
A B A C A D
AB AC AD
= = =
. Khối tứ diện
A B C D
đồng dạng với khối tứ diện
ABCD
theo tỷ số
1
3
k =
.
Do đó
3
3
11
3 27
V
k
V

= = =


.
Công thức 8: So sánh bằng công thức thể tích khối chóp
Ví dụ 9: Cho khối tứ diện đều
ABCD
có thể tích
V
. Gọi
,,M N P
lần lượt là trọng tâm các tam giác
,,ABC ACD ADB
và
V
là thể tích khối tứ diện
AMNP
. Tính tỉ số
V
V
.
A.
8
81
V
V
=
. B.
6
81
V
V
=
. C.
4
27
V
V
=
. D.
4
9
V
V
=
.
Lời giải
Chn B
Ta có mặt phẳng
( )
MNP
cắt các mặt của tứ diện theo các đoạn giao tuyến
,EF FH
và
HE
do vậy
thiết diện là tam giác
EFH
. Ta dễ có
( ) ( )
//MNP BCD
và
( )
( )
( )
( )
2
;;
3
d A MNP d A BCD=
Chuyên đề: Tỉ số thể tích
Trang 18/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Ta cũng có
2
1 1 2 1
.
4 4 3 9
MNP EFH BCD BCD
S S S S

= = =


Do đó
( )
( )
( )
( )
1 2 6
; . ; .
3 81 81
AMNP MNP BCD ABCD
V d A MNP S d A BCD S V= = =
.
Ví dụ 10: Cho khối tứ diện đều
ABCD
có độ dài cạnh bằng
a
. Gọi
,,M N P
lần lượt là trọng tâm các tam giác
,,ABC ACD ADB
. Tính thể tích
V
khối tứ diện
AMNP
.
A.
3
2
72
a
V =
. B.
3
22
81
a
V =
. C.
3
2
144
a
V =
. D.
3
2
162
a
V =
.
Lời giải
Chn D
Ta có mặt phẳng
( )
MNP
cắt các mặt của tứ diện theo các đoạn giao tuyến
,EF FH
và
HE
do vậy
thiết diện là tam giác
EFH
. Ta dễ có
( ) ( )
//MNP BCD
và
( )
( )
( )
( )
2
;;
3
d A MNP d A BCD=
Ta cũng có
2
1 1 2 1
.
4 4 3 9
MNP EFH BCD BCD
S S S S

= = =


Do đó
( )
( )
( )
( )
33
1 2 6 6 2 2
; . ; . .
3 81 81 81 12 162
AMNP MNP BCD ABCD
aa
V d A MNP S d A BCD S V= = = = =
.
Ví dụ 11: Cho khối chóp tứ giác
.S ABCD
có thể tích
V
. Gọi
, , ,M N P Q
lần lượt là trọng tâm các tam giác
, , ,SAB SBC SCD SDA
. Gọi
V
là thể tích khối tứ diện
.S MNPQ
. Tính tỉ số
V
V
.
A.
8
81
V
V
=
. B.
4
9
V
V
=
. C.
8
27
V
V
=
. D.
4
27
V
V
=
.
Lời giải
Chn D
Khối chóp tứ giác
.S ABCD
có diện tích đáy là
S
, chiều cao
h
ta có
3
Sh
V =
.
Chuyên đề: Tỉ số thể tích
Trang 19/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Mặt phẳng
( )
MNPQ
cắt các cạnh
, , ,SA SB SC SD
lần lượt tại
, , ,E F G H
ta có
1
2
MNPQ EFGH
SS=
và
2
2
3
EGFGH
SS

=


và
( )
( )
( )
( )
22
,,
33
d S MNPQ d S ABCD h==
.
Do đó
( )
( )
2
1 1 1 2 2 4 4 4
; . . . .
3 3 2 3 3 3.27 27 27
MNPQ
Sh V V
V d S MNPQ S S h
V

= = = = =


.
Công thức 9: Định lí Meneleus trong không gian
. . . 1
MA ND PC QB
MB NA PD QC
=
.
B. ĐỀ THI
Câu 1. Cho khối hộp
.ABCD ABC D
có thể tích
V
. Các điểm
,,M N P
là các điểm thỏa mãn
4AB AM=
,
3AD AN=
,
2AA AP
=
. Tính thể tích của khối tứ diện
AMNP
.
A.
6
V
. B.
144
V
. C.
72
V
. D.
48
V
.
Lời giải
Chn C
Chuyên đề: Tỉ số thể tích
Trang 20/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Ta có
1 1 1 1 1 1
4 3 2 24 24 3 72
AMNP ABDA ABDA A BDA
AM AN AP V
V V V V V
AB AD AA
= = = = =
.
Câu 2. Cho tứ diện
ABCD
có các cạnh
AB
,
AC
và
AD
đôi một vuông góc. Các điểm
,,M N P
lần lượt là
trung điểm các đoạn thẳng
,,BC CD BD
. Cho biết
4 , 6 , 7AB a AC a AD a===
. Tính thể tích
V
của
khối tứ diện
AMNP
.
A.
3
7Va=
. B.
3
28Va=
. C.
3
14Va=
. D.
3
21Va=
.
Lời giải
Chn A
Ta có
( )
( )
( )
( )
.
1 1 1 1
,,
3 3 4 4
A MNP MNP BCD ABCD
V S d A MNP S d A MNP V= = =
3
11
7
46
AB AC AD a= =
.
Câu 3. Cho khối chóp
.S ABC
, các điểm
,,A B C
lần lượt thuộc các tia
,,SA SB SC
và không trùng với
S
.
Hỏi khẳng định nào dưới đây đúng?
A.
.
.
1
..
3
S A B C
S ABC
V
SA SB SC
V SA SB SC
=
. B.
.
.
..
S A B C
S ABC
V
SA SB SC
V SA SB SC
=
.
C.
.
.
..
S A B C
S ABC
V
SA SB SC
V SA SB SC
=
. D.
.
.
1
..
3
S A B C
S ABC
V
SA SB SC
V SA SB SC
=
.
Lời giải
Chuyên đề: Tỉ số thể tích
Trang 21/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Chn B
Câu hỏi lí thuyết.
Câu 4. Cho hình chóp
.S ABCD
có
, , ,M N P Q
lần lượt là trung điểm các cạnh
, , ,SA SB SC SD
. Mệnh đề nào
sau đây đúng?
A.
.
.
1
2
S MNPQ
S ABCD
V
V
=
. B.
.
.
1
4
S MNPQ
S ABCD
V
V
=
. C.
.
.
1
8
S MNPQ
S ABCD
V
V
=
. D.
.
.
1
16
S MNPQ
S ABCD
V
V
=
.
Lời giải
Chn C
C'
A'
B'
D'
A
D
C
B
S
Ta thấy hai khối đa diện
.S MNPQ
và
.S ABCD
đồng dạng theo tỉ số
1
2
nên
3
.
.
11
28
S MNPQ
S ABCD
V
V

==


.
Câu 5. Cho tứ diện
ABCD
có các góc tại đỉnh
A
vuông;
6 , 9 , 3AB a AC a AD a===
. Gọi
,,M N P
lần lượt
là trọng tâm các tam giác
,,ABC ACD ADB
. Tính thể tích
V
của khối tứ diện
AMNP
.
A.
3
8Va=
. B.
3
4Va=
. C.
3
6Va=
. D.
3
2Va=
.
Lời giải
Chn D
P
N
M
I
K
H
B
D
C
A
Gọi
,,H I K
lần lượt là trọng tâm các cạnh
,,BC CD DB
. Ta thấy khai khối đa diện
AMNP
và
AHIK
đồng dạng theo tỉ số
2
3
nên
3
28
3 27
AMNP
AHIK
V
V

==


8
27
AMNP AHIK
VV=
.
Ta có
1
4
AHIK HIK
ABCD BCD
VS
VS
==
(do hai khối chóp có chung đường cao kẻ từ
A
)
Chuyên đề: Tỉ số thể tích
Trang 22/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
12
4 27
AIHK ABCD AMNP ABCD
V V V V = =
.
Mà
3
11
. . 6 .9 .3 27
66
ABCD
V AB AC AD a a a a= = =
.
Vậy
33
2
27 2
27
AMNP
V a a==
.
Câu 6. Cho khối tứ diện
ABCD
có thể tích
V
và các điểm
,,M N P
là các điểm thỏa mãn
2AM AB=
,
3AN AC=
,
4AP AD=
. Hỏi khẳng định nào dưới đây là khẳng định đúng?
A.
24
AMNP
V
V =
. B.
8
AMNP
VV=
. C.
24
AMNP
VV=
. D.
8
AMNP
V
V =
.
Lời giải
Chn C
D
B
A
M
P
N
C
Ta có
. . 2.3.4 24
AMNP
ABCD
V
AM AN AP
V AB AC AC
= = =
24
AMNP
VV=
.
Câu 7. Cho hình chóp
.S ABC
có đáy là tam giác vuông cân tại
B
,
2AC a=
,
( )
SA ABC⊥
và
SA a=
. Điểm
I
thuộc cạnh
SB
sao cho
1
3
SI SB=
. Thể tích khối tứ diện
SAIC
bằng
A.
3
2
9
a
. B.
3
9
a
. C.
3
3
a
. D.
3
2
3
a
.
Lời giải
Chn B
Chuyên đề: Tỉ số thể tích
Trang 23/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
S
A
C
B
I
Ta có
3
1 1 1 1
. . . . .
3 3 9 2 9
SAIC SABC ABC
SI a
V V S SA AB BC
SB
= = = =
.
Câu 8. Cho tứ diện
OABC
có
OA OB OC a= = =
và đôi một vuông góc. Gọi
,N,PM
lần lượt là trung điểm
các cạnh
,,AB BC CA
. Tính thể tích
V
của khối tứ diện
OMNP
.
A.
3
4
a
V =
B.
3
24
a
V =
. C.
3
6
a
V =
. D.
3
12
a
V =
.
Lời giải
Chn B
N
M
P
A
O
C
B
Ta có:
( )
( )
1
;.
3
OMNP MNP
V d O MNP S=
( )
( )
11
;.
34
ABC
d O ABC S=
1
4
OABC
V=
11
. . . .
46
OAOB OC=
3
24
a
=
Câu 9. Cho hình chóp
.S ABC
có chiều cao bằng 9, diện tích đáy bằng 5. Gọi
M
là trung điểm cạnh
SB
và
điểm
N
trên cạnh
SC
sao
2NS NC=
. Thể tích
V
của khối chóp
.ABMNC
A.
15V =
. B.
5V =
. C.
30V =
D.
10V =
.
Lời giải
Chn D
Chuyên đề: Tỉ số thể tích
Trang 24/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
M
S
A
C
B
N
Ta có
.
.
. . . .
1 2 1
..
2 3 3
2 2 1
. .5.9 10
3 3 3
S AMN
S ABC
A BMNC S ABC S AMN S ABC
V
SM SN
V SB SC
V V V V
= = =
= − = = =
.
Câu 10. Cho khối tứ diện
ABCD
có thể tích
V
và điểm
E
trên cạnh
AB
sao cho
3AE EB=
. Tính thể tích
của khối tứ diện
EBCD
.
A.
3
V
B.
4
V
. C.
2
V
. D.
5
V
.
Lời giải
Chn B
A
C
B
D
E
Ta có
3
.
4
AECD ABCD
AE
V V V
AB
==
3
1
44
EBCD
V
VV

= − =


.
Câu 11. Cho khối lăng trụ
.ABC A B C
. Đường thẳng đi qua trọng tâm của tam giác
ABC
và song song với
BC
cắt các cạnh
AB
,
AC
lần lượt tại
D
,
E
. Mặt phẳng
( )
A DE
chia khối lăng trụ thành hai phần,
tính tỉ số thể tích (số bé chia số lớn) của chúng.
Chuyên đề: Tỉ số thể tích
Trang 25/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
A.
2
3
. B.
4
23
. C.
4
9
. D.
4
27
.
Lời giải
Chn B
Ta có
2
'.
'.
'. . ' ' '
2
.
3
1
3
A ADE
ADE
A ABC ABC
A ABC ABC A B C
V
S
AD AE
V S AB AC
VV

= = =


=
'. . ' ' '
4
27
A ADE ABC A B C
VV=
Do đó
1
2
4
4
27
4
23
1
27
V
V
==
−
.
Câu 12. Cho tứ diện
ABCD
có thể tích
V
. Xét điểm
P
thuộc cạnh
AB
, điểm
Q
thuộc cạnh
BC
và điểm
R
thuộc cạnh
BD
sao cho
2
PA
PB
=
,
3
QB
BC
=
,
4
RB
RD
=
. Tính thể tích của khối tứ diện
BPQR
.
A.
5
V
. B.
4
V
. C.
3
V
. D.
6
V
.
Lời giải
Chn A
Ta có
.
.
.
1 3 4 1
..
3 4 5 5
B PQR
B PQR
B ACD
V
BP BQ BR
VV
V BA BC BD
= = =
.
Câu 13. Cho hình chóp tứ giác
.S ABCD
có đáy
ABCD
là hình bình hành. Các điểm
A
,
C
thỏa mãn
1
3
SA SA
=
,
1
5
SC SC
=
. Mặt phẳng
( )
P
chứa đường thẳng
AC

cắt các cạnh
SB
,
SD
lần lượt tại
B
,
D
và đặt
.
.
S A B C D
S ABCD
V
k
V
=
. Giá trị nhỏ nhất của
k
là?
Chuyên đề: Tỉ số thể tích
Trang 26/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
A.
1
60
. B.
1
30
. C.
4
15
. D.
15
16
.
Lời giải
Chn A
Đặt
SB
x
SB
=
,
SD
y
SD
=
Ta có
SB SD SA SC
SB SD SA SC
+ = +
8xy + =
.
Ta có
.
.
1
15
S A B C
S ABC
V
Vx
=
. . .
11
15 30
S A B C S ABC S ABCD
V V V
xx
= =
.
Ta có
.
.
1
15
S A D C
S ADC
V
Vy
=
. . .
11
15 30
S A D C S ADC S ABCD
V V V
yy
= =
.
Ta có
.
.
1 1 1
30
S A B C D
S ABCD
V
k
V x y

= = +


Ta có
( )
11
4xy
xy

+ +


1 1 1
2xy
+
1
60
k
.
Vậy giá trị nhỏ nhất của
k
là
1
60
khi
4xy==
.
Câu 14. Cho hình chóp tứ giác
.S ABCD
có đáy
ABCD
là hình bình hành. Các điểm
A
,
C
thỏa mãn
1
3
SA SA
=
,
1
5
SC SC
=
. Mặt phẳng
( )
P
chứa đường thẳng
AC

cắt các cạnh
SB
,
SD
lần lượt tại
B
,
D
và đặt
.
.
S A B C D
S ABCD
V
k
V
=
. Giá trị lớn nhất của
k
là?
A.
4
105
. B.
1
30
. C.
4
15
. D.
4
27
.
Lời giải
Chn A
Đặt
SB
x
SB
=
,
SD
y
SD
=
Chuyên đề: Tỉ số thể tích
Trang 27/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Ta có
SB SD SA SC
SB SD SA SC
+ = +
8xy + =
8yx = −
.
Ta có
.
.
1
15
S A B C
S ABC
V
Vx
=
. . .
11
15 30
S A B C S ABC S ABCD
V V V
xx
= =
.
Ta có
.
.
1
15
S A D C
S ADC
V
Vy
=
. . .
11
15 30
S A D C S ADC S ABCD
V V V
yy
= =
.
Ta có
.
.
1 1 1
30
S A B C D
S ABCD
V
k
V x y

= = +


4
15xy
=
( )
4
15 8xx
=
−
( )
2
4
15 8xx
=
−+
.
Ta có
1 , 8xy
81x −
7x
.
Xét hàm số
( )
2
8f x x x= − +
trên đoạn
1;7
.
( )
28f x x
= − +
;
( )
0fx
=
0 1;7
4 1;7
x
x
=
=
Tính
( )
17f =
;
( )
77f =
;
( )
4 32f =
.
k
đạt giá trị lớn nhất khi
( )
fx
đạt giá trị nhỏ nhất.
( )
min 7fx=
max
44
15.7 105
k ==
.
Câu 15. Cho tứ diện đều có chiều cao
h
, ở ba góc của tứ diện người ta cắt đi các tứ diện bằng nhau có chiều
cao
x
để khối đa diện còn lại có thể tích bằng một nửa thể tích của khối đa diện đều ban đầu . Tìm
x
.
A.
3
2
h
x =
. B.
3
3
h
x =
. C.
4
4
h
x =
. D.
3
6
h
x =
.
Lời giải
Chn D
Gọi cạnh của khối tứ diện đều ban đầu là
a
.
Ta có
22
AO AB BO=−
2
2
3
3
a
a

=−



6
3
a
=
6
3
a
h=
36
2
6
hh
a = =
.
33
23
12 8
ABCD
ah
V ==
.
Thể tích của ba khối tứ diện đều có chiều cao
x
được cắt ra là
33
3 3 3
3.
88
xx
V ==
.
Ta có
33
3 3 1 3
8 2 8
xh
=
3
3
6
h
x=
3
6
h
x=
.
Chuyên đề: Tỉ số thể tích
Trang 28/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Câu 16. Cho tứ diện đều có chiều cao
h
, ở bốn góc của tứ diện người ta cắt đi các tứ diện đều bằng nhau có
chiều cao
x
để khối đa diện còn lại có thể tích bằng
3
4
thể tích của khối đa diện ban đầu. Tìm
x
.
A.
3
4
h
x =
. B.
3
16
h
x =
. C.
3
12
h
x =
. D.
3
6
h
x =
.
Lời giải
Chn C
Gọi cạnh của khối tứ diện đều ban đầu là
a
, ta có
2
2
32
33
a
h a a

= − =



3
2
ah=
.
Thể tích của khối tứ diện ban đầu là
2
3
1 3 3
. . .
3 2 4 8
h
V h h

==



.
Do đó tổng thể tích của ba khối tứ diện đều có chiều cao
x
được cắt ra là
3
3
8
x
.
Theo giả thiết ta có
33
3
31
.
8 4 8
12
x h h
x= =
.
Câu 17. Mặt phẳng đi qua trọng tâm của một tứ diện, song song với một mặt của tứ diện và chia khối tứ diện
đã cho thành hai phần. Tính tỉ số thể tích (số bé chia số lớn) của hai phần đó.
A.
2
3
. B.
5
7
. C.
27
37
. D.
3
4
.
Lời giải
Chn C
Gọi
G
là trọng tâm của tứ diện
ABCD
,
A
là trọng tâm tam giác
BCD
.
Giả sử mặt phẳng qua
G
song song với
( )
BCD
cắt các cạnh
,,AB AC AD
lần lượt tại
,,M N P
ta có
3
4
AM AN AP AG
AB AC AD AA
= = = =
.
Chuyên đề: Tỉ số thể tích
Trang 29/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Do đó
2
3
4
MNP BCD
SS

=


và
( )
( )
( )
( )
3
,,
4
d A MNP d A BCD=
.
Suy ra
2
3 3 27
4 4 64
AMNP ABCD ABCD
V V V
==
1
2
27 / 64 27
1 27 / 64 37
V
V
= =
−
.
Câu 18. Cho khối hộp
.ABCD A B CD
. Lấy điểm
E
thuộc cạnh
BB
sao cho
4
BB
BE
=
, điểm
F
thuộc cạnh
DD
sao cho
3
4
DD
DF
=
. Mặt phẳng qua ba điểm
,,A E F
chia khối hộp thành hai phần. Tính tỉ số
hai phần ấy.
A.
2
. B.
1
. C.
3
2
. D.
4
3
.
Lời giải
Chn B
Ta thấy thiết diện của
( )
AEF
và hình hộp là tứ giác
'AFC E
.
Ta có
. ' . ' ' ' '
4
ABCD AFC E ABCD A B C D
x y z t
VV
+ + +
=
trong đó
. ' . ' ' ' '
0 1 ' 3 1
0; ; 1;
' ' 4 ' ' 4 2
ABCD AFC E ABCD A B C D
BE CC DF
x y z t V V
AA BB CC DD
= = = = = = = = =
.
Vậy tỉ lệ thể tích của hai khối là 1.
Câu 19. Cho khối hộp chữ nhật
. ' ' ' 'ABCD A B C D
có
4 ; 6 ; ' 7AB a AD a AA a= = =
. Các điểm
,,M N P
thỏa
mãn
2 ; 3 ; 4 'AM AB AN AD AP AA= = =
. Tính thể tích
V
của khối tứ diện
AMNP
.
A.
3
168Va=
. B.
3
672Va=
. C.
3
336Va=
. D.
3
1008Va=
.
Lời giải
Chn D
Ta có tứ diện
AMNP
vuông tại
A
nên
3
11
. . ' .8 .18 .28 672
66
V AB AD AA a a a a= = =
.
Chuyên đề: Tỉ số thể tích
Trang 30/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Câu 20. Cho hình chóp
.S ABCD
có đáy là hình bình hành. Gọi
'C
là trung điểm của
SC
. Mặt phẳng
( )
P
chứa
'AC
cắt các cạnh
,SB SD
lần lượt tại
', 'BD
. Đặt
. ' ' '
.
S B C D
S ABCD
V
m
V
=
.Giá trị nhỏ nhất của
m
bằng
A.
2
27
. B.
4
27
. C.
1
9
. D.
2
9
.
Lời giải
Chn C
Đặt
' ' ' 1 '
1; ; ;
2
SA SB SC SD
xy
SA SB SC SD
= = = =
. Ta có
11
3
' ' '
SA SC SD SB
SA SC SD SB x y
+ = + + =
Có
. ' ' ' . ' ' '
..
1 ' ' ' 1
..
2 2 4
S B C D S B C D
S ABCD S BCD
VV
SB SC SD
m xy
V V SB SC SD
= = = =
.
1 1 2 4 1
3
99
xy m
xy
xy
= +
.
Câu 21. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành. Gọi
C
là trung điểm cạnh
SC
. Mặt phẳng
( )
P
chứa đường thẳng
AC
cắt các cạnh
SB
,
SD
lần lượt tại
B
,
D
. Đặt
.
.
S B C D
S ABCD
V
m
V
=
. Giá trị lớn
nhất của
m
bằng
A.
1
9
. B.
1
8
. C.
3
8
. D.
4
9
.
Lời giải
Chn B
Đặt
1
SA
x
SA
==
;
SB
y
SB
=
;
1
2
SC
z
SC
==
;
SD
t
SD
=
. Ta có
1 1 1 1
x z y t
+ = +
1 1 1 1
1 2 3
y t y t
+ = + + =
.
Mà
..
..
11
..
2 2 4
S B C D S B C D
S ABCD S BCD
VV
SB SC SD
m yt
V V SB SC SD
= = = =
.
11
3
31
t
y
y t t
= − =
−
,
1
1
3
t




( )
( )
( )
2
1
;1
3
11
max
4 3 1 2 8
t
m f t f t f
t



= = = =

−

.
Câu 22. Cho khối hộp
.ABCD A BC D
có thể tích
V
. Tính thể tích khối tứ diện
AB CD

.
A.
3
4
V
. B.
6
V
. C.
3
V
. D.
4
V
.
Chuyên đề: Tỉ số thể tích
Trang 31/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Lời giải
Chn C
Ta có
( )
. . . .
4.
63
AB CD A A B D C C B D B ACB D ADC
VV
V V V V V V V
= − + + + = − =
.
Câu 23. Cho khối hộp
.ABCD A BC D
có thể tích
V
. Các điểm
M
,
N
,
P
thỏa mãn
2AM AC=
,
3AN AB
=
,
4AP AD
=
. Tính thể tích của khối tứ diện
AMNP
.
A.
8V
. B.
4V
. C.
6V
. D.
18V
.
Lời giải
Chn A
Ta có
. . . 2.3.4. 8
3
AMNP ACB D
AM AN AP V
V V V
AC AB AD

= = =

.
Câu 24. Cho khối tứ diện đều
.S ABC
cạnh bằng
a
. Mặt phẳng
( )
P
đi qua
S
và trọng tâm của tam giác
ABC
cắt các cạnh
AB
,
AC
lần lượt tại
M
,
N
. Đặt
.
.
S AMN
S ABC
V
m
V
=
. Giá trị nhỏ nhất của
m
bằng
A.
2
3
. B.
2
9
. C.
4
9
. D.
1
3
.
Lời giải
Chn C
Đặt
AM
x
AB
=
,
AN
y
AC
=
,
( )
, 0;1xy
. Gọi
O
là trọng tâm ta giác
ABC
và
D
là trung điểm cạnh
AB
, giả sử
AM AD
. Ta có
.
AMN
ABC
S
AM AN
m xy
S AB AC
= = =
.
Áp dụng định lí Meneleuys cho tam giác
ACD
ta có
2
. . 1 .2. 1
a
xa
MD OC NA ya
MA OD NC xa a ya
−
= =
−
( ) ( )
2 1 1x y x y − = −
32xy x y xy = +
4
9
m xy =
.
Câu 25. Cho hình chóp
.S ABC
có
M
,
N
,
P
lần lượt là các điểm thỏa mãn
2SM SA=
,
3SP SC=
và
SN kSB=
. Biết
.
.
1
6
S MNP
S ABC
V
V
=
. Tìm
k
.
A.
1
36
k =
. B.
1k =
. C.
1
6
k =
. D.
36k =
.
Chuyên đề: Tỉ số thể tích
Trang 32/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Lời giải
Chn A
Ta có
.
.
1
. . 6
6
S MNP
S ABC
V
SM SN SP
k
V SA SB SC
= = =
1
36
k=
.
Câu 26. Cho khối tứ diện đều
ABCD
. Gọi
, , , , ,M N P Q R S
lần lượt là trung điểm của các cạnh
, , , , ,AB AC AD BC CD DB
. Biết thể tích của khối bát diện đều
MQNPSR
bằng
3
9 2 cm
. Tính độ dài
cạnh của tứ diện đều
ABCD
.
A.
2 cm
. B.
3 cm
. C.
6 cm
. D.
3
2 cm
.
Lời giải
Chn C
P
N
M
S
Q
R
B
D
C
A
Gọi
.A BCD
VV=
Ta có:
.
.
.
11
..
88
A MNP
A MNP
A BCD
V
AM AN AP
VV
V AB AC AD
= = =
Tương tự
. . .
1 1 1
;;
8 8 8
B MQS C NQR D PRS
V V V V V V= = =
. . . .
1
4.
82
MQNPSR A MNP B MQS C NQR D PRS
V
V V V V V V V V= − − − − = − =
Theo giả thiết
9 2 9 2 18 2
2
MQNPSR
V
VV= = =
.
Đặt độ dài cạnh của tứ diện là
a
, ta có:
3
2
18 2 6
12
a
Va= = =
Vậy
6 cma =
.
Chuyên đề: Tỉ số thể tích
Trang 33/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Câu 27. Cho khối tứ diện đều
ABCD
có cạnh bằng
a
. Gọi
,MN
lần lượt là các điểm trên cạnh
1
, : , 2
2
AM AN
AB AC
BM CN
==
. Mặt phẳng
( )
chứa
MN
, song song với
AD
chia khối tứ diện thành
hai khối đa diện, trong đó khối đa diện chứa đỉnh
A
có thể tích
V
. Tính
V
A.
3
42
108
a
V =
. B.
3
52
108
a
V =
. C.
3
42
81
a
V =
. D.
Lời giải
Chn A
F
E
A
C
D
B
M
N
Ta có
( ) ( )
( )
( ) ( )
2
/ / ,
3
//
N ACD
DE AN
ACD NE AD E CD
DC AC
AD


= = =


( ) ( )
( )
( ) ( )
1
/ / ,
3
//
M ABD
DF AM
ABD MF AD F BD
DB AB
AD


= = =


.
Như vậy thiết diện của tứ diện
ABCD
cắt bởi
( )
là tứ giác
MNEF
.
.
..
.
1 2 2 2
.
3 3 9 9
A MND
A MND A BCD
A BCD
V
AM AN
VV
V AB AC
= = = =
. (1)
..
..
21
14
93
;
39
ABC ABC ABC
D MNF D MNB MNB ABC AMN BCN
D MNB D ABC ABC ABC ABC
S S S
V V S S S S
DF
V DB V S S S
−−
−−
= = = = = =
. . .
1 4 4
.
3 9 27
D MNF A BCD A BCD
V V V = =
. (2)
..
..
2 1 2 1
. . ;
3 3 9 3
D EFN D CBN CBN
D CBN D CBA CBA
V V S
DE DF CN
V DC DB V S CA
= = = = = =
. . .
1 2 2
.
3 9 27
D EFN A BCD A BCD
V V V = =
. (3)
Cộng (1), (2), (3) theo vế ta được:
Chuyên đề: Tỉ số thể tích
Trang 34/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
. . . . . .
2 4 2
9 27 27
A MND D MNF D EFN A BCD A BCD A BCD
V V V V V V+ + = + +
3 3 3
.
12 12 2 2 4 2
.
27 27 12 27 108
A BCD
a a a
VV = = = =
.
Câu 28. Cho khối tứ diện đều
ABCD
có cạnh bằng
a
. Gọi
,MN
lần lượt là trung điểm các cạnh
,AB BC
và
E
là điểm thuộc tia đối của tia
DB
sao cho
BE
k
BD
=
. Tìm
k
để mặt phẳng
( )
MNE
chia khối tứ diện
thành hai khối đa diện, trong đó khối đa diện chứa đỉnh
B
có thể tích
3
11 2
294
a
V =
A.
6
5
k =
. B.
6k =
. C.
4k =
. D.
5k =
.
Lời giải
Chn C
P
Q
M
N
B
D
C
A
E
Gọi
P EN CD
Q EM AD
=
=
suy ra thiết diện của tứ diện
ABCD
cắt bởi
( )
MNE
là tứ giác
MNPQ
.
Ta có:
.
.BNM
.
E DPQ
E
V
ED EP EQ
V EB EN EM
=
(1)
Theo giả thiết:
1BE ED k
k
BD EB k
−
= =
; (1.1)
Ta thấy:
( ) ( )
//
/ / / /
MN AC
EQ EP
PQ MN AC
EMN ACD PQ
EM EN
=
=
(1.2)
Xét
EAB
có
EM
là trung tuyến
1
2 1 2 2
1
12
2 2 2 2 1
k
EB EM EM k EQ k
k
ED EQ EQ k EM k
+
−−
−
+ = = = =
−−
(1.3)
Chuyên đề: Tỉ số thể tích
Trang 35/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Thay (1.1) (1.2) (1.3) vào (1):
( )
22
2
.
2
..
1 2 2 1 2 2 8 11 4
. 1 .
2 1 2 1
21
E DPQ
E BNM E BNM
V
k k V k k k k
V k k V k k
kk
− − − − − +
= = − =
−−
−
.(2)
Lại có:
( )
( )
( )
( )
.
.
,.
..
4
D, .
BMN
E BMN
D ABC
ABC
d E BMN S
V
EB BM BN k
V DB BA BC
d ABC S
= = =
(2.1)
Từ (2) và (2.1) suy ra
( ) ( )
22
22
.
8 11 4 8 11 4
.
4
2 1 4 2 1
A BCD
V k k k k k
V
k k k
− + − +
==
−−
Như vậy
( ) ( )
3
22
2
22
3
11 2
4
8 11 4 22 8 11 4
294
40 187 108 0
27
49
2
4 2 1 4 2 1
40
12
a
k
k k k k
kk
k
a
kk
=
− + − +
= = − + =
=
−−
Vậy
4k =
.
Câu 29. Cho hình chóp
.S ABC
. Trên cạnh
SA
lấy các điểm
,MN
sao cho
SM MN NA==
. Gọi
( ), ( )

là
các mặt phẳng song song với mặt phẳng
( )
ABC
và lần lượt đi qua
,MN
. Khi đó hai mặt phẳng
( ), ( )

chia khối chóp đã cho thành 3 phần. Nếu phần trên có thể tích bằng
3
10 dm
thì thể tích của
hai phần còn lại lần lượt là
A.
3
80 dm
và
3
190 dm
. B.
3
70 dm
và
3
190 dm
.
C.
3
70 dm
và
3
200 dm
. D.
3
80 dm
và
3
180 dm
.
Lời giải
Chn B
Gọi
( ) , ( ) , ( ) , ( ) E SB F SC G SB H SC
= = = =
thì theo đề ta có:
3
.
10 dm
S MEF
V =
3
.
..
.
111
. . . . 27 270
333
dm
S MEF
S ABC S MEF
S ABC
V
SM SE SF
VV
V SA SB SC
= = = =
.
3
.
..
.
111
. . . . 8 80 .
222
dm
S MEF
S NGH S MEF
S NGH
V
SM SE SF
VV
V SN SG SH
= = = =
Do đó
3
..
70 , dm
NGHMEF S NGH S MEF
V V V= − =
3
.ABC .NGH
270 80 190 . dm
NGHABC S S
V V V= − = − =
Vậy thể tích của hai khối đa diện còn lại lần lượt là
3
70 dm
và
3
190 dm
.
Chuyên đề: Tỉ số thể tích
Trang 36/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Câu 30. Cho hình chóp
.S ABCD
có đáy là hình bình hành. Trên cạnh
SA
lấy các điểm
,MN
sao cho
SM MN NA==
. Hai mặt phẳng
( ), ( )

song song với
( )
ABCD
và lần lượt đi qua
,MN
chia khối
chóp đã cho thành ba phần. Nếu phần trên có thể tích bằng
3
10 dm
thì phần ở giữa có thể tích là
A.
3
70 dm
. B.
3
80 dm
. C.
3
180 dm
. D.
3
190 dm
.
Lời giải
Chn A
Gọi
( ) , ( ) , ( ) , ( ) , ( ) , ( ) P SD Q SC R SB E SD F SC G SB
= = = = = =
thì theo đề ta có:
3
.
10 dm
S MPQR
V =
. . .
,
S NEFG S NEF S NGF
V V V=+
.
..
.
. . 2.2.2 8
S NEF
S NEF S MPQ
S MPQ
V
SN SE SF
VV
V SM SP SQ
= = =
,
.
..
.
. . 2.2.2 8
S NGF
S NEF S MRQ
S MRQ
V
SN SG SF
VV
V SM SR SQ
= = =
( )
3
. . . . . . . .
8 8 8 8 80 . dm
S NEFG S NEF S NGF S MPQ S MRQ S MPQ S MRQ S MPQR
V V V V V V V V = + = + = + = =
Vậy thể tích của khối chóp cụt
.NEFG MPQR
là
3
..
80 10 70 dm
S NEFG S MPQR
V V V= − = − =
.
Câu 31. Cho hình chóp
.S ABCD
có đáy là hình chữ nhật,
2AB a=
,
BC a=
,
2SA SB SC SD a= = = =
. Giả
sử
E
thuộc cạnh
SC
sao cho
2SE EC=
,
F
là điểm thuộc cạnh
SD
sao cho
1
3
SF FD=
. Thể tích
khối đa diện
SABEF
bằng:
A.
3
53
36
a
. B.
3
3
18
a
. C.
3
23
9
a
. D.
3
23
27
a
.
Lời giải
Chn A.
Chuyên đề: Tỉ số thể tích
Trang 37/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Vì
2SA SB SC SD a= = = =
nên hình chiếu vuông góc hạ từ đỉnh
S
xuống đáy trùng với tâm đường
tròn ngoại tiếp đáy, tức là trùng với điểm
O AC BD=
.
Ta có:
22
2 2 2
43
2
42
a a a
SO SA AO a
+
= − = − =
3
.
13
..
33
S ABCD ABCD
a
V SO S = =
.
Ta có:
3 3 3
. . .
2 3 2 1 3 5 3
. . . . . .
3 6 3 4 6 36
S ABEF S ABE S AEF SABC SACD
SE SE SF a a a
V V V V V
SC SC SD
= + = + = + =
.
Câu 32. Cho tứ diện
ABCD
có
60BAC CAD DAB= = =
,
( )
8AB cm=
,
( )
9AC cm=
,
( )
10AD cm=
. Gọi
1 1 1 1
, , , A B C D
lần lượt là trọng tâm của các tam giác
, , , BCD ACD ABD ABC
. Tính thể tích
V
của
khối tứ diện
1 1 1 1
A B C D
:
A.
( )
3
20 2V cm=
. B.
( )
3
20 2
3
V cm=
. C.
( )
3
20 2
9
V cm=
. D.
( )
3
60 2V cm=
.
Lời giải
Chn C
Lấy các điểm
,BC

lần lượt trên các tia
,AB AC
sao cho
10AB AC AD
= = =
.
Chuyên đề: Tỉ số thể tích
Trang 38/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Khi đó:
. ' . '
18
..
25
ABCD A B C D A B C D
AB AC
V V V
AB AC
==

Trong đó
AB C D

là tứ diện đều cạnh
10a cm=
, do đó thể tích của nó là
3
3
2 250 2
12 3
a
cm=
.
Vì vậy
60 2
ABCD
V =
và hai khối tứ diện
ABCD
và
1 1 1 1
A B C D
đồng dạng theo tỉ số
1
3
.
Do đó:
( )
1 1 1 1
3
1 20 2
27 9
A B C D ABCD
V V cm==
.
Câu 33. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật. Một mặt phẳng song song với đáy cắt các
cạnh bên
, , , SA SB SC SD
lần lượt tại
, , , M N P Q
. Gọi
, , , M N P Q
lần lượt là hình chiếu của
, , , M N P Q
trên mặt phẳng đáy. Tìm tỉ số
SM
SA
để thể tích khối đa diện
.MNPQ M N P Q
đạt giá trị
lớn nhất.
A.
3
4
. B.
2
3
. C.
1
2
. D.
1
3
.
Lời giải
Chn B.
Đặt
( )
01
SM
xx
SA
=
, kí hiệu
,Vh
lần lượt là thể tích và chiều cao của khối chóp đã cho.
Theo định l Ta-let, ta có:
MN NP PQ QM SM
x
AB BC CD DA SA
= = = = =
Và
( )
( )
( )
( )
,
1
,
d M ABCD
AM
x
SA
d S ABCD
= = −
( )
( )
( )
,1d M ABCD x h = −
.
Vì vậy
( )
( )
( ) ( )
22
.
. . , . 1 . . 3 1
MNPQ M N P Q
V MN MQ d M ABCD x x h AB AD x x V
= = − = −
Theo BDT Co-si, ta có:
( ) ( )
3
2
1 1 2 2 4
1 . . 2 2
2 2 3 27
x x x
x x x x x
+ + −

− = − =


.
Do đó,
.
4
9
MNPQ M N P Q
VV
.
Chuyên đề: Tỉ số thể tích
Trang 39/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Dấu “=” xảy ra
2
22
3
x x x = − =
.
Câu 34. Cho hình chóp
.S ABC
. Một mặt phẳng song song với đáy
( )
ABC
cắt các cạnh bên
, , SA SB SC
lần
lượt tại
, , M N P
. Gọi
, , M N P
lần lượt là hình chiếu của
, , M N P
trên mặt phẳng đáy. Tìm tỉ số
SM
SA
để thể tích khối đa diện
.MNP M N P
đạt giá trị lớn nhất.
A.
3
4
. B.
2
3
. C.
1
2
. D.
1
3
.
Lời giải
Chn B.
Đặt
( )
01
SM
xx
SA
=
, kí hiệu
,Vh
lần lượt là thể tích và chiều cao của khối chóp đã cho.
Theo định l Ta-let, ta có:
MN NP PQ SM
x
AB BC CD SA
= = = =
Và
( )
( )
( )
( )
,
1
,
d M ABC
AM
x
SA
d S ABC
= = −
( )
( )
( )
,1d M ABC x h = −
.
Vì vậy
( )
( )
( ) ( )
22
.
. , . 1 . 3 1
MNP M N P MNP ABC
V S d M ABCD x x h S x x V
= = − = −
Theo BDT Co-si, ta có:
( ) ( )
3
2
1 1 2 2 4
1 . . 2 2
2 2 3 27
x x x
x x x x x
+ + −

− = − =


.
Do đó,
.
4
9
MNP M N P
VV
.
Dấu “=” xảy ra
2
22
3
x x x = − =
.
Câu 35. Cho hình chóp
.S ABC
. Một mặt phẳng
( )
P
song song với đáy
( )
ABC
cắt các cạnh bên
, , SA SB SC
lần lượt tại
, , M N P
. Tìm tỉ số
SM
SA
để
( )
P
chia khối chóp đã cho thành hai khối đa diện có thể tích
bằng nhau.
Chuyên đề: Tỉ số thể tích
Trang 40/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
A.
3
1
2
. B.
3
1
4
. C.
1
2
. D.
1
4
.
Lời giải
Chn A.
Đặt
( )
01
SM
xx
SA
=
Theo định l Ta-let, ta có:
SM SN SP
x
SA SB SC
= = =
Và
3
. . .
. . .
S MNP S ABC S ABC
SM SN SP
V V x V
SA SB SC
==
Theo giả thiết,
..
1
2
S MNP S ABC
VV=
nên
3
3
11
2
2
xx= =
Câu 36. Cho hình chóp
.S ABC
có tất cả các cạnh đều bằng
a
, một mặt phẳng
( )
P
song song với mặt đáy
( )
ABC
cắt các cạnh bên
,,SA SB SC
lần lượt tại
,,M N P
. Tính diện tích tam giác
MNP
biết mặt
phẳng
( )
P
chia khối chóp đã cho thành hai khối đa diện có diện tích bằng nhau.
A.
2
3
8
MNP
a
S =
. B.
2
3
16
MNP
a
S =
. C.
2
3
3
42
MNP
a
S =
. D.
2
4
3
44
MNP
a
S =
.
Lời giải
C
B
A
P
N
M
S
Chn D
Chuyên đề: Tỉ số thể tích
Trang 41/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Mặt phẳng
( )
P
song song với
( )
ABC
và cắt các cạnh bên
,,SA SB SC
lần lượt tại
,,M N P
.
Theo Ta-let ta có:
0
SM SN SP
x
SA SB SC
= = =
.
Do đó
3
.
. . 0
S MNP
SABC
V
SM SN SP
x
V SA SB SC
= =
.
Theo giả thiết:
3
.
3 3 3
1 1 1 1
22
2 2 2
S MNP
SABC
V
MN SM a
x x MN
V AB SA
= = = = = =
.
Vì tam giác
ABC
đều cạnh
a
nên tam giác
MNP
là tam giác đều có cạnh bằng
3
2
a
.
Vậy
2
2
3
4
3
3
2
4
44
MNP
a
a
S



==
.
Câu 37. Một viên đá có dạng khối chóp tứ giác đều có tất cả các cạnh bằng
a
. Người ta cưa viên đá theo mặt
phẳng song song với mặt đáy của khối chóp để chia viên đá thành hai phần có thể tích bằng nhau. Tính
diện tích thiết diện viên đá bị cưa bởi mặt phẳng nói trên.
A.
2
3
4
a
. B.
2
3
2
a
. C.
2
2
a
. D.
2
3
22
a
.
Lời giải
O
D
C
B
A
S
Q
P
N
M
Chn D
Giả sử cắt viên đá khối chóp tứ giác đều
.S ABCD
theo mặt phẳng
( )
MNPQ
song song với
( )
ABCD
như hình vẽ.
Theo Ta-let ta có:
0
SM SN SP SQ
x
SA SB SC SD
= = = =
.
Theo giả thiết ta có:
. . . .
.
. . . .
1 1 1 1
.
2 2 2 2 2
S MNPQ S MNP S MPQ S MPQ
S MNP
S ABCD S ABC S ABC S ACD
V V V V
V
SM SP SN SQ
V V V V SA SC SB SD
+

= = + = + =


.
3
3 3 3
1 1 1
2
2
4 4 4
MN SM a
x x MN
AB SA
= = = = =
.
Vì
ABCD
là hình vuông nên
MNPQ
là hình vuông cạnh
3
4
a
. Vậy
2
2
33
4 2 2
MNPQ
aa
S

==


.
Chuyên đề: Tỉ số thể tích
Trang 42/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Câu 38. Cho tứ diện
ABCD
có thể tích bằng
12
và
G
là trọng tâm tam giác
BCD
. Tính thể tích của khối
chóp
.AGBC
.
A.
3V =
. B.
4V =
. C.
6V =
. D.
5V =
.
Lời giải
Chn B
G
A
B
C
D
Ta có
.
.
1
3
A GBC GBC
A BCD BCD
VS
VS
==
..
1
4
3
A GBC A BCD
VV = =
.
Câu 39. Cho hình lăng trụ tam giác
.ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
, cạnh
2AC a=
.
Biết
AC
tạo với mặt phẳng
( )
ABC
góc
60
và
4AC
=
. Tính thể tích
V
của khối đa diện
ABCB C

.
A.
8
3
V =
. B.
16
3
V =
. C.
83
3
V =
. D.
16 3
3
V =
.
Lời giải
Chn B
H
A
A'
C
C'
B
B'
Ta có
( )
2
2
11
2 2 4
22
ABC
S AC= = =
và
( )
( )
, .sin60 2 3d C ABC C H AC
= = =
.
Chuyên đề: Tỉ số thể tích
Trang 43/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Khi đó,
..ABCB C ABC A B C A A B C
V V V
=−
..
1
3
ABC A B C ABC A B C
VV
=−
.
2
3
ABC A B C
V
=
2 16 3
.4.2 3
33
==
.
Câu 40. Cho tứ diện
ABCD
có thể tích bằng
54
, gọi
,,M N P
lần lượt là trọng tâm các tam giác
ABC
,
ACD
,
ADB
. Tính thể tích của khối tứ diện
AMNP
.
A.
27
2
V =
. B.
4V =
. C.
9V =
. D.
16V =
.
Lời giải
Chn B
N
P
M
F
D
E
A
B
C
D
Gọi
,,D E F
lần lượt là trung điểm các cạnh
,,BC CD DB
.
Ta có
33
2 2 1 2 2
. .54 4
3 3 4 27 27
AMNP ADEF ABCD ABCD
V V V V
= = = = =
.
Câu 41. Cho hình hộp
.ABCD A BC D
có đáy
ABCD
là hình thoi cạnh bằng
6
và góc nhọn bằng
45
, cạnh
bên của hình hộp bằng
10
và tạo với mặt phẳng đáy một góc
45
. Tính thể tích khối đa diện
ABCDDB

.
A.
180V =
. B.
60V =
. C.
90V =
. D.
120V =
.
Lời giải
Chn D
Gọi
AH
là đường cao của hình hộp
Chuyên đề: Tỉ số thể tích
Trang 44/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Khi đó
( )
( )
; 45AA ABCD A AH

= =
.sin45 5 2A H AA

= =
.
2
6 .sin45 18 2
ABCD
S = =
Nên
.
. 180
ABCD A B C D ABCD
V S A H
==
.
..ABCDD B A BDD B C BDD B
V V V
=+
. . .
2 2 2
. 120
3 3 3
ABD A B D BCD B C D ABCD A B C D
V V V
= + = =
.
Câu 42. Cho khối lăng trụ tam giác
.ABC A B C
, gọi
M
,
N
lần lượt thuộc các cạnh bên
AA
,
CC
sao cho
MA MA
=
,
4NC NC
=
. Gọi
G
là trọng tâm tam giác
ABC
. Hỏi trong bốn khối tứ diện
GA B C
,
BB MN
,
ABB C

và
A BCN
, khối tứ diện nào có thể tích nhỏ nhất?
A. Khối
A BCN
. B. Khối
GAB C
. C. Khối
ABB C

. D. Khối
BB MN
.
Lời giải
Chn A
Đặt
.ABC A B C
VV
=
.
Ta có
( )
G ABC
nên
.
1
3
G A B C
VV
=
.
. . .
1 1 2 1
..
2 2 3 3
BB MN M BB N A BB N A BB C C
V V V V V V
= = = = =
.
.
1 1 2 1
.
2 2 3 3
ABB C A BB C C
V V V V
= = =
.
Ta có
4
5
CBN
CBC
S
CN
S CC
==
nên
4 4 1 4 1 2 4
. . .
5 5 2 5 2 3 15
A BCN A BCC A BCC B
V V V V V
= = = =
Vậy khối tứ diện
A BCN
có thể tích nhỏ nhất.
Câu 43. Cho khối lăng trụ tam giác
.ABC A B C
có thể tích bằng
60
. Gọi
M
,
N
,
P
lần lượt thuộc các cạnh
bên
AA
,
BB
,
CC
sao cho
2MA MA
=
,
3NB NB
=
,
4PC PC
=
. Tính thể tích khối đa diện
BCMNP
.
A.
40
. B.
30
. C.
31
. D.
85
3
.
Lời giải
Chn C
Chuyên đề: Tỉ số thể tích
Trang 45/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Gọi
d
là khoảng cách giữa
BB
và
CC
.
Ta có
( )
1
.
2
BCPN
S CP BN d=+
1 3 4 1 31 31
. . . . .
2 4 5 2 20 40
BCC B
BB CC d BB d S


= + = =


.
Do đó
. . .
31 31 2 31 2
. . . .60 31
40 40 3 40 3
BCMNP M BCPN M BCC B ABC A B C
V V V V
= = = = =
.
Câu 44. Cho khối tứ diện đều
ABCD
có cạnh bằng
a
. Gọi
M
,
N
lần lượt là trung điểm của các cạnh
AB
,
BC
và
E
đối xứng với điểm
B
qua
D
. Mặt phẳng
( )
MNE
chia khối tứ diện
ABCD
thành hai khối
đa diện, trong đó khối đa diện chứa đỉnh
A
có thể tích
V
. Tính
V
.
A.
3
13 2
216
a
V =
. B.
3
72
216
a
V =
. C.
3
2
18
a
V =
. D.
3
11 2
216
a
V =
.
Lời giải
Chn D
Gọi
P CD NE=
,
Q AD ME=
, khi đó
( )
MNE
chia hình chóp là hai khối đa diện gồm
ACMNPQ
và
BMNDQP
.
Dễ dàng chứng minh được
P
,
Q
lần lượt là trọng tâm tam giác
EBC
và
EAB
. Khi đó:
2
3
EQ EP
EM EN
==
.
Ta có
. . . .
1 2 2 2
. . . . .
2 3 3 9
E DQP E BMN E BMN E BMN
ED EQ EP
V V V V
EB EM EN
= = =
. . .
7
9
BMNDQP E BMN E DQP E BMN
V V V V = − =
.
Lại có
1
4
BMN ABC
SS

=
,
( )
( )
( )
( )
;
2
;
d E ABC
EB
DB
d D ABC
==
Chuyên đề: Tỉ số thể tích
Trang 46/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Nên
( )
( )
( )
( )
.
.
;.
11
2.
42
;.
BMN
E BMN
D ABC
ABC
d E ABC S
V
V
d D ABC S
= = =
Suy ra
..
7 1 7
. . .
9 2 18
BMNDQP D ABC D ABC
V V V==
33
..
11 11 2 11 2
..
18 18 12 216
ACMNPQ D ABC DMBDQP D ABC
aa
V V V V V = = − = = =
.
Câu 45. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành và có thể tích bằng
48
. Kí hiệu
M
,
N
lần
lượt là các điểm thuộc cạnh
AB
,
CD
sao cho
MA MB=
,
2ND NC=
. Tính thể tích
V
của khối chóp
.S MBCN
.
A.
40V =
. B.
8V =
. C.
20V =
. D.
28V =
.
Lời giải
Chn C
Gọi
d
là khoảng cách giữa
AB
và
CD
.
Ta có
( )
1 1 1 1 1 5 5
. . . . . . .
2 2 2 3 2 6 12
MBCN ABCD
S BM CN d AB CD d AB d S

= + = + = =


.
Nên
..
55
.48 20
12 12
S MBCN S ABCD
VV= = =
.
Câu 46. Cho khối hộp
.ABCD AB C D
tâm
I
, các điểm
M
,
N
,
P
,
Q
lần lượt là trug điểm của các cạnh
AB
,
BC
,
CD
,
DA
. Tính thể tích của phầ khối hộp nằm ngoài khối nón
.I MNPQ
.
A.
11
12
V
. B.
5
6
V
. C.
3
4
V
. D.
7
8
V
.
Lời giải
Chn A
Ta có
1 1 4 1
1
4 8 8 2
AMQ ABD ABCD MNPQ ABCD ABCD
S S S S S S

= = = − =


và
h
là chiều cao của hình chóp đã
cho.
Vì vậy
( )
( )
.
1 1 1
. , . .
3 3 2 2 12
I MNPQ MNPQ ABCD
hV
V S d I ABCD S= = =
.
Vậy Thể tích cần tính là
11
12
V
.
Câu 47. Cho khối chóp
.S ABCD
có thể tích
V
và đáy
ABCD
là hình bình hành. Kí hiệu
S
là điểm thỏa mãn
2SS DC
=
. Tính thể tích phần chung của hai khối chóp
.S ABCD
và
.S ABCD
.
A.
5
9
V
. B.
4
9
V
. C.
3
V
. D.
2
V
.
Chuyên đề: Tỉ số thể tích
Trang 47/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Lời giải
Chn B
Ta có
/ / / /CD AB SS
do đó
S D SC C

=
,
S A SB B

=
.
Vì
//BC BC

và
12
23
B B AB SB
B S SS SB

= = =

.
Phần chung của hai khối chóp là
.ABCD B C

.
Ta có
( )
. . . .ABCD B C S ADC B A ABC A ADC
V V V V V V
= − = − +
và theo công thức tỷ số thể tích ta có
2
..
2 4 1 2
.
3 9 2 9
S AB C S ABC
V V V V


= = =


và
..
2 2 1 1
.
3 3 2 3
S ADC S ADC
V V V V
= = =
.
Vậy
.
2 1 5 4
9 3 9 9
S ADC B ABCDC B
V V V V V V
= + = =
.
Câu 48. Cho hình lăng trụ
.ABC A B C
có thể tích
V
. Các điểm
M
,
N
,
P
trên các cạnh
AA
,
BB
,
CC
sao
cho
1
2
AM
AA
=
,
1
3
BN
BB
=
,
2
3
CP
CC
=
. Tính thể tích của khối đa diện
.ABC MNP
.
A.
1
2
V
. B.
7
16
V
. C.
7
18
V
. D.
11
18
V
.
Lời giải
Chn A
Ta có
. . .ABC NMP M ABC M BCPN
V V V=+
Trong đó
( )
( )
.
11
,.
36
M ABC ABC
V d M ABC S V==
Chuyên đề: Tỉ số thể tích
Trang 48/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
. . .
BCPN
M BCPN M BCC B A BCC B
BCC B
S
BP CN
V V V
S BB CC

+
==

+
21
21
33
.
1 1 3 3
VV
+
==
+
.
Vậy
.
1 1 1
6 3 2
ABC MNP
V V V

= + =


.
Câu 49. Cho hình lăng trụ
.ABC A B C
có thể tích
V
. Các điểm
M
,
N
,
P
trên các cạnh
AA
,
BB
,
CC
sao
cho
1
2
AM
AA
=
,
2
3
BN CP
BB CC
==

. Tính thể tích của khối đa diện
.ABC MNP
.
A.
2
3
V
. B.
9
16
V
. C.
20
27
V
. D.
11
18
V
.
Lời giải
Chn D
Ta có
. . .ABC NMP M ABC M BCPN
V V V=+
Trong đó
( )
( )
.
11
,.
36
M ABC ABC
V d M ABC S V==
. . .
BCPN
M BCPN M BCC B A BCC B
BCC B
S
BP CN
V V V
S BB CC

+
==

+
2 2 4
.
3 3 9
VV==
.
Vậy
.
1 4 11
6 9 18
ABC MNP
V V V

= + =


.
Câu 50. Cho hình lăng trụ
.ABC A B C
có thể tích
V
. Các điểm
M
,
N
,
P
trên các cạnh
AA
,
BB
,
CC
sao
cho
AM
x
AA
=
,
BN
y
BB
=
,
CP
z
CC
=
. Biết thể tích của khối đa diện
.ABC MNP
bằng
1
2
V
. Mệnh đề nào
sau đây đúng?
A.
1x y z+ + =
. B.
2x y z+ + =
. C.
3
2
x y z+ + =
. D.
2
3
x y z+ + =
.
Lời giải
Chn C
Chuyên đề: Tỉ số thể tích
Trang 49/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Ta có
. . .ABC NMP M ABC M BCPN
V V V=+
Trong đó
( )
( )
.
1
,.
33
M ABC ABC
x
V d M ABC S V==
. . .
BCPN
M BCPN M BCC B A BCC B
BCC B
S
BP CN
V V V
S BB CC

+
==

+
2
.
1 1 3 3
y z y z
VV
++
==
+
.
Khi đó
.
3
ABC MNP
x y z
VV
++
=
.
Vậy
.
1 1 3
2 3 2 2
ABC MNP
x y z
V V V V x y z
++
= = + + =
.
Câu 51. Cho khối tứ diện
OABC
có
,,OA OB OC
đôi một vuông góc và
1, 2, 3OA OB OC= = =
. Gọi
,,D E F
lần lươt là chân đường cao hạ từ đỉnh
O
xuống các cạnh
,,BC CA AB
. Thể tích khối tứ diện
ODEF
bằng
A.
36
325
. B.
276
325
. C.
289
325
. D.
49
325
.
Lời giải
Chn A
C
O
B
A
D
E
F
*Ta có
2
2
91
10 10
CE CO AE
CA CA AC
= = =
,
2
2
94
13 13
CD CO BD
CB CB BC
= = =
,
2
2
14
55
AF AO BF
AB AB BA
= = =
.
* Ta có thể tích khối tứ diện
0
1
: . . 1
6
OABC V OAOB OC==
.
*
. 0 0
1
..
50
A OEF
AO AE AF
V V V
AO AC AB
==
,
C. 0 0
81
..
130
OED
CO CE CD
V V V
CO CA CB
==
,
. 0 0
16
..
65
B ODF
BO BD BF
V V V
BO BC BA
==
.
Vậy
00
1 81 16 36 36
1
50 130 65 325 325
ODEF
V V V

= − − − = =


.
Chuyên đề: Tỉ số thể tích
Trang 50/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Câu 52. Cho tứ diện đều
ABCD
có cạnh bằng
1
. Gọi
,MN
lần lượt là trung điểm các cạnh
,AB BC
. Điểm
P
trên cạnh
CD
sao cho
2PD CP=
. Mặt phẳng
( )
MNP
cắt
AD
tại
Q
. Tính thể tích khối đa diện
BMNPQD
.
A.
2
16
. B.
23 2
432
. C.
2
48
. D.
13 2
432
.
Lời giải
Chn B
M
N
A
C
B
D
P
Q
*Có
( ) ( )
// // //MN AC MNP ACD PQ MN AC =
. Ta chia khối đa diện thánh các khối tứ diện
. . .BMNPQD D PQB B MNQ B PQN
V V V V= + +
.
*Thể tích khối tứ diện đều đã cho là
0
2
12
V =
.
*Ta có
2
. 0 0 0
24
..
39
D PQB
DP DQ DB
V V V V
DC DA DB

= = =


.
Và
. . . 0 0 0
1 1 1 1
. . . .
4 4 4 12
ACQ
B MNQ B ACQ B ACQ
ACD
S
BM BN BQ AQ
V V V V V V
BA BC BQ S AD
= = = = =
.
Và
. . . 0 0 0
1 1 1 2 1
. . . .
2 2 2 9 9
PQC
B PQN B PQC B PQC
ADC
S
BP BQ BN
V V V V V V
BP BQ BC S
= = = = =
.
Vậy
0
4 1 1 23 2 23 2
.
9 12 9 36 12 432
BMNPQD
VV

= + + = =


.
Câu 53. Cho tứ diện đều
ABCD
có cạnh bằng
10cm
. Trên các cạnh
,AB AC
lần lượt lấy các điểm
,MN
sao
cho
8cm, 9cmAM AN==
. Thể tích khối tứ diện
AMND
bằng
A.
3
250 2
cm
3
V =
. B.
3
60 2 cmV =
. C.
3
180 2 cmV =
. D.
3
250 2 cmV =
.
Lời giải
Chn B
Chuyên đề: Tỉ số thể tích
Trang 51/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
D
B
C
A
M
N
Ta có
3
3
8 9 10 2
. . . . 60 2 cm
10 10 12
AMND ABCD
AM AN
VV
AB AC
= = =
.
Câu 54. Cho hình lập phương
.ABCD A BC D
cạnh
2a
, gọi
M
là trung điểm của
BB
và
P
thuộc cạnh
DD
sao cho
1
4
DP DD
=
. Mặt phẳng
( )
AMP
cắt tích khối đa diện
AMNPBCD
bằng
A.
3
2Va=
. B.
3
3Va=
. C.
3
11
3
Va=
. D.
3
9
4
Va=
.
Lời giải
Chn B
*Thể tích khói lập phương
3
0
8Va=
. Ta có
11
0; ; ;
24
AA BM CN DP
x y z t
AA BB CC DD
= = = = = = =
.
*Ta có
x z y t+ = +
và
( ) ( )
3
0
0
1 1 3 3
3
4 2 8 8
AMNPBCD
AMNPBCD
V
x y z t y t V V a
V
= + + + = + = = =
.
Câu 55. Cho tứ diện
ABCD
đều cạnh bằng
1
. Gọi
,MN
lần lượt là trung điểm các cạnh
,AB BC
. Điểm
P
trên cạnh
CD
sao cho
2PC PD=
. Mặt phẳng
( )
MNP
cắt
AD
tại
Q
. Thể tích khối đa diện
BMNPQD
bằng
A.
11 2
216
. B.
2
27
. C.
52
108
. D.
72
216
.
Lời giải
Chn D
Chuyên đề: Tỉ số thể tích
Trang 52/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
M
N
A
C
B
D
P
Q
*Có
( ) ( )
// //MN AC MNP ACD PQ MN =
. Ta chia khối đa diện thánh các khối tứ diện
. . .BMNPQD D PQB B MNQ B PQN
V V V V= + +
.
*Thể tích khối tứ diện đều đã cho là
0
2
12
V =
.
Ta có
2
. 0 0 0
11
..
39
D PQB
DP DQ DB
V V V V
DC DA DB

= = =


.
Và
. . . 0 0 0
1 1 1 1
. . . .
4 4 4 6
ACQ
B MNQ B ACQ B ACQ
ACD
S
BM BN BQ AQ
V V V V V V
BA BC BQ S AD
= = = = =
.
Và
. . . 0 0 0
1 1 1 2 1
. . . .
2 2 2 9 9
PQC
B PQN B PQC B PQC
ADC
S
BP BQ BN
V V V V V V
BP BQ BC S
= = = = =
.
Vậy
0
1 1 1 7 2 7 2
.
9 6 9 18 12 216
BMNPQD
VV

= + + = =


.
Câu 56. Cho khối chóp
.S ABC
có
, 60 , 90 , 120SA SB SC a ASB BSC CSA= = = = = =
. Gọi
,MN
lần là các
điểm trên cạnh
AB
và
SC
sao cho
CN AM
SC AB
=
. Khi khoảng cách giữa
M
và
N
nhỏ nhất, tính thể tích
V
của khối chóp
.S AMN
.
A.
3
2
72
a
V =
. B.
3
52
72
a
V =
. C.
3
52
432
a
V =
. D.
3
2
432
a
V =
.
Lời giải
Chn C
Ta có thể tích của khối chóp
.S ABC
là
22
33
0
1 1 2
1
6 2 2 12
aa
V
= − − − =
.
Chuyên đề: Tỉ số thể tích
Trang 53/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Đặt
( )
0 1
CN AM
mm
SC AB
= =
, ta có
22
, , , , , 0,
22
aa
SA a SB b SC c a b c a a b b c c a= = = = = = = = = −
.
Theo đẳng thức trên ta có sự biểu diễn vectơ
( )
( )
1 , SN m c SM SA AM a mAB a m b a= − = + = + = + −
.
(1 ) [ ( )] ( 1) (1 )MN SN SM m c a m b a m a mb m c = − = − − + − = − − + −
.
Do đó
( )
( )
2
2
2 2 2
11
3 5 3
1
( 1) (1 )
2
m a mb m c
a
MN m m a−−= = + +− −
.
Dấu bằng đạt tại
( )
33
00
5 5 1 2 5 2
. 1 . .
6 6 6 12 432
SAMC
SN SN AM a a
m V V V m m V
SC SC AB
= = = = − = =
.
Câu 57. Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,3a SA a=
vuông góc với đáy. Mặt phẳng qua
A
vuông góc với
SC
cắt các cạnh
,,SB SC SD
lần lượt tại
,,M N P
. Thể tích khối đa diện
SAMNP
bằng
A.
3
33
20
a
. B.
3
3
24
a
. C.
3
3
10
a
. D.
3
53
24
a
.
Lời giải
Chn A
Có
, , SB AM SC AN SD AP⊥ ⊥ ⊥
và
2 2 2
2 2 2
3 3 3
1, , ,
4 5 4
SA SM SA SN SA SP SA
x y z t
SA SB SB SC SC SD SD
= = = = = = = = = = =
.
Vậy
3
..
1 1 1 1 3 3
4 20
S AMNP S ABCD
xyzt a
VV
x y z t

= + + + =


.
Câu 58. Cho khối lăng trụ
.ABC A B C
có thể tích bằng
1
. Gọi
,MN
lần lượt là trung điểm các đoạn
thẳng
AA
và
BB
. Đường thẳng
CM
cắt đường thẳng
CA
tại
P
, đường thẳng
CN
cắt đường
thẳng
CB
tại
Q
. Thể tích của khối đa diện lồi
A MPB NQ
bằng
A.
1
. B.
1
3
. C.
1
2
. D.
2
3
.
Lời giải
Chn D
Chuyên đề: Tỉ số thể tích
Trang 54/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Ta có
A
là trung điểm của
PC
;
B
là trung điểm của
QC
. Do đó
. . . .
14
4 4.
33
C PQ
C C PQ C A B C C A B C ABC A B C
C A B
S
V V V V
S
= = = =
.
Mặt khác
. . .
11
1
2
22
3 3 3
A B C MNC ABC A B C ABC A B C
A M B N C C
A A BB C C
V V V
++
++
= = =
.
Do đó
..
4 2 2
3 3 3
A MPB NQ C C PQ A B C MNC
V V V
= − = − =
.
Câu 59. Cho khối chóp tứ giác đều
.S ABCD
có tất cả các cạnh bằng
a
. Gọi
M
là điểm đối xứng của
C
qua
D
,
N
là trung điểm của cạnh
SC
. Mặt phẳng
( )
BMN
chia khối chóp
.S ABCD
thành hai khối đa
diện. Tính thể tích
V
của khối đa diện chứa đỉnh
S
.
A.
3
15 2
144
a
V =
. B.
3
72
72
a
V =
. C.
3
11 2
144
a
V =
. D.
3
72
144
a
V =
.
Lời giải
Chn B
Chuyên đề: Tỉ số thể tích
Trang 55/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Gọi
O AC BD=
( )
SO ABCD⊥
;
P MB AD=
và
Q SD MN=
suy ra
Q
là trọng tâm của
tam giác
SMC
1
3
QD
SD
=
( )
( )
( )
( )
,
1
3
,
d Q ABCD
d S ABCD
=
.
Mặt phẳng
( )
BMN
chia khối chóp
.S ABCD
thành hai khối đa diện, trong đó khối đa diện chứa đỉnh
S
là
SABPQN
.
Ta có
( )
( )
22
2
,
2
a
d S ABCD SO SA AO= = − =
.
( )
( )
3
2
.
1 1 2
, . .
3 3 6
S ABCD ABCD
a
V d S ABCD S SO AB = = =
.
Có
( )
( )
( )
( )
3
.
1 1 1 . 2
, . . , .
3 3 2 2 12
N BCM BCM
MD BC a
V d N ABCD S d S ABCD= = =
.
Lạ có
( )
( )
( )
( )
3
.
1 1 1 . 2
, . . , .
3 3 3 2 72
Q DMP DMP
MD PA a
V d Q DMP S d S ABCD= = =
.
Mà
. . .SABPQN S ABCD Q DMP N BCM
V V V V= + −
3 3 3 3
2 2 2 7 2
6 72 12 72
SABPQN
a a a a
V = + − =
.
Câu 60. Cho khối chóp tam giác
.S ABC
có thể tích
V
. Gọi
M
,
N
,
P
,
H
lần lượt là trung điểm các cạnh
AB
,
BC
,
CA
,
SA
. Tính thể tích khối chóp
.H MNP
.
A.
1
12
V
. B.
1
24
V
. C.
1
8
V
. D.
3
8
V
.
Lời giải
Chn C
Ta có
( )
( )
.
1
,.
3
S ABC ABC
V V d S ABC S==
.
Lại có
( )
( )
( )
( )
( )
( )
.
1 1 1 1 1 1 1
, . . , . ,
3 3 2 4 8 3 8
H MNP MNP ABC ABC
V d H MNP S d S ABC S d S ABC S V

= = = =


.
Chuyên đề: Tỉ số thể tích
Trang 56/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
TỶ SỐ THỂ TÍCH KHỐI ĐA DIỆN
(ĐỀ SỐ 02)
Câu 1. Cho hình chóp
.S ABC
có
2SC a=
và
( )
SC ABC⊥
. Đáy
ABC
là tam giác vuông cân tại
B
và
2AB a=
. Mặt phẳng
( )
đi qua
C
và vuông góc với
SA
,
( )
cắt
,SA SB
lần lượt tại
,DE
. Tính
thể tích khối chóp
.S CDE
.
A.
3
4
9
a
. B.
3
8
27
a
. C.
3
2
9
a
. D.
3
16
27
a
.
Lời giải
Chn C
Ta có
( )
3
2
2
.
1 1 1 1 1 2
. . . . . .2 . . 2
3 3 2 3 2 3
S ABC ABC
a
V SC S SC AB a a= = = =
.
Lại có
2 2 2 2
.
2 2 2 2 2 2
.
4 4 1
. . .
3
4 2 4 4
S DEC
S ABC
V
SD SE SC SC a a
V SA SB
SA SB a a a a
= = = =
++
.
Do đó
3
..
12
39
S DEC S ABC
a
VV==
.
Câu 2. Cho hình chóp
.S ABC
có
2SC a=
và
( )
SC ABC⊥
. Đáy
ABC
là tam giác vuông cân tại
B
và
2AB a=
. Mặt phẳng
( )
đi qua
C
và vuông góc với
SA
,
( )
cắt
,SA SB
lần lượt tại
,DE
. Tính
thể tích khối đa diện
ABCDE
.
A.
3
4
9
a
. B.
3
8
27
a
. C.
3
2
9
a
. D.
3
19
27
a
.
Lời giải
Chn A
Chuyên đề: Tỉ số thể tích
Trang 57/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Ta có
( )
3
2
2
.
1 1 1 1 1 2
. . . . . .2 . . 2
3 3 2 3 2 3
S ABC ABC
a
V SC S SC AB a a= = = =
.
Lại có
2 2 2 2
.
2 2 2 2 2 2
.
4 4 1
. . .
3
4 2 4 4
S DEC
S ABC
V
SD SE SC SC a a
V SA SB
SA SB a a a a
= = = =
++
.
Do đó
3
..
12
39
S DEC S ABC
a
VV==
. Suy ra
3 3 3
..
2 2 4
3 9 9
ABCDE S ABC S DEC
a a a
V V V= − = − =
.
Câu 3. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
2a
,
2SA a=
,
( )
SA ABCD⊥
. Mặt
phẳng
( )
P
đi qua
A
vuông góc với
SC
cắt
,,SB SC SD
lần lượt tại
,,H K J
. Tính thể tích khối chóp
.S AHKJ
.
A.
3
4
27
a
. B.
3
8
27
a
. C.
3
8
9
a
. D.
3
4
9
a
.
Lời giải
Chn D
Ta có
( )
3
2
.
1 1 4
. . .2 . 2
3 3 3
S ABCD ABCD
a
V SAS a a= = =
và
,,AH SB AK SC AJ SD⊥ ⊥ ⊥
và
1
SA
x
SA
==
,
2
2
2
3
SH SA
y
SB
SB
= = =
,
2
2
1
2
SK SA
z
SC
SC
= = =
,
2
2
2
3
SJ SA
t
SD
SD
= = =
.
Do đó
.
.
1 1 1 1 1 1 2 1 2 3 3 1
. .1. . . 1 2
4 4 3 2 3 2 2 3
S AHKJ
S ABCD
V
xyzt
V x y z t


= + + + = + + + =




3
..
14
39
S AHKJ S ABCD
a
VV = =
.
Câu 4. Cho hình chóp
.S ABCD
có đáy
ABCD
là tứ giác lồi với
O
là giao điểm của
AC
và
BD
. Gọi
, , ,M N P Q
lần lượt là trọng tâm của các tam giác
, , ,SAB SBC SCD SDA
. Gọi
12
,VV
lần lượt là thể tích
của các khối chóp
.S ABCD
và
.O MNPQ
. Khi đó tỉ số
1
2
V
V
là
A.
8
. B.
27
4
. C.
27
2
. D.
9
.
Lời giải
Chn C
Chuyên đề: Tỉ số thể tích
Trang 58/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
O
N
P
Q
M
F
G
H
E
A
D
B
C
S
Gọi
, , ,E F G H
lần lượt là trung điểm của
, , ,AB BC CD DA
.
Ta có
2
24
39
MNPQ EFGH EFGH
S S S

==


(do hai tứ giác
MNPQ
và
EFGH
đồng dạng theo tỉ số
2
3
).
Mà
12
29
EFGH ABCD MNPQ ABCD
S S S S= =
.
Suy ra
( )
( )
( )
( )
1
2
,
9 27
. 3.
22
,
ABCD
MNPQ
d S ABCD
S
V
VS
d O MNPQ
= = =
.
Câu 5. Cho khối lăn trụ tam giác
.ABC A B C
có thể tích
V
. Các điểm
,MN
lần lượt thuộc các cạnh
,BB CC

sao cho
11
;
24
MB NC
BB CC
==

. Thể tích khối chóp tứ giác
.ABMNC
là
A.
3
V
. B.
3
8
V
. C.
6
V
. D.
4
V
.
Lời giải
Chn D
N
M
C'
A'
B
C
A
B'
Ta có
.
1 1 1 1 1
3 3 2 4 4
ABCMN
ABC A B C
V
AA BM CN
V AA BB CC
= + + = + =
.
Vậy
4
ABCMN
V
V =
.
Chuyên đề: Tỉ số thể tích
Trang 59/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Câu 6. Cho khối lăng trụ tam giác
. ' ' 'ABC A B C
. Mặt phẳng qua điểm
A
và điểm
P
thuộc cạnh
'BB
đồng
thời song song cạnh
BC
, chia khối lăng trụ thành hai khối đa diện có thể tích bằng nhau. Tính tỉ số
'
PB
PB
A.
3
. B.
2
. C.
6
. D.
4
Lời giải
Chn A.
Đặt
'
BP
x
BB
=
, Do
//PQ BC
nên
''
BP CQ
x
BB CC
==
Áp dụng công thức tỉ số thể tích ta có
( )
. ' ' '
1 1 2
3 ' ' 3 3
ABCQP
ABC A B C
V
BP CQ x
xx
V BB CC

= + = + =


.
Mà giả thiết cho
' ' 'ABCQP APQA B C
VV=
nên suy ra
. ' ' '
1
2
ABCQP
ABC A B C
V
V
=
1 2 3
2 3 4
x
x = =
Suy ra
33
4 3 3 ' 3 ' 3
' 4 ' 4 '
BP BP PB
BP PB PB PB PB
BB BP PB PB
= = = + = =
+
Câu 7. Cho khối hộp
. ' ' ' 'ABCD A B C D
. Mặt phẳng qua
D
, điểm
Q
thuộc cạnh
'AA
, điểm
R
thuộc cạnh
'CC
sao cho
1
'3
QA
QA
=
,
3
'
RC
RC
=
chia khối hộp thành hai phần. Tính thể tích của phần chứa mặt đáy
( )
DABC
.
A.
3
V
. B.
2
3
V
. C.
4
V
. D.
2
V
.
Lời giải
Chn D
R
Q
D'
C'
A'
C
A
D
B
B'
Chuyên đề: Tỉ số thể tích
Trang 60/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Ta có: Vì
. ' ' ' 'ABCD A B C D
là khối hộp nên chứng minh được:
( )
''ADQ C B R c g c = − −
.
Suy ra:
'DQ RB=
.
Chứng minh tương tự ta có:
( )
' ' 'A B Q CDR c g c B Q DR = − − =
.
Do đó: tứ giác
'B QDR
là hình bình hành.
Nên
/ / 'QD B R
( )
'B DQR
.
Ta có:
'
' ' ' '
AQ CR BB DD
AA CC BB DD
+ = +
hay:
1
10
4'
CR
CC
+ = +
Suy ra:
3
'4
CR
CC
=
.
Mặt phẳng
( )
DQR
chia khối hộp thành
.'ABCDQB R
và
' . ' ' 'DQB R A C D
.
Áp dụng công thức tính nhanh tỉ số thể tích ta có:
.'
. ' ' ' '
ABCD QB R
ABCD A B C D
V
V
1'
4 ' ' ' '
AQ BB CR DD
AA BB CC DD

= + + +


=
1 1 3
10
4 4 4

= + + +


1
2
=
.
Vậy:
.'
.'
. ' ' ' '
11
22
ABCD QB R
ABCD QB R
ABCD A B C D
V
VV
V
= =
.
Câu 8. Cho hình chóp
.S ABCD
có thể tích
V
với đáy
ABCD
là hình bình hành. Mặt phẳng qua
,,A M P
cắt
cạnh
SC
tại
N
với
,MP
là các điểm thuộc
SB
,
SD
sao cho
1
2
SM
SB
=
,
2
3
SP
SD
=
. Tính thể tích khối đa
diện
.ABCDMNP
.
A.
23
30
V
. B.
7
30
V
. C.
14
15
V
. D.
1
15
V
.
Lời giải
Chn A
P
I
O
N
C
S
B
D
A
Q
M
Ta có công thức cho bài toán tổng quát: cho hình chóp
.S ABCD
đáy là hình bình hành. Mặt phẳng
( )
cắt các cạnh
, , ,SA SB SC SD
lần lượt tại
, , ,M N P Q
như hình vẽ.
Đặt:
, , ,
SM SN SP SQ
x y z t
SA SB SC SD
= = = =
. Khi đó ta có:
1 1 1 1
x z y t
+ = +
.
Áp dụng vào bài toán ta có:
Chuyên đề: Tỉ số thể tích
Trang 61/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
N
I
O
M
C
A
D
B
S
P
( )
AMNP
là mặt phẳng cắt nên:
1
SA
SA
=
,
1
2
SM
SB
=
,
SN
x
SC
=
,
2
3
SP
SD
=
.
Suy ra:
1 1 1 1 1 5 2
12
1 2 5
23
x
xx
+ = + = =
.
Khi đó:
1 2 1
1. .
2 5 5
SAMN
SABC
V
V
==
;
2 2 4
1. .
5 3 15
SANP
SACD
V
V
==
.
Nên:
SAMN SANP
SABC SACD
VV
VV
+
1 4 7
5 15 15
= + =
hay:
.
.D
7
1
15
2
S AMNP
S ABC
V
V
=
.
.D
7
30
S AMNP
S ABC
V
V
=
.
Do đó:
.
.
23
30
AMNP BCD
S ABCD
V
V
=
.
Câu 9. Cho hình hộp
. ' ' ' 'ABCD A B C D
có thể tích
V
. Các điểm
,,M N P
trên các cạnh
', ', 'AA BB CC
sao
cho
1
'2
AM
AA
=
,
1
'3
BN
BB
=
,
2
'3
CP
CC
=
. Mặt phẳng
( )
qua ba điểm
,,M N P
cắt cạnh
'DD
tại
Q
. Tính
thể tích của khối đa diện
.ABCD MNPQ
.
A.
7
12
V
. B.
7
8
V
. C.
11
12
V
. D.
5
12
V
.
Lời giải
Chn A
F
Q
E
M
D
C
A
C'
A'
D'
B'
B
N
P
Công thức tính nhanh: ta có:
' ' ' '
AM CP BN DQ
AA CC BB DD
+ = +
.
Suy ra:
1 2 1
2 3 3 '
DQ
DD
+ = +
5
'6
DQ
DD
=
.
Chuyên đề: Tỉ số thể tích
Trang 62/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Do đó tỉ số thể tích:
.
. ' ' ' '
1
2 ' '
ABCD MNPQ
ABCD A B C D
V
AM CP
V AA CC

=+


1 1 2
.
2 2 3

=+


7
12
=
.
Vậy:
.
7
12
ABCD MNPQ
VV=
.
Câu 10. Cho hình hộp
.ABCD A B C D
có thể tích
V
. Các điểm
M
,
N
,
P
,
Q
trên các cạnh
AA
,
BB
,
CC
sao cho
AM
x
AA
=
,
BN
y
BB
=
,
CP
z
CC
=
. Mặt phẳng
( )
qua ba điểm
M
,
N
,
P
cắt cạnh
DD
tại
Q
sao cho
DQ
t
DD
=
. Tính thể tích của khối đa diện
.ABCD MNPQ
.
A.
( )
.
3
4
ABCD MNPQ
x y z t
VV
+ + +
=
. B.
( )
.
3
8
ABCD MNPQ
x y z t
VV
+ + +
=
.
C.
.
8
ABCD MNPQ
x y z t
VV
+ + +
=
. D.
.
4
ABCD MNPQ
x y z t
VV
+ + +
=
.
Lời giải
Chn D
Ta có tứ giác
MNPQ
là hình bình hành.
Gọi
E
,
F
lần lượt là giao điểm của
AC
và
BD
;
MP
và
NQ
.
Khi đó
AMPC
,
BNQD
là các hình thang nên
2BN DQ AM CP EF+ = + =
hay có
x z y t+ = +
.
Ta có
. . .ABC MNP N ABC N ACPM
V V V=+
..
33
ABC A B C ABC A B C
y x z
VV
+
=+
66
y x z
VV
+
=+
6
x y z
V
++
=
.
Tương tự ta có
.
6
ACD MPQ
x z t
VV
++
=
.
Do đó
. . .ABCD MNPQ ABCC MNP ACD MPQ
V V V=+
66
x y z x z t
VV
+ + + +
=+
22
6
x z y t
V
+ + +
=
.
4 4 2 2
12
x z y t
V
+ + +
=
( )
3 3 2 2
12
x z x z y t
V
+ + + + +
=
( )
3 3 2 2
12
x z y t y t
V
+ + + + +
=
.
3 3 3 3
12
x z y t
V
+ + +
=
4
x y z t
V
+ + +
=
.
Vậy
.
4
ABCD MNPQ
x y z t
VV
+ + +
=
.
Chuyên đề: Tỉ số thể tích
Trang 63/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Câu 11. Cho khối hộp
.ABCD A B C D
có
= 4AC a
và
00
60 , 120BAD A AD A AB

= = =
. Biết tất cả các
cạnh của khối hộp bằng nhau. Tính thể tích
V
của khối chóp đã cho.
A.
3
8
3
Va=
. B.
3
32
3
Va=
. C.
3
16Va=
. D.
3
32Va=
.
Lời giải
120
0
120
0
60
0
4a
D'
C'
B'
A'
D
C
B
A
Chn C
Gọi
x
là độ dài cạnh của khối hộp. Theo qui tắc hình hộp ta có
( ) ( )
2
2
2 2 2
2 . . .AC AC AB AD AA AB AD AA AB AD AD AA AA AB
= = + + = + + + + +
2 2 2 2 2
111
3 2 2 4 2 2
222
x x x x x a x a

= + − − = = =


.
Do đó
( )
3
222
3
33
.
22
1 1 1 1 1 1
6. 1 2 16
2 2 2 2 2 2
22
A A BD
a
x
V V x a
= = + − − − − − = = =
.
Câu 12. Cho khối hộp
.ABCD A B C D
có
ABD
là tam giác đều cạnh
a
. Các mặt phẳng
( ) ( ) ( )
,,ADD A ABB A A BD
cùng tạo với mặt phẳng đáy các góc bằng
0
60
và hình chiếu vuông góc
của
A
lên mạt phẳng đáy nằm khác phía với điểm
A
so vói đường thẳng
BD
. Tính thể tích
V
của
khối chóp đã cho.
A.
3
33
4
a
. B.
3
3
4
a
. C.
3
3
12
a
. D.
3
33
2
a
.
Lời giải
Chuyên đề: Tỉ số thể tích
Trang 64/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
a
a
a
D'
C'
B'
A'
D
C
B
A
Chn A
Ta có
( )( )
−−
= = = =
3
.
6 tan
3 3 3
6. 2 3
3 2 2 2 4
A A BD
p p b p c
a a a a
VV
Câu 13. Cho hình chóp
.S ABCD
có thể tích
V
và đáy
ABCD
là hình bình hành. Mặt phẳng qua
A
và trung
điểm
N
cạnh
SC
các cạnh
SB
,
SD
lần lượt tại
M
,
P
. Tính thể tích nhỏ nhất của khối chóp
.S AMNP
.
A.
8
V
. B.
3
8
V
. C.
4
V
. D.
3
V
.
Lời giải
Chn D
Đặt
1
SA
x
SA
==
;
SM
y
SB
=
;
1
2
SN
z
SC
==
;
SP
t
SD
=
. Ta có
1 1 1 1
x z y t
+ = +
1 1 1 1
1 2 3
y t y t
+ = + + =
.
Do đó
( )
.
1 1 1 1 1 1 1 3
3 3 .1.
4 4 2 4
S AMNP
V xyzt V yt V ytV
x y z t

= + + + = + =


.
Mà
2
33
yt
yt
yt
+
=
4
9
yt
.
3
S AMNP
V
V
.
Chuyên đề: Tỉ số thể tích
Trang 65/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Câu 14. Cho khối hộp
.ABCD A B CD
có thể tích
V
. Mặt phẳng qua
A
,
M
là trung điểm cạnh
CC
cắt các
cạnh
BB
,
DD
lần lượt tại
P
,
Q
. Tính thể tích khối của khối đa diện
.ABCD PMQ
.
A.
3
4
V
. B.
2
V
. C.
4
V
. D.
8
V
.
Lời giải
Chn C
Ta có
0
AA
x
AA
==
,
BP
y
BB
=
,
1
2
CM
z
CC
==
,
DQ
t
DD
=
và
1
0
22
x z y t
+ = + = + =
.
Do đó
.
11
0
22
4 4 4
ABCD PMQ
x t z t V
V V V
++
+ + +
= = =
.
Câu 15. Cho hình chóp
.S ABC
có
30ASB BSC CSA= = =
và
SA SB SC a= = =
. Mặt phẳng
( )
P
qua
A
cắt
hai cạnh
SB
,
SC
lần lượt tại
B
,
C
sao cho chu vi tam giác
AB C

nhỏ nhất. Gọi
1
V
,
2
V
lần lượt là
thể tích các khối chóp
.S AB C

,
.S ABC
. Tính tỉ số
1
2
V
V
.
A.
1
2
3 2 2
V
V
=−
. B.
1
2
31
V
V
=−
. C.
1
2
4 2 3
V
V
=−
. D.
1
2
21
V
V
=−
.
Lời giải
Chn C
Đặt
SB
x
SB
=
;
SC
y
SC
=
. Ta có
1
2
V
xy
V
=
.
Theo định lí hàm cosin ta được
2 2 2 2
3AB a a x a x
= + −
;
2 2 2 2
3AC a a y a y
= + −
;
2 2 2 2 2
3B C a x a y a xy

= + −
.
Khi đó chu vi của
ABC

là
2 2 2 2 2 2 2 2 2 2 2 2 2
2 3 3 3p a a x a x a a y a y a x a y a xy= + − + + − + + −
2 2 2 2
3 1 3 1 3a x x y y x y xy

= − + + − + + + −


Chuyên đề: Tỉ số thể tích
Trang 66/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
22
22
2
3 1 3 1
31
2 2 2 2
a y y x x x x


= − + + − + + − +


2
2
2
3 3 1 1
31
2 2 2 2
a x x x x




− + + + − +







( )
( )
22
3 1 1 . . 3 1 2a x x x x a f x a f a

= − + + − + = − =


.
Dấu bằng đặt tại
3
2
; 3 1
3
2
yx
xx
y
−
= = −
−
31xy = = −
.
Khi đó
( )
2
1
2
3 1 4 2 3
V
V
= − = −
.
Câu 16. Cho hình chóp
.S ABC
có
30 , 60
OO
ASB BSC CSA= = =
và
SA SB SC a= = =
. Mặt phẳng
( )
P
qua
A
cắt
,SB SC
lần lượt tại
,BC

sao cho chu vi tam giác
AB C

nhỏ nhất. Gọi
12
,VV
lần lượt là thể
tích các khối chóp
. , .S AB C S ABC

. Tính tỉ số
1
2
V
V
.
A.
1
2
3 3 5
V
V
=−
. B.
1
2
3 3 5
2
V
V
−
=
. C.
1
2
4 2 3
V
V
=−
. D.
1
2
3 3 2
2
V
V
−
=
.
Lời giải
Chn B
Đặt
,
SB SC
xy
SB SC

==
, ta có
1
2
V
xy
V
=
và theo định lí hàm số côsin ta có:
2 2 2 2 2 2 2 2 2 2 2 2 2
3 , ,AB a a x a x AC a a y a y B C a x a y a xy
= + − = + − = + −
.
Khi đó chu vi tam giác là:
2 2 2 2 2 2 2 2 2 2 2 2 2
23p a a x a x a a y a y a x a y a xy= + − + + − + + −
2 2 2 2
3 1 1a x x y y x y xy

= − + + − + + + −


22
22
2
1 3 1 3
31
2 2 2 2
a x x y x y x


= − + + − + + − +


2
2
2
1 1 3 3
31
2 2 2 2
a x x x x




− + + − + +







( )
31
23
2
af x af

−
= = +



.
Dấu ”=” đạt tại
31
2
x
−
=
và
1
31
2
, 2 3
1
2
2
xy
x x y
y
−
−
= = = −
−
.
Chuyên đề: Tỉ số thể tích
Trang 67/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Khi đó
( )
1
2
3 1 3 3 5
23
22
V
V
−−
= − =
.
Câu 17. Cho tứ diên
ABCD
có thể tích
V
. Các điểm
,,M N P
lần lượt thuộc các cạnh
,,AB AC BD
thoả mãn
12
,
23
AM AN BP
AB AC BD
= = =
. Gọi
S
là giao điểm của
AD
và mặt phẳng
( )
MNP
. Tính thể tích khối tứ
diện
AMNS
.
A.
2
3
V
. B.
3
V
. C.
3
4
V
. D.
4
V
Lời giải
Chn A
Trong mặt phẳng
( )
ABD
gọi
S MP AD=
. Trong mặt phẳng
( )
ACD
gọi
Q SN CD=
Ta có
1
1 1.2 1
2
MA PB SD SD SD
MB PD SA SA SA
= = =
.
Do đó
.
1 2 2
2
2 3 3
A MNS
AM AN AS
V V V V
AB AC AD
= = =
Chọn A.
Câu 18. Cho khối chóp
.S ABC
có
6, 2, 4, 2 10SA SB SC AB= = = =
và
00
90 , 60 ,ASB BSC==
0
120ASC =
.
Mặt phẳng
( )
P
qua
B
và trung điểm
N
của
SC
, vuông góc với mặt phẳng
( )
SAC
cắt cạnh
SA
tại
M
. Tính tỉ số thể tích
.
.
S MBN
S ABC
V
V
.
A.
2
9
. B.
2
5
. C.
1
6
. D.
1
4
.
Lời giải
Chn C
Chuyên đề: Tỉ số thể tích
Trang 68/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
S
C
A
B
N
M
*Đặt
SM
k
SA
=
ta có
.
.
1
.
2
S MBN
S ABC
V
SM SN
k
V SA SC
==
.
Các góc
0 0 0
90 , 60 , 120ASB BSC ASC= = =
.
Đặt
6, 2, 4
,,
. 0, . 4, . 12
a b c
SA a SB b SC c
a b c b a c
= = =
= = =
= = = −
.
Vì
( ) ( )
BMN SAC⊥
nên kẻ
( ) ( )
BH MN H MN BH SAC⊥ ⊥
và ta có biểu diễn véctơ cho ba
điểm
,,M H N
thẳng hàng:
( )
( )
( )
( )
1
11
2
x
BH xBM x BN x SM SB x SN SB kxa b c
−
= + − = − + − − = − +
.
Giải điều kiện vuông góc ta có
( )
( )
1
1
.0
36 0 6 1 0
.0
2
3
12 4 8 1 0
1
1
.0
.0
3
2
x
a kxa b c
k
kx x
BH SA
kx x
x
BH SC
x
c kxa b c
−

− + =
=

− − − =
=
− − + − =
−

=

=
− + =


.
Vậy
.
.
1 1 1
.
2 3 6
S MBN
S ABC
V
V
==
.
Câu 19. Cho hình chóp
.S ABC
có
,MN
lần lượt là trung điểm các cạnh
,SB SC
. Gọi
1
V
là thể tích khối chóp
.S AMN
và
2
V
là thể tích khối chóp
.ABCNM
. Tính tỉ số
1
2
V
V
.
A.
1
2
4
V
V
=
. B.
1
2
3
V
V
=
. C.
1
2
1
3
V
V
=
. D.
1
2
1
4
V
V
=
.
Lời giải
Chn C
Chuyên đề: Tỉ số thể tích
Trang 69/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
N
M
S
B
C
A
*Ta có
11
1 2 1
2
1 1 1 3 1
. . ;
2 2 4 4 3
VV
SM SN
V V V V V V
V SB SC V
= = = = − = =
.
Câu 20. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
, cạnh bên
SA
vuông góc với mặt phẳng
đáy
( )
ABC
. Gọi
,HK
lần lượt là hình chiếu vuông góc của
A
lên
,SB SC
. Gọi
1
V
là thể tích khối
chóp
.S AHK
và
2
V
là thể tích khối chóp
.ABCKH
. Biết
1
2
81
19
V
V
=
. Tính thể tích
V
của khối chóp
.S ABC
.
A.
3
3
4
a
V =
. B.
3
3
6
a
V =
. C.
3
33
4
a
V =
. D.
3
3
2
a
V =
.
Lời giải
Chn A
S
B
C
A
H
K
Ta có
11
2
81 81 81
19 81 19 100
VV
VV
= = =
+
.
Mặt khác
( )
2 2 4
1
2
22
22
81
. . 3
100
V
SH SK SA SA SA
SA a
V SB SC SB SC
SA a
= = = = =
+
.
Vì vậy
23
1 1 3 3
. .3 .
3 3 4 4
ABC
aa
V SA S a= = =
.
Câu 21. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh bằng
1
, mặt bên
SAB
là một tam giác cân
tại
S
và nằm trong mặt phẳng vuông góc với mặt phẳng đáy
( )
ABC
. Gọi
H
là hình chiếu vuông góc
của
A
lên
SC
. Biết
.
.
16
19
S AHB
S ABC
V
V
=
. Tính thể tích
V
của khối chóp
.S ABC
.
Chuyên đề: Tỉ số thể tích
Trang 70/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
A.
3
12
. B.
3
6
. C.
3
4
. D.
3
2
.
Lời giải
Chn B
Gọi
O
là trung điểm
AB
, ta có
( )
SO ABC⊥
và
( )
SC AH
SC AHB SC OH
SC AB
⊥
⊥ ⊥
⊥
.
Suy ra:
2 2 2
1
2 2 2
2
16
2
3
9
4
V
SH SO SO SO
SO
V SC SC SO OC
SO
= = = = = =
+
+
.
Vì vậy:
( )
1 1 3 3
. .2.
3 3 4 6
V SO dt ABC= = =
.
Câu 22. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành và có thể tích bằng
V
. Gọi
,,M N P
lần
lượt là các điểm trên các cạnh
,,SA SB SC
sao cho
1 2 1
,,
2 3 3
SM SN SP
SA SB SC
= = =
. Mặt phẳng
( )
MNP
cắt
cạnh
SD
tại điểm
Q
. Tính thể tích khối đa diện
.ABCD MNPQ
.
A.
5
63
V
. B.
10
63
V
. C.
53
63
V
. D.
58
63
V
.
Lời giải
Chn D
Chuyên đề: Tỉ số thể tích
Trang 71/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Đặt
1 2 1
, , ,
2 3 3
SM SN SP SQ
x y z t
SA SB SC SD
= = = = = = =
.
Ta có tỷ số:
1 1 1 1 2
7
SA SC SB SD
t
SM SQ SN SP x t y z
+ = + + = + =
.
Vậy
( )
. . .
1 1 1 5
2 2 2 63
S MNPQ S MNP S PMQ
V V V xyz V ztx V xz y t V V= + = + = + =
Suy ra
.
5 58
1
63 63
ABCD MNPQ
V
VV

= − =


Câu 23. Cho hình chóp
.S ABCD
có đáy
ABCD
là một tứ giác lồi. Trên cạnh
SA
lấy điểm
M
sao cho
3
4
SM
SA
=
. Mặt phẳng
( )
song song với mặt phẳng
( )
ABCD
và qua
M
chia khối chóp thành hai
khối đa diện. Nếu thể tích khối đa diện chứa đỉnh
A
là
2
100 dm
thì thể tích của khối đa diện còn lại
là?
A.
( )
3
324
7
dm
. B.
( )
3
2700
37
dm
. C.
( )
3
3700
27
dm
. D.
( )
3
2025
64
dm
.
Lời giải
Chn B
Chuyên đề: Tỉ số thể tích
Trang 72/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Gọi
,,N P Q
lần lượt là giao điểm của mặt phẳng
( )
và các cạnh
,,SB SC SD
.
Ta có:
( ) ( ) ( )
2
39
4 16
dt MNPQ dt ABCD dt ABCD

==


và
( ) ( )
3
S,MNPQ ,
4
kc kc S ABCD=
.
Suy ra:
( ) ( ) ( ) ( )
..
1 1 9 3 27
, . . ,
3 3 16 4 64
S MNPQ S ABCD
V kc S MNPQ dt MNPQ dt ANBCD kc S ABCD V= = =
.
Vậy:
( )
.
3
.
.
27 27 27 2700
.100
64 27 37 3 37
S MNPQ
S MNPQ
ABCD MNPQ
V
V dm
V
= = = =
−
.
Câu 24. Cho khối chóp
.S ABCD
có đáy là hình chữ nhật,
3 , ,AB a AD a SA==
vuông góc với đáy và
SA a=
. Mặt phẳng
( )
qua
A
vuông góc với
SC
cắt
,,SB SC SD
lần lượt
,,M N P
. Tính thể tích
khối chóp
.S AMNP
.
A.
3
33
40
a
. B.
3
3
40
a
. C.
3
3
10
a
. D.
3
3
30
a
.
Lời giải
Chn B
.
Chuyên đề: Tỉ số thể tích
Trang 73/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Ta có
( )
,,SC SC AM SC AN SC AP
⊥ ⊥ ⊥ ⊥
.
Mặt khác:
( ) ( )
CB SAB AM CB AM SBC AM SB⊥ ⊥ ⊥ ⊥
.
Tương tự
AP SD⊥
.
Thể tích khối chóp ban đầu là
3
2
13
3
33
a
V a a==
.
Tính các tỷ số:
2
2
22
1
1; ;
34
SA SM SA a
xy
SA SB SB a a

= = = = =

+

22
22
2 2 2 2 2
11
;
3 5 2
SN SA a SP SA a
zt
SC SC a a a SD SD a a
= = = = = = = =
+ + +
.
Vậy
3
.
1 1 1 1 3
4 40
S AMNP
xyzt a
VV
x y z t

= + + + =


.
Câu 25. Cho khối chóp
.S ABCD
có thể tích
V
và có đáy là hình bình hành. Điểm
'S
thỏa mãn
( )
'0SS kDC k=
. Biết thể tích phần chung của hai khối chóp
.S ABCD
và
'.S ABCD
là
7
25
V
. Tìm
k
.
A.
9k =
. B.
6k =
. C.
11k =
. D.
4k =
.
Lời giải
Chn D
Ta có
/ / / / ' ' ' , ' 'AB CD SS B S A SB C S D SC = =
.
Theo Ta lét ta có:
' ' ' ' '
' ' 1
B S C S SS SB SC k
k
B B C D DC SB SC k
= = = = =
+
.
Suy ra ta có:
''
1, , , 1
11
SA SB k SC k SD
x y z t
SA SB k SC k SD
= = = = = = = =
++
.
Chuyên đề: Tỉ số thể tích
Trang 74/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Vậy ta có:
( )
( )
2
''
2
21
1 1 1 1 1
.1.1. .
4 1 1 1 2
21
11
SABC B
kk
kk
V V V
kk
kk
kk
kk


+
= + + + =

++
+

++

.
Suy ra thể tích phần chung là:
( )
( )
2
. ' '
2
21
7
' 1 4
25
21
S ADC B
kk
V V V V V k
kk

+
= − = − = =


+

.
Câu 26. Khối hộp
.ABCD A BC D
có tất cả các mặt là các hình thoi cạnh
a
, các góc xuất phát từ đỉnh
A
đều
bằng
60
o
. Tính thể tích
V
của khối hộp đã cho.
A.
3
2
3
a
V =
. B.
3
3
6
a
V =
. C.
3
2
2
a
V =
. D.
3
2
6
a
V =
.
Lời giải
Chn C
Ta có
1
cos cos cos
2
AB AD AA a
BAD A AD A AB
= = =

= = =
Ta có
.
6
A ABD
VV
=
222
3
1 1 1 1 1 1
1 2. . .
2 2 2 2 2 2
a
= + − − −
3
2
2
a
=
.
Câu 27. Khối hộp
.ABCD A B CD
có tất cả các mặt là các hình thoi cạnh
a
, các góc
60BAD =
,.
120A AB A AD

= =
. Tính thể tích
V
của khối hộp đã cho.
A.
3
2
3
a
V =
. B.
3
3
6
a
V =
. C.
3
2
2
a
V =
. D.
3
2
6
a
V =
.
Lời giải
Chn C
Chuyên đề: Tỉ số thể tích
Trang 75/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Ta có
11
cos ;cos cos
22
AB AD AA a
BAD A AD A AB
= = =

= = = −
Ta có
.
6
A ABD
VV
=
222
3
1 1 1 1 1 1
1 2. . .
2 2 2 2 2 2
a
= + − − − − − − −
3
2
2
a
=
.
Câu 28. Cho hình chóp tứ giác đều
.S ABCD
. Mặt phẳng
( )
P
qua
A
vuông góc với
SC
cắt
,,SB SC SD
lần
lượt tại
,,B C D
và
2
3
SB
SB
=
. Gọi
,VV
lần lượt là thể tích của khối chóp
.S AB C D
và
.S ABCD
.
Tính tỉ số
V
V
A.
4
9
V
V
=
. B.
2
9
V
V
=
. C.
1
3
V
V
=
. D.
2
3
V
V
=
.
Lời giải
Chn C
Gọi
O AC BD=
Ta kẻ
AC SC
⊥
tại
C
, gọi
H AC SO

=
.
Theo giả thiết
( ) ( )
//BD SAC BD SC BD P⊥ ⊥
Vậy
( ) ( )
//P SBD B D BD

=
và
SB SD SH
H
SB SD SO
= =
là trọng tâm tam giác
SBD
do đó
C
là
trung điểm cạnh
SC
Vậy ta có
2 1 2
1, , ,
3 2 3
SA SB SC SD
x y z t
SA SB SC SD
= = = = = = = =
Do đó
1 1 1 1 1
43
V xyzt
V x y z t

= + + + =


.
Câu 29. Cho hình chóp tứ giác đều
.S ABCD
. Mặt phẳng
( )
P
qua
A
vuông góc với
SC
cắt
,,SB SC SD
lần
lượt tại
,,B C D
và
2
;
3
SB
AB a
SB
==
. Tính thể tích
V
của khối chóp
.S AB C D
.
A.
3
6
18
a
V =
. B.
3
6
27
a
V =
. C.
3
26
27
a
V =
. D.
3
6
9
a
V =
.
Lời giải
Chn A
Chuyên đề: Tỉ số thể tích
Trang 76/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Gọi
O AC BD=
Ta kẻ
AC SC
⊥
tại
C
, gọi
H AC SO

=
.
Theo giả thiết
( ) ( )
//BD SAC BD SC BD P⊥ ⊥
Vậy
( ) ( )
//P SBD B D BD

=
và
2
3
SB SD SH
H
SB SD SO
= = =
là trọng tâm tam giác
SBD
do đó
C
là trung điểm cạnh
SC
Vậy ta có
2 1 2
1, , ,
3 2 3
SA SB SC SD
x y z t
SA SB SC SD
= = = = = = = =
Do đó
00
1 1 1 1 1
43
xyzt
V V V
x y z t

= + + + =


.
Tam giác cân
SAC
có
AC SC
⊥
tại trung điểm
SC
do đó nó là tam giác đều.
Vậy
23
22
0
6 1 6 6
2 2a .
2 2 3 2 6
a a a a
SA AC a h V a= = = − = = =
Vậy
3
6
18
a
V =
.
Câu 30. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành, thể tích
V
. Gọi
P
là trung điểm cạnh
SC
.
Một mặt phẳng chứa
AP
cắt các cạnh
,SB SD
lần lượt tại
,MN
. Tính tỉ số
SM
SB
biết thể tích của
khối chóp
.S AMNP
bằng
27
56
V
.
A.
3
4
SM
SB
=
. B.
3
7
SM
SB
=
. C.
3
5
SM
SB
=
. D.
3
8
SM
SB
=
.
Lời giải
Chn B
Chuyên đề: Tỉ số thể tích
Trang 77/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Gọi
O AC BD=
;
H AC SO

=
.
Với
1
1, 0;1 , ,
2
SA SM SP SN
x y z t
SA SB SC SD
= = = = = =
Ta có
1 1 1 1 1 1
12
31
y
t
x z y t y t y
+ = + + = + =
−
1
1
3
y




Do đó
( )
2
1 1 1 1 3
4 4 3 1
SAMNP
xyzt y
V V V
x y z t y

= + + + =

−

.
Theo giả thiết ta có phương trình
( )
2
3 27 3 1
1
4 3 1 56 7 3
y
V V y y
y

= =

−

.
Câu 31. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật với
,AB a AD b==
và cạnh bên
SA c=
vuông góc với mặt đáy
( )
ABCD
. Gọi
M
là một điểm trên cạnh
SA
sao cho
AM x=
( )
0 xc
.
Tìm
x
để mặt phẳng
( )
MBC
chia khối chóp đã cho thành hai khối đa diện có thể tích bằng nhau.
A.
( )
32
2
c
x
−
=
. B.
( )
23
2
ab
x
c
−
=
. C.
( )
35
2
c
x
−
=
. D.
( )
51
2
ab
x
c
−
=
.
Lời giải
Chn C
M
A
B
D
C
S
N
Qua
M
kẻ đường thẳng song song với
AD
cắt
SD
tại
N
. Khi đó
( )
MBC
cắt hình chóp theo thiết
diện là hình thang vuông
MNCB
tại
M
và
B
.
Ta có
SM SN c x
SA SD c
−
==
.
.A
..
S MBC
S BC
V
SM SB SC SM c x
V SA SB SC SA c
−
= = =
. .A
2
S MBC S BCD
cx
VV
c
−
=
.
Chuyên đề: Tỉ số thể tích
Trang 78/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Lại có:
2
.
.AD
. . .
S MNC
SC
V
SM SN SC SM SN c x
V SA SD SC SA SD c
−

= = =


( )
2
. .A
2
2
S MNC S BCD
cx
VV
c
−
=
.
Do đó
( )
2
. .A
2
2
2
S MNBC S BCD
cx
cx
VV
c
c

−
−

=+


( )
2
2
.A
2
1
2
2
S BCD
c cx c x
V
c

− + −

=


Từ giả thiết suy ra:
( )
( )
2
2
22
2
35
1 3 0
2
c
c cx c x
x cx c x
c
−
− + −
= − + = =
.
Câu 32. Cho hình hộp
.ABCD A B CD
có
,,M N P
lần lượt là trung điểm ba cạnh
,,A B BB DD
. Mặt phẳng
( )
MNP
cắt
AA
tại
I
. Biết thể tích khối tứ diện
IANP
là
V
. Tính thể tích khối hộp.
A.
6V
. B.
12V
. C.
4V
. D.
2V
.
Lời giải
Chn C
Mặt phẳng
( )
MNP
cắt
AD

tại
Q
theo tính chất giao tuyến ta có
//MQ NP
. Do đó
IA BN
=
và
,MQ
lần lượt là trung điểm các đoạn
,IN IP
Khi đó:
1
. . .
12
IA MQ IA MQ
IA IM IQ
V V V V
IA IN IP

= =
.
Ta có:
( )
( )
( )
( )
.'
1 1 1 1 1
. , . . , . .
3 3 2 8 48
IA MQ A MQ ABCD ABCD A B C D
V d I A B C D S d A ABCD S V
= = =
Từ đó suy ra:
. ' . '
11
.4
48 12
ABCD A B C D ABCD A B C D
V V V V
= =
.
Câu 33. Cho hình chóp tứ giác đều
.S ABCD
. Gọi
H
là hình hộp chữ nhật có bốn đỉnh là bốn trung điểm của
các cạnh bên
, , ,SA SB SC SD
và bốn đỉnh còn lại nằm trong đáy
ABCD
. Biết thể tích khối hộp
H
là
V
. Tính thể tích của khối hộp đã cho.
A.
4
3
V
. B.
2V
. C.
8
3
V
. D.
6V
.
Lời giải
Chn C
Chuyên đề: Tỉ số thể tích
Trang 79/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Gọi các điểm như hình vẽ.
Ta có
( )
( )
.
1 1 3
,
4 2 8
M N P Q ABCD S ABCD
V S MM S d S ABCD V
= = =
.
Suy ra
.
8
3
S ABCD
VV=
.
Câu 34. Cho khối lăng trụ
.ABC A B C
có thể tích
V
. Hai mặt phẳng
( )
ACB
và
( )
BA C

chia khối lăng trụ
đã cho thành bốn phần. Tính thể tích của phần có thể tích lớn nhất
A.
2
V
. B.
3
5
V
. C.
5
12
V
. D.
2
5
V
.
Lời giải
Chn C
Hai mặt phẳng
( )
ACB
và
( )
BA C

chia khối lăng trụ thành các khối
B MBN
,
MNCCA A

,
MNBCA
,
MNBCA
.
Trong đó
1 1 1
4 4 12
B MBN
B MBN B ABC
B ABC
V B M B B B N
V V V
V B A B B B C

= = = =
.
Suy ra
31
44
MNCC A A B ABC B MBN B ABC
V V V V V
= − = =
.
Tương tự,
1 1 1
3 12 4
MNB A C BA B C BMNB
V V V V V V
= − = − =
.
Do đó
1 1 1 5
1
12 4 4 12
MNCC A A B MBN MNCC A A MNB A C
V V V V V V V

= − − − = − − − =


.
Chuyên đề: Tỉ số thể tích
Trang 80/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Câu 35. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang với
//AB CD
và
4CD AB=
. Gọi
M
là một
điểm trên cạnh
SA
sao cho
0 AM SA
. Tìm tỉ số
SM
SA
sao cho mặt phẳng
( )
CDM
chia khối chóp
thành hai khối đa diện có thể tích bằng nhau.
A.
3 13
2
SM
SA
−+
=
. B.
4 26
2
SM
SA
−+
=
. C.
3 17
2
SM
SA
−+
=
. D.
4 23
2
SM
SA
−+
=
.
Lời giải
Chn B
Từ
M
kẻ đường thẳng song song với
AB
, cắt
SB
tại
N
. Khi đó mặt phẳng
( )
CDM
chia khối chóp
thành hai khối đa diện
.,S CMND CMNDBA
.
Đặt
,0 1
SM SN
xx
SA SB
= =
.
Ta có
.
. . . .
.
41
4,
55
S ADC ADC
S ADC S ABCD S ABC S ABCD
S ABC ABC
V S AD
V V V V
V S AB
= = = = =
.
Mặt khác
.
4
5
SMCD
SMCD S ABCD
SACD
V SM x
VV
V SA
= =
.
2
2
5
SMNC
SMNC SABC
SABC
V SM SN x
x V V
V SA SB
= = =
.
Vậy
2
.
.
4
5 5 2
S ABCD
SMNCD S ABCD
x x V
VV

= + =


.
Suy ra
2
4 1 4 26
5 2 2
xx
x
+ − +
= =
.
Câu 36. Cho hình chóp
.S ABC
có thể tích
V
. Lấy hai điểm
,MN
lần lượt nằm trên hai cạnh
,SA SB
sao cho
12
,
33
SM SN
SA SB
==
. Mặt phẳng
( )
qua
MN
và song song với
SC
chia khối chóp
.S ABC
thành hai
khối đa diện. Tính thể tích của khối đa diện có thể tích lớn hơn.
A.
5
6
V
. B.
5
8
V
. C.
5
9
V
. D.
7
12
V
.
Lời giải
Chn C
Chuyên đề: Tỉ số thể tích
Trang 81/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
E
I
A
C
B
S
M
N
D
Kéo dài
MN
cắt
AB
tại
I
. Kẻ
//MD SC
,
ID
cắt
BC
tại
E
.
Ta có tứ giác
MNED
là thiết diện của hình chóp với mặt phẳng
( )
.
Trong tam giác
SAB
ta có
. . 1 4
MS IA NB IA
MA IB NS IB
= =
.
Do đó
.
.
.
2 2 4 16
. . . .
3 3 3 27
A MDI
A MDI
A SCB
V
AM AD AI
VV
V AS AC AB
= = =
.
Mặt khác
..
.
1 1 1 1 1
. . . .
4 2 2 16 27
IBNE
I BNE A MDI
I AMD
V
IB IN IE
V V V
V IA IM ID
= = = =
.
Do đó
.
16 1 5
27 27 9
AMD BNE
V V V

= − =


.
Câu 37. Cho hình chóp
.S ABC
. Lấy hai điểm
,MN
lần lượt nằm trên hai cạnh
,SA SB
sao cho
1
,
3
SM SN
x
SA SB
==
. Mặt phẳng
( )
qua
MN
và song song với
SC
chia khối chóp
.S ABC
thành hai
khối đa diện có thể tích bằng nhau. Tìm
x
.
A.
45
3
x
−
=
. B.
8 10
6
x
−
=
. C.
45
6
x
−
=
. D.
8 10
9
x
−
=
.
Lời giải
Chn B.
Chuyên đề: Tỉ số thể tích
Trang 82/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
E
I
A
C
B
S
M
N
D
Kéo dài
MN
cắt
AB
tại
I
. Kẻ
//MD SC
,
ID
cắt
BC
tại
E
.
Ta có tứ giác
MNED
là thiết diện của hình chóp với mặt phẳng
( )
.
Trong tam giác
SAB
ta có
2
. . 1
1
MS IA NB IA x
MA IB NS IB x
= =
−
.
Do đó
( )
.
.
.
2 2 2 8
. . . .
3 3 1 9 3 1
A MDI
A MDI
A SCB
V
AM AD AI x x
VV
V AS AC AB x x
= = =
−−
.
Trong tam giác
AMI
có
( )
31
. . 1
31
x
SM NI BA NI
SA NM BI NM x
−
= =
−
.
Do đó
( ) ( )
2
3
.
.
3 1 1
1
. . .
2 2 3 1
IBNE
I BNE
I AMD
xx
V
IB IN IE x
VV
V IA IM ID x x

−−
−
= = =

−

.
Suy ra
( )
( )
( )
( )
33
.
11
8 1 8 1 8 10
9 3 1 3 1 2 9 3 1 3 1 2 6
AMD BNE
xx
xx
V V V x
x x x x

−−
−
= − = − = =

− − − −


Câu 38. Cho khối lập phương
.ABCD A BC D
có thể tích bằng
V
. Gọi
,EF
lần lượt là trung điểm của các
cạnh
,B C C D
. Mặt phẳng
( )
AEF
chia khối lập phương thành hai phần. Tính thể tích của phần có
thể tích nhỏ hơn.
A.
3
8
V
. B.
25
72
V
. C.
5
16
V
. D.
9
32
V
.
Lời giải
Chn B.
Chuyên đề: Tỉ số thể tích
Trang 83/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Ta có:
1 1 1 1
, , ,
2 2 3 3
D G D A B H B A B K B B D I D D
= = = =
.
Và
93
88
A HG A B C D AGHA
S S V V
= =
.
Mà
1 1 1 1 3 1 25
..
3 2 12 72 8 36 72
EB HK GFD I A IFEB KD
V V V V V V V

= = = = − =


.
Câu 39. Cho hình chóp
.S ABCD
có đáy có đáy ABCD là hình bình hành và thể tích bằng
V
. Gọi
,MN
lần
lượt là các điểm di động trên các cạnh
,AB AD
sao cho
24
AB AD
AM AN
+=
. Gọi
.S AMN
VV
=
. Tìm giá trị
nhỏ nhất của
V
.
A.
1
4
V
. B.
1
6
V
. C.
1
8
V
. D.
1
3
V
.
Lời giải
Chn A.
Chuyên đề: Tỉ số thể tích
Trang 84/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Đặt
1 2 2
,4
41
AM AN x
x y y
AB AD x y x
= = + = =
−
.
Có
2
..
..
1 1 1 1
. . . 4 1 2
2 2 2 2 4 1 16 4 1 4
S AMN S AMN
S ABCD S ABD
VV
AM AN x V V
xy V xyV V x
V V AB AD x x

= = = = = = − + +

−−

.
Câu 40. Cho hình chóp
.S ABCD
có đáy có đáy ABCD là hình bình hành và thể tích bằng
V
. Gọi
,MN
lần
lượt là các điểm di động trên các cạnh
,AB AD
sao cho
24
AB AD
AM AN
+=
. Gọi
.S MBCDN
VV
=
. Tìm giá
trị lớn nhất của
V
.
A.
1
4
V
. B.
2
3
V
. C.
3
4
V
. D.
1
3
V
.
Lời giải
Chn C.
Đặt
1 2 2
,4
41
AM AN x
x y y
AB AD x y x
= = + = =
−
.
Có
2
. . .
. . .
1 1 1
1 1 1 . . 1 1 1 .
2 2 2 2 4 1
S MBCDN S AMN S AMN
S ABCD S ABCD S ABD
V V V
AM AN x
xy V xy V V
V V V AB AD x


= − = − = − = − = − = −


−


13
4 1 2
16 4 1 4
VV
Vx
x

= − − + +

−

.
Câu 41. Cho khối tứ diện đều
ABCD
có cạnh bằng
a
. Gọi
,MN
lần lượt là trung điểm các cạnh
,AB BC
và
E
là điểm đối xứng với
B
qua
D
. Mặt phẳng
( )
MNE
chia khối tứ diện
ABCD
thành hai khối đa
diện, trong đó khối đa diện chứa đỉnh
A
có thể tích
V
. Tính
V
A.
3
13 2
216
a
V =
. B.
3
72
216
a
V =
. C.
3
2
18
a
V =
. D.
3
11 2
216
a
V =
.
Lời giải
Chn D
Chuyên đề: Tỉ số thể tích
Trang 85/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Ta có
3
0
2
12
ABCD
a
VV==
Dễ thấy
,PQ
là trọng tâm các tam giác
,BEC ABE
2
3
EQ EP
EM EN
= =
.
.
2
..
9
E QPD
E BMN
V
ED EQ EP
V EB EM EN
= =
.
7
9
BMQPN E BMN
VV=
Mà
( )
( )
( )
( )
. . .
1 1 1 1
, . . , .
3 3 2 2
E BMN M BEN BEN BDC A BCD
V V d M BEN S d A BCD S V

= = = =
3
0 0 0
7 1 7 11 11 2
.
9 2 18 18 216
BMQPN AMNCPQ
a
V V V V V = = = =
.
Câu 42. Cho khối tư diện đều
ABCD
có cạnh bằng
a
. Gọi
,MN
lần lượt là trung điểm các cạnh
,AB AC
sao
cho
1
,2
2
AM AN
BM CN
==
. Mặtt phẳng
( )
chứa
MN
, song song với
AD
chia khối tứ diện
ABCD
thành hai khối đa diện, trong đó khối đa diện chứa đỉnh
A
có thể tích
V
. Tính
V
A.
3
42
108
a
V =
. B.
3
52
108
a
V =
. C.
3
42
81
a
V =
. D.
3
11 2
342
a
V =
.
Lời giải
Chn A
Chuyên đề: Tỉ số thể tích
Trang 86/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Ta có:
3
0
2
12
ABCD
a
VV==
Dễ thấy
,,BC MN PQ
đồng quy tại
S
Áp dụng định lí Mênêlauyt cho
ABC
với
,,M N P
thẳng hàng, suy ra
1
4
SC
SB
=
.
.
1 1 1 1
. . . .
4 2 2 16
S CNP
S BMQ
V
SC SN SP
V SB SM SQ
= = =
.
15
16
BMQPNC S BMQ
VV=
Mà
. . . .
4 2 2 16
. . . . .
3 3 3 27
S BMQ A BCD A BCD A BCD
BS BM BQ
V V V V
BC BA BD
= = =
3
0 0 0
15 16 5 4 4 2
.
16 27 9 9 108
BMQPNC ADQPNM
a
V V V V V = = = =
.
Câu 43. Cho khối tứ diện đều
ABCD
có cạnh bằng
a
. Gọi
,MN
lần lượt là trung điểm các cạnh
,AB BC
và
E
là điểm thuộc tia đối của tia
DB
sao cho
BE
k
BD
=
. Tìm
k
để mặt phẳng
( )
MNE
chia khối tứ diện
ABCD
thành hai khối đa diện, trong đó khối đa diện chứa đỉnh
B
có thể tích
3
11 2
294
a
V =
.
A.
6
5
k =
. B.
6k =
. C.
4k =
. D.
5k =
.
Lời giải
Chn C
Chuyên đề: Tỉ số thể tích
Trang 87/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Thể tích của khối tứ diện đều
ABCD
là
3
0
2
12
a
V =
.
0 0 0
11
2 2 4
BMNE
BM BN BE k
V V kV V
BA BC BD
= = =
.
Theo Thales ta có
2
0
2
1 2( 1) 4( 1) 1
1
2 1 (2 1) 4
( 1)
2
EDPQ BMNE
EP EQ k k EP EQ ED ED k k k
V V V
EN EM k EN EM EM EB k k
k
− − − −
= = = = =
−−
−+
Do đó
23
0 0 0
22
4( 1) 1 4( 1)
.1
4 (2 1) 4 4 (2 1)
.
BMNPDQ
k k k k k k
V V V V
k k k k

− − −
= − = −

−−

.
Theo giả thiết ta có
3
. 0 0
2
22 4( 1) 22
14
49 4 (2 1) 49
B MNPDQ
kk
V V V V k
kk

−
= − = =

−

.
Câu 44. Cho hình lăng trụ đứng
.ABC A B C
có thể tích
V
. Các điểm
,,M N P
trên các cạnh
,,'AA BB CC

sao cho
12
,
23
AM BN CP
AA BB CC
= = =
. Tính thể tích của khối đa diện
.ABC MNP
A.
2
3
V
. B.
9
16
V
. C.
20
27
V
. D.
11
18
V
.
Lời giải
Chn D
Chuyên đề: Tỉ số thể tích
Trang 88/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Ta có
. . .ABC MNP M ABC M BCPN
V V V=+
.
Trong đó
( )
( )
.
11
,.
36
M ABC ABC
V d M ABC S V
==
.
. . .
2 2 4
..
3 3 9
BCPN
M BCPN M BCC B A BCC B
BCC B
S
BP CN
V V V V V
S BB CC

+
= = = =

+
.
Vậy
.
1 4 11
6 9 18
ABC MNP
V V V

= + =


.
Câu 45. Cho hình chóp
.S ABCD
có đáy là hình bình hành và có thể tích
V
. Goị
M
là trung điểm của
SB
,
P
là điểm thuộc cạnh
SD
sao cho
2SP DP=
. Mặt phẳng
( )
AMP
cắt cạnh
SC
tại
N
. Tính thể tích
của khối đa diện
ABCDMNP
theo
V
.
A.
23
30
ABCDMNP
VV=
. B.
19
30
ABCDMNP
VV=
. C.
2
5
ABCDMNP
VV=
. D.
7
30
V
.
Lời giải
Chn A
Gọi
O
là tâm của hình bình hành
ABCD
. Gọi
I MP SO N AI SC= =
.
Ta có
Chuyên đề: Tỉ số thể tích
Trang 89/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
17
..
3 2 2 2 12
SPM SPI SMI SPI SMI
SDB SDB SDO SBO
S S S S S
SP SM SI SP SM SI
SD SB S S S S SO SD SB SO
+

= = = = + = + =


.
4
7
SI
SO
=
.
Suy ra
22
..
2 2 2 2 7 7
SAN SAI SNI SAI SNI
SAC SAC SAO SAO
S S S S S
SN SI SI SN SN
SC S S S S SO SO SC SC
+
== = = + = + = +
.
2
5
SN
SC
=
.
Suy ra
. . . . 7
2 2 . . 2 . . 30
SAMNP SAMP SMNP SAMP SMNP
SABD SBCPD
V V V V V
SA SM SP SM SN SP
V V V V SA SB SD SB SC SD
+
= = + = + =
.
23
30
ABCDMNP
VV=
.
Câu 46. Cho khối chóp
.S ABC
có tất cả các cạnh bằng nhau và bằng
a
. Gọi
,MN
lần lượt là trung điểm của
các cạnh
,AB SC
. Các điểm
,PQ
trên các đường thẳng
,SA BN
sao cho
//PQ CM
. Tính thể tích
V
của khối chóp
.S BNP
.
A.
3
2
36
a
V =
. B.
3
2
72
a
V =
. C.
3
2
18
a
V =
. D.
3
2
9
a
V =
.
Lời giải
Chn B
A
C
B
S
M
N
P
Q
Đặt
,,SA a SB b SC c= = =
. Ta có:
( )
1 1 1 1
2 2 2 2
CM SM SC SA SB SC a b c= − = + − = + −
và
( ) ( )
( )
11
2
1
2
SP kSA ka
m
SQ mSN m SB c m b
m
PQ SQ SP ka m b c
==
= + − = + −
= − = − + − +
.
Theo giả thiết bài toán ta có hai véc tơ
,PQ CM
cùng phương, ta có:
Chuyên đề: Tỉ số thể tích
Trang 90/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
( )
1 1 1 4 1
2
1;
11
2 2 2 1 3 3
22
m
m k m
ka m b c n a b c m k
−−

− + − + = + − = = = =

−

Do đó:
33
.
1 1 2 2
. . . .
3 2 12 72
S ABC
SP SN a a
VV
SA SC
= = =
. Chọn B.
Câu 47.
Cho khối hộp
.ABCD A B C D
có tất cả các mặt đều là hình thoi,
6,AC a
=
60BAD A AD A AB

= = =
. Tính thể tích
V
của khối hộp đã cho.
A.
3
62Va=
. B.
3
32Va=
. C.
3
23Va=
. D.
3
63Va=
.
Lời giải
Chn D
Đặt cạnh của hình hộp là
x
.
, 60AB AD BAD BAD= =
là tam giác đều
.BD AB AD x= = =
Tương tự ta có
AD AB AA x
= = =
. Do đó tứ diện
ABDA
là tứ diện đều cạnh bằng
x
.
Theo quy tắc hình hộp ta có:
AC AB AD AA

= + +
( ) ( )
2
2
2 2 2
2 . . .AC AC AB AD AA AB AD AA AB AD AB AA AD AA
= = + + = + + + + +
2 2 2 2
111
3 2 6 6 6
222
x x x x x a x a

= + + + = = =


.
Do đó:
( )
3
3
.
2. 6
6 6. 6 3
12
A ABD
a
V V a
= = =
.
Câu 48. Cho hình chóp
.S ABCD
có thể tích
V
, đáy là hình bình hành. Mặt phẳng
( )
đi qua
A
, điểm
M
thuộc cạnh
SB
thỏa mãn
2SM MB=
và trọng tâm
G
của tam giác
SAC
cắt các cạnh
,SC SD
lần
lượt tại
,NP
. Tính thể tích của khối chóp
.S AMNP
.
A.
2
3
V
. B.
3
V
. C.
2
9
V
. D.
4
9
V
.
Lời giải
Chn B
Chuyên đề: Tỉ số thể tích
Trang 91/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
G
O
A
D
B
C
S
M
N
P
Ta có
AG
cắt
SC
tại trung điểm
N
của
SC
.
Với
21
1, , ,
32
SA SM SN SP
x y z t
SA SB SC SD
= = = = = = =
ta có:
1 1 1 1 2
3
t
x z y t
+ = + =
.
Do đó:
.
1 1 1 1
..
43
S AMNP
xyzt V
VV
x y z t

= + + + =


. Chọn B.
Câu 49. Cho hình chóp
.S ABCD
có thể tích
V
, đáy là hình bình hành tâm
O
. Mặt phẳng
( )
đi qua
A
, trung
điểm
I
của
SO
cắt các cạnh
,,SB SC SD
lần lượt tại
,,M N P
. Tính thể tích nhỏ nhất của khối chóp
.S AMNP
.
A.
18
V
. B.
3
V
. C.
6
V
. D.
3
8
V
.
Lời giải
Chn C
O
A
D
B
C
S
I
M
N
P
Với
1, , ,
SA SM SN SP
x y z t
SA SB SC SD
= = = = =
ta có:
1 1 1 1
x z y t
+ = +
và xét tam giác
SAC
ta có :
( )
1 1 1 1
..
2 2 4
SO SC
SO SA SC SI SA SN SI SA SN
SI SN z
= + = + = +
.
Mặt khác ba điểm
,,A I N
thẳng hàng nên
1 1 1
1
4 4 3
z
z
+ = =
.
Do đó :
1 1 1 1
4
1
1 4 1
3
t
y
y t t
+ = + = =
−
.
Chuyên đề: Tỉ số thể tích
Trang 92/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Vì vậy
( )
( )
( )
2
.
1
;1
4
1 1 1 1 2 1
. min
4 3 4 1 2 6
S AMNP
xyzt t V
V V f t V f t f
x y z t t




= + + + = = = =


−


.
Dấu bằng đạt tại
11
,
22
ty==
. Tức là mặt phẳng
( )
đi qua trung điểm các cạnh
,SB SD
.
Chọn C.
Câu 50. Cho khối tứ diện đều
ABCD
cạnh
a
. Gọi
E
là điểm đối xứng của
A
qua
D
. Mặt phẳng qua
CE
và
vuông góc với mặt phẳng
( )
ABD
cắt cạnh
AB
tại điểm
F
. Tính thể tích
V
của khối tứ diện
AECF
.
A.
3
2
30
a
V =
. B.
3
2
60
a
V =
. C.
3
2
40
a
V =
. D.
3
2
15
a
V =
.
Lời giải
Chn D
K
B
D
C
A
E
M
M
G
F
Gọi
G
là trọng tâm tam giác
( )
ABD CG ABD⊥
.
Do đó :
( )
F EG AB CEF=
là mặt phẳng cần dựng.
Ta có :
11
// 3
33
MG MD KD KG GD KB
GD BE
MB ME KB KE BE KD
= = = = = =
.
Vì
,,F K E
thẳng hàng nên ta có :
12
. . 1 .3. 1
23
FA KB ED FA FA
FB KD EA FB FB
= = =
33
2 2 2 2
. . .2.
5 5 12 15
ABCD
AF AF AE a a
VV
AB AB AD
= = = =
. Chọn D.
Câu 51. Cho khối lăng trụ
.ABC A B C
có chiều cao bằng
8
và đáy làm tam giác đều cạnh bằng
4
.
Gọi
,,M N P
lần lượt là trung điểm các cạnh
,,B C C A A B
. Thể tích khối đa diện có các
đỉnh là
, , , , ,A B C M N P
bằng
A.
21 3
. B.
12 3
. C.
24 3
. D.
83
.
Lời giải
Chọn D
Chuyên đề: Tỉ số thể tích
Trang 93/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
M
P
N
B
C
A'
C'
B'
A
Ta có
2
.
43
4 3 32 3
4
ABC ABC A B C
SV
Các hình chóp
. , . , .A A NP B B MP C C MN
các hình chóp bằng nhau và có đáy là tam giác đều
có cạnh bằng
2
23
23
4
A NP
S
, chiều cao bằng
8
.
thể tích
.
1 8 3
.8
33
A A NP A NP
VS
.
3 32 3 8 3 24 3
ABCMNP ABCA B C A A MP
V V V
. Chọn C
Câu 52. Cho lăng trụ
.ABC A B C
có chiều cao là
8
đáy là tam giác đều cạnh
6
. Gọi
,,M N P
lần lượt
là tâm các mặt bên
,,ABB A ACC A BCC B
. Thể tích khối đa diện có các đỉnh là các
điểm
, , , , ,A B C M N P
bằng
A.
27 3
. B.
21 3
. C.
30 3
. D.
36 3
.
Lời giải
Chọn D
M
K
P
I
L
N
B
C
A'
C'
B'
A
Ta có
2
.
63
9 3 72 3
4
ABC ABC A B C
SV
Chuyên đề: Tỉ số thể tích
Trang 94/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Gọi
,,I K L
lần lượt là trung điểm của
,,AA BB CC
. Từ đó ta có:
. . . . .ABCMNP ABC A B C B KMP A IMN C LPN A B C IKL
V V V V V V
Trong đó
..
1
36 3
2
A B C IKL ABC A B C
VV
.
. . .
.
1 1 1 1 1
. . . . .72 3 3 3
8 8 8 3 24
B KMP
B KMP B B A C ABC A B C
B B A C
V
BK BM BP
V V V
V BB BA BC
Mà
. . .B KMP A IMN C LPN
V V V
72 3 3.3 3 36 3 27 3
ABCMNP
V
. Chọn A
Câu 53. Cho khối lăng trụ
.ABC A B C
có thể tích
V
,trên các cạnh
,,AA BB CC
lần lượt lấy các
điểm
,,M N P
sao cho
1 2 1
,,
2 3 6
AM AA BN BB CP CC
.Thể tích khối đa diện
ABCMNP
bằng
A.
2
5
V
. B.
4
9
V
. C.
2
V
. D.
5
9
V
.
Lời giải
Chọn B
Có
.
1 2 1 4
,,
2 3 6 3 9
ABC MNP
xyz
AM BN CP
x y z V V V
AA BB CC
.Chọn đáp án B
Câu 54. Cho khối chóp
.S ABCD
có đáy
ABCD
là hình bình hành và có thể tích bằng 1.Gọi
,MN
lần
lượt là các điểm trên các cạnh
,SB SD
sao cho
,2MS MB ND NS
. Mặt phẳng
CMN
chia
khối chóp đã cho thành hai phần,thể tích của phần có thể tích nhỏ hơn bằng
A.
2
25
. B.
1
12
. C.
3
25
. D.
5
48
.
Lời giải
Chọn D
Chuyên đề: Tỉ số thể tích
Trang 95/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Ta có
11
1; ; ;
23
SC SM SP SN
x y z t
SC SB SA SD
và
1 1 1 1 1 1
1 2 3
4
z
x z y t z
.
Khi đó
..
1 1 1 1 5
4 48
S CMPN S ABCD
xyzt
VV
x y z t
.Chọn đáp án D.
Câu 55. Cho khối lăng trụ
.ABC A B C
có thể tích
V
.Các điểm
,,M N E
lần lượt là các điểm nằm
trên cạnh
,,A B A C AB
sao cho
3 , , 3MA MB NC NA EB EA
.Mặt phẳng
MNE
cắt
AC tại F. Thể tích khối đa diện lồi
BEFCC MNB
bằng
A.
59
72
V
. B.
5
24
V
. C.
3
8
V
. D.
41
72
V
.
Lời giải
ChọnA
Goị
,Sh
lần
lượt là diện tích đáy và chiều cao của lăng trụ
đã cho
/ / MNMNE ABC EF
và
AEF
đồng Có
với
'A MN
theo tỷ số
1
'3
AE
k
AM
Do đó dạng
2
3 1 3 1 1 3
. . . ; S .
4 2 8 3 9 8 24
A MN ACB AEF A MN
A M A N S S S
S S S S
A B A C
Do đó áp dụng công thức thể tích khối chóp cụt ta có
.
3 3 13 13
. . . .h
3 3 24 24 8 8 72 72
AEF A MN AEF AEF A MN A MN
h h S S S S
V S S S S S V
.
Vì vậy
..
13 59
1.
72 72
BEFCC MNB ABC A B C AEF A MN
V V V V V
Chọn đáp án A.
Câu 56. Cho khối chóp
.S ABC
có thể tích
V
.Mặt phằng
P
song song với đáy cắt các cạnh
,,SA SB SC
lần luotj tại
,,D E F
.Gọi
1 1 1
,,D E F
tương ứng là hình chiếu vuông góc của
,,D E F
lên mp
ABC
(tham khảo hình vẽ).Khối đa diện
1 1 1
.DEF D E F
có thể tích lớn nhất
bằng
Chuyên đề: Tỉ số thể tích
Trang 96/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
A.
6
V
. B.
12
V
. C.
4
9
V
. D.
2
3
V
.
Lời giải
Chọn C
Đặt
0 1 ;
SD SE SF
xx
SA SB SC
ta cũng có
2
DEF ABC
DE EF FD
x S x S
AB BC CA
.
Và
,
1 , 1 ,
,
d D ABC
AD AS SD
x d D ABC x d S ABC
AS AS
d S ABC
.
Vì vậy
1 1 1
22
.
.d , . 1 , 1 .3
DEF D E F DEF ABC
V S D ABC x S x d S ABC x x V
3
3 3 2 2 4
. . . 2 2
2 2 3 9
V V x x x V
x x x
.
Dấu bằng đạt tại
2
22
3
x x x
.Chọn đáp án C.
Câu 57. Cho khối chóp
.S ABC
có đáy là tam giác vuông tại
C
, cạnh bên
SA
vuông góc với đáy. Biết
2SA AB a
. Gọi
,HK
lần lượt là hình chiếu của
A
lên
,SB SC
. Khối chóp
.S AHK
có thể
tích lớn nhất bằng
A.
3
2
6
a
. B.
3
3
6
a
. C.
3
3
3
a
. D.
3
2
3
a
.
Lời giải
Chọn A
Chuyên đề: Tỉ số thể tích
Trang 97/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Đặt
2 2 2 2
4CA x CB AB CA a x
22
11
.4
22
ABC
S CA CB x a x
.
Do đó
22
.
11
.4
33
S ABC ABC
V S SA ax a x
.
Ta có
22
2 2 3 2 2
22
. . .
2 2 2
22
4 4 1 2 4
. . . . 4
3
84
34
S AHK S ABC S ABC
SH SK SA SA a a a x a x
V V V ax a x
SB SC SB SC
a a x
ax
.
Dùng bất đẳng thức AM-GM có:
2 2 2 2 2 2 2 2 2 2
4 4 2 2 4 .2 2 2 4a x a x x a x x x a x
.
Suy ra:
33
.
2 1 2
.
36
22
S AHK
aa
V
.
Câu 58. Cho khối lăng trụ
.ABC A B C
có thể tích bằng
1
. Gọi
,MN
lần lượt là trung điểm
,AA BB
. Đường thẳng
CM
cắt đường thẳng
AC
tại
P
, đường thẳng
CN
cắt đường
thẳng
BC
tại
Q
. Thể tích khối đa diện lồi
A B MNPQ
bằng
A.
1
3
. B.
1
2
. C.
3
4
. D.
2
3
.
Lời giải
Chọn D
Chuyên đề: Tỉ số thể tích
Trang 98/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
* Ta có:
.A B MNPQ C C PQ CMNA B C
V V V
(1).
* Dễ thấy
,AB
lần lượt là trung điểm
,C P C Q
nên
4
C PQ A B C
SS
. Do đó
. . .
44
4
33
C C PQ C C A B A B C ABC
V V V
(2).
* Vì
1
2
ABNM A B NM ABB A
S S S
nên
. . .
1 1 2 1
.
2 2 3 3
C ABNM C A B BA A B C ABC
V V V
Suy ra
..
2
3
CMNC A B A B C ABC C ABNM
V V V
(3).
* Từ (1), (2) và (3), ta được:
4 2 2
3 3 3
A B MNPQ
V
.
Câu 59. Cho hình chóp
.S ABCD
có đáy là hình bình hành và có thể tích là
V
. Gọi
P
là điểm trên
cạnh
SC
sao cho
5SC SP
. Một mặt phẳng qua
AP
cắt hai cạnh
SB
và
SD
lần lượt tại
M
và
N
. Gọi
1
V
là thể tích của khối chóp
.S AMPN
. Giá trị lớn nhất của
1
V
V
bằng
A.
1
15
. B.
1
25
. C.
3
25
. D.
2
25
.
Lời giải
Chọn C
Chuyên đề: Tỉ số thể tích
Trang 99/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Đặt
1
SA
x
SA
;
SM
y
SB
;
1
5
SP
z
SC
;
0 , 1
SN
t y t
SD
Khi đó,
1 1 1 1 1
61
6 1 6
t
yt
y t x z t
Chứng minh:
1 . .
1 1 1 1 1
4
S AMPN S ABCD
V V xyzt V
x y z t
Ta có:
.
. . .
.
11
. . . .
22
S AMP
S AMP S ABC S ABCD
S ABC
V
SA SM SP
xyz V xyz V xyz V xyzV
V SA SB SC
.
. . .
.
11
. . . .
22
S APN
S APN S ACD S ABCD
S ACD
V
SA SP SN
xzt V xzt V xzt V xztV
V SA SC SD
. . .
1 1 1 1
22
S AMPN S AMP S APN
V V V xyz xzt V xyzt
ty
(*)
Mặt khác:
.
. . .
.
11
. . . .
22
S AMN
S AMN S ABD S ABCD
S ABD
V
SA SM SN
xyt V xyt V xyt V xytV
V SA SB SD
.
. . .
.
11
. . . .
22
S MNP
S MNP S BDC S ABCD
S BDC
V
SM SN SP
ytz V yzt V yzt V yztV
V SB SD SC
. . .
1 1 1 1
22
S AMPN S AMN S MNP
V V V xyt yzt V xyzt
zx
(**)
Chuyên đề: Tỉ số thể tích
Trang 100/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Cộng hai vế của (*) và (**), ta có:
. . . .
1 1 1 1 1 1 1 1 1 1
2
24
S AMPN S ABCD S AMPN S ABCD
V xyzt V V xyzt V
x y z t x y z t
(đpcm)
Ta có:
2
1
1 . .
1 1 1 1 1 3 3 3
4 5 5
5 6 1
S AMPN S ABCD
V
t
V V xyzt V ytV yt
x y z t V
t
.
Xét hàm số
2
3
5 6 1
t
ft
t
trên
1
;1
6
2
2
1
0 ;1
6
3 6 2
0
5
11
61
;1
36
t
tt
ft
t
t
.
Bảng biến thiên:
Vậy
1
;1
6
3
max 1
25
f t f
Câu 60. Cho khối chóp
.S ABCD
có đáy là hình bình hành và có thể tích là
1
. Gọi
,MN
lần lượt là
trung điểm các cạnh
AD
và
SC
; đường thẳng
BM
cắt
AC
tại
P
. Thể tích của khối tứ diện
ABNP
bằng
A.
1
16
. B.
1
12
. C.
1
8
. D.
1
24
.
Lời giải
Chọn B
Chuyên đề: Tỉ số thể tích
Trang 101/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Xét tam giác
ABD
có
P
là trọng tâm
11
36
ABP ABD ABCD
S S S
.
1 1 1
N, . . , .
1 1 1
3 63
.
12 122
A ABCDBNP AB S ABCP D
V d ABP S d B D VS SAC
Câu 61. Cho lăng trụ tam giác
.ABC A B C
có thể tích bằng
72
. Gọi
M
là trung điểm cạnh
AB
; các
điểm
N
,
P
thỏa mãn
3
4
B N B C
,
1
4
BP BC
. Đường thẳng
NP
cắt
BB
tại
E
; đường
thẳng
ME
cắt
AB
tại
Q
. Thể tích khối đa diện
ACPQA C NM
bằng:
A.
55
. B.
59
. C.
52
. D.
56
.
Lời giải
Chọn B
Thể tích khối lăng trụ đã cho là
0
72V S h
. Ta có
1
1
4
3
3
4
BC
EP EQ EB BP
EN EM EB B N
BC
;
Do đó
1 3 3
. . .
2 4 8
B MN B A C
B M B N
S S S S
B A B C
;
2
1 1 3 1
.
3 9 8 24
BQP B MN
S S S S
.
Vì vậy khối chóp cụt
.BQP B MN
có thể tích là:
Chuyên đề: Tỉ số thể tích
Trang 102/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
.
3 1 3 1 13
13
3 3 8 24 8 24 72
BQP B MN B MN BQP B MN BQP
hh
V S S S S S S S S Sh
.
Do đó:
..
72 13 59
ACPQA C NM ABC A B C BQP B MN
V V V
. Chọn đáp án B.
Cách 2: Dùng tỉ số thể tích có:
.0
1 1 3 3 3
. , . .
3 3 8 2 16
E B MN B MN
V S d E B MN S h V
. . 0
1 3 1
. . .
27 16 144
E BQP E B MN
EB EQ EP
V V Sh V
EB EM EN
. . . 0 0
3 1 13
13
16 144 72
BQP B MN E B MN E BQP
V V V V V
Vì vậy
..
72 13 59
ACPQA C NM ABC A B C BQP B MN
V V V
. Chọn đáp án B
Câu 62. Cho khối lăng trụ tam giác
.ABC A B C
. Các mặt phẳng
ABC
và
ABC
chia khối lăng
trụ đã cho thành
4
khối đa diện. Kí hiệu
1
H
,
2
H
lần lượt là các khối đa diện có thể tích lớn
nhất, nhỏ nhất. Giá trị của
1
2
H
H
V
V
bằng:
A.
4
. B.
2
. C.
5
. D.
3
.
Lời giải
Chọn C
Gọi
E AC A C
;
F BC B C
có
4
khối đa diện cần tìm là:
ABCEF
;
ABB A EF
;
A B C EF
;
CEFC
.
Đặt
.ABC A B C
VV
ta có
.
3
C A B C
V
V
;
2
3
ABB A C
V
V
.
Theo công thức tỉ số thể tích có:
Chuyên đề: Tỉ số thể tích
Trang 103/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
.
11
. . .
2 2 3 12
CEFC C A B C
CE CF V V
VV
CA CB
.
3 12 4
A B C EF C A B C CEFC
V V V
V V V
.
Và với
1
CA
x
CA
;
1
CB
y
CB
;
1
2
CF
z
CB
;
1
2
CE
t
CA
theo công thức tính nhanh tỉ số thể tích có :
.
1 1 1 1 1 1 1 1 2
. .1.1. . 1 1 2 2 .
4 4 2 2 3 4
C ABEF ABB A C
VV
V xyzt V
x y z t
.
Suy ra:
.
25
3 4 12
ABB A EF ABB A C C ABEF
V V V
V V V
1
5
12
H
V
V
;
1
2
2
5
12
H
H
H
V
V
V
V
.
Chọn đáp án C.
Câu 63. Cho khối chóp
.S ABCD
có đáy là hình bình hành thể tích bằng
1
. Gọi
M
là điểm đối xứng
của
C
qua
B
;
N
là trung điểm cạnh
SC
. Mặt phẳng
MDN
chia khối chóp
.S ABCD
thành
hai khối đa diện, thể tích của khối đa diện chứ đỉnh
S
bằng:
A.
1
6
. B.
5
8
. C.
12
19
. D.
7
12
.
Lời giải
Chọn D
• Gọi
P MN SB P
là trọng tâm của
SCM
vì là giao của hai đường trung tuyến
SB
,
MN
.
• Gọi
Q MD AB Q
là trung điểm của
MD
.
• Ta có:
. . . .
..
..
1 1 2 5
1 . .
2 2 3 6
BCDQNP M CDN M BQP M CDN M CDN
M CDN M CDN
MB MQ MP
V V V V V
MC MD MN
VV
.
• Mặt khác :
Chuyên đề: Tỉ số thể tích
Trang 104/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
. . .
..
,
.
,
1
.
1 1 1
2
..
. 2 2 2
MCD
M CDN N MCD S ABCD
ABCD
S ABCD S ABCD
d N ABCD
S
V V V
S
d S ABCD
CD CM
VV
CD CB
.
• Vậy
.
5 5 7
1
12 12 12
BCDQNP SANPQD S ABCD BCDQNP
V V V V
. Chọn đáp án D.
Câu 64. Cho hình lăng trụ
. ' ' 'ABC A B C
có đường cao bằng
8
và đáy là tam giác đều cạnh bằng
6
.
Gọi
,MN
lần lượt là trung điểm của các cạnh
', '.AA BB
Đường thẳng
CM
cắt đường thẳng
''AC
tại
P
; đường thẳng
CN
cắt đường thẳng
''BC
tại
Q
. Thể tích của khối đa diện có các
đỉnh là các điểm
, , , , , 'A B C P Q C
bằng
A.
120 3.
B.
140 3.
C.
168 3.
D.
192 3.
Lời giải
Chọn C
Ta có
1 ' ' ' '
''
AC MA
PA AC A C A
PA MA
là trung điểm
'.PC
Tương tự
'B
là
'QC
. Khối
chóp cụt
.'ABC PQC
có chiều
8h
, diện tích đáy
2
1 2 ' 1
3
.6 9 3, 4. 36 6.
4
ABC PQC
S S S S S
Do đó
. ' 1 2 1 2
8
9 3 36 3 9 3.36 3 168 3.
33
ABC PQC
h
V S S S S
Vậy chọn C
Câu 65. Cho hình hộp
. ' ' ' 'ABCD A B C D
có đường cao bằng
8
và đáy là hình vuông cạnh bằng
6
. Gọi
, , ,M N P Q
lần lượt là tâm của các mặt
' ', ' ', ' ', ' 'ABB A BCC B CDD C DAA D
.Thể tích của khối
đa diện có các đỉnh là các điểm
, , , , , , , ,A B C D M N P Q
bằng
A.
108.
B.
168.
C.
96.
D.
120.
Lời giải
Chọn D
Chuyên đề: Tỉ số thể tích
Trang 105/105
Giáo viên: Nguyễn Hoàng Việt
Website: http://luyenthitracnghiem.vn
0905193688
Thể tích khối hộp đã cho
2
6 .8 288.V
Gọi
, , ,E F G H
lần lượt là trung điểm của
AA', ', ', 'BB CC DD
Ta có
. . . .ACBDMNPQ ABCDGH A MNQ B MFN C NGP D PHQ
V V V V V V
. . . .
. ' ' '
1
,
2
. . .
' ' '
1 1 1 1 1
...
2 2 2 6 48
ABCDGH A MNQ B MFN C NGP D PHQ
D D C A
V V V V V V
DH DP DQ
V
DD DC DA
VV
Vậy
1 1 1 1 1 5
120
2 48 48 48 48 12
ACBDMNPQ
V V V V V V V
Vậy chọn D
| 1/105
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Chuyên đề: Tỉ số thể tích Trang 1/105
MỘT SỐ ỨNG DỤNG HAY VỀ TỶ SỐ THỂ TÍCH TRONG VIỆC
GIẢI TOÁN TRẮC NGHIỆM
Từ khi Bộ Giáo Dục và Đào Tạo chuyển hướng sang thi trắc nghiệm, việc dạy và học môn
toán cũng có sự thay đổi để đáp ứng đối với kì thi. Giáo viên phải dạy học sinh hiểu rõ bản chất
và cách làm nhanh nhất để đi đến kết quả. Còn học sinh mong muốn mình giải quyết một bài
toán với con đường đơn giản nhất và đáp số chính xác nhất. Sau đây tôi xin biên soạn lại một
vấn đề rất hay gặp trong các kì thi thử và thi THPTQG, giúp các em học sinh giải quyết rất
nhanh các bài toán liên quan đến thể tích khối đa diện.. I. KIẾN THỨC CƠ SỞ.
+) Hai hình chóp có cùng diện tích đáy thì tỷ số thể tích của chúng chính là tỷ số của đường cao và ngược lại.
+) Với khối chóp tam giác ta có tính chất quen thuộc sau.
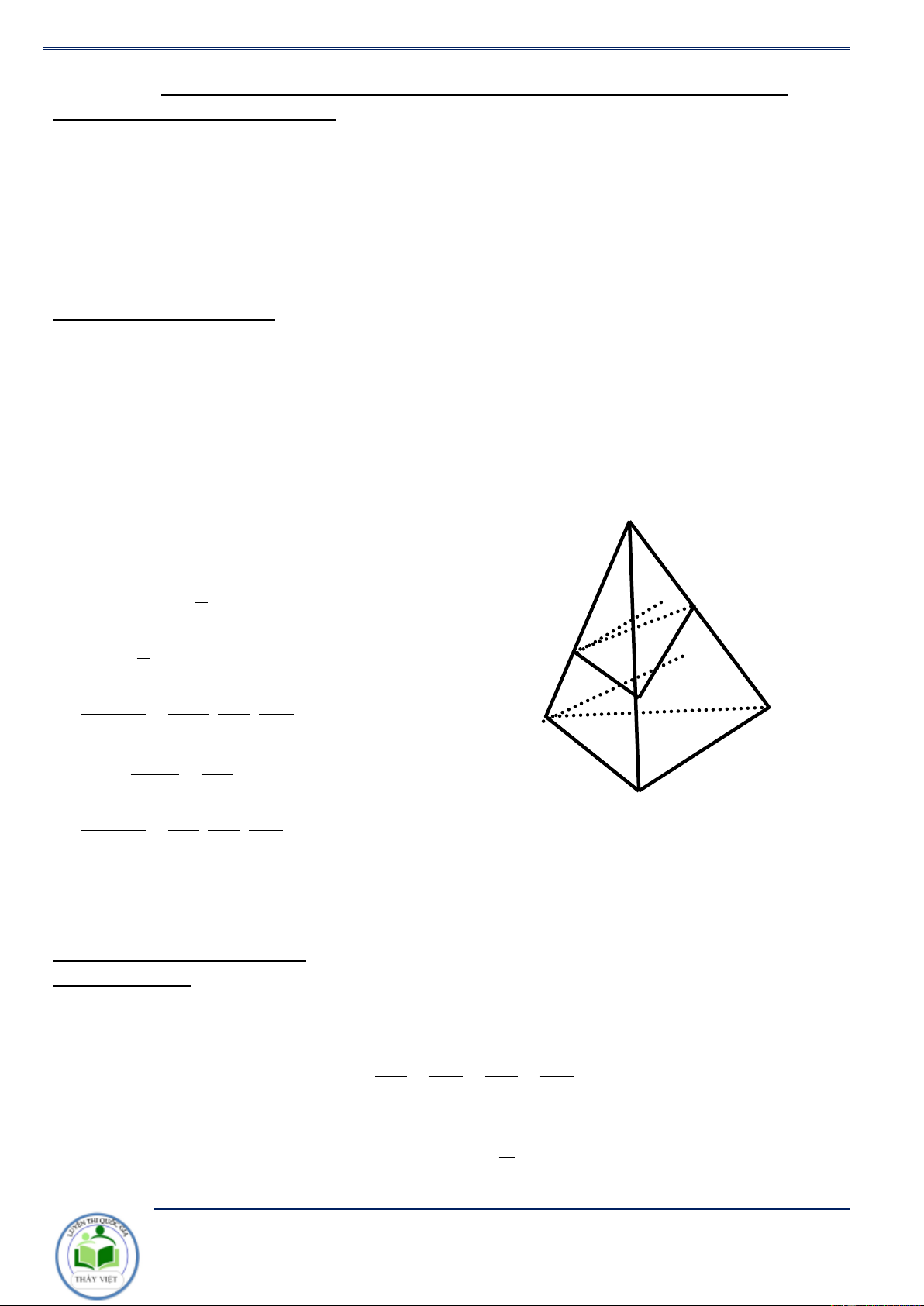
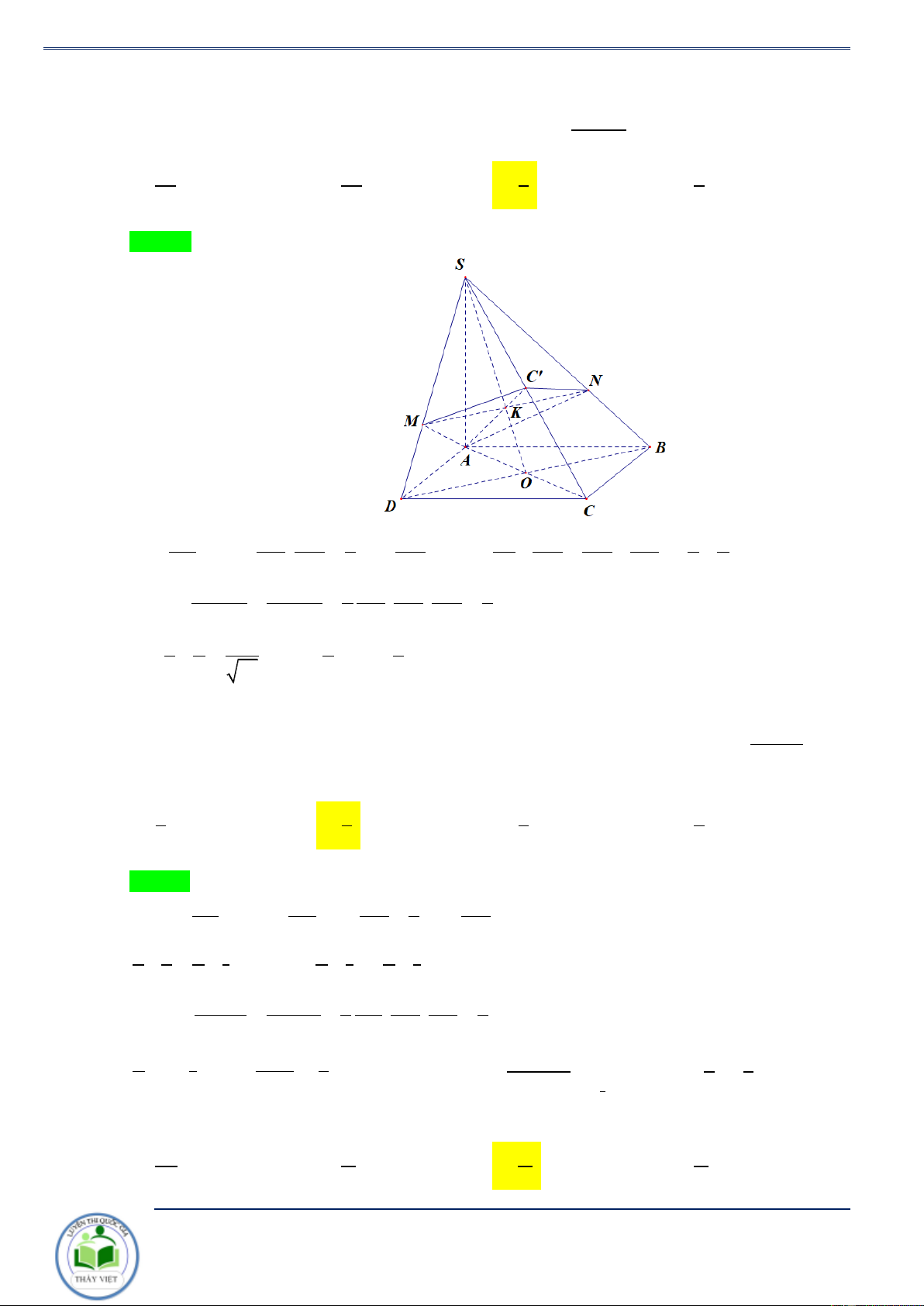
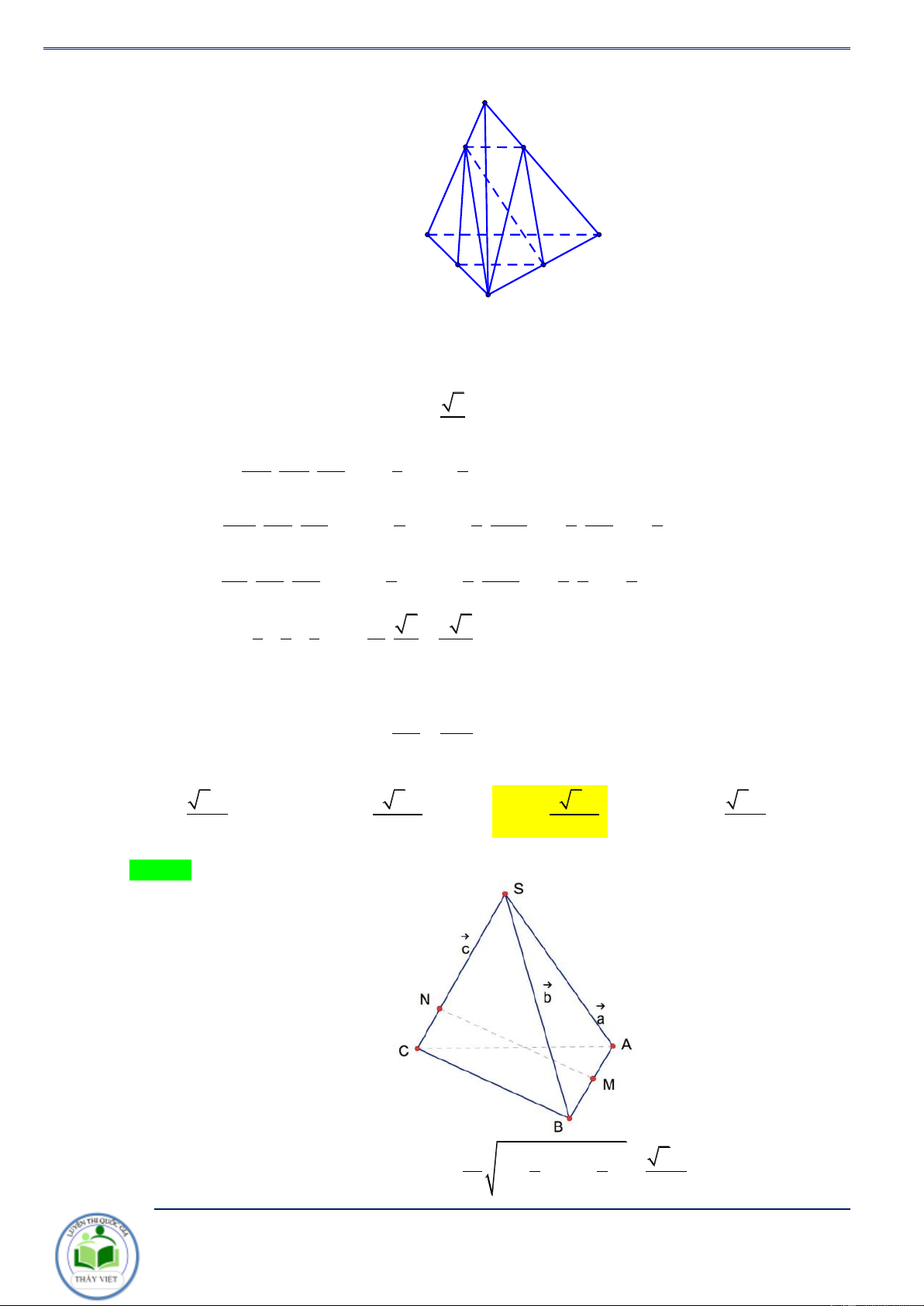
Cho khối chóp tam giác S.ABC . Mặt phẳng ( P) cắt các đường thẳng S , A S , B SC lần lượt tại V
SA' SB ' SC '
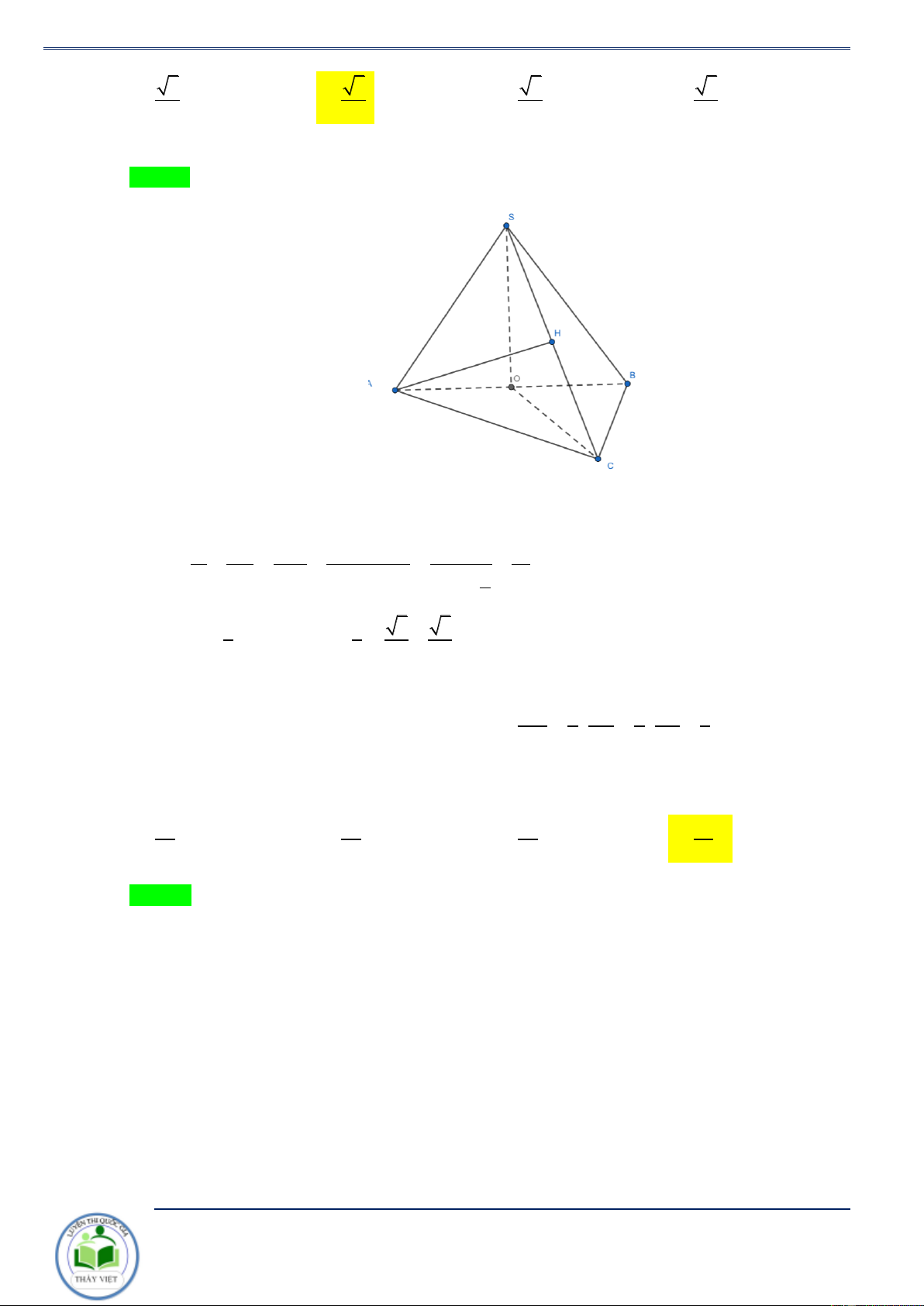
A', B',C ' . Khi đó ta có S.A'B'C ' = . . (*). V SA SB SC S . ABC Chứng minh. S
Gọi H,H ' lần lượt là hình chiếu của , A A'
trên mp (SBC ) . 1 H’ V =V = AH.S .
B SC.sin BSC và C’ S . ABC . A SBC 6 1 V
= A'H '.SB'.SC '.sin B'SC ' A’
A'.SB 'C ' 6 H V
AH ' SB ' SC ' B’
S . A' B 'C '  = . . C V AH SB SC A S . ABC A' H ' SA' Rõ ràng = AH SA B V
SA' SB ' SC '
S . A' B 'C '  = . . V SA SB SC S . ABC
Đây là kết quả quen thuộc và nó là bài toán
mở đầu cho rất nhiều ứng dụng hay sau này. \
II. MỘT SỐ TÍNH CHẤT . 1. Tính chất 1.
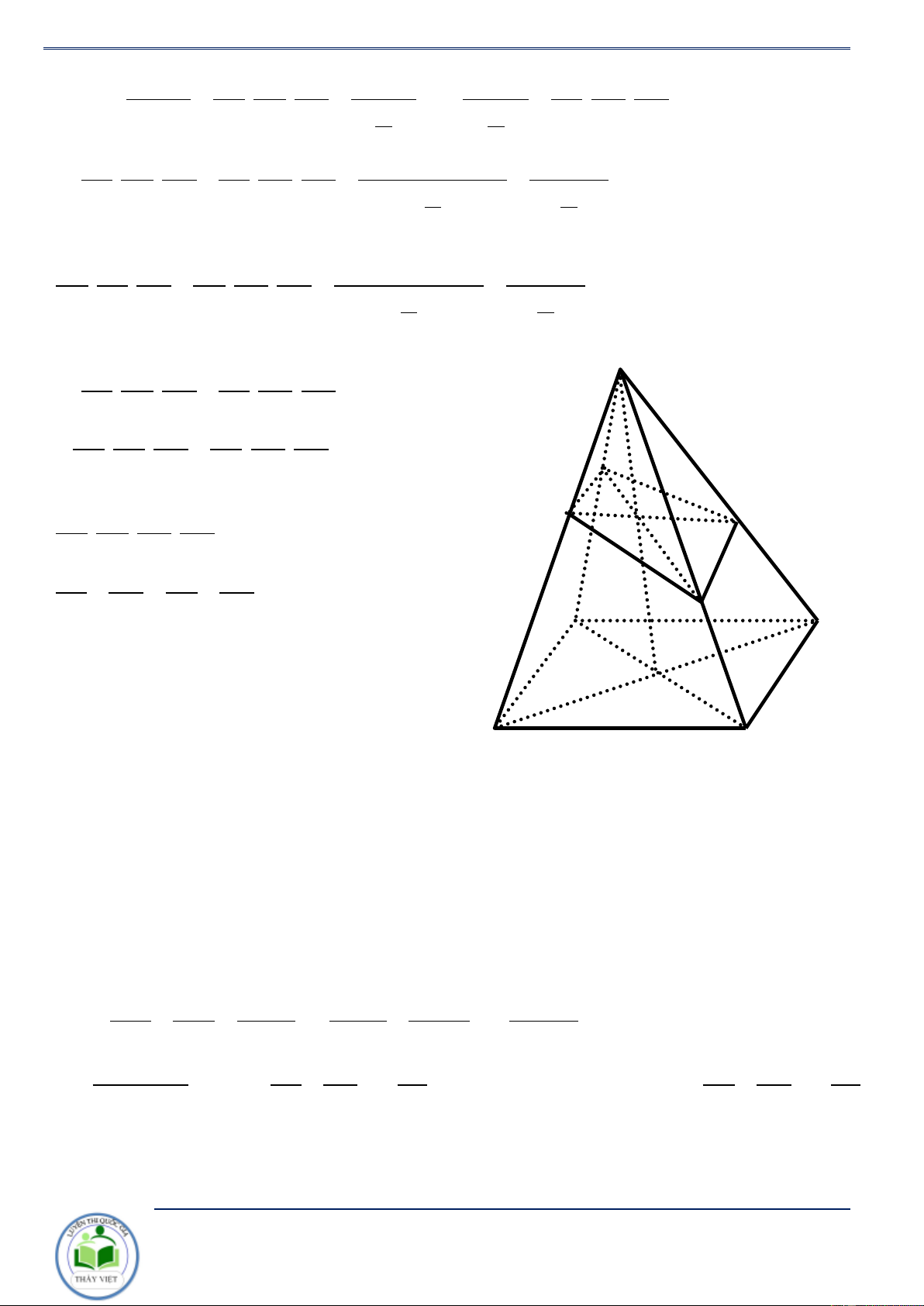
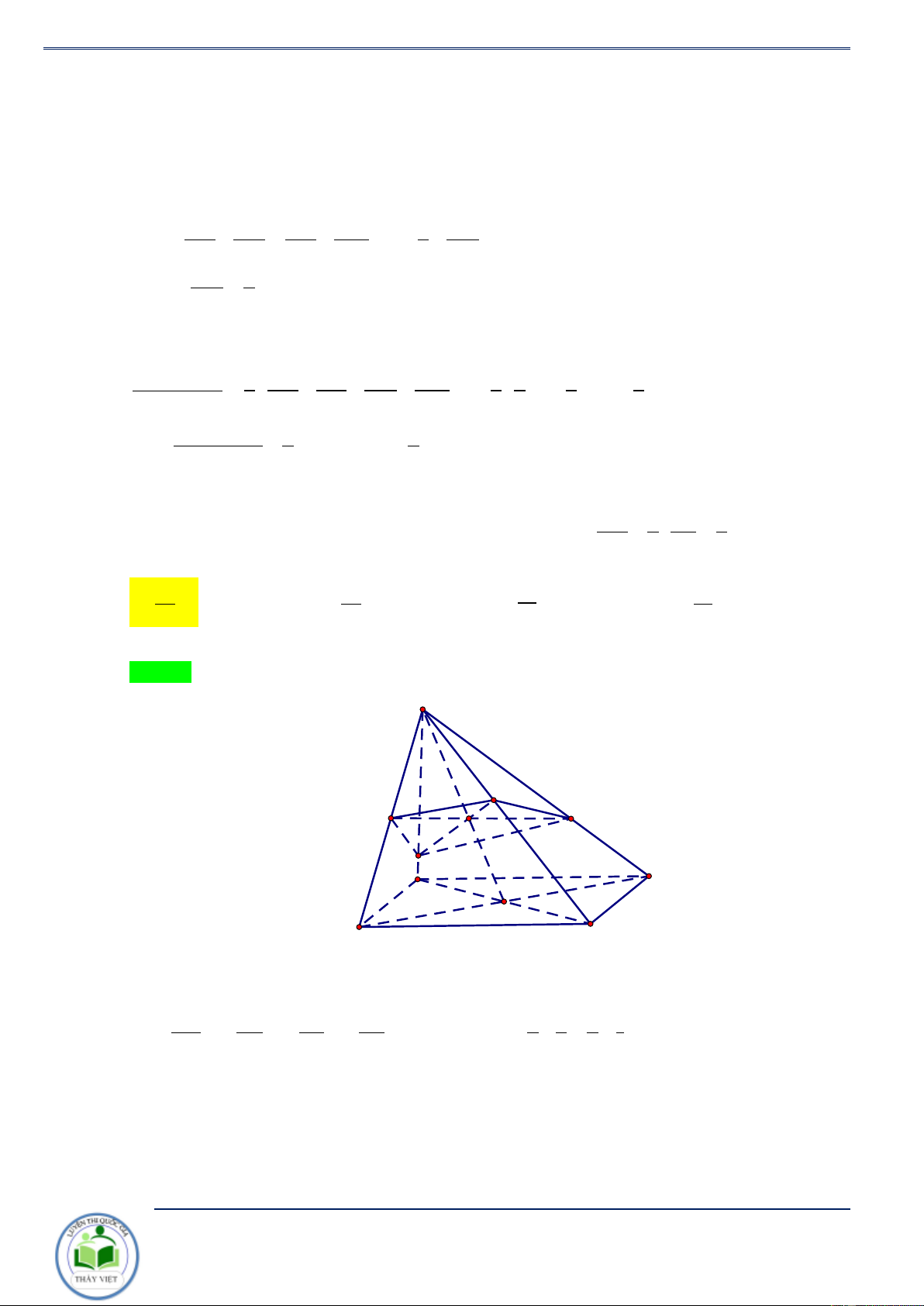
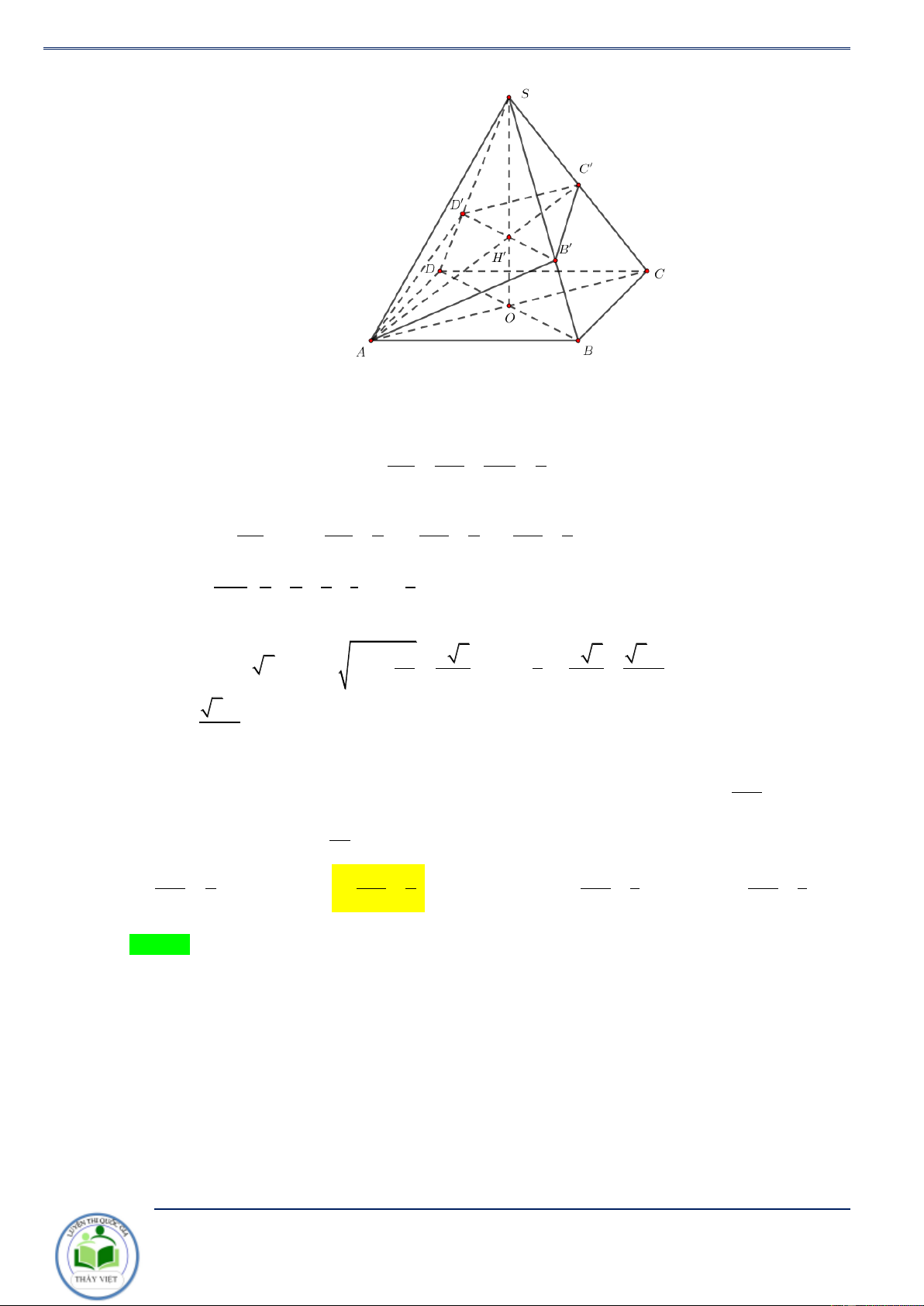
Cho hình chóp S.ABCD , đáy ABCD là hình bình hành. Mặt phẳng ( P) S , A S , B SC,SD lần
lượt tại A', B',C', D' . Khi đó ta có SA SC SB SD + = + SA' SC ' SB ' SD ' Chứng minh. Đặt V V =V V =V =V =V = S.ABCD S.ABC S.ADC S .BAD S .BCD 2
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 2/105 V
SA' SB ' SC ' V V
SA' SD ' SC '
Ta có S.A'B'C '
S . A' B 'C ' = . . =
S . A' D 'C ' và = . . V SA SB SC V V SA SD C S SABC 2 2
SA' SB ' SC '
SA' SC ' SD ' V +V V
S . A' B 'C '
S . A'C ' D '
S . A' B 'C ' D '  . . + . . = = ( ) 1 SA SB SC SA SC SD V V 2 2 Tượng tự ta có
SB ' SA' SD '
SB ' SC ' SD ' V +V V
S .B ' A' D '
S .B 'C ' D '
S . A' B 'C ' D ' . . + . . = = (2) SB SA SD SB SC SD V V 2 2 Từ (1), (2) S
SA' SB ' SC '
SA' SC ' SD '  . . + . . SA SB SC SA SC SD
SB ' SA' SD '
SB ' SC ' SD ' = . . + . . (3) SB SA SD SB SC SD D’
Nhân vào hai vế của (3) với SA SB SC SD A’ C’ . . . ta được I
SA' SB ' SC ' SD ' SA SC SB SD + = + SA' SC ' SB ' SD ' B’ C D
Suy ra điều phải chứng minh. O A B
Tính chất 1 ta chỉ áp dụng cho chóp có đáy là hình bình hành.
Việc chứng minh Tính chất 1 như trên là ta đã áp dụng tính chất (*). Tuy nhiên ta có thể chứng
minh Tính chất 1 nhanh gọn như sau :
Gọi O là tâm hình bình hành, I là giao điểm của SO và ( A'B'C 'D'). S S 2S SA'.SI SC '.SI SA'.SC ' Ta có SA'I SC ' I SA'C ' + =  + = 2.
. Nhân cả hai vế của đẳng thức sau S S S S . A SO SC.SO S . A SC SAO SCO SAC S . A SC.SO SA SC SO SB SD SO cho ta được + = 2.
. Chứng minh tương tự ta có + = 2. .
SA'.SC '.SI SA' SC ' SI SB ' SD ' SI
Vậy ta có điều phải chứng minh.
*) Cách chứng minh này còn cho ta kết quả mạnh hơn là
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 3/105
Kết quả 1 : Cho hình chóp S.ABCD , đáy ABCD là hình bình hành. Mặt phẳng (P) S , A S ,
B SC,SD lần lượt tại A', B',C ', D' . Khi đó ta có SA SC SB SD SO + = + = 2. . SA' SC ' SB ' SD ' SI
Kết quả trên còn có thể được chứng minh bằng nhiều cách khác nữa. Nó là kết quả rất hay và
được ứng dụng nhiều trong hình học không gian.
Tính chất 1 được ứng dụng rất nhiều trong bài toán tìm thiết diện cũng như thể tích khối đa diện. SA SB SC SD Đặt x = ; y = ; z = ; t =
(x, y,z,t  0)(**) SA' SB ' SC ' SD '
Vận dụng Tính chất (*) và Tính chất 1 ta có V V V
1  SA' SB ' SC '
SA' SD ' SC ' 
S . A' B 'C ' D '
S . A' B 'C '
S . A ' D 'C ' = + = . . + . .   V 2V 2V 2  SA SB SC SA SD SC S . ABCD S . ABC S . ADC 1  1 1  y + t
x + y + z + t = + = =  
do x + z = y + t . Ta có 2  xyz xtz  2xyz 4xyz + + + Kết V x y z t
quả 2 : S.A'B'C 'D' =
với x, y, z,t được xác định như (* ) * . V 4xyzt S . ABCD
Chú ý : Nếu A', B',C', D' lần lượt thuộc các cạnh S , A S , B SC,SD thì ,
x y, z,t  1.
Kết quả 2 được áp dụng vào giải quyết các bài toán thể tích khối chóp có đáy là hình bình hành
một cách rất nhanh gọn và đơn giản thay cho việc phải chia khối chóp tứ giác loại này thành các
khối chóp tam giác để sử dụng Tính chất (*)
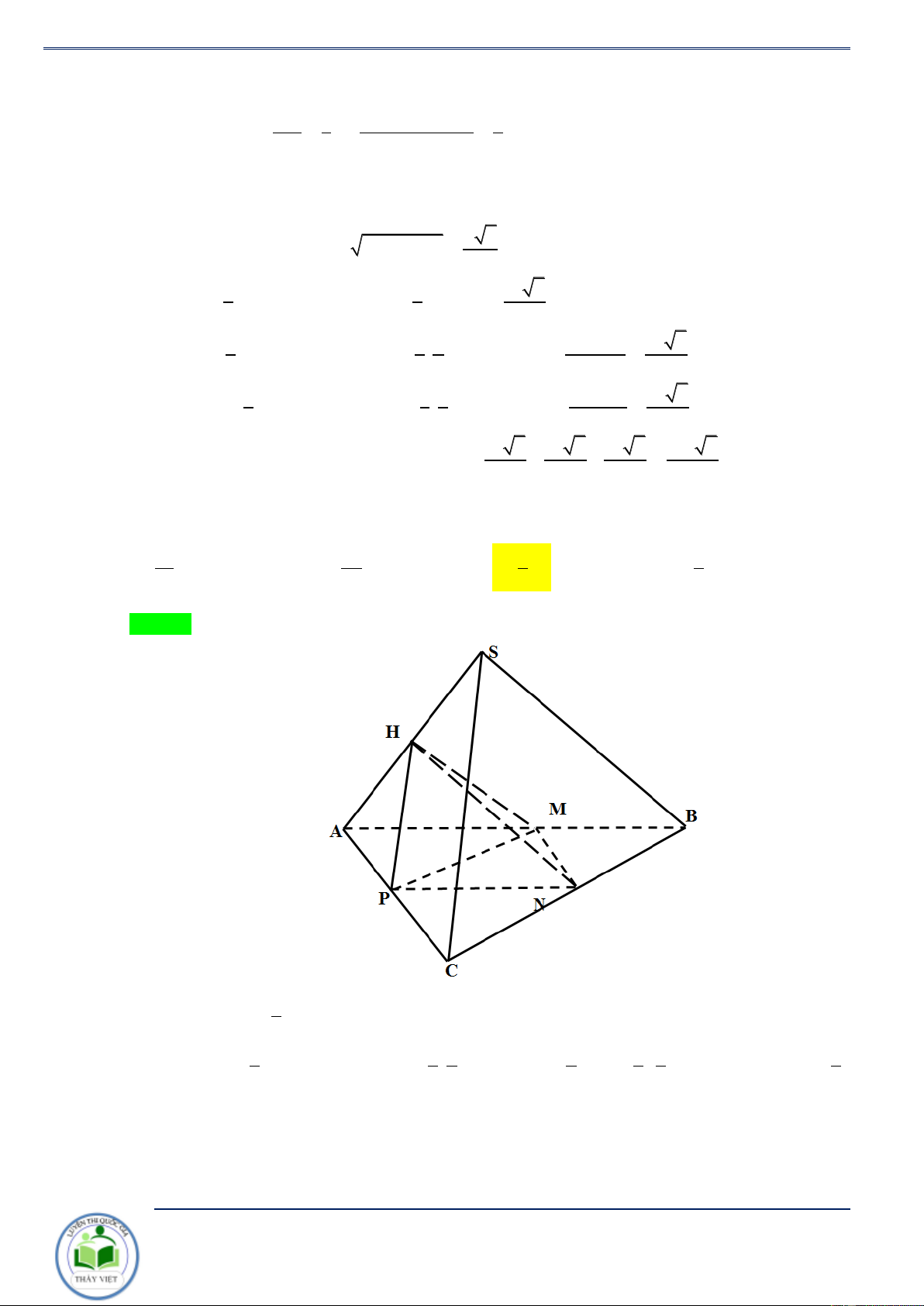
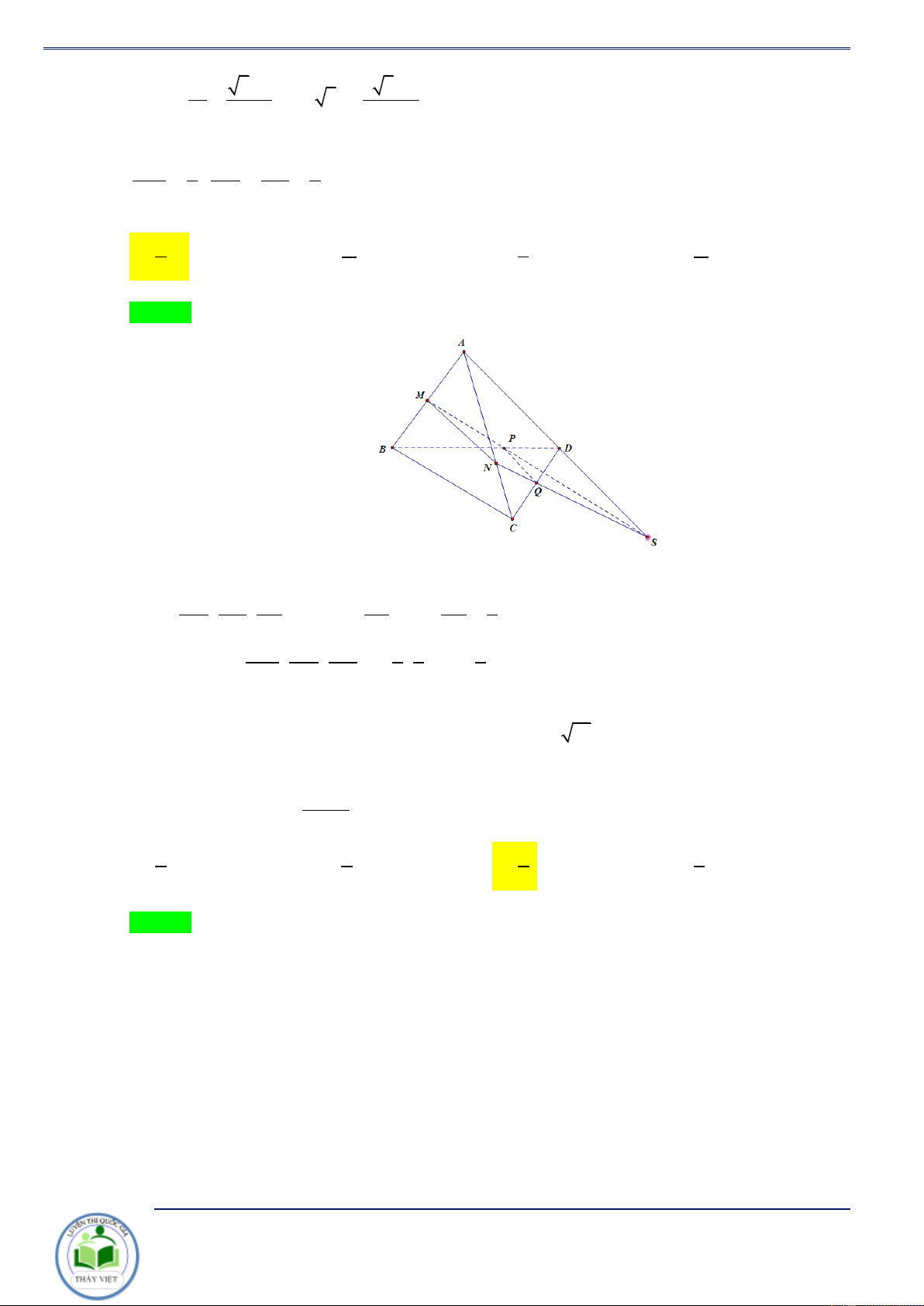
Ví dụ 1. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm SB , điểm V
P thuộc cạnh SD sao cho SP = 2PD . Mặt phẳng ( AMP) cắt SC tại N . Tỷ số S.AMNP VS.ABCD bằng Giải. S Ta có SA SC SB SD SC 3 + = +  1+ = 2 + SA SN SM SP SN 2 N P SC 5  = M SN 2 5 3 D 1 + 2 + + A Vậy V 7 S.AMNP 2 2 = = V 5 3 30 S . ABCD 4.1.2. . 2 2 B C
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 4/105
Ví dụ 2. Cho hình chóp S.ABCD có thể tích bằng V , đáy ABCD là hình vuông. Cạnh
SA ⊥ ( ABCD) và SC hợp với đáy một góc bằng 30 . Mặt phẳng ( P) đi qua A và vuông góc
với SC , cắt các cạnh S ,
B SC, SD lần lượt tại E, F, K . Thể tích khối chóp S.AEFK bằng Giải. 2 2 SA SE SB SB Ta có 2 SA = S . E SB  =  = 2 2 SB SB SE SA 2 Tương tự SD SD = SB SD nên = 2 SK SA SE SK 2 SC SC Mà = = 4 2 SF SA ( do SCA vuông tại 0 , A SCA = 30 ) SC SB SD SB SD 5 nên +1= + = 5  = = SF SE SK SE SK 2 V 10 1 V V S . AEFK S . ABCD = =  V = = . S . V 5 5 10 AEFK 10 10 S . ABCD 4.1.4. . 2 2
Ví dụ 3. Cho khối chóp S.ABCD có đáy ABCD là hình bình hành. Mặt phẳng (P) chứa cạnh
AB và đi qua điểm M trên SC chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau. Tính tỷ số SM k = . SC Giải. AB  (P)
Gọi N = (P)  SC ta có  nên MN CD . AB CD SM SC SD 1 Ta có k =  = = SC SM SN k 1 1 1 + 1 + + Khi đó V 1 SABMN k k = = V 1 2 SABCD 4. 2 k 1 1 1 1 + 5 5 −1 − −1= 0  =  k = . 2 k k k 2 2
Ví dụ 4. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. I nằm trên SC sao cho IS = 2IC .
Mặt phẳng (P) chứa cạnh AI cắt cạnh S ,
B SD lần lượt tại M , N . Gọi V ',V lần lượt là thể tích V
khối chóp S.AMIN và S.ABCD . Tính giá trị nhỏ nhất của tỉ số thể tích ' V Giải.
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 5/105 Đặt SB SD = x,
= y x, y 1. SM SN 3 5 5
Ta có  x + y = 1+ =  x + y = 2 2 2 Ta có 3 x + y +1 + V ' 5 5 8 2 = =  = 2 V 3 6xyx + y  15 4 . x . y 1. 6 2    2  Dấu bằng xảy ra khi 5 x = y = . 4
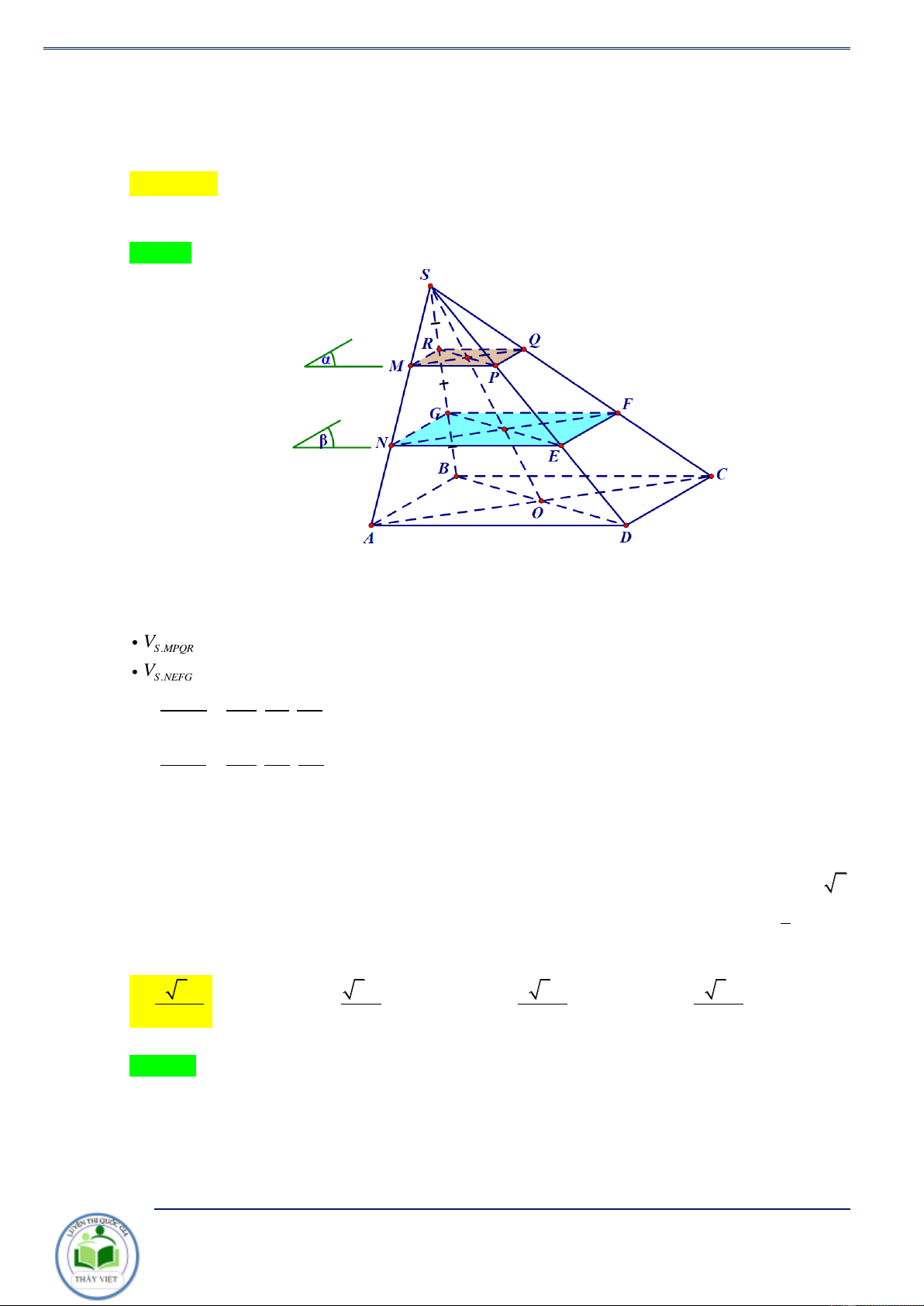
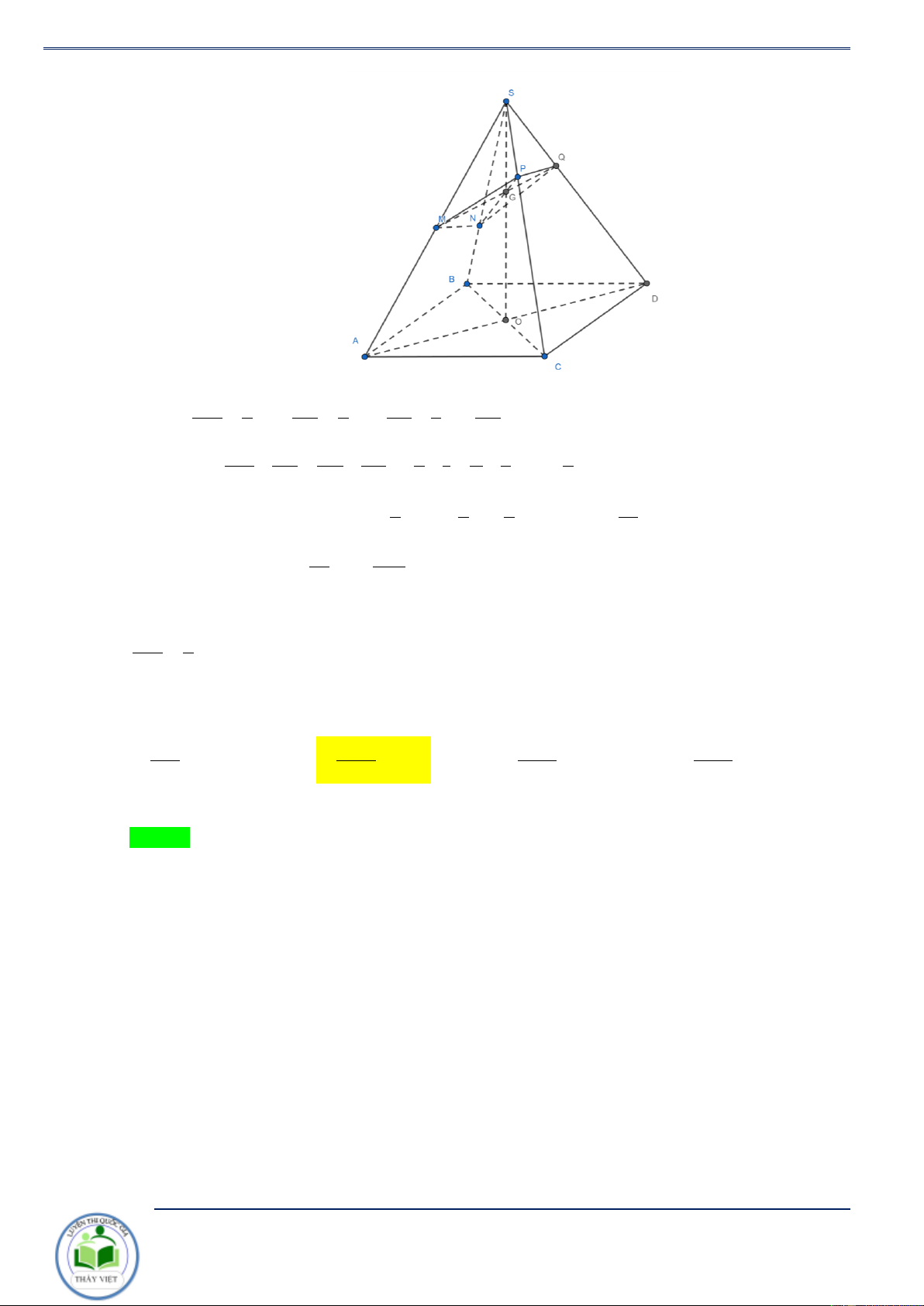
Ví dụ 5. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Mặt phẳng ( )
thay đổi luôn đi qua B , trung điểm I của SO và cắt các cạnh S ,
A SC và SD lần lượt tại V M , N và .
P Tính GTNN và GTLN cùa tỷ số S.BMPN . VS.ABCD Giải. Đặt SA SC = x,
= y x, y 1. SM SN SA SC SB SD SO Ta có + = + = 2. = 4 SM SN SB SP SI SD Nên
= 3; x + y = 4. Từ đó SP V 8 2 2 S .BMPN = = = V 4. . x .3 y .1 3xy 3x 4 − x S . ABCD ( )
Từ x + y = 4  x = 4 − y  3 vì y 1. Xét 2 4 − 2x f ( x) 2 =   f '(x) ( ) = = 0  x = 2
x ( − x) , 1 x 3 3 4 3x(4 − x) 2    2 1 Ta có f ( )
1 = f (3) = ; f (2) = . 9 6
Vậy VS.BMPN đạt GTNN, GTLN lần lượt là 1 2 , . V 6 9 S . ABCD
Nhận xét. Qua năm ví dụ trên ta thấy sự lợi hại của Kết quả 2 đem lại. Vừa nhanh, dễ sử dụng
mà hiệu quả thì cực tốt. Rất hợp cho học sinh trong việc làm bài trắc nghiệm.
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 6/105
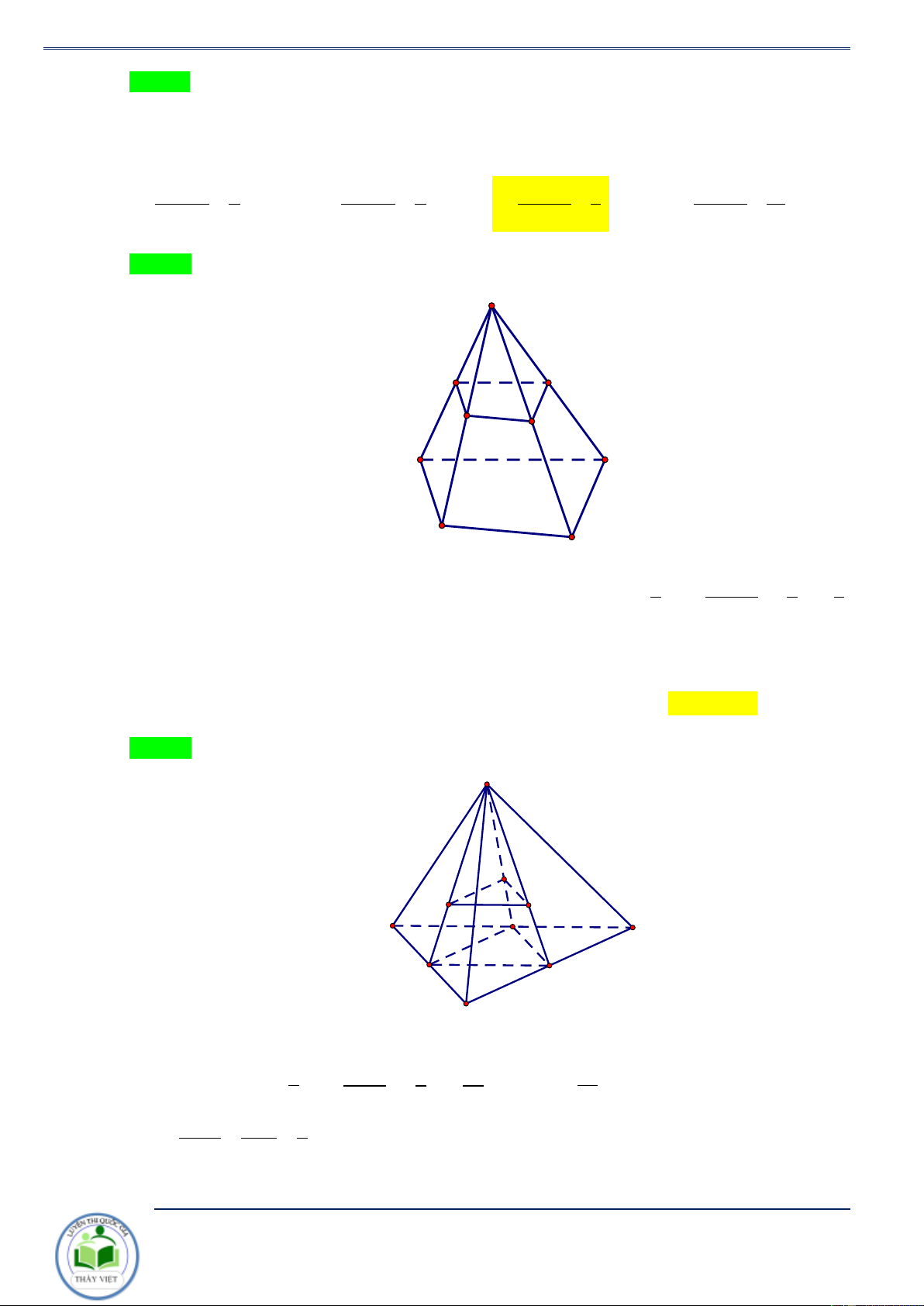
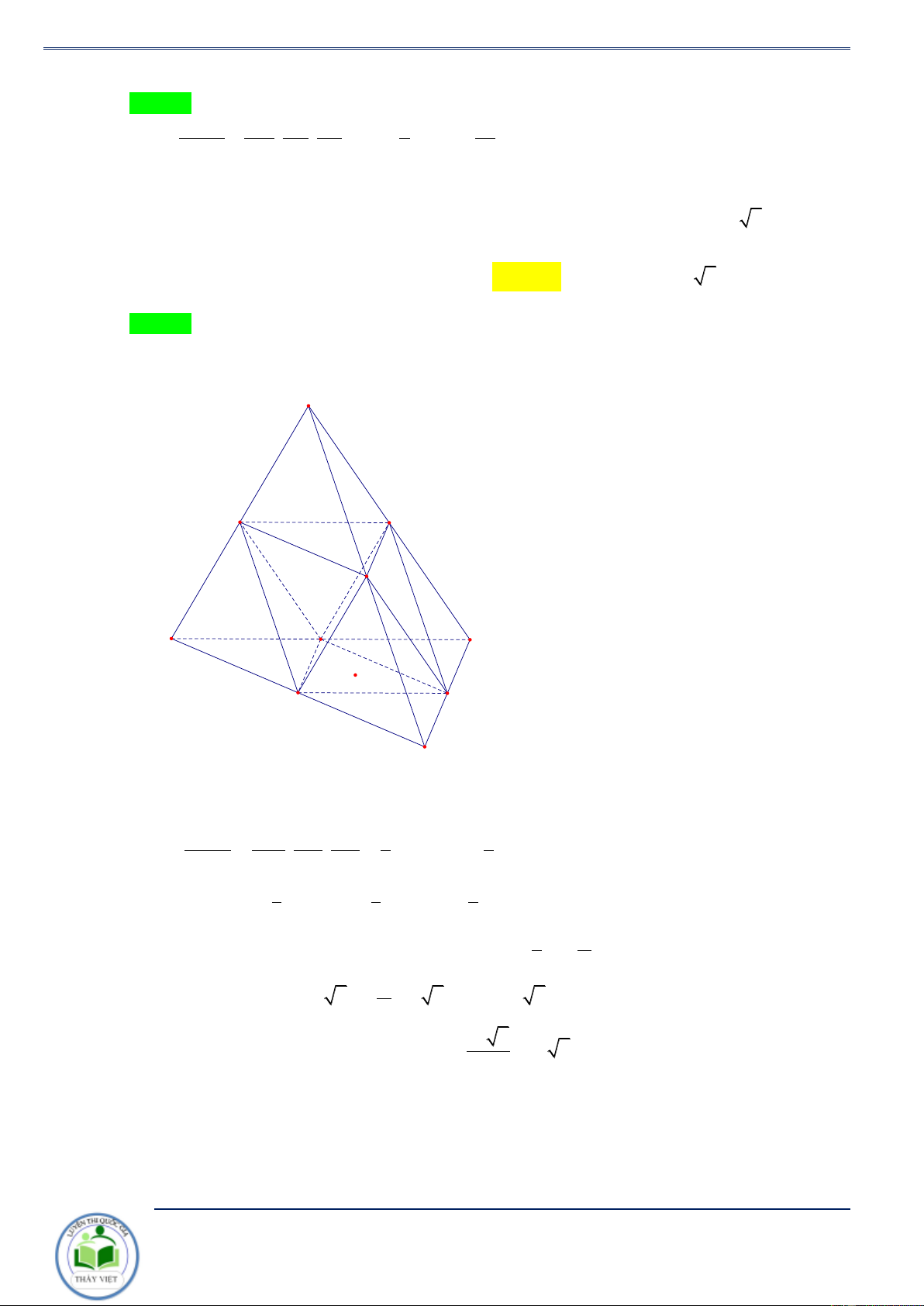
2. Tính chất 2. Cho lăng trụ ABC.A B C có các điểm M, N,P lần lượt thuộc các cạnh 1 1 1 AM BN CP V x + y + z
AA , BB ,CC sao cho = x, = y,
= z . Khi đó ta có tỷ số ABCMNP = . 1 1 1 AA BB CC V 3 1 1 1 ABC. 1 A 1 B 1 C
Chứng minh. Ta có V = V +V , đặt ABCMNP M . ABC M .BCPN V = V ABC. 1 A 1 B 1 C 2V dễ thấy V = . A BC 1 C 1 B 3 + Ta có
1 d(M;(ABC)).SABC V
1 d (M ;( ABC)) 1 AM 1 M . ABC 3 = = . = = x V
d ( A ;( ABC).S
3 d ( A ;( ABC) 3 AA 3 1 ABC 1 1 x Suy ra V = .V 1 . M . ABC ( ) 3
Do AM / / (BCC A V =V 1 1 ) M .BCPN . A BCPN Nên
1 (CP + BN).d( ; P BB ) 1 V V S yBB + zCC y + z M .BCPN . A BCPN BCPN 2 1 1 = = = = = BB = CC V V S
BB .d P, BB 2BB 2 . A BCC B . A BCC B BCC B 1 ( 1 ) ( 1 1 ) 1 1 1 1 1 1 1 V y + z y + z 2V y + z M .BCPN  = V = . = .V 2 . M .BCPN ( ) V 2 2 3 3 . A BC 1 C 1 B + + + + Vậy từ ( ) x y z V x y z 1 ,(2) ta có V =V +V = . ABCMNP V  = . ABCMNP M . ABC M .BCPN 3 V 3 ABC. 1 A 1 B 1 C + Đặc biệt V x V y z : . A MNP M . = , BCPN = . V 3 V 3 ABC. 1 A 1 B 1 C ABC. 1 A 1 B 1 C
Ví dụ 6. Cho khối lăng trụ ABC.A BC
  , có M,N,P lần lượt thuộc các cạnh AA ,BB ,CC sao cho AM = MA ,
BN = 3NB ,CP = 3PC. Đặt V là thể tích của khối đa diện ABCMNP , V là thể 1 2
tích của khối đa diện còn lại. T V ính tỉ số 1 . V2
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 7/105 Giải. Ta có MA 1 BN 3 MA = MA 
= ;BN = 3NB  = ; AA 2 BB 4 CP 3 CP = 3PC  = CC 4 Đặt V = V ABC. A BC   Suy ra 1 3 3 + + V 2 2 1 1 2 4 4 =
= V = V V =V −V = V 1 2 1 V 3 3 3 3 V1  = 2 V 2
Ví dụ 7. Cho khối lăng trụ ABC.A BC
  có thể tích bằng V , các điểm M,N,P lần lượt thuộc
các cạnh AA , BB ,CC sao cho AM = 2MA , BN = 3NB ,CP = .
x PC . Đặt V là thể tích của khối 1 đa diện V 3
ABC.MNP , tính giá trị của x để 1 = . V 5 Giải. Ta có AM 2 BN 3 MA = 2MA 
= ;BN = 3NB  = ; AA 3 BB 4 CP x CP = xPC  = CCx + 1 Suy ra 2 3 x + + V 3 17 x 9 + 1 3 4 x 1 = =  + = V 3 5 12 x +1 5 . x 23 23  =  x = . x + 1 60 37
Ví dụ 8. Cho khối lăng trụ ABC.A BC
  có thể tích bằng 3
60cm , các điểm M , N, P lần lượt
thuộc các cạnh AA , BB ,CC sao cho AM = 2MA , BN = 3NB ,CP = 4PC . Thể tích của khối đa diện B . C MNP .
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 8/105 Giải. Ta có AM 2 BN 3 MA = 2MA 
= ;BN = 3NB  = ; AA 3 BB 4 CP 4 CP = 4PC  = CC 5 Nên 2 3 4 + + V 133 ABCMNP 3 4 5 = = V 3 180
ABCA' B 'C ' 133 133 V = .60 = ABCMNP 180 3 1 1 2 2 40 Mà V
= d M; ABC .S
= . d A'; ABC .S = .V = . M . ABC ( ( )) ABC ( ( )) ABC
ABC. A' B 'C ' 3 3 3 9 3 Vậy 133 40 V = − = 3 cm BCMNP ( 3 1 ). 3 3
Nhận xét. Các bài toán dạng này sẽ xuất hiện nhiều khối không phải là các khối có công thức
tính thể tích như chóp hay lăng trụ.. Thay vì việc phải phân chia các khối này thành các khối có
công thức tính, nay ta có ngay một kết quả rất nhanh và chính xác. Ví dụ 9.
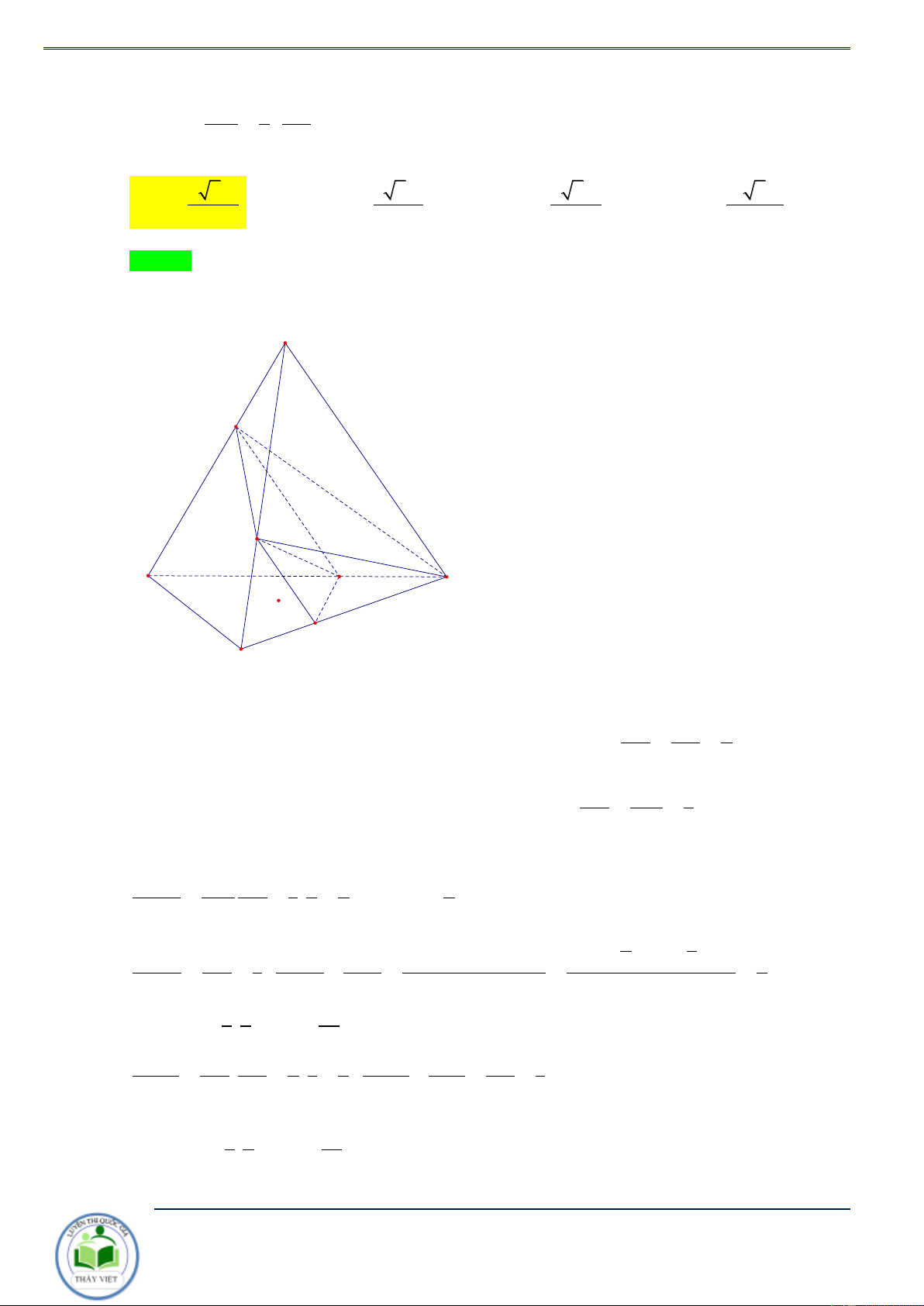
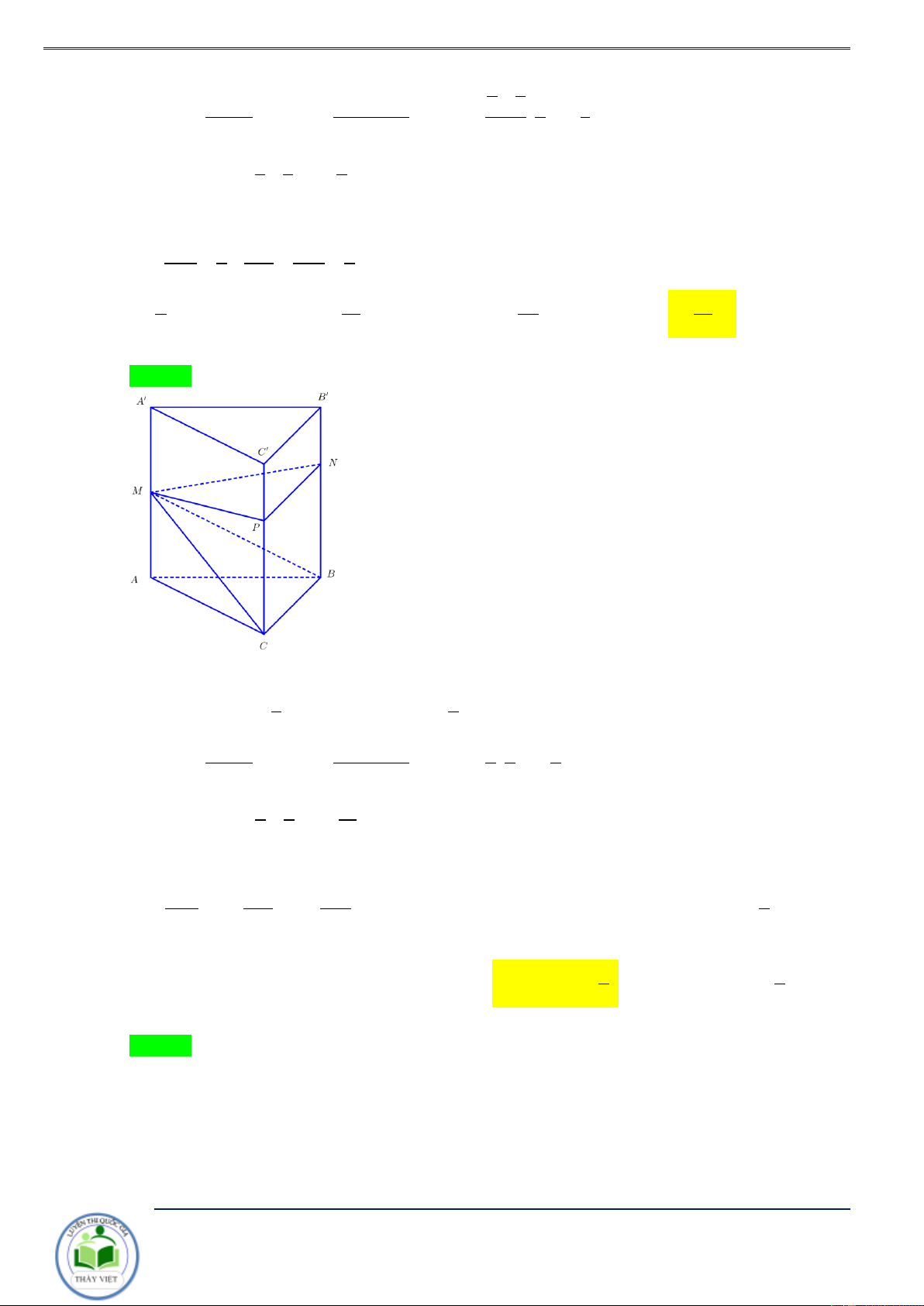
Cho lăng trụ AB .
C A' B'C ' có G,G ' lần
lượt là trọng tâm của B ABC, A  'B'C . A Mặt phẳng ( ) G
cắt AA', BB',CC ',GG '
lần lượt tại M , N, , P I . Chứng minh M C rằng AM BN CP GI + + = 3. N AA' BB ' CC ' GG ' I Chứng minh. Đặt AM BN CP GI x = , y = , z = ,t = ; AA' BB ' CC ' GG ' B’ P V = V
ABC. A' B 'C ' Dễ thấy A’ G’ V V =V =V =
AGB. A'G ' B '
CGB.C 'G ' B '
AGC. A'G 'C ' 3 C’ V x + y + t V
z + y + t V z + y + t Ta có AGBMIN = . Tương tụ ta có CGBPIN = ; CGAPIN = V 3 V 3 V 3
VAGB.A'G 'B' C
V GB.C 'G'B' C
V GA.C 'G ' A'
Cộng vế với vế cả 3 đẳng thức trên ta được 3V x + y + t z + y + t z + y + t
2 x + y + z ABCMNBP ( ) = + + = + t V 3 3 3 3
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 9/105 3V x + y + z x + y + z Mà ABCMNBP = 3.
= x + y + z nên t =
. Ta được điều phải chứng minh. V 3 3
Từ kết quả trên ta có V GI ABCMNBP = . V GG '
ABC. A' B 'C '
Nhận xét. Dựa vào kết quả trên ta thấy rẳng chỉ cần biết ( ) cắt GG' tại vị trí điểm I xác định
là ta đã biết ( ) chia lăng trụ thành hai phần với tỉ số bao nhiêu rồi.
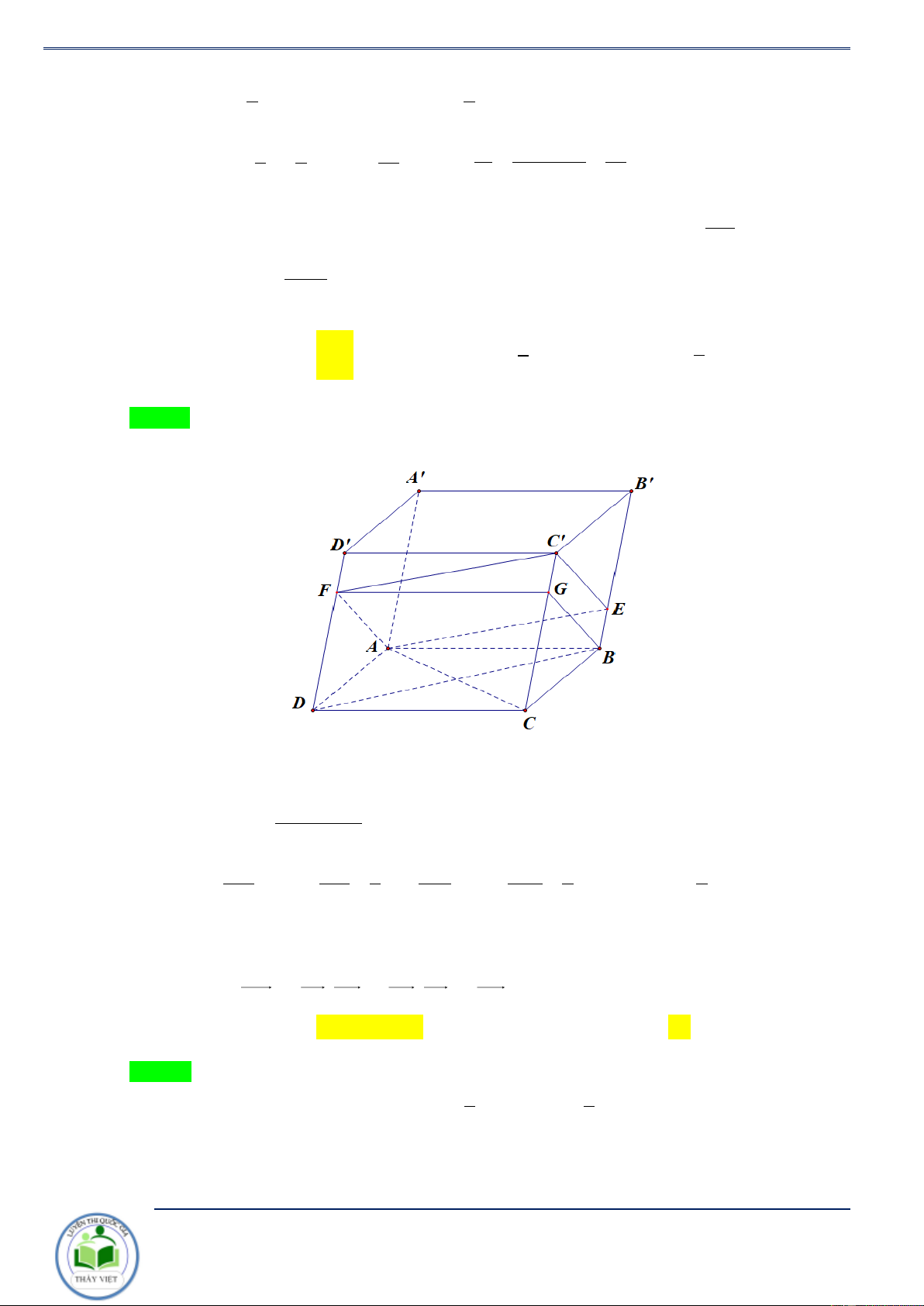
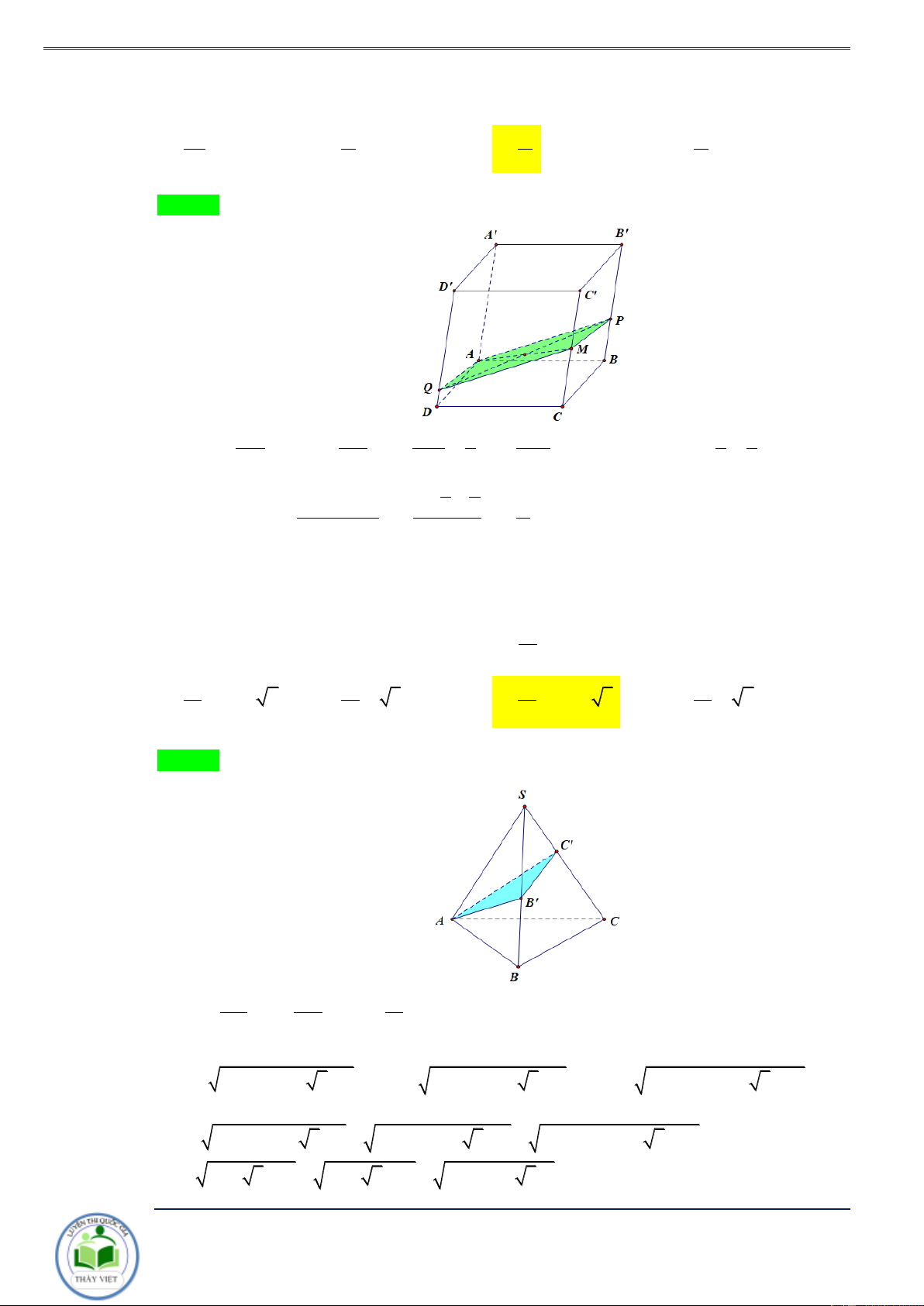
3. Tính chất 3. Cho hình hộp ABC .
D A' B'C ' D' . Mặt phẳng ( ) cắt
các cạnh AA', BB',CC', DD' lần lượt tại M , N, , P Q sao cho AM BN CP DQ = x, = y, = z, = t . ' ' ' ' AA BB CC DD Khi đó ta có :
a. x + z = y + t. V
x + y + z + t x + z y + t b. ABCDMNQP = = = V 4 2 2
ABCD. A' B 'C ' D ' Chứng minh.
a. Dễ thấy tứ giác MNPQ là hình bình hành. Gọi I,O lần lượt là tâm của hình bình hành MNPQ
và hình vuông ABCD . Ta có OI là đường trung bình của hình thang AMPC nên AM + CP BN + DQ OI = . Tương tự OI = , do đó 2 2
AM + CP = BN + DQ  A
x A'+zCC'=yBB'+tDD'  x + z = y + t
b. Áp dụng Tính chất 2 ta có V x + y + t 2V x + y + t V + + ABDMNQ ABDMNPQ ABDMNQ x y t =  =  = V 3 V 3 V 6
ABD. A' B ' D '
ABCD. A' B 'C ' D '
ABCD. A' B 'C ' D ' V + + tương tự BCDNPQ y z t = V 6
ABCD. A' B 'C ' D ' Do đó, V V V + + + + + + + + + ABCDMNPQ ABDMNQ BCDNPQ x y t y z t x y z t y t = + = + = V V V 6 6 6
ABCD. A' B 'C ' D '
ABCD. A' B 'C ' D '
ABCD. A' B 'C ' D '
x + y + z + t
x + y + z + t + 2
x + y + z + t = = 6 4 V
x + y + z + t OI Chú ý : ABCDMNQP = = . V 4 OO '
ABCD. A' B 'C ' D '
Nhận xét. Một kết quả tương tự như Tính chất 2. Ở lăng trụ là tổng ba tỉ số chia ba, còn hình hộp là chia bốn.
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 10/105
Và cũng chỉ cần biết ( ) cắt đoạn thẳng nối hai tâm đáy ở đâu là ta đã tìm được tỷ số hai khối
tạo thành do ( ) cắt hình hộp. Tuy nhiên, Tính chất 3 cũng khẳng định chỉ cần biết hai tỉ số ở
hai cạnh bên đối diện của hình hộp mà ( ) cắt là ta cũng tìm được tỉ số thể tích các khối.
Ví dụ 10. Cho khối hộp chữ nhật ABC . D A BCD
  có thể tích bằng 2110 . Biết A M  = M ,
A DN = 3ND và CP = 2C P
 . Mặt phẳng (MNP) chia khối hộp đã cho thành hai khối
đa diện. Thể tích khối đa diện nhỏ hơn bằng bao nhiêu. Giải. (MNP) cắt ’ BB tại Q .
Từ giải thiết ta có AM 1 CP 2 = ; = . AA' 2 CC ' 3 Do đó AM CP 1 2 + + VABCDMNPQ 7 AA' CC ' 2 3 = = = V 2 2 12
ABCD. A' B 'C ' D ' 7 7385 V = .2110 = ABCDMNPQ 12 6 Vậy 7385 5275 V = 2110 − =
A' B 'C ' D ' MNPQ 6 6
Ví dụ 11. Cho hình lập phương ABC . D A BCD
  có N là trung điểm CC . Mặt phẳng ( ) đi
qua AN , cắt các cạnh BB ', DD lần lượt tại M , P . ( ) chia khối lập phương thành hai phần có
thể tích tương ứng bằng V
V và V V V . Tính tỉ số 2 2 ( 1 2 ) 1 V1 Từ giải thiết ta có AA CN 1 + 0 + V 1 ABCDPNM AA' CC ' 2 = = = V 2 2 4
ABCD. A ' B 'C ' D ' V 1 V Nên ABCDPNM 2 =  = 3 V 3 V
AMNPA' B 'C ' D ' 1
Kết luận. Việc áp dụng các tính chất trên vào lớp các bài toán thể tích tương ứng rất là hữu ích.
Nó làm cho việc giải toán trắc nghiệm của các em học sinh nhanh gọn và nhẹ nhàng hơn nhiều
so với việc giải truyền thống. Hy vọng nó sẽ giúp các em đạt kết quả cao nhất trong các kỳ thi sắp tới.
III. MỘT SỐ BÀI TẬP ÁP DỤNG .
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 11/105
TỶ SỐ THỂ TÍCH KHỐI ĐA DIỆN (ĐỀ SỐ 01) A. LÝ THUYẾT
1. Một số kiến thức cần biết
Kiến thức cần nhớ đối với khối lăng trụ tam giác và khối hộp V 2V V = , V = AABC   3 A'.BCC B 3 V V V = , V = AABD   6 BDA C 3 2 2 BH
AB CH AC
Tam giác ABC vuông tại A có đường cao AH có = , =     BC
BC CB BC
Định lý menelaus: Ba điểm D, E, F lần lượt nằm trên 3 đường thẳng chứa 3 cạnh BC,C , A AB của FA DB EC
tam giác ABC , khi đó ,
A B C thẳng hàng khi và chỉ khi . . = 1 FB DC EA Công thức 1: V S
Hai khối chóp có chung đỉnh và chung mặt đáy 1 1 = V S 2 2
Hai khối chóp S.A A ...A và S.B B ...B có chung đỉnh và hai mặt đáy cùng nằm trên một mặt phẳng, 1 2 n 1 2 n V S
ta có S.A A ...A A A ...A 1 2 n 1 2 n = V S S. 1 B 2 B ... n B 1 B 2 B ... n B
Ví dụ 1: Cho khối chóp S.ABC có thể tích V . Gọi M , N , P lần lượt là trung điểm các cạnh BC ,CA, AB và V
V  là thể tích khối chóp S.MNP . Tính tỉ số . V V  3 V  1 V  1 V  1 A. = . B. = . C. = . D. = . V 4 V 3 V 2 V 4 Lời giải Chọn D 2 V S  1  1 Ta có: MNP = = =   . Chọn đáp án D. V S  2  4 ABC
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 12/105
Ví dụ 2: Cho khối chóp S.ABCD có thể tích V . Gọi M , N , P ,Q lần lượt là trung điểm các cạnh AB , BC , V
CD , DA . Gọi V  là thể tích khối chóp S.MNPQ . Tính tỉ số . V V  3 V  1 V  1 V  1 A. = . B. = . C. = . D. = . V 4 V 8 V 2 V 4 Lời giải Chọn D V SMNPQ 1 Ta có: =
= . Chọn đáp án C. V S 2 ABCD
Ví dụ 3: Cho khối chóp S.ABCD có thể tích V và đáy ABCD là hình vuông tâm I . Các điểm P ,Q lần lượt
trên các cạnh AB , AD sao cho PIQ = 90 ( P , Q không phải là đỉnh của hình vuông). Tính thể tích
của khối chóp tứ giác S.APIQ . V V V V A. . B. . C. . D. . 2 3 4 6 Lời giải Chọn C V S S APIQ APIQ 1 V Ta có: . = =  V = . Chọn đáp án C. S . V S 4 APIQ 4 ABCD
Công thức 2 : Công thức Simson (tỷ số thể tích) Cho khối chóp tam giác S.ABC . Gọi A , B ,C lần 1 1 1 V lượt là các điể SA SB SC
m nằm trên các cạnh SA, SB , SC ta có : S.A B C 1 1 1 1 1 1 = . . . V SA SB SC S . ABC
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 13/105
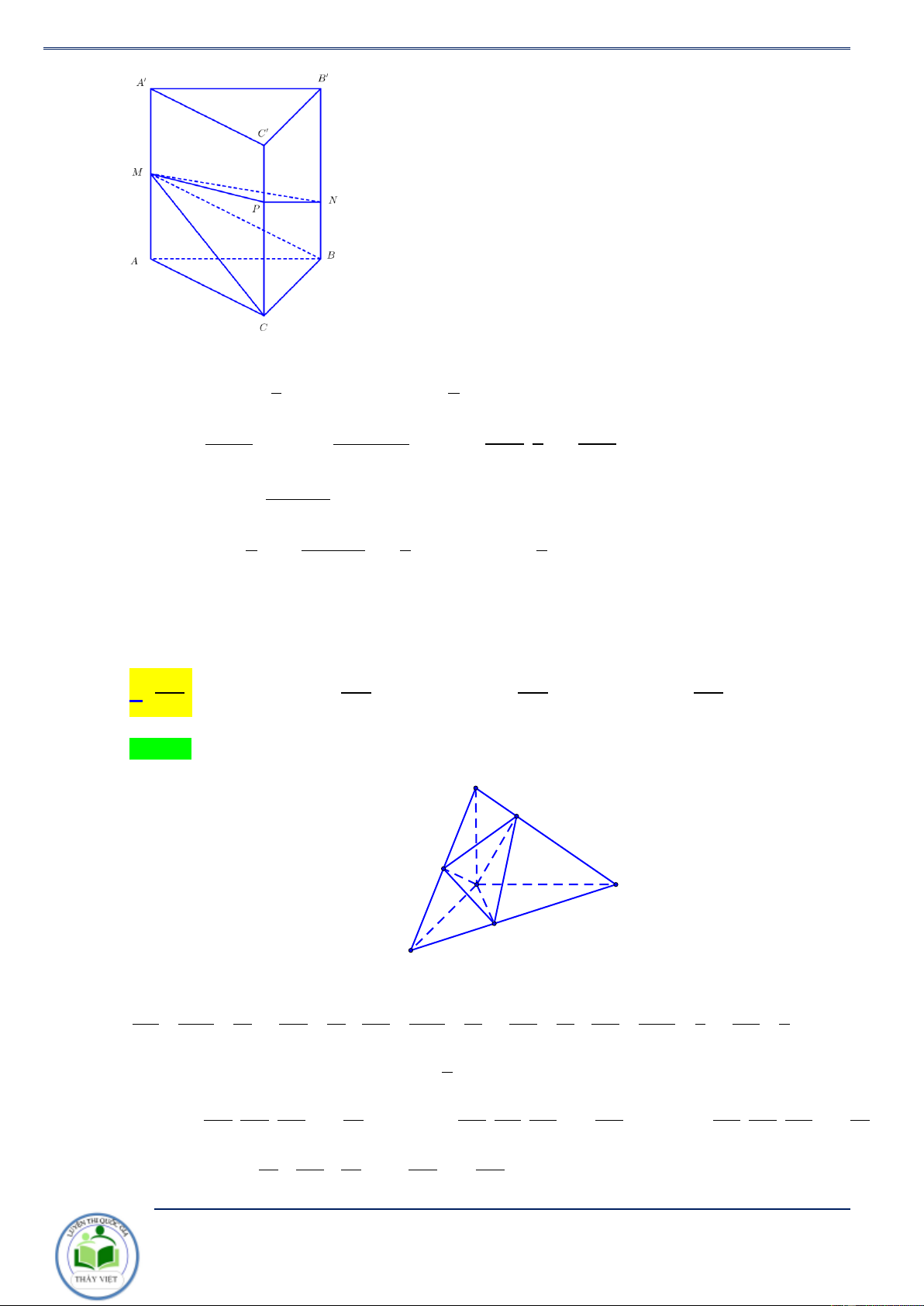
Ví dụ 4: Cho khối tứ diện ABCD có thể tích V . Gọi V  là thể tích của khối tám mặt có các đỉnh là trung điểm V
các cạnh của khối tứ diện ABCD . Tính tỷ số . V V  3 V  1 V  1 V  1 A. = . B. = . C. = . D. = . V 4 V 8 V 2 V 4 Lời giải Chọn B 3 AM AN AP  1  V Ta có: V = . . .V = V = . . A MNP   AB AC AD  2  8 Tương tự V V V ta có: V = ;V = ;V = . B.M SQ C.NQR D. 8 8 PSR 8 ' Do đó, V V V 1 ' V = V − 4. =  = . 8 2 V 2 SB V
Công thức 3: Cắt khối chóp bởi mặt phẳng song song với đáy sao cho
1 = k thì SB B ...B 1 2 n 3 = k (Đây S A V 1 S 1 A 2 A ... n A
là trường hợp đặc biệt cho hai khối đa diện đồng dạng theo tỷ sồ k .
Công thức 4: Mặt phẳng cắt cắt các cạnh của khối lăng trụ tam giác ' ' '
ABCA B C lần lượt tạ M ; N; P AM BN CP x + y + z sao cho = x, = y, = z. V = V    . AABBCC Ta có ABC.MNP ABC. 3 A B C
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 14/105
Ví dụ 5: Cho khối lăng trụ tam giác ' ' '
ABCA B C có thể tích V . Các điểm M ; N lần lượt thuộc các cạnh MB 1 NC 1 ' ' BB ;CC sao cho = x, = V là? ' BB 2 CC
. Thể tích của khối chóp tứ giác 4 . A BMNC V 3V V V A. . B. . C. . D. . 3 8 6 4 Lời giải Chọn D 1 1 + + 0 x + y + z V Ta có 2 4 V = V = V = . Chọn đáp án D. . A BMNC 3 3 4
Công thức 5: Mặt phẳng cắt các cạnh của khối hộp ABC . D A BCD
  lần lượt tại M , N, P,Q sao cho AM BN CP DQ + + + = x y z t x, = y, = z, = t V = V + = +     và x z y t . AABBCCDD
ta có ABCD.MNPQ ABCD. 4 A B C D
Chứng minh: Xem bài giảng:
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 15/105
Ví dụ 6: Cho hình lập phương ABC . D A BCD
  cạnh 2a , gọi M là trung điểm của BB và P thuộc cạnh 1
DD sao cho DP =
DD . Mặt phẳng ( AMP) cắt CC tại N . Thể tích khối đa diện AMNPQBCD 4 bằng. 11 9 A. 3 2a . B. 3 3a . C. 3 a . D. 3 a . 3 4 Lời giải Chọn B AA BM 1 CN DP 1
Thể tích khối lập phương 3
V = 8a . Có x = = 0, y = = , z = ,t = = 0 AABB 2 CCDD và 4 1 1 3
x + z = y + t  0 + z = +  z = . 2 4 4 1 3 1 0 + + + + + + Khi đó x y z t 2 4 4 3 3 V = V =
.8a = 3a . Chọn đáp án B. AMNPBCD 0 4 4
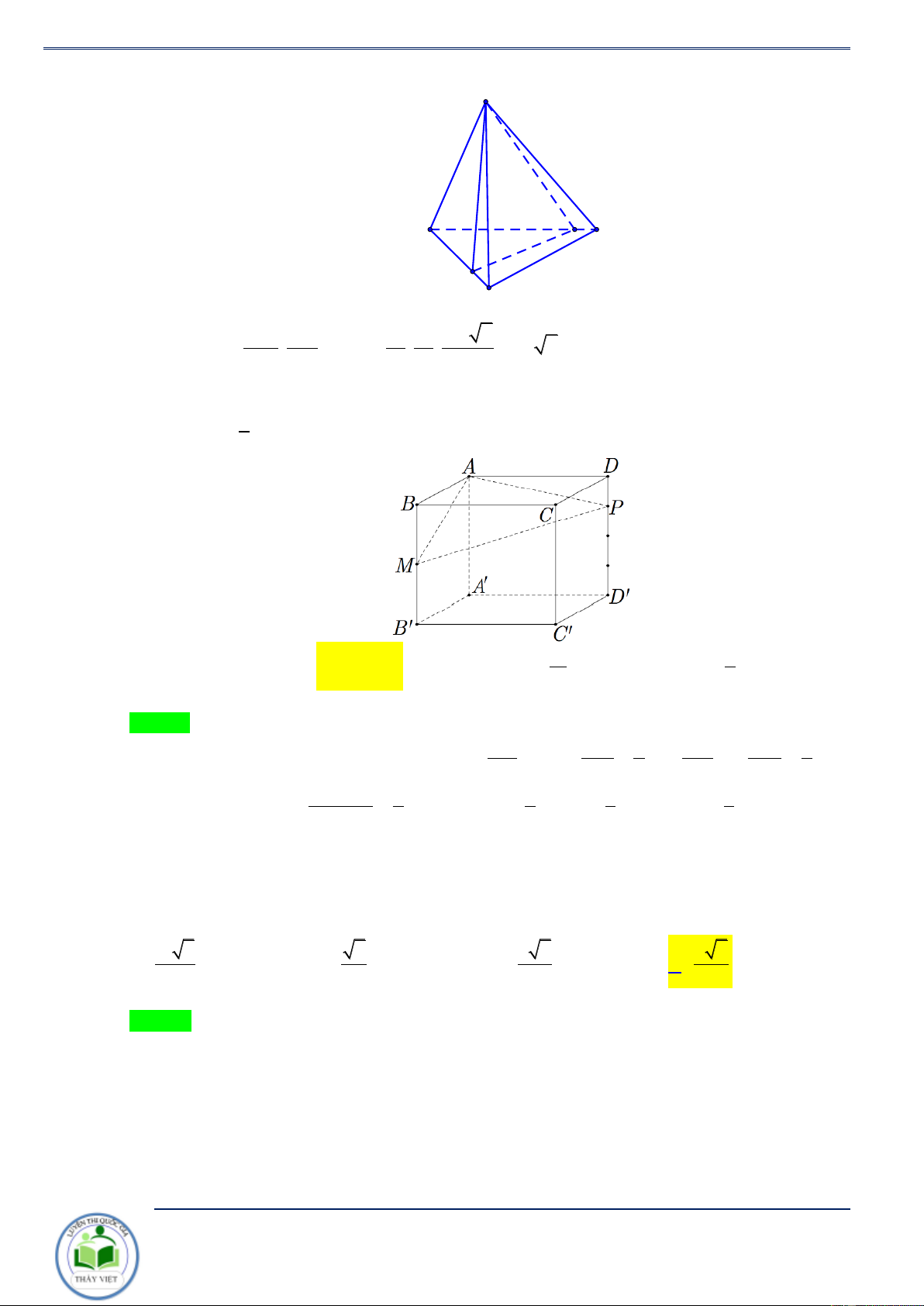
Ví dụ 7: Người ta cần cắt một khối hộp lập phương thành hai khối đa diện bởi mặt phẳng đi qua A ( như hình
vẽ ) sao cho phần thể tích của khối đa diện chứa đỉnh B bằng một nửa thể tích của khối đa diện còn lại. Tính tỉ số CN k = CC .
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 16/105 1 2 3 1 A. k = . B. k = . C. k = . D. k = . 3 3 4 2 Lời giải Chọn B
Gọi V  là thể tích khối đa diện chứa đỉnh B và V là thể tích khối lập phương. AA CN +   + Theo giả thiết, ta có 1 0 k 1 2 V  = V và AA CC V  = V =
V = V k = . 3 2 2 3 3
Công thức 6: Mặt phẳng cắt các cạnh cử khối chóp tứ giác .
S ABCD có đáy là hình bình hành lần lượt   tại SM SN SP SQ xyzt 1 1 1 1
M , N , P,Q sao cho = x; = y; = z; = t . Ta có V = + + + V   SA SB SC SD S.MNPQ S . 4 ABCDx y z t  1 1 1 1 và + = + . x z y t
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 17/105 Công thức 7: V
Hai khối đa diện đồng dạng với tỷ số k có 1 3 = k . V2
Ví dụ 8: Cho khối tứ diện ABCD có thể tích V . Gọi V  là thể tích của khối tứ diện có bốn đỉnh là trọng tâm 
các mặt bên của khối tứ diện ABCD. Tính tỷ số V V V  8 V  1 V  4 V  4 A. = . B. = . C. = . D. = . V 27 V 27 V 27 V 9 Lời giải Chọn B
Gọi A , B ,C , D lần lượt là trọng tâm các mặt (BCD),( ACD),( ABD),( ABC); Ta có ABA C   A D   1 = =
= . Khối tứ diện A BCD
  đồng dạng với khối tứ diện ABCD theo tỷ số 1 k = . AB AC AD 3 3 3   Do đó V 1 1 3 = k = =   . V   3  27
Công thức 8: So sánh bằng công thức thể tích khối chóp
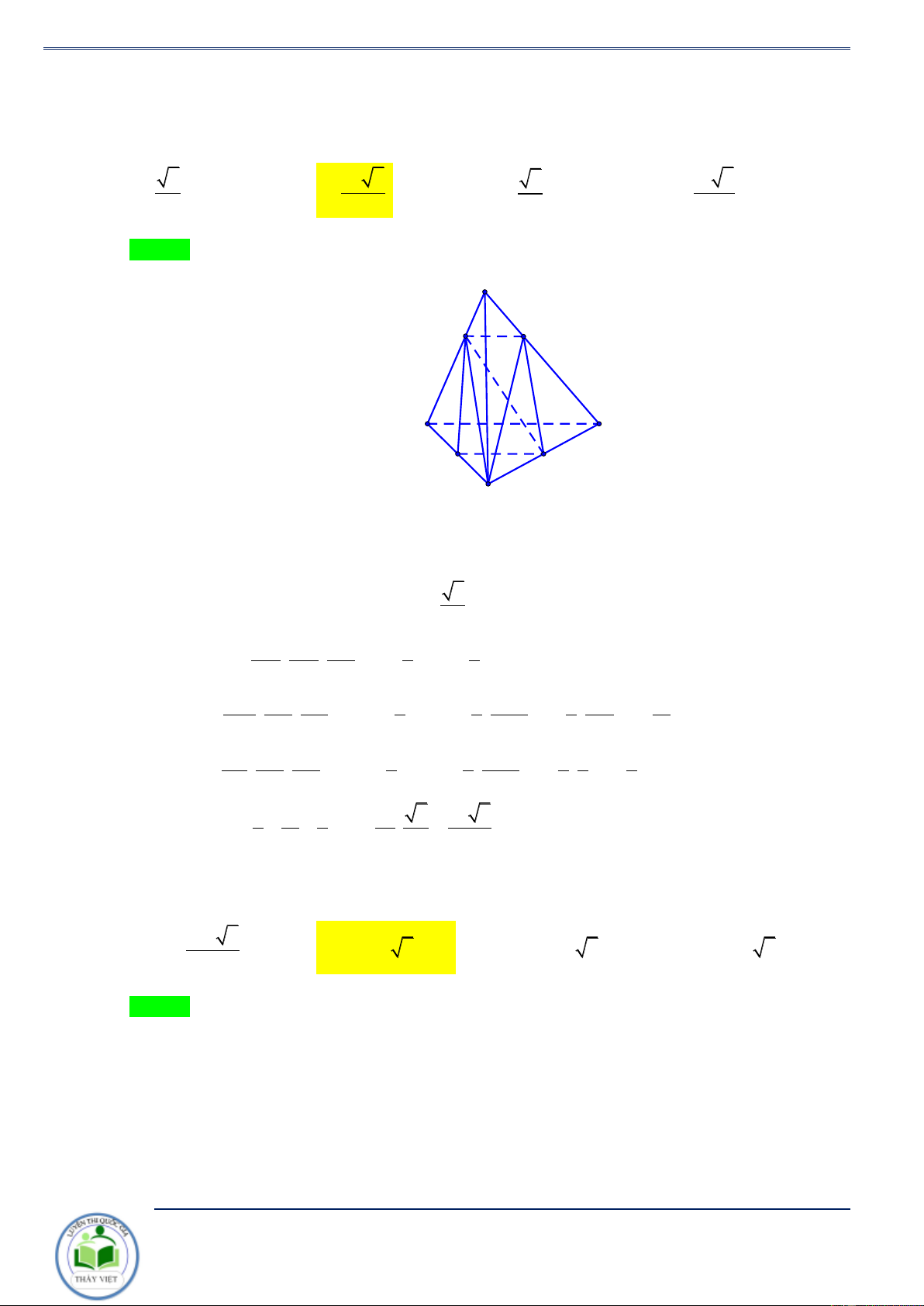
Ví dụ 9: Cho khối tứ diện đều ABCD có thể tích V . Gọi M, N,P lần lượt là trọng tâm các tam giác 
ABC, ACD, ADB và V  là thể tích khối tứ diện AMNP . Tính tỉ số V . V V  8 V  6 V  4 V  4 A. = . B. = . C. = . D. = . V 81 V 81 V 27 V 9 Lời giải Chọn B
Ta có mặt phẳng (MNP) cắt các mặt của tứ diện theo các đoạn giao tuyến EF,FH và HE do vậy thiết diện là tam giác 2
EFH . Ta dễ có (MNP) // (BCD) và d ( ;
A (MNP)) = d ( ; A (BCD)) 3
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 18/105 2   Ta cũng có 1 1 2 1 S = S = . S = S MNP   4 EFH 4  3 BCD  9 BCD Do đó 1 V = d A MNP S = d A BCD S = V . AMNP ( ( )) 2 MNP ( ( )) 6 ; . ; . 3 81 BCD 81 ABCD
Ví dụ 10: Cho khối tứ diện đều ABCD có độ dài cạnh bằng a . Gọi M, N,P lần lượt là trọng tâm các tam giác
ABC, ACD, ADB . Tính thể tích V khối tứ diện AMNP . 3 2a 3 2 2a 3 2a 3 2a A. V = . B. V = . C. V = . D. V = . 72 81 144 162 Lời giải Chọn D
Ta có mặt phẳng (MNP) cắt các mặt của tứ diện theo các đoạn giao tuyến EF,FH và HE do vậy thiết diện là tam giác 2
EFH . Ta dễ có (MNP) // (BCD) và d ( ;
A (MNP)) = d ( ; A (BCD)) 3 2   Ta cũng có 1 1 2 1 S = S = . S = S MNP   4 EFH 4  3 BCD  9 BCD Do đó a a V = d A MNP S = d A BCD S = V = = . AMNP ( ( )) MNP ( ( )) 3 3 1 2 6 6 2 2 ; . ; . . 3 81 BCD 81 ABCD 81 12 162
Ví dụ 11: Cho khối chóp tứ giác .
S ABCD có thể tích V . Gọi M , N , P,Q lần lượt là trọng tâm các tam giác 
SAB, SBC, SCD, SDA. Gọi V  là thể tích khối tứ diện S.MNPQ . Tính tỉ số V . V V  8 V  4 V  8 V  4 A. = . B. = . C. = . D. = . V 81 V 9 V 27 V 27 Lời giải Chọn D Khối chóp tứ giác Sh .
S ABCD có diện tích đáy là S , chiều cao h ta có V = . 3
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 19/105 Mặt phẳng ( 1
MNPQ) cắt các cạnh S ,
A SB, SC, SD lần lượt tại E, F ,G, H ta có S = S và MNPQ 2 EFGH 2  2  2 2 S =
S và d (S,(MNPQ)) = d (S,( ABCD)) = h . EGFGH    3  3 3 2    Do đó 1 V  =
d (S (MNPQ)) 1 1 2 2 4Sh 4V V 4 ; .S = . . S. h = =  =   . 3 MNPQ 3 2  3  3 3.27 27 V 27
Công thức 9: Định lí Meneleus trong không gian MA ND PC QB . . . =1 . MB NA PD QC B. ĐỀ THI Câu 1. Cho khối hộp ABC . D A BCD
  có thể tích V . Các điểm M , N, P là các điểm thỏa mãn AB = 4AM ,
AD = 3AN , AA = 2 AP . Tính thể tích của khối tứ diện AMNP . V V V V A. . B. . C. . D. . 6 144 72 48 Lời giải Chọn C
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 20/105 AM AN AP 1 1 1 1 1 1 V Ta có V =   V =    =  =  =  VV V AMNP ABDA AB AD AA . 4 3 2 ABDA 24 A BDA 24 3 72 Câu 2.
Cho tứ diện ABCD có các cạnh AB , AC và AD đôi một vuông góc. Các điểm M , N , P lần lượt là
trung điểm các đoạn thẳng BC,CD, BD . Cho biết AB = 4a, AC = 6a, AD = 7a . Tính thể tích V của
khối tứ diện AMNP . A. 3 V = 7a . B. 3 V = 28a . C. 3 V = 14a . D. 3 V = 21a . Lời giải Chọn A 1 1 1 1 Ta có V =  Sd , A MNP =   Sd , A MNP = V . A MNP MNP ( ( )) BCD ( ( )) 3 3 4 4 ABCD 1 1 3
=   AB AC AD = 7a . 4 6 Câu 3.
Cho khối chóp S.ABC , các điểm A ,
B ,C lần lượt thuộc các tia S ,
A SB, SC và không trùng với S .
Hỏi khẳng định nào dưới đây đúng? V       1 SA SB SC V    SA SB SC
A. S.A B C = . . S A B C = . . . V
3 SASBSC . B. . V SA SB SC S . ABC S . ABC V       SA SB SC V    1 SA SB SC
C. S.A B C = . . S A B C = . . . V
SASBSC . D. . V 3 SA SB SC S . ABC S . ABC Lời giải
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 21/105 Chọn B Câu hỏi lí thuyết. Câu 4.
Cho hình chóp S.ABCD có M , N, P,Q lần lượt là trung điểm các cạnh ,
SA SB, SC, SD . Mệnh đề nào sau đây đúng? V V V V S MNPQ 1 S MNPQ 1 S MNPQ 1 S MNPQ 1 A. . = . B. . = . C. . = . D. . = . V 2 V 4 V 8 V 16 S . ABCD S . ABCD S . ABCD S . ABCD Lời giải Chọn C S A' D' B' C' A D B C 3 1 V   S MNPQ 1 1
Ta thấy hai khối đa diện S.MNPQ và S.ABCD đồng dạng theo tỉ số nên . = =   . 2 V  2  8 S.ABCD Câu 5.
Cho tứ diện ABCD có các góc tại đỉnh A vuông; AB = 6a, AC = 9a, AD = 3a . Gọi M , N , P lần lượt
là trọng tâm các tam giác ABC, ACD, ADB . Tính thể tích V của khối tứ diện AMNP . A. 3 V = 8a . B. 3 V = 4a . C. 3 V = 6a . D. 3 V = 2a . Lời giải Chọn D A P M N B D K H I C
Gọi H , I , K lần lượt là trọng tâm các cạnh BC, CD, DB . Ta thấy khai khối đa diện AMNP và AHIK 3   đồ 2 V 2 8 8 ng dạng theo tỉ số nên AMNP = =    V = V . 3 AMNP AHIK V  3  27 27 AHIK V S 1 Ta có AHIK HIK =
= (do hai khối chóp có chung đường cao kẻ từ A ) V S 4 ABCD BCD
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 22/105 1 2  V = VV = V . AIHK 4 ABCD AMNP 27 ABCD 1 1 Mà 3 V = A . B AC.AD = 6 .9 a .3 a a = 27a . ABCD 6 6 2 Vậy 3 3 V = 27a = 2a . AMNP 27 Câu 6.
Cho khối tứ diện ABCD có thể tích V và các điểm M , N, P là các điểm thỏa mãn AM = 2AB ,
AN = 3AC , AP = 4AD . Hỏi khẳng định nào dưới đây là khẳng định đúng? V V A. V = . B. V = 8V . C. V = 24V . D. V = . AMNP 24 AMNP AMNP AMNP 8 Lời giải Chọn C A D B C M P N V AM AN AP Ta có AMNP = . . = 2.3.4 = 24 V = 24V . V AB AC AC AMNP ABCD Câu 7.
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B , AC = 2a , SA ⊥ ( ABC) và SA = a . Điểm 1
I thuộc cạnh SB sao cho SI =
SB . Thể tích khối tứ diện SAIC bằng 3 3 2a 3 a 3 a 3 2a A. . B. . C. . D. . 9 9 3 3 Lời giải Chọn B
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 23/105 S I C A B 3 SI 1 1 1 1 a Ta có V = .V = . .S = S . A A . B BC = . SAIC SABC SB 3 3 ABC 9 2 9 Câu 8.
Cho tứ diện OABC có OA = OB = OC = a và đôi một vuông góc. Gọi M , N, P lần lượt là trung điểm
các cạnh AB, BC,CA . Tính thể tích V của khối tứ diện OMNP . 3 a 3 a 3 a 3 a A. V = B. V = . C. V = . D. V = . 4 24 6 12 Lời giải Chọn B A P M O C N B 1 1 1 Ta có: V = d O MNP S = d ( ;
O ( ABC )). S OMNP ( ;( )). 3 MNP 3 4 ABC 1 3 = 1 1 a V = . . . OA . OB OC = 4 OABC 4 6 24 Câu 9.
Cho hình chóp S.ABC có chiều cao bằng 9, diện tích đáy bằng 5. Gọi M là trung điểm cạnh SB và
điểm N trên cạnh SC sao NS = 2NC . Thể tích V của khối chóp . A BMNC
A. V =15 . B. V = 5.
C. V = 30 D. V =10 . Lời giải Chọn D
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 24/105 S M N C A BV SM SN 1 2 1 S . AMN = . = . = V SB SC 2 3 3 Ta có S . ABC  .  2 2 1 V = V −V = V = . .5.9 =10 . A BMNC S .ABC S .AMN S .  3 ABC 3 3
Câu 10. Cho khối tứ diện ABCD có thể tích V và điểm E trên cạnh AB sao cho AE = 3EB . Tính thể tích
của khối tứ diện EBCD . V V V V A. B. . C. . D. . 3 4 2 5 Lời giải Chọn B A E C D B AE 3  3  V Ta có V = .V = V V = 1− V = . AECD ABCD   AB 4 EBCD  4  4
Câu 11. Cho khối lăng trụ AB . C A BC
 . Đường thẳng đi qua trọng tâm của tam giác ABC và song song với
BC cắt các cạnh AB , AC lần lượt tại D , E . Mặt phẳng ( A D
E) chia khối lăng trụ thành hai phần,
tính tỉ số thể tích (số bé chia số lớn) của chúng.
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 25/105 2 4 4 4 A. . B. . C. . D. . 3 23 9 27 Lời giải Chọn B 2 V S AD AE  2  A '. ADE ADE  = = . =   V S AB AC  3  4 Ta có A '. ABC ABC   V = V A '. ADE
ABC. A ' B ' C '  1 27 V = V A '. ABC
ABC. A ' B ' C '  3 4 V Do đó 4 1 27 = = . V 4 23 2 1 − 27
Câu 12. Cho tứ diện ABCD có thể tích V . Xét điểm P thuộc cạnh AB , điểm Q thuộc cạnh BC và điểm R thuộc cạnh PA QB RB BD sao cho = 2 , = 3,
= 4 . Tính thể tích của khối tứ diện BPQR . PB BC RD V V V V A. . B. . C. . D. . 5 4 3 6 Lời giải Chọn A VB PQR BP BQ BR 1 3 4 1 Ta có . = = . .  V = V . B. V BA BC BD 3 4 5 PQR 5 B.ACD
Câu 13. Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình bình hành. Các điểm A , C thỏa mãn 1 1 SA = SA , SC =
SC . Mặt phẳng ( P) chứa đường thẳng A C
  cắt các cạnh SB , SD lần lượt tại 3 5 V
B , D và đặt
S . AB CD k   =
. Giá trị nhỏ nhất của k là? VS.ABCD
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 26/105 1 1 4 15 A. . B. . C. . D. . 60 30 15 16 Lời giải Chọn A Đặt SB = SD x = y SB , SDSB SD SA SC Ta có + = +  x + y = . SBSDSASC 8 V    1 1 1 Ta có S.A B C =  V = =    V V . V 15x S . A B C S . ABC S . 15x 30 ABCD x S . ABC V    1 1 1 Ta có S.A D C =  V = =    V V . V 15 y S . A D C S . ADC S . 15y 30 ABCD y S . ADC V       1 1 1 Ta có S . A B C D k = = +   V 30  x y S . ABCD   1 1 1
Ta có ( x + y) 1 1 +  4    +  1  k  .  x y x y 2 60 1
Vậy giá trị nhỏ nhất của k là
khi x = y = 4 . 60
Câu 14. Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình bình hành. Các điểm A , C thỏa mãn 1 1 SA = SA , SC =
SC . Mặt phẳng ( P) chứa đường thẳng A C
  cắt các cạnh SB , SD lần lượt tại 3 5 V
B , D và đặt
S . AB CD k   =
. Giá trị lớn nhất của k là? VS.ABCD 4 1 4 4 A. . B. . C. . D. . 105 30 15 27 Lời giải Chọn A Đặt SB = SD x = y SB , SD
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 27/105 SB SD SA SC Ta có + = +
x + y =  y = 8 − x . SBSDSASC 8 V    1 1 1 Ta có S.A B C =  V = =    V V . V 15x S . A B C S . ABC S . 15x 30 ABCD x S . ABC V    1 1 1 Ta có S.A D C =  V = =    V V . V 15 y S . A D C S . ADC S . 15y 30 ABCD y S . ADC V       1 1 1 4 4 4 Ta có S . A B C D k = = +   = = = . V 30  x y  15xy 15x (8 − x) 15( 2 −x + 8x) S . ABCD
Ta có 1  x, y  8  8 − x 1  x  7 .
Xét hàm số f (x) 2
= −x +8x trên đoạn 1;7. x = 01;7 f ( x) = 2
− x +8 ; f (x) = 0   x = 4  1;7 Tính f ( )
1 = 7 ; f (7) = 7 ; f (4) = 32 .
k đạt giá trị lớn nhất khi f ( x) đạt giá trị nhỏ nhất. 4 4
min f ( x) = 7  k = = . max 15.7 105
Câu 15. Cho tứ diện đều có chiều cao h , ở ba góc của tứ diện người ta cắt đi các tứ diện bằng nhau có chiều
cao x để khối đa diện còn lại có thể tích bằng một nửa thể tích của khối đa diện đều ban đầu . Tìm x . h h h h A. x = . B. x = . C. x = . D. x = . 3 2 3 3 4 4 3 6 Lời giải Chọn D
Gọi cạnh của khối tứ diện đều ban đầu là a . 2  a 3  a 6 a h h Ta có 2 2 AO = AB − BO 2 = a −     = 6  h = 3 6  a = = . 3   3 3 6 2 3 3 a 2 h 3 V = = . ABCD 12 8 3 3 x 3 x 3 3
Thể tích của ba khối tứ diện đều có chiều cao x được cắt ra là V = 3. = . 8 8 3 3 x 3 3 1 h 3 3 h h Ta có = 3  x =  x = . 8 2 8 6 3 6
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 28/105
Câu 16. Cho tứ diện đều có chiều cao h , ở bốn góc của tứ diện người ta cắt đi các tứ diện đều bằng nhau có 3
chiều cao x để khối đa diện còn lại có thể tích bằng
thể tích của khối đa diện ban đầu. Tìm x . 4 h h h h A. x = . B. x = . C. x = . D. x = . 3 4 3 16 3 12 3 6 Lời giải Chọn C 2  
Gọi cạnh của khối tứ diện đều ban đầu là a 3 2 3 a , ta có 2 h = a −   = a    a = h . 3 3   2 2 3  
Thể tích của khối tứ diện ban đầu là 1 3 3 h V = . h  . .h =   . 3 2 4 8   3
Do đó tổng thể tích của ba khối tứ diện đều có chiều cao 3x
x được cắt ra là . 8 3 3
Theo giả thiết ta có 3x 1 h h = .  x = . 3 8 4 8 12
Câu 17. Mặt phẳng đi qua trọng tâm của một tứ diện, song song với một mặt của tứ diện và chia khối tứ diện
đã cho thành hai phần. Tính tỉ số thể tích (số bé chia số lớn) của hai phần đó. 2 5 27 3 A. . B. . C. . D. . 3 7 37 4 Lời giải Chọn C
Gọi G là trọng tâm của tứ diện ABCD, A là trọng tâm tam giác BCD.
Giả sử mặt phẳng qua G song song với (BCD) cắt các cạnh AB, AC, AD lần lượt tại M , N, P ta có AM AN AP AG 3 = = = = AB AC AD AA . 4
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 29/105 2   Do đó 3 3 S = S và d ( ,
A (MNP)) = d ( , A ( BCD)) . MNP    4 BCD  4 2  3   3  27 V 27 / 64 27 Suy ra V = V = V 1  = = . AMNP      4   4 ABCD  64 ABCD V 1− 27 / 64 37 2 BB
Câu 18. Cho khối hộp ABC . D A BCD
  . Lấy điểm E thuộc cạnh BB sao cho BE =
, điểm F thuộc cạnh 4 3DD
DD sao cho DF =
. Mặt phẳng qua ba điểm ,
A E, F chia khối hộp thành hai phần. Tính tỉ số 4 hai phần ấy. 3 4 A. 2 . B. 1. C. . D. . 2 3 Lời giải Chọn B
Ta thấy thiết diện của ( AEF) và hình hộp là tứ giác AFC 'E .
x + y + z + t Ta có V = V
ABCD. AFC ' E
ABCD. A' B 'C ' D ' 4 0 BE 1 CC ' DF 3 1 trong đó x = = 0; y = = ; z = = 1;t = =  V = V .
ABCD. AFC ' E
ABCD. A' B 'C ' D ' AA' BB ' 4 CC ' DD ' 4 2
Vậy tỉ lệ thể tích của hai khối là 1.
Câu 19. Cho khối hộp chữ nhật ABC .
D A' B'C ' D' có AB = 4 ; a AD = 6 ;
a AA ' = 7a . Các điểm M , N , P thỏa mãn AM = 2A ; B AN = 3A ;
D AP = 4AA' . Tính thể tích V của khối tứ diện AMNP . A. 3 V = 168a . B. 3 V = 672a . C. 3 V = 336a . D. 3 V = 1008a . Lời giải Chọn D 1 1
Ta có tứ diện AMNP vuông tại A nên 3 V = A . B A . D AA ' = .8 .18 a .28 a
a = 672a . 6 6
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 30/105
Câu 20. Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi C ' là trung điểm của SC . Mặt phẳng ( P) V
chứa AC ' cắt các cạnh SB, SD lần lượt tại B ', D ' . Đặt
S .B 'C ' D ' m =
.Giá trị nhỏ nhất của m bằng VS.ABCD 2 4 1 2 A. . B. . C. . D. . 27 27 9 9 Lời giải Chọn C Đặ SA' SB ' SC ' 1 SD ' SA SC SD SB 1 1 t = 1; x = ; = ; y = . Ta có + = +  + = 3 SA SB SC 2 SD SA SC ' SD ' SB ' x y V V
1 SB ' SC ' SD ' 1 Có
S .B 'C ' D '
S .B 'C ' D ' m = = = . . = xy . V 2V 2 SB SC SD 4 S . ABCD S .BCD 1 1 2 4 1 3 = + 
xy   m  . x y xy 9 9
Câu 21. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi C là trung điểm cạnh SC . Mặt phẳng ( V
P) chứa đường thẳng AC cắt các cạnh SB , SD lần lượt tại B , D . Đặt S .B CD m   = . Giá trị lớn VS.ABCD nhất của m bằng 1 1 3 4 A. . B. . C. . D. . 9 8 8 9 Lời giải Chọn B     Đặ SA SB SC 1 SD t x = =1; y = ; z = = ; t = . Ta có SA SB SC 2 SD 1 1 1 1 + = + 1 1 1 1  1+ 2 = +  + = 3. x z y t y t y t V       V    1 SB SC SD 1 Mà S .B C D S .B C D m = = = . . = yt . V 2V 2 SB SC SD 4 S . ABCD S .BCD 1 1 t 2 =  1  t  1  1 3 −  y = ,  t  1 
  m = f (t) =  max f t = f =   . y t 3t −1  3  4(3t − ) ( )  1 1    ;1 2 8    3 
Câu 22. Cho khối hộp ABC . D A BCD
  có thể tích V . Tính thể tích khối tứ diện AB CD . 3V V V V A. . B. . C. . D. . 4 6 3 4
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 31/105 Lời giải Chọn C V V Ta có V = − + + + = − =   V V    V    V V V . AB CD ( 4. . A A B D C.C B D B .ACB D .ADC ) 6 3
Câu 23. Cho khối hộp ABC . D A BCD
  có thể tích V . Các điểm M , N , P thỏa mãn AM = 2AC ,
AN = 3AB , AP = 4AD . Tính thể tích của khối tứ diện AMNP . A. 8V . B. 4V . C. 6V . D. 18V . Lời giải Chọn A AM AN AP V Ta có V = . . .V = =   2.3.4. 8V AMNP ACB D AC ABAD . 3
Câu 24. Cho khối tứ diện đều S.ABC cạnh bằng a . Mặt phẳng ( P) đi qua S và trọng tâm của tam giác ABC V
cắt các cạnh AB , AC lần lượt tại M , N . Đặt S . AMN m =
. Giá trị nhỏ nhất của m bằng VS.ABC 2 2 4 1 A. . B. . C. . D. . 3 9 9 3 Lời giải Chọn C Đặ AM AN t x = , y =
, ( x, y 0 
;1 ) . Gọi O là trọng tâm ta giác ABC và D là trung điểm cạnh AB AC
AB , giả sử AM AD . Ta có S AM AN AMN m = = . = xy . S AB AC ABC
Áp dụng định lí Meneleuys cho tam giác ACD ta có a xa − MD OC NA 2 ya . . =1 .2. =1  (2x − )
1 y = x (1− y)  3xy = x + y  2 xy MA OD NC xa a − ya 4
m = xy  . 9
Câu 25. Cho hình chóp S.ABC có M , N , P lần lượt là các điểm thỏa mãn SM = 2SA, SP = 3SC và V 1
SN = kSB . Biết S.MNP = . Tìm k . V 6 S . ABC 1 1 A. k = . B. k = 1. C. k = . D. k = 36 . 36 6
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 32/105 Lời giải Chọn A V SM SN SP 1 1 Ta có S.MNP = . . = 6k =  k = . V SA SB SC 6 36 S . ABC
Câu 26. Cho khối tứ diện đều ABCD . Gọi M , N, P,Q, R, S lần lượt là trung điểm của các cạnh
AB, AC, AD, BC,CD, DB . Biết thể tích của khối bát diện đều MQNPSR bằng 3 9 2 cm . Tính độ dài
cạnh của tứ diện đều ABCD . A. 2 cm . B. 3 cm . C. 6 cm . D. 3 2 cm . Lời giải Chọn C A M P N B D S Q R C Gọi V = V . A BCD V AM AN AP 1 1 Ta có: . A MNP = . . =  V = V . V AB AC AD 8 A MNP 8 . A BCD Tươn 1 1 1 g tự V = V; V = V; V = V B.MQS C.NQR D. 8 8 PRS 8 1 V V = V −V −V −V −V = V − 4. V = MQNPSR . A MNP B.MQS C.NQR D.PRS 8 2 V Theo giả thiết V = 9 2  = 9 2  V = 18 2 . MQNPSR 2 3 Đặt độ a 2
dài cạnh của tứ diện là a , ta có: V = = 18 2  a = 6 12 Vậy a = 6 cm .
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 33/105
Câu 27. Cho khối tứ diện đều ABCD có cạnh bằng a . Gọi M , N lần lượt là các điểm trên cạnh AM 1 AN AB, AC : = ,
= 2 . Mặt phẳng ( ) chứa MN , song song với AD chia khối tứ diện thành BM 2 CN
hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V . Tính V 3 4 2a 3 5 2a 3 4 2a 3 11 2a A. V = . B. V = . C. V = . D. V = 108 108 81 342 Lời giải Chọn A A M N B F D E CN   () (ACD)  DE AN  Ta có   ( )  ( ACD) 2 = NE AD E CD = =   AD / /  () / / ,  DC AC 3  M   ( ) (ABD)  ( ) (     ABD) DF AM 1 = MF AD F BD = =   . AD / /  ( ) / / ,  DB AB 3 
Như vậy thiết diện của tứ diện ABCD cắt bởi ( ) là tứ giác MNEF . V AM AN 1 2 2 2 . A MND = = . =  V = V . (1) . A MND . V AB AC 3 3 9 9 A BCD . A BCD 2 1 S − S − S V DF 1 ABC ABC ABC V S S − S − S 4 D.MNF D.MNB MNB ABC AMN BCN 9 3 = = ; = = = = V DB 3 V S S S 9 D.MNB D. ABC ABC ABC ABC 1 4 4  V = . V = V . (2) D.MNF . A BCD . 3 9 27 A BCD V DE DF 2 1 2 V S CN 1 D.EFN D. = . = . = ; CBN CBN = = = V DC DB 3 3 9 V S CA 3 D.CBN D.CBA CBA 1 2 2  V = . V = V . (3) D.EFN . A BCD . 3 9 27 A BCD
Cộng (1), (2), (3) theo vế ta được:
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 34/105 2 4 2 V +V +V = V + V + V . A MND D.MNF D.EFN . A BCD . A BCD . 9 27 27 A BCD 3 3 3 12 12 a 2 a 2 4a 2  V = V = . = = . . 27 A BCD 27 12 27 108
Câu 28. Cho khối tứ diện đều ABCD có cạnh bằng a . Gọi M , N lần lượt là trung điểm các cạnh AB, BC và BE
E là điểm thuộc tia đối của tia DB sao cho
= k . Tìm k để mặt phẳng (MNE) chia khối tứ diện BD 3 11 2a
thành hai khối đa diện, trong đó khối đa diện chứa đỉnh B có thể tích V = 294 6 A. k = . B. k = 6 . C. k = 4 . D. k = 5 . 5 Lời giải Chọn C A M Q D E B P N C
P = EN CD Gọi 
suy ra thiết diện của tứ diện ABCD cắt bởi (MNE) là tứ giác MNPQ . Q  = EM AD V ED EP EQ Ta có: E.DPQ = . (1) V EB EN EM E. BNM BE ED k − 1 Theo giả thiết: = k  = ; (1.1) BD EB kMN / / ACEQ EP Ta thấy: ( (1.2)  ) ( )
PQ / /MN / / AC  = EMN ACD = PQ EM EN k +1 EB EM EM − 2k −1 EQ 2k − 2 Xét EAB
có EM là trung tuyến k 1  +1 = 2  = =  = ED EQ EQ 2 2k − 2 EM 2k −1 (1.3)
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 35/105
Thay (1.1) (1.2) (1.3) vào (1): 2 2 2 V −  −  −  −  − + E.DPQ k 1 2k 2 V k 1 2k 2 8k 11k 4 = .  = 1− . =     .(2) V k  2k −1  V k  2k −1  − E BNM E BNM k (2k )2 . . 1 Lại có: V
d ( E,( BMN )).S EB BM BN k . BMN E BMN = = . . = (2.1) V
d D, ABC .S DB BA BC 4 D. ABC ( ( )) ABC 2 2 V
8k −11k + 4 k 8k −11k + 4 Từ (2) và (2.1) suy ra = = V − − A BCD k (2k ) . 2 1 4 4(2k )2 . 1 3 11 2ak = 4 2 2 − + − + Như vậ 8k 11k 4 22 8k 11k 4 y 294 2  =  =
 40k −187k +108 = 0  27 3 2a 4(2k − )2 1 49 4(2k − )2 1 k =  40 12 Vậy k = 4 .
Câu 29. Cho hình chóp S.ABC . Trên cạnh SA lấy các điểm M , N sao cho SM = MN = NA . Gọi ( ), ( ) là
các mặt phẳng song song với mặt phẳng ( ABC) và lần lượt đi qua M , N . Khi đó hai mặt phẳng
( ), ( ) chia khối chóp đã cho thành 3 phần. Nếu phần trên có thể tích bằng 3 10 dm thì thể tích của
hai phần còn lại lần lượt là A. 3 80 dm và 3 190 dm . B. 3 70 dm và 3 190 dm . C. 3 70 dm và 3 200 dm . D. 3 80 dm và 3 180 dm . Lời giải Chọn B
Gọi E = ()  SB, F = ()  SC, G = ( )  SB, H = ( )  SC thì theo đề ta có: 3 V = 10 dm S .MEF V SM SE SF 1 1 1 S .MEF 3 = . . = . .  V = 27V = 270 dm . S . ABC S . V SA SB SC 3 3 3 MEF S . ABC V SM SE SF 1 1 1 S .MEF 3 = . . = . .  V = 8V = 80 dm . S .NGH S . V SN SG SH 2 2 2 MEF S .NGH Do đó 3 V = V −V = 70 dm , 3 V = V −V = 270 −80 =190 dm . NGHMEF S .NGH S .MEF NGHABC S .ABC S .NGH
Vậy thể tích của hai khối đa diện còn lại lần lượt là 3 70 dm và 3 190 dm .
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 36/105
Câu 30. Cho hình chóp S.ABCD có đáy là hình bình hành. Trên cạnh SA lấy các điểm M , N sao cho
SM = MN = NA. Hai mặt phẳng ( ), ( ) song song với ( ABCD) và lần lượt đi qua M , N chia khối
chóp đã cho thành ba phần. Nếu phần trên có thể tích bằng 3
10 dm thì phần ở giữa có thể tích là A. 3 70 dm . B. 3 80 dm . C. 3 180 dm . D. 3 190 dm . Lời giải Chọn A
Gọi P = ()  SD, Q = ()  SC, R = ()  SB, E = ( )  SD, F = ( )  SC, G = ( )  SB thì theo đề ta có: 3 V =10 dm S.MPQR V =V +V , S.NEFG S.NEF S.NGF V SN SE SF S.NEF = . . = 2.2.2 V = 8V , S.NEF S .MPQ V SM SP SQ S.MPQ V SN SG SF S.NGF = . . = 2.2.2 V = 8V S.NEF S.MRQ V SM SR SQ S.MRQV = V +V = 8V + 8V = 8 V +V = V = S NEFG S NEF S NGF S MPQ S MRQ ( S MPQ S MRQ) 3 8 80 dm . . . . . . . . S .MPQR
Vậy thể tích của khối chóp cụt NEF . G MPQR là 3 V = V −V = 80 −10 = 70 dm . S.NEFG S.MPQR
Câu 31. Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB = 2a , BC = a , SA = SB = SC = SD = 2a . Giả 1
sử E thuộc cạnh SC sao cho SE = 2EC , F là điểm thuộc cạnh SD sao cho SF = FD . Thể tích 3
khối đa diện SABEF bằng: 3 5 3a 3 3a 3 2 3a 3 2 3a A. . B. . C. . D. . 36 18 9 27 Lời giải Chọn A.
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 37/105
Vì SA = SB = SC = SD = 2a nên hình chiếu vuông góc hạ từ đỉnh S xuống đáy trùng với tâm đường
tròn ngoại tiếp đáy, tức là trùng với điểm O = AC BD . 2 2 4a + a 3a Ta có: 2 2 2 SO = SA − AO = 2a − = 4 2 3 1 3aV = . . SO S = . S . ABCD 3 ABCD 3 Ta có: 3 3 3 SE SE SF 2  3a  2 1  3a  5 3a V = V +V = .V + . .V = .  + . .  = . S . ABEF S . ABE S . AEF SABC SACD     SC SC SD 3 6 3 4 6 36    
Câu 32. Cho tứ diện ABCD có BAC = CAD = DAB = 60 , AB = 8(cm) , AC = 9(cm) , AD =10(cm) . Gọi
A , B , C , D lần lượt là trọng tâm của các tam giác BCD, ACD, ABD, ABC . Tính thể tích V của 1 1 1 1
khối tứ diện A B C D : 1 1 1 1 20 2 20 2 A. V = ( 3 20 2 cm ). B. V = ( 3
cm ) . C. V = ( 3
cm ) . D. V = ( 3 60 2 cm ) . 3 9 Lời giải Chọn C Lấy các điểm B ,
C lần lượt trên các tia AB, AC sao cho AB = AC = AD =10 .
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 38/105 AB AC 18 Khi đó: V = . .V =   V ABCD . A B 'C D . A B '   ABAC 25 C D Trong đó AB CD
 là tứ diện đều cạnh a =10cm, do đó thể tích của nó là 3 a 2 250 2 3 = cm . 12 3 1 Vì vậy V
= 60 2 và hai khối tứ diện ABCD và A B C D đồng dạng theo tỉ số . ABCD 1 1 1 1 3 Do đó 1 20 2 : 3 V = V = cm . 1 A 1 B 1 C 1 D ABCD ( ) 27 9
Câu 33. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Một mặt phẳng song song với đáy cắt các cạnh bên ,
SA SB, SC, SD lần lượt tại M , N , P, Q . Gọi M ,
N , P , Q lần lượt là hình chiếu của SM
M , N , P, Q trên mặt phẳng đáy. Tìm tỉ số
để thể tích khối đa diện MNP . Q M NPQ   đạt giá trị SA lớn nhất. 3 2 1 1 A. . B. . C. . D. . 4 3 2 3 Lời giải Chọn B. Đặ SM t
= x(0  x  )
1 , kí hiệu V , h lần lượt là thể tích và chiều cao của khối chóp đã cho. SA Theo đị MN NP PQ QM SM nh lý Ta-let, ta có: = = = = = x AB BC CD DA SA
d (M ,( ABCD)) AM Và =
= −  d (M ,( ABCD)) = (1− x)h.
d (S ( ABCD)) 1 x , SA Vì vậy V = = − = −     MN.M . Q d M ABCD x x h AB AD x x V M N P Q ( ,( )) 2.(1 ) 2 . . 3 1 MNPQ. ( ) 3 1
1  x + x + 2 − 2x  4 Theo BDT Co-si, ta có: 2 x (1− x) = . x . x (2 − 2x)  =   . 2 2  3  27 Do đó 4 , V      V . MNPQ.M N P Q 9
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 39/105 2
Dấu “=” xảy ra  x = 2 − 2x x = . 3
Câu 34. Cho hình chóp S.ABC . Một mặt phẳng song song với đáy ( ABC) cắt các cạnh bên S ,
A SB, SC lần
lượt tại M , N, P . Gọi M , N , P lần lượt là hình chiếu của M , N, P trên mặt phẳng đáy. Tìm tỉ số
SM để thể tích khối đa diện MN . P M NP
  đạt giá trị lớn nhất. SA 3 2 1 1 A. . B. . C. . D. . 4 3 2 3 Lời giải Chọn B. Đặ SM t
= x(0  x  )
1 , kí hiệu V , h lần lượt là thể tích và chiều cao của khối chóp đã cho. SA Theo đị MN NP PQ SM nh lý Ta-let, ta có: = = = = x AB BC CD SA
d (M ,( ABC )) AM Và =
= −  d (M ,( ABC)) = (1− x)h .
d (S ( ABC )) 1 x , SA Vì vậy V = = − = −    S .d M ABCD x x h S x x V M N P MNP ( ,( )) 2.(1 ) 2 . 3 1 MNP. ABC ( ) 3 1
1  x + x + 2 − 2x  4 Theo BDT Co-si, ta có: 2 x (1− x) = . x . x (2 − 2x)  =   . 2 2  3  27 Do đó 4 , V     V . MNP.M N P 9 2
Dấu “=” xảy ra  x = 2 − 2x x = . 3
Câu 35. Cho hình chóp S.ABC . Một mặt phẳng (P) song song với đáy ( ABC) cắt các cạnh bên S ,
A SB, SC SM
lần lượt tại M , N , P . Tìm tỉ số
để (P) chia khối chóp đã cho thành hai khối đa diện có thể tích SA bằng nhau.
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 40/105 1 1 1 1 A. . B. . C. . D. . 3 2 3 4 2 4 Lời giải Chọn A. Đặ SM t
= x(0  x  ) 1 SA Theo đị SM SN SP nh lý Ta-let, ta có: = = = x SA SB SC SM SN SP 1 Và 3 V = . . V = x .V Theo giả thiết, V = V nên S .MNP S . ABC S . ABC SA SB SC S .MNP S . 2 ABC 1 1 3 x =  x = 3 2 2
Câu 36. Cho hình chóp S.ABC có tất cả các cạnh đều bằng a , một mặt phẳng (P) song song với mặt đáy
(ABC) cắt các cạnh bên S ,
A SB, SC lần lượt tại M , N , P . Tính diện tích tam giác MNP biết mặt
phẳng (P) chia khối chóp đã cho thành hai khối đa diện có diện tích bằng nhau. 2 a 3 2 a 3 2 a 3 2 a 3 A. S = . B. S = . C. S = . D. S = . MNP 8 MNP 16 MNP 3 MNP 4 2 4 4 4 Lời giải S M P N A C B Chọn D
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 41/105
Mặt phẳng (P) song song với ( ABC) và cắt các cạnh bên S ,
A SB, SC lần lượt tại M , N , P . SM SN SP Theo Ta-let ta có: = = = x  0 . SA SB SC Do đó V SM SN SP S .MNP 3 = . . = x  0 . V SA SB SC SABC Theo giả thiết: V 1 1 1 MN SM 1 a S .MNP 3
=  x =  x =  = =  MN = . 3 3 3 V 2 2 AB SA SABC 2 2 2 a
Vì tam giác ABC đều cạnh a nên tam giác MNP là tam giác đều có cạnh bằng . 3 2 2  a  3   2 3 Vậy  2  a 3 S = = . MNP 4 4 4 4
Câu 37. Một viên đá có dạng khối chóp tứ giác đều có tất cả các cạnh bằng a . Người ta cưa viên đá theo mặt
phẳng song song với mặt đáy của khối chóp để chia viên đá thành hai phần có thể tích bằng nhau. Tính
diện tích thiết diện viên đá bị cưa bởi mặt phẳng nói trên. 2 a 2 a 2 a 2 a A. . B. . C. . D. . 3 4 3 2 2 3 2 2 Lời giải S M Q N P A D O B C Chọn D
Giả sử cắt viên đá khối chóp tứ giác đều S.ABCD theo mặt phẳng (MNPQ) song song với ( ABCD) như hình vẽ. SM SN SP SQ Theo Ta-let ta có: = = = = x  0 . SA SB SC SD Theo giả thiết ta có: V V +V V V   S .MNPQ 1 S .MNP S .MPQ 1 S .MPQ 1 SM SP SN SQ 1 S .MNP =  =  + =  . + =   . V 2 2V 2 V V 2 SA SC SB SD  2 S . ABCD S. ABC S. ABC S. ACD 1 1 MN SM 1 a 3  2x =  x =  = =  MN = . 3 3 3 2 4 AB SA 4 4 2 a 2  a a
Vì ABCD là hình vuông nên MNPQ là hình vuông cạnh . Vậy S = =   . 3 MNPQ 4 3 3  4  2 2
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 42/105
Câu 38. Cho tứ diện ABCD có thể tích bằng 12 và G là trọng tâm tam giác BCD . Tính thể tích của khối chóp . AGBC . A. V = 3. B. V = 4 . C. V = 6 . D. V = 5. Lời giải Chọn B A B D G C V S 1 1 Ta có . A GBC GBC = =  V = V = 4 . V S 3 . A GBC . 3 A BCD . A BCD BCD
Câu 39. Cho hình lăng trụ tam giác AB . C A BC
  có đáy ABC là tam giác vuông cân tại A , cạnh AC = a 2 .
Biết AC tạo với mặt phẳng ( ABC) góc 60 và AC = 4. Tính thể tích V của khối đa diện ABCB C   . 8 16 8 3 16 3 A. V = . B. V = . C. V = . D. V = . 3 3 3 3 Lời giải Chọn B B' A' C' B A H C 1 1 Ta có S = AC =
= và d (C ,( ABC)) = C H
 = AC .sin 60 = 2 3 . ABC (2 2)2 2 4 2 2
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 43/105 Khi đó, 1 2 V = − = − = 2 16 3 = =   V    V V    V V .4.2 3 . ABCB C ABC.A B C . A A BC   ABC. A B C ABC.       3 A B C . 3 ABC A B C 3 3
Câu 40. Cho tứ diện ABCD có thể tích bằng 54 , gọi M , N, P lần lượt là trọng tâm các tam giác ABC , ACD ,
ADB . Tính thể tích của khối tứ diện AMNP . 27 A. V = . B. V = 4 . C. V = 9. D. V =16 . 2 Lời giải Chọn B A P M N B D F D E C
Gọi D, E, F lần lượt là trung điểm các cạnh BC,CD, DB . 3 3  2   2  1 2 2 Ta có V = V = . V = V = .54 = 4 . AMNP      3 ADEF
 3  4 ABCD 27 ABCD 27
Câu 41. Cho hình hộp ABC . D A BCD
  có đáy ABCD là hình thoi cạnh bằng 6 và góc nhọn bằng 45, cạnh
bên của hình hộp bằng 10 và tạo với mặt phẳng đáy một góc 45. Tính thể tích khối đa diện ABCDD B   .
A. V =180 .
B. V = 60 .
C. V = 90. D. V =120 . Lời giải Chọn D
Gọi AH là đường cao của hình hộp
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 44/105
Khi đó ( AA ;( ABCD)) = A A
H = 45  A H
 = AA.sin 45 = 5 2 . 2 S = 6 .sin 45 =18 2 ABCD Nên V =  =     S .A H 180 . ABCD.A B C D ABCD 2 2 2 V = + = + = =   V   V .V    V    V     120 . ABCDD B . A BDD B C.BDD B   ABD. A B D BCD.B C D ABCD. 3 3 3 A B C D
Câu 42. Cho khối lăng trụ tam giác AB . C A BC
 , gọi M , N lần lượt thuộc các cạnh bên AA , CC sao cho
MA = MA , NC = 4NC. Gọi G là trọng tâm tam giác ABC . Hỏi trong bốn khối tứ diện GA BC   , BB MN , ABB C   và A B
CN , khối tứ diện nào có thể tích nhỏ nhất? A. Khối A BCN . B. Khối GA BC   . C. Khối ABB C   . D. Khối BB MN . Lời giải Chọn A Đặt V = V . ABC. A BC   1
Ta có G ( ABC) nên V =    V . G. A B C 3 1 1 2 1 V = = = = =  VV  .V   . V V . BB MN M .BB N . A BB N . 2 A BB C C 2 3 3 1 1 2 1 V = = =   V   . V V . ABB C . 2 A BB C C 2 3 3 S CN 4 4 4 1 4 1 2 4 Ta có CBN = = V = = = =  V   . V    . . V V S  nên A BCN A BCC A BCC BCC 5 5 5 2 5 2 3 15 CBC
Vậy khối tứ diện A B
CN có thể tích nhỏ nhất.
Câu 43. Cho khối lăng trụ tam giác AB . C A BC
  có thể tích bằng 60 . Gọi M , N , P lần lượt thuộc các cạnh
bên AA , BB , CC sao cho MA = 2MA , NB = 3NB, PC = 4PC . Tính thể tích khối đa diện BCMNP . 85 A. 40 . B. 30 . C. 31. D. . 3 Lời giải Chọn C
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 45/105
Gọi d là khoảng cách giữa BB và CC . 1   Ta có S = CP + 1 3 4 1 31 31 BN d = . BB + CC .d = . BB .d = .S . BCPN ( ).     2 2  4 5  2 20 40 BCC B 31 31 2 31 2 Do đó V = V = V = = =   . .V    . .60 31. BCMNP M .BCPN M .BCC B ABC. 40 40 3 A B C 40 3
Câu 44. Cho khối tứ diện đều ABCD có cạnh bằng a . Gọi M , N lần lượt là trung điểm của các cạnh AB ,
BC và E đối xứng với điểm B qua D . Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối
đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V . Tính V . 3 13 2a 3 7 2a 3 2a 3 11 2a A. V = . B. V = . C. V = . D. V = . 216 216 18 216 Lời giải Chọn D
Gọi P = CDNE , Q = AD ME , khi đó (MNE) chia hình chóp là hai khối đa diện gồm
ACMNPQ và BMNDQP .
Dễ dàng chứng minh được P , Q lần lượt là trọng tâm tam giác EBC và EAB . Khi đó: EQ EP 2 = = . EM EN 3 ED EQ EP 1 2 2 2 Ta có V = . . .V = . . V = V E.DQP E.BMN E.BMN E. EB EM EN 2 3 3 9 BMN 7  V = V −V = V . BMNDQP E.BMN E.DQP E. 9 BMN 1
d ( E;( ABC )) EB Lại có S = S = =  , 2 BMN  4 ABC d ( ; D ( ABC )) DB
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 46/105 V
d ( E;( ABC )).S BMN 1 1 Nên E.BMN = = 2. = V d ; D ABC .S 4 2 D. ABC ( ( )) ABC  7 1 7 Suy ra V = . .V = .V BMNDQP D. ABC D. 9 2 18 ABC 3 3 11 11 2a 11 2aV = V = V −V = .V = . = . ACMNPQ D. ABC DMBDQP D. 18 ABC 18 12 216
Câu 45. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích bằng 48 . Kí hiệu M , N lần
lượt là các điểm thuộc cạnh AB , CD sao cho MA = MB , ND = 2NC . Tính thể tích V của khối chóp S.MBCN .
A. V = 40 .
B. V = 8 .
C. V = 20 . D. V = 28 . Lời giải Chọn C
Gọi d là khoảng cách giữa AB và CD. 1 1  1 1  1 5 5 Ta có S = BM + CN d = AB + CD d = AB d = S . MBCN ( ). . . . . . .   2 2  2 3  2 6 12 ABCD 5 5 Nên V = V = .48 = 20 . S .MBCN S . 12 ABCD 12
Câu 46. Cho khối hộp ABC . D A BCD
  tâm I , các điểm M , N , P , Q lần lượt là trug điểm của các cạnh
AB , BC , CD , DA . Tính thể tích của phầ khối hộp nằm ngoài khối nón I.MNPQ . 11V 5V 3V 7V A. . B. . C. . D. . 12 6 4 8 Lời giải Chọn A 1 1  4  1 Ta có S = S = SS = 1− S = S
và h là chiều cao của hình chóp đã AMQ   4 ABD 8 ABCD MNPQ  8 ABCD  2 ABCD cho. Vì vậy 1 1 1 h V V = S .d I , ABCD = . S . = . I .MNPQ MNPQ ( ( )) 3 3 2 ABCD 2 12
Vậy Thể tích cần tính là 11V . 12
Câu 47. Cho khối chóp S.ABCD có thể tích V và đáy ABCD là hình bình hành. Kí hiệu S là điểm thỏa mãn
SS = 2DC . Tính thể tích phần chung của hai khối chóp S.ABCD và S .ABCD . 5V 4V V V A. . B. . C. . D. . 9 9 3 2
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 47/105 Lời giải Chọn B
Ta có CD / / AB / /SS do đó S D
 SC = C, S A
 SB = B. B BAB 1 SB 2 Vì B C   / /BC và = =  = B SSS . 2 SB 3
Phần chung của hai khối chóp là ABC . D B C  . Ta có V = − = − +   V V   V V   V
và theo công thức tỷ số thể tích ta có ABC . D B C S.ADC B ( .AABC . A ADC ) 2  2  4 1 2 2 2 1 1 V = = = = = =   V . V V và VV . V V . S . AB C   S.  3 ABC  9 2 9 S . ADC S . 3 ADC 3 2 3 Vậy 2 1 5 4 V = + =  =   V V V V   V . S . ADC B 9 3 9 ABCDC B 9
Câu 48. Cho hình lăng trụ AB . C A BC
  có thể tích V . Các điểm M , N , P trên các cạnh AA , BB , CC sao AM 1 BN 1 CP 2 cho = = = ABC MNP . AA , 2 BB , 3 CC
. Tính thể tích của khối đa diện . 3 1 7 7 11 A. V . B. V . C. V . D. V . 2 16 18 18 Lời giải Chọn A Ta có V =V +V ABC.NMP M .ABC M .BCPN Trong đó 1 1 V
= d M , ABC .S = V M . ABC ( ( )) 3 ABC 6
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 48/105 2 1 + S BP + CN 2 1 BCPN V = V = 3 3 = =   V . V V . M .BCPN M .BCC B . A BCC B   S  +  +   BB CC 1 1 3 3 BCC B   Vậy 1 1 1 V = + V = V . ABC.MNP    6 3  2
Câu 49. Cho hình lăng trụ AB . C A BC
  có thể tích V . Các điểm M , N , P trên các cạnh AA , BB , CC sao AM 1 BN CP 2 cho = = = ABC MNP . AA , 2 BBCC
. Tính thể tích của khối đa diện . 3 2 9 20 11 A. V . B. V . C. V . D. V . 3 16 27 18 Lời giải Chọn D Ta có V =V +V ABC.NMP M .ABC M .BCPN Trong đó 1 1 V
= d M , ABC .S = V M . ABC ( ( )) 3 ABC 6 S BP + CN 2 2 4 BCPN V = V = = =   V . V V . M .BCPN M .BCC B . A BCC B   S  +    BB CC 3 3 9 BCC B   Vậy 1 4 11 V = + V = V . ABC.MNP    6 9  18
Câu 50. Cho hình lăng trụ AB . C A BC
  có thể tích V . Các điểm M , N , P trên các cạnh AA , BB , CC sao AM BN CP 1 cho = x = y = z
ABC MNP bằng V . Mệnh đề nào AA , BB , CC
. Biết thể tích của khối đa diện . 2 sau đây đúng? 3 2
A. x + y + z = 1 .
B. x + y + z = 2 .
C. x + y + z = .
D. x + y + z = . 2 3 Lời giải Chọn C
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 49/105 Ta có V =V +V ABC.NMP M .ABC M .BCPN Trong đó 1 x V
= d M , ABC .S = V M . ABC ( ( )) 3 ABC 3 S BP + CN y + z 2 y + z BCPN V = V = = =   V . V V . M .BCPN M .BCC B . A BCC B   S  +  +   BB CC 1 1 3 3 BCC B + + Khi đó x y z V = V . ABC.MNP 3 + + Vậy 1 x y z 1 3 V = V V =
V x + y + z = . ABC.MNP 2 3 2 2
Câu 51. Cho khối tứ diện OABC có O ,
A OB,OC đôi một vuông góc và OA = 1,OB = 2,OC = 3 . Gọi D, E, F
lần lươt là chân đường cao hạ từ đỉnh O xuống các cạnh BC, C ,
A AB . Thể tích khối tứ diện ODEF bằng 36 276 289 49 A. . B. . C. . D. . 325 325 325 325 Lời giải Chọn A C D E O B F A *Ta có 2 CE CO 9 AE 1 2 2 = =  = CD CO 9 BD 4 AF AO 1 BF 4 , = =  = , = =  = . 2 CA CA 10 AC 10 2 CB CB 13 BC 13 2 AB AB 5 BA 5 * Ta có thể tích 1
khối tứ diện OABC :V = O . A O . B OC = 1. 0 6 AO AE AF 1 CO CE CD 81 BO BD BF 16 *V = . . V = V , V = . . V = V ,V = . . V = V . . A OEF 0 0 AO AC AB 50 C.OED 0 0 CO CA CB 130 B.ODF 0 0 BO BC BA 65   Vậy 1 81 16 36 36 V = 1− − − V = V = . ODEF   0 0  50 130 65  325 325
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 50/105
Câu 52. Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M , N lần lượt là trung điểm các cạnh AB, BC . Điểm P
trên cạnh CD sao cho PD = 2CP . Mặt phẳng (MNP) cắt AD tại Q . Tính thể tích khối đa diện BMNPQD . 2 23 2 2 13 2 A. . B. . C. . D. . 16 432 48 432 Lời giải Chọn B D P Q A C M N B
*Có MN // AC  (MNP) ( ACD) = PQ // MN // AC . Ta chia khối đa diện thánh các khối tứ diện V = V +V +V . BMNPQD D.PQB B.MNQ B.PQN
*Thể tích khối tứ diện đều đã cho là 2 V = . 0 12 2 DP DQ DB  2  4 *Ta có V = . . V = V = V . D.PQB 0   0 0 DC DA DB  3  9 BM BN BQ 1 1 SACQ 1 AQ 1 Và V = . . V = V = . V = . V = V . B.MNQ B. ACQ B. ACQ 0 0 0 BA BC BQ 4 4 S 4 AD 12 ACD BP BQ BN 1 1 SPQC 1 2 1 Và V = . . V = V = . V = . V = V . B.PQN B.PQC B.PQC 0 0 0 BP BQ BC 2 2 S 2 9 9 ADC   Vậy 4 1 1 23 2 23 2 V = + + V = . = . BMNPQD   0  9 12 9  36 12 432
Câu 53. Cho tứ diện đều ABCD có cạnh bằng 10cm . Trên các cạnh AB, AC lần lượt lấy các điểm M , N sao
cho AM = 8cm, AN = 9cm . Thể tích khối tứ diện AMND bằng 250 2 A. 3 V = cm . B. 3 V = 60 2 cm . C. 3 V =180 2 cm . D. 3 V = 250 2 cm . 3 Lời giải Chọn B
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 51/105 D N A C M B 3 AM AN 8 9 10 2 Ta có 3 V = . .V = . . = 60 2 cm . AMND ABCD AB AC 10 10 12
Câu 54. Cho hình lập phương ABC . D A BCD
  cạnh 2a , gọi M là trung điểm của BB và P thuộc cạnh DD 1 sao cho DP =
DD . Mặt phẳng ( AMP) cắt tích khối đa diện AMNPBCD bằng 4 11 9 A. 3 V = 2a . B. 3 V = 3a . C. 3 V = a . D. 3 V = a . 3 4 Lời giải Chọn B AA BM 1 CN DP 1
*Thể tích khói lập phương 3
V = 8a . Ta có x = = 0; y = = ; z = ;t = = 0 AABB 2 CCDD . 4 V 1 1 3 3
*Ta có x + z = y + t và AMNPBCD =
(x + y + z +t) = ( y +t) 3 =  V = V = 3a . AMNPBCD 0 V 4 2 8 8 0
Câu 55. Cho tứ diện ABCD đều cạnh bằng 1. Gọi M , N lần lượt là trung điểm các cạnh AB, BC . Điểm P
trên cạnh CD sao cho PC = 2PD . Mặt phẳng (MNP) cắt AD tại Q . Thể tích khối đa diện BMNPQD bằng 11 2 2 5 2 7 2 A. . B. . C. . D. . 216 27 108 216 Lời giải Chọn D
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 52/105 D P Q A C M N B
*Có MN // AC  (MNP) ( ACD) = PQ // MN . Ta chia khối đa diện thánh các khối tứ diện V = V +V +V . BMNPQD D.PQB B.MNQ B.PQN
*Thể tích khối tứ diện đều đã cho là 2 V = . 0 12 2 DP DQ DB  1  1 Ta có V = . . V = V = V . D.PQB 0   0 0 DC DA DB  3  9 BM BN BQ 1 1 SACQ 1 AQ 1 Và V = . . V = V = . V = . V = V . B.MNQ B. ACQ B. ACQ 0 0 0 BA BC BQ 4 4 S 4 AD 6 ACD BP BQ BN 1 1 SPQC 1 2 1 Và V = . . V = V = . V = . V = V . B.PQN B.PQC B.PQC 0 0 0 BP BQ BC 2 2 S 2 9 9 ADC   Vậy 1 1 1 7 2 7 2 V = + + V = . = . BMNPQD   0  9 6 9  18 12 216
Câu 56. Cho khối chóp S.ABC có SA = SB = SC = , a ASB = 60 ,  BSC = 90 ,
CSA =120 . Gọi M , N lần là các điể CN AM
m trên cạnh AB và SC sao cho =
. Khi khoảng cách giữa M và N nhỏ nhất, tính thể tích SC AB
V của khối chóp S.AMN . 3 2a 3 5 2a 3 5 2a 3 2a A. V = . B. V = . C. V = . D. V = . 72 72 432 432 Lời giải Chọn C 2 2 3 3 a  1   1  2a
Ta có thể tích của khối chóp S.ABC là V = 1− − − = . 0     6  2   2  12
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 53/105 Đặ CN AM t =
= m (0  m  ) 1 , ta có SC AB 2 2 a a
SA = a, SB = ,
b SC = c, a = b = c = a, a b =
, b c = 0, c a = − . 2 2
Theo đẳng thức trên ta có sự biểu diễn vectơ SN = (1− m) ,
c SM = SA + AM = a + mAB = a + m (b − a).
MN = SN − SM = (1− m)c −[a + m(b − a)] = (m −1)a − mb + (1− m)c . Do đó = ( a MN
(m −1)a − mb + (1− )
m c) = (3m − 5m + 3) 2 2 11 2 2 2 a  . 12 5 SN SN AM 5 1 2a 5 2a
Dấu bằng đạt tại m =  V = V = .
V = m m − V = = . SAMC ( ) 3 3 1 . . 0 0 6 SC SC AB 6 6 12 432
Câu 57. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA = 3a vuông góc với đáy. Mặt phẳng qua A
vuông góc với SC cắt các cạnh SB, SC, SD lần lượt tại M , N , P . Thể tích khối đa diện SAMNP bằng 3 3 3a 3 3a 3 3a 3 5 3a A. . B. . C. . D. . 20 24 10 24 Lời giải Chọn A
Có SB ⊥ AM , SC ⊥ AN , SD ⊥ AP và 2 2 2 SA SM SA 3 SN SA 3 SP SA 3 x = =1, y = = = , z = = = ,t = = = . 2 2 2 SA SB SB 4 SC SC 5 SD SD 4 3 xyzt  1 1 1 1  3 3a Vậy V = + + + V = . S . AMNP   S. 4 ABCDx y z t  20
Câu 58. Cho khối lăng trụ AB . C AB C
  có thể tích bằng 1 . Gọi M , N lần lượt là trung điểm các đoạn
thẳng AA và BB . Đường thẳng CM cắt đường thẳng CA tại P , đường thẳng CN cắt đường
thẳng CB tại Q . Thể tích của khối đa diện lồi AMPBNQ bằng 1 1 2 A. 1. B. . C. . D. . 3 2 3 Lời giải Chọn D
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 54/105
Ta có A là trung điểm của PC ; B là trung điểm của QC . Do đó SC PQ 1 4 V = = = =  V    4V    4. V . C.C PQ C.A B C C.A B C ABC.    S    3 A B C 3 C A B A MB NC C  1 1 + + + +1    2 Mặt khác A A BB C C 2 2 V = = =    V    V . A B C .MNC ABC. A B C ABC.    3 3 A B C 3 Do đó 4 2 2 V = − = − =   VV . A MPB NQ C.C PQ A BC  .MNC 3 3 3
Câu 59. Cho khối chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a . Gọi M là điểm đối xứng của C qua
D , N là trung điểm của cạnh SC . Mặt phẳng (BMN ) chia khối chóp S.ABCD thành hai khối đa
diện. Tính thể tích V của khối đa diện chứa đỉnh S . 3 15 2a 3 7 2a 3 11 2a 3 7 2a A. V = . B. V = . C. V = . D. V = . 144 72 144 144 Lời giải Chọn B
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 55/105
Gọi O = AC BD SO ⊥ ( ABCD) ; P = MB AD và Q = SD MN suy ra Q là trọng tâm của QD 1
d (Q,( ABCD)) 1 tam giác SMC  =  = . SD 3
d (S,( ABCD)) 3
Mặt phẳng (BMN ) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S là SABPQN . a 2
Ta có d (S,( ABCD)) 2 2
= SO = SA − AO = . 2 1 aV = d S ABCD S = SO AB = . S ABCD ( ,( )) 3 1 2 2 . . . 3 ABCD 3 6 1 1 1 M . D BC a 2 Có V = d N ABCD S = d S ABCD = . N BCM ( ,( )). . BCM ( ,( )) 3 . . 3 3 2 2 12 1 1 1 M . D PA a 2 Lạ có V = d Q DMP S = d S ABCD = . Q DMP ( ,( )). . DMP ( ,( )) 3 . . 3 3 3 2 72 3 3 3 3 a 2 a 2 a 2 7a 2 Mà V = V +V −V V = + − = . SABPQN S . ABCD Q.DMP N .BCM SABPQN 6 72 12 72
Câu 60. Cho khối chóp tam giác S.ABC có thể tích V . Gọi M , N , P , H lần lượt là trung điểm các cạnh
AB , BC , CA , SA . Tính thể tích khối chóp H.MNP . 1 1 1 3 A. V . B. V . C. V . D. V . 12 24 8 8 Lời giải Chọn C 1 Ta có V = V
= d S, ABC .S . S . ABC ( ( )) 3 ABC 1 1 1 1 1  1  1 Lại có V
= d H, MNP .S
= . d S, ABC . S = d S, ABC S = V . H .MNP ( ( )) MNP ( ( )) ABC  ( ( ))  3 3 2 4 8  3 ABC  8
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 56/105
TỶ SỐ THỂ TÍCH KHỐI ĐA DIỆN (ĐỀ SỐ 02) Câu 1.
Cho hình chóp S.ABC có SC = 2a và SC ⊥ ( ABC) . Đáy ABC là tam giác vuông cân tại B và
AB = a 2 . Mặt phẳng ( ) đi qua C và vuông góc với SA , ( ) cắt S ,
A SB lần lượt tại D, E . Tính
thể tích khối chóp S.CDE . 3 4a 3 8a 3 2a 3 16a A. . B. . C. . D. . 9 27 9 27 Lời giải Chọn C 1 1 1 1 1 2a Ta có V = .SC.S
= .SC. .AB = .2 . a . a = . S ABC ABC ( 2) 3 2 2 . 3 3 2 3 2 3 2 2 2 2 V Lại có SD SE SC SC 4a 4a 1 S .DEC = . = . = . = . 2 2 2 2 2 2 V SA SB SA SB 4a + 2a 4a + 4a 3 S . ABC 3 Do đó 1 2a V = V = . S .DEC S . 3 ABC 9 Câu 2.
Cho hình chóp S.ABC có SC = 2a và SC ⊥ ( ABC) . Đáy ABC là tam giác vuông cân tại B và
AB = a 2 . Mặt phẳng ( ) đi qua C và vuông góc với SA , ( ) cắt S ,
A SB lần lượt tại D, E . Tính
thể tích khối đa diện ABCDE . 3 4a 3 8a 3 2a 3 19a A. . B. . C. . D. . 9 27 9 27 Lời giải Chọn A
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 57/105 1 1 1 1 1 2a Ta có V = .SC.S
= .SC. .AB = .2 . a . a = . S ABC ABC ( 2) 3 2 2 . 3 3 2 3 2 3 2 2 2 2 V Lại có SD SE SC SC 4a 4a 1 S .DEC = . = . = . = . 2 2 2 2 2 2 V SA SB SA SB 4a + 2a 4a + 4a 3 S . ABC 3 3 3 3 Do đó 1 2a 2a 2a 4a V = V = . Suy ra V = V −V = − = . S .DEC S . 3 ABC 9 ABCDE S .ABC S .DEC 3 9 9 Câu 3.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a 2 , SA = 2a , SA ⊥ ( ABCD) . Mặt
phẳng ( P) đi qua A vuông góc với SC cắt SB, SC, SD lần lượt tại H , K, J . Tính thể tích khối chóp S.AHKJ . 3 4a 3 8a 3 8a 3 4a A. . B. . C. . D. . 27 27 9 9 Lời giải Chọn D 1 1 4a SA Ta có V = .S . A S = .2 . a a =
và AH ⊥ SB, AK ⊥ SC, AJ ⊥ SD và x = = 1, S ABCD ABCD ( 2) 3 2 . 3 3 3 SA 2 SH SA 2 2 SK SA 1 2 SJ SA 2 y = = = , z = = = , t = = = . 2 SB SB 3 2 SC SC 2 2 SD SD 3     Do đó V 1 1 1 1 1 1 2 1 2 3 3 1 S . AHKJ = .xyzt + + + = .1. . . 1 + + 2 + =     V 4  x y z t  4 3 2 3  2 2  3 S . ABCD 3 1 4aV = V = . S . AHKJ S . 3 ABCD 9 Câu 4.
Cho hình chóp S.ABCD có đáy ABCD là tứ giác lồi với O là giao điểm của AC và BD . Gọi
M , N , P, Q lần lượt là trọng tâm của các tam giác SAB, SBC, SCD, SDA . Gọi V ,V lần lượt là thể tích 1 2 V
của các khối chóp S.ABCD và .
O MNPQ . Khi đó tỉ số 1 là V2 27 27 A. 8 . B. . C. . D. 9 . 4 2 Lời giải Chọn C
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 58/105 S Q P M N A D H E G O C F B
Gọi E, F,G, H lần lượt là trung điểm của AB, BC,CD, DA . 2  2  4 Ta có S = S = S
(do hai tứ giác MNPQ và EFGH đồng dạng theo tỉ số 2 ). MNPQ    3 EFGH  9 EFGH 3 1 2 Mà S = SS = S . EFGH 2 ABCD MNPQ 9 ABCD V
d (S,( ABCD)) S 9 27 Suy ra 1 = . ABCD = 3. = . V d O, MNPQ S 2 2 2 ( ( )) MNPQ Câu 5.
Cho khối lăn trụ tam giác AB . C A BC
  có thể tích V . Các điểm M , N lần lượt thuộc các cạnh MB 1 NC 1 BB ,  CC sao cho = ; = BB 2 CC
. Thể tích khối chóp tứ giác . A BMNC là 4 V 3V V V A. . B. . C. . D. . 3 8 6 4 Lời giải Chọn D B C A N M B' C' A' V 1  AA BM CN  1  1 1  1 Ta có ABCMN = + + = + =     . V        3 AA BB CC  3  2 4  4 ABC. A B C Vậy V V = . ABCMN 4
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 59/105 Câu 6.
Cho khối lăng trụ tam giác AB .
C A' B'C ' . Mặt phẳng qua điểm A và điểm P thuộc cạnh BB ' đồng
thời song song cạnh BC , chia khối lăng trụ thành hai khối đa diện có thể tích bằng nhau. Tính tỉ số PB PB ' A. 3 . B. 2 . C. 6 . D. 4 Lời giải Chọn A. Đặt BP = BP CQ
x , Do PQ / / BC nên = = x BB ' BB ' CC ' V  
Áp dụng công thức tỉ số thể tích ta có ABCQP 1 BP CQ 1 = + = ( + ) 2x x x =   . V
3  BB ' CC '  3 3
ABC. A' B 'C ' V Mà giả thiết cho ABCQP 1 1 2x 3 V = V nên suy ra =  =  x = ABCQP
APQA' B 'C ' V 2 2 3 4
ABC. A' B 'C ' BP 3 BP 3 PB Suy ra = 
=  4BP = 3PB + 3PB '  PB = 3PB '  = 3 BB ' 4 BP + PB ' 4 PB ' Câu 7. Cho khối hộp ABC .
D A' B'C ' D' . Mặt phẳng qua D , điểm Q thuộc cạnh AA' , điểm R thuộc cạnh QA 1 RC CC ' sao cho = ,
= 3 chia khối hộp thành hai phần. Tính thể tích của phần chứa mặt đáy QA' 3 RC ' ( D ABC ) . V 2V V V A. . B. . C. . D. . 3 3 4 2 Lời giải Chọn D A D Q C B A' D' R B' C'
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 60/105 Ta có: Vì ABC .
D A' B'C ' D' là khối hộp nên chứng minh được: ADQ = C
 'B'R(c − g −c) .
Suy ra: DQ = RB ' .
Chứng minh tương tự ta có: A
 'B'Q = C
DR(c − g −c)  B'Q = DR .
Do đó: tứ giác B 'QDR là hình bình hành.
Nên QD / / B ' R B '(DQR) . AQ CR BB ' DD 1 CR Ta có: + = + hay: + =1+ 0 AA ' CC ' BB ' DD ' 4 CC ' CR 3 Suy ra: = . CC ' 4
Mặt phẳng (DQR) chia khối hộp thành AB .
CD QB ' R và DQB ' .
R A'C ' D ' .
Áp dụng công thức tính nhanh tỉ số thể tích ta có: V    
ABCD.QB ' R 1 AQ BB ' CR DD = + + + 1 1 3 1   = = +1+ + 0   = . V 4  AA' BB ' CC ' DD '  4  4 4  2
ABCD. A' B 'C ' D ' V Vậy:
ABCD.QB ' R 1 1 = V = V . ABCD.QB ' V 2 R 2
ABCD. A' B 'C ' D ' Câu 8.
Cho hình chóp S.ABCD có thể tích V với đáy ABCD là hình bình hành. Mặt phẳng qua , A M , P cắt SM 1 SP 2
cạnh SC tại N với M , P là các điểm thuộc SB , SD sao cho = ,
= . Tính thể tích khối đa SB 2 SD 3 diện ABC . D MNP . 23 7 14 1 A. V . B. V . C. V . D. V . 30 30 15 15 Lời giải Chọn A S P N Q I M D A O C B
Ta có công thức cho bài toán tổng quát: cho hình chóp S.ABCD đáy là hình bình hành. Mặt phẳng
() cắt các cạnh ,
SA SB, SC, SD lần lượt tại M , N , P,Q như hình vẽ. Đặt: SM SN SP SQ = x, = y, = z,
= t . Khi đó ta có: 1 1 1 1 + = + . SA SB SC SD x z y t
Áp dụng vào bài toán ta có:
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 61/105 S N M P I D A O B C ( SA SM 1 SN SP 2
AMNP) là mặt phẳng cắt nên: = 1, = , = x , = . SA SB 2 SC SD 3 1 1 1 1 1 5 2 Suy ra: + = +  =  x = . 1 x 1 2 x 2 5 2 3 Khi đó: V 1 2 1 V 2 2 4
SAMN = 1. . = ; SANP = 1. . = . V 2 5 5 V 5 3 15 SABC SACD V V V 7 V 7 Nên: SAMN SANP + 1 4 7 = + = hay: S . AMNP = S . AMNP  = . V V 5 15 15 1 15 V 30 SABC SACD V S . ABCD S . ABCD 2 Do đó: V 23 AMNP.BCD = . V 30 S . ABCD Câu 9. Cho hình hộp ABC .
D A' B'C ' D' có thể tích V . Các điểm M , N, P trên các cạnh AA', BB ',CC ' sao AM 1 BN 1 CP 2 cho = , = ,
= . Mặt phẳng ( ) qua ba điểm M , N, P cắt cạnh DD' tại Q . Tính AA ' 2 BB ' 3 CC ' 3
thể tích của khối đa diện AB . CD MNPQ . 7 7 11 5 A. V . B. V . C. V . D. V . 12 8 12 12 Lời giải Chọn A A' D' Q C' B' M F P N E A D B C
Công thức tính nhanh: ta có: AM CP BN DQ + = + . AA' CC ' BB ' DD ' 1 2 1 DQ DQ Suy ra: + = + 5  = . 2 3 3 DD ' DD ' 6
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 62/105 V    
Do đó tỉ số thể tích: ABCD.MNPQ 1 AM CP = + 1 1 2 7   = . +   = . V 2  AA' CC '  2  2 3  12
ABCD. A' B 'C ' D ' Vậy: 7 V = V . ABCD.MNPQ 12
Câu 10. Cho hình hộp ABC . D A BCD
  có thể tích V . Các điểm M , N , P , Q trên các cạnh AA , BB , CCAM BN CP sao cho = x = y = z
 qua ba điểm M , N , P cắt cạnh DD tại Q AA , BB , CC . Mặt phẳng ( ) DQ sao cho = t ABCD MNPQ . DD
. Tính thể tích của khối đa diện .
3( x + y + z + t )
3( x + y + z + t ) A. V = V . B. V = V . ABCD.MNPQ 4 ABCD.MNPQ 8
x + y + z + t
x + y + z + t C. V = V . D. V = V . ABCD.MNPQ 8 ABCD.MNPQ 4 Lời giải Chọn D
Ta có tứ giác MNPQ là hình bình hành.
Gọi E , F lần lượt là giao điểm của AC và BD ; MP và NQ .
Khi đó AMPC , BNQD là các hình thang nên BN + DQ = AM + CP = 2EF hay có x + z = y +t . y x + z y x + z x + y + z Ta có V = V +V = V + = + =    V V V V . ABC.MNP N .ABC N .ACPM ABC. A B C ABC.    3 3 A B C 6 6 6 x + z + t Tương tự ta có V = V . ACD.MPQ 6 x + y + z x + z + t
x + z + y + t Do đó V = V +V = V + 2 2 V = V . ABCD.MNPQ ABCC.MNP ACD.MPQ 6 6 6
4x + 4z + 2 y + 2t
3x + 3z + ( x + z) + +
3x + 3z + ( y + t ) + + = 2 y 2t 2 y 2t V = V = V . 12 12 12
3x + 3z + 3y + 3t + + + = x y z t V = V . 12 4
x + y + z + t Vậy V = V . ABCD.MNPQ 4
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 63/105
Câu 11. Cho khối hộp ABC . D A B C 
D có AC = 4a và 0 0 BAD = 60 , A AD = A A
B =120 . Biết tất cả các
cạnh của khối hộp bằng nhau. Tính thể tích V của khối chóp đã cho. 8 32 A. 3 V = a . B. 3 V = a . C. 3
V = 16a . D. 3
V = 32a . 3 3 Lời giải A B 600 1200 1200 D C 4a A' B' D' C' Chọn C
Gọi x là độ dài cạnh của khối hộp. Theo qui tắc hình hộp ta có 2 AC =
AC = ( AB + AD + AA)2 2 2 2
= AB + AD + AA + 2(A .
B AD + AD .AA + AA .AB)  1 1 1  2 2 2 2 2 = 3x + 2 x − x − x
= 2x = 4a x = 2 2a   .  2 2 2  2 2
 1  1  1   1   1   1 ax 3 ( )3 2 2 2 3 Do đó 3 V = 6.V = + − − − − − = = =  x 1 2 16a . A A BD          
 2  2  2   2   2   2  2 2 .
Câu 12. Cho khối hộp ABC . D A B C 
D có ABD là tam giác đều cạnh a . Các mặt phẳng (ADD A  ),(ABB A  ),(A B
D) cùng tạo với mặt phẳng đáy các góc bằng 0
60 và hình chiếu vuông góc
của A lên mạt phẳng đáy nằm khác phía với điểm A so vói đường thẳng BD . Tính thể tích V của
khối chóp đã cho. 3 3a 3 3 a 3 3 a 3 3 3a 3 A. . B. . C. . D. . 4 4 12 2 Lời giải
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 64/105 A a B a a D C B' A' D' C' Chọn A
6p( p − b)( p − c)tan 3 3a a a 3a 3 Ta có V = 6.V = = 2 3 = A.  A BD 3 2 2 2 4
Câu 13. Cho hình chóp S.ABCD có thể tích V và đáy ABCD là hình bình hành. Mặt phẳng qua A và trung
điểm N cạnh SC các cạnh SB , SD lần lượt tại M , P . Tính thể tích nhỏ nhất của khối chóp S.AMNP . V 3V V V A. . B. . C. . D. . 8 8 4 3 Lời giải Chọn D Đặt SA SM SN 1 SP x = = 1; y = ; z = = ; t = . Ta có SA SB SC 2 SD 1 1 1 1 + = + 1 1 1 1  1+ 2 = +  + = 3. x z y t y t y t   Do đó 1 1 1 1 1 1 1 3 V = xyzt + + + V = 3 + 3 yt.1. V = ytV . S . AMNP   ( ) 4  x y z t  4 2 4 y + t 2 yt 4 V Mà yt =   yt   V  . 3 3 9 S . AMNP 3
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 65/105
Câu 14. Cho khối hộp ABC . D A BCD
  có thể tích V . Mặt phẳng qua A , M là trung điểm cạnh CC cắt các
cạnh BB , DD lần lượt tại P , Q . Tính thể tích khối của khối đa diện ABC . D PMQ . 3V V V V A. . B. . C. . D. . 4 2 4 8 Lời giải Chọn C AA BP CM 1 DQ 1  Ta có x = = 0 y = z = = t =
x + z = y + t = 0 + = . AA , BB , CC , 2 DD và 2 2 1 1 0 + + + + + Do đó x t z t 2 2 V V = V = V = . ABCD.PMQ 4 4 4
Câu 15. Cho hình chóp S.ABC có ASB = BSC = CSA = 30 và SA = SB = SC = a . Mặt phẳng ( P) qua A cắt
hai cạnh SB , SC lần lượt tại B, C sao cho chu vi tam giác AB C
  nhỏ nhất. Gọi V , V lần lượt là 1 2 thể tích các khối chóp V S.AB C
  , S.ABC . Tính tỉ số 1 . V2 V V V V A. 1 = 3 − 2 2 . B. 1 = 3 −1 . C. 1 = 4 − 2 3 . D. 1 = 2 −1 . V V V V 2 2 2 2 Lời giải Chọn C   Đặt SB SC V x = ; y = . Ta có 1 = xy . SB SC V2
Theo định lí hàm cosin ta được 2 2 2 2 AB =
a + a x − 3a x ; 2 2 2 2
AC = a + a y − 3a y ; 2 2 2 2 2 B C
  = a x + a y − 3a xy . Khi đó chu vi của AB C   là 2 2 2 2 2 2 2 2 2 2 2 2 2
2 p = a + a x − 3a x + a + a y − 3a y + a x + a y − 3a xy  2 2 2 2  = a x − 3x +1 +
y − 3y +1 + x + y − 3xy  
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 66/105 2 2   2 2  3   1   3   1   2  = a  − y  + +       y − x  + x + x − 3x +1     2 2 2 2            2   2  3 3   1 1   2   a  − x  +
+ x + x − 3x +1      2 2 2 2         2 2  = a
x − 3x +1 + x − x +1 = . a f ( x)  . a f   ( 3−1)=a 2  . 3 y − x Dấu bằng đặt tại 2 x =
; x = 3 −1  x = y = 3 −1 . 3 − y 2 Khi đó V = ( 3 − )2 1 1 = 4 − 2 3 . V2
Câu 16. Cho hình chóp S.ABC có = 30O, = = 60O ASB BSC CSA
và SA = SB = SC = a . Mặt phẳng ( P) qua
A cắt SB, SC lần lượt tại B ,
C sao cho chu vi tam giác AB C
  nhỏ nhất. Gọi V ,V lần lượt là thể 1 2 V
tích các khối chóp S.AB C
 , S.ABC . Tính tỉ số 1 . V2 V V 3 3 − 5 V V 3 3 − 2 A. 1 = 3 3 − 5 . B. 1 = . C. 1 = 4 − 2 3 . D. 1 = . V V 2 V V 2 2 2 2 2 Lời giải Chọn B   V Đặ SB SC t x = , y =
, ta có 1 = xy và theo định lí hàm số côsin ta có: SB SC V2 2 2 2 2 2 2 2 2 2 2 2 2 2
AB = a + a x − 3a x, AC = a + a y − a y, B C
  = a x + a y − a xy .
Khi đó chu vi tam giác là: 2 2 2 2 2 2 2 2 2 2 2 2 2
2 p = a + a x − 3a x + a + a y − a y + a x + a y − a xy  2 2 2 2  = a x − 3x +1 + y − y +1 +
x + y − xy   2 2   2 2  1   3   1   3   2  = a x − 3x +1 + y − +     + x − y +       x    2 2 2 2            2   2  1 1   3 3   2   a x − 3x +1 + x − +    + x     2 2 2 2         −  = af (x) 3 1  af   = 2 + 3   . 2   1 x − y 3 −1 3 −1
Dấu ”=” đạt tại x = và 2 x =  x = , y = 2 − 3 . 2 1 2 y − 2
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 67/105 − − Khi đó V 3 1 3 3 5 1 = (2− 3) = . V 2 2 2
Câu 17. Cho tứ diên ABCD có thể tích V . Các điểm M , N, P lần lượt thuộc các cạnh AB, AC, BD thoả mãn AM 1 AN BP 2 = , =
= . Gọi S là giao điểm của AD và mặt phẳng (MNP) . Tính thể tích khối tứ AB 2 AC BD 3 diện AMNS . 2 V 3 V A. V . B. . C. V . D. 3 3 4 4 Lời giải Chọn A
Trong mặt phẳng ( ABD) gọi S = MP AD. Trong mặt phẳng ( ACD) gọi Q = SN CD MA PB SD SD SD 1 Ta có   = 1 1.2 = 1 = . MB PD SA SA SA 2 Do đó AM AN AS 1 2 2 V =   V =   2V = V . A MNS AB AC AD 2 3 3 Chọn A.
Câu 18. Cho khối chóp S.ABC có SA = 6, SB = 2, SC = 4, AB = 2 10 và 0 0
ASB = 90 , BSC = 60 , 0 ASC = 120 .
Mặt phẳng (P) qua B và trung điểm N của SC , vuông góc với mặt phẳng (SAC) cắt cạnh SA tại V
M . Tính tỉ số thể tích S.MBN . VS.ABC 2 2 1 1 A. . B. . C. . D. . 9 5 6 4 Lời giải Chọn C
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 68/105 S N M B A C *Đặt SM V SM SN 1 k = ta có S.MBN = . = k . SA V SA SC 2 S . ABC Các góc 0 0 0
ASB = 90 , BSC = 60 , ASC =120 .
a = 6, b = 2, c = 4 
Đặt SA = a, SB = b, SC = c   .
 .ab = 0, .cb = 4, .ac = 12 −
Vì (BMN ) ⊥ (SAC) nên kẻ BH ⊥ MN (H MN )  BH ⊥ (SAC) và ta có biểu diễn véctơ cho ba
điểm M , H , N thẳng hàng: ( − =
+ − x) BN = x(SM − SB)+ ( − x)(SN − SB) 1 x BH xBM 1 1 = kxa − b + c . 2
Giải điều kiện vuông góc ta có   1− x   1 . a kxa − b + c = 0    k = BH.SA = 0   2  3
 6kx − 0 − 6(1− x) = 0  3        . BH.SC = 0   1− x   1 − 2kx − 4 + 8  (1− x) = 0 1  . c kxa − b + c = 0 x =     2    3 Vậy V 1 1 1 S .MBN = . = . V 2 3 6 S . ABC
Câu 19. Cho hình chóp S.ABC có M , N lần lượt là trung điểm các cạnh SB, SC . Gọi V là thể tích khối chóp 1 V
S.AMN và V là thể tích khối chóp .
A BCNM . Tính tỉ số 1 . 2 V2 V V V 1 V 1 A. 1 = 4 . B. 1 = 3 . C. 1 = . D. 1 = . V V V 3 V 4 2 2 2 2 Lời giải Chọn C
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 69/105 S N M A C B V SM SN 1 1 1 3 V 1 *Ta có 1 1 = .
= .  V = V ;V = V −V = V  = . 1 2 1 V SB SC 2 2 4 4 V 3 2
Câu 20. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , cạnh bên SA vuông góc với mặt phẳng
đáy ( ABC) . Gọi H, K lần lượt là hình chiếu vuông góc của A lên SB, SC . Gọi V là thể tích khối 1 V 81
chóp S.AHK và V là thể tích khối chóp . A BCKH . Biết 1 =
. Tính thể tích V của khối chóp 2 V 19 2 S.ABC . 3 a 3 3 a 3 3 3a 3 3 a 3 A. V = . B. V = . C. V = . D. V = . 4 6 4 2 Lời giải Chọn A S K H A C B V 81 V 81 81 Ta có 1 1 =  = = V 19 V 81+ . 19 100 2 2 2 4 Mặt khác V SH SK SA SA SA 81 1 = . = . = =  SA = 3a . 2 2 V SB SC SB SC ( 2 2 SA + a )2 100 2 3 Vì vậy 1 1 a 3 a 3 V = S . A S = .3 . a = . 3 ABC 3 4 4
Câu 21. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là một tam giác cân
tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy ( ABC) . Gọi H là hình chiếu vuông góc V 16
của A lên SC . Biết S.AHB =
. Tính thể tích V của khối chóp S.ABC . V 19 S . ABC
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 70/105 3 3 3 3 A. . B. . C. . D. . 12 6 4 2 Lời giải Chọn B SC ⊥ AH
Gọi O là trung điểm AB , ta có SO ⊥ ( ABC) và 
SC ⊥ ( AHB)  SC ⊥ OH . SC ⊥ AB 2 2 2 V SH SO SO SO 16 Suy ra: 1 = = = = =  SO = 2 . 2 2 2 V SC SC SO + OC 3 2 9 SO + 4 1 1 3 3 Vì vậy: V = S .
O dt ( ABC ) = .2. = . 3 3 4 6
Câu 22. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích bằng V . Gọi M , N , P lần lượ SM 1 SN 2 SP 1
t là các điểm trên các cạnh S ,
A SB, SC sao cho = , = ,
= . Mặt phẳng (MNP) cắt SA 2 SB 3 SC 3
cạnh SD tại điểm Q . Tính thể tích khối đa diện AB . CD MNPQ . 5 10 53 58 A. V . B. V . C. V . D. V . 63 63 63 63 Lời giải Chọn D
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 71/105 Đặ SM 1 SN 2 SP 1 SQ t x = = , y = = , z = = ,t = . SA 2 SB 3 SC 3 SD SA SC SB SD 1 1 1 1 2 Ta có tỷ số: + = +  + = +  t = . SM SQ SN SP x t y z 7 1 1 1 5 Vậy V = V +V
= xyz V + ztx V = xz y + t V = V S .MNPQ S .MNP S .PMQ ( ) 2 2 2 63  5  58V Suy ra V = 1− V = ABCD.MNPQ    63  63
Câu 23. Cho hình chóp S.ABCD có đáy ABCD là một tứ giác lồi. Trên cạnh SA lấy điểm M sao cho SM 3
= . Mặt phẳng ( ) song song với mặt phẳng ( ABCD) và qua M chia khối chóp thành hai SA 4
khối đa diện. Nếu thể tích khối đa diện chứa đỉnh A là 2
100 dm thì thể tích của khối đa diện còn lại là? 324 2700 3700 2025 A. ( 3 dm ). B. ( 3 dm ) . C. ( 3 dm ). D. ( 3 dm ) . 7 37 27 64 Lời giải Chọn B
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 72/105
Gọi N , P, Q lần lượt là giao điểm của mặt phẳng ( ) và các cạnh SB, SC, SD . 2  3  9 3
Ta có: dt (MNPQ) = dt  
(ABCD) = dt (ABCD) và kc(S,MNPQ) = kc(S, ABCD).  4  16 4 1 1 9 3 27 Suy ra: V
= kc S, MNPQ dt MNPQ = .
dt ANBCD . kc S, ABCD = V . S .MNPQ ( ) ( ) ( ) ( ) S . 3 3 16 4 64 ABCD VS MNPQ 27 27 27 2700 Vậy: . = =  V = .100 = dm . S MNPQ ( 3 . ) V 64 − 27 37 3 37 ABCD.MNPQ
Câu 24. Cho khối chóp S.ABCD có đáy là hình chữ nhật, AB = 3a, AD = a, SA vuông góc với đáy và
SA = a . Mặt phẳng ( ) qua A vuông góc với SC cắt SB, SC, SD lần lượt M , N, P . Tính thể tích
khối chóp S.AMNP . 3 3 3a 3 3a 3 3a 3 3a A. . B. . C. . D. . 40 40 10 30 Lời giải Chọn B .
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 73/105
Ta có SC ⊥ ( )  SC ⊥ AM, SC ⊥ AN, SC ⊥ AP .
Mặt khác: CB ⊥ (SAB)  AM ⊥ CB AM ⊥ (SBC)  AM ⊥ SB .
Tương tự AP ⊥ SD . 3
Thể tích khối chóp ban đầu là 1 3a 2 V = 3a a = . 3 3 2 2   Tính các tỷ số: SA SM SA a 1 x = =1; y = = = ;   2 2 SA SB SB a + 3a 4 2 2 2 2 SNSA a 1 SPSA a 1 z = = = = ;t = = = =     . 2 2 2 2 2 SCSC
a + 3a + a 5 SDSD a + a 2 3   Vậy xyzt 1 1 1 1 3a V = + + + V = . S . AMNP   4  x y z t  40
Câu 25. Cho khối chóp S.ABCD có thể tích V và có đáy là hình bình hành. Điểm S ' thỏa mãn 7
SS ' = k DC (k  0) . Biết thể tích phần chung của hai khối chóp S.ABCD và S '.ABCD là V . Tìm 25 k . A. k = 9 . B. k = 6 . C. k = 11. D. k = 4 . Lời giải Chọn D
Ta có AB / /CD / /SS '  B ' = S ' A SB, C ' = S ' D SC . B ' S C ' S SS ' SB ' SC ' k Theo Ta lét ta có: = = = k  = = . B ' B C ' D DC SB SC k +1 SA SB ' k SC ' k SD Suy ra ta có: x = =1, y = = , z = = ,t = = 1 SA SB k +1 SC k + . 1 SD
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 74/105   2 1 k k  1 1 1 1  k (2k + ) 1 Vậy ta có: V = .1.1. .  + + + V = V . SABC ' B ' 4 k +1 k +1 1 2 k k   2k (k + )2 1  k +1 k +1 
Suy ra thể tích phần chung là: 2  k (2k + ) 1  7
V ' = V −V = 1− V = V k = 4 .
S .ADC ' B '  2k  (k )2 1  + 25 
Câu 26. Khối hộp ABC . D A BCD
  có tất cả các mặt là các hình thoi cạnh a , các góc xuất phát từ đỉnh A đều
bằng 60o . Tính thể tích V của khối hộp đã cho. 3 2a 3 3a 3 2a 3 2a A. V = . B. V = . C. V = . D. V = . 3 6 2 6 Lời giải Chọn C
AB = AD = AA = a  Ta có  1
cos BAD = cos A AD = cos A AB =  2 2 2 2 1 1 1  1   1   1  3 2a Ta có V = 6V 3 = a 1+ 2. . . − − − = . A .  ABD       2 2 2  2   2   2  2
Câu 27. Khối hộp ABC . D A BCD
  có tất cả các mặt là các hình thoi cạnh a , các góc BAD = 60,. A AB = A A
D =120. Tính thể tích V của khối hộp đã cho. 3 2a 3 3a 3 2a 3 2a A. V = . B. V = . C. V = . D. V = . 3 6 2 6 Lời giải Chọn C
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 75/105
AB = AD = AA = a  Ta có  1 1 cos BAD = ;cos A AD = cos A AB = −  2 2 2 2 2
1  1   1   1   1   1  3 2a Ta có V = 6V 3 = a 1+ 2. . − . − − − − − − = . A .  ABD          
2  2   2   2   2   2  2
Câu 28. Cho hình chóp tứ giác đều .
S ABCD . Mặt phẳng (P) qua A vuông góc với SC cắt SB, SC, SD lần  lượt tại SB 2 B ,
C ,D và
= . Gọi V ,V lần lượt là thể tích của khối chóp S.AB CD   và . S ABCD . SB 3  Tính tỉ số V V V  4 V  2 V  1 V  2 A. = . B. = . C. = . D. = . V 9 V 9 V 3 V 3 Lời giải Chọn C
Gọi O = AC BD
Ta kẻ AC ⊥ SC tại C , gọi H = AC SO.
Theo giả thiết BD ⊥ (SAC)  BD ⊥ SC BD// (P)    Vậy ( SB SD SH
P)  (SBD) = B D  //  BD và = =
H  là trọng tâm tam giác SBD do đó C là SB SD SO
trung điểm cạnh SC    Vậy ta có SA SB 2 SC 1 SD 2 x = = 1, y = = , z = = ,t = = SASB 3 SC 2 SD 3    Do đó V xyzt 1 1 1 1 1 = + + + =   . V 4  x y z t  3
Câu 29. Cho hình chóp tứ giác đều .
S ABCD . Mặt phẳng (P) qua A vuông góc với SC cắt SB, SC, SD lần  lượt tại SB 2 B ,
C ,D và AB = a;
= . Tính thể tích V của khối chóp S.AB CD  . SB 3 3 6a 3 6a 3 2 6a 3 6a A. V = . B. V = . C. V = . D. V = . 18 27 27 9 Lời giải Chọn A
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 76/105
Gọi O = AC BD
Ta kẻ AC ⊥ SC tại C , gọi H = AC SO.
Theo giả thiết BD ⊥ (SAC)  BD ⊥ SC BD// (P)    Vậy ( SB SD SH 2
P)  (SBD) = B D  //  BD và = =
=  H  là trọng tâm tam giác SBD do đó CSB SD SO 3
là trung điểm cạnh SC    Vậy ta có SA SB 2 SC 1 SD 2 x = = 1, y = = , z = = ,t = = SASB 3 SC 2 SD 3   Do đó xyzt 1 1 1 1 1 V = + + + V = V   . 0 0 4  x y z t  3
Tam giác cân SAC có AC ⊥ SC tại trung điểm SC do đó nó là tam giác đều. 2 3 Vậy a a 6 1 a 6 6a 2 2
SA = AC = 2a h = 2a − = V = a . = 0 2 2 3 2 6 3 Vậy 6a V = . 18
Câu 30. Cho hình chóp .
S ABCD có đáy ABCD là hình bình hành, thể tích V . Gọi P là trung điểm cạnh SC .
Một mặt phẳng chứa AP cắt các cạnh SB, SD lần lượt tại M , N . Tính tỉ số SM biết thể tích của SB
khối chóp S.AMNP bằng 27V . 56 SM 3 SM 3 SM 3 SM 3 A. = . B. = . C. = . D. = . SB 4 SB 7 SB 5 SB 8 Lời giải Chọn B
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 77/105
Gọi O = AC BD; H = AC SO. Với SA SM SP SN x = = y =   1 1, 0;1 , z = = ,t = SASB SC 2 SD 1 1 1 1 1 1 y  1  Ta có
+ = + 1+ 2 = +  t =  y  1   x z y t y t 3y − 1  3  2   Do đó xyzt 1 1 1 1 3y V = + + + V = V . SAMNP   4  x y z t  4 (3y − ) 1 2  
Theo giả thiết ta có phương trình 3y 27 3 1 ( =  =     . y − )V V y y 1 4 3 1 56 7  3 
Câu 31. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, AD = b và cạnh bên SA = c
vuông góc với mặt đáy ( ABCD) . Gọi M là một điểm trên cạnh SA sao cho AM = x (0  x c) .
Tìm x để mặt phẳng (MBC) chia khối chóp đã cho thành hai khối đa diện có thể tích bằng nhau. (3− 2)c (2− 3)ab (3− 5)c ( 5 − )1ab A. x = . B. x = . C. x = . D. x = . 2 2c 2 2c Lời giải Chọn C S M N A D B C
Qua M kẻ đường thẳng song song với AD cắt SD tại N . Khi đó (MBC) cắt hình chóp theo thiết
diện là hình thang vuông MNCB tại M và B . SM SN c − x V SM SB SC SM c − x Ta có = = S.MBC  = . . = = SA SD c V SA SB SC SA c S. A BC c − xV = V . S .MBC S . A 2 BCD c
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 78/105 2 V  −  Lại có SM SN SC SM SN c x : S.MNC = . . = . =   V SA SD SC SA SDc S. AD C (c − x)2  V = V . S .MNC 2 S . A 2 BCD c  − −   − + −  c x (c x)2 1 c cx (c x)2 2 Do đó V =  + V =  V S.MNBC 2 S. A  2c 2 BCD c  2 . A     2 2 S BCD c   − + ( − )2 2 3 − 5 c c cx c x 2 2 ( ) Từ giả thiết suy ra:
= 1  x − 3cx + c = 0  x = . 2 c 2
Câu 32. Cho hình hộp ABC . D A BCD
  có M , N, P lần lượt là trung điểm ba cạnh A B
 , BB , DD . Mặt phẳng
(MNP) cắt AA tại I . Biết thể tích khối tứ diện IANP là V . Tính thể tích khối hộp. A. 6V . B. 12V . C. 4V . D. 2V . Lời giải Chọn C
Mặt phẳng (MNP) cắt AD tại Q theo tính chất giao tuyến ta có MQ / /NP . Do đó IA = BN và
M , Q lần lượt là trung điểm các đoạn IN , IP  Khi đó: IA IM IQ 1 V =  =  . . .V V V . IA MQ IA MQ IA IN IP 12 1 1 1 1 1 Ta có: V =     =  =  .d I A B C D S d A ABCD S V IA MQ ( ,( )). . A MQ ( ,( )). . ABCD ABCD.A BCD  ' 3 3 2 8 48 Từ đó suy ra: 1 1 .V =  =    V V    4V . ABCD. A B C D ' ABCD.A B C D ' 48 12
Câu 33. Cho hình chóp tứ giác đều .
S ABCD . Gọi H là hình hộp chữ nhật có bốn đỉnh là bốn trung điểm của các cạnh bên S , A S ,
B SC, SD và bốn đỉnh còn lại nằm trong đáy ABCD . Biết thể tích khối hộp H là
V . Tính thể tích của khối hộp đã cho. 4V 8V A. . B. 2V . C. . D. 6V . 3 3 Lời giải Chọn C
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 79/105
Gọi các điểm như hình vẽ. 1 1 3 Ta có V = S   =   =     MM S d S ABCD V . M N P Q ABCD ( ,( )) S . 4 2 8 ABCD 8 Suy ra V = V . S . ABCD 3
Câu 34. Cho khối lăng trụ AB . C A BC
  có thể tích V . Hai mặt phẳng ( ACB) và (BA C
 ) chia khối lăng trụ
đã cho thành bốn phần. Tính thể tích của phần có thể tích lớn nhất V 3V 5V 2V A. . B. . C. . D. . 2 5 12 5 Lời giải Chọn C
Hai mặt phẳng ( ACB) và (BA C
 ) chia khối lăng trụ thành các khối B MBN , MNCC AA  , MNBCA, MNB CA   .    Trong đó V B M B B B N 1 1 1 B MBN =   =  V = =  V V V    .  B A B B B C 4 B MBN 4 B ABC 12 B ABC 3 1 Suy ra V = − = =   V V V V . MNCC A A B ABC B MBN 4 B ABC 4 Tương tự, 1 1 1 V = − = − =    V    VV V V . MNB A C BA B C BMNB 3 12 4   Do đó 1 1 1 5 V = − − − = − − − =   V V V   V    1 V V . MNCC A A B MBN MNCC A A MNB A C    12 4 4  12
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 80/105
Câu 35. Cho hình chóp .
S ABCD có đáy ABCD là hình thang với AB//CD và CD = 4AB . Gọi M là một
điểm trên cạnh SA sao cho 0  AM SA. Tìm tỉ số SM sao cho mặt phẳng (CDM ) chia khối chóp SA
thành hai khối đa diện có thể tích bằng nhau. SM 3 − + 13 SM −4 + 26 SM 3 − + 17 SM 4 − + 23 A. = . B. = . C. = . D. = . SA 2 SA 2 SA 2 SA 2 Lời giải Chọn B
Từ M kẻ đường thẳng song song với AB , cắt SB tại N . Khi đó mặt phẳng (CDM ) chia khối chóp
thành hai khối đa diện S.CMN , D CMNDBA . Đặt SM SN x = = , 0  x  1 . SA SB V S AD 4 1 Ta có S.ADC ADC = = = 4  V = V ,V = V . S . ADC S . ABCD S . ABC S . V S AB 5 5 ABCD S . ABC ABC Mặt khác V SM 4x SMCD =  V = V . SMCD S . V SA 5 ABCD SACD 2 V SM SN x SMNC 2 =  = x V = V . SMNC V SA SB 5 SABC SABC 2   Vậy 4x x VS.ABCD V = + V = . SMNCD   S.  5 5 ABCD  2 2 4x + x 1 −4 + 26 Suy ra =  x = . 5 2 2
Câu 36. Cho hình chóp S.ABC có thể tích V . Lấy hai điểm M , N lần lượt nằm trên hai cạnh S , A SB sao cho SM 1 SN 2 = ,
= . Mặt phẳng ( ) qua MN và song song với SC chia khối chóp S.ABC thành hai SA 3 SB 3
khối đa diện. Tính thể tích của khối đa diện có thể tích lớn hơn. 5V 5V 5V 7V A. . B. . C. . D. . 6 8 9 12 Lời giải Chọn C
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 81/105 S M N D A C E B I
Kéo dài MN cắt AB tại I . Kẻ MD//SC , ID cắt BC tại E .
Ta có tứ giác MNED là thiết diện của hình chóp với mặt phẳng ( ) . MS IA NB IA
Trong tam giác SAB ta có . . =1 = 4 . MA IB NS IB Do đ V AM AD AI 2 2 4 16 ó . A MDI = . . = . .  V = V . . V AS AC AB 3 3 3 A MDI 27 . A SCB Mặt khác V IB IN IE 1 1 1 1 1 IBNE = . . = . .  V = V = V . I .BNE . V IA IM ID 4 2 2 16 A MDI 27 I . AMD   Do đó 16 1 5 V = − V = V . AMD.BNE    27 27  9
Câu 37. Cho hình chóp S.ABC . Lấy hai điểm M , N lần lượt nằm trên hai cạnh S , A SB sao cho SM 1 SN = ,
= x . Mặt phẳng ( ) qua MN và song song với SC chia khối chóp S.ABC thành hai SA 3 SB
khối đa diện có thể tích bằng nhau. Tìm x . 4 − 5 8 − 10 4 − 5 8 − 10 A. x = . B. x = . C. x = . D. x = . 3 6 6 9 Lời giải Chọn B.
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 82/105 S M N D A C E B I
Kéo dài MN cắt AB tại I . Kẻ MD//SC , ID cắt BC tại E .
Ta có tứ giác MNED là thiết diện của hình chóp với mặt phẳng ( ) . MS IA NB IA 2x
Trong tam giác SAB ta có . . =1 = . MA IB NS IB 1− x Do đó V AM AD AI 2 2 2x 8x . A MDI = . . = . . V = V . . V AS AC AB 3 3 1 A MDI − x 9 3x −1 . A SCB ( ) SM NI BA NI 3(1− x)
Trong tam giác AMI có . . =1 = . SA NM BI NM 3x −1 V IB IN IE
1− x 3(1− x) 2  (1− x)3 Do đó IBNE = . . = .  V = V . I . V IA IM ID 2x 2 BNE 3x −1 I . AMD    −  8x (1 x)3 1 8x (1− x)3 1 8 − 10 Suy ra V =  − V = V  − =  x = AMD.BNE 9(3x − ) 1 3x −1  2 9(3x − ) 1 3x −1 2 6  
Câu 38. Cho khối lập phương ABC . D A BCD
  có thể tích bằng V . Gọi E, F lần lượt là trung điểm của các cạnh B C  ,C D
  . Mặt phẳng (AEF) chia khối lập phương thành hai phần. Tính thể tích của phần có thể tích nhỏ hơn. 3V 25V 5V 9V A. . B. . C. . D. . 8 72 16 32 Lời giải Chọn B.
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 83/105 1 1 1 1 Ta có: D G  = D A  , B H  = B A  , B K  = B B
 , D I = D D  . 2 2 3 3 9 3 Và S =  =  S     VV . A HG 8 A B C D AGHA 8 1 1 1 1  3 1  25 Mà V = = =  = − =  V  . . V V V    V V . EB HK GFD I   3 2 12 72 A IFEB KD  8 36  72
Câu 39. Cho hình chóp S.ABCD có đáy có đáy ABCD là hình bình hành và thể tích bằng V . Gọi M , N lần
lượt là các điểm di độ AB AD
ng trên các cạnh AB, AD sao cho + 2
= 4 . Gọi V =V . Tìm giá trị AM AN S.AMN
nhỏ nhất của V . 1 1 1 1 A. V . B. V . C. V . D. V . 4 6 8 3 Lời giải Chọn A.
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 84/105 Đặt AM AN 1 2 2x = , x
= y  + = 4  y = . AB AD x y 4x −1 Có 2 V V 1 AM AN 1 1 x V  1  V S . AMN S . AMN = = . .
= xy V  = xyV = .V = 4x −1+ + 2    . V 2V 2 AB AD 2 2 4x −1 16  4x −1  4 S . ABCD S . ABD
Câu 40. Cho hình chóp S.ABCD có đáy có đáy ABCD là hình bình hành và thể tích bằng V . Gọi M , N lần
lượt là các điểm di độ AB AD
ng trên các cạnh AB, AD sao cho + 2
= 4 . Gọi V =V . Tìm giá AM AN S.MBCDN
trị lớn nhất của V . 1 2 3 1 A. V . B. V . C. V . D. V . 4 3 4 3 Lời giải Chọn C. Đặt AM AN 1 2 2x = , x
= y  + = 4  y = . AB AD x y 4x −1 Có 2 V V V 1 AM AN 1  1   xS.MBCDN S.AMN S. =1− =1 AMN − =1− . .
=1− xy V = 1− xy V =   1− .V V V 2V 2 AB AD 2  2   4x −1 S.ABCD S.ABCD S.ABD V  1  3V = V − 4x −1+ + 2    . 16  4x −1  4
Câu 41. Cho khối tứ diện đều ABCD có cạnh bằng a . Gọi M , N lần lượt là trung điểm các cạnh AB, BC và
E là điểm đối xứng với B qua D . Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa
diện, trong đó khối đa diện chứa đỉnh A có thể tích V . Tính V 3 13 2a 3 7 2a 3 2a 3 11 2a A. V = . B. V = . C. V = . D. V = . 216 216 18 216 Lời giải Chọn D
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 85/105 3 2a Ta có V = V = 0 ABCD 12 EQ EP 2
Dễ thấy P, Q là trọng tâm các tam giác BEC, ABE  = = EM EN 3 VE QPD ED EQ EP 2 7 .  = . . =  V = V V EB EM EN 9 BMQPN E. 9 BMN E.BMN 1 1 1 1 Mà V = V
= d M , BEN .S = . d , A BCD .S = V E.BMN M .BEN ( ( )) BEN ( ( )) BDC . 3 3 2 2 A BCD 3 7 1 7 11 11 2aV = . V = V V = V = . BMQPN 0 0 AMNCPQ 0 9 2 18 18 216
Câu 42. Cho khối tư diện đều ABCD có cạnh bằng a . Gọi M , N lần lượt là trung điểm các cạnh AB, AC sao AM 1 AN cho = ,
= 2 . Mặtt phẳng ( ) chứa MN , song song với AD chia khối tứ diện ABCD BM 2 CN
thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V . Tính V 3 4 2a 3 5 2a 3 4 2a 3 11 2a A. V = . B. V = . C. V = . D. V = . 108 108 81 342 Lời giải Chọn A
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 86/105 3 2a
Ta có: V = V = 0 ABCD 12
Dễ thấy BC, MN, PQ đồng quy tại S
Áp dụng định lí Mênêlauyt cho SC 1 ABC
với M , N , P thẳng hàng, suy ra = SB 4 V SC SN SP 1 1 1 1 15 S.CNP  = . . = . . =  V = V V SB SM SQ 4 2 2 16 BMQPNC S . 16 BMQ S.BMQ BS BM BQ 4 2 2 16 Mà V = . . .V = . . V = V S .BMQ . A BCD . A BCD . BC BA BD 3 3 3 27 A BCD 3 15 16 5 4 4 2aV = .
V = V V = V = . BMQPNC 0 0 ADQPNM 0 16 27 9 9 108
Câu 43. Cho khối tứ diện đều ABCD có cạnh bằng a . Gọi M , N lần lượt là trung điểm các cạnh AB, BC và BE
E là điểm thuộc tia đối của tia DB sao cho
= k . Tìm k để mặt phẳng (MNE) chia khối tứ diện BD 3 11 2a
ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh B có thể tích V = . 294 6 A. k = . B. k = 6 . C. k = 4 . D. k = 5 . 5 Lời giải Chọn C
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 87/105 3 a 2
Thể tích của khối tứ diện đều ABCD là V = . 0 12 BM BN BE 1 1 k V =   V =
  kV = V . BMNE 0 0 0 BA BC BD 2 2 4 Theo Thales ta có 2 EP EQ k −1 2(k −1) EP EQ ED ED 4(k −1) k −1 k = = =  V =    V =   V EDPQ BMNE 2 0 EN EM 1 2k −1 EN EM EM EB (2k −1) k 4 (k −1) + 2 2 3 k 4(k −1) k −1 k k  4(k −1)  Do đó V = V − . . V = V 1−  . BMNPDQ 0 2 0 0 2 4 (2k −1) k 4 4  k(2k −1)  3 22 k  4(k −1)  22
Theo giả thiết ta có V = V V 1−  = V k = 4 . B.MNPDQ 0 0 2 49 4 
k(2k −1)  49
Câu 44. Cho hình lăng trụ đứng AB . C A BC
  có thể tích V . Các điểm M , N, P trên các cạnh AA , BB ,CC ' AM 1 BN CP 2 sao cho = , = = ABC MNP AA 2 BBCC
. Tính thể tích của khối đa diện . 3 2 9 20 11 A. V . B. V . C. V . D. V . 3 16 27 18 Lời giải Chọn D
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 88/105 Ta có V =V +V . ABC.MNP M .ABC M .BCPN Trong đó 1 1 V
= d M , ABC .S = V . M . ABC ( ( ))  3 ABC 6 S BP + CN 2 2 4 BCPN V = .V = = =   V   . V V . M .BCPN M .BCC B A.BCC B S  +    BB CC 3 3 9 BCC B  1 4  11 Vậy V = + V = V . ABC.MNP    6 9  18
Câu 45. Cho hình chóp S.ABCD có đáy là hình bình hành và có thể tích V . Goị M là trung điểm của SB ,
P là điểm thuộc cạnh SD sao cho SP = 2DP . Mặt phẳng ( AMP) cắt cạnh SC tại N . Tính thể tích
của khối đa diện ABCDMNP theo V . 23 19 2 7 A. V = V . B. V = V . C. V = V . D. V . ABCDMNP 30 ABCDMNP 30 ABCDMNP 5 30 Lời giải Chọn A
Gọi O là tâm của hình bình hành ABCD . Gọi I = MP SO N = AI SC . Ta có
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 89/105 1 SP SM S S + S S S SI SP SM  7 SI = . SPM SPI SMI SPI SMI = = = + = + = .   . 3 SD SB S S 2S 2S 2SO SD SB  12 SO SDB SDB SDO SBO SI 4  = . SO 7 Suy ra SN S S + S S S SI SI SN 2 2 SN SAN SAI SNI SAI SNI == = = + = + . = + . . SC S S 2S 2S 2SO 2SO SC 7 7 SC SAC SAC SAO SAO SN 2  = . SC 5 V V +V V V . SA SM .SP SM .SN.SP 7 Suy ra SAMNP SAMP SMNP SAMP SMNP = = + = + = . V V 2V V 2 . SA . SB SD 2 . SB SC.SD 30 SABD SBCPD 23  V = V . ABCDMNP 30
Câu 46. Cho khối chóp S.ABC có tất cả các cạnh bằng nhau và bằng a . Gọi M , N lần lượt là trung điểm của
các cạnh AB , SC . Các điểm P , Q trên các đường thẳng SA, BN sao cho PQ // CM . Tính thể tích V
của khối chóp S.BNP . 3 2a 3 2a 3 2a 3 2a A. V = . B. V = . C. V = . D. V = . 36 72 18 9 Lời giải Chọn B S N Q P A C M B Đặ 1 1 1 1
t SA = a , SB = b , SC = c . Ta có: CM = SM − SC =
(SA+SB)−SC = a+ b− c 2 2 2 2 
SP = kSA = ka   m
và SQ = mSN + (1− m) SB =
c + (1− m)b . 2   = − = − +  ( m PQ SQ SP k a 1− m)b + c  2
Theo giả thiết bài toán ta có hai véc tơ PQ ,CM cùng phương, ta có:
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 90/105 m   − − −ka + ( − m) m 1 1 k 1 m 4 1 2 1 b + c = n a + b − c  = =  m = ;k =   2  2 2 1 1  1 − 3 3 2 2 3 3 Do đó: SP SN 1 1 2a 2a V = . .V = . . = . Chọn B. S . ABC SA SC 3 2 12 72      =
Câu 47. Cho khối hộp ABC .
D A B C D có tất cả các mặt đều là hình thoi, AC 6a , BAD = A AD = A A
B = 60 . Tính thể tích V của khối hộp đã cho. A. 3 V = 6 2a . B. 3 V = 3 2a . C. 3 V = 2 3a . D. 3 V = 6 3a . Lời giải Chọn D
Đặt cạnh của hình hộp là x . AB = A ,
D BAD = 60  B
ADlà tam giác đều BD = AB = AD = . x Tương tự ta có A D  = A B  = A A
 = x. Do đó tứ diện ABDA là tứ diện đều cạnh bằng x .
Theo quy tắc hình hộp ta có: AC = AB + AD + AA 2
AC = AC = (AB + AD + AA)2 2 2 2
= AB + AD + AA + 2(A . B AD + A . B AA + A . D AA)  1 1 1  2 2 2 2 = 3x + 2 x + x + x
= x 6 = 6a x = 6a   .  2 2 2  2.( 6a)3 Do đó: 3 V = 6V = =  6. 6 3a . A .ABD 12
Câu 48. Cho hình chóp S.ABCD có thể tích V , đáy là hình bình hành. Mặt phẳng ( ) đi qua A , điểm M
thuộc cạnh SB thỏa mãn SM = 2MB và trọng tâm G của tam giác SAC cắt các cạnh SC , SD lần
lượt tại N , P . Tính thể tích của khối chóp S.AMNP . 2V V 2V 4V A. . B. . C. . D. . 3 3 9 9 Lời giải Chọn B
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 91/105 S M N G P D A O B C
Ta có AG cắt SC tại trung điểm N của SC . Với SA SM 2 SN 1 SP 1 1 1 1 2 x = =1, y = = , z = = ,t = ta có: + = +  t = . SA SB 3 SC 2 SD x z y t 3   Do đó: xyzt 1 1 1 1 V V = . + + + .V = . Chọn B. S .AMNP   4  x y z t  3
Câu 49. Cho hình chóp S.ABCD có thể tích V , đáy là hình bình hành tâm O . Mặt phẳng ( ) đi qua A , trung
điểm I của SO cắt các cạnh SB , SC , SD lần lượt tại M , N , P . Tính thể tích nhỏ nhất của khối chóp S.AMNP . V V V 3V A. . B. . C. . D. . 18 3 6 8 Lời giải Chọn C S N P I M D A O B C Với SA SM SN SP 1 1 1 1 x = =1, y = , z = , t = ta có:
+ = + và xét tam giác SAC ta có : SA SB SC SD x z y t 1     SO =
(SA+SC) SO 1 SC 1 1  .SI = SA + .SN SI = SA + SN     . 2 SI 2  SN  4  z  Mặt khác ba điểm 1 1 1
A, I , N thẳng hàng nên + = 1  z = . 4 4z 3 Do đó 1 1 1 1 t : + = + = 4  y = . y t 1 1 4t −1 3
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 92/105 2     Vì vậy xyzt 1 1 1 1 2t 1 V V = . + + + V = f t =
V  min f t = f = . S.AMNP   ( )   4  x y z t  3(4t − ) ( )  1 1    ;1 2 6    4  Dấu bằng đạt tại 1 1 t = , y =
. Tức là mặt phẳng ( ) đi qua trung điểm các cạnh SB , SD . 2 2 Chọn C.
Câu 50. Cho khối tứ diện đều ABCD cạnh a . Gọi E là điểm đối xứng của A qua D . Mặt phẳng qua CE và
vuông góc với mặt phẳng ( ABD) cắt cạnh AB tại điểm F . Tính thể tích V của khối tứ diện AECF . 3 2a 3 2a 3 2a 3 2a A. V = . B. V = . C. V = . D. V = . 30 60 40 15 Lời giải Chọn D A F M G B D K M C E
Gọi G là trọng tâm tam giác ABD CG ⊥ ( ABD) .
Do đó : F = EG AB  (CEF ) là mặt phẳng cần dựng. MG MD 1 KD KG GD 1 KB Ta có : =
=  GD // BE  = = =  = 3 . MB ME 3 KB KE BE 3 KD FA KB ED FA 1 FA 2
Vì F , K , E thẳng hàng nên ta có : . . =1  .3. =1  = FB KD EA FB 2 FB 3 3 3 AF 2 AF AE 2 2a 2a  =  V = . .V = .2. = . Chọn D. AB 5 ABCD AB AD 5 12 15
Câu 51. Cho khối lăng trụ AB .
C A B C có chiều cao bằng 8 và đáy làm tam giác đều cạnh bằng 4 .
Gọi M, N, P lần lượt là trung điểm các cạnh B C ,C A , A B . Thể tích khối đa diện có các
đỉnh là A, B,C, M, N, P bằng A. 21 3 . B. 12 3 . C. 24 3 . D. 8 3 . Lời giải Chọn D
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 93/105 N A' C' P M B' A C B 2 4 3 Ta có S 4 3 V 32 3 ABC ABC. 4 A B C Các hình chóp . A A NP, . B B MP, .
C C MN các hình chóp bằng nhau và có đáy là tam giác đều 2 2 3 có cạnh bằng 2 S 3 , chiều cao bằng 8 . A NP 4 1 8 3 thể tích V S .8 A.A NP 3 A NP 3 V V 3V 32 3 8 3 24 3 . Chọn C ABCMNP ABCA B C A.A MP
Câu 52. Cho lăng trụ AB .
C A B C có chiều cao là 8 đáy là tam giác đều cạnh 6 . Gọi M, N, P lần lượt
là tâm các mặt bên ABB A , ACC A , BCC B . Thể tích khối đa diện có các đỉnh là các
điểm A, B,C, M, N, P bằng A. 27 3 . B. 21 3 . C. 30 3 . D. 36 3 . Lời giải Chọn D A' C' B' N I L M P K A C B 2 6 3 Ta có S 9 3 V 72 3 ABC ABC. 4 A B C
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 94/105
Gọi I,K, L lần lượt là trung điểm của AA , BB ,CC . Từ đó ta có: V V V V V V ABCMNP ABC.A B C B.KMP A.IMN C.LPN A B C .IKL 1 Trong đó V V 36 3 A B C .IKL ABC. 2 A B C V BK BM BP 1 1 1 1 1 B.KMP . . V V . .V .72 3 3 3 B.KMP B.B A C ABC. V BB BA BC 8 8 8 3 A B C 24 B.B A C Mà V V V B.KMP A.IMN C.LPN V 72 3 3.3 3 36 3 27 3 . Chọn A ABCMNP
Câu 53. Cho khối lăng trụ ABC . A B C có thể tích V ,trên các cạnh AA , BB ,CC lần lượt lấy các 1 2 1
điểm M , N , P sao cho AM AA , BN BB , CP
CC .Thể tích khối đa diện 2 3 6 ABCMNP bằng 2V 4V V 5V A. . B. . C. . D. . 5 9 2 9 Lời giải Chọn B AM 1 BN 2 CP 1 xyz 4 Có x , y , z V V V .Chọn đáp án B ABC. AA 2 BB 3 CC 6 MNP 3 9
Câu 54. Cho khối chóp .
S ABCDcó đáy ABCD là hình bình hành và có thể tích bằng 1.Gọi M , N lần
lượt là các điểm trên các cạnh SB,SD sao cho MS MB, ND
2NS . Mặt phẳng CMN chia
khối chóp đã cho thành hai phần,thể tích của phần có thể tích nhỏ hơn bằng 2 1 3 5 A. . B. . C. . D. . 25 12 25 48 Lời giải Chọn D
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 95/105 SC SM 1 SP SN 1 Ta có x 1; y ; z ; t và SC SB 2 SA SD 3 1 1 1 1 1 1 1 2 3 z . x z y t z 4 xyzt 1 1 1 1 5 Khi đó V V .Chọn đáp án D. S. CMPN S. 4 ABCD x y z t 48
Câu 55. Cho khối lăng trụ AB .
C A B C có thể tích V .Các điểm M , N , E lần lượt là các điểm nằm
trên cạnh A B , A C , AB sao cho MA 3MB , NC NA , EB
3EA .Mặt phẳng MNE cắt
AC tại F. Thể tích khối đa diện lồi BEFCC MNB bằng 59 5 3 41 A. V . B. V . C. V . D. V . 72 24 8 72 Lời giải ChọnA Goị S, h lần
lượt là diện tích đáy và chiều cao của lăng trụ đã cho Có MNE ABC
EF / / MN và AEF đồng AE 1 dạng
với A' MN theo tỷ số k Do đó A' M 3 2 A M A N 3 1 3S 1 1 3S S S . S . .S ; S S . A MN ACB A B A C 4 2 8 AEF 3 A MN 9 8 24
Do đó áp dụng công thức thể tích khối chóp cụt ta có h h S S 3S 3S 13 13 V S S .S S . . . S h V . AEF. A MN 3 AEF AEF A MN A MN 3 24 24 8 8 72 72 13 59 Vì vậy V V V 1 V
V . Chọn đáp án A. BEFCC MNB ABC.A B C AEF.A MN 72 72
Câu 56. Cho khối chóp .
S ABC có thể tích V .Mặt phằng P song song với đáy cắt các cạnh
SA, SB, SC lần luotj tại D , E , F .Gọi D , E , F tương ứng là hình chiếu vuông góc của 1 1 1
D, E, F lên mp ABC (tham khảo hình vẽ).Khối đa diện DEF . D E F có thể tích lớn nhất 1 1 1 bằng
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 96/105 V V 4V 2V A. . B. . C. . D. . 6 12 9 3 Lời giải Chọn C SD SE SF DE EF FD Đặt x 0 x 1 ; ta cũng có 2 x S x S . SA SB SC DEF ABC AB BC CA d D , ABC AD AS SD Và 1 x d D , ABC 1 x d S , ABC . d S , ABC AS AS Vì vậy 2 2 V S .d D , ABC x S . 1 x d S , ABC
x 1 x .3V DEF. D E F DEF ABC 1 1 1 3 3V 3V x x 2 2x 4V . . x . x 2 2x . 2 2 3 9 2
Dấu bằng đạt tại x 2 2x x .Chọn đáp án C. 3
Câu 57. Cho khối chóp .
S ABC có đáy là tam giác vuông tại C , cạnh bên SA vuông góc với đáy. Biết SA AB
2a . Gọi H, K lần lượt là hình chiếu của A lên S , B SC . Khối chóp . S AHK có thể
tích lớn nhất bằng 3 2a 3 3a 3 3a 3 2a A. . B. . C. . D. . 6 6 3 3 Lời giải Chọn A
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 97/105 1 1 Đặt 2 2 2 2 CA x CB AB CA 4a x 2 2 S C . A CB x 4a x . ABC 2 2 1 1 Do đó 2 2 V S .SA ax 4a x . S.ABC 3 ABC 3 Ta có 2 2 2 2 3 2 2 SH SK SA SA 4a 4a 1 2 2 2a x 4a x V . V . V . . ax 4a x . S.AHK S.ABC S.ABC 2 2 2 2 2 SB SC SB SC 8a 4a x 3 3 4a x
Dùng bất đẳng thức AM-GM có: 2 2 2 2 2 2 2 2 2 2 4a x 4a x 2x 2 4a x .2x 2 2x 4a x . 3 3 2a 1 2a Suy ra: V . . S.AHK 3 2 2 6
Câu 58. Cho khối lăng trụ AB .
C A B C có thể tích bằng 1 . Gọi M, N lần lượt là trung điểm
AA , BB . Đường thẳng CM cắt đường thẳng A C tại P , đường thẳng CN cắt đường
thẳng B C tại Q . Thể tích khối đa diện lồi A B MNPQ bằng 1 1 3 2 A. . B. . C. . D. . 3 2 4 3 Lời giải Chọn D
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 98/105 * Ta có: V V V (1). A B MNPQ C.C PQ CMNA B C
* Dễ thấy A , B lần lượt là trung điểm C P,C Q nên S 4S . Do đó C PQ A B C 4 4 V 4V V (2). C.C PQ C.C A B A B C . 3 ABC 3 1 1 1 2 1 * Vì S S S nên V V . V ABNM A B NM 2 ABB A C.ABNM C .A B BA A B C . 2 2 3 ABC 3 2 Suy ra V V V (3). CMNC A B A B C .ABC C.ABNM 3 4 2 2
* Từ (1), (2) và (3), ta được: V . A B MNPQ 3 3 3
Câu 59. Cho hình chóp .
S ABCDcó đáy là hình bình hành và có thể tích là V . Gọi P là điểm trên
cạnh SC sao cho SC
5SP . Một mặt phẳng
qua AP cắt hai cạnh SB và SD lần lượt tại V
M và N . Gọi V bằng
1 là thể tích của khối chóp .
S AMPN . Giá trị lớn nhất của 1 V 1 1 3 2 A. . B. . C. . D. . 15 25 25 25 Lời giải Chọn C
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 99/105 SA SM SP 1 SN Đặt x 1 ; y ; z ; t 0 y,t 1 SA SB SC 5 SD 1 1 1 1 t 1 Khi đó, 6 y t 1 y t x z 6t 1 6 1 1 1 1 1 Chứng minh: V V xyzt V 1 S.AMPN S. 4 ABCD x y z t Ta có: V SA SM SP 1 1 S.AMP . . xyz V xy . z V xy . z V xyzV S.AMP S.ABC S. V SA SB SC 2 ABCD 2 S.ABC V SA SP SN 1 1 S.APN . . xzt V xzt.V xzt. V xztV S.APN S.ACD S. V SA SC SD 2 ABCD 2 S.ACD 1 1 1 1 V V V xyz xzt V xyzt (*) S.AMPN S.AMP S.APN 2 2 t y Mặt khác: V SA SM SN 1 1 S.AMN . . xyt V xyt.V xyt. V xytV S.AMN S.ABD S. V SA SB SD 2 ABCD 2 S.ABD V SM SN SP 1 1 S.MNP . . ytz V yzt.V yzt. V yztV S.MNP S.BDC S. V SB SD SC 2 ABCD 2 S.BDC 1 1 1 1 V V V xyt yzt V xyzt (**) S.AMPN S.AMN S.MNP 2 2 z x
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 100/105
Cộng hai vế của (*) và (**), ta có: 1 1 1 1 1 1 1 1 1 1 2V xyzt V V xyzt V (đpcm) S.AMPN S.ABCD S.AMPN S. 2 x y z t 4 ABCD x y z t 2 1 1 1 1 1 3 V 3 3t Ta có: 1 V V xyzt V ytV yt . 1 S.AMPN S. 4 ABCD x y z t 5 V 5 5 6t 1 2 3t 1 Xét hàm số f t trên ;1 5 6t 1 6 1 t 0 ;1 2 3 6t 2t 6 f t 0 . 2 5 6t 1 1 1 t ;1 3 6 Bảng biến thiên: 3 Vậy max f t f 1 1;1 25 6
Câu 60. Cho khối chóp .
S ABCDcó đáy là hình bình hành và có thể tích là 1 . Gọi M, N lần lượt là
trung điểm các cạnh AD và SC ; đường thẳng BM cắt AC tại P . Thể tích của khối tứ diện ABNP bằng 1 1 1 1 A. . B. . C. . D. . 16 12 8 24 Lời giải Chọn B
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 101/105 1 1
Xét tam giác ABD có P là trọng tâm S S S ABP 3 ABD 6 ABCD 1 1 1 1 1 1 V
d N, ABP .S . d S, B A D C . .S V ABNP ABP ABCD S. 3 3 2 6 12 ABCD 12
Câu 61. Cho lăng trụ tam giác AB .
C A B C có thể tích bằng 72 . Gọi M là trung điểm cạnh A B ; các 3 1
điểm N , P thỏa mãn B N B C , BP
BC . Đường thẳng NP cắt BB tại E ; đường 4 4
thẳng ME cắt AB tại Q . Thể tích khối đa diện ACPQA C NM bằng: A. 55 . B. 59 . C. 52 . D. 56 . Lời giải Chọn B 1 BC EP EQ EB BP 1
Thể tích khối lăng trụ đã cho là V Sh 72 . Ta có 4 ; 0 EN EM EB B N 3 3 B C 4 2 B M B N 1 3 3 1 1 3 1 Do đó S . S . .S S ; S S . S S . B MN B A C B A B C 2 4 8 BQP 3 B MN 9 8 24
Vì vậy khối chóp cụt BQ .
P B MN có thể tích là:
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 102/105 h h 3 1 3 1 13 V S S S S S S S S Sh 13 . BQP.B MN 3 B MN BQP B MN BQP 3 8 24 8 24 72 Do đó: V V V 72 13 59 . Chọn đáp án B. ACPQA C NM ABC.A B C BQP.B MN
Cách 2: Dùng tỉ số thể tích có: 1 1 3 3 3 V S .d E , B MN . . S h V . E B MN B MN 0 3 3 8 2 16 EB EQ EP 1 3 1 V . . V . Sh V . E BQP . E B MN 0 EB EM EN 27 16 144 3 1 13 V V V V V 13 BQP.B MN E.B MN E.BQP 0 0 16 144 72 Vì vậy V V V 72 13 59 . Chọn đáp án B ACPQA C NM ABC.A B C BQP.B MN
Câu 62. Cho khối lăng trụ tam giác AB .
C A B C . Các mặt phẳng ABC và A B C chia khối lăng
trụ đã cho thành 4 khối đa diện. Kí hiệu H , H lần lượt là các khối đa diện có thể tích lớn 1 2 V H
nhất, nhỏ nhất. Giá trị của 1 bằng: V H2 A. 4 . B. 2 . C. 5 . D. 3 . Lời giải Chọn C Gọi E AC A C ; F BC
B C có 4 khối đa diện cần tìm là:
ABCEF ; ABB A EF ; A B C EF ; CEFC . Đặt V V ABC.A B C V 2V ta có V ; V . C.A B C 3 ABB A C 3
Theo công thức tỉ số thể tích có:
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 103/105 CE CF 1 1 V V V . V . . CEFC C.A B C CA CB 2 2 3 12 V V V V V V . A B C EF C.A B C CEFC 3 12 4 CA CB CF 1 CE 1 Và với x 1 ; y 1 ; z ; t CA CB CB 2 CA 2
theo công thức tính nhanh tỉ số thể tích có : 1 1 1 1 1 1 1 1 2V V V xyzt .V .1.1. . 1 1 2 2 . . C.ABEF 4 ABB A C x y z t 4 2 2 3 4 2V V 5V 5V V V H Suy ra: V V V V ; 1 V 5 . ABB A EF ABB A C C.ABEF 3 4 12 H H 1 12 2 12 V H2 Chọn đáp án C.
Câu 63. Cho khối chóp .
S ABCD có đáy là hình bình hành thể tích bằng 1 . Gọi M là điểm đối xứng
của C qua B ; N là trung điểm cạnh SC . Mặt phẳng MDN chia khối chóp . S ABCD thành
hai khối đa diện, thể tích của khối đa diện chứ đỉnh S bằng: 1 5 12 7 A. . B. . C. . D. . 6 8 19 12 Lời giải Chọn D • Gọi P MN SB
P là trọng tâm của SCM vì là giao của hai đường trung tuyến SB , MN . • Gọi Q MD AB
Q là trung điểm của MD . • Ta có: MB MQ MP V V V V . . V BCDQNP M.CDN M.BQP M.CDN M.CDN MC MD MN . 1 1 2 5 1 . . V V M.CDN M. 2 2 3 6 CDN • Mặt khác :
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 104/105 S d N , ABCD MCD V V . V M.CDN N.MCD S. S d S , ABCD ABCD ABCD . 1 . CD CM 1 1 1 2 . .V V S.ABCD S. . CD CB 2 2 ABCD 2 • 5 5 7 Vậy V V V V 1 . Chọn đáp án D. BCDQNP SANPQD S. 12 ABCD BCDQNP 12 12
Câu 64. Cho hình lăng trụ AB .
C A' B'C' có đường cao bằng 8 và đáy là tam giác đều cạnh bằng 6 .
Gọi M, N lần lượt là trung điểm của các cạnh AA', BB'. Đường thẳng CM cắt đường thẳng
A'C' tại P ; đường thẳng CN cắt đường thẳng B'C' tại Q . Thể tích của khối đa diện có các đỉnh là các điểm , A ,
B C, P,Q,C'bằng A. 120 3. B. 140 3. C. 168 3. D. 192 3. Lời giải Chọn C AC MA Ta có 1 PA' AC A'C '
A' là trung điểm PC'. Tương tự B' là QC ' . Khối PA' MA'
chóp cụt ABC.PQC ' có chiều h 8 , diện tích đáy 3 2 S S .6 9 3,S S 4.S 36 6. 1 ABC 2 PQC' 1 4 h 8 Do đó V S S S S 9 3 36 3 9 3.36 3 168 3. Vậy chọn C ABC.PQC' 1 2 1 2 3 3
Câu 65. Cho hình hộp ABC .
D A' B'C' D' có đường cao bằng 8 và đáy là hình vuông cạnh bằng 6 . Gọi
M, N, P,Q lần lượt là tâm của các mặt ABB' A', BCC' B',CDD'C', DAA' D' .Thể tích của khối
đa diện có các đỉnh là các điểm , A , B C, ,
D M, N, P, , Q bằng A. 108. B. 168. C. 96. D. 120. Lời giải Chọn D
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tỉ số thể tích Trang 105/105
Thể tích khối hộp đã cho 2 V 6 .8 288. Gọi ,
E F,G, H lần lượt là trung điểm của
AA', BB', CC', DD' Ta có V V V V V V ACBDMNPQ ABCDGH A.MNQ B.MFN C.NGP D.PHQ 1 V V , V V V V ABCDGH A.MNQ B.MFN C.NGP D. 2 PHQ DH DP DQ . . .V
D.D'C ' A'
DD' DC ' DA' 1 1 1 1 1 . . . V V 2 2 2 6 48 1 1 1 1 1 5 Vậy V V V V V V V 120 ACBDMNPQ 2 48 48 48 48 12 Vậy chọn D
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn