TƯ DUY TOÁN HỌC 4.0 – LUYỆN THI ĐẠI HỌC NĂM 2021
NẮM TRỌN
CHUYÊN ĐỀ
HÌNH HỌC OXYZ
SỐ PHỨC
(Dùng cho học sinh 11,12 và luyện thi Đại học năm 2021)
………………………………………………………………
………………………………………………………………
………………………………………………………………
………………………………………………………………
………………………………………………………………
TÀI LIỆU LƯU HÀNH NỘI BỘ THÁNG 10/2020


LỜI NÓI ĐẦU
Các em học sinh, quý thầy cô và bạn đọc thân mến !
Kỳ thi THPT Quốc Gia là một trong những kỳ thi quan trọng nhất đối với mỗi chúng ta. Để có
thể tham dự và đạt được kết quả cao nhất thì việc trang bị đầy đủ kiến thức và kĩ năng cần thiết là
một điều vô cùng quan trọng. Thấu hiểu được điều đó, chúng tôi đã cúng nhau tiến hành biên soạn
bộ sách “ Nắm trọn các chuyên đề môn Toán 2021 ” giúp các em học sinh ôn luyện và hoàn
thiện những kiến thức trọng tâm phục vụ kỳ thi, làm tài liệu giảng dạy và tham khảo cho quý thầy
cô trước sự thay đổi về phương pháp dạy học và kiểm tra của Bộ Giáo dục và Đào tạo.
Bộ sách chúng tôi biên soạn gồm 4 quyển:
• Quyển 1: Nắm chọn chuyên đề Hàm số
• Quyển 2: Nắm trọn chuyên đề Mũ – Logarit và Tích phân
• Quyển 3: Hình học không gian
• Quyển 4: Hình học Oxyz và Số phức
Trong mỗi cuốn sách, chúng tôi trình bày một cách rõ ràng và khoa học – tạo sự thuận lợi nhất
cho các em học tập và tham khảo. Đầu tiên là tóm tắt toàn bộ lý thuyết và phương pháp giải các
dạng toán. Tiếp theo là hệ thống các ví dụ minh họa đa dạng, tiếp cận xu hướng ra đề của kỳ thi
THPT Quốc Gia các năm gần đây bao gồm 4 mức độ: Nhận biết, Thông hiểu, Vận dụng và Vận
dụng cao. Cuối cùng là phần bài tập rèn luyện từ cơ bản đến nâng cao để các em hoàn thiện kiến
thức, rèn tư duy và rèn luyện tốc độ làm bài. Tất cả các bài tập trong sách chúng tôi đều tiến hành
giải chi tiết 100% để các em tiện lợi cho việc so sánh đáp án và tra cứu thông tin.
Để có thể biên soạn đầy đủ và hoàn thiện bộ sách này, nhóm tác giả có sưu tầm, tham khảo một
số bài toán trích từ đề thi của các Sở, trường Chuyên trên các nước và một số bài toán của các
thầy/cô trên toàn quốc. Chân thành cảm ơn quý thầy cô đã sáng tạo ra các bài toán hay và các
phương pháp giải toán hiệu quả nhất.
Mặc dù nhóm tác giả đã tiến hành biên soạn và phản biện kĩ lưỡng nhất nhưng vẫn không tránh
khỏi sai sót. Chúng tôi rất mong nhận được những ý kiến phản hồi và đóng góp từ quý thầy cô,
các em học sinh và bạn đọc để cuốn sách trở nên hoàn thiện hơn. Mọi ý kiến đóng góp, quý vị vui
lòng gửi về địa chỉ:
• Gmail: Blearningtuduytoanhoc4.0@gmail.com
• Fanpage: 2003 – ÔN THI THPT QUỐC GIA
Cuối cùng, nhóm tác giả xin gửi lời chúc sức khỏe đến quý thầy cô, các em học sinh và quý bạn
đọc. Chúc quý vị có thể khai thác hiệu quả nhất các kiến thức khi cầm trên tay cuốn sách này !
Trân trọng./
NHÓM TÁC GIẢ


A. PHẦN I: HÌNH TỌA ĐỘ OXYZ
Trang
CHỦ ĐỀ 1: HỆ TỌA ĐỘ TRONG KHÔNG GIAN.................................................
1
Dạng 1. Điểm và vecto trong hệ tọa độ Oxyz..........................................................................
5
Dạng 2. Tích vô hướng và ứng dụng.........................................................................................
28
Dạng 3. Phương trình mặt cầu....................................................................................................
39
Dạng 4. Cực trị...............................................................................................................................
59
CHỦ ĐỀ 2: PHƯƠNG TRÌNH MẶT PHẲNG....................................................
79
Dạng 1. Xác định vecto pháp tuyến, tính tích có hướng của mặt phẳng............................
84
Dạng 2. Viết phương trình mặt phẳng......................................................................................
91
Dạng 3. Tìm tọa độ điểm liên quan đến mặt phẳng...............................................................
114
Dạng 4. Góc và khoảng cách liên quan đến mặt phẳng.........................................................
123
Dạng 5. Vị trí tương đối giữa hai mặt phẳng, giữa mặt cầu và mặt phẳng........................
140
Dạng 6. Cực trị liên quan đến mặt phẳng................................................................................
165
CHỦ ĐỀ 3: PHƯƠNG TRÌNH ĐƯỜNG THẲNG...........................................
185
Dạng 1. Xác định vecto chỉ phương của đường thẳng..........................................................
191
Dạng 2. Viết phương trình đường thẳng..................................................................................
200
Dạng 3. Tìm tọa độ điểm liên quan đến đường thẳng...........................................................
231
Dạng 4. Góc và khoảng cách liên quan đến đường thẳng.....................................................
247
Dạng 5. Vị trí tương đối giữa hai đường thẳng, giữa đường thẳng và mặt phẳng..........
257
Dạng 6. Bài toán liên quan giữa đường thẳng – mặt phẳng – mặt cầu...............................
271
Dạng 7. Cực trị liên quan đến đường thẳng............................................................................
314
CHỦ ĐỀ 4: ỨNG DỤNG CỦA PHƯƠNG PHÁP TỌA ĐỘ.......................
347
Dạng 1. Tọa độ hóa Hình học không gian................................................................................
353
Dạng 2. Bài toán đại số.................................................................................................................
367
CHỦ ĐỀ 5: TỔNG HỢP VỀ HÌNH TỌA ĐỘ OXYZ......................................
372
Đề bài...............................................................................................................................................
372
Đáp án..............................................................................................................................................
381
B. PHẦN II: SỐ PHỨC………………………...……………………………………….
405
Dạng toán 1: Xác định các yếu tố cơ bản của số phức….…………………………………...
406
Dạng toán 2: Phép toán cộng, trừ, nhân hai số phức...……………………………………...
424
Dạng toán 3: Phép chia hai số phức…………………………………………………………...
437
MỤC LỤC

Dạng toán 4: BT quy về giải PT, HPT và tập hợp điểm biễu diễn số phức……...………
448
Dạng toán 5: Phương trình bậc hai với hệ số thực……………………………..……………
468
Dạng toán 6: Cực trị số phức……………………………………………………...……………
482

PHẦN I
HÌNH HỌC OXYZ

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
1
CHỦ ĐỀ 1 : HỆ TRỤC TỌA ĐỘ OXYZ
➢ Trong không gian xét hệ trục
Oxyz
, có trục
Ox
vuông góc với trục
Oy
tại
O
, và trục
Oz
vuông
góc với mặt phẳng
Oxy
tại
O
. Các vectơ đơn vị trên từng trục
Ox
,
Oy
,
Oz
lần lượt là
( )
1;0;0 ,i =
( )
0;1;0 ,j =
( )
0;0;1k =
.
▪ Nếu
1 2 3
a a i a j a k= + +
thì
( )
1 2 3
;;a a a a=
.
▪
( ; ; )
M M M M M M
M x y z OM x i y j z k = + +
▪ Cho
( )
;;
A A A
A x y z
và
( )
;;
B B B
B x y z
▪ Ta có:
( ; ; )
B A B A B A
AB x x y y z z= − − −
và
2 2 2
( ) ( ) ( )
B A B A B A
AB x x y y z z= − + − + −
.
▪
M
là trung điểm
AB
thì
M
;;
2 2 2
A B A B A B
x x y y z z+ + +
.
➢ Trong không gian với hệ tọa độ
Oxyz
. Cho
1 2 3
( ; ; )a a a a=
và
1 2 3
( ; ; )b b b b=
ta có
▪
11
22
33
ab
a b a b
ab
=
= =
=
1 1 2 2 3 3
( ; ; )a b a b a b a b =
1 2 3
. ( ; ; )k a ka ka ka=
▪
1 1 2 2 3 3
. . os(a; )a b a b c b a b a b a b= = + +
222
1 2 3
a a a a= + +
▪
1 1 2 2 3 3
2 2 2 2 2 2
1 2 3 1 2 3
. . .
os os(a, )
.
a b a b a b
c c b
a a a b b b
++
==
+ + + +
(với
0 , 0ab
)
▪
a
và
b
vuông góc
1 1 2 2 3 3
. 0 . . . 0a b a b a b a b = + + =
▪
a
và
b
cùng phương
11
22
33
:
a kb
k R a kb a kb
a kb
=
= =
=
➢ Tích có hướng của
1 2 3
( ; ; )a a a a=
và
1 2 3
( ; ; )b b b b=
là
2 3 3 2 3 1 1 3 1 2 2 1
, ( ; ; )a b a b a b a b a b a b a b
= − − −
▪
a
và
b
cùng phương
,0ab
=
a
,
b
,
c
đồng phẳng
, . 0a b c
=
▪ Diện tích tam giác :
1
[ , ]
2
ABC
S AB AC=
▪ Thể tích tứ diện
ABCD
V =
1
[ , ].
6
AB AC AD
▪ Thể tích khối hộp:
' ' ' '
.ABCD A B C D
V
=
[ , ]. 'AB AD AA
➢ Một số kiến thức khác
▪ Nếu
M
chia đoạn
AB
theo tỉ số
k
(
MA kMB=
) thì ta có :
;;
1 1 1
A B A B A B
M M M
x kx y ky z kz
x y z
k k k
− − −
= = =
− − −
Với
( )
1k
▪
G
là trọng tâm của tam giác
ABC
;;
3 3 3
A B C A B C A B C
G G G
x x x y y y z z z
x y z
+ + + + + +
= = =
▪
G
là trọng tâm của tứ diện
ABCD
0GA GB GC GD+ + + =
LÍ THUYẾT

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
2
Lời giải
Chọn B
Ta có:
( )
.
cos ,
.
uv
uv
uv
=
( )
2
2 2 2 2
12
1 1 2 . 1
m
m
−
=
+ + − +
2
1 2 2
2
6. 1
m
m
−
==
+
2
1 2 3 1mm − = −
22
4 4 1 3 3m m m − + = +
(điều kiện
1
2
m
).
2
4 2 0mm − − =
26
26
m
m
=−
=+
. Đối chiếu điều kiện ta có
26m =−
.
Lời giải
Chọn D
Ta có:
2 3 2;2 3 2; 4 3 2u a mb m m
và
2 ; 2; 2 2v ma b m m m
.
Khi đó:
. 0 4 2 3 2 2 4 3 2 2 2 0u v m m m m m
.
2
9 2 6 6 2 0mm
26 2
6
m
.
Lời giải
Chọn C
VÍ DỤ MINH HỌA
VÍ DỤ 1: Trong không gian với hệ tọa độ
Oxyz
, cho vectơ
( )
1;1; 2u =−
,
( )
1;0;vm=
. Tìm
m
để góc
giữa hai vectơ
,uv
bằng
45
.
A.
2m =
. B.
26m =−
. C.
26m =+
. D.
.
VÍ DỤ 2: Trong không gian
Oxyz
, cho hai véc tơ
2;1; 2a
,
0; 2; 2b
. Tất cả giá trị của
m
để hai véc tơ
23u a mb
và
v ma b
vuông góc với nhau là
A.
26 2
6
. B.
26 2
6
. C.
11 2 26
18
. D.
26 2
6
.
VÍ DỤ 3: Trong mặt phẳng tọa độ
Oxyz
, cho bốn điểm
( )
0; 1;2A −
,
( )
2; 3;0B −
,
( )
2;1;1C −
,
( )
0; 1;3D −
Gọi
( )
L
là tập hợp tất cả các điểm
M
trong không gian thỏa mãn đẳng thức
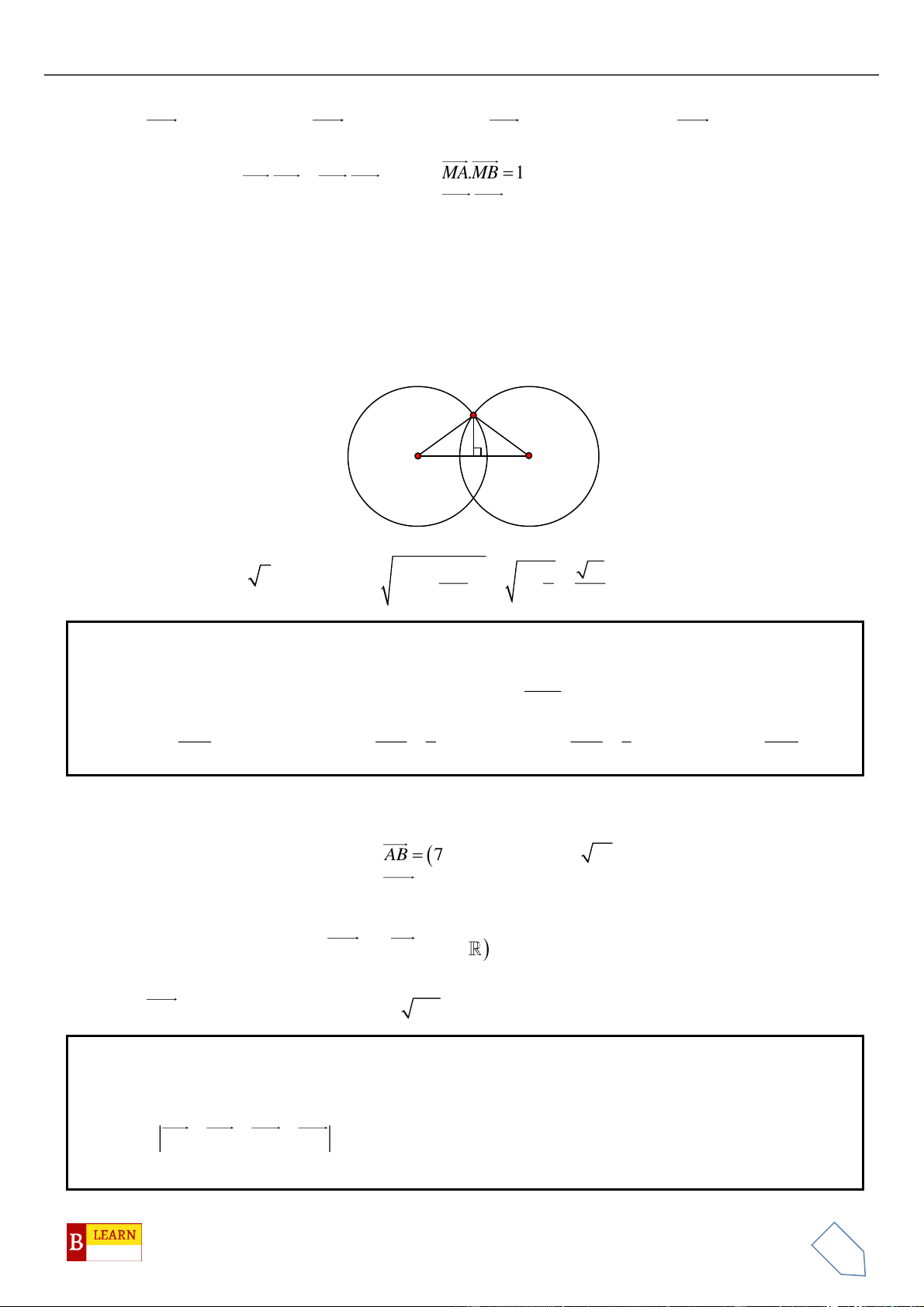
. . 1MAMB MC MD==
. Biết rằng
( )
L
là một đường tròn, đường tròn đó có bán kính
r
bằng
bao nhiêu?
A.
3
2
r =
. B.
5
2
r =
. C.
11
2
r =
. D.
7
2
r =
.
.
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
3
Gọi
( )
;;M x y z
là tập hợp các điểm thỏa mãn yêu cầu bài toán. Ta có
( )
; 1; 2AM x y z= + −
,
( )
2; 3;BM x y z= − +
,
( )
2; 1; 1CM x y z= + − −
,
( )
; 1; 3DM x y z= + −
.
Từ giả thiết:
.1
. . 1
.1
MAMB
MAMB MC MD
MC MD
=
= =
=
( ) ( )( ) ( )
( ) ( )( ) ( )( )
2 1 3 2 1
2 1 1 1 3 1
x x y y z z
x x y y z z
− + + + + − =
+ + + − + − − =
2 2 2
2 2 2
2 4 2 2 0
2 4 1 0
x y z x y z
x y z x z
+ + − + − + =
+ + + − + =
Suy ra quỹ tích điểm
M
là đường tròn giao tuyến của mặt cầu tâm
( )
1
1; 2;1I −
,
1
2R =
và mặt cầu
tâm
( )
2
1;0;2I −
,
2
2R =
.
Ta có:
12
5II =
. Dễ thấy:
2
2
12
1
5 11
4
2 4 2
II
rR
= − = − =
.
Lời giải
Chọn B
( ) ( )
; 0 ; M Oxz M x z
;
( )
( )
7 ; 3 ; 1 59
2 ; 3 ; 1
AB AB
AM x z
= =
= + − −
.
,,A B M
thẳng hàng
( )
. AM k AB k =
2 7 9
3 3 1
10
x k x
kk
z k z
+ = = −
− = − =
− = =
( )
9 ; 0 ; 0M−
.
( )
14 ; 6 ; 2 118 2.BM BM AB= − − − = =
.
Lời giải
1
I
2
I
M
VÍ DỤ 4: Trong không gian với hệ tọa độ Oxyz, cho hai điểm
( )
2;3;1A −
và
( )
5; 6; 2B
. Đường thẳng
AB
cắt mặt phẳng
( )
Oxz
tại điểm
M
. Tính tỉ số
AM
BM
.
A.
2
AM
BM
=
. B.
1
2
AM
BM
=
. C.
1
3
AM
BM
=
. D.
3
AM
BM
=
.
.
VÍ DỤ 5: Trong không gian với hệ trục tọa độ
Oxyz
, cho bốn điểm
( )
2; 3;7A −
,
( )
0;4;1B
,
( )
3;0;5C
và
( )
3;3;3D
. Gọi
M
là điểm nằm trên mặt phẳng
( )
Oyz
sao cho biểu thức
MA MB MC MD+ + +
đạt giá trị nhỏ nhất. Khi đó tọa độ của
M
là:
A.
( )
0;1; 2M −
. B.
( )
0;1;4M
. C.
( )
0;1; 4M −
. D.
( )
2;1;0M
.
.
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
4
Chọn B
Ta có:
( )
2;7; 6AB = − −
,
( )
1;3; 2AC =−
,
( )
1;6; 4AD =−
nên
, . 4 0AB AC AD
= −
.
Suy ra:
AB
,
AC
,
AD
không đồng phẳng.
Gọi
G
là trọng tâm tứ diện
ABCD
. Khi đó
( )
2;1;4G
.
Ta có:
44MA MB MC MD MG MG+ + + = =
.
Do đó
MA MB MC MD+ + +
nhỏ nhất khi và chỉ khi
MG
ngắn nhất.
Vậy
M
là hình chiếu vuông góc của
G
lên mặt phẳng
( )
Oyz
nên
( )
0;1;4M
.
Hướng dẫn giải
Chọn C
Ta có
( )
6;0;0DA =
,
( )
0;2;0DB =
,
( )
0;0;3DC =
nên tứ diện $ABCD$ là tứ diện vuông đỉnh
D
.
Giả sử
( )
1; 2; 3M x y z+ + +
.
Ta có
( )
2
22
6MA x y z= − + +
6x−
6 x−
,
( )
2
22
2MB x y z= + − +
2y−
2 y−
.
( )
2
22
3MC x y z= + + −
3z−
3 z−
,
( )
2 2 2
33MD x y z= + +
( )
2
x y z + +
x y z + +
.
Do đó
( ) ( ) ( ) ( )
6 2 3 11P x y z x y z − + − + − + + + =
.
Vậy
P
đạt giá trị nhỏ nhất bằng $11$, khi và chỉ khi
0
60
20
30
0
x y z
x
y
z
x y z
= = =
−
−
−
+ +
0x y z = = =
.
Khi đó
( )
1;2;3M
suy ra
2 2 2
1 2 3OM = + +
14=
.
Chọn C
Ta có
( )
4; 2; 1AB = − −
,
( )
2;0;1AD =
,
( )
, 2; 6;4AB AD
= − −
,
( )
1;1; 4AC m=−
Để
A
,
B
,
C
,
D
là bốn đỉnh của một hình tứ diện khi
, . 0AB AD AC
2 6 4 16 0m − − + −
6m
.
VÍ DỤ 6: Trong không gian với hệ tọa độ
Oxyz
, cho bốn điểm
( )
7;2;3A
,
( )
1;4;3B
,
( )
1;2;6C
,
( )
1;2;3D
và điểm
M
tùy ý. Tính độ dài đoạn khi biểu thức
3P MA MB MC MD= + + +
đạt giá trị
nhỏ nhất.
A.
3 21
4
OM =
. B.
26OM =
. C.
14OM =
. D.
5 17
4
OM =
.
OM
VÍ DỤ 7: Trong không gian
Oxyz
, cho bốn điểm
( )
1;1;4A
,
( )
5; 1;3B −
,
( )
2;2;Cm
,
( )
3;1;5D
. Tìm tất cả
giá trị thực của tham số
m
để
A
,
B
,
C
,
D
là bốn đỉnh của một hình tứ diện.
A.
6m
. B.
6m
. C.
6m
. D.
6m =
.
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
5
DẠNG 1. ĐIỂM VÀ VECTO TRONG HỆ TRỤC TỌA ĐỘ
Câu 1. Trong không gian với hệ trục
Oxyz
cho ba điểm
1;2; 3 , 1;0;2 , ; ; 2A B C x y
thẳng hàng.
Khi đó
xy
bằng
A.
1xy
. B.
17xy
. C.
11
5
xy
. D.
11
5
xy
.
Câu 2. Tìm tọa độ véctơ
u
biết rằng
0ua+=
và
( )
1; 2;1a =−
.
A.
( )
3; 8;2u = − −
. B.
( )
1; 2;8u =−
. C.
( )
1;2; 1u = − −
. D.
( )
6; 4; 6u = − −
.
Câu 3. Trong không gian
Oxyz
, cho ba điểm
( )
1;0;2−A
,
( )
2;1; 3−B
và
( )
1; 1;0−C
. Tìm tọa độ điểm
D
sao cho
ABCD
là hình bình hành.
A.
( )
0;2; 1−D
. B.
( )
2; 2;5−−D
. C.
( )
2;2;5−D
. D.
( )
2;2; 5D −
.
Câu 4. Trong không gian
,Oxyz
cho điểm
( )
1;1;1A
. Tìm tọa độ hình chiếu vuông góc của
A
trên mặt
phẳng
( )
Oxz
.
A.
( )
1;1;0
. B.
( )
0;1;1
. C.
( )
1;0;1
. D.
( )
0;1;0
.
Câu 5. Trong không gian
Oxyz
, cho
( )
3;1;2A −
, tọa độ điểm
'A
đối xứng với điểm
A
qua trục
Oy
là
A.
( )
3; 1; 2−−
. B.
( )
3; 1;2−
. C.
( )
3;1; 2−
. D.
( )
3; 1;2−−
.
Câu 6. Trong không gian với hệ trục tọa độ
Oxyz
, cho ba điểm
( ) ( ) ( )
1;2; 1 ; 2; 1;3 ; 3;5;1A B C− − −
. Tìm
tọa độ điểm
D
sao cho tứ giác
ABCD
là hình bình hành.
A.
( )
4; 8; 5D −−
B.
( )
4; 8; 3D −−
.
C.
( )
2;8; 3D −−
.
D.
( )
2;2;5D −
.
Câu 7. Trong không gian
Oxyz
, cho đường thẳng
3 1 1
:
2 1 2
x y z
d
− + −
==
và điểm
( )
1;2; 3M −
. Gọi
1
M
là hình chiếu vuông góc của
M
lên đường thẳng
d
. Độ dài đoạn thẳng
1
OM
bằng
A.
22
. B.
6
. C.
3
. D.
2
.
Câu 8. Trong không gian
Oxyz
, cho hai điểm
( )
2;4;1A −
và
( )
4;5;2B
. Điểm
C
thỏa mãn
OC BA=
có tọa độ là
A.
( )
6; 1; 1− − −
. B.
( )
2; 9; 3− − −
. C.
( )
6; 1;1
. D.
( )
2; 9;3
.
Câu 9. Trong không gian với hệ toạn độ
Oxyz
, cho
( ) ( ) ( )
1;1;2 , 2; 1;1 , 3;2; 3A B C−−
. Tìm tọa độ điểm
D
để tứ giác
ABCD
là hình bình hành.
A.
( )
4;2; 4−
. B.
( )
0; 2;6−
. C.
( )
2;4; 2−
. D.
( )
4;0; 4−
.
Câu 10. Trong không gian
Oxyz
, cho hai điểm
( )
3;1; 2A −
,
( )
2; 3;5B −
. Điểm
M
thuộc đoạn
AB
sao cho
2MA MB=
, tọa độ điểm
M
là
BÀI TẬP RÈN LUYỆN

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
6
A.
7 5 8
;;
3 3 3
M
−
. B.
( )
4;5; 9M −
. C.
3 17
; 5;
22
M
−
. D.
( )
1; 7;12M −
.
Câu 11. Trong không gian với hệ tọa độ
Oxyz
, gọi
a
,
b
,
c
lần lượt là khoảng cách từ điểm
( )
1;3;2M
đến
ba mặt phẳng tọa độ
( )
Oxy
,
( )
Oyz
,
( )
Oxz
. Tính
23
P a b c= + +
?
A.
32P =
. B.
18P =
. C.
30P =
. D.
12P =
.
Câu 12. Cắt một hình trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh
bằng
3a
. Tính diện tích toàn phần của hình trụ đã cho.
A.
2
9a
. B.
2
27
2
a
. C.
2
9
2
a
. D.
2
13
6
a
.
Câu 13. Trong không gian
(ox )yz
cho
2 3 ,OA i j k= − +
điểm
(3; 4;1)B −
và điểm
(2;0; 1).C −
Tọa độ trọng
tâm của tam giác ABC là
A.
(1; 2;3).−
B.
( 2;2; 1).−−
C.
(2; 2;1).−
D.
( 1;2; 3).−−
Câu 14. Trong không gian vói hệ trục tọa độ
Oxyz
, cho hình thang cân
ABCD
có hai đáy
AB
,
CD
thỏa
mãn
2CD AB=
và diện tích bằng
27
, đỉnh
( )
1; 1;0A −−
, phương trình đường thẳng chứa cạnh
CD
là
2 1 3
2 2 1
x y z− + −
==
. Tìm tọa độ điểm
D
biết
BA
xx
.
A.
( )
2; 5;1D −−
. B.
( )
3; 5;1D −−
. C.
( )
2; 5;1D −
. D.
( )
3; 5;1D −
.
Câu 15. Trong không gian
Oxyz
, cho
23OA i j k= − +
, điểm
( )
3; 4;1B −
và điểm
( )
2;0; 1C −
. Tọa độ
trọng tâm tam giác
ABC
là
A.
( )
1; 2;3−
. B.
( )
2;2; 1−−
. C.
( )
2; 2;1−
. D.
( )
1;2; 3−−
.
Câu 16. Trong không gian
Oxyz
, cho
23AO i j k= − +
, điểm
( )
3; 4;1B −
( )
2;0; 1C −
và
điểm
( )
;;D a b c
sao cho
B
là trọng tâm tam giác
ACD
. Khi đó
P a b c= + +
bằng
A.
1
. B.
3−
. C.
1−
. D.
3
.
Câu 17. Trong không gian
Oxyz
, cho hình hộp
.ABCD A B C D
biết
( )
1;0;1A
,
( )
2;1;2B
,
( )
1; 1;1D −
,
( )
4;5; 5C
−
. Tọa độ của điểm
A
là:
A.
( )
4;6; 5A
−
. B.
( )
3;4; 1A
−−
. C.
( )
3;5; 6A
−
. D.
( )
3;5;6A
.
Câu 18. Trong không gian
Oxyz
, cho hai điểm
( )
2; 2;1A −
,
( )
0;1;2B
. Tọa độ điểm
M
thuộc mặt phẳng
( )
Oxy
sao cho ba điểm
A
,
B
,
M
thẳng hàng là
A.
( )
4; 5;0M −
. B.
( )
2; 3;0M −
. C.
( )
0;0;1M
. D.
( )
4;5;0M
.
Câu 19. Trong không gian
Oxyz
, véctơ
u
vuông góc với hai véctơ
( )
1;1;1a =
và
( )
1; 1;3b =−
; đồng thời
u
tạo với tia
Oz
một góc tù và độ dài véctơ
u
bằng 3. Tìm véctơ
u
.
A.
66
6; ;
22
−−
. B.
66
6; ;
22
−
. C.
66
6; ;
22
−
. D.
66
6; ;
22
−−
.
Câu 20. Trong hệ trục tọa độ
Oxyz
, cho các điểm
(1; 1;1),N(2;0; 1),P( 1;2;1)M − − −
. Xét điểm
Q
sao cho
tứ giác
MNPQ
là một hình bình hành. Tọa độ
Q
là

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
7
A.
( 2;1;3)−
B.
( 2;1;3)−
C.
( 2;1; 3)−−
D.
(4;1;3)
Câu 21. Trong không gian
Oxyz
, cho ba điểm
( )
3;5; 1A −
,
( )
7; ;1Bx
và
( )
9;2;Cy
. Để
A
,
B
,
C
thẳng
hàng thì giá trị
xy+
bằng
A.
5
. B.
6
. C.
4
. D.
7
.
Câu 22. Trong không gian với hệ trục tọa độ cho hai điểm Hình chiếu
vuông góc của trung điểm của đoạn trên mặt phẳng là điểm nào dưới đây?
A. . B. . C. . D.
Câu 23. Trong không gian
Oxyz
, cho điểm
( )
2; 5;4M −
. Trong các phát biểu sau, phát biểu nào sai?
A. Khoảng cách từ
M
đến mặt phẳng tọa độ
( )
xOz
bằng
5
.
B. Khoảng cách từ
M
đến trục
Oz
bằng
29
.
C. Tọa độ điểm
M
đối xứng với
M
qua mặt phẳng
( )
yOz
là
( )
2;5; 4M
−
.
D.Tọa độ điểm
M
đối xứng với
M
qua trục
Oy
là
( )
2; 5; 4M
− − −
.
Câu 24. Trong không gian
Oxyz
cho ba điểm
( )
1;1;2A −
,
( )
0;1; 1B −
,
( )
2; ; 2C x y+−
thẳng hàng. Tổng
xy+
bằng
A.
7
3
. B.
8
3
−
. C.
2
3
−
. D.
1
3
−
.
Câu 25. Trong hệ trục tọa độ Oxyz, cho điểm
( )
2;1;1H
. Gọi các điểm
,,A B C
lần lượt ở trên các trục tọa
độ
,,Ox Oy Oz
sao cho
H
là trực tâm của tam giác
ABC
. Khi đó hoành độ điểm
A
là:
A.
3−
. B.
5−
. C. 3. D. 5
Câu 26. Trong không gian với hệ tọa độ
Oxyz
, biết
2u =
;
1v =
và góc giữa hai vectơ
u
và
v
bằng
2
3
. Tìm
k
để vectơ
p ku v=+
vuông góc với vectơ
q u v=−
.
A.
2
5
k =
. B.
5
2
k =
. C.
2k =
. D.
2
5
k =−
.
Câu 27. Trong không gian với hệ tọa độ
Oxyz
, cho hình hộp
. ' ' ' 'ABCD A B C D
với
( )
2;1;3 ,A −
( )
2;3;5 ,C
( ) ( )
' 2;4; 1 , ' 0;2;1BD−
. Tìm tọa độ điểm
B
.
A.
( )
1; 3;3B −
. B.
( )
1;3;3B −
. C.
( )
1;3; 3C −
. D.
( )
1;3;3B
.
Câu 28. Trong không gian
Oxyz
, cho bốn điểm
( )
1;2;0A −
,
( )
3;1;0B
,
( )
0;2;1C
và
( )
1;2;2D
. Trong đó có
ba điểm thẳng hàng là
A.
A
,
C
,
D
. B.
A
,
B
,
D
. C.
B
,
C
,
D
. D.
A
,
B
,
C
.
Câu 29. Trong không gian tọa độ
Oxyz
, cho hai điểm
( )
1;0;0A
,
( )
5;0;0B
. Gọi
( )
H
là tập hợp các điểm
M
trong không gian thỏa mãn
.0MAMB =
. Khẳng định nào sau đây là đúng?
A.
( )
H
là một đường tròn có bán kính bằng
4
.
B.
( )
H
là một mặt cầu có bán kính bằng
4
.
C.
( )
H
là một đường tròn có bán kính bằng
2
.
,Oxyz
( ) ( )
2;3;4 , 8; 5;6 .AB−−
I
AB
( )
Oyz
( )
3; 1;5N −
( )
0; 1;5M −
( )
0;0;5Q
( )
3;0;0 .P

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
8
D.
( )
H
là một mặt cầu có bán kính bằng
2
.
Câu 30. Trong không gian với hệ tọa độ
Oxyz
, cho các vectơ
( ) ( )
2; 1;3 , 1;3; 2a m b n= − = −
. Tìm
,mn
để
các vectơ
,ab
cùng hướng.
A.
3
7;
4
mn= = −
. B.
4; 3mn= = −
. C.
1; 0mn==
. D.
4
7;
3
mn= = −
.
Câu 31. Trong không gian
Oxyz
, cho
( )
−1;1; 3A
,
( )
−3; 1;1B
. Gọi
G
là trọng tâm tam giác
OAB
,véc
tơ
OG
có độ dài bằng:
A.
25
3
. B.
25
5
. C.
35
3
. D.
35
2
.
Câu 32. Trong không gian vói hệ trục tọa độ
Oxyz
, cho hình thang cân
ABCD
có hai đáy
AB
,
CD
thỏa
mãn
2CD AB=
và diện tích bằng
27
, đỉnh
( )
1; 1;0A −−
, phương trình đường thẳng chứa cạnh
CD
là
2 1 3
2 2 1
x y z− + −
==
. Tìm tọa độ điểm
D
biết hoành độ điểm
B
lớn hơn hoành độ điểm
A
.
A.
( )
2; 5;1D −−
. B.
( )
3; 5;1D −−
. C.
( )
2; 5;1D −
. D.
( )
3; 5;1D −
.
Câu 33. Trong không gian với hệ trục tọa độ
Oxyz
cho hai điểm
( )
2;3;2A
,
( )
2; 1;4B −−
. Tìm tọa độ điểm
E
thuộc trục
Oz
sao cho
E
cách đều hai điểm
,AB
.
A.
1
0;0;
2
. B.
1
0;0;
3
. C.
( )
0;0; 1−
. D.
( )
0;0;1
.
Câu 34. Trong không gian với hệ tọa độ
Oxyz
, cho
( )
1;0;2A
,
( )
3;1;4B
,
( )
3; 2;1C −
. Tìm tọa độ điểm
S
, biết
SA
vuông góc với
( )
ABC
, mặt cầu ngoại tiếp tứ diện
.S ABC
có bán kính bằng
3 11
2
và
S
có cao độ âm.
A.
( )
4;6; 4S −
. B.
( )
4; 6; 4S −−
. C.
( )
4;6; 4S −−
. D.
( )
4; 6; 4S −−−
.
Câu 35. Trong không gian
Oxyz
, cho hình thang cân
ABCD
có các đáy lần lượt là
,AB CD
. Biết
( )
3;1; 2A −
,
( )
1;3;2B −
,
( )
6;3;6C −
và
( )
;;D a b c
với
;;abc
. Tính
T a b c= + +
.
A.
3T =−
. B.
1T =
. C.
3T =
. D.
1T =−
.
Câu 36. Trong không gian
Oxyz
, cho tam giác
ABC
với
( )
1;2;5A
,
( )
3;4;1B
,
( )
2;3; 3C −
. Gọi
G
là
trọng tâm tam giác
ABC
và
M
là điểm thay đổi trên
( )
mp Oxz
. Độ dài
GM
ngắn nhất bằng
A.
2
. B.
3
. C.
4
. D.
1
.
Câu 37. Trong không gian
Oxyz
cho các điểm
( )
5;1;5A
,
( )
4;3;2B
,
( )
3; 2;1C −−
. Điểm
( )
;;I a b c
là
tâm đường tròn ngoại tiếp tam giác
ABC
. Tính
2a b c++
?
A.
1
. B.
3
. C.
6
. D.
9−
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
9
Câu 38. Trong không gian với hệ tọa
Oxyz
, cho vectơ
( )
1; 2;4a =−
,
( )
0 0 0
;;b x y z=
cùng phương với
vectơ
a
. Biết vectơ
b
tạo với tia
Oy
một góc nhọn và
21b =
. Giá trị của tổng
0 0 0
x y z++
bằng
A.
3−
. B.
6
. C.
6−
. D.
3
.
Câu 39. Trong không gian
Oxyz
cho
( )
4; 2;6A −
,
( )
2;4;2B
,
( )
: 2 3 7 0M x y z
+ − − =
sao cho
.MAMB
nhỏ nhất. Tọa độ của
M
bằng
A.
29 58 5
;;
13 13 13
. B.
( )
4;3;1
. C.
( )
1;3;4
. D.
37 56 68
;;
3 3 3
−
.
Câu 40. Trong không gian với hệ tọa độ
Oxyz
, cho hình thang
ABCD
có hai đáy
, AB CD
; có tọa độ ba
đỉnh
( ) ( ) ( )
1;2;1 , 2;0; 1 , 6;1;0A B C−
. Biết hình thang có diện tích bằng
62
. Giả sử đỉnh
( )
;;D a b c
, tìm mệnh đề đúng?
A.
6abc+ + =
. B.
5abc+ + =
. C.
8abc+ + =
. D.
7abc+ + =
.
Câu 41. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )
: 3 0x y z
+ + − =
và đường thẳng
12
:
1 2 1
x y z
d
+−
==
−
. Gọi
là hình chiếu vuông góc của
d
trên
( )
và
( )
1;a;ub=
là một vectơ
chỉ phương của
với
,ab
. Tính tổng
ab+
.
A.
0
. B.
1
. C.
1−
. D.
2−
.
Câu 42. Trong không gian
Oxyz
, cho hình lăng trụ tam giác đều
.ABC A B C
có
( )
3; 1;1A
−
, hai đỉnh
,BC
thuộc trục
Oz
và
1AA
=
(
C
không trùng với
O
). Biết véctơ
( )
; ;2u a b=
với
,ab
là
một véctơ chỉ phương của đường thẳng
AC
. Tính
22
T a b=+
.
A.
5T =
. B.
16T =
. C.
4T =
. D.
9T =
.
Câu 43. Trong không gian , cho hai điểm và . Biết là tâm của
đường tròn nội tiếp tam giác . Giá trị của bằng
A. 1. B. 3. C. 2. D. 0.
Câu 44. Trong không gian , cho ba điểm , , . Bán kính đường tròn
nội tiếp tam giác thuộc nửa khoảng
A. . B. . C. . D. .
Câu 45. Trong không gian , cho ba điểm , , . Độ dài đường phân
giác trong đỉnh của tam giác là
A. . B. . C. . D. .
Câu 46. Trong không gian
Oxyz
, cho mặt phẳng
( )
P
:
20xy−+=
và hai điểm
( )
1;2;3A
,
( )
1;0;1B
.
Điểm
( ) ( )
; ; 2C a b P−
sao cho tam giác
ABC
có diện tích nhỏ nhất. Tính
ab+
Oxyz
(1;2; 2)A −
8 4 8
;;
333
B
( ; ; )I a b c
OAB
a b c−+
Oxyz
(1;0;0)A
( )
2;2; 2B −
11 4 8
;;
3 3 3
C
ABC
1
0;
2
1
;1
2
3
1;
2
3
;2
2
Oxyz
( 1;0;0)A −
( )
0;2; 2B −
5 4 8
;;
3 3 3
C
A
ABC
12 2
7
12 3
7
13 2
7
13 3
7

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
10
A. 0. B.
3−
. C. 1. D. 2.
Câu 47. Trong không gian tọa độ
Oxyz
, cho hai điểm
(1;0;0)A
,
(5;6;0)B
và
M
là điểm thay đổi trên
mặt cầu
( )
2 2 2
:1S x y z+ + =
. Tập hợp các điểm
M
trên mặt cầu
( )
S
thỏa mãn
22
3 48MA MB+=
có bao nhiêu phần tử?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 48. Trong không gian
Oxyz
, cho
3= + −OA i j k
,
( )
2;2;1B
. Tìm tọa độ điểm
M
thuộc trục tung
sao cho
22
MA MB+
nhỏ nhất.
A.
( )
0; 2;0M −
. B.
3
0; ;0
2
M
. C.
( )
0; 3;0M −
. D.
( )
0; 4;0M −
.
Câu 49. Trong không gian
Oxyz
cho hai điểm
( )
1;5;0A
,
( )
3;3;6B
và đường thẳng
11
:
2 1 2
x y z
d
+−
==
−
. Điểm
( )
;;M a b c
thuộc đường thẳng
d
sao cho chu vi tam giác
MAB
nhỏ
nhất. Khi đó biểu thức
23a b c++
bằng
A.
5
. B.
7
. C.
9
. D.
3
.
Câu 50. Trong không gian
Oxyz
, cho các điểm
( )
0;4 2 ;0A
,
( )
0;0;4 2B
, điểm
( )
C Oxy
và tam giác
OAC
vuông tại
C
, hình chiếu vuông góc của
O
trên
BC
là điểm
H
. Khi đó điểm
H
luôn thuộc
đường tròn cố định có bán kính bằng
A.
22
. B.
4
. C.
3
. D.
2
.
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
11
ĐÁP ÁN CHI TIẾT
Câu 1. Chọn A
Có
2; 2;5 , 1; 2;1AB AC x y
.
, , A B C
thẳng hàng
, AB AC
cùng phương
3
1 2 1
5
1
8
2 2 5
5
x
xy
xy
y
.
Câu 2. Chọn C
Ta có
( )
0 1;2; 1u a u a+ = = − = − −
.
Câu 3. Chọn B
Gọi
( )
;;D a b c
;
( )
3;1; 5=−AB
;
( )
2; 1; 2= − −AC
Vì
31
21
−
nên
AB
không cùng phương
AC
tồn tại hình bình hành
ABCD
.
Suy ra
ABCD
là hình bình hành khi
3 1 2
1 1 2
55
aa
AB DC b b
cc
= − = −
= = − − = −
− = − =
. Vậy
( )
2; 2;5−−D
.
Câu 4. Chọn C
Vì
( )
1;1;1A
nên tọa độ hình chiếu vuông góc của
A
trên mặt phẳng
( )
Oxz
là
( )
1;0;1
.
Câu 5. Chọn C
Gọi
( )
; ; , '( '; '; ')A x y z A x y z
là điểm đối xứng với điểm A qua trục
Oy
.
Điểm
'A
đối xứng với điểm
A
qua trục
Oy
nên
'
'
'
xx
yy
zz
=−
=
=−
. Do đó
( )
' 3;1; 2A =−
.
Câu 6. Chọn B
Ta có
( )
1; 3; 4AB −
;
( )
4; 3; 2AC −
nên
;AB AC
không cùng phương hay
,,A B C
không thẳng
hàng. Gọi
( )
;;D x y z
( )
3 ; 5 ; 1DC x y z− − − −
.
Lúc đó,
ABCD
là hình bình hành khi và chỉ khi
1 3 4
3 5 8 .
4 1 3
xx
AB DC y y
zz
= − − = −
= − = − =
= − = −
Vậy
( )
4;8; 3D −−
.
Câu 7. Chọn B

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
12
Cách 1: Phương trình tham số của đường thẳng
d
là:
32
1
12
xt
yt
zt
=+
= − +
=+
.
Một vtcp của
d
là
( )
2;1;2u =
.
Gọi
( )
là mặt phẳng đi qua điểm
( )
1;2; 3M −
và vuông góc với đường thẳng
d
. Khi đó
( )
có vtpt là
( )
2;1;2nu==
.
Phương trình mặt phẳng
( )
:
( ) ( ) ( )
2 1 1 2 2 3 0 2 2 2 0x y z x y z− + − + + = + + + =
.
1
M
là hình chiếu vuông góc của
M
lên đường thẳng
d
nên
1
M
là giao điểm của
d
và
( )
.
Xét hệ phương trình:
( )
( )
( )
( )
3 2 1
12
1 2 3
2 2 2 0 4
xt
yt
zt
x y z
=+
= − +
=+
+ + + =
Thay
( ) ( ) ( )
1 , 2 , 3
vào
( )
4
ta được:
( ) ( )
2 3 2 1 2 1 2 2 0t t t+ − + + + + =
9 9 0 1tt + = = −
.
Suy ra
( )
1
1
2 1; 2; 1
1
x
yM
z
=
= − − −
=−
.
Độ dài đoạn thẳng
1
OM
là:
( ) ( )
22
2
1
1 2 1 6OM = + − + − =
.
Cách 2: Phương trình tham số của đường thẳng
d
là:
32
1
12
xt
yt
zt
=+
= − +
=+
.
Một vtcp của
d
là
( )
2;1;2u =
.
( ) ( )
1 1 1
3 2 ; 1 ;1 2 2 2 ; 3 ;4 2M d M t t t MM t t t + − + + = + − + +
.
Ta có
11
. 0 4 4 3 8 4 0 1MM u MM u t t t t⊥ = + − + + + = = −
.
Suy ra
( )
1
1; 2; 1M −−
Độ dài đoạn thẳng
1
OM
là:
( ) ( )
22
2
1
1 2 1 6OM = + − + − =
.
Câu 8. Chọn A
Gọi
( )
;;C x y z
. Ta có
( )
;;OC x y z=
,
( )
6; 1; 1BA = − − −
.
Khi đó
6
1
1
x
OC BA y
x
=−
= = −
=−
. Vậy
( )
6; 1; 1C − − −
.
Câu 9. Chọn C
Gọi tọa độ điểm
( )
;;D x y z
. Ta có:
( )
1; 1; 2AD x y z= − − −
,
( )
1;3; 4BC =−
.
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
13
Tứ giác
ABCD
là hình bình hành
1 1 2
1 3 4
2 4 2
xx
AD BC y y
zz
− = =
= − = =
− =− =−
. Vậy
( )
2;4; 2D −
.
Câu 10. ChọnA
Gọi
( )
;;M x y z
.
Vì điểm
M
thuộc đoạn
AB
sao cho
2=MA MB
2AM MB=
( )
( )
( )
7
3
3 2 2
5 7 5 8
1 2 3 ; ;
3 3 3 3
2 2 5
8
3
x
xx
y y y M
zz
z
=
− = −
− = − − = − −
+ = −
=
. Vậy
7 5 8
;;
3 3 3
M
−
.
Câu 11. Chọn C
Với
( )
; ; ( )
o o o
A x y z Oxyz
. Khi đó
( )
( )
,
o
d A Oxy z=
,
( )
( )
,
o
d A Oxz y=
,
( )
( )
,
o
d A Oyz x=
.
Theo bài ra ta có:
( )
( )
;2a d M Oxy==
;
( )
( )
;1b d M Oyz==
,
( )
( )
;3c d M Oxz==
.
2 3 2 3
2 1 3 30P a b c= + + = + + =
.
Câu 12. Chọn B
Do thiết diện qua trục của hình trụ là một hình vuông có cạnh bằng
3a
nên ta có bán kính đáy
3
2
a
R =
và độ dài đường sinh
3la=
.
Diện tích toàn phần hình trụ là:
2
2
27
22
2
tp
a
S R Rl
= + =
.
Câu 13. Chọn C
Ta có
2 3 (1; 2;3).OA i j k A= − + = −
Gọi G là trọng tâm của tam giác ABC ta có
1 3 2
2
33
240
2
33
3 1 1
1
33
A B C
G
A B C
G
A B C
G
xxx
x
yyy
y
zzz
z
++
++
= = =
++
− − +
= = = −
++
+−
= = =
. Vậy
(2; 2;1).G −
Câu 14. Chọn A
A
B
D
C
R
l
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
14
Gọi điểm
H
là hình chiếu vuông góc của
A
lên đường thẳng
CD
.
Khi đó
( )
2 2 ; 1 2 ;3H t t t+ − + +
( )
3 2 ;2 ;3AH t t t + +
.
Đường thẳng
CD
có vtcp là:
( )
2;2;1u
. Ta có:
( ) ( )
. 0 2 3 2 2.2 3 0 1 0; 3;2AH u AH u t t t t H⊥ = + + + + = = − −
3AH=
.
Đường thẳng
AB
đi qua
A
và song song với
CD
phương trình
AB
là:
11
2 2 1
x y z++
==
( )
1 2 ; 1 2 ; 3 6B AB B a a a AB a CD a − + − + = =
Theo bài ra ta có:
2
36
. .3 27 2
2
22
ABCD
a
aa
AB CD
S AH a
a
=
+
+
= = =
=−
Với
( )
2 5; 5; 2aB= − − − −
.
Với
( )
2 3;3; 2aB= −
Ta có:
( )
1
2; 5;1
2
DH AB D= − −
Câu 15. Chọn C
Từ
( )
2 3 1; 2;3OA i j k A= − + −
Tọa độ trọng tâm
G
của tam giác
ABC
là
2
3
2
3
1
3
A B C
G
A B C
G
A B C
G
xxx
x
yyy
y
zzz
z
++
==
++
= = −
++
==
Vậy tọa độ trọng tâm
( )
2; 2;1−
.
Câu 16. Chọn A
Câu 17. Chọn C
Gọi
( )
;;A a b c
. ' ' ' 'ABCD A B C D
là hình hộp
AC AB AD AA AA AC AB AD
= + + = − −
( )
1;1;1AB =
,
( )
0; 1;0AD =−
,
( )
3;5; 6AC
=−
( )
2;5; 7AC AB AD
− − = −
( )
1; ; 1AA a b c
= − −
A
B
D
C
H

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
15
( )
1 2 3
1 5 5
1 7 6
aa
bb
cc
− = =
= =
− = − = −
. Vậy:
( )
3;5; 6A
−
.
Câu 18. Chọn A
Ta có
( ) ( )
; ;0M Oxy M x y
;
( ) ( )
2;3;1 ; 2; 2; 1AB AM x y= − = − + −
.
Để
A
,
B
,
M
thẳng hàng thì
AB
và
AM
cùng phương , khi đó :
2 2 1
2 3 1
xy− + −
==
−
4
5
x
y
=
=−
. Vậy
( )
4; 5;0M −
.
Câu 19. Chọn A
Ta có
a
và
b
không cùng phương đồng thời
( ) ( )
// , 4; 2; 2 2 ; ;
ua
u a b u k k k
ub
⊥
= − − = − −
⊥
.
Do
222
6
3 4 3
2
u k k k k= + + = =
. Mặt khác
u
tạo với tia
Oz
một góc tù nên
( )
cos , 0uk
( )
. 0 2 .0 .1 0u k k k + −
( )
.1 0 0kk −
. Suy ra
6
2
k =
.
Vậy
66
6; ;
22
u
=−
.
Câu 20. Chọn A
Gọi
( ; ; ).Q x y z
Ta có
(1;1; 2), ( 1 ;2 ;1 ).MN QP x y z= − = − − − −
Tứ giác
MNPQ
là một hình bình hành
1 1 2
1 2 1 .
2 1 3
xx
MN QP y y
zz
= − − = −
= = − =
− = − =
Vậy,
( 2;1;3)Q −
.
Câu 21. Chọn A
Ta có
( )
4; 5;2AB x=−
,
( )
6; 3; 1AC y= − +
.
Ba điểm
A
,
B
,
C
thẳng hàng
:.k AB k AC =
( )
46
53
21
k
xk
ky
=
− = −
=+
2
3
3
2
k
x
y
=
=
=
.
Vậy
5xy+=
.
Câu 22. Chọn B
Vì là trung điểm của đoạn nên .
Khi đó hình chiếu của lên là .
Câu 23. Chọn C
I
AB
( )
3; 1;5I −
I
( )
Oyz
( )
0; 1;5M −

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
16
+) Ta có khoảng cách từ
M
đến mặt phẳng tọa độ
( )
xOz
bằng
55−=
nên A đúng.
+) Khoảng cách từ
M
đến trục
Oz
bằng
( )
2
2
2 5 29+ − =
nên B đúng.
+) Tọa độ hình chiếu vuông góc của điểm
M
lên mặt phẳng
( )
yOz
là
( )
0; 5;4I −
.
Suy ra tọa độ điểm
'M
đối xứng với
M
qua mặt phẳng
( )
yOz
là
( )
' 2; 5;4M −−
nên C sai.
+) Tọa độ hình chiếu vuông góc của điểm
M
lên trục
Oy
là
( )
0; 5;0J −
.
Suy ra tọa độ điểm
'M
đối xứng với
M
qua trục
Oy
là
( )
' 2; 5; 4M − − −
nên D đúng.
Câu 24. Chọn C
Ta có
( )
1;0; 3AB =−
,
( )
2; 1; 1BC x y= + − −
.
Ba điểm
,,A B C
thẳng hàng
AB
và
BC
cùng phương
:k BC kAB =
2
10
13
xk
y
k
+=
− =
− = −
5
3
1
1
3
x
y
k
−
=
=
=
2
3
xy + = −
.
Câu 25. Chọn C
Giả sử
( ) ( ) ( )
;0;0 ; 0; ;0 ; 0;0;A a B b C c
. Khi đó mặt phẳng
( )
:1
x y z
ABC
a b c
+ + =
Ta có:
( ) ( )
( ) ( )
2 ;1;1 ; 2;1 ;1
0; ; ; ;0;
AH a BH b
BC b c AC a c
= − = −
= − = −
Vì
H
là trực tâm của tam giác
ABC
nên
( )
2 1 1
1
3
. 0 0 6
2 0 6
.0
H ABC
a
abc
AH BC b c b
a c c
BH AC
+ + =
=
= − + = =
− + = =
=
Vậy
( )
3;0;0A
Câu 26. Chọn A
Ta có:
( )
2
. 2.1.cos , 2.cos 1
3
u v u v
= = = −
.
Vectơ
p ku v=+
vuông góc với vectơ
q u v=−
khi và chỉ khi:
( )( )
.0p q ku v u v= + − =
( )
22
1 . 0ku k u v v + − − =
( )
4 1 1 0kk − − − =
2
5
k=
.
Câu 27. Chọn D
Gọi
( )
;;B x y z
là điểm cần tìm.
Gọi
I
và
'I
lần lượt là trung điểm
AC
và
''BD
( )
0;2;4I
và
( )
' 1;3;0I
.
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
17
( ) ( )
' 1; 1;4 ; ' 2; 4; 1I I B B x y z= − − = − − +
Ta có:
21
' ' 4 1
14
x
B B I I y
z
− = −
= − = −
+=
1
3
3
x
y
z
=
=
=
. Vậy
( )
1;3;3B
.
Câu 28. Chọn A
Ta có:
( )
1;0;1AC =
,
( )
2;0;2AD =
Mà
0AC AD=
, nên hai vecto
AC
,
AD
cùng phương, hay ba điểm
,,A C D
thẳng hàng.
Nhận xét: Có thể vẽ phát họa lên hệ tọa độ
Oxyz
để nhìn nhận dễ dàng hơn.
Câu 29. Chọn D
+ Gọi
I
là trung điểm
AB
( )
3;0;0I
.
Ta có :
( ) ( )
. 0 . 0MA MB MI IA MI IB= + + =
( ) ( )
.0MI IA MI IA + − =
22
0MI IA − =
22
11
. 5 1 2
22
MI IA MI AB = = = − =
.
Suy ra tập hợp điểm
M
trong không gian là mặt cầu tâm
I
, bán kính bằng 2.
Vậy
( )
H
là một mặt cầu có bán kính bằng
2
.
Câu 30. Chọn A
a
và
b
cùng hướng
a kb=
( )
( )
22
0 1 3 7
3
32
4
kk
k m k m
kn
n
==
− = =
=−
=−
. Vậy
3
7;
4
mn= = −
Câu 31. Chọn A
G là trọng tâm tam giác
OAB
nên tọa độ
−
42
; 0;
33
G
.
Ta có:
= + + =
16 4 2 5
0
9 9 3
OG
Câu 32. Chọn A
Gọi điểm
H
là hình chiếu vuông góc của
A
lên đường thẳng
CD
.
Khi đó
( )
2 2 ; 1 2 ;3H t t t+ − + +
( )
3 2 ;2 ;3AH t t t + +
.
A
B
D
C
H
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
18
Đường thẳng
CD
có vtcp là:
( )
2;2;1u
. Ta có:
( ) ( )
. 0 2 3 2 2.2 3 0 1 0; 3;2AH u AH u t t t t H⊥ = + + + + = = − −
3AH=
.
Đường thẳng
AB
đi qua
A
và song song với
CD
phương trình
AB
là:
11
2 2 1
x y z++
==
( )
1 2 ; 1 2 ; 3 6B AB B a a a AB a CD a − + − + = =
Theo bài ra ta có:
2
36
. .3 27 2
2
22
ABCD
a
aa
AB CD
S AH a
a
=
+
+
= = =
=−
Với
( )
2 5; 5; 2aB= − − − −
. Với
( )
2 3;3; 2aB= −
Ta có:
( )
2 2; 5;1DH AB D= − −
Câu 33. Chọn D
Gọi
( )
0;0;E t Oz
. Ta có
( )
22
4 17 8 21 1 0;0;1 .AE BE t t t t t E= − + = − + =
Câu 34. Chọn A.
Ta có
( )
2;1;2AB =
,
( )
2; 2; 1AC = − −
( )
, 3;6; 6 .AB AC
= −
Do
SA
vuông góc với nên một VTCP của đường thẳng
SA
được chọn là
( )
; 3;6; 6 .u AB AC
= = −
Đường thẳng
SA
qua
( )
1;0;2A
và có VTCP
( )
3;6; 6u =−
nên có phương trình tham số là:
( )
13
6
26
xt
y t t
zt
=+
=
=−
.
Do
. 4 2 2 0AB AC AB AC= − − = ⊥
ABC
vuông tại
A
.
Gọi
M
là trung điểm
,BC
khi đó
M
là tâm đường tròn ngoại tiếp tam giác
ABC
. Gọi
d
là
đường thẳng qua
M
và song song với
SA
nên
( )
d ABC⊥
, suy ra
d
là trục đường tròn ngoại
tiếp
ABC
.
Trong mặt phẳng
( )
SAM
vẽ đường trung trực của
SA
cắt
d
tại
I
và cắt
SA
tại
N
.
Mặt phẳng
( )
ABC
qua
A
và có một VTPT
( )
; 3;6; 6n AB AC
= = −
nên có phương trình tổng
quát là:

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
19
( ) ( )
3 1 6 6 2 0 2 2 3 0x y z x y z− + − − = + − + =
( )
2
0; 3; 3 18 18BC BC BC= − − = =
.
Ta có
2 2 2 2 2
99 1 9
4 4 2
R IA AM IM BC IM= + = + =
.
Do
S SA
nên
( )
1 3 ;6 ;2 6S t t t+−
, mà
29SA IM SA= =
( )
( )
( )
( )
2
22
1 3 12 2 2 6 3
d , 9 9
1 2 2
t t t
S ABC
+ + − − +
= =
+ − +
( )
( )
1 4;6; 4
27 27
1 2; 6;8
tS
t
tS
= −
=
= − − −
, mà cao độ của
S
âm nên
( )
4;6; 4S −
thỏa mãn.
Câu 35. Chọn A
Cách 1: Ta có
( ) ( )
4;2;4 ; 6; 3; 6AB CD a b c= − = + − −
Do
ABCD
là hình thang cân nên
CD k AB=
( )
k
hay
6 3 6
2 1 2
a b c+ − −
==
−
2
a
b
ca
−
=
=−
. Vậy
;;
2
a
D a a
−
−
.
Lại có
( ) ( ) ( )
2
2 2 2
2 2 2 2
9 2 8 1 3 2
2
a
AC BD AC BD a a
= = − + + = + + + + +
2
6
4 60 0
10
a
aa
a
=
+ − =
=−
. Với
( )
10 10;5;10aD= − −
. Kiểm tra thấy:
AB CD=
.
Với
( )
6 6; 3; 6aD= − −
. Kiểm tra thấy:
( )
3.AB CD−=
. Do đó,
6 3 6 3T a b c= + + = − − = −
.
Cách 2
Ta có
( ) ( )
4;2;4 ; 6; 3; 6AB CD a b c= − = + − −
Do
ABCD
là hình thang cân nên
;AB CD
ngược hướng hay
6 3 6
0
2 1 2
a b c+ − −
==
−
2
6
a
b
ca
a
−
=
= −
−
. Vậy
;;
2
a
D a a
−
−
với
6a −
.
Lại có

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
20
( ) ( ) ( )
2
2 2 2
2 2 2 2
9 2 8 1 3 2
2
a
AC BD AC BD a a
= = − + + = + + + + +
2
6
4 60 0
10( )
a
aa
aL
=
+ − =
=−
. Với
( )
6 6; 3; 6aD= − −
.
Do đó,
6 3 6 3T a b c= + + = − − = −
.
Cách 3
+ Viết phương trình mặt phẳng trung trực của đoạn thẳng
AB
+ Gọi mp
( )
là mặt phẳng trung trực của đoạn thẳng
AB
, suy ra mp
( )
đi qua trung điểm
( )
1;2;0I
của đoạn thẳng
AB
và có một vectơ pháp tuyến là
( )
1
2;1;2
2
n AB= = −
, suy ra phương
trình của mp
( )
là :
( )
: 2 2z 0xy
− + + =
.
+ Vì
,CD
đối xứng nhau qua mp
( )
nên
( )
6; 3; 6 6; 3; 6 3D a b c T a b c− − = = − = − = + + = −
Công thức trắc nghiệm: Xác định toạ độ điểm
( )
1 1 1
;;M x y z
là điểm đối xứng của điểm
( )
0 0 0
;;M x y z
qua mp
( )
: z 0ax by c d
+ + + =
( )
2 2 2
0abc+ +
( )
10
0 0 0
10
2 2 2
10
2a
z
2,
2
x x k
ax by c d
y y bk k k
abc
z z ck
=−
+ + +
= − = −
++
=−
.
Câu 36. Chọn B
Do
G
là trọng tâm tam giác
ABC
( )
2;3;1G
.
Gọi
H
là hình chiếu vuông góc của
G
trên mặt phẳng
( )
Oxz
, khi đó
GH
là khoảng cách từ
G
đến mặt phẳng
( )
Oxz
, ta có:
( )
( )
,3GH d G Oxz==
Với
M
là điểm thay đổi trên mặt phẳng
( )
Oxz
, ta có
3GM GH=
, do đó
GM
ngắn nhất
MH
. Vậy độ dài
GM
ngắn nhất bằng
3
.
Câu 37. Chọn B
Cách 1:
( )
1;2; 3AB = − −
,
( )
8; 3; 4AC = − − −
.
Gọi
M
,
N
lần lượt là trung điểm
AB
,
AC
97
;2;
22
1
1; ;3
2
M
N
−
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
21
Gọi
n
là véc tơ pháp tuyến của mặt phẳng
( )
ABC
( )
, 17;20;19n AB AC
= = −
.
( )
: 17 20 19 30 0ABC x y z− + + − =
.
I
là tâm đường tròn ngoại tiếp tam giác
ABC
( )
IM AB
IN AC
I ABC
⊥
⊥
( ) ( ) ( )
( ) ( ) ( ) ( ) ( )
97
. 1 2 .2 . 3 0
22
1
1 . 8 . 3 3 . 4 0
2
17 20 19 30 0
a b c
a b c
a b c
− − + − + − − =
− − + − − − + − − =
− + + − =
2 3 11
37
8 3 4
2
17 20 19 30
a b c
a b c
a b c
− + =
+ + =
− + + =
1
1
2
3
a
b
c
=
=−
=
.
Vậy
1
2 1 2. 3 3
2
a b c
+ + = + − + =
.
Cách 2:
Ta có
( )
1;2; 3AB = − −
và
( )
7; 5; 1 . 0BC AB BC ABC= − − − =
vuông tại
B
.
Vì
I
là tâm đường tròn ngoại tiếp
ABC
nên
I
là trung điểm của
AC
.
Vậy
11
1; ;3 2 1 2. 3 3
22
I a b c
− + + = + − + =
.
Câu 38. Chọn A
Do
,ab
cùng phương và nên ta có
( )
.0b k a k=
0
0
0
2
4
xk
yk
zk
=
= −
=
.
Suy ra
0 0 0 0 0 0
1 2 4 3
x y z x y z++
= = =
−
( )
( )
( )
0 0 0 0
0 0 0 0
0 0 0 0
1
3
2
3
4
3
x x y z
y x y z
z x y z
= + +
= − + +
= + +
.
Theo giả thiết vectơ
b
tạo với tia
Oy
một góc nhọn nên
.0bj
với
( )
0;1;0j =
, do đó
0
0y
.
Mà
0 0 0 0
23
y x y z++
=
−
nên
0 0 0
0x y z+ +
.
Lại có
21b =
, suy ra
( )
2
2 2 2
0 0 0 0 0 0
21
9
x y z x y z+ + = + +
21=
( )
2
0 0 0
9x y z + + =
.
Vậy
0 0 0
3x y z+ + = −
.
Câu 39. Chọn B
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
22
Gọi
I
là trung điểm
( )
3;1;4AB I
. Gọi
H
là hình chiếu của
I
xuống mặt phẳng
( )
.
Ta có
( ) ( ) ( )
2 2 2 2
. . .MA MB MI IA MI IB MI MI IA IB IA MI IA= + + = + + − = −
.
Do
IA
không đổi nên
.MAMB
nhỏ nhất khi
MI
nhỏ nhất
MI IH M H =
.
Gọi
là đường thẳng đi qua
I
và vuông góc với mặt phẳng
( )
. Khi đó
nhận
( )
( )
1;2; 3n
=−
làm vectơ chỉ phương. Do đó
có phương trình
3
12
43
xt
yt
zt
=+
=+
=−
.
( )
3 ;1 2 ;4 3H H t t t + + −
.
( ) ( ) ( ) ( )
3 2 1 2 3 4 3 7 0H t t t
+ + + − − − =
( )
1 4;3;1tH =
.
Vậy
( )
4;3;1M
.
Câu 40. Chọn C
Cách 1:
( ) ( ) ( )
1; 2; 2 ; 5; 1; 1 ; 6 ;1 ; .AB AC DC a b c= − − = − − = − − −
Ta có
1 9 2 9 2 3 2
, 6 2 .
2 2 2 2
ABC ACD
S AB AC S
= = = − =
AB
//
CD
nên
AB
và
DC
cùng phương, cùng chiều
12 2
13 2
61
06
1 2 2
1
0
ca
ba
a b c
a
b
c
=−
=−
−−
= =
−
( )
, 0;9 54;54 9 .AC AD a a
= − −
D
C
B
A
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
23
19
3 2 1 3 2
3
, 54 9 3 .
17
2 2 2
3
ACD
a
S AC AD a
a
=
= = − =
=
So với điều kiện suy ra:
17
8.
3
a a b c= + + =
Cách 2:
Ta có
( )
162
3; , .
3
AB h d C AB= = =
( ) ( )
162
6 2 3 1.
26
ABCD
h
S AB CD CD CD= + = + =
Suy ra
17 5 2
3 ; ; 8.
3 3 3
AB DC D a b c
= + + =
Câu 41. Chọn C
Cách 1.
Ta có mặt phẳng
( )
nhận vectơ
( )
1;1;1n
=
là vectơ pháp tuyến, đường thẳng
d
đi qua điểm
( )
0; 1;2A =−
và nhận
( )
1;2; 1
d
u =−
là vectơ chỉ phương.
Gọi
( )
là mặt phẳng chứa đường thẳng
d
và vuông góc với mặt phẳng
( )
.
Ta có
( )
3;2;1
d
n n u
= = −
.
Khi đó đường thẳng
là giao tuyến của hai mặt phẳng
( )
và
( )
. Do đó một vectơ chỉ phương
của đường thẳng
là
( )
1; 4;5u n n
= = − −
.
Mà
( )
1;a;ub=
nên
4a =
,
5b =−
. Vậy
1ab+ = −
.
Cách 2.
Dễ dàng tính được tọa độ giao điểm của đường thẳng
d
và mặt phẳng
( )
là
( )
1;1;1I =
. Trên
đường thẳng lấy điểm
( )
0; 1;2A =−
và gọi
H
là hình chiếu vuông góc của
A
trên mặt phẳng
( )
. Phương trình đường thẳng đi qua
A
và
H
có dạng:
0
1
2
xt
yt
zt
=+
= − +
=+
.
I
H
A
d
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
24
Tọa độ của là
H
nghiệm của hệ
0
1
2
30
xt
yt
zt
x y z
=+
= − +
=+
+ + − =
2
3
t =
. Vậy
2 1 8
;;
3 3 3
H
−
.
Đường thẳng
đi qua hai điểm
I
và
H
nhận vectơ
1 4 5
;;
3 3 3
IH
−−
=
là vectơ chỉ phương nên
cũng nhận vectơ
( )
1;4; 5u
=−
là vectơ chỉ phương. Vậy
1ab+ = −
.
Câu 42. Chọn B
Gọi
M
là trung điểm
BC
.
Khi đó có
AM BC
AA BC
⊥
⊥
BC A M
⊥
tại
M
M
là hình chiếu của
A
trên trục
Oz
( )
3; 1;1A
−
( )
0;0;1M
và
2AM
=
.
Ta có:
22
AM A M AA
=−
3=
. Mà tam giác
ABC
đều nên
3
3
2
AM BC==
2BC=
1MC=
. Vì
C
thuộc trục
Oz
và
C
không trùng với
O
nên gọi
( )
0;0;Cc
,
0c
.
( )
0;0; 1MC c=−
1MC c = −
;
1MC =
11c − =
0(L)
2
c
c
=
=
( )
0;0;2C
.
( )
3;1;1AC
=−
là một véctơ chỉ phương của đường thẳng
AC
( )
2 3;2;2u =−
cũng là một véctơ chỉ phương của đường thẳng
AC
.
Vậy
22
2 3; 2 16.a b T a b= − = = + =
Câu 43. Chọn D
Tính được ; ; .
M
A
C
B
A'
B'
C'
3OA =
4OB =
5AB =

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
25
Ta có: .
Vậy, , suy ra .
Câu 44. Chọn B
Câu 45. Chọn A
Câu 46. Chọn A
( ) ( )
; ; 2C a b P−
( )
2 0 2 ; 2; 2a b b a C a a − + = = + + −
.
( )
0; 2; 2AB = − −
,
( )
1; ; 5AC a a= − −
( )
, 10 2 ; 2 2;2 2AB AC a a a
= + − + −
.
( ) ( )
22
2
2 10 2 2 2
1 12 24 108
,
2 2 2
ABC
aa
aa
S AB AC
+ + −
++
= = =
( )
2
3 2 9aa= + +
( )
2
3 1 24a= + +
26
với
a
.
Do đó
min 2 6
ABC
S
=
khi
1a =−
. Khi đó ta có
( )
1;1; 2C −−
0ab + =
.
Câu 47. Chọn B
Cách 1:
▪ Mặt cầu
( )
2 2 2
:1S x y z+ + =
có tâm
( )
0;0;0O
, bán kính
1R =
.
▪
Ta tìm điểm
( )
;;I x y z
thỏa mãn
30IA IB+=
.
▪ Có
( )
1 ; ;IA x y z= − − −
,
( )
5 ;6 ;IB x y z= − − −
;
30IA IB+=
( )
( )
( )
3 1 5 0
3 6 0
30
xx
yy
zz
− + − =
− + − =
− − =
4 8 0
4 6 0
40
x
y
z
− + =
− + =
−=
2
3
2
0
x
y
z
=
=
=
3
2; ;0
2
I
. Suy ra
13
2
IA =
,
3 13
2
IB =
.
Do đó
22
22
3 48 3 48MA MB MA MB+ = + =
( ) ( )
22
3 48MI IA MI IB + + + =
( )
2 2 2
4 3 2 3 48MI IA IB MI IA IB + + + + =
2 2 2
4 3 48MI IA IB + + =
3
2
MI=
.
Ta thấy
5
2
OI =
nên điểm
I
nằm ngoài mặt cầu
( )
S
. Ta có
OI R MI OM MI= + = +
, suy ra có
một điểm
M
thuộc đoạn
OI
thỏa mãn đề bài .
Cách 2:
Gọi
( )
0 0 0
;;M x y z
thuộc mặt cầu
( )
S
và thỏa mãn
22
3 48MA MB+=
.
. . . 0OA IB OB IA AB IO+ + =
( ) ( )
( ) ( )
( ) ( )
8
3 4 1 5 0
3
4
3 4 2 5 0
3
8
3 4 2 5 0
3
x x x
y y y
z z z
− + − + − =
− + − + − =
− + − − + − =
1
1
0
x
y
z
=
=
=
(1;1;0)I
0a b c− + =

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
26
Ta có:
22
3 48MA MB+=
( ) ( ) ( )
2 2 2
2 2 2
0 0 0 0 0 0
3 1 5 6 48x y z x y z
− + + + − + − + =
2 2 2
0 0 0 0 0
4 4 4 16 12 16 0x y z x y + + − − + =
2 2 2
0 0 0 0 0
4 3 4 0x y z x y + + − − + =
.
Suy ra
M
thuộc mặt cầu
( )
S
tâm
3
2; ;0
2
I
, bán kính
3
2
R
=
.
Mặt khác
M
thuộc mặt cầu
( )
S
tâm
( )
0;0;0O
, bán kính
1R =
.
Ta thấy:
5
2
OI R R
= = +
mặt cầu
( )
S
và
( )
S
tiếp xúc ngoài nhau tại
M
Có duy nhất một điểm
M
thỏa mãn đề bài.
Câu 48. Chọn B
Cách 1: Do
M Oy
nên
( )
0; ;0My
. Tính
( )
2 2 2
2 6 20+ = − + =MA MB y y f y
.
Do đó
( )
fy
nhỏ nhất
3
2
=y
. Vậy
3
0; ;0
2
M
.
Cách 2: Ta có:
( )
1;1; 3−A
. Gọi
I
là trung điểm của
AB
. Suy ra
33
; ; 1
22
I
=−
.
Khi đó:
22
22
+ = +MA MB MA MB
( ) ( )
22
= + + +MI IA MI IB
( )
2 2 2
2 2 .= + + + +MI IA IB MI IA IB
2 2 2
2= + +MI IA IB
2
29=+MI
.
Do đó
22
+MA MB
đạt giá trị nhỏ nhất khi và chỉ khi
MI
có độ dài ngắn nhất, điều này xảy ra
khi và chỉ khi
M
là hình chiếu vuông góc của
I
trên trục tung.
Phương trình mặt phẳng
( )
P
đi qua
I
và vuông góc với trục tung là
( )
33
0. 1. 0. 1 0
22
− + − + + =
x y z
hay
( )
3
:0
2
−=Py
.
Phương trình tham số của trục tung là
0
0
x
yt
z
=
=
=
.
Tọa độ điểm
M
cần tìm là nghiệm
( )
;;x y z
của hệ phương trình:
0
0
3
0
2
x
yt
z
y
=
=
=
−=
0
3
2
0
x
y
z
=
=
=
. Vậy
3
0; ;0
2
M
.
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
27
Câu 49. Chọn B
Ta có
44AB =
không đổi. Do đó chu vi tam giác
MAB
nhỏ nhất khi
()MA MB+
đạt giá trị nhỏ
nhất.
( ) ( )
1+2t;1 t;2tM d M − −
.
( )
( )
2
2
2
9 20 3 2 5= + = +MA t t
,
( )
( )
2
2
2
9 36 56 6 3 2 5MB t t t= − + = − +
.
Chọn
( )
( )
( )
2
2
3t;2 5;0 3 2 5u u t= = +
.
Chọn
( )
( )
( )
2
2
6 3 ;2 5;0 6 3 2 5v t v t= − = − +
( )
6;4 5;0 2 29+ = + =u v u v
.
Theo tính chất vecto
2 29u v u v+ + =
.
Dấu
""=
xảy ra khi và chỉ khi
u
cùng hướng với
v
1t =
.
Suy ra
2 29MA MB u v+ = +
.
Do đó
MA MB+
đạt giá trị nhỏ nhất bằng
2 29
khi
1t =
( )
1;0;2M
.
Vậy
2 3 1 2.0 3.2 7a b c+ + = + + =
.
Câu 50. Chọn D
Dễ thấy
B Oz
. Ta có
( )
A Oxy
và
( )
C Oxy
, suy ra
( )
OB OAC⊥
.
Ta có
AC OC
AC OB
⊥
⊥
( )
AC OBC⊥
, mà
( )
OH OBC
. Suy ra
AC OH⊥
( )
1
.
Mặt khác ta có
OH BC⊥
( )
2
, .
Từ
( )
1
và
( )
2
suy ra
( )
OH ABC⊥
OH AB⊥
và
OH HA⊥
.
Với
OH AB⊥
suy ra
H
thuộc mặt phẳng
( )
P
với
( )
P
là mặt phẳng đi qua
O
và vuông góc
với đường thẳng
AB
. Phương trình của
( )
P
là:
0yz−=
.
Với
OH HA⊥
OHA
vuông tại
H
. Do đó
H
thuộc mặt cầu
( )
S
có tâm
( )
0;2 2 ;0I
là
trung điểm của
OA
và bán kính
22
2
OA
R ==
.
Do đó điểm
H
luôn thuộc đường tròn
( )
T
cố định là giao tuyến của mp
( )
P
với mặt cầu
( )
S
.
Giả sử
( )
T
có tâm
K
và bán kính
r
thì
( )
( )
,2IK d I P==
và
22
2r R IK= − =
.
Vậy điểm
H
luôn thuộc đường tròn cố định có bán kính bằng
2
.
H
I
O
C
A
B
P
(
T
)
K
I
H

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
28
DẠNG 2. TÍCH VÔ HƯỚNG VÀ ỨNG DỤNG
Câu 1. Trong không gian
Oxyz
, cho hai điểm
( 2;1; 3)A −−
và
B(1;0; 2)−
. Độ dài đoạn thẳng
AB
bằng
A.
33
. B.
11
. C.
11
. D.
27
.
Câu 2. Trong không gian cho . Sin của góc giữa và bằng
A. . B. . C. . D. .
Câu 3. Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
( )
1;0;1A
và
( )
4;2; 2B −
. Độ dài đoạn thẳng
AB
bằng
A.
22
. B.
4
. C.
2
. D.
22
.
Câu 4. Trong không gian tọa độ
Oxyz
, góc giữa hai vectơ
i
và
( )
3;0;1u =−
là
A.
0
30
. B.
0
120
. C.
0
60
. D.
0
150
.
Câu 5. Trong không gian với hệ trục tọa độ
Oxyz
, cho
( )
2;0;0 ;A
( )
0;3;1 ;B
( )
3;6;4C −
. Gọi
M
là điểm
nằm trên đoạn
BC
sao cho
2MC MB=
. Độ dài
AM
là
A.
29
. B.
33
. C.
30
. D.
27
.
Câu 6. Cho hai vec tơ
( ) ( )
1; 2;3 , 2;1;2 .ab= − = −
Khi đó tích vô hướng
( )
.a b b+
bằng
A.
12
. B.
2
. C.
11
. D.
10
.
Câu 7. Trong không gian
Oxyz
, cho các vectơ
( )
5; 3; 2a =−
và
( )
; 1; 3b m m= − +
. Có bao nhiêu giá trị
nguyên dương của
m
để góc giữa hai vectơ
a
và
b
là góc tù?
A.
2
. B.
3
. C.
1
. D.
5
.
Câu 8. Trong không gian với hệ tọa độ
Oxyz
, cho tam giác
ABC
có
( )
1;0;0A
,
( )
0;0;1B
,
( )
2;1;1C
.
Diện tích tam giác
ABC
bằng:
A.
11
2
. B.
7
2
. C.
6
2
. D.
5
2
.
Câu 9. Trong không gian với hệ tọa độ
,Oxyz
cho hình hộp
. ' ' ' 'ABCD A B C D
có
( )
0;0;0 ,A
( )
;0;0 ,Ba
( )
0;2 ;0 ,Da
( )
' 0;0;2Aa
với
0.a
Độ dài đoạn thẳng
'AC
là
A.
3 a
. B.
3
2
a
. C.
2 a
. D.
a
.
Câu 10. Trong không gian với hệ tọa độ
Oxyz
, cho
32OA i j k= + −
và
( )
; 1; 4B m m −−
. Tìm tất cả giá trị
của tham số
m
để độ dài đoạn
3AB =
.
A.
2m =
hoặc
3m =
. B.
1m =
hoặc
4m =
.
C.
1m =
hoặc
2m =
. D.
3m =
hoặc
4m =
.
Câu 11. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )
:2 3 3 0P x y z− + + =
. Gọi
M
,
N
lần
lượt là giao điểm của mặt phẳng
( )
P
với các trục
Ox
,
Oz
. Tính diện tích tam giác
OMN
.
A.
9
4
. B.
9
2
. C.
3
2
. D.
3
4
.
Oxyz
( ) ( )
2;3; 1 ; 2; 1;3ab− − −
a
b
2
7
−
35
7
35
7
−
2
7

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
29
Câu 12. Trong không gian với hệ tọa độ
Oxyz
, cho véc tơ
( ) ( )
1;1; 2 , 1;0;u v m= − =
. Tìm tất c giá trị của
m
để góc giữa
u
,
v
bằng
45
.
A.
2m =
. B.
26m =
. C.
26m =−
. D.
26m =+
.
Câu 13. Trong không gian tọa độ
Oxyz
góc giữa hai vectơ
i
và
( )
3;0;1u =−
là
A.
120
. B.
30
. C.
60
. D.
150
.
Câu 14. Trong không gian với hệ tọa độ
Oxyz
, cho hình hộp
.ABCD A B CD
có
( )
0;0;0A
,
( )
;0;0Ba
;
( )
0;2 ;0Da
,
( )
0;0;2Aa
với
0a
. Độ dài đoạn thẳng
AC
là
A.
a
. B.
2 a
. C.
3 a
. D.
3
2
a
.
Câu 15. Trong không gian
Oxyz
, cho hai điểm
( )
2; 1;3A −
,
( )
3;2; 4B −
. Vectơ
AB
có tọa độ là
A.
( )
1; 3; 7−−
. B.
( )
1;3; 7−
. C.
( )
1;3; 7−−
. D.
( )
1; 3; 7− − −
.
Câu 16. Trong mặt phẳng tọa độ
Oxyz
, cho bốn điểm
( )
0; 1;2A −
,
( )
2; 3;0B −
,
( )
2;1;1C −
,
( )
0; 1;3D −
. Gọi
( )
L
là tập hợp tất cả các điểm
M
trong không gian thỏa mãn đẳng thức
. . 1MA MB MC MD==
. Biết rằng
( )
L
là một đường tròn, tính bán kính đường tròn đó?
A.
5
2
r =
. B.
11
2
r =
. C.
3
2
r =
. D.
7
2
r =
.
Câu 17. Trong không gian với hệ trục tọa độ
Oxyz
cho hình thang
ABCD
vuông tại
A
và
B
. Ba đỉnh
( )
1;2;1A
,
( )
2;0; 1B −
,
( )
6;1;0C
và đỉnh
( )
;;D a b c
. Biết rằng hình thang có diện tích là
62
,
tính
abc++
?
A.
6abc+ + =
. B.
8abc+ + =
. C.
12abc+ + =
. D.
7abc+ + =
.
Câu 18. Trong không gian với hệ trục tọa độ
Oxyz
, cho điểm
( )
1;2;5M
. Mặt phẳng
( )
P
đi qua điểm
M
và cắt trục tọa độ
Ox
,
Oy
,
Oz
tại
A
,
B
,
C
sao cho
M
là trực tâm tam giác
ABC
. Thể
tích của tứ diện
OABC
là
A.
10
6
. B.
450
. C.
10
. D.
45
.
Câu 19. Trong không gian với hệ tọa độ
Oxyz
, cho hai đường thẳng
1
12
:
1 2 1
x y z
d
−+
==
−
và
2
21
:
2 1 2
x y z
d
+−
==
−
. Phương trình mặt phẳng
( )
P
chứa
( )
1
d
sao cho góc giữa
( )
P
và đường
thẳng
( )
2
d
là lớn nhất là:
0− + + =ax y cz d
. Giá trị của biểu thức
T a c d= + +
bằng
A.
0=T
. B.
3=T
. C.
13
4
=−T
. D.
6=−T
.
Câu 20. Trong không gian
Oxyz
, cho hai điểm
( )
2;1; 2A −−
,
( )
1;1;0B −
và mặt phẳng
( )
: 1 0P x y z+ + + =
. Điểm
C
thuộc
( )
P
sao cho tam giác
ABC
vuông cân tại
B
. Cao độ của
điểm
C
bằng

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
30
A.
1
hoặc
2
3
−
. B.
1−
hoặc
2
3
. C.
3−
hoặc
1
3
. D.
1−
hoặc
1
3
−
.
Câu 21. Trong không gian
Oxyz
, cho mặt cầu
( )
2 2 2
9
: 2 4 2 0
2
S x y z x y z+ + + − − + =
và hai điểm
( ) ( )
0;2;0 , 2; 6; 2AB−−
. Điểm
( )
;;M a b c
thuộc
( )
S
thỏa mãn tích
.MAMB
có giá trị nhỏ nhất.
Tổng
abc++
bằng
A.
1−
B.
1
C.
3
D.
2
Câu 22. Trong không gian
Oxyz
, cho mặt cầu
( )
2
22
( ):( 2) ( 1) 2 9S x y z+ + − + + =
và hai điểm
( )
( )
2;0; 2 2 , 4; 4;0AB− − − −
. Biết rằng tập hợp các điểm
M
thuộc
()S
sao cho
2
. 16MA MO MB+=
là một đường tròn. Bán kính của đường tròn đó bằng
A.
3
. B.
2
. C.
22
. D.
5
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
31
ĐÁP ÁN CHI TIẾT
Câu 1. Chọn C
Ta có
2 2 2
(3; 1;1) 3 ( 1) 1 11AB AB= − = + − + =
.
Câu 2. Chọn D
;
Câu 3. Chọn A
Với
( )
1;0;1A
,
( )
4;2; 2B −
ta được
( ) ( ) ( )
2 2 2
4 1 2 0 2 1 22AB = − + − + − − =
.
Vậy độ dài đoạn thẳng
AB
bằng
22
.
Câu 4. Chọn D
Gọi
là góc giữa hai vectơ
i
và
( )
3;0;1u =−
, ta có :
0
.3
cos 150
2
.
iu
iu
−
= = =
.
Câu 5. Chọn A
Giả sử
( )
;;M a b c
( )
; 3; 1 ;BM a b c = − −
( )
3;3;3BC =−
.
Ta có
M
là điểm nằm trên đoạn
BC
sao cho
2MC MB=
1
3
BM BC=
( )
1
. 3 1
3
1
1
3 .3 4
3
c2
1
c 1 .3
3
a
a
bb
= − = −
=−
− = =
=
−=
( )
1;4;2M−
.
Do đó
( )
3;4;2AM =−
29AM=
.
Câu 6. Chọn C
Ta có
( )
( )
( ) ( )
1; 1;5 . 1. 2 1 .1 2.5 11.a b a b b+ = − − + = − − + − + =
Câu 7. Chọn A
Góc giữa hai vectơ
a
và
b
là góc tù khi và chỉ khi
( )
cos , 0ab
.0ab
( ) ( ) ( )
5. 3. 1 2 . 3 0mm + − + − +
3 9 0m −
3m
.
Vì m là số nguyên dương nên
1; 2m
. Vậy có 2 giá trị m nguyên dương thỏa yêu cầu bài toán.
Câu 8. Chọn C
( )
1;0;1AB =−
,
( )
1;1;1AC =
( )
; 1;2; 1AB AC
= − −
16
;
22
ABC
S AB AC
= =
.
Câu 9. Chọn A
( )
42
cos ;
7
4 9 1. 4 1 9
ab
−
= = −
+ + + +
( ) ( )
2
35
sin ; 1 cos ;
7
a b a b= − =
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
32
Từ giả thiết ta có
. ' ' ' 'ABCD A B C D
là hình hộp chữ nhật nên
( )
;2 ;2AC AB AD AA a a a
= + + =
Vậy
( )
; 2 ; 2AC a a a
=
2 2 2
' 4 +4a 3AC AC a a a
= = + =
.
Câu 10. Chọn B
( )
3 2 3;1; 2OA i j k A= + − −
( ) ( ) ( )
2 2 2
2
3 2 2 2 10 17AB m m m m= − + − + − = − +
.
2
1
3 2 10 17 3
4
m
AB m m
m
=
= − + =
=
.
Câu 11. Chọn A
Cách 1.
Mặt phẳng
( )
:2 3 3 0P x y z− + + =
cắt các trục
Ox
,
Oz
lần lượt tại
3
;0;0
2
M
=−
,
( )
0;0; 3N =−
.
Suy ra:
3
;0;0
2
OM
=−
,
( )
0;0; 3ON =−
9
, 0; ;0
2
OM ON
= −
.
Vậy diện tích tam giác
OMN
là
19
,
24
S OM ON
==
.
Cách 2.
Ta có
3
2
OM =
,
3ON =
.
Vì hai điểm
M
,
N
lần lượt thuộc trục
Ox
,
Oz
nên tam giác
OMN
vuông tại
O
.
Do đó, diện tích tam giác
OMN
là:
19
.
24
S OM ON==
.
Câu 12. Chọn C
+
( ) ( )
2
, 45 cos ,
2
u v u v= =
.2
2
.
uv
uv
=
2
1 2 1
2
6. 1
m
m
−
=
+
( )
2
3 1 1 2mm + = −
22
1 2 0
3 3 1 4 4
m
m m m
−
+ = − +
2
1
2
4 2 0
m
mm
− − =
26m = −
.
Câu 13. Chọn D
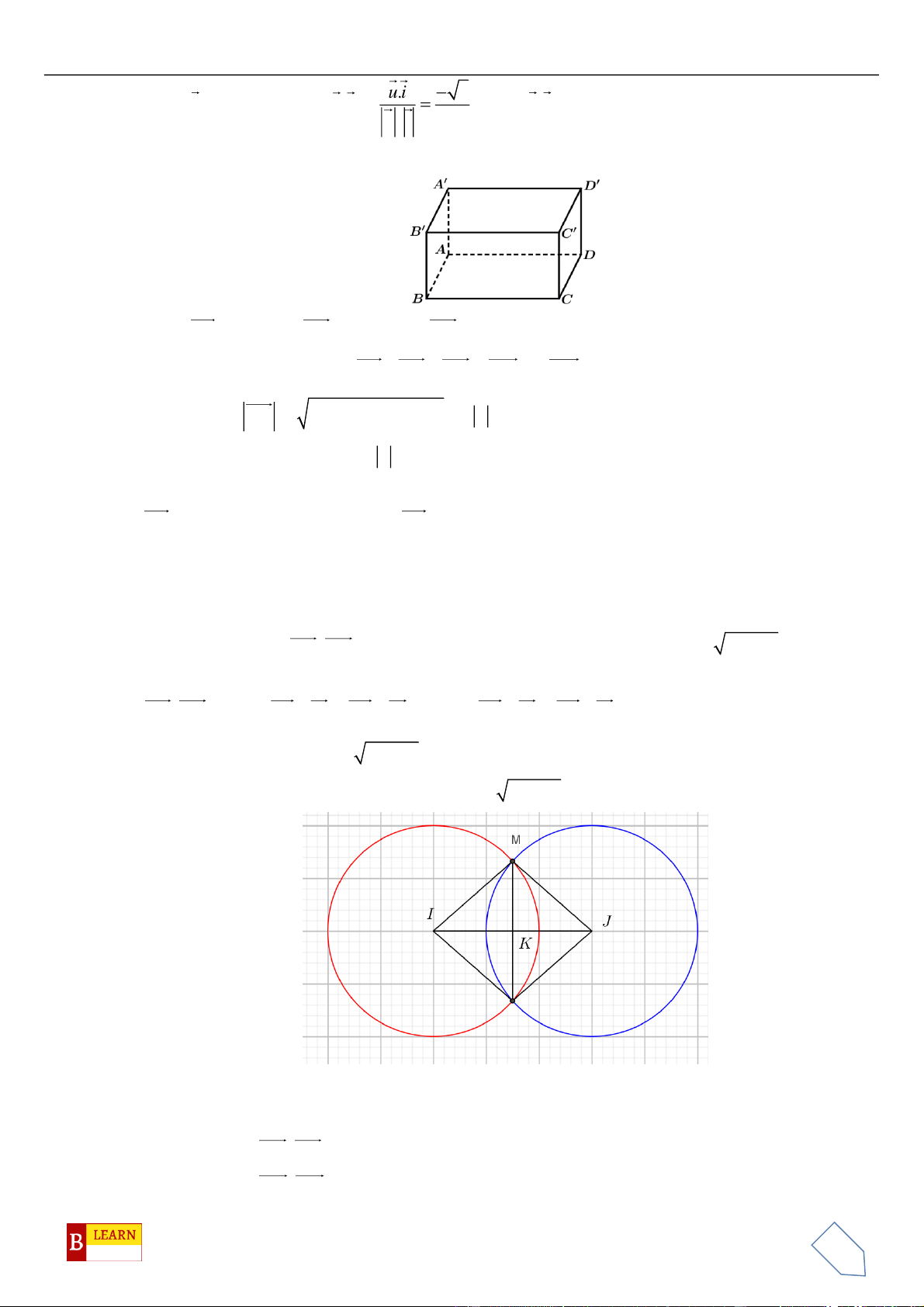
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
33
Ta có
( )
1;0;0i =
( )
.3
cos ,
2
.
ui
ui
ui
−
==
. Vậy
( )
, 150ui =
.
Câu 14. Chọn C
Ta có
( )
;0;0AB a=
;
( )
0;2 ;0AD a=
;
( )
0;0;2AA a
=
.
Theo quy tắc hình hộp ta có
AB AD AA AC
+ + =
( )
;2 ;2AC a a a
=
.
Suy ra
AC AC=
( ) ( )
22
2
2 2 3a a a a= + + =
.
Vậy độ dài đoạn thẳng
3AC a
=
.
Câu 15. Chọn B
( )
( )
3 2;2 1 ; 4 3AB = − − − − −
. Vậy
( )
1;3; 7AB =−
.
Câu 16. Chọn D
▪ Trước tiên, ta xét bài toán phụ sau:
“Trong không gian cho đoạn thẳng
AB
bất kì, có trung điểm
I
. Chứng minh rằng tập hợp các
điểm
M
thỏa mãn
.0MA MB k=
là một mặt cầu tâm
I
và bán kính
2
R k IA=+
”.
Thật vậy:
( )( ) ( )( )
22
.MA MB k MI IA MI IB k MI IA MI IA k MI IA k= + + = + − = − =
22
MI k IA = +
hay
2
IM k IA=+
.
Suy ra
M
thuộc mặt cầu tâm
I
, bán kính
2
R k IA=+
.
▪ Áp dụng: Có
( )
1; 2;1I −
và
( )
1;0;2J −
lần lượt là trung điểm của đoạn thẳng
AB
và
CD
Sử dụng kết quả bài toán trên, ta có:
+ Từ điều kiện
.1MA MB =
, suy ra
M
thuộc mặt cầu tâm
I
, bán kính
1
2R =
. (1)
+ Từ điều kiện
.1MC MD =
, suy ra
M
thuộc mặt cầu tâm
J
, bán kính
2
2R =
. (2)

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
34
Ta có
1 2 1 2
0 3 4R R IJ R R− = = + =
. (3)
Từ (1), (2) và (3) suy ra
M
thuộc đường tròn giao tuyến của hai mặt cầu nêu trên.
+ Gọi
K
là tâm của đường tròn giao tuyến.
Suy ra bán kính cần tìm
2
2 2 2
37
2
22
r KM IM IK
= = − = − =
.
Câu 17. Chọn A
Ta có
( )
1; 2; 2AB = − −
,
( )
4;1;1BC =
3AB=
,
32BC =
.
Mặt khác, hình thang
ABCD
vuông tại
A
và
B
, suy ra
( )
6 2 2
2
ABCD
AB AD BC
S AD
+
= = =
1
3
AD BC=
.
Với
( )
1; 2; 1AD a b c= − − −
ta được
17
1 .4
33
17
2 .1
33
14
1 .1
33
aa
bb
cc
− = =
− = =
− = =
7 7 4
;;
333
D
.
Vậy
6abc+ + =
.
Câu 18. Chọn B
Mặt phẳng
( )
P
đi qua điểm
M
và cắt trục tọa độ
Ox
,
Oy
,
Oz
tại
A
,
B
,
C
. Gọi
( )
,0,0Aa
;
( )
0, ,0Bb
;
( )
0,0,Cc
. Phương trình mặt phẳng
( )
P
có dạng:
( )
11
x y z
a b c
+ + =
.
Do
( )
1;2;5M
thuộc mặt phẳng
( )
P
nên thay vào
( )
1
ta có:
( )
1 2 5
1 2
a b c
+ + =
.
Mặt khác
M
là trực tâm tam giác
ABC
nên
AM BC
BM AC
⊥
⊥
.0
.0
AM CB
BM AC
=
=
.
Ta có
( )
1 ;2;5AM a=−
;
( )
1;2 ;5BM b=−
;
( )
0; ;CB b c=−
;
( )
;0;AC a c=−
.
Khi đó :
2 5 0
50
bc
ac
−=
− + =
5
2
5
bc
ac
=
=
. Thay vào (2) ta có:
1 4 5
1
55c c c
+ + =
6c=
30
15
6
a
b
c
=
=
=
.
Vậy thể tích tứ diện
OABC
là:
11
..
66
V OAOB OC abc==
1
.30.15.6 450
6
==
(đơn vị thể tích).
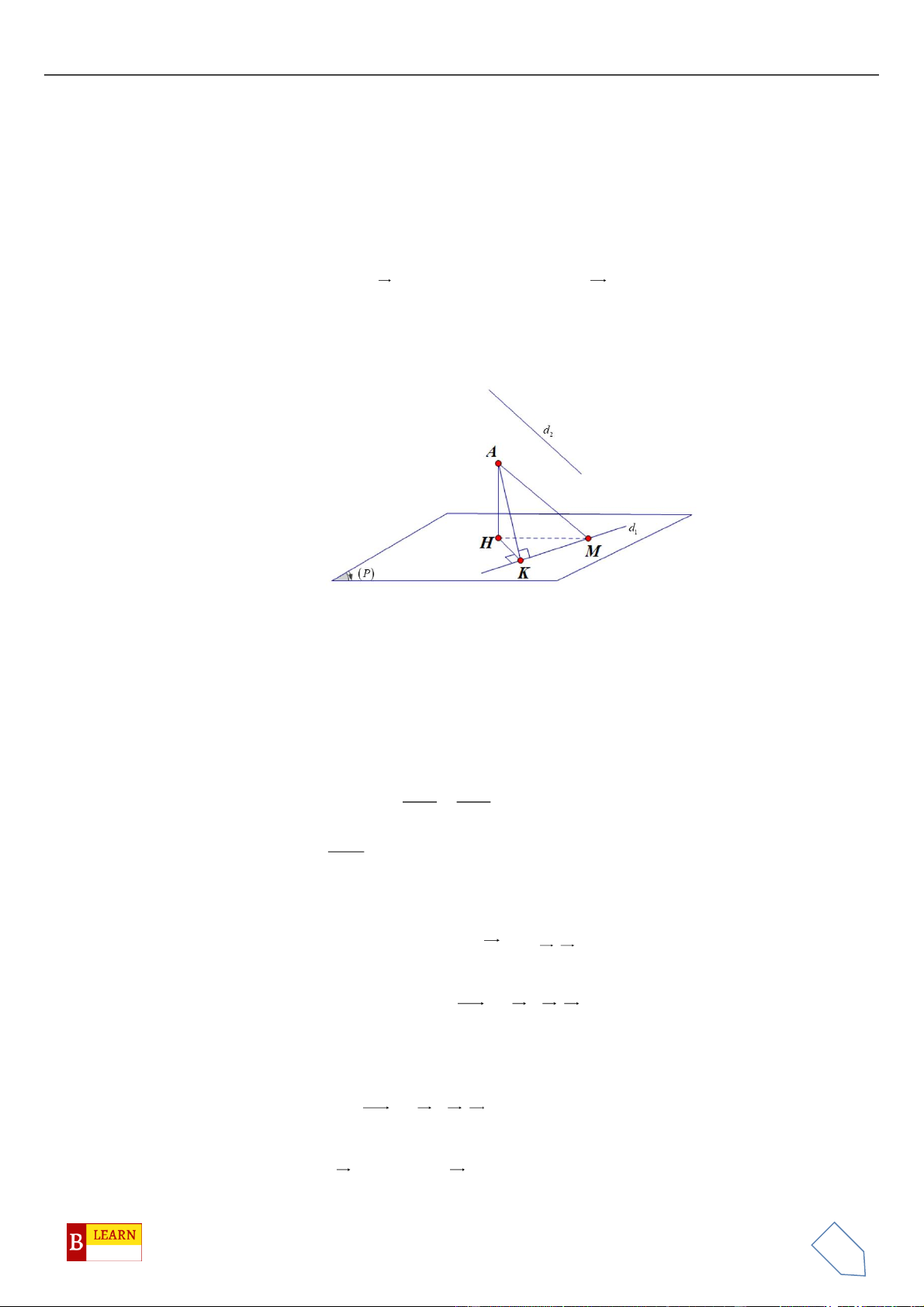
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
35
Câu 19. Chọn B
Ta xét bài toán tổng quát như sau:
Bài toán: Cho hai đường thẳng
1
d
,
2
d
không song song. Viết phương trình mặt phẳng
( )
P
chứa
1
d
và tạo với đường thẳng
2
d
một góc lớn nhất.
Phương pháp giải
Giả sử
1
d
có vectơ chỉ phương
1
u
,
2
d
có vectơ chỉ phương
2
u
.
Trước hết ta xét trường hợp
1
d
và
2
d
chéo nhau.
Gọi là một điểm nào đó thuộc
1
d
, dựng đường thẳng qua và song song với
2
d
. Lấy điểm
A
cố định trên đường thẳng đó. Gọi
H
là hình chiếu của
A
lên mặt phẳng
P
,
K
là hình chiếu
của
A
lên đường thẳng
1
d
.
Góc giữa mặt phẳng và đường thẳng
2
d
là .
Ta có
( ) ( )
2
sin , sin
AH AK
d P HMA
AM AM
= =
(do
AH AK
). Góc
( )
2
,dP
lớn nhất khi
( )
2
sin ,dP
lớn nhất. Do
AK
AM
không đổi suy ra
( )
2
sin ,dP
lớn nhất .
Mặt phẳng cần tìm là mặt phẳng chứa
1
d
và vuông góc với mặt phẳng , hay vectơ
pháp tuyến của vuông góc với hai vectơ
1
u
và
12
,uu
.
Nên ta chọn vectơ pháp tuyến của là
( )
1 1 2
,,
P
n u u u
=
.
Trường hợp
1
d
và
2
d
cắt nhau tại , bài toán giải tương tự như trên. Kết luận không thay đổi:
vectơ pháp tuyến của là
( )
1 1 2
,,
P
n u u u
=
.
Áp dụng vào bài 45 ta có
( )
1
1;2; 1=−u
;
( )
2
2; 1;2=−u
.
M
M
( )
P
AMH
HK
( )
P
( )
AKM
( )
P
( )
P
M
( )
P

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
36
( )
12
; 3; 4; 5
= − −
uu
( )
( ) ( )
1 1 2
; ; 14;2; 10 2 7; 1;5
= = − − = − −
P
n u u u
.
Mặt phẳng
()P
chứa
1
d
nên mặt phẳng
()P
đi qua điểm
(1; 2;0)−A
.
Phương trình mặt phẳng
( )
:7 5 9 0P x y z− + − =
. Suy ra
7 5 9 3a c d+ + = + − =
.
Câu 20. Chọn A
Gọi tọa độ
( )
;;C a b c
.
Vì điểm
C
thuộc
( )
: 1 0P x y z+ + + =
nên
1a b c= − − −
hay tọa độ
C
có dạng
( ) ( ) ( ) ( )
22
22
1; ; ; 1; 1C b c b c BC b c b c BC b c b c− − − = − − − = + + − +
.
Ta có
( )
2
1; 0; 2 5AB AB= =
. Do tam giác
ABC
vuông cân tại
B
nên
( )
( ) ( ) ( )
22
22
2
1
.0
1 5 2
bc
AB BC
BC AB
b c b c
=
=
=
+ + − + =
Thay
( )
1
vào
( )
2
ta có
2
1
6 2 4 0
2
3
c
cc
c
=
− − =
=−
( 3;1;1)
.
1 2 2
;;
3 3 3
C
C
Vậy cao độ của điểm
C
là
1
hoặc
2
3
.
Câu 21. Chọn B
Cách 1:
( )
( )
;2 ;
2 ; 6; 2
MA a b c
MB a b c
= − − −
= − − − − −
( ) ( )( ) ( )
2 2 2
. 2 2 6 2 2 4 2 12MA MB a a b b c c a b c a b c P = − − + − − − − − − = + + − + + − =
2 2 2
2 4 2 12 0a b c a b c P + + − + + − − =
( ) ( ) ( )
2 2 2
1 2 1 18a b c P − + + + + = +
Nếu
18 0P +
18P −
thì không tồn tại điểm
M
.
Nếu
18 0P+=
18P = −
thì
( )
1; 2; 1M −−
không thỏa mãn
( )
MS
.
Nếu
18 0P+
18P −
thì
M
thuộc mặt cầu
( )
S
có tâm
( )
1; 2; 1I
−−
và bán kính
18RP
=+
.Khi đó
M
là điểm chung của hai mặt cầu:
( )
2 2 2
9
: 2 4 2 0
2
S x y z x y z+ + + − − + =
có tâm
( )
1;2;1I −
và bán kính
6
2
R =
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
37
( )
2 2 2
2 4 2 12 0S x y z x y z P
+ + − + + − − =
có tâm
( )
1; 2; 1I
−−
và bán kính
18RP
=+
.
Tồn tại điểm
M
khi và chỉ khi hai mặt cầu
( )
S
và
( )
S
có điểm chung
66
18 2 6 18
22
R R II R R P P
− + − + + +
.
9
36
18
9 39
2
2
22
56
6
18
2 6 18 2 6
2
2
P
P
P
P
P
−
+
−
+
− − +
(thỏa mãn
18P −
)
Khi đó
9
2
P
−
=
đạt được khi hai mặt cầu trên tiếp xúc ngoài tại
( )
;;M a b c
thỏa mãn:
6
13
2
30
34
36
2
R OI OI
MI MI MI MI MI MI OM
R
+
= − = − = − + = =
11
;1;
22
M
−
.
Khi đó
9
min
2
P
−
=
11
;1; 1.
22
M a b c
− + + =
Cách 2:
( )
2 2 2
9
2 4 2 0
2
M S a b c a b c + + + − − + =
( ) ( ) ( )
2 2 2
3
1 2 1
2
a b c + + − + − =
.
( )
2 2 2
9
2 4 2
2
M S a b c a b c + + = − + + −
.
( )
( )
;2 ;
2 ; 6; 2
MA a b c
MB a b c
= − − −
= − − − − −
( ) ( )( ) ( )
2 2 2
. 2 2 6 2 2 4 2 12MA MB a a b b c c a b c a b c= − − + − − − − − − = + + − + + −
.
9
. 2 4 2 2 4 2 12
2
MAMB a b c a b c = − + + − − + + − =
33
4 8 4
2
a b c P− + + − =
.
( ) ( ) ( )
33 15
4 8 4 4 1 8 2 4 1
22
P a b c a b c= − + + − = − + + − + − +
.
( ) ( ) ( )
15
4 1 8 2 4 1
2
P a b c − = − + + − + −
.
Áp dụng bất đẳng thức Bunhiacốpxki cho hai bộ số
4;8;4−
và
1; 2; 1a b c+ − −
, ta có
( ) ( ) ( ) ( ) ( ) ( ) ( )
2
2
2 2 2
15
4 1 8 2 4 1 16 64 16 1 2 1 144
2
P a b c a b c
− = − + + − + − + + + + − + − =
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
38
15 9 39
12 12
2 2 2
PP − − −
.
33 9
4 8 4
9
22
1 2 1
2
4 8 4
a b c
P
a b c
− + + − = −
= −
+ − −
==
−
2
1
4 8 4
10
12
2
1
2
0
a
a b c
ab
ac
b
c
=−
− + + =
+=
+=
=
=
.
Khi đó
9
min
2
P =−
11
;1; 1.
22
M a b c
− + + =
Câu 22. Chọn C
Mặt cầu
()S
có tâm
( )
2;1; 2I −−
, bán kính
3R =
.
Với mọi điểm
( )
; ; ( )M x y z S
ta có
3MI =
.
Theo đề bài
2
. 16MA MO MB+=
( ) ( )( )
2
16MI IA MI IO MI IB + + + + =
.
( )
( )
22
2 2 . 16 *MI IA MI IA IB IO IO IB + + + + + =
.
Có
( ) ( ) ( )
0; 1; 2 , 2; 1; 2 , 2; 5; 2IA IO IB= − − = − = − −
,
( )
2 ;1 ; 2MI x y z= − − − − −
( )
2 0; 8;0IA IB IO + + = −
,
( )
2 8( 1)MI IA IB IO y+ + = −
,
.3IO IB =
.
Do đó
(*) 2.9 3 8( 1) 3 16 0yy + + − + = =
hay
M
thuộc mặt phẳng
( ): 0Py=
.
Tập hợp điểm
M
là đường tròn giao tuyến của mặt phẳng
( )
P
và mặt cầu
()S
.
Do
( ;( )) 1d I P =
suy ra bán kính của đường tròn
22
3 1 2 2r = − =
.
Cách 2.
Mặt cầu
()S
có tâm
( )
2;1; 2I −−
, bán kính
3R =
. Gọi
( )
;;M x y z
.
()MS
( ) ( )
( )
2
22
2 1 2 9x y z + + − + + =
2 2 2
4 2 2 2 2 0x y z x y z + + + − + − =
(1)
2
. 16MA MO MB+=
( )
( )
( ) ( )
2
2
22
2 2 2 4 4 16x y z x x y y z + + + + + + + + + =
2 2 2
4 2 2 2 2 0x y z x y z + + + + + − =
(2)
Từ (1) và (2) ta có hệ:
2 2 2
2 2 2
4 2 2 2 2 0
4 2 2 2 2 0
x y z x y z
x y z x y z
+ + + − + − =
+ + + + + − =
0y=
hay
M
thuộc mặt phẳng
( ): 0Py=
.
Tập hợp điểm
M
là đường tròn giao tuyến của mặt phẳng
( )
P
và mặt cầu
()S
.
Do
( ;( )) 1d I P =
suy ra bán kính của đường tròn
22
3 1 2 2r = − =
.
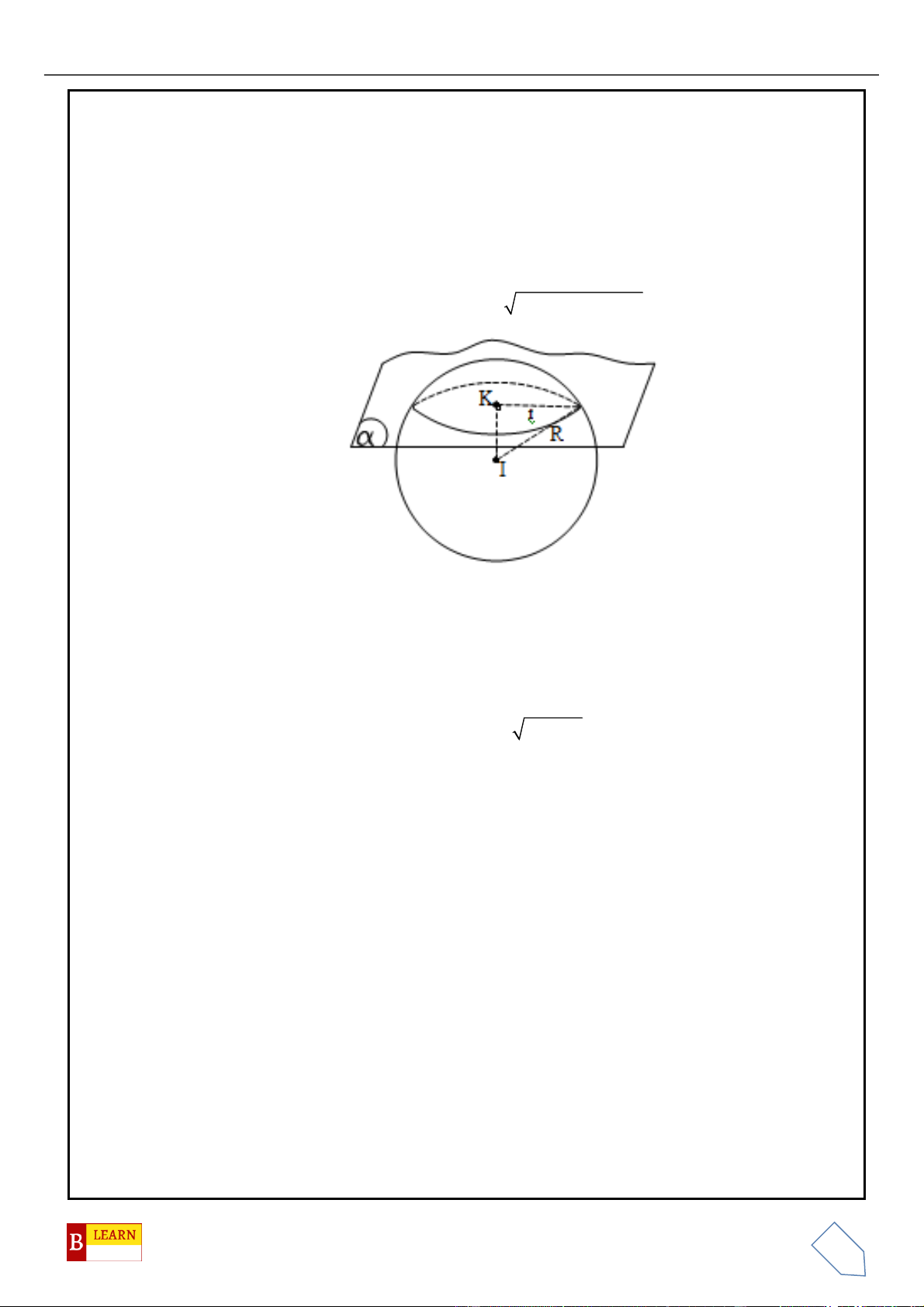
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
39
MẶT CẦU TRONG KHÔNG GIAN
❖ Trong không gian với hệ trục Oxyz:
▪ Mặt cầu (S) tâm
( )
;;I a b c
bán kính
R
có phưong trình là :
( ) ( ) ( )
2 2 2
2
x a y b z c R− + − + − =
.
▪ Phương trình :
2 2 2
2 2 2 0x y z ax by cz d+ + + + + + =
với
2 2 2
0a b c d+ + −
là phương
trình mặt cầu tâm
( )
;;I a b c
, bán kính
2 2 2
R A B C D= + + −
.
❖ Vị
trí
tương
đối
của
mặt
phẳng
( )
và
mặt
cầu
( )
S
:
▪
( )
( )
,d I R
khi và chỉ khi
( )
không cắt mặt cầu
( )
S
.
▪
( )
( )
,d I R
=
khi và chỉ khi
( )
tiếp xúc mặt cầu
( )
S
.
▪
( )
( )
,d I R
khi và chỉ khi
( )
cắt mặt cầu
( )
S
theo giao tuyến là đường tròn nằm trên
mặt phẳng (P) có tâm K và có bán kính
22
.r R d=−
❖ Vị trí tương đối giữa mặt cầu và đường thẳng.
▪ Cho mặt cầu
( )
;S O R
và đường thẳng
. Gọi
H
là hình chiếu của
O
lên
và
d OH=
là khoảng cách từ
O
đến
▪ Nếu
dR
thì
cắt mặt cầu tại 2 điểm phân biệt
▪ Nếu
dR=
thì
cắt mặt cầu tại 1 điểm duy nhất
▪ Nếu
dR
thì
không cắt mặt cầu

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
40
DẠNG 3. MẶT CẦU TRONG KHÔNG GIAN
Câu 1: Trong không gian gian Oxyz, cho mặt cầu
( )
S
tâm
( ; ; )I a b c
bán kính bằng 1, tiếp xúc với mặt
phẳng
( )
Oxz
. Khẳng định nào sau đây đúng?
A.
1a =
. B.
1abc+ + =
. C.
1b =
. D.
1c =
.
Câu 2: Trong không gian với hệ trục tọa độ
Oxyz
, cho điểm
( ) ( )
1;1;2 , 3;2; 3AB−
. Mặt cầu
( )
S
có tâm
I
thuộc
Ox
và đi qua hai điểm
,AB
có phương trình.
A.
2 2 2
8 2 0x y z x+ + − + =
. B.
2 2 2
8 2 0x y z x+ + + + =
.
C.
2 2 2
4 2 0x y z x+ + − + =
. D.
2 2 2
8 2 0x y z x+ + − − =
.
Câu 3: Trong không gian
Oxyz
, cho hai điểm
( )
1;2;3A
,
( )
1;4;1B −
. Phương trình mặt cầu có đường kính
AB
là
A.
( ) ( ) ( )
2 2 2
1 4 1 12x y z+ + − + − =
. B.
( ) ( ) ( )
2 2 2
1 2 3 12x y z− + − + − =
.
C.
( ) ( )
22
2
3 2 3x y z+ − + − =
. D.
( ) ( )
22
2
3 2 12x y z+ − + − =
.
Câu 4: Trong không gian
Oxyz
, cho điểm
( )
1; 2;3I −
. Viết phương trình mặt cầu tâm
I
, cắt trục
Ox
tại hai điểm
A
và
B
sao cho
23AB =
.
A.
( ) ( ) ( )
2 2 2
1 2 3 16x y z− + + + − =
. B.
( ) ( ) ( )
2 2 2
1 2 3 20x y z− + + + − =
.
C.
( ) ( ) ( )
2 2 2
1 2 3 25x y z− + + + − =
. D.
( ) ( ) ( )
2 2 2
1 2 3 9x y z− + + + − =
.
Câu 5: Trong không gian với hệ tọa độ
Oxyz
, phương trình nào sau đây không phải phương trình mặt
cầu?
A.
2 2 2
2 2 2 2 4 6 5 0x y z x y z+ + + − + + =
. B.
2 2 2
20x y z x y z+ + − + − =
.
C.
2 2 2
3 7 5 1 0x y z x y z+ + − + + − =
. D.
2 2 2
3 4 3 7 0x y z x y z+ + + − + + =
.
Câu 6: Trong không gian
Oxyz
, cho điểm
( )
2;3;4A −
,
( )
6;1;2B
. Viết phương trình mặt cầu có đường
kính
AB
.
A.
( ) ( ) ( )
2 2 2
2 2 3 18x y z+ + + + + =
. B.
( ) ( ) ( )
2 2 2
2 2 3 18x y z− + − + − =
.
C.
( ) ( ) ( )
2 2 2
2 2 3 3 2x y z+ + + + + =
. D.
( ) ( ) ( )
2 2 2
2 2 3 3 2x y z− + − + − =
.
Câu 7: Trong không gian với hệ tọa độ
Oxyz
, phương trình nào sau đây không phải phương trình mặt
cầu?
A.
2 2 2
3 3 3 2 0x y z x+ + − =
. B.
2 2 2
2 1 0x y z x y z+ + − + − − =
.
C.
2 2 2
8 2 1 0x y z x y+ + − + + =
. D.
2 2 2
2 4 6 7 0x y z x y z+ − + − + + =
.
Câu 8: Trong không gian
Oxyz
, cho hai điểm
( )
1;1;1A
và
( )
1; 2; 3I
. Phương trình của mặt cầu tâm
I
và đi qua
A
là
A.
( ) ( ) ( )
2 2 2
1 2 3 29x y z− + − + − =
. B.
( ) ( ) ( )
2 2 2
1 1 1 5x y z− + − + − =
.
C.
( ) ( ) ( )
2 2 2
1 1 1 25x y z− + − + − =
. D.
( ) ( ) ( )
2 2 2
1 2 3 5x y z− + − + − =
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
41
Câu 9: Trong không gian
Oxyz
, xét mặt cầu
( )
S
có phương trình dạng
2 2 2
4 2 2 10 0x y z x y az a+ + − + − + =
. Tập hợp các giá trị thực của
a
để
( )
S
có chu vi đường tròn
lớn bằng
8
là
A.
1;10
. B.
2; 10−
. C.
1;11−
. D.
1; 11−
.
Câu 10: Trong không gian
Oxyz
, mặt cầu có tâm
( )
1;2; 1I −
và tiếp xúc với mặt phẳng
( ):2 2 8 0P x y z− − − =
có phương trình là
A.
( ) ( ) ( )
2 2 2
( ) : 1 2 1 3S x y z+ + + + − =
. B.
( ) ( ) ( )
2 2 2
( ) : 1 2 1 3S x y z− + − + + =
.
C.
( ) ( ) ( )
2 2 2
( ) : 1 2 1 9S x y z− + − + + =
. D.
( ) ( ) ( )
2 2 2
( ) : 1 2 1 9S x y z+ + + + − =
.
Câu 11: Trong không gian
O,xyz
mặt cầu có tâm
1;1;1I
và diện tích bằng
4
có phương
trình là
A.
( ) ( ) ( )
2 2 2
1 1 1 4x y z− + − + − =
. B.
( ) ( ) ( )
2 2 2
1 1 1 1x y z+ + + + + =
.
C.
( ) ( ) ( )
2 2 2
1 1 1 4x y z+ + + + + =
. D.
( ) ( ) ( )
2 2 2
1 1 1 1x y z− + − + − =
.
Câu 12: Trong không gian cho . Gọi là tâm mặt cầu tiếp
xúc với mặt phẳng đồng thời đi qua các điểm . Tìm biết
A. . B. . C. . D. .
Câu 13: Trong không gian cho . là điểm khác sao cho
đôi một vuông góc. là tâm mặt cầu ngoại tiếp tứ diện . Tính
A. . B. . C. . D. .
Câu 14: Trong không gian
,Oxyz
cho hai điểm
( ) ( )
1; 2;3 , 0; 4;6 .AB−−
Phương trình mặt cầu tâm
A
đi
qua điểm
B
là
A.
( ) ( ) ( )
2 2 2
2
1 2 3 14x y z− + + + − =
. B.
( ) ( ) ( )
2 2 2
1 2 3 14x y z− + + + − =
.
C.
( ) ( ) ( )
2 2 2
0 4 6 14xyz− + + + − =
. D.
( ) ( ) ( )
2 2 2
0 4 6 14xyz− + + + − =
.
Câu 15: Trong không gian
Oxyz
, cho hai điểm
( )
1;0; 1A −
,
( )
3; 2;1B −−
. Gọi
( )
S
là mặt cầu có tâm
I
thuộc mặt phẳng
( )
Oxy
, bán kính
11
và đi qua hai điểm
A
,
B
. Biết
I
có tung độ âm, phương
trình mặt cầu
( )
S
là
A.
2 2 2
6 2 0x y z y+ + + − =
. B.
2 2 2
4 7 0x y z y+ + + − =
.
C.
2 2 2
4 7 0x y z y+ + + + =
. D.
2 2 2
6 2 0x y z y+ + + + =
.
Câu 16: Trong không gian
Oxyz
, có tất cả bao nhiêu giá trị nguyên của
m
để
( ) ( )
2 2 2 2
2 2 2 1 3 5 0x y z m x m z m+ + + + − − + − =
là phương trình của một mặt cầu?
A. 4. B.
6
. C.
5
. D.
7
.
Oxyz
( ) ( ) ( )
2;1;4 ; 5;0;0 ; 1; 3;1M N P −
( )
;;I a b c
( )
Oyz
, , M N P
c
5abc+ +
3
2
4
1
Oxyz
( ) ( ) ( )
2;0;0 ; 0; 2;0 ; 0;0; 2A B C− − −
D
O
, , DA DB DC
( )
;;I a b c
ABCD
S a b c= + +
4−
1−
2−
3−

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
42
Câu 17: Trong không gian hệ tọa độ
Oxyz
, tìm tất cả các giá trị của
m
để phương trình
2 2 2
2 2 4 0x y z x y z m+ + − − − + =
là phương trình của một mặt cầu.
A.
6m
. B.
6m
. C.
6m
. D.
6m
.
Câu 18: Trong không gian với hệ tọa độ
,Oxyz
tìm tất cả các giá trị của tham số
m
để phương trình
2 2 2
4 2 6 13 0x y z x my z+ + − + + + =
là phương trình của mặt cầu.
A.
0m
. B.
0m
. C.
m
. D.
0m
.
Câu 19: Trong không gian với hệ tọa độ
Oxyz
, tìm
m
để phương trình
2 2 2
2 2( 2) 2( 3) 8 37 0x y z mx m y m z m+ + − + − − + + + =
là phương trình của một mặt cầu.
A.
2 hay 4mm −
. B.
2 hay 4mm −
.
C.
4 hay 2mm − −
. D.
4 hay 2mm −
.
Câu 20: Trong không gian với hệ tọa độ
Oxyz
, tìm tất cả các giá trị của
m
để phương trình
2 2 2
2 4 6 0x y z x y z m+ + − − − + =
là phương trình mặt cầu.
A.
14m
. B.
14m
. C.
14m
. D.
14m
.
Câu 21: Trong không gian Oxyz, cho mặt cầu
2 2 2
( ): 9S x y z+ + =
và mặt phẳng
( ):4 2 4 7 0.P x y z+ + + =
Hai mặt cầu có bán kính là
1
R
và
2
R
chứa đường tròn giao tuyến của
( )
S
và
()P
đồng thời cùng tiếp xúc với mặt phẳng
( ):3 4 20 0.Q y z− − =
Tổng
12
RR+
bằng
A.
63
8
. B.
35
8
. C.
5
. D.
65
8
.
Câu 22: Cho đường thẳng
1 2 2
:
1 2 1
x y z
d
− − −
==
−
và điểm
( )
1;2;1A
. Tìm bán kính của mặt cầu có tâm
I
nằm trên
d
, đi qua
A
và tiếp xúc với mặt phẳng
( )
: 2 2 1 0P x y z− + + =
.
A.
2R =
. B.
4R =
. C.
1R =
. D.
3R =
.
Câu 23: Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 1 2 1 9S x y z− + − + + =
và hai
điểm
( ) ( )
4;3;1 , 3;1;3AB
;
M
là điểm thay đổi trên
( )
S
. Gọi
,mn
là giá trị lớn nhất, nhỏ nhất
cảu biểu thức
22
2P MA MB=−
. Xác định
( )
mn−
.
A.
64
. B.
60
. C.
68
. D.
48
.
Câu 24: Trong không gian
Oxyz
, mặt cầu qua bốn điểm
( )
5;3;3A
,
( )
1;4;2B
,
( )
2;0;3C
,
( )
4;4; 1D −
, có
phương trình là
( ) ( ) ( )
2 2 2
x a y b z c D− + − + − =
. Giá trị
abc++
bằng
A.
5
. B.
7
. C.
4
. D.
6
.
Câu 25: Trong không gian
Oxyz
, cho điểm
( ) ( )
3;0;0 ; 0; 2;0AB−
và
( )
0;0; 4C −
. Mặt cầu ngoại tiếp tứ
diện
OABC
có diện tích bằng
A.
116
. B.
29
. C.
16
. D.
29
4
.
Câu 26: Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 1 1 2 4S x y z− + − + + =
và điểm
( )
1;1; 1A −
. Ba mặt phẳng thay đổi đi qua
A
và đôi một vuông góc với nhau, cắt mặt cầu
( )
S

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
43
theo ba giao tuyến là các đường tròn
( ) ( ) ( )
1 2 3
,,C C C
. Tổng bình phương bán kính của ba đường
tròn
( )
1
C
,
( )
2
C
,
( )
3
C
là
A.
10
. B.
11
. C.
12
. D.
13
.
Câu 27: Cho đường thẳng
d
:
1 2 2
3 2 2
x y z+ − −
==
−
. Viết phương trình mặt cầu tâm
( )
1;2; 1I −
cắt
d
tại
các điểm
A
,
B
sao cho
23AB =
.
A.
( ) ( ) ( )
2 2 2
1 2 1 25x y z− + − + + =
. B.
( ) ( ) ( )
2 2 2
1 2 1 4x y z− + − + + =
.
C.
( ) ( ) ( )
2 2 2
1 2 1 9x y z− + − + + =
. D.
( ) ( ) ( )
2 2 2
1 2 1 16x y z− + − + + =
.
Câu 28: Trong không gian
Oxyz
, cho mặt cầu
2 2 2
1x y z+ + =
cắt mặt phẳng
( )
: 2y 2z 1 0Px+ − + =
theo
giao tuyến là đường tròn
( )
C
. Mặt cầu chứa đường tròn
( )
C
và qua điểm
( )
1;1;1A
có tâm là
điểm
( )
;;I a b c
, giá trị
abc++
bằng
A.
0,5
. B.
1−
. C.
0,5−
. D. 1.
Câu 29: Cho mặt cầu
( ) ( ) ( ) ( ) ( )
2 2 2
: 2 1 2 2 1 6 2 0S x y z m x m y m z m+ + − + + − + + − + =
. Biết rằng khi
m
thay đổi mặt cầu
( )
S
luôn chứa một đường tròn cố định. Tọa độ tâm
I
của đường tròn đó là
A.
( )
1;2;1I
. B.
( )
1; 2; 1I − − −
. C.
( )
1;2; 1I −
. D.
( )
1; 2;1I −−
.
Câu 30: Trong không gian
Oxyz
, cho mặt phẳng
( )
: 2 2 3 0P x y z− − − =
và mặt phẳng
( )
: 2 2 6 0Q x y z− − + =
. Gọi
( )
S
là một mặt cầu tiếp xúc với cả hai mặt phẳng. Bán kính của
( )
S
bằng.
A.
3
. B.
9
2
. C.
3
2
. D. 9.
Câu 31: Trong không gian
Oxyz
, cho mặt cầu
( )
2 2 2
: ( 3) 8+ + − =S x y z
và hai điểm
( )
4;4;3A
,
( )
1;1;1B
Tập hợp tất cả các điểm
M
thuộc
( )
S
sao cho
2=MA MB
là một đường tròn
( )
C
. Bán kính của
( )
C
bằng
A.
7
. B.
6
. C.
22
. D.
3
.
Câu 32: Trong không gian cho mặt cầu có phương trình . Từ điểm ta
kẻ các tiếp tuyến đến với các tiếp điểm thuộc đường tròn
( )
. Từ điểm di động nằm ngoài
và nằm trong mặt phẳng chứa
( )
, kẻ các tiếp tuyến đến với các tiếp điểm thuộc đường
tròn
( )
'
. Biết khi
( )
và
( )
'
có cùng bán kính thì luôn thuộc một đường tròn cố định. Tính
chiều dài quảng đường khi di chuyển đúng vòng theo cùng một chiều trên đường tròn
đó.
A. . B. . C. . D. .
S
2 2 2
1x y z
2019;0;0A
S
M
S
S
M
l
M
2019
4
2. 2019 1
2019
l
2019l
8152722l
4076361l
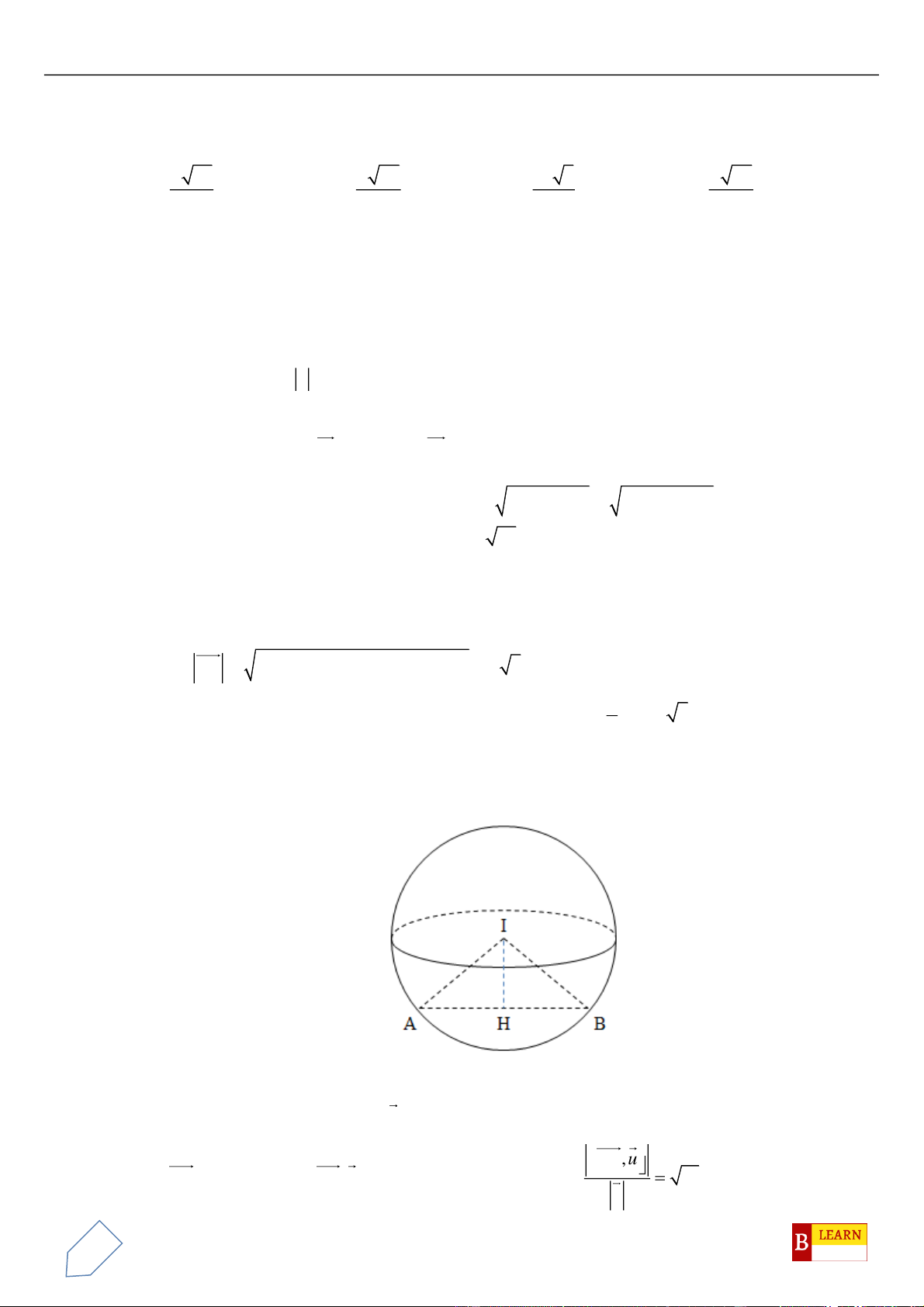
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
44
Câu 33: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SAD
là tam giác đều và nằm
trong mặt phẳng với đáy. Gọi
M
và
N
lần lượt là trung điểm của
BC
và
CD
. Bán kính của mặt
cầu ngoại tiếp hình chóp
.S CMN
bằng
A.
93
12
a
. B.
29
8
a
. C.
53
12
a
. D.
37
6
a
.
ĐÁP ÁN CHI TIẾT
Câu 1: Chọn C
Ta có phương trình
( )
:0Oxz y =
.
Do mặt cầu
( )
S
tâm
( ; ; )I a b c
bán kính bằng 1, tiếp xúc với mặt phẳng
( )
Oxz
nên
( )
( )
, 1 1d I Oxz b= =
.
Câu 2: Chọn A
Gọi
( )
;0;0I a Ox
( ) ( )
1 ;1;2 ; 3 ;2; 3IA a IB a − − −
.
Do
( )
S
đi qua hai điểm
,AB
nên
( ) ( )
22
1 5 3 13IA IB a a= − + = − +
4 16 4aa = =
( )
S
có tâm
( )
4;0;0I
, bán kính
14R IA==
.
( ) ( )
2
2 2 2 2 2
: 4 14 8 2 0.S x y z x y z x − + + = + + − + =
Câu 3: Chọn C
Ta có
( ) ( ) ( )
2 2 2
1 1 4 2 1 3 2 3.AB = − − + − + − =
Gọi
I
là trung điểm của
AB
khi đó
( )
0;3;2I
. Bán kính
1
3
2
R AB==
.
Phương trình mặt cầu cần tìm là
( ) ( )
22
2
3 2 3x y z+ − + − =
.
Câu 4: Chọn A
Gọi
H
là trung điểm
AB
IH AB⊥
tại
H
( )
( )
( )
;
;
I Ox
I AB
IH d d = =
.
Ox
có một véc tơ chỉ phương là
( )
1;0;0u =
, chọn điểm
( )
2;0;0M Ox
.
( ) ( )
( )
,
,
1;2; 3 , 0; 3;2 13
I Ox
IM u
IM IM u IH d
u
= − = − = = =
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
45
( Cách khác: Gọi
H
là hình chiếu vuông góc của
I
lên trục
Ox
( )
1;0;0H
13IH=
) mà
1
3
2
HA AB==
.
Nên bán kính mặt cầu cần tìm là
22
4R IA IH HA= = + =
.
Vậy phương trình mặt cầu cần tìm là:
( ) ( ) ( )
2 2 2
1 2 3 16x y z− + + + − =
.
Câu 5: Chọn B
Mặt cầu có tâm
I
và bán kính R
Vì mặt cầu nhận
OA
làm đường kính do đó tâm
I
là trung điểm của
OA
Ta có
2 2 2
(1; 2;3); 14 ( ):( 1) ( 2) ( 3) 14
2
OA
I R S x y z− = = − + + + − =
.
Câu 6: Chọn B
Mặt cầu có đường kính
AB
nên tâm
I
là trung điểm
AB
. Suy ra
( )
2;2;3I
.
Mặt khác
1
2
r AB=
( ) ( ) ( )
2 2 2
1
2
B A B A B A
x x y y z z= − + − + −
32=
.
Vậy phương trình mặt cầu cần tìm là:
( ) ( ) ( )
2 2 2
2 2 3 18x y z− + − + − =
.
Câu 7: Chọn D
Phương trình ở đáp án D không đúng dạng (1) do hệ số của
2 2 2
,,x y z
không bằng nhau.
Câu 8: Chọn D
Vì mặt cầu tâm
I
đi qua
A
nên có bán kính
( ) ( ) ( )
2 2 2
1 1 1 2 1 3 5R IA= = − + − + − =
Phương
trình mặt cầu tâm
( )
1;2;3I
đi qua
A
là :
( ) ( ) ( )
( )
( ) ( ) ( )
2
2 2 2 2 2 2
1 2 3 5 1 2 3 5x y z x y z− + − + − = − + − + − =
Câu 9: Chọn C
Đường tròn lớn có chu vi bằng
8
nên bán kính của
( )
S
là
8
4
2
=
.
Từ phương trình của
( )
S
suy ra bán kính của
( )
S
là
2 2 2
2 1 10aa+ + −
.
Do đó:
2 2 2
1
2 1 10 4
11
a
aa
a
=−
+ + − =
=
.
Câu 10: Chọn C
Do mặt cầu tiếp xúc với mặt phẳng nên bán kính mặt cầu là:
( )
( )
2 4 1 8
; 3 3
4 4 1
d I P r r
− + −
= = =
++
Vậy phương trình mặt cầu là:
( ) ( ) ( )
2 2 2
( ) : 1 2 1 9S x y z− + − + + =
Câu 11: Chọn D
Gọi
R
là bán kính mặt cầu, suy ra diện tích mặt cầu là
2
4 R
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
46
Theo đề bài mặt cầu có diện tích là
4
nên ta có
2
4 4 1RR
= =
.
Mặt cầu có tâm
1;1;1I
và bán kính
1R =
nên có phương trình:
( ) ( ) ( )
2 2 2
1 1 1 1x y z− + − + − =
.
Câu 12: Chọn C
Mặt cầu tiếp xúc với mặt phẳng đồng thời đi qua các điểm nên
hoặc
So sánh với điều kiện ta có
Câu 13: Chọn B
Gọi
Vì đôi một vuông góc nên
là tâm mặt cầu ngoại tiếp tứ diện
ABCD
nên
( ) ( )
( ) ( )
( )
22
2 2 2 2
22
2 2 2 2
2 2 2
2
22
22
22
4 4 4
2
3 3 3
c
IA IB
IA IC
IA I
a b c a b c
a b c a b
a b c a
D
bc
+ + + =
=
=
=
+ + + +
+ + +
+ + + = + + +
+ + + = +
1
3
16
4 4 8
3
ab
a c a b c
aa
=
= = = = −
+ = +
. Vậy
1abc+ + = −
.
Câu 14: Chọn B
Mặt cầu tâm
( )
1; 2;3A −
đi qua
( )
0; 4;6B −
có bán kính
( )
2
22
1 2 3 14.R AB= = + − + =
Phương trình mặt cầu là:
( ) ( ) ( )
2 2 2
1 2 3 14.x y z− + + + − =
( )
Oyz
, , M N P
( )
( )
;d I Oyz IM IN IP= = =
( )
( )
( ) ( ) ( )
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
2 2 2
2
2 2 2 2
22
2 2 2 2
22
214
;
5 2 1 4
5 1 3 1
a a b c
d I Oyz IM
IN IM a b c a b c
IN IP
a b c a b c
= − + − + −
=
= − + + = − + − + −
=
− + + = − + + + −
( ) ( ) ( )
2 2 2
2
214
3 4 2
4 3 7
a a b c
a b c
a b c
= − + − + −
− − =
+ − =
3
1
2
a
b
c
=
= −
=
5
3
4
a
b
c
=
=−
=
5abc+ +
2c =
( )
;;D x y z
( ) ( ) ( )
= 2; ; ; = ; 2; ; = ; ; 2DA x y z DB x y z DC x y z + + +
, , DA DB DC
( ) ( )
( ) ( )
( ) ( )
2
2
2
.0
2 2 0
4
. 0 2 2 0
3
2 2 0
.0
DA DB
x x y y z
DA DC x x y z z x y z
x y y z z
DB DC
=
+ + + + =
= + + + + = = = = −
+ + + + =
=
( )
;;I a b c

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
47
Câu 15: Chọn A
Gọi
( ) ( )
; ;0 ; 0I a b Oxy b
.
Ta có
( )
1 ; ; 1IA a b= − − −
,
( )
3 ; 2 ;1IB a b= − − − −
.
Do mặt cầu
( )
S
hai điểm
A
,
B
nên
11IA IB==
22
2
11
11
IA IB
IA IB
IA
IA
=
=
=
=
( ) ( ) ( )
2 2 2
2
2 3 2 3
1 1 11 1 2 3 10 0
a b b a
a b a a
+ = − = − −
− + + = − + − − − =
2
23
23
0; 3
0
2; 1
5 10 0
2
ba
ba
ab
a
ab
aa
a
= − −
= − −
= = −
=
= − =
+=
=−
.
Đối chiếu điều kiện ta có
( ) ( )
2 2 2
0; 3;0 : 6 2 0.I S x y z y− + + + − =
Câu 16: Chọn D
Phương trình
( ) ( )
2 2 2 2
2 2 2 1 3 5 0x y z m x m z m+ + + + − − + − =
có dạng
2 2 2
2 2 2x y z ax by cz d+ + − − − +
với
( )
2
2 , 0, 1, 3 5a m b c m d m= − + = = − = −
.
Điều kiện để phương trình đã cho là phương trình mặt cầu:
2 2 2
0a b c d+ + −
( ) ( )
22
2
2 1 3 5 0m m m + + − − +
2
2 10 0mm − + +
1 11 1 11m − +
.
Do
m
nên suy ra
2; 1;0;1;2;3;4m − −
.
Vậy có 7 giá nguyên của
m
thoả mãn yêu cầu bài toán.
Câu 17: Chọn C
Phương trình
2 2 2
2 2 4 0x y z x y z m+ + − − − + =
là một phương trình mặt cầu
2 2 2
1 1 2 0m + + −
6m
.
Câu 18: Chọn B
Để phương trình
2 2 2
4 2 6 13 0x y z x my z+ + − + + + =
là phương trình của mặt cầu thì
2 2 2
4 3 13 0 0 0m m m+ + −
.
Câu 19: Chọn A
Câu 20: Chọn C
Câu 21: Chọn D
Mặt cầu
( )
S
có tâm
( )
0;0;0O
, bán kính
3R =
.
Gọi
( )
( ) ( )PCS =
là đường tròn tâm
K
, bán kính
( )
2
22
7 5 11
,( ) 9
66
r R d O P
= − = − =
.
Gọi
d
là đường thẳng qua
O
và vuông góc với
( )
P
. Khi đó
2
( ): (t )
2
xt
d y t
zt
=
=
=
.
Gọi
I
là tâm mặt cầu chứa đường tròn giao tuyến của
( )
S
và
()P
. Khi đó
Id
(2 ; ;2 )I t t t
.
Theo bài ra
( ) ( )
( )
2
2
2
2
22
3 8 20 8 2 8 7
275
,( ) ,( )
6 36
34
t t t t t
d I Q d I P r
− − + + +
= + = +
+

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
48
22
22
36 4 18 7 275 288 36 252 0 8 7 0t t t t t t + = + + − − = − − =
1
7
8
t
t
=
=−
.
Với
( )
1 ,( ) 5t d I Q= =
; Với
( )
7 25
,( )
88
t d I Q= − =
.
Vậy có hai mặt cầu chứa đường tròn giao tuyến của
( )
S
và
()P
đồng thời cùng tiếp xúc với mặt
phẳng
( )
Q
, bán kính hai mặt cầu đó lần lượt là
1
5R =
,
2
25
8
R =
. Khi đó
12
65
.
8
RR+=
Câu 22: Chọn D
Tâm
I
nằm trên
d
nên
( )
1 ;2 2 ;2I t t t+ − +
.
Mặt cầu đi qua
A
và tiếp xúc với mặt phẳng
( )
P
nên
( )
( )
;AI d I P R==
.
( )
( )
( )
( )
2
22
2
2
1 4 4 4 2 1
; 4 1
1 2 2
t t t
AI d I P t t t
+ − + + + +
= + + + =
+ − +
( )
( )
2
22
72
6 2 1 9 6 2 1 7 2
3
t
t t t t t
+
+ + = + + = +
.
( )
2
2 1 0 1 2;0;3t t t I − + = =
. Vậy bán kính mặt cầu
3R AI==
.
Câu 23: Chọn B
Mặt cầu
( )
S
có tâm
( )
1;2; 1I −
và bán kính
3R =
. Lấy điểm
E
sao cho
20AE BE−=
( )
5;5; 1E−
. Dễ thấy điểm
E
là điểm ngoài của
( )
S
.
Khi đó
( ) ( )
22
2 2 2 2 2
2 2 2P MA MB ME AE ME BE ME AE BE= − = − − − = + −
.
P
lớn nhất và nhỏ nhất khi và chỉ khi
ME
lớn nhất và nhỏ nhất.
max 8; min 2ME IE R ME IE R= + = = − =
. Do đó
2 2 2 2
max 64 2 ; min 4 2m P AE BE n P AE BE= = + − = = + −
suy ra
60mn−=
.
Câu 24: Chọn D
Cách 1:
Mặt cầu
( )
S
có tâm
( )
;;I a b c
( )
S
có dạng:
( )
2 2 2 2 2 2
2 2 2 0 0x y z ax by cz e a b c e+ + − − − + = + + −
.
Ta có:
( )
( )
( )
( )
10 6 6 43 3
2 8 4 21 2
4 6 13 1
8 8 2 33 5
AS
a b c e a
BS
a b c e b
a c e c
CS
a b c e e
DS
+ + − = =
+ + − = =
+ − = =
+ − − = =
.
3 2 1 6abc + + = + + =
.
Cách 2:
Mặt cầu
( )
S
có tâm
( )
;;I a b c
.
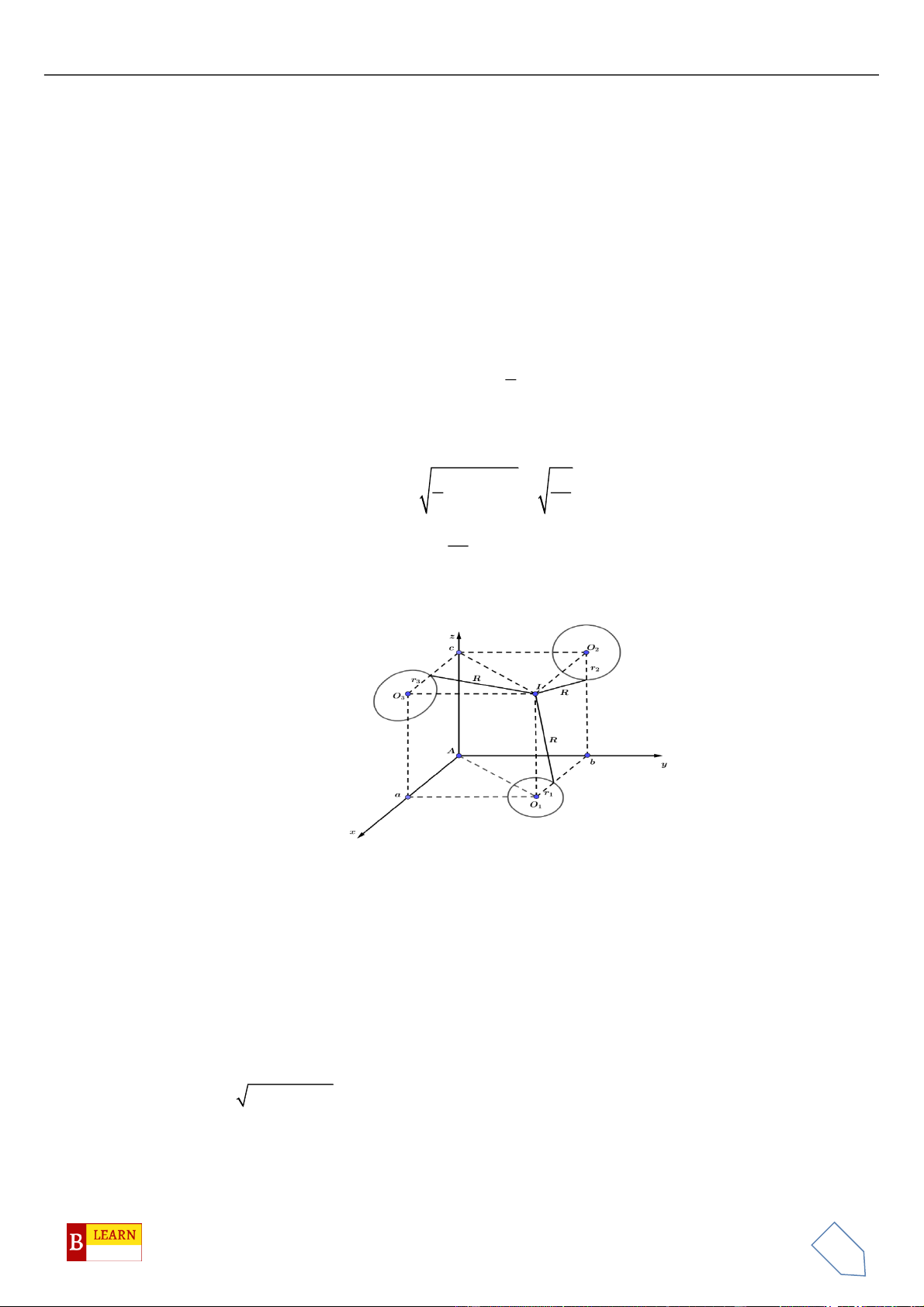
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
49
Khi đó:
22
22
22
8 2 2 22 3
6 6 30 2
2 2 8 10 1
AI BI
a b c a
AI BI CI DI AI CI a b b
a b c c
AI DI
=
− + = =
= = = = + = =
− + = =
=
.
3 2 1 6abc + + = + + =
.
Câu 25: Chọn B
Gọi phương trình mặt cầu đi qua 4 điểm
,,,O A B C
có dạng là:
2 2 2
2 2 2 0x y z ax by cz d+ + − − − + =
.
Do mặt cầu đi qua 4 điểm
,,,O A B C
nên thay lần lượt tọa độ
,,,O A B C
vào phương trình mặt cầu,
ta có hệ phương trình:
0
9 6a 0
4 4 0
16 8 0
d
d
bd
cd
=
− + =
+ + =
− + =
0
3
2
1
2
d
a
b
c
=
=
=−
=
.
Do đó ta có bán kính mặt cầu là
9 29
1 4 0
44
R = + + − =
.
Nên diện tích mặt cầu là
2
29
S 4 4 . 29
4
R
= = =
.
Câu 26: Chọn B
Mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 1 1 2 4S x y z− + − + + =
có tâm
( )
1;1; 2I −
và bán kính
2R =
.
Vì ba mặt phẳng thay đổi qua
( )
1;1; 1A −
và đôi một vuông góc với nhau nên ba mặt phẳng này
cắt nhau theo ba giao tuyến là ba đường thẳng đôi một vuông góc với nhau tại
A
. Chọn hệ trục
tọa độ
Axyz
sao cho gốc tọa độ là điểm
A
và các trục tọa độ lần lượt trùng với các đường thẳng
giao tuyến của ba mặt phẳng đã cho.
Gọi
( )
;;I a b c
là tọa độ tâm mặt cầu
()S
ứng với hệ trục tọa độ
Axyz
.
Suy ra
2 2 2 2 2 2
11IA a b c a b c= + + = + + =
. Không mất tính tổng quát ta giả sử mặt cầu
()S
cắt các mặt phẳng
( )
Axy
,
( )
Ayz
,
( )
Axz
theo các đường tròn lần lượt có tâm là
1
O
,
2
O
,
3
O
tương
ứng với bán kính là
1
r
,
2
r
,
3
r
.
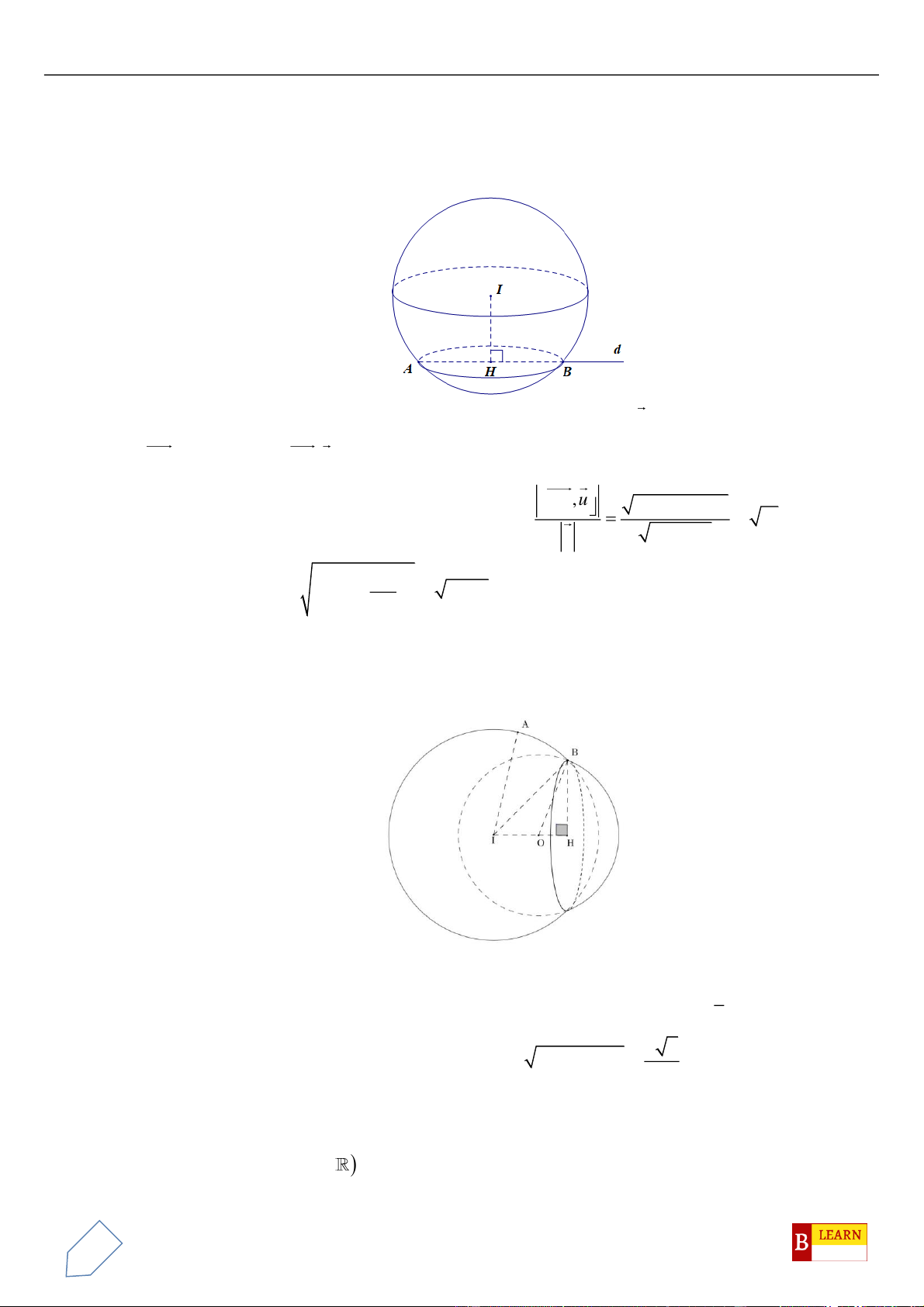
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
50
Ta có
2 2 2 2
11
4r R IO c= − = −
,
2 2 2 2
22
4r R IO a= − = −
,
2 2 2 2
33
4r R IO b= − = −
.
Suy ra
( )
2 2 2 2 2 2
1 2 3
12 12 1 11r r r a b c+ + = − + + = − =
Câu 27: Chọn D
Đường thẳng
d
đi qua điểm
( )
1;2;2M −
và có vectơ chỉ phương
( )
3; 2;2u =−
.
( ) ( )
2;0;3 , 6;13;4IM IM u
= − =
. Gọi
H
là trung điểm
AB IH AB⊥
.
Khoảng cách từ tâm
I
đến đường thẳng
d
là:
,
36 169 16
13
944
IM u
IH
u
++
= = =
++
.
Suy ra bán kính
2
2
13 3 4
2
AB
R IH
= + = + =
.
Phương trình mặt cầu tâm
( )
1;2; 1I −
và có bán kính
4R =
là
( ) ( ) ( )
2 2 2
1 2 1 16x y z− + − + + =
.
Câu 28: Chọn A
Ta có hình vẽ sau:
Mặt cầu
( )
2 2 2
:1S x y z+ + =
có tâm
( )
0;0;0O
, bán kính
1R OB==
.
Khoảng cách từ điểm
( )
0;0;0O
đến mặt phẳng
( )
P
là:
( )
( )
1
,
3
d O P OH==
.
Bán kính đường tròn giao tuyến
( )
C
là:
22
22
3
r BH OB OH= = − =
.
Gọi
d
là đường thẳng qua tâm
( )
0;0;0O
và vuông góc với mặt phẳng
( )
P
.
Khi đó
( )
:2
2
xt
d y t t
zt
=
=
=−
lại có điểm
Id
do ba điểm
,,I O H
thẳng hàng.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
51
Suy ra
( )
;2 ; 2I t t t−
,
( )
1;2 1; 2 1IA t t t= − − − −
,
( ) ( ) ( )
2 2 2
1 2 1 2 1IA t t t= − + − + − −
Ta có:
( )
( )
( )
2
22
4 4 1 9 1
,
3
1 2 2
t t t t
IH d I P
+ + + +
= = =
+ + −
,
22
IB BH IH=+
2
2
91
22
33
t
+
=+
.
Mặt cầu chứa đường tròn
( )
C
và qua điểm
( )
1;1;1A
có tâm là điểm
( )
;;I a b c
có bán kính
IA IB=
( ) ( ) ( )
2
2
2 2 2
91
22
1 2 1 2 1
33
t
t t t
+
− + − + − − = +
( ) ( ) ( )
2 2 2
1 2 1 2 1t t t − + − + − −
=
2
91
8
93
t +
+
1
2
t=
.
Suy ra tâm
1
;1; 1
2
I
−
. Vậy
1
2
abc+ + =
.
Cách 2.
Măt cầu chứa dường tròn
( )
2 2 2
1
:
2 2 1 0
x y z
C
x y z
+ + =
+ − + =
có dạng:
( ) ( )
2 2 2
: 1 2 2 1 0S x y z m x y z
+ + − + + − + =
( ) ( ) ( )
1;1;1 3 1 1 2 2 1 0 1.A S m m
− + + − + = = −
( )
2 2 2
' : 2 2 1 0S x y z x y z + + − − + − =
. Suy ra tâm
1
;1; 1
2
I
−
. Vậy
1
2
abc+ + =
.
Câu 29: Chọn D
Ta có
( ) ( ) ( ) ( )
2 2 2
2 1 2 2 1 6 2 0x y z m x m y m z m+ + − + + − + + − + =
( ) ( ) ( ) ( )
2 2 2
1 1 1 15 2 2 6 0x y z m x y z − + + + + − + − − + − =
Khi đó đường tròn cố định
( )
C
cần tìm là giao điểm của mặt phẳng
( )
: 2 2 6 0P x y z− − + − =
và
mặt cầu
( ) ( ) ( ) ( )
2 2 2
' : 1 1 1 15 0S x y z− + + + + − =
.
Mặt cầu
( )
'S
có tâm
(1; 1; 1)J −−
nên độ tâm
I
của đường tròn
( )
C
là hình chiếu vuông góc của
J
trên mặt phẳng
( )
P
.
Gọi
là đường thẳng qua
J
và vuông góc với
( )
P
, ta có:
1 1 1
:
2 1 2
x y z− + +
= =
−−
( )
2 1; 1;2 1I I t t t − + − − −
, mặt khác
( )
IP
nên
2 2 6 0 1
I I I
x y z t− − + − = =
Vậy
( 1; 2;1)I −−
.
Câu 30: Chọn C
Dễ thấy mặt phẳng
()P
song song mặt phẳng
()Q
.
Lấy điểm
( )
(1; 1;0)AP−
. Ta có:
( ) ( )
( )
( )
( )
1 2 6
; ; 3
1 4 4
d P Q d A Q
++
= = =
++
.
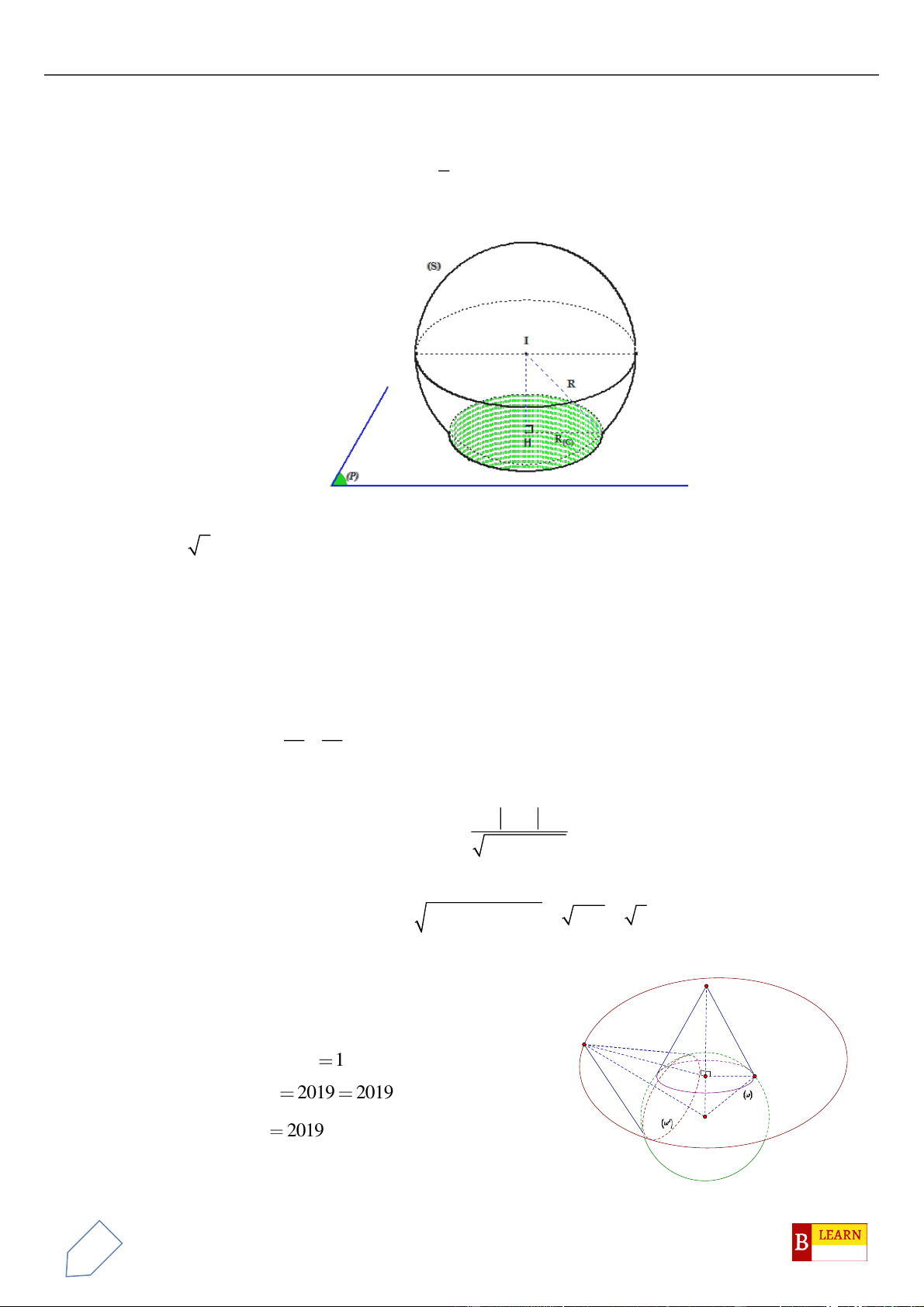
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
52
Do mặt cầu
()S
tiếp xúc với hai mặt phẳng song song nên khoảng cách giữa hai mặt phẳng song
song đó chính bằng đường kính của
()S
.
Vậy mặt cầu
( )
S
có bán kính là
( )
3
2
S
R =
.
Câu 31: Chọn A
Từ phương trình mặt cầu
( )
2 2 2
: ( 3) 8+ + − =S x y z
, suy ra mặt cầu có tâm
( )
0;0;3I
và bán kính
22=R
.
Gọi
( )
;;M x y z
là điểm thuộc
( )
S
sao cho
2=MA MB
. Theo giả thiết, ta có :
( )
( )
( ) ( ) ( ) ( ) ( ) ( )
2
22
2 2 2 2 2 2
38
2
4 4 3 4 1 1 1
+ + − =
=
− + − + − = − + − + −
x y z
MS
MA MB
x y z x y z
( )
( )
2
22
2
22
2 2 2
38
38
2 29
20
0
33
+ + − =
+ + − =
−=
+ + − − =
x y z
x y z
z
z
x y z
.
Khoảng cách từ tâm
( )
0;0;3I
đến mặt phẳng
( )
: 2 0−=Pz
là:
( )
( )
2 2 2
32
,1
0 0 1
d I P R
−
= =
++
.
Do đó đường tròn
( )
C
là giao tuyến của mặt phẳng
( )
P
và mặt cầu
( )
S
.
Đường tròn
( )
C
có bán kính
( )
( )
( )
22
, 8 1 7
C
R R d I P= − = − =
.
Câu 32: Chọn C
Từ giả thiết ta có:
Bán kính mặt cầu , tâm mặt cầu .
Khoảng cách .
Như vậy ta có .
Áp dụng bài toán ta có bán kính mà đường tròn
di động trên đó là
1R
0;0;0O
2019 2019AO R
2019k
47.1
M
E
I
M
A
H

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
53
. Chu vi của đường tròn di động là .
Vậy chiều dài quảng đường là: .
Câu 33: Chọn A
Chọn hệ tọa độ
Oxyz
như hình vẽ.
( )
1 1 1 3
1;0;0 , ; ;0 , 1; ;0 , 0;0;
2 2 2 2
M N C S
.
Gọi
( )
;;I x y z
là tâm mặt cầu ngoại tiếp hình chóp
.S CMN
MI NI CI SI = = =
.
Ta có:
( )
1 1 1 3
1; ; , ; ; , 1; ; , ; ;
2 2 2 2
MI x y z NI x y z CI x y z SI x y z
= − = − − = − − = −
.
Từ
MI NI CI SI= = =
ta có hệ:
( )
( )
( )
22
2
2 2 2
2 2 2
2
22
2
2
2
2 2 2
11
3
1
22
4
1 1 1 1
1
2 2 2 4
53
13
1
12
22
x y z x y z
x
x y z x y z y
z
x y z x y z
− + + = − + − +
=
− + − + = − + − + =
=
− + − + = + + −
.
3 1 5 3 1 1 5 3
; ; ; ;
4 4 12 4 4 12
I IM
= − −
.
Bán kính mặt cầu ngoại tiếp hình chóp
.S CMN
là:
93
12
R IM==
.
44
1 2019 1
2019
k
rR
k
M
2Cr
4
2019 1
2019.2 2019.2. 8152722
2019
lr

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
54
DẠNG 4. CỰC TRỊ LIÊN QUAN ĐẾN HỆ TRỤC TOẠ ĐỘ
Câu 1. Trong hệ trục tọa độ
Oxyz
, cho bốn điểm
( ) ( ) ( ) ( )
0; 2;1 ; 1;0; 2 ; 3;1; 2 ; 2; 2; 1A B C D− − − − − −
. Câu
nào sau đây sai?
A. Bốn điểm
, , ,A B C D
không đồng phẳng. B. Tam giác
ACD
là tam giác vuông tại
A
.
C. Góc giữa hai véctơ
AB
và
CD
là góc tù. D. Tam giác
ABD
là tam giác cân tại
B
.
Câu 2. Trong không gian
Oxyz
, cho điểm
( )
1;2;3A
, mặt phẳng
( )
P
:
2 5 0x y z+ + + =
. Mặt cầu tâm
( )
;;I a b c
thỏa mãn đi qua
A
, tiếp xúc với mặt phẳng
( )
P
và có bán kính nhỏ nhất. Tính
abc++
A.
2
. B.
2−
. C.
3
2
. D.
3
2
−
.
Câu 3. Trong không gian
( )
Oxyz
, cho mặt cầu
( )
:S
2 2 2
6 4 2 5 0x y z x y z+ + − + − + =
và mặt phẳng
( )
: 2 2 11 0P x y z+ + + =
. Tìm điểm
M
trên mặt cầu
( )
S
sao cho khoảng cách từ
M
đến mặt
phẳng
( )
P
là ngắn nhất.
A.
( )
0;0;1M
. B.
( )
2; 4; 1M −−
. C.
( )
4;0;3M
. D.
( )
0; 1;0M −
.
Câu 4. Trong không gian
Oxyz
, cho điểm
( )
1;2;3A
, mặt phẳng
( )
P
:
2 5 0x y z+ + + =
. Mặt cầu tâm
( )
;;I a b c
thỏa mãn đi qua
A
, tiếp xúc với mặt phẳng
( )
P
và có bán kính nhỏ nhất. Tính
abc++
A.
2
. B.
2−
. C.
3
2
. D.
3
2
−
.
Câu 5. Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
( )
1;4;5A
,
( )
3;4;0B
,
( )
2; 1;0C −
và mặt
phẳng
( )
:3 3 2 29 0P x y z+ − − =
. Gọi
( )
;;M a b c
là điểm thuộc
( )
P
sao cho
2 2 2
3MA MB MC++
đạt giá trị nhỏ nhất. Tính tổng
abc++
.
A.
8
. B.
10
. C.
10−
. D.
8−
.
Câu 6. Trong không gian với hệ trục
Oxyz
, cho tam giác
ABC
với
( )
2;0; 3A −
;
( )
1; 2; 4B −−
;
( )
2; 1;2C −
. Biết điểm
( )
;;E a b c
là điểm để biểu thức
P EA EB EC= + +
đạt giá trị nhỏ nhất.
Tính
T a b c= + +
A.
3T =
. B.
1T =
. C.
0T =
. D.
1T =−
.
Câu 7. Trong không gian
Oxyz
, cho mặt phẳng
( )
:2 2 14 0P x y z− + − =
và mặt cầu
( )
2 2 2
: 2 4 2 3 0S x y z x y z+ + − + + − =
. Gọi tọa độ điểm
( ; ; )M a b c
thuộc mặt cầu
( )
S
sao cho
khoảng cách từ
M
đến mặt phẳng
( )
P
là lớn nhất. Tính giá trị biểu thức
.K a b c= + +
A.
1K =
. B.
2K =
. C.
5K =−
. D.
2K =−
.
Câu 8. Trong không gian
Oxyz
, cho hai đường thẳng
1
4 1 5
:
3 1 2
x y z− − +
= =
−−
và
2
23
:.
1 3 1
x y z−+
= =
Trong tất cả các mặt cầu tiếp xúc với cả hai đường thẳng
1
và
2
. Gọi
( )
S
là mặt cầu có bán
kính nhỏ nhất. Bán kính của mặt cầu
( )
S
là
A.
12
. B.
6
. C.
24
. D.
3
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
55
Câu 9. Trong không gian với hệ trục toạ độ
Oxyz
, cho hai điểm
( )
1;3;4A −
,
( )
9; 7;2B −
. Tìm trên trục
Ox
toạ độ điểm
M
sao cho
22
MA MB+
đạt giá trị nhỏ nhất.
A.
( )
5;0;0M
. B.
( )
2;0;0M −
. C.
( )
4;0;0M
. D.
( )
9;0;0M
.
Câu 10. Trong không gian
Oxyz
, cho các điểm
(6;0;0)A
,
(0;3;0)B
và mặt phẳng
( ): 2 2 0P x y z− + =
.
Gọi
d
là đường thẳng đi qua
(2; 2; 0)M
, song song với
()P
và tổng khoảng cách từ
A
,
B
đến
đường thẳng
d
đạt giá trị nhỏ nhất. Vectơ nào dưới đây là một vectơ chỉ phương của
d
?
A.
1
( 10;3;8)u =−
. B.
2
(14 ; 1; 8)u = − −
. C.
3
(22 ; 3; 8)u =−
. D.
4
( 18; 1; 8)u = − −
.
Câu 11. Trong không gian với hệ trục tọa độ
Oxyz
, cho các mặt cầu
( )
1
S
,
( )
2
S
,
( )
3
S
có bán kính
1r =
và lần lượt có tâm là các điểm
( )
0;3; 1A −
,
( )
2;1; 1B −−
,
( )
4; 1; 1C −−
. Gọi
( )
S
là mặt cầu tiếp
xúc với cả ba mặt cầu trên. Mặt cầu
( )
S
có bán kính nhỏ nhất là bao nhiêu?
A.
10R =
. B.
10 1R =−
. C.
2 2 1R =−
. D.
22R =
.
Câu 12. Trong không gian
Oxyz
, cho mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 1 2 2 4S x y z− + + + − =
và mặt phẳng
( )
: 2 1 0P x y z− + − =
. Gọi
M
là một điểm bất kì trên mặt cầu
( )
S
. Khoảng cách từ
M
đến
( )
P
có giá trị nhỏ nhất bằng
A.
46
2
3
−
. B.
0
. C.
62−
. D.
2 6 2−
.
Câu 13. Cho
x
,
y
,
z
,
a
,
b
,
c
là các số thực thay đổi thỏa mãn
( ) ( ) ( )
2 2 2
3 2 1 2x y z+ + − + + =
và
1abc+ + =
. Giá trị nhỏ nhất của biểu thức
( ) ( ) ( )
2 2 2
P x a y b z c= − + − + −
là
A.
32−
. B.
32+
. C.
5 2 6−
. D.
5 2 6+
.
Câu 14. Trong không gian
Oxyz
, cho hai điểm
( ) ( )
1;2;1 , 2; 1;3AB−
và điểm
( )
; ;0M a b
sao cho
22
MA MB+
nhỏ nhất. Giá trị của
ab+
bằng
A.
3.
B.
2.
C.
1.
D.
2.−
Câu 15. Trong không gian
Oxyz
cho mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 4 2 4 1S x y z− + − + − =
. Điểm
( )
;;M a b c
thuộc
( )
S
. Tìm giá trị nhỏ nhất của
2 2 2
abc++
.
A.
25
. B.
29
. C.
24
. D.
26
.
Câu 16. Trong không gian
Oxyz
, cho
( )
0 ;1;1A
,
( )
2 ; 1;1B −
,
( )
4 ;1;1C
và
( )
: 6 0P x y z+ + − =
. Xét điểm
( )
;;M a b c
thuộc
( )
mp P
sao cho
2MA MB MC++
đạt giá trị
nhỏ nhất. Giá trị của
24a b c++
bằng:
A.
6
. B.
12
. C.
7
. D
5
.
Câu 17. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
3 1 3
:
1 2 3
x y z
d
− − −
==
và hai điểm
( )
2;0;3A
,
( )
2; 2; 3B −−
. Biết điểm
( )
0 0 0
;;M x y z
thuộc
d
thỏa mãn
4 4 2 2
.P MA MB MA MB=++
nhỏ nhất. Tìm
0
y
.
A.
0
3y =
. B.
0
2y =
. C.
0
1y =
. D.
0
1y =−
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
56
Câu 18. Trong không gian với hệ tọa độ
Oxyz
cho ba điểm
( ) ( ) ( )
8;5; 11 , 5;3; 4 , 1;2; 6A B C− − −
và mặt
( ) ( ) ( ) ( )
2 2 2
: 2 4 1 9S x y z− + − + + =
. Gọi điểm
( )
;;M a b c
là điểm trên
( )
S
sao cho
MA MB MC−−
đạt giá trị nhỏ nhất. Hãy tìm
ab+
.
A.
6
. B.
2
. C.
4
. D. 9.
Câu 19. Trong không gian
Oxyz
, cho các điểm
(4; 2;4)A −
,
( 2;6;4)B −
,
(5; 1; 6)C −−
. Xét các điểm M
thuộc mặt phẳng
( )
Oxy
sao cho
o
90AMB =
, đoạn thẳng
CM
có độ dài lớn nhất bằng
A.
73
. B.
53
. C.
10
. D.
8
.
Câu 20. Trong không gian với hệ trục tọa độ
Oxyz
, cho
4
điểm
( )
2;4; 1A −
,
( )
1;4; 1B −
,
( )
2;4;3C
,
( )
2;2; 1D −
, biết
( )
;;M x y z
để
2 2 2 2
MA MB MC MD+ + +
đạt giá trị nhỏ nhất thì
x y z++
bằng
A.
6
. B.
21
4
. C.
8
. D.
9
.
Câu 21. Trong không gian
Oxyz
, cho ba điểm
( )
10; 5;8A −−
,
( )
2;1; 1B −
,
( )
2;3;0C
và mặt phẳng
( )
: 2 2 9 0P x y z+ − − =
. Xét
M
là điểm thay đổi trên
( )
P
sao cho
2 2 2
23MA MB MC++
đạt giá
trị nhỏ nhất. Tính
2 2 2
23MA MB MC++
.
A.
54
.
B.
282
.
C.
256
.
D.
328
.
Câu 22. Trong không gian
Oxyz
cho mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 2 1 1 9S x y z− + − + − =
và điểm
( ) ( )
; ; M a b c S
sao cho biểu thức
22P a b c= + +
đạt giá trị nhỏ nhất. Tính
T a b c= + +
.
A.
2
. B.
1
. C.
2−
. D.
1−
.
Câu 23. Trong không gian
Oxyz
, cho mặt cầu
( ) ( ) ( )
22
2
: 3 4 4.S x y y+ − + + =
Xét hai điểm
M
,
N
di
động trên
( )
S
sao cho
1.MN =
Giá trị nhỏ nhất của
22
OM ON−
bằng
A.
10−
. B.
4 3 5−−
. C.
5−
. D.
6 2 5.−−
Câu 24. Cho điểm
( )
3;5; 5A −−
,
( )
5; 3;7B −
và mặt phẳng
( )
:0x y z
+ + =
. Xét điểm
M
thay đổi trên
( )
, giá trị lớn nhất của
22
2MA MB−
bằng
A.
398
. B.
379
. C.
397
. D.
498
.
Câu 25. Trong không gian
Oxyz
cho đường thẳng
3
:
2 2 1
x y z
d
+
==
−
và mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 3 2 5 36S x y z− + − + − =
. Gọi
là đường thẳng đi qua
( )
2;1;3A
, vuông góc với
đường thẳng
d
và cắt
( )
S
tại hai điểm có khoảng cách lớn nhất. Khi đó đường thằng
có một
véctơ chỉ phương là
( )
1; ;u a b=
. Tính
ab+
.
A.
4
. B.
2−
. C.
1
2
−
. D.
5
.
Câu 26. Trong không gian
Oxyz
, cho ba điểm
( )
1;2;2A −
,
( )
3; 1; 2B −−
,
( )
4;0;3C −
. Tìm tọa độ điểm
I
trên mặt phẳng
( )
Oxz
sao cho biểu thức
25IA IB IC−+
đạt giá trị nhỏ nhất.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
57
A.
37 19
;0;
44
I
−
. B.
27 21
;0 ;
44
I
−
. C.
37 23
;0 ;
44
I
−
. D.
25 19
;0 ;
44
I
−
.
Câu 27. Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
( )
1;3;4A −
,
( )
3;1;0B
. Gọi
M
là điểm trên
mặt phẳng
( )
Oxz
sao cho tổng khoảng cách từ
M
đến
A
và
B
là ngắn nhất. Tìm hoành độ
0
x
của điểm
M
.
A.
0
4x =
. B.
0
3x =
. C.
0
2x =
. D.
0
1x =
.
Câu 28. Trong không gian , cho và hai điểm , . Giả sử , là
hai điểm thay đổi trong mặt phẳng sao cho cùng hướng với và . Giá trị
lớn nhất của bằng
A. . B. . C. . D. .
Câu 29. Cho mặt cầu và hai điểm . Gọi là điểm
thuộc mặt mặt cầu Tính giá trị nhỏ nhất của biểu thức
A. B. C. D.
Câu 30. Trong không gian với hệ trục tọa độ
Oxyz
, cho
( ) ( ) ( )
;0;0 , 0; ;0 , 0;0;A a B b C c
A, B, C với
, , 0abc
sao cho
21+=+++++ CABCABOCOBOA
. Giá trị lớn nhất của V
O.ABC
bằng
A.
1
.
108
B.
1
.
486
C.
1
.
54
D.
1
.
162
Câu 31. Trong không gian
Oxyz
, cho
( )
1; 1;2A −
,
( )
2;0;3B −
,
( )
0;1; 2C −
. Gọi
( )
;;M a b c
là điểm thuộc
mặt phẳng
( )
Oxy
sao cho biểu thức
. 2 . 3 .S MAMB MB MC MC MA= + +
đạt giá trị nhỏ nhất. Khi
đó
12 12T a b c= + +
có giá trị là
A.
3T =
. B.
3T =−
. C.
1T =
. D.
1T =−
.
Câu 32. Trong không gian với hệ tọa độ
Oxyz
, gọi điểm
( )
;;M a b c
thuộc mặt cầu
( )
2 2 2
: 2 4 4 7 0S x y z x y z+ + − − − − =
sao cho biểu thức
2 3 6T a b c= + +
đạt giá trị lớn nhất. Khi
đó giá trị biểu thức
2P a b c= − +
bằng
A.
12
7
. B.
8
. C.
6
. D.
51
7
.
Câu 33. Trong không gian
Oxyz
cho hai điểm
(2; 3;2)−A
,
( 2;1;4)−B
và mặt cầu
2 2 2
( ):( 1) ( 4) 12S x y z+ + + − =
. Điểm
( ; ; )M a b c
thuộc mặt cầu
()S
sao cho
.MA MB
nhỏ nhất,
tính
abc++
.
A.
7
3
. B.
4−
. C.
1
. D.
4
.
Câu 34. Trong không gian
Oxyz
, cho hai điểm
( )
2; 2; 4A −
,
( )
3; 3; 1B −−
và mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 1 3 3 3S x y z− + − + − =
. Xét điểm
M
thay đổi thuộc mặt cầu
( )
S
, giá trị nhỏ nhất
của
22
23MA MB+
bằng
A. 103. B. 108. C. 105. D. 100.
Oxyz
( )
1; 1;0a =−
( )
4;7;3A −
( )
4;4;5B
M
N
( )
Oxy
MN
a
52MN =
AM BN−
17
77
7 2 3−
82 5−
2 2 2
( ):( 1) ( 4) 8S x y z+ + − + =
(3;0;0), (4;2;1)AB
M
( ).S
2.MA MB+
6.
2 6.
6 2.
3 2.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
58
Câu 35. Cho hình lập phương
.ABCD A BC D
có cạnh bằng
1
. Các điểm
M
,
N
lần lượt thuộc các đoạn
AB
và
AD
sao cho hai mặt phẳng
( )
MAC
và
( )
NAC
vuông góc với nhau. Tìm giá trị nhỏ
nhất của thể tích khối chóp
.A A MC N
.
A.
31
3
+
. B.
52
3
−
. C.
31
3
−
. D.
21
3
−
.
Câu 36. Trong không gian với hệ trục
Oxyz
, cho mặt cầu
( ) ( ) ( )
22
2
: 1 4 8S x y z+ + − + =
và điểm
( ) ( )
3;0;0 ; 4;2;1AB
. Điểm
M
thay đổi nằm trên mặt cầu, tìm giá trị nhỏ nhất của biểu thức
2P MA MB=+
.
A.
22P =
. B.
32P =
. C.
42P =
. D.
62P =
.
Câu 37. Trong không gian
Oxyz
, cho các điểm
( ) ( )
2 ;2 ;0 , 0;0;A t t B t
với
0.t
Cho điểm
P
di động thỏa
mãn
. . . 3OP AP OP BP AP BP+ + =
. Biết rằng có giá trị
a
t
b
=
với
,ab
nguyên dương và
a
b
tối
giản sao cho
OP
đạt giá trị lớn nhất là 3. Tính giá trị
2Q a b=+
?
A.
5
. B.
13
. C.
11
. D.
9
.
Câu 38. Trong không gian
,Oxyz
cho bốn điểm
( ) ( ) ( )
3;0;0 , 0;2;0 , 0;0;6A B C
và
( )
1;1;1 .D
Gọi
là
đường thẳng đi qua
D
và thỏa mãn tổng khoảng cách từ các điểm
, , A B C
đến
là lớn nhất, hỏi
đi qua điểm nào trong các điểm dưới đây?
A.
( )
1; 2;1 .M −−
B.
( )
5;7;3 .M
C.
( )
3;4;3 .M
D.
( )
7;13;5 .M
Câu 39. Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
( ) ( ) ( ) ( )
2
2 2 2
: 1 1
4
m
m
S x y z m− + − + − =
và hai
điểm
( )
2;3;5A
,
( )
1;2;4B
. Tìm giá trị nhỏ nhất của
m
để trên
( )
m
S
tồn tại điểm
M
sao cho
22
9MA MB−=
.
A.
1m =
. B.
33m =−
. C.
8 4 3m =−
. D.
43
2
m
−
=
.
Câu 40. Trong không gian với hệ trục
Oxyz
, cho mặt cầu
( ) ( ) ( )
22
2
: 1 4 8S x y z+ + − + =
và điểm
( ) ( )
3;0;0 ; 4;2;1AB
. Điểm
M
thay đổi nằm trên mặt cầu, tìm giá trị nhỏ nhất của biểu thức
2P MA MB=+
.
A.
22P =
. B.
32P =
. C.
42P =
. D.
62P =
.
Câu 41. Trong không gian
Oxyz
, cho các điểm
( ) ( )
1;1;2 ; 0; 1; 3AB−−
. Xét điểm
M
thay đổi trên mặt
phẳng
( )
Oxz
, giá trị nhỏ nhất của
23OM MA MB++
bằng?
A.
1
. B.
3
2
. C.
1
2
. D.
1
4
.
Câu 42. Trong không gian
Oxyz
, cho hai mặt cầu
2 2 2
1
( ): 2 4 2 2 0S x y z x y z+ + − + − + =
và
2 2 2
2
( ): 2 4 2 4 0S x y z x y z+ + − + − − =
. Xét tứ diện
ABCD
có hai đỉnh
A
,
B
nằm trên
1
()S
; hai
đỉnh
C
,
D
nằm trên
2
()S
. Thể tích khối tứ diện
ABCD
có giá trị lớn nhất bằng
A.
32
. B.
23
. C.
63
. D.
62
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
59
ĐÁP ÁN CHI TIẾT
Câu 1. Chọn A
( ) ( ) ( ) ( ) ( )
1;2; 3 ; 5; 3;1 ; 3;3; 3 ; 3; 2;1 ; 2;0; 2AB CD AC BD AD= − = − − = − = − − = − −
Ta có:
( )
, 3; 6; 3AB AC
= − −
( ) ( )( )
, . 2 .3 0.6 2 3 0AB AC AD
= − + + − − =
.
,,AB AC AD
đồng phẳng hay bốn điểm
, , ,A B C D
đồng phẳng. Vậy đáp án A sai.
Lại có
( ) ( ) ( )
. 3. 2 3.0 3 . 2 0AC AD AC AD= − + + − − = ⊥
.
tam giác
ACD
là tam giác vuông tại
A
. Vậy đáp án B đúng.
Mặt khác:
( ) ( ) ( )
( ) ( )
. 1. 5 2. 3 3 .1 14 0 , 0 ,AB CD cos AB CD AB CD= − + − + − = −
là góc
tù. Vậy đáp án C đúng.
14AB BD hay AB BD= = =
tam giác
ABD
là tam giác cân tại
B
. Vậy đáp án D đúng.
Câu 2. Chọn A
Đường thẳng
đi qua
A
và vuông góc với mặt phẳng
( )
P
có phương trình là:
12
2
3
xt
yt
zt
=+
=+
=+
Gọi
( )
HP=
ta có:
( )
1 2 ;2 ;3H t t t+ + +
và
( )
HP
nên ta có:
( ) ( ) ( )
2 1 2 2 3 5 0t t t+ + + + + + =
6 12 0t + =
2t = −
( )
3;0;1H−
Mặt cầu tâm
I
đi qua
A
, tiếp xúc với mặt phẳng
( )
P
và có bán kính nhỏ nhất nên có đường kính
là đoạn
AH
với
H
là hình chiếu của
A
lên mặt phẳng
( )
P
.
Gọi
( )
;;I a b c
là tọa độ trung điểm của
AH
ta có:
( )
1;1;2I −
2abc + + =
.
Câu 3. Chọn B
Mặt cầu
( )
S
có tâm
( )
3; 2;1I −
và bán kính
3R =
.
Ta có:
( )
( )
,4d I P R=
nên mặt phẳng
( )
P
không cắt mặt cầu
( )
S
.
Gọi
d
là đường thẳng đi qua
I
và vuông góc với mặt phẳng
( )
P
.
A
I
H
P
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
60
Suy ra phương trình đường thẳng
3
: 2 2
12
xt
d y t
zt
=+
= − +
=+
.
Gọi
1
M
,
2
M
là các giao điểm của
d
và
( )
S
.
Khi đó tọa độ điểm
1
M
,
2
M
ứng với
t
là nghiệm của phương trình
( ) ( ) ( ) ( ) ( ) ( )
2 2 2
3 2 2 1 2 6 3 4 2 2 2 1 2 5 0t t t t t t+ + − + + + − + + − + − + + =
1
1
t
t
=
=−
.
Với
( )
1
1 4;0;3tM=
( )
( )
1
,7d M P=
.
Với
( )
2
1 2; 4; 1tM= − − −
( )
( )
2
,1d M P=
.
Với mọi điểm
M
thuộc
( )
S
ta luôn có
( )
( )
( )
( )
( )
( )
21
, , ,d M P d M P d M P
.
Khoảng cách từ
M
đến mặt phẳng
( )
P
ngắn nhất bằng 1 khi
2
MM
.
Vậy
( )
2; 4; 1M −−
.
Câu 4. Chọn A
Đường thẳng
đi qua
A
và vuông góc với mặt phẳng
( )
P
có phương trình là:
12
2
3
xt
yt
zt
=+
=+
=+
Gọi
( )
HP=
ta có:
( )
1 2 ;2 ;3H t t t+ + +
và
( )
HP
nên ta có:
( ) ( ) ( )
2 1 2 2 3 5 0t t t+ + + + + + =
6 12 0t + =
2t = −
( )
3;0;1H−
Mặt cầu tâm
I
đi qua
A
, tiếp xúc với mặt phẳng
( )
P
và có bán kính nhỏ nhất nên có đường kính
là đoạn
AH
với
H
là hình chiếu của
A
lên mặt phẳng
( )
P
.
Gọi
( )
;;I a b c
là tọa độ trung điểm của
AH
ta có:
( )
1;1;2I −
2abc + + =
.
Câu 5. Chọn A
Gọi
( )
;;
H H H
H x y z
là điểm thỏa mãn
30HA HB HC+ + =
.
Khi đó:
( )
( )
( ) ( )
1 3 3 2 0
2
4 4 3 1 0 1
1
5 3 0
H H H
H
H H H H
H
H H H
x x x
x
y y y y
z
z z z
− + − + − =
=
− + − + − − = =
=
− + − + − =
( )
2;1;1H
.
A
I
H
P

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
61
Ta có:
( ) ( ) ( )
2 2 2
2 2 2
33T MA MB MC MH HA MH HB MH HC= + + = + + + + +
( )
2 2 2 2
5 3 2 3MH HA HB HC MH HA HB HC= + + + + + +
2 2 2 2
53MH HA HB HC= + + +
.
Suy ra
T
đạt giá trị nhỏ nhất
MH
nhỏ nhất
M
là hình chiếu của
H
lên
( )
P
.
Phương trình đường thẳng
d
đi qua
( )
2;1;1H
và vuông góc với
( )
P
là
( )
23
1 3 ,
12
xt
y t t
zt
=+
= +
=−
.
Tọa độ của điểm
M
thỏa mãn hệ phương trình
2 3 5
1 3 4
1 2 1
3 3 2 29 0 1
x t x
y t y
z t z
x y z t
= + =
= + =
= − = −
+ − − = =
( )
5;4; 1M −
. Vậy
8abc+ + =
.
Câu 6. Chọn B
Gọi
G
là trọng tâm tam giác
ABC
( )
1; 1;1G−
.
Ta có:
P EA EB EC= + +
3 3 0EG EG= =
min
0P=
khi
( )
1; 1;1EG−
1T=
, chọn B.
Câu 7. Chọn C
Mặt cầu
( )
S
có tâm
( )
1; 2; 1I = − −
và có bán kính
3R =
.
Mặt phẳng
( )
P
có véctơ pháp tuyến
( )
2; 1;2n =−
.
Gọi
d
là đường thẳng đi qua
I
và vuông góc với mặt phẳng
( )
P
thì đường thẳng
d
có phương
trình tham số là
12
2
12
xt
yt
zt
=+
= − −
= − +
.
Điểm
M
thuộc mặt cầu
()S
sao cho khoảng cách từ
M
đến mặt phẳng
()P
là lớn nhất khi và
chỉ khi
M
là giao điểm của đường thẳng
d
và mặt cầu
( )
S
.
Khi đó tọa độ điểm
M
là nghiệm của hệ phương trình
2 2 2
12
2
12
2 4 2 3 0
xt
yt
zt
x y z x y z
=+
= − −
= − +
+ + − + + − =
12
2
12
1
1
xt
yt
zt
t
t
=+
= − −
= − +
=
=−
.
Với
( ) ( )
( )
6 3 2 14
1 3; 3;1 d , 1
3
t M M P
+ + −
= − = =
.
Với
( ) ( )
( )
2 1 6 14
1 1; 1; 3 d , 7
3
t M M P
− + − −
= − − − − = =
.
Vậy
( )
1; 1; 3M −−−
thỏa mãn nên
1, 1, 3 5a b c K a b c= − = − = − = + + = −
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
62
Câu 8. Chọn B
Cách 1: Gọi
I
là tâm mặt cầu tiếp xúc với cả hai đường thẳng
1
và
2
.
Q
là tiếp điểm của
1
với mặt cầu;
R
là tiếp điểm của
2
với mặt cầu.
J
là trung điểm của
QR
.
Ta có:
R IQ JQ R=
nhỏ nhất khi và chỉ khi
I
trùng
J
hay
QR
là đoạn vuông góc chung
của
1
và
2
, khi đó tâm mặt cầu
I
là trung điểm của đoạn vuông góc chung,
2R
bằng độ dài
đoạn vuông góc chung.
Gọi
( )
( )
1
2
4 3 ;1 ; 5 2 ,
2 ; 3 3 ; , .
Q a a a a
R b b b b
+ − − −
+ − +
Khi đó ta có vec tơ chỉ phương
( )
1
3; 1; 2u
= − −
,
( )
2
1;3;1u
=
,
( )
3 2 ; 3 4 ; 2 5 .RQ a b a b a b= − + − − + − − −
Theo giả thiết đề bài ta có:
( )
1
2
.0
1
2; 2;4 2 6 6.
1
2
.0
RQ u
a
RQ
RQ RQ R
b
RQ u
⎯⎯→ ⎯⎯→
⎯⎯→
⎯⎯→ ⎯⎯→
=
=−
= − = = =
=
=
Cách 2: Gọi hai mặt phẳng song song và lần lượt chứa
1
và
2
là
( )
P
và
( )
Q
.
Mặt cầu có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng
1
và
2
sẽ tiếp xúc với
( )
P
và
( )
Q
nên đường kính hình cầu là khoảng cách giữa hai mặt phẳng
( )
P
và
( )
Q
hay là khoảng cách
từ
2
tới mặt phẳng
( )
P
.
Khi đó ta có
( ) ( )
12
3; 1; 2 ; 1;3;1VTCP u u
= − − =
và
( )
2
2; 3;0N = −
.
Véc-tơ pháp tuyến của
( )
P
là
( ) ( )
1 1 2
11
; 5; 5;10 1; 1;2
55
u u u
= = − = −
Ta có phương trình mặt phẳng
( )
P
là
2z 7 0xy− + + =
.
Vậy
( ) ( )
( )
( )
( )
( )
( )
2
, , , 2 6d P Q d P d N P= = =
. Suy ra bán kính mặt cầu là
6R =
.
Câu 9. Chọn C
Gọi
( )
;0;0M x Ox
;
( )
2
2 2 2
1 3 4MA x= + + +
;
( )
2
2 2 2
9 7 2MB x= − + +
.
Suy ra
( )
2
2 2 2
2 16 160 2 4 128 128,MA MB x x x x+ = − + = − +
.
Nên
22
MA MB+
đạt giá trị nhỏ nhất là 128 khi
4x =
. Vậy
( )
4;0;0M =
Câu 10. Chọn B
Gọi
()Q
là mặt phẳng đi qua
(2; 2;0)M
và song song với
()P
.
Phương trình mặt phẳng
()Q
là:
1( 2) 2( 2) 2( 0) 0− − − + − =x y z
2 2 2 0x y z− + + =
.
Theo bài ra
()dQ
.
Gọi
A
,
B
lần lượt là hình chiếu của
A
,
B
trên
()Q
. Khoảng cách từ
A
,
B
đến
d
lần lượt là
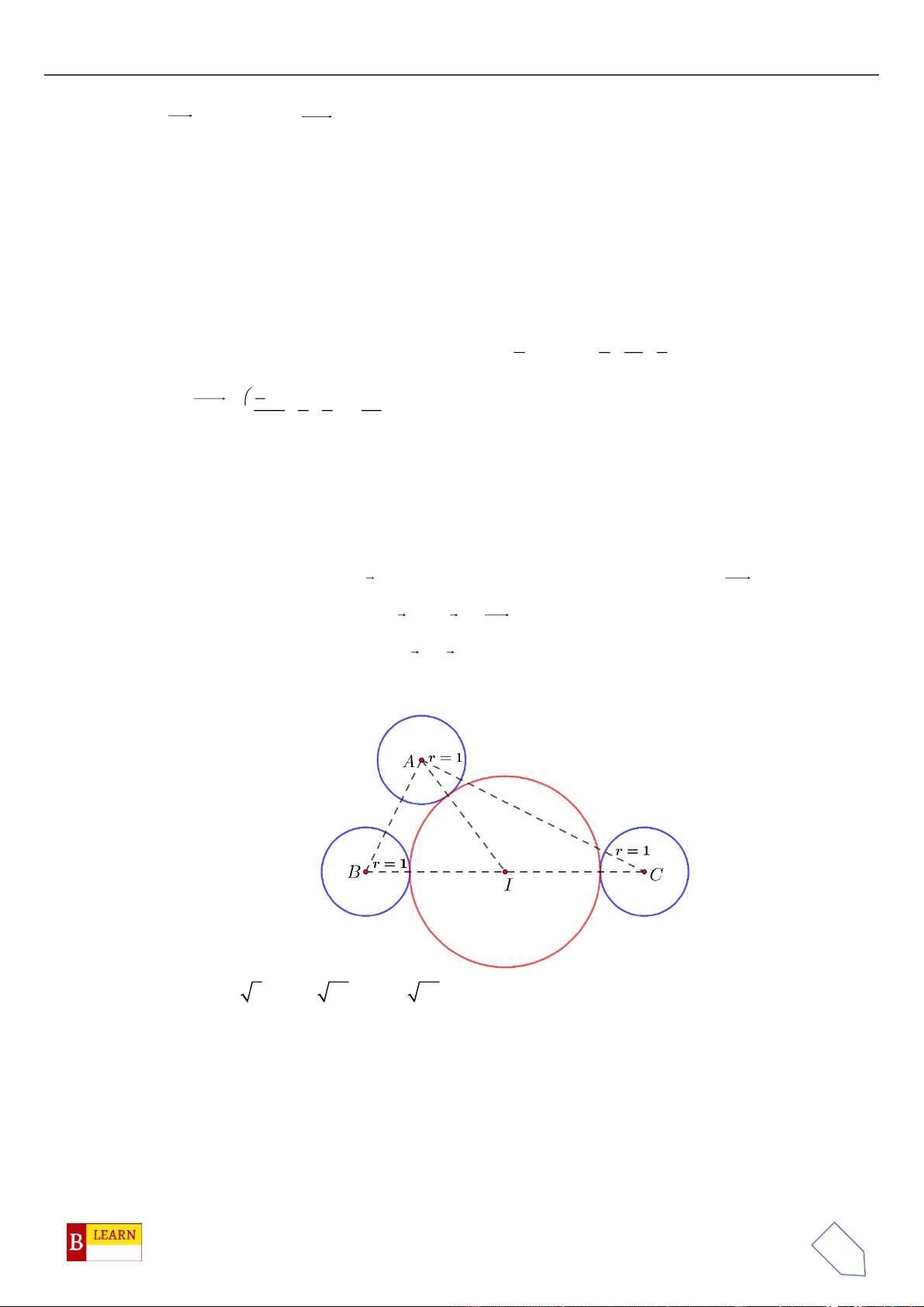
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
63
1
k
,
2
k
. Khi đó
12
k k AA BB
+ +
.
Vì
( 6 ; 3; 0)AB =−
,
( 4 ; 2 ; 0)AM =−
là hai vectơ cùng phương nên
A
,
B
và
M
thẳng hàng.
Do đó, dấu bằng xảy ra khi
d
đi qua
A
,
B
.
Ta có hai cách sau để tìm tọa độ vectơ chỉ phương của
d
.
Cách 1: Tìm
B
.
Đường thẳng đi qua
B
và vuông góc với
()Q
có phương trình:
32
2
xt
yt
zt
=
=−
=
( )
;3 2 ;2B t t t
−
()BQ
suy ra
4
2(3 2 ) 2(2 ) 2 0
9
t t t t− − + + = =
4 19 8
;;
9 9 9
B
=
.
Từ đó
14 1 8 1
; ; (14; 1; 8)
9 9 9 9
MB
−−
= = − −
.
Do vậy, một vectơ chỉ phương của
d
là
(14; 1; 8)−−
.
Cách 2: Ta thấy
d
là giao của hai mặt phẳng:
()Q
và
()R
với
()R
là mặt phẳng chứa
A
,
B
và vuông góc với
()Q
. Do đó vectơ chỉ phương của
d
cùng phương với tích có hướng của hai
véc tơ pháp tuyến tương ứng của
()Q
và
()R
.
Vectơ pháp tuyến của
()Q
là
()
(1; 2 ; 2)
Q
n =−
. Vectơ chỉ phương của
AB
là
( 6 ; 3; 0)AB =−
.
Nên vectơ pháp tuyến của
()R
là
( ) ( )
[ , ] ( 6 ; 12 ; 9) 3(2 ; 4 ; 3).
RQ
n n AB= = − − − = −
Từ đó vec tơ chỉ phương của
d
là
( ) ( )
[ , ] ( 14 ;1;8)
QR
nn=−
.
Câu 11. Chọn B
Ta có:
8; 32 ; 40AB AC BC= = =
2 2 2
AB AC BC + =
ABC
vuông tại
A
.
Thấy 3 mặt cầu
( )
1
S
,
( )
2
S
,
( )
3
S
có đôi một nằm ngoài nhau.
Khi đó: Mặt cầu
( )
S
tiếp xúc với 3 mặt cầu
( )
1
S
,
( )
2
S
,
( )
3
S
và có bán kính nhỏ nhất
( )
S
có tâm thuộc
( )
mp ABC
và
( )
S
tiếp xúc ngoài với 3 mặt cầu
( )
1
S
,
( )
2
S
,
( )
3
S
( )
S
có tâm
I
thuộc
( )
mp ABC
và
IA IB IC==
( )
S
có tâm
( )
1;0; 1I −
, (trong đó
I
là trung điểm của
BC
).

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
64
Vậy mặt cầu
( )
S
có bán kính nhỏ nhất
min
10 1R IA r= − = −
.
Câu 12. Chọn C
Mặt cầu
( )
S
có tâm
( )
1; 2;2I −
và bán kính
2R =
.
( )
( )
,6d I P R=
suy ra mặt phẳng
( )
P
không cắt mặt cầu
( )
S
.
Điểm
( )
MS
thỏa mãn
( )
( )
,d M P
nhỏ nhất bằng
( )
( )
, 6 2d I P R− = −
.
Câu 13. Chọn C
Giả sử
( )
;;M x y z
và
( )
;;N a b c
.
Khi đó
( ) ( ) ( )
2 2 2
2
P x a y b z c MN= − + − + − =
.
Vì
( ) ( ) ( )
2 2 2
3 2 1 2x y z+ + − + + =
nên
M
thuộc mặt cầu
( )
S
có tâm
( )
3;2; 1I −−
và bán kính
2R =
.
Vì
1abc+ + =
nên
N
thuộc mặt phẳng
( )
: 1 0P x y z+ + − =
.
Ta có
( )
( )
3 2 1 1
;3
111
d I P R
− + − −
= =
++
mặt phẳng
( )
P
không cắt mặt cầu
( )
S
.
( )
( )
( )
2
2
2
min min ; 3 2 5 2 6P MN d I P R
= = − = − = −
.
Câu 14. Chọn B
Ta có:
( ) ( ) ( ) ( )
2 2 2 2
2 2 2 2
22
22
1 2 1 2 1 3
2 6 2 2 20
31
2 2 15 15.
22
MA MB a b a b
a a b b
ab
+ = − + − + + − + − − +
= − + − +
= − + − +
Đẳng thức xảy ra khi
3
2
1
2
a
b
=
=
khi đó
2.ab+=
Câu 15. Chọn A

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
65
Mặt cầu
( )
S
có tâm
( )
4;2;4I
, bán kính
1R =
2 2 2
OM a b c= + +
Ta có
OM OI IM OI R − = −
Nên
OM
nhỏ nhất khi
OM =
OI R−=
222
4 2 4 1+ + −
5=
Vậy giá trị nhỏ nhất của
2 2 2
25abc+ + =
.
Câu 16. Chọn B
Ta có
2T MA MB MC= + +
2 2 4 2MI IA MI IB MI IC MI IA IB IC= + + + + + = + + +
Tìm tọa độ điểm
( )
;;
I I I
I x y z
sao cho
20IA IB IC+ + =
( )
( )
( )
0 2 2 4 0
1 2 1 1 0
1 2 1 1 0
I I I
I I I
I I I
x x x
y y y
z z z
− + − + − =
− + − − + − =
− + − + − =
2
0
1
I
I
I
x
y
z
=
=
=
( )
2 ; 0 ;1I
4T MI=
mà điểm
M
thuộc
( )
mp P
Vậy giá trị nhỏ nhất của biểu thức đạt được khi điểm
M
là hình chiếu của điểm
I
lên
( )
mp P
.
( )
( )
,
222
2 0 1 6
min 4. 4. 4 3
111
IP
Td
+ + −
= = =
++
.
Đường thẳng
IM
đi qua điểm
I
và nhận vectơ
( )
( )
1;1;1
P
n =
làm vectơ chỉ phương.
( )
2
1
xt
y t t
zt
=+
=
=+
. Gọi điểm
( )
2 ; ;1M t t t IM+ +
mà
( )
MP
2 1 6 0t t t + + + + − =
1t=
( )
3;1; 2M
.
Vậy giá trị của
24a b c+ + =
2.3 4.1 2 12+ + =
Câu 17. Chọn D
Vì
Md
nên
( )
3;2 1;3 3M t t t+ + +
.
Suy ra
( )
1; 2 1; 3MA t t t= − − − − −
,
( )
1; 2 3; 3 6MB t t t= − − − − − −
.
( ) ( ) ( )
22
2 2 2
1 2 1 9 14 6 2 1MA t t t t t= + + + + = + +
.
( ) ( ) ( ) ( )
2 2 2
22
1 2 3 3 6 14 50 46 2MB t t t t t= + + + + + = + +
.
Ta có
( )
2
4 4 2 2 2 2 2 2
. 3 .P MA MB MA MB MB MA MA MB= + + = − +
Thay
( )
1
và
( )
2
vào
P
ta được
( )
( )( )
2
22
44 44 3 14 6 2 14 50 46P t t t t t= + + + + + +
( ) ( ) ( ) ( ) ( )
2 2 2
2
44 1 3 14 1 10 22 1 14 1 10 22 1t t t t t
= + + + + − + + + + +
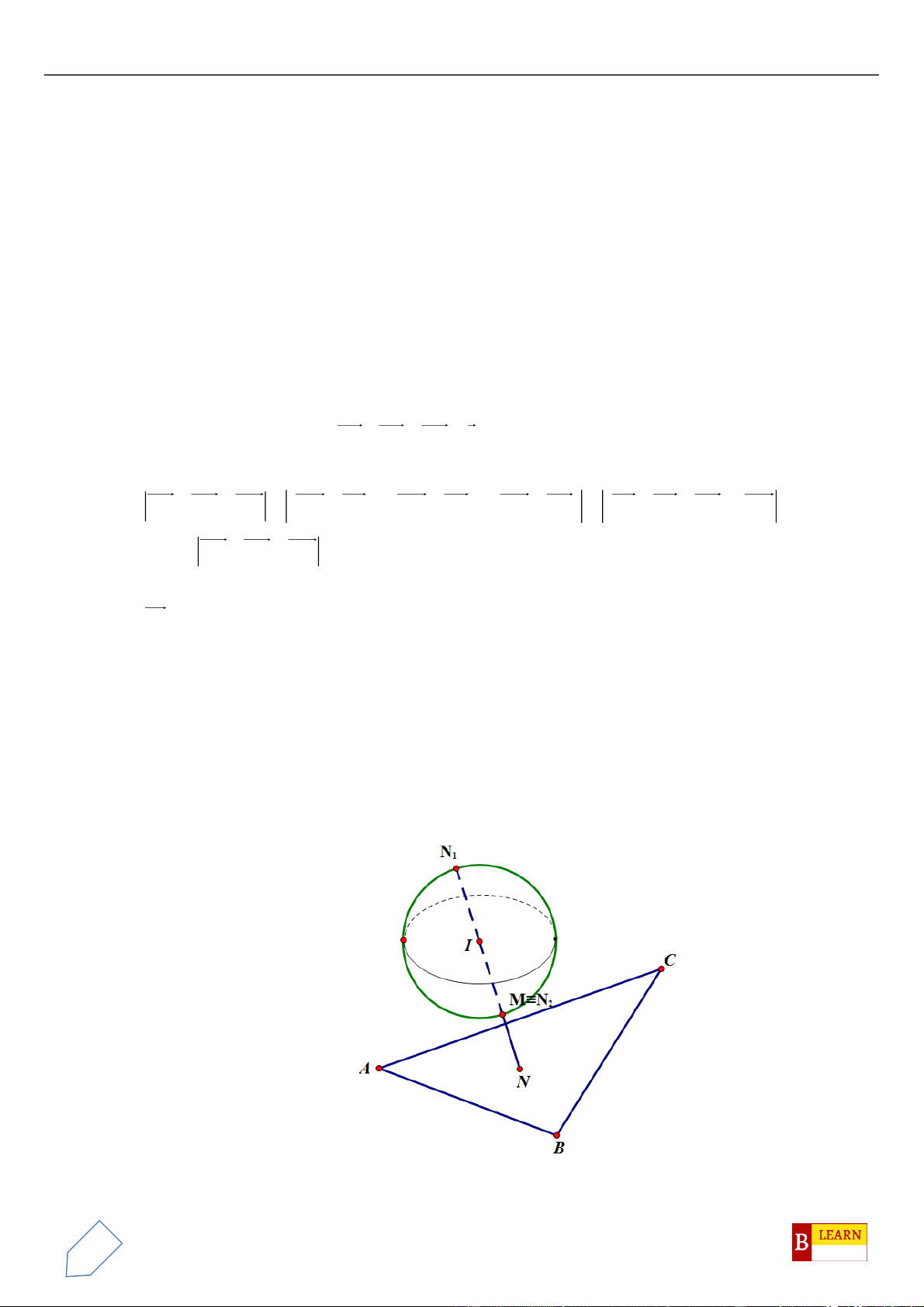
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
66
( ) ( ) ( )
2
2 2 2
2
1936 1 3 14 1 10 22 1t t t
= + + + + − +
( ) ( ) ( ) ( )
2 4 2 2
1936 1 3 196 1 280 1 100 484 1t t t t
= + + + + + + − +
( ) ( )
42
588 1 1324 1 300tt= + + + +
. Đặt
( )
2
2
1 , 0 588 1324 300, 0u t u P u u u= + = + +
.
Xét hàm số
( )
2
588 1324 300, 0f u u u u= + +
có
( )
' 1176 1324 0, 0f u u u= +
cho nên
( ) ( )
0 , 0f u f u
.
Ta được
( )
min
0 300Pf==
khi
0
0 1 0 1 2.( 1) 1 1u t t y= + = = − = − + = −
. Vậy
0
1y =−
.
Câu 18. Chọn B
Gọi
N
là điểm thỏa mãn
0NA NB NC− − =
, suy ra
( )
2;0;1N −
.
Khi đó:
( ) ( ) ( ) ( )
MA MB MC MN NA MN NB MN NC NA NB NC MN MN− − = + − + − + = − − − =
.
Suy ra
MA MB MC−−
nhỏ nhất khi
MN
nhỏ nhất. Mặt cầu
( )
S
có tâm
( )
2;4; 1I −
, suy ra:
( ) ( )
4;4; 2 2;2; 1NI = − = −
. Phương trình
22
42
1
xt
NI y t
zt
=+
= = +
= − −
. Thay phương trình NI vào phương
trình
( )
S
ta được:
( ) ( ) ( )
2 2 2
2
1
2 2 9 1
1
t
t t t t
t
=
+ + − = =
=−
.
Suy ra
NI
cắt
( )
S
tại hai điểm phân biệt
( ) ( )
12
3;6; 2 , 0;2;0NN−
.
Vì
12
NN NN
nên MN nhỏ nhất khi và chỉ khi
2
MN
. Vậy
( )
0;2;0M
là điểm cần tìm.
Suy ra:
2.ab+=
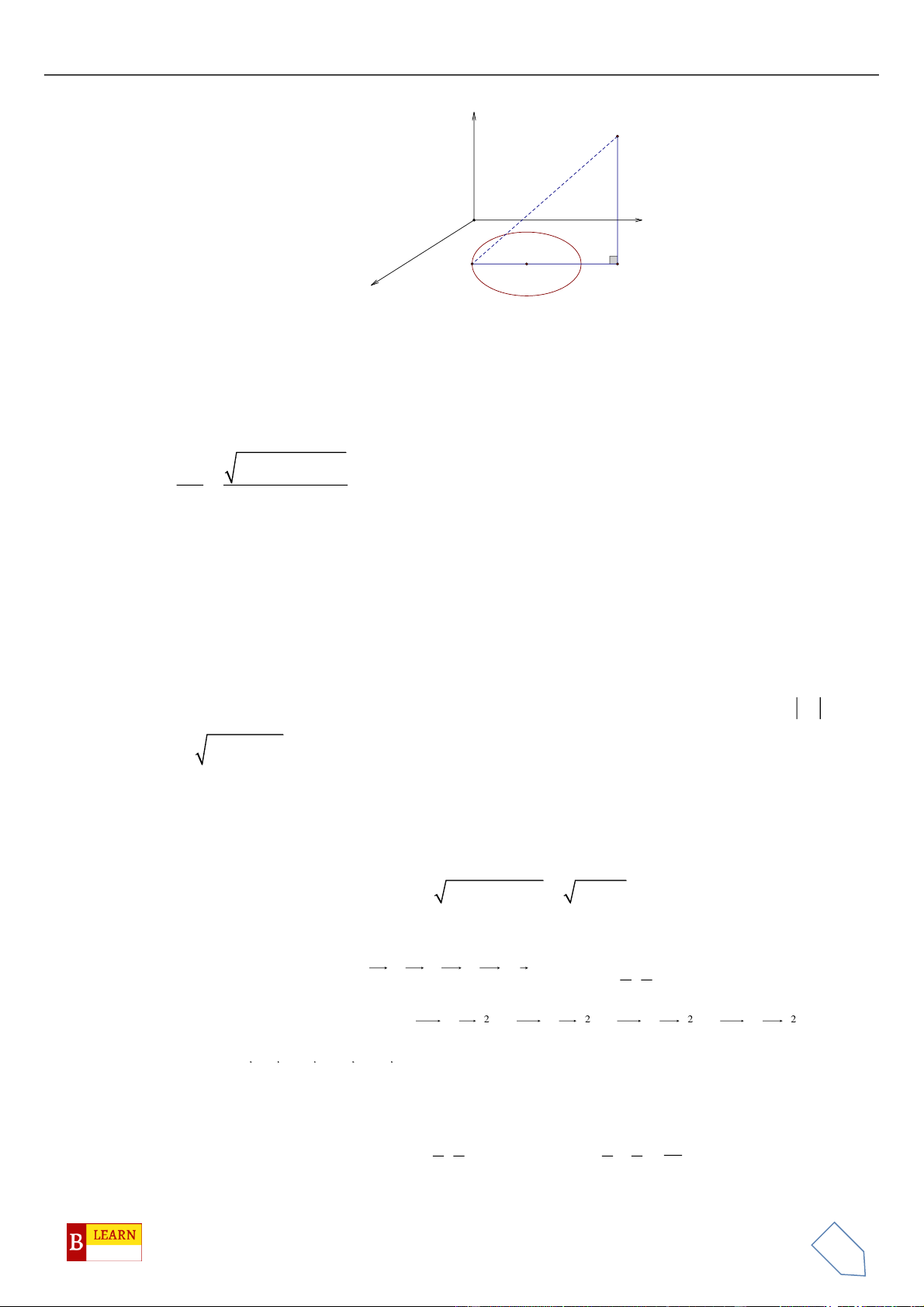
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
67
Câu 19.
Chọn C
Giả sử
( )
; ;0M x y
. Gọi
I
là trung điểm
AB
(1;2;4)I
.
Do
MA MB⊥
tại
M
, suy ra
M
thuộc mặt cầu tâm
I
bán kính
( )
2
22
6 8 0
5
22
AB
R
− + +
= = =
.
Mặt khác
M Oxy
suy ra toa độ điểm M thỏa mãn
( ) ( ) ( )
2 2 2
1 2 4 25
0
x y z
z
− + − + − =
=
( ) ( )
22
1 2 9
0
xy
z
− + − =
=
. Suy ra M thuộc đường trong
( )
C
có tâm
( )
1;2;0H
và bán kính
3R =
Gọi
C
là hình chiếu của
C
lên
( )
Oxy
, suy ra
( )
5; 1;0C
−
,
66CC
= − =
.
( )
2
2
4 3 5HC
= + − =
CM
lớn nhất khi và chỉ khi
CM
lớn nhất.
CM
lớn nhất bằng
( )
5 3 8HC R
+ = + =
.
Suy ra độ dài đoạn
CM
lớn nhất bằng
2 2 2 2
8 6 10C M CC
+ = + =
.
Câu 20. Chọn B
Xét điểm
( )
;;I a b c
thỏa mãn
0IA IB IC ID+ + + =
. Khi đó
77
; ;0
42
I
.
Ta có
2 2 2 2
MA MB MC MD+ + +
( ) ( ) ( ) ( )
2 2 2 2
MI IA MI IB MI IC MI ID= + + + + + + +
( )
2 2 2 2 2
42MI MI IA IB IC ID IA IB IC ID= + + + + + + + +
2 2 2 2 2 2 2 2 2
4MI IA IB IC ID IA IB IC ID= + + + + + + +
( vì
2
0MI
với mọi điểm
M
)
Dấu
""=
xảy ra
MI
tức là
7 7 7 7
; ;0
4 2 4 2
M x y z
+ + = +
21
4
=
.
Câu 21. Chọn B
x
z
y
M
O
H
C'
C

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
68
Gọi
( )
;;I x y z
là điểm thỏa mãn
2 3 0IA IB IC+ + =
.
Ta có
( )
10 ; 5 ;8IA x y z= − − − − −
,
( )
2 ;1 ; 1IB x y z= − − − −
,
( )
2 ;3 ;IC x y z= − − −
.
Khi đó,
( ) ( ) ( )
( ) ( ) ( )
( ) ( ) ( )
10 2 2 3 2 0
5 2 1 3 3 0
8 2 1 3 0
x x x
y y y
z z z
− − + − + − =
− − + − + − =
− + − − + − =
0
1
1
x
y
z
=
=
=
( )
0;1;1I
.
Với điểm
M
thay đổi trên
( )
P
, ta có
2 2 2
23MA MB MC++
( ) ( ) ( )
2 2 2
23MI IA MI IB MI IC= + + + + +
( )
2 2 2 2
6 2 3 2 2 3MI IA IB IC MI IA IB IC= + + + + + +
2 2 2 2
6 2 3MI IA IB IC= + + +
(Vì
2 3 0IA IB IC+ + =
).
Ta lại có
2 2 2
23IA IB IC++
185 2.8 3.9= + +
228=
.
Do đó,
2 2 2
23MA MB MC++
đạt giá trị nhỏ nhất
MI
đạt giá trị nhỏ nhất
M
là hình chiếu vuông góc của
I
trên
( )
P
.
Khi đó,
( )
( )
,3MI d I P==
.
Vậy giá trị nhỏ nhất của
2 2 2
23MA MB MC++
bằng
2
6 228MI +
6.9 228=+
282=
.
Giá trị nhỏ nhất của
2 2 2
23MA MB MC++
đạt được khi và chỉ khi
M
là hình chiếu vuông góc của
I
trên
( )
P
.
Lưu ý thêm cách tìm điểm
M
như sau:
Gọi
là đường thẳng qua
I
và vuông góc với
( )
P
. Phương trình của
:
12
12
xt
yt
zt
=
=+
=−
.
Ta có
( )
MP=
. Xét phương trình
( ) ( )
2 1 2 2 1 2 9 0t t t+ + − − − =
9 9 0t − =
1t=
( )
1;3; 1M −
.
Câu 22. Chọn D
Cách 1:
Ta có
( ) ( ) ( ) ( ) ( )
2 2 2
; ; 2 1 1 9M a b c S a b c − + − + − =
.
Áp dụng bất đẳng thức Bunhiacopski ta có
( ) ( ) ( )
( )
( ) ( ) ( )
2
2 2 2
222
1. 2 2. 1 2. 1 1 2 2 2 1 1a b c a b c
− + − + − + + − + − + −
( ) ( ) ( ) ( ) ( ) ( )
2
1. 2 2. 1 2. 1 9.9 9 1. 2 2. 1 2. 1 9a b c a b c − + − + − − − + − + −
3 2 2 15abc − + +
hay
3 15P−
.
Vậy
( ) ( ) ( )
min
1
2 1 1
1 2 2
31
1. 2 2. 1 2. 1 9
1
a
a b c
Pb
a b c
c
=
− − −
==
= − = −
− + − + − = −
=−
.
Khi đó
( ) ( )
1 1 1 1T a b c= + + = + − + − = −
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
69
Cách 2:
Mặt cầu
( )
S
có tâm
( )
2;1;1I
, bán kính
3R =
. Để
( ) ( )
;;M a b c S
đồng thời
22P a b c= + +
đạt giá trị nhỏ nhất thì
M
phải là điểm chung giữa
( )
S
và mặt phẳng
( )
: 2 2 0Q x y z P+ + − =
.
Suy ra
( )
( )
; 6 9 3 15d I R P P
− −
. Ta có
3P =−
khi
1a =
,
1b =−
,
1c =−
.
Vậy
1T a b c= + + = −
.
Câu 23. Chọn A
Cách 1:
Mặt cầu
( ) ( ) ( )
22
2
: 3 4 4.S x y y+ − + + =
có tâm
( )
0;3; 4I −
, bán kính
2R =
.
Ta có:
( ) ( ) ( )
22
22
2OM ON OI IM OI IN OI IM IN− = + − + = −
, (vì
IM IN R==
)
( )
2 . 2. .NM.cos , 2 .NM 10OI NM OI OI NM OI= = − = −
.
Dấu “=” xảy ra khi hai véc tơ
OI
,
NM
ngược hướng.
Vậy giá trị nhỏ nhất của biểu thức
22
OM ON−
là
10−
.
Cách 2:
Xét điểm
( )
;;M x y z
,
( )
;;N a b c
ta có
( )
( )
( ) ( ) ( )
( ) ( ) ( )
( ) ( ) ( )
22
2
22
2
2 2 2
3 4 4 1
3 4 4 2
1
1(3)
x y z
MS
N S a b c
MN
x a y b z c
+ − + + =
+ − + + =
=
− + − + − =
.
Lấy
( ) ( )
12−
theo vế có:
( ) ( )
2 2 2 2 2 2
6 8 .x y z a b c y b z c+ + − − − = − − −
Kết hợp sử dụng bất đẳng thức Cauchy – Schwarz (Bunhiacopski) và (3) ta có
( ) ( )
2 2 2 2 2 2 2 2
68OM ON x y z a b c y b z c− = + + − − − = − − −
( )
( ) ( )
( )
( )
( ) ( )
( )
2 2 2 2
2 2 2 2 2
6 8 6 8 ( ) 10.y b z c y a y b z c − + − + − − + − + − + − = −
Dấu bằng đạt tại
( ) ( )
( ) ( )
( ) ( ) ( )
22
2
22
2
2 2 2
3 4 4
3 4 4
1
.
0
0
68
x y z
a b c
x a y b z c
xa
y b z c
k
+ − + + =
+ − + + =
− + − + − =
−=
−−
= =
−
Chọn đáp án A.
*Một cách tương tự mở rộng cho min – max của
22
.
+OM ON
Câu 24. Chọn C
Cách 1.
Gọi
H
là điểm thỏa mãn
20HA HB−=
( )
13; 11;19H −
.
Ta tính:
2
1088HA =
;
2
272HB =
;
( )
( )
d , 7 3H
=
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
70
Ta có:
( ) ( )
22
22
22MA MB MH HA MH HB− = + − +
.
( )
2 2 2 2 2
2 2 2 2MA MB MH MH HA HB HA HB− = − + − + −
2 2 2
2 544MA MB MH− = − +
.
( )
( )
2 2 2
2 d , 544 397MA MB H
− − + =
.
Vậy giá trị lớn nhất của
22
2 397MA MB−=
khi
M
là hình chiếu vuông góc của
H
trên
( )
.
Cách 2.
Gọi
( ) ( )
;;M a b c
0abc+ + =
a b c= − −
.
Ta tính
( ) ( ) ( )
2 2 2
2
3 5 5MA a b c= − − + − + − −
;
( ) ( ) ( )
2 2 2
2
5 3 7MB a b c= − + − − + −
.
2 2 2 2 2
2 26 22 38 107MA MB a a b b c c− = − + − − − + −
.
( )
2 2 2 2
2 2 2 24 2 12 107MA MB b b c c c− = − − + − + −
.
2
2 2 2
24 3
2 2 36 181
22
c
MA MB b c c
+
− = − + − + +
( )
2
2
22
24 3
2 2 12 397
22
c
MA MB b c
+
− = − + − − +
22
2 397MA MB−
.
Giá trị lớn nhất của
22
2 397MA MB−=
khi
12; 18; 6c b a= = − =
.
Vậy giá trị lớn nhất của
22
2 397MA MB−=
khi
( )
6; 18;12M −
.
Câu 25. Chọn D
Gọi
( )
là mặt phẳng đi qua
A
và vuông góc
d
. Suy ra
( )
:2 2 3 0x y z
+ − − =
.
đi qua
A
và vuông với
d
nên
nằm trong
( )
.
Vì
cắt
( )
S
tại hai điểm có khoảng cách lớn nhất nên
đi qua tâm
K
của đường tròn giao
tuyến của
( )
và
( )
S
.
Ta có:
K
là hình chiếu vuông góc của tâm
I
của mặt cầu lên
( )
nên
23 14 47
;;
9 9 9
K
.
Khi đó:
( )
5 5 20
; ; 1;1;4
9 9 9
AK u
= =
.
Câu 26. Chọn B
Chọn điểm
K
sao cho
2 5 0KA KB KC− + =
.
Khi đó:
( ) ( ) ( )
( ) ( ) ( )
( ) ( ) ( )
1 2 3 5 4 0
2 2 1 5 0 0
2 2 2 5 3 0
K K K
K K K
K K K
x x x
y y y
z z z
− − − − + − − =
− − − − + − =
− − − − + − =
27
4
1
21
4
K
K
K
x
y
z
=−
=
=
27
21
;1;
44
K
−
.
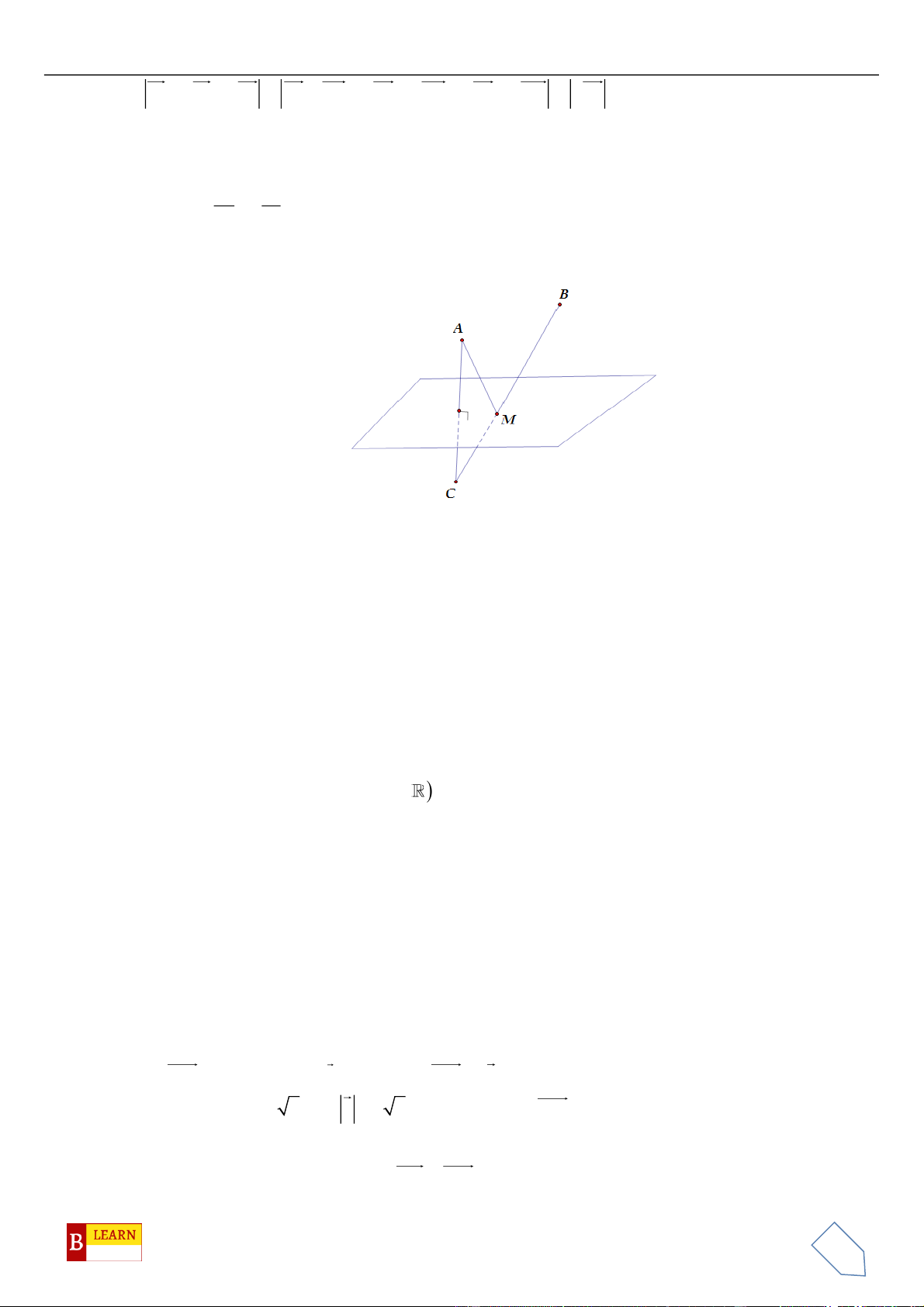
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
71
2 5 2 2 5 5 4 4IA IB IC IK KA IK KB IK KC IK IK− + = + − − + + = =
.
IK
đạt giá trị nhỏ nhất khi
K
là hình chiếu vuông góc của
I
lên mặt phẳng
( )
Oxz
.
Vậy
27 21
;0;
44
I
−
.
Câu 27. Chọn C
Mặt phẳng
( )
Oxz
có phương trình
0y =
.
Vì
. 3 0
AB
yy=
nên
A
,
B
nằm cùng phía với mặt phẳng
( )
Oxz
.
Lấy điểm
C
đối xứng với
A
qua
( )
Oxz
. Suy ra
( )
1; 3;4C −−
.
Khi đó
MA MB+
nhỏ nhất khi và chỉ khi
MC MB+
nhỏ nhất. Suy ra
M
là giao điểm của đường
thẳng
BC
với mặt phẳng
( )
Oxz
.
Đường thẳng
BC
:
( )
1
3,
4
xt
y t t
zt
= − +
= − +
=−
.
Tọa độ điểm
( )
;;M x y z
là nghiệm của hệ :
1
3
30
4
0
xt
yt
t
zt
y
= − +
= − +
− + =
=−
=
3t=
.
( )
0
2;0;1 2Mx =
.
Câu 28. Chọn A
Vì cùng hướng với nên .
Hơn nữa, . Suy ra .
Gọi là điểm sao cho .
MN
a
0:t MN ta =
5 2 . 5 2MN t a= =
5t=
( )
5; 5;0MN =−
( )
;;A x y z
AA MN
=
45
75
30
x
y
z
+=
− = −
−=
1
2
3
x
y
z
=
=
=
( )
1;2;3A
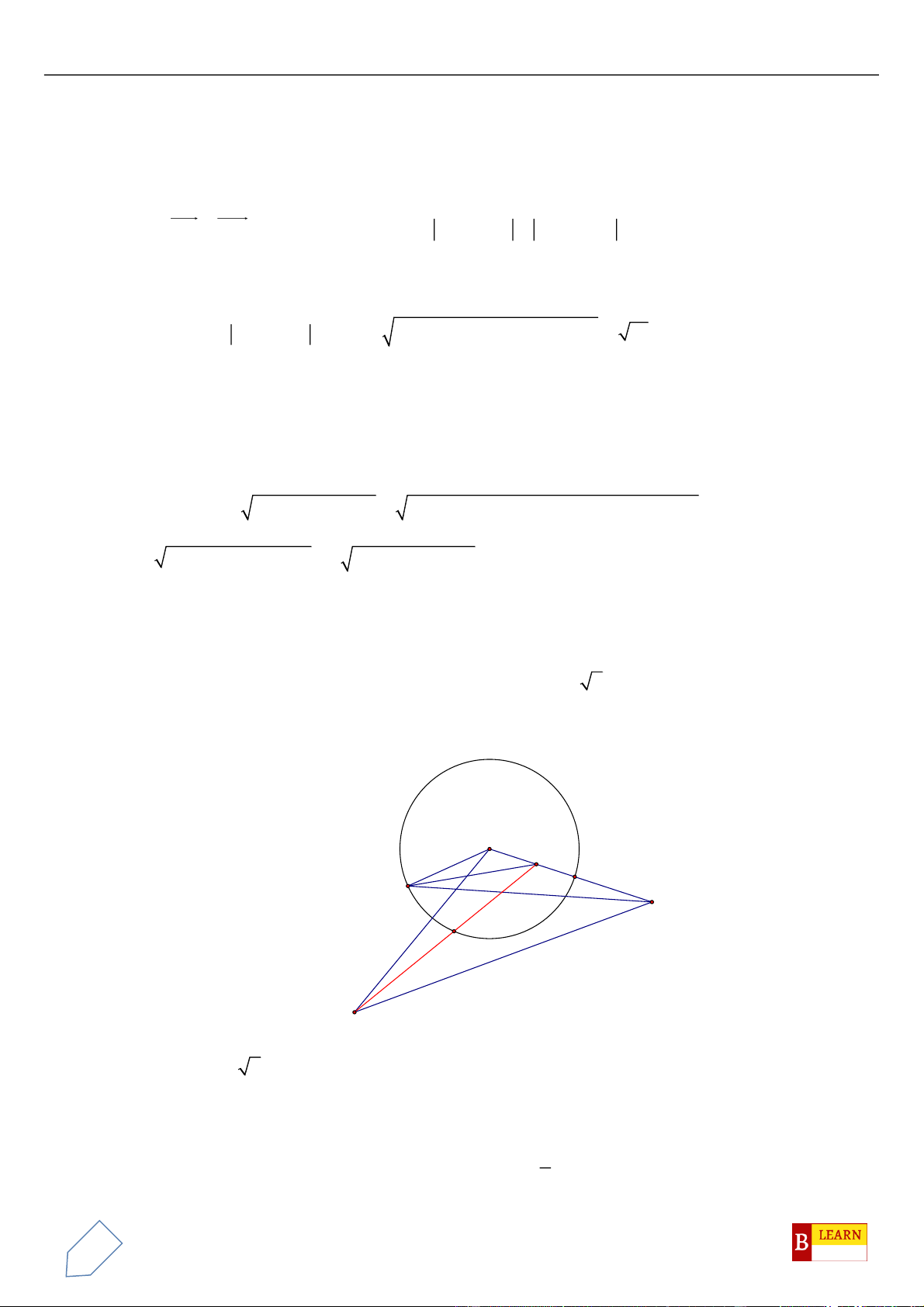
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
72
Dễ thấy các điểm , đều nằm cùng phía so với mặt phẳng vì chúng đều có cao độ
dương. Hơn nữa vì cao độ của chúng khác nhau nên đường thẳng luôn cắt mặt phẳng
tại một điểm cố định.
Từ suy ra nên dấu bằng xảy ra khi
là giao điểm của đường thẳng với mặt phẳng .
Do đó , đạt được khi
.
Câu 29. Chọn C
Cách 1: Gọi ta có
Do đó
với
Dễ thấy nằm trong mặt cầu, nằm ngoài mặt cầu nên nhỏ nhất
khi thẳng hàng.
Vậy, giá trị nhỏ nhất của biểu thức là
Cách 2:
Ta có với là tâm mặt cầu.
Gọi lần lượt là trung điểm của và
+ là điểm nằm trên đường thẳng ta có
A
B
( )
Oxy
'AB
( )
Oxy
AA MN
=
AM A N
=
''AM BN A N BN A B− = −
N
'AB
( )
Oxy
( ) ( ) ( )
2 2 2
max ' 4 1 4 2 5 3 17AM BN A B− = = − + − + − =
( )
N A B Oxy
=
( ; ; ) ( ),M a b c S
2 2 2 2 2 2
( 1) ( 4) 8 2 8 9a b c a b c a b+ + − + = + + = − + −
2 2 2 2 2 2 2 2 2
( 3) 4( ) 3( ) 6 9MA a b c a b c a b c a= − + + = + + − + + − +
2 2 2 2 2 2
2 6 9 2 ( 3) 2 'a b c b a b c MB+ + − + = + − + =
'(0;3;0).B
'B
B
2 2( ' )MA MB MB MB+ = +
', ,B M B
2MA MB+
2 ' 6 2.BB =
M
0
E
I
A
B
B'
M
4 2,IA =
I
(1;2;0), '(0;3;0)EB
IA
.IE
M
IA
1
'.
2
MB MA=

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
73
+ là điểm không nằm trên đường thẳng ta có nên ,
ta có
Dễ thấy nằm trong mặt cầu, nằm ngoài mặt cầu nên nhỏ nhất
khi thẳng hàng.
Vậy, giá trị nhỏ nhất của biểu thức là
Câu 30. Chọn D
Ta có
2 2 2 2 2 2
, ; ; , , .OA a OB b OC c AB a b BC b c CA c a= = = = + = + = +
11
. . . . .
66
OABC
V OAOB OC a b c==
2 2 2 2 2 2
1 2 1 2.OA OB OC AB BC CA a b c a b b c c a+ + + + + = + + + + + + + + + = +
Áp dụng bất đẳng thức Côsi ta có:
3
3,a b c abc+ +
( )( )( )
2 2 2 2 2 2 2 2 2 2 2 2
63
6
3 3 2 .2 .2 3 2. .a b b c c a a b b c c a ab bc ac abc+ + + + + + + + =
Suy ra
2 2 2 2 2 2
33
3 3 2.a b c a b b c c a abc abc+ + + + + + + + +
( )
33
1 1 1 1 1
1 2 3 1 2 .
3 27 6 162 162
OABC
abc abc abc abc V + +
Dấu bằng xảy ra
2 2 2 2 2 2
0; 0; 0
12
abc
abc
a b c a b b c c a
= =
+ + + + + + + + = +
1
.
3
abc = = =
Vậy giá trị lớn nhất của
OABC
V
bằng
1
.
162
Câu 31. Chọn D
Ta có
( ) ( )
;;M a b c Oxy
nên
0c =
. Do đó
( )
; ;0M a b
.
( )
1 ; 1 ;2MA a b= − − −
,
( )
2 ; ;3MB a b= − − −
,
( )
;1 ; 2MC a b= − − −
( )( ) ( )( )
22
. 1 2 1 6 4MA MB a a b b a a b b= − − − + − − − + = + + + +
( )( ) ( )( )
22
. 2 1 6 2 6MB MC a a b b a a b b= − − − + − − − = + + − −
( )( ) ( )( )
22
. 1 1 1 4 5MC MA a a b b a a b= − − + − − − − = − + −
Suy ra
( ) ( )
2 2 2 2 2 2 2 2
4 2 2 6 3 5 6 2 6 23S a a b b a a b b a a b a a b b= + + + + + + + − − + − + − = + + − −
22
1 1 557 557
66
6 12 24 24
S a b
= + + − − −
.
M
IA
'IMB IAM
'1
2
MB IM
MA IA
==
1
'.
2
MB MA=
'B
B
2 2( ' )MA MB MB MB+ = +
', ,B M B
0
MM
2MA MB+
2 ' 6 2.BB =

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
74
Do đó
S
đạt giá trị nhỏ nhất là
557
24
−
khi
1
6
a =−
và
1
12
b =
Khi đó
11
12 12 12. 12. 0 1
6 12
T a b c
= + + = − + + = −
.
Câu 32. Chọn C
Ta có
( )
2 2 2
: 2 4 4 7 0S x y z x y z+ + − − − − =
( ) ( ) ( )
2 2 2
1 2 2 16x y z − + − + − =
.
Vì điểm
( ) ( ) ( ) ( )
2 2 2
1 2 2 16M S a b c − + − + − =
.
( )
*
Xét
( ) ( ) ( )
2 3 6 2 1 3 2 6 2 20T a b c a b c= + + = − + − + − +
( )
( ) ( ) ( )
( )
2 2 2
2 2 2
2 3 6 1 2 3 20 7.4 20 48a b c + + − + − + − + = + =
.
Dấu bằng xảy ra khi
12
1 2 2
0 2 3
2 3 6
26
at
a b c
t b t
ct
=+
− − −
= = = = +
=+
, thay vào phương trình
( )
*
ta
được:
2 2 2
4
4 9 36 16
7
t t t t+ + = =
.
Do đó
15 26 38
;;
7 7 7
M
và
15 26 38
2 2. 6
7 7 7
P a b c= − + = − + =
.
Câu 33. Chọn C
Mặt cầu
2 2 2
( ):( 1) ( 4) 12S x y z+ + + − =
có tâm
( 1;0;4)−I
, bán kính
12R =
.
Gọi
(0; 1;3)−C
là trung điểm của
AB
.
Ta có
( )( )
.MAMB IA IM IB IM= − −
( )
2
.IA IB IM IM IA IB= + − +
2
. 2 .IAIB R IM IC= + −
( )
2
. 2. . . ,IA IB R R IC cos IM IC= + −
.
Vì
,,,,I A B R C
không đổi nên
.MA MB
nhỏ nhất khi
( )
,1cos IM IC =
lớn nhất hay hai véctơ
,IM IC
cùng hướng.
Cách 1: Đường thẳng
IC
có véctơ chỉ phương
( )
1; 1; 1= − −IC
Phương trình đường thẳng
IC
:
1
4
xt
yt
zt
= − +
=−
=−
Điểm
M
thuộc đường thẳng
IC
nên
( )
1 ; ;4= − + − −M t t t
Điểm
M
thuộc mặt cầu nên
( )
2
22
( 1 1) (4 4) 12t t t− + + + − + − − =
2
2
3 12
2
t
t
t
=
=
=−
Khi
2t =−
thì
( )
3;2;6−M
và
( )
2;2;2=−IM
2IM IC = −
nên hai véctơ
,IM IC
không cùng
hướng.
Khi
2t =
thì
( )
1; 2;2−M
và
( )
2; 2; 2= − −IM
2IM IC=
nên hai véctơ
,IM IC
cùng hướng.
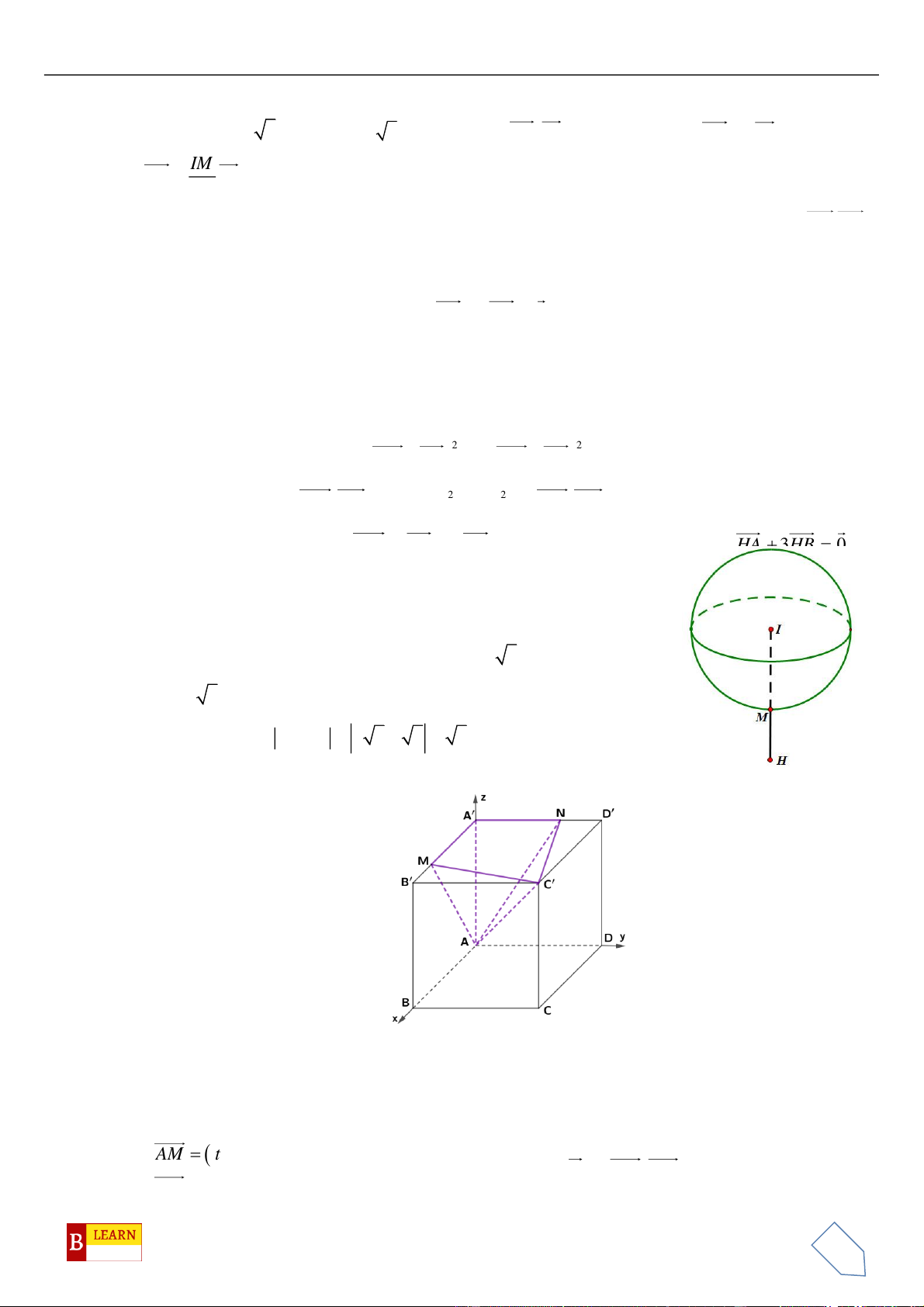
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
75
Vậy
( )
1; 2;2−M
hay
1abc+ + =
.
Cách 2:
3=IC
,
23==IM R
và hai véctơ
,IM IC
cùng hướng nên
2IM IC=
(Tổng quát
IM
IM IC
IC
=
) hay
C
là trung điểm của đoạn thẳng
IM
. Suy ra
( )
1; 2;2M −
hay
1abc+ + =
.
Bình luận: Bài toán cũng có thể ra ở dạng Điểm
( ; ; )M a b c
thuộc mặt cầu
()S
sao cho
.MA MB
lớn nhất, tính
abc++
.
Câu 34. Chọn C
Gọi
( )
;;H x y z
là điểm thỏa mãn:
2 3 0HA HB+=
.
( ) ( )
( ) ( )
( ) ( )
2 2 3 3 0
2 2 3 3 0
2 4 3 1 0
xx
yy
zz
− + − − =
− + − =
− + − − =
( )
1
1 1;1;1
1
x
yH
z
=−
= −
=
Xét
( ) ( )
22
22
2 3 2 3P MA MB MH HA MH HB= + = + + +
( ) ( )
2 2 2 2
2 2 . 3 2 .MH HA MH HA MH HB MH HB= + + + + +
( )
2 2 2
5 2 3 . 2 3MH HA HB MH HA HB= + + + +
2 2 2
5 2 3MH HA HB= + +
(vì
2 3 0HA HB+=
)
2
5 90MH=+
Để
2
5 90P MH=+
nhỏ nhất
MH
nhỏ nhất.
Mặt cầu
( )
S
có tâm
( )
1;3;3I
, bán kính
3R =
.
23IH R=
nên điểm
H
nằm ngoài mặt cầu
( )
S
.
Khi đó:
min
2 3 3 3MH IH R= − = − =
. Vậy
min
5.3 90 105P = + =
.
Câu 35. Chọn C
Chọn hệ trục tọa độ
Axyz
như hình vẽ, ta có:
( )
0;0;0A
,
( )
0;0;1A
,
( )
1;1;1C
.
( )
;0;1 , 0;1M t A B t
,
( )
0; ;1 , 0;1N m A D m
.(
M
,
N
lần lượt thuộc đoạn
AB
,
AD
)
( )
( )
;0;1
1;1;1
AM t
AC
=
=
( )
AMC
có một vectơ pháp tuyến là
( )
1
; 1;1 ;n AM AC t t
= = − −
.
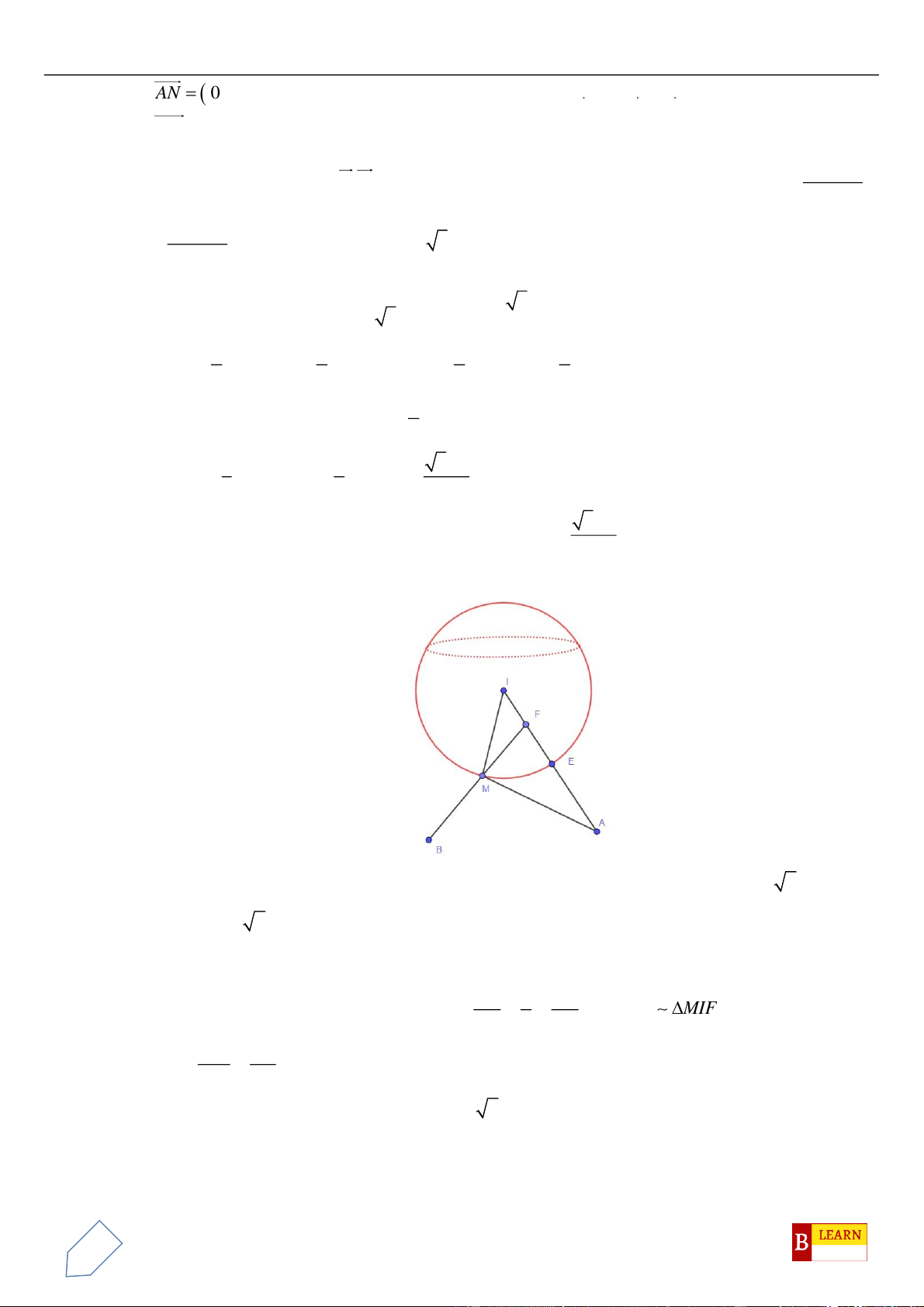
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
76
( )
( )
0; ;1
1;1;1
AN m
AC
=
=
( )
ANC
có một vectơ pháp tuyến là
( )
2
; 1;1;n AN AC m m
= = − −
.
( ) ( )
MAC NAC
⊥
12
.0nn=
2m t mt + + =
( )
2
2
4
Cauchy
mt
m t mt m t
+
= + + + +
( )
2
20
4
mt
mt
+
+ + −
2 3 2mt + −
vì
, 0;1mt
.
Dấu
""=
xảy ra khi
31
2 3 2
tm
tm
tm
=
= = −
+ = −
.
( )
11
.1
22
B MC
S B M B C t
= = −
,
( )
11
.1
22
D NC
S D N D C m
= = −
,
1
A B C D
S
=
.
( )
1
2
A MC N A B C D B MC D NC
S S S S m t
= − − = +
.
( )
.
1 1 3 1
.
3 6 3
A A MC N A MC N
V AA S t m
−
= = +
.
Vậy giá trị nhỏ nhất của thể tích khối chóp
.A A MC N
là
31
3
−
.
Câu 36. Chọn D
Nhận xét: điểm
,AB
nằm ngoài mặt cầu
( )
S
. Mặt cầu
( )
S
có tâm
( )
1;4;0 , 2 2IR−=
.
Ta có:
( ) ( )
4 2 2 , 1;2;0IA R E IA S E= = =
(Do
E
là trung điểm của
IA
).
Gọi
F
là trung điểm của
( )
0;3;0IE F
.
Tam giác
IFM
và
IMA
có
AIM
chung và
1
2
IF IM
AIM MIF
IM IA
= =
.
Suy ra
22
MA AI
MA MF
FM MI
= = =
.
Ta có:
( )
2 2 2 6 2MA MB MF MB FB+ = + =
.
Vì
F
nằm trong
( )
S
và
B
nằm ngoài
( )
S
nên dấu
'' ''=
xảy ra khi
( )
M BF S=
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
77
Câu 37. Chọn C
Ta có:
.0OAOB =
nên
. . . 3OP AP OP BP AP BP+ + =
( ) ( ) ( ) ( )
. . . 3OP OP OA OP OP OB OP OA OP OB − + − + − − =
( )
2
3 3 2 1OP OP OA OB
= + +
.
Giả sử
( )
;;P x y z
thì phương trình (1) trở thành
( )
( ) ( )
( )
2 2 2 2 2 2
3 3 2 2 2 3 2 4 4 1x y z t x y z t x y z+ + = + + + + + + + +
Hay
22
3 3 6 2 1 0OP tOP OP tOP + − −
22
11t t OP t t − + + +
Từ giả thiết suy ra
2
4
13
3
t t t+ + = =
. Vậy
2 11Q a b= + =
.
Câu 38. Chọn B
Phương trình mặt phẳng
( )
ABC
là
1 2 3 6 0
3 2 6
x y z
x y z+ + = + + − =
.
Dễ thấy
( )
D ABC
. Gọi
,,H K I
lần lượt là hình chiếu của
,,A B C
trên
Δ
.
Do
Δ
là đường thẳng đi qua
D
nên
,,AH AD BK BD CI CD
.
Vậy để khoảng cách từ các điểm
,,A B C
đến
Δ
là lớn nhất thì
Δ
là đường thẳng đi qua
D
và
vuông góc với
( )
ABC
. Vậy phương trình đường thẳng
Δ
là
( )
12
13
1
xt
y t t
zt
=+
= +
=+
. Kiểm tra ta thấy
điểm
( )
5;7;3 .M
Câu 39. Chọn C
Gọi
( )
;;M x y z
, suy ra
22
9MA MB−=
( ) ( ) ( ) ( ) ( ) ( )
2 2 2 2 2 2
2 3 5 1 2 4 9x y z x y z
− + − + − − − + − + − =
40x y z+ + − =
Suy ra: Tập các điểm
( )
;;M x y z
thỏa mãn
22
9MA MB−=
là mặt phẳng
( )
: 4 0P x y z+ + − =
Trên
( )
m
S
tồn tại điểm
M
sao cho
22
9MA MB−=
khi và chỉ khi
( )
m
S
và
( )
P
có điểm chung
( )
( )
;d I P R
1 1 4
2
111
mm+ + −
++
2 2 3mm −
2
16 16 0mm − +
8 4 3 8 4 3m − +
Vậy giá trị nhỏ nhất của
m
là
8 4 3−
.
Câu 40. Chọn D
Nhận xét: điểm
,AB
nằm ngoài mặt cầu
( )
S
. Mặt cầu
( )
S
có tâm
( )
1;4;0 , 2 2IR−=
.
Ta có:
( ) ( )
4 2 2 , 1;2;0IA R E IA S E= = =
(Do
E
là trung điểm của
IA
).
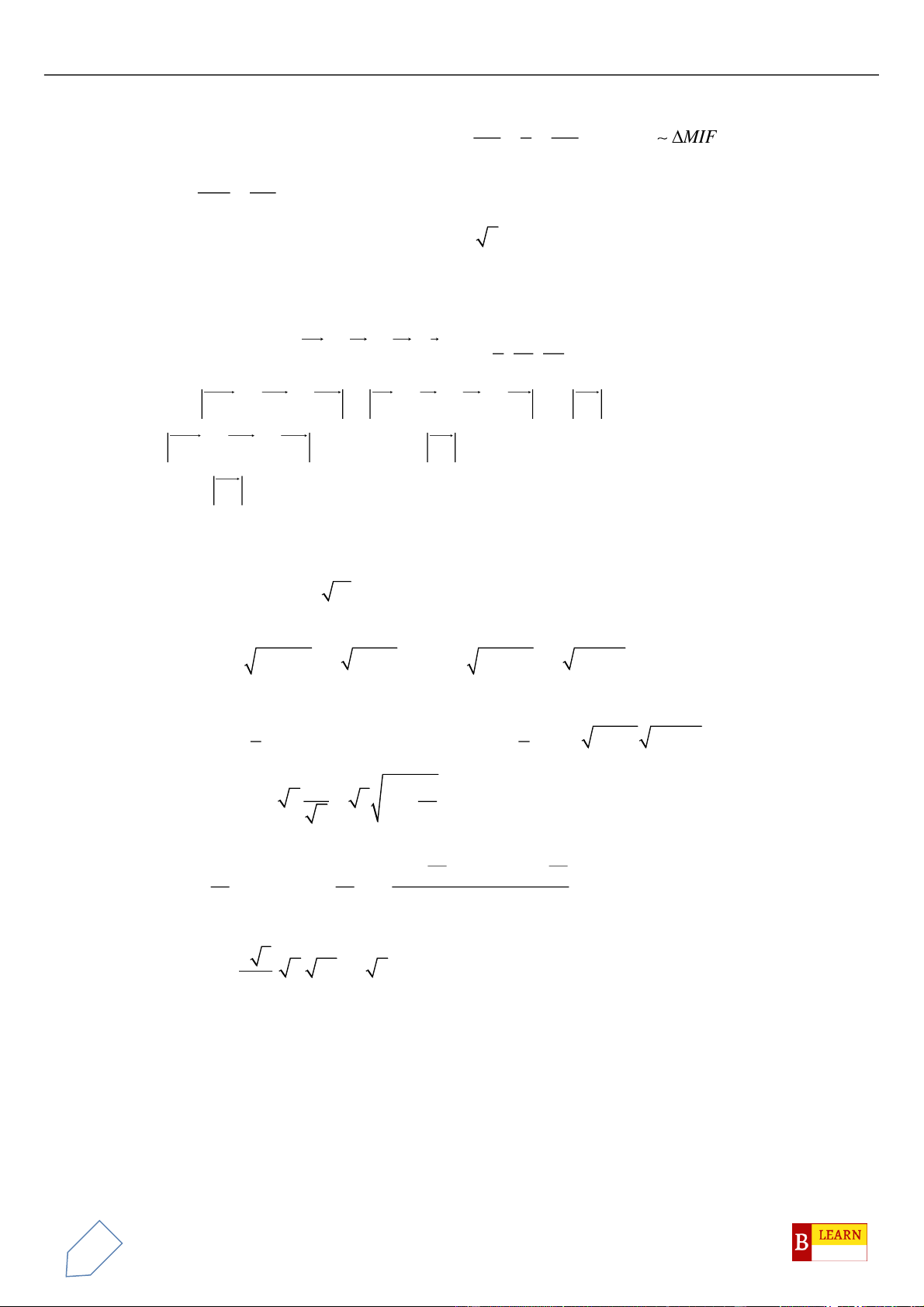
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
78
Gọi
F
là trung điểm của
( )
0;3;0IE F
.
Tam giác
IFM
và
IMA
có
AIM
chung và
1
2
IF IM
AIM MIF
IM IA
= =
.
Suy ra
22
MA AI
MA MF
FM MI
= = =
.
Ta có:
( )
2 2 2 6 2MA MB MF MB FB+ = + =
.
Vì
F
nằm trong
( )
S
và
B
nằm ngoài
( )
S
nên dấu
'' ''=
xảy ra khi
( )
M BF S=
.
Câu 41. Chọn A
Chọn
( )
;;I a b c
thỏa
2 3 0OI IA IB+ + =
1 1 5
;;
2 4 4
I
−−
.
Ta có :
23OM MA MB++
2 3 4OI IA IB MI= + + +
4 MI=
.
23OM MA MB + +
nhỏ nhất
4 MI
nhỏ nhất
( )
MI Oxz⊥
.
Lúc đó
( )
( )
4 4 ; 1MI d I Oxz==
.
Câu 42. Chọn D
Mặt cầu
1
()S
có tâm
(1; 2;1)I −
và bán kính là
1
2R =
. Mặt cầu
2
()S
cũng có tâm
(1; 2;1)I −
nhưng bán kính là
2
10R =
.
Gọi
a
,
b
lần lượt là khoảng cách từ tâm
I
đến hai đường thẳng
AB
,
CD
.
Ta có
2 2 2
1
2 2 4AB R a a= − = −
,
2 2 2
2
2 2 10CD R b b= − = −
và
( , ) ( , ) ( , )d AB CD d I AB d I CD a b + = +
. Thêm nữa:
sin( , ) 1.AB CD
Ta có
22
12
. . ( , ).sin( , ) ( ) 4 10
63
ABCD
V AB CD d AB CD AB CD a b a b= + − −
.
Ta có:
2
2
23
2
2
bb
a b a a+ = + +
và
( )
3
22
22
22
22
45
22
4 5 27
2 2 3
bb
aa
bb
aa
+ + − + −
+ − − =
.
Vậy
23
. 2. 27 6 2
3
ABCD
V =
.
Dấu bằng đạt được tại
1a =
,
2b =
và hai đường
,AB CD
vuông góc với

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
79
CHỦ ĐỀ 2 : PHƯƠNG TRÌNH MẶT PHẲNG
❖ Trong không gian
Oxyz
phương trình dạng
0Ax By Cz D+ + + =
với
2 2 2
0A B C+ +
đuợc gọi là
phương trình tổng quát của mặt phẳng
▪ Phương trình mặt phẳng (P) :
( )
:0P Ax By Cz D+ + + =
với
2 2 2
0A B C+ +
. Có vecto pháp
tuyến là
( ; ; )n A B C=
▪ Mặt phẳng
( )
P
đi qua điểm
( )
;;
o o o o
M x y z
và nhận vectơ
( ; ; )n A B C=
,
0n
làm vectơ pháp
tuyến có dạng
( ) ( ) ( ) ( )
0
:0
oo
P A x x B y y C z z− + − + − =
▪ Nếu
( )
P
có cặp vectơ
1 2 3 1 2 3
( ; ; ) b ( ; ; )a a a a b b b==
không cùng phương ,có giá song song hoặc
nằm trên
( )
P
thì vectơ pháp tuyến của
( )
P
được xác định
,n a b
=
❖ Các trường hợp riêng của mặt phẳng :
Trong không gian
Oxyz
cho mp(
)
:
0Ax By Cz D+ + + =
, với
2 2 2
0A B C+ +
. Khi đó:
▪
0D =
khi và chỉ khi (
)
đi qua gốc tọa độ.
▪
0, 0, 0, 0A B C D=
khi và chỉ khi
()
song song với trục
Ox
▪
0, 0, 0, 0A B C D= =
khi và chỉ khi
()
song song mp
( )
Oxy
▪
, , , 0A B C D
. Đặt
,,
D D D
a b c
A B C
= − = − = −
Khi đó
( ): 1
x y z
a b c
+ + =
❖ Vị trí tương đối của hai mặt phẳng
Trong không gian
Oxyz
cho mp(
)
:
0Ax By Cz D+ + + =
và (
’):
' ' ' '
0A x B y C z D+ + + =
▪ (
) cắt (
’)
''
''
''
AB A B
BC B C
CB C B
(
) // (
’)
''
''
''
AB A B
BC B C
CB C B
=
=
=
và
''AD A D
▪ (
) ≡ (
’)
''
''
''
''
AB A B
BC B C
CB C B
AD A D
=
=
=
=
▪ Đặc biệt: (
)
⊥
(
’)
12
. 0 . ' . ' . ' 0n n A A B B C C = + + =
❖ Góc giữa hai mặt phẳng:
Gọi
là góc giữa hai mặt phẳng
( )
0 90
oo
( )
:0P Ax By Cz D+ + + =
và
( )
: ' ' ' ' 0Q A x B y C z D+ + + =
▪
P
P
2 2 2 2 2 2
PQ
n.
A.A' . ' . '
os = cos(n , )
n . n
. ' ' '
Q
Q
n
B B C C
cn
A B C A B C
++
==
+ + + +
LÍ THUYẾT
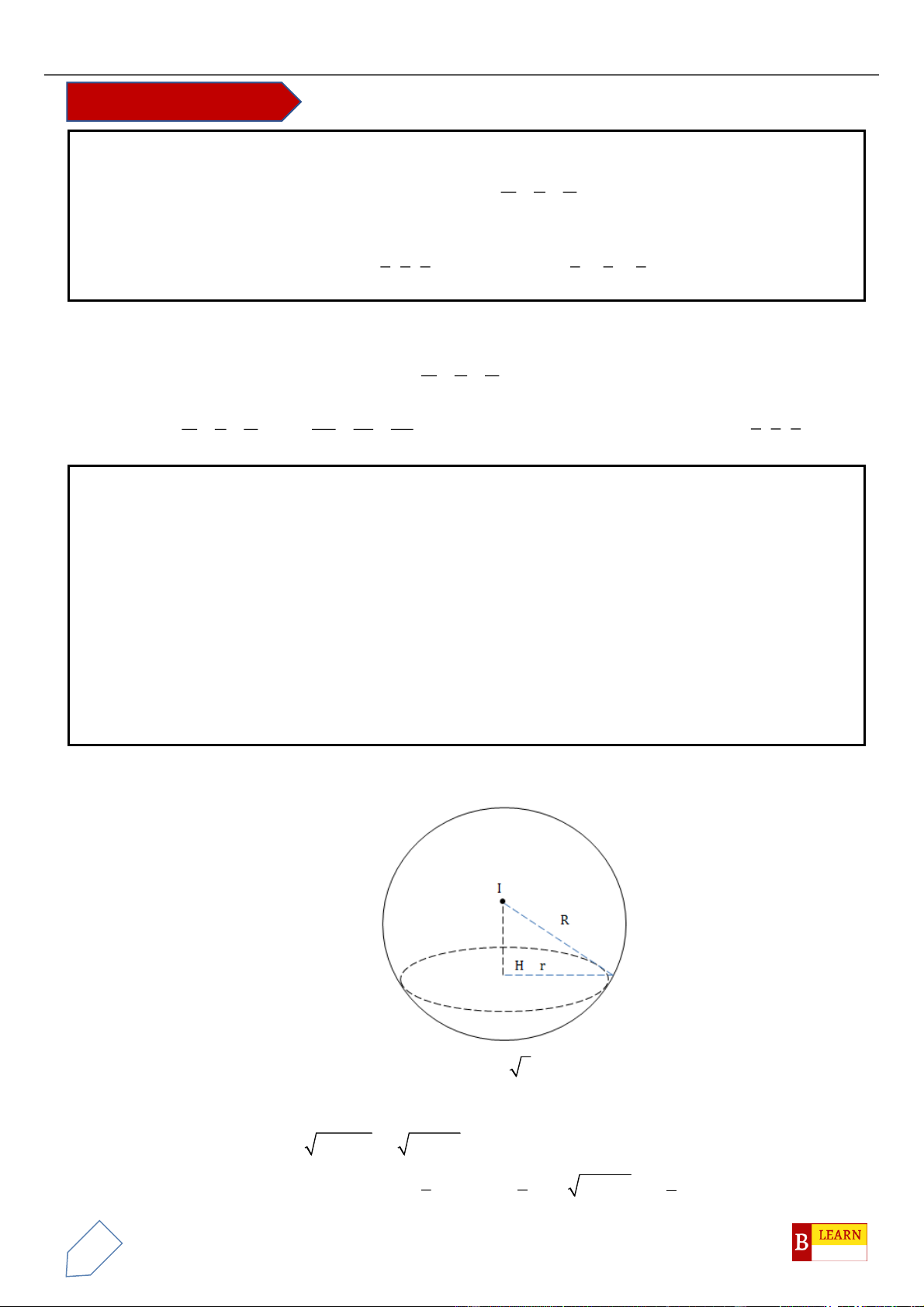
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
80
Lời giải
Chọn B
Phương trình mặt phẳng
( )
MNP
là:
1
x y z
m n p
+ + =
.
Mà:
1 1 1 1 1 1
31
3 3 3m n p m n p
+ + = + + =
. Vậy mặt phẳng
( )
MNP
luôn đi qua
111
;;
333
E
.
Lời giải
Chọn A
Mặt cầu
( )
S
có tâm
( )
1; 2;3I −
và bán kính
23R =
.
Gọi
r
là bán kính đường tròn
( )
C
và
H
là hình chiếu của
I
lên
( )
Q
.
Đặt
IH x=
ta có
22
r R x=−
2
12 x=−
Vậy thể tích khối nón tạo được là
( )
( )
1
..
3
C
V IH S=
(
)
2
2
1
. . 12
3
xx
=−
( )
3
1
12
3
xx
=−
.
VÍ DỤ MINH HỌA
VÍ DỤ 1: Trong không gian với hệ trục tọa độ
Oxyz
, cho ba điểm
( )
;0;0Mm
,
( )
0; ;0Nn
và
( )
0;0;Pp
Với
m
,
n
,
p
là các số dương thay đổi thỏa
1 1 1
3
m n p
+ + =
. Mặt phẳng
( )
MNP
luôn đi qua
điểm:
A.
( )
3;3;3F
. B.
111
;;
333
E
. C.
111
;;
333
H
− − −
. D.
( )
1;1;1G
.
VÍ DỤ 2: Trong không gian
Oxyz
, cho mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 1 2 3 12S x y z− + + + − =
và mặt phẳng
( )
:2 2 3 0P x y z+ − − =
. Gọi
( )
Q
là mặt phẳng song song với
( )
P
và cắt
( )
S
theo thiết diện là
đường tròn
( )
C
sao cho khối nón có đỉnh là tâm của mặt cầu và đáy là hình tròn giới hạn bởi
( )
C
có thể tích lớn nhất. Phương trình của mặt phẳng
( )
Q
là
A.
2 2 1 0
2 2 11 0
x y z
x y z
+ − − =
+ − + =
. B.
2 2 6 0
2 2 3 0
x y z
x y z
+ − − =
+ − + =
.
C.
2 2 4 0
2 2 17 0
x y z
x y z
+ − − =
+ − + =
. D.
2 2 2 0
2 2 8 0
x y z
x y z
+ − + =
+ − + =
.
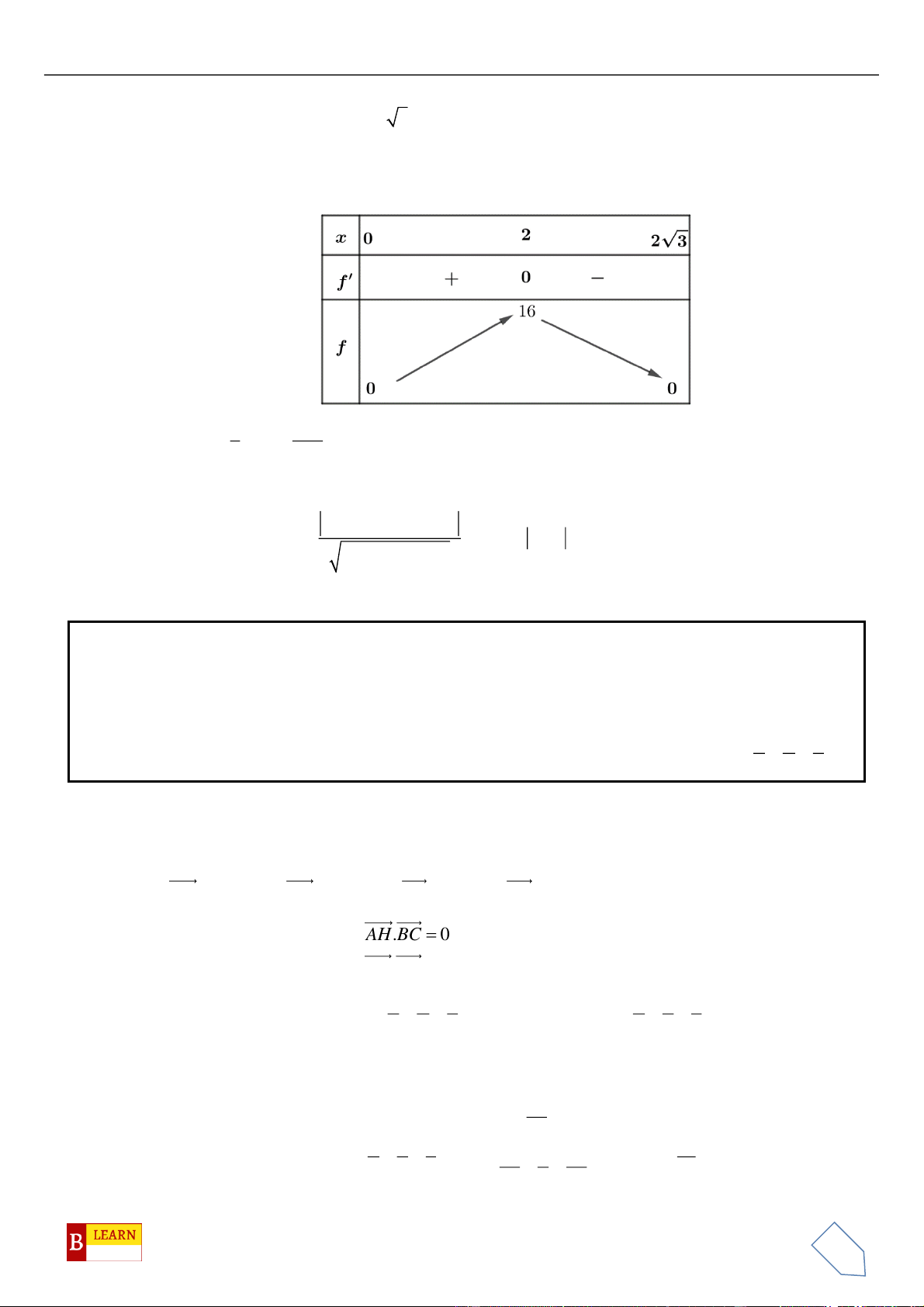
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
81
Gọi
( )
3
12f x x x=−
với
( )
0;2 3x
. Thể tích nón lớn nhất khi
( )
fx
đạt giá trị lớn nhất
Ta có
( )
2
12 3f x x
=−
;
( )
0fx
=
2
12 3 0x − =
2x =
2x=
.
Bảng biến thiên :
Vậy
max
1
16
3
V
=
16
3
=
khi
2x IH==
.
Mặt phẳng
( ) ( )
//QP
nên
( )
:2 2 0Q x y z a+ − + =
Và
( )
( )
;d I Q IH=
( )
( )
2
22
2.1 2 2 3
2
2 2 1
a+ − − +
=
+ + −
56a −=
11
1
a
a
=
=−
.
Vậy mặt phẳng
( )
Q
có phương trình
2 2 1 0x y z+ − − =
hoặc
2 2 11 0x y z+ − + =
.
Lời giải
Chọn B
Giả sử
( ) ( ) ( )
;0;0 , 0; ;0 , 0;0;cA a B b C
( ) ( ) ( ) ( )
1 ;2;3 ; 1;2 ;3 ; 0; b;c ; a;0;cAH a BH b BC AC − − − −
Do
H
là trực tâm nên ta có:
. 0 2 3 0
30
.0
AH BC b c
ac
BH AC
= − + =
− + =
=
Phương trình mặt phẳng
( )
:1
x y z
ABC
a b c
+ + =
. Vì
( )
1 2 3
1.H ABC
abc
+ + =
Do đó ta có hệ phương trình:
2
2 3 0 14
2
3 0 7
3
1 2 3 14
1 2 9
1
1
3
22
ab
b c a
b
a c c b
c
abc
b b b
=
− + = =
− + = = =
+ + = =
+ + =
.
VÍ DỤ 3: Trong không gian với trục hệ tọa độ
Oxyz
, cho điểm
( )
1;2;3H
là trực tâm của
ABC
với
,,A B C
là ba điểm lần lượt nằm trên các trục
,,Ox Oy Oz
(khác gốc tọa độ). Phương trình mặt
phẳng đi qua ba điểm
,,A B C
là
A.
3 2 9 0x y z+ + − =
B.
2 3 14 0x y z+ + − =
C.
3 2 10 0x y z+ + − =
D.
1
1 2 3
x y z
+ + =
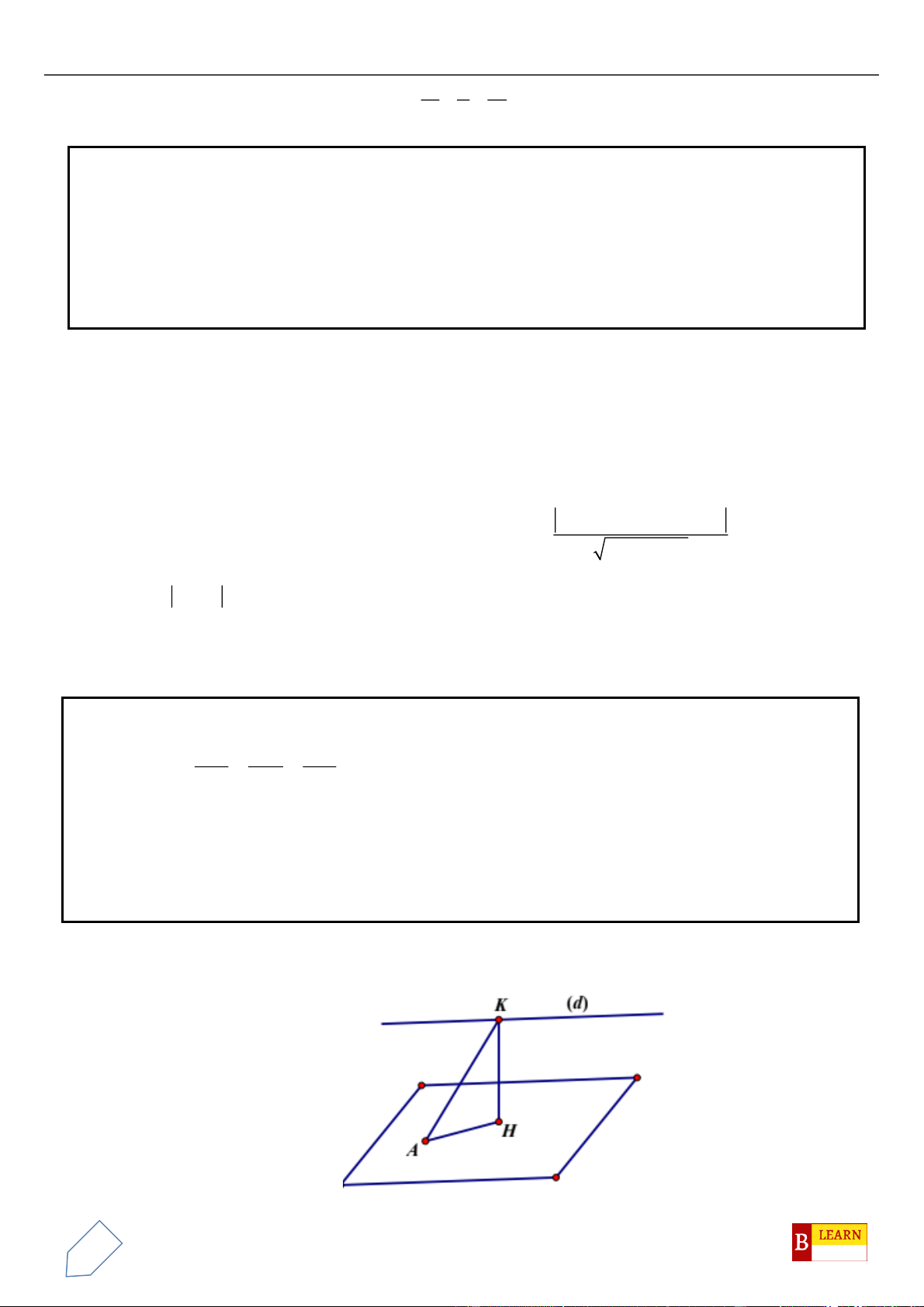
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
82
Vậy phương trình mặt phẳng
( )
3
: 1 2 3 14 0.
14 7 14
x y z
ABC x y z+ + = + + − =
Lời giải
Chọn D
Mặt cầu
( )
S
có tâm
( )
1; 2; 3I −−
và bán kính
2R =
.
Gọi
( )
Q
là mặt phẳng song song với mặt phẳng
( )
P
và đồng thời tiếp xúc với mặt cầu
( )
S
.
Phương trình
( )
Q
có dạng:
2 2 0x y z D− − + =
( )
5D −
.
( )
Q
tiếp xúc với
( )
S
khi và chỉ khi
( )
( )
,d I Q R=
( ) ( )
222
1 2. 2 2. 3
2
1 2 2
D− − − − +
=
++
11 6D + =
11 6
11 6
D
D
+=
+ = −
5
17
D
D
=−
=−
.
Đối chiếu điều kiện suy ra
17D =−
.
Vậy phương trình của
( )
Q
là
2 2 17 0 2 2 17 0x y z x y z− − − = − + + + =
.
Lời giải
Chọn C
VÍ DỤ 4: Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt phẳng
( )
P
có phương trình
2 2 5 0x y z− − − =
và mặt cầu
( )
S
có phương trình
( ) ( ) ( )
2 2 2
1 2 3 4x y z− + + + + =
. Tìm
phương trình mặt phẳng song song với mặt phẳng
( )
P
và đồng thời tiếp xúc với mặt cầu
( )
S
A.
2 2 1 0x y z− − + =
. B.
2 2 5 0x y z− + + + =
.
C.
2 2 23 0x y z− − − =
. D.
2 2 17 0x y z− + + + =
.
VÍ DỤ 5: Trong không gian với hệ tọa độ
Ozyz
cho điểm
( )
2; 1; 2A −−
và đường thẳng
( )
d
có phương
trình
1 1 1
1 1 1
x y z− − −
==
−
. Gọi
( )
P
là mặt phẳng đi qua điểm
A
, song song với đường thẳng
( )
d
và khoảng cách từ đường thẳng
d
tới mặt phẳng
( )
P
là lớn nhất. Khi đó mặt phẳng
( )
P
vuông góc với mặt phẳng nào sau đây?
A.
3 2 10 0x y z+ + + =
. B.
2 3 1 0x y z− − − =
.
C.
3 2 0xz+ + =
. D.
60xy− − =
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
83
Gọi
( )
;;K x y z
là hình chiếu vuông góc của
A
lên
d
. Tọa độ của
K
là nghiệm của hệ
1 1 1
1 1 1
1 0 1
x y x
y z y
x y z z
− + = − =
− = − + =
− + − = =
( )
1;1;1K
.
Ta có
( ) ( )
( )
( )
( )
, , 14d d P d K P KH KA= = =
. Nên khoảng cách từ
d
đến
( )
P
đạt giá trị lớn
nhất bằng
14
khi mặt phẳng
( )
P
qua
A
và vuông góc với
KA
. Khi đó có thể chọn VTPT của
( )
P
là
KA
. Vậy
( )
P
vuông góc với mặt phẳng
3 2 0xz+ + =
.
Lời giải
Chọn C
Vì
( )
AP
nên ta
8 2 0b c d+ + =
82d b c = − −
( ) ( )
: 8 2 0P x by cz b c + + − + =
.
Do
( )
P
tiếp xúc với mặt cầu
( )
S
nên
( )
( )
;d I P R=
22
5 11 5
62
1
bc
bc
−+
=
++
.
Ta có:
( )
( )
( ) ( )
2 2 2 2
5 11 5 4 1 4
9 7 23 8 2
;
11
b c b c
b c b c
d B P
b c b c
− + + − +
− + − −
==
+ + + +
( )
( )
2 2 2 2
5 11 5 1 4
;4
11
b c b c
d B P
b c b c
− + − +
+
+ + + +
( )
( )
22
14
; 6 2 4
1
bc
d B P
bc
−+
+
++
( )
( )
( )
( )
22
22
1 1 16 1
; 6 2 4
1
Cosi Svac
bc
d B P
bc
−
+ + + +
+
++
( )
( )
; 18 2d B P
.
Dấu “=” xảy ra khi
22
1
1
4
4
5 11 5
62
0
1
c
b
b
c
bc
d
bc
=−
= − =
=
−+
=
=
++
.
Vậy
max
18 2P =
khi
3b c d+ + =
.
VÍ DỤ 6: Trong không gian
( )
Oxyz
, cho hai điểm
( )
0;8;2A
,
( )
9; 7;23B −
và mặt cầu
( )
S
có phương
trình
( ) ( ) ( ) ( )
2 2 2
: 5 3 7 72S x y z− + + + − =
. Mặt phẳng
( )
:0P x by cz d+ + + =
đi qua điểm
A
và tiếp xúc với mặt cầu
( )
S
sao cho khoảng cách từ
B
đến mặt phẳng
( )
P
lớn nhất. Giá
trị của
b c d++
khi đó là
A.
2b c d+ + =
. B.
4b c d+ + =
. C.
3b c d+ + =
. D.
1b c d+ + =
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
84
DẠNG 1. VECTO CHỈ PHƯƠNG, TÍCH CÓ HƯỚNG VÀ ỨNG DỤNG CỦA PT MẶT PHẲNG
Câu 1. Xét đường thẳng
d
xác định bởi
1
2
x
yz
=
+=
và đường thẳng
'd
xác định bởi
0x
yz
=
=
. Tính bán
kính bé nhất
R
của mặt cầu tiếp xúc với cả
d
và
'd
.
A.
1R =
. B.
1
2
R =
. C.
2R =
. D.
2R =
.
Câu 2. Trong không gian với hệ tọa độ
Oxyz
phương trình nào sau đây không phải là phương trình của
một mặt cầu?
A.
2 2 2
2 4 3 0x y z x y z+ + + − + − =
. B.
2 2 2
2 2 2 0x y z x y z+ + − − − =
.
C.
2 2 2
2 2 2 4 8 6 3 0x y z x y z+ + + + + + =
. D.
2 2 2
2 4 4 10 0x y z x y z+ + − + − + =
.
Câu 3. Trong không gian
Oxyz
có tất cả bao nhiêu giá trị nguyên
m
để phương trình
2 2 2 2
4 2 2 9 28 0x y z mx my mz m+ + + + − + − =
là phương trình mặt cầu?
A.
7
. B.
8
. C.
9
. D.
6
.
Câu 4. Tìm phương trình mặt phẳng đi qua điểm
( )
1;4; 3M −
và chứa trục
Oy
?
A.
30yz+=
. B.
0x y z− − =
. C.
30xz+=
. D.
30xz+=
.
Câu 5. Trong không gian với hệ trục tọa độ
Oxyz
cho các điểm
( ) ( ) ( )
0;1;2 , 2; 2;1 , 2;0;1A B C−−
.
Phương trình mặt phẳng đi qua 3 điểm
,,A B C
là
0ax by cz d+ + + =
với
22
21a b c+ + =
và
0.a
Khi đó
a b c d+ + +
bằng:
A.
2
. B.
4
. C.
5
. D.
3
.
Câu 6. Trong không gian
Oxy
, cho mặt cầu
2 2 2
( ): 2 4 6 5 0S x y z x y z+ + − − − + =
. Thể tích của
()S
bằng
A.
12
. B.
9
. C.
36 .
D.
36.
Câu 7. Trong không gian
Oxy
, cho mặt cầu
2 2 2
( ): 2 4 6 5 0S x y z x y z+ + − − − + =
. Thể tích của
()S
bằng
A.
12
. B.
9
. C.
36 .
. D.
36.
Câu 8. Trong không gian với hệ trục tọa độ
Oxyz
, cho điểm
( )
1;0;2I
và đường thẳng
1
:
2 1 1
x y z
d
−
==
−
. Gọi
( )
S
là mặt cầu có tâm
I
, tiếp xúc với đường thẳng
d
. Bán kính của
( )
S
bằng
A.
25
3
. B.
5
3
. C.
42
3
. D.
30
3
.
Câu 9. Trong không gian với hệ toạ độ
Oxyz
, cho các mặt cầu
( ) ( ) ( )
1 2 3
,,S S S
có bán kính
1r =
và lần
lượt có tâm là các điểm
( ) ( ) ( )
0;3; 1 , 2;1; 1 , 4; 1; 1A B C− − − − −
. Gọi
( )
S
là mặt cầu tiếp xúc với cả
ba mặt cầu trên. Mặt cầu
( )
S
có bán kính nhỏ nhất là
A.
10R =
. B.
22R =
. C.
2 2 1R =−
. D.
10 1R =−
.
BÀI TẬP RÈN LUYỆN

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
85
Câu 10. Phương trình
2 2 2 2
2 4 2 5 0x y z mx y mz m m+ + − + + + + =
là phương trình mặt cầu khi
A.
4m
. B.
1m
. C.
1
4
m
m
. D.
1
4
m
m
.
Câu 11. Trong không gian
Oxyz
, cho hai điểm
( )
1;5; 2A −
,
( )
3;1;2B
. Viết phương trình mặt phẳng trung
trực của đoạn thẳng
AB
.
A.
2 3 4 0xy+ + =
. B.
2 2 8 0x y x− + − =
.
C.
2 2 8 0x y z− + + =
. D.
2 2 4 0x y z− + + =
.
Câu 12. Trong không gian với hệ trục tọa độ
Oxyz
, phương trình mặt phẳng đi qua điểm
( )
1;2; 3A −
có
vectơ pháp tuyến
( )
2; 1;3n =−
là :
A.
2 3 9 0x y z− + + =
. B.
2 3 4 0x y z− + − =
. C.
2 4 0xy− − =
. D.
2 3 4 0x y z− + + =
.
Câu 13. Trong không gian , đường thẳng có phương trình nào sau đây song song với mặt phẳng
A. . B. .
C. . D. .
Câu 14. Trong không gian , mặt phẳng nào trong các mặt phẳng sau song song với đường thẳng
A. . B. .
C. . D. .
Câu 15. Cho không gian
Oxyz
, viết phương trình đoạn chắn mặt phẳng đi qua điểm
( ) ( ) ( )
2,0,0 ; 0, 3,0 ; 0,0,2A B C−
A.
1
2 3 2
x y z
+ + =
. B.
1
2 3 2
x y z
+ + =
−
. C.
1
3 2 2
x y z
+ + =
−
. D.
1
2 2 3
x y z
+ + =
−
.
Câu 16. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
( )
1;2; 2H −
. Mặt phẳng
( )
đi qua
H
và cắt
các trục
,,Ox Oy Oz
lần lượt tại các điểm
,,A B C
sao cho
H
là trực tâm của tam giác
ABC
. Tính
diện tích mặt cầu ngoại tiếp tứ diện
OABC
.
A.
243
. B.
81
. C.
81
2
. D.
243
2
.
Câu 17. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
12
:
1 2 1
x y z
d
+−
==
−
và mặt phẳng
( )
: 2 2 2 0P x y z− − − =
.
( )
Q
là mặt phẳng chứa
d
và tạo với mặt phẳng
( )
P
một góc nhỏ nhất.
Gọi
( )
; ;1
Q
n a b=
là một vectơ pháp tuyến của
( )
Q
. Đẳng thức nào đúng?
A.
0ab+=
. B.
1ab− = −
. C.
1ab−=
. D.
2ab+ = −
.
Oxyz
Oxz
1
1
( ): 2
3
x
d y t t
z
2
1
( ): 2
3
x
d y t t
z
3
2
( ): 0
62
xt
d y t
zt
4
12
( ): 3
53
xt
d y t
zt
Oxyz
1 2 3
( ):
1 2 3
x y z
d
( ): 2 3 5P z y z
( ):3 2 5Q x y z
( ):3 3 5x y z
( ):
3 3 0x y z
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
86
ĐÁP ÁN CHI TIẾT
Câu 1. Chọn B
Ta có VTCP của đường thẳng
d
là
( )
, 0; 1;1
d
u i m
= = −
với
( )
1;0;0i =
,
( )
0;1;1m =
.
Suy ra đường thẳng
d
đi qua điểm
( )
1;1;1M
, có vtcp
( )
0; 1;1
d
u =−
nên có phương trình tham số
là:
( )
1
:1
1
x
d y t t
zt
=
= −
=+
.
Tương tự, đường thẳng
'd
đi qua điểm
( )
' 0;1;1M
, có vtcp
( )
'
, 0;1;1
d
u i n
==
với
( )
1;0;0i =
,
( )
0;1; 1n =−
nên có phương trình tham số là:
( )
0
': 1 ' '
1'
x
d y t t
zt
=
= +
=+
.
Ta có
'
, . 2 0
dd
u u MM
=
,dd
chéo nhau.
Do đó mặt cầu tiếp xúc với cả
d
và
d
có đường kính nhỏ nhất bằng khoảng cách giữa
d
và
d
.
Ta có:
'
'
,.
( , ) 1
,
dd
dd
u u MM
ddd
uu
==
.
Suy ra, bán kính bé nhất
R
của mặt cầu tiếp xúc với cả
d
và
d
là:
1
2
R =
.
Câu 2. Chọn D
Phương trình
2 2 2
2 2 2 0x y z ax by cz d+ + − − − + =
là phương trình của một mặt cầu nếu
2 2 2
0a b c d+ + −
.
Xét đáp án D ta thấy:
1, 2, 2, 10a b c d= = − = =
2 2 2
10a b c d + + − = −
nên chọn D
Câu 3. Chọn A
Ta có
2 2 2 2
4 2 2 9 28 0x y z mx my mz m+ + + + − + − =
( ) ( ) ( )
2 2 2
2
2 28 3x m y m z m m + + + + − = −
( )
1
.
( )
1
là phương trình mặt cầu
2
28 28
28 3 0
33
mm − −
.
Do
m
nguyên nên
3; 2; 1;0;1;2;3m − − −
.
Vậy có
7
giá trị của
m
thỏa mãn yêu cầu bài toán .
Câu 4. Chọn C
Gọi mặt phẳng cần tìm là
( )
.
Do
( )
đi qua điểm
( )
1;4; 3M −
và chứa trục
Oy
nên
( )
có một vectơ pháp tuyến là
( )
, 3;0; 1n j OM
= = − −
.
Vậy phương trình mặt phẳng
( )
:
( ) ( ) ( )
3 1 0 4 3 0 3 0x y z x z− − + − − + = + =
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
87
Câu 5. Chọn C
Ta có
( ) ( )
2; 3; 1 , 2; 1; 1AB AC= − − = − − −
( )
, 2;4; 8 .AB AC
= −
( )
1
1
, 1;2; 4
2
n AB AC
= = −
là một vectơ pháp tuyến của mặt phẳng
( )
ABC
.
Theo giả thiết , mặt phẳng
( )
ABC
có phương trình
0ax by cz d+ + + =
nên
( )
2
;;n a b c=
cũng là
một vectơ pháp tuyến của mặt phẳng
( )
.ABC
Do đó tồn tại số thực
\0k
sao cho
21
.2
4
ak
n k n b k
ck
=
= =
=−
. Vì
0a
nên
0.ka=
Vì
( ) ( )
2;0;1C ABC−
nên ta có:
2 4 0 6k k d d k− − + = =
.
Lại có
22
21a b c+ + =
nên
( )
2 2 2
1 (nhan)
4 16 21 20 21 0 .
21
loai
20
k
k k k k k
k
=
+ + = + − =
=−
Với
1k =
thì
2 4 6 5 5.a b c d k k k k k+ + + = + − + = =
Vậy
5.a b c d+ + + =
Câu 6. Chọn C
Mặt cầu
()S
có tâm
(1;2;3)I
bán kính
3r =
. Thể tích của
()S
là:
3
4
. .3 36
3
V
==
.
Câu 7. Chọn C
Mặt cầu
()S
có tâm
(1;2;3)I
bán kính
3r =
. Thể tích của
()S
là:
3
4
. .3 36
3
V
==
.
Câu 8. Chọn D
Đường thẳng
1
:
2 1 1
x y z
d
−
==
−
có vectơ chỉ phương là
( )
2; 1;1u =−
và đi qua điểm
( )
1;0;0A
.
Khi đó
( ) ( )
0;0;2 , 2;4;0AI AI u
= =
,
, 2 5AI u
=
.
Do
( )
S
là mặt cầu có tâm
I
, tiếp xúc với đường thẳng
d
nên bán kính mặt cầu
( )
S
là
( )
,
2 5 30
;
3
6
AI u
R d I d
u
= = = =
.
Câu 9. Chọn D
Gọi
D
là tâm mặt cầu
( )
S
thì
1AD BD CD R= = = +
.Suy ra điểm
D
thuộc trục
đường tròn ngoại tiếp tam giác
ABC
. Suy ra
R
nhỏ nhất khi và chỉ khi
D
trùng với tâm
I
đường
tròn ngoại tiếp
ABC
. Vì
( )
D mp ABC
có
phương trình:
1z =−
nên ta đặt
( )
, , 1D x y −
, ta có
hệ sau:
D
≡
I
D
C
B
A

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
88
( ) ( ) ( )
( ) ( ) ( )
( )
2 2 2
2
2 2 2
2
3 2 1
1
1;0; 1
0
3 4 1
x y x y
x
D
y
x y x y
+ − = + + −
=
−
=
+ − = − + +
. Vậy
1 10 1R AD= − = −
.
Câu 10. Chọn C
Ta có
2
22
24
22
5
am
b
cm
d m m
− = −
−=
−=
=+
2
2
5.
am
b
cm
d m m
=
=−
=−
=+
Để phương trình đã cho là phương trình mặt cầu thì
2 2 2
0a b c d+ + −
2
5 4 0mm− +
1
4
m
m
.
Câu 11. Chọn D
Ta có:
( )
2; 4;4AB =−
là một VTPT của mặt phẳng trung trực đoạn thẳng
AB
.
Gọi
I
là trung điểm của
AB
( )
2;3;0I
.
Mặt phẳng trung trực của đoạn thẳng
AB
đi qua điểm
I
và có VTPT
( )
2; 4;4n =−
nên có
phương trình là:
( ) ( ) ( )
2 2 4 3 4 0 0x y z− − − + − =
2 2 4 0x y z − + + =
.
Câu 12. Chọn A
Phương trình mặt phẳng đi qua điểm
( )
1;2; 3A −
có vectơ pháp tuyến
( )
2; 1;3n =−
là :
( ) ( ) ( )
2 1 1 2 3 3 0 2 3 9 0x y z x y z− − − + + = − + + =
.
Câu 13. Chọn D
Mặt phẳng có một véctơ pháp tuyến là véctơ .
Nếu một đường thẳng song song với mặt phẳng thì véctơ chỉ phương của mặt phẳng đó phải
vuông góc với véctơ , khi đó đáp án C và D thỏa mãn
Mặt khác, lấy , vì nên nhận đáp án D.
Câu 14. Chọn C
Đường thẳng có một véctơ chỉ phương là véctơ , và đi qua điểm .
Mặt phẳng và đều có véctơ pháp tuyến vuông góc với véctơ , và , nên mặt
phẳng song song đường thẳng .
Câu 15. Chọn B
Ta có: phương trình đoạn chắn mặt phẳng đi qua điểm
( ) ( ) ( )
− 2,0,0 ; 0, 3,0 ; 0,0, 2A B C
là:
1
2 3 2
x y z
+ + =
−
.
Câu 16. Chọn D
Oxz
0;1;0j
Oxz
j
(1;3;5)A
4
()d
()A Oxz
()d
(1;2;3)u
( 1; 2; 3)A
()
()
u
()A
()
()d

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
89
Mặt phẳng
( )
cắt các trục
,,Ox Oy Oz
lần lượt tại các điểm
( )
;0;0Aa
,
( )
0; ;0Bb
,
( )
0;0;Cc
.
Do
H
là trực tâm tam giác
ABC
nên
, , 0abc
.
Khi đó phương trình mặt phẳng
( )
:
1
x y z
a b c
+ + =
.
Mà
( ) ( )
1;2; 2H
−
nên:
1 2 2
1
a b c
+ − =
( )
1
.
Ta có:
( )
1 ;2; 2AH a= − −
,
( )
1;2 ; 2BH b= − −
,
( )
0; ;BC b c=−
,
( )
;0;AC a c=−
.
Lại có
H
là trực tâm tam giác
ABC
, suy ra
.0
.0
AH BC
BH AC
=
=
hay
2
bc
ac
=−
=−
(2)
.
Thay
( )
2
vào
( )
1
ta được:
1 2 2 9
1
22
c
c c c
+ − = = −
−−
, khi đó
9
9,
2
ab==
.
Vậy
( )
9;0;0A
,
9
0; ;0
2
B
,
9
0;0;
2
C
−
.
Khi đó, giả sử mặt cầu ngoại tiếp tứ diện
OABC
có phương trình là:
2 2 2
2 2 2 0x y z a x b y c z d
+ + − − − + =
. Với
( ) ( ) ( )
2 2 2
0a b c d
+ + −
Vì 4 điểm
,,,O A B C
thuộc mặt cầu nên ta có hệ phương trình:
0
0
9
18 81
2
81
9
9
4
4
81
9
9
4
4
d
d
ad
a
bd
b
cd
c
=
=
− + = −
=
− + = −
=
+ = −
=−
.
Phương trình mặt cầu ngoại tiếp tứ diện
OABC
là:
2 2 2
99
90
22
x y z x y z+ + − − + =
, có tâm
9 9 9
;;
2 4 4
I
−
và bán kính
222
9 9 9 9 6
0
2 4 4 4
R
= + + − =
.
Vậy diện tích mặt cầu ngoại tiếp tự diện
OABC
là
2
2
9 6 243
4 4 .
42
SR
= = =
.
Câu 17. Chọn D
Cách 1
Gọi
d
là giao tuyến của
( )
P
và
( )
Q
,
B
là giao
điểm của
d
và
( )
P
. Suy ra
B
cố định và
Bd
Trên đường thẳng
d
lấy điểm
A
không trùng với
B
Gọi
H
là hình chiếu vuông góc của
A
lên mặt phẳng
( )
P
,
E
là hình chiếu vuông góc của
H
lên
d
.
P
d'
d
H
E
B
A

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
90
Ta có
( ) ( )
;AH P BE P AH BE⊥ ⊥
. Mà
BE EH⊥
. Suy ra
BE EA⊥
Vậy góc giữa
( )
P
và
( )
Q
là góc
AEH
Ta có tam giác
AEH
vuông tại H và
AH
không đổi
Vì vậy, góc
AEH
nhỏ nhất
EH
lớn nhất. Mà
EH BH
;
BH
không đổi
Suy ra
EH
lớn nhất
E
trùng với
B
d
vuông góc với
BH
. Từ đó ,
d
vuông góc với
d
Vậy
( )
Q
là mặt phẳng chứa
d
và tạo với mặt phẳng
( )
P
một góc nhỏ nhất khi và chỉ khi
( )
Q
chứa
d
và
d
Ta có
( )
2; 1; 2
P
n = − −
là một vectơ pháp tuyến của
( )
P
;
( )
1;2;1
d
u =−
là một vectơ chỉ phương
của
d
( )
; 3;0;3
Pd
nu
=
( )
1;0;1
d
u
=
là một vectơ chỉ phương của
d
( )
; 2; 2;2
dd
uu
= − −
( )
1; 1;1
Q
n = − −
là một vectơ pháp tuyến của mặt phẳng
( )
Q
Suy ra
1; 1 2a b a b= − = − + = −
.
Cách 2. Ta có:
( )
1;2;1
d
u =−
là một vectơ chỉ phương của
d
( )
; ;1
Q
n a b=
là một vectơ pháp tuyến của
( )
Q
( )
2; 1; 2
P
n = − −
là một vectơ pháp tuyến của
( )
P
( )
Q
là mặt phẳng chứa
d
nên
( )
. 0 2 1 0 2 1 1
Q d Q d
n u n u a b a b⊥ = − + + = = +
Gọi
là góc giữa
( )
P
và
( )
Q
( )
22
22
cos cos ;
3. 1
PQ
ab
nn
ab
−−
= =
++
( )
2
Thay
( )
1
vào
( )
2
ta có
2 2 2
4 2 2
cos
3 4 4 1 1 5 4 2
b b b
b b b b b
+ − −
==
+ + + + + +
2
2
1 1 1
4 2 3
1
5
2 1 3
bb
b
= =
++
++
Góc
nhỏ nhất
cos
lớn nhất
1
cos
3
=
Khi đó
1
1 0 1b
b
+ = = −
. Suy ra
1a =−
. Vậy
2ab+ = −
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
91
DẠNG 2. VIẾT PHƯƠNG TRÌNH MẶT PHẲNG
Câu 1. Trong không gian
Oxyz
, cho điểm
( )
2;2;3M
. Mặt phẳng
( )
P
đi qua
M
và cắt các trục tọa độ
Ox
,
Oy
,
Oz
lần lượt tại các điểm
A
,
B
,
C
không trùng với gốc tọa độ sao cho
M
là trực tâm
của tam giác
ABC
. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng
( )
P
.
A.
2 3 9 0.x y z+ + + =
B.
2 2 3 14 0x y z+ + + =
.
C.
2 9 0x y z+ + − =
. D.
3 2 14 0x y z+ + − =
.
Câu 2. Trong không gian với hệ toạ độ
Oxyz
, viết phương trình mặt phẳng
( )
chứa trục
Ox
và đi qua
điểm
( )
2; 1;3M −
.
A.
( )
: 3 0yz
− + =
. B.
( )
:2 1 0xz
− + =
.
C.
( )
: 2 3 0x y z
+ + − =
. D.
( )
:3 0yz
+=
.
Câu 3. Trong không gian
Oxyz
, cho
( )
2;0;0A
,
( )
0;4;0B
,
( )
0;0;6C
,
( )
2;4;6D
. Gọi
( )
P
là mặt phẳng
song song với
( )
mp ABC
,
( )
P
cách đều
D
và mặt phẳng
( )
ABC
. Phương trình của
( )
P
là
A.
6 3 2 24 0x y z+ + − =
. B.
6 3 2 12 0x y z+ + − =
.
C.
6 3 2 0x y z+ + =
. D.
6 3 2 36 0x y z+ + − =
.
Câu 4. Viết phương trình mặt phẳng
( )
đi qua
( )
2;1; 3M −
, biết
( )
cắt trục
,,Ox Oy Oz
lần lượt tại
,,ABC
sao cho tam giác
ABC
nhận
M
làm trực tâm
A.
2 5 6 0.x y z+ + − =
B.
2 6 23 0.x y z+ − − =
C.
2 3 14 0.x y z+ − − =
D.
3 4 3 1 0.x y z+ + − =
Câu 5. Trong không gian với hệ tọa độ
Oxyz
, viết phương trình mặt phẳng
( )
P
đi qua hai điểm
( )
2;1;1A
,
( )
1; 2; 3B − − −
và vuông góc với mặt phẳng
( )
Q
:
0x y z+ + =
.
A.
0x y z− − =
. B.
30xy+ − =
. C.
10xy− − =
. D.
40x y z+ + − =
.
Câu 6. Trong không gian
Oxyz
, viết phương trình mặt phẳng
( )
P
đi qua điểm
( )
1;2;3M
và song song
với mặt phẳng
( )
: 2 3 1 0Q x y z− + + =
A.
2 3 6 0x y z− + + =
. B.
2 3 16 0x y z− + + =
.
C.
2 3 6 0x y z− + − =
. D.
2 3 16 0x y z− + − =
.
Câu 7. Trong không gian
Oxyz
, phương trình nào dưới đây là phương trình mặt phẳng vuông góc với
trục
Oz
?
A.
2 3 0+=y
. B.
2 3 0+=z
. C.
2 2 3 0+ + =xy
. D.
2 3 0+=x
.
Câu 8. Trong không gian
Oxyz
, cho hai điểm
( ) ( )
1;3; 4 , 1;2;2AB−−
. Phương trình mặt phẳng trung
trực của đoạn
AB
là?
A.
4 2 12z 7 0xy+ + + =
. B.
4 2 12z 7 0xy− + + =
.
C.
4 2 12z 17 0xy+ − − =
. D.
4 2 12z 17 0xy− − − =
.
Câu 9. Trong không gian
,Oxyz
cho hai điểm
( ) ( )
3; 1;1 , 1;2;4 .AB−
Viết phương trình mặt phẳng
( )
P
đi qua
A
và vuông góc với đường thẳng
.AB

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
92
A.
( )
:2 3 3 16 0.P x y z− − − =
B.
( )
:2 3 3 6 0.P x y z− − − =
C.
( )
: 2 3 3 6 0.P x y z− + + − =
D.
( )
: 2 3 3 16 0.P x y z− + + − =
Câu 10. Trong không gian với hệ tọa độ
Oxyz
cho hai mặt phẳng
( )
: 3 2 2 7 0x y z
− + + =
và
( )
:5 4 3 1 0x y z
− + + =
. Phương trình mặt phẳng đi qua
O
đồng thời vuông góc với cả
( )
và
( )
có phương trình là
A.
2 2 1 0x y z+ − + =
. B.
2 2 0x y z+ − =
. C.
2 2 0x y z− − =
. D.
2 2 0x y z− + =
.
Câu 11. Trong không gian
Oxyz
, phương trình mặt phẳng
( )
P
song song và cách mặt phẳng
( )
: 2 2z 3 0Q x y+ + − =
một khoảng bằng 1; đồng thời
( )
P
không qua
O
là
A.
2 2 1 0x y z+ + + =
. B.
220x y z+ + =
.
C.
2 2 6 0x y z+ + − =
. D.
2 2 3 0x y z+ + + =
.
Câu 12. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
23
: 5 4 ;
67
xt
d y t t
zt
=+
= −
= − +
và điểm
( )
1;2;3A −
. Phương trình mặt phẳng qua
A
và vuông góc với
d
là
A.
3 4 7 10 0x y z− + + =
. B.
3 4 7 16 0x y z− + + =
.
C.
3 4 7 16 0x y z− + − =
. D.
3 4 7 10 0x y z− + − =
.
Câu 13. Trong không gian
Oxyz
, mặt phẳng đi qua điểm
( )
1;1;2A −
và song song với hai đường thẳng
1 1 3
:
2 2 1
x y z− + −
= =
,
31
':
1 3 1
x y z−+
= =
có phương trình là
A.
4 10 0x y z− − + =
. B.
4 8 0x y z+ + − =
. C.
4 6 0x y z− + − =
. D.
4 8 0x y z+ − + =
.
Câu 14. Trong không gian
Oxyz
, cho
( ) ( )
0;1;1 , 1;0;0AB
và mặt phẳng
( )
: 3 0P x y z+ + − =
.
( )
Q
là
mặt phẳng song song với
( )
P
đồng thời đường thẳng
AB
cắt
( )
Q
tại
C
sao cho
2CA CB=
. Mặt
phẳng
( )
Q
có phương trình là:
A.
4
0
3
x y z+ + − =
hoặc
0x y z+ + =
. B.
0x y z+ + =
.
C.
4
0
3
x y z+ + − =
. D.
20x y z+ + − =
hoặc
0x y z+ + =
.
Câu 15. Trong không gian
Oxyz
, viết phương trình của mặt phẳng
( )
P
đi qua điểm
( )
2;1; 3M −
, đồng
thời vuông góc với hai mặt phẳng
( )
: 3 0Q x y z+ + =
,
( )
:2 0R x y z− + =
?
A.
2 3 14 0x y z+ − − =
. B.
4 5 3 22 0x y z+ − − =
.
C.
4 5 3 22 0x y z+ − + =
. D.
4 5 3 12 0x y z− − − =
.
Câu 16. Trong không gian với hệ trục tọa độ
Oxyz
, viết phương trình mặt phẳng vuông góc với mặt phẳng
( )
:2 3 2 0x y z
− + − =
và chứa đường thẳng
12
:
1 2 1
x y z
d
+−
==
−−
.
A.
10x y z+ + − =
. B.
3 3 0x y z+ − + =
.
C.
30x y z− + − =
. D.
2 3 0x y z+ − + =
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
93
Câu 17. Trong không gian Oxyz, cho hai điểm
( )
1; 1;0A −
,
( )
0;1;1B
. Gọi
( )
là mặt phẳng chứa đường
thẳng
12
:
2 1 1
x y z
d
−−
==
−
và song song với đường thẳng AB. Điểm nào dưới đây thuộc mặt phẳng
( )
?
A.
( )
6; 4; 1M −−
. B.
( )
6; 4;2N −
. C.
( )
6; 4;3P −
. D.
( )
6; 4;1Q −
.
Câu 18. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )
: 1 0P x y z+ + + =
và hai điểm
( ) ( )
1; 1;2 ; 2;1;1AB−
. Mặt phẳng
( )
Q
chứa
,AB
và vuông góc với mặt phẳng
( )
P
, mặt phẳng
( )
Q
có phương trình là:
A.
3 2 3 0x y z− − + =
. B.
20x y z+ + − =
. C.
3 2 3 0x y z− − − =
. D.
0xy− + =
.
Câu 19. Trong không gian
Oxyz
, cho ba điểm
( )
2;0;0A
,
( )
0;3;0B
và
( )
0;0; 1C −
. Phương trình của
mặt phẳng
( )
P
đi qua điểm
( )
1;1;1D
và song song với mặt phẳng
( )
ABC
là
A.
2 3 6 1 0xyz+ − + =
. B.
3 2 6 1 0x y z+ − + =
.
C.
3 2 5 0x y z+ − =
. D.
6 2 3 5 0x y z+ − − =
.
Câu 20. Trong không gian
,Oxyz
cho mặt phẳng
( )
P
chứa điểm
( )
3; 1; 2A −
và đường thẳng
: 1 .
32
xt
d y t
zt
=
=+
=−
Mặt phẳng
( )
P
có phương trình là
A.
3 5 8 0x y z− − + =
. B.
2 2 6 0x y z+ − − =
.
C.
40x y z+ + − =
. D.
2 7 0x y z− + − =
.
Câu 21. Trong không gian với hệ tọa độ , cho hai mặt phẳng ,
.Mặt phẳng vuông góc với cả và đồng thời cắt trục tại điểm
có hoành độ bằng 3. Phương trình của mp là:
A.
. B.
. C.
. D. .
Câu 22. Trong không gian
Oxyz
, cho hai điểm
( ) ( )
3;1; 1 , 2; 1;4AB−−
. Phương trình mặt phẳng
( )
OAB
với
O
là gốc tọa độ là
A.
3 14 5 0x y z+ + =
. B.
3 14 5 0x y z− + =
. C.
3 14 5 0x y z+ − =
. D.
3 14 5 0x y z− − =
.
Câu 23. Trong không gian
Oxyz
, mặt phẳng
()P
đi qua điểm
(1;0;2)A
và vuông góc với đường thẳng
12
:
2 1 3
−+
==
−
x y z
d
có phương trình là
A.
2 3 8 0+ − + =x y z
. B.
2 3 8 0− + − =x y z
. C.
2 3 8 0− + + =x y z
. D.
2 3 8 0+ − − =x y z
.
Câu 24. Trong không gian
Oxyz
, phương trình mặt phẳng
( )
P
đi qua điểm
( )
2;1; 3B −
, đồng thời vuông
góc với hai mặt phẳng
( )
: 3 0Q x y z+ + =
và
( )
:2 0R x y z− + =
là:
A.
4 5 3 22 0x y z+ − − =
. B.
4 5 3 12 0x y z− − − =
.
C.
2 3 14 0x y z+ − − =
. D.
4 5 3 22 0x y z+ − + =
.
Oxyz
( ): 3 2 1 0P x y z− + − =
( ): 2 0Q x z− + =
( )
()P
()Q
Ox
( )
30x y z
30x y z
2 6 0xz
2 6 0xz

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
94
Câu 25. Trong không gian
Oxyz
, mặt phẳng
z 18 0ax by c+ + − =
cắt ba trục toạ độ tại
,,A B C
sao cho
tam giác
ABC
có trọng tâm
( )
1; 3;2G −−
. Giá trị
ac+
bằng
A.
3
. B.
5
. C.
5−
. D.
3−
.
Câu 26. Trong không gian
Oxyz
, cho điểm
( )
1; 3;2M −
. Hỏi có bao nhiêu mặt phẳng đi qua
M
và cắt
các trục tọa độ tại
A
,
B
,
C
mà
0OA OB OC= =
?
A.
3
. B.
1
. C.
4
. D.
2
.
Câu 27. Trong không gian với hệ trục
Oxyz
, cho mặt cầu
( ) ( ) ( )
22
2
: 1 2 9S x y z− + + − =
. Mặt phẳng tiếp
xúc với mặt cầu tại điểm
( )
1;3;2A
có phương trình là
A.
4 0.xy+ − =
B.
3 0.y−=
C.
3 1 0.y −=
D.
1 0.x −=
Câu 28. Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 1 2 3 12S x y z− + + + − =
và mặt
phẳng
( ):2 2 3 0P x y z+ − − =
. Viết phương trình mặt phẳng song song với
( )
P
và cắt
( )
S
theo
thiết diện là đường tròn
( )
C
sao cho khối nón có đỉnh là tâm mặt cầu và đáy là hình tròn
( )
C
có
thể tích lớn nhất.
A.
( ):2 2 2 0Q x y z+ − + =
hoặc
( ):2 2 8 0Q x y z+ − + =
.
B.
( ):2 2 1 0Q x y z+ − − =
hoặc
( ):2 2 11 0Q x y z+ − + =
.
C.
( ):2 2 6 0Q x y z+ − − =
hoặc
( ):2 2 3 0Q x y z+ − + =
.
D.
( ):2 2 2 0Q x y z+ − + =
hoặc
( ):2 2 2 0Q x y z+ − + =
.
Câu 29. Trong không gian
Oxyz
, cho mặt cầu
( ) ( )
2
22
: 1 4S x y z+ + − =
và điểm
( )
2;2;2A
. Từ
A
kẻ ba
tiếp tuyến
AB
,
AC
,
AD
với
B
,
C
,
D
là các tiếp điểm. Viết phương trình mặt phẳng
( )
BCD
.
A.
2 2 1 0x y z+ + − =
. B.
2 2 3 0x y z+ + − =
.
C.
2 2 1 0x y z+ + + =
. D.
2 2 5 0x y z+ + − =
.
Câu 30. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
( )
;;H a b c
với
, , 0abc
. Mặt phẳng
()P
chứa
điểm
H
và lần lượt cắt các trục
,,Ox Oy Oz
tại
,,A B C
thỏa mãn
H
là trực tâm của tam giác
ABC
. Phương trình của mặt phẳng
()P
là
A.
2 2 2
x y z ab bc ca
a b c abc
++
+ + =
B.
3
x y z
a b c
+ + =
.
C.
2 2 2
0ax by cz a b c+ + − − − =
. D.
2 2 2 3 3 3
0a x b y c z a b c+ + − − − =
.
Câu 31. Trong không gian với hệ tọa độ
Oxyz
. Viết phương trình mặt phẳng
( )
P
đi qua điểm
( )
1;2;3M
và cắt các trục
,,Ox Oy Oz
lần lượt tại ba điểm
,,A B C
khác với gốc tọa độ
O
sao cho biểu thức
2 2 2
1 1 1
OA OB OC
++
có giá trị nhỏ nhất.
A.
( )
: 2 14 0P x y z+ + − =
. B.
( )
: 2 3 14 0P x y z+ + − =
.
C.
( )
: 2 3 11 0P x y z+ + − =
. D.
( )
: 3 14 0P x y z+ + − =
.
Câu 32. Trong không gian
Oxyz
, mặt phẳng
( )
: 27 0P ax by cz+ + − =
qua hai điểm
( )
3;2;1A
,
( )
3;5;2B −
và vuông góc với mặt phẳng
( )
:3 4 0Q x y z+ + + =
. Tính tổng
S a b c= + +
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
95
A.
2S =
. B.
12S =−
. C.
4S =−
. D.
2S =−
.
Câu 33. Trong không gian
Oxyz
12
:
1 2 1
x y z
d
+−
==
−
và mặt phẳng
( )
:2 2 4 0P x y z− − + =
.Mặt phẳng
chứa đường thẳng
d
và tạo với mặt phẳng
( )
P
góc với số đo nhỏ nhất có phương trình là
A.
20xz− − =
. B.
20xz+ − =
. C.
3 1 0x y z+ + − =
. D.
30x y z+ − + =
.
Câu 34. Trong không gian
Oxyz
, cho hai điểm
(1;2;1)A
và
(3; 1;5)B −
. Mặt phẳng
()P
vuông góc với
đường thẳng
AB
và cắt các trục
Ox
,
Oy
và
Oz
lần lượt tại các điểm
D
,
E
và
F
. Biết thể tích
của tứ diện
ODEF
bằng
3
2
, phương trình mặt phẳng
()P
là
A.
3
2 3 4 36 0x y z− + =
. B.
3
2 3 4 0
2
x y z− + + =
.
C.
2 3 4 12 0x y z− + =
. D.
2 3 4 6 0x y z− + =
.
Câu 35. Trong không gian
Oxyz
, có bao nhiêu mặt phẳng qua điểm
( )
4; 4;1M −
và chắn trên ba trục tọa
độ
Ox
,
Oy
,
Oz
theo ba đoạn thẳng có độ dài theo thứ tự lập thành cấp số nhân có công bội bằng
1
2
?
A. 1. B. 2. C. 3. D. 4.
Câu 36. Trong không gian
Oxyz
, cho mặt cầu
( )
2 2 2
: 2 4 6 2 0S x y z x y z+ + − − − − =
. Viết phương trình
mặt phẳng
( )
chứa
Oy
cắt mặt cầu
( )
S
theo thiết diện là đường tròn có chu vi bằng
8
.
A.
( )
:3 0xz
−=
. B.
( )
:3 0xz
+=
.
C.
( )
: 3 0xz
−=
. D.
( )
:3 2 0xz
+ + =
.
Câu 37. Cho mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 1 2 5 16S x y z− + − + + =
và điểm
( )
1;2; 1A −
. Điểm
( )
;;B a b c
thuộc
mặt cầu sao cho
AB
có độ dài lớn nhất. Tính
abc++
.
A.
6−
. B.
2
. C.
2−
. D.
12
.
Câu 38. Trong không gian với hệ tọa độ
Oxyz
, cho các điểm
(1;0;0), (0;1;0)AB
. Mặt phẳng đi qua các
điểm
,AB
đồng thời cắt tia
Oz
tại
C
sao cho tứ diện
OABC
có thể tích bằng
1
6
có phương trình
dạng
0x ay bz c+ + + =
. Tính giá trị
32a b c+−
.
A.
16
. B.
1
. C.
10
. D.
6
Câu 39. Trong không gian với hệ trục tọa độ
Oxyz
, cho hai mặt phẳng
( )
1
:3 4 2 0Q x y z− + + =
và
( )
2
:3 4 8 0Q x y z− + + =
. Phương trình mặt phẳng
( )
P
song song và cách đều hai mặt phẳng
( )
1
Q
và
( )
2
Q
là:
A.
( )
:3 4 10 0P x y z− + + =
. B.
( )
:3 4 5 0P x y z− + + =
.
C.
( )
:3 4 10 0P x y z− + − =
. D.
( )
:3 4 5 0P x y z− + − =
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
96
Câu 40. Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
1;2;1 , 3; 4;0AB
, mặt phẳng
: 46 0P ax by cz
. Biết rằng khoảng cách từ
,AB
đến mặt phẳng
P
lần lượt bằng
6
và
3
. Giá trị của biểu thức
T a b c
bằng
A.
3
. B.
6
. C.
3
. D.
6
.
Câu 41. Trong không gian
Oxyz
, mặt phẳng qua ba điểm
( )
1;3;2A
,
( )
2;5;9B
,
( )
3;7; 2C −−
có phương
trình là
30x ay bz c+ + + =
. Giá trị
abc++
bằng
A.
6−
. B.
3
. C.
3−
. D.
6
.
Câu 42. Trong không gian
Oxyz
, cho ba điểm
( )
10;1;1A
,
( )
10;4;1B
và
( )
10;1;5C
. Gọi
( )
1
S
là mặt
cầu có tâm
A
, bán kính bằng
1
; gọi
( )
2
S
là mặt cầu có tâm
B
, bán kính bằng
2
và
( )
3
S
là mặt
cầu có tâm
C
, bán kính bằng
4
. Hỏi có bao nhiêu mặt phẳng tiếp xúc với cả ba mặt cầu
( )
1
S
,
( )
2
S
,
( )
3
S
?
A.4. B.7. C.2. D. 3.
Câu 43. Trong không gian
Oxyz
, biết mặt phẳng
24 0ax by cz+ + − =
qua
( )
1;2;3A
và vuông góc với
hai mặt phẳng
( )
:3 2 4 0P x y z− + + =
,
( )
:5 4 3 1 0Q x y z− + + =
. Giá trị
abc++
bằng
A.
8
. B.
9
. C.
10
. D.
12
.
Câu 44. Trong không gian
Oxyz
, cho hinh lập phương
1 1 1 1
.ABCD ABC D
biết
( )
0;0;0A
,
( )
1;0;0B
,
( )
0;1;0D
,
( )
1
0;0;1A
. Gọi
( )
: 3 0P ax by cz+ + − =
là phương trình mặt phẳng chứa
1
CD
và tạo
với mặt phẳng
( )
11
BB D D
một góc có số đo nhỏ nhất. Giá trị của
= + +T a b c
bằng
A.
1−
. B.
6
. C.
4
. D.
3
.
Câu 45.
Trong không gian
Oxyz
, cho ba điểm
( )
1;2;4M
;
( )
0;1;2N
;
( )
2;1;3P
và mặt phẳng
( )
:0x Ay Bz C
+ + + =
. Biết
( )
song song với
OP
và đi qua hai điểm
M
,
N
. Giá trị của
biểu thức
A B C+−
là
A.
1
. B.
1−
. C.
5−
. D.
0
.
Câu 46. Trong không gian
Oxyz
, biết mặt phẳng
50ax by cz+ + + =
qua hai điểm
( )
3;1; 1A −
,
( )
2; 1;4B −
và vuông góc với
( )
:2 3 4 0P x y z− + + =
. Giá trị của
a b c−+
bằng
A.
9
. B.
12
. C.
10
. D.
8
.
Câu 47. Trong không gian
Oxyz
, cho mặt cầu
2 2 2
( ) ( ) ( ) 2): 1 1 1 1(S x y z− + − + − =
và mặt phẳng
: 2 0( 2 11)P x y z− + + =
. Xét điểm
M
di động trên
()P
; các điểm
,,A B C
phân biệt di động trên
()S
sao cho
,,AM BM CM
là các tiếp tuyến của
()S
. Mặt phẳng
()ABC
luôn đi qua điểm cố
định nào dưới đây?
A.
111
;;
422
−−
. B.
( )
0; 1;3−
. C.
3
;0;2
2
. D.
( )
0;3; 1−
.
Câu 48. Mặt phẳng
( )
P
đi qua điểm
( )
1;1;1M
cắt các tia
Ox
,
Oy
,
Oz
lần lượt tại
( )
;0;0Aa
,
( )
0; ;0Bb
( )
0;0;Cc
sao cho thể tích khối tứ diện
OABC
nhỏ nhất. Khi đó
23a b c++
bằng

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
97
A.
12
. B.
21
. C.
15
. D.
18
.
Câu 49. Trong không gian
Oxyz
, cho hình chóp
.S ABC
có
32SC AB==
, đường thẳng
AB
có
phương trình
11
1 4 1
x y z−+
==
−
và góc giữa đường thẳng
SC
và mặt phẳng đáy bằng
60
. Khi ba
điểm
,,A B C
cùng với ba trung điểm của ba cạnh bên của hình chóp
.S ABC
nằm trên một mặt
cầu thì mặt phẳng
( )
ABC
có phương trình là
A.
10yz+ + =
. B.
4 14 0x y z+ − − =
.C.
2 7 8 0x y z− − − =
. D.
4 14 0x y z+ − + =
.
Câu 50. Trong không gian
Oxyz
, cho bốn điểm
( )
1;1;1A
,
( )
1;0; 2B −−
,
( )
2; 1;0C −
,
( )
2;2;3D −
. Hỏi có
bao nhiêu mặt phẳng song song với
,AB CD
và cắt 2 đường thẳng
,AC BD
lần lượt tại
,MN
thỏa mãn
2
2
1
BN
AM
AM
=−
.
A.
0
. B.
2
. C.
3
. D.
1
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
98
ĐÁP ÁN CHI TIẾT
Câu 1. Chọn B
Ta có
( )
OA OB
OA OBC OA BC
OA OC
⊥
⊥ ⊥
⊥
Mặt khác
BC AM⊥
suy ra
( )
BC OAM BC OM⊥ ⊥
.
Ta có
( )
OB OA
OB OAC OB AC
OB OC
⊥
⊥ ⊥
⊥
Mặt khác
AC BM⊥
suy ra
( )
AC OBM AC OM⊥ ⊥
.
Từ đó, ta có
( )
OM ABC⊥
hay
( )
OM P⊥
nên
( )
P
nhận
( )
2;2;3OM =
làm một véctơ pháp
tuyến.
Phương trình mặt phẳng
( )
P
:
( ) ( ) ( )
2 2 2 2 3 3 0 2 2 3 17 0x y z x y z− + − + − = + + − =
.
Trong các đáp án, ta chọn mặt phẳng song song với mặt phẳng
( )
P
là mặt phẳng có phương trình
2 2 3 14 0x y z+ + + =
. Các đáp án A, C, D loại vì các mặt phẳng đó không nhận
( )
2;2;3OM =
làm một véctơ pháp tuyến.
Câu 2. Chọn D
Cách 1: Ta có
( )
( )
1;0;0
2; 1;3
i
OM
=
=−
( )
, 0; 3; 1i OM
= − −
.
Do đó
( )
qua điểm
O
và có 1 véc tơ pháp tuyến là
( )
0;3;1n =
.
Vậy phương trình mặt phẳng
( )
là
( ) ( )
3 0 0 0yz− + − =
hay
30yz+=
.
Vậy chọn phương án D.
Cách 2
Mặt phẳng
( )
chứa
Ox
nên loại B và C.
Thay toạ độ điểm
M
vào phương trình ở phương án A và D. Suy ra chọn phương án D.
Câu 3. Chọn A
Phương trình
( )
mp ABC
:
1
2 4 6
x y z
+ + =
6 3 2 12 0x y z + + − =
.
Mặt phẳng
( )
P
song song với mặt phẳng
( )
ABC
nên phương trình có dạng:
6 3 2 0x y z d+ + + =
,
12d −
.
Mặt phẳng
( )
P
cách đều
D
và mặt phẳng
( )
ABC
( ) ( )
( )
( )
( )
,,d ABC P d D P=
( )
( )
( )
( )
,,d A P d D P=
2 2 2 2 2 2
6.2 6.2 3.4 2.6
6 3 2 6 3 2
dd+ + + +
=
+ + + +
12 36dd + = +
24d = −
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
99
Vậy phương trình mặt phẳng
( )
P
:
6 3 2 24 0x y z+ + − =
.
Câu 4. Chọn C
Giả sử
( ) ( ) ( )
;0;0 , 0; ;0 , 0;0; , 0.A a B b C c abc
Khi đó mặt phẳng
( )
có dạng:
1
x y z
a b c
+ + =
.
Do
( ) ( )
2 1 3
11M
a b c
+ − =
Ta có:
( ) ( ) ( ) ( )
2 ;1; 3 , 2;1 ; 3 , 0; ; , ;0;AM a BM b BC b c AC a c= − − = − − = − = −
Do
M
là trực tâm tam giác
ABC
nên:
( )
3
. 0 3 0
2
3
2 3 0
.0
2
bc
AM BC b c
c
ac
a
BM AC
=−
= − − =
− − =
=−
=
Thay
( )
2
vào
( )
1
ta có:
4 1 3 14
1 7, 14.
3 3 3
c a b
c c c
− − − = = − = =
Do đó
( )
3
: 1 2 3 14 0.
7 14 14
x y z
x y z
+ − = + − − =
Câu 5. Chọn C
( )
3; 3; 4AB = − − −
. Một vectơ pháp tuyến của
( )
Q
là
( )
( )
1;1;1
Q
n =
.
Vì
( )
( ) ( )
P AB
PQ
⊥
nên
( )
( )
, 1; 1;0
Q
n AB n
= = −
là một vectơ pháp tuyến của
( )
P
.
Vậy phương trình
( )
P
là:
( ) ( ) ( )
1 2 1 1 0 1 0 1 0x y z x y− − − + − = − − =
.
Câu 6. Chọn C
( ) ( )
//PQ
( ) ( )
( )
1; 2;3
PQ
nn= = −
.
( )
( )
( )
( )
qua 1;2;3
VTPT 1; 2;3
P
M
P
n
=−
( ) ( ) ( ) ( )
: 1 2 2 3 3 0P x y z− − − + − =
( )
: 2 3 6 0P x y z− + − =
.
Câu 7. Chọn B
Mặt phẳng
( )
vuông góc với trục
Oz
có
1
vectơ pháp tuyến là
( )
0;0;1=n
.
Trong 4 đáp án chỉ có mặt phẳng
2 3 0+=z
là có 1 vectơ pháp tuyến là
( )
0;0;1=n
.
Câu 8. Chọn C
Ta có trung điểm của đoạn thẳng
AB
là
5
0; ; 1
2
I
−
. Véc tơ
( )
2; 1;6AB −−
.
Phương trình mặt phẳng trung trực của
AB
đi qua
I
nhận
AB
làm VTPT có phương trình:
( ) ( )
5
2 0 1 6 1 0 4 2 12 17 0
2
x y z x y z
− − − − + + = + + − =
.
Câu 9. Chọn B

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
100
Mặt phẳng
( )
P
đi qua
A
và vuông góc với đường thẳng
AB
nhận
( 2;3;3)AB =−
làm vecto
pháp tuyến, do đó, phương trình mặt phẳng
()P
là
( ) ( ) ( )
2 3 3 1 3 1 0x y z− − + + + − =
2 3 3 6 0x y z − + + + =
hay
2 3 3 6 0.x y z− − − =
Câu 10. Chọn B
Gọi mặt phẳng phải tìm là
( )
P
. Khi đó véc tơ pháp tuyến của
( )
P
là:
( )
, 2; 1; 2
P
n n n
= = −
.
Phương trình của
( )
P
là
2 -2 0x y z+=
.
Câu 11. Chọn C
Vì
( ) ( )
//PQ
nên
( ) ( )
( )
1; 2; 2
PQ
nn==
;
( )
: 2 2 0Q x y z d+ + + =
.
( ) ( )
222
3 3 6
3
1 1 3 3
3 3 0
1 2 2
PQ
dd
d
dd
dd
− − = = −
−−
= = − − =
− − = − =
++
Vì
( )
P
không qua
O
nên
6c =−
suy ra
( )
: 2 2 6 0Q x y z+ + − =
. Vậy đáp án C đúng.
Câu 12. Chọn D
Gọi
( )
P
là mặt phẳng cần tìm. Ta có: đường thẳng
d
có một VTCP
( )
3; 4;7
d
u =−
Và
( ) ( )
P d P⊥
có một VTPT
( )
( )
3; 4;7
P
d
nu= = −
Khi đó
( )
P
qua điểm
( )
1;2;3A −
và nhận
( )
( )
3; 4;7
P
n =−
làm VTPT có phương trình là
( ) ( ) ( )
3 1 4 2 7 3 0 3 4 7 10 0x y z x y z+ − − + − = − + − =
.
Câu 13. Chọn D
Vì
()
song song với
và
'
nên
()
có cặp VTCP
1
2
(2;2;1)
(1;3;1)
u
u
=
=
Suy ra
()
có một VTPT
12
[ . ] ( 1; 1;4)n u u= = − −
Mặt phẳng
()
đi qua điểm
( )
1;1;2A −
và có một VTPT
( 1; 1;4)n = − −
có phương trình là:
1( 1) 1.( 1) 4( 2) 0x y z− + − − + − =
4 8 0x y z − − + − =
4 8 0x y z + − + =
.
Câu 14. Chọn A
Vì
, , A B C
thẳng hàng và
2CA CB=
nên
( )
2; 1; 1
22
2 1 1
;;
2 3 2
3 3 3
C
CA CB OC OB OA
C
CA CB OC OB OA
− −
= = −
= − = +
Mặt phẳng
( )
Q
qua
C
song song với mặt phẳng
( )
P
nên phương trình của mặt phẳng
( )
Q
là:
4
0
3
x y z+ + − =
hoặc
0x y z+ + =
.
Câu 15. Chọn B

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
101
Mặt phẳng
( )
Q
có vectơ pháp tuyến là
( )
1;1;3a =
và mặt phẳng
( )
R
có vectơ pháp tuyến là
( )
2; 1;1b =−
.
( )
P
vuông góc với hai mặt phẳng
( )
Q
và
( )
R
nên một vectơ pháp tuyến của
( )
P
là
( )
; 4;5; 3n a b
= = −
.
( )
P
qua
( )
2;1; 3M −
có vectơ pháp tuyến
n
nên có phương trình
( ) ( ) ( )
4 2 5 1 3 3 0x y z− + − − + =
hay
4 5 3 22 0x y z+ − − =
.
Câu 16. Chọn A
Đường thẳng
d
đi qua
( )
0; 1;2M −
và có vectơ chỉ phương
( )
1;2; 1u −−
.
Mặt phẳng
( )
có vectơ pháp tuyến
( )
2; 3;1n
−
.
Giả sử
( )
là mặt phẳng vuông góc với
( )
và chứa
d
.
Khi đó
( )
đi qua
M
và có vectơ pháp tuyến
nn
⊥
,
nu
⊥
.
( )
đi qua
( )
0; 1;2M −
và nhận
( )
, 1;1;1nu
=
là một vectơ pháp tuyến.
phương trình
( )
: 1 0x y z
+ + − =
.
Câu 17. Chọn C
Ta có
( ) ( )
1;2;1 ; 2; 1;1
d
AB u= − = −
.
Theo giả thiết
( )
( )
( )
( )
( ) ( )
( ) ( )
//
; 3;3; 3 3 1;1; 1
d
d
AB
AB n
n AB u n
d
un
⊥
= = − = −
⊥
.
Phương trình mặt phẳng
( )
là:
( )
1 0 1 0x y z x y z+ + − = + − + =
.
Thay từng tọa độ điểm M, N, P, Q vào phương trình mặt phẳng
( )
, suy ra điểm P thuộc
( )
.
Câu 18. Chọn A
Mặt phẳng
( )
P
có 1 véc tơ pháp tuyến là
(1;1;1)
p
n =
. Véc tơ
(1;2; 1)AB =−
.
Gọi
n
là một véc tơ pháp tuyến của
( )
Q
, do
( )
Q
vuông góc với
( )
P
nên
n
có giá vuông góc với
p
n
, mặt khác véc tơ
AB
có giá nằm trong mặt phẳng
( )
Q
nên
n
cũng vuông góc với
AB
Mà
p
n
và
AB
không cùng phương nên ta có thể chọn
n
=
( )
, 3;2;1
P
n AB
=−
, mặt khác
( )
Q
đi
qua
( )
1; 1;2A −
nên phương trình của mặt phẳng
( )
Q
là:
( ) ( )
3 1 2 1 1( 2) 0 3 2 3 0x y z x y z− − + + + − = − − − =
.
Câu 19. Chọn B
Ta có phương trình mặt phẳng
( )
ABC
là
( )
1 3 2 6 6 0
2 3 1
x y z
x y z+ + = + − − =
−
.
Do
( )
P
song song với
( )
ABC
nên phương trình của
( )
P
có dạng
( )
3 2 6 0 6x y z d d+ − + = −
.
Mặt khác
( )
P
đi qua điểm
( )
1;1;1D
suy ra
1 0 1dd− + = =
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
102
Vậy phương trình mặt phẳng
( )
P
là
3 2 6 1 0x y z+ − + =
.
Câu 20. Chọn C
( )
1;1; 2
d
u =−
là VTCP của
d
và
( )
0;1;3Md
.
( )
3; 2; 1MA = − −
.
,
d
u MA
=
1 2 2 1 1 1
;;
2 1 1 3 3 2
− −
− − − −
( )
5; 5; 5= − − −
( )
5 1;1;1=−
.
Vậy phương trình của
( )
P
đi qua
( )
3; 1; 2A −
và có VTPT
( )
( )
1; 1; 1
P
n =
là
( ) ( ) ( )
1 3 1 1 1 2 0x y z− + + + − =
40x y z + + − =
.
Câu 21. Chọn A
có vectơ pháp tuyến , có vectơ pháp tuyến .
Vì mặt phẳng vuông góc với cả và nên có một vectơ pháp tuyến là
.
Vì mặt phẳng cắt trục tại điểm có hoành độ bằng 3 nên đi qua điểm .
Vậy đi qua điểm và có vectơ pháp tuyến nên có phương trình:
.
Câu 22. Chọn D
Ta có:
( ) ( ) ( )
3;1; 1 , 2; 1;4 ; 3; 14; 5OA OB OA OB
= − = − = − −
là VTPT của
( )
OAB
Mặt phẳng
( )
OAB
có VTPT là
( )
3; 14 ; 5−−
và đi qua
( )
0;0;0O
nên có phương trình:
3 14 5 0x y z− − =
.
Câu 23. Chọn B
Véctơ
(2; 1;3)=−u
là một véctơ chỉ phương của đường thẳng
d
, vì
()Pd⊥
nên
()P
nhận
(2; 1;3)=−u
làm một véctơ pháp tuyến. Vậy phương trình mặt phẳng
()P
là
2( 1) ( 0) 3( 2) 0 2 3 8 0− − − + − = − + − =x y z x y z
.
Câu 24. Chọn A
( )
1
1;1;3n =
và
( )
2
2; 1;1n =−
lần lượt là các vectơ pháp tuyến của hai mặt phẳng
( )
Q
và
( )
R
.
Vì mặt phẳng
( )
P
vuông góc với hai mặt phẳng
( )
Q
và
( )
R
nên ta chọn vectơ pháp tuyến mặt
phẳng
( )
P
là
12
;n n n
=
( )
4;5; 3=−
.
()P
( )
1; 3;2
P
n =−
( )
Q
( )
1;0; 1
Q
n =−
( )
( )
P
( )
Q
( )
( ) ( )
; 3;3;3 3 1;1;1
PQ
nn
==
( )
Ox
( )
( )
3;0;0M
( )
( )
3;0;0M
( )
1;1;1n
=
( )
30x y z+ + − =

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
103
Mà mặt phẳng
( )
P
đi qua điểm
( )
2;1; 3B −
nên phương trình mặt phẳng
( )
P
là
( ) ( ) ( )
4 2 5 1 3 3 0x y z− + − − + =
4 5 3 22 0x y z+ − − =
.
Câu 25. Chọn D
Giả sử mặt phẳng
( )
: z 18 0P ax by c+ + − =
cắt 3 trục toạ độ
,,Ox Oy Oz
lần lượt tại
,,A B C
.
Do
( )
;0;0
A
A Ox A x
;
( )
0; ;0
B
B Oy B y
;
( )
0;0;
C
C Oz C z
.
Vì
( )
1; 3;2G −−
là trọng tâm tam giác
ABC
nên :
( ) ( ) ( )
00
1
3
3
00
3 9 3;0;0 , 0; 9;0 , 0;0;6 .
3
6
00
2
3
A
A
B
B
C
C
x
x
y
y A B C
z
z
++
=−
=−
++
= − = − − −
=
++
=
Do
( )
,,A B C P
nên mp
( )
P
có phương trình:
1 6 2 3 18 0
3 9 6
x y z
x y z+ + = − − + − =
−−
.
Suy ra:
6; 3ac= − =
. Vậy
3ac+ = −
.
Câu 26. Chọn A
Gọi
( )
;0;0Aa
,
( )
0; ;0Bb
,
( )
0;0;Cc
. Từ đó ta có
OA a=
,
OB b=
,
OC c=
Mặt phẳng qua các điểm
A
,
B
,
C
có phương trình theo đoạn chắn:
( )
1
x y z
P
a b c
+ + =
.
Vì
( )
MP
nên
1 3 2
1
a b c
− + =
. Vì
OA OB OC a b c= = = =
Từ đó ta có hệ phương trình:
1 3 2
1
a b c
abc
− + =
==
1 3 2
1
a b c
ab
bc
− + =
=
=
1 3 2
1
a b c
ab
ab
bc
bc
− + =
=
=−
=
=−
1 3 2
1
1 3 2
1
1 3 2
1
1 3 2
1
a b c
abc
a b c
a b c
a b c
a b c
a b c
abc
− + =
==
− + =
= = −
− + =
= − =
− + =
= − = −
4
6
2
a b c
a b c
abc
= = − = −
= − = =
= − = − =
.
Vậy có 3 mặt phẳng thỏa mãn.
Câu 27. Chọn B
Gọi
I
là tâm của mặt cầu. Khi đó
( )
1;0;2I
.
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
104
Mặt phẳng
( )
tiếp xúc với
( )
S
tại điểm
( )
1;3;2A
nên nhận
( )
0;3;0IA =
làm véctơ pháp tuyến.
Mặt khác mặt phẳng
()
đi qua điểm
( )
1;3;2A
nên có phương trình tổng quát
( )
: 3 0y
−=
.
Câu 28. Chọn B
( ) ( ) ( )
/ / : 2 2 0( 3)P x y z d d
+ − + = −
.
Mặt cầu
( )
S
có tâm
( )
1; 2;3I −
, bán kính
23R =
.
Gọi
( )
H
là khối nón thỏa đề bài với đường sinh
23lR==
.
Đặt
( )
( , )x h d I
==
. Khí đó bán kính đường tròn đáy hình nón :
2
12rx=−
.
Thể tích khối nón:
2
()
1
(12 )
3
H
V x x
=−
, với
0 2 3x
.
Xét sự biến thiên của hàm số :
2
1
( ) (12 )
3
f x x x
=−
trên
0 2 3x
.
Khi đó
()fx
đạt giá trị lớn nhất tại
2x =
, hay
( ,( )) 2dI
=
Vậy :
2 2 2
5 6 11
2.1 2.( 2) 3
( ,( )) 2 2
5 6 1
2 2 ( 1)
dd
d
dI
dd
− = =
+ − − +
= =
− = − = −
+ + −
.
Câu 29. Chọn D
Mặt cầu
( ) ( )
2
22
: 1 4S x y z+ + − =
có tâm
( )
0;0;1I
và bán kính
2R =
.
Do
AB
,
AC
,
AD
là ba tiếp tuyến của mặt cầu
( )
S
với
B
,
C
,
D
là các tiếp điểm nên:
AB AC AD
IA
IB IC ID R
==
= = =
là trục của đường tròn ngoại tiếp
( )
BCD IA BCD ⊥
.
x
2
3
M
I
H
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
105
Khi đó mặt phẳng
( )
BCD
có một vectơ pháp tuyến
( )
2;2;1n IA==
.
Gọi
J
là tâm của đường tròn ngoại tiếp
BCD J IA
và
IJ BJ⊥
.
Ta có:
IBA
vuông tại
B
và
BJ IA⊥
nên:
2
2
44
.
39
IB
IB IJ IA IJ IJ IA
IA
= = = =
.
Đặt
( ) ( )
; ; ; ; 1J x y z IJ x y z = −
,
( )
2;2;1IA =
.
4 8 8 13
;;
9 9 9 9
IJ IA J
=
.
Mặt phẳng
( )
BCD
đi qua
8 8 13
;;
9 9 9
J
và có véctơ pháp tuyến
( )
2;2;1n =
có phương trình:
8 8 13
2 2 0 2 2 5 0
9 9 9
x y z x y z
− + − + − = + + − =
.
Câu 30. Chọn C
Cách 1:
Gọi
( )
0
;0;0Ax
,
( )
0
B 0; ;0y
,
( )
0
C 0;0; z
. Khi đó mặt phẳng
()P
có phương trình theo đoạn
chắn là:
0 0 0
1
x y z
x y z
+ + =
.
Ta có :
( )
0
;;AH a x b c=−
,
( )
00
0; ;BC y z=−
,
( )
0
;;BH a b y c=−
,
( )
00
;0;AC x z=−
.
Vì
H
là trực tâm tam giác
ABC
nên ta có hệ:
( )
2 2 2
0
00
00
2 2 2
0 0 0 0 0
2 2 2
0
0 0 0
0
00
. =0
0
. =0 0
1
1
abc
c
y
yz
b
b
AH BC
by cz
c a b c
BH AC ax cz x z x
aa
a b c
H ABC
a b c
abc
z
x y z
cc
z
c
zz
ab
++
=
=
− + =
++
− + = = =
+ + =
++
+ + =
=
Thay vào phương trình mặt phẳng
()P
ta được:
2 2 2 2 2 2 2 2 2
1
ax by cz
a b c a b c a b c
+ + =
+ + + + + +
.
Hay
( )
2 2 2
:0P ax by cz a b c+ + − − − =
.
Cách 2 : Ta chứng minh được
( )
OH ABC⊥
hay
( )
OH P⊥
. Do đó mặt phẳng
()P
qua
H
và
nhận
( )
;;OH a b c
làm véc tơ pháp tuyến có phương trình là :
( ) ( ) ( )
2 2 2
00a x a b y b c z c ax by cz a b c− + − + − = + + − − − =
.
Câu 31. Chọn B
Gọi
H
là trực tâm
ABC
.
Ta có:
( ) ( )
1
BH AC
AC OBH AC OH
OB AC
⊥
⊥ ⊥
⊥
.
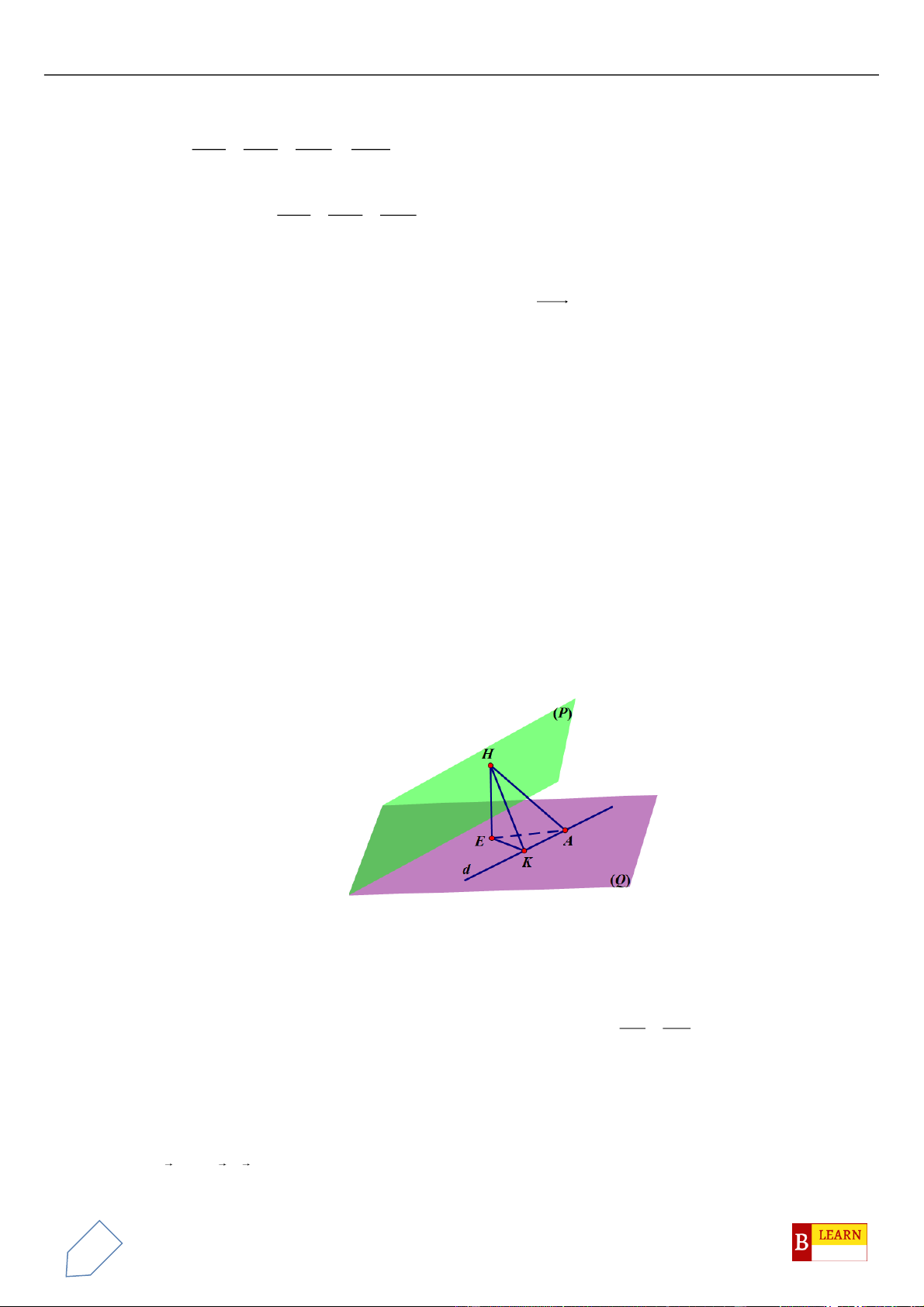
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
106
Chứng minh tương tự ta có:
( )
2BC OH⊥
. Từ
( ) ( ) ( )
1 , 2 OH ABC⊥
.
Ta có:
2 2 2 2
1 1 1 1
OA OB OC OH
+ + =
.
Vậy để biểu thức
2 2 2
1 1 1
OA OB OC
++
đạt giá trị nhỏ nhất thì
OH
đạt giá trị lớn nhất.
Mà
OH OM
nên suy ra
OH
đạt giá lớn nhất bằng
OM
hay
HM
.
Vậy
( )
OM ABC⊥
( )
P
có 1 vectơ pháp tuyến là
( )
1;2;3OM =
.
Phương trình mặt phẳng
( )
P
:
( ) ( ) ( )
1 1 2 2 3 3 0 2 3 14 0x y z x y z− + − + − = + + − =
.
Câu 32. Chọn B
Do
( )
P
đi qua
A
nên
3 2 27 0a b c+ + − =
; Do
( )
P
đi qua
B
nên
3 5 2 27 0a b c− + + − =
Do
( ) ( )
PQ⊥
nên
30abc+ + =
Từ đó , ta có hệ phương trình
3 2 27 6
3 5 2 27 27
3 0 45
a b c a
a b c b
a b c c
+ + = =
− + + = =
+ + = = −
.
Khi đó
6 27 45 12S a b c= + + = + − = −
.
Câu 33. Chọn D
Lấy điểm
( )
0; 1;2A −
thuộc đường thẳng
d
.
Gọi
H
là hình chiếu vuông góc của
A
lên mặt phẳng
( )
P
.
Gọi
,EK
lần lượt là hình chiếu vuông góc của
H
lên mặt phẳng
( )
Q
và đường thẳng
d
.
Ta có:
( ) ( ) ( ) ( )
(
)
,,AH P HE Q P Q AHE
⊥ ⊥ = =
. Xét
cos
HE HK
HA HA
=
Để
có số đo nhỏ nhất khi
cos
lớn nhất
EK
. Lúc đó mặt phẳng
( )
Q
chứa đường thẳng
d
và vuông góc với mặt phẳng
( )
HAK
.
Mặt phẳng
( )
AHK
là mặt phẳng chứa đường thẳng
d
và vuông với mặt phẳng
( )
P
,
AHK d P
n u n
=
là một vectơ pháp tuyến của mặt phẳng
( )
AHK

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
107
Suy ra một vectơ pháp tuyến của mặt phẳng
( )
Q
( )
, 6; 6;6
Q d AHK
n u n
= = − −
phương trình
mặt phẳng
( )
Q
:
30x y z+ − + =
.
Câu 34. Chọn D
Vì
()AB P⊥
nên mặt phẳng
()P
có một véc tơ pháp tuyến là
(2; 3;4)AB =−
, do đó phương trình
mặt phẳng
()P
có dạng
2 3 4 0x y z d− + + =
, từ đây tìm được
( ;0;0)
2
d
D −
,
(0; ;0)
3
d
E
,
(0;0; )
4
d
F −
suy ra
2
d
OD =
,
3
d
OE =
,
4
d
OF =
. Mặt khác tứ diện
ODEF
có
,,OD OE OF
đôi
một vuông góc nên
1
..
6
ODEF
V OD OE OF=
3
()
3
66
144 2
d
dd = = =
.Vậy phương trình
mặt phẳng
()P
là
2 3 4 6 0x y z− + =
.
Câu 35. Chọn C
Gọi
( ) ( ) ( )
;0;0 , 0; ;0 , 0;0;A a B b C c
là giao điểm của mặt phẳng
( )
P
và các trục tọa độ.
( )
:1
x y z
P
a b c
+ + =
Theo giả thiết có:
( )
4 4 1
1
8, 4, 2
8, 4, 2
11
11
16, 8, 4
24
24
MP
a b c
a b c
a b c
OC OB OA
a b c
c b a
− + =
= − = − =
= = − = −
==
= = − =
==
.
Vậy có 3 mặt phẳng thỏa mãn.
Câu 36. Chọn A
( )
S
có tâm
( )
1;2;3I
, bán kính
4R =
. Đường tròn thiết diện có bán kính
4r =
.
mặt phẳng
( )
qua tâm
I
.
( )
chứa
Oy
( )
:0ax cz
+ =
. Mà
( )
3 0 3I a c a c
+ = = −
.
Chọn
( )
1 3 :3 0c a x z
= − = − =
.
Câu 37. Chọn A
+ Mặt cầu
( )
S
có tâm
( )
1;2; 5I −
và bán kính
4R =
.
+ Gọi
là đường thẳng đi qua 2 điểm
A
và
I
. Véc tơ chỉ phương của đường thẳng
là
( )
0;0;4u IA==
.
phương trình đường thẳng
là:
( )
1
2.
14
x
yt
zt
=
=
= − +
+ Vì
( )
1;2; 1A −
thuộc mặt cầu
( )
S
nên
AB
có độ dài lớn nhất
AB
là đường kính
B
là
giao điểm còn lại của đường thẳng
và mặt cầu
( )
S
.
+
( )
1;2; 1 4 .B B t − +
( ) ( ) ( ) ( )
2 2 2
0
1 1 2 2 1 4 5 16
2
t
B S t
t
=
− + − + − + + =
=−
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
108
+ Với
( )
0 1;2; 1tB= −
.
+ Với
( )
2 1;2; 9tB= − −
.
Vậy
1 2 9 6abc+ + = + − = −
.
Cách 2: Vì
( )
1;2; 1A −
thuộc mặt cầu
( )
S
nên
AB
có độ dài lớn nhất
AB
là đường kính, tức
là
I
là trung điểm của đoạn
AB
.
Câu 38. Chọn D
Mặt phẳng đi qua các điểm
,AB
đồng thời cắt tia
Oz
tại
( )
0;0;Cc
,
0c
có phương trình là
1
11
x y z
c
+ + =
.
Mặt khác:
1 1 1
. . . 1
6 6 6
OABC
V OAOB OC c= = =
.
Vậy phương trình mặt phẳng cần tìm có dạng
1 1 0
1 1 1
x y z
x y z+ + = + + − =
.
Vậy
1ab==
,
1c =−
3 2 1 3.1 2 6a b c + − = + + =
.
Câu 39. Chọn B
Gọi
( )
;;M x y z
là điểm thuộc mặt phẳng
( )
P
cần tìm.
Ta có
( )
( )
( )
( )
12
,,d M Q d M Q=
3 4 2 3 4 8
26 26
x y z x y z− + + − + +
=
3 4 5 0x y z − + + =
.
Vậy phương trình mặt phẳng
( )
P
là:
3 4 5 0− + + =x y z
.
Câu 40. Chọn B
Gọi
,HK
lần lượt là hình chiếu của
,AB
trên mặt phẳng
( )
P
.
Khi đó theo giả thiết ta có:
3AB =
,
6AH =
,
3BK =
.
Do đó
,AB
ở cùng phía với mặt phẳng
( )
P
Lại có:
AB BK AK AH H K+
.
Suy ra
,,A B H
là ba điểm thẳng hàng và
B
là trung điểm của
AH
nên tọa độ
( )
5;6; 1H −
.
Vậy mặt phẳng
P
đi qua
( )
5;6; 1H −
và nhận
( )
2;2; 1AB =−
là VTPT có nên phương trình
( ) ( ) ( )
2 5 2 6 1 1 0 2 2 23 0x y z x y z− + − − + = + − − =
.
Theo bài ra thì
( )
: 4 4 2 46 0P x y z− − + + =
, nên
4, 4, 2abc= − = − =
.
Vậy
6T a b c
.
Câu 41. Chọn A
( )
1;2;7AB =
,
( )
4;4; 4AC = − −
.
Mặt phẳng
( )
ABC
qua điểm
( )
1;3;2A
và có một vectơ pháp tuyến là
( )
; 36; 24;12n AB AC
= = − −
.
Vậy phương trình mặt phẳng
( )
ABC
:
( ) ( ) ( )
36 1 24 3 12 2 0xyz− − − − + − =
hay
3 2 7 0x y z+ − − =
.
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
109
2
16
7
a
b a b c
c
=
= − + + = −
=−
.
Câu 42. Chọn C
Giả sử
( )
mp P
là mặt phẳng tiếp xúc với cả ba mặt cầu
( )
1
S
,
( )
2
S
,
( )
3
S
.
Xét vị trí tương đối giữa
3
mặt cầu
( )
1
S
,
( )
2
S
,
( )
3
S
có bán kính lần lượt là
1, 2, 4
.
12
3 1 2AB R R= = + = +
Mặt cầu
( )
1
S
và
( )
2
S
tiếp xúc ngoài.
13
4 1 4AC R R= + = +
Mặt cầu
( )
1
S
và
( )
3
S
cắt nhau.
23
5 2 4BC R R= + = +
Mặt cầu
( )
2
S
và
( )
3
S
cắt nhau.
Từ vị trí trên ta có nhận xét: tâm của cả ba mặt cầu phải nằm về cùng
1
phía so với
( )
mp P
.
Có hai
( )
mp P
thỏa mãn đề bài
Chọn đáp án C.
Câu 43. Chọn D
Gọi
( )
là mặt phẳng cần tìm và
( )
n
là một véc tơ pháp tuyến của mặt phẳng
( )
.
Mặt phẳng
( )
:3 2 4 0P x y z− + + =
có véc tơ pháp tuyến
( )
3; 2;1
P
n −
; mặt phẳng
( )
:5 4 3 1 0Q x y z− + + =
có véc tơ pháp tuyến
( )
5; 4;3
Q
n −
.
Ta có:
( ) ( )
( ) ( )
P
Q
⊥
⊥
( )
( )
; 2; 4; 2
PQ
n n n
= = − − −
.
Mặt phẳng
( )
qua
A
có véc tơ pháp tuyến
( )
n
nên có phương trình là:
( ) ( ) ( )
2 1 4 2 2 3 0x y z− − − − − − =
2 4 2 16 0x y z− − − + =
( )
:3 6 3 24 0x y z
+ + − =
.
Vậy
3 6 3 12abc+ + = + + =
.
Câu 44. Chọn C
Từ giả thiết ta có
( )
1;1;0C
,
( )
1
1;0;1B
,
( )
1
0;1;1D
.
Gọi
d
là giao tuyến của
( )
P
và
( )
11
BB D D
,
E
là trung
điểm của
AC
;
K
là hình chiếu vuông góc của
E
trên
d
. Ta
có
( ) ( ) ( )
( )
11
,
d CE
d ECK P BB D D EKC
d EK
⊥
⊥ =
⊥
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
110
Do đó
( ) ( )
( )
11
1
1
sin , sin
2
CE CE
P BB D D EKC
CK CD
= = =
suy ra góc giữa mặt phẳng
( )
P
và
( )
11
BB D D
nhỏ nhất bằng
30
. Dấu "=" xảy ra khi
d
vuông góc với
1
CD
, mặt khác
d
vuông góc
với
AC
suy ra
d
cùng phương với
1
,CD AC
. Do đó
( )
1
1;0;1CD =−
;
( )
1;1;0AC =
;
( )
11
, , 1;2;1
P
n CD AC CD
==
Vậy
( )
: 2 3 0P x y z+ + − =
, do đó
4.abc+ + =
Câu 45.
Chọn B
Ta có
( )
2;1;3OP =
;
( )
1; 1; 2MN = − − −
Từ đề bài ta có vectơ pháp tuyến của mặt phẳng
( )
là
( )
, 1;1; 1n OP MN
= = −
Mặt phẳng
( )
đi qua
( )
1;2;4M
và nhận
( )
1;1; 1n =−
vectơ pháp tuyến nên phương trình tổng
quát
( )
là:
( ) ( ) ( )
1 2 4 0 1 0x y z x y z− + − − − = + − + =
.
Vậy
1, 1, 1A B C= = − =
1A B C + − = −
.
Câu 46. Chọn A
Ta có:
( )
1; 2;5AB = − −
,
( )
2; 1;3
P
n =−
. Gọi
( )
:
50ax by cz+ + + =
.
Ta có: mặt phẳng
( )
nhận
( )
, 1;13;5
P
n AB n
= = −
làm vectơ pháp tuyến.
Do đó
( )
: 13 5 0x y z D
− + + + =
.
Mặt phẳng
( )
qua
( )
3;1; 1A −
nên:
( )
3 13.1 5. 1 0D− + + − + =
5D = −
.
( )
: 13 5 5 0x y z
− + + − =
hay
( )
: 13 5 5 0x y z
− − + =
.
Suy ra
1a =
;
13b =−
;
5c =−
.
Vậy
9a b c− + =
.
Câu 47. Chọn D
Mặt cầu
( )
S
có tâm
( )
1;1;1I
bán kính
23R =
.
Xét điểm
( ) ( )
;; ; ; ;M a b c A x y z
ta có hệ điều kiện:
( ) ( ) ( )
2 2 2
2 2 2
2 1 1 12
2 2 11 0
x y z
AI AM IM
a b c
− + − + − =
+=
− + + =
( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( )
( )
2 2 2
2 2 2 2 2 2
2 1 1 12 1
12 1 1 1 2
2 2 11 0 3
x y z
x a y b z c a b c
a b c
− + − + − =
+ − + − + − = − + − + −
−+
+
=
Lấy – theo vế có:
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
111
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
2 2 2 2 2 2 2 2 2
1 1 1 12 12 1 1 1x y z x a y b z c a b c
− + − + − − + − + − + − = − − + − + −
( ) ( ) ( )
1 1 1 9 0a x b y c z a b c − + − + − − − − − =
.
Vậy mặt phẳng qua ba tiếp điểm là
( ) ( ) ( ) ( )
: 1 1 1 9 0 Q a x b y c z a b c− + − + − − − − − =
.
Kết hợp với suy ra mặt phẳng này luôn đi qua điểm cố định
( )
0;3; 1−
.
Câu 48. Chọn D
Từ giả thiết ta có
0, 0, 0abc
và thể tích khối tứ diện
OABC
là
1
6
OABC
V abc=
.
Ta có phương trình đoạn chắn mặt phẳng
( )
P
có dạng
1
x y z
a b c
+ + =
.
Mà
( )
1 1 1
1MP
abc
+ + =
.
Áp dụng bất đẳng thức côsi cho ba số ta có:
3
1 1 1 1
1 3 27abc
a b c abc
= + +
.
Do đó
19
62
=
OABC
V abc
. Đẳng thức xảy ra khi và chỉ khi
3abc= = =
.
Vậy
9
min 3
2
OABC
V
abc= = = =
. Khi đó
2 3 18a b c+ + =
.
Câu 49. Chọn C
Gọi
,HK
lần lượt là hình chiếu của
S
lên mặt phẳng
( )
ABC
và đường thẳng
AB
.
góc giữa
SC
và mặt phẳng
( )
ABC
là góc
60SCH =
.
33
.sin60
2
SH SC = =
Gọi
( )
1 ;4 ; 1K t t t AB+ − −
( )
;4 3; 3SK t t t = − − −
.
Gọi
AB
u
là một vectơ chỉ phương của đường thẳng
AB
. Theo đề ra
( )
1;4; 1
AB
u =−
.
Ta có
1 3 3
. 0 16 12 3 0 ;2;
2 2 2
AB
SK AB SK u t t t t K
⊥ = + − + + = = −
1 7 1 49 3 3
; 1; 1
2 2 4 3
2
SK SK
= − − = + + =
SK SH H K =
.
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
112
Khi đó
( )
SK ABC⊥
. Chọn vectơ pháp tuyến của
( )
mp ABC
là
17
; 1;
22
n SK
= = − −
, ta có
phương trình mặt phẳng
( )
ABC
là:
( )
1 3 7 3
2 0 2 7 8 0
2 2 2 2
x y x x y z
− − − − + = − − − =
Cách 2:
( )
ABC
chứa điểm
( )
1;0; 1M −
nên loại đáp án B, D. Vecto pháp tuyến của
( )
ABC
vuông góc với vecto chỉ phương của đường thẳng
AB
nên chọn C. Phương án nhiễu kém!
Nhận xét: Khi 6 điểm
,,A B C
cùng với ba trung điểm của ba cạnh bên của hình chóp
.S ABC
nằm trên một mặt cầu thì các mặt bên của hình chóp cụt là hình thang cân suy ra
SA SB SC==
.
Mà
( )
SK ABC⊥
nên
K
là tâm đường tròn ngoại tiếp
ABC
. Do đó
ABC
vuông tại
C
nên tâm
mặt cầu qua 6 điểm
,,A B C
cùng với ba trung điểm của ba cạnh bên của hình chóp
.S ABC
là
K
. Đề nên hỏi phương trình mặt cầu đi qua 6 điểm trên.
Câu 50. Chọn D
Cách 1:
Ta dễ dàng chứng minh được 4 điểm
, , ,A B C D
tạo thành tứ diện. Gọi
()
là mặt phẳng cần tìm,
ta xác định mặt phẳng
()
như sau:
Xét
()
và
( )
ABC
có
( )
( )
//
M AB
AB
giao tuyến của
()
và
( )
ABC
là
Mx
trong đó
//Mx AB
,
Mx AB K=
Tương tự ta có giao tuyến của
()
và
( )
BCD
là
Ky
trong đó
//Ky CD
,
Ky BD N=
( )
() KMN

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
113
Ta có:
BN BK AM
BD BC AC
==
30
5
6
BN AM BN BD
BD AC AM AC
= = = =
Vậy từ giả thiết:
2
2
1
BN
AM
AM
=−
2
66AM AM AC = = =
.
M
là điểm đối xứng của
C
qua
A
.
Vậy chỉ có 1 mặt phẳng thỏa mãn yêu cầu bài toán.
Cách 2:
Ta dễ dàng chứng minh được 4 điểm
, , ,A B C D
tạo thành tứ diện.
Vì mặt phẳng
()
song song với
,AB CD
và cắt 2 đường thẳng
,AC BD
lần lượt tại
,MN
nên
theo định lí Talet trong không gian ta có:
30
5
6
BN BD
AM AC
= = =
Vậy từ giả thiết:
2
2
1
BN
AM
AM
=−
2
66AM AM AC = = =
.
M
là điểm đối xứng của
C
qua
A
.
Vậy chỉ có 1 mặt phẳng thỏa mãn yêu cầu bài toán.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
114
DẠNG 3. TÌM TỌA ĐỘ ĐIỂM LIÊN QUAN ĐẾN MẶT PHẲNG
Câu 1. Trong không gian
Oxyz
, cho điểm
( )
1;4;2M
và mặt phẳng
( )
: 1 0x y z
+ + − =
. Xác định tọa
độ điểm
H
là hình chiếu vuông góc của điểm
M
trên mặt phẳng
( )
.
A.
4 5 1
;;
3 3 3
H
−−
. B.
( )
1;4; 4H −
. C.
( )
1;2;0H −
. D.
( )
3;6;4H
.
Câu 2. Trong không gian
Oxyz
, cho hai điểm
( )
1;7;3A
,
( )
2;1;9B
. Trung điểm
M
của
AB
có tọa độ
là:
A.
3
;4;6
2
M
. B.
( )
3;8;12M
. C.
( )
1; 6;6M −
. D.
1
; 3;3
2
M
−
.
Câu 3. Trong không gian
Oxyz
, hình chiếu của điểm
( )
1;2;3M
trên mặt phẳng
( )
Oxy
là
A.
(1;2;0)
. B.
(1;0;3)
. C.
(0;2;3)
. D.
(0;0;3)
.
Câu 4. Trong không gian với hệ trục tọa độ
Oxyz
, cho điểm
( )
1; 2;3M −
. Tìm tọa độ điểm
A
là hình
chiếu vuông góc của
M
lên mặt phẳng
( )
Oyz
.
A.
( )
1; 2;3A −
. B.
( )
1; 2;0A −
. C.
( )
1;0;3A
. D.
( )
0; 2;3A −
.
Câu 5. Trong không gian
Oxyz
, cho mặt phẳng
( ):2 6 0P x y z+ − − =
. Điểm nào sau đây không thuộc
mặt phẳng
( )
P
?
A.
( )
0;3; 3−
. B.
( )
3;0;0
. C.
( )
3;1;1
. D.
( )
3;2; 2−
.
Câu 6. Trong không gian với hệ tọa độ
Oxyz
, mặt cầu
( )
S
qua bốn điểm
( )
3;3;0A
,
( )
3;0;3B
,
( )
0;3;3C
,
( )
3;3;3D
. Phương trình mặt cầu
( )
S
là
A.
2 2 2
3 3 3 3 3
2 2 2 2
x y z
− + − + − =
. B.
2 2 2
3 3 3 27
2 2 2 4
x y z
− + + + − =
.
C.
2 2 2
3 3 3 27
2 2 2 4
x y z
− + − + + =
D.
2 2 2
3 3 3 27
2 2 2 4
x y z
− + − + − =
.
Câu 7. Cho
4
điểm
( )
2; 1;3A −−
,
( )
2;3;1B
,
( )
1;2;3C
,
( )
4;1;3D −
. Hỏi có bao nhiêu điểm trong bốn
điểm đã cho thuộc mặt phẳng
( )
: 3 6 0x y z
+ + − =
?
A.
3
. B.
2
. C.
4
. D.
1
.
Câu 8. Trong không gian
Oxyz
, mặt phẳng
3 5 2 0x y z− + − =
đi qua điểm nào sau đây?
A.
( )
1;2; 1M −
. B.
( )
1;1; 1N −
. C.
( )
2;0; 3P −
. D.
( )
1;0; 1Q −
.
Câu 9. Trong không gian
Oxyz
, mặt phẳng
( )
: 2 3 10 0P x y z− + − =
cắt trục
Ox
tại điểm có hoành độ
bằng
A. 10. B.
10−
. C. 5. D. 0.
Câu 10. Trong không gian
Oxyz
, cho mặt phẳng
( )
: 2 5 0P x y z− + − =
. Điểm nào dưới đây thuộc
( )
P
?
A.
( )
2; 1;5 .Q −
B.
( )
0;0; 5 .P −
C.
( )
1;1;6 .M
D.
( )
5;0;0 .N −

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
115
Câu 11. Trong không gian với hệ tọa độ
Oxyz
, cho
( )
2;0;0A
,
( )
1;1;1M
. Mặt phẳng
( )
P
thay đổi qua
AM
cắt các tia
Oy
,
Oz
lần lượt tại
B
,
C
. Khi mặt phẳng
( )
P
thay đổi thì diện tích tam giác
ABC
đạt giá trị nhỏ nhất bằng bao nhiêu?
A.
56
. B.
26
. C.
46
. D.
36
.
Câu 12. Trong không gian
Oxyz
, cho tam giác
ABC
với
( )
1;0;0A
,
( )
0;0;1B
và
( )
2;1;1C
. Gọi
( )
;;I a b c
là tâm đường tròn ngoại tiếp tam giác. Khi đó
2++a b c
bằng
A.
2
. B.
4
. C.
3
. D.
5
.
Câu 13. Trong không gian
Oxyz
cho hai mặt phẳng
( )
: 2 3 0P x y z− + − =
,
( )
: 2 3 0Q x y z− + + =
có bao
nhiêu điểm
M
có hoành độ nguyên thuộc
Ox
sao cho tổng khoảng cách từ
M
đến hai mặt phẳng
( )
P
,
( )
Q
bằng khoảng cách giữa
( )
P
và
( )
Q
.
A.
2
. B.
4
. C.
6
. D.
7
.
Câu 14. Trong không gian với hệ trục tọa độ
Oxyz
, cho hai điểm
( )
3;1;7A
,
( )
5;5;1B
và mặt phẳng
( )
:2 4 0P x y z− − + =
. Điểm
M
thuộc
( )
P
sao cho
35MA MB==
. Biết
M
có hoành độ
nguyên, ta có
OM
bằng
A.
22
. B.
23
. C.
32
. D.
4
.
Câu 15. Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
( )
1;0;0A
,
( )
0;0;1B
và mặt phẳng
( )
:2 2 5 0P x y z− − + =
. Tìm tọa độ điểm
C
trên trục
Oy
sao cho mặt phẳng
( )
ABC
hợp với mặt
phẳng
( )
P
một góc
45
là
A.
22
0; ;0
0
C
+
−
. B.
1
0; ;0
4
C
. C.
22
0; ;0
2
C
+
. D.
1
0; ;0
4
C
−
.
Câu 16. Trong không gian
Oxyz
cho
( )
1; 1;0A −−
,
( )
0;1;0B
,
( )
;;M a b c
với
( )
0b
thuộc mặt phẳng
( )
: 2 0P x y z+ + + =
sao cho
2AM =
và mặt phẳng
( )
ABM
vuông góc với mặt phẳng
( )
.P
Khi đó
2
24T a b c= − +
bằng
A.
8−
. B.
7
. C.
28
. D.
17−
.
Câu 17. Trong không gian với hệ tọa độ
Oxyz
,cho hai điểm
(1;0;2), (3;1; 1).AB−
và mặt phẳng
( ): 1 0.P x y z+ + − =
Gọi
( ; ; ) ( )M a b c P
sao cho
32MA MB−
đạt giá trị nhỏ nhất. Tính
9a 3 6 .S b c= + +
A.
4.
B.
3.
C.
2.
D.
1.
Câu 18. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
( )
4;1;9M
. Gọi
( )
P
là mặt phẳng đi qua
M
và
cắt 3 tia
,,Ox Oy Oz
lần lượt tại các điểm
,,A B C
sao cho
( )
OA OB OC++
đạt giá trị nhỏ nhất.
Tính khoảng cách
d
từ điểm
( )
0;1;3I
đến mặt phẳng
( )
P
.
A.
34
5
d =
. B.
36
5
d =
. C.
24
7
d =
. D.
30
7
d =
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
116
Câu 19. Trong không gian
Oxyz
cho ba điểm
( )
0;1;1A
;
( )
1;1;0B
;
( )
1;0;1C
và mặt phẳng
( )
: 1 0P x y z+ − − =
. Điểm
M
thuộc
( )
P
sao cho
MA MB MC==
. Thể tích khối chóp
.M ABC
là
A.
1
4
. B.
1
2
. C.
1
6
. D.
1
.
3
Câu 20. Trong không gian
Oxyz
cho ba điểm
( ) ( ) ( )
2;0;1 , 1;0;0 , 1;1;1A B C
và mặt phẳng
( )
: 2 0P x y z+ + − =
. Điểm
( )
;;M a b c
nằm trên mặt phẳng
( )
P
thỏa mãn
MA MB MC==
. Tính
23T a b c= + +
.
A.
5T =
. B.
4T =
. C.
3T =
. D.
2T =
.
Câu 21. Trong không gian
Oxyz
, cho mặt phẳng
( )
:3 3 2 37 0P x y z− + + =
và các điểm
( )
4;1;5A
,
( )
3;0;1B
,
( )
1;2;0C −
. Biết rằng có điểm
( )
;;M a b c
thuộc mặt phẳng
( )
P
để biểu thức
. . .MAMB MB MC MC MA++
đạt giá trị nhỏ nhất. Biểu thức
2 2 2
a b c+−
có giá trị là
A.
69
. B.
61
. C.
18
. D.
22
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
117
ĐÁP ÁN CHI TIẾT
Câu 1. Chọn C
Mặt phẳng
( )
có vectơ pháp tuyến
( )
1;1;1n =
.
Vì
( )
MH
⊥
nên đường thẳng
MH
có vectơ chỉ phương
( )
1;1;1u =
.
Phương trình đường thẳng
MH
là:
( )
1
4
2
xt
y t t
zt
=+
= +
=+
( )
1 ;4 ;2H t t t + + +
.
Mà
( )
1 4 2 1 0 2H t t t t
+ + + + + − = = −
. Vậy
( )
1;2;0H −
.
Câu 2. Chọn A
Trung điểm
M
của
AB
có tọa độ là:
1 2 7 1 3 9 3
; ; ;4;6
2 2 2 2
+ + +
=
.
Câu 3. Chọn A
Mặt phẳng
( )
Oxy
có phương trình là
0=z
. Phương trình đường thẳng
( )
d
đi qua điểm
M
và
vuông góc với mặt phẳng
( )
Oxy
là :
1
2
=
=
=
x
y
zt
Gọi
I
là giao điểm của
( )
d
và mặt phẳng
( )
Oxy
. Vì
( )
Id
nên
( )
1;2;It
.
Do
( ) ( )
0 1;2;0I Oxy t I =
. Vậy hình chiếu của
M
lên mặt phẳng
( )
Oxy
là
( )
1;2;0I
.
Câu 4. Chọn D
Tọa độ điểm
A
là hình chiếu vuông góc của
M
lên mặt phẳng
( )
Oyz
là
( )
0; 2;3A −
.
Câu 5. Chọn D
Ta có:
2.3 2 ( 2) 6 4 0+ − − − =
nên điểm
( )
3;2; 2−
không thuộc mặt phẳng
( )
P
.
Câu 6. Chọn D
Gọi phương trình mặt cầu
( )
( )
2 2 2 2 2 2
: 2 2 2 0 0S x y z ax by cz d a b c d+ + − − − + = + + −
Vì mặt cầu đi qua 4 điểm nên:
18 6 6 0
18 6 6 0
18 6 6 0
27 6 6 6 0
a b d
a c d
b c d
a b c d
− − + =
− − + =
− − + =
− − − + =
6 6 18
6 6 18
6 6 18
6 6 6 27
a b d
a c d
b c d
a b c d
− − + = −
− − + = −
− − + = −
− − − + = −
3
2
3
2
3
2
0
a
b
c
d
=
=
=
=
Suy ra tâm
333
;;
222
I
bán kính
222
3 3 3 3 3
2 2 2 2
R
= + + =
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
118
Vậy phương trình mặt cầu
2 2 2
3 3 3 27
2 2 2 4
x y z
− + − + − =
.
Câu 7. Chọn B
Thay lần lượt
4
điểm vào phương trình mặt phẳng ta thấy:
( )
2; 1;3A −−
:
2 1 3.3 6 0− − + − =
A
thuộc mặt phẳng
( )
.
( )
2;3;1B
:
2 3 3.1 6 2+ + − =
B
không thuộc mặt phẳng
( )
.
( )
1;2;3C
:
1 2 3.3 6 6+ + − =
C
không thuộc mặt phẳng
( )
.
( )
4;1;3D −
:
4 1 3.3 6 0− + + − =
D
thuộc mặt phẳng
( )
.
Vậy có
2
điểm trong
4
điểm trên thuộc mặt phẳng
( )
.
Câu 8. Chọn D
Thay lần lượt tọa độ các điểm vào phương trình mặt phẳng.
Ta nhận thấy tọa độ điểm
Q
thỏa mãn phương trình, suy ra điểm
Q
thuộc mặt phẳng đã cho.
Câu 9. Chọn A
Gọi
( ) ( )
;;
A A A
P Ox A x y z=
0
A
y=
và
0
A
z =
.
( )
2.0 3.0 10 0 10
AA
A P x x − + − = =
.
Câu 10. Chọn C
Thay tọa độ các điểm
Q
,
P
,
M
,
N
vào phương trình mặt phẳng
( )
P
Ta có với tọa độ của điểm
M
thì
1 2.1 6 5 0− + − =
.Vậy
( )
MP
.
Câu 11. Chọn C
Giả sử
(0; ;0); (0;0; )B b C c
với (
, 0).bc
Phương trình mặt phẳng
( )
P
đi qua 3 điểm
A
,
B
,
C
là:
1
2
x y z
bc
+ + =
.
Do
(1;1;1) ( )MP
1 1 1
22
bc
bc
bc
+ = + =
.
Ta có:
( 2; ;0), ( 2;0; )AB b AC c= − = −
.
Diện tích tam giác
ABC
là:
2 2 2 2
11
, 4( )
22
ABC
S AB AC b c b c
= = + +
.
Mặt khác,
22
0 16
24
b c bc
bc bc bc
+
−
;
22
2 32b c bc+
.
Do đó,
2
1
16 4.32 4 6
2
ABC ABC
SS +
. Vậy
min
46
ABC
S =
.
Câu 12. Chọn C
Ta có
( )
1;0;1AB =−
,
( )
1;1;1AC =
.
Mặt phẳng
( )
ABC
có VTPT
( )
, 1;2; 1
= = − −
n AB AC
đi qua
A
có phương trình là:
( )
1 1 2 0 2 1 0− − + − = − + − + =x y z x y z
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
119
Ta có
( )
=
=
IA IB
IB IC
I mp ABC
( ) ( )
( ) ( ) ( ) ( )
22
2 2 2 2
2 2 2 2
22
11
1 2 1 1
2 1 0
− + + = + + −
+ + − = − + − + −
− + − + =
a b c a b c
a b c a b c
a b c
1
2 2 0
1
4 2 5
2
2 1 0
1
=
− + =
+ = =
− + − + =
=
a
ac
a b b
a b c
c
1
1; ;1 2 1 1 1 3
2
+ + = + + =
I a b c
.
Câu 13. Chọn D
Do
( )
;0;0M Ox M a
,
a
.
Lấy
( ) ( )
0; 3;0AP−
. Do
( ) ( ) ( ) ( )
( )
( )
( )
( )
( )
2
22
33
/ / , , 6
1 1 2
P Q d P Q d A Q
− − +
= = =
+ − +
.
Ta có :
( )
( )
( )
( )
( ) ( )
( )
( ) ( )
22
2 2 2 2
33
, , , 6
1 1 2 1 1 2
aa
d M P d M Q d P Q
−+
+ = + =
+ − + + − +
3 3 6aa − + + =
( )
1
.
+ TH1 : Với
3a −
thì
( )
1 3 3 6 3a a a − − − = = −
( )
tm
.
+ TH2 : Với
33a−
thì
( )
1 3 3 6 6 6aa − + + + = =
luôn đúng.
Do
a
nên
2; 1;0;1;2a − −
.
+ TH3 : Với
3a
thì
( )
1 3 3 6 3a a a − + + = =
( )
tm
.
Vậy có
7
điểm
M
có hoành độ nguyên thuộc
Ox
thỏa mãn yêu cầu bài toán.
Câu 14. Chọn A
Gọi
( )
;;M a b c
với
a
,
b
,
c
.
Ta có:
( )
3; 1; 7AM a b c= − − −
và
( )
5; 5; 1BM a b c= − − −
.
Vì
( )
35
MP
MA MB
==
( )
22
2
35
MP
MA MB
MA
=
=
nên ta có hệ phương trình sau:
( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( )
2 2 2 2 2 2
2 2 2
2 4 0
3 1 7 5 5 1
3 1 7 35
abc
a b c a b c
a b c
− − + =
− + − + − = − + − + −
− + − + − =
( ) ( ) ( )
2 2 2
24
4 8 12 8
3 1 7 35
abc
a b c
a b c
− − = −
+ − = −
− + − + − =
( ) ( ) ( )
2 2 2
2
3 1 7 35
bc
ca
a b c
=
= +
− + − + − =
2
2
2
3 14 0
ba
ca
aa
=+
= +
−=
0
2
2
a
b
c
=
=
=
, (do
a
).
Ta có
( )
2;2;0M
. Suy ra
22OM =
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
120
Câu 15. Chọn D
Gọi
( )
0; ;0C c Oy
.
Ta có:
( )
1;0;1AB =−
,
( )
1; ;0AC c=−
.
Vectơ pháp tuyến của mặt phẳng
( )
ABC
là:
( )
, ; 1;
ABC
n AB AC c c
= = − − −
.
Vectơ pháp tuyến của mặt phẳng
( )
P
là:
( )
2; 2; 1
P
n = − −
.
Theo giả thiết ta có:
( ) ( )
( )
cos , cos , cos45
ABC P
ABC P n n= =
( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( )
2 2 2 2 2
2
.2 1 . 2 . 1
2
2
2 2 1 . 1
cc
cc
− + − − + − −
=
+ − + − − + − + −
2
2
2
2
3 2 1
c
c
−+
=
+
( )
( )
2
2
2
1
2
9 2 1
c
c
−
=
+
2
16 8 1 0cc + + =
( )
2
4 1 0c + =
1
4
c = −
.
Vậy tọa độ điểm
C
là:
1
0; ;0
4
C
−
.
Câu 16. Chọn D
( )
( )
1;2;0
1;b 1;c
AB
AM a
=
= + +
( )
( )
, 2 ; ; 2 1
ABM
n AB AM c c a b
= = − − + −
Ta có hệ phương trình:
( ) ( )
( ) ( )
( )
( ) ( )
( )
( )
22
2
2 0 1
;;
2 1 1 2 2
.0
2 1 0 3
ABM P
abc
M a b c P
AM a b c
nn
abc
+ + + =
= + + + + =
=
− + + − =
Từ
( )
1
và
( )
3
suy ra
1a =−
. Do đó:
( )
2 2 2
11
1
0
2
2 1 2 4 0
b c c b
c
b
b
b c b b b
+ = − = − −
=
=−
+ + = + =
Vậy
( )
1; 2;1M −−
nên
2
2 4 17T a b c= − + = −
.
Câu 17. Chọn B
Gọi
( ; ; )I m n p
là điểm thỏa mãn:
3 2 0.IA IB−=
Ta có
(1 ; ;2 ); (3 ;1 ; 1 ).IA m n p IB m n p= − − − = − − − −
3(1 ) 2(3 ) 0 3
3 2 0 3( ) 2(1 ) 0 2 ( 3; 2;8).
3(2 ) 2( 1 ) 0 8
m m m
IA IB n n n I
p p p
− − − = = −
− = − − − = = − − −
− − − − = =
Ta có
3 2 3( ) 2( ) .MA MB MI IA MI IB MI MI− = + − + = =
Khi đó,
32MA MB−
đạt giá trị nhỏ nhất,
()MP
MI
nhỏ nhất,
()MP
M
là hình chiếu vuông góc của
I
trên
( ).P

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
121
Gọi
là đường thẳng qua
I
và vuông góc với
( ).P
Khi đó
nhận vectơ pháp tuyến của
()P
là
(1;1;1)n =
làm vecto chỉ phương
3
: 2 .
8
xt
yt
zt
= − +
= − +
=+
Tọa độ
M
là nghiệm của hệ
11
3
11
3
2
8
3
9a 3 6 3.
88
3
22
3
10
22
2
3
3
3
a
xt
x
yt
b S b c
zt
y
x y z
c
z
t
=−
= − +
=−
= − +
= − = + + =
=+
=−
+ + − =
=
=
=−
Câu 18. Chọn C
Gọi
( ) ( ) ( )
;0;0 , 0; ;0 , 0;0;A a B b C c
với
, , 0abc
.
Ta có phương trình
( )
:1
x y z
P
a b c
+ + =
và
( )
OA OB OC a b c+ + = + +
.
Vì
( ) ( )
4 1 9
4;1;9 1MP
a b c
+ + =
(1).
Áp dụng bất đẳng thức Cauchy-Schwarz (Bunhiacôpxki) ta có
( )
2
2
2 1 3
2 1 3 . . .a b c
a b c
+ + = + +
( )
4 1 9
abc
a b c
+ + + +
.
Kết hợp với (1) suy ra
36abc+ +
.
Dấu bằng xảy ra khi và chỉ khi
2 1 3
4 1 9
1
abc
a b c
==
+ + =
12
6
18
a
b
c
=
=
=
.
Do đó
OA OB OC++
đạt giá trị nhỏ nhất bằng 36 khi và chỉ khi
12, 6, 18a b c= = =
.
Khi đó phương trình
( )
:1
12 6 18
x y z
P + + =
.
Vậy khoảng cách cần tìm là
( )
( )
2 2 2
13
1
24
6 18
,
7
1 1 1
12 6 18
d d I P
+−
= = =
++
.
Nhận xét.
Có thể sử dụng hệ quả bất đẳng thức Cauchy-Schwarz dưới dạng sau
( )
2
2 2 2
abc
abc
x y z x y z
++
+ +
++
với
,,abc
và
, , 0x y z
.
Dấu
""=
xảy ra khi và chỉ khi
a b c
x y z
==
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
122
Khi đó
2 2 2
213
1
a b c
= + +
( )
2
213
36
a b c a b c
++
=
+ + + +
suy ra
36abc+ +
.
Câu 19. Chọn C
Gọi điểm
( ; ; )M x y z
.
Vì điểm
M
thuộc
( )
P
sao cho
MA MB MC==
nên
2 2 2 2 2 2
2 2 2 2 2 2
10
()
( 1) ( 1) ( 1) ( 1)
( 1) ( 1) ( 1) ( 1)
x y z
MP
MA MB x y z x y z
MA MC
x y z x y z
+ − − =
= + − + − = − + − +
=
+ − + − = − + + −
1 0 1
0 1 (1;1;1)
01
x y z x
x z y M
x y z
+ − − = =
− = =
− = =
Ta có
( ) ( )
1;0;0 ; 0;0;1 , (0; 1;0)MA MB MA MB
= = = −
;
( )
0;1;0 , . 1MC MA MB MC
= = −
.
11
,.
66
M ABC
V MA MB MC
==
.
Câu 20. Chọn B
Ta có:
( )
( ) ( ) ( )
( ) ( ) ( ) ( ) ( )
2 2 2
2 2 2 2 2
22
2 2 2 2 2
2
20
2 1 1
2 1 1 1 1
abc
MP
AM BM a b c a b c
AM CM
a b c a b c
+ + − =
= − + + − = − + +
=
− + + − = − + − + −
2 2 1
2 2 4 2 0
2 2 2 1 1
a b c a b c a
a c a c b
a b a b c
+ + = + + = =
− − = − + = =
− + = − − = =
. Vậy
2 3 1 0 3 4T a b c= + + = + + =
.
Câu 21. Chọn B
Gọi
I
là điểm thỏa
0IA IB IC+ + =
( )
2;1;2I
.
Khi đó ta có
. . .P MAMB MB MC MC MA= + +
( )( ) ( )( ) ( )( )
MI IA MI IB MI IB MI IC MI IC MI IA= + + + + + + + +
( )
2
3 2 . . . .MI MI IA IB IC IA IB IB IC IC IA= + + + + + +
2
3 . . .MI IAIB IB IC IC IA= + + +
.
Vậy
P
đạt GTNN
MI
đạt GTNN
M
là hình chiếu của
I
lên mặt phẳng
( )
P
.
Gọi
là đường thẳng qua
I
và vuông góc với
( )
P
23
: 1 3
22
xt
yt
zt
=+
= −
=+
.
Ta có
M
nên
( )
2 3 ;1 3 ;2 2M t t t+ − +
.
Vì
( )
MP
nên
( ) ( ) ( )
3 2 3 3 1 3 2 2 2 37 0t t t+ − − + + + =
2t = −
( )
4;7; 2M − −
Vậy
2 2 2
61a b c+ − =
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
123
DẠNG 4. GÓC – KHOẢNG CÁCH LIÊN QUAN ĐẾN MẶT PHẲNG
Câu 1. Trong không gian , biết hình chiếu của lên mặt phẳng là Số đo góc
giữa mặt phẳng với mặt phẳng là
A. . B. . C. . D. .
Câu 2. Trong không gian
Oxyz
, cho mặt phẳng
( )
: 3 1 0P x y− + + =
. Tính góc tạo bởi
( )
P
với trục
Ox
.
A.
0
60
. B.
0
30
. C.
0
120
. D.
0
150
.
Câu 3. Trong không gian Oxyz, cho tứ diện
ABCD
với
( )
1;2;1A =
,
( )
2;1;3B =
,
( )
3;2;2C =
,
( )
1;1;1D =
. Độ dài chiều cao
DH
của tứ diện bằng
A.
3 14
14
. B.
14
14
. C.
4 14
7
. D.
3 14
7
.
Câu 4. Trong không gian
Oxyz
, cho mặt phẳng
:4 3 2 28 0x y z
và điểm
0;1;2I
. Viết
phương trình của mặt cầu
S
có tâm
I
và tiếp xúc với mặt phẳng .
A.
22
2
: 1 2 29S x y z
. B.
22
2
: 1 2 29S x y z
.
C.
22
2
: 1 2 841S x y z
. D.
22
2
: 1 2 29S x y z
.
Câu 5. Trong không gian
Oxyz
, cho hai mặt phẳng
( ): 2 2 10 0P x y z+ + − =
và
( ): 2 2 3 0Q x y z+ + − =
.
Điểm
M
là giao của mặt phẳng
()P
với trục
Oz
. Khoảng cách từ
M
tới mặt phẳng
()Q
bằng
A.
8
3
. B.
7
3
. C.
3
. D.
4
3
.
Câu 6. Trong không gian với hệ tọa độ
Oxyz
, mặt cầu
( )
S
có tâm
( )
1;2;1I −
và tiếp xúc với mặt phẳng
( )
: 2 2 2 0P x y z− − − =
có phương trình là
A.
( ) ( ) ( )
2 2 2
1 2 1 9x y z− + + + + =
. B.
( ) ( ) ( )
2 2 2
1 2 1 3x y z+ + − + − =
.
C.
( ) ( ) ( )
2 2 2
1 2 1 9x y z+ + − + − =
. D.
( ) ( ) ( )
2 2 2
1 2 1 3x y z+ + − + + =
.
Câu 7. Trong không gian
Oxyz
, khoảng cách giữa
( ): 2 2 0P x y z+ + =
và
( ): 2 2 12 0Q x y z+ + − =
bằng:
A.
2
. B.
3
. C.
1
. D.
4
.
Câu 8. Trong không gian
Oxyz
, khoảng cách giữa hai mặt phẳng
( )
:
2 2 4 0x y z− − − =
và
( )
:
4 2 4 4 0x y z− + + − =
bằng
A.
6
. B.
2
. C.
4
3
. D.
10
3
.
Câu 9. Trong không gian cho hệ trục tọa độ
Oxyz
, tất cả các điểm
M
nằm trên
Oz
có khoảng cách đến
mặt phẳng
( )
:2 2 2 0P x y z− − − =
bằng 2 là
A.
(0;0; 4)M −
. B.
( ) ( )
0;0;0 , 0;0; 2MM−
.
C.
( )
0;0;2M
. D.
( ) ( )
0;0;2 , 0;0; 4MM−
Oxyz
O
P
2; 1; 2 .H
P
: 5 0Q x y
30
90
60
45

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
124
Câu 10. Phương trình mặt cầu tâm
( )
3; 2;4I −
và tiếp xúc với
( )
P
:
2 2 4 0x y z− + + =
là:
A.
( ) ( ) ( )
2 2 2
400
x 3 y 2 z 4
9
+ + − + + =
. B.
( ) ( ) ( )
2 2 2
20
x 3 y 2 z 4
3
+ + − + + =
.
C.
( ) ( ) ( )
2 2 2
400
x 3 y 2 z 4
9
− + + + − =
. D.
( ) ( ) ( )
2 2 2
20
x 3 y 2 z 4
3
− + + + − =
.
Câu 11. Trong không gian
,Oxyz
cho các điểm
( ) ( ) ( )
3;0;0 , 0; 3;0 , 0;0;6 .A B C−−
Tính khoảng cách từ
điểm
( )
1; 3; 4M −−
đến mặt phẳng
( )
.ABC
A.
4.
B.
2.
C.
1.
D.
3.
Câu 12. Trong không gian
Oxyz
, cho đường thẳng
1
:
1 1 2
x y z
d
−
==
−
song song với mặt phẳng
( )
: 2 0P x y z+ + + =
. Khoảng cách giữa
d
và
( )
P
bằng
A.
23
. B.
3
3
. C.
23
3
. D.
3
.
Câu 13. Trong không gian Oxyz, mặt cầu tâm
(1;2; 1)I −
tiếp xúc với mặt phẳng
( ): 2 2 1 0P x y z− + − =
có bán kính bằng
A. 2. B. 4. C.
4
3
. D. 9.
Câu 14. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )
P
có phương trình:
3 4 2 4 0x y z+ + + =
và điểm
( )
1; 2;3A −
. Tính khoảng cách
d
từ
A
đến
( )
P
.
A.
5
9
d =
. B.
5
29
d =
. C.
5
29
d =
. D.
5
3
d =
.
Câu 15. Trong không gian
Oxyz
, cho ba điểm
( )
1;0;0A
,
( )
0;2;0B
và
( )
0,0,3C
. Khoảng cách từ gốc tọa
độ đến mp
( )
ABC
bằng
A.
3
5
. B.
1
3
. C.
6
11
. D.
6
7
.
Câu 16. Trong không gian tọa độ
Oxyz
, cho điểm
( ; ; )A a b c
với
, , \{0}abc
. Xét là mặt phẳng thay
đổi đi qua điểm
A
. Khoảng cách lớn nhất từ điểm
O
đến mặt phẳng bằng
A.
2 2 2
abc
. B.
2 2 2
2 abc
. C.
2 2 2
3 abc
. D.
2 2 2
4 abc
.
Câu 17. Trong không gian tọa độ
Oxyz
cho điểm
(1;2;3)M
. Mặt phẳng thay đổi đi qua điểm
M
, cắt cá
c trục tọa độ
,,Ox Oy Oz
lần lượt tại các điểm
,,A B C
. Tìm GTNN của
2 2 2
1 1 1
Q
OA OB OC
A.
14
. B.
1
14
. C.
14
. D.
1
14
.
Câu 18. Trong không gian
Oxyz
khoảng cách giữa hai mặt phẳng
( )
: 2 3 1 0P x y z+ + − =
và
( )
: 2 3 6 0Q x y z+ + + =
là
A.
7
14
B.
8
14
C.
14
D.
5
14

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
125
Câu 19. Trong không gian
Oxyz
, cho mặt phẳng
()P
đi qua hai điểm
(1;2;3); (3; 1;1)AB−
và song song với
đường thẳng
1 2 3
:
2 1 1
x y z
d
− + −
==
−
. Khoảng cách từ gốc tọa độ đến mặt phẳng
()P
bằng
A.
37
101
. B.
5
77
. C.
37
101
D.
5 77
77
Câu 20. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )
:3 2 5 0P x y z− − + =
và đường thẳng
1 7 3
:
2 1 4
x y z− − −
= =
. Gọi
( )
Q
là mặt phẳng chứa đường thẳng
và song song với
( )
P
. Tính
khoảng cách giữa hai mặt phẳng
( )
P
và
( )
Q
.
A.
9
14
. B.
9
14
. C.
3
14
. D.
3
14
.
Câu 21. Trong không gian , khoảng cách giữa hai mặt phẳng và
bằng:
A. . B. . C. . D. .
Câu 22. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )
: 2 2 3 0P x y z− + + =
và điểm
( )
1; 2;3A −
. Gọi
( ) ( )
;;M a b c P
sao cho
4AM =
. Tính
abc++
.
A.
2
3
. B.
2
. C.
8
3
. D.
12
.
Câu 23. Trong không gian tọa độ Oxyz, cho tứ diện
ABCD
với
( ) ( ) ( )
1; 2;4 , 4; 2;0 , 3; 2;1A B C− − − − −
và
( )
1;1;1D
. Độ cao của tứ diện kẻ từ
D
bằng
A. 3. B. 1. C. 2. D.
1/ 2
Câu 24. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
5 7 12
:
2 2 1
x y z
d
− + −
==
−
và mặt phẳng
( )
: 2 3 3 0x y z
+ − − =
. Gọi
M
là giao điểm của
d
với
( )
,
A
thuộc
d
sao cho
14AM =
.
Tính khoảng cách từ
A
đến
( )
.
A. 2. B. 3. C. 6. D.
14
.
Câu 25. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
5 7 12
:
2 2 1
x y z
d
− + −
==
−
và mặt phẳng
( )
: 2 3 3 0x y z
+ − − =
. Gọi
M
là giao điểm của
d
với
( )
,
A
thuộc
d
và cách
( )
một
khoảng bằng 3. Tính độ dài đoạn thẳng
AM
.
A.
2 14
3
. B. 3. C.
2 14
. D.
14
.
Câu 26. Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
( )
S
có tâm
A
thuộc đường thẳng
5 7 12
:
2 2 1
x y z
d
− + −
==
−
và cắt mặt phẳng
( )
: 2 3 3 0x y z
+ − − =
theo một đường tròn có bán
kính bằng
5
. Biết rằng giao điểm
M
của
d
với
( )
cũng thuộc
( )
S
, tính bán kính của
( )
S
Oxyz
( ): 2 2 10 0P x y z+ + − =
( ): 2 2 3 0Q x y z+ + − =
7
3
5
3
3
4
3

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
126
A.
2 14
3
. B. 3. C.
2 14
. D.
14
.
Câu 27. Trong không gian
Oxyz
, cho hai mặt phẳng song song
( )
P
và
( )
Q
lần lượt có phương trình
20x y z− + =
và
2 7 0x y z− + − =
. Khoảng cách giữa hai mặt phẳng
( )
P
và
( )
Q
bằng
A.
76
. B.
7
6
. C.
7
. D.
67
.
Câu 28. Khoảng cách giữa hai mặt phẳng
( )
: 2 2 4 0x y z
− − − =
và
( )
: 2 2 2 0x y z
− − + =
là
A.
2
. B.
6
. C.
10
3
. D.
4
3
.
Câu 29. Trong hệ trục toạ độ
Oxyz
, cho điểm
( )
2; 1; 2H
. Điểm
H
là hình chiếu vuông góc của gốc toạ
độ
O
xuống mặt phẳng
( )
P
, số đo góc giữa mặt phẳng
( )
P
và mặt phẳng
( )
: 11 0Q x y+ − =
là
A.
90
. B.
30
. C.
60
. D.
45
.
Câu 30. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )
P
có phương trình:
10ax by cz+ + − =
với
0c
đi qua
2
điểm
( )
0;1;0A
,
( )
1;0;0B
và tạo với
( )
Oyz
một góc
60
. Khi đó
abc++
thuộc khoảng nào dưới đây?
A.
( )
5;8
. B.
( )
8;11
. C.
( )
0;3
. D.
( )
3;5
.
Câu 31. Trong không gian
Oxyz
, cho mặt cầu
2 2 2
( ):( 1) ( 2) 4S x y z− + + + =
và đường thẳng
2
:.
1
xt
d y t
z m t
=−
=
= − −
Tổng các giá trị thực của tham số
m
để
d
cắt
( )
S
tại hai điểm phân biệt
,AB
và các tiếp diện của
( )
S
tại
,AB
tạo với nhau một góc lớn nhất bằng
A.
1,5−
. B.
3
. C.
1−
. D.
2,25−
.
Câu 32. Cho khối chóp
.S ABCD
có đáy là hình bình hành,
3AB =
,
4AD =
,
120BAD =
. Cạnh bên
23SA =
vuông góc với mặt phẳng đáy
( )
ABCD
. Gọi
M
,
N
,
P
lần lượt là trung điểm các
cạnh
SA
,
AD
và
BC
,
là góc giữa hai mặt phẳng
( )
SAC
và
( )
MNP
. Chọn khẳng định đúng
trong các khẳng định sau đây:
A.
( )
60 ; 90
. B.
( )
0 ; 30
. C.
( )
30 ; 45
. D.
( )
45 ; 60
.
Câu 33. Trong không gian với hệ tọa độ
Oxyz
, mặt phẳng
( )
đi qua điểm
( )
1;2;1M
và cắt các tia
,,Ox Oy Oz
lần lượt tại
,,A B C
sao cho độ dài
,,OA OB OC
theo thứ tự tạo thành một cấp số nhân
có công bội bằng 2. Tính khoảng cách từ gốc tọa độ O tới mặt phẳng
( )
.
A.
4
21
. B.
21
21
. C.
3 21
7
. D.
9 21
.
Câu 34. Trong không gian với hệ tọa độ
Oxyz
, cho các điểm
( )
0;2;1A
,
( )
6;0;3B
,
( )
2;1;1C
. Khoảng
cách từ
C
đến mặt phẳng trung trực của đoạn
AB
bằng

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
127
A.
7
11
. B.
6
11
. C.
5
11
. D.
4
11
.
Câu 35. Trong không gian
Oxyz
, khoảng cách giữa hai mặt phẳng
( )
: 6 3 2 1 0P x y z+ + − =
và
( )
11
: 8 0
23
Q x y z+ + + =
bằng
A.
7
. B.
8
. C.
9
. D.
6
.
Câu 36. Trong không gian
Oxyz
, cho tứ diện
ABCD
với
( )
1, 2,0A −
;
( )
3,3,2B
;
( )
1,2,2C −
;
( )
3,3,1D
.
Độ dài đường cao của tứ diện
ABCD
hạ từ đỉnh
D
xuống mặt phẳng
( )
ABC
bằng
A.
9
72
B.
9
7
C.
9
14
D.
9
2
Câu 37. Trong không gian
Oxyz
cho
( )
1 2 1M ; ; −
. Gọi
( )
P
là mặt phẳng đi qua điểm
M
và cách gốc
tọa độ
O
một khoảng lớn nhất. Mặt phẳng
( )
P
cắt các trục tọa độ tại các điểm
A,B,C
. Tính thể
tích
V
của khối cầu ngoại tiếp tứ diện
OABC
.
A.
27 6
. B.
216 6
. C.
972
. D.
243
2
.
Câu 38. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )
P
đi qua điểm
( )
2;3;5M
cắt các tia
,,Ox Oy Oz
lần lượt tại ba điểm
,,A B C
sao cho
,,OA OB OC
theo thứ tự lập thành cấp số nhân có
công bội bằng
3
. Khoảng cách từ
O
đến mặt phẳng
( )
P
là
A.
16
91
. B.
24
91
. C.
32
91
. D.
18
91
.
Câu 39. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
11
:
2 1 3
−+
==
x y z
d
và mặt phẳng
( )
:2 0+ − =P x y z
. Mặt phẳng
( )
Q
chứa đường thẳng
d
và vuông góc với mặt phẳng
( )
P
.
Khoảng cách từ điểm
( )
0;0;0O
đến mặt phẳng
( )
Q
bằng
A.
1
3
. B.
1
3
. C.
1
5
. D.
1
5
.
Câu 40. Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt phẳng
( ) ( ) ( )
2
: 1 1 1 0
m
P mx m m y m z+ + + − − =
(
m
là tham số) và đường thẳng
d
có vec-tơ chỉ phương
( )
1; 2; 3u =
. Đường thẳng
song song với mặt phẳng
( )
Oxy
,
vuông góc với
d
và cắt mặt
phẳng
( )
m
P
tại một điểm cố định. Tính khoảng cách
h
từ
( )
1; 5; 0A −
đến đường thẳng
.
A.
52h =
. B.
19h =
. C.
21h =
. D.
25h =
.
Câu 41. Trong không gian
Oxyz
, cho
( )
1;2;2A
,
( )
2;1;2B
,
( )
1;5;1C −
,
( )
3;1;1D
và
( )
0; 1;2E −
. Có bao
nhiêu mặt phẳng cách đều năm điểm đã cho?
A. Vô số. B.
1
. C.
2
. D.
3
.
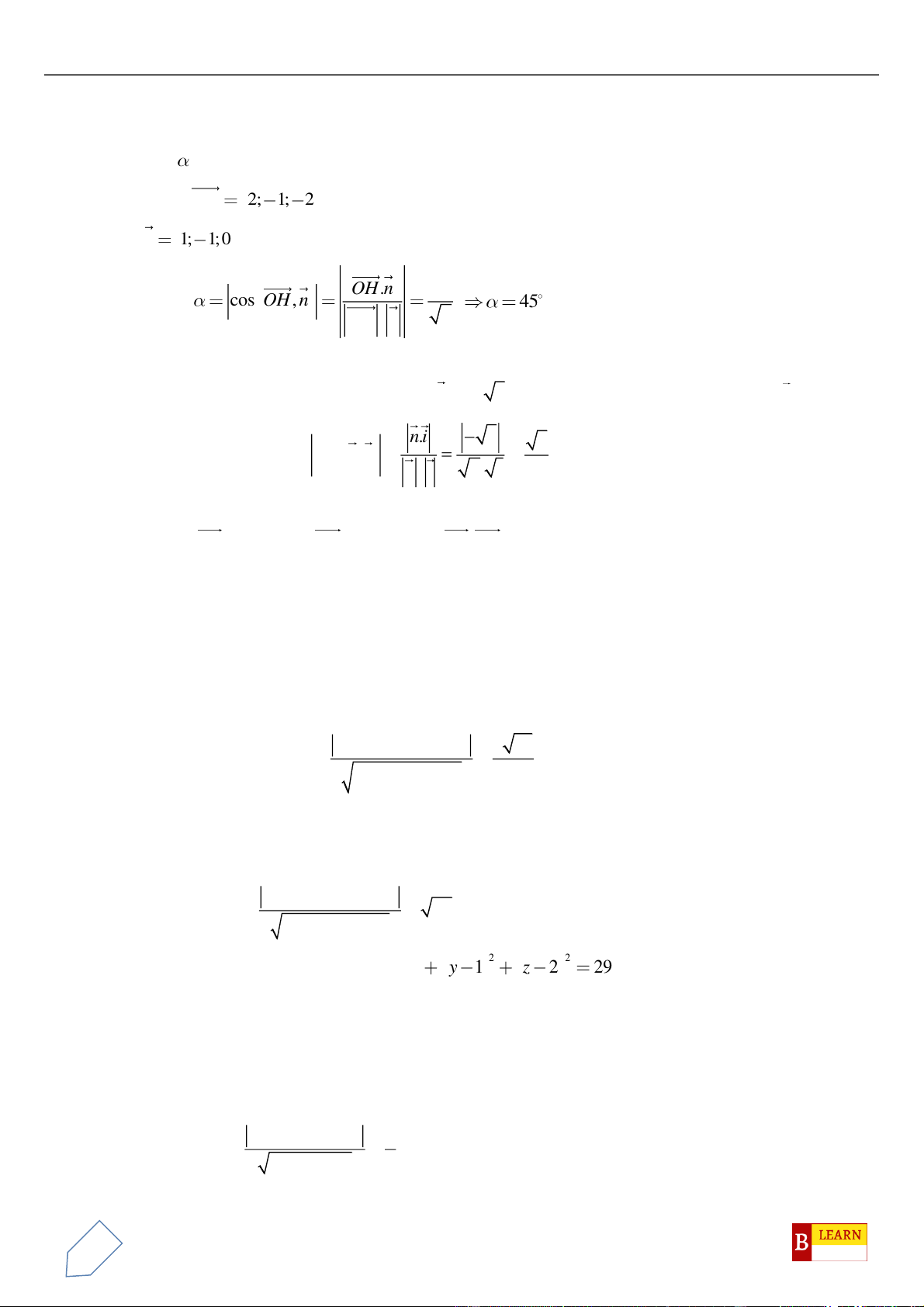
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
128
ĐÁP ÁN CHI TIẾT
Câu 1. Chọn D
Gọi là góc giữa mặt phẳng với mặt phẳng
Ta có là véctơ pháp tuyến của mặt phẳng
là véctơ pháp tuyến của mặt phẳng
và
Câu 2. Chọn A
Mặt phẳng
( )
P
có véc tơ pháp tuyến là
( )
3;1;0n =−
; trục
Ox
có véc tơ chỉ phương
( )
1;0;0i =
Ta có:
( )
( )
( )
( )
( )
0
3
.
3
sin ; cos ; ; 60 .
2
4. 1
.
ni
P Ox n i P Ox
ni
−
= = = = =
Câu 3. Chọn A
Ta có
( )
1; 1;2=−AB
,
( )
2;0;1=AC
( )
; 1;3;2
= −
AB AC
là một vectơ pháp tuyến của mặt
phẳng
( )
ABC
. Suy ra phương trình mặt phẳng
( )
ABC
là
( ) ( ) ( )
1 1 3 2 2 1 0− − + − + − =x y z
3 2 7 0 − + + − =x y z
.
Độ dài chiều cao DH của tứ diện ABCD là khoảng cách từ D đến
( )
ABC
. Suy ra
( )
( )
( )
2
22
1.1 3.1 2.1 7
3 14
,
14
1 3 2
DH d D ABC
− + + −
= = =
− + +
Câu 4. Chọn A
Vì mặt cầu
( )
S
tiếp xúc với mặt phẳng
()
nên có bán kính là:
2 2 2
4.0 3.1 2.2 28
( ,( )) 29.
4 ( 3) 2
R d I
− + +
= = =
+ − +
Vậy phương trình mặt cầu
( )
S
là:
22
2
1 2 29x y z
.
Câu 5. Chọn B
Điểm
M
là giao điểm của
( )
: 2 2 10 0P x y z+ + − =
với trục
0
:0
x
Oz y
zt
=
=
=
. Suy ra
(0;0;5)M
.
( )
( )
222
0 2.0 2.5 3
7
,
3
1 2 2
d M Q
+ + −
==
++
.
Câu 6. Chọn C
P
Q
2; 1; 2OH
P
1; 1;0n
Q
.1
cos cos ,
2
.
OH n
OH n
OH n
45
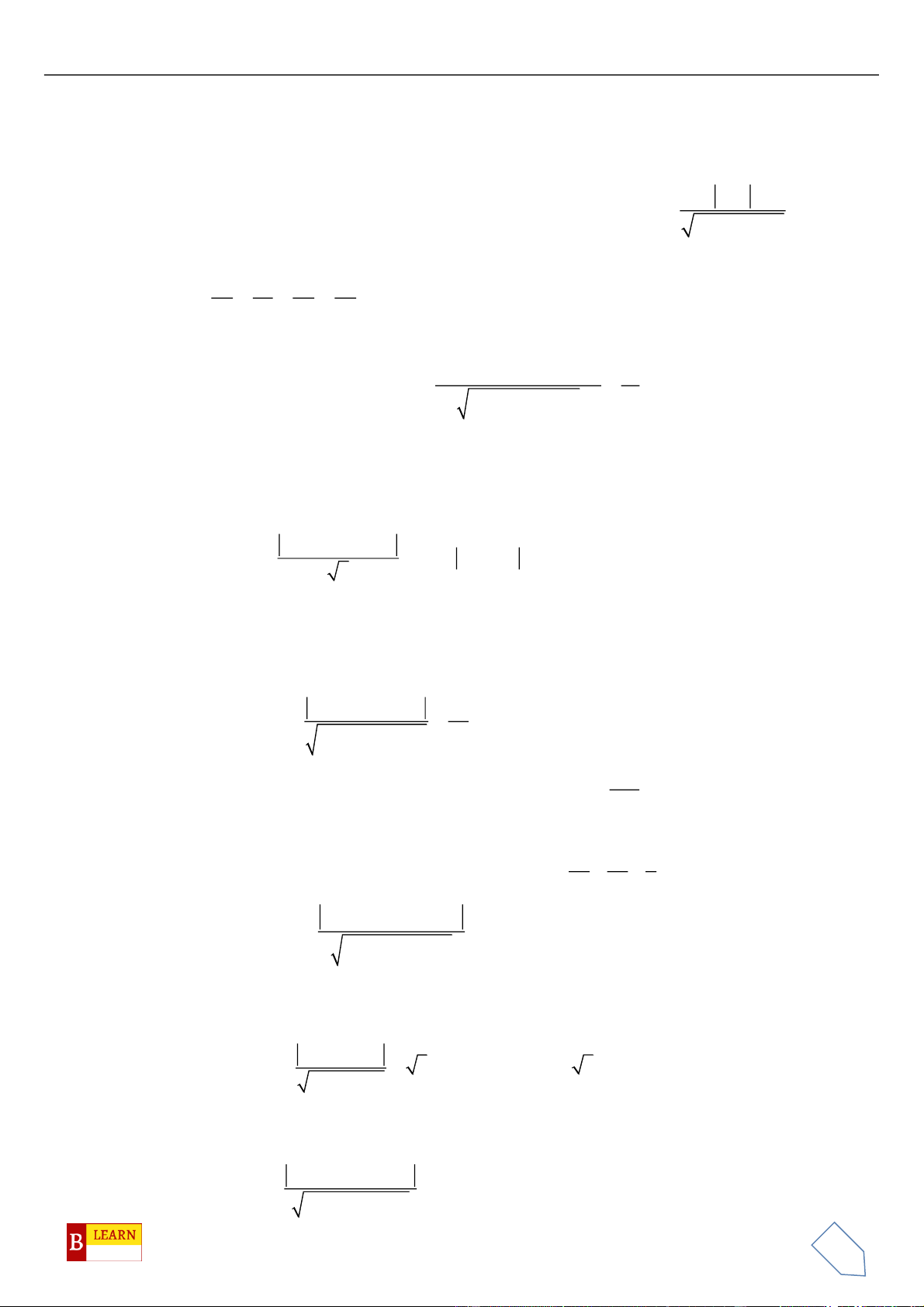
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
129
Bán kính của mặt cầu
( )
S
là
( )
( )
,3R d I P==
. Vậy phương trình mặt cầu
( )
S
là
( ) ( ) ( )
2 2 2
1 2 1 9x y z+ + − + − =
.
Câu 7. Chọn D
Lấy
( ) ( )
0;0;0OP
. Vì
( )
( ) / /PQ
, nên
( ) ( )
( )
( )
( )
222
12
, , 4
1 2 2
d P Q d O Q
−
= = =
++
.
Câu 8 Chọn B
Ta thấy:
2 1 2 4
4 2 4 4
− − −
= =
−−
. Do đó
( )
song song với
( )
.
Điểm
( )
2;0;0M
thuộc
( )
, khi đó khoảng cách giữa hai mặt phẳng
( )
và
( )
bằng
( )
( )
( )
2
22
| 4 2 2 0 4 0 4| 12
,2
6
4 2 4
dM
− + + −
= = =
− + +
.
Câu 9. Chọn D
( )
0;0;M Oz M a
Vì
M
nằm trên
Oz
có khoảng cách đến mặt phẳng
( )
:2 2 2 0P x y z− − − =
bằng 2 nên ta có
( )
2 2 6 4
2.0 0 2. 2
;(P) 2 2 2. 2 6
2 2 6 2
9
aa
a
d M a
aa
− − = = −
− − −
= = − − =
− − = − =
( ) ( )
0;0;2 , 0;0; 4MM−
.
Câu 10. Chọn C
Vì mặt cầu tiếp xúc với
( )
P
nên
( )
( )
d;I P R=
( )
2
22
2.3 2 2.4 4
20
3
2 1 2
R
+ + +
= =
+ − +
.
Vậy phương trình mặt cầu
( )
S
:
( ) ( ) ( )
2 2 2
400
3 2 4
9
x y z− + + + − =
.
Câu 11. Chọn B
Ta có phương trình mặt phẳng
( )
ABC
theo đoạn chắn là
1 2 2 6 0
3 3 6
x y z
x y z+ + = + − + =
−−
.
Suy ra
( )
( )
( )
( )
2
22
2.1 2. 3 4 6
, 2.
2 2 1
d M ABC
+ − + +
==
+ + −
Câu 12. Chọn D
Nhận thấy:
( )
//dP
. Gọi
( )
1;0;0Md
suy ra
( )
( )
( )
( )
;;d d P d M P=
.
Ta có:
( )
( )
222
1 0 0 2
;3
111
d M P
+++
==
++
. Vậy
( )
( )
;3d d P =
.
Câu 13. Chọn A
Mặt cầu tâm
(1;2; 1)I −
tiếp xúc với mặt phẳng
( ): 2 2 1 0P x y z− + − =
2 2 2
1 2.2 2( 1) 1
( ,( )) 2.
1 ( 2) 2
R d I P
− + − −
= = =
+ − +
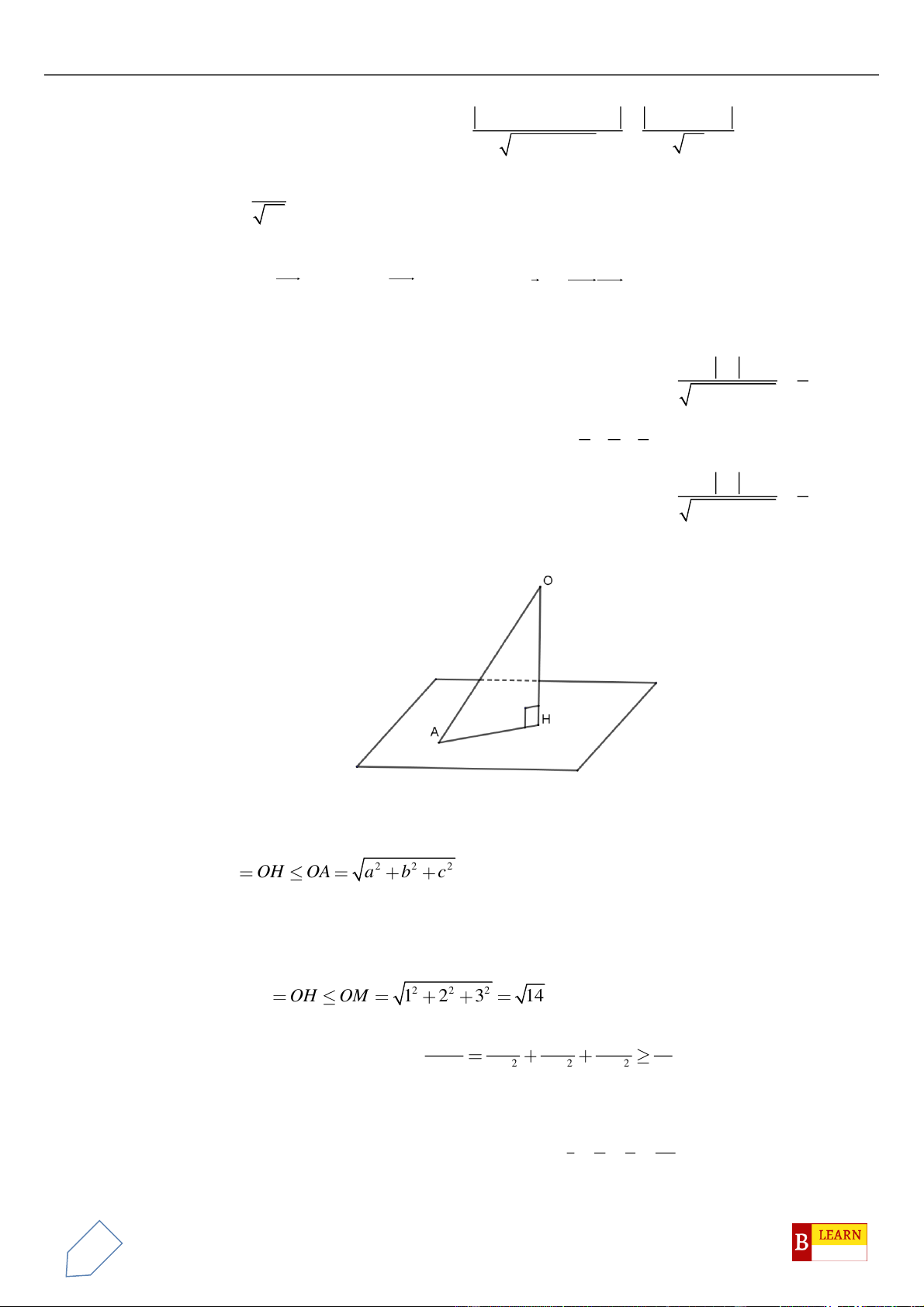
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
130
Câu 14. Chọn C
Khoảng cách
d
từ
A
đến
( )
P
là
222
3 4 2 4 3 8 6 4
( ,( ))
29
3 4 2
A A A
x y z
d A P
+ + + − + +
==
++
5
( ,( ))
29
d A P=
.
Câu 15. Chọn D
Cách 1: Ta có:
( 1;2;0), ( 1;0;3)AB AC= − = −
( )
, 6;3;2n AB AC
= =
là một véc tơ pháp
tuyến của mp
( )
ABC
. Phương trình mp
( )
ABC
là:
( )
6 1 3 2 0 6 3 2 6 0x y z x y z− + + = + + − =
.
Do đó khoảng cách từ gốc tọa độ đến mp
( )
ABC
bằng:
( )
2 2 2
6
6
;( )
7
632
d O ABC
−
==
++
.
Cách 2: Viết phương trình của mp
( )
ABC
theo đoạn chắn:
1
1 2 3
x y z
+ + =
hay
6 3 2 6 0x y z+ + − =
.
Do đó khoảng cách từ gốc tọa độ đến mp
( )
ABC
bằng:
( )
2 2 2
6
6
;( )
7
632
d O ABC
−
==
++
.
Câu 16. Chọn A
Xét (P) là một mặt phẳng đi qua
A
, gọi
H
là hình chiếu vuông góc của
O
lên mặt phẳng (P). Khi
đó,
2 2 2
(0,(P))d OH OA a b c
Câu 17. Chọn D
Xét (P) là một mặt phẳng đi qua
M
, gọi
H
là hình chiếu vuông góc của
O
lên mặt phẳng (P).
Khi đó,
2 2 2
(0,(P)) 1 2 3 14d OH OM
Dễ thấy
OABC
là tứ diện vuông nên
2 2 2 2
1 1 1 1 1
14OH OA OB OC
Câu 18. Chọn A
( )
: 2 3 1 0P x y z+ + − =
( )
: 2 3 6 0Q x y z+ + + =
. Ta có:
1 2 3 1
1 2 3 6
−
= =
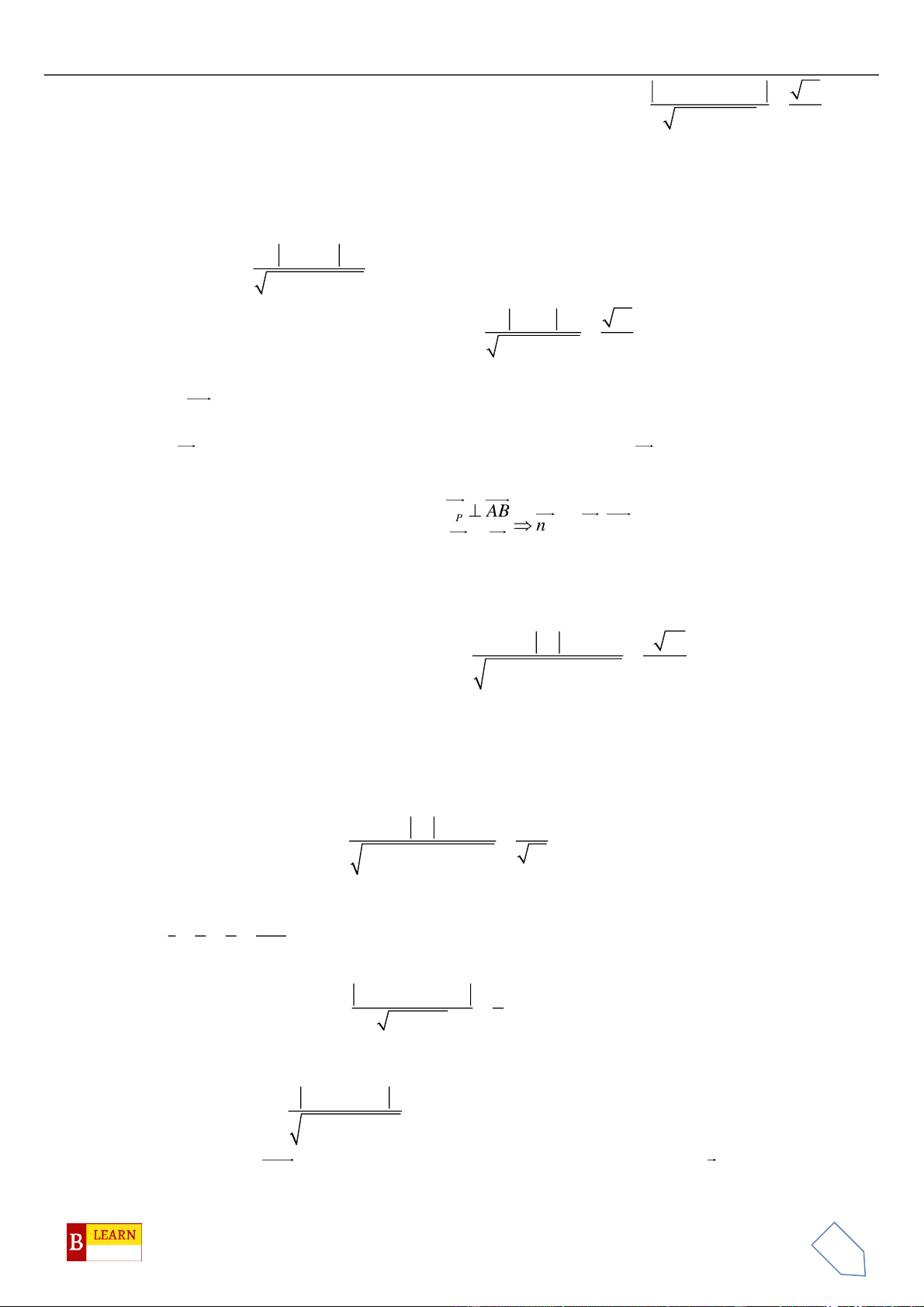
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
131
( )
P
//
( )
Q
nên chọn A
( ) ( )
1;0;0 P
. Vì
( )
P
//
( )
Q
nên d
( )
( )
,AQ
2 2 2
1 2.0 3.0 6
14
2
1 2 3
+ + +
==
++
.
Các giải trắc nghiệm:
Công thức tính nhanh:
( ) ( )
12
: 0; 0P Ax By Cz D Q Ax By Cz D+ + + = + + + =
d
( ) ( )
( )
;PQ
=
21
2 2 2
DD
A B C
−
++
( )
P
//
( )
Q
áp dụng công thức: d
( ) ( )
( )
;PQ
2 2 2
16
14
2
1 2 3
−−
==
++
.
Câu 19. Chọn D
Ta có
(2; 3; 2)AB = − −
Gọi
P
n
là VTPT của mặt phẳng (P), VTCP của đường thẳng d là
(2; 1;1)
d
u =−
Theo đề bài ta có
( ) ( )
( )
;
; (5;6; 4)
//
P
Pd
Pd
A P B P n AB
n u AB
dP
nu
⊥
= = −
⊥
Mặt phẳng
( )
P
qua
A
có phương trình là:
5( 1) 6( 2) 4( 3) 0x y z− + − − − =
5 6 4 5 0x y z + − − =
. Khi đó
( )
2
22
5
5 77
( ,( ))
77
(5) 6 ( 4)
d O P
−
==
+ + −
.
Câu 20. Chọn A
Đường thẳng
đi qua
( )
1;7;3A
.
Do
( )
Q
là mặt phẳng chứa đường thẳng
và song song với
( )
P
nên :
( ) ( )
( )
( )
( )
;;d Q P d A P=
( ) ( )
22
2
9
9
14
3 2 1
−
==
+ − + −
.
Câu 21. Chọn A
Vì nên . Chọn .
Câu 22. Chọn A
Ta có:
( )
( )
( )
2
2
2 4 3 3
,4
2 2 1
d A P AM
+ + +
= = =
+ − +
M
là hình chiếu vuông góc của
A
lên
( )
P
.
( )
MP
và
( )
1; 2; 3AM a b c= − + −
cùng phương với VTPT của
( )
P
( )
2; 2;1n =−
.
1 2 2 10
1 2 2 3
−
==
−
( ) / / (Q)P
(0;0;5) ( )MP
( ) ( )
0 2.0 2.5 3
7
( ), ( ) , ( ) .
3
1 4 4
d P Q d M Q
+ + −
= = =
++
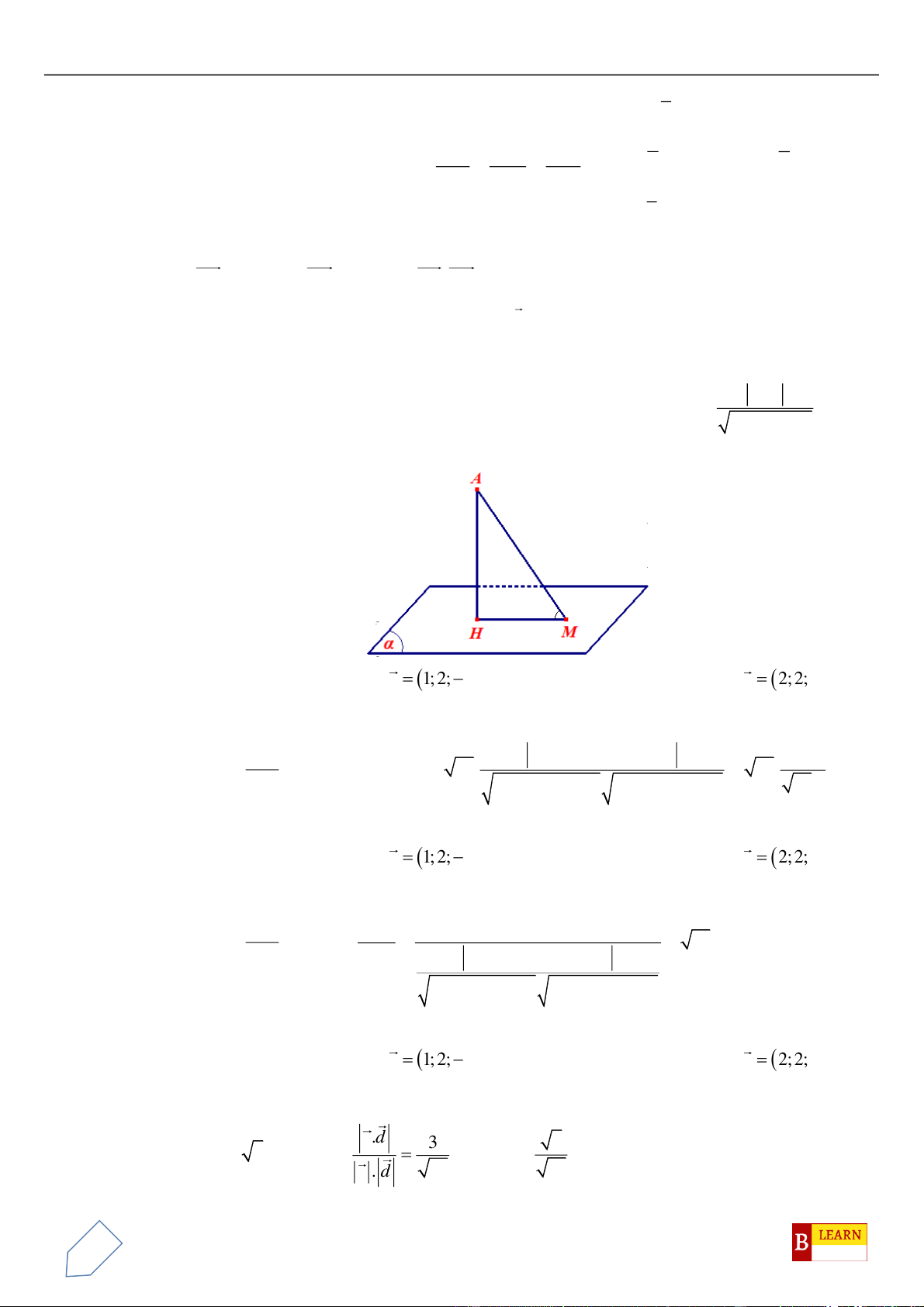
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
132
Tọa độ của
M
là nghiệm của hệ:
5
3
2 2 3 0
2
123
3
2 2 1
5
3
a
a b c
b
a b c
c
=−
− + + =
=
− + −
==
−
=
2
3
abc + + =
.
Câu 23. Chọn A
Ta có:
( ) ( ) ( )
3;0; 4 , 4;0; 3 , , 0; 25;0AB AC AB AC
− − − = −
.
Chọn vecto pháp tuyến của mặt phẳng
( )
ABC
là
( )
0;1;0n
.
Phương trình mặt phẳng
( )
ABC
là:
20y +=
.
Độ cao
h
của tứ diện kẻ từ
D
bằng khoảng cách từ
D
đến
( )
ABC
. Vậy
2 2 2
12
3
0 1 0
h
+
==
++
.
Câu 24. Chọn B
( )
có một vectơ pháp tuyến là
( )
1;2; 3n =−
và
d
có một vectơ chỉ phương là
( )
2;2; 1u =−
.
Gọi
là góc giữa
( )
và
d
,
H
là hình chiếu của
A
trên
( )
.
Ta có
sin
AH
AM
=
( )( )
( ) ( )
22
2 2 2 2
1.2 2.2 3 1
9
sin 14. 14. 3
14.3
1 2 3 2 2 1
AH AM
+ + − −
= = = =
+ + − + + −
Câu 25. Chọn D
( )
có một vectơ pháp tuyến là
( )
1;2; 3n =−
và
d
có một vectơ chỉ phương là
( )
2;2; 1u =−
.
Gọi
là góc giữa
( )
và
d
,
H
là hình chiếu của
A
trên
( )
.
Ta có
sin
AH
AM
=
( )( )
( ) ( )
22
2 2 2 2
3
14
sin
1.2 2.2 3 1
1 2 3 2 2 1
AH
AM
= = =
+ + − −
+ + − + + −
Câu 26. Chọn D
( )
có một vectơ pháp tuyến là
( )
1;2; 3n =−
và
d
có một vectơ chỉ phương là
( )
2;2; 1u =−
.
Gọi
là góc giữa
( )
và
d
,
H
là hình chiếu của
A
trên
( )
.
Ta có
5MH =
và
.
3
sin
14
.
nd
nd
==
5
cos
14
=
.
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
133
Mà
cos
MH
AM
=
5
14
cos
5
14
MH
AM
= = =
.
Câu 27. Chọn B
Ta có
( ) ( )
( )
( )
2
22
70
7
;
6
2 1 1
d P Q
−
==
+ − +
.
Câu 28. Chọn A
Nhận thấy hai mặt phẳng trên là song song nhau.
Lấy điểm
( ) ( )
0;0; 2A
−
.
Ta có
( ) ( )
( )
( )
( )
( ) ( )
22
2
6
; ; 2
2 1 2
d d A
= = =
+ − + −
.
Câu 29. Chọn D
Ta có
H
là hình chiếu vuông góc của
O
xuống mặt phẳng
( )
P
nên
( )
OH P⊥
. Do đó
( )
2; 1; 2OH =
là một vectơ pháp tuyến của mặt phẳng
( )
P
.
Mặt phẳng
( )
Q
có một vectơ pháp tuyến là
( )
1; 1; 0n =
.
Gọi
là góc giữa hai mặt phẳng
( ) ( )
, PQ
.
Ta có
2 2 2 2 2 2
.
2.1 1.1 2.0
2
cos 45
2
.
2 1 2 . 1 1 0
OH n
OH n
++
= = = =
+ + + +
.
Vây góc giữa hai mặt phẳng
( ) ( )
, PQ
là
45
.
Câu 30. Chọn C
Mặt phẳng
( )
P
đi qua hai điểm
A
,
B
nên
10
1
10
b
ab
a
−=
= =
−=
.
Và
( )
P
tạo với
( )
Oyz
góc
60
nên
( ) ( )
( )
2 2 2
1
cos ,
2
.1
a
P Oyz
abc
==
++
(*).
Thay
1ab==
vào phương trình được
2
2 2 2cc+ = = −
.
Khi đó
( )
2 2 0;3abc+ + = −
.
Câu 31. Chọn C
Mặt cầu
( )
S
có tâm
( )
1;0; 2I −
và bán kính
2R =
.
Các tiếp diện của
( )
S
tại
A
và
B
tạo với nhau một góc lớn nhất ( bằng
90
)
IA IB⊥
( )
,2
2
R
d I d = =
Đường thẳng
d
đi qua điểm
( )
2;0; 1Mm−
và có một VTCP
( )
1;1; 1u = − −
.
Suy ra:
( )
1;0; 1IM m=+
,
( )
, 1; ;1IM u m m
= − − −
.
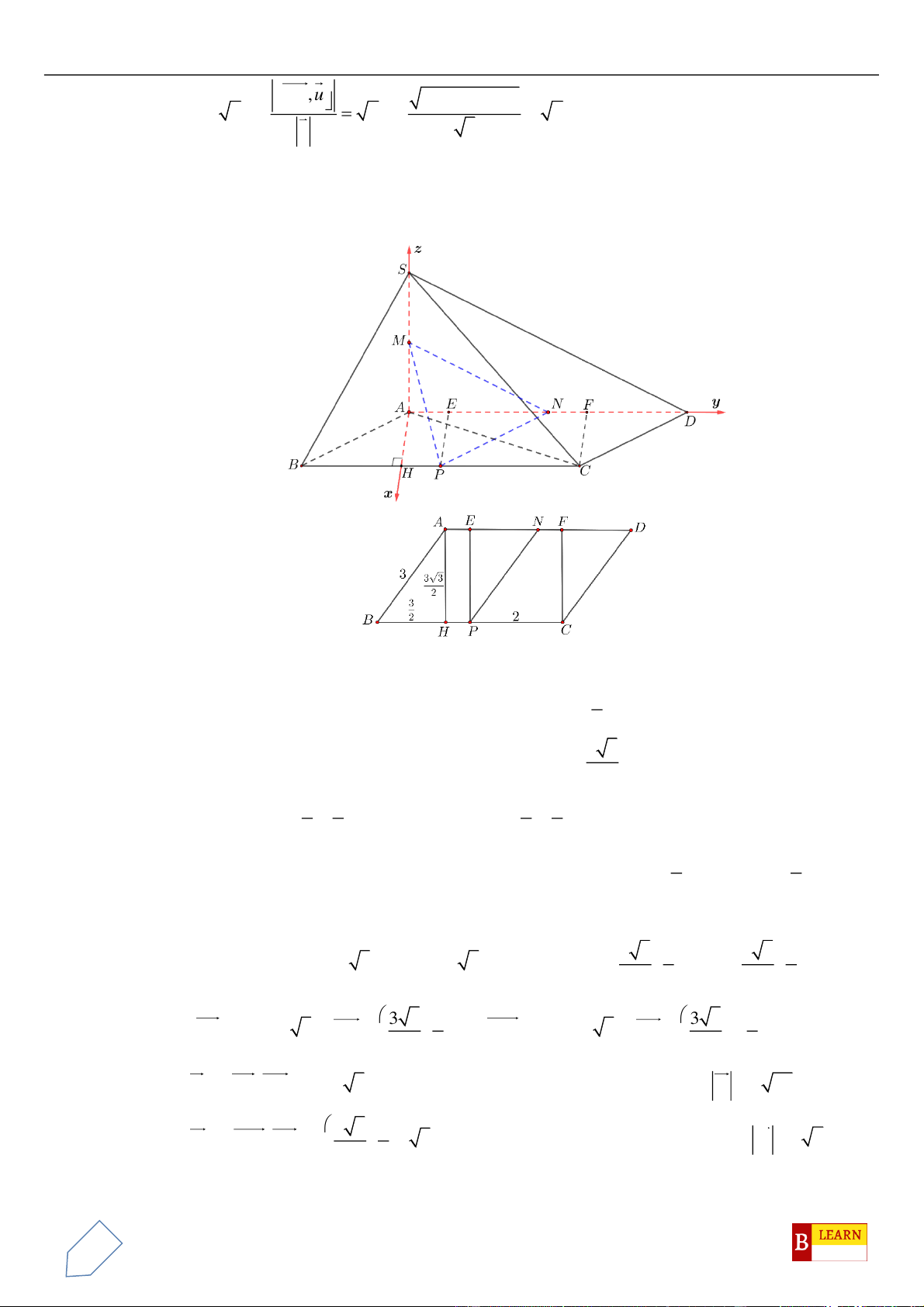
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
134
( )
2
2
,
1
2 2 2
, 2 2 2 2 0
2
3
IM u
m
mm
d I d m m
m
u
=
++
= = = + − =
=−
.
Vậy tổng các giá trị thực của tham số
m
bằng
1−
.
Câu 32. Chọn A
Cách 1:
Trong mặt phẳng
( )
ABCD
, dựng tia
Ax AD⊥
nên
Ax BC⊥
tại
H
.
ABH
vuông tại
H
có:
3
.cos 3.cos60
2
33
.sin 3.sin60
2
BH AB ABH
AH AB ABH
= = =
= = =
.
31
2
22
HP BP BH= − = − =
,
35
4
22
HC BC BH= − = − =
.
Dựng hình chữ nhật
AHPE
và hình chữ nhật
AHCF
nên
1
2
AE HP==
,
5
2
AF HC==
.
Chọn hệ trục tọa độ
Axyz
như hình vẽ.
Ta có:
( )
0; 0; 0A
,
( )
0; 0; 2 3S
,
( )
0; 0; 3M
,
( )
0; 2; 0N
,
3 3 5
; ; 0
22
C
,
3 3 1
; ; 0
22
P
.
Ta có:
( )
0; 0; 2 3AS =
,
3 3 5
; ; 0
22
AC
=
,
( )
0; 2; 3NM =−
,
3 3 3
; ; 0
22
NP
=−
.
Chọn
( )
1
, 5 3;9; 0n AS AC
= = −
là một vectơ pháp tuyến của
( )
SAC
1
2 39n=
.
Chọn
2
3 3 9
, ; ; 3 3
22
n NM NP
==
là một vectơ pháp tuyến của
( )
MNP
2
36n=
.
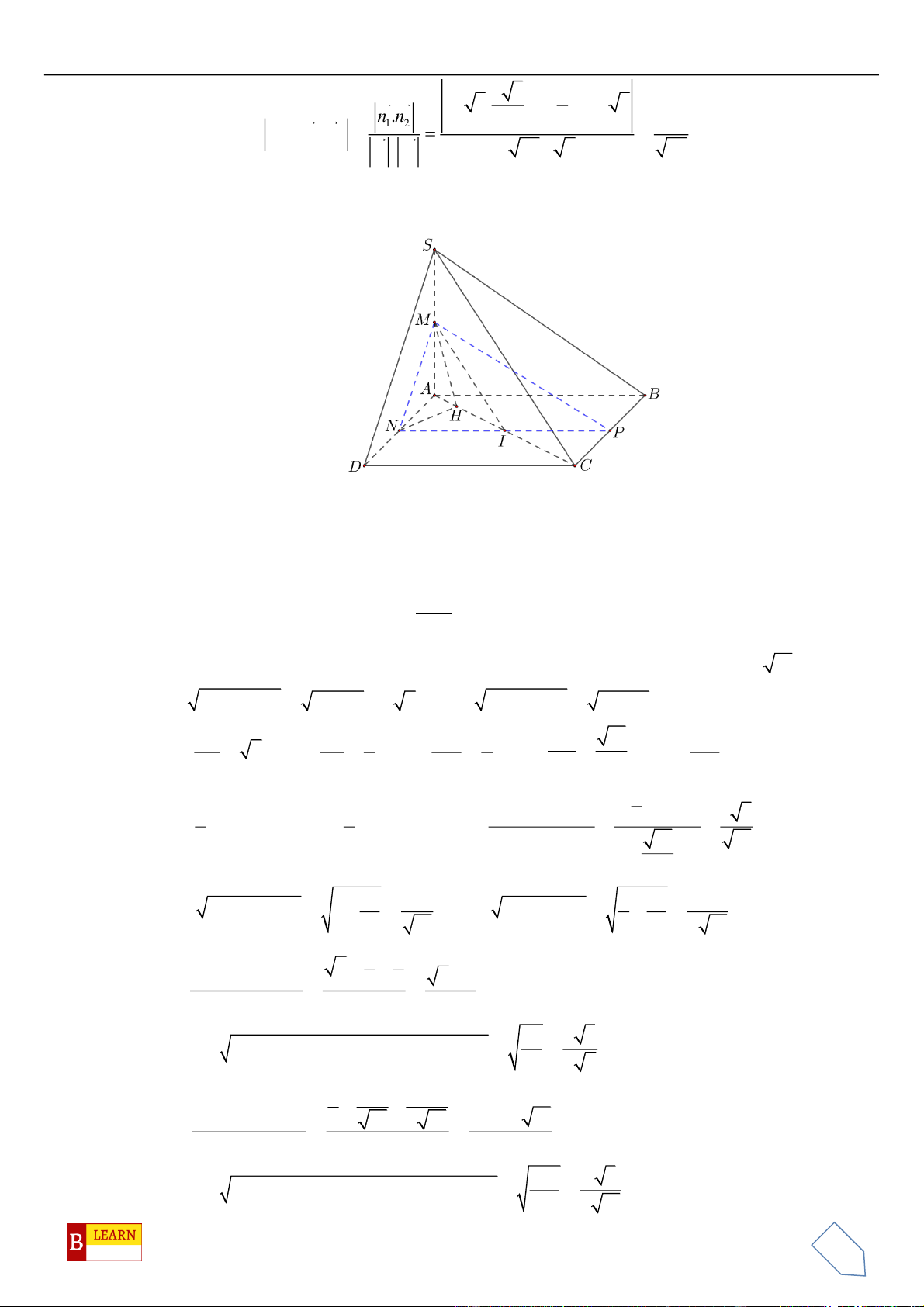
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
135
Khi đó:
( )
12
12
12
3 3 9
5 3. 9. 0.3 3
.
22
1
cos cos ,
2 39.3 6 26
.
nn
nn
nn
− + +
= = = =
.
Vậy:
78 41'24''
.
Cách 2:
Gọi
I AC NP=
và dựng
NH AC⊥
tại
H
.
Ta có:
( )
,NH AC NH SA NH SAC⊥ ⊥ ⊥
tại
H
.
Khi đó:
HMI
là hình chiếu vuông góc của
NMI
lên mặt phẳng
( )
SAC
.
Do đó:
.cos cos
HMI
HMI MNI
MNI
S
SS
S
= =
.
Ta có:
2 2 2
2. . .cos 16 9 2.3.4.cos60 13 13AC AB BC AB BC ABC AC= + − = + − = =
.
22
12 16 2 7SD SA AD= + = + =
,
22
12 13 5SC SA AC= + = + =
.
7
2
SD
MN ==
,
5
22
SC
MI ==
,
3
22
DC
NI ==
,
13
22
AC
AI ==
,
2
2
AD
AN ==
.
3
2. .sin60
1 1 . .sin60 3 3
2
. . .sin . .
22
13 13
2
NAI
NA NI
S NA NI ANI NH AI HN
AI
= = = = =
.
22
36 8
7
13
13
MH MN NH= − = − =
,
22
9 36 3
4 13
2 13
HI NI NH= − = − =
.
*
1
53
7
74
22
2 2 2
NM MI NI
p
++
+ + +
= = =
( ) ( ) ( )
1 1 1 1
27 3 3
. . .
8
22
MNI
S p p MN p MI p NI = − − − = =
.
*
2
5 8 3
65 19 13
2
13 2 13
2 2 52
MI IH HM
p
++
+ + +
= = =
( ) ( ) ( )
2 2 2 2
27 3 3
. . .
208
4 13
MIH
S p p MI p HI p MH = − − − = =
.
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
136
Vậy:
3 3 2 2 1
cos .
4 13 3 3 26
==
. Suy ra:
78 41'24''
.
Câu 33. Chọn C
Đặt
OA a=
( )
0a
. Khi đó
2OB a=
,
4OC a=
.
Áp dụng phương trình mặt phẳng theo đoạn chắn ta có mặt phẳng
( )
có phương trình
1
24
x y z
aaa
+ + =
.
Do
( ) ( )
1;2;1M
nên
1 2 1
1
24aaa
+ + =
99
1
44
a
a
= =
(thỏa mãn
0a
).
Phương trình tổng quát của mặt phẳng
( )
là:
4 2 9 0x y z+ + − =
.
Suy ra:
( )
( )
2 2 2
4.0 2.0 0 9
3 21
;
7
4 2 1
dO
+ + −
==
++
.
Câu 34. Chọn D
Gọi
( )
là mặt phẳng trung trực của đoạn
AB
nên
( )
qua
( )
3;1;2I
là trung điểm
AB
và nhận
( )
6; 2;2AB =−
là một vectơ pháp tuyến.
Phương trình
( )
có dạng
( ) ( ) ( )
3 3 1 1 1 2 0x y z− − − + − =
3 10 0x y z − + − =
.
( )
( )
( )
2
22
3 10
;
3 1 1
C C C
x y z
dC
− + −
=
+ − +
3.2 1 1 10
9 1 1
− + −
=
++
4
11
=
.
Câu 35. Chọn A
Vì
6 3 2 1
11
18
23
−
= =
( ) ( )
//PQ
nên
( ) ( )
( )
( )
( )
;;d P Q d M Q=
với
( ) ( )
0;1; 1MP−
( ) ( )
( )
( )
( )
22
2
1 1 1 1
8 0 8
2 3 2 3
; ; 7
49
11
1
36
23
M M M
x y z
d P Q d M Q
+ + + + − +
= = = =
++
.
Câu 36. Chọn A
Ta có:
z
y
x
O
M
A
B
C
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
137
Mặt phẳng
( )
ABC
có
( )
; 1, 4,9n AB AC
= = −
là véc-tơ pháp tuyến
( )
ABC
và đi qua điểm
( )
1, 2,0A −
nên có phương trình dạng:
( ) ( ) ( )
1 1 4 2 9 0 4 9 9 0x y z x y z− − + + − − + − =
Độ dài đường cao của tứ diện
ABCD
hạ từ điểm
D
:
( )
( )
( ) ( )
22
2 2 2 2
4 9 9 3 4.3 9.1 9
9
,
72
1 4 9 1 4 9
D D D
x y z
d D ABC
− + − − + −
= = =
+ − + + − +
Câu 37. Chọn D
Gọi
H
là hình chiếu của
O
mặt phẳng
( )
P
. Khi đó:
( )
( )
d O , P OH=
.
Trong tam giác vuông
OHM
:
OH OM
nên
( )
( )
d O , P
đạt giá trị lớn nhất khi
( )
( )
d O , P OM=
hay
( )
OM P⊥
.
Phương trình mặt phẳng
( )
P
qua
( )
1 2 1M ; ; −
và nhận
( )
1 2 1OM ; ;=−
làm véc tơ pháp tuyến
là
2 6 0x y z+ − − =
.
( )
P
cắt các trục
Ox,Oy ,Oz
lần lượt tại
( )
600A ; ;
,
( )
0 3 0B ; ;
,
( )
0 0 6C ; ; −
.
Xét tứ diện
OABC'
với
6OC' =
,
6OA =
,
3OB =
.
Gọi
I
là trung điểm của
AB
, trong mp
( )
OAB
. Gọi
d
qua
I
và song song trục
Oz
.
Lấy
H
là trung điểm
OC'
. Mặt phẳng trung trực của
OC'
qua
H
cắt
d
tại G.
Suy ra :
GC' GO GA GB R= = = =
.
Tam giác vuông
OAB
:
22
1 1 45
63
2 2 2
OI AB= = + =
45
2
OI HG = =
.
1
3
2
OH OC'==
.
Tam giác vuông
OHG :
22
9
2
R OG HG OH= = + =
.
Thể tích
V
của khối cầu ngoại tiếp tứ diện
OABC
bằng thể tích khối cầu ngoại tiếp tứ diện
OABC'
là
3
4 243
32
VR
==
(đvtt).
Câu 38. Chọn C

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
138
Vì
( )
P
cắt các tia
,,Ox Oy Oz
lần lượt ở
,,A B C
nên ta gọi tọa độ các điểm là
( ) ( ) ( )
;0;0 , 0; ;0 , 0;0;A a B b C c
với
, , 0abc
.
Khi đó phương trình mặt phẳng
( )
:1
x y z
P
a b c
+ + =
.
Vì
( ) ( )
2 3 5
2;3;5 1MP
abc
+ + =
.
Vì đô dài các đoạn
,,OA OB OC
lập thành cấp số nhân với công bội bằng
3
3
39
ba
c b a
=
==
32
2 3 5 32
1
3
3 9 9
32
b
a
a a a
c
=
+ + = =
=
Khi đó ta có phương trình mặt phẳng
( )
:1
32 32
32
93
x y z
P + + =
Hay
( )
:9 3 32 0P x y z+ + − =
. Do đó:
( )
( )
2 2 2
32
32
;
91
9 3 1
d O P
−
==
++
.
Bình luận:
Bài này có thể dùng cách khác như sau:
Khoảng cách từ
O
đến
( )
ABC
:
( ) ( )
2 2 2 2
1 1 1 1 9
91
39
a
h
ha
aa
= + + =
Mà
32
9
a =
(theo trên). từ đó tìm được
32
91.
h =
.
Câu 39. Chọn C
+ Đường thẳng
11
:
2 1 3
−+
==
x y z
d
đi qua điểm
( )
1;0; 1−M
và có một vectơ chỉ phương là
( )
2;1;3u =
.
+ Mặt phẳng
( )
:2 0+ − =P x y z
có một vectơ pháp tuyến là
( )
( )
2;1; 1
P
n =−
.
+ Gọi
( )
Q
n
là một vectơ pháp tuyến của mặt phẳng
( )
Q
.
Vì mặt phẳng
( )
Q
chứa đường thẳng
d
và vuông góc với mặt phẳng
( )
P
nên
( )
( ) ( )
⊥
⊥
Q
QP
nu
nn
và
( )
Q
đi qua điểm
( )
1;0; 1−M
.
Do đó mặt phẳng
( )
Q
có một vectơ pháp tuyến
( ) ( )
( ) ( )
4;8;0 4 1; 2;0= = − = − −
QP
n u n
.
Phương trình của mặt phẳng
( )
Q
là:
( ) ( )
1. 1 2 0 0 2 1 0− − − = − − =x y x y
.
+ Vậy khoảng cách từ điểm
( )
0;0;0O
đến mặt phẳng
( )
Q
bằng
( )
( )
( )
2
2
0 2.0 1
1
;
5
12
−−
==
+−
d O Q
.
Câu 40. Chọn C
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
139
Ta có
( ) ( ) ( ) ( )
2
2
1 1 1 0 2 1 0mx m m y m z m y z m x y z z+ + + − − = + + + − + − =
.
Giả sử
( )
0 0 0
;;M x y z
là điểm cố định mà mặt phẳng
( )
m
P
luôn đi qua.
( ) ( )
2
0 0 0 0 0 0
2 1 0m y z m x y z z m + + + − + − =
00
0 0 0
0
0
20
10
yz
x y z
z
+=
+ − =
−=
0
0
0
3
1
1
x
y
z
=
= −
=
. Suy ra
( )
3; 1;1M −
.
Vì
cắt mặt phẳng
( )
m
P
tại một điểm cố định và
M
là điểm cố định mà mặt phẳng
( )
m
P
luôn đi
qua nên
( )
3; 1;1M −
.
Mặt phẳng
( )
Oxy
có vec-tơ pháp tuyến là
( )
0; 0;1n =
.
Vì
( )
// Oxy
d
⊥
nên
có vec-tơ chỉ phương
( )
1
, 2; 1; 0u u n
= = −
.
Vậy
đi qua
( )
3; 1;1M −
và có vec-tơ chỉ phương
( )
1
2; 1; 0u =−
.
Do vậy ta có
( )
1
1
,
d , 21
u AM
hA
u
= = =
.
Câu 41. Chọn D
Ta có:
( )
1; 1;0AB =−
,
( )
4; 4;0CD =−
,
( )
2; 1; 1AD = − −
,
( )
3;4; 1BC = − −
. Nhận thấy
4CD AB=
và
AD BC
bốn điểm
, , ,A B C D
tạo thành một hình thang hai đáy là
AB
và
CD
Mặt khác
2;3; 1AC
và
( )
, 1;1;1AB AC
=
nên
( )
: 5 0ABC x y z+ + − =
Suy ra
( )
E ABC
. Vậy
5
điểm
, , , ,A B C D E
tạo thành hình chóp có đỉnh là
E
.
Gọi
,MN
;
,PQ
;
,RS
lần lượt là trung điểm của
,AC BD
;
,EB EA
;
,EC ED
.
Ta dễ chứng minh được các mặt phẳng
( )
MNQP
,
( )
MNSR
,
( )
PQRS
là các mặt phẳng thỏa mãn
yêu cầu bài toán. Vậy có
3
mặt phẳng cách đều
5
điểm đã cho.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
140
DẠNG 5. VÍ TRÍ TƯƠNG ĐỐI GIỮA 2 MẶT PHẲNG, MẶT CẦU
VỚI MẶT PHẲNG
Câu 1. Trong không gian với hệ tọa độ
Oxyz
cho hai đường thẳng
1
12
:
2 1 2
x y z
d
−+
==
−
,
2
21
:
2 1 2
x y z
d
+−
==
−−
. Xét vị trí tương đối của hai đường thẳng đã cho.
A. Chéo nhau. B. Trùng nhau. C. Song song. D. Cắt nhau.
Câu 2. Trong không gian
Oxyz
, cho mặt cầu
( )
2 2 2
: 6 4 12 0S x y z x y+ + − + − =
. Mặt phẳng nào sau đây
cắt
( )
S
theo một đường tròn có bán kính
3r =
?
A.
4 3 4 26 0x y z− − − =
. B.
2 2 12 0x y z+ − + =
.
C.
3 4 5 17 20 2 0x y z− + − + =
. D.
30x y z+ + + =
.
Câu 3. Trong không gian
Oxyz
, cho hai mặt phẳng
( )
: 1 0x y z
+ + − =
và
( )
:2 1 0x y mz m
− + − + =
, với
m
là tham số thực. Giá trị của
m
để
( ) ( )
⊥
là
A.
1−
. B.
0
. C.
1
. D.
4−
.
Câu 4. Trong không gian với hệ tọa độ
Oxyz
. Cho điểm
( )
1;2; 2I −
và mặt phẳng
( )
P
:
2 2 5 0x y z+ + + =
. Viết phương trình mặt cầu tâm
I
cắt mặt phẳng
( )
P
theo giao tuyến là một
đường tròn có diện tích bằng
16
.
A.
( ) ( ) ( )
2 2 2
2 2 1 36x y z− + − + − =
. B.
( ) ( ) ( )
2 2 2
1 2 2 9x y z− + − + + =
.
C.
( ) ( ) ( )
2 2 2
1 2 2 25x y z− + − + + =
. D.
( ) ( ) ( )
2 2 2
1 2 2 16x y z− + − + + =
.
Câu 5. Trong không gian
Oxyz
, cho mặt
2 2 2
( ): 2 4 6 4 0S x y z x y z m+ + + + − − + =
. Tìm số thực
m
để
mặt phẳng
( ):2 2 1 0P x y z− + + =
cắt
( )
S
theo một đường tròn có bán kính bằng
3
.
A.
3m =
. B.
2m =
. C.
1m =
. D.
4m =
.
Câu 6. Trong không gian
Oxyz
, cho điểm
( )
3; 1;4I −
và mặt cầu
( ) ( ) ( )
22
2
1
: 1 2 1S x y z− + + − =
.
Phương trình của mặt cầu
( )
S
có tâm
I
và tiếp xúc ngoài với mặt cầu
( )
1
S
là
A.
( ) ( ) ( )
2 2 2
3 1 4 4x y z− + − + − =
. B.
( ) ( ) ( )
2 2 2
3 1 4 16x y z− + − + − =
.
C.
( ) ( ) ( )
2 2 2
3 1 4 4x y z− + + + − =
. D.
( ) ( ) ( )
2 2 2
3 1 4 2x y z− + + + − =
.
Câu 7. Trong không gian
Oxyz
, có bao nhiêu số thực
m
để mặt phẳng
( )
: 2 2 1 0P x y z+ − − =
song song
với mặt phẳng
( )
:2 ( 2) 2 0Q x m y mz m+ + − − =
?
A.
1
. B.
0
. C. Vô số. D.
2
.
Câu 8. Trong không gian với hệ trục tọa độ
Oxyz
, khoảng cách từ tâm mặt cầu
( )
2 2 2
: 4 4 4 1 0S x y z x y z+ + − − − − =
đến mặt phẳng
( )
: 2 2 10 0P x y z+ + − =
bằng
A.
4
3
. B.
7
3
. C.
0
. D.
8
3
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
141
Câu 9. Cho mặt cầu
( )
S
có đường kính
10 cm
và mặt phẳng
( )
P
cách tâm mặt cầu một khoảng
4cm
.
Khẳng định nào sau đây sai?
A.
( )
P
và
( )
S
có vô số điểm chung. B.
( )
P
tiếp xúc với
( )
S
.
C.
( )
P
cắt
( )
S
theo một đường tròn bán kính
3cm
. D.
( )
P
cắt
( )
S
.
Câu 10. Trong hệ trục tọa độ
Oxyz
, cho mặt cầu
( )
2 2 2
: 2 4 6 0S x y z x y z+ + − − − =
cắt các trục
Ox
,
Oy
,
Oz
lần lượt tại các điểm
A
,
B
,
C
. Phương trình mặt phẳng
( )
ABC
là
A.
1
2 4 6
x y z
− − =
. B.
1
2 4 6
x y z
+ + =
. C.
0
2 4 6
x y z
− − =
. D.
1
2 4 6
x y z
+ − =
.
Câu 11. Trong không gian
Oxyz
, cho mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 2 1 1 12S x y z+ + + + − =
. Mặt phẳng nào sau
đây cắt mặt cầu
( )
S
theo giao tuyến là một đường tròn?
A.
( )
1
: 2 0P x y z+ − + =
. B.
( )
2
: 2 0P x y z+ − − =
.
C.
( )
3
: 10 0P x y z+ − + =
. D.
( )
4
: 10 0P x y z+ − − =
.
Câu 12. Trong không gian
Oxyz
, mặt cầu
( )
S
có tâm
( )
1;2; 3I −
và tiếp xúc với mặt phẳng
( )
Oyz
có
phương trình là
A.
( ) ( ) ( )
2 2 2
1 2 3 1x y z+ + + + − =
. B.
( ) ( ) ( )
2 2 2
1 2 3 1x y z− + − + + =
.
C.
( ) ( ) ( )
2 2 2
1 2 3 13x y z+ + + + − =
. D.
( ) ( ) ( )
2 2 2
1 2 3 13x y z− + − + + =
.
Câu 13. Trong không gian
Oxyz
, cho mặt cầu
( )
S
:
( ) ( ) ( )
2 2 2
2 1 2 4x y z− + + + + =
và mặt phẳng
( )
P
:
4 3 0x y m− − =
. Tìm tất cả các giá trị thực của tham số
m
để mặt phẳng
( )
P
và mặt cầu
( )
S
có
đúng
1
điểm chung.
A.
1m =
. B.
1m =−
hoặc
21m =−
.
C.
1m =
hoặc
21m =
. D.
9m =−
hoặc
31m =
.
Câu 14. Phương trình mặt phẳng
()P
chứa trục
Oz
và cắt mặt cầu
2 2 2
( ): 2 2 2 6 0S x y z x y z+ + − + − − =
theo đường tròn có bán kính bằng
3
là
A.
0xy+=
. B.
0xy−=
. C.
20xy+=
. D.
20xy−=
.
Câu 15. Trong không gian hệ tọa độ
Oxyz
, cho mặt phẳng
( )
: 2 2 3 0Q x y z+ + − =
và mặt phẳng
( )
P
không qua
O
, song song mặt phẳng
( )
Q
và
( ) ( )
( )
; 1.d P Q =
Phương trình mặt phẳng
( )
P
là
A.
2 2 3 0x y z+ + + =
. B.
2 2 0x y z+ + =
.
C.
2 2 1 0x y z+ + + =
. D.
2 2 6 0x y z+ + − =
.
Câu 16. Trong không gian
Oxyz
, cho mặt cầu
( )
S
:
( ) ( ) ( )
2 2 2
2 4 1 4xyz− + − + − =
và mặt phẳng
( )
P
:
3 1 0x my z m+ + − − =
. Tìm tất cả các giá trị thực của tham số
m
để mặt phẳng
( )
P
cắt mặt cầu
( )
S
theo giao tuyến là đường tròn có đường kính bằng
2
.
A.
1m =
. B.
1m =−
hoặc
2m =−
.
C.
1m =
hoặc
2m =
. D.
1m =−
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
142
Câu 17. Trong không gian với hệ trục tọa độ
Oxyz
cho các điểm
( )
0 ;1;2A
,
( )
2; 2 ;1B −
,
( )
2 ; 0;1C −
.
Phương trình mặt phẳng đi qua
A
và vuông góc
BC
với là
A.
2 1 0xy− − =
. B.
2 3 0yz− + − =
. C.
2 1 0xy− + =
. D.
2 5 0yz+ − =
.
Câu 18. Trong mặt phẳng tọa độ
Oxyz
, cho mặt cầu
()S
:
2 2 2
( 2) ( 1) 9x y z− + + + =
và mặt phẳng
()P
có
phương trình
2 2 3 0x y z− − − =
. Biết mặt phẳng
()P
cắt mặt cầu
()S
theo giao tuyến là đường
tròn
()C
. Tính bán kính
r
của
()C
A.
5r =
. B.
2r =
. C.
22r =
. D.
2r =
.
Câu 19. Trong không gian với hệ trục tọa độ
Oxyz
, cho hai mặt phẳng
( )
P
:
2 4 3 0x by z+ + − =
và
( )
Q
:
3 2 1 0ax y z+ − + =
,
( )
,ab
. Với giá trị nào của
a
và
b
thì hai mặt phẳng
( )
P
và
( )
Q
song
song với nhau.
A.
1a =
;
6b =−
. B.
1a =−
;
6b =−
. C.
3
2
a =−
;
9b =
. D.
1a =−
;
6b =
.
Câu 20. Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt phẳng
: 2 2 1 0P x y z
; hai điểm
1;0;0A
,
1;2;0B
và mặt cầu
22
2
: 1 2 25S x y z
. Viết phương trình mặt phẳng
vuông góc với mặt phẳng
P
, song song với đường thẳng
AB
, đồng thời cắt mặt cầu
S
theo đường tròn có bán kính bằng
22r
.
A.
2 2 3 11 0;2 2 3 23 0x y z x y z
. B.
2 2 3 11 0;2 2 3 23 0x y z x y z
.
C.
2 2 3 11 0;2 2 3 23 0x y z x y z
. D
2 2 3 11 0;2 2 3 23 0x y z x y z
.
Câu 21. Trong không gian hệ tọa độ
Oxyz
, cho hai đường thẳng
1
11
:
1 2 1
x y z
d
−+
==
−
và
2
23
:
1 2 2
x y z
d
−+
==
. Viết phương trình đường thẳng
đi qua điểm
( )
1;0;2A
cắt
1
d
và vuông
góc với
2
d
.
A.
12
:
2 3 4
x y z−−
= =
−
. B.
3 3 2
:
2 3 4
x y z− − +
= =
−
.
C.
5 6 2
:
2 3 4
xyz− − −
= =
−−
. D.
12
:
2 3 4
x y z−−
= =
−−
.
Câu 22. Trong không gian
Oxyz
, mặt phẳng
( )
:2 2 0P x y z+ + − =
vuông góc với mặt phẳng nào dưới
đây?
A.
2 2 0x y z− − − =
. B.
20x y z− − − =
. C.
20x y z+ + − =
. D.
2 2 0x y z+ + − =
.
Câu 23. Trong không gian
Oxyz,
cho mặt cầu
( ) ( ) ( )
22
2
: 1 2 4− + + =S x y z+
và điểm
( )
3;1;2M
. Điểm
A
di chuyển trên mặt cầu
( )
S
thỏa mãn
.3=−OAMA
thì điểm
A
thuộc mặt phẳng nào trong các
mặt phẳng sau?
A.
6 2 0.−x+ y+ z =
B.
3 3 0.−x+ y+2z =
C.
5 2 4 0.−−x+ y z =
D. Không tồn tại mặt phẳng thỏa mãn.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
143
Câu 24. Trong không gian
Oxyz
, cho mặt cầu
( )
2 2 2
: 2 4 6 2 0S x y z x y z+ + − − − − =
và mặt phẳng
( )
: 4 3 12 10 0x y z
+ − + =
. Lập phương trình mặt phẳng
( )
thỏa mãn đồng thời các điều kiện:
tiếp xúc với
( )
S
; song song với
( )
và cắt trục
Oz
ở điểm có cao độ dương.
A.
4 3 12 78 0x y z+ − − =
. B.
4 3 12 26 0x y z+ − − =
.
C.
4 3 12 78 0x y z+ − + =
. D.
4 3 12 26 0x y z+ − + =
.
Câu 25. Trong không gian
Oxyz,
cho mặt cầu
( ) ( ) ( )
22
2
: 1 2 9− + + =S x y z+
và điểm
( )
3;1;2M
. Điểm
A
di chuyển trên mặt cầu
( )
S
thỏa mãn
.2=OAMA
thì điểm
A
thuộc mặt phẳng nào trong các
mặt phẳng sau?
A.
6 2 0.−x+ y+ z =
B.
3 3 0.−x+ y+2z =
C.
5 2 4 0.−−x+ y z =
D.
2 4 1 0.−−x z =
Câu 26. Trong không gian
Oxyz
, cho điểm
( )
1;2;5I
và mặt phẳng
( )
: 2 2 2 0x y z
− + + =
. Phương trình
mặt cầu tâm
I
và tiếp xúc với
( )
là
A.
( ) ( ) ( )
2 2 2
1 2 5 3x y z− + − + − =
. B.
( ) ( ) ( )
2 2 2
1 2 5 3x y z+ + + + + =
.
C.
( ) ( ) ( )
2 2 2
1 2 5 9x y z− + − + − =
. D.
( ) ( ) ( )
2 2 2
1 2 5 9x y z+ + + + + =
.
Câu 27. Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt phẳng
( )
Q
song song với mặt phẳng
( )
P
:
2 2 17 0x y z− + − =
. Biết mặt phẳng
( )
Q
cắt mặt cầu
( )
S
:
( ) ( )
22
2
2 1 25x y z+ + + − =
theo một
đường tròn có chu vi bằng
6
. Khi đó mặt phẳng
( )
Q
có phương trình là:
A.
2 2 7 0x y z− + + =
. B.
2 2 17 0x y z− + + =
.
C.
2 7 0x y z− + − =
. D.
2 2 17 0x y z− + − =
.
Câu 28. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
( )
:2 2 3 0P x y z− + − =
và điểm
( )
1;3; 1I −
. Gọi
( )
S
là mặt cầu tâm
I
và cắt mặt phẳng
( )
P
theo một đường tròn cho chu vi bằng
2.
Viết
phương trình mặt cầu
( )
S
.
A.
( ) ( ) ( ) ( )
2 2 2
: 1 3 1 5.S x y z− + − + + =
B.
( ) ( ) ( ) ( )
2 2 2
: 1 3 1 5.S x y z+ + + + − =
C.
( ) ( ) ( ) ( )
2 2 2
: 1 3 1 3.S x y z− + − + + =
D.
( ) ( ) ( ) ( )
2 2 2
: 1 3 1 5.S x y z− + − + + =
Câu 29. Trong không gian với hệ tọa độ Oxyz, cho hai điểm
(3; 2;6), (0;1;0)AB−
và mặt cầu
2 2 2
( ):( 1) ( 2) ( 3) 25S x y z− + − + − =
. Mặt phẳng
( ): 2 0P ax by cz+ + − =
đi qua A, B và cắt theo
giao tuyến là đường tròn có bán kính nhỏ nhất. Tính
T a b c= + +
.
A.
3T =
B.
5T =
C.
2T =
D.
4T =
Câu 30. Trong không gian
,Oxyz
cho mặt phẳng
( )
: 2 7 0P x y z− + + =
và mặt cầu
( )
2 2 2
: 2 4 10 0S x y z x z+ + − + − =
. Gọi
( )
Q
là mặt phẳng song song với mặt phẳng
( )
P
và cắt
mặt cầu
( )
S
theo giao tuyến là đường tròn có chu vi bằng
6
. Hỏi
( )
Q
đi qua điểm nào trong số
các điểm sau?
A.
( )
6;0;1M
. B.
( )
3;1;4N −
. C.
( )
2; 1;5J −−
. D.
( )
4; 1; 2K −−
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
144
Câu 31. Cho hai mặt cầu
( )
2 2 2
1
:6S x y z+ + =
và
( ) ( ) ( ) ( )
2 2 2
2
: 1 1 1 6S x y z− + − + − =
. Biết rằng mặt
phẳng
( ) ( )
: 6 0 0P ax by cz a+ + + =
vuông góc với mặt phẳng
( )
:3 2 1 0Q x y z+ + − =
đồng
thời tiếp xúc với cả hai mặt cầu đã cho. Tích
abc
bằng
A.
2−
. B.
2
. C.
0
. D.
1
.
Câu 32. Trong không gian
Oxyz
, mặt cầu tâm
( )
1; 2; 1I −
và cắt mặt phẳng
( )
:2 2 1 0P x y z− + − =
theo
một đường tròn có bán kính bằng
8
có phương trình là
A.
( ) ( ) ( )
2
22
1 2 1 9x y z+ + + + − =
. B.
( ) ( ) ( )
2
22
1 2 1 9x y z− + − + + =
.
C.
( ) ( ) ( )
2
22
1 2 1 3x y z+ + + + − =
. D.
( ) ( ) ( )
2
22
1 2 1 3x y z− + − + + =
.
Câu 33. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) ( )
: 1 10 0P mx m y z+ − + − =
và mặt
phẳng
( )
:2 2z 3 0Q x y+ − + =
. Với giá trị nào của m thì và vuông góc với nhau?
A.
2m =−
. B.
2m =
. C.
1m =
. D.
1m =−
.
Câu 34. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) ( )
: 1 10 0P mx m y z+ − + − =
và mặt
phẳng
( )
:2 2z 3 0Q x y+ − + =
. Với giá trị nào của m thì và vuông góc với nhau?
A.
2m =−
. B.
2m =
. C.
1m =
. D.
1m =−
.
Câu 35. Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
()S
có tâm
(2;1;1)I
và mặt phẳng
( ):2 2 2 0P x y z+ + + =
. Biết mặt phẳng
()P
cắt mặt cầu
()S
theo giao tuyến là một đường tròn có
bán kính bằng
1
. Viết phương trình của mặt cầu
()S
.
A.
2 2 2
( ):( 2) ( 1) ( 1) 8S x y z+ + + + + =
. B.
2 2 2
( ):( 2) ( 1) ( 1) 10S x y z+ + + + + =
.
C.
2 2 2
( ):( 2) ( 1) ( 1) 8S x y z− + − + − =
. D.
2 2 2
( ):( 2) ( 1) ( 1) 10S x y z− + − + − =
.
Câu 36. Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt cầu
( )
2 2 2
: 2 2 1 0S x y z x z+ + − + + =
và
đường thẳng
2
:
1 1 1
x y z
d
−
==
−
. Hai mặt phẳng
( )
P
và
( )
Q
chứa
d
và tiếp xúc với mặt cầu
( )
S
tại
A
và
B
. Gọi
( )
;;H a b c
là trung điểm
AB
. Giá trị
abc++
bằng
A.
1
6
. B.
1
3
. C.
2
3
. D.
5
6
.
Câu 37. Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng
( )
P :mx 2y z 1 0+ − + =
(
m
là tham
số). Mặt phẳng
( )
P
cắt mặt cầu
( ) ( ) ( )
22
2
S : x 2 y 1 z 9− + − + =
theo một đường tròn có bán kính
bằng
2
. Tìm tất cả các giá trị thực của tham số
m
?
A.
m1=
. B.
m 2 5= +
. C.
m4=
. D.
m 6 2 5=
.
Câu 38. Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt phẳng
( )
P
:
2 2 7 0x y z+ − − =
và mặt cầu
( )
S
:
2 2 2
2 4 6 11 0x y z x y z+ + − + − − =
. Mặt phẳng
( )
Q
song song với
( )
P
và cắt
( )
S
theo một
đường tròn có chu vi bằng
6
có phương trình là
A.
( )
:2 2 17 0Q x y z+ − + =
. B.
( )
:2 2 7 0Q x y z+ − + =
.
C.
( )
:2 2 19 0Q x y z+ − − =
. D.
( )
:2 2 17 0Q x y z+ − − =
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
145
Câu 39. Trong không gian
Oxyz
, cho ba điểm
( ) ( ) ( )
;0;0 , 0; ;0 , 0;0;A a B b C c
với
, , 0.abc
Biết rằng
mặt phẳng
( )
ABC
đi qua điểm
244
;;
333
M
và tiếp xúc với mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 1 2 2 1.S x y z− + − + − =
Thể tích khối tứ diện
OABC
bằng:
A.
4
. B.
6
. C.
9
. D.
12
.
Câu 40. Trong không gian với hệ trục tọa độ
Oxyz
, cho đường thẳng
2
:
2 1 4
x y z
d
−
==
−
và mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 1 2 1 2S x y z− + − + − =
. Hai mặt phẳng
( )
P
và
( )
Q
chứa
d
và tiếp xúc với
( )
S
.
Gọi
M
,
N
là tiếp điểm. Tính độ dài đoạn thẳng
MN
.
A.
22
. B.
4
3
. C.
6
. D.
4
.
Câu 41. Trong không gian
Oxyz
, cho mặt cầu
( ) ( ) ( )
( )
2
22
: 2 1 2 9S x y z+ + − + + =
và hai điểm
( )
( )
2;0; 2 2 , 4; 4;0AB− − − −
. Biết rằng tập hợp các điểm
M
thuộc
( )
S
sao cho
2
. 16MA MO MB+=
là một đường tròn. Bán kính của đường tròn đó bằng
A. . B. . C. . D. .
Câu 42. Trong không gian
Oxyz
, cho điểm
( )
2; 5; 2I −−
và mặt phẳng
( )
:2 2 1 0P x y z+ + − =
. Phương
trình mặt cầu có tâm
I
và tiếp xúc với mặt phẳng
( )
P
là:
A.
2 2 2
( 2) ( 5) (z 2) 16xy− + + + + =
. B.
2 2 2
( 2) ( 5) (z 2) 4xy− + + + + =
.
C.
2 2 2
( 2) ( 5) (z 2) 4xy+ + − + − =
. D.
2 2 2
( 2) ( 5) (z 2) 2xy− + + + + =
Câu 43. Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
( )
2 2 2
: 2 4 6 3 0S x y z x y z m+ + + − − + − =
.
Tìm số thực
m
để
( )
:2 2 8 0x y z − + − =
cắt
( )
S
theo một đường tròn có chu vi bằng
8
.
A.
3m =−
. B.
4m =−
. C.
1m =−
. D.
2m =−
.
Câu 44. Biết rằng trong không gian với hệ tọa độ
Oxyz
có hai mặt phẳng
( )
P
và
( )
Q
cùng thỏa mãn các
điều kiện sau: đi qua hai điểm
( )
1;1;1A
và
( )
0; 2;2B −
, đồng thời cắt các trục tọa độ
,Ox Oy
tại
hai điểm cách đều
O
. Giả sử
( )
P
có phương trình
1 1 1
0x b y c z d+ + + =
và
( )
Q
có phương trình
2 2 2
0x b y c z d+ + + =
. Tính giá trị biểu thức
1 2 1 2
bb c c+
.
A.7. B.-9. C.-7. D.9.
Câu 45. Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
( )
S
đi qua điểm
( )
2;5; 2M −
và tiếp xúc với
các mặt phẳng
( )
:1x
=
,
( )
:1y
=
,
( )
:1z
=−
. Bán kính của mặt cầu
( )
S
bằng
A.
4
. B.
32
. C.
1
. D.
3
.
Câu 46. Trong không gian
O,xyz
mặt cầu tâm
( )
1;2;1I −
tiếp xúc với mặt phẳng
( )
: 2 2 2 0P x y z− − − =
có phương trình là
( ) ( ) ( )
2 2 2
x a y b z c d− + − + − =
. Giá trị
T a b c d= + + +
bằng
A.
11
. B.
5
. C.
1
. D.
13
.
3
2
22
5

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
146
Câu 47. Trong không gian
Oxyz
, cho mặt cầu
( )
S
có tâm thuộc trục
Oz
. Biết mặt phẳng
( )
Oxy
và mặt
phẳng
( )
:
2z =
lần lượt cắt
( )
S
theo hai đường tròn có bán kính 2 và 4. Phương trình của
( )
S
A.
( )
2
22
2 16x y z+ + − =
. B.
( )
2
22
4 16x y z+ + − =
.
C.
( )
2
22
4 20x y z+ + − =
. D.
( )
2
22
2 20x y z+ + − =
.
Câu 48. Trong không gian tọa độ
Oxyz
, mặt cầu tâm
( )
4;9;16I
tiếp xúc với mặt phẳng
( )
Oyz
có phương
trình là
A.
( ) ( ) ( )
2 2 2
4 9 16 4x y z+ + + + + =
. B.
( ) ( ) ( )
2 2 2
4 9 16 4x y z− + − + − =
.
C.
( ) ( ) ( )
2 2 2
4 9 16 16x y z+ + + + + =
. D.
( ) ( ) ( )
2 2 2
4 9 16 16x y z− + − + − =
.
Câu 49. Trong không gian
Oxyz
, cho các mặt phẳng
( )
:2 4 7 0P x y z+ − − =
,
( )
:4 5 14 0Q x y z+ + − =
,
( )
: 2 2 2 0R x y z+ − − =
và
( )
: 2 2 4 0S x y z+ − + =
.
Biết mặt cầu
( ) ( ) ( )
2 2 2
x a y b z c D− + − + − =
có tâm nằm trên
( )
P
và
( )
Q
, cùng tiếp xúc với
( )
R
và
( )
S
. Giá trị
abc++
bằng
A.
2
. B.
3
. C.
5
. D.
4
.
Câu 50. Trong không gian với hệ trục toạ độ
Oxyz
, cho điểm
(2;1;2)A
và mặt cầu
2 2 2
( ): ( 1) ( 1) 9S x y z+ − + − =
. Mặt phẳng thay đổi luôn đi qua
A
cắt
()S
theo thiết diện là đường
tròn. Hãy tìm bán kính của đường tròn có chu vi nhỏ nhất.
A.
3
2
. B.
1
2
. C.
2
. D.
3
.
Câu 51. Trong không gian với hệ trục toạ độ
Oxyz
, cho điểm
(2;1;2)A
và mặt cầu
2 2 2
( ): ( 1) ( 1) 9S x y z+ − + − =
. Mặt phẳng thay đổi luôn đi qua
A
cắt
()S
theo thiết diện là đường
tròn. Hãy tìm bán kính của đường tròn có chu vi nhỏ nhất.
A.
3
2
. B.
1
2
. C.
2
. D.
3
.
Câu 52. Trong không gian
,Oxyz
cho mặt phẳng
( )
: 6 0P x z− + =
và hai mặt cầu
( )
2 2 2
1
: 25S x y z+ + =
;
( )
2 2 2
2
: 4 4 7 0.S x y z x z+ + + − + =
Biết rằng tập hợp tâm
I
các mặt cầu tiếp xúc với cả hai
mặt cầu
( )
1
S
,
( )
2
S
và tâm I nằm trên
( )
P
là một đường cong. Tính diện tích hình phẳng giới hạn
bởi đường cong đó.
A.
7
3
. B.
7
9
. C.
9
7
. D.
7
6
.
Câu 53. Trong không gian
Oxyz
, cho
( )
P
2 2 5 0x y z+ − + =
và 2 mặt cầu
( )
1
S
:
( ) ( )
22
2
2 1 1x y z− + + + =
,
( )
2
S
:
( ) ( ) ( )
2 2 2
4 2 3 4x y z+ + + + − =
. Gọi
,,M A B
lần lượt thuộc
mặt phẳng
( )
P
và hai mặt cầu
( )
1
S
,
( )
2
S
. Tìm giá trị nhỏ nhất
S MA MB=+
.
A.
=
mi n
11S
. B.
=−
min
2 14 3S
. C.
=−
min
15 3S
. D.
=−
min
3 6 3S
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
147
ĐÁP ÁN CHI TIẾT
Câu 1. Chọn C
Đường thẳng
1
d
có véc tơ chỉ phương
( )
1
2;1; 2u =−
và đi qua điểm
( )
1
1;0; 2M −
.
Đường thẳng
2
d
có véc tơ chỉ phương
( )
2
2; 1;2u = − −
.
Do
1
u
cùng phương với
2
u
nên ta có
( )
12
12
//
,1
dd
dd
.
Thay tọa độ
1
M
vào phương trình
2
d
ta được:
1 2 1 2
2 1 2
+ − −
==
−−
, (mệnh đề sai).
Suy ra
( )
12
,2Md
. Từ
( )
1
và
( )
2
, ta có
12
//dd
.
Câu 2. Chọn C
Mặt cầu
( )
S
có phương trình
2 2 2
6 4 12 0x y z x y+ + − + − =
có tâm
( )
3; 2;0I −
và bán kính
5R =
.
Ta gọi khoảng cách từ tâm
I
của mặt cầu tới các mặt phẳng ở các đáp án là
h
, khi đó để mặt
phẳng cắt mặt cầu
( )
S
theo một đường tròn có bán kính
3r =
thì
22
25 9 4h R r= − = − =
.
Đáp án A loại vì
18 4 26
4
26
h
−
=
. Đáp án B loại vì
14
4
3
h =
.
Chọn đáp án C vì
4.h =
Đáp án D loại vì
13
4
3
h
+
=
.
Câu 3. Chọn A
Mặt phẳng
( )
có véctơ pháp tuyến
( )
1;1;1n
=
và
( )
có véctơ pháp tuyến
( )
2 ; 1;nm
=−
( ) ( )
1 0 1n n m m
⊥ ⊥ + = = −
.
Câu 4. Chọn C
Ta có:
( )
( )
2 2 2
2.1 2.2 2 5
;3
2 2 1
d d I P
+ − +
= = =
++
.
Bán kính của đường tròn giao tuyến là:
16 4
S
r
= = =
.
Mặt cầu tâm
I
cắt mặt phẳng
( )
P
theo giao tuyến là một đường tròn nên ta có:
2 2 2
9 16 25R d r= + = + =
5R=
.
Vậy phương trình mặt cầu tâm
I
, bán kính
5R =
là:
( ) ( ) ( )
2 2 2
1 2 2 25x y z− + − + + =
.
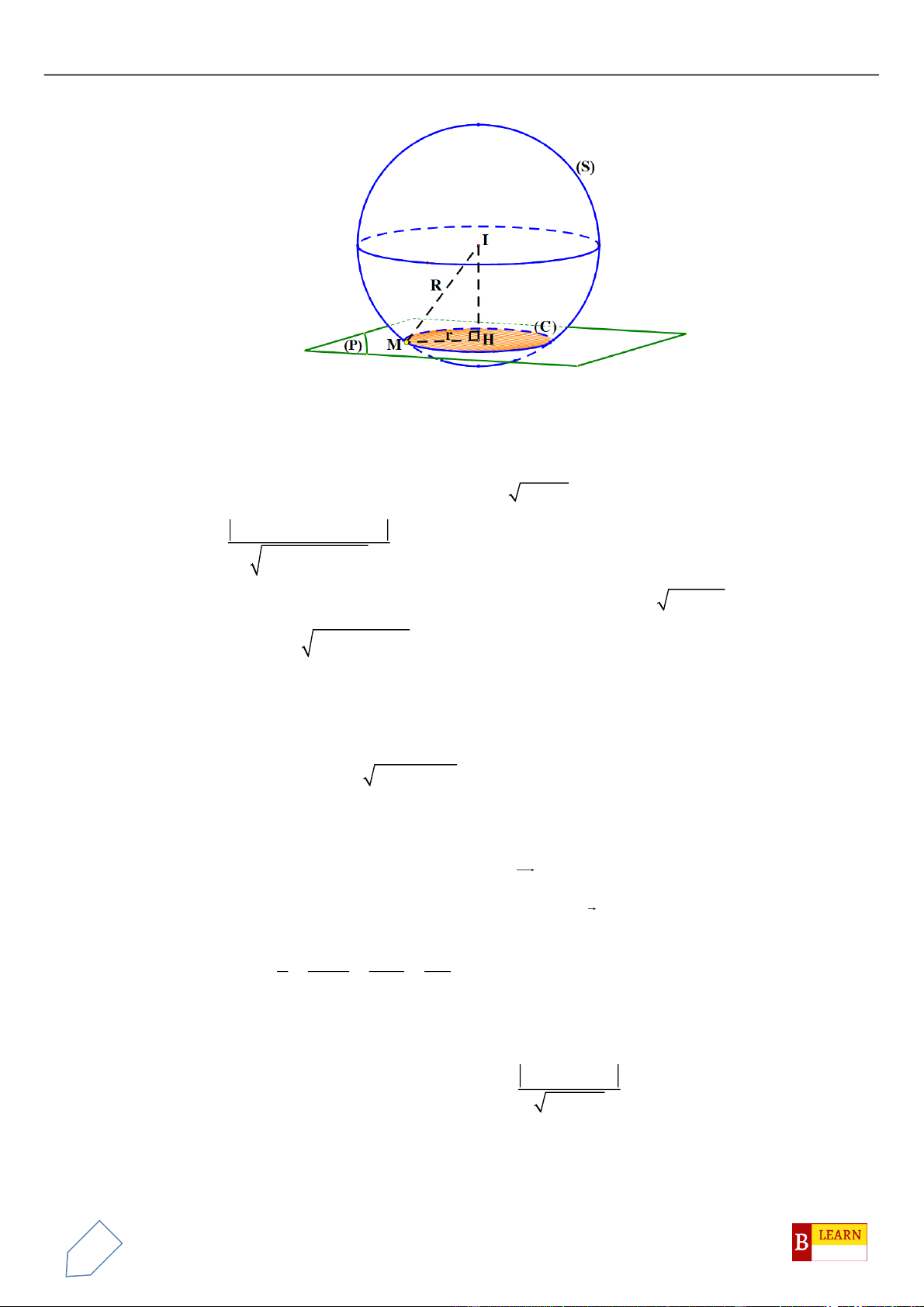
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
148
Câu 5. Chọn A
2 2 2
2 4 6 4 0x y z x y z m+ + + + − − + =
2 2 2
2.( 1). 2.( 2). 2.3. ( 4) 0x y z x y z m+ + − − − − − + − + =
1a =−
,
-2b =
,
3c =
,
-4dm=+
Điều kiện:
2 2 2
0a b c d+ + −
10 0m+
10m −
.
Mặt cầu
()S
có tâm
( )
1; 2;3I −−
, bán kính
10 .Rm=+
( )
2
22
2.( 1) 2.( 2)
(,
31
2
2
)
21
()d I P
− − − + +
=
+ − +
=
.
()P
cắt
( )
S
theo một đường tròn có bán kính bằng
3
22
( ,( )) 3d I P R=−
.
( )
2
10 32 m= + −
.
3m =
( thỏa mãn điều kiện). Vậy
3m =
là giá trị cần tìm.
Câu 6. Chọn C
Gọi
1
I
là tâm mặt cầu
( )
1
S
và
1
R
là bán kính mặt cầu
( )
1
S
.
Tính được khoảng cách
2 2 2
11
2 1 2 3 1II R= + + = =
nên điểm
I
nằm ngoài mặt cầu
( )
1
S
Suy ra bán kính của mặt cầu
( )
S
là
11
2R II R= − =
.
Câu 7. Chọn B
Mặt phẳng
( )
: 2 2 1 0P x y z+ − − =
có
1
VTPT là
( )
1;2; 2
P
n =−
.
Mặt phẳng
( )
:2 ( 2) 2 0Q x m y mz m+ + − − =
có 1 VTPT là
( )
2; 2; 2
Q
n m m= + −
.
Để
( )
P
//
( )
Q
thì
1 2 2 1
2 2 2m m m
−−
= =
+ − −
2
2
m
m
m
=
.
Suy ra không có giá trị thực của
m
thỏa mãn yêu cầu đề bài.
Câu 8. Chọn C
Mặt cầu
( )
S
có tâm
( )
2;2;2I
, do đó
( )
( )
2 4 4 10
, 0.
1 4 4
d I P
++−
==
++
Câu 9. ChọnB
Vì bán kính của mặt cầu là
5R =
,
( )
( )
;4d d I P R= =
(với
I
là tâm mặt cầu)

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
149
Do đó
( )
P
cắt
( )
S
theo một đường tròn bán kính là
2 2 2 2
5 4 3r R d= − = − =
.
Vậy
( )
P
không tiếp xúc với
( )
S
.
Câu 10. Chọn B
Gọi điểm
( )
;0;0Aa
là giao điểm của mặt cầu và trục hoành trong đó
0a
.
Khi đó
( )
( )
2
0
20
2
al
aa
an
=
− =
=
. Do đó
( )
2;0;0A
.
Gọi điểm
( )
0; ;0Bb
là giao điểm của mặt cầu và trục tung trong đó
0b
.
Khi đó
( )
( )
2
0
40
4
bl
bb
bn
=
− =
=
. Do đó
( )
0;4;0B
.
Gọi điểm
( )
0;0;Cc
là giao điểm của mặt cầu và trục
Oz
trong đó
0c
.
Khi đó
( )
( )
2
0
60
6
cl
cc
cn
=
− =
=
. Do đó
( )
0;0;6C
.
Phương trình mặt phẳng đi qua ba điểm
A
,
B
,
C
là
1
2 4 6
x y z
+ + =
.
Câu 11. Chọn A
Mặt cầu
( )
S
có tâm
( )
2; 1;1I −−
, bán kính
12R =
.
Ta có:
( )
( )
1
2 1 1 2
2
, 12
33
d I P R
− − − +
= = =
.
Vậy mặt phẳng
( )
1
P
cắt mặt cầu
( )
S
theo giao tuyến là một đường tròn.
Câu 12. Chọn B
Phương trình mặt phẳng
( )
Oyz
là
0x =
.
Do mặt cầu
( )
S
tiếp xúc với mặt phẳng
( )
Oyz
nên:
( )
( )
,
222
1.1 0.2 0.( 3)
1
1 0 0
I Oyz
d R R R
+ + −
= = =
++
.
Khi đó phương trình mặt cầu cần tìm là:
( ) ( ) ( )
2 2 2
1 2 3 1x y z− + − + + =
.
Câu 13. Chọn C
Ta có mặt cầu
( )
S
:
( ) ( ) ( )
2 2 2
2 1 2 4x y z− + + + + =
có tâm , bán kính .
Mặt phẳng
( )
P
và mặt cầu
( )
S
có đúng
1
điểm chung khi và chỉ khi mặt phẳng
( )
P
tiếp xúc với
mặt cầu
( )
S
.
Câu 14. Chọn A
Vì mặt phẳng
()P
chứa trục
Oz
nên phương trình mặt phẳng
()P
có dạng
0ax by+=
( )
22
0ab+
.
( )
2; 1; 2I −−
2R =
( )
( )
,d I P R=
( )
22
4.2 3. 1
2
43
m− − −
=
+
11 10m − =
1
21
m
m
=
=

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
150
Mặt cầu
()S
có tâm
(1; 1;1)I −
và bán kính
3R =
. Mặt khác mặt cầu
()S
cắt mặt phẳng
()P
theo
giao tuyến là đường tròn có bán kính bằng 3 nên mặt phẳng
()P
đi qua tâm
(1; 1;1)I −
của măt
cầu.
Ta có
( )
.1 .( 1) 0 a bI P a b + − = =
. Vì
22
0ab+
nên chọn
11ab= =
.
Vậy phương trình mặt phẳng
()P
là:
0xy+=
.
Câu 15. Chọn D
Gọi phương trình mặt phẳng
( )
P
có dạng
2 2 0x y z d+ + + =
Với
0; 3dd −
.
Có
( ) ( )
( )
222
3
0
; 1 1
6
1 2 2
d
d
d P Q
d
+
=
= =
=−
++
.
Kết hợp điều kiện
( )
P
có dạng:
2 2 6 0x y z+ + − =
.
Câu 16. Chọn A
Mặt cầu
( )
S
:
( ) ( ) ( )
2 2 2
2 4 1 4xyz− + − + − =
có tâm
( )
2; 4;1I
, bán kính .
Ta có
( )
( )
2
2 4 1 3 1
,
11
mm
d I P
m
+ + − −
=
++
2
2
2
m
m
+
=
+
Mặt phẳng
( )
P
cắt mặt cầu
( )
S
theo giao tuyến là đường tròn có đường kính bằng
2
nên bán
kính đường tròn giao tuyến
1r =
.
Ta có
( )
( )
2 2 2
,R d I P r=+
( )
2
2
2
41
2
m
m
+
= +
+
( )
22
4 4 3 2m m m + + = +
2
2 4 2 0mm − + =
1m=
.
Câu 17. Chọn C
Ta có
( )
4;2 ; 0BC =−
là một vectơ pháp tuyến của mặt phẳng cần tìm.
Vì mặt phẳng đi qua
A
nên có phương trình:
( ) ( )
4 0 2 1 0 2 1 0x y x y− − + − = − + =
.
Câu 18. Chọn C
Mặt cầu
()S
có tâm
(2;0; 1)I −
, bán kính
3R =
.
Khi đó, ta có
( )
( ) ( )
22
2
2.2 0 2 1 3
( ;( )) 1
2 1 2
d I P
− − − −
==
+ − + −
và
2 2 2
( ;( )) 8r R d I P= − =
22r=
.
Câu 19. Chọn B
Gọi
P
n
,
Q
n
lần lượt là vectơ pháp tuyến của mặt phẳng
( )
P
và
( )
Q
. Ta có :
( )
2; ;4
P
nb=
và
( )
;3; 2
Q
na=−
.
Cách 1.
Ta có
( ) ( )
//
3 .1
PQ
n kn
PQ
k
=
−
( ) ( )
2; ;4 ;3; 2
3 .1
b k a
k
=−
−
2.
3.
4 2.
3
ka
bk
k
k
=
=
=−
−
2
1
6
k
a
b
=−
= −
=−
.
2R =

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
151
Cách 2.
Ta có
( ) ( )
0
//
31
PQ
nn
PQ
=
−
( ) ( )
2 12;4 4;6 0;0;0b a ab − − + − =
1
6
a
b
=−
=−
.
Câu 20. Chọn A
Mặt cầu
22
2
: 1 2 25S x y z
có tâm
1;2;0I
và bán kính
5R
.
Khoảng cách từ điểm
I
đến mặt phẳng là
22
, 17d I R r
.
Vectơ pháp tuyến của mặt phẳng
P
là
1;2; 2n
, vectơ
2;2;0AB
.
Vì mặt phẳng vuông góc với mặt phẳng
P
và song song với đường thẳng
AB
nên vectơ
pháp tuyến của mặt phẳng là
, 4;4;6n n AB
.
Suy ra, phương trình mặt phẳng có dạng
:2 2 3 0x y z D
.
Ta có:
6
,
17
D
dI
6
17
17
D
6 17
6 17
D
D
11
23
D
D
.
Do đó, phương trình mặt phẳng là
2 2 3 11 0x y z
hoặc
2 2 3 23 0x y z
.
Dễ thấy,
A
nên song song với đường thẳng
AB
.
Vậy phương trình mặt phẳng là
2 2 3 11 0x y z
hoặc
2 2 3 23 0x y z
.
Câu 21. Chọn B
Gọi
( )
P
là mặt phẳng qua điểm
( )
1;0;2A
và vuông góc với
2
d
.
Phương trình mặt phẳng
( )
P
:
( ) ( ) ( )
1 1 2 0 2 2 0x y z− + − + − =
2 2 5 0x y z + + − =
Phương trình tham số của đường thẳng
1
d
:
1
12
xt
yt
zt
=+
= − +
=−
Gọi
B
là giao điểm của
( )
P
và đường thẳng
1
d
, khi đó tọa độ điểm
B
thỏa hệ:
2 2 5 0
1
12
x y z
xt
yt
zt
+ + − =
=+
= − +
=−
2
3
3
2
t
x
y
z
=
=
=
=−
( )
3;3; 2B−
.
Vì đường thẳng
đi qua điểm
( )
1;0;2A
, cắt
1
d
và vuông góc với
2
d
nên đường thẳng
đi qua
2 điểm
A
và
B
.
( )
2;3; 4AB =−
Phương trình đường thẳng
đi qua
B
nhận
( )
2;3; 4AB =−
làm vecto chỉ phương là:
3 3 2
:
2 3 4
x y z− − +
= =
−
.
Câu 22. Chọn B
Mặt phẳng
( )
P
có một vectơ pháp tuyến
( )
2;1;1
P
n =
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
152
Mặt phẳng
( )
: 2 0Q x y z− − − =
có một vectơ pháp tuyến
( )
1; 1; 1
Q
n = − −
.
Mà
. 2 1 1 0
PQ
nn= − − =
( ) ( )
PQ
n n P Q ⊥ ⊥
.
Vậy mặt phẳng
20x y z− − − =
là mặt phẳng cần tìm.
Câu 23. Chọn D
Cách 1
Gọi
A
có tọa độ là
( )
;;A x y z
.
( )
;;=OA x y z
,
( )
3 1 2 .= − − −MA x ; y ;z
Vì
( )
;;A x y z
thuộc mặt cầu
( )
S
nên ta có
( ) ( )
22
2
1 2 4− + + =x y z+
.
Ta có
( ) ( ) ( )
. 3 3 1 2 3.= − − − − = −OA MA x x + y y + z z
2 2 2
3 2 3 = 0 + + − − −x y z x y z+
( ) ( )
22
2
1 2 4 6z 2 = 0 − + + − − − − +x y z+ x y
( ) ( )
22
2
1 2 4 6z 2 − + + − = −x y z+ x+ y+
6 2 0. − =x+ y+ z
Điểm
A
thuộc mặt phẳng
( )
: 6 2 0 − =x+ y+ z
(1)
Ta thấy
( ) ( ) ( )
22
2
: 1 2 4− + + =S x y z+
có tâm
( )
1;0; 2−I
bán kính
2R=
( )
( )
13
2
38
= =d I, R
suy ra
( ) ( )
= S
suy ra (1) vô l. Vậy không có mặt phẳng chứa
điểm
A
thỏa mãn yêu cầu
A
di chuyển trên mặt cầu
( )
S
và
. 3.=−OAMA
Cách 2
Gọi
A
có tọa độ là
( )
;;A x y z
.
( )
;;=OA x y z
,
( )
3 1 2 .= − − −MA x ; y ;z
Vì
( )
;;A x y z
thuộc mặt cầu
( )
S
nên ta có
( ) ( )
22
2
1 2 4− + + =x y z+
.
Ta có
( ) ( ) ( )
. 3 3 1 2 3.= − − − − = −OA MA x x + y y + z z
( )
22
2
2 2 2
3 1 1
3 2 3 = 0 y z 1
2 2 2
+ + − − − − + − + − =
x y z x y z+ x
.
Suy ra
A
thuộc mặt cầu
( )
S'
có tâm
31
; ;1
22
I'
bán kính
2
2
R' =
Ta có
( ) ( ) ( )
22
2
: 1 2 4− + + =S x y z+
có tâm
( )
1;0; 2−I
bán kính
2R=
Ta thấy
38 2
2
22
II' = > + = R+ R'
suy ra
( ) ( )
. = S S'
Vậy không có mặt phẳng chứa điểm
A
thỏa mãn yêu cầu
A
di chuyển trên mặt cầu
( )
S
và
. 3.=−OAMA
Câu 24. Chọn C
Mặt cầu
( )
S
có: tâm
( )
1;2;3I
, bán kính
2 2 2
1 2 3 2 4R = + + + =
.
Vì
( ) ( )
nên phương trình mp
( )
có dạng:
( )
4 3 12 0, 10x y z d d+ − + =
.
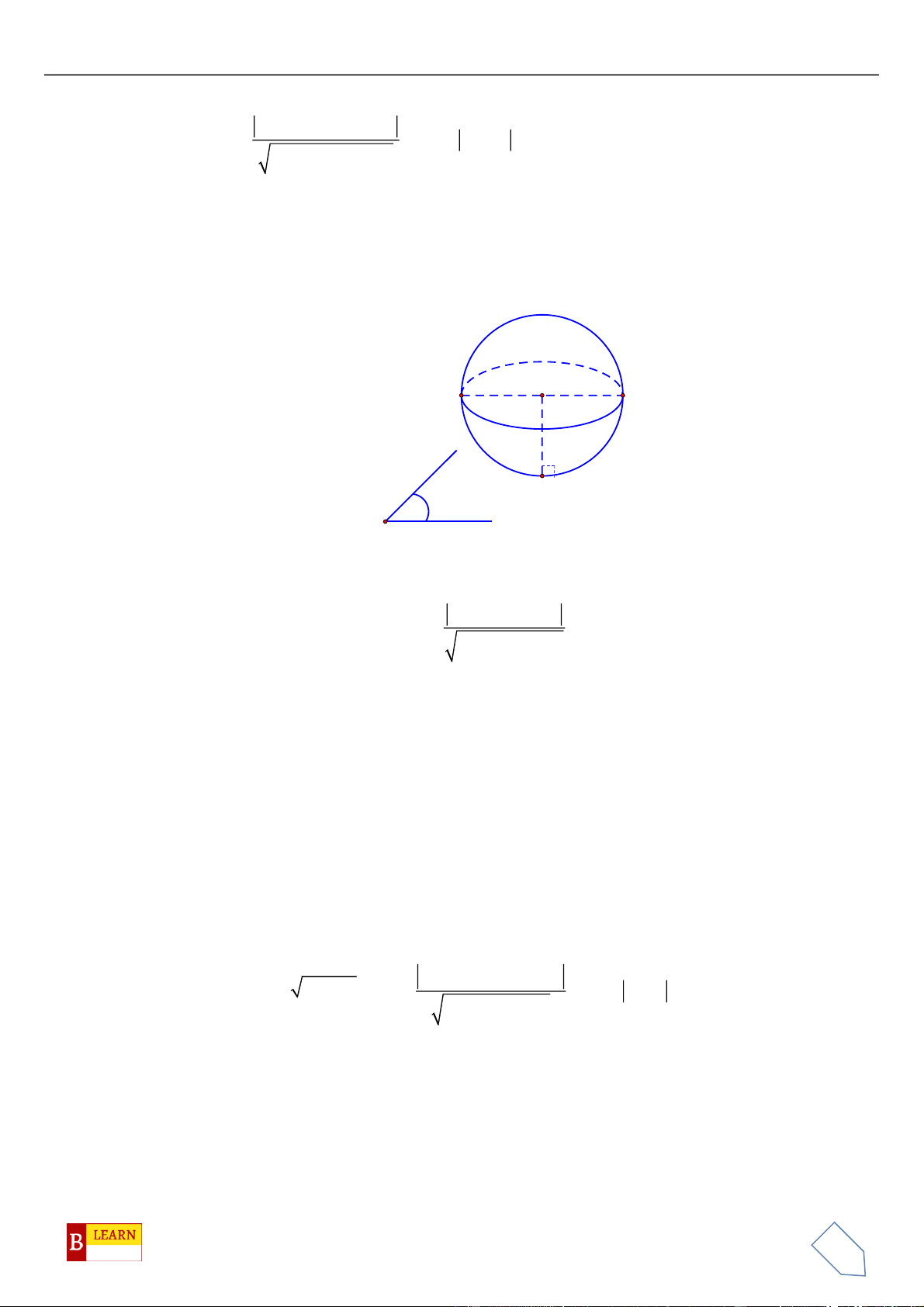
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
153
Vì
( )
tiếp xúc mặt cầu
( )
S
nên:
( )
( )
( )
,
2
22
4.1 3.2 12.3
26
4 26 52
78
4 3 12
I
d
d
d R d
d
+ − +
=−
= = − =
=
+ + −
.
Do
( )
cắt trục
Oz
ở điểm có cao độ dương nên chọn
78d =
.
Vậy mp
( )
:
4 3 12 78 0x y z+ − + =
.
Câu 25. Chọn A
Câu 26. Chọn C
Từ tọa độ tâm
( )
1;2;5I
ta loại được hai đáp án B, D.
Mặt khác theo bài ta có
( )
( )
( )
2
22
1 2.2 2.5 2
,3
1 2 2
R d I
−++
= = =
+ − +
nên đáp án A loại.
Vậy phương trình mặt cầu cần tìm có phương trình
( ) ( ) ( )
2 2 2
1 2 5 9x y z− + − + − =
.
Vậy chọn C
Câu 27. Chọn A
Do mặt phẳng
( )
Q
song song với mặt phẳng
( )
P
nên mặt phẳng
( )
Q
có dạng:
( )
2 2 0, 17x y z D D− + + = −
.
Mặt cầu
( )
S
có tâm
( )
0; 2;1I −
và bán kính
5R =
.
Đường tròn giao tuyến có chu vi bằng
6
, suy ra:
2 6 3rr
= =
.
Do đó:
( )
( )
22
,4d I Q R r= − =
( )
( )
( )
( )
2
22
7
2.0 2. 2 1
4 5 12
17
2 2 1
D TM
D
D
DL
=
− − + +
= + =
=−
+ − +
.
Vậy phương trình mặt phẳng
( )
Q
là:
2 2 7 0x y z− + + =
.
* Phân tích bài toán
- Đây là bài toán về sự tương giao của mặt cầu với mặt phẳng.
- Để giải quyết bài toán này chúng ta cần nhớ lại kiến sau:
d
R
α( )
I
H
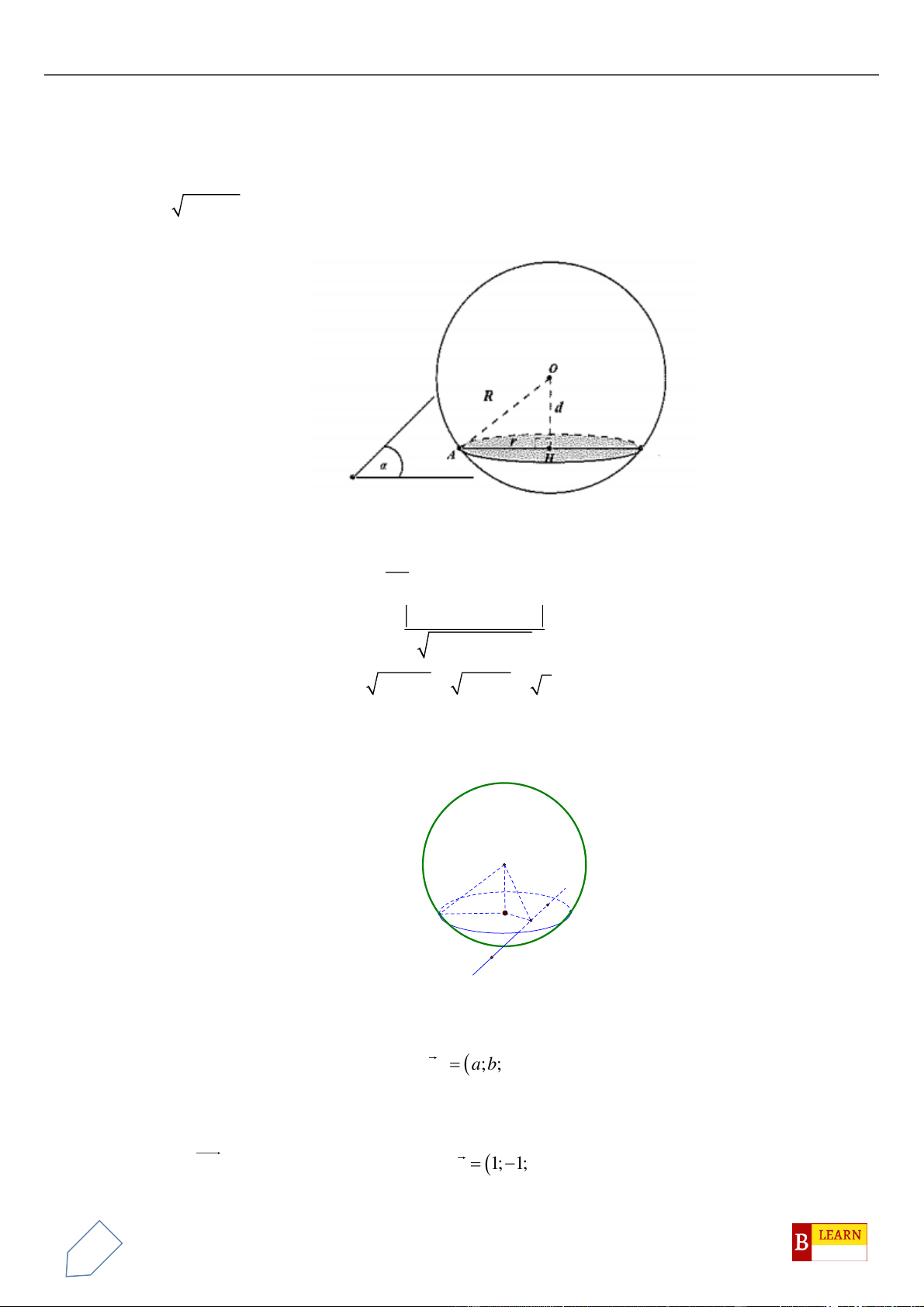
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
154
Cho mặt cầu
( )
;S O R
và một mặt phẳng
( )
. Gọi
H
là hình chiều vuông góc của
O
lên
( )
và
( )
( )
,d d O OH
==
. Khi đó
Nếu
dR
thì mặt phẳng cắt mặt cầu theo thiết diện là một đường tròn có tâm
H
và bán kính
22
r R d=−
.
Câu 28. Chọn D
Bán kính của đường tròn là:
2
1
2
r
==
.
Khoảng cách từ
I
đến
( )
P
là:
2 2 2
2.1 3 2.( 1) 3
2
2 ( 1) 2
d
− + − −
==
+ − +
.
Bán kính mặt cầu
( )
S
là:
2 2 2 2
1 2 5.R r d= + = + =
Phương trình mặt cầu
( )
S
là:
( ) ( ) ( ) ( )
2 2 2
: 1 3 1 5.S x y z− + − + − =
Câu 29. Chọn A
Mặt cầu
( )
S
có tâm
( )
1;2;3 ,I
bán kính
5.R =
Mặt phẳng
( )
P
có vec-tơ pháp tuyến
( )
;;
P
n a b c=
Theo giả thiết
( ) ( )
0;1;0 : 2 0 2.B P b b − = =
Ta có:
( )
3;3; 6AB = − −
cùng phương với
( )
1; 1;2u =−
.
H
I
K
A
B
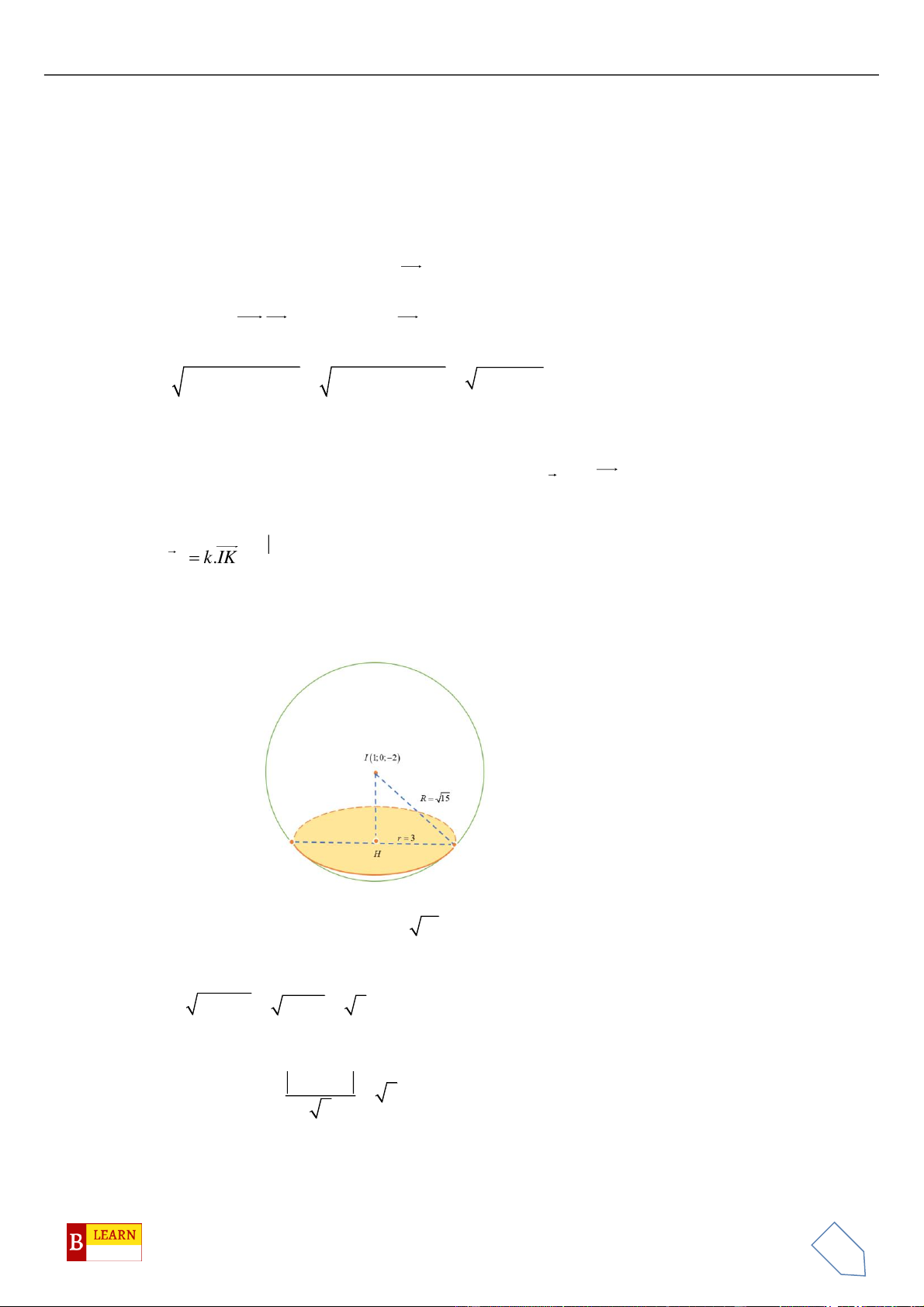
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
155
Phương trình đường thẳng
:1
2
xt
AB y t
zt
=
=−
=
Gọi
r
là bán kính đường tròn giao tuyến.
K
là hình chiếu vuông góc của
I
lên đường thẳng
,AB
H
là hình chiếu vuông góc của
I
lên
( )
P
Ta có:
( ) ( )
;1 ;2 1; 1;2 3K AB K t t t IK t t t − = − − − −
( )
. 0 1 0; 2; 1IK AB AB IK t IK⊥ = = = − −
.
( )
( )
( )
( )
2 2 2 2
, 25 , 25r R d I P d I P IH= − = − = −
.
Ta có:
min max
r IH
.
Mà
( )
max
IH IK IH IK H K P IK = ⊥
P
n
và
IK
cùng phương.
00
0
. 2 1
1
1
P
aa
a
n k IK b k k
c
c k c
==
=
= = − = −
=
= − =
0 2 1 3.t a b c = + + = + + =
Câu 30. Chọn C
Mặt cầu
( )
S
có tâm
( )
1;0; 2 , 15IR−=
.
Gọi đường tròn giao tuyến của
( )
S
và
( )
Q
có bán kính là
r
, theo đề bài
2 6 3.C r r
= = =
22
15 9 6IH R r= − = − =
.
( ) ( ) ( ) ( )
// : 2 0 7P Q Q x y z D D − + + =
.
( )
( )
( )
( )
7
12
,6
5/
6
Dl
D
d I Q IH
D t m
=
−+
= =
=−
( )
: 2 5 0Q x y z − + − =
.
Thay các điểm ở đáp án vào phương trình
( )
Q
J
thỏa mãn.
Câu 31. Chọn A

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
156
Ta có:
( )
1
S
có tâm
( )
1
0;0;0I
và bán kính
1
6R =
( )
2
S
có tâm
( )
2
1;1;1I
và bán kính
2
6R =
Mặt phẳng
( ) ( )
: 6 0 0P ax by cz a+ + + =
có vectơ pháp tuyến
( )
( )( )
; ; 0
P
n a b c a=
Mặt phẳng
( )
:3 2 1 0Q x y z+ + − =
có vectơ pháp tuyến
( )
( )
3;2;1
Q
n =
Vì Mặt phẳng
( )
P
và mặt phẳng
( )
Q
vuông góc nhau
( ) ( )
( )
. 0 3 2 0 1
PQ
n n a b c= + + =
Mặt phẳng
( )
P
đồng thời tiếp xúc với cà hai mặt cầu nên
( )
( )
( )
( )
11
22
;
;
d I P R
d I P R
=
=
2 2 2
2 2 2
6
6
6
6
abc
abc
abc
=
++
+ + +
=
++
2 2 2
2 2 2
0
| 6| 6
12
6
6
+ + =
+ + + =
+ + = −
+ + =
+ + =
abc
abc
abc
abc
abc
(2)
Từ (1) và (2)
TH1:
2 2 2 2 2 2
3 2 0 1
0 2 2
1
6 4 6
+ + = = =
+ + = = − = −
=
+ + = + + =
a b c c a c
a b c b a b
a
a b c a a a
2 = −abc
TH2:
2 2 2 2 2 2 2
3 2 0 24 24
12 12 2 12 2
6 (12 2 ) ( 24) 6 5 96 684 0(VN)
+ + = = − = −
+ + = − = − = −
+ + = + − + − = − + =
a b c c a c a
a b c b a b a
a b c a a a a a
Ta chọn đáp án A.
Cách khác :
Ta có:
( )
1
S
có tâm
( )
1
0;0;0I
và bán kính
1
6R =
( )
2
S
có tâm
( )
2
1;1;1I
và bán kính
2
6R =
; Mặt phẳng
( )
:3 2 1 0Q x y z+ + − =
có vectơ pháp
tuyến
( )
( )
3;2;1
Q
n =
.
Vì
12
36II =
nên hai mặt cầu cắt nhau mà
12
6RR==
nên mặt phẳng
( )
P
tiếp xúc với cả
hai mặt cầu khi
( )
P
song song với
12
II
.
Ta lại có mặt phẳng
( )
P
vuông góc với mặt phẳng
( )
Q
nên mặt phẳng
( )
P
nhận
( )
( )
12
, 1;2; 1
Q
I I n
= − −
làm vectơ pháp tuyến.
Vì
( )
P
có vectơ pháp tuyến
( )
( )( )
; ; 0
P
n a b c a=
nên
2
1 2 1
ba
a b c
ca
=−
= =
=
−−
.
Khi đó phương trình mặt phẳng
( )
P
được viết lại là:
2 6 0ax ay az− + + =
.
Mặt phẳng
( )
P
tiếp xúc với mặt cầu
( )
1
S
nên
( )
( )
11
6
, 6 1
6
d I P R a
a
= = =
.
Suy ra phương trình mặt phẳng
( )
:1 2 6 0P x y z− + + =
. Vậy tích
2abc =−
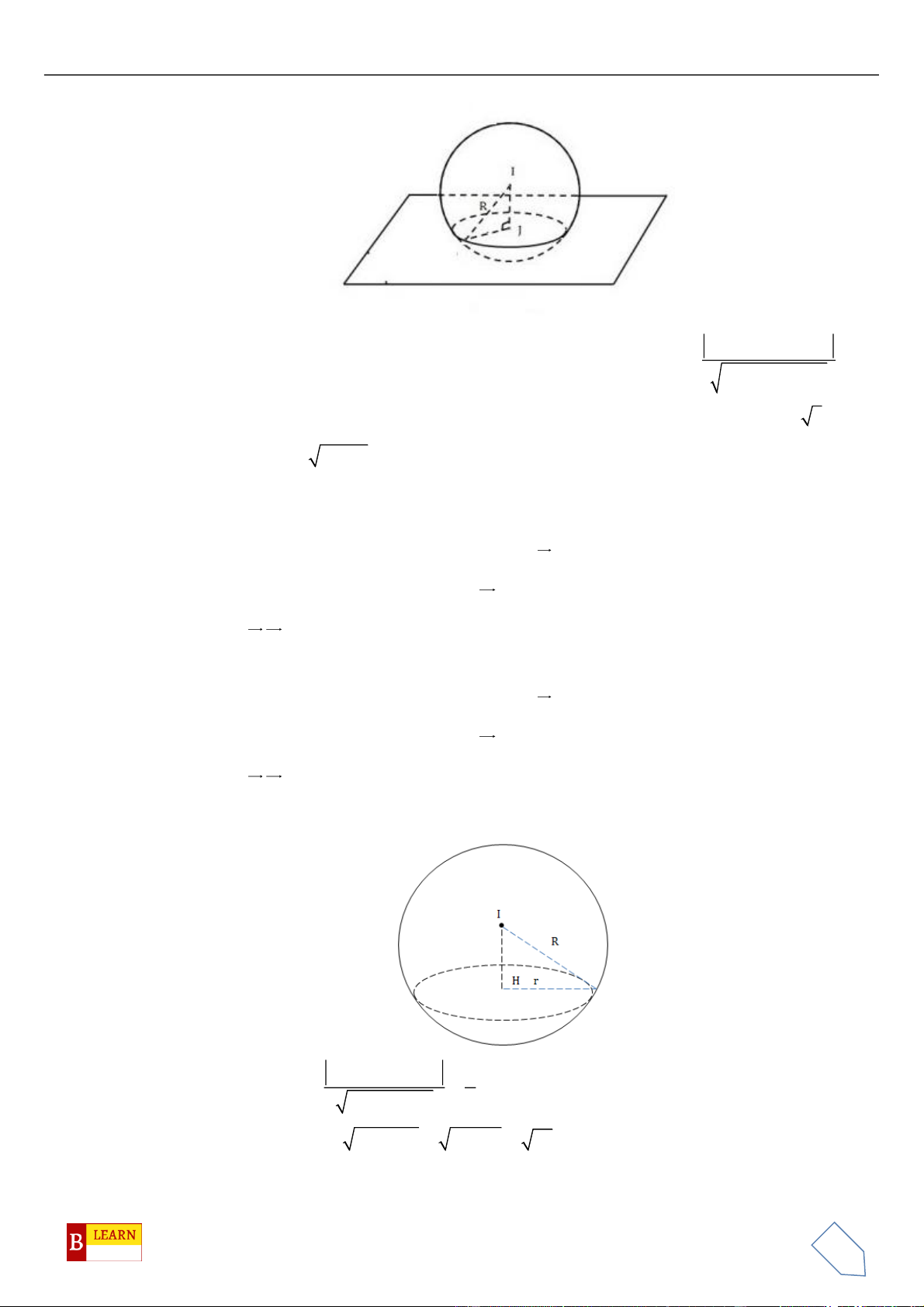
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
157
Câu 32. Chọn B
Gọi
J
là hình chiếu của điểm
I
lên mặt phẳng
( )
P
ta có
( )
( )
( )
( )
2
22
2.1 2 2 1 1
IJ , 1
2 1 2
d I P
− + − −
= = =
+ − +
.
Mặt cầu tâm
( )
1; 2; 1I −
và cắt mặt phẳng
( )
P
theo một đường tròn có bán kính bằng
8
ta có
bán kính mặt cầu
2
8 IJ 3R = + =
.
Phương trình mặt cầu cần tìm
( ) ( ) ( )
2
22
1 2 1 9x y z− + − + + =
.
Câu 33. Chọn C
( ) ( )
: 1 10 0P mx m y z+ − + − =
có vectơ pháp tuyến
( )
1
; 1;1n m m=−
.
( )
:2 2z 3 0Q x y+ − + =
có vectơ pháp tuyến
( )
2
2;1; 2n =−
.
( ) ( )
12
. 0 2 1 2 0 1P Q n n m m m⊥ = + − − = =
.
Câu 34. Chọn C
( ) ( )
: 1 10 0P mx m y z+ − + − =
có vectơ pháp tuyến
( )
1
; 1;1n m m=−
.
( )
:2 2z 3 0Q x y+ − + =
có vectơ pháp tuyến
( )
2
2;1; 2n =−
.
( ) ( )
12
. 0 2 1 2 0 1P Q n n m m m⊥ = + − − = =
.
Câu 35. Chọn D
Ta có:
( )
( )
2 2 2
2.2 1 2.1 2
9
;3
3
2 1 2
+ + +
= = = =
++
IH d I P
,
Suy bán kính mặt cầu
2 2 2 2
3 1 10R IH r= + = + =
Phương trình mặt câu:
2 2 2
( ) : ( 2) ( 1) ( 1) 10− + − + − =S x y z
Câu 36.
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
158
Chọn B
Mặt cầu
( )
S
có tâm
( )
1;0; 1I −
và bán kính
( )
2
22
1 0 1 1 1R = + + − − =
.
Mặt phẳng
( )
đi qua
I
và vuông góc với đường thẳng
d
có phương trình:
( ) ( ) ( )
1 1 1 0 1 1 0 2 0x y z x y z− + − − + = + − − =
.
Gọi
K
là hình chiếu của
I
trên
d
, do
( )
;2 ;K d K t t t + −
và
( ) ( ) ( )
2 2 0 0 0;2;0K P t t t t K + + − − − = =
.
Mặt phẳng
( )
cắt
( )
S
theo đường tròn lớn
( )
C
, có
( )
,A B C
và
H IK AB=
.
( ) ( ) ( )
2 2 2
0 1 2 0 0 1 6IK = − + − + + =
2
11
.1
66
IH
IH IK IA IH IK
IK
= = = =
( vì
,IH IK
cùng hướng).
( )
( )
( )
15
1 0 1
66
1 1 1
0 2 0
6 3 3
15
1 0 1
66
aa
b b a b c
cc
− = − =
− = − = + + =
+ = + = −
.
Câu 37. Chọn D
Từ
( ) ( ) ( )
22
2
S : x 2 y 1 z 9− + − + =
ta có tâm
( )
2;1;0I =
bán kính
3R =
. Gọi
H
là hình chiếu vuông góc của
I
trên
( )
P
và
( ) ( ) ( )
;P S C H r=
với
2r =
Ta có
( )
( )
;IH d I P=
22
2 2 0 1 2 3
4 1 5
mm
IH
mm
+ − + +
==
+ + +
Theo yêu cầu bài toán ta có
2 2 2
R IH r=+
( )
2
2
23
94
5
m
m
+
=+
+
2
6 2 5
12 16 0
6 2 5
m
mm
m
=−
− + =
=+
.
P
Q
H
I
A
B
K
A
I
H
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
159
Câu 38. Chọn A
Ta có mặt cầu
( )
S
có tâm
( )
1; 2;3I −
, bán kính
1 4 9 11 5R = + + + =
.
Đường tròn
( )
C
có chu vi bằng
6
nên có bán kính là:
6
3
2
C
r
==
.
Mặt phẳng
( )
Q
song song với mp
( )
P
nên phương trình mặt phẳng
( )
Q
là:
2 2 0x y z D+ − + =
( )
7D −
.
Vì
( )
Q
cắt
( )
S
theo giao tuyến là đường tròn
( )
C
nên
( )
( )
( )
( )
( )
( )
2 2 2
, 3 25 , , 4
C
r R d I Q d I Q d I Q= − = − =
( )
2.1 2 2 3
17
4 5 12
7
4 4 1
D
D
D
D
+ − − +
=
= − =
=−
++
Kết hợp điều kiện
7D −
ta có phương trình
( )
:2 2 17 0Q x y z+ − + =
.
Câu 39. Chọn C
Mặt cầu
( )
S
có tâm
( )
1;2;2I
bán kính
1R =
.
Ta có
222
2 4 4
1 2 2 1
3 3 3
IM R
= − + − + − = =
Suy ra mặt phẳng
( )
ABC
tiếp xúc với mặt cầu
( )
S
tại điểm
M
.
Nên mặt phẳng
( )
ABC
có véctơ pháp tuyến
1 2 2
;;
3 3 3
MI
.
Phương trình mặt phẳng
( )
2 4 4
:1 2 2 0 1
3 3 3 6 3 3
x y z
ABC x y z
− + − + − = + + =
.
Suy ra
6; 3; 3a b c= = =
. Vậy
1
9.
6
OABC
V abc==
Câu 40. Chọn B
d
nằm trên hai mặt phẳng
()P
và
()Q
nên
d
chính là giao tuyến của hai mặt phẳng đó
Mặt cầu
( )
S
có tâm
( )
1;2;1I
và bán kính
2R =
.
Mặt phẳng
( )
đi qua
I
và vuông góc với đường thẳng
d
có phương trình:

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
160
( ) ( ) ( )
2 1 1 2 4 1 0 2 4 4 0x y z x y z− − − + − = − + − =
.
Gọi
K
là hình chiếu của
I
trên
d
, do
( )
2 2 ; ;4K d K t t t + −
và
( )
K
( )
2. 2 2 4.4 4 0t t t + + + − =
( )
0 2;0;0tK =
.
Mặt phẳng
( )
cắt
( )
S
theo giao tuyến là đường tròn lớn
( )
C
. Ta có
( )
,M N C
và gọi
H IK MN=
. Suy ra
H
là trung điểm của
MN
.
( ) ( ) ( )
2 2 2
2 1 0 2 0 1 6IK = − + − + − =
.
Ta có
2
2
.2
6
IH IK IM IH= = =
nên
2
2
2 2 4
2 2 2 2
3
63
MN HM IM
= = − = − =
.
Câu 41. Chọn C
Gọi là điểm thuộc mặt cầu .Vì nên
.
Ta thấy rằng tọa độ thỏa phương trình cũng là phương trình mặt cầu.
Như vậy điểm nằm trên giao tuyến của hai mặt cầu và ,đó là một đường tròn.
Để tìm bán kính của đường tròn giao tuyến ta làm như sau:
Bằng cách khử đi từ phương trình và ta được phương trình
Phương trình là phương trình của một mặt phẳng.
Như vậy điểm nằm trên giao tuyến của mặt cầu (hoặc của cũng được) với mặt phẳng
.
Mặt cầu có tâm và bán kính .
Khoảng cách từ tâm đến mặt phẳng là: .
Vậy bán kính đường tròn giao tuyến là .
Câu 42. Chọn B
Ta có:
( )
( )
( ) ( )
2.2 5 2 2 1
6
;2
3
4 1 4
d I P
+ − + − −
= = =
++
.
Mặt cầu có tâm
( )
2; 5; 2I −−
và có
2R =
nên
( ) ( ) ( ) ( )
2 2 2
: 2 5 2 4S x y z− + + + + =
.
Câu 43. Chọn A
Mặt cầu
( )
S
có tâm
( )
1;2;3I −
, bán kính
17Rm=−
(điều kiện
17m
).
( )
;;M x y z
( )
S
2
. 16MA MO MB+=
( )
( )
2
2
2 2 2 2
2 2 2 4 4 16x y z x y z x y+ + + + + + + + + =
2 2 2
2 2 2 8 4 4 2 12 16x y z x y z + + + + + + =
( )
2 2 2
4 2 2 2 2 0 x y z x y z S
+ + + + + − =
M
( )
S
M
( )
S
( )
S
2 2 2
,,x y z
( )
S
( )
S
( )
0 yP=
( )
P
M
( )
S
( )
S
( )
P
( )
S
( )
2;1; 2I −−
3R =
I
( )
P
( )
( )
,1d d I P==
22
9 1 2 2r R d= − = − =

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
161
Khoảng cách từ tâm
I
đến mặt phẳng
( )
là:
( )
( )
=, 2.dI
Đường tròn giao tuyến có bán kính là:
8
4
2
r
==
.
Ta có
( )
( )
2 2 2
, 17 4 16 3R d I r m m= + − = + = −
(thỏa mãn).
Câu 44. ChọnB
Cách 1
Xét mặt phẳng
( )
có phương trình
0x by cz d+ + + =
thỏa mãn các điều kiện: đi qua hai điểm
( )
1;1;1A
và
( )
0; 2;2B −
, đồng thời cắt các trục tọa độ
,Ox Oy
tại hai điểm cách đều
O
.
Vì
( )
đi qua
( )
1;1;1A
và
( )
0; 2;2B −
nên ta có hệ phương trình:
( )
10
*
2 2 0
b c d
b c d
+ + + =
− + + =
Mặt phẳng
( )
cắt các trục tọa độ
,Ox Oy
lần lượt tại
( )
;0;0 , 0; ;0
d
M d N
b
−
−
.
Vì
,MN
cách đều
O
nên
OM ON=
. Suy ra:
d
d
b
=
.
Nếu
0d =
thì chỉ tồn tại duy nhất một mặt phẳng thỏa mãn yêu cầu bài toán (mặt phẳng này sẽ đi
qua điểm
O
).
Do đó để tồn tại hai mặt phẳng thỏa mãn yêu cầu bài toán thì:
1
d
db
b
= =
.
▪ Với
1b =
,
( )
24
*
2 2 6
c d c
c d d
+ = − =
+ = = −
. Ta được mặt phẳng
( )
P
:
4 6 0x y z+ + − =
▪ Với
1b =−
,
( )
02
*
2 2 2
c d c
c d d
+ = = −
+ = − =
. Ta được mặt phẳng
( )
Q
:
2 2 0x y z− − + =
Vậy:
( ) ( )
1 2 1 2
1. 1 4. 2 9bb c c+ = − + − = −
.
Cách 2 ;
( )
1; 3;1AB = − −
Xét mặt phẳng
( )
có phương trình
0x by cz d+ + + =
thỏa mãn các điều kiện: đi qua hai điểm
( )
1;1;1A
và
( )
0; 2;2B −
, đồng thời cắt các trục tọa độ
,Ox Oy
tại hai điểm cách đều
O
lần lượt tại
,MN
. Vì
,MN
cách đều
O
nên ta có 2 trường hợp sau:
TH1:
( ;0;0), (0; ;0)M a N a
với
0a
khi đó
( )
chính là
( )
P
. Ta có
( ; ;0)MN a a=−
, chọn
1
( 1;1;0)u =−
là một véc tơ cùng phương với
MN
. Khi đó
1
, ( 1; 1; 4)
P
n AB u
= = − − −
,
suy ra
( )
1
: 4 0P x y z d+ + + =
TH2:
( ;0;0), (0; ;0)M a N a−
với
0a
khi đó
( )
chính là
( )
Q
. Ta có
( ; ;0)MN a a=
, chọn
2
(1;1;0)u =
là một véc tơ cùng phương với
MN
. Khi đó
2
, ( 1;1;2)
Q
n AB u
= = −
,
suy ra
( )
2
: 2 0Q x y z d− − + =
. Vậy:
( ) ( )
1 2 1 2
1. 1 4. 2 9bb c c+ = − + − = −
.
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
162
Câu 45. Chọn D
Gọi
( )
;;I a b c
là tâm mặt cầu
( )
S
.
Do
( )
S
tiếp xúc với cả ba mặt phẳng
( )
,
( )
,
( )
nên ta có
1 1 1a b c R− = − = + =
.
Mặt khác, ta lại có
( ) ( ) ( )
2 2 2
2 5 2R IM a b c= = − + − + − −
.
Do đó ta có hệ:
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( )
2 2 2 2
2 2 2 2
2 2 2 2
2 5 2 1
2 5 2 1 1
2 5 2 1
a b c a
a b c b
a b c c
− + − + − − = −
− + − + − − = −
− + − + − − = +
.
Quan sát ta thấy rằng
( ) ( )
( ) ( )
( ) ( )
22
22
22
3
1 2 1 0
2
1 5 3 1 0
3
1 2 1 0
2
a a a a
b b b b
c c c c
− − −
− − −
+ + − +
.
Do đó
1 1 1 1 1 1a b c a b c− = − = + − = − = − −
.
Từ
( )
( ) ( ) ( ) ( )
2 2 2 2
1 1 1
1
2 5 2 1
a b c
a b c a
− = − = − −
− + − + + = −
4
4
4
a
b
c
=
=
=−
. Vậy
3R IM==
.
Câu 46. Chọn A
Gọi
R
là bán kính mặt cầu. Do mặt cầu tiếp xúc với mặt phẳng
( )
P
nên ta có:
( )
( )
,d I P R=
( ) ( )
22
2
1 2.2 2.1 2
1 2 2
R
− − − −
=
+ − + −
3R=
. Suy ra
9d =
.
Từ
( ) ( ) ( )
2 2 2
x a y b z c d− + − + − =
và tâm
( )
1;2;1I −
suy ra
1a =−
;
2b =
;
1c =
.
Vậy
T a b c d= + + +
1 2 1 9 11= − + + + =
.
Câu 47. Chọn C
Giả sử mặt cầu
( )
S
có bán kính
R
và có tâm
( )
0;0;Ic
(vì tâm
I
thuộc trục
Oz
).
Ta có:
( )
( )
;d I Oxy c=
và
( )
( )
;2d I c
=−
.
Vì mặt phẳng
( )
Oxy
cắt
( )
S
theo đường tròn có bán kính bằng 2 nên
( )
( )
( )
2
2
; 4 4R d I Oxy c= + = +
.
Vì mặt phẳng
( )
:
2z =
cắt
( )
S
theo đường tròn có bán kính bằng 4 nên
( )
( )
( )
( )
2
2
; 16 2 16R d I c
= + = − +
.
Suy ra:
( )
2
2
4 2 16 4 16 4c c c c+ = − + = =
( )
0;0;4I
và
20R =
.
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
163
Vậy phương trình mặt cầu
( )
S
là:
( )
2
22
4 20x y z+ + − =
.
Câu 48. Chọn D
Phương trình mặt phẳng
( )
Oyz
là
0x =
.
Vì mặt cầu tiếp xúc với mặt phẳng
( )
Oyz
có bán kính
( )
( )
,4R d I Oyz==
.
Vậy phương trình mặt cầu cần tìm là
( ) ( ) ( )
2 2 2
4 9 16 16x y z− + − + − =
.
Câu 49. Chọn C
Gọi
( )
;;I a b c
là tâm của mặt cầu
( ) ( ) ( ) ( )
2 2 2
:S x a y b z c D
− + − + − =
.
Vì
I
nằm trên
( )
P
và
( )
Q
nên:
2 4 7 0
4 5 14 0
a b c
a b c
+ − − =
+ + − =
( )
1
Mặt khác,
( )
S
cùng tiếp xúc với
( )
R
và
( )
S
nên:
( )
( )
( )
( )
,,d I R d I S=
2 2 2 2 2 4
33
a b c a b c+ − − + − +
=
2 2 2 2 2 4 2 4
2 2 2 2 2 4 2 2 1 0
a b c a b c
a b c a b c a b c
+ − − = + − + − =
+ − − = − − + − + − + =
2 2 1 0a b c + − + =
( )
2
Từ
( )
1
và
( )
2
ta được hệ:
2 4 7 0
4 5 14 0
2 2 1 0
a b c
a b c
a b c
+ − − =
+ + − =
+ − + =
1
3
3
a
b
c
=−
=
=
5abc + + =
.
Câu 50. Chọn C
Mặt cầu
()S
có tâm là
(0;1;1)I
bán kính
3R =
. Vì
53IA =
nên điểm
A
nằm trong mặt cầu.
Gọi
H
và
r
lần lượt là tâm và bán kính của đường tròn thiết diện.
Khi đó, ta luôn có
2 2 2 2 2
4r R IH R IA= − − =
(vì
H
trùng với
A
hoặc
AIH
vuông tại
H
nên
IH IA
).
Vậy đường tròn có chu vi nhỏ nhất thì có bán kính nhỏ nhất
2r =
khi
A
trùng với
H
.
Câu 51. Chọn C
Mặt cầu
()S
có tâm là
(0;1;1)I
bán kính
3R =
. Vì
53IA =
nên điểm
A
nằm trong mặt cầu.
Gọi
H
và
r
lần lượt là tâm và bán kính của đường tròn thiết diện.
Khi đó, ta luôn có
2 2 2 2 2
4r R IH R IA= − − =
(vì
H
trùng với
A
hoặc
AIH
vuông tại
H
nên
IH IA
).
Vậy đường tròn có chu vi nhỏ nhất thì có bán kính nhỏ nhất
2r =
khi
A
trùng với
H
.
Câu 52. Chọn B
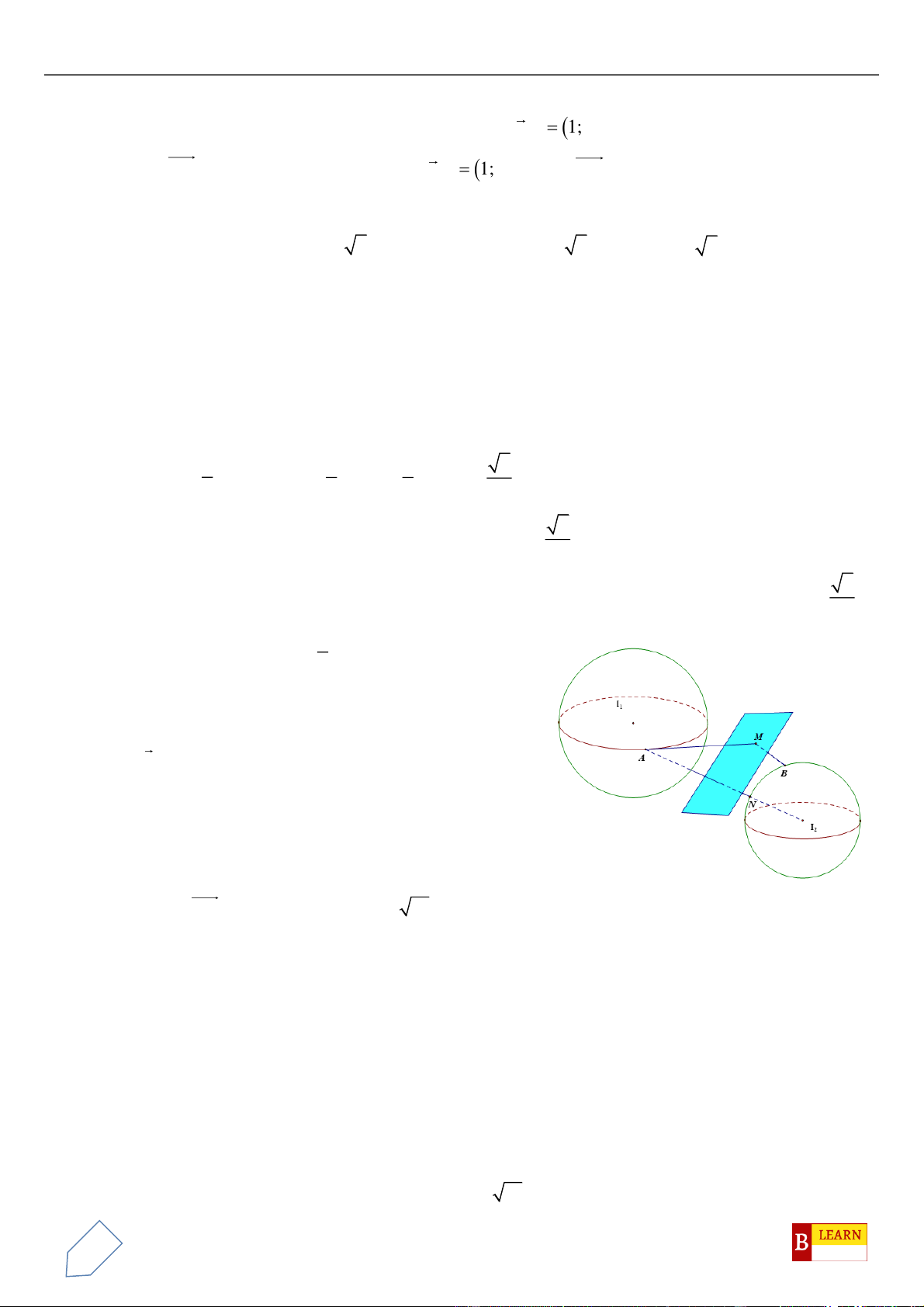
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
164
Mặt cầu
( )
1
S
có tâm
( )
0;0;0O
, bán kính
1
5R =
. Mặt cầu
( )
2
S
có tâm
( )
2;0;2K −
, bán kính
2
1R =
, mặt phẳng
( )
P
có
1
vectơ pháp tuyến là
( )
( )
1;0 ; 1
P
n =−
.
Vì
( )
2;0;2OK =−
cùng phương với
( )
( )
1;0 1
P
n =−
nên
OK
vuông góc với mặt phẳng
( )
P
Gọi
H
là hình chiếu vuông góc của
O
lên mặt phẳng
( )
P
nên
O
,
K
,
H
thẳnghàng.
Ta có
( )
( )
1
; 3 2OH d O P R= =
,
( )
( )
2
;2KH d K P R= =
,
22OK =
,
21
OK R R+
( )
P
cắt
( )
1
S
và
( )
P
không cắt
( )
2
S
và
( )
1
S
chứa
( )
2
S
.
Do đó mặt cầu tâm
I
phải tiếp xúc trong với
( )
1
S
tại
A
và tiếp xúc ngoài với
( )
2
S
tại
B
.
Gọi
R
là bán kính với mặt cầu tâm
I
.
Suy ra:
1
5OI R R R= − = −
và
2
1KI R R R= + = +
.
Ta có
2 2 2 2 2
IH OI OH KI KH= − = −
( ) ( )
22
2
5 18 1 2IH R R = − − = + −
12 8R=
2
3
R=
2
2
27
12
39
IH
= + − =
7
3
IH=
.
Khi đó
I
thuộc mặt cầu
( )
3
S
tâm
H
, bán kính
3
7
3
R =
.
Mà
I
thuộc mặt phẳng
( )
P
nên
I
thuộc đường tròn giao tuyến và có bán kính là
3
7
3
rR==
Vậy diện tích là
2
7
9
r
=
.
Câu 53. Chọn B
Mặt phẳng
( )
P
có một vectơ pháp tuyến là
( )
1;2; 2
P
n =−
.
Mặt cầu
( )
1
S
có tâm
( )
1
2;0; 1I −
và bán kính
1
1R =
Mặt cầu
( )
2
S
có tâm
( )
2
4; 2;3I −−
và bán kính
2
2R =
.
Ta có
( )
1 2 1 2 1 2
6; 2;4 2 14I I I I R R= − − = +
suy ra
( )
1
S
,
( )
2
S
nằm ngoài nhau.
Ta có
( )( )
1 1 1 2 2 2
2 2 5 2 2 5 0
I I I I I I
x y z x y z+ − + + − +
nên
1
I
,
2
I
nằm về hai phía đối với mặt phẳng
( )
P
.
Ngoài ra
( )
11
,3d I P R=
,
( )
22
,3d I P R=
.
Gọi
,NP
lần lượt là giao điểm của đoạn thẳng
12
II
với hai mặt cầu
( )
1
S
và
( )
2
S
.
Ta có
1 2 1 2 1 2 1 2
MA MB AI BI I I MA MB NI PI I N NP PI MA MB NP+ + + + + + + + +
.
Đẳng thức xảy ra khi và chỉ khi
AN
,
BP
và
,,M N P
thẳng hàng.
Khi đó
( )
1 2 1 2
min
2 14 3MA MB NP I I R R+ = = − − = −
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
165
DẠNG 6. CỰC TRỊ LIÊN QUAN ĐẾN MẶT PHẲNG
Câu 1. Trong không gian
Oxyz
, cho ba điểm
(1;1;1)A
,
( 1; 2; 0)B −
,
(3; 1; 2)C −
và
M
là điểm thuộc
mặt phẳng
( )
:2 2 7 0x y z
− + + =
. Tính giá trị nhỏ nhất của
3 5 7P MA MB MC= + −
.
A.
min
20P =
. B.
min
5P =
. C.
min
25P =
. D.
min
27P =
.
Câu 2. Trong không gian
Oxyz
, cho hai điểm
( )
2;0;1A
,
( )
2;8;3B −
và điểm
( )
;;M a b c
di động trên
mặt phẳng
( )
Oxy
. Khi
MA MB+
đạt giá trị nhỏ nhất thì giá trị
3a b c++
bằng
A.
2
. B.
3
. C.
5
. D.
4
.
Câu 3. Trong không gian với hệ trục tọa độ
Oxyz
, Cho hai điểm
( ) ( )
3;5; 5 , 5; 3;7AB− − −
và mặt phẳng
( )
:0P x y z+ + =
. Tìm tọa độ điểm
M
trên mặt phẳng
( )
P
sao cho
22
2MA MB−
lớn nhất.
A.
( )
2;1;1M −
. B.
( )
2; 1;1M −
. C.
( )
6; 18;12M −
. D.
( )
6;18;12M −
.
Câu 4. Trong không gian
Oxyz
, cho hai điểm
(2; 2;4)A −
,
( 3;3; 1)B −−
và mặt phẳng
( );2 2 8 0P x y z− + − =
. Xét
M
là điểm thay đổi thuộc
()P
, giá trị nhỏ nhất của
22
23MA MB+
bằng
A.
145
. B.
108
. C.
105
. D.
135
.
Câu 5. Trong không gian với hệ trục tọa độ
Oxyz
, cho tam giác
ABC
với
( )
2;1;3A
,
( )
1; 1;2B −
,
( )
3; 6;1C −
. Điểm
( )
;;M x y z
thuộc mặt phẳng
( )
Oyz
sao cho
2 2 2
MA MB MC++
đạt giá trị nhỏ
nhất. Tính giá trị biểu thức
P x y z= + +
.
A.
0P =
. B.
2P =
. C.
6P =
. D.
2P =−
.
Câu 6. Cho
( ) ( )
4;5;6 ; 1;1;2AB
,
M
là một điểm di động trên mặt phẳng
( )
:2 2 1 0P x y z+ + + =
.
Khi đó
MA MB−
nhận giá trị lớn nhất là?
A.
77
. B.
41
. C.
7
. D.
85
.
Câu 7. Trong không gian
Oxyz
, cho ba điểm
( )
0;1;2A
,
( )
1;1;1B
,
( )
2; 2;3C −
và mặt phẳng
( )
: 3 0P x y z− + + =
. Gọi
( )
;;M a b c
là điểm thuộc mặt phẳng
( )
P
thỏa mãn
MA MB MC++
đạt giá trị nhỏ nhất. Giá trị của
23a b c++
bằng
A.
7
. B.
5
. C.
3
. D.
2
.
Câu 8. Trong không gian
Oxyz
, cho các điểm
( )
00M m; ;
,
( )
00N ;n;
,
( )
00P ; ; p
không trùng với gốc
tọa độ và thỏa mãn
2 2 2
3m n p+ + =
. Tìm giá trị lớn nhất của khoảng cách từ
O
đến mặt phẳng
( )
MNP
.
A.
1
3
. B.
3
. C.
1
3
. D.
1
27
.
Câu 9. Trong không gian
Oxyz
, cho các điểm
( )
1;4;5A
,
( )
0;3;1B
,
( )
2; 1;0C −
và mặt phẳng
( )
:3 3 2 15 0P x y z− − − =
. Gọi
;;M a b c
là điểm thuộc mặt phẳng
P
sao cho tổng các bình
phương khoảng cách từ
M
đến A, B, C nhỏ nhất. Tính
abc
.
A.
5
. B.
5−
. C.
3
. D.
3−
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
166
Câu 10. Trong không gian
Oxyz
, cho mặt phẳng
( )
:3 5 0P x y z+ − + =
và hai điểm
( )
1;0;2A
,
( )
2; 1;4B −
. Tập hợp các điểm
M
nằm trên mặt phẳng
( )
P
sao cho tam giác
MAB
có diện tích
nhỏ nhất.
A.
7 4 7 0
3 5 0
x y z
x y z
− − + =
− + − =
. B.
7 4 14 0
3 5 0
x y z
x y z
− − + =
+ − + =
.
C.
7 4 7 0
3 5 0
x y z
x y z
− − + =
+ − + =
.
D.
7 4 5 0
3 5 0
x y z
x y z
− − + =
+ − + =
.
Câu 11. Trong hệ trục
,Oxyz
cho điểm
( )
1;3;5 ,−A
( )
2;6; 1 ,−B
( )
4; 12;5−−C
và mặt phẳng
( )
: 2 2 5 0.+ − − =P x y z
Gọi
M
là điểm di động trên
( )
.P
Gía trị nhỏ nhất của biểu thức
= + +S MA MB MC
là
A.
42.
B.
14.
C.
14 3.
D.
14
.
3
Câu 12. Trong không gian với hệ tọa độ
,Oxyz
cho mặt phẳng
( )
: 2 2 3 0P x y z− + − =
và mặt cầu
( )
2 2 2
: 2 4 2 5 0S x y z x y z+ + + − − + =
. Giả sử
( )
MP
và
( )
NS
sao cho
MN
cùng phương
với vectơ
( )
1;0;1u =
và khoảng cách giữa
M
và
N
lớn nhất. Tính
.MN
A.
3MN =
. B.
1 2 2MN =+
. C.
32MN =
. D.
14MN =
.
Câu 13. Trong không gian với hệ tọa độ
Oxyz
, gọi
( )
: 3 0P ax by cz+ + − =
là mặt phẳng đi qua hai điểm
( ) ( )
0; 1;2 , 1;1;3MN−−
và không đi qua điểm
( )
0;0;2H
. Biết rằng khoảng cách từ
H
đến mặt
phẳng
( )
P
đạt giá trị lớn nhất. Tổng
2 3 12T a b c= − + +
bằng
A.
16−
. B.
8
. C.
12
. D.
16
.
Câu 14. Trong không gian với hệ tọa độ
Oxyz
,
cho hai điểm
( )
3;1;1M
,
( )
4;3;4N
và đường thẳng
7 3 9
:
1 2 1
x y z− − −
= =
−
. Gọi
( )
;;I a b c
là điểm thuộc đường thẳng
sao cho chu vi tam giác
IMN
nhỏ nhất. Tính
T a b c= + +
.
A.
23
3
T =
. B.
29T =
. C.
19T =
. D.
40
3
T =
.
Câu 15. Trong không gian Oxyz, cho hai điểm
(1; 3;0)A −
,
(5; 1; 2)B −−
và mặt phẳng
( ) : 1 0P x y z+ + − =
. Xét các điểm
M
thuộc
()P
, giá trị lớn nhất của biểu thức
| MA MB|−
bằng:
A.
3
. B.
2
. C.
25
. D.
26
Câu 16. Trong không gian
,Oxyz
cho mặt cầu
2 2 2
( ): ( 3) ( 6) 45S x y z+ − + − =
và
( )
1;4;5M
. Ba đường
thẳng thay đổi
1
d
,
2
d
,
3
d
nhưng luôn đôi một vuông góc tại
O
cắt mặt cầu tại điểm thứ hai lần
lượt là
A
,
B
,
C
. Khoảng cách lớn nhất từ
M
đến mặt phẳng
( )
ABC
là
A. 3. B.
5
. C. 4. D.
6
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
167
Câu 17. Trong không gian với hệ tọa độ
Oxyz
, cho điểm và mặt phẳng
. Tìm giá trị lớn nhất của khoảng cách
từ A đến mặt phẳng
( )
P
.
A. . B. . C. . D. .
Câu 18. Trong không gian , cho điểm , đường thẳng và mặt cầu
. Mặt phẳng chứa đường thẳng thỏa mãn khoảng
cách từ điểm đến lớn nhất. Mặt cầu cắt theo đường tròn có bán kính bằng
A. . B. . C. . D. .
Câu 19. Trong không gian
,Oxyz
cho hai điểm
( )
1;2;3 ,A
( )
2;3;4B
và mặt cầu
( )
2 2 2
: 100.S x y z+ + =
Phương trình mặt phẳng qua hai điểm
,AB
và cắt mặt cầu
( )
S
theo một đường tròn có bán kính
nhỏ nhất là
A.
2 3 0.x y z+ − + =
B.
2 0.xz− + =
C.
1 0.yz− + =
D.
2 0.x y z− + =
Câu 20. Trong không gian , cho hai điểm , . Giả sử là điểm thay đổi trong mặt
phẳng Tìm giá trị lớn nhất của biểu thức
A. . B. . C. . D. .
Câu 21. Trong không gian , cho và mặt phẳng . Tìm tọa độ
điểm sao cho đạt giá trị lớn nhất.
A. . B. . C. . D. .
Câu 22. Cho mặt phẳng và hai điểm . Biết sao cho
đạt giá trị nhỏ nhất. Khi đó, hoành độ của điểm là
A. . B. . C. . D. .
Câu 23. Trong không gian
Oxyz
, cho điểm
( )
1;2;3M
. Mặt phẳng
( )
:0P x Ay Bz C+ + + =
chứa trục
Oz
và cách điểm
M
một khoảng lớn nhất, khi đó tổng
A B C++
bằng
A.
6
. B.
3−
. C.
3
. D.
2
.
Câu 24. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
( )
;;A a b c
với
a
,
b
,
c
là các số thực dương
thỏa mãn
( )
( )
2 2 2
5 9 2+ + = + +a b c ab bc ca
và
( )
3
22
1
=−
+
++
a
Q
bc
abc
có giá trị lớn nhất. Gọi
M
,
N
,
P
lần lượt là hình chiếu vuông góc của
A
lên các tia
Ox
,
Oy
,
Oz
. Phương trình mặt
phẳng
( )
MNP
là
A.
4 4 12 0+ + − =x y z
. B.
3 12 12 1 0+ + − =x y z
.
C.
440+ + =x y z
. D.
3 12 12 1 0+ + + =x y z
.
( )
3; 2;4A −
( )
( ) ( )
( )
2 2 2
: 2 4 1 2 3 1 1 0P m m x m m y m z m+ − + − + − + + =
5
29
33
21
Oxyz
( )
2; 3;4A −
12
:
2 1 2
x y z
d
−+
==
( ) ( ) ( ) ( )
2 2 2
: 3 2 1 20S x y z− + − + + =
( )
P
d
A
( )
P
( )
S
( )
P
5
1
4
2
Oxyz
( )
1;2;3A
( )
4;4;5B
M
( ):2 2 2019 0.P x y z+ + + =
.P AM BM=−
17
77
7 2 3−
82 5−
Oxyz
( ) ( )
1;1;0 , 3; 1;4AB−
( )
: 1 0x y z
− + + =
( )
M
MA MB−
( )
1;3; 1M −
3 5 1
;;
4 4 2
M
−
1 2 2
;;
3 3 3
M
−
( )
0;2;1M
( )
: 2 1 0x y z
− + − =
( ) ( )
0; 1;1 , 1;1; 2AB−−
( )
M
MA MB+
M
x
M
1
3
M
x =
1
M
x =−
2
M
x =−
2
7
M
x =

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
168
Câu 25. Trong không gian
Oxyz
, cho hai điểm
( )
1;0;0A −
và
( )
2;3;4B
. Gọi
( )
P
là mặt phẳng chứa
đường tròn giao tuyến của hai mặt cầu
( ) ( ) ( )
22
2
1
: 1 1 4S x y z− + + + =
và
( )
2 2 2
2
: 2 2 0S x y z y+ + + − =
. Xét
M
,
N
là hai điểm bất kỳ thuộc mặt phẳng
( )
P
sao cho
1MN =
. Giá trị nhỏ nhất của
AM BN+
bằng
A. 5. B. 3. C. 6. D. 4.
Câu 26. Trong không gian với hệ trục tọa độ
Oxyz
, cho
(1; 2;1)M
. Viết phương trình mặt phẳng
()P
qua
M
cắt các trục
,,Ox Oy Oz
lần lượt tại
,,A B C
sao cho
++
2 2 2
1 1 1
OA OB OC
đạt giá trị nhỏ nhất.
A.
+ + − =( ) : 2 3 8 0P x y z
. B.
+ + =( ) : 1
1 2 1
y
xz
P
.
C.
+ + − =( ) : 4 0P x y z
. D.
+ + − =( ) : 2 6 0P x y z
.
Câu 27. Trong không gian Oxyz, cho các điểm
( )
1;1;1A
,
( )
2;3;4B
,
( )
3;2;4C
,
( )
2; 1; 3D − − −
. Mặt
phẳng
( )
P
thay đổi nhưng luôn qua
D
và không cắt cạnh nào của tam giác
ABC
. Khi tổng các
khoảng cách từ
A
,
B
,
C
đến
( )
P
là lớn nhất thì
( )
P
có một phương trình dạng
29 0ax by cz+ + + =
. Tính tổng
a b c++
.
A. 9. B. 5. C. 13. D. 14.
Câu 28. Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
( )
0; 2; 1A −−
,
( )
2; 4;3B −−
,
( )
1;3; 1C −
và mặt
phẳng
( )
: 2 3 0P x y z+ − − =
. Biết điểm
( ) ( )
;;M a b c P
thỏa mãn
2T MA MB MC= + +
đạt
giá trị nhỏ nhất. Tính
S a b c= + +
.
A.
1S =−
. B.
1
2
S =
. C.
0S =
. D.
1
2
S =−
.
Câu 29. Trong không gian
Oxyz
, cho ba điểm
(1;1;1)A
,
( 2;3;4)B −
và
( 2;5;1)C −
. Điểm
( ; ;0)M a b
thuộc
mặt phẳng
( )
Oxy
sao cho
2 2 2
MA MB MC++
đạt giá trị nhỏ nhất. Tổng
22
T a b=+
bằng
A.
10T =
. B.
25T =
. C.
13T =
. D.
17T =
.
Câu 30. Trong không gian
Oxyz
, cho ba điểm
(1;1;1)A
,
( 2;3;4)B −
và
( 2;5;1)C −
. Điểm
( ; ;0)M a b
thuộc
mặt phẳng
( )
Oxy
sao cho
2 2 2
MA MB MC++
đạt giá trị nhỏ nhất. Tổng
22
T a b=+
bằng
A.
10T =
. B.
25T =
. C.
13T =
. D.
17T =
.
Câu 31. Trong không gian
Oxyz
, cho ba điểm
( )
2;0;6A
,
( )
2;4;0B
và
( )
0;4;6C
. Biết
M
là điểm để
biểu thức
MA MB MC MO+ + +
đạt giá trị nhỏ nhất, phương trình đường thẳng
đi qua hai điểm
( )
3;0; 1H −
và
M
là
A.
31
:
2 1 3
x y z−+
= =
−
. B.
31
:
1 1 3
x y z−+
= =
.
C.
31
:
1 3 1
x y z−+
= =
−
. D.
31
:
1 1 2
x y z−+
= =
−−
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
169
Câu 32. Trong không gian
Oxyz
, cho hai điểm
( )
3; 2;2A −
,
( )
2;2;0B −
và mặt phẳng
( )
:2 2 3 0P x y z− + − =
. Xét các điểm
M
,
N
di động trên
( )
P
sao cho
1MN =
. Giá trị nhỏ nhất
của biểu thức
22
23MA NB+
bằng
A.
49,8
. B.
45
. C.
53
. D.
55,8
.
Câu 33. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) ( )
: 1 2 1 0P mx m y z m+ + − − − =
, với
m
là tham số. Gọi
( )
T
là tập hợp các điểm
m
H
là hình chiếu vuông góc của điểm
( )
3;3;0H
trên
( )
P
. Gọi
,ab
lần lượt là khoảng cách lớn nhất, khoảng cách nhỏ nhất từ
O
đến một điểm thuộc
( )
T
. Khi đó,
ab+
bằng
A.
52
. B.
33
. C.
82
. D.
42
.
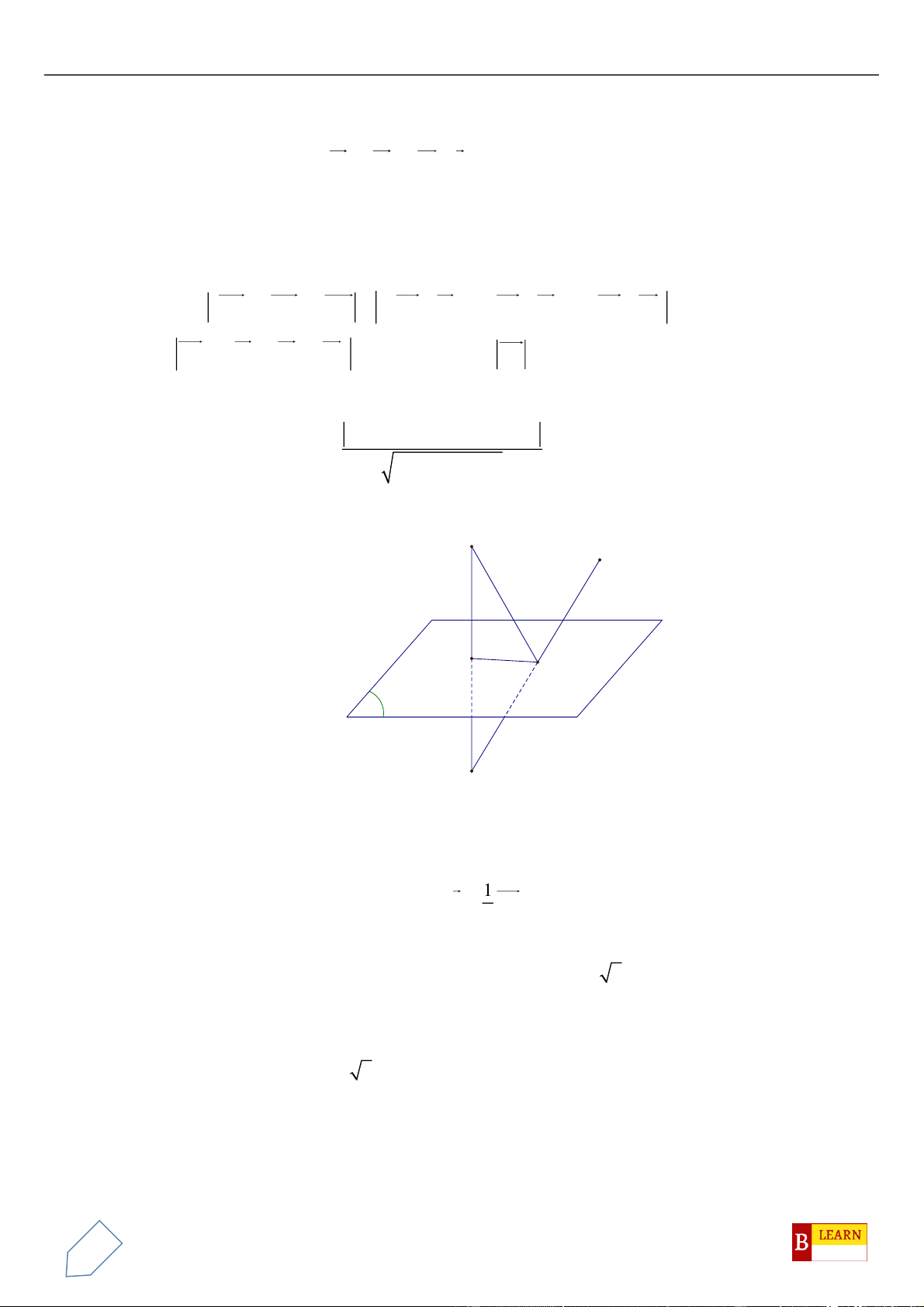
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
170
ĐÁP ÁN CHI TIẾT
Câu 1. Chọn D
Gọi
( )
;;I x y z
sao cho
3 5 7 0IA IB IC+ − =
( )
1
.
Ta có:
( ) ( ) ( )
( ) ( ) ( )
( ) ( ) ( )
3 1 5 1 7 3 0
23
3 1 5 2 7 1 0 20
11
3 1 5 0 7 2 0
x x x
x
y y y y
z
z z z
− + − − − − =
=−
− + − − − − = =
=−
− + − − − =
. Suy ra
( )
23;20; 11I −−
.
Xét
( ) ( ) ( )
3 5 7 3 5 7P MA MB MC MI IA MI IB MI IC= + − = + + + − +
.
( )
3 5 7P MI IA IB IC= + + −
.
Từ
( )
1
ta có
P MI MI==
.
min
P
khi
MI
ngắn nhất hay
M
là hình chiếu vuông góc của
I
lên mặt phẳng
( )
.
Khi đó:
( )
( )
( ) ( )
( )
min
2
22
2. 23 20 2. 11 7
, 27
2 1 2
P d I
− − + − +
= = =
+ − +
.
Câu 2. Chọn B
Dễ thấy hai điểm
,AB
nằm về cùng một phía so với mặt phẳng
( )
Oxy
.
Gọi
C
là điểm đối xứng với
A
qua
( )
Oxy
suy ra
( )
2;0; 1C −
.
Đường thẳng
BC
đi qua
( )
2;0 1C −
và
( )
1
1;2;1
4
u CB= = −
làm vecto chỉ phương có phương
trình là:
2
2
1
xt
yt
zt
=−
=
= − +
. Khi đó
46MA MB MC MB BC+ = + =
.
Đẳng thức xảy ra khi và chỉ khi
,,M B C
thẳng hàng.
Suy ra
( ) ( )
min 4 6MA MB M Oxy BC+ = =
nên tọa độ điểm
( )
;;M x y z
thỏa mãn hệ:
2
1
2
2
1
0
0
xt
x
yt
y
zt
z
z
=−
=
=
=
= − +
=
=
. Vậy
( )
1;2;0 1, 2, 0 3 3M a b c a b c = = = + + =
.
Oxy
A
C
M
B

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
171
Câu 3. Chọn C
Cách 1.
Gọi
( )
;;M a b c
thuộc mặt phẳng
( )
:0P x y z+ + =
nên ta có
0a+b+c =
( ) ( ) ( ) ( ) ( ) ( )
2 2 2 2 2 2
22
2 3 5 5 2 5 3 7MA MB a b c a b c
− = − − + − + − − − − + − − + −
2 2 2
26 22 38 107a b c a b+ c= − − − + − −
( ) ( ) ( )
2 2 2
13 11 19 544a b+ c
= − − + + − +
.
Theo bất đẳng thức Bunnhia ta có
( ) ( ) ( ) ( ) ( ) ( )
2 2 2
0 21 13 11 19 3 13 11 19a+b+c a + b + + c a + b + + c
= − = − − − −
( ) ( ) ( )
2 2 2
13 11 19 147a + b + + c − −
( ) ( ) ( )
2 2 2
22
2 13 11 19 544 397MA MB a b+ c
− = − − + + − +
Dấu bằng xảy ra khi:
13 11 19
7
1 1 1
a b + c−−
= = = −
6
18
12
a
b
c
=
= −
=
( )
6; 18;12M−
.
Cách 2.
(Căn cứ vào đề cho đáp án sẵn tọa độ điểm
M
)
M
thuộc mặt phẳng
( )
:0P x y z+ + =
nên loại B, D.
Với
( )
22
2;1;1 2 149M MA MB− − = −
, với
( )
22
6; 18;12 2 397M MA MB− − =
Từ đó loại A. Vậy đáp án là C.
Cách 3.
Ta có thể dùng tâm tỷ cự như sau:
Gọi
I
thỏa mãn
20IA IB−=
( )
20IO OA IO OB + − + =
2OI OB OA = −
( )
13; 11;19I−
.
Khi đó:
22
2MA MB−
( ) ( )
22
2MA MB=−
( ) ( )
22
2MI IA MI IB= + − +
( )
2 2 2
2MI IA IB= − + −
lớn
nhất khi
I
là hình chiếu vuông góc của
M
lên
( ) ( )
6; 18;12PM−
.
Câu 4. Chọn D
Gọi
I
là điểm thỏa điều kiện :
2 3 0IA IB+=
. Khi đó
( 1;1;1)I −
.
T=
22
23MA MB+
22
2 2 2 2 2
2 3 2( ) 3( ) 5 2 3MA MB MI IA MI IB MI IA IB= + = + + + = + +
.
T đạt giá trị nhỏ nhất
min
MI
.
Mà
()MP
nên
min
MI
M
là hình chiếu của
I
lên mặt phẳng
( )
P
2 2 2
2.( 1) 1 2.1 8
(I,( )) 3
2 ( 1) 2
MI d P
− − + −
= = =
+ − +
.
Khi đó:
2 2 2
min
5 2 3 135T MI IA IB= + + =
.
Câu 5. Chọn A

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
172
Gọi
I
là điểm thỏa
0IA IB IC+ + =
( )
2; 2;2I−
.
2 2 2
MA MB MC++
( ) ( ) ( )
2 2 2
MI IA MI IB MI IC= + + + + +
( )
2 2 2 2
3 2 .MI IA IB IC MI IA IB IC= + + + + + +
2 2 2 2
3MI IA IB IC= + + +
.
Mà
( )
M Oyz
2 2 2
MA MB MC + +
đạt giá trị nhỏ nhất
M
là hình chiếu của
I
lên
( )
Oyz
( )
0; 2;2M−
. Vậy
0 2 2 0P = − + =
.
Câu 6. Chọn B
Ta có
MA MB AB−
với mọi điểm
( )
MP
Vì
( ) ( )
2.4 5 2.6 1 . 2.1 1 2.2 1 208 0+ + + + + + =
nên hai điểm
,AB
nằm cùng phía với
( )
P
Dấu
""=
xảy ra khi và chỉ khi
( )
M AB P=
Khi đó,
MA MB−
nhận giá trị lớn nhất là:
( ) ( ) ( )
2 2 2
4 1 5 1 6 2 41AB = − + − + − =
.
Câu 7. Chọn C
Ta có trọng tâm của tam giác
ABC
là
( )
1;0;2G
. Khi đó:
33MA MB MC MG MG+ + = =
.
Vậy
min
min
MA MB MC MG M+ +
là hình chiếu vuông góc của
G
trên mặt phẳng
( )
P
.
Gọi
d
là đường thẳng qua
G
và vuông góc với
( )
P
, ta có phương trình đường thẳng
d
là:
1
2
xt
yt
zt
=+
=−
=+
. Giá trị
t
ứng với tọa độ điểm
M
là nghiệm của phương trình:
( ) ( ) ( )
1 2 3 0 3 6 0 2t t t t t+ − − + + + = + = = −
.
Vậy
( )
1;2;0M −
. Khi đó:
2 3 1 2.2 3.0 3a b c+ + = − + + =
.
Câu 8. Chọn C
Do
M
,
N
,
P
không trùng với gốc tọa độ nên
0m
,
0n
,
0p
.
Phương trình mặt phẳng
( )
MNP
là:
1 1 1
1 1 0
x y z
x y z
m n p m n p
+ + = + + − =
( )
( )
2 2 2
1
1 1 1
d O, MNP
m n p
=
++
Áp dụng bất đẳng thức Côsi cho ba số dương
2
m
,
2
n
,
2
p
và ba số dương
2
1
m
,
2
1
n
,
2
1
p
ta có:
2 2 2 2 2 2
3
3m n p m n p+ +
và
3
2 2 2 2 2 2
1 1 1 1
3
m n p m n p
+ +
( )
2 2 2
2 2 2
1 1 1
9m n p
m n p
+ + + +
; Mà
2 2 2
3m n p+ + =
suy ra:

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
173
2 2 2 2 2 2
2 2 2
1 1 1 1 1 1 1 1
33
1 1 1 3
m n p m n p
m n p
+ + + +
++
( )
( )
1
3
d O, MNP
. Dấu bằng xảy ra khi và chỉ khi
2 2 2
1m n p= = =
.
Vậy giá trị lớn nhất của khoảng cách từ
O
đến mặt phẳng
( )
MNP
là
1
3
. Chọn C
Câu 9. Chọn C
Ta có:
1;2;2I
là trọng tâm của tam giác ABC.
MA, MB, MC là khoảng cách từ M đến các điểm A, B, C.
Xét
2 2 2
2 2 2
MA MB MC MA MB MC
=
2 2 2
MI IA MI IB MI IC
2 2 2 2
3 2 . 2 . 2 .MI IA IB IC MI IA MI IB MI IC
2 2 2 2
3 2 .MI IA IB IC MI IA IB IC
2 2 2 2
3 2 .0MI IA IB IC MI
(do I là trọng tâm của tam giác ABC nên
0IA IB IC
)
2 2 2 2
3MI IA IB IC
.
Mà
2 2 2
IA IB IC
có giá trị không đổi nên
2 2 2
MA MB MC
đạt giá trị nhỏ nhất khi MI ngắn
nhất. Khi đó M là hình chiếu vuông góc của I lên mặt phẳng
P
.
Gọi
d
là đường thẳng đi qua M và I , vuông góc với mặt phẳng
P
.
Đường thẳng
( )
d
đi qua điểm
( )
1;1;1I
, nhận véc tơ pháp tuyến của
( )
P
là
( )
3; 3; 2
P
n = − −
là
một véc tơ chỉ phương nên phương trình tham số của
d
là
13
: 2 3
22
xt
d y t t
zt
.
M P d
.
1 3 ;2 3 ;2 2M d M t t t
.
Mặt khác
( )
MP
nên:
3 1 3 3 2 3 2 2 2 15 0 1t t t t
.
Do đó
4; 1;0M
. Suy ra
3abc
.
Câu 10. Chọn C
Ta có:
( )
;( )
1
.
2
MAB
M AB
S d AB
=
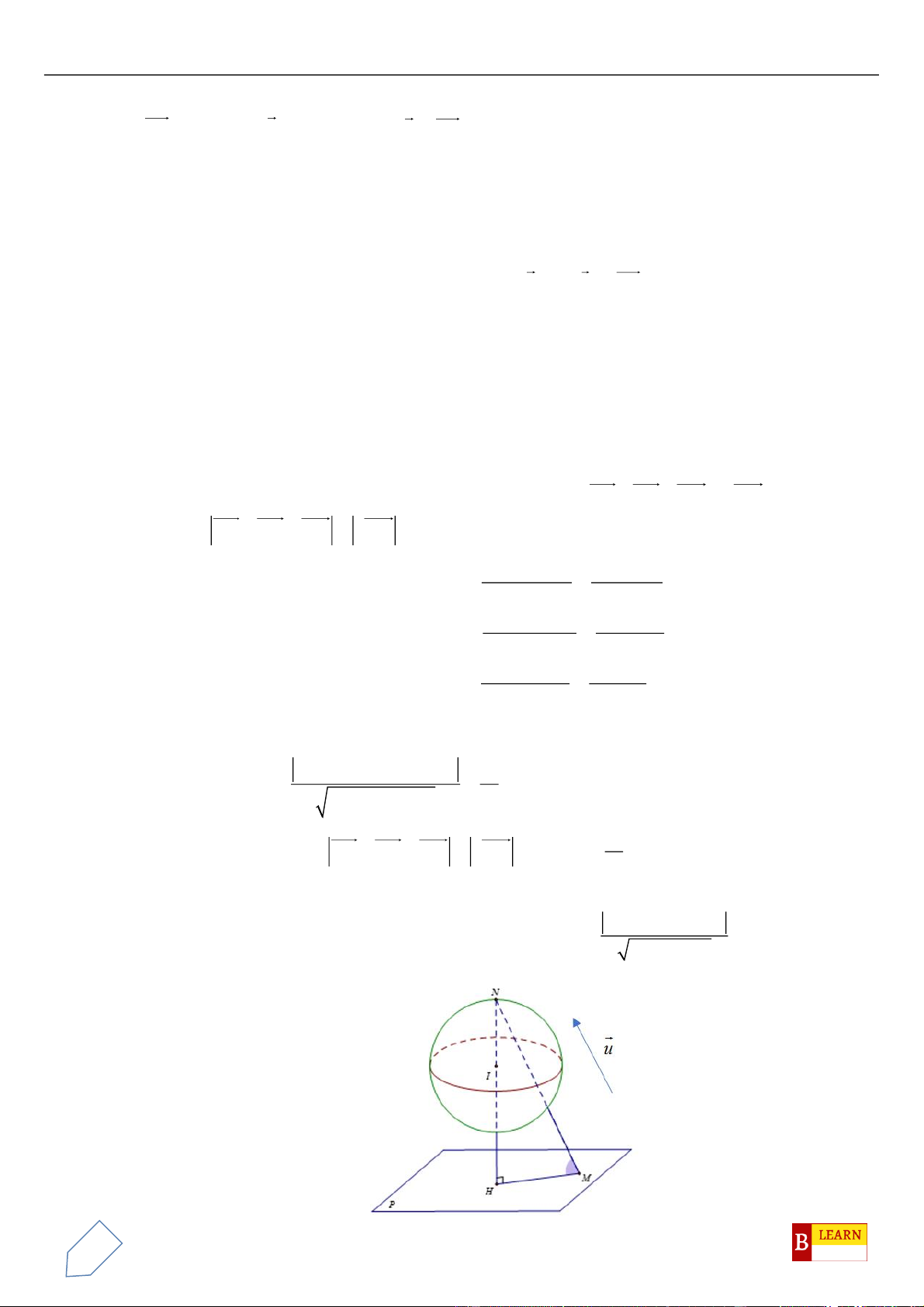
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
174
Ta có: Diện tích tam giác
MAB
nhỏ nhất
( )
;( )M AB
d
nhỏ nhất.
( )
1; 1;2AB =−
;
( )
( )
3;1; 1
P
n =−
( )
. 0.
P
n AB=
AB
song song với mặt phẳng
( )
.P
Mà
( )
;( )M AB
d
ngắn nhất,
M
( )
.P
Nên
M
thuộc giao tuyến của mặt phẳng
( )
P
và mặt phẳng
( )
.Q
Với
( )
Q
là mặt phẳng vuông góc với
( )
P
và đi qua
AB
.
Mặt phằng
( )
Q
vuông góc với
( )
P
đi qua
AB
( ) ( )
( )
; 1; 7; 4 .
QP
n n AB
= = − −
( ) ( ) ( )
: 7 4 0 1 7.0 4.2 0 7 : 7 4 7 0
A A A
A Q Q x y z c c c Q x y z − − + = − − + = = − − + =
( )
( )
7 4 7 0
.
3 5 0
MQ
x y z
M
x y z
MP
− − + =
+ − + =
Câu 11. Chọn B
Gọi
( )
1 1 1
;;G x y z
là trọng tâm tam giác
.ABC
Vì
G
là trọng tâm tam giác
ABC
và
M
là điểm tùy nên
3.+ + =MA MB MG MG
Vậy
3 3 .= + + = =S MA MB MC MG MG
Do
G
là trọng tâm tam giác
ABC
nên
( )
1
1
1
1 2 4
1
33
3 6 12
1 1; 1;3 .
33
5 1 5
3
33
++
− + −
= = = −
++
+−
= = = − − −
++
−+
= = =
A B C
A B C
A B C
xxx
x
yyy
yG
zzz
z
Vì
G
cố định nên
3=S MG
đạt giá trị nhỏ nhất khi và chỉ khi
MG
nhỏ nhất. Tức là
( )
.⊥MG P
Ta có:
( )
( )
( )
( )
2
22
1.1 2. 1 2.3 5
14
,.
3
1 2 2
− + − − −
= = =
+ + −
d G P MG
Vậy giá trị nhỏ nhất
14
3 3 3. 14.
3
= + + = = = =S MA MB MC MG MG
Câu 12. Chọn C
( )
S
có tâm
( )
1;2;1I −
và bán kính
1R =
. Ta có:
( )
( )
222
1 2.2 2.1 3
d , 2
1 2 2
I P R
− − + −
= =
++
.
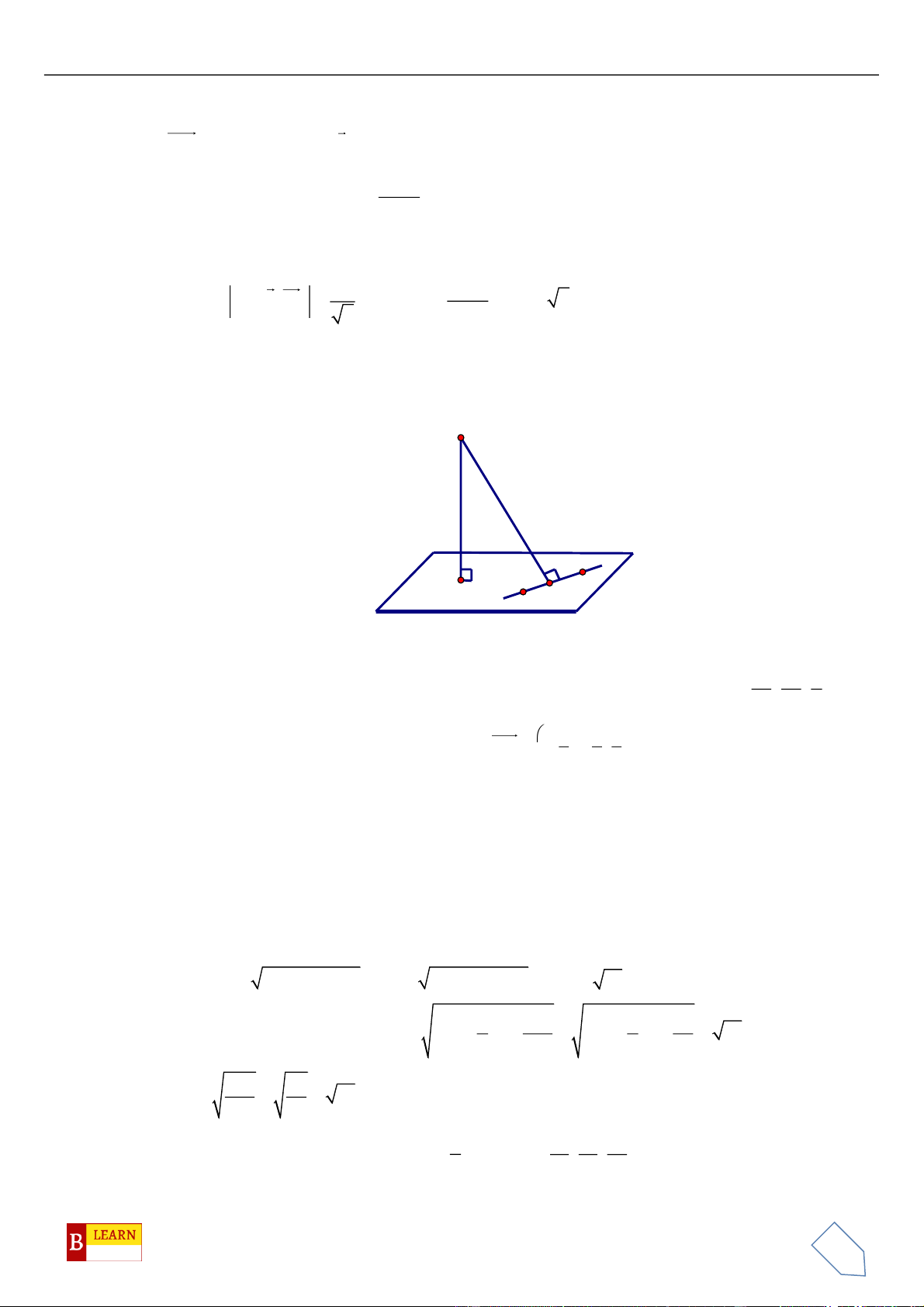
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
175
Gọi
H
là hình chiếu vuông góc của
N
trên mặt phẳng
( )
P
và
là góc giữa
MN
và
NH
.
Vì
MN
cùng phương với
u
nên góc
có số đo không đổi,
HNM
=
.
Có
1
.cos .
cos
HN MN MN HN
= =
nên
MN
lớn nhất
HN
lớn nhất
( )
( )
,3HN d I P R= + =
.
Có
( )
1
cos cos ,
2
P
un
==
nên
1
32
cos
MN HN
==
.
Câu 13. Chọn D
Gọi
K
là hình chiếu của
H
lên
( )
P
,
E
là hình chiếu của
H
lên
MN
.
Ta có :
( )
( )
;d H P HK=
và
( )
;d H MN HE=
,
HK HE
(không đổi) .
Vậy
( )
( )
;d H P
lớn nhất khi
KE
, với
E
là hình chiếu của
H
lên
MN
1 1 7
;;
3 3 3
E
−−
.
Vậy mặt phẳng
( )
P
cần tìm là mặt phẳng nhận
1 1 1
;;
3 3 3
HE
= − −
làm vectơ pháp tuyến và đi qua
M
( )
: 3 0P x y z − − + − =
. Vậy
1
1 16
1
a
bT
c
=−
= − =
=
.
Câu 14. Chọn C
Cách 1.
Ta có
I
;
( )
7 ;3 2 ;9I t t t+ − +
.
Ta tính:
2
6 16 84MI t t= + +
;
2
6 16 34NI t t= + +
;
14MN =
.
Gọi
C
là chu vi tam giác
IMN
;
22
4 220 4 70
6 6 14
3 3 3 3
C t t
= + + + + + +
.
Hay
220 70
14
33
C + +
.
Chu vi tam giác
IMN
nhỏ nhất khi
4
3
t =−
; khi đó
17 17 23
;;
3 3 3
I
hay
19T =
.
Cách 2.
M
H
K
E
N
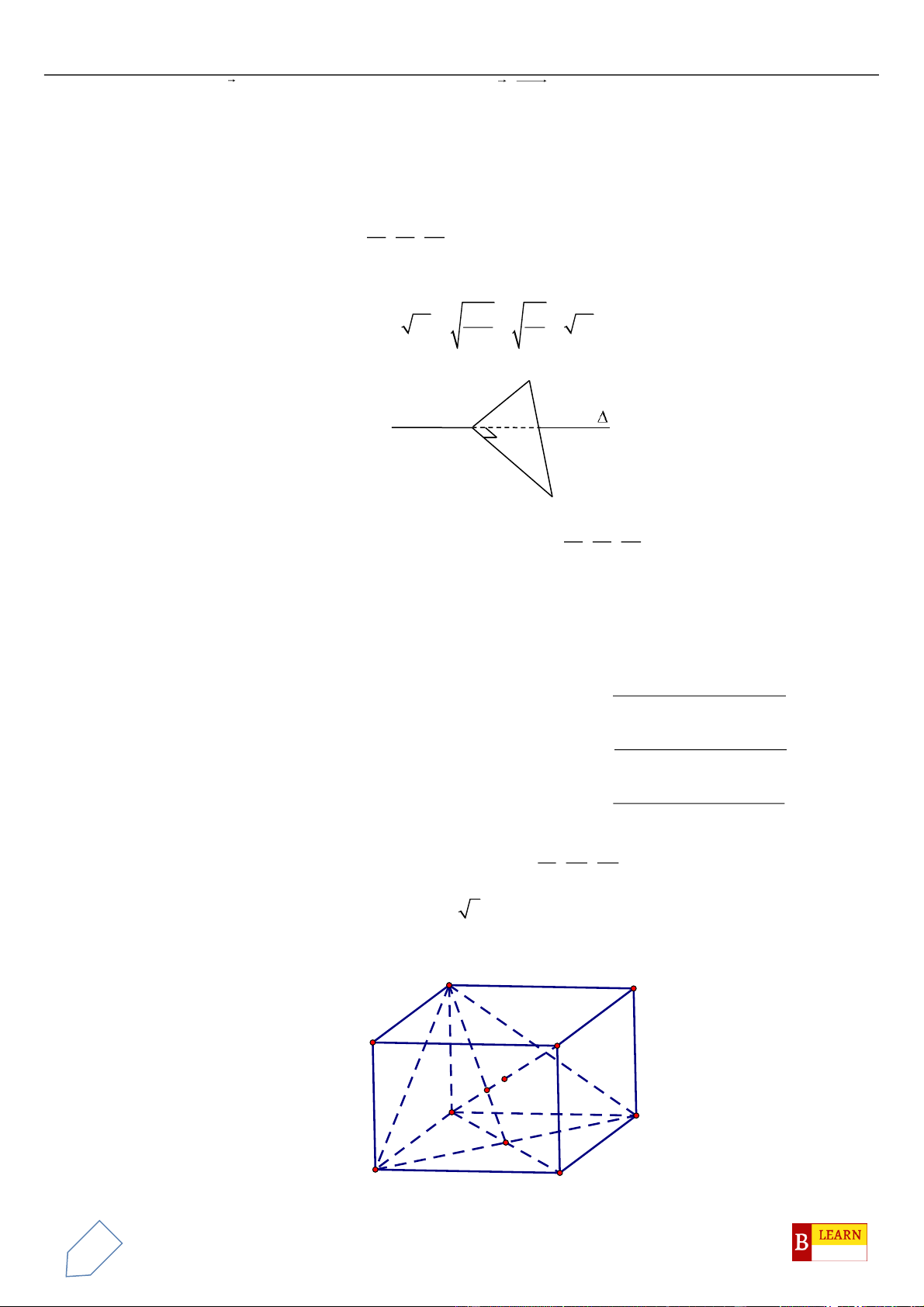
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
176
Gọi véc tơ
u
là véc tơ chỉ phương của
ta có
0u MN=
.
Đường thẳng
MN
vuông góc với
.
Gọi
( )
là mặt phẳng chứa
MN
và vuông góc với
.
Phương trình mặt phẳng
( )
chứa
MN
vuông góc với
là:
2 2 0x y z− + − =
.
Mặt phẳng
( )
cắt
tại
17 17 23
;;
3 3 3
H
.
Gọi điểm
I
; Gọi
C
là chu vi tam giác
IMN
. Ta có:
C MI NI MN= + +
220 70
14 14
33
MH NH + + = + +
.
Vậy chu vi tam giác
IMN
nhỏ nhất khi
IH
. Hay
17 17 23
;;
3 3 3
I
. Vậy
19T =
.
Câu 15. Chọn C
Nhận xét:
( 1)(x ) 0
A A C B B C
x y z y z+ + − + +
suy ra
A
và
B
khác phía với mặt phẳng
()P
Áp dụng công thức tính nhanh:Tọa độ điểm đối xứng của
0 0 0
( ; ; )M x y z
qua
(P) : ax 0by cz d+ + + =
là điểm
1 1 1
'( ; ; )M x y z
với
2
2
2
0 0 0
10
22
0 0 0
10
22
0 0 0
10
22
2 ( )
2 ( )
2 ( )
a ax by cz d
xx
abc
b ax by cz d
yy
abc
c ax by cz d
zz
abc
+ + +
=−
++
+ + +
=−
++
+ + +
=−
++
Gọi
'B
là điểm đối xứng của
B
qua
()P
suy ra
13 5 8
' ; ;
3 3 3
B
−−
Ta có
| MA MB | | MA MB' | AB' 2 5− = − =
Câu 16. Chọn D
I
H
B
C'
O
O'
C
A'
B'
A
M
I
N

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
177
Mặt cầu
( )
S
có tâm
( )
0;3;6I
, bán kính
35R =
.
Tứ diện
OABC
vuông đỉnh
O
và nội tiếp mặt cầu
( )
S
nên gọi
O
,
A
,
B
,
C
lần lượt là các
điểm đối xứng với
O
,
A
,
B
,
C
qua tâm
I
thì
.OBAC AC O B
là hình hộp chữ nhật nội tiếp mặt
cầu
( )
S
và đường chéo
OO
của hình hộp cắt mặt chéo tam giác
ABC
tại trọng tâm
H
của tam
giác
ABC
và
( )
12
0;2;4
33
OH OO OI H
= =
.
Mặt phẳng
( )
ABC
thay đổi, luôn đi qua
( )
0;2;4H
nên
( )
( )
,6d M ABC MH=
.
( )
( )
,6d M ABC =
khi mặt phẳng
( )
ABC
vuông góc với
MH
.
Câu 17. Chọn C
Gọi là điểm cố định mà mặt phẳng
( )
P
luôn đi qua.
Ta có
. Ta có
Do đó khoảng cách từ khoảng cách từ A đến mặt phẳng
( )
P
đạt giá trị lớn nhất bằng
khi tại .
Câu 18. Chọn D
Gọi là hình chiếu vuông góc của trên , là hình chiếu vuông góc của trên . Ta có
. Vậy mặt phẳng thỏa mãn yêu cầu đề bài phải chứa và vuông góc với .
Gọi . Ta có ,
.
Vậy mặt phẳng có vecto pháp tuyến và đi qua điểm .
Phương trình mặt phẳng .
( )
0 0 0
;;M x y z
( ) ( )
( )
2 2 2
0 0 0
2 4 1 2 3 1 1 0 m m x m m y m z m m+ − + − + − + + =
( ) ( )
2
0 0 0 0 0 0 0
1 2 4 6 2 1 0 x y m x y z m y z m − + + − + + − + =
0 0 0
0 0 0 0
0 0 0
1 0 2
2 4 6 0 1
2 1 0 0
x y x
x y z y
y z z
− + = = −
− + = = −
− + = =
( )
2; 1;0M − −
( )
( )
,d A P AM
29AM =
( )
AM P⊥
M
P
d
H'
H
A
H
A
d
H
A
( )
P
AH AH
( )
P
d
AH
( )
1 2 ; 2 ;2 ,H t t t t+ − +
( )
2 1;1 ;2t 4AH t t= − + −
( )
2;1;2
d
u =
. 0 9 9 0 1
d
AH u t t= − = =
( )
P
( )
1;2; 2AH =−
( )
1; 2;0Bd−
( )
: 2 2 3 0P x y z+ − + =
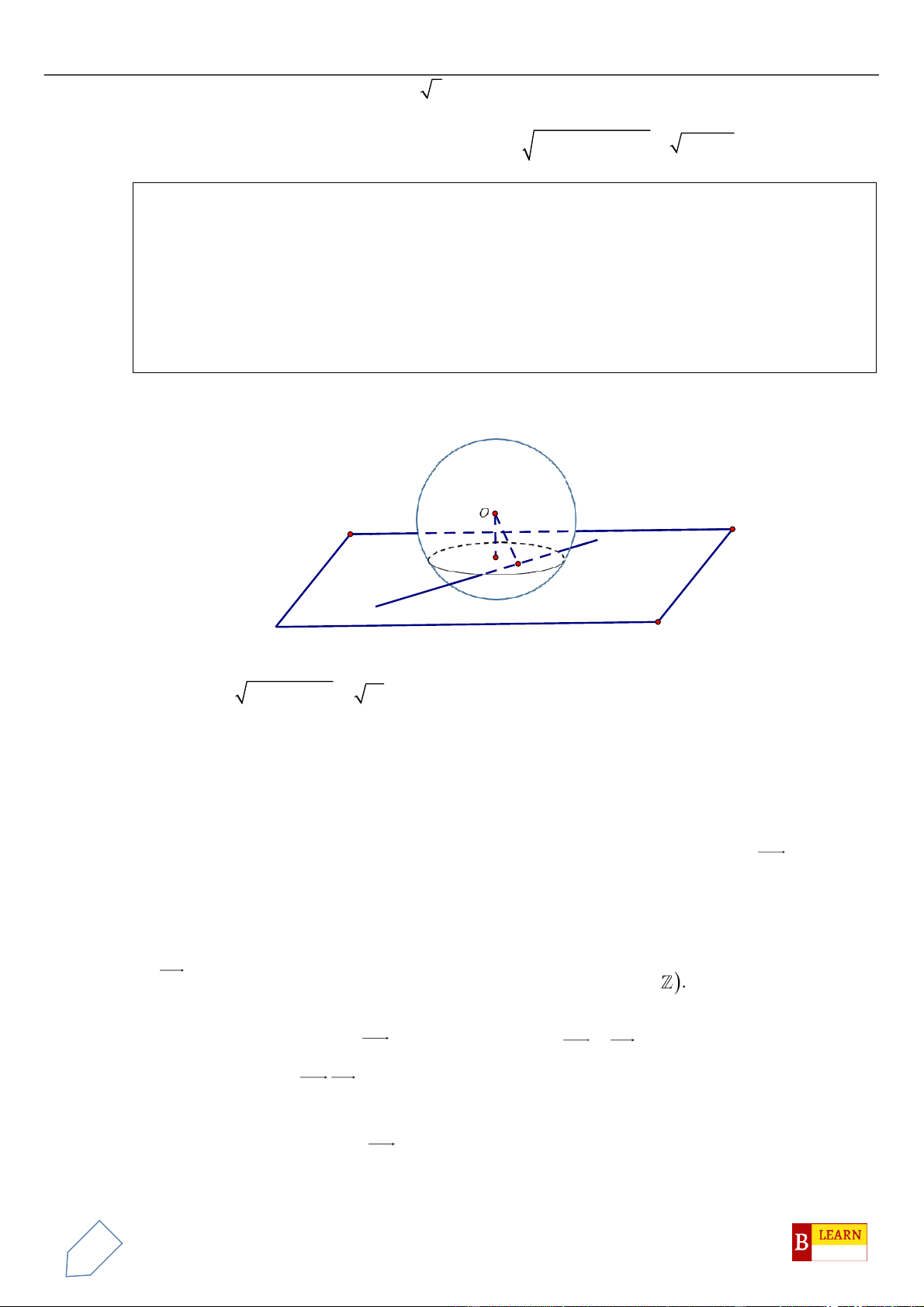
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
178
Mặt cầu có tâm . Ta có .
Vậy cắt theo đường tròn có bán kính
Phân tích: Bài có nhiều hướng giải,như đưa về phương trình chùm mặt phẳng rồi đánh giá max –
min, tuy nhiên dùng hình học là đơn giản hơn cả.
Yêu cầu các em nắm vững được vị trí tương đối của điểm, đường, mặt và mặt cầu trong không
gian.
Trong các dạng bài chứa điểm, chứa đường, thỏa mãn khoảng cách max thì nhìn chung khoảng
cách max chính là khoảng cách từ điểm- đường ,điểm – điểm theo dữ kiện đề bài.
Câu 19. Chọn B
Mặt cầu
( )
S
có tâm
( )
0;0;0O
và có bán kính
10.R =
Ta có
2 2 2
1 2 3 14OA R= + + =
suy ra
A
nằm trong mặt cầu, nên đường thẳng
AB
luôn cắt
mặt cầu tại
2
điểm phân biệt.
Gọi
( )
P
là mặt phẳng cần tìm,
r
là bán kính đường tròn giao tuyến,
H
là hình chiếu vuông góc
của
O
lên
( )
P
và
K
là hình chiếu vuông góc của
O
lên đường thẳng
.AB
Do
2 2 2
100r OH R+ = =
nên
r
nhỏ nhất khi
OH
lớn nhất.
Từ
OH OK
suy ra
OH
lớn nhất khi
HK
và
( )
P
là mặt phẳng qua
A
nhận
OK
làm vectơ
pháp tuyến.
Ta có:
+
( )
1;1;1AB =
nên đường thẳng
AB
có phương trình
( )
1
2 .
3
xt
y t t
zt
=+
= +
=+
+ Gọi
( )
1 ;2 ;3K t t t+ + +
thì
( )
1 ;2 ;3OK t t t= + + +
, do
OK AB⊥
nên
. 0 1 2 3 0 2OK AB t t t t= + + + + + = = −
Suy ra
( )
1;0;1K −
.
+
( )
P
qua
( )
1;2;3A
và nhận
( )
1;0;1OK −
làm vectơ pháp tuyến nên có phương trình
2 0 2 0x z x z− + − = − + =
.
( )
S
( )
3;2; 1 , 2 5IR−=
( )
( )
,4d I P R=
( )
S
( )
P
( )
( )
22
, 20 16 2r R d I P= − = − =
H
K

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
179
Câu 20. Chọn A
Ta có: nên các điểm đều nằm cùng phía
so với mặt phẳng và đường thẳng luôn cắt mặt phẳng tại một điểm cố định.
Từ bất đẳng thức véc tơ Ta có Dấu bằng xảy ra khi là
giao điểm của đường thẳng với mặt phẳng .
Do đó , đạt được khi .
Câu 21. Chọn B
Ta có: nên hai điểm và
cùng nằm về một phía của mặt phẳng .
Ta có , nên lớn nhất khi và chỉ khi .
Phương trình đường thẳng : , do đó tọa độ điểm là nghiệm của hệ phương trình
. Do đó .
Câu 22. Chọn D
Ta có: nên hai điểm và
nằm khác phía so với mặt phẳng . Nên đạt giá trị nhỏ nhất khi .
Phương trình đường thẳng : , do đó tọa độ điểm là nghiệm của hệ phương
trình
2 / 7
2 / 7
3/ 7
1/ 7
t
x
y
z
=
=
=−
=
.Do đó ,
.
Câu 23. Chọn D
Vì
( )
P
chứa trục
Oz
nên luôn có
( )
( )
( )
;;d M P d M Oz
.
( )( )
2 2 2019 2 2 2019 0
A A A B B B
x y z x y z+ + + + + +
,AB
()P
AB
()P
| | | | .u v u v− −
.AM BM AB−
M
AB
()P
( ) ( ) ( )
2 2 2
4 1 4 2 5 3 17
Max
AM BM AB− = = − + − + − =
( )
M AB P=
( )( ) ( )( )
1 1 1 1 0 1 3 1 4 1 0
A A A B B B
x y z x y z− + + − + + = − + + + + +
A
B
( )
26MA MB AB− =
MA MB−
( )
M AB
=
AB
12
12
4
xt
yt
zt
=+
=−
=
M
12
12
4
10
xt
yt
zt
x y z
=+
=−
=
− + + =
1
8
3
4
5
4
1
2
t
x
y
z
=−
=
=
=−
3 5 1
;;
4 4 2
M
−
( )( ) ( )( )
2 1 2 1 0 1 2.1 1 1 1 4 1 0
A A A B B B
x y z x y z− + − − + − = + + − − − −
A
B
( )
MA MB+
( )
M AB
=
AB
12
13
xt
yt
zt
=
= − +
=−
M
12
13
2 1 0
xt
yt
zt
x y z
=
= − +
=−
− + − =
2 3 1
;;
7 7 7
M
−
2
7
M
x =
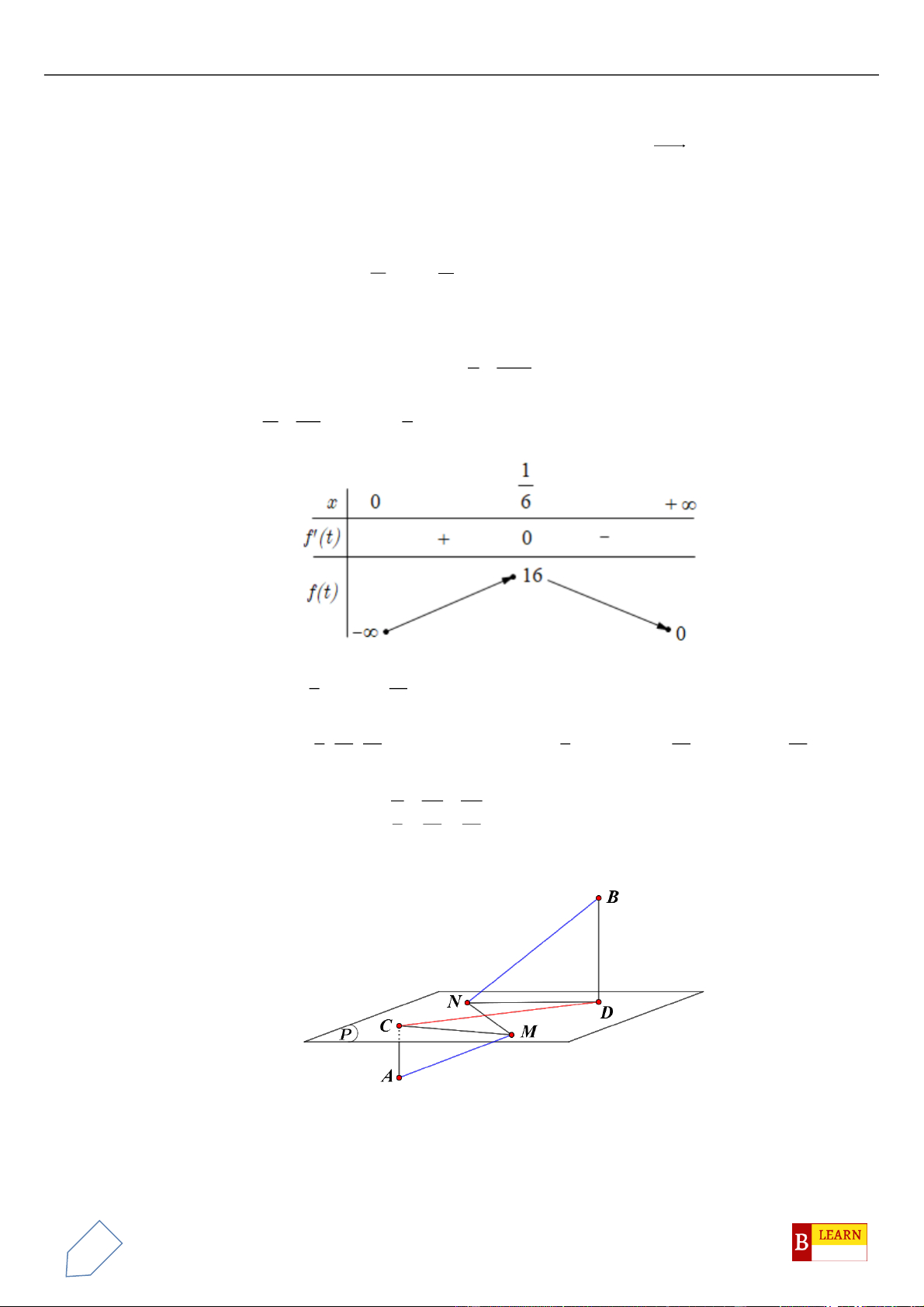
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
180
Suy ra
( )
( )
;d M P
đạt giá trị lớn nhất bằng
( )
;d M Oz MH=
, với
H
là hình chiếu của
M
trên
trục
Oz
.
Dễ có
( )
0;0;3H
. Vậy
( )
P
đi qua
( )
0;0;3H
, có véc tơ pháp tuyến
( )
1; 2;0MH −−
.
( )
: 2 0 2 0 2; 0 2P x y x y A B C A B C− − = + = = = = + + =
Câu 24. Chọn B
Đặt
=+t b c
( )
0t
;
2
22
2
+
t
bc
;
2
4
t
bc
.
( )
( )
2 2 2
5 9 2a b c ab bc ca+ + = + +
( ) ( )
2
2
5 5 9 28 + + − + =a b c a b c bc
2 2 2
5 5 9 7 + − a t at t
( )( )
5 2 0 + − a t a t
2at
. Vậy
( )
3
41
27
− =Q f t
tt
với
0t
.
Ta có
( )
24
41
0
9
= − + =ft
tt
1
6
=t
(vì
0t
). Ta có bảng biến thiên
Vậy
16=
max
Q
1
3
=a
;
1
12
==bc
.
Suy ra tọa độ điểm
1 1 1
;;
3 12 12
A
; tọa độ các điểm
1
;0;0
3
M
;
1
0; ;0
12
N
;
1
0;0;
12
P
.
Phương trình mặt phẳng
( )
MNP
1
1 1 1
3 12 12
+ + =
x y z
3 12 12 1 0 + + − =x y z
.
Câu 25. Chọn A
Xét hệ
( ) ( )
22
2
2 2 2
1 1 4
2 2 0
x y z
x y z y
− + + + =
+ + + − =
2 2 2
2 2 2
2 2 2 0
2 2 0
x y z x y
x y z y
+ + − + − =
+ + + − =
0x=
Vậy
( )
:0Px=
( )
(
P
chính là mặt phẳng
( )
)
Oyz
.
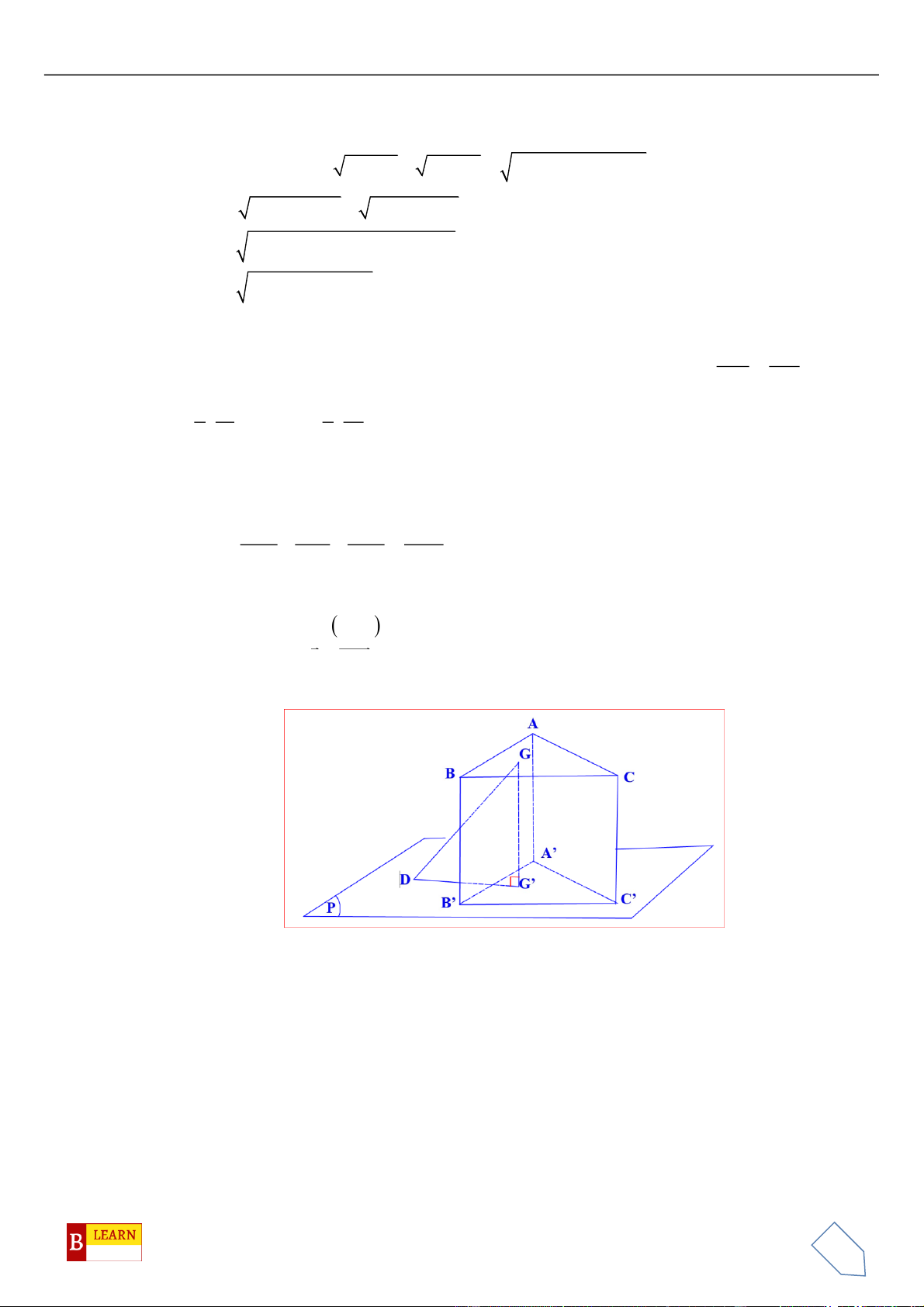
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
181
Gọi
( )
0;0;0C
và
( )
0;3;4D
lần lượt là hình chiếu vuông góc của
( )
1;0;0A −
và
( )
2;3;4B
trên
mặt phẳng
( )
P
. Suy ra
1AC =
,
2BD =
,
5CD =
.
Áp dụng bất đẳng thức
( ) ( )
22
2 2 2 2
a b c d a c b d+ + + + + +
, ta được
( ) ( )
( )
2 2 2 2
22
2
9
AM BN AC CM BD DN
AC BD CM DN
CM DN
+ = + + +
+ + +
+ +
Lại có
5CM MN ND CD+ + =
nên suy ra
4CM ND+
. Do đó
5AM BN+
.
Đẳng thức xảy ra khi
C
,
M
,
N
,
D
thẳng hàng theo thứ tự đó và
AC BD
CM DN
=
, tức là
4 16
0; ;
5 15
M
và
7 28
0; ;
5 15
N
. Vậy giá trị nhỏ nhất của
AM BN+
là 5.
Câu 26. Chọn D
Gọi
H
là hình chiếu của gốc tọa độ
O
lên mặt phẳng
( )
P
, do tứ diện
OABC
là tứ diện vuông tại
O
nên ta có
+ + =
2 2 2 2
1 1 1 1
OA OB OC OH
nhỏ nhất khi và chỉ khi
OH
lớn nhất.
Mặt khác
( )
( )
,OH d O P OM=
.
Vậy mặt phẳng
( )
( )
( )
( )
1;2;1
: : 2 6 0
1;2;1
M
P P x y z
n OM
+ + − =
==
.
Câu 27. Chọn C
* Gọi
A
,
B
,
C
lần lượt là hình chiếu của
A
,
B
,
C
xuống
( )
P
.
Gọi
G
là trọng tâm
ABC
( )
2;2;3G
.
Gọi
G
là hình chiếu của
G
xuống mặt phẳng
( )
P
.
* Tổng khoảng cách từ
A
,
B
,
C
xuống
( )
P
, theo giả thiết thì
( ) ( )
//P ABC
nên
3d AA BB CC GG
= + + =
( )
max
max
d GG
.
Mà
GG GD
(mối quan hệ đường xiên – hình chiếu)

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
182
( )
max
d G D P
qua
( )
2; 1; 3D − − −
nhận
( )
4;3;6DG =
là véc tơ pháp tuyến nên có
phương trình:
( ) ( ) ( )
4 2 3 1 6 3 0x y z+ + + + + =
hay
( )
: 4 3 6 29 0P x y z+ + + =
. Từ đó suy ra
4a =
;
3b =
;
6c =
. Vậy
4 3 6 13a b c+ + = + + =
.
Câu 28. Chọn C
Cách 1:
Ta có
2 2 2 2 2 2
2 4 4 4 2T MA MB MC a b c a b c= + + = + + = + +
( )
( )
2
2 2 2
2
22
2
3
2 2 2 6
2
1 1 2
a b c
abc
+−
= + + = =
+ + −
2T MA MB MC= + +
đạt giá trị nhỏ nhất bằng
6
1
1 1 2 2
2 3 0 1
a b c
ab
a b c c
= = = =
−
+ − − = = −
Cách 2:
Gọi
I
là trung điểm của
AB
,
J
là trung điểm của
IC
. Tính được
( ) ( )
1; 3;1 , 0;0;0IJ−−
.
Khi đó
2 2 2 4 4T MA MB MC MI MC MJ MJ= + + = + = =
. Do đó
T
đạt giá trị nhỏ nhất khi
M
là hình chiếu vuông góc của
J
trên
( )
P
.
Gọi
là đường thẳng đi qua
J
và vuông góc với
( )
P
. Khi đó
có phương trình
2
xt
yt
zt
=
=
=−
. Tọa
độ của
M
là nghiệm của hệ phương trình
1
2
2 3 0
1
1 1 1 1
; ; 1 1 0
2
2 2 2 2
1
2
2
1
t
x y z
xt
x
MS
yt
y
zt
z
=
+ − − =
=
=
− = + − =
=
=
=−
=−
Câu 29. Chọn A
Ta có
( )
1;3;2G −
là trọng tâm tam giác
ABC
.
Khi đó
( ) ( ) ( )
( )
2 2 2
2 2 2
2 2 2
2 2 2 2
2 2 2 2
32
3
G
MA MB MC MA MB MC
MG GA MG MG
GA GB GC MG GA GB GC
G
B GC
MG
MG A GB GC
+ + = + +
+ + + + +=
+ + + + +
++= +
=+

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
183
Do đó
2 2 2
MA MB MC++
nhỏ nhất khi và chỉ khi
MG
nhỏ nhất
M là hình chiếu của G lên
mặt phẳng
( )
Oxy
. Do hình chiếu vuông góc của G lên mặt phẳng
( )
Oxy
có tọa độ
( )
1;3;0−
Vậy
( )
1;3;0M −
. Từ đó
( )
2
2
1 103T += − =
.
Câu 30. Chọn A
Ta có
( )
1;3;2G −
là trọng tâm tam giác
ABC
.
Khi đó
( ) ( ) ( )
( )
2 2 2
2 2 2
2 2 2
2 2 2 2
2 2 2 2
32
3
G
MA MB MC MA MB MC
MG GA MG MG
GA GB GC MG GA GB GC
G
B GC
MG
MG A GB GC
+ + = + +
+ + + + +=
+ + + + +
++= +
=+
Do đó
2 2 2
MA MB MC++
nhỏ nhất khi và chỉ khi
MG
nhỏ nhất
M là hình chiếu của G lên
mặt phẳng
( )
Oxy
. Do hình chiếu vuông góc của G lên mặt phẳng
( )
Oxy
có tọa độ
( )
1;3;0−
Vậy
( )
1;3;0M −
. Từ đó
( )
2
2
1 103T += − =
.
Câu 31. Chọn D
Ta có:
( )
. . .cos ;a b a b a b=
.
Do
( )
cos ; 1ab
nên:
..a b a b
. Dấu bằng xảy ra khi
a
,
b
cùng hướng.
Gọi
G
là là điểm thỏa mãn
0GA GB GC GO+ + + =
. Khi đó, tọa độ
G
là
1
4
3
4
2
4
A B C O
G
A B C O
G
A B C O
G
x x x x
x
y y y y
y
z z z z
z
+ + +
==
+ + +
==
+ + +
==
( )
1;2;3 14G GA GB GC GO = = = =
.
Đặt
T MA MB MC MO= + + +
.
14 14 14 14 14T MA MB MC MO = + + +
. . . .GAMA GB MB GC MC GO MO= + + +
. . . .GAMA GB MB GC MC GO MO + + +
( ) ( ) ( ) ( )
. . . .GA MG GA GB MG GB GC MG GC GO MG GO= + + + + + + +
( )
2 2 2 2
.GA GB GC GO MG GA GB GC GO= + + + + + + +
2 2 2 2
56 4 14GA GB GC GO T= + + + =
.
Giá trị nhỏ nhất
T MA MB MC MO= + + +
bằng
4 14
khi 4 cặp véc tơ:
GA
và
MA
;
GB
và
MB
;
GC
và
MC
;
GO
và
MO
cùng hướng. Khi đó
M
trùng với
G
.
( )
1;2;3M
. Đường thẳng
có một véctơ chỉ phương
( )
1
1; 1; 2
2
u MH= = − −
.
Vậy phương trình đường thẳng
là:
31
1 1 2
x y z−+
==
−−
.
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
184
Câu 32. Chọn A
Gọi
,HK
lần lượt là hình chiếu vuông góc của
,AB
lên mặt phẳng
( )
P
.
Theo định lí Pitago có
2 2 2 2 2 2
2 2 2 2 2 2
( ,( )) 9
.
( ,( )) 9
MA MH HA MH d A P MH
NB NK KB NK d B P NK
= + = + = +
= + = + = +
Đặt
2 2 2 2
, 2 3 2( 9) 3( 9).MH a NK b MA NB a b= = + = + + +
Mặt khác theo bất đẳng thức đường gấp khúc ta có:
3 1 3 2 .HM MN NK HK a b b a+ + = + + −
Do đó
( ) ( )
2 2 2 2 2
2 3 2 9 3 (2 ) 9 5 12 57 49,8.MA NB a a a a+ + + − + = − +
Vậy giá trị nhỏ nhất
22
23MA NB+
bằng
49,8
khi
1,2; 0,8ab==
và các điểm
,MN
thuộc đoạn
thẳng
HK
.
Câu 33. Chọn D
Ta có
( ) ( )
: 1 2 1 0P mx m y z m+ + − − − =
,
m
( ) ( )
20
: 2 1 0
10
xy
P m x y y z
yz
+ − =
+ − + − − =
− − =
.
Vậy mặt phẳng
( )
P
luôn chứa đường thẳng
( )
2
:
1
xt
yt
zt
=−
=
= − +
.
Gọi
( )
2 ; ; 1K t t t− − +
là hình chiếu của
H
lên đường thẳng
( )
,
( )
1 ; 3; 1HK t t t= − − − − +
.
Vì
( )
HK ⊥
nên:
( )
1 3 1 0 1t t t t− − − + − − + = =
( )
1;1;0K
.
Gọi mặt phẳng
( )
là mặt phẳng đi qua
K
và vuông góc với đường thẳng
( )
.
( )
:0x y z
− + + =
( )
OQ
. Vậy:
m
H
thuộc mặt cầu đường kính
HK
.
+
( )
m
HQ
.
( )
T
là một đường tròn tâm
( )
2;2;0I
, bán kính
2
2
HK
R ==
và
22OI =
.
Vậy:
32a OI R= + =
;
2b OI R= − =
42ab + =
.
K
I
H
H
m
P

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
185
CHỦ ĐỀ 3 : PHƯƠNG TRÌNH ĐƯỜNG THẲNG
❖ Phương trình ttham số của đường thẳng
đi qua điểm
( )
;;
o o o o
M x y z
và có vectơ chỉ phương
1 2 3
( ; ; )a a a a=
,
0a
có dạng là :
01
02
03
(t R)
x x a t
y y a t
z z a t
=+
= +
=+
.
❖ Nếu
1 2 3
,,a a a
đều khác không .Phương trình đường thẳng
viết dưới dạng chính tắc như sau:
0 0 0
1 2 3
x x y y z z
a a a
− − −
==
❖ Vị trí tương đối giữa hai đường thẳng
▪ Trong không gian
Oxyz
cho hai đường thẳng
''
1
1
''
22
''
03
3
'
: ': '
'
o
o
oo
o
x x a t
x x a t
d y y a t d y y a t
z z a t
z z a t
=+
=+
= + = +
=+
=+
có VTCP
u
đi qua
o
M
và
'
d
có vtcp
'u
đi qua
'
o
M
▪
( )
( )
'
dd
[ , ']=0
M'
o
uu
d
( )
( )
'
dd
0
[ , ']=0
M'
uu
d
▪
( )
d
cắt
( )
'
d
'
0
, ' 0
, ' . 0
o
uu
u u M M
=
( )
d
chéo
( )
'
d
'
00
, ' . 0u u M M
❖ Vị trí tương đối của đường thẳng và mặt phẳng
▪ Trong không gian
Oxyz
cho đường thẳng
d
đi qua điểm
( )
;;
o o o
M x y z
và có vectơ chỉ phương
1 2 3
( ; ; )a a a a=
và mặt phẳng
( )
:0Ax By Cz D
+ + + =
có vecto pháp tuyến
( ; ; )n A B C=
▪
( )
d
cắt
( )
.0an
▪
( )
d
//
( )
.0
()
an
M
=
▪
( )
d
nằm trên mặt phẳng
( )
.0
()
an
M
=
❖ Khoảng cách từ điểm đến mặt phẳng
▪ Khoảng cách từ
( )
;;
o o o o
M x y z
đến mặt phẳng
( )
:0Ax By Cz D
+ + + =
cho bởi công thức
0 0 0
0
2 2 2
Ax
( , )
By Cz D
dM
A B C
+ + +
=
++
❖ Khoảng cách từ một điểm đến một đường thẳng
▪ Khoảng cách từ đường thẳng
d
đi qua điểm
o
M
có VTCP
u
đến điểm
M
cho bởi công
thức
0
[M , ]
( , )
Mu
dM
u
=
LÍ THUYẾT
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
186
❖ Khoảng cách giữa hai đường thẳng chéo nhau
▪ Trong không gian
Oxyz
cho đường thẳng
d
đi qua
( )
;;
o o o
M x y z
; có VTCP
1 2 3
( ; ; )a a a a=
và đường thẳng
'
d
đi qua
( )
' ' ' '
;;
o o o
M x y z
có VTCP
' ' ' '
1 2 3
( ; ; )a a a a=
. Khi đó khoảng cách giữa
hai đường thẳng này là :
[ , ']. '
( , ')
[ , ']
hop
day
a a MM
V
ddd
S
aa
==
❖ Góc giữa hai đường thẳng:
▪ Trong không gian
Oxyz
cho hai đường thẳng
() đi qua
( )
;;
o o o
M x y z
có VTCP
1 2 3
( ; ; )a a a a=
(’) đi qua
( )
' ' ' '
;;
o o o
M x y z
có VTCP
1 2 3
' ( ' ; ' ; ' )a a a a=
▪ Khi đó góc giữa hai đường thẳng này được cho bởi công thức sau đây:
1 1 2 2 3 3
2 2 2 2 2 2
1 2 3 1 2 3
.'
. ' . ' . '
os os( , ')
.'
. ' ' '
aa
a a a a a a
c c a a
aa
a a a a a a
++
= = =
+ + + +
❖ Góc giữa đường thẳng và mặt phẳng:
▪ Trong không gian
Oxyz
cho hai đường thẳng
() đi qua
o
M
có VTCP
1 2 3
( ; ; )a a a a=
, mặt phẳng
( )
có VTPT
( ; ; )n A B C=
▪ Gọi
là góc hợp bởi () và mặt phẳng
( )
, khi đó góc giữa đường thẳng và mặt phẳng là
1 2 3
2 2 2 2 2 2
1 2 3
Aa +Ba +Ca
sin os( , )
A.
c a n
B C a a a
==
+ + + +
▪ NOTE: Cho tam giác
ABC
▪ Đường phân giác trong của góc
BAC
có vectơ chỉ phương là
11
u AB AC
AB AC
=+
.
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
187
Lời giải
Cách 1
Gọi
( )
P
là mặt phẳng qua
A
và vuông góc với
'
,dB
là hình chiếu của
B
lên
( )
P
Khi đó đường thẳng
chính là đường thẳng AB’ và
B'Au =
Ta có
( )
( 2; 2;1)
: (P): 2 2 9 0
(2;2; 1)
Pd
Qua A
P x y z
VTPT n u
−−
+ − + =
= = −
Gọi
'
d
là đường thẳng qua
B
và song song
'
d
12
' 2 2
3
xt
d y t
zt
=+
= +
= − −
'
B
là giao điểm của
'
d
và
( )
P
'( 3; 2; 1) ' (1;0;2)B u B A − − − = =
Chọn A
Cách 2: TƯ DUY TOÁN HỌC 4.0
Không cần viết phương trình mặt phẳng
( )
P
qua
A
và vuông góc với
d
.
Gọi
'
d
là đường thẳng qua
B
và song song
'
d
12
' 2 2
3
xt
d y t
zt
=+
= +
= − −
''
Bd
( )
' 2 3; 2 4; 4B A t t t = − − − − +
'
AB d⊥
. ' 0 2 ' (1;0;2)
d
u B A t u B A = = − = =
.
Lời giải
Chọn C
Phương trình tham số của đường phân giác trong góc
A
:
64
63
xt
yt
zt
=
=−
=−
.
( )
d
VÍ DỤ MINH HỌA
VÍ DỤ 1: Trong không gian với hệ tọa độ Oxyz, cho hai điểm
( 2; 2;1),A −−
( )
1; 2; 3B −
và đường thẳng
15
:
2 2 1
x y z
d
+−
==
−
. Tìm vectơ chỉ phương
u
của đường thẳng
qua A, vuông góc với d
đồng thời cách điểm B một khoảng bé nhất.
A.
(1;0;2)u =
B.
(2;2; 1)u =−
C.
(25; 29; 6)u = − −
D.
(2;1;6)u =
VÍ DỤ 2: Trong không gian với hệ tọa độ
Oxyz
, cho tam giác
ABC
có phương trình đường phân giác
trong góc
A
là:
66
1 4 3
x y z−−
==
−−
. Biết rằng điểm
( )
0;5;3M
thuộc đường thẳng
AB
và
điểm
( )
1;1;0N
thuộc đường thẳng
AC
. Vectơ nào sau đây là vectơ chỉ phương của đường
thẳng
AC
.
A.
( )
0;1; 3u =−
. B.
( )
1;2;3u =
. C.
( )
0;1;3u =
. D.
( )
0; 2;6u =−
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
188
Gọi
D
là điểm đối xứng với
M
qua
( )
d
. Khi đó
D AC
đường thẳng
AC
có một vectơ chỉ
phương là
ND
. Ta xác định điểm
D
.
Gọi
K
là giao điểm
MD
với
( )
d
. Ta có
( )
;6 4 ;6 3K t t t−−
;
( )
;1 4 ;3 3MK t t t= − −
.
Ta có
d
MK u⊥
với
( )
1; 4; 3
d
u = − −
nên
( ) ( )
4 1 4 3 3 3 0t t t− − − − =
1
2
t=
.
19
;4;
22
K
.
K
là trung điểm
MD
nên
2
2
2
D K M
D K M
D K M
x x x
y y y
z z z
=−
=−
=−
1
3
6
D
D
D
x
y
z
=
=
=
hay
( )
1;3;6D
.
Một vectơ chỉ phương của
AC
là
( )
0; 2; 6DN = − −
. Hay
( )
0;1;3u =
là vectơ chỉ phương.
Lời giải
Chọn D
Đường thẳng
2 5 2
:
3 5 1
x y z
d
+ − −
==
−−
có một VTCP
( )
3; 5; 1u = − −
.
Mặt phẳng
( )
:2 2 0P x z+ − =
vó một VTPT
( )
2; 0; 1n
.
Đường thẳng
có một VTCP
( )
, 5 1; 1; 2a u n
= = − −
.
Đường thẳng
có phương trình
1 3 4
:
1 1 2
x y z− + −
= =
−
.
Lời giải
Chọn A
Cách 1:
Gọi là giao điểm của và .
, VTPT của là .
.
( )
2 2 ; 2 ; 3A t t t d+ + +
d
( )
1 2 ; ; 3MA t t t= + +
( )
( )
( )
1;1;1n
=
( )
( )
MA n
⊥
( )
. 0 1 2 3 0 1MA n t t t t
= + + + + = = −
VÍ DỤ 3: Trong không gian tọa độ
Oxyz
, cho điểm
( )
1; 3; 4M −
, đường thẳng
2 5 2
:
3 5 1
x y z
d
+ − −
==
−−
và mặt phẳng
( )
:2 2 0P x z+ − =
. Viết phương trình đường thẳng
qua
M
vuông góc với
d
và song song với
( )
P
.
A.
1 3 4
:
1 1 2
x y z− + −
= =
−
. B.
1 3 4
:
1 1 2
x y z− + −
= =
−−
.
C.
1 3 4
:
1 1 2
x y z− + −
= =
− − −
. D.
1 3 4
:
1 1 2
x y z− + −
= =
−
.
VÍ DỤ 4: Trong không gian với hệ toạ độ , cho đường thẳng nằm trong mặt phẳng
đồng thời đi qua điểm và cắt đường thẳng
. Một vectơ chỉ phương của là.
A.
( )
1;1; 2u =−
B.
( )
1;0; 2u =−
C.
( )
1;1;2u =−
D.
( )
1; 1;2u = − −
Oxyz
( )
: 3 0x y z
+ + − =
( )
1;2;0M
2 2 3
:
2 1 1
x y z
d
− − −
==
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
189
. Vậy .
Cách 2:
Gọi . .
. .
Lời giải
Chọn C
Đường thẳng
d
đi qua điểm
( )
1; 2; 5A −
và vuông góc với mặt phẳng
( )
:2 3 4 5 0P x y z+ − + =
nên nhận
( )
2; 3; 4u =−
là véctơ chỉ phương
Phương trình đường thẳng
d
là
12
: 2 3
54
xt
d y t
zt
=+
=+
= − −
.
Lời giải
Chọn D
Gọi
( )
Q
là mặt phẳng đi qua
( )
2;2; 3M −
và song song với mặt phẳng
( )
P
.
Suy ra
( )
:2 3 0Q x y z+ + − =
. Do
( )
// P
nên
( )
Q
.
( )
,dN
đạt giá trị nhỏ nhất
đi qua
N
, với
N
là hình chiếu của
N
lên
( )
Q
.
Gọi
d
là đường thẳng đi qua
N
và vuông góc
( )
P
,
42
:2
1
xt
d y t
zt
= − +
=+
=+
.
Ta có
Nd
( )
4 2 ;2 ;1N t t t
− + + +
;
( )
4
3
N Q t
=
4 10 7
;;
333
N
−
.
( )
;;u a b c=
cùng phương
10 4 16
;;
333
MN
=−
.
Do
a
,
b
nguyên tố cùng nhau nên chọn
( )
5;2;8u =−
. Vậy
15abc+ + =
.
( ) ( )
1; 1; 2 1 1; 1; 2MA − − = − −
( )
1; 1; 2
d
u =−
( )
Bd
=
( )
2 2 ; 2 ; 3B d B t t t + + +
( ) ( )
2 2 2 3 3 0 1 0;1;2B t t t t B
+ + + + + − = = −
( ) ( )
1;1; 2 1;1; 2
d
BM u− −
VÍ DỤ 5: Trong không gian với hệ tọa độ
Oxyz
, phương trình của đường thẳng
d
đi qua điểm
( )
1; 2; 5A −
và vuông góc với mặt phẳng
( )
:2 3 4 5 0P x y z+ − + =
là
A.
2
: 3 2
45
xt
d y t
zt
=+
=+
= − −
. B.
12
: 2 3
54
xt
d y t
zt
=+
=+
= − +
. C.
12
: 2 3
54
xt
d y t
zt
=+
=+
= − −
. D.
2
: 3 2
45
xt
d y t
zt
=+
=+
=+
.
VÍ DỤ 5: Trong không gian với hệ tọa độ
Oxyz
, cho các điểm
( )
2;2; 3M −
và
( )
4;2;1N −
. Gọi
là
đường thẳng đi qua
M
, nhận vecto
( )
;;u a b c=
làm vectơ chỉ phương và song song với mặt
phẳng
( )
:2 0P x y z+ + =
sao cho khoảng cách từ
N
đến
đạt giá trị nhỏ nhất. Biết
a
,
b
là hai số nguyên tố cùng nhau. Khi đó
abc++
bằng:
A.
14
. B.
13
. C.
16
. D.
15
.
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
190
Lời giải
Chọn B
( ) ( )
12
1 2 ; ; 2 ; 1 ; 2 3 ;2 2A d A a a a B d B b b b + − − + − + −
có vectơ chỉ phương
( )
2 ;3 2; 2 4AB b a b a b a= − − − − + +
( )
P
có vectơ pháp tuyến
( )
1;1;1
P
n =
Vì
( )
// P
nên
. 0 1
PP
AB n AB n b a⊥ = = −
.Khi đó
( )
1;2 5;6AB a a a= − − − −
( ) ( ) ( )
2
2 2 2
2
5 49 7 2
1 2 5 6 6 30 62 6 ;
2 2 2
AB a a a a a a a
= − − + − + − = − + = − +
Dấu
""=
xảy ra khi
5 5 9 7 7
6; ; , ;0;
2 2 2 2 2
a A AB
= − = −
Đường thẳng
đi qua điểm
59
6; ;
22
A
−
và vec tơ chỉ phương
( )
1;0;1
d
u =−
Lời giải
Chọn C
( )
1
S
có tâm
( )
1
3; 2; 2I
, bán kính
1
2R =
.
( )
2
S
có tâm
( )
2
1; 0; 1I
, bán kính
2
1R =
.
Ta có:
1 2 1 2
3I I R R= = +
, do đó
( )
1
S
và
( )
2
S
tiếp xúc ngoài với nhau tại điểm
5 2 4
;;
3 3 3
A
.
Vì
d
tiếp xúc với hai mặt cầu, đồng thời cắt đoạn thẳng nối hai tâm
12
II
nên
d
phải tiếp xúc với
hai mặt cầu tại
A
12
d I I⊥
. Mặt khác
( )
;d d O d OA=
max
d OA=
khi
d OA⊥
.
Khi đó,
d
có một vectơ chỉ phương là
( )
12
, 6; 3; 6I I OA
= − −
( )
2; 1; 2u = −
.Vậy
2S =
.
VÍ DỤ 5: Trong không gian với hệ tọa độ
Oxyz
cho hai đường thẳng
1
12
:
2 1 1
x y z
d
−+
==
−
và
2
1 2 2
:
1 3 2
x y z
d
− + −
==
−
. Gọi
là đường thẳng song song với
( )
: 7 0P x y z+ + − =
và cắt
12
, dd
lần lượt tại hai điểm
,AB
sao cho
AB
ngắn nhất. Phương trình của đường thẳng
là.
A.
12
5
9
xt
y
zt
=−
=
= − +
. B.
6
5
2
9
2
xt
y
zt
=−
=
= − +
. C.
6
5
2
9
2
x
yt
zt
=
=−
= − +
. D.
62
5
2
9
2
xt
yt
zt
=−
=+
= − +
.
VÍ DỤ 5: Cho
2
mặt cầu
( ) ( ) ( ) ( )
2 2 2
1
: 3 2 2 4S x y z− + − + − =
,
( ) ( ) ( )
22
2
2
: 1 1 1S x y z− + + − =
. Gọi
d
là đường thẳng đồng thời tiếp xúc với hai mặt cầu trên, cắt đoạn thẳng nối tâm hai mặt cầu và
cách gốc tọa độ
O
một khoảng lớn nhất. Nếu
( )
; 1;u a b=
là một vectơ chỉ phương của
d
thì
tổng
23S a b=+
bằng bao nhiêu?
A.
0S =
B.
4S =
C.
2S =
D.
1S =

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
191
DẠNG 1. TÌM VECTO CHỈ PHƯƠNG CỦA ĐƯỜNG THẲNG
Câu 1. Trong không gian
Oxyz
, cho hai mặt phẳng
( )
: 6 0P x y− − =
và
( )
Q
. Biết rằng điểm
( )
2; 1; 2H −−
là hình chiếu vuông góc của gốc tọa độ
( )
0;0;0O
xuống mặt phẳng
( )
Q
. Số đo góc
giữa mặt phẳng
( )
P
và mặt phẳng
( )
Q
bằng
A.
45
. B.
60
. C.
30
. D.
90
.
Câu 2. Trong không gian với hệ tọa độ
Oxyz
, phương trình mặt phẳng vuông góc với đường thẳng
22
1 2 3
x y z−+
==
−
và đi qua điểm
( )
3; 4;5A −
là
A.
3 4 5 26 0x y z− + − − =
. B.
2 3 26 0x y z− + + =
.
C.
3 4 5 26 0x y z− + − =
. D.
2 3 26 0x y z− + − + =
.
Câu 3. Trong không gian với hệ tọa độ
,Oxyz
véctơ nào trong 4 phương án dưới đây là một véc tơ chỉ
phương của đường thẳng có phương trình
1 3 3
3 2 1
x y z
.
A.
3
3; ;1
2
a
=
. B.
( )
9;2; 3a =−
. C.
( )
3;2;1a =
. D.
2
3; ;1
3
a
=
.
Câu 4. Trong không gian với hệ tọa độ
,Oxyz
véctơ nào trong 4 phương án dưới đây là một véc tơ chỉ
phương của đường thẳng có phương trình
1 3 3
3 2 1
x y z
.
A.
3
3; ;1
2
a
=
. B.
( )
9;2; 3a =−
. C.
( )
3;2;1a =
. D.
2
3; ;1
3
a
=
.
Câu 5. Trong không gian
Oxyz
, cho tam giác
ABC
có
( )
2;3;3A
, phương trình đường trung tuyến kẻ
từ
B
là
3 3 2
1 2 1
x y z− − −
==
−−
, phương trình đường phân giác trong của góc
C
là
2 4 2
2 1 1
x y z− − −
==
−−
. Biết rằng
( )
; ; 1u m n=−
là một vectơ chỉ phương của đường thẳng
AB
.
Tính giá trị của biểu thức
22
T m n=+
.
A.
5T =
. B.
10T =
. C.
2T =
. D.
1T =
.
Câu 6. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 1
:
2 1 3
x y z
d
− − +
==
và một mặt
phẳng
( )
: 3 0P x y z+ + − =
. Đường thẳng
'd
là hình chiếu của
d
theo phương
Ox
lên
( )
P
,
'd
nhận
( )
; ;2019u a b=
là một vec tơ chỉ phương . Xác định tổng
( )
ab+
A.
2019
. B.
2020−
. C.
2018
. D.
2019−
.
BÀI TẬP RÈN LUYỆN

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
192
Câu 7. Trong không gian
Oxyz
, cho đường thẳng
11
:
2 3 1
x y z++
= =
−
và hai điểm
( )
1;2; 1A −
,
( )
3; 1; 5B −−
. Gọi
d
là đường thẳng đi qua điểm
A
và cắt đường thẳng
sao cho khoảng cách
từ
B
đến đường thẳng
d
lớn nhất,
( )
1; ;u a b=
là vectơ chỉ phương của
d
. Giá trị của
a
b
bằng
A.
2−
. B.
1
2
−
. C.
2
. D.
1
2
.
Câu 8. Trong không gian
Oxyz
, gọi
d
là hình chiếu vuông góc của đường thẳng
1 2 3
:
2 3 1
x y z
d
+ − +
==
trên mặt phẳng tọa độ
Oxy
. Vecto nào dưới đây là một vecto chỉ phương của
d
?
A.
( )
2;3;0u =
. B.
( )
2;3;1u =
. C.
( )
2;3;0u =−
. D.
( )
2; 3;0u =−
.
Câu 9. Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt phẳng
( )
: 2 2 2 0P x y z+ − + =
, điểm
( )
1;1; 2A −
và đường thẳng
122
:
2 1 3
x y z
d
+ − +
==
−
. Đường thẳng
qua
A
cắt
d
và
( )
P
lần
lượt tại hai điểm
M
và
N
sao cho
2AM AN=
, khi đó một vectơ chỉ phương của
là?
A.
( )
8;4; 3u = − −
. B.
( )
8; 4; 9u = − − −
. C.
( )
8; 4; 9u = − −
. D.
( )
8; 4;9u =−
.
Câu 10. Trong không gian
Oxyz
, cho điểm
( )
1;1;1A
và mặt phẳng
( ): 2 0P x y+=
. Gọi
là đường
thẳng đi qua
A
, song song với
()P
và cách điểm
( )
1;0;2B −
một khoảng ngắn nhất. Hỏi
nhận
vecto nào dưới đây là vecto chỉ phương ?
A.
( )
6;3; 5u =−
. B.
( )
6; 3;5u =−
. C.
( )
6;3;5u =
. D.
( )
6; 3; 5u = − −
.
Câu 11. Trong không gian tọa độ
Oxyz
, cho hai điểm
( )
3;1;1A
,
( )
7;3;9B
và mặt phẳng
( )
P
:
30x y z+ + + =
. Điểm
( ) ( )
;;M x y z P
sao cho
MA MB+
đạt giá trị nhỏ nhất. Giá trị
x y z++
bằng
A. – 3. B. 3. C. 0. D. 2.
Câu 12. Trong không gian tọa độ
Oxyz
cho hai đường thẳng
( )
1
21
:
1 3 2
x y z
d
−+
==
,
( )
2
15
:
3 1 3
x y z
d
+−
==
−
và điểm
(1; 0; 2)M
.
,AB
là hai điểm lần lượt trên
1
()d
và
2
()d
sao cho
tam giác
MAB
vuông tại
.M
Khi
,AB
thay đổi thì trung điểm
I
của đoạn
AB
sẽ thuộc một
đường thẳng. Tìm vectơ chỉ phương của đường thẳng đó.
A.
( )
5;9;17u =−
. B.
( )
3;1;5u =−
. C.
( )
1;5;9u =
. D.
( )
1;4;4u =
.
Câu 13. Trong không gian , cho đường thẳng và 2 điểm ,
. Gọi là đường thẳng đi qua , vuông góc với và thỏa mãn khoảng cách từ
đến là nhỏ nhất. Một vectơ chỉ phương của có tọa độ
A. . B. . C. . D. .
Oxyz
3 4 2
:
2 1 1
x y z
d
− − −
==
( )
6;3; 2A −
( )
1;0; 1B −
B
d
A
( )
1;1; 3−
( )
1; 1; 1−−
( )
1;2; 4−
( )
2; 1; 3−−

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
193
Câu 14. Trong không gian Oxyz, cho mặt cầu
( ) ( ) ( ) ( )
2 2 2
2
: 1 2 1 3S x y z− + − + − =
, mặt phẳng
( )
: 3 0P x y z− + + =
và điểm
( )
1;0; 4N −
thuộc
( )
P
. Một đường thẳng
đi qua
N
nằm trong
( )
P
cắt
( )
S
tại hai điểm
A
,
B
thỏa mãn
4AB =
. Gọi
( )
1; ;u b c=
,
( )
0c
là một vecto chỉ
phương của
, tổng
bc+
bằng
A.
1
. B.
3
. C.
1−
. D.
45
.
Câu 15. Trong không gian cho ba đường thẳng \
. Đường thẳng vuông góc với đồng thời cắt tương ứng tại
sao cho độ dài nhỏ nhất. Biết rằng có một vectơ chỉ phương Giá trị bằng
A. B. C. D.
Oxyz
1
:,
1 1 2
x y z
d
+
==
−
1
31
:,
2 1 1
x y z−−
= =
2
12
:
1 2 1
x y z−−
= =
d
12
,
,HK
HK
( )
; ;1 .u h k
hk−
0.
4.
6.
2.−
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
194
ĐÁP ÁN CHI TIẾT
Câu 1. Chọn A
Mặt phẳng
( )
P
có một vectơ pháp tuyến
( )
1; 1;0n −
.
Vì
( )
2; 1; 2H −−
là hình chiếu vuông góc của gốc tọa độ
( )
0;0;0O
xuống mặt phẳng
( )
Q
nên
( )
Q
nhận
( )
2; 1; 2OH −−
là vectơ pháp tuyến.
Ta có
( ) ( )
( )
cos ,PQ
( )
cos ,n OH=
.
.
nOH
n OH
=
( ) ( ) ( )
( ) ( ) ( )
2 2 2
2 2 2
1.2 1 . 1 0. 2
1 1 0 . 2 1 2
+ − − + −
=
+ − + + − + −
3
32
=
2
2
=
.
Vậy góc giữa mặt phẳng
( )
P
và mặt phẳng
( )
Q
bằng
45
.
Câu 2. Chọn D
Gọi
( )
P
là mặt phẳng cần tìm.
( )
P
qua
( )
3; 4;5A −
và có VTPT
( )
1; 2;3
d
nu=−
(do
( )
Pd⊥
).
Vậy
( )
P
có phương trình:
( ) ( ) ( )
1 3 2 4 3 5 0xyz− − + + − =
2 3 26 0x y z − + − =
.
Câu 3. Chọn B
Ta có
1 3 3 1 3
3 2 1 9 2 3
x y z x y z
Vậy một véc tơ chỉ phương của đường thẳng là
( )
9;2; 3a =−
.
Câu 4. Chọn B
Ta có
1 3 3 1 3
3 2 1 9 2 3
x y z x y z
Vậy một véc tơ chỉ phương của đường thẳng là
( )
9;2; 3a =−
.
Câu 5. Chọn D
Cách 1:
Đặt
3 3 2
:
1 2 1
x y z
BM
− − −
==
−−
và
2 4 2
:
2 1 1
x y z
CD
− − −
==
−−
Giả sử
( )
2 2 ;4 ;2C c c c+ − −
75
2 ; ;
22
cc
Mc
−−
+
là trung điểm của cạnh
AC
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
195
Vì
M BM
nên
75
32
23
22
1
1 2 1
cc
c
c
−−
−−
+−
= = =
−−
( ) ( )
4;3;1 , 3;3;2CM
Gọi
( )
là mặt phẳng qua điểm
M
và vuông góc với đường phân giác
CD
( )
:2 1 0x y z
− − − =
. Khi đó
( )
73
3; ;
22
CD H
=
Gọi
N
là điểm đối xứng với
M
qua
CD
( )
3;4;1N
( )
1;1;0CN = −
Do
CD
là đường phân giác trong của góc
C
nên
N BC
phương trình tham số của cạnh
BC
đi qua điểm
C
và nhận vectơ
CN
làm VTCP là:
4
3
1
xt
yt
z
=−
=+
=
( ) ( )
2;5;1 0;2; 2BM BC B AB = = −
Do đó đường thẳng
AB
có một VTCP là
( ) ( )
0;1; 1 ; ; 1u m n= − = −
Vậy
22
1T m n= + =
.
Cách 2:
Gọi
( )
P
là mặt phẳng qua
A
và vuông góc với
CD
( )
:2 2 0P x y z − − + =
( ) ( )
2;4;2CD P H=
. Gọi
N
là điểm đối xứng với
A
qua
CD
H
là trung điểm của
AN
( )
2;5;1N
Do
CD
là đường phân giác trong của góc
C
nên điểm
N BC
Thay tọa độ điểm
N
vào phương trình đường trung tuyến
BM
, ta được:
2 3 5 3 1 2
1 2 1
− − −
==
−−
N BM
mà
BM BC B B N =
Nên đường thẳng
AB
nhận vectơ
( ) ( )
1
0;1; 1 ; ; 1
2
u AN m n= = − = −
. Vậy
22
1T m n= + =
.
Câu 6. Chọn D
Ta có
( )
2;1;3
d
u =
là một vectơ chỉ phương của đường thẳng
d
.
Mặt phẳng
( )
'P
chứa d và hình chiếu
'd
có VTPT
( )
'
; 0;3; 1
Pd
n u i
= = −
.
VTCP
( ) ( )
''
. 4; 1; 3 2692;673;2019
d P P
u n n
= = − − = −
. Vậy
2019ab+ = −
.
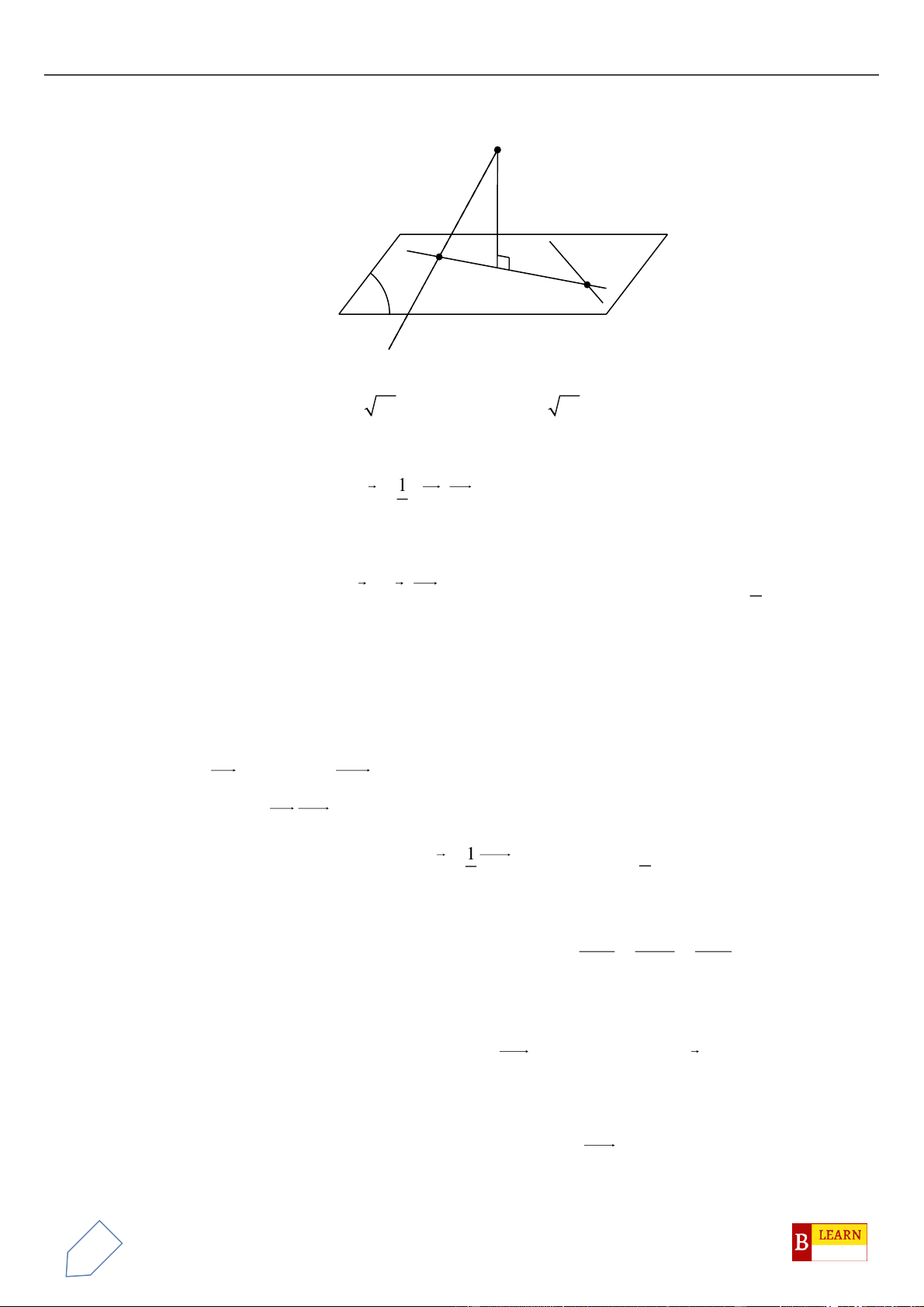
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
196
Câu 7. Chọn A
Cách 1:
Gọi
H
là hình chiếu vuông góc của
B
trên đường thẳng
d
.
Khi đó
( ) ( )
( )
, 29 max , 29= = =d B d BH AB d B d
đạt được khi
H A d AB ⊥
.
Gọi
( )
P
là mặt phẳng chứa
và đi qua
A
. Lấy điểm
( )
1;0; 1E −−
thuộc đường thẳng
.
( )
P
có một vectơ pháp tuyến
( )
1
, 1; 1; 1
2
n u EA
= = − −
.
Vì đường thẳng
d
đi qua
A
và cắt
nên
d
nằm trong
( )
P
.
Suy ra đường thẳng
d
nhận
( )
, 1;2; 1u n AB
= = −
làm vectơ chỉ phương. Vậy
2
a
b
=−
.
Cách 2:
Gọi
H
là hình chiếu vuông góc của
B
trên đường thẳng
d
.
Khi đó
( ) ( )
( )
, max ,= =d B d BH AB d B d AB
đạt được khi
⊥ d AB H A
.
Gọi M là giao điểm của hai đường thẳng
d
và
. Suy ra
( 1 2 ;3 ; 1 )M t t t− + − −
.
Ta được
(2; 3; 4), ( 2 2 ;3 2; ).AB AM t t t= − − = − + − −
Do
⊥d AB
nên
. 0 2( 2 2 ) 3(3 2) 4 0 2.AB AM t t t t= − + − − + = =
Suy ra một vectơ chỉ phương của
d
là
1
(1;2; 1).
2
u AM= = −
Vậy
2
a
b
=−
.
Câu 8. Chọn A
Tọa độ giao điểm
I
của
d
và
( )
Oxy
là nghiệm của hệ :
1 2 3
2 3 1
0
x y z
z
+ − +
==
=
.
Giải hệ trên ta được
( )
5;11;0I
. Gọi
( )
1;2; 3Md− −
. Khi đó hình chiếu của
M
lên
( )
Oxy
là
( )
1;2;0M
−
. Do đó
d
là đường thẳng
IM
có
( )
6; 9;0IM
= − −
. Suy ra
( )
2;3;0u =
cũng là một
vectơ chỉ phương của
d
.
Câu 9. Chọn D
Ta có
( )
1 2 ;2 ; 2 3d M M d M t t t = − + − − +
;
( )
2 2 ;1 ;3AM t t t= − + −
.
d
P
H
Δ
A
B
M

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
197
Vì
22AM AN AM AN= = −
( )
( )
( )
2 2 2 1
1 2 1
3 2 2
N
N
N
tx
ty
tz
− + = − −
− = − −
= − +
2
11
22
3
2
2
N
N
N
xt
yt
zt
=−
= +
= − −
1 1 3
2 ; ; 2
2 2 2
N t t t
− + − −
.
Mặt khác
( ) ( ) ( )
1 1 3
2 2 2 2 2 0 3
2 2 2
P N N P t t t t
= − + + − − − + = = −
.
Với
( )
3 8;4; 9t AM= − = − −
. Vậy một vectơ chỉ phương của
là
( )
8; 4;9u =−
.
Câu 10. Chọn D
Gọi
()Q
chứa
và song song với
()P
. Suy ra
()Q
có phương trình:
1 2( 1) 0 2 3 0x y x y− + − = + − =
.
Khi đó
( )
min
;d B BH=
với
H
là hình chiếu của
B
lên mặt phẳng
()Q
.
Đường thẳng
BH
đi qua
B
, vuông góc với mặt phẳng
()Q
có phương trình
1
2,
2
xt
y t t
z
= − +
=
=
.
Tọa độ giao điểm
H
của đường thẳng
BH
và mặt phẳng
()Q
là nghiệm của hệ:
1
2
2
2 3 0
xt
yt
z
xy
= − +
=
=
+ − =
. Giải hệ trên ta được
18
; ;2
55
H
−
.
Do đó
là đường thẳng
AH
có
63
; ; 1
55
AH
= − −
.
Suy ra
( )
6; 3; 5u = − −
cũng là một vecto chỉ phương của
.
Câu 11. Chọn A
Gọi
I
là điểm thỏa mãn
0IA IB+=
thì
I
là trung điểm của
AB
. Suy ra
( )
5;2;5I
.
Khi đó:
MA MB+
MI IA MI IB= + + +
2 MI=
.
MA MB+
đạt giá trị nhỏ nhất
MI
đạt giá trị nhỏ nhất
M
là hình chiếu vuông góc của
I
lên mặt phẳng
( )
P
.
Gọi
( )
d
là đường thẳng đi qua
I
và vuông góc
( )
P
. Suy ra
( ) ( )
M d P=
( )
d
:
5
2
5
xt
yt
zt
=+
=+
=+
( )
5 ;2 ;5M t t t + + +
.
( )
MP
nên
5 2 5 3 0t t t+ + + + + + =
3 15 0t + =
5t = −
( )
0; 3;0M−
.
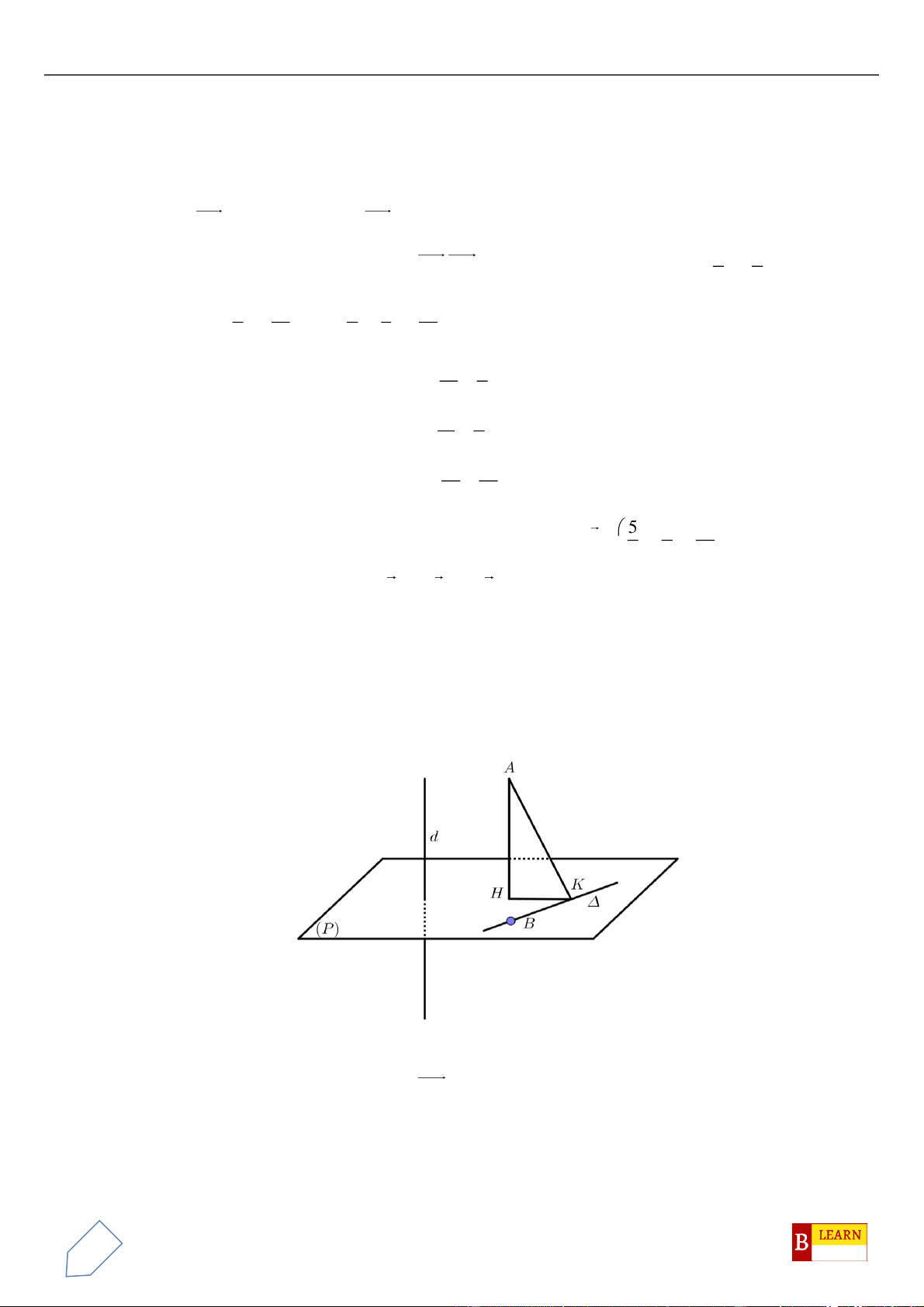
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
198
Vậy
3x y z+ + = −
.
Trắc nghiệm: Vì
( ) ( )
;;M x y z P
nên
30x y z+ + + =
3x y z + + = −
.
Câu 12. Chọn A
Gọi
1
( 2;3 ;2 1) ( )A t t t d+ −
và
2
(3 ' 1; ' 5; 3 ') ( )B t t t d− + −
.
Khi đó
( 1;3 ;2 3), (3 ' 2; ' 5; 3 ' 2).MA t t t MB t t t= + − = − + − −
Vì tam giác
MAB
vuông tại
M
nên
. 0 9 12 ' 4 0MAMB t t= + + =
44
'.
39
tt = − −
Do đó
4 14 4 8 17
' ; 4 ' ; '
3 9 3 3 9
A t t t
− + − − − −
.
Tọa độ trung điểm
I
của
AB
là
55
18 6
11 3
62
17 17
86
xt
yt
zt
=+
=−
= − −
.
Suy ra điểm
I
thuộc một đường thẳng có vectơ chỉ phương
5 3 17
;;
6 2 6
v
= − −
.
Chọn vec tơ chỉ phương khác là
6uv=−
hay
( )
5;9;17 .u =−
Câu 13. Chọn A
Gọi là mặt phẳng qua và vuông góc với nên .
Gọi là hình chiếu của lên , ta có:
Ta có: nên .
Dấu đẳng thức xảy ra khi và chỉ khi .
Vậy một vectơ chỉ phương của là .
Câu 14. Chọn D
( )
P
B
d
( )
:2 1 0P x y z+ + − =
H
A
( )
P
( )
2;1; 4H −
( )
P
( ) ( )
( )
;;d A d A P
H
( )
1;1; 3BH =−
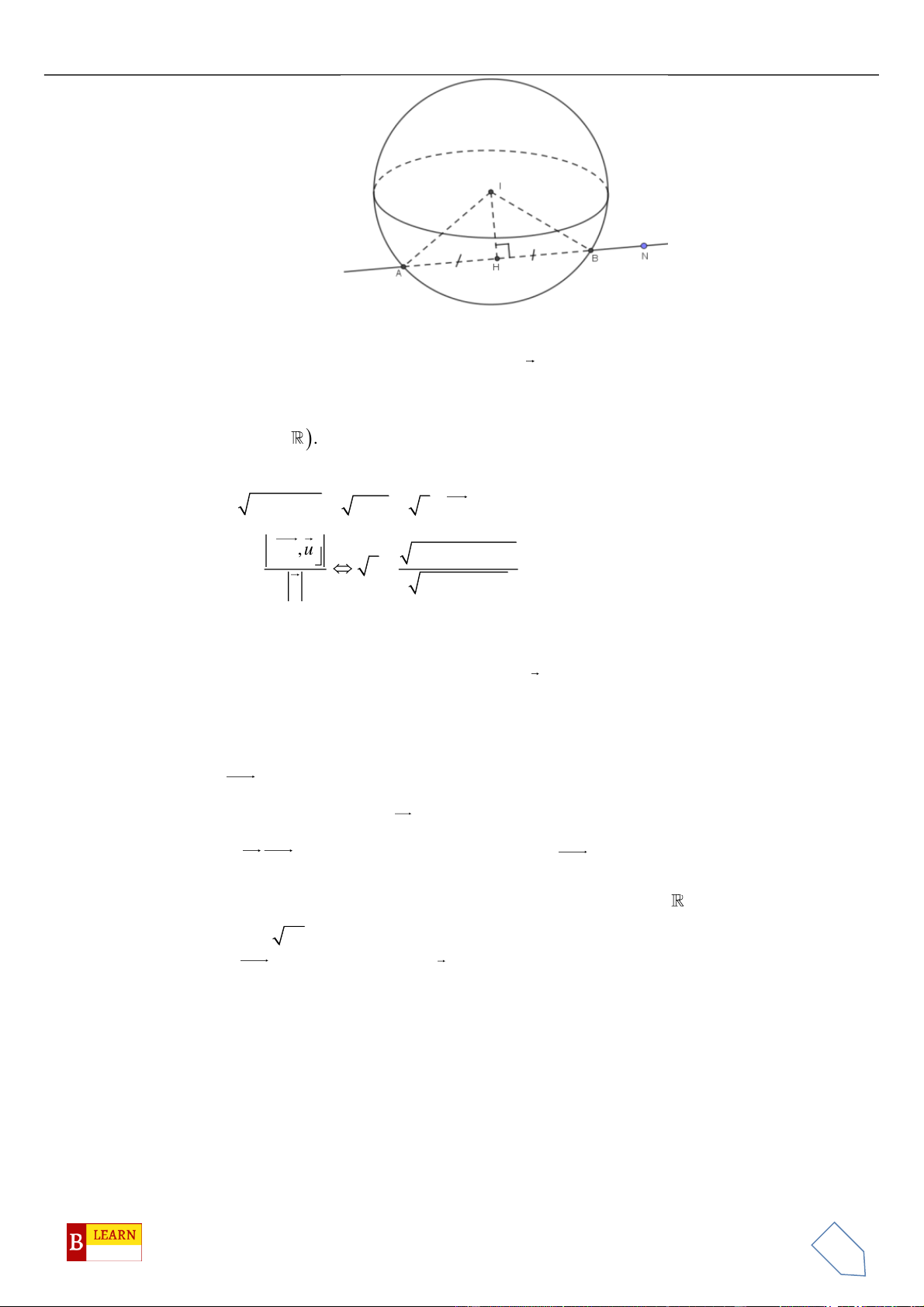
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
199
Mặt cầu
( )
S
có tâm
( )
1;2;1I
và bán kính
3R =
. Gọi
H
là trung điểm
AB
.
Đường thẳng
đi qua
N
và có vecto chỉ phương
( )
1; ;u b c=
ta có phương trình:
( )
1
:.
4
xt
y bt t
z ct
=+
=
= − +
( )
1 0 1P b c b c − + = = +
.
Ta có:
22
9 4 5IH R HB= − = − =
,
( )
0; 2; 5IN = − −
.
( )
2
2
2 2 2
,
9 30 54
,5
2 2 2
22
10 10 10 9 30 54 20 44 0 .
2
IN u
cc
IH d I
u
cc
c
c c c c c c
c
++
= = =
++
=
+ + = + + − − =
=−
Vì
0c
nên ta chọn
22c =
. Vậy vecto chỉ phương
( )
1;23;22u =
.
Câu 15. Chọn A
Gọi ; Gọi .
Tính được .
Đường thẳng có một VTCP là .
Vì
Tính được
Suy ra đạt được khi .
Khi đó ta có , suy ra
( )
1
3 2 ; ;1H H t t t + +
( )
2
1 ;2 2 ;K K m m m + +
( )
2 2;2 2; 1HK m t m t m t= − − − + − −
d
( )
1;1; 2
d
u =−
d ⊥
.0
d
u HK =
( )
2 0 2 4; 2; 3 .m t m t HK t t − + = = − = − − − −
( ) ( ) ( ) ( )
2 2 2 2
2
4 2 3 2 1 27 27,HK t t t t= − − + − + − = + +
27,minHK =
1t =−
( )
3; 3; 3HK = − − −
( )
1;1;1 1 0.u h k h k = = − =
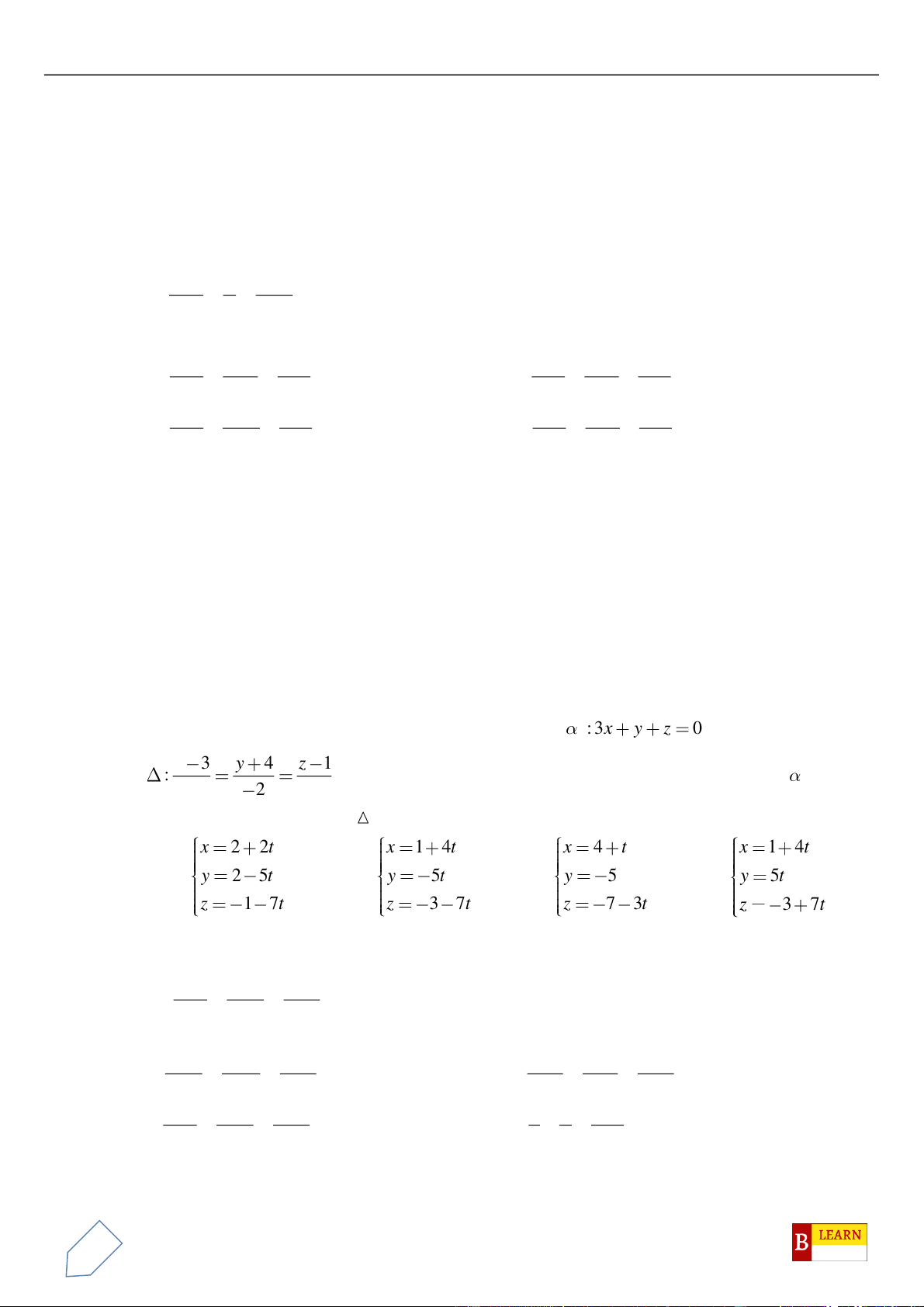
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
200
DẠNG 2. VIẾT PHƯƠNG TRÌNH ĐƯỜNG THẲNG
Câu 1. Trong không gian với hệ tọa độ
Oxyz
, phương trình tham số trục
Oz
là
A.
0
0
x
yt
z
=
=
=
. B.
0
0
xt
y
z
=
=
=
. C.
0z =
. D.
0
0
x
y
zt
=
=
=
.
Câu 2. Trong không gian với hệ tọa độ
Oxyz
cho mặt phẳng
( ): 2 4 0P x y z+ + − =
và đường thẳng
12
:.
2 1 3
x y z
d
++
==
Đường thẳng
nằm trong mặt phẳng
()P
đồng thời cắt và vuông góc với
đường thẳng
d
có phương trình là
A.
1 1 1
5 1 2
x y z− + −
==
−
. B.
1 1 1
5 2 3
x y z− − −
==
.
C.
1 3 1
5 1 3
x y z+ + −
==
−
. D.
1 1 1
5 1 3
x y z− − −
==
−−
.
Câu 3. Trong không gian tọa độ
Oxyz
, cho hai điểm
( )
1;2;3A
;
( )
3;0;1B
. Mặt phẳng trung trực của đoạn
thẳng
AB
có phương trình tổng quát là
A.
40x y z− − + =
. B.
10x y z− − + =
. C.
20x y z− − − =
. D.
10x y z+ − − =
.
Câu 4. Trong không gian
Oxyz
cho điểm
( )
2; 1;1A −
và mặt phẳng
( )
:2 2 1 0P x y z− + + =
. Viết đường
thẳng
đi qua
A
và vuông góc với mặt phẳng
( )
P
A.
22
:1
12
xt
yt
zt
=−
= − +
=−
. B.
22
:1
1
xt
yt
zt
=+
= − +
=−
. C.
22
:1
2
xt
yt
zt
=+
= − −
=+
. D.
24
: 1 2
1
xt
yt
zt
=+
= − +
=+
Câu 5. Trong không gian
Oxyz
, cho mặt phẳng
:3 0x y z
và đường thẳng
3 4 1
:
1 2 2
x y z
. Phương trình của đường thẳng
d
nằm trong mặt phẳng , cắt và
vuông góc với đường thẳng là:
A.
22
: 2 5
17
xt
d y t
zt
. B.
14
:5
37
xt
d y t
zt
. C.
4
:5
73
xt
dy
zt
. D.
14
:5
37
xt
d y t
zt
.
Câu 6. Trong hệ tọa độ
Oxyz
, lập phương trình đường vuông góc chung
của hai đường thẳng
1
1 3 2
:
1 1 2
x y z
d
− − −
==
−
và
2
3
:
13
xt
d y t
zt
=−
=
= − −
.
A.
2 2 4
1 3 2
x y z− − −
==
−−
. B.
3 1 2
1 1 1
x y z− + −
==
−
.
C.
1 3 2
3 1 1
x y z− − −
==
−
. D.
1
1 6 1
x y z +
==
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
201
Câu 7. Trong không gian
Oxyz
, cho đường thẳng
1
:2
32
xt
d y t
zt
=−
= − +
=+
và mặt phẳng
( )
: 2 3 2 0P x y z− + − =
.
Đường thẳng
nằm trong mặt phẳng
( )
P
đồng thời cắt và vuông góc đường thẳng
d
có phương
trình là:
A.
57
: 6 5
5
xt
d y t
zt
=+
= − +
= − +
. B.
57
: 6 5
5
xt
d y t
zt
=+
= − −
= − +
. C.
17
: 2 5
3
xt
d y t
zt
=+
= − +
=+
. D.
17
:5
1
xt
d y t
zt
= − +
=
=+
.
Câu 8. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 3 1
:
3 4 1
x y z
d
+ − +
==
−
và mặt phẳng
( )
:2 2 12 0P x y z+ − − =
. Viết phương trình đường thẳng
d
là hình chiếu vuông góc của đường
thẳng
d
trên mặt phẳng
( )
P
A.
1 2 3
:
2 1 2
x y z
d
+ + −
==
−
B.
1 4 3
:
3 4 1
x y z
d
− − +
==
−
.C.
42
:
3 1 1
x y z
d
−−
==
−
. D.
1 4 2
:
3 4 1
x y z
d
− − −
==
−
.
Câu 9. Trong không gian Oxyz, cho hai đường thẳng
1
22
:
1 1 1
x y z
d
−−
==
−
;
2
21
:
1 2 3
x y z
d
−+
==
−
Phương trình đường thẳng
cắt
12
,dd
lần lượt tại
A
và
B
sao cho
AB
nhỏ nhất là
A.
32
2
xt
yt
zt
=
=−
=−
. B.
2
12
xt
yt
zt
= − −
= − +
=−
. C.
1
12
2
xt
yt
zt
=+
= − −
=−
. D.
2
12
xt
yt
zt
=−
=+
=−
.
Câu 10. Trong không gian
,Oxyz
cho đường thẳng
1
1
:2
3
xt
d y t
z
=+
=+
=
và
2
1
: 2 7 .
3
x
d y t
zt
=
=+
=+
Phương trình đường
phân giác của góc nhọn giữa
1
d
và
2
d
là
A.
1 2 3
5 12 1
x y z− − −
==
−
. B.
1 2 3
5 12 1
x y z− − −
==
−
.
C.
1 2 3
5 12 1
x y z− − −
==
−
. D.
1 2 3
5 12 1
x y z− − −
==
.
Câu 11. Trong không gian với hệ tọa độ
Oxyz
, phương trình đường thẳng đi qua điểm
( )
1; 0;1M
và vuông
góc với hai đường thẳng
1
:4
3
xt
d y t
zt
=
= − +
=−
và
2
12
: 3 2
4
xt
d y t
zt
=−
= − +
=−
là:
A.
11
3 3 4
x y z−−
==
−
. B.
11
1 3 4
x y z−−
==
−
. C.
11
1 3 4
x y z−−
==
−
. D.
11
1 3 4
x y z−−
==
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
202
Câu 12. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )
:3 2 0P x y z+ − =
và hai đường thẳng
1
16
:
1 2 1
x y z
d
+−
==
−
và
2
124
:
3 1 4
x y z
d
− − +
==
−−
. Đường thẳng vuông góc với
( )
P
cắt cả hai
đường thẳng
1
d
và
2
d
có phương trình là
A.
21
3 1 2
x y z+−
==
−
. B.
54
3 1 2
x y z+−
==
.
C.
2 8 1
3 1 2
x y z+ − −
==
−
. D.
1 2 2
3 1 2
x y z− − −
==
−
.
Câu 13. Trong không gian
Oxyz
, cho mặt phẳng
( ): 3 0P x y z+ + − =
và đường thẳng
21
:
2 1 3
x y z
d
++
==
−
. Hình chiếu vuông góc của đường thẳng d trên
()P
có phương trình là:
A.
12
.
5 8 13
x y z−−
==
−
B.
12
.
2 7 5
x y z−−
==
−
C.
12
.
4 3 7
x y z−−
==
−
D.
12
.
2 3 5
x y z−−
==
−
Câu 14. Cho đường thẳng
d
:
21
2 3 2
x y z−+
==
−
và mặt phẳng
()P
:
20x y z− − − =
. Phương trình hình
chiếu vuông góc của
d
trên
()P
là
A.
1
12
23
xt
yt
zt
=−
=+
= − −
. B.
1
12
23
xt
yt
zt
=−
=+
= − +
.
C.
1
12
23
xt
yt
zt
=−
=−
= − −
. D.
1
12
23
xt
yt
zt
=−
=+
=−
.
Câu 15. Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
( )
2; 3; 1A −−
và
( )
4; 1;3B −
. Phương trình mặt
phẳng trung trực của đoạn thẳng
AB
là
A.
2 9 0x y z+ + − =
. B.
2 3 0x y z+ + + =
. C.
2 3 0x y z+ + − =
. D.
2 2 4 3 0x y z+ + − =
.
Câu 16. Trong không gian
Oxyz
,
cho điểm
( )
1;2;3A
và đường thẳng
3 1 7
:
2 1 2
x y z
d
− − +
==
−
. Đường
thẳng đi qua
A
, vuông góc với
d
và cắt trục
Ox
có phương trình là
A.
1
22
32
=+
=+
=+
xt
yt
zt
. B.
12
2
3
= − +
=
=
xt
yt
zt
. C.
12
2
= − +
=−
=
xt
yt
zt
. D.
1
22
33
=+
=+
=+
xt
yt
zt
.
Câu 17. Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt phẳng
( )
:2 2 9 0P x y z+ − + =
và đường
thẳng
1 3 3
:
1 2 1
x y z
d
− + −
==
−
. Phương trình tham số của đường thẳng
đi qua
( )
0; 1;4A −
,
vuông góc với
d
và nằm trong
( )
P
là:
A.
5
:1
45
xt
yt
zt
=
= − +
=+
. B.
2
:
42
xt
yt
zt
=
=
=−
. C.
:1
4
=
= −
=+
xt
y
zt
. D.
: 1 2
4
xt
yt
zt
=−
= − +
=+
.
Câu 18. Trong không gian
Oxyz
, cho tam giác
ABC
có
( )
2;1; 1 ,A −
( )
2;3;1B −
và
( )
0; 1;3C −
. Gọi
d
là đường thẳng đi qua tâm đường tròn ngoại tiếp tam giác
ABC
và vuông góc với mặt phẳng
( )
ABC
. Phương trình đường thẳng
d
là

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
203
A.
1 1 2
1 1 1
x y z+ − −
==
.B.
1
1 1 1
x y z+
==
. C.
2
2 1 1
x y z−
==
−
. D.
1
1 1 1
x y z−
==
.
Câu 19. Đường thẳng
là giao của hai mặt phẳng
50xz+ − =
và
2 3 0x y z− − + =
thì có phương trình
là
A.
21
1 3 1
x y z++
==
−
. B.
21
1 2 1
x y z++
==
−
C.
2 1 3
1 1 1
x y z− − −
==
−
. D.
2 1 3
1 2 1
x y z− − −
==
−
.
Câu 20. Trong không gian
Oxyz
, đường thẳng
Oy
có phương trình tham số là
A.
( )
xt
y t t
zt
=
=
=
. B.
( )
0
2
0
x
y t t
z
=
= +
=
. C.
( )
0
0
x
yt
zt
=
=
=
. D.
( )
0
0
xt
yt
z
=
=
=
.
Câu 21. Trong không gian tọa độ
Oxyz
, viết phương trình tham số của đường thẳng đi qua điểm
( )
1;2;3M
và song song với giao tuyến của hai mặt phẳng
( )
:3 3 0P x y+ − =
,
( )
:2 3 0Q x y z+ + − =
.
A.
1
23
3
xt
yt
zt
=+
=+
=+
. B.
1
23
3
xt
yt
zt
=+
=−
=−
. C.
1
23
3
xt
yt
zt
=−
=−
=+
. D.
1
23
3
xt
yt
zt
=+
=−
=+
.
Câu 22. Trong không gian tọa độ
Oxyz
, cho hai điểm
( )
1;0;1A −
,
( )
2;1;1B −
. Phương trình mặt phẳng
trung trực của đoạn
AB
là
A.
20xy−+=
. B.
10xy+ + =
. C.
10xy− + − =
. D.
20xy+ − =
.
Câu 23. Đường thẳng
đi qua điểm
( )
3;1;1M
, nằm trong mặt phẳng
( )
: 3 0x y z
+ − − =
và tạo với đường thẳng
1
: 4 3
32
x
d y t
zt
=
=+
= − −
một góc nhỏ nhất thì phương trình
của
là
A.
1
2
x
yt
zt
=
=−
=
. B.
85
34
2
xt
yt
zt
=+
= − −
=+
. C.
12
1
32
xt
yt
zt
=+
=−
=−
. D.
15
14
32
xt
yt
zt
=+
=−
=+
.
Câu 24. Trong không gian
Oxyz
, phương trình đường thẳng đi qua
( )
1;2;4A
song song với
( )
P
:
2 4 0x y z+ + − =
và cắt đường thẳng
:d
2 2 2
3 1 5
x y z− − −
==
có phương trình:
A.
1
2
42
xt
y
zt
=+
=
=−
. B.
12
2
42
xt
y
zt
=+
=
=+
. C.
12
2
44
xt
y
zt
= − −
=
=+
. D.
1
2
42
xt
y
zt
=−
=−
=+
.
Câu 25. Trong không gian
Oxyz
cho đường thẳng
31
:
2 1 1
x y z
d
++
==
−
và mặt phẳng
( )
: x y 3z 2 0.P + − − =
Gọi
d
là đường thẳng nằm trong
( )
P
, cắt và vuông góc với
d
. Đường
thẳng
'd
có phương trình là:
A.
11
2 5 1
x y z++
==
−−
. B.
11
2 5 1
x y z++
==
−
. C.
11
2 5 1
x y z++
==
− − −
. D.
11
2 5 1
x y z++
==
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
204
Câu 26. Trong không gian
Oxyz
, cho
( )
2;3; 1M −
và đường thẳng
3
:
2 4 1
x y z
d
−
==
. Đường thẳng qua
M
vuông góc với
d
và cắt
d
có phương trình là
A.
2 3 1
5 6 32
x y z− − +
==
B.
2 3 1
6 5 32
x y z− − +
==
−
C.
2 3 1
5 6 32
x y z− − +
==
−
D.
2 3 1
6 5 32
x y z− − +
==
−
Câu 27. Trong hệ tọa độ
Oxyz
, lập phương trình đường vuông góc chung
của hai đường thẳng
1
1 3 2
:
1 1 2
x y z
d
− − −
==
−
và
2
3
:
13
xt
d y t
zt
=−
=
= − −
.
A.
2 2 4
1 3 2
x y z− − −
==
−−
. B.
3 1 2
1 1 1
x y z− + −
==
−
.
C.
1 3 2
3 1 1
x y z− − −
==
−
. D.
1
1 6 1
x y z +
==
.
Câu 28. rong không gian
Oxyz
, cho đường thẳng
1 1 3
:
1 2 2
x y z
d
+ − −
==
−
và mặt phẳng
( )
:2 2 3 0P x y z− + − =
, phương trình đường thẳng
nằm trong mặt phẳng
( )
P
, cắt
d
và vuông
góc với
d
là
A.
22
15
56
zt
yt
zt
=−
=−
= − −
. B.
22
15
56
zt
yt
zt
= − −
= − −
=−
. C.
22
15
56
zt
yt
zt
= − +
= − +
=−
. D.
22
15
56
zt
yt
zt
= − −
=−
=+
.
Câu 29. Trong không gian
Oxyz
, đường thẳng qua
( )
1;2; 1M −
và song song với hai mặt phẳng
( )
: 8 0P x y z+ − − =
,
( )
:2 5 3 0Q x y z− + − =
có phương trình là
A.
1 2 1
4 7 3
x y z− − +
==
−−
. B.
1 2 1
4 7 3
x y z− − +
==
−
.
C.
1 2 1
4 7 3
x y z− − +
==
. D.
1 2 1
4 7 3
x y z− + −
==
−
.
Câu 30. Trong không gian
Oxyz
cho mặt phẳng
( )
: 3 0P x y z+ + − =
và đường thẳng
12
:
1 2 1
x y z
d
+−
==
−
. Hình chiếu vuông góc của
d
trên mặt phẳng
( )
P
có phương trình là
A.
1 1 1
1 4 5
x y z+ + +
==
−−
. B.
1 1 1
3 2 1
x y z− − −
==
−−
.
C.
1 1 1
1 4 5
x y z− − −
==
−
. D.
1 4 5
1 1 1
x y z− − +
==
.
Câu 31. Trong không gian
Oxyz
, cho điểm
( )
1;0;2A
và đường thẳng
11
:
1 1 2
x y z
d
−+
==
. Phương
trình đường thẳng
đi qua
A
, vuông góc và cắt
d
là:
A.
12
1 1 1
x y z−−
==
. B.
12
1 1 1
x y z−−
==
−
.
C.
12
2 2 1
x y z−−
==
. D.
12
1 3 1
x y z−−
==
−
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
205
Câu 32. Trong không gian
Oxyz
, cho đường thẳng
1 3 1 1
: , ,2
2 1 2 2 2
x y z
dm
mm
− + +
= = −
+−
và mặt phẳng
( )
: 6 0P x y z+ + − =
. Gọi đường thẳng
là hình chiếu vuông góc của
d
lên mặt phẳng
( )
P
. Có
bao nhiêu số thực
m
để đường thẳng
vuông góc với giá của véctơ
( 1;0;1)a =−
?
A.
2
. B.
1
. C.
3
. D.
0
.
Câu 33. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
22
:
1 1 1
x y z+−
= =
−
và mặt phẳng
( )
: 2 3 4 0P x y z+ − + =
. Phương trình tham số của đường thẳng
d
nằm trong
( )
P
, cắt và vuông
góc đường thẳng
là
A.
32
1
1
xt
yt
zt
= − +
=−
=+
. B.
13
23
1
xt
yt
zt
=−
= − +
= − +
. C.
33
12
1
xt
yt
zt
= − −
=+
=+
. D.
3
12
1
xt
yt
zt
= − +
=−
=−
.
Câu 34. Trong không gian tọa độ
Oxyz
, cho điểm
( )
3;3; 3A −−
thuộc mặt phẳng
( )
có phương trình
2 – 2 15 0x y z+ + =
và mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 2 3 5 100S x y z− + − + − =
. Đường thẳng
qua
A
, nằm trên mặt phẳng
( )
cắt
()S
tại
M
,
N
. Để độ dài
MN
lớn nhất thì phương trình đường
thẳng
là
A.
3 3 3
1 4 6
x y z+ − +
==
. B.
3 3 3
16 11 10
x y z+ − +
==
−
.
C.
35
3
38
xt
y
zt
= − +
=
= − +
. D.
3 3 3
1 1 3
x y z+ − +
==
.
Câu 35. Trong không gian toạ độ
Oxyz
, cho điểm
( )
1;2;4A
và hai điểm
,MB
thoả mãn
. . 0MAMA MB MB+=
. Giả sử điểm
M
thay đổi trên đường thẳng
3 1 4
:
221
x y z
d
+ − +
==
. Khi
đó điểm
B
thay đổi trên đường thẳng có phương trình là:
A.
1
7 12
:
2 2 1
x y z
d
++
==
. B.
2
1 2 4
:
2 2 1
x y z
d
− − −
==
.
C.
3
:
2 2 1
x y z
d ==
. D.
4
5 3 12
:
2 2 1
x y z
d
− − −
==
.
Câu 36. Trong không gian , cho 2 đường thẳng , và mặt phẳng
. Đường thẳng vuông góc với mặt phẳng , cắt
và có phương trình
là
A. . B. .
C. . D. .
Oxyz
12
:
13
xt
d y t
zt
= − −
=
= − +
2
: 1 2
2
xt
d y t
zt
=+
= − +
=−
( )
: 2 0P x y z+ + + =
( )
P
d
d
3 1 2
1 1 1
x y z− − +
==
1 1 1
1 1 4
x y z− − −
==
−−
2 1 1
1 1 1
x y z+ + −
==
1 1 4
2 2 2
x y z+ − −
==
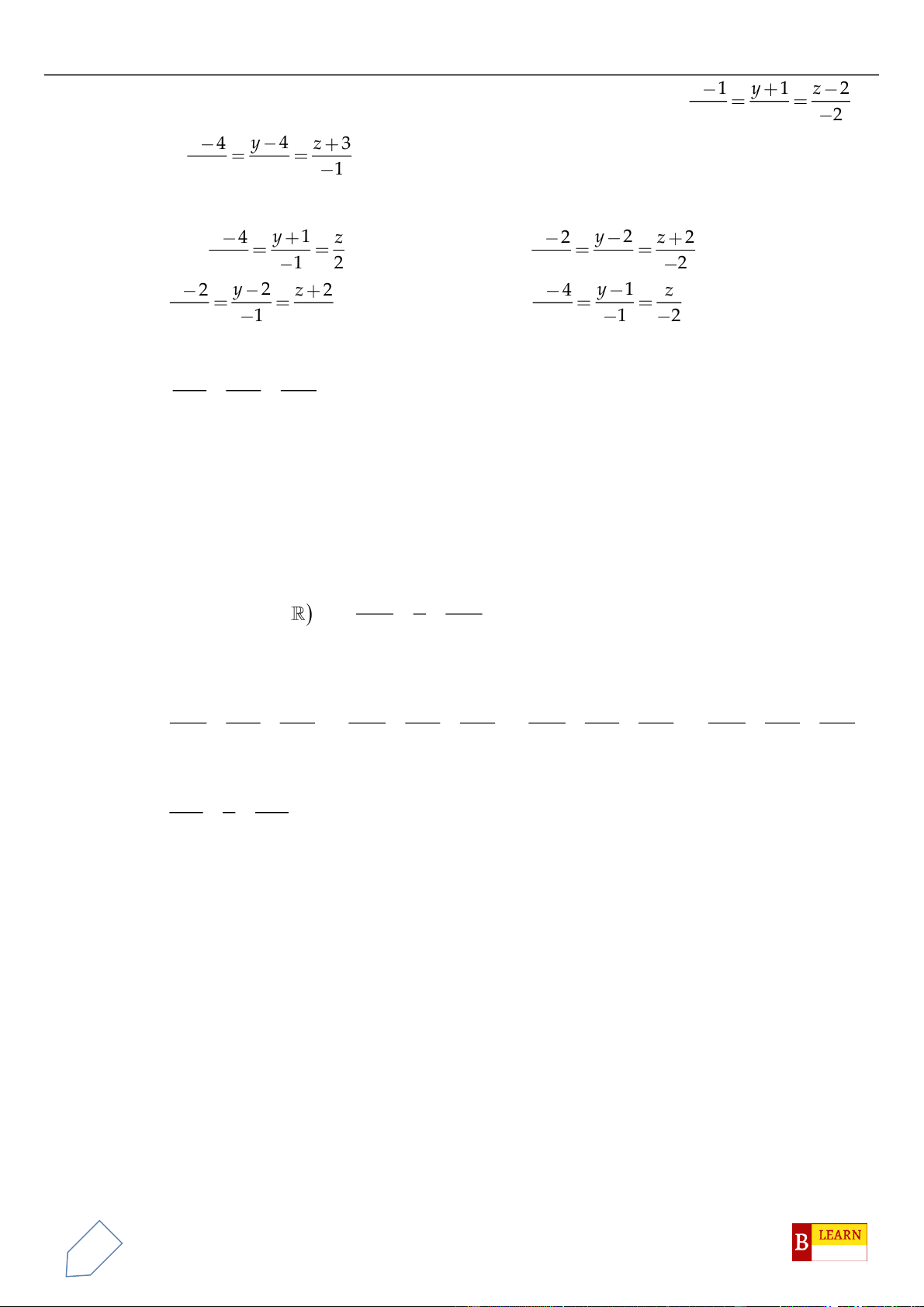
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
206
Câu 37. Trong không gian
Oxyz
, cho hai đường thẳng chéo nhau
1
1
12
:
3 2 2
y
xz
d
,
2
4
43
:
2 2 1
y
xz
d
. Phương trình đường vuông góc chung của hai đường thẳng
12
,dd
là
A.
1
1
4
:
2 1 2
y
xz
d
. B.
2
22
6 3 2
y
xz
.
C.
2
22
2 1 2
y
xz
. D.
1
4
2 1 2
y
xz
.
Câu 38. Trong không gian với hệ trục
Oxyz
, cho mặt phẳng
( )
: 5 4 0P x y z+ − + =
và đường thẳng
1 1 5
:
2 1 6
x y z
d
+ + +
==
. Hình chiếu vuông góc của đường thẳng
d
trên mặt phẳng
( )
P
có
phương trình là
A.
23
22
xt
yt
zt
= − +
= − +
=−
. B.
2
22
xt
yt
zt
= − −
=+
=
. C.
13
2
1
xt
yt
zt
=+
=
=+
. D.
3
2
1
xt
y
zt
=+
=
=+
.
Câu 39. Trong không gian
Oxyz
, cho hai đường thẳng
1
d
,
2
d
và mặt phẳng (
) có phương trình:
( )
1
13
:2
12
xt
d y t t
zt
=+
= +
= − +
,
2
24
:
3 2 2
x y z
d
−−
==
−−
,
( ): 2 0x y z
+ − − =
.
Phương trình đường thẳng
nằm trong mặt phẳng (
), cắt cả hai đường thẳng
1
d
và
2
d
là
A.
2 1 3
8 7 1
x y z+ − +
==
−
B.
2 1 3
8 7 1
x y z− + −
==
−−
C.
2 1 3
8 7 1
x y z+ − +
==
−
D.
2 1 3
8 7 1
x y z− + −
==
−
.
Câu 40. Trong không gian
Oxyz
, cho điểm
( )
1;3;2A
, mặt phẳng
( )
: 2 0P x y z+ − + =
và đường thẳng
11
:
2 1 1
x y z
d
−+
==
−
. Viết phương trình đường thẳng
cắt
( )
P
và
d
lần lượt tại
M
,
N
sao cho
A
là trung điểm của
MN
.
A.
1
:3
22
xt
yt
zt
=+
= −
=−
. B.
1
:3
22
xt
yt
zt
=+
= +
=−
. C.
1
:3
22
xt
yt
zt
= − +
= −
=−
. D.
1
:3
22
xt
yt
zt
=+
= − −
=−
.
Câu 41. Trong không gian với hệ tọa độ
Oxyz
, cho tam giác
ABC
có
( ) ( ) ( )
1;1;2 , 2;3;1 , 3; 1;4A B C−−
.
Viết phương trình đường cao của tam giác
ABC
kẻ từ đỉnh
B
A.
2
3
1
xt
yt
zt
= − −
=+
=−
. B.
2
3
1
xt
y
zt
= − +
=
=−
. C.
2
3
1
xt
yt
zt
= − −
=+
=+
. D.
2
3
1
xt
yt
zt
= − +
=−
=+
.
Câu 42. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
( )
1;2;3A
và mặt phẳng
( )
:2 4 1 0P x y z+ − + =
. Đường thẳng
( )
d
đi qua điểm
A
, song song với mặt phẳng
( )
P
, đồng thời cắt trục
Oz
. Viết
phương trình tham số của đường thẳng
( )
d
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
207
A.
15
26
3
xt
yt
zt
=+
=−
=+
. B.
2
2
xt
yt
zt
=
=
=+
. C.
13
22
3
xt
yt
zt
=+
=+
=+
. D.
1
26
3
xt
yt
zt
=−
=+
=+
.
Câu 43. Trong không gian Oxyz, cho điểm
( )
2;1;3E
, mặt phẳng
( )
P
đi qua ba điểm
3
;0;0
2
A
,
3
0; ;0
2
B
,
( )
0;0; 3C −
và mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 3 2 5 36S x y z− + − + − =
. Gọi
là đường
thẳng đi qua điểm
E
, nằm trong
( )
P
và cắt
( )
S
tại hai điểm có khoảng cách nhỏ nhất. Phương
trình
là
A.
29
19
38
xt
yt
zt
=+
=+
=+
. B.
25
13
3
xt
yt
z
=−
=+
=
. C.
2
1
3
xt
yt
z
=+
=−
=
. D.
24
13
33
xt
yt
zt
=+
=+
=−
.
Câu 44. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
( )
2;1;5A −
và hai mặt phẳng
( )
:2 3 7 0,P x y z+ + − =
( )
:3 2 1 0Q x y z− − + =
. Gọi
M
là điểm nằm trên mặt phẳng
( )
P
và
điểm
N
nằm trên mặt phẳng
( )
Q
thỏa mãn
2AN AM=
. Khi
M
di động trên mặt phẳng
( )
P
thì
quỹ tích điểm
N
là một đường thẳng có phương trình là
A.
35
8 11
67
xt
yt
zt
= − −
= − +
=−
. B. . C. . D. .
Câu 45. Trong không gian
,Oxyz
cho điểm
1; 1;2A
và hai đường thẳng
1
12
:;
2 1 1
x y z
d
2
1
: 1 2
25
xt
d y t
zt
. Viết phương trình đường thẳng đi qua
A
vuông góc với
1
d
và
2
.d
A.
45
32
57
xt
yt
zt
= − +
= − +
= − +
B.
17
1 11
23
xt
yt
zt
=−
= − +
=+
. C.
1
12
2
x
yt
zt
=
= − +
=+
. D.
7
11
32
xt
yt
zt
= − +
=−
=+
Câu 46. Trong không gian
,Oxyz
cho điểm
2;1;0M
và đường thẳng
11
:
2 1 1
x y z
d
. Viết
phương trình đường thẳng đi qua điểm
M
cắt và vuông góc với đường thẳng
.d
A.
21
.
1 4 1
x y z−−
==
B.
21
.
1 4 1
x y z−−
==
−
C.
21
.
2 4 1
x y z−−
==
−
D.
21
.
1 4 2
x y z−−
==
−−
Câu 47. Trong không gian
Oxyz
, cho mặt phẳng
( )
:2 3 2 12 0x y z
+ − + =
. Gọi
,,A B C
lần lượt là giao
điểm của
( )
với ba trục tọa độ, đường thẳng
d
đi qua tâm đường tròn ngoại tiếp tam giác
ABC
và vuông góc với
( )
có phương trình là
A.
3 2 3
2 3 2
x y z+ − −
==
−
B.
3 2 3
2 3 2
x y z+ − −
==
−
C.
3 2 3
2 3 2
x y z+ + −
==
−
. D.
3 2 3
2 3 2
x y z− − +
==
−
.
7 11
85
67
xt
yt
zt
=+
= − −
=−
7 11
85
87
xt
yt
zt
=+
= − −
= − −
25
3 11
17
xt
yt
zt
=+
=+
= − −
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
208
Câu 48. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
( )
2;1;1A
và hai đường thẳng
1
3
:1
2
xt
dy
zt
=+
=
=−
,
2
32
:3
0
xt
d y t
z
=+
=+
=
. Phương trình đường thẳng đi qua
,A
vuông góc với
1
d
và cắt
2
d
là
A.
12
.
2 1 2
x y z−−
==
−
B.
2 1 1
1 1 1
x y z− − −
==
−−
.
C.
2 1 1
2 1 2
x y z− − −
==
. D.
12
1 1 1
x y z−−
==
−
.
Câu 49. Trong không gian
Oxyz
cho hai đường thẳng
1
11
:,
1 1 2
x y z
d
−−
==
−
2
13
:
2 4 2
x y z
d
−−
==
−−
. Viết
phương trình đường phân giác của những góc tù tạo bởi
12
,dd
.
A.
13
3 5 4
x y z−−
==
−−
. B.
13
1 1 1
x y z−−
==
−
.
C.
11
2 1 1
x y z−−
==
. D.
13
2 1 1
x y z−−
==
.
Câu 50. Trong không gian với hệ tọa độ
Oxyz
cho tam giác
ABC
biết
( )
2;1;0A
,
( )
3;0;2B
,
( )
4;3; 4C −
. Viết phương trình đường phân giác trong của góc
A
.
A.
2
1
0
x
yt
z
=
=+
=
. B.
2
1
x
y
zt
=
=
=
. C.
2
1
0
xt
y
z
=+
=
=
. D.
2
1
xt
y
zt
=+
=
=
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
209
ĐÁP ÁN CHI TIẾT
Câu 1. Chọn D
Oz
có vec tơ chỉ phương là
( )
0;0;1u =
, đối chiếu 4 phương án, chỉ có D là phương án thích hợp.
Câu 2. Chọn D
Gọi
A
là giao điểm của
d
và
.
Ta có
Ad
( )
2 1; ;3 2A t t t − −
( )
P
, mà
A
nên
( )
AP
( ) ( )
2 1 2. 3 2 4 0 1t t t t − + + − − = =
. Vậy
( )
1;1;1A
.
( )
P
có vtpt
( )
1;2;1n =
và đường thẳng
d
có vtcp
( )
2;1;3
d
u =
.
Ta có
( )
d
P
⊥
suy ra
có 1 vtcp
( )
, 5; 1; 3
d
u n u
= = − −
đi qua
( )
1;1;1A
và nhận
( )
5; 1; 3u
= − −
làm vtcp.
Vậy
có phương trình
1 1 1
5 1 3
x y z− − −
==
−−
.
Câu 3. Chọn B
Gọi
I
là trung điểm đoạn thẳng
AB
( )
2;1;2I
.
Ta có
( )
2; 2; 2AB = − −
AB
cùng phương với
( )
1; 1; 1n = − −
.
( )
là mặt phẳng trung trực của đoạn thẳng
( )
AB
đi qua
( )
2;1;2I
và nhận
n
làm vectơ
pháp tuyến. Vậy phương trình mặt phẳng
( )
là:
10x y z− − + =
.
Câu 4. Chọn A
Đường thẳng
vuông góc với mặt phẳng
( )
:2 2 1 0P x y z− + + =
nên ta chọn véctơ pháp tuyến
của
( )
P
là
( )
2; 1;2n =−
làm véc tơ chỉ phương.
Đường thẳng
đi qua
( )
2; 1;1A −
Phương trình tham số của đường thẳng
là
22
1
12
xt
yt
zt
=−
= − +
=−
.
Câu 5. Chọn B
Phương trình tham số của đường thẳng
3
: 4 2
12
xt
yt
zt
.
Đường thẳng có vectơ chỉ phương là
1; 2;2u
.
Mặt phẳng có vectơ pháp tuyến là
3;1;1n
.
Gọi
I
là giao điểm của đường thẳng và mặt phẳng
Xét phương trình
3 3 4 2 1 2 0t t t
2t
. Suy ra tọa độ điểm
1;0; 3I
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
210
Vì đường thẳng
d
nằm trong mặt phẳng , cắt đường thẳng nên đường thẳng
d
đi qua điểm
1;0; 3I
.
Đường thẳng
d
vuông góc với mặt phẳng , vuông góc với đường thẳng nên đường thẳng
d
có một vectơ chỉ phương là
, 4;5;7v u n
.
Vậy phương trình đường thẳng
14
:5
37
xt
d y t
zt
.
Câu 6. Chọn A
Gọi:
( )
1
1 ';3 ';2 2 'd M t t t = + − +
,
( )
2
3 ; ; 1 3d N t t t = − − −
( )
3 1 '; 3 '; 3 3 2 'MN t t t t t t = − − − − + − − −
.
12
,dd
lần lượt có 2 vectơ chỉ phương là
( ) ( )
12
1; 1;2 , 3;1; 3uu= − = − −
.
Vì
là đường vuông góc chung của
12
;dd
nên
1
2
.0
6 ' 10 4 ' 1
10 ' 19 9 1
.0
MN u
t t t
t t t
MN u
=
− − = =
+ = − = −
=
( ) ( ) ( )
2;2;4 , 3; 1;2 , 1; 3; 2M N MN − = − −
. Vậy phương trình
2 2 4
:
1 3 2
x y z− − −
= =
−−
.
Câu 7. Chọn A
Gọi
Ad=
( )
1 ; 2 ;3 2A t t t− − + +
.
Vì
( )
P
( )
AP
nên
( ) ( )
1 2 2 3 3 2 2 0t t t− − − + + + − =
4t =−
( )
5; 6; 5A −−
.
Ta có
( )
( )
()
1;1;2
1; 2;3
d
P
u
n
=−
=−
( )
()
, 7;5;1
dP
u u n
==
.
Đường thẳng
d
có phương trình là :
57
6 5 ,
5
xt
y t t
zt
=+
= − +
= − +
.
Câu 8. Chọn B
Ta có :
d//(P)
nên
//dd
. Do đó
( )
3; 4;1
dd
uu
= = −
.
( )
1;3; 1Md− −
.
M
là hình chiếu vuông góc của
M
trên
( )
P
.
Gọi
a
là đường thẳng đi qua điểm
M
và vuông góc với
( )
P
.
Khi đó đường thẳng
a
có phương trình
12
3
12
xt
yt
zt
= − +
=+
= − −
.
Tọa độ điểm
M
là nghiệm của hệ phương trình
12
1
3
4
12
3
2 2 12 0
xt
x
yt
y
zt
z
x y z
= − +
=
=+
=
= − −
=−
+ − − =
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
211
Phương trình đường thẳng
d
là
1 4 3
:
3 4 1
x y z
d
− − +
==
−
Câu 9. Chọn A
Ta có
AB
ngắn nhất khi
AB
là đoạn vuông góc chung của
1
d
và
2
d
.
Gọi
( ) ( )
12
2 ;2 ; ; 2 ; 1 2 ; 3A a a a d B b b b d+ + − + − + −
( )
;2 3; 3AB b a b a b a − − − − +
.
12
,dd
lần lượt có các véc tơ chỉ phương là
( )
1
1;1; 1
d
u =−
và
( )
2
1;2; 3
d
u =−
Ta có:
( )
1
2
.0
1( ) 1(2 3) 1( 3 ) 0 6 3 3 0
1( ) 2(2 3) 3( 3 ) 0 14 6 6 0
.0
1 (1;1;1)
1; 2; 1
0 (2; 1;0)
d
d
AB u
b a b a b a b a
b a b a b a b a
AB u
aA
AB
bB
=
− + − − − − + = − − =
− + − − − − + = − − =
=
=−
= − −
=−
Do
( )
1; 2; 1AB = − −
nên vectơ chỉ phương của đường thẳng
cùng phương với vectơ
AB
, ta
loại 2 đáp án B, D .
Thay tọa độ 2 điểm
,AB
vào đáp án A và C ta chỉ thấy đáp án A thỏa mãn .
Câu 10. Chọn D
Đường thẳng
1
d
,
2
d
lần lượt có vectơ chỉ phương là
12
1 1 7 1
; ; 0 , 0 ; ; .
2 2 5 2 5 2
uu
==
Khi đó đường phân giác của góc nhọn giữa
1
d
và
2
d
có một vectơ chỉ phương là
( )
( )
12
5 2 5;12 ;1u u u= + =
(Từ đây có thể chọn được đáp án D).
Ta có hai đường thẳng
1
d
và
2
d
cắt nhau tại
( )
1; 2 ; 3M
nên phương trình đường phân giác của
góc nhọn giữa
1
d
và
2
d
là
1 2 3
.
5 12 1
x y z− − −
==
Câu 11. Chọn D
Đường thẳng
1
d
,
2
d
lần lượt nhận
( )
1
1;1; 1u =−
,
( )
2
2; 2; 1u = − −
làm véctơ chỉ phương.
Đường thẳng
d
cần tìm vuông góc với hai đường thẳng
1
d
,
2
d
nên véctơ chỉ phương của
d
là:
( )
12
, 1; 3; 4u u u
==
.
Phương trình đường thẳng
d
là
11
1 3 4
x y z−−
==
.
Câu 12. Chọn A
( )
1 1 1
1
16
: : 6 2 1 ;6 2 ;
1 2 1
xt
x y z
d d y t M d M t t t
zt
= − −
+−
= = = + − − +
−
=
( )
2 2 1
1 3 '
124
: : 2 ' 1 3 ';2 '; 4 4 '
3 1 4
4 4 '
xt
x y z
d d y t N d N t t t
zt
=−
− − +
= = = − − − − +
−−
= − +

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
212
( )
2 3 '; 4 2 '; 4 4 'MN t t t t t t= + − − − − − − +
( )
:3 2 0P x y z+ − =
có VTPT
( )
3;1; 2n −
Đường thẳng
( )
d
vuông góc với
( )
P
cắt cả hai đường thẳng
1
d
tại
M
và cắt
2
d
tại
N
suy ra
( )
2 3 ' 3 2 1 3
4 2 ' ' 1 1;2; 2 : 2 ;
4 4 ' 2 1 2 2
t t k t x s
MN kn t t k t M d y s s
t t k k z s
+ − = = − = +
= − − − = = − = +
− − + = − = − = − −
Chọn
( )
21
1 2;1;0 :
3 1 2
x y z
s A d d
+−
= − − = =
−
.
Câu 13. Chọn B
Ta có vtcp của đường thẳng
d
là
2; 1;3u
.
Vtpt của mặt phẳng
P
là
1;1;1
P
n
Gọi
Q
là mặt phẳng chứa
d
và vuông góc với
P
. Khi đó
; 4;1;3
Q
QP
QP
nu
n u n
nn
.Điểm
2; 1;0M d M Q
.
Phương trình mặt phẳng
: 4 2 1 3 0 4 3 7 0Q x y z x y z
Hình chiếu vuông góc của đường thẳng d trên
()P
là
d P Q
.
Khi đó vtcp của
d
là
; 2; 7;5
PQ
d
u n n
.Điểm
0;1;2N P Q
Câu 14. Chọn A
Đường thẳng
d
có véc tơ chỉ phương
( )
2; 3;2
d
u =−
.
Mặt phẳng
()P
có véc tơ pháp tuyến
( )
1; 1; 1
P
n = − −
.
Mặt phẳng
()Q
chứa
d
và vuông góc với
()P
;
Đường thẳng
'
d
là hình chiếu vuông góc của
d
trên
()P
,
( ) ( )
'd P Q=
Véc tơ pháp tuyến của mặt phẳng
()Q
là
( )
'
, 5;4;1
Q d P
n u n
==
Véc tơ chỉ phương của
'
d
là
( ) ( )
'
, 3; 6;9 3 1;2; 3
d P Q
u n n
= = − = − − −
Ta thấy đường thẳng
'
d
thuộc
()P
nên điểm
00
' ( )M d M P
. Thay tọa độ điểm
( )
0
1;1; 2M −
ở đáp án A thấy thỏa mãn phương trình
()P
.
Câu 15. Chọn C
Gọi
M
là trung điểm
AB
( )
3; 2;1M−
. Ta có
( ) ( )
2;2;4 2 1;1;2AB ==
.
Mặt phẳng trung trực của đoạn thẳng
AB
qua
( )
3; 2;1M −
và có một véctơ pháp tuyến
( )
1;1;2n =
có phương trình là: 1.
(
𝑥 − 3
)
+ 1.
(
𝑦 + 2
)
+ 2
(
𝑧 − 1
)
= 0 ⇔
2 3 0x y z+ + − =
.
Câu 16. Chọn B
Đường thẳng
d
có véc tơ chỉ phương
( )
2;1; 2
d
u =−
. Gọi đường thẳng cần tìm là
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
213
Gọi
( )
;0;0Ma
là điểm thuộc trục
Ox
mà đường thẳng
đi qua, suy ra
( )
1 ;2;3MA a=−
là
một véc tơ chỉ phương của
. Vì đường thẳng
vuông góc với
d
nên:
( ) ( ) ( )
. 0 1 .2 2.1 3. 2 0 1 1;0;0
dd
MA MA au aMu⊥ = − + + − = = − −
.
Đường thẳng
đi qua
( )
1;0;0M −
, nhận
( )
2;2;3MA =
làm một véc tơ chỉ phương suy ra
có phương trình
( )
12
2
3
xt
y t t
zt
= − +
=
=
.
Cách 2:
Mặt phẳng
()P
đi qua
(1;2;3)A
và vuông góc với
d
nên
( )
P
nhận vectơ chỉ phương của
d
( )
2;1; 2=−
d
u
làm một vetơ pháp tuyến.
Phương trình mặt phẳng
()P
:
( ) ( ) ( )
2 1 1 2 2 3 0 2 2 2 0− + − − − = + − + =x y z x y z
.
Tọa độ giao điểm
M
của trục
Ox
và mặt phẳng
()P
là nghiệm hệ phương trình:
0
0
2 2 2 0
=
=
=
+ − + =
xt
y
z
x y z
( )
1 1;0;0 = − −tM
.
Đường thẳng cần tìm đi qua hai điểm
, AM
nên nhận vectơ
( ) ( )
2; 2; 3 2;2;3AM = − − − = −
làm vectơ chỉ phương, có phương trình tham số:
12
2
3
= − +
=
=
xt
yt
zt
,
t
.
Câu 17. Chọn C
Ta thấy :
( )
AP
. Mặt phẳng
( )
P
có véctơ pháp tuyến
( )
2;1; 2n =−
, đường thẳng
d
có véctơ
chỉ phương
( )
1;2;1
d
u =−
Vì đường thẳng
đi qua
( )
0; 1;4−A
, vuông góc với
d
và nằm trong
( )
P
nên đường thẳng
có véctơ chỉ phương là
( )
5;0;5,
d
u u n
=
=
hay
( )
1;0;1u
=
Khi đó, phương trình tham số của đường thẳng
:1
4
=
= −
=+
xt
y
zt
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
214
Câu 18. Chọn B
Ta có:
( )
4;2;2 16 4 4 2 6AB AB= − = + + =
;
( )
2; 2;4 4 4 16 2 6AC AC= − − = + + =
4 16 4 2 6BC = + + =
Vậy tam giác
ABC
đều nên tâm đường tròn ngoại tiếp là trọng tâm
( )
0;1;1G
.
Do đó phương trình đường thẳng
d
qua
( )
0;1;1G
có véctơ chỉ phương
( )
, 12. 1;1;1u AB AC
==
hay,
:1
1
xt
d y t
zt
=
=+
=+
Vậy đường thẳng
d
đi qua điểm
( )
1;0;0A −
và có véctơ chỉ phương
( )
1;1;1u =
nên chọn B.
Câu 19. Chọn C
( )
: 5 0P x z+ − =
có vectơ pháp tuyến
( )
1
1;0;1n =
.
( )
: 2 3 0Q x y z− − + =
có vectơ pháp tuyến
( )
2
1; 2; 1n = − −
.
Ta có:
( )
12
, 2;2; 2nn
=−
.
Gọi
u
là một vectơ chỉ phương của
, thì
1
un⊥
và
2
un⊥
.
Suy ra
u
cùng phương với
12
,nn
. Chọn
( )
1;1; 1u =−
.
Lấy
( )
2;1;3M
thuộc mặt phẳng
( )
P
và
( )
Q
.
Đường thẳng
đi qua
( )
2;1;3M
có một véctơ chỉ phương
( )
1;1; 1u =−
.
Vậy phương trình
là:
2 1 3
1 1 1
x y z− − −
==
−
.
Nhận xét: Với 4 đáp án của đề, sau khi chọn
( )
1;1; 1u =−
thì ta đã có thể chọn C là đáp án.
Câu 20. Chọn B
Đường thẳng
Oy
đi qua điểm
( )
0 ; 2 ; 0A
và nhận vectơ đơn vị
( )
0; 1; 0j =
làm vectơ chỉ
phương nên có phương trình tham số là
( ) ( )
0 0. 0
2 1. 2
0 0. 0
x t x
y t t y t t
z t z
= + =
= + = +
= + =
.
Câu 21. Chọn D
Gọi đường thẳng cần tìm là
d
.
Mặt phẳng
( )
P
có vectơ pháp tuyến
( )
( )
3;1;0
P
n =
.
Mặt phẳng
( )
Q
có vectơ pháp tuyến
( )
( )
2;1;1
Q
n =
.
Suy ra
( ) ( )
( )
, 1; 3;1
PQ
nn
=−
là một vectơ chỉ phương của đường thẳng
d
Vậy phương trình tham số của đường thẳng
d
là:
1
23
3
xt
yt
zt
=+
=−
=+
.
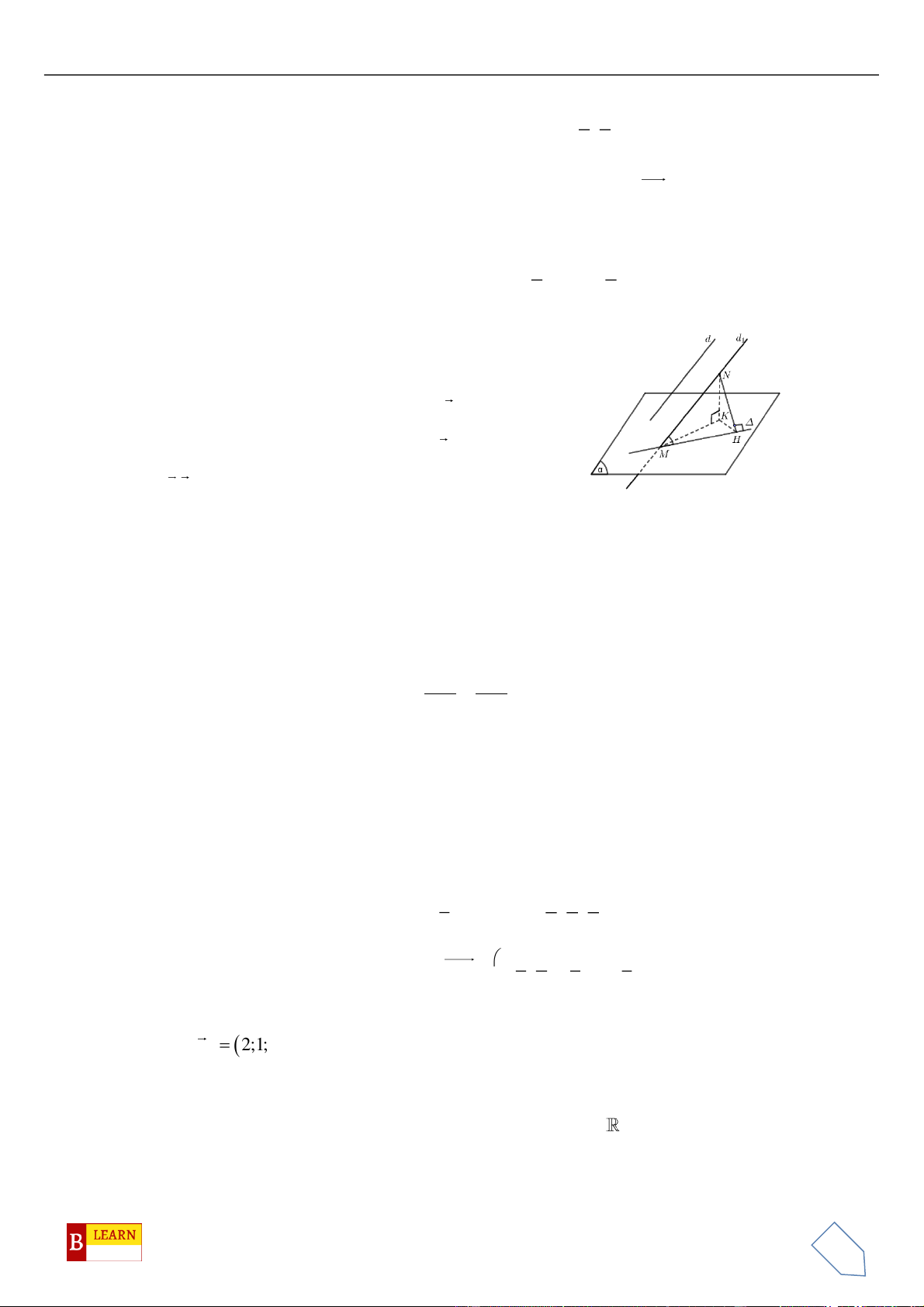
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
215
Câu 22. Chọn A
Gọi
I
là trung điểm của
AB
. Khi đó
I
có tọa độ là:
31
; ;1
22
I
−
.
Mặt phẳng trung trực của đoạn
AB
đi qua điểm
I
và nhận vectơ
( )
1;1;0AB =−
làm vectơ pháp
tuyến.
Nên mặt phẳng trung trực đoạn
AB
có dạng:
31
0
22
xy
− + + − =
20xy − + − =
20xy − + =
.
Câu 23. Chọn B
Đường thẳng
d
có vectơ chỉ phương là
( )
0;3; 2u =−
.
Mặt phẳng
( )
có vectơ pháp tuyến là
( )
1;1; 1n =−
.
Vì
( ) ( )
. 0.1 3.1 2 . 1 5 0un= + + − − =
nên
d
cắt
( )
.
Gọi
1
d
là đường thẳng đi qua
M
và
1
d
//
d
, suy ra
1
d
có phương trình:
3
13
12
x
yt
zt
=
=+
=−
.
Lấy
( )
1
3;4; 1Nd−
. Gọi
K
,
H
lần lượt là hình chiếu vuông góc của
N
trên mặt phẳng
( )
và
đường thẳng
.
Ta có:
( )
,d NMH=
và
sin .
NH NK
NMH
MN MN
=
Do vậy
( )
,d
nhỏ nhất khi
KH
hay
là đường thẳng
MK
.
Đường thẳng
NK
có phương trình:
3
4
1
xt
yt
zt
=+
=+
= − −
.
Tọa độ điểm
K
ứng với
t
là nghiệm của phương trình:
( ) ( ) ( )
5
3 4 1 3 0
3
t t t t+ + + − − − − = = −
. Suy ra
4 7 2
;;
333
K
.
Đường thẳng
có vectơ chỉ phương là
( )
5 4 1 1
; ; 5; 4;1
3 3 3 3
MK
= − − = − −
Chọn B
Câu 24. Chọn A
Ta có:
( )
2;1;1=
P
n
là một vec tơ pháp tuyến của mặt phẳng
( )
P
.
Phương trình tham số của đường thẳng
d
là:
23
2,
25
xt
y t t
zt
=+
= +
=+
.
Gọi
là đường thẳng cần tìm. Gọi
M
là giao điểm của
và
d
( )
2 3 ;2 ;2 5M t t t + + +

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
216
( )
1 3 ; ; 2 5AM t t t = + − +
Do
( )
// P
nên
( ) ( )
. 0 2 1 3 2 5 0 12 0 0
P
AM n t t t t t= + + + − + = = =
( )
1;0; 2AM = −
.
Phương trình đường thẳng
đi qua
( )
1;2;4A
và nhận
( )
1;0; 2AM =−
là một vec tơ chỉ phương
là:
1
2,
42
xt
yt
zt
=+
=
=−
.
Câu 25. Chọn B
Vectơ chỉ phương của đường thẳng
d
là:
(2;1; 1)u −
.
Vectơ pháp tuyến của mặt phẳng
( )
P
là
(1;1; 3)n −
.
Do đường thẳng
d
là đường thẳng nằm trong
( )
P
, cắt và vuông góc với
d
, nên đường thẳng
d
có vectơ chỉ phương là:
' , ( 2;5;1)u u n
= = −
.
Gọi
N
là giao điểm của
d
và
N( 3 2 ; 1 ; ).d t t t
− + − + −
Do đường thẳng
d
nằm trong
( )
P
nên
( )
NP
( 1;0; 1)N − −
.
Phương trình chính tắc của
d
là:
11
2 5 1
x y z++
==
−
.
Câu 26. Chọn D
Cách 1:
Đường thẳng
d
có vectơ chỉ phương
( )
2;4;1
d
u =
và đi qua điểm
( )
0;0;3A
,
( )
2;3; 4AM =−
Gọi
u
là vectơ chỉ phương của đường thẳng
qua
M
vuông góc với
d
và cắt
d
.
Khi đó
, . 0
d
u AM u
=
hay
,
d
u u AM
⊥
và
d
uu⊥
.
Gọi
( )
, 19;10; 2
d
v u AM
= = − −
,
( )
, 18;15; 96
d
vu
=−
, chọn
( )
6;5; 32u =−
.
Vậy phương trình đường thẳng
cần tìm là
2 3 1
6 5 32
x y z− − +
==
−
.
Cách 2:
Gọi
( )
là mặt phẳng qua
M
và vuông góc
d
( )
:2 4 15 0x y z
+ + − =
.
Gọi
( )
Hd
=
8 16 25
;;
7 7 7
H
.
Gọi
là đường thẳng qua
M
vuông góc với
d
và cắt
d
. Khi đó
MH
.
Ta có
6 5 32
;;
7 7 7
MH
= − −
, chọn
( )
6;5; 32u =−
làm vectơ chỉ phương của
.
Vậy phương trình đường thẳng
cần tìm là
2 3 1
6 5 32
x y z− − +
==
−
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
217
Cách 3:
Gọi
là đường thẳng qua
M
vuông góc với
d
và cắt
d
tại
H
. Khi đó
MH
.
Ta có
2
:4
3
xt
d y t
zt
=
=
=+
( )
2 ;4 ;3H t t t+
,
( )
2 2;4 3;4MH t t t= − − +
.
d ⊥
.0
d
uu
=
.0
d
u MH=
( ) ( ) ( )
2 2 2 4 4 3 1 4 0t t t − + − + + =
4
7
t=
.
Suy ra
6 5 32
;;
7 7 7
MH
= − −
, chọn
( )
6;5; 32u
=−
làm vectơ chỉ phương của
.
Vậy phương trình đường thẳng
cần tìm là
2 3 1
6 5 32
x y z− − +
==
−
.
Câu 27. Chọn A
Gọi:
( )
1
1 ';3 ';2 2 'd M t t t = + − +
,
( )
2
3 ; ; 1 3d N t t t = − − −
( )
3 1 '; 3 '; 3 3 2 'MN t t t t t t = − − − − + − − −
.
12
,dd
lần lượt có 2 vectơ chỉ phương là
( ) ( )
12
1; 1;2 , 3;1; 3uu= − = − −
.
Vì
là đường vuông góc chung của
12
;dd
nên
1
2
.0
6 ' 10 4 ' 1
10 ' 19 9 1
.0
MN u
t t t
t t t
MN u
=
− − = =
+ = − = −
=
( ) ( ) ( )
2;2;4 , 3; 1;2 , 1; 3; 2M N MN − = − −
Vậy phương trình
2 2 4
:
1 3 2
x y z− − −
= =
−−
.
Câu 28. Chọn B
Mặt phẳng
( )
P
có vecto pháp tuyến
( )
2; 2;1n =−
.
Đường thẳng
d
đi qua
( )
1;1;3M −
và có vecto chỉ phương
( )
1;2; 2u =−
nên phương trình tham
số của
d
là:
1
12
32
xt
yt
zt
= − +
=+
=−
.Gọi
( )
IP
I
Id
Id
Id
=
( )
I d P=
.
Vì
( )
1 ;1 2 ;3 2I d I t t t − + + −
, mà
( ) ( )
1 2; 1;5I P t I = − − −
.
Gọi
v
là vecto chỉ phương của đường thẳng
.
Vì
( )
P
vn
d
vu
⊥
⊥
⊥
nên ta chọn
( )
, 2; 5; 6v u n
= = − − −
.
I
d
P
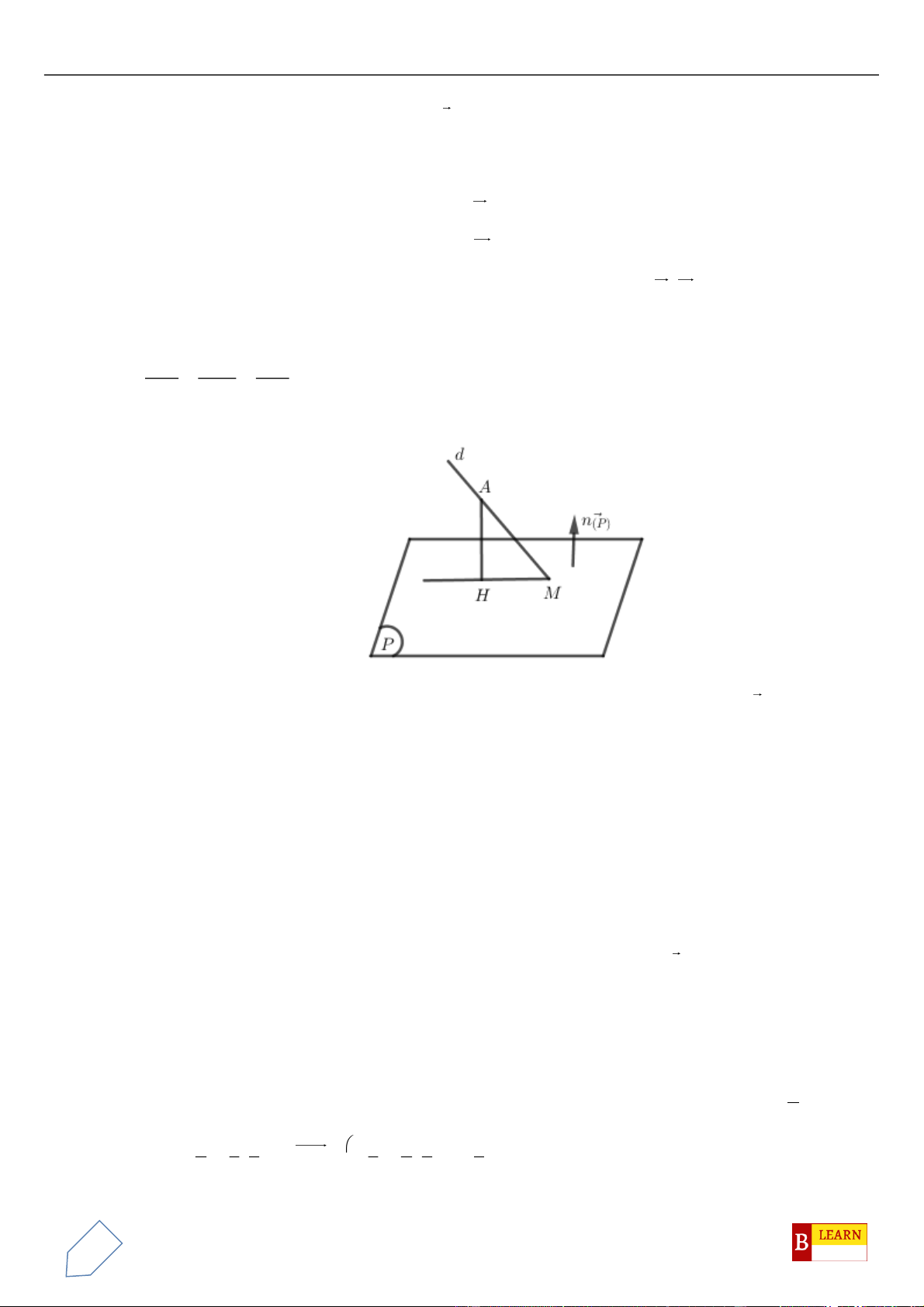
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
218
Vậy
đi qua
( )
2; 1;5I −−
và có VTCP
( )
2; 5; 6v = − − −
nên có PT tham số là:
22
15
56
zt
yt
zt
= − −
= − −
=−
.
Câu 29. Chọn A
Mặt phẳng
( )
P
có một vectơ pháp tuyến là
( )
1
1;1; 1n =−
.
Mặt phẳng
( )
Q
có một vectơ pháp tuyến là
( )
2
2; 1;5n =−
.
Đường thẳng
d
song song với
( )
P
và
( )
Q
có vectơ chỉ phương là
( )
12
, 4; 7; 3nn
= − −
.
Đường thẳng
d
đi qua điểm
( )
1;2; 1M −
nên phương trình của đường thẳng
d
là
1 2 1
4 7 3
x y z− − +
==
−−
.
Câu 30. Chọn C
Phương trình đường thẳng
d
qua
(0; 1;2)A −
, có 1 véc tơ chỉ phương
(1;2; 1)a =−
là
( )
1
11
1
12
2
xt
y t t R
zt
=
= − +
=−
.
Gọi
M
là giao điểm của đường thẳng
d
và mặt phẳng
()P
.
Ta có
( )
1 1 1
; 1 2 ;2M t t t d− + −
và
( ) ( )
1 1 1
( ) 1 2 2 3 0M P t t t + − + + − − =
1
1t=
( )
1;1;1M
.
Gọi
H
là hình chiếu vuông góc của
A
lên mặt phẳng
( )
P
.
Đường thẳng chứa
AH
đi qua
( )
0; 1;2A −
và nhận vectơ pháp tuyến
( )
( )
1;1;1
P
n =
của
( )
P
làm
vectơ chỉ phương có phương trình là
( )
2
22
2
1
2
xt
y t t R
zt
=
= − +
=+
.
Lại có
( )
2 2 2
; 1 ;2 ( )H t t t AH− + +
và
( ) ( )
2 2 2 2
2
( ) 1 2 3 0
3
H P t t t t + − + + + − = =
( )
2 1 8 1 4 5 1
; ; ; ; 1;4; 5
3 3 3 3 3 3 3
H MH
− = − − = − −
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
219
Hình chiếu cần tìm là đường thẳng
()MH
, đi qua
( )
1;1;1M
và có một véc tơ chỉ phương
( )
1;4; 5b =−
là
1 1 1
.
1 4 5
x y z− − −
==
−
Câu 31. Chọn B
Gọi
d
u
là vectơ chỉ phương của đường thẳng
d
( )
1;1;2
d
u=
.
Gọi
B
là giao điểm của
và
d
. Vì
Bd
nên
( )
1; ;2 1B t t t+−
.
Khi đó vectơ chỉ phương của
là
( )
; ;2 3u AB t t t
= = −
.
Vì
vuông góc với
d
nên
( )
. 0 2 3 .2 0 6 6 1
d
u u t t t t t
= + + − = = =
Suy ra
( )
1;1; 1u
=−
. Khi đó phương trình đường thẳng
là
12
1 1 1
x y z−−
==
−
.
Câu 32. Chọn B
Cách 1:
Ta có VTCP của đường thẳng
d
là
( )
2 1;2; 2
d
u m m= + −
.
VTPT của mặt phẳng
( )
P
là
( )
1;1;1
P
n =
Gọi
()
, (4 ; 3;2 1).
( ) ( )
Q d P
Qd
n u n m m m
QP
= = − − − −
⊥
Khi đó
( ) ( ) , ( 3 2;3 5;7).
PQ
P Q u n n m m
= = = − − −
Vì
vuông góc với giá của véctơ
a
nên ta có
. 0 1( 3 2) 7 0 3.u a m m
= − − − + = = −
Cách 2:
Ta có:
d
có VTCP là
( )
2 1;2; 2
d
u m m= + −
.
là hình chiếu vuông góc của
d
lên mặt phẳng
( )
P
và vuông góc với giá của véc tơ
a
nên
d
vuông góc với giá của véc tơ
a
.
Khi đó
( )
. 0 2 1 2 0 3
d
a u m m m= − + + − = = −
.
Câu 33. Chọn D
Gọi
d
u
là vectơ chỉ phương của đường thẳng
d
.
Đường thẳng
có vectơ chỉ phương
( )
1;1; 1u
=−
.
Mặt phẳng
( )
P
có vectơ pháp tuyến
( )
( )
1;2; 3
P
n =−
.
Vì đường thẳng
d
nằm trong
( )
P
và vuông góc đường thẳng
nên
( )
d
d
P
uu
un
⊥
⊥
.
Suy ra
( )
( )
, 1;2;1
d
P
u u n
= = −
.
Gọi
I
là giao điểm của đường thẳng
và mặt phẳng
( )
P
.
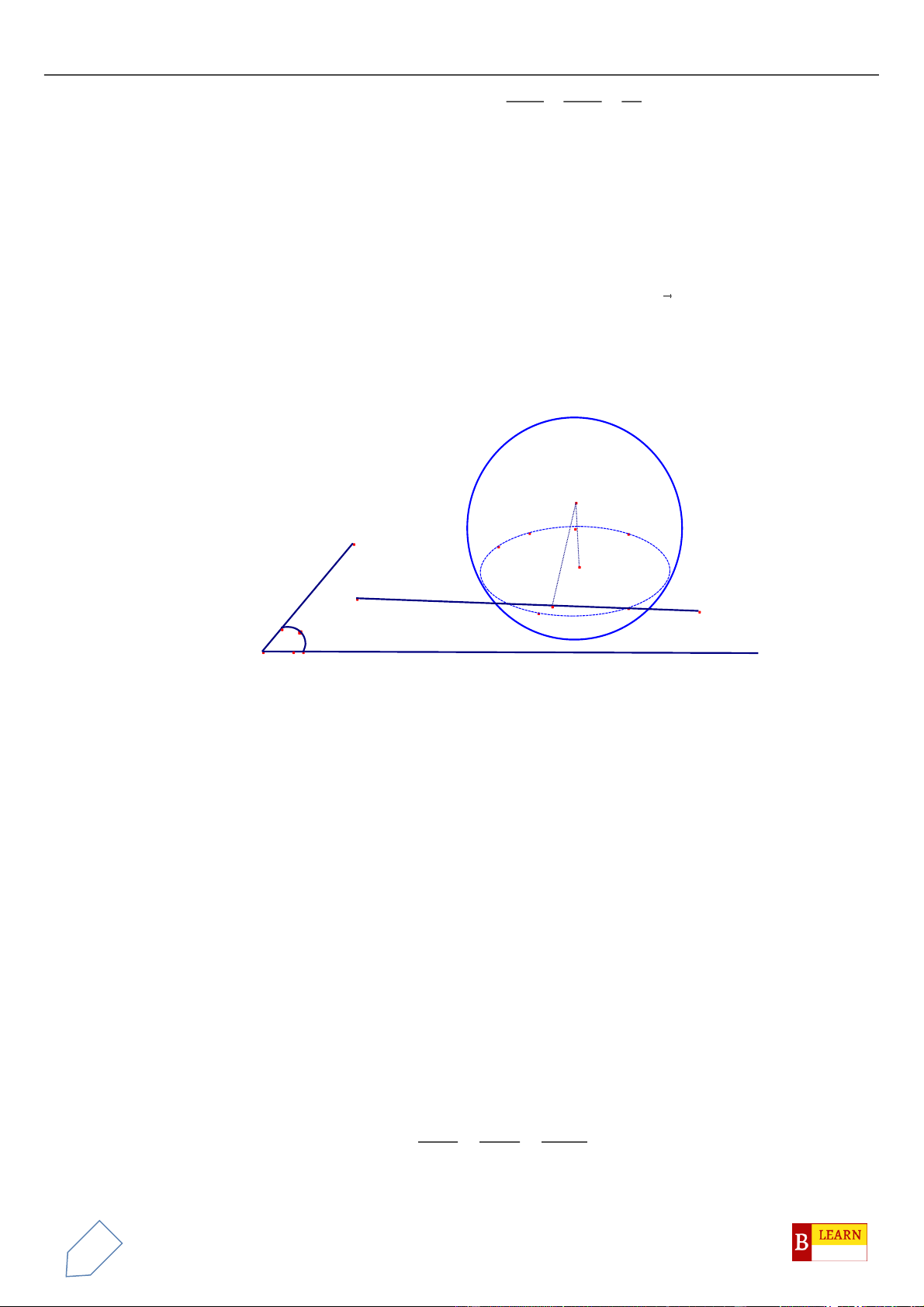
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
220
Tọa độ điểm
I
là nghiệm của hệ phương trình
22
1 1 1
2 3 4 0
x y z
x y z
+−
==
−
+ − + =
( )
3;1;1I−
.
Vì đường thẳng
d
nằm trong
( )
P
và cắt đường thẳng
nên đường thẳng
d
đi qua điểm
I
.
Vậy phương trình đường thẳng
d
là:
3
12
1
xt
yt
zt
= − +
=−
=−
.
Lưu ý: Đây là câu hỏi trắc nghiệm nên chỉ cần tính vectơ chỉ phương
d
u
là có thể chọn đáp án.
Câu 34. Chọn A
Mặt cầu
( )
S
có tâm
( )
2;3;5I
bán kính
10R =
.
Gọi
H
,
K
lần lượt là hình chiếu vuống góc của
I
lên
và mặt phẳng
( )
.
( )
IK
⊥
nên phương trình đường thẳng
IK
đi qua
I
và vuông góc với mặt phẳng
( )
là.
Phương trình tham số đường thẳng
IK
:
22
32
5
xt
yt
zt
=+
=−
=+
.
Tọa độ điểm
K
là nghiệm hệ phương trình
22
32
5
2 2 15 0
xt
yt
zt
x y z
=+
=−
=+
− + + =
( )
2;7;3K −
.
Vì
( )
nên
IH IK
. Do đó,
IH
nhỏ nhất khi
H
trùng với
K
.
Để
MN
lớn nhất thì
IH
phải nhỏ nhất. Khi đó, đường thẳng
cần tìm đi qua
A
và
K
.
Đường thẳng
có phương trình là:
3 3 3
1 4 6
x y z+ − +
==
.
Câu 35. Chọn A
A
K
I
H

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
221
Từ
. . 0MAMA MB MB+=
ta suy ra
,,M A B
thẳng hàng. Hơn nữa:
22
. . 0 . . . .MA MA MB MB MA MA MB MB MA MA MB MB MA MB+ = = − = − =
Vậy
M
là trung điểm
AB
.
Vì
Md
nên toạ độ
( )
3 2 ;1 2 ; 4M t t t− + + − +
( )
t
. Đặt toạ độ
( )
;;B x y z
ta có:
( )
( )
( )
1 2 3 2
74
7 12
2 2 1 2 4
2 2 1
12 2
4 2 4
xt
xt
x y z
y t y t
zt
zt
+ = − +
+=
++
+ = + = = =
+=
+ = − +
. Vậy
1
Bd
.
Câu 36. Chọn A
Tổng quát bài toán: Viết phương trình đường thẳng vuông góc với mặt phẳng , cắt hai
đường thẳng và cho trước.
Gọi tọa độ điểm theo , tọa độ điểm theo .
Đường thẳng vuông góc với mặt phẳng nên và cùng phương suy ra được và
.
Tìm được tọa độ và suy ra phương trình đường thẳng .
Lời giải
Mặt phẳng có vectơ pháp tuyến là .
Gọi là đường thẳng cần tìm và có nên , có
nên .
Ta có .
Do nên , cùng phương
.
Đường thẳng đi qua điểm và có vectơ chỉ phương nên có phương trình
.
Câu 37. Chọn C
Hai đường thẳng
12
,dd
có VTCP là
1
3; 2 ; 2u
và
2
2 ; 2 ; 1u
.
( )
P
d
d
Ad=
A
t
Bd
=
B
t
( )
P
AB
P
n
t
t
A
B
( )
P
( )
1;1;1n =
Ad=
Ad
( )
1 2 ; ; 1 3A t t t− − − +
Bd
=
Bd
( )
2 ; 1 2 ; 2B t t t
+ − + −
( )
2 3;2 1; 2 3 1AB t t t t t t
= + + − − − − +
( )
P⊥
AB
n
2 3 2 1 2 3 1
1 1 1
t t t t t t
+ + − − − − +
= =
34
2 4 2
tt
tt
− = −
+=
1
1
t
t
=−
=
( )
( )
1; 1; 4
3;1; 2
A
B
−−
−
B
( )
1;1;1n =
3 1 2
1 1 1
x y z− − +
==

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
222
Lấy điểm
1
1 3 ; 1 2 ; 2 2A t t t d
và
2
4 2 ; 4 2 ; 3B u u u d
AB
là đường thẳng vuông góc chung của hai đường thẳng
12
,dd
khi
1
2
.0
.0
AB u
AB u
12 17 29
9 12 21
ut
ut
1
1
u
t
4 ;1; 0
2 ; 2 ; 2
2 ;1; 2
A
B
AB
.Vậy phương trình đường vuông góc chung của hai đường thẳng
12
,dd
là
2
22
2 1 2
y
xz
.
Câu 38. Chọn C
Gọi đường thẳng
d
là hình chiếu vuông góc của đường thẳng
d
trên mặt phẳng
( )
P
Đường thẳng
d
đi qua điểm
( )
1; 1; 5A − − −
và có véc tơ chỉ phương
( )
2;1;6
d
u =
.
Mặt phẳng
( )
P
có véc tơ pháp tuyến
( )
()
1;1; 5
P
n =−
.
Gọi
( )
Q
là mặt phẳng chứa
d
và vuông góc với
( )
P
( ) ( )
P Q d
=
.
Véc tơ pháp tuyến của
( )
Q
là
( )
(Q) ( )
, 11; 16; 1
Pd
n n u
= = − −
.
Phương trình của mặt phẳng
( )
Q
là :
11 16 10 0x y z− − − =
.
Do
( ) ( )
P Q d
=
nên véc tơ chỉ phương của đường thẳng
d
là
( ) ( )
' ( ) ( )
, 81; 54; 27 27 3;2;1
d Q P
u n n
= = − − − =−
,
suy ra
d
có véc tơ chỉ phương là
( )
1
3;2;1u =
.
Kiểm tra với điểm
( )
1;0;1B
thuộc đường thẳng ở khẳng định C ta thấy
( ) ( )
,B P B Q
.
Do đó phương trình của
d
là :
13
2
1
xt
yt
zt
=+
=
=+
,
t
Câu 39. Chọn A
Vì đường thẳng
cắt cả hai đường thẳng
1
d
và
2
d
nên ta gọi
M
và
N
lần lượt là giao điểm của
với
1
d
và
2
d
. Hơn nữa, vì đường thẳng
nằm trong mặt phẳng (
) nên
( )
,MN
.
Tìm tọa độ điểm
M
.
Vì
1
Md
nên tọa độ điểm
M
có dạng
( )
1 3 ;2 ; 1 2M t t t+ + − +
với
t
.
Vì
( ) ( )
1 3 ;2 ; 1 2M t t t
+ + − +
nên
1 3 2 1 2 2 0 1t t t t
.
Do đó
( )
2;1; 3M −−
.
Tìm tọa độ điểm
N
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
223
( )
22
23
24
: : 0 2
3 2 2
42
xt
x y z
d d y t t
zt
=−
−−
= = = +
−−
=−
.
Vì
2
Nd
nên tọa độ điểm
N
có dạng
( )
2 3 ; 2 ; 4 2N t t t
−−
với
t
.
Vì
( ) ( )
2 3 ; 2 ; 4 2N t t t
− −
nên
( ) ( ) ( )
2 3 2 4 2 2 0 4t t t t
− + − − − = =
.
Do đó
( )
10;8; 4N −−
. Ta có:
8 ; 7 ; 1NM
.
Đường thẳng
đi qua
( )
2;1; 3M −−
và nhận
8 ; 7 ; 1NM
làm vectơ chỉ phương nên
có
phương trình là
2 1 3
8 7 1
x y z+ − +
==
−
.
Câu 40. Chọn A
Gọi
( )
2 1; ; 1N t t t+ − −
. Vì
A
là trung điểm của
MN
, suy ra
( )
1 2 ;6 ;5M t t t− − +
.
Điểm
M
nằm trong mặt phẳng
( )
P
, suy ra
1 2 6 5 2 0t t t− + − − − + =
1t =
.
Suy ra tọa độ điểm
( )
3;1; 2N −
. Ta có
( )
2;2;4NA =−
, chọn
( )
1; 1; 2u
= − −
.
Phương trình đường thẳng
qua
A
, có véc-tơ chỉ phương
u
là
1
3
22
xt
yt
zt
=+
=−
=−
.
Câu 41. Chọn B
Cách 1.Gọi
( )
;;H a b c
là hình chiếu vuông góc của
B
trên
AC
.
Ta có :
( ) ( ) ( )
2; 3; 1 , 2; 2;2 , 1; 1; 2BH a b c AC AH a b c= + − − = − = − − −
H
là hình chiếu vuông góc của
B
trên
.0BH AC
AC
H AC
=
( ) ( ) ( )
41
2 2 2 3 2 1 0
23
1 1 2
10
2 2 2
a b c a
a b c
a b b
abc
a c c
− + = − = −
+ − − + − =
+ = =
− − −
==
− = − =
−
Nên
( )
1;3;0H −
,
( )
1;0; 1BH =−
Đường cao
BH
đi qua
B
và có VTCP
( )
1;0; 1BH =−
có phương trình là:
( )
2
3
1
xt
yt
zt
= − +
=
=−

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
224
Cách 2. Đường thẳng
AC
đi qua
A
và có VTCP
( )
2; 2;2AC =−
hay ta có thể chọn véc tơ chỉ
phương của
AC
là
( )
1; 1;1U =−
nên phương trình của đường thẳng AC là:
( )
1
1
2
xt
y t t
zt
=+
= −
=+
Gọi
H
là hình chiếu vuông góc của
B
trên
AC
nên ta gọi
( )
1 ;1 ;2H t t t+ − +
( )
3 ; 2 ;1BH t t t = + − − +
Ta có:
( ) ( )( ) ( )
. 0 2 3 2 2 2 1 0 1BH AC BH AC t t t t⊥ = + + − − − + + = = −
( ) ( )
1;3;0 ; 1;0; 1H BH − = −
Vậy đường thẳng
BH
đi qua
B
và có VTCP
( )
1;0; 1BH =−
có PT là:
( )
2
3
1
xt
yt
zt
= − +
=
=−
Câu 42. Chọn B
Giả sử đường thẳng
( )
d
cắt trục
Oz
tại điểm
( )
0;0;Ba
(
a
là số thực).
Suy ra đường thẳng
( )
d
nhận
( )
1;2;3BA a−
là một vecto chỉ phương.
Mà
( )
d
song song với mặt phẳng
( )
P
và
( )
2;1; 4n −
là một vecto pháp tuyến của
( )
P
nên:
.0BA n BAn⊥ =
( )
2.1 1.2 4 3 0 2aa + − − = =
.
Suy ra đường thẳng
( )
d
đi qua điểm
( )
1;2;3A
và nhận
( )
1;2;1BA
là một vecto chỉ phương có
phương trình tham số là:
1
22
3
xt
yt
zt
=+
=+
=+
.
Từ dữ kiện
( )
d
nhận
( )
1;2;1BA
là một vecto chỉ phương ta loại được đáp án A, C, D.
Thử lại thấy điểm
( )
0;0;2
thuộc đường thẳng
1
22
3
xt
yt
zt
=+
=+
=+
nên đáp án B là đáp án đúng.
Câu 43. Chọn C
Cách 1:

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
225
Mặt phẳng
( )
P
đi qua ba điểm
3
;0;0
2
A
,
3
0; ;0
2
B
,
( )
0;0; 3C −
nên phương trình
( )
P
là
22
1 2 2 3 0
3 3 3
x y z
x y z+ + = + − − =
−
. Dễ thấy
( )
EP
.
Mặt cầu
( )
S
có tâm
( )
3;2;5I
, bán kính
6R =
.
Giả sử
K
là hình chiếu của
I
lên
( )
P
, ta có:
( )
( )
/
2
22
2.3 2.2 5 3
2
3
2 2 1
IP
IK d
+ − −
= = =
+ + −
.
Do đó
IK R
nên
( )
S
và
( )
P
cắt nhau và giao tuyến của chúng là đường tròn tâm
K
.
Lại có
( ) ( ) ( )
2 2 2
2 3 1 2 3 5 6IE = − + − + − =
IE R
, nên
E
nằm trong mặt cầu
( )
S
. Mà
( )
EP
nên
E
nằm trong đường tròn giao tuyến của
( )
S
và
( )
P
.
Giả sử
cắt
( )
S
tại
D
và
G
,
F
là hình chiếu của
K
lên
. Qua
E
kẻ đường thẳng vuông góc
với
EK
, nằm trên
( )
P
, cắt
( )
S
tại
M
và
N
. Ta có
KF KE
DG MN
(theo tính chất mối
quan hệ giữa dây cung và khoảng cách từ dây cung tới tâm).
Mà
MN
không đổi nên
DG
nhỏ nhất khi và chỉ khi
EF
. Khi đó
KE⊥
, ngoài ra
( )
IK P IK⊥ ⊥
, do đó
( )
IKE ⊥
IE⊥
.
Vậy
u IE
⊥
;
P
un
⊥
, mà
( )
1; 1; 2IE = − − −
,
( )
2;2; 1
P
n =−
Ta có:
( )
; 5; 5;0
P
IE n
=−
, chọn
( )
1; 1;0u
=−
.
Vì
đi qua
( )
2;1;3E
nên phương trình
là
2
1
3
xt
yt
z
=+
=−
=
.
Cách 2:
Mặt phẳng
( )
P
đi qua ba điểm
3
;0;0
2
A
,
3
0; ;0
2
B
,
( )
0;0; 3C −
nên phương trình
( )
P
là
22
1 2 2 3 0
3 3 3
x y z
x y z+ + = + − − =
−
. Dễ thấy
( )
EP
.
Thay tọa độ điểm
E
vào vế trái của phương trình
()S
ta được :
2 2 2
1 1 2 6 36+ + =
. Do đó
E
nằm trong mặt cầu
()S
.
Gọi
,MN
là giao điểm của
và mặt cầu
()S
. Khi đó ta có:
22
2 ( ( , ))MN R d I= −
, với
,RI
lần lượt là bán kính và tâm của mặt cầu
()S
.
Do đó
MN
nhỏ nhất khi
( , )dI
lớn nhất.
Ta lại có:
( , )d I IE
, với
IE
cố định.
Do đó:
max ( , ) IEdI=
. Khi đó:
u IE
⊥
;
P
un
⊥
, mà
( )
1; 1; 2IE = − − −
,
( )
2;2; 1
P
n =−
Ta có:
( )
; 5; 5;0
P
IE n
=−
, chọn
( )
1; 1;0u
=−
.
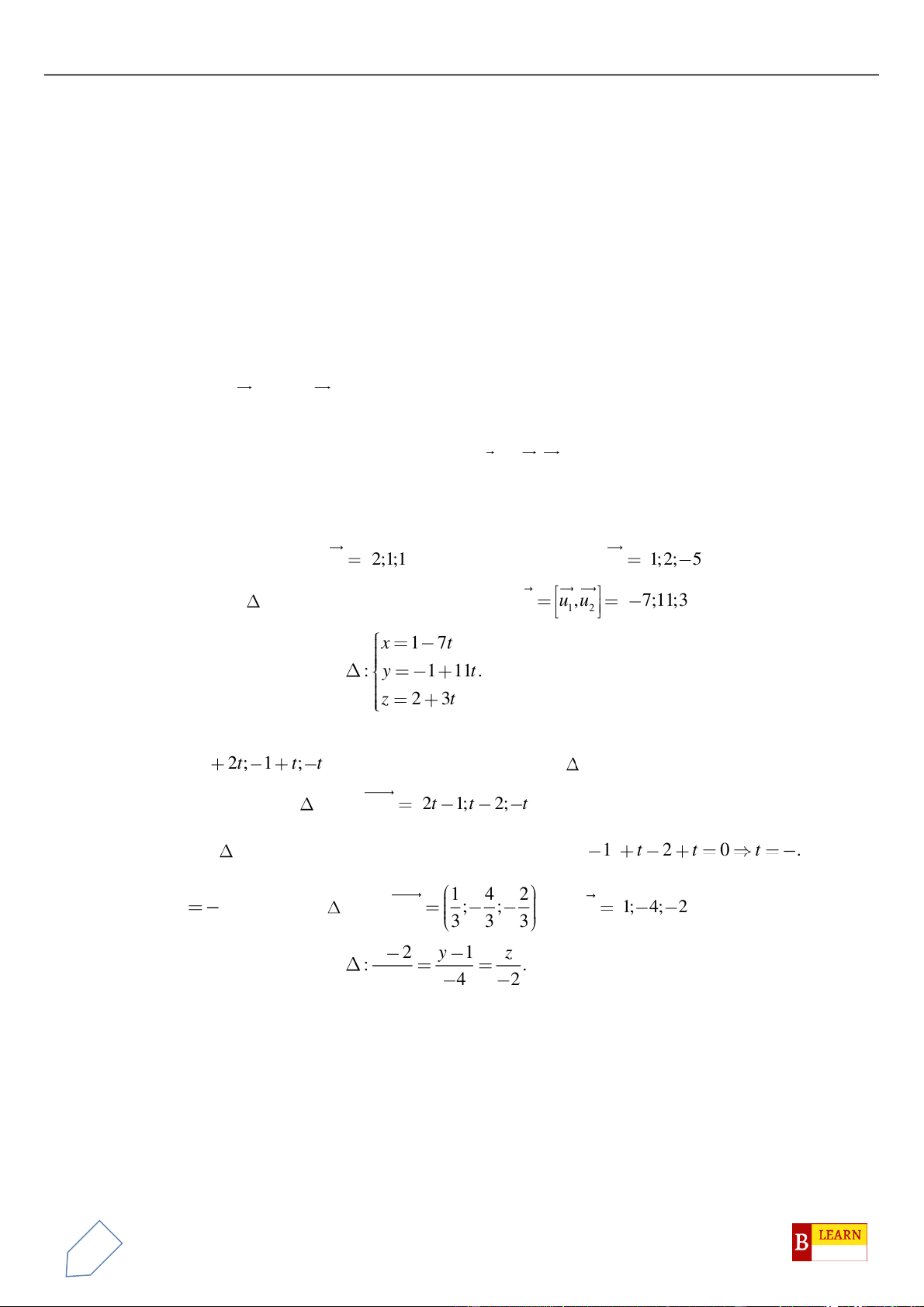
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
226
Ngoài ra
đi qua
( )
2;1;3E
nên phương trình
là
2
1
3
xt
yt
z
=+
=−
=
.
Câu 44. Chọn D
Ta có phép vị tự tâm
A
tỉ số biến điểm
M
thành điểm
N
mà
M
là điểm nằm trên mp
( )
P
Suy ra điểm
N
nằm trên mp
( )
'P
là ảnh của mặt phẳng
( )
P
qua phép vị tự tâm
A
tỉ số .
Ta có , phép vị tự tâm
A
tỉ số biến
B
thành và
( ) ( )
/ / 'PP
Do đó
N
thuộc hai mặt phẳng
( )
Q
và
( )
'P
nên
N
thuộc giao tuyến
d
của hai mặt phẳng
( )
Q
và
( )
'P
với lần lượt là vectơ pháp tuyến của hai mặt phẳng
( )
'P
và
( )
Q
và
d
có vectơ chỉ phương .
Câu 45. Chọn B
Đường thẳng
1
d
có vtcp
1
2;1;1u
, đường thẳng
2
d
có vtcp
2
1;2; 5u
.
Đường thẳng vuông góc với
1
d
và
2
d
nên nhận
12
, 7;11;3u u u
làm vectơ chỉ phương.
Phương trình đường thẳng
17
: 1 11 .
23
xt
yt
zt
Câu 46. Chọn D
Gọi
1 2 ; 1 ;N t t t
là giao điểm của đường thẳng và đường thẳng
.d
Lúc đó đường thẳng nhận
2 1; 2;MN t t t
làm vectơ chỉ phương.
Mặt khác vuông góc với đường thẳng
d
nên ta có:
2
2 2 1 2 0 .
3
t t t t
Với
2
3
t
đường thẳng nhận
1 4 2
;;
3 3 3
MN
hoặc
1; 4; 2u
làm vtcp.
Phương trình đường thẳng
21
:.
1 4 2
x y z
Câu 47. Chọn C
Cách 1:
Ta có: mặt phẳng
( )
:2 3 2 12 0x y z
+ − + =
( ) ( )
( ) ( )
( ) ( )
6;0;0
0; 4;0
0;0;6 .
Ox A
Oy B
Oz C
= −
= −
=
2
2
( ) ( )
2;0;1BP
2
( ) ( )
' 6;1; 3 'BP−
( )
' :2 3 4 0P x y z + + − =
( ) ( )
12
2;1;3 , 3; 2; 1nn−−
( )
2;3; 1Cd −
( )
12
; 5;11; 7u n n
= = −
25
: 3 11
17
xt
d y t
zt
=+
= +
= − −
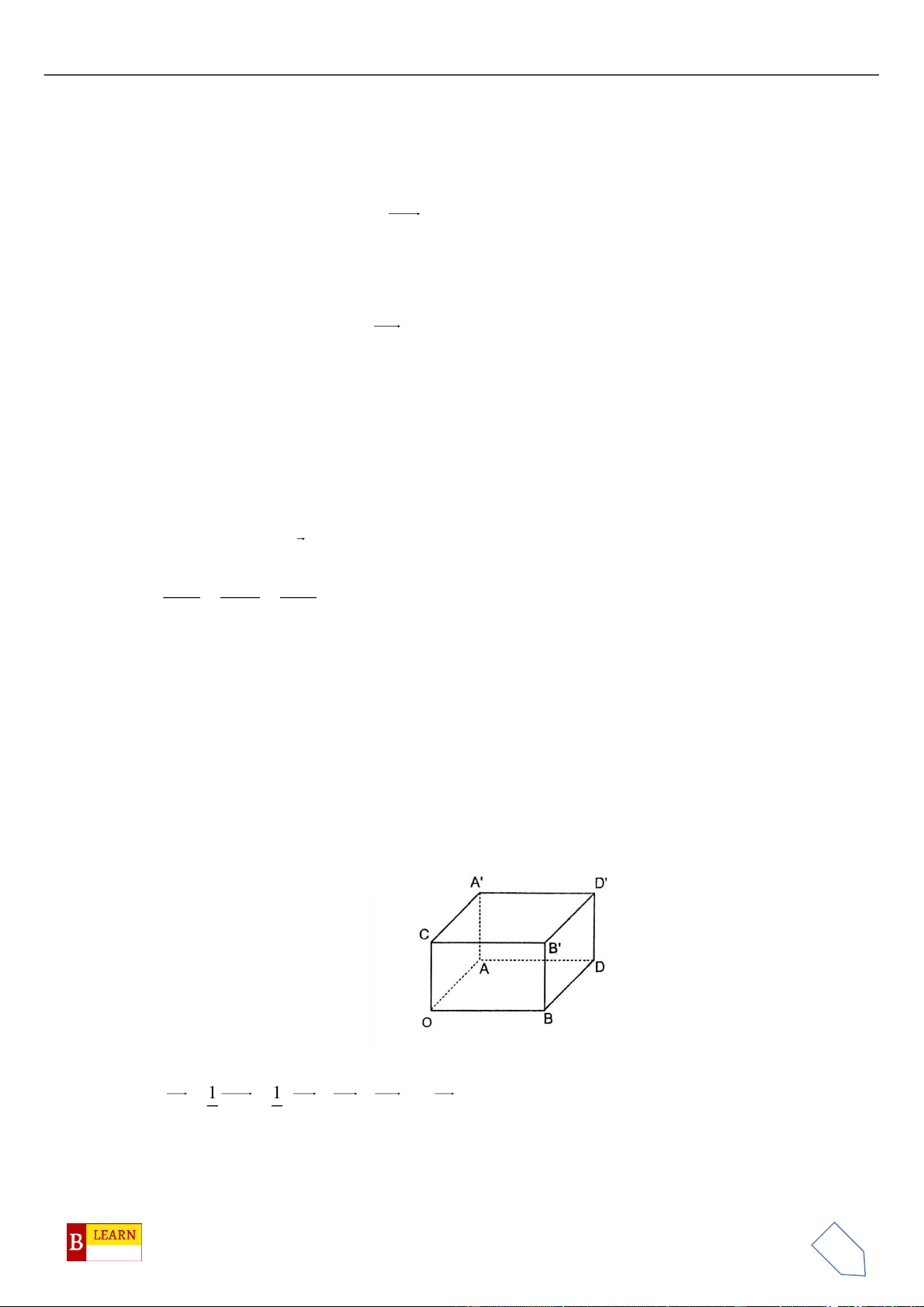
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
227
Mà đường thẳng
d
đi qua tâm đường tròn ngoại tiếp tam giác
ABC
và vuông góc với mặt phẳng
( )
ABC
nên đường thẳng
d
là tập hợp các điểm cách đều 3 đỉnh
,,A B C
trong không gian
đường thẳng
d
là giao tuyến của các mp trung trực của các đoạn thẳng
,,AB AC BC
.
Gọi
( )
P
là mặt phẳng trung trực của đoạn thẳng
AB
Mặt phẳng
( )
P
đi qua trung điểm
( )
3; 2;0M −−
của
AB
và nhận
( )
3; 2;0AM =−
là vectơ pháp tuyến
Phương trình của mặt
phẳng
( )
P
là:
3 2 5 0xy− + =
.
Gọi
( )
Q
là mặt phẳng trung trực của đoạn thẳng
AC
Mặt phẳng
( )
Q
đi qua trung điểm
( )
3;0;3N −
của
AC
và nhận
( )
3;0;3AN =
là vectơ pháp tuyến
Phương trình của mặt phẳng
( )
Q
là:
0xz+=
.
Lấy điểm
( )
1; ;E y z−
thuộc đường thẳng
d
, vì đường thẳng
d
là giao tuyến của hai mặt phẳng
( )
P
và
( )
Q
nên tọa độ điểm
E
thỏa mãn hệ:
( )
3 2 5 0 1
1;1;1
1 0 1
yy
E
zz
− − + = =
−
− + = =
Đường thẳng
d
vuông góc với mặt phẳng
( )
:2 3 2 12 0x y z
+ − + =
nên đường thẳng
d
có 1
véctơ chỉ phương là
( )
2;3; 2u =−
, đồng thời
d
đi qua điểm
( )
1;1;1E −
nên phương trình của
d
là
3 2 3
2 3 2
x y z+ + −
==
−
.
Cách 2:
Ta có: mặt phẳng
( )
:2 3 2 12 0x y z
+ − + =
( ) ( )
( ) ( )
( ) ( )
6;0;0
0; 4;0
0;0;6 .
Ox A
Oy B
Oz C
= −
= −
=
Mà đường thẳng
d
đi qua tâm đường tròn ngoại tiếp tam giác
ABC
và vuông góc với mặt phẳng
( )
ABC
nên đường thẳng
d
là tập hợp các điểm cách đều 3 đỉnh
,,A B C
trong không gian.
Nhận xét: 3 cạnh
,,OA OB OC
đôi một vuông góc
dựng hình hộp chữ nhật
. ' ' 'OADBCA D B
Dễ thấy tâm mặt cầu ngoại tiếp hình hộp là trung điểm
I
của đường chéo
'OD
( )
( ) ( )
11
' 3; 2;3 3; 2;3 .
22
OI OD OA OB OC OI I = = + + = − − − −
Mà
I
là tâm mặt cầu ngoại tiếp của hình hộp
I
cách đều 3 đỉnh
,,A B C
I
nằm trên
đường thẳng
d
cần tìm.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
228
Đường thẳng
d
vuông góc với mặt phẳng
( )
:2 3 2 12 0x y z
+ − + =
nên đường thẳng
d
có 1
véctơ chỉ phương là
( )
2;3; 2u =−
, đồng thời
d
đi qua điểm
( )
1;1;1E −
nên phương trình của
d
là
3 2 3
2 3 2
x y z+ + −
==
−
.
Câu 48. Chọn D
Đường thẳng
1
d
có VTCP
( )
1
1;0; 1
d
u =−
.
Giả sử
( )
P
là mặt phẳng qua
A
và vuông góc với
( )
1
: 2 1 0 1 0d P x z x z − − + = − − =
Gọi
B
là giao điểm của
( )
P
và
2
.d
Tọa độ
B
là nghiệm của hệ phương trình:
( )
3 2 1
31
1;2;0
02
1 0 0
x t t
y t x
B
zy
x z z
= + = −
= + =
==
− − = =
.
Đường thẳng cần tìm là đường thẳng
:AB
Ta có
( )
1;1; 1AB = − −
hay VTCP của đường thẳng cần tìm là
( )
1; 1;1u =−
Đường thẳng cần tìm đi qua
( )
1;2;0B
và có VTCP là
( )
1; 1;1u =−
Suy ra phương trình đường thẳng cần tìm:
12
1 1 1
x y z−−
==
−
.
Cách 2:
Gọi
là đường thẳng cần tìm.
cắt
2
d
tại
B
.
Ta có
( )
2
3 2 ;3 ;0B d B t t
+ +
.
Đường thẳng
có vectơ chỉ phương là
( )
1 2 ;2 ; 1AB t t
= + + −
,
1
d
có vectơ chỉ phương là
( )
1
1;0; 1u =−
.
Ta có
1 1 1
. 0 1 2 0 1 0 1d AB u AB u t t
⊥ ⊥ = + + + = = −
. Suy ra
( )
1;1; 1AB = − −
.
Đường thẳng cần tìm đi qua
( )
1;2;0B
và có VTCP là
( )
1; 1;1u =−
Suy ra phương trình đường thẳng cần tìm:
12
1 1 1
x y z−−
==
−
.
Câu 49. Chọn D
Ta viết phương trình tham số của
( ) ( )
12
12
: 1 , : 4
1 2 3 2
x t x s
d y t t d y s s
z t z s
= = −
= − = −
= + = +
.
Tìm giao điểm của hai đường thẳng
1
d
và
2
d
.
Ta có
12
1
14
0
1 2 3 2
ts
t
ts
s
ts
=−
=
− = −
=
+ = +
suy ra
( )
1;0;3I
là giao điểm của hai đường thẳng
1
d
và
2
d
.
Lấy
( )
1
0;1;1 6.A d IA =
Gọi
( )
2
1 2 ; 4 ;3 2B s s s d− − +
sao cho
6IB =
.
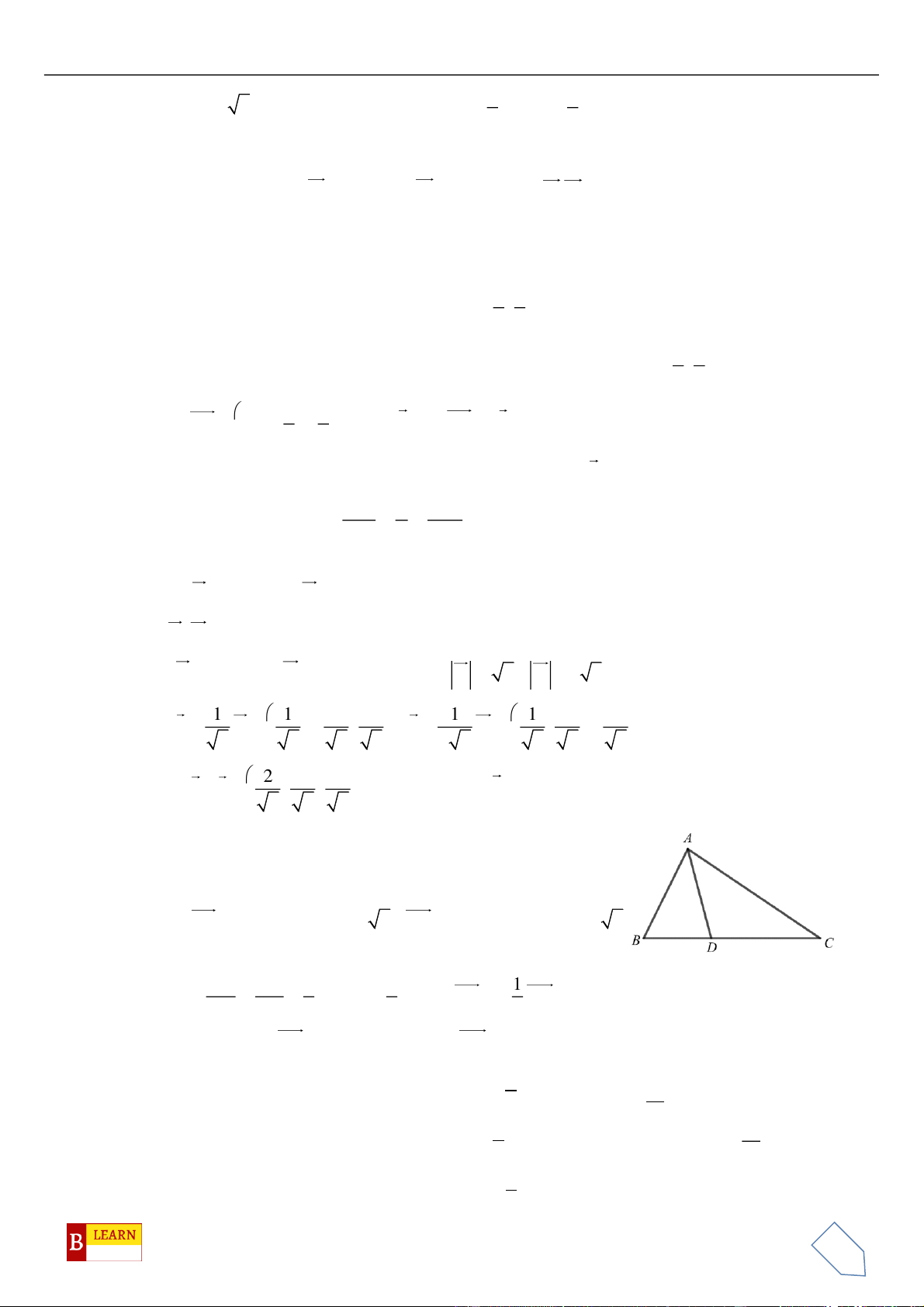
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
229
Ta có
2 2 2 2
11
6 4 16 4 6 .
42
IB s s s s s= + + = = =
Vậy có 2 điểm thỏa mãn
( )
( )
0; 2;4
2;2;2
B
B
−
.
Với
( )
0; 2;4B −
ta có
( ) ( )
1;1; 2 , 1; 2;1IA IB− − − −
. 3 0IAIB AIB= −
là góc tù
Theo yêu cầu bài toán ta viết phương trình của đường phân giác của góc
AIB
với
( )
0; 2;4B −
(không cần xét trường hợp kia) .
Gọi
M
là trung điểm của
AB
suy ra
15
0; ;
22
M
−
, khi đó phương trình đường phân giác cần
tìm là phương trình đường thẳng đi qua hai điêm
( )
1;0;3I
và
15
0; ;
22
M
−
.
Ta có
11
1; ;
22
IM
= − − −
, chọn
( )
2 2;1;1u IM u= − =
làm vectơ chỉ phương của đường phân
giác. Vậy đường phân giác đi qua điểm
( )
1;0;3I
và nhận
( )
2;1;1u =
làm vectơ chỉ phương có
phương trình chính tắc là:
13
2 1 1
x y z−−
==
.
Nhận xét: Có thể tìm vectơ chỉ phương của đường phân giác như sau:
Ta có
( ) ( )
12
1; 1;2 ; 2;4; 2uu= − = −
lần lượt là véctơ chỉ phương của hai đường thẳng
1
d
và
2
d
.
Vì
12
. 6 0uu= −
nên góc giữa hai vectơ đó là góc tù.
Xét
( ) ( )
12
1; 1;2 ; 2;4; 2uu= − = −
. Ta có
1
6u =
,
2
26u =
.
Đặt
1
1 1 1 2
;;
6 6 6 6
au
= = −
;
2
1 1 2 1
;;
2 6 6 6 6
bu
= = −
.
Ta có
2 1 1
;;
666
ab
+=
nên có thể chọn
( )
2;1;1u =
là VTCP của đường phân giác.
Câu 50. Chọn C
Cách 1:
Ta có
( )
1; 1;2 6AB AB= − =
,
( )
2;2; 4 2 6AC AC= − =
.
Giả sử đường phân giác trong của góc
A
cắt
BC
tại
D
.
Khi đó:
1 1 1
2 2 2
DB AB
DB DC DB DC
DC AC
= = = = −
(*) (vì
D
nằm giữa
B
và
C
).
Gọi
( ) ( )
; ; 3 ; ;2D x y z DB x y z = − − −
,
( )
4 ;3 ; 4DC x y z= − − − −
.
Thay vào (*) ta được hệ phương trình
( )
( )
( )
1
10
34
2
3
1
31
2
0
1
24
2
xx
x
y y y
z
zz
− = − −
=
− = − − =
=
− = − − −
. Vậy
10
;1;0
3
D
.
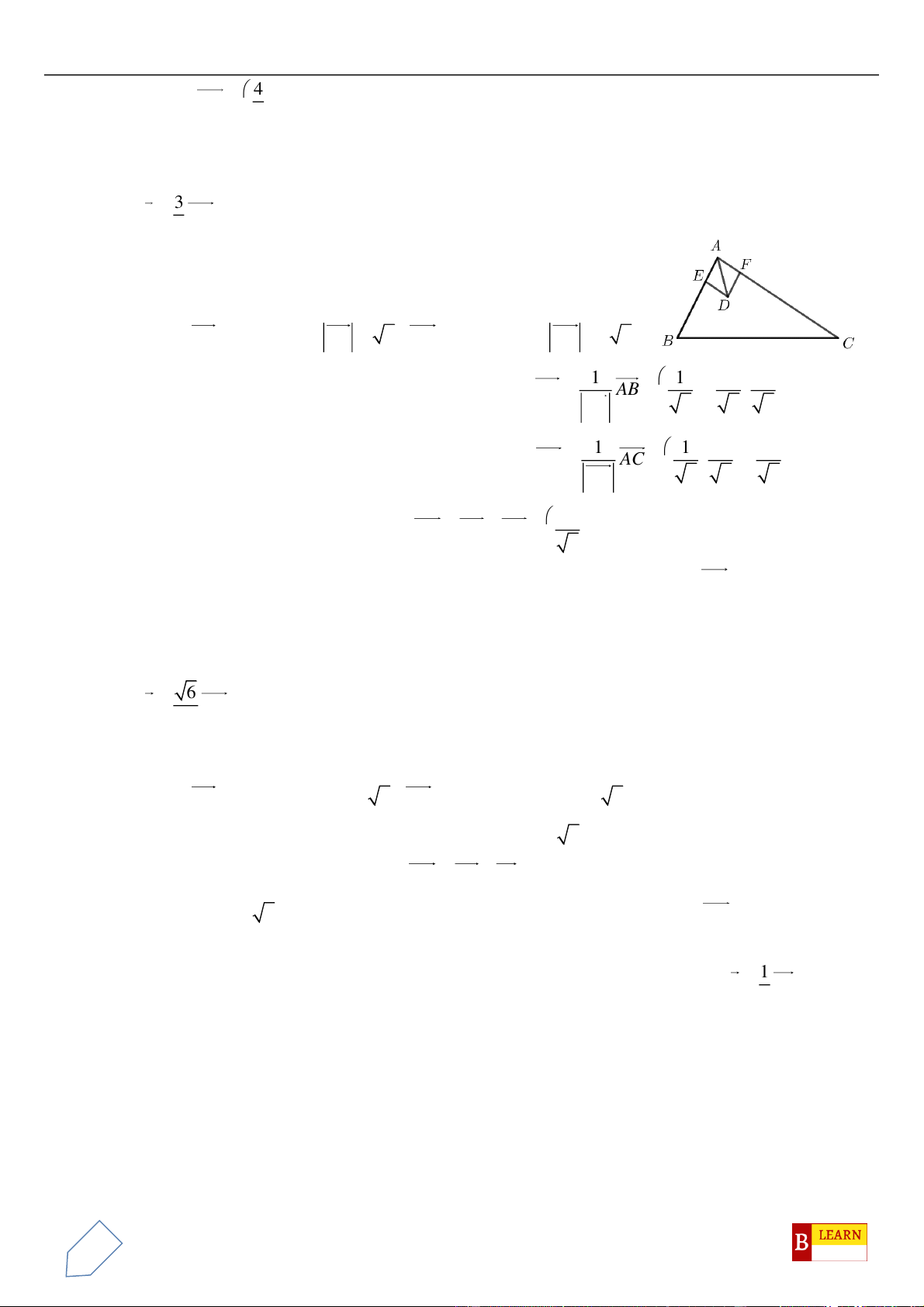
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
230
Suy ra
4
;0;0
3
AD
=
.
Đường phân giác trong của góc
A
đi qua điểm
( )
2;1;0A
và có vectơ chỉ phương
( )
3
1;0;0
4
u AD==
nên có phương trình là:
2
1
0
xt
y
z
=+
=
=
.
Cách 2:
Ta có
( )
1; 1;2 6AB AB= − =
,
( )
2;2; 4 2 6AC AC= − =
.
Lấy điểm
E
trên cạnh
AB
sao cho
1AE =
. Khi đó
1 1 1 2
;;
6 6 6
AE AB
AB
= = −
.
Lấy điểm
F
trên cạnh
AC
sao cho
1AF =
. Khi đó
1 1 1 2
;;
6 6 6
AF AC
AC
= = −
.
Dựng hình bình hành
AEDF
, ta có
2
;0;0
6
AD AE AF
= + =
.
Vì
1AE AF==
nên hình bình hành
AEDF
cũng là hình thoi. Do đó
AD
là một vectơ chỉ
phương của đường phân giác trong của góc
A
của tam giác
ABC
.
Vậy đường phân giác trong của góc
A
đi qua điểm
( )
2;1;0A
và có vectơ chỉ phương là
( )
6
1;0;0
2
u AD==
nên có phương trình là:
2
1
0
xt
y
z
=+
=
=
.
Cách 3:
Ta có
( )
1; 1;2 6AB AB= − =
,
( )
2;2; 4 2 6AC AC= − =
.
Gọi
I
là trung điểm
AC
. Ta có
( )
3;2; 2I =−
và
6AI =
.
Dựng hình bình hành
ABKI
, ta có
( )
2;0;0AK AB AI= + =
.
Vì
6AB AI==
nên hình bình hành
ABKI
cũng là hình thoi. Do đó
AK
là một vectơ chỉ
phương của đường phân giác trong của góc
A
của tam giác
ABC
.
Vậy đường phân giác trong của góc
A
đi qua điểm
( )
2;1;0A
và có VTCP là
( )
1
1;0;0
2
u AI==
nên có phương trình là:
2
1
0
xt
y
z
=+
=
=
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
231
DẠNG 3. TÌM TỌA ĐỘ ĐIỂM LIÊN QUAN ĐẾN ĐƯỜNG THẲNG
Câu 1. Trong không gian
Oxyz
, cho đường thẳng
( )
12
:2
22
xt
d y t t
zt
=+
= −
= − +
và điểm
( )
1;2;Mm
. Tìm giá trị
tham số
m
để điểm
M
thuộc đường thẳng
d
.
A.
2m =
. B.
2m =−
. C.
1m =
. D.
0m =
.
Câu 2. Trong không gian
Oxyz
, cho đường thẳng
21
:
1 2 2
x y z
d
−−
==
−
và mặt phẳng
( )
: 2 5 0P x y z+ − − =
. Tọa độ giao điểm của
d
và
( )
P
là
A.
( )
2;1; 1−
. B.
( )
3; 1; 2−−
. C.
( )
1;3; 2−
. D.
( )
1;3;2
Câu 3.
Trong không gian
Oxyz
cho đường thẳng
12
:
2 1 1
x y z−+
= =
−
và điểm
( )
4;1;1A −
. Gọi
'A
là hình
chiếu của
A
trên
. Mặt phẳng nào sau đây vuông góc với
'?AA
A.
2 2 0xy− − =
. B.
4 7 1 0x y z− + − =
. C.
3 3 0x y z− + + + =
. D.
4 1 0x y z− + + =
.
Câu 4. Trong không gian
Oxyz
, đường thẳng
12
3
xt
yt
zt
=−
=
=−
không đi qua điểm nào dưới đây?
A.
( )
3; 1;4Q −
. B.
( )
1;1;2N −
. C.
( )
1;0;3M
. D.
( )
3; 1;2P −
.
Câu 5. Trong không gian tọa độ
Oxyz
, cho mặt phẳng
( ):2 2 7 0P x y z− − + =
và điểm
(1;1; 2)A −
. Điểm
( ; ; 1)H a b −
là hình chiếu vuông góc của
()A
trên
()P
. Tổng
ab+
bằng
A.
2
. B.
3
. C.
1−
. D.
3−
.
Câu 6. Trong không gian với hệ tọa độ
Oxyz
, gọi
( )
là mặt phẳng chứa đường thẳng
23
( ):
1 1 2
x y z
d
−−
==
và vuông góc với mặt phẳng
( )
: 2z 1 0xy
+ − + =
. Hỏi giao tuyến của
( )
và
( )
đi qua điểm nào ?
A.
( )
0;1;3
. B.
( )
2;3;3
. C.
( )
5;6;8
D.
( )
1; 2;0−
Câu 7. Trong không gian
Oxyz
, cho đường thẳng
42
:3
1
xt
d y t
zt
=−
= − +
=−
( )
t
, giao điểm của
d
với mặt
phẳng
( )
Oxy
có tọa độ là
A.
( )
4; 3;0−
. B.
( )
2; 2;0−
. C.
( )
0; 1; 1−−
. D.
( )
2;0; 2−−
.
Câu 8. Trong không gian
Oxyz
, cho điểm
1;1;6A
và đường thẳng
2
: 1 2
2
xt
yt
zt
. Hình chiếu
vuông góc của điểm
A
lên đường thẳng là
A.
3; 1;2M
. B.
11; 17;18H
. C.
1;3; 2N
. D.
2;1;0K
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
232
Câu 9. Trong không gian với hệ trục tọa độ
Oxyz
, cho hai đường thẳng
1
:
12
x at
d y t
zt
=+
=
= − +
và
1
: 2 2
3
xt
d y t
zt
= − −
=+
=−
. Giá trị của
a
để hai đường thẳng
d
và
d
cắt nhau là
A.
2a =−
. B.
1a =−
. C.
0a =
. D.
1a =
.
Câu 10. Trong không gian với hệ tọa độ
Oxyz
. Đường thẳng
1
2
xt
d y t
zt
=
=−
=+
đi qua điểm nào sau sau đây?
A.
( )
1; 1;1K −
. B.
( )
1;1;2E
. C.
( )
1;2;0H
. D.
( )
0;1;2F
.
Câu 11. Trong không gian với hệ trục tọa độ
Oxyz
, cho
( )
1; 2;3A −
,
( )
2;0; 1B −
và mặt phẳng
( )
: 1 0P x y z+ + − =
. Tọa độ giao điểm
C
của đường thẳng
AB
và mặt phẳng
( )
P
là
A.
( )
2;0; 1C −
. B.
( )
1;1; 1C −
. C.
( )
0;2; 1C −
. D.
( )
2; 1;0C −
.
Câu 12. Trong không gian với hệ tọa độ
Oxyz
, tìm tọa độ hình chiếu
B
của điểm
( )
5;3; 2B −
trên đường
thẳng
13
:
2 1 1
x y z
d
−−
==
−
.
A.
( )
1;3;0B
. B.
( )
5;1;2B
. C.
( )
3;2;1B
. D.
( )
9;1;0B
.
Câu 13. Trong không gian với hệ trục tọa độ
Oxyz
, cho đường thẳng
1
:
2 1 1
x y z
d
+
==
−
và mặt phẳng
( )
: 2 2 5 0x y z
− − + =
. Tìm điểm
A
trên
d
có hoành độ dương sao cho khoảng cách từ
A
đến
( )
bằng
3
.
A.
( )
4; 2;1A −
. B.
( )
2;1; 2A −−
. C.
( )
2; 1; 0A −
. D.
( )
0; 0; 1A −
.
Câu 14. Trong không gian
Oxyz
, cho điểm
( )
3; 2 ; 1M −
. Hình chiếu vuông góc của điểm
M
lên trục
Oz
là điểm:
A.
( )
3
3; 0 ; 0M
. B.
( )
4
0 ; 2 ; 0M
. C.
( )
1
0 ; 0 ; 1M −
. D.
( )
2
3; 2 ; 0M
.
Câu 15. Trong không gian
Oxyz
, cho điểm
( )
3; 2 ;1M −−
. Hình chiếu vuông góc của điểm
M
lên mặt
phẳng
( )
Oxy
là điểm:
A.
( )
3
3; 0 ; 0M −
. B.
( )
4
0 ; 2 ;1M −
. C.
( )
1
0 ; 0 ;1M
. D.
( )
2
3; 2 ; 0M −−
.
Câu 16. Trong không gian với hệ trục tọa độ
Oxyz
, phương trình của mặt phẳng
( )
P
đi qua điểm
( )
2;1; 3B −
, đồng thời vuông góc với hai mặt phẳng
( )
: 3 0Q x y z+ + =
,
( )
:2 0R x y z− + =
là
A.
4 5 3 22 0x y z+ − + =
. B.
4 5 3 12 0x y z− − − =
.
C.
2 3 14 0x y z+ − − =
. D.
4 5 3 22 0x y z+ − − =
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
233
Câu 17. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
( )
1;2;2A
và đường thẳng
6 1 5
:
2 1 1
x y z
d
− − −
==
. Tìm tọa độ điểm
B
đối xứng với
A
qua
d
.
A.
( )
3;4; 4B −−
. B.
( )
2; 1;3B −
. C.
( )
3;4; 4B −
. D.
( )
3; 4;4B −
.
Câu 18. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
6 1 5
:
2 1 1
x y z
d
− − −
==
và mặt phẳng
( )
: 2 3 4 0P x y z+ + + =
. Viết phương trình đường thẳng
d
là hình chiếu vuông góc của
d
trên
( )
P
.
A.
6
25
23
xt
yt
zt
=−
= − −
=+
. B.
6
25
23
xt
yt
zt
=
= − −
=+
. C.
6
25
23
xt
yt
zt
=−
= − +
=+
. D.
6
25
23
xt
yt
zt
=−
= − −
=−
.
Câu 19. Trong không gian , cho đường thẳng và hai điểm và
. Gọi là điểm thuộc đường thẳng sao cho diện tích tam giác bằng
. Giá trị của tổng bằng
A. . B. . C. . D. .
Câu 20. Trong không gian , cho đường thẳng và hai điểm và
. Gọi là điểm thuộc đường thẳng sao cho tam giác vuông tại A.
Giá trị của tổng bằng
A. . B. . C. . D. .
Câu 21 . Trong không gian , cho đường thẳng và mặt phẳng
. Gọi là điểm thuộc đường thẳng sao cho khoảng cách từ đến
mặt phẳng bằng . Nếu có hoành độ âm thì tung độ của bằng.
A. . B. . C. . D. .
Câu 22. Trong không gian , cho tam giác có . Đường cao
kẻ từ của tam giác đi qua điểm nào trong các điểm sau?
A. . B. . C. . D. .
Câu 23. Trong không gian , cho tam giác có . Đường phân
giác trong kẻ từ của tam giác đi qua điểm nào trong các điểm sau?
A. . B. . C. . D. .
Câu 24. Trong không gian , cho . Đường cao của tứ
diện kẻ từ đi qua điểm nào trong các điểm sau?
A. . B. . C. . D. .
Oxyz
12
:
2 1 1
x y z
d
+−
==
−
( 1;3;1)A −
( )
0;2; 1B −
( )
;;C m n p
d
ABC
22
m n p++
1−
2
3
5−
Oxyz
12
:
2 1 1
x y z
d
+−
==
−
( 1;3;1)A −
( )
0;2; 1B −
( )
;;C m n p
d
ABC
2m n p++
0
2
3
5−
Oxyz
12
:
1 2 3
x y z
d
++
==
( )
: 2 2 3 0P x y z+ − + =
M
d
M
( )
P
2
M
M
3−
21−
3
1−
Oxyz
ABC
( ) ( ) ( )
0;0;1 , 3;2;0 , 2; 2;3A B C−−
B
ABC
( )
1;2; 2P −−
( )
1;3;4M −
( )
0;3; 2N −
( )
5;3;3Q −
Oxyz
ABC
( ) ( ) ( )
1;2;3 , 3; 1;2 , 2; 1;1A B C−−
A
ABC
( )
0;4;4P
( )
2;0;1M
( )
1;5;5N −
( )
3; 2;2Q −
Oxyz
( ) ( ) ( ) ( )
1;0;0 , 0;2;0 , 0;0;3 , 2; 3;1A B C D −−
ABCD
D
( )
4;0;3P
( )
8; 6;0M −−
( )
8;3;5N
( )
2;5; 3Q −

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
234
Câu 25. Trong không gian , cho tam giác vuông tại . Gọi là hình chiếu của điểm
lên cạnh . Mặt phẳng đi qua đường phân giác trong của góc của
tam giác và vuông góc với mặt phẳng chứa tam giác . Điểm thuộc
đường trung tuyến . Tìm tọa độ điểm
A. . B. . C. . D. .
Câu 26. Trong không gian , cho tam giác cân tại . Gọi là trọng tâm của tam
giác . Mặt phẳng đi qua cạnh và vuông góc với mặt phẳng chứa tam
giác . Phương trình đường thẳng đi qua có dạng là . Tìm tọa độ điểm
A. . B. . C. . D. .
Câu 27. Gọi
( )
;;M a b c
là giao điểm của đường thẳng
1 1 3
:
1 2 2
x y z
d
+ − −
==
−
và mặt phẳng
( )
:2 2 3 0P x y z− + − =
. Khi đó tổng
T a b c= + +
bằng
A. 5. B. 4. C. 6. D. 2.
Câu 28. Trong không gian với hệ tọa độ
Oxyz
, tìm tọa độ điểm
A
đối xứng với điểm
( )
1;0;3A −
qua mặt
phẳng
( )
: 3 2 7 0P x y z+ − − =
.
A.
( )
1; 6;1A
−−
. B.
( )
0;3;1A
. C.
( )
1;6; 1A
−
. D.
( )
11;0; 5A
−
.
Câu 29. Trong không gian
,Oxyz
cho đường thẳng
1 1 1
:
3 2 1
x y z
d
− − −
==
−−
và điểm
( )
5;0;1A
. Điểm đối
xứng của
A
qua đường thẳng
d
có tọa độ là
A.
( )
1;1;1
. B.
( )
5;5;3−
. C.
( )
4; 1;0−
. D.
( )
3; 2; 1−−
.
Câu 30. Trong không gian
Oxyz
, cho hình thoi
ABCD
với
( ) ( )
1 2 1 2 3 2A ; ; ,B ; ;−
. Tâm
I
của hình thoi
thuộc đường thẳng
12
1 1 1
x y z
d:
+−
==
−−
. Đỉnh nào sau đây là đỉnh
D
của hình thoi?
A.
( )
0 1 2D ; ;
. B.
( )
2 1 0D ; ;−−
. C.
( )
0 1 2D ; ;−−
. D.
( )
2 1 0D ; ;
.
Câu 31. Trong không gian với hệ trục tọa độ
Oxyz
, cho đường thẳng
1
:
2 1 1
x y z
d
và mặt phẳng
:2 2 2 0.P x y z
Có bao nhiêu điểm
M
thuộc
d
sao cho
M
cách đều gốc tọa độ
O
và
mặt phẳng
P
?
A. 4. B. 0. C. 2. D. 1.
Oxyz
ABC
A
( )
5;5;2H
A
BC
( )
50P x y z+ + − =
AJ
A
ABC
ABC
( )
2; 1;0K −−
AM
A
50 29 64
;;
3 4 2
A
−
50 29 64
;;
3 2 2
A
−
50 29 64
;;
9 4 2
A
−
50 29 64
;;
3 3 3
A
−
Oxyz
ABC
A
5 4 1
;;
3 3 3
G
ABC
( )
50P x y z+ + − =
BC
ABC
BG
5
3
4
3
1
4
3
xt
yt
zt
=+
=−
=−
C
5 9 3
;;
3 4 2
C
−
50 9
; ;5
32
C
97
3; ;
42
C
−
16
;3; 1
3
C
−

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
235
ĐÁP ÁN CHI TIẾT
Câu 1. Chọn B
Md
112
22
22
t
t
mt
=+
=−
= − +
0
0
2
t
t
m
=
=
=−
.
Vậy
2m =−
thì điểm
M
thuộc đường thẳng
d
.
Câu 2. Chọn D
Xét hệ:
2
12
2
2 5 0
xt
yt
zt
x y z
=−
=+
=
+ − − =
( )
2 2 1 2 2 5 0t t t − + + − − =
1t=
( )
1;3;2A
là tọa độ giao
điểm của đường thẳng và mặt phẳng.
Câu 3.
Chọn C
Ta có
( )
2;1; 1u
=−
là một vec tơ chỉ phương của đường thẳng
.
Giả sử
( )
' 1 2 ; ; 2A t t t+ − −
là hình chiếu của
A
trên
.
Khi đó
( )
' 5 2 ; 1; 3 tA A t t= + − − −
, theo đề bài ta có
( )
' '. 0 2 5 2 1 3 0 6 12 0 2AA u AA u t t t t t
⊥ = + + − + + = + = = −
hay
( )
' 3; 2;0A −−
và
( )
' 1; 3; 1AA = − −
. Mặt phẳng
( )
P
có vec tơ pháp tuyến
n
vuông góc với
'AA
khi
( )
. ' 0n k AA k=
.
Xét đáp án C có
( )
1;3;1 'n AA= − = −
nên thỏa mãn yêu cầu bài toán.
Câu 4. Chọn D
Thay tọa độ từng điểm vào phương trình đường thẳng
d
đã cho, ta thấy
,,Q N M
thuộc đường
thẳng
d
.
Thay tọa độ điểm
P
vào phương trình đường thẳng
d
đã cho, ta có:
3 1 2
1
23
t
t
t
=−
−=
=−
1
1
1
t
t
t
=−
= −
=
( vô nghiệm ). Vậy
Pd
.
Câu 5. Chọn A
Gọi
là đường thẳng đi qua
A
và vuông góc mặt phẳng
()P
. Ta chọn một vectơ pháp tuyến của
là
(2; 2; 1)n = − −
.
Phương trình của đường thẳng
là
12
12
2
xt
yt
zt
=+
=−
= − −
,
tR
Gọi
( ) ( )HP=
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
236
Khi đó tọa độ điểm
H
là nghiệm hệ phương trình
1 2 1
1 2 3
21
2 2 7 0 1
x t x
y t y
z t z
x y z t
= + = −
= − =
= − − = −
− − + = = −
( 1;3; 1)H − −
Vậy
1a =−
,
3b =
nên tổng
2ab+=
.
Câu 6. Chọn B
(1;1;2)
d
u
là một VTCP của đường thẳng d
(1;1; 2)n
−
là một VTPT của
( )
; ( 4;4;0)
d
n u n
= = −
;
( )
(2;3;0)A d A
Phương trình mặt phẳng
( ): 4( 2) 4( 3) 0( 0) 0 4x 4 4 0 1 0x y z y x y
− − + − + − = − + − = − + =
.
Giả sử
( ) ( )
( ; ; )M x y z
. Khi đó tọa độ M thỏa mãn hệ
x- 1 0
2z 1 0
y
xy
+=
+ − + =
Thay các đáp án vào hệ trên ta thấy
(2;3;3)M
thỏa mãn. Chọn đáp án B.
Câu 7. Chọn B
Tọa độ giao điểm
I
của
d
với mặt phẳng
( )
Oxy
là nghiệm của hệ phương trình:
42
3
1
0
xt
yt
zt
z
=−
= − +
=−
=
2
2
0
1
x
y
z
t
=
=−
=
=
. Do đó
( )
2; 2;0I −
.
Câu 8. Chọn A
Gọi
2 ;1 2 ;2M t t t
là hình chiếu vuông góc của
A
lên đường thẳng .
Ta có
3 ; 2 ;2 6AM t t t
và véc tơ chỉ phương của đường thẳng là
1; 2; 2u
.
Có
. 0 3 4 4 12 0 1 3; 1;2AM u AM u t t t t M
.
Câu 9. Chọn B
Đường thẳng
d
có một VTCP
( )
;1;2
d
aa=
;
d
có một véctơ chỉ phương
( )
1;2; 1
d
a
= − −
.
Nhận thấy
12
21
−
nên
d
a
,
d
a
không cùng phương nên
( )
, 5; 2;2 1
dd
a a a a
= − − +
.
Lấy
( )
1;0; 1Md−
,
( )
1;2;3Nd
−
( )
2;2;4MN = −
.
d
cắt
d
khi và chỉ khi
, . 0
dd
a a MN
=
( ) ( ) ( ) ( )
5 . 2 2 2 4 2 1 0aa − − + − + + =
1a = −
.
Câu 10. Chọn D
Thay tọa độ của
( )
1; 1;1K −
vào PTTS của
d
ta được
11
1 1 2 :
1 2 1
tt
tt
tt
==
− = − =
= + = −
không tồn tại
t
.
Do đó,
.Kd

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
237
Thay tọa độ của
( )
1;1;2E
vào PTTS của
d
ta được
11
1 1 0:
2 2 0
tt
tt
tt
==
= − =
= + =
không tồn tại
t
.
Do đó,
.Ed
Thay tọa độ của
( )
1;2;0H
vào PTTS của
d
ta được
11
2 1 1:
0 2 2
tt
tt
tt
==
= − = −
= + = −
không tồn tại
t
.
Do đó,
.Hd
Thay tọa độ của
( )
0;1;2F
vào PTTS của
d
ta được
00
1 1 0 0.
2 2 0
tt
t t t
tt
==
= − = =
= + =
Do đó,
Fd
. Vậy, ta chọn D.
Câu 11. Chọn A
Ta có:
( )
1;2; 4AB =−
. Đường thằng
AB
đi qua điểm
( )
1; 2;3A −
và có vectơ chỉ phương
AB
có
phương trình tham số là:
( )
1
2 2
34
xt
y t t
zt
=+
= − +
=−
.
Gọi
C
là giao điểm của
AB
và
( )
P
( )
1 ; 2 2 ;3 4C t t t + − + −
mà
C
( )
P
nên:
1 2 2 3 4 1 0 1t t t t+ − + + − − = =
.
Vậy
( )
2;0; 1C −
.
Câu 12. Chọn C
Đường thẳng
13
:
2 1 1
x y z
d
−−
==
−
có VTCP
( )
2; 1;1u =−
, có PT tham số là:
12
:3
xt
d y t
zt
=+
=−
=
.
( )
1 2 ;3 ;B d B t t t
+ −
, để
B
là hình chiếu của
B
trên
d
thì
.0BB u BB u
⊥ =
.
( )
2 2 4 2 0t t t − + + + =
66t=
1t=
( )
3;2;1B
.
Câu 13. Chọn C
Vì
(2 , , 1 ); 0A d A t t t t − − +
. Ta có:
1
27
( ,( )) 3 3
8
3
t
t
dA
t
=
+
= =
=−
Vì
0t
nên chọn t = 1. Vậy
(2; 1;0)A −
Câu 14. Chọn C
Hình chiếu của điểm
( )
;;M a b c
lên trục
Oz
là điểm
( )
0 ; 0 ; c
nên chọn C
Câu 15. Chọn D
Hình chiếu của điểm
( )
;;M a b c
lên trục
Oxy
là điểm
( )
; ; 0ab
nên chọn D

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
238
Câu 16. Chọn D
Véc tơ pháp tuyến của mặt phẳng
( )
Q
và
( )
R
lần lượt là
( )
( )
1;1;3
2; 1;1
Q
R
n
n
=
=−
.
( ) ( )
( ) ( )
PQ
PR
PQ
nn
PR
nn
⊥
⊥
⊥
⊥
( )
, 4;5; 3 .
P Q R
VTPT n n n
= = −
Mặt phẳng
( )
P
đi qua điểm
( )
2;1; 3B −
và véc tơ pháp tuyến
( )
4;5; 3
P
n =−
có phương trình:
( ) ( ) ( )
4 2 5 1 3 3 0 4 5 3 22 0x y z x y z− + − − + = + − − =
.
Câu 17. Chọn D
Từ phương trình đường thẳng
d
ta có véc tơ chỉ phương của
d
là
( )
2;1;1u
Gọi
H
là hình chiếu của
A
trên
d
, suy ra
( ) ( )
6 2 ;1 ;5 5 2 ; 1 ;3H t t t AH t t t+ + + + − + +
. Khi
đó
.0AH u AH u⊥ =
( ) ( ) ( )
2 5 2 1 3 0 2t t t t+ + − + + + = = −
.Với
2t =−
thì
( )
2; 1;3H −
Gọi
B
là điểm đối xứng với
A
qua
d
thì
H
là trung điểm
( )
3; 4;4AB B−
.
Câu 18. Chọn A
Gọi
( )
I d P=
, khi đó toạ độ điểm
I
là nghiệm của hệ phương trình:
( )
6 2 3
10
0; 2;2
52
2 3 4 0 2
x t t
y t x
I
z t y
x y z z
= + = −
= + =
−
= + = −
+ + + = =
.
Lấy
( )
6;1;5Ad
, gọi
là đường thẳng đi qua
A
và vuông góc với
( )
P
suy ra PT đường thẳng
có dạng:
62
13
5
xt
yt
zt
=+
=+
=+
. Gọi
( )
JP=
, ta tính được
18 29 23
; ; ;
7 7 7
J
−−
.
Khi đó đường thẳng
d
đi qua 2 điểm
,IJ
có PTTS là:
6
25
23
xt
yt
zt
=−
= − −
=+
.
TƯ DUY TOÁN HỌC 4.0 giải nhanh như sau:
Cho
( )
:
0ax by cz d+ + + =
;
( )
;;A m n k
. Gọi
H
là hình chiếu của
A
lên
( )
.
Khi đó
( )
2 2 2
;;
am bn ck d
h
abc
H m ah n bh k ch
+ + +
=−
++
+ + +
Câu 19. Chọn C
Phương trình tham số của đường thẳng .
12
:
2
xt
d y t
zt
= − +
=
=−

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
239
Vì thuộc nên tọa độ của có dạng .
Ta có và .Suy ra .
Diện tích tam giác là .
Theo bài ra ta có .
.
Với thì nên . Vậy giá trị của tổng
Câu 20. Chọn A
Vì nên tọa độ của có dạng
Ta có và
Vì vuông tại A nên .
.
Câu 21 . Chọn A
Phương trình tham số của đường thẳng
Vì nên tọa độ của có dạng .
Vì khoảng cách từ đến mặt phẳng bằng nên
Vì có tung độ âm nên
C
d
C
( )
1 2 ; ;2C t t t− + −
( )
1; 1; 2AB −−
( )
2 ; 3;1AC t t t−−
( )
, 3 7; 3 1;3 3AB AC t t t
= − − − −
ABC
2 2 2
11
, (3 7) ( 3 1) (3 3)
22
ABC
S AB AC t t t
= = − + − − + −
2
1
2 2 27 54 59 2 2
2
ABC
S t t= − + =
2
27 54 59 32tt − + =
2
( 1) 0t − =
1t=
1t =
( )
1;1;1C
1; 1; 1m n p= = =
3m n p+ + =
Cd
C
( )
1 2 ; ;2C t t t− + −
( )
1; 1; 2AB −−
( )
2 ; 3;1AC t t t−−
ABC
1
. 0 2 3 2 2 0 3 1 0
3
AC AB t t t t t
−
= − + − + = + = =
5
3
5 1 4 1 5 2 7
; ; 2 0
3 3 3 3 3 3 3
7
3
m
C n m n p
p
−
=
− − − − −
= + + = + + =
=
: 1 2
23
xt
d y t
zt
=
= − +
= − +
Md
M
( )
; 1 2 ; 2 3M t t t− + − +
M
( )
P
2
( ) ( )
( )
2
2
2 1 2 2 2 3 3
2
1 2 2
t t t+ − + − − + +
=
+ + −
2 4 4 6 3
2
1 4 4
t t t− + + − +
=
++
( )
( )
1 1; 3; 5
56
5
2 5 6
56
3
11 11;21;31
tM
t
t
t
t
tM
= − − − −
−=
−
= − =
− = −
=
M
( )
1; 3; 5M − − −
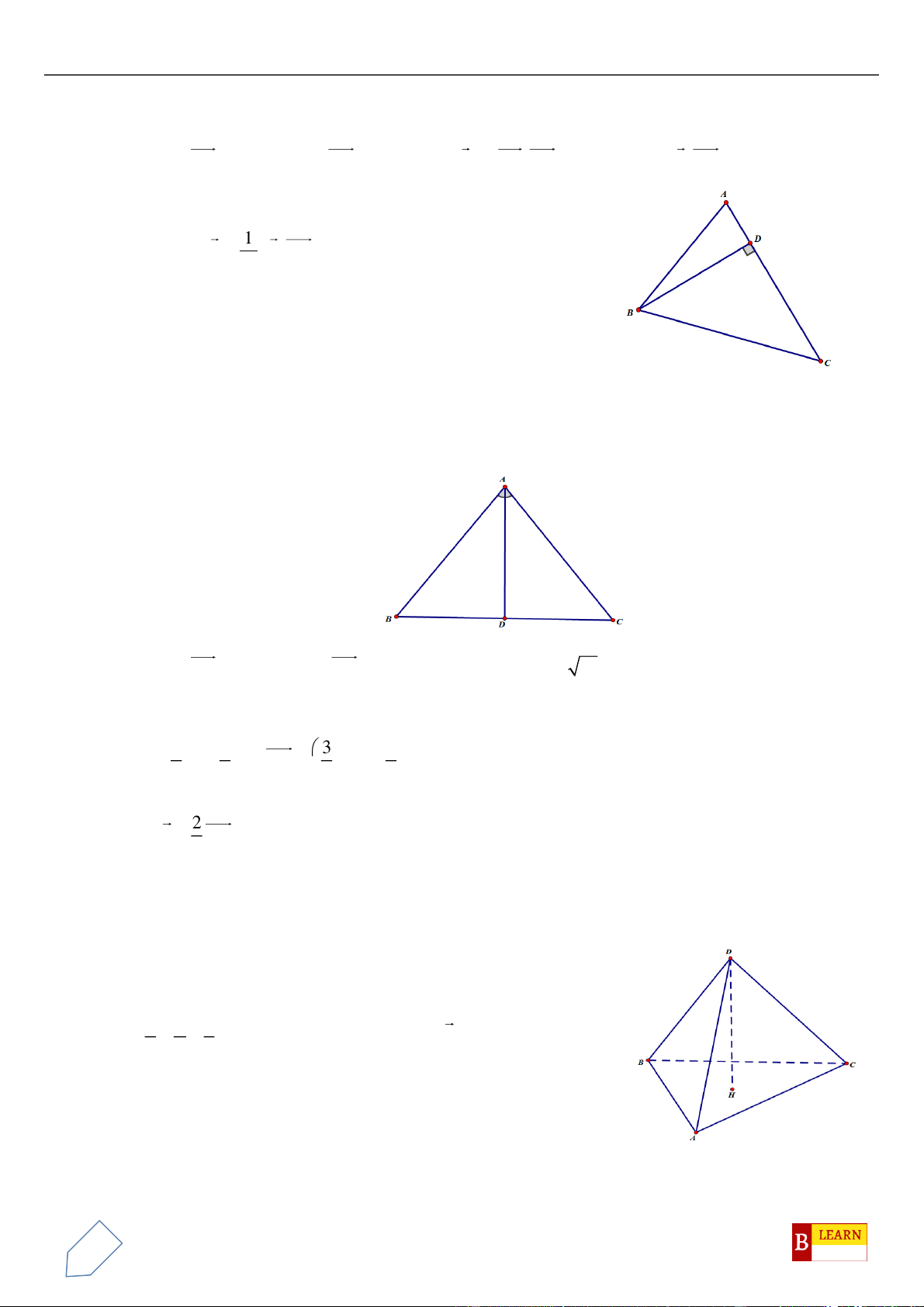
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
240
Câu 22. Chọn A
Ta có .
Một vectơ chỉ phương của đường cao kẻ từ của tam giác
là .
Phương trình đường cao kẻ từ là:
Ta thấy điểm thuộc đường thẳng trên.
Câu 23. Chọn A
Ta có tức tam giác cân tại .
Do đó gọi là chân đường phân giác trong kẻ từ
thì
cũng là trung điểm nên
. Chọn một vectơ chỉ phương của đường phân giác trong
là . Vậy phương trình là :
Ta thấy điểm thuộc đường thẳng trên.
Câu 24. Chọn A
Phương trình mặt phẳng theo đoạn chắn là
là vectơ
pháp tuyến của mặt phẳng .
( ) ( ) ( ) ( )
3;2; 1 , 2; 2;2 , , 2;4;2 , 12;0; 12AB AC n AB AC n AC
= − − = − = = = −
B
ABC
( )
1
, 1;0; 1
12
u n AC
= = −
B
3
2.
xt
y
zt
= − +
=
=−
( )
1;2; 2P −−
( ) ( )
2; 3; 1 , 1; 3; 2 = 14AB AC AB AC= − − = − − =
ABC
A
D
A
D
BC
5 3 3 3
; 1; ; 3;
2 2 2 2
D AD
− = − −
AD
( )
2
1; 2; 1
3
u AD= = − −
AD
1
2 2 .
3
xt
yt
zt
=+
=−
=−
( )
0;4;4P
( )
ABC
1
1 2 3
x y z
+ + =
6 3 2 6 0x y z + + − =
( )
6;3;2n=
( )
ABC
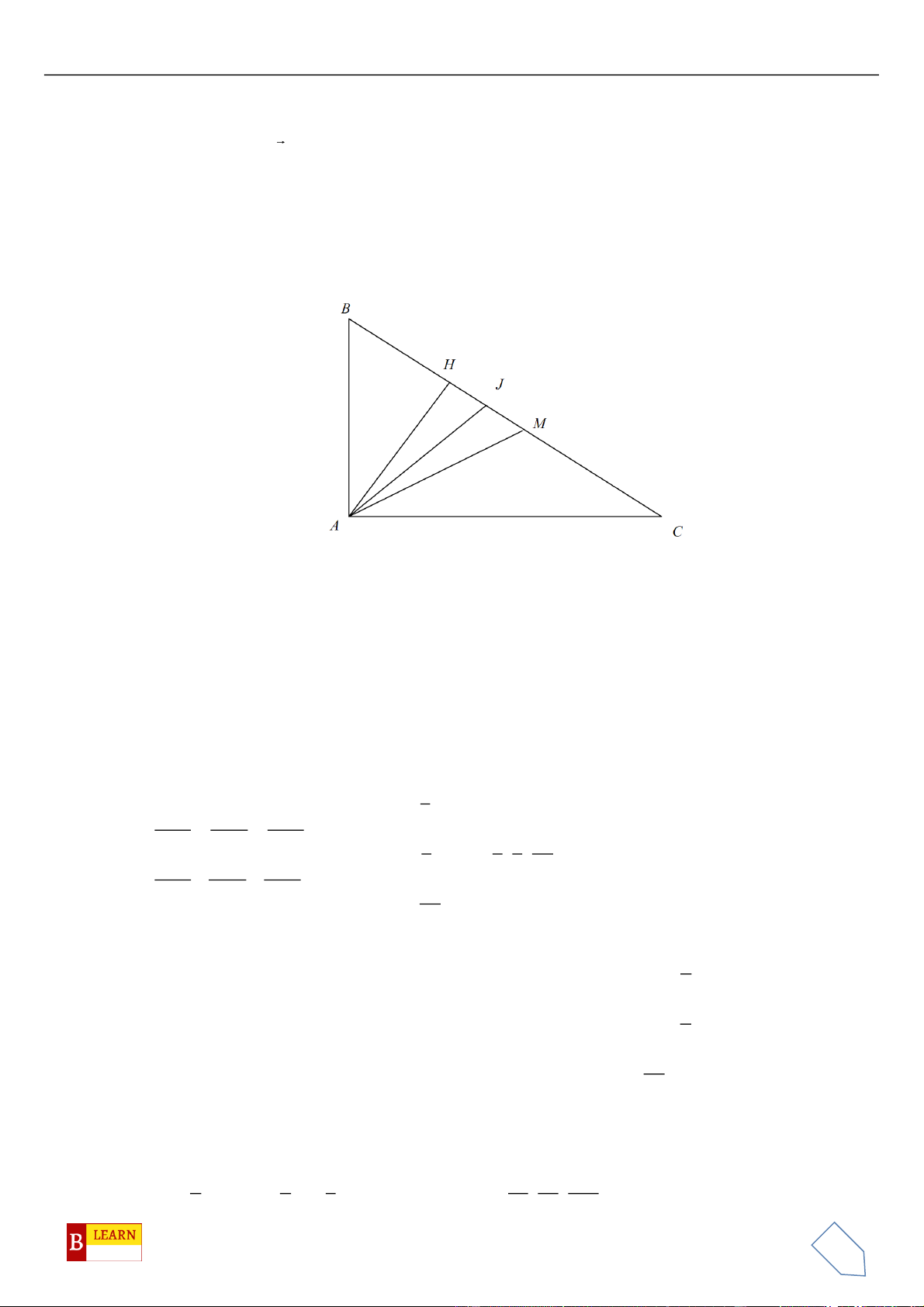
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
241
Đường cao của tứ diện kẻ từ đi qua và nhận vectơ pháp tuyến của mặt
phẳng là làm vectơ chỉ phương có phương trình là
Ta thấy điểm thuộc đường thẳng trên.
Câu 25. Chọn D
Do tam giác vuông tại và là đường trung tuyến nên ta có
và mà là phân giác nên dễ dàng có được
Hay cũng là phân giác của tam giác . Vậy ta có điểm đối xứng của qua sẽ thuộc
. Gọi là điểm đối xứng với qua ta có tọa độ điểm bằng cách giải hệ:
Phương trình đường thẳng đi qua và nên có dạng
Ta có là giao điểm của mặt phẳng và đường thẳng . Vậy
ABCD
D
( )
2; 3;1D −−
( )
ABC
( )
6;3;2n =
26
3 3 .
12
xt
yt
zt
= − +
= − +
=+
( )
4;0;3P
ABC
A
AM
MA MC MB==
MCA MAC BAH==
AJ
HAJ MAJ=
AJ
HAM
H
AJ
AM
( )
;;E x y z
H
AJ
E
1
5 5 2 3
1 1 1 8
1 1 1
;;
5 5 2
3 3 3 3
50
8
2 2 2
3
x
x y z
yE
x y z
z
=
− − −
==
−
=
+ + +
+ + − =
−
=
AM
K
E
7
2
3
4
1
3
8
3
xt
yt
zt
= − +
= − +
−
=
A
( )
P
AM
7 4 8 50 29 64
2 1 5 0 8 ; ;
3 3 3 3 3 3
t t t t A
−
− + + − + − − = =

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
242
Câu 26. Chọn D
Ta có chính là giao điểm của đường thẳng và mặt phẳng
Gọi là trung điểm của , ta có vuông góc với đường thẳng vậy nó cũng vuông
góc với mặt phẳng . Vậy phương trình đường thẳng là
Ta có điểm M chính là giao điểm của với mặt phẳng .Vậy ta có tọa độ điểm
Mà lại là trung điểm vậy ta có tọa độ của là
Câu 27. Chọn D
Tọa độ
( )
;;M a b c
thỏa hệ phương trình
2 3 2
1 1 3
41
1 2 2
2 2 3 0
2 2 3 5
a b a
a b c
b c b
a b c
a b c c
− = − = −
+ − −
==
+ = = −
−
− + − =
− + = =
.
Vậy
2T a b c= + + =
.
Câu 28. Chọn C
Gọi
là đường thẳng đi qua điểm
A
và vuông góc với mặt phẳng
( )
P
.
Phương trình tham số của đường thẳng
là
1
3
32
xt
yt
zt
= − +
=
=−
.
Gọi
H
là hình chiếu của
A
trên mặt phẳng
( )
P
. Suy ra
( )
HP=
.
Tham số
t
ứng với tọa độ điểm
H
là nghiệm của phương trình
( ) ( )
1 3.3 2 3 2 7 0t t t− + + − − − =
1t=
.
Do đó
( )
0;3;1H
.
Điểm
A
đối xứng với điểm
A
qua mặt phẳng
( )
P
khi và chỉ khi
H
là trung điểm của đoạn thẳng
AA
. Suy ra
( )
1;6; 1A
=−
.
Câu 29. Chọn D
Cách 1.
Gọi
A
là điểm đối xứng với
A
qua
d
.
B
BG
( )
P
5 4 1 2 7 13
4 5 0 1 ; ;
3 3 3 3 3 3
t t t t B
+ + − + − − = = −
M
BC
GM
BC
( )
P
GM
5
3
4
3
1
3
xt
yt
zt
=+
=+
=+
GM
( )
P
M
5 4 1 4 8 5
5 0 3; ;
3 3 3 3 3 3
t t t t M
+ + + + + − = =
M
BC
C
16
;3; 1
3
C
−

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
243
Gọi
( )
P
là mặt phẳng qua
A
và vuông góc với đường thẳng
d
.
Ta có phương trình mặt phẳng
( )
P
là
( ) ( )
3 5 2 1 0 3 2 14 0x y z x y z− − − − = − − − =
.
Gọi
H
là hình chiếu của
A
trên
d
, dễ có
( )
H d P=
.Vì
Hd
nên
( )
1 3 ;1 2 ;1H t t t+ − −
.
Lại có
( )
HP
nên
( ) ( ) ( )
3 1 3 2 1 2 1 14 0 14 14 1t t t t t+ − − − − − = = =
.
Suy ra
( )
4; 1;0H −
, mà
H
là trung điểm của
AA
nên
( )
3; 2; 1A
−−
.
Cách 2.
Gọi
H
là hình chiếu của
A
trên
d
, ta có
( ) ( )
1 3 ;1 2 ;1 3 4;1 2 ; tH t t t AH t t+ − − = − − −
.
Đường thẳng
d
có véc tơ chỉ phương là
( )
3; 2; 1u = − −
.
Ta có
( ) ( ) ( )
. 0 3 4 3 2 1 2 0 14 14 1AH u t t t t t= − + − − − − = = =
.
Suy ra
( ) ( )
4; 1;0 3; 2; 1HA
− − −
.
Câu 30. Chọn B
Gọi
( )
12I t; t; t d− − − +
là tâm của hình thoi
ABCD
.
Xét
( ) ( )
2 1 3 3IA t;t ; t ;IB t ;t ; t= + − − = + + −
.
Vì
ABCD
là hình thoi nên
2
0 3 9 6 0 2 1IA IB IA.IB t t t ;t⊥ = + + = = − = −
.
Do
D
đối xứng
B
qua
I
nên:
Với
( ) ( )
1 0 1 1 2 1 0t I ; ; D ; ;= − − −
. (Đáp án B)
Với
( ) ( )
2 1 2 0 0 1 2t I ; ; D ; ;= − −
.
Câu 31. Chọn D
Vì
Md
nên
( 2 ;1 ; )M t t t
;
2
6 2 1MO t t
2
22
2 2 1 2 2
,1
2 1 2
t t t
d M P t
.
M
cách đều gốc tọa độ
O
và mặt phẳng
P
nên
,MO d M P
hay
2
6 2 1 1t t t
2
2
6 2 1 1 0t t t t
. Vậy có 1 điểm
M
.
Câu 32. Chọn C
Cách 1:
Ta có
( )
2; 2;2 , 2 3.= − − =AB AB
Phương trình đường thẳng
1'
: 4 '
2'
xt
AB y t
zt
=+
=+
=−
.
Gọi
N
là hình chiếu của
M
lên trên đường thẳng
AB
. Khi đó
1
.
2
AMB
S AB MN=
Suy ra,
AMB
S
đạt giá trị nhỏ nhất khi và chỉ khi
MN
nhỏ nhất, hay
MN
là đường vuông góc chung
của hai đường thẳng
AB
và
d
.
( )
5 4 ;2 2 ;4 − + +M d M t t t
;
( )
1 ;4 ;2
+ + −N AB N t t t

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
244
( )
4 4; 2 2; 2
= + − − + + − − −MN t t t t t t
.
Vì
MN
là đường vuông góc chung của hai đường thẳng
AB
và
d
nên
.0
01
21 3 18 0 1
.0
AB
d
MN u
t t t
t t t
MN u
=
+ = =
− − + = = −
=
6=MN
.
( )
1
min .2 3. 6 3 2
2
= =
AMB
S dvdt
.
Cách 2:
Ta có
( )
2; 2;2= − −AB
;
( )
5 4 ;2 2 ;4 − + +M d M t t t
.
( )
4 4 ; 2 2 ;2 = − − + +AM t t t
.
( ) ( ) ( )
( )
22
2
2
2
11
; 6 ;12 6 ;12 12 3 2 2 2
22
3 6 12 8 3 6 1 2 3 2.
AMB
S AB AM t t t t t t
t t t
= = − − − = + − + −
= − + = − +
Dấu bằng xảy ra khi và chỉ khi
1t =
hay
( )
1;4;5M
. Vậy
( )
min 3 2
AMB
S dvdt=
.
Câu 33. Chọn D
Có
. . . .
DO DB AO AB
AD AB AO AB AO
BO BO AO AB AB AO
= + = +
++
(trong đó
D
là chân đường phân giác trong hạ từ
A
xuống
OB
)
( )
3 5 2 14 5 12 24
. ; ; . 1; 2;2 0; ;
8 3 3 3 8 8 8
AD
−
= + − − = −
Chọn
( )
0; 1;2u =−
là vecto chỉ phương của đường thằng
AD
phương trình đường thẳng
AD
là:
1
2
22
x
yt
zt
=
=−
= − +
.
Tương tự:
..
OB OA
OT OA OB
OA OB OA OB
=+
++
.
( )
4 3 8 4 8 12 12
. 1;2; 2 . ; ; ; ;0
7 7 3 3 3 7 7
OT
= − + =
.
(trong đó
T
là chân đường phân giác trong hạ từ
O
xuống cạnh
AB
).
Chọn
( )
1;1;0v =
là vecto chỉ phương của đường thẳng
OT
.
phương trình đường thẳng
OT
là:
0
xt
yt
z
=
=
=
.
I
là tâm đường tròn nội tiếp của tam giác
OAB
I
là giao điểm của
AD
và
OT
.
Xét hệ phương trình giao điểm của
AD
và
OT
:
1
1
2
1
2 2 0
s
s
ts
t
t
=
=
− =
=
− + =
( )
1;1;0I
.
Vậy
1 1 0 0a b c− + = − + =
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
245
Cách 2
Ta có
( )
;;I a b c
;
3OA =
;
4OB =
;
5AB =
.
Sử dụng kết quả:
. . . 0BO IA OAIB AB IO+ + =
( ) ( )
( ) ( )
( ) ( )
8
4. 1 3. 5. 0
3
4
4. 2 3. 5. 0
3
8
4. 2 3. 5. 0
3
x x x
y y y
z z z
− + − + − =
− + − + − =
− − + − + − =
1
1
0
x
y
z
=
=
=
( )
1;1;0I
.
Vậy
1 1 0 0a b c− + = − + =
.
Câu 34. Chọn C
Vì
( )
( )
( )
( )
; 2 ;d B P d A P=
và
( )
P
cắt đoạn
AB
tại
I
nên
( )
( )
( )
7
5 2 1
3
2 4 2 2 0 4
5
1 2 3
3
a
aa
BI AI b b b a b c
cc
c
=
− = − −
= − + = − − = + + =
+ = − −
=
.
Câu 35. Chọn B
Mặt cầu
( )
1
:S
2 2 2
9x y z+ + =
có tâm
( )
0; 0; 0O
, bán kính
1
3R =
.
Md
( )
1 ; 1 2 ; 2 3M a a a + + −
.
Do
,MA
,MB
MC
là những tiếp tuyến tại
,A
,B
C
với mặt cầu
( )
1
S
.
Suy ra
2 2 2 2
9MA MB MC OM= = = −
.
Khi đó
,A
,B
C
( )
2
S
có tâm là
M
, bán kính
2
2
9R OM=−
.
Ta có phương trình
( )
2
:S
( )
( )
( )
( )
( )
( )
2 2 2
2
1 2 1 2 3 9x a y a z a OM− + + − + + − − = −
.
( )
2
:S
( ) ( ) ( )
2 2 2
2 1 2 2 1 2 2 3 9 0x y z a x a y a z+ + − + − + − − + =
.
Mặt khác theo giả thiết
,A
,B
C
cùng thuộc mặt cầu
( )
1
S
.
Suy ra tọa độ
,A
,B
C
thỏa mãn hệ:
( ) ( ) ( )
2 2 2
2 2 2
90
2 1 2 2 1 2 2 3 9 0
x y z
x y z a x a y a z
+ + − =
+ + − + − + − − + =
.
Do đó phương trình mặt phẳng
( )
ABC
là:
( ) ( ) ( )
2 1 2 2 1 2 2 3 18 0a x a y a z+ + + + − − =
.
( )
D ABC
( ) ( ) ( )
2 1 2 2 1 4 2 3 18 0a a a + + + + − − =
1a = −
.
Với
1a =−
, ta có
( )
0; 1;5M −
. Khi đó
2 2 2
0 0 0
26T x y z= + + =
.
Câu 32. Trong hệ trục tọa độ
Oxyz
, cho điểm
( ) ( )
1;4;2 , 1;2;4−AB
đường thẳng
54
: 2 2
4
xt
d y t
zt
=−
=+
=+
và điểm
M
thuộc
d
. Tìm giá trị nhỏ nhất của diện tích tam giác
AMB
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
246
A.
23
. B.
22
. C.
32
. D.
62
.
Câu 33. Trong không gian
Oxyz
, cho hai điểm
( )
1;2; 2A −
và
8 4 8
;;
333
B
. Biết
( )
;;I a b c
là tâm của
đường tròn nội tiếp tam giác
OAB
. Giá trị của
a b c−+
bằng
A. 1. B. 3. C. 2. D. 0.
Câu 34. Trong không gian với hệ trục tọa độ
Oxyz
, cho hai điểm
( )
1;2;3A
,
( )
5; 4; 1B −−
và mặt phẳng
( )
P
qua
Ox
sao cho
( )
( )
( )
( )
; 2 ;d B P d A P=
,
( )
P
cắt
AB
tại
( )
;;I a b c
nằm giữa
AB
. Tính
a b c++
.
A.
12
. B.
6
. C.
4
. D.
8
.
Câu 35. Trong không gian
Oxyz
, cho mặt cầu
2 2 2
9x y z+ + =
và điểm
( )
0 0 0
; ; M x y z
thuộc đường thẳng
1
: 1 2 .
23
xt
d y t
zt
=+
=+
=−
Ba điểm
,A
,B
C
phân biệt cùng thuộc mặt cầu sao cho
,MA
,MB
MC
là tiếp
tuyến của mặt cầu. Biết rằng mặt phẳng
( )
ABC
đi qua
( )
1; 1; 2D
. Tổng
2 2 2
0 0 0
T x y z= + +
bằng
A.
30
. B.
26
. C.
20
. D.
21
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
247
DẠNG 4. GÓC – KHOẢNG CÁCH LIÊN QUAN ĐỂ ĐƯỜNG THẲNG
Câu 1. Trong không gian , cho hai đường thẳng và
. Góc giữa hai đường thẳng bằng
A. . B. . C. . D. .
Câu 2. Trong không gian
Oxyz
, cho hai đường thẳng
1
1 2 3
:
2 1 2
x y z− + −
= =
−
và
2
3 1 2
:
1 1 4
x y z+ − +
= =
−
. Góc giữa hai đường thẳng
12
,
bằng
A.
0
30
. B.
0
45
. C.
0
60
. D.
0
135
.
Câu 3. Trong không gian với hệ trục tọa độ
yOx z
, cho đường thẳng
32
:
2 1 1
x y z−−
= =
và mặt phẳng
( )
:3 4 5 8 0x y z
+ + + =
. Góc giữa đường thẳng
và mặt phẳng
( )
có số đo là:
A.
45
. B.
90
. C.
30
. D.
60
.
Câu 4. Trong không gian Oxyz, mặt phẳng chứa trục Ox và đi qua điểm
( )
1;1; 1A −
có phương trình là:
A.
10z +=
. B.
0yz+=
. C.
0xz+=
. D.
0xy−=
.
Câu 5. Mặt phẳng
( )
P
đi qua
( )
0; 1;4A −
và song song với giá của hai véctơ
( ) ( )
3;2;1 , 3;0;1uv= = −
là?
A.
2 3 14 0x y z− + − =
. B.
30x y z− − + =
.
C.
3 3 15 0x y z− + − =
. D.
3 3 9 0x y z− + − =
.
Câu 6. Trong không gian , cho đường thẳng và mặt phẳng . Góc
giữa đường thẳng
và mặt phẳng bằng
A. . B. . C. . D. .
Câu 7. Trong không gian với hệ trục tọa độ , cho đường thẳng và mặt phẳng
. Gọi là góc giữa đường thẳng và mặt phẳng . Khi đó, góc
bằng
A. . B. . C. . D. .
Câu 8. Trong không gian với hệ trục tọa độ , gọi là góc hợp bởi đường thẳng
và mặt phẳng . Khi đó, giá trị bằng bao nhiêu
A. . B. . C. . D. .
Câu 9. Trong không gian
Oxyz
, cho mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 1 1 1 1S x y z− + − + − =
và điểm
(2;2;2)A
. Xét
các điểm
M
thuộc
()S
sao cho đường thẳng
AM
luôn tiếp xúc với
()S
.
M
luôn thuộc một mặt
phẳng cố định có phương trình là
Oxyz
1
1 2 3
:
2 1 2
x y z− + −
= =
−
2
3 1 2
:
1 1 4
x y z+ − +
= =
−
12
,
0
30
0
45
0
60
0
135
Oxyz
:
1 2 1
x y z
= =
−
( )
: 2 0x y z
− + =
( )
30
60
150
120
Oxyz
2 1 1
:
1 2 3
x y z
d
− − +
==
−
( )
: 2 3 0x y z
− + − =
d
( )
0
0
0
45
0
90
0
60
Oxyz
3 4 3
:
1 2 1
x y z
d
− − +
==
−
( )
:2 1 0P x y z+ + − =
cos
1
2
−
3
2
−
3
2
1
2
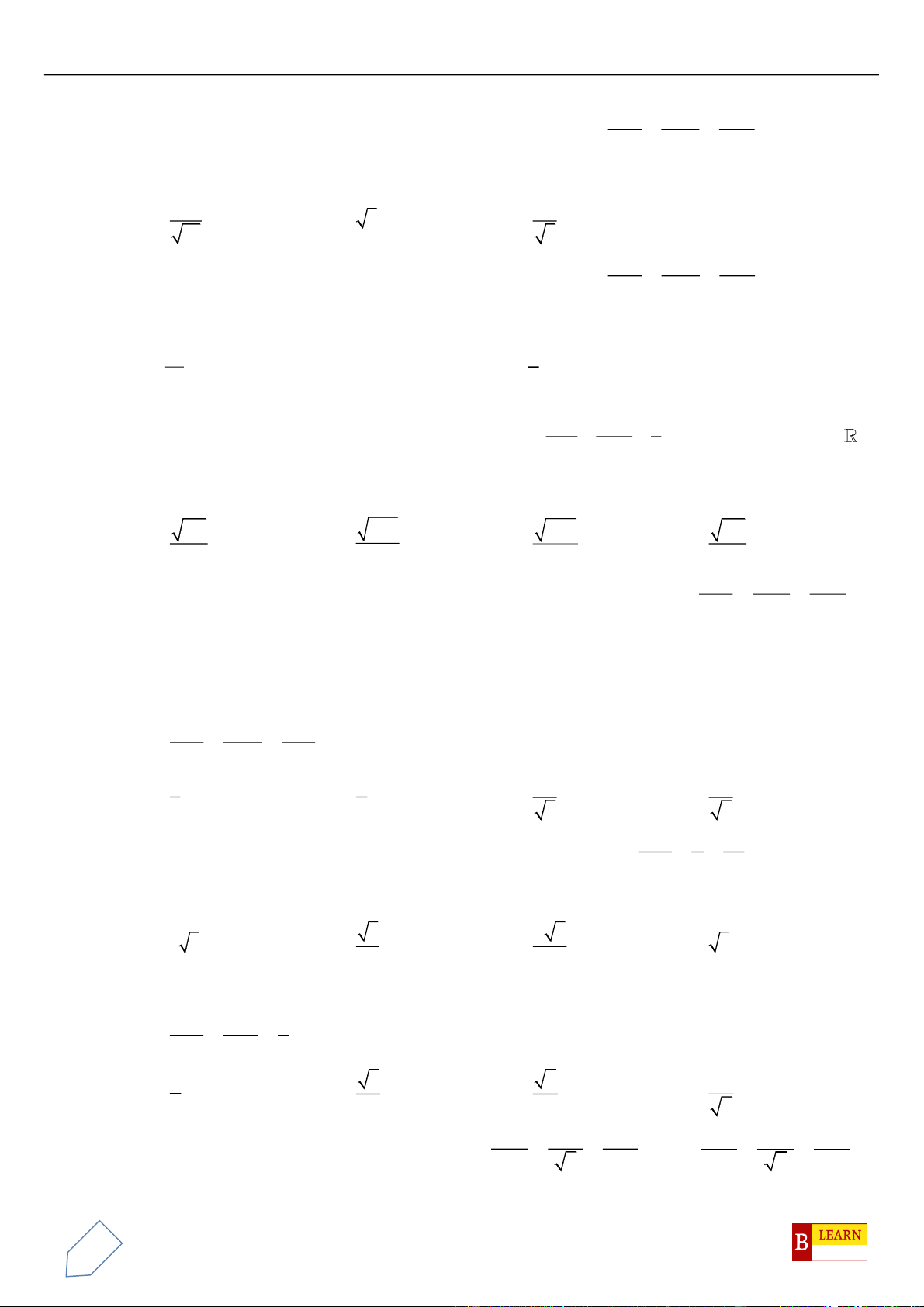
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
248
A.
– 6 0x y z+ + =
. B.
40x y z+ + − =
. C.
3 3 3 –8 0x y z+ + =
. D.
3 3 3 – 4 0x y z+ + =
.
Câu 10. Trong không gian
Oxyz
, khoảng cách giữa đường thẳng
1 2 3
:
2 3 1
x y z
d
− − +
==
và mặt phẳng
( )
: 1 0P x y z− + + =
bằng:
A.
3
14
. B.
3
. C.
1
3
. D.
0
.
Câu 11. Trong không gian
Oxyz
, khoảng cách giữa đường thẳng
1 2 3
:
2 2 3
x y z
d
+ − +
==
−
và mặt phẳng
( )
: 2 2 5 0P x y z− + − =
bằng
A.
16
3
. B.
2
. C.
5
3
. D.
3
.
Câu 12. Trong không gian
Oxyz
, cho hai đường thẳng
1
12
:
2 1 1
x y z
d
−+
==
−
và
2
14
: 1 2 ,
22
xt
d y t t
zt
=+
= − −
=+
.
Khoảng cách giữa hai đường thẳng đã cho bằng
A.
87
6
. B.
174
6
C.
174
3
D.
87
3
Câu 13. Trong không gian với hệ tọa độ
Oxyz
, khoảng cách giữa đường thẳng
1 3 2
:
2 2 1
x y z− − −
= =
và
mặt phẳng
( ): 2 2 4 0P x y z− + + =
là
A.
0
. B.
1
. C.
3
. D.
2
.
Câu 14. Trong không gian
Oxyz
, cho mặt phẳng
( )
: 2 2 1 0P x y z− + + =
và đường thẳng
1 2 1
:
2 2 1
x y z− + −
= =
. Khoảng cách giữa
và
( )
P
bằng
A.
8
3
. B.
7
3
. C.
6
3
. D.
8
3
.
Câu 15. Trong không gian
Oxyz
, khoảng cách giữa đường thẳng
1
:
1 1 2
x y z
d
−
==
−
và mặt phẳng
( )
: 2 0P x y z+ + + =
bằng:
A.
2 3.
B.
3
.
3
C.
23
.
3
D.
3.
Câu 16. Trong không gian
Oxyz
, mặt phẳng
( )
P
đi qua hai điểm
( )
2;1;0A
,
( )
3;0;1B
và song song với
11
:
1 1 2
x y z−+
= =
−
. Tính khoảng cách giữa
và mặt phẳng
( )
P
.
A.
3
2
. B.
3
2
. C.
2
2
. D.
3
2
.
Câu 17. Trong không gian
Oxyz
, hai đường thẳng
1
2 1 3
:
11
2
x y z
d
− + −
==
và
2
5 3 5
:
1
2
x y z
d
m
+ + −
==
tạo với nhau góc
60
, giá trị của tham số
m
bằng

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
249
A.
1m =−
. B.
3
2
m =
. C.
1
2
m =
. D.
1m =
.
Câu 18. Trong không gian
Oxyz
cho đường thẳng
( )
d
là giao tuyến của hai mặt phẳng
( ): .sin cos 0;( ): .cos sin 0; 0;
2
P x z Q y z
− + = − − =
. Góc giữa
()d
và trục
Oz
là:
A.
30
. B.
45
. C.
60
. D.
90
.
Câu 19. Trong không gian
Oxyz
, gọi
d
là đường thẳng đi qua điểm
( )
1; 1;2A −
, song song với mặt phẳng
( )
:2 3 0P x y z− − + =
, đồng thời tạo với đường thẳng
11
:
1 2 2
x y z+−
= =
−
một góc lớn nhất.
Phương trình đường thẳng
d
là
A.
112
4 5 3
x y z− + −
==
−
. B.
112
4 5 3
x y z− + −
==
−
.C.
112
4 5 3
x y z+ + −
==
−
. D.
112
4 5 3
x y z− + −
==
Câu 20. Trong không gian
Oxyz
, cho hai đường thẳng:
1
3 2 1
:
4 1 1
x y z
d
− + +
==
−
và
2
12
:
6 1 2
x y z
d
−−
==
−
. Khoảng cách giữa chúng bằng
A.
5
. B.
4
. C.
2
. D.
3
.
Câu 21. Trong không gian
Oxyz
, cho hai điểm
( )
2 2 1M ; ;−−
,
( )
1 2 3A ; ;−
và đường thẳng
15
2 2 1
x y z
d:
+−
==
−
. Tìm vectơ chỉ phương
u
của đường thẳng
đi qua
M
, vuông góc với
đường thẳng
d
đồng thời cách điểm
A
một khoảng nhỏ nhất.
A.
( )
2 2 1u ; ;−
. B.
( )
3 4 4u ; ;−
. C.
( )
2 1 6u ; ;
. D.
( )
1 0 2u ; ;
.
Câu 22. Trong không gian
Oxyz
, cho mặt phẳng phẳng
( )
: 2 2 1 0− + − =P x y z
và đường thẳng
11
:
1 2 1
−+
==
−
x y z
d
. Biết điểm
( )
;;A a b c
( )
0c
là điểm nằm trên đường thẳng
d
và cách
( )
P
một khoảng bằng 1. Tính tổng
= + +S a b c
A.
2=S
. B.
2
5
=−S
. C.
4=S
. D.
12
5
=S
.
Câu 24. Trong không gian
Oxyz
, cho điểm
(10;2;1)A
và đường thẳng
11
:
2 1 3
x y z
d
−−
==
. Gọi
()P
là
mặt phẳng đi qua điểm
A
, song song với đường thẳng
d
sao cho khoảng cách giữa
d
và
()P
lớn nhất. Khoảng cách từ điểm
( 1;2;3)M −
đến mặt phẳng
()P
bằng
A.
533
2765
. B.
97 3
15
. C
2 13
13
. D.
76 790
790
.
Câu 25. Trong không gian Oxyz, cho ba điểm
( ) ( )
1;2;3 , 1;2;0AB
và
( )
1;3;4M −
. Gọi
d
là đường thẳng
qua B vuông góc với
AB
đồng thời cách
M
một khoảng nhỏ nhất. Một véc tơ chỉ phương của
d
có dạng
( )
2; ;u a b
. Tính tổng
ab+
.
A.
1
. B.
2
. C.
1.−
D.
2.−
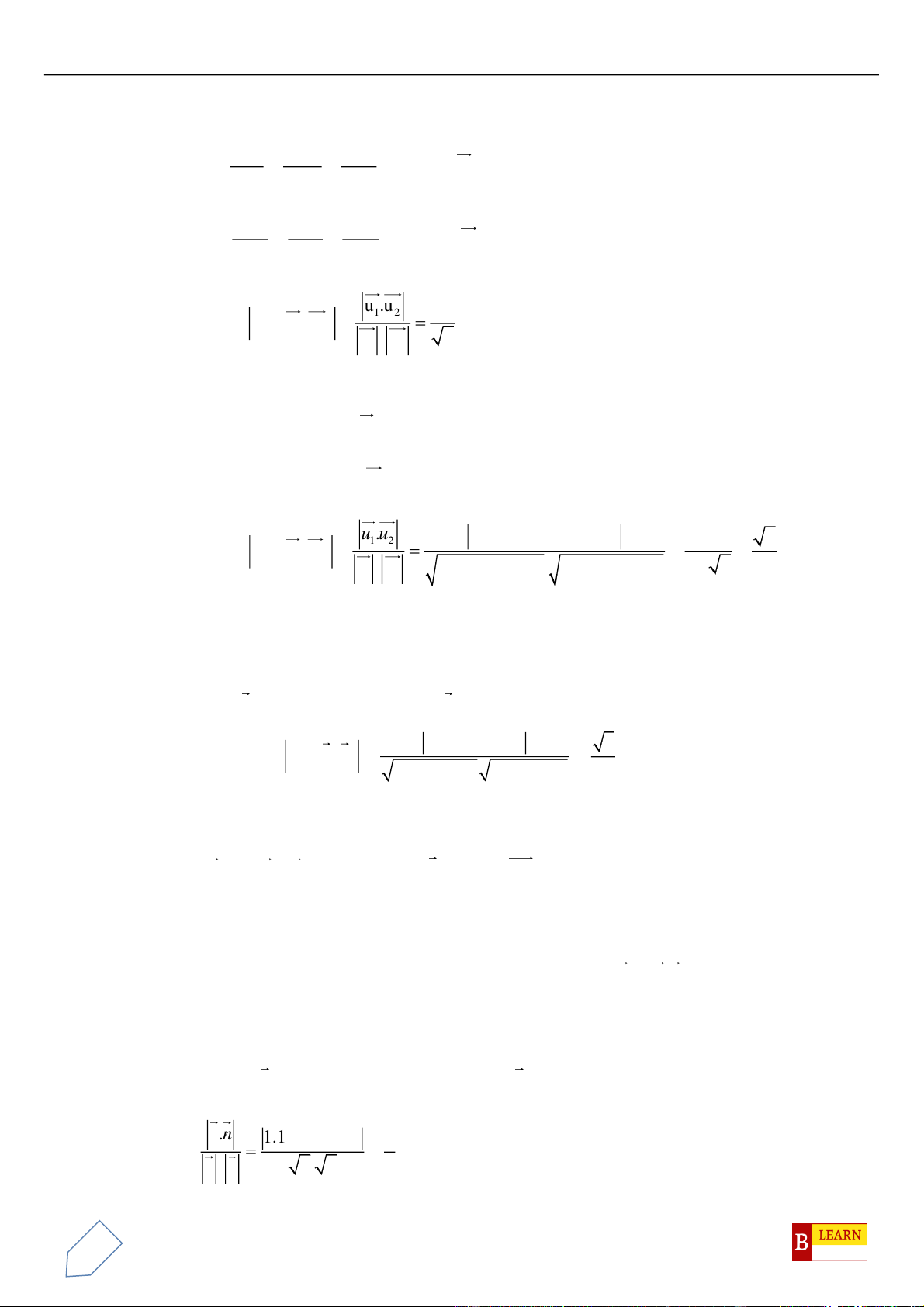
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
250
ĐÁP ÁN CHI TIẾT
Câu 1. Chọn B
Đường có VTCP
Đường có VTCP
.
Câu 2. Chọn B
Véc tơ chỉ phương của
1
là
( )
1
2;1;2u =−
Véc tơ chỉ phương của
2
là
( )
2
1;1; 4u =−
( )
( )
( ) ( )
( ) ( )
12
1 2 1 2
22
2 2 2 2
12
.
2 .1 1.1 2. 4
92
cos , cos ,
2
3.3 2
.
2 1 2 . 1 1 4
uu
uu
uu
− + + −
= = = = =
− + + + + −
.
Do đó góc giữa hai đường thẳng
1
và
2
là
0
45
.
Câu 3. Chọn D
có VTCP
( )
2;1;1u =
.
( )
có VTPT
( )
3;4;5n =
.
Ta có:
( )
( )
sin , cos ;nu
=
2 2 2 2 2 1
3.2 4.1 5.1
3 4 5 2 1 1
++
=
+ + + +
3
2
=
( )
; 60
=
.
Câu 4. Chọn B
Gọi
( )
là mặt phẳng chứa trục Ox và đi qua điểm
( )
1;1; 1A −
.
Khi đó :
( )
( )
, 0;1;1n i OA
==
, với
( )
1;0;0i
,
( )
1;1; 1OA −
.
Phương trình mặt phẳng
( )
:
0yz+=
.
Câu 5. Chọn C
Phương trình mặt phẳng
( )
P
,
( ) ( ) ( )
0; 1;4 đi qua có , 2; 6;6 2 1; 3;3AnVTP uvT
− = = − = −
( )
: 3 3 15 0.P x y z− + − =
Câu 6. Chọn A
có VTCP là và có VTPT là .
1
1 2 3
:
2 1 2
x y z− + −
= =
−
1
( 2;1;2)u =−
2
3 1 2
:
1 1 4
x y z+ − +
= =
−
2
(1;1; 4)u =−
( )
( )
12
1 2 1 2
12
u .u
1
cos , cos u ,u
2
u . u
= = =
( )
12
, 45
o
=
d
( )
1;2; 1u =−
( )
P
( )
1; 1;2n =−
0
.
1.1 2.1 1.2
1
sin 30 .
2
6. 6
.
un
un
−−
= = = =

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
251
Câu 7. Chọn C
có VTCP là và có VTPT là .
Vì nên đường thẳng vuông góc với mặt phẳng
Câu 8. Chọn C
có VTCP là và có VTPT là .
Vì là góc không tù nên từ
Câu 9. Chọn B
( )
S
có tâm
( )
1;1;1I
và bán kính
1R =
.
Do
1 1 1 3IA R= + + =
nên điểm
A
nằm ngoài mặt cầu
( )
S
.
AMI
vuông tại
M
:
22
3 1 2AM AI IM= − = − =
.
M
thuộc mặt cầu
( )
S
có tâm
A
bán kính
2
.
Ta có phương trình
( )
S
( ) ( ) ( )
2 2 2
: 2 2 2 2x y z− + − + − =
. Ta có
( ) ( )
M S S
.
Tọa độ của
M
thỏa hệ phương trình
( ) ( ) ( )
( ) ( ) ( )
( )
2 2 2
2 2 2
1 1 1 1
2 2 2 2
x y z
I
x y z
− + − + − =
− + − + − =
.
Ta có
( )
2 2 2
2 2 2
2 2 2 2 0
4 4 4 10 0
x y z x y z
I
x y z x y z
+ + − − − + =
+ + − − − + =
2 2 2 8 0x y z + + − =
40x y z + + − =
Suy ra
( )
: 4 0M P x y z + + − =
.
Câu 10. Chọn B
Đường thẳng
d
có VTCP là :
( )
2;3;1u
và đi qua điểm
( )
1;2; 3M −
Mặt phẳng
( )
P
có VTPT là :
( )
1; 1;1−n
. Ta có :
( )
( )
.0
//
=
un
dP
MP
Câu 11. Chọn A
Đường thẳng
d
có vectơ chỉ phương
( )
2;2;3u =−
.
d
( )
1; 2;3u =−
( )
( )
1;2; 3n = − −
un=−
d
( )
: 2 3 0.x y z
− + − =
d
( )
1;2; 1u =−
( )
P
( )
2;1;1n =
.
1.2 2.1 1.1
13
sin cos .
22
6. 6
.
un
un
+−
= = = =
I
A
M
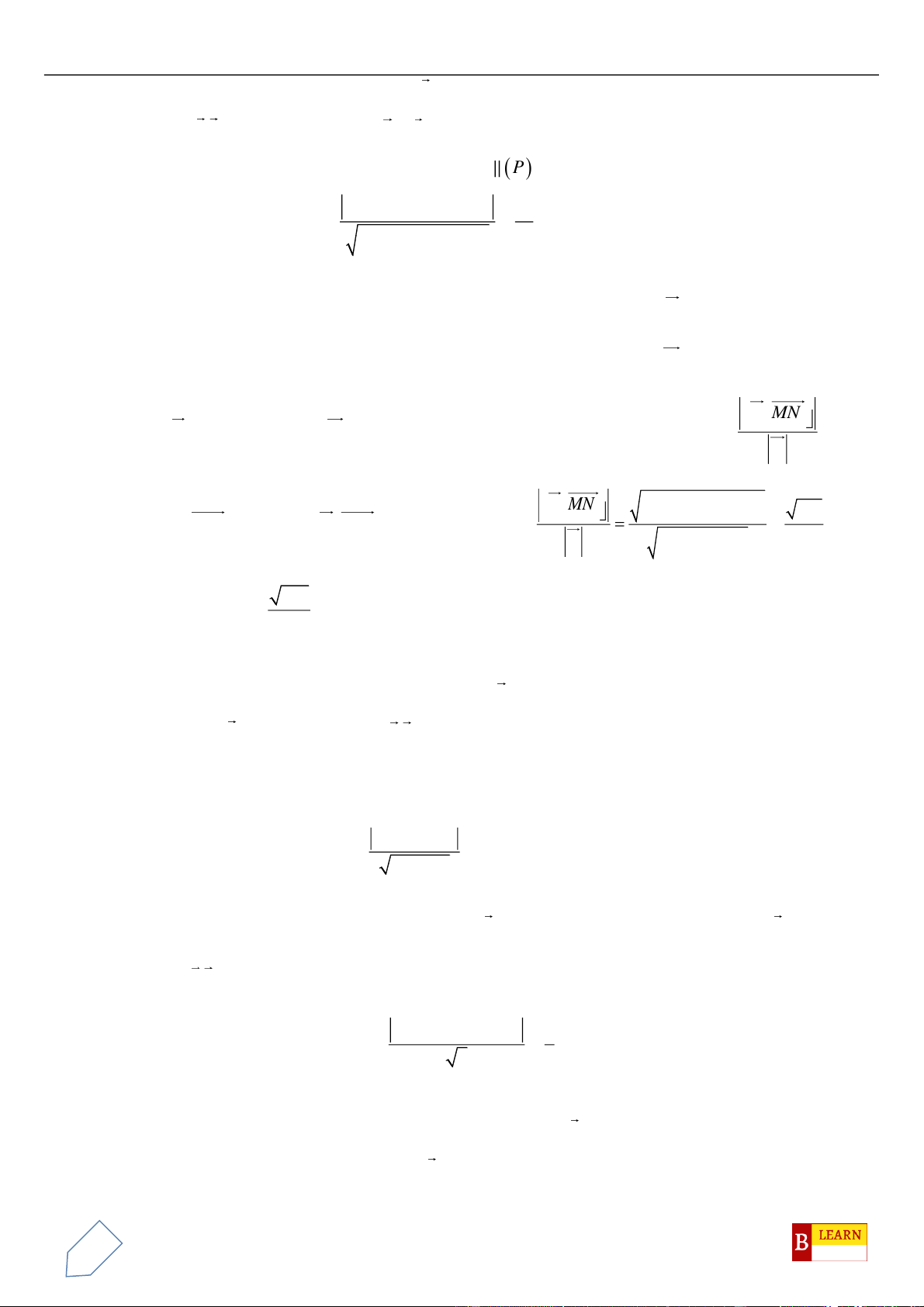
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
252
Mặt phẳng
( )
P
có vectơ pháp tuyến
( )
1; 2;2n =−
.
Ta có:
( )
. 2 4 6 0un= − − + =
un⊥
d
song song hoặc nằm trong mặt phẳng
( )
P
.
Lấy
( ) ( )
1;2; 3Ad− −
, ta thấy
( )
AP
nên
( )
dP
. Khi đó:
( ) ( )
,,d d P d A P=
( )
( ) ( )
22
2
1 2.2 2. 3 5
16
.
3
1 2 2
− − + − −
==
+ − + −
Câu 12. Chọn B
Đường thẳng
1
d
đi qua điểm
( )
1; 2;0M −
và có một vectơ chỉ phương
( )
1
2; 1;1u =−
.
Đường thẳng
2
d
đi qua điểm
( )
1; 1;2N −
và có một vectơ chỉ phương
( )
2
4; 2;2u =−
.
Do
1
u
cùng phương với
2
u
và
2
Md
nên
12
//dd
từ đó
( ) ( )
1
1 2 1
1
,
;;
u MN
d d d d N d
u
==
.
Ta có
( )
0;1;2MN =
,
( )
1
, 3; 4;2u MN
= − −
suy ra
( ) ( )
( )
22
2
1
2
2
1
,
3 4 2
174
6
2 1 1
u MN
u
− + − +
==
+ − +
.
Vậy
( )
12
174
;
6
d d d =
.
Câu 13. Chọn B
Mặt phẳng
()P
có một véc tơ pháp tuyến là
( )
1; 2;2n =−
, đường thẳng
có một véc tơ chỉ
phương là
( )
2;2;1u =
. Ta thấy
. 2 4 2 0nu= − + =
nên mặt phẳng
()P
và đường thẳng
song
song hoặc đường thẳng
nằm trong mặt phẳng
()P
.
Do
( )
1;3;2M
mà
( )
MP
nên đường thẳng
song song
()P
.
Vậy
( ) ( )
1 6 4 4
,( ) ,( ) 1
1 4 4
d P d M P
− + +
= = =
++
.
Câu 14. Chọn A
Đường thẳng
qua
( )
1; 2;1M −
và có VTCP
( )
2;2;1u =
; mặt phẳng
( )
P
có VTPT
( )
1; 2;2n =−
Ta có
.0nu=
và
( )
MP
nên đường thẳng
( )
// P
Suy ra
( )
( )
( )
( )
( )
1 2 2 2.1 1
8
,,
3
9
d P d M P
− − + +
= = =
Câu 15. Chọn D
Đường thẳng
d
qua
( )
1;0;0M
và có vec-tơ chỉ phương
( )
1;1; 2a =−
.
Mặt phẳng
( )
P
có vec-tơ pháp tuyến
( )
1;1;1n =
.
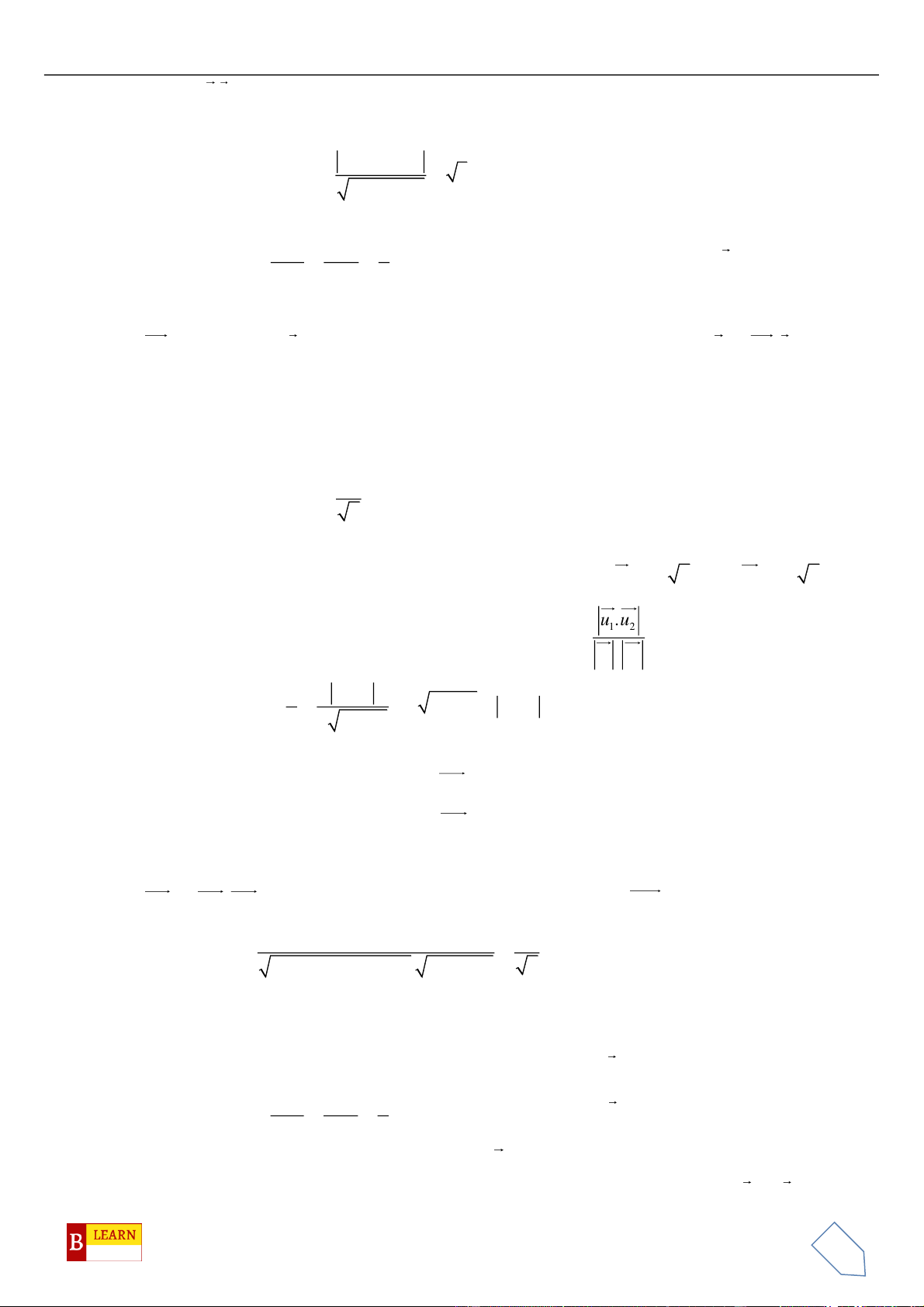
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
253
Ta có:
( )
( )
. 1.1 1.1 2.1 0
/ / .
an
dP
MP
= + − =
( )
( )
( )
( )
222
1 0 0 2
, , 3.
111
d d P d M P
+++
= = =
++
Câu 16. Chọn D
Đường thẳng
11
:
1 1 2
x y z−+
= =
−
đi qua
( )
1; 1;0M −
và có vectơ chỉ phương
( )
1; 1;2u =−
.
Mặt phẳng
( )
P
đi qua hai điểm
( )
2;1;0A
,
( )
3;0;1B
và song song với
nhận hai vectơ
( )
1;1; 1BA = − −
và
( )
1; 1;2u =−
làm cặp vectơ chỉ phương nên
( )
P
nhận
( )
, 1;1;0n BA u
==
làm vectơ pháp tuyến.
Do đó, mặt phẳng
( )
P
có phương trình:
( )
: 3 0P x y+ − =
Khoảng cách giữa
và mặt phẳng
( )
P
bằng khoảng cách từ
( )
1; 1;0M −
tới mặt phẳng
( )
P
( )
( )
( )
( )
3
,,
2
d P d M P = =
.
Câu 17. Chọn A
Ta có vectơ chỉ phương của hai đường thẳng
12
,dd
lần lượt là
( )
1
1; 2;1u =
và
( )
2
1; 2;um=
.
Theo công thức tính góc tạo bởi hai đường thẳng thì
12
12
.
.
uu
cos
uu
=
với
( )
12
,dd
=
.
Từ giả thiết suy ra
2 2 2
2
3
1
3 3 3 6 9 1
2
23
m
m m m m m m
m
+
= + = + + = + + = −
+
.
Câu 18. Chọn B
Mặt phẳng
( )
P
có vectơ pháp tuyến là
( )
( )
1;0; sin
P
n
=−
Mặt phẳng
( )
Q
có vectơ pháp tuyến là
( )
( )
0;1; cos
Q
n
=−
( )
d
là giao tuyến của
( )
P
và
( )
Q
nên vectơ chỉ phương của
( )
d
là:
( ) ( ) ( )
( )
; sin ;cos ;1
d P Q
u n n
==
; vectơ chỉ phương của
( )
Oz
là
()
(0;0;1)
Oz
u =
2 2 2 2
| 0.sin 0.cos 1.1| 1
cos(d, ) ( , ) 45
2
sin cos 1 . 0 0 1
Oz d Oz
++
= = =
+ + + +
Vậy góc giữa
( )
d
và trục
( )
Oz
là:
45
.
Câu 19. Chọn D
Mặt phẳng
( )
:2 3 0P x y z− − + =
có một véctơ pháp tuyến là
( )
( )
= 2; 1; 1
P
n −−
.
Đường thẳng
11
:
1 2 2
x y z+−
= =
−
có một véctơ chỉ phương là
( )
1; 2;2u
=−
.
Giả sử đường thẳng
d
có vectơ chỉ phương là
d
u
.
Do
( )
0 , 90d
mà theo giả thiết
d
tạo
góc lớn nhất
( )
, 90
d
d u u
= ⊥
.
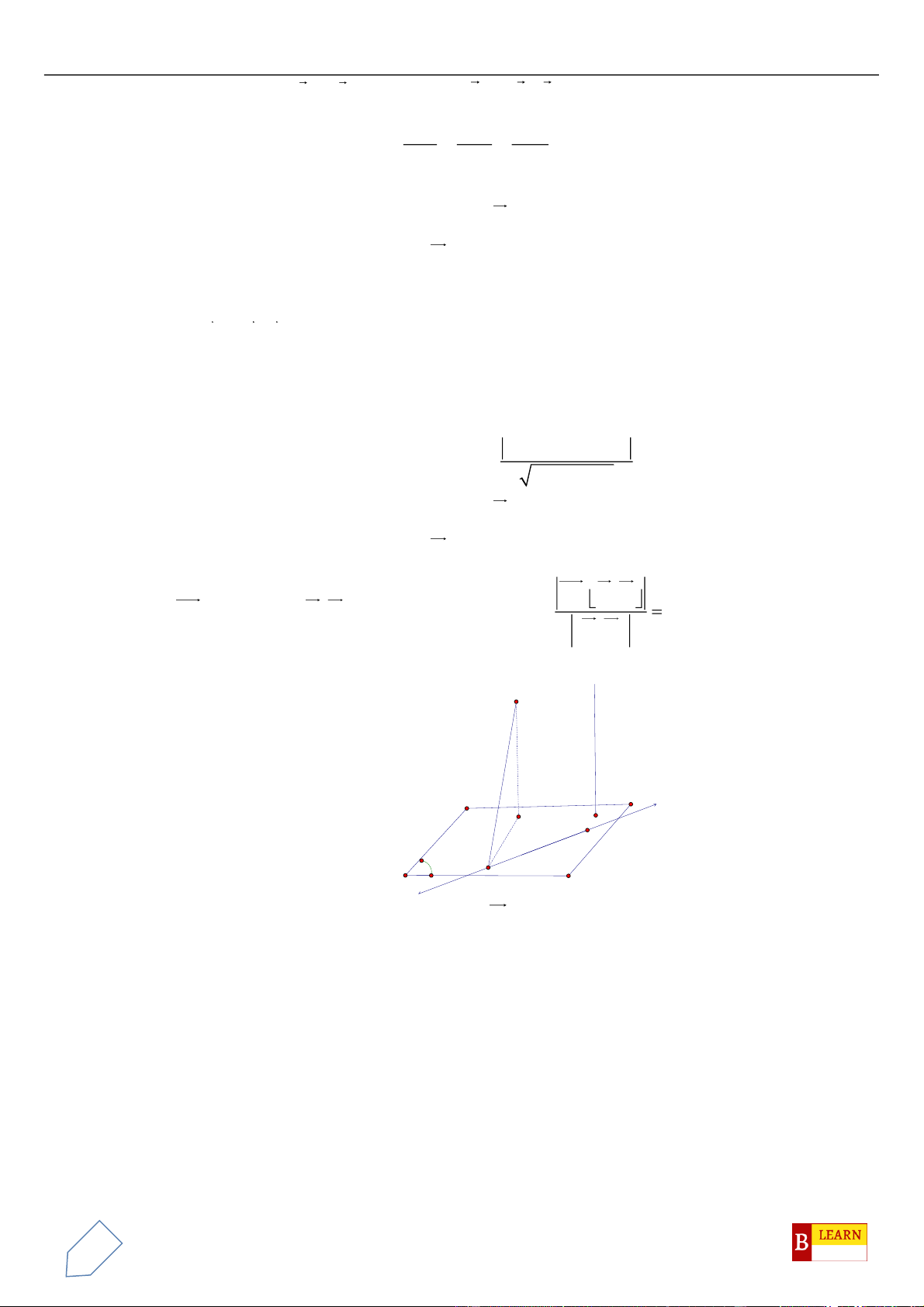
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
254
Lại có
( )
// dP
nên
( )
dP
un⊥
. Do đó chọn
( )
( )
, 4; 5; 3
dP
u u n
==
.
Vậy phương trình đường thẳng
112
:
4 5 3
x y z
d
− + −
==
.
Câu 20. Chọn D
Cách 1: Đường thẳng
1
d
có vecto chỉ phương
( )
1
4;1;1u =−
và đi qua điểm
( )
3; 2; 1A −−
.
Đường thẳng
2
d
có vecto chỉ phương
( )
2
6;1;2u =−
và đi qua điểm
( )
0;1;2B
.
Gọi mặt phẳng chứa
1
d
và song song với
2
d
là
( )
P
.
Ta có:
( )
12
; 1;2;2
P
u u u
==
.
Vì
( )
P
chứa
1
d
nên
( )
AP
, ta suy ra phương trình mặt phẳng
( )
P
là:
( ) ( ) ( )
1 3 2 2 2 1 0 2 2 3 0x y z x y z− + + + + = + + + =
.
Ta suy ra:
( ) ( )
( )
( )
( )
1 2 2
222
0.1 2.1 2.2 3
; ; ; 3
1 2 2
d d d d d P d B P
+ + +
= = = =
++
.
Cách 2: Đường thẳng
1
d
có vecto chỉ phương
( )
1
4;1;1u =−
và đi qua điểm
( )
3; 2; 1A −−
.
Đường thẳng
2
d
có vecto chỉ phương
( )
2
6;1;2u =−
và đi qua điểm
( )
0;1;2B
.
Có:
( )
3;3;3AB =−
;
( )
12
; 1;2;2uu
=
.Vậy
( )
12
12
12
.,
;3
,
AB u u
d d d
uu
==
.
Câu 21. Chọn D
Đường thẳng
()d
có một vectơ chỉ phương là
( )
2;2; 1
d
u =−
.
Gọi
( )
P
là mặt phẳng chứa
M
và vuông góc với đường thẳng
d
. Gọi
H
là hình chiếu kẻ từ
A
xuống mặt phẳng
( )
P
. Gọi
K
là hình chiếu vuông góc kẻ từ
A
đến đường thẳng
. Suy ra
( )
;d A AK=
. Vì
(P)AH AH HK⊥ ⊥
nên
AK AH
(A/ )d AH
.
Do đó khoảng cách từ
A
đến đường thẳng
đạt giá trị nhỏ nhất khi
K
trùng với
H
, khi đó
đường thẳng cần tìm là
MH
.
Phương trình của mặt phẳng
()P
là
( ) ( ) ( ) ( )
:2 2 2 2 1 0 2 2 9 0P x y z x y z+ + + − − = + − + =
(
P
)
d
A
H
M
K
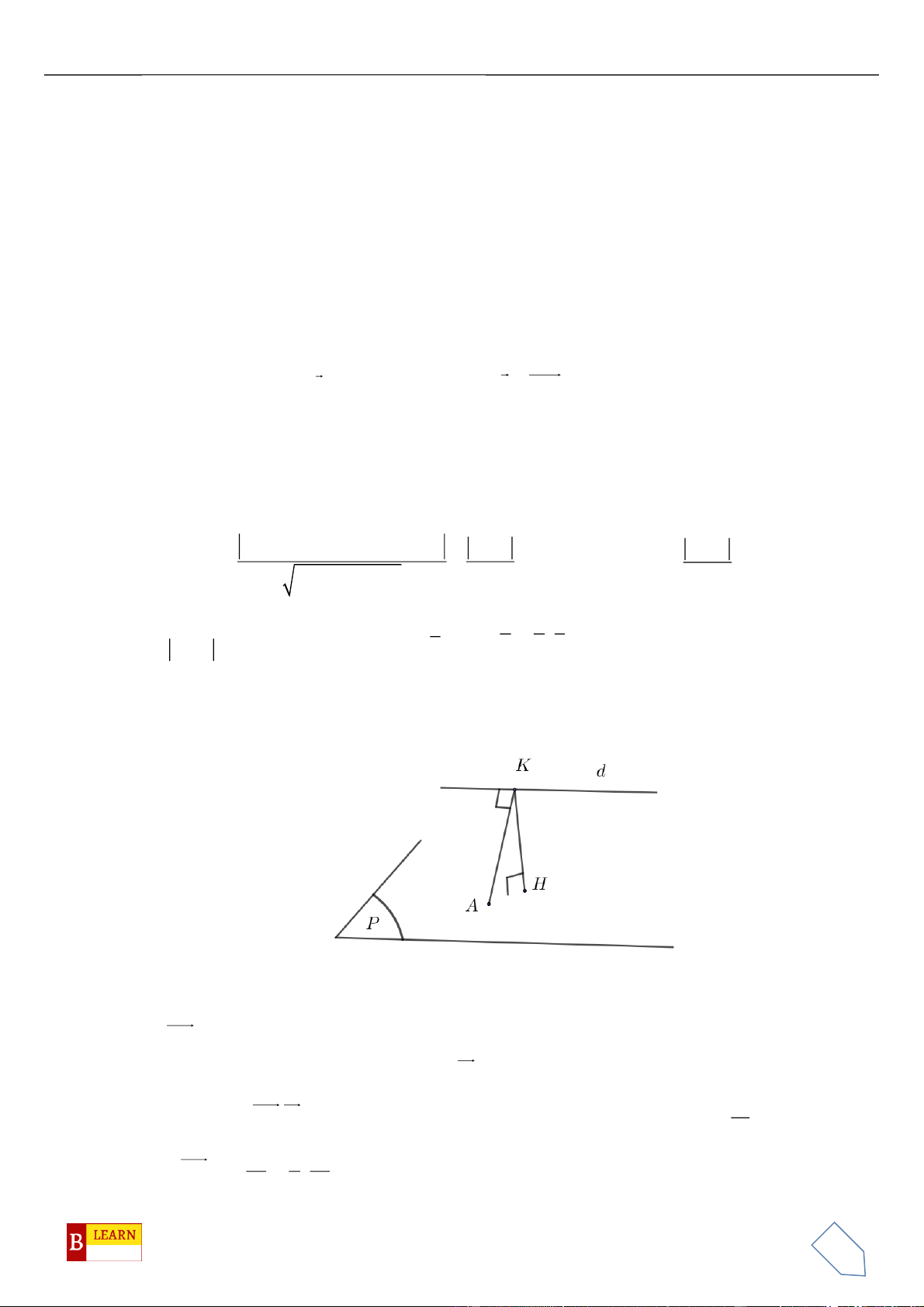
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
255
Phương trình đường thẳng
AH
là
12
22
3
xt
yt
zt
=+
=+
= − −
Vì
( )
H P AH=
nên tọa độ của
H
là bộ ba
( ; ; )x y z
thỏa hệ
( )
( )
( )
( )
1 2 1
2 2 2
33
2 2 9 0 4
==
=+
= − −
+ − + =
xt
yt
zt
x y z
.
Thay
(1),(2),(3)
vào
(4)
ta được
( ) ( ) ( )
2 1 2 2 2 2 3 9 0 9 18 0 2t t t t t+ + + − − − + = + = = −
( )
3 2 1H ; ; − − −
Vậy vectơ chỉ phương
u
của đường thẳng
là
( )
1 0 2u HM ; ;==
.
Câu 22. Chọn A
Ta có
1
: 1 2
=+
= − +
=−
xt
d y t
zt
. Gọi
( )
1 ; 1 2 ;+ − + − A t t t d
( )
( )
( ) ( )
( )
2
22
1 2 1 2 2 1
25
,
3
1 2 2
+ − − + + − −
−
==
+ − +
t t t
t
d A P
mà
( )
( )
,1=d A P
25
1
3
−
=
t
( )
4 7 1
1
;;
2 5 3
5 5 5
2 5 3
5
2 5 3
1
2;1; 1
−
−=
=−
− =
− = −
=
−
A
t
t
t
t
t
A
. Vì
( )
0 2;1; 1 −cA
Vậy
2=S
.
Câu 23. Chọn A
Gọi
K
là hình chiếu vuông góc của
A
lên đường thẳng
d
và
H
là hình
chiếu vuông góc của
K
lên mặt phẳng
()P
. Vì
Kd
nên ta đặt
(1 2 ; ;1 3 )K t t t++
(2 9; 2;3 )AK t t t = − −
.
Véc tơ chỉ phương của đường thẳng
d
là
(2;1;3)
d
u =
.
Vì
. 0 2(2 9) 1.( 2) 3.3 0
d
AK d AK u t t t⊥ = − + − + =
10
14 20 0
7
tt − = =
.
Vậy
43 4 30
( ; ; )
7 7 7
AK = − −
. Khoảng cách giữa
d
và
()P
là độ dài đoạn thẳng

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
256
HK
mà
HK AK
nên khoảng cách giữa
d
và
()P
lớn nhất bằng
AK
khi
H
trùng
A
, lúc đó
()AK P⊥
nên
()P
có véc tơ pháp tuyến
43 4 30
( ; ; )
7 7 7
AK = − −
,
ta chọn véctơ pháp tuyến
()P
là
(43;4; 30)
p
n =−
. Khi đó phương trình mặt phẳng
()P
là
43( 10) 4( 2) 30.( 1) 0x y z− + − − − =
43 4 30 408 0x y z + − − =
.
Vậy ta có
533
( ;( ))
2765
d M P =
.
Câu 24. Chọn C
Cách 1.
( )
0;0; 3AB =−
;
( )
2; ;
d
u a b=
.
. 0 0
d
d AB AB u b⊥ = =
( )
2; ;0
d
ua=
( )
2;1;4BM =−
( )
, 4 ;8; 2 2
d
BM u a a
= − − −
( )
,
,
d
d
BM u
d d M d
u
= =
( )
2
2
2
22
16 64 2 2
20 8 68
44
aa
aa
aa
+ + +
++
==
++
( )
2
2
5 2 17
2. 2
4
aa
fa
a
++
==
+
Xét
( )
2
2
5 2 17
4
aa
fa
a
++
=
+
có
( )
( )
2
2
2
1
2 6 8
0
4
4
a
aa
fa
a
a
=−
− + +
= =
=
+
Vì hàm
( )
fa
liên tục trên nên
( )
fa
có GTNN
( ) ( )
1 , 4ff=−
;
( ) ( )
1 4, 4 5,25ff− = =
.
Vậy
( )
min
d f a
đạt GTNN
1a = −
1a b C + = −
Cách 2.
d AB⊥
nên d nằm trong mặt phẳng (P) qua B và vuông góc
( )
0;0; 3AB =−
Có phương trình:
( ) ( ) ( )
0 1 0 2 3 0 0x y z− + − − − =
hay
( ) ( )
:0P z P=
trùng
( )
xOy
Khoảng cách từ
( )
1;3;4M −
đến
( )
P
nhỏ nhất khi và chỉ khi
( )
d
đi qua
H
là hình chiếu của
( )
1;3;4M −
xuống
( )
xOy
( )
1;3;0H−
. Vậy
( )
d
có vtcp là
( )
2;1;0BH =−
Gt cho
( )
d
có vtcp dạng
( ) ( )
2; ; // 2; 1;0u a b −−
1, 0 1a b a b C = − = + = −
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
257
DẠNG 5. VỊ TRÍ TƯƠNG ĐỐI GIỮA HAI ĐƯỜNG THẲNG, ĐƯỜNG
THẲNG VỚI MẶT CẦU
Câu 1: Trong không gian
,Oxyz
cho đường thẳng
1 2 3
:
2 4 1
x y z
d
− − −
==
và mặt phẳng
( ): 2 5 0,x y z
− + − =
mệnh đề nào dưới đây là đúng?
A.
/ /( ).d
B.
( ).d
C.
d
cắt
()
và
d
không vuông góc với
( ).
D.
( ).d
⊥
Câu 2: Tọa độ giao điểm
M
của đường thẳng
12 9 1
:
4 3 1
x y z
d
− − −
==
và mặt phẳng
( )
: 3 5 2 0P x y z+ − − =
là
A.
( )
1;0;1
. B.
( )
0;0; 2−
. C.
( )
1;1;6
. D.
( )
12;9;1
.
Câu 3: Trong không gian
Oxyz
, tìm tọa độ điểm
M
là giao điểm của đường thẳng
1
:2
xt
d y t
zt
=+
= − +
=−
với mặt
phẳng
( )
: 4 0P x y z− − − =
.
A.
( )
1; 2;0M −
. B.
( )
4;0;0M
. C.
( )
3;0; 1M −
. D.
( )
2; 1; 1M −−
.
Câu 4: Cho đường thẳng
112
:
2 1 2
x y z− + −
= =
nằm trong mặt phẳng
3 3 0mx ny z+ + + =
. Tổng
mn+
bằng
A.
1
. B.
2
. C.
2−
. D.
1−
.
Câu 5: Trong không gian tọa độ
Oxyz
, cho hai đường thẳng
1
112
:
1 2 1
− + −
==
x y z
d
và
2
2
3 9 2
:
48
xyz
d
m
+ + +
==
( )
0m
. Tập hợp các giá trị
m
thỏa mãn
12
//dd
có số phần tử là:
A.
1
. B.
0
. C.
3
. D.
2
.
Câu 6: Trong không gian với hệ tọa độ
Oxyz
, cho hai đường thẳng
1
: 2 3
3
xt
d y t
zt
=+
=+
=−
và
2 2 '
': 2 '
1 3 '
xt
d y t
zt
=−
= − +
=+
.
Tìm tọa độ giao điểm
M
của
d
và
'd
.
A.
( )
0; 1;4M =−
. B.
( )
1;0;4M =−
. C.
( )
4;0; 1M =−
. D.
( )
0;4; 1M =−
.
Câu 7: Trong không gian , cho đường thẳng và mặt phẳng
. Tọa độ giao điểm của và là
A. . B. . C. . D. .
Câu 8: Trong không gian tọa độ
Oxyz
, xét vị trí tương đối của hai đường thẳng
12
1 1 3 3 2
: , :
2 2 3 1 2 1
x y z x y z− + − − +
= = = =
−−
Oxyz
21
:
1 2 2
x y z
d
−−
==
−
( )
: 2 5 0P x y z+ − − =
d
( )
P
( )
2;1; 1−
( )
3; 1; 2−−
( )
1;3; 2−
( )
1;3;2

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
258
A.
1
song song với
2
. B.
1
chéo với
2
. C.
1
cắt
2
. D.
1
trùng với
2
.
Câu 9: Trong không gian với hệ toạ độ
Oxyz
, cho đường thẳng
15
:
1 3 1
x y z
d
+−
==
−−
và mặt phẳng
( )
:3 3 2 6 0P x y z− + − =
. Mệnh đề nào dưới đây đúng?
A.
d
cắt và không vuông góc với
( )
P
. C.
d
song song với
( )
P
.
B.
d
vuông góc với
( )
P
. D.
d
nằm trong
( )
P
.
Lời giải
Chọn A
Đường thẳng
d
nhận
( )
1; 3; 1u = − −
làm một vectơ chỉ phương.
Mặt phẳng
( )
P
nhận
( )
3; 3;2n =−
làm một vectơ pháp tuyến.
Do
.0un
và hai vectơ này không cùng phương nên đường thẳng
d
cắt và không vuông góc với
( )
P
.
Câu 10: Trong không gian
Oxyz
, cho đường thẳng
1 2 1
:
2 1 1
x y z
d
− + +
==
−
. Hỏi
d
song song với mặt
phẳng nào dưới đây?
A.
3 4 0x y z+ + + =
. B.
2 4 7 0x y z+ + + =
. C.
3 7 5 0x y z+ + + =
. D.
3 4 5 0x y z+ + + =
.
Câu 11: Trong không gian
Oxyz
, cho điểm
( )
2;1;1A
và mặt phẳng
( )
: 2 3 0P x y z− − + =
. Mặt phẳng đi
qua điểm
A
, vuông góc với mặt phẳng
( )
P
và song song với trục
Oz
có phương trình là
A.
2 1 0x y z+ − + =
. B.
10z −=
. C.
10xy− − =
. D.
30xy+ − =
.
Câu 12: Trong không gian với hệ trục tọa độ
,Oxyz
cho đường thẳng có phương trình
2 1 1
:.
1 1 1
x y z
d
− − −
==
−
Xét mặt phẳng
( )
( )
2
: 1 7 0,P x my m z+ + − − =
với
m
là tham số thực.
Tìm
m
sao cho đường thẳng
d
song song với mặt phẳng
( )
.P
A.
1m =
. B.
1m =−
. C.
1
2
m
m
=−
=
. D.
2m =
.
Câu 13: Trong không gian tọa độ
Oxyz
, cho đường thẳng
1 2 9
d:
1 3 1
x y z− − −
==
−
và mặt phẳng
( )
có
phương trình
2
2 19 0m x my z− − + =
với
m
là tham số. Tập hợp các giá trị
m
sao cho đường
thẳng
d
song song với mặt phẳng
( )
là
A.
2
. B.
1;2
. C.
1
. D.
.
Câu 14: Trong không gian với hệ tọa độ
Oxyz
cho mặt phẳng
( )
: 2 5 0Q x y z− + − =
và mặt cầu
( ) ( ) ( )
22
2
: 1 2 15S x y z− + + + =
. Mặt phẳng
( )
P
song song với mặt phẳng
( )
Q
và cắt mặt cầu
( )
S
theo giao tuyến là một đường tròn có chu vi bằng
6
đi qua điểm nào sau đây?
A.
( )
2; 2;1−
. B.
( )
1; 2;0−
. C.
( )
0; 1; 5−−
. D.
( )
2;2; 1−−
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
259
Câu 15: Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 3
d:
2 1 2
x y z
mm
− + +
==
−
và mặt phẳng
(P): x+3y-2z+1=0
. Với giá trị nào của m thì đường thẳng
d
vuông góc mặt phẳng
(P)
.
A.
m = 2
. B.
m = -1
. C.
m = 1
. D.
m = 0
.
Câu 16: Trong không gian
Oxyz
cho đường thẳng
( )
1
:1
1
x
d y t t
zt
=
= +
= − +
và hai mặt phẳng
( ) ( )
: 1 0, :2 4 0.P x y z Q x y z− + + = + − − =
Khẳng định nào sau đây đúng?
A.
( )
//dP
. B.
( )
//dQ
. C.
( ) ( )
P Q d=
. D.
( )
dP⊥
.
Câu 17: Trong không gian
Oxyz
, cho đường thẳng
d
1
12
xt
yt
zt
=
=−
= − +
và mặt phẳng
( )
: 3 2 0x y z
+ + − =
. Khẳng định nào sau đây là đúng?
A. Đường thẳng
d
cắt mặt phẳng
( )
.
B. Đường thẳng
d
nằm trên mặt phẳng
( )
.
C. Đường thẳng
d
vuông góc với mặt phẳng
( )
.
D. Đường thẳng
d
song song với mặt phẳng
( )
.
Câu 18: Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
( )
3;2;1A
,
( )
3;0;0M
và mặt phẳng
( )
: 3 0P x y z+ + − =
. Đường thẳng
đi qua điểm
M
, nằm trong mặt phẳng
( )
P
sao cho
khoảng cách từ điểm
A
đến
là nhỏ nhất. Gọi véc tơ
( )
;;u a b c=
là một véc tơ chỉ phương của
(
,,abc
là các số nguyên có ước chung lớn nhất là 1). Tính
P a b c= + +
A.
1−
B.
1
C.
2
D.
0
Câu 19: Trong không gian cho hai mặt phẳng và hai
đường thẳng . Đường thẳng song song với hai mặt
phẳng và cắt tương ứng tại . Độ dài đoạn bằng
A. . B. C. D.
Câu 20: Trong không gian với hệ tọa độ
Oxyz
, cho điểm
( )
2;1;0M
và đường thẳng
11
:
2 1 1
x y z−+
= =
−
. Phương trình tham số của đường thẳng
d
đi qua
M
, cắt và vuông góc với
là
A.
2
: 1 4
2
xt
d y t
zt
=+
=−
=−
. B.
22
:1
xt
d y t
zt
=+
=+
=−
. C.
2
:1
xt
d y t
zt
=−
=+
=
. D.
1
: 1 4
2
xt
d y t
zt
=+
= − −
=
.
Oxyz
( )
: 2 1 0,P x y z+ − − =
( )
:2 2 0,P x y z+ − + =
1
11
:,
2 1 2
x y z−+
= =
2
21
:
1 1 2
x y z−−
= =
−
( ) ( )
;PQ
12
,
,HK
HK
8 11
7
5
6.
11
.
7

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
260
Câu 21: Trong không gian
Oxyz
, cho điểm
( )
2 ;5 ; 3A
và đường thẳng
12
:
2 1 2
x y z
d
−−
==
. Gọi
()P
là
mặt phẳng chứa
d
sao cho khoảng cách từ điểm
A
đến
()P
lớn nhất. Khoảng cách từ gốc tọa độ
O
đến
()P
bằng
A.
1
2
. B.
3
6
. C.
11 2
6
. D.
2
.
Câu 22: Trong không gian
Oxyz
, cho hai đường thẳng
1
1 3 1
d:
1 1 1
x y z− − +
==
−
và
2
13
d:
2 2 1
x m y z− + −
==
−
. Có bao nhiêu giá trị của tham số m để hai đường thẳng
1
d
,
2
d
có đúng
một điểm chung?
A.
2
. B.
0
. C.
1
. D. vô số.
Câu 23: Trong không gian
Oxyz
cho đường thẳng
1 3 1
:
2 1 2 2
x y z
d
mm
− + +
==
+−
và mặt phẳng
( )
: 6 0P x y z+ + − =
, hai điểm
( )
2;2;2A
,
( )
1;2;3B
thuộc
( )
P
. Giá trị của
m
để
AB
vuông
góc với hình chiếu của
d
trên
( )
P
là?
A.
1m =
. B.
1m =−
. C.
2m =
. D.
3m =−
.
Câu 24: Trong không gian
Oxyz
, cho mặt phẳng
( )
:2 2 3 0P x y z− + + =
và hai đường thẳng
1
11
:
3 1 1
x y z
d
−+
==
−
;
2
2 1 3
:
1 2 1
x y z
d
− − +
==
−
. Xét các điểm
A
,
B
lần lượt di động trên
1
d
và
2
d
sao cho
AB
song song với mặt phẳng
( )
P
. Tập hợp trung điểm của đoạn thẳng
AB
là
A. Một đường thẳng có vectơ chỉ phương
( )
9;8; 5u = − −
.
B. Một đường thẳng có vectơ chỉ phương
( )
5;9;8u =−
.
C. Một đường thẳng có vectơ chỉ phương
( )
1; 2; 5u = − −
.
D. Một đường thẳng có vectơ chỉ phương
( )
1;5; 2u =−
.
Câu 25: rong không gian
Oxyz
, cho hai đường thẳng
1
1 2 1
:
2 2 1
x y z
d
− − +
==
−−
và
2
:0
xt
dy
zt
=
=
=−
. Mặt phẳng
( )
P
qua
1
d
, tạo với
2
d
một góc
45
và nhận vectơ
( )
1; ;n b c
làm một vec tơ pháp tuyến. Xác
định tích
.bc
.
A.
4−
. B.
4
. C.
4
hoặc
0
. D.
4−
hoặc
0
.
Câu 26: Trong không gian
Oxyz
, cho hai điểm
( ) ( )
1;2; 3 , 2; 2;1AB− − −
và mặt phẳng
( )
:2 2 9 0x y z
+ − + =
. Xét điểm
M
thuộc
( )
sao cho tam giác
AMB
vuông tại
M
và độ dài
đoạn thẳng
MB
đạt giá trị lớn nhất. Phương trình đường thẳng
MB
là
A.
2
22
12
xt
yt
zt
= − −
= − +
=+
. B.
22
2
12
xt
yt
zt
= − +
= − −
=+
. C.
2
2
12
xt
y
zt
= − +
=−
=+
. D.
2
2
1
xt
yt
z
= − +
= − −
=
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
261
Câu 27: Trong không gian với hệ tọa độ
Oxyz
, cho hai đường thẳng
12
1
1
: ; : 2
2 1 3
xt
x y z
d d y t
zm
=+
−
= = = +
=
.
Gọi
S
là tập tất cả các số
m
sao cho
1
d
và
2
d
chéo nhau và khoảng cách giữa chúng bằng
5
19
. Tính tổng các phần tử của
S
.
A.
11−
. B.
12
. C.
12−
. D.
11
.
Câu 28: Trong không gian với hệ trục tọa độ
Oxyz
cho hai đường thẳng
1
4
4
62
xt
d y t
zt
=+
= − −
=+
;
2
5 11 5
:
2 4 2
x y z
d
− − −
==
. Đường thẳng
d
đi qua
( )
5; 3;5A −
cắt
12
;dd
lần lượt ở
,BC
.Tính tỉ
sô
AB
AC
.
A.
2
. B.
3
. C.
1
2
. D.
1
3
.
Câu 29: Trong không gian
Oxyz
, cho điểm
(1;0;2)A
và đường thẳng
11
:
1 1 2
x y z
d
−+
==
. Đường thẳng
đi qua
A
, vuông góc và cắt
d
có phương trình là
A.
2 1 1
:
2 2 1
x y z− − −
= =
. B.
2 1 1
:
1 1 1
x y z− − −
= =
−
.
C.
12
:
1 1 1
x y z−−
= =
. D.
12
:
1 3 1
x y z−−
= =
−
.
Câu 30: Trong không gian
Oxyz
, cho ba điểm
( ) ( ) ( )
3;0;0 , 0;4;0 , 0;0;A B C c
với
c
là số thực thay đổi
khác
0
. Khi
c
thay đổi thì trực tâm
H
của tam giác
ABC
luôn thuộc một đường tròn cố định.
Bán kính của đường tròn đó bằng
A.
5
2
. B.
5
4
. C.
12
5
. D.
6
5
.
Câu 31: Trong không gian với hệ tọa độ
Oxy
, cho đường thẳng
12
:.
1 1 2
x y z
d
−+
==
−
Mặt phẳng
( )
P
đi
qua điểm
( )
2;0; 1M −
và vuông góc với
d
có phương trình là
A.
( )
: 2 0P x y z− + =
. B.
( )
: 2 2 0P x y− − =
.
C.
( )
: 2 0P x y z− − =
. D.
( )
: 2 0P x y z+ + =
.
Câu 32: Trong không gian với hệ trục tọa độ
Oxyz
, cho điểm
( )
2; 1;2M −
và mặt cầu
( ) ( )
2
22
: 1 9S x y z− + + =
. Mặt phẳng
( )
P
đi qua
M
cắt
( )
S
theo giao tuyến là một đường tròn
có bán kính nhỏ nhất có phương trình là
A.
2 5 0x y z− + − =
. B.
2 7 0x y z− + − =
. C.
2 7 0x y z− + − =
. D.
2 5 0x y z+ + − =
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
262
ĐÁP ÁN CHI TIẾT
Câu 1: Chọn B
Ta có
12
: 2 4 , .
3
xt
d y t t
zt
=+
= +
=+
Xét hệ phương trình:
1 2 (1)
2 4 (2)
.
3 (3)
2z 5 0(*)
xt
yt
zt
xy
=+
=+
=+
− + − =
Thay,, vào ta được
1 2 (2 4 ) 2(3 ) 5 0.t t t+ − + + + − =
Phương trình này có vô số nghiệm. Do đó,
đường thẳng
d
nằm trong mặt phẳng
( ).
Câu 2: Chọn B
Gọi
( )
4 12;3 9; 1M t t t d+ + +
.
Ta có:
( ) ( ) ( ) ( ) ( )
3 4 12 5 3 9 1 2 0 3 0;0; 2M P t t t t M + + + − + − = = − −
.
Câu 3: Chọn D
Gọi
( )
1; 2 ;M t t t d+ − + −
.
Ta có:
( ) ( ) ( ) ( ) ( )
1 2 4 0 1 2; 1; 1M P t t t t M + − − + − − − = = − −
.
Câu 4: Chọn D
Lấy 2 điểm
( )
1; 1;2A −
và
( )
3;0;4B
thuộc đường thẳng
.
Đặt mặt phẳng
( )
: 3 3 0P mx ny z+ + + =
.
Vì
( )
P
nên
A
,
B
thuộc
( )
P
. Thay tọa độ
A
,
B
vào phương trình mặt phẳng
( )
P
ta có hệ
phương trình:
9 0 4
3 15 0 5
m n n
mm
− + = =
+ = = −
. Vậy
1mn+ = −
.
Câu 5: Chọn B
Đường thẳng
1
d
qua
(1; 1;2)A −
và có vectơ chỉ phương là
( )
1
1;2;1u =
.
Đường thẳng
2
d
qua
( 3; 9; 2)B − − −
và có một vectơ chỉ phương là
( )
2
2
4;8;um=
.
Đường thẳng
12
//dd
khi và chỉ khi
1
u
cùng phương với
2
u
và hai đường thẳng
1
d
và
2
d
không
trùng nhau.
Ta thấy điểm
( 3; 9; 2)B − − −
nằm trên
2
d
và
3 1 9 1 2 2
1 2 1
− − − + − −
==
nên
B
cũng nằm trên
đường thẳng
1
d
Do đó hai đường thẳng này luôn có điểm chung nên không thể song song.
Câu 6: Chọn A
Tọa độ giao điểm
M
của và
'd
ứng với
t
và
't
là nghiệm của hệ:
d

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
263
1 2 2 ' 2 ' 1
1
2 3 2 ' 3 ' 4
'1
3 1 3 ' 3 ' 2
t t t t
t
t t t t
t
t t t t
+ = − + =
=−
+ = − + − = −
=
− = + + =
. Vậy
( )
0; 1;4M =−
.
Câu 7: Chọn D
Giả sử .
Vì .
Câu 8: Chọn C
Vì
22
12
−−
nên vectơ chỉ phương
( )
1
2;2;3u =
của đường thẳng
1
không cùng phương với
vectơ chỉ phương
( )
2
1; 2;1u = − −
của
2
. Tức là
1
chéo với
2
hoặc
1
cắt
2
.
Lấy
( )
1
1; 1;0M −
,
( )
2
3;3; 2N −
. Ta có:
( )
2;4; 2MN =−
.
Khi đó:
12
; . 0u u MN
=
. Suy ra
12
,,u u MN
đồng phẳng.
Vậy
1
cắt
2
.
Câu 9: Chọn A
Đường thẳng
d
nhận
( )
1; 3; 1u = − −
làm một vectơ chỉ phương.
Mặt phẳng
( )
P
nhận
( )
3; 3;2n =−
làm một vectơ pháp tuyến.
Do
.0un
và hai vectơ này không cùng phương nên đường thẳng
d
cắt và không vuông góc với
( )
P
.
Câu 10: Chọn C
Ta có:
d
có một véc tơ chỉ phương
( )
2;1; 1
d
u −
và đi qua điểm
( )
1; 2; 1A −−
.
( ) ( )
.0
*
A (P)
dP
un
dP
=
Kiểm tra điều kiện
( )
*
ta thấy mp
( )
:3 7 5 0P x y z+ + + =
thỏa mãn.
Câu 11: Chọn D
Giả sử
( )
là mặt phẳng cần tìm và
( )
có 1 VTPT là
n
.
Mặt phẳng
( )
: 2 3 0P x y z− − + =
có 1 VTPT là
( )
1
1; 1; 2n = − −
.
Trục
Oz
có 1 VTCP
( )
0;0;1k =
. Ta có:
( ) ( )
P
⊥
nên
1
nn⊥
.
( )
/ / Oz
nên
nk⊥
.
Do đó, ta có thể chọn VTPT của mặt phẳng
( )
:
( )
1
, 1; 1;0n n k
= = − −
.
Vậy mặt phẳng
( )
đi qua điểm
A
và có 1 VTPT
n
nên phương trình mặt phẳng
( )
là:
( ) ( )
2 1 0xy− − − − =
30xy+ − =
.
Câu 12: Chọn C
( )
d P M=
( )
2 ;1 2 ;2M t t t − +
( )
MP
( )
2 2 1 2 2 5 0t t t − + + − − =
1t=
( )
1;3;2M

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
264
Đường thẳng
d
có VTCP là
( )
1;1; 1u =−
và mặt phẳng
( )
P
có VTPT là
( )
2
1; ; 1n m m=−
.
/ /( )dP
22
1
. 0 1 1 0 2 0 .
2
m
u n u n m m m m
m
=−
⊥ = + − + = − − =
=
Câu 13: Chọn A
Ta có vectơ chỉ phương của đường thẳng
d
là
( )
1;3; 1u =−
.
Vectơ pháp tuyến mặt phẳng
( )
là
( )
2
; ; 2n m m= − −
.
Gọi
( )
1;2;9Md
. Đường thẳng
d
song song với mặt phẳng
( )
khi:
( )
2
2
3 2 0
.0
2 1 0
mm
un
M
mm
− + =
=
− +
1
2
2
1
m
m
m
m
=
=
=
.
Câu 14: Chọn D
Mặt cầu
( )
S
có tâm
( )
1;0; 2I −
và bán kính
15R =
.
Đường tròn có chu vi bằng
6
nên có bán kính
6
3
2
r
==
.
Mặt phẳng
( )
P
song song với mặt phẳng
( )
Q
nên phương trình mặt phẳng
( )
P
có dạng:
20x y z D− + + =
,
5D −
.
Vì mặt phẳng
( )
P
cắt mặt cầu
( )
S
theo giao tuyến là một đường tròn có chu vi bằng
6
nên
( )
( )
( )
( )
22
; ; 6d I P R r d I P= − =
( )
2
22
1 6 7
1 2.0 2
6 1 6
1 6 5
1 2 1
DD
D
D
DD
− = =
− − +
= − =
− = − = −
+ − +
.
Đối chiếu điều kiện ta được
7D =
. Do đó phương trình mặt phẳng
( )
: 2 7 0P x y z− + + =
.
Nhận thấy điểm có tọa độ
( )
2;2; 1−−
thuộc mặt phẳng
( )
P
.
Câu 15: Chọn B
Yêu cầu bài toán tương đương
( ;2 1;2)
d
u m m −
cùng phương
(1;3; 2)
P
n −
hay
2 1 2
11
1 3 2
mm
m
−
= = = − = −
−
Câu 16: Chọn C
Ta có đường thẳng
d
đi qua
( )
1;1; 1M −
và có véctơ chỉ phương
( )
0;1;1u =
.
Mặt phẳng
( )
P
có véc tơ pháp tuyến
( )
( )
1; 1;1
P
n =−
.
Mặt phẳng
( )
Q
có véc tơ pháp tuyến
( )
( )
2;1; 1
P
n =−
.
Nhận xét:
( ) ( )
. 0 1 1 0
PP
u n u n= − + = ⊥
. Hơn nữa
( )
MP
nên
( )
dP
. Tương tự
( )
dQ
.
Vậy
( ) ( )
d P Q=
.
Câu 17: Chọn B
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
265
Thay
1
12
xt
yt
zt
=
=−
= − +
vào phương trình
3 2 0x y z+ + − =
ta được:
( )
3 1 1 2 2 0 0 0 0t t t t+ − − + − = + =
đường thẳng
d
nằm trên mặt phẳng
( )
.
Câu 18: Chọn D
Gọi
H
là hình chiếu vuông góc của
A
trên mặt phẳng
( )
P
. Khi đó
AH
là khoảng cách từ A đến
( )
P
. Suy ra đường thẳng
cần tìm chính là đường thẳng nằm trong
( )
P
đi qua
M
và
H
Đường thẳng
d
đi qua
A
và vuông góc với
( )
P
là
3
2
1
xt
yt
zt
=+
=+
=+
(
t
là tham số)
Ta có
()H P d=
thay phương trình tham số
d
vào phương trình mặt phẳng ta được
3 2 1 3 0 1t t t t+ + + + + − = = −
Vậy
( )
2;1;0H
là hình chiếu vuông góc của
A
trên
( )
P
Đường thẳng
nhận
MH
làm véc tơ chỉ phương
.
( )
1;1;0 0MH a b c= − + + =
Câu 19: Chọn A
Tính
Gọi nên
+Vì song song với 2 mặt phẳng nên suy ra
tính ra được . Suy ra .
Câu 20: Chọn A
Vectơ chỉ phương của
là
( )
2;1; 1u
=−
.
Gọi
( )
;;H x y z
là hình chiếu của
M
lên
, suy ra tọa độ của
H
thỏa
( ) ( ) ( )
( )
7
3
2 .2 1 .1 . 1 0
25
.0
1
1 2 1 2 3
3
1
1
2
3
x
x y z
x y z
MH u
x y x y y
H
yz
yz
z
=
− + − + − =
+ − =
=
− = + − = = −
+ = −
+ = −
=−
.
( )
, 1; 1; 3
PQ
u n n
= = − − −
( ) ( )
2 ;1 ; 1 2 ; ;2 ;1 2H t t t K m m m+ − + − +
( )
2;1 ;2 2 2HK m m t m t= − − − + −
( ) ( )
;PQ
.HK k u=
2 1 2 2 2
1 1 3
m t m t m t− − − + −
==
23
;
77
mt
−
==
8 11
7
HK =
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
266
Ta có
1 4 2
;;
3 3 3
MH
= − −
, suy ra vectơ chỉ phương của
d
là
( )
1; 4; 2
d
n = − −
.
Phương trình tham số của đường thẳng
d
có vectơ chỉ phương
( )
1; 4; 2
d
n = − −
và đi qua điểm
( )
2;1;0M
là
2
: 1 4
2
xt
d y t
zt
=+
=−
=−
.
Câu 21: Chọn A
Gọi
K
là hình chiếu của
A
lên đường thẳng
d
.
H
là hình chiếu của
A
lên mặt phẳng
()P
.
Khi đó
( )
,( )d A P AH AK=
không đổi.
Vậy khoảng cách từ điểm
A
đến
()P
lớn nhất khi
HK
. Khi đó
()AK P⊥
.
Giả sử
( )
1 2 ; ; 2 2K t t t d+ +
. Suy ra
( )
1 2 ; 5 ; 1 2AK t t t= − + − + − +
.
Ta có:
( )
2;1; 2 . 0
dd
AK u AK u⊥ = =
( ) ( ) ( )
2 1 2 5 2 1 2 0 1 3;1;4t t t t K − + − + + − + = =
và
( )
1; 4 ;1AK =−
.
Mặt phẳng
()P
có phương trình:
( ) ( ) ( ) ( )
1
1 4 0 2 4 3 0 ;( )
2
x y z x y z d O P− − − + − − + − = =
.
Câu 22: Chọn C
Đường thẳng
1
d
đi qua điểm
( )
1
M 1;3; 1−
có vectơ chỉ phương
( )
1
1; 1;1u =−
.
Đường thẳng
2
d
đi qua điểm
( )
2
M ; 1;3m −
có vectơ chỉ phương
( )
2
2; 2;1u =−
.
Ta có
( )
( )
12
12
; 1;1;0
M M 1; 4;4
uu
m
=
= − −
;
1
d
cắt
2
d
khi
( )
12
1 2 1 2
; 1;1;0 0
5
; .M M 5 0
uu
m
u u m
=
=
= − =
.
Câu 23: Chọn D
Ta có
( )
2 1;2; 2
d
u m m= + −
,
( )
1;1;1
P
n =
và
( )
1;0;1AB =−
.
Giả sử
d
vuông góc với
( )
P
, khi đó
d
u
và
P
n
cùng phương
1
2 1 2
2 1 2 2
2
22
1 1 1
4
m
m
mm
m
m
+=
=
+−
= =
−=
=
.
Vậy
d
không vuông góc với
( )
P
.
d
(
P
A
H
K

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
267
Khi đó với
( )
AB P
,
AB
vuông góc với hình chiếu của
d
lên
( )
P
khi và chỉ khi
AB
vuông
góc với
d
( ) ( ) ( )
0 1 2 1 0 2 1 2 0 3
d
AB u m m m = − + + + − = = −
.
Câu 24: Chọn A
Mặt phẳng
( )
P
có vectơ pháp tuyến là
( )
2; 1;2n =−
.
Phương trình tham số của đường thẳng
1
3
: 1 (
1
xa
d y a a
za
=
=−
= − +
là tham số,
a
)
Phương trình tham số của đường thẳng
2
2
: 1 2 (
3
xb
d y b b
zb
=+
=−
= − +
là tham số,
b
)
Ta có:
( )
1
3 ;1 ; 1A d A a a a − − +
;
( )
2
2 ;1 2 ; 3B d B b b b + − − +
.
( )
3 2; 2 ; 2AB b a a b b a = − + − − −
.
Theo GT:
( )
( )
( ) ( ) ( )
3
2 3 2 2 2 2 0
2
0
/ / 0
,
0
0
a
b
b a a b b a
AB n
a
AB P a
A B P
b
b
=
− + − − + − − =
⊥
.
Suy ra
33
2 ;1 3 ; 3
22
aa
Ba
+ − − +
.
Gọi
I
là trung điểm của đoạn thẳng
AB
, ta có:
2
2
2
AB
I
AB
I
AB
I
xx
x
yy
y
zz
z
+
=
+
=
+
=
3
32
2
2
1 1 3
2
3
13
2
2
I
I
I
a
a
x
aa
y
a
a
z
++
=
− + −
=
− + − +
=
9
1
4
12
5
2
4
I
I
I
xa
ya
za
=+
= −
= − +
hay
95
1 ;1 2 ; 2
44
I a a a
= + − − +
.
Suy ra tập hợp điểm
I
là đường thẳng
9
1
4
: 1 2
5
2
4
xa
ya
za
=+
= −
= − +
Đường thẳng
( )
có một vectơ chỉ phương là:
( )
9;8; 5u = − −
.
Câu 25: Chọn A
( ) ( )
12
2; 2; 1 , 1;0; 1uu= − − = −
lần lượt là vectơ chỉ phương của
12
,dd
. Theo bài ra ta có
( )
( )
( )
1
22
.0
cos ; sin ;
nu
n u d P
=
=
( ) ( )
( )
22
2.1 2 1 0
1.1 0. 1
1
2
1 . 2
bc
bc
bc
+ − + − =
+ + −
=
++
( )
2
22
22
11
cb
c b c
=−
− = + +
2
2
b
c
=
=−
.
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
268
Câu 26: Chọn C
Ta có
( )
B
và gọi
H
là hình chiếu của điểm
A
lên mặt phẳng
( )
. Khi đó, tọa độ điểm
H
là nghiệm của hệ phương trình
2 2 9 0
( 3; 2; 1)
1 2 3
2 2 1
x y z
H
x y z
+ − + =
− − −
− − +
==
−
.
Xét hai tam giác vuông
;AHB AMB
có
2 2 2 2
5MB AB AM AB AH BH= − − = =
. Dấu
bằng xảy ra khi và chỉ khi
(1;0;2)M H MB =
.
Vậy phương trình đường thẳng
MB
là
2
2
12
xt
y
zt
= − +
=−
=+
.
Câu 27: Chọn C
1
d
đi qua điểm
( )
1;0;0M
, có VTCP
( )
1
2;1;3u =
.
2
d
đi qua điểm
( )
1;2;Nm
, có VTCP
( )
2
1;1;0u =
.
( )
12
, 3;3;1uu =−
;
( )
0;2;MN m=
.
1
d
và
2
d
chéo nhau khi và chỉ khi
12
, . 0 6u u MN m −
.
Mặt khác
( )
12
5
,
19
d d d =
12
12
,.
5
,
19
u u MN
uu
=
6
5
19 19
m +
=
1
11
m
m
=−
=−
.
Khi đó tổng các phần tử của
m
là
12−
.
Câu 28: Chọn C
( )
1
4 ; 4 ;6 2B d B t t t + − − +
. PT tham số của
2
52
: 11 4
52
xs
d y s
zs
=+
=+
=+
.
( )
2
5 2 ;11 4s;5 2C d C s s + + +
. Khi đó:
(1 ; 1 ;2 1); (2s;4s 14;2s)AB t t t AC= − − − + = +
.
Do
,,ABC
thẳng hàng
,AB AC
cùng phương
:k AB k AC =
1 2 2
1 4 14 3
2 1 2 1
2
t ks t
t ks k s
t ks
k
− = = −
− − = + = −
+=
=
. Do đó:
11
.
22
AB
AB AC
AC
= =
( )
H
B
M
A
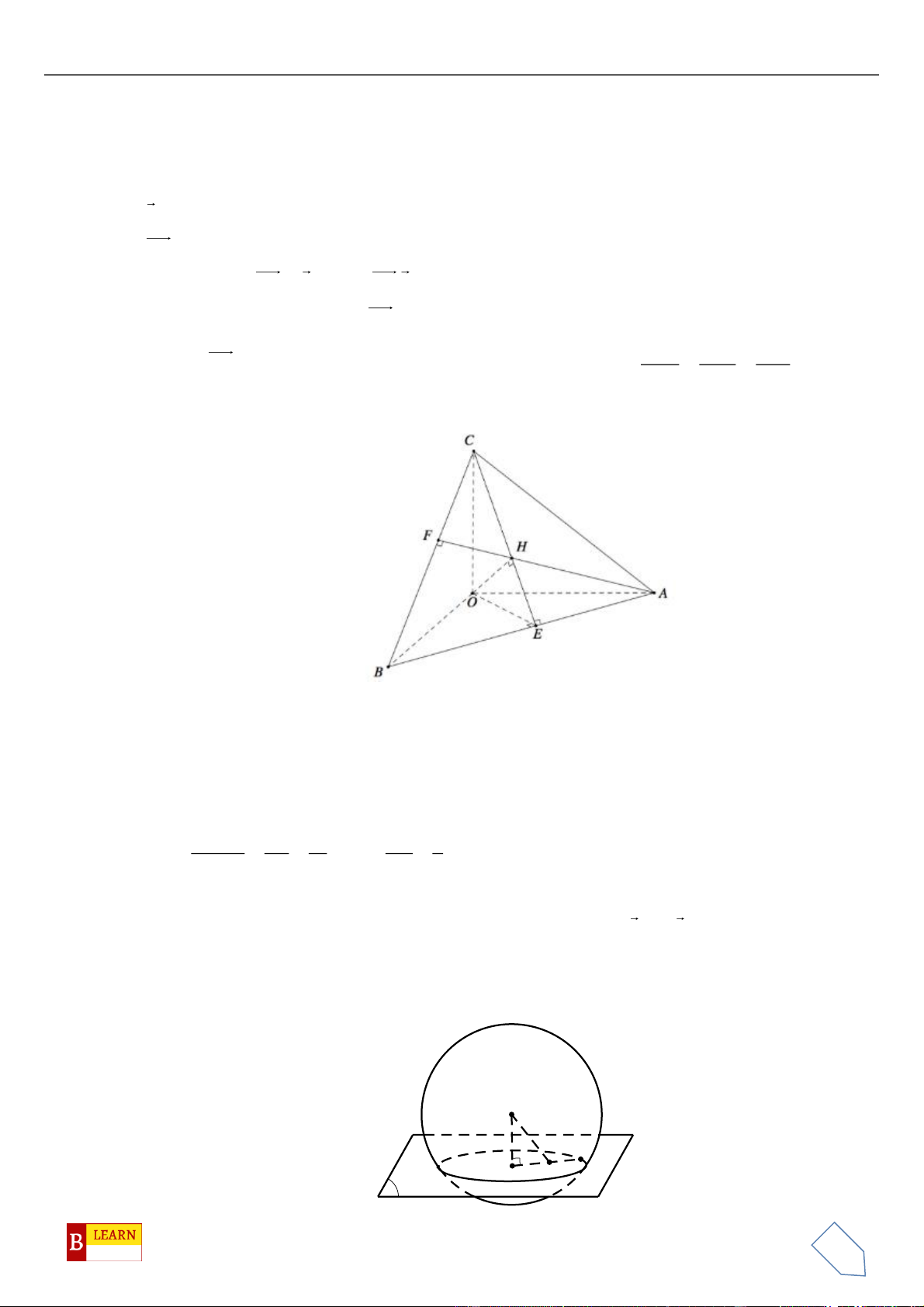
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
269
Câu 29: Chọn B
Ta có phương trình tham số của đường thẳng
1
:
12
xt
d y t
zt
=+
=
= − +
và d có vectơ chỉ phương là
(1;1;2)u =
. Gọi
B
là giao điểm của
và
d
khi đó tọa độ của
(1 ; ; 1 2 )B t t t+ − +
.
( ; ; 3 2 )AB t t t= − +
Vì
d⊥
nên
AB u⊥
suy ra
.0AB u =
hay
2( 3 2 ) 0 1t t t t+ + − + = =
( )
2;1;1B
.
Vectơ chỉ phương của
là
(1;1; 1)AB =−
. Đường thẳng
đi qua
( )
2;1;1B
và có vectơ chỉ
phương
(1;1; 1)AB =−
nên có phương trình đường thẳng
là
2 1 1
:
1 1 1
x y z− − −
= =
−
.
Câu 30: Chọn D
Kẻ
,CE AB⊥
AF BC H CE AF⊥ =
và
()OH ABC OH HE⊥ ⊥
;
()AB OCE AB OE⊥ ⊥
.
Vì điểm
O
và điểm
E
cố định nên
H
di động trên đường tròn đường kính
OE
nằm trong mặt
phẳng
( ) ( )
,OCE OE Oz=
.
Tam giác vuông
OAB
vuông tại
O
và có
OE AB⊥
nên ta có:
. 3.4 12 6
.
5 5 2 5
OAOB OE
OE R
AB
= = = = =
Câu 31: Chọn A
( )
P
vuông góc với
d
nên VTCP của
d
là một VTPT của
( )
P
:
( )
( )
1; 1;2
Pd
nu= = −
Phương trình mặt phẳng
( )
P
:
( ) ( )
2 2 1 0 : 2 0x y z P x y z− − + + = − + =
.
Câu 32: Chọn B
P
H
I
M

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
270
Mặt cầu
( )
S
có tâm
( )
1;0;0I
,
bán kính
3R =
.
Giả sử đường tròn giao tuyến có tâm
H
, bán kính
r
. Khi đó
H
là hình chiếu của
I
trên
( )
P
Ta có
( )
1; 1;2IM =−
6IM=
.
Do
( )
2 2 2 2 2 2 2 2 2 2
33r R IH R IM MH R IM MH MH= − = − − = − + = +
. Suy ra
r
nhỏ nhất
bằng 3 khi và chỉ khi
MH
nhỏ nhất
MH
.
Khi đó
( )
P
là mặt phẳng qua
M
và vuông góc với
IM
.
Phương trình mặt phẳng
( )
P
là
( ) ( )
1.( 2) 1. 1 2. 2 0x y z− − + + − =
hay
2 7 0x y z− + − =

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
271
DẠNG 6. BÀI TOÁN LIÊN QUAN ĐƯỜNG THẲNG, MẶT PHẲNG, MẶT CẦU
Câu 1: Trong hệ trục tọa độ
Oxyz
, mặt phẳng
( )
P
đi qua điểm
( )
1;7;2A
và cách
( )
2;4; 1M −−
một
khoảng lớn nhất có phương trình là
A.
( )
:3 3 3 10 0P x y z+ + − =
. B.
( )
: 1 0P x y z+ + − =
.
C.
( )
: 10 0P x y z+ + − =
. D.
( )
: 10 0P x y z+ + + =
.
Câu 2: Tính khoảng cách giữa đường thẳng
13
:
2 1 2
x y z
d
−+
==
và mặt phẳng
( ) : 2 2 1 0P x y z+ − + =
.
A.
7
.
3
B.
8
.
3
C.
5
.
3
D.
1
.
3
Câu 3: Trong không gian
Oxyz
, mặt cầu
( ) ( )
2
22
( : 2 17S x y z+ + + =
cắt trục
Oz
tại hai điểm
,AB
. Độ
dài đoạn
AB
bằng
A.
4 13
. B.
2 17
. C.
23
. D.
17
.
Câu 4: Trong không gian với hệ toạ độ
Oxyz
, cho điểm
( )
1; 3;4M −
, đường thẳng
d
có phương trình:
2 5 2
3 5 1
x y z+ − −
==
−−
và mặt phẳng
( )
P
:
2 2 0xz+ − =
. Viết phương trình đường thẳng
qua
M
vuông góc với
d
và song song với
( )
P
.
A.
:
1 3 4
1 1 2
x y z− + −
==
−−
. B.
:
1 3 4
1 1 2
x y z− + −
==
− − −
.
C.
:
1 3 4
1 1 2
x y z− + −
==
−
. D.
:
1 3 4
1 1 2
x y z− + +
==
−
.
Câu 5: Bán kính mặt cầu tâm
( )
1;3;5I
và tiếp xúc đường thẳng
:1
2
xt
d y t
zt
=
= − −
=−
là
A.
14
. B.
14
. C.
7
. D.
7
.
Câu 6: Trong không gian với hệ tọa độ
,Oxyz
cho điểm
(1;3;1)A
, đường thẳng
1 1 2
:
1 2 3
x y z− − −
= =
và mặt phẳng
( )
3: 20xyP − − =
. Phương trình đường thẳng đi qua
A
, vuông góc với
và song
song với mặt phẳng
( )
P
là
A.
13
36
15
xt
yt
zt
=+
=−
=−
. B.
13
36
15
xt
yt
zt
=+
=+
=+
. C.
13
36
15
xt
yt
zt
=−
=−
=+
. D.
13
36
15
xt
yt
zt
=−
=+
=+
.
Câu 7: Trong không gian với hệ trục tọa độ
Oxyz
, cho điểm
( )
1; 2;3A −
và đường thẳng
d
có phương
trình
1 2 3
2 1 1
x y z+ − +
==
−
. Tính bán kính của mặt cầu
( )
S
có tâm
A
và tiếp xúc với đường thẳng
d
.
A.
52
. B.
45
. C.
25
. D.
10 2
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
272
Câu 8: Trong không gian
Oxyz
, cho mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 1 2 1 45S x y z− + − + + =
và mặt phẳng
( )
: 13 0P x y z+ − − =
. Mặt cầu
( )
S
cắt mặt phẳng
( )
P
theo giao tuyến là đường tròn có tâm
( )
;;I a b c
thì giá trị của
abc++
bằng
A.
5
. B.
2
. C.
11−
. D.
1
.
Câu 9: Trong không gian
Oxyz
, cho mặt phẳng
( )
: 2 3 7 0P x y z+ + − =
và hai đường thẳng
12
3 2 2 1 1 2
: ; : .
2 1 4 3 2 3
x y z x y z
dd
+ + + + + −
= = = =
−−
Đường thẳng vuông góc với
( )
P
và cắt cả hai
đường thẳng
12
;dd
có phương trình là.
A.
76
.
1 2 3
x y z+−
==
B.
5 1 2
.
1 2 3
x y z+ + −
==
C.
4 3 1
1 2 3
x y z+ + +
==
. D.
3 2 2
123
x y z+ + +
==
.
Câu 10: Trong không gian
Oxyz
, cho đường thẳng
122
:
1 2 1
x y z
d
− − +
==
−
. Mặt phẳng nào sau đây vuông
góc với đường thẳng
d
.
A.
( )
: 2 1 0T x y z+ + + =
. B.
( )
: 2 1 0P x y z− + + =
.
C.
( )
: 2 1 0Q x y z− − + =
. D.
( )
: 1 0R x y z+ + + =
.
Câu 11: Biết rằng hai mặt phẳng
( )
: 2 3 1 0+ + + =P x y z
và
( ) ( ) ( )
: 1 3 6 1 0+ + + + + =Q m x m y z
song
song với nhau. Giá trị của
m
bằng
A.
1−
. B.
1
. C.
2
. D.
0
.
Câu 12: Trong không gian với hệ tọa độ
Oxyz
, cho điểm
( )
1; 1;0A −
và đường thẳng
11
:
2 1 3
x y z
d
+−
==
−
. Viết phương trình mặt phẳng chứa
A
và
d
.
A.
0x y z+ + =
. B.
2 3 2 0x y z+ + + =
.C.
2 1 0x y z+ + − =
. D.
2 1 0x y z+ + + =
.
Câu 13: Trong không gian
Oxyz
, cho
( )
:2 2 1 0P x y z+ + − =
,
( ) ( )
0;0;4 , 3;1;2AB
. Một mặt cầu
( )
S
luôn đi qua
,AB
và tiếp xúc với
( )
P
tại
C
. Biết rằng,
C
luôn thuộc một đường tròn cố định bán
kính
r
. Tính bán kính
r
của đường tròn đó.
A.
14 5
3
. B.
4
2 244651
3
r =
. C.
2 244651
9
r =
. D.
2024
3
r =
.
Câu 14: Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt cầu
( ):S
2 2 2
2 2 1 0x y z x z+ + − + + =
và
đường thẳng
2
:
1 1 1
x y z
d
−
==
−
. Hai mặt phẳng
()P
,
()P
chứa
d
và tiếp xúc với
()S
tại
T
,
T
. Tìm tọa độ trung điểm
H
của
TT
.
A.
717
;;
6 3 6
H
−
. B.
5 2 7
;;
6 3 6
H
−
. C.
5 1 5
;;
6 3 6
H
−
. D.
5 1 5
;;
6 3 6
H
−
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
273
Câu 15: Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt cầu
2 2 2
( ): 2 4 6 3 0S x y z x y z m+ + + − − + − =
. Tìm số thực
m
để
( )
: 2 2 8 0x y z
− + − =
cắt
( )
S
theo một đường tròn có chu vi bằng
8
.
A.
4m =−
. B.
1m =−
C.
2m =−
. D.
3m =−
.
Câu 16: Trong không gian
Oxyz
, cho mặt phẳng
( ) ( ) ( ) ( ) ( )
: 1 1 1 3 2 8 0P m x m y m z m+ + − − + − − =
và
điểm
( )
4; 2; 7A −−
. Khi
m
thay đổi, biết tập hợp hình chiếu của
A
trên mặt phẳng
( )
P
là một
đường tròn, đường kính của đường tròn đó bằng
A.
35
. B.
73
. C.
37
. D.
53
.
Câu 17: Trong không gian với hệ tọa độ
Oxyz
, biết
( )
P
là mặt phẳng cách đều hai đường thẳng
1
2
:
1 1 1
x y z
d
−
==
−
và
2
12
:
2 1 1
x y z
d
−−
==
−−
. Điểm nào sau đây thuộc mặt phẳng
( )
P
A.
1
;1;0
2
M
. B.
1
1; ;0
2
N
−
. C.
1
;0;1
2
P
−
. D.
1
1;0;
2
Q
−
.
Câu 18: Trong không gian với hệ tọa độ
Oxyz
viết phương trình mặt phẳng tiếp xúc với mặt cầu
( ) ( )
22
2
1 2 6x y z− + + + =
đồng thời song song với hai đường thẳng
1
21
:
3 1 1
x y z
d
−−
==
−−
,
2
22
:
1 1 1
x y z
d
+−
==
−
.
A.
2 3 0
2 9 0
x y z
x y z
− + − =
− + + =
. B.
2 3 0
2 9 0
x y z
x y z
+ + − =
+ + + =
. C.
2 9 0x y z+ + + =
. D.
2 9 0x y z− + + =
.
Câu 19: Trong không gian với hệ trục tọa độ
Oxyz
, cho
2
điểm
( ) ( )
1;2;3 , 2;4;4MA
và hai mặt phẳng
( )
: 2 1 0P x y z+ − + =
,
( )
: 2 4 0.Q x y z− − + =
Viết phương trình đường thẳng
đi qua
M
, cắt
( ), ( )PQ
lần lượt tại
,BC
sao cho tam giác
ABC
cân tại
A
và nhận
AM
làm đường trung tuyến.
A.
1 2 3
1 1 1
x y z− − −
==
−−
. B.
1 2 3
2 1 1
x y z− − −
==
−
.
C.
1 2 3
1 1 1
x y z− − −
==
−
. D.
1 2 3
1 1 1
x y z− − −
==
−−
.
Câu 20: Trong không gian
Oxyz
, cho hai điểm
( ) ( )
1;2; 1 , 3;0;3AB−
. Biết mặt phẳng
( )
P
đi qua điểm
A
và cách
B
một khoảng lớn nhất. Phương trình mặt phẳng
( )
P
là:
A.
2 2 5 0x y z− + + =
. B.
2 3 0x y z− + + =
. C.
2 2 4 3 0x y z− + + =
.D.
2 2 0x y z− + =
.
Câu 21: Trong không gian
Oxyz
, cho mặt phẳng
( )
: 4 0P x y z+ − − =
và điểm
( )
2; 1;3A −
. Gọi
là
đường thẳng đi qua
A
và song song với
( )
P
, biết
có một vectơ chỉ phương là
( )
;;u a b c=
,
đồng thời
đồng phẳng và không song song với
Oz
. Tính
a
c
.
A.
2
a
c
=
. B.
2
a
c
=−
. C.
1
2
a
c
=−
. D.
1
2
a
c
=
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
274
Câu 22: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
( )
: 3 0P x y z+ + − =
và đường thẳng
12
:
1 2 1
x y z
d
+−
==
−
. Đường thẳng
'd
đối xứng với
d
qua mặt phẳng
( )
P
có phương trình là
A.
1 1 1
1 2 7
x y z+ + +
==
−
. B.
1 1 1
1 2 7
x y z− − −
==
.
C.
1 1 1
1 2 7
x y z− − −
==
−
. D.
1 1 1
1 2 7
x y z+ + +
==
.
Câu 23: Trong không gian
Oxyz
, cho các đường thẳng
( )
1
1
:0
5
xt
dy
zt
=+
=
= − +
;
( )
2
0
: 4 2
53
x
d y t
zt
=
=−
=+
. Biết mặt
cầu
( ) ( ) ( )
2 2 2
2
x a y b z c R− + − + − =
nhận đoạn vuông góc chung của
( )
1
d
và
( )
2
d
làm
đường kính. Giá trị
2a b c++
bằng
A.
6
. B.
8
. C.
7
. D.
5
.
Câu 24: Trong không gian Oxyz, cho hai điểm
(1;2;3)A
,
( 1;2;1)B −
và mặt phẳng
( ): 0P x y z+ + =
. Gọi
M là giao điểm của đường thẳng AB và mặt phẳng (P). Tính tỉ số
AM
BM
.
A. 1. B. 2. C. 3. D. 4.
Câu 25: Cho đường thẳng
1 2 2
:
1 2 1
x y z
d
− − −
==
−
và điểm
( )
1;2;1A
. Tìm bán kính của mặt cầu có tâm
I
nằm trên
d
, đi qua
A
và tiếp xúc với mặt phẳng
( )
: 2 2 1 0P x y z− + + =
.
A.
2R =
. B.
4R =
. C.
1R =
. D.
3R =
.
Câu 26: Trong không gian Oxyz, cho hai đường thẳng
1
4 1 5
:
3 1 2
x y z
d
− − +
==
−−
và
2
23
:
1 3 1
x y z
d
−+
==
.
Viết phương trình mặt cầu (
S
) có bán kính nhỏ nhất và tiếp xúc với cả hai đường thẳng đã cho.
A.
2 2 2
( ):( 2) ( 1) ( 1) 24S x y z− + − + + =
. B.
2 2 2
( ):( 2) ( 1) ( 1) 24S x y z+ + + + − =
.
C.
2 2 2
( ):( 2) ( 1) ( 1) 6S x y z− + − + + =
. D.
2 2 2
( ):( 2) ( 1) ( 1) 6S x y z+ + + + − =
.
Câu 27: Trong không gian
Oxyz
, cho đường thẳng
1 2 3
:
1 2 1
x y z
d
− − −
==
và mặt phẳng
( )
: 2 0x y z
+ − − =
. Đường thẳng nằm trong mặt phẳng
( )
, đồng thời vuông góc và cắt đường
thẳng
d
có phương trình là
A.
3
5 2 5
:
3 2 1
x y z− − −
= =
−
. B.
1
2 4 4
:
3 2 1
x y z+ + +
= =
−−
.
C.
2
2 4 4
:
1 2 3
x y z− − −
= =
−
. D.
4
11
:
3 2 1
x y z−−
= =
−
.
Câu 28: Trong không gian
Oxyz
cho điểm
( )
1; 2;3I −
và mặt phẳng
( ):2 2 1 0P x y z− + − =
. Mặt cầu
( )
S
tâm
I
tiếp xúc với
( )
P
có phương trình là
A.
( ) ( ) ( )
2 2 2
1 2 3 9x y z− + + + − =
. B.
( ) ( ) ( )
2 2 2
1 2 3 3x y z+ + − + + =
.
C.
( ) ( ) ( )
2 2 2
1 2 3 3x y z− + + + − =
. D.
( ) ( ) ( )
2 2 2
1 2 3 9x y z+ + − + + =
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
275
Câu 29: Trong không gian tọa độ
Oxyz
,cho điểm
( )
0;0; 2A −
và đường thẳng
có phương trình là
2 2 3
.
2 3 2
x y z+ − +
==
Phương trình mặt cầu tâm
A
, cắt
tại hai điểm
B
và
C
sao cho
8BC =
là
A.
( ) ( ) ( )
2 2 2
2 3 1 16x y z+ + − + + =
. B.
( )
2
22
2 25x y z+ + + =
.
C.
( )
2
22
2 25x y z+ + + =
. D.
( )
2
22
2 16x y z+ + + =
.
Câu 30: Trong không gian
Oxyz
, cho mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 1 1 2 3S x y z+ + − + + =
và hai đường thẳng
21
:
1 2 1
x y z
d
−−
==
−
,
1
:.
1 1 1
x y z −
= =
−
Phương trình nào dưới đây là phương trình mặt phẳng cắt
mặt cầu
( )
S
theo giao tuyến là một đường tròn
( )
C
có bán kính bằng
1
và song song với
d
và
.
A.
30yz+ + =
. B.
10xy+ + =
. C.
10xz+ − =
. D.
10xz+ + =
.
Câu 31: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
( )
: 3 0P x y z+ − − =
và hai điểm
( )
1;1;1M
,
( )
3; 3; 3N −−−
. Mặt cầu
( )
S
đi qua
, MN
và tiếp xúc với mặt phẳng
( )
P
tại điểm
Q
. Biết rằng
Q
luôn thuộc một đường tròn cố định. Tìm bán kính của đường tròn đó.
A.
2 11
3
R =
. B.
6R =
. C.
2 33
3
R =
. D.
4R =
.
Câu 32: Cho đường thẳng
d
:
1 2 2
3 2 2
x y z+ − −
==
−
. Viết phương trình mặt cầu tâm
( )
1;2; 1I −
cắt
d
tại
các điểm
A
,
B
sao cho
23AB =
.
A.
( ) ( ) ( )
2 2 2
1 2 1 25x y z− + − + + =
. B.
( ) ( ) ( )
2 2 2
1 2 1 4x y z− + − + + =
.
C.
( ) ( ) ( )
2 2 2
1 2 1 9x y z− + − + + =
. D.
( ) ( ) ( )
2 2 2
1 2 1 16x y z− + − + + =
.
Câu 33: Trong không gian với hệ trục tọa độ
Oxyz
, cho điểm
( )
2;1;1M
, mặt phẳng
( )
: 4 0x y z
+ + − =
và mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 3 3 4 16S x y z− + − + − =
. Phương trình đường thẳng
đi qua
M
và nằm
trong
( )
cắt mặt cầu
( )
S
theo một đoạn thẳng có độ dài nhỏ nhất. Đường thẳng
đi qua điểm
nào trong các điểm sau đây?
A.
( )
4; 3;3−
. B.
( )
4; 3; 3−−
. C.
( )
4;3;3
. D.
( )
4; 3; 3− − −
.
Câu 34: Trong không gian với hệ trục tọa độ
Oxyz
, cho điểm
( )
1;3;2A −
và đường thẳng
d
có phương
trình
14
2
xt
yt
zt
=−
=
=+
. Mặt phẳng
( )
P
chứa điểm
A
và đường thẳng
d
có phương trình nào dưới đây?
A.
2 2 1 0.x y z− + + =
B.
0.x y z+ − =
C.
3 2 10 23 0.x y z− − − + =
D.
2 3 4 0.x y z− + + =

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
276
Câu 35: Trong không gian với hệ trục tọa độ
Oxyz
, cho điểm
( )
1;3;2A −
và đường thẳng
d
có phương
trình
14
2
xt
yt
zt
=−
=
=+
. Mặt phẳng
( )
P
chứa điểm
A
và đường thẳng
d
có phương trình nào dưới đây?
A.
2 2 1 0.x y z− + + =
B.
0.x y z+ − =
C.
3 2 10 23 0.x y z− − − + =
D.
2 3 4 0.x y z− + + =
Câu 36: Cho mặt cầu:
.
( )
2 2 2
: 2 4 6 0S x y z x y z m+ + + − + + =
. Tìm
m
để cắt đường thẳng
( )
12
:
1 2 2
x y z+−
= =
−−
tại hai điểm
,AB
sao cho tam giác
IAB
vuông.
A.
1m =−
. B.
10m =
. C.
20m =−
. D.
4
9
m =−
.
Câu 37: Trong không gian
,Oxyz
cho hai đường thẳng
1 2 2
: ; : 1 2
1 3 2
x t x t
d y t d y t
z t z t
= − − = +
= = − +
= − + = −
và mặt phẳng
( )
: 2 0.P x y z+ + + =
Đường thẳng vuông góc với mặt phẳng
( )
P
và cắt cả hai đường thẳng
,dd
có phương trình là
A.
3 1 2
1 1 1
x y z− − +
==
. B.
1 1 1
1 1 4
x y z− − −
==
−−
.
C.
2 1 1
1 1 1
x y z+ + −
==
. D.
1 1 4
2 2 2
x y z+ − −
==
.
Câu 38: Trong không gian Oxyz, cho ba đường thẳng
( ) ( )
12
3 1 2 1 4
: , :
2 1 2 3 2 1
x y z x y z
dd
− + − + +
= = = =
− − −
và
( )
3
32
:
4 1 6
x y z
d
+−
==
−
. Đường thẳng song song
3
d
, cắt
1
d
và
2
d
có phương trình là
A.
3 1 2
4 1 6
x y z− + −
==
. B.
3 1 2
4 1 6
x y z− + −
==
−−
.
C.
14
4 1 6
x y z+−
==
−
. D.
14
4 1 6
x y z−+
==
−
.
Câu 39: Trong không gian với hệ trục
Oxyz
cho hai đường thẳng
1
1 1 1
:
2 1 2
x y z+ + +
= =
và
2
1 1 1
:
2 2 1
x y z− − −
= =
. Tính diện tích mặt cầu có bán kính nhỏ nhất, đồng thời tiếp xúc với cả
hai đường thẳng
1
và
2
.
A.
16
17
. B.
4
17
. C.
16
17
. D.
4
17
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
277
Câu 40: Trong không gian Oxyz, cho tam giác đều ABC với
( )
6;3;5A
và đường thẳng BC có phương trình
tham số
1
2
2
xt
yt
zt
=−
=+
=
. Gọi
là đường thẳng qua trọng tâm G của tam giác ABC và vuông góc với
mặt phẳng
( )
ABC
. Điểm nào dưới đây thuộc đường thẳng
?
A.
( )
1; 12;3M −−
. B.
( )
3; 2;1N −
. C.
( )
0; 7;3P −
. D.
( )
1; 2;5Q −
.
Câu 41: Trong không gian
Oxyz
, cho hai điểm
( )
1;2; 1A −
và
( )
3;0;5B
. Điểm
( )
;;M a b c
thuộc mặt
phẳng
( )
: 2 2 10 0P x y z− + − =
sao cho tam giác
MAB
cân tại
M
và có diện tích bằng
11 2
.
Tính
S a b c= + +
.
A.
7
3
S =
. B.
19
3
S =
. C.
1S =−
. D.
1
3
S =−
.
Câu 42: Trong không gian với hệ trục tọa độ
,Oxyz
cho hai điểm
2;1;3A
,
6;5;5B
. Gọi
S
là mặt cầu
đường kính
AB
. Mặt phẳng
P
vuông góc với
AB
tại
H
sao cho khối nón đỉnh
A
và đáy là
hình tròn tâm
H
có thể tích lớn nhất, biết rằng
:2 0P x by cz d
với
,,b c d
. Tính
S b c d
.
A.
18S =
. B.
18S =−
. C.
12S =−
. D.
24S =
.
Câu 43: Trong không gian
Oxyz
, cho mặt phẳng
( )
: 4 0Py−=
. Có bao nhiêu đường thẳng
d
song song
với ba mặt phẳng
( )
xOy
,
( )
zOx
,
( )
P
đồng thời cách đều 3 mặt phẳng đó.
A.
1
. B.
2.
C.
3
. D.
4
.
Câu 44: Trong không gian
Oxyz
, cho điểm
( )
2; 3;4M −
, mặt phẳng
( )
: 2 12 0P x y z− + − =
và mặt cầu
( )
S
có tâm
( )
1;2;3I
, bán kính
5R =
. Phương trình nào dưới đây là phương trình đường thẳng đi
qua
M
, nằm trong
( )
P
và cắt
( )
S
theo dây cung dài nhất?
A.
2
32
43
xt
yt
zt
=+
= − +
=+
. B.
23
39
43
xt
yt
zt
=+
= − −
=+
. C.
13
12
15
xt
yt
zt
=+
=−
=+
. D.
3
2
5
xt
yt
zt
=+
= − +
=+
.
Câu 45: Trong không gian
Oxyz
, cho mặt phẳng
( )
: 2 2 3 0P x y z− + − =
và mặt cầu
( )
2 2 2
: 2 4 2 5 0S x y z x y z+ + + − − + =
. Xét hai điểm
,MN
thay đổi với
( )
MP
và
( )
NS
sao cho vectơ
MN
cùng phương với vectơ
( )
1;0;1u =
. Độ dài đoạn
MN
lớn nhất bằng
A.
3
. B.
32
. C.
52
. D.
2
.
Câu 46: Trong không gian
Oxyz
, cho điểm
( )
1;1;1E
, mặt cầu
( )
2 2 2
:4S x y z+ + =
và mặt phẳng
( )
: 3 5 3 0P x y z− + − =
. Gọi
là đường thẳng đi qua
E
, nằm trong
( )
P
và cắt
( )
S
tại hai điểm
A
,
B
sao cho
OAB
là tam giác đều. Phương trình của
là

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
278
A.
12
1
1
xt
yt
zt
=+
=+
=+
. B.
14
13
1
xt
yt
zt
=+
=+
=+
. C.
12
1
1
xt
yt
zt
=+
=−
=−
. D.
1
1
12
xt
yt
zt
=+
=+
=−
.
Câu 47: Trong không gian với hệ tọa độ
,Oxyz
cho mặt phẳng
( )
:3 4 5 1 0P x y z+ + + =
và ba điểm
( ) ( ) ( )
2;5; 3 , 2;1;1 , 2;0;1 .A B C−−
Tìm điểm
( )( )
;b;c 0D a b
là điểm nằm trên
( )
P
sao cho có
vô số mặt phẳng
( )
Q
đi qua hai điểm
,CD
và thỏa mãn khoảng cách từ điểm
A
đến mặt phẳng
( )
Q
gấp
3
lần khoảng cách từ
B
đến
( )
.Q
Tính
.T abc=
A.
0
. B.
16
. C.
12
. D.
16−
.
Câu 48: Trong không gian hệ tọa độ
Oxyz
, cho hai điểm
( ) ( )
1;1;1 , 2;2;1AB
và mặt phẳng
( )
: 2 0P x y z+ + =
. Mặt cầu
( )
S
thay đổi qua
,AB
và tiếp xúc với
( )
P
tại
H
. Biết
H
chạy trên
1 đường tròn cố định. Tìm bán kính của đường tròn đó.
A.
32
. B.
23
. C.
3
. D.
3
2
Câu 49: Trong không gian
Oxyz
cho đường thẳng
11
:
1 1 2
− + −
==
x y z m
d
và mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 1 1 2 9S x y z− + − + − =
. Đường thẳng
d
cắt mặt cầu
( )
S
tại hai điểm phân biệt
E
,
F
sao cho độ dài đoạn thẳng
EF
lớn nhất khi
0
=mm
. Hỏi
0
m
thuộc khoảng nào dưới đây?
A.
( )
1;1−
. B.
1
;1
2
. C.
1
1;
2
−−
. D.
( )
0;2
.
Câu 50: Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
12
:
2 1 1
x y z
d
+−
==
, mặt phẳng
( )
: 2 5 0P x y z+ − + =
và
( )
1; 1;2A −
. Đường thẳng
cắt
d
và
( )
P
lần lượt tại
M
và
N
sao
cho
A
là trung điểm của đoạn thẳng
MN
. Một vectơ chỉ phương của
là
A.
( )
4; 5; 13u =−
. B.
( )
2; 3; 2u =
. C.
( )
1; 1; 2u =−
. D.
( )
3; 5; 1u =−
.
Câu 51: Trong không gian với hệ tọa độ
,Oxyz
cho mặt phẳng
( )
: 2 2 2 0− + − =P x y z
và điểm
( )
1; 2; 1I −−
. Viết phương trình mặt cầu
( )
S
có tâm
I
và cắt mặt phẳng
( )
P
theo giao tuyến là
đường tròn có bán kính bằng
5.
A.
( ) ( ) ( ) ( )
2 2 2
: 1 2 1 25.+ + − + + =S x y z
B.
( ) ( ) ( ) ( )
2 2 2
: 1 2 1 16.+ + − + + =S x y z
C.
( ) ( ) ( ) ( )
2 2 2
: 1 2 1 34.− + + + − =S x y z
D.
( ) ( ) ( ) ( )
2 2 2
: 1 2 1 34.+ + − + + =S x y z
Câu 52: Trong không gian
Oxyz
, cho mặt phẳng
( )
: 1 0P x y z+ − − =
và hai đường thẳng
12
11
: , :
1 1 1 1 1 3
x y z x y z−+
= = = =
−−
. Biết rằng
12
,dd
nằm trong mặt phẳng
( )
P
, cắt
2
và cách
1
một khoảng bằng
6
2
. Gọi
( ) ( )
12
; ;1 , 1; ;u a b u c d==
lần lượt là vectơ chỉ phương của
12
,dd
. Tính
S a b c d= + + +
.
A.
0S =
. B.
2S =
. C.
4S =
. D.
1S =
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
279
Câu 53: Trong không gian với hệ trục tọa độ
Oxyz
, cho đường thẳng
11
:
2 1 1
x y z
d
−−
==
−
cắt mặt phẳng
( )
: 2 6 0P x y z+ + − =
tại điểm
M
. Mặt cầu
( )
S
có tâm
( )
;;I a b c
với
0a
thuộc đường thẳng
d
và tiếp xúc với mặt phẳng
( )
P
tại điểm
A
. Tìm tổng
T a b c= + +
khi biết diện tích tam giác
IAM
bằng
33
.
A.
2T =−
. B.
1
2
T =
. C.
8T =
. D.
0T =
.
Câu 54: Trong không gian tọa độ
Oxyz
, cho điểm
( )
2;4;2A
và mặt cầu
( )
2
22
21x y z+ + + =
. Gọi
S
là
tập hợp các đường thẳng trong không gian đi qua điểm
A
cắt mặt cầu tại hai điểm phân biệt
,BC
thỏa mãn
12AB AC+=
. Số phần tử của
S
là
A. 3. B. 0. C. 1. D. 2.
Câu 55: Trong không gian
Oxyz
, cho mặt phẳng
( )
( ) ( )
22
:2 1 1 10 0P mx m y m z+ + + − − =
và điểm
( )
2;11; 5A −
. Biết rằng khi
m
thay đổi, tồn tại hai mặt cầu cố định tiếp xúc với mặt phẳng
( )
P
và
cùng đi qua
A
. Tổng bán kính của 2 mặt cầu đó bằng:
A.
12 3
. B.
12 2
. C.
10 3
. D.
10 2
.
Câu 56: Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
( )
6;0;0M
,
( )
0;6;0N
,
( )
0;0;6P
. Hai mặt
cầu có phương trình
( )
2 2 2
1
: 2 2 1 0S x y z x y+ + − − + =
và
( )
2 2 2
2
: 8 2 2 1 0S x y z x y z+ + − + + + =
cắt nhau theo đường tròn
( )
C
. Hỏi có bao nhiêu mặt cầu
có tâm thuộc mặt phẳng chứa
( )
C
và tiếp xúc với ba đường thẳng
,,MN NP PM
.
A.
1
. B.
3
. C. Vô số. D.
4
.
Câu 57: Cho hai đường thẳng
2
:
22
x
d y t
zt
=−
=
=+
( )
t
,
3 1 4
:
1 1 1
x y z− − −
= =
−
và mặt phẳng
( )
: 2 0P x y z+ − + =
. Gọi
d
,
lần lượt là hình chiếu của
d
và
lên mặt phẳng
( )
P
. Gọi
( )
;;M a b c
là giao điểm của hai đường thẳng
d
và
. Biểu thức
.a bc+
bằng
A.
4
. B.
5
. C.
3
. D.
6
.
Câu 58: Trong không gian
Oxyz
, cho mặt cầu
( )
2 2 2
: 2 2 1 0S x y z y z+ + − + + =
và hai điểm
( )
2;0;0A
,
( )
3;1; 1B −
. Hai mặt phẳng
( )
P
và
( )
P
chứa đường thẳng
AB
, tiếp xúc với
( )
S
tại
T
và
T
.
( )
;;H a b c
là trung điểm đoạn
TT
. Tính
2a b c++
.
A.
2
2.
3
a b c+ + =
B.
2
2.
3
a b c+ + =−
C.
1
2.
2
a b c+ + =−
D.
1
2.
2
a b c+ + =
Câu 59: Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 1 1 2 9S x y z− + + + − =
và điểm
( )
1;3; 1M −
. Biết rằng các tiếp điểm của các tiếp tuyến kẻ từ
M
tới mặt cầu đã cho luôn thuộc
một đường tròn
( )
C
có tâm
( )
;;J a b c
. Tính
2abc++
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
280
A.
134
25
. B.
116
25
. C.
84
25
. D.
62
25
.
Câu 60: Trong không gian
Oxyz
, cho hai mặt cầu
( ) ( )
12
,SS
có phương trình lần lượt là
( )
2 2 2 2 2 2
12
: 25;( ): ( 1) 4.S x y z S x y z+ + = + + − =
Một đường thẳng
d
vuông góc với véc tơ
(1; 1;0)u =−
tiếp xúc với mặt cầu
( )
2
S
và cắt mặt cầu
( )
1
S
theo một đoạn thẳng có độ dài bằng
8
. Hỏi véc tơ nào sau đây là véc tơ chỉ phương của
?d
A.
( )
1
1;1; 3u =
. B.
( )
2
1;1; 6u =
. C.
3
(1;1;0)u =
. D.
( )
4
1;1; 3u =−
.
Câu 61: Trong không gian với hệ tọa độ
Oxyz
, cho hai mặt phẳng song song
( )
:2 2 1 0,P x y z− + − =
( )
:2 2 5 0Q x y z− + + =
và điểm
( )
1;1;1A −
nằm trong khoảng giữa hai mặt phẳng này. Gọi
( )
S
là mặt cầu đi qua
A
và tiếp xúc với cả
( )
P
và
( )
.Q
Biết khi
( )
S
thay đổi thì tâm
I
của nó luôn
thuộc đường tròn
( )
C
cố định. Diện tích hình tròn giới hạn bởi
( )
C
là
A.
2
3
. B.
4
9
. C.
16
9
. D.
8
9
.
Câu 62: Trong không gian Oxyz, xét số thực
(0;1)m
và hai mặt phẳng
( )
:2 2 10 0x y z
− + + =
và
( )
: 1.
11
x y z
mm
+ + =
−
Biết rằng, khi m thay đổi có hai mặt cầu cố định tiếp xúc đồng thời với cả
hai mặt phẳng
( ) ( )
,
. Tổng bán kính của hai mặt cầu đó bằng
A.
6
. B.
3
. C.
9
D.
12
.
Câu 63: Trong không gian
Oxyz
, cho mặt cầu
()S
:
2 2 2
( 1) ( 2) ( 3) 27x y z− + + + − =
. Gọi
()
là mặt
phẳng đi qua hai điểm
(0;0; 4)A −
,
(2;0;0)B
và cắt
()S
theo giao tuyến là đường tròn
()C
. Xét
các khối nón có đỉnh là tâm của
()S
và đáy là
()C
. Biết rằng khi thể tích của khối nón lớn nhất
thì mặt phẳng
()
có phương trình dạng
0ax by z d+ − + =
. Tính
P a b d= − −
.
A.
4P =−
. B.
8P =
. C.
0P =
. D.
4P =
.
Câu 64: Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
( ) ( ) ( ) ( )
2 2 2
14
: 1 2 3
3
S x y z− + − + − =
và
đường thẳng
4 4 4
:
3 2 1
x y z
d
− − −
==
. Gọi
( ) ( )
0 0 0 0
; ; 0A x y z x
là điểm nằm trên đường thẳng
d
sao cho từ
A
kẻ được 3 tiếp tuyến đến mặt cầu
( )
S
có các tiếp điểm
,,B C D
sao cho
ABCD
là tứ diện đều. Tính giá trị của biểu thức
0 0 0
P x y z= + +
.
A.
6P =
. B.
16P =
. C.
12P =
. D.
8P =
.
Câu 65: Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
,,P Q R
lần lượt di động trên ba trục tọa độ
,Ox
,Oy
Oz
sao cho
2 2 2
1 1 1 1
8OP OQ OR
+ + =
. Biết mặt phẳng
( )
PQR
luôn tiếp xúc với mặt cầu
( )
S
cố định. Đường thẳng
d
thay đổi nhưng luôn đi qua
13
; ;0
22
M
và cắt
( )
S
tại hai điểm
,AB
phân biệt. Diện tích lớn nhất của tam giác
AOB
là

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
281
A.
15
. B.
5
. C.
17
. D.
7
.
Câu 66: Trong không gian
Oxyz
, cho đường thẳng
3 1 2
:
1 3 1
x y z− − −
= =
−
. Có tất cả bao nhiêu giá trị
thực của
m
để phương trình
2 2 2 2
4 2 2( 1) 2 8 0x y z x my m z m m+ + − + − + + + + =
là phương
trình của một mặt cầu
( )
S
sao cho có duy nhất một mặt phẳng chứa Δ và cắt
( )
S
theo giao tuyến
là một đường tròn có bán kính bằng 1.
A.
1
. B.
6
. C.
7
. D.
2
.
Câu 67: Trong không gian
Oxyz
, cho hai mặt cầu
2 2 2
1
( ):( 1) ( 1) ( 2) 16S x y z− + − + − =
và
2
( ) :S
2 2 2
( 1) ( 2) ( 1) 9x y z+ + − + + =
cắt nhau theo giao tuyến là một đường tròn với tâm là
( ; ; )I a b c
. Tính
abc++
A.
7
4
. B.
1
4
−
. C.
10
3
. D.
1
.
Câu 68: Trong không gian với hệ trục tọa độ
Oxyz
, cho điểm
( )
3;3; 3M −−
thuộc mặt phẳng
( )
:2 2 15 0x y z
− + + =
và mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 2 3 5 100S x y z− + − + − =
. Đường thẳng
qua
M
, nằm trên mặt phẳng
( )
cắt
( )
S
tại
,AB
sao cho độ dài
AB
lớn nhất. Viết phương trình
đường thẳng
.
A.
3 3 3
113
x y z+ − +
==
. B.
3 3 3
1 4 6
x y z+ − +
==
.
C.
3 3 3
16 11 10
x y z+ − +
==
−
. D.
3 3 3
5 1 8
x y z+ − +
==
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
282
ĐÁP ÁN CHI TIẾT
Câu 1: Chọn C
Ta có:
( )
( )
,d M P MA
Nên
( )
( )
ax
,
m
d M P MA=
khi
A
là hình chiếu của
M
trên mặt phẳng
( )
P
.
Suy ra
( ) ( )
3; 3; 3AM P AM⊥ = − − −
là vectơ pháp tuyến của
( )
P
.
( )
P
đi qua
( )
1;7;2A
và nhận
( )
3; 3; 3AM = − − −
là vectơ pháp tuyến nên có phương trình
( ) ( ) ( )
3 1 3 7 3 2 0 10 0x y z x y z− − − − − − = + + − =
.
Câu 2: Chọn B
Ta có:
( )
( )
( )
2;1;2
. 2.1 1.2 2. 2 0
1;2; 2
d
dP
P
u
un
n
=
= + + − =
=−
.
Do đó đường thẳng
d
đi qua điểm
( )
1;0; 3M −
và song song với mặt phẳng
( )
P
nên ta có
khoảng cách giữa
d
và
( )
P
là
( )
( )
( )
( )
( )
( )
2
22
1 2.0 2. 3 1
8
; ; .
3
1 2 2
d d P d M P
+ − − +
= = =
+ + −
Câu 3: Chọn B
Gọi
M
là giao điểm của
( )
S
với trục
Oz
.Ta có
M Oz
( )
0;0;tM
. Mà
( )
MS
nên:
( )
2
22
0 0 2 17t+ + + =
( )
2
2 17 2 17tt + = + =
2 17
2 17
t
t
= − −
= − +
.
Suy ra tọa độ các giao điểm là:
( )
0;0; 2 17A −−
,
( )
0;0; 2 17B −+
2 17AB=
.
Câu 4: Chọn C
Ta có
(3; 5; 1)
d
u = − −
là véc tơ chỉ phương của
d
.
( )
()
2;0;1
P
n =
là véc tơ pháp tuyến của
( )
P
.
( )
( )
, 5; 5;10
d
p
un
= − −
.
Do
vuông góc với
d
và song song với
( )
P
nên
( )
1;1; 2u =−
là véctơ chỉ phương của
.
Khi đó, phương trình của
là
1 3 4
1 1 2
x y z− + −
==
−
.
Câu 5: Chọn A
Đường thẳng
d
đi qua
( )
0; 1;2M −
và có véc tơ chỉ phương
( )
1; 1; 1u = − −
.
( ) ( )
1;4;3 , 1;4; 5MI MI u
= − −
.
( )
( ) ( )
( ) ( )
22
2
22
2
,
1 4 5
; 14
1 1 1
MI u
R d I d
u
− + + −
= = = =
+ − + −
.
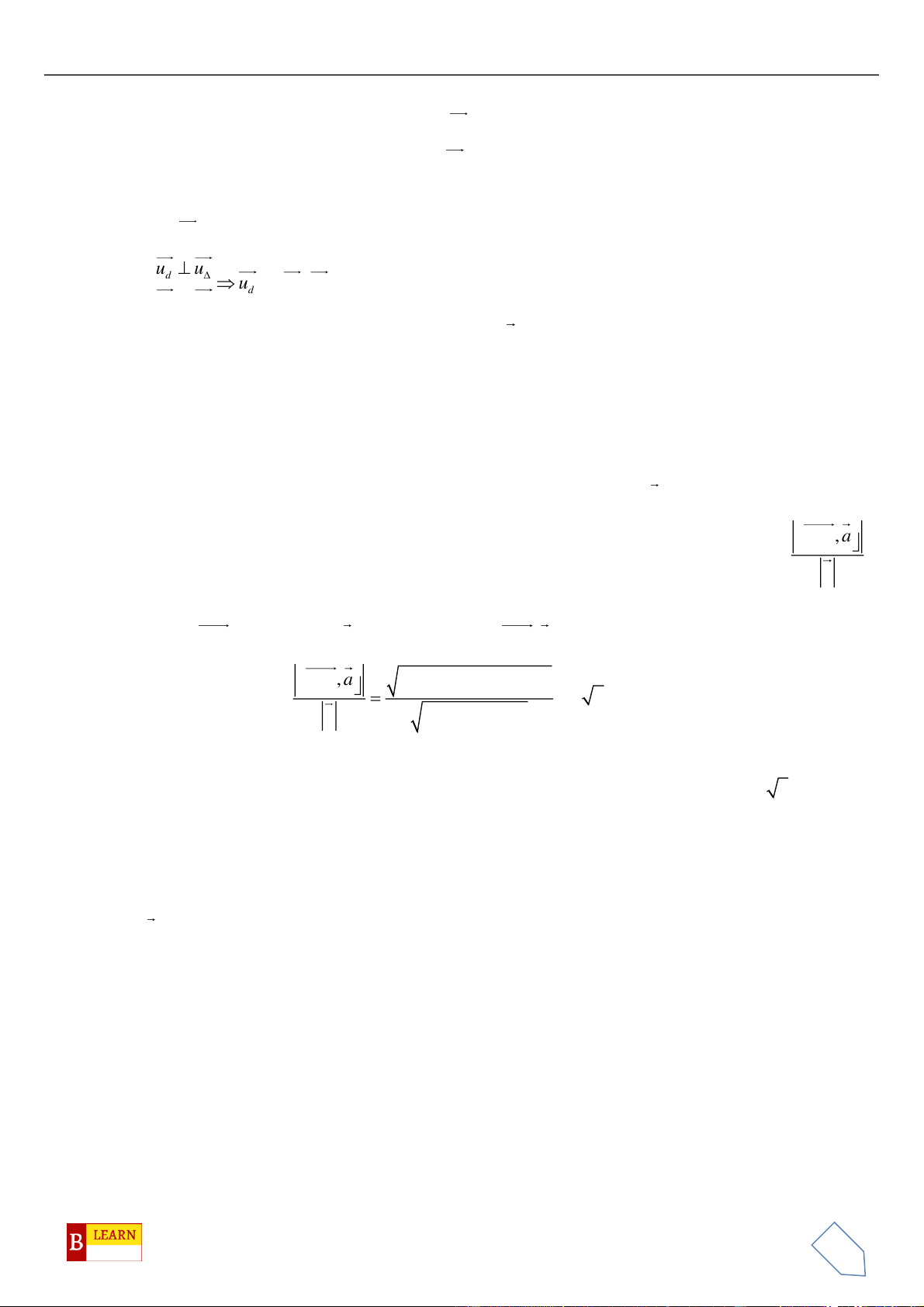
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
283
Câu 6: Chọn C
Đường thẳng
có vec tơ chỉ phương là
( )
1;2;3u
=
.
Mặt phẳng
( )
P
có vec tơ pháp tuyến là
( )
2; 1;0
P
n =−
.
Gọi
()d
là đường thẳng đi qua
A
, vuông góc với
và song song với mặt phẳng
( )
P
.
Gọi
d
u
là một vec tơ chỉ phương của đường thẳng
()d
, ta có:
( )
, 3;6; 5
d
dP
dP
uu
u u n
un
⊥
= = −
⊥
.
Đường thẳng
()d
qua
(1;3;1)A
và cũng nhận
( )
3; 6;5a = − −
làm vec tơ chỉ phương nên có
phương trình là
( )
13
3 6 .
15
xt
y t t R
zt
=−
= −
=+
Câu 7: Chọn A
Đường thẳng
d
đi qua điểm
( )
1;2; 3M −−
và có véctơ chỉ phương
( )
2;1; 1a =−
.
Bán kính của mặt cầu
( )
S
có tâm
A
và tiếp xúc với đường thẳng
d
là
( )
,
,
AM a
R d A d
a
==
.
Ta có:
( )
2;4; 6AM = − −
,
( )
2;1; 1a =−
suy ra
( )
, 2; 14; 10AM a
= − −
.
Vậy
( )
( ) ( )
( )
22
2
2
22
,
2 14 10
, 5 2
2 1 1
AM a
R d A d
a
+ − + −
= = = =
+ + −
.
Câu 8: Chọn A
Mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 1 2 1 45S x y z− + − + + =
có tâm
( )
1;2; 1A −
và bán kính
35R =
.
Mặt cầu
( )
S
cắt mặt phẳng
( )
P
theo giao tuyến là đường tròn có tâm
( )
;;I a b c
nên
I
là hình
chiếu vuông góc của
A
trên mặt phẳng
( )
P
.
Đường thẳng
AI
đi qua
A
, vuông góc với mặt phẳng
( )
P
nên
AI
có vectơ chỉ phương là
( )
1;1; 1n =−
.
Phương trình đường thẳng
AI
có dạng:
1
2
1
xt
yt
zt
=+
=+
= − −
.
Tọa độ của
I
là nghiệm của hệ:
1
2
1
13 0
xt
yt
zt
x y z
=+
=+
= − −
+ − − =
3
4
5
4
t
x
y
z
=
=
=
=−
( )
4;5; 4I −
.
Ta có
4 5 4 5abc+ + = + − =
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
284
Câu 9: Chọn B
Gọi
là đường thẳng cần tìm. Giả sử
cắt
12
;dd
lần lượt tại
A
và
B
Do
( )
1
3 2 ; 2 ; 2 4A d A a a a − + − − − −
;
( )
2
1 3 ; 1 2 ;2 3B d B b b b − + − + +
( )
2 2 3 ;1 2 ;4 4 3AB a b a b a b − + + + + +
Do
( ) ( )
/ / 1;2;3
P
P AB n ⊥
2 2 3
1 2 2
4 4 3 3
a b k
a b k
a b k
− + =
+ + =
+ + =
1
2
2
a
b
k
=−
= −
=−
( )
( )
5; 1;2
7; 5; 4
A
B
−−
− − −
Đường thẳng
đi qua
A
và nhận vecto
P
n
làm vecto chỉ phương có phương trình là:
5 1 2
.
1 2 3
x y z+ + −
==
Câu 10: Chọn B
Đường thẳng vuông góc với mặt phẳng nếu vectơ chỉ phương của đường thẳng cùng phương với
vectơ pháp tuyến của mặt phẳng.
Đường thẳng
d
có một vectơ chỉ phương là
( )
1 ; 2 ; 1u =−
.
Mặt phẳng
( )
T
có một vectơ pháp tuyến là
( )
1 ; 1 ; 2
T
n =
. Do
1 2 1
1 1 2
−
nên
u
không cùng
phương với
T
n
. Do đó
d
không vuông góc với
( )
T
.
Mặt phẳng
( )
P
có một vectơ pháp tuyến là
( )
1 ; -2 ; 1
P
n =
. Do
1 2 1
1 2 1
−
==
−
nên
u
cùng phương
với
P
n
. Do đó
d
vuông góc với
( )
P
.
Mặt phẳng
( )
Q
có một vectơ pháp tuyến là
( )
1 ; -2 ; -1
Q
n =
. Do
1 2 1
1 2 1
−
=
−−
nên
u
không cùng
phương với
Q
n
. Do đó
( )
d
không vuông góc với
( )
Q
.
Mặt phẳng
( )
R
có một vectơ pháp tuyến là
( )
1 ; 1 ; 1
R
n =
. Do
1 2 1
111
−
nên
u
không cùng
phương với
R
n
. Do đó
( )
d
không vuông góc với
( )
R
.
Câu 11: Chọn B
Mặt phẳng
( )
P
nhận
( )
1
1;2;3=n
làm véctơ pháp tuyến.
Mặt phẳng
( )
Q
nhận
( )
2
1; 3;6= + +n m m
làm véctơ pháp tuyến.
Theo giả thiết ta có
( ) ( )
1
1 3 6 1
// 1.
0
1 2 3 1
=
++
= = =
m
mm
P Q m
m
Câu 12: Chọn A
Đường thẳng
d
đi qua điểm
( )
1;1;0M −
và có một véc tơ chỉ phương là
( )
2;1; 3u =−
.
( )
2; 2;0MA =−
. Ta có:
;MA u
( )
6;6;6=
cùng phương với
( )
1;1;1n =
.
chứa
d
và đi qua
A
nên nhận
( )
1;1;1n =
làm một véc tơ pháp tuyến.
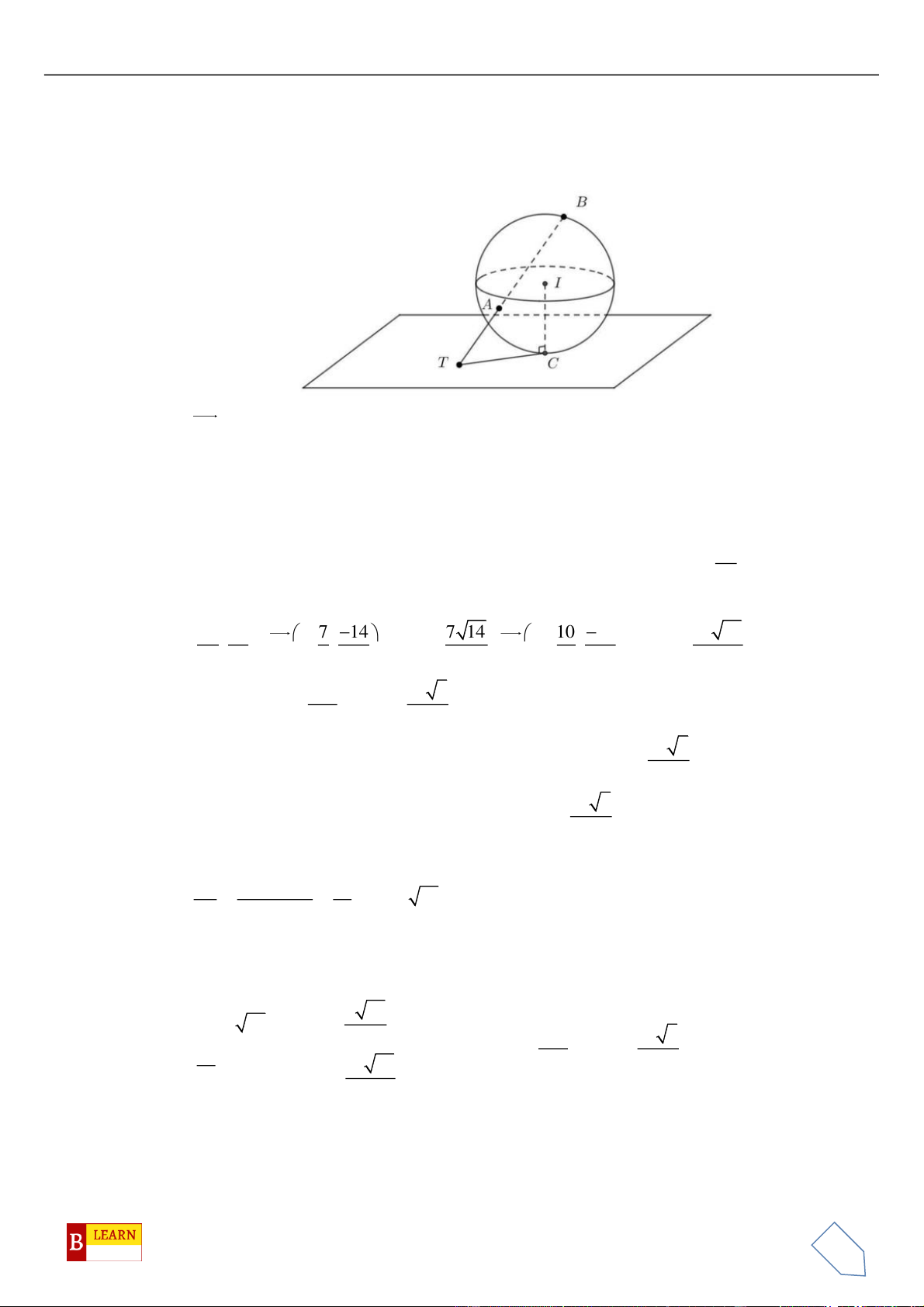
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
285
Phương trình mặt phẳng
()P
là:
( ) ( ) ( )
1. 1 1. 1 1. 0 0 0x y z x y z− + + + − = + + =
.
Câu 13: Chọn A
Cách 1:
Ta có
( )
3;1; 2AB −
là véc tơ chỉ phương của đường thẳng
AB
.
Phương trình tham số của đường thẳng AB là
3
42
xt
yt
zt
=
=
=−
.
Giả sử
AB
cắt
( )
P
tại
( )
3 ; ;4 2T t t t−
. Do
T
( )
7
:2 2 1 0
3
P x y z t
−
+ + − = =
.
Khi đó
7 26 7 14 7 14 10 20 10 14
7; ; ; 7; ; ; 10; ;
3 3 3 3 3 3 3 3
T TA TA TB TB
− − −
− = =
.
Ta có
2
980 14 5
.
93
TC TATB TC= = =
.
Điểm
C
thuộc mặt phẳng
( )
P
và cách điểm
T
cố định một khoảng
14 5
3
.
Vậy
C
luôn thuộc một đường tròn cố định bán kính
r =
14 5
3
.
Cách 2:
Ta có
( )
( )
( )
( )
,
7
; 14
, 10
d A P
TA
AB
TB d B P
= = =
.
Giả sử
AB
cắt
( )
P
tại
T
. Suy ra A nằm giữa B và
T
.
Khi đó ta có
7
14
14
3
10 14
3
7
10
T
TB TA
TA TB
A
TB
−=
=
=
=
2
980 14 5
.
93
TC TATB TC = = =
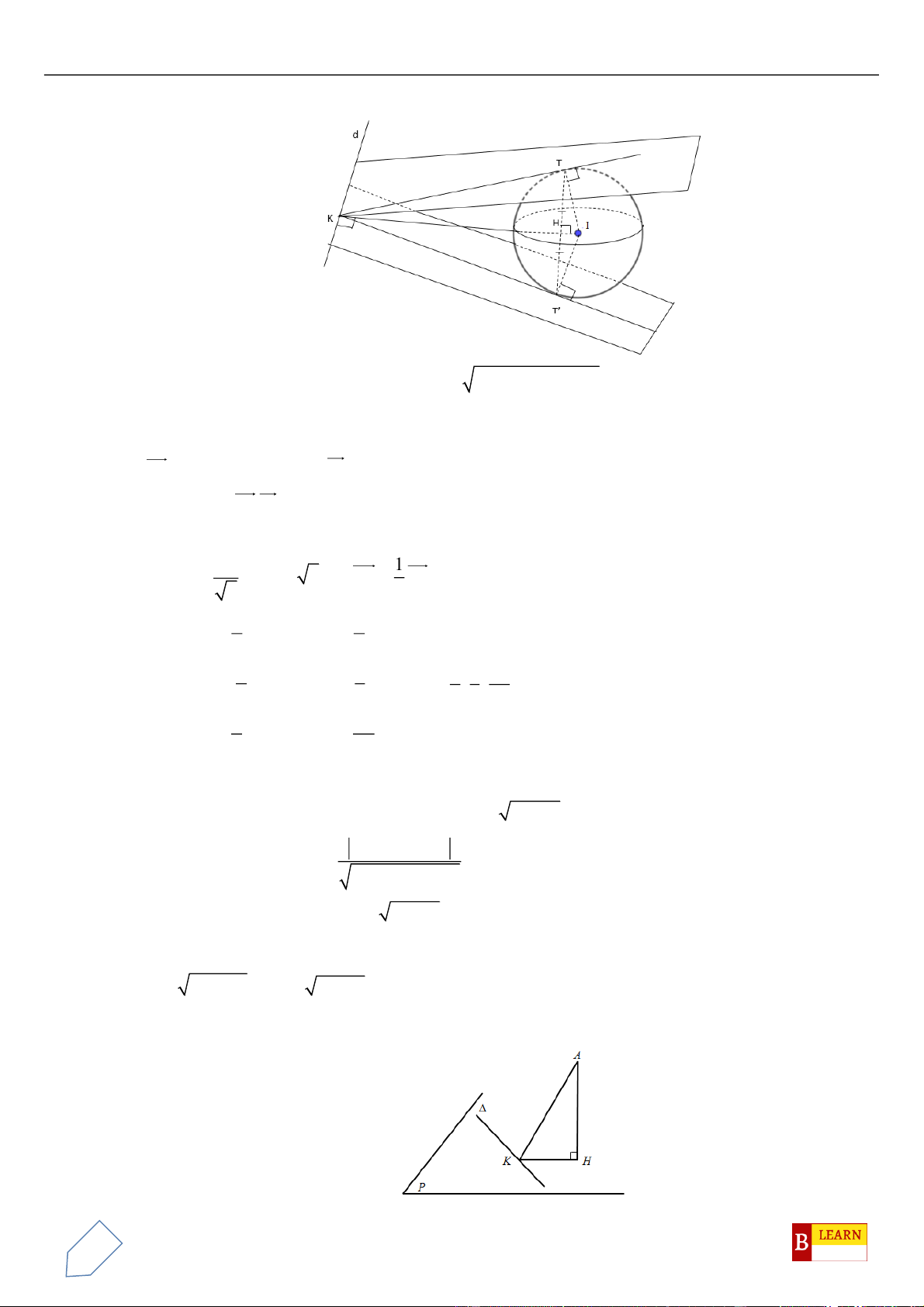
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
286
Câu 14: Chọn C
Mặt cầu
()S
tâm
(1;0; 1)I −
, bán kính
2 2 2
1 0 ( 1) 1 1R = + + − − =
.
Gọi
K
là hình chiếu vuông góc của
I
lên
d
.
Kd
nên ta có thể giả sử
( ;2 ; )K t t t+−
( 1;2 ; 1)IK t t t= − + − +
,
(1;1; 1)
d
u =−
là một véctơ chỉ phương của đường thẳng
d
IK d⊥
. 0 1 2 1 0
d
IK u t t t = − + + + − =
0t=
.
(0;2;0)K
ITK
vuông tại
T
có
TH
là đường cao nên
2
.IT IH IK=
.
1
6
IH=
( )
6IK =
1
6
IH IK=
. Giả sử
( ; ; )H x y z
1
1 .( 1)
6
1
0 .2
6
1
1 .1
6
x
y
z
− = −
− =
+=
5
6
1
3
5
6
x
y
z
=
=
−
=
Vậy
5 1 5
;;
6 3 6
H
−
Câu 15: Chọn D
Mặt cầu
()S
có: Tâm
( )
1;2;3I −
, bán kính
17Rm=−
.
Khoảng cách
( )
2 2 2
2 2 6 8
;( ) 2
2 ( 1) 2
dI
− − + −
==
+ − +
.
( ) ( ) ( )
;( ) 17 2S d I R m
−
13m
( )
*
Mặt khác,
( ) ( ) ( )
,S C H r
=
có chu vi bằng
8
nên
4r =
.
hay
22
4 13 4 3R d m m− = − = = −
thỏa mãn
( )
*
. Vậy
3m =−
.
Câu 16: Chọn D

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
287
Gọi
là đường thẳng cố định nằm trong mặt phẳng
( )
P
.
Ta có
( ) ( )
3 8 2 0m x y z x y z− − + + + − − =
nên phương trình
thỏa mãn hệ sau:
3 8 0
20
x y z
x y z
− − + =
+ − − =
. Chọn
zt=
suy ra
có phương trình
23
5
xt
yt
zt
=−
= − +
=
.
Gọi
K
là hình chiếu của
A
trên
.
( )
2 3; t 5;tK K t − − +
( )
2 1; t 7;t 7AK t = + − + −
.
( ) ( )( ) ( )
. 0 2 2 1 1 7 7 0 2 1;3;2AK u t t t t K
= + + − − + + − = =
.
Gọi
H
là hình chiếu của
A
trên mặt phẳng
( )
P
. Ta có
( )
AHK⊥
mà
cố định, điểm
A
cố
định nên mặt phẳng
( )
AHK
cố định.
Khi
m
thay đổi ta luôn có
AHK
là một góc vuông. Do
AK
cố định nên điểm
H
luôn nằm trên
đường tròn đường kính
53AK =
.
Câu 17: Chọn B
1
d
có véc tơ chỉ phương
( )
1;1;1u =−
và đi qua điểm
( )
2;0;0A
.
2
d
có véc tơ chỉ phương
( )
2; 1; 1v = − −
và đi qua điểm
( )
0;1;2B
.
Ta có:
( )
, 0;1; 1uv
=−
,
( )
2;1;2AB =−
,
, . 1 0u v AB
= −
1
d
và
2
d
chéo nhau
có duy
nhất một mặt phẳng
( )
P
song song và cách đều
12
,dd
.
( )
P
đi qua trung điểm
1
1; ;1
2
I
của đoạn AB và nhận
( )
, 0;1; 1uv
=−
làm véc tơ pháp tuyến,
vậy
( )
:2 2 1 0P y z− + =
, chỉ có điểm
( )
NP
,
Câu 18: Gọi
( )
P
là mặt phẳng cần tìm có vectơ pháp tuyến là
n
.
Đường thẳng
1
d
,
2
d
có vectơ chỉ phương lần lượt là
( )
1
3; 1; 1u = − −
và
( )
2
1;1; 1u =−
.
Mặt cầu
( ) ( ) ( )
22
2
: 1 2 6S x y z− + + + =
có tâm
( )
1;0; 2I −
, bán kính
6R =
.
Do
( )
( )
1
2
//
//
Pd
Pd
1
2
nu
nu
⊥
⊥
. Suy ra
n
cùng phương với
12
,uu
.
Có
12
,uu
( )
2;2;4=
, nên chọn
( )
1;1;2n =
.
Khi đó phương trình tổng quát của mặt phẳng
( )
P
có dạng:
20x y z d+ + + =
.
Mặt phẳng
( )
P
tiếp xúc với mặt cầu
( )
S
( )
( )
,d I P R=
( )
2 2 2
1 0 2. 2
6
1 1 2
d+ + − +
=
++
36d − =
9
3
d
d
=
=−
.
Vậy có hai mặt phẳng thỏa mãn đề là
( )
1
P
:
2 3 0x y z+ + − =
và
( )
2
P
:
2 9 0x y z+ + + =
.
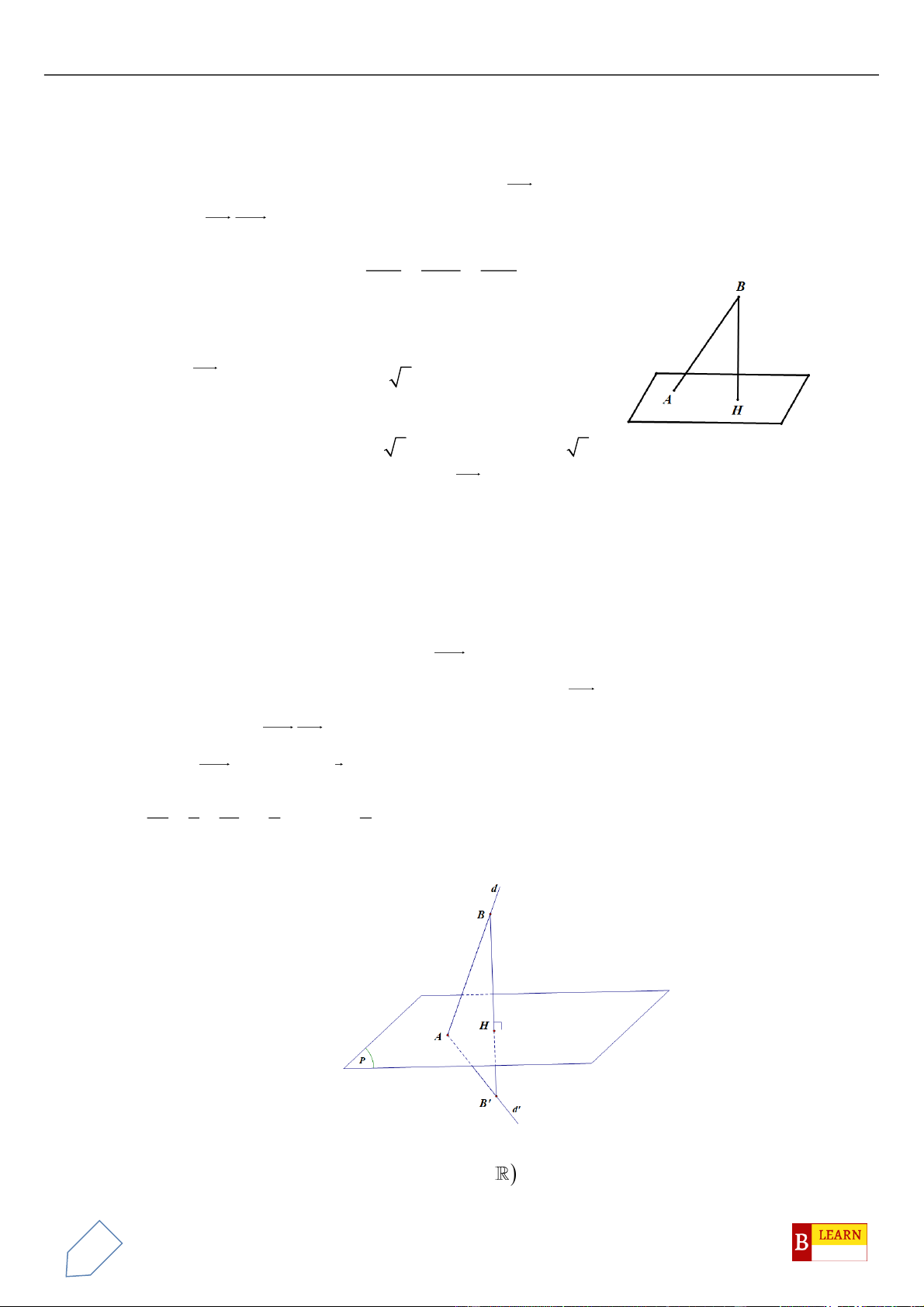
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
288
Câu 19: Chọn C
Điểm
B
thuộc mặt
()P
nên
( )
2 1; ;B c b b c−−
vì
( )
1;2;3M
là trung điểm
BC
nên
( )
3 2 ;4 ;6C c b b c− + − −
. Do
C
thuộc mặt
(Q)
nên
3 7 0 3 7c c c b− − = = −
. Khi đó
(5 15; ;3 7)B b b b−−
,
( 5 17;4 ;13 3 )C b b b− + − −
.
( 10 32; 2 4; 6 20)BC b b b− + − + − +
.
ABC
cân tại
A
nên
. 0 20 60 0 3 (0;3;2).BC AM b b B= − = =
Đường thẳng
đi qua
(1;2;3)M
và
(0;3;2)B
có phương trình là
1 2 3
1 1 1
x y z− − −
==
−
.
Câu 20: Chọn B
Ta có
( )
2; 2;4 2 6AB AB= − =
.
Gọi
H
là hình chiếu vuông góc của
B
trên mặt phẳng
( )
P
.
Ta có
( )
( )
( )
( )
, 2 6 , 2 6d B P BH BA maxd B P= = =
, đạt được khi
HA
.
Khi đó mặt phẳng
( )
P
đi qua
A
và nhận
( )
2; 2;4AB =−
là véctơ pháp tuyến.
Suy ra phương trình mặt phẳng
( )
P
là
( ) ( ) ( )
2 1 2 2 4 1 0 2 3 0x y z x y z− − − + + = − + + =
.
Câu 21: Chọn A
Ta có
( )
2; 1;3A −
,
( )
2; 1;3A −
Oz
. Mà
đồng phẳng và không song song với
Oz
nên
cắt
Oz
tại một điểm. Gọi
( )
0
0;0;Mz
là giao điểm của
và
Oz
.
Khi đó
có một vectơ chỉ phương là
( )
0
2;1; 3AM z−−
.
( )
: 4 0P x y z+ − − =
suy ra
( )
P
có vectơ pháp tuyến là
( )
( )
1;1; 1
P
n =−
.
Vì
( )
// P
nên
( )
.0
P
AM n =
( ) ( ) ( )
0
2 .1 1.1 3 . 1 0z − + + − − =
0
2z=
.
Suy ra
( )
2;1; 1AM = − −
.
( )
;;u a b c=
cũng là một vectơ chỉ phương của
nên ta có:
2.
2 1 1
a b c a
c
= = =
−−
Vậy
2.
a
c
=
Câu 22: Chọn C
Phương trình tham số của
( )
: 1 2
2
=
= − +
=−
xt
d y t t
zt
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
289
Giả sử
A
là giao điểm của
d
và
( )
P
tọa độ của
A
là nghiệm hệ phương trình:
( )
12
1;1;1
2
30
=
= − +
=−
+ + − =
xt
yt
A
zt
x y z
.
Lấy điểm
( )
0; 1;2−Bd
, Gọi
H
là hình chiếu của
B
trên
( )
P
.
Đường thẳng
chứa
BH
vuông góc với
( )
P
có phương trình
( )
'
: 1 ' '
2'
xt
y t t
zt
=
= − +
=+
.
Khi đó
( )
HP=
Tọa độ
H
là nghiệm của hệ phương trình
'
1'
2'
30
xt
yt
zt
x y z
=
= − +
=+
+ + − =
2 1 8
;;
3 3 3
−
H
.
Gọi
B
là điểm đối xứng với
B
qua
( )
4 1 10
;;
3 3 3
PB
1 2 7
;;
3 3 3
AB
=−
.
Đường thẳng
'd
đối xứng với
d
qua mặt phẳng
( )
P
đi qua
2
điểm
,AB
có véc tơ chỉ phương
( )
1; 2; 7u =−
'd
có phương trình là
1 1 1
1 2 7
x y z− − −
==
−
.
Câu 23: Chọn B
Gọi
MN
là đoạn vuông góc chung của
( )
1
d
và
( )
2
d
,
( ) ( )
12
;M d N d
.
Khi đó
( )
1 ;0; 5M t t+ − +
,
( )
0;4 2 ;5 3N t t
−+
và
( ) ( )
12
,MN d MN d⊥⊥
.
Đường thẳng
( )
1
1
:0
5
xt
dy
zt
=+
=
= − +
có một vectơ chỉ phương là
( )
1
1;0;1u =
, đường thẳng
( )
2
0
: 4 2
53
x
d y t
zt
=
=−
=+
có một vectơ chỉ phương là
( )
2
0; 2;3u =−
.
( )
1; 4 2 ; 3 10MN t t t t
= − − − − + +
.
( ) ( )
12
,MN d MN d⊥⊥
suy ra
1
2
.0
2 3 9 3
3 13 22 1
.0
MN u
t t t
t t t
MN u
=
− + = − =
− + = − = −
=
.
Suy ra
( )
4;0; 2M −
,
( )
0;6;2N
.
Mặt cầu
( ) ( ) ( )
2 2 2
2
x a y b z c R− + − + − =
có đường kính
MN
suy ra tâm
( )
2;3;0I
là trung
điểm của
MN
. Suy ra
2; 3; 0 2 8a b c a b c= = = + + =
.
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
290
Câu 24: Chọn C
Cách 1: Ta có
( ) ( )
1
2;0; 2 : 2
3
xt
AB AB y t
zt
=+
= − − =
=+
( )
1 ;2;3M AB M t t + +
;
( )
1 2 3 0 3M P t t t + + + + = = −
.
Vậy
( )
32
2;2;0 3
2
AM
M
BM
− = =
.
Cách 2: Do
( )
AB P M =
( )
( )
( )
( )
,
1 2 3
3
1 2 1
,
d A P
AM
BM
d B P
++
= = =
− + +
.
Câu 25: Chọn D
Tâm
I
nằm trên
d
nên
( )
1 ;2 2 ;2I t t t+ − +
.
Mặt cầu đi qua
A
và tiếp xúc với mặt phẳng
( )
P
nên
( )
( )
;AI d I P R==
.
( )
( )
( )
( )
2
22
2
2
1 4 4 4 2 1
; 4 1
1 2 2
t t t
AI d I P t t t
+ − + + + +
= + + + =
+ − +
( )
( )
2
22
72
6 2 1 9 6 2 1 7 2
3
t
t t t t t
+
+ + = + + = +
( )
2
2 1 0 1 2;0;3t t t I − + = =
.
Vậy bán kính mặt cầu
3R AI==
.
Câu 26: Chọn C
Mặt cầu tiếp xúc đồng thời hai đường thẳng và có bán kính nhỏ nhất chính là mặt cầu có đường
kính là đoạn vuông góc chung của hai đường thẳng.
Gọi
1
2
(4 3 ;1 ; 5 2 )
(2 ; 3 3 ; )
A a a a d
B b b b d
+ − − −
+ − +
là chân đoạn vuông góc chung của hai đường thẳng.
Ta có
( 3 2;3 4; 2 5)AB b a b a b a= − − + − + +
và
1
2
.0
3( 3 2) 1(3 4) 2( 2 5) 0 1
1( 3 2) 3(3 4) 1( 2 5) 0 1
.0
ABu
b a b a b a a
b a b a b a b
ABu
=
− − − + − − + + = = −
− − + + − + + + = =
=
.
Khi đó
222
224
(1;2; 3), (3;0;1) (2;1; 1), 6.
22
AB
A B I R
++
− − = = =
Vậy:
2 2 2
( ):( 2) ( 1) ( 1) 6.S x y z− + − + + =
Câu 27: Chọn A
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
291
Phương trình tham số của đường thẳng
d
là
1
22
3
xt
yt
zt
=+
=+
=+
.
Đường thẳng
d
có vectơ chỉ phương là
( )
1;2;1
d
u =
.
Mặt phẳng
( )
có vectơ pháp tuyến là
( )
1;1; 1n =−
.
Gọị
I
là giao điểm của đường thẳng
d
và mặt phẳng
( )
.
Ta có:
( )
1 ;2 2 ;3I d I t t t + + +
.
Mặt khác
( ) ( )
1 2 2 3 2 0 1 2;4;4I t t t t I
+ + + − − − = =
.
Vì đường thẳng cần tìm
nằm trong mặt phẳng
( )
, đồng thời vuông góc và cắt đường thẳng
d
nên
đi qua điểm
( )
2;4;4I
và có vectơ chỉ phương
( )
, 3; 2;1
d
u n u
= = −
.
Phương trình chính tắc của
:
2 4 4
3 2 1
x y z− − −
==
−
.
Đối chiếu đáp án ta thấy đường thẳng
3
của đáp án A có vtcp
( )
3; 2;1−
, và khi thay toạ độ
( )
2;4;4I
vào phương trình
3
thì thỏa mãn. Vậy Chọn A
Câu 28: Chọn A
Mặt cầu
( )
S
tâm
I
tiếp xúc với
( )
P
nên có bán kính:
( )
( )
( )
( )
2
22
2.1 2 2.3 1
, 3.
2 1 2
R d I P
− − + −
= = =
+ − +
Phương trình mặt cầu
( )
S
có tâm
( )
1; 2;3I −
và bán kính
3R =
là:
( ) ( ) ( )
2 2 2
1 2 3 9.x y z− + + + − =
Câu 29: Chọn B
Gọi
( )
S
là mặt cầu tâm
( )
0;0; 2A −
và có bán kính
R
.
Đường thẳng
đi qua
( )
2;2;3M −
có véc tơ chỉ phương
( )
2;3;2u =
.
Gọi là
H
trung điểm
BC AH BC⊥
.
Ta có:
( )
,
.
A
MAu
AH d
u
==
.Với
( )
( )
( )
2; 2;1
. 7; 2;10
2;3;2
MA
MAu
u
=−
= − −
=
.
( ) ( )
22
2
2 2 2
7 2 10
3.
232
AH
− + − +
= =
++
+Bán kính mặt cầu
( )
S
là:
2 2 3 2
3 4 5R AB AH HB= = + = + =
.
Vậy phương trình mặt cầu
( )
S
là:
( )
2
22
2 25x y z+ + + =
.
C
B
A
H
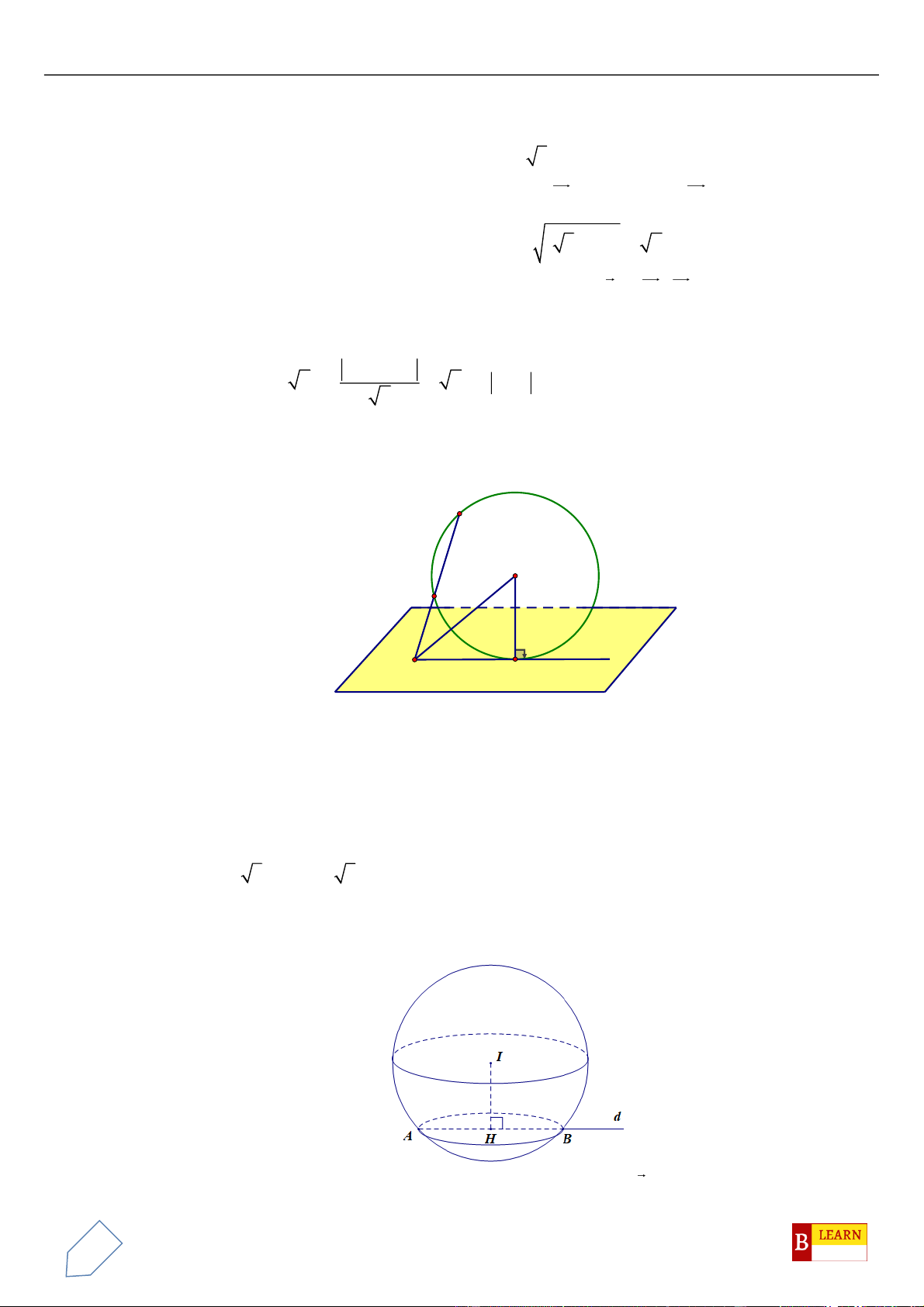
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
292
Câu 30: Chọn D
Gọi
( )
là mặt phẳng cần tìm.
Mặt cầu
( )
S
có tâm
( )
1;1; 2I −−
và bán kính
3.R =
Đường thẳng
d
và
có vectơ chỉ phương lần lượt là
( )
1;2; 1
d
u =−
và
( )
1;1; 1u
=−
.
Khoảng cách từ
I
đến mặt phẳng
( )
:
( )
( )
( )
2
2
, 3 1 2dI
= − =
.
Vì
( )
song song với
d
và
nên
( )
có vectơ pháp tuyến
( )
, 1;0;1
d
n u u
==
.
Suy ra phương trình mặt phẳng
( )
có dạng:
0x z d+ + =
.
Ta có:
( )
( )
3 2 5
12
, 2 2 3 2
3 2 1
2
dd
d
d I d
dd
− = =
− − +
= = − =
− = − =
.
Vậy phương trình mặt phẳng
( )
là:
50xz+ + =
hoặc
10xz+ + =
.
Câu 31: Chọn B
Từ tọa độ các điểm
M
và
N
suy ra phương trình đường thẳng
MN
là:
x y z==
.
Gọi
( )
A MN P=
, tọa độ
A
là nghiệm hệ phương trình
30
3
x y z
x y z
x y z
+ − − =
= = =
==
.
Suy ra
( )
3;3;3A
.
Các điểm
,,M N Q
cùng thuộc một đường tròn nên ta có
2
.AM AN AQ=
.
Với
23AM =
,
63AN =
thì
2
36 6AQ AQ= =
.
Vậy điểm
Q
luôn thuộc một đường tròn cố định có tâm
( )
3;3;3A
và bán kính
6R =
.
Câu 32: Chọn D
Đường thẳng
d
đi qua điểm
( )
1;2;2M −
và có vectơ chỉ phương
( )
3; 2;2u =−
.
P)
M
I
Q
A
N
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
293
( ) ( )
2;0;3 , 6;13;4IM IM u
= − =
. Gọi
H
là trung điểm
AB IH AB⊥
.
Khoảng cách từ tâm
I
đến đường thẳng
d
là:
,
36 169 16
13
944
IM u
IH
u
++
= = =
++
.
Suy ra bán kính
2
2
13 3 4
2
AB
R IH
= + = + =
.
Phương trình mặt cầu tâm
( )
1;2; 1I −
và có bán kính
4R =
là
( ) ( ) ( )
2 2 2
1 2 1 16x y z− + − + + =
.
Câu 33: Chọn A
Mặt cầu
( )
S
có tâm
( )
3;3;4I
, mặt phẳng
( )
có vectơ pháp tuyến
( ) ( )
1;1;1 , 1;2;3n MI==
.
Gọi
H
là hình chiếu vuông góc của
I
lên
. Khi đó
( )
,d I IH IM =
.
Để
cắt mặt cầu
( )
S
theo một đoạn thẳng có độ dài nhỏ nhất
( )
,dI
lớn nhất khi
IM⊥
.
Khi đó
có vectơ chỉ phương là
( )
, 1; 2;1u n MI
= = −
.
Phương trình đường thẳng
là:
2
12
1
xt
yt
zt
=+
=−
=+
.
Do đó đường thẳng đi qua điểm có tọa độ
( )
4; 3;3−
.
Câu 34: Chọn C
Đường thẳng
d
đi qua điểm
( )
1;0;2M
và có vectơ chỉ phương
( )
4;1;1u =−
.
Ta có:
( )
2; 3;0AM =−
;
( )
, 3; 2; 10AM u
= − − −
.
Mặt phẳng
()P
chứa điểm
A
và đường thẳng
d
có vectơ pháp tuyến
( )
, 3; 2; 10AM u
= − − −
.
Vậy phương trình mặt phẳng
()P
là
( ) ( ) ( )
3 1 2 3 10 2 0x y z− + − − − − =
3 2 10 23 0x y z − − − + =
.
Câu 35: Chọn C
Đường thẳng
d
đi qua điểm
( )
1;0;2M
và có vectơ chỉ phương
( )
4;1;1u =−
.
Ta có:
( )
2; 3;0AM =−
;
( )
, 3; 2; 10AM u
= − − −
.
Mặt phẳng
()P
chứa điểm
A
và đường thẳng
d
có vectơ pháp tuyến
( )
, 3; 2; 10AM u
= − − −
.
Vậy phương trình mặt phẳng
()P
là
( ) ( ) ( )
3 1 2 3 10 2 0x y z− + − − − − =
3 2 10 23 0x y z − − − + =
.
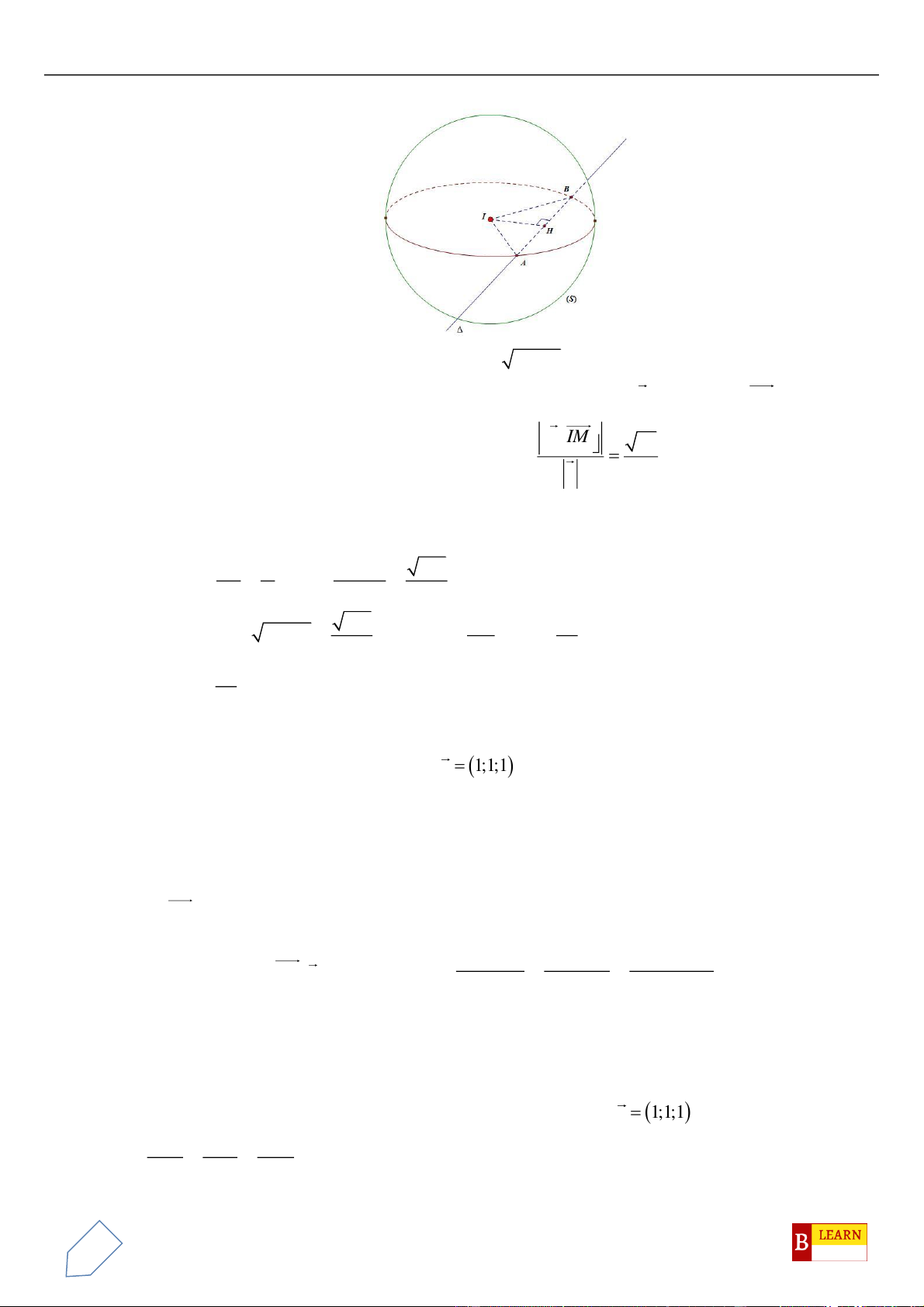
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
294
Câu 36: Chọn D
Mặt cầu
( )
S
có tâm
( )
1;2; 3 ,I −−
bán kính
( )
14 , 1Rm=−
. Điều kiện:
14 0 14mm−
.
Đường thẳng
( )
đi qua điểm
( )
1;0;2M −
, có vecto chỉ phương
( ) ( )
1;2; 2 , 0; 2;5u IM= − − = −
Khoảng cách từ tâm
I
đến đường thẳng
( )
là
,
65
3
u IM
d IH
u
= = =
, với
H
là
trung điểm
AB
.
Vì tam giác
IAB
vuông cân, ta có
0
45IBA =
. Trong tam giác vuông
IHB
có:
( )
0
0
130
sin45 , 2
sin45 3
IH d d
R
IB R
= = = =
Từ
( ) ( )
130 130 4
1 , 2 14 14 .
3 9 9
m m m
−
− = − = =
Thỏa mãn điều kiện
Vậy
4
.
9
m
−
=
Câu 37: Chọn A
Mặt phẳng
( )
P
có vectơ pháp tuyến là
( )
1;1;1 .n =
Gọi
là đường thẳng cần tìm và
,A d B d
= =
Vì
,A d B d
nên gọi
( )
1 2 ; ; 1 3A t t t− − − +
và
( )
2 ; 1 2 ; 2B t t t
+ − + −
( )
2 3; 2 1; 2 3 1 .AB t t t t t t
= + + − − − − +
Do
( )
P⊥
nên
,AB n
cùng phương
2 3 2 1 2 3 1
1 1 1
t t t t t t
+ + − − − − +
= =
( )
( )
1; 1; 4
3 4 1
.
2 4 2 1
3; 1; 2
A
t t t
t t t
B
−−
− = − = −
+ = =
−
Đường thẳng
đi qua điểm
B
và có vectơ chỉ phương
( )
1;1;1n =
nên có phương trình
3 1 2
.
1 1 1
x y z− − +
==

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
295
Câu 38: Chọn B
Gọi d là đường thẳng cần tìm
Phương trình tham số của
1
d
là
( )
1
32
:1
22
xa
d y a
za
=+
= − +
=−
Phương trình tham số của
2
d
là
( )
2
13
:2
4
xb
d y b
zb
= − +
=−
= − −
-Gọi
( )
1
3 2 ; 1 ;2 2A d d A a a a= + − + −
;
( )
2
1 3b; 2 ; 4 bB d d B b= − + − − −
( )
4 3 2 ; 2b 1 ; 6 2AB b a a b a = − + − − + − − − +
-Véc tơ chỉ phương của
3
d
là
( )
3
4; 1;6u =−
Vì d song song với
3
d
nên ta có
AB
cùng phương với
3
u
4 3 2 2b 1
0
4 3 2 2b 1 6 2
41
2b 1 6 2
0
4 1 6
16
b a a
a
b a a b a
a b a
b
− + − − + −
=
=
− + − − + − − − +
−
= =
− + − − − +
=
−
=
−
( ) ( ) ( ) ( )
3; 1;2 ; 1;0; 4 4;1; 6 :A B AB d − − − = − −
3 1 2
4 1 6
x y z− + −
==
−−
Câu 39: Chọn D
Gọi
;AB
là hai điểm thuộc lần lượt
1
và
2
sao cho
AB
là đoạn thẳng vuông góc chung giữa 2
đường. Gọi
M
là trung điểm
AB
. Dễ có mặt cầu tâm
M
bán kính
2
AB
R =
tiếp xúc với hai đường
thẳng
1
và
2
là mặt cầu có bán kính bé nhất.
Ta có tọa độ theo tham số của
;AB
lần lượt là:
1 1 1
(2 1; 1;2 1)A t t t− − −
và
2 2 2
(2 1;2 1; 1)B t t t+ + +
2 1 2 1 2 1
(2 2 2;2 2; 2 2)AB t t t t t t − + − + − +
.
Có
1
(2;1;2)u
và
2
(2;2;1)u
lần lươt là 2 vectơ chỉ phương của
1
và
2
nên
1
2
AB u
AB u
⊥
⊥
2 1 2 1 2 1
2 1 2 1 2 1
(2 2 2).2 (2 2).1 ( 2 2).2 0
(2 2 2).2 (2 2).2 ( 2 2).1 0
t t t t t t
t t t t t t
− + + − + + − + =
− + + − + + − + =
.
1
21
21
2
10
8 9 10 0
17
9 8 10 0 10
17
t
tt
tt
t
=
− + =
− + = −
=
3 7 3
( ; ; )
17 17 17
A
−
;
3 3 7
B( ; ; )
17 17 17
−−
6 4 4
( ; ; )
17 17 17
AB
−
.
222
( 6) 4 4
1 17
.
2 2 17 17
AB
R
− + +
= = =
.
Diện tích mặt cầu cần tính là
2
2
14
4 . 4. .
17
17
SR
= = =
.
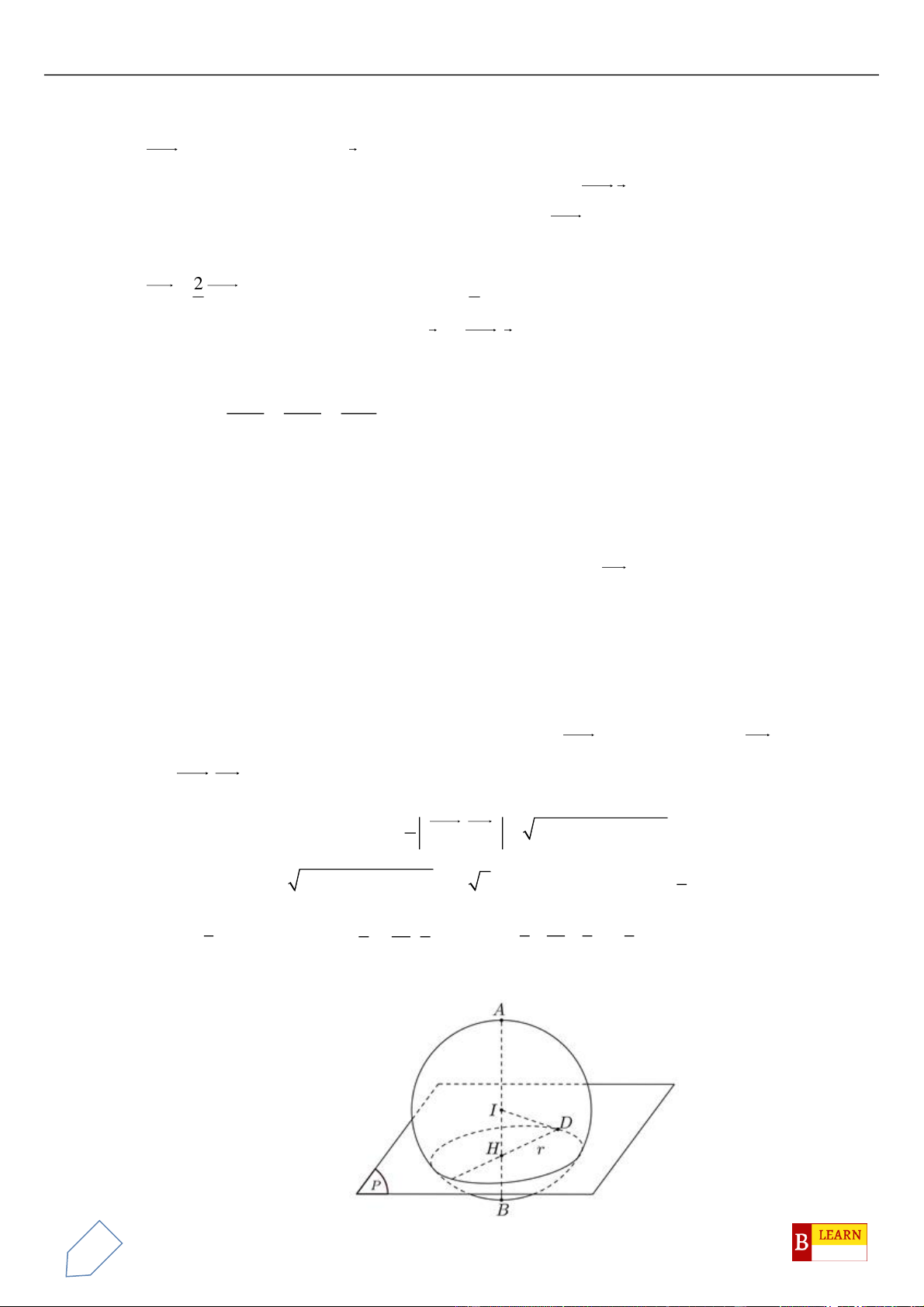
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
296
Câu 40: Chọn D
Gọi
( )
1 ;2 ;2M t t t BC− +
là trung điểm của cạnh BC.
( )
5; 1;2 5AM t t t= − − − −
;
( )
1;1;2
d
u =−
.
Vì tam giác ABC đều nên
AM BC⊥
và
G AM
, suy ra
.0
d
AM u =
.
5 1 4 10 0 1t t t t + + − + − = =
, suy ra
( )
0;3;2M
;
( )
6;0; 3AM = − −
.
Vì G là trọng tâm tam giác nên
( ) ( ) ( )
22
; ; 6;0; 3 2;3;3
33
G A G A G A
AG AM x x y y z z G= − − − = − −
Phương trình mp ABC có một vtpt là
( ) ( )
; 3;15; 6 3 1;5; 2
d
n AM u
= = − = −
Phương trình đường thẳng
đi qua trọng tâm G của tam giác ABC và vuông góc với mặt phẳng
( )
ABC
là
2 3 3
1 5 2
x y z− − −
==
−
.
Thử từng tọa độ điểm vào ptdt
thì điểm
Q
thỏa mãn.
Câu 41: Chọn D
Tam giác
MAB
cân tại
M
MA MB M =
nằm trên mặt phẳng
( )
Q
là mặt phẳng trung trực
của đoạn
AB
.
Mặt phẳng
( )
Q
đi qua trung điểm
( )
2;1;2I
của
AB
và nhận
( )
2; 2;6AB −
làm vec tơ pháp tuyến
có phương trình là:
( )
: 3 7 0Q x y z− + − =
.
Khi đó
M
nằm trên đường thẳng là giao tuyến của hai mặt phẳng
( )
P
và mặt phẳng
( )
Q
.
tọa độ
M
thỏa mãn hệ phương trình
2 2 10 0 3 7 0
3 7 0 3 0
x y z x y z
x y z y z
− + − = − + − =
− + − = + + =
.
Đặt
3 ; 4 4z t y t x t= = − − = −
( )
4 4 ; 3 ;M t t t− − −
.
( )
3 4 ; 5 ; 1AM t t t− − − +
;
( )
2; 2;6AB −
( )
, 4 28;26 16;10 4AM AB t t t
= − − − +
.
Diện tích tam giác
MAB
:
2
1
, 198 132 264
2
MAB
S AM AB t t
= = − +
.
Từ giả thiết suy ra
22
1
198 132 264 11 2 9 6 1 0
3
t t t t t− + = − + = =
.
Với
1
3
t =
ta được điểm
8 10 1
;;
3 3 3
M
−
. Vậy
8 10 1 1
3 3 3 3
S = − + = −
.
Câu 42: Chọn B

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
297
Cách 1.
Ta có
( )
4;4;2AB =
. Điểm
H
thuộc đoạn
AB
và không trùng với hai đầu mút nên ta giả sử
( )
, 0 1AH t AB t=
.
Khi đó tọa độ của điểm
H
là
( )
2 4 ;1 4 ;3 2H t t t+ + +
và
6AH tAB t==
.
Tâm của mặt cầu là trung điểm của
AB
có tọa độ
( )
4;3;4I
, bán kính
3R IA==
.
Bán kính đường tròn đáy của nón là
( )
2
2 2 2
9 9 2 1 6r R IH t t t= − = − − = −
.
Thể tích khối nón:
( )
( )
3
2 2 2
1 1 2 2 32
.36. .6 36 2 2 36 .
3 3 3 3
t t t
V r AH t t t t t
+ + −
= = − = − =
Đẳng thức xảy ra khi và chỉ khi
2
22
3
t t t= − =
. Khi đó
14 11 13
;;
3 3 3
H
.
Mặt phẳng
( )
P
qua
H
, nhận
AB
làm véc tơ pháp tuyến có phương trình:
14 11 13
2 2 0 2 2 21 0
3 3 3
x y z x y z
.
Do đó:
2
1 18.
21
b
c b c d
d
Cách 2
Ta có
4;4;2AB
.
Gọi
I
là trung điểm
4;3;4 .AB I
Bán kính mặt cầu là
3R IA
.
Giả sử
IH t
. Xét điểm
H
đối xứng với
H
qua
I
thì mặt phẳng qua
,HH
cắt mặt cầu với
đường tròn có cùng bán kính nên thể tích khối nón sẽ lớn hơn nếu
H
nằm khác phía
A
so với
điểm
I
. Khi đó chiều cao của nón là
3 0 3AH t t
.
Bán kính mặt nón là:
2 2 2
9r R IH t
.
Thể tích khối nón là:
2 2 3 2
11
. . 9 3 3 9 27
3 3 3
π
V π r h π t t t t t
.
Xét hàm số
32
3 9 27f t t t t
Có
2
1
3 6 9 0
3
t
f t t t
t loai
.
Bảng biến thiên
0;3
max 1 32f t f
. Khi đó
1 4.IH AH
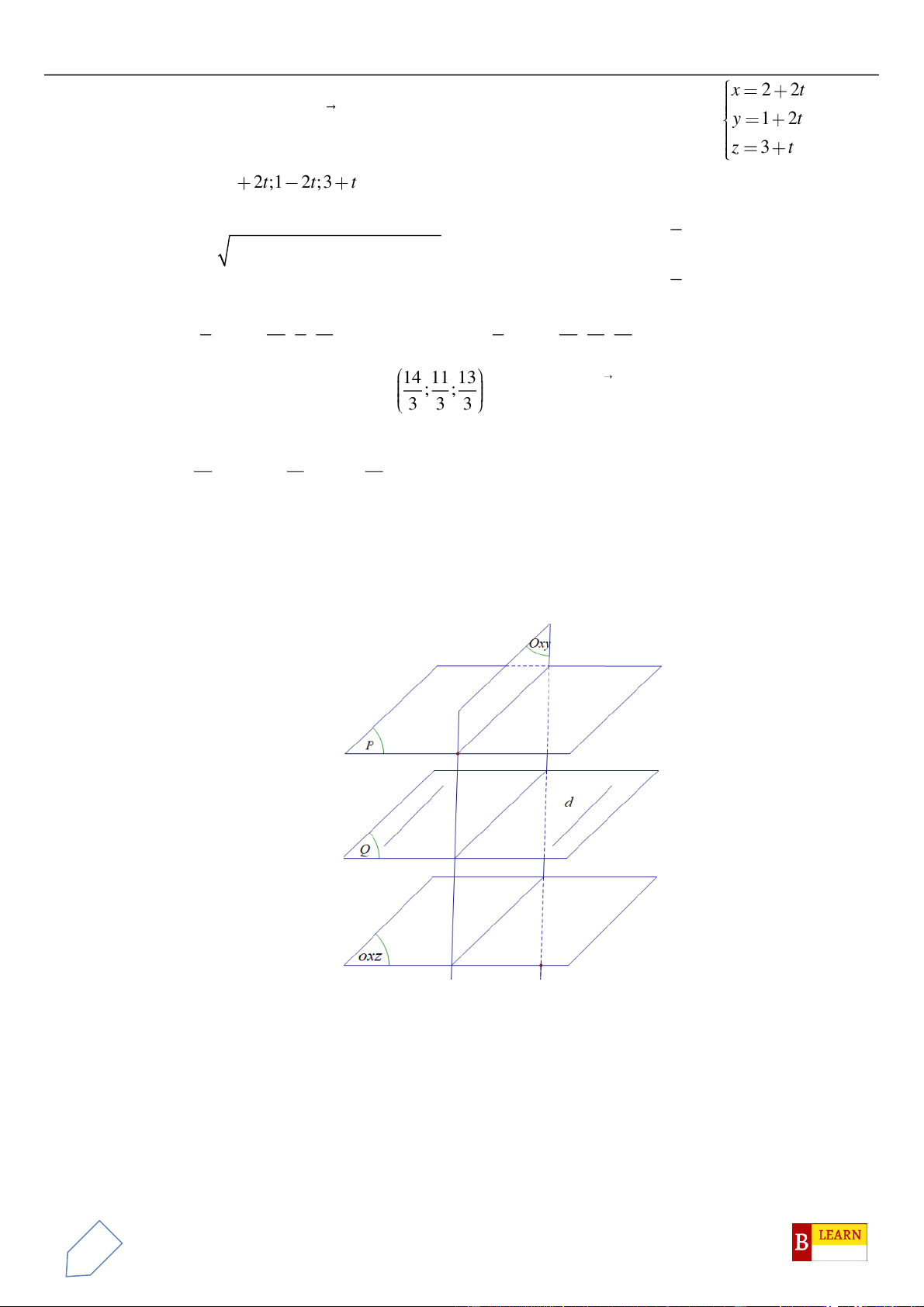
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
298
Đường thẳng
AB
nhận
2;2;1u
làm vectơ chỉ phương nên có phương trình
22
12
3
xt
yt
zt
Suy ra
2 2 ;1 2 ;3H t t t
.
Mà
( ) ( ) ( )
2 2 2
2
4
3
2 2 2 2 1 1 9 18 8 0
2
3
t
IH t t t t t
t
=
= − + − + − = − + =
=
Với
2 10 7 11
; ; 2.
3 3 3 3
t H AH
= =
Với
4 14 11 13
; ; 4.
3 3 3 3
t H AH
= =
Khi đó, mặt phẳng
P
đi qua
14 11 13
;;
3 3 3
H
và nhận vectơ
2;2;1u
làm vectơ pháp tuyến nên
có phương trình là
14 11 13
2 2 0 2 2 21 0
3 3 3
x y z x y z
− + − + − = + + − =
.
Do đó:
2
1 18.
21
b
c b c d
d
=
= + + = −
=−
.
Câu 43: Chọn B
Vì
( ) ( )
//P xOz
nên đường thẳng
d
sẽ nằm trên mặt phẳng cách đều 2 mặt phẳng
( ) ( )
;P xOz
.
Do đó
d
thuộc mặt phẳng
( )
: 2 0Qy−=
.
Mà mặt phẳng
( )
xOy
vuông góc với hai mặt phẳng
( ) ( )
;P xOz
. Do đó có 2 đường thẳng
d
thỏa
mãn đề bài.
Câu 44: Chọn D
Thay tọa độ
( )
2; 3;4M −
vào phương trình của
( )
P
, dễ thấy
( )
MP
.
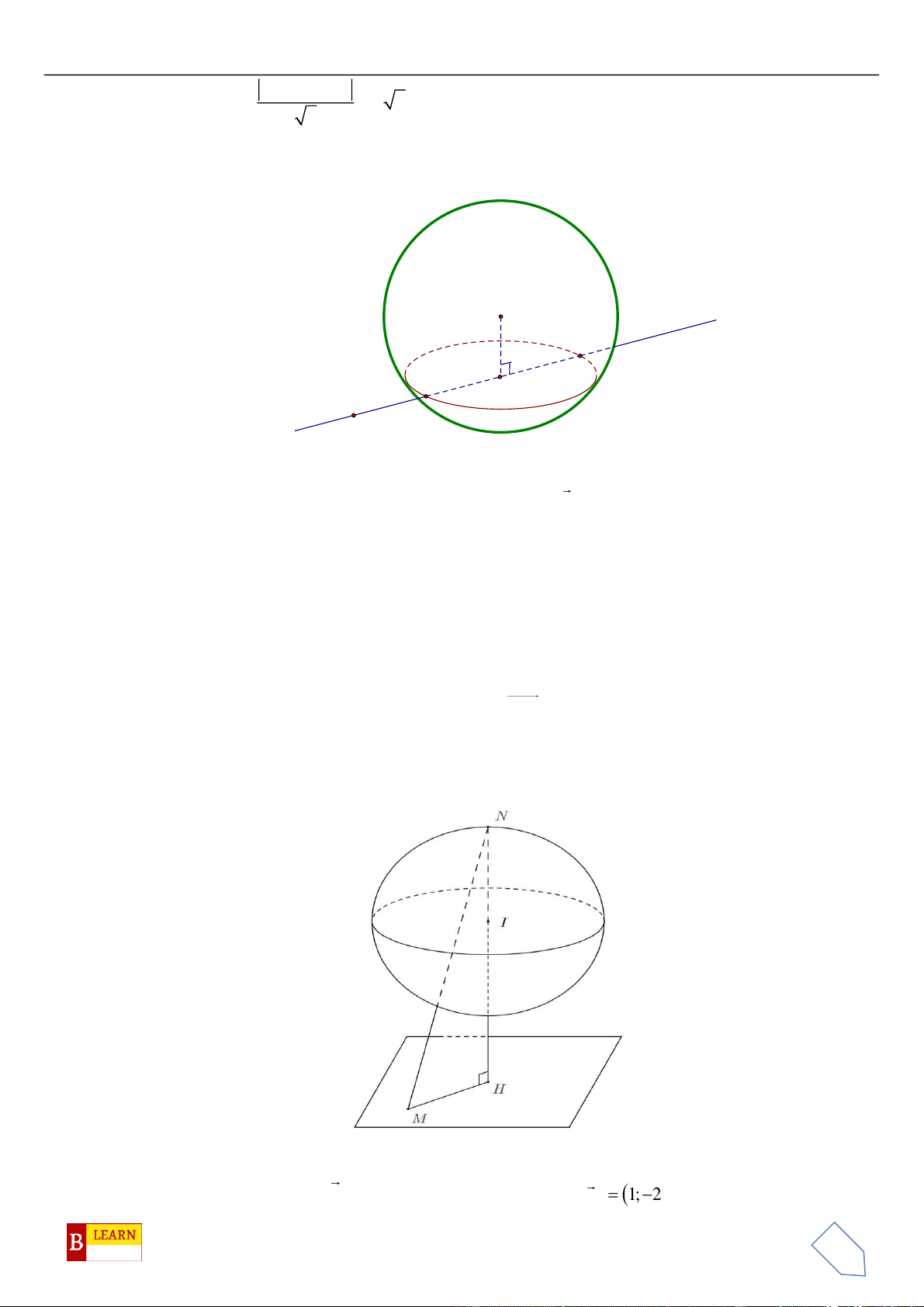
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
299
Ta có
( )
( )
,
1 4 3 12
2 6 5
6
IP
d
− + −
= =
, do đó mặt phẳng
( )
P
cắt mặt cầu
( )
S
theo giao tuyến là
một đường tròn. Vậy đường thẳng đi qua qua
M
, nằm trong
( )
P
và cắt
( )
S
theo dây cung dài
nhất khi và chỉ khi đường thẳng đó qua tâm
H
của đường tròn giao tuyến.
Đường thẳng
IH
đi qua
( )
1,2,3I
nhận VTPT của
( )
P
( )
1; 2;1n −
làm VTCP:
1
22
3
xt
yt
zt
=+
=−
=+
.
Do vậy ta có
( )
H IH P=
nên ta có hệ:
12
2 2 3
32
2 12 0 5
x t t
y t x
z t y
x y z z
= + =
= − =
= + = −
− + − = =
hay
( )
3; 2;5H −
.
Vậy đường thẳng cần tìm qua
( )
3; 2;5H −
nhận
( )
1;1;1MH
làm vtcp có dạng
3
2
5
xt
yt
zt
=+
= − +
=+
.
Câu 45: Chọn B
( )
S
có tâm
( )
1;2;1I −
, bán kính
1R =
.
Đường thẳng
MN
nhận
( )
1;0;1u =
làm VTCP,
( )
P
nhận
( )
1; 2;2
p
n =−
làm VTPT.
M
B
H
A
I
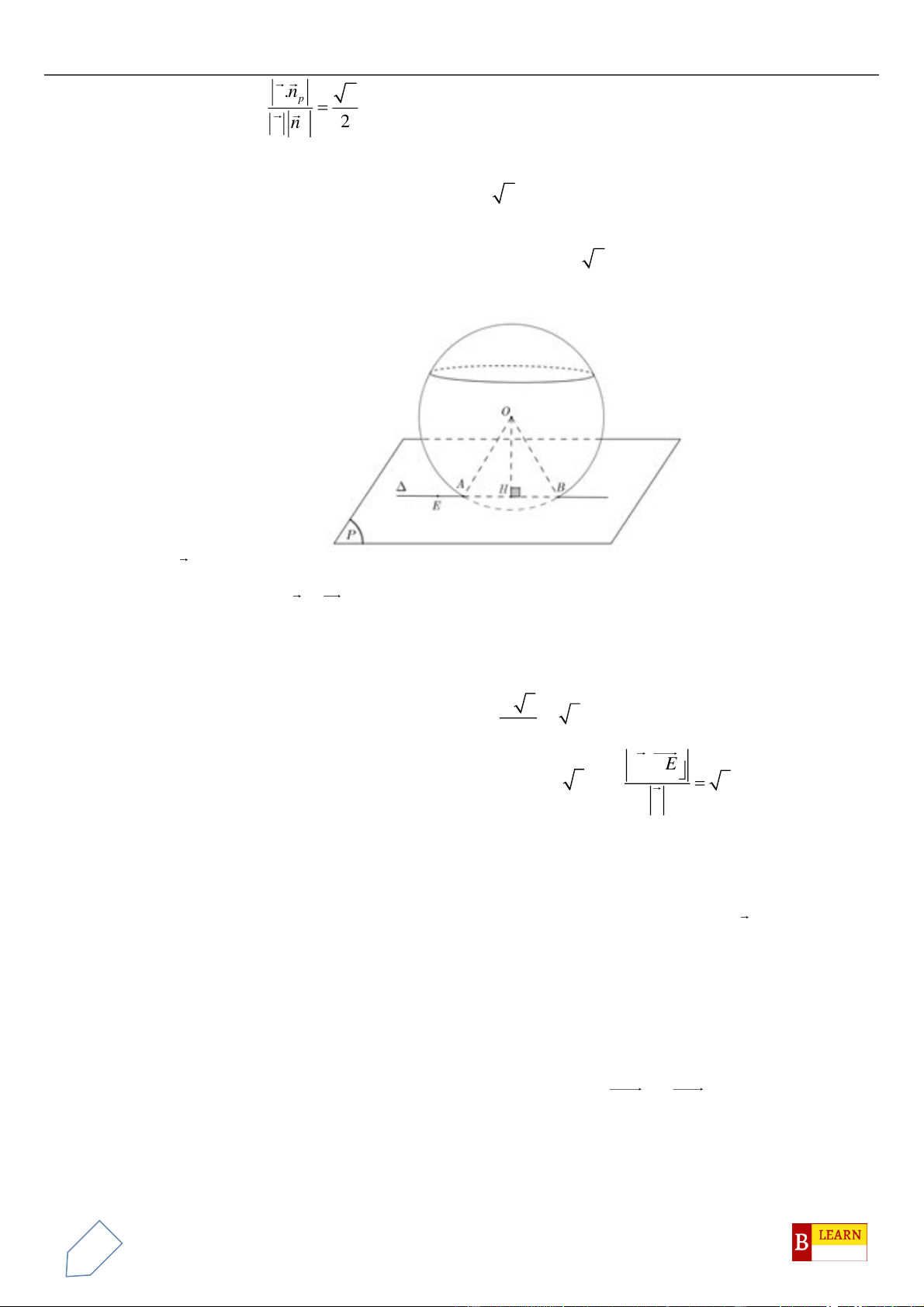
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
300
( )
( )
.
2
sin ,
2
p
p
un
MN P
un
==
( )
( )
, 45MN P =
.
Gọi
H
là hình chiếu vuông góc của
N
lên
( )
P
.
Suy ra
MNH
vuông cân tại
H
2MN NH=
. Do đó
MN
lớn nhất khi
NH
lớn nhất.
Mà
NH
lớn nhất khi
NH
đi qua tâm
I
của
( )
S
, khi đó
NH NI IH R IH= + = +
.
( )
( )
,2IH d I P==
nên
1 2 3
max
NH = + =
. Vậy
32
max
MN =
.
Câu 46: Chọn C
Gọi
( )
;;=u a b c
là một VTCP của đường thẳng
(
2 2 2
0abc+ +
).
+) Vì
( )
P
nên
P
un⊥
3 5 0a b c− + =
35a b c=−
.
+) Mặt cầu
( )
S
có tâm
( )
0;0;0O
và bán kính
2R =
.
Gọi
H
là hình chiếu vuông góc của
O
trên
AB
.
Ta có
OAB
là tam giác đều cạnh
R
nên
3
2
R
OH =
3=
.
Hay khoảng cách từ
O
đến đường thẳng
bằng
3OH =
,
3
u OE
u
=
.
( ) ( ) ( )
( )
2 2 2
2 2 2
3a b b c c a a b c− + − + − = + +
( )
2
0abc+ + =
0abc + + =
.
Thay vào ta được
3 5 0b c b c− + + =
bc=
2ac = −
.
Chọn
1c =−
, khi đó
1b =−
và
2a =
. Ta được một vectơ chỉ phương của
là
( )
2; 1; 1= − −u
.
Vậy phương trình của đường thẳng
là
12
1
1
xt
yt
zt
=+
=−
=−
.
Câu 47: Chọn B
Trường hợp 1:
,AB
cùng phía với
( )
:Q
Gọi
( )
;y;zMx
thỏa
3.AM BM=
Suy ra:
( )
( )
( )
2 3 2
5 3 1
3 3 1
xx
yy
zz
− = +
− = −
+ = −
4
1
3
x
y
z
=−
= −
=
( )
4; 1;3M − −

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
301
Đường thẳng
MC
qua
( )
2;0;1C
và có VTCP
( )
6;1; 2u MC= = −
.Phương trình
26
:
12
xt
MC y t
zt
=+
=
=−
Gọi
( )
2 6 ; ;1 2 .D t t t MC+ −
( ) ( ) ( )
3 2 6 4. 5 1 2 1 0D P t t t + + + − + =
( )
1 4; 1;3tD = − − −
Trường hợp 2:
,AB
khác phía với
( )
:Q
Gọi
( )
;y;zMx
thỏa
3.AM BM=−
Suy ra:
( )
( )
( )
2 3 2
5 3 1
3 3 1
xx
yy
zz
− = − +
− = − −
+ = − −
1
2
0
x
y
z
=−
=
=
( )
1;2;0M−
Đường thẳng
MC
qua
( )
2;0;1C
và có VTCP
( )
3; 2;1u MC= = −
.Phương trình
23
:2
1
xt
MC y t
zt
=+
=−
=+
Gọi
( )
2 3 ; 2 ;1 .D t t t MC+ − +
( ) ( ) ( ) ( )
3 2 3 4. 2 5 1 1 0D P t t t + + − + + + =
( )
2 4;4; 1tD = − − −
16.abc=
.
Câu 48: Chọn B
Có
(1;1;1), (2;2;1)AB
Phương trình AB:
1
1
1
xt
yt
z
=+
=+
=
Gọi
K
là giao điểm của
AB
và
( )
P
( )
1; 1;1K −−
Có Mặt cầu
( )
S
tiếp xúc với
( )
P
tại
H
HK
là tiếp tuyến của
( )
S
2
. 12 2 3KH KA KB KH= = =
không đổi
Biết
H
chạy trên 1 đường tròn bán kính
23
không đổi
Câu 49: Chọn A
Đường thẳng d đi qua
( )
Mm−1; 1;
và có một vtcp
(1;1;2)=u
.
Mặt cầu
( )
S
có tâm
( )
I 1;1;2
và bán kính
= 3R
. Gọi
K
là hình chiếu vuông góc của
I
lên
đường thẳng
d
thì
K
cũng là trung điểm
EF
. Khi đó:
2
22
9
4
+ = =
EF
IK R
. Để
EF
lớn nhất thì
IK
nhỏ nhất. Mà
( )
2
[ , ]
2 12
,
6
+
= = =
u IM
m
IK d I d
u
nên
IK
nhỏ nhất khi
0=m
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
302
Câu 50: Chọn B
Ta có
12
12
:
2 1 1
2
xt
x y z
d y t
zt
= − +
+−
= = =
=+
. Do đó
Md
( )
1 2 ; ;2M t t t − + +
.
Vì
( )
1; 1;2A −
là trung điểm
MN
( )
3 2 ; 2 ;2N t t t − − − −
.
Mặt khác
( )
NP
( )
3 2 2 2 2 5 0t t t − − − − − + =
( )
2 3;2;4tM =
( )
2;3;2AM=
là
một vectơ chỉ phương của
.
Câu 51: Chọn D
Gọi
M
là điểm nằm trên đường tròn giao tuyến của
( )
S
và
( )
.P
Ta có
.=IM R
Áp dụng công
thức tính bán kính mặt cầu trong trường hợp mặt cầu
( )
S
giao với mặt phẳng
( )
P
theo giao tuyến
là đường tròn có bán kính
r
là
( )
( )
( )
2 2 2 2
;
*
IP
IM R d r= = +
Ta có:
( )
( )
( )
( )
;
2
22
1 2.2 2. 1 2
3.
1 2 2
− − + − −
= = =
+ − +
IP
d IH
Từ
( )
2 2 2
* 3 5 34R = + =
. Vậy phương trình mặt cầu
( )
S
thỏa mãn yêu cầu đề bài là
( ) ( ) ( )
2 2 2
1 2 1 34.+ + − + + =x y z
Câu 52: Chọn A
Gọi
M
là giao điểm của mặt phẳng
( )
P
và đường thẳng
2
( )
0;0; 1M−
d
P
M
N
A
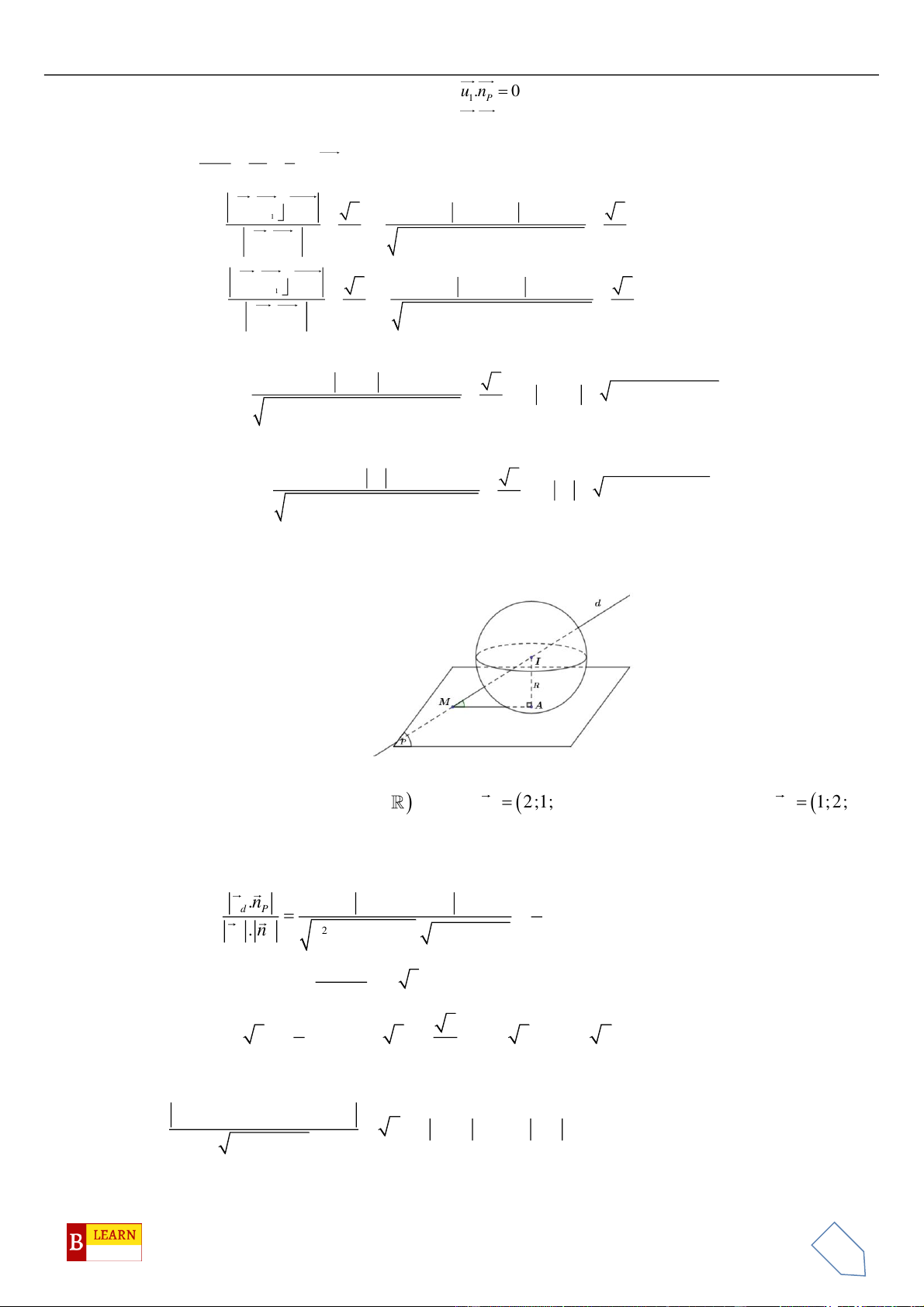
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
303
Do
12
,dd
nằm trong mặt phẳng
( )
P
nên:
( )
( )
1
2
1 0 1
.0
1 0 2
.0
P
P
ab
un
cd
un
+ − =
=
− + =
=
Từ
( ) ( )
1
1
1
: 1; 1;1 , 1;0;0
1 1 1
x y z
uN
−
= = − −
−−
( )
( ) ( ) ( )
( )
1
1
1
11
2 2 2
1
,.
21
66
,3
22
,
11
u u MN
ba
dd
uu
b a b a
−+
= = =
+ + + + −
( )
( ) ( ) ( )
( )
1
1
2
21
2 2 2
2
,.
21
66
,4
22
,
11
u u MN
dc
dd
uu
d c c d
+−
= = =
+ + − + +
Từ
( )
11ba = −
.
Thay vào
( )
3
( ) ( ) ( )
2
2 2 2
33
6
6 6 36 36 36 0 1
2
2 1 1 2
a
a a a a b
a a a
−
= − = − + = =
− + + + −
Từ
( )
21dc = +
Thay vào
( )
4
( ) ( ) ( )
2
2 2 2
3
6
6 36 36 36 1 0
2
2 1 2 1
c
c c c c d
c c c
= = + + = − =
+ + − + +
Vậy
0S a b c d= + + + =
.
Câu 53: Chọn D
Đường thẳng
( )
12
: 1 ,
xt
d y t t
zt
=+
= +
=−
có vtcp
( )
2;1; 1
d
u =−
. Mặt phẳng
( )
P
có vtpt
( )
1;2;1
P
n =
Khi đó: Góc giữa đường thẳng
d
và mặt phẳng
( )
P
là
IMA
( )
2
2 2 2 2 2
. 2.1 1.2 1.1
1
sin 30
.2
2 1 1 . 1 2 1
dP
dP
un
IMA IMA
un
+−
= = = =
+ + − + +
.
Ta có:
3
tan30
IA
IA R MA R= = =
.
Mà
2
13
3 3 . 3 3 3 3 6
22
IAM
S IAMA R R
= = = =
.
Mặt khác:
( )
1 2 ;1 ;I t t t d+ + −
và
( )
( )
,d I P R=
( ) ( )
( ) ( )
( )
2 2 2
1 2 2 1 6
3 7;4; 3
6 3 3 6 1 2
1 1;0;1
1 2 1
t t t
t I L
tt
tI
+ + + + − −
= −
= − = − =
= − −
++
1, 0, 1a b c = − = =
. Vậy
0T a b c= + + =
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
304
Câu 54: Chọn C
Từ giả thiết ta có mặt cầu tâm
( )
0;0; 2 , 1IR−=
. Tính được
6AI R=
, suy ra
A
nằm ngoài mặt
cầu. Gọi
là đường thẳng đi qua
A
và cắt mặt cầu tại hai điểm
,BC
.
Xét mặt phẳng
( )
,AI
cắt mặt cầu theo giao tuyến là đường tròn
( )
C
.
Ta chứng minh
22
.AB AC AI R=−
.
Thật vậy, gọi là điểm
D
đối xứng với
C
qua
I
, ta có
DB AC⊥
.
Ta có
( )
. . . . . .AB AC AB AC AD DB AC AD AC DB AC AD AC= = + = + =
( )
1
.
Mặt khác
( ) ( ) ( ) ( )
22
22
. . .AD AC AI ID AI IC AI ID AI ID AI ID AI R= + + = + − = − = −
( )
2
.
Từ
( )
1
và
( )
2
suy ra
22
. 35AB AC AI R= − =
( )
3
.
Theo giả thiết và
( )
3
ta có
12 5 7
. 35 7 5
AB AC AB AB
AB AC AC AC
+ = = =
= = =
.
Suy ra
22BC AC AB R= − = =
.
Từ trên suy ra
đi qua tâm
I
, như vậy có 1 đường thẳng thỏa mãn bài toán.
Câu 55: Chọn B
Giả sử mặt cầu cố định tiếp xúc với mặt phẳng
( )
P
có dạng
( ) ( ) ( )
2 2 2
2
x a y b z c R− + − + − =
với
0R
.
Vì mặt cầu tiếp xúc với mặt phẳng
( )
( ) ( )
22
:2 1 1 10 0P mx m y m z+ + + − − =
và đi qua điểm
( )
2;11; 5A −
nên
( ) ( ) ( ) ( )
( )
( )
( ) ( )
( ) ( )
( )
2 2 2
2
22
22
2 2 2
2 11 5 1
2 1 1 10
;2
4 1 1
a b c R
ma m b m c
d I P R
m m m
− + − + − − =
+ + + − −
==
+ + + −
( ) ( )
( )
( )
( )
22
2
2
2 2 10 2. 1
2 2 10 2 0
2 2 10 2 0
m b c ma b c R m
m b c R ma b c R
m b c R ma b c R
+ + + − − = +
+ − + + − − − =
+ + + + − − + =
Trường hợp 1:
( )
2
2 2 10 2 0m b c R ma b c R+ − + + − − − =

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
305
Vì với mọi
m
tồn tại hai mặt cầu cố định tiếp xúc với mặt phẳng
( )
P
nên
0
2 0 0
2 0 2 5
10 0
10 2 0 2 5
a
b c R a
a b c R c
b c b c
b c R b R
=
+ − = =
= + = = −
− − − − =
− − − = = +
.
Khi đó
( )
( )
2
22
1 4 6 2 12 2 40 0R R R R + − = − + =
.
Vậy tổng bán kính của 2 mặt cầu là
12 2
.
Trường hợp 2:
( )
2
2 2 10 2 0m b c R ma b c R+ + + + − − + =
Vì với mọi
m
tồn tại hai mặt cầu cố định tiếp xúc với mặt phẳng
( )
P
nên
0
2 0 0
2 0 2 5
10 0
10 2 0 5 2
a
b c R a
a b c R c
b c b c
b c R b R
=
+ + = =
= + = − = −
− − − − =
− − + = = −
Khi đó
( )
( )
2
22
1 4 6 2 12 2 40 0 10 2 2 2R R R R R R + + = + + = = − = −
.
Vậy tổng bán kính của 2 mặt cầu là
12 2
.
Câu 56: Chọn C
Giả sử mặt cầu
( )
S
có tâm
( )
IC
và tiếp xúc với ba đường thẳng
,,MN NP PM
.
Gọi
H
là hình chiếu vuông góc của
I
trên
( )
MNP
.
Ta có:
( )
S
tiếp xúc với ba đường thẳng
,,MN NP PM
( ) ( ) ( )
, , ,d I MN d I NP d I PM = =
( ) ( ) ( )
, , ,d H MN d H NP d H PM = =
H
là tâm đường tròn nội tiếp hoặc tâm đường tròn bàng tiếp của tam giác
MNP
.
( )
MNP
có phương trình là
1
6 6 6
x y z
+ + =
hay
60x y z+ + − =
.
( ) ( ) ( )
12
C S S=
Tọa độ các điểm thuộc trên
( )
C
thỏa mãn hệ phương trình:
2 2 2
2 2 2
2 2 1 0
8 2 2 1 0
x y z x y
x y z x y z
+ + − − + =
+ + − + + + =
3 2 0x y z − − =
.
Do đó, phương trình chứa mặt phẳng chứa
( )
C
là
( )
:3 2 0x y z
− − =
.
Vì
( ) ( )
1.3 1. 2 1. 1 0+ − + − =
( ) ( )
MNP
⊥
.
( )
1
. Có:
62MN NP PM= = =
MNP
đều.
Gọi
G
là trọng tâm tam giác
MNP
( )
2;2;2G
và
G
là tâm đường tròn nội tiếp tam giác
MNP
. Thay tọa độ của điểm
G
vào phương trình mặt phẳng
( )
, ta có:
( )
G
.
Gọi
là đường thẳng vuông góc với
( )
MNP
tại
G
.Vì
( ) ( )
( )
MNP
G
⊥
( )
.
Khi đó:
I
( ) ( )
,,d I MN d I NP=
( )
,d I PM r==
Mặt cầu tâm
I
bán kính
r
tiếp xúc với ba đường thẳng
MN
,
NP
,
PM
.
Vậy có vô số mặt cầu có tâm thuộc mặt phẳng chứa
( )
C
và tiếp xúc với ba đường thẳng
,,MN MP PM
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
306
Câu 57: Chọn B
Do
d
là hình chiếu của
d
lên mặt phẳng
( )
P
khi đó
d
là giao tuyến của mặt phẳng
( )
P
và mặt
phẳng
( )
chứa
d
và vuông góc với mặt phẳng
( )
P
.
một vec tơ pháp tuyến của mặt phẳng
( )
là
( )
( )
, 3;2; 1
dP
n u n
= = − −
.
Phương trình mặt phẳng
( )
đi qua
( )
2;0;2A −
và có một vec tơ pháp tuyến
( )
( )
3;2; 1n
= − −
là
3 2 4 0x y z− + + =
.
Do
là hình chiếu của
lên mặt phẳng
( )
P
khi đó
là giao tuyến của mặt phẳng
( )
P
và mặt
phẳng
( )
chứa
và vuông góc với mặt phẳng
( )
P
.
một vec tơ pháp tuyến của mặt phẳng
( )
là
( )
( )
, 0; 2; 2
P
n u n
= = − −
.
Phương trình mặt phẳng
( )
đi qua
( )
3;1;4B
và có một vec tơ pháp tuyến
( )
( )
0; 2; 2n
= − −
là
50yz+ − =
.
Tọa độ điểm
M
là nghiệm của hệ phương trình
2 0 1
3 2 4 0 2
5 0 3
x y z x
x y z y
y z z
+ − + = = −
− + + = =
+ − = =
.
Vậy
( )
1;2;3M −
. 1 2.3 5a bc + = − + =
.
Câu 58: Chọn C
Đường thẳng AB đi qua điểm
( )
2;0;0A
và có VTCP
( )
1;1; 1AB =−
có dạng:
( )
2
:
xt
AB y t t
zt
=+
= +
=−
.
( )
S
có tâm
( )
0;1; 1I −
và bán kính
1R=
.
( )
.
IT AB
ITT AB
IT AB
⊥
⊥
⊥
Gọi
( )
.0IK AB
K ITT AB
K AB
=
=
.
( ) ( )
2 ; ; , 2 ; 1; 1K t t t AB IK t t t+ − = + − − +
,
. 2 1 1 0 0IK AB t t t t K A= + + − + − = =
.
Ta có,
( )
2
22
2 1 1 6IA= + − + =
,
IA TT
⊥
và
;;I A H
thẳng hàng. Mặt khác,
IAT
vuông tại
T
nên theo hệ thức lượng
2
1
6
IT
IH
IA
==
1 6 1 1 1 1 5 5
; ; ; ;
3 6 6 3 6 6
6
IH
IH IA IA H
IA
= = = − −
.
Vậy
1
2.
2
a b c+ + =−
Câu 59: Chọn C
Ta có:
( )
( )
1; 1;2
:.
3
I
S
R
−
=
Khi đó
5IM R=
M
nằm ngoài mặt cầu.
Tâm
( )
;;J a b c
nằm trên
( )
1
: 1 4
23
x
MI y t t
zt
=
= − +
=−
nên
( )
1; 1 4t;2 3tJ − + −
.
J
K
I
M
H
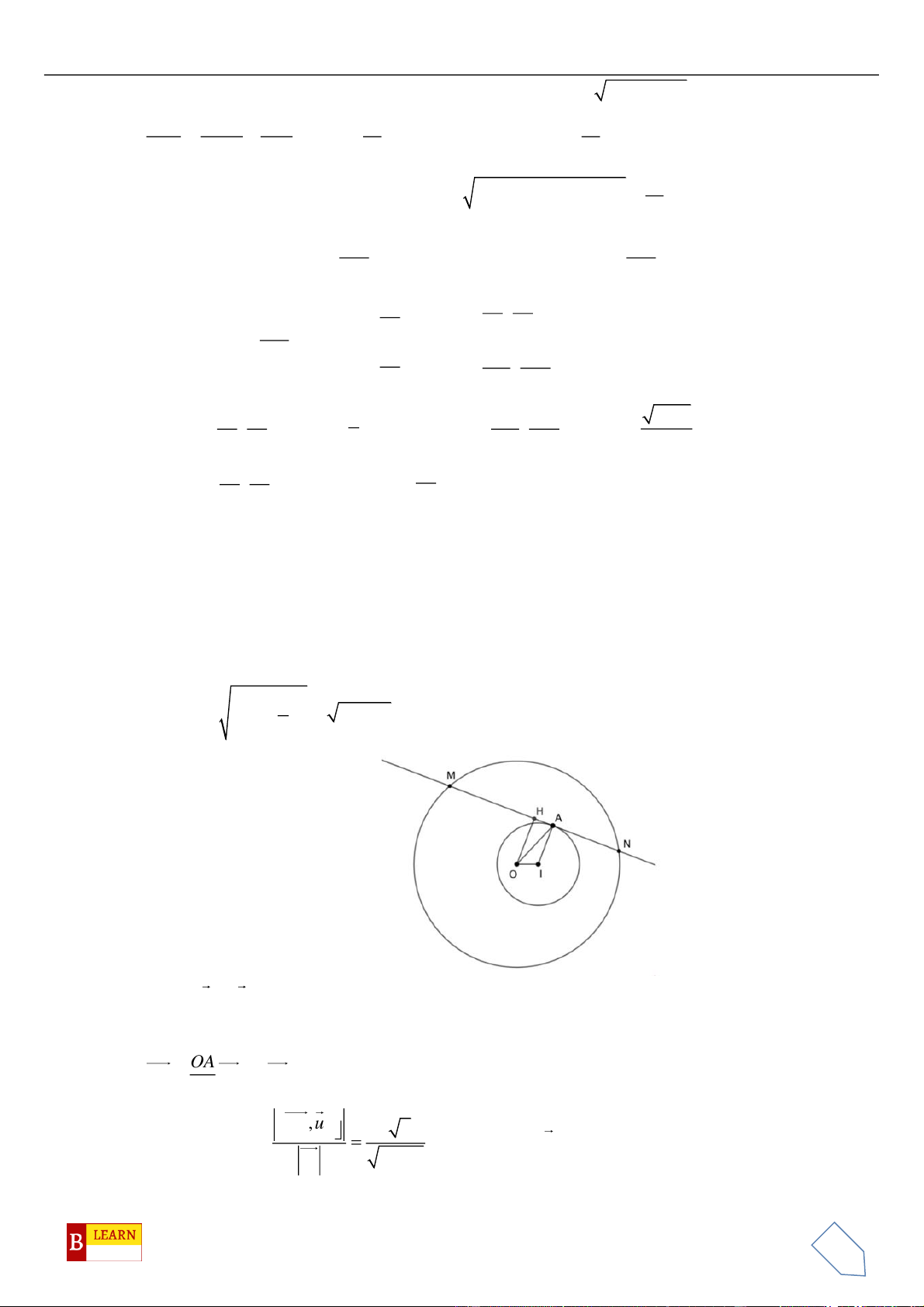
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
307
Xét tam giác
MHI
vuông tại
H
có:
5; 3MI IH==
22
4MH MI HI = − =
.
2 2 2
1 1 1 12
5
HJ
HJ HM HI
= + =
.
2
16
.
5
MJ MI MH MJ= =
.
Mặt khác,
( )
( )
1;3; 1
1; 1 4t;2 3t
M
J
−
− + −
( ) ( )
22
16
4 4 3 3
5
MJ t t = − + + − =
.
( ) ( )
22
256
4 4 3 3
25
tt − + + − =
22
256
16 32 16 9 18 9
25
t t t t − + + − + =
2
369
25 50 0
25
tt − + =
9
25
41
25
t
t
=
=
11 23
1; ;
25 25
139 73
1; ;
25 25
J
J
−
.
Với
11 23
1; ;
25 25
J
thì
9
5
IJ IM=
. Với
139 73
1; ;
25 25
J
−
thì
1097
5
IJ IM=
.
Vậy
11 23
1; ;
25 25
J
nên:
84
2
25
abc+ + =
.
Câu 60: Chọn C
Hai mặt cầu , có tâm lần lượt là là gốc toạ độ O, điểm I và bán kính lần lượt là
12
5; 2RR==
.
Gọi A là tiếp điểm của d và , ta có IA = R2 = 2.
Vì d cắt
( )
1
S
theo một đoạn thẳng có độ dài bằng 8 nên
2
2
1
8
(O;d) 25 16 3.
2
dR
= − = − =
Vì
(1;1; ),
d
d u u x⊥ =
ta có:
( , ) 1 2 OA 3 , ,OI IA OA d O d O I A+ → +
thẳng hàng.
3 (0;0;3) (0;0;3).
OA
OA OI OI A
OI
= = =
Do đó
2
,
32
( ; ) 3 0 (1;1;0).
2
d
d
d
OA u
d O d x u
u
x
= = = = =
+
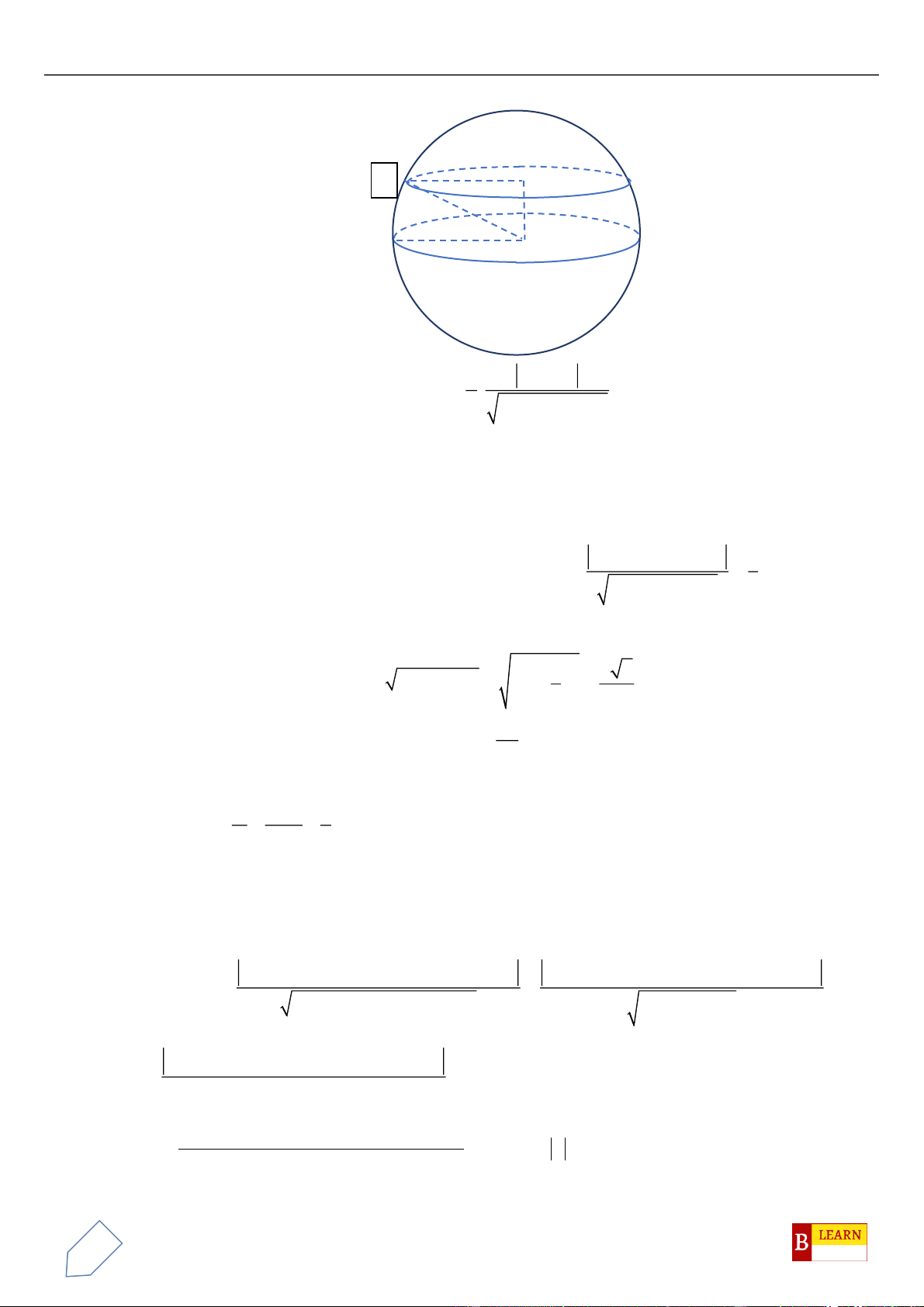
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
308
Câu 61: Chọn D
Bán kính mặt cầu
( )
S
:
( ) ( )
( )
( )
( )
2
22
51
1
, . 1
2
2 1 2
R d P Q
−−
= = =
+ − +
Tâm
I
của mặt cầu
( )
S
nằm trên mặt phẳng
( )
R
cách đều
( )
P
và
( )
.Q
Phương trình mặt phẳng
( )
: 2 2 2 0R x y z− + + =
Tâm
I
của mặt cầu
( )
S
nằm trên mặt cầu
( )
'
S
có tâm
A
bán kính
1R IA==
Gọi
K
là hình chiếu của
A
trên
( )
R
( )
( )
( )
( )
2
22
2. 1 1 2.1 2
1
,
3
2 1 2
AK d A R
− − + +
= = =
+ − +
Tâm
I
của mặt cầu
( )
S
nằm trên đường tròn
( )
C
là giao của mặt cầu
( )
'
S
và mặt phẳng
( )
R
có tâm
K
và bán kính
2
2 2 2
1 2 2
1
33
r KI AI AK
= = − = − =
Diện tích hình tròn giới hạn bởi
( )
C
là:
2
8
9
r
=
.
Câu 62: ChọnC
Ta có
( ) ( )
22
: 1 0 :(1 ) ( ) 0.
11
x y z
m x my m m z m m
mm
+ + − = − + + − − + =
−
Gọi
( )
0 0 0
;;I x y z
là tâm,
R
là bán kính mặt cầu tiếp xúc đồng thời với cả hai mặt phẳng
( ) ( )
,
. Khi đó:
( )
( )
( )
( )
,,R d I d I==
.
( )
( )
( )
2 2 2 2
0 0 0 0 0 0
2 2 2 2 2
2
(1 ) ( ) (1 ) ( )
,
(1 ) ( )
1
m x my m m z m m m x my m m z m m
dI
m m m m
mm
− + + − − + − + + − − +
==
− + + −
−+
22
0 0 0
2
(1 ) ( )
1
m x my m m z m m
mm
− + + − − +
=
−+
Đặt
( )
( )
22
0 0 0
2
1
1
m x my m m z m m
k R k
mm
− + + − − +
= =
−+
Ta cần tìm
( )
0 0 0
;;x y z
sao cho
A
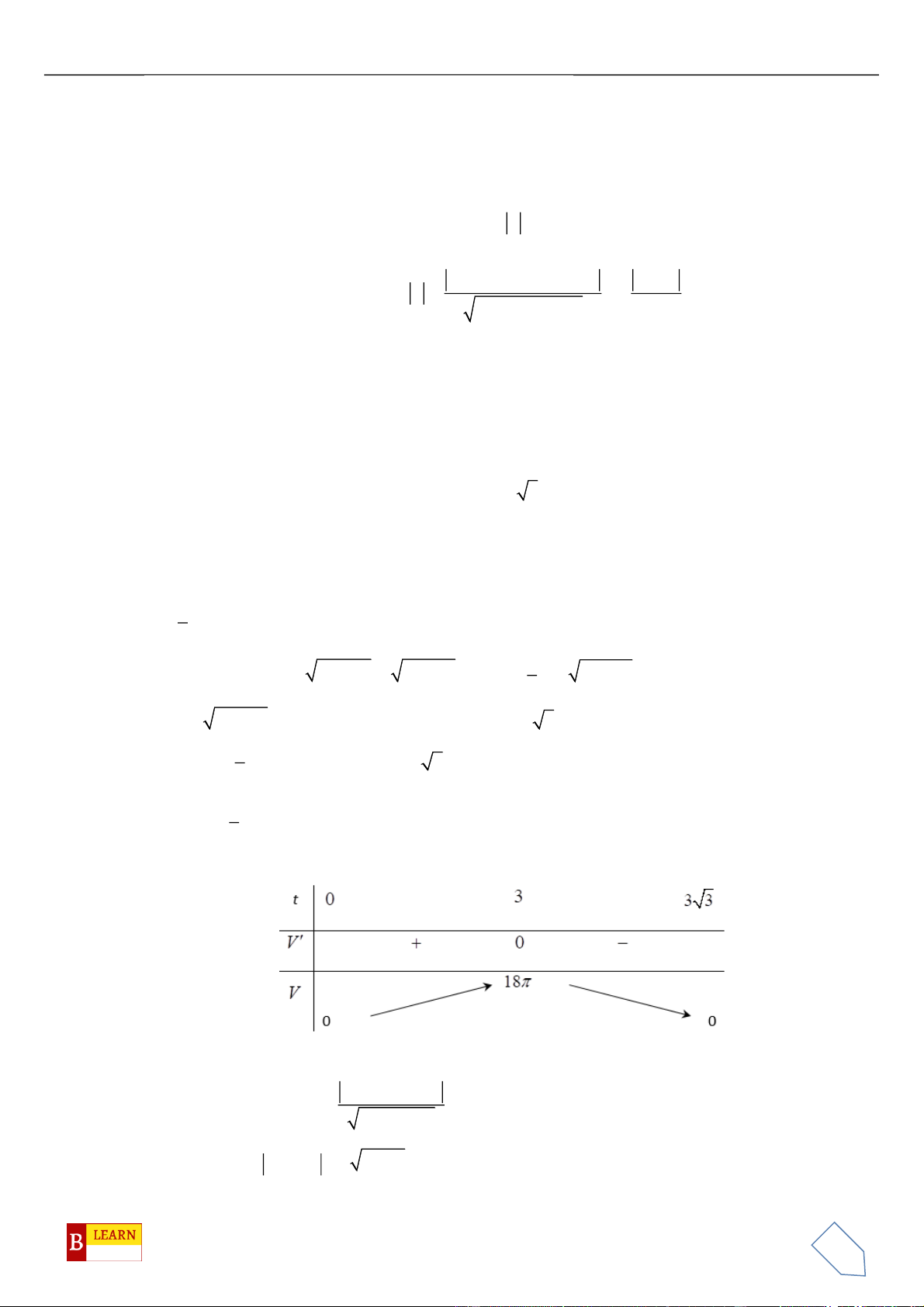
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
309
2 2 2
0 0 0
(1 ) ( ) ( 1),m x my m m z m m k m m m− + + − − + = − +
( ) ( )
22
0 0 0 0 0
1 1 ,z m x y z m x km km k m − + − + + − + = − +
( )
00
0 0 0 0
00
1
; ;1
1
1
z k x k
I k k k
x y z k y k
Rk
x k z k
− = =
−
− + + − = − =
=
= = −
Khi đó:
2 2 2
2 2(1 ) 10 12
(I,( )) (I,( ))
3
2 ( 1) 2
k k k k
R d d k
− + − + −
= = =
+ − +
( )
11
2
2
( 6; 6;7), 6
12 3 6
.
3;3; 2 , 3
12 3 3
IR
k k k
IR
k k k
− − =
− = − = −
−=
− = =
Tổng bán kính của hai mặt cầu bằng
6 3 9.+=
Câu 63: Chọn D
Mặt cầu
()S
có tâm
( )
1; 2;3I −
và bán kính
33R =
.
Vì
()
đi qua 2 điểm
(0;0; 4)A −
,
(2;0;0)B
nên ta có
.0 .0 4 0 4
.2 .0 0 0 2
a b d d
a b d a
+ + + = = −
+ − + = =
.
Gọi
r
,
h
lần lượt là bán kính đáy và chiều cao của khối nón. Khi đó thể tích của khối nón là
2
1
3
V r h
=
.
Ta có
2 2 2
( ,( )) 27h d I R r r
= = − = −
22
1
27
3
V r r
=−
.
Đặt
2 2 2
27 27t r r t= − = −
, điều kiện:
0 3 3t
.
Khi đó
( )
2
1
27
3
V t t
=−
,
( )
0 3 3t
.
Ta có
( )
( )
( )
2
3
1
27 3 0
3
3
tn
Vt
tl
=
= − =
=−
.
Bảng biến thiên:
Thể tích khối nón lớn nhất khi
2
3 18 3t r h= = =
.
Mặt khác
( )
22
23
,( ) 3
1
a b d
h d I
ab
− − +
= = =
++
Mà
22
2
2 5 3 5 4 4 0 2
4
a
b b b b b
d
=
− − = + − + = =
=−
.
Vậy
2 2 4 4P a b d= − − = − + =
.
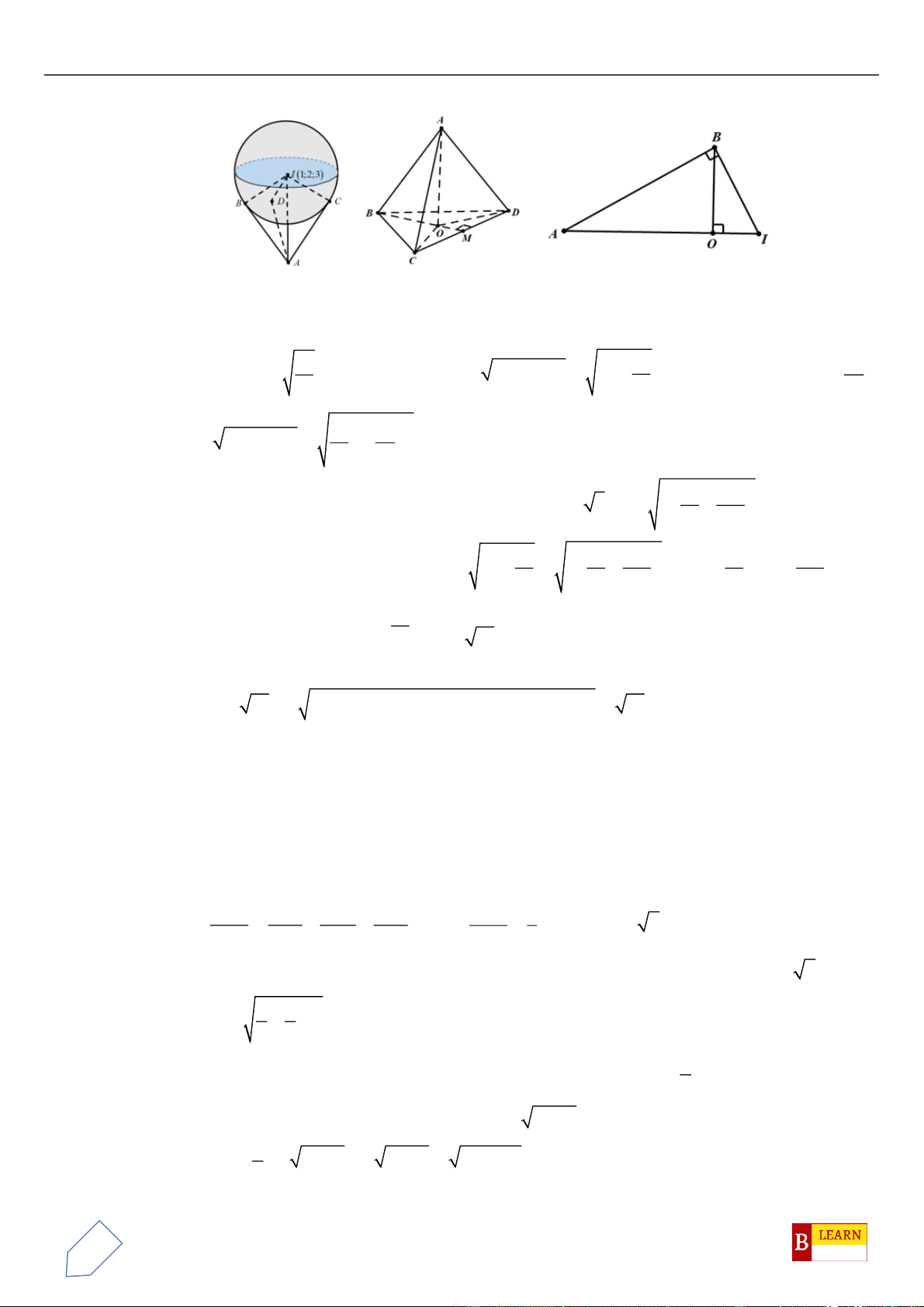
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
310
Câu 64: Chọn C
Gọi
I
là tâm của mặt cầu
( )
1;2;3I
. Gọi
O
là giao điểm của mặt phẳng
( )
BCD
và đoạn
AI
.
Khi đó
O
là tâm đường tròn ngoại tiếp tam giác
BCD
.
Đặt
14
3
AI x x
=
. Ta có
2 2 2
14
3
AB AI IB x= − = −
,
2
14
.
3
IB IO IA IO
x
= =
2
22
14 14
33
OB IB IO
x
= − = −
2 2 2 2
2
14 196
2 . .cos120 3 3 3
39
BD OB OD OB OD OB BD OB
x
= + − = = = −
Do
ABCD
là tứ diện đều nên
22
22
14 14 196 14 196
3 14
3 3 9 3 3
AB BD x x
xx
= − = − − = −
2
42
2
14
3 56 196 0 14
3
14
x
x x x
x
=
− + = =
=
. Gọi tọa độ điểm
( )
4 3 ;4 2 ;4A t t t+ + +
.
Suy ra
( ) ( ) ( )
2 2 2
14 4 3 1 4 2 2 4 3 14AI t t t= + − + + − + + − =
2
0
14 28 14 14
2
t
tt
t
=
+ + =
=−
( )
( )
4;4;4
2;0;2
A
A
−
Do
0
0x
nên điểm
A
có tọa độ
( )
4;4;4A
12P=
.
Câu 65: Chọn D
Gọi
H
là hình chiếu vuông góc của điểm
O
trên mặt phẳng
( )
PQR
.
Dễ thấy
2 2 2 2
1 1 1 1
OH OP OQ OR
= + +
suy ra
2
11
8OH
=
hay
22OH =
.
Khi đó suy ra mặt phẳng
( )
PQR
luôn tiếp xúc với mặt cầu
( )
S
tâm
O
, bán kính
22R =
.
Ta có
13
01
44
OM R= + + =
nên điểm
M
nằm trong mặt cầu
( )
S
.
Gọi
I
là trung điểm của
AB
, do tam giác
OAB
cân tại
O
nên
1
.
2
OAB
S OI AB
=
.
Đặt
OI x=
, vì
OI OM
nên
01x
và
2
28AB x=−
.
Ta có
2 2 2 4
1
.2 8 8 8
2
OAB
S x x x x x x
= − = − = −
.
Xét hàm số
( )
24
8f x x x=−
với
01x
.
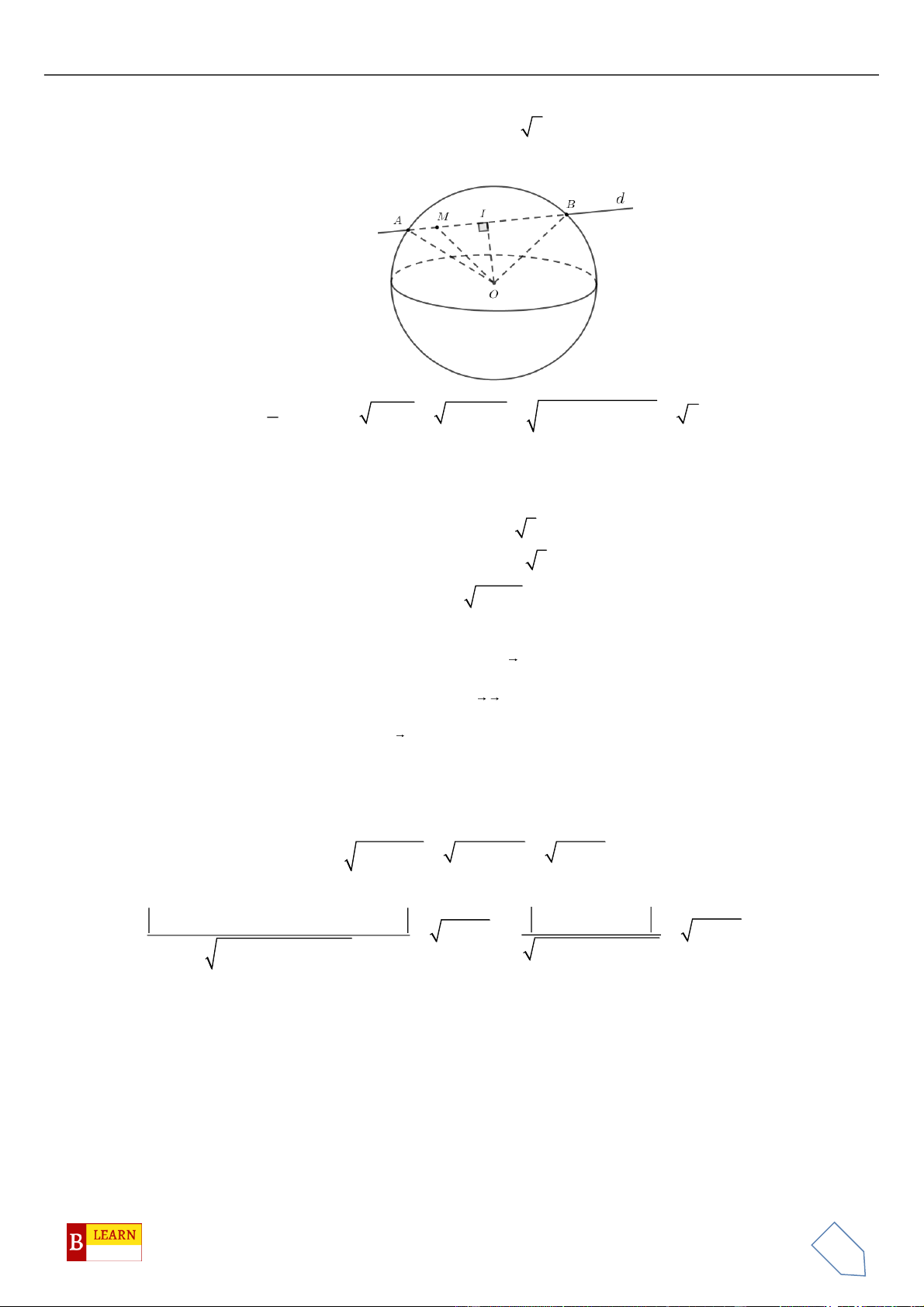
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
311
Có
( )
( )
32
16 4 4 4 0f x x x x x
= − = −
với mọi
(
0;1x
( ) ( )
17f x f=
.
Suy ra diện tích của tam giác
OAB
lớn nhất bằng
7
đạt được khi
M
là trung điểm của
AB
.
Cách 2.
( )
2 2 4 2 2 2
1
. 8 8 7 1 7
2
OAB
S OI AB x x x x x x x
= = − = − = + −
với
(
0;1x
.
Câu 66: Chọn D
Điều kiện của
m
để
( )
S
là phương trình mặt cầu là
( ) ( )
( )
22
22
3
2 1 2 8 0
3
m
m m m m
m
+ − + + − + +
−
Mặt cầu
( )
S
có tâm
( )
2; ; 1I m m−+
,
2
3Rm=−
Gọi
( )
P
là mặt phẳng chứa Δ và cắt
( )
S
theo giao tuyến là một đường tròn
( )
C
có bán kính
( )
1
C
R =
thì mặt phẳng
( )
P
có véctơ pháp tuyến
( )
;;n a b c=
với
( )
22
0abc+ +
.
Vì mặt phẳng
( )
P
chứa đưởng thẳng
Δ nên
.0nu
=
30a b c + − =
( )
3 ; ; 3c a b n a b a b = + = +
Mặt khác
( ) ( )
3;1;2AP
( ) ( ) ( ) ( )( )
: 3 1 3 2 0P a x b y a b z − + − + + − =
Hay
( ) ( )
: 3 5 7 0.P ax by a b z a b+ + + − − =
Theo giả thiết
( )
( )
( )
2 2 2 2
, 3 1 4
C
d I P R R m m= − = − − = −
Vậy có điều kiện:
( )( )
( )
2
2
22
2 3 1 5 7
4
3
a bm a b m a b
m
a b a b
− + + + − −
=−
+ + +
( )( )
2
22
22
4
2 10 6
m a b
m
a b ab
−+
= −
++
▪ Nếu
2m =
đẳng thức luôn đúng, tức vô số mặt phẳng.
▪ Nếu
2m
ta có
( )( ) ( )
( )
2
22
2 2 2 2 10 6m a b m a b ab− + = + + +
( ) ( ) ( )
22
6 2 10 6 28 0m a m ab m b + + + + + =
▪ Nếu
2
6 8 8 0m ab b= − − =
0
ab
b
=
=
có hai mặt phẳng.
▪ Nếu
6m −
, điều kiện là
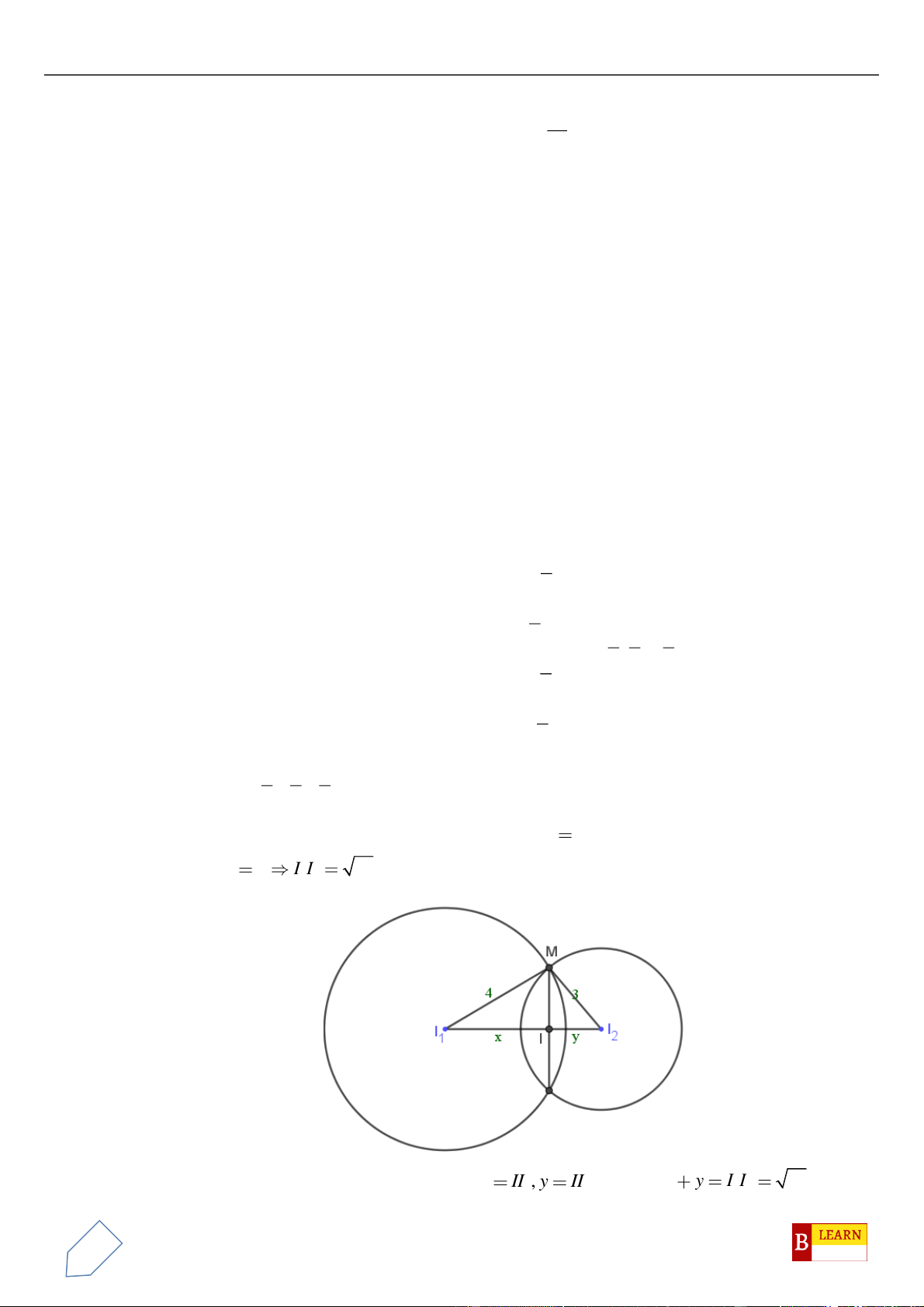
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
312
( ) ( )( )
2
2
0 10 6 6 28 0
34
5
a
m
m m m
m
=−
= + − + + =
=−
.
Vậy có hai giá trị thực của tham số
m
thoả mãn.
Câu 67: Chọn D
Cch 1: Mặt cầu
1
()S
có tâm là
1
(1;1;2)I
Xét hệ phương trình:
2 2 2
2 2 2
2 2 2
2 2 2
( 1) ( 1) ( 2) 16
2 2 4 10 0 (1)
2 4 2 3 0 (2)
( 1) ( 2) ( 1) 9
x y z
x y z x y z
x y z x y z
x y z
− + − + − =
+ + − − − − =
+ + + − + − =
+ + − + + =
Lấy trừ ta được:
4 2 6 7 0 ( )x y z P− + + =
đường tròn tâm
I
thuộc mặt phẳng
()P
.
Gọi
d
là đường thẳng đi qua
1
I
và vuông góc với mặt phẳng
()P
.
Phương trình đường thẳng
d
là:
12
1
23
xt
yt
zt
=+
=−
=+
. Khi đó,
()I d P=
.
Xét hệ phương trình:
1
2
4 2 6 7 0
7
12
1 7 1
4
( ; ; )
11
2 4 4
4
23
3
4
x
x y z
y
xt
I
yt
z
zt
t
=−
− + + =
=
=+
− −
=−
=−
=+
=−
1 7 1
1
2 4 4
abc + + = − + − =
.
Cch 2: Mặt cầu
1
()S
có tâm là
1
(1;1;2)I
, bán kính
R
1
4
; mặt cầu
2
()S
có tâm là
2
( 1;2; 1)I −−
bán kính
R
2
3
II
12
14
Giả sử
M
là điểm thuộc đường tròn tâm
I
,
,x II y II
12
. Khi đó,
x y I I
12
14
và

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
313
( )( )x y x y x y x y x y
2 2 2 2 2 2
14
4 3 7 7
2
xy
x
xy
14
3 14
14
4
2
.( )
.
.( )
II
II
II
xx
I I I I y y
zz
1 1 2
31
12
42
3 3 7
11
4 4 4
31
23
44
1 7 1
1
2 4 4
abc + + = − + − =
.
Câu 68: Chọn B
Ta có: Mặt cầu
( )
S
có tâm
( )
2;3;5I
, bán kính
10R =
.
( )
( )
( )
2
22
2.2 2.3 5 15
,6
2 2 1
d I R
− + +
= =
+ − +
( ) ( ) ( )
;S C H r
=
,
H
là hình chiếu của
I
lên
( )
.
Gọi
1
là đường thẳng qua
I
và vuông góc với
( )
1
có VTCP là
( )
1
2; 2;1u
=−
.
PTTS
1
22
: 3 2
5
xt
yt
zt
=+
= −
=+
. Tọa độ
H
là nghiệm của hệ:
22
32
5
2 2 15 0
xt
yt
zt
x y z
=+
=−
=+
− + + =
2
7
3
x
y
z
=−
=
=
( )
2;7;3H−
.
Ta có
AB
có độ dài lớn nhất
AB
là đường kính của
( )
C
MH
.
Đường thẳng
MH
đi qua
( )
3;3; 3M −−
và có VTCP
( )
1;4;6MH =
.
Suy ra phương trình
3 3 3
:.
1 4 6
x y z+ − +
= =

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
314
DẠNG 7. CỰC TRỊ LIÊN QUAN ĐẾN ĐƯỜNG THẲNG
Câu 1: Trong không gian với hệ tọa độ
Oxyz
cho điểm
( )
2; 1; 2A −−
và đường thẳng
( )
d
có phương
trình
1 1 1
1 1 1
x y z− − −
==
−
. Gọi
( )
P
là mặt phẳng đi qua điểm
A
, song song với đường thẳng
( )
d
và khoảng cách từ
d
tới mặt phẳng
( )
P
là lớn nhất. Khi đó mặt phẳng
( )
P
vuông góc với mặt
phẳng nào sau đây?
A.
60xy− − =
. B.
3 2 10 0x y z+ + + =
.
C.
2 3 1 0x y z− − − =
. D.
3 2 0xz+ + =
.
Câu 2: Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
( )
2; 2;1 ,M −−
( )
1;2; 3A −
và đường thẳng
15
:
2 2 1
x y z
d
+−
==
−
. Tìm một vectơ chỉ phương
u
của đường thẳng
đi qua
M
, vuông góc với đường thẳng
d
đồng thời cách điểm
A
một khoảng bé nhất.
A.
( )
2;2; 1u =−
. B.
( )
1;7; 1u =−
. C.
( )
1;0;2u =
. D.
( )
3;4; 4u =−
.
Câu 3: Trong không gian với hệ toạ độ
Oxyz
, gọi
( )
P
là mặt phẳng đi qua hai điểm
( )
1; 7; 8A −−
,
( )
2; 5; 9B −−
sao cho khoảng cách từ điểm
( )
7; 1; 2M −−
đến
( )
P
đạt giá trị lớn nhất. Biết
( )
P
có một véctơ pháp tuyến là
( )
; ;4n a b=
, khi đó giá trị của tổng
ab+
là
A.
1−
. B.
3
. C.
6
. D.
2
.
Câu 4: Trong không gian với hệ tọa độ
Oxyz
, cho điểm
( )
3; 1;0A −
và đường thẳng
2 1 1
:
1 2 1
x y z
d
− + −
==
−
. Mặt phẳng
( )
chứa
d
sao cho khoảng cách từ
A
đến
( )
lớn nhất có
phương trình là
A.
20x y z+ − − =
. B.
0x y z+ − =
. C.
10x y z+ − + =
. D.
2 5 0x y z− + + + =
.
Câu 5: 4 Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
( )
3;0;1A −
,
( )
1; 1;3B −
và mặt phẳng
( )
: 2 2 5 0P x y z− + − =
. Viết phương trình chính tắc của đường thẳng
d
đi qua
A
, song song
với mặt phẳng
( )
P
sao cho khoảng cách từ
B
đến
d
nhỏ nhất.
A.
31
:
26 11 2
x y z
d
+−
==
−
. B.
31
:
26 11 2
x y z
d
+−
==
−
.
C.
31
:
26 11 2
x y z
d
+−
==
. D.
31
:
26 11 2
x y z
d
+−
==
−−
.
Câu 6: Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
d
có phương trình
12
1
xt
yt
zt
= − −
=
=+
và điểm
( )
1;2;3A
. Mặt phẳng
( )
P
chứa
d
sao cho
( )
( )
,d A P
lớn nhất. Khi đó tọa độ vectơ pháp tuyến
của mặt phẳng
( )
P
là
A.
( )
1;1;1
. B.
( )
1;2;3
. C.
( )
1; 1;1−
. D.
( )
0;1;1
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
315
Câu 7: Trong không gian với hệ tọa độ
Oxyz
cho hai mặt phẳng
( ): 2 2 1 0,P x y z+ − + =
( ): ( 1) 2019 0Q x my m z+ + − + =
. Khi hai mặt phẳng
( )
P
,
( )
Q
tạo với nhau một góc nhỏ nhất thì
mặt phẳng
( )
Q
đi qua điểm
M
nào sau đây?
A.
( )
2019; 1;1M −
. B.
( )
0; 2019;0M −
. C.
( )
2019;1;1M −
. D.
( )
0;0; 2019M −
.
Câu 8: Viết phương trình đường thẳng
a
đi qua
( )
4; 2; 1M −
, song song với mặt phẳng
( ):3 4 12 0x y z− + − =
và cách
( )
2; 5; 0A −
một khoảng lớn nhất.
A.
4
2
1
xt
yt
zt
=−
= − +
=+
. B.
4
2
1
xt
yt
zt
=+
= − −
= − +
. C.
14
12
1
xt
yt
zt
=+
=−
= − +
. D.
4
2
1
xt
yt
zt
=+
= − +
=+
.
Câu 9: Trong không gian
Oxyz
cho mặt cầu
( )
S
có phương trình
2 2 2
4 2 2 3 0x y z x y z+ + − + − − =
và
điểm
( )
5;3; 2A −
. Một đường thẳng
d
thay đổi luôn đi qua
A
và luôn cắt mặt cầu tại hai điểm
phân biệt
,.MN
Tính giá trị nhỏ nhất của biểu thức
4.S AM AN=+
A.
min
30S =
. B.
min
20S =
. C.
min
34 3S =−
. D.
min
5 34 9S =−
.
Câu 10: Trong không gian
Oxyz
, cho tam giác nhọn
ABC
có đường phân giác trong góc
A
song song
với đường thẳng
( )
2
:1
4
x
d y t
zt
=
= − +
=−
. Đường thẳng
AC
có một véctơ chỉ phương
( )
1
1;2; 1u =−
. Biết
đường thẳng
AB
có một véctơ chỉ phương
( )
2
;;u a b c=
với
,,abc
. Biểu thức
2 2 2
P a b c= + +
có giá trị nhỏ nhất bằng
A.
10
. B.
6
. C.
2
. D.
14
.
Câu 11: Trong không gian với hệ tọa độ
Oxyz
cho hai điểm
( )
2; 2;4A −
,
( )
3;3; 1B −−
và đường thẳng
52
:
2 1 1
x y z
d
−−
==
−−
. Xét
M
là điểm thay đổi thuộc
d
, giá trị nhỏ nhất của
22
23MA MB+
bằng
A.
14
. B.
160
. C.
4 10
. D.
18
.
Câu 12: Trong không gian với hệ trục tọa độ
()Oxyz
cho ba điểm
(1;0;3)A
;
( 3;1;3)B
;
(1;5;1)C
. Gọi
( ; ; )
o o o
M x y z
thuộc mặt phẳng tọa độ
()Oxy
sao cho biểu thức
2T MA MB MC
có giá trị
nhỏ nhất. Khi đó tính giá trị
oo
xy
?
A.
8
5
oo
xy
. B.
8
5
oo
xy
. C.
2
oo
xy
. D.
2
oo
xy
.
Câu 13: Trong không gian
Oxyz
, cho đường thẳng
35
:2
22
xy
dz
−−
= = +
và hai điểm
( )
4;3;0A
,
( )
1;9;3B
. Điểm
( )
;;M a b c
nằm trên
d
sao cho
MA MB+
nhỏ nhất. Khi đó, tổng
abc++
thuộc khoảng nào dưới đây:
A.
( )
9;10
. B.
( )
4;5
. C.
( )
2;3
. D.
( )
7;8
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
316
Câu 14: Trong không gian
Oxyz
cho hai điểm
( ) ( )
2; 2;1 , 1;2; 3AB− − −
và đường thẳng
15
:
2 2 1
x y z+−
= =
−
. Tìm véctơ chỉ phương của đường thẳng
d
đi qua
A
vuông góc với đường
thẳng
đồng thời cách điểm
B
một khoảng cách bé nhất.
A.
( )
2;2; 1u −
. B.
( )
1;0;2u
. C.
( )
2;1;6u
. D.
( )
25; 29; 6u −−
.
Câu 15: Trong không gian
,Oxyz
cho đường thẳng
21
:
1 2 1
x y z
d
−+
==
−
và điểm
( )
2;1;2A
. Gọi
là
đường thẳng đi qua
,A
vuông góc với
d
đồng thời khoảng cách giữa
d
và
là lớn nhất. Biết
( ; ;4)v a b=
là một véc- tơ chỉ phương của
. Tính giá trị
ab+
.
A.
2.
B.
8.−
C.
2.−
D.
4.−
Câu 16: Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt phẳng
( )
:2 3 0P x y z+ + − =
và điểm
( )
1;2;2A
. Gọi M là giao điểm của mặt phẳng
( )
P
và trục
oy
. Viết phương trình đường thẳng
d
nằm trong mặt phẳng
( )
P
, đi qua M sao cho khoảng cách từ điểm
A
đến đường thẳng
d
có giá
trị lớn nhất.
A.
3
:.
1 1 1
x y z
d
−
==
−−
B.
3
:.
1 3 1
x y z
d
−
==
−
C.
3
:.
2 3 1
x y z
d
−
==
−−
D.
3
:.
1 1 3
x y z
d
−
==
−
Câu 17: Cho hai số
12
,zz
thoả mãn điều kiện
12
3 4 2; 1z i z z− − = − =
. Giá trị nhỏ nhất của biểu thức bằng
22
12
P z z=−
là
A.
6 2 5−−
. B.
5−
. C.
85−
. D.
10−
.
Câu 18: Trong không gian
Oxyz
, cho ba điểm
(0;0;4), (3;2;6), (3; 2;6).A B C −
Gọi
M
là điểm di động
trên mặt cầu
2 2 2
( ): 4.S x y z+ + =
Giá trị nhỏ nhất của biểu thức
MA MB MC++
bằng
A.
2 34
. B.
65
. C.
4 10
. D.
2 29
.
Câu 19: Trong không gian
Oxyz
, cho điểm
( )
3;3; 3A −−
, thuộc mặt phẳng
( )
:2 2 15 0x y z
− + + =
và
mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 2 3 5 100S x y z− + − + − =
. Gọi
là đường thẳng đi qua
A
, nằm trong
( )
và cắt
( )
S
tại hai điểm
B
,
C
. Để độ dài BC lớn nhất thì
có phương trình là
A.
3 3 3
:
1 4 6
x y z+ − +
= =
. B.
3 3 3
:
16 11 10
x y z+ − +
= =
−
.
C.
35
:3
38
xt
y
zt
= − +
=
= − +
. D.
3 3 3
:
113
x y z+ − +
= =
.
Câu 20: Trong không gian
Oxyz
, cho đường thẳng
11
:.
2 1 1
x y z−−
= =
−−
Hai điểm
,MN
lần lượt di động
trên các mặt phẳng
( )
:2x
=
,
( )
:2z
=
sao cho trung điểm
K
của
MN
luôn thuộc đường
thẳng Δ. Giá trị nhỏ nhất của độ dài
MN
bằng

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
317
A.
85
5
. B.
45
5
. C.
35
5
. D.
95
5
.
Câu 21: Trong không gian với hệ tọa độ
Oxyz
, cho
2
điểm
( ) ( )
1;4;2 , 1;2;4AB−
và đường thẳng
12
:
1 1 2
x y z
d
−+
==
−
. Viết phương trình đường thẳng
qua
A
cắt
d
sao cho khoảng cách từ
B
đến
là nhỏ nhất.
A.
1 15
4 18
2 19
xt
yt
zt
=−
=−
=−
. B.
15
48
29
xt
yt
zt
=−
=+
=−
C.
15
48
29
xt
yt
zt
=+
=−
=−
. D.
1 15
4 18
2 19
xt
yt
zt
=+
=+
=−
.
Câu 22: Trong không gian với hệ tọa độ
Oxyz
cho hai điểm
( )
1;2; 3A −
,
( )
2; 2;1B −−
và mặt phẳng
( )
:2 2 9 0x y z+ − + =
. Gọi
M
là điểm thay đổi trên mặt phẳng
( )
sao cho
M
luôn nhìn đoạn
AB dưới một góc vuông. Xác định phương trình đường thẳng
MB
khi
MB
đạt giá trị lớn nhất.
A.
2
22
12
xt
yt
zt
= − −
= − +
=+
. B.
22
2
12
xt
yt
zt
= − +
= − −
=+
. C.
2
2
12
xt
y
zt
= − +
=−
=+
. D.
2
2
1
xt
yt
z
= − +
= − −
=
.
Câu 23: Trong không gian với hệ trục tọa độ , cho mặt phẳng , điểm
và đường thẳng . Viết phương trình đường thẳng đi qua song song với
sao cho khoảng cách giữa và lớn nhất.
A. . B. . C. . D. .
Câu 24: Trong không gian
Oxyz
, cho đường thẳng
11
:
2 1 1
x y z
d
−+
==
−
và hai điểm
( ) ( )
1;2;3 ; 1;0;2AB−
. Phương trình đường thẳng
đi qua
B
, cắt
d
sao cho khoảng cách từ
A
đến
đạt giá trị lớn
nhất là
A.
12
3 1 4
x y z+−
==
. B.
12
3 1 4
x y z+−
==
−−
. C.
12
1 1 1
x y z+−
==
−−
. D.
12
8 1 14
x y z+−
==
−−
.
Câu 25: Cho đường thẳng và Tìm tọa độ điểm thuộc
sao cho đạt giá trị nhỏ nhất.
A. B. C. D.
Câu 26: Cho đường thẳng
và hai điểm
Biết điểm
thuộc
sao cho biểu thức
đạt giá trị lớn nhất. Khi đó tổng
bằng:
A.
8
. B. . C. . D. .
Oxyz
( )
: 1 0P x y z+ − + =
( )
1; 1;2A −
14
:
2 1 3
x y z+−
= =
−
d
A
( )
P
d
1 40
: 1 29
2 69
xt
d y t
zt
=+
= − +
=+
1 40
: 1 29
2 11
xt
d y t
zt
=+
= − −
=+
1
: 1 2
23
xt
d y t
zt
=+
= − +
=−
1 21
: 1 10
2 31
xt
d y t
zt
=+
= − +
=+
1 1 2
:
1 1 2
x y z+ − +
= =
−
(1;1;0),A
(3; 1;4).B −
M
MA MB+
( 1;1; 2).M −−
11
; ;1 .
22
M
−
33
; ; 3 .
22
M
−−
(1; 1;2).M −
1 1 2
:
1 1 2
x y z+ − +
= =
−
(1;1;0),A
( 1;0;1).B −
( ; ; )M a b c
T MA MB=−
a b c−+
8 33+
33
8
3
+
4 33
8
3
+

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
318
Câu 27: Cho đường thẳng
và hai điểm Biết điểm
thuộc sao
cho biểu thức
đạt giá trị lớn nhất là Khi đó, bằng bao nhiêu?
A. . B. . C. . D. .
Câu 28: Cho mặt phẳng và hai điểm . Gọi là điểm thuộc mặt
phẳng sao cho đạt giá trị nhỏ nhất. Khi đó giá trị của là:
A. . B. . C. . D. .
Câu 29: Cho mặt phẳng và hai điểm . Biết
thuộc mặt phẳng sao cho đạt giá trị nhỏ nhất. Khi đó, giá trị của biểu thức
bằng bao nhiêu?
A. . B. . C. . D. .
Câu 30: Trong không gian
Oxyz
, cho hai điểm
( )
9; 6; 11A
,
( )
5; 7; 2B
và điểm
M
di động trên mặt
cầu
( ) ( ) ( ) ( )
2 2 2
: 1 2 3 36S x y z− + − + − =
. Giá trị nhỏ nhất của
2MA MB+
bằng
A.
105
. B.
2 26
. C.
2 29
. D.
102
.
Câu 31: Trong không gian
,Oxyz
cho điểm
( )
0;1;9A
và mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 3 4 4 25.S x y z− + − + − =
Gọi
( )
C
là giao tuyến của
( )
S
với mặt phẳng
( )
.Oxy
Lấy hai điểm
,MN
trên
( )
C
sao cho
2 5.MN =
Khi tứ diện
OAMN
có thể tích lớn nhất thì đường thẳng
MN
đi qua điểm nào trong
số các điểm dưới đây?
A.
( )
5;5;0 .
B.
1
;4;0 .
5
−
C.
12
; 3;0 .
5
−
D.
( )
4;6;0 .
Câu 32: Cho mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 2 1 3 9S x y z− + − + − =
và hai điểm
( )
1 ; 1 ; 3A
,
( )
21 ; 9 ; 13B −
.
Điểm
( )
; ; M a b c
thuộc mặt cầu
( )
S
sao cho
22
3MA MB+
đạt giá trị nhỏ nhất. Khi đó giá trị
của biểu thức
..T ab c=
bằng
A.
3
. B.
8
. C.
6
. D.
18−
.
Câu 33: Trong không gian với hệ trục tọa độ
Oxyz
, cho điểm
( )
2;5;3A
, đường thẳng
12
:
2 1 2
−−
==
x y z
d
. Biết rằng phương trình mặt phẳng
( )
P
chứa
d
sao cho khoảng cách từ
A
đến mặt phẳng
( )
P
lớn nhất, có dạng
30+ + − =ax by cz
. Khi đó tổng
= + +T a b c
bằng
A.
3
. B.
3−
. C.
2−
. D.
5−
.
Câu 34: Trong không gian
Oxyz
cho mặt phẳng
( ): 1 0Py−=
, đường thẳng
1
:2
1
x
yt
z
=
= −
=
và hai điểm
( )
1; 3;11A −−
,
1
;0;8
2
B
. Hai điểm
,MN
thuộc mặt phẳng
()P
sao cho
( ; ) 2dM=
và
2NA NB=
. Tìm giá trị nhỏ nhất của đoạn
MN
.
1
:
1 1 1
x y z−
= =
(0;1; 3),A −
( 1;0;2).B −
M
T MA MB=−
max
.T
max
T
max
3T =
max
23T =
max
33T =
max
2T =
( )
: 1 0x y z
− + + =
( ) ( )
1;1;0 , 3; 1;4AB−
M
( )
P MA MB=+
P
5P =
6P =
7P =
8P =
( )
: 3 5 0x y z
+ − − =
( ) ( )
1; 1;2 , 5; 1;0AB− − −
( )
;;M a b c
( )
MA MB+
23T a b c= + +
5T =
3T =−
7T =−
9T =−

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
319
A.
min
1MN =
. B.
min
2MN =
. C.
min
2
2
MN =
. D.
min
2
3
MN =
.
Câu 35: Trong không gian
Oxyz
, cho mặt cầu
( )
2 2 2
:1S x y z+ + =
. Điểm
M
nằm trên
( )
S
có tọa độ
dương, mặt phẳng
( )
P
tiếp xúc với
( )
S
tại
M
, cắt các tia
,,Ox Oy Oz
tại các điểm
,,A B C
. Giá
trị nhỏ nhất của biểu thức
( )( )( )
2 2 2
1 1 1T OA OB OC= + + +
là
A.
24
. B.
27
. C.
64
. D.
8
.
Câu 36: Trong không gian
Oxyz
cho đường thẳng
1 2 3
:
2 3 4
x y z
d
− − −
==
và mặt cầu
( )
S
:
( ) ( ) ( )
2 2 2
3 4 5 729x y z+ + + + + =
. Cho biết điểm
( )
2; 2; 7A −−−
, điểm
B
thuộc giao tuyến của
mặt cầu
( )
S
và mặt phẳng
( )
:2 3 4 107 0P x y z+ + − =
. Khi điểm
M
di động trên đường thẳng
d
giá trị nhỏ nhất của biểu thức
MA MB+
bằng
A.
5 30
. B.
27
. C.
5 29
. D.
742
.
Câu 37: Trong không gian
Oxyz
, cho hai điểm
( 2; 2;1)M −−
,
(1;2; 3)A −
và đường thẳng
16
:
2 2 1
x y z
d
+−
==
−
. Gọi
là đường thẳng qua
M
, vuông góc với đường thẳng
d
, đồng thời
cách
A
một khoảng bé nhất. Khoảng cách bé nhất đó là
A.
29
. B.
6
. C.
5
. D.
34
9
.
Câu 38: Trong không gian
Oxyz
, cho mặt cầu
2 2 2
( ):( 1) ( 1) ( 1) 6S x y z
tâm I. Gọi
()
là mặt
phẳng vuông góc với đường thẳng
13
:
1 4 1
x y z
d
và cắt mặt cầu
()S
theo đường tròn
()C
sao cho khối nón có đỉnh
I
, đáy là đường tròn
()C
có thể tích lớn nhất. Biết
()
không đi qua
gốc tọa độ, gọi
( , , )
H H H
H x y z
là tâm của đường tròn
()C
. Giá trị của biểu thức
H H H
T x y z
bằng
A.
1
3
. B.
4
3
. C.
2
3
. D.
1
2
.
Câu 39: Trong không gian
Oxyz
, cho đường thẳng
1 1 2
:
2 1 1
x y z
d
+ − −
==
−−
. Gọi
( )
là mặt phẳng chứa
đường thẳng
d
và tạo với mặt phẳng
( )
Oxy
một góc nhỏ nhất. Khoảng cách từ
( )
0;3; 4M −
đến
mặt phẳng
( )
bằng
A.
30
. B.
26
. C.
20
. D.
35
.
Câu 40: Trong không gian
Oxyz
cho hai điểm
(1;2; 1)A −
,
(7; 2;3)B −
và đường thẳng
d
có phương trình
1 2 2
3 2 2
x y z+ − −
==
−
. Điểm
I
thuộc
d
sao cho
AI BI+
nhỏ nhất. Hoành độ của điểm
I
là
A.
2
. B.
0
. C.
4
. D.
1
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
320
Câu 41: Trong không gian
Oxyz
, cho đường thẳng
43
: 3 4
0
xt
d y t
z
=−
=+
=
. Gọi
A
là hình chiếu vuông góc của
O
trên
d
. Điểm
M
di động trên tia
Oz
, điểm
N
di động trên đường thẳng
d
sao cho
MN OM AN=+
. Gọi
I
là trung điểm đoạn thẳng
OA
. Trong trường hợp diện tích tam giác
IMN
đạt giá trị nhỏ nhất, một véctơ pháp tuyến của mặt phẳng
( )
,Md
có tọa độ là
A.
( )
4;3;5 2
. B.
( )
4;3;10 2
. C.
( )
4;3;5 10
. D.
( )
4;3;10 10
.
Câu 42: Trong không gian
Oxyz
, cho các điểm
( ) ( ) ( )
2;2;2 , 2;4; 6 , 0;2; 8A B C−−
và mặt phẳng
( )
:0P x y z+ + =
. Xét các điểm
M
thuộc mặt phẳng
( )
P
sao cho
90AMB=
, đoạn thẳng
CM
có độ dài lớn nhất bằng
A.
2 15
. B.
2 17
. C. 8. D. 9.
Câu 43: Trong không gian
Oxyz
, cho đường thẳng
3 4 2
:
2 1 1
x y z
d
− − −
==
và 2 điểm
( )
6;3; 2A −
,
( )
1;0; 1B −
. Gọi
là đường thẳng đi qua
B
, vuông góc với
d
và thỏa mãn khoảng cách từ
A
đến
là nhỏ nhất. Một vectơ chỉ phương của
có tọa độ
A.
( )
1;1; 3−
. B.
( )
1; 1; 1−−
. C.
( )
1;2; 4−
. D.
( )
2; 1; 3−−
.
Câu 44: Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
( )
;0;0Aa
,
( )
0, ,0Bb
,
( )
0,0,Cc
với
a
,
b
,
c
là những số dương thay đổi thỏa mãn
2 2 2
4 16 49a b c+ + =
. Tính tổng
2 2 2
S a b c= + +
khi
khoảng cách từ
O
đến mặt phẳng
( )
ABC
đạt giá trị lớn nhất.
A.
51
5
S =
. B.
49
4
S =
. C.
49
5
S =
. D.
51
4
S =
.
Câu 45: Trong không gian
Oxyz
, cho điểm
( )
2; ;3;4A −
, đường thẳng
12
:
2 1 2
x y z
d
−+
==
và mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 3 2 1 20S x y z− + − + + =
. Mặt phẳng
( )
P
chứa đường thẳng
d
thỏa mãn khoảng
cách từ điểm
A
đến
( )
P
lớn nhất. Mặt cầu
( )
S
cắt
( )
P
theo đường tròn có bán kính bằng
A.
5
. B.
1
. C.
4
. D.
2
.
Câu 46: Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
( )
A 0; 1;1
,
( )
B 3; 0;-1
,
( )
C 0; 21; -19
và mặt
cầu
( ) ( ) ( ) ( )
2 2 2
: 1 1 1 1S x y z− + − + − =
.
( )
; ; M a b c
là điểm thuộc mặt cầu
( )
S
sao cho biểu
thức
2 2 2
32T MA MB MC= + +
đạt giá trị nhỏ nhất. Tính tổng
abc++
.
A.
14
5
abc+ + =
. B.
0abc+ + =
. C.
12
5
abc+ + =
. D.
12abc+ + =
.
Câu 47: Trong không gian với hệ tọa độ
Oxyz
cho điểm
( )
2;2; 2A −−
và điểm
( )
3; 3;3B −
.
Điểm M thay đổi trong không gian thỏa mãn
2
3
MA
MB
=
. Điểm
( )
;;N a b c
thuộc mặt phẳng
( )
: 2 2 6 0P x y z− + − + =
sao cho
MN
nhỏ nhất. Tính tổng
T a b c= + +
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
321
A.
6
. B.
2−
. C.
12
. D.
6−
.
Câu 48: Trong không gian
Oxyz
, cho hai điểm
( )
0; 1;2A −
,
( )
1;1;2B
và đường thẳng
11
:
1 1 1
x y z
d
+−
==
. Biết
( )
;;M a b c
thuộc đường thẳng
d
sao cho tam giác
MAB
có diện tích nhỏ nhất. Khi đó, giá
trị
23T a b c= + +
bằng:
A.
5
. B.
3
. C.
4
. D.
10
.
Câu 49: Trong không gian
Oxyz
, cho hai điểm
( )
0; 1;2A −
,
( )
1;1;2B
và đường thẳng
11
:
1 1 1
x y z
d
+−
==
. Biết
( )
;;M a b c
thuộc đường thẳng
d
sao cho tam giác
MAB
có diện tích bằng
5
6
. Khi đó,
giá trị
23T a b c= + +
bằng:
A.
5
. B.
3
. C.
4
. D.
10
.
Câu 50: Trong không gian
Oxyz
, cho hai điểm
( )
0; 1;2A −
,
( )
1;1;2B
và đường thẳng
11
:
1 1 1
x y z
d
+−
==
. Có bao nhiêu điểm
M
thuộc đường thẳng
d
sao cho tam giác
MAB
có diện tích bằng
1
.
A.
0
. B.
1
. C.
2
. D. Vô số.
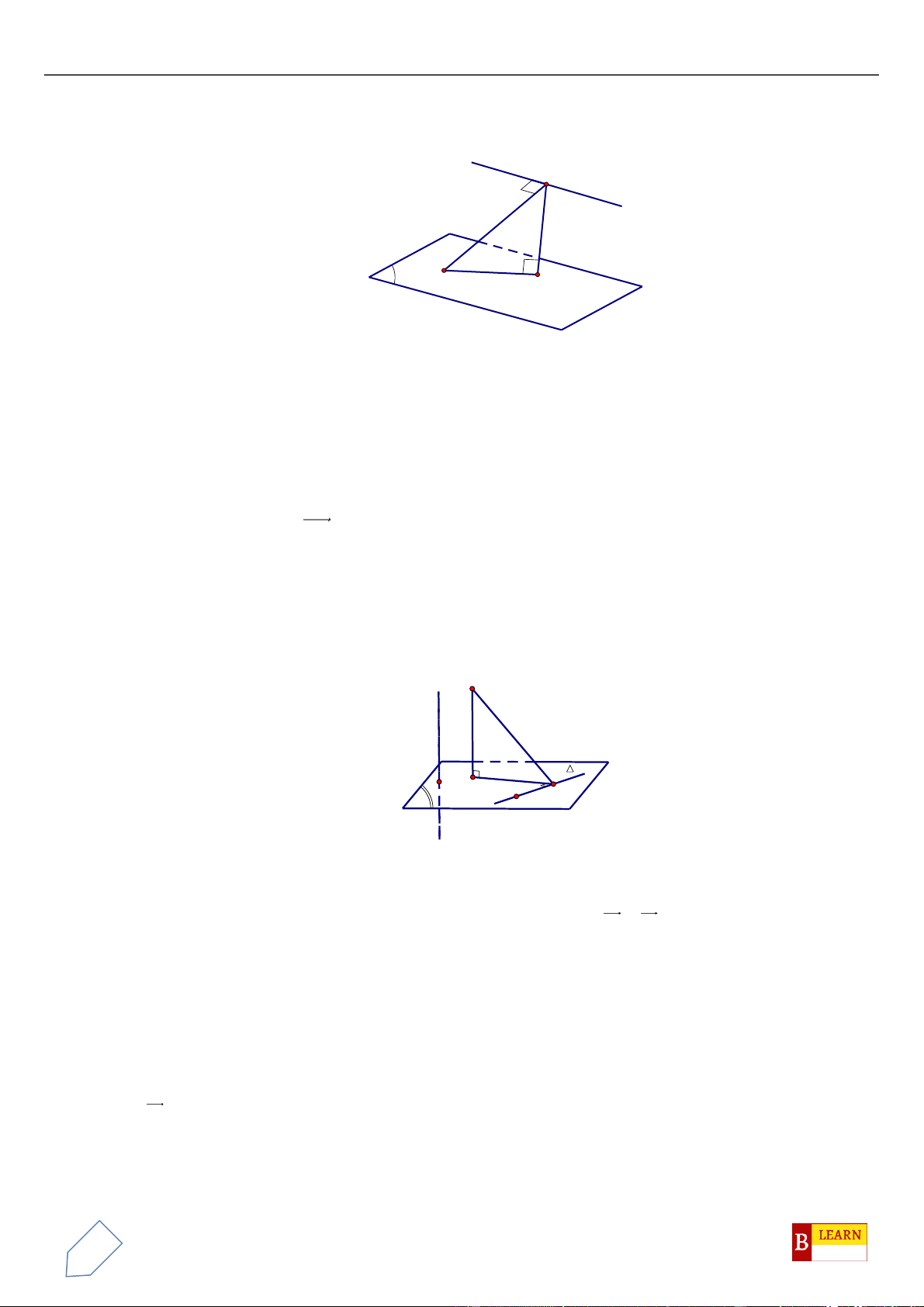
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
322
ĐÁP ÁN CHI TIẾT
Câu 1: Chọn D
Gọi
H
là hình chiếu của
A
lên đường thẳng
d
. Ta suy ra
( )
1;1;1H
.
Gọi
( )
P
là mặt phẳng đi qua điểm
A
và
( )
P
song song với đường thẳng
d
. Gọi
K
là hình chiếu
của
H
lên mặt phẳng
( )
P
. Do
( )
// dP
nên ta có
( )
( )
( )
( )
,,d d P d H P HK==
.
Ta luôn có bất đẳng thức
HK HA
. Như vậy khoảng cách từ
( )
d
đến
( )
P
lớn nhất bằng
AH
.
Và khi đó
( )
P
nhận
( )
1;2;3AH =−
làm vectơ pháp tuyến.
Do
( )
P
đi qua
( )
2; 1; 2A −−
nên ta có phương trình của
( )
P
là:
2 3 10 0x y z− − − =
.
Do đó
( )
P
vuông góc với mặt phẳng có phương trình:
3 2 0xz+ + =
.
Câu 2: Chọn C
Xét
( )
P
là mặt phẳng qua
M
và
( )
Pd⊥
.
Mặt phẳng
( )
P
qua
( )
2; 2;1M −−
và có vectơ pháp tuyến
( )
2;2; 1
Pd
nu= = −
nên có phương
trình:
( )
:2 2 9 0P x y z+ − + =
.
Gọi
,H
K
lần lượt là hình chiếu của
A
lên
( )
P
và
. Khi đó:
AK AH const=
nên
min
AK
khi và chỉ khi
KH
. Đường thẳng
AH
đi qua
( )
1,2, 3A −
và có vectơ chỉ phương
( )
2;2; 1
d
u =−
nên
AH
có phương trình tham số:
12
22
3
xt
yt
zt
=+
=+
= − −
.
Vì
( )
1 2 ;2 2 ; 3H AH H t t t + + − −
.
d
P
A
K
H
d
P
A
H
K
M

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
323
Lại
( ) ( ) ( ) ( ) ( )
2 1 2 2 2 2 3 9 0 2 3; 2; 1H P t t t t H + + + − − − + = = − − − −
.
Vậy
( )
1;0;2u HM==
.
Câu 3: Chọn B
Phương trình tham số của đường thẳng
AB
là
1
72
8
xt
yt
zt
=+
= − +
= − −
.
Gọi
H
,
K
lần lượt là hình chiếu của
M
trên
( )
P
và đường thẳng
AB
.
Ta tìm được điểm
( )
3; 3; 10K −−
. Ta luôn có bất đẳng thức
( )
( )
,d M P MH MK=
.
Dấu bằng xảy ra khi và chỉ khi
HK
. Khi đó
( ) ( )
4; 2; 8 2 2;1;4MH = − − − = −
.
Mặt phẳng
( )
P
có một vectơ pháp tuyến là
( )
2;1;4n =
. Vậy ta có
3ab+=
.
Câu 4: Chọn B
Gọi
,HK
lần lượt là hình chiếu của
A
lên
( )
và
d
. Khi đó ta có
AH AK
.
Vì
Hd
nên
( )
2 ; 1 2 ;1H t t t− − + +
( )
1 ;2 ;1AH t t t = − − +
.
Do
AH d⊥
nên ta có
( )
1 2.2 1 0t t t− − − + + + =
1
3
t = −
. Khi đó
2 2 2
;;
3 3 3
AH
= − −
.
Khoảng cách từ
A
đến
( )
lớn nhất khi và chỉ khi
AH AK=
. Do đó
( )
có vectơ pháp tuyến
là
( )
1;1; 1n =−
. Vậy
( )
:
( ) ( ) ( )
1 2 1 1 1 1 0x y z− + + − − =
0x y z + − =
.
Vẫn là đánh giá bất đẳng thức
AH AK
nói trên, nhưng bài toán sau đây lại phát biểu hơi khác
một chút.
Câu 5: Chọn A
Ta thấy rằng
d
đi qua
A
và
d
song song với
( )
P
nên
d
luôn nằm trong mặt phẳng
( )
Q
qua
A
và
( ) ( )
// QP
. Như vậy bây giờ ta chuyển về xét trong mặt phẳng
( )
Q
để thay thế cho
( )
P
. Ta
lập được phương trình mặt phẳng
( )
: 2 2 1 0Q x y z− − + =
.
Gọi
,HK
lần lượt là hình chiếu của
B
lên
( )
Q
và
d
. Ta tìm được
1 11 7
;;
9 9 9
H
−
. Ta luôn có
được bất đẳng thức
( )
;d B d BK BH=
nên khoảng cách từ
B
đến
d
bé nhất bằng
BH
.
d
Q
P
B
H
K
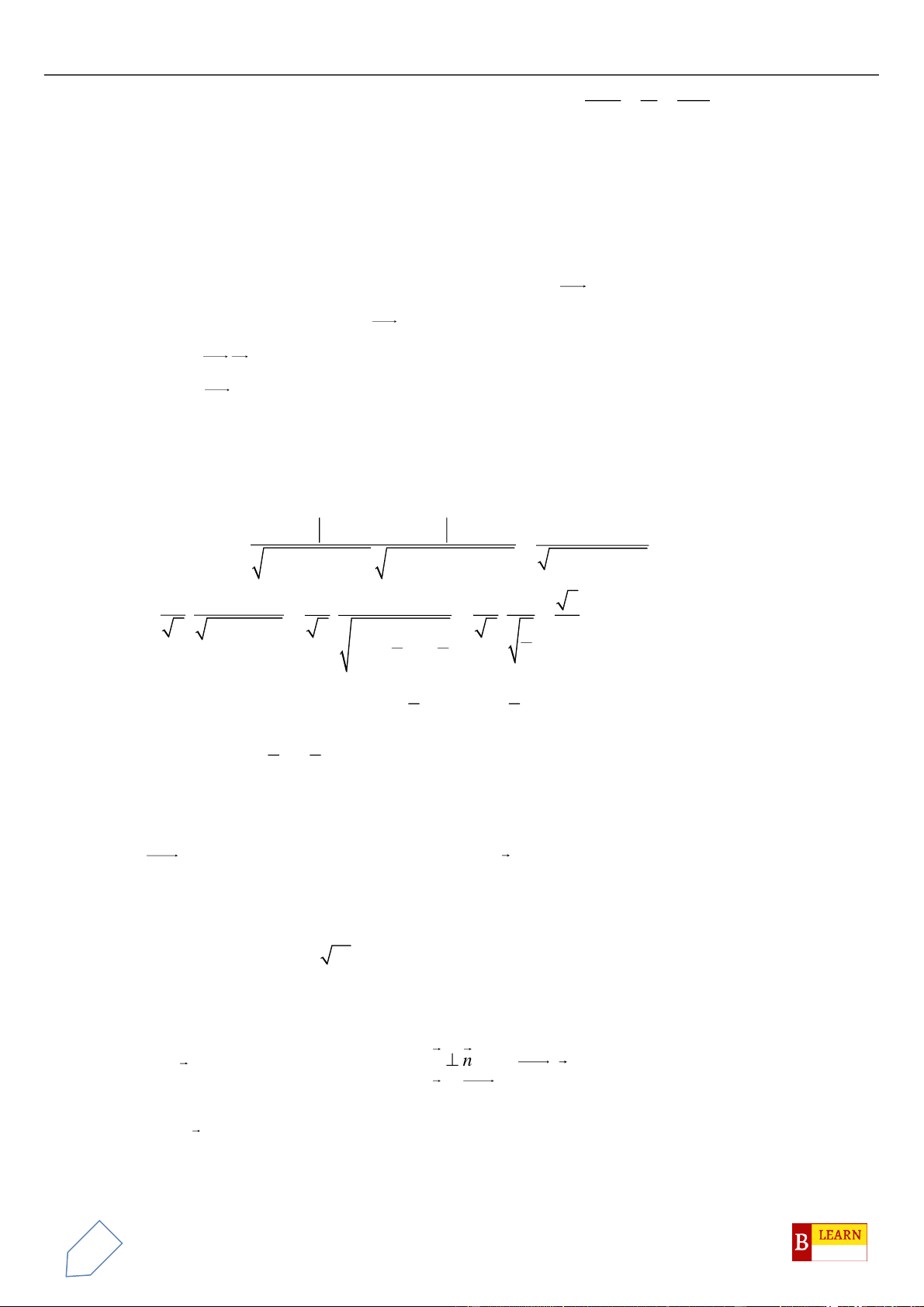
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
324
Đường thẳng
d
bây giờ đi qua
,AH
nên có phương trình
31
26 11 2
x y z+−
==
−
.
Câu 6: Chọn A
Gọi
H
là hình chiếu vuông góc của
A
trên
( )
P
và
K
là hình chiếu vuông góc của
A
trên
d
.
Ta có:
( )
( )
,d A P AH AK=
.
Suy ra:
( )
( )
,d A P
lớn nhất bằng
AK
khi và chỉ khi
H
trùng
K
.
Khi đó tọa độ vectơ pháp tuyến của mặt phẳng
( )
P
là:
AK
.
Lấy
( )
1 2 ; ;1K t t t d− − +
và
( )
2 2; 2; 2AK t t t= − − − −
.
Lại có:
( )( ) ( ) ( )
. 0 2 2 2 1. 2 1. 2 0 0
d
AK u t t t t= − − − + − + − = =
.
Suy ra:
( )
2; 2; 2AK = − − −
. Vậy vectơ pháp tuyến của mặt phẳng
( )
P
là:
( )
1;1;1
.
Câu 7: Chọn C
Gọi
là góc giữa hai mặt phẳng
( )
P
và
( )
Q
. Vì
0 90
nên
nhỏ nhất khi và chỉ khi
cos
lớn nhất.
Ta có
( )
( ) ( )
22
2 2 2 2
1 2 2 1
cos
1 2 2 . 1 1
mm
mm
+ − −
=
+ + − + + −
2
1
=
2 2 2mm−+
2
11
=.
2
1mm−+
2
11
=.
2
13
24
m
−+
1 1 6
.,
3
23
4
m =
.
Dấu
“”=
xảy ra khi và chỉ khi
11
0
22
mm− = =
.
Khi đó
( )
11
: 2019 0
22
Q x y z+ − + =
. Dễ thấy điểm
( )
2019;1;1M −
thuộc mặt phẳng
( )
Q
.
Vậy mặt phẳng
( )
Q
đi qua điểm
( )
2019;1;1M −
.
Câu 8: Chọn D
( )
6; 7;1AM =−
, vectơ pháp tuyến của
( )
là
(3; 4;1)n =−
.
Gọi
H
là hình chiếu vuông góc của
A
trên
a
.
( )
; 86d A a AH AM= =
( )
;d A a
lớn nhất khi
HM
.
Khi đó
a
là đường thẳng đi qua
M
, song song với
( )
và vuông góc với
AM
.
Gọi
u
là vectơ chỉ phương của
a
un
u AM
⊥
⊥
;
( ) ( )
, 3; 3; 3 3 1;1;1AM n
= − − − = −
.
Chọn
( )
1;1;1u =
. Đáp án D thỏa mãn.
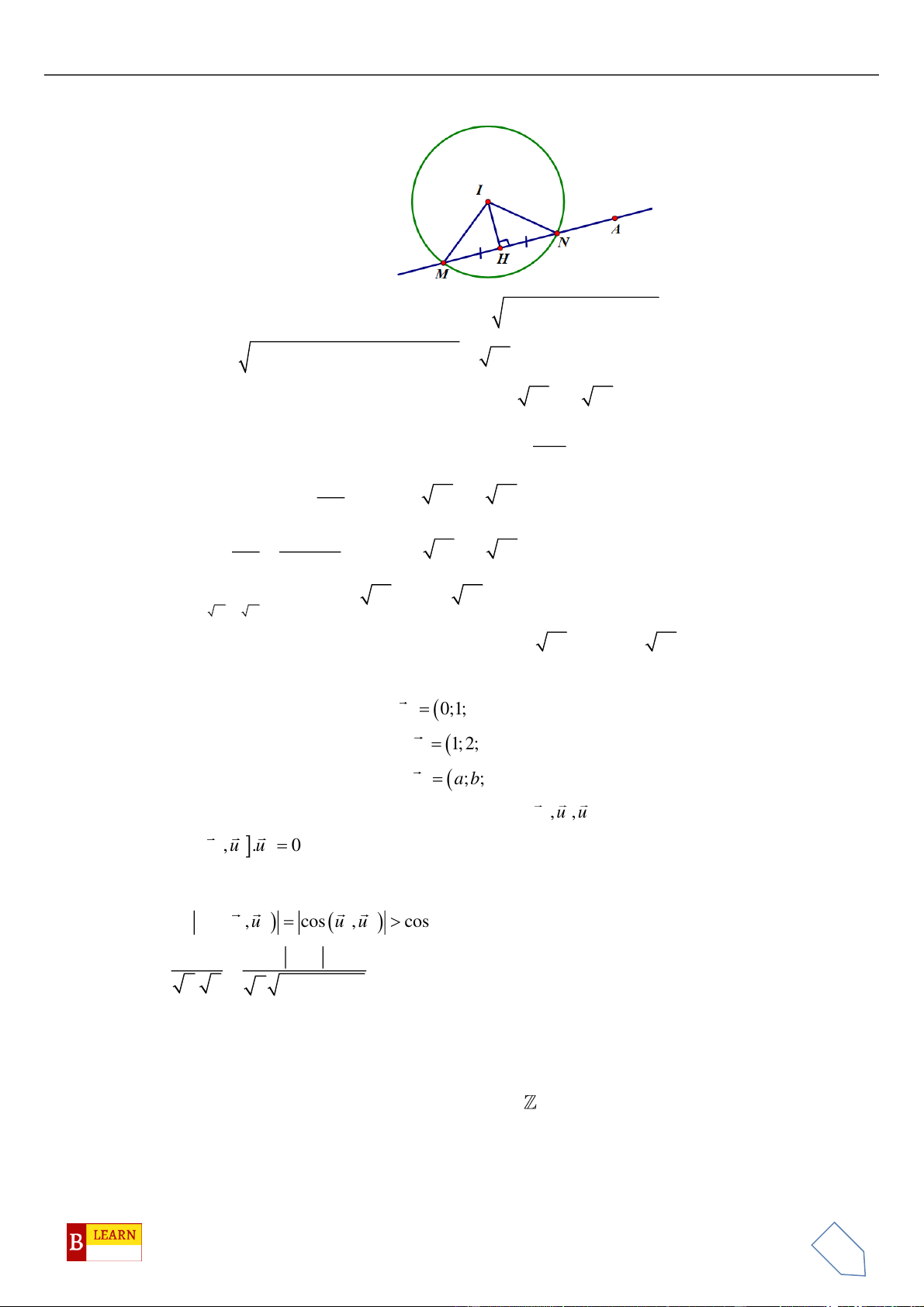
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
325
Câu 9: Chọn D
Mặt cầu
( )
S
có tâm
( )
2; 1;1 ,I −
bán kính
( ) ( )
2
22
2 1 1 3 3.R = + − + − − =
Ta có:
( ) ( ) ( )
2 2 2
2 5 1 3 1 2 34AI R= − + − − + + =
nên
A
nằm ngoài mặt cầu
( )
.S
Ta lại có:
4.S AM AN=+
Đặt
AM x=
với
34 3; 34 3x
− +
Mà
22
. 34 9 25AM AN AI R= − = − =
suy ra:
25
AN
AM
=
Do đó:
( )
100
S f x x
x
= = +
với
34 3; 34 3x
− +
( )
2
22
100 100
' 1 0, 34 3; 34 3
x
f x x
xx
−
= − = − +
Do đó:
( )
( )
34 3; 34 3
min 34 3 5 34 9.f x f
−+
= + = −
Dấu “=” xảy ra
, , ,A M N I
thẳng hàng và
34 3; 34 3.AM AN= + = −
Câu 10: Chọn B
Đường thẳng
d
có một VTCP là
( )
0;1; 1
d
u =−
.
Đường thẳng
AC
có một VTCP là
( )
1
1;2; 1u =−
.
Đường thẳng
AB
có một VTCP là
( )
2
;;u a b c=
với
( )
2 2 2
0*abc+ +
Do
d
là đường phân giác của góc
A
nên ba véc tơ
12
,,
d
u u u
đồng phẳng
Suy ra
12
, . 0
d
u u u =
0abc− − =
a b c = +
.
Do tam giác
ABC
nhọn nên
( ) ( )
00
, 45 , , 45AC d AB d
.
Ta có
( ) ( )
0
12
cos , cos , cos45
dd
u u u u=
.
2 2 2
3
2. 6
2
bc
abc
−
=
++
( ) ( )
2 2 2 2 2
3 2 2a b c b bc c + + = − +
.
Từ và suy ra
( )
2
22
3 4 0b c b c bc+ + + + =
22
2 5 2 0b bc c + + =
2
2
bc
cb
=−
=−
.
Trường hợp 1: Với
2bc=−
ta được
ac=−
.
Khi đó
2 2 2 2
6P a b c c= + + =
. Do điều kiện và
c
ta được
2
66Pc=
. Nên
min
6P =
.
Trường hợp 2: Với
2cb=−
ta được
ab=−
.
Khi đó
2 2 2 2
6P a b c b= + + =
. Tương tự trên ta có
min
6P =
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
326
Câu 11: Chọn B
Ta có
( )
5 2 ;2 ;M d M t t t + − −
,
( )
t
.
( )
3 2 ;4 ; 4AM t t t = + − − −
,
( )
8 2 ; 1 ; 1BM t t t= + − − −
.
( ) ( ) ( ) ( ) ( ) ( )
( )
2 2 2 2 2 2
22
2
2
2 3 2 3 2 4 4 3 8 2 1 1
30 120 280 30 2 160 160
MA MB t t t t t t
t t t
+ = + + − + − − + + + − − + −
= + + = + +
Dấu
'' ''=
xảy ra khi và chỉ khi
2t =−
.
Vậy giá trị nhỏ nhất của
22
23MA MB+
bằng
160
.
Câu 12: Chọn C
Trung điểm của BC là
1;3;2I
suy ra
2 2 2T MA MI MA MI
.
Điểm đối xứng với
I
qua mặt phẳng
Oxy
là
1;3; 2D
.
Nhận xét:
,AI
cùng phía so với mặt phẳng
Oxy
nên
,DA
khác phía với
Oxy
.
Ta có
22T MA MI MA MD AD
không đổi.
Dấu “=” xảy ra khi
, , A M D
thẳng hàng với
M
nằm giữa
A
và
D
.
M AD Oxy
.
Đường thẳng
()AD
qua điểm
(1;0;3)A
, có một véc tơ chỉ phương
(2; 3;5)DA =−
là
12
3 ( )
35
xt
y t t
zt
=+
= −
=+
. Mặt phẳng
:0Oxy z
.
Lúc đó
( ) ( )
1 2 ; 3 ;3 5M t t t AD+ − +
và
( )
3
5
M Oxy t = −
.
00
19
; ;0 2
55
M x y
.
Câu 13: Chọn D
Ta có:
( )
2 3;2 5; 2M d M t t t + + −
.
( ) ( ) ( ) ( ) ( ) ( )
2 2 2 2 2 2
2 1 2 2 2 2 2 2 4 5T MA MB AM BM t t t t t t= + = + = − + + + − + + + − + −
Oxy
M
I
A
D
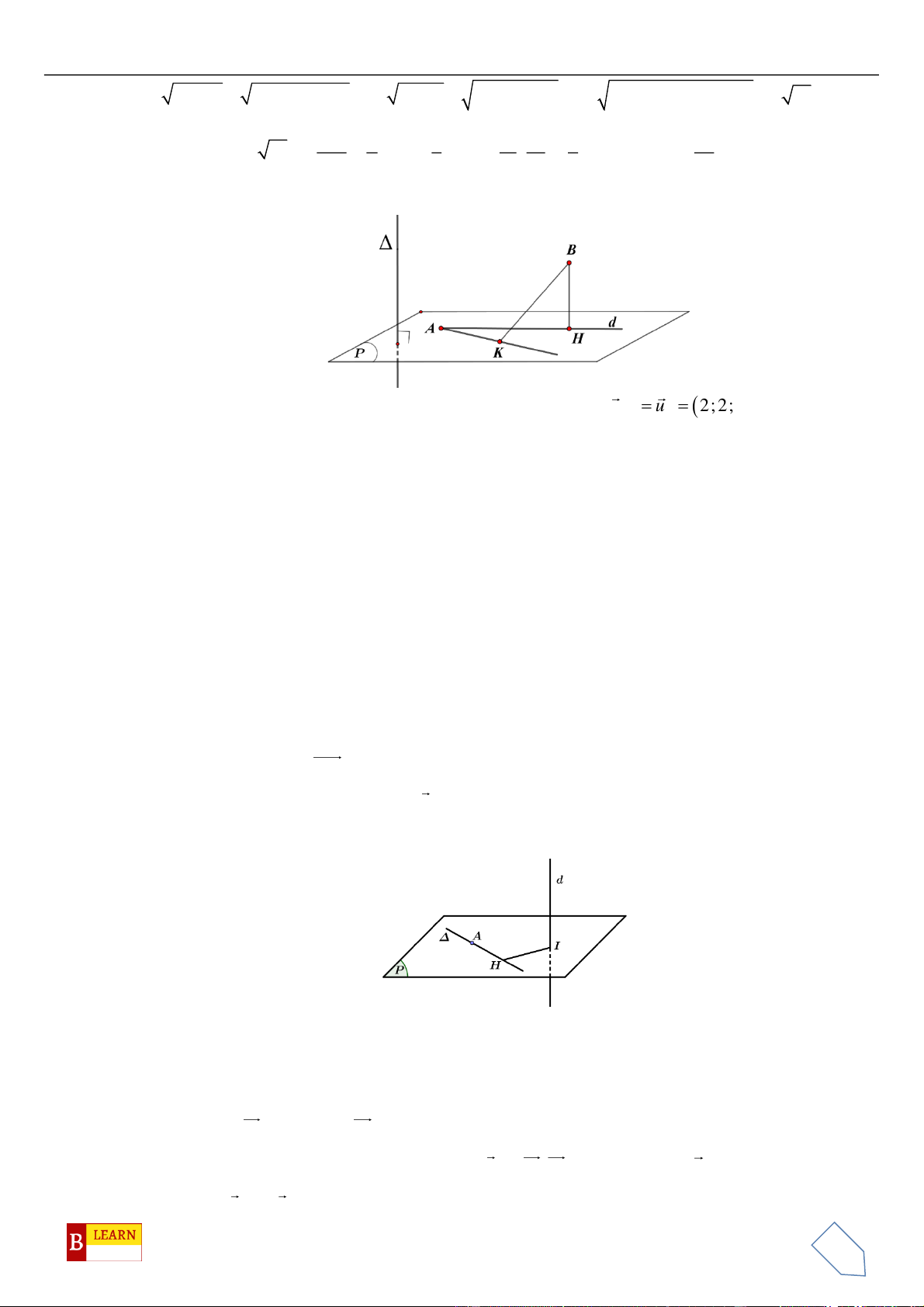
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
327
( )
( )
( ) ( )
2 2 2
2 2 2 2 2
9 9 9 18 45 3 1 1 2 3. 1 1 2 3 10t t t t t t t= + + − + = + + − + + − + + =
.
Do đó:
( )
min
1 1 11 17 5 23
3 10 ; ; 7,7 7;8
1 2 3 3 3 3 3
t
T t M a b c
t
= = = − + + =
−
.
Câu 14: Chọn B
Gọi
( )
P
là mặt phẳng đi qua
A
và vuông góc với
. Chọn
( )
()
2;2; 1
P
nu
= = −
.
( )
P
có phương trình:
( ) ( ) ( )
2 2 2 2 1 0 2 2 9 0x y z x y z+ + + − − = + − + =
.
Khi đó mọi đường thẳng
d
đi qua
A
và vuông góc
thì
d
nằm trong
( )
P
.
Gọi
,KH
lần lượt là hình chiếu vuông góc của
B
lên
d
và
( )
P
.
Ta có khoảng cách từ
B
đến
d
là
( )
( )
, 6BH PB dBK ==
.
Dấu bằng xảy ra khi
d
đi qua
A
và
H
.
Tìm
H
là hình chiếu vuông góc của
B
trên
( )
P
.
Đường thẳng
a
đi qua
( )
1;2; 3B −
và vuông góc với
( )
P
, có phương trình:
12
22
3
xt
yt
zt
=+
=+
= − −
.
Có
( )
H a P=
( ) ( ) ( )
2 1 2 2 2 2 3 9 0 9 18 0t t t t + + + − − − + = + =
2t = −
( )
3; 2; 1H − − −
và
( )
1;0; 2AH = − −
là một véctơ chỉ phương của
d
.
Vậy một véctơ chỉ phương của
d
là
( )
1;0;2u
.
Câu 15: Chọn B
Gọi
( )
P
là mặt phẳng qua
,A
vuông góc với
d
( )
: 2 2 0P x y z − + + − =
. Suy ra
( )
P
Gọi
( ) ( )
1;1;1I d P I=
,
,H
là hình chiếu vuông góc của
I
lên
.
Ta có
( )
;d d IH IA =
. Dấu bằng xảy ra khi
.HA
d
có VTCP
( )
1;2;1
d
u =−
,
( )
1;0;1IA =
Vậy
( )
max ,d d IA=
khi
có 1 VTCP là
, (2;2; 2)
d
u u IA
= = −
mà
( ; ;4)v a b=
là 1 VTCP
của
nên
2 4, 4v u a b= − = − = −
8ab + = −
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
328
Câu 16: Chọn A
( ) ( )
0;3;0M P oy M=
. Gọi H là chân đường vuông góc hạ từ điểm A lên đường thẳng
d
Ta có
( )
;AH d A d=
. Xét trong tam giác vuông
AHM
có
max H MAH AM AH
( )
; max AMd A d d ⊥
. Suy ra vecto chỉ phương của d:
;
dP
u AM n
=
.
( ) ( ) ( ) ( )
2;1;1 , 1;1; 2 3;3;3 3 1; 1; 1
Pd
n AM u= = − − = − = − − −
.
Câu 17: Chọn D
3 4 2zi− − =
Tập hợp điểm biểu diễn số phức
z
là đường tròn tâm
( )
3;4I
bán kính
2R =
.
Đặt
( )
12
, , , , ,z a bi z c di a b c d= + = +
được biểu diễn bởi điểm
( ) ( )
; , ;M a b N c d
.
12
11z z MN− = =
.
( ) ( )
22
22
22
12
P z z OM ON OI IM OI IN= − = − = + − +
( )
( )
2 2 2 2
2 . 2 . 2 . .P OI OI IM IM OI OI IN IN OI IM OI IN = + + − + + = − =
( )
2 2 . 2. .P OI IM IN OI NM OI MN = − = −
10P −
Dấu bằng xảy ra khi
,OI NM
ngược hướng.
Giá trị nhỏ nhất của biểu thức bằng
22
12
P z z=−
là
10−
.
Câu 18: Chọn A
Với điểm
( )
; ; ( )M x y z S
thì
2 2 2
40x y z+ + − =
và điểm
( )
3;0;6I
là trung điểm
BC
và
22MA MB MC MA MI MA MI+ + = + = +
2 2 2 2 2 2
( 4) 2 ( 3) ( 6)x y z x y z= + + − + − + + −
2 2 2 2 2 2 2 2 2
( 4) 3 4 2 ( 3) ( 6)x y z x y z x y z
= + + − + + + − + − + + −
2 2 2 2 2 2
2 ( 1) ( 3) ( 6)x y z x y z
= + + − + − + + −
2 2 2
2 ( 3 ) ( ) ( 1 6 ) 2 34x x y y z z + − + − + − + − =
Dấu bằng đạt tại
( )
2 2 2
1
0
36
3 127 15 9 5 127
0 ; ; ;0;
34 34
4
xz
k
xz
y x y z
x y z
−
= =
−−
−+
= =
+ + =
.
Câu 19: Chọn A
Mặt cầu
( )
S
có tâm
( )
2;3;5I
và bán kính
10R =
.
Gọi
H
là hình chiếu của
I
trên mặt phẳng
( )
,
Khi đó,
BC
lớn nhất khi nó là đường kính của đường tròn giao tuyến tâm
H
BC
đi qua
A
,
H
α
(S)
Δ
A
C
B
H
O
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
329
Phương trình
IH
đi qua
I
và vuông góc
( )
22
32
5
xt
yt
zt
=+
=−
=+
thay vào
( )
( )
2 2;7;3tH = − −
Ta có:
( )
1;4;6AH =
. Vậy phương trình của
là
3 3 3
:.
1 4 6
x y z+ − +
= =
Câu 20: Chọn A
Gọi
( ) ( )
2; ; ;M a b
( ) ( )
; ;2N c d
khi đó trung điểm của
MN
là
22
;;
2 2 2
c a d b
K
+ + +
.
Vì
K
thuộc
nên
( )
22
4 2 2
c a d b
tt
+ + −
= = =
−−
22
2
42
a d t
bt
ct
+ = −
= −
=−
.
Khi đó
( ) ( ) ( )
2 2 2
22MN c a d b= − + − + −
( ) ( ) ( )
2 2 2
4 4 2 2t a d t= − + − + +
( ) ( )
2
22
2
3 64 8 5
20 24 20 4 5
55
5
t t a d t a d
= − + + − = − + + −
.
Dấu bằng xảy ra khi và chỉ khi
22
2
42
0
3
5
a d t
bt
ct
ad
t
+ = −
=−
=−
−=
=
2
5
6
5
2
5
ad
b
c
==
= −
=
26
2; ; ,
55
M
−
22
; ;2
55
N
. Đối chiếu chọn đáp án A.
Câu 21: Chọn D
Đường thẳng
12
:
1 1 2
x y z
d
−+
==
−
đi qua điểm
( )
1; 2;0M −
và nhận
( )
1;1;2u =−
làm một véc
tơ chỉ phương.
Gọi
( )
P
là mặt phẳng chứa
d
và
A
.
Khi đó
( )
1;1;2u =−
và
( )
0; 6; 2AM = − −
không cùng
phương và có giá song song hoặc chứa trong
( )
P
. Suy ra có véc tơ pháp tuyến của mặt phẳng
( )
P
là
( )
()
10; 2;6,
P
n u AM
= = −
.
Phương trình mặt phẳng
( )
:5 3 7 0P x y z− + − =
Gọi
,KH
lần lượt là hình chiếu vuông góc của
B
trên
( )
P
và
,
ta luôn có
BH BK
,
suy ra
BH
nhỏ nhất khi
H
trùng
K
.
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
330
Đường thẳng qua
B
vuông góc với
( )
P
có phương trình:
( ) ( )
15
:2
43
xt
BK y t t
zt
R
= − +
=−
+
=
.
Tọa độ điểm
K
là nghiệm của hệ phương trình
( ) ( )
2
35
15
15
5
2
2
5 68 146
7
; ; .
43
4 3 68
7 35 35
35
5 1 5 2 3 4 3 7 0
5 3 7 0
146
35
t
xt
xt
x
yt
yt
K
zt
zt
y
t t t
x y z
z
=
= − +
= − +
=−
=−
=−
−
=+
=+
=
− + − + + + − =
− + − =
=
Ta có
12 72 76
;;
7 35 35
AK
= − −
, đường thẳng
đi qua
( )
1;4;2A
, nhận
35
4
AKu
=−
hay
( )
15;18; 19u
=−
làm một véc tơ chỉ phương, suy ra có phương trình
( ) ( )
1 15
: 4 18
2 19
xt
y t t R
zt
=+
= +
=−
.
Câu 22: Chọn C
Ta có
( )
M
và
90AMB =
suy ra
M
nằm trên đường tròn
( )
C
là giao tuyến của mặt phẳng
và mặt cầu
( )
S
đường kính
AB
.
Lại có
( )
B
suy ra
B
và
M
cùng nằm trên đường tròn
C
.
Khi đó
MB
lớn nhất khi và chỉ khi
MB
là đường kính của đường tròn
( )
C
.
Gọi
I
là tâm mặt cầu
( )
S
suy ra
1
; 0; 1
2
I
,
H
là tâm đường tròn
( )
C
.
có một vectơ pháp tuyến là
( )
( )
2;2; 1n −
.
Đường thẳng
IH
vuông góc với
( )
nên nhận
( )
( )
2;2; 1n −
là vectơ chỉ phương.
I
H
B
A
M

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
331
Phương trình tham số của đường thẳng
1
2
2
:2
1
xt
IH y t
zt
= − +
=
= − −
.
Ta có
1
2 ;2 ; 1
2
H t t t
− + − −
.
( ) ( ) ( )
1
2 2 2 2 1 9 0
2
H t t t
− + + − − − + =
1t = −
. Suy ra
5
; 2; 0
2
H
.
Phương trình đường thẳng
BM
đi qua
B
nhận
( )
11
;0; 1 1;0;2
22
BH
= − − = −
làm vectơ chỉ
phương là:
2
2
12
xt
y
zt
= − +
=−
=+
.
Câu 23: Chọn A
Mặt phẳng qua và song song với có phương trình: .
Đường thẳng có vtcp là , có vtpt là .
Phương trình tham số của .
Gọi
là giao điểm của và . Tọa độ điểm ứng với là nghiệm phương trình:
.
Xét đường thẳng là đường thẳng đi qua song song với . Phương trình của là:
.
Gọi là hình chiếu vuông góc của lên
. Ta có .
Khi đó .
Đường thẳng có vectơ chỉ phương .
Phương trình đường thẳng .
Câu 24: Chọn D
A
( )
P
20x y z+ − + =
( )
d
( )
2;1; 3u =−
( )
( )
1;1; 1n
=−
12
:
43
xt
yt
zt
= − +
=
=−
B
B
t
( )
1
1 2 4 3 2 0
2
t t t t− + + − − + = =
15
0; ;
22
B
1
A
1
12
1
23
xt
yt
zt
=+
= − +
=−
H
B
1
( )
1 2 , 1 ,2 3H t t t + − + −
3
1 2 ; ; 3
2
BH t t t
= + − −
3
. 0 2 4 9 0
2
BI u t t t= + + − + =
1
28
t=
( )
1
13 43 3 1 1
; ; 26; 43;3
14 28 28 28 28
BH u
−
= = − =
d
( )
1
; 40;29;69
d
u u n
==
1 40
: 1 29
2 69
xt
d y t
zt
=+
= − +
=+
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
332
Ta có:
( ) ( )
1;0; 1 2;0; 3C d C BC − = −
,
( )
2;1; 1
d
u =−
.
Gọi
( )
P
là mặt phẳng chứa
B
và đường thẳng
d
. Gọi
H
là hình chiếu kẻ từ
A
xuống mặt
phẳng
( )
P
và
n
là vectơ pháp tuyến của mặt phẳng
( )
P
( )
; 3; 4;2
d
n BC u
= = −
.
Gọi
K
là hình chiếu vuông góc kẻ từ
A
đến đường thẳng
. Suy ra
( )
;d A AK=
.
Ta thấy
ABK
vuông tại
K
nên
AK AB
.
AK
đạt giá trị lớn nhất khi
K
trùng với
B
, khi đó
AK AB=
.
Do đó:
( )
; 8;1;14u BA n
= = −
Vậy phương trình đường thẳng
:
12
8 1 14
x y z+−
==
−−
.
Câu 25. Chọn D
Ta có: cùng phương với và
// và đồng phẳng.
Xét mặt phẳng chứa và :
Gọi là điểm đối xứng của qua ; là mặt phẳng qua , vuông góc với
Khi đó, giao điểm của với là trung điểm của
có phương trình:
Giả sử ,
là trung điểm của
Ta có: khi và chỉ khi trùng với là
giao điểm của và
d
P
( )
A
H
K
B
C
( )
2; 2;4AB −
( )
1; 1;2u −
(1;1;0)A
AB
AB
AB
A
A
( )
A
H
( )
AA
( )
20x y z− + =
( )
1 ;1 ; 2 2H t t t− + − − +
( ) ( )
1 0;0;0H t H
=
H
( )
1; 1;0AA A
− −
( )
min
MA MB MA MB A B MA MB A B
+ = + + =
M
0
M
AB
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
333
Đường thẳng đi qua , có phương trình: . Mà
Giải hệ phương trình:
Vậy, để đạt giá trị nhỏ nhất thì .
Câu 26. Chọn D
qua và có vectơ chỉ phương
.
nên
không đồng phẳng
Vì điểm
thuộc
nên ta có . Lúc đó
Đặt . Ta có .
Tức là .
Đẳng thức xảy ra khi và chỉ khi .
Với ta có .
Câu 27. Chọn C
Ta có , phương trình đường thẳng
là .
AB
( )
1; 1;0A
−−
1
1
xt
y
zt
= − +
=−
=
1
:1
22
xt
yt
zt
= − +
= −
= − +
11
2
1 1 2
2
2 2 2 2
t t t t
t
tt
t
t t t t
− + = − + =
=
− = − =
=
− + = − + =
( )
0
1; 1;2M−
MA MB+
( )
1; 1;2M −
C( 1;1; 2),−−
(1; 1;2)u =−
( 2; 1;1);AB = − −
( 2;0; 2)AC = − −
;0AB u AC
;AB
M
( 1 ;1 ; 2 2 ),M t t t− + − − +
t
( ) ( ) ( ) ( ) ( )
2 2 2 2 2
2
2 2 2 1 2 3P MA MB t t t t t t= − = − + + − − − + − + −
22
6 12 8 6 14 10 .t t t t= − + − − +
( )
2
2
1 7 11
61
3 6 6
P t t
= − + − − +
3
1; ,
3
ut
=−
7 11
;
66
vt
=−
| | | |u v u v− −
2
2
1 3 11
6.
6 3 6
P
+ −
3
1 33
3
3
7
3
11
6
6
t
t
t
−
= = +
−
4 33
4 4 8
3
a b c t− + = − = +
( )
1; 1; 5AB = − −
AB
1 ( )
35
xt
y t t
zt
=−
= −
= − +

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
334
Xét vị trí tương đối giữa
và ta có
cắt
tại .
Suy ra là trung điểm .
. Dấu “=” xảy ra khi
hoặc . Do đó .
Câu 28. Chọn B
Ta có: nên hai điểm và
cùng nằm về một phía của mặt phẳng .
Gọi là hình chiếu vuông góc của lên mặt phẳng .PT đường thẳng : .
Do đó tọa độ điểm là nghiệm của hệ phương trình .
Do đó . Gọi đối xứng với qua , suy ra .
Ta có .
Câu 29. Chọn C
Ta có: nên hai điểm
và cùng nằm về một phía của mặt phẳng .
Gọi là hình chiếu vuông góc của lên mặt phẳng .
Phương trình đường thẳng : .
Do đó tọa độ điểm là nghiệm của hệ phương trình .
AB
AB
1 1 1
;;
2 2 2
C
−−
1 1 5 1
;;
2 2 2 2
AC AC AB C
= − − =
AB
T MA MB AB= −
MA
MB
max
27 3 3T AB= = =
( )( ) ( )( )
1 1 1 1 0 1 3 1 4 1 0
A A A B B B
x y z x y z− + + − + + = − + + + + +
A
B
( )
H
A
( )
AH
1
1
xt
yt
zt
=+
=−
=
H
1
1
10
xt
yt
zt
x y z
=+
=−
=
− + + =
1
3
2
3
4
3
1
3
t
x
y
z
=−
=
=
=−
2 4 1
;;
3 3 3
H
−
A
A
( )
1 5 2
;;
3 3 3
A
−
6MA MB MA MB A B P A B
+ = + = =
( )( ) ( )( )
3 5 3 5 1 1 3.2 5 5 1 3.0 5 0
A A A B B B
x y z x y z+ − − + − − = − − − − − − −
A
B
( )
H
A
( )
AH
1
1
23
xt
yt
zt
=+
= − +
=−
H
1
1
23
3 5 0
xt
yt
zt
x y z
=+
= − +
=−
+ − − =
1
2
0
1
t
x
y
z
=
=
=
=−
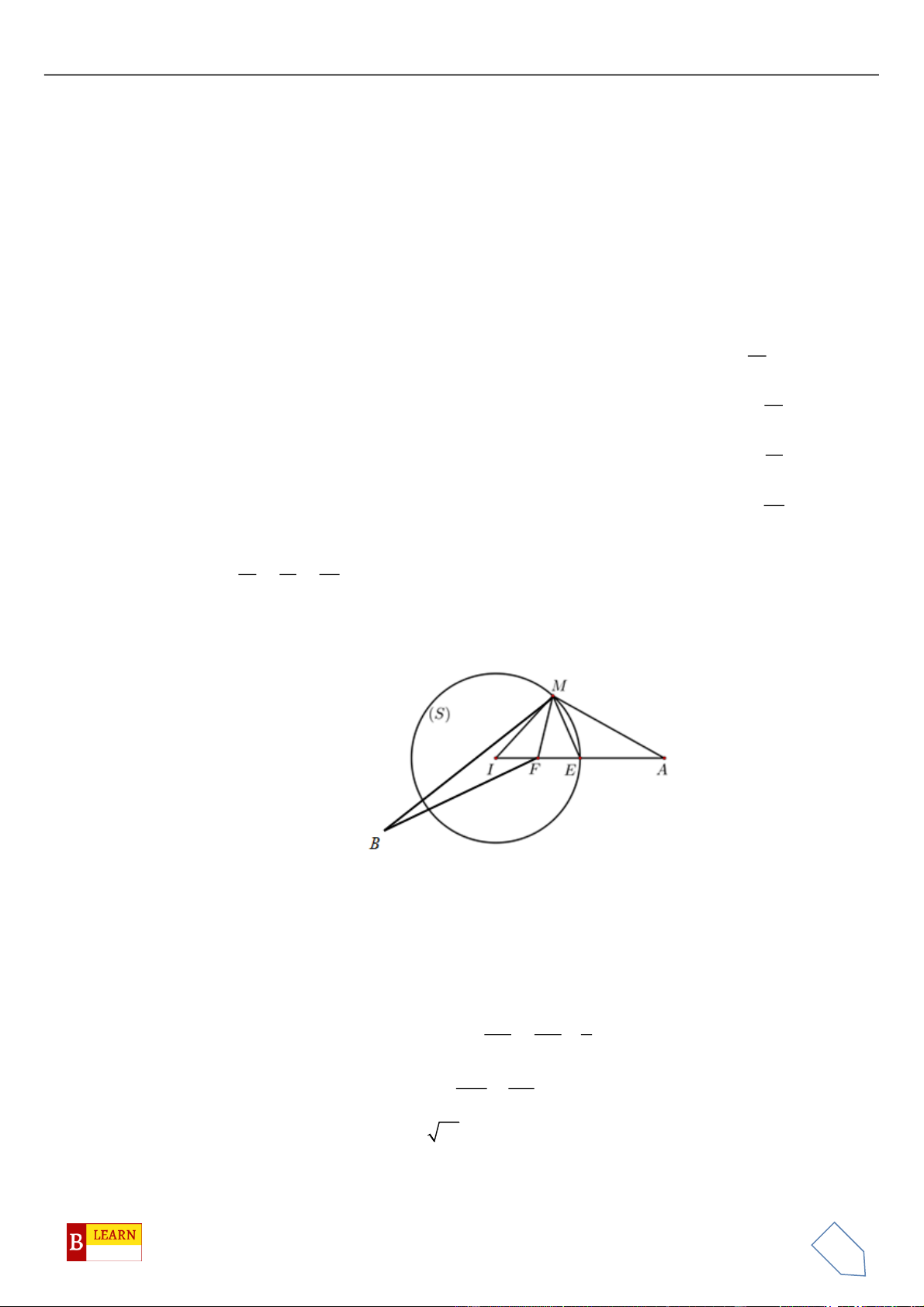
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
335
Do đó .
Gọi đối xứng với qua , suy ra .
Ta có nên nhỏ nhất khi .
Phương trình đường thẳng : .
Do đó tọa độ điểm là nghiệm của hệ phương trình .
Do đó , .
Câu 30. Chọn C
Mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 1 2 3 36S x y z− + − + − =
có tâm
( )
1; 2; 3I
và bán kính
6R =
.
Nhận xét
12 2IA R==
.
Gọi
E
là giao điểm của
IA
và mặt cầu
( )
S
suy ra
E
là trung điểm của
IA
nên
( )
5; 4; 7E
.
Gọi
F
là trung điểm của
IE
suy ra
( )
3; 3; 5F
.
MIF
và
AIM
có góc
AIM
chung và có
1
2
IF IM
IM IA
==
.
Nên
AIM
đồng dạng
( )
. .cMIF c g
2 2 .
MA AI
MA MF
MF MI
= = =
( )
2 2 2 2 29MA MB MF MB BF+ = + =
.
Dấu bằng xảy ra khi
M
là giao điểm
FB
và mặt cầu
( )
.S
( )
2;0; 1H −
A
A
( )
( )
3;1; 4A
−
MA MB MA MB A B
+ = +
MA MB+
( )
M A B
=
AB
34
1
43
xt
yt
zt
=−
=−
= − +
M
34
1
43
3 5 0
xt
yt
zt
x y z
=−
=−
= − +
+ − − =
12
11
15
11
1
11
20
11
t
x
y
z
=
=−
=−
=−
15 1 20
;;
11 11 11
M
− − −
2 3 7T a b c= + + = −
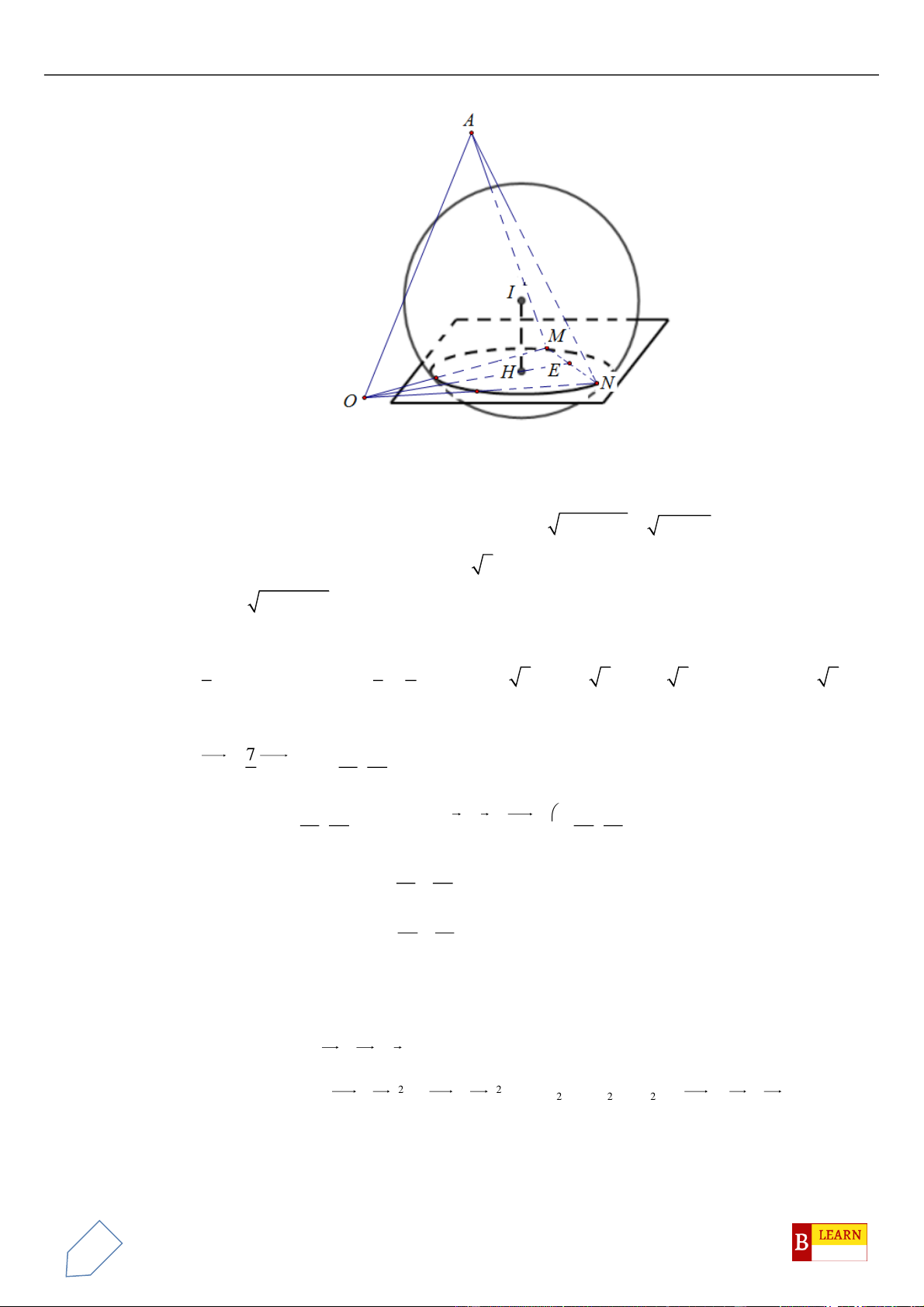
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
336
Câu 31. Chọn A
( ) ( ) ( ) ( )
2 2 2
: 3 4 4 25S x y z− + − + − =
có tâm
( )
3;4;4I
và bán kính
5.R =
Gọi
H
là hình chiếu vuông góc của
I
lên
( ) ( )
3;4;0 .Oxy H
Đường tròn
( )
C
có tâm là
( )
3;4;0H
và bán kính
22
25 16 3.r R IH= − = − =
Gọi
E
là trung điểm của
,MN
suy ra
5ME =
và
.HE MN⊥
22
5, 2.OH HE r ME= = − =
Suy ra
O
nằm ngoài
( )
.C
Gọi
K
là hình chiếu vuông góc của
O
lên
.MN
( )
( )
1 1 1
; . .9. .
3 3 2
OAMN OMN
V d A Oxy S OK MN
==
( )
3 5. 3 5. 3 5. 21 5.OK OE OH HE= + =
Đẳng thức xảy ra khi
KE
và
,,O H E
thẳng hàng (
H
nằm trong đoạn
OE
).
Khi đó:
7 21 28
; ;0 .
5 5 5
OE OH E
=
MN
đi qua điểm
21 28
; ;0
55
E
và nhận
28 21
; ;0
55
u k OE
= = −
làm một vectơ chỉ phương.
Do đó
MN
có phương trình:
21 28
55
28 21
55
0
xt
yt
z
=−
=+
=
. Vậy,
MN
đi qua điểm
( )
5;5;0 .
Câu 32. Chọn B
Gọi điểm
I
thỏa mãn
( )
3 0 6 ; 3 ; 1IA IB I+ = −
.
Khi đó
( ) ( ) ( )
22
2 2 2 2 2
3 3 4 3 2 . 3MA MB MI IA MI IB MI IA IB MI IA IB+ = + + + = + + + +
2 2 2
43MI IA IB= + +
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
337
Do
22
3IA IB+
không đổi vì ba điểm
;;A B I
cố định nên
22
3MA MB+
đạt giá trị nhỏ nhất khi
MI
nhỏ nhất. Khi đó
M
là giao điểm của đường thẳng
IJ
với mặt cầu
( )
S
, (
( )
2 ; 1 ; 3J
là tâm của
mặt cầu
( )
S
). Ta có phương trình đường thẳng
IJ
là
22
1
32
xt
yt
zt
=+
=+
=−
( )
( )
( )
1
2
4; 2 ; 1
0 ; 0 ; 5
M
IJ S
M
=
.
Kiểm tra
( )
12
39IM IM
nên
( )
1
4;2;1M
là điểm cần tìm. Vậy
. . 8T abc==
.
Câu 33. Chọn C
Gọi
K
,
H
lần lượt là hình chiếu vuông góc của
A
lên mặt phẳng
( )
P
, đường thẳng
d
.
Ta có:
AH AK
.
Suy ra, mặt phẳng
( )
P
chứa
d
sao cho khoảng cách từ
A
đến mặt phẳng
( )
P
lớn nhất khi và
chỉ khi
( )
P
đi qua điểm
H
và vuông góc
AH
. Gọi
( )
1 2 ; ;2 2H t t t d+ +
ta có:
.0
d
AH u =
với
( )
2;1;2
d
u =
là vectơ chỉ phương của đường thẳng
d
1t=
( )
3;1;4H
.
Nên
( )
P
đi qua điểm
( )
3;1;4H
nhận
( )
1; 4;1AH =−
làm vectơ pháp tuyến có phương trình là:
4 3 0x y z− + − =
. Vậy
1 4 1 2T a b c= + + = − + = −
.
Câu 34. Chọn A
Ta có
( )
()
( ) 1;1;1
P
PI
⊥
=
.
Vì
( )
;2dM=
nên điểm
M
thuộc mặt trụ tròn xoay
()H
có trục là đường thẳng
.
Khi đó
M
nằm trên giao của mặt phẳng
()P
và mặt trụ
()H
là đường tròn
()C
có tâm
( )
1;1;1I
và bán kính
2R =
. Giả sử
( )
;;N x y z
.
Do
2 2 2 2 2
2 4 2 2 14 42 0NA NB NA NB x y z x y z= = + + − − − + =
.
Suy ra
N
nằm trên mặt cầu
()S
có tâm
( )
1;1;7J
và bán kính
3R
=
.
Mặt khác:
()
()
NP
JP
, do đó
N
nằm trên giao của mặt phẳng
()P
và mặt cầu
()S
là đường tròn
()C
có tâm
( )
1;1;7J
và bán kính
3R
=
.
Bài toán đã cho trở thành: ‘Trên mặt phẳng
()P
cho hai điểm
,MN
. Biết
M
thuộc đường tròn
()C
có tâm
( )
1;1;1I
, bán kính
2R =
và
N
thuộc đường tròn
()C
có tâm
( )
1;1;7J
, bán kính
3R
=
. Tìm giá trị nhỏ nhất của đoạn
MN
.”
Từ hình vẽ trên, dễ thấy
( )
min
IJ 6 (2 3) 1MN IM JN= − + = − + =
.
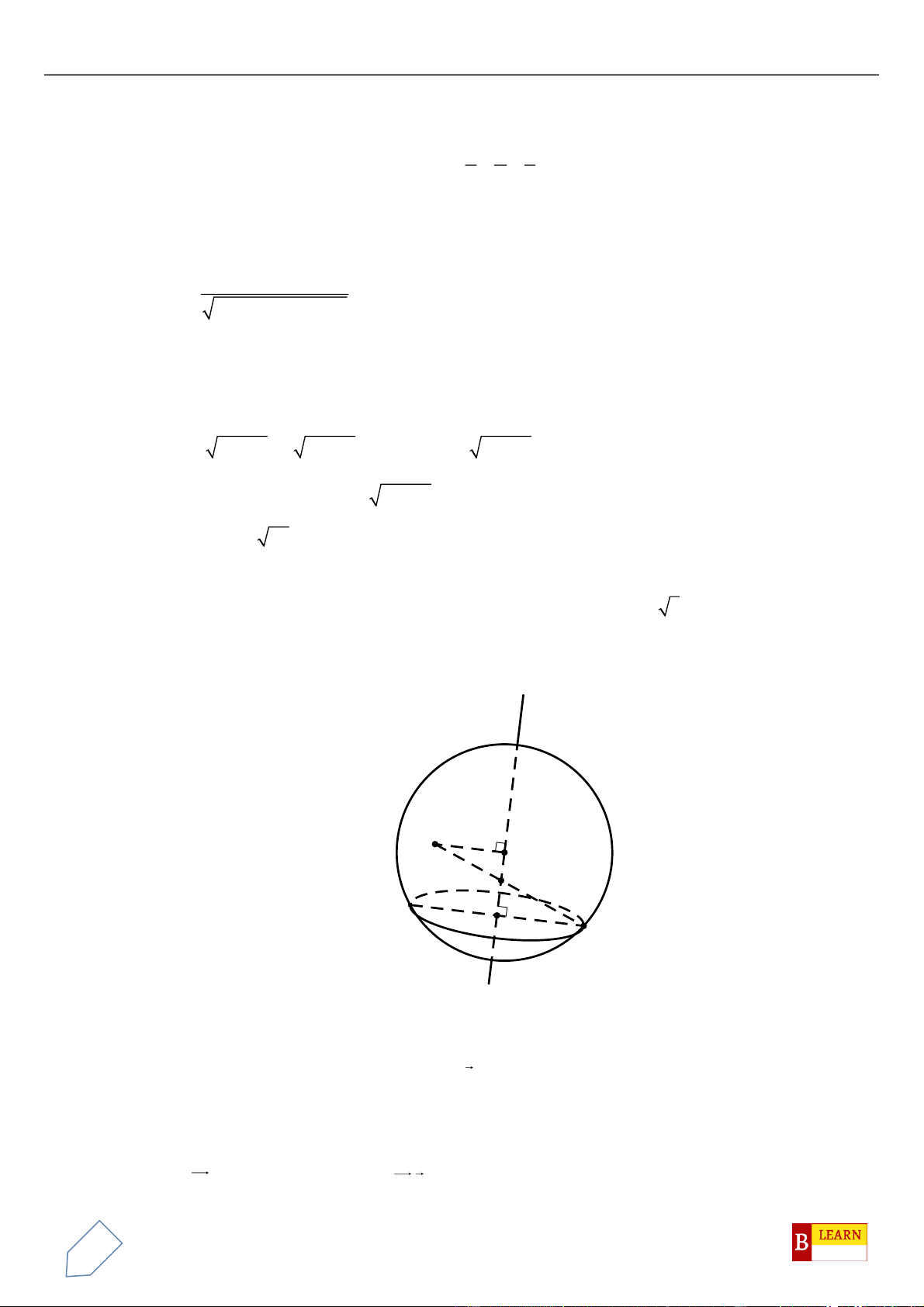
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
338
Câu 35. Chọn C
Gọi
( ) ( ) ( )
;0;0 , 0; ;0 , 0;0;A a B b C c
( )
0, 0, 0abc
.
Khi đó phương trình mặt phẳng
( )
ABC
là
10
x y z
bcx acy abz abc
a b c
+ + = + + − =
.
Mặt cầu
( )
S
có tâm
( )
0;0;0O
và bán kính
1R =
.
Mặt phẳng
( )
P
tiếp xúc với
( )
S
nên
( )
( )
,d O P R=
hay
( )
( )
,1d O ABC =
.
Khi đó
( )
2 2 2 2 2 2 2 2 2
2 2 2 2 2 2
11
abc
a b c a b b c c a
b c a c a b
= = + +
++
.
Ta có :
( )( )( ) ( )( )( )
2 2 2 2 2 2
1 1 1 1 1 1T OA OB OC a b c= + + + = + + +
.
2 2 2 2 2 2 2 2 2 2 2 2
1T a b c a b b c a c a b c= + + + + + + +
.
(
)
3
3 3 3
2 2 2 4 4 4 2 2 2 2 2 2
1 3 3 1T a b c a b c a b c a b c + + + = +
.
Mặt khác từ suy ra
3
2 2 2 4 4 4 6 6 6 4 4 4 2 2 2
3 27 27a b c a b c a b c a b c a b c
.
Suy ra
( )
3
3
1 27 64T + =
.
Vậy giá trị nhỏ nhất của
T
bằng 64 khi:
2 2 2
2 2 2
3
27
abc
a b c a b c
abc
==
= = = = =
=
.
Câu 36.
Chọn A
Mặt cầu
( )
S
có tâm
( )
3; 4; 5I − − −
và bán kính
27R =
.
Đường thẳng
d
có 1 véc-tơ chỉ phương là
( ) ( )
2;3;4u d P= ⊥
.
Gọi
K
là giao điểm của mặt phẳng
( )
P
và đường thẳng
d
. Vì
Id
nên
K
là tâm của đường
tròn giao tuyến và
KB d⊥
.
Ta có
( )
1;2; 2 3IA IA= − =
và
.0IAu IA d= ⊥
.
d
M
K
I
B
A
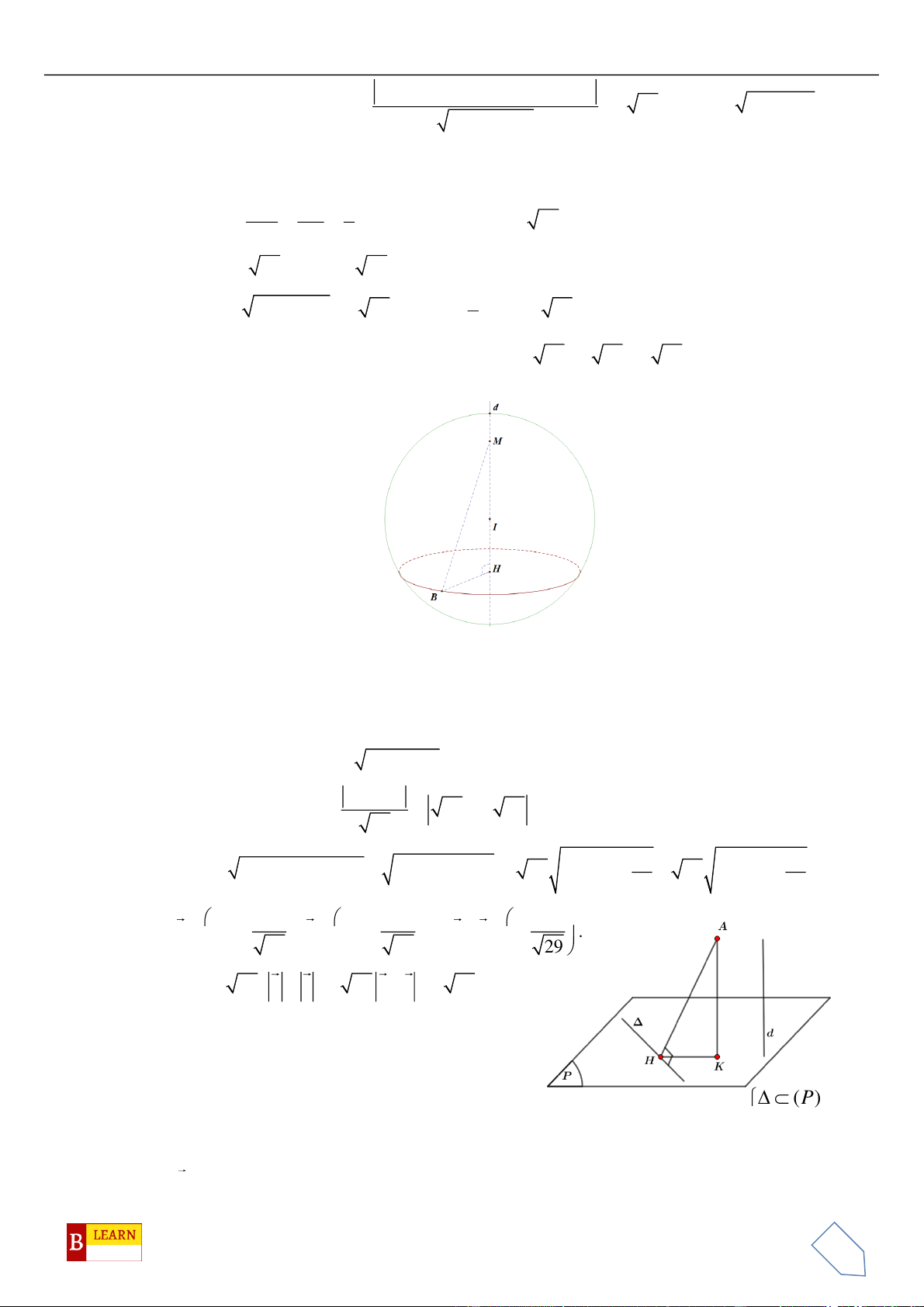
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
339
Ta tính được
( )
( )
( ) ( ) ( )
2 2 2
2. 3 3. 4 4 5 107
d , 5 29
234
IK I P
− + − + − −
= = =
++
và
22
2KB R IK= − =
.
Do
M
di động trên đường thẳng
d
và
B
thuộc đường tròn giao tuyến nên biểu thức
MA MB+
nhỏ nhất khi và chỉ khi
M AB d=
.
Khi đó, ta có
3
2
MI IA
MK KB
==
và
5 29MI MK IK+ = =
.
Suy ra
3 29MI =
,
2 29MK =
.
Ta có
22
3 30AM IA MI= + =
2
2 30
3
BM AM = =
.
Vậy giá trị nhỏ nhất của
MA MB+
là
3 30 2 30 5 30AM BM+ = + =
.
Cách 2:
Ta có
( )
S
có tâm
( )
3; 4; 5I − − −
,
bán kính
27R =
.
Dễ thấy
d
đi qua
( )
3; 4; 5I − − −
và vuông góc với
( )
P
.
( )
P
cắt
( )
S
theo đường tròn có bán kính
2r =
.
( )
1 2 ;2 3 ;3 4M d M t t t + + +
.
Ta có
22
.T MA MB MA MH r= + = + +
Lại có
29 87
( ;( )) 29 3 29
29
t
MH d M P t
−
= = = −
.
Suy ra
( )
2
2
29 116 125 29 3 4T t t t= + + + − +
( ) ( )
22
94
29 2 29 3 .
29 29
tt= + + + − +
Xét
3
2;
29
ut
=+
,
2
3;
29
vt
=−
5
5;
29
uv
+ =
.
Do đó
( )
29 29 5 50T u v u v= + + =
.
Câu 37. Chọn B
Gọi
()P
là mặt phẳng chứa
qua
M
và vuông góc với đường thẳng
d
, khi đó
()P
d
⊥
.
Với
(2;2; 1)
d
u =−
là một véctơ chỉ phương của đường thẳng
d
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
340
Chọn một véc tơ pháp tuyến của
()P
là
()
(2;2; 1)
P
d
nu=−=
. Ta có
()P
:
2 2 9 0.x y z+ − + =
Gọi
,KH
lần lượt là hình chiếu vuông góc của
A
lên mp
()P
và đường thẳng
.
Ta thấy
( )
;.d A AH AK =
Nên
( )
;Min d A AK=
khi và chỉ khi
HK
.
Mà
( )
( )
2 2 2
2.1 2.2 3 9
; 6.
2 2 ( 1)
AK d A P
+ + +
= = =
+ + −
Vậy
( )
; 6Min d A =
.
Câu 38. Chọn A
Mặt cầu
()S
có tâm
(1; 1;1)I
, bán kính
6R
.
Gọi
x
là khoảng cách từ
I
đến mặt phẳng
()
,
06x
. Khi đó, thể tích khối nón đỉnh
I
,
đáy là đường tròn
()C
là:
3
2
1
62
33
x
V x x x
Xét hàm số
3
( ) 2 ,
3
x
f x x
với
06x
có
2
'( ) 2; '( ) 0 2f x x f x x
Hàm số
()y f x
liên tục trên
0; 6
, có
(0) ( 6) 0, ( 2) 2f f f
, nên
0; 6
( ) 2Max f x
đạt được khi
2x
.
Gọi
(1; 4;1)u
là một véc tơ chỉ phương của đường thẳng
d
. Vì
()IH
nên tồn tại số thực
k
sao cho
IH ku
, suy ra
2 1 1
| |. | |
33
18
IH k u k k
.
Với
1
:
3
k
1 4 7 4
;;
3 3 3 3
IH u H
( ): 4 6 0x y z
Với
1
:
3
k
1 2 1 2
;;
3 3 3 3
IH u H
( ): 4 0x y z
. Vậy
1
3
H H H
x y z
Câu 39. Chọn A
Có góc tạo bởi đường thẳng
d
và mặt phẳng
( )
Oxy
là
( )
( )
; Oxdy
góc tạo bởi mặt phẳng
( )
và mặt phẳng
( )
Oxy
là
( ) ( )
( )
; Oxy
.
Ta có
( )
( )
( ) ( )
( )
; Ox ; Oxd y y
( ) ( )
( )
( )
( )
( ) ( )
( )
min
; Ox ; Ox ; Oxy d y y
=
( )
( )
( )
( )
.
1 30
sin , cos ,
6
6
.
d
d
uk
dd
uk
= = =
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
341
Gọi VTPT của
( )
là
( )
2 2 2
;b;c , 0n a a b c= + +
Vì
( )
2 0 2d u n a b c c a b
⊥ − − = = −
( ) ( )
( )
( )
2
22
.
2
30
cos Ox ,
6
.
2
nk
ab
y
nk
a b a b
−
= = =
+ + −
( ) ( )
2 2 2 2
36 4 4 30 5 4 2a ab b a ab b − + = − +
( )
2
22
6 24 24 0 6 2 0 2a ab b a b a b + + = + = = −
. Chọn
( )
2; 1;5n =−
.
Vậy
( )
đi qua
( )
1;1;2Ad−
và có VTPT
( )
2; 1;5n =−
( )
:2 5 7 0x y z
− + − =
.
( )
( )
,
30
30
30
M
d
==
.
Câu 40. Chọn A
Đường thẳng
d
có véctơ chỉ phương
( )
3; 2;2
d
u =−
.
Ta thấy
Ad
và
( ) ( )
6; 4;4 2 3; 2;2AB = − = −
. Suy ra
//AB d
.
Gọi
A
là điểm đối xứng với
A
qua
d
. Ta có
AI BI A I BI A B
+ = +
. Dấu
""=
xảy ra khi
A
,
I
,
B
thẳng hàng.
Vậy
( )
min AI BI A B
+=
trong đó
I A B d
=
Gọi
H
là hình chiếu vuông góc của
A
lên đường thẳng
d
. Ta tìm được
( )
1;2;2H −
Do
H
là trung điểm
AA
nên suy ra
( )
' 3;2;5A −
.
Do
//AB d
nên
I
là trung điểm
AB
nên suy ra
( )
2;0;4I
.
Cách 2: Tìm tọa độ điểm
H
trong bài này từ nhận xét sau:
Từ phương trình đường thẳng
d
ta thấy
d
đi qua điểm
( )
1;2;2H −
.
Có
( )
4;0;6AH =−
và
( )
3; 2;2
d
u =−
thỏa mãn
.0
d
AH u AH d= ⊥
.
Vậy
H
là hình chiếu của
A
lên đường thẳng
d
.
Câu 41. Chọn A
Theo đề
( )
( )
( )
0;0;
4 3 ;3 4 ;0
M Oz M m
N d N t t
d Oxy
− +
.
Vì
A
là hình chiếu vuông góc của
O
trên
d
nên tìm được
( )
4;3;0A
.
I
là trung điểm đoạn
thẳng
3
2; ;0
2
OA I
.
Mặt khác
( ) ( ) ( )
22
2
3 4 4 3 5 *MN OM AN t t m m t= + − + + + = +
d
I
H
A
A'
B

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
342
( )
55
2 5 0
22
mt mt m t
t
= = =
.
Trên tia đối của tia
Oz
, lấy điểm
H
thỏa
OH AN=
. Ta chứng minh được
IMH IMN =
.
Khi đó
( )
1 5 5
.5
2 4 4
IMN IMH
S S IO MH MN m t
= = = = +
do
( )
*.
5 5 25 1 25 2
5.
4 2 4 2 4
tt
tt
= + = +
Dấu
""=
đạt tại
1 2 5 2
.
2 2 2
t t m
t
= = =
Vậy
52
0;0;
2
M
.
Ta có
( )
52
4;3; ; 3;4;0
2
d
MA u
= − = −
.
Mặt phẳng
( )
,Md
có một VTPT
( )
15 2 5 2
; 10 2; ;25 4;3;5 2
22
d
n MA u
= = =
.
Câu 42. Chọn B
Vì
90AMB=
nên ta có điểm
M
thuộc mặt cầu
( )
S
.
Mặt cầu
( )
S
có tâm
( )
2;3; 2I −
là trung điểm của
AB
và bán kính
1
17
2
R AB==
.
Mặt khác điểm
M
thuộc mặt phẳng
( )
P
nên ta có tập hợp điểm
M
là đường tròn
( ) ( ) ( )
C S P=
.
Đường tròn
( )
C
có tâm
O
là hình chiếu của điểm
( )
2;3; 2I −
lên mặt phẳng
( )
P
và có bán kính
( )
( )
22
, 17 3 14r R d I P= − = − =
.
Tìm tọa độ điểm
O
:
Gọi
( )
d
là đường thẳng đi qua điểm
I
và vuông góc với mặt phẳng
( )
P
. Phương trình đường
thẳng
( )
d
là:
2
3
2
xt
yt
zt
=+
=+
= − +
.
Vì
O
là hình chiếu của điểm
( )
2;3; 2I −
lên mặt phẳng
( )
P
nên
( ) ( )
O d P=
.
Xét
(2 ) (3 ) ( 2 t) 0 3t 3 0 1 (1;2; 3)t t t O+ + + + − + = + = =− −
.
Vậy đường tròn
( )
C
nằm trên mặt phẳng
( )
P
có tâm
(1;2; 3)O −
bán kính
14r =
.
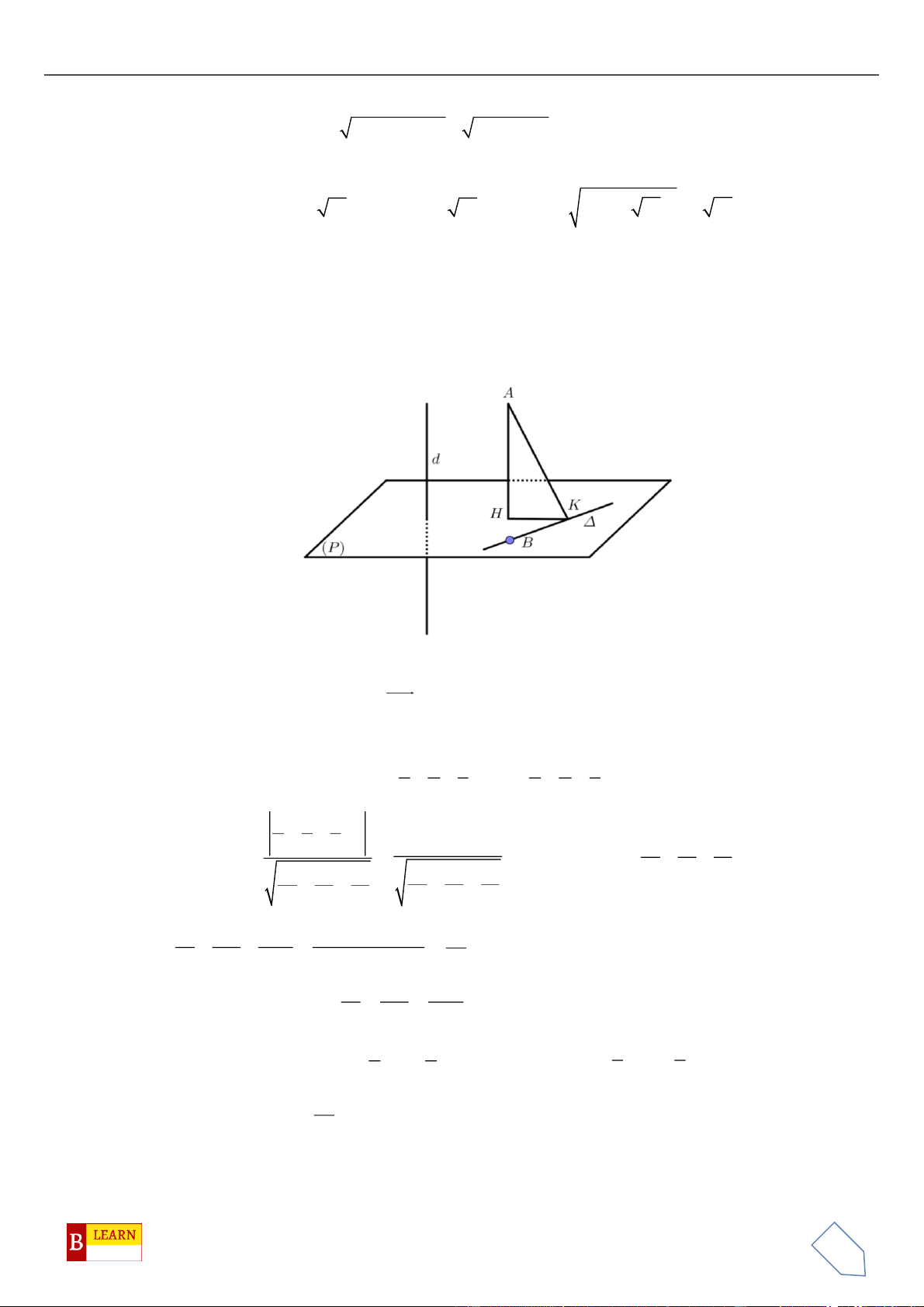
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
343
Gọi
H
là hình chiếu của điểm
C
lên mặt phẳng
( )
P
. Tương tự tìm tọa độ điểm
O
ta có
( )
2;4; 6H −
. Ta có
2 2 2
12CM CH HM HM= + = +
.
Do đó
CM
đạt giá trị lớn nhất khi và chỉ khi
HM
lớn nhất.
Ta có
max
2 14 2 14HM HO r HM + =
( )
2
max
12 2 14 2 17CM = + =
.
Câu 43. Chọn A
Gọi
( )
P
là mặt phẳng qua
B
và vuông góc với
d
;
( )
:2 1 0P x y z+ + − =
.
Gọi
H
là hình chiếu của
A
lên
( )
P
, ta có:
( )
2;1; 4H −
Ta có:
( )
P
nên
( ) ( )
( )
;;d A d A P
;
Dấu đẳng thức xảy ra khi và chỉ khi
H
.
Một vectơ chỉ phương của
là
( )
1;1; 3BH =−
.
Câu 44. Chọn B
Phương trình mặt phẳng
( )
ABC
:
1
x y z
a b c
+ + =
10
x y z
a b c
+ + − =
.
( )
( )
2 2 2
0 0 0
1
;
1 1 1
a b c
d O ABC
abc
++−
=
++
2 2 2
1
1 1 1
P
abc
==
++
.
max
P
2 2 2
1 1 1
T min
abc
= + +
.
( )
2
2 2 2 2 2 2
1 2 4
1 4 16
4 16 4 16
T
a b c a b c
++
= + +
++
2
7
1
49
==
.
min
1S =
. Dấu bằng xảy ra
2 2 2
1 2 4
4 16a b c
==
22
2ba=
;
22
4ca=
.
2 2 2
4 16 49a b c+ + =
22
2
4 16 49
24
aa
a + + =
2
7a=
,
2
7
2
b =
,
2
7
4
c =
.
Vậy
2 2 2
49
4
S a b c= + + =
.
Câu 45. Chọn D
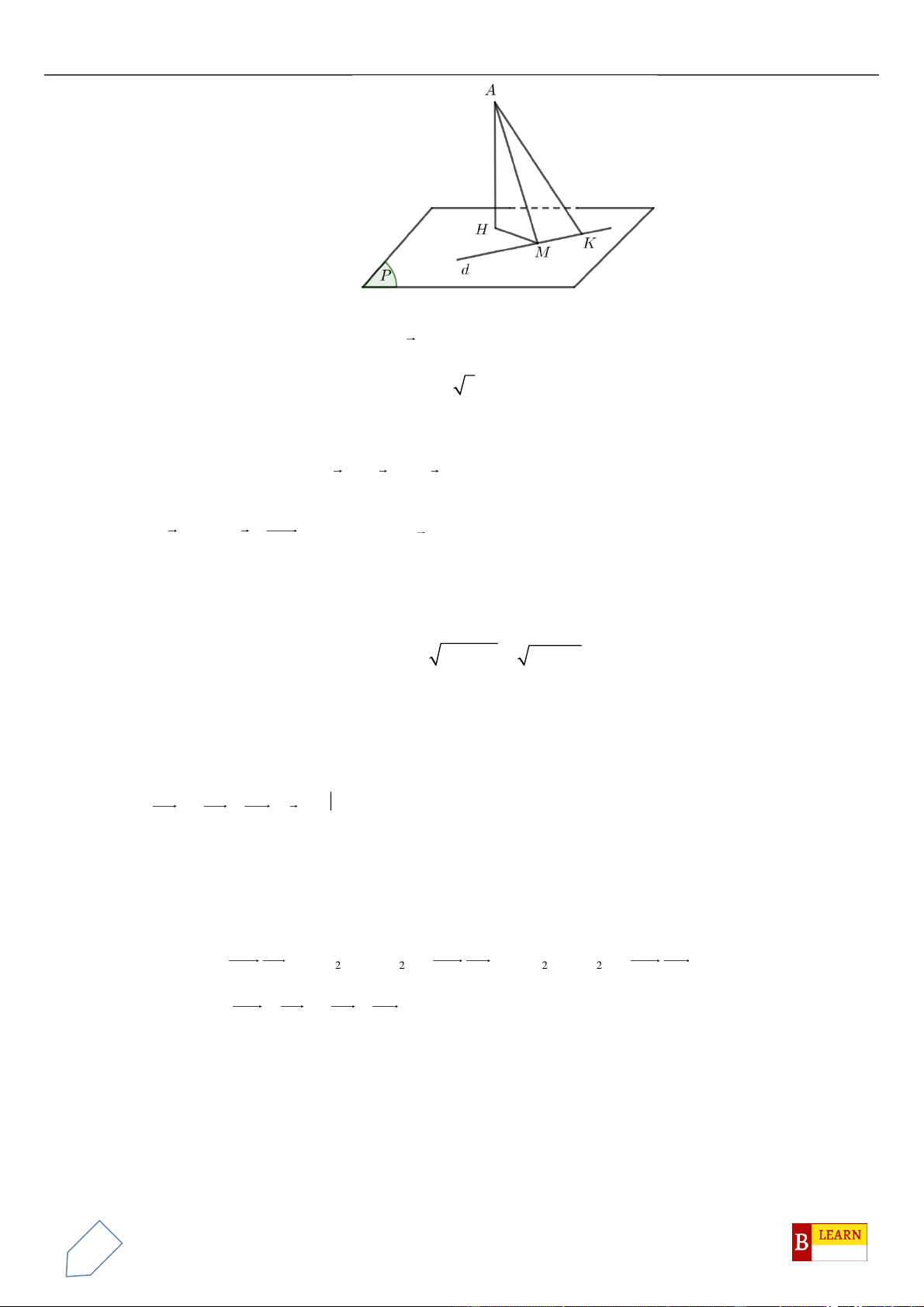
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
344
Ta có:
d
đi qua
( )
1; 2;0M −
và có VTCP
( )
2;1;2
d
u =
.
( )
S
có tâm
( )
3;2; 1I −
và bán kính
25R =
.
Ta có:
( )
( )
( )
;;d A P d A d
. Dấu “
=
” xảy ra khi
( )
P
chứa
d
và vuông góc với
AK
.
Khi đó:
( )
P
có VTPT là
( )
,
P AKM d
n n u
=
.
Vì
( )
( )
, 6;6;3
AKM d
n u AM
= = −
( ) ( )
9;18; 18 9 1;2; 2
P
n = − = −
.
( ) ( ) ( )
: 1 2 2 2 0P x y z − + + − =
( )
: 2 2 3 0P x y z + − + =
. Ta có:
( )
( )
;4d d I P==
.
Vậy bán kính đường tròn cần tìm:
22
20 16 2r R d= − = − =
.
Câu 46. Chọn A
( ) ( ) ( ) ( )
2 2 2
: 1 1 1 1S x y z− + − + − =
có tâm
( )
1;1; 1I
. Gọi
( )
;;G x y z
là điểm thỏa mãn
( ) ( ) ( )
( ) ( ) ( )
( ) ( ) ( )
3 0 2 3 0 0
1
3 2 0 3 1 2 0 21 0 4
3
3 1 2 1 19 0
x x x
x
GA GB GC y y y y
z
z z z
− + − + − =
=
+ + = − + − + − = =
=−
− + − − + − − =
( )
1; 4; 3G−
.
Ta có:
2 2 2
32T MA MB MC= + +
2 2 2 2 2 2
3 6 . 3 2 4 . 2 2 .MG MGGA GA MG MGGB GB MG MGGC GC= + + + + + + + +
( )
2 2 2 2
6 2 3 2 3 2MG MG GA GB GC GA GB GC= + + + + + +
2 2 2 2
6 3 2MG GA GB GC= + + +
min
T
M
là giao điểm của đường thẳng
IG
và mặt cầu
( )
S
, sao cho
M
và
G
cùng phía với
I
Phương trình đường thẳng
1
: 1 3
14
x
IG y t
zt
=
=+
=−
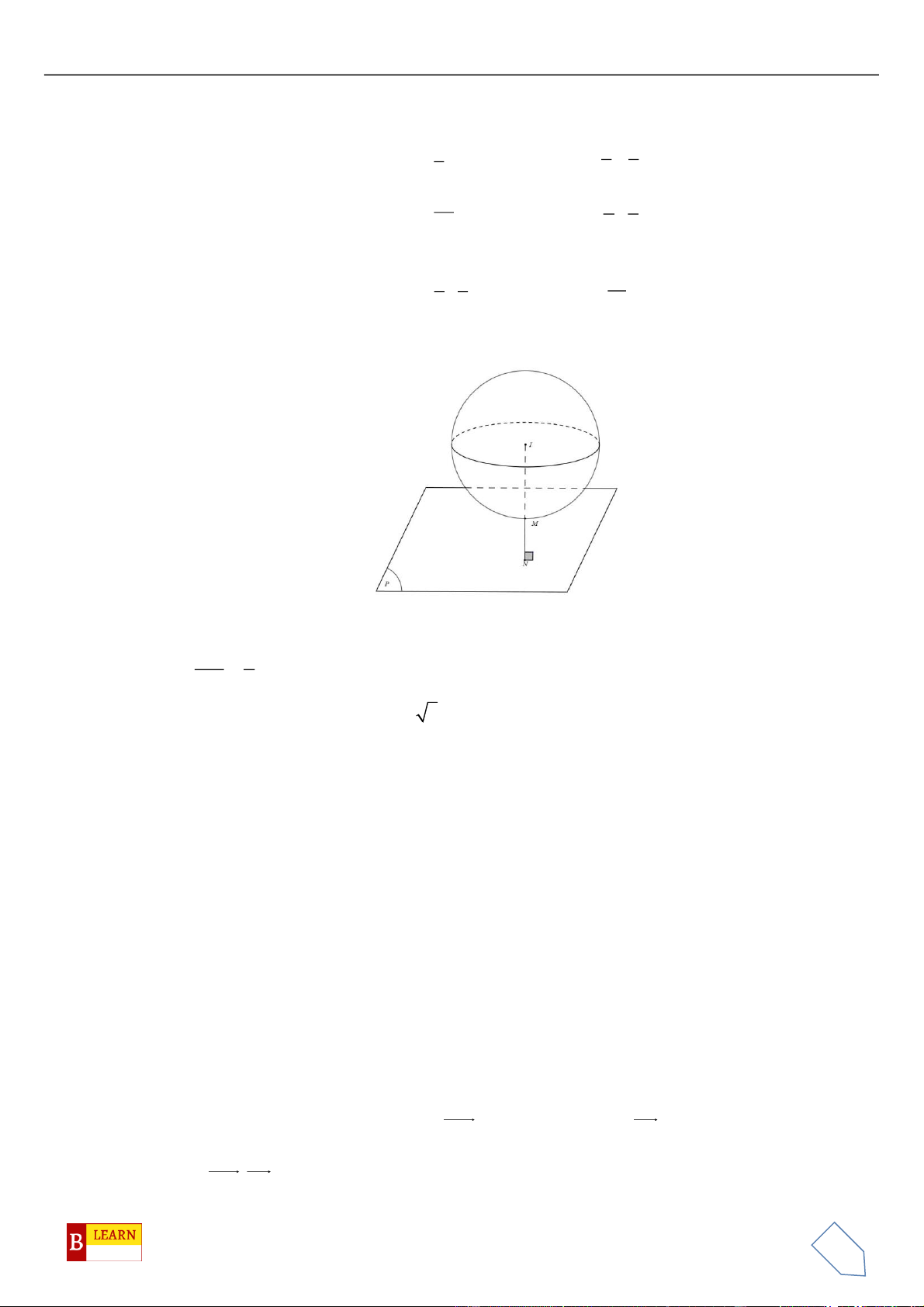
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
345
( )
M IG S=
nên tọa độ
M
là nghiệm của hệ
( ) ( ) ( )
2 2 2
1
1
13
5
14
1
5
1 1 1 1
x
t
yt
zt
t
x y z
=
=
=+
=−
−
=
− + − + − =
. Khi đó :
1
2
81
1; ;
55
29
1; ;
55
M
M
Vì
12
M G M G
nên điểm
1
81
1; ;
55
MM
. Vậy
14
5
abc+ + =
.
Câu 47. Chọn B
Gọi
( )
;;M x y z
.
Ta có
( ) ( ) ( )
2 2 2
22
2
9 4 6 6 6 108
3
MA
MA MB x y z
MB
= = + + − + + =
. Vậy điểm
M
thuộc mặt
cầu tâm
( )
6;6; 6I −−
bán kính
63R =
.
Vậy
MN
nhỏ nhất khi
,MN
thuộc đường thẳng đi qua tâm
I
và vuông góc với mặt phẳng
( )
P
.
Gọi
( )
d
là đường thẳng đi qua tâm
I
và vuông góc với mặt phẳng
( )
P
.
Khi đó
( )
6
: 6 2
62
xt
d y t
zt
= − −
=+
= − −
. Tọa độ điểm
N
là nghiệm của hệ phương trình
6
62
62
2 2 6 0
xt
yt
zt
x y z
= − −
=+
= − −
− + − + =
6
62
62
6 12 4 12 4 6 0
xt
yt
zt
ttt
= − −
=+
= − −
+ + + + + + =
2
2
2
4
x
y
z
t
=−
=−
=
=−
.
( )
2; 2;2N − −
. Do đó
2 2 2 2T = − − + = −
.
Câu 48. Chọn D
Vì
Md
nên
( )
1 ; ;1M t t t− + +
. Ta có
( )
1 ; 1; 1AM t t t= − + + −
,
( )
1;2;0AB =
.
Do đó:
( )
, 2 2 ; 1; 3AM AB t t t
= − − −
. Diện tích tam giác
MAB
:

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
346
1
,
2
S AM AB
=
( ) ( ) ( )
2 2 2
1
2 2 1 3
2
t t t= − + − + −
2
1
6 16 14
2
tt= − +
2
1 4 10
6
2 3 3
t
= − +
5
6
. Dấu bằng xảy ra khi
4
3
t =
.
Do đó diện tích tam giác
MAB
nhỏ nhất khi
147
;;
3 3 3
M
. Khi đó
2 3 10T a b c= + + =
.
Câu 49. Chọn D
Vì
Md
nên
( )
1 ; ;1M t t t− + +
.
Ta có
( )
1 ; 1; 1AM t t t= − + + −
,
( )
1;2;0AB =
. Do đó:
( )
, 2 2 ; 1; 3AM AB t t t
= − − −
Diện tích tam giác
MAB
:
1
,
2
S AM AB
=
( ) ( ) ( )
2 2 2
1
2 2 1 3
2
t t t= − + − + −
2
1
6 16 14
2
tt= − +
5
6
=
4
3
t=
. Do đó
147
;;
3 3 3
M
. Khi đó
2 3 10T a b c= + + =
.
Câu 50. Chọn C
Vì
Md
nên
( )
1 ; ;1M t t t− + +
. Ta có
( )
1 ; 1; 1AM t t t= − + + −
,
( )
1;2;0AB =
.
Do đó:
( )
, 2 2 ; 1; 3AM AB t t t
= − − −
. Diện tích tam giác
MAB
:
1
,
2
S AM AB
=
( ) ( ) ( )
2 2 2
1
2 2 1 3
2
t t t= − + − + −
2
1
6 16 14
2
tt= − +
1=
1
5
3
t
t
=
=
.
Do đó
( )
0;1;2M
hoặc
2 5 8
;;
3 3 3
M
.
Vậy có hai điểm
M
thuộc
d
để tam giác
MAB
có diện tích bằng
1
.
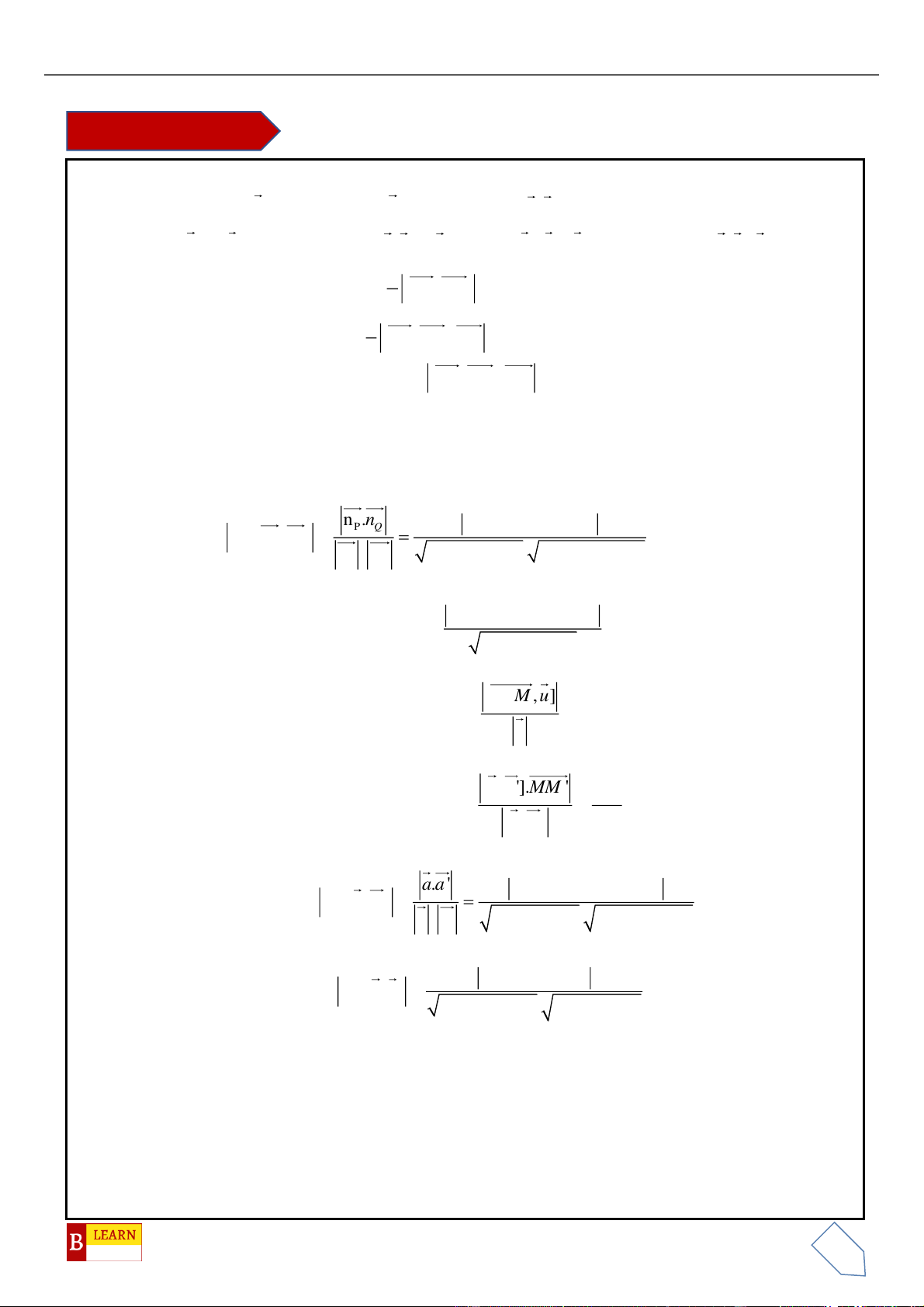
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
347
CHỦ ĐỀ 4 : TỌA ĐỘ HÓA VÀ BÀI TOÁN ĐẠI SỐ
➢ LƯU Ý MỘT SỐ CÔNG THỨC SAU ĐÂY
❖ Tích có hướng của
1 2 3
( ; ; )a a a a=
và
1 2 3
( ; ; )b b b b=
là
2 3 3 2 3 1 1 3 1 2 2 1
, ( ; ; )a b a b a b a b a b a b a b
= − − −
▪
a
và
b
cùng phương
,0ab
=
a
,
b
,
c
đồng phẳng
, . 0a b c
=
▪ Diện tích tam giác :
1
[ , ]
2
ABC
S AB AC=
▪ Thể tích tứ diện
ABCD
V =
1
[ , ].
6
AB AC AD
▪ Thể tích khối hộp:
' ' ' '
.ABCD A B C D
V
=
[ , ]. 'AB AD AA
❖ Góc giữa hai mặt phẳng:
▪ Gọi là góc giữa hai mặt phẳng
và
▪
❖ Khoảng cách từ điểm đến mặt phẳng
0 0 0
0
2 2 2
Ax
( , )
By Cz D
dM
A B C
+ + +
=
++
❖ Khoảng cách từ một điểm đến một đường thẳng
0
[M , ]
( , )
Mu
dM
u
=
❖ Khoảng cách giữa hai đường thẳng chéo nhau
[ , ']. '
( , ')
[ , ']
hop
day
a a MM
V
ddd
S
aa
==
❖ Góc giữa hai đường thẳng:
1 1 2 2 3 3
2 2 2 2 2 2
1 2 3 1 2 3
.'
. ' . ' . '
os os( , ')
.'
. ' ' '
aa
a a a a a a
c c a a
aa
a a a a a a
++
= = =
+ + + +
❖ Góc giữa đường thẳng và mặt phẳng:
1 2 3
2 2 2 2 2 2
1 2 3
Aa +Ba +Ca
sin os( , )
A.
c a n
B C a a a
==
+ + + +
❖ Mẹo nhớ công thức về góc trong hình học Oxyz:
▪ Cùng loại dùng Cos (Góc giữa đường thẳng với đường thẳng, mặt phẳng với mặt phẳng)
▪ Khác loại dung Sin (Góc giữa đường thẳng và mặt phẳng)
( )
0 90
oo
( )
:0P Ax By Cz D+ + + =
( )
: ' ' ' ' 0Q A x B y C z D+ + + =
P
P
2 2 2 2 2 2
PQ
n.
A.A' . ' . '
os = cos(n , )
n . n
. ' ' '
Q
Q
n
B B C C
cn
A B C A B C
++
==
+ + + +
LÍ THUYẾT
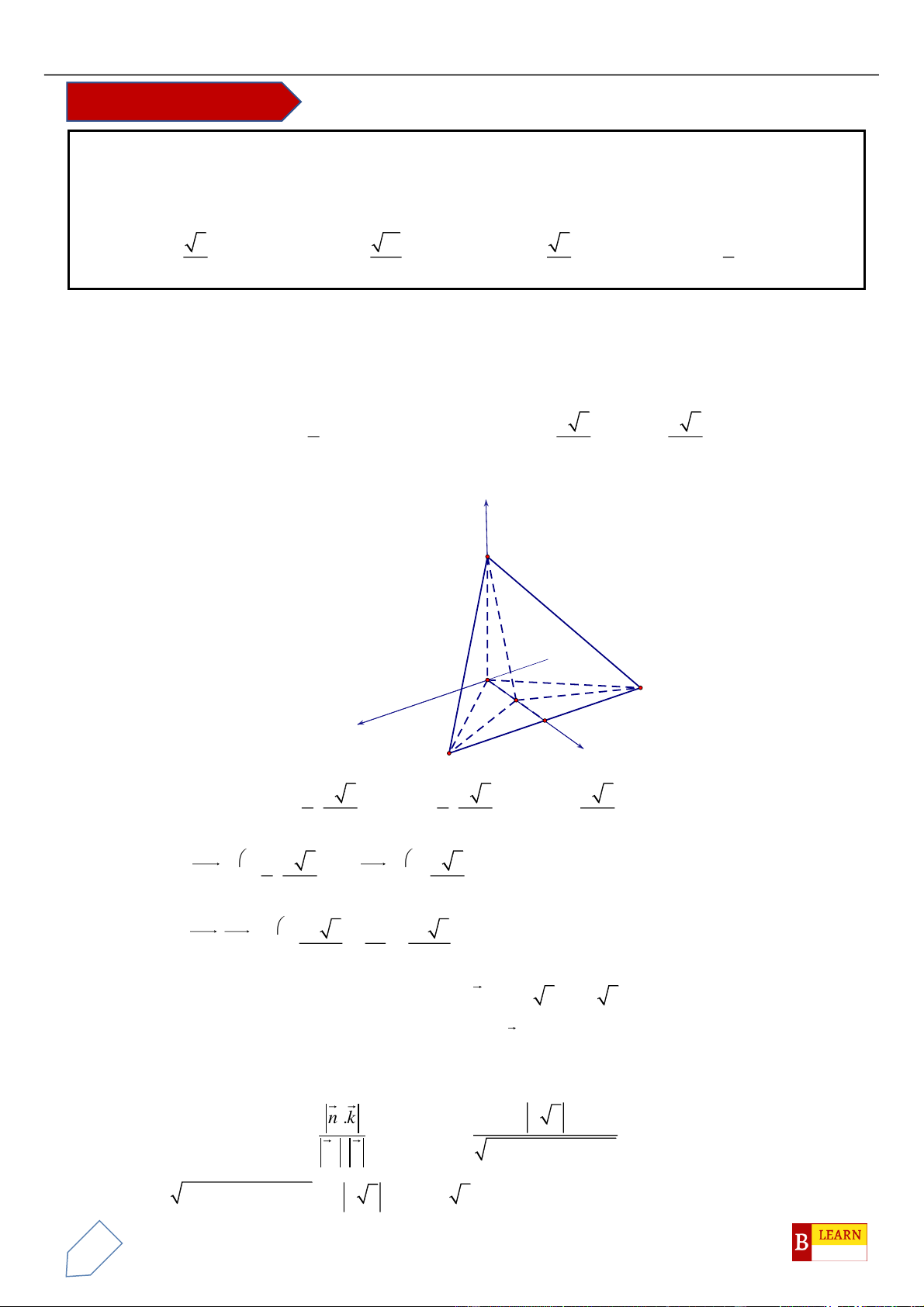
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
348
Lời giải
Chọn B
Từ
M
là trung điểm của
BC
và
H
là trung điểm của
AM
,
HB HC=
suy ra
AM BC⊥
, hay
tam giác
ABC
cân đỉnh
A
.
Đặt
2
a
BC a BM= =
. Do
30HBC =
suy ra
33
63
aa
HM AM= =
. Đặt
SA b=
.
Đặt hệ trục tọa độ như hình vẽ:
Ta có
( )
0;0;0A
,
3
; ;0
23
aa
B
,
3
; ;0
23
aa
C
−
;
3
0; ;0
6
a
H
,
( )
0;0;Sb
.
Ta có
3
; ;0
26
aa
HC
=−
;
3
0; ;
6
a
SH b
=−
.
Nên
2
33
, ; ;
6 2 12
ab ab a
HC SH
= − − −
.
Suy ra
( )
SHC
có một véc-tơ pháp tuyến là
( )
1
2 3;6 ; 3n b b a=
.
Mặt phẳng
( )
HBC
có một véc-tơ pháp tuyến là
( )
0;0;1k =
.
Góc giữa mặt phẳng
( )
SHC
và mặt phẳng
( )
HBC
bằng
60
nên
( ) ( )
( )
1
1
.
cos ,
.
nk
SHC HBC
nk
=
2 2 2
3
cos60
12 36 3
a
b b a
=
++
2 2 2
12 36 3 2 3b b a a + + =
3 / 4ba=
.
z
y
x
H
M
S
A
B
C
VÍ DỤ MINH HỌA
VÍ DỤ 1: Cho hình chóp
.S ABC
có
SA
vuông góc với mặt phẳng đáy. Gọi
M
là trung điểm của
BC
và
H
là trung điểm của
AM
. Biết
HB HC=
,
30HBC =
; góc giữa mặt phẳng
( )
SHC
và
mặt phẳng
( )
HBC
bằng
60
.Tính côsin của góc giữa đường thẳng
BC
và mặt phẳng
( )
SHC
A.
3
2
. B.
13
4
. C.
3
4
. D.
1
2
.
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
349
Khi đó
1
3 3 3
; ; 3
22
aa
na
=
, đường thẳng
BC
có véc-tơ chỉ phương
( )
1;0;0i =
.
Gọi
là góc giữa đường thẳng
BC
và mặt phẳng
( )
SHC
, ta có
1
22
1
2
3
.
3
2
sin
4
.
9 27
3
44
a
ni
ni
aa
a
= = =
++
. Do đó
2
2
3 13
cos 1 sin 1
44
= − = − =
.
Lời giải
Chọn A
Chọn hệ trục tọa độ
Oxyz
như hình vẽ. Khi đó
3
0;0;
2
S
;
;0;0
2
a
A
−
;
;0;0
2
a
B
;
; ;0
2
a
Ca
;
; ;0
2
a
Da
−
suy ra
3
0;0;
6
a
G
;
3
;;
4 2 4
aaa
M
;
3
;;
4 2 4
aaa
N
−
VÍ DỤ 2: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, mặt bên
SAB
là tam giác đều
và nằm trong mặt phẳng vuông góc với mặt phẳng
( )
ABCD
. Gọi
G
là trọng tâm của tam
giác
SAB
và
,MN
lần lượt là trung điểm của
,SC SD
(tham khảo hình vẽ bên). Tính côsin
của góc giữa hai mặt phẳng
( )
GMN
và
( )
ABCD
.
A.
2 39
13
. B.
13
13
. C.
2 39
39
. D.
3
6
.
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
350
Ta có mặt phẳng
( )
ABCD
có vectơ pháp tuyến là
( )
0;0;1k =
, mặt phẳng
( )
GMN
có vectơ pháp
tuyến là
3
; 0; ;
24 4
aa
n GM GN
= = −
Gọi
là góc giữa hai mặt phẳng
( )
GMN
và
( )
ABCD
, ta có
.
cos
.
nk
nk
=
1
4
39
24
=
2 39
13
=
.
Lời giải
Chọn A
Ta có
2 2 2 o
2. . .cos60AH BH BA BH BA= + −
22
2
13
2. . .
4 2 2 4
a a a
aa= + − =
3
2
a
AH=
.
o
tan60
SH
AH
=
.3SH AH=
3
2
a
=
.
Chuẩn hóa và chọn hệ trục tọa độ sao cho
( )
0;0;0H
,
3
;0;0
2
C
,
3
0; ;0
2
A
,
3
0;0;
2
S
,
1
;0;0
2
B
−
,
13
;0;
22
SB
= − −
39
;0;
44
SD
= − −
33
;0;
44
D
− −
.
Ta có
3 3 3
;;
424
DA
=
( )
3;2; 3u=
là một vtcp của
AD
.
33
;0;
22
SC
=−
( )
1;0; 1v = −
là một vtcp của
SC
. Ta có
.0uv=
AD SC⊥
Vậy góc giữa hai đường thẳng
AD
và
SC
bằng
o
90
.
VÍ DỤ 3: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
A
,
o
60ABC =
,
2BC a=
. Gọi
D
là điểm thỏa mãn
32SB SD=
. Hình chiếu của
S
trên mặt phẳng
( )
ABC
là điểm
H
thuộc
đoạn
BC
sao cho
4BC BH=
. Biết
SA
tạo với đáy một góc
o
60
. Góc giữa hai đường thẳng
AD
và
SC
bằng
A.
o
90
. B.
o
30
. C.
o
60
. D.
o
45
.
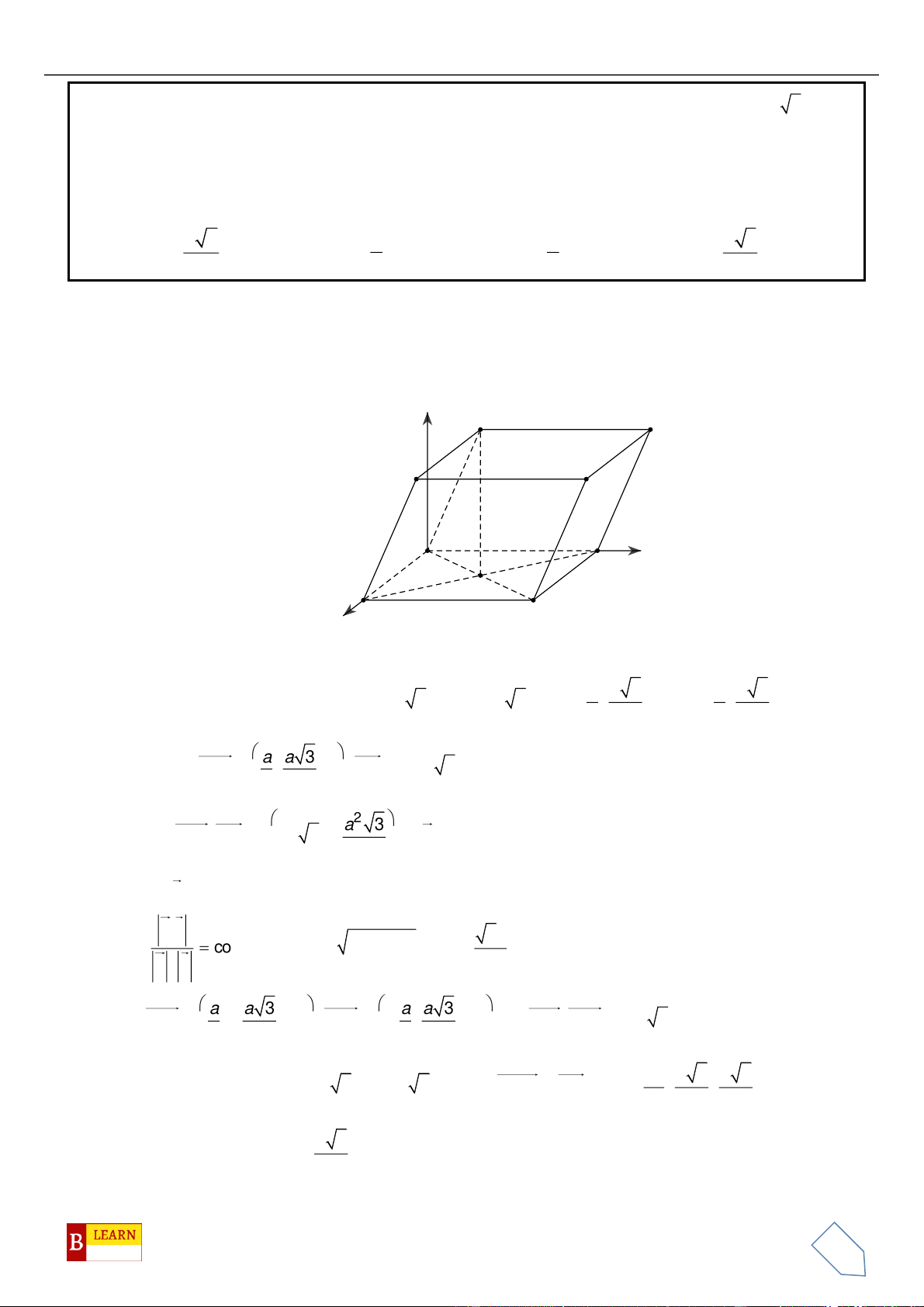
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
351
Lời giải
Chọn D
Gọi là tâm của đáy và đặt .
Chọn hệ trục như hình vẽ
Tọa độ các điểm:
,
Suy ra
là VTPT của
Và là VTPT của nên theo giả thiết đề bài ta có:
Phương trình . Vì
Vậy .
H
ABCD
1
A H x=
x
y
z
D
1
C
1
B
1
H
B
A
D
C
A
1
(
)
3
(0;0;0), ( ;0;0), (0; 3;0), ; 3;0 , ; ;0
22
aa
A B a D a C a a H
1
3
;;
22
aa
Ax
(
)
1
3
; ; , 0; 3;0
22
aa
AA x AD a
==
( )
2
1
3
, 3;0; 2 ;0;
2
a
AA AD ax n x a
= =
1
()A AD
(0;0;1)k =
()ABCD
0 2 2
.
3
cos60 2 4
2
.
nk
a
a x a x
nk
= = + =
(
)
1 1 1 1
33
; ; , ; ; , 3 ; ;0
2 2 2 2
a a a a
A B x A D x A B A D a x ax
= − − = − − =
1
( ) : 3 3 0A BD x y a+ − =
1 1 1
3 3 3
;;
2 2 2
a a a
A B A B B
=
( )
11
3
,( )
2
a
d B A BD =
VÍ DỤ 4: Cho lăng trụ có đáy là hình chữ nhật. , . Hình
chiếu vuông góc của điểm trên mặt phẳng trùng với giao điểm và .
Góc giữa hai mặt phẳng và bằng . Tính khoảng cách từ điểm
đến mặt phẳng theo .
A.
2
2
a
. B.
4
a
. C.
2
a
. D.
3
2
a
.
1 1 1 1
.A BCD A B C D
ABCD
AB a=
3AD a=
1
A
( )
ABCD
AC
BD
( )
11
ADD A
( )
ABCD
0
60
1
B
( )
1
A BD
a
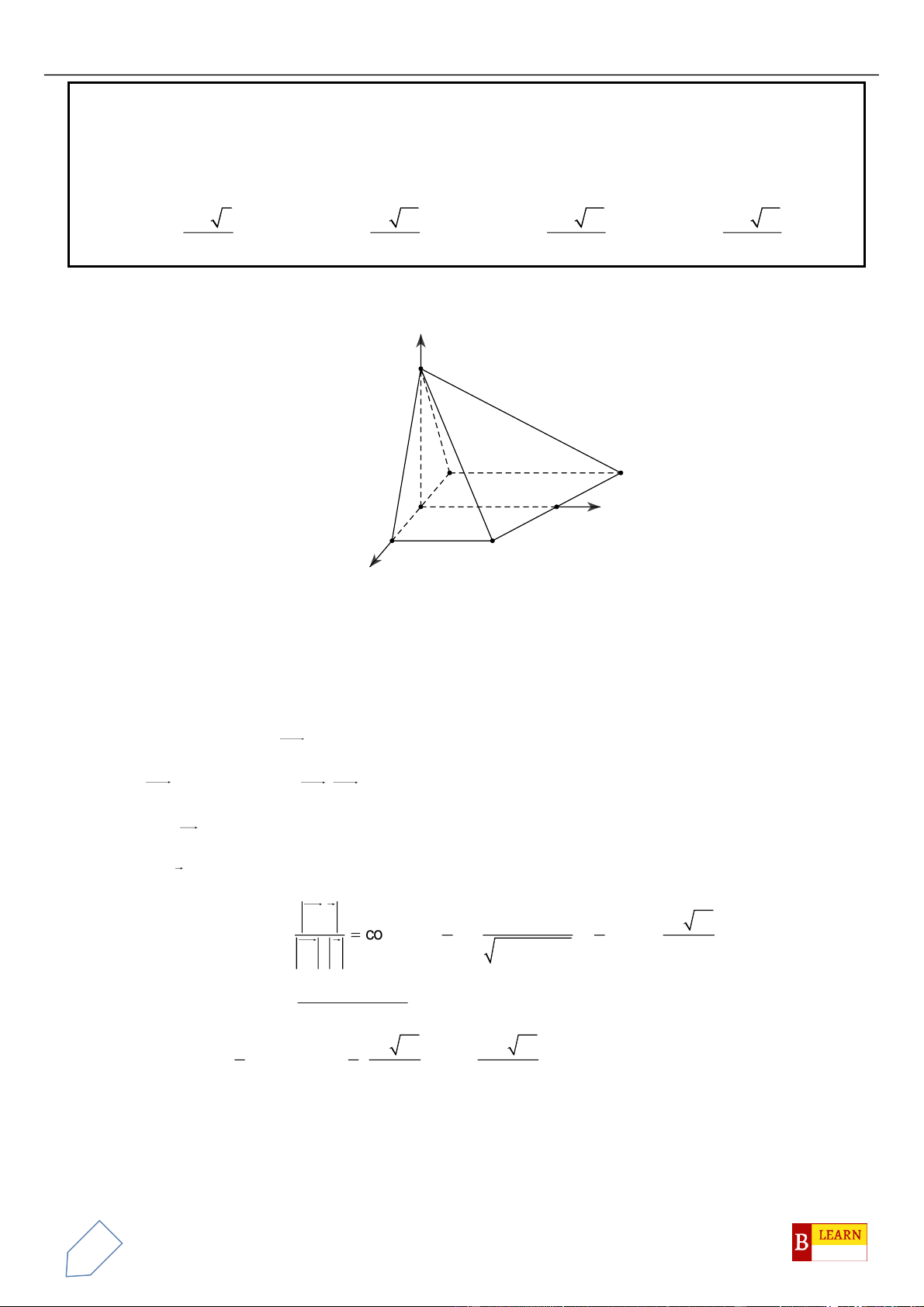
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
352
Lời giải
Chọn C
Vì hai mặt phẳng và cùng vuông góc với đáy
nên .
Đặt , tọa độ các điểm là:
. Suy ra
Nên là VTPT của mặt phẳng .
Mà là VTPT của mặt đáy nên theo giả thiết đề bài ta có
Mặt khác: nên thể tích khối chóp là
.
y
x
z
I
A
B
D
S
C
( )
SDI
( )
SCI
()SI ABCD⊥
,0SI x x=
( ) ( )
−0;0;0 , ;0;0 ,I A a
( ) ( ) ( )
−;0;0 , ; ;0 , ;2 ;0 ,B a C a a D a a
( )
0;0;Sx
( )
=−; ; ,SC a a x
( )
=−2 ; ;0CD a a
(
)
=
2
, ;2 ;3SC CD ax ax a
( )
1
;2 ;3n x x a=
()SCD
(0;0;1)k =
1
0
22
1
.
1 3 1 3 15
cos60
2 2 5
.
59
nk
aa
x
nk
xa
= = = =
+
2
()
3
2
ABCD
AB BC AD
Sa
+
==
3
2
.
1 1 3 15 3 15
. . .3
3 3 5 5
S ABCD ABCD
aa
V SI S a= = =
VÍ DỤ 5: Cho hình chóp
.S ABCD
có đáy là hình thang vuông tại
A
và
B
;
2,AB AD a CB a= = =
, góc
giữa hai mặt phẳng
( )
SBC
và
( )
ABCD
bằng
60
o
. Gọi
I
là trung điểm của cạnh
AB
. Biết hai
mặt phẳng và cùng vuông góc với mặt phẳng
( )
ABCD
, tính thể tích khối chop
.S ABCD
theo .
A.
3
33
5
a
. B.
3
15
5
a
. C.
3
3 15
5
a
. D.
3
8 15
5
a
.
( )
SDI
( )
SCI
a

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
353
Câu 1: Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông cân,
AB AC a==
,
AA h
=
( )
,0ah
. Tính khoảng cách giữa hai đường thẳng chéo nhau
AB
và
BC
theo
a
,
h
.
A.
22
5
ah
ah+
. B.
22
5
ah
ah+
. C.
22
2
ah
ah+
. D.
22
ah
ah+
.
Câu 2: Trong không gian
Oxyz
, mặt phẳng
( )
: 3 4 12 0P x y z+ − − =
cắt trục
Ox
tại
A
, cắt trục
Oz
tại
B
. Chu vi tam giác
OAB
bằng
A. 6. B. 12. C. 36. D. 5.
Câu 3: Xác định
m
để bốn điểm
( )
1;1; 4A
,
( )
5; 1; 3B −
,
( )
2 ; 2 ;Cm
và
( )
3;1; 5D
tạo thành tứ diện.
A.
m
. B.
4m
. C.
6m
. D.
0m
.
Câu 4: Trong không gian
Oxyz
, cho 3 điểm
( )
1;2; 3A −
,
( )
4;2;5B −
,
( )
;2;1Ma
với
a
là tham số. Biết
rằng điểm
M
thuộc đường thẳng
AB
, tìm
a
.
A.
3
2
a =−
. B.
6a =−
. C.
6a =
. D.
3
2
a =
.
Câu 5: Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )
: 3 0P x y z+ − − =
và hai điểm
( )
1;1;1 ,M
( )
3; 3; 3N −−−
. Mặt cầu
( )
S
đi qua hai điểm
,MN
và tiếp xúc với mặt phẳng
( )
P
tại
điểm
Q
. Biết rằng
Q
luôn thuộc một đường tròn cố định. Tính bán kính R của đường tròn đó.
A.
2 11
.
3
R =
. B.
2 33
.
3
R =
. C.
6R =
. D.
4R =
Câu 6: Trong không gian với hệ trục tọa độ
Oxyz
,cho tứ diện
ABCD
có tọa độ các điểm
( )
1;1;1A
,
( )
2;0;2B
( )
1; 1;0C −−
,
( )
0;3;4D
. Trên các cạnh
AB
,
AC
,
AD
lần lượt lấy các điểm
B
,
C
,
D
sao cho
4+ + =
AB AC AD
AB AC AD
và tứ diện
AB C D
có thể tích nhỏ nhất. Phương trình mặt
phẳng
( )
B C D
là
A.
16 40 44 39 0x y z− − + =
. B.
16 40 44 39 0x y z− − − =
.
C.
16 40 44 39 0x y z+ + − =
. D.
16 40 44 39 0x y z+ − + =
.
Câu 7: Cho hình chóp tứ giác đều
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, tâm
O
. Gọi
M
và
N
lần lượt là trung điểm của hai cạnh
SA
và
BC
, biết
6
2
a
MN =
. Khi đó giá trị sin của góc giữa
đường thẳng
MN
và mặt phẳng
( )
SBD
bằng
A.
2
5
. B.
3
3
. C.
5
5
. D.
3
.
Câu 8: Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
2 2 2
: 1 2 3 4S x y z
. Xét
đường thẳng
1
:
( 1)
xt
d y mt
z m t
với
m
là tham số thực. Giả sử
P
và
'P
là hai mặt phẳng chứa

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
354
d
, tiếp xúc với
S
lần lượt tại
T
và
'.T
Khi
m
thay đổi, tính giá trị nhỏ nhất của độ dài đoạn
thẳng
'TT
.
A. 2. B.
2 11
3
. C.
4 13
5
.
D.
22
.
Câu 9: Cho hình hộp đứng
.ABCD A B C D
có đáy là hình thoi, tam giác
ABD
đều. Gọi
,MN
lần lượt
là trung điểm
BC
và
CD
, biết rằng
MN B D
⊥
. Gọi
là góc tạo bởi đường thẳng
MN
và
mặt đáy
( )
ABCD
, khi đó giá trị
cos
bằng
A.
1
cos
3
=
. B.
3
cos
2
=
. C.
1
cos
10
=
. D.
1
cos
2
=
.
Câu 10: Trong không gian với hệ trục tọa độ
Oxyz
, gọi
()P
là mặt phẳng chứa đường thẳng
12
:
1 1 2
x y z
d
−+
==
−−
và tạo với trục
Oy
góc có số đo lớn nhất. Điểm nào sau đây thuộc mặt
phẳng
()P
A.
( 3;0;4)E −
. B.
(3;0;2)M
. C.
( 1; 2; 1)N − − −
. D.
(1;2;1)F
.
Câu 11: Trong không gian
Oxyz
, cho điểm
,,A B C
. Trên đường thẳng
d
vuông góc với mặt phẳng tại
A
lấy một điểm
S
. Gọi
,HK
lần lượt là hình chiếu vuông góc của
A
lên
,SB SC
. Biết khi
S
di
động trên
d
thì đường thẳng
HK
luôn đi qua một điểm cố định
D
. Tính độ dài đoạn thẳng
AD
.
A.
33AD =
. B.
62AD =
. C.
36AD =
. D.
63AD =
.
Câu 12: Trong không gian
Oxyz
, cho hình lập phương
.ABCD A B C D
có tọa độ
( )
1;2;1A
,
( )
3;6; 3C
−
. Gọi
M
là một điểm bất kỳ thuộc mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 2 4 1 1S x y z− + − + + =
.
Tính tổng các khoảng cách từ điểm
M
đến tất cả các mặt của hình lập phương .
A.
23
. B.
33
. C.
63
. D.
12
.
Câu 13: Trong không gian tọa độ
Oxyz
, cho ba điểm
( )
2;1;2A
,
( )
2; 3;1B −
,
( )
3;2;2C
và mặt phẳng
( )
: 3 0x y z
− + =
. Gọi
A
,
B
,
C
lần lượt là hình chiếu vuông góc của
A
,
B
,
C
lên
( )
.
D
là điểm sao cho
AB CD
là hình bình hành. Diện tích hình bình hành
AB CD
bằng
A.
3
22
B.
4
11
. C.
8
11
. D.
6
22
.
Câu 14: Trong không gian
Oxyz
, cho điểm
( )
1;0;0A
,
( )
0; 1;0B −
,
( )
0;0;1C
,
( )
1; 1;1D −
. Mặt cầu tiếp
xúc
6
cạnh của tứ diện
ABCD
cắt
( )
ACD
theo thiết diện có diện tích
S
. Chọn mệnh đề đúng?
A.
3
S
=
. B.
6
S
=
. C.
4
S
=
. D.
5
S
=
.
Câu 15: Cho hình lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác cân tại
C
,
2=AB a
,
=AA a
, góc
giữa
BC
và
( )
ABB A
bằng
60
. Gọi
N
là trung điểm
AA
và
M
là trung điểm
BB
. Tính
khoảng cách từ điểm
M
đến mặt phẳng
( )
BC N
.
.ABCD A B C D

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
355
A.
2 74
37
a
. B.
74
37
a
. C.
2 37
37
a
. D.
37
37
a
.
Câu 16:
Cho tứ diện SABC có SA vuông góc với mặt phẳng,
3,SA AB cm==
5BC cm=
và diện tích tam
giác SAC bằng
2
6cm
. Một mặt phẳng
( )
thay đổi qua trọng tâm G của tứ diện cắt các cạnh AS,
AB, AC lần lượt tại
,,M N P
. Tính giá trị nhỏ nhất
m
T
của biểu thức
2 2 2
1 1 1
T
AM AN AP
= + +
.
A.
8
17
m
T =
. B.
41
144
m
T =
. C.
1
10
m
T =
. D.
1
34
m
T =
.
Câu 17: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, cạnh bên
2=SA a
và vuông góc
với mặt phẳng đáy. Gọi
M
là trung điểm cạnh
SD
. Tang của góc tạo bởi hai mặt phẳng
()AMC
và
()SBC
bằng
A.
3
2
. B.
23
3
. C.
5
5
. D.
25
5
Câu 18: Trong không gian với hệ trục tọa độ
Oxyz
cho mặt phẳng
:2 2 2 0P x y z
và mặt phẳng
:2 2 10 0Q x y z
song song với nhau. Biết
(1;2;1)A
là điểm nằm giữa hai mặt phẳng
( )
P
và
( )
Q
. Gọi
( )
S
là mặt cầu qua
A
và tiếp xúc với cả hai mặt phẳng
( )
P
và
( )
Q
. Biết rằng
khi
( )
S
thay đổi thì tâm của nó luôn nằm trên một đường tròn. Tính bán kính
r
của đường tròn
đó
A.
42
3
r
. B.
22
3
r
. C.
5
3
r
. D.
25
3
r
.
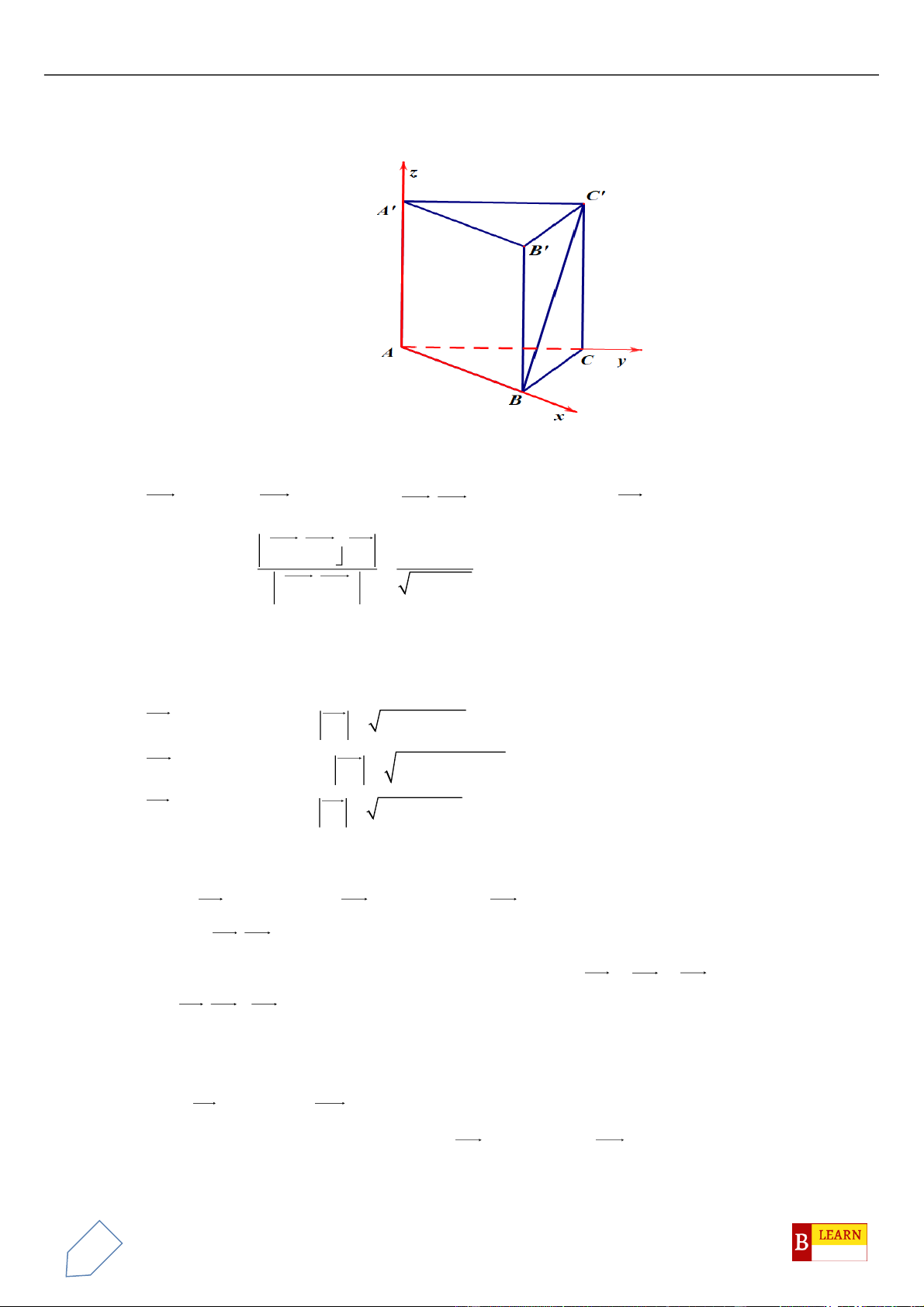
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
356
ĐÁP ÁN CHI TIẾT
Câu 1: Chọn A
Chọn hệ trục tọa độ như hình vẽ.
( )
0;0;0A
;
( )
0;0;Ah
;
( )
0; ;0Ca
;
( )
;0;0Ba
;
( )
;0;B a h
;
( )
0; ;C a h
.
( )
;0;AB a h
=
;
( )
;;BC a a h
=−
;
( )
2
; ; 2 ;AB BC ah ah a
= − −
;
( )
;0;0AB a=
.
( )
22
;.
;
5
;
d
AB BC AB
ah
AB BC
ah
AB BC
==
+
.
Câu 2: Chọn B
Ta có:
( )
A P Ox=
( )
4;0;0A
;
( )
B P Oz=
( )
0;0; 3B−
.
( )
4;0;0OA =
222
4 0 0 4OA OA = = + + =
.
( )
0;0; 3OB =−
( )
2
22
0 0 3 3OB OB = = + + − =
.
( )
4;0;3BA =
2 2 2
4 0 3 5AB BA = = + + =
.
Khi đó chu vi tam giác
OAB
bằng:
OA OB AB++
4 3 5 12= + + =
.
Câu 3: Chọn C
Ta có:
(4; 2; 1)AB = − −
,
(1;1; 4)AC m=−
,
(2; 0 ;1)AD =
.
Suy ra:
, ( 2 ; 6 ; 4)AB AD
= − −
4 điểm
A
,
B
,
C
,
D
tạo thành tứ diện
3 vectơ
AB
,
AC
,
AD
không đồng phẳng
, . 0 2.1 ( 6).1 4( 4) 0 6AB AD AC m m
− + − + −
Vậy
6m
.
Câu 4: Chọn A
Ta có
( )
5;0;8AB =−
;
( )
1;0;4AM a=−
.
Vì điểm
M
thuộc đường thẳng
AB
nên
AB
cùng phương
AM
.
Cách 1:
Áp dụng tính chất của tích có hướng giữa 2 vec tơ ta có:
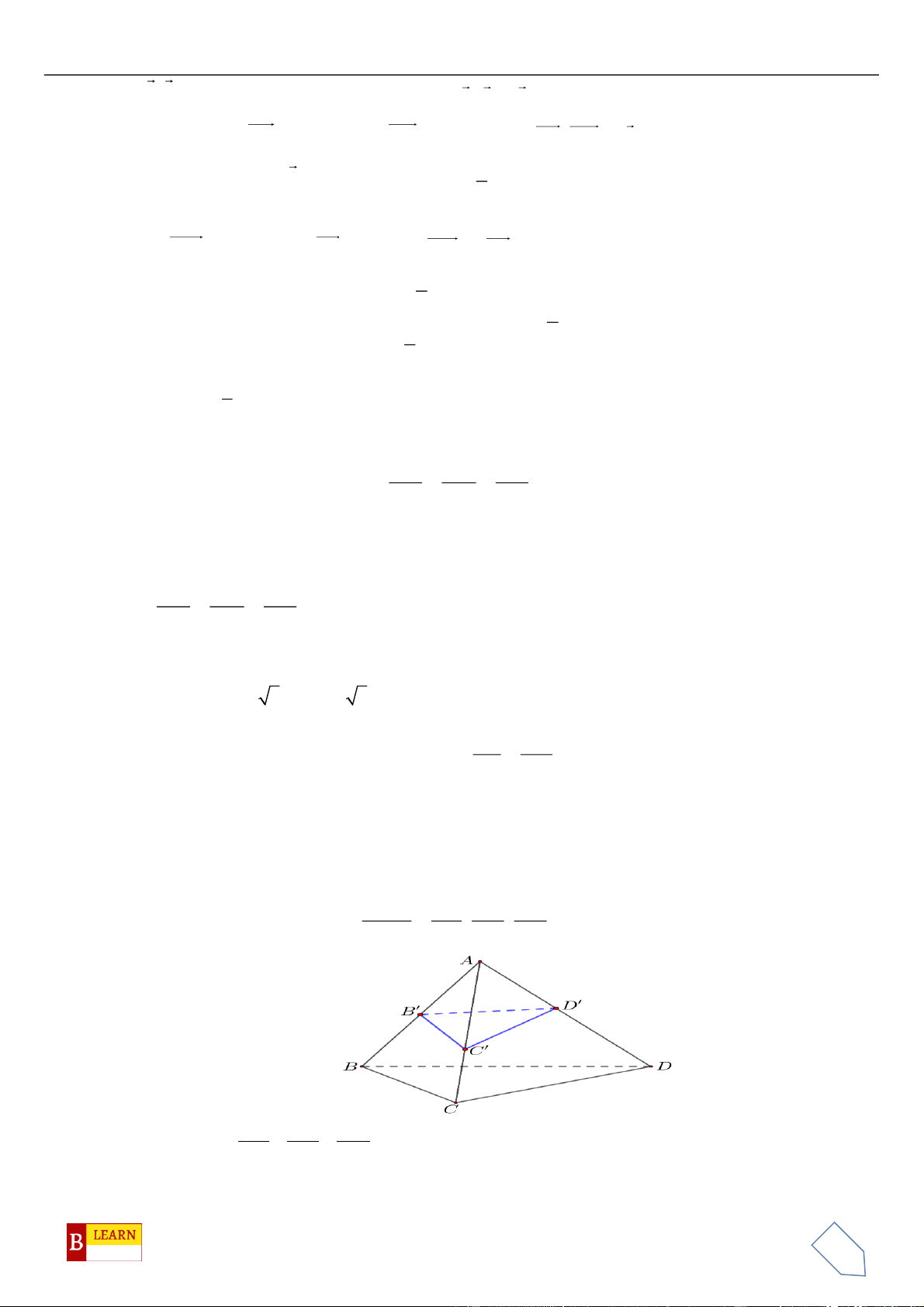
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
357
,ab
cùng phương với nhau tương đương
,0ab
=
.
Khi đó ta có:
AB
cùng phương
AM
tương đương
,0AB AM
=
( )
0;8 12;0 0a + =
3
8 12 0
2
aa + = = −
.
Cách 2:
Vì
AM
cùng phương
AB
nên ta có:
AM kAB=
( )
51
00
84
luôn
ka
k g
k
đún
− = −
=
=
1
2
1
5. 1
2
k
a
=
− = −
3
2
a = −
.
Vậy
3
2
a =−
.
Câu 5: Chọn C
Phương trình đường thẳng
1 1 1
:
1 1 1
x y z
MN
− − −
==
Gọi
( )
.E MN P=
Suy ra
tọa độ điểm
E
thỏa hệ:
( )
3
1 1 1
3 3;3;3
1 1 1
30
3
x
x y z
yE
x y z
z
=
− − −
==
=
+ − − =
=
.
Suy ra
2 3; 6 3.EM EN==
Ta có
EQM
và
ENQ
đồng dạng, suy ra
2
. 36
EQ EM
EQ EM EN
EN EQ
= = =
6EQ=
. Do đó điểm
Q
thuộc đường tròn tâm E, bán kính
6.R =
Câu 6: Chọn D
Trên các cạnh
AB
,
AC
,
AD
của tứ diện
ABCD
lần lượt có các điểm
B
,
C
,
D
. Áp dụng
công thức tỉ số thể tích ta có
=
AB C D
ABCD
V
AB AC AD
V AB AC AD
.
Từ giả thiết
4+ + =
AB AC AD
AB AC AD
, áp dụng bất đẳng thức
AM GM−
ta có:
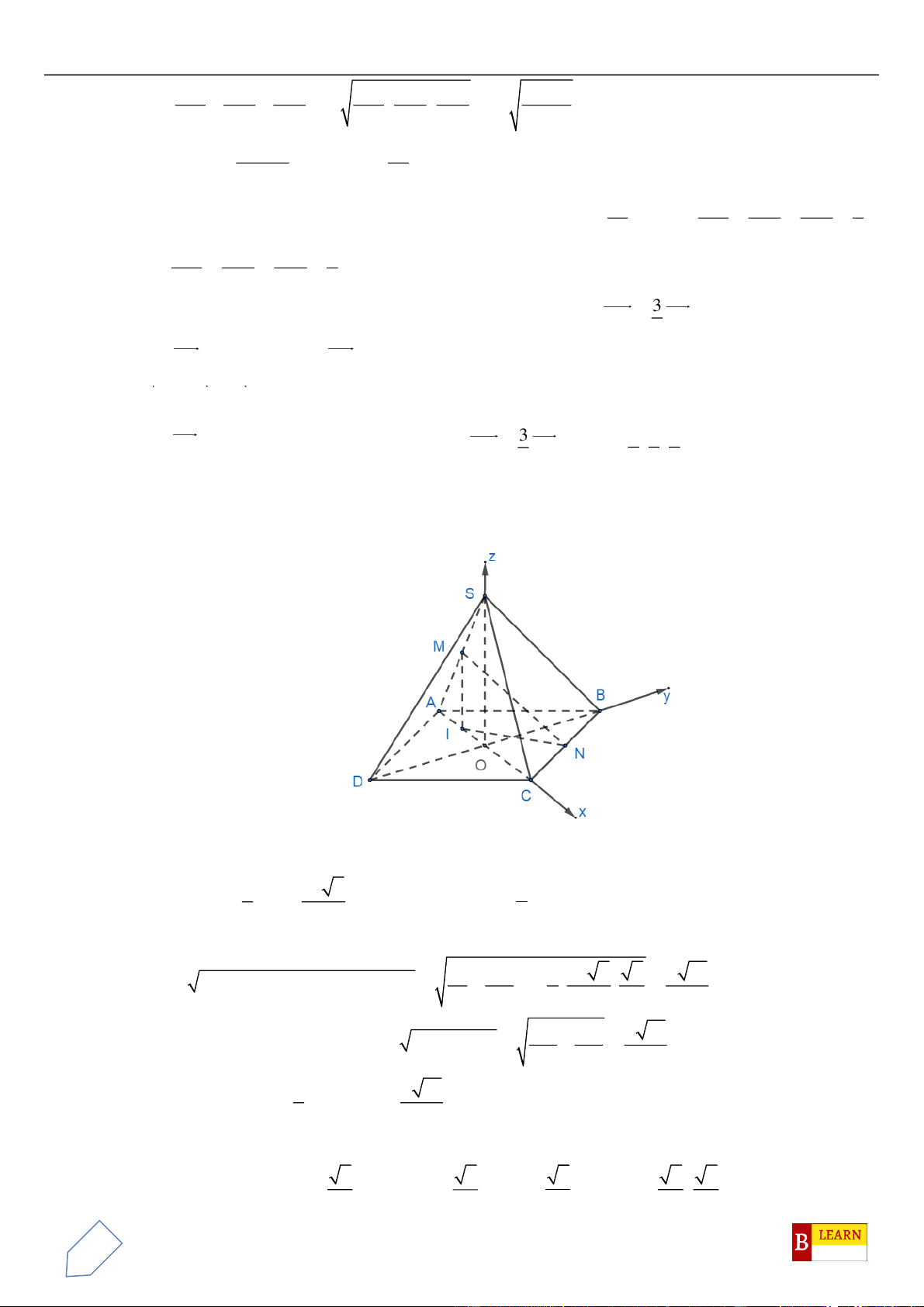
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
358
3
3
4 3. 3.
= + + =
ABCD
AB C D
V
AB AC AD AB AC AD
AB AC AD AB AC AD V
' ' '
' ' '
27
64 27
64
ABCD
AB C D ABCD
AB C D
V
VV
V
.
Do
ABCD
V
cố định nên
' ' 'AB C D
V
nhỏ nhất
' ' ' '
27 4
64 3
= = = =
A B C D ABCD
AB AC AD
VV
AB AC AD
3
4
= = =
AB AC AD
AB AC AD
( )
B C D
song song với
( )
BCD
và đi qua điểm
B
thoả
3
4
=AB AB
.
Có
( )
3; 1; 2BC = − − −
,
( )
2;3;2BD =−
, suy ra vectơ pháp tuyến của mặt phẳng
( )
B C D
là
( )
, 4;10; 11n BC BD
= = −
.
Có
( )
1; 1;1AB =−
, giả sử
( )
' ; ;B x y z
. Do
3
4
=AB AB
nên
717
' ; ;
444
B
.
Vậy phương trình
( )
B C D
là:
16 40 44 39 0x y z+ − + =
.
Câu 7: Chọn B
Gọi
I
hình chiếu của
M
lên
( )
ABCD
, suy ra
I
là trung điểm của
AO
.
Khi đó
3 3 2
44
a
CI AC==
. Xét
CNI
có:
2
a
CN =
,
45
o
NCI =
.
Áp dụng định lý cosin ta có:
22
22
9 3 2 2 10
2 . .cos45 2. . .
4 8 2 4 2 4
o
a a a a a
NI CN CI CN CI= + − = + − =
.
Xét
MIN
vuông tại
I
nên
22
22
3 5 14
2 8 4
a a a
MI MN NI= − = − =
.
Mà
1 14
/ / ,
22
a
MI SO MI SO SO= =
.
Chọn hệ trục tọa độ
Oxyz
như hình vẽ:
Ta có:
( )
0;0;0O
,
2
0; ;0
2
B
,
2
0; ;0
2
D
−
,
2
;0;0
2
C
,
22
; ;0
44
N
,
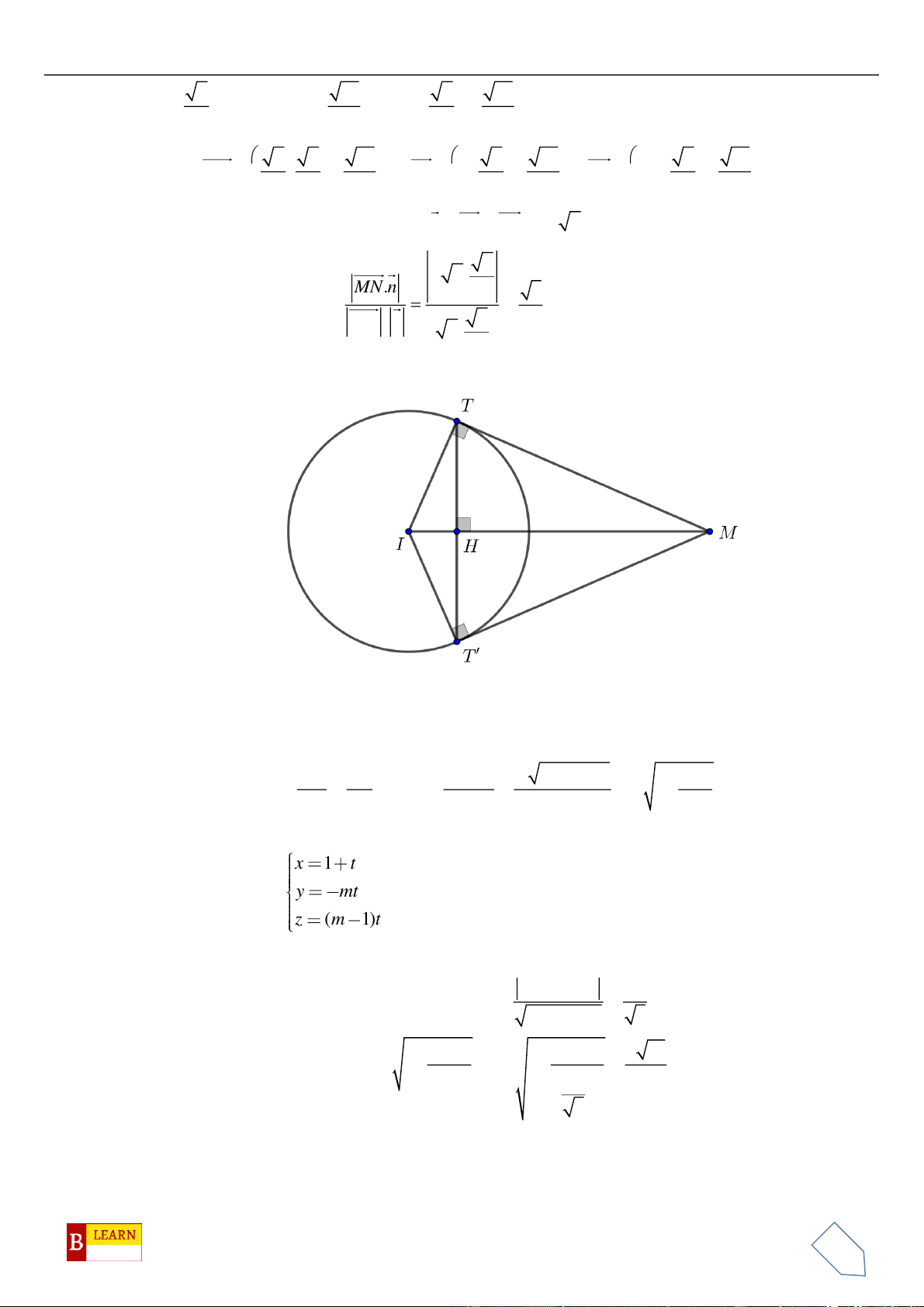
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
359
2
;0;0
2
A
−
,
14
0;0;
4
S
,
2 14
;0;
44
M
−
.
Khi đó
2 2 14
;;
2 4 4
MN
=−
,
2 14
0; ;
22
SB
=−
,
2 14
0; ;
22
SD
= − −
.
Vectơ pháp tuyến mặt phẳng
( )
SBD
:
( )
7 ;0;0n SB SD= = −
.
Suy ra
( )
( )
2
7.
.
2
3
sin ,
3
6
.
7.
2
MN n
MN SBD
MN n
−
= = =
.
Câu 8: Chọn C
Mặt cầu
( )
S
có tâm
( )
1;2;3I
, bán kính
2R =
. Mặt phẳng
( )
'ITT
cắt
d
tại điểm
M
. Gọi
H
là
giao điểm của
TT
và
MI
.
Vì
~TIH MIT
nên ta có:
2 2 2
2
.
1
TH TI TM TI R MI R R
TH R
TM MI MI MI MI
−
= = = = −
Do
2TT TH
=
nên
min min min
TT TH MI
Nhận xét rằng với
1
( 1)
xt
y mt
z m t
ta có:
( )
1 1 1x y z t mt m t+ + = + − + − =
nên khi
m
thay đổi ta luôn có
( ) ( )
: 1 0d P x y z + + − =
cố định. Vì thế
( )
( )
min
222
1 2 3 1
5
,
3
111
MI d I P
+ + −
= = =
++
Từ đó ta có:
22
min min
2
2
min
2 4 13
2 2 1 2.2 1
5
5
3
R
TT TH R
MI
= = − = − =
Ta kiểm tra điều kiện đủ của bài toán, tức là chứng minh rằng hình chiếu vuông góc của
I
lên
( )
P
thuộc vào đường thẳng
d
.
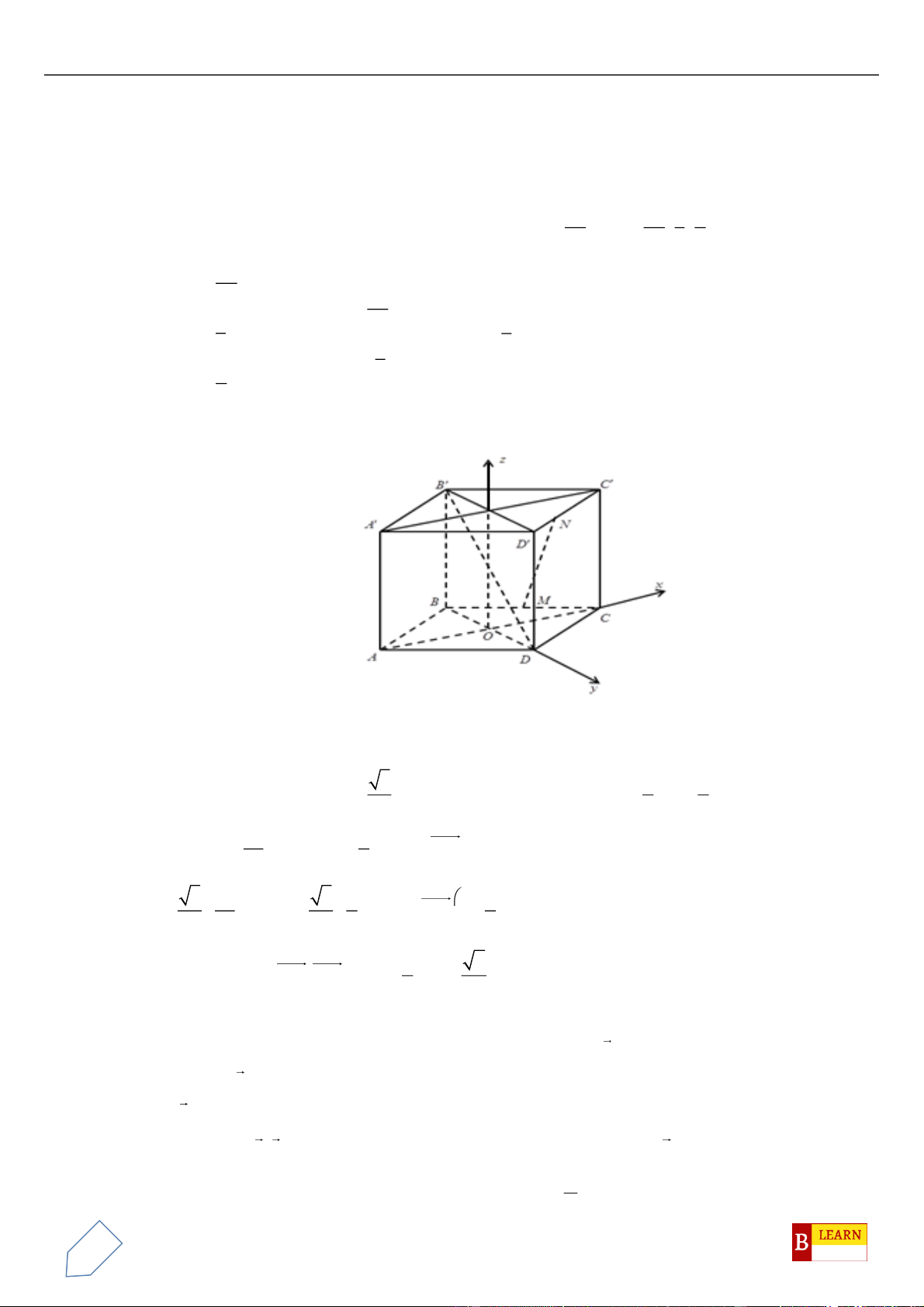
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
360
Gọi
d
là đường thẳng qua
I
và vuông góc với
( )
P
ta có:
1
:2
3
xt
d y t
zt
=+
=+
=+
Gọi
M
là hình chiếu vuông góc của
I
lên
( )
P
ta có:
( )
M d P
=
suy ra:
( ) ( ) ( )
5 2 1 4
1 2 3 1 0 ; ;
3 3 3 3
t t t t M
−−
+ + + + + − = =
Xét hệ:
( )
2
1
5
3
1
3
1
3
4
5
1
3
t
t
mt
m
mt
−
=+
−
=
= −
=
=−
. Vậy với
1
5
m =
thì độ dài của
TT
nhỏ nhất.
Câu 9: Chọn A
Đặt cạnh hình thoi
ABCD
là
1
, chiều cao hình hộp
( )
0.hh=
Gọi
O
là giao điểm hai đường chéo
AC
và
BD
của hình thoi.
Tam giác
ABD
đều
3 1 1
, 1, .
2 2 2
AO CO BD AB BO DO BD = = = = = = =
Ta có
( )
11
0; ; , 0; ; 0 0;1; .
22
B h D B D h
−
−
3 1 3 1 1
; ; 0 , ; ; 0; ; .
4 4 4 4 2
M N h MN h
−
Vì
2
12
.
22
MN B D MN B D h h
⊥ = =
Câu 10: Cách 1:
Đường thẳng
d
qua điểm
(1; 2;0)M −
, có véc tơ chỉ phương
(1; 1; 2)a = − −
và trục
Oy
có véc tơ
chỉ phương
(0;1;0)j =
.
Gọi
( )
2 2 2
; ; ( 0)n A B C A B C= + +
là một véc tơ pháp tuyến của mặt phẳng
()P
.
Vì
( ) . 0 1. ( 1). ( 2). 0 2d P a n A B C A B C = + − + − = = +
( 2 ; ; )n B C B C = +
.
Gọi
là góc giữa mặt phẳng
()P
và trục
Oy
0
2
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
361
Ta có
2
22
2 2 2
.
sin
2 4 5
.
( 2 )
nj
B
B
B BC C
nj
B C B C
= = =
++
+ + +
22
11
26
2 4. 5 5
55
C C C
B B B
==
+ + + +
( 0)B
.
Vì hàm số
sin
tăng liên tục trên
0;
2
nên
đạt giá trị lớn nhất khi
sin
lớn nhất
Lúc đó
2
26
5
55
C
B
++
đạt giá trị nhỏ nhất bằng
6
5
khi và chỉ khi
2
0
5
C
B
+=
.
Chọn
5 2; 1 (1;5; 2)B C A n= = − = = −
.
Phương trình mặt phẳng
()P
qua điểm
(1; 2;0)M −
, có véc tơ pháp tuyến
(1;5; 2)n =−
là
1.( 1) 5.( 2) 2( 0) 0 5 2 9 0x y z x y z− + + − − = + − + =
.
Thế tọa độ
( 1; 2; 1)N − − −
vào phương trình mặt phẳng
()P
:
1 5( 2) 2( 1) 9 0− + − − − + =
.
Vậy điểm
( 1; 2; 1)N − − −
thuộc mặt phẳng
()P
.
Cách 2:
Xét bài toán tổng quát: Cho hai đường thẳng
12
,
phân biệt và không song song với nhau. Viết
phương trình mặt phẳng
( )
P
chứa đường thẳng
1
và tạo với
2
một góc lớn nhất.
Phương pháp giải:
▪ Vẽ một đường thẳng
3
bất kỳ song song với
2
và cắt
1
tại
M
. Gọi
B
là điểm cố định
trên
3
và
H
là hình chiếu vuông góc của
B
lên mp
( )
P
, kẻ
1
BA ⊥
▪
( )
( )
2
, P BMH=
.
sin
HB BA
BMH
BM BM
=
không đổi
Suy ra
BMH
lớn nhất khi
HA
Khi đó
( )
12
,BMH =
và
( )
P
chứa
1
và vuông góc với mặt phẳng
( )
12
,
.
Vậy
( )
P
có VTPT là:
1 2 1
,,u u u
Áp dụng:
( ) ( ) ( )
1; 1; 2 ; 0;1;0 , , , 1;5; 2
d d d
u j n u j u
= − − = = = −
. Phương trình mặt phẳng
()P
qua
điểm
(1; 2;0)M −
, có véc tơ pháp tuyến
(1;5; 2)n =−
là
5 2 9 0xyz+ − + =
Vậy điểm
( 1; 2; 1)N − − −
thuộc mặt phẳng
()P
.
1
3
2
P
B
H
A
M
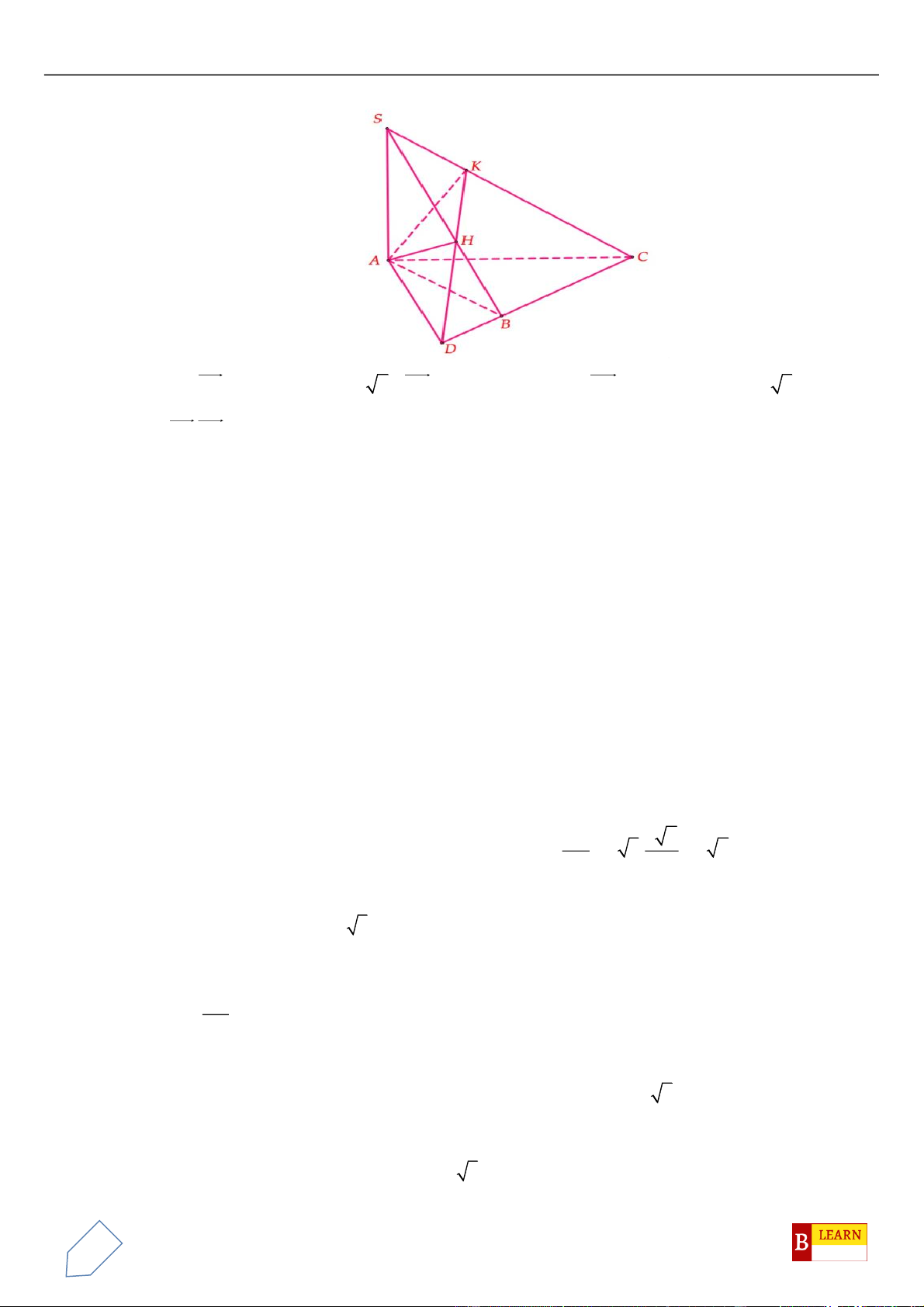
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
362
Câu 11: Chọn C
Ta có:
( )
3;0;3 , 3 2= − =AB AB
;
( )
2; 1;2 , 3= − =BC BC
;
( )
1; 1;5 , 3 3= − − =AC AC
Vì
. 0 ABC= AB BC
vuông tại B
Ta có:
( )
⊥
⊥ ⊥
⊥
BC AB
BC SAB BC AH
BC SA
.
Ta có:
( )
⊥
⊥ ⊥
⊥
AH SB
AH SBC AH SC
AH BC
.
Ta có:
( )
⊥
⊥
⊥
SC AH
SC AHK
SC AK
.
Do đó: Gọi D là giao điểm của HK và BC thì
⊥SC AD
Ta có:
( )
⊥
⊥ ⊥
⊥
AD SA
AD SAC AD AC
AD SC
Vì D nằm trong mặt phẳng và D là giao điểm của BC và đường thẳng vuông góc với AC tại A nên
D cố định.
Trong ΔDAC vuông tại A, ta có:
32
.tan . 3 3. 3 6
3
= = = =
AB
AD AC C AC
BC
. Đáp án C
Câu 12: Chọn C
Ta có
'6AC =
nên
23AB =
.
Mặt cầu
( )
S
có tâm
( )
2;4; 1I −
trùng với tâm hình lập phương và có bán kính
1
2
AB
R =
nên mặt cầu
( )
S
nằm trong hình lập phương .
Với mọi điểm
M
nằm trong hình lập phương , tổng các khoảng cách từ điểm
M
đến
6
mặt của hình lập phương bằng
3 6 3AB =
.
Vậy từ một điểm
M
bất kỳ thuộc mặt cầu
( )
S
, tổng các khoảng cách từ điểm
M
đến
6
mặt của
hình lập phương
.ABCD A B C D
bằng
63
.
.ABCD A B C D
.ABCD A B C D
.ABCD A B C D
.ABCD A B C D
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
363
Câu 13: Chọn C
Ta có
( )
0; 4; 1AB = − −
,
( )
1;1;0AC =
.
( )
, 1; 1;4
ABC
n AB AC
= = −
1 3 2
,
22
ABC
S AB AC
= =
.
( ) ( )
( )
.
4 22
cos ,
33
ABC
ABC
nn
ABC
nn
==
( ) ( )
( )
3 2 4 22 4
.cos , .
2 33
11
A B C ABC
S S ABC
= = =
.
8
2
11
A B C D A B C
SS
= =
.
Câu 14: Chọn B
Nhận thấy
2AB AC BC DA DB DC= = = = = =
nên
ABCD
là tứ diện đều cạnh
2
.
Theo giả thiết giao tuyến của mặt cầu tiếp xúc
6
cạnh của tứ diện với
( )
ACD
là đường tròn nội
tiếp tam giác
ACD
.
Gọi
r
là bán kính hình tròn nội tiếp tam giác
ACD
,
32
22
AC CD AD
p
++
==
.
Khi đó diện tích tam giác đều
ACD
,
2
3
4
ACD
AC
S pr pr
= =
3 3 2 6
.
2 2 6
rr = =
.
Diện tích thiết diện
2
2
6
.
66
Sr
= = =
.
Cách 2:
Vì
ABCD
là tứ diện đều nên
( )
ACD
cắt mặt cầu theo giao tuyến là đường tròn nội tiếm
ACD
. Suy ra tâm đường tròn này trùng với trọng tâm tam giác đều
ACD
và bán kính
1 3 6
3 2 6
AC
r ==
. Diện tích thiết diện
2
2
6
.
66
Sr
= = =
.
Câu 15: Chọn A
Gọi
,HK
lần lượt là là trung điểm cạnh
''AB
và
AB
. Từ giả thiết ta có:
' 2 ' .tan60 6
o
HB a HB a HC HB a= = = =

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
364
Mặt khác:
', ' và HC HB HK
đôi một vuông góc nhau.
Tọa độ hóa:
(0;0;0)H
,
'(0; 6;0)Ca
,
'( ;0;0)Aa−
,
( ;0; )A a a−
,
;0;
2
a
Na
−
,
'( ;0;0)Ba
,
( ;0; )B a a
,
;0;
2
a
Ma
.
Xét mặt phẳng
( ' )BC N
có
' ( ; 6; )
( 6; 3; 4 6)
2 ;0;
2
C B a a a
vtpt n
a
BN a
=−
= − −
= − −
Phương trình
( ' )BC N
là:
6( ) 3 4 6 0
2
a
x a y z
+ − − − =
.
Khoảng cách từ M đến
( ' )BC N
là:
6( ) 3.0 4 6( )
2 6 2 74
22
( ;( ' ))
37
6 9 96 111
aa
aa
aa
d M BC N
+ − − −
= = =
++
.
Câu 16:
Chọn A
Vì tam giác
SAC
vuông tại
A
2
4
SAC
S
AC cm
SA
= =
.
Vì
2 2 2
AC AB BC+=
nên tam giác
ABC
vuông tại
A
.
Chọn hệ trục
Oxyz
như hình vẽ
Ta có
( ) ( ) ( ) ( )
0;0;0 , 3;0;0 , 0;4;0 , 0;0;3A B C S
.
Vì
G
là trọng tâm của tứ diện
SABC
nên ta có:
3
44
33
1 ;1;
4 4 4
3
44
S A B C
G
S A B C
G
S A B C
G
x x x x
x
y y y y
yG
z z z z
z
+++
==
+++
= =
+++
==
.
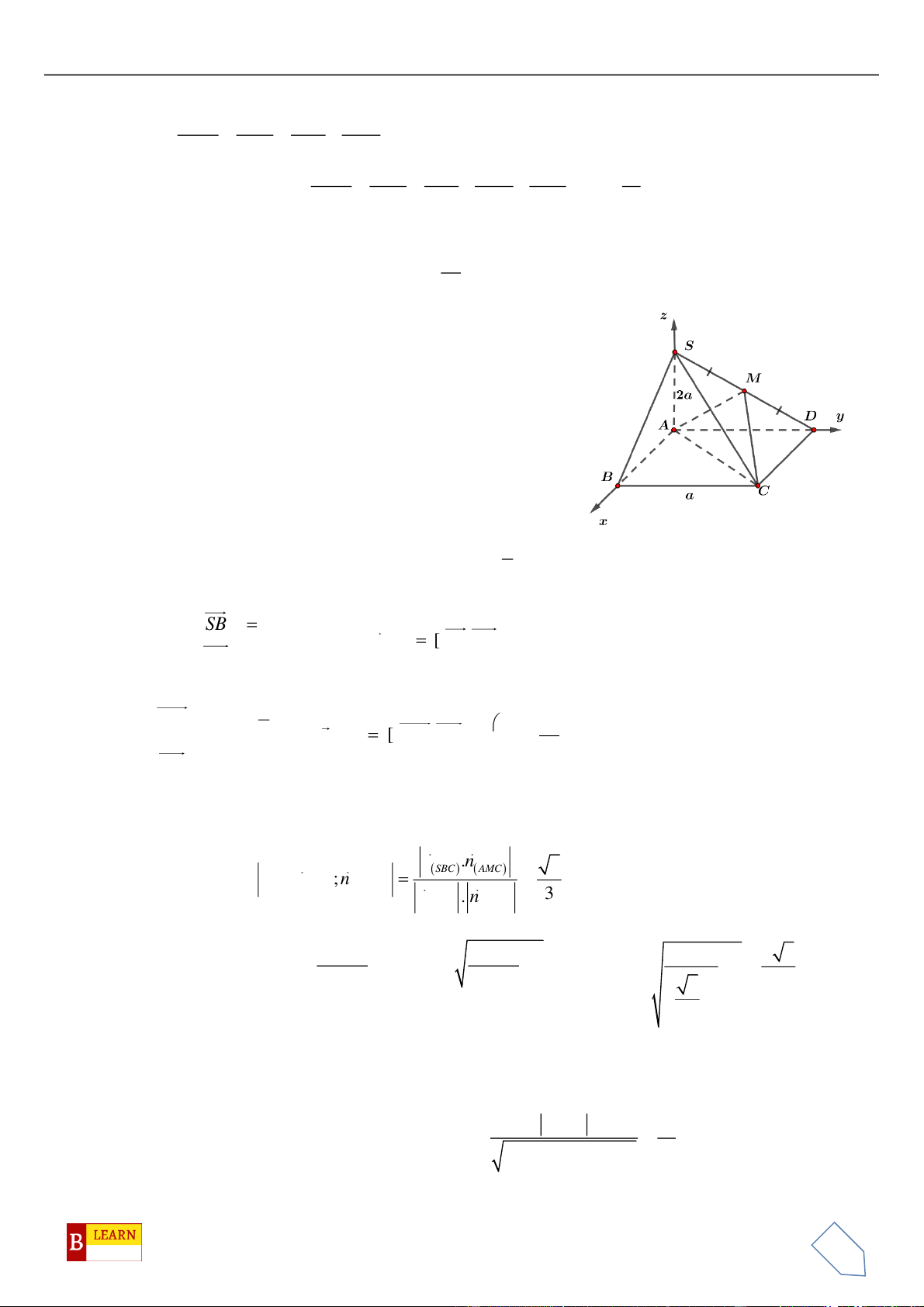
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
365
Gọi
H
là hình chiếu của điểm
A
lên mặt phẳng
( )
. Theo tính chất của tam diện vuông ta có:
2 2 2 2
1 1 1 1
T
AM AN AP AH
= + + =
.
mà
AH AG
2 2 2 2 2
1 1 1 1 1
T
AM AN AP AH AG
= + + =
8
17
T
.
Dấu “=” xảy ra khi
HG
tức mặt phẳng
( )
đi qua điểm
G
và vuông góc với đường thẳng
OG
. Vậy giá trị nhỏ nhất của
T
bằng
8
17
.
Câu 17: Chọn D
Để thuận tiện trong việc tính toán ta chọn
1a =
.
Trong không gian, gắn hệ trục tọa độ
Oxyz
như hình vẽ
sao cho gốc
O
trùng với điểm
A
, tia
Ox
chứa đoạn
thẳng
AB
, tia
Oy
chứa đoạn thẳng
AD
, tia
Oz
chứa
đoạn thẳng
AS
. Khi đó:
(0;0;0)A
,
(1;0;0)B
,
(1;1;0)C
(0;0;2)S
,
(0;1;0)D
.
Vì
M
là trung điểm
SD
nên tọa độ
M
là
1
0; ;1
2
M
.
Ta có
(1;0; 2)
(0;1;0)
=−
=
SB
BC
( )
[ ; ] =(2;0;1)=
SBC
n SB BC
.
( )
1
0; ;1
1
2
[ ; ] = 1;1;
2
(1;1;0)
=
−
= −
=
AMC
AM
n AM AC
AC
Gọi
là góc giữa hai mặt phẳng
()AMC
và
()SBC
.
Suy ra
( ) ( )
( )
( ) ( )
( ) ( )
.
5
cos cos ;
3
.
= = =
SBC AMC
SBC AMC
SBC AMC
nn
nn
nn
.
Mặt khác,
2
22
11
1 tan tan 1
cos cos
+ = = −
. Vậy
2
1 2 5
tan 1 .
5
5
3
= − =
Câu 18: Chọn A
Điểm
( )
1;0;0M
là 1 điểm thuộc
( )
P
.
Vì
( ) ( )
//PQ
nên
( ) ( )
( )
( )
( )
( ) ( )
22
2
2 10
12
, , 4
3
2 1 2
d P Q d M Q
+
= = = =
+ − + −
.
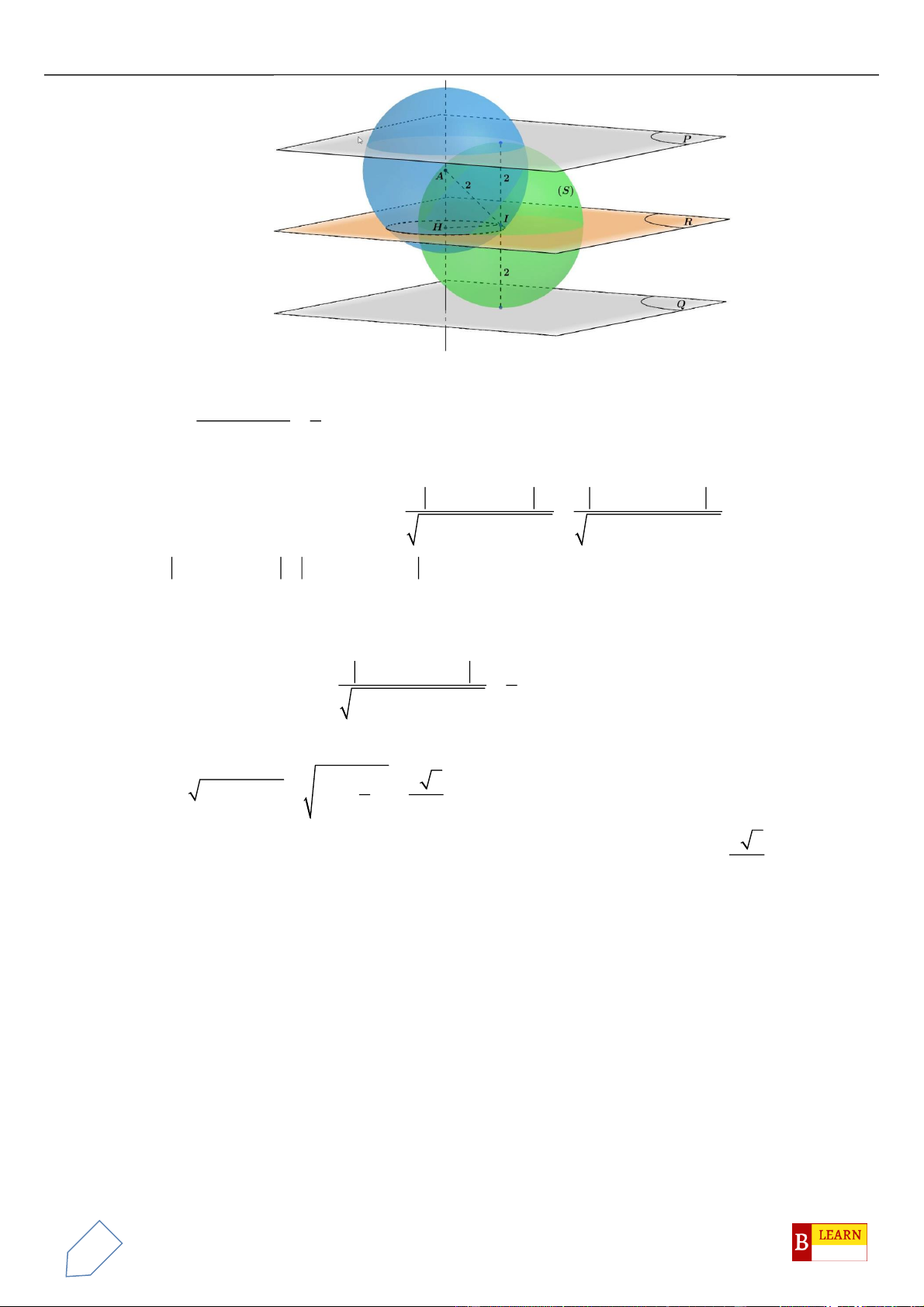
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
366
Giả sử
( )
;;I a b c
là tâm của
( )
S
. Vì
( )
S
tiếp xúc với cả
( )
P
và
( )
Q
nên bán kính mặt cầu
( )
S
là
( ) ( )
( )
,
4
2
22
d P Q
R = = =
.
Do đó
2IA =
nên
I
luôn thuộc mặt cầu
( )
T
tâm
A
, bán kính
2
.
Ngoài ra
( )
( )
( )
( )
( ) ( ) ( ) ( )
2 2 2 2
22
2 2 2 2 2 10
,,
2 1 2 2 1 2
a b c a b c
d I P d I Q
− − − − − +
= =
+ − + − + − + −
2 2 2 2 2 10a b c a b c − − − = − − +
( )
2 2 2 2 2 10a b c a b c − − − = − − − +
2 2 4 0a b c − − + =
. Do đó
I
luôn thuộc mặt phẳng
( )
:2 2 4 0R x y z− − + =
.
Gọi
H
là hình chiếu vuông góc của
A
lên
( )
R
. Vì
( )
,AR
cố định nên
H
cố định.
Ta có:
( )
( )
( ) ( )
22
2
2.1 2 2.1 4
2
,
3
2 1 2
AH d A R
− − +
= = =
+ − + −
.
Mà
( )
AH R AH HI⊥ ⊥
, do đó
AHI
vuông tại
H
nên
2
2 2 2
2 4 2
2
33
HI AI AH
= − = − =
.
Vậy
I
luôn thuộc đường tròn tâm
H
, nằm trên mặt phẳng
( )
R
, bán kính
42
3
r =
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
367
BÀI TOÁN ĐẠI SỐ
Câu 1: Trong không gian
Oxyz
cho mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 1 2 1 6− + − + + =S x y z
tiếp xúc với hai mặt
phẳng
( )
: 2 5 0+ + + =P x y z
,
( )
:2 5 0− + − =Q x y z
lần lượt tại
A
và
B
. Độ dài đoạn thẳng
AB
là
A.
26
. B.
3
. C.
32
. D.
23
.
Câu 2: Trong không gian với hệ tọa độ
Oxyz
, cho tứ diện
ABCD
có
( )
1;1;6A −
,
( )
3; 2; 4B − − −
,
( )
1;2; 1C −
,
( )
2; 2;0D −
. Điểm
( )
;;M a b c
thuộc đường thẳng
CD
sao cho tam giác
ABM
có
chu vi nhỏ nhất. Tính
abc++
.
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 3: Trong không gian Oxyz, cho điểm
( )
1; 3;0A −
và mặt cầu
2 2 2
( ):( 2) ( 6) 50S x y z− + + + =
tâm I.
Xét các điểm M thuộc sao cho góc
AMI
lớn nhất, M luôn thuộc mặt phẳng có phương trình là
A.
3 10 0.xy− − =
B.
2 10 0.xy− − =
C.
10 0.xy− − =
D.
2 10 0.xy− − =
Câu 4: Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
để hệ phương trình:
( ) ( )
2 2 2
22
2 1 2 2 0
2 9 0
m m x m y m m
x y x
+ + − + − − =
+ + − =
có hai nghiệm thực phân biệt
( )
11
;xy
,
( )
22
;xy
sao
cho biểu thức
( ) ( )
22
1 2 1 2
x x y y− + −
đạt giá trị nhỏ nhất. Tổng giá trị của tất cả các phần tử thuộc
S
bằng
A.
1
. B.
2
. C.
1−
. D.
0
.
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
368
ĐÁP ÁN CHI TIẾT
Câu 1: Chọn C
Mặt cầu
( )
S
có tâm
( )
1;2; 1−I
, mặt phẳng
( )
P
có một VTPT là
( )
( )
1;1;2=
P
n
, mặt phẳng
( )
Q
có một VTPT là
( )
( )
2 ; 1;1=−
Q
n
. Gọi
d
là đường thẳng đi qua tâm
I
và vuông góc với mặt
phẳng
( )
P
suy ra đường thẳng
d
nhận
( )
( )
1;1;2
P
n =
làm một véctơ chỉ phương. Phương trình
tham số của đường thẳng
d
là
1
: 2 ,
12
=+
= +
= − +
xt
d y t t
zt
.
Ta có:
( )
= A d P A d
nên ta gọi
( )
1 ;2 ; 1 2A t t t+ + − +
.
Vì
( )
AP
nên ta có:
( )
1 2 2 1 2 5 0+ + + + − + + =t t t
1 = −t
( )
0;1; 3−A
.
Gọi
'd
là đường thẳng đi qua tâm
I
và vuông góc với mặt phẳng
( )
Q
. Suy ra đường thẳng
'd
nhận
( )
( )
2; 1;1
Q
n =−
làm một véctơ chỉ phương. Phương trình tham số của đường thẳng
'd
là
12
': 2 ' ,
1
xt
d y t t
zt
=+
= −
= − +
. Ta có:
( )
'B d Q B d
=
nên ta gọi
( )
1 2 ;2 ; 1B t t t
+ − − +
.
Vì
( )
BQ
nên ta có:
( ) ( ) ( ) ( )
2 1 2 2 1 5 0 1 3;1;0t t t t B
+ − − + − + − = =
.
Vậy
( ) ( ) ( )
2 2 2
3 0 1 1 0 3 3 2= − + − + + =AB
.
Câu 2: Chọn A
Gọi
ABM
C
là chu vi của tam giác
ABM
.
( )
2; 3; 10AB = − − −
113AB=
( )
2; 3; 10AB = − − −
,
( )
1; 4;1CD =−
. 2 12 10 0ABCD = − + − =
AB CD⊥
.
Gọi
( )
P
là mặt phẳng chứa đường thẳng
AB
và vuông góc với đường thẳng
CD
.
H
là giao điểm của
( )
P
và đường thẳng
CD
.
Phương trình mặt phẳng
( )
P
qua
( )
1;1;6A −
có véc tơ pháp tuyến
( )
1; 4;1CD =−
là:
4 1 0x y z− + − =
.
A
B
H
D
C
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
369
Phương trình đường thẳng
CD
:
1
24
1
xt
yt
zt
=+
=−
= − +
.
( )
1 ;2 4 ; 1H CD H t t t + − − +
.
( ) ( )
1 4 2 4 1 1 0H P t t t + − − − + − =
1
2
t=
31
;0;
22
H
−
.
Với
M CD
, ta có
AM AH
BM BH
AM BM AH BH + +
.
113
ABM
C AB AM BM AH BH= + + + +
,
M CD
.
Suy ra
113
ABM
minC AH BH= + +
, đạt được
MH
31
;0;
22
M
−
.
Vậy
1abc+ + =
.
Câu 3: Chọn A
Mặt cầu có tâm
(2; 6;0), 5 2IR−=
và
10.IA =
Ta có
2 2 2 2 2 2 2 2
40 2 .40 2
cos .
2 . 2 .
10 2 10 2 5
MA MI IA MA R IA MA MA
AMI
MAMI MA R
MA MA
+ − + − +
= = = =
Do đó
2
arccos .
5
AMI
Dấu “=” xảy ra khi
2
40 2 10.MA MA= =
Gọi
( )
2 2 2
2 2 2
()
( 2) ( 6) 50
; ; 3 10 0.
2 10
( 1) ( 3) 40
MS
x y z
M x y z x y
MA
x y z
− + + + =
− − =
=
− + + + =
Vậy
( ): 3 10 0.M P x y − − =
Câu 4: Chọn C
Xét
( ) ( )
( )
( )
2 2 2
22
2 1 2 2 0 1
2 9 0 2
m m x m y m m
x y x
+ + − + − − =
+ + − =
Do
( ) ( )
22
22
2 1 0,m m m m+ + −
nên
( )
1
là phương trình của đường thẳng
và phương
trình
( )
2
là phương trình của đường tròn
( )
C
có tâm
( )
1;0I −
, bán kính
10R =
Để
cắt
( )
C
tại hai điểm phân biệt
( )
11
;A x y
,
( )
22
;B x y
( )
; (*)d I R
d
A
B
I
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
370
Ta có
( ) ( )
22
12
2
12
x x y yAB − + −=
nhỏ nhất khi
( )
;dI
lớn nhất
Có
( )
( ) ( )
( ) ( )
( ) ( )
22
2 2 2 2
2 2 2 2
2 2 1
2 2 1
; 2 2
2 1 2 1
m m m
m
d I R
m m m m m m
+ + −
+
= =
+ + − + + −
. Dấu bằng xảy ra
khi
2 2 2
13
2
2 1 2 2 1 0
13
2
m
m m m m m
m
−−
=
+ = − + − =
−+
=
.
Suy ra
1 3 1 3
;
22
S
=
− − −
+
. Do đó tổng giá trị các phần tử thuộc
S
bằng
1−
.
Xét
( ) ( )
( )
( )
2 2 2
22
2 1 2 2 0 1
2 9 0 2
m m x m y m m
x y x
+ + − + − − =
+ + − =
Do
( ) ( )
22
22
2 1 0,m m m m+ + −
nên
( )
1
là phương trình của đường thẳng
và phương
trình
( )
2
là phương trình của đường tròn
( )
C
có tâm
( )
1;0I −
, bán kính
10R =
Nghiệm của hệ phương trình là tọa độ giao điểm của
và
( )
C
.
Ta có:
( ) ( )
2 2 2
2 1 2 2 0m m x m y m m+ + − + − − =
( ) ( )
2
1 2 1 2 0m x y m x y − + + − + − =
Thấy:
10
1
10
2
20
xy
x
x
y
y
− + =
=
− =
=
−=
thì phương trình luôn đúng với mọi
m
.
Suy ra: Đường thẳng
luôn đi qua điểm
( )
1;2H
.
Mà
8 10IH R= =
nên điểm
H
nằm trong đường tròn
( )
C
.
Khi đó, đường thẳng
đi qua
H
luôn cắt đường tròn
( )
C
tại 2 điểm phân biệt
( )
11
;A x y
và
( )
22
;B x y
.
Ta có:
( ) ( )
22
12
2
12
x x y yAB − + −=
nhỏ nhất
AB
nhỏ nhất
AB IH⊥
hay
( )
2;2IH =
là một véctơ pháp tuyến của đường thẳng

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
371
22
21
22
m m m+−
=
2
2 2 1 0mm + − =
13
2
13
2
m
m
−−
=
−+
=
Vậy
1 3 1 3
;
22
S
=
− − −
+
nên tổng giá trị các phần tử thuộc
S
bằng
1−
.
Nhận xét: Phương trình
2
2 2 1 0mm+ − =
(
,ac
trái dấu) có 2 nghiệm phân biệt nên theo Vi-et,
tổng hai nghiệm đó bằng
1−
.
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
372
ĐỀ THI: TỔNG HỢP HÌNH HỌC OXYZ
Câu 1. Trong không gian với hệ tọa độ
Oxyz
, cho ba vectơ
2 3 5a i j k= + −
,
34b j k= − +
,
2c i j= − −
.
Khẳng định nào sau đây đúng?
A.
( ) ( ) ( )
2;3; 5 , 3;4;0 , 1; 2;0a b c= − = − = − −
.
B.
( ) ( ) ( )
2;3; 5 , 3;4;0 , 0; 2;0a b c= − = − = −
.
C.
( ) ( ) ( )
2;3; 5 , 0; 3;4 , 1; 2;0a b c= − = − = − −
.
D.
( ) ( ) ( )
2;3; 5 , 1; 3;4 , 1; 2;1a b c= − = − = − −
.
Câu 2. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
( )
0;1;3a =
và
( )
2;3;1b =−
. Nếu
2 3 4x a b+=
thì tọa độ của vectơ
x
là:
A.
95
4; ;
22
x
= − −
. B.
95
4; ;
22
x
=−
. C.
95
4; ;
22
x
=−
. D.
95
4; ;
22
x
= − −
.
Câu 3. Trong không gian với hệ tọa độ
Oxyz
, cho các vectơ
( ) ( )
1;0; 2 , 2;1;3ab= − = −
,
( )
3;2; 1c =−
,
( )
9;0; 11d =−
.
m
,
n
,
p
là ba số thực sao cho
..m a n b pc d+ + =
. Khi đó tổng
m n p++
bằng
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 4. Gọi
là góc giữa hai vectơ
( )
1;2;0a =
và
( )
2;0; 1b =−
, khi đó
cos
bằng:
A. 0. B.
2
5
−
. C.
2
5
. D.
2
.
5
Câu 5. Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
( )
−2; 3; 1M
,
( )
−1;1;1N
,
( )
−1; 1; 2Pm
.
Với những giá trị nào của
m
thì tam giác
MNP
vuông tại
N
?
A.
= 3m
. B.
= 2m
. C.
= 1m
. D.
= 0m
Câu 6. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
( )
=−2 ;1; 2a
và
( )
=−0; 2; 2b
. Tất cả
giá trị của
m
để hai vectơ
=+23u a mb
và
=−v ma b
vuông góc là.
A.
+26 2
6
. B.
+26 2
6
. C.
26 2
6
. D.
2
6
.
Câu 7. Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
( )
1;2;0A
,
( )
2;1;2B
,
( )
1;3;1−C
. Bán kính
đường tròn ngoại tiếp tam giác
ABC
.
A.
3 10
. B.
3 10
5
. C.
10
5
. D.
10
.
Câu 8. Trong không gian với hệ tọa độ
Oxyz
, cho năm điểm tạo thành một hình chóp có đáy là tứ giác
với
( )
0;0;3A
,
( )
2; 1;0−B
,
( )
3;2;4C
,
( )
1;3;5D
,
( )
4;2;1E
. Đỉnh của hình chóp tương ứng là.
A. Điểm
C
. B. Điểm
A
. C. Điểm
B
. D. Điểm
D
.
Câu 9. Trong không gian với hệ tọa độ
Oxyz
, cho hình lăng trụ
.
ABC A B C
có tọa độ các
đỉnh
( )
0;0;0A
,
( )
0; ;0Ba
,
3
; ;0
22
aa
C
và
( )
0;0;2
Aa
. Gọi
D
là trung điểm cạnh
BB
và
M
di động trên cạnh
AA
. Diện tích nhỏ nhất của tam giác
MDC
là.
A.
2
3
4
a
. B.
2
5
4
a
. C.
2
6
4
a
. D.
2
15
4
a
.
Câu 10. Trong không gian với hệ tọa độ
,Oxyz
cho bốn điểm
( )
1; 1;2A −
,
( )
2;1;0B
,
( )
1;1;1C −
,
( )
2;3;1D
. Gọi
( )
L
là tập hợp tất cả các điểm
M
trong không gian thỏa mãn đẳng thức

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
373
2 2 2 2
100MA MB MC MD+ + + =
. Biết rằng
( )
L
là một mặt cầu, mặt cầu đó có bán kính
R
bằng
bao nhiêu?
A.
10R =
. B.
21R =
. C.
3R =
. D.
13R =
.
Câu 11. Trong không gian với hệ tọa độ
,Oxyz
cho hai điểm
1
0; 3;
2
M
−
,
3
2; 1;
2
N
−
và mặt phẳng
( )
: 3 0.P x y z− − − =
Gọi
là đường thẳng thay đổi nằm trong mặt phẳng
( )
,P
các điểm
H
,
K
lần lượt là hình chiếu vuông góc của
M
,
N
trên
.
Biết rằng khi
MH NK=
thì trung điểm
của
HK
luôn thuộc một đường thẳng
d
cố định, phương trình của
d
là:
A.
3
1
7
xt
yt
z
= − −
=−
=−
. B.
3
1
7
xt
yt
z
= − +
=+
=−
. C.
3
1
7
xt
yt
z
= − −
=−
=−
. D.
3
1
7
xt
yt
z
= − −
=+
=−
.
Câu 12. Trong không gian với hệ tọa độ
,Oxyz
cho mặt phẳng
( )
:2 2 4 0P x y z+ − + =
và các điểm
( )
2;1;2A
,
( )
3; 2;2 .B −
Điểm
M
thuộc mặt phẳng
( )
P
sao cho các đường thẳng
MA
,
MB
luôn
tạo với mặt phẳng
( )
P
các góc bằng nhau. Biết rằng điểm
M
luôn thuộc đường tròn
( )
C
cố định.
Tìm tọa độ tâm của đường tròn
( )
.C
A.
74 97 62
;;
27 27 27
−
. B.
10 14
; 3;
33
−
. C.
17 17 17
;;
21 21 21
−
. D.
32 49 2
;;
9 9 9
−
.
Câu 13. Phương trình mặt phẳng trung trực của đoạn
AB
với
( )
1;1;2A
,
( )
1; 3;2B −
là
A.
10y −=
. B.
30y +=
. C.
20y −=
. D.
10y +=
.
Câu 14. Phương trình mặt phẳng
( )
P
qua ba điểm
( )
1;2;3A
,
( )
3;5;4B
và
( )
3;0;5C
là
A.
4 5 13 0x y z− − − =
. B.
8 2 10 25 0x y z− − − =
.
C.
8 2 10 25 0x y z− − + =
. D.
4 5 13 0x y z− − + =
.
Câu 15. Phương trình mặt phẳng
( )
P
qua hai điểm
( )
2;1; 3A −
,
( )
3;2; 1B −
và vuông góc với mặt phẳng
( )
: 2 3 4 0Q x y z+ + − =
là
A.
60x y z+ − + =
. B.
12 0x y z+ − + =
. C.
12 0x y z+ − − =
. D.
60x y z+ − − =
.
Câu 16. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )
:3 4 8 0P x y z− + − =
. Tọa độ giao điểm
M
của
( )
P
và trục
Oy
là
A.
( )
0;2;0M
. B.
( )
0;0;8M
. C.
8
;0;0
3
M
. D.
( )
0; 2;0M −
.
Câu 17. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
( )
1;4;1M
.
( )
P
là mặt phẳng qua
M
và cắt các
tia
Ox
,
Oy
,
Oz
lần lượt tại các điểm
,,A B C
sao cho thể tich khối tứ diện
OABC
nhỏ nhất. Phương trình mặt phẳng
( )
P
là
A.
4 4 12 0x y z+ + − =
. B.
4 3 12 0x y z+ + − =
.C.
4 4 12 0x y z+ + + =
. D.
4 4 12 0x y z+ + − =
.
Câu 18. Trong không gian với hệ tọa độ
Oxyz
, cho hai đường thẳng
1
21
:
1 2 1
x y z
d
−+
==
và
2
3
:
2 2 1
x y z
d
−
==
−
.
( )
P
là mặt phẳng chứa
1
d
và tạo với
2
d
một góc lớn nhất. Phương trình mặt
phẳng
( )
P
là
A.
13 10 7 36 0x y z− + + =
. B.
13 10 7 36 0x y z− + − =
.
C.
13 10 7 36 0x y z+ + − =
. D.
13 10 7 36 0x y z− − + + =
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
374
Câu 19. Trong không gian
Oxyz
, cho điểm
( )
1;3; 1M −
và mặt phẳng
( )
: 2 2 1P x y z− + =
. Gọi
N
là
hình chiếu vuông góc của
M
trên
( )
P
. Viết phương trình mặt phẳng trung trực của đoạn
MN
.
A.
2 2 3 0x y z− + + =
. B.
2 2 1 0x y z− + + =
.
C.
2 2 3 0x y z− + − =
. D.
2 2 2 0x y z− + + =
.
Câu 20. Trong không gian với hệ trục
Oxyz
, cho hai điểm
( )
0; 1;2M −
,
( )
1;1;3N −
. Một mặt phẳng
( )
P
đi qua
M
,
N
sao cho khoảng cách từ điểm
( )
0;0;2K
đến mặt phẳng
( )
P
đạt giá trị lớn nhất.
Tìm tọa độ véctơ pháp tuyến
n
của mặt phẳng
( )
P
.
A.
( )
1; 1;1n =−
. B.
( )
1;1; 1n =−
. C.
( )
2; 1;1n =−
. D.
( )
2;1; 1n =−
.
Câu 21. Trong không gian với hệ tọa độ
Oxyz
, gọi
( )
P
là mặt phẳng đi qua điểm
( )
1;4;9M
, cắt các tia
,,Ox Oy Oz
tại
,,A B C
sao cho biểu thức
OA OB OC++
có giá trị nhỏ nhất. Mặt phẳng
( )
P
đi
qua điểm nào dưới đây?
A.
( )
12;0;0
.
B.
( )
6;0;0
. C.
( )
0;6;0
.
D.
( )
0;0;12
.
Câu 22. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )
: 5 0P x y z− + − =
và
( )
: 2 5 0Q x y z+ + + =
. Mặt phẳng
( )
R
vuông góc với
( )
P
và
( )
Q
có véc tơ pháp tuyến là
A.
( )
3; 2 ; 1n =−
. B.
( )
1; 2 ; 4n = − −
. C.
( )
1;1; 0n =
. D.
( )
2 ;1; 3n =−
.
Câu 23. Trong không gian với hệ tọa độ
Oxyz
, cho hai mặt phẳng
( )
: 2 2 5 0P x y z+ + − =
và
( )
: 2 2 7 0Q x y z− + − + =
. Phương trình mặt phẳng
( )
chứa giao tuyến hai mặt phẳng trên và
song song với trục
Oy
là
A.
5 6 17 0xz+ − =
. B.
3 17 0y +=
.
C.
5 6 17 0xz+ + =
. D.
5 3 6 17 0x y z+ + + =
.
Câu 24. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
( )
0 ;8; 2A
và mặt cầu (S) có phương trình
( ) ( ) ( ) ( )
2 2 2
: 5 3 7 72S x y z− + + + − =
và điểm
( )
9 ; 7 ; 23B −
. Viết phương trình mặt phẳng
( )
P
qua
A
và tiếp xúc với
( )
S
sao cho khoảng cách từ
B
đến
( )
P
lớn nhất. Giả sử
( )
1; ;n m n=
là một véc tơ pháp tuyến của
( )
P
, hãy tính tích
.mn
biết
,mn
là các số nguyên.
A.
.2mn=
. B.
.2mn=−
. C.
.4mn=
. D.
.4mn=−
.
Câu 25. Trong không gian hệ tọa độ Oxyz, cho đường thẳng
2 2 3
:
2 3 2
x y z
d
+ − +
==
. Điểm nào thuộc
đường thẳng
d
.
A.
( )
0 ; 5 ; 1−M
. B.
( )
1; 2 ; 1−N
. C.
( )
2 ; 0;1P
. D.
( )
1;1; 2−−Q
.
Câu 26. Cho đường thẳng
12
:
2 1 1
x y z−+
= =
−
và hai điểm
(0; 1;3),−A
(1; 2;1).−B
Tìm tọa độ điểm
M
thuộc đường thẳng
sao cho
22
2MA MB+
đạt giá trị nhỏ nhất.
A.
(1; 0; 2).−M
B.
(3;1; 3).−M
C.
( 1; 1; 1).− − −M
D.
(5; 2; 4).−M
Câu 27. Trong không gian
Oxyz
, cho
( )
1; 1;0a =−
và hai điểm
( )
4 ;7 ; 3A −
,
( )
4 ;4 ;5B
. Giả sử
M
,
N
là hai điểm thay đổi trong mặt phẳng
( )
Oxy
sao cho
MN
cùng hướng với
a
và
52MN =
. Giá
trị lớn nhất của
AM BN−
bằng.
A.
17
. B.
77
. C.
7 2 3−
. D.
82 5−
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
375
Câu 28. Trong không gian với hệ trục tọa độ
Oxyz
, cho điểm
( )
1; 2;5A −
và mặt phẳng
( )
:2 3 9 0P x z− − =
. Phương trình đường thẳng
d
đi qua điểm
A
và vuông góc với mặt phẳng
( )
P
là
A.
12
23
59
xt
yt
zt
=+
= − −
=−
. B.
12
23
5
xt
yt
z
=+
= − −
=
. C.
12
2
53
xt
y
zt
=+
=−
=−
. D.
2
2
35
xt
yt
zt
=+
=−
= − +
.
Câu 29. Trong không gian với hệ trục tọa độ
Oxyz
, cho hai mặt phẳng
( )
:3 4 0P x y z− + + =
và
( )
:2 5 6 0Q x y− + =
. Lập phương trình đường thẳng là giao tuyến của hai mặt phẳng
( )
P
và
( )
Q
.
A.
35
2
5 13
xt
yt
zt
= − +
=
=−
. B.
35
2
5 13
xt
yt
zt
= − +
=−
=−
. C.
35
12
5 13
xt
yt
zt
= − +
=+
=−
. D.
35
2
5 13
xt
yt
zt
=+
=
=−
.
Câu 30. Trong không gian với hệ trục tọa độ
Oxyz
, cho điểm
5 1 1
;;
2 2 2
A
−
, mặt phẳng
( )
:2 2 2 3 0P x y z− + − =
và mặt cầu
( )
2 2 2
:9S x y z+ + =
. Gọi
d
là đường thẳng đi qua điểm
A
, nằm trong
( )
P
và cắt
( )
S
tại hai điểm
B
,
C
sao cho
3BC =
. Phương trình đường thẳng
d
là:
A.
5
2
1
2
1
6
2
xt
yt
zt
=+
=+
= − −
. B.
3
1
5
6
2
xt
yt
zt
=+
=+
=+
. C.
3
1
5
6
2
xt
yt
zt
=+
= − +
=+
. D.
3
1
5
6
2
xt
yt
zt
=+
=+
= − +
.
Câu 31. Trong không gian với hệ tọa độ
Oxyz
, viết phương trình đường thẳng
d
biết
d
song song với
73
:4
42
yz
dx
−−
− = =
−
, đồng thời cắt cả hai đường thẳng
1
d
và
2
d
với
1
: 1 2
xt
d y t
zt
=
= − +
=
(
t
: tham số) và
2
11
:
23
yz
dx
−−
==
−
.
A.
2
34
22
xu
yu
zu
=+
=+
=−
. B.
2
34
22
xu
yu
zu
=+
=−
=−
. C.
2
34
22
xu
yu
zu
=−
=+
=−
. D.
2
34
22
xu
yu
zu
=+
=+
=+
.
Câu 32. Trong không gian với hệ tọa độ
Oxyz
, cho hai đường thẳng
1
d
và
2
d
với
1
23
:3
42
xt
d y t
zt
=+
= − +
=−
(
t
: tham
số) và
2
41
:
3 1 2
x y z
d
−+
==
−
. Viết phương trình đường thẳng
d
nằm trong mặt phẳng chứa hai
đường thẳng
1
d
và
2
d
, đồng thời cách đều hai đường thẳng đó.
A.
33
2
22
xu
yu
zu
=+
= − −
=−
. B.
33
2
22
xu
yu
zu
=+
=−
=−
. C.
33
2
22
xu
yu
zu
=+
= − +
=−
. D.
33
2
22
xu
yu
zu
=−
= − −
=−
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
376
Câu 33. Trong không gian với hệ tọa độ
Oxyz
, cho hai đường thẳng đường thẳng
1
1
: 2 2
xt
d y t
zt
= − +
= − +
=
và
2
22
:1
1
xt
d y t
zt
=+
=+
=+
(
t
và
t
: tham số) và mặt phẳng
( )
: 2 5 0P x y z+ − + =
. Lập phương trình đường
thẳng
d
song song với mặt phẳng
( )
P
và cắt hai đường thẳng
1
d
và
2
d
tại
A
,
B
sao cho độ dài
AB
đạt giá trị nhỏ nhất.
A.
1xu
yu
zu
=+
=−
=
. B.
1
2
2
xu
yu
zu
=+
=+
=+
. C.
12
2
xu
yu
zu
=+
=
=
. D.
14
2
xu
yu
zu
=−
=−
=−
.
Câu 34. Đường thẳng
đi qua điểm
( )
1;4;2A −
và vuông góc với hai đường thẳng
1
3 4 2
:
253
x y z
d
+ + −
==
và
2
11
:
2 2 4
x y z
d
+−
==
có phương trình là
A.
1 4 2
:
7 1 3
x y z+ − −
= =
−−
. B.
1 4 2
:
7 1 3
x y z− − −
= =
−−
.
C.
1 4 2
:
7 1 3
x y z+ − −
= =
−
. D.
1 4 2
:
7 1 3
x y z+ − −
= =
−−
.
Câu 35. Đường thẳng
đi qua điểm
( )
3; 1;2A −−
, vuông góc với đường thẳng
1
7 1 9
:
3 6 2
x y z
d
− − −
==
−−
và cắt đường thẳng
2
3 1 1
:
5 3 2
x y z
d
− − +
==
có phương trình là
A.
3 1 2
:
6 2 3
x y z− − +
= =
−
. B.
3 1 2
:
6 2 3
x y z+ + −
= =
−
.
C.
6 2 3
:
3 1 2
x y z+ + −
= =
−−
. D.
3 1 2
:
6 2 3
x y z+ + −
= =
−−
.
Câu 36. Đường thẳng
đi qua điểm
( )
2;1;1A −
, và cắt đường thẳng
2 1 5
:
1 3 2
x y z
d
+ − +
==
−
tại điểm
M
có tọa độ thỏa mãn
35
ABM
S
=
với
( )
3; 1;2B −−
. Phương trình của đường thẳng
là
A.
2 1 1
:
2 6 3
x y z− + −
= =
− − −
. B.
2 1 1
:
2 6 3
x y z− + −
= =
−
.
C.
2 1 1
:
2 6 3
x y z+ − +
= =
. D.
2 1 1
:
2 6 3
x y z+ − −
= =
−
.
Câu 37. Cho hình lập phương
.ABCD A BCD
có
( ) ( ) ( ) ( )
0;0;0 , 3;0;0 , 0;3;0 , 0;0;3A B D A
. Mặt cầu
tiếp xúc với tất cả các cạnh của hình lập phương có phương trình là
A.
( )
222
333
:9
222
S x x x
− + − + − =
. B.
( ) ( ) ( ) ( )
222
: 1 1 1 18S x x x− + − + − =
.
C.
( ) ( ) ( ) ( )
222
: 1 1 1 9S x x x− + − + − =
. D.
( )
222
3 3 3 9
:
2 2 2 2
S x x x
− + − + − =
.
Câu 38. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )
: 5 0P x y z+ + + =
. Mặt cầu
( )
S
có bán
kính
4R =
và cắt mặt phẳng
( )
P
theo giao tuyến là đường tròn
( )
C
có tâm
( )
1; 2; 4H −−
bán
kính
13r =
, biết rằng tâm mặt cầu
( )
S
có hoành độ dương. Phương trình mặt cầu
( )
S
là:

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
377
A.
( ) ( ) ( ) ( )
2 2 2
: 2 1 3 16S x y z− + + + + =
. B.
( ) ( ) ( ) ( )
2 2 2
: 2 3 5 16S x y z− + + + + =
.
C.
( ) ( ) ( ) ( )
2 2 2
: 1 2 4 16S x y z− + + + + =
. D.
( ) ( ) ( ) ( )
2 2 2
: 2 3 5 13S x y z− + + + + =
.
Câu 39. Trong không gian
Oxyz
, cho mặt cầu
( )
S
tâm
( )
1;2; 3I −
và điểm
( )
1; 2;1M −−
sao cho từ
M
có thể kẻ được ba tiếp tuyến
MA
,
,MB MC
đến mặt cầu
( )
S
(
A
,
,BC
là các tiếp điểm ) thỏa
mãn
60AMB =
;
90BMC =
;
120CMA =
. Phương trình mặt cầu
( )
S
là
A.
2 2 2
2 4 6 13 0x y z x y z+ + + + − − =
. B.
2 2 2
2 4 6 13 0x y z x y z+ + − − + + =
.
C.
2 2 2
2 4 6 1 0x y z x y z+ + − − + − =
. D.
2 2 2
2 4 6 13 0x y z x y z+ + − − + − =
.
Câu 40. Cho đường thẳng
11
:
1 2 1
x y z
d
−+
==
−
và điểm
( )
5;4; 2A −
. Tìm phương trình mặt cầu đi qua
điểm
A
và có tâm là giao điểm của
d
với mặt phẳng
( )
Oxy
.
A.
( ) ( ) ( ) ( )
2 2 2
: 1 1 2 65S x y z+ + − + + =
. B.
( ) ( ) ( )
22
2
: 1 1 9S x y z+ + − + =
.
C.
( ) ( ) ( )
22
2
: 1 2 64S x y z− + + + =
. D.
( ) ( ) ( )
22
2
: 1 1 65S x y z+ + + + =
.
Câu 41. Trong không gian với hệ tọa độ
Oxyz
, cho mặt mặt phẳng
( )
:P
2 2 10 0x y z+ − + =
và mặt cầu
( )
S
có tâm
( )
2;1;3I
. Biết mặt mặt phẳng
( )
P
cắt mặt cầu
( )
S
theo giao tuyến là một đường tròn
bán kính bằng
4
. Viết phương trình của mặt cầu
( )
S
.
A.
( ) ( ) ( )
2 2 2
2 1 3 36x y z+ + + + + =
. B.
( ) ( ) ( )
2 2 2
2 1 3 25x y z+ + + + + =
.
C.
( ) ( ) ( )
2 2 2
2 1 3 36x y z− + − + − =
. D.
( ) ( ) ( )
2 2 2
2 1 3 25x y z− + − + − =
.
Câu 42. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
( )
3;0; 2A −
và mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 1 2 3 25S x y z− + + + + =
. Đường thẳng
d
đi qua
A
và cắt mặt cầu
( )
S
tại hai điểm
phân biệt
,MN
. Độ dài nhỏ nhất của
MN
là
A.
8
. B.
10
. C.
4
. D.
6
.
Câu 43. Trong không gian với hệ tọa độ
,Oxyz
cho mặt cầu
( )
S
có phương trình
2 2 2
2 4 4 0x y z x y z m+ + − + − − =
có bán kính
5.R =
Tìm giá trị của
m
.
A.
4m =
. B.
4m =−
. C.
16m =
. D.
16m =−
.
Câu 44. Trong không gian với hệ trục
Oxyz
, cho hai đường thẳng
1
4 1 5
:
3 1 2
x y z
d
− − +
==
−−
và
2
23
:
1 3 1
x y z
d
−+
==
. Mặt cầu có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng và có
phương trình
A.
2 2 2
20x y z x y z+ + + + − =
. B.
2 2 2
4 2 2 0x y z x y z+ + + + − =
.
C.
2 2 2
4 2 2 0x y z x y z+ + − − + =
. D.
2 2 2
20x y z x y z+ + − − + =
.
Câu 45. Trong không gian với hệ tọa độ
,Oxyz
cho mặt phẳng
( )
: 2 2 5 0P x y z− + + =
và các điểm
( )
0;0;4A
,
( )
2;0;0B
. Mặt cầu
( )
S
có bán kính nhỏ nhất đi qua
;;A B O
và tiếp xúc với mặt phẳng
( )
P
có tâm là
A.
( )
1;2;2
. B.
19
1; ;2
4
−
. C.
( )
1; 2;2−
. D.
19
1; ;2
4
.
Câu 46. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 1
:
112
x y z
d
− − −
==
,
( )
2;1;4A
. Gọi
( )
;;H a b c
là điểm thuộc
d
sao cho
AH
có độ dài nhỏ nhất. Tính
3 3 3
T a b c= + +
.
A.
8T =
. B.
62T =
. C.
13T =
. D.
5T =
.
1
d
2
d

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
378
Câu 47. Trong không gian với hệ trục toạ độ
Oxyz
, cho phương trình hai đường thẳng
:
1 1 2
x y z
= =
và
11
:
2 1 1
x y z+−
= =
−
.Gọi
M
là điểm thuộc
và
N
là điểm thuộc thuộc
sao cho đường thẳng
MN
song song với mặt phẳng
( ): 0P x y z− + =
và độ dài
2MN =
. Số cặp điểm
;MN
thỏa
mãn bài toán là
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 48. Trong không gian với hệ toạ độ Oxyz, cho đường thẳng
2
1
Δ:
1 2 1
x m y z m− + +
==
−
và hai điểm
( 1;4;1), (3; 2;0).MN−−
Gọi
( )
;;H a b c
, K lần lượt là hình chiếu vuông góc của M, N lên Δ sao
cho khối tứ diện
HKNM
có thể tích nhỏ nhất. Khi đó, giá trị
2T a b c= − +
bằng
A.
3−
. B.
5
. C.
8.−
D.
8.
Câu 49. Trong không gian với hệ tọa độ Oxyz, cho hai điểm
(2;1;1)A
,
( )
0;3; 1B −
và điểm C nằm trên
mặt phẳng Oxy sao cho ba điểm A, B, C thẳng hàng. Điểm C có tọa độ là
A.
( )
1;2;3
. B.
( )
1;2;1
. C.
( )
1;2;0
. D.
( )
1;1;0
.
Câu 50. Cho mặt cầu
2 2 2
( ): 2 2 0S x y z x+ + − − =
và mặt phẳng
( ): 1 0P x z+ + =
. Mặt phẳng (P) cắt
()S
theo giao tuyến là một đường tròn có tọa độ tâm là
A.
( )
1; 1;0−
. B.
( )
0; 1;0−
. C.
( )
0;1; 1−
. D.
( )
0;0; 1−
.
Câu 51. Trong không gian với hệ tọa độ
Oxyz
, cho tam giác
ABC
có
(3;1;0)A
,
B
nằm trên mặt phẳng
()Oxy
và có hoành độ dương,
C
nằm trên trục
Oz
và
(2;1;1)H
là trực tâm của tam giác
ABC
.
Toạ độ các điểm
B
,
C
thỏa mãn yêu cầu bài toán là:
A.
( ) ( )
3;1;0 , 0;0; 3BC−
. B.
( ) ( )
1;3;0 , 0;0; 3BC−
.
C.
( ) ( )
3; 3;0 , 0;0;1BC−
. D.
( ) ( )
1; 3;0 , 0;0;1BC−
.
Câu 52. Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
( )
0;1;1A
,
( )
3;0; 1B −
,
( )
0;5; 6C −
và mặt cầu
( ) ( )
2
22
1
( ): 1 y 1 z 2
2
Sx
− + − + + =
. Biết điểm
( )
;;M x y z
thuộc mặt cầu
(S)
và thỏa mãn giá trị
của
32T MA MB MC= + +
đạt giá trị nhỏ nhất. Khi đó tổng
P x y z= + +
bằng:
A.
3P =
. B.
5
2
P =
. C.
3
2
P =
. D.
3P =−
.
Câu 53. Trong không gian tọa độ
Oxyz
, cho mặt phẳng
( )
P
đi qua
( )
1;2;0A −
và cách
điểm
( )
1; 2; 2B −−
một khoảng lớn nhất có phương trình là
0ax by cz d+ + + =
, với
,,a b c
. Nếu
1a =
thì giá trị của
d
bằng
A.
5−
. B.
5
. C.
6
. D.
6−
.
Câu 54. Trong không gian tọa độ
Oxyz
, cho hai điểm
( )
1;2;2A
,
( )
5;4;4B
và mặt phẳng
( )
P
:
2 6 0x y z+ − + =
. Gọi điểm
( )
;;M a b c
thuộc
( )
P
sao cho
22
MA MB+
nhỏ nhất. Khi đó giá trị
abc++
bằng
A.
5
. B.
3
. C.
2−
. D.
4
.
Câu 55. Trong không gian tọa độ
Oxyz
, gọi
( )
P
là mặt phẳng cắt các tia
,,Ox Oy Oz
lần lượt tại
( ) ( ) ( )
;0;0 , 0; ;0 , 0;0;A a B b C c
sao cho
2 2 2
12abc+ + =
và diện tích tam giác
ABC
lớn nhất.
Mặt phẳng
( )
P
đi qua điểm nào sau đây?
A.
( )
2;0;2
. B.
( )
3;0;3
. C.
( )
2;2;0
. D.
( )
1;0;1
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
379
Câu 56. Cho hình chóp
.S ABC
, có
SC
vuông góc với đáy
( )
ABC
, tam giác
ABC
vuông tại
A
, các điểm
,MN
lần lượt thuộc
,SA BC
sao cho
AM CN=
. Biết
2SC CA AB a= = =
. Tìm giá trị của
MN
ngắn nhất?
A.
6
.
6
a
B.
6
3
a
. C.
6
2
a
. D.
3
6
a
.
Câu 57. Cho hình hộp đứng
' ' ' '
.ABCD ABC D
,
'
2AA AB=
, đáy
ABCD
là hình vuông. Tìm
M
thuộc cạnh
AB
sao cho
''
A MC
là góc lớn nhất?
A.
( )
1;0;0M
. B.
( )
1;0;1M
. C.
( )
0;1;0M
. D.
( )
0;0;1M
.
Câu 58. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang vuông, đường cao
, 2 ,AB a BC a SA a= = =
và vuông góc với đáy,
.SC BD⊥
Gọi
M
thuộc
SA
,
DE
là đường cao
tam giác
BDM
.Giả sử
( )
0MA x x a=
, xác định
x
để
DE
lớn nhất.
A.
2xa=
. B.
2
a
x =
. C.
3xa=
. D.
xa=
.
Câu 59. Trong không gian với hệ tọa độ
,Oxyz
cho hai đường thẳng
1 1 1
:
1 2 2
x y z− − +
= =
−
và
12
: 1 2 ,
1
xt
d y t t
zt
=+
= − +
=+
. Khẳng định nào sau đây là khẳng định đúng?
A.
cắt
d
và
vuông góc với
d
. B.
và
d
chéo nhau,
vuông góc với
d
.
C.
cắt
d
và
không vuông góc với
d
. D.
và
d
chéo nhau nhưng không vuông góc.
Câu 60. Trong không gian với hệ tọa độ
,Oxyz
cho hai đường thẳng
1
:
2 2 1
x y m z n− + −
= =
−
và
16
: 3 6
63
xt
d y t
zt
=+
=−
=−
. Tính giá trị biểu thức
22
K m n=+
, biết hai đường thẳng
và
d
trùng nhau.
A.
30K =
. B.
45K =
. C.
55K =
. D.
73K =
.
Câu 61. Viết phươngg trình mặt cầu (S) tâm
( )
4, 2, 1I −
nhận đường thẳng
( )
D
:
21
1
22
xz
y
−−
= + =
làm tiếp tuyến.
A.
( ) ( ) ( )
2 2 2
4 2 1 4xyz− + − + + =
B.
( ) ( ) ( )
2 2 2
4 2 1 16xyz− + − + + =
C.
( ) ( ) ( )
2 2 2
4 2 1 9xyz− + − + + =
D.
( ) ( ) ( )
2 2 2
4 2 1 3xyz− + − + + =
Câu 62. Trong không gian
Oxyz
cho hai đường thẳng
1
1
:2
x
yt
zt
=
= +
=−
,
2
4
: 3 2
1
xt
yt
zt
=+
= −
=−
. Gọi
( )
S
là mặt
cầu có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng
1
và
2
. Bán kính mặt cầu
( )
S
.
A.
10
2
B.
11
2
C.
3
2
D.
2
Câu 63. Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
( ) ( ) ( )
;0;0 , 0; ;0 , 0;0;A a B b C c
với
,,abc
là các số thực khác 0, mặt phẳng (ABC) đi qua điểm
(2;4;5)M
. Biết rằng mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 1 2 3 25S x y z− + − + − =
cắt mặt phẳng
( )
ABC
theo giao tuyến là một đường tròn
có chu vi
8
. Giá trị của biểu thức
abc++
bằng
A.
40
. B.
4
. C.
20
. D.
30
.
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
380
Câu 64. Trong không gian
Oxyz
, cho ba điểm
( )
2;1; 1A −−
,
( )
3;4; 3B −
,
( )
2;1; 2C −
và đường thẳng
1 1 1
:
1 2 1
x y z− − −
= =
−−
. Gọi
( )
là mặt phẳng chứa
sao cho
A
,
B
,
C
ở cùng phía đối với mặt
phẳng
( )
. Gọi
1
d
,
2
d
,
3
d
lần lượt là khoảng cách từ
A
,
B
,
C
đến
( )
. Giá trị lớn nhất của
1 2 3
T d d d= + +
là
A.
max
21
2
T =
. B.
max
354
2
T =
. C.
max
14
2
T =
. D.
max
203
2
T =
.
Câu 65. Trong không gian
Oxyz
, cho đường thẳng
2
( ): 2 ( 1) ( , )
2 2 (2 3)
xt
d y m m t m t
z m m t
=+
= + + −
= − + + −
. Gọi
( , , ) ( ):2 2 8 0I a b c P x y z + + − =
là tâm mặt cầu
()S
luôn tiếp xúc với
( ),dm
. Biết
()S
có
bán kính là
R
. Tính
2
2T a b c R= + + −
.
A.
1−
. B. 0. C. 1. D. 2.
Câu 66. Cho
2 2 2
( ):( 1) ( 2) ( 3) 4, (2;1;2), (4; 3; 4), (4; 3; 2)S x y z I A B+ + + + + = − − − −
. Gọi
M
là điểm nằm
trên
()S
và cách đều
,AB
. Biết
( )
max
1
, , ,
13
MI a b a b a b= +
. Tính
10T b a=−
.
A. 56. B. 57. C. 58. D. 59.
Câu 67. Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
( )
2 2 2
: 2 4 6 13 0S x y z x y z+ + − − + − =
và
đường thẳng
1 2 1
:
1 1 1
x y z
d
+ + −
==
. Điểm
( )
;;M a b c
( )
0a
nằm trên đường thẳng
d
sao cho
từ
M
kẻ được ba tiếp tuyến
MA
,
MB
,
MC
đến mặt cầu
( )
S
(
A
,
B
,
C
là các tiếp điểm) và
60AMB =
,
90BMC =
,
120CMA =
. Tính
3 3 3
abc++
.
A.
3 3 3
173
9
abc+ + =
. B.
3 3 3
112
9
abc+ + =
. C.
3 3 3
8abc+ + = −
. D.
3 3 3
23
9
abc+ + =
.
Câu 68. Trong không gian với hệ tọa độ
Oxyz
, xét tứ diện
ABCD
có các cặp cạnh đối diện bằng nhau và
D
khác phía với
O
so với
( )
;ABC
đồng thời
A
,
B
,
C
lần lượt là giao điểm của các trục
Ox
,
Oy
,
Oz
và
( ): 1
25
x y z
m m m
++=
+−
(với
2m −
,
0m
,
5m
). Tìm khoảng cách ngắn nhất
từ tâm mặt cầu ngoại tiếp
I
của tứ diện
ABCD
đến
.O
A.
30
. B.
13
2
. C.
26
. D.
26
2
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
381
ĐÁP ÁN CHI TIẾT
1
.
C
2
.
A
3
.
A
4
.
D
5
.
D
6
.
A
7
.
B
8
.
A
9
.
C
1
0
.
B
1
1
.
C
1
2
.
A
1
3
.
D
1
4
.
D
1
5
.
D
1
6
.
D
1
7
.
A
1
8
.
B
1
9
.
A
2
0
.
B
2
1
.
B
2
2
.
D
2
3
.
A
2
4
.
D
2
5
.
A
2
6
.
C
2
7
.
A
2
8
.
C
2
9
.
A
3
0
.
B
3
1
.
A
3
2
.
C
3
3
3
4
.
A
3
5
.
B
3
6
.
D
3
7
.
D
3
8
.
A
3
9
.
D
4
0
.
D
4
1
.
D
4
2
.
A
4
3
.
C
4
4
.
C
4
5
.
A
4
6
.
B
4
7
.
B
4
8
.
C
4
9
.
C
5
0
.
D
5
1
.
A
5
2
.
C
5
3
.
B
5
4
.
A
5
5
.
D
5
6
.
B
5
7
.
A
5
8
.
D
5
9
.
B
6
0
.
B
6
1
.
B
6
2
.
B
6
3
.
A
6
4
.
B
6
5
.
B
6
6
.
B
6
7
.
B
6
8
.
D
Câu 1. Chọn C
( )
2 3 5 2;3; 5a i j k a= + − = −
.
( )
3 4 0; 3;4b j k b= − + = −
.
( )
2 1; 2;0c i j c= − − = − −
.
Câu 2. Chọn A
( )
3 3 9 9 5
2 3 4 2 4;6;2 0; ; 4; ;
2 2 2 2 2
x a b x b a
+ = = − = − − = − −
.
Câu 3. Chọn A
( ) ( ) ( ) ( )
..
;0; 2 2 ; ;3 3 ;2 ; 9;0; 11
2 3 9 2
2 0 2 1.
2 3 11 1
m a n b pc d
m m n n n p p p
m n p m
n p n m n p
m n p p
+ + =
− + − + − = −
− + = =
+ = = − + + =
− + − = − =
Câu 4. Chọn D
. 2 2
. cos cos .
5
5. 5
ab
a b a b
ab
= = = = =

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
382
Câu 5. Chọn D
( 3; 2;2); (2; 2;1).MN NP m
Tam giác
MNP
vuông tại
N
. 0 6 2 4 2 0 0.MN NP m m = − − + + = =
Câu 6. Chọn A
. 3 2; . 9; . 4.a b a a b b= − = =
Hai vectơ
23u a mb=+
và
v ma b=−
vuông góc
22
2
. 0 2 . 2 . 3 . 3 . 0 18 6 2 9 2 12 0
26 2
3 2 2 2 2 0 .
6
u v ma a a b m a b mb b m m m
m m m
= − + − = + − − =
+
− + + = =
Câu 7. Chọn B
Ta có:
( )
1; 1;2=−AB
,
( )
2;1;1 6AC AB AC= − = =
; có
14=BC
.
Lại có:
( )
, 3; 5; 1AB AC
= − − −
.
Diện tích tam giác
ABC
là
1 35
,
22
==
ABC
S AB AC
.
Ta lại có công thức
. . . . 6. 6. 14 3 10
4 4 5
35
4.
2
ABC ABC
ABC ABC
AB AC BC AB AC BC
SR
RS
= = = =
.
Câu 8. Chọn A
Xét đáp án A chọn điểm
C
là đỉnh, ta có:
( )
2; 1; 3= − −AB
,
( )
1;3;2=AD
,
( )
4;2; 2=−AE
,
( )
3;2;1=AC
.
Với
( )
, . 4.7 2.7 2.7 0
, 7; 7;7
, . 3.7 2.7 1.7 14
= − − =
= −
= − + =
AB AD AE
AB AD
AB AD AC
Suy ra
A
,
B
,
D
,
E
đồng phẳng. Vậy điểm
C
là đỉnh của hình chóp.
Câu 9. Chọn C
Theo giả thiết, ta có
3
; ;2
22
=
aa
CC AA C a
,
( )
0; ;D a a
và
( ) ( )
0;0; 0 2M t t a
.
Ta có
3
;;
22
aa
DC a
=−
,
( )
0; ;= − −DM a t a
.
Vì vậy
( )
2
2
2 2 2
2 3 6
1 4 12 15 6
,
2 4 4 4
−+
−+
= = =
MDC
a t a a
a t at a a
S DC DM
.
Suy ra
2
6
4
MDC
a
MinS
=
khi
3
2
ta=
.
Câu 10. Chọn B
Giả sử
( )
;;M x y z
. Khi đó:
( ) ( ) ( )
2 2 2
2
112MA x y z= − + + + −
,
( ) ( )
22
22
21MB x y z= − + − +
,
( ) ( ) ( )
2 2 2
2
1 1 1MC x y z= + + − + −
,
( ) ( ) ( )
2 2 2
2
2 3 1MD x y z= − + − + −
.
Ta có:
2 2 2 2 2 2 2
100 4 4 4 8 8 8 28 100MA MB MC MD x y z x y z+ + + = + + − − − + =
( ) ( ) ( )
2 2 2
1 1 1 21 21x y z MI − + − + − = =
, với
( )
1;1;1I
.
Vậy tập hợp tất cả các điểm
M
thỏa mãn đẳng thức đã cho là mặt cầu tâm
( )
1;1;1I
, bán kính
21R =
.
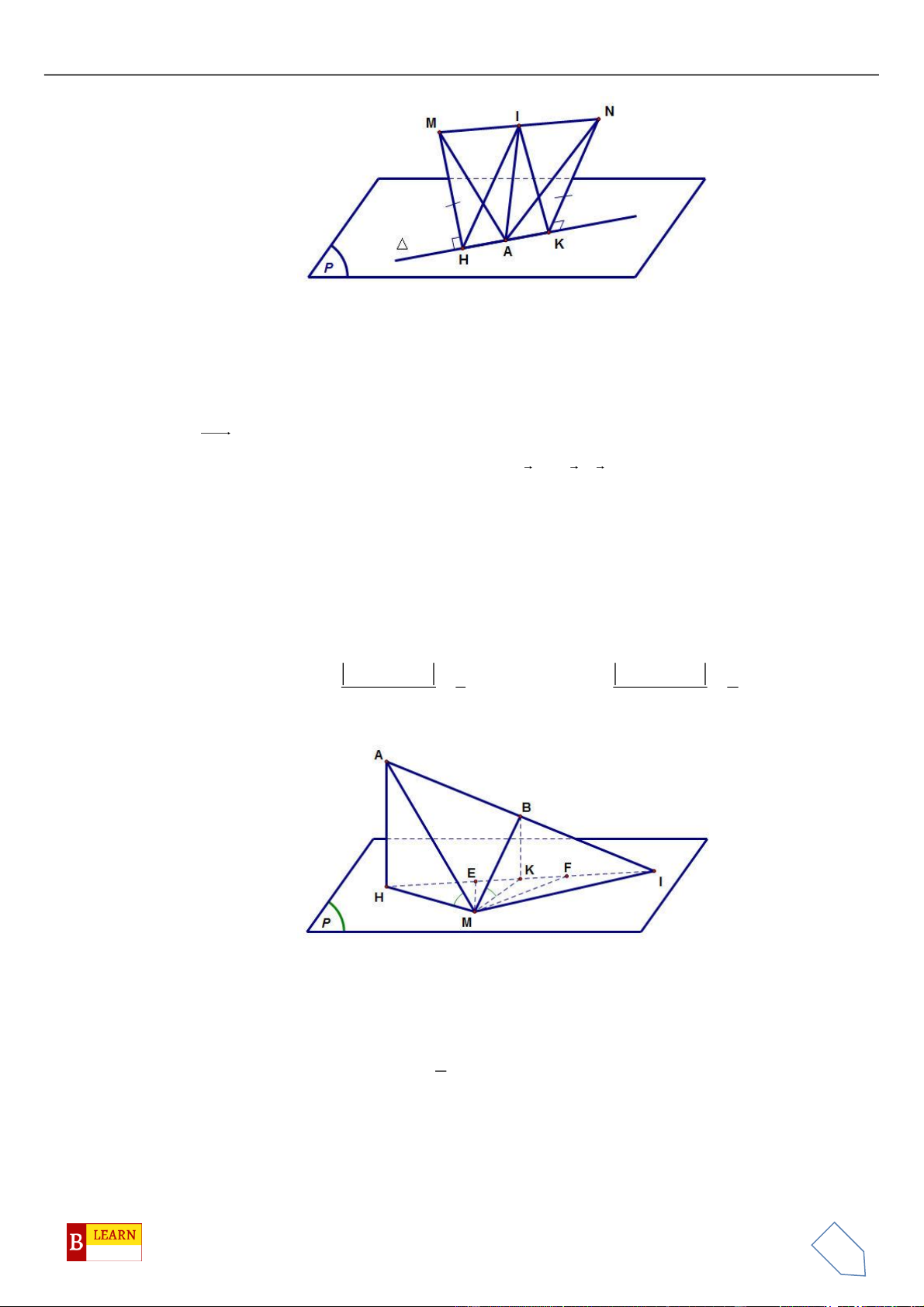
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
383
Câu 11. Chọn C
Gọi
I
,
A
lần lượt là trung điểm của
MN
và
.HK
Ta có
( )
.. HAM KAN c g c AM AN = =
tam giác
MAN
cân tại
A
AI MN⊥
AI
luôn thuộc mặt phẳng trung trực
( )
Q
của đoạn thẳng
MN
là giao tuyến của hai mặt phẳng
( )
P
và
( )
Q
.
Ta có:
( )
2; 2; 1MN = − −
,
( )
1;2; 1I −
. Phương trình mặt phẳng
( )
:2 2 1 0Q x y z− − + =
.
( ) ( )
d P Q=
nên
d
có một véctơ chỉ phương
( )
; 1; 1;0
d P Q
u n n
= = − −
và
d
đi qua điểm
( )
3;1; 7E −−
. Do đó phương trình tham số của
d
là:
3
1
7
xt
yt
z
= − −
=−
=−
.
Câu 12. Chọn A
Cách 1:
Gọi
H
,
K
lần lượt là hình chiếu của
A
,
B
lên
( )
P
AMH BMK=
.
Ta có:
( )
( )
( )
( )
4 2 2 4 6 4 2 4
84
; ; ; 2.
3 3 3 3
AH d A P BK d B P AH BK
+ − + − − +
= = = = = = =
2.HM MK=
(do
AHM
đồng dạng với
BKM
(g.g) vì giả thiết cho
AMH BMK=
).
Lấy điểm
I
là điểm đối xứng của
H
qua
K
;
E
thuộc đoạn
HK
sao cho
2HE KE=
;
F
thuộc
đoạn
KI
sao cho
2FI KF=
.
Khi đó:
A
,
B
,
I
,
H
,
E
,
K
,
F
đều là các điểm cố định.
* Ta chứng minh:
M
di chuyển trên đường tròn tâm
F
, đường kính
IE
:
Gọi
N
là điểm đối xứng của
M
qua
K
HMN
cân tại
M
.
E
nằm trên trung tuyến
HK
và
2
3
HE HK=
E
là trọng tâm
HMN
ME HN⊥
.
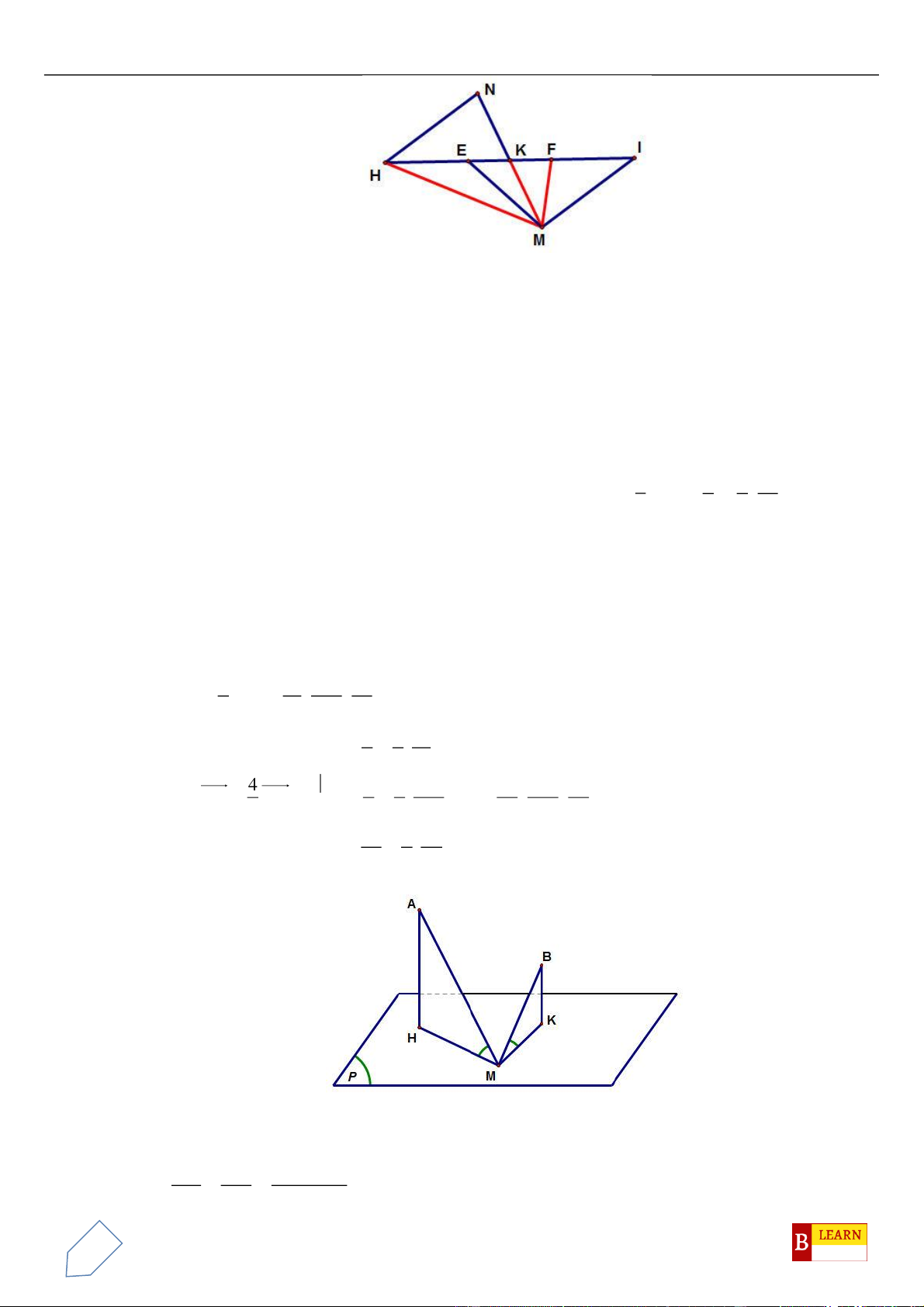
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
384
Mà
//HN MI ME MI⊥
.
Dễ dàng chứng minh
F
là trung điểm của
EI
M
di chuyển trên đường tròn tâm
F
đường kính
EI
(thuộc mặt phẳng
( )
P
).
* Tìm tọa độ điểm
F
:
Phương trình đường cao
AH
là:
22
12
2
xt
yt
zt
=+
=+
=−
.
Khi đó ta gọi
( )
1 1 1
2 2 ;1 2 ;2H t t t AH+ + −
.
Ta có:
( ) ( ) ( ) ( )
1 1 1 1
8
2 2 2 2 1 2 2 4 0
9
H P t t t t + + + − − + = = −
2 7 26
;;
9 9 9
H
−
.
Phương trình đường cao
BK
là:
32
22
2
xt
yt
zt
=+
= − +
=−
.
Khi đó ta gọi
( )
2 2 2
3 2 ; 2 2 ;2K t t t+ − + −
.
( ) ( ) ( ) ( )
2 2 2
2 3 2 2 2 2 2 4 0K P t t t + + − + − − + =
2
4 19 26 22
;;
9 9 9 9
tK
−
= −
.
Ta có:
2 4 17
.
9 3 9
4 7 4 19 74 97 62
. ; ;
3 9 3 9 27 27 27
26 4 4
.
9 3 9
F
F
F
x
HF HK y F
z
−=
−−
= + =
−
−=
.
Cách 2:
Gọi
H
,
K
lần lượt là hình chiếu vuông góc của
A
,
B
trên
( )
.P
Khi đó ta có
AMH BMK=
. Suy ra
AMH BMK∽
( )
( )
( )
( )
,
2 2 .
,
d A P
MA AH
MA MB
MB BK
d B P
= = = =

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
385
Gọi
( )
; ; .M x y z
Khi đó ta có:
( ) ( ) ( ) ( ) ( ) ( )
2 2 2 2 2 2
2 2 1 2 2 3 2 2MA MB x y z x y z= − + − + − = − + + + −
( )
2 2 2
20
6 4 59 0 .
3
x y z x y z S + + − + − + =
Suy ra
M
thuộc đường tròn giao tuyến của
( )
P
với mặt cầu
( )
.S
Mặt cầu
( )
S
có tâm
10
; 3;2 .
3
I
−
Tâm
H
của đường tròn
( )
C
là hình chiếu vuông góc của
I
trên
( )
.P
Từ đó ta tìm được
74 97 62
;;
27 27 27
H
−
.
Câu 13. Chọn D
Gọi
I
là trung điểm của
AB
, suy ra
( )
1; 1;2I −
.
Khi đó mặt phẳng trung trực
( )
P
của đoạn
AB
qua
I
và nhận
( ) ( )
0; 4;0 4 0;1;0AB = − = −
làm
vectơ pháp tuyến.
Ta có phương trình:
( ) ( ) ( ) ( ) ( )
:0. 1 1. 1 0. 2 0 : 1 0P x y z P y− + + + − = + =
.
Câu 14. Chọn D
Gọi
n
là một vectơ pháp tuyến của mặt phẳng
( )
P
ta có
n AB
n AC
⊥
⊥
nên chọn
( ) ( )
, 8; 2; 10 2 4; 1; 5n AB AC
= = − − = − −
. Khi đó mặt phẳng
( )
P
qua
( )
1;2;3A
và nhận
( )
4; 1; 5n = − −
làm vectơ pháp tuyến.
Ta có phương trình:
( ) ( ) ( ) ( ) ( )
:4. 1 1. 2 5. 3 0 :4 5 13 0P x y z P x y z− − − − − = − − + =
.
Câu 15. Gọi
n
là vectơ pháp tuyến của mặt phẳng
( )
P
ta có
( ) ( )
, 1; 1;1 1 1;1; 1
Q
Q
n AB
n AB n
nn
⊥
= = − − = − −
⊥
Khi đó mặt phẳng
( )
P
qua
( )
2;1; 3A −
và nhận
( )
1;1; 1n =−
làm vectơ pháp tuyến.
Ta có phương trình:
( ) ( ) ( ) ( ) ( )
: 2 1 3 0 : 6 0P x y z P x y z− + − − + = + − − =
.
Câu 16. Chọn D
Ta có phương trình trục
Oy
:
0
0
x
yt
z
=
=
=
.
Tọa độ giao điểm
M
của
( )
P
và trục
Oy
là nghiệm
( )
;;x y z
của hệ phương trình:
( )
0
2 0;2;0
0
3 4 8 0
x
yt
tM
z
x y z
=
=
=
=
− + − =
.
Câu 17. Chọn A
Gọi
( )
;0;0a
,
( )
0; ;0b
,
( )
0;0;c
lần lượt là tọa độ các điểm
,,A B C
(
0a
,
0b
,
0c
).
Thể tích khối tứ diện
OABC
là:
1
6
V abc=
.
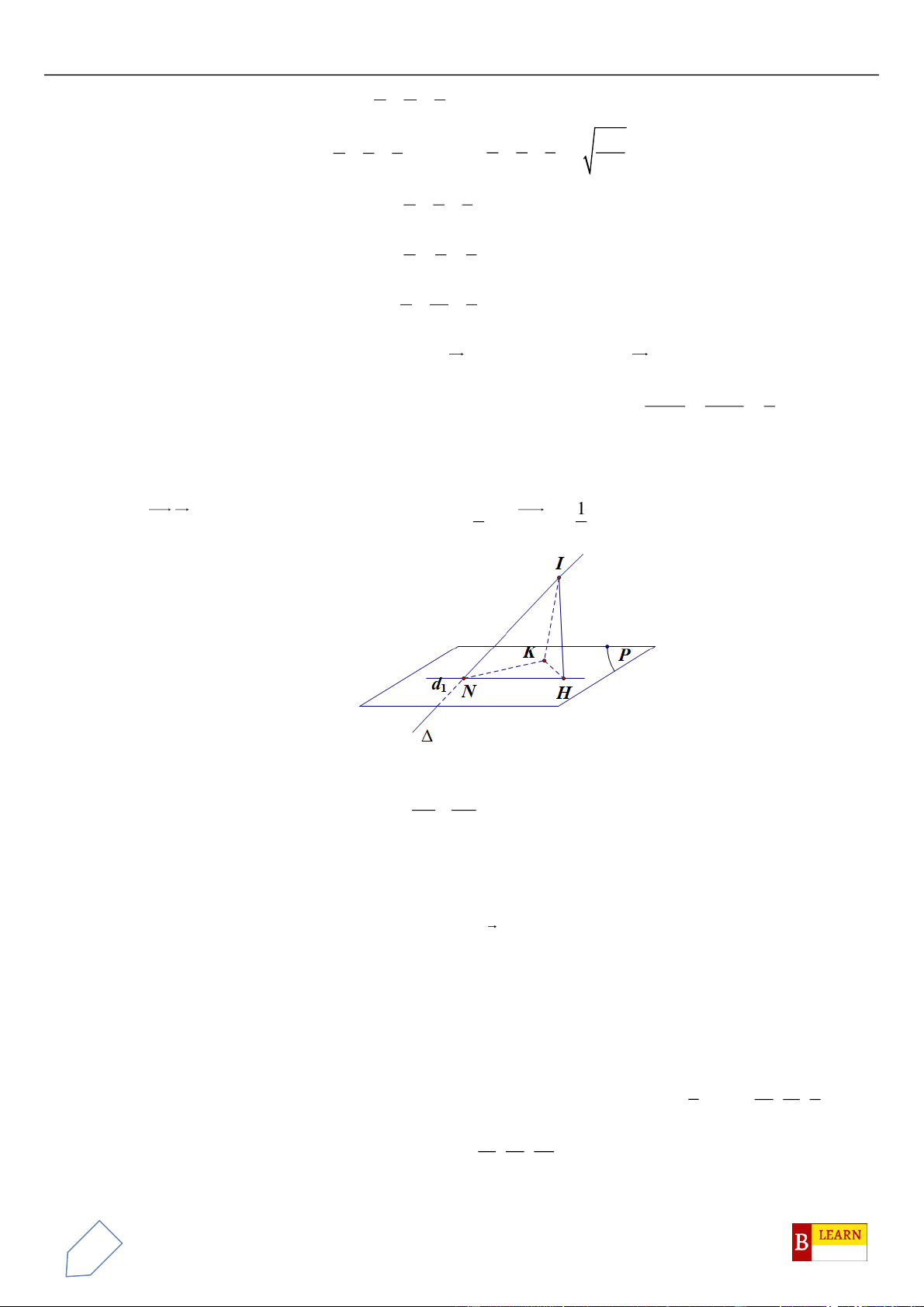
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
386
Phương trình mặt phẳng
( )
: 1.
x y z
P
a b c
+ + =
Điểm
( ) ( )
1 4 1
1;4;1 1MP
abc
+ + =
3
1 4 1 4
1 3 108abc
a b c abc
= + +
.
18V
. Dấu bằng xảy ra khi:
1 4 1
1
3
1 4 1 12
ac
abc
b
abc
+ + =
==
=
==
.
Phương trình mặt phẳng
( )
: 1 4 4 12 0
3 12 3
x y z
P x y z+ + = + + − =
.
Câu 18. Chọn B
Ta có
1
d
đi qua
( )
2; 1;0N −
và có vtcp
( )
1
1;2;1u =
,
2
d
có vtcp
( )
2
2; 2;1u =−
.
Gọi là
đường thẳng qua
( )
2; 1;0N −
và song song với
2
21
:
2 2 1
x y z
d
−+
= =
−
.
Khi đó
( ) ( )
2
;( ) ;( )d P P=
.
Gọi
( )
4; 3;1I −
,
( )
2 ; 1 2 ;H t t t+ − +
là hình chiếu của
I
lên
1
d
.
1
1
. 0 2 4 4 1 0
6
IH u t t t t= − + + + − = = −
( )
1
13; 10;7
6
IH = − −
.
Gọi
K
là hình chiếu của
I
lên
( )
P
.
Khi đó:
( )
;( )INK P=
và
INK
IK IH
IN IN
=
( Không đổi).
Vậy
( )
;( )P
lớn nhất khi
KH
( ) ( ) ( )
:13 2 10( 1) 7 6 0 3 10 36 0P x y z x y z − − + + − = − + − =
.
Câu 19. Chọn A
Ta có véc tơ pháp tuyến của mặt phẳng
( )
P
là
( )
1; 2;2n =−
.
Phương trình đường thẳng
đi qua
( )
1;3; 1M −
và vuông góc với mặt phẳng
( )
P
là
1
32
12
xt
yt
zt
=+
=−
= − +
.
Gọi
N
là hình chiếu vuông góc của
M
trên
( )
P
ta có
( )
1 ;3 2 ; 1 2N t t t+ − − +
.
Thay tọa độ
N
vào phương trình mặt phẳng
( )
P
ta được
9 8 0t −=
8
9
t=
17 11 7
;;
9 9 9
N
Gọi
I
là trung điểm của
MN
khi đó ta có
13 19 1
;;
9 9 9
I
−
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
387
Do mặt phẳng trung trực của đoạn thẳng
MN
song song với mặt phẳng
( )
P
nên véc tơ pháp tuyến
của
( )
P
cũng là véc tơ pháp tuyến của mặt phẳng trung trực của đoạn
MN
.
Phương trình mặt phẳng trung trực của đoạn thẳng
MN
đi qua
13 19 1
;;
9 9 9
I
−
và có một véc tơ pháp
tuyến là
( )
1; 2;2n =−
là
2 2 3 0x y z− + + =
.
Cách 2. TƯ DUY TOÁN HỌC 4.0
Lấy
( ) ( )
1;0;0KP
, gọi
31
1; ;
22
E
−
là trung điểm
MK
. Mặt phẳng cần tìm đi qua
E
và có cùng
vectơ pháp tuyến với
( )
P
nên có phương trình:
( )
31
1 2 2 0 2 2z 3 0
22
x y z x y
− − − + + = − + + =
.
Câu 20. Chọn B
Ta có:
( )
1;2;1MN =−
.
Đường thẳng
( )
d
qua hai điểm
M
,
N
có phương trình tham số
12
2
xt
yt
zt
=−
= − +
=+
.
Gọi
I
là hình chiếu vuông góc của
K
lên đường thẳng
( )
; 1 2 ;2d I t t t − − + +
.
Khi đó ta có
( )
; 1 2 ;KI t t t= − − +
.
Do
( )
1 1 1 1 1
. 0 2 4 0 ; ; 1;1; 1
3 3 3 3 3
KI MN KI MN t t t t KI
⊥ = − + + = = = − − = − −
.
Ta có
( )
( )
( )
( )
( )
;;
max
d K P KI d K P KI KI P = ⊥
( )
1;1; 1n =−
.
Câu 21. Chọn B
Giả sử
( )
;0;0A a Ox
,
( )
0; ;0B b Oy
,
( )
0;0;C c Oz
và
( )
, , 0abc
.
Ta có
OA OB OC a b c+ + = + +
.
Phương trình mặt phẳng
( )
P
có dạng:
1
x y z
a b c
+ + =
.
Ta có:
( ) ( )
1 4 9
1;4;9 1MP
a b c
+ + =
.
( )
( ) ( ) ( )
( )
( )
2 2 2
2 2 2
2
1 4 9 1 4 9
1 2 3a b c a b c
a b c a b c
+ + + + = + + + + + +
( )
2
1 2 3abc + + + +
.
P
(
)
M
N
K
I
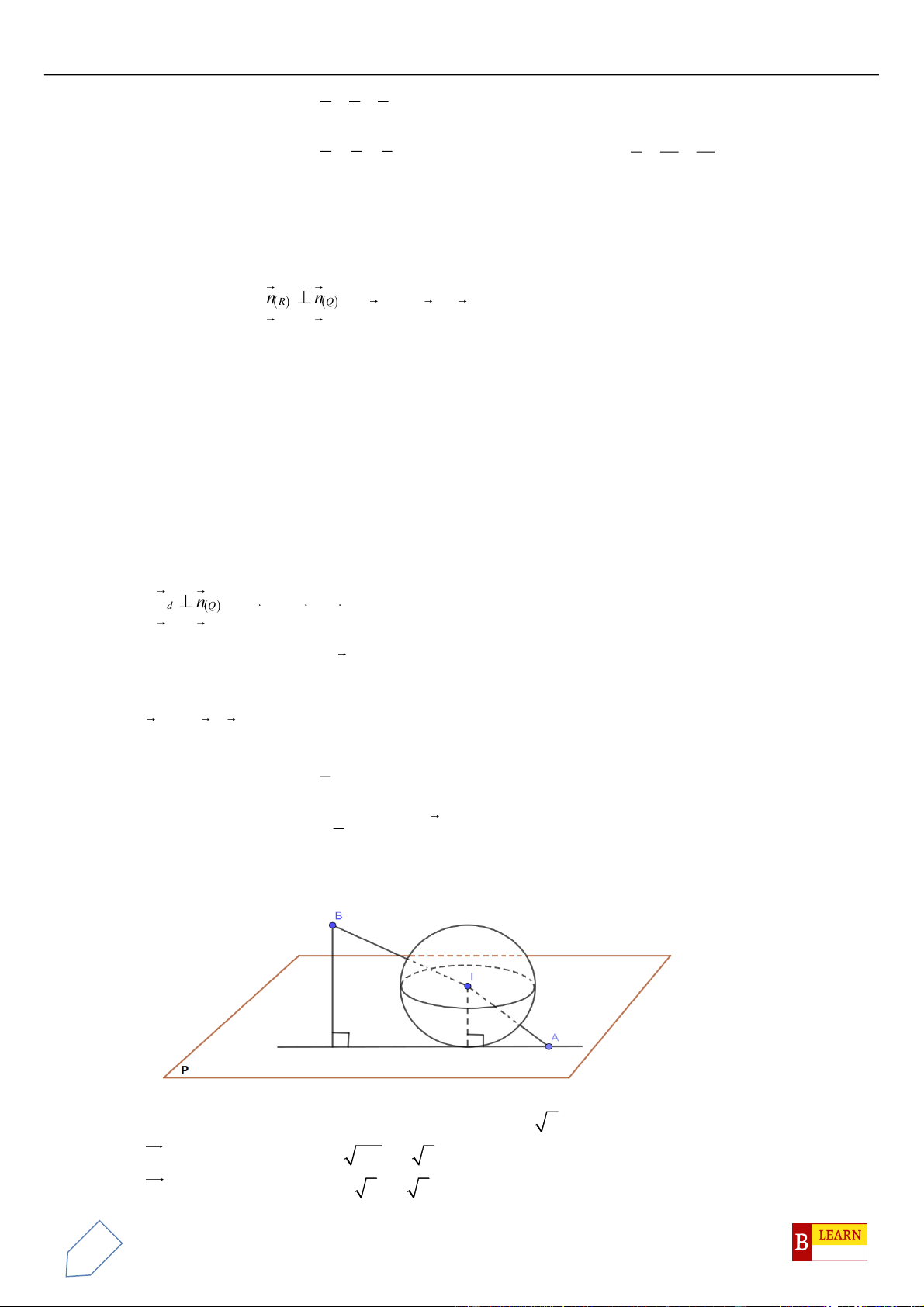
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
388
Dấu
""=
xảy ra khi:
( )
2
1 4 9
1
6
1 2 3
12
18
1 2 3
a b c
a
b
abc
c
abc
+ + =
=
= = =
=
+ + = + +
( )
:1
6 12 18
x y z
P + + =
(Thỏa).
Vậy mặt phẳng
( )
P
đi qua điểm
( )
6;0;0
.
Câu 22. Chọn D
( ) ( )
( ) ( )
( ) ( )
( ) ( )
RQ
RP
RQ
nn
RP
nn
⊥
⊥
⊥
⊥
( ) ( ) ( )
( )
, 2 ;1; 3
R P Q
n n n
= = −
.
Câu 23. Chọn A
Cách 1:
Vì trắc nghiệm nên mình nêu phương pháp cũ: Phương trình chùm mp.
Phương tình mặt phẳng
( )
có dạng:
( ) ( )
2 2 5 2 2 7 0m x y z n x y z+ + − + − + − + =
( ) ( ) ( ) ( )
2 2 2 2 5 7 0 *m n x m n y m n z m n − + + + − − + =
.
Vì
( )
song song với
Oy
nên hệ số
y
trong phương trình (*) bằng
0
, tức
20mn+=
.
Ta chọn
2m =−
,1n =
nên ta có phương trình của
( )
là
5 6 17 0xz+ + =
.
Cách 2:
Do
( )
chứa giao tuyến
d
của hai mặt phẳng nên
( )
( )
dQ
dP
un
un
⊥
⊥
( ) ( )
( )
, 6 ; 2 ;5
d P Q
u n n
= = −
là một vec tơ chỉ phương của
d
.
Oy
có véc tơ chỉ phương
( )
0 ;1; 0j =
.
Do mặt phẳng
( )
chứa
d
và song song trục
Oy
nên véc tơ pháp tuyến được xác định:
( )
( )
, 5; 0 ; 6
d
n u j
= = − −
.
Chọn điểm
9
2 ; 0 ;
2
M
−
thuộc giao tuyến hai mặt phẳng.
Mp
( )
qua
9
2 ; 0 ;
2
M
−
và nhận
( )
( )
5 ; 0 ; 6n
= − −
làm vecto pháp tuyến nên có phương
trình:
5 6 17 0xz+ − =
.
Câu 24. Chọn D
Cách 1.
Mặt cầu
( )
S
có tâm
(5; 3; 7)I −
và bán kính
62R =
.
( )
5;11; 5IA = − −
171 6 2IA =
nên điểm
A
nằm ngoài mặt cầu.
( )
4; 4;16IB =−
12 2 6 2IB =
nên điểm
B
nằm ngoài mặt cầu.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
389
A
,
I
,
B
không thẳng hàng. Mặt phẳng
( )
P
qua
A
và tiếp xúc với
( )
S
nên khi
( )
P
thay đổi thì
tập hợp các đường thẳng qua
A
và tiếp điểm tạo thành hình nón
Gọi
( )
( )
( ,( )) , .sinAB P d B P AB
= =
đạt giá trị lớn nhất
, , ,A B I H
đồng phẳng
( ) ( )
AIB P⊥
.(
H
là hình chiếu của
B
lên
()P
)
Mặt phẳng
( )
P
qua
A
và nhận
( )
1; ;n m n=
làm véc tơ pháp tuyến nên có phương trình:
8 2 0x my nz m n+ − − − =
.
Mặt phẳng
( )
P
tiếp xúc với
( )
S
( )
( )
,d I P R=
( )
( )
2
22
22
5 11 5
6 2 5 11 5 72 1
1
nm
n m m n
mn
−+
= − + = + +
++
( )
22
49 47 110 50 110 47 0 1m n mn n m − − + − − =
.
Ta có:
( )
, 156;70; 24IA IB
=−
.
Gọi
1
n
là véc tơ pháp tuyến của mp
( )
AIB
, Chọn
1
(13;5; 2).n =−
Do
( ) ( ) ( )
1
. 0 13 5 2 0 2AIB P n n m n⊥ = + − =
.
Thế (2) vào (1) ta được phương trình:
( )
2
1
2079 8910 6831 0
6831
2079
m
mm
m loai
=−
+ + =
−
=
.
Thay
1m =−
vào (2) suy ra
4.n =
Vậy
.4mn=−
.
Cách 2. TƯ DUY TOÁN HỌC 4.0
Mặt cầu
( )
S
có tâm
(5; 3; 7)I −
và bán kính
62R =
.
Mặt phẳng
( )
P
qua
A
và nhận
( )
1; ;n m n=
làm véc tơ pháp tuyến nên có phương trình:
8 2 0x my nz m n+ + − − =
.
Mặt phẳng
( )
P
tiếp xúc với
( )
S
( )
( )
,d I P R=
22
5 11 5
62
1
nm
mn
−+
=
++
( )
( )
2 2 2 2
2 2 2 2 2
2 2 2 2
21 15 9 5 11 5 4 16 4
,
11
5 11 5 4 4 1
(4 ( 1) 1 )( 1)
6 2 4
11
18 2
n m n m m n
d B P
m n m n
n m n m
nm
m n m n
− + − + − + +
= =
+ + + +
− + + − +
+ − + + +
+
+ + + +
=
Dấu bằng xảy ra khi
1
1; 4
4 1 1
nm
mn= = = − =
−
. Vậy
.4mn=−
Câu 25. Chọn A
Thay tọa độ điểm
( )
0 ; 5 ; 1−M
vào đường thẳng
d
ta được
2 3 2
1
2 3 2
= = =
. Vậy điểm
( )
0 ; 5 ; 1−M
thuộc đường thẳng
d
.
Câu 26. Chọn C
( )
2 1; ; 2M M t t t + − −
, khi đó
( ) ( ) ( ) ( ) ( ) ( )
2 2 2 2 2 2
22
2 2 1 1 5 2 2 2 3
+ = + + + + + + + + + +
MA MB t t t t t t
( )
2
2
18 36 53 18 1 35 35t t t= + + = + +
. Dấu bằng xảy ra khi
( )
1 1; 1; 1tM= − − − −
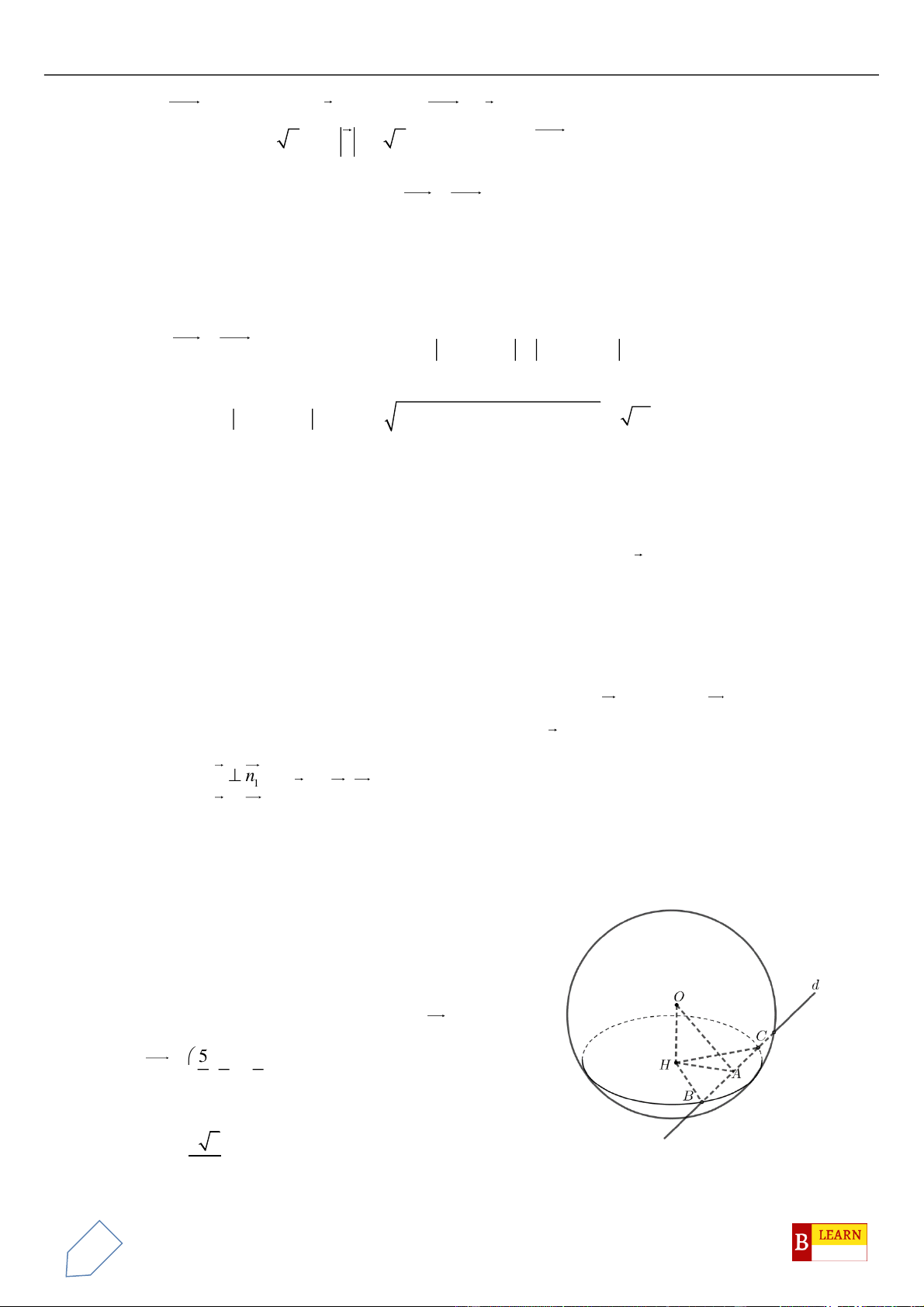
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
390
Câu 27. Chọn A
Vì
MN
cùng hướng với
a
nên
0:t MN ta =
.
Hơn nữa,
5 2 . 5 2MN t a= =
5t=
. Suy ra
( )
5; 5;0MN =−
.
Gọi
( )
;;A x y z
là điểm sao cho
AA MN
=
44
75
30
x
y
z
+=
− = −
−=
1
2
3
x
y
z
=
=
=
( )
1; 2 ; 3
A
.
Dễ thấy các điểm
A
,
B
đều nằm cùng phía so với mặt phẳng
( )
Oxy
vì chúng đều có cao độ
dương. Hơn nữa vì cao độ của chúng khác nhau nên đường thẳng
'AB
luôn cắt mặt phẳng
( )
Oxy
tại một điểm cố định.
Từ
AA MN
=
suy ra
AM A N
=
nên
''AM BN A N BN A B− = −
dấu bằng xảy ra khi
N
là giao điểm của đường thẳng
'AB
với mặt phẳng
( )
Oxy
.
Do đó
( ) ( ) ( )
2 2 2
max ' 4 1 4 2 5 3 17AM BN A B− = = − + − + − =
, đạt được khi
( )
N A B Oxy
=
.
Câu 28. Chọn C
Vì đường thẳng
d
vuông góc với mặt phẳng
( )
P
nên
d
nhận véc tơ pháp tuyến của mặt phẳng
( )
P
làm một véc tơ chỉ phương.
Do đó đường thẳng
d
đi qua điểm
A
và có véc tơ chỉ phương là
( )
2;0; 3u =−
.
Vậy phương trình đường thẳng
d
là:
12
2
53
xt
y
zt
=+
=−
=−
.
Câu 29. Chọn A
Mặt phẳng
( )
P
và
( )
Q
có các véc tơ pháp tuyến lần lượt là
( )
1
3; 1;1n =−
;
( )
2
2; 5;0n =−
.
Gọi
d
là giao tuyến của hai mặt phẳng
( )
P
và
( )
Q
,
u
là một véc tơ chỉ phương của
d
.
Khi đó
1
2
un
un
⊥
⊥
12
,u n n
=
( )
5;2; 13=−
.
Gọi
Ad
Tọa độ điểm
A
thỏa mãn hệ phương trình:
3 4 0
2 5 6 0
x y z
xy
− + + =
− + =
( )
3;0;5A−
.
Vậy phương trình đường thẳng
d
là:
35
2
5 13
xt
yt
zt
= − +
=
=−
.
Câu 30. Chọn B
Mặt phẳng
( )
P
có véc tơ pháp tuyến
( )
1; 1;1
P
n =−
;
5 1 1
;;
2 2 2
OA
=−
Mặt cầu
( )
S
có tâm
( )
0; 0; 0O
và bán kính
3R =
.
33
2
OA R=
A
nằm trong mặt cầu
( )
S
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
391
Gọi
E
là hình chiếu của
O
lên
BC
. Vì
3BC R OB OC= = = =
nên tam giác
OBC
là tam giác
đều
. 3 3 3
22
R
OE OA = = =
.
Suy ra
EA
BC OA⊥
d
có véc tơ chỉ phương là
11
, ; ; 3
22
P
u OA n
= = − − −
Vậy phương trình đường thẳng
d
là:
5
2
1
2
1
6
2
xt
yt
zt
=+
=+
−
=+
.
Ta thấy đường thẳng
d
đi qua điểm
5
3;1;
2
E
.
Câu 31. Chọn A
d
có VTCP
( )
1;4; 2u =−
,
2
d
có phương trình tham số:
12
13
xt
yt
zt
=
=−
=+
.
Giả sử
A
và
B
lần lượt là giao điểm của
d
với
1
d
và
2
d
( )
; 1 2 ;A t t t − +
và
( )
;1 2 ;1 3B t t t
−+
.
Ta có:
( )
;2 2 2 ;1 3AB t t t t t t
= − − − + −
.
Do
//dd
nên vectơ
u
và vectơ
AB
cùng phương
2
2 2 2 1 3
'1
1 4 2
t
t t t t t t
t
=
− − − + −
= =
=
−
.
Do đó,
( )
2;3;2A
.
Vậy
d
là đường thẳng đi qua
( )
2;3;2A
và nhận
( )
1;4; 2u =−
là VTCP nên
d
có phương trình
là
2
34
22
xu
yu
zu
=+
=+
=−
(
u
: tham số).
Câu 32. Chọn C
Ta có:
1
d
có VTCP
( )
3;1; 2u =−
và
( )
1
2; 3;4Ad−
.
2
d
có VTCP
( )
3;1; 2u =−
và
( )
2
4; 1;0Bd−
.
Dễ thấy
2
Ad
. Do đó,
12
//dd
.
Do
12
//dd
và
d
cách đều
1
d
và
2
d
nên d có VTCP là VT
( )
3;1; 2u =−
.
Gọi
I
là trung điểm của
AB
nên
( )
3; 2;2Id−
.
Vậy
d
là đường thẳng đi qua
I
và có VTCP là vectơ
( )
3;1; 2u =−
nên
d
có phương trình là:
33
2
22
xu
yu
zu
=+
= − +
=−
(
u
: tham số).
Câu 33. Chọn B
Vì
1
Ad
;
2
Bd
( )
1 ; 2 2 ;A t t t− + − +
và
( )
2 2 ;1 ;1B t t t
+ + +
.
Ta có:
( )
3 2 ;3 2 ;1AB t t t t t t
= + − + − + −
.

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
392
Mặt phẳng
( )
P
có VTPT
( )
1;1; 2n =−
;
( )
//AB P
( )
AB n
AP
⊥
.
AB n⊥
.0AB n =
( )
3 2 3 2 2 1 0t t t t t t
+ − + + − − + − =
4tt
=−
.
Suy ra
( )
5; 1; 3AB t t= − − − −
.
Do đó,
( ) ( ) ( ) ( )
2 2 2 2
5 1 3 2 2 27 3 3AB t t t= − + − − + − = − +
.
min 3 3AB=
khi
2t =
.
Khi đó,
( )
1;2;2A
( )
P
;
( )
3; 3; 3AB = − − −
.
Vậy
d
là đường thẳng đi qua
A
và có VTCP là vectơ
( )
1;1;1u =
nên
d
có phương trình là:
1
2
2
xu
yu
zu
=+
=+
=+
(
u
: tham số).
Câu 34. Chọn A
Đường thẳng
1
d
có VTCP
( )
1
2;5;3u =
.
Đường thẳng
2
d
có VTCP
( )
2
2;2;4u =
.
Vì
( )
1
12
2
, 14; 2; 6
d
u u u
d
⊥
= = − −
⊥
là một VTCP của đường thẳng
.
1 14
: 4 2
26
xt
yt
zt
= − +
= −
=−
(Với
t
là tham số) hay
1 4 2
:
7 1 3
x y z+ − −
= =
−−
.
Câu 35. Chọn B
Ta có: VTCP của đường thẳng
1
d
là
( )
1
3;6; 2u = − −
.
VTCP của đường thẳng
2
d
là
( )
2
5;3;2u =
.
Gọi
( )
2
3 5 ;1 3 ; 1 2B d B t t t= + + − +
.
( )
6 5 ;2 3 ; 3 2AB t t t = + + − +
.
Vì
1
B
d
⊥
nên
11
.0AB u AB u⊥ =
.
( ) ( ) ( )
3 6 5 6 2 3 2 3 2 0 0t t t t − + + + − − + = =
( )
6;2; 3AB = −
.
Đường thẳng
đi qua điểm
( )
3; 1;2A −−
và nhận
( )
6;2; 3AB =−
làm VTCP nên có phương
trình là
3 1 2
:
6 2 3
x y z+ + −
= =
−
.
Câu 36. Chọn D
Ta có:
( )
2 ;1 3 ; 5 2M d M t t t= − + + − −
.
( ) ( )
1; 2;1 ; ;3 ; 6 2AB AM t t t= − − = − −
.
( )
, 12 ; 6 ;AB AM t t t
= + − − −
Ta có:
35
ABM
S
=
1
; 3 5
2
AB AM
=
.
( ) ( )
22
2
12 6 6 5t t t + + − − + =
2
3 36 180 180tt + + =
2
0
12 0
12
t
tt
t
=
+ =
=−
.
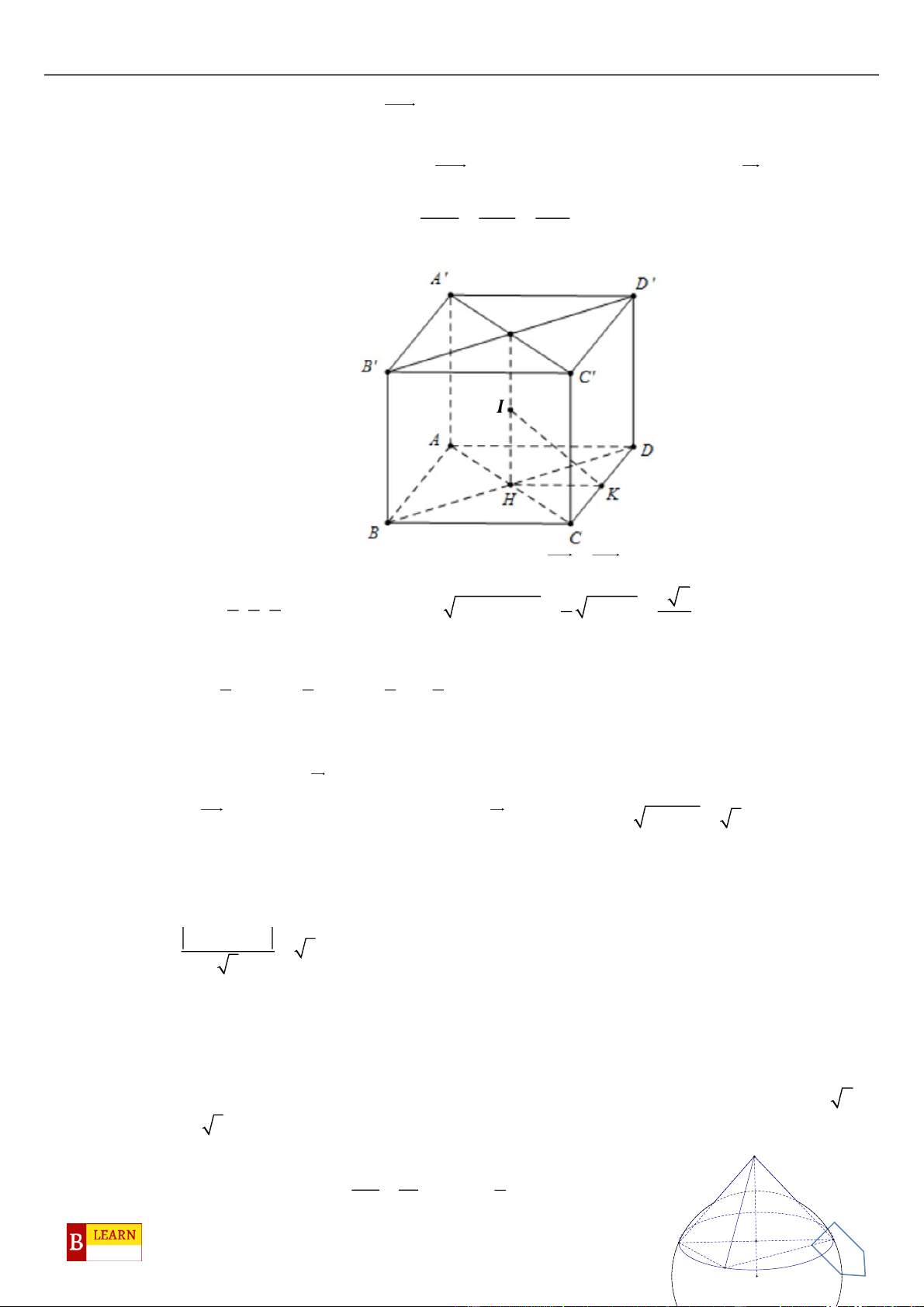
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
393
+ Với
( ) ( )
0 2;1; 5 0;0; 6t M AM= − − = −
:
2
1
1
x
y
zt
=−
=−
=−
(Với
t
là tham số).
+ Với
( ) ( )
12 14; 35;19 12; 36;18t M AM= − − − = − −
VTCP của
là
( )
2;6; 3u
=−
.
Phương trình đường thẳng
là:
2 1 1
2 6 3
x y z+ − −
==
−
.
Câu 37. Chọn D
Tâm
I
của mặt cầu là tâm
I
hình lập phương. Ta có
AB DC=
( )
3;3;0C
và
I
là trung điểm
AC
333
;;;
222
I
. Bán kính là
2 2 2 2
1 3 2
33
22
IK IH HK= + = + =
.
Mặt cầu tiếp xúc với tất cả các cạnh của hình lập phương có phương trình là
( )
222
3 3 3 9
:
2 2 2 2
S x x x
− + − + − =
.
Câu 38. Chọn A
Gọi
( )
;;I a b c
( )
0a
là tâm mặt cầu
( )
S
.
( )
P
có một VTPT là
( )
1
1;1;1n =
.
Ta có:
( )
1; 2; 4HI a b c= − + +
cùng phương
1
n
và
( )
22
,3d I P R r= − =
.
( ) ( )
1 2 3 3 2 0
1 4 5 5 1 3
2 8 3 5
5
3
3
a b a b a b a a
a c a c a c b n b l
a b c a b c c c
abc
− = + − = − = = =
− = + − = − = = − = −
+ + = − + + = − = − = −
+ + +
=
( )
2; 1; 3I − −
Vậy:
( ) ( ) ( ) ( )
2 2 2
: 2 1 3 16S x y z− + + + + =
.
Câu 39. Chọn D
Mặt cầu
( )
S
có tâm
( )
1;2; 3I −
và bán kính
R
.
Đặt
MA a=
, do
60AMB =
;
90BMC =
;
120CMA =
nên
AB a=
,
2BC a=
,
3AC a=
Tam giác
ABC
vuông tại
B
Tâm
K
đường tròn ngoại tiếp tam giác
ABC
là
trung điểm
AC
.
2 2 2
MK MC KC=−
22
2
3
42
aa
a= − =
2
a
MK=
.
K
A
C
I
M
B

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
394
Trong tam giác vuông
MIC
ta có
2
2
.2
2
a
MK MI MC MI a
a
= = =
.
63MI a= =
2 2 2 2 3
3 27MI MC R R a= + = =
33R=
.
Phương trình mặt cầu
( )
S
là
2 2 2
2 4 6 13 0x y z x y z+ + − − + − =
.
Câu 40. Chọn D
Gọi
I
là tâm mặt cầu. Theo giả thiết, ta có
( )
1; 1;0I −−
.
Bán kính
( ) ( ) ( )
2 2 2
5 1 4 1 2 65IA = + + + + − =
.
Câu 41. Chọn D
( )
( )
( )
2
22
4 1 6 10
;3
2 1 2
d I P
+ − +
==
+ + −
. Khi đó bán kính mặt cầu bằng
22
3 4 5+=
.
Câu 42. Chọn A
Mặt cầu có tâm
( )
1; 2; 3I −−
và bán kính
5R =
.
Ta có:
3IA R=
nên
A
nằm trong mặt cầu. Gọi
H
là trung điểm đoạn
MN
, ta có:
2MN MH=
và
2 2 2
MH R IH=−
. Nên
min
MN
khi
max
IH
. Ta luôn có
IH IA
nên
max
3IH IA==
.Ta có:
2
25 9 16 4MH MH= − = =
8MN=
.
Câu 43. Chọn C
Mặt cầu
( )
S
có tâm
( )
1; 2;2I −
.
Theo đề bài ta có:
1 4 4Rm= + + +
5=
16m=
.
Câu 44. Chọn C
Ta có
( ) ( )
12
3; 1; 2 ; 1;3;1uu−−
lần lượt là véctơ chỉ phương của đường thẳng và .
Mặt cầu có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng và là mặt cầu nhận đoạn
vuông góc chung của và là đường kính.
Gọi
( )
1
4 3 ;1 ; 5 2A a a a d+ − − −
và
( )
2
2 ; 3 3 ;B b b b d+ − +
( )
3 2;3 4; 2 5AB b a b a b a = − − + − + +
.
AB
là đoạn vuông góc chung của và khi và chỉ
khi
1
2
.0
7 6 0 1
2 11 9 0 1
.0
AB u
a b a
a b b
AB u
=
+ + = = −
+ − = =
=
Suy ra
( ) ( )
1;2; 3 ; 3;0;1AB−
.
Mặt cầu
( )
S
có tâm
( )
2;1; 1I −
là trung điểm của
AB
, có bán kính
6R IA==
.
Vậy phương trình
( )
S
:
2 2 2
4 2 2 0x y z x y z+ + − − + =
.
Câu 45. Chọn A
Gọi
( )
1;0;2I
là trung điểm của
AB
suy ra
I
là tâm của đường tròn ngoại tiếp tam giác
OAB
.
Gọi
d
là đường thẳng qua
I
và vuông góc với
( ) ( )
OAB Oxz
, suy ra
d
có phương trình
1
2
x
yt
z
=
=
=
. Gọi
E
là tâm mặt cầu
( )
S
, suy ra
( )
1; ;2E d E t
Ta có:
2
5EB t=+
và
( )
( )
11
;
3
t
d E P
−+
=
.
1
d
2
d
1
d
2
d
1
d
2
d
1
d
2
d

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
395
Khi đó
22
2
11
5 8 22 76 0
19
3
4
t
t
t t t
t
=
−+
+ = + − =
=−
Với
( )
2 1;2;2 3t E R EB= = =
.
Với
19 19 441
1; ;2 3
4 4 4
t E R EB
= − − = =
.
Vậy chọn đáp án
A
.
Câu 46. Chọn B
Phương trình tham số của đường thẳng
( )
1
:2
12
xt
d y t t
zt
=+
= +
=+
.
( )
1 ;2 ;1 2H d H t t t + + +
.
Độ dài
( ) ( ) ( ) ( )
2 2 2 2
2
1 1 2 3 6 12 11 6 1 5 5AH t t t t t t= − + + + − = − + = − +
.
Độ dài
AH
nhỏ nhất bằng
5
khi
1t =
( )
2;3;3H
.
Vậy
2a =
,
3b =
,
3c =
3 3 3
62abc + + =
.
Câu 47. Chọn B
Ta có:
:
1 1 2
x y z
= =
đi qua
(0;0;0)O
và có một VTCP là
( )
1;1;2u =
.
11
:
2 1 1
x y z+−
= =
−
đi qua
( 1;0;1)M −
và có một VTCP là
( )
' 2;1;1u =−
.
Vì
( )
; ;2M M t t t
,
( )
' 1 2 ; ;1N N u u u − − +
Mặt phẳng
( )
P
có một vectơ pháp tuyến là
( )
1; 1;1n −
. Vì
MN
song song với
( )
P
nên
.0MN n t u= = −
.
22
0
14 8 2 2 14 8 2 2
4
.
7
u
MN u u u u
u
=
= + + = + + =
=−
) 0 (0;0;0) ( )u M P+ =
(loại ).
4 4 4 8 1 4 3
) ; ; ; ; ; . ( ) (tm) .
7 7 7 7 7 7 7
u M N M P
+ = − −
Câu 48. Chọn C
Mặt phẳng
()P
qua điểm
M
vuông góc Δ là
2 8 0.x y z− + + =
Mặt phẳng
( )
Q
qua
N
vuông
góc với
là
2 7 0.x y z− + − =
Do đó
2 2 2
8 ( 7)
15
(( ),( )) .
6
1 2 1
HK d P Q
−−
= = =
++
Đường thẳng Δ qua điểm
2
( ; 1; )A m m−−
và véctơ chỉ phương
(1; 2;1).u −
Đường thẳng
MN
qua điểm
( 1;4;1)M −
có véctơ chỉ phương
(4; 6; 1).MN −−
Góc giữa hai đường thẳng này là
.
15 15 31
cos sin .
106
6 53 318
.
u MN
u MN
= = = =
Khoảng cách giữa hai đường thẳng
MN
và
HK
là
2
,.
2 8 19
11
.
93 93
,
u MN AM
mm
d
u MN
−+
= =

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
396
Do đó
1 1 15 11 31 55
. . .sin . . 53. . .
6 6 106 12
6 93
HKMN
V HK MN d
= =
Dấu
'' ''=
xảy ra khi
2m =
. Khi đó phương trình đường thẳng
2 1 4
Δ : .
1 2 1
x y z− + +
==
−
Đường thẳng Δ véctơ chỉ phương
(1; 2;1).u −
Vì
H
là hình chiếu của
M
lên Δ nên
2 5 16
. 0 ( ; ; )
3 3 3
uHMH = −
.
2 8.T a b c= − + = −
Câu 49. Chọn C
Do C nằm trên Oxy nên
( )
; ;0C x y
A, B, C thẳng hàng
AC
cùng phương
AB
2 1 0 1
2 2 2
xy− − −
= =
−−
Suy ra
1, 2xy==
Chọn đáp án C.
Câu 50. Chọn D
Mặt cầu
( )
S
có tâm
( )
1,0,0I
và bán kính
3R =
.
Gọi
là đường thẳng qua
I
và vuông góc với
()P
pt
:
1
0
xt
y
zt
=+
=
=
.
Gọi
H
là tâm đường tròn giao tuyến. Ta có
()HP=
tọa độ
H
là nghiệm của hệ pt:
1
0
0
0 (0;0; 1)
1
10
xt
x
y
yH
zt
z
xz
=+
=
=
= −
=
=−
+ + =
.
Câu 51. Chọn A
Giả sử .
là trực tâm của tam giác
( Vì ). Vậy
Câu 52. Chọn C
Gọi là điểm thỏa mãn , khi đó .
.
Do đó nhỏ nhất khi nhỏ nhất là một trong hai giao điểm của đường thẳng qua
và mặt cầu với là tâm của .
( )
( ; ;0) ( ), 0 , (0;0; )B x y Oxy x C z Oz
H
ABC
,,
⊥
⊥
AH BC
CH AB
AB AC AH ñoàng phaúng
.0
.0
, . 0
AH BC
CH AB
AB AH AC
=
=
=
0
2x 7 0
x 3 0
xz
y
y yz z
+=
+ − =
− + − =
3
1
3
x
y
z
=
=
=−
0x
( ) ( )
3;1;0 , 0;0; 3 .BC−
I
3 2 0IA IB IC+ + =
45
1; ;
36
I
−
( ) ( ) ( )
3 2 3 2 6 6T MA MB MC MI IA MI IB MI IC MI MI= + + = + + + + + = =
T
MI
M
IE
(S)
1
1;1;
2
E
−
(S)
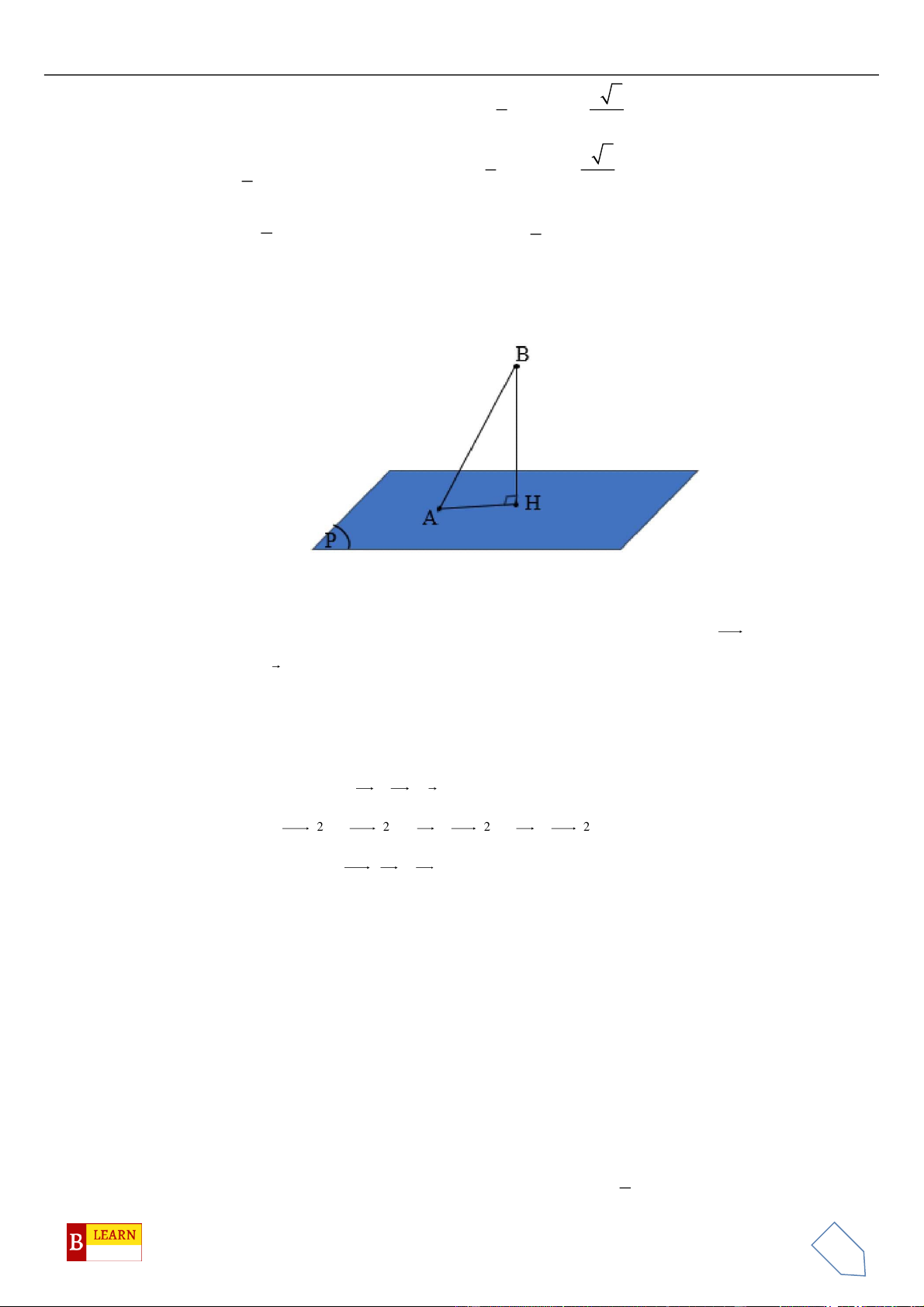
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
397
.
Vậy là điểm cần tìm.
Câu 53. Chọn B
Gọi là hình chiếu vuông góc của lên .
Khi đó: .
Vậy lớn nhất khi trùng .
đi qua và vuông góc với đoạn thẳng nên nhận làm
một VTPT. Hay cũng là một VTPT của .
Phương trình mặt phẳng là: .
Dựa vào phương trình của ta có khi thì .
Câu 54. Chọn A
Gọi là điểm thõa mãn: . Khi đó là trung điểm của nên .
.
.
Vì không đổi nên nhỏ nhất khi nhỏ nhất.
là hình chiếu của lên .
Khi đó đường thẳng qua và vuông góc với nên có phương trình: .
Tọa độ giao điểm của đường thẳng và ứng với
t
là nghiệm của phương trình:
.
Giao điểm tìm được chính là hình chiếu của lên . Vậy nên .
Câu 55. Chọn D
Gọi là hình chiếu vuông góc của lên . Khi đó: .
( )
1
:1
1
2
x
IE y t
zt
=
=+
= − −
11
22
3 2 2
1;2;
23
(S)
1 4 2
1;0;
23
M IM
M IE
M IM
− =
=
=
1
3
1;2;
2
M
−
3
.
2
P x y z= + + =
H
B
( )
P
( )
;( )d B P BH BA const= =
( )
;( )d B P
H
A
( )
P
( )
1;2;0A −
AB
( )
P
( )
2; 4; 2AB −−
( )
1; 2; 1n −−
( )
P
( )
P
( ) ( )
1 2 2 0 2 5 0x y z x y z+ − − − = − − + =
( )
P
1a =
5d =
I
0IA IB+=
I
AB
( )
3;3;3I
( ) ( ) ( ) ( )
2 2 2 2
22
MA MB MA MA IA IM IB IM+ = + = − + −
( )
2 2 2 2 2 2
2 2 2IA IB IM IM IA IB IA IB IM= + + − + = + +
22
IA IB+
22
MA MB+
IM
M
I
( )
P
IM
( )
3;3;3I
( )
P
32
3
3
xt
yt
zt
=+
=+
=−
IM
( )
P
( ) ( ) ( )
2 3 2 3 3 6 0 6 12 0 2t t t t t+ + + − − + = + = = −
I
( )
P
( )
1;1;5M −
5abc+ + =
I
A
BC
1
.
2
ABC
S AI BC=
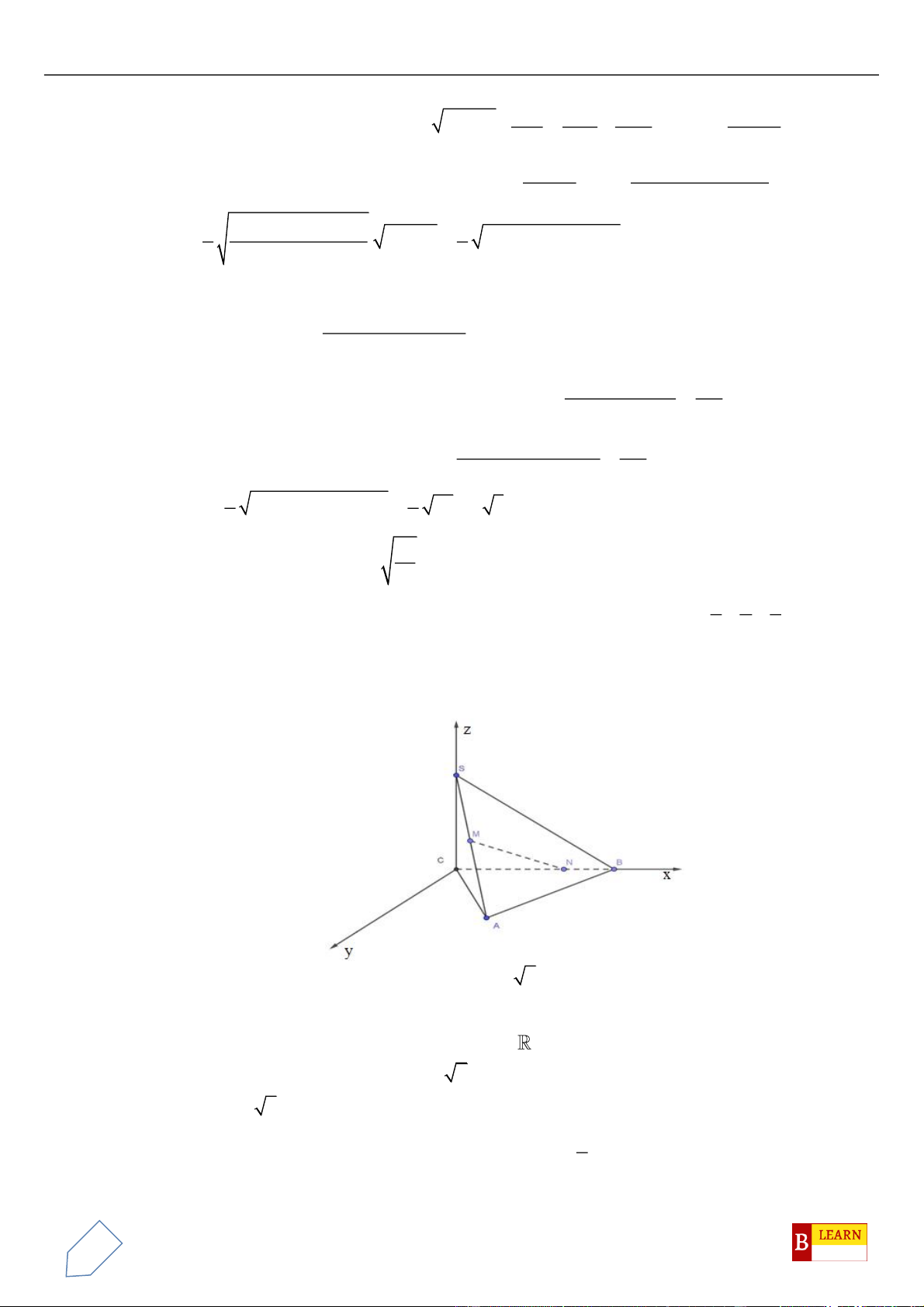
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
398
Ta có vuông tại nên: , .
Ta có vuông tại nên: .
.
Vì .
. (1)
Mà: . (2)
Từ (1) và (2) suy ra:
.
nhỏ nhất khi: .
Vậy đi qua 3 điểm có phương trình là: .
Kiểm tra thấy đi qua điểm .
Câu 56. Chọn B
Cho hệ trục tọa độ , .
Khi đó
Phương trình đường thẳng là: ,
Giả sử nên
OBC
O
22
BC b c=+
22
2
2 2 2 2 2
1 1 1 bc
OI
OI OB OC b c
= + =
+
IOC
O
2 2 2 2 2 2 2 2
2 2 2 2
2 2 2 2
b c a b b c a c
IA OI OA a
b c b c
++
= + = + =
++
2 2 2 2 2 2
2 2 2 2 2 2 2 2
22
11
.
22
ABC
a b b c a c
S b c a b b c a c
bc
++
= + = + +
+
2 2 2 2 4 4 4 2 2 2 2 2 2
12 12 2 2 2a b c a b c a b b c a c+ + = = + + + + +
( )
2 4 4 4
2 2 2 2 2 2
12
2
abc
a b b c a c
− + +
+ + =
( ) ( ) ( )
( )
2
2 2 2
2
2
4 4 4 2 2 2 4 4 4
12
3
33
abc
a b c a b c a b c
++
+ + + + + + =
( )
2 4 4 4
2
2 2 2 2 2 2
12
12
48
23
abc
a b b c a c
− + +
+ + = =
2 2 2 2 2 2
11
48 2 3
22
ABC
S a b b c a c = + + =
ABC
S
= = = =
12
a b c 2
3
( )
P
( ) ( ) ( )
2;0;0 , 0;2;0 , 0;0;2A B C
1
2 2 2
x y z
+ + =
( )
P
( )
1;0;1
Cxyz
,B Cx S Cz
( ) ( ) ( )
( )
; ;0 , 2 ;0;0 , 0;0;0 , 0;0; 2A a a B a C S a
SA
2
x a t
y a t
zt
=−
=−
=
t
( )
; ; 2M a t a t t SA− −
AM u=
2 2 2 2 2 2
24
2
u
u AM t t t t t= = + + = =
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
399
; do
.
Min .
Cách khác: TƯ DUY TOÁN HỌC 4.0
Lấy ,
Vì và nên
Suy ra Min khi
Câu 57. Chọn A
Chọn hệ trục như hình vẽ
;
; ; ;
;
.
max
là trung điểm
Nhận xét: Hình vẽ trên hệ trục lại chọn sai so với lời giải
Câu 58. Chọn D
2
;;
2 2 2
u u u
M a a
−−
( )
;0;0N BC N u
NC AM=
22
2
2
3
2 2 2
u u u
MN a a
= − + − +
2
2
2
2 2 2
3
3 3 3
a a a
u
= − +
6
3
a
MN =
( )
0 0 0 0
; ; 2 ; 0;M a t a t t t a− −
( )
0 0 0 0
; ; 2 2AM t t t AM t= − − =
N BC
NC AM=
( )
2 ;0;0
o
Nt
( )
( )
22
00
3 ; ; 2 12 8 2 , 0;
o o o o
MN t a t a t MN t at a t a= − − − = − +
6
3
a
MN =
2
3
o
a
t =
Axyz
'
21AB AA= =
( )
2;0;0B Ax B
( )
0;2;0D Ay D
( )
''
0;0;1A Az A
( )
2;2;0C
( )
;0;0M AB M x
02x
( )
'
;0;1MA x−
( )
'
2 ;2;1MC x−
''
''
''
.
cos
.
MA MC
AMC
MA MC
=
( )
( )
( )
2
22
22
1
(2 ) 1
0
1. 2 4 1 1. 2 5
x
xx
x x x x
−
− − +
= =
+ − + + + − +
''
2
AMC
''
1.
2
AMC x
= =
( )
1;0;0M
.AB
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
400
Cho hệ trục như hình vẽ,
Gọi ta có: ; .
Vì và nên .
Ta có lớn nhất nhỏ nhất
lớn nhất
Nhận xét: Một lần nữa hình vẽ lại chọn sai tọa độ so với lời giải
Câu 59. Chọn B
đi qua điểm , có véctơ chỉ phương là .
đi qua điểm , có véctơ chỉ phương là .
Ta có suy ra vuông góc với .
Mặt khác .
Suy ra và chéo nhau.
Vậy và chéo nhau, vuông góc với
.
Câu 60. Chọn B
đi qua điểm có véctơ chỉ phương là .
có véctơ chỉ phương là .
Vì nên cùng phương với .
Vậy đường thẳng và trùng nhau khi và chỉ khi nằm trên .
Dó đó
Suy ra .
Câu 61. Chọn B
qua có vecto chỉ phương
Axyz
, , .D Ax B Ay S Az
( ) ( ) ( ) ( )
0;0;0 , 0; ;0 , ;2 ;0 , 0;0; .A B a C a a S a
( )
0a
( )
;0;0
D
Dx
( )
2 ; ;SC a a a−
( )
; ;0
D
BD x a−
'2
. 0 2 . 0 .
2
DD
a
SC BD SC BD a x a x⊥ = − = =
M SA
AM x=
( )
0;0;Mx
2
22
,
4
5.
2
BD BM
aa
DE
xa
BM
= = −
+
DE
2
22
4a
xa
+
22
xa+
xa=
( )
1;1; 1A −
( )
1; 2;2u
=−
d
( )
1; 1;1B −
( )
2;2;1
d
u =
. 1.2 2.2 2.1 0
dd
u u u u
= − + = ⊥
d
( ) ( ) ( )
; 6;3;6 , 0; 2;2 ; . 6.0 3. 2 6.2 6 0
dd
u u AB u u AB
= − = − = − + − + =
d
d
d
( )
1; m;nA −
( )
2;2;1u
=−
d
( )
6; 6; 3
d
u = − −
2 2 1
6 6 3
−
==
−−
u
d
u
d
( )
1; m;nA −
3
1 1 3 6
6
6 6 3
m
mn
n
=−
− − − −
= =
=
−−
( )
2
2 2 2
6 3 45K m n= + = + − =
( )
D
( )
2, 1,1A −
( )
2,1,2 3aa= =
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
401
. Chọn B
Câu 62. Chọn B
, .
Ta có
VTCP của đường thẳng là .
VTCP của đường thẳng là .
Ta có
. Suy ra .
Mặt cầu có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng và có đường kính bằng độ
dài đoạn nên có bán kính .
Câu 63. Chọn A
Phương trình mặt phẳng là .
Vì mặt phẳng đi qua điểm nên ta có và có vectơ pháp tuyến
.
Mặt cầu có tâm và bán kính .
Ta có nên (1)
Gọi là hình chiếu của trên mặt phẳng .
Khi đó giao tuyến của với mặt cầu là đường tròn tâm có chu vi bằng suy ra
bán kính .
Ta có (2)
Vì và nên (3)
Từ (1), (2) ta có . Do đó (3) phải xảy ra đẳng thức hay .
Khi đó nên là vectơ pháp tuyến của .
( ) ( )
2, 3, 2 , 8,8,4 , 12AI a AI a AI
= − = − =
( )
( )
( ) ( ) ( ) ( )
= = = − + − + + =
2 2 2
12
, 4 : 4 2 1 16
3
R d I D S x y z
1
A
( )
1;2 ;A t t + −
2
B
( )
4 ;3 2 ;1B t t t
+ − −
( )
3 ;1 2 ;1AB t t t t t
= + − − − +
1
( )
1
0;1; 1u =−
2
( )
2
1; 2; 1u = − −
1
2
.0
.0
ABu
ABu
=
=
( )
( ) ( )
1 2 1 0
3 2 1 2 1 0
t t t t
t t t t t
− − − − + =
+ − − − − − + =
20
60
tt
tt
− − =
+=
0tt
= =
( )
3;1;1AB =
11AB=
1
2
AB
11
22
AB
r ==
I
M
H
K
( )
ABC
1
x y z
a b c
+ + =
( )
ABC
(2;4;5)M
2 4 5
1
a b c
+ + =
1 1 1
;;n
abc
=
( )
S
( )
1;2;3I
5R =
( )
1;2;2IM =
3IM =
H
I
( )
ABC
( )
ABC
( )
S
H
8
4r =
2 2 2 2
5 4 3IH R r= − = − =
( )
IH ABC⊥
( )
M ABC
IM IH
3IM IH==
MH
( )
IM ABC⊥
IM
( )
ABC

CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
402
Suy ra .
Vì nên . Từ đó suy ra .
Vậy .
Câu 64. Chọn B
Gọi G là trọng tâm tam giác ABC suy ra .
Ta có (Theo tính chất hình thang)
Do đó .
Gọi là hình chiếu của lên đường thẳng , ta có .
. Vậy .
Câu 65. Chọn B
.
đúng .
luôn đi qua điểm .
Lấy ta được: .
tiếp xúc tại .
qua và vuông góc với
tọa độ điểm thỏa:
.
.
Câu 66. Chọn B
có tâm , bán kính .
cách đều là mặt phẳng trung trực của .
qua là trung điểm và có VTPT .
: đường tròn tâm là hình chiếu của trên .
(Vì nên ).
Ta có (Vì 4.2-3.1-2-3=0) .
( )
0n k IM k=
1
1
2
1
2
k
a
k
b
k
c
=
=
=
2 4 5
1
abc
+ + =
1
2 8 10 1
20
k k k k+ + = =
20, 10, 10a b c= = =
40abc+ + =
(1;2; 2)G −
1 2 3
3 ( ;( ))T d d d d G
= + + =
( )
( )
( )
( )
3 ; 3 ;T d G d G
=
( )
1 ;1 2 ;1H t t t+ − −
G
( )
; 2 1;3GH t t t= − − −
( ) ( )
1
. 0 2 2 1 3 0
6
GH u t t t t
= − − − − − = =
max
354
3
2
T GH==
2 2 2 2
( ):
1 1 2 3
x y m z m
d
mm
− − − + −
==
−−
( 1) 2 2 2 ( 1) 4(1)
(2 3) 4 6 2 2 2 ( 1) 3 4(2)
m x m y m m x y x
m x m z m m x z x
− − + = − − − = + −
− − + = + − − = + −
(1),(2)
1 0 1
4 0 3
3 4 0 1
xx
m x y y
x z z
− = =
+ − = =
+ − = =
()d
(1;3;1)M
2(1) (2)−
2 4 0 2 4 0y z x x y z− − − = − + + =
( )
( ) : 2 4 0,d x y z m
− + + =
()S
()d
M
IM
M
1 3 1
( ) :
1 2 1
x y z
IM
− − −
= =
−
()I IM P=
I
1 3 1
6
(2;1;2), ( ,( )) 6
1 2 1
6
2 2 8 0
x y z
I R d I
x y z
− − −
==
= = =
−
+ + − =
2 1.2 2 6 0T = + + − =
2 2 2
( ):( 1) ( 2) ( 3) 4S x y z+ + + + + =
( 1; 2; 3)J − − −
2R =
M
,AB
()M
AB
()
(0;0; 3)N −
AB
( 8;6;2) 2(4; 3; 1)n AB= = − = − − −
( ):4 3 3 0x y z
− − − =
( ) ( ) ( )M S M C
H
J
()
4 6 3 3
2
( ,( ))
16 9 1 26
d J R
− + + −
= =
++
M
()I
max
IM IH r = +
CHUYÊN ĐỀ: HÌNH TỌA ĐỘ TRONG KHÔNG GIAN OXYZ.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
403
qua và vuông góc với .
Tọa độ của thỏa: .
, .
.
Câu 67. Chọn B
Mặt cầu có tâm và bán kính .
Gọi là đường tròn giao tuyến của mặt phẳng
và mặt cầu .
Đặt khi đó , ,
do đó vuông tại nên trung điểm
của là tâm đường tròn và , , thẳng hàng.
Vì nên đều do đó
suy ra .
Lại có nên , .
Mà nên .
Do nên suy ra . Vậy .
Câu 68. Chọn D
Dựng hình hộp chữ nhật . Gọi là giao điểm các đường chéo của hình hộp, dễ
thấy chính là tâm mặt cầu ngoại tiếp tứ diện
Ta có , , suy ra .
Bán kính .
IH
J
()
1 2 3
:
4 3 1
x y z
IH
+ + +
= =
−−
()H IH
=
H
1 2 3
17 23 38
;;
4 3 1
13 13 13
4 3 3 0
x y z
H
x y z
+ + +
==
− − −
−−
− − − =
22
4 50
( ,( )) 4
26 13
r R d J
= − = − =
557
13
IH =
max
1
( 50 557) 50, 557 57
13
IM a b T = + = = =
( )
S
( )
1;2; 3I −
33R =
( )
C
( )
ABC
( )
S
MA MB MC x= = =
AB x=
2BC x=
3CA x=
ABC
B
H
AC
( )
C
H
I
M
120AMC =
AIC
33x R x= =
2 2 6IM AM x= = =
Md
( )
1 ; 2 ;1M t t t− + − + +
( )
1t
6IM =
( ) ( ) ( )
2 2 2
2
0
2 4 4 36 3 4 0
4
3
t
t t t t t
t
=
− + − + + = − =
=
0a
4
3
t =
1 2 7
;;
3 3 3
H
−
3 3 3
112
9
abc+ + =
I
C
M
D
P
A
Q
O
B
.OAQBCMDP
I
I
ABCD
( )
;0;0Am
( )
0; 2;0Bm+
( )
0;0; 5Cm−
( )
; 2; 5D m m m+−
2
1 1 26
3 6 29
2 2 2
R OD m m= = − +

CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
404
PHẦN II
SỐ PHỨC
CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
405
XÁC ĐỊNH CÁC YẾU TỐ CƠ BẢN
1. Phần thực, phần ảo của số phức, số phức liên hợp
• Số phức có dạng
( )
2
, , 1= + = −z a bi a b R i
. Phần thực của
z
là
a
, phần ảo của
z
là
b
và
i
được
gọi là đơn vị ảo.
• Số phức liên hợp của
z
là
z a bi a bi= + = −
.
22
.z z a b=+
Tổng và tích của
z
và
z
luôn là một số thực.
z z z z
1 2 1 2
.
..z z z z
1 2 1 2
.
z
z
z
z
1
1
2
2
.
• Lưu ý:
; ; ;
n n n n
i i i i i i
4 4 1 4 2 4 3
11
; với
nN
.
2. Hai số phức bằng nhau
• Cho hai số phức
1 1 1
z a b i=+
,
2 2 2
z a b i=+
( )
1 2 2 2
, , ,a a b b R
. Khi đó:
12
12
12
aa
zz
bb
=
=
=
3. Biểu diễn hình học của số phức, môđun của số phức
• Biễu diễn hình học của số phức.
▪ Số phức
( )
,z a bi a b R= +
được biểu diễn bởi điểm
( )
;M a b
trong mặt phẳng tọa độ.
▪
z
và
z
được biểu diễn bởi hai điểm đối xứng nhau qua trục
Ox
.
• Mô đun của số phức.
▪ Mô đun của số phức
z
là
22
z OM a b= = +
.
▪ Ta có :
.z z z=
;
zz=
.
LÝ THUYẾT

CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
406
Lời giải
CÁC CÂU HỎI TRẮC NGHIỆM LẤY RA TỪ TÀI LIỆU
Câu 1: Cho số phức
12zi=−
. Tìm phần ảo của số phức
z
.
A. 2. B.
2−
. C.
1−
. D. 1.
Câu 2: Tìm các số thực
,xy
thỏa mãn
( )( ) ( ) ( )( )
3 2 4 1 2− − − − = + +i x yi i i x yi
A.
3, 1= = −xy
. B.
3, 1= − = −xy
. C.
1, 3= − =xy
. D.
3, 1==xy
.
Câu 3: Cho hai số phức
1
2zi=+
,
2
13zi=−
. Tính mô-đun của số phức
2
12
w z z=−
.
A.
7w =
. B.
5w =
. C.
19w =
. D.
53w =
.
Câu 4: Cho số phức
z
thỏa mãn
( )
23z i z=+
. Tính
z
.
A.
5z =
. B.
35
2
z =
. C.
5z =
. D.
10z =
.
Câu 5: Cho số phức
z
thỏa mãn
2 6 2 .+ = +z z i
Điểm biểu diễn số phức
z
có tọa độ là
A.
( )
2; 2−
. B.
( )
2; 2−−
. C.
( )
2;2
. D.
( )
2;2−
.
Câu 6: Tìm mô đun của số phức
z
, biết
( )
2 3 17 9z i z i− + = − +
.
A.
26z =
. B.
17z =
. C.
29z =
. D.
5z =
.
Câu 7: Tìm tất cả các số thực
,xy
để hai số phức
2 5 2 11
12
9 4 10 , 8 20z y xi z y i= − − = +
là hai số phức liên
hợp của nhau.
A.
2
2
x
y
=
=
. B.
2
2
x
y
=
=
. C.
2
2
x
y
=−
=
. D.
2
2
x
y
=−
=
.
Câu 8: Biết số phức
z
thỏa mãn.
1
1
3
1
z
zi
zi
zi
−
=
−
−
=
+
. Số phức
z
bằng:
A.
1zi=+
. B.
1zi=−
. C.
1zi= − −
. D.
1zi= − +
Câu 9: Tính môđun của số phức
z
, biết:
( )
1 2 2 12 .i z i i− + − = −
VÍ DỤ MINH HỌA
VÍ DỤ 1. Giải các phương trình sau:
a)
−+
=
2
45
3 9.
xx
b)
− + −
=
2
3 8 2 1
39
x x x
.
c)
+
−
=
2
28
4
3
1
2 16
x
x
. d)
( )
−
−−
=
22
1
8 8 5
2 .5 0,001. 10
x
xx
.
e)
++
+ = +
11
2 2 3 3
x x x x
.
f)
+
+ − =
1
12.3 3.15 5 20
x x x
.

CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
407
A.
5
. B.
7
. C.
1
2
. D.
2 2.
Câu 10: Nếu
z a bi=+
( )
,ab
có số phức nghịch đảo
1
4
a bi
z
−
−
=
thì
A.
22
2ab+=
. B.
22
4ab+=
. C.
22
8ab+=
. D.
22
16ab+=
.
Câu 11: Cho số phức
z a bi=+
với
,ab
thỏa mãn
3z i z i− + =
. Giá trị của
ab+
bằng
A.
1−
. B.
7
. C.
5
. D.
12
.
Câu 12: Cho
i
là đơn vị ảo. Nghiệm của phương trình
2
31
2
i
zi
i
+
+ − =
−
là
A.
23
.
15 5
i−
B.
23
.
15 5
i+
C.
22
.
15 5
i−−
D.
23
.
15 5
i−+
Câu 13: Có bao nhiêu số phức
z
thỏa mãn
2
2
2018 2019z z z−=
?
A. Vô số. B.
2
. C.
1
. D.
0
.
Câu 14: Có bao nhiêu số phức
z
thỏa mãn
2
2
2018 2019z z z−=
?
A. Vô số. B.
2
. C.
1
. D.
0
.
Câu 15: Cho hai số phức
34zi=−
và
( )
2z m mi
= + +
( )
m
thỏa mãn
z iz
=
. Tổng tất cả các giá trị
của
m
bằng
A.
1−
. B.
46
2
. C.
0
. D.
2−
.
Câu 16: Có bao nhiêu số phức
z
thỏa mãn đồng thời các điều kiện:
1z =
và
2
4 2 3z +=
.
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 17: Cho số phức
( )
,z a bi a b= +
thỏa mãn
2 3 3z iz i+ = +
. Tính giá trị biểu thức:
( ) ( )
2019 2019
.P a i b i= + + −
A.
1010
2−
. B.
1009
2−
. C.
1011
2−
. D.
1008
2−
.
Câu 18: Có bao nhiêu số phức
z
thỏa mãn
12z i z i+ + = −
và
1z =
A. 0. B. 2. C. 1. D. 4.
Câu 19: Tìm hai số thực
x
và
y
thỏa mãn
( ) ( )
3 2 3 4 3x yi i x i+ + − = −
với
i
là đơn vị ảo.
A.
3;x =
1y =−
. B.
2
;
3
x =
1y =−
. C.
3;x =
3y =−
. D.
3;x =−
1y =−
.
Câu 20: Có bao nhiêu số phức
z
thỏa mãn
2
20zz+=
.
A.
1
. B.
4
. C.
2
. D.
3
.
Câu 21: Với mọi số thuần ảo
z
, số
2
2
zz+
là
A. số thực dương. B. số thực âm. C. số 0. D. số thuần ảo khác 0.
Câu 22: Cho số phức
10 2zi=−
. Phần thực và phần ảo của số phức
z
là:
A. Phần thực bằng
10−
và phần ảo bằng
2i−
. B. Phần thực bằng
10−
và phần ảo bằng
2−
.

CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
408
C. Phần thực bằng
10
và phần ảo bằng
2
. D. Phần thực bằng
10
và phần ảo bằng
2i
.
Câu 23: Cho số phức
( )( )
2 3 4
32
ii
z
i
−−
=
+
. Tìm tọa độ điểm biểu diễn của số phức
z
trên mặt phẳng
Oxy
.
A.
( )
1;4
. B.
( )
1;4−
. C.
( )
1; 4−−
. D.
( )
1; 4−
.
Câu 24: Cho số phức
z
có phần thực là số nguyên và
z
thỏa mãn
2 7 3z z i z− = − + +
. Tính mô-đun của
số phức
2
1 zz
= − +
bằng
A.
37
=
. B.
457
=
. C.
425
=
. D.
445
=
.
Câu 25: Cho số phức
z a bi=+
( )
,ab
thỏa mãn
2 3 4z iz z+ = −
. Tính
S ab=
.
A.
3
2
S =
. B.
3
2
S =−
. C.
3
4
S =
. D.
3
4
S =−
.
Câu 26: Cho số phức
z a bi=+
( )
, , 0a b a
thỏa
( )
. 12 13 10z z z z z i− + − = +
. Tính
S a b=+
.
A.
7S =
. B.
17S =
. C.
17S =−
. D.
5S =
.
Câu 27: Có bao nhiêu số phức
z
thỏa mãn
2
24= + +z z z
và
1 3 3− − = − +z i z i
?
A.
4
. B.
3
. C.
1
. D.
2
.
Câu 28: Cho hai số phức z và w khác 0 thoả mãn
35z w w+=
và
2 2 2 .z wi z w wi− = − −
Phần thực
của số phức
z
w
bằng
A. 1. B.
3−
. C.
1−
. D. 3.
Câu 29: Cho số phức
z
thoả mãn
22
21z z i+ = −
. Tính môđun của số phức
2zi++
.
A.
1
. B.
3
. C.
4
. D.
2
.
Câu 30: Số phức
z a bi=+
,
,ab
là nghiệm của phương trình
( )
( )
11
1
z iz
i
z
z
−+
=
−
. Tổng
22
T a b=+
bằng
A.
4
. B.
4 2 3−
. C.
3 2 2+
. D.
3
.
Câu 31: Gọi là tập hợp tất cả các số nguyên sao cho tồn tại số phức phân biệt thỏa mãn
đồng thời các phương trình và . Tổng tất cả các phần tử của là
A. . B. . C. . D. .
Câu 32: Gọi là tập hợp tất cả các số sao cho tồn tại đúng một số phức thỏa mãn đồng thời các
phương trình và . Tích tất cả các phần tử của là
A. . B. . C. . D. .
Câu 33: Gọi là tập hợp tất cả các số nguyên sao cho tồn tại số phức phân biệt thỏa mãn
đồng thời các phương trình và . Số các phần tử của là
A. . B. . C. . D. .
S
m
2
12
,zz
1z z i− = −
21z m m+ = +
S
1
4
2
3
S
m
z
21z i z+ + = +
2
2 3 2 5 9z i m m− + = − +
S
6
5
2
3
S
m
2
12
,zz
( )
3 4 25 20iz+ + =
25z m i+ + =
S
8
7
6
5

CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
409
Câu 34: Trên mặt phẳng phức, tập hợp điểm biểu diễn số phức z thỏa mãn
( )
2 3 2zi+ − =
là đường tròn
có phương trình nào sau đây?
A.
22
4 6 9 0x y x y+ − − + =
. B.
22
4 6 11 0x y x y+ − + + =
.
C.
22
4 6 11 0x y x y+ − − + =
. D.
22
4 6 9 0x y x y+ + − + =
.
Câu 35: Tìm số phức z biết rằng điểm biểu diễn của z nằm trên đường tròn có tâm O, bán kính bằng 5 và
nằm trên đường thẳng .
A.
3 4 .zi=−
B.
3 4 .zi=+
C.
4 3 .zi=+
D.
4 3 .zi=−
Câu 36: Cho số thực
,xy
thỏa mãn
( ) ( )( )
2 3 2 1,x yi i x y+ + − + =
với
i
là đơn vị ảo là
A.
1, 2xy= = −
. B.
2, 1xy= = −
. C.
1, 2xy= − =
. D.
2, 1xy= − =
Câu 37: Cho số phức
( )
2
36z m m m i= + + − −
với
m
. Gọi
( )
P
là tập hợp các điểm biểu diễn số phức
z
trong mặt phẳng tọa độ. Diện tích hình phẳng giới hạn bởi
( )
P
và trục hoành bằng
A.
125
6
. B.
17
6
. C. 1. D.
55
6
.
Câu 38: Cho các số phức
z
thỏa mãn
12z +=
. Biết rằng tập hợp các điểm biểu diễn các số phức
( )
18w i z i= + +
là một đường tròn. Bán kính
r
của đường tròn đó là
A.
9
. B.
36
. C.
6
. D.
3
.
Câu 39: Gọi
1
z
,
2
z
là hai trong các số phức thỏa mãn
1 2 5zi− + =
và
12
8zz−=
. Tìm mô đun của số
phức
12
24w z z i= + − +
.
A.
6w =
. B.
10w =
. C.
16w =
. D.
13w =
.
Câu 40: Cho số phức z thoả mãn
11z −
và
zz−
có phần ảo không âm. Tập hợp các điểm biểu diễn số
phức
z
là một miền phẳng. Tính diện tích
S
của miền phẳng này
A.
S
=
. B.
2S
=
. C.
1
2
S
=
. D.
1S =
.
Câu 41: Cho số phức
3
( ) ,z m m m i= + −
với
m
là tham số thực thay đổi. Tập hơp tất cả các điểm biểu diễn
số phức
z
là đường cong
()C
.Tính diện tích hình phẳng giới hạn bởi
()C
và trục hoành.
A.
1
2
. B.
1
4
. C.
3
4
. D.
3
2
.
Câu 42: Phần gạch trong hình vẽ dưới là hình biểu diễn của tập các số phức thỏa mãn điều kiện nào sau
đây?
: 2 5 0d x y− + =
CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
410
A.
68z
. B.
2 4 4 4zi + +
. C.
2 4 4 4zi − −
. D.
4 4 4 16zi − −
.
Câu 43: Xét số phức
z
thỏa mãn
2z
zi
+
+
là số thuần ảo. Biết rằng tập hợp các điểm biểu diễn của số phức
z
là một đường tròn, tâm
I
của đường tròn có tọa độ là
A.
3
1;
2
I
. B.
1
1;
2
I
−−
. C.
( )
2;1I
. D.
1
;1
2
I
.
Câu 44: Gọi
12
,zz
là hai trong các số phức
z
thỏa mãn
3 5 5zi− + =
và
12
6zz−=
. Tìm môđun của số
phức
12
6 10z z i
= + − +
.
A.
10
=
. B.
32
=
. C.
16
=
. D.
8
=
.
Câu 45: Xét các số phức
z
thỏa mãn
( )
( )
22z i z++
là số thuần ảo. Biết rằng tập hợp các điểm biểu diễn
số phức
( )
1 2019 2019w i z i= + + −
là một đường tròn, bán kính đường tròn là
A.
2
. B.
1
. C.
2019 2
. D.
4
.
Câu 46: Trong mặt phẳng tọa độ
Oxy
gọi hình
()H
là tập hợp các điểm biểu diễn số phức
z
thỏa mãn điều kiện
| 2 | 2
10
zi
xy
+ −
+ +
. Tính diện tích
()S
của hình phẳng
()H
A.
4S
=
. B.
1
4
S
=
. C.
1
2
S
=
. D.
2S
=
.
Câu 47: Cho số phức
z
thỏa mãn:
23zi+ − =
. Tập hợp các điểm trong mặt phẳng tọa độ
( )
Oxy
biểu
diễn số phức
1 z
=+
là
A. Đường tròn tâm
( )
2;1I −
bán kính
3.R =
B. Đường tròn tâm
( )
2; 1I −
bán kính
3.R =
C. Đường tròn tâm
( )
1; 1I −−
bán kính
9.R =
D. Đường tròn tâm
( )
1; 1I −−
bán kính
3.R =
Câu 48: Cho
12
,zz
là hai số phức thỏa mãn điều kiện
| z 5 3i| 5− − =
đồng thời
12
| | 8zz−=
. Tập hợp các điểm
biểu diễn số phức
12
w z z=+
trong mặt phẳng tọa độ
Oxy
là đường tròn có phương trình
A.
22
( 10) ( 6) 36xy− + − =
. B.
22
( 10) ( 6) 16xy− + − =
.

CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
411
C.
22
53
( ) ( ) 9
22
xy− + − =
. D.
22
5 3 9
( ) ( )
2 2 4
xy− + − =
.
1.A
2.A
3.D
4.C
5.A
6.C
7.C
8.B
9.A
10.B
11.B
12.A
13.B
14.B
15.D
16.D
17.A
18.B
19.A
20.D
21.C
22.C
23.C
24.B
25.D
26.B
27.B
28.A
29.D
30.C
31.D
32.A
33.B
34.D
35.B
36.C
37.A
38.C
39.A
40.C
41.A.D
42
43.B
44.D
45.A
46.D
47.D
48.A
Câu 1: Chọn A
Ta có
1 2 1 2z i z i= − = +
.
Vậy
z
có phần ảo
2b =
.
Câu 2: Chọn A
Có:
( )( ) ( ) ( )( ) ( ) ( )
3 2 4 1 2 3 2 4 2 3 4 2 2i x yi i i x yi x y x y i x y x y i− − − − = + + − − + − − + = − + +
3 2 4 2 4 3
2 3 4 2 3 5 4 1
x y x y x y x
x y x y x y y
− − = − − = =
− − + = + − − = − = −
. Vậy khẳng định đúng là A
Câu 3: Chọn D
Ta có:
( ) ( )
2
2
12
2 1 3 2 7w z z i i i= − = + − − = +
.
22
2 7 53w = + =
.
Câu 4: Chọn C
Đặt
( )
;z a bi a b= +
, suy ra
z a bi=−
. Thay vào đẳng thức
( )
23z i z=+
ta có:
( ) ( ) ( )
21
2 3 2 2 3
2 3 2
a b a
a bi i a bi a bi b a i
b a b
==
+ = − + + = + +
= + =
.
Vậy
12zi=+
, suy ra
22
1 2 5z = + =
.
Câu 5: Chọn A
Gọi số phức
z x yi=+
với
,x y
. Theo bài ra ta có
( ) ( )
2
2 6 2 3 6 2 .
2
=
+ + − = + − = +
=−
x
x yi x yi i x yi i
y
Vậy điểm biểu diễn số phức
z
có tọa độ là
( )
2; 2 .−
Câu 6: Chọn C
Gọi
( )
, ,z a bi a b= +
. Suy ra
z a bi=−
.
Ta có
( )
2 3 17 9z i z i− + = − +
( ) ( )( )
2 3 17 9a bi i a bi i + − + − = − +
2 2 3 3 17 9a bi a bi ai b i + − + − − = − +
3 17
3 3 9
ab
ab
− − = −
− + =
2
5
a
b
=
=
Suy ra
25zi=+
. Do đó
29z =
.

CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
412
Câu 7: Chọn C
Ta có:
2 5 2 11 2 2
12
9 4 10 8 20 9 4 10 8 20z z y xi y i y xi y i= − − = − − − = +
22
2
9 4 8
2
10 20
x
yy
y
x
=−
−=
=
−=
. Vậy:
2
2
x
y
=−
=
.
Câu 8: Chọn B
Giả sử
2
, , , 1z a bi a b i= + = −
.
Ta có:
( ) ( )
( ) ( )
22
22
22
22
11
2 2 0
1
8
1
1
1
3
3
80
31
1
− + = + −
=
− + =
= =
=
−=
+
−
=
−=
−−
−
−+
++
−
=
+
a b a
z
z z i
zi
zi
b
ab
ab
b
a b b
zi
zi
zi
a
Do đó
11z i z i= + = −
Câu 9: Chọn A
Ta có:
( )
( )( )
( )
2
2
2 11 1 2
2 11
1 2 2 12 4 3
12
12
ii
i
i z i i z i
i
− − +
−−
− + − = − = = = −
−
+−
( )
2
2
3 4 5z = + − =
.
Câu 10: Chọn B
Ta có:
1
4
a bi
z
−
−
=
1
4
a bi
z
−
=
1
4
a bi
a bi
−
=
+
( )( )
4a bi a bi + − =
22
4ab + =
.
Câu 11: Chọn B
Ta có:
22
3 3 .z i z i a bi i a b i− + = + − + = +
( )
(
)
22
31a b i a b i − + + = +
22
30
3
4
1
a
a
b
b a b
−=
=
=
+ = +
. Vậy
3 4 7ab+ = + =
.
Câu 12: Chọn A
Ta có:
( )( )
22
2
3 1 3 1
25
ii
i
z i z i
i
+ − −
+
+ − = + − =
−
3 4 2 9 2 3
3 1 3 .
5 5 15 5
− − −
= − + = = −
ii
z i z z i
Câu 13: Chọn B
Đặt
z a bi=+
( )
,ab
.
Ta có
( )
2 2 2 2
2
2
2018 2019 (1)
2018 2019
2 2018 0 (2)
a b a a b
z z z
ab b
− − = +
− =
− =
.
Từ
(2)
ta được
0
1009
b
a
=
=
.
Thay
0b =
vào
(1)
ta được
2
0
2018 2018
1
a
aa
a
=
− =
=−
.
Do đó trường hợp này ta có 2 số phức thỏa yêu cầu là
0; 1zz= = −
.

CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
413
Thay
1009a =
vào
(1)
ta được
2
2018.1009.1010 2020b−=
vô nghiệm do
b
.
Vậy có
2
số phức
z
thỏa mãn.
Câu 14: Chọn B
Đặt
z a bi=+
( )
,ab
.
Ta có
( )
2 2 2 2
2
2
2018 2019 (1)
2018 2019
2 2018 0 (2)
a b a a b
z z z
ab b
− − = +
− =
− =
.
Từ
(2)
ta được
0
1009
b
a
=
=
.
Thay
0b =
vào
(1)
ta được
2
0
2018 2018
1
a
aa
a
=
− =
=−
.
Do đó trường hợp này ta có 2 số phức thỏa yêu cầu là
0; 1zz= = −
.
Thay
1009a =
vào
(1)
ta được
2
2018.1009.1010 2020b−=
vô nghiệm do
b
.
Vậy có
2
số phức
z
thỏa mãn.
Câu 15: Chọn D
Ta có:
.z iz i z
==
( )
2
2
25mm + + =
2
2 4 21 0mm + − =
2 46
2
2 46
2
m
m
−+
=
−−
=
.
Tổng tất cả các giá trị của
m
là
2−
.
Câu 16: Chọn D
Gọi số phức
z a bi=+
(
a
,
b
). Ta có
2 2 2
4 4 2z a b abi+ = − + +
.
Từ giả thiết, ta suy ra:
( )
22
2
2 2 2 2
1
4 4 12
ab
a b a b
+=
− + + =
( )
22
2
2 2 2 2
1
8 8 4
ab
a b a b
+=
+ + − = −
2
22
22
2
3 13
;
44
3
3 13
;
1
16
44
13
8 8 5
3 13
;
16
44
3 13
;
44
ab
a
ab
ab
ab
b
ab
ab
==
=
= = −
+=
− = −
=
= − =
= − = −
.
Vậy có 4 số phức
z
thỏa mãn bài toán.
Câu 17: Chọn A
Ta có:
( ) ( )
2 3 3 2 3 3 2 2 3 3+ = + + + − = + + + + = +z iz i a bi i a bi i a b a b i i
2 3 1
.
2 3 1
+ = =
+ = =
a b a
a b b
CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
414
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
( )( ) ( )( ) ( ) ( )
( )
( )
1009 1009
2019 2019 2019 2019 2 2
1009 1009
1009 1009
1009 2 2 1009 1010
1 1 1 1 1 1
1 2 1 2 2 1 2 1
2 2 2 2 .
= + + − = + + − = + + + − −
= + + − − = + − −
= + − + = − = −
P a i b i i i i i i i
i i i i i i i i
i i i i
Câu 18: Chọn B
Gọi
( )
,z a bi a b= +
z a bi = −
.
Ta có:
( ) ( ) ( )
( )
2 2 2
2
2
2
22
1
1
12
0
1 1 2
1
0
11
1
1
1
b
ab
z i z i
a
zi
a b a b
z
b
bb
ab
z
a
= −
=+
+ + = −
=
=−
+ + + = + +
=
=
+ + =
+=
=
=
Vậy có 2 số phức
zi=−
và
1z =
thỏa mãn.
Câu 19: Chọn A
Ta có
( ) ( )
3 2 3 4 3x yi i x i+ + − = −
( ) ( )
3 3 4 2 1 3 0x x y i + − + − + =
( ) ( )
3 2 2 0x y i − + + =
30
2 2 0
x
y
−=
+=
3
1
x
y
=
=−
.
Câu 20: Chọn D
Gọi
z a bi=+
,
( )
,ab
Khi đó
2
20zz+=
2 2 2 2
2 2 0a b a b abi − + + + =
22
2 2 2 2
22
0
0
0
20
0
20
2
0
20
0
20
2
a
a
b
bb
a
a b a b
b
b
ab
a
aa
b
=
=
=
− + =
=
− + + =
=
=
=
=
+=
=−
.
Vậy có 3 số phức
z
cần tìm.
Câu 21: Chọn C
Ta có
( ) ( )
2
2 2 2
0z bi b z z bi b= + = + =
.
Câu 22: Chọn C
Số phức
10 2zi=+
nên phần thực bằng 10 phần ảo bằng 2.
Câu 23: Chọn C
Ta có
( )( )
2 3 4
32
ii
z
i
−−
=
+
( ) ( )
8 3 2 12
32
i
i
− − +
=
+
5 14
32
i
i
−
=
+
( )( )
( )( )
5 14 3 2
3 2 3 2
ii
ii
−−
=
+−
( ) ( )
15 28 10 42
94
i− − +
=
+
13 52
13
i−−
=
14i= − −
.
CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
415
Vậy điểm biểu diễn số phức
z
trên mặt phẳng
Oxy
là
( )
1; 4M −−
.
Câu 24: Chọn B
Đặt
( )
,,z a bi a b= +
.
Ta có:
2 7 3z z i z− = − + +
( )
22
2 7 3a b a bi i a bi + − − = − + + +
( )
22
22
3 7 0
3 7 3 0
30
a b a
a b a b i
b
+ − + =
+ − + + − =
−=
2
9 3 7
3
aa
b
+ = −
=
22
7
3
9 9 42 49
3
a
a a a
b
+ = − +
=
( )
( )
7
3
4
5
4
3
a
aN
aL
b
=
=
=
3
4
b
a
=
=
.
Vậy
2
4 3 1 4 21 457z i z z i
= + = − + = + =
.
Câu 25: Chọn D
Cách 1
Ta có:
2 3 4z iz z+ = −
( ) ( )
22
2 3 4a b i a bi a bi + + + = − +
.
(
)
( )
22
2 3 3 4a b b a i a bi + − + = − −
.
22
22
1
3
3
2 3 4
2
1
3
3 2 3 3 4
2
a
ba
ba
a b b a
aa
a b a a a a
b
=
=−
=−
+ − = −
=−
= − + + = −
=−
.
Vậy
3
4
S =−
.
Cách 2
( )
2 3 4 3 1 4 2z iz z i z z+ = − + = −
.
Lấy môđun 2 vế ta có:
( )
4 2 2
3 1 4 2 4 2 2 1
4 2 2
zz
i z z z z z
zz
− =
+ = − − = =
− = −
42
13
22
31
z
zi
i
−
= = −
+
. Vậy
3
4
S =−
.
Câu 26: Chọn B
Ta có
z a bi=+
( )
, , 0a b a
. Khi đó phương trình ban đầu trở thành
2 2 2 2
12 2 13 10a b a b bi i+ − + + = +
2 2 2 2
12 13
2 10
a b a b
b
+ − + =
=

CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
416
22
12
13
5
5
a
ab
b
b
=
+=
=
=
. Vậy
17.S a b= + =
Câu 27: Chọn B
Gọi
,,z a bi a b R= +
. Khi đó theo giả thiết ta có hệ.
( ) ( ) ( ) ( )
2
2
22
2 2 2 2
2
4
44
2 2 4
2
4
1 1 3 3
2
0, 2
5 8 16
24 2
,
4
55
2
8 14
,
55
a
aa
a b a
a
a b a b
b
ab
a a a
ab
a
b
ab
−
+ = +
+ = +
−
− + − = − + +
=
= =−
−=
= =
−
=
= − = −
Vậy có
3
số phức
z
thỏa mãn.
Câu 28: Chọn A
Đặt
,
z
a bi
w
=+
với
,a b R
. Theo giả thiết ta có:
3
5 3 5
2 2 2
2 2 2
z w z
ww
z wi z w wi z z
ii
w w w w
+
= + =
− − −
= − = − −
22
22
2 2 2 2
( 3) 25 1
( 3) 25
.
3
4 4 0
( 2) ( 2) ( 2)
a b a
ab
b
a
a b a b
+ + = =
+ + =
=
−=
+ − = − + −
Vậy phần thực của số phức
z
w
bằng 1.
Câu 29: Chọn D
Gọi
( , )z x yi x y= +
. Ta có:
22
21z z i+ = −
22
21x yi x yi i + + = + −
2 2 2 2
2 ( 1) ( 1)x y x y
+ + = + −
22
4 2 1 0x x y y + + + + =
22
( 2) ( 1) 4xy + + + =
Do đó
22
2 ( 2) ( 1) 4 2z i x y+ + = + + + = =
.
Câu 30: Chọn C
Cách 1: Điều kiện:
1, 0zz
( )
( )
11
1
z iz
i
z
z
−+
=
−
( )
( )
2
11
1
z iz z
i
z
−+
=
−
( )
1
1
iz z
i
z
+
=
+
( )
2
1z z i z i + = +

CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
417
( )
(
)
2 2 2 2
1a bi a b i a b i − + + = + +
2 2 2 2
0
1
a
b a b a b
=
− + + = + +
2
1(*)b b b − = +
Với
(*)
2
0 1 1b b b z i = = − =
.
Với
(*)
2
0 2 1 0 1 2b b b b − − = = +
( )
12zi = +
.
Vậy
( )
2
2 2 2
0 1 2 3 2 2T a b= + = + + = +
.
Cách 2:
Điều kiện:
1, 0zz
( )
( )
11
1
z iz
i
z
z
−+
=
−
( )
( )
2
11
1
z iz z
i
z
−+
=
−
( )
1
1
iz z
i
z
+
=
+
( )
2
1z z i z i + = +
( )
2
1z z z i = − + +
.
Lấy môđun hai vế ta được:
( )
2
2
2
1z z z= − + +
2
2
1
12
1
= − + +
= +
− = − + +
z z z
z
z z z
2
22
3 2 2.a b z + = = +
Câu 31: Chọn D
Ta có
Trường hợp 1: .
Trường hợp 2:
Đặt
Ta có
Xét trong hệ tọa độ , là phương trình đường thẳng , là phương trình đường tròn
tâm , bán kính
Yêu cầu bài toán xảy ra khi và chỉ khi hệ phương trình, có hai nghiệm phân biệt khi và chỉ khi
đường thẳng cắt đường tròn tại hai điểm phân biệt
Kết hợp với và
Vậy tổng các phần tử của tập bằng 3.
Câu 32: Chọn A
Ta có luôn đúng với mọi .
2 1 0z m m+ = +
1 0 2 0 2 2m z m z m+ = + = = − =
10m+
z x yi=+
( )
( ) ( ) ( )
22
2
0 1
1
21
2 1 2
xy
z z i
z m m
x m y m
− =
− = −
+ = +
+ + = +
Oxy
:0d x y−=
( )
C
( )
2 ;0Im−
1Rm=+
d
( )
C
( )
22
2
, 1 2 2 1
2
m
d I d m m m m = + + +
2
2 1 0 1 2 1 2m m m − − − +
10m+
0;1;2m m S =
S
2
5 9 0mm− +
m
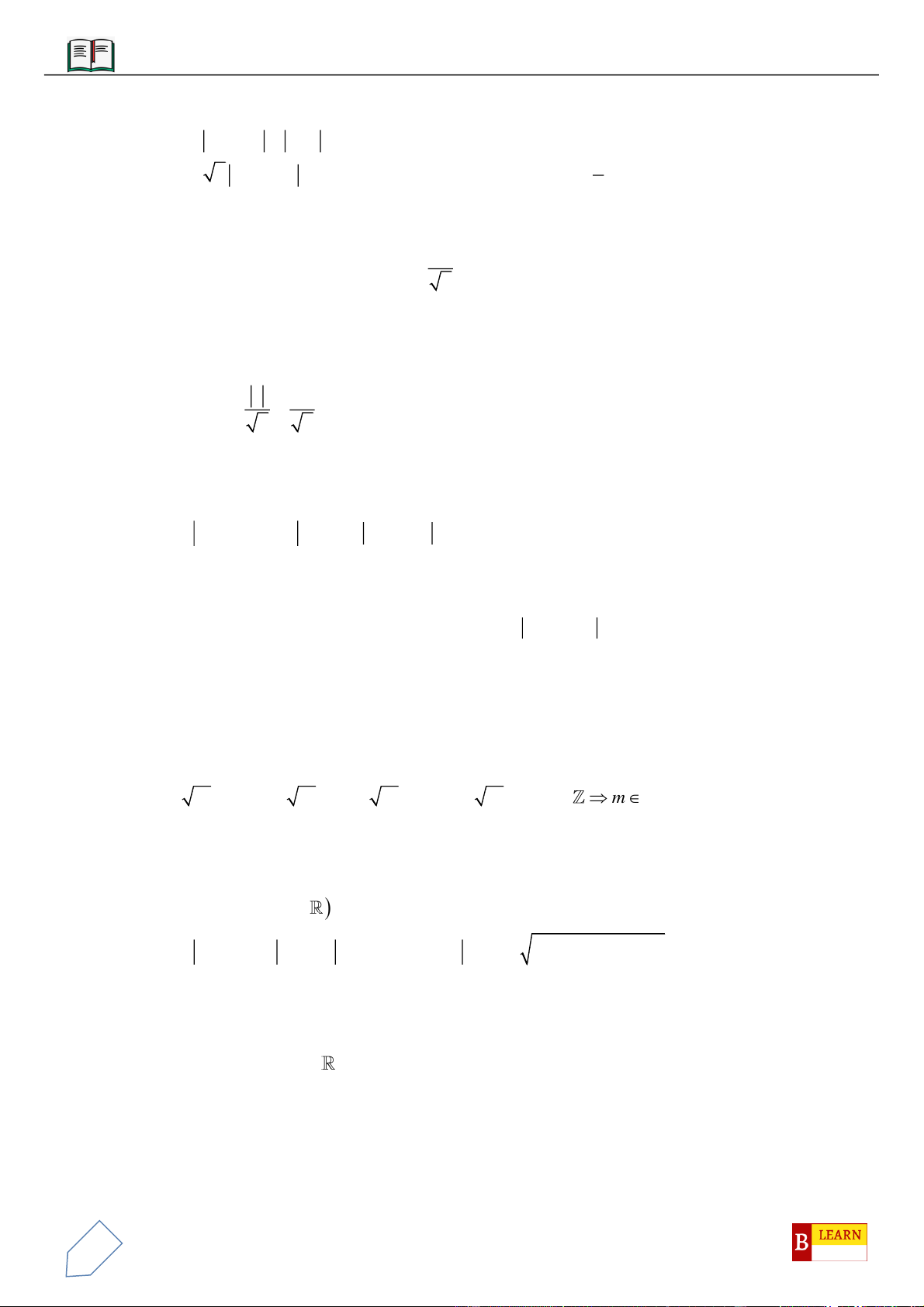
CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
418
Đặt
Ta có
Xét trong hệ tọa độ , là phương trình đường thẳng , là phương trình đường
tròn tâm , bán kính
Yêu cầu bài toán xảy ra khi và chỉ khi hệ phương trình, có nghiệm duy nhất khi và chỉ khi đường
thẳng tiếp xúc với đường tròn
Vậy tích các phần tử của tập bằng 6.
Câu 33: Chọn D
Ta có
tập hợp các điểm biểu diễn số phức thỏa mãn là đường tròn tâm , bán kính
Tập hợp các điểm biểu diễn số phức thỏa mãn là đường tròn tâm ,
bán kính .
Yêu cầu bài toán xảy ra khi hai đường tròn cắt nhau tại hai điểm phân biệt
mà
số các phần từ của là 7.
Câu 34: Chọn D
Gọi
( )
,z x yi x y= +
.
Ta có
( ) ( ) ( ) ( ) ( )
22
2 3 2 2 3 2 2 3 2z i x y i x y+ − = + + − = + + − =
( ) ( )
22
22
2 3 4 4 6 9 0x y x y x y + + − = + + − + =
.
Câu 35: Chọn A
Giả sử
,,z x yi x y= +
. Khi đó
,xy
là nghiệm của hệ pt:
22
2 5 0
3
4
25
xy
x
y
xy
− + =
=
=
+=
.
Suy ra:
34zi=+
.
Câu 36: Chọn C
( ) ( )( ) ( )
( )
5 3 1 0
1
2 3 2 1 5 3 1 2 0 .
20
2
xy
x
x yi i x y x y x y i
xy
y
+ − =
=−
+ + − + = + − − + =
− + =
=
z x yi=+
( )
( ) ( )
( )
( )
2
22
2
2
2 0 1
21
1
3 2 5 9 2
2 3 2 5 9
2
xy
z i z
x y m m
z i m m
+ + =
+ + = +
− + + = − +
− + = − +
Oxy
: 2 0d x y+ + =
( )
C
( )
3; 2I −
( )
2
1
59
2
R m m= − +
d
( )
C
( )
( )
22
2
3
1
, 5 9 5 6 0
3
22
m
d I d m m m m
m
=
= = − + − + =
=
2;3S=
S
( )
3 4 25 10 3 4 2i z z i+ + = + − =
z
( )
3;4I −
2R =
z
25z m i+ + =
( )
;2Jm−−
5R =
( ) ( )
;2 , ;5IJ
( ) ( )
22
3 7 9 3 36 49 3 13IJ m m − + −
13 3 13 3 13 3 13mm − − − +
0;1;2;3;4;5;6m m S =
S

CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
419
Câu 37: Chọn A
Gọi
( )
;M x y
( )
;xy
là điểm biểu diễn số phức
z
. Từ bài ra ta có:
2
3
6
xm
y m m
=+
= − −
( ) ( )
2
2
3
3
76
3 3 6
mx
mx
y x x
y x x
=−
=−
= − +
= − − − −
Vậy
( )
P
là một Parabol có phương trình:
2
76y x x= − +
.
Hoành độ giao điểm của
( )
P
và trục hoành là nghiệm của phương trình:
2
1
7 6 0
6
x
xx
x
=
− + =
=
Diện tích hình phẳng giới hạn bởi
( )
P
và trục hoành bằng:
6
2
1
125
76
6
S x x dx= − + =
.
Câu 38: Chọn C
Gọi
( )
,w x yi x y= +
Theo đề bài ta có:
( ) ( ) ( )
( )
( )
1 8 1 8 1 8 1 1 8w i z i w i i z w i i z i= + + − = + − = + + − +
( )
( ) ( )
( ) ( )
( )
1 8 1 8 1 1 1 8 1 8 1w i i i z x y i i z − + + = + + + + − + = + +
( )
( ) ( )
( )
( )
2 2 2
22
2
1 1 8 1 8 .2 1 1 8 36x y x y + + − + = + + + − + =
Vậy tập hợp các điểm biểu diễn số phức
( )
18w i z i= + +
là một đường tròn có bán kính
6.r =
Câu 39: Chọn A
Gọi
,AB
lần lượt là điểm biểu diễn số phức
1
z
,
2
z
. Gọi
E
là trung điểm của
AB
.
Do
1 2 5zi− + =
nên
,AB
thuộc đường tròn tâm
( )
1; 2I −
, bán kính
5R =
. Gọi
C
là điểm biểu
diễn số phức
w
ta có
2OC OA OB OI= + −
2 2 2OE OI IE= − =
.
22
2 2 2 25 16 6w IE IB EB= = − = − =
.
Câu 40: Chọn C
Đặt
( , )z x yi x y= +
theo giả thiết ta có
( ) ( ) 2z z x yi x yi yi− = + − − =
và
( )
2
2
11
11
20
0
x yi
xy
y
y
+ −
− +
.
CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
420
Vậy tập hợp các điểm biểu diễn số phức
z
là nửa hình tròn tâm
(1;0)I
,
1R =
.
Vì vậy
2
.
22
R
S
==
Câu 41: Chọn A
Đặt
( , )z x yi x y= +
.
Ta có:
3
()z m m m i= + −
3
()x yi m m m i + = + −
3
xm
y m m
=
=−
3
y x x = −
.
Vậy tập hợp tất cả các điểm biểu diễn số phức z là đường cong
()C
có dạng:
3
y x x=−
.
Phương trình hoành độ giao điểm:
3
0xx−=
0
1
1
x
x
x
=
=
=−
.
Diện tích phẳng giới hạn bởi đường cong
()C
và trục hoành:
01
33
10
1 1 1
( ) ( )
4 4 2
S x x dx x x
−
= − − − = + =
Câu 42: Chọn C
Dễ thấy điểm
( )
4;4I
là tâm của hai đường tròn.
Đường tròn nhỏ có phương trình là:
( ) ( )
22
4 4 4xy− + − =
.
Đường tròn to có phương trình là:
( ) ( )
22
4 4 16xy− + − =
.
Vậy tập hợp điểm biểu diễn số phức thỏa mãn đề bài là
2 4 4 4zi − −
.
Câu 43: Chọn B
Đặt
z x yi=+
, với
x
,
y
.
Ta có
( )
( )
( ) ( )
22
2 . 1
2
22
1 ( 1)
x yi x y i
x yi
z x yi
z i x yi i x y i x y
+ + − +
++
+ + +
= = =
+ + + + + + +
CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
421
( ) ( ) ( )( )
22
2 2 2 2 2 2
2 1 2 1
2 2 2
( 1) ( 1) ( 1)
x x y y x y xy i
x y x y x y
i
x y x y x y
+ + + − + + −
+ + + + +
= = −
+ + + + + +
.
Số phức
2z
zi
+
+
là số thuần ảo
22
22
2
0
( 1)
x y x y
xy
+ + +
=
++
( )
2
2
22
15
2 0 1
24
x y x y x y
+ + + = + + + =
. Vậy tâm
1
1;
2
I
−−
.
Câu 44: Chọn D
Tập hợp điểm biểu diễn số phức
z
thỏa mãn
3 5 5zi− + =
là đường tròn
( )
C
tâm
( )
3; 5I −
bán
kính
5R =
.
Gọi
,MN
lần lượt là điểm biểu diễn của số phức
12
,zz
suy ra
,MN
nằm trên đường tròn
( )
C
.
Gọi
H
là trung điểm của
MN
suy ra
IH MN⊥
Do
22
12
6 6 3 4z z MN MH NH IH IM MH− = = = = = − =
.
( ) ( )
1 2 1 2
6 10 3 5 3 5 2 2 8.
= + − + = − − + − − = + = = =z z i z i z i IM IN IH IH
Câu 45: Chọn A
Gọi số phức
z a bi=+
,
( )
,ab
.
Ta có:
( )
( )
( ) ( )
2 2 2 2z i z a b i a bi+ + = + + + −
( ) ( ) ( )( )
2 2 2 2a a b b a b ab i= + + + + + + −
.
( )
( )
22z i z++
là số thuần ảo nên
( ) ( ) ( ) ( )
22
2 2 0 1 1 2a a b b a b+ + + = + + + =
.
Gọi số phức
( )
, ,w x yi x y= +
.
Ta có
( )
1 2019 2019x yi i z i+ = + + −
( )( )
1 2019 2019i a bi i= + + + −
( )
2019 2019x yi a b a b i + = − + + + −
2019
2019
x a b
y a b
= − +
= + −
2
2.2019
2
xy
a
yx
b
+
=
−+
=
.
CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
422
Khi đó
( ) ( )
22
1 1 2ab+ + + =
22
2.2019
1 1 2
22
x y y x+ − +
+ + + =
22
4038 4042 8160789 0x y x y + − + + =
.
Vậy, tập hợp điểm biểu diễn số phức
w
là đường tròn có bán kính
22
2019 2021 8160789 2R = + − =
.
Câu 46: Chọn D
Gọi
2
( , ; 1)z x yi x y i= + = −
. Theo đề bài, ta có:
| 2 | 2zi+ −
| 2 | 2x yi i + + −
( ) ( )
| 2 1 | 2x y i + + −
( ) ( )
22
2 1 2xy + + −
( ) ( )
22
2 1 4xy + + −
. Đây là hình tròn tâm
( )
2;1I −
, bán kính
2R =
.
Ta lại có,
1 0 1x y y x+ + − −
. Đây là nửa mặt phẳng có bờ là đường thẳng
1yx= − −
và
chứa gốc tọa độ
( )
0;0O
.
Vì đường thẳng
1yx= − −
đi qua tâm
( )
2;1I −
của hình tròn nên phần diện tích cần tính bằng một
nửa diện tích của hình tròn.
Diện tích của hình tròn là:
22
. .2 4SR
= = =
.
Diện tích cần tính là:
1
11
. .4 2
22
SS
= = =
.
Câu 47: Chọn D
Đặt
( )
,x yi x y
= +
( )
;M x y
là điểm biểu diễn của số phức
.
Ta có:
1 z
=+
( )
11z z x yi
= − = − +
( )
1z x yi = − −
.
Do
23zi+ − =
( 1) 2 3x yi i − − + − =
( ) ( )
1 1 3x y i + − + =
( ) ( )
22
1 1 9xy + + + =
.
Vậy tập hợp các điểm biểu diễn số phức
là đường tròn tâm
( )
1; 1I −−
và bán kính
3R =
.
Câu 48: Chọn A
Đặt
z x yi=+
. Khi đó
22
| z 5 3i| 5 | x 5 (y 3)i| 5 ( 5) ( 3) 25xy− − = − + − = − + − =
()C
Gọi A, B lần lượt là 2 điểm biểu diễn số phức
12
,zz
A, B thuộc đường tròn
()C
có tâm I, bán kính R = 5 và
12
| | 8 8z z AB− = =

CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
423
Gọi H là điểm biểu diễn số phức
12
w=
2
zz+
H là trung điểm AB
4
2
AB
AH = =
Xét tam giác AIH vuông tại H có AH = 4, AI = 5 nên
2 2 2 2
5 4 3IH IA AH= − = − =
H thuộc đường tròn
()C
có tâm I, bán kính
3R
=
Gọi M là điểm biểu diễn số phức
12
w = +zz
2OM OH=
M là ảnh của H qua phép vị tự tâm O, tỉ số k = 2 với O là gốc tọa độ
Từ và
tập hợp M là đường tròn
()C
là ảnh của
()C
phép vị tự tâm O, tỉ số k = 2
Giả sử đường tròn
()C
có tâm J và bán kính
R
2.5 10
2.3 6
2.R 6
a
b
R
==
= =
==
Phương trình đường tròn
()C
là
22
( 10) ( 6) 36xy− + − =

CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
424
CÁC PHÉP TOÁN SỐ PHỨC
Câu 1: Cho số phức
12zi=+
. Tìm tổng phần thực và phần ảo của số phức
2w z z=+
.
A. 3. B. 5. C. 1. D. 2.
Câu 2: Trên tập số phức, cho biểu thức
( )( )
1A a bi i= − −
(
, ab
là số thực). Khẳng định nào sau đây
đúng?
A.
( )
.A a b a b i= + − +
B.
( )
.A a b b a i= − + + −
C.
( )
.A a b a b i= − − −
D.
( )
.A a b a b i= − − +
Câu 3: Kí hiệu
12
,zz
là hai nghiệm của phương trình
2
4 5 0zz− + =
. Giá trị của
22
12
zz+
bằng
A.
6
. B.
10
. C.
25
. D.
4
.
Câu 4: Tìm các số thực
x
,
y
thỏa mãn
( )
2 1 2 1x y i i− + − = +
với
i
là đơn vị ảo.
A.
1; 1xy==
. B.
1; 2xy==
. C.
1; 3xy==
. D.
1; 3xy= − =
.
Câu 5: Tìm số phức
z
biết
4 5 27 7z z i+ = −
.
A.
37zi= − +
. B.
37zi= − −
. C.
37zi=−
. D.
37zi=+
.
Câu 6: Cho số phức . Môđun của số phức là
A.
370
10
. B.
10
10
. C.
10
. D.
31
10 10
i
−
+
.
Câu 7: Cho
12
2 4 , 3 5= + = −z i z i
. Xác định phần thực của
2
12
.=w z z
A.
120−
. B.
32−
. C.
88
. D.
152−
.
Câu 8: Cho các số thực
x
,
y
thỏa mãn
( )
4 3 2 4 2i x yi− = +
. Tính giá trị của
P x y=+
.
A.
4P =
. B.
7P =
. C.
1P =−
. D.
8P =
.
Câu 9: Cho
( )
2
2
1.
zz
w
zz
−
=
+
với
z
là số phức tùy ý cho trước với phần thực và phần ảo khác 0. Mệnh đề
nào dưới đây đúng?
A.
w
là số ảo. B.
1w =−
. C.
1w =
. D.
w
là số thực.
Câu 10: Các số thực
x
,
y
thỏa mãn đẳng thức
( ) ( )
3 5 1 2 9 16x i y i i+ − + = +
trong đó
2
1i =−
. Giá trị của
biểu thức
T x y=−
là
A.
3
. B.
5
. C.
0
. D.
1
.
Câu 11: Biết phương trình
2
0z bz c+ + =
( )
,bc
có một nghiệm phức là
1
12zi=+
. Khi đó.
A.
2bc+=
. B.
3bc+=
. C.
1bc+=
. D.
7bc+=
.
Câu 12: Cho ba số phức
1 2 3
;;z z z
thỏa mãn
1 2 3
1 2 3
0
22
3
z z z
z z z
+ + =
= = =
. Tính
3
3
i
zi
i
=−
+
z

CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
425
2 2 2
1 2 2 3 3 1
A z z z z z z= + + + + +
A.
22
3
. B.
22
. C.
8
3
. D.
3
8
.
Câu 13: Kí hiệu
1
;z
2
z
là hai nghiệm phức của phương trình
2
3 1 0zz− + =
. Tính
12
P z z=+
.
A.
14
3
P =
. B.
2
3
P =
. C.
3
3
P =
. D.
23
3
P =
.
Câu 14: Cho số phức
z
thỏa mãn phương trình
( ) ( )
2
3 2 2 4i z i i+ + − = +
. Tìm tọa độ điểm
M
biểu diễn
số phức
z
.
A.
( )
1;1M −
. B.
( )
1; 1M −−
. C.
( )
1;1M
. D.
( )
1; 1M −
.
Câu 15: Tìm số phức
z
thỏa mãn
(2 ) 3 5z i z i+ + = −
.
A.
23zi=+
. B.
23zi= − +
. C.
23zi=−
. D.
23zi= − −
.
Câu 16: Cho số phức
( ) ( )
2
1 1 2 .z i i= + +
Số phức
z
có phần ảo là
A.
2i
. B.
4
. C.
2
. D.
4−
.
Câu 17: Cho số phức
1z
thỏa mãn
3
1z =
. Tính
( )( )
2018 2018
11z z z z− + + −
.
A. 1. B. Đáp số khác. C. 4. D. 2.
Câu 18: Có bao nhiêu số phức
z
thỏa mãn điều kiện
5 5 6z i z i+ + − =
, biết
z
có môđun bằng
5
?
A.
3
. B.
4
. C.
2
. D.
0
.
Câu 19: Cho hai số phức
z
,
w
thỏa mãn
17zw+=
,
2 58zw+=
và
2 5 2zw−=
. Giá trị của biểu
thức
..P z w z w=+
bằng
A.
1
. B.
2
. C.
4
. D.
3
.
Câu 20: Tính tổng phần thực của tất cả các số phức
0z
thỏa mãn
5
7z i z
z
+ = −
.
A.
2
. B.
2−
. C.
3−
. D.
3
.
Câu 21: Cho hai số phức
1
z
,
2
z
khác
0
thỏa mãn
1
2
z
z
là số thuần ảo và
12
10zz−=
. Giá trị lớn nhất của
12
zz+
bằng
A.
10
. B.
10 2
. C.
10 3
. D.
20
.
Câu 22: Cho các số phức thỏa mãn và . Điểm biểu diễn cho số phức có
hoành độ bằng
A. . B. . C. . D. .
Câu 23: Tìm số phức
z
thỏa mãn
2 3 2z i z+ − =
.
A.
2zi=+
. B.
2zi=−
. C.
32zi=−
. D.
3zi=+
.
Câu 24: Môđun của số phức
z
thỏa mãn
15z −=
và
( )
17 5 . 0z z z z+ − =
bằng
z
2021
2 2 3 1iz i z− = −
1z =
z
4−
4
1−
1
CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
426
A.
53
. B.
34
. C.
29
và
13
. D.
29
.
Câu 25: Cho số phức
u
,
v
thỏa mãn:
10uv==
và
3 4 2019uv−=
. Ta có
43uv+
là
A.
2890
. B.
2981
. C.
2891
. D.
2982
.
Câu 26: Cho khai triển
( )
2019
2 3 2019
0 1 2 3 2019
3 ...x a a x a x a x a x+ = + + + + +
. Hãy tính tổng
0 2 4 6 2016 2018
...S a a a a a a= − + − + + −
.
A.
0
. B.
2019
2
. C.
( )
1009
3
. D.
1009
2
.
Câu 27: Biết rằng
a
;
b
là các số thực thỏa mãn
( )
2017
13a bi i+ = +
. Giá trị của
ab+
bằng:
A.
( )
672
1 3 .8+
. B.
( )
671
1 3 .8+
. C.
( )
672
3 1 .8−
. D.
( )
671
3 1 .8−
.
Câu 28: Cho số phức
z
thỏa mãn
4z z z z+ + − =
. Gọi
,Mm
lần lượt là giá trị lớn nhất, nhỏ nhất của
22P z i= − −
. Đặt
A M n=+
. Mệnh đề nào sau đây đúng?
A.
)
4;3 3A
. B.
( )
34;6A
. C.
( )
2 7; 33A
. D.
( )
6; 42A
.
Câu 29: Cho các số phức
12
,zz
thỏa mãn
1
6z =
và
2
2z =
. Gọi
,MN
lần lượt là các điểm biểu diễn của
các số phức
1
z
và
2
iz
. Biết
60MON =
. Tính
22
12
9T z z=+
.
A.
T =
36 2
. B.
36 3T =
. C.
24 3
. D. 18.
Câu 30: Xét các số phức
z
thỏa mãn
( )
( )
2 z z i−+
là số thuần ảo. Tập hợp tất cả các điểm biểu diễn của
z
trong mặt phẳng tọa độ là
A. Đường tròn có tâm
1
1;
2
I
, bán kính
5
2
R =
.
B. Đường tròn có tâm
1
1;
2
I
, bán kính
5
2
R =
nhưng bỏ đi hai điểm
( )
2;0A
,
( )
0;1B
.
C. Đường tròn có tâm
1
1;
2
I
−−
, bán kính
5
2
R =
.
D. Đường tròn có tâm
( )
2;1I
, bán kính
5R =
.
Câu 31:
Cho số phức
z
thỏa mãn
( )
2 14
3 1 3
i
i z i
z
−+
+ = + −
. Khẳng định nào sau đây đúng?
A.
3
2
2
z
. B.
13
4
4
z
. C.
7 11
45
z
. D.
3
1
2
z
.
Câu 32: Cho các số phức thỏa mãn và Môđun bằng
A. . B. . C. . D. .
Câu 33: Gọi
S
là tập hợp tất cả các số phức
z
có phần thực và phần ảo là các số nguyên thỏa mãn hai
điều kiện:
3 4 2zi− −
và
z z z z+−
. Số phần tử của tập
S
là
A.
11
. B.
12
. C.
13
. D.
10
.
12
,zz
12
3zz==
12
2.zz−=
12
zz+
2
3
2
22
CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
427
BẢNG ĐÁP ÁN
1.B
2.D
3.B
4.C
5.D
6.B
7.D
8.A
9.A
10.B
11.B
12.C
13.D
14.C
15.C
16.C
17.C
18.B
19.B
20.D
21.B
22.C
23.A
24.B
25.B
26.A
27.A
28.B
29.B
30.A
31.C
32.D
33.D
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Chọn B
Ta có
1 2 1 2z i z i= + = −
, khi đó
( ) ( )
2 2 1 2 1 2 3 2w z z i i i= + = + + − = +
.
Phần thực của số phức
w
là 3, phần ảo của số phức
w
là 2.
Tổng phần thực và phần ảo là:
3 2 5+=
.
Câu 2: Chọn D
( )( )
2
1A a bi i a ai bi bi= − − = − − +
( ) ( )
a b a b i= − − +
.
Câu 3: Chọn B
Ta có
1
2
2
2
4 5 0
2
zi
zz
zi
=+
− + =
=−
nên
22
12
10zz+=
.
Câu 4: Chọn C
Ta có
( )
2 1 1 1
2 1 2 1
2 1 3
xx
x y i i
yy
− = =
− + − = +
− = =
.
Câu 5: Chọn D
Giả sử
( )
,z a bi a b R= +
, khi đó
4( ) 5( ) 27 7 9 27 7a bi a bi i a bi i+ + − = − − = −
9 27 3
37
77
aa
zi
bb
==
= +
− = − =
.
Câu 6: Chọn B
Ta có:
3 1 3 3 1 9 1 10
3 3 10 10 10 100 100 10
ii
z i z z i z
ii
−
= − = = = + = + =
++
Câu 7: Chọn D
Ta có
2
22
3 5 16 30z i z i= + = − +
( )( )
2
12
. 2 4 16 30 152 4w z z i i i = = + − + = − −
.
Vậy phần thực của
w
là
152−
.
Câu 8: Chọn A
Ta có
( )
4 3 2 4 2i x yi− = +
8 12 4 2i x yi − + = +
48
2 12
x
y
=−
=
2
6
x
y
=−
=
4P x y = + =
.
Câu 9: Chọn A
Gọi số phức
z x yi=+
,
( )
,xy
z x yi = −
.

CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
428
Ta có:
( )
2
2
1.
zz
w
zz
−
=
+
( ) ( )
22
22
1
x yi x yi
xy
+ − −
=
++
2 2 2 2
22
22
1
x xyi y x xyi y
xy
+ − − + +
=
++
22
4
1
xy
i
xy
=
++
.
Vậy
w
là số ảo.
Câu 10: Chọn B
Ta có
( ) ( )
3 5 1 2 9 16x i y i i+ − + = +
( ) ( )
3 9 5 2 16 0x y x y i − − + − − =
3 9 0
5 2 16 0
xy
xy
− − =
− − =
2
3
x
y
=
=−
. Suy ra
5T x y= − =
.
Câu 11: Chọn B
Vì phương trình
2
0z bz c+ + =
nhận
1
12zi=+
là nghiệm nên ta có:
( ) ( )
( ) ( )
2
1 2 1 2 0 3 4 2 0
3 0 3
3 2 4 0
2 4 0 2
i b i c i b bi c
b c b c
b c b i
bb
+ + + + = − + + + + =
+ − = + =
+ − + + =
+ = = −
Câu 12: Chọn C
1 2 3
1 2 3 1 3 2
3 2 1
0
z z z
z z z z z z
z z z
=−
=−
=−
+
+ + = +
+
.
2
2 2 2 2 2 2 2 2 2
1 2 2 3 3 1 1 2 3 1 2 3
2 2 8
3.
33
A z z z z z z z z z z z z
= + + + + + − + − + − = + + = =
=
.
Câu 13: Chọn D
Cách 1:
Ta có
2 2 2
1 1 1 11
3 1 0 0
3 3 6 36
z z z z z
− + = − + = − = −
22
1 11
1 11
66
6 36
1 11
66
zi
zi
zi
=+
− =
=−
.
Khi đó
22
22
1 11 1 11 2 3
6 6 6 6 3
P
= + + + − =
.
Cách 2:
Theo tính chất phương trình bậc 2 với hệ số thực, ta có
1
;z
2
z
là hai số phức liên hợp nên
22
1 2 1 2
.z z z z==
. Mà
12
1
.
3
zz=
suy ra
12
3
3
zz==
. Vậy
12
23
3
P z z= + =
.
Câu 14: Chọn C
Ta có phương trình:
2
(3 2 ) (2 ) 4i z i i+ + − = +
( ) ( )
2
3 2 2 4i z i i + = − − + +
( )
3 2 1 5i z i + = +
15
1
32
i
z z i
i
+
= = +
+
.

CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
429
Vậy điểm
M
biểu diễn số phức
z
có tọa độ là
( )
1;1M
.
Câu 15: Chọn C
Gọi
( )
;z a bi a b= +
, theo đề bài ta có:
( )
(2 ) 3 5a bi i a bi i+ + + − = +
2 2 3 5a bi a b ai bi i + + + + − = +
3 3 5a b ai bi i + + − = +
3 3 2
53
a b a
a b b
+ = =
− = = −
. Vậy
23zi=−
.
Câu 16: Chọn C
Ta có
( ) ( ) ( )
2
1 1 2 2 1 2 4 2 .z i i i i i= + + = + = − +
Do đó phần ảo của
z
là
2.
Câu 17: Chọn C
Ta có:
( )
672
3 2018 3 2 2
1.z z z z z= = =
( )
( )
32
1 1 1 0z z z z= − + + =
, mà
1z
nên
2
10zz+ + =
Do đó,
( )( ) ( )( )
2018 2018 2 2
1 1 1 1z z z z z z z z− + + − = − + + −
( )( )
2 2 2
1 2 1 2z z z z z z= + + − + + −
( )
23
2 . 2 4 4z z z= − − = =
.
Câu 18: Chọn B
Gọi
z a bi=+
với
a
,
b
. Ta có hệ phương trình sau:
( ) ( )
5 5 6 5 5 6
5
5
z i z i a b i a b i
z
a bi
+ + − = + + + + − =
=
+=
( ) ( )
22
22
2 2 2 2
22
22
5 5 6
2 5 5 2 5 5 6
5
5
a b a b
a b b a b b
ab
ab
+ + + + − =
+ + + + + − + =
+=
+=
22
10 2 5 10 2 5 6
5
bb
ab
+ + − =
+=
,
2
2
22
22
2 2 2 2
2
16
100 20 64
20 2 100 20 36 100 20 8
5
9
5
55
5
a
b
bb
ab
a b a b
b
=
−=
+ − = − =
+=
+ = + =
=
4
5
4
4 4 4 4
5
5 5 5 5
3 3 3 3
3
5 5 5 5
5
3
5
a
a
a a a a
b b b b
b
b
=
=−
= = = − = −
= = − = = −
=
=−
.

CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
430
Kết hợp với điều kiện ta có bốn số phức cần tìm là:
43
55
zi=+
,
43
55
zi=−
,
43
55
zi= − +
,
43
55
zi= − −
.
Câu 19: Chọn B
Ta có
2
.z z z=
,
1 2 1 2
zaz b az bz+ = +
nên
2 58zw+=
2
2 58zw + =
( )
( )
2 2 58z w z w + + =
22
2 . 2 . 4 58z z w z w w + + + =
22
2 4 58z P w + + =
.
Tương tự
2 5 2zw−=
22
2 4 50z P w − + =
.
Khi đó
22
22
2 4 58
2 4 50
z P w
z P w
+ + =
− + =
48P=
2P=
.
Câu 20: Chọn D
Ta có:
5
7z i z
z
+ = −
. Chia hai vế cho
i
ta được:
5
7z i zi
z
+ = − +
.
Hay
( ) ( )
( )
2
5 5 25
1 7 1 7 2 49z i i z i i z
zz
z
− = − − − = − − = +
Bình phương 2 vế, ta được:
2
2
25
2 49z
z
= +
42
2 49 25 0zz− − =
2
2
25 (t/m)
1
(kt/m)
2
z
z
=
=−
.
Do
0z
nên
5z =
. Thế
5z =
vào đề bài ta được:
( )
5
7 1 7
5
z i z z i z
+ = − + = −
.
Đặt
z x yi
, với
,xy
.
Thế vào ta được:
( )
17x yi i x yi+ + = − −
( )
17y x i x yi − + + = − −
7
1
yx
xy
− = −
+ = −
7
1
xy
xy
−=
+ = −
3
4
x
y
=
=−
.
Dễ thấy số phức
34i
thỏa mãn yêu cầu bài toán.
Vậy tổng phần thực của các số phức cần tìm là
3
.
Câu 21: Chọn B
Cách 1:
Vì
1
2
z
z
là số thuần ảo nên
1
2
z
ai
z
=
12
z aiz=
.
Ta có
12
10zz−=
22
10aiz z−=
2
1 10z ai −=
2
2
1 10za+=
2
2
10
1
z
a
=
+
.

CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
431
Từ
12
z aiz=
12
2
10
1
a
z aiz
a
==
+
.
Do đó
12
22
10
10
11
a
zz
aa
+ = +
++
( )
2
10 1
1
a
a
+
=
+
( )
( )
2
2
10 1 1 1
1
a
a
++
+
10 2
.
Đẳng thức xảy ra
1a =
12
z iz=
. Vậy
( )
12
10 2max z z+=
.
Cách 2:
Đặt
1 1 1
=+z a b i
,
2 2 2
=+z a b i
. Gọi
A
,
B
lần lượt là điểm biểu diễn của
1
z
,
2
z
.
( )
11
; A a b
,
( )
22
;B a b
( ) ( )
1 1 2 2
; , ; OA a b OB a b
.
( )( )
1 1 2 2
1 1 2
22
2
22
.
+−
==
a bi a b i
z z z
z
zz
là số thuần ảo
1 2 1 2
0 . 0 + = =a a bb OAOB
OAB
vuông
tại
O
.
12
10− = =z z AB
.
( ) ( )
2 2 2 2 2
12
. 1 1 2 10 2+ = + + + = =z z OA OB OA OB AB
.
Đẳng thức xảy ra
=OA OB
. Vậy
( )
12
10 2max z z+=
.
Câu 22: Chọn C
Giả sử .
Ta có
.
Mặt khác: . Thay vào được .
Câu 23: Chọn A
Đặt
z x yi=+
(
x
,
y
), suy ra
z x yi=−
.
Ta có
( ) ( )
2 3 2 2 3 2 2z i z x y i x yi+ − = + + − = −
.
Đồng nhất hệ số ta có
2 2 2
3 2 1
x x x
y y y
+ = =
− = − =
. Vậy số phức
2zi=+
.
Câu 24: Chọn B
Đặt
( )
;z a bi a b R= +
Ta có
( )
15
17 5 . 0
z
z z z z
−=
+ − =
( )
( )
2
2
22
1 25
17.2 5 0
ab
a a b
− + =
− + =
( )
( )
22
22
2 24 0
17.2 5 0
a b a
a a b
+ − − =
− + =
( )
( )
22
22
5 2 24 0
17.2 5 0
a b a
a a b
+ − − =
− + =
( )
( )
22
34 5 2 24 0
5 17.2
aa
a b a
+ − − =
+=
22
5
34
a
ab
=
+=
Suy ra
22
34z a b= + =
.
z a bi=+
( )
;ab
2021
2 2 3 1iz i z− = −
( )
( )
( )
1010
2
2 2 3 1i a bi i i a bi + − = − −
( ) ( )
2 2 2 3 1 3a i b a bi − − = − −
( ) ( )
22
22
2 2 4 3 1 9a b a b − + = − +
( )
( )
22
5 2 3 0 1a b a + + − =
1z =
( )
22
12ab + =
5.1 2 3 0 1aa+ − = = −

CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
432
Câu 25: Chọn B
Ta có
( )( )
2
3 4 2019 3 4 2019 3 4 3 4 2019u v u v u v u v− = − = − − =
( )
( ) ( ) ( ) ( )
22
3 4 3 4 2019 9 12 16 2019u v u v u uv uv v − − = − + + =
. Suy ra
481
12
uv uv+=
.
Tương tự như trên ta có
( )( ) ( )
( ) ( ) ( ) ( )
22
2
4 3 4 3 4 3 4 3 4 3 16 12 9 2981u v u v u v u v u v u uv uv v+ = + + = + + = + + + =
.
Do đó:
4 3 2981uv+=
.
Câu 26: Chọn A
Với mọi
k
, ta có:
4
1
k
i =
,
41k
ii
+
=
,
42
1
k
i
+
=−
,
43k
ii
+
=−
và
( )
4
1
k
i−=
,
( )
41k
ii
+
− = −
,
( )
42
1
k
i
+
− = −
,
( )
43k
ii
+
−=
Xét khai triển
( )
2019
2 3 2019
0 1 2 3 2019
3 ...x a a x a x a x a x+ = + + + + +
Thay
xi=
ta được:
( )
2019
0 1 2 3 4 5 6 2018 2019
3 ...i a a i a a i a a i a a a i+ = + − − + + − − − −
( ) ( )
0 2 4 2018 1 3 5 2019
...... ......a a a a a a a a i= − + − − + − + − −
Mà
( )
2019
2019
2019 2019
2019 2019
3 2 cos .sin 2 cos .sin 0
6 6 6 6
i i i i
+ = + = + = +
Suy ra
0 2 4 6 2018
... 0a a a a a− + − + − =
Câu 27: Chọn A
Ta có:
13
1 3 2 2 cos .sin
2 2 3 3
i i i
+ = + = +
( )
2017
2017
2017
1 3 2 cos .sin
33
ii
+ = +
2017
2017 2017
2 cos .sin
33
i
=+
2016
2 .2. cos .sin
33
i
=+
( )
672
8 1 3i=+
672 672
8 8 3i=+
672
672
8
83
a
b
=
=
.
( )
672
1 3 8ab + = +
.
Câu 28: Chọn B
Giả sử
( )
,z x yi x y= +
. Khi đó
4z z z z+ + − =
2 2 4xy + =
2xy + =
2 khi 0, 0
2 khi 0, 0
2 khi 0, 0
2 khi 0, 0
x y x y
x y x y
x y x y
x y x y
+ =
+ = −
− =
− + =
Hình biểu diễn hệ nói trên là hình vuông
ABCD
như trong hình vẽ
CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
433
Khi đó
22P z i EM= − − =
với
( )
2;2E
và
( )
;M x y
.
Dễ thấy
( )
min ; 2; max 20m P d E AB EH M P ED= = = = = = =
.
Do đó
( )
2 20 34;6Mm+ = +
.
Câu 29: Chọn B
Trong mặt phẳng tọa độ
Oxy
, gọi
,MN
lần lượt là điểm biểu diễn các số phức
1
z
và
2
iz
, gọi
,EF
lần lượt là các điểm biểu diễn các số phức
2
3iz
và
2
3iz−
.
Theo bài ra ta có:
1
6z =
nên tập hợp các điểm
M
là đường tròn tâm
O
, bán kính
6R =
, gọi là đường tròn
( )
1
C
;
2 2 2
2 . 2z iz i z= = =
do đó tập hợp các điểm
N
biểu diễn số phức
2
iz
thuộc đường tròn tâm
O
, bán kính
2r
, gọi là đường tròn
( )
2
C
.
Lại thấy :
2
36iz
và
2
36iz
suy ra các điểm
E
,
F
thuộc đường tròn
( )
1
C
.
Hơn nữa:
2
3iz
và
2
3iz−
là các số phức đối nên
EF
là một đường kính của
( )
1
C
.
Mặt khác :
3OE ON=
nên
N
nằm giữa
O
và
E
60MOE =
, suy ra tam giác
MOE
là tam
giác đều cạnh bằng
6
và tam giác
MEF
vuông tại
M
.
Khi đó :
( )
2
2 2 2
1 2 1 2 1 2 1 2
9 3 3 . 3 .T z z z iz z iz z iz ME MF= + = − = − + =
.

CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
434
Nhận thấy:
2
6 . 3
. 2. 4. 4. 36 3
4
MEF MOE
ME MF S S
= = = =
. Vậy
36 3T =
.
Câu 30: Chọn A
Gọi
( )
,;z x yi x y= +
.
Ta có
( )
( )
( )( ) ( )
22
2 2 2 2 2z z i x yi x yi i x y x y x y i− + = − − − + = − − + + − + −
.
Các số phức
z
thỏa mãn
( )
( )
2 z z i−+
là số thuần ảo khi
22
20x y x y− − + + =
Hay
( )
2
2
15
1
24
xy
− + − =
.
Suy ra tập hợp tất cả các điểm biểu diễn của
z
trong mặt phẳng tọa độ là đường tròn có tâm
1
1;
2
I
, bán kính
5
2
R =
.
Câu 31:
Chọn C
Phân tích: Nếu đặt
( )
;z x yi x y= +
thì thấy khối lượng tính toán lớn và đi đến một phương
trình rất phức tạp. Nghĩ đến phép lấy mô đun hai vế của một biểu thức số phức là phép suy rA.
Ta có:
( ) ( )
2 14
3 1 3 0
i
i z i z
z
−+
+ = + −
( ) ( )
( )
3 1 3 2 14z z z i i − + + = − +
.
Sau khi lấy mô đun hai vế ta được một phương trình theo ẩn
0z
.
( ) ( ) ( ) ( )
22
. 3 1 3 2 14 . 3 1 3 10 2z z z i i z z z− + + = − + − + + =
.
2
42
2
42
20 0
2(L)
5 (L)
zz
zz
z
z
= =
+ − =
=−
=−
.
Thử lại
2z =
ta được
68
55
zi=+
thỏa yêu cầu bài toán.
Câu 32: Chọn D
Cách 1:
Gọi các số phức .
Ta có: ; .
Ta có: ; .
.
Do đó: .
1 1 1 2 2 2 1 1 2 2
, ( , , , )z a b i z a b i a b a b= + = +
( ) ( )
1 2 1 2 1 2
z z a a b b i− = − + −
( ) ( )
1 2 1 2 1 2
z z a a b b i+ = + + +
2 2 2 2
1 1 1 1 1
33z a b a b= + = + =
2 2 2 2
2 2 2 2 2
33z a b a b= + = + =
( ) ( )
22
1 2 1 2 1 2
22z z a a b b− = − + − =
( ) ( )
22
1 2 1 2
4a a b b − + − =
2 2 2 2
1 1 2 2 1 2 1 2
2 2 4a b a b a a b b + + + − − =
1 2 1 2
2 2 2a a b b + =
( ) ( )
22
1 2 1 2 1 2
z z a a b b+ = + + +
2 2 2 2
1 1 2 2 1 2 1 2
2 2 8 2 2a b a b a a b b= + + + + + = =
CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
435
Cách 2:
Cách 3:
Gọi lần lượt là điểm biểu diễn số phức . Khi đó tam giác cân có
. Gọi là trung điểm của . Khi đó là đường cao của tam giác
; ; .
Cách 4:
Gọi lần lượt là điểm biểu diễn 2 số phức . Khi đó tam giác có
; .
Mà .
Vậy .
Cách 5:
Ta có .
.
.
Cách 6: Chọn đại diện
Chọn .
Cách 7:
( )
( ) ( )
2 2 2
1 2 1 2 1 2 1 2 1 2 2 1
4z z z z z z z z z z z z− = − − = + − + =
( )
( )
2 2 2
1 2 1 2 1 2 1 2 1 2 2 1
8z z z z z z z z z z z z+ = + + = + + + =
12
22zz + =
,AB
2
12
,zz
OAB
3, 2OA OB AB= = =
I
AB
OI
OAB
22
2OI OA AI= − =
12
2 2 2z z OI+ = =
,AB
12
,zz
OAB
3, 2OA OB AB= = =
2 2 2
12
2.T z z OA OB T OA OB OAOB= + = + = + +
( )
2 2 2 2 2 2
. . .cos , . . 1
2 . 2
OA OB AB OA OB AB
OAOB OAOB OA OB OAOB
OAOB
+ − + −
= = = =
2
8 2 2TT= =
2 2 2 2
1 2 1 2 1 2
22z z z z z z+ + − = +
2 2 2 2
1 2 1 2 1 2
2 2 2.3 2.3 4 8T z z z z z z = + = + − − = + − =
22T =
1
12
2
3
3 2 6
3 2 2
3 2 6
33
33
z
z z i
zi
=
+ = + + =
=+

CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
436
Gọi lần lượt là điểm biểu diễn 2 số phức . Khi đó tam giác có
. Gọi là trung điểm của .
Ta có .
Cách 8: Tính nhanh.
Tổng quát
Vậy .
Câu 33: Chọn D
Gọi
( )
,z a bi a b= +
là số phức thỏa mãn bài toán.
Ta có
( ) ( )
22
3 4 2
22
ab
ab
− + −
( ) ( )
22
3 4 4ab
ab
− + −
. Suy ra
,
15
26
ab
a
b
ab
.
Bảng giá trị thỏa mãn
a
1
2
3
4
b
4
3
4
5
3
4
5
6
4
5
Vậy tập
S
có tất cả
10
phần tử.
,AB
12
,zz
OAB
3, 2OA OB AB= = =
I
AB
2 2 2
12
2 2 2 2 2
24
OA OB AB
T z z OA OB OI OI
+
= + = + = = = − =
( )
22
2 2 2 2 2 2
1 2 1 2 1 2 1 2
mz nz m z n z mn z z z z+ = + + + − −
( )
2 2 2 2 2 2
2
1 2 1 2 1 2 1 2
8 2 2T z z z z z z z z T= + = + + + − − = =

CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
437
PHÉP CHIA SỐ PHỨC
Câu 1: Cho số phức
z
thỏa mãn
( ) ( )
1 2 3i z i z+ − − =
. Môđun của số phức
2
1
iz
w
i
−
=
−
là?
A.
122
5
. B.
3 10
2
. C.
45
4
. D.
122
2
.
Câu 2: Cho số phức
2 3 2017
1 2 3 4 ... 2018z i i i i= + + + + +
có phần thực là
a
và phần ảo là
b
. Tính
ba−
.
A.
1
. B.
1−
. C.
1010
. D.
2017−
.
Câu 3: Có bao nhiêu số phức
z
thỏa mãn
( ) ( )
5 2 6z z i i i z− − + = −
?
A.
1
. B.
3
. C.
4
. D.
2
.
Câu 4: Cho số phức
12zi=−
. Điểm biểu diễn của số phức
w iz=
trên mặt phẳng tọa độ là:
A.
( )
1;2Q
. B.
( )
2;1N
. C.
( )
1; 2M −
. D.
( )
2;1P −
.
Câu 5: Cho số phức
z
thỏa mãn
2
24zz=+
. Tìm giá trị lớn nhất của
z
.
A.
15+
. B.
1 3 5+
. C.
35+
. D.
6 13+
.
Câu 6: Cho số phức
z
thỏa mãn
( )
2 8 5i z i+ + − =
. Tập hợp các điểm biểu diễn số phức là một đường
tròn tâm
I
có tọa độ là:
A.
( )
3; 2I −
. B.
( )
3;2I −
. C.
( )
8;1I −
. D.
( )
8; 1I −
.
Câu 7: Tính diện tích hình phẳng giới hạn bởi các điểm biểu diễn các số phức thỏa mãn
2 4 10z i z i+ − + − − =
.
A.
15
. B.
12
. C.
20
. D. Đáp án khác.
Câu 8: Tập hợp các điểm biểu diễn của số phức
z
thỏa mãn
1 2 2z i z i+ − = − +
là một đường thẳng có
phương trình
A.
30xy+=
. B.
30xy−=
. C.
0xy−=
. D.
0xy+=
.
Câu 9: Cho số phức
z
thỏa mãn:
( ) ( )
2
3 2 2 4+ + − = +i z i i
. Hiệu phần thực và phần ảo của số phức
z
là
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 10: Cho số phức
z
thỏa mãn
12z −=
;
( )
w 1 3 2iz= + +
. Tập hợp các điểm biểu diễn số phức
w
là một đường tròn, bán kính của đường tròn đó bằng
A.
5
. B.
3
. C.
4
. D.
2
.
Câu 11: Xét các số phức
z
thỏa mãn
( )( )
−+42z i z
là số thuần ảo. Biết rằng tập hợp tất cả các điểm biểu
diễn của
z
là một đường tròn. Tìm tọa độ tâm của đường tròn đó.
A.
( )
−−1; 2
. B.
( )
−1; 2
. C.
( )
1; 2
. D.
( )
−1; 2
.
Câu 12: Xét các số phức
z
thỏa mãn
( )
( )
22z i z++
là số thuần ảo. Biết rằng tập hợp tất cả các điểm biểu
diễn của
z
là một đường tròn, tâm của đường tròn đó có tọa độ là
A.
( )
1; 1−
. B.
( )
1;1
. C.
( )
1;1−
. D.
( )
1; 1−−
.
CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
438
Câu 13: Có bao nhiêu số phức
z
thỏa mãn
2
3
10
4
z z i i+ − − =
?
A.
1
. B.
3
. C.
2
. D.
0
.
Câu 14: Có bao nhiêu số phức
z
thỏa mãn
1 10zi− + =
và
2
4
z
z
−
−
là số thuần ảo.
A.
4.
B.
2.
C.
3.
D.
1.
Câu 15: Tính tổng của tất cả các giá trị của tham số
m
để tồn tại duy nhất số phức
z
thoả mãn đồng thời
zm=
và
2
43z m mi m− + =
.
A.
4
. B.
6
. C.
9
. D.
10
.
Câu 16: Cho số phức
( )
( )
1
,
1 2 1
m
zm
mi
+
=
+−
. Tìm các giá trị của
m
để
| | 1zi−
.
A.
0
. B.
1
. C.
4
. D. vô số.
Câu 17: Hai điểm
N
,
M
trong hình vẽ bên dưới lần lượt là điểm biểu diễn số phức
1
z
,
2
z
.
Biết
2 2 5ON OM==
. Giá trị của
22
12
zz+
bằng
A.
5 13
. B.
5 37
. C.
5 21
. D.
5 11
.
Câu 18: Cho số phức
z
thay đổi thỏa mãn
1 2.z −=
Biết rằng tập hợp các số phức
( )
1 3 2w i z= + +
là
đường tròn có bán kính bằng
.R
Tính
.R
A.
8R =
. B.
2R =
. C.
16R =
. D.
4R =
.
Câu 19: Trong mặt phẳng
Oxy
, gọi là hình biểu diễn tập hợp các số phức z thỏa mãn
7 10zz−
. Diện
tích của hình bằng
A.
5
2
. B.
25
12
. C.
7
2
. D.
5
.
Câu 20: Xét các số phức
z
thỏa mãn điều kiện
( )( )
1z i z i+ − −
là số thực. Biết rằng tập hợp các điểm biểu
diễn hình học của
z
là một đường thẳng. Hệ số góc của đường thẳng đó là
A.
1−
. B.
1
. C.
2−
. D.
2
.
Câu 21: Cho số phức
z
thỏa mãn
1 3 3 2zi− + =
. Biết rằng số phức
( )
( )
2019
1 3 2019w i z i= − + +
có tập
hợp các điểm biểu diễn thuộc đường tròn
( )
C
. Diện tích
S
của hình tròn
( )
C
bằng
A.
18
. B.
36
. C.
9
. D.
12
.

CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
439
Câu 22: Cho số phức
z
có mô đun bằng
22
. Biết rằng tập hợp điểm trong mặt phẳng tọa độ biểu diễn
các số phức
( )( )
w = 1 1i z i− + −
là đường tròn có tâm
I
, bán kính
R
. Tổng
a b R++
bằng:
A. 5. B. 7. C. 1. D. 3.
Câu 23: Cho số phức
z
thỏa mãn
3.=z
Biết rằng tập hợp điểm biểu diễn số phức
=+w z i
là một đường
tròn. Tìm tọa độ tâm của đường tròn đó.
A.
( )
0;1
. B.
( )
0; 1−
. C.
( )
1;0−
. D.
( )
1;0
.
Câu 24: Xét các số phức
z
thỏa mãn
( )
1
1
zi
z z i
−+
++
là số thực. Tập hợp các điểm biểu diễn của số phức
w
2
z
=
là parabol có đỉnh
A.
13
;
44
I
−
. B.
11
;
22
I
−
. C.
13
;
22
I
−
. D.
11
;
44
I
−
.
Câu 25: Cho số phức
z
thỏa mãn
1 2 2zi− + =
. Tập hợp điểm biểu diễn số phức
1
z
w
i
=
−
trong mặt
phẳng toạ độ
Oxy
là đường tròn có tâm là
A.
13
;
22
I
−
. B.
13
;
22
I
−
. C.
31
;
22
I
−−
. D.
31
;
22
I
.
Câu 26: Trong mặt phẳng tọa độ
Oxy
, gọi
( )
H
là tập hợp các điểm biểu diễn hình học của số phức
z
thỏa mãn
12
4 3 2 2
zz
zi
+
− −
. Diện tích của hình phẳng
( )
H
là
A.
44−
. B.
88−
. C.
24−
. D.
84−
.
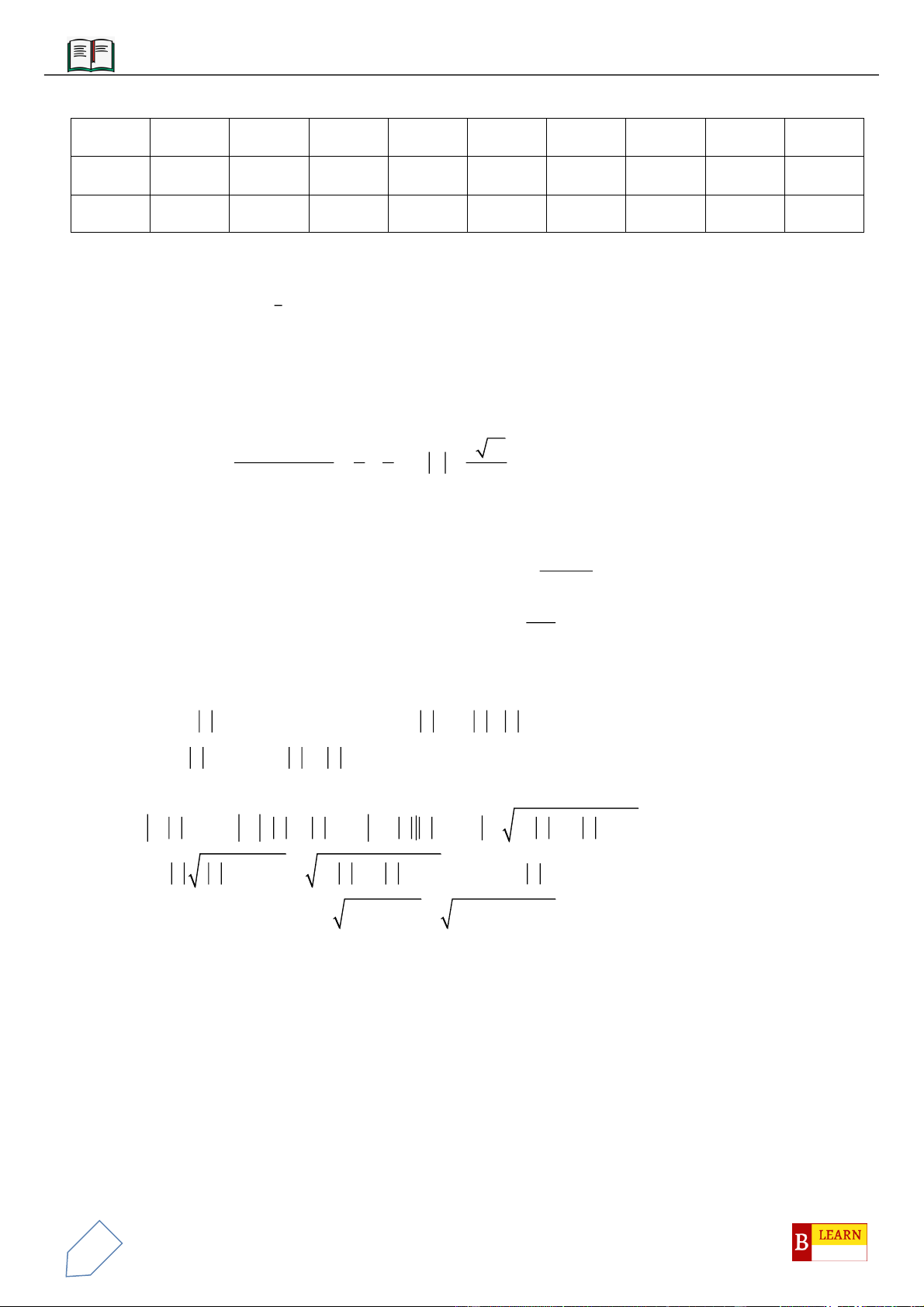
CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
440
BẢNG ĐÁP ÁN
1.B
2.C
3..B
4.B
5.A
6.C
7.C
8.B
9.D
10.C
11.B
12.D
13.A
14.D
15.D
16.A
17.A
18.D
19.C
20.C
21.B
22.D
23.A
24.A
25.B
26.C
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Chọn B
Gọi
z a bi z a bi= + = −
, ta có
( )( ) ( )( )
1 2 3i a bi i a bi+ + − − − =
( )
( )
22
2 2 3 3 2 3 0a bi ai bi a bi ai bi a a b i+ + + − − − + = − − + + =
3 0 3
32
2 3 0 2
aa
zi
a b b
− − = = −
= − +
+ = =
Khi đó
( )
2 3 2
9 3 3 10
1 2 2 2
− − +
= = + =
−
ii
w i w
i
.
Câu 2: Chọn A
Ta có:
2 3 2017
1 2 3 4 ... 2018z i i i i= + + + + +
2 3 2017 2018
1 2 3 ... 2017 2018iz i i i i i = + + + + +
2 2017 2018
1 ... 2018z iz i i i i − = + + + + −
( )
2018
2018
1
1 2018
1
i
i z i
i
−
− = −
−
Mà
( )
( )
1009
1009
2018 2
11ii= = − = −
. Do đó,
( )
2
1 2018 1009 1010
1
i z z i
i
− = + = +
−
Vậy
1009, 1010ab==
hay
1ba−=
.
Câu 3: Chọn B
Ta có:
( ) ( )
5 2 6 5 2 6z z i i i z z z z z i i z iz− − + = − − − + = −
( ) ( )
( )
6 5 2 *z z i z z i − + = + −
.
Mô đun hai vế của biểu thức ta được:
( ) ( ) ( )
2
2
6 5 2 6 25 2z z i z z i z z i z z− + = + − − + = + −
( ) ( )
( )
22
2
6 1 25 2 **z z z z − + = + −
. Đặt
zt=
,
0t
.
Phương trình trở thành:
( ) ( )
22
2
6 1 25 2t t t t− + = + −
.
Bình phương hai vế ta được:
( ) ( )
( ) ( )
( )
( )
22
2 2 2 2 2 2
4 3 2 3 2
6 1 25 2 12 36 1 25 4 4
12 11 4 4 0 1 11 4 0
t t t t t t t t t t
t t t t t t t
− + = + − − + + = + − +
− + + − = − − + =
32
10
11 4 0
t
tt
−=
− + =
.Suy ra
1
10,967
0,621
0,588
t
t
t
t
=
−
Kết hợp với điều kiện
0t
ta có 3 giá trị của
t
thỏa mãn.

CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
441
Từ suy ra, ứng với mỗi
zt=
sẽ có một số phức
( )
52
6
t t i
z
ti
+−
=
−+
thỏa mãn đề bài.
Vậy có
3
số phức
z
thỏa mãn yêu cầu bài toán.
Câu 4: Chọn B
( )
1 2 2w iz i i i= = − = +
.
Vậy điểm biểu diễn của số phức
w
là
( )
2;1N
.
Câu 5: Chọn A
Cách 1: Đặt:
( )
;z x yi x y= +
.
Ta có:
2
24zz=+
( )
( )
2
2
2 2 2 2
2 4 2x y x y xy + = − + +
( ) ( )
2
2 2 2 2 2 2
4 4 4x y x y x y + = − + +
( )
2
2 2 2 2
4 12 16 0x y x y + + − + =
( ) ( )
2
2 2 2 2 2
12 16 16 0x y x y x − + + + − =
22
6 2 5 6 2 5xy − + +
22
6 2 5 1 5z x y = + + = +
.
Vậy giá trị lớn nhất của
z
là
15+
khi
( )
15zi=+
.
Cách 2: Áp dụng bắt đẳng thức trong số phức ta có:
1 2 1 2
z z z z+ −
22
22
4 4 4 4z z z z + − − = − = −
khi
2z
Theo đề ta có:
22
2
2 4 4 4z z z z= + − −
2
24zz −
2
2 4 0zz − −
1 5 1 5z − +
Vậy giá trị lớn nhất của
z
là
15+
.
Câu 6: Chọn B
Giả sử số phức
z x yi=+
,
,xy
Ta có:
( )
85
2 8 5 3 2 5
22
i
i z i z z i
ii
−
+ + − = + = + − =
++
Giả sử số phức
z x yi=+
,
,xy
Ta có:
( ) ( )
22
3 2 5 3 2 5z i x y+ − = + + − =
.
Vậy tập hợp điểm biểu diễn số phức
z
là đường tròn tâm
( )
3;2I −
, bán kính:
5R =
Câu 7: Chọn C
Gọi
( )
;M x y
là điểm biểu diễn của số phức
( )
,.z x yi x y= +
Ta có:
2 4 10z i z i+ − + − − =
( ) ( )
2 1 4 1 10.x y i x y i + + − + − + − =
( ) ( ) ( ) ( )
2 2 2 2
2 1 4 1 10x y x y + + − + − + − =
Đặt
( ) ( ) ( )
2
2
2;1 , 4;1 4 2 0 6.A B AB− = + + =
Khi đó phương trình trở thành:
10.MA MB+=
Khi đó tập hợp những điểm
M
thỏa mãn phương trình là một elip với.
Độ dài trục lớn
10
2 10 5.
2
aa= = =
Tiêu cự
6
2 6 3.
2
c AB c= = = =

CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
442
Độ dài trục bé
2b
với
2 2 2 2 2
5 3 16 4.b a c b= − = − = =
Vậy diện tích hình phẳng giới hạn bởi các điểm biểu diễn các số phức thỏa mãn
2 4 10z i z i+ − + − − =
là diện tích Elip trên:
4.5 20S ab
= = =
.
Câu 8: Chọn B
Gọi số phức
z
thỏa mãn đề bài là
( )
,z x yi x y= +
.
Từ giả thiết
1 2 2z i z i+ − = − +
suy ra
( ) ( )
1 2 2 1x y i x y i+ + − = − + −
.
Suy ra:
( ) ( ) ( ) ( )
2 2 2 2
1 2 2 1 6 2 0 3 0x y x y x y x y+ + − = − + − − = − =
.
Vậy tập hợp các điểm biểu diễn của số phức
z
là đường thẳng có phương trình
30xy−=
.
Câu 9: Chọn D
Gọi số phức
=+z a bi
( )
, ab
.
Ta có
( ) ( )
2
3 2 2 4+ + − = +i z i i
( )( ) ( )
2
3 2 4 2 + + = + − −i a bi i i
.
( )
3 2 2 3 4 3 4 − + + = + − +a b a b i i i
( )
3 2 2 3 1 5 − + + = +a b a b i i
.
321
2 3 5
−=
+=
ab
ab
1
1
=
=
a
b
0 − =ab
.
Vậy hiệu phần thực và phần ảo của số phức
z
là
0
.
Cách 2:
( ) ( )
2
3 2 2 4+ + − = +i z i i
( )
2
42
1
32
ii
zi
i
+ − −
= = +
+
.
Phần thực
1a =
, phần ảo
1b =
0ab − =
.
Câu 10: Chọn C
Cách 1.
Giả sử
w a bi=+
với
,ab
.
Ta có
( )
1 3 2a bi i z+ = + +
( )
33
2
1
1 3 1 3
a b i
a bi
zz
ii
− + −
−+
= − =
++
.
Ta có
( )
33
1 2 2
13
a b i
z
i
− + −
− = =
+
( )
( )
2
2
33
2
2
ab− + −
=
( )
( )
2
2
3 3 16ab − + − =
.
Do đó tập hợp các điểm biểu diễn số phức
w
là đường tròn
( )
( )
2
2
3 3 16xy− + − =
.
Suy ra bán kính của đường tròn đó là
4
.
Cách 2.
Ta có
( )
w 2 1 3iz− = +
( )
( )
w 2 1 3 1 3 1i i z− − − = + −
.
Suy ra
( )
( )
w 3 3 1 3 1i i z− − = + −
( )
w 3 3 1 3 . 1i i z − + = + −
( )
w 3 3 4i − + =
.
Do đó tập hợp các điểm biểu diễn số phức
w
là đường tròn có tâm
( )
3; 3I
, bán kính
4R =
.
Câu 11: Chọn B

CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
443
Gọi
( )
,z x yi x y= +
.
Ta có
( )
( )
( ) ( ) ( ) ( ) ( )( )
4 2 4 2 = 2 4 2 4z i z x y i x yi x x y y x y i xyi− + = + − + − + + − + + − −
Theo yêu cầu bài toán ta có
( ) ( )
22
2 4 0 2 4 0x x y y x y x y+ + − = + + − =
.
Vậy tập hợp tất cả các điểm biểu diễn của
z
là một đường tròn có tâm
( )
1;2 , 5IR−=
.
Câu 12: Chọn D
Gọi
z x yi=+
,
,xy
.
Ta có
( )
( )
( )( )
2 2 2 2z i z x yi i x yi+ + = + + − +
( ) ( )
22x y i x yi= + + + −
( ) ( ) ( )( )
2 2 2 2x x y y x y xy i= + + + + + + −
.
( )
( )
22z i z++
là số thuần ảo
( ) ( )
2 2 0x x y y + + + =
( ) ( )
22
1 1 2xy + + + =
.
Vậy tập hợp các điểm biểu diễn của số phức
z
là đường tròn tâm
( )
1; 1I −−
.
Câu 13: Chọn A
Biến đổi
2
3
10
4
z z i i+ − − =
2
3
1
4
z z i
= + −
. Lấy môđun hai vế ta có:
( )
2
2 2 2 4 4 2 2 2
3 9 3 5
1 1 16 40 25 0 0
4 16 2 4
z z z z z z z z z
= + − = + − + − + = =
Thay vào
2
3
1
4
z z i
= + −
1
1
2
zi = −
.
Câu 14: Chọn D
Đặt
( )
;z a bi a b= +
. Điều kiện
4z=
.
( ) ( ) ( )
22
1
1 10 : 1 1 10z i C a b− + = − + + =
có tâm
( )
1
1; 1I −
và bán kính
1
10R =
.
( )( )
( )
2
2
24
22
44
4
a bi a bi
z a bi
z a bi
ab
− + − −
− − +
==
− − +
−+
là số thuần ảo khi
( )( )
2
2 4 0a a b− − + =
.
Do đó,
( ) ( )
2
2
2
: 3 1C a b− + =
có tâm
( )
2
3;0I
và bán kính
2
1R =
.
Ta có,
( ) ( )
( )
2
2
1 2 1 2
3 1 0 1 5I I R R= − + − − = +
nên
( )
2
C
cắt
( )
1
C
tại hai điểm phân biệt.
Vì
( ) ( )
12
40z i C C= +
nên có duy nhất số phức thỏa yêu cầu bài.
Câu 15: Chọn D
Đặt
( )
,z x yi x y= +
. Ta có điểm biểu diễn
z
là
( )
;M x y
.
Với
0m =
, ta có
0z =
, thoả mãn yêu cầu bài toán.
Với
0m
, ta có:
zm=
M
thuộc đường tròn
( )
1
C
tâm
( )
0;0 ,I
bán kính
Rm=
( ) ( )
22
24
4 3 4 3z m mi m x m y m m− + = − + + =
M
thuộc đường tròn
( )
2
C
tâm
( )
4 ; 3 ,I m m
−
bán kính
2
Rm
=
.
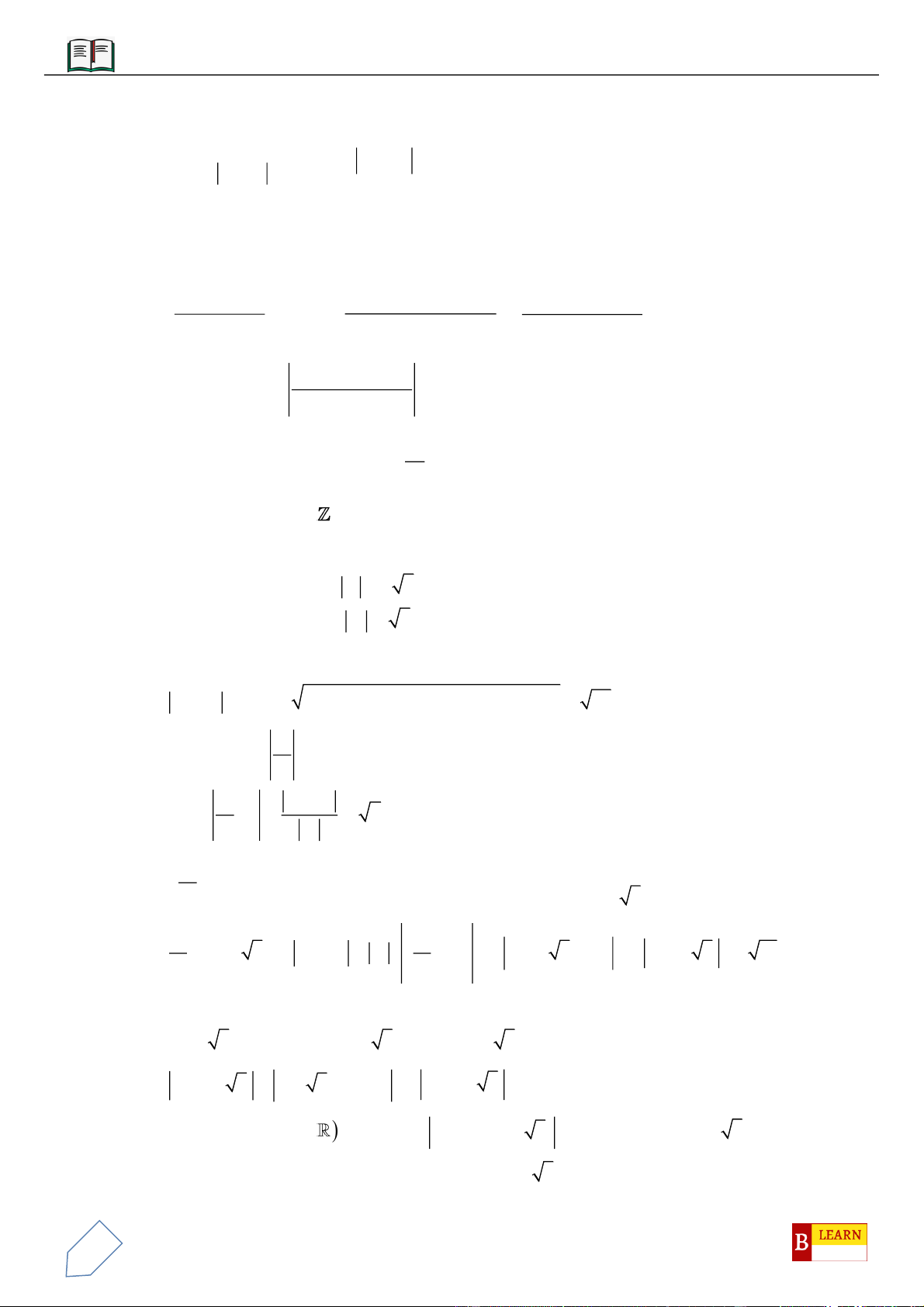
CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
444
Có duy nhất một số phức
z
thoả mãn yêu cầu bài toán khi và chỉ khi
( )
1
C
và
( )
2
C
tiếp xúc nhau
2
2
5
4
.
5
6
0
m m m
II R R
m
m m m
II R R
m
m
=+
=+
=
=−
=−
=
Kết hợp với
0m =
, suy ra
0;4;6m
. Vậy tổng tất cả các giá trị của
m
là
10
.
Câu 16: Chọn A
( )
1
1 2 1
m
z
mi
+
=
+−
( )
( )
1 1 2
12
m m i m
zi
m mi
+ − − +
− =
−+
( )
3 1 1
12
m m i
m mi
+ − −
=
−+
.
Ta có:
( )
( )
3 1 1
| | 1 1
12
m m i
zi
m mi
+ − −
−
−+
( ) ( ) ( ) ( )
2 2 2 2
3 1 1 1 2m m m m + + − − +
.
( )( )
1 5 1 0mm + +
1
1;
5
m
−
−
.
Vậy không tồn tại
m
thỏa mãn điều kiện đề bài.
Câu 17: Chọn A
Từ giả thiết ta có:
1
2
25
5
120
ON z
OM z
MON
==
==
=
22
12
2 . .cos 35z z MN OM ON OM ON MON − = = + − =
Khi đó
1
2
12
1
22
2
17
z
z
zz
z
zz
=
−
− = =
.
Đặt
22
22
1
22
2
1
4
4
2 5 7
3
( 1) 7
a
ab
ab
z
a bi
z
a
b
ab
=−
+=
+=
= +
− + =
=
− + =
( )
2
2
2 2 2
11
1 2 2
22
1 3 1 5 1 3 1 5 1 2 3 5 13
zz
i z z z i i
zz
= − + = + = − + = − =
.
Câu 18: Chọn D
( )
1 3 2w i z= + +
( )
( )
1 3 1 3 3w i z i = + − + +
( )
( )
3 3 1 3 1w i i z − − = + −
( )
3 3 4 *wi − − =
.
Đặt
w x yi=+
( )
,xy
thì:
( )
( )
* 3 3 4x i y − + − =
( )
( )
2
2
3 3 16xy − + − =
.
Vậy tập hợp các số phức
w
là đường tròn tâm
( )
3; 3I
, bán kính
4R =
.
Câu 19: Chọn B

CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
445
Đặt
z x yi=+
( )
,xy
z x yi = −
. Từ:
7 10zz−
22
22
36 64 100 1
100 100
36 64
xy
xy + +
.
Do đó: là hình Elip:
22
22
1
55
34
xy
+=
có trục lớn và trục bé lần lượt
10 5
2 ;2
32
ab==
.
Theo công thức tính diện tích Elip ta có:
5 5 25
.
3 4 12
S ab
= = =
.
Câu 20: Chọn C
Gọi
z x yi=+
,
( )
;xy
.
Ta có
( )( ) ( )( )
( )
( )
22
1 1 1 2 1z i i x yi i x yi i x x y xz yi+ − − = + + − − − = + + − − + +
.
Số phức
( )( )
1z zii+ − −
là số thực khi
2 1 0xy+ + =
Suy ra tập hợp tất cả các điểm biểu diễn của
z
trong mặt phẳng tọa độ là đường thẳng có phương
trình
2 1 0 2 1x y y x+ + = = − −
. Do đó hệ số góc của đường thẳng là
2−
.
Câu 21: Chọn B
Ta có:
1 3 3 2zi− + =
1 3 3 2zi− + =
1 3 3 2zi − − =
.
Mà
( )
( )
( )
( )
( )
( )
2019
1 3 2019 1 1 3 1 6 2019w i z i i z i i= − + + = + − − + + +
hay
( )
( )
1 1 3 2014 7w i z i i= + − − + +
( )
( )
2014 7 1 1 3w i i z i − − = + − −
.
Suy ra:
( )
( )
2014 7 1 1 3w i i z i− − = + − −
2014 7 1 1 3 2.3 2 6w i i z i − − = + − − = =
2014 7 6wi − − =
.
Vậy tập hợp điểm biểu diễn là đường tròn
( )
C
có tâm
( )
2014;7I
và bán kính
6R =
.
Suy ra diện tích
S
của hình tròn
( )
C
bằng:
2
36SR
==
.
Câu 22: Chọn D
Gọi
(
w = x yi x+
,
)
y
. Theo bài ra ta có:
w 1 2
1
i
z
i
−+
=
−
( ) ( )
12
1
x y i
z
i
− + +
=
−
( ) ( )
12
1
x y i
z
i
− + +
=
−
( ) ( )
12
22
1
x y i
i
− + +
=
−
.
( ) ( )
22
12
22
2
xy− + +
=
( ) ( )
22
1 2 16 − + + =xy
Tập hợp điểm biểu diễn cho số phức
w
là đường tròn có tâm
I
và bán kính
R =
4.
Vậy tổng
3a b R+ + =
Câu 23: Chọn A
Giả sử
( )
,= + w x yi x y
Ta có
= + = −w z i z w i
Mà
3 3 3= = − =z z w i
( ) ( )
2
2
1 3 1 9. + − = + − =x y i x y
Vậy tập hợp điểm biểu diễn số phức
w
là đường tròn tâm
( )
0;1I
, bán kính
3.=r
Câu 24: Chọn A
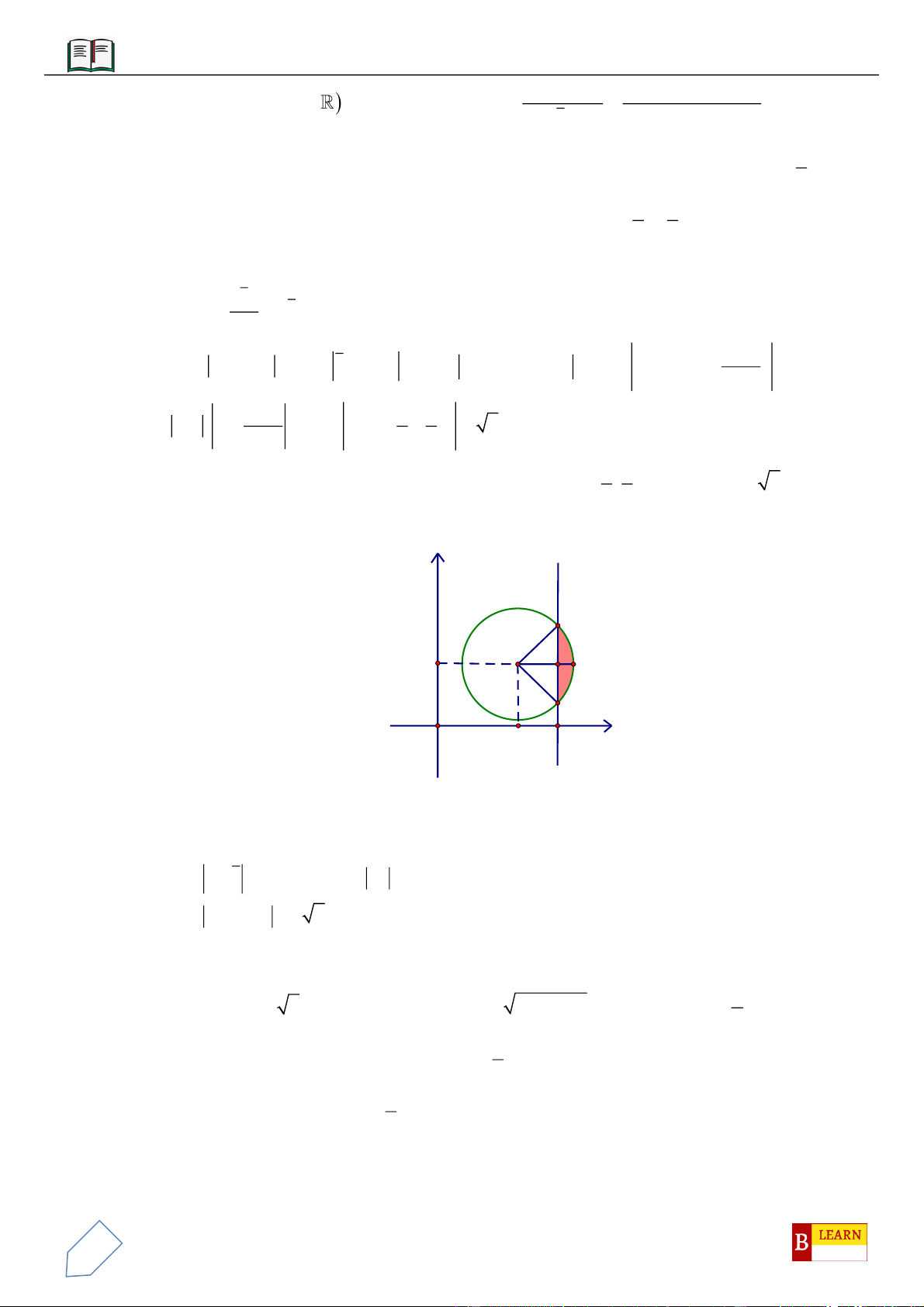
CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
446
Gọi
( )
w , ,x yi x y= +
( )
( ) ( )
2 1 2 1
1
2 2 2
14
1
x y i
zi
z w x yi
xi
z z i
− + +
−+
= = + =
+
++
là số thực
( ) ( ) ( )
2 1 2 1 1 4x y i xi − + + −
là số thực
2
8 4 2 1 0x x y− + + + =
2
1
42
2
y x x = − −
Vậy tập hợp điểm biểu diễn cho số phức
w
là parabol có đỉnh
13
;
44
I
−
.
Câu 25: Chọn B
Ta có:
( )
1
1
z
w z i w
i
= = −
−
Khi đó:
1 2 2 1 2 2z i z i− + = − − =
( ) ( )
12
1 1 2 2 1 . 2
1
i
i w i i w
i
+
− − − = − − =
−
1 2 1 3
1 . 2 2
1 2 2
i
i w w i
i
+
− − = − − + =
−
.
Tập hợp điểm biểu diễn số phức
w
là đường tròn có tâm
13
;
22
I
−
, bán kính
2R =
.
Câu 26: Chọn C
Cách 1:
Trong mặt phẳng tọa độ
Oxy
, điểm biểu diễn số phức
z x yi=+
là điểm
( )
;M x y
.
Ta có
12
4 3 2 2
zz
zi
+
− −
( ) ( )
22
2 12
4 3 8
x
xy
− + −
( ) ( )
22
6
6
4 3 8
x
x
xy
−
− + −
.
Hình phẳng
( )
H
là hình tô đậm trên hình vẽ.
Ta có
22IA IB==
,
2ID =
và
22
2 2 4AB AD IA ID= = − =
, suy ra
2
AIB
=
.
Gọi
1
S
là diện tích hình quạt
AIB
. Ta có
2
1
1
2
4
SR
==
.
Diện tích tam giác
AIB
là
2
1
.4
2
S IA IB==
.
Vậy diện tích hình phẳng
( )
H
là
( )
12
24
H
S S S= − = −
.
Cách 2:
x
y
D
6
O
A
B
I
3
4
M

CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
447
Hình phẳng
( )
H
được biểu thị là phần tô màu trên hình vẽ, là hình giới hạn bởi đường tròn
( )
C
có tâm
( )
4;3I
, bán kính
22R =
và đường thẳng
6x =
.
Ta có
( ) ( )
22
4 3 8xy− + − =
( ) ( )
22
3 8 4yx − = − −
( )
2
3 8 4yx = − −
.
( )
C
cắt đường thẳng
3y =
tại 2 điểm có tọa độ
( )
4 2 2;3
Gọi
0
S
là diện tích của hình phẳng giới hạn bởi các đường
( )
2
3 8 4yx= + − −
,
3y =
,
6x =
,
4 2 2x =+
. Ta có
( )
( )
( )
4 2 2
2
0
6
2. 2. 8 4 d 2,2831
H
S S x x
+
= = − −
.

CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
448
BÀI TOÁN QUY VỀ GIẢI PT, HPT VÀ ĐIỂM BIỂU DIỄN SP
Câu 1: Có bao nhiêu số phức
z
thỏa mãn
( )
6 8 2zi− + =
và
. 64zz=
.
A.
3
. B.
4
. C.
2
. D.
1
.
Câu 2: Cho số thực
,x
y
thỏa mãn
(2 )i (1 2i) 3 7ix y y− + − = +
với
i
là đơn vị ảo. Giá trị của
2
x xy−
bằng
A. 30. B. 40. C. 10. D. 20.
Câu 3: Cho số phức z thỏa mãn
3 (1 ) 1 5z i z i+ + = −
. Tìm mô đun của z
A.
5z =
. B.
5z =
. C.
13z =
. D.
10z =
.
Câu 4: Cho số phức
z
thỏa mãn điều kiện
( )
2
1 2 4 20i z z i+ + = −
. Tìm
z
.
A.
25z =
. B.
7z =
. C.
4z =
. D.
5z =
.
Câu 5: Có bao nhiêu số phức
z
thỏa mãn
( ) ( )
1 2 13 2i z i z i+ + − = +
?
A. 4. B. 3. C. 2. D. 1.
Câu 6: Cho số phức
z
thỏa mãn:
( )
1 2 . 15− + = +z i z i i
. Tìm môđun của số phức
z
?
A.
5=z
. B.
4=z
. C.
25=z
. D.
23=z
.
Câu 7: Có bao nhiêu số phức
z
thỏa mãn điều kiện
.2z z z+=
và
2?z =
A. 2. B. 3. C. 1. D. 4.
Câu 8: Có bao nhiêu số phức
z
thỏa mãn
2 3 1z i z i− + = + −
và
( )
2
25z z z+ + =
?
A.
1
. B.
0
. C.
2
. D.
4
.
Câu 9: Cho số phức
( )
,z a bi a b= +
thỏa
( )
2 3 2 16 3 .i z z i+ + = +
Tính giá trị biểu thức
3.P a b=+
A.
11P =−
. B.
17P =
. C.
1P =−
. D.
1P =
.
Câu 10: Cho số phức
z
thỏa mãn
( )
3 . . 7 6i z i z i+ − = −
. Môđun của số phức
z
bằng
A.
25
. B.
25
. C.
5
. D.
5
.
Câu 11: Cho số phức
z
thoả mãn
( ) ( )
1 2 2 3 4 12z i z i i+ − − = − +
. Tìm toạ độ điểm
M
biểu diễn số phức
z
.
A.
( )
3;1M
. B.
( )
3; 1M −
. C.
( )
1;3M −
. D.
( )
1;3M
.
Câu 12: Cho số phức
z
thoả mãn
( )
1 3 3 5 7i z z i+ − = − +
. Điểm nào sau đây trong các điểm
, , ,M N P Q
biểu diễn cho số phức
z
?
CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
449
A. Điểm
M
. B. Điểm
N
. C. Điểm
P
. D. Điểm
Q
.
Câu 13: Cho số phức
z
thoả mãn
( ) ( )
2 3 1 2 8i z i z i+ − − = − +
. Khoảng cách từ điểm biểu diễn cho số
phức
z
trên mặt phẳng toạ độ
Oxy
đến điểm
( )
1;2M
bằng
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 14: Cho các số thực
,ab
thỏa mãn
( ) ( )
2 5 7 3i a i b a i
− − = + +
, với
i
là đơn vị ảo. Tính
−ab
A.
2
. B.
6
. C.
12
. D.
3
.
Câu 15: Cho số phức
z
thỏa mãn
2 7 3z z i z− = − + +
. Tnh
z
.
A.
5z =
. B.
3z =
. C.
13
4
z =
. D.
25
4
z =
.
Câu 16: Tnh mô đun của số phức
z
thỏa mãn
( ) ( )
1 2 1 4 0z i z i i+ + − + − =
với
i
là đơn vị ảo.
A.
6
. B.
5
. C.
2
. D.
3
.
Câu 17: Tìm tập hợp
T
gồm tất cả các số phức
z
thỏa mãn đồng thời hai điều kiện
2z =
và
2
z
là số
thuần ảo.
A.
1 ;1 ; 1 ;1T i i i i= − − − − + +
. B.
1 ;1T i i= − +
.
C.
1Ti= − +
. D.
1Ti= − −
.
Câu 18: Cho số phức
( )
,= + z a bi a b
thỏa mãn
( )
1 2 3 2+ + = +i z z i
. Tính
=+P a b
.
A.
1=P
. B.
1
2
=−P
. C.
1
2
=P
. D.
1=−P
.
Câu 19: Cho số phức
z a bi=+
( )
, ab
thỏa mãn
1 3 0z i z i+ + − =
. Tính
23S a b=+
.
A.
6S =−
. B.
6S =
. C.
5S =−
. D.
5S =
.
Câu 20: Gọi
S
là tập hợp các số phức
z
thỏa mãn điều kiện
4
zz=
. Số phần tử của
z
là
A.
7
. B.
6
. C.
5
. D.
4
.
Câu 21: Cho số phức
( , ; , 0)z a bi a b a b= +
thỏa mãn
5
4 2 2 .
3
z z i z
+ = −
Tính
2
.
2
ab
S
ab
+
=
−
A.
2 2 3S = − −
. B.
2 2 2S =−
. C.
2 2 2S =−
. D.
2 2 3S =+
.

CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
450
Câu 22: Có bao nhiêu số phức
z
thỏa mãn
( 2 3 ) 4 (4 5 ) .z z i i i z− + + = +
A. 1. B. 2. C. 4. D. 3.
Câu 23: Giả sử
12
,zz
là hai nghiệm phức của phương trình
2 1 2 1 3i z z i z i
và
12
1zz
. Tính
12
23M z z
.
A.
19M
. B.
19M
. C.
25M
. D.
5M
.
Câu 24: Tìm mô đun của số phức số
z
biết
( )( )
( )
( )
2 1 1 1 1 2 2z i z i i− + + + − = −
.
A.
1
9
. B.
2
3
. C.
2
9
. D.
1
3
.
Câu 25: Có bao nhiêu số phức
z
thỏa mãn
2
z z z z z= + + −
và
2
z
là số thuần ảo.
A. 4. B. 2. C. 3. D. 5.
Câu 26: Có bao nhiêu số phức
z
thỏa mãn
+ + − =z z z z3 2 12
và
+ − = − +z i z i2 3 4
?
A. 1. B. 4. C. 3. D. 2.
Câu 27: Cho số phức
z
không phải là số thực và
2
2
24
24
zz
zz
−+
++
là số thực. Có bao nhiêu số phức
z
thỏa mãn
2
z z z z z+ + − =
?
A.
0
. B.
2
. C.
4
. D.
8
.
Câu 28: Cho số phức
z
thỏa mãn
5z =
và
3 3 10z z i+ = + −
. Tìm số phức
w 4 3zi= − +
.
A.
w 3 8i= − +
. B.
w 1 3i=+
. C.
w 1 7i= − +
. D.
w 4 8i= − +
.
Câu 29: Cho các số phức
z
thỏa mãn hai điều kiện
2z =
và
2
z
là số thuần ảo. Tổng bình phương phần
thực của tất cả các số phức
z
đó bằng
A.
5
. B.
4
. C.
2
. D.
3
.
Câu 30: Có bao nhiêu số phức thỏa mãn ?
A. 4. B. 2. C. 1. D. 3.
Câu 31: Trong các số phức
z
thỏa mãn
4 3 8 5 2 38z i z i+ − + − − =
. Tìm giá trị nhỏ nhất của
24zi−−
.
A.
1
2
. B.
5
2
. C.
2
. D.
1
.
Câu 32: Trong mặt phẳng
Oxy
, tập hợp điểm biểu diễn các số phức
z
thỏa mãn
2 1 2z z z− = − +
là hình
gồm:
A. hai đường thẳng. B. hai đường tròn. C. một đường tròn. D. một đường thẳng.
Câu 33: Cho số phức
z
thỏa mãn
2
3 i . 9z z z+ +
. Tìm tập hợp điểm biểu diễn số phức
thỏa mãn
1iz
= + −
z
( )
2
2019
11z z z i z z i− + − + + =
CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
451
A. Hình tròn
( )
2
2
5 73
1
8 64
xy
− + +
. B. Đường tròn
( )
2
2
5 73
1
8 64
xy
− + +
.
C. Đường tròn
( ) ( )
22
1 3 9xy− + +
. D. Hình tròn
( ) ( )
22
1 3 9xy− + +
.
Câu 34: Biết phương trình
4 3 2
0x ax bx cx d+ + + + =
,
( )
, , ,a b c d
nhận
1
1zi= − +
và
2
12zi=+
là
nghiệm. Tính
a b c d+ + +
.
A.
10
. B.
9
. C.
7−
. D.
0
.
Câu 35: Tìm tập hợp tất cả các giá trị của tham số
m
để có đúng 4 số phức
z
thỏa mãn đồng thời các điều
kiện
2
z z z z z+ + − =
và
zm=
.
A.
2; 2 2
. B.
2;2 2
. C.
2
. D.
( )
2;2 2
.
Câu 36: Cho các số phức
z
thỏa mãn
2020
2 1 2z i z i− = − +
. Tập hợp các điểm biểu diễn số phức
w 2 1 4zi= − +
trên mặt phẳng tọa độ là một đường thẳng. Khoảng cách từ
( )
2; 3I −
đến đường
thẳng đó bằng
A.
10 3
3
. B.
18 5
5
. C.
10 5
5
. D.
18 13
13
.
Câu 37: Hình phẳng giới hạn bởi tập hợp điểm biểu diễn các số phức
z
thỏa mãn
3 3 10zz− + + =
có
diện tích bằng
A.
12
. B.
20
. C.
15
. D.
25
.
Câu 38: Cho số phức
z
có
2z =
. Biết tập hợp biểu diễn các số phức
( )
3 3 4w i i z= + − −
là một đường
tròn, bán knh đường tròn đó bằng
A.
52
. B.
55
. C.
10
. D.
25
.
Câu 39: Cho số phức
z
thỏa mãn
( )
2z i z+=
. Mệnh đề nào dưới đây đúng?
A.
13
22
z
. B.
35
22
z
. C.
1
2
z
. D.
57
22
z
.
Câu 40: Cho số phức
( )
2
31z m m i= + + −
,với
m
là tham số thực thay đổi. Tập hợp các điểm biểu diễn số
phức
z
thuộc đường cong
( )
C
. Tnh diện tch hình phẳng giới hạn bởi
( )
C
và trục hoành.
A.
2
3
. B.
8
3
. C.
1
3
. D.
4
3
.
Câu 41: Cho hai số phức
12
,zz
khác
0
, thỏa mãn
22
1 2 1 2
z z z z+=
.
,MN
lần lượt là hai điểm biểu diễn số
phức
12
,zz
trên mặt phẳng
Oxy
. Mệnh đề nào sau đây đúng?
A. Tam giác
OMN
nhọn và không đều. B. Tam giác
OMN
đều.
C. Tam giác
OMN
tù. D. Tam giác
OMN
vuông.
Câu 42: Cho số phức
z
thỏa mãn điều kiện
2 3 3zi− +
. Trong mặt phẳng
Oxy
, tập hợp điểm biểu diễn
số phức
21w z i= + −
là hình tròn có diện tích
A.
25S
=
. B.
16S
=
. C.
9S
=
. D.
36S
=
.

CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
452
Câu 43: Cho số phức
z
thỏa mãn
( )
( )
1 3 1 3 25z i z i+ − + + =
. Biết tập hợp các điểm biểu diễn của số phức
z
là một đường tròn có tâm
( )
;I a b
và bán kính
c
. Tổng
abc++
bằng
A. 9. B. 3. C. 2. D. 7.
Câu 44: Cho các số phức
1
z
,
2
z
thỏa mãn phương trình
2 3 5zi− − =
và
12
6zz−=
. Biết rằng tập hợp
các điểm biểu diễn số phức
12
w z z=+
là một đường tròn. Tnh bán knh đường tròn đó.
A.
8R =
. B.
4R =
. C.
22R =
. D.
2R =
.
Câu 45: Cho các số phức thỏa mãn . Tập hợp các điểm biểu diễn số phức
trên mặt phẳng tọa độ là một đường thẳng. Khoảng cách từ đến đường
thẳng đó bằng
A. . B. . C. . D. .
Câu 46: Cho số phức z thỏa mãn điều kiện
3 4 2zi− +
. Trong mặt phẳng
Oxy
tập hợp các điểm biểu
diễn số phức
w 2 1zi= + −
là hình tròn có diện tích là
A.
25S
=
. B.
9S
=
. C.
12S
=
. D.
16S
=
.
Câu 47: Gọi
S
là tập tất cả các giá trị thực của tham số
m
để tồn tại 4 số phức
z
thỏa mãn
2z z z z+ + − =
và
( ) ( )
2z z z z m+ − + −
là số thuần ảo. Tổng các phần tử của
S
là.
A.
21+
. B.
21
2
+
. C.
3
2
. D.
1
2
.
z
2020
2 1 2z i z i− = − +
2 1 4w z i= − +
( )
2; 3I −
18 5
5
18 13
13
10 3
3
10 5
5
CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
453
BẢNG ĐÁP ÁN
1. D
2. B
3. D
4. D
5.D
6.A
7.C
8.C
9.C
10..C
11.B
12.B
13.A
14.B
15.A
16.B
17.A
18.D
19.A
20.C
21.A
22.A
23.A
24.B
25.D
26.D
27.C
28.C
29.B
30.D
31.D
32.A
33.A
34.B
35.A
36.C
37.B
38.C
39.A
40.C
41.B
42.D
43.D
44.A
45.D
46.D
47.C
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Chọn D
Gọi
( )
,z x yi x y= +
.
Khi đó:
( )
( ) ( ) ( )
( )
22
22
6 8 2
6 8 4 1
64 2
. 64
zi
xy
xy
zz
− + =
− + − =
+=
=
Trong mặt phẳng tọa độ
Oxy
thì:
( )
1
là phương trình của đường tròn
( )
1
C
có tâm
( )
6;8I
, bán kính
1
2R =
.
( )
2
là phương trình của đường tròn
( )
2
C
có tâm
( )
0;0O
, bán kính
2
8R =
.
Vì
22
12
6 8 10OI R R= + = = +
nên đường tròn
( )
1
C
và
( )
2
C
tiếp xúc ngoài nhau như hình vẽ.
Suy ra hệ phương trình
( ) ( )
1 , 2
có nghiệm duy nhất.
Vậy có đúng
1
số phức thỏa mãn ycbt.
Chú ý: Ta có thể tìm nghiệm của hệ phương trình
( ) ( )
1 , 2
như sau:
Hệ
( ) ( )
2
22
2
2
2
24
3 4 40 0
12 96 16 0
24 32
5
32
55
5
1 , 2
64 0
64 0
zi
xy
x
xy
x y x y
xy
y
=
+ − =
+ − + − =
=
=+
+
+ − =
−=
.
Câu 2: Chọn B
Ta có
(2 )i (1 2i) 3 7ix y y− + − = +
3 (2 3 7) 0y x y i − + − − =
30
2 3 7 0
y
xy
−=
− − =
3
8
y
x
=
=
.
2
40x xy − =
.
Câu 3: Chọn D

CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
454
Gọi
z a bi z a bi= + = −
3 (1 ) 1 5 3( ) (1 )( ) 1 5
3 3 1 5 (4 ) ( 2 )i 1 5
4 1 1
1 3 10
2 5 3
z i z i a bi i a bi i
a bi a bi ai b i a b a b i
a b a
z i z
a b b
+ + = − − + + + = −
− + + + − = − − + − = −
− = =
= + =
− = − =
Câu 4: Chọn D
Gọi
z a bi=+
với
,ab
.
Ta có
( ) ( )( )
2
1 2 4 20 1 4 4 4 20i z z i i a bi a bi i+ + = − + − + + − = −
3 4 20 4
4 3 4 3
a b a a
a b b b
− − + = − =
− − = =
4 3 5z i z = + =
.
Câu 5: Chọn D
Gọi
( )
;z x yi x y= +
, khi đó ta có:
( ) ( )
1 2 13 2i z i z i+ + − = +
( )( ) ( )( )
1 2 13 2i x yi i x yi i + + + − − = +
( ) ( )
2 2 13 2x y x y i x y x y i i − + + + − − + = +
3 2 13 2x y yi i − − = +
3 2 13 3
22
x y x
yy
− = =
− = = −
. Vậy
32zi=−
.
Câu 6: Chọn A
Đặt
=+z a bi
,
( , )ab
, ta có:
( )
1 2 . 15− + = +z i z i i
( )( ) ( )
1 2 . 15 + − + − = +a bi i a bi i i
2 2 15 − + + + + = +a ai bi b ai b i
( ) ( )
3 15 + + − = +a b b a i i
3 15 3
14
+ = =
− = =
a b a
b a b
3 4 5 = + =z i z
.
Câu 7: Chọn C
Cách 1: Lưu ý:
2
.z z z=
. Đặt
z x yi=+
( )
,xy
.
Theo đề ta có
22
22
2
2
x y x yi
xy
+ + + =
+=
( )
22
42
4
x yi
xy
+ + =
+=
( ) ( )
( )
2
2
1
22
2
44
4
x y C
x y C
+ + =
+=
Số số phức
z
thỏa mãn yêu cầu bài toán là số giao điểm của hai đường tròn
( )
1
C
và
( )
2
C
.
Đường tròn
( )
1
C
có tâm
( )
1
4;0I −
, bán kính
1
2R =
, đường tròn
( )
2
C
có tâm
( )
2
0;0I
, bán kính
2
2R =
.
Kiểm tra thấy
1 2 1 2
I I R R=+
. Vậy hai đường tròn tiếp xúc ngoài, số giao điểm là 1.
Cách 2: Ta có:
. 2 . 1 2 1 1 1 1z z z z z z z+ = + = + = + =
Vậy số phức
z
thỏa mãn 2 phương trình
2
11
z
z
=
+=
Gọi
A
là điểm biểu diễn của số phức
z
thì
A
là giao điểm của đường tròn
( )
1
C
tâm
( )
0;0O
, bán kính
2R =
và đường tròn
( )
2
C
tâm
( )
1;0I −
, bán kính
1R
=
.

CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
455
Mặt khác ta có
1OI R R
= = −
( )
1
C
và
( )
2
C
tiếp xúc trong, vậy số giao điểm là 1.
Câu 8: Chọn C
Cách 1.
Đặt
z x yi=+
(
x
,
y
). Ta có
2 3 1z i z i− + = + −
( ) ( ) ( ) ( )
2 2 2 2
2 3 1 1x y x y − + + = + + −
6 8 11 0xy − − =
6 11
8
x
y
−
=
.
( )
2
25z z z+ + =
( )
22
25x y x yi x yi + + + + − =
22
4 5 0x y x + + − =
.
Thay vào, ta được
2
2
6 11
4 5 0
8
x
xx
−
+ + − =
2
100 124 199 0xx + − =
31 4 371
50
31 4 371
50
x
x
−+
=
−−
=
.
Với
31 4 371
50
x
−+
=
92 3 371
50
y
−+
=
31 4 371 92 3 371
50 50
zi
− + − +
=+
.
Với
31 4 371
50
x
−−
=
92 3 371
50
y
−−
=
31 4 371 92 3 371
50 50
zi
− − − −
=+
.
Vậy có hai số phức thỏa mãn yêu cầu bài toán.
Cách 2.
Từ và suy ra số các số phức
z
thỏa mãn yêu cầu bài toán bằng số giao điểm của đường thẳng
:6 8 11 0xy − − =
với đường tròn
( )
22
: 4 5 0C x y x+ + − =
.
Đường tròn
( )
C
có tâm
( )
2;0I −
và bán kính
3R =
.
Ta có
( )
22
12 11
,
68
dI
−−
=
+
23
10
=
R
nên
cắt
( )
C
tại hai điểm phân biệt.
Do đó, có hai số phức thỏa mãn yêu cầu bài toán.
Câu 9: Chọn C
Ta có:
( ) ( )( ) ( )
2 3 2 16 3 2 3 2 16 3i z z i i a bi a bi i+ + = + + + + − = +
( )
1
4 3 3 16 3
4
a
a b ai i
b
=
− + = +
=−
. Vậy
3 1.P a b= + = −
Câu 10: Chọn C
Đặt
z x yi=+
( )
;xy
z x yi = −
.
Khi đó
( )
3 . . 7 6i z i z i+ − = −
( )( ) ( )
3 7 6i x yi i x yi i + + − − = −
( )
3 2 3 7 6x y yi i − + = −
.
3 2 7
36
xy
y
−=
=−
1
2
x
y
=
=−
12zi = −
. Vậy
( )
2
2
1 2 5z = + − =
.
Câu 11: Chọn B
Giả sử
( )
,z a bi a b= +
. Suy ra
z a bi=−
.

CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
456
Khi đó:
( ) ( )
1 2 2 3 4 12z i z i i+ − − = − +
( )( ) ( )( )
1 2 2 3 4 12a bi i a bi i i + + − − − = − +
( )
5 3 4 12a b a b i i − + + + = − +
43
5 3 12 1
a b a
a b b
− + = − =
+ = = −
.
Do đó điểm
M
biểu diễn số phức
z
có toạ độ là
( )
3; 1−
.
Câu 12: Chọn B
Giả sử
( )
,z a bi a b= +
. Suy ra
z a bi=−
.
Khi đó:
( )
1 3 3 5 7i z z i+ − = − +
( )( ) ( )
1 3 3 5 7i a bi a bi i + + − − = − +
( )
2 3 3 4 5 7a b a b i i − − + + = − +
2 3 5 1
3 4 7 1
a b a
a b b
− − = − =
+ = =
.
Do đó điểm biểu diễn cho số phức
z
có toạ độ là
( )
1;1
là điểm
N
trên hình vẽ.
Câu 13: Chọn A
Giả sử
( )
,z a bi a b= +
. Suy ra
z a bi=−
.
Khi đó:
( ) ( )
2 3 1 2 8i z i z i+ − − = − +
( )( ) ( )( )
2 3 1 2 8i a bi i a bi i + + − − − = − +
( )
2 3 4 2 8a b a b i i − + + = − +
2 2 0
3 4 8 2
a b a
a b b
− = − =
+ = =
.
Do đó điểm
N
biểu diễn cho số phức
z
có toạ độ là
( )
0;2
.
Ta có khoảng cách cần tìm là
1MN =
.
Câu 14: Chọn B
( ) ( )
2 5 7 3i a i b a i
− − = + +
( ) ( )
7 2 5 3a i b a i + − = + +
( )
7
7
13 7 6.
3 2 5
13
b
b
ab
aa
a
=
=
− = − =
+ = −
=
Câu 15: Chọn A
Gọi
z a bi=+
,
( )
,ab
.
( )
22
22
27
2 7 3 2 7 3
23
a b a a
z z i z a b a bi i a bi
bb
+ − = − +
− = − + + + − − = − + + +
=+
( )
2
2
2
3
3
4
3 7 0
3
9 3 7
9 3 7
b
b
a
a
b
aa
aa
=
=
=
−
=
+ = −
+ = −
4 3 5z i z = + =
.
Câu 16: Chọn B
Giả sử:
z x yi=+
,
,xy
.
Ta có:
( ) ( )
1 2 1 4 0z i z i i+ + − + − =
( )( ) ( )( )
1 2 1 4 0x yi i x yi i i+ + + − − + − =
( ) ( )
2 3 4 1 0x y x i− + + − =
2 3 4 0
10
xy
x
− + =
−=
2
1
y
x
=
=
1 2 5z i z
.
Câu 17: Chọn A
Đặt
( , )z x yi x y= +
( )
2
2 2 2
2z x yi x y xyi = + = − −
.

CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
457
Khi đó
2z =
22
2xy + =
;
2
z
là số thuần ảo nên ta có
22
0xy−=
.
Từ đó ta có hệ
22
22
2
0
xy
xy
+=
−=
2
22
1
0
x
xy
=
−=
2
1
1
x
y
=
=
1, 1
1, 1
1, 1
1, 1
xy
xy
xy
xy
==
= = −
= − =
= − = −
.
Câu 18: Chọn D
Ta có:
( )
1 2 3 2+ + = +i z z i
( )( ) ( )
1 2 3 2 + + + − = +i a bi a bi i
2 2 3 2 + + − + − = +a bi ia b a bi i
33
2
−=
−=
ab
ab
1
2
3
2
=
=−
a
b
. Vậy
1= + = −P a b
.
Câu 19: Chọn A
Ta có
1 3 0z i z i+ + − =
( )
(
)
22
1 3 0a b a b i + + + − + =
.
22
10
30
a
b a b
+=
+ − + =
( )
2
1
1 3 *
a
bb
=−
+ = +
.
( )
( )
2
2
3
*
13
b
bb
−
+ = +
3
4
3
b
b
−
=−
4
3
b = −
. Vậy
1
4
3
a
b
=−
=−
2 3 6S a b = + = −
.
Câu 20: Chọn C
Ta có:
4
zz=
4
zz=
( )
3
10zz − =
0
1
z
z
=
=
;
0z =
0z=
.
1z =
4
1z=
( )( )
22
1 1 0zz − + =
1
1
z
z
zi
zi
=−
=
=
=−
S
có 5 phần tử.
Câu 21: Chọn A
Đặt
( , ; , 0)z a bi a b R a b= +
, ta có
22
5
( ) 4( ) ( 2 2 ).
3
a bi a bi i a b+ + − = − +
2 2 2 2
5
5 3 2 2( )
3
a bi a b a b i − = + − +
22
22
5
5 (1)
3
3 2 2( ) (2)
a a b
b a b
=+
− = − +
. Từ đó suy ra
0a
,
0b
.
Chia cho được
2 2 2
2 2 0 2 2 3.
2 2 2
b a S
+
= = = − −
−

CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
458
Câu 22: Chọn A
Đặt
( )
0t z t=
.
Ta có:
( )
2 3 4 (4 5 ) ( 4 5 ) 2 (3 4)z i t i i z z t i t t i− + + = + − − = − +
Lấy môđun 2 vế ta được:
2 2 2
( 4 5 ) 2 (3 4) ( 4) 25 4 (3 4)z t i t t i t t t t− − = − + − + = + +
( ) ( )
2 2 2 2
4 3 2
0
0
( 4) 25 4 (3 4)
8 28 24 16 0
t
t
t t t t
t t t t
− + = + +
− + − − =
32
0
( 2)( 6 16 8) 0
t
t t t t
− − + + =
2t=
Với
2t =
,ta có:
2( 2 3 ) 4 (4 5 ) 2[ 2 ( 3) ] 4 (4 5 )( )
2 4 4 2
2( 2) (2 10) 4 5 (5 4 ) 2
5 2 10 0
− + + = + − + + + = + +
− = − =
− + + = − + + =
+ = =
z i i i z x y i i i x yi
x y x
x y x y x y z
x y y
Vậy có duy nhất 1 số phức
z
thỏa yêu cầu.
Câu 23: Chọn A
2 1 2 1 3 2 1 2 10i z z i z i z z z i
22
4 2 2
2 1 2 10 5 5 10 0 1 1z z z z z z z
Gọi
1 1 1 2 2 2
,z a bi z a b i
.
Ta có:
2 2 2 2
1 2 1 1 2 2
11z z a b a b
Ta có:
22
1 2 1 2 1 2 1 2 1 2
1
11
2
z z a a b b a a b b
Ta có:
22
1 2 1 2 1 2 1 2 1 2
2 3 2 3 2 3 2 3 2 3M z z a a b b i a a b b
2 2 2 2
1 1 1 2 1 2 2 2
4 12 9 19a b a a bb a b
. Vậy Chọn A
Câu 24: Chọn B
Ta có
( )( )
( )
( )
2 1 1 1 1 2 2z i z i i− + + + − = −
( ) ( )
2 1 1 1 1 2 2z i i i z i i + − − + − + − = −
.
( ) ( ) ( )
2 1 2 1 1z i i z + = − −
.
Đặt
z a bi=+
với
;ab
.
Ta có:
( ) ( )( ) ( )
2 1 2 1 2 2 2 2z i a bi i a b a b i+ = + + = − + +
.
( )
2 1 iz−−
=
( )( ) ( )
2 1 2i a bi a b a b i− − − = − + + +
.
Do đó
( )
2 2 2
1
22
a b a b
a b a b
− = − +
+ = +
3 3 2
0
ab
ab
−=
+=
1
3
1
3
a
b
=
=−
.

CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
459
Vậy
11
33
zi=−
22
1 1 2
3 3 3
z
= + − =
.
Câu 25: Chọn D
Giả sử
( )
;,z a bi a b= +
, khi đó ta có
2 2 2
2z a b abi= − +
là số thuần ảo khi và chỉ khi
22
ab=
( )
1ab=
Khi đó
z a bi=−
suy ra
2 , 2z z a z z b+ = − =
.
Ta có
2
2
2z z ab==
nên kết hợp với giả thiết suy ra
( )
2ab a b=+
Kết hợp
( )
1
và
( )
2
ta được hệ
ab
ab a b
=
=+
2
2aa
ab
=
=
2
0
ab
ab
= =
==
2
2
2
2
0
ab
ab
ab
ab
ab
==
= = −
= − =
= − = −
==
Vậy có 5 số phức thỏa mãn.
Câu 26: Chọn D
Đặt
z a bi z a bi= + = −
Từ giả thiết ta có
( ) ( ) ( ) ( )
+ + − =
+=
+ + − = − + −
+ − = − +
z z z z
a bi
a b i a b i
z i z i
3 2 12
3 2 2 2 12
2 3 4 1
2 3 4
( ) ( ) ( ) ( )
( )
,
+ =
+ =
−=
+ + − = − + −
ab
ab
ab
a b a b
2 2 2 2
3 2 6
3 2 6
1
31
2 3 4 1
Trường hợp 1:
0, 0ab
thì
( )
=
+=
−=
=
a
ab
ab
b
8
3 2 6
9
1
3 1 5
3
= +zi
85
93
Trường hợp 2:
0, 0ab
thì
( )
−=
=−
−=
=−
ab
a
ab
b
4
3 2 6
1
3
31
5
,
Trường hợp 3:
0, 0ab
thì
( )
− + =
=
−=
=
ab
a
ab
b
8
3 2 6
1
3
31
7
,
Trường hợp 4:
0, 0ab
thì
( )
=−
− − =
−=
=−
a
ab
ab
b
4
3 2 6
9
1
3 1 7
3
= − −zi
47
93
Vậy có 2 số phức thỏa mãn
Câu 27: Cho số phức
z
không phải là số thực và
2
2
24
24
zz
zz
−+
++
là số thực. Có bao nhiêu số phức
z
thỏa mãn
2
z z z z z+ + − =
?

CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
460
A.
0
. B.
2
. C.
4
. D.
8
.
Lời gii
Chọn B
Cch 1.
Ta có
2
2
24
24
zz
zz
−+
++
là số thực nên
22
22
2 4 2 4
2 4 2 4
z z z z
zzzz
− + − +
=
+ + + +
( )( ) ( )( )
2 2 2 2
2 4 2 4 2 4 2 4z z z z z z z z− + + + = + + − +
22
4 . 4 . 16 16 0z z z z z z − − + =
( ) ( )
2
40z z z z z − − − =
( )
( )
2
40z z z − − =
2
4z=
vì
0zz−
( )
1
Đặt
z a bi=+
với
0b
,
a
2
z z z z z+ + − =
2 2 4ab + =
( )
2
Từ
( )
1
và
( )
2
ta có
22
4
2
ab
ab
+=
+=
.0
2
ab
ab
=
+=
0
2
a
b
=
=
0
2
0
2
a
b
a
b
=
=
=
=−
.
Cch 2.
Đặt
z a bi=+
với
,ab
. Do
z
là số thực nên
0b
2
2
24
24
zz
zz
−+
++
( ) ( )
( ) ( )
2
2
24
24
a bi a bi
a bi a bi
+ − + +
=
+ + + +
( )
( )
( )
( )
22
22
2 4 2 2
2 4 2 2
a b a ab b i
a b a ab b i
− − + + −
=
− + + + +
2
2
24
24
zz
zz
−+
++
là số thực nên phần ảo bằng
0
( )
( ) ( )
( )
2 2 2 2
2 4 2 2 2 2 2 4 0a b a ab b ab b a b a − − − + + + − − + + =
( )
22
4 4 0b a b − +=
22
4ab +=
do
0b
.
Mặt khác
2
z z z z z+ + − =
22
22a b a b+ = +
( )
22
2 a b a b+ = +
( ) ( )
2
2 2 2 2
42a ab b a b + + = +
Thay
( )
1
vào
( )
2
ta có
( )
4 4 2 16ab+=
0ab=
0
0
a
b
=
=
mà
0b
nên nhận
0a =
Với
0a =
ta được
2b =
nên
2zi=
Câu 28: Chọn D
Gọi
( )
,z x yi x y= +
.
Ta có
( )
( ) ( ) ( )
22
2 2 2
2
5
25
5
3 3 10 3 3 10
3 3 10
x yi
xy
z
z z i x yi x y i
x y x y
+ =
+=
=
+ = + − + + = + + −
+ + = + + −
CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
461
2 2 2 2
0
25 25 5 0
5
20 100 5
x
x y x
y
yy
=
+ = = − =
=
==
. Suy ra
5zi=
.
Từ đó ta có
w 4 3 4 3 5 4 8z i i i i= − + = − + + = − +
.
Câu 29: Chọn B
Đặt
( )
,z x yi x y= +
.
Ta có:
( )
2
2 2 2
2z x yi x y xyi= + = − +
là số thuần ảo khi
22
0x y x y− = =
.
Mặt khác:
2 2 2 2
2 2 2z x y x y= + = + =
.
Suy ra:
2 2 2
1
1
1
1
21
1
1
1
1
x
y
x
y
x y x y
x y y
x
y
x
y
=
=
=−
=
= =
+ = =
=
=−
=−
=−
.
Vậy tổng bình phương phần thực bằng 4.
Câu 30: Chọn D
Giả sử , .
Ta có: , , .
.
Do đó
. Vậy có 3 số phức thỏa mãn yêu cầu bài toán.
Câu 31: Chọn D
z a bi=+
( )
,ab
z a bi = −
11z a bi− = − +
2z z bi−=
2z z a+=
( )
1009
2019 2
i i i=
( )
1009
1 ii= − = −
( )
2
2019
11z z z i z z i− + − + + =
( )
( )
( ) ( )
2
22
2
1 2 . 2 1a b b i a i − + + + − =
( )
2
2
1 2 2 1a b b i ai − + + − =
( )
2
2
11
2 2 0
ab
ba
− + =
−=
22
20a a b
ab
− + =
=
2
2 2 0bb
ab
−=
=
0
1
b
b
ab
=
=
=
0
0
1
1
1
1
a
b
a
b
a
b
=
=
=
=
=
=−
z

CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
462
Gọi
( )
( )
( )
( )
11
22
0
;
4 3 4;3
8 5 8;5
2 4 2;4
z x yi M x y
z i F
z i F
z i A
= +
= − + −
= +
= +
. Ta thấy:
12
0
2
zz
z
+
=
A
là trung điểm của
12
FF
.
Theo giả thiết, ta có:
4 3 8 5 2 38z i z i+ − + − − =
12
2 38MF MF+=
.
Suy ra, tập hợp điểm
M
biểu diễn số phức
z
là Elip
( )
E
có:
12
22
2 38
38
2
37
2
1
a
zz
c
b a c
==
−
==
= − =
.
Ta có:
24z i MA− − =
. Vì
A
là tâm Elip và
M
di chuyển trên Elip nên
min 1AM b==
.
Vậy giá trị nhỏ nhất của
24zi−−
bằng 1.
Câu 32: Chọn A
Đặt
z x yi=+
với
,xy
.
Số phức
z
có điểm biểu diễn
( )
;M x y
.
Ta có
2 1 2z z z− = − +
( )
2 1 2x yi x yi x yi + − = + − − +
( )
2
22
2 1 4 4x y y − + = +
( )
2
2 22
4 1 4 4 4 4
0
80
2
x
xxx y y
x
− +
=
−=+ =
=
.
Vậy tập hợp các điểm biểu diễn các số phức
z
là hai đường thẳng có phương trình
0x =
và
2x =
.
Câu 33: Chọn A
Gọi
( )
i, ,x y x y
= +
. Theo đề bài ta có
1iz
= + −
( ) ( ) ( ) ( )
1 1 i 1 1 iz x y z x y = − + + = − − +
Từ đó ta có:
2
3 i . 9z z z+ +
( ) ( ) ( ) ( )
22
3 1 1 i i 1 1 9x y x y − − + + − + + +
( ) ( ) ( ) ( )
2
22
3 1 3 2 i 1 1 9x y x y − − + − + + +
( )
2
2
5 73
1
8 64
xy
− + +
Vậy tập hợp điểm biểu diễn số phức
là hình tròn
( )
2
2
5 73
1
8 64
xy
− + +
.
Câu 34: Chọn B
Xét phương trình
4 3 2
0x ax bx cx d+ + + + =
( )
1
,
( )
, , , .a b c d
Nhận thấy: Nếu
z
là nghiệm của
( )
1
thì
z
cũng là nghiệm của
( )
1
.
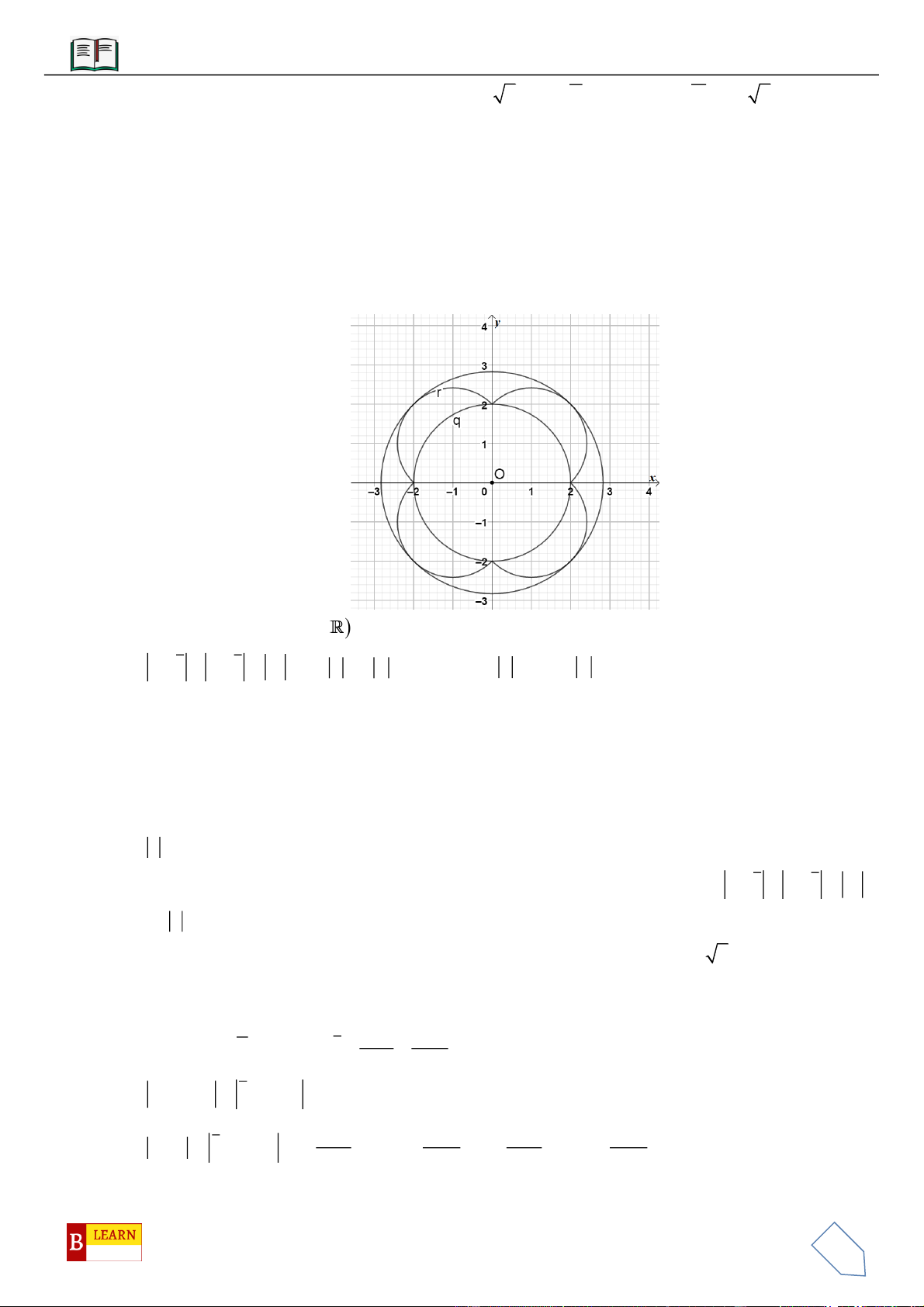
CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
463
Do đó,
( )
1
có bốn nghiệm
1
1zi= − +
,
2
12zi=+
,
31
1z z i= = − −
,
42
12z z i= = −
.
Mà
13
13
2
.2
zz
zz
+ = −
=
và
24
24
2
.3
zz
zz
+=
=
.
Do đó
4 3 2
x ax bx cx d+ + + + =
( )( )
22
2 2 2 3x x x x+ + − +
4 3 2 4 2
26x ax bx cx d x x x + + + + = + + +
.
Suy ra
0a =
,
1b =
,
2c =
,
6d =
hay
9a b c d+ + + =
.
Câu 35: Chọn A
Giả sử
( )
,z x yi x y= +
. Khi đó
2
z z z z z+ + − =
22
22x y x y + = +
( ) ( )
22
1 1 2xy − + − =
( ) ( )
( ) ( )
( ) ( )
( ) ( )
22
22
22
22
1 1 2 khi 0, 0
1 1 2 khi 0, 0
1 1 2 khi 0, 0
1 1 2 khi 0, 0
x y x y
x y x y
x y x y
x y x y
− + − =
+ + + =
− + + =
+ + − =
.
( )
2 2 2
,0z m x y m m= + =
.
Điều kiện cần và đủ để có đúng 4 số phức
z
thỏa mãn đồng thời các điều kiện
2
z z z z z+ + − =
và
zm=
là đường tròn
( )
2 2 2
:C x y m+=
có đúng 4 điểm chung với cả 4 phần đường tròn trên.
Dựa vào đồ thị ta thấy có hai trường hợp thỏa mãn đó là
2m =
hoặc
22m =
.
Câu 36: Chọn C
Đặt
w a bi=+
;,a b R
2 1 4a bi z i + = − +
14
22
ab
zi
+−
= +
2020
2 1 2z i z i− = − +
hay
( ) ( ) ( )
2 2 2 2
2 2 2
2
1 4 1 4
2 1 2 2 1 2
2 2 2 2
3 4 1 2 6 0
+ − + −
− = − + − + = − + +
− + − = − + + − =
a b a b
z z i
a b a b a b
CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
464
Vậy tập hợp các điểm biểu diễn số phức
w
là đường thẳng
( )
d
:
2 6 0xy+ − =
Khoảng cách từ
(2; 3)I
đến
( )
d
là:
2 2.3 6
10 5
5
14
−−
=
+
.
Câu 37: Chọn B
Gọi
( )
;M x y
là điểm biểu diễn số phức
z x yi=+
,
( )
,xy
.
Gọi
( )
3;0A
,
( )
3;0B −
lần lượt là điểm biểu diễn cho các số phức
1
3z =
và
2
3z =−
. Khi đó
6AB =
.
3 3 10 10z z MA MB AB− + + = + =
.
Do đó quỹ tích của điểm
M
là đường Elip có bán trục lớn
5a =
, nửa tiêu cự
3c =
và bán trục nhỏ
là
4b =
.
Vậy diện tích hình Elip là
20S ab
==
.
Câu 38: Chọn C
Gọi số phức
( )
,w x yi x y= +
.
Ta có:
( ) ( ) ( )
3 3 4 3 3 4 3 3 4 3 10w i i z w i i z w i i z w i= + − − − − = − + − − = − + − − =
( ) ( ) ( ) ( )
2 2 2 2
3 1 10 3 1 100x y x y − + − = − + − =
.
Vậy tập hợp biểu diễn các số phức
w
là một đường tròn có bán kính bằng
10
.
Câu 39: Chọn A
Gọi
0zm=
. Khi đó
( )
2z i z+=
được viết lại thành
( )
2m i z+=
.
Lấy module 2 vế ta có
( )
2
2 2 2 4 2
2
11
. 2 1 2 1 2 2 0
2 (VN)
mm
m i z m m m m m m
m
= =
+ = + = + = + − =
=−
Do
0m
nên ta có
1m =
, suy ra
1z =
. Vậy
13
22
z
.
Câu 40: Chọn D
Xét
z x yi=+
với
,xy
.
Mà
( )
2
31z m m i= + + −
2
3
1
xm
ym
=+
=−
( )
2
2
3
3 1 6 8
xm
y x x x
−=
= − − = − +
Vậy tập hợp các điểm biểu diễn số phức
z
thuộc đường cong
( )
C
:
2
68y x x= − +
Xét phương trình hoành độ giao điểm của
( )
C
và trục
Ox
.
2
2
6 8 0
4
x
xx
x
=
− + =
=
Diện tích giới hạn bởi
( )
C
và trục hoành là:

CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
465
( )
44
22
22
6 8 6 8S x x dx x x dx= − + = − − +
4
3
2
2
4
38
33
x
xx
= − − + =
Câu 41: Chọn B
Cách 1
22
1 2 1 2
z z z z+=
( )
2
1 2 1 2
z z z z − = −
2
1 2 1 2
.z z z z − =
2
.MN OM ON=
( )
1
Lại có:
22
1 2 1 2
z z z z+=
( )
2
1 2 1 2
z z z z = −
2
1 2 1 2
.z z z z = −
2
.OM ON MN=
( )
2
Tương tự ta có:
2
.ON OM MN=
( )
3
Từ
( )
2
và
( )
3
ta có:
2
2
OM ON
OM ON
ON OM
= =
.
( )
4
Từ
( )
1
và
( )
4
ta có:
22
MN OM MN OM= =
.
Từ đó suy ra:
OM ON MN==
. Vậy
OMN
đều.
Cách 2
Ta có
2
2 2 2 2 2
1 2 1 2 1 1 2 2 1 2 2
13
00
24
z z z z z z z z z z z
+ = − + = − + =
.
1 2 2 1 2 2
1 3 1 3
0
2 2 2 2
z z iz z z iz
− − − + =
12
12
13
22
13
22
z i z
z i z
=+
=−
( )
1
1 2 2
1 2 2
13
22
13
22
z z i z
z z i z
− = − +
− = − −
12
zz − =
2
z
MN ON=
.
( )
2
Cũng từ
( )
1
ta suy ra
12
z z OM ON= =
.
( )
3
Từ
( )
2
và
( )
3
suy ra
OMN
đều.
Cách 3
Chọn
1
13zi=+
và
2
13zi= − +
.
Ta có
( ) ( )
22
22
12
1 3 1 3 4z z i i+ = + + − + =
và
( )( )
12
1 3 1 3 4z z i i= + − + =
Suy ra
22
1 2 1 2
z z z z+=
nên hai số phức
12
,zz
thỏa mãn yêu cầu đề bài.
Khi đó
( )
1; 3M
và
( )
1; 3N −
, ta có
2OM ON MN= = =
. Vậy
OMN
đều.
Câu 42: Chọn D
Gọi
( )
;M x y
là điểm biểu diễn cho số phức
w
.
Ta có
( )
2 2 3 4 6 1w z i i i= − + + − + −
( )
5 7 2 2 3w i z i − + = − +
.
Khi đó
5 7 2 2 3 6w i z i− + = − +
( ) ( )
22
5 7 36xy − + +
.
tập hợp các điểm
M
trên mặt phẳng
Oxy
là hình tròn tâm
( )
5; 7I −
bán kính
6R =
.
Vậy diện tch hình tròn là
2
36SR
==
.

CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
466
Câu 43: Chọn D
Giả sử
z x yi=+
với
x
,
y
.
Ta có
( )
( )
( ) ( ) ( ) ( )
1 3 1 3 25 1 3 1 3 25z i z i x y i x y i+ − + + = + + − + − − =
( ) ( )
22
1 3 25xy + + − =
.
Tập các điểm biểu diễn số phức
z
là đường tròn tâm
( )
1;3I −
, bán knh bằng
5
.
Vậy
1 3 5 7abc+ + = − + + =
.
Câu 44: Chọn A
Giả sử
A
,
B
lần lượt là các điểm biểu diễn số phức
1
z
,
2
z
trên mặt phẳng tọa độ
Oxy
. Theo giả
thiết ta có
A
,
B
thuộc đường tròn tâm
( )
2;3I
, bán kính
5r =
và
6AB =
.
Gọi
M
là trung điểm của
AB
khi đó
M
cũng là điểm biểu diễn số phức
12
22
zz
w
u
+
==
.
Lại có
2
2 2 2 2
16 4
2
AB
IM IA AM r IM
= − = − = =
.
Vậy
M
thuộc đường tròn tâm
( )
2;3I
bán kính
'4r =
.
Suy ra các điểm biểu diễn số phức
12
2w z z u= + =
là một đường tròn bán kính
28Rr
==
Câu 45: Chọn D
Giả sử và .
Ta có
.
Theo giả thiết: .
.
Thay vào ta được: .
Vậy: .
Câu 46: Chọn D
w 2 1zi= + −
( )
w1
2
i
z
−−
=
( )
w1
3 4 3 4
2
i
i z i
−−
− + = − +
w 7 9
34
2
i
zi
−+
= − +
w 7 9
34
2
i
zi
−+
= − +
Ta được
( )
w 7 9
3 4 2
2
i
zi
−−
= − +
( )
w 7 9 4i − −
.
Do đó tập hợp điểm biểu diễn biểu diễn số phức
w
là hình tròn tâm
( )
7; 9I −
, bán knh bằng
4
.
Vậy diện tch hình tròn là
16S
=
.
z a bi=+
( )
;ab
w x yi=+
( )
;xy
2020
2 1 2z i z i− = − +
( )
1010
2
2 1 2a bi i a bi i + − = − − +
( ) ( ) ( )
2 2 2
2
2 1 2a b a b − + = − + −
( )
2 4 1 0 1ab − + =
2 1 4w z i= − +
( )
2 1 4x yi a bi i + = − − +
( )
2 1 4 2x yi a b i + = − + −
21
42
xa
yb
=−
=−
1
2
4
2
x
a
y
b
+
=
−
=
( )
2
( )
2
( )
1
14
2. 4. 1 0
22
xy+−
− + =
( )
2 6 0xy + − =
( )
10 5
,
5
dI=
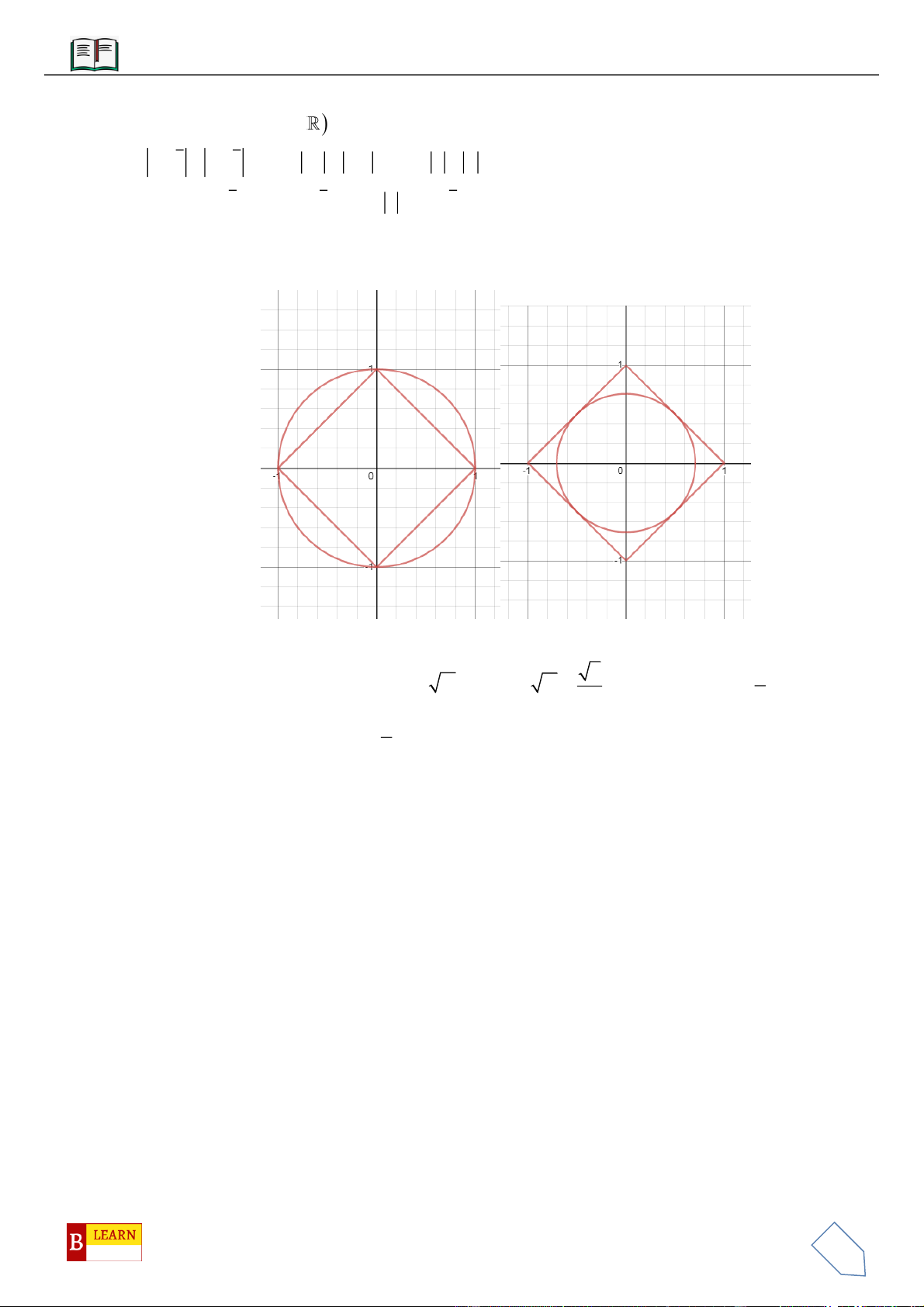
CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
467
Câu 47: Chọn C
Đặt
( )
,,z x yi x y= +
.
2 2 2 2 1z z z z x yi x y+ + − = + = + =
.
Đặt
( ) ( )
2
2z z z z z m z z z m
= + − + − = + − −
.
z
là số thuần ảo nên có phần thực bằng 0. Tức là:
22
x y m+=
.
Tập hợp các điểm
( )
;M x y
thỏa mãn là hình vuông tâm là gốc tọa
Để có 4 cặp số
( )
;xy
thỏa mãn đồng thời và thì phải là một đường tròn nội tiếp hoặc ngoại tiếp
hình vuông nói trên. Tức là
0m
và
1m =
hoặc
2
2
m =
1m=
hoặc
1
2
m =
Vậy tổng các phần tử của
S
là
3
2
.

CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
468
PHƯƠNG TRÌNH BẬC HAI HỆ SỐ THỰC
Câu 1: Gọi
12
,zz
là hai nghiệm phức của phương trình
2
2 7 0zz− + =
. Tính
1 2 2 1
..S z z z z=+
.
A.
1
2
. B.
27
4
. C.
2
. D.
7
2
.
Câu 2: Phương trình nào dưới đây nhận hai số phức và làm nghiệm?
A. . B. . C. . D. .
Câu 3: Gọi
12
,zz
là hai nghiệm phức của phương trình
2 2020
2 2 0zz+ + =
. Giá trị của
12
zz+
bằng
A.
2021
2
. B.
1011
2
. C.
2020
2
. D.
1010
2
.
Câu 4: Cho số phức
13
22
zi
. Phương trình bậc hai với hệ số thực nhận
z
và
z
làm nghiệm là
A.
2
20zz
. B.
2
2 2 0zz
. C.
2
10zz
. D.
2
10zz
.
Câu 5: Biết phương trình
2
0z mz n+ + =
có một nghiệm là
1zi=+
. Tính môđun của số phức
z m ni=+
.
A.
22
. B.
4
. C.
16
. D.
8
.
Câu 6: Gọi
12
,zz
là hai nghiệm phức của phương trình
2
2 3 3 0zz+ + =
. Giá trị của biểu thức
22
12
zz+
bằng
A.
3
18
. B.
9
8
−
. C.
3
. D.
9
4
−
.
Câu 7: Cho phương trình
2
0z bz c+ + =
có hai nghiệm
1
z
;
2
z
thỏa mãn
21
42z z i− = +
. Gọi
A
,
B
là
điểm biểu diễn các nghiệm của phương trình
2
2 4 0z bz c− + =
. Tính độ dài đoạn
AB
.
A.
85
. B.
25
. C.
45
. D.
5
.
Câu 8: Kí hiệu
n
là số các giá trị của tham số
a
sao cho phương trình
2
30z az+ + =
, có hai nghiệm phức
1
z
,
2
z
thỏa mãn
22
12
5zz+ = −
. Tìm
n
.
A.
0n =
. B.
1n =
. C.
2n =
. D.
3n =
.
Câu 9: Ký hiệu
1
z
,
2
z
là hai nghiệm phức của phương trình
2
2 4 9 0zz− + =
. Tính
12
11
P
zz
=+
.
A.
9
4
P =−
. B.
4
9
P =
. C.
9
4
P =
. D.
4
9
P =−
.
Câu 10: Phương trình
2
0z az b+ + =
; với
,ab
là các tham số thực nhận số phức
1 i+
là một nghiệm. Tính
ab−
?
A.
2−
. B.
4−
. C.
4
. D.
0
.
Câu 11: Biết rằng hai số phức
1
z
,
2
z
thỏa mãn
1
3 4 1zi− − =
và
2
1
34
2
zi− − =
. Số phức
z
có phần thực
là
a
và phần ảo là
b
thỏa mãn
3 2 12ab−=
. Giá trị nhỏ nhất của
12
22P z z z z= − + − +
bằng:
12i+
12i−
2
2 3 0zz+ + =
2
2 3 0zz− − =
2
2 3 0zz− + =
2
2 3 0zz+ − =
CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
469
A.
9945
11
P =
. B.
5 2 3P =−
. C.
9945
13
P =
. D.
5 2 5P =+
.
Câu 12: Gọi
1
z
và
2
z
là hai nghiệm phức của phương trình
2
3 2 27 0zz− + =
. Giá trị của
1 2 2 1
z z z z+
bằng
A.
2
. B.
6
. C.
36
. D.
6
.
Câu 13: Gọi
12
,zz
là
2
nghiệm phức của phương trình
2
4 8 5 0− + =zz
. Giá trị của biểu thức
22
12
+zz
là
A.
2
. B.
5
. C.
5
2
D.
3
2
.
Câu 14: Gọi
1
z
,
2
z
là hai nghiệm phức của phương trình
2
2 6 17 0zz−+=
. Giá trị của
12
zz−
bằng
A.
34
. B.
3
. C.
34
2
. D.
5
.
Câu 15: Gọi
12
,zz
là hai nghiệm phức của phương trình
2
4 5 0zz− + =
. Giá trị của biểu thức
( ) ( )
2019 2019
12
11zz− + −
bằng
A.
1009
2
. B.
1010
2
. C.
0
. D.
1010
2−
.
Câu 16: Có bao nhiêu giá trị dương của số thực
a
sao cho phương trình
22
3 2 0z z a a+ + − =
có nghiệm
phức
0
z
thỏa
0
3z =
.
A.
3
. B.
2
. C.
1
. D.
4
.
Câu 17: Trong các số phức
z
thỏa mãn
1 1 2z i z i− + = + −
, số phức
z
có mô đun nhỏ nhất có phần ảo
là
A.
3
10
. B.
3
5
. C.
3
5
−
. D.
3
10
−
.
Câu 18: Cho
12
,zz
là các nghiệm phức của phương trình
2
2 4 11 0zz− + =
. Tính giá trị biểu thức
( )
22
12
2
12
zz
P
zz
+
=
+
A.
9
2
. B.
11
4
. C.
11
2
. D.
9
4
.
Câu 19: Có tất cả bao nhiêu số phức
z
thỏa mãn
4+ + − =z z z z
và
2 2 3 2.− − =zi
A.
7
. B.
3
. C.
2
. D.
5
.
Câu 20: Tổng môđun các nghiệm phức của phương trình
2
4 5 0zz+ + =
bằng
A.
5
. B.
3
. C.
25
. D.
23
.
Câu 21: Gọi
S
là tổng các giá trị thực của
m
để phương trình
2
9 6 1 0z z m+ + − =
có nghiệm phức thỏa
mãn
1z =
. Tính
S
.
A.
20
. B.
12
. C.
14
. D.
8
.

CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
470
Câu 22: Cho số phức
z
thoả mãn
3 4 5zi− − =
và biểu thức
22
2P z z i= + − −
đạt giá trị lớn nhất. Tính
zi+
A.
61
. B.
41
. C.
53
. D.
35
.
Câu 23: Cho hai số phức
,zw
thỏa mãn
3 2 2z −=
,
4 2 2 2wi−=
. Biết rằng
zw−
đạt giá trị nhỏ
nhất khi
0
zz=
,
0
ww=
. Tính
00
3zw−
.
A.
22
. B.
42
. C. 1. D.
62
.
Câu 24: Cho số phức
z
thỏa mãn
3 2 12z z z z+ + −
. Gọi
,Mm
lần lượt là giá trị lớn nhất, nhỏ nhất
của
43zi−+
. Giá trị của
.Mm
bằng
A. 28. B. 24. C. 26. D. 20.
Câu 25: Cho hai số phức
12
,zz
thỏa mãn
1
3 5 2zi− + =
và
2
1 2 4iz i− + =
.Tìm giá trị lớn nhất của biểu
thức
1
23
z
T iz z=+
A.
313
. B.
313 8+
. C.
313 16+
. D.
313 2 5+
.
Câu 26: Cho số phức
z
thỏa mãn
22
21z iz z z i
. Giá trị nhỏ nhất của
2zi
là
A.
22
. B.
2
. C.
2
. D.
1
5
2
.
Câu 27: Cho hai số phức
12
,zz
thoả mãn
11
2 4 7 6 2z i z i+ − + − − =
và
2
1 2 1iz i− + =
. Tìm giá trị nhỏ
nhất của biểu thức
12
T z z=+
.
A.
21−
. B.
21+
. C.
2 2 1+
. D.
2 2 1−
.
Câu 28: Gọi
1
z
và
2
z
là hai nghiệm phức của phương trình
( )
2
3 4 4 25 0.z i z i− + − − + =
Tính giá trị của
biểu thức
22
12
.A z z=+
A.
50.A =
B.
70.A =
C.
13.A =
D.
8.A =
Câu 29: Gọi
S
là tập tất cả các nghiệm phức của phương trình
4 3 2
2 ( 1) 2 0z iz i z z i− + − + − =
. Tổng các
phần tử của
S
bằng
A.
1
. B.
1 i+
. C.
i
. D.
2i
.
Câu 30: Kí hiệu
1 2 3 4
; ; ;z z z z
là bốn nghiệm phức của phương trình
( )( ) ( )
2 2 2 2
3 6 3 3 9 02z z z z zzz −++ +− + + =
. Giá trị của biểu thức
1 2 3 4
z z z z+ + +
bằng
A.
( )
2 3 1 2+
. B.
2
. C.
( )
2 2 1 2+
. D.
( )
2 3 1 3+
.
Câu 31: Cho số phức
,zw
khác 0 thỏa mãn
0zw+
và
1 3 6
z w z w
+=
+
. Khi đó
z
w
bằng:
A. 3. B.
1
3
. C.
3
. D.
1
3
.

CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
471
BẢNG ĐÁP ÁN
1.B
2.C
3.B
4.D
5.A
6.D
7.C
8.C.
9.B
10.B
11.C
12.A
13.C
14.D
15.D
16.B
17.D
18.B
19.B
20.C
21.B
22.A
23.D
24.B
25.C
26.B
27.D
28.B
29.C
30.C
31.D
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Chọn B
Vì phương trình
2
2 7 0zz− + =
có hệ số thực và
0
nên
12
zz=
và
21
zz=
.
Do đó:
( )
2
2
22
1 2 1 2 1 2 1 2 1 2
1 7 27
. . 2 . 2.
2 2 4
S z z z z z z z z z z
= + = + = + − = − =
.
Câu 2: Chọn C
Đặt và .
Ta có: là nghiệm của phương trình .
Câu 3: Chọn B
Nhận xét:
20
1
20
2
12
12
.2zz
zz
zz
=
=
=
. Ta có:
2
11
zz=
, mặt khác
2
1 1 1 1
0
2
202
. . 2z z z z z= = =
nên
1010
1
2z =
.
Vậy
10
1
10 1 1
2
01
2.2 2zz+ = =
.
Câu 4: Chọn D
Ta có:
1 3 1 3
2 2 2 2
z i z i
1
.1
S z z
P z z
.
Theo Vi-et ta có
z
và
z
là nghiệm của phương trình
22
. 0 1 0z S z P z z
.
Câu 5: Chọn A
Vì
1zi=+
là nghiệm của phương trình
2
0z mz n+ + =
nên:
( ) ( ) ( )
2
02
1 1 0 2 0
2 0 2
m n m
i m i n m n m i
mn
+ = = −
+ + + + = + + + =
+ = =
.
22
22z m n = + =
.
Câu 6: Chọn D
Cách 1: Phương trình
2
2 3 3 0zz+ + =
có hai nghiệm
12
3 21 3 21
;
4 4 4 4
z i z i= − + = − −
Suy ra biểu thức
22
22
12
3 21 3 21 9
4 4 4 4 4
z z i i
+ = − + + − − = −
1
12zi=+
2
12zi=−
( ) ( )
( )( )
12
12
1 2 1 2 2
. 1 2 1 2 3
z z i i
z z i i
+ = + + − =
= + − =
12
,zz
2
2 3 0zz− + =

CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
472
Cách 2: Áp dụng định lý Viet cho phương trình:
2
2 3 3 0zz+ + =
. Ta có:
12
12
3
2
3
.
2
zz
zz
−
+=
=
Biểu thức
( )
2
2
22
1 2 1 2 1 2
3 3 9
2 .z 2.
2 2 4
z z z z z
−−
+ = + − = − =
.
Câu 7: Chọn C
Phương trình
2
0z bz c+ + =
có hai nghiệm
1
z
;
2
z
nên
12
z z b+ = −
;
12
z z c=
.
( )
22
1 2 1 2
2 4 0 2 4 0z bz c z z z z z z− + = + + + =
( )( )
12
2 2 0z z z z + + =
1
2
2
2
zz
zz
=−
=−
. Suy ra
1 2 1 2
2 2 2 4 5AB z z z z= − + = − + =
.
Câu 8: Chọn C
Ta có
12
,zz
là hai nghiệm phức của phương trình
2
30z az+ + =
12
12
3
z z a
zz
+ = −
=
.
Khi đó
( )
2
2 2 2
1 2 1 2 1 2
2 5 1 0z z z z z z a+ = + − = − − =
1
1
a
a
=
=−
.
Vậy có 2 giá trị của
a
thỏa mãn
2n=
.
Câu 9: Chọn B
Ta có
1 2 1 2
9
2, .
2
z z z z+ = =
. Do đó
12
1 2 1 2
1 1 4
.9
zz
P
z z z z
+
= + = =
.
Câu 10: Chọn B
Cách 1:
( )
2
01z az b+ + =
.
Phương trình
( )
1
nhận
1zi=+
là nghiệm. Thay
1zi=+
vào
( )
1
ta được:
( ) ( )
2
1 1 0 2 0i a i b i a ai b+ + + + = + + + =
( ) ( 2) 0a b a i + + + =
0
20
ab
a
+=
+=
2
2
a
b
=−
=
.
Vậy
4ab− = −
.
Câu 11: Chọn C
Gọi
A
là điểm biểu diễn của số phức
1
z
suy ra
A
thuộc đường tròn
( )
C
tâm
(3;4)I
, bán kính
1R =
.
Gọi
A
là điểm đối xứng của
A
qua đường thẳng
d
.
22
1
3 4 2 6 8 1
2
z i z i− − = − − =
.
Gọi
B
là điểm biểu diễn của số phức
2
2z
suy ra
B
thuộc đường tròn
( )
1
C
tâm
(6;8)J
bán kính
1
1R =
.
Gọi
M
là điểm biểu diễn của số phức
z
suy ra
M
thuộc đường thẳng
d
:
3 2 12 0xy− − =
.
Ta có: điểm
I
,
J
cùng phía so với đường thẳng
d
và đường thẳng
d
không có điểm chung với
đường tròn
( )
C
và đường tròn
( )
1
C
.

CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
473
Gọi
( )
2
C
là đường tròn tâm
K
đối xứng với đường tròn
( )
C
qua đường thẳng
d
.
Khi đó điểm
K
đối xứng với điểm
I
qua đường thẳng
d
.
Ta tìm được
105 8
;
13 13
K
,
9945
13
JK =
.
Khi đó:
12
2 2 2 ' 2 ' 2P z z z z MA MB MA MB A B= − + − + = + + = + + +
Suy ra
min
9945
' 2 1 1 2
13
P A B JK JK= + = − − + = =
.
Câu 12: Chọn A
Ta có:
12
2
3
zz+=
và
12
.9zz=
. Mặt khác:
1 2 1 2 1 2
. 9 3z z z z z z= = = = =
.
Do đó
( )
1 2 2 1 1 2 1 2
2
.3 .3 3 3. 2
3
z z z z z z z z+ = + = + = =
.
Câu 13: Chọn C
Ta có
1
1
1,
2
=+zi
2
1
1
2
=−zi
nên ta có
22
12
5
2
zz+=
.
Câu 14: Chọn D
Ta có:
2
35
22
2 6 17 0
35
22
zi
zz
zi
=+
− + =
=−
Do đó:
12
3 5 3 5
55
2 2 2 2
z z i i i
− = + − − = =
.
Câu 15: Chọn D
Xét phương trình
( )
2
1
2
2
2
4 5 0 2 1
2
zi
z z z
zi
=+
− + = − = −
=−
Khi đó ta có:
( ) ( ) ( ) ( )
2019 2019 2019 2019
12
1 1 1 1z z i i− + − = + + −
( ) ( )
( )
( ) ( )
( )
1009 1009
22
1 . 1 1 . 1i i i i= + + + − −
( ) ( ) ( ) ( )
1009 1009
1 . 2 1 . 2i i i i= + + − −
( ) ( ) ( )
( )
( )
1009 1010
1010
2 1 1 2 2i i i i= + − − = = −
.
Câu 16: Chọn B
d
A
H
M
B
A'
I
J
K
CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
474
Phương trình
22
3 2 0z z a a+ + − =
có
2
4 8 3aa = − + +
.
Xét 2 trường hợp:
Trường hợp 1.
2
2 7 2 7
0 4 8 3 0
22
a a a
−+
− + +
.
Khi đó, phương trình có nghiệm
0
z
thì
0
z
.
Theo đề bài:
0
0
0
3
3
3
z
z
z
=
=
=−
.
0
3z =−
, thay vào phương trình ta được
2
0
2
2
a
aa
a
=
−
=
.
0
3z =
, thay vào phương trình ta được
2
2 6 0aa− + =
.
Kết hợp điều kiện
0a
và điều kiện suy ra
2a =
.
Trường hợp 2.
2
27
2
0 4 8 3 0
27
2
a
aa
a
−
− + +
+
.
Khi đó, phương trình có nghiệm phức
0
z
thì
0
z
cũng là một nghiệm của phương trình.
Ta có
2
2 2 2
0
00
1
. 2 2 2 3 0
3
a
z z a a z a a a a
a
=−
= − = − − − =
=
.
Kết hợp điều kiện
0a
và điều kiện suy ra
3a =
.
Vậy có 2 giá trị
a
dương thỏa mãn là
2a =
;
3a =
.
Câu 17: Chọn D
Gọi
z x yi=+
,
( )
,xy
được biểu diễn bởi điểm
( )
;M x y
.
( ) ( ) ( ) ( )
1 1 2 1 1 1 2z i z i x y i x y i− + = + − − + + = + − +
( ) ( ) ( ) ( )
2 2 2 2
3
1 1 1 2 4 2 3 0 2
2
x y x y x y y x − + + = + + + + + = = − −
.
Cách 1:
22
2 2 2 2
3 9 3 9 3 5
2 5 6 5 ,
2 4 5 20 10
z x y x x x x x x
= + = + − − = + + = + +
.
Suy ra
35
10
min z =
khi
33
;
5 10
xy= − = −
.
Vậy phần ảo của số phức
z
có mô đun nhỏ nhất là
3
10
−
.
Cách 2:
Trên mặt phẳng tọa độ
Oxy
, tập hợp điểm biểu diễn số phức
z
là đường thẳng
: 4 2 3 0d x y+ + =
.
Ta có
z OM=
.
z
nhỏ nhất
OM
nhỏ nhất
M
là hình chiếu của
O
trên
d
.
Phương trình đường thẳng
OM
đi qua
O
và vuông góc với
d
là:
20xy−=
.
CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
475
Tọa độ của
M
là nghiệm của hệ phương trình:
3
4 2 3 0
5
2 0 3
10
x
xy
xy
y
=−
+ + =
−=
=−
33
;
5 10
M
− −
. Hay
33
5 10
zi= − −
.
Vậy phần ảo của số phức
z
có mô đun nhỏ nhất là
3
10
−
.
Nhận xét: Ta có thể tìm tập hợp điểm biểu diễn số phức
z
như sau:
( ) ( )
1 1 2 1 1 2z i z i z i z i− + = + − − − = − − −
( )
*
Gọi
M
biểu diễn số phức
z
, điểm
( )
1; 1A −
biểu diễn số phức
1 i−
, điểm
( )
1; 2B −−
biểu diễn
số phức
12i−−
.
Khi đó
( )
* MA MB=
. Suy ra tập hợp điểm biểu diễn số phức
z
là đường trung trực của đoạn
thẳng
AB
có phương trình
: 4 2 3 0d x y+ + =
.
Câu 18: Chọn B
Cách 1.
2
32
1
2
2 4 11 0
32
1
2
zi
zz
zi
=+
− + =
=−
.
( )
22
22
22
12
22
12
3 2 3 2
11
11 11
22
11
22
44
2 3 2 2 3 2
2
zz
P
zz
ii
−
+ + +
+
+
= = = =
+
+ + −
.
Cách 2.
2
32
1
2
2 4 11 0
32
1
2
zi
zz
zi
=+
− + =
=−
.
22
1 2 1 1 1 2 1 2
2
11
2.
11 11
2
. .z ; 2
2 2 4
z z z z z z z P= = = = + = = =
.
Câu 19: Chọn B
Cách 1:
Với
4 2 2 4 2.= + + + − = + = + =z a bi z z z z a b a b
Khi đó
22
2 2 3 2 ( 2) ( 2) 18.− − = − + − =z i a b
Vậy ta có hệ
CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
476
( )
( )
( )
( )
( )
22
22
2( , 0) 1
2( 0, 0) 2
2
2( 0, 0) 3
( 2) ( 2) 18
2( 0, 0) 4
( 2) ( 2) 18 *
a b a b
a b a b
ab
a b a b
ab
a b a b
ab
+ =
− + =
+=
− =
− + − =
− − =
− + − =
Từ
( ) ( )
1 , *
ta có hệ
( )
( )
( )
( )
( )
2
2
2 , 0
2 , 0
1 2 2 1 2 2
2 18
1 2 2
a b a b
a b a b
b a l
bb
bl
= −
= −
= + = −
+ − =
=−
.
Từ
( ) ( )
2 , *
ta có hệ
( )
( ) ( )
( )
( )
22
2 0, 0
2 0, 0
3 2 2 1 2 2
4 2 18
3 2 2 1 2 2
a b a b
a b a b
b a l
bb
ba
= −
= −
= + = +
− + − =
= − = −
.
Từ
( ) ( )
3 , *
ta có hệ
( )
( )
( )
( )
2
2
2 0, 0
2 0, 0
1 2 2
2 18
1 2 2 3 2 2
a b a b
a b a b
bl
bb
ba
= +
= +
=+
+ − =
= − = −
.
Từ
( ) ( )
4 , *
ta có hệ
( )
( ) ( )
( )
22
2 0, 0
2 0, 0
11
4 2 18
a b a b
a b a b
ba
bb
= − −
= − −
= − = −
+ + − =
.
Vậy có 3 số phức thỏa mãn yêu cầu bài toán.
Cách 2:
Với
;,z x yi x y= +
42z z z z x y+ + − = + =
. Khi đó tập hợp điểm biểu diễn số phức
z
là 4 cạnh hình vuông
ABCD
.
( ) ( )
22
2 2 3 2 2 2 18z i x y− − = − + − =
. Tập hợp điểm biểu diễn số phức
z
là đường tròn
tâm
( )
2;2 , 3 2IR=
.
Dựa vào hình vẽ, ta thấy có 3 số phức thỏa mãn yêu cầu bài toán tương ứng với 3 điểm biểu diễn
,,M N P
.
Câu 20: Chọn C
8
6
4
2
2
4
6
15
10
5
5
10
15
P
M
I
B
A
D
C
N
CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
477
2
4 5 0zz+ + =
2
2
zi
zi
= − +
= − −
.
Vậy tổng môđun các nghiệm phức của phương trình
2
4 5 0zz+ + =
bằng:
2 2 2 5ii− + + − − =
.
Câu 21: Chọn B
Ta có:
2
9 6 1 0z z m+ + − =
( )
*
.
Trường hợp 1:
( )
*
có nghiệm thực
( )
0 9 9 1 0 1mm
− −
.
1
1
1
z
z
z
=
=
=−
.
1 16zm= =
.
14zm= − =
.
Trường hợp 2:
( )
*
có nghiệm phức
( )
0z a bi b= +
( )
0 9 9 1 0 1mm
− −
.
Nếu
z
là một nghiệm của phương trình
2
9 6 1 0z z m+ + − =
thì
z
cũng là một nghiệm của
phương trình
2
9 6 1 0z z m+ + − =
.
Ta có
2
1
1 1 .z 1 1 1 8
9
cm
z z z m
a
−
= = = = = = −
.
Vậy tổng các giá trị thực của
m
bằng
12
.
Câu 22: Chọn A
Gọi
z x yi=+
với
,xy
.
Vì
( ) ( )
22
3 4 5 3 4 5z i x y− − = − + − =
.
Vậy tập hợp điểm biểu diễn của số phức
z
là đường tròn tâm
( )
3;4I
, bán kính
5R =
.
Ta có
( ) ( )
22
22
22
2 2 1 4 2 3P z z i x y x y x y= + − − = + + − − − = + +
( ) ( )
4 12 2 8 23 4 3 2 4 23x y x y= − + − + = − + − +
.
Áp dụng bất đẳng thức Bunhiacopxki cho 4 số:
4, 3,2, 4xy−−
ta có:
( ) ( ) ( ) ( )
22
23 4 3 2 4 16 4. 3 4 10P x y x y− = − + − + − + − =
33P
Max 33P=
khi
34
2 4 10 5
42
4 2 30 5
4 2 30
xy
x y x
x y y
xy
−−
− = − =
=
+ = =
+=
1 5 6 61zi + = + =
.
Câu 23: Chọn D
Ta có: +
3 2 2z −=
, suy ra tập hợp điểm biểu diễn
M
biểu diễn số phức
z
là đường tròn có
tâm
( )
3 2;0I
, bán kính
2r =
.
4 2 2 2wi−=
, suy ra tập hợp điểm biểu diễn
N
biểu diễn số phức
w
là đường tròn có tâm
( )
0;4 2J
, bán kính
22R =
.
Ta có
min minz w MN−=
.
5 2; 2; 2 2IJ IM r NJ R= = = = =
.

CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
478
Mặt khác
IM MN NJ IJ+ +
MN IJ IM NJ − −
hay
5 2 2 2 2 2 2MN − − =
.
Suy ra
min 2 2MN =
khi
, , ,I M N J
thẳng hàng và
,MN
nằm giữa
,IJ
.
Cách 1:
Khi đó ta có:
00
33z w OM ON− = −
và
32IN =
13
;
55
IM IJ IN IJ = =
.
Mặt khác
ON OI IN=+
3
5
OI IJ=+
;
( )
33OM OI IM= + =
13
33
55
OI IJ OI IJ
+ = +
.
Suy ra
00
33z w OM ON− = −
33
32
55
OI IJ OI IJ OI
= + − + =
62=
.
Cách 2:
Ta có
3 3 0IN IM IM IN= − =
.
Do đó
( ) ( )
00
3 3 3 2 2. 2.3 2 6 2.z w OM ON OI IM OI IN OI OI− = − = + − + = = = =
Cách 3:
0
12 2
1 12 2 4 2
5
5 5 5
42
5
M
M
x
IM
IM IJ IM IJ z i
IJ
y
=
= = = +
=
.
0
62
3 6 2 12 2
5
5 5 5
12 2
5
N
N
x
IN
IN IJ IN IJ w i
IJ
y
=
= = = +
=
.
Suy ra
00
3 6 2 6 2zw− = =
.
Câu 24: Chọn B
Đặt
,z x yi=+
( )
;Rxy
,
( )
;P x y
là điểm biểu diễn của số phức
z
.
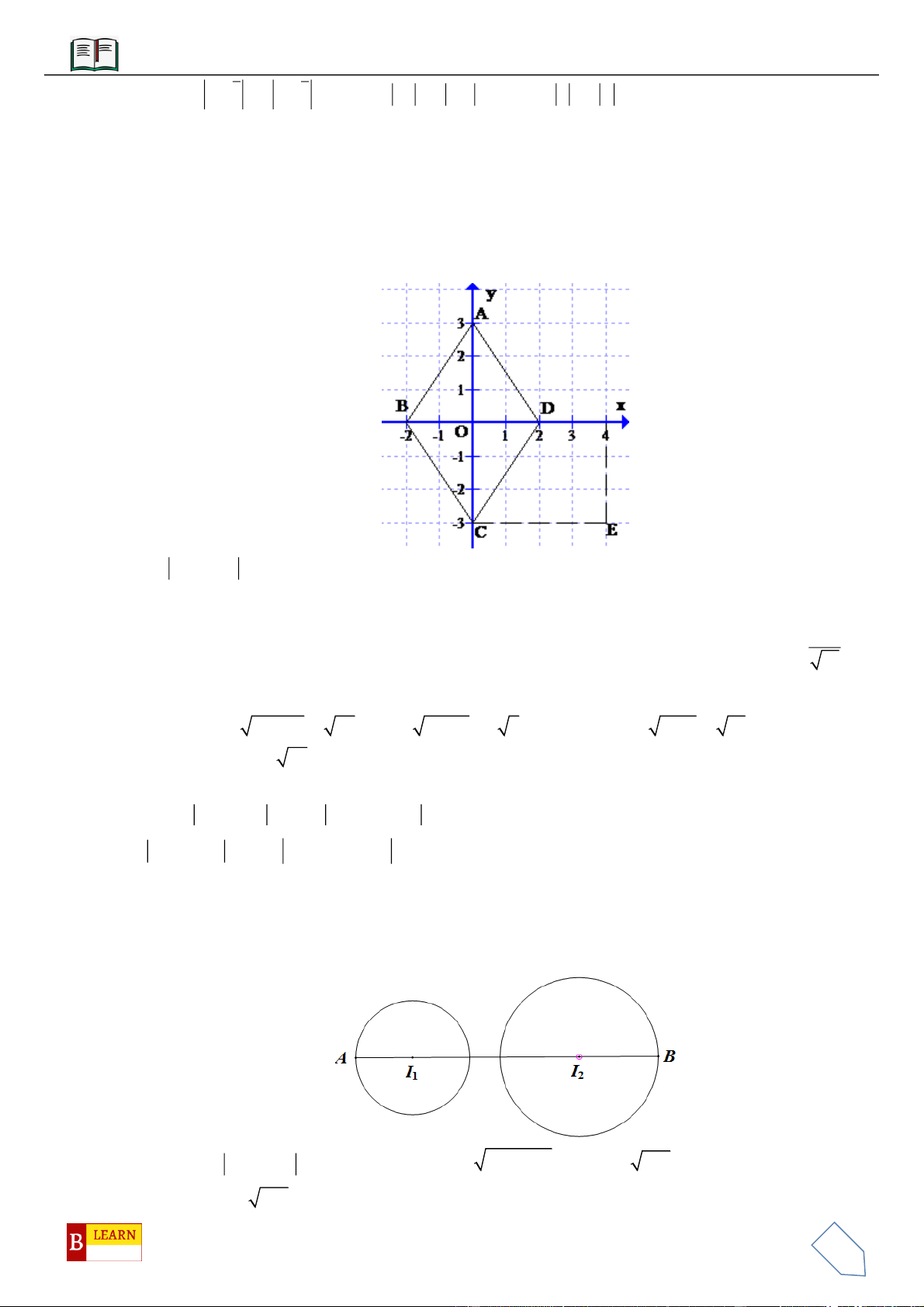
CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
479
Ta có
3 2 12z z z z+ + −
3 2 2 2 12x yi +
3 2 6xy +
( )
1
.
Khi
0; 0xy
, ta có
( )
1 3 2 6xy +
.
Khi
0; 0xy
, ta có
( )
1 3 2 6xy − −
.
Khi
0; 0xy
, ta có
( )
1 3 2 6xy − +
.
Khi
0; 0xy
, ta có
( )
1 3 2 6xy −
.
Suy ra quỹ tích điểm
P
là hình thoi
ABCD
cùng miền trong của nó.
+)
43z i EP− + =
với
( )
4; 3E −
là điểm biều diễn của số phức
1
43zi=−
.
Từ hình vẽ ta có
( )
min ,m EP d E CD==
.
Đường thẳng
CD
có phương trình
3 2 6 0xy− − =
, suy ra
12
13
m =
.
max max , , ,EP EA EB EC ED=
.
Lại có
16 36 52EA = + =
,
9 36 3 5EB = + =
,
4EC =
,
9 4 13ED = + =
.
Do đó
52M EA==
. Vậy
. 24Mm=
.
Câu 25: Chọn C
Ta có
( )
11
3 5 2 2 6 10 4 1z i iz i− + = + + =
( ) ( )
22
1 2 4 3 6 3 12 2iz i z i− + = − − − =
Gọi
A
là điểm biểu diễn số phức
1
2,iz
B
là điểm biểu diễn số phức
2
3z−
Từ
( )
1
và
( )
2
suy ra điểm
A
nằm trên đường tròn tâm
( )
1
6; 10I −−
, bán kính
1
4R =
, điểm
B
nằm trên đường tròn tâm
( )
2
6;3I
, bán kính
2
12R =
Ta có
22
1 1 2 1 2
2 3 12 13 4 12 313 16
z
T iz z AB I I R R= + = + + = + + + = +
Vậy
max 313 16.T =+
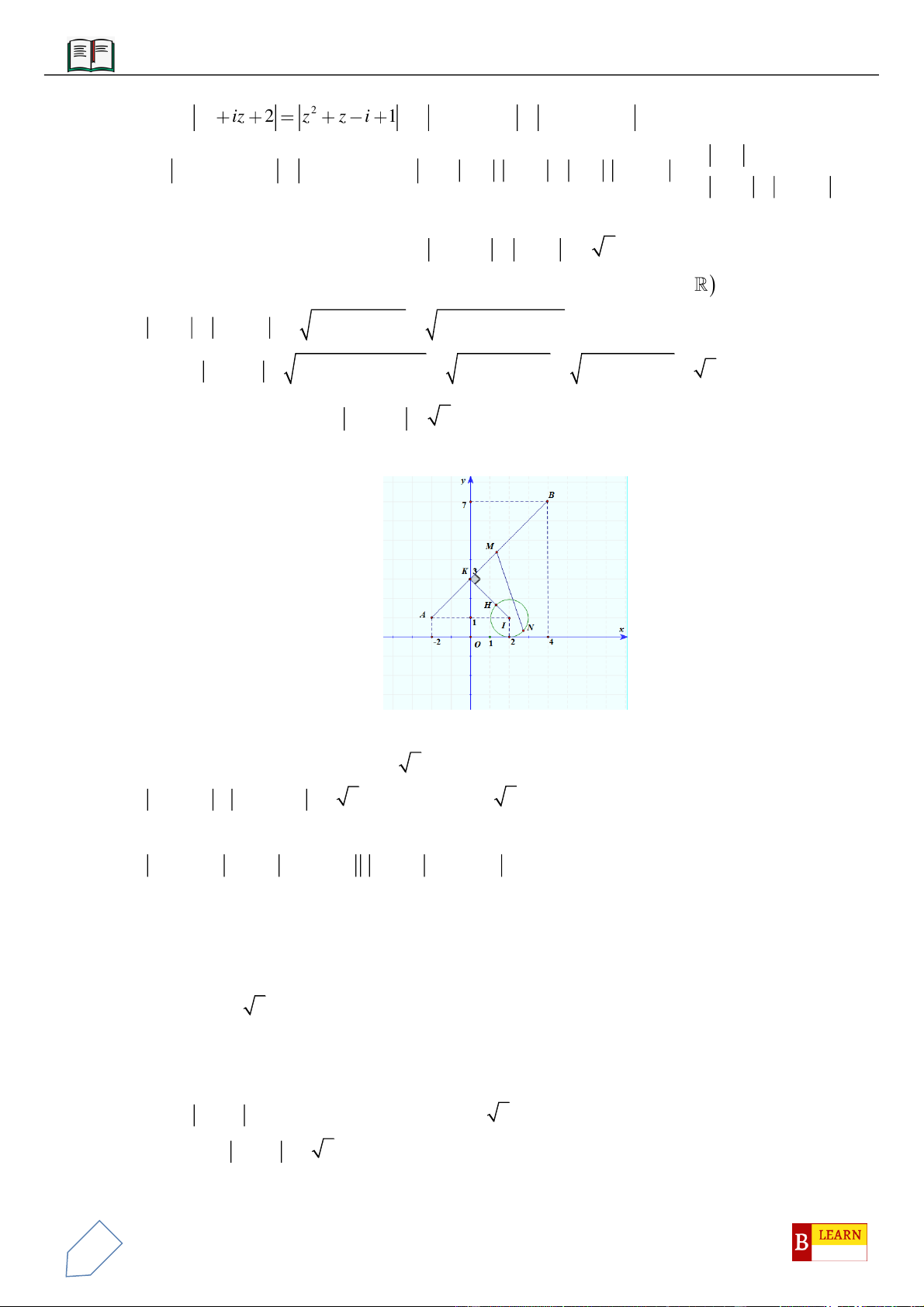
CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
480
Câu 26: Chọn B
Ta có
22
21z iz z z i
2 2 2 2
2z iz i z z i i + − = + − −
( )( ) ( )( )
21z i z i z i z i − + = − + +
. 2 . 1z i z i z i z i − + = − + +
( )
( )
01
2 1 2
zi
z i z i
− =
+ = + +
.
Giải phương trình
(1)
: Ta có
2 2 2 2 2z i z i i= − + = − =
( )
*
.
Giải phương trình
( )
2
: Đặt
( )
,,z x yi x y= +
, ta có
( ) ( ) ( )
2 2 2
2
2 1 2 1 1 1z i z i x y x y y x+ = + + + + = + + + = −
Khi đó
( ) ( ) ( ) ( )
2 2 2 2
2
2 2 1 2 2 1 2 2z i x y x x x− + = − + + = − + = − +
Từ
( )
*
và
( )
**
ta có
22min z i− + =
. Dấu
""=
xảy ra khi
1
0
x
y
=
=
hay
1z =
.
Câu 27: Chọn D
Gọi
M
là điểm biểu diễn số phức
1
z
và
( )
2;1A −
;
( )
4;7B
lần lượt là hai điểm biểu diễn hai số
phức
2 i−+
,
47i+
. Ta có
62AB =
. Phương trình đường thẳng
AB
là
: 3 0d x y− + =
.
11
2 4 7 6 2z i z i+ − + − − =
62MA MB + =
MA MB AB + =
. Do đó tập hợp các điểm
biểu diễn số phức
1
z
là đoạn thẳng
AB
.
2 2 2
1 2 1 1 2 1 2 1iz i iz i i z i− + = − + = − − − =
.
Gọi
N
là điểm biểu diễn số phức
2
z−
và
( )
2;1I
là điểm biểu diễn số phức
2 i+
. Ta có
1IN =
Suy ra tập hợp các điểm biểu diễn số phức
2
z−
là đường tròn
( )
C
có phương trình:
( ) ( )
22
2 1 1xy− + − =
.
( )
, 2 2 1d I AB =
, suy ra
AB
không cắt đường tròn.
Gọi
K
là hình chiếu của
( )
2;1I
lên
AB
. Dễ thấy
K
nằm trên đoạn thẳng
AB
.
Gọi
H
là giao điểm của đoạn
IK
với đường tròn
( )
C
.
Ta có
( )
12
, 2 2 1z z MN KH d I AB R+ = = − = −
.
Suy ra
12
2 2 1.min z z+ = −
Câu 28: Chọn B

CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
481
Có
( )
2
3 4 4 25 0z i z i− + − − + =
2
( ) 3 4( ) 25 0z i z i + − − + + =
2
( ) 10( ) 34 0z i z i + − + + =
53
53
z i i
z i i
+ = +
+ = −
1
2
52
54
zi
zi
=+
=−
22
12
A z z=+
22
5 2 5 4 70.ii= + + − =
Câu 29: Chọn C
Ta có:
4 3 2
2 ( 1) 2 0z iz i z z i− + − + − =
( )
( )
2
2
.0z i z i − + =
22
0
0
zi
z i z i
−=
+ = = −
22
22
22
22
zi
zi
zi
=
= −
= − +
Khi đó, tập các nghiệm phức của phương trình đã cho:
2 2 2 2
;;
2 2 2 2
S i i i
= − + −
Tổng các phần tử của
S
bằng:
2 2 2 2
2 2 2 2
i i i i
+ − + + − =
.
Câu 30: Chọn A
Ta có
( )( ) ( )
2 2 2 2
3 6 3 3 092+− + + −++=z z z z zz z
( ) ( )( )
2 2 2 2
9 2 3 6 3 3 0 − + + − + + + =z z z z z z z
( ) ( )( )
( )
2
2
2
2
2 2 2
2
2
9 6 3
36
9 2 4 3 6 3 3 6 3
2
2
2
9 6 3
33
2
z
zz
z
z
z z z z z z
zz
z z z
+ − +
−+
= + − − + + + = −
+ + −
= = + +
==
.
Với
22
3 6 4 6 0zz z z z=− + − + =
.
Phương trình có hai nghiệm
1
2 2zi=+
và
2
2 2zi=−
Với
22
3 3 2 3 0zz z z z=+ + + + =
.
Phương trình có hai nghiệm là
3
21zi= − −
và
4
21zi= − +
f
Vậy
( )
1 2 3 4
2 2 2 2 1 2 1 2 2 3 1 2z z z z i i i i+ + + = + + − + − − + − + = +
.
Câu 31: Chọn D
Với hai số phức
,zw
khác 0 thỏa mãn
w0z +
, ta có:
( )( )
22
2
1 3 6 3 6
3 6 3 2 0
12
33
3 2. 1 0
12
33
wz
w z z w zw z zw w
z w z w zw z w
z
i
zz
w
ww
z
i
w
+
+ = = + + = − + =
++
=−
− + =
=+
Suy ra
2
2
1 2 1
33
3
z
w
= + =
.

CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
482
CỰC TRỊ SỐ PHỨC
Câu 1: Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
2zi
P
z
+
=
với
z
là số phức khác
0
và thỏa mãn
2z
. Tính tỉ số
M
m
.
A.
3
M
m
=
. B.
4
3
M
m
=
. C.
5
3
M
m
=
. D.
2
M
m
=
.
Câu 2: Trong các số phức
z
thỏa mãn điều kiện
23z i z i− = − +
, số phức
0
z
có môđun nhỏ nhất. Phần
ảo của
0
z
là
A.
2
3
. B.
4
3
. C.
3
2
. D.
3
4
.
Câu 3: Cho tất cả các số phức
( )
i, ,z x y x y= +
thỏa mãn
2i 1 izz+ − = +
. Biết
z
được biểu diễn
bởi điểm
M
sao cho
MA
ngắn nhất với
( )
1;3A
. Tìm
P 2 3xy=+
.
A. 9. B. 11. C.
3−
. D. 5.
Câu 4: Cho số phức
z
thỏa mãn
1z =
. Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
biểu thức
2
11P z z z= + + − +
. Tính
.Mm
.
A.
13 3
4
. B.
39
4
. C.
33
. D.
13
4
.
Câu 5: Gọi
M
là điểm biểu diễn số phức
( )
2
1
22z a a a i= + − +
và
N
là điểm biểu diễn số phức
2
z
biết
22
26z i z i− − = − −
. Tìm độ dài ngắn nhất của đoạn
MN
.
A.
25
. B.
65
5
. C. 1. D. 5.
Câu 6: Cho số phức
z
và
w
biết chúng đồng thời thỏa mãn hai điều kiện:
( )
1
21
1
iz
i
+
+=
−
và
w iz=
.
Tìm giá trị lớn nhất của
M z w=−
A.
33M =
. B.
3M =
. C.
32M =
. D.
23
.
Câu 7: Cho số phức
z
thỏa mãn
2
22z iz−=
. Giá trị lớn nhất của biểu thức
1P iz=+
bằng
A.
2
. B.
3
. C.
3
. D.
2
.
Câu 8: Với ai số phức
12
,zz
thỏa mãn
12
86z z i+ = +
và
12
2zz−=
. Giá trị lớn nhất của biểu thức
12
P z z=+
là:
A.
5 3 5+
. B.
2 26
. C.
46
. D.
34 3 2+
.
Câu 9: Xét tập hợp
S
các số phức
z x yi=+
( )
,xy
thoả mãn điều kiện
( )( )
3 1 2 2z z i i− = + +
.
Biểu thức
( )
2Q z z x= − −
đạt giá trị lớn nhất là
M
và đạt được tại
0 0 0
z x y i=+
. Tính giá trị
2
00
.T M x y=
.
CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
483
A.
93
2
T =−
. B.
93
4
T =
. C.
93
2
T =
. D.
93
4
T =−
.
Câu 10: Cho số phức
z
thỏa mãn
( )( )
2
2 5 1 2 3 1z z z i z i− + = − + + −
. Tính
min w
, với
22w z i= − +
.
A.
1
min
2
w =
. B.
min 1w =
. C.
3
min
2
w =
. D.
min 2w =
.
Câu 11: Xét các số phức
z
thỏa mãn
21zi− − =
. Gọi
,mM
là giá trị nhỏ nhất và lớn nhất của
z
. Giá
trị
Mm+
bằng:
A.
3
. B.
2
. C.
1 2 5+
. D.
25
.
Câu 12: Xét các số phức
z
thỏa mãn
1z =
, giá trị nhỏ nhất của biểu thức
2
4
1
2
zz++
bằng
A.
2
8
. B.
1
8
. C.
1
16
. D.
1
4
.
Câu 13: Cho hai số phức
12
;zz
thỏa mãn
12
zz
và
22
1 1 2 2
5 4 0z z z z− + =
. Gọi
,MN
lần lượt là điểm biểu
diễn của số phức
2
1,
zz
thỏa mãn diện tích tam giác
OMN
bằng 12. Giá trị nhỏ nhất của biểu thức
12
2P z z=−
là
A.
14 3
. B.
21 2
. C.
14 6
3
. D.
76
.
Câu 14: Cho số phức
z
có
1z =
. Giá trị lớn nhất của biểu thức
22
1P z z z z= − + + +
là
A.
13
4
. B.
3
. C.
3
. D.
11
4
.
Câu 15: Xét số phức
z
thỏa mãn
( )
10
1 2 2 .i z i
z
+ = − +
Mệnh đề nào dưới đây đúng?
A.
3
2.
2
z
B.
2.z
C.
1
.
2
z
D.
13
.
22
z
Câu 16: Cho số phức
z
thỏa mãn
2 4 2z i z i− − = −
và biểu thức
2iz i+−
đạt giá trị nhỏ nhất. Tìm phần
ảo của số phức
z
.
A.
2
2
. B.
5
2
−
. C.
3
2
−
. D.
5
2
.
Câu 17: Xét các số phức
z
thỏa mãn
1 3 2zi− − =
. Số phức
z
mà
1z −
nhỏ nhất là
A.
15zi=+
. B.
1zi=+
. C.
13zi=+
. D.
1zi=−
.
Câu 18: Cho các số phức và thỏa mãn . Tìm giá trị lớn nhất của .
A. . B. . C. . D. .
Câu 19: Cho số phức và thỏa mãn . Tính giá trị lớn nhất của
z
w
( )
21
w
z
i z i+ = + −
w1Ti= + −
42
3
2
3
22
3
2
z
w
( )
12
z
i z i
w
+ = + −
2T w i=−
CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
484
A. . B. . C. . D.
Câu 20: Cho số phức và thỏa mãn . Tính giá trị lớn nhất của
A. . B. . C. . D.
Câu 21: Cho
z
là số phức thỏa mãn
2z z i=+
. Giá trị nhỏ nhất của
1 2 1 3z i z i− + + + +
là
A.
52
. B.
13
. C.
29
. D.
5
.
Câu 22: Cho
1
z
,
2
z
là các số phức khác
0
thỏa mãn
1 1 2 2
9z z z z=
. Gọi
M
,
N
lần lượt là điểm biểu diễn
các số phức
1
z
và
2
z
. Biết tam giác
OMN
có diện tích bằng
6
, giá trị nhỏ nhất của
12
zz+
bằng
A.
8
. B.
6
. C.
42
. D.
32
.
Câu 23: Các số phức
1
z
,
2
z
thỏa mãn
( )
1
11
2
1
zi
w
z z i
+−
=
++
là số thực và
2
4z 8 13 4i+ + =
. Giá trị nhỏ nhất
của biểu thức
12
P z z=+
bằng
A.
21
16
. B.
37
4
. C. 0. D.
37 4
4
−
.
Câu 24: Cho các số phức
z
và
w
thỏa mãn
( )
31
1
z
i z i
w
− = + −
−
. Tìm giá trị lớn nhất
T w i=+
.
A.
2
2
. B.
32
2
. C.
2
. D.
1
2
.
Câu 25: Cho số phức
z
thỏa mãn điều kiện
22z z i+ = +
. Biết giá trị nhỏ nhất của biểu thức
1 2 3 4 5 6A z i z i z i= − − + − − + − −
được viết dạng
17
2
ab+
với
a
,
b
là số hữu tỉ. Giá trị của
3ab−
bằng
A.
4
. B.
2
. C.
1
. D.
3
.
Câu 26: Trong các số phức z thoả mãn
3 4 2zi− − =
có hai số phức
12
,zz
thỏa mãn
12
1.zz−=
Giá trị
nhỏ nhất của
22
12
zz−
bằng
A.
10−
. B.
4 3 5−−
. C.
5−
. D.
6 2 5−−
.
Câu 27: Cho số phức
z a bi=+
,
( , )ab
thỏa mãn
2 2 3 1.zi+ − =
Khi biểu thức
2 2 3P z z= + + −
đạt giá trị lớn nhất thì giá trị của
ab−
bằng
A.
3−
. B.
2
. C.
2−
. D.
3
.
Câu 28: Cho số phức
z
thỏa mãn
1 2 4 6 9z i z i− − + − − =
, giá trị lớn nhất của
10 14zi−−
là
A.
17
. B.
20
. C.
15
. D.
12
.
Câu 29: Xét các số phức thỏa mãn .Giá trị nhỏ nhất của bằng
A. B. C. D.
5
2
3
+
5
3
5
5
3
+
5
z
w
( )
3 2 1
13
z
i z i
iw i
+ = + −
−+
Tw=
2
11
3
+
2
10
5
+
5
2
5
13
5
+
,zw
2, 2 5 1z iw i= − + =
2
4z wz−−
4.
( )
2 29 3 .−
8.
( )
2 29 5 .−

CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
485
Câu 30: Cho các số phức
,zw
thỏa mãn
35
5
wi+=
và
5 (2 )( 4)w i z= + −
. Tìm giá trị lớn nhất của biểu
thức
2 6 2P z i z i= − + − −
.
A. 7. B.
2 53
. C.
2 58
D.
4 13
.
Câu 31: Cho hai số phức
12
,zz
thỏa mãn
12
2 3 5 2 3 3z i z i+ + = + + =
. Gọi
0
m
là giá trị lớn nhất của phần
thực số phức
1
2
23
23
zi
zi
++
++
. Tìm
0
m
.
A.
0
3
5
m =
. B.
0
81
25
m =
. C.
0
3m =
. D.
0
5m =
.
Câu 32: Cho số phức
z
thỏa mãn
( ) ( )
1 2 1 2 4 2i z i z+ + + + − =
. Gọi
max ;n minm z z==
và số
phức
w m ni=+
. Tính
2018
w
A.
1009
4
. B.
1009
5
. C.
1009
6
. D.
1009
2
.
Câu 33: Cho số phức
z
thỏa mãn
( )
1 1 3 3 2i z i+ + − =
. Giá trị lớn nhất của biểu thức
2 6 2 3P z i z i= + + + − −
bằng
A.
56
. B.
( )
15 1 6+
. C.
65
. D.
10 3 15+
.
Câu 34: Hai số phức
z
,
w
thay đổi nhưng luôn thỏa mãn đẳng thức
( )
2
2019 2019
1 2 1 2 2
zi
i z iz i
w
+
+ − − = + −
. Giá trị lớn nhất của
w
là
A.
2019 2
4
. B.
2019 2
2
. C.
2019
. D. Đáp án khác.
CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
486
BẢNG ĐÁP ÁN
1.C
2.C
3.A
4.A
5.B
6.C
7.C
8.B
9.D
10.B
11.D
12.B
13.D
14.A
15.D
16.D
17.B
18.A.
19.A
20.B
21.B
22.A
23.D
24.B
25.C
26.A
27.A
28.A
29.C
30.C
31.D
32.C
33.C
34.A
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Chọn C
Ta có
2 2 2
2 1 1 3 5
22
22
z i z i z i
zi
P P P P
z z z z z z
+ − +
+
= = − +
.
Vậy
5
3
M
m
=
.
Câu 2: Chọn C
Giả sử
( )
0
,,z x yi x y= +
.
Ta có:
( ) ( ) ( )
2 3 1 2 3z i z i x y i x y i− = − + + − = − + − +
( ) ( ) ( )
2 2 2
2
1 2 3x y x y + − = − + − +
3yx = − +
.
( )
2
2
2 2 2 2
0
3 9 3
3 2 6 9 2
22
2
z x y x x x x x
= + = + − + = − + = − +
.
Vậy
0
min
3
2
z =
khi và chỉ khi
0
3 3 3 3
2 2 2 2
x y z i= = = +
, suy ra phần ảo của
0
z
bằng
3
2
.
Câu 3: Chọn A
Gọi
( )
;M x y
là điểm biểu diễn số phức
( )
i, ,z x y x y= +
.
Ta có:
2i 1 izz+ − = +
i 2i 1 i ix y x y + + − = + +
( ) ( ) ( )
1 2 i 1 ix y x y − + + = + +
( ) ( ) ( )
2 2 2
2
1 2 1x y x y − + + = + +
20xy − − =
.
Dễ thấy tập hợp các điểm M biểu diễn số phức
z
là đường thẳng:
20xy− − =
( )
;2M x x−
( )
1;x 5MA x= − −
( ) ( )
( )
2
22
2
1 5 2 12 26 2 3 2 8 8MA x x x x x = − + − = − + = − +
Suy ra:
min
8MA =
khi
2 3 2 0 3 1x x y− = = =
. Vậy
P 2 3 2.3 3.1 9xy= + = + =
Câu 4: Chọn A
Giả sử
z x yi=+
,
( )
,x y R
.
Do
1z =
22
1xy + =
22
1xy + =
. Suy ra
, 1;1xy−
.
Ta có
2
.1z z z==
. Thay vào
P
ta được:

CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
487
( )
2
1 . 1 1 1 . 1 1 1P z z z z z z z z z z z z z z z z= + + − + = + + − + = + + + − = + + + −
( )
2
2
1 2 1 2 2 2 1x y x x x= + + + − = + + −
.
Xét hàm số
( )
2 2 2 1y f x x x= = + + −
Ta có
( )
1
2 2 2 1 1
2
1
2 2 2 1 1
2
x x khi x
y f x
x x khi x
+ − + −
==
+ + −
.
( )
11
21
2
22
11
21
2
22
khi x
x
fx
khi x
x
− −
+
=
+
+
( )
1
1
2
'0
1
20
22
x
fx
x
−
=
−=
+
1
1
2
1
22
2
x
x
−
+=
7
8
x = −
Bảng biến thiên của hàm số
( )
fx
trên
1;1−
Suy ra
( )
( )
1;1
1;1
min 3
14
max
3
m f x
M f x
−
−
==
==
. Vậy
13 3
.
4
Mm=
.
Câu 5: Chọn B
Gọi
( )
;M x y
. Từ điều kiện
( )
2
1
22z a a a i= + − +
suy ra
M
thuộc parabol
( )
2
: 2 2P y x x= − +
Gọi
( )
;N x y
. Từ điều kiện
22
26z i z i− − = − −
suy ra
N
thuộc đường thẳng
: 2 8 0d x y− − =
.
Gọi
là tiếp tuyến của
( )
P
mà song song với
: 2 8 0d x y− − =
.
Gọi
( )
;
oo
M x y
là tiếp điểm mà tại đó tiếp tuyến
// d
. Ta có
22yx
=−
.
Do
// d
nên
( )
2 2 2 2 2
o o o
y x x x
= − = =
suy ra
2
o
y =
.
Phương trình tiếp tuyến
có dạng:
( ) ( ) ( )
. 2 2 2 2 2
o o o
y y x x x y y x y x
= − + = − + = −
.
Khi đó:
( ) ( )
min , ;MN d d d A d= =
với
A
. Chọn
( )
1;0A
ta có:
( )
2
2
2.1 0 8
65
min
5
21
MN
−−
==
+−
3
13
4
3
3
+
1
x
y'
y
1
0
7
8
1
2
+
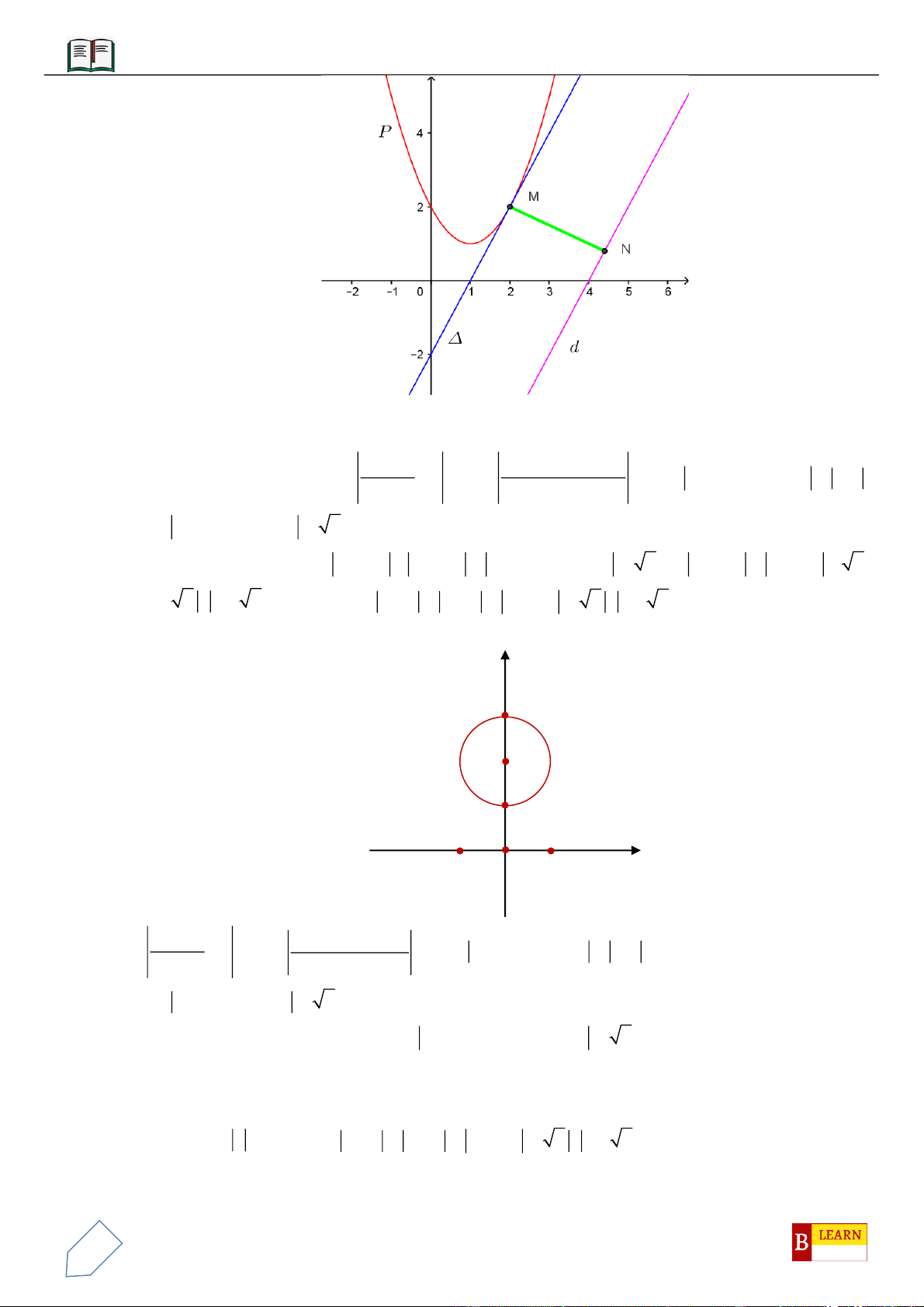
CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
488
Câu 6: Chọn C
Cch 1.
Ta có:
( )
1
21
1
iz
i
+
+=
−
( ) ( )
1 2 1
1
1
i z i
i
+ + −
=
−
( ) ( )
1 2 1 1i z i i + + − = −
( ) ( )
1 2 1 2i z i + + − =
.
Mặt khác:
( ) ( ) ( ) ( )
1 2 1 1 2 1 2i z i i z i+ − − + + − =
( ) ( )
1 2 1 2i z i + − +
2 3 2z
. Khi đó:
( )
1 2 3 2M z w z iz i z z= − = − = − =
.
Cách 2.
( )
1
21
1
iz
i
+
+=
−
(1 ) 2(1 )
1
1
i z i
i
+ + −
=
−
(1 ) 2(1 ) 1i z i i + + − = −
(1 ) 2(1 ) 2i z i + + − =
( )
1
Đặt
z x yi=+
thay vào
( )
1
ta được
( )
1 ( ) 2(1 i) 2i x yi+ + + − =
( )
2
2
2 ( 2) 2x y x y − + + + − =
22
( 2) 1xy + − =
.
Tập hợp điểm biểu diễn số phức
z
trên hệ trục tọa độ là đường tròn tâm
(0;2)I
bán kính
1R =
.
Khi đó:
13z
( )
1 2 3 2M z w z iz i z z= − = − = − =
.
Câu 7: Chọn C
O
1−
1
1
2
3
x
y
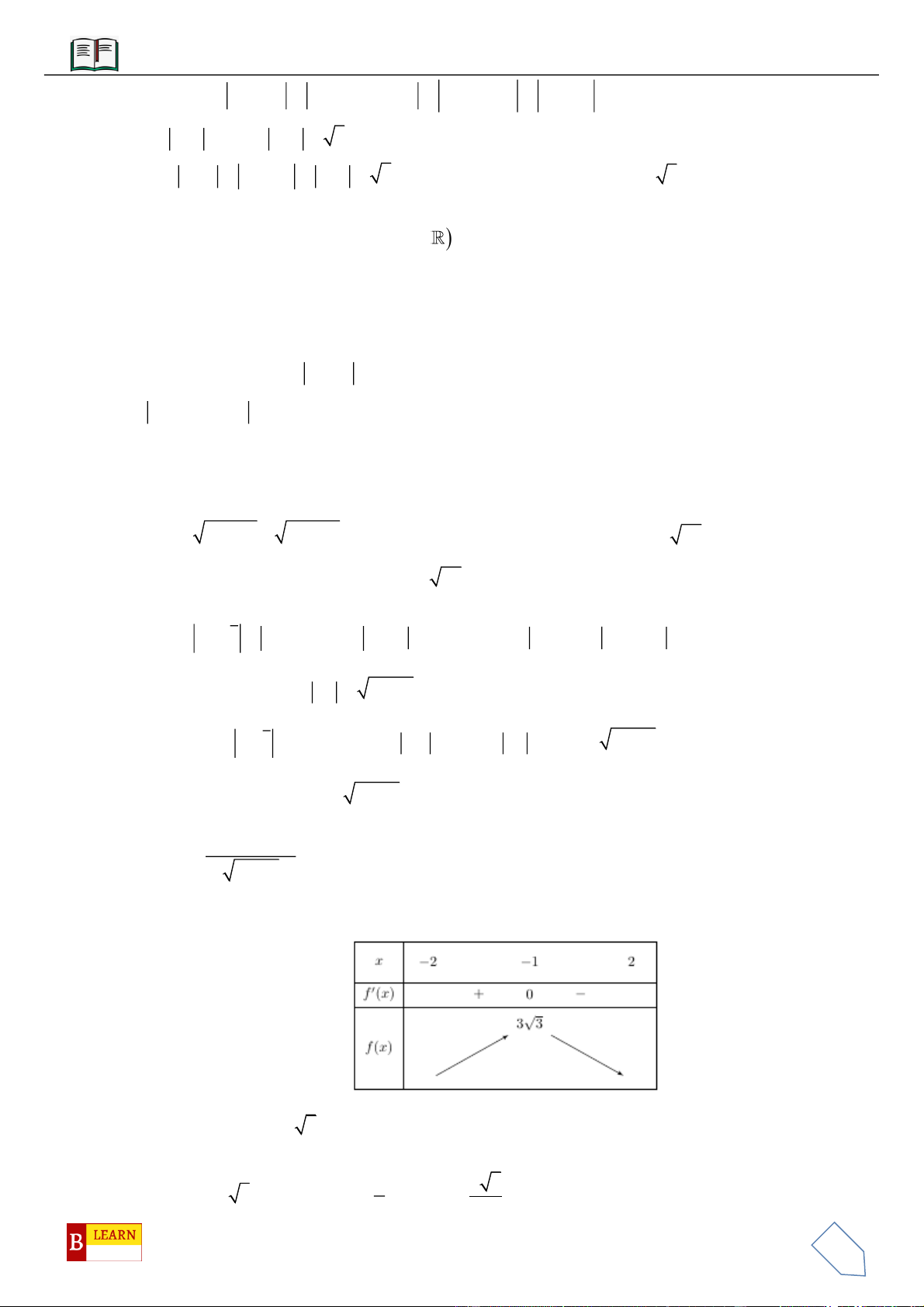
CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
489
Ta có:
( ) ( )
22
2 2 2
2 2 2 1 1 1z iz z iz i z i z i= − = − + + = − + − −
.
2
33z i z i − −
.
( )
13P iz i z i z i= + = − = −
. Vậy giá trị nhỏ nhất của
P
bằng
3
.
Câu 8: Chọn B
Đặt
( )
12
, , , , ,z a bi z c di a b c d= + = +
.
Ta có:
12
86z z i+ = +
nên
8
86
6
ac
a bi c di i
bd
+=
+ + + = +
+=
.
Do đó
( ) ( ) ( )
22
2 2 2 2
100 100 2 2 1 .a c b d a b c d ac bd+ + + = + + + = − −
Vì
12
2zz−=
nên ta có:
( ) ( ) ( )
22
2 2 2 2
2 4 4 2 2 2 .a bi c di a c b d a b c d ac bd+ − − = − + − = + + + = + +
Cộng và ta được:
( )
2 2 2 2
2 104a b c d+ + + =
.
Áp dụng bất đẳng thức
( )
( )
2
22
2 x y x y+ +
ta có:
(
)
( )
2
2 2 2 2 2 2 2 2 2
2 104P a b c d a b c d= + + + + + + =
. Do đó
2 26P
.
Vậy giá trị lớn nhất của biểu thức là
2 26
.
Câu 9: Chọn D
Ta có
( )( )
3 1 2 2z z i i− = + +
3 3 4x yi x yi+ − + =
2 4 4x yi+=
22
44xy+=
2
24yx=−
( )
22x−
.
Khi đó
( )
2Q z z x= − −
( ) ( ) ( )
2
2 2 2 2 4 2Q yi x y x x x= − = − = − −
.
Xét hàm số
( )
2
( ) 2 4f x x x= − −
với
2;2x −
.
2
2
2 2 4
()
4
xx
fx
x
−−
=
−
;
1
( ) 0
2
x
fx
x
=−
=
=
.
Ta có bảng biến thiên
Nên
2;2
( ) 3 3 ( 1)
x
Max f x f
−
= = −
.
Vậy
33M =
;
0
1x =−
;
2
0
3
4
y =
93
4
T =−
.
CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
490
Câu 10: Chọn B
Ta có
( )( )
2
2 5 1 2 3 1z z z i z i− + = − + + −
( ) ( )( )
2
1 4 1 2 3 1z z i z i − + = − + + −
( )( ) ( )( )
1 2 1 2 1 2 3 1z i z i z i z i − + − − = − + + −
1 2 1 2 1 2 3 1z i z i z i z i − + − − = − + + −
1 2 0
1 2 3 1
zi
z i z i
− + =
− − = + −
Trường hợp 1:
1 2 0 1 2z i z i− + = = −
2 2 1 2 2 2 1 1w z i i i w = − + = − − + = − =
Trường hợp 2:
( ) ( )
1 2 3 1 2 2 1 4 2 2 1z i z i z i i z i i− − = + − − + + − = − + + +
1 4 1w i w i + − = + +
Gọi
( )
;w x yi x y= +
thì
( ) ( ) ( ) ( )
2 2 2 2
3
1 4 1 1
2
x y x y y + + − = + + + =
.
Khi đó
2
2 2 2
33
22
w x y x
= + = +
. Đẳng thức xảy ra
0x=
. Suy ra:
3
min
2
w =
Từ và suy ra
min 1w =
.
Câu 11: Chọn D
Ta có:
( ) ( )
22z z i i= − − + +
.
Áp dụng bất đẳng thức
1 2 1 2 1 2
z z z z z z− + +
ta có:
2 2 2 2 1 5 1 5 5 1 1 5z i i z z i i z z− − − + − − + + − + − +
Vậy
5 1, 5 1mM= − = +
, do đó
25Mm+=
.
Câu 12: Chọn B
Theo đề
1z =
. Đặt
cos sinz x i x=+
( )
x
. Suy ra
( )
4
4
cos sin cos4 sin 4z x i x x i x= + = +
.
Khi đó
( )
2
2
4
11
cos4 cos sin4 sin
22
z z x x x x i
+ + = + + + +
( )
2
2
1
cos4 cos sin4 sin
2
x x x x
= + + + +
9
cos4 2cos3 cos
4
x x x= + + +
4 3 2
9
8cos 8cos 8cos 5cos 1
4
x x x x= + + − − +
( )
9
4
ft=+
. Với
( )
4 3 2
8 8 8 5 1, 1;1f t t t t t t= + − − + −
.
( )
1;1
9 9 1 11 1
min
4 4 4 8
f t f
−
−+
+ = + =
.
Câu 13: Chọn D
Vì
22
1 1 2 2
5 4 0z z z z− + =
( )
12
zz
suy ra
12
4zz=
2
7Pz=
Mặt khác
1
. .sin
2
OMN
S OM ON MON
=
12
1
12 sin
2
z z MON=
2
2
sin 6z MON=
.

CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
491
2
6
77
sin
Pz
MON
= =
. Nên
2
7Pz=
nhỏ nhất khi
sinMON
lớn nhất
sin 1MON=
.
Khi đó
76P =
.
Câu 14: Chọn A
Giả sử
( )
,z x yi x y= +
. Theo giả thiết ta có
22
1xy+=
.
Ta có:
( )
2 2 2 2 2
1 1 1 . 1 1 1 1P z z z z z z z z z z z z z z z= − + + + = − + + + = − + + + = − + + +
.
( )
2
2 2 2
1 1 1 2 1 2 2z x yi x y x y x x− = + − = − + = + − + = −
.
( )
2 2 2 2
1 2 1 2 2 1z z x y xyi x yi x x y x i+ + = − + + + + = + + +
( ) ( ) ( )
( )
2 2 2
2 2 2 2 2
1 2 1 2 1 2 1 2 1z z x x y x x x y x + + = + + + = + + = +
.
Suy ra
2 2 2 1P x x= − + +
. Xét hàm số
( )
2 2 2 1f x x x= − + +
trên đoạn
1;1−
.
Trên
1
1;
2
−−
;
( ) ( )
11
2 2 2 1 2 0, 1;
2
22
f x x x f x x
x
= − − − = − − − −
−
.
Mặt khác hàm số
( )
2 2 2 1f x x x= − − −
liên tục trên
1
1;
2
−−
.
Do đó hàm số nghịch biến trên
1
1;
2
−−
( ) ( )
1
1 3, 1;
2
f x f x
− = − −
.
( )
1
1;
2
max 3
x
fx
− −
=
.
Trên
1
;1
2
−
( ) ( ) ( )
1 1 7
2 2 2 1 2 0 2 2
28
22
f x x x f x f x x x
x
= − + + = − + = − = =
−
.
Có:
1
3
2
f
−=
;
7 13
84
f
=
;
( )
13f =
( )
1
;1
2
13
max
4
x
fx
−
=
.
Từ và
( )
1;1
13
max
4
x
fx
−
=
hay
max
13
4
P =
.
Câu 15: Chọn D
Ta có:
( )
10
1 2 2 .i z i
z
+ = − +
( ) ( )
10
2 2 1z i z
z
+ + − =
lấy môđun hai vế
( ) ( )
22
10 1 3
2 2 1 1 ; .
22
z z z
z
= + + − =
Câu 16: Chọn D
Gọi
z a bi=+
( )
,ab
. Khi đó:
( ) ( ) ( )
2 2 2
2
2 4 2 2 4 2 4z i z i a b a b a b− − = − − + − = + − = −
.
( ) ( ) ( ) ( )
2 2 2 2
2
2 2 1 2 3 2 10 13iz i b a b b b b+ − = − + − = − + − = − +
2
5 1 2
2
2 2 2
b
= − +
.
CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
492
Vậy giá trị nhỏ nhất của
2iz i+−
là
2
2
khi
5
2
b =
;
3
2
a =
.
Câu 17: Chọn B
Gọi
z x yi=+
,
,xy
. Khi đó
( )
; M x y
là điểm biểu diễn của số phức
z
.
Theo bài ra ta có
( ) ( )
22
1 3 2 1 3 4z i x y− − = − + − =
.
Suy ra tập hợp điểm
M
là đường tròn tâm
( )
1; 3I
bán kính
2R =
.
Khi đó
( )
2
2
11z x y I M
− = − + =
với
( )
1; 0I
.
1z −
nhỏ nhất khi
IM
ngắn nhất hay
I
,
M
,
I
thẳng hàng,
M
nằm giữa
I
và
I
.
Phương trình đường thẳng
II
là
1x =
.
Tọa độ giao điểm của đường thẳng
II
với đường tròn tâm
I
bán kính
2R =
là
( )
1
1; 1M
và
( )
1
1; 5M
. Thử lại ta thấy
( )
1
1; 1M
thỏa mãn. Vậy
1zi=+
.
Câu 18: Chọn A
Cách 1
Ta có:
.
Vì . Đặt .
Ta có: .
Khi đó: .
( )
21
w
z
i z i+ = + −
( ) ( )
2 1 1
w
z
z z i − + + =
( ) ( )
2 1 1
w
z
z z i − + + =
( ) ( )
22
2 1 1
w
z
zz − + + =
2
5 2 2
w
z
zz − + =
2
5 2 2 0zz− +
z
0z
tz=
( )
0t
2
1 5 2 2
w
tt
t
−+
=
2
22
5
tt
= − +
2
1 1 9
2
22t
= − +
3
2
0t
2
w
3
w1Ti= + −
w1i + −
2
2
3
+
42
3
=
CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
493
Dấu đẳng thức xảy ra .
Vậy .
Cách 2
Ta có:
.
Vì . Đặt .
Ta có: .
Suy ra tập hợp các điểm biểu diễn cho số phức là hình tròn tâm , bán kính .
Khi đó:
Dễ thấy điểm nằm ngoài đường tròn tâm , suy ra đạt giá trị lớn nhất khi
và chỉ khi . Vậy .
Câu 19: Chọn A
Cách 1
Ta có:
Đánh giá: . Đặt
Ta có:
Khi đó ta có:
( ) ( )
w 1 , 0
2
w
3
2
k i k k
z
= −
=
=
2
2
3
k=
1
3
k=
11
w
33
i = −
42
max
3
T =
( )
21
w
z
i z i+ = + −
( ) ( )
2 1 1
w
z
z z i − + + =
( ) ( )
2 1 1
w
z
z z i − + + =
( ) ( )
22
2 1 1
w
z
zz − + + =
2
5 2 2
w
z
zz − + =
2
5 2 2 0zz− +
z
0z
tz=
( )
0t
2
1 5 2 2
w
tt
t
−+
=
2
22
5
tt
= − +
2
1 1 9
2
22t
= − +
3
2
0t
2
w
3
w
( )
0;0O
2
3
R =
w1T i MI= + − =
( )
0;2I
( )
O;CR
T MI=
5 6 5
2
33
T MI IO R
+
= = + = + =
42
max
3
T =
( )
12
z
i z i
w
+ = − +
( )
21
z
z z i
w
− + + =
( ) ( )
22
21
z
zz
w
− + + =
2
2 2 5
z
zz
w
− + =
2
2 2 5 0,z z z− +
0z
tz=
( )
0t
2
2
2
1 2 2 5 2 5 1 1 9 3
25
55
5
tt
w t t t t
−+
= = − + = − +
5
3
w
5
2 2 2
3
w i w i− + − +
CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
494
Dấu đẳng thức xảy ra
Vậy: .
Cách 2
Ta có:
Đánh giá: . Đặt
Ta có:
Suy ra tập hợp các điểm biểu diễn cho số phức là hình tròn tâm , bán kính .
Khi đó:
Dễ thấy điểm nằm ngoài đường tròn tâm , suy ra đạt giá trị lớn nhất khi
và chỉ khi .
Vậy .
Câu 20: Chọn B
Ta có:
Đánh giá: . Đặt
Ta có:
Khi đó ta có:
( ) ( )
2 , 0
5
3
5
w k i k k
w
z
= −
=
=
55
2
36
kk = =
5
2
wi = −
5
2
3
MaxT =+
( )
12
z
i z i
w
+ = − +
( )
21
z
z z i
w
− + + =
( ) ( )
22
21
z
zz
w
− + + =
2
2 2 5
z
zz
w
− + =
2
2 2 5 0,z z z− +
0z
tz=
( )
0t
2
2
2
1 2 2 5 2 5 1 1 9 3
25
55
5
tt
w t t t t
−+
= = − + = − +
5
3
w
w
( )
0;0O
5
3
R =
w2T i MI=−=
( )
0;2I
( )
O;CR
T MI=
5
2
3
T MI IO R= = + = +
5
max 2
3
T =+
( )
3 2 1
13
z
i z i
iw i
+ = + −
−+
( )
3 1 2 1
13
z
z z i
iw i
− + + =
−+
( ) ( )
( )
22
3 1 2 1
3
z
zz
i w i
− + + =
++
2
13 2 2
3
z
zz
wi
− + =
++
2
13 2 2 0,z z z− +
0z
tz=
( )
0t
2
2
2
1 13 2 2 2 2 1 1 25 5
13 2
3 2 2
2
tt
w i t t t t
−+
= = − + = − +
++
2
3
5
wi + +
2
3 ( 3 ) 3 3 10
5
w w i i w i i= + + + − − + + + − − +

CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
495
Dấu đẳng thức xảy ra
Vậy:
Câu 21: Chọn B
Đặt
( )
,z a bi a b= +
.
Ta có:
( )
2
2 2 2
22z z i a b a b= + + = + +
4 4 0 1bb + = = −
z a i = −
.
Xét:
1 2 1 3 1 1 2z i z i a i a i− + + + + = − + + + +
( ) ( )
22
22
1 1 1 2aa= − + + + +
.
Áp dụng BĐT Mincôpxki:
( ) ( ) ( ) ( )
2 2 2 2
22
1 1 1 2 1 1 1 2a a a a− + + + + − + + + +
4 9 13= + =
.
Suy ra:
1 2 1 3z i z i− + + + +
đạt GTNN là
13
khi
( )
1
2 1 1
3
a a a− = + =
.
Nhận xét: Bài toán trên có thể được giải quyết bằng cách đưa về bài toán hình học phẳng.
Câu 22: Chọn A
Từ giả thiết:
1 1 2 2
9z z z z=
( )
1
Lấy mođun hai vế ta được:
22
1 2 1 2
93z z z z= =
.
Thay
12
3zz=
vào
( )
1
ta được
12
3zz=
.
Gọi
2
z a bi=+
( )
,ab
1
33z a bi = +
,
2
z a bi=−
.
Điểm
( )
3 ;3M a b
,
( )
;N a b−
1
3 3 3
2
OMN
S ab ab a b= − − =
.
Mà
6
OMN
S =
nên
2ab=
và
22
12
4 4 4z z a bi a b+ = + = +
4 2 8ab=
.
Suy ra
12
min 8zz+=
.
Lưu ý công thức tính diện tích tam giác
OAB
với
( )
12
;OA a a=
,
( )
12
;OB b b=
là
1 2 2 1
1
2
OAB
S a b a b=−
.
Câu 23: Chọn D
Đặt
1
z x yi=+
,
( )
,xy
, ta có
( ) ( )
3 3 , , 0
2
3
5
2
w i k i k k
wi
z
+ + = − −
+ + =
=
21
10
5
55
kk = =
( )
1 3 1
3 3 3 1
5 5 5 5 5 5
w i i w i
+ + = − − = − + − +
2
10
5
MaxT =+
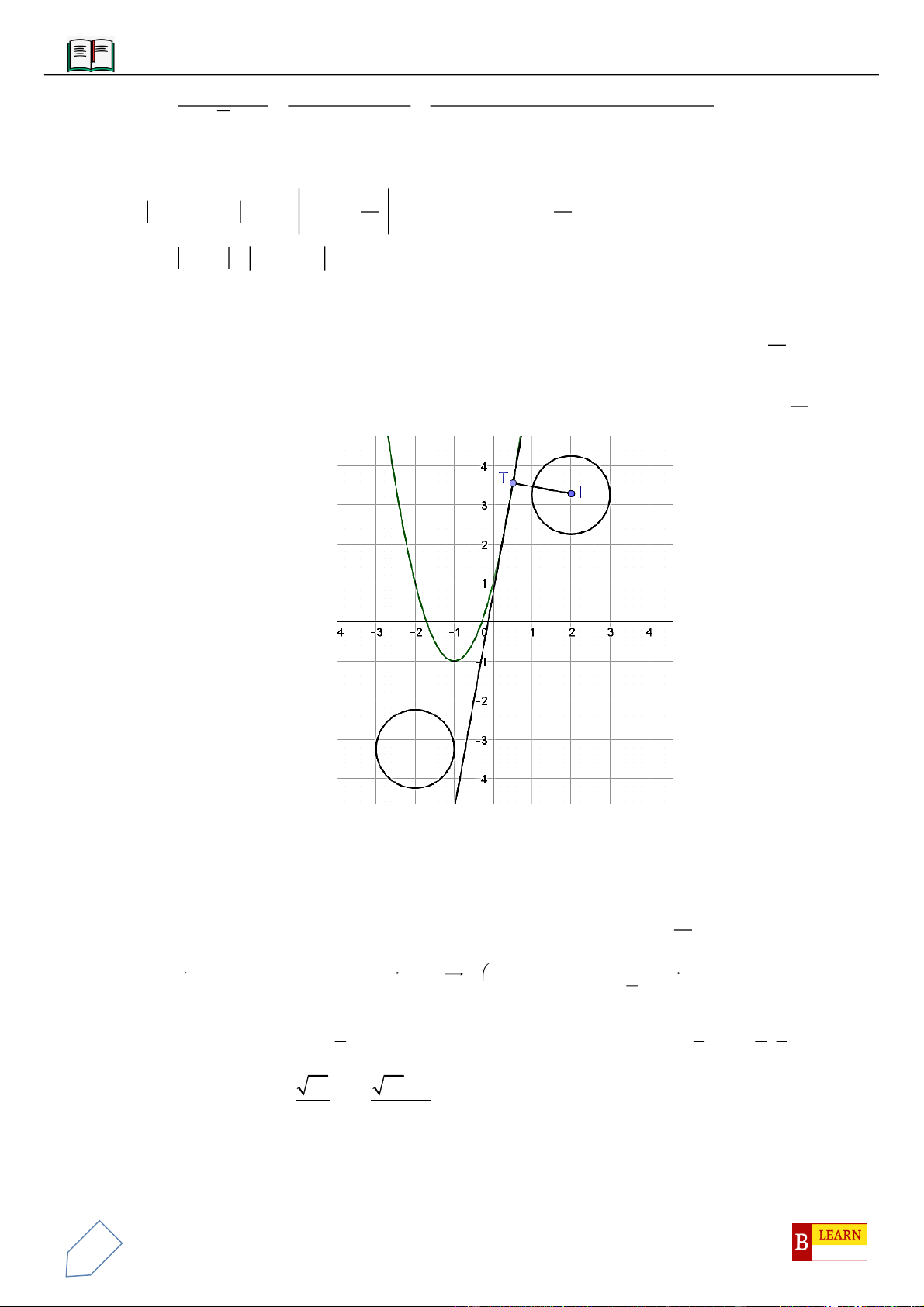
CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
496
( )
( ) ( )
( ) ( )
1
2
11
2 2 1 1 2 2
21
2
1 2 1 4
1
x x y y x x i
x y i
zi
w
xi x
z z i
+ + − + − − +
+ + −
+−
= = =
++
++
.
Vì
w
là số thực nên
( )
2
1 2 2 0 2 4 1y x x y x x− − + = = + +
.
( )
2
2
22
13 13
4z 8 13 4 z 2 1 2 1
44
i i x y
+ + = + + = + + + =
.
( )
1 2 1 2
P z z z z= + = − −
Gọi
M
là điểm biểu diễn của
1
z
thì điểm
M
thuộc parabol
( )
2
: 2 4 1P y x x= + +
.
Gọi
N
là điểm biểu diễn của
2
z
thì điểm
N
thuộc đường tròn
( ) ( )
2
2
13
: 2 1
4
C x y
+ + + =
Gọi
1
N
là điểm biểu diễn của
2
z−
thì điểm
1
N
thuộc đường tròn
( ) ( )
2
2
1
13
: 2 1
4
C x y
− + − =
Phương trình tiếp tuyến
của
( )
P
tại
( )
2
0 0 0
,2 4 1 ,T x x x++
( )
0
1x −
là
( )( )
2
0 0 0 0
4 4 2 4 1y x x x x x= + − + + +
( )
2
00
4 4 2 1 0x x y x + − − + =
.
Khi đó:
( )
1min
min
P MN T
là hình chiếu vuông góc của
I
lên
, với
13
2,
4
I
là tâm
( )
1
C
IT
cùng phương với VTPT
n
, với
2
0 0 0
9
2,2 4
4
IT x x x
= − + −
,
( )
0
4 4, 1nx
= + −
( )
2
0 0 0 0
9
4 4 2 4 2
4
x x x x
+ + − = −
32
0 0 0
8 24 8 11 0x x x + + − =
0
1 1 7
,
2 2 2
xT
=
Vậy
37 37 4
1
44
min
P IT R
−
= − = − =
.
Câu 24: Chọn B
Điều kiện:
1w
.
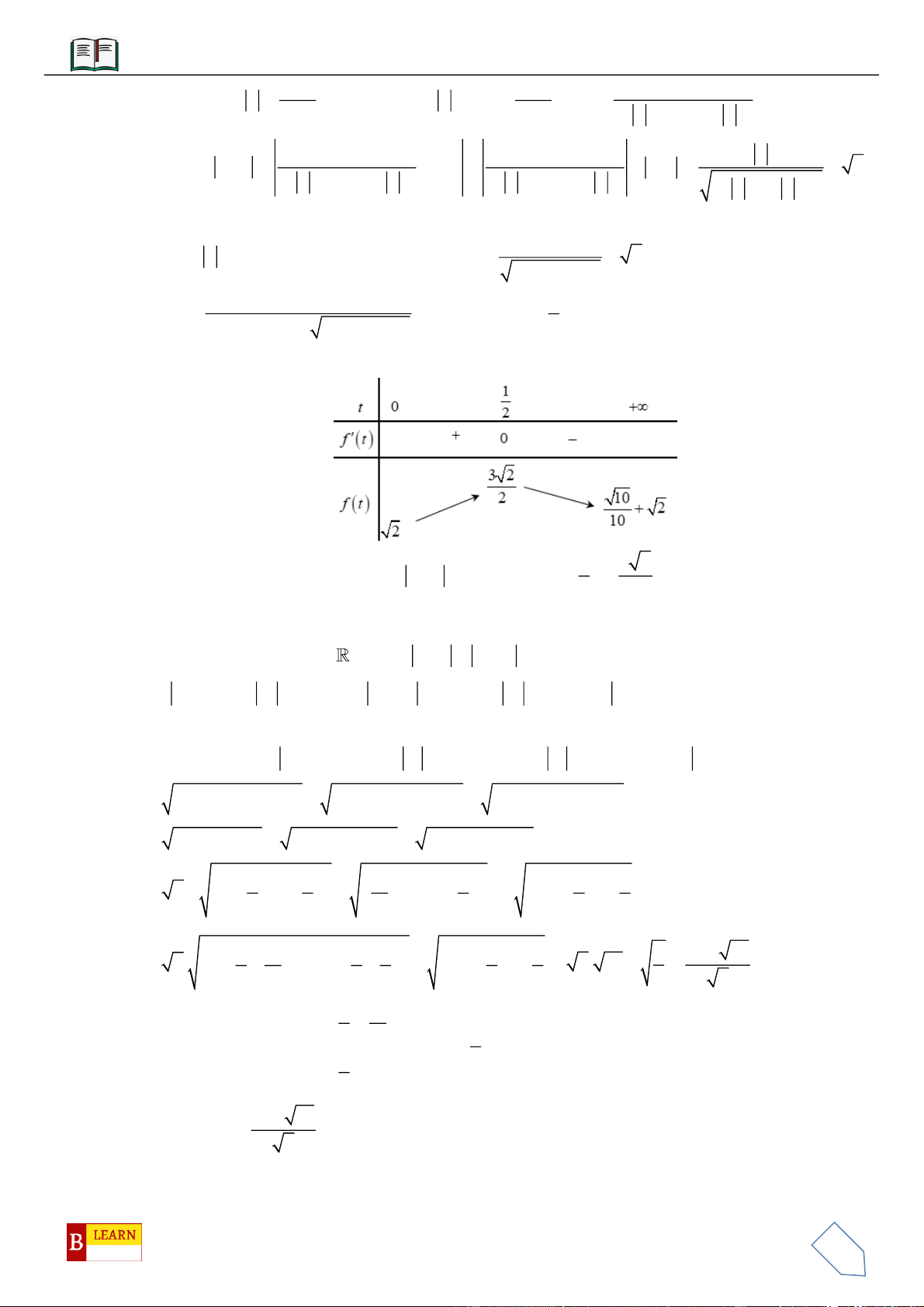
CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
497
Ta có:
( )
31
1
z
i z i
w
− = + −
−
( )
31
1
z
i z i
w
− − + =
−
( ) ( )
1
3 1 1
z
w
z z i
= +
− + −
.
Vậy
T w i=+
( ) ( ) ( ) ( )
11
3 1 1 3 1 1
zz
ii
z z i z z i
= + + + +
− + − − + −
2
2
10 8 2
z
zz
+
−+
.
Đặt
tz=
điều kiện:
0t
. Xét hàm số
( )
2
2
10 8 2
t
ft
tt
=+
−+
.
( )
( )
22
42
10 8 2 10 8 2
t
ft
t t t t
−+
=
− + − +
;
( )
1
0
2
f t t
= =
.
Bảng biến thiên:
Dựa vào bảng biến thiên ta có
)
( )
0;
1 3 2
max
22
T w i f t f
+
= + = =
.
Câu 25: Chọn C
Gọi
z x yi=+
với
x
,
y
. Ta có:
22z z i+ = +
( ) ( )
22x yi x yi i + + = + +
( ) ( )
22x yi x y i + + = + +
( ) ( )
22
22
22x y x y + + = + +
xy=
hay
z x xi=+
Khi đó ta có:
( ) ( ) ( ) ( ) ( ) ( )
1 2 3 4 5 6A x x i x x i x x i= − + − + − + − + − + −
( ) ( ) ( ) ( ) ( ) ( )
2 2 2 2 2 2
1 2 3 4 5 6x x x x x x= − + − + − + − + − + −
2 2 2
2 6 5 2 14 25 2 22 61x x x x x x= − + + − + + − +
2 2 2 2 2
3 1 11 1 7 1
2. 2
2 2 2 2 2 2
x x x
= − + + − + + − +
2 2 2
3 11 1 1 7 1
2. 2
2 2 2 2 2 2
x x x
− + − + + + − +
1 1 2 17
2. 17
2
2
+
+ =
.
Dấu bằng xảy ra khi
3 11
7
22
7
2
0
2
xx
x
x
− = −
=
−=
.
Vậy:
1 2 17
min .
2
A
+
=
Suy ra
1a =
,
2b =
nên
31ab−=
.
Câu 26: Chọn A

CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
498
Đặt
( )
1
2
, , ,
z a bi
a b c d
z c di
=+
=+
. Theo đề ta có:
( ) ( ) ( )
( ) ( ) ( )
( ) ( ) ( )
22
22
22
3 4 4 1
3 4 4 2
13
ab
cd
a c b d
− + − =
− + − =
− + − =
Khi lấy – theo vế có
( ) ( )
2 2 2 2
6 8 .a b c d a c b d+ − − = − + −
Kết hợp sử dụng bất đẳng thức Cauchy – Schwarz và sử dụng ta có:
( ) ( )
( )
( ) ( )
22
22
2 2 2 2 2 2
12
6 8 6 8 10.z z a b c d a c b d a c b d
− = + − − = − + − − + − + − = −
Vậy
giá trị nhỏ nhất của
22
12
zz−
là
10−
khi
( ) ( )
( ) ( )
( ) ( )
22
22
22
3 4 4
3 4 4
1
0
68
ab
cd
a c b d
a c b d
k
− + − =
− + − =
− + − =
−−
= =
.
Tồn tại 2 cặp số phức thỏa mãn là:
1
2
1
2
27 4 15 144 12 15
10 40
33 4 15 176 12 15
10 40
27 4 15 144 12 15
10 40
33 4 15 176 12 15
10 40
zi
zi
zi
zi
−+
=+
−+
=+
+−
=+
+−
=+
.
Câu 27: Chọn A
Theo giả thiết có:
2( ) 2 3 1a bi i+ + − =
(2 2) (2 3) 1a b i + + − =
( )
2
2
2 2 (2 3) 1.ab + + − =
2
2
31
( 1)
24
ab
+ + − =
( )
*
Cách 1:
( )
*
22
3 2 3a b a b + = − − +
. Từ
( )
*
suy ra
2
31
1 2.
24
bb
−
Khi đó biến đổi và sử dụng bất đẳng thức Bunhiacopxki ta được:
2 2 2 2
2 2 3 2 ( 2) ( 3)P z z a b a b= + + − = + + + − +
2 2 2 2
2 4 4 6 9a b a a b a= + + + + + − +
2 ( 3 2 3 ) 4 4 ( 3 2 3 ) 9 6a b a a b a= − − + + + + − − + + −
2 2 3 1 8 3 6a b a b= + + + − + +
8 12 4 8 3 6 (1 1)(8 12 4 8 3 6)a b a b a b a b= + + + − + + + + + − + +
2(15 10) 2(15.2 10) 4 5.b= + + =
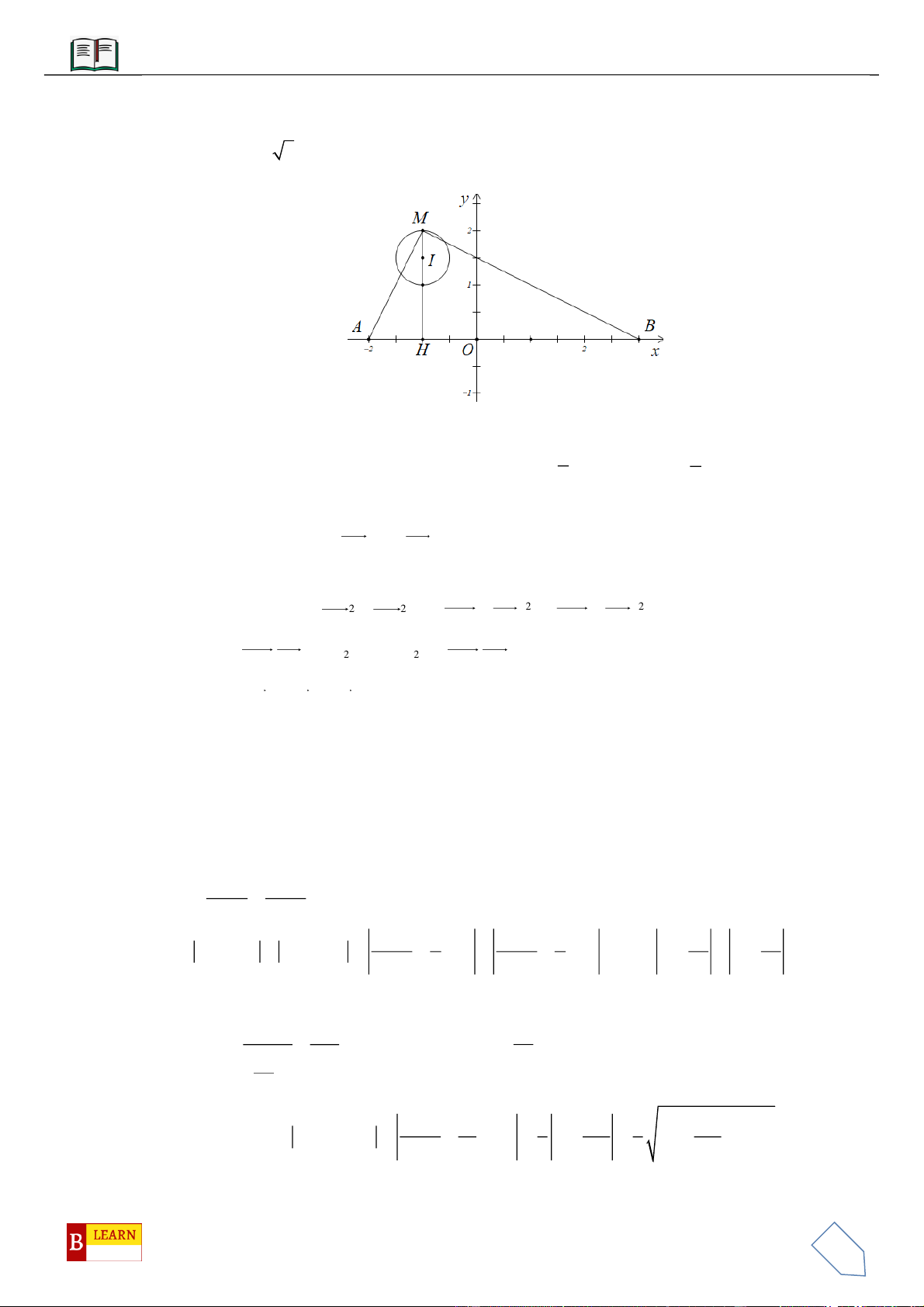
CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
499
Dấu “ = ” xảy ra khi
8 12 4 8 3 6 1
22
a b a b a
bb
+ + = − + + = −
==
.
Suy ra
45MaxP =
khi
1, 2ab= − =
.
Vậy
3.ab− = −
Cách 2:
Gọi
( )
;M a b
là điểm biểu diễn hình học của số phức
z
.
Từ
( )
*
suy ra
M
thuộc đường tròn
( )
C
có tâm
3
1;
2
I
−
bán kính
1
2
R =
.
Gọi
( ) ( )
2; 0 , 3; 0AB−
và
( )
1; 0H −
.
Khi đó
2P MA MB=+
và
4HB HA=−
.
Theo bất đẳng thức Bunhiacopxki ta được:
( ) ( )
( )
2
2 2 2
2 1 1 4P MA MB MA MB= + + +
.
Ta có:
22
22
44MA MB MA MB+ = +
( ) ( )
22
4 MH HA MH HB= + + +
( ) ( )
2 2 2 2
4 8 . 2 .MH MH HA HA MH MH HB HB= + + + + +
( )
( )
2 2 2
5 2 4MH MH HA HB HA HB= + + + +
( )
2 2 2
5MH HA HB= + +
.
Do các điểm
,,H A B
cố định và
0P
nên
P
lớn nhất khi
MH
là lớn nhất
M
là giao điểm của đường thẳng
IH
với đường tròn
( )
C
(
I
nằm giữa
M
và
H
).
Dễ dàng tìm được
( )
1; 2M −
hay
1; 2ab= − =
. Vậy
3.ab− = −
Câu 28: Chọn A
Cách 1:
Đặt
58
3 4 2
wi
z
i
+
=+
−
.
Ta có
3 3 25 25
1 2 4 6 2 2 9 45
3 4 2 3 4 2 2 2
ww
z i z i i i w w
ii
− − + − − = + + + − − = + + − =
−−
.
Đặt
w x yi=+
và gọi
( )
;M x y
là điểm biểu diễn
w
. Khi đó tập hợp điểm
M
là elip có phương
trình là
( )
22
2
:1
350
45
2
xy
E +=
. Suy ra
22
56
350
81
yx=−
( )
1
.
Mặt khác ta có
2
2
15 1 125 1 125
10 14 10
3 4 2 5 2 5 2
w
T z i i w x y
i
= − − = − − = − = − +
−
.

CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
500
Suy ra
2
22
1 125 56 1 25 17025
350 125
5 2 81 5 81 4
T x x x x
= − + − = − +
.
Từ
( )
1
ta có
45 45
22
x−
. Xét hàm số
( )
2
25 17025
125
81 4
f x x x= − +
trên đoạn
45 45
;
22
−
.
( )
50
125
81
f x x
=−
. Xét
( )
405 45 45
0;
2 2 2
f x x
= = −
.
Ta có
45
7225
2
f
−=
;
45
1600
2
f
=
.
Vậy giá trị lớn nhất của
T
bằng
1 45
17
52
f
−=
.
Cách 2:
Ta có
10 14 1 2 9 12 1 2 15z i z i i z i− − − − + − − = − − +
.
Ta có
10 14 4 6 6 8 4 6 10z i z i i z i− − − − + − − = − − +
.
Suy ra
2 10 14 9 15 10 34 10 14 17z i z i− − + + = − −
.
Dấu
'' ''=
xảy ra khi
12
55
zi= − +
. Vậy max
10 14 17zi− − =
.
Cách 3:
Gọi
( )
;M x y
là điểm biểu diễn số phức
z
. Gọi
( )
1
1;2F
và
( )
2
4;6F
. Suy ra
12
9MF MF+=
.
Suy ra tập hợp điểm biểu diễn
z
là Elip và có
12
5FF =
.
Ta có
10 14P z i MA= − − =
với
( )
10;14A
.
Ta có
( )
1
9;12FA=
,
( )
1 2 1 1 2 1
3;4 3F F F A F F F= =
,
A
,
2
F
thẳng hàng và có
12
1
2
5
15
10
FF
FA
FA
=
=
=
.
Ta có
22
7 10 17MA MF F A + + =
. Dấu
'' ''=
xảy ra khi
M
,
1
F
,
2
F
thẳng hàng và
1 1 2 2
MF FF MF+=
.
Câu 29: Chọn C
Ta có:
Đặt: . Khi đó:
Ta có:
Gọi lần lượt là điểm biểu diễn và .
Dẫn đến: với , thuộc đường tròn có tâm và có bán kính
2 5 1 5 2 1; 2 . 4iw i w i z z z− + = + + = = =
( )
, ; , , ,z x iy w a ib x y a b= + = +
( ) ( )
22
22
4
5 2 1
xy
ab
+=
+ + + =
( )
2
4
42z wz z z w z z w
z
− − = − − = − −
,AB
zz−
w
( )
0;2Ay
22y−
B
( )
5; 2I −−
1.R =

CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
501
Khi đó: . Ta có:
Giá trị nhỏ nhất của
Nhận xét:
Ta xem bài toán trên gồm 3 giả thiết:
Việc đầu tiên, ta rút gọn các giả thiết của bài toán.
Từ , ta gọi là điểm biểu diễn của , là điểm biểu diễn của .
Bài toán trở thành tìm độ dài nhỏ nhất.
Câu 30: Chọn C
Cách 1.
Ta có
5 (2 )( 4)w i z= + −
5 5 5 (2 )( 4)w i i i z + = + + −
5 (2 ) 8w i i z i + = + − +
.
Đặt
z x yi=+
với
,xy
ta được
(2 )( ) 8 3 5i x yi i+ + − + =
2 8 ( 2 1) 3 5x y x y i − − + + + =
22
(2 8) ( 2 1) 45x y x y − − + + + =
2 2 2 2
4 64 4 32 16 4 1 4 2 4 45x y xy x y x y xy x y + + − − + + + + + + + =
22
5 5 30 20 20 0x y x y + − + + =
22
( 3) ( 2) 9xy − + + =
Đặt
3sin 3
3cos 2
x
y
=+
=−
. Khi đó
2 2 2 2
( 2) ( 6) ( 2) 18sin 24cos 34 18sin 24cos 34P x y x y
= + − + − + − = − + + − − +
Áp dụng bất đẳng thức Bunhia Copsky ta có
22
1 1 . 48cos 68 2 58P
+ − +
Dấu bằng xảy ra khi
18sin 24cos 34 18sin 24cos 34
11
cos 1
− + − − +
=
=−
cos 1
sin 0
=−
=
.
Suy ra
max 2 58P =
khi
35zi=−
.
Cách 2.
Ta có
5 (2 )( 4)w i z= + −
5 5 5 (2 )( 4)w i i i z + = + + −
5 (2 ) 8w i i z i + = + − +
.
B
d
I
A
2
42z wz AB− − =
( )
min
,4AB d I d R= − =
2
4 8.z wz− − =
2 . 4z z z= =
2 5 1 5 2 1iw i w i− + = + + =
( )
2
4 2 *z wz z w z− − = − −
( )
*
A
zz−
B
w
AB
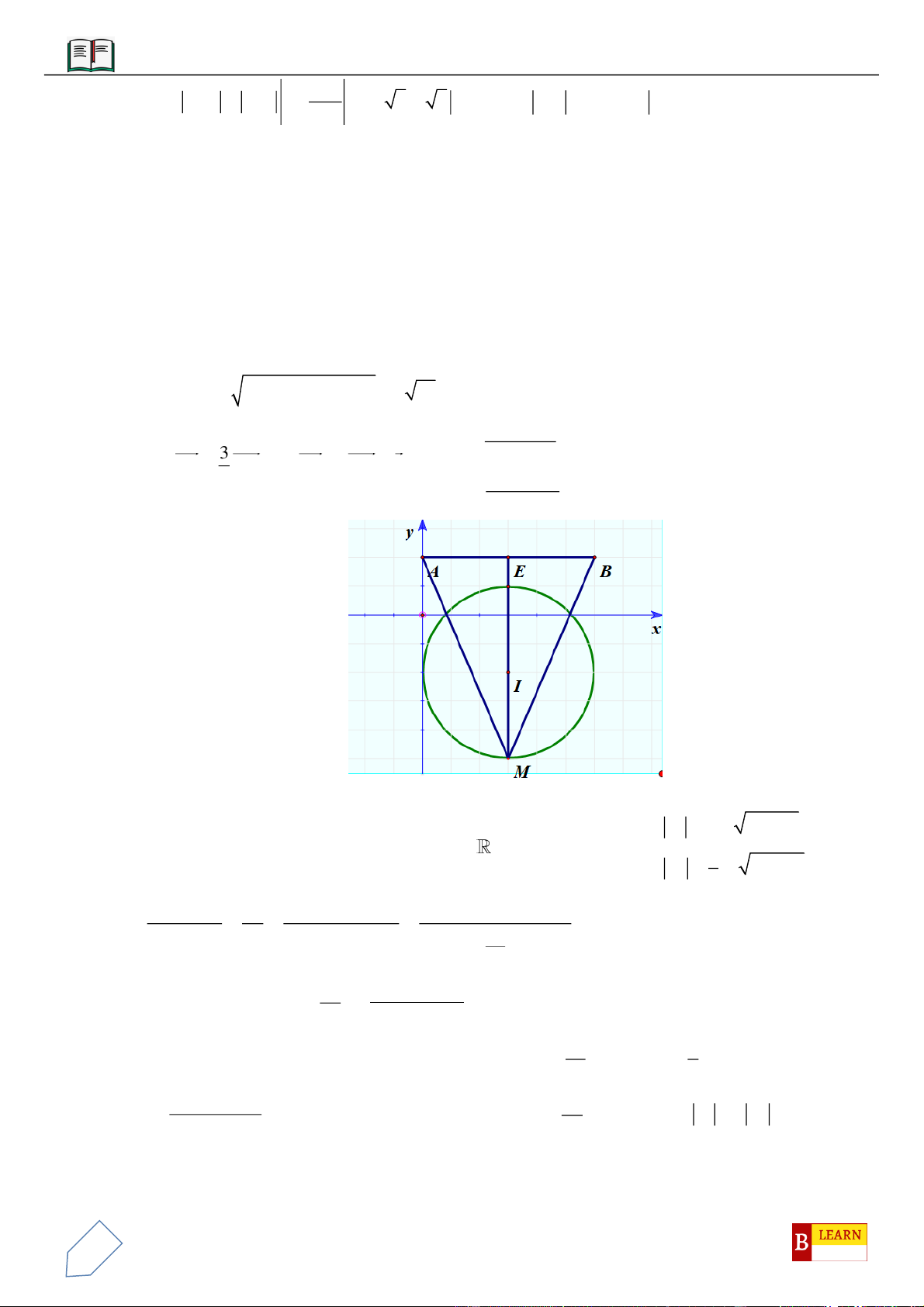
CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
502
8
52
2
i
w i i z
i
−
+ = + −
+
( )
3 5 5 3 2zi = − −
( )
3 2 3zi − − =
.
Khi đó tập hợp các điểm biểu diễn số phức
z
là đường tròn tâm
( )
3; 2I −
và bán kính
3R =
.
Gọi
( )
;M x y
là điểm biểu diễn số phức
z
;
( )
0;2A
là điểm biểu diễn số phức
1
2zi=
;
( )
6;2B
là điểm biểu diễn số phức
2
62zi=+
.
( )
3;2E
là trung điểm của đoạn thẳng
AB
.
Ta có
P MA MB=+
( )
( )
2
2 2 2 2 2
24P MA MB MA MB ME AB= + + = +
.
Khi đó
P
đạt giá trị lớn nhất khi
ME
đạt giá trị lớn nhất hay
ME R IE=+
.
Vậy
( )
2
2
max
4 2 58P R IE AB= + + =
khi
3
7 3 0
7
MI ME MI ME= − =
73
4
73
4
IE
M
IE
M
xx
x
yy
y
−
=
−
=
3
5
M
M
x
y
=
=−
.
Câu 31: Chọn D
Đặt
11
22
23
23
w z i a bi
w z i c di
= + + = +
= + + = +
với
, , ,a b c d
, theo giả thiết ta có:
22
1
22
2
3
3
5
w a b
w c d
= = +
= = +
.
( )( ) ( )
11
22
22
23
9
23
25
a bi c di ac bd bc ad i
z i w
z i w c d
+ − + + −
++
= = =
+ + +
.
Phần thực của số phức
1
2
w
w
là
( )
25
9
ac bd+
.
Ta có
( )
( )( )
( )
22
2 2 2 2
99
9.
25 5
ac bd a b c d ac bd ac bd+ + + + +
.
( )
25
5
9
ac bd+
. Dấu
""=
xảy ra khi
ad bc=
hay
1
2
w
w
là số thực và
12
53ww==
.
Vậy
0
5m =
.
Câu 32: Chọn C

CHUYÊN ĐỀ: SỐ PHỨC.
Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.
503
Gọi
( )
,z x yi x y= +
.
Ta có
( ) ( )
1 2 1 2 4 2i z i z+ + + + − =
( ) ( )( ) ( ) ( )( )
1 1 1 1 1 1 4 2i z i i i z i i + + + − + + − + − =
( )( ) ( )( )
1 1 1 1 4 2i z i i z i + + − + + − + =
1 1 1 1 4 2i z i i z i + + − + + − + =
( ) ( ) ( ) ( )
2 2 2 2
1 1 4 1 1 1 1 4(*)z i z i x y x y + − + − + = + + − + − + + =
.
Gọi
( ) ( ) ( )
12
; ,F 1;1 , 1; 1M x y F−−
. Ta có
12
4MF MF + =
.
Do đó tập hợp điểm
M
biểu diễn cho số phức
z
là một Elip có hai tiêu điểm là
12
,FF
; tiêu cự
bằng
12
1
2
2
FF =
; độ dài trục lớn bằng
12
4MF MF+=
; một nửa độ dài trục bé bằng
2
.
Ta có
max 2mz==
;
n min 2z==
( )
2018
2018
1009
2 2 6 6 6w i w w = + = = =
.
Câu 33: Chọn C
Ta có
( )
1 1 3 3 2 1 2 3i z i z i+ + − = − − =
nên tập hợp điểm
M
biểu diễn số phức
z
là đường
tròn tâm
(1;2)I
, bán kính
3R =
.
Đặt
1 2 , 1a z i b i= − − = +
.
Ta có
( )
( )
2 2 2 2
2 2 2 2
2 3 9 3 . .
2 3 . .
z i a b a b a b a b
z i a b a b a b a b
+ + = + = + + +
− − = − = + − +
2 2 2 2 2 2
2 3 2 3 3 3 4 12 60z i z i a b a b a b + + + − − = + + − = + =
.
Khi đó
( )
( )
22
3 2. 3 1 2 3 3 6 5P a b a b a b a b= + + − + + + − =
.
Câu 34: Chọn A
Ta có:
z i z i− = +
nên
2
2
2
21z iz z i z i− − = − = +
.
Như vậy:
( ) ( )
( )
2
2
2019
2019 2019
1 2 1 2 2 1 2 2
zi
zi
i z iz i i z i i
ww
+
+
+ − − = + − + + = + −
( )
( )
( )
( )
2 2 2
2019 2019
1 2 2 2 2
z i z i
i z i i z i z i i
ww
++
+ + + − = + − + + + =
.
Điều kiện:
0w
suy ra
0zi+
hay
0zi+
.
Đặt
,0t z i t= +
ta có
( )
( )
22
2019
22
zi
t t i
w
+
− + + =
. Lấy môđun hai vế ta được:
( ) ( ) ( ) ( )
2 2 2 2
2 2 2 2
2019
2019
2 2 2 2
zi
t
t t t t
ww
+
− + + = − + + =
( ) ( )
2 2 4
22
2019 2019
28
22
tt
ww
t
tt
= =
+
− + +
2019 2019 2
4
22
t
ww
t
.
Vậy
2009 2
max
4
w =
khi
44
2 8 4 2 2t t t z i= = = − =
.

CHUYÊN ĐỀ: SỐ PHỨC.
Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.
Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”
504
Bấm Tải xuống để xem toàn bộ.




