Nắm trọn chuyên đề thể tích khối đa diện ôn thi THPT Quốc gia môn Toán

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

1 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

1. Một số định nghĩa cần nhớ

• Hình lăng trụ là hình có hai đáy là hai đa giác bằng nhau nằm trên hai mặt phẳng song song với

nhau và các mặt bên đều là các hình bình hành.

• Hình lăng trụ đứng

Định nghĩa: Hình lăng trụ đứng là hình lăng trụ có cạnh bên vuông góc với mặt đáy.

Tính chất: Các mặt bên của hình lăng trụ đứng là các hình chữ nhật và vuông góc với mặt đáy.

• Hình lăng trụ đều

Định nghĩa. Hình lăng trụ đều là hình lăng trụ đứng có đáy là đa giác đều.

Tính chất. Các mặt bên của hình lăng trụ đều là các hình chữ nhật bằng nhau và vuông góc với

mặt đáy.

• Hình hộp là hình lăng trụ có đáy là hình bình hành.

• Hình hộp đứng

Định nghĩa. Hình hộp đứng là hình hộp có cạnh bên vuông góc với mặt đáy.

Tính chất. Hình hộp đứng có

2

đáy là hình bình hành, 4 mặt xung quanh là 4 hình chữ nhật.

• Hình hộp chữ nhật

Định nghĩa. Hình hộp chữ nhật là hình hộp đứng có đáy là hình chữ nhật.

Tính chất. Hình hộp chữ nhật có

6

mặt là

6

hình chữ nhật.

• Hình lập phương

Định nghĩa. Hình lập phương là hình hộp chữ nhật

2

đáy và

4

mặt bên đều là hình vuông

Tính chất. Hình lập phương có

6

mặt đều là hình vuông.

• Hình chóp là hình có đáy là một đa giác và các mặt bên là các tam giác có chung một đỉnh.

2. Thể tích khối đa diện

1. Công thức tính thể tích khối chóp

1

.

3

V S h=

Trong đó:

S

là diện tích đáy,

h

là chiều cao khối

chóp.

• Chú ý: Nếu khối chóp cần tính thể tích chưa biết chiều

cao thì ta phải xác định được vị trí chân đường cao trên

đáy.

2

THỂ TÍCH KHỐI ĐA DIỆN

8

CHỦ ĐỀ

TÓM TẮT LÝ THUYẾT

A

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 2

▪ Chóp có cạnh bên vuông góc chiều cao chính là cạnh bên.

▪ Chóp có hai mặt bên vuông góc đáy đường cao là giao tuyến của hai mặt bên vuông góc

đáy.

▪ Chóp có mặt bên vuông góc đáy chiều cao của mặt bên vuông góc đáy.

▪ Chóp đều chiều cao hạ từ đỉnh đến tâm đa giác đáy.

▪ Chóp có hình chiếu vuông góc của một đỉnh lên xuống mặt đáy thuộc cạnh mặt đáy đường

cao là từ đỉnh tới hình chiếu.

2. Công thức tính thể tích khối lăng trụ

.V B h=

Trong đó:

B

là diện tích đáy,

h

là hiều cao khối lăng trụ.

• Thể tích khối hộp chữ nhật:

..V a b c=

Trong đó:

, , a b c

là ba kích thước của khối hộp chữ nhật.

• Thể tích khối lập phương:

3

Va=

Trong đó

a

là độ dài cạnh của hình lập phương.

3. Tỷ số thể tích

Cho khối chóp

.S ABC

và

,,A B C

  

là các điểm tùy ý lần lượt thuộc

,,SA SB SC

, ta có:

Công thức tỉ số thể tích:

. ' ' '

.

' ' '

..

S A B C

S ABC

V

SA SB SC

V SA SB SC

=

(hay gọi là công thức Simson)

Phương pháp này được áp dụng khi khối chóp không xác đinh được chiều cao một cách dễ dàng

hoặc khối chóp cần tính là một phần nhỏ trong khối chóp lớn và cần chú ý đến một số điều kiện

sau:

▪ Hai khối chóp phải cùng chung đỉnh.

▪ Đáy hai khối chóp phải là tam giác.

▪ Các điểm tương ứng nằm trên các cạnh tương ứng.

Định lý Menelaus: Cho ba điểm thẳng hàng

. . 1

FA DB EC

FB DC EA

=

với

DEF

là một đường thẳng cắt

ba đường thẳng

,,BC CA AB

lần lượt tại

,,D E F

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

3 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

4. Một số công thức tính nhanh thể tích và tỷ số thế tích khối chóp và khối lăng trụ.

➢ Công thức 1 : Thể tích tứ diện đều cạnh

a

:

3

.

2

12

S ABC

a

V =

.

➢ Công thức 2 : Với tứ diện

ABCD

có

,,AB a AC b AD c= = =

đôi một vuông góc thì thể tích của

nó là

1

6

ABCD

V abc=

.

➢ Công thức 3 : Với tứ diện

ABCD

có

,,AB CD a BC AD b AC BD c= = = = = =

thì thể tích của

nó là

( )( )( )

2 2 2 2 2 2 2 2 2

2

12

ABCD

V a b c b c a a c b= + − + − + −

.

➢ Công thức 4 : Cho khối chóp

.S ABC

có

, , , , ,SA a SB b SC c BSC CSA ASB

  

= = = = = =

thì

thể tích của nó là

2 2 2

.

1 2cos cos cos cos cos cos

6

S ABC

abc

V

     

= + − − −

.

➢ Công thức 5 : Mặt phẳng cắt các cạnh của khối lăng trụ tam giác

.ABC A B C

  

lần lượt tại

,,M N P

sao cho

,,

AM BN CP

x y z

AA BB CC

= = =

  

thì ta có

..

3

ABC MNP ABC A B C

x y z

VV

  

++

=

.

➢ Công thức 6 : Mặt phẳng cắt các cạnh của khối hộp

.ABCD A B C D

   

lần lượt tại

, , ,M N P Q

sao

cho

,,,

AM BN CP DQ

x y z t

AA BB CC DD

= = = =

   

thì ta có

..

4

ABCD MNPQ ABCD A B C D

x y z t

VV

   

+ + +

=

và

x z y t+ = +

.

➢ Công thức 7 : Mặt phẳng cắt các cạnh của khối chóp tứ giác

.S ABCD

có đáy là hình bình hành

lần lượt tại

, , ,M N P Q

sao cho

, , ,

SM SN SP SQ

x y z t

SA SB SC SD

= = = =

thì ta có công thức sau đây

..

1 1 1 1

4

S MNPQ S ABCD

xyzt

VV

x y z t



= + + +





và

1 1 1 1

x z y t

+ = + +

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 4

Câu 1: Cho hình chóp tứ giác đều có cạnh bên gấp đôi cạnh đáy. Tỉ lệ giữa diện tích xung quanh và diện

tích đáy của hình chóp này bằng

A.

15.

B.

3.

C.

4 3.

D.

3.

 Lời giải

…………………………………………………………………

………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 2: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông tâm

O

, cạnh

a

. Cạnh

SA

vuông góc với

đáy, góc

60SBD =

. Thể tích khối chóp đã cho bằng

A.

3

2

3

a

. B.

3

2

a

. C.

3

a

. D.

3

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 3: Cho hình chóp tam giác

.S AB C

có đáy là tam giác đều cạnh

a

. Cạnh bên

SA

vuông góc với

đáy

( )

ABC

và có

2SA a=

. Thể tích khối chóp

SABC

bằng

A.

3

2

a

. B.

2

3

6

a

. C.

3

12

a

. D.

3

6

12

a

.

S

C

A

B

D

VÍ DỤ MINH HỌA

B

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

5 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 4: Cho hình chóp

.S AB C

có đáy

ABC

là tam giác vuông cân tại

A

, cạnh huyền bằng

2a

và

3SA a=

,

SA

vuông góc với đáy. Thể tích

V

của khối chóp đã cho bằng

A.

3

4

3

a

V =

. B.

3

46

3

a

V =

. C.

3

6

a

V =

. D.

3

22Va=

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 5: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

. Biết

( )

SA ABCD⊥

và

3SA a=

. Thể tích khối chóp

.S ABCD

là

A.

3

a

. B.

3

3a

. C.

3

4

a

. D.

3

12

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 6

Câu 6: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật,

AB a

,

3AD a

,

SA

vuông góc

với đáy và mặt phẳng

SBC

tạo với đáy một góc

60

. Tính thể tích

V

của khối chóp

.S ABCD

A.

3

a

V

. B.

3

3Va

. C.

3

a

V

. D.

3

Va

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 7: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật,

SA

vuông góc với đáy,

,2AB a AD a==

. Góc giữa

SB

và đáy bằng

0

45

. Thể tích của khối chóp

.S ABCD

bằng

A.

3

2

3

a

. B.

3

a

. C.

3

2

6

a

. D.

3

2

3

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 8: Cho hình chóp

.S ABCD

có

SA

vuông góc đáy, hai mặt phẳng

( )

SAB

và

( )

SBC

vuông góc với

nhau,

3SB a=

, góc giữa

SC

và

( )

SAB

là

45

và

30ASB =

. Gọi thể tích khối chóp

.S ABCD

là

V

. Tỉ số

3

a

V

là

A.

8

3

. B.

83

3

. C.

23

3

. D.

4

3

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

7 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 9: Cho khối chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

3a

, cạnh

SA

vuông góc với mặt

phẳng

( )

ABC D

và

SB

tạo với đáy một góc

60

o

. Tính thể tích của khối chóp

.S ABCD

.

A.

3

9a

. B.

3

9

2

a

. C.

3

3a

. D.

3

4

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 10: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

, cạnh bên

SA

vuông góc với mặt

phẳng đáy, góc giữa

SA

và mặt phẳng

( )

SBD

bằng

45

. Thể tích khối chóp

.S AB D

bằng

A.

3

6

4

a

. B.

3

12

a

. C.

3

4

a

. D.

3

2

12

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 8

Dạng 1: Mở đầu về thể tích khối đa diện

Dựa vào kiến thức được nêu trong phần lý thuyết

Câu 1: Thể tích khối lập phương là

3

27cm

. Diện tích toàn phần của hình lập phương tương ứng bằng

A.

2

54cm

. B.

2

36cm

. C.

2

16cm

. D.

2

9cm

.

Câu 2: Cho khối chóp có thể tích bằng

3

30cm

và chiều cao bằng

5cm

. Diện tích đáy của khối chóp đã

cho bằng

A.

6.cm

B.

18 .cm

C.

24 .cm

D.

12 .cm

Câu 3: Cho hình lập phương có cạnh bằng

3

. Tổng diện tích các mặt của hình lập phương đã cho bằng

A.

54

. B.

12

. C.

36

. D.

24

.

Câu 4: Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng

a

, có thể tích

( )

3

9

.

4

V dm=

Tính giá trị

của

a

.

A.

( )

33a dm=

. B.

( )

3a dm=

. C.

( )

3 dm

. D.

( )

9 dm

.

Câu 5: Cho khối chóp tam giác đều có cạnh đáy bằng

2a

và thể tích bằng

3

a

. Chiều cao của khối chóp

đã cho bằng

A.

3a

. B.

23a

. C.

3

a

. D.

3

2

a

.

Câu 6: Cho hình lập phương có cạnh bằng 2. Tổng diện tích các mặt của hình lập phương đó bằng

A.

16

. B.

12

. C.

4

. D.

24

.

Câu 7: Cho hình lăng trụ đứng có diện tích đáy là

2

3a

, độ dài cạnh bên là

2a

. Khi đó thể tích của

khối lăng trụ bằng

A.

3

6a

. B.

3

3a

. C.

3

2a

. D.

3

6

3

a

.

Câu 8: Cho hình lập phương có cạnh bằng

2

. Tổng diện tích các mặt của hình lập phương đã cho bằng

A.

16

. B.

12

. C.

4

. D.

24

.

Câu 9: Mệnh đề nào sau đây sai?

A. Hai khối hộp chữ nhật có diện tích toàn phần bằng nhau thì có thể tích bằng nhau.

B. Hai khối lăng trụ có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau.

C. Hai khối lập phương có diện tích toàn phần bằng nhau thì có thể tích bằng nhau.

D. Hai khối chóp có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau.

Câu 10: Trong các mệnh đề sau, mệnh đề nào sai?

A. Thể tích khối chóp có đường cao

h

và diện tích đáy

B

là

1

3

V Bh=

.

B. Thể tích khối lăng trụ có đường cao

h

và diện tích đáy

B

là

.V B h=

.

C. Thể tích khối tứ diện có đường cao

h

và diện tích đáy

B

là

1

6

V Bh=

.

D. Thể tích khối lập phương cạnh

a

là

3

Va=

.

BÀI TẬP TRẮC NGHIỆM

C

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

9 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 11: Khối chóp

.S AB CD

có tất cả các cạnh bằng nhau và có thể tích bằng

16

3

. Tính cạnh của khối

chóp.

A.

22

. B.

2

. C.

3

. D.

2

.

Câu 12: Cho khối lăng trụ có diện tích đáy

2

6Ba=

và chiều cao

2ha=

. Thể tích của khối lăng trụ đã

cho bằng

A.

3

8a

. B.

3

4

3

a

. C.

3

4a

. D.

3

12a

.

Câu 13: Cho khối lăng trụ có thể tích bằng

3

24a

và chiều cao bằng

3a

. Diện tích một mặt đáy của khối

lăng trụ đã cho bằng

A.

2

16a

. B.

2

8a

. C.

2

6a

. D.

2

72a

.

Câu 14: Tính tổng diện tích các mặt của một hình bát diện đều cạnh

a

.

A.

2

23a

. B.

2

4a

. C.

2

3a

. D.

2

43a

.

Câu 15: Tổng diện tích tất cả các mặt của hình bát diện đều cạnh bằng

2a

là

A.

2

2 3.a

B.

2

8 3.a

C.

2

3.a

D.

2

43a

Câu 16: Cho hình lăng trụ đứng

.ABC A B C

  

có đáy là tam giác đều cạnh

a

và cạnh bên

2a

. Tính diện

tích xung quanh hình trụ ngoại tiếp hình lăng trụ đứng

.ABC A B C

  

.

A.

2

3a



. B.

2

3

a



. C.

2

23

3

a



. D.

2

43

3

a



.

Câu 17: Cho hình lăng trụ đứng

.ABCD A B C D

   

với đáy là hình thoi có cạnh bằng

4a

,

6AA a



=

,

0

120BCD =

. Gọi

,,M N K

lần lượt là trung điểm của

,,AB B C BD

  

. Tính thể tích khối đa diện

lồi có các đỉnh là các điểm

, , , , ,A B C M N K

.

A.

3

9a

. B.

3

16 3a

. C.

3

93a

. D.

3

12 3a

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

1 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Dạng 2: Thể tích khối chóp có cạnh bên vuông góc với đáy

▪ Một hình chóp có một cạnh bên vuông góc với đáy thì cạnh bên đó chính là đường cao.

▪ Một hình chóp có hai mặt bên kề nhau cùng vuông góc với đáy thì cạnh bên là giao tuyến của hai

mặt đó vuông góc với đáy.

Câu 1: Cho hình chóp

SABCD

có đáy

ABCD

là hình chữ nhật với

3,AB a AD a==

, cạnh

SA

có độ

dài bằng

2a

và vuông góc với mặt phẳng đáy. Tính thể tích khối chóp

SABCD

A.

3

a

. B.

3

2

3

a

. C.

3

a

. D.

3

23

3

a

.

 Lời giải

…………………………………………………………………

………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 2: Cho khối chóp

.S ABC

có đáy là tam giác đều cạnh bằng

3

, tam giác

SAC

đều và nằm trong

mặt phẳng vuông góc với mặt phẳng đáy. Thể tích của khối chóp đã cho bằng

A.

3

12

. B.

33

8

. C.

33

4

. D.

3

8

.

 Lời giải

…………………………………………………………………

………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 3: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật, tam giác

SCD

đều và nằm trong mặt

phẳng vuông góc với đáy,

CD a=

,

3BC a=

. Thể tích khối chóp

.S ABCD

bằng

A.

3

2

a

. B.

3

6

a

. C.

3

2

a

. D.

3

a

.

VÍ DỤ MINH HỌA

B

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 2

 Lời giải

…………………………………………………………………

………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 4: Cho hình chóp

.S ABCD

có đáy là hình chữ nhật, mặt bên

SAD

là tam giác đều cạnh

4a

và nằm

trong mặt phẳng vuông góc với mặt phẳng đáy. Góc giữa mặt phẳng

( )

SBC

và mặt phẳng

( )

ABC D

là

o

30

. Thể tích của khối chóp

.S ABCD

là

A.

3

24 3a

. B.

3

16 3a

. C.

3

43a

. D.

3

48 3a

.

 Lời giải

…………………………………………………………………

………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 5: Cho hình chóp

.S AB C

có

SAB

và

ABC

là hai tam giác đều cạnh

a

và nằm trong hai mặt phẳng

vuông góc với nhau. Tính theo

a

thể tích của khối chóp

..S ABC

A.

3

2

3

a

. B.

3

a

. C.

3

a

. D.

3

3a

.

 Lời giải

…………………………………………………………………

………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

3 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 6: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh bằng

3,a

tam giác

SBC

vuông

tại

S

và nằm trong mặt phẳng vuông góc với đáy, đường thẳng

SD

tạo với mặt phẳng

( )

SBC

một góc

60

. Thể tích của khối chóp đã cho bằng

A.

3

3.a

B.

3

6.a

C.

3

6

.

6

a

D.

3

6

.

3

a

 Lời giải

…………………………………………………………………

………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 7: Cho hình chóp

.S ABCD

có đáy là hình chữ nhật,

=AB a

,

2=AD a

. Tam giác SAB cân tại S và

nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng

( )

ABCD

bằng

45

. Thể tích của khối chóp

.S ABCD

là:

A.

3

17

9

a

. B.

3

17

3

a

. C.

3

17

3

a

. D.

3

17

6

a

.

 Lời giải

…………………………………………………………………

………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

………………………………………………………………

…………………………………………………………………

………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 4

Câu 1: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

. Biết

( )

SA ABCD⊥

và

3SA a=

. Thể tích của khối chóp

.S ABCD

là:

A.

3

12

a

. B.

3

3a

. C.

3

a

. D.

3

4

a

.

Câu 2: Cho khối chóp

.S AB C

có đáy

ABC

là tam giác vuông cân tại

A

,

( )

2, 12,AB SA SA ABC= = ⊥

. Tính thể tích khối chóp

.S AB C

?

A.

8

. B.

16

. C.

24

. D.

6

.

Câu 3: Cho khối tứ diện

ABCD

có

,,AB AC AD

đôi một vuông góc và

2 , 3= = =AB AC a AD a

. Thể

tích

V

của khối tứ diện đó là:

A.

3

4=Va

. B.

3

2=Va

. C.

3

=Va

. D.

3

3=Va

.

Câu 4: Cho khối chóp

.S ABC

có đáy là tam giác đều cạnh

a

,

( )

SA ABC⊥

,

SA a=

(tham khảo hình

vẽ bên dưới).

Thể tích của khối chóp đã cho bằng:

A.

3

4

a

. B.

3

6

a

. C.

3

3a

. D.

3

12

a

.

Câu 5: Cho hình chóp

.S ABC

có đáy là tam giác đều cạnh

2a

, cạnh bên

SA

vuông góc với đáy và

3SA a=

. Tính thể tích

V

của khối chóp

.S ABC

A.

3

1

2

Va=

. B.

3

4

Va=

. C.

3

22Va=

. D.

3

Va=

.

Câu 6: Cho tứ diện

SABC

có các cạnh

, , SA SB SC

đôi một vuông góc với nhau. Biết

3,SA a=

4 , 5 .SB a SC a==

Tính theo

a

thể tích

V

của khối tứ diện

.SABC

A.

3

5.Va=

B.

2

5

.

2

a

V =

C.

3

10 .Va=

D.

3

20 .Va=

Câu 7: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác đều cạnh

a

. Biết

( )

SA ABC⊥

và

3SA a=

.

Tính thể tích khối chóp

.S ABC

A.

4

a

. B.

3

2

a

. C.

3

4

a

. D.

3

4

a

.

Câu 8: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

2a

,

( )

SA ABCD⊥

,

2SA a=

.

Tính thể tích khối chóp

.S ABCD

BÀI TẬP TRẮC NGHIỆM

C

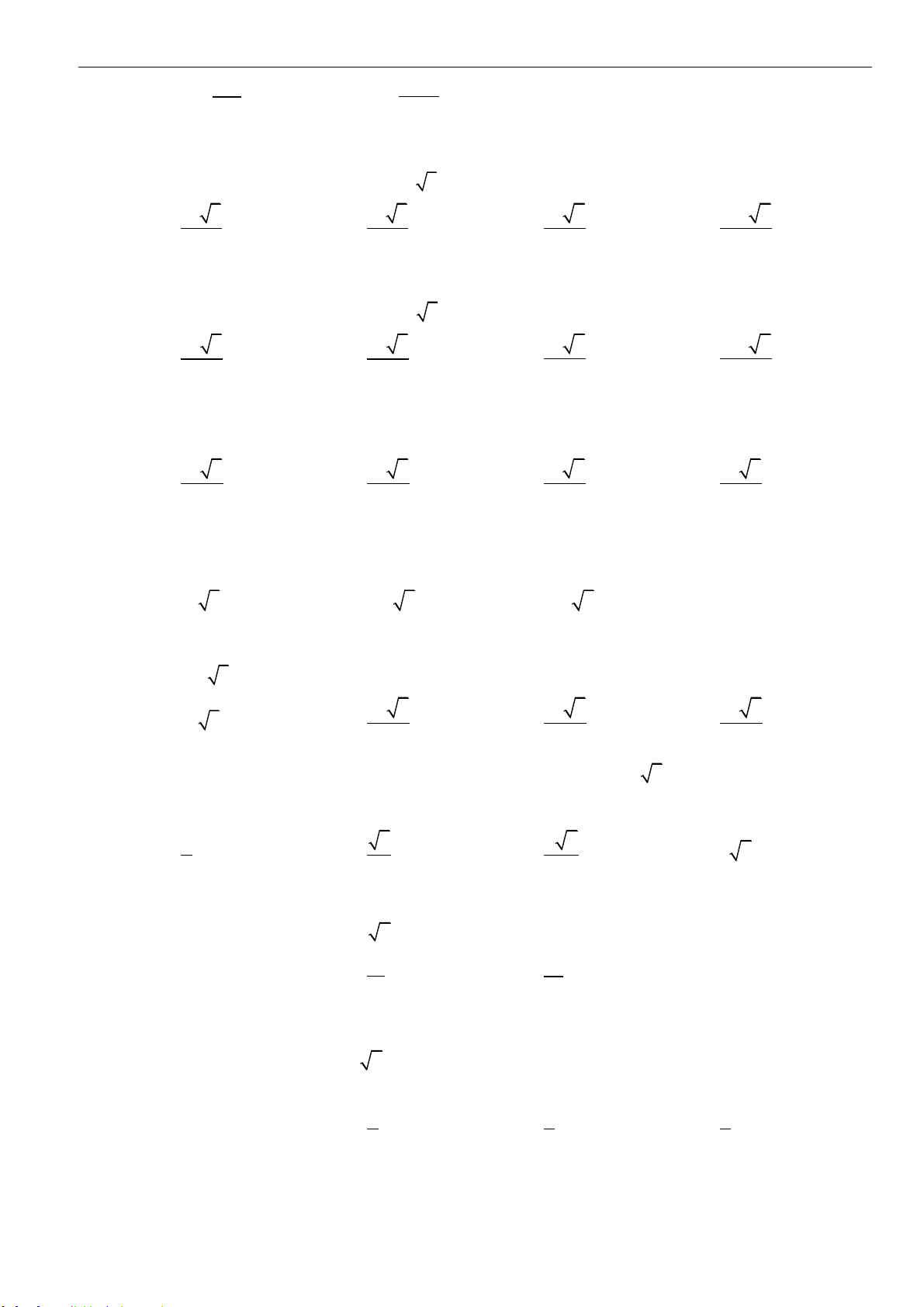
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

5 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

A.

3

4

3

a

V =

. B.

3

4

3

a

V



=

. C.

3

4Va=

. D.

3

4Va



=

.

Câu 9: Cho khối chóp

.S ABC

có đáy

ABC

là tam giác đều cạnh

a

, hai mặt bên

( )

SAB

và

( )

SAC

cùng vuông góc với đáy và

3SC a=

. Thể tích khối chóp bằng

A.

3

4

a

. B.

3

2

a

. C.

3

6

12

a

. D.

3

26

9

a

.

Câu 10: Cho khối chóp

.S ABC

có đáy

ABC

là tam giác đều cạnh

a

, hai mặt bên

( )

SAB

và

( )

SAC

cùng vuông góc với đáy và

3SC a=

. Thể tích khối chóp bằng

A.

3

4

a

. B.

3

2

a

. C.

3

2

6

1

a

. D.

3

26

9

a

.

Câu 11: Cho hình chóp

.S AB C

có đáy là tam giác đều cạnh bằng

a

. Cạnh bên

SC

vuông góc với mặt

phẳng

( )

,ABC SC a=

. Thể tích khối chóp

.S AB C

bằng

A.

3

a

. B.

3

9

a

. C.

3

2

12

a

. D.

3

12

a

.

Câu 12: Cho khối chóp

.S ABCD

có đáy là hình thoi cạnh

2a

,

0

60ABC =

, cạnh bên

SA

vuông góc với

mặt phẳng đáy, mặt bên

( )

SCD

tạo với đáy một góc

0

60

. Thể tích khối chóp

.S AB C

bằng

A.

3

3a

. B.

3

33a

. C.

3

23a

. D.

3

2a

.

Câu 13: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

. Biết

( )

SA ABCD⊥

và

3SA a=

. Thể tích của khối chóp

.S ABCD

là:

A.

3

3a

. B.

3

12

a

. C.

3

a

. D.

3

6

a

.

Câu 14: Cho khối chóp

.S ABCD

có đáy là hình chữ nhật

, 3,AB a AD a SA==

vuông góc với mặt đáy

và

SC

tạo với mặt phẳng

( )

SAB

một góc

0

30

. Thể tích của khối chóp đã cho bằng

A.

3

4

3

a

. B.

3

6

3

a

. C.

3

26

3

a

. D.

3

26a

.

Câu 15: Cho tứ diện

SABC

có các mặt

,SAB SBC

là các tam giác cân tại S và

,,SA SB SC

đôi một

vuông góc với nhau,

2AB a=

. Thể tích của khối tứ diện đã cho bằng

A.

3

2a

. B.

3

a

. C.

3

6

a

. D.

3

a

.

Câu 16: Cho khối chóp

.S AB CD

có

( )

SA ABCD⊥

, đáy

ABCD

là hình thang,

/ / ,AB CD

,7SA AD DC a BC a= = = =

. Tam giác

SBC

vuông tại

C

, tam giác

SCD

vuông tại

D

. Thể

tích khối chóp đã cho bằng

A.

3

2a

. B.

3

4

3

a

. C.

3

2

3

a

. D.

3

1

2

a

.

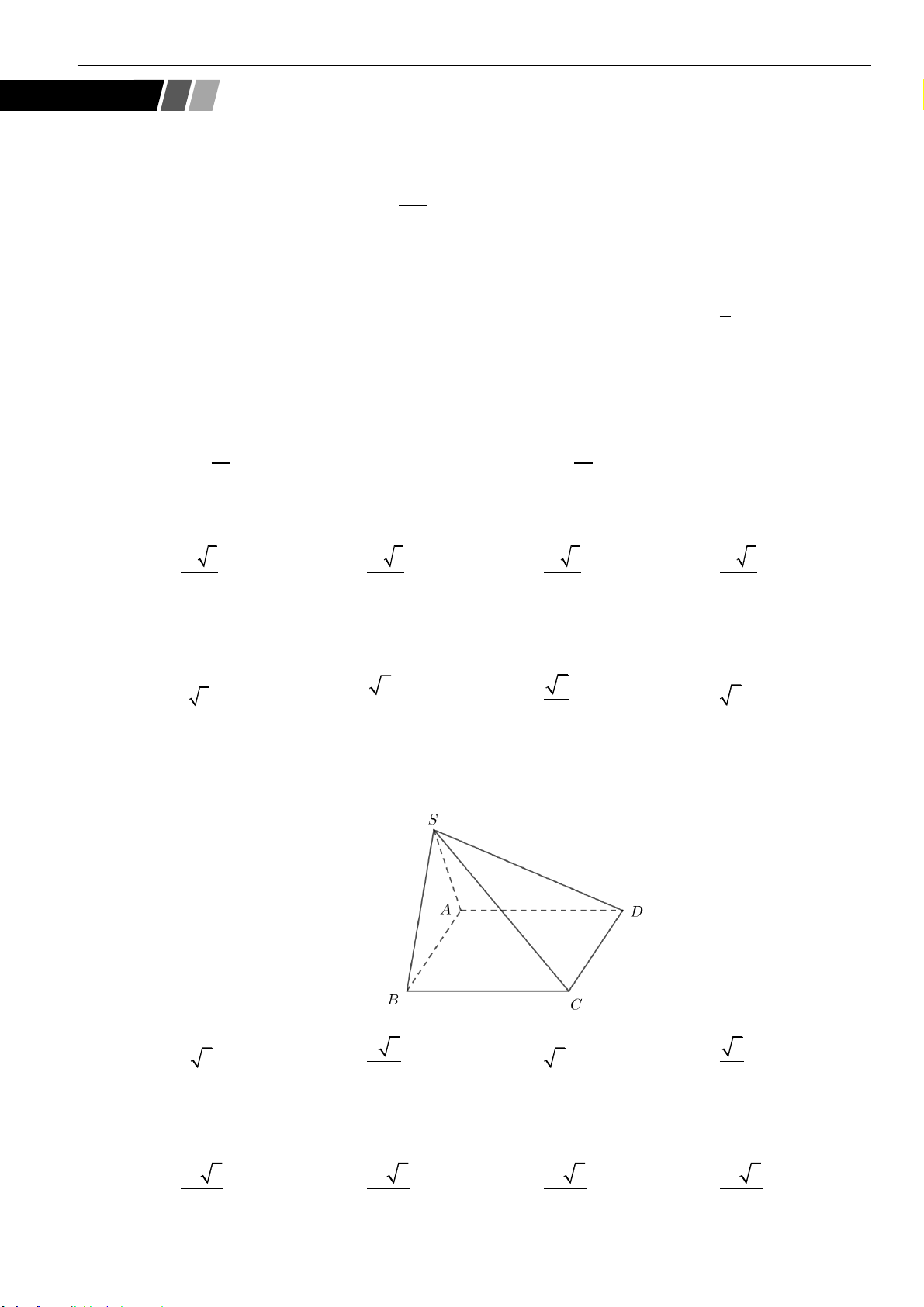
Câu 17: Cho khối chóp

.S ABCD

có đáy

ABCD

là hình vuông,

( )

SA ABCD⊥

và

SA a=

, góc giữa

đường thẳng

SC

và mặt phẳng

( )

ABC D

bằng

30

o

(tham khảo hình vẽ). Thể tích khối chóp

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 6

.S ABCD

bằng

A.

3

2

a

. B.

3

4

a

. C.

3

6

a

. D.

3

6

a

.

Câu 18: Cho khối chóp

.S AB C

có đáy

ABC

là tam giác vuông tại

B

và

3, 4BC BA==

. Cạnh bên

5SA =

vuông góc với đáy, khi đó thể tích khối chóp bằng

A.

60V =

. B.

20V =

. C.

30V =

. D.

10V =

.

Câu 19: Cho khối chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

. Hai mặt phẳng

( )

SAB

và

( )

SAD

cùng vuông góc với đáy. Tính thể tích khối chóp

.S ABCD

biết rằng

3SC a=

.

A.

3

ABCD

Va=

. B.

3

SABCD

a

V =

. C.

3

9

SABCD

a

V =

. D.

3

SABCD

a

V =

.

Câu 20: Cho khối chóp

.S ABCD

có

ABCD

là hình chữ nhật tâm

O

;

22AC AB a==

;

SA

vuông góc

với mặt phẳng đáy. Tính thể tích khối chóp

.S ABCD

biết rằng

5.SD a=

A.

3

.

5

3

S ABCD

a

V =

B.

3

.

15

3

S ABCD

a

V =

C.

3

.

6

3

S ABCD

a

V =

D.

3

.

6

S ABCD

Va=

Câu 21: Cho hình chóp

SABC

có đáy

ABC

là tam giác vuông tại

B

,

AB a=

,

5AC a=

,

( )

SA ABC⊥

và

3SA a=

. Thể tích khối chóp

SABC

bằng

A.

3

a

V =

. B.

3

3Va=

. C.

3

2

a

V =

D.

3

5

3

a

V =

.

Câu 22: Cho hình chóp tam giác

.S AB C

có đáy

ABC

là tam giác vuông tại

B

,

3AB a=

,

60ACB =

, cạnh bên

SA

vuông góc với mặt đáy và

SB

hợp với mặt đáy một góc

30

. Tính thể tích

V

của khối chóp

.S AB C

.

A.

3

18

a

V =

. B.

3

6

a

V =

. C.

3

6

a

V =

. D.

3

9

a

V =

.

Câu 23: Cho hình chóp

.S ABC

có cạnh bên

SA

vuông góc với mặt phẳng đáy

( )

ABC

. Biết

SA a=

, tam

giác

ABC

là tam giác vuông cân tại

A

,

2AB a=

. Tính theo

a

thể tích

V

của khối chóp

..S ABC

A.

3

6

a

V =

. B.

3

2

a

V =

. C.

3

2

3

a

V =

. D.

3

2Va=

.

Câu 24: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật

AB a=

và

3AD a=

, cạnh bên

SA

vuông góc với đáy. Tính thể tích

V

của khối chóp

.S ABCD

biết góc giữa hai mặt phẳng

( )

SBD

và

( )

ABC D

bằng

60

.

Câu 25: Cho khối chóp

.S ABCD

có đáy là hình chữ nhật,

,2AB a AD a==

,

SA

vuông góc với đáy, góc

giữa cạnh bên

SC

và đáy bằng

30

. Tính thể tích của khối chóp đã cho.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

7 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

A.

3

2 15

3

Va=

. B.

3

2

3

Va=

. C.

3

2 15

9

Va=

. D.

3

2 15Va=

.

Câu 26: Cho hình chóp

.S AB C

có đáy

ABC

là tam giác đều cạnh

a

. Hai mặt

( )

SAB

và

( )

SAC

cùng

vuông góc với đáy và

3SB a=

. Tính thể tích

.S AB C

.

A.

3

6

4

a

. B.

3

6

12

a

. C.

3

6

3

a

. D.

3

26

9

a

.

Câu 27: Cho hình chóp

.S AB C

có đáy

ABC

là tam giác cân tại

A

,

23BC a=

,

0

120BAC =

, cạnh bên

SA

vuông góc với mặt đáy và

2SA a=

. Tính thể tích

V

của khối chóp

.S AB C

.

A.

3

23

3

a

V =

. B.

3

3Va=

. C.

3

2

a

V =

. D.

3

6

a

V =

Câu 28: Cho hình chóp

.S ABC

, đáy là tam giác vuông cân tại

B

,

AB a=

,

SA

vuông góc với đáy, góc

giữa

SC

và đáy bằng

45



. Thể tích khối chóp

.S ABC

bằng

A.

3

2

6

a

. B.

3

2

a

. C.

3

6

a

. D.

3

2

a

.

Câu 29: Cho khối chóp

.S ABCD

có đáy

ABCD

là hình vuông,

SA

vuông góc với mặt phẳng đáy và

3SA a=

. Biết góc giữa đường thẳng

SD

và mặt phẳng

()SAC

bằng

30 .

Thể tích khối chóp đã

cho bằng

A.

3

27a

. B.

3

a

. C.

3

3a

. D.

3

9a

.

Câu 30: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật

2AB a=

và

4AD a=

, cạnh bên

SA

vuông góc với đáy. Tính thể tích

V

của khối chóp

.S ABCD

biết góc giữa hai mặt phẳng

( )

SBD

và

( )

ABCD

bằng

0

30

.

A.

3

15

5

a

. B.

3

8 15

15

a

. C.

3

8 15

45

a

. D.

3

a

.

Câu 31: Cho hình chóp

.S AB C

có đáy là tam giác vuông tại

, 3 , 10,B BC a AC a==

cạnh bên

SA

vuông góc với đáy. Góc giữa mặt phẳng

( )

SBC

và mặt phẳng đáy bằng

30 .

o

Tính thể tích khối

chóp

.S AB C

là

A.

3

.

6

a

B.

3

.

3

a

C.

3

.

2

a

D.

3

3.a

Câu 32: Cho hình chóp

.S ABCD

có đáy là hình vuông cạnh

2a

,cạnh bên

SA

vuông góc với mặt phẳng

đáy, góc giữa

SC

với mặt phẳng

()SAB

bằng

30



. Thể tích của khối chóp

.S ABCD

bằng

A.

3

2

3

a

. B.

3

8

3

a

. C.

3

82

3

a

. D.

3

22

3

a

.

Câu 33: Cho hình chóp

.S ABC

có tam giác

ABC

đều cạnh

a

,

( )

SA ABC⊥

. Gọi

M

là điểm trên cạnh

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 8

AB

sao cho

2

3

AM

AB

=

. Biết khoảng cách giữa hai đường thẳng

SM

và

BC

bằng

13

a

. Tính

thể tích khối chóp

.S ABC

.

A.

3

6

a

. B.

3

4

a

. C.

3

23

3

a

. D.

3

2

a

.

Câu 34: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh bằng

a

,

( )

SA ABCD⊥

. Góc giữa

hai mặt phẳng

( )

SBC

và

( )

SCD

bằng



với

9

cos

16



=

. Thể tích của khối chóp

.S ABCD

bằng:

A.

3

7

3

a

. B.

3

57

3

a

. C.

3

57

9

a

. D.

3

7

9

a

.

Câu 35: Cho hình chóp

.S ABC

có

SA

vuông góc với đáy, mặt phẳng

()SAB

vuông góc với mặt phẳng

()SBC

, góc giữa hai mặt phẳng

()SAC

và

()SBC

bằng

0

60

,

2;SB a=

0

45 .BSC =

Tính thể

tích khối chóp

.S ABC

A.

3

2

4

a

. B.

3

2

a

. C.

3

2

a

. D.

3

53

.

2

a

Câu 36: Cho hình chóp

.S ABC

có đáy là tam giác

ABC

vuông tại

A

,

,2AB a BC a==

và

SB

vuông

góc với mặt phẳng

( )

ABC

. Biết góc giữa hai mặt phẳng

( )

SAC

và

( )

SBC

bằng

0

60

. Thể tích

của khối chóp

.S ABC

bằng

A.

3

2

6

a

. B.

3

6

12

a

. C.

3

6

4

a

. D.

3

2

a

.

Câu 37: Cho tam giác

ABC

đều cạnh

a

, gọi

d

là đường thẳng qua

A

và vuông góc với mặt phẳng

( )

ABC

. Trên

d

lấy điểm

S

và đặt

( )

,0AS x x=

. Gọi

H

và

K

lần lượt là trực tâm của các

tam giác

ABC

và

SBC

. Biết

HK

cắt

d

tại điểm

S



. Khi

SS



ngắn nhất thì khối chóp

.S ABC

có thể tích bằng

A.

3

6

a

. B.

3

8

a

. C.

3

2

27

a

. D.

3

6

24

a

.

Câu 38: Cho hình chóp

.S AB C

có đáy là tam giác đều có cạnh bằng

4

,

SA

vuông góc với đáy, khoảng

cách từ

A

đến mặt phẳng

( )

SBC

bằng

3

. Thể tích

V

của khối chóp

.S AB C

là

A.

83V =

. B.

16 2

3

V =

. C.

83

3

V =

. D.

16 3

3

V =

.

Câu 39: Cho hình chóp

.S ABCD

, mặt đáy

ABCD

là hình vuông cạnh

a

. Cạnh bên

SA

vuông góc với

mặt đáy. Gọi

,HK

lần lượt là hình chiếu vuông góc của

A

lên

,SB SD

. Tính theo

a

thể tích

khối chóp

.S ABCD

biết góc giữa hai mặt phẳng

( )

ABC D

và

( )

AHK

là

30

.

A.

3

2

3

a

. B.

3

6

2

a

. C. . D.

3

6

9

a

.

Câu 40: Cho hình chóp

SABC

có đáy

ABC

là tam giác vuông cân tại

B

,

2BC a=

. Biết

( )

SA ABC⊥

, góc giữa

SC

và đáy bằng

60

. Thể tích khối chóp

SABC

bằng

3

6

3

a

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

9 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

A.

3

6

a

. B.

3

a

. C.

3

12

a

. D.

3

23

3

a

.

Câu 41: Cho chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật. Biết

( )

SA ABCD⊥

,

22AB BC a==

, góc

giữa

( )

SBD

và đáy bằng

30

. Thể tích của khối chóp

.S ABCD

là

A.

3

15

a

. B.

3

4 15

45

a

. C.

3

15

45

a

. D.

3

4 15

15

a

.

Câu 42: Cho hình chóp

.S AB C

có tam giác

ABC

vuông cân tại B, AC =

22a

, SA

vuông góc với mặt

phẳng

()ABC

, góc giữa 2 mặt phẳng

()SAC

và

()SBC

bằng

0

60

. Tính thể tích của khối chóp

.S ABC

A.

3

1

3

a

. B.

3

a

. C.

3

5

3

a

D.

3

4

3

a

Câu 43: Cho hình chóp có đáy là tam giác vuông cân tại . Cạnh bên vuông

góc với mặt phẳng đáy. Gọi lần lượt là trung điểm của Góc giữa hai mặt phẳng

và là . Biết . Thể tích khối chóp bằng

A. . B. . C. . D. .

Câu 44: Cho hình chóp

.,S ABCD

đáy

ABCD

là hình vuông cạnh

,a

SA

vuông góc với đáy. Khoảng

cách giữa hai đường thẳng

BD

và

SC

là

.

2

a

Tính thể tích khối chóp

..S ABCD

A.

3

2

3

a

. B.

3

6

a

. C.

3

2a

. D.

3

2

3

a

.

Câu 45: Cho khối chóp

.S ABC

có cạnh bên

SA

vuông góc với mặt phẳng đáy, đáy là tam giác cân tại

,A

độ dài đường trung tuyến

AD a=

, cạnh bên

SB

tạo với mặt phẳng đáy góc

0

45

và tạo với

mặt phẳng

( )

SAD

góc

0

30 .

Thể tích khối chóp

.S ABC

bằng

A.

3

2

.

9

a

B.

3

2

.

3

a

C.

3

2.a

D.

3

3 2.a

Câu 46: Cho hình chóp

.S AB C

có

( )

SA ABC⊥

, hai mặt phẳng

( )

SAB

và

( )

SBC

vuông góc với nhau.

;

2

aa

SA AB==

, góc tạo bởi hai mặt phẳng

( )

SAC

và

( )

SBC

là

0

60

. Tính theo

a

thể tích

khối chóp

.S AB C

.

A.

3

24

a

B.

3

4

a

C.

3

12

a

D.

3

12

a

Câu 47: Cho khối chóp

.S ABCD

có đáy

ABCD

là hình bình hành và

SA

vuông góc với mặt phẳng đáy.

Biết

o

2 , 2 , 45AB a AD a ABC= = =

và góc giữa hai mặt phẳng

( )

SBC

,

( )

SCD

bằng

o

30

.

Thể tích khối chóp đã cho bằng

A.

3

3a

. B.

3

a

. C.

3

2

3

a

. D.

3

4

a

.

.S ABC

,B

2AB a=

SA

,M

N

,SB

.SC

( )

AMN

( )

ABC



2

cos

3



=

.S ABC

3

2

a

3

5

3

a

3

7

3

a

3

2

3

a

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 10

Câu 48: Cho hình chóp

.S AB CD

có đáy

ABCD

là hình vuông cạnh

,a

3SA a=

và

SA

vuông góc với

mặt phẳng đáy. Mặt phẳng

( )

P

đi qua điểm

A

và vuông góc với

SC

cắt

,SB

,SC

SD

lần lượt

tại

,B



,C



.D



Thể tích khối chóp

.S AB C D

  

bằng

A.

3

33

20

a

. B.

3

93

20

a

. C.

3

33

10

a

. D.

3

33

40

a

.

Câu 49: Cho khối chóp

.S ABCD

có đáy là hình vuông cạnh

x

và

SA ABCD

. Khoảng cách từ điểm

A

đến mặt phẳng

( )

SCD

bằng

2a

. Biết thể tích nhỏ nhất của khối chóp

.S ACD

là

3

,,

m

a m n

n

. Tính

P m n

.

A.

10

. B.

9

. C.

8

. D.

11

.

Câu 50: Cho hình chóp

.S ABCD

có đáy là hình chữ nhật và

()SA ABC D⊥

. Gọi

M

là trung điểm của

CD

. Trung tuyến

CN

của tam giác

SC M

kéo dài cắt

SD

tại

P

. Biết rằng

3AB =

,

5

cos( ,( ))

26

SC ABCD =

và

12

( ,( ))

13

d C SBD =

. Tính

.S ANP

V

.

A.

1

2

. B.

1

3

. C.

1

12

. D.

1

6

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

11 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

1 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Dạng 3: Thể tích khối chóp có mặt bên vuông góc với đáy

Bài toán: Cho hình chóp có mặt phẳng

( )

P

( mặt phẳng

( )

P

chứa đỉnh hình chóp). Mặt phẳng

( )

P

vuông góc với mặt đáy của hình chóp. Cách tìm đường cao của hình chóp như thế nào?

Cách tìm đường cao hình chóp:

• Bước 1: Tìm giao tuyến của mặt phẳng

( )

P

và mặt phẳng đáy

• Bước 2: Từ đỉnh

S

của hình chóp kẻ đoạn thẳng

SH

vuông góc với giao tuyến

d

Lưu ý: Chúng ta phải đặc biệt lưu ý đến tính chất hình học của mặt phẳng

( )

P

để xác định được cụ thể,

tính chất của chân đường cao

H

.

Câu 1: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác cân tại

A

,

, 120AB a BAC= = 

, tam giác

SAB

đều và nằm trong mặt phẳng vuông góc với

( )

ABC

. Thể tích khối chóp

.S ABC

bằng

A.

3

2

a

. B.

3

2

a

. C.

3

8

a

. D.

3

a

.

 Lời giải

…………………………………………………………………

………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 2: Cho hình chóp

.S ABC

có

SAB

và

ABC

là hai tam giác đều cạnh

a

và nằm trong hai mặt phẳng

vuông góc với nhau. Tính theo

a

thể tích của khối chóp

..S ABC

A.

3

2

3

a

. B.

3

a

. C.

3

a

. D.

3

3a

.

 Lời giải

…………………………………………………………………

………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

VÍ DỤ MINH HỌA

B

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 2

Câu 3: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh bằng

3,a

tam giác

SBC

vuông

tại

S

và nằm trong mặt phẳng vuông góc với đáy, đường thẳng

SD

tạo với mặt phẳng

( )

SBC

một góc

60

. Thể tích của khối chóp đã cho bằng

A.

3

3.a

B.

3

6.a

C.

3

6

.

6

a

D.

3

6

.

3

a

 Lời giải

…………………………………………………………………

………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 4: Cho hình chóp

.S ABCD

có đáy là hình vuông cạnh

2a

, tam giác

SAB

cân tại

S

và nằm trong

mặt phẳng vuông góc với đáy,

2SC a=

. Thể tích khối chóp

.S ABCD

là:

A.

3

2

a

. B.

3

6

3

a

. C.

3

2

3

a

. D.

3

6

4

a

.

 Lời giải

…………………………………………………………………

………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 5: Cho hình chóp

.S ABCD

có đáy là hình chữ nhật,

AB a=

,

2AD a=

. Tam giác SAB cân tại S và

nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng

( )

ABCD

bằng

45

. Thể tích của khối chóp

.S ABCD

là:

A.

3

17

9

a

. B.

3

17

3

a

. C.

3

17

3

a

. D.

3

17

6

a

.

 Lời giải

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

3 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

…………………………………………………………………

………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 6: Cho hình chóp

.S ABCD

có đáy là hình vuông cạnh

a

. Hình chiếu của đỉnh

S

trên mặt phẳng

đáy là

H

sao cho

3AB AH=

. Góc giữa cạnh

SD

và mặt phẳng

( )

ABCD

bằng

45



. Tính thể

tích

V

của khối chóp

.S HCD

.

A.

3

2

9

a

V =

. B.

3

10

9

a

V =

. C.

3

10

6

a

V =

. D.

3

10

18

a

V =

.

 Lời giải

…………………………………………………………………

………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 7: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật với

BC a=

; tam giác

SAB

đều và

nằm trong mặt phẳng vuông góc với đáy. Gọi

M

là trung điểm của

AB

,

I

là tâm mặt cầu

ngoại tiếp hình chóp

.S ABCD

. Biết góc giữa đường thẳng

IM

và mặt phẳng

( )

SAB

bằng

O

60

. Tính thể tích khối chóp

.S ABCD

.

A.

3

3a

. B.

3

2

a

. C.

3

6

a

. D.

3

2

a

 Lời giải

…………………………………………………………………

………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

…………………………………………………………

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 4

Câu 8: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông tại

A

và có

,3AB a BC a==

. Mặt bên

SAB

là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng

( )

ABC

. Tính thể tích

V

của khối khóp

.S ABC

.

A.

3

26

12

a

V =

. B.

3

6

a

V =

. C.

3

6

12

a

V =

. D.

3

6

4

a

V =

.

 Lời giải

…………………………………………………………………

………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 9: Cho hình chóp

.S ABCD

có đáy ABCD là hình chữ nhật,

AB a=

,

3AD a=

, tam giác SAB cân

tại S và nằm trong mặt phẳng vuông góc với đáy, khoảng cách giữa AB và SC bằng

3

2

a

. Tính thể

tích V của khối chóp

.S ABCD

.

A.

3

3a

. B.

3

23a

. C.

3

a

. D.

3

33a

.

 Lời giải

…………………………………………………………………

………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

5 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 10: Cho tứ diện

MNPQ

. Biết rằng mặt phẳng

( )

MNP

vuông góc với mặt phẳng

( )

NPQ

, đồng thời

MNP

và

NPQ

là hai tam giác đều có cạnh bằng

8a

. Tính theo

a

thể tích

V

của khối tứ

diện

MNPQ

.

A.

3

64Va=

. B.

3

128Va=

. C.

3

64 3Va=

. D.

3

192Va=

.

 Lời giải

…………………………………………………………………

………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 6

Câu 1: Cho tứ diện

SABC

có các cạnh

SA

,

SB

,

SC

đôi một vuông góc với nhau. Biết

3SA a=

,

4SB a=

,

5SC a=

. Tính theo

a

thể tích

V

của khối tứ diện

SABC

.

A.

3

10Va=

. B.

3

5

2

a

V =

. C.

3

20Va=

. D.

3

5Va=

.

Câu 2: Cho tứ diện

OABC

có

OA

,

OB

,

OC

đôi một vuông góc với nhau,

1OA =

,

2OB =

,

3OC =

.

Thể tích khối tứ diện

OABC

là

A.

1

. B.

2

. C.

6

. D.

2

3

.

Câu 3: Cho hình chóp

.S ABC

có đáy là tam giác cân tại

A

,

AB AC a==

,

120BAC =

. Mặt bên

SAB

là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Thể tích

V

của khối chóp

.S ABC

là

A.

3

8

a

V =

. B.

3

Va=

. C.

3

2

a

V =

. D.

3

2Va=

.

Câu 4: Cho khối chóp

.S ABC

có đáy là tam giác đều cạnh

a

, tam giác

SAB

vuông cân tại

S

và nằm

trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp

.S ABC

theo

a

.

A.

3

24

a

. B.

3

8

a

. C.

3

6

a

. D.

3

12

a

.

Câu 5: Cho khối chóp

.S ABC

có đáy là tam giác đều cạnh

2a

, mặt bên

SBC

là tam giác vuông cân

tại

S

và

( )

SBC

vuông góc với mặt phẳng

( )

ABC

. Thể tích của khối chóp đã cho bằng

A.

3

33a

. B.

3

a

. C.

3

12

a

. D.

3

3a

.

Câu 6: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật với

2,AB a AD a==

. Mặt bên

()SAB

là

tam giác đều và vuông góc với mặt đáy. Thể tích khối chóp

.S ABC

bằng

A.

3

23a

. B.

3

23

3

a

. C.

3

3a

. D.

3

a

.

Câu 7: Cho hình chóp

.S ABC

có

ABC

cân tại

A

và

120 ,BAC AC a=  =

. Cạnh bên

SC

vuông

góc với mặt đáy và

SC a=

. Thể tích khối chóp

.S ABC

bằng

A.

3

6

a

. B.

3

4

a

. C.

3

12

a

. D.

3

2

a

.

BÀI TẬP TRẮC NGHIỆM

C

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

7 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 8: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật,

, 2 .AB a AD a==

Tam giác

SAB

là

tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Thể tích của khối chóp

.S ABCD

bằng

A.

3

.

3

a

B.

3

.

6

a

C.

3

2

.

3

a

D.

3

.

3

a

Câu 9: Cho hình chóp

SABC

có đáy

ABC

là tam giác vuông tại

B

,

AB a=

,

5AC a=

,

( )

SA ABC⊥

và

3SA a=

. Thể tích khối chóp

SABC

bằng

A.

3

a

V =

. B.

3

3Va=

. C.

3

2

a

V =

D.

3

5

3

a

V =

.

Câu 10: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật;

SAB

đều cạnh

a

và nằm trong mặt

phẳng vuông góc với

( )

ABCD

. Biết

SC

tạo với

( )

ABCD

một góc bằng

30

. Tính thể tích

V

của khối chóp

.S ABCD

.

A.

3

6

3

a

V =

. B.

3

6

a

V =

. C.

3

a

V =

. D.

3

6

a

V =

.

Câu 11: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông tại

A

và có

AB a

,

3BC a

. Mặt

bên

SAB

là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng

ABC

. Tính theo

a

thể tích của khối chóp

.S ABC

.

A.

3

6

.

12

a

V

B.

3

6

4

a

V

. C.

3

6

8

a

V

. D.

3

6

a

V

.

Câu 12: Cho tứ diện

ABCD

có

ABC

là tam giác đều cạnh

,a

tam giác

BCD

cân tại

D

và nằm trong

mặt phẳng vuông góc với

( )

.ABC

Biết

AD

hợp với mặt phẳng

( )

ABC

một góc

0

60 .

Tính thể

tích

V

của khối tứ diện

.ABCD

A.

3

.

6

=

a

V

B.

3

.

12

=

a

V

C.

3

.

8

=

a

V

D.

3

.

24

=

a

V

Câu 13: Cho hình chóp

.S ABC

có đáy là tam giác vuông tại B. Biết tam giác SAB là tam giác đều và nằm

trong mặt phẳng vuông góc với mặt phẳng đáy (ABC).Biết

, 3AB a AC a==

. Thể tích khối

chóp

.S ABC

là

A.

3

4

a

. B.

3

6

4

a

. C.

3

2

6

a

. D.

3

6

12

a

.

Câu 14: Cho hình chóp

.S ABCD

có

ABCD

là hình chữ nhật, tam giác

SBC

đều cạnh

a

nằm trong mặt

phẳng vuông góc với

( )

ABCD

biết góc giữa

SD

và mặt phẳng

( )

ABCD

bằng

45

. Thể tích

hình chóp

.S ABCD

là

A.

3

6

4

a

. B.

3

a

. C.

3

4

a

. D.

3

6

12

a

.

Câu 15: Cho khối chóp

.S ABC

có

H

là trung điểm của

AB

, biết

SH ABC

,

SA SB AB BC CA a

. Thể tích của khối chóp đã cho là

A.

3

4

a

. B.

3

4

a

. C.

3

8

a

. D.

3

8

a

.

Câu 16: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật với

2AB a=

,

AD a=

. Mặt bên

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 8

( )

SAB

là tam giác đều và vuông góc với mặt đáy.

Thể tích của khối chóp

.S ABC

bằng

A.

3

23a

. B.

3

23

3

a

. C.

3

3a

. D.

3

a

.

Câu 17: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật, tam giác

SAD

vuông tại

S

và nằm

trong mặt phẳng vuông góc với mặt phẳng đáy. Cho biết

AB a=

,

2SA SD=

, mặt phẳng

( )

SBC

tạo với mặt phẳng đáy một góc

60

. Tính thể tích của khối chóp

.S ABCD

.

A.

3

5

2

a

. B.

3

5a

. C.

3

15

2

a

. D.

3

2

a

.

Câu 18: Hình chóp

.S ABCD

đáy là hình chữ nhật có

2 3; 2AB a AD a==

. Mặt bên

( )

SAB

là tam giác

đều và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối chóp

.S ABD

là

A.

3

23

3

a

. B.

3

43a

. C.

3

4a

. D.

3

23a

.

Câu 19: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật, mặt bên

SAD

là tam giác đều cạnh

2a

và nằm trong mặt phẳng vuông góc với mặt phẳng

()ABCD

. Góc giữa mặt phẳng

()SBC

và mặt phẳng

()ABCD

là

30

. Thể tích của khối chóp

.S ABCD

là:

A.

3

23

3

a

. B.

3

23a

. C.

3

43

3

a

. D.

3

a

.

Câu 20: Trong không gian cho tam giác đều

SAB

và hình chữ nhật

ABCD

với

2AD a=

nằm trên hai

mặt phẳng vuông góc. Gọi



là góc giữa hai mặt phẳng

( )

SAB

và

( )

SCD

. Biết

22

tan

3



=

.

Thể tích của khối chóp

.S ABC

là

A.

3

2

a

V =

. B.

3

3Va=

. C.

3

8

a

V =

D.

3

2

12

a

V =

.

Câu 21: Cho hình chóp

.S ABC

có mặt phẳng

( )

SAC

vuông góc với mặt phẳng

( )

ABC

, tam giác

SAB

là tam giác đều cạnh

3a

;

3BC a=

. Đường thẳng

SC

tạo với mặt phẳng

( )

ABC

một góc

60

. Thể tích khối chóp

.S ABC

bằng

A.

3

a

. B.

3

6

2

a

. C.

3

6

a

. D.

3

26a

.

Câu 22: Cho khối chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

2a

, tam giác

SAD

cân tại

S

và

nằm trong mặt phẳng vuông góc với đáy. Góc giữa

( )

SBC

và mặt đáy bằng

0

60

. Tính thể tích

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

9 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

khối chóp

.S ABCD

.

A.

3

23

3

a

. B.

3

43

3

a

. C.

3

83

3

a

. D.

3

23a

.

Câu 23:

Cho hình chóp

.S ABC

có đáy là tam giác vuông cân tại

A

, mặt bên

SBC

là tam giác đều cạnh

a

và

( )

SBC

vuông góc với mặt đáy. Thể tích khối chóp đó là

A.

3

4

a

. B.

3

24

a

. C.

3

8

a

. D.

3

12

a

.

Câu 24: Cho hình chóp

.S ABC

có đáy là tam giác vuông cân tại

A

, cạnh

2BC a=

. Gọi

M

là trung điểm

của

BC

, hình chiếu vuông góc của

S

lên mặt phẳng

( )

ABC

là trung điểm của

AM

, tam giác

SAM

vuông tại

S

. Thể tích khối chóp

.S ABC

là

A.

3

.

2

a

B.

3

.

6

a

C.

3

.

3

a

D.

3

.

9

a

Câu 25: Cho hình chóp

.S ABCD

có đáy là hình chữ nhật, tam giác

SAB

vuông tại

S

và nằm trong mặt

phẳng vuông góc với mặt phẳng đáy. Biết

2 , 2AB SA BC a==

và mặt phẳng

( )

SCD

tạo với mặt

phẳng đáy một góc

0

60

. Thể tích của khối chóp

.S ABCD

tính theo

a

bằng

A.

3

32 3

3

a

. B.

3

16 3a

. C.

3

16a

. D.

3

32

3

a

.

Câu 26: Cho hình chóp

.S ABC

có mặt phẳng

()SAC

vuông góc với mặt phẳng

()ABC

,

SAB

là tam giác

đều cạnh

3a

,

3BC a=

, đường thẳng

SC

tạo với mặt phẳng

()ABC

góc

60



. Thể tích của

khối chóp

.S ABC

bằng

A.

3

6

2

a

. B.

3

a

. C.

3

26a

. D.

3

6

a

.

Câu 27: Cho hình chóp

.S ABCD

có đáy là hình vuông cạnh bằng

2

, tam giác

SAB

là tam giác đều và

tam giác

SCD

vuông tại

S

. Tính thể tích

V

của khối chóp

.S ABCD

.

A.

23

3

V =

. B.

83

3

V =

. C.

43

3

V =

. D.

23V =

.

Câu 28: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác đều, hình chiếu vuông góc của đỉnh

S

trên mặt

đáy là trung điểm

H

của cạnh

AB

. Biết

3

2

a

SH =

và mặt phẳng

( )

SAC

vuông góc với mặt

phẳng

()SBC

. Thể tích khối chóp

.S ABC

bằng

A.

3

4

a

. B.

3

16

a

. C.

3

2

a

. D.

3

8

a

.

Câu 29: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh bằng

a

, mặt bên

SAB

là tam giác

đều,

3SC SD a==

. Thể tích khối chóp

.S ABCD

bằng

A.

3

2

3

a

. B.

3

2

6

a

. C.

3

6

a

. D.

3

2

a

.

Câu 30: Cho hình chóp

.S ABCD

có đáy là hình thoi cạnh

a

góc

0

120BAD =

, tam giác

SAB

cân tại

S

và nằm trong mặt phẳng vuông góc với mặt đáy, góc giữa

SCD

và mặt đáy bằng

0

60

. Tính thể

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 10

tích khối chóp

.S ABCD

.

A.

3

4

a

V

. B.

3

12

a

V

. C.

3

4

a

V

. D.

3

2

a

V

.

Câu 31: Cho hình chóp tứ giác

.S ABCD

có đáy là hình vuông, mặt bên

( )

SAB

là tam giác đều và nằm

trong mặt phẳng vuông góc với mặt đáy. Biết khoảng cách từ điểm

A

đến mặt phẳng

( )

SCD

bằng

3a

. Tính thể tích

V

của khối chóp

A.

3

7 21

6

a

. B.

3

7 21

2

a

. C.

3

77

6

a

. D.

3

37

2

a

.

Câu 32: Hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

. Tam giác

SAD

cân và nằm trong mặt

phẳng vuông góc với đáy. Gọi

M

là trung điểm của

CD

, cạnh bên

SB

hợp với đáy góc

60

.

Tính theo

a

thể tích

V

của khối chóp

.S ABM

A.

3

15

4

a

V =

. B.

3

15

6

a

V =

. C.

3

15

12

a

V =

. D.

3

15

3

a

V =

.

Câu 33: Cho hình chóp

.S ABCD

có đáy là hình thang cân,

2AB a=

,

AD BC CD a= = =

. Mặt bên

SAB

là tam giác đều và nằm trong mặt phẳng vuông góc với

( )

.ABCD

Tính bán kính

R

của mặt cầu

ngoại tiếp khối chóp

.S ABC

.

A.

23

3

a

R =

B.

Ra=

C.

3

a

R =

D.

2

3

a

R =

Câu 34: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thang vuông tại

A

và

B

;

4AB BC a==

. Tam

giác

SAB

đều và nằm trong mặt phẳng vuông góc với mặt phẳng

( )

ABCD

. Gọi

H

là trung

điểm của

AB

, biết khoảng cách từ

C

đến mặt phẳng

( )

SHD

bằng

10a

. Tính thể tích khối

chóp

.S ABCD

.

A.

3

10 10

3

a

V =

. B.

3

10 3Va=

. C.

3

40 3

3

a

V =

. D.

3

20 3

3

a

V =

.

Câu 35: Cho hình chóp

.S ABCD

có đáy là hình chữ nhật, tam giác

SAB

cân tại

S

và nằm trong mặt

phẳng vuông góc với mặt phẳng đáy;

H

là trung điểm của

AB

. Biết

2SD a=

và lần lượt tạo

với các mặt phẳng

( )

ABCD

và

( )

SHC

các góc bằng

30

. Thể tích khối chóp

.S ABCD

bằng

A.

3

6

a

. B.

3

a

. C.

3

23

3

a

. D.

3

6

a

.

Câu 36: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh là

2.a

Mặt bên

SAB

là tam giác cân

nằm trong mặt phẳng vuông góc với đáy. Khoảng cách từ

A

đến

( )

SCD

là

.a

Tính thể tích khối

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

11 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

chóp

.S ABCD

.

A.

3

83a

. B.

3

83

5

a

. C.

3

83

7

a

. D.

3

83

9

a

.

Câu 37: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác đều, hình chiếu vuông góc của đỉnh

S

trên mặt

đáy là trung điểm

H

của cạnh

AB

. Biết

3

2

a

SH =

và mặt phẳng

( )

SAC

vuông góc với mặt

phẳng

( )

SBC

. Thể tích khối chóp

.S ABC

bằng

A.

4

a

. B.

4

16

a

. C.

4

2

a

. D.

4

3

8

a

.

Câu 38: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác đều, hình chiếu vuông góc của đỉnh

S

trên mặt

đáy là trung điểm

H

của cạnh

AB

. Biết

3

2

a

SH =

và mặt phẳng

( )

SAC

vuông góc với mặt

phẳng

( )

SBC

. Thể tích của khối chóp

.S ABC

bằng

A.

3

.

2

a

. B.

3

.

4

a

. C.

3

.

16

a

. D.

3

.

8

a

.

Câu 39: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật, tam giác

SAB

vuông tại

S

và nằm

trong mặt phẳng vuông góc với đáy. Biết

2 , 2AB SA BC a==

và mặt phẳng

( )

SCD

tạo với mặt

phẳng đáy một góc

60

. Thể tích khối chóp

.S ABCD

tính theo

a

bằng

B.

3

16 3a

. B.

3

32 3

3

a

. C.

3

32

3

a

. D.

3

16a

.

Câu 40: Cho hình chóp

.S ABC

có

SA

vuông góc với đáy, mặt phẳng

()SAB

vuông góc với mặt phẳng

()SBC

, góc giữa hai mặt phẳng

()SAC

và

()SBC

bằng

0

60

,

2;SB a=

0

45 .BSC =

Gọi thể tích

khối chóp

.S ABC

là

.V

Khi đó tỉ số

3

a

V

bằng

A.

2

4

. B.

2

. C.

3

2

. D.

53

.

2

Câu 41: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật, tam giác

SAB

là tam giác đều cạnh

a

và nằm trong mặt phẳng vuông góc với đáy. Gọi H, K lần lượt là trung điểm của AB, CD.

Biết góc giữa KS và DA bằng

30

. Thể tích khối chóp

.S ABCD

A.

3

4

a

B.

3

2

a

C.

3

36

a

D.

3

53

36

a

Câu 42: Cho khối chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

. Tam giác

SAB

cân tại

S

và nằm

trong mặt phẳng vuông góc với mặt đáy. Biết khoảng cách từ điểm

A

đến mặt phẳng

( )

SCD

bằng

2

a

. Thể tích của khối chóp đã cho bằng

A.

3

a

. B.

3

3a

. C.

3

a

. D.

3

1

3

a

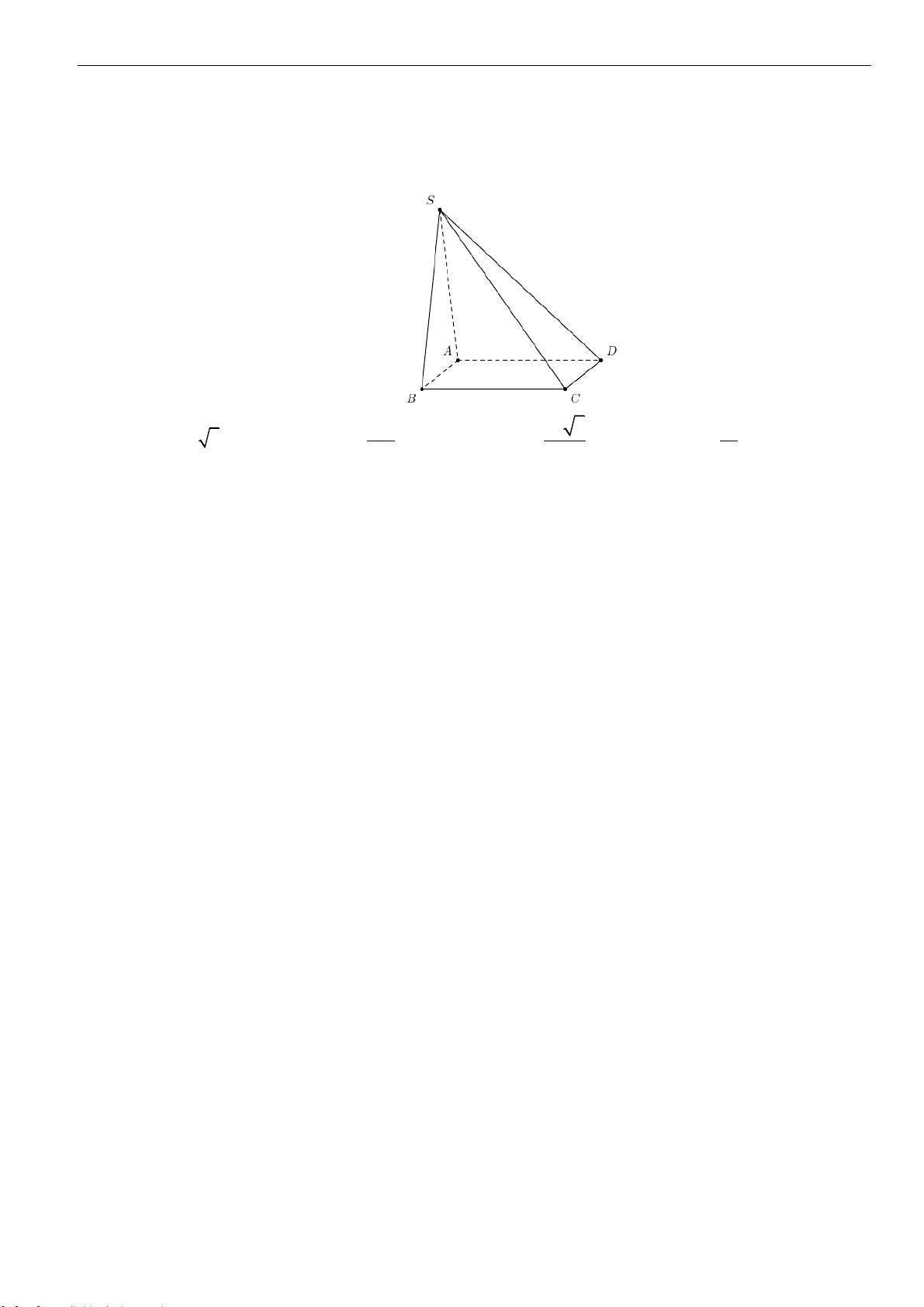
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 12

Câu 43: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

2a

,

( ) ( )

SAB ABCD⊥

. Gọi



là

góc tạo bởi mặt phẳng

( )

SAB

và mặt phẳng

( )

SCD

, với

tan 2



=

. Gọi

( )

P

là mặt phẳng chứa

CD

và vuông góc với

( )

ABCD

. Trên

( )

P

lấy điểm

M

bất kỳ, thể tích khối tứ diện

.S ABM

bằng

A.

3

3a

. B.

3

2

3

a

. C.

3

a

. D.

3

4

a

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

1 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Dạng 4: Thể tích khối chóp đều

Công thức tính thể tích khối chóp đều và một số công thức giải nhanh:

• Chiều cao

h

khối chóp xác định bởi

22

d

h b R=−

, trong đó

d

R

là bán kính đường tròn ngoại tiếp

đa giác đáy và

b

là độ dài cạnh bên.

• Khối tứ diện đều cạnh

a

có

3

2

12

a

V =

và

3

8

h

V =

, trong đó

6

3

a

h =

là chiều cao khối tứ diện

đều.

• Khối chóp tam giác đều cạnh đáy bằng

a

, cạnh bên bằng

b

có

2 2 2

3

12

a b a

V

−

=

• Khối chóp tứ giác đều cạnh đáy bằng

a

, cạnh bên bằng

b

có

( )

2 2 2

22

6

a b a

V

−

=

• Khối chóp tứ giác đều có tất cả các cạnh bằng

a

, có

3

2

6

a

V =

• Khối bát diện đều cạnh

a

là hợp của hai khối chóp tứ giác đều có tất cả các cạnh bằng

a

có

3

2

3

a

V =

• Khối chóp lục giác đều cạnh đáy bằng

a

, cạnh bên bằng

b

có

( )

2 2 2

3

2

a b a

V

−

=

Câu 1: Cho hình chóp tứ giác đều có tất cả các cạnh bằng

a

. Thể tích của khối chóp tương ứng tính

theo

a

sẽ bằng

A.

3

2

a

. B.

3

2

6

a

. C.

3

2

3

a

. D.

3

2

12

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 2: Cho khối chóp tam giác đều có cạnh đáy bằng

a

và cạnh bên tạo với đáy một góc

o

60

. Thể tích

khối chóp đó bằng

A.

3

12

a

. B.

3

6

a

. C.

3

36

a

. D.

3

4

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

VÍ DỤ MINH HỌA

B

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 2

Câu 3: Cho hình chóp tứ giác đều S.ABCD có chiều cao bằng

3a

và độ dài cạnh bên bằng

5a

. Thể

tích của khối chóp

.S ABCD

bằng

A.

3

45

3

a

. B.

3

43

3

a

. C.

3

83

3

a

. D.

3

43a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 4: Cho hình chóp đều

.S ABCD

có đáy là hình vuông cạnh

2a

, cạnh bên bằng

3a

. Tính thể tích

khối chóp

.S ABCD

.

A.

3

43a

. B.

3

43

3

a

. C.

3

4

3

a

. D.

3

4a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 5: Cho hình chóp tam giác đều

.S ABC

có cạnh đáy bằng

2,a

cạnh bên tạo với đáy một góc

0

60 .

Tính theo

a

thể tích khối chóp

..S ABC

A.

3

3a

. B.

3

a

. C.

3

23a

. D.

3

23

3

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

3 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 6: Cho hình chóp đều

.S ABCD

có cạnh đáy bằng

a

, biết góc giữa cạnh bên và mặt đáy bằng

45

. Tính thể tích

V

của khối chóp

.S ABC

.

A.

3

2

6

Va=

. B.

3

2

12

Va=

. C.

3

2

3

Va=

. D.

3

2Va=

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 7: Cho hình chóp đều

.S ABCD

có cạnh đáy bằng

3a

, cạnh bên bằng

33

2

a

và

O

là tâm của đáy.

Gọi

,,M N P

và

Q

lần lượt là hình chiếu vuông góc của

O

trên các mặt phẳng

( )

SAB

,

( )

SBC

,

( )

SCD

và

( )

SDA

. Thể tích của khối chóp

.O MNPQ

bằng

A.

3

9

16

a

. B.

3

2

3

a

. C.

3

9

32

a

. D.

3

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 8: Cho khối chóp tứ giác đều

.S ABCD

có diện tích xung quanh gấp 2 lần diện tích đáy, diện tích

đáy bằng

2

4a

. Thể tích của khối chóp

.S ABC

tương ứng bằng

A.

3

43

3

a

. B.

3

23

3

a

. C.

3

83

3

a

. D.

3

56

3

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 4

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 9: Cho khối chóp tứ giác đều có cạnh đáy bằng

2a

và diện tích xung quanh bằng

2

8a

. Thể tích

của khối chóp đó bằng

A.

3

23

.

3

a

B.

3

4 3 .a

C.

3

43

.

3

a

D.

3

2 3 .a

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 10: Cho hình chóp tứ giác đều

.S ABCD

có cạnh bên bằng

2a

, góc giữa mặt bên và mặt đáy bằng

60

. Thể tích khối chóp

.S ABCD

là

A.

3

32

15 5

a

. B.

3

32 3

15 5

a

. C.

3

32 5

15

a

. D.

3

32 15

15

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

BÀI TẬP TRẮC NGHIỆM

C

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

5 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 1: Cho khối chóp tam giác đều có cạnh đáy bằng

2a

và thể tích bằng

3

a

. Chiều cao của khối chóp

đã cho bằng

A.

3a

. B.

23a

. C.

3

a

. D.

3

2

a

.

Câu 2: Cho khối chóp tam giác đều có cạnh đáy bằng

a

, chiều cao bằng

3a

. Thể tích khối chóp bằng

A.

3

4

a

. B.

3

12

a

. C.

3

6

a

. D.

3

4

a

.

Câu 3: Cho hình chóp có đáy là tam giác đều cạnh

3cm

, chiều cao

5.cm

Thế tích khối chóp đó là

A.

3

15 3

4

cm

. B.

45cm

. C.

3

45cm

. D.

3

45 3

4

cm

.

Câu 4: Cho hình chóp tứ giác đều

.S ABCD

có cạnh đáy bằng

a

và đường cao bằng

3.a

Thể tích khối

chóp

.S ABCD

bằng

A.

3

.a

B.

3

3.a

C.

2

3a

D.

2

a

Câu 5: Tính thể tích khối chóp tam giác đều có độ dài cạnh đáy bằng a và chiều cao bằng

3

a

là

A.

3

12

a

V =

. B.

3

12

a

V =

. C.

3

4

a

V =

. D.

3

4

a

V =

.

Câu 6: Tính thể tích khối chóp tứ giác đều có cạnh đáy bằng

2a

và có mặt bên tạo với mặt đáy một góc

bằng

0

60

A.

3

4

3

a

. B.

3

43

3

a

. C.

3

4

33

a

. D.

3

43a

.

Câu 7: Cho khối chóp đều

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

. Biết diện tích tam giác

SAC

là

2

2a

, thể tích của khối chóp đã cho bằng

A.

3

2

3

a

. B.

3

a

. C.

3

22a

. D.

3

4

3

a

.

Câu 8: Cho hình chóp tứ giác đều có cạnh đáy bằng

2a

và cạnh bên tạo với đáy góc

60



. Thể tích của

khối chóp đó bằng

A.

3

46

3

a



B.

3

a



C.

3

4

3

a



D.

3

23

3

a



Câu 9: Thể tích của khối chóp có đáy là tam giác đều cạnh

a

và chiều cao

4a

bằng

A.

3

4

3

a

. B.

3

4a

. C.

3

3a

. D.

3

a

.

Câu 10:

Thể tích của khối tứ diện đều cạnh

a

là?

A.

3

2

4

a

. B.

3

12

a

. C.

3

2

12

a

. D.

3

4

a

.

Câu 11: Thể tích của khối tứ diện đều cạnh

a

là

A.

3

2

4

a

. B.

3

12

a

. C.

3

2

12

a

. D.

3

4

a

.

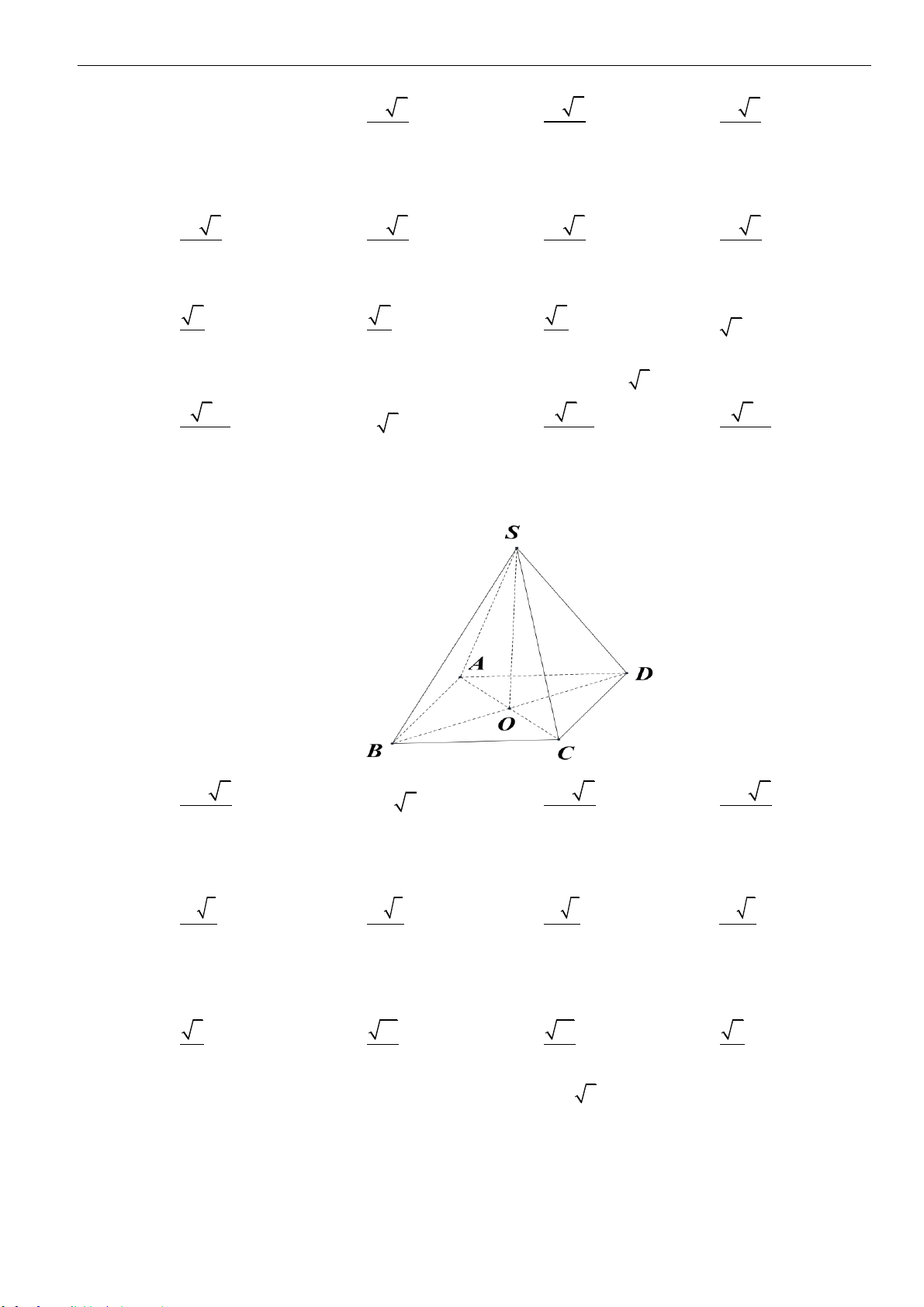
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 6

Câu 12: Tính thể tích khối chóp tứ giác đều có tất cả các cạnh bằng

a

là

A.

3

a

. B.

3

2

3

a

. C.

3

2

6

a

. D.

3

2

a

.

Câu 13: Cho khối chóp đều

.S ABC

có cạnh đáy là

a

, mặt bên tạo với đáy một góc

0

60

. Thể tích khối

chóp

.S ABC

là

A.

3

24

a

. B.

3

4

a

. C.

3

8

a

. D.

3

12

a

.

Câu 14: Thể tích của khối chóp đều

.S ABCD

có tất cả các cạnh bằng

a

là

A.

3

2

a

. B.

3

2

3

a

. C.

3

2

6

a

. D.

3

2a

.

Câu 15: Thể tích của khối chóp tứ giác đều

.S ABCD

có chiều cao bằng

3a

và độ dài cạnh bên 3a bằng

A.

3

83

3

a

. B.

3

43a

. C.

3

45

3

a

. D.

3

43

3

a

.

Câu 16: Cho hình chóp tứ giác đều

.S ABCD

có cạnh đáy bằng

2a

, góc giữa cạnh bên và mặt đáy bằng

30

. Khi đó thể tích của khối chóp bằng

A.

3

46

9

a

. B.

3

46a

. C.

3

46

3

a

. D.

3

26

9

a

.

Câu 17: Cho hình chóp tam giác đều

.S ABC

có đáy

ABC

là tam giác đều cạnh

.a

Biết góc giữa mặt

bên và mặt đáy là

60

. Thể tích của khối chóp này bằng

A.

3

12

a

B.

3

24

a

. C.

3

8

a

. D.

3

6

a

.

Câu 18: Cho khối chóp đều có tất cả 5 mặt có diện tích bằng nhau và bằng

2

a

. Thể tích của khối chóp

tương ứng bằng:

A.

3

2

a

. B.

3

15

2

a

. C.

3

15

6

a

. D.

3

6

4

a

.

Câu 19: Cho hình chóp tứ giác đều

.S ABCD

có cạnh đáy bằng

6a

, góc giữa cạnh bên và mặt đáy bằng

60

. Tính thể tích

V

của khối chóp

.S ABCD

.

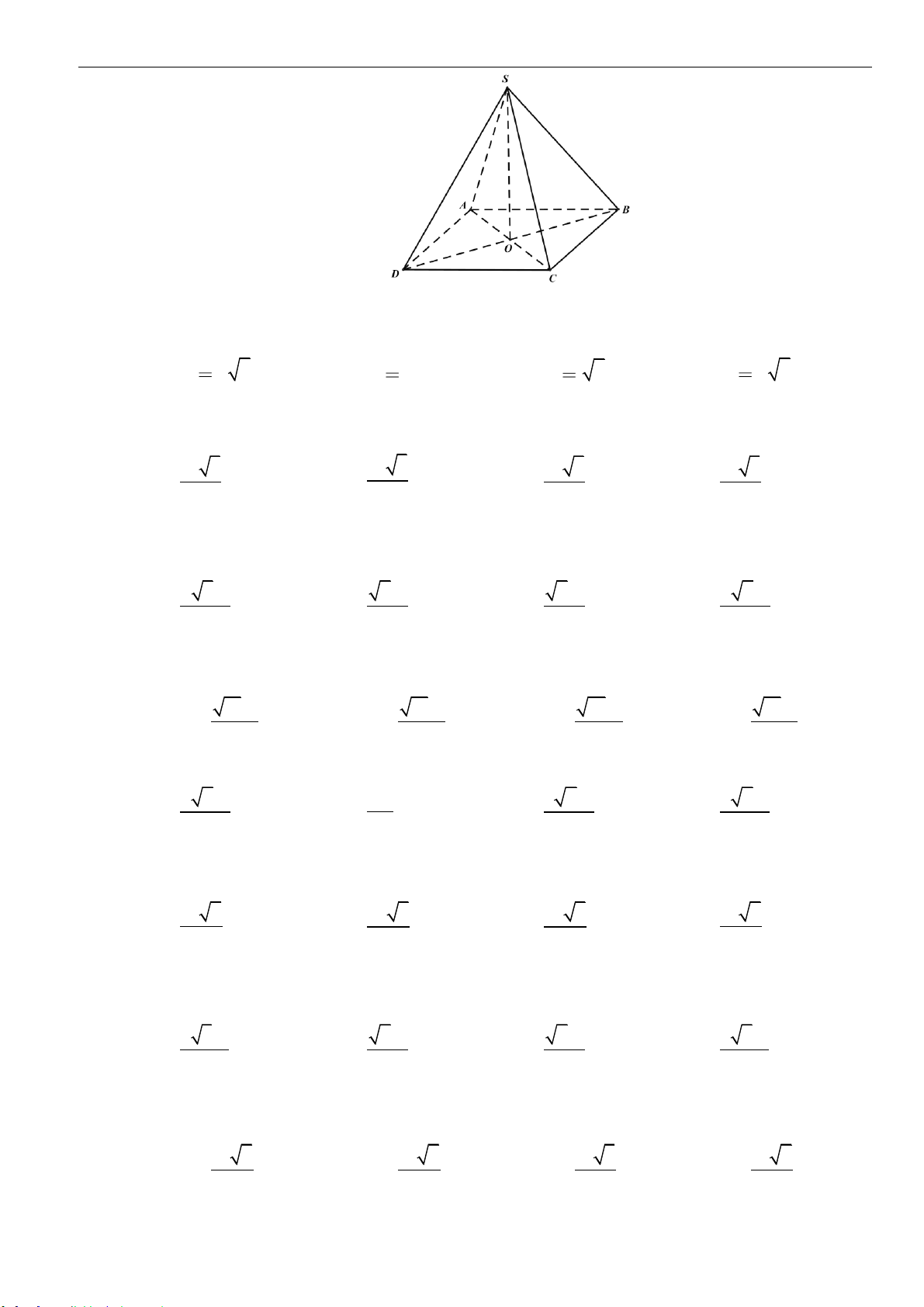
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

7 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

A.

3

3Va=

. B.

3

2Va=

. C.

3

6Va=

. D.

3

9Va=

.

Câu 20: Khối chóp tam giác đều có chiều cao bằng

9dm

và cạnh đáy bằng

2dm

có thể tích là

A.

3

9 3dmV

. B.

3

12dmV

. C.

3

3dmV

. D.

3

3 3dmV

.

Câu 21: Cho khối chóp đều

.S ABC

có cạnh đáy bằng

a

và các cạnh bên hợp với đáy một góc

0

60

. Tính

thể tích của khối chóp

.S ABC

A.

3

12

a

. B.

3

4

a

. C.

3

36

a

. D.

3

2

a

.

Câu 22: Cho hình chóp đều

.S ABCD

đáy là hình vuông cạnh

a

. Biết

60SBD =

. Tính thể tích khối

chóp

.S ABCD

.

A.

3

23

3

a

. B.

3

6

a

. C.

3

6

3

a

. D.

3

46

3

a

.

Câu 23: Cho khối chóp tam giác đều

.S ABC

có cạnh đáy bằng

a

và cạnh bên bằng

2a

. Tính thể tích

V

của khối chóp

.S ABC

.

A.

3

11

6

a

V =

. B.

3

11

4

a

V =

. C.

3

13

12

a

V =

. D.

3

11

12

a

V =

.

Câu 24: Cho khối chóp tứ giác đều có tất cả các cạnh bằng

2a

. Thể tích của khối chóp đã cho bằng

A.

3

22

3

a

. B.

3

8

3

a

. C.

3

82

3

a

. D.

3

42

3

a

.

Câu 25: Cho hình chóp đều

.S ABCD

có cạnh đáy bằng

a

và cạnh bên tạo với đáy một góc

60

. Thể

tích của hình chóp đều đó là

A.

3

6

a

. B.

3

6

a

. C.

3

2

a

. D.

3

6

2

a

.

Câu 26: Cho hình chóp đều

.S ABCD

đáy là hình vuông cạnh

a

. Biết

60SBD =

. Tính thể tích khối

chóp

.S ABCD

.

A.

3

23

3

a

. B.

3

6

a

. C.

3

6

3

a

. D.

3

46

3

a

.

Câu 27: Cho hình chóp tứ giác đều

.S ABCD

có cạnh đáy bằng

a

và mặt bên tạo với mặt phẳng đáy một

góc

0

60

. Tính thể tích

V

của khối chóp

.S ABCD

.

A.

3

6

2

=

a

V

. B.

3

6

3

=

a

V

. C.

3

2

=

a

V

. D.

3

6

=

a

V

.

Câu 28: Cho hình chóp tam giác đều

.S ABC

có cạnh đáy bằng

a

và mặt bên tạo với đáy một góc

0

45

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 8

Tính thể tích của khối chóp

.S ABC

?

A.

3

8

a

. B.

3

12

a

. C.

3

4

a

. D.

3

24

a

.

Câu 29: Cho khối chóp đều

.S ABCD

có

6AC a=

và góc tạo bởi hai mặt phẳng

( )

SAB

và

( )

SCD

bằng

0

60

. Thể tích khối chóp đã cho bằng:

A.

3

108 3a

. B.

3

96a

. C.

3

36 3a

. D.

3

27 6a

.

Câu 30: Cho khối chóp đều

.S ABCD

có

4AC a=

, hai mặt phẳng

()SAB

và

()SCD

vuông góc với

nhau. Thể tích của khối chóp đã cho bằng

A.

3

16 2

3

a

. B.

3

82

3

a

. C.

3

16a

D.

3

16

3

a

.

Câu 31: Cho khối chóp tứ giác đều

.S ABCD

có

4AC a=

, hai mặt phẳng

( )

SAB

và

( )

SBC

tạo với nhau

một góc

0

60

. Thể tích của khối chóp đã cho bằng

A.

3

22

3

a

B.

3

22a

. C.

3

16a

. D.

3

82

3

a

.

Câu 32: Cho hình chóp đều

.S ABC

có cạnh đáy bằng

.a

Gọi E, F lần lượt là trung điểm của các cạnh

SB, SC. Biết rằng mặt phẳng

( )

AEF

vuông góc với mặt phẳng

( )

.SBC

Thể tích khối chóp

.S ABC

bằng

A.

3

5

24

a

. B.

3

5

8

a

. C.

3

5

12

a

. D.

3

5

16

a

.

Câu 33: Cho hình chóp tam giác đều

.S ABC

có cạnh bên bằng

2cm

, các điểm

,DE

lần lượt là trung

điểm của

,SA SC

, đồng thời

AE

vuông góc với

BD

. Thể tích khối chóp

.S ABC

bằng

A.

3

4 21

cm

27

. B.

3

4 21

cm

7

. C.

3

4 21

cm

3

. D.

3

4 21

cm

9

.

Câu 34: Cho hình chóp tứ giác đều

.S ABCD

, đáy tâm

O

,

3SA SB SC SD a= = = =

. Gọi

,MN

lần

lượt là trung điểm cạnh

,CD AB

. Biết khoảng cách từ

M

đến

( )

SNC

bằng

510

51

a

. Tính thể

tích khối chóp

.S ABCD

.

A.

3

10

6

a

. B.

3

10

2

a

. C.

3

5

2

a

. D.

3

5

6

a

.

Câu 35: Cho hình chóp đều

.S ABC

có đáy

ABC

là tam giác đều cạnh

.a

Gọi

,E

F

lần lượt là trung

điểm của các cạnh

,SB

.SC

Biết mặt phẳng

( )

AEF

vuông góc với mặt phẳng

( )

.SBC

Thể tích

khối chóp

.S ABC

bằng

A.

3

5

.

8

a

B.

3

.

24

a

C.

3

5

.

24

a

D.

3

15

.

27

a

Câu 36: Cho hình chóp tam giác đều

.S ABC

có cạnh

2AB a=

. Các cạnh bên tạo với đáy một góc

60

.

Thể tích của khối chóp

.S ABC

bằng

A.

3

23a

. B.

3

23

3

a

. C.

43

. D.

3

43

3

a

.

Câu 37: Xét khối tứ diện đều

ABCD

có cạnh

AB x=

. Với giá trị nào của

x

thì thể tích khối tứ diện

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

9 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

ABCD

bằng

3

3a

A.

26xa=

. B.

6xa=

. C.

2x =

. D.

32xa=

.

Câu 38: Cho hình chóp đều

.S ABCD

với

O

là tâm đáy. Khoảng cách từ

O

đến mặt bên bằng 1 và góc

giữa mặt bên với đáy bằng

0

45

. Thể tích của khối chóp

.S ABCD

bằng

A.

42

3

V =

. B.

82

3

V =

. C.

23V =

. D.

43

3

V =

.

Câu 39: Cho khối chóp đều

.S ABCD

có

2AB a=

. Gọi

,MN

lần lượt là trung điểm

,SC SD

, hai mặt

phẳng

( )

AMN

và

( )

SCD

vuông góc với nhau. Thể tích của khối chóp đã cho bằng

A.

3

4

3

3a

. B.

3

43a

. C.

3

8

3

a

D.

3

4

3

2a

.

Câu 40: Cho khối chóp tam giác đều

.S ABC

có cạnh đáy bằng

2a

. Gọi

,MN

lần lượt là trung điểm các

cạnh

,SB SC

. Biết mặt phẳng

( )

AMN

vuông góc với mặt phẳng

( )

SBC

. Thể tích của khối chóp

.S ABC

bằng:

A.

3

5

.

3

a

B.

3

5.a

C.

3

5

.

9

a

D.

3

3 5.a

Câu 41: Cho hình chóp tứ giác đều

.S ABCD

có cạnh đáy bằng

a

, tâm của đáy là

O

. Gọi

M

và

N

lần

lượt là trung điểm của

SA

và

BC

. Biết góc giữa đường thẳng

MN

và mặt phẳng

( )

ABCD

bằng

0

60

. Tính thể tích khối chóp

.S ABCD

.

A.

3

10

6

a

. B.

3

30

2

a

. C.

3

30

6

a

. D.

3

10

3

a

Câu 42: Cho khối chóp đều

.S ABC

có cạnh đáy bằng

a

, hai mặt phẳng

( )

SAC

và

( )

SBC

vuông góc

với nhau. Thể tích khối chóp đã cho bằng

A.

3

2

24

a

. B.

3

8

2a

. C.

3

2

5

1

a

. D.

3

5

4

a

.

Câu 43: Cho hình chóp tứ giác đều

.S ABCD

có cạnh đáy bằng

a

. Gọi

M

,

N

lần lượt là trung điểm

của

SA

và

CD

. Cho biết

MN

tạo với mặt đáy một góc bằng

30

. Tính thể tích khối chóp

.S ABCD

.

A.

3

30

18

a

. B.

3

15

3

a

. C.

3

5

12

a

. D.

3

15

5

a

.

Câu 44: Cho hình chóp đều

.S ABCD

có cạnh đáy bằng

a

, góc giữa hai mặt phẳng

( )

SBC

và

( )

SCD

bằng

0

60

. Tính thể tích khối chóp

.S ABCD

theo

a

.

A.

3

2

a

. B.

3

6

a

. C.

3

2

12

a

. D.

3

2

4

a

.

Câu 45: Cho khối chóp đều

.S ABCD

có

6AC a=

. Gọi

,MN

lần lượt là trung điểm cạnh

SB

và

SD

.

Biết

( )

AMC

và

( )

CMN

cùng vuông góc nhau. Tính thể tích khối chóp đã cho.

A.

3

72a

. B.

3

108a

. C.

3

36a

. D.

3

216a

.

Câu 46: Cho khối chóp đều

.S ABCD

có

4AC a=

, hai mặt phẳng

( )

SAB

và

( )

SCD

vuông góc với

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 10

nhau. Thể tích khối chóp đã cho bằng

A.

3

16 2

3

a

. B.

3

82

3

a

. C.

3

16a

. D.

3

16

3

a

.

Câu 47: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác đều cạnh

1

, biết khoảng cách từ

A

đến

( )

SBC

là

6

4

, từ

B

đến

( )

SCA

là

15

10

, từ

C

đến

( )

SAB

là

30

20

và hình chiếu vuông góc

H

của

S

xuống đáy nằm trong tam giác

ABC

. Tính thể tích khối chóp

.S ABC

V

.

A.

1

12

. B.

1

36

. C.

1

24

. D.

1

48

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

1 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Dạng 5: Tổng hợp về thể tích khối chóp

Câu 1: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Diện tích đáy và chiều cao của khối

lần lượt

S

và

h

. Tính thể tích của khối chóp

.S ABC

là

A.

1

3

Sh

. B.

1

6

Sh

. C.

2

3

Sh

. D.

Sh

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 2: Cho hình chóp

.S ABC

có đáy là tam giác đều cạnh

2a

và có thể tích bằng

3

3a

. Tính chiều cao

h

của hình chóp đã cho.

A.

33

2

a

h =

. B.

3

a

h =

. C.

3ha=

. D.

23ha=

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 3: Khối chóp

.S ABCD

có đáy là hình vuông cạnh bằng

2a

, chân đường cao trùng với trung điểm

H

của

AB

, mặt bên

( )

SCD

tạo với mặt đáy một góc

0

30

. Gọi

M

là trung điểm của

SC

. Thể

tích khối chóp

.H BCM

là

A.

3

2

3

a

. B.

3

8

a

. C.

3

9

a

. D.

3

6

3

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

VÍ DỤ MINH HỌA

B

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 2

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 4: Cho hình chóp

.S ABC

có

3AB a=

,

4BC a=

,

5CA a=

, các mặt bên cùng tạo với đáy một góc

60

, hình chiếu vuông góc của

S

lên mặt phẳng

( )

ABC

thuộc miền trong tam giác

ABC

. Tính

thể tích khối chóp

.S ABC

.

A.

3

23a

. B.

3

63a

. C.

3

12 3a

. D.

3

22a

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 5: Cho tứ diện

ABCD

có

ABC

,

ABD

và

ACD

là các tam giác vuông tương ứng tại

,AB

và

C

.

Góc giữa

AD

và

( )

ABC

bằng

45

;

AD BC⊥

và khoảng cách giữa

AD

và

BC

bằng

a

. Tính

thể tích khối tứ diện

ABCD

.

A.

3

6

a

. B.

3

43

3

a

. C.

3

2

6

a

. D.

3

42

3

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

3 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 6: Cho tứ diện

ABCD

có

AD

vuông góc với mặt phẳng

( )

ABC

. Biết

3AD a=

,

2AB a=

,

4AC a=

và

60BAC =

. Gọi

,HK

lần lượt là hình chiếu của

B

lên

AC

và

CD

. Đường thẳng

HK

cắt

AD

tại

E

. Thể tích khối tứ diện

BCDE

bằng

A.

3

52 3

9

a

. B.

3

3a

. C.

3

26 3

9

a

. D.

3

19 3

6

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 7: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thoi cạnh bằng

a

. Biết rằng

, , 3,SA a SA AD SB a AC a= ⊥ = =

. Thể tích khối chóp

.S ABCD

bằng.

A.

3

2

a

. B.

3

2

3

a

. C.

3

2

6

a

. D.

3

6

2

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 8: Cho khối chóp

.S ABCD

có đáy là hình vuông cạnh bằng

2

. Tam giác

SAB

là tam giác đều, tam

giác

SCD

vuông tại

S

. Tính thể tích

V

của khối chóp đã cho.

A.

43

3

V =

. B.

23V =

. C.

83

3

V =

. D.

23

3

V =

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 4

Câu 9: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thoi, hai đường chéo

23AC a=

,

2BD a=

và

cắt nhau tại

O

, hai mặt phẳng

( )

SAC

và

( )

SBD

cùng vuông góc với mặt phẳng

ABCD

. Biết

khoảng cách từ điểm

O

đến mặt phẳng

( )

SAB

bằng

3

4

a

. Tính thể tích

V

của khối chóp

.S ABCD

.

A.

3

12

a

V =

. B.

3

6

a

V =

. C.

3

2

6

a

V =

. D.

3

a

V =

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 10: Cho hình chóp tam giác

.S ABC

có

2SA a=

và

SA

tạo với mặt phẳng

( )

ABC

góc

30

. Tam giác

ABC

vuông cân tại

B

,

G

là trọng tâm tam giác

ABC

. Hai mặt phẳng

( )

SGB

và

( )

SGC

cùng

vuông góc với mặt phẳng đáy. Tính thể tích của khối chóp

.S ABC

theo

a

.

A.

3

9

10

a

. B.

3

9

40

a

. C.

3

27

10

a

. D.

3

81

10

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

…………………………………………………………

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

5 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 1: Cho khối chóp có diện tích đáy

B

và chiều cao

h

. Thể tíc

V

của khối chóp đã cho được tính

theo công thức nào dưới đây?

A.

V Bh=

. B.

2

3

V Bh=

. C.

3V Bh=

. D.

1

3

V Bh=

.

Câu 2: Thể tích của khối chóp tam giác bằng

6

, diện tích đáy bằng

2

. Chiều cao của khối chóp bằng?

A.

18

. B.

1

. C.

3

. D.

9

.

Câu 3: Tính thể tích khối chóp có đáy là tam giác đều cạnh

a

và chiều cao của khối chóp bằng

3a

.

A.

3

4

a

. B.

3

a

. C.

3

3a

. D.

3

12

a

.

Câu 4: Cho khối chóp có diện tích đáy

B

và chiều cao

h

. Thể tích

V

của khối chóp đã cho được tính

theo công thức vào dưới đây?

A.

1

2

V Bh=

. B.

1

3

V Bh=

. C.

4

3

V Bh=

. D.

V Bh=

.

Câu 5: Cho khối chóp có diện tích đáy

5S =

, chiều cao

3h =

. Thể tích khối chóp đã cho bằng

A.

5

. B.

12

. C.

15

. D.

35

.

Câu 6: Cho hình chóp

.S ABC

có

, 3, 2, 2 .AB a BC a AC a SA SB SC a= = = = = =

Tính thể tích khối

chóp

..S ABC

A.

3

26

24

a

. B.

3

26

12

a

. C.

3

26

4

a

. D.

3

26

8

a

.

Câu 7: Cho khối chóp

.S ABCD

có

( )

SA ABCD⊥

, đáy

ABCD

là hình thang,

//AB CD

,

,2SA AD DC a BC a= = = =

. Tam giác

SBC

vuông tại

C

, tam giác

SCD

vuông tại

D

. Thể

tích khối chóp đã cho bằng

A.

3

2a

. B.

3

4

3

a

. C.

3

2

3

a

. D.

3

1

2

a

.

Câu 8: Cho hình chóp

.S ABCD

,có

AC

vuông góc với

BD

và

3cmAC =

,

4cmBD =

.Khoảng cách từ

điểm

S

đến mặt phẳng

( )

ABC

bằng

9cm

. Thể tích khối chóp

.S ABCD

bằng

A.

3

36cm

. B.

3

18cm

. C.

3

54cm

. D.

3

6cm

.

Câu 9: Cho hình chóp

.S ABC

có tất cả các mặt bên cùng hợp với đáy một góc

60 .

Biết rằng mặt phẳng

đáy là tam giác

ABC

đều cạnh

.a

Tính thể tích khối chóp đã cho.

A.

3

.

24

a

B.

3

.

8

a

C.

3

.

12

a

D.

3

.

4

a

Câu 10: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

. Hình chiếu vuông góc của đỉnh

S

lên đáy

()ABCD

là trọng tâm của tam giác

ABD

. Biết góc tạo bởi cạnh

SC

với đáy bằng

60



. Thể tích khối chóp

.S ABC

bằng:

A.

3

4

a

. B.

3

2

3

a

. C.

3

6

a

. D.

3

a

.

Câu 11: Cho hình chóp

.S ABC

có các cạnh bên

,,SA SB SC

tạo với đáy các góc bằng nhau và bằng

60

BÀI TẬP TRẮC NGHIỆM

C

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 6

. Biết

13 , 14AB a AC a==

và

15BC a=

. Tính thể tích

V

của khối chóp

.S ABC

.

A.

3

455 3

6

Va=

. B.

3

455 3Va=

. C.

3

455 3

3

a

. D.

3

455 3

2

Va=

.

Câu 12: Cho hình chóp

.S ABC

có đáy là tam giác đều cạnh bằng

a

, tam giác

SAB

cân tại

S

và thuộc

mặt phẳng vuông góc với mặt phẳng

( )

ABC

, góc giữa hai mặt phẳng

( )

SCA

và

( )

SCB

bằng

0

60

. Gọi

H

là trung điểm của đoạn

AB

. Trong các mệnh đề sau, mệnh đề nào đúng:

A. Thể tích khối chóp

.S ABC

bằng

3

2

16

a

. B. Thể tích khối chóp

.B SHC

bằng

3

2

16

a

.

C. Thể tích khối chóp

.S AHC

bằng

3

2

64

a

. D. Không tồn tại hình chóp đã cho.

Câu 13: Cho khối chóp

.S AB C

có đáy

ABC

là tam giác cân đỉnh

A

,

120BAC =

và

AB a=

. Các cạnh

bên

,,SA SB SC

bằng nhau và góc giữa

SA

với mặt phẳng đáy bằng

60

. Thể tích khối chóp đã

cho bằng

A.

3

4

a

. B.

3

4

a

. C.

3

4

a

. D.

3

3a

.

Câu 14: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thoi, có

0

3, 60AC a ABC==

. Biết rằng

SA SC=

,

SB SD=

và khoảng cách từ

A

mặt phẳng

( )

SBC

bằng

6

2

a

. Tính thể tích khối chóp

.S ABC

bằng:

A.

3

36

8

a

. B.

3

96

16

a

. C.

3

3 15

40

a

. D.

3

36

16

a

.

Câu 15: Cho tứ diện

MNPQ

. Biết rằng mặt phẳng

()MNP

vuông góc với mặt phẳng

()NPQ

, đồng thời

MNP

và

NPQ

là 2 tam giác đều cạnh

4a

. Tính theo

a

thể tích

V

của khối tứ diện

MNPQ

.

A.

3

24 3Va=

. B.

3

24Va=

. C.

3

83Va=

. D.

3

8Va=

.

Câu 16: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật, tam giác

SAD

vuông tại

S

và nằm

trong mặt phẳng vuông góc với mặt phẳng đáy. Biết

,2AB a SA SD==

và mặt phẳng

( )

SBC

tạo với mặt phẳng đáy một góc

60

. Thể tích khối chóp

.S ABCD

bằng

A.

3

5

2

a

. B.

3

2

a

. C.

3

5a

. D.

3

15

2

a

.

Câu 17: Cho hình chóp

.S ABCD

có đáy là hình vuông cạnh

2

,

SAB

đều,

SCD

vuông tại

S

.Tính thể

tích

V

của khối chóp

.S ABCD

.

A.

23

3

V =

. B.

83

3

V =

. C.

43

3

V =

. D.

23V =

.

Câu 18: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật,

1AB =

,

20AD =

,

SA SB=

,

SC SD=

. Biết mặt phẳng

( )

SAB

và

( )

SCD

vuông góc nhau đồng thời tổng diện tích của hai

tam giác

SAB

và

SCD

bằng

3

. Thể tích khối chóp

.S ABCD

bằng

A.

8

3

. B.

13

6

. C.

26

3

. D.

13

2

.

Câu 19: Cho hình chóp

.S AB C

có đáy

ABC

là tam giác vuông cân tại

B

và

BA BC a==

,

SA AB⊥

và

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

7 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

SC CB⊥

. Biết góc giữa hai mặt phẳng

( )

SAB

và

( )

SBC

là



thỏa mãn

9

cos

16



=

Thể tích

khối chóp

.S AB C

bằng

A.

3

5

18

a

. B.

3

7

9

a

. C.

3

7

6

a

. D.

3

7

18

a

.

Câu 20: Cho tứ diện

ABCD

có

=AB a

,

5=AC a

,

90DAB CBD= = 

,

135ABC =

. Biết góc giữa

hai mặt phẳng

( )

ABD

và

( )

BCD

bằng

30

. Thể tích khối tứ diện

ABCD

bằng

A.

3

2

a

. B.

3

32

a

. C.

3

23

a

. D.

3

6

a

.

Câu 21: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thoi cạnh

a

và

60ABC =

. Biết

SA SB SC==

và góc giữa mặt bên

( )

SCD

và mặt đáy bằng

60

. Thể tích của khối chóp

.S ABCD

bằng

A.

3

2

a

. B.

3

6

a

. C.

3

2

a

. D.

3

2

6

a

.

Câu 22: Cho hình chóp

.S ABC

có đáy là tam giác

ABC

đều cạnh

a

, tam giác

SBA

vuông tại

B

, tam

giác

SAC

vuông tại

C

. Biết góc giữa hai mặt phẳng

( )

SAB

và

( )

ABC

bằng

60

. Thể tích khối

chóp

.S ABC

bằng

A.

3

8

a

. B.

3

12

a

. C.

3

6

a

. D.

3

4

a

.

Câu 23: Cho hình chóp

.S AB C

có đáy

ABC

là tam giác vuông tại

C

, cạnh

SA

vuông góc với mặt đáy

và

2SA AB a==

,

30CAB =

. Gọi

H

là hình chiếu vuông góc của

A

trên

SC

,

B



là điểm đối

xứng của

B

qua mặt phẳng

( )

SAC

. Thể tích của khối chóp

.H A B B



bằng

A.

3

7

a

. B.

3

63

7

a

. C.

3

43

7

a

. D.

3

23

7

a

.

Câu 24: Cho hình chóp

.S ABCD

có đáy là hình thang vuông tại

A

và

B

. Hình chiếu vuông góc của

S

trên mặt phẳng

( )

ABC D

trùng với trung điểm của

.AB

Biết

,AB a=

2,BC a=

10.BD a=

Góc

giữa hai mặt phẳng

( )

SBD

và mặt phẳng đáy là

30 .

Tính thể tích

V

của khối chóp

.S ABCD

theo

.a

A.

3

3 30

2

a

V =

B.

3

30

4

a

V =

C.

3

30

24

a

V =

D.

3

30

8

a

V =

Câu 25: Cho khối chóp tứ giác đều

.S ABCD

có

22BD a=

, gọi

M

là trung điểm của

DC

, góc giữa

SM

và mặt phẳng

( )

ABCD

bằng

0

60

. Thể tích

V

của khối chóp

.S ABCD

bằng,

A.

3

33

2

a

V =

B.

3

42

3

a

V =

C.

3

43

3

a

V =

D.

3

6

a

V =

Câu 26: Cho hình chóp tứ giác đều

.S ABCD

có cạnh đáy bằng

a

, tâm của đáy là

O

. Gọi

M

và

N

lần

lượt là trung điểm của

SA

và

BC

. Biết góc giữa đường thẳng

MN

và mặt phẳng

( )

ABCD

bằng

0

60

. Tính thể tích khối chóp

.S ABCD

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 8

A.

3

10

6

a

B.

3

30

2

a

C.

3

30

6

a

D.

3

10

3

a

Câu 27: Cho hình chóp

.S ABCD

với đáy

ABCD

là hình thang vuông tại

A

và

D

, đáy nhỏ của hình

thang là

CD

, cạnh bên

15SC a=

. Tam giác

SAD

là tam giác đều cạnh

2a

và nằm trong mặt

phẳng vuông góc với đáy hình chóp. Gọi

H

là trung điểm cạnh

AD

, khoảng cách từ

B

tới mặt

phẳng

( )

SHC

bằng

26a

. Tính thể tích

V

của khối chóp

.S ABCD

.

A.

3

46Va=

. B.

3

12 6Va=

. C.

3

86Va=

. D.

3

24 6Va=

.

Câu 28: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật, tam giác

SAB

đều và nằm trong mặt

phẳng vuông góc với đáy, biết khoảng cách giữa hai đường thẳng

SB

và

CD

bằng

a

và

0

30BDC =

. Tính thể tích của khối chóp

.S ABCD

.

A.

3

33

2

a

. B.

3

6

9

a

. C.

3

6

a

. D.

3

2

a

.

Câu 29: Cho khối chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật, tam giác

SAB

cân tại

S

và nằm trong

mặt phẳng vuông góc với

( )

ABC D

. Biết

2,BD a AB a==

, khoảng cách giữa

AB

và

SD

bằng

2a

. Tính thể tích khối chóp

.S ABCD

.

A.

3

a

. B.

3

32a

. C.

3

2

3

a

. D.

3

2a

.

Câu 30: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật,

AB a=

,

2BC a=

.

SA

vuông góc với

mặt phẳng đáy. Biết khoảng cách giữa hai đường thẳng

BD

và

SC

bằng

23

31

a

. Tính thể tích

của khối chóp

.S ABCD

.

A.

3

3a

. B.

3

a

. C.

3

23

3

a

. D.

3

23a

Câu 31: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

. Gọi

;MN

lần lượt là trung điểm

của

AB

và

AD

;

H

là giao điểm của

CN

và

DM

. Biết

SH

vuông góc với mặt phẳng

( )

ABC D

và khoảng cách giữa hai đường thẳng

DM

và

SC

bằng

2 57

19

a

. Tính thể tích khối

chóp

.S ABCD

?

A.

3

a

. B.

3

6

9

a

. C.

3

a

. D.

3

33a

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

1 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Dạng 6: Tỷ số thể tích khối chóp

Cho khối chóp

.S ABC

và

,,A B C

  

là các điểm tùy ý lần lượt thuộc

,,SA SB SC

, ta có:

Công thức tỉ số thể tích:

. ' ' '

.

' ' '

..

S A B C

S ABC

V

SA SB SC

V SA SB SC

=

(hay gọi là công thức Simson)

Phương pháp này được áp dụng khi khối chóp không xác đinh được chiều cao một cách dễ dàng

hoặc khối chóp cần tính là một phần nhỏ trong khối chóp lớn và cần chú ý đến một số điều kiện sau:

▪ Hai khối chóp phải cùng chung đỉnh.

▪ Đáy hai khối chóp phải là tam giác.

▪ Các điểm tương ứng nằm trên các cạnh tương ứng.

Định lý Menelaus: Cho ba điểm thẳng hàng

. . 1

FA DB EC

FB DC EA

=

với

DEF

là một đường thẳng cắt ba

đường thẳng

,,BC CA AB

lần lượt tại

,,D E F

.

Chú ý: (Áp dụng cho khối chóp với mọi đáy)

▪ Hai hình chóp có cùng chiều cao thì tỉ số thể tích chính là tỉ số diện tích đáy tương ứng.

▪ Hai hình chóp có cùng diện tích đáy thì tỉ số thể tích chính là tỉ số đường cao tương ứng.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 2

Câu 1: Cho khối tứ diện

ABCD

có thể tích

V

và điểm

E

trên cạnh

AB

sao cho

3AE EB=

. Khi đó

thể tích khối tứ diện

EBCD

bằng

A.

3

V

. B.

5

V

. C.

4

V

. D.

2

V

.

 Lời giải

…………………………………………………………………

………………………………………………………………

……………………………………………………………

Câu 2: Cho hình chóp

.S ABC

. Gọi

M

,

N

,

P

lần lượt là trung điểm của

SA

,

SB

,

SC

. Tỉ số

.

S ABC

S MNP

V

bằng

A.

3

2

. B. 8. C.

1

8

. D. 6.

 Lời giải

…………………………………………………………………

………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 3: Cho hình chóp

.S ABCD

có đáy là hình bình hành. Gọi

G

là trọng tâm tam giác

SAB

và

,MN

lần lượt là trung điểm của

,SC SD

. Biết thể tích khối chóp

.S ABCD

là

V

, tính thể tích khối

chóp

.S GMN

.

A.

8

V

. B.

4

V

. C.

6

V

. D.

12

V

.

 Lời giải

…………………………………………………………………

………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

VÍ DỤ MINH HỌA

B

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

3 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 4: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông cân tại

,,A AB a SA=

vuông góc với đáy,

góc hợp bởi

SB

và đáy bằng

60

. Gọi

,HK

lần lượt là hình chiếu vuông góc của

A

trên các

đường thẳng chứa cạnh

,SB SC

. Gọi

12

,VV

lần lượt là thể tích các khối đa diện

SAHK

và

ABCKH

. Tỉ số

1

2

V

bằng

A.

7

9

. B.

7

16

. C.

9

7

. D.

9

16

.

 Lời giải

…………………………………………………………………

………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 5: Cho khối tứ diện

ABCD

có thể tích

V

. Gọi

, , ,M N P Q

lần lượt là trung điểm các cạnh

AB

,

AC

,

BC

,

AD

. Tính thể tích tứ diện

MNPQ

theo

V

.

A.

3

8

V

. B.

4

V

. C.

8

V

. D.

12

V

.

 Lời giải

…………………………………………………………………

………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 6: Cho tứ diện

ABCD

. Gọi

,M

N

là trung điểm của

,,AB AC

lấy điểm

P

thuộc cạnh

AD

sao

cho

2

3

AP AD

. Khi đó tỉ số

AMNP

ABCD

V

bằng

A.

1

.

6

B.

1

.

8

C.

1

.

3

D.

1

.

4

 Lời giải

…………………………………………………………………

……………………………………………………………

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 4

…………………………………………………………………

………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 7: Cho hình chóp

.S ABC

có đáy là tam giác

ABC

vuông cân tại

,A

12=SB

,

SB

vuông góc với

mặt phẳng

( )

ABC

. Gọi

, DE

lần lượt là các điểm thuộc các đoạn

, SA SC

sao cho

2 , ==SD DA ES EC

. Biết

23=DE

, hãy tính thể tích khối chóp

.B ACED

.

A.

96

5

. B.

144

5

. C.

288

5

. D.

192

5

.

 Lời giải

…………………………………………………………………

………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 8: Cho hình chóp

.S ABCD

có đáy là hình vuông cạnh

a

,

SA

vuông góc với đáy, côsin góc hợp

bởi

SD

và mặt phẳng đáy

( )

ABCD

bằng

1

3

. Gọi

E

;

F

lần lượt là hình chiếu của

A

lên

SB

;

SD

. Mặt phẳng

( )

AEF

chia khối chóp thành hai phần. Tính thể tích phần khối chóp không

chứa đỉnh

S

:

A.

3

2

9

a

V =

. B.

3

2

4

a

V =

. C.

3

22

9

a

V =

. D.

3

2

6

a

V =

.

 Lời giải

…………………………………………………………………

………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

5 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 1: Cho khối chóp

.S ABC

có thể tích

V

. Các điểm

A



,

B



,

C



tương ứng là trung điểm các cạnh

SA

,

SB

,

SC

. Thể tích khối chóp

.S A B C

  

bằng

A.

8

V

. B.

2

V

. C.

4

V

. D.

16

V

.

Câu 2: Cho khối chóp

.S ABC

có thể tích

V

. Gọi

,MN

lần lượt là trung điểm của

SA

và

BC

. Tính

thể tích khối chóp

.M ANC

theo

V

.

A.

8

V

. B.

6

V

C.

12

V

. D.

4

V

.

Câu 3: Cho tứ diện

MNPQ

. Gọi

,IJ

và

K

lần lượt là trung điểm của

,MN MP

và

MQ

(tham khảo hình

vẽ). Tỉ số thể tích

MIJK

MNPQ

V

là:

A.

1

8

. B.

1

4

. C.

1

6

. D.

1

3

.

Câu 4: Cho hình chóp

SABC

có đáy là tam giác cân tại

,A AB a=

và góc

A

bằng

0

30

. Cạnh bên

2SA a=

và

( )

SA ABC⊥

. Gọi

,MN

lần lượt là trung điểm của các cạnh

SB

và

SC

. Khi đó thể

tích khối đa diện có các đỉnh

, , , ,A B C M N

bằng

A.

3

4

a

. B.

3

12

a

. C.

3

8

a

. D.

3

8

a

.

Câu 5: Cho khối chóp

.S ABC

. Trên ba cạnh

,,SA SB SC

lần lượt lấy ba điển

,,A B C

  

sao cho

2 , 3 , 4SA SA SB SB SC SC

  

= = =

. Mặt phẳng

( )

ABC

  

chia khối chóp thành hai khối. Gọi

V

và

V



lần lượt là thể tích các khối đa diện

.S A B C

  

và

.ABC A B C

  

. Khi đó tỉ số

V



là:

A.

1

59

. B.

1

12

. C.

1

23

. D.

1

24

.

Câu 6: Cho tứ diện

ABCD

. Các điểm

,,M N P

lần lượt thuộc các cạnh

,,AB AC AD

sao cho

, 2 , 3 .MA MB NA NC PA PD

Biết thể tích khối tứ diện

AMNP

bằng

V

thì khối tứ diện

ABCD

tính theo

V

có giá trị là

A.

6.V

B.

4.V

C.

8.V

D.

12 .V

Câu 7: Cho hình chóp

.S ABCD

. Gọi

, , ,A B C D

   

theo thứ tự là trung điểm của

, , ,SA SB SC SD

. Tính

tỉ số thể tích của hai khối chóp

.S A B C D

   

và

.S ABCD

.

BÀI TẬP TRẮC NGHIỆM

C

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 6

A.

1

16

. B.

1

4

. C.

1

8

. D.

1

2

.

Câu 8: Cho lăng trụ tam giác

.ABC A B C

  

. Biết diện tích mặt bên

( )

ABB A



bằng

15

, khoảng cách từ

C

đến mặt phẳng

( )

ABB A



bằng

6

. Thể tích khối lăng trụ

.ABC A B C

  

bằng

A.

60

. B.

45

. C.

90

. D.

30

Câu 9: Cho khối tứ diện

ABCD

có thể tích

V

và điểm

E

thỏa mãn

3EA EB=−

. Khi đó thể tích khối

tứ diện

EBCD

bằng

A.

2

V



B.

3

V



C.

5

V



D.

4

V



Câu 10: Cho khối chóp

.S ABC

có đáy

ABC

là tam giác đều cạnh

a

,

2SA a=

và vuông góc với mặt

phẳng

( )

ABC

. Trên cạnh

,SB SC

lần lượt lấy các điểm

,MN

sao cho

12

,

23

SM SN

SB SC

==

(tham

khảo hình vẽ). Thể tích của khối chóp

.S AMN

bằng

A.

3

36

a

. B.

3

9

a

. C.

3

18

a

. D.

3

a

.

Câu 11: Cho hình chóp

.S ABC

, trên các cạnh

,,SA SB SC

lần lượt lấy các điểm

,,A B C

  

sao cho

2 , 4 ,SA AA SB BB SC CC

     

= = =

. Gọi

1

V

là thể tích khối chóp

.S A B C

  

,

2

V

là thể tích khối

chóp

.S ABC

. Tính

1

2

V

A.

1

2

4

15

V

=

. B.

1

2

1

24

V

=

. C.

1

2

8

15

V

=

. D.

1

2

1

16

V

=

.

Câu 12: Cho hình chóp

.S ABC

có

SA

vuông góc với đáy,

3=SA a

, đáy

ABC

là tam giác đều cạnh bằng

a

.

,,M N P

lần lượt là trùng điểm của các cạnh bên

,,SA SB SC

. Tính thể tích khối đa diện

MNP ABC

.

A.

3

8

a

. B.

3

33

16

a

. C.

3

73

32

a

. D.

3

6

a

.

Câu 13: Cho khối chóp

.S ABC

. Trên ba cạnh

,,SA SB SC

lần lượt lấy ba điểm

’, ,A B C



sao cho

2 , 4 , 5SA SA SB SB SC SC

  

= = =

. Tính tỉ số

. ' ' '

.

S A B C

S ABC

V

A.

1

10

. B.

1

40

. C.

1

8

. D.

1

20

.

Câu 14: Cho hình chóp

.S ABC

, gọi

,,M N P

lần lượt là trung điểm của cạnh

,,SA SB SC

. Biết thể tích

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

7 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

khối chóp

.S MNP

bằng

5

.

Khi đó thể tích của khối đa diện

.MNP ABC

bằng:

A.

40

. B.

10

. C.

35

. D.

25

.

Câu 15: Cho hình chóp tứ giác

.S ABCD

có đáy

ABCD

là hình bình hành tâm

I

. Gọi

1

V

,

2

V

lần lượt là

thể tích của khối chóp

.S ABI

và

.S ABCD

. Khẳng định nào sau đây đúng?

A.

1

2

1

6

V

=

. B.

1

2

1

2

V

=

. C.

1

2

1

8

V

=

. D.

1

2

1

4

V

=

.

Câu 16: Cho tứ diện đều

ABCD

có cạnh bằng

a

. Gọi

,,M N P

lần lượt là trung điểm của các cạnh

,,AB AC AD

và điểm

O

tùy ý trên mặt phẳng

()BCD

. Thể tích tứ diện

OMNP

bằng

A.

3

2

96

a

. B.

3

2

24

a

. C.

3

2

48

a

. D.

3

2

36

a

.

Câu 17: Cho khối chóp

.S ABC

. Gọi

'A

,

'C

lần lượt là trung điểm của

SA

và

SC

. Khi đó tỉ số thể tích

của hai khối chóp

. ' 'S BA C

và

.S ABC

bằng

A.

1

2

. B.

1

3

. C.

1

4

. D.

1

6

.

Câu 18: Cho khối tứ diện đều

ABCD

có cạnh bằng

a

. Gọi

M

là điểm trên cạnh

AB

sao cho thể tích

khối

AMCD

bằng

3

2

18

a

. Phát biểu nào sau đây đúng?

A.

32MA MB=

. B.

3MA MB=

. C.

3MA MB=

. D.

2MA MB=

.

Câu 19: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành và

M

là trung điểm cạnh bên

SC

.

Gọi

()P

là mặt phẳng chứa

AM

và song song với

BD

, mặt phẳng

()P

cắt

SB

và

SD

lần lượt

tại

B



và

D



. Tính tỷ số

.

S AB MD

S ABCD

V



.

A.

1

6

. B.

1

3

. C.

3

4

. D.

2

3

.

Câu 20: Cho hình chóp đều

.S ABCD

. Mặt phẳng

( )

P

chứa

AB

và đi qua trọng tâm

G

của tam giác

SAC

cắt

,SC SD

lần lượt tại

,MN

. Tỉ lệ

.

S ABMN

S ABCD

V

T

V

=

có giá trị là

A.

1

.

2

B.

3

.

8

C.

1

.

4

D.

3

.

4

Câu 21: Cho hình chóp

.S ABCD

có thể tích bằng

2

và đáy

ABCD

là hình bình hành. Lấy các điểm

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 8

,MN

lần lượt thuộc các cạnh

,SB SD

thỏa mãn

( )

01

SM SN

kk

SB SD

= =  

. Mặt phẳng

( )

AMN

cắt

cạnh

SC

tại

P

. Biết khối chóp

.S AMPN

có thể tích bằng

1

3

, khi đó giá trị của

k

bằng

A.

1

2

. B.

1

3

. C.

2

3

. D.

1

4

.

Câu 22: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông tâm

O

. Gọi

H

và

K

lần lượt là trung

điểm của

,SB SD

. Tỷ số thể tích

.

AOHK

S ABCD

V

bằng

A.

1

12

. B.

1

6

. C.

1

8

. D.

1

4

.

Câu 23: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật. Mặt phẳng

( )



đi qua

,AB

và trung

điểm

M

của

SC

. Mặt phẳng

( )



chia khối chóp đã cho thành hai phần có thể tích lần lượt là

12

,VV

với

12

VV

. Tính tỉ số

1

2

V

.

A.

1

2

1

4

V

=

. B.

1

2

3

8

V

=

. C.

1

2

5

8

V

=

. D.

1

2

3

5

V

=

.

Câu 24: Cho hình chóp tứ giác

.S ABCD

đáy là hình bình hành có thể tích bằng

V

. Lấy điểm

B



,

D



lần lượt là trung điểm của cạnh

SB

và

SD

. Mặt phẳng qua

( )

AB D



cắt cạnh

SC

tại

C



. Khi

đó thể tích khối chóp

.S AB C D

  

bằng

A.

3

V

B.

2

3

V

. C.

3

V

. D.

6

V

.

Câu 25: Cho hình chóp

.S ABCD

có đáy là hình thang vuông tại

A

và

B

.

2,AB BC a==

4AD a=

.

Mặt phẳng

( )



đi qua

A

và trung điểm các cạnh

SB

,

SC

chia khối chóp

.S ABCD

thành hai

khối đa diện. Gọi

V

là thể tích khối đa diện chứa đỉnh

S

,

V



là thể tích khối đa diện không chứa

đỉnh

S

. Tỉ số

V



bằng

A.

5

12

. B.

5

7

. C.

7

12

. D.

7

5

.

Câu 26: Cho khối chóp tứ giác đều

.S ABCD

có cạnh đáy

AB a=

, cạnh bên

2SA a=

. Gọi

M

và

N

lần

lượt là trung điểm

,SA SC

. Mặt phẳng

( )

BMN

cắt

SD

tại

K

.

Thể tích khối chóp

.S MNK

bằng

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

9 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

A.

3

14

112

a

. B.

3

14

84

a

. C.

3

14

12

a

. D.

3

14

144

a

.

Câu 27: Cho hình chóp

.S ABCD

có đáy là hình bình hành. Gọi

,MN

là trung điểm của

,.SA SB

Mặt

phẳng

()MNCD

chia hình chóp đã cho thành hai phần. Tỉ số thể tích hai phần là (số bé chia số

lớn).

A.

3

5

. B.

3

4

. C.

1

3

. D.

4

5

.

Câu 28: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

,

SA

vuông góc với đáy,

2SA a=

. Gọi

, BD



lần lượt là hình chiếu vuông góc của

A

lên

, SB SD

. Mặt phẳng

( )

AB D



cắt

SC

tại

C



. Thể tích khối chóp

.S AB C D

  

là

A.

3

22

3

a

V =

. B.

3

23

3

a

V =

. C.

3

2

9

a

V =

. D.

3

23

9

a

V =

.

Câu 29: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Gọi

,M

N

lần lượt là trung điểm

của các cạnh

,SA

SD

. Mặt phẳng

( )



chứa

MN

cắt các cạnh

,SB

SC

lần lượt tại

,Q

P

. Đặt

SQ

x

SB

=

,

1

V

là thể tích khối chóp

.,S MNPQ

V

là thể tích khối chóp

.S ABCD

. Tìm

x

để

1

2

VV=

.

A.

1

2

x =

. B.

2x =

. C.

1 41

4

x

−+

=

. D.

1 33

4

x

−+

=

.

Câu 30: Cho tứ diện

ABCD

, trên các cạnh

BC

,

BD

,

AC

lần lượt lấy các điểm

M

,

N

,

P

sao cho

3BC BM=

,

3

2

BD BN=

,

2AC AP=

. Mặt phẳng

( )

MNP

chia khối tứ diện

ABCD

thành hai

phần có thể tích là

1

V

,

2

V

. Tính tỉ số

1

2

V

.

A.

1

2

26

13

V

=

. B.

1

2

26

19

V

=

. C.

1

2

3

19

V

=

. D.

1

2

15

19

V

=

.

Câu 31: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật

, 3,AB a AD a SA a= = =

và

SA

vuông góc với mặt phẳng

( )

ABCD

. Gọi

,HK

lần lượt là hình chiếu vuông góc của

A

lên

,SB SD

. Mặt phẳng

( )

AHK

cắt

SC

tại điểm

P

. Thể tích của khối

.S AHPK

là:

A.

3

40

a

. B.

3

120

a

. C.

3

60

a

. D.

3

30

a

.

Câu 32: Cho hình chóp

.S ABCD

có đáy là hình bình hành tâm

O

. Gọi

,EF

lần lượt là trung điểm của

,SA SC

và

G

là trọng tâm của tam giác

ABC

. Mặt phẳng

( )

EFG

chia khối chóp

.S ABCD

thành hai phần có thể tích lần lượt là

12

,VV

với

1

V

là thể tích khối đa diện chứa đỉnh

S

. Tỉ số

1

2

V

bằng

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 10

A.

1

2

31

59

=

V

. B.

1

2

31

49

=

V

. C.

1

2

25

59

=

V

. D.

.

25

49

=

O AEMF

V

.

Câu 33: Cho tứ diện

ABCD

có thể tích là

3

27cm

. Điểm

M

di động trên

BC

(

M

khác

,BC

), điểm

S

di động trên đường thẳng

CD

. Một mặt phẳng qua

M

song song với hai đường thẳng

,AB CD

đồng thời cắt

,,AC AD BD

lần lượt tại

,,N P Q

. Gọi

V

là thể tích của khối chóp

.S MNPQ

. Khi

,MN

thay đổi thì thể tích lớn nhất của

V

bằng

A.

12

. B.

18

. C.

4

. D.

8

.

Câu 34: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

,

SA

vuông góc với mặt phẳng

( )

ABCD

. Góc giữa hai mặt phẳng

( )

SBD

và

( )

ABCD

bằng

60

. Gọi

M

là điểm đối xứng

của

C

qua

B

và

N

là trung điểm của

SC

. Mặt phẳng

( )

MND

chia khối chóp

.S ABCD

thành hai khối đa diện, trong đó khối đa diện chứa đỉnh

S

có thể tích

1

V

, khối đa diện còn lại có

thể tích

2

V

. Tính tỉ số

2

1

V

A.

2

1

7

5

V

=

. B.

2

1

7

9

V

=

. C.

2

1

9

7

V

=

. D.

2

1

5

7

V

=

.

Câu 35: Cho khối chóp

.S ABCD

có đáy

ABCD

là hình bình hành, có thể tích

3

24cm

. Gọi

E

là trung

điểm của

SC

. Một mặt phẳng chứa

AE

cắt các cạnh

SB

và

SD

lần lượt tại

M

và

N

. Tìm

giá trị nhỏ nhất của thể tích khối chóp

.S AMEN

.

A.

3

9cm

. B.

3

8 cm

. C.

3

6 cm

. D.

3

7 cm

.

Câu 36: Cho hình chóp

.S ABC

thỏa mãn

, 2 , 60 , 90SA a SB SC a ASB ASC= = = =  = 

và

1

cos

23

BSC =

. Thể tích khối chóp đã cho là:

A.

3

26

9

a

V =

. B.

3

2

6

a

V =

. C.

3

6

4

a

V =

. D.

3

23

3

a

V =

.

Câu 37: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật. Một mặt phẳng thay đổi luôn song

song với mặt phẳng chứa đa giác đáy và cắt các cạnh bên

SA

,

SB

,

SC

,

SD

lần lượt tại

I

,

J

,

K

,

L

. Gọi

E

,

F

,

G

,

H

lần lượt là hình chiếu vuông góc của

I

,

J

,

K

,

L

lên mặt phẳng

( )

ABCD

. Thể tích khối đa diện

.IJKL EFGH

đạt giá trị lớn nhất khi

SI a

SA b

=

(

,*a b N

,

a

b

là

phân số tối giản). Giá trị biểu thức

22

T a b=+

bằng

A.

10T =

. B.

5T =

. C.

13T =

. D.

25T =

.

Câu 38: Cho hình chóp

.S ABCD

có đáy là hình bình hành, gọi

G

là trọng tâm tam giác

SAD

, mặt

phẳng

( )



chứa

BG

và song song với

AC

cắt

,,SA SD SC

lần lượt tại

,,A D C

  

. Tỉnh số

.

S A BC D

S ABCD

V

  

bằng

A.

3

8

. B.

9

20

. C.

5

16

. D.

117

128

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

11 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 39: Cho hình chóp tứ giác đều

.S ABCD

có đáy là hình vuông tâm

O

, cạnh đáy bằng

2a

, góc giữa

hai mặt phẳng

( )

SAB

và

( )

ABCD

bằng

o

45

. Gọi

M

,

N

,

P

lần lượt là trung điểm của

SA

,

SB

và

AB

. Thể tích khối tứ diện

DMNP

bằng

A.

3

6

a

. B.

3

12

a

. C.

3

2

a

. D.

3

4

a

.

Câu 40: Cho lăng trụ

. ' ' 'ABC A B C

có thể là

V

. Gọi

M

là điểm nằm trên cạnh

'BB

sao cho

2 3 'MB MB=

, điểm

N

nằm trên cạnh

AA'

sao cho

4'AN NA=

, điểm

P

nằm trên cạnh

'CC

sao cho

3'CP C P=

. Các đường thẳng

NM

và

PM

cắt các cạnh

''AB

và

''CB

lần lượt tại

H

và

K

. Hãy tính theo

V

thể tích của khối tứ diện

'MB HK

.

A.

16

105

V

. B.

6

35

V

. C.

4

15

V

. D.

2

7

V

.

Câu 41: Cho tứ diện

ABCD

. Hai điểm

,MN

lần lượt di động trên hai đoạn thẳng

BC

và

BD

sao cho

2. 3. 10

BC BD

BM BN

+=

. Gọi

12

,VV

lần lượt là thể tích của các khối tứ diện

ABMN

và

ABCD

. Tìm

giá trị nhỏ nhất của

1

2

.

V

A.

3

.

8

B.

2

.

7

C.

6

.

25

D.

5

.

8

Câu 42: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông cân tại

B

,

AB a=

,

AB SA⊥

,

BC SC⊥

. Gọi

,MN

lần lượt là trung điểm của

SC

,

AC

. Góc giữa hai mặt phẳng

( )

BMN

và

( )

SAB

là



thỏa mãn

5

cos

3



=

. Thể tích khối chóp

.S BMN

bằng bao nhiêu?

A.

3

24

a

. B.

3

a

. C.

3

12

a

. D.

3

6

a

.

Câu 43: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

2a

. Hình chiếu vuông góc của

S

với mặt phẳng đáy là trung điểm cạnh

AB

và

( )

SCD

tạo với đáy một góc

0

60

. Mặt phẳng chứa

AB

và vuông góc với

( )

SCD

cắt

,SC SD

lần lượt tại

M

và

N

. Thể tích của khối chóp

.S ABMN

bằng

A.

3

21

4

a

. B.

3

73

2

a

. C.

3

21 3

4

a

. D.

3

73

4

a

.

Câu 44: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành và có thể tích là

V

. Gọi

M

là một

điểm trên cạnh

AB

sao cho

MA

x

AB

=

,

01x

. Mặt phẳng

( )



qua

M

và song song với

( )

SBC

chia khối chóp

.S ABCD

thành hai phần, trong đó phần chứa điểm

A

thể tích bằng

4

27

V

. Tính giá trị của biểu thức

1

x

P

x

−

=

+

.

A.

1

2

. B.

1

5

. C.

1

3

. D.

3

5

.

Câu 45: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành có thể tích là

V

. Gọi

M

là một điểm

trên

AB

sao cho

,0 1

MA

xx

AB

=  

. Mặt phẳng

( )



qua

M

và song song với

( )

SBC

chia khối

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 12

chóp

.S ABCD

thành hai phần, trong đó phần chứa điểm

A

có thể tích bằng

4

27

V

. Tính giá trị

của biểu thức

1

x

P

x

−

=

+

.

A.

1

2

. B.

1

5

C.

1

3

. D.

3

5

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

1 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Dạng 7: Thể tích khối lăng trụ đứng

Câu 1: Lăng trụ đứng

.ABC A B C

  

có đáy

ABC

là tam giác vuông tại

A

,

2BC a=

,

AB a=

. Mặt bên

BB C C



là hình vuông. Khi đó thể tích lăng trụ là

A.

3

a

. B.

3

2a

. C.

3

23a

. D.

3

3a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 2: Cho hình lăng trụ đứng

.ABC A B C

  

có đáy

ABC

là tam giác vuông tại

C

,

3AB a=

,

2BC a=

. Góc giữa

BC



và mặt phẳng

( )

ABC

bằng

60

. Tính thể tích khối lăng trụ đó.

A.

3

2 15a

. B.

3

2 15

3

a

. C.

3

15a

. D.

3

15

3

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 3: Cho khối lăng trụ đứng

.ABC A B C

  

có đáy

ABC

là tam giác vuông cân tại

, 2 2.C BC =

Góc

giữa đường thẳng

AB



và mặt phẳng

( )

BCC B



bằng

30 .

Thể tích của khối lăng trụ đã cho bằng

A.

12

. B.

4

. C.

42

. D.

16

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

VÍ DỤ MINH HỌA

B

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 2

Câu 4: Cho khối lăng trụ đứng

.ABC A B C

  

có đáy là tam giác

ABC

vuông tại

A

,

AC a=

,

60ACB =

. Đường thẳng

BC



tạo với mặt phẳng

( )

A C CA



một góc

30

. Tính thể tích khối

lăng trụ đã cho.

A.

3

2

a

. B.

3

23a

. C.

3

6a

. D.

3

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 5: Cho khối lăng trụ tam giác đều

.ABC A B C

  

có

AB a=

, góc giữa đường thẳng

AB



và mặt

phẳng

( )

BCC B



bằng

30

. Thể tích khối lăng trụ đã cho bằng

A.

3

2

a

. B.

3

4

a

. C.

3

6

12

a

. D.

3

6

4

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 6: Cho hình hộp đứng

.ABCD A B C D

   

có đáy

ABCD

là hình vuông. Gọi

S

là tâm hình vuông

A B C D

   

. Gọi

M

và

N

lần lượt là trung điểm của

SA

và

BC

. Biết rằng, nếu

MN

tạo với mặt

phẳng

( )

ABC D

một góc bằng

0

60

và

AB a=

thì thể tích khối chóp

.S ABC

bằng

A.

3

30

12

a

. B.

3

30

3

a

. C.

3

30a

. D.

3

2

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

3 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 7: Cho lăng trụ đứng

.ABC A B C

  

có đáy

ABC

là tam giác đều cạnh bằng

2.a

Biết diện tích tam

giác

A BC



bằng

2

23a

. Tính thể tích khối lăng trụ

.ABC A B C

  

.

A.

3

93a

. B.

3

63a

. C.

3

33a

D.

3

3a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 8: Cho lăng trụ đứng

.ABC A B C

  

có đáy

ABC

là tam giác vuông tại

A

. Khoảng cách từ đường

thẳng

AA



đến mặt phẳng

( )

BCC B



bằng khoảng cách từ điểm

C

đến mặt phẳng

( )

ABC



và

cùng bằng

1

. Góc giữa hai mặt phẳng

( )

ABC



và

( )

ABC

bằng



. Tính

tan



khi thể tích khối

lăng trụ

.ABC A B C

  

nhỏ nhất.

A.

tan 2



=

. B.

tan 3



=

. C.

1

tan

3



=

. D.

1

tan

2



=

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 9: Cho khối lăng trụ đứng

.ABC A B C

  

có

60BAC =

,

3AB a=

và

4AC a=

. Gọi

M

là trung

điểm của

BC



, biết khoảng các từ

M

đến mặt phẳng

( )

B AC



bằng

3 15

10

a

. Thể tích khối lăng

trụ bằng

A.

3

4a

B.

3

27a

C.

3

7a

D.

3

9a

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 4

Câu 1: Một khối lăng trụ có thể tích bằng

V

, diện tích mặt đáy bằng

S

. Chiều cao của khối lăng trụ đó

bằng

A.

S

V

. B.

3V

S

. C.

V

S

. D.

3

S

V

.

Câu 2: Thể tích khối hộp chữ nhật có các kích thước 2, 3, 4 là

A.

6

. B.

8

. C.

72

. D.

24

.

Câu 3: Cho khối lăng trụ có diện tích đáy bằng 5 và chiều cao bằng 3. Thể tích của khối lăng trụ đã cho

bằng

A.

45

. B.

24

. C.

5

. D.

15

.

Câu 4: Khối lăng trụ có diện tích đáy là

2

6 cm

và có chiều cao là

3 cm

thì có thể tích

V

là

A.

3

6 cmV =

. B.

3

108 cmV =

. C.

3

54 cmV =

. D.

3

18 cmV =

.

Câu 5: Khối hộp chữ nhật có cách kích thước lần lượt là

, 2 , 3a a a

có thể tích bằng

A.

3

32

5

a

. B.

3

6a

. C.

3

2a

. D.

2

6a

.

Câu 6: Cho khối hộp chữ nhật

. ' ' ' 'ABCD A B C D

có

1 , ' 3 , 2= = =AB m AA m BC m

. Thể tích của khối

hộp đã cho bằng

A.

3

3m

. B.

3

6m

. C.

3

35m

. D.

3

5m

.

Câu 7: Thể tích khối lăng trụ có diện tích đáy bằng

B

và chiều cao bằng

h

là

A.

4

.

3

V B h=

. B.

1

.

2

V B h=

. C.

1

.

3

V B h=

. D.

.V B h=

.

Câu 8: Cho khối hộp chữ nhật có ba kích thước là

4,5,6

. Thể tích của khối hộp đã cho bằng:

A.

120

. B.

80

. C.

40

. D.

60

.

Câu 9: Khối lập phương

.ABCD A B C D

   

có độ dài đoạn

A C a



=

. Thể tích khối đó là

A.

3

.

9

a

B.

3

.

6

a

C.

3

.

3

a

D.

3

.a

Câu 10: Cho khối lăng trụ đứng

. ' ' 'ABC A B C

có

'BB a=

, đáy

ABC

là tam giác vuông tại

A

và

2 , 3AB a AC a==

. Tính thể tích

V

của khối lăng trụ đã cho.

A.

3

.a

B.

3

6.a

C.

3

3.a

D.

3

2.a

Câu 11: Cho khối lăng trụ có diện tích đáy

2

3Ba=

và chiều cao

ha=

. Thể tích của khối lăng trụ đã

cho bằng

A.

3

4

a

. B.

3

a

. C.

3

33a

. D.

3

3a

.

Câu 12: Cho một hình hộp chữ nhật có 3 kích thước bằng 12,15 và 20. Tính thể tích của hình hộp chữ

nhật đó.

A.

3600V =

. B.

1800V =

. C.

60V =

. D.

2880V =

.

Câu 13: Cho khối lăng trụ đứng

.ABC A B C

  

có đáy

ABC

là tam giác vuông cân tại

B

. Biết

2C A a



=

và

45AC C



=

(tham khảo hình vẽ). Thể tích của khối lăng trụ đã cho bằng

BÀI TẬP TRẮC NGHIỆM

C

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

5 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

A.

3

6

a

. B.

3

12

a

. C.

3

4

a

. D.

3

2

a

.

Câu 14: Cho lăng trụ đứng

.ABC A B C

  

có đáy là tam giác đều cạnh bằng

2

. Mặt phẳng

()AB C



tạo

với mặt đáy bằng

45



. Thể tích lăng trụ

.ABC A B C

  

bằng

A.

3

B.

42

C.

6

D.

22

Câu 15: Cho hình lăng trụ đứng

.ABC A B C

  

có tất cả các cạnh bằng

a

. Tính thể tích

V

của khối lăng

trụ

.ABC A B C

  

.

A.

3

2

a

V =

. B.

3

2

3

a

V =

. C.

3

2

a

V =

. D.

3

4

a

V =

.

Câu 16: Một khối lăng trụ có chiều cao bằng

2a

và diện tích đáy bằng

2

2a

. Tính thể tích khối lăng trụ.

A.

3

4

3

a

V =

. B.

3

2

3

a

V =

. C.

3

2aV =

. D.

3

4Va=

.

Câu 17: Cho khối lăng trụ tam giác đều, cạnh bên có độ dài gấp hai lần cạnh đáy. Biết tổng diện tích các

mặt của khối lăng trụ là

( )

2

12 3 a+

. Tính theo

a

thể tích

V

của khối lăng trụ đã cho

A.

3

6Va=

. B.

3

6

3

a

V =

. C.

3

6

8

Va=

. D.

3

26Va=

.

Câu 18: Cho khối hộp đứng

1 1 1 1

.ABCD A B C D

có đáy

ABCD

là hình thoi cạnh

a

,

120

o

ABC =

, đường

thẳng

1

AC

tạo với mặt phẳng

( )

ABC D

một góc

60

o

. Tính thể tích khối hộp đã cho

A.

3

2

a

B.

3

2

a

C.

3

2

a

D.

3

33

2

a

Câu 19: Cho lăng trụ đứng

.ABC A B C

  

có đáy

ABC

là tam giác đều cạnh

3a

. Gọi

M

là trung điểm

của

BC

,

3A M a



=

. Thể tích khối lăng trụ

.ABC A B C

  

bằng

A.

3

27

8

a



B.

3

93

8

a



C.

3

9

8

a



D.

3

33

8

a



Câu 20: Cho hình lăng trụ tam giác đều

. ' ' 'ABC A B C

có cạnh đáy bằng

2

, một mặt bên có diện tích

bằng

42

. Thể tích khối lăng trụ đã cho bằng

A.

2 6.

B.

46

.

3

C.

26

.

3

D.

4 6.

Câu 21: Cho khối lăng trụ đứng

.ABC A B C

  

có

BB a



=

, đáy

ABC

là tam giác vuông cân tại

B

và

2AC a=

. Thể tích

V

của khối lăng trụ đã cho là

A.

3

Va=

. B.

3

a

V =

. C.

3

6

a

V =

. D.

3

2

a

V =

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 6

Câu 22: Cho khối lăng trụ đứng

.ABC A B C

  

có

BB a



=

, đáy

ABC

là tam giác vuông cân tại

B

và

BA BC a==

. Tính theo

a

thể tích

V

của khối lăng trụ đã cho.

A.

3

Va=

. B.

3

2

a

V =

. C.

3

a

V =

. D.

3

6

a

V =

.

Câu 23: Cho khối lăng trụ đứng

.ABC A B C

  

có đáy là tam giác đều cạnh

a

và

AA 2a



=

. Thể tích của

khối lăng trụ đã cho bằng

A.

3

.

3

a

. B.

3

.

6

a

. C.

3

3a

. D.

3

.

2

a

Câu 24: Cho khối lăng trụ đứng

.ABC A B C

  

có

BB a



=

, đáy

ABC

là tam giác vuông cân tại

B

và

2AC a=

. Tính thể tích

V

của khối lăng trụ đã cho.

A.

3

Va=

. B.

3

a

V =

. C.

3

2

a

V =

. D.

3

6

a

V =

.

Câu 25: Cho hình lập phương

.ABCD A B C D

   

cạnh

3a

. Gọi

M

là một điểm trên mặt phẳng

( )

A B C D

   

(tham khảo hình vẽ). Thể tích khối chóp

.M ABCD

.

A.

3

9a

. B.

3

a

. C.

3

3a

. D.

3

8a

.

Câu 26: Cho lăng trụ đứng

. ' ' 'ABC A B C

có đáy

ABC

là tam giác vuông cân tại

B

và

2AC a=

, biết

rằng

( )

'A BC

hợp với đáy

( )

ABC

một góc

45

o

.Thể tích lăng trụ là:

A.

3

2

a

. B.

3

a

. C.

3

3a

. D.

3

2a

.

Câu 27: Cho hình lăng trụ đứng

.ABC A B C

  

có đáy là

ABC

vuông tại

A

, biết

AB a=

,

2AC a=

và

3A B a



=

. Thể tích của khối lăng trụ

.ABC A B C

  

bằng

A.

3

22

3

a

. B.

3

5

3

a

. C.

3

5a

. D.

3

22a

.

Câu 28: Cho khối hộp chữ nhật

. ' ' ' 'ABCD A B C D

có đáy là hình vuông,

22AC a=

, góc giữa hai mặt

phẳng

( )

'C BD

và

( )

ABCD

bằng

0

45

. Thể tích của khối hộp chữ nhật đã cho bằng:

A.

3

42a

. B.

3

42

3

a

. C.

3

32a

. D.

3

32

3

a

.

Câu 29: Cho lăng trụ đứng

.ABC A B C

  

. Biết rằng góc giữa hai mặt phẳng

( )

A BC



và

()ABC

là

30

,

tam giác

A B C



đều và có diện tích bằng

3

. Thể tích khối lăng trụ

.ABC A B C

  

bằng

A.

23

B. 6. C.

33

4

. D.

3

4

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

7 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 30: Cho lăng trụ đứng

.ABC A B C

  

. Biết rằng góc giữa hai mặt phẳng

( )

A BC



và

( )

ABC

là

30

,

tam giác

A B C



đều và diện tích bằng

3

. Thể tích khối lăng trụ

.ABC A B C

  

bằng

A.

23

. B.

6

. C.

33

4

. D.

3

4

.

Câu 31: Cho lăng trụ đứng

.ABC A B C

  

có đáy là tam giác

ABC

vuông tại

A

,

, 2AB a AC a==

. Góc

giữa hai mặt phẳng

( )

A B C



và

( )

ABC

bằng

60

. Thể tích

V

của khối lăng trụ

.ABC A B C

  

theo

a

.

A.

3

2 15

5

Va=

. B.

3

2 15

15

Va=

. C.

3

2 15

45

Va=

. D.

3

6 15

45

Va=

.

Câu 32: Cho hình hộp

.ABCD A B C D

   

có đáy

ABCD

là hình thoi có cạnh bằng

a

và góc

0

60ABC =

.

Cạnh bên

2

3

a

AA



=

;

A



cách đều các đỉnh

,,A B C

. Tính theo

a

thể tích của khối hộp

.ABCD A B C D

   

.

A.

3

2

a

. B.

3

6

a

. C.

3

16 3a

. D.

3

83a

.

Câu 33: Cho hình lăng trụ đứng

.ABC A B C

  

có đáy là tam giác vuông cân đỉnh

A

, mặt bên là

BCC B



hình vuông, khoảng cách giữa

AB



và

CC



bằng

a

. Thể tích khối lăng trụ

.ABC A B C

  

là

A.

3

2a

. B.

3

2

3

a

. C.

3

a

. D.

3

2

a

.

Câu 34: Cho hình hộp đứng

.ABCD A B C D

   

có đáy là hình thoi, góc

60BAD =

đồng thời

AA a



=

.

Gọi

G

là trọng tâm tam giác

BCD

. Biết rằng khoảng cách từ

G

đến mặt phẳng

( )

A BD



bằng

21

a

. Tính thể tích khối hộp

.ABCD A B C D

   

theo

a

.

A.

2

6

a



. B.

3

6

a



. C.

2

a



. D.

3

2

a



.

Câu 35: Cho khối lăng trụ đứng

. ' ' 'ABC A B C

có đáy

ABC

là tam giác vuông cân tại

A

và

2aBC =

.

Góc giữa đường thẳng

'AB

với

( )

ABC

bằng

30

o

. Tính thể tích của khối lăng trụ đã cho?

A.

3

6

a

. B.

3

6a

. C.

3

6

9

a

. D.

3

6

3

a

Câu 36: Cho khối lăng trụ đứng

.ABC A B C

  

có đáy

ABC

là tam giác vuông cân tại

,A

AB a=

. Biết

khoảng cách từ

A

đến mặt phẳng

( )

A BC



bằng

3

a

. Tính thể tích của khối lăng trụ

..ABC A B C

  

A.

3

a

. B.

3

2

a

. C.

3

2

3

a

. D.

3

9

a

.

Câu 37: Cho hình hộp đứng

.ABCD A B C D

   

có đáy là hình vuông cạnh

a

, góc giữa mặt phẳng

( )

D AB



và mặt phẳng

( )

ABB A



bằng

30

. Thể tích khối hộp

.ABCD A B C D

   

bằng

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 8

A.

3

18

a

. B.

3

3a

. C.

3

a

. D.

3

9

a

.

Câu 38: Cho khối hộp chữ nhật

.ABCD A B C D

   

có

2AB a=

,

3BC a=

. Góc giữa hai mặt phẳng

( )

A B CD



và

( )

ABC D

bằng

45

. Thể tích khối hộp chữ nhật bằng

A.

3

12a

. B.

3

18 2a

. C.

3

18a

. D.

3

6 13a

.

Câu 39: Cho khối lăng trụ đứng

.ABC A B C

  

có đáy là tam giác đều. Mặt phẳng

()A BC



tạo với đáy một

góc

30

và tam giác

A BC



có diện tích bằng

32

. Thể tích của khối lăng trụ đã cho bằng

A.

64 3

. B.

64 3

3

. C.

128

. D.

128

3

.

Câu 40: Cho khối lăng trụ đứng

. ' ' 'ABC A B C

có đáy là tam giác vuông tại

A

;

; 60AC b ACB= = 

.

Đường thẳng

'BC

tạo với mặt phẳng

( ' ' )AA C C

một góc

30

. Tính thể tích của khối lăng trụ

đã cho theo

b

.

A.

3

6

3

b

. B.

3

26b

. C.

3

6

b

. D.

3

6b

.

Câu 41: Cho khối hộp đứng

.ABCD A B C D

   

có đáy là hình thoi cạnh đáy bằng

2cm

, góc

30BAD



=

,

góc giữa

AC



và mặt phẳng đáy bằng

45

. Thể tích khối hôp đã cho bằng

A.

4 2 3−

. B.

2 2 3+

. C.

2 2 3−

. D.

4 2 3+

.

Câu 42: Cho khối hộp chữ nhật

.ABCD A B C D

   

có đáy là hình vuông. Gọi

M

là trung điểm của

BB



,

góc giữa hai mặt phẳng

( )

MAC

và

( )

A B C D

   

bằng

0

30

. Thể tích của khối hộp chữ nhật bằng

3

32 3

3

a

. Tính độ dài cạnh hình vuông.

A.

3a

. B.

23a

. C.

2a

. D.

22a

.

Câu 43: Cho lăng trụ đứng

.ABCD A B C D

   

có đáy là hình chữ nhật,

,2CD a CB a==

, góc giữa hai

mặt phẳng

( )

'C BD

và

( )

ABC D

bằng

60

. Thể tích của khối hộp chữ nhật đã cho bằng

A.

3

2a

. B.

3

22a

. C.

3

32a

. D.

3

3a

.

Câu 44: Cho lăng trụ tam giác đều

.ABC A B C

  

có

2AA



=

, góc giữa đường thẳng

AB



và mặt phẳng

( )

AA C C



bằng

45

. Tính thể tích

V

của lăng trụ

.ABC A B C

  

.

A.

23V =

. B.

43V =

. C.

32V =

. D.

72V =

.

Câu 45: Cho hình hộp chữ nhật

1 1 1 1

.ABCD A B C D

có

2AB =

,

4AD =

, cosin của góc giữa

AC

và

1

DA

bằng

4

30

. Tính thể tích khối hộp chữ nhật

1 1 1 1

.ABCD A B C D

.

A.

16 2

. B.

24

30

. C.

16

. D.

32 2

.

Câu 46: Cho hình lăng trụ đứng

.ABC A B C

  

có đáy

ABC

là tam giác đều cạnh

a

. Khoảng cách từ tâm

O

của tam giác

ABC

đến mặt phẳng

( )

A BC



bằng

6

a

. Thể tích khối lăng trụ bằng

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

9 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

A.

3

32

4

a

. B.

3

32

8

a

. C.

3

32

28

a

. D.

3

32

16

a

Câu 47: Cho khối hộp chữ nhật

.ABCD A B C D

   

có đáy là hình vuông cạnh

a

. Khoảng cách từ

A

đến

mặt phẳng

( )

A B CD



bằng

25

5

a

. Tính thể tích

V

của khối hộp chữ nhật đã cho.

A.

3

2.Va=

. B.

3

2

.

3

a

V =

. C.

3

2

V

a

=

. D.

3

32Va=

.

Câu 48: Cho lăng trụ đứng

.ABC A B C

  

có

7, 30AC a ABC= = 

,

AB AA



=

. Gọi

M

là trung điểm

của

BB



, khoảng cách giữa hai đường thẳng

AM

và

CC



bằng

3a

. Thể tích của khối lăng trụ

đứng

.ABC A B C

  

là

A.

3

53

3

a

. B.

3

25

2

a

. C.

3

25 3

6

a

. D.

3

53

6

a

Câu 49: Cho hình hộp đứng

.ABCD A B C D

   

có cạnh

2AA



=

, đáy

ABCD

là hình thoi với

ABC

là tam

giác đều cạnh bằng 4. Gọi

,,M N P

lần lượt là trung điểm của

,,B C C D DD

    

và

Q

thuộc cạnh

BC

sao cho

3QC QB=

. Tính thể tích tứ diện

MNPQ

.

A.

33

. B.

33

2

. C.

3

4

. D.

3

2

.

Câu 50: Cho lăng trụ đứng

.ABC A B C

  

có đáy là tam giác

ABC

là tam giác vuông cân tại

A

, cạnh

BC a=

. Gọi

M

là trung điểm của cạnh

AA



, biết hai mặt phẳng

()MBC

và

()MB C



vuông

góc với nhau, thể tích khối lăng trụ

.ABC A B C

  

bằng

A.

3

2

8

a

. B.

3

4

a

. C.

3

2

24

a

. D.

3

8

a

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

1 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Dạng 8: Thể tích khối đa diện đều

Câu 1: Cho hình lăng trụ tam giác đều

.ABC A B C

  

có

,AB a=

góc giữa đường thẳng

AC



và mặt

phẳng

( )

ABC

bằng

45 .

Thể tích khối lăng trụ

.ABC A B C

  

bằng

A.

3

12

a

. B.

3

4

a

. C.

3

2

a

. D.

3

6

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 2: Cho lăng trụ đều

.ABC A B C

  

có cạnh đáy bằng

a

,

AC



tạo với mặt phẳng

( )

ABC

góc

60

.

Tính thể tích của khối lăng trụ

.ABC A B C

  

theo

a

.

A.

3

4

a

. B.

3

12

a

. C.

3

4

a

. D.

3

4

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 3: Cho hình lăng trụ tam giác đều

. ' ' 'ABC A B C

có diện tích xung quanh bằng tổng diện tích hai

đáy và bằng

18 3

. Thể tích khối lăng trụ

. ' ' 'ABC A B C

tính theo đơn vị thể tích bằng

A.

18 3

. B.

27

. C.

36 3

. D.

64

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

VÍ DỤ MINH HỌA

B

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 2

Câu 4: Cho lăng trụ đứng

.ABC A B C

  

có đáy là tam giác đều cạnh

a

. Mặt phẳng

( )

AB C



tạo với mặt

phẳng

( )

ABC

một góc

60

. Thể tích khối lăng trụ

.ABC A B C

  

bằng

A.

3

2

a

. B.

3

33

4

a

. C.

3

8

a

. D.

3

33

8

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 5: Lăng trụ tam giác đều có độ dài tất cả các cạnh bằng

3

. Thể tích khối lăng trụ đã cho bằng

A.

27 3

4

. B.

93

8

. C.

93

2

. D.

27 3

12

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 6: Cho lăng trụ tứ giác đều

. ' ' ' 'ABCD A B C D

có cạnh đáy bằng

a

, góc giữa

'AB

và mặt phẳng

''A ACC

bằng

0

30

. Tính thể tích khối lăng trụ đã cho.

A.

3

Va=

. B.

3

3Va=

. C.

3

2Va=

. D.

3

2Va=

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 7: Cho lăng trụ tam giác đều

. ' ' 'ABC A B C

có cạnh đáy bằng

a

. Mặt phẳng

( )

'A BC

hợp với mặt

phẳng đáy một góc

0

45

. Tính thể tích khối lăng trụ

. ' ' 'ABC A B C

.

A.

3

8

a

B.

3

8

a

C.

3

4

a

D.

3

8

a

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

3 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 8: Cho hình lăng trụ đều

.ABC A B C

  



Biết khoảng cách từ điểm

C

đến mặt phẳng

( )

ABC



bằng

,a

góc giữa hai mặt phẳng

( )

ABC



và

( )

BCCB



bằng



với

1

cos .

23



=

Tính thể tích khối

lăng trụ

.ABC A B C

  



A.

3

32

4

a

V =

. B.

3

2

8

3a

V =

. C.

3

2

a

V =

. D.

3

2

3a

V =

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 9: Cho hình lăng trụ tam giác đều

.ABC A B C

  

có cạnh đáy bằng

a

. Đường thẳng

BC



tạo với mặt

phẳng

( )

ACC A



góc



thỏa mãn

cot 2



=

. Thể tích khối lăng trụ

.ABC A B C

  

bằng

A.

3

33

8

a

. B.

3

4 11

3

a

. C.

3

11

8

a

. D.

3

2 33

3

a

.

 Lời giải

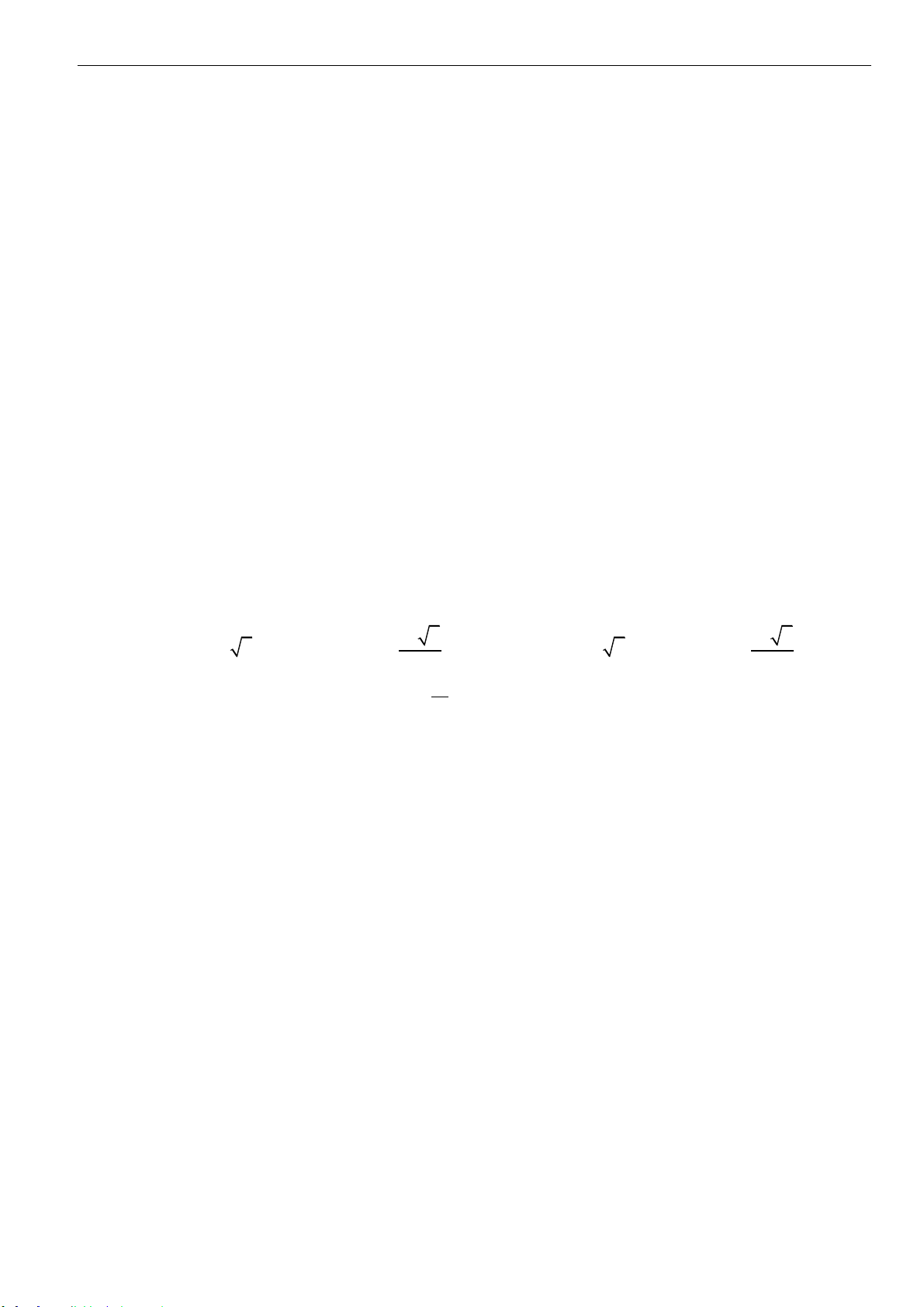
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 4

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 10: Cho hình lăng trụ tam giác đều

.ABC A B C

  

có

2,AB a=

đường thẳng

AB



tạo với mặt phẳng

( )

BCC B



một góc

30 .

Tính thể tích

V

của khối lăng trụ đã cho.

A.

3

6Va=

. B.

3

6

3

a

V =

. C.

3

26Va=

. D.

3

6

2

a

V =

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

5 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 1: Thể tích

V

khối lập phương cạnh

3a

là

A.

3

81Va=

. B.

3

9Va=

. C.

3

Va=

. D.

3

27Va=

.

Câu 2: Cho khối lăng trụ đứng

.ABC A B C

  

có tam giác

ABC

đều cạnh

a

và độ dài cạnh bên

2a

. Tính

thể tích

V

của khối lăng trụ

.ABC A B C

  

.

A.

3

4

a

V =

. B.

3

23Va=

. C.

3

2

a

V =

. D.

3

3Va=

.

Câu 3: Cho lăng trụ đều

. ' ' 'ABC A B C

có cạnh đáy bằng

2a

, độ dài cạnh bên bằng

3a

. Thể tích

V

của khối lăng trụ bằng

A.

3

4

a

V =

. B.

3

4

a

V =

. C.

3

Va=

. D.

3

3Va=

.

Câu 4: Thể tích khối lập phương có cạnh bằng

2

bằng

A.

8

3

. B.

4

. C.

6

. D.

8

.

Câu 5: Thể tích khối lập phương cạnh

2a

bằng

A.

3

32a

. B.

3

16a

. C.

3

64a

. D.

3

8a

.

Câu 6: Cho khối lập phương có thể tích bằng

64.

Cạnh của khối lập phương đã cho bằng

A.

4 2.

B.

4.

C.

32.

D.

8.

Câu 7: Thể tích của một khối lập phương có cạnh bằng

1m

là

A.

3.Vm=

B.

3

1.Vm=

C.

3

1

.

3

Vm=

D.

2

1Vm=

Câu 8: Cho khối lăng trụ tứ giác đều có cạnh đáy bằng

a

, chiều cao bằng

2a

. Thể tích khối lăng trụ đã

cho bằng

A.

3

4a

. B.

3

4

3

a

. C.

3

2

3

a

. D.

3

2a

.

Câu 9: Thể tích của khối lập phương cạnh

4a

bằng

A.

3

16a

. B.

3

64a

. C.

3

4a

. D.

3

a

.

Câu 10: Thể tích khối lập phương có cạnh bằng 3 là

A.

36

. B.

9

. C.

27

. D.

81

.

Câu 11: Cho khối lăng trụ đứng có chiều cao bằng

3

và đáy là tam giác đều có độ dài cạnh bằng

2

. Tính

thể tích khối lăng trụ đã cho

A.

3

. B.

33

. C.

3

. D.

6

.

Câu 12: Thể tích khối lập phương cạnh

3a

bằng

A.

3

3a

. B.

3

27a

. C.

3

a

. D.

3

9a

.

Câu 13: Cho

( )

H

là lăng trụ tam giác đều có tất cả các cạnh bằng nhau, thể tích của

( )

H

bằng

3

4

. Độ

dài cạnh của khối lăng trụ

( )

H

là

A.

3

. B.

3

4

. C.

1

. D.

3

16

3

.

BÀI TẬP TRẮC NGHIỆM

C

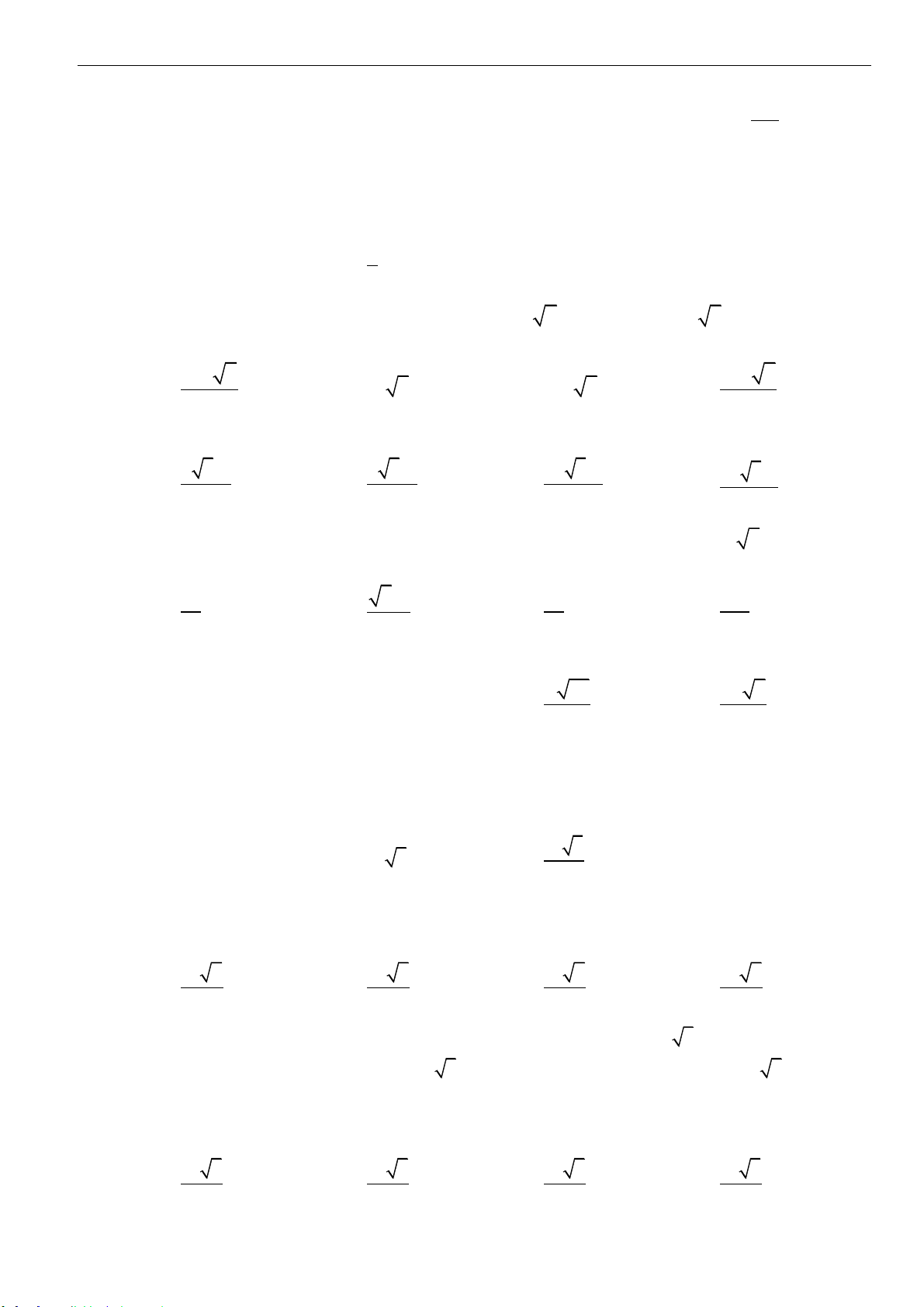
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 6

Câu 14:

Khối lập phương có cạnh bằng

2a

thì có thể tích

V

là

A.

3

4Va=

. B.

3

Va=

. C.

3

8Va=

. D.

3

8

3

a

V =

.

Câu 15: Thể tích của khối lập phương cạnh

2

bằng

A.

6

. B.

8

. C.

2

. D.

4

.

Câu 16: Khối lập phương đơn vị có thể tích bằng

A.

3

. B.

1

3

. C.

1

. D.

12

.

Câu 17: Cho hình lăng trụ tứ giác đều có cạnh đáy bằng

2a

, cạnh bên bằng

5a

. Thể tích của khối

lăng trụ đó bằng

A.

3

25

9

a

. B.

3

5a

. C.

3

25a

. D.

3

25

3

a

.

Câu 18: Cho lăng trụ tam giác đều có độ dài tất cả các cạnh bằng

3a

. Thể tích khối lăng trụ đã cho bằng

A.

3

93

2

a

. B.

3

93

4

a

. C.

3

27 3

2

a

. D.

3

27 3

4

a

.

Câu 19: Cho khối lăng trụ đều

. ' ' 'ABC A B C

có cạnh đáy bằng

a

, cạnh bên bằng

3a

. Thể tích của

khối lăng trụ bằng

A.

3

a

. B.

3

4

a

. C.

3

6

a

. D.

3

4

a

.

Câu 20: Thể tích của khối lập phương cạnh

2a

bằng

A.

3

.a

B.

3

8.a

C

.

31

.

4

a

D.

25

.

5

a

Câu 21: Thể tích của khối lập phương cạnh

3a

bằng

A.

3

3a

. B.

3

a

. C.

3

27a

. D.

3

9a

.

Câu 22: Thể tích của khối lăng trụ đều có cạnh đáy bằng

2a

, cạnh bên bằng

a

là:

A.

3

8a

. B.

3

3a

. C.

3

a

. D.

3

2a

.

Câu 23: Cho lăng trụ tam giác đều

.ABC A B C

  

có cạnh đáy bằng

a

. Góc tạo bởi đường thẳng

AB



và

mặt phẳng

( )

AA C



bằng

0

30

. Thể tích khối lăng trụ bằng

A.

3

6

4

a

. B.

3

2

a

. C.

3

6

12

a

. D.

3

4

a

.

Câu 24: Tính thể tích

V

của khối lập phương

.ABCD A B C D

   

biết

23AC a



=

.

A.

3

Va=

. B.

3

24 3Va=

. C.

3

8a

. D.

3

33Va=

.

Câu 25: Cho hình lăng trụ tam giác đều

.ABC A B C

  

có

AB a=

, góc giữa đường thẳng

AC



và mặt

phẳng

( )

ABC

bằng

45

. Thể tích khối lăng trụ

.ABC A B C

  

bằng

A.

3

4

a

. B.

3

6

a

. C.

3

12

a

. D.

3

2

a

.

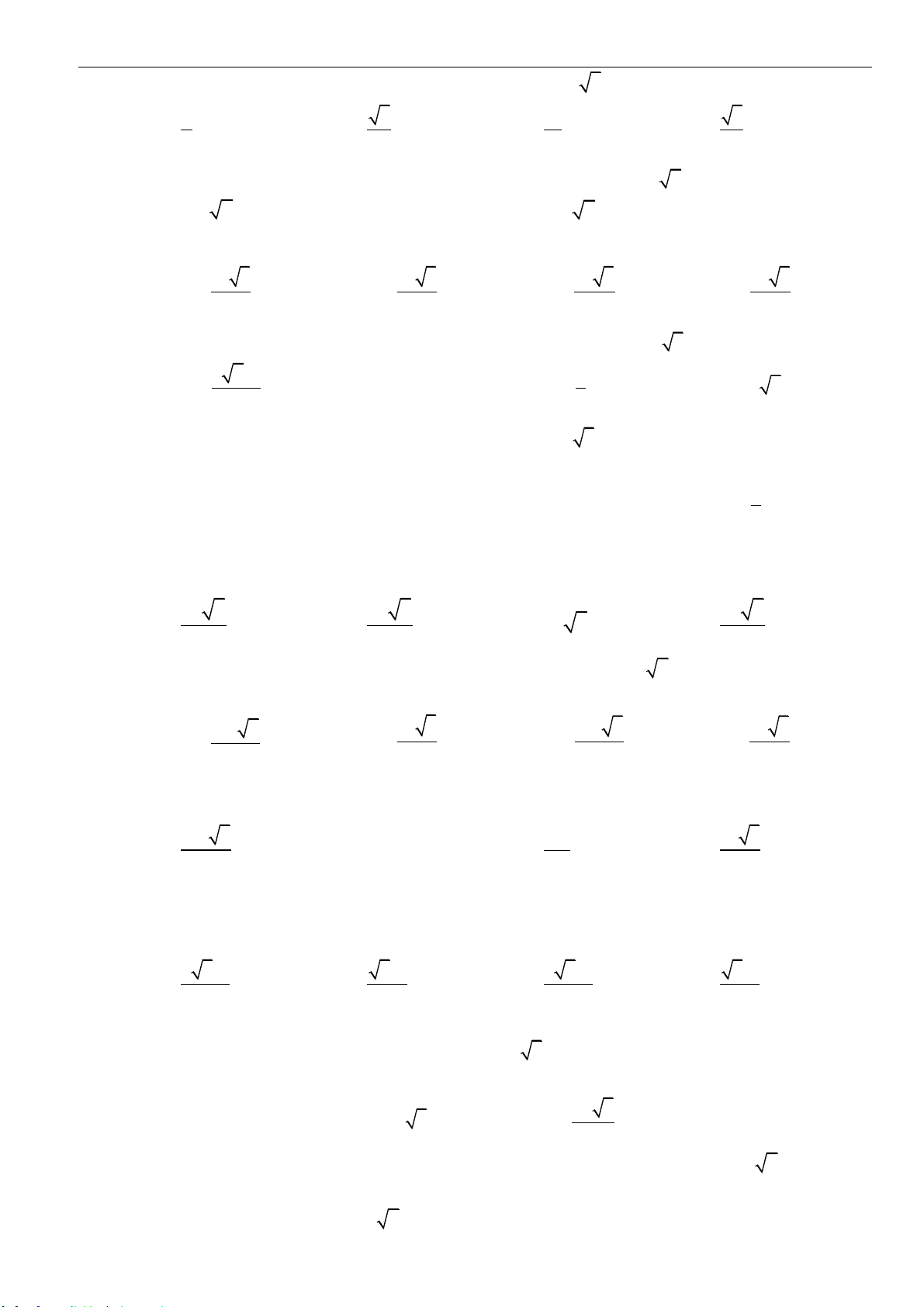
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

7 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 26: Cho lăng trụ tam giác đều có độ dài tất cả các cạnh bằng

3

. Thể tích khối lăng trụ đã cho bằng

A.

9

4

. B.

3

4

. C.

9

12

. D.

3

8

.

Câu 27: Cho một khối lập phương

.ABCD A B C D

   

có đường chéo

6AC a



=

có thể tích là

A.

3

22a

. B.

3

a

. C.

3

66a

. D.

3

4a

.

Câu 28: Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng

a

.

A.

3

2

a

V =

. B.

3

4

a

V =

. C.

3

12

a

V =

. D.

3

6

a

V =

.

Câu 29: Tính thể tích

V

của khối lập phương

.ABCD A B C D

  

, biết

3AC a



=

A.

3

36

4

a

V =

. B.

3

Va=

. C.

3

1

3

Va=

. D.

3

33Va=

.

Câu 30: Cho hình lập phương

.ABCD A B C D

   

có

23AC a



=

. Tính thể tích hình lập phương

.ABCD A B C D

   

.

A.

3

8Va=

. B.

3

4Va=

. C.

3

Va=

. D.

3

8

3

Va=

.

Câu 31: ) Cho khối lăng trụ tam giác đều

.ABC A B C

  

có

AB a=

và

' 2 .AA a=

Thể tích của khối lăng

trụ

.ABC A B C

  

bằng

A.

3

2

a

. B.

3

6

a

. C.

3

3a

. D.

3

12

a

.

Câu 32: Cho khối lăng trụ tam giác đều

.ABC A B C

  

, biết

AB a=

,

7AB a



=

. Thể tích

V

của khối lăng

trụ là

A.

3

32

4

a

V =

. B.

3

4

a

V =

. C.

3

33

4

a

V =

. D.

3

a

V =

.

Câu 33: Cho lăng trụ tam giác đều

.ABC A B C

  

có cạnh bên bằng

2a

. Đáy

ABC

nội tiếp đường tròn

bán kính

Ra=

. Tính thể tích khối lăng trụ đã cho.

A.

3

33

2

a

. B.

3

3a

. C.

3

2

a

. D.

3

2

a

.

Câu 34: Cho hình lăng trụ đều

.ABC A B C

  

, đáy là tam giác đều cạnh

a

góc giữa hai mặt phẳng

( )

A BC



và

( )

ABC

bằng

60



. Thể tích của khối lăng trụ

.ABC A B C

  

bằng

A.

3

33

4

a

. B.

3

4

a

. C.

3

33

8

a

. D.

3

8

a

.

Câu 35: Cho hình lăng trụ lục giác đều

.ABCDEF A B C D E F

     

có cạnh đáy bằng

a

, biết thể tích của

khối lăng trụ

.ABCDEF A B C D E F

     

là

3

33Va=

. Tính chiều cao

h

của khối lăng trụ

.ABCDEF A B C D E F

     

.

A.

2ha=

. B.

3ha=

. C.

23

3

a

h =

. D.

ha=

.

Câu 36: Cho khối lập phương

. ' ' ' 'ABCD A B C D

có diện tích mặt chéo

''ACC A

bằng

2

22a

. Thể tích

của khối lập phương

. ' ' ' 'ABCD A B C D

bằng

A.

3

2a

. B.

3

22a

. C.

3

a

. D.

3

8a

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 8

Câu 37: Cho khối lăng trụ đều

.ABC A B C

  

có cạnh đáy bằng

2a

. Khoảng cách từ điểm

A



đến mặt

phẳng

( )

AB C



bằng

a

. Thể tích khối lăng trụ đã cho là

A.

3

32

2

a

. B.

3

32

8

a

. C.

3

2

a

. D.

3

32

6

a

.

Câu 38: Cho hình lập phương

.ABCD A B C D

   

có khoảng cách giữa hai đường thẳng

AB



và

BD

bằng

23

.

3

a

Thể tích của khối lập phương

.ABCD A B C D

   

bằng

A.

3

8a

. B.

3

36

4

a

. C.

3

33a

. D.

3

a

.

Câu 39: Cho hình lăng trụ đều

.ABC A B C

  

có cạnh đáy bằng

23

3

a

. Đường thẳng

BC



tạo với mặt

phẳng

( )

ACC A



góc



thỏa mãn

cot 2



=

. Thể tích khối lăng trụ

.ABC A B C

  

bằng

A.

3

4

11

3

a

. B.

3

1

11

9

a

. C.

3

1

11

3

a

. D.

3

2

11

3

a

.

Câu 40: Cho lăng trụ tứ giác đều

.ABCD A B C D

   

. Biết khoảng cách và góc giữa hai đường thẳng

AC

và

DC



lần lượt là

21

7

a

và



,

2

cos

4



=

. Tính thể tích lăng trụ

.ABCD A B C D

   

A.

3

21

6

a

. B.

3

7

2

a

. C.

3

15

2

a

. D.

3

3a

.

Câu 41: Cho hình lăng trụ đều

.ABC A B C

  

. Biết cosin góc giữa hai mặt phẳng

( )

ABC



và

( )

BCC B



bằng

1

23

và khoảng cách từ điểm C đến mặt phẳng

( )

ABC



bằng

a

. Thể tích khối lăng trụ

.ABC A B C

  

bằng:

A.

3

32

8

a

. B.

3

2

a

. C.

3

32

4

a

. D.

3

32

2

a

.

Câu 42: Cho khối bát diện đều có cạnh

a

. Gọi

, , ,M N P Q

lần lượt là trọng tâm của các tam giác

, , ,SAB SBC SCD SDA

; gọi

, , ,M N P Q

   

lần lượt là trọng tâm của các tam giác

, , ,S AB S BC S CD S DA

   

(như hình vẽ dưới). Thể tích của khối lăng trụ

.MNPQ M N P Q

   

là

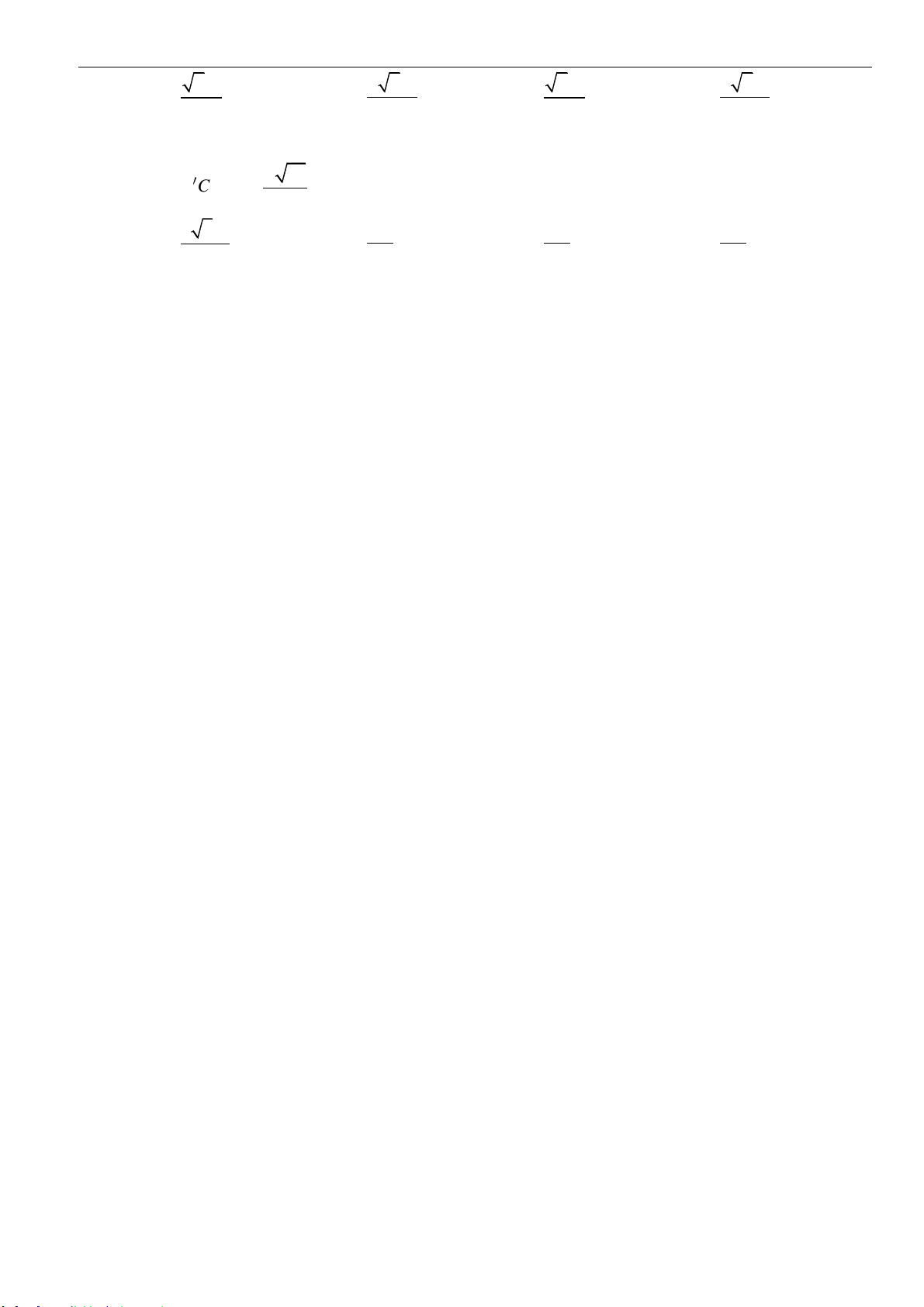
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

9 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

A.

3

2

72

a

. B.

3

22

81

a

. C.

3

2

24

a

. D.

3

22

27

a

.

Câu 43: Cho hình lăng trụ đều

.ABC A B C

  

có cạnh đáy

a

; biết khoảng cách giữa hai đường thẳng

AB

và

AC

bằng

15

5

a

. Thể tích của khối lăng trụ

.ABC A B C

  

tính theo

a

bằng:

A.

3

33

8

a

. B.

3

2

a

. C.

3

8

a

. D.

3

4

a

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

1 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Dạng 9: Thể tích khối lăng trụ xiên

Câu 1: Cho hình lăng trụ

. ' ' 'ABC A B C

có đáy

ABC

là tam giác vuông cân tại

B

và

2AC a=

. Hình

chiếu vuông góc của

'A

trên mặt phẳng

( )

ABC

là trung điểm

H

của cạnh

AB

và

'2AA a=

. Thể tích của khối lăng trụ đã cho bằng?

A.

3

3a

. B.

3

22a

. C.

3

6

2

a

. D.

3

6

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 2: Cho khối lăng trụ

.ABC A B C

  

có thể tích bằng

( )

3

18 cm

. Gọi

,,M N P

theo thứ tự là trung

điểm các cạnh

,,CC BC B C

  

. Khi đó thể tích

V

của khối chóp

.A MNP



là

A.

( )

3

9 cm

. B.

( )

3

3 cm

. C.

( )

3

12 cm

. D.

( )

3

6 cm

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 3: Cho lăng trụ

.ABC A B C

  

có đáy

ABC

là tam giác vuông tại

B

và

A A A B A C

  

==

. Biết rằng

,3AB a BC a==

và mặt phẳng

( )

A BC



tạo với mặt phẳng đáy một góc

60

. Thể tích khối

lăng trụ

.ABC A B C

  

bằng?

A.

3

4

a

. B.

3

2

a

C.

3

a

. D.

3

4

a

 Lời giải

VÍ DỤ MINH HỌA

B

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 2

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 4: Cho lăng trụ tam giác

.ABC A B C

  

có đáy là tam giác đều cạnh

a

. Hình chiếu vuông góc của

A



trên mặt phẳng

( )

ABC

trùng với trọng tâm tam giác

ABC

. Biết khoảng cách giữa

AA



và

BC

bằng

3

4

a

. Khi đó thể tích khối lăng trụ là

A.

3

12

a

. B.

3

6

a

. C.

3

a

. D.

3

24

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 5: Cho hình lăng trụ

.ABC A B C

  

có đáy là tam giác đều cạnh

a

. Hình chiếu vuông góc của

A



xuống

mặt phẳng

( )

ABC

là trung điểm

H

của đoạn

AB

. Mặt bên

()AA C C



tạo với đáy 1 góc

45

.

Tính thể tích khối lăng trụ

.ABC A B C

  

.

A.

3

33

16

a

. B.

3

8

a

. C.

3

16

a

. D.

3

33

8

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

3 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 6: Cho hình lăng trụ

.ABC A B C

  

có đáy

ABC

là tam giác đều cạnh

a

, hình chiếu vuông góc của

A



trên

( )

ABC

là trung điểm của cạnh

AB

, góc giữa đường thẳng

AC



với mặt phẳng đáy bằng

60

. Thể tích khối lăng trụ

.ABC A B C

  

bằng

A.

3

2

4

a

. B.

3

33

4

a

. C.

3

4

a

. D.

3

33

8

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

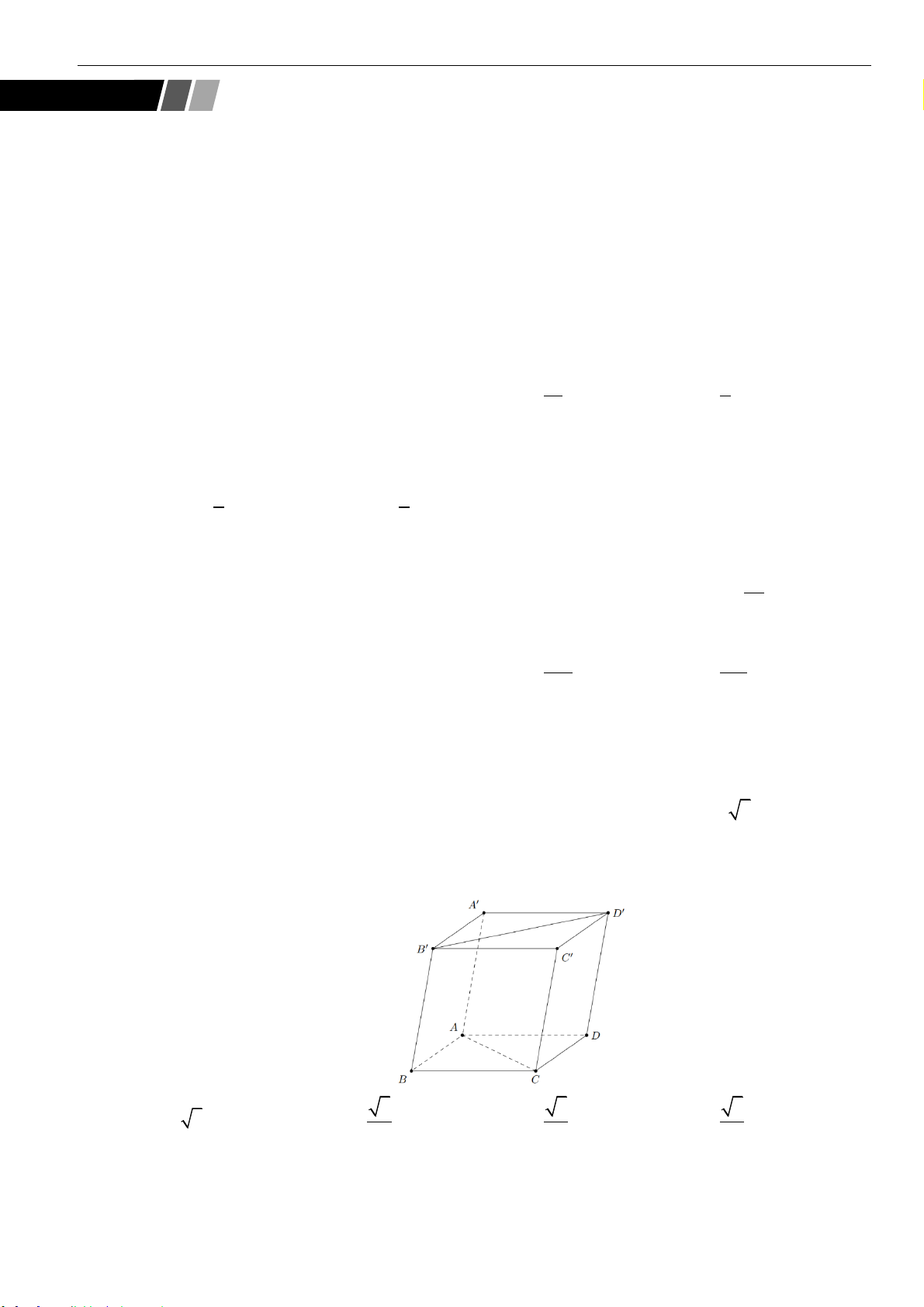
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 4

Câu 1: Cho khối lăng trụ có thể tích

45V =

và diện tích đáy

9B =

. Chiều cao của khối lăng trụ đã cho

bằng

A.

20

. B.

10

. C.

15

. D.

5

.

Câu 2: Một lăng trụ có diện tích đáy bằng 5 và chiều cao bằng 6 có thể tích bằng.

A.

12

. B.

30

. C.

10

. D.

18

.

Câu 3: Một khối lăng trụ có diện tích đáy

5B =

và chiều cao

6h =

. Thể tích của khối lăng trụ đó bằng

A.

25

. B.

10

. C.

15

. D.

30

.

Câu 4: Cho khối lăng trụ có đáy là hình vuông cạnh

a

và chiều cao bằng

4a

. Thể tích của khối lăng

trụ đã cho bằng ?

A.

3

4a

. B.

3

16a

. C.

3

16

3

a

. D.

3

4

3

a

.

Câu 5: Cho khối lăng trụ có diện tích đáy

B

và chiều cao

h

. Thể tích

V

của khối lăng trụ đã cho được

tính theo công thức nào dưới đây?

A.

1

3

V Bh=

. B.

4

3

V Bh=

. C.

6V Bh=

. D.

V Bh=

.

Câu 6: Cho hình hộp

.ABCD A B C D

   

có đáy

ABCD

là hình chữ nhật tâm

O

. Hình chiếu vuông góc

của

A



lên

( )

ABCD

trùng với

O

. Biết

2AB a=

,

BC a=

, cạnh bên

AA



bằng

3

2

a

. Thể tích của

khối hộp

.ABCD A B C D

   

bằng

A.

3

2a

. B.

3

3a

. C.

3

4

3

a

. D.

3

2

a

.

Câu 7: Cho lăng trụ

.ABC A B C

  

có diện tích tam giác

A BC



bằng 4, khoảng cách từ

A

đến

BC

bằng

3, góc giữa hai mặt phẳng

( )

A BC



và

( )

ABC

  

bằng

30

. Thể tích khối lăng lăng trụ

.ABC A B C

  

bằng

A.

12

. B.

6

. C.

2

. D.

33

.

Câu 8: Cho khối lăng trụ

.ABCD A B C D

   

có đáy là hình thoi cạnh

a

,

120BAD =

, khoảng cách giữa

hai đường thẳng

BD



và

AC

bằng

2a

. Thể tích của khối lăng trụ đã cho bằng

A.

3

3a

. B.

3

6

a

. C.

3

2

a

. D.

3

a

.

Câu 9: Cho khối lăng trụ tam giác

. ' ' 'ABC A B C

. Mặt bên

( )

''BCC B

có diện tích bằng 10, khoảng cách

từ

'A

đến mặt phẳng

( )

''BCC B

bằng 6. Tính thể tích khối lăng trụ đã cho.

BÀI TẬP TRẮC NGHIỆM

C

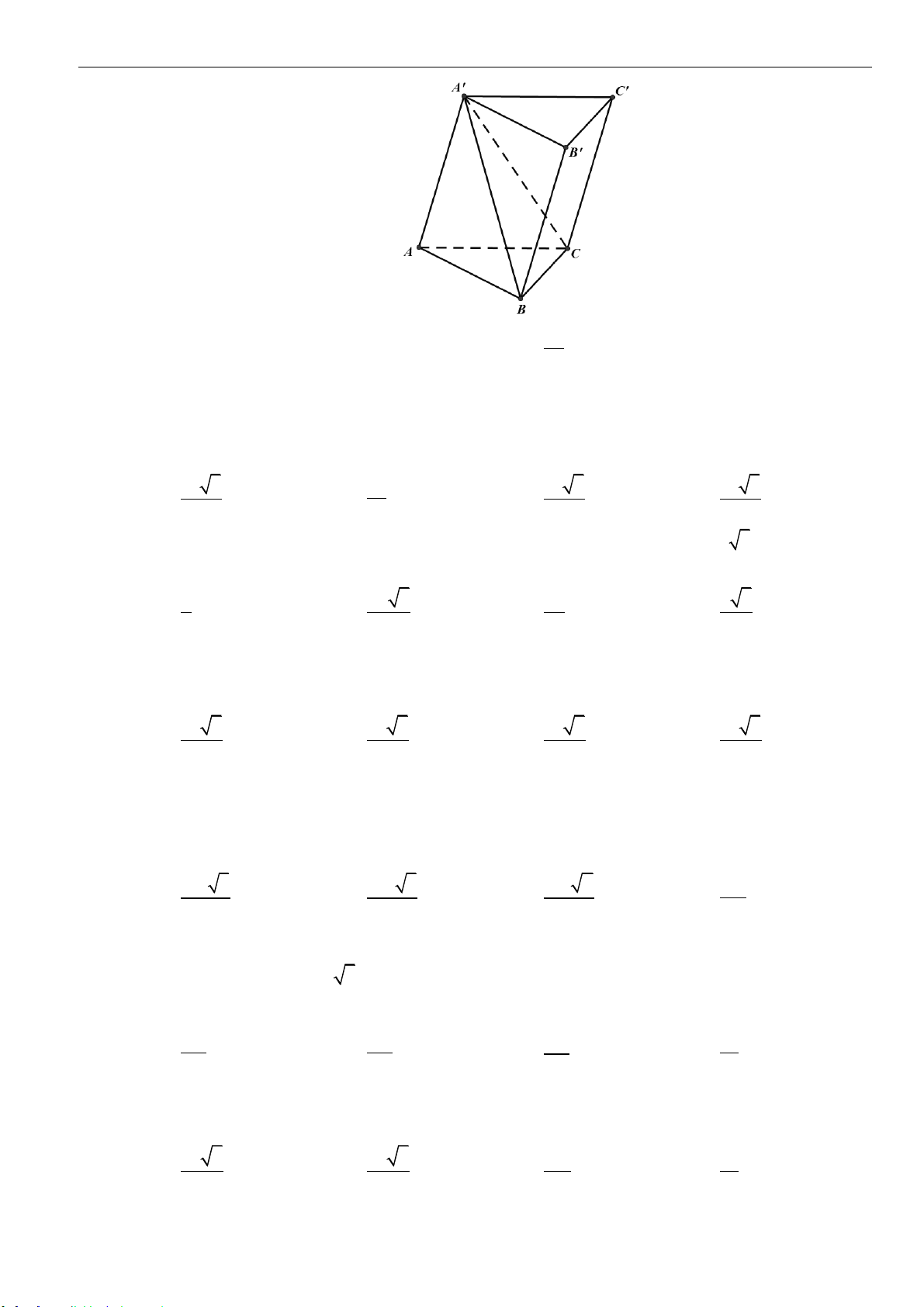
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

5 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

A.

40

. B.

30

. C.

40

3

. D.

60

.

Câu 10: Cho hình lăng trụ

.ABC A B C

  

có đáy là tam giác đều cạnh

a

, góc giữa cạnh bên và mặt phẳng

đáy bằng

30



. Hình chiếu của

A



xuống mặt phẳng

( )

ABC

trùng với trung điểm của

BC

. Tính

thể tích khối lăng trụ

.ABC A B C

  

.

A.

3

24

a

. B.

3

8

a

. C.

3

8

a

. D.

3

4

a

.

Câu 11: Một khối lăng trụ tam giác có đáy là tam giác đều cạnh 3, cạnh bên bằng

23

và tạo với mặt

phẳng đáy một góc

30 .

Khi đó thể tích khối lăng trụ là?

A.

9

.

4

B.

27 3

.

4

C.

27

.

4

D.

93

.

4

Câu 12: Cho khối lăng trụ tam giác

.ABC A B C

  

có đáy là tam giác đều cạnh

a

. Độ dài cạnh bên bằng

4

a

. Mặt phẳng

( )

BCC B



vuông góc với đáy và

30B BC



=

. Thể tích khối chóp

.ACC B



bằng

A.

3

2

a

. B.

3

12

a

. C.

3

18

a

. D.

3

6

a

.

Câu 13: Cho khối lăng trụ

.ABCD A B C D

   

có đáy

ABCD

là hình thoi cạnh

a

,

60ABC =

. Chân đường

cao hạ từ

B



trùng với tâm

O

của đáy

ABCD

, góc giữa mặt phẳng

( )

BB C C



với đáy bằng

60

. Thể tích khối lăng trụ đã cho bằng

A.

3

33

8

a

. B.

3

23

9

a

. C.

3

32

8

a

. D.

3

4

a

.

Câu 14: Cho khối lăng trụ

.ABC A B C

  

có đáy

ABC

là tam giác vuông tại

B

và

A A A B A C

  

==

. Biết

rằng

AB a=

và

3BC a=

và mặt phẳng

( )

A BC



tạo với mặt phẳng đáy một góc bằng

60

.

Thể tích khối lăng trụ

.ABC A B C

  

bằng

A.

2

3

2

a

. B.

2

3

2

a

. C.

2

3

4

a

. D.

2

4

a

.

Câu 15: Cho hình lăng trụ

.

  

ABC A B C

có tất cả các cạnh bằng

a

, các cạnh bên tạo với đáy góc

60

.

Tính thể tích khối lăng trụ

.

  

ABC A B C

bằng

A.

3

24

a

. B.

3

8

a

. C.

3

8

a

. D.

3

8

a

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 6

Câu 16: Cho khối lăng trụ

.ABCD A B C D

   

có đáy

ABCD

là hình vuông cạnh

a

. Hình chiếu của

B



lên

( )

mp ABCD

trùng với giao điểm của

AC

và

BD

, biết góc giữa hai mặt phẳng

( )

ABA



và

( )

ABCD

bằng

60

. Tính thể tích khối lăng trụ

.ABCD A B C D

   

.

A.

3

a

. B.

3

6

a

. C.

3

2

a

. D.

3

6

2

a

.

Câu 17: Cho hình lăng trụ tam giác

.ABC A B C

  

có đáy

ABC

là tam giác vuông tại

B

,

3 , 5AB a AC a==

, hình chiếu của

A



xuống mặt phẳng

( )

ABC

là trọng tâm tam giác

ABC

.

Biết mặt bên

ACC A



hợp với mặt đáy

ABC

  

một góc

0

60

, thể tích khối lăng trụ

.ABC A B C

  

là

A.

3

24 3

5

a

. B.

3

83

5

a

. C.

3

12 3

5

a

. D.

3

63

5

a

.

Câu 18: Cho khối hộp

.ABCD A B C D

   

có đáy

ABCD

là hình thoi cạnh

a

,

120ABC =

. Hình chiếu

vuông góc của

D



lên

( )

ABCD

trùng với giao điểm của

AC

và

BD

, góc giữa hai mặt phẳng

( )

ADD A



và

( )

A B C D

   

bằng

45

. Thể tích khối hộp đã cho bằng

A.

3

8

a

. B.

3

1

8

a

. C.

3

16

a

. D.

3

4

a

.

Câu 19: Cho lăng trụ

.ABCD A B C D

   

có đáy

ABCD

là hình chữ nhật tâm

O

và

AB a=

,

3AD a=

;

AO



vuông góc với đáy

( )

ABCD

. Cạnh bên

AA



hợp với mặt đáy

( )

ABCD

một góc

45

. Tính

theo

a

thể tích

V

của khối lăng trụ đã cho

A.

3

a

V =

. B.

3

6

a

V =

. C.

3

3Va=

. D.

3

6

2

a

V =

.

Câu 20: Cho hình lăng trụ

. ' ' ' 'ABCD A B C D

có đáy ABCD là hình thoi cạnh

2a

,

0

60ABC =

. Chân đường

cao hạ từ

'B

trùng với

O

của đáy

ABCD

, góc giữa mặt phẳng

( )

''BB C C

với đáy bằng

0

60

. Thể

tích lăng trụ bằng

A.

3

16 3

9

a

. B.

3

32a

. C.

3

33a

. D.

3

6a

.

Câu 21: Cho hình lăng trụ

.ABC A B C

  

cạnh bên có độ dài bằng

4

,

BB



tạo với đáy góc

0

60

. Hình chiếu

vuông góc của

A



trên mặt phẳng

( )

ABC

trùng với trọng tâm

G

của tam giác

ABC

. Biết

khoảng cách từ điểm

A



đến các đường thẳng

BB



và

CC



bằng nhau và bằng

3

. Tính thể tích

khối lăng trụ

.ABC A B C

  

.

A.

18 3 

B.

93

C.

63

D.

12 3 

Câu 22: Cho lăng trụ

. ' ' 'ABC A B C

có đáy tam giác

ABC

vuông tại

A

,

,2AB a BC a==

, biết hình

chiếu của

'A

lên mặt phẳng

( )

ABC

trùng với trung điểm của cạnh

BC

. Góc giữa

'AA

và mặt

phẳng

( )

ABC

bằng

0

60

. Khi đó thể tích của hình trụ

. ' ' 'ABC A B C

bằng:

A.

3

1

2

a

. B.

3

1

6

a

. C.

3

2

a

. D.

3

1

3

a

.

Câu 23: Cho hình lăng trụ

.ABC A B C

  

có đáy là tam giác đều cạnh

a

. Hình chiếu vuông góc của

A

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

7 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

trên mặt phẳng

( )

ABC

  

trùng với trung điểm

H

của

BC



. Biết rằng góc giữa

AA



và mặt

phẳng

( )

ABC

  

bằng

60

. Thể tích của khối lăng trụ

.ABC A B C

  

bằng

A.

3

33

8

a

. B.

3

33

4

a

. C.

3

4

a

. D.

3

8

a

.

Câu 24: Cho lăng trụ

.ABC A B C

  

có đáy

ABC

là tam giác đều. Điểm

M

là trung điểm cạnh

AB

, tam

giác

MA C



đều cạnh

23a

và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối lăng trụ

.ABC A B C

  

là

A.

3

10 3a

. B.

3

43a

. C.

3

12 3a

. D.

3

83a

.

Câu 25: Cho lăng trụ

.ABC A B C

  

có đáy là tam giác đều cạnh

a

. Hình chiếu vuông góc của điểm

A



lên mặt phẳng

( )

ABC

trùng với trọng tâm tam giác

ABC

. Biết khoảng cách giữa hai đường

thẳng

AA



và

BC

bằng

3

4

a

. Khi đó thể tích của khối lăng trụ là

A.

3

.

12

a

B.

3

.

6

a

C.

3

.

3

a

D.

3

.

24

a

Câu 26: Cho hình hộp có

3, 4, ' 5AB AD AA= = =

,

0

60''BAD DAA A AB= = =

.

Thể tích khối hộp đã cho là

A.

30 2

. B.

60

. C.

30

. D.

60 3

.

Câu 27: Cho lăng trụ

.ABC A B C

  

có đáy

ABC

là tam giác vuông cân tại

A

. Mặt phẳng

( )

ACC A



vuông góc đáy,

2BC a=

và

C A C C CA



==

. Thể tích của khối lăng trụ

.ABC A B C

  

là

A.

3

12

a

. B.

3

2

a

. C.

3

3a

. D.

3

4

a

.

Câu 28: Cho hình lăng trụ

.ABC A B C

  

có đáy là tam giác đều cạnh

.a

Hình chiếu của

A



lên mặt phẳng

( )

ABC

trùng với trung điểm cạnh

,AB

góc giữa

AA



và mặt đáy của hình lăng trụ đã cho bằng

60 .

Tính thể tích

V

của khối chóp

..A BCC B

  

A.

3

.

4

a

V =

B.

3

.

8

a

V =

C.

3

.

4

a

V =

D.

3

.

8

a

V =

Câu 29: Cho hình lăng trụ

.ABC A B C

  

có

AA AB AC

  

==

. Tam giác

ABC

vuông cân tại

A

có

2BC a=

. Khoảng cách từ

A



đến mặt phẳng

( )

BCC B



là

3

a

. Tính thể tích khối lăng trụ đã

cho.

A.

3

2

a

V =

. B.

3

2

6

a

V =

. C.

3

6

a

V =

. D.

3

a

V =

.

Câu 30: Cho khối lăng trụ tam giác

. ' ' 'ABC A B C

có đáy

ABC

là tam giác đều. Biết

'AA AB a==

. Các

mặt bên

( ' )A AB

và

( ' )A AC

cùng hợp với đáy

()ABC

1 góc

0

60

. Thể tích khối lăng trụ

. ' ' 'ABC A B C

bằng?

A.

3

37

28

a

. B.

3

37

4

a

. C.

3

7

a

. D.

3

7

28

a

Câu 31: Cho lăng trụ

.ABC A B C

  

có đáy là tam giác vuông cân tại

B

,

2AC a=

. Hình chiếu vuông góc

. ' ' ' 'ABCD A B C D

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 8

của

A



lên mặt phẳng

( )

ABC

là điểm

H

thuộc cạnh

AC

sao cho

1

3

AH AC=

. Mặt bên

( )

ABB A



tạo với đáy một góc

60

. Thể tích khối lăng trụ là

A.

3

9

a

. B.

3

6

9

a

. C.

3

6

3

a

. D.

3

a

.

Câu 32: Cho hình lăng trụ

.ABC A B C

  

có đáy

ABC

là tam giác đều cạnh là

a

. Tam giác

A AB



cân tại

A



và nằm trong mặt phẳng vuông góc với mặt đáy, mặt bên

( )



AA C C

tạo với mặt phẳng

( )

ABC

một góc

45



. Thể tích của khối lăng trụ

.ABC A B C

  

là

A.

3

32

a

V =

. B.

3

4

a

V =

. C.

3

8

a

V =

. D.

3

16

a

V =

.

Câu 33: Cho hình lăng trụ

.ABC A B C

  

có

A A A B A C

  

==

. Tam giác

ABC

vuông cân tại

A

có

2BC a=

. Hai mặt phẳng

()A ABB



và

()ABC



vuông góc nhau. Tính thể tích khối lăng trụ đã

cho.

A.

3

2

a

V =

. B.

3

2

6

a

V =

. C.

3

2

a

V =

. D.

3

6

a

V =

.

Câu 34: Cho hình hộp

. ' ' ' 'ABCD A B C D

,

0

2 , , 60AB a BC a ABC= = =

. Hình chiếu vuông góc của

điểm

'A

lên mặt phẳng

( )

ABCD

là trung điểm

O

của cạnh

AC

. Góc giữa hai mặt phẳng

( )

''ABB A

và

( )

ABCD

bằng

0

60

. Thể tích của hình hộp đã cho bằng

A.

3

2

a

. B.

3

37

4

a

. C.

3

2

a

. D.

3

33

4

a

.

Câu 35: Cho hình lăng trụ

.ABCD A B C D

   

có đáy

ABCD

là hình thoi tâm

O

cạnh

a

,

60ABC =

.

Hình chiếu vuông góc của

A



lên mặt phẳng

ABCD

trùng với tâm

O

. Góc giữa mặt phẳng

( )

ADD A



và mặt đáy

( )

ABCD

bằng

60

. Tính thể tích lăng trụ

.ABCD A B C D

   

.

A.

3

4

a

. B.

3

4

a

. C.

3

33

8

a

. D.

3

8

a

.

Câu 36: Cho hình lăng trụ

.ABCD A B C D

   

có đáy

ABCD

là hình chữ nhật tâm

O

có

2AB a=

,

4AC a=

và

A A A B A C

  

==

. Biết hai mặt phẳng

( )

A AC



và

( )

DA C



tạo với nhau góc

30

.

Tính thể tích khối lăng trụ đã cho.

A.

3

63a

. B.

3

12 2a

. C.

3

62a

. D.

3

12 3a

.

Câu 37: Cho hình lăng trụ

.ABCD A B C D

   

có đáy là hình thang vuông tại

,AB

( )

//BC AD

, góc giữa hai

mặt phẳng

( )

ABCD

và

( )

AA B B



bằng

90

và

12, 16, 5BC AD CD= = =

,tam giác

ABA





đều. Thể tích của khối lăng trụ đã cho là

A.

126 3

. B.

252

. C.

63 3

. D.

410

.

Câu 38: Lăng trụ tam giác

.ABC A B C

  

có đáy là tam giác đều cạnh

a

, góc giữa cạnh bên và mặt đáy

bằng

30

. Hình chiếu của

A



lên

( )

ABC

là trung điểm

I

của

BC

. Thể tích khối lăng trụ là

A.

3

12

a

. B.

3

6

a

. C.

3

2

a

. D.

3

8

a

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

9 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 39: Cho lăng trụ tam giác

.ABC A B C

  

có đáy là tam giác đều cạnh

a

. Độ dài cạnh bên bằng

4a

.

Mặt phẳng

( )

BCC B



vuông góc với đáy và góc giữa hai đường thẳng

'AA

và

BC

bằng

0

30

.

Thể tích khối lăng trụ đã cho là

A.

3

9

a

. B.

3

a

. C.

3

6

a

. D.

3

2

a

.

Câu 40: Cho hình lăng trụ

.ABCD A B C D

   

có

ABCD

là hình chữ nhật. Tính thể tích khối lăng trụ đã

cho biết

A A A B A D

  

==

và

, 3, 2AB a AD a AA a



= = =

A.

3

3a

. B.

3

a

. C.

3

3a

. D.

3

33a

.

Câu 41: Cho hình lăng trụ

.ABC A B C

  

có đáy là tam giác đều cạnh

a

. Hình chiếu vuông góc của điểm

A



lên mặt phẳng

( )

ABC

trùng với trọng tâm tam giác

ABC

. Biết khoảng cách giữa hai đường

thẳng

AA



và

BC

bằng

3

4

a

. Tính theo

a

thể tích

V

của khối lăng trụ

.ABC A B C

  

.

A.

3

6

a

V =

. B.

3

12

a

V =

. C.

3

a

V =

. D.

3

24

a

V =

.

Câu 42: Cho hình lăng trụ tứ giác đều

.ABCD A B C D

   

có đáy là hình vuông; khoảng cách và góc giữa

hai đường thẳng

AC

và

DC



lần lượt bằng

37

7

a

và



với

2

cos

4



=

. Thể tích khối lăng trụ

đã cho bằng

A.

3

3a

. B.

3

9a

. C.

3

33a

. D.

3

3a

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

1 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Dạng 10: Tỷ số thể tích khối lăng trụ

Câu 1: Cho khối lăng trụ tam giác

.ABC A B C

  

có thể tích

V

. Thể tích của khối chóp

.B ACC A



bằng

A.

2

3

V

. B.

1

3

V

. C.

1

2

V

. D.

3

4

V

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 2: Cho hình hộp

.ABCD A B C D

   

. Tính tỷ số thể tích của khối tứ diện

BDA C



và khối hộp

.ABCD A B C D

   

.

A.

1

5

. B.

2

3

. C.

1

3

. D.

2

5

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 3: Cho hình hộp

.ABCD A B C D

   

, gọi

,,M N P

lần lượt là trung điểm của các đoạn thẳng

,,AB A D B C

   

. Tỷ số thể tích của khối

MNPD



và khối hộp

.ABCD A B C D

   

bằng

A.

1

6

. B.

1

8

. C.

1

24

. D.

1

12

.

VÍ DỤ MINH HỌA

B

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 2

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 4: Cho khối hộp

. ' ' ' 'ABCD A B C D

có thể tích bằng

V

. Thể tích của khối tứ diện

''A BC D

bằng

A.

2

V

. B.

6

V

. C.

3

V

. D.

4

V

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

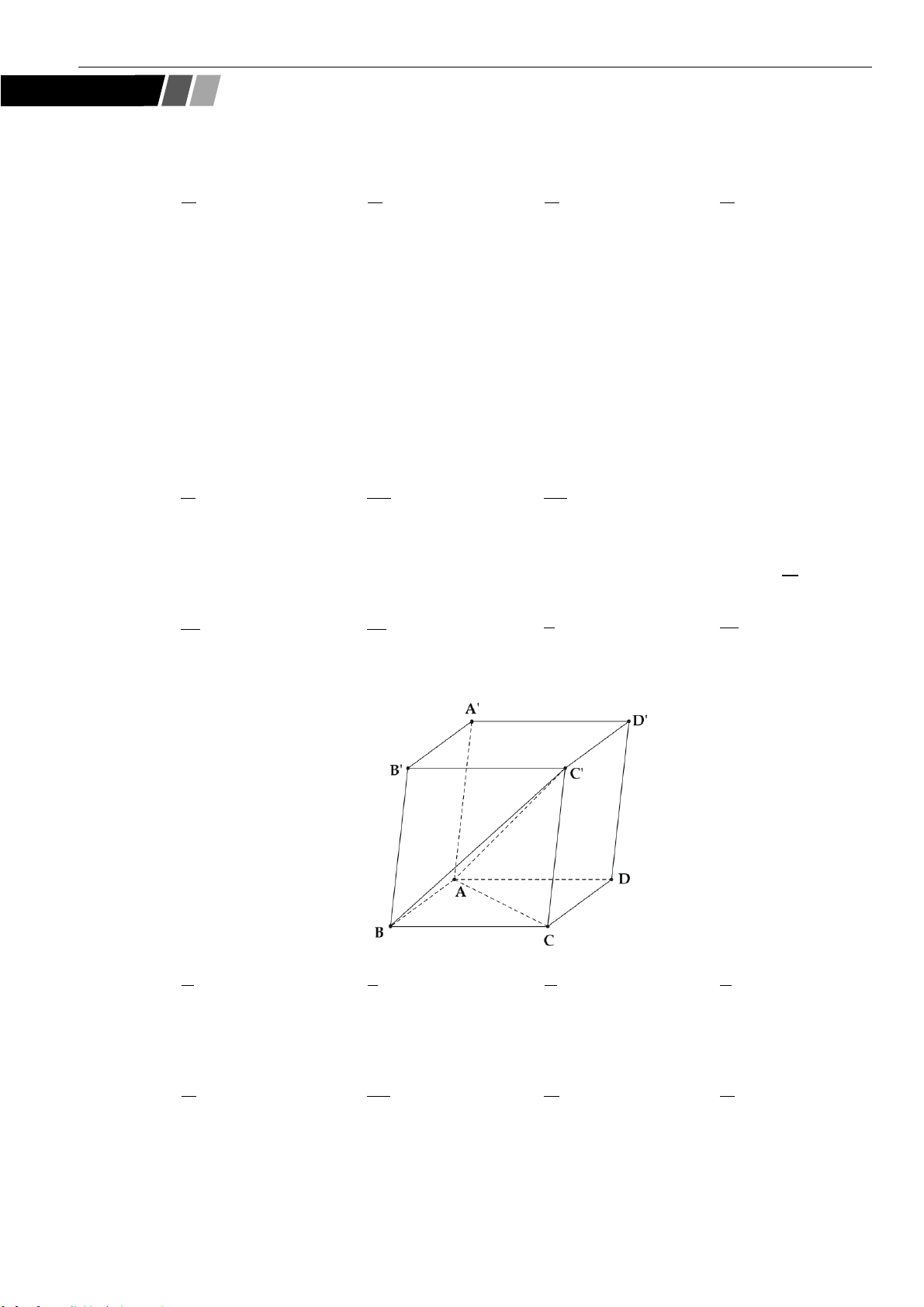
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

3 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 1: Cho khối lăng trụ

.ABC A B C

  

có thể tích

V

và

M

là trung điểm của cạnh

AA



, thể tích khối

chóp

.M ABC

là

A.

6

V

. B.

4

V

. C.

2

V

. D.

3

V

.

Câu 2: Cho lăng trụ

.ABC A B C

  

biết diện tích mặt bên

( )

ABB A



bằng

15

, khoảng cách từ

C

đến mặt

phẳng

( )

ABB A



bằng

6

. Thể tích của khối lăng trụ

.ABC A B C

  

bằng

A.

60

. B.

45

. C.

90

. D.

30

.

Câu 3: Cho lăng trụ

.ABC A B C

  

, gọi

M

,

N

lần lượt là trung điểm của cạnh

AA



và

BC

. Biết khối

tứ diện

AMNB

có thể tích là

3

3a

. Tính thể tích lăng trụ

.ABC A B C

  

.

A.

3

9a

. B.

3

12a

. C.

3

36a

. D.

3

18a

.

Câu 4: Cho khối lăng trụ tam giác

.ABC A B C

  

. Biết thể tích của khối chóp

.A ABC



bằng

.V

Thể tích

khối lăng trụ

.ABC A B C

  

là

A.

.

3

V

B.

3

.

2

V

C.

2

.

3

V

D.

3.V

Câu 5: Cho hình lăng trụ

.

  

ABC A B C

có thể tích bằng

V

. Gọi

M

là trung điểm cạnh



BB

, điểm

N

thuộc cạnh



CC

sao cho

2



=CN C N

. Khối chóp

.A BCNM

có thể tích là

1

V

. Tính

1

V

.

A.

7

12

. B.

5

18

. C.

1

3

. D.

7

18

.

Câu 6: Cho khối hộp

.ABCD A B C D

   

có thể tích bằng

1

. Thể tích của khối tứ diện

ABC C



bằng

A.

2

3

. B.

1

3

. C.

1

2

. D.

1

6

.

Câu 7: Cho khối lăng trụ tam giác

.ABC A B C

  

có thể tích là

V

. Gọi

M

là trung điểm cạnh

AA



. Khi

đó thể tích khối chóp

.M BCC B



là

A.

2

V

. B.

2

3

V

. C.

3

V

. D.

6

V

.

Câu 8: Cho hình hộp

.ABCD A B C D

   

có

O AC BD=

. Với thể tích khối chóp

.A AOD



là

3

a

thì thể

tích khối hộp

.ABCD A B C D

   

là

A.

3

6a

. B.

3

12a

. C.

3

3a

. D.

3

4a

.

BÀI TẬP TRẮC NGHIỆM

C

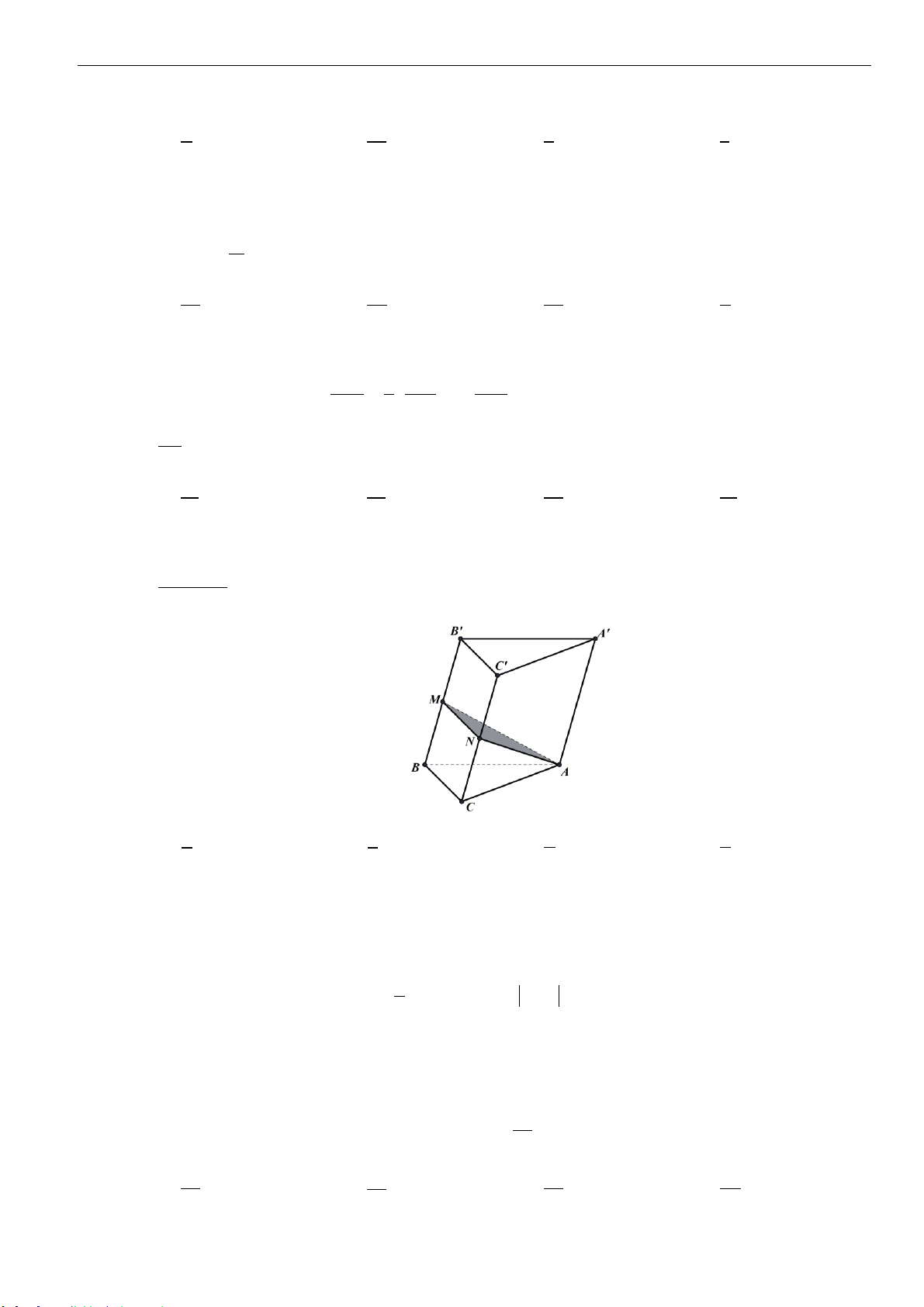
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 4

Câu 9: Cho hình lăng trụ đứng

. ' ' 'ABC A B C

. Gọi I là trung điểm BC. Tính tỉ số thể tích khối tứ diện

A’ABI và thể tích khối lăng trụ đã cho.

A.

1

4

. B.

1

12

. C.

1

6

. D.

1

3

.

Câu 10: Cho khối lăng trụ tam giác

.ABC A B C

  

có thể tích

V

. Gọi

M

là trung điểm của

AA



,

N

là

trung điểm

AM

,

P

nằm trên

BB



sao cho

4BP B P



=

. Gọi thể tích khối đa diện

MNBCC P



là

1

V

. Tỉ số

1

V

bằng

A.

41

60

. B.

37

49

. C.

41

57

. D.

2

3

.

Câu 11: Cho lăng trụ

. ' ' 'ABC A B C

có thể tích là

V

.

,,M N P

là các điểm lần lượt nằm trên các cạnh

', ', 'AA BB C C

sao cho

1

'3

AM

AA

=

,

'

BN

x

BB

=

,

'

CP

y

CC

=

. Biết thể tích khối đa diện

.ABC MNP

bằng

2

3

V

. Giá trị lớn nhất của

xy

bằng:

A.

17

21

. B.

25

36

. C.

5

24

. D.

9

16

.

Câu 12: Cho lăng trụ

. ' ' 'ABC A B C

. Gọi

,MN

lần lượt là trung điểm của

'BB

và

'CC

. Tỉ số thể tích

. ' ' '

ABCMN

ABC A B C

V

là

A.

1

6

. B.

1

3

. C.

1

2

. D.

2

3

.

Câu 13: Cho hình lăng trụ tam giác

.ABC A B C

  

có thể tích là

V

và độ dài cạnh bên

6AA



=

đơn vị. Cho

điểm

1

A

thuộc cạnh

AA



sao cho

1

2AA =

. Các điểm

1

B

,

1

C

lần lượt thuộc cạnh

BB



,

CC



sao

cho

11

,BB x CC y==

, ở đó

,xy

là các số thực dương thỏa mãn

12.xy =

Biết rằng thể tích của

khối đa diện

1 1 1

.ABC A B C

bằng

1

.

2

V

Giá trị của

xy−

bằng

A.

3

. B.

4

. C.

1

. D.

0

.

Câu 14: Cho hình lập phương

. ' ' ' 'ABCD A B C D

. Gọi

M

là điểm thuộc đoạn

'CC

thỏa mãn

'4CC CM=

. Mặt phẳng

( ' )AB M

chia khối lập phương thành hai phần có thể tích

1

V

và

2

V

.

Gọi

2

V

là phần có chứa điểm

B

. Tính tỉ số

1

2

V

k

V

=

.

A.

32

25

. B.

7

16

. C.

25

7

. D.

7

32

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

5 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 15: Cho hình lăng trụ

.ABC A B C

  

. Gọi

M

,

N

,

P

lần lượt là các điểm thuộc các cạnh

AA



,

BB



,

CC



sao cho

2AM MA



=

,

2NB NB



=

,

PC PC



=

. Gọi

1

V

,

2

V

lần lượt là thể tích của hai khối

đa diện

ABCMNP

và

A B C MNP

  

. Tính tỉ số

1

2

V

.

A.

1

2

V

=

. B.

1

2

1

V

=

. C.

1

2

1

2

V

=

. D.

1

2

3

V

=

.

Câu 16: Cho khối lăng trụ tam giác

.ABC A B C

  

có thể tích

V

. Gọi

,,M N P

lần lượt là trung điểm của

các cạnh

;;A B BC CC

  

. Mặt phẳng

( )

MNP

chia khối lăng trụ đã cho thành

2

phần, phần chứa

điểm

B

có thể tích là

1

V

. Tỉ số

1

V

bằng

A.

61

144

. B.

37

144

. C.

49

144

. D.

25

144

.

Câu 17: Cho hình lập phương

. ' ' ' 'ABCD A B C D

. Gọi

,MN

lần lượt là trung điểm

''BA

và

'BB

. Mặt

phẳng

( )

P

đi qua

MN

và tạo với mặt phẳng

( )

''ABB A

một góc



sao cho

tan 2=

. Biết

( )

P

cắt các cạnh

'DD

và

DC

. Khi đó mặt phẳng

( )

P

chia khối lập phương thành hai phần,

gọi thể tích phần chứa điểm

A

là

1

V

và phần còn lại có thể tích

2

V

. Tỉ số

1

2

V

là

A.

1

2

1

V

=

. B.

1

2

V

=

. C.

1

2

1

3

V

=

. D.

1

2

1

2

V

=

.

Câu 18: Cho khối hộp

. ' ' ' 'ABCD A B C D

, điểm

M

thuộc cạnh

'CC

sao cho

'3CC CM=

. Mặt phẳng

( )

'AB M

chia khối hộp thành hai khối đa diện.

1

V

là thể tích khối đa diện chứa đỉnh

'A

,

2

V

là

thể tích khối đa diện chứa đỉnh

B

. Tính tỉ số

1

2

V

?

A.

13

41

. B.

41

108

. C.

13

8

. D.

41

13

.

Câu 19: Cho lăng trụ

.ABCD A B C D

   

có

ABCD

là hình thang đáy

,AB CD

sao cho

2AB CD=

. Gọi

,MN

lần lượt thuộc cạnh

,AA DD



sao cho

34

;

43

AM DN

MA ND

==



, mặt phẳng

( )

BMN

chia khối

lăng trụ thành hai khối đa diện, gọi

1

V

là thể tích của khối đa diện có chứa đỉnh

2

;AV

là thể tích

khối đa diện còn lại. Biết

1

2

V

a

Vb

=

. Giá trị của biểu thức

2ab+

bằng

A.

167

. B.

211

. C.

293

. D.

208

.

Câu 20: Cho hình hộp

.ABCD A B C D

   

có thể tích bằng

V

. Điểm

M

là trung điểm cạnh

CC



. Mặt

phẳng

( )

P

chứa

AM



cắt các cạnh

,BB DD



lần lượt tại

,NP

chia khối hộp thành hai phần.

Thể tích phần chứa đỉnh

C



bằng

A.

2

V

. B.

3

V

. C.

6

V

. D.

4

V

.

Câu 21: Cho lăng trụ

.ABC A B C

  

có thể tích bằng

V

. Gọi

M

,

N

,

P

lần lượt là các điểm thuộc

AA



,

V

ũ

V

ă

n

B

ắ

c

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 6

BB



,

AC



sao cho

1

2

AM B N C P

A M BN A P



= = =



. Gọi

Q

là trung điểm

BC

. Thể tích khối tứ diện

MNPQ

bằng

A.

2

9

V

. B.

1

3

V

. C.

2

7

V

. D.

2

3

V

.

Câu 22: Cho hình hộp

ABCD A B C D

   



có đáy

ABCD

là hình thoi tâm

O

, cạnh bằng

a

và

60BAC =

.

Gọi

, IJ

lần lượt là tâm của các mặt bên

, ABB A CDD C

   

. Biết

7

2

a

AI =

,

2AA a



=

và góc

giữa hai mặt phẳng

( ) ( )

,ABB A A B C D

     

bằng

60

. Tính theo

a

thể tích khối tứ diện

AOIJ

.

A. . B. . C. . D. .

Câu 23: Cho lăng trụ

. ' ' '.ABC A B C

Điểm

M

thỏa mãn

1

.

2

B M B A

  

=−

,

D

là trung điểm của

'BB

và

E

là trung điểm của

AC



. Mặt phẳng

( )

MDE

chia khối lăng trụ

. ' ' 'ABC A B C

thành hai khối

đa diện có thể tích là

12

,VV

(

1

V

là thể tích khối đa diện chứa đỉnh

A

). Biết tỉ số

1

2

V

a

Vb

=

(

,ab

là

các số nguyên dương và

a

b

là phân số tối giản), tính

2ab+

.

A.

2 193ab+=

. B.

2 144ab+=

. C.

2 187ab+=

. D.

2 239ab+=

.

Câu 24: Cho hình lập phương

. ' ' ' 'ABCD A B C D

. Gọi

M

là một điểm trên cạnh

BC

sao cho

2BM MC=

,

E

là giao điểm của

AM

và

CD

,

F

là giao điểm của

DM

và

BE

. Mặt phẳng

( )



đi qua trung điểm của

''AD

và vuông góc với

CF

chia khối lập phương ra thành hai phần

có thể tích là

( )

1 2 1 2

,,V V V V

. Đặt

1

2

V

a

Vb

=

với

,ab

là các số nguyên dương và phân số

a

b

tối

giản. Giá trị

ab−

bằng

A.

7−

. B.

11−

. C.

10−

. D.

5−

.

Câu 25: Cho khối lăng trụ tam giác

.ABC A B C

  

có thể tích là

V

. Gọi

,IJ

lần lượt là trung điểm của

hai cạnh

AA



và

BB



. Khi đó thể tích khối đa diện

ABCIJC



bằng

A.

2

3

V

. B.

3

5

V

. C.

3

4

V

. D.

4

5

V

.

Câu 26: Cho hình lăng trụ

.ABC A B C

  

. Gọi

,MN

lần lượt là trung điểm của

CC



và

BB



. Tính tỉ số

.

ABCMN

ABC A B C

V

  

.

A.

1

2

. B.

2

3

. C.

1

3

. D.

1

6

.

Câu 27: Cho hình lăng trụ tam giác

.ABC A B C

  

có thể tích là

V

. Gọi

M

là trung điểm

AA



và

N

là

trung điểm của

AB

. Mặt phẳng

( )

MNC



chia lăng trụ thành hai phần trong đó phần chứa đỉnh

A

có thể tích

V



. Thể tích của khối

V



theo

V

là

A.

11

25

VV



=

. B.

1

5

VV



=

. C.

13

36

VV



=

. D.

5

7

VV



=

.

3

33

64

a

3

48

a

3

32

a

3

192

a

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

7 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 28: Cho hình lăng trụ

.'ABC A B C



có thể tích

V

. Gọi

M

là điểm nằm trên cạnh

BB



sao cho

23MB MB



=

, điểm

N

nằm trên cạnh

AA



sao cho

4AN NA



=

, điểm

P

nằm trên cạnh

CC



sao cho

3CP PC



=

. Các đường thẳng

NM

,

PM

lần lượt cắt các cạnh

AB



và

CB



lần lượt

tại

H

,

K

. Hãy tính theo

V

thể tích của khối tứ diện

MB H K



?

A.

16

105

V

. B.

6

35

V

. C.

4

15

V

. D.

2

7

V

.

Câu 29: Cho hình lăng trụ

.ABC A B C

  

có

.A ABC



là hình chóp tam giác đều, cạnh đáy

1AB =

, cạnh

bên

2AA



=

. Tính thể tích khối chóp

.A BB C C

  

.

A.

11

.

6

B.

26

.

3

C.

23

.

3

D.

15

3

.

Câu 30: Cho khối lăng trụ

. ' ' 'ABC A B C

có

P

là trọng tâm tam giác

' ' 'A B C

và

Q

là trung điểm của

.BC

Gọi

12

,VV

lần lượt là thể tích hai khối tứ diện

'B PAQ

và

'A ABC

. Tính tỉ số

1

2

.

V

A.

1

3

. B.

2

3

. C.

1

6

. D.

1

2

.

Câu 31: Cho hình lập phương

.ABCD A B C D

   

, gọi

I

là trung điểm của

BB



. Mặt phẳng

( )

DIC



chia

khối lập phương thành 2 phần. Tính tỷ số thể tích phần bé chia phần lớn.

A.

7

17

. B.

1

3

. C.

1

2

. D.

1

7

.

Câu 32: Cho lăng trụ tam giác

.

  

ABC A B C

.

,MN

lần lượt là trung điểm

,;AB AC P

thuộc đoạn



CC

sao cho

.=



CP

x

CC

Tìm

x

để mặt phẳng

( )

MNP

chia khối lăng trụ thành hai khối đa diện có tỉ lệ

thể tích là

1

2

.

A.

8

5

. B.

5

8

. C.

4

5

. D.

5

4

.

Câu 33: Cho khối hộp

.ABCD A B C D

   

có thể tích

V

. Gọi

,,M N P

lần lượt là trung điểm của

AB

,

BC



DD



. Gọi thể tích khối tứ diện

CMNP

là

V



. Khi đó thể tích

V



bằng:

A.

1

64

. B.

3

64

. C.

1

16

. D.

3

16

.

Câu 34: Cho lăng trụ tam giác đều

. ' ' 'ABC A B C

. Trên tia đối của tia

''BA

lấy điểm

M

sao cho

1

' ' '

2

B M B A=

. Gọi

,NP

lần lượt là trung điểm của

' ', 'A C BB

. Mặt phẳng

()MN P

chia khối

trụ

. ' ' 'ABC A B C

thành hai khối đa diện, trong đó khối đa diện có chứa đỉnh

'A

có thể tích

1

V

và

khối đa diện chứa đỉnh

'C

có thể tích

2

V

. Tỉ số

1

2

V

bằng

A.

95

144

. B.

97

59

. C.

49

144

. D.

49

95

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

1 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Dạng 11: Góc, khoảng cách liên quan đến thể tích khối đa diện

Câu 1: Cho hình lăng trụ tứ giác

.ABCD A B C D

   

có đáy

ABCD

là hình vuông cạnh

a

và thể tích bằng

3

3a

. Tính chiều cao

h

của lăng trụ đã cho.

A.

ha=

. B.

9ha=

. C.

3

a

h =

. D.

3ha=

.

 Lời giải

…………………………………………………………………

……………………………………………………………

Câu 2: Cho khối chóp đều

.S ABC

có cạnh đáy bằng

a

. Gọi

M

là trung điểm

SA

. Biết thể tích khối

chóp bằng

3

2

a

, khoảng cách từ điểm

M

đến mặt phẳng

( )

ABC

bằng

A.

3a

. B.

3a

. C.

3

a

. D.

23a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 3: Lăng trụ

.ABC A B C

  

có đáy

ABC

là tam giác vuông cân tại

A

,

AB a=

, biết thể tích của lăng

trụ

.ABC A B C

  

là

3

4

3

a

V =

. Tính khoảng cách

h

giữa

AB

và

BC



.

A.

3

8

a

h =

. B.

2

3

a

h =

. C.

8

3

a

h =

. D.

3

a

h =

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

VÍ DỤ MINH HỌA

B

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 2

Câu 4: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

2.a

Tam giác

SAB

cân tại

S

và

( )

SAB

vuông góc với

( )

.ABCD

Giả sử thể tích của khối chóp

.S ABCD

bằng

3

4

.

3

a

Gọi



là

góc giữa đường thẳng

SC

và mặt phẳng

( )

.ABCD

Mệnh đề nào sau đây đúng?

A.

15

cos .

5



=

B.

6

cos .

6



=

C.

30

cos .

6



=

D.

35

cos .

5



=

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 5: Cho hình chóp

SABCD

có đáy

ABCD

là hình vuông cạnh bằng

a

. Hình chiếu vuông góc của

đỉnh

S

lên đáy

()ABCD

là trọng tâm tam giác

ACD

và góc tạo bởi

SB

với đáy

()ABCD

bằng

30

o

. Thể tích khối chóp

SABD

bằng

A.

3

6

27

a

. B.

3

26

27

a

. C.

3

9

a

. D.

3

6

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

3 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 6: Cho hình chóp

.S ABC

có

,,SA SB SC

đôi một vuông góc với nhau và

SA a=

,

2SB a=

,

3SC a=

. Gọi

,,M N P

lần lượt là trung điểm của

,,AB BC CA

. Khoảng cách từ

M

đến mặt

phẳng

( )

SNP

.

A.

13

2

a

. B.

15

2

a

. C.

6

7

a

. D.

13

2

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 7: Cho hình hộp

.ABCD A B C D

   

có tất cả các cạnh đều bằng

a

và

0

60 .BAA DAA BAD



= = =

Gọi

G

là trọng tâm của tam giác

A BC



. Khoảng cách từ

G

đến mặt phẳng

( )

DA C



bằng

A.

22

66

a

. B.

4 11

11

a

. C.

2 11

11

a

. D.

22

.

11

a

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 8: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

,

SA

vuông góc với đáy. Biết thể

tích khối chóp

.S ABCD

bằng

3

a

. Khoảng cách từ

D

đến mặt phẳng

()SBC

bằng

A.

2

a

. B.

3

2

a

. C.

2

a

. D.

2 39

13

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 4

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 9: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thoi tâm

O

,

2AC a=

,

23BD a=

,

( )

SO ABCD⊥

. Biết khoảng cách từ

O

đến mặt phẳng

( )

SBC

bằng

3

4

a

. Tính thể tích của

khối chóp

.S ABCD

theo

a

.

A.

3

a

. B.

3

6

a

. C.

3

12

a

. D.

3

4

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 10: Cho hình chóp tam giác

SABC

có đáy là tam giác đều cạnh

6

. Biết khoảng cách từ

B

đến mặt

phẳng

( )

SAC

bằng

3

; khoảng cách giữa hai đường thẳng

SB

và

AC

bằng

2

. Khoảng cách từ

điểm

S

đến mặt phẳng

( )

ABC

nằm trong khoảng nào dưới đây?

A.

5 11

;

48







. B.

11 3

;

82







. C.

75

;

84







. D.

3 13

;

28







.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

5 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 1: Thể tích của khối chóp tam giác bằng

6

, biết diện tích đáy bằng

2

. Chiều cao của khối chóp

bằng

A.

18

. B.

1

. C.

3

. D.

9

.

Câu 2: Cho hình chóp có thể tích

3

36V cm=

và diện tích đáy

2

6.B cm=

Chiều cao của khối chóp là

A.

72h cm=

. B.

18h cm=

. C.

6h cm=

. D.

1

2

h cm=

.

Câu 3: Cho khối lăng trụ

( )

H

có diện tích đáy bằng 4, thể tích bằng

4

3

. Tính chiều cao

h

của khối lăng

trụ.

A.

1h =

. B.

1

3

h =

. C.

3h =

. D.

9h =

.

Câu 4: Cho khối chóp có thể tích

32V =

và đáy là hình vuông có cạnh bằng

4

. Chiều cao của khối

chóp đã cho bằng

A.

8

. B.

2

. C.

4

. D.

6

.

Câu 5: Khối chóp có thể tích bằng

144

và diện tích đáy bằng

12

thì chiều cao của nó bằng

A.

24

. B.

4

. C.

12

. D.

36

.

Câu 6: Cho hình lăng trụ lục giác đều

.ABCDEF A B C D E F

     

có cạnh đáy bằng

a

, biết thể tích của

khối lăng trụ

.ABCDEF A B C D E F

     

là

3

33Va=

. Tính chiều cao

h

của khối lăng trụ lục giác

đều đó.

A.

3ha=

. B.

2ha=

. C.

23

3

a

h =

. D.

ha=

.

Câu 7: Cho khối chóp tam giác đều. Nếu tăng cạnh đáy lên hai lần và giảm chiều cao đi bốn lần thì thể

tích khối chóp đó sẽ

A. Không thay đổi. B. Giảm đi hai lần. C. Tăng lên hai lần. D. Giảm đi ba lần.

Câu 8: Một hình lập phương có thể tích bằng

3

33a

thì cạnh của khối lập phương đó bằng

A.

3a

. B.

3a

. C.

33a

. D.

3

a

.

Câu 9: Khối lăng trụ có diện tích đáy bằng

2

20cm

và thể tích bằng

2

60cm

thì chiều cao bằng

A.

30cm

. B.

3cm

. C.

9cm

. D.

1cm

.

Câu 10: Khối chóp có chiều cao bằng

7cm

và thể tích bằng

3

28cm

thì diện tích đáy bằng

A.

2

12cm

. B.

2

36cm

. C.

2

4cm

. D.

2

15cm

.

Câu 11: Cho hình lăng trụ tam giác

.ABC A B C

  

có các cạnh bên hợp với đáy những góc bằng

0

60

, đáy

ABC

là tam giác đều cạnh

a

và

A



cách đều

,,A B C

. Tính khoảng cách giữa hai đáy của hình

lăng trụ.

A.

a

. B.

2a

. C.

3

2

a

. D.

2

3

a

.

BÀI TẬP TRẮC NGHIỆM

C

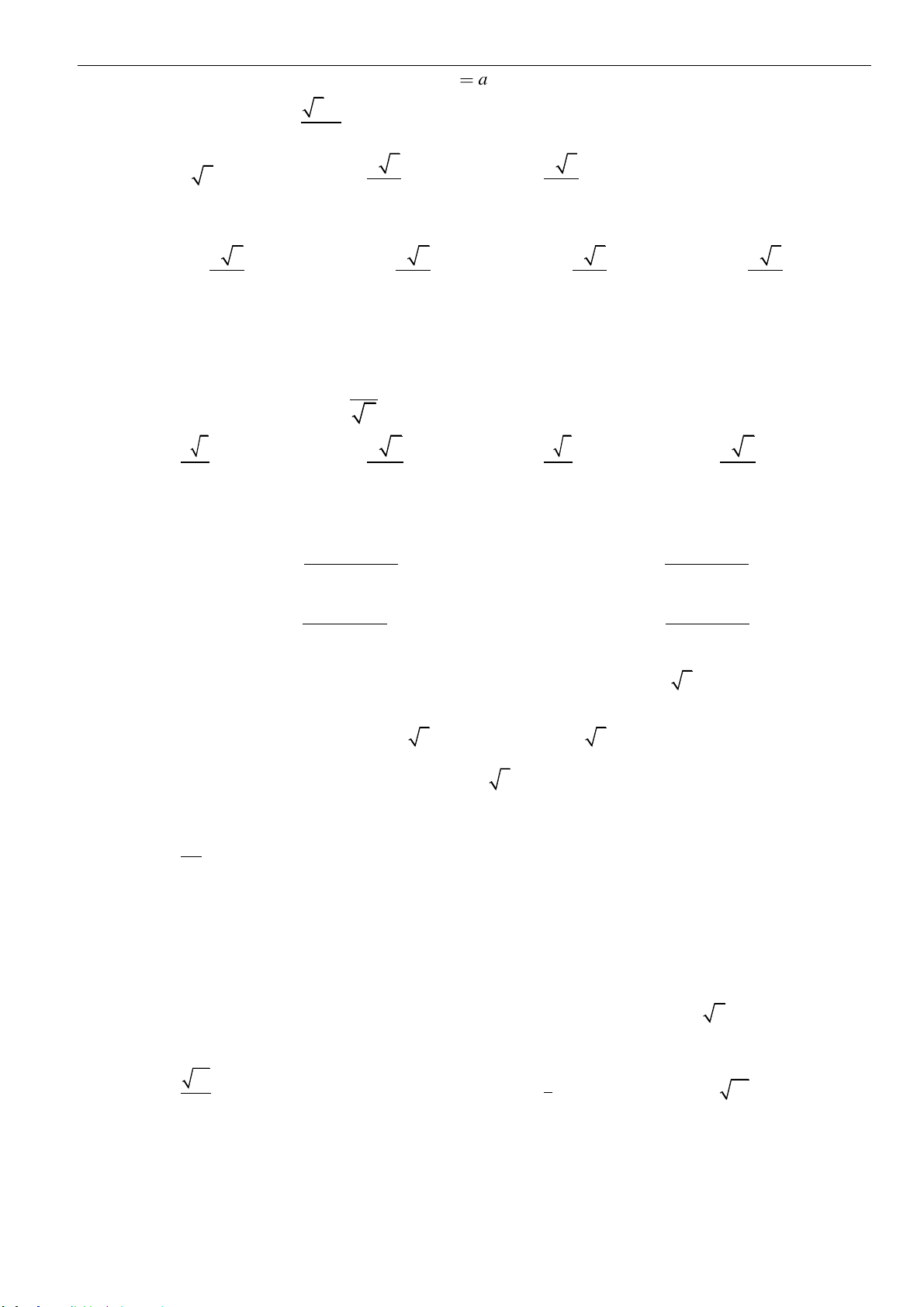
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 6

Câu 12: Cho khối chóp tam giác

.S ABC

có

BC a

và tam giác

ABC

vuông cân tại

B

. Biết thể tích

khối chóp đó bằng

3

6

a

. Khoảng cách từ

S

đến mặt phẳng

ABC

là

A.

3a

. B.

3

a

. C.

3

2

a

. D.

3a

.

Câu 13: Cho tứ diện đều cạnh

.a

Tính độ dài đường cao

h

của tứ diện đều.

A.

6

3

a

h =

. B.

6

2

a

h =

. C.

3

2

a

h =

. D.

3

a

h =

.

Câu 14: Cho hình chóp

.S ABCD

có

ABCD

là hình thang vuông tại

A

và

D

,

AB AD a==

,

2CD a=

. Hình chiếu của

S

lên mặt phẳng

( )

ABCD

trùng với trung điểm của

BD

. Biết thể

tích tứ diện

SBCD

bằng

3

6

a

. Tính khoảng cách từ

A

đến mặt phẳng

( )

SBC

.

A.

3

2

a

. B.

2

6

a

. C.

3

6

a

. D.

6

4

a

.

Câu 15: Cho hình lập phương

.ABCD A B C D

   

. Khoảng cách từ điểm

A

đến mặt phẳng

( )

A B D



là

A.

( )

.

3

,

ABCD A B C D

A BD

V

d A A BD

S

   



=

. B.

( )

.

,

ABCD A B C D

A BD

V

d A A BD

S

   



=

.

C.

( )

.

,

3

ABCD A B C D

A BD

V

d A A BD

S

   



=

. D.

( )

.

,

2

ABCD A B C D

A BD

V

d A A BD

S

   



=

.

Câu 16: Cho khối chóp có đáy là tam giác đều cạnh

a

và có thể tích là

3

3Va=

. Chiều cao

h

của khối

chóp đã cho bằng

A.

10ha=

. B.

12 3ha=

. C.

10 3ha=

. D.

12ha=

.

Câu 17: Cho hình tứ diện

ABCD

có

, 3,AB a CD a==

góc giữa hai đường thẳng

,AB CD

bằng

0

60 ,

thể tích của khối tứ diện

ABCD

là

3

.a

Tính khoảng cách giữa hai đường thẳng

,.AB CD

A.

2

3

a

. B.

2a

. C.

3a

. D.

4a

.

Câu 18: Cho khối chóp tứ giác có thể tích

3

2Va=

,

đáy là hình vuông có cạnh bằng

a

. Tính chiều cao

khối chóp.

A.

2a

. B.

6a

. C.

3a

. D.

a

.

Câu 19: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

,

32SA a=

và

SA

vuông góc

với mặt phẳng

( )

ABC D

. Tính

tan

góc tạo bởi đường thẳng

SC

và mặt phẳng

( )

SAD

?

A.

19

. B.

3

. C.

1

3

. D.

19

.

Câu 20: Cho khối lăng trụ tam giác đều

. ' ' 'ABC A B C

có cạnh đáy bằng

2a

, chiều cao bằng

a

. Tính số

đo góc tạo bởi hai mặt phẳng

( )

''AB C

và

( )

ABC

?

A.

0

45

. B.

0

60

. C.

0

30

. D.

0

26 33'

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

7 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 21: Một khối trụ có thể tích bằng

16 .



Nếu chiều cao khối trụ tăng lên hai lần và giữ nguyên bán

kính đáy thì được khối trụ mới có diện tích xung quanh bằng

16 .



Bán kính đáy của khối trụ

ban đầu là

A.

1r =

. B.

4r =

. C.

3r =

. D.

8r =

.

Câu 22: Cho hình chóp tứ giác đều

.S ABCD

có đáy là hình vuông cạnh

a

. Gọi

M

là trung điểm của

SD

. Khoảng cách từ

M

đến mặt phẳng

()SAC

bằng

A.

2

a

. B.

4

a

. C.

2

4

a

. D.

2

a

.

Câu 23: Cho hình chóp

.S ABCD

có đáy là hình thang vuông tại

A

và

D

,

,2AB AD a CD a= = =

. Hình

chiếu của đỉnh

S

lên mặt

( )

ABC D

trùng với trung điểm của

BD

. Biết thể tích khối chóp

.S ABCD

bằng

3

2

.

2

a

Khoảng cách từ điểm

A

đến mặt phẳng

( )

SBC

bằng

A.

5

2

a

. B.

5

a

. C.

10

5

a

. D.

10

2

a

.

Câu 24: Cho hình chóp tứ giác đều

.S ABCD

có cạnh đáy bằng

a

và thể tích bằng

3

23

a

. Tính góc giữa

mặt bên và mặt đáy của hình chóp

.S ABCD

.

A.

30

B.

45

C.

60

D.

75

Câu 25: Cho hình chóp tứ giác đều

.S ABCD

,

O

là giao điểm của

AC

và

BD

. Biết mặt bên của hình

chóp là tam giác đều và khoảng cách từ

O

đến mặt bên là

a

. Tính thể tích khối chóp

.S ABCD

theo

a

.

A.

3

23a

. B.

3

43a

. C.

3

63a

. D.

3

83a

.

Câu 26: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thoi và thể tích bằng

2

. Gọi

,MN

lần lượt là

các điểm nằm trên

SB

và

SD

sao cho

SM SN

k

SB SD

==

. Mặt phẳng

( )

AMN

cắt cạnh

SC

tại

Q

. Tìm giá trị của

k

để thể tích khối chóp

.S AMNQ

bằng

2

3

A.

2

3

k =

. B.

1

8

k =

. C.

1

4

k =

. D.

2

4

k =

.

Câu 27: Cho lăng trụ

.ABC A B C

có đáy là tam giác đều cạnh

a

, hình chiếu vuông góc của điểm

A

lên mặt phẳng

ABC

trùng với trung điểm của đường trung tuyến

AM

trong

ABC

, biết

thể tích lăng trụ bằng

3

3a

16

. Tính khoảng cách giữa đường thẳng

AA

và

BC

.

A.

3

,

4

a

d AA BC

B

.

3

,

8

a

d AA BC

C

.

6

,

4

a

d AA BC

D.

6

,

2

a

d AA BC

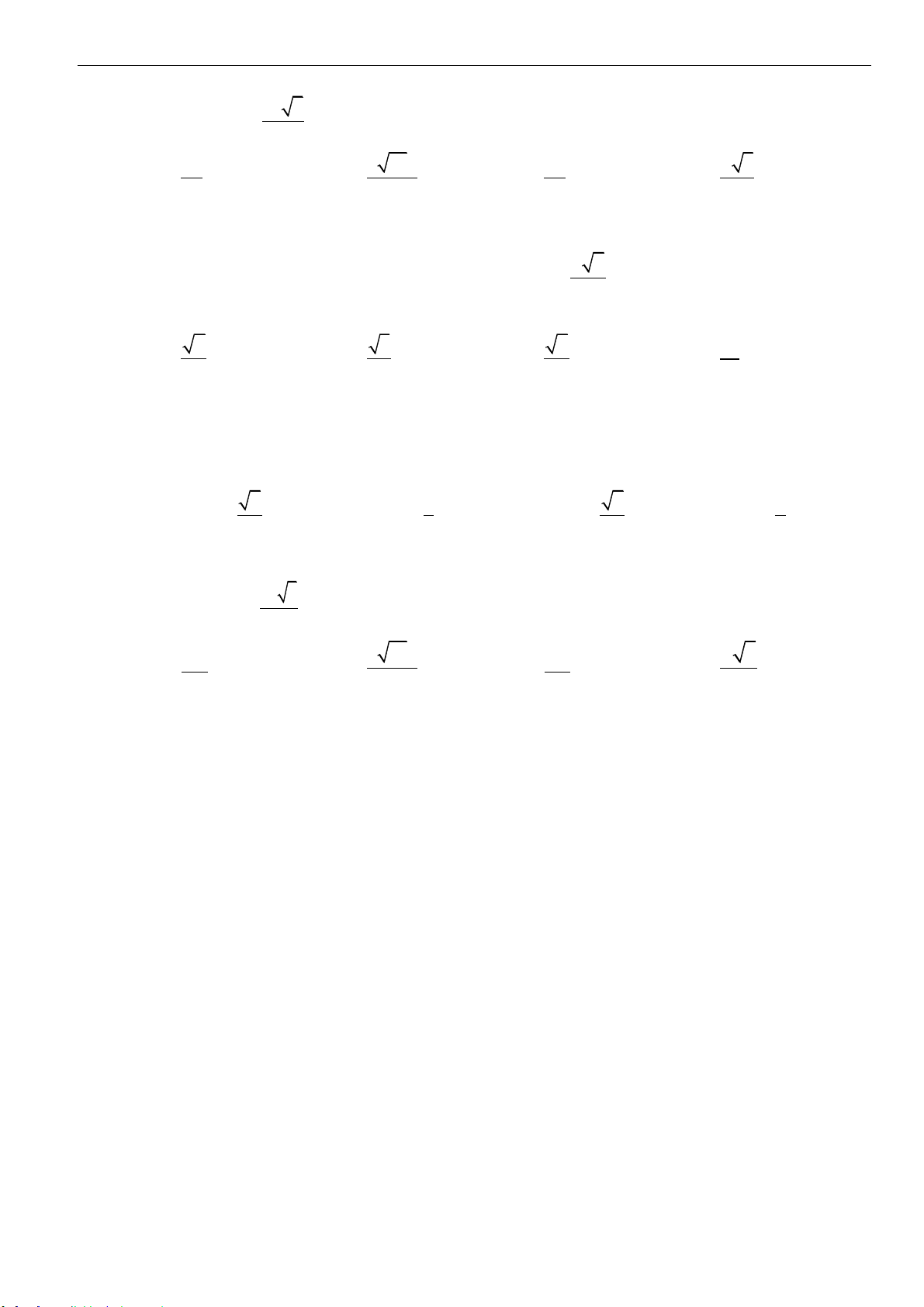
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 8

Câu 28: Cho hình chóp

.S ABC

, có

==SA SB SC

, đáy là tam giác đều cạnh

a

. Biết thể tích khối chóp

.S ABC

bằng

3

a

. Khoảng cách giữa hai đường thẳng

SA

và

BC

bằng

A.

4

7

a

. B.

3 13

13

a

. C.

6

7

a

. D.

3

4

a

.

Câu 29: Cho khối chóp

.S ABCD

có đáy

ABCD

là hình thoi cạnh

,a

0

60ABC =

,

SA

vuông góc với

đáy và khoảng cách từ

A

đến mặt phẳng

( )

SBC

bằng

2

.

2

a

Thể tích của khối chóp

.S ABCD

bằng

A.

3

2

4

a

. B.

3

6

a

. C.

3

6

a

. D.

3

a

.

Câu 30: Cho hình chóp

.S ABCD

có đáy là hình thang vuông tại

A

và

B

,

, 2AB BC AD AB==

. Biết

SA

vuông góc với mặt phẳng đáy,

2SA a=

và thể tích khối chóp

.S ABCD

bằng

3

3a

. Gọi



là

góc giữa hai mặt phẳng

( )

SCD

và

( )

ABCD

, tính

tan



.

A.

6

tan

2



=

. B.

1

tan

3



=

. C.

6

tan

3



=

. D.

2

tan

3



=

.

Câu 31: Cho hình chóp

.S AB C

, có

==SA SB SC

, đáy là tam giác đều cạnh

a

. Biết thể tích khối chóp

.S AB C

bằng

3

a

. Khoảng cách giữa hai đường thẳng

SA

và

BC

bằng

A.

4

7

a

. B.

3 13

13

a

. C.

6

7

a

. D.

3

4

a

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

1 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Dạng 12: Cực trị khối đa diện

Câu 1: Cho tứ diện

ABCD

có

ABC

và

ABD

là các tam giác đều cạnh bằng

a

không đổi. Độ dài

CD

thay đổi. Tính giá trị lớn nhất đạt được của thể tích khối tứ diện

ABCD

.

A.

3

8

a

. B.

3

2

12

a

. C.

3

8

a

. D.

3

12

a

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Câu 2: Cho một hình lập phương

( )

H

và một hình lăng trụ tam giác đều

( )

L

có tổng độ dài các cạnh

bằng nhau. Tỷ lệ thể tích khối lăng trụ

( )

L

và khối lập phương

( )

H

tương ứng có giá trị lớn nhất

bằng

A.

16 3

27

. B.

17 3

24

. C.

32

27

. D.

83

9

.

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

VÍ DỤ MINH HỌA

B

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 2

Câu 3: Cho hình chóp tứ giác đều

.S ABCD

có các cạnh bên bằng

a

, góc tạo bởi mặt phẳng bên và mặt

phẳng đáy là



với

0;

2













. Thể tích khối chóp

.S ABCD

đạt giá trị lớn nhất là

A.

3

47

.

49

a

B.

3

43

.

27

a

C.

3

23

.

9

a

D.

3

4 15

.

75

a

 Lời giải

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

…………………………………………………………………

……………………………………………………………

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

3 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 1: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật

3, 2AB a SA SB SC SD a= = = = =

.Giá trị lớn nhất của thể tích khối chóp

.S ABCD

bằng:

A.

3

13

12

a

. B.

3

13 2

12

a

. C.

3

13 6

12

a

. D.

3

13 3

12

a

.

Câu 2: Cho hình chóp đều

.S ABCD

có cạnh bên bằng

a

, góc hợp bởi đường cao

SH

của hình chóp và

mặt bên bằng



. Tìm



để thể tích

.S ABCD

là lớn nhất.

A.

30

. B.

60

. C.

45

. D.

75

.

Câu 3: Cho khối chóp

.S ABCD

, có đáy

là hình chữ nhật cạnh

25AB a=

và tất cả các cạnh bên của

hình chóp bằng

5a

. Thể tích lớn nhất của khối chóp đã cho bằng

A.

3

20 5

3

a

. B.

3

8

3

a

. C.

3

40 5

3

a

. D.

3

15 5a

.

Câu 4: Cho khối chóp

.S ABCD

có đáy là hình bình hành, một cạnh của hình bình hành bằng

a

và các

cạnh bên đều bằng

2a

. Thể tích của khối chóp có giá trị lớn nhất là

A.

3

7

12

a

. B.

3

8a

. C.

3

26

3

a

. D.

3

26a

.

Câu 5: Cho khối chóp tứ giác đều

.S ABCD

có tất cả các cạnh đều bằng

1

. Gọi

,MN

lần lượt là các

điểm thuộc các cạnh

,BC CD

sao cho

1MN =

. Tìm giá trị nhỏ nhất của thể tích khối tứ diện

.S AMN

.

A.

42

24

−

. B.

3

12

. C.

2

12

. D.

12

+

.

Câu 6: Một tứ diện

ABCD

có

ABC

và

DBC

là hai tam giác đều cạnh

a

, cạnh

AD

thay đổi. Khi thể

tích tứ diện đạt giá trị lớn nhất, gọi



giữa hai mặt

( )

ADB

và

( )

ADC

. Tính

cos



.

A.

1

5

cos



=

. B.

5

7

cos



=

. C.

6

7

cos



=

. D.

1

5

cos



=

.

Câu 7: Cho lăng trụ

.ABC A B C

  

có thể tích là

V

.

M

,

N

,

P

là các điểm lần lượt nằm trên các cạnh

AA



,

BB



,

CC



sao cho

1

3

AM

AA

=



,

BN

x

BB

=



,

CP

y

CC

=



. Biết thể tích khối đa diện

.ABC MNP

bằng

2

3

V

. Giá trị lớn nhất của

.xy

bằng

A.

17

21

. B.

9

16

. C.

25

36

. D.

5

24

.

Câu 8: Trên cạnh

AD

của hình vuông

ABCD

cạnh

1

, người ta lấy điểm

M

sao cho

( )

01AM x x=  

và trên nửa đường thẳng

Ax

vuông góc với mặt phẳng chứa hình vuông,

người ta lấy điểm

S

với

SA y=

thỏa mãn

0y 

và

22

1xy+=

. Biết khi

M

thay đổi trên đoạn

AD

thì thể tích của khối chóp

.S ABCM

đạt giá trị lớn nhất bằng

m

n

với

*

,mn

và

,mn

nguyên tố cùng nhau. Tính

T m n=+

.

A.

11

. B.

17

. C.

27

. D.

35

.

BÀI TẬP TRẮC NGHIỆM

C

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 4

Câu 9: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng

a

. Gọi O là tâm của tứ giác ABCD

Một mẳng phẳng thay đổi và vuông góc với SO cắt các cạnh SO, SA, SB, SC, SD lần lượt tại I,

M, N, P, Q. Một hình trụ có một đáy nội tiếp tứ giác MNPQ và một đáy nằm trên hình vuông

ABCD

. Khi thể tích của khối trụ lớn nhất thì đội dài đoạn SI bằng

A.

2

a

SI =

. B.

32

2

a

SI =

. C.

3

a

SI =

. D.

2

3

a

SI =

.

Câu 10: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông,

1AB =

, cạnh bên

1SA =

và vuông góc

với mặt phẳng đáy

( )

ABCD

. Kí hiệu

M

là điểm di động trên đoạn

CD

và

N

là điểm di động

trên đoạn

CB

sao cho

45MAN =

. Thể tích nhỏ nhất của khối chóp

.S AMN

là

A.

21

3

−

. B.

21

9

+

. C.

21

6

+

. D.

21

9

−

.

Câu 11: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh a,

SA a=

và

SA

vuông góc với mặt

phẳng đáy. Gọi

M

và

N

lần lượt là hai điểm di chuyển trên các cạnh

BC

và

DC

sao cho

45 .MAN =

Tìm giá trị nhỏ nhất của thể tích khối chóp

..S AMN

A.

( )

3

21

3

a−

. B.

3

6

a

. C.

( )

3

31

3

a−

. D.

3

2

3

a

.

Câu 12: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành, có thể tích là

V

. Gọi

M

là trung

điểm của cạnh

SA

,

N

là điểm trên cạnh

SB

sao cho

3SN NB=

. Mặt phẳng

( )

P

thay đổi đi

qua các điểm

,MN

và cắt các cạnh

,SC SD

lần lượt tại hai điẻm phân biệt

,PQ

. Tìm giá trị lớn

nhất của thể tích khối chóp

.S MNPQ

.

A.

3

V

. B.

27

80

V

. C.

27

40

V

. D.

6

V

.

Câu 13: Cho hình hộp chữ nhật

. ' ' ' 'ABCD A B C D

có diện tích toàn phần bằng 18 và độ dài đường chéo

' 18AC =

. Thể tích lớn nhất của khối hộp chữ nhật

. ' ' ' 'ABCD A B C D

là

A.

max

8V =

. B.

max

3V =

. C.

max

4V =

. D.

max

8V =

.

Câu 14: Cho hình lăng trụ

.ABC A B C

  

, có đáy là tam giác đều và thể tích bằng

V

. Gọi

,,E F I

là các

điểm lần lượt di động trên các cạnh

,,AB BC CA

sao cho

AE BF CI==

. Thể tích khối chóp

.A EFI



đạt giá trị nhỏ nhất bằng

A.

9

V

. B.

6

V

. C.

4

V

. D.

12

V

.

Câu 15: Một khối gỗ dạng hình chóp

.O ABC

CÓ

,,OA OB OC

đôi một vuông góc với nhau.

3 , 6 , 12OA cm OB cm OC cm= = =

. Trên mặt đáy

ABC

người ta đánh dấu một điểm

M

sau đó

người cắt gọt khối gỗ để thu được một khối hộp chữ nhật có

OM

là một đường chéo, đồng thời

hình hộp có ba mặt trên ba mặt bên của hình chóp (tham khảo hình vẽ). Khối hộp chữ nhật thu

được có thể tích lớn nhất bằng bao nhiêu?

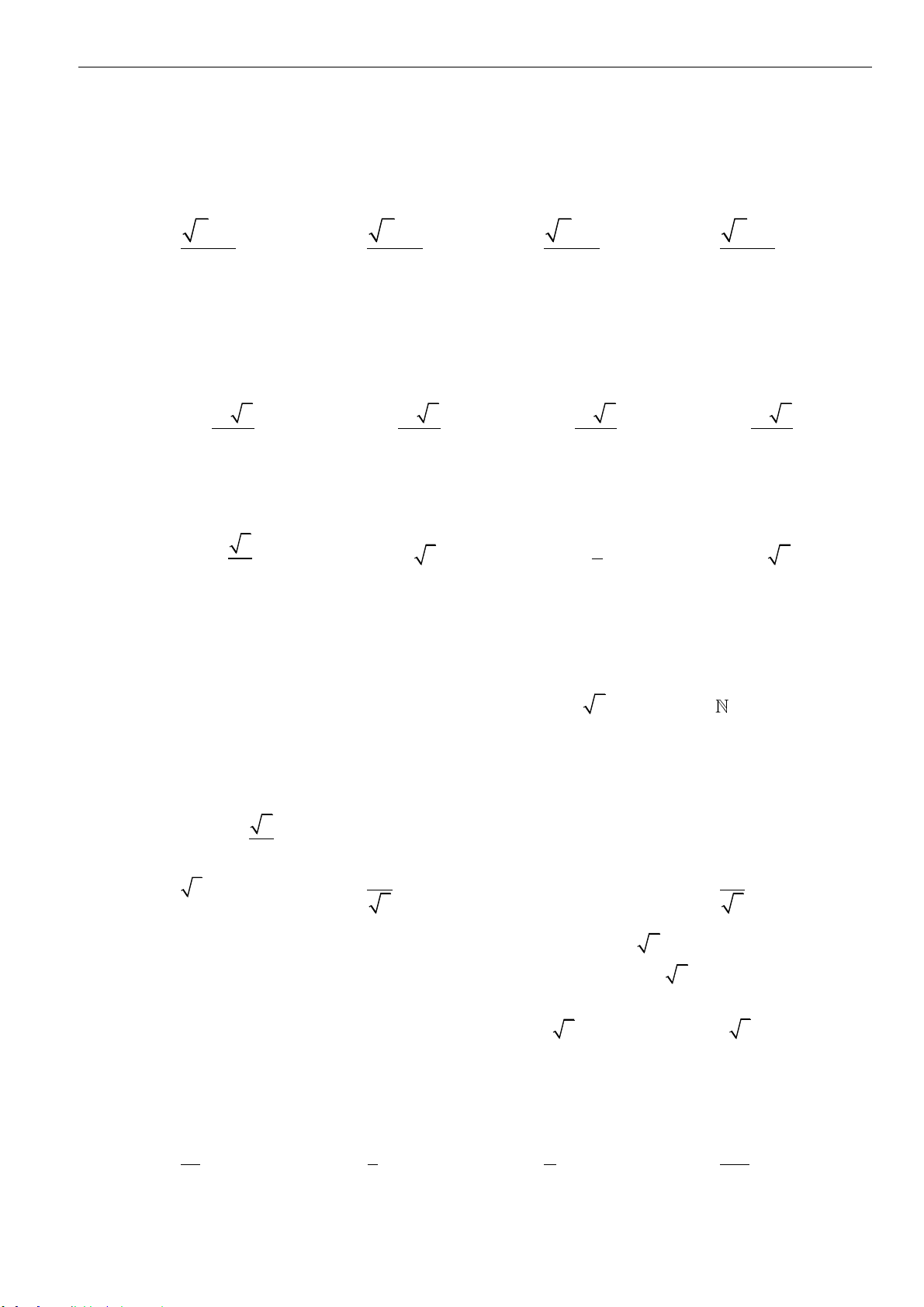
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

5 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

A.

3

12 .cm

B.

3

36 .cm

C.

3

24 .cm

D.

3

8.cm

Câu 16: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông,

1AB =

, cạnh bên

1SA =

và vuông

góc với mặt phẳng đáy

()ABCD

. Kí hiệu

M

là điểm di động trên đoạn

CD

và

N

là điểm di

động trên đoạn

CB

sao cho góc

MAN

bằng

45

. Thể tích nhỏ nhất của khối chóp

.S AMN

là

A.

21

3

−

. B.

21

9

+

. C.

21

6

+

. D.

21

9

−

.

Câu 17: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

,

SA

vuông góc với mặt đáy

( )

ABCD

và góc giữa

SC

với mặt phẳng

( )

SAB

bằng

30

. Gọi

M

là điểm di động trên cạnh

CD

và

H

là hình chiếu vuông góc của

S

lên đường thẳng

BM

. Khi điểm

M

di động trên

cạnh

CD

thì thể tích chóp

.S ABH

lớn nhất là

A.

3

2

15

a

V =

. B.

3

2

6

a

V =

. C.

3

2

8

a

V =

. D.

3

2

12

a

V =

.

Câu 18: Cho tứ diện đều có cạnh bằng 3, điểm

M

thuộc miền trong đa diện, gọi

1 2 3 4

; ; ;d d d d

là khoảng

cách từ

M

đến 4 mặt của tứ diện. Tìm giá trị nhỏ nhất của

2222

1 2 3 4

P d d d d= + + +

?

A.

min

3

2

P =

. B.

min

3P =

. C.

min

3

2

P =

. D.

min

6P =

.

Câu 19: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh bằng

2

,

2SA =

và

SA

vuông góc

với mặt phẳng đáy

( )

ABCD

. Gọi

,MN

là hai điểm thay đổi trên hai cạnh

,AB AD

sao cho mặt

phẳng

( )

SMC

vuông góc với mặt phẳng

( )

SNC

. Biết rằng khi thể tích khối chóp

.S AMCN

đạt

giá trị nhỏ nhất thì biểu thức

2022 2021P AM AN a b a= − = −

với

,ab

. Tính

ab+

.

A.

4

. B.

5

. C.

6

. D.

2

.

Câu 20: Cho hình chóp

.S ABC

có đáy là tam giác đều cạnh bằng 2,

SA

vuông góc với mặt phẳng chứa

đáy. Gọi

M

là trung điểm của

AB

và



là góc giữa đường thẳng

SM

và mặt phẳng

( )

SBC

.

Biết

6

sin

8



=

, hãy tìm giá trị lớn nhât của thể tích khối chóp

.S ABC

.

A.

3

. B.

4

3

. C.

1

. D.

1

3

.

Câu 21: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác đều cạnh bằng

6

. Biết rằng các mặt bên của

hình chóp có diện tích bằng nhau và một trong các cạnh bên bằng

32

. Tính thể tích nhỏ nhất

của khối chóp

.S ABC

A.

4

. B.

3

. C.

22

. D.

23

.

Câu 22: Cho hình chóp

.S ABC

có

4SA =

,

2AB =

,

1AC =

và

( )

SA ABC⊥

. Gọi

O

là tâm đường tròn

ngoại tiếp tam giác

ABC

. Mặt cầu tâm

O

, đi qua

A

và cắt các tia

SB

,

SC

lần lượt tại

D

và

E

. Khi độ dài đoạn thẳng

BC

thay đổi, giá trị lớn nhất của thể tích khối chóp

.S ADE

là

A.

64

85

. B.

8

3

. C.

4

3

. D.

256

255

.

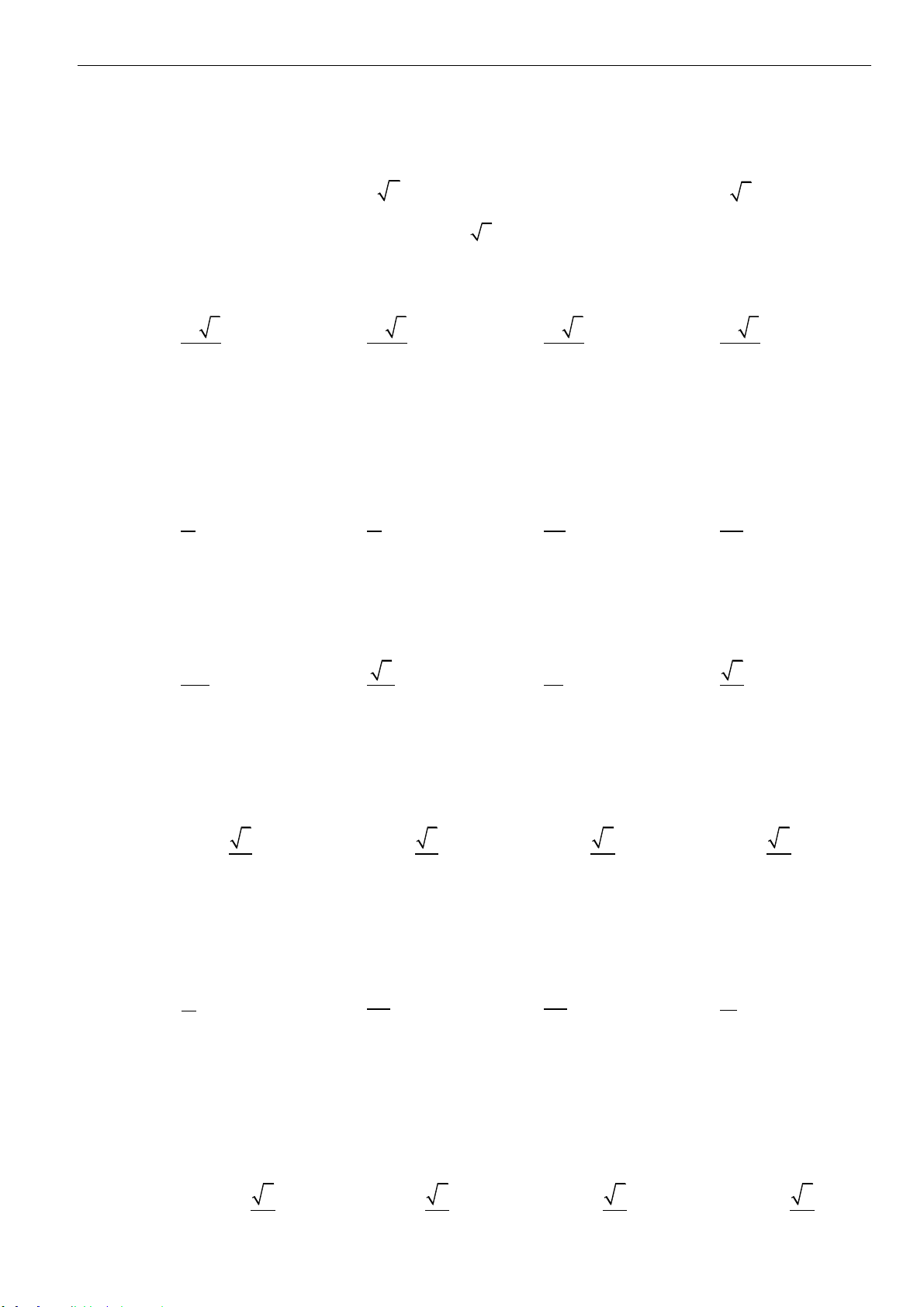
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 6

Câu 23: Cho tam giác

OAB

đều cạnh

2a

. Trên đường thẳng

d

qua

O

và vuông góc với mặt phẳng

( )

OAB

lấy điểm

M

sao cho

OM x=

. Gọi

,EF

lần lượt là hình chiếu vuông góc của

A

trên

MB

và

OB

. Gọi

N

là giao điểm của

EF

với đường thẳng

d

. Tìm

x

sao cho tứ diện

ABMN

có thể tích nhỏ nhất.

A.

a

. B.

2a

. C.

2a

. D.

3a

.

Câu 24: Cho hình chóp

.S ABC

có

, 3, 60 .AB a BC a ABC



= = =

Hình chiếu vuông góc của

S

lên mặt

phẳng

()ABC

là một điểm thuộc cạnh

.BC

Góc giữa đường thẳng

SA

và mặt phẳng

()ABC

bằng

45



. Thể tích khối chóp

.S ABC

đạt giá trị nhỏ nhất bằng

A.

3

12

a

. B.

3

8

a

. C.

3

6

a

. D.

3

a

.

Câu 25: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành, có thể tích là

V

. Gọi

M

là trung

điểm của cạnh

SA

,

N

là điểm trên cạnh

SB

sao cho

2SN NB=

. Mặt phẳng

( )

P

thay đổi đi

qua các điểm

,MN

và cắt các cạnh

,SC SD

lần lượt tại hai điểm phân biệt

,KQ

. Tìm giá trị

lớn nhất của thể tích khối chóp

.S MNKQ

.

A.

2

V

. B.

3

V

. C.

3

4

V

. D.

2

3

V

.

Câu 26: Cho tam giác đều

ABC

có cạnh bằng

1

. Gọi

d

là đường thẳng vuông góc với mặt phẳng

( )

ABC

tại

A

. Trên đường thẳng

d

lấy điểm

S

. Gọi

P

và

Q

lần lượt là trực tâm của tam giác

ABC

và

SBC

. Thể tích tứ diện

PQBC

lớn nhất bằng:

A.

1

144

. B.

3

144

. C.

1

48

. D.

6

72

.

Câu 27: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông tại

C

,

2SA AB==

. Cạnh bên

SA

vuông góc với mặt phẳng đáy

( )

ABC

. Gọi

,HK

lần lượt là hình chiếu của

A

lên

SB

và

SC

. Tính thể tích lớn nhất

max

V

của khối chóp

.S AHK

.

A.

max

3

V =

. B.

max

3

6

V =

. C.

max

2

6

V =

. D.

max

2

3

V =

.

Câu 28: Cho hình chóp

.S ABC

. Mặt phẳng

()P

song song với đáy và cắt các cạnh

,,SA SB SC

lần lượt

,,D E F

. Gọi

1, 1 1

,,D E F

tương ứng là hình chiếu của

,,D E F

lên mặt phẳng đáy (tham khảo hình

vẽ)

V

là thể tích khối chóp

.S ABC

. Giá trị lớn nhất của thể tích khối đa diện

1 1 1

.DEF D E F

bằng

A.

6

V

. B.

4

9

V

. C.

2

3

V

. D.

12

V

.

Câu 29: Cho hình chóp có đáy là hình thang,

// , 2 ,AB CD AB CD=

45ABC =

. Hình chiếu

vuông góc của đỉnh

S

lên mặt phẳng

( )

ABCD

là trung điểm của cạnh

AB

và

SC BC⊥

,

SC a=

. Gọi góc giữa hai mặt phẳng

( )

SBC

và

( )

ABCD

là



. Khi



thay đổi, tìm

cos



để

thể tích khối chóp

.S ABCD

có giá trị lớn nhất.

A.

6

cos

3



=−

. B.

6

cos

3



=

. C.

3

cos

3



=

. D.

6

cos

3



=

.

.S ABCD

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

7 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 30: Cho hình chóp

.S ABC

có đáy là tam giác đều cạnh bằng 2,

SA

vuông góc với mặt phẳng chứa

đáy. Gọi

M

là trung điểm của

AB

và

φ

là góc giữa đường thẳng

SM

và mặt phẳng

( )

SBC

.

Biết rằng

6

sinφ

8

=

, tìm giá trị lớn nhất của thể tích khối chóp

.S ABC

.

A.

3

. B.

4

3

. C. 1. D.

1

3

.

Câu 31: Cho

,xy

là những số thực dương không đổi. Xét hình chóp

.S ABC

có

,SA x BC y==

và các

cạnh còn lại đều bằng 1. Khi thể tích khối chóp

.S ABC

đạt giá trị lớn nhất thì tích

.xy

bằng

A.

1

3

. B.

4

3

. C.

43

3

. D.

23

.

Câu 32: Cho hình chóp

.S ABC

,

O

là trung điểm của

AB

. Điểm

M

di động trên cạnh

SB

. Đặt

SM

x

SB

=

. Mặt phẳng qua

A

,

M

song song với

OC

, cắt

SC

tại

N

. Thể tích khối chóp

ABMN

lớn nhất khi

A.

31x =−

. B.

1x =

. C.

35x =−

. D.

12x = − +

.

Câu 33: Cho hình chóp

.S ABC

có

SA x=

,

BC y=

,

1AB AC SB SC= = = =

. Thể tích khối chóp

.S ABC

lớn nhất khi

xy+

bằng

A.

3

. B.

2

3

. C.

4

3

. D.

43

.

Câu 34: Cho tam giác

OAB

đều cạnh

2a

. Trên đường thẳng

d

qua

O

và vuông góc với mặt phẳng

( )

OAB

lấy điểm

M

sao cho

OM x=

. Gọi

,EF

lần lượt là hình chiếu vuông góc của

A

trên

MB

và

OB

. Gọi

N

là giao điểm của

EF

và

d

. Tìm

x

để thể tích tứ diện

ABMN

có giá trị nhỏ

nhất.

A.

2

=

a

x

. B.

6

12

=

a

x

. C.

3

2

=

a

x

. D.

2=xa

.

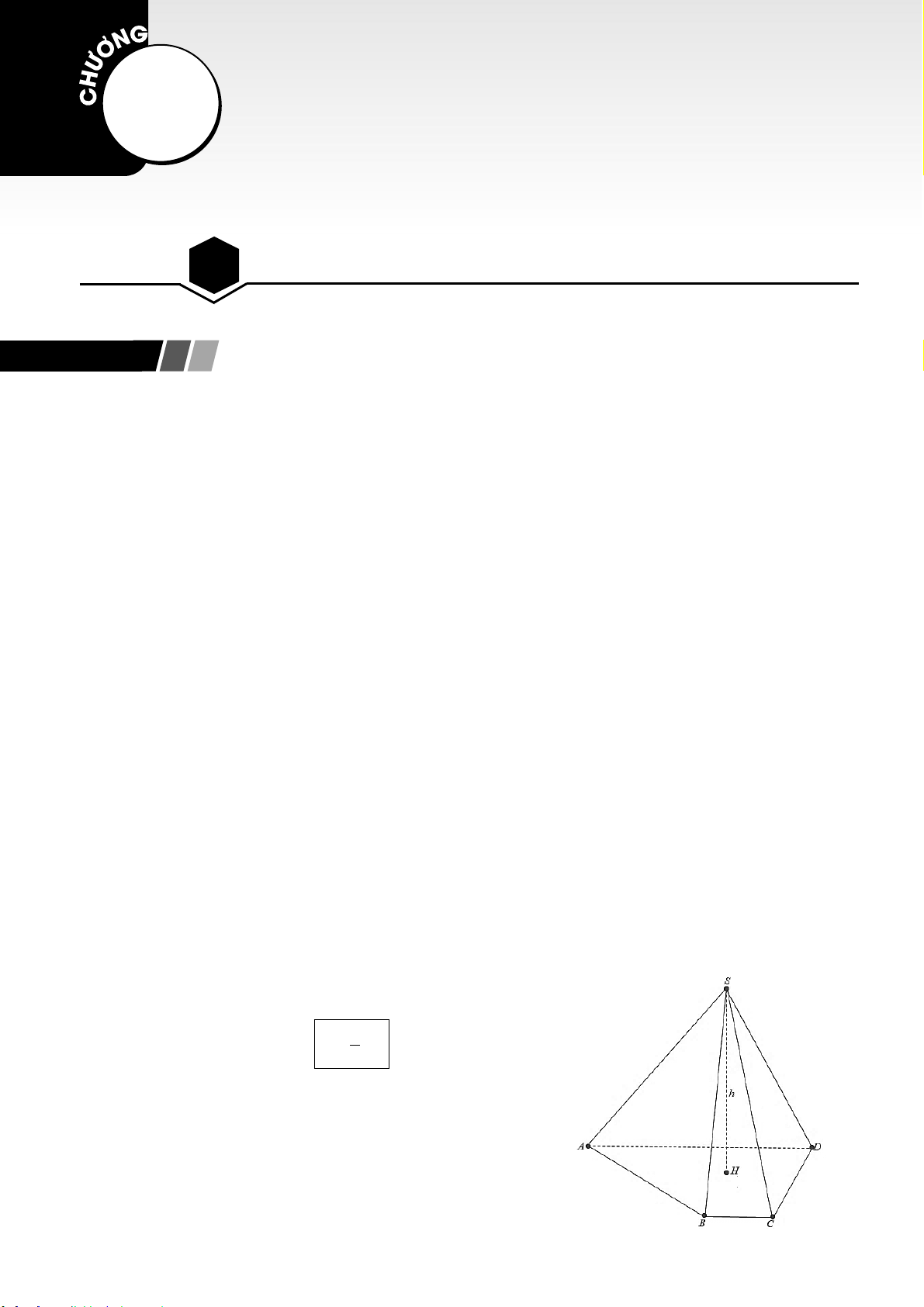
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

1 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

1. Một số định nghĩa cần nhớ

• Hình lăng trụ là hình có hai đáy là hai đa giác bằng nhau nằm trên hai mặt phẳng song song với

nhau và các mặt bên đều là các hình bình hành.

• Hình lăng trụ đứng

Định nghĩa: Hình lăng trụ đứng là hình lăng trụ có cạnh bên vuông góc với mặt đáy.

Tính chất: Các mặt bên của hình lăng trụ đứng là các hình chữ nhật và vuông góc với mặt đáy.

• Hình lăng trụ đều

Định nghĩa. Hình lăng trụ đều là hình lăng trụ đứng có đáy là đa giác đều.

Tính chất. Các mặt bên của hình lăng trụ đều là các hình chữ nhật bằng nhau và vuông góc với

mặt đáy.

• Hình hộp là hình lăng trụ có đáy là hình bình hành.

• Hình hộp đứng

Định nghĩa. Hình hộp đứng là hình hộp có cạnh bên vuông góc với mặt đáy.

Tính chất. Hình hộp đứng có

2

đáy là hình bình hành, 4 mặt xung quanh là 4 hình chữ nhật.

• Hình hộp chữ nhật

Định nghĩa. Hình hộp chữ nhật là hình hộp đứng có đáy là hình chữ nhật.

Tính chất. Hình hộp chữ nhật có

6

mặt là

6

hình chữ nhật.

• Hình lập phương

Định nghĩa. Hình lập phương là hình hộp chữ nhật

2

đáy và

4

mặt bên đều là hình vuông

Tính chất. Hình lập phương có

6

mặt đều là hình vuông.

• Hình chóp là hình có đáy là một đa giác và các mặt bên là các tam giác có chung một đỉnh.

2. Thể tích khối đa diện

1. Công thức tính thể tích khối chóp

1

.

3

V S h=

Trong đó:

S

là diện tích đáy,

h

là chiều cao khối

chóp.

• Chú ý: Nếu khối chóp cần tính thể tích chưa biết chiều

cao thì ta phải xác định được vị trí chân đường cao trên

đáy.

2

THỂ TÍCH KHỐI ĐA DIỆN

8

CHỦ ĐỀ

TÓM TẮT LÝ THUYẾT

A

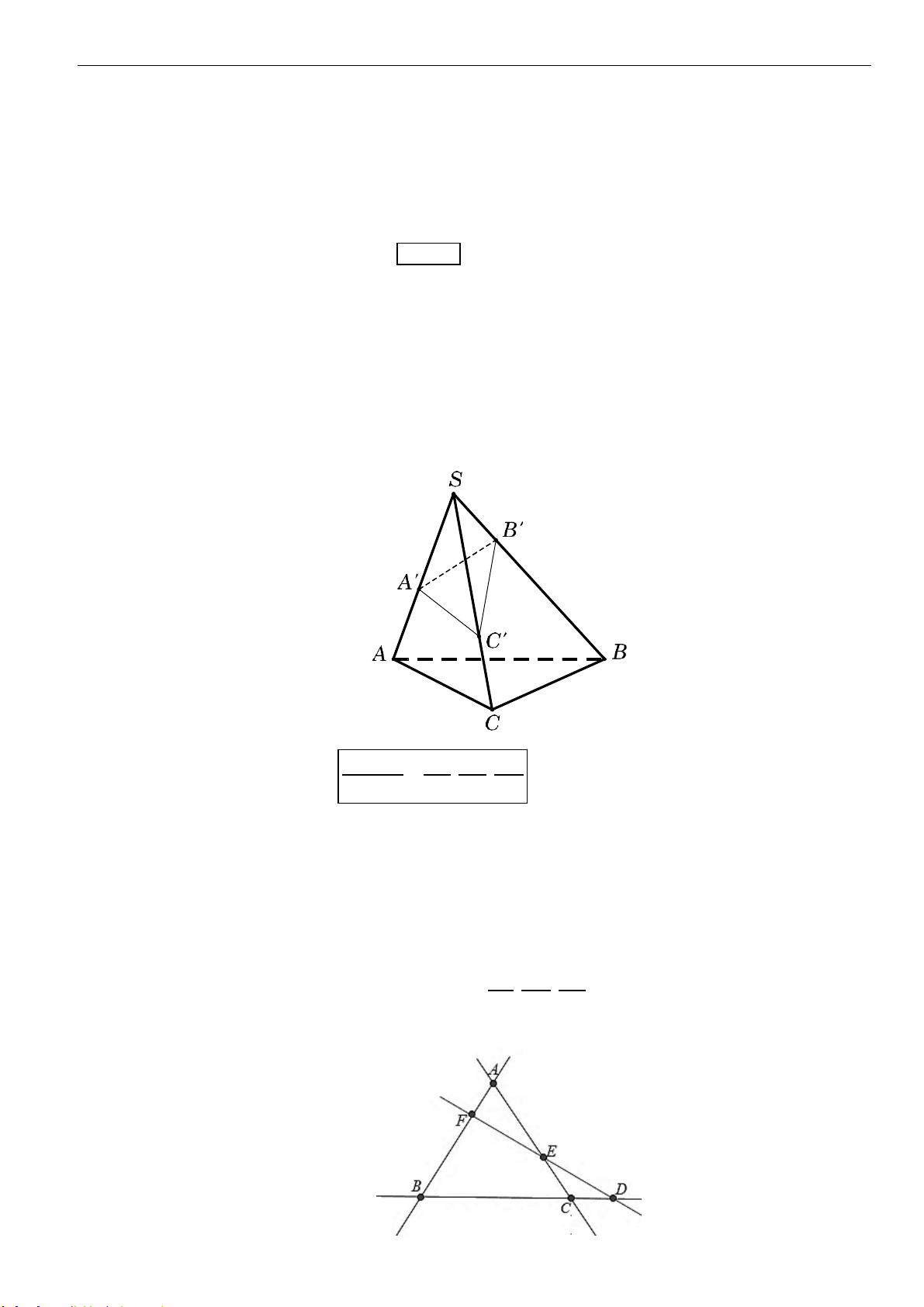
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 2

▪ Chóp có cạnh bên vuông góc chiều cao chính là cạnh bên.

▪ Chóp có hai mặt bên vuông góc đáy đường cao là giao tuyến của hai mặt bên vuông góc

đáy.

▪ Chóp có mặt bên vuông góc đáy chiều cao của mặt bên vuông góc đáy.

▪ Chóp đều chiều cao hạ từ đỉnh đến tâm đa giác đáy.

▪ Chóp có hình chiếu vuông góc của một đỉnh lên xuống mặt đáy thuộc cạnh mặt đáy đường

cao là từ đỉnh tới hình chiếu.

2. Công thức tính thể tích khối lăng trụ

.V B h=

Trong đó:

B

là diện tích đáy,

h

là hiều cao khối lăng trụ.

• Thể tích khối hộp chữ nhật:

..V a b c=

Trong đó:

, , a b c

là ba kích thước của khối hộp chữ nhật.

• Thể tích khối lập phương:

3

Va=

Trong đó

a

là độ dài cạnh của hình lập phương.

3. Tỷ số thể tích

Cho khối chóp

.S ABC

và

,,A B C

  

là các điểm tùy ý lần lượt thuộc

,,SA SB SC

, ta có:

Công thức tỉ số thể tích:

. ' ' '

.

' ' '

..

S A B C

S ABC

V

SA SB SC

V SA SB SC

=

(hay gọi là công thức Simson)

Phương pháp này được áp dụng khi khối chóp không xác đinh được chiều cao một cách dễ dàng

hoặc khối chóp cần tính là một phần nhỏ trong khối chóp lớn và cần chú ý đến một số điều kiện

sau:

▪ Hai khối chóp phải cùng chung đỉnh.

▪ Đáy hai khối chóp phải là tam giác.

▪ Các điểm tương ứng nằm trên các cạnh tương ứng.

Định lý Menelaus: Cho ba điểm thẳng hàng

. . 1

FA DB EC

FB DC EA

=

với

DEF

là một đường thẳng cắt

ba đường thẳng

,,BC CA AB

lần lượt tại

,,D E F

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

3 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

4. Một số công thức tính nhanh thể tích và tỷ số thế tích khối chóp và khối lăng trụ.

➢ Công thức 1 : Thể tích tứ diện đều cạnh

a

:

3

.

2

12

S ABC

a

V =

.

➢ Công thức 2 : Với tứ diện

ABCD

có

,,AB a AC b AD c= = =

đôi một vuông góc thì thể tích của

nó là

1

6

ABCD

V abc=

.

➢ Công thức 3 : Với tứ diện

ABCD

có

,,AB CD a BC AD b AC BD c= = = = = =

thì thể tích của

nó là

( )( )( )

2 2 2 2 2 2 2 2 2

2

12

ABCD

V a b c b c a a c b= + − + − + −

.

➢ Công thức 4 : Cho khối chóp

.S ABC

có

, , , , ,SA a SB b SC c BSC CSA ASB

  

= = = = = =

thì

thể tích của nó là

2 2 2

.

1 2cos cos cos cos cos cos

6

S ABC

abc

V

     

= + − − −

.

➢ Công thức 5 : Mặt phẳng cắt các cạnh của khối lăng trụ tam giác

.ABC A B C

  

lần lượt tại

,,M N P

sao cho

,,

AM BN CP

x y z

AA BB CC

= = =

  

thì ta có

..

3

ABC MNP ABC A B C

x y z

VV

  

++

=

.

➢ Công thức 6 : Mặt phẳng cắt các cạnh của khối hộp

.ABCD A B C D

   

lần lượt tại

, , ,M N P Q

sao

cho

,,,

AM BN CP DQ

x y z t

AA BB CC DD

= = = =

   

thì ta có

..

4

ABCD MNPQ ABCD A B C D

x y z t

VV

   

+ + +

=

và

x z y t+ = +

.

➢ Công thức 7 : Mặt phẳng cắt các cạnh của khối chóp tứ giác

.S ABCD

có đáy là hình bình hành

lần lượt tại

, , ,M N P Q

sao cho

, , ,

SM SN SP SQ

x y z t

SA SB SC SD

= = = =

thì ta có công thức sau đây

..

1 1 1 1

4

S MNPQ S ABCD

xyzt

VV

x y z t



= + + +





và

1 1 1 1

x z y t

+ = + +

.

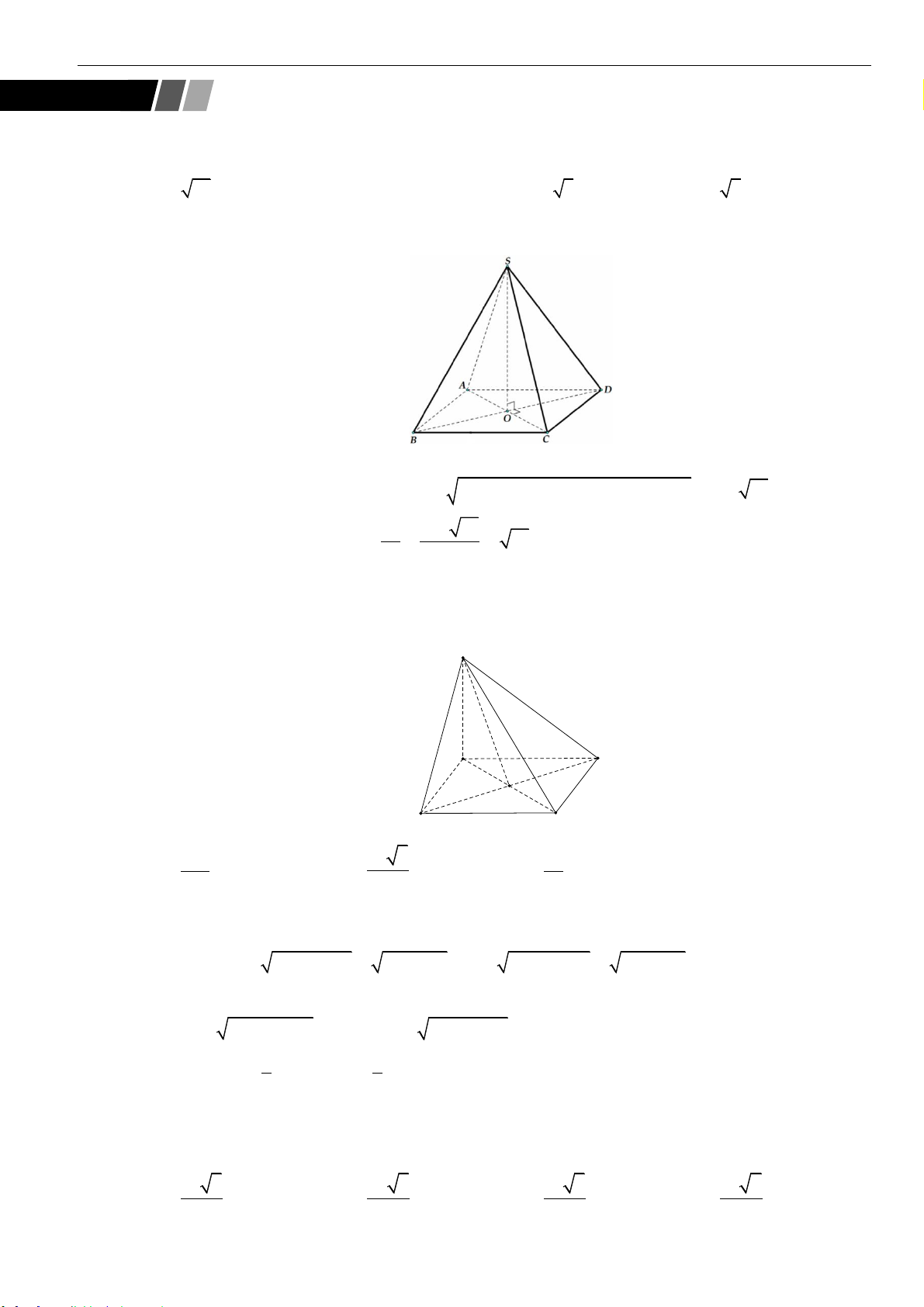
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 4

Câu 1: Cho hình chóp tứ giác đều có cạnh bên gấp đôi cạnh đáy. Tỉ lệ giữa diện tích xung quanh và diện

tích đáy của hình chóp này bằng

A.

15.

B.

3.

C.

4 3.

D.

3.

Lời giải

Chọn A

Gọi độ dài cạnh đáy là

2a



độ dài cạnh bên bằng

4.a

Diện tích xung quanh:

( )( )( )

2

1

4. 4. 5 5 4 5 4 5 2 4 15.

SAB

S S a a a a a a a a



= = − − − =

Diện tích đáy:

2

4.Sa=

Vậy

2

1

2

4 15

15.

4

S

a

Sa

==

Câu 2: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông tâm

O

, cạnh

a

. Cạnh

SA

vuông góc với

đáy, góc

60SBD =

. Thể tích khối chóp đã cho bằng

A.

3

2

3

a

. B.

3

2

a

. C.

3

a

. D.

3

a

.

Lời giải

Chọn C

Dễ thấy

2 2 2 2 2 2 2 2

;SB SA AB SA a SD SA AD SA a= + = + = + = +

.

Từ đó suy ra

SBD

cân tại

S

, kết hợp với

60SBD =

ta được

SBD

đều.

Do vậy

2 2 2 2

AB AD BD SB AB SA SA AD a+ = = = +  = =

.

Vậy

3

.

11

..

33

S ABCD

V SA AB AD a==

.

Câu 3: Cho hình chóp tam giác

.S AB C

có đáy là tam giác đều cạnh

a

. Cạnh bên

SA

vuông góc với

đáy

( )

ABC

và có

2SA a=

. Thể tích khối chóp

SABC

bằng:

A.

3

2

a

. B.

2

3

6

a

. C.

3

12

a

. D.

3

6

12

a

.

S

C

A

B

D

VÍ DỤ MINH HỌA

B

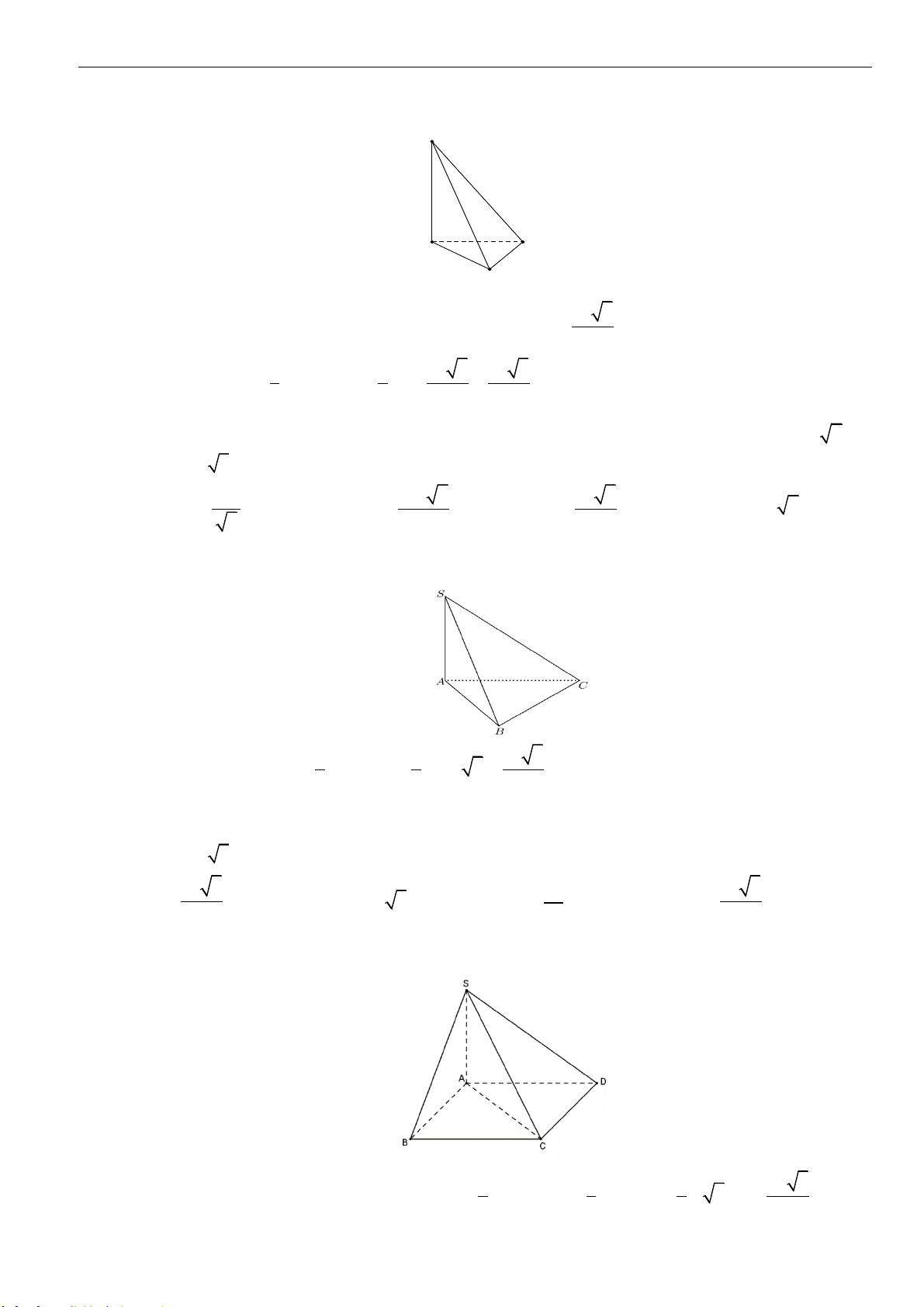
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

5 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Lời giải

Chọn B

Vì

ABC

là tam giác đều có cạnh bằng

a

nên

2

3

4

ABC

a

S



=

.

Khi đó

23

1 1 3 3

2

3 3 4 6

SABC ABC

aa

V SA S a



=   =   =

.

Câu 4: Cho hình chóp

.S AB C

có đáy

ABC

là tam giác vuông cân tại

A

, cạnh huyền bằng

2a

và

3SA a=

,

SA

vuông góc với đáy. Thể tích

V

của khối chóp đã cho bằng

A.

3

4

3

a

V =

. B.

3

46

3

a

V =

. C.

3

6

a

V =

. D.

3

22Va=

.

Lời giải

Chọn C

Ta có

3

1 1 3

. . . 3

3 6 6

ABC

a

AB a V S SA a a a



=  = = =

.

Câu 5: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

. Biết

( )

SA ABCD⊥

và

3SA a=

. Thể tích khối chóp

.S ABCD

là

A.

3

a

. B.

3

3a

. C.

3

4

a

. D.

3

12

a

.

Lời giải

Chọn A

Thể tích khối chóp

.S ABCD

là

3

22

.

1 1 1 3

. . . 3.

3 3 3 3

S ABCD ABCD

a

V SAS SA AB a a= = = =

.

a

2a

a

S

A

B

C

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 6

Câu 6: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật,

AB a

,

3AD a

,

SA

vuông góc

với đáy và mặt phẳng

SBC

tạo với đáy một góc

60

. Tính thể tích

V

của khối chóp

.S ABCD

A.

3

a

V

. B.

3

3Va

. C.

3

a

V

. D.

3

Va

.

Lời giải

Chọn D

Ta có

; 60SBC ABCD SBA

Xét

SAB

vuông tại

A

ta có

tan tan60 3

SA SA

SBA SA a

AB a

.

Vậy thể tích khối chóp

.S ABCD

là

3

11

. . . 3. . 3

33

ABCD

V SAS a a a a

.

Câu 7: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật,

SA

vuông góc với đáy,

,2AB a AD a==

. Góc giữa

SB

và đáy bằng

0

45

. Thể tích của khối chóp

.S ABCD

bằng

A.

3

2

3

a

. B.

3

a

. C.

3

2

6

a

. D.

3

2

3

a

.

Lời giải

Chọn A

Ta có

( )

0

, 45SBA SB ABCD==

. Suy ra

SAB

vuông cân tại

A

SA AB a = =

.

3

.

12

. . .

33

S ABCD

a

V SA AB AD==

.

Câu 8: Cho hình chóp

.S ABCD

có

SA

vuông góc đáy, hai mặt phẳng

( )

SAB

và

( )

SBC

vuông góc với

nhau,

3SB a=

, góc giữa

SC

và

( )

SAB

là

45

và

30ASB =

. Gọi thể tích khối chóp

.S ABCD

là

V

. Tỉ số

3

a

V

là

A.

8

3

. B.

83

3

. C.

23

3

. D.

4

3

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

7 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Lời giải

Chọn A

Ta có

( ) ( ) ( )

SA ABC SAB ABC⊥  ⊥

.

Ta có

( ) ( ) ( ) ( )

( ) ( )

( )

;SBC SAB ABC SAB

BC SAB

SBC ABC BC

⊥⊥





⊥



=





.

Khi đó

( )

, , 45SC SAB SC SB BSC= = = 

BSC

vuông cân tại

B

3.BC a=

Ta có

3

.sin

2

a

AB SB ASB==

2

1 1 3 3

3.

2 2 2 4

ABC

aa

S AB BC a=  =   =

Ta có

3

.cos .

2

a

SA SB ASB==

Vậy

2 3 3

.

1 1 3 3 3 8

3 3 4 2 8 3

S ABC ABC

a a a a

V S SA

V

= =   =  =

.

Câu 9: Cho khối chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

3a

, cạnh

SA

vuông góc với mặt

phẳng

( )

ABC D

và

SB

tạo với đáy một góc

60

o

. Tính thể tích của khối chóp

.S ABCD

.

A.

3

9a

. B.

3

9

2

a

. C.

3

3a

. D.

3

4

a

.

Lời giải

Chọn C

Ta có

( )

SA ABCD

AB

SB ABCD B

⊥









=





là hình chiếu của

SB

lên

( )

ABC D

( )

,,SB ABCD SB AB SBA = =

do

SAB

vuông ở

( )

A SA ABCD SA AB⊥  ⊥

60

o

SBA=

.

Tam giác

SAB

vuông ở

tan tan 3

SA

A SBA SA AB SBA a

AB

 =  = =

.

Vậy

( )

2

3

.

11

. .3 . 3 3

33

S ABCD ABCD

V SA S a a a= = =

.

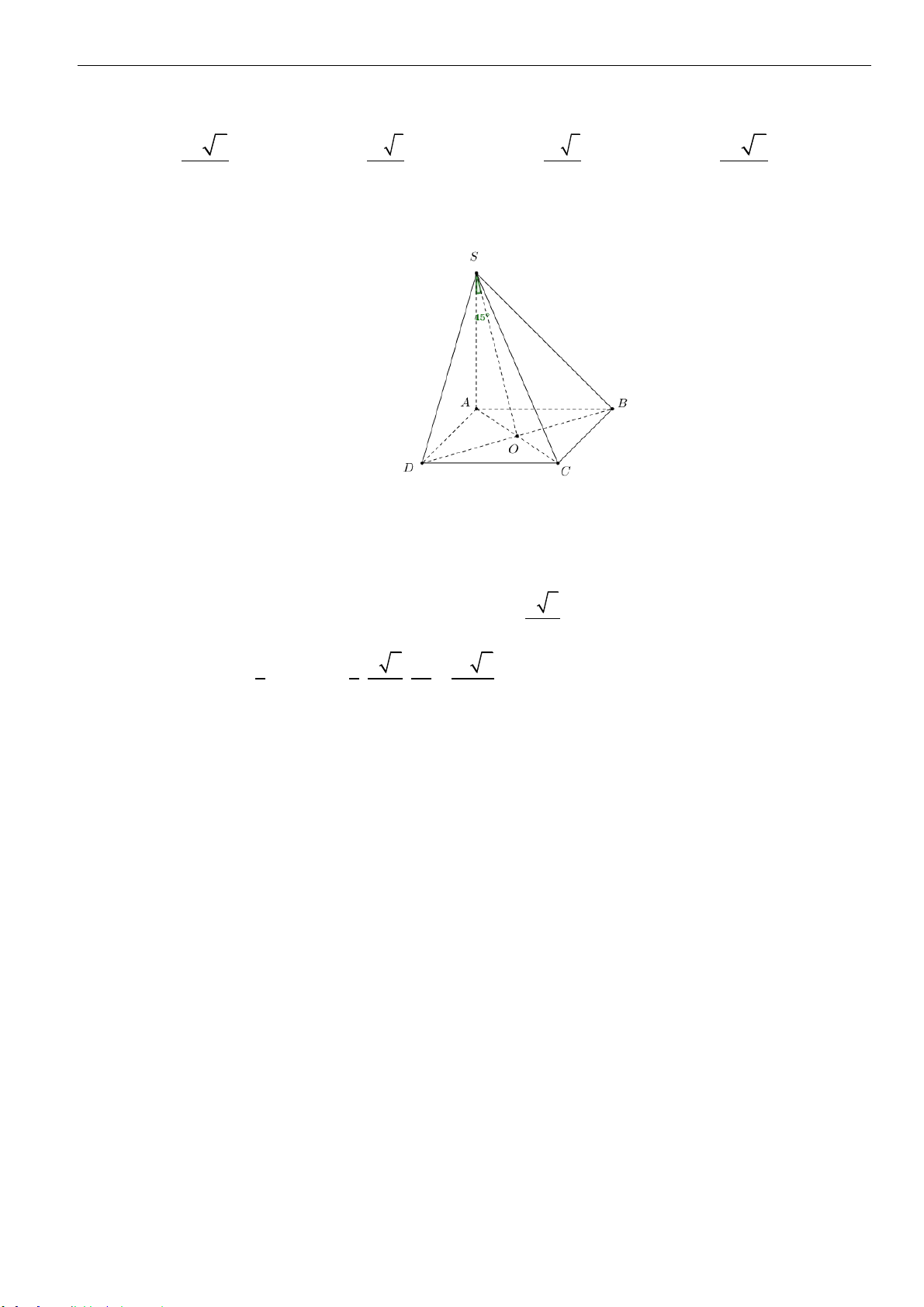
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 8

Câu 10: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

, cạnh bên

SA

vuông góc với mặt

phẳng đáy, góc giữa

SA

và mặt phẳng

( )

SBD

bằng

45

. Thể tích khối chóp

.S AB D

bằng

A.

3

6

4

a

. B.

3

12

a

. C.

3

4

a

. D.

3

2

12

a

Lời giải

Chọn D

Giao điểm của

SA

và mặt phẳng

( )

SBD

là

S

.

Gọi

O

là trung điểm

BD

thì

⊥AO BD

.

Có

⊥SA BD

nên

( )

⊥SAO BD

. Từ đó góc giữa

SA

và mặt phẳng

( )

SBD

là góc

45 = ASO

Xét tam giác

SAO

vuông cân tại

A

:

2

==

a

SA AO

Vậy

23

.

1 1 2 2

. . . . .

3 3 2 2 12

= = =

S ABD ABD

a a a

V SAS

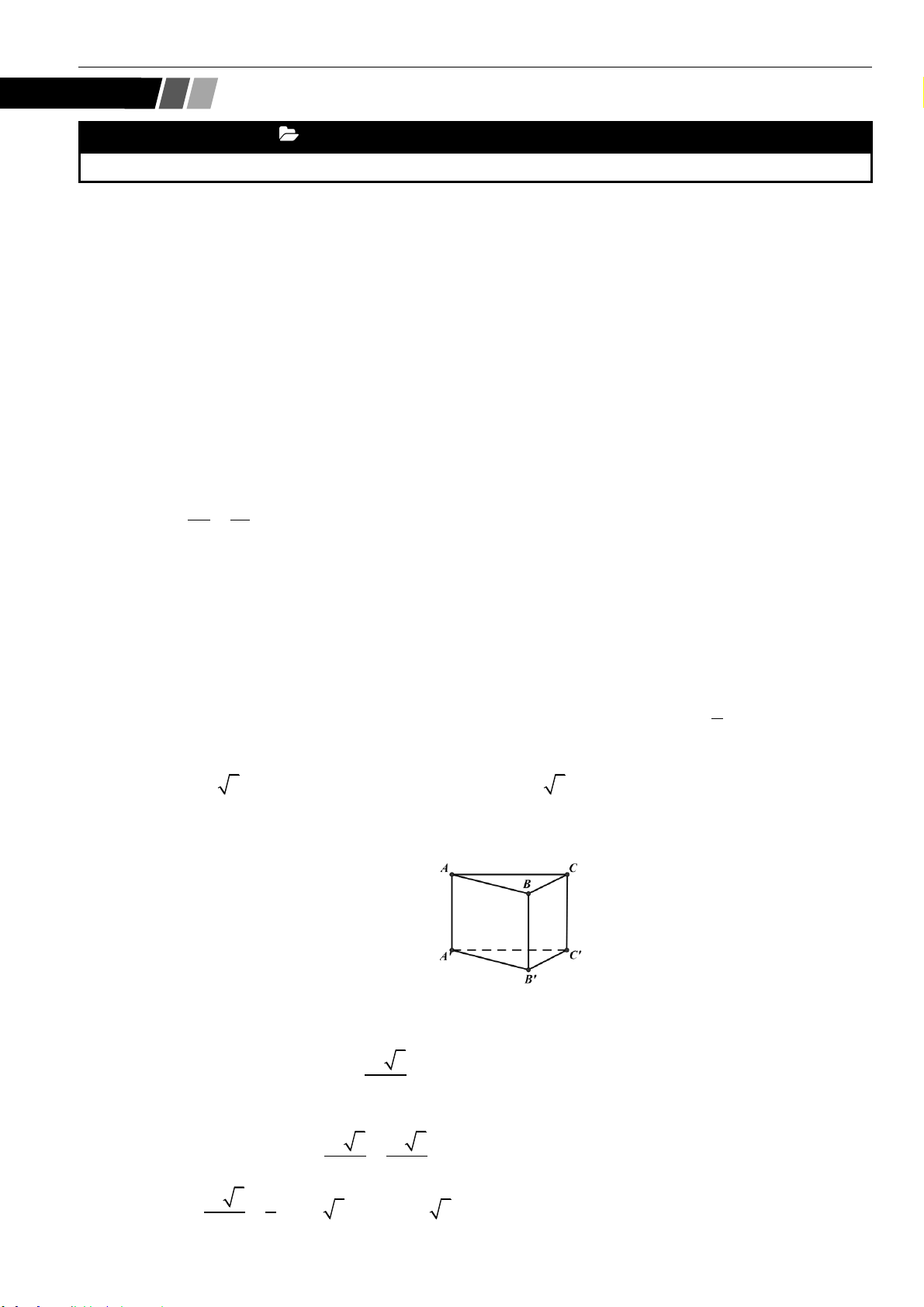
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

9 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Dạng 1: Mở đầu về thể tích khối đa diện

Dựa vào kiến thức được nêu trong phần lý thuyết

Câu 1: Thể tích khối lập phương là

3

27cm

. Diện tích toàn phần của hình lập phương tương ứng bằng

A.

2

54cm

. B.

2

36cm

. C.

2

16cm

. D.

2

9cm

.

Lời giải

Chon A

3

27V cm=

suy ra cạnh của hình lập phương bằng

3

.

Diện tích toàn phần của hình lập phương là

2

3 .6 54=

.

Câu 2: Cho khối chóp có thể tích bằng

3

30cm

và chiều cao bằng

5cm

. Diện tích đáy của khối chóp đã

cho bằng

A.

6.cm

B.

18 .cm

C.

24 .cm

D.

12 .cm

Lời giải

Chọn B

3 90

18 .

5

V

S cm

h

= = =

Câu 3: Cho hình lập phương có cạnh bằng

3

. Tổng diện tích các mặt của hình lập phương đã cho bằng

A.

54

. B.

12

. C.

36

. D.

24

.

Lời giải

Chọn A

Tổng diện tích các mặt của hình lập phương là:

2

6.3 54S ==

.

Câu 4: Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng

a

, có thể tích

( )

3

9

.

4

V dm=

Tính giá trị

của

a

.

A.

( )

33a dm=

. B.

( )

3a dm=

. C.

( )

3 dm

. D.

( )

9 dm

.

Lời giải

Chọn C

Lăng trụ đều

. ' ' 'ABC A B C

là lăng trụ đứng và có đáy

ABC

là tam giác đều.

Chiều cao lăng trụ

'h AA a==

.

Diện tích đáy

ABC

:

2

3

4

ABC

a

S =

.

Thể tích khối lăng trụ đều

. ' ' 'ABC A B C

là:

23

. ' ' '

33

..

44

ABC A B C ABC

aa

V h S a= = =

.

Ta có

( )

3

39

3 9 3 .

44

a

a a dm=  =  =

BÀI TẬP TRẮC NGHIỆM

C

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 10

Câu 5: Cho khối chóp tam giác đều có cạnh đáy bằng

2a

và thể tích bằng

3

a

. Chiều cao của khối chóp

đã cho bằng

A.

3a

. B.

23a

. C.

3

a

. D.

3

2

a

.

Lời giải

Chọn A

Ta có

1

3

V Sh= 

Suy ra

3

2

33

(

3

4

)

3

2

a

Va

h

S

a 

= = =

.

Câu 6: Cho hình lập phương có cạnh bằng 2. Tổng diện tích các mặt của hình lập phương đó bằng

A.

16

. B.

12

. C.

4

. D.

24

.

Lời giải

Chọn D

Hình lập phương có diện tích toàn phần:

2

6.2 24

.

Câu 7: Cho hình lăng trụ đứng có diện tích đáy là

2

3a

, độ dài cạnh bên là

2a

. Khi đó thể tích của

khối lăng trụ bằng

A.

3

6a

. B.

3

3a

. C.

3

2a

. D.

3

6

3

a

.

Lời giải

Chọn A

Ta có:

23

3 . 2 6V a a a==

.

Câu 8: Cho hình lập phương có cạnh bằng

2

. Tổng diện tích các mặt của hình lập phương đã cho bằng

A.

16

. B.

12

. C.

4

. D.

24

.

Lời giải

Chọn D

Hình lập phương có 6 mặt là hình vuông có các cạnh bằng nhau.

Do đó tổng diện tích các mặt là

2

2 .6 24S

.

Câu 9: Mệnh đề nào sau đây sai?

A. Hai khối hộp chữ nhật có diện tích toàn phần bằng nhau thì có thể tích bằng nhau.

B. Hai khối lăng trụ có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau.

C. Hai khối lập phương có diện tích toàn phần bằng nhau thì có thể tích bằng nhau.

D. Hai khối chóp có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau.

Lời giải

Chọn A

Ta có thể tích khối lăng trụ bằng

.Bh

, với

B

là diện tích đáy,

h

là chiều cao. Do đó B đúng.

Thể tích khối chóp bằng

1

.

3

Bh

, với

B

là diện tích đáy,

h

là chiều cao. Do đó D đúng.

Hai khối lập phương có diện tích toàn phần

2

6.canh

bằng nhau, thì cạnh

a

bằng nhau do đó thể

tích bằng nhau. Suy ra C đúng.

Vậy chọn phương án A sai.

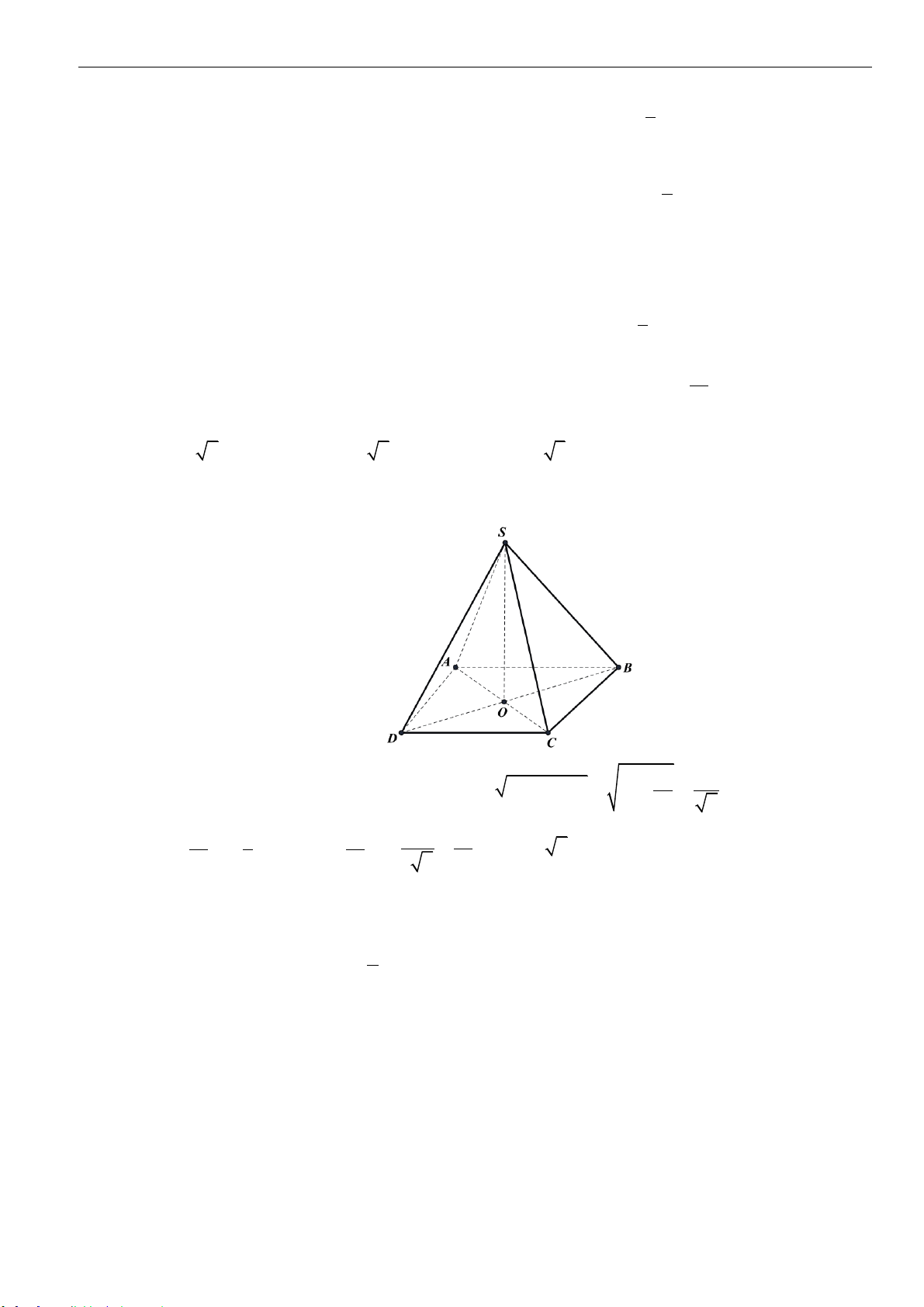
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

11 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 10: Trong các mệnh đề sau, mệnh đề nào sai?

A. Thể tích khối chóp có đường cao

h

và diện tích đáy

B

là

1

3

V Bh=

.

B. Thể tích khối lăng trụ có đường cao

h

và diện tích đáy

B

là

.V B h=

.

C. Thể tích khối tứ diện có đường cao

h

và diện tích đáy

B

là

1

6

V Bh=

.

D. Thể tích khối lập phương cạnh

a

là

3

Va=

.

Lời giải

Chọn C

Thể tích khối tứ diện có đường cao

h

và diện tích đáy

B

là

1

3

V Bh=

.

Câu 11: Khối chóp

.S AB CD

có tất cả các cạnh bằng nhau và có thể tích bằng

16

3

. Tính cạnh của khối

chóp.

A.

22

B.

2

. C.

3

. D.

2

.

Lời giải

Chọn A

Đặt độ dài cạnh hình chóp là

x

. Ta có:

2

2 2 2

2

xx

SO SA AO x= − = − =

.

16

3

V =

1 16

. .S

33

ABCD

SO=

3

16

3

32

x

=

22x=

.

Câu 12: Cho khối lăng trụ có diện tích đáy

2

6Ba=

và chiều cao

2ha=

. Thể tích của khối lăng trụ đã

cho bằng

A.

3

8a

. B.

3

4

3

a

. C.

3

4a

. D.

3

12a

.

Lời giải

Chọn D

Thể tích của khối lăng trụ có diện tích đáy

2

6Ba=

và chiều cao

2ha=

là:

23

. 6 .2 12V B h a a a= = =

.

Câu 13: Cho khối lăng trụ có thể tích bằng

3

24a

và chiều cao bằng

3a

. Diện tích một mặt đáy của khối

lăng trụ đã cho bằng

A.

2

16a

. B.

2

8a

. C.

2

6a

. D.

2

72a

.

Lời giải

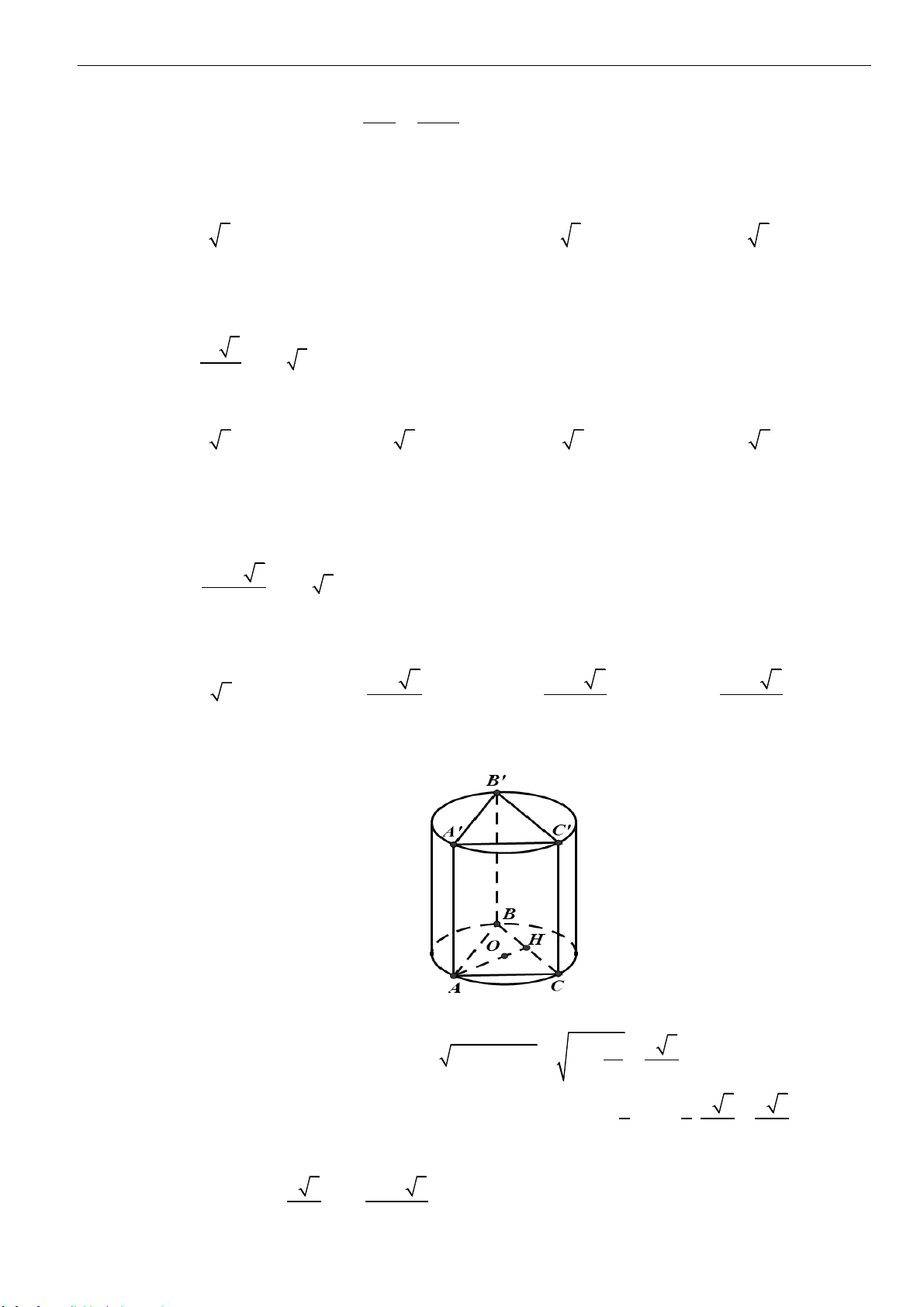
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 12

Chọn B

Ta có

3

2

24

.8

3

LT

LT ð ð

V

a

V S h S a

ha

=  = = =

.

Vậy diện tích một mặt đáy của khối lăng trụ đã cho bằng

2

8a

.

Câu 14: Tính tổng diện tích các mặt của một hình bát diện đều cạnh

a

.

A.

2

23a

. B.

2

4a

. C.

2

3a

. D.

2

43a

.

Lời giải

Chọn A

Một hình bát diện đều là hình có 8 mặt đều là tam giác đều có cạnh

a

.

2

3

8. 2 3

4

a

Sa==

.

Câu 15: Tổng diện tích tất cả các mặt của hình bát diện đều cạnh bằng

2a

là

A.

2

2 3.a

B.

2

8 3.a

C.

2

3.a

D.

2

43a

Lời giải

Chọn B

Hình bát diện đều có

8

mặt là các tam giác đều cạnh bằng

2a

.

Tổng diện tích tất cả các mặt của hình bát diện đều cạnh bằng

2a

là:

2

(2 ) 3

8. 8 3

4

a

Sa==

.

Câu 16: Cho hình lăng trụ đứng

.ABC A B C

  

có đáy là tam giác đều cạnh

a

và cạnh bên

2a

. Tính diện

tích xung quanh hình trụ ngoại tiếp hình lăng trụ đứng

.ABC A B C

  

.

A.

2

3a



. B.

2

3

a



. C.

2

23

3

a



. D.

2

43

3

a



.

Lời giải

Chọn D

Gọi

H

là trung điểm

BC

khi đó ta có

AH BC⊥

.

Xét

ABH

vuông tại

H

ta có

2

2 2 2

3

42

aa

AH AB BH a= − = − =

.

Gọi

( )

,OR

là đường tròn ngoại tiếp

ABC

khi đó ta có:

2 2 3 3

.

3 3 2 3

aa

R AH= = =

.

Vậy diện tích xung quang hình trụ ngoại tiếp hình lăng trụ đứng

.ABC A B C

  

là

2

3 4 3

2 2 . .2

33

xq

aa

S Rh a





= = =

.

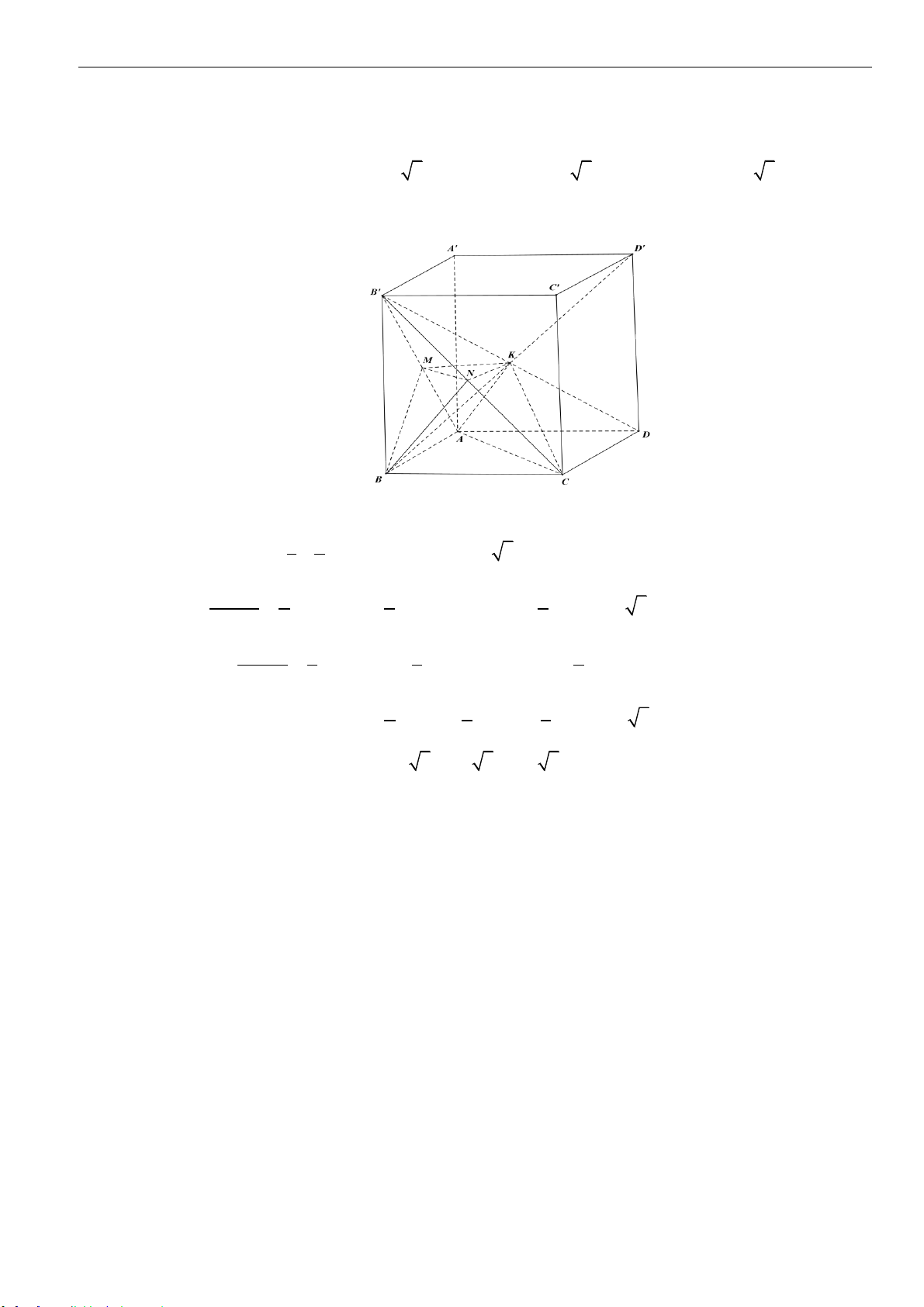
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

13 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 17: Cho hình lăng trụ đứng

.ABCD A B C D

   

với đáy là hình thoi có cạnh bằng

4a

,

6AA a



=

,

0

120BCD =

. Gọi

,,M N K

lần lượt là trung điểm của

,,AB B C BD

  

. Tính thể tích khối đa diện

lồi có các đỉnh là các điểm

, , , , ,A B C M N K

.

A.

3

9a

. B.

3

16 3a

. C.

3

93a

. D.

3

12 3a

Lời giải

Chọn C

Ta có:

00

120 60BCD ABC=  =

.

03

..

11

. .4 .4 .sin60 .6 8 3

32

B ABC B ACD

V V a a a a





= = =





.

Ta có:

3

.

. . .

.

1 1 3

63

4 4 4

B BMN

B BMN B ABC MNABC B ABC

B ABC

V

V V V V a

V



  



=  =  = =

.

Mặt khác:

.

. . .

.

1 1 7

8 8 8

B KMN

B KMN B DAC MNKACD B DAC

B DAC

V

V V V V

V



  



=  =  =

3

. . . .

7 1 3

33

8 2 8

MNKAC MNKACD K ACD B DAC B DAC B DAC

V V V V V V a

  

 = − = − = =

.

Vậy

3 3 3

6 3 3 3 9 3

MNKABC MNABC MNKAC

V V V a a a= + = + =

.

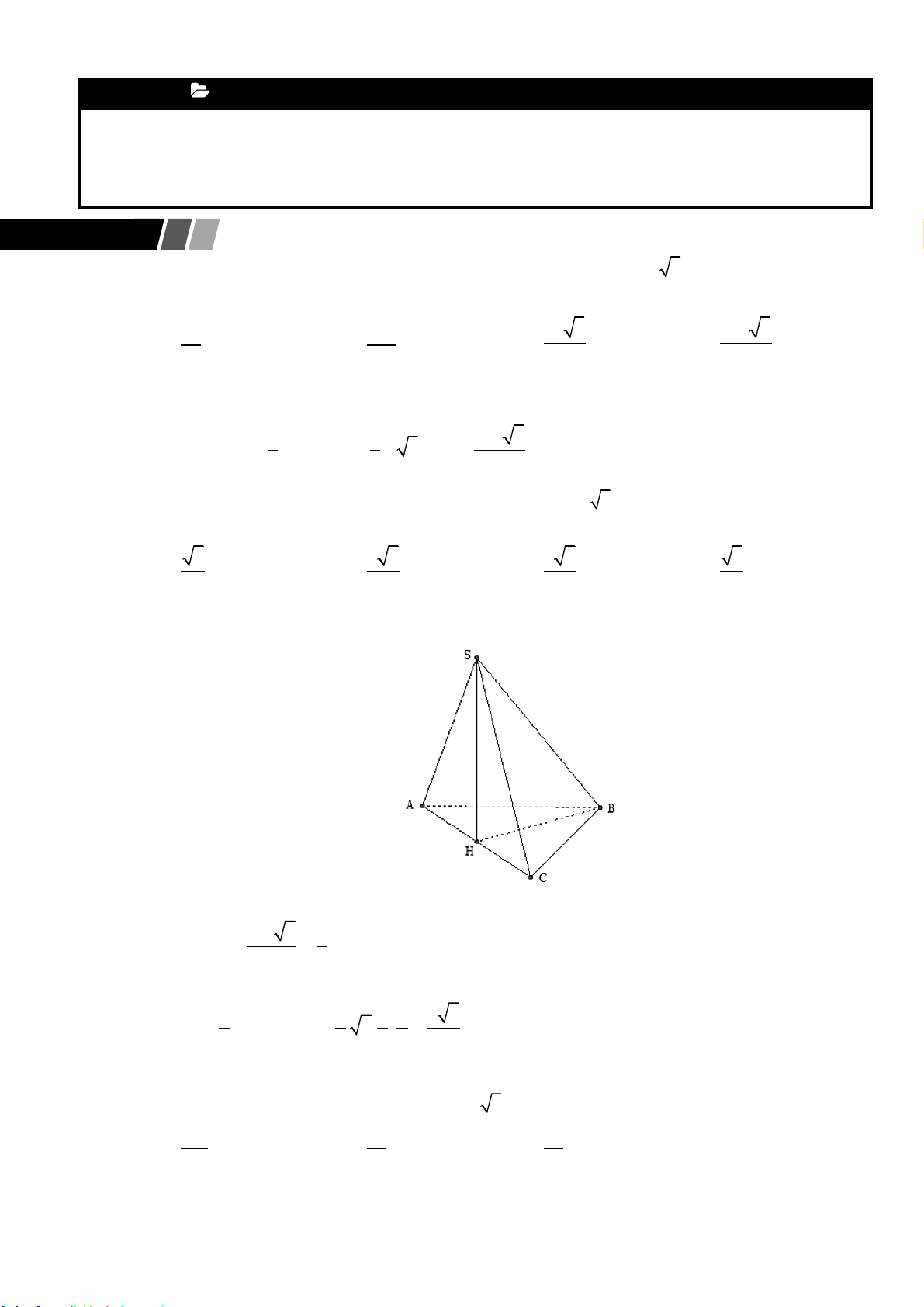
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

1 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Dạng 2: Thể tích khối chóp có cạnh bên vuông góc với đáy

▪ Một hình chóp có một cạnh bên vuông góc với đáy thì cạnh bên đó chính là đường cao.

▪ Một hình chóp có hai mặt bên kề nhau cùng vuông góc với đáy thì cạnh bên là giao tuyến của hai

mặt đó vuông góc với đáy.

Câu 1: Cho hình chóp

SABCD

có đáy

ABCD

là hình chữ nhật với

3,AB a AD a==

, cạnh

SA

có độ

dài bằng

2a

và vuông góc với mặt phẳng đáy. Tính thể tích khối chóp

SABCD

A.

3

a

. B.

3

2

3

a

. C.

3

a

. D.

3

23

3

a

.

Lời giải

Chọn D

Ta có

3

1 1 2 3

. . 3. .2

3 3 3

SABCD SABCD

a

V S SA a a a= = =

Câu 2: Cho khối chóp

.S ABC

có đáy là tam giác đều cạnh bằng

3

, tam giác

SAC

đều và nằm trong

mặt phẳng vuông góc với mặt phẳng đáy. Thể tích của khối chóp đã cho bằng

A.

3

12

. B.

33

8

. C.

33

4

. D.

3

8

.

Lời giải

Chọn B

Gọi

H

là trung điểm của

AC

, hai tam giác

SAC

và

ABC

là hai tam giác đều, bằng nhau và

33

22

AB

HS HB= = =

.

Ba đường thẳng

AC

,

HS

,

HB

đôi một vuông góc với nhau, suy ra:

.

1 1 3 3 3 3

. . 3. .

6 6 2 2 8

S ABC

V AC HB HS= = =

.

Câu 3: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật, tam giác

SCD

đều và nằm trong mặt

phẳng vuông góc với đáy,

CD a=

,

3BC a=

. Thể tích khối chóp

.S ABCD

bằng

A.

3

2

a

. B.

3

6

a

. C.

3

2

a

. D.

3

a

.

Lời giải

Chọn C

VÍ DỤ MINH HỌA

B

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 2

Gọi

I

là trung điểm

CD

SI CD⊥

.

Ta có

( ) ( )

( )

;

SCD ABCD

SCD ABCD CD

SI SCD SI CD

⊥





=





⊥



( )

SI ABCD⊥

.

Do đó

3

.

1 1 3

. . . . 3

3 3 2 2

S ABCD ABCD

aa

V SI S a a= = =

.

Câu 4: Cho hình chóp

.S ABCD

có đáy là hình chữ nhật, mặt bên

SAD

là tam giác đều cạnh

4a

và nằm

trong mặt phẳng vuông góc với mặt phẳng đáy. Góc giữa mặt phẳng

( )

SBC

và mặt phẳng

( )

ABCD

là

o

30

. Thể tích của khối chóp

.S ABCD

là

A.

3

24 3a

. B.

3

16 3a

. C.

3

43a

. D.

3

48 3a

.

Lời giải

Chọn B

Gọi

H

là trung điểm của

( )

2 3,AD SH a SH ABCD = ⊥

.

Gọi

K

là trung điểm của

BC

( ) ( )

( )

0

, 30SBC ABCD SKH SKH =  =

0

66

tan30

SH

HK a AB a = =  =

. Vậy

3

1

. 16 3

3

ABCD

V SH S a==

.

Câu 5: Cho hình chóp

.S ABC

có

SAB

và

ABC

là hai tam giác đều cạnh

a

và nằm trong hai mặt phẳng

vuông góc với nhau. Tính theo

a

thể tích của khối chóp

..S ABC

A.

3

2

3

a

. B.

3

a

. C.

3

a

. D.

3

3a

.

Lời giải

Chọn C

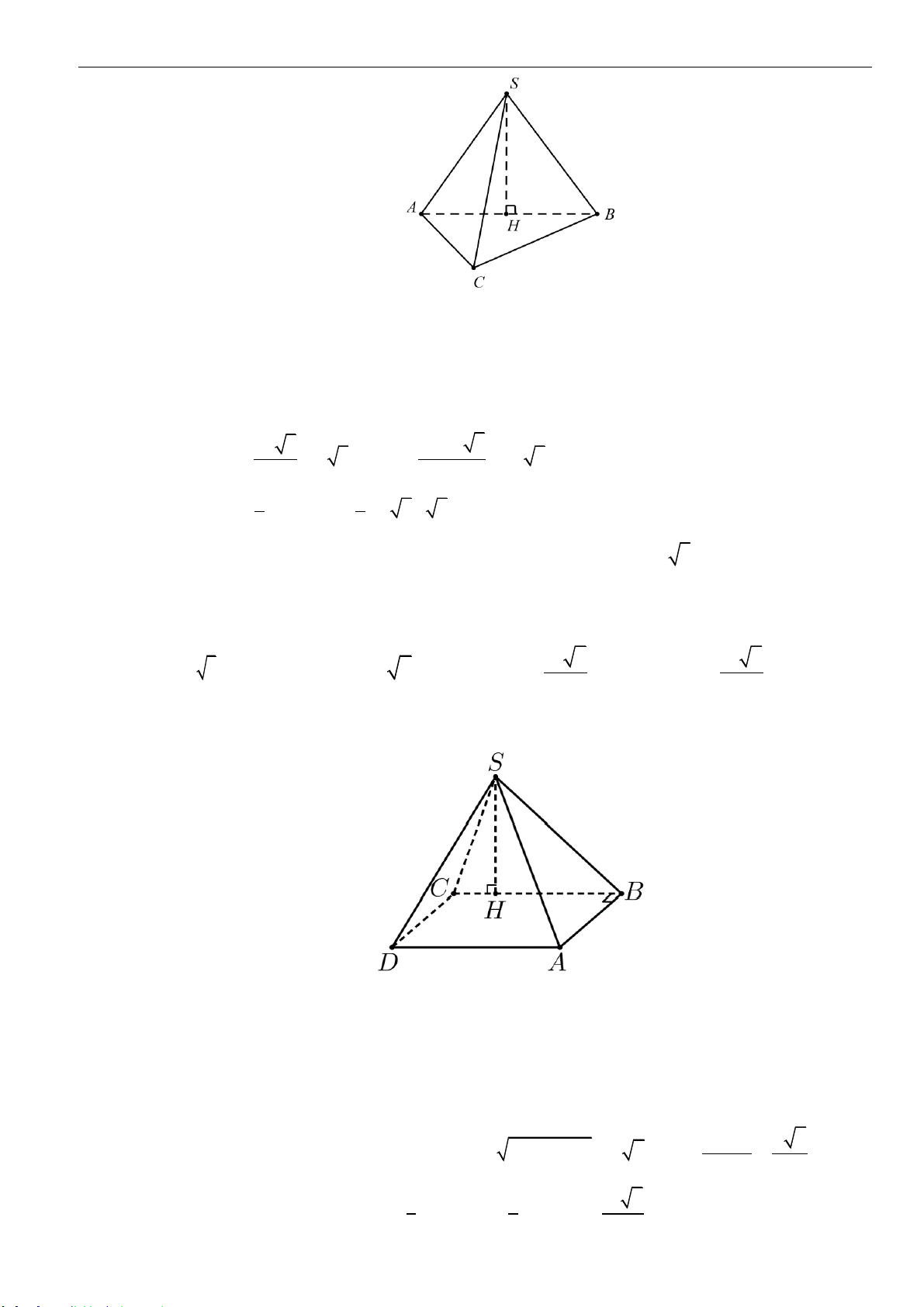
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

3 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Gọi

H

là trung điểm của

AB

. Suy ra

SH AB⊥

.

Ta có:

( ) ( )

SAB ABC

SAB ABC AB

SH AB

⊥





=





⊥



( )

SH ABC⊥

.

Ta có:

( )

2

23

3, 3

24

ABC

a

SH a S a



= = = =

.

Vậy

23

.

11

. . 3. 3

33

S ABC ABC

V S SH a a a



= = =

.

Câu 6: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh bằng

3,a

tam giác

SBC

vuông

tại

S

và nằm trong mặt phẳng vuông góc với đáy, đường thẳng

SD

tạo với mặt phẳng

( )

SBC

một góc

60

. Thể tích của khối chóp đã cho bằng

A.

3

3.a

B.

3

6.a

C.

3

6

.

6

a

D.

3

6

.

3

a

Lời giải

Chọn D

Kẻ

.SH BC⊥

Từ giả thiết suy ra

( )

SH ABCD⊥

.

Xác định được hình chiếu vuông góc của

D

lên

( )

SBC

là điểm

C

.

Do đó:

( )

60,,SD SBC SD SC DSC= = = 

.

Tam giác vuông

SCD

vuông tại

C

có

.cotSC DC DSC a==

.

Tam giác vuông

SBC

vuông tại

S

có

22

.

2,

3

6SB SC a

SB BC SC a SH

BC

= − = = =

.

Vậy thể tích khối chóp:

3

2

.

11

..

3 3 3

6

S ABCD ABCD

a

V S SH AB SH= = =

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 4

Câu 7: Cho hình chóp

.S ABCD

có đáy là hình chữ nhật,

=AB a

,

2=AD a

. Tam giác SAB cân tại S và

nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng

( )

ABCD

bằng

45

. Thể tích của khối chóp

.S ABCD

là:

A.

3

17

9

a

. B.

3

17

3

a

. C.

3

17

3

a

. D.

3

17

6

a

.

Lời giải

Chọn C

Ta có có:

2

.2==

ABCD

S AB AD a

.

Gọi M là trung điểm của AB, khi đó

( )

⊥  ⊥SM AB SM ABCD

.

Do đó

( )

(

)

( )

, , 45= = = SC ABCD SC MC SCM

.

Khi đó

2

17

4

42

= = + =

aa

SM MC a

.

Vậy

3

2

.

1 1 17 17

. . .2

3 3 2 3

= = =

S ABCD ABCD

aa

V SM S a

.

A

B

C

D

S

M

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

5 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 1: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

. Biết

( )

SA ABCD⊥

và

3SA a=

. Thể tích của khối chóp

.S ABCD

là:

A.

3

12

a

. B.

3

3a

. C.

3

a

. D.

3

4

a

.

Lời giải

Chọn C

Thể tích khối chóp

.S ABCD

là:

3

22

.

1 1 3

. . . 3. .

3 3 3

S ABCD

a

V SA AB a a= = =

Câu 2: Cho khối chóp

.S ABC

có đáy

ABC

là tam giác vuông cân tại

A

,

( )

2, 12,AB SA SA ABC= = ⊥

. Tính thể tích khối chóp

.S ABC

?

A.

8

. B.

16

. C.

24

. D.

6

.

Lời giải

Chọn A

Thể tích khối chóp là

1 1 1

. . . .2.2.12 8

3 3 2

V S h= = =

.

Câu 3: Cho khối tứ diện

ABCD

có

,,AB AC AD

đôi một vuông góc và

2 , 3= = =AB AC a AD a

. Thể

tích

V

của khối tứ diện đó là:

A.

3

4=Va

. B.

3

2=Va

. C.

3

=Va

. D.

3

3=Va

.

Lời giải

Chọn B

Do khối tứ diện

ABCD

có

,,AB AC AD

đôi một vuông góc nên

3

1

. . 2

6

==

ABCD

V AB AC AD a

.

Câu 4: Cho khối chóp

.S ABC

có đáy là tam giác đều cạnh

a

,

( )

SA ABC⊥

,

SA a=

(tham khảo hình

vẽ bên dưới). Thể tích của khối chóp đã cho bằng:

A.

3

4

a

. B.

3

6

a

. C.

3

3a

. D.

3

12

a

.

Lời giải

Chọn D

Vì

( )

SA ABC⊥

nên ta có

SA

là đường cao của hình chóp hay

h SA a==

.

Do đáy của hình chóp là tam giác đều cạnh

a

nên ta có:

2

3

4

a

S =

.

Khi đó thể tích của khối chóp đã cho là:

1

.

3

V S h=

23

1 3 3

..

3 4 12

aa

a==

(đvtt).

BÀI TẬP TRẮC NGHIỆM

C

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 6

Câu 5: Cho hình chóp

.S ABC

có đáy là tam giác đều cạnh

2a

, cạnh bên

SA

vuông góc với đáy và

3SA a=

. Tính thể tích

V

của khối chóp

.S ABC

A.

3

1

2

Va=

. B.

3

4

Va=

. C.

3

22Va=

. D.

3

Va=

.

Lời giải

Chọn D

Ta có tam giác đều cạnh

2a

nên

2

43

3

4

ABC

a

Sa



==

.

Thể tích

V

của khối chóp

.S ABC

bằng

23

.

11

. 3. 3

33

S ABC ABC

V SAS a a a



= = =

.

Câu 6: Cho tứ diện

SABC

có các cạnh

, , SA SB SC

đôi một vuông góc với nhau. Biết

3,SA a=

4 , 5 .SB a SC a==

Tính theo

a

thể tích

V

của khối tứ diện

.SABC

A.

3

5.Va=

B.

2

5

.

2

a

V =

C.

3

10 .Va=

D.

3

20 .Va=

Lời giải

Chọn C

Thể tích của khối tứ diện là:

3

11

. . .3 .4 .5 10 .

66

V SA SB SC a a a a= = =

Câu 7: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác đều cạnh

a

. Biết

( )

SA ABC⊥

và

3SA a=

.

Tính thể tích khối chóp

.S ABC

A.

4

a

. B.

3

2

a

. C.

3

4

a

. D.

3

4

a

.

Lời giải

Ta có:

23

.

31

.

4 3 4

ABC S ABC ABC

aa

S V SAS=  = =

Câu 8: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

2a

,

( )

SA ABCD⊥

,

2SA a=

.

Tính thể tích khối chóp

.S ABCD

A.

3

4

3

a

V =

. B.

3

4

3

a

V



=

. C.

3

4Va=

. D.

3

4Va



=

.

Lời giải

Chọn A

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

7 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Diện tích hình vuông

ABCD

là:

( )

2

22

ABCD

S a a==

Thể tích khối chóp

.S ABCD

là:

3

2

.

1 1 4

. .2 .2

3 3 3

S ABCD ABCD

a

V SA S a a= = =

Câu 9: Cho khối chóp

.S ABC

có đáy

ABC

là tam giác đều cạnh

a

, hai mặt bên

( )

SAB

và

( )

SAC

cùng vuông góc với đáy và

3SC a=

. Thể tích khối chóp bằng

A.

3

4

a

. B.

3

2

a

. C.

3

6

12

a

. D.

3

26

9

a

.

Lời giải

Chọn C

Ta có

( ) ( )

( )

SAB ABC

SAC ABC SA ABC

SAB ABC SA

⊥





⊥  ⊥





=



Xét

SAC

vuông tại

A

ta có:

2 2 2 2

32SA SC AC a a a= − = − =

Diện tích của tam giác

ABC

là

2

3

4

a

Thể tích khối chóp

23

.

1 1 3 6

. . . 2.

3 3 4 12

S ABC ABC

aa

V SA S a



= = =

.

Câu 10: Cho khối chóp

.S ABC

có đáy

ABC

là tam giác đều cạnh

a

, hai mặt bên

( )

SAB

và

( )

SAC

cùng vuông góc với đáy và

3SC a=

. Thể tích khối chóp bằng

A.

3

4

a

. B.

3

2

a

. C.

3

2

6

1

a

. D.

3

26

9

a

.

Lời giải

Chọn C

B

A

C

S

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 8

Ta có

( ) ( )

SAB SAC SA

SAB ABC

SAC ABC

=





⊥





⊥



( )

SA ABC⊥

.

Trong tam giác

SAC

vuông tại

A

có

22

2SA SC AC a= − =

.

Diện tích tam giác

ABC

là

2

3

4

ABC

a

S



=

.

Thể tích khối chóp

.S ABC

là

23

1 1 3 6

. . 2.

3 3 4 12

ABC

aa

V SAS a



= = =

.

Câu 11: Cho hình chóp

.S ABC

có đáy là tam giác đều cạnh bằng

a

. Cạnh bên

SC

vuông góc với mặt

phẳng

( )

,ABC SC a=

. Thể tích khối chóp

.S ABC

bằng

A.

3

a

. B.

3

9

a

. C.

3

2

12

a

. D.

3

12

a

.

Lời giải

Chọn D

Do đáy là tam giác đều nên niện tích đáy

2

3

4

a

B =

và chiều cao

h SC a==

Vậy thể tích khối chóp đã cho

3

13

.

3 12

a

V B h==

.

Câu 12: Cho khối chóp

.S ABCD

có đáy là hình thoi cạnh

2a

,

0

60ABC =

, cạnh bên

SA

vuông góc với

mặt phẳng đáy, mặt bên

( )

SCD

tạo với đáy một góc

0

60

. Thể tích khối chóp

.S ABC

bằng

A.

3

3a

. B.

3

33a

. C.

3

23a

. D.

3

2a

.

Lời giải

Chọn A

Gọi

I

là trung điểm của

CD

.

Vì

ABCD

là hình thoi có

00

60 60 ,ABC ADC AD DC=  = =

ACD

đều

AI CD⊥

.

Vậy

( ) ( )

0

; 60SCD ABCD SIA==

. Vì

ACD

đều

3

2

AI AD a = =

.

SAI

vuông tại

:A

.tan 3. 3 3SA AI SIA a a= = =

.

Dễ thấy

ABC

đều:

22

3

4

ABC

S AB a



==

. Vậy

23

.

11

. .3 . 3 3

33

S ABC ABC

V SA S a a a



= = =

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

9 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 13: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

. Biết

( )

SA ABCD⊥

và

3SA a=

. Thể tích của khối chóp

.S ABCD

là:

A.

3

3a

. B.

3

12

a

. C.

3

a

. D.

3

6

a

.

Lời giải

Chọn C

Ta có

3

2

.

13

.

33

S ABCD

a

V AB SA==

.

Câu 14: Cho khối chóp

.S ABCD

có đáy là hình chữ nhật

, 3,AB a AD a SA==

vuông góc với mặt đáy

và

SC

tạo với mặt phẳng

( )

SAB

một góc

0

30

. Thể tích của khối chóp đã cho bằng

A.

3

4

3

a

. B.

3

6

3

a

. C.

3

26

3

a

. D.

3

26a

.

Lời giải

Chọn C

Ta có:

 

()

BC AB

BC SA BC SAB

AB SA A



⊥



⊥  ⊥





=



SB

là hình chiếu của SC trên (SAB)

( )

0

, 30SC SAB CSB = =

Vì

SBC

vuông tại

3

tan30

BC

B SB a = =

Xét

SAB

vuông tại

A

, ta có:

22

22SA SB AB a= − =

Thể tích khối chóp là:

3

1 1 2 6

. . 3.2 2

3 3 3

V Bh a a a a= = =

.

Câu 15: Cho tứ diện

SABC

có các mặt

,SAB SBC

là các tam giác cân tại S và

,,SA SB SC

đôi một

vuông góc với nhau,

2AB a=

. Thể tích của khối tứ diện đã cho bằng

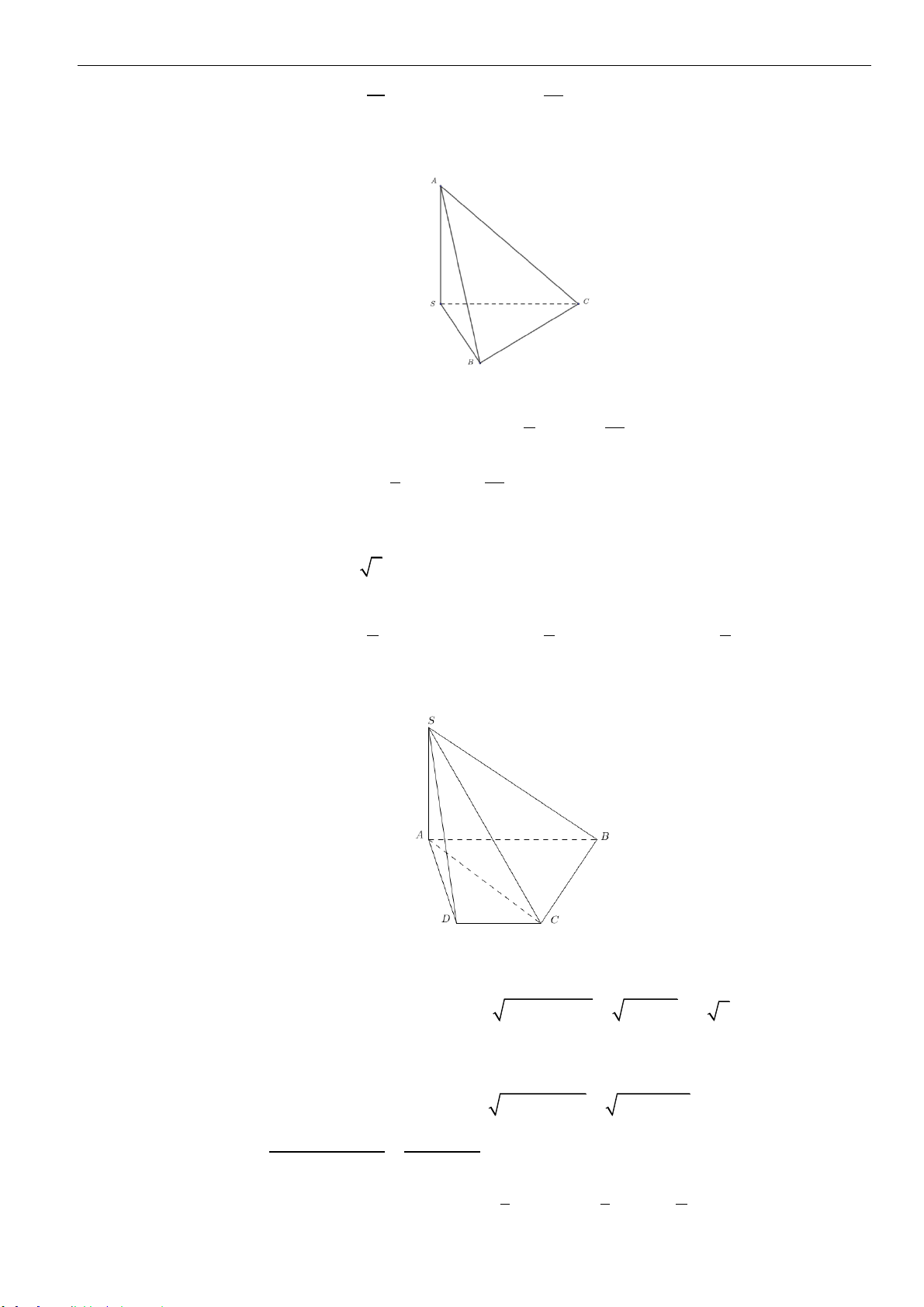
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 10

A.

3

2a

. B.

3

a

. C.

3

6

a

. D.

3

a

.

Lời giải

Chọn C

Do

SA SB⊥

,

SAB

cân tại

S

2 2 2

22SA AB a SA SB a = =  = =

.

Do

SBC

cân tại

S

nên

2

1

.

22

SBC

a

SC SB a S SB SC



= =  = =

.

Thể tích khối tứ diện bằng

3

1

.

36

SBC

a

V SAS



==

.

Câu 16: Cho khối chóp

.S ABCD

có

( )

SA ABCD⊥

, đáy

ABCD

là hình thang,

/ / ,AB CD

,7SA AD DC a BC a= = = =

. Tam giác

SBC

vuông tại

C

, tam giác

SCD

vuông tại

D

. Thể

tích khối chóp đã cho bằng

A.

3

2a

. B.

3

4

3

a

. C.

3

2

3

a

. D.

3

1

2

a

.

Lời giải

Chọn C

Ta có:

( ) ( )

CD SA

CD SAD CD AD SAD

CD SD

⊥



 ⊥  ⊥ 



⊥



Suy ra, tam giác

ACD

vuông tại

2 2 2 2

2D AC AD DC a a a = + = + =

( ) ( )

BC SA

BC SAC BC AC SAC

BC SC

⊥



 ⊥  ⊥ 



⊥



Suy ra, tam giác

ABC

vuông tại

2 2 2 2

2 7 3C AB AC BC a a a = + = + =

Ta có:

( ) ( )

2

. 3 .

2

22

ABCD

CD AB AD a a a

Sa

++

= = =

.

Thể tích của khối chóp

.S ABCD

là:

23

.

1 1 2

. . . .2

3 3 3

S ABCD ABCD

V SA S a a a= = =

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

11 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 17: Cho khối chóp

.S ABCD

có đáy

ABCD

là hình vuông,

( )

SA ABCD⊥

và

SA a=

, góc giữa

đường thẳng

SC

và mặt phẳng

( )

ABCD

bằng

30

o

(tham khảo hình vẽ). Thể tích khối chóp

.S ABCD

bằng

A.

3

2

a

. B.

3

4

a

. C.

3

6

a

. D.

3

6

a

.

Lời giải

Chọn A

( )

SA ABCD⊥

( )

(

)

, 30

O

SC ABCD SCA = =

.

Xét tam giác vuông

SAC

, ta có:

.cot30 3

o

AC SA a==

. Suy ra:

3

22

AC a

AB ==

.

2

3

.

1 1 3

. . .

3 3 2

2

S ABCD ABCD

aa

V SA S a



= = =





.

Câu 18: Cho khối chóp

.S ABC

có đáy

ABC

là tam giác vuông tại

B

và

3, 4BC BA==

. Cạnh bên

5SA =

vuông góc với đáy, khi đó thể tích khối chóp bằng

A.

60V =

. B.

20V =

. C.

30V =

. D.

10V =

.

Lời giải

Chọn D

Ta có

1 1 1 1 1

. . . . . .3.4.5 10

3 3 2 3 2

ABC

V S SA BA BC SA= = = =

.

Câu 19: Cho khối chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

. Hai mặt phẳng

( )

SAB

và

( )

SAD

cùng vuông góc với đáy. Tính thể tích khối chóp

.S ABCD

biết rằng

3SC a=

.

A.

3

ABCD

Va=

. B.

3

SABCD

a

V =

. C.

3

9

SABCD

a

V =

. D.

3

SABCD

a

V =

.

Lời giải

Chọn D

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 12

Ta có

( ) ( )

( )

SAB ABCD

SAD ABCD SA ABCD

SAB SAD SA

⊥





⊥  ⊥





=



.

ABCD

là hình vuông cạnh

a

nên

2AC a=

.

Tam giác

SAC

vuông tại

A

nên

22

SA SC AC a= − =

.

3

2

.

11

..

3 3 3

S ABCD ABCD

a

V SA S SA AB= = =

.

Câu 20: Cho khối chóp

.S ABCD

có

ABCD

là hình chữ nhật tâm

O

;

22AC AB a==

;

SA

vuông góc

với mặt phẳng đáy. Tính thể tích khối chóp

.S ABCD

biết rằng

5.SD a=

A.

3

.

5

3

S ABCD

a

V =

B.

3

.

15

3

S ABCD

a

V =

C.

3

.

6

3

S ABCD

a

V =

D.

3

.

6

S ABCD

Va=

Lời giải

Chọn C

Ta có:

2 2 .AC AB a AB a= =  =

Do

ABCD

là hình chữ nhật

.AB BC⊥

Xét

ABC

vuông tại

B

có

( )

2

2 2 2

2 3.BC AC AB BC a a a= −  = − =

Xét

SAD

vuông tại

A

có

( ) ( )

22

5 3 2.SA SD AD SA a a a= −  = − =

Do

( )

SA ABCD⊥

suy ra

SA

là đường cao của khối chóp.

Thể tích khối chóp

.S ABCD

là

3

.

1 1 6

3 3 3

S ABCD ABCD

a

V SA S SA AB BC=  =   = 

Câu 21: Cho hình chóp

SABC

có đáy

ABC

là tam giác vuông tại

B

,

AB a=

,

5AC a=

,

( )

SA ABC⊥

và

3SA a=

. Thể tích khối chóp

SABC

bằng

A.

3

a

V =

. B.

3

3Va=

. C.

3

2

a

V =

D.

3

5

3

a

V =

.

Lời giải

Chọn A

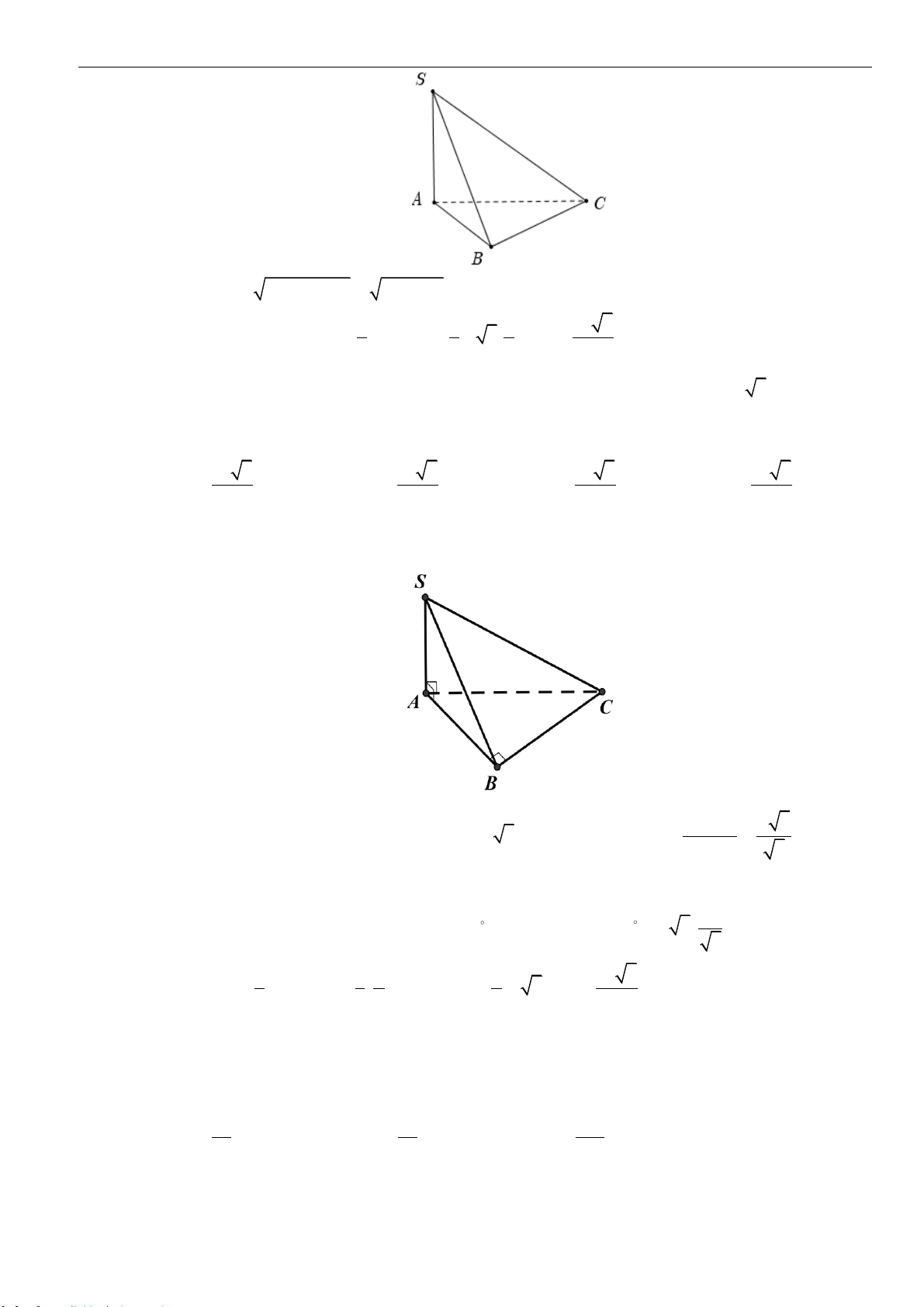
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

13 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Ta có:

2 2 2 2

52BC AC AB a a a= − = − =

.

Thể tích khối chóp là:

3

1 1 1 3

. . . 3. . .2

3 3 2 3

ABC

a

V SA S a a a= = =

.

Câu 22: Cho hình chóp tam giác

.S ABC

có đáy

ABC

là tam giác vuông tại

B

,

3AB a=

,

60ACB =

, cạnh bên

SA

vuông góc với mặt đáy và

SB

hợp với mặt đáy một góc

30

. Tính thể tích

V

của khối chóp

.S ABC

.

A.

3

18

a

V =

. B.

3

6

a

V =

. C.

3

6

a

V =

. D.

3

9

a

V =

.

Lời giải

Chọn C

Ta có

ABC

là tam giác vuông tại

B

,

3AB a=

,

60ACB =

0

3

tan60

3

AB a

BC a = = =

.

Vì

( )

SA ABC⊥

AB

là hình chiếu vuông góc của

SB

lên mặt phẳng

( )

ABC

.

Khi đó

( )

, , 30SB ABC SB AB SBA= = =

1

.tan30 3.

3

SA AB a a = = =

.

Vậy

3

.

1 1 1 1 3

. . . . . 3. .

3 3 2 6 6

S ABC ABC

a

V S SA BA BC SA a a a



= = = =

.

Câu 23: Cho hình chóp

.S ABC

có cạnh bên

SA

vuông góc với mặt phẳng đáy

( )

ABC

. Biết

SA a=

, tam

giác

ABC

là tam giác vuông cân tại

A

,

2AB a=

. Tính theo

a

thể tích

V

của khối chóp

..S ABC

A.

3

6

a

V =

. B.

3

2

a

V =

. C.

3

2

3

a

V =

. D.

3

2Va=

.

Lời giải

Chọn C

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 14

Diện tích tam giác

ABC

vuông cân tại

A

là

2

11

. 2 .2 2

22

ABC

S AB AC a a a= = =

.

Thể tích khối chóp

.S ABC

là:

3

2

.

1 1 2

. . .2

3 3 3

S ABC ABC

a

V SAS a a= = =

.

Câu 24: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật

AB a=

và

3AD a=

, cạnh bên

SA

vuông góc với đáy. Tính thể tích

V

của khối chóp

.S ABCD

biết góc giữa hai mặt phẳng

( )

SBD

và

( )

ABCD

bằng

60

.

Lời giải

Kẻ

AH BD⊥

( )

H BD

. Vì

( ) ( )

( )

SBD ABCD BD

BD SH SBC

BD AH ABCD

=





⊥





⊥



Suy ra

( ) ( )

( )

,;SBD ABCD SH AH=

60SHA= = 

Xét

ABD

vuông tại

A

có

2

22

. 3 3 10

10

AD AB a a

AH

a

AD AB

= = =

+

.

Xét

SAH

vuông tại

A

có

3 10 3 30

.tan60 . 3

10 10

aa

SA AH=  = =

.

Khi đó thể tích khối chóp

.S ABCD

là:

3

2

1 1 3 30 3 30

. . .3

3 3 10 10

ABCD

aa

V SAS a= = =

.

Câu 25: Cho khối chóp

.S ABCD

có đáy là hình chữ nhật,

,2AB a AD a==

,

SA

vuông góc với đáy, góc

giữa cạnh bên

SC

và đáy bằng

30

. Tính thể tích của khối chóp đã cho.

A.

3

2 15

3

Va=

. B.

3

2

3

Va=

. C.

3

2 15

9

Va=

. D.

3

2 15Va=

.

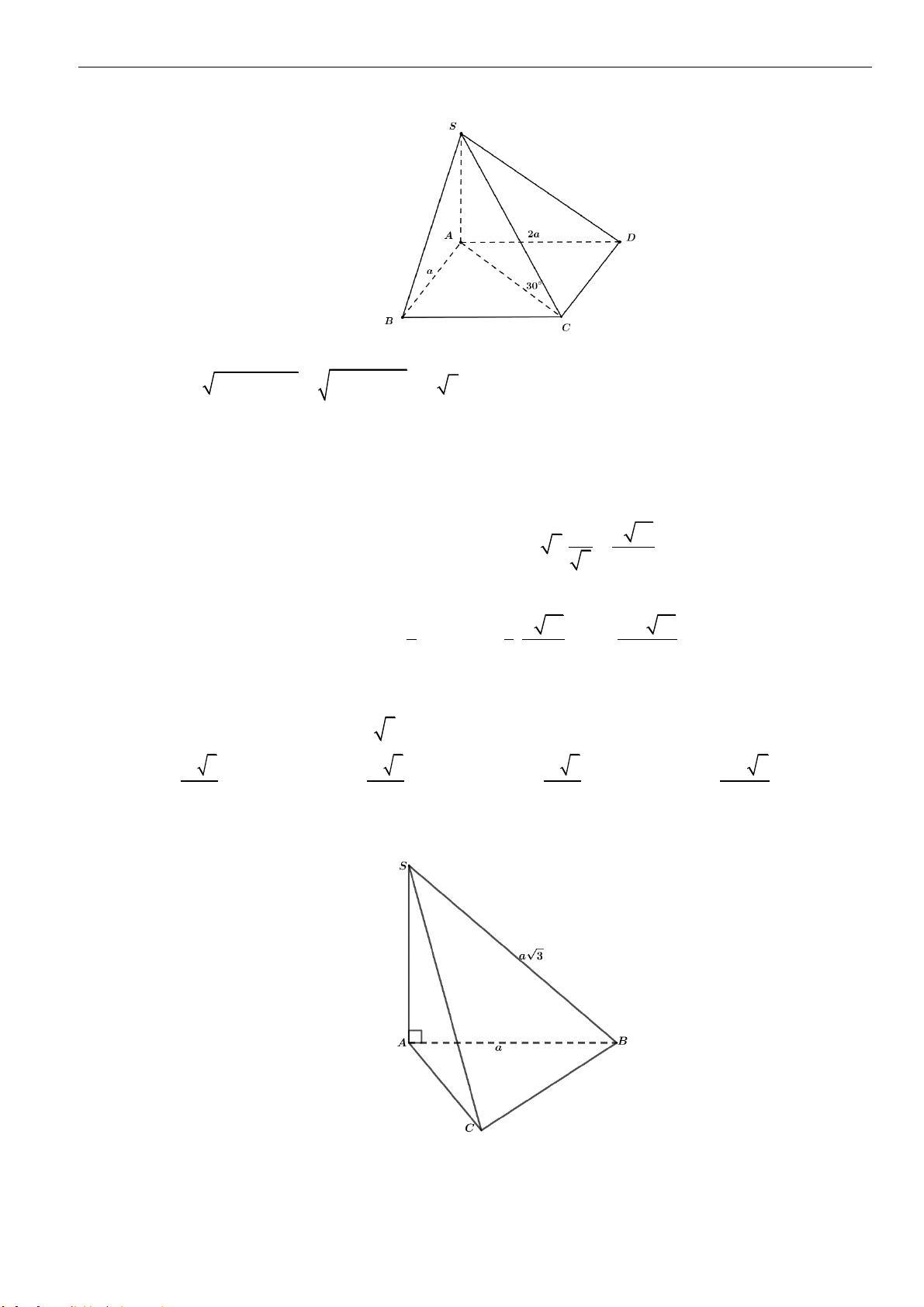
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

15 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Lời giải

Chọn C

Áp dụng định lý Pytago cho tam giác vuông

ABC

ta được:

( )

2

2 2 2

25AC AB BC a a a= + = + =

Ta có

( )

SA ABCD⊥

A

là hình chiếu vuông góc của

S

trên

( )

ABCD

AC

là hình chiếu vuông góc của

SC

trên

( )

ABCD

( )

, ; 30SC ABCD SC AC SCA = = = 

Xét tam giác vuông

SAC

có:

1 15

.tan 5.

3

a

SA AC SCA a= = =

Diện tích đáy

ABCD

là:

2

.2

ABCD

S AB AD a==

Khi đó thể tích khối chóp là:

3

2

1 1 15 2 15

. . .2

3 3 3 9

ABCD

aa

V SAS a= = =

Câu 26: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác đều cạnh

a

. Hai mặt

( )

SAB

và

( )

SAC

cùng

vuông góc với đáy và

3SB a=

. Tính thể tích

.S ABC

.

A.

3

6

4

a

. B.

3

6

12

a

. C.

3

6

3

a

. D.

3

26

9

a

.

Lời giải

Chọn B

Ta có:

( ) ( )

SAB ABC

SAC ABC

SAC SAB SA

⊥





⊥





=



( )

SA ABC⊥

tại

A

.

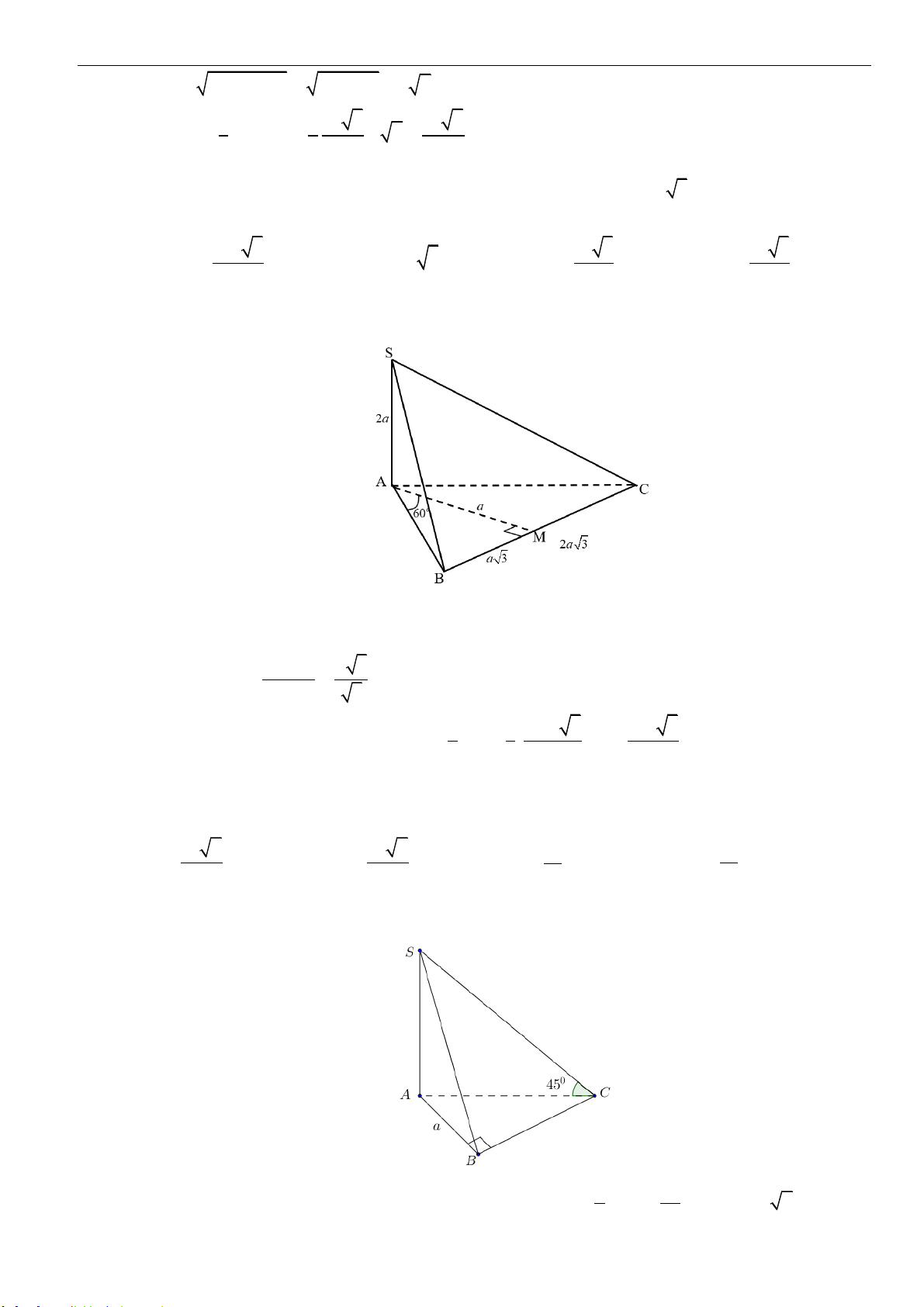
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 16

2 2 2 2

32SA SB AB a a a= − = − =

.

23

.

1 1 3 6

. . 2

3 3 4 12

S ABC ABC

aa

V S SA a= = =

.

Câu 27: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác cân tại

A

,

23BC a=

,

0

120BAC =

, cạnh bên

SA

vuông góc với mặt đáy và

2SA a=

. Tính thể tích

V

của khối chóp

.S ABC

.

A.

3

23

3

a

V =

. B.

3

3Va=

. C.

3

2

a

V =

. D.

3

6

a

V =

Lời giải

Chọn A

Trong tam giác

ABC

kẻ đường cao

AM

vuông góc

BC

.

Do tam giác

ABC

cân tại

A

,

0

120BAC =

nên

0

60BAM =

.

Do đó:

3

tan60

3

o

BM a

AM a= = =

Vậy thể tích khối chóp

.S ABC

là:

3

1 1 .2 3 2 3

. . .2

3 3 2 3

a a a

V B h a= = =

.

Câu 28: Cho hình chóp

.S ABC

, đáy là tam giác vuông cân tại

B

,

AB a=

,

SA

vuông góc với đáy, góc

giữa

SC

và đáy bằng

45



. Thể tích khối chóp

.S ABC

bằng

A.

3

2

6

a

. B.

3

2

a

. C.

3

6

a

. D.

3

2

a

.

Lời giải

Chọn A

Đáy là tam giác vuông cân tại

B

nên diện tích đáy

2

1

22

ABC

a

S AB==

và

2AC a=

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

17 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Góc giữa

SC

và đáy bằng

45



nên

2SA AC a==

Thể tích cảu khối chóp là

23

1 1 2

. 2.

3 3 2 6

ABC

aa

V SAS a= = =

.

Câu 29: Cho khối chóp

.S ABCD

có đáy

ABCD

là hình vuông,

SA

vuông góc với mặt phẳng đáy và

3SA a=

. Biết góc giữa đường thẳng

SD

và mặt phẳng

()SAC

bằng

30 .

Thể tích khối chóp đã

cho bằng

A.

3

27a

. B.

3

a

. C.

3

3a

. D.

3

9a

.

Lời giải

Chọn D

Gọi độ dài cạnh hình vuông

ABCD

là

x

( )

0x 

.

Gọi

( ) ( )

( )

, 30

DO AC

O AC BD DO SAC SD SAC OSD

DO SA

⊥



=    ⊥  = = 



⊥



.

Do đó

1

tan

3

OD

OSD

OS

==

2

1

2

3

2

9

2

x

ax

=



+





3xa=



3

.

1

.9

3

S ABCD ABCD

V S SA a==

.

Câu 30: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật

2AB a=

và

4AD a=

, cạnh bên

SA

vuông góc với đáy. Tính thể tích

V

của khối chóp

.S ABCD

biết góc giữa hai mặt phẳng

( )

SBD

và

( )

ABCD

bằng

0

30

.

A.

3

15

5

a

. B.

3

8 15

15

a

. C.

3

8 15

45

a

. D.

3

a

.

Lời giải

Chọn C

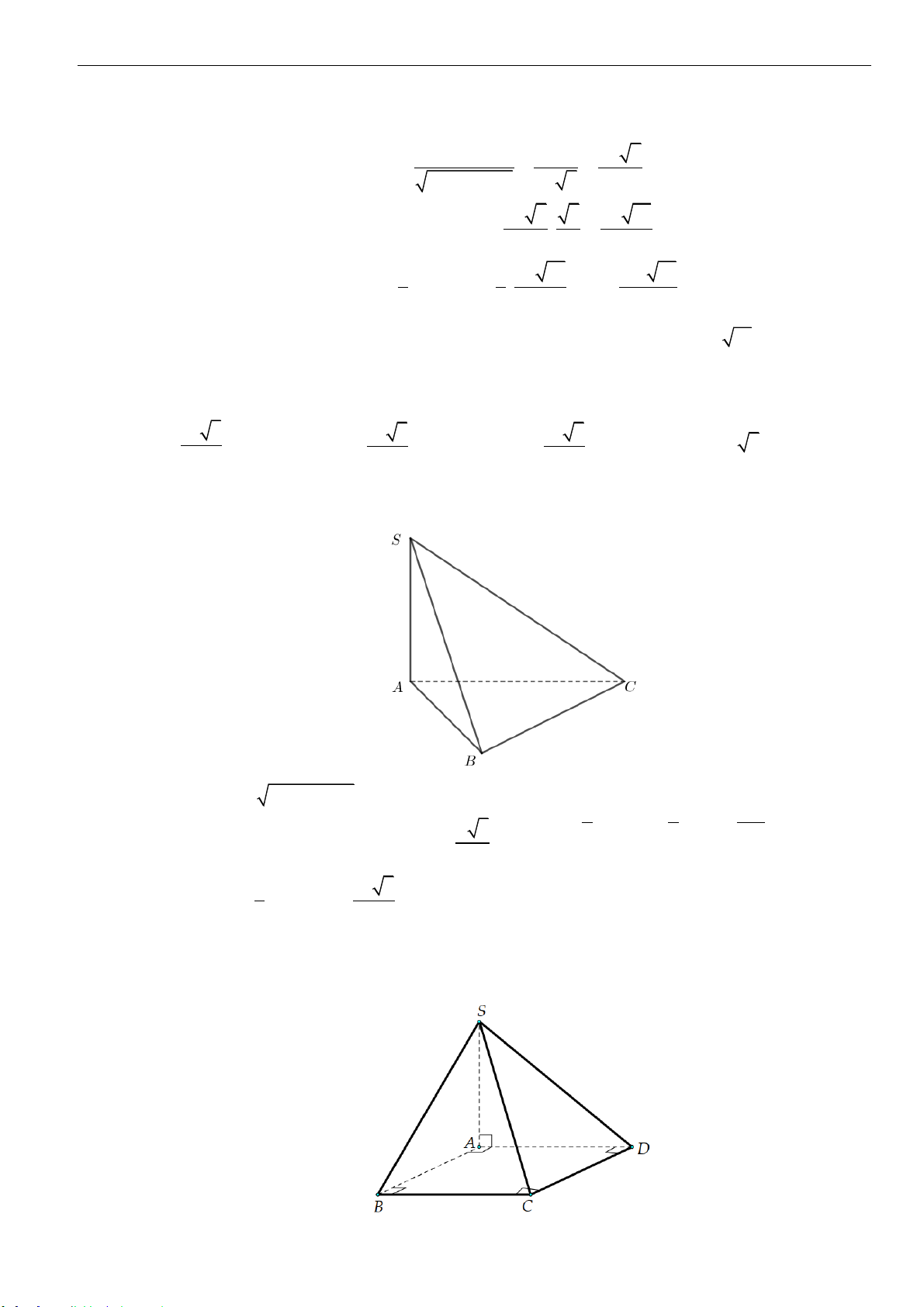
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 18

Kẻ

AE BD⊥

.

( ) ( )

(

)

0

30 ,SBD ABCD SEA==

.

Xét

ABD

vuông tại

A

có

2

22

. 8 4 5

5

25

AD AB a a

AE

a

AD AB

= = =

+

.

Xét

SAE

vuông tại

A

có

0

4 5 3 4 15

.tan30 .

5 3 15

aa

SA AE= = =

.

Khi đó thể tích

.S ABCD

là

3

2

1 1 4 15 8 15

. . .2

3 3 15 45

ABCD

aa

V SAS a= = =

.

Câu 31: Cho hình chóp

.S ABC

có đáy là tam giác vuông tại

, 3 , 10,B BC a AC a==

cạnh bên

SA

vuông góc với đáy. Góc giữa mặt phẳng

( )

SBC

và mặt phẳng đáy bằng

30 .

o

Tính thể tích khối

chóp

.S ABC

là

A.

3

.

6

a

B.

3

.

3

a

C.

3

.

2

a

D.

3

3.a

Lời giải

Chọn A

Ta có

22

3

30 .tan30

3

oo

AB AC BC a

a

SBA SA AB



= − =





=  = =





và

2

1 1 3

. .3 .

2 2 2

ABC

a

S AB BC a a



= = =

Vậy

3

.

13

. . .

36

S ABC ABC

a

V S SA



==

Câu 32: Cho hình chóp

.S ABCD

có đáy là hình vuông cạnh

2a

,cạnh bên

SA

vuông góc với mặt phẳng

đáy, góc giữa

SC

với mặt phẳng

()SAB

bằng

30



. Thể tích của khối chóp

.S ABCD

bằng

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

19 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

A.

3

2

3

a

. B.

3

8

3

a

. C.

3

82

3

a

. D.

3

22

3

a

.

Lời giải

Chọn C

Ta có:

( )

0

; 30

SC SAB S

SC SAB SC SB CSB

CB SAB

=





  = = =



⊥





.

Xét tam giác

SBC

vuông tại

B

có:

0

2

tan30 2 3

tan30

3

BC BC a

SB a

SB

=  = = =

.

Xét tam giác

SAB

vuông tại

A

có:

( )

2

2 3 4 2 2SA a a a= − =

.

Thể tích khối chóp

3

2

.

1 1 8 2

. . .2 2.4

3 3 3

S ABCD ABCD

a

V SA S a a= = =

.

Câu 33: Cho hình chóp

.S ABC

có tam giác

ABC

đều cạnh

a

,

( )

SA ABC⊥

. Gọi

M

là điểm trên cạnh

AB

sao cho

2

3

AM

AB

=

. Biết khoảng cách giữa hai đường thẳng

SM

và

BC

bằng

13

a

. Tính

thể tích khối chóp

.S ABC

.

A.

3

6

a

. B.

3

4

a

. C.

3

23

3

a

. D.

3

2

a

.

Lời giải

Chọn A

Gọi

I

là trung điểm của

BC

,

23

:,

33

AN a

N AC G MN AI AG

AC

 = =   =

.

Ta có

( ) ( )

( )

1

, , , ,

2

d SM BC d BC SMN d B SNM d A SMN= = =

Suy ra

( )

2

,

13

a

d A SMN =

Gọi

K

là hình chiếu vuông góc của

A

lên

SG

.

Khi đó

( )

,MN AG MN SA MN SAG MN AK⊥ ⊥  ⊥  ⊥

. Vậy

( )

AK SMN⊥

, hay

( )

2

,

13

a

d A SMN AK==

.

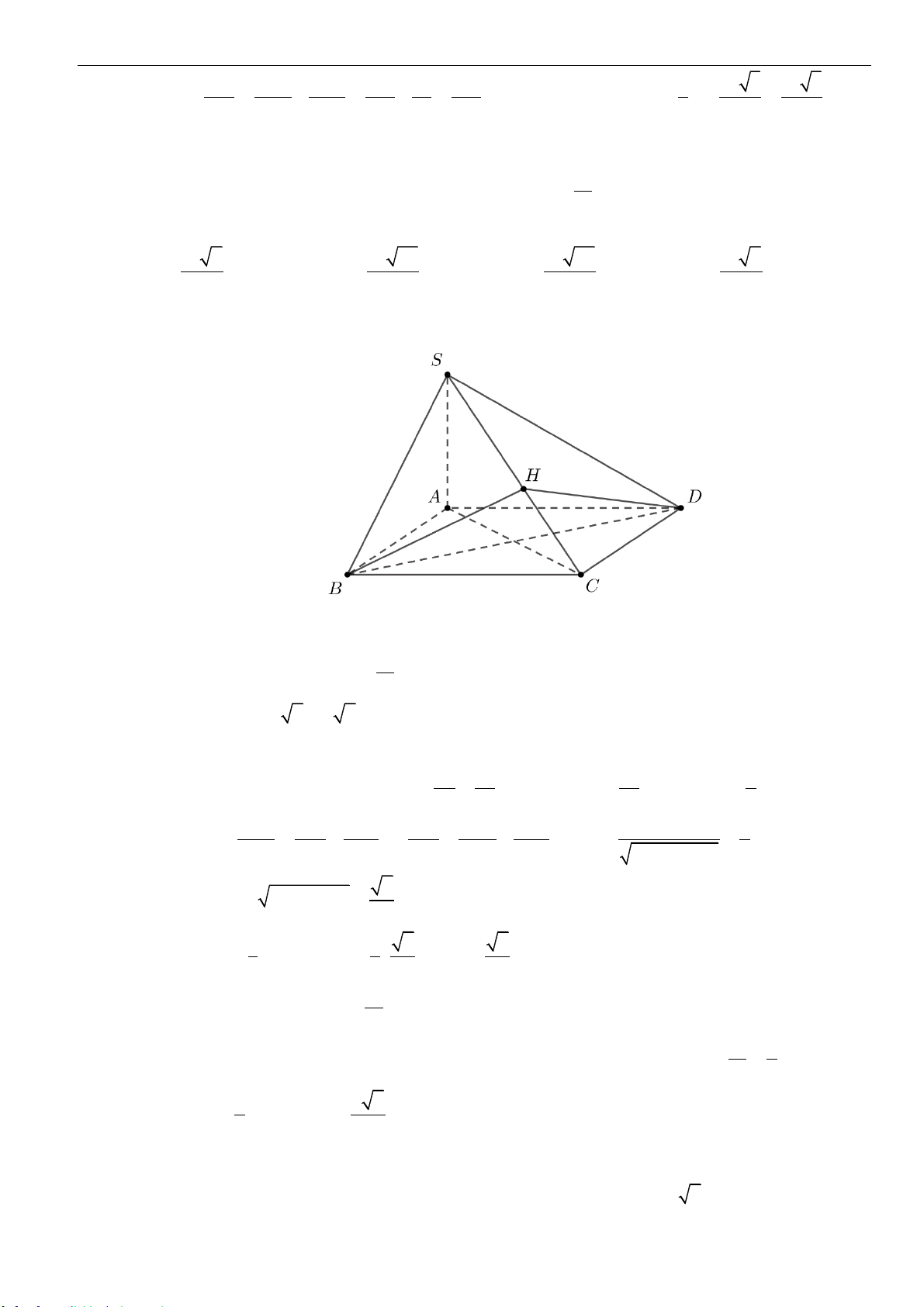
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 20

Ta có

2 2 2 2 2 2

1 1 1 13 3 1

2

44

SA a

SA AK AG a a a

= − = − =  =

. Vậy

23

.

1 3 3

.2 .

3 4 6

S ABC

aa

Va==

.

Câu 34: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh bằng

a

,

( )

SA ABCD⊥

. Góc giữa

hai mặt phẳng

( )

SBC

và

( )

SCD

bằng



với

9

cos

16



=

. Thể tích của khối chóp

.S ABCD

bằng:

A.

3

7

3

a

. B.

3

57

3

a

. C.

3

57

9

a

. D.

3

7

9

a

.

Lời giải

Chọn D

Dựng

BH SC⊥

( )

SC BHD SC DH ⊥  ⊥

( ) ( )

( )

,,SBC SCD BH DH=

Trường hợp 1:

9

cos

16

BHD =−

Ta có:

22BD AC a==

suy ra

222

2 cosBD BH DH BH DH BHD= + −  

Mà

( )

BH DH SBC SDC=  = 

Nên

2 2 2

9 25

2

16 8

BD BH BH BH BH BH



−

= + −   =

22

84

2

25 5

BH a BH a =  =

Mặt khác:

2 2 2 2 2 2

22

1 1 1 1 1 1 4

3

BH BC

SB a

BH SB BC SB BH BC

BC BH



= +  = −  = =

−

Khi đó:

22

7

3

SA SB AB a= − =

3

.

1 1 7 7

3 3 3 9

S ABCD

V SA AB AD a a a a =   =    =

Trường hợp 2:

9

cos

16

BHD =

Ta có:

2 2 2 2 2

97

2 cos 2

16 8

BD BH DH BH DH BHD BH BH BH BH BH



= + −   = + −   =

22

8 4 7

2

77

BH a BH a BC =  = 

(vô lý)

Câu 35: Cho hình chóp

.S ABC

có

SA

vuông góc với đáy, mặt phẳng

()SAB

vuông góc với mặt phẳng

()SBC

, góc giữa hai mặt phẳng

()SAC

và

()SBC

bằng

0

60

,

2;SB a=

0

45 .BSC =

Tính thể

tích khối chóp

.S ABC

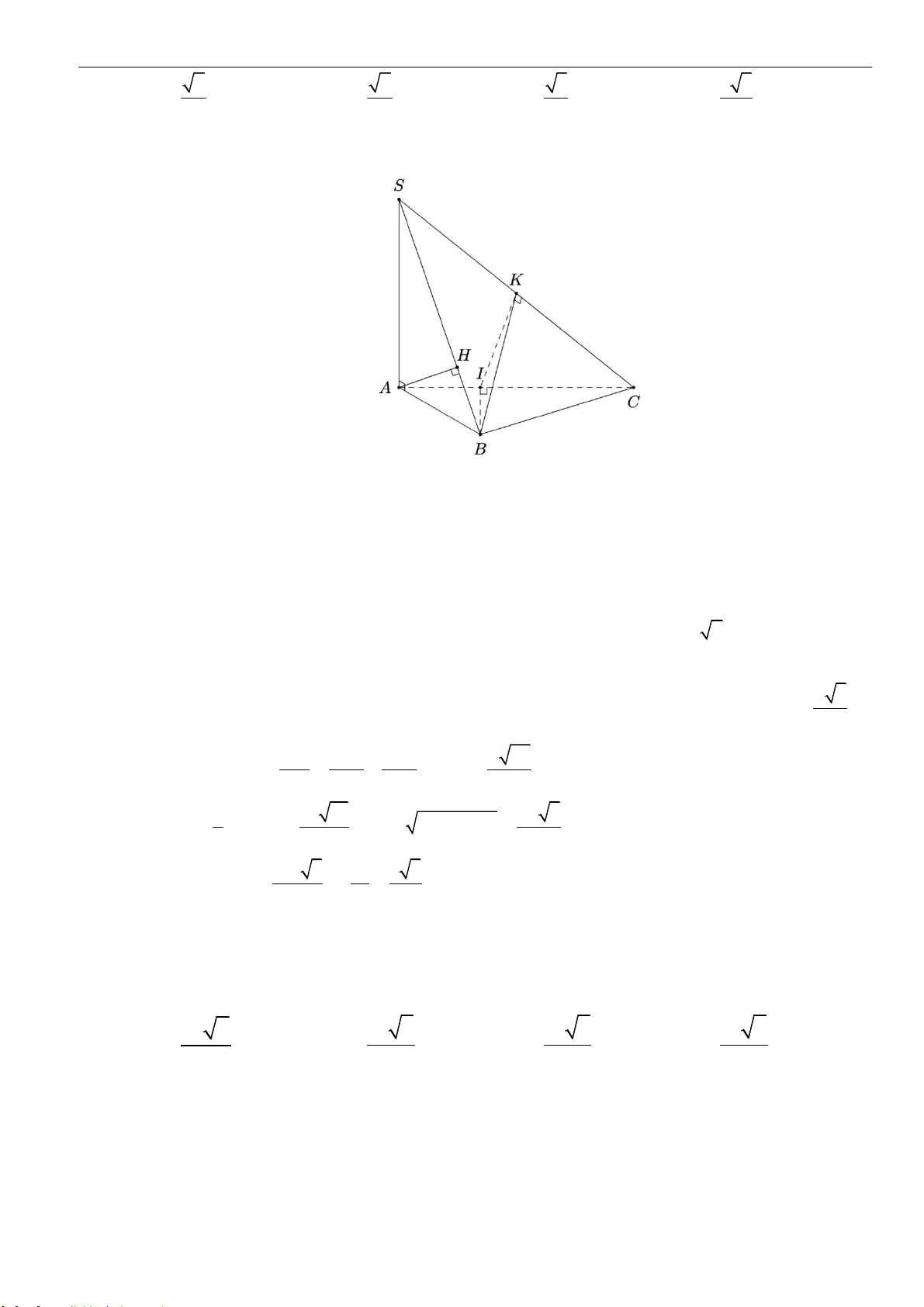
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

21 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

A.

3

2

4

a

. B.

3

2

a

. C.

3

2

a

. D.

3

53

.

2

a

Lời giải

Chọn D

Dựng

AH SB⊥

( ) ( )H SB AH SBC  ⊥

Ta có:

()

BC SA

BC SAB ABC

BC AH

⊥



 ⊥  



⊥



vuông tại

.B

Dựng

BI AC⊥

()I AC BI SC  ⊥

Dựng

BK SC⊥

( ) ( )K SC SC BIK  ⊥

. Suy ra:

0

(( );( )) 60 .SAC SBC BKI==

Ta lại có:

SBC

vuông cân tại

B

0

( 45 ; ) 2.BSC BC SB SB BC a= ⊥  = =

Suy ra:

BK a=

(

K

là trung điểm của

)SC

Do

()

BI SC

BI SAC BI IK

BI AC

⊥



 ⊥  ⊥



⊥



nên

BIK

vuông tại

I

0

3

.sin60 .

2

a

BI BK = =

ABC

tại

B

2 2 2

1 1 1 30

.

5

a

AB

BI AB BC

 = +  =

2

1 15

.;

25

ABC

a

S AB BC



==

22

25

5

a

SA SB AB= − =

.

33

.

2 3 5 3

.

15 2

S ABC

aa

VV

V

 = =  =

Câu 36: Cho hình chóp

.S ABC

có đáy là tam giác

ABC

vuông tại

A

,

,2AB a BC a==

và

SB

vuông

góc với mặt phẳng

( )

ABC

. Biết góc giữa hai mặt phẳng

( )

SAC

và

( )

SBC

bằng

0

60

. Thể tích

của khối chóp

.S ABC

bằng

A.

3

2

6

a

. B.

3

6

12

a

. C.

3

6

4

a

. D.

3

2

a

.

Lời giải

Chọn B

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 22

Kẻ

( )

1

AH BC

AK SC

⊥







⊥





. Ta có:

( )

AH SBC AH SC⊥  ⊥

.

Khi đó:

( ) ( )

2SC AHK SC KH⊥  ⊥

.

Từ

( ) ( )

1 , 2

suy ra: Góc giữa hai mặt phẳng

( )

SAC

và

( )

SBC

là

0

60AKH =

Tam giác vuông

ABC

có:

22

2

, 2 3

3

..

2

3

.

2

AB a BC a AC BC AB a

a

AH BC AB AC AH

AC CH CB CH a

= =  = − =

=  =

Xét tam giác vuông

AHK

vuông tại

H

:

0

3

1

2

tan tan60

2

a

AH

K HK a

HK HK

=  =  =

.

Xét tam giác vuông

HKC

vuông tại

K

:

22

2KC HC HK a= − =

.

Khi đó:

2

tan

2

SB KH

C SB a

BC KC

= =  =

.

Vậy:

3

.

1 1 1 6

. . . . . . .

3 3 2 12

S ABC ABC

a

V S SB AB AC SB= = =

Câu 37: Cho tam giác

ABC

đều cạnh

a

, gọi

d

là đường thẳng qua

A

và vuông góc với mặt phẳng

( )

ABC

. Trên

d

lấy điểm

S

và đặt

( )

,0AS x x=

. Gọi

H

và

K

lần lượt là trực tâm của các

tam giác

ABC

và

SBC

. Biết

HK

cắt

d

tại điểm

S



. Khi

SS



ngắn nhất thì khối chóp

.S ABC

có thể tích bằng

A.

3

6

a

. B.

3

8

a

. C.

3

2

27

a

. D.

3

6

24

a

.

Lời giải

Chọn D

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

23 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Gọi

,AI



lần lượt là trung điểm của

BC

và

AC

,

B



là chân đường cao của tam giác

SBC

hạ từ

đỉnh

B

.

Xét tam giác

SA S



có

H

là trực tâm, ta có

2

33

. . .

2 3 2

AS AH a a a

S AH A AS AS AS AA AH

AA AS



   

   =  = = =



∽

Theo bất đẳng thức Cauchy ta có:

2

2 . 2 2

2

a

SS SA AS AS AS a

  

= +  = =

Dấu “

=

” xảy ra khi

2

a

SA AS x



= = =

.

Do đó

SS



ngắn nhất khi

2

a

x =

. Khi đó

23

.

1 1 2 3 6

. . .

3 3 2 4 24

S ABC ABC

a a a

V SAS= = =

.

Câu 38: Cho hình chóp

.S ABC

có đáy là tam giác đều có cạnh bằng

4

,

SA

vuông góc với đáy, khoảng

cách từ

A

đến mặt phẳng

( )

SBC

bằng

3

. Thể tích

V

của khối chóp

.S ABC

là

A.

83V =

. B.

16 2

3

V =

. C.

83

3

V =

. D.

16 3

3

V =

.

Lời giải

Gọi

M

là trung điểm của

BC

, suy ra

( )

1AM BC⊥

.

Ta có

( ) ( )

2SA ABC SA BC⊥  ⊥

.

Từ

( ) ( )

1 , 2

suy ra

( )

BC SAM⊥

.

Kẻ

AH SM⊥

, vì

( )

AH SAM

nên

AH BC⊥

.

Do đó

( )

AH SBC⊥

, suy ra

( )

,3d A SBC AH==

.

ABC

là tam giác đều cạnh bằng

4

nên

43

23

2

AM ==

,

2

4 . 3

43

4

ABC

S ==

.

Tam giác

SAM

vuông tại

A

, ta có:

2 2 2

1 1 1

AH SA AM

=+

( ) ( )

22

2 2 2

1 1 1 1 1 1

4

3 2 3

SA AH AM

 = − = − =

2SA=

.

Thể tích khối chóp:

1 1 8 3

. .4 3.2

3 3 3

ABC

V S SA= = =

.

Câu 39: Cho hình chóp

.S ABCD

, mặt đáy

ABCD

là hình vuông cạnh

a

. Cạnh bên

SA

vuông góc với

mặt đáy. Gọi

,HK

lần lượt là hình chiếu vuông góc của

A

lên

,SB SD

. Tính theo

a

thể tích

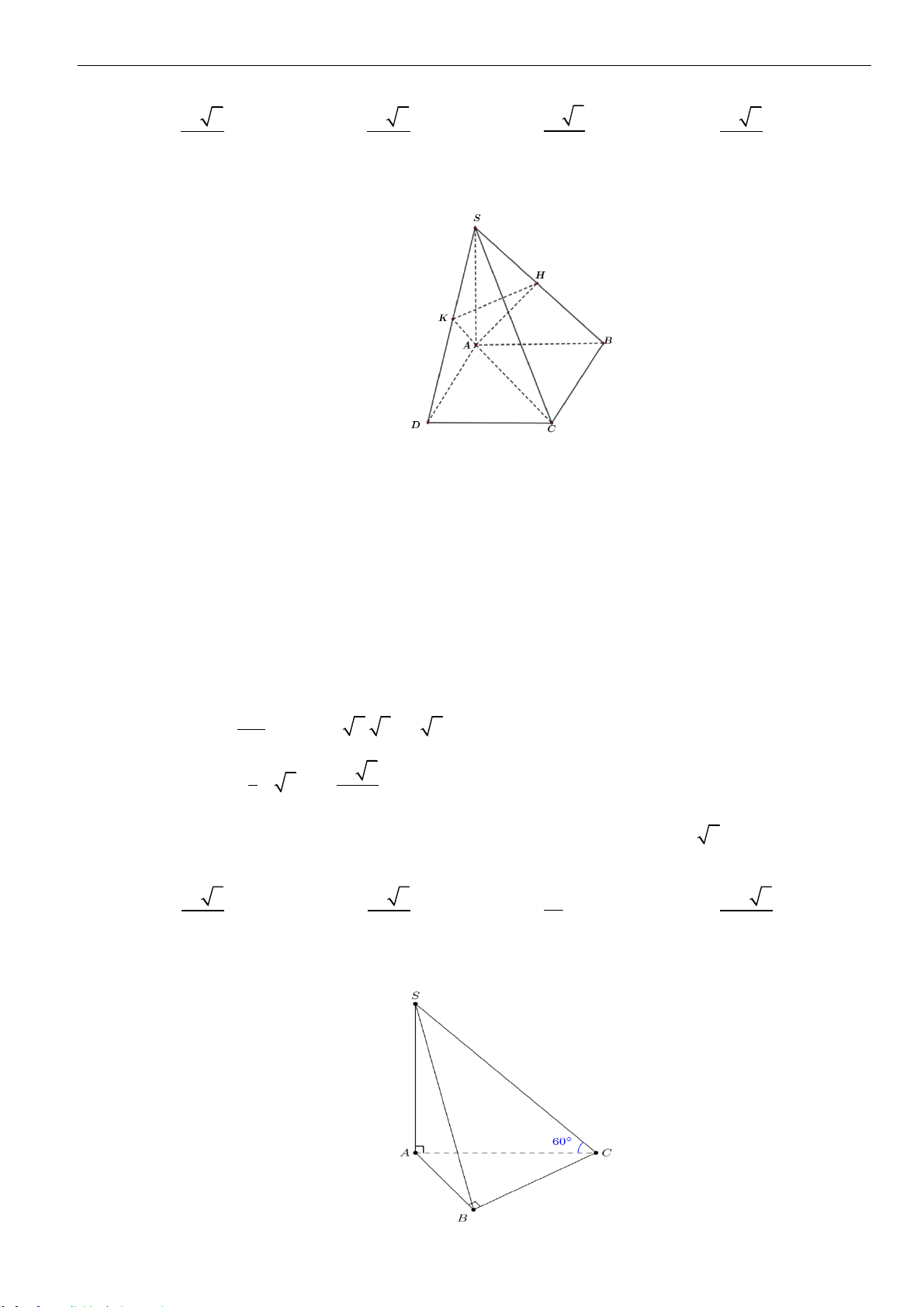
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 24

khối chóp

.S ABCD

biết góc giữa hai mặt phẳng

( )

ABCD

và

( )

AHK

là

30

.

A.

3

2

3

a

. B.

3

6

2

a

. C. . D.

3

6

9

a

.

Lời giải

Chọn C

Ta có:

( )

BC AB

BC SAB BC AH

BC SA

⊥



 ⊥  ⊥



⊥



Khi đó

( ) ( )

1

AH BC

AH SBC SC AH

AH SB

⊥



 ⊥  ⊥



⊥



Tương tự

( )

2SC AK⊥

Từ (1) và (2) suy ra

( ) ( )

3SC AHK⊥

Theo giả thiết

( ) ( )

4SA ABCD⊥

Từ (3) và (4) suy ra góc giữa hai mặt phẳng

( )

ABCD

và

( )

AHK

là

( )

, 30SC SA ASC



= = = 

tan 2. 3 6

AC

SA a a

SA



 =  = =

3

2

.

16

. 6.

33

S ABCD

a

V a a = =

.

Câu 40: Cho hình chóp

SABC

có đáy

ABC

là tam giác vuông cân tại

B

,

2BC a=

. Biết

( )

SA ABC⊥

, góc giữa

SC

và đáy bằng

60

. Thể tích khối chóp

SABC

bằng

A.

3

6

a

. B.

3

a

. C.

3

12

a

. D.

3

23

3

a

.

Lời giải

Chọn D

3

6

3

a

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

25 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Ta có

( )

, 60

SC ABC C

SC ABC SCA

SA ABC

=





 = = 



⊥





.

Vì

ABC

là tam giác vuông cân tại

B

,

( ) ( )

22

2 2 2AC AB BC a a a= + = + =

.

Tam giác

SAC

vuông tại

tan60 .tan60 2 3

SA

A SA AC a

AC

  =  =  =

.

Tam giác

ABC

vuông tại

2

11

. . 2. 2

22

ABC

B S AB BC a a a = = =

.

Vậy

3

2

1 1 2 3

. . .2 3.

3 3 3

SABC ABC

a

V SA S a a= = =

.

Câu 41: Cho chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật. Biết

( )

SA ABCD⊥

,

22AB BC a==

, góc

giữa

( )

SBD

và đáy bằng

30

. Thể tích của khối chóp

.S ABCD

là

A.

3

15

a

. B.

3

4 15

45

a

. C.

3

15

45

a

. D.

3

4 15

15

a

.

Lời giải

Chọn B

Kẻ

AI BD⊥

tại

I

.

Ta có

()

BD AI

BD SAI BD SI

BD SA

⊥



 ⊥  ⊥



⊥



.

Ta có

( ) ( )

( )

, , 30

SBD ABCD BD

AI BD SBD ABCD AI SI SIA

SI BD

=





⊥  = = = 





⊥



.

22

5BD AD AB a= + =

;

. 2 5

5

AD AB

AI a

BD

==

.

2 5 3 2 15

.tan .

5 3 15

SA AI SIA a a= = =

.

3

.

1 1 2 15 4 15

. . . .2 .

3 3 15 45

S ABCD ABCD

V S SA a a a a= = =

.

Câu 42: Cho hình chóp

.S ABC

có tam giác

ABC

vuông cân tại B, AC =

22a

, SA

vuông góc với mặt

phẳng

()ABC

, góc giữa 2 mặt phẳng

()SAC

và

()SBC

bằng

0

60

. Tính thể tích của khối chóp

.S ABC

A.

3

1

3

a

. B.

3

a

. C.

3

5

3

a

D.

3

4

3

a

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 26

Lời giải

Chọn D

Gọi M là trung điểm của AC ⇒

BM AC⊥

. Ta có:

()

BM AC

BM SAC BM SC

BM SA

⊥



 ⊥  ⊥



⊥



.

Kẻ

BH SC⊥

tại H. Ta có:

.

SC BM

SC MH

SC BH

⊥



⊥



⊥



Vậy góc giữa 2 mặt phẳng

()SAC

và

()SBC

là góc

0

60BHM =

Từ giả thiết

22AC a=

. nên AB = BC = 2a và BM = MC =

2a

Xét tam giác BMH vuông tại M:

0

6

tan .

tan60 3

BM BM a

BHM MH

MH

=  = =

22

23

.

3

a

CH CM MH= − =

Xét hai tam giác đồng dạng

,CAS CHM

(tam giác vuông có chung góc nhọn

C

), do đó:

.

2

SA AC MH AC

SA a

MH CH CH

=  = =

. Thể tích khối chóp:

3

.

1 1 4

. . . .

3 2 3

S ABC

V SA AB BC a==

.

Câu 43: Cho hình chóp có đáy là tam giác vuông cân tại . Cạnh bên vuông

góc với mặt phẳng đáy. Gọi lần lượt là trung điểm của Góc giữa hai mặt phẳng

và là . Biết . Thể tích khối chóp bằng

A. . B. . C. . D. .

Lời giải

Chọn C

.S ABC

,B

2AB a=

SA

,M

N

,SB

.SC

( )

AMN

( )

ABC



2

cos

3



=

.S ABC

3

2

a

3

5

3

a

3

7

3

a

3

2

3

a

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

27 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Vì

nên giao tuyến của và là đường thẳng đi qua và song song với

Ta có

Suy ra

Đặt .

Xét tam giác vuông có .

Áp dụng định lí Côsin cho , ta có

.

Thể tích khối chóp đã cho bằng .

Câu 44: Cho hình chóp

.,S ABCD

đáy

ABCD

là hình vuông cạnh

,a

SA

vuông góc với đáy. Khoảng

cách giữa hai đường thẳng

BD

và

SC

là

.

2

a

Tính thể tích khối chóp

..S ABCD

A.

3

2

3

a

. B.

3

6

a

. C.

3

2a

. D.

3

2

3

a

.

Lời giải

Chọn D

Gọi

O AC BD=

.

Vẽ

OH SC⊥

( )

H SC

(1).

Ta có

( )

BD AC

BD SAC BD OH

BD SA

⊥



 ⊥  ⊥



⊥



(2).

Từ (1) và (2) ta có

OH

là đoạn vuông góc chung của

BD

và

.SC

Vậy

( )

,

2

a

d BD SC OH==

.

Xét hai tam giác đồng dạng

CHO

và

CAS

ta có

( ) ( )

( )

||

A AMN ABC

MN AMN

BC ABC

MN BC



















( )

AMN

( )

ABC

d

A

,BC

.MN

( )

AB BC AB d

BC SAB BC AM AM d









⊥  ⊥

⊥  ⊥ ⊥





( ) ( )

(

)

( )

, , .AMN ABC AM AB MAB==

( )

,0SA x x=

,SAB

22

2

ax

SB a x BM AM

+

= +  = =

ABM

2 2 2 2

22

2 2 2

cos 7

2. . 3 3

2

2. . 2

2

AM AB BM a

MAB x a

AM AB

ax

a

+−

= =  =  =

+

3

22

1 1 1 7

. . .2 . 7

3 2 6 3

a

V AB SA a a= = =

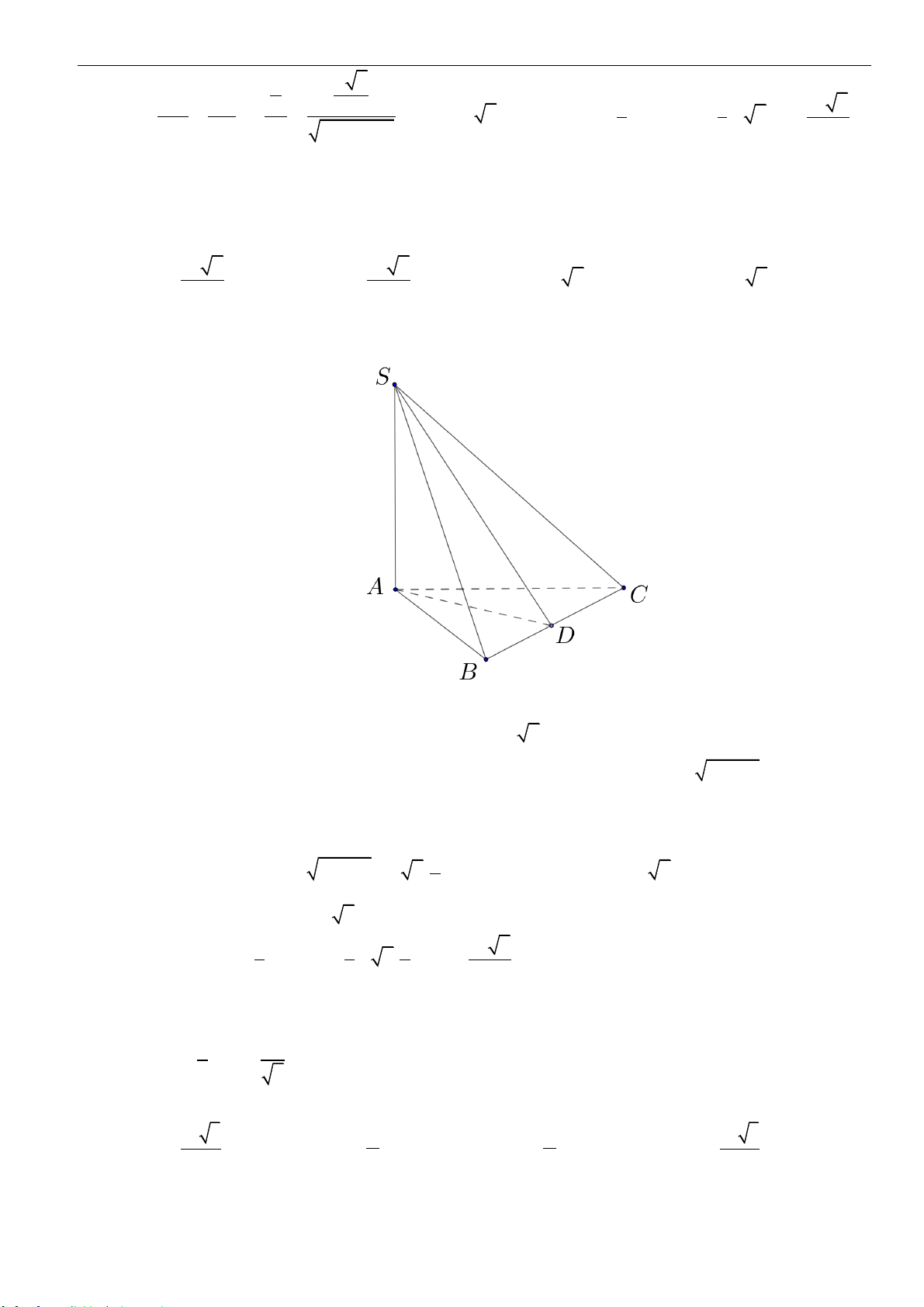
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 28

22

2

22

2

aa

OH CO

SA a

SA SC SA

SA a

=  =  =

+

. Vậy

3

2

.

1 1 2

. . . 2.

3 3 3

S ABCD ABCD

a

V SAS a a= = =

.

Câu 45: Cho khối chóp

.S ABC

có cạnh bên

SA

vuông góc với mặt phẳng đáy, đáy là tam giác cân tại

,A

độ dài đường trung tuyến

AD a=

, cạnh bên

SB

tạo với mặt phẳng đáy góc

0

45

và tạo với

mặt phẳng

( )

SAD

góc

0

30 .

Thể tích khối chóp

.S ABC

bằng

A.

3

2

.

9

a

B.

3

2

.

3

a

C.

3

2.a

D.

3

3 2.a

Lời giải

Chọn B

Ta có vì

( )

SA ABC⊥

nên

( )

, , 45SB ABC SB AB SBA= =  = 

suy ra tam giác

SAB

vuông

cân tại

A

. Đặt

( )

0 , 2;AB x x SA x SB x=   = =

Do tam giác

ABC

cân tại

A

nên

AD BC⊥

,

22

BD x a=−

. Ta có:

( )

,BD AD BD SA BD SAD⊥ ⊥  ⊥

, suy ra

( )

, , 30 .SB SAD SB SD BSD= =  = 

Xét tam giác vuông

SBD

có:

( )

2 2 2 2 2

1

.sin30 2. 2 2.

2

BD SB x a x x a x x a=   − =  − =  =

Suy ra

BD a=

;

2SA a=

Vậy

3

.

1 1 1 2

. . 2. . .2 .

3 3 2 3

S ABC ABC

a

V SA S a a a= = =

Câu 46: Cho hình chóp

.S ABC

có

( )

SA ABC⊥

, hai mặt phẳng

( )

SAB

và

( )

SBC

vuông góc với nhau.

;

2

aa

SA AB==

, góc tạo bởi hai mặt phẳng

( )

SAC

và

( )

SBC

là

0

60

. Tính theo

a

thể tích

khối chóp

.S ABC

.

A.

3

24

a

B.

3

4

a

C.

3

12

a

D.

3

12

a

Lời giải

Chọn A

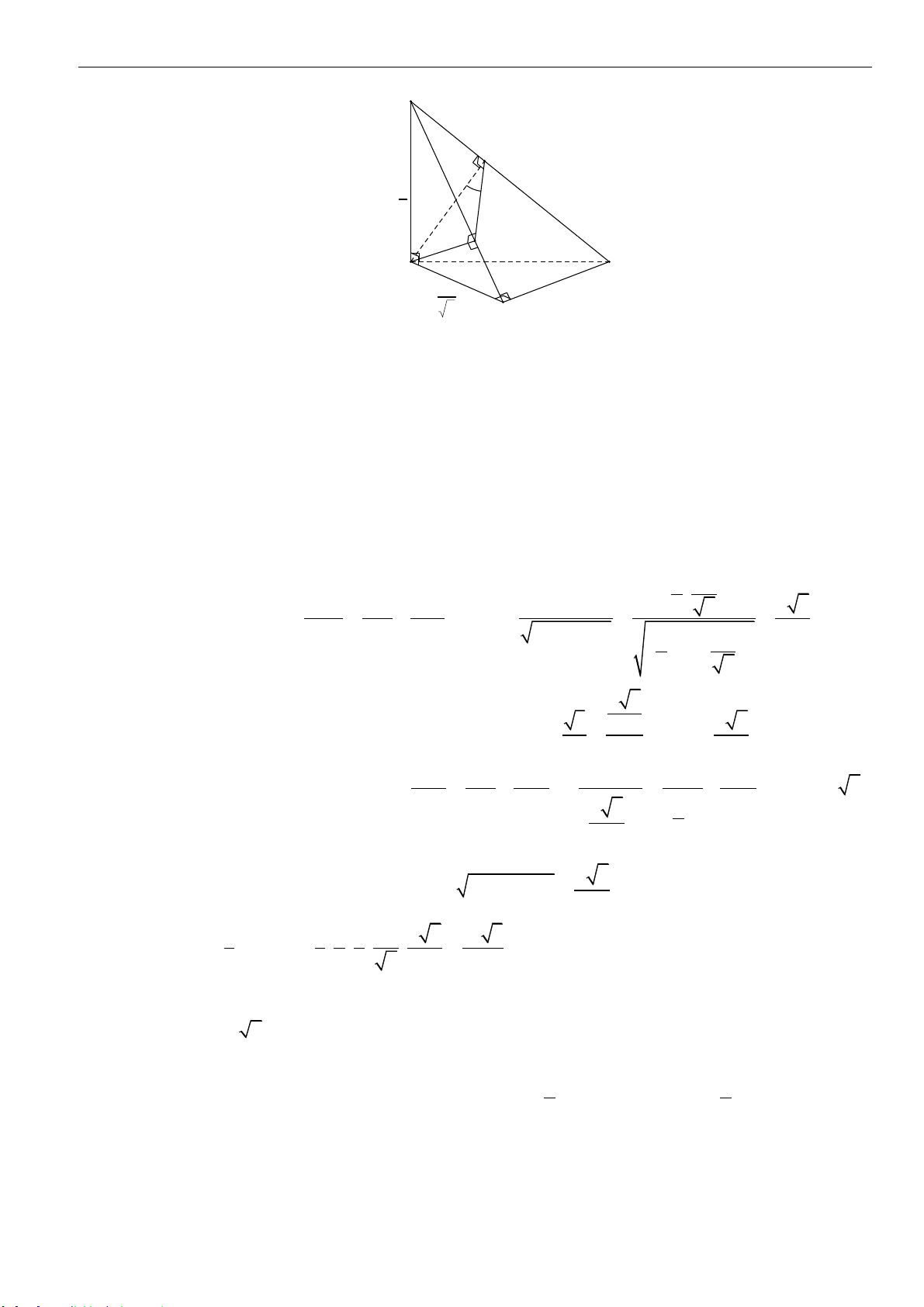
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

29 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Ta có

( ) ( ) ( )

SA ABC SAB ABC⊥  ⊥

. Ta có

( ) ( )

( )

SAB SBC

SAB ABC BC SAB

SBC ABC BC

⊥





⊥  ⊥





=



Gọi

,HE

lần lượt là chân đường cao hạ từ

A

xuống

,SB SC

, vì

( ) ( )

SAB SBC⊥

và

( ) ( ) ( )

SAB SBC SB AH SBC AH SC =  ⊥  ⊥

Ta có

,SC AH SC AE SC EH⊥ ⊥  ⊥

nên

( ) ( )

0

; 60SAC SBC AEH==

Xét tam giác

SAB

:

2 2 2

2

.

1 1 1 . 6

2

6

2

aa

SA AB a

AH

AH SA AB

SA AB

aa

= +  = = =

+



+





Xét tam giác

AHE

vuông tại

H

:

0

6

32

6

sin sin 60

23

a

AEH AE

AE

= = =  =

Xét tam giác

SAC

vuông tại

A

:

22

2 2 2 2

1 1 1 1 1 1

2

3

AC a

AE SA AC AC

a

= +  = +  =

   





Xét tam giác

ABC

vuông tại

B

:

22

6

2

a

BC AC AB= − =

Vậy

3

1 1 1 6 3

. . . . .

3 3 2 2 2 24

2

ABC

a a a a

V SAS= = =

.

Câu 47: Cho khối chóp

.S ABCD

có đáy

ABCD

là hình bình hành và

SA

vuông góc với mặt phẳng đáy.

Biết

o

2 , 2 , 45AB a AD a ABC= = =

và góc giữa hai mặt phẳng

( )

SBC

,

( )

SCD

bằng

o

30

.

Thể tích khối chóp đã cho bằng

A.

3

3a

. B.

3

a

. C.

3

2

3

a

. D.

3

4

a

.

Lời giải

Chọn C

60

°

a

2

a

2

A

C

B

S

E

H

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 30

Gọi

K

là hình chiếu vuông góc của

A

trên

BC

o

2

.cos45 2 .

2

BK AB a a = = =

.

Khi đó

K

là trung điểm của

BC

và

AK BC⊥

nên

2AC AB a==

Nhận thấy tam giác

,ABC ACD

là các tam giác vuông lần lượt tại

A

và

C

.

Ta có:

( ) ( )

,BC SAK CD SAC⊥⊥

suy ra

( ) ( ) ( ) ( )

,SBC SAK SCD SAC⊥⊥

.

Gọi

,IH

lần lượt là hình chiếu vuông góc của

A

lên

,SK SC

Khi đó

( ) ( )

,AI SBC AH SCD⊥⊥

.

Dẫn đến

AI IH⊥

hay tam giác

AIH

vuông tại

I

.

Góc giữa hai mặt phẳng

( )

SBC

,

( )

SCD

bằng

o

30IAH =

.

Gọi

h SA=

,

2 2 2 2

. 2 .

,

2

a h a h

AI AH

a h a h

==

++

Ta có

22

23

cos

2

2.

AI a h

IAH h a

AH

ah

+

=  =  =

+

.

Diện tích hình bình hành

ABCD

là

2

.2S AK AD a==

.

Thể tích khối chóp

23

1 1 2

.2 . .

3 3 3

V Sh a a a= = =

Câu 48: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

,a

3SA a=

và

SA

vuông góc với

mặt phẳng đáy. Mặt phẳng

( )

P

đi qua điểm

A

và vuông góc với

SC

cắt

,SB

,SC

SD

lần lượt

tại

,B



,C



.D



Thể tích khối chóp

.S AB C D

  

bằng

A.

3

33

20

a

. B.

3

93

20

a

. C.

3

33

10

a

. D.

3

33

40

a

.

Lời giải

Chọn A

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

31 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Ta có:

2

.

1

. 3.

3

S ABCD

V a a=

( ) ( )

( )

,.AC SC do SC P AC P



⊥ ⊥ 

( ) ( )

( )

,

.

,

AD SC do SC P AD P

AD SD

AD CD do CD AD CD SA





⊥ ⊥ 





⊥





⊥ ⊥ ⊥





( ) ( )

( )

,

.

,

AB SC do SC P AB P

AB SB

AB BC do BC AB BC SA





⊥ ⊥ 





⊥





⊥ ⊥ ⊥





Trong

SAB

vuông tại

A

có:

2

3

..

4

SB SA

SA SB SB

SB SB



=  = =

Trong

SAD

vuông tại

A

có:

2

3

'. .

4

SD SA

SA SD SD

SD SD



=  = =

Trong

SAC

vuông tại

A

có:

2

3

..

5

SC SA

SA SC SC

SC SC



=  = =

.

9

.

20

S AB C

S ABC

V

SB SC

V SB SC



==

và

.

9

..

20

S AC D

S ACD

V

SC SD

V SC SD



==

. . . . . ' . '

. . . . .

2.

9

.

10

S AB C S AC D S AB C S AC D S AB C D S AB C D

S ABC S ACD S ABC S ABC S ABCD

V V V V V V

V V V V V

           

+

 + = = = =

Vậy

3

. ' .

9 3 3

.

20 20

S AB C D S ABCD

a

VV



==

.

Câu 49: Cho khối chóp

.S ABCD

có đáy là hình vuông cạnh

x

và

SA ABCD

. Khoảng cách từ điểm

A

đến mặt phẳng

( )

SCD

bằng

2a

. Biết thể tích nhỏ nhất của khối chóp

.S ACD

là

3

,,

m

a m n

n

. Tính

P m n

.

A.

10

. B.

9

. C.

8

. D.

11

.

Lời giải

Chọn C

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 32

Kẻ

AH SD

1

. Ta có

CD SAD

AH CD

AH SAD

2

Từ

1

và

2

ta có

AH SCD

suy ra

,2d A SCD AH a

.

Xét

SAD

ta có

2 2 2 2 2 2

1 1 1 1 1 1

AH AS AD AS AH AD

22

.2

2

AD AH ax

AS

AD AH

xa

.

Diên tích tam giác

ACD

là

2

1

.

22

ACD

x

S ADCD

Vậy thể tích của khối chóp

.S ACD

là

3

2

.

2 2 2 2

1 1 1 2 2

. . . . .

3 3 2 6

22

S ACD ACD

ax a x

V SA S x

x a x a

= = =

−−

.

Xét hàm số

( )

3

22

2

x

fx

xa

=

−

với

2xa

.

( )

( ) ( )

4 2 2

2 2 2 2

26

22

x x a

fx

x a x a

−



=

−−

,

( ) ( )

0 ( )

0 3

3

x KTM

f x x a KTM

xa

=







=  = −



=



.

Bảng biến thiên:

Vậy ta có

8P m n= + =

.

Câu 50: Cho hình chóp

.S ABCD

có đáy là hình chữ nhật và

()SA ABCD⊥

. Gọi

M

là trung điểm của

CD

. Trung tuyến

CN

của tam giác

SCM

kéo dài cắt

SD

tại

P

. Biết rằng

3AB =

,

5

cos( ,( ))

26

SC ABCD =

và

12

( ,( ))

13

d C SBD =

. Tính

.S ANP

V

.

A.

1

2

. B.

1

3

. C.

1

12

. D.

1

6

.

Lời giải

Chọn D

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

33 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Áp dụng định lý Menelaus cho tam giác

SMD

với cát tuyến

CNP

ta có

.

1 1 1 1 1

1 2 1 1

2 3 2 3 6

S ANP

S AMD

V

SP DC MN SP SP SP SN SP

PD CM NS PD PD SD V SM SD

  =    =  =  =  =  =  =

Gọi

O

là giao điểm của

AC

và

BD

. Kẻ

AK BD⊥

tại

,K AH AK⊥

tại

H

.

Ta có:

2 2 2

2

11

9 ,tan( ,( )) 1

cos ( ,( )) 5

AC AB AD AD SC ABCD

SC ABCD

= + = + = − =

.

AC

là hình chiếu của

SC

trên

()ABCD

2

11

tan( ,( )) tan( , ) tan 9

55

SA

SC ABCD SC AC SCA SA AD

AC

 = = = =  = +

2

3

9

AB AD AD

AK

AC

AD



 = =

+

( )

2

42

2 2 2

2

13

9

5

.9

9

3

243 81

19

9

25 9

AD

SA AK SA AK AD

AD

AH AD

SK AD AD

SA AK AD

AD

+

+

+

= = = =

++

+

++

+

Ta có:

()

BD AK

BD SAK BD AH

BD SA

⊥



 ⊥  ⊥



⊥



mà ( ) ( ,( )) . SK AH AH SBD d A SBD AH⊥  ⊥  =

( ,( ))

( ) 1 ( ,( ))

( ,( ))

d C SBD CO

AC SBD O d C SBD AH

d A SBD AO

 =  = =  =

( )

22

2

4 2 4 2

9

12 9 16

3

13 243 81 169 243 81

AD AD

AD

AD AD AD AD

+

 =  =

+ + + +

42

153 2367 1296 0 4 1AD AD AD SA − − =  =  =

.

1 1 1 1 1 1 1

1 4 3 1 .

3 3 2 6 2 3 6

S AMD AMD S ANP

V SA S AD MD AB V



 =   =    =   =  =  =

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 34

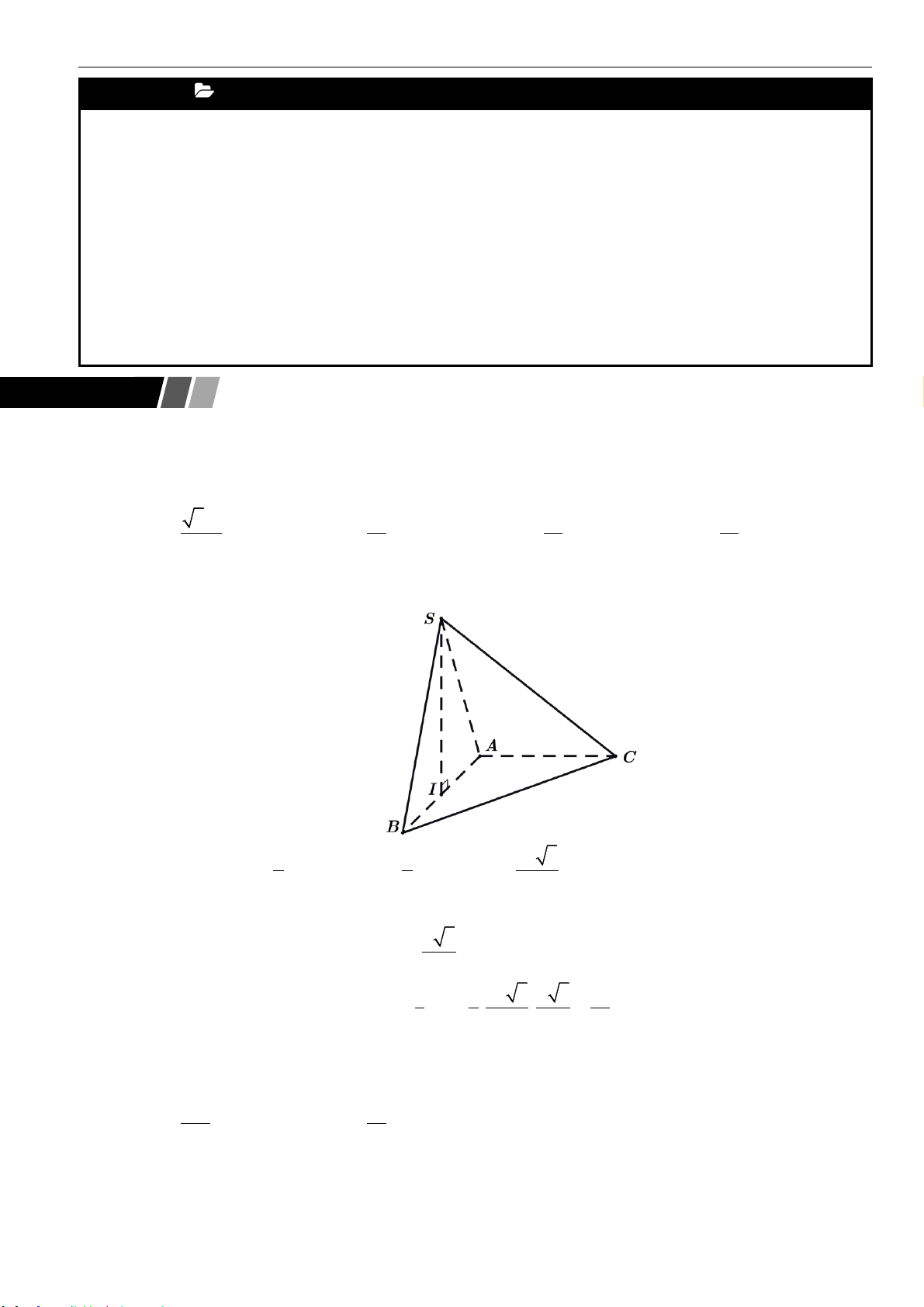
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

1 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Dạng 3: Thể tích khối chóp có mặt bên vuông góc với đáy

Bài toán: Cho hình chóp có mặt phẳng

( )

P

( mặt phẳng

( )

P

chứa đỉnh hình chóp). Mặt phẳng

( )

P

vuông góc với mặt đáy của hình chóp. Cách tìm đường cao của hình chóp như thế nào?

Cách tìm đường cao hình chóp:

• Bước 1: Tìm giao tuyến của mặt phẳng

( )

P

và mặt phẳng đáy

• Bước 2: Từ đỉnh

S

của hình chóp kẻ đoạn thẳng

SH

vuông góc với giao tuyến

d

Lưu ý: Chúng ta phải đặc biệt lưu ý đến tính chất hình học của mặt phẳng

( )

P

để xác định được cụ thể,

tính chất của chân đường cao

H

.

Câu 1: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác cân tại

A

,

, 120AB a BAC= = 

, tam giác

SAB

đều và nằm trong mặt phẳng vuông góc với

( )

ABC

. Thể tích khối chóp

.S ABC

bằng

A.

3

2

a

. B.

3

2

a

. C.

3

8

a

. D.

3

a

.

Lời giải

Chọn C

Ta có:

2

1 1 3

. .sin .sin120

2 2 4

ABC

a

S AB AC A a



= =  =

.

Gọi

I

là trung điểm của đoạn thẳng

AB

, tam giác

SAB

đều và nằm trong mặt phẳng vuông góc

với

( )

ABC

()SI ABC⊥

3

2

a

SI=

.

Thể tích khối chóp

.S ABC

là

23

1 1 3 3

..

3 3 4 2 8

a a a

V Bh= = =

.

Câu 2: Cho hình chóp

.S ABC

có

SAB

và

ABC

là hai tam giác đều cạnh

a

và nằm trong hai mặt phẳng

vuông góc với nhau. Tính theo

a

thể tích của khối chóp

..S ABC

A.

3

2

3

a

. B.

3

a

. C.

3

a

. D.

3

3a

.

Lời giải

Chọn C

VÍ DỤ MINH HỌA

B

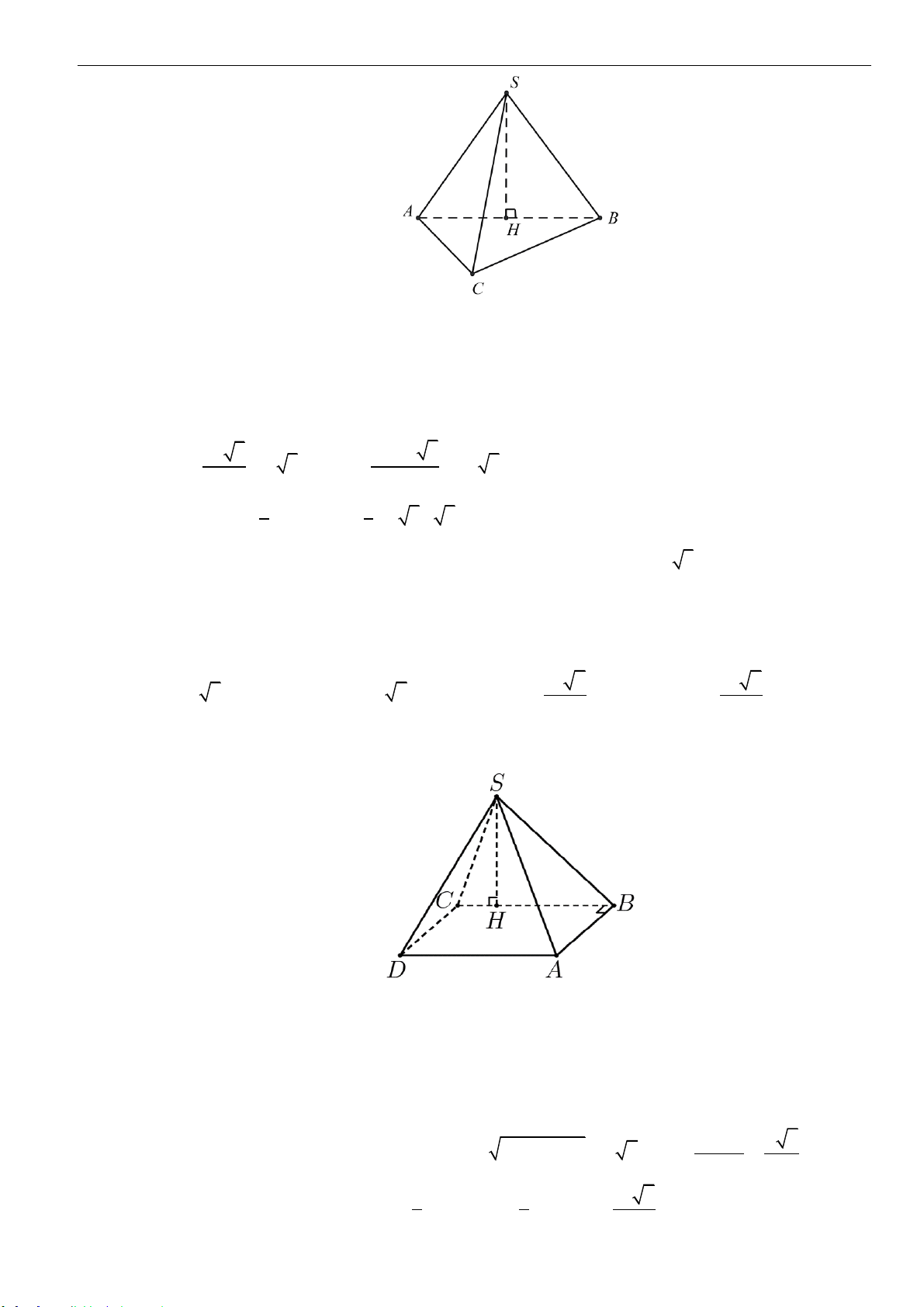
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 2

Gọi

H

là trung điểm của

AB

. Suy ra

SH AB⊥

.

Ta có:

( ) ( )

SAB ABC

SAB ABC AB

SH AB

⊥





=





⊥



( )

SH ABC⊥

.

( )

2

23

3, 3

24

ABC

a

SH a S a



= = = =

.

Vậy

23

.

11

. . 3. 3

33

S ABC ABC

V S SH a a a



= = =

.

Câu 3: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh bằng

3,a

tam giác

SBC

vuông

tại

S

và nằm trong mặt phẳng vuông góc với đáy, đường thẳng

SD

tạo với mặt phẳng

( )

SBC

một góc

60

. Thể tích của khối chóp đã cho bằng

A.

3

3.a

B.

3

6.a

C.

3

6

.

6

a

D.

3

6

.

3

a

Lời giải

Chọn D

Kẻ

.SH BC⊥

Từ giả thiết suy ra

( )

SH ABCD⊥

.

Xác định được hình chiếu vuông góc của

D

lên

( )

SBC

là điểm

C

.

Do đó:

( )

60,,SD SBC SD SC DSC= = = 

.

Tam giác vuông

SCD

vuông tại

C

có

.cotSC DC DSC a==

.

Tam giác vuông

SBC

vuông tại

S

có

22

.

2,

3

6SB SC a

SB BC SC a SH

BC

= − = = =

.

Vậy thể tích khối chóp:

3

2

.

11

..

3 3 3

6

S ABCD ABCD

a

V S SH AB SH= = =

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

3 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 4: Cho hình chóp

.S ABCD

có đáy là hình vuông cạnh

2a

, tam giác

SAB

cân tại

S

và nằm trong

mặt phẳng vuông góc với đáy,

2SC a=

. Thể tích khối chóp

.S ABCD

là:

A.

3

2

a

. B.

3

6

3

a

. C.

3

2

3

a

. D.

3

6

4

a

.

Lời giải

Chọn B

Gọi

H

là trung điểm của

AB

.

Theo bài tam giác

SAB

cân tại

S

nên ta có

SH AB⊥

Ta có:

( ) ( )

SAB ABCD AB

SH SAB SH ABCD

SH AB

=





  ⊥





⊥



Xét tam giác

BHC

vuông tại

B

có:

( )

2

22

2 10

2

22

aa

HC BH BC a



= + = + =





Xét tam giác

SHC

vuông tại

H

có:

2

2 2 2

10 6

4

22

aa

SH SC HC a



= − = − =





Vậy

( )

3

2

.

1 6 6

. 2 .

3 2 3

S ABCD

aa

Va==

Câu 5: Cho hình chóp

.S ABCD

có đáy là hình chữ nhật,

AB a=

,

2AD a=

. Tam giác SAB cân tại S và

nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng

( )

ABCD

bằng

45

. Thể tích của khối chóp

.S ABCD

là:

A.

3

17

9

a

. B.

3

17

3

a

. C.

3

17

3

a

. D.

3

17

6

a

.

Lời giải

Chọn C

A

B

C

D

S

M

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 4

Ta có có:

2

.2

ABCD

S AB AD a==

.

Gọi M là trung điểm của AB, khi đó

( )

SM AB SM ABCD⊥  ⊥

.

Do đó

( )

(

)

( )

, , 45SC ABCD SC MC SCM= = = 

.

Khi đó

2

17

4

42

aa

SM MC a= = + =

.

Vậy

3

2

.

1 1 17 17

. . .2

3 3 2 3

S ABCD ABCD

aa

V SM S a= = =

.

Câu 6: Cho hình chóp

.S ABCD

có đáy là hình vuông cạnh

a

. Hình chiếu của đỉnh

S

trên mặt phẳng

đáy là

H

sao cho

3AB AH=

. Góc giữa cạnh

SD

và mặt phẳng

( )

ABCD

bằng

45



. Tính thể

tích

V

của khối chóp

.S HCD

.

A.

3

2

9

a

V =

. B.

3

10

9

a

V =

. C.

3

10

6

a

V =

. D.

3

10

18

a

V =

.

Lời giải

Chọn D

Ta có

( ) ( )

(

)

0

, 45SH ABCD SD ABCD SDH⊥  = =

.

Lại có

22

10

3

a

HD AH AD= + =

;

0

10 10

.tan .tan45

33

aa

SH HD SDH= = =

.

Diện tích tam giác

HCD

là

2

1

..

22

HCD

a

S BC CD



==

.

Vậy

23

.

1 1 10 10

. . . .

3 3 3 2 18

S HCD HCD

a a a

V SH S



= = =

.

Câu 7: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật với

BC a=

; tam giác

SAB

đều và

nằm trong mặt phẳng vuông góc với đáy. Gọi

M

là trung điểm của

AB

,

I

là tâm mặt cầu

ngoại tiếp hình chóp

.S ABCD

. Biết góc giữa đường thẳng

IM

và mặt phẳng

( )

SAB

bằng

O

60

. Tính thể tích khối chóp

.S ABCD

.

A.

3

3a

. B.

3

2

a

. C.

3

6

a

. D.

3

2

a

Lời giải

Chọn C

a

45

0

O

C

B

D

A

H

S

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

5 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Gọi

O

là tâm của hình chữ nhật,

G

là trọng tâm tam giác

SAB

, suy ra

,OG

là các tâm đường

tròn giao tuyến của mặt cầu ngoại tiếp hình chóp

.S ABCD

và các mặt phẳng

( ) ( )

,ABCD SAB

.

Trong mặt phẳng

( )

SMN

(

N

là trung điểm của

CD

), dựng các trục đường tròn ngoại tiếp đáy

và tam giác

SAB

cắt nhau tại

I

, suy ra

I

là tâm mặt cầu.

( )

IG SAB⊥

, suy ra góc giữa đường

thẳng

IM

và mặt phẳng

( )

SAB

là góc

GMI

.

Đặt

33

tan 3 3

26

x x IG

AB x SM GM IMG IG MG

GM

=  =  =  = =  =

.

33

.3

2 6 2

a x a

x a SM=  =  =

.

Vậy

3

2

.

1 1 3 3

. . .

3 3 2 6

S ABCD ABCD

aa

V SM S a= = =

.

Câu 8: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông tại

A

và có

,3AB a BC a==

. Mặt bên

SAB

là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng

( )

ABC

. Tính thể tích

V

của khối khóp

.S ABC

.

A.

3

26

12

a

V =

. B.

3

6

a

V =

. C.

3

6

12

a

V =

. D.

3

6

4

a

V =

.

Lời giải

Chọn C

Gọi

K

là trung điểm của đoạn

AB

. Vì

SAB

là tam giác đều nên

SK AB⊥

.

( ) ( )

SAB ABC⊥

theo giao tuyến

AB

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 6

( )

.

1

.

3

S ABC ABC

SK ABC V SK S



⊥  =

.

ABC

vuông tại

A

có

22

, 3 2AB a BC a AC BC AB a= =  = − =

2

1 1 2

. . 2

2 2 2

ABC

a

S AB AC a a



= = =

.

SAB

là tam giác đều

3

2

a

SK=

.

23

.

1 1 3 2 6

. . .

3 3 2 2 12

S ABC ABC

a a a

V SK S



= = =

.

Câu 9: Cho hình chóp

.S ABCD

có đáy ABCD là hình chữ nhật,

AB a=

,

3AD a=

, tam giác SAB cân

tại S và nằm trong mặt phẳng vuông góc với đáy, khoảng cách giữa AB và SC bằng

3

2

a

. Tính thể

tích V của khối chóp

.S ABCD

.

A.

3

3a

. B.

3

23a

. C.

3

a

. D.

3

33a

.

Lời giải

Chọn A

Gọi H, I lần lượt là trung điểm của AB, CD, kẻ

HK SI⊥

.

Vì tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Suy ra

( )

SH ABCD⊥

.

( ) ( )

CD HI

CD SIH CD HK HK SCD

CD SH

⊥



 ⊥  ⊥  ⊥



⊥



( ) ( )

( )

, , ,CD AB d AB SC d AB SCD d H SCD HK = = =

Suy ra

3

;3

2

a

HK HI AD a= = =

Trong tam giác vuông SHI ta có

22

.

3

HI HK

SH a

HI HK

==

−

Vậy

23

.

11

. 3 . 3 3

33

S ABCD ABCD

V SH S a a a= = =

.

O

A

B

C

D

S

H

I

K

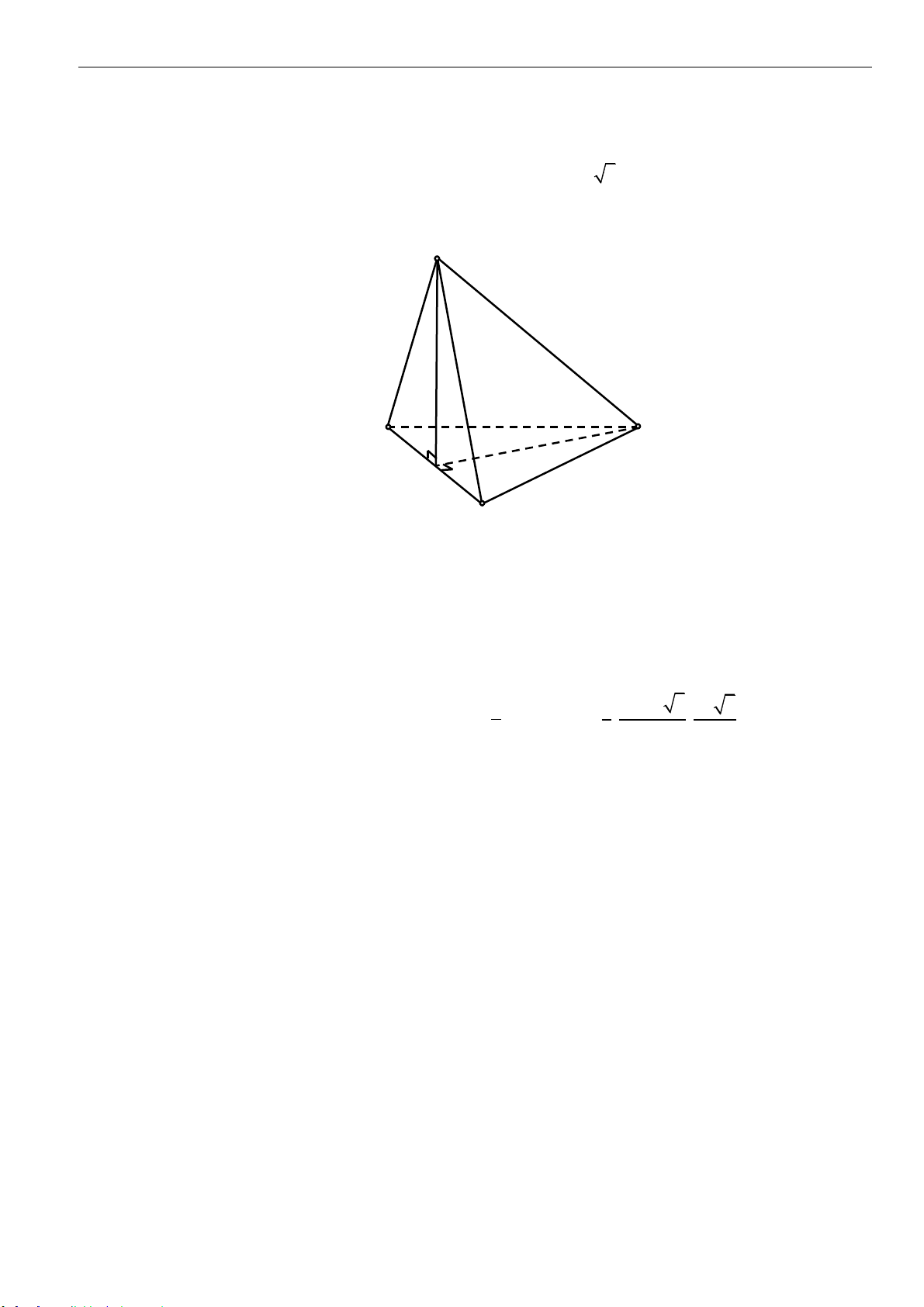
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

7 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 10: Cho tứ diện

MNPQ

. Biết rằng mặt phẳng

( )

MNP

vuông góc với mặt phẳng

( )

NPQ

, đồng thời

MNP

và

NPQ

là hai tam giác đều có cạnh bằng

8a

. Tính theo

a

thể tích

V

của khối tứ

diện

MNPQ

.

A.

3

64Va=

. B.

3

128Va=

. C.

3

64 3Va=

. D.

3

192Va=

.

Lời giải

Chọn A

Gọi

H

là trung điểm cạnh

NP

.

Do tam giác

MNP

đều nên

MH NP⊥

( )

1

Mà

( ) ( )

( )

2

MNP NPQ

MNP NPQ NP

⊥







=





Từ

( )

1

và

( )

2

suy ra

( )

MH NPQ⊥

hay

MH

là đường cao của hình chóp

Vậy thể tích của khối tứ diện

MNPQ

là

1

.

3

NPQ

V S MH=

( )

2

83

1 8 3

..

3 4 2

a

=

3

64 .a=

M

N

P

Q

H

8a

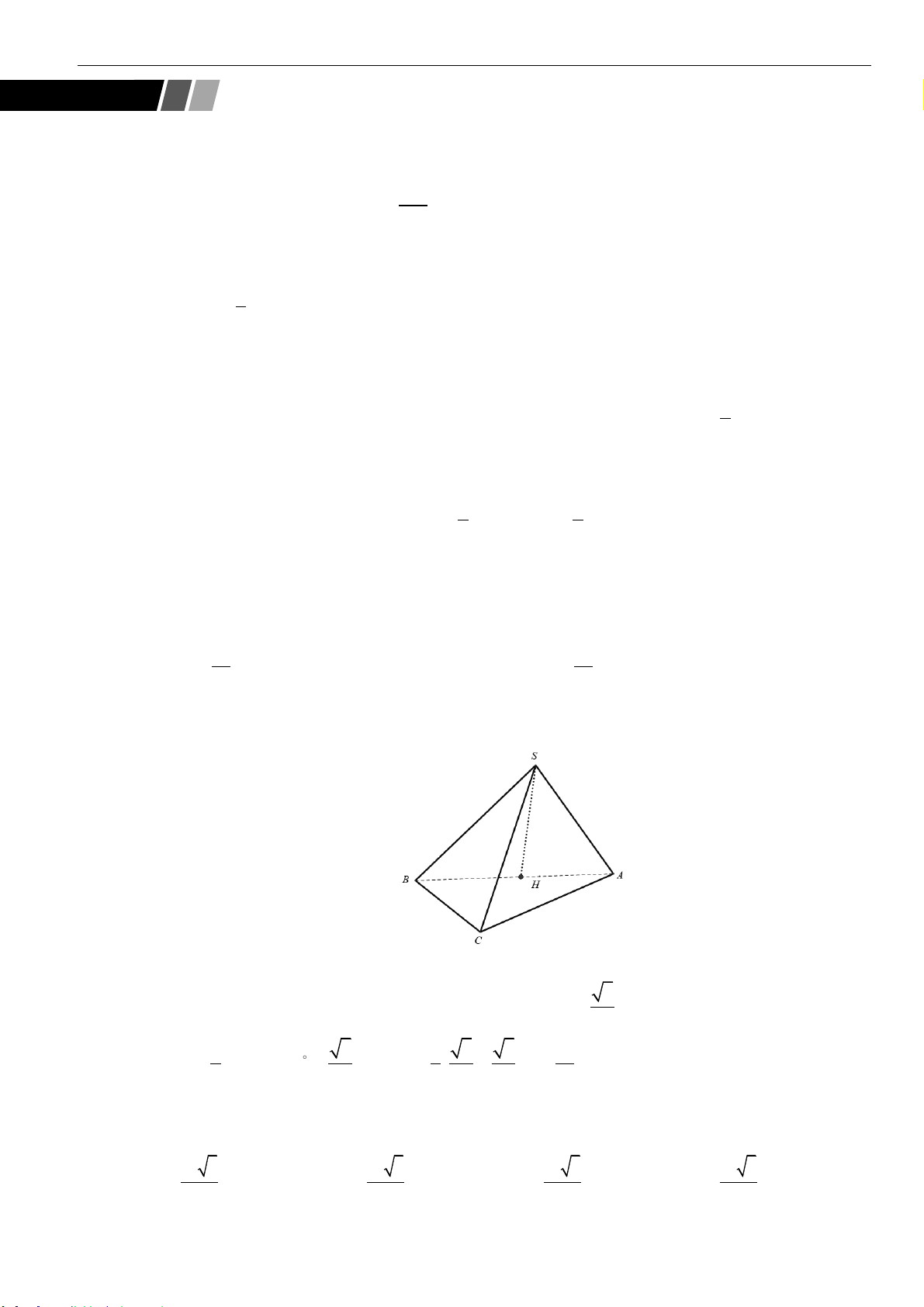
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 8

Câu 1: Cho tứ diện

SABC

có các cạnh

SA

,

SB

,

SC

đôi một vuông góc với nhau. Biết

3SA a=

,

4SB a=

,

5SC a=

. Tính theo

a

thể tích

V

của khối tứ diện

SABC

.

A.

3

10Va=

. B.

3

5

2

a

V =

. C.

3

20Va=

. D.

3

5Va=

.

Lời giải

Chọn A

Ta có

3

1

.3 .4 .5 10

6

V a a a a==

.

Câu 2: Cho tứ diện

OABC

có

OA

,

OB

,

OC

đôi một vuông góc với nhau,

1OA =

,

2OB =

,

3OC =

.

Thể tích khối tứ diện

OABC

là

A.

1

. B.

2

. C.

6

. D.

2

3

.

Lời giải

Chọn A

Thể tích khối tứ diện

OABC

là

11

. . .1.2.3 1

66

OABC

V OAOBOC= = =

(đvtt).

Câu 3: Cho hình chóp

.S ABC

có đáy là tam giác cân tại

A

,

AB AC a==

,

120BAC =

. Mặt bên

SAB

là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Thể tích

V

của khối chóp

.S ABC

là

A.

3

8

a

V =

. B.

3

Va=

. C.

3

2

a

V =

. D.

3

2Va=

.

Lời giải

Chọn A

Vì tam giác

SAB

đều nên gọi

H

là trung điểm của

AB SH AB⊥

. Mặt bên

SAB

nằm trong

mặt phẳng vuông góc với mặt đáy

( )

3

,.

2

SH ABC SH a ⊥ =

3

22

1 3 1 3 3

. .sin120 . . .

2 4 3 2 4 8

ABC

a

S a a a V a a= =  = =

.

Câu 4: Cho khối chóp

.S ABC

có đáy là tam giác đều cạnh

a

, tam giác

SAB

vuông cân tại

S

và nằm

trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp

.S ABC

theo

a

.

A.

3

24

a

. B.

3

8

a

. C.

3

6

a

. D.

3

12

a

.

Lời giải

BÀI TẬP TRẮC NGHIỆM

C

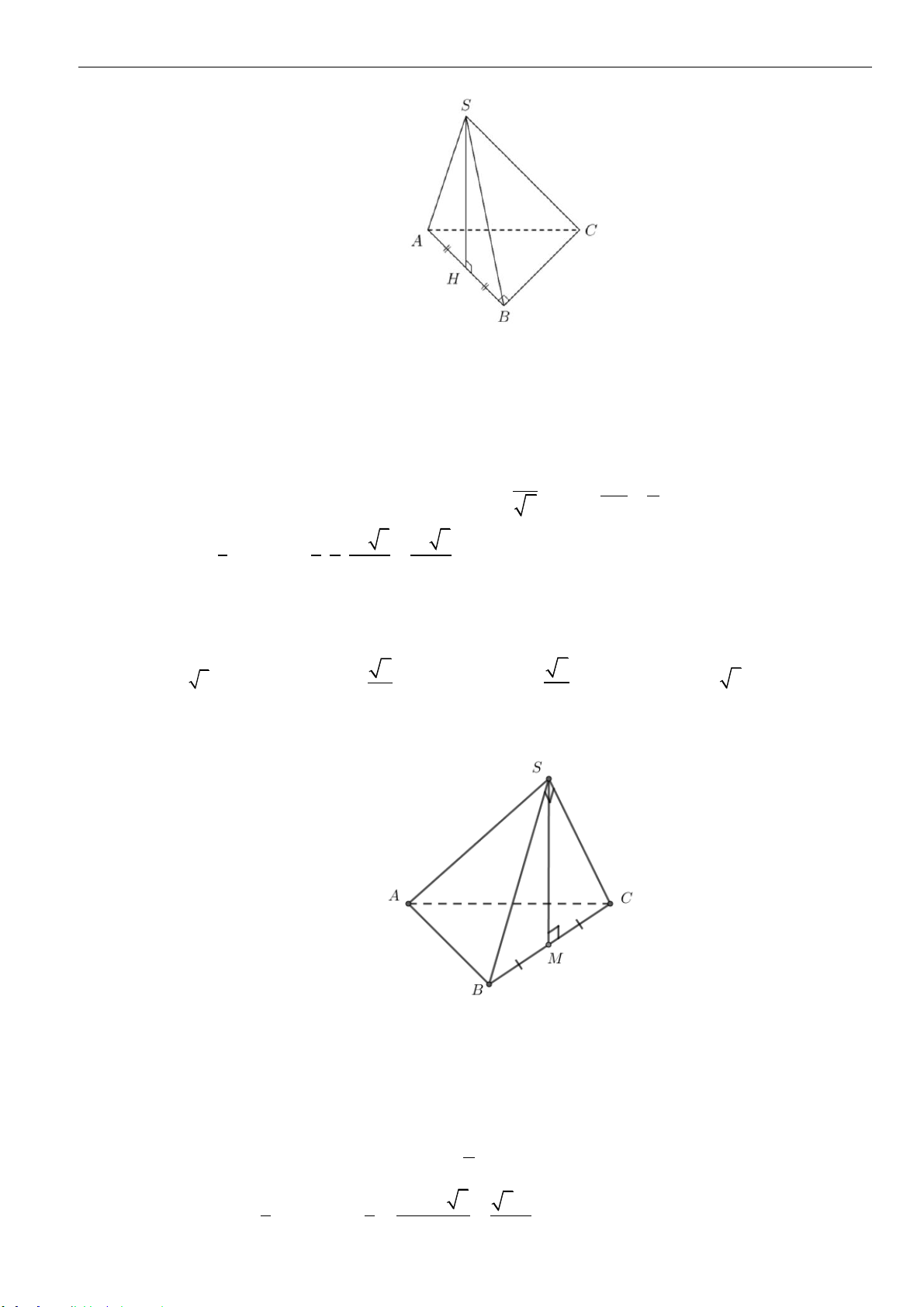
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

9 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Chọn A

Vì tam giác

SAB

cân tại

S

nên hạ

SH AB⊥



H

là trung điểm

AB

.

Vì

( ) ( )

( ) ( ) ( )

SAB ABC

SAB ABC AB SH ABC

SH AB

⊥





 =  ⊥





⊥



Tam giác

SAB

vuông cân tại

S

nên

2

a

SA SB==

;

22

AB a

SH ==

22

.

1 1 3 3

. . .

3 3 2 4 24

S ABC ABC

a a a

V SH S= = =

Câu 5: Cho khối chóp

.S ABC

có đáy là tam giác đều cạnh

2a

, mặt bên

SBC

là tam giác vuông cân

tại

S

và

( )

SBC

vuông góc với mặt phẳng

( )

ABC

. Thể tích của khối chóp đã cho bằng

A.

3

33a

. B.

3

a

. C.

3

12

a

. D.

3

3a

.

Lời giải

Chọn B

Dựng

SM BC⊥

, ta có

( ) ( )

( )

.

ABC

ABC BC

ABC

SM BC

S

B

BC

SBC

SM

SM C









⊥

=

⊥





⊥



Do

SBC

vuông cân ở

S

, suy ra

1

.

2

SM BC a==

.

Vậy

( )

2

3

.

.3

1 1 3

. . . .

3 3 4 3

2

S ABC SBC

a

V

a

SM S a= = =

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 10

Câu 6: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật với

2,AB a AD a==

. Mặt bên

()SAB

là

tam giác đều và vuông góc với mặt đáy. Thể tích khối chóp

.S ABC

bằng

A.

3

23a

. B.

3

23

3

a

. C.

3

3a

. D.

3

a

.

Lời giải

Chọn D

Vì tam giác

SAB

là tam giác đều và vuông góc với mặt phẳng đáy nên

()SH ABCD⊥

.

Ta có

3

.sin60 2 . 3

2

SH SA a a



= = =

Vậy

3

..

1 1 1 1 3

. . . . . 3.2 .

2 2 3 6 3

S ABC S ABCD

V V SH AB BC a a a a= = = =

.

Câu 7: Cho hình chóp

.S ABC

có

ABC

cân tại

A

và

120 ,BAC AC a=  =

. Cạnh bên

SC

vuông

góc với mặt đáy và

SC a=

. Thể tích khối chóp

.S ABC

bằng

A.

3

6

a

. B.

3

4

a

. C.

3

12

a

. D.

3

2

a

.

Lời giải

Chọn C

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

11 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Ta có

2

1 1 3 3

. .sin120 . . .

2 2 2 4

ABC

a

S AB AC a a



=  = =

.

Vậy

23

.

1 1 3 3

. . .

3 3 4 12

S ABC ABC

aa

V S SC a



= = =

.

Câu 8: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật,

, 2 .AB a AD a==

Tam giác

SAB

là

tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Thể tích của khối chóp

.S ABCD

bằng

A.

3

.

3

a

B.

3

.

6

a

C.

3

2

.

3

a

D.

3

.

3

a

Lời giải

Chọn A

Lấy

H AB

sao cho

SH AB⊥

(do tam giác

SAB

đều nên

H

cũng là trung điểm của

AB

)

( ) ( )

( )

( ) ( )

( )

SH AB

AB SAB ABCD

SH ABCD

SH SAB

SAB ABCD

⊥





=



⊥







⊥



.

Ta có

3

2

a

SH =

;

2

.2

ABCD

S AB AD a==

.

Vậy

3

.

13

.

33

S ABCD ABCD

a

V S SH==

.

Câu 9: Cho hình chóp

SABC

có đáy

ABC

là tam giác vuông tại

B

,

AB a=

,

5AC a=

,

( )

SA ABC⊥

và

3SA a=

. Thể tích khối chóp

SABC

bằng

A.

3

a

V =

. B.

3

3Va=

. C.

3

2

a

V =

D.

3

5

3

a

V =

.

Lời giải

Chọn A

Ta có:

2 2 2 2

52BC AC AB a a a= − = − =

.

Thể tích khối chóp là:

3

1 1 1 3

. . . 3. . .2

3 3 2 3

ABC

a

V SA S a a a= = =

.

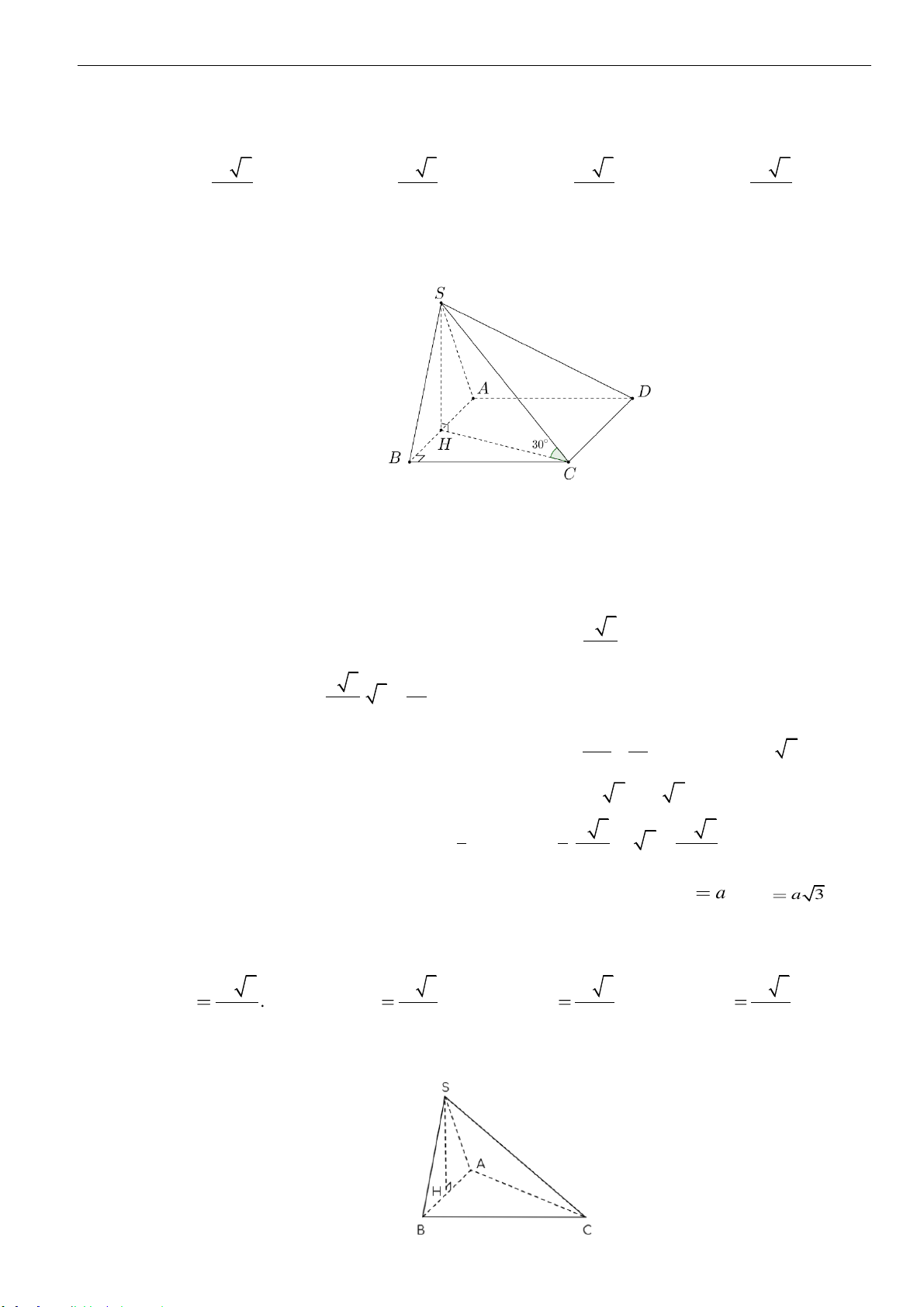
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 12

Câu 10: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật;

SAB

đều cạnh

a

và nằm trong mặt

phẳng vuông góc với

( )

ABCD

. Biết

SC

tạo với

( )

ABCD

một góc bằng

30

. Tính thể tích

V

của khối chóp

.S ABCD

.

A.

3

6

3

a

V =

. B.

3

6

a

V =

. C.

3

a

V =

. D.

3

6

a

V =

.

Lời giải

Chọn D

Gọi

H

là trung điểm của

AB

. Vì tam giác

SAB

đều nên

SH AB⊥

.

( ) ( )

( ) ( ) ( )

SAB ABCD AB

SAB ABCD SH ABCD

SH AB

=





⊥  ⊥





⊥



. Suy ra

( )

, 30SC ABCD SCH= = 

.

Vì

SH

là đường cao của tam giác đều cạnh

a

nên

3

2

a

SH =

.

33

.cot30 . 3

22

aa

CH SH =  = =

.

Trong tam giác vuông

BHC

, ta có:

22

2 2 2 2

9

22

44

aa

BC HC HB a BC a= − = − =  =

.

Diện tích của hình chữ nhật

ABCD

là

2

. . 2 2

ABCD

S AB BC a a a= = =

.

Vậy thể tích hình chóp

.S ABCD

là

3

2

1 1 3 6

. . . 2

3 3 2 6

ABCD

aa

V SH S a= = =

.

Câu 11: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông tại

A

và có

AB a

,

3BC a

. Mặt

bên

SAB

là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng

ABC

. Tính theo

a

thể tích của khối chóp

.S ABC

.

A.

3

6

.

12

a

V

B.

3

6

4

a

V

. C.

3

6

8

a

V

. D.

3

6

a

V

.

Lời giải

Chọn A

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

13 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Vì tam giác

SAB

đều và nằm trong mặt phẳng vuông góc với mặt phẳng

ABC

nên đường cao

SH

của tam giác

SAB

(

H

là trung điểm

AB

) là đường cao của hình chóp.

Ta có

SAB

đều có cạnh

3

.

2

a

AB a SH=  =

Ta lại có

2 2 2 2 2

1 1 1

3 2 . . . . 2 2.

2 2 2

ABC

AC BC AB a a a S AB AC a a a



= − = − =  = = =

Từ đó

3

2

.

1 1 1 3 6

. . . 2.

3 3 2 2 12

S ABC ABC

aa

V S SH a



= = =

.

Câu 12: Cho tứ diện

ABCD

có

ABC

là tam giác đều cạnh

,a

tam giác

BCD

cân tại

D

và nằm trong

mặt phẳng vuông góc với

( )

.ABC

Biết

AD

hợp với mặt phẳng

( )

ABC

một góc

0

60 .

Tính thể

tích

V

của khối tứ diện

.ABCD

A.

3

.

6

=

a

V

B.

3

.

12

=

a

V

C.

3

.

8

=

a

V

D.

3

.

24

=

a

V

Lời giải

Chọn C

Ta có:

2

3

4

ABC

a

S

.

Gọi

H

là trung điểm của

BC

, khi đó:

( )

DH ABC⊥

( )

, , 60AD ABC AD AH DAH= = = 

.

3

2

a

AH =

;

33

.tan60 . 3

22

aa

DH AH=  = =

.

23

1 1 3 3 3

. . . .

3 3 4 2 8

ABCD ABC

a a a

V S DH= = =

.

Câu 13: Cho hình chóp

.S ABC

có đáy là tam giác vuông tại B. Biết tam giác SAB là tam giác đều và nằm

trong mặt phẳng vuông góc với mặt phẳng đáy (ABC).Biết

, 3AB a AC a==

. Thể tích khối

chóp

.S ABC

là

A.

3

4

a

. B.

3

6

4

a

. C.

3

2

6

a

. D.

3

6

12

a

.

Lời giải

Chọn D

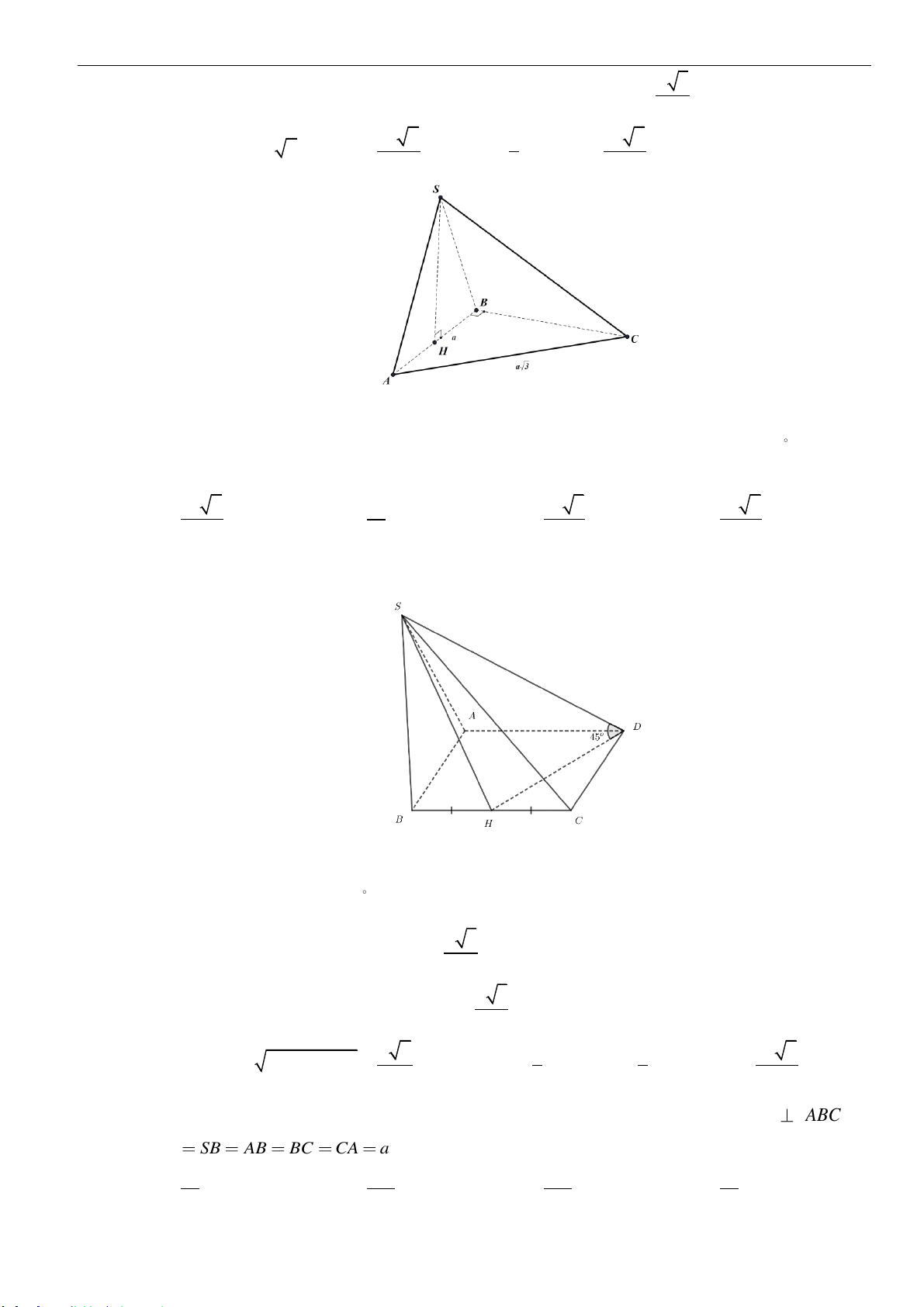
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 14

Gọi H là trung điểm của AB, từ giả thiết suy ra

3

( ), SH=

2

a

SH ABC⊥

. Trong tam giác vuông

ABC có

23

.

2 1 6

2 . .

2 3 12

ABC S ABC ABC

aa

BC a S V SH S=  =  = =

Câu 14: Cho hình chóp

.S ABCD

có

ABCD

là hình chữ nhật, tam giác

SBC

đều cạnh

a

nằm trong mặt

phẳng vuông góc với

( )

ABCD

biết góc giữa

SD

và mặt phẳng

( )

ABCD

bằng

45

. Thể tích

hình chóp

.S ABCD

là

A.

3

6

4

a

. B.

3

a

. C.

3

4

a

. D.

3

6

12

a

.

Lời giải

Chọn D

Gọi

H

là trung điểm của cạnh

BC SH BC⊥

. Mà

( ) ( ) ( )

SBC ABCD SH ABCD⊥  ⊥

và

( )

(

)

, 45SD ABCD SDH==

Tam giác

SBC

đều cạnh

a

nên

3

2

a

SH =

.

Tam giác

SHD

vuông cân tại

3

2

a

H HD=

Suy ra

22

2

a

CD DH CH= − =

. Vậy

3

.

1 1 6

. . . . .

3 3 12

S ABCD ABCD

a

V SH S SH BC CD= = =

.

Câu 15: Cho khối chóp

.S ABC

có

H

là trung điểm của

AB

, biết

SH ABC

,

SA SB AB BC CA a

. Thể tích của khối chóp đã cho là

A.

3

4

a

. B.

3

4

a

. C.

3

8

a

. D.

3

8

a

.

Lời giải

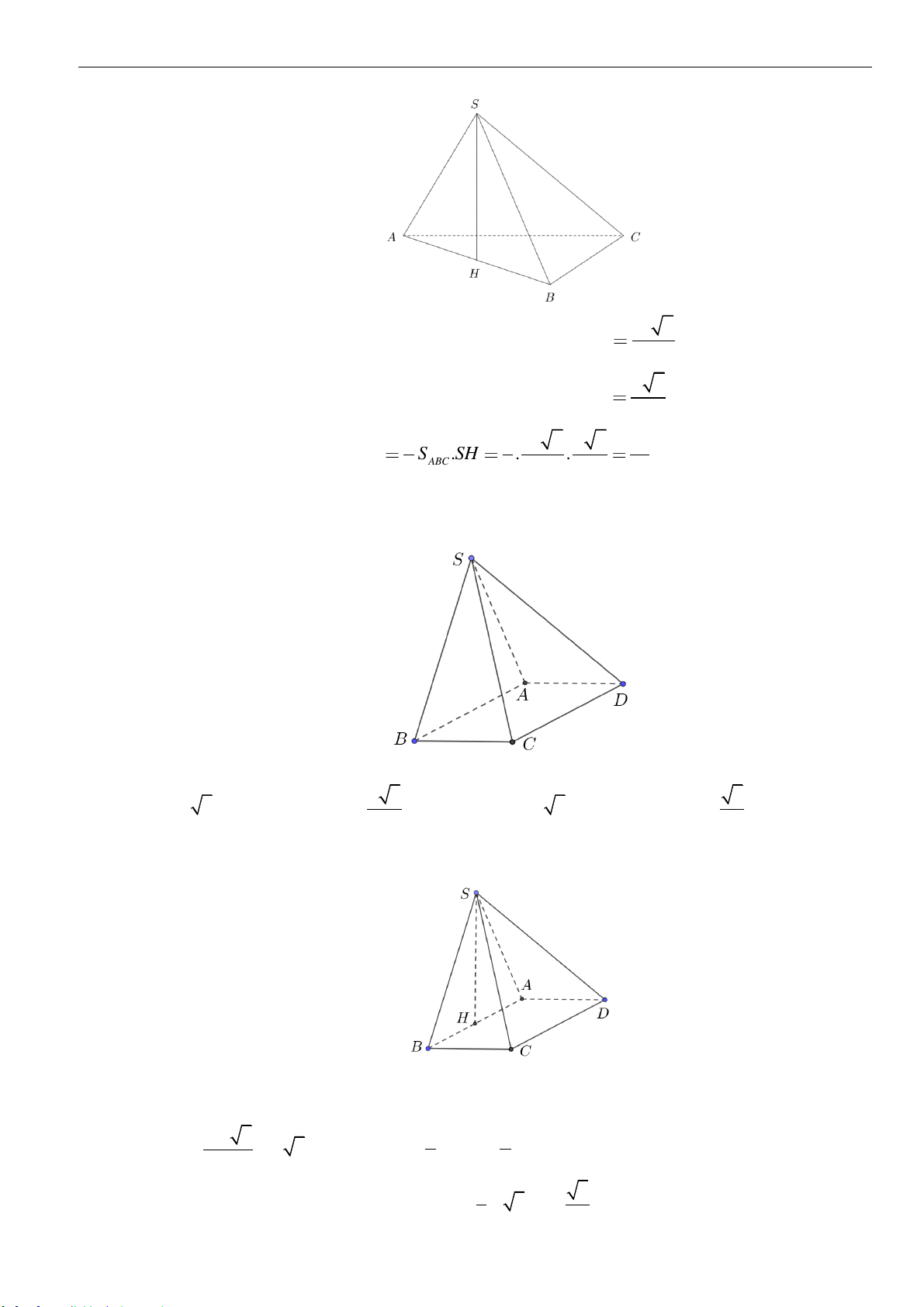
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

15 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Chọn D

Vì tam giác

ABC

đều với cạnh bằng

a

nên có diện tích

ABC

a

S

2

3

4

.

Vì tam giác

SAB

đều với cạnh bằng

a

nên có đường cao

a

SH

3

2

.

Do đó, thể tích khối chóp là

. . .

ABC

a a a

V S SH

23

1 1 3 3

3 3 4 2 8

.

Câu 16: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật với

2AB a=

,

AD a=

. Mặt bên

( )

SAB

là tam giác đều và vuông góc với mặt đáy.

Thể tích của khối chóp

.S ABC

bằng

A.

3

23a

. B.

3

23

3

a

. C.

3

3a

. D.

3

a

.

Lời giải

Chọn D

Gọi

SH

là đường cao của tam giác

SAB

.

Vì mặt bên

( )

SAB

là tam giác đều và vuông góc với đáy nên ta có

( )

SH ABCD⊥

và

3

2

AB

SH a==

. Ta có

2

11

.2 .

22

ABC ABCD

S S a a a



= = =

.

Vậy thể tích của khối chóp

.S ABC

là

23

13

. 3.

33

V a a a==

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 16

Câu 17: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật, tam giác

SAD

vuông tại

S

và nằm

trong mặt phẳng vuông góc với mặt phẳng đáy. Cho biết

AB a=

,

2SA SD=

, mặt phẳng

( )

SBC

tạo với mặt phẳng đáy một góc

60

. Tính thể tích của khối chóp

.S ABCD

.

A.

3

5

2

a

. B.

3

5a

. C.

3

15

2

a

. D.

3

2

a

.

Lời giải

Chọn A

Gọi

H

là hình chiếu của

S

trên

AD

và

K

là hình chiếu của

H

trên

BC

.

Ta có:

( ) ( )

( )

SAD ABCD

SH ABCD

SH AD

⊥





⊥



⊥





.

HK BC

BC SK

SH BC

⊥



⊥



⊥



. Do đó góc tạo bởi hai mặt phẳng

( )

SBC

và

( )

ABCD

là góc

60SKH =

,

.tan60 3SH HK a=  =

2 2 2

1 1 1

SH SA SD

=+

22

15

34a SD

=



15

2

a

SD =

,

15SA a=

,

53

2

a

AD =

.

1

.

3

S ABCD ABCD

V SH S=

=

3

1 5 3 5

3. .

3 2 2

aa

aa =

.

Câu 18: Hình chóp

.S ABCD

đáy là hình chữ nhật có

2 3; 2AB a AD a==

. Mặt bên

( )

SAB

là tam giác

đều và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối chóp

.S ABD

là

A.

3

23

3

a

. B.

3

43a

. C.

3

4a

. D.

3

23a

.

Lời giải

Chọn D

Gọi

H

là trung điểm của

AB

( )

SH ABCD⊥

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

17 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Tam giác

SAB

là tam giác đều cạnh

23a

nên

2 3 3

3

2

a

SH a



==

.

Vậy thể tích khối chóp

SABD

là

3

1 1 1

3 2 3 2 2 3

3 3 2

ABD

V SH S a a a a=   =     =

.

Câu 19: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật, mặt bên

SAD

là tam giác đều cạnh

2a

và nằm trong mặt phẳng vuông góc với mặt phẳng

()ABCD

. Góc giữa mặt phẳng

()SBC

và mặt phẳng

()ABCD

là

30

. Thể tích của khối chóp

.S ABCD

là:

A.

3

23

3

a

. B.

3

23a

. C.

3

43

3

a

. D.

3

a

.

Lời giải

Chọn B

Gọi

I

là trung điểm của

AD

()SI AD SI ABCD ⊥  ⊥

.

Gọi

M

là trung điểm của

BC

, ta có:

( )

BC MI

BC SIM BC SM

BC SI

⊥



 ⊥  ⊥



⊥



.

Khi đó:

( ) ( )

( )

,

SBC ABCD BC

SM SBC SM BC

MI ABCD MI BC

=





⊥





⊥



( ) ( )

( )

, , 30SBC ABCD SM MI SMI = = = 

Vì

SAD

đều cạnh

2a

nên

2SA AD a==

và

( )

2

2 2 2

23SI SA AI a a a= − = − =

.

Xét

SIM

vuông tại

I

ta có:

3

tan30

SI

IM a==



.

Lại có

3AB IM a==

. Vậy thể tích của khối chóp

.S ABCD

là:

3

1 1 1

. . . .2 .3 . 3 2 3

3 3 3

ABCD

V S SI AD AB SI a a a a= = = =

(đvtt).

Câu 20: Trong không gian cho tam giác đều

SAB

và hình chữ nhật

ABCD

với

2AD a=

nằm trên hai

mặt phẳng vuông góc. Gọi



là góc giữa hai mặt phẳng

( )

SAB

và

( )

SCD

. Biết

22

tan

3



=

.

Thể tích của khối chóp

.S ABC

là

A.

3

2

a

V =

. B.

3

3Va=

. C.

3

8

a

V =

D.

3

2

12

a

V =

.

Lời giải

Chọn B

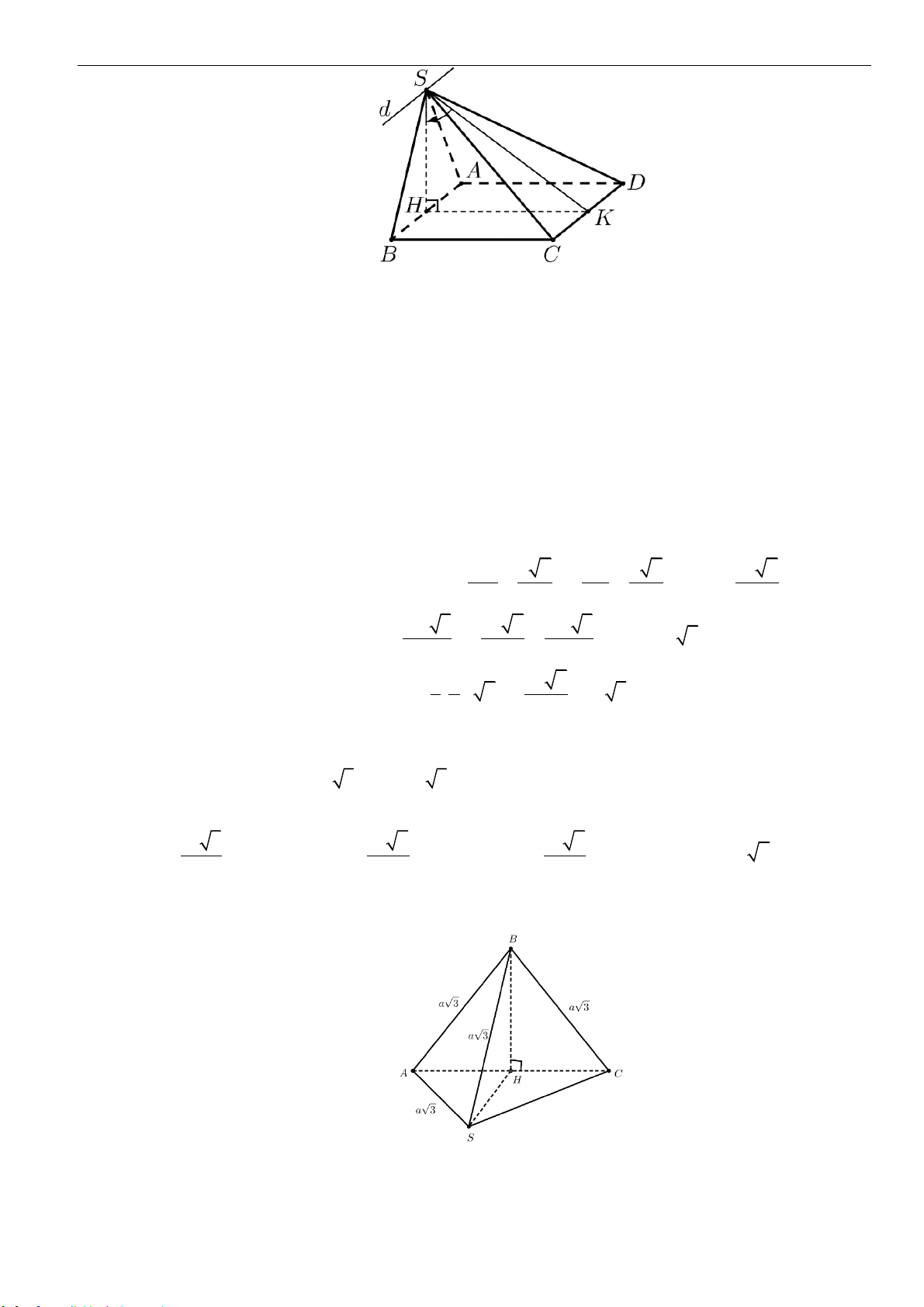
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 18

Dễ dàng xác định giao tuyến của hai mặt phẳng

( )

SAB

và

( )

SCD

là đường thẳng

d

đi qua

S

và song song với

,AB

.CD

Gọi

,H

K

lần lượt là trung điểm của

,AB

.CD

Trong mặt phẳng

( )

SAB

có

.SH AB SH d⊥  ⊥

Vì

( )

.

CD HK

CD SHK CD SK d SK

CD SH

⊥



 ⊥  ⊥  ⊥



⊥



Ta có

( ) ( )

( )

, .

,

SAB SCD d

SH d SH SAB

SK d SK SCD

=





⊥





⊥



Do đó

( ) ( )

(

)

( )

, , .SAB SCD SH SK HSK==

Xét tam giác vuông

,SHK

có

2 2 2 2 2 3 2

tan

3 3 2

HK a a

HSK SH

SH SH

= =  =  =

.

Xét tam giác đều

SAB

có:

3 3 2 3

6

2 2 2

AB a AB

SH AB a=  =  =

Thể tích khối chóp

.S ABC

bằng

3

1 1 3 2

. 6.2 . 3

3 2 2

a

V a a a==

.

Câu 21: Cho hình chóp

.S ABC

có mặt phẳng

( )

SAC

vuông góc với mặt phẳng

( )

ABC

, tam giác

SAB

là tam giác đều cạnh

3a

;

3BC a=

. Đường thẳng

SC

tạo với mặt phẳng

( )

ABC

một góc

60

. Thể tích khối chóp

.S ABC

bằng

A.

3

a

. B.

3

6

2

a

. C.

3

6

a

. D.

3

26a

.

Lời giải

Chọn C

Gọi

H

là trung điểm của

AC

. Vì

ABC

cân tại

B

nên

BH AC⊥

.

Mặt khác

( ) ( )

SAC ABC⊥

( )

BH SAC⊥

.

Ta thấy

BHA BHS BHC =  = 

HA HC HS = =

SAC

vuông tại

S

.

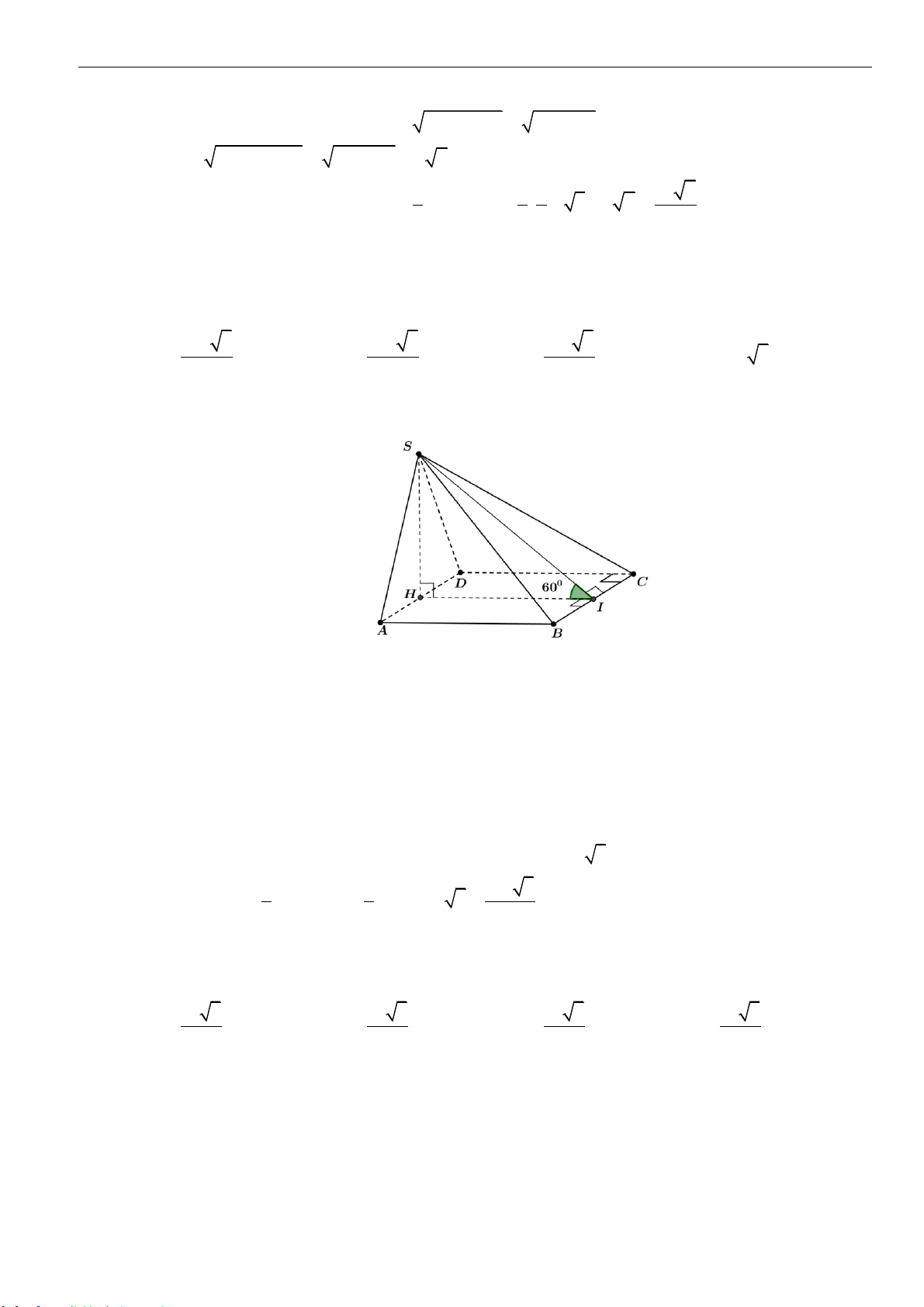
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

19 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Góc giữa đường thẳng

SC

và mặt phẳng

( )

ABC

là góc

60SCA =

.

Ta có

.cot 60SC SA a=  =

;

2 2 2 2

32AC SA SC a a a= + = + =

AH HC a = =

.

2 2 2 2

32BH BC HC a a a= − = − =

.

Thể tích khối chóp

.B SAC

là

3

1 1 1 6

. . . . 3. . 2

3 3 2 6

SAC

a

V S BH a a a



= = =

.

Câu 22: Cho khối chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

2a

, tam giác

SAD

cân tại

S

và

nằm trong mặt phẳng vuông góc với đáy. Góc giữa

( )

SBC

và mặt đáy bằng

0

60

. Tính thể tích

khối chóp

.S ABCD

.

A.

3

23

3

a

. B.

3

43

3

a

. C.

3

83

3

a

. D.

3

23a

.

Lời giải

Chọn C

Gọi

H

là trung điểm của

AD

. Vì tam giác

SAD

cân tại

S

nên

SH AD⊥

. Hai mặt phẳng

( )

SAD

và

( )

ABCD

vuông góc nhau và cắt nhau theo giao tuyến

AD

có

( )

SH SAD

mà

SH AD⊥

nên

( )

SH ABCD⊥

.

Gọi

I

là trung điểm của

BC

ta có

( )

BC HI

BC SHI BC SI

BC SH

⊥



 ⊥  ⊥



⊥



suy ra góc giữa hai

mặt phẳng

( )

SBC

và mặt đáy

( )

ABCD

là góc

0

60SIH =

.

Xét tam giác

SHI

vuông tại

H

có

0

.tan60 2 3SH HI a==

.

Vậy

( )

3

2

.

1 1 8 3

. 2 .2 3

3 3 3

S ABCD ABCD

a

V S SH a a= = =

.

Câu 23:

Cho hình chóp

.S ABC

có đáy là tam giác vuông cân tại

A

, mặt bên

SBC

là tam giác đều cạnh

a

và

( )

SBC

vuông góc với mặt đáy. Thể tích khối chóp đó là

A.

3

4

a

. B.

3

24

a

. C.

3

8

a

. D.

3

12

a

.

Lời giải

Chọn B

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 20

Gọi H là trung điểm của BC mà tam giác

SBC

đều cạnh a nên

SH BC⊥

và

3

2

a

SH =

.

Do

( ) ( ) ( )

SBC ABC SH ABC⊥  ⊥

Ta có

2

1

.

24

22

ABC

BC a a

AB AC S AB AC= = =  = =

Vậy

23

.

1 1 3 3

.

3 3 2 4 24

S ABC ABC

a a a

V SH S= = =

.

Câu 24: Cho hình chóp

.S ABC

có đáy là tam giác vuông cân tại

A

, cạnh

2BC a=

. Gọi

M

là trung điểm

của

BC

, hình chiếu vuông góc của

S

lên mặt phẳng

( )

ABC

là trung điểm của

AM

, tam giác

SAM

vuông tại

S

. Thể tích khối chóp

.S ABC

là

A.

3

.

2

a

B.

3

.

6

a

C.

3

.

3

a

D.

3

.

9

a

Lời giải

Chọn B

Gọi

H

là trung điểm của

AM

. Theo giả thiết:

( )

SH ABC⊥

.

Ta có:

ABC

vuông cân tại

A

1

2

AM BC a = =

.

Mà

SAM

vuông tại

S

và

H

là trung điểm của

1

.

22

a

AM SH AM = =

3

.

1 1 1

. . . . . .

3 3 2 6

S ABC ABC

a

V SH S SH AM BC = = =

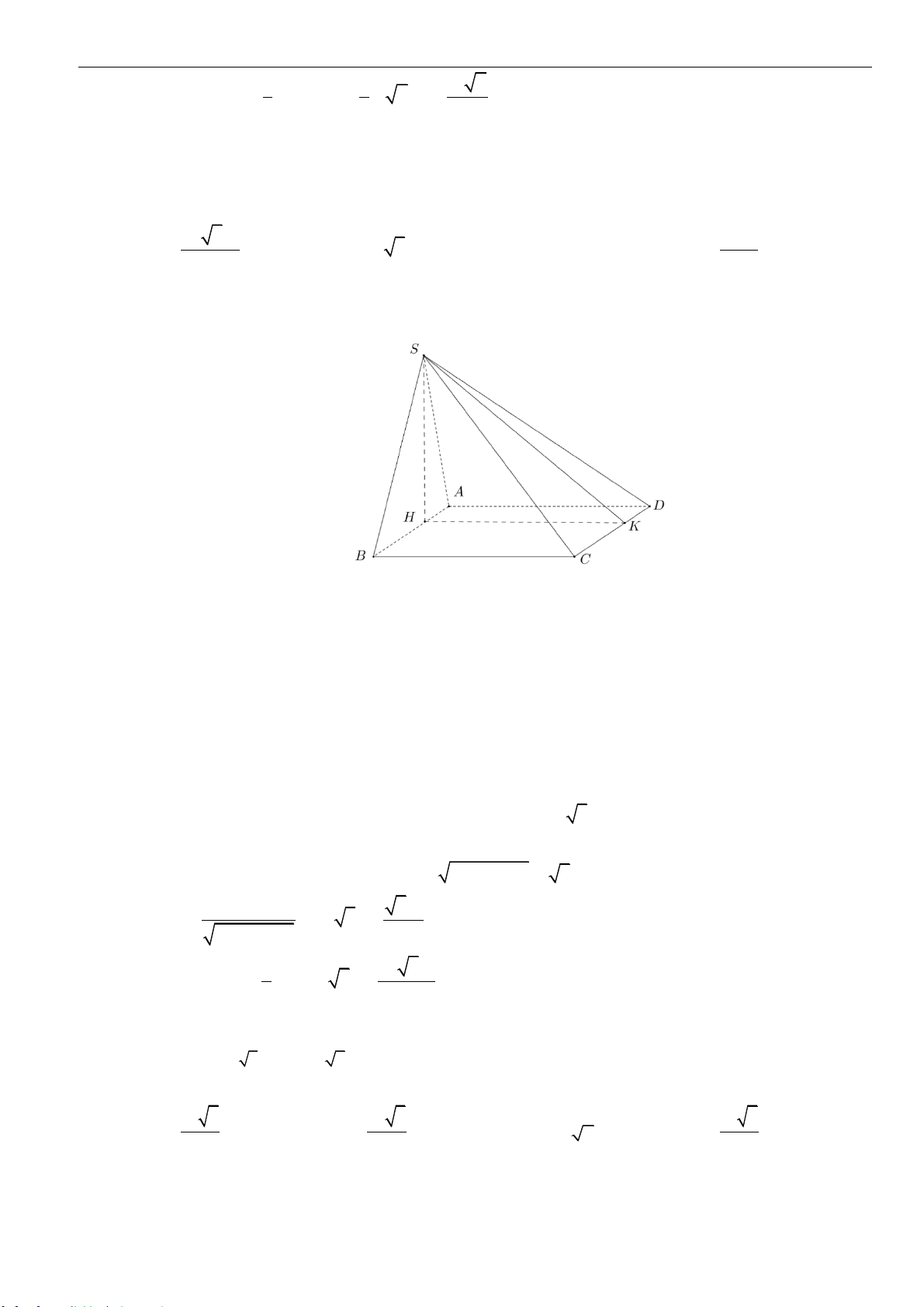
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

21 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Ta có

3

2

.

1 1 2

. . . 2.

3 3 3

S ABCD ABCD

a

V SH S a a= = =

.

Câu 25: Cho hình chóp

.S ABCD

có đáy là hình chữ nhật, tam giác

SAB

vuông tại

S

và nằm trong mặt

phẳng vuông góc với mặt phẳng đáy. Biết

2 , 2AB SA BC a==

và mặt phẳng

( )

SCD

tạo với mặt

phẳng đáy một góc

0

60

. Thể tích của khối chóp

.S ABCD

tính theo

a

bằng

A.

3

32 3

3

a

. B.

3

16 3a

. C.

3

16a

. D.

3

32

3

a

.

Lời giải

Chọn D

Kẻ

SH AB⊥

Ta có

( ) ( )

( ) ( ) ( )

SAB ABCD

SAB ABCD AB SH ABCD

SH AB

⊥





 =  ⊥





⊥



.

Ta có

( ) ( )

( )

0

; 60

SCD ABCD CD

HK CD SCD ABCD SKH

SK CD

=





⊥  = =





⊥



Xét tam giác

SKH

vuông tại

H

:

0

.tan60 2 3SH HK a==

Đặt

SA x=

Xét tam giác

SAB

vuông tại

S

:

22

3SB AB SA x= − =

2

22

.3

2 3 4

2

SA AB x

SH x x a

x

SA AB

=  =  =

+

. Suy ra

2

16

ABCD

Sa=

Vậy

3

2

.

1 32 3

.16 .2 3

33

S ABCD

a

V a a==

.

Câu 26: Cho hình chóp

.S ABC

có mặt phẳng

()SAC

vuông góc với mặt phẳng

()ABC

,

SAB

là tam giác

đều cạnh

3a

,

3BC a=

, đường thẳng

SC

tạo với mặt phẳng

()ABC

góc

60



. Thể tích của

khối chóp

.S ABC

bằng

A.

3

6

2

a

. B.

3

a

. C.

3

26a

. D.

3

6

a

.

Lời giải

Chọn D

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 22

Gọi

O

là trung điểm của

AC

, vì

BA BC=

nên

BO AC⊥

.

Mà

( ) ( )SAC SAB⊥

nên

()BO SAC⊥

.

Khi đó, các tam giác vuông

BOA

,

BOC

,

BOS

bằng nhau nên

OA OC OS==

.

Suy ra tam giác

SAC

vuông tại

S

.

Vì

()SAC

vuông góc với

()ABC

và góc giữa

SC

và mặt phẳng

()ABC

bằng

60



nên góc

60SCA



=

.

Như vậy

2

2sin

AC SA

OS OA OC a

SCA

= = = = =

.

Suy ra

22

2BO SB OS a= − =

.

Diện tích

SAC

tính bằng công thức

2

1 1 3

sin 3 2 sin30 .

2 2 2

S SA AC SAC a a a



=   =    =

Như vậy

3

16

36

SAC

V BO S a=   =

.

Câu 27: Cho hình chóp

.S ABCD

có đáy là hình vuông cạnh bằng

2

, tam giác

SAB

là tam giác đều và

tam giác

SCD

vuông tại

S

. Tính thể tích

V

của khối chóp

.S ABCD

.

A.

23

3

V =

. B.

83

3

V =

. C.

43

3

V =

. D.

23V =

.

Lời giải

Chọn A

Gọi

,EF

lần lượt là trung điểm

,AB CD

. Gọi

H

là chân đường cao của hình chóp,

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

23 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

( )

H ABCD

.

Ta có

( )

,AB SE AB EF AB SEF⊥ ⊥  ⊥

do đó

H EF

.

Tam giác

SCD

vuông tại

S

và có trung tuyến

SF

nên

1

2

SF CD==

.

Tam giác

SEF

có

3, 2, 1SE EF SF= = =

nên tam giác

SEF

vuông tại

S

.

Do đó

..SH EF SE SF=

. 3.1 3

22

SE SF

SH

EF

 = = =

.

Vậy thể tích khối chóp là

2

1 1 3 2 3

. .2 .

3 3 2 3

ABCD

V S SH= = =

.

Câu 28: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác đều, hình chiếu vuông góc của đỉnh

S

trên mặt

đáy là trung điểm

H

của cạnh

AB

. Biết

3

2

a

SH =

và mặt phẳng

( )

SAC

vuông góc với mặt

phẳng

()SBC

. Thể tích khối chóp

.S ABC

bằng

A.

3

4

a

. B.

3

16

a

. C.

3

2

a

. D.

3

8

a

.

Lời giải

Chọn A

Ta có:

( )

AB HC

AB SHC AB SC

AB SH

⊥



 ⊥  ⊥



⊥



.

Kẻ

HK SC⊥

tại

K

Có:

( )

;

SC HK

SC AKB SC KB SC AK

SC AB

⊥



 ⊥  ⊥ ⊥



⊥



.

Suy ra

( )

0

( );( ) 90SAC SBC AKB==

.

Đặt

AB x=

,

AKB

vuông tại

K

có

H

là trung điểm của

1

22

x

AB KH AB = =

.

ABC

đều nên

3

2

x

CH =

.

Xét tam giác

SHC

vuông tại

H

có:

HK

là đường cao

222

1 1 1

HK SH HC

 = +

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 24

2 2 2

1 1 1

2

33

2

22

xa

x

ax

 = +  =

     



   



   

.

Thể tích khối chóp:

3

.

1 1 1 1 3 3

. . . . . . 2. 2.

3 3 2 6 2 2 4

S ABC ABC

aa

V SH S SH CH AB a a= = = =

.

Câu 29: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh bằng

a

, mặt bên

SAB

là tam giác

đều,

3SC SD a==

. Thể tích khối chóp

.S ABCD

bằng

A.

3

2

3

a

. B.

3

2

6

a

. C.

3

6

a

. D.

3

2

a

.

Lời giải

Chọn B

Gọi

,EF

lần lượt là trung điểm của

AB

và

CD

.

Từ giả thiết ta có:

( ) ( )

,SE AB SF CD SEF ABCD⊥ ⊥  ⊥

.

Kẻ

SH EF⊥

tại H. Khi đó

( )

SH ABCD⊥

.

Vì

SAB

đều cạnh

a

nên

3

2

a

SE =

.

Vì

SCD

cân, có

3SC SD a==

nên

11

2

a

SF =

.

Vì

ABCD

là hình vuông cạnh

a

nên

EF a=

.

Xét

SEF

, theo công thức hê-rông ta có:

2

4

SEF

a

S



=

.

Mà

2

12

.

22

SEF

S

a

S SH EF SH

EF



=  = =

.

Vậy thể tích khối chóp

.S ABCD

là:

3

2

1 1 2 2

. . . .

3 3 2 6

ABCD

aa

V SH S a= = =

.

Câu 30: Cho hình chóp

.S ABCD

có đáy là hình thoi cạnh

a

góc

0

120BAD =

, tam giác

SAB

cân tại

S

và nằm trong mặt phẳng vuông góc với mặt đáy, góc giữa

SCD

và mặt đáy bằng

0

60

. Tính thể

tích khối chóp

.S ABCD

.

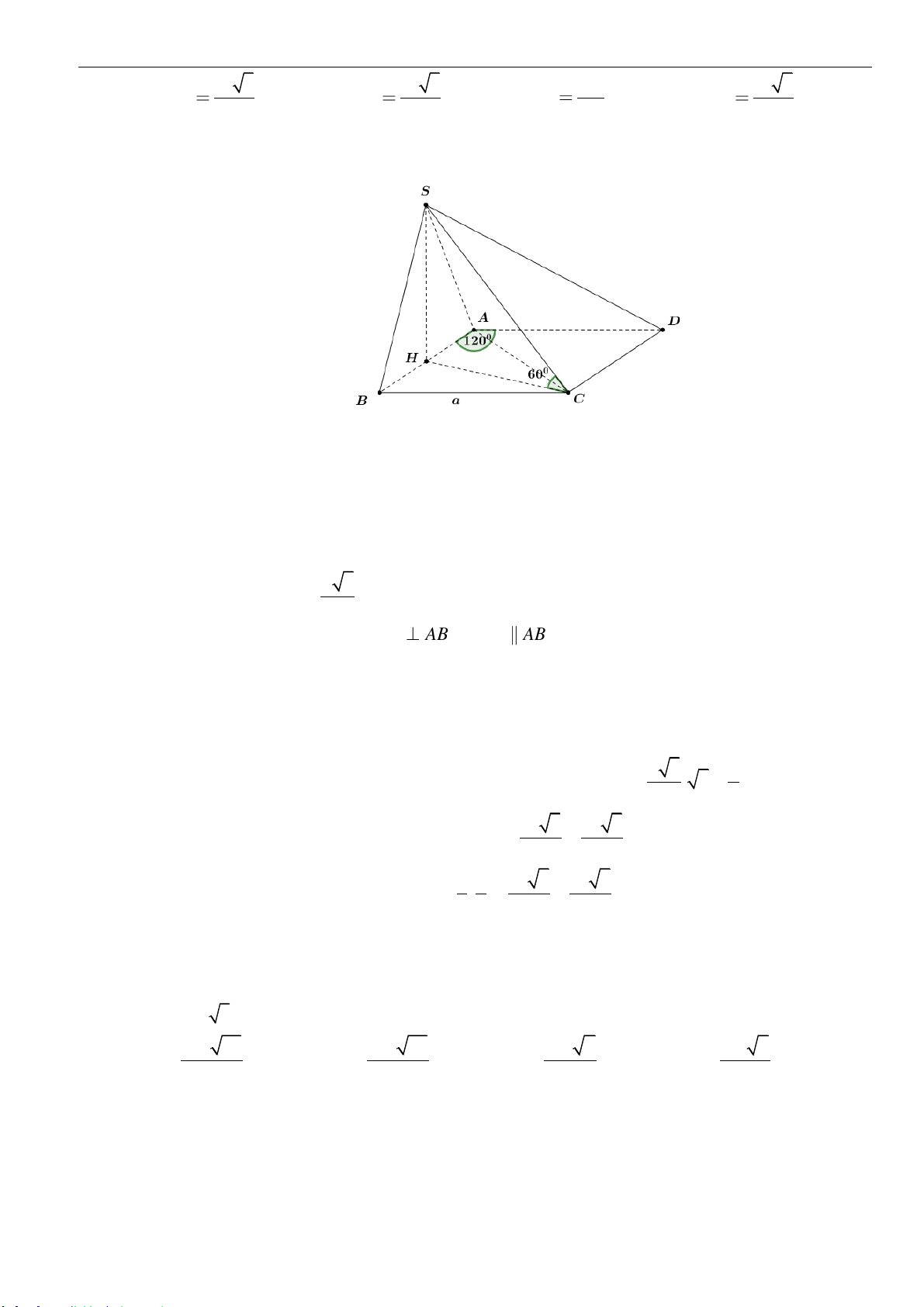
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

25 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

A.

3

4

a

V

. B.

3

12

a

V

. C.

3

4

a

V

. D.

3

2

a

V

.

Lời giải

Chọn A

Gọi

H

là trung điểm của đoạn

AB

.

Vì

SAB

là tam giác cân đỉnh

S

nên

SH AB⊥

, mà

( ) ( ) ( ) ( )

,SAB ABCD SAB ABCD AB⊥  =

suy ra

( )

SH ABCD⊥

.

Vì đáy

ABCD

là hình thoi cạnh

a

và có góc

0

120BAD =

nên tam giác

BAC

là tam giác đều

cạnh

a

, suy ra

3

2

a

CH =

.

Vì

BAC

là tam giác đều nên

CH AB

mà

CD AB

suy ra

CH CD⊥

.

Vì

;CD CH CD SH⊥⊥

suy ra

CD SC⊥

.

Vì

( ) ( )

;;CD CH CD SC SCD ABCD CD⊥ ⊥  =

suy ra góc giữa hai mặt phẳng

( )

SCD

và

( )

ABCD

bằng góc giữa hai đường thẳng

SC

và

HC

suy ra góc

0

60SCH =

.

Xét tam giác

SHC

vuông tại

H

ta có

0

33

.tan60 . 3

22

a

SH HC SH a=  = =

.

Diện tích hình thoi

ABCD

là:

22

33

2 2.

42

ABCD ABC

aa

SS= = =

Vậy thể tích khối chóp

.S ABCD

là:

23

1 3 3 3

. . .

3 2 2 4

aa

Va==

.

Câu 31: Cho hình chóp tứ giác

.S ABCD

có đáy là hình vuông, mặt bên

( )

SAB

là tam giác đều và nằm

trong mặt phẳng vuông góc với mặt đáy. Biết khoảng cách từ điểm

A

đến mặt phẳng

( )

SCD

bằng

3a

. Tính thể tích

V

của khối chóp

A.

3

7 21

6

a

. B.

3

7 21

2

a

. C.

3

77

6

a

. D.

3

37

2

a

.

Lời giải

Chọn A

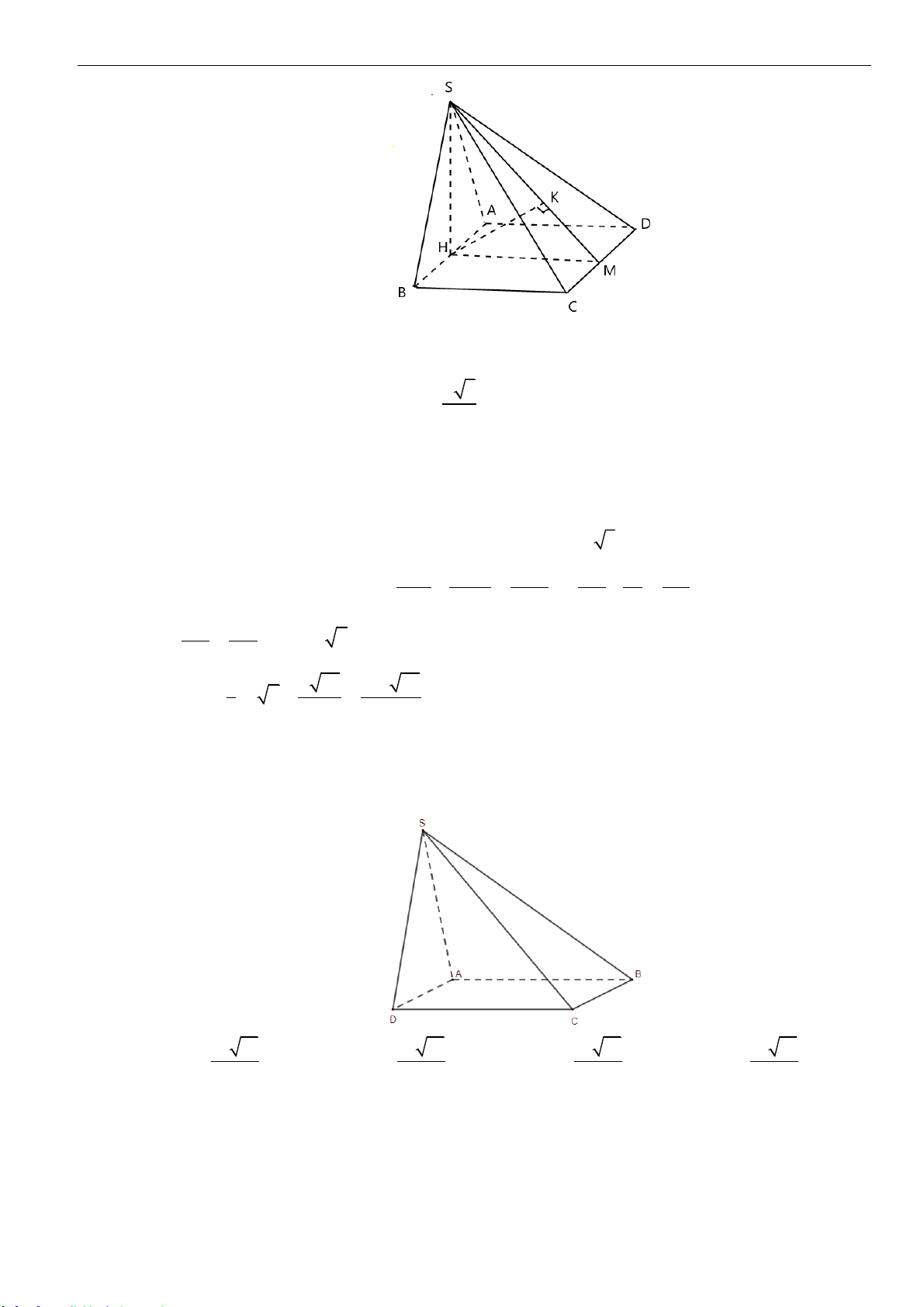
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 26

Gọi cạnh của hình vuông

ABCD

là

x

.

,HM

là trung điểm của

,AB CD

. Do tam giác

SAB

đều và nằm trong mặt phẳng vuông góc với

đáy nên

SH

vuông góc với

AB

,

3

2

x

SH =

,

( )

SH ABCD⊥

.

( ) ( )

( )

// , ,AH SCD d A SCD d H SCD=

.

Kẻ

HK SM⊥

(1),

( )

CD MH

CD SHM CD HK

CD SH

⊥



 ⊥  ⊥



⊥



(2).

Từ (1) và (2)

( )

HK SDC⊥

hay

( )

, 3.d H SDC HK a==

Trong tam giác vuông

SHM

:

2 2 2 2 2 2

1 1 1 4 1 1

33SH HM HK x x a

+ =  + =

22

71

7.

33

xa

 =  =

( )

3

2

.

1 21 7 21

7.

3 2 6

S ABCD

aa

Va==

Câu 32: Hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

. Tam giác

SAD

cân và nằm trong mặt

phẳng vuông góc với đáy. Gọi

M

là trung điểm của

CD

, cạnh bên

SB

hợp với đáy góc

60

.

Tính theo

a

thể tích

V

của khối chóp

.S ABM

A.

3

15

4

a

V =

. B.

3

15

6

a

V =

. C.

3

15

12

a

V =

. D.

3

15

3

a

V =

.

Lời giải

Chọn C

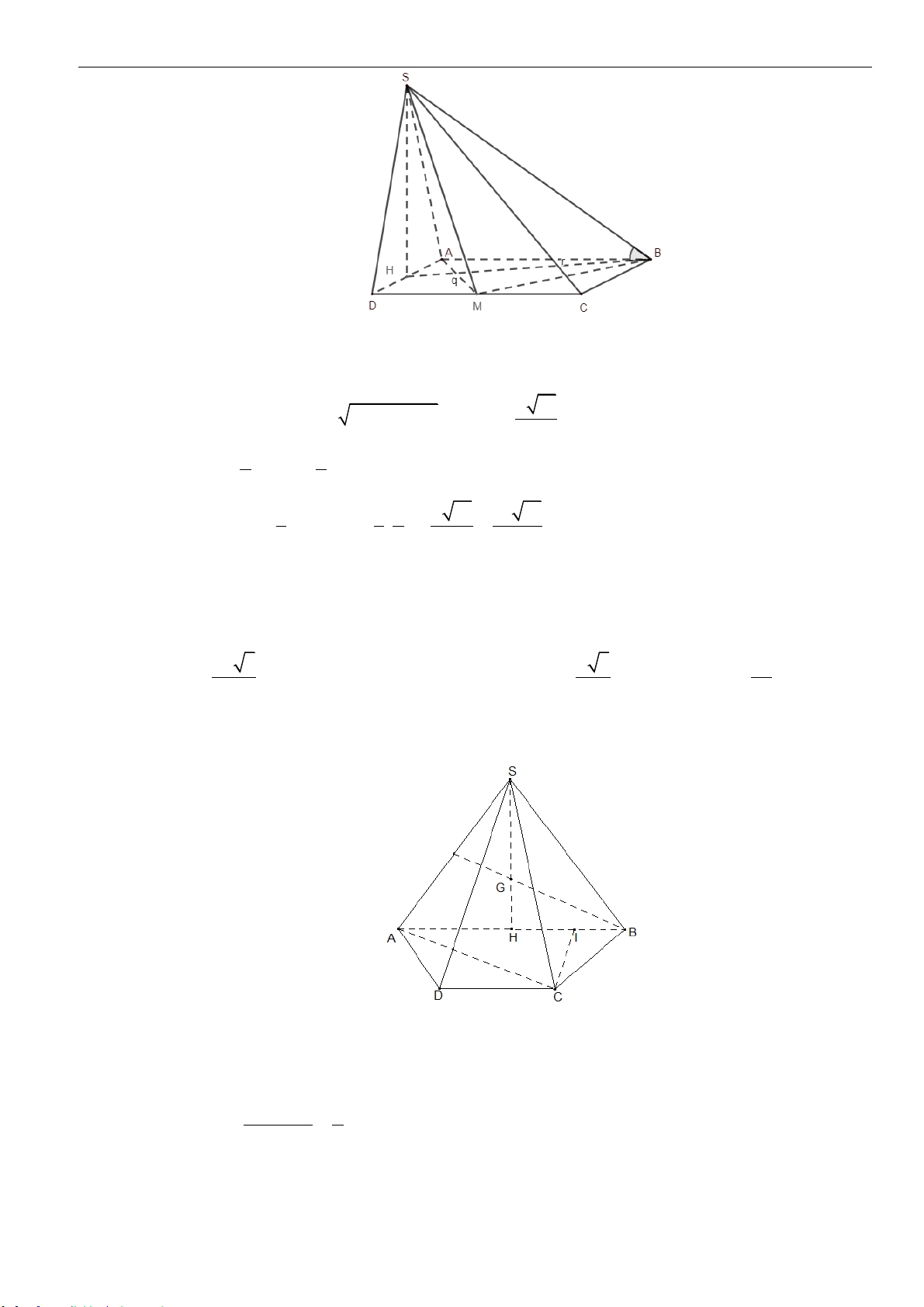
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

27 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Gọi

H

là trung điểm của

AD

( )

SH AD SH ABCD ⊥  ⊥

.

Khi đó ta có:

( )

, , 60SB ABCD SB HB SBH= = = 

22

15

.tan .tan60

2

a

SH HB SBH AH AB = = +  =

.

Có

2

11

22

ABM ABCD

S S a==

3

2

.

1 1 1 15 15

. . .

3 3 2 2 12

S ABM ABM

aa

V V S SH a = = = =

Câu 33: Cho hình chóp

.S ABCD

có đáy là hình thang cân,

2AB a=

,

AD BC CD a= = =

. Mặt bên

SAB

là tam giác đều và nằm trong mặt phẳng vuông góc với

( )

.ABCD

Tính bán kính

R

của mặt cầu

ngoại tiếp khối chóp

.S ABC

.

A.

23

3

a

R =

B.

Ra=

C.

3

a

R =

D.

2

3

a

R =

Lời giải

Chọn A

Do

AB

và

CD

không bằng nhau nên hai đáy của hình thang là

AB

và

CD

. Gọi

H

là trung

điểm của

AB

. Khi đó

SH

vuông góc với

AB

nên

SH

vuông góc với

( )

.ABCD

Gọi

I

là chân đường cao của hình thang

ABCD

từ đỉnh

C

của hình thang

ABCD

.

Ta có

22

AB CD a

BI

−

==

Do

22

.BI BC a BC==

. Từ đó ta có tam giác

ABC

vuông tại

C

.

Do đó

SH

chính là trục đường trong ngoại tiếp của tam giác

ABC

.

Mặt khác do tam giác

SAB

đều nên tâm mặt cầu ngoại tiếp hình chóp

.S ABC

chính là trọng tâm

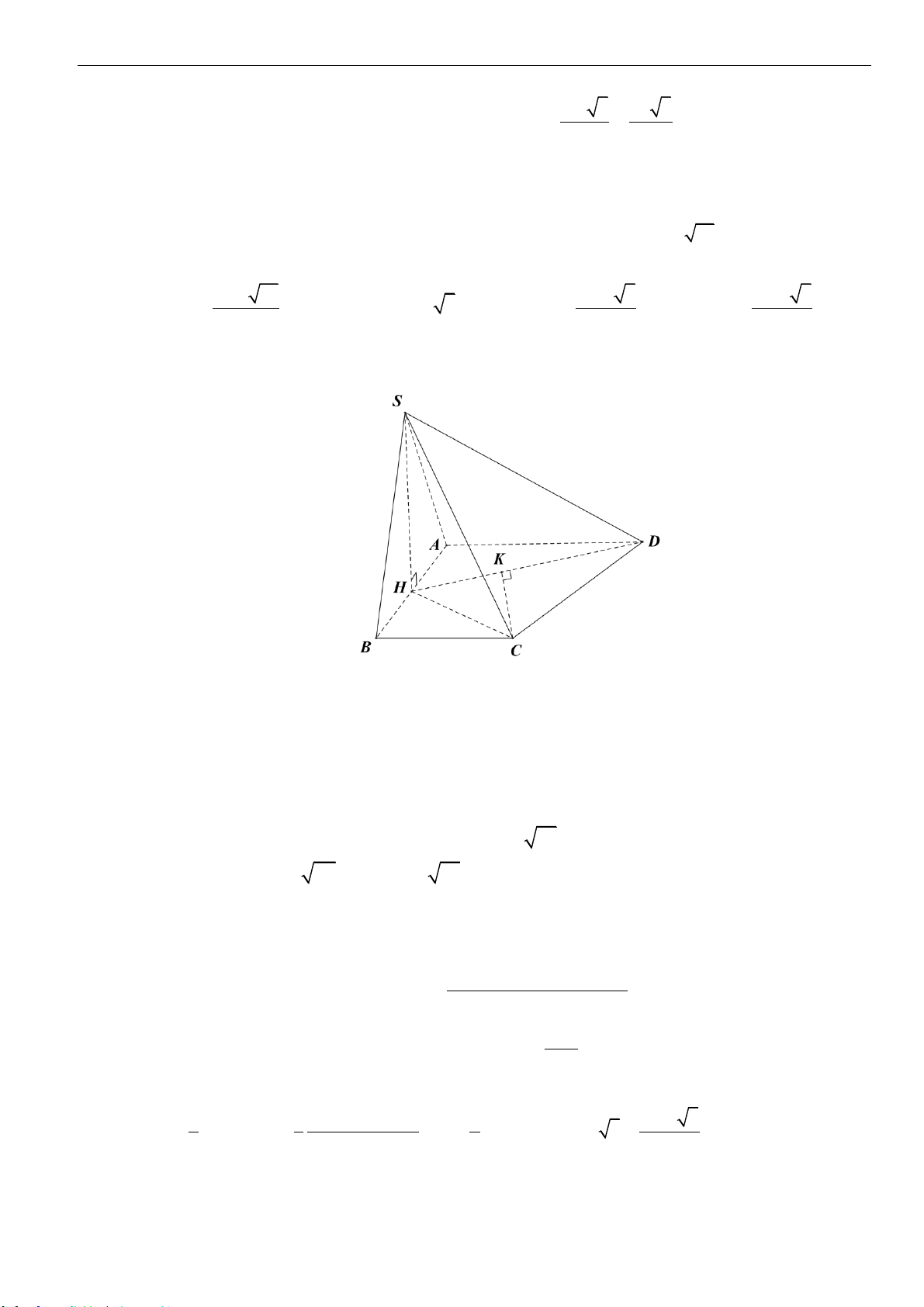
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 28

G

của tam giác

SAB

.

Bán kính mặt cầu ngoại tiếp hình chóp

.S ABC

là

3 2 3

33

AB a

R ==

.

Câu 34: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thang vuông tại

A

và

B

;

4AB BC a==

. Tam

giác

SAB

đều và nằm trong mặt phẳng vuông góc với mặt phẳng

( )

ABCD

. Gọi

H

là trung

điểm của

AB

, biết khoảng cách từ

C

đến mặt phẳng

( )

SHD

bằng

10a

. Tính thể tích khối

chóp

.S ABCD

.

A.

3

10 10

3

a

V =

. B.

3

10 3Va=

. C.

3

40 3

3

a

V =

. D.

3

20 3

3

a

V =

.

Lời giải

Chọn C

Tam giác

SAB

cân nên

SH AB⊥

Ta có:

) ( )

( ) ( ) ( )

SAB ABCD

SAB ABCD AB SH ABCD

SH AB

⊥





 =  ⊥





⊥



Kẻ

,CK HD K HD⊥

mà

()SH ABCD SH CK⊥  ⊥

.

Do đó

( ) ( ,( )) 10CK SHD d C SHD CK a⊥  = =

Tính được

20 10CH a HK a CK=  = =

. Do đó tam giác

CHK

vuông cân tại

K

Nên

45 45 tan 1KHC DHC DHC



=  =  =

Tam giác

BHC

vuông tại

B

nên

tan 2BHC =

và

tan tan

tan tan( ) 3

1 tan .tan

BHC CHD

BHD BHC CHD

BHC CHD

+

= + = = −

−

Mà

180BHD AHD



+=

. Do đó

tan 3 3 6

AD

AHD AD a

AH

=  =  =

Vậy thể tích khối chóp là :

( )

3

1 1 1 40 3

. . . 6 4 4 .2 3

3 3 2 6 3

ABCD

AD BC AB

a

V S SH SH a a a a

+

= = = + =

Câu 35: Cho hình chóp

.S ABCD

có đáy là hình chữ nhật, tam giác

SAB

cân tại

S

và nằm trong mặt

phẳng vuông góc với mặt phẳng đáy;

H

là trung điểm của

AB

. Biết

2SD a=

và lần lượt tạo

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

29 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

với các mặt phẳng

( )

ABCD

và

( )

SHC

các góc bằng

30

. Thể tích khối chóp

.S ABCD

bằng

A.

3

6

a

. B.

3

a

. C.

3

23

3

a

. D.

3

6

a

.

Lời giải

Chọn B

Do tam giác

SAB

cân tại

S

,

H

là trung điểm cạnh

AB

nên

SH AB⊥

.

Mặt khác

( ) ( ) ( ) ( )

, SAB ABCD SAB ABCD AB⊥  =

nên

( )

SH ABCD⊥

.

( )

(

)

, 30SD ABCD SDH = = 

.

Gọi

I

là hình chiếu của

D

lên

HC

.

( )

DI HC

DI SHC

DI SH

⊥



⊥



⊥



( )

(

)

, 30SD SHC DSI = = 

.

Tam giác

SHD

vuông tại

H

có:

.cos30 2 .cos30 3 3HD SD a a HC a=  =  =  =

.sin30 2 .sin30SH SD a a=  =  =

Trong tam giác vuông

SID

có

.sin30 2 .sin30DI SD a a=  =  =

.

2

13

. . 2 3

22

HDC ABCD HDC

a

S HC DI S S a = =  = =

.

Vậy

3

.

13

..

33

S ABCD ABCD

a

V S SH==

.

Câu 36: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh là

2.a

Mặt bên

SAB

là tam giác cân

nằm trong mặt phẳng vuông góc với đáy. Khoảng cách từ

A

đến

( )

SCD

là

.a

Tính thể tích khối

chóp

.S ABCD

.

A.

3

83a

. B.

3

83

5

a

. C.

3

83

7

a

. D.

3

83

9

a

.

Lời giải

Chọn D

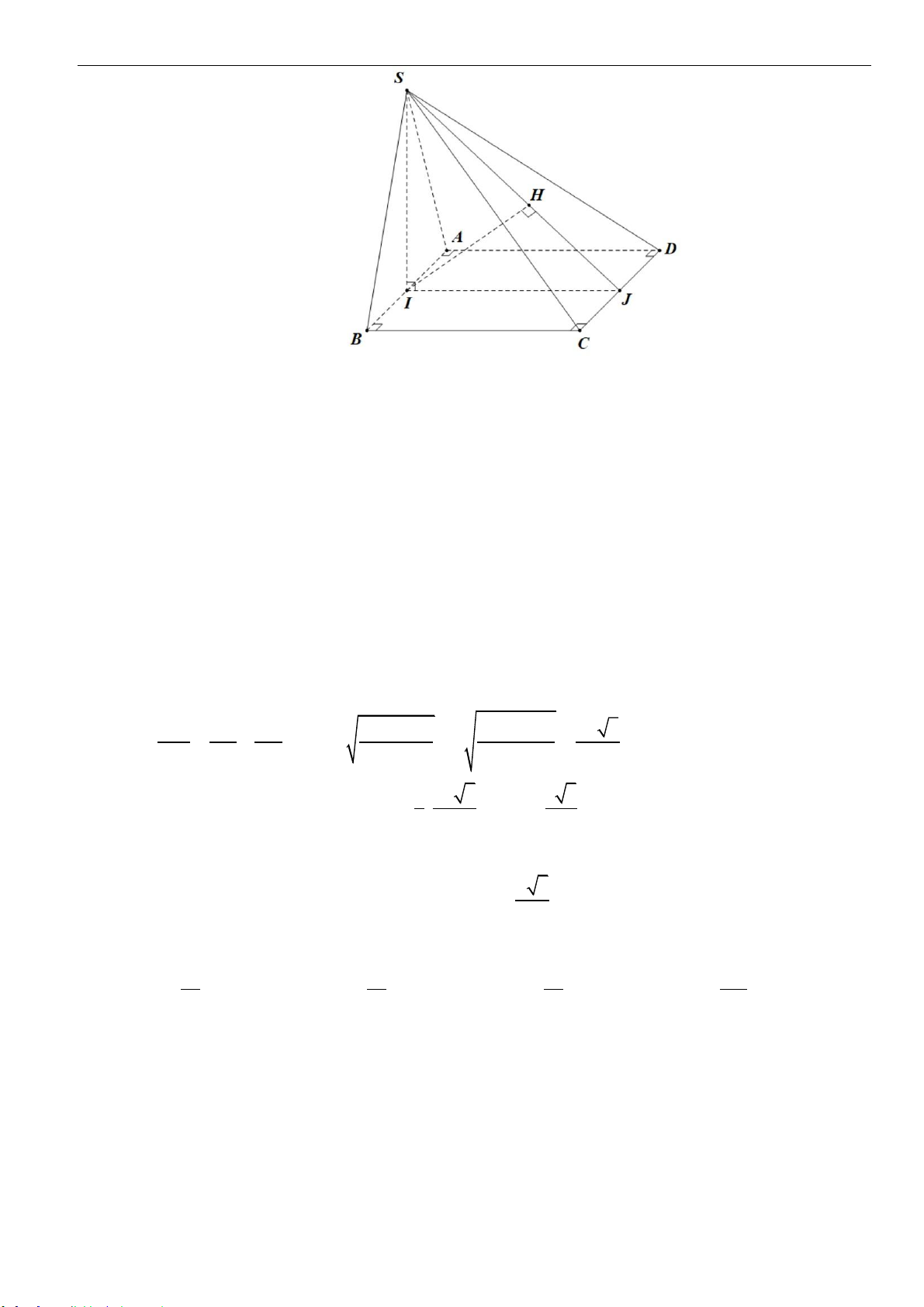
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 30

Gọi

,IJ

lần lượt là trung điểm của

,.AB CD

Suy ra

IJ AD a==

Ta có:

( ) ( )

( ) ( ) ( )

SAB ABCD

SAB ABCD AB SI ABCD

SI AB

⊥





 =  ⊥





⊥



.

Vì

( )

// DAB SC

nên

( )

,,d A SCD d I SCD=

.

Gọi

H

là chân đường vuông góc hạ từ

I

đến

SJ

. Khi đó:

( )

D , D

D

,

IH SJ

IH CD C IJ C SI

IH SCD

SJ C J

SJ CD SCD

⊥





⊥ ⊥ ⊥



⊥



=







( )

,d I SCD IH a = =

Xét tam giác

SIJ

vuông tại

,I

đường cao

IH

, ta có:

( )

2

22

2

2 2 2 2 2

2

2.

1 1 1 . 2 3

.

3

2

aa

IJ IH a

SI

IH IJ SI IJ IH

aa

= +  = == =

−

Thể tích khối chóp

.S ABCD

:

( )

2

3

1 2 3 8 3

. . 2

3 3 9

a

V a a==

.

Câu 37: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác đều, hình chiếu vuông góc của đỉnh

S

trên mặt

đáy là trung điểm

H

của cạnh

AB

. Biết

3

2

a

SH =

và mặt phẳng

( )

SAC

vuông góc với mặt

phẳng

( )

SBC

. Thể tích khối chóp

.S ABC

bằng

A.

4

a

. B.

4

16

a

. C.

4

2

a

. D.

4

3

8

a

.

Lời giải

Chọn A

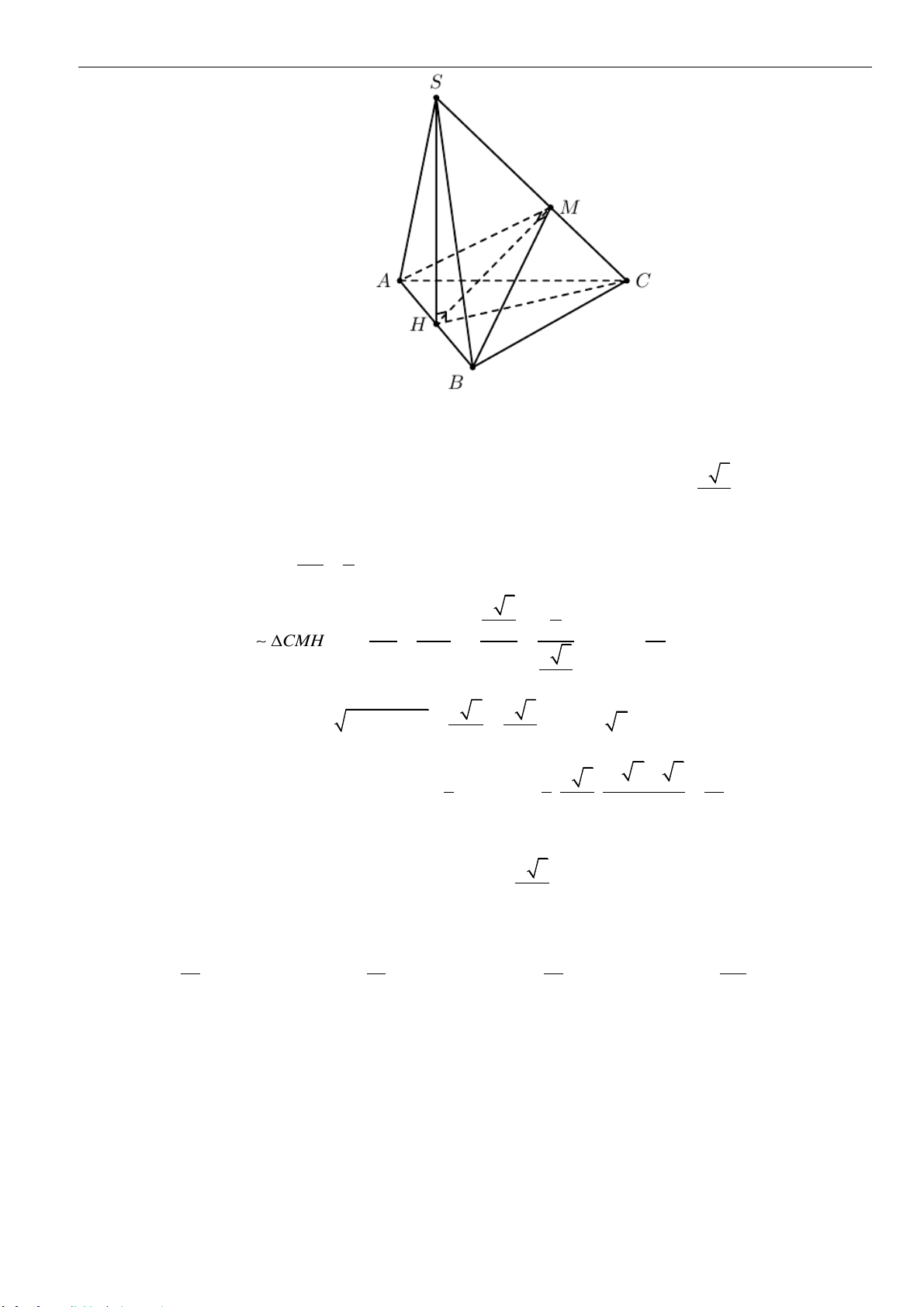
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

31 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Kẻ

( )

MB SC M SC⊥

. Ta có

( )

SH AB

AB SHC AB SC

HC AB

⊥



 ⊥  ⊥



⊥



.

Do đó

( )

SC AMB SC MH⊥  ⊥

và

0

90AMB =

. Đặt

3

2

x

AB x HC=  =

.

Trong

AMB

vuông tại

M

có

MH AB⊥

tại trung điểm

H

của

AB

nên

AMB

vuông cân tại

M

. Suy ra

22

AB x

MH ==

.

Ta có

CHS CMH

nên

3

22

2

3

2

ax

SH HM a

SC

SC HC SC

x

=  =  =

.

Trong

SHC

có

22

63

2

22

ax

HC SC SH x a= − = =  =

.

Vậy thể tích khối chóp

.S ABC

là

( )

2

3

23

1 1 3

. . . .

3 3 2 4 4

ABC

a

aa

V SH S= = =

.

Câu 38: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác đều, hình chiếu vuông góc của đỉnh

S

trên mặt

đáy là trung điểm

H

của cạnh

AB

. Biết

3

2

a

SH =

và mặt phẳng

( )

SAC

vuông góc với mặt

phẳng

( )

SBC

. Thể tích của khối chóp

.S ABC

bằng

A.

3

.

2

a

. B.

3

.

4

a

. C.

3

.

16

a

. D.

3

.

8

a

.

Lời giải

Chọn B

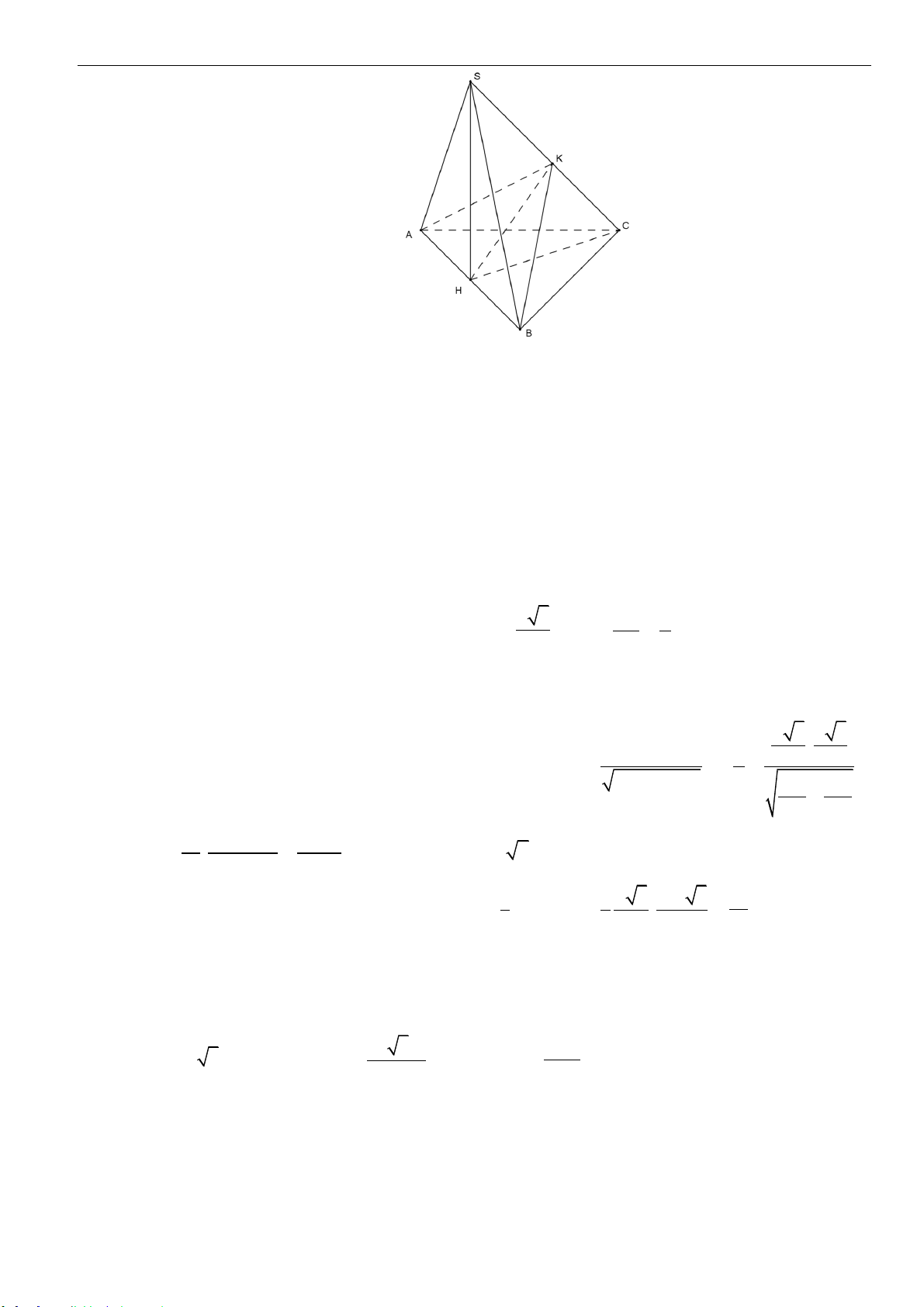
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 32

Ta có

H

là trung điểm cạnh

AB

,

SH AB⊥

SAB

cân tại

S SA SB=

.

Trong tam giác

SAC

kẻ

( )

;AK SC K SC⊥

Ta có:

( ) ( )

( )

;

SAC SBC

SAC SBC SC AK SBC

AK SAC AK SC

⊥





 =  ⊥





⊥



AK BK⊥

( )

1

.

Mà

SAC SBC = 

AK BK=

( )

2

và

AK SC

BK SC

⊥





⊥



.

Từ

( )

1

và

( )

2

AKB

vuông cân tại

K

.

Gọi cạnh tam giác

ABC

là

x

( )

,0x 

3

2

x

HC=

;

22

AB x

HK ==

.

Mà

AK SC

BK SC

⊥





⊥



( )

SC ABK⊥

SC HK⊥

.

Xét tam giác

SHC

vuông tại

H

đường cao

HK

có:

22

.SH HC

HK

SH HC

=

+

22

33

.

22

2

33

44

ax

x

ax

=

+

2 2 2 2 2

3 3 9

.

4 4 16

x a x a x+

=

22

2xa=

.

Vậy thể tích khối chóp

.S ABC

bằng:

2

.

1 1 3 2 3

..

3 3 2 4

S ABC ABC

aa

V SH S



==

3

4

a

=

.

Câu 39: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật, tam giác

SAB

vuông tại

S

và nằm

trong mặt phẳng vuông góc với đáy. Biết

2 , 2AB SA BC a==

và mặt phẳng

( )

SCD

tạo với mặt

phẳng đáy một góc

60

. Thể tích khối chóp

.S ABCD

tính theo

a

bằng

B.

3

16 3a

. B.

3

32 3

3

a

. C.

3

32

3

a

. D.

3

16a

.

Lời giải

Chọn B

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

33 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Kẻ

( )

SH AB H AB⊥

,

( )

HK CD K CD⊥

.

Ta có

( ) ( ) ( )

SAB ABCD SH ABCD⊥  ⊥

.

Có

( )

HK CD

CD SHK

SH CD

⊥



⊥



⊥



CD SK⊥

( ) ( )

(

)

; 60SCD ABCD SKH = = 

.

Xét

SHK

vuông tại

H

có:

.tan 2 .tan60 2 3SH HK SKH a a= =  =

.

Xét

SAB

vuông tại

S

, có

..SH AB SB SA=

Mà

2AB SA=

nên

.2 .SH SA SB SA=

43SB a=

.

Mặt khác

2 2 2

SB SA AB+=

22

3SB SA=

48SA a AB a =  =

.

Khi đó diện tích mặt đáy là:

2

. 8 .2 16

ABCD

S AB BC a a a= = =

.

Thể tích khối chóp

.S ABCD

là:

3

2

.

1 1 32 3

. 2 3.16

3 3 3

S ABCD ABCD

a

V SH S a a= = =

(đvtt).

Câu 40: Cho hình chóp

.S ABC

có

SA

vuông góc với đáy, mặt phẳng

()SAB

vuông góc với mặt phẳng

()SBC

, góc giữa hai mặt phẳng

()SAC

và

()SBC

bằng

0

60

,

2;SB a=

0

45 .BSC =

Gọi thể tích

khối chóp

.S ABC

là

.V

Khi đó tỉ số

3

a

V

bằng

A.

2

4

. B.

2

. C.

3

2

. D.

53

.

2

Lời giải

Chọn D

Dựng

AH SB⊥

( ) ( )H SB AH SBC  ⊥

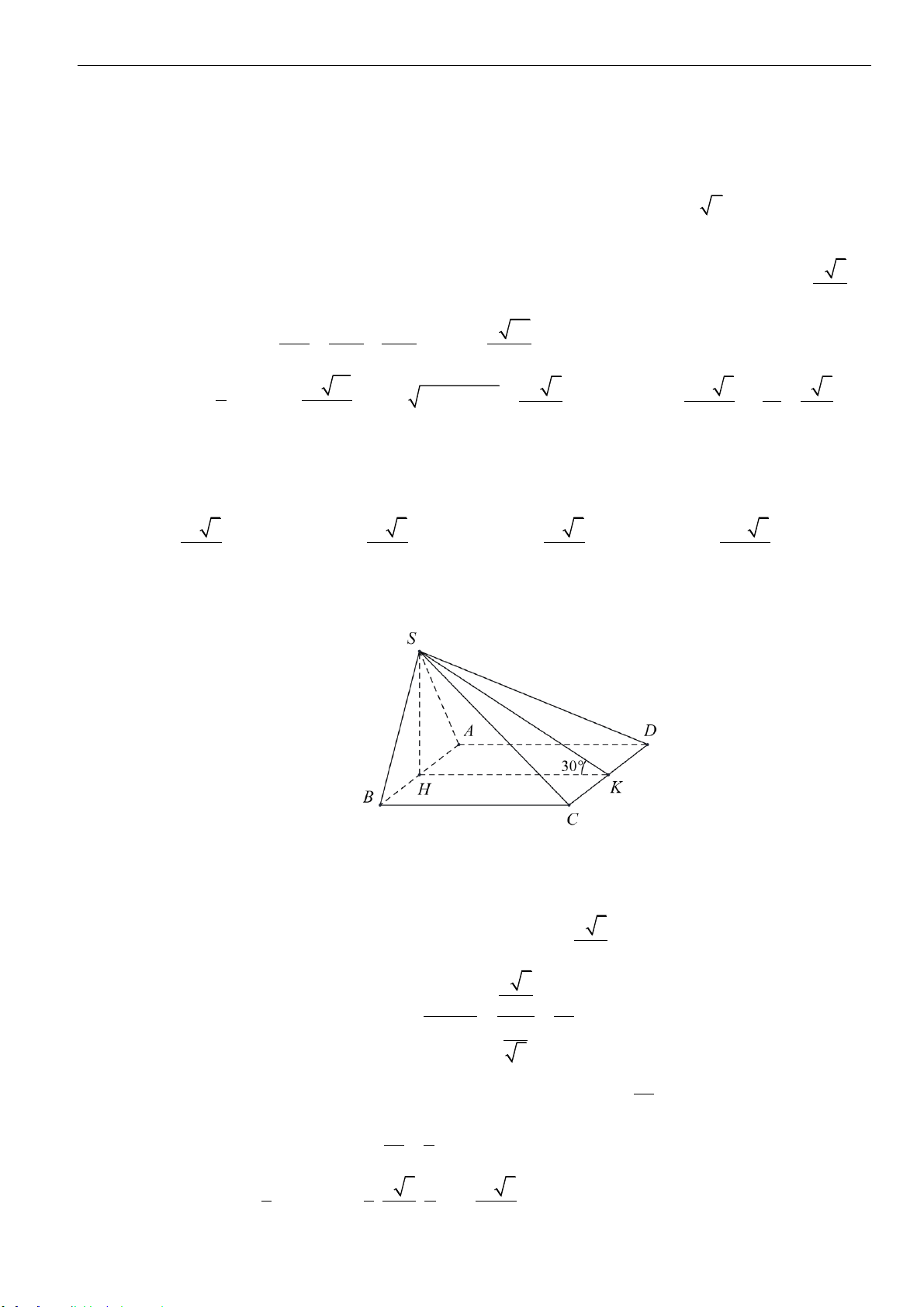
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 34

Ta có:

()

BC SA

BC SAB ABC

BC AH

⊥



 ⊥  



⊥



vuông tại

.B

Dựng

BI AC⊥

()I AC BI SC  ⊥

Dựng

BK SC⊥

( ) ( )K SC SC BIK  ⊥

. Suy ra:

0

(( );( )) 60 .SAC SBC BKI==

Ta lại có:

SBC

vuông cân tại

B

0

( 45 ; ) 2.BSC BC SB SB BC a= ⊥  = =

Suy ra:

BK a=

(

K

là trung điểm của

)SC

Do

()

BI SC

BI SAC BI IK

BI AC

⊥



 ⊥  ⊥



⊥



nên

BIK

vuông tại

I

0

3

.sin60 .

2

a

BI BK = =

ABC

tại

B

2 2 2

1 1 1 30

.

5

a

AB

BI AB BC

 = +  =

2

1 15

.;

25

ABC

a

S AB BC



==

22

25

5

a

SA SB AB= − =

33

.

2 3 5 3

.

15 2

S ABC

aa

VV

V

 = =  =

Câu 41: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật, tam giác

SAB

là tam giác đều cạnh

a

và nằm trong mặt phẳng vuông góc với đáy. Gọi H, K lần lượt là trung điểm của AB, CD.

Biết góc giữa KS và DA bằng

30

. Thể tích khối chóp

.S ABCD

A.

3

4

a

B.

3

2

a

C.

3

36

a

D.

3

53

36

a

Lời giải

Chọn A

Góc giữa 2 đường thẳng

KS

và

DA

là góc giữa hai đường thẳng

KS

và

KH

và là góc

( )

, 30KS KH SKH= = 

.

Tam giác

SAB

là tam giác đều cạnh

a

nên ta có:

3

2

a

SH =

Xét

SHK

vuông tại

H

, có

3

2

1

tan30 2

3

a

SH a

HK = = =



.

,HK

lần lượt là trung điểm của

,AB CD

nên

3

2

a

HK BC AD= = =

.

Diện tích:

2

33

..

22

ABCD

a

S AB AD a a= = =

.

Vậy

3

2

.

1 1 3 3 3

. . .

3 3 2 2 4

S ABCD ABCD

aa

V SH S a= = =

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

35 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 42: Cho khối chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

. Tam giác

SAB

cân tại

S

và nằm

trong mặt phẳng vuông góc với mặt đáy. Biết khoảng cách từ điểm

A

đến mặt phẳng

( )

SCD

bằng

2

a

. Thể tích của khối chóp đã cho bằng

A.

3

a

. B.

3

3a

. C.

3

a

. D.

3

1

3

a

Lời giải

Chọn D

Gọi H là trung điểm của AB

SH AB⊥

Ta có:

( ) ( )

( ) ( ) ( )

SAB ABCD

SAB ABCD AB SH ABCD

SH AB

⊥





 =  ⊥





⊥



.

Gọi I là trung điểm của

.CD

Suy ra

;HI a HI CD=⊥

.

Gọi K là hình chiếu của H lên SI. Ta có:

( )

CD HI

CD SH SH ABCD

⊥







⊥⊥





( )

CD SHI CD HK ⊥  ⊥

mà

( )

HK SI HK SCD⊥  ⊥

.

Ta có

( ) ( )

( )

2

/ / / / ; ;

2

a

AH CD AH SCD d A SCD d H SCD HK  = = =

.

Xét tam giác SHI vuông tại H có HK là đường cao

2 2 2 2 2 2

1 1 1 2 1 1

SH a

HK SH HI a SH a

= +  = +  =

.

Thể tích khối chóp:

23

.

1 1 1

..

3 3 3

S ABCD ABCD

V SH S a a a= = =

.

Câu 43: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

2a

,

( ) ( )

SAB ABCD⊥

. Gọi



là

góc tạo bởi mặt phẳng

( )

SAB

và mặt phẳng

( )

SCD

, với

tan 2



=

. Gọi

( )

P

là mặt phẳng chứa

CD

và vuông góc với

( )

ABCD

. Trên

( )

P

lấy điểm

M

bất kỳ, thể tích khối tứ diện

.S ABM

bằng

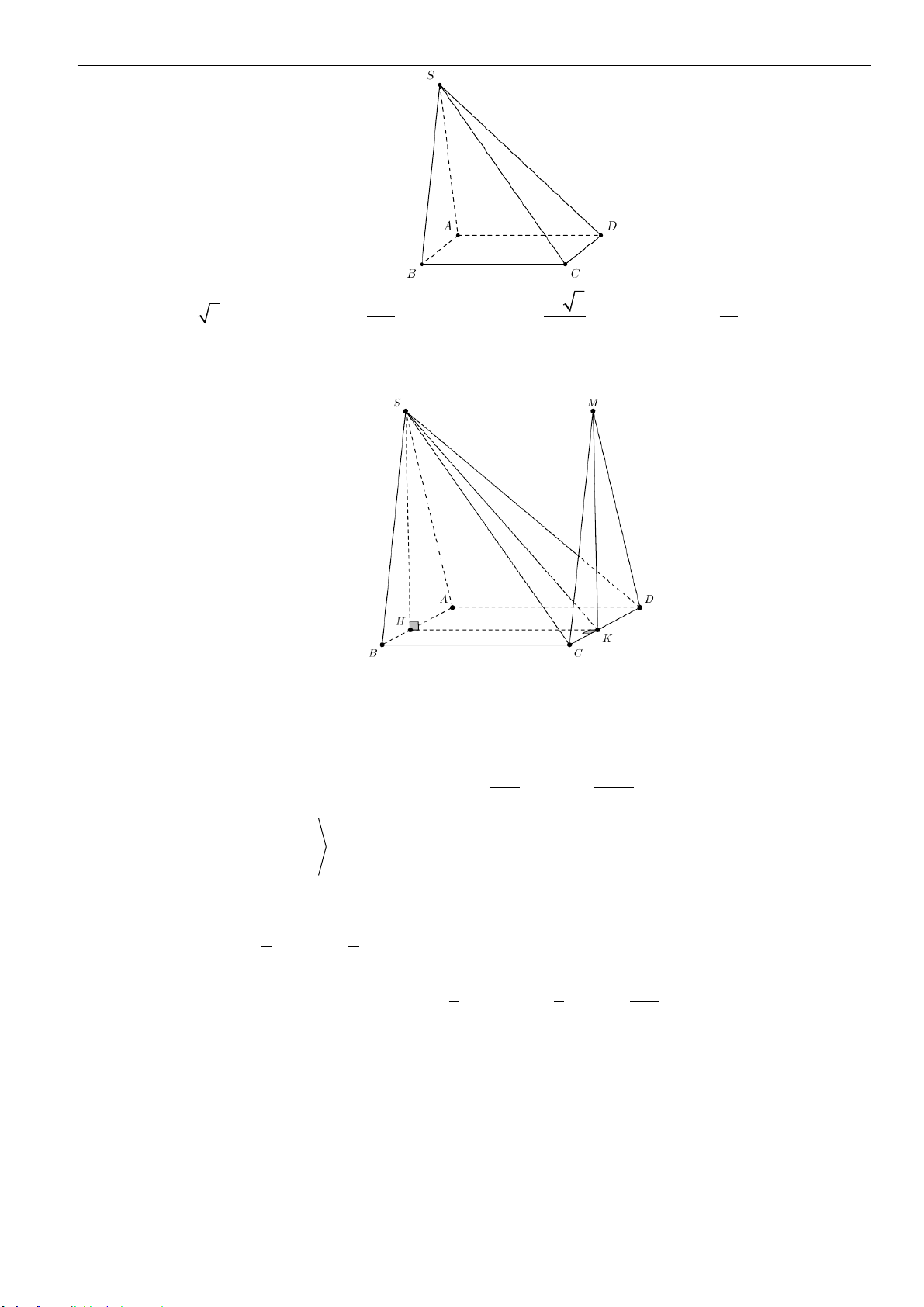
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 36

A.

3

3a

. B.

3

2

3

a

. C.

3

a

. D.

3

4

a

.

Lời giải

Chọn B

Gọi

H

là hình chiếu của

S

đường thẳng

AB

. Suy ra

( )

SH ABCD⊥

.

Gọi

K

là hình chiếu vuông góc của

S

đường thẳng

CD

.

Khi đó góc tạo bởi mặt phẳng

( )

SAB

và mặt phẳng

( )

SCD

là

HSK



=

.

Trong

SHK

vuông tại

H

ta có

tan

HK HK

HSK SH a

SH



=  = =

.

Do

( ) ( )

//

P ABCD

P SAB

SAB ABCD

⊥



⊥

.

Khi đó

( )

d , =d , 2M SAB K SAB HK a==

.

Ta có

2

11

. . .2

22

SAB

S SH AB a a a



= = =

.

Vậy thể tích khối chóp

.S ABM

là

3

2

1 1 2

. . . .2

3 3 3

SAB

a

V S HK a a



= = =

.

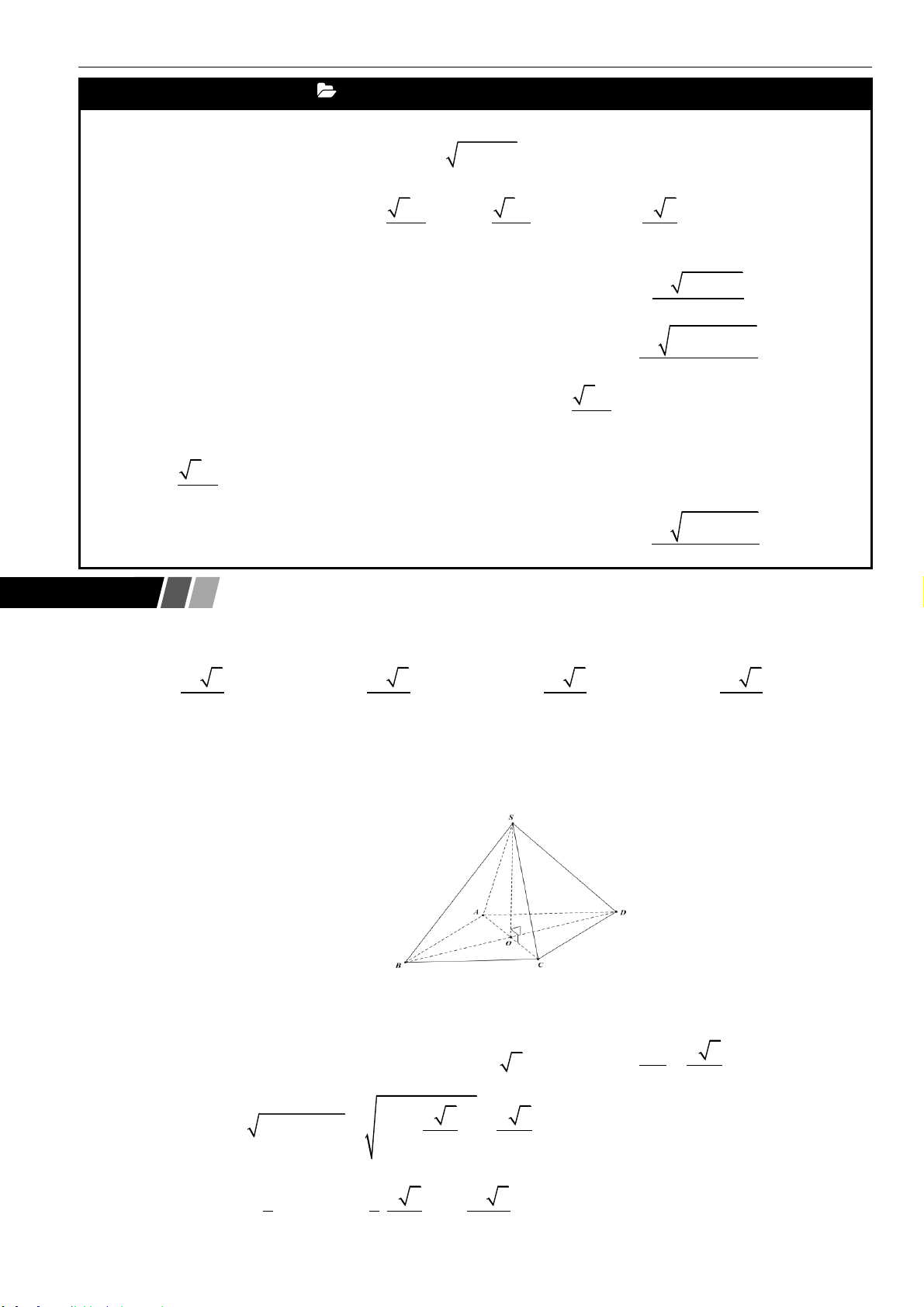
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

1 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Dạng 4: Thể tích khối chóp đều

Công thức tính thể tích khối chóp đều và một số công thức giải nhanh:

• Chiều cao

h

khối chóp xác định bởi

22

d

h b R=−

, trong đó

d

R

là bán kính đường tròn ngoại tiếp

đa giác đáy và

b

là độ dài cạnh bên.

• Khối tứ diện đều cạnh

a

có

3

2

12

a

V =

và

3

8

h

V =

, trong đó

6

3

a

h =

là chiều cao khối tứ diện

đều.

• Khối chóp tam giác đều cạnh đáy bằng

a

, cạnh bên bằng

b

có

2 2 2

3

12

a b a

V

−

=

• Khối chóp tứ giác đều cạnh đáy bằng

a

, cạnh bên bằng

b

có

( )

2 2 2

22

6

a b a

V

−

=

• Khối chóp tứ giác đều có tất cả các cạnh bằng

a

, có

3

2

6

a

V =

• Khối bát diện đều cạnh

a

là hợp của hai khối chóp tứ giác đều có tất cả các cạnh bằng

a

có

3

2

3

a

V =

• Khối chóp lục giác đều cạnh đáy bằng

a

, cạnh bên bằng

b

có

( )

2 2 2

3

2

a b a

V

−

=

Câu 1: Cho hình chóp tứ giác đều có tất cả các cạnh bằng

a

. Thể tích của khối chóp tương ứng tính

theo

a

sẽ bằng

A.

3

2

a

. B.

3

2

6

a

. C.

3

2

3

a

. D.

3

2

12

a

.

Lời giải

Chọn B

Gọi khối chóp tứ giác đều là

.S ABCD

như hình vẽ.

Gọi

O

là tâm hình vuông

ABCD

, suy ra

()SO ABCD⊥

.

Do

ABCD

là hình vuông cạnh

a

nên

2

22

BD a

BD a OD OB=  = = =

.

Ta có

2

2 2 2

22

aa

SO SD OD a



= − = − =





và

2

ABCD

Sa=

.

Vậy

3

2

1 1 2 2

. . .

3 3 2 6

SABCD ABCD

aa

V SO S a= = =

.

VÍ DỤ MINH HỌA

B

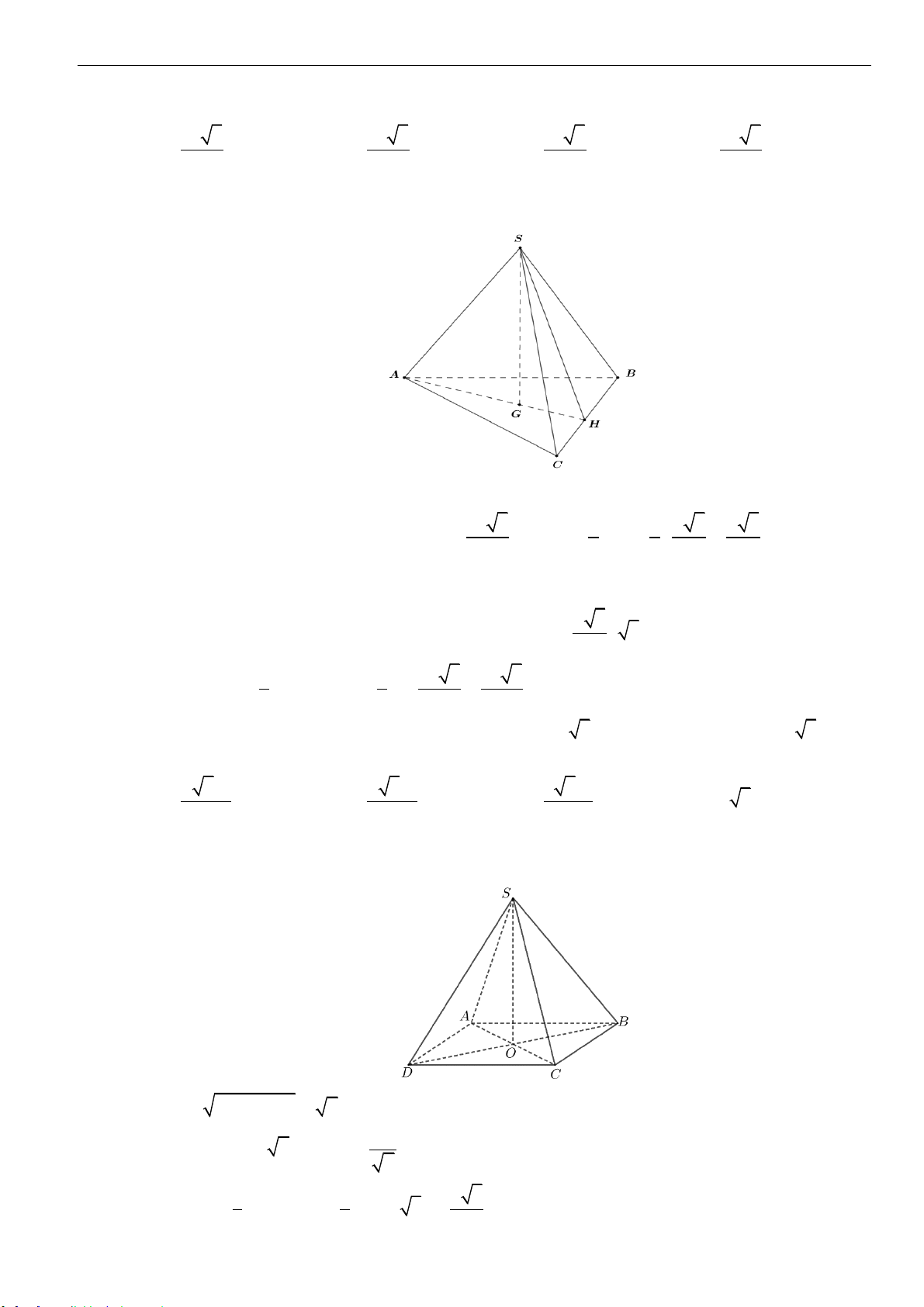
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 2

Câu 2: Cho khối chóp tam giác đều có cạnh đáy bằng

a

và cạnh bên tạo với đáy một góc

o

60

. Thể tích

khối chóp đó bằng

A.

3

12

a

. B.

3

6

a

. C.

3

36

a

. D.

3

4

a

.

Lời giải

Chọn A

Gọi

H

là trung điểm

BC

và

G

là trọng tâm tam giác

ABC

. Ta có

( )

SG ABC⊥

.

Tam giác

ABC

đều cạnh

a

nên

2

3

4

ABC

a

S



=

và

2 2 3 3

3 3 2 3

aa

AG AH= =  =

.

( )

o

, 60SA ABC SAG==

.

Trong tam giác vuông

SGA

, ta có

3

.tan 3

3

a

SG AG SAG a= =  =

.

Vậy

23

.

1 1 3 3

3 3 4 12

S ABC ABC

aa

V SG S a



=   =   =

.

Câu 3: Cho hình chóp tứ giác đều S.ABCD có chiều cao bằng

3a

và độ dài cạnh bên bằng

5a

. Thể

tích của khối chóp

.S ABCD

bằng

A.

3

45

3

a

. B.

3

43

3

a

. C.

3

83

3

a

. D.

3

43a

.

Lời giải

Chọn B

22

2BO SB SO a= − =

.

2 2 2 2

2

BD

BD BO a AB a= =  = =

.

( )

2

3

.

1 1 4 3

. . 2 . 3

3 3 3

S ABCD ABCD

V S SO a a a= = =

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

3 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 4: Cho hình chóp đều

.S ABCD

có đáy là hình vuông cạnh

2a

, cạnh bên bằng

3a

. Tính thể tích

khối chóp

.S ABCD

.

A.

3

43a

. B.

3

43

3

a

. C.

3

4

3

a

. D.

3

4a

.

Lời giải

Chọn C

Ta có

11

2 2 2

22

OD BD a a= =  =

.

Xét tam giác

SOD

vuông tại

O

, ta có

( ) ( )

22

32SO SD OD a a a= − = − =

.

Diện tích hình vuông

ABCD

:

( )

2

24

ABCD

S a a==

.

Thể tích khối chóp

.S ABCD

là

23

.

1 1 4

4

3 3 3

S ABCD ABCD

V S SO a a a=   =   =

.

Câu 5: Cho hình chóp tam giác đều

.S ABC

có cạnh đáy bằng

2,a

cạnh bên tạo với đáy một góc

0

60 .

Tính theo

a

thể tích khối chóp

..S ABC

A.

3

3a

. B.

3

a

. C.

3

23a

. D.

3

23

3

a

.

Lời giải

Chọn D

Ta có:

2 2 2 3 2 3

..

3 3 2 3

aa

AO AI= = =

Mà

( )

0

, 60 .SA ABC SAO==

0

23

.tan60 . 3 2

3

SO AO a a = = =

Suy ra

( )

2

3

.

23

1 2 3

.2 . .

3 4 3

S ABC

a

Va==

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 4

Câu 6: Cho hình chóp đều

.S ABCD

có cạnh đáy bằng

a

, biết góc giữa cạnh bên và mặt đáy bằng

45

. Tính thể tích

V

của khối chóp

.S ABC

.

A.

3

2

6

Va=

. B.

3

2

12

Va=

. C.

3

2

3

Va=

. D.

3

2Va=

.

Lời giải

Chọn B

Gọi

O

là tâm hình vuông

ABCD

. Ta có:

( )

SO ABCD⊥

OB

là hình chiếu của

SB

lên mặt

phẳng

( )

ABCD

. Suy ra:

( )

, , 45SB ABCD SB OB SBO= = = 

.

Ta có:



SOB

vuông cân tại

O



2

.

2

a

SO OB==

Vậy

.

1

.

3

S ABC ABC

V SO S=

2

1 2 1

..

3 2 2

a

a=

3

2

12

a=

.

Câu 7: Cho hình chóp đều

.S ABCD

có cạnh đáy bằng

3a

, cạnh bên bằng

33

2

a

và

O

là tâm của đáy.

Gọi

,,M N P

và

Q

lần lượt là hình chiếu vuông góc của

O

trên các mặt phẳng

( )

SAB

,

( )

SBC

,

( )

SCD

và

( )

SDA

. Thể tích của khối chóp

.O MNPQ

bằng

A.

3

9

16

a

. B.

3

2

3

a

. C.

3

9

32

a

. D.

3

a

.

Lời giải

Chọn C

Gọi

, , ,E F G H

theo thứ tự là trung điểm của

, , ,AB BC CD DA

.

Ta có:

( ) ( ) ( )

AB SO

AB SOE SAB SOE

AB OE

⊥



 ⊥  ⊥



⊥



.

Mặt khác:

( ) ( )

SAB SOE SE=

đồng thời

M

là hình chiếu vuông góc của

O

lên mặt phẳng

( )

SAB

nên

OM SE⊥

tại

M

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

5 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Ta có:

22

3 3 3 2 3

2 2 2

a a a

SO SA OA OE

   

= − = − = =

   

   

.

Khi đó tam giác

SOE

vuông cân tại

O



M

là trung điểm

SE

.

Chứng minh tương tự ta cũng có

,,N P Q

lần lượt là trung điểm của các cạnh

,,SF SG SH

.

Khi đó

13

( ,( )) ( ,( ))

24

a

d O MNPQ d S MNPQ SO= = =

,

2

1 1 9

4 8 8

MNPQ EFGH ABCD

a

S S S= = =

.

Suy ra

23

.

1 1 3 9 9

. ( ,( )) .

3 3 4 8 32

O MNPQ MNPQ

a a a

V S d O MNPQ=  =  =

.

Vậy

3

.

9

32

O MNPQ

a

V =

.

Câu 8: Cho khối chóp tứ giác đều

.S ABCD

có diện tích xung quanh gấp 2 lần diện tích đáy, diện tích

đáy bằng

2

4a

. Thể tích của khối chóp

.S ABC

tương ứng bằng

A.

3

43

3

a

. B.

3

23

3

a

. C.

3

83

3

a

. D.

3

56

3

a

.

Lời giải

Chọn B

Diện tích hình vuông

ABCD

:

22

42

ABCD

S AB a AB a= =  =

.

Gọi

M

là trung điểm cạnh

AB

.

Diện tích xung quanh của khối chóp

.S ABCD

:

2

1

4. 4. . . 8 2

2

SAB

S SM AB a SM a



= =  =

.

Gọi

O

là giao điểm hai đường chéo của hình vuông

ABCD

, trong tam giác vuông

SOM

có

2 2 2 2

33SO SM OM a SO a= − =  =

.

3

2

..

1 1 1 1 2 3

. . . . . 3.4

2 2 3 6 3

S ABC S ABCD ABCD

a

V V SO S a a= = = =

.

Câu 9: Cho khối chóp tứ giác đều có cạnh đáy bằng

2a

và diện tích xung quanh bằng

2

8a

. Thể tích

của khối chóp đó bằng

A.

3

23

.

3

a

B.

3

4 3 .a

C.

3

43

.

3

a

D.

3

2 3 .a

Lời giải

Chọn C

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 6

Xét hình chóp

.S ABCD

thỏa các giả thiết. Gọi

O

là tâm của hình vuông

ABCD

và

I

là trung

điểm

CD

. Ta có

2

11

. 2 . .2 2

22

SCD

S SI CD a SI a SI a=  =  =

.

Dễ thấy

OI a=

và tam giác

SOI

vuông tại

O

. Suy ra

22

3SO SI OI a= − =

.

23

.

1 1 4 3

. 3.4 .

3 3 3

S ABCD ABCD

V SO S a a a= = =

Câu 10: Cho hình chóp tứ giác đều

.S ABCD

có cạnh bên bằng

2a

, góc giữa mặt bên và mặt đáy bằng

60

. Thể tích khối chóp

.S ABCD

là

A.

3

32

15 5

a

. B.

3

32 3

15 5

a

. C.

3

32 5

15

a

. D.

3

32 15

15

a

.

Lời giải

ABCD

là hình vuông có tâm

O

và cạnh bằng

x

.

Gọi

M

là trung điểm của

BC

. Góc giữa

( )

SBC

và

( )

ABCD

là góc

SMO

bằng

60

.

Ta có

22

2 2 2 2

4 , 4

42

xx

SM a SO a= − = −

.

Và

2

14

24

cos cos60

4

5

4

xx

OM a

SMO x

SM

x

a

=   =  =  =

−

.

Suy ra

2

23

4

2

5

xa

SO a= − =

.

Vậy

3

2

.

1 32 3

.

3

15 5

S ABCD

a

V SO AB==

.

O

M

D

C

B

A

S

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

7 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 1: Cho khối chóp tam giác đều có cạnh đáy bằng

2a

và thể tích bằng

3

a

. Chiều cao của khối chóp

đã cho bằng

A.

3a

. B.

23a

. C.

3

a

. D.

3

2

a

.

Lời giải

Chọn A

Diện tích đáy của hình chóp là

( )

2

2 . 3

3

4

a

Sa==

.

Chiều cao của khối chóp là

3

2

33

3

Va

ha

S

a

= = =

.

Câu 2: Cho khối chóp tam giác đều có cạnh đáy bằng

a

, chiều cao bằng

3a

. Thể tích khối chóp bằng

A.

3

4

a

. B.

3

12

a

. C.

3

6

a

. D.

3

4

a

.

Lời giải

Chọn D

Gọi

H

là trọng tâm tam giác

ABC

, suy ra

( )

SH ABC⊥

Ta có

3SH a=

,

2

3

4

ABC

a

S =

. Vậy

23

13

. . 3

3 4 4

aa

Va==

Câu 3: Cho hình chóp có đáy là tam giác đều cạnh

3cm

, chiều cao

5.cm

Thế tích khối chóp đó là

A.

3

15 3

4

cm

. B.

45cm

. C.

3

45cm

. D.

3

45 3

4

cm

.

Lời giải

Chọn A

Tam giác đều cạnh

3

2

3 3 9 3

44

ABC

S cm = =

.

Thế tích khối chóp là

3

.

1 1 9 3 15 3

. . .5.

3 3 4 4

S ABC ABC

V h S cm= = =

.

Câu 4: Cho hình chóp tứ giác đều

.S ABCD

có cạnh đáy bằng

a

và đường cao bằng

3.a

Thể tích khối

chóp

.S ABCD

bằng

A.

3

.a

B.

3

3.a

C.

2

3a

D.

2

a

Lời giải

BÀI TẬP TRẮC NGHIỆM

C

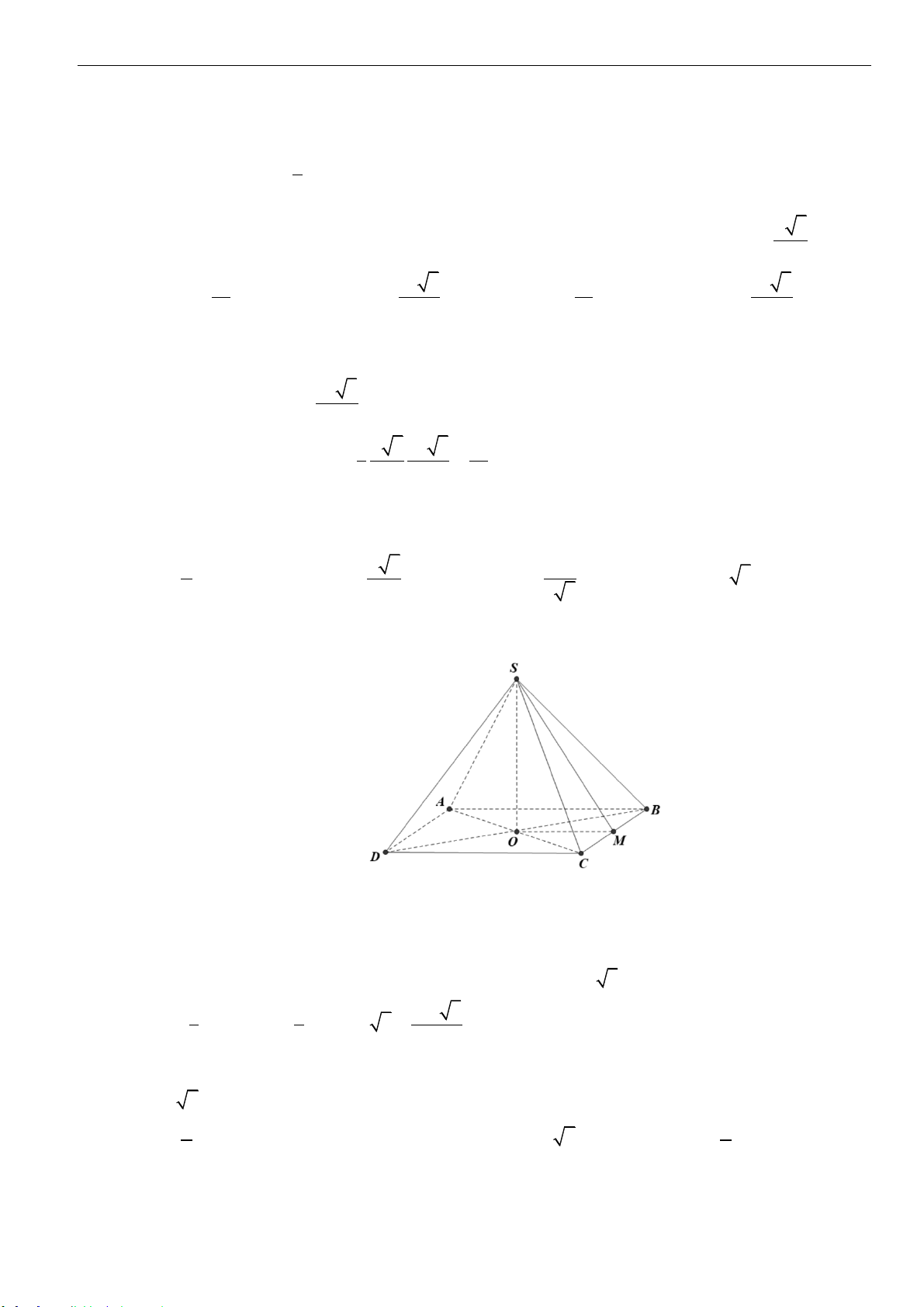
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 8

Chọn A

Vì

.S ABCD

là hình chóp tứ giác đều, đường cao bằng

3a

nên có đáy

ABCD

là hình vuông.

Khi đó, diện tích đáy

2

ABCD

Sa=

.

Thể tích

23

.

1

.3

3

S ABCD

V a a a==

.

Câu 5: Tính thể tích khối chóp tam giác đều có độ dài cạnh đáy bằng a và chiều cao bằng

3

a

là

A.

3

12

a

V =

. B.

3

12

a

V =

. C.

3

4

a

V =

. D.

3

4

a

V =

.

Lời giải

Chọn A

Diện tích đáy là:

2

3

4

a

S =

Thể tích khối chóp là:

23

1 3 3

3 3 4 12

a a a

V ==

.

Câu 6: Tính thể tích khối chóp tứ giác đều có cạnh đáy bằng

2a

và có mặt bên tạo với mặt đáy một góc

bằng

0

60

A.

3

4

3

a

. B.

3

43

3

a

. C.

3

4

33

a

. D.

3

43a

.

Lời giải

Chọn B

Gọi hình chóp tứ giác đều là

.S ABCD

và

O

là tâm của hình vuông

ABCD

cạnh là

2a

,

M

là

trung điểm của

BC

OM a=

và góc giữa mặt bên và mặt đáy là

0

60SMO =

,

SOM

vuông tại

0

.cos .tan60 3O SO OM SMO a a = = =

( )

3

2

1 1 4 3

. . . 2 . 3

3 3 3

ABCD

a

V S SO a a= = =

.

Câu 7: Cho khối chóp đều

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

. Biết diện tích tam giác

SAC

là

2

2a

, thể tích của khối chóp đã cho bằng

A.

3

2

3

a

. B.

3

a

. C.

3

22a

. D.

3

4

3

a

.

Lời giải

Chọn A

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

9 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Gọi

( )

,,O AC BD SO ABCD SO AC BD=   ⊥ ⊥

.

3

2

.

1 1 2

. 2 2 .

2 3 3

SAC S ABCD ABCD

a

S SO AC a SO a V SO S= =  =  = =

.

Câu 8: Cho hình chóp tứ giác đều có cạnh đáy bằng

2a

và cạnh bên tạo với đáy góc

60



. Thể tích của

khối chóp đó bằng

A.

3

46

3

a



B.

3

a



C.

3

4

3

a



D.

3

23

3

a



Lời giải

Chọn A

Giả sử khối chóp tứ giác đều là

.S ABCD

có đáy

ABCD

là hình vuông cạnh

2a

. Gọi

O

là tâm

của đáy ta có

()SO ABCD⊥

. Khi đó tất cả các cạnh bên đều tạo với đáy các góc bằng nhau. Xét

cạnh bên

SB

và

()ABCD

, ta có

( ,( )) 60SB ABCD SBO



==

.

Xét tam giác

SBO

vuông tại

O

,

60SBO



=

,

1

2

OB BD a==

, do đó

.tan60 2. 3 6SO OB a a



= = =

.

Vậy

3

2

.

1 1 4 6

. . . 6.(2 )

3 3 3

S ABCD ABCD

a

V SO S a a= = =

.

Câu 9: Thể tích của khối chóp có đáy là tam giác đều cạnh

a

và chiều cao

4a

bằng

A.

3

4

3

a

. B.

3

4a

. C.

3

3a

. D.

3

a

.

Lời giải

Chọn D

Công thức tính thể tích khối chóp:

1

.,

3

V B h=

trong đó B là diện tích đáy, h là chiều cao của

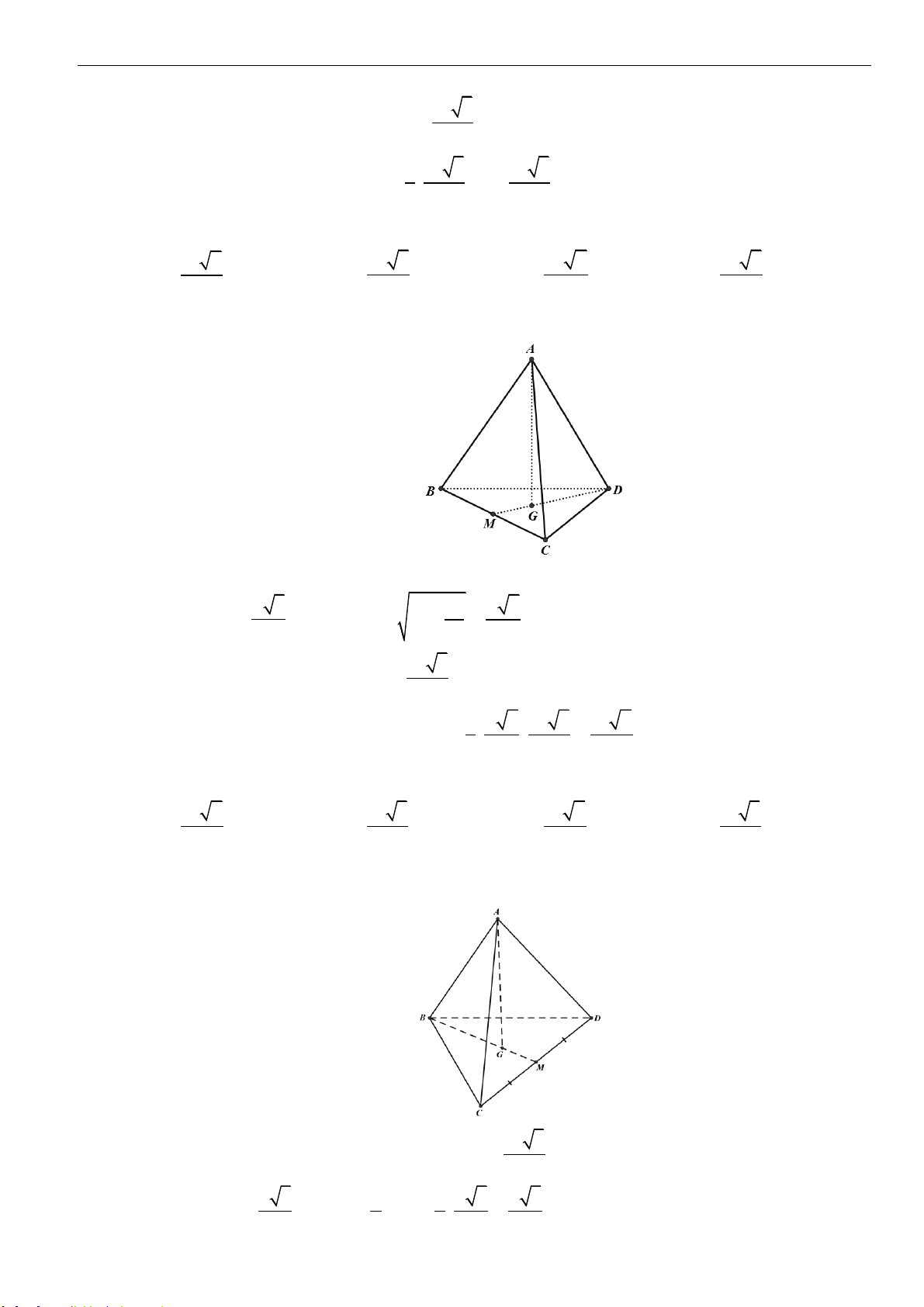
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 10

khối chóp.

Diện tích tam giác đều cạnh a là

2

3

.

4

a

B =

Chiều cao của khối chóp là

4.ha=

Khi đó, thể tích khối chóp là

23

1 3 3

. .4 .

3 4 3

aa

Va==

Câu 10:

Thể tích của khối tứ diện đều cạnh

a

là?

A.

3

2

4

a

. B.

3

12

a

. C.

3

2

12

a

. D.

3

4

a

.

Lời giải

Xét tứ diện đều

ABCD

cạnh

a

. Gọi

G

là trọng tâm tam giác

BCD

.

Ta có

3

a

DG =

, suy ra

2

6

33

aa

AG a= − =

.

Diện tích tam giác

BCD

:

2

3

4

BCD

a

S =

.

Thể tích khối tứ diện đều cạnh

a

là:

23

1 6 3 2

..

3 3 4 12

a a a

V ==

.

Câu 11: Thể tích của khối tứ diện đều cạnh

a

là

A.

3

2

4

a

. B.

3

12

a

. C.

3

2

12

a

. D.

3

4

a

.

Lời giải

Chọn C

Vì khối tứ diện đều nên diện tích đáy:

2

3

4

BCD

a

S



=

.

Ta có:

3

2

a

BM =

2 2 3 3

.

3 3 2 3

aa

BG BM = = =

.

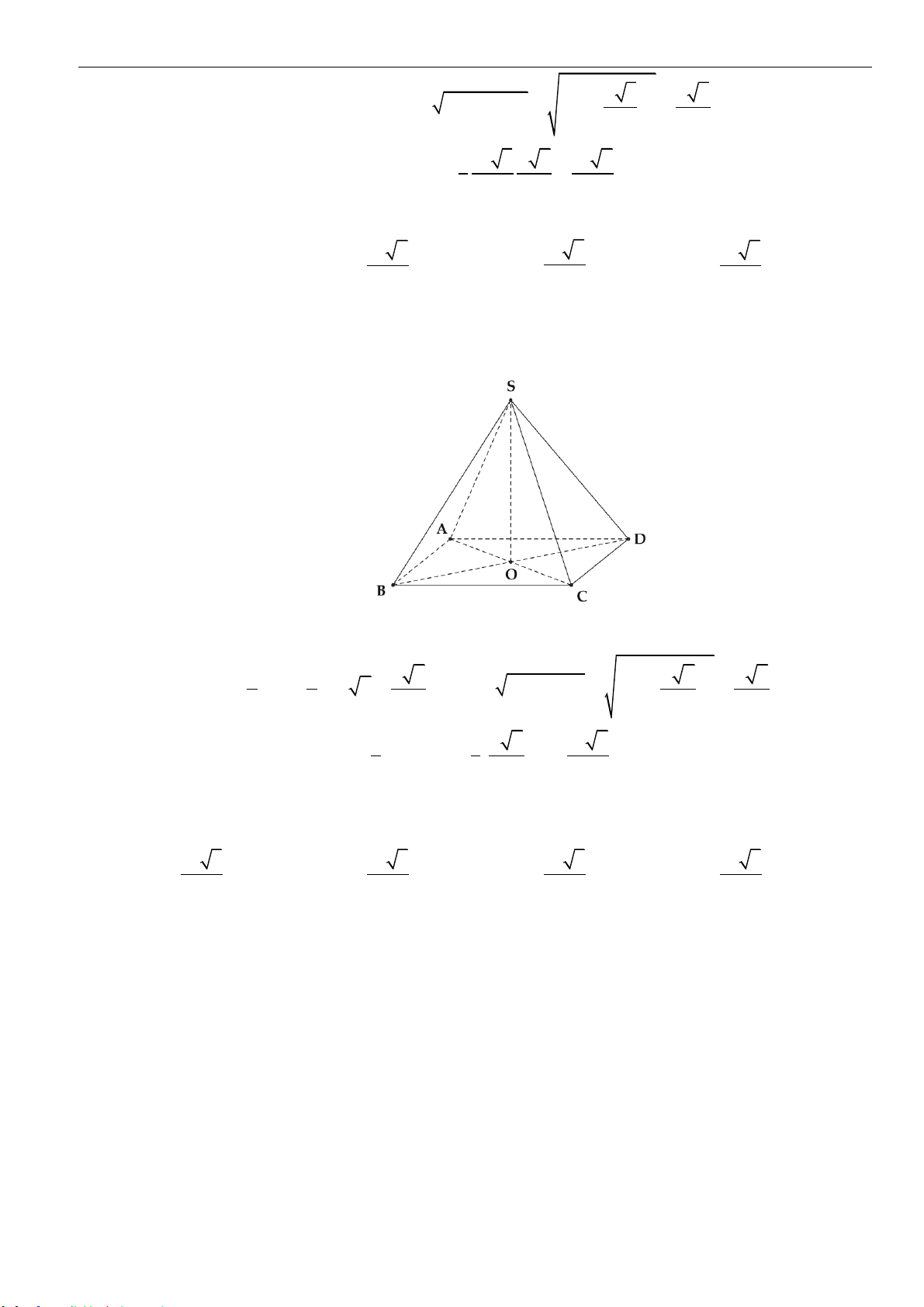
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

11 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Trong

ABG

vuông tại G có:

2

2 2 2

36

33

aa

AG AB BG a



= − = − =





.

Theo công thức, thể tích khối chóp:

23

1 3 6 2

3 4 3 12

a a a

V ==

.

Câu 12: Tính thể tích khối chóp tứ giác đều có tất cả các cạnh bằng

a

là

A.

3

a

. B.

3

2

3

a

. C.

3

2

6

a

. D.

3

2

a

.

Lời giải

Chọn C

Gỉa sử

.S ABCD

là khối chóp tứ giác đều có tất cả các cạnh bằng

a

.

Trong

( )

ABCD

, gọi

O AC BD=

suy ra

( )

SO ABCD⊥

.

Ta có

2

2 2 2

1 1 2 2 2

.2

2 2 2 2 2

a a a

OA AC AB SO SA OA a



= = =  = − = − =





.

Thể tích khối chóp

3

2

.

1 1 2 2

. . .

3 3 2 6

S ABCD ABCD

aa

V SO S a= = =

.

Câu 13: Cho khối chóp đều

.S ABC

có cạnh đáy là

a

, mặt bên tạo với đáy một góc

0

60

. Thể tích khối

chóp

.S ABC

là

A.

3

24

a

. B.

3

4

a

. C.

3

8

a

. D.

3

12

a

.

Lời giải

Chọn A

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 12

Gọi

M

là trung điểm

BC

. Do

ABC

đều

⊥AM BC

.

Lại có

SBC

là tam giác cân tại

S

do

.S ABC

là chóp đều

⊥BC SM

.

Vậy

( ) ( )

( )

;;SBC ABC SM AM=

.

Gọi

G

là trọng tâm

ABC

. Do

.S ABC

là chóp đều

( )

⊥SG ABC

.

Ta có:

0

tan tan60=  =

SG SG

SMG

GM GM

.

3 3 3

3.

3 2 3 2

 = = = =

AM AB a

SG GM

.

Vậy

23

.

1 1 3 3

. . .

3 3 2 4 24



= = =

S ABC ABC

a a a

V SG S

.

Câu 14: Thể tích của khối chóp đều

.S ABCD

có tất cả các cạnh bằng

a

là

A.

3

2

a

. B.

3

2

3

a

. C.

3

2

6

a

. D.

3

2a

.

Lời giải

Chọn C

Ta có

2

ABCD

Sa=

và

2

.

22

BD

OD a==

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

13 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Vì tam giác

SOD

vuông tại

O

nên

2

2 2 2

22

.

22

SO SD OD a a a



= − = − =





Vậy

3

.

12

. . .

36

S ABCD ABCD

V S SO a==

Câu 15: Thể tích của khối chóp tứ giác đều

.S ABCD

có chiều cao bằng

3a

và độ dài cạnh bên 3a bằng

A.

3

83

3

a

. B.

3

43a

. C.

3

45

3

a

. D.

3

43

3

a

.

Lời giải

Chọn B

Trong hình chóp tứ giác đều, đáy là hình vuông, hình chiếu của đỉnh xuống mặt đáy trùng với

tâm

O

của hình vuông

ABCD

.

3; 3 6SO a SA a AO a= =  =

( ĐL Py-ta-go)

2

6 2 6 12

2

ABCD

AC

AO a AC a S a=  =  = =

2

.

11

. 3.12 4 3

33

S ABCD ABCD

V SO S a a a



= = =

.

Câu 16: Cho hình chóp tứ giác đều

.S ABCD

có cạnh đáy bằng

2a

, góc giữa cạnh bên và mặt đáy bằng

30

. Khi đó thể tích của khối chóp bằng

A.

3

46

9

a

. B.

3

46a

. C.

3

46

3

a

. D.

3

26

9

a

.

Lời giải

Chọn A

Gọi

O

là tâm của hình vuông

ABCD

. Khi đó,

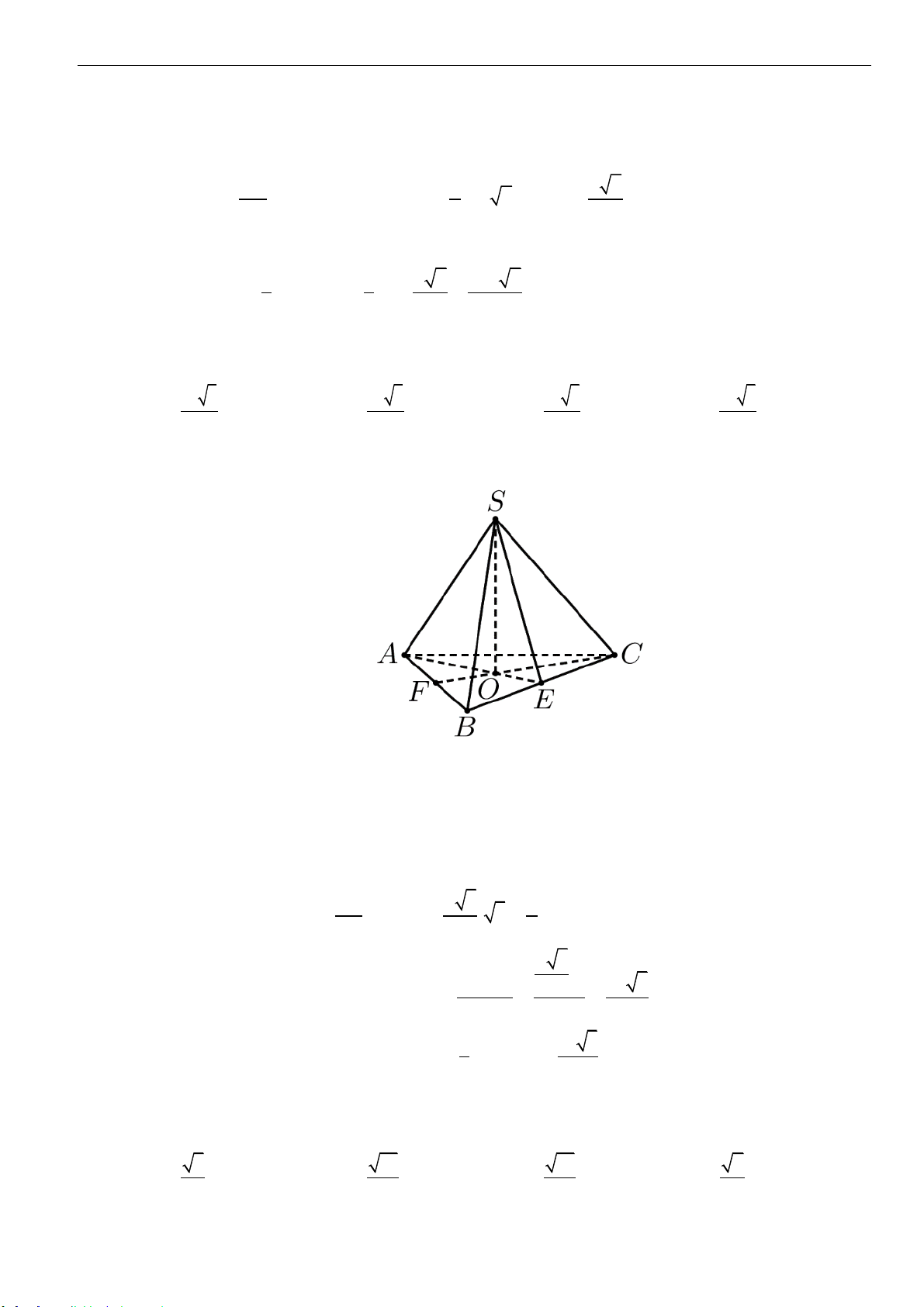
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 14

( )

(

)

0

.

, 30

h SO

SO ABCD

SD ABCD SDO

=





⊥



==





Xét tam giác

SOD

vuông tại

O

, ta có

0

16

tan .tan .2 . 2.tan30 .

23

SO a

SDO SO OD SDO a

OD

=  = = =

Ta lại có:

( )

2

2 4 .

ABCD

S a a==

Vậy

3

2

.

1 1 6 4 . 6

. . .4 . .

3 3 3 9

S ABCD ABCD

aa

V S SO a= = =

.

Câu 17: Cho hình chóp tam giác đều

.S ABC

có đáy

ABC

là tam giác đều cạnh

.a

Biết góc giữa mặt

bên và mặt đáy là

60

. Thể tích của khối chóp này bằng

A.

3

12

a

B.

3

24

a

. C.

3

8

a

. D.

3

6

a

.

Lời giải

Chọn B

Ta có:

( ) ( )

(

)

( )

, , 60

SBC ABC BC

AE BC SBC ABC SE AE SEA

SE BC

=





⊥  = = = 





⊥



Tam giác

SOE

vuông tại

O

0

3

.tan .tan60 . 3 .

3 6 2

AE a a

SO OE SEO = = = =

Diện tích tam giác đều

ABC

là

2

3

.

.3

2

2 2 4

ABC

a

AE BC a

S



= = =

.

Vậy thể tích khối chóp

.S ABC

:

3

.

13

..

3 24

S ABC ABC

a

V S SO



==

Câu 18: Cho khối chóp đều có tất cả 5 mặt có diện tích bằng nhau và bằng

2

a

. Thể tích của khối chóp

tương ứng bằng:

A.

3

2

a

. B.

3

15

2

a

. C.

3

15

6

a

. D.

3

6

4

a

.

Lời giải

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

15 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Chọn C

Theo đề bài,

.S ABCD

là khối chóp đều nên

ABCD

là hình vuông và

SA SB SC SD= = =

.

Gọi

O

là giao điểm của

AC

và

BD

, khi đó:

( )

SO ABCD⊥

.

Diện tích các mặt đều bằng

2

a

nên ta có:

2

ABCD SBC

S S a



==

.

Với

2

ABCD

S a AB BC CD DA a=  = = = =

,

22

AB a

OH ==

.

Gọi

H

là trung điểm của

BC

, khi đó:

2

12

.2

2

SBC

a

S BC SH SH a

a



=  = =

.

Áp dụng định lí Pytago cho tam giác

SOH

vuông tại

O

ta được:

( )

2

22

15

2

22

aa

SO SH OH a



= − = − =





.

Thể tích khối chóp

.S ABCD

là:

23

.

1 15 15

..

3 2 6

S ABCD

a

V a a==

.

Câu 19: Cho hình chóp tứ giác đều

.S ABCD

có cạnh đáy bằng

6a

, góc giữa cạnh bên và mặt đáy bằng

60

. Tính thể tích

V

của khối chóp

.S ABCD

.

A.

3

3Va=

. B.

3

2Va=

. C.

3

6Va=

. D.

3

9Va=

.

Lời giải

Chọn C

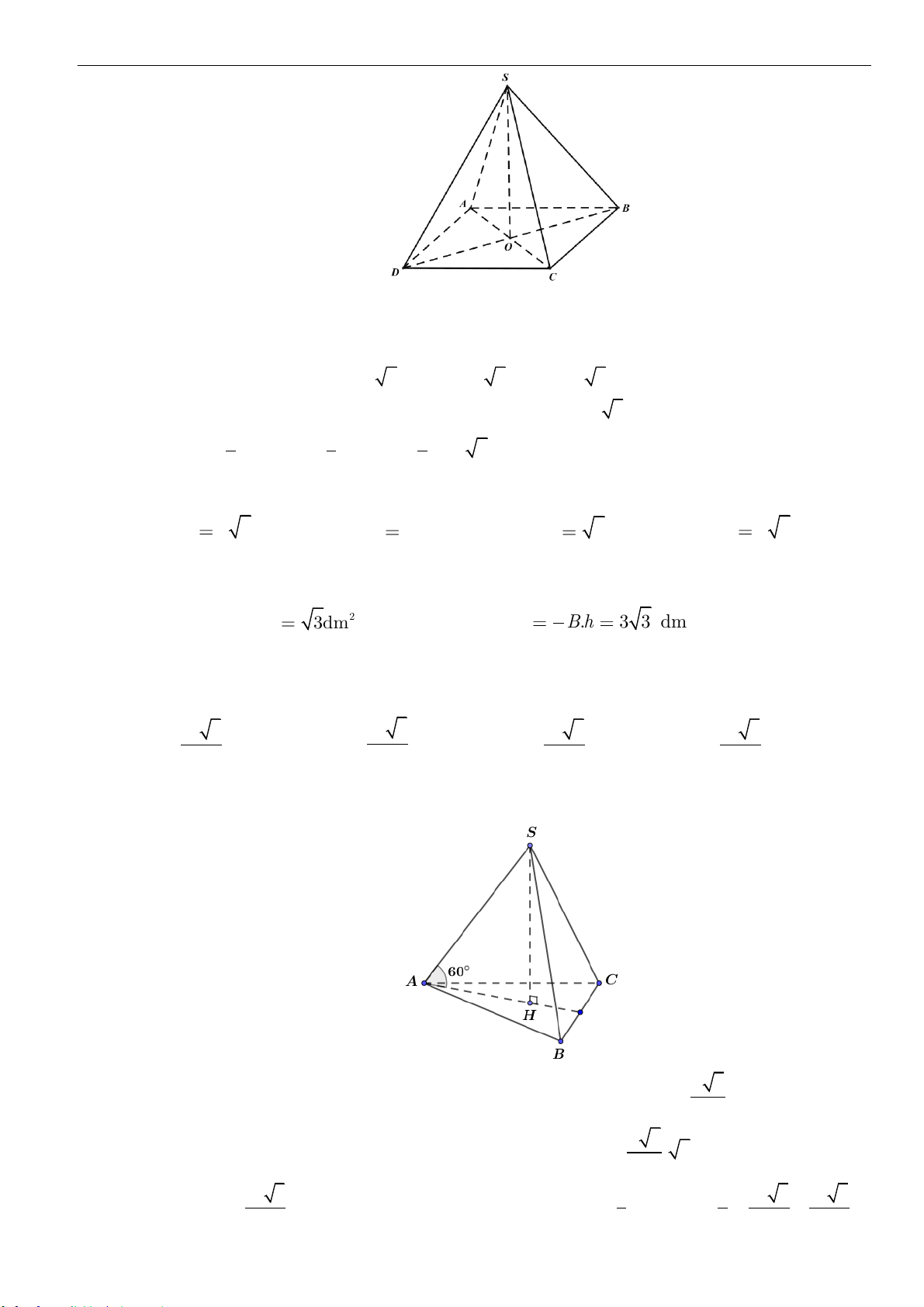
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 16

Gọi

O

là tâm hình vuông

ABCD

suy ra

( )

SO ABCD⊥

.

Do đó,

OB

là hình chiếu của

SB

trên

( )

ABCD

( )

,,SB ABCD SB OB SBO = =

.

ABCD

là hình vuông cạnh

6a

2 3 3BD a OB a =  =

.

Xét tam giác

SOB

vuông tại

O

ta có

.tan 3.tan60 3SO OB SBO a a= =  =

.

( )

2

23

.

1 1 1

. . .3 . 6 6

3 3 3

S ABCD ABCD

V SO S SO AB a a a= = = =

.

Câu 20: Khối chóp tam giác đều có chiều cao bằng

9dm

và cạnh đáy bằng

2dm

có thể tích là

A.

3

9 3dmV

. B.

3

12dmV

. C.

3

3dmV

. D.

3

3 3dmV

.

Lời giải

Chọn D

Diện tích đáy

2

3dmB

. Thể tích khối chóp

3

1

. 3 3 dm

3

V B h

.

Câu 21: Cho khối chóp đều

.S ABC

có cạnh đáy bằng

a

và các cạnh bên hợp với đáy một góc

0

60

. Tính

thể tích của khối chóp

.S ABC

A.

3

12

a

. B.

3

4

a

. C.

3

36

a

. D.

3

2

a

.

Lời giải

Chọn A

Gọi H là trọng tâm tam giác

ABC

khi đó ta có

( )

SH ABC⊥

và

3

a

AH =

. Theo giả thiết thì

ta có

0

60SAH =

. Xét tam giác

SAH

ta có

0

3

.tan60 . 3

3

a

SH AH a= = =

. Diện tích tam giác

ABC

bằng

2

3

4

a

. Vậy thể tích của khối chóp

.S ABC

là

23

1 1 3 3

. . . .

3 3 4 12

ABC

aa

V SH S a



= = =

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

17 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 22: Cho hình chóp đều

.S ABCD

đáy là hình vuông cạnh

a

. Biết

60SBD =

. Tính thể tích khối

chóp

.S ABCD

.

A.

3

23

3

a

. B.

3

6

a

. C.

3

6

3

a

. D.

3

46

3

a

.

Lời giải

Chọn B

Gọi

O

tâm của hình vuông

ABCD

.

Hình chóp

.S ABCD

đều nên

( )

SO ABCD⊥

.

Hình vuông

ABCD

có cạnh bằng

a

2=BD a

.

Ta có

SBD

là tam giác đều nên

36

.2

22

SO a a==

.

Thể tích khối chóp

.S ABCD

là

3

2

6

11

3

6

3

6

2

=  =   =

ABCD

a

V SO S a a

.

Câu 23: Cho khối chóp tam giác đều

.S ABC

có cạnh đáy bằng

a

và cạnh bên bằng

2a

. Tính thể tích

V

của khối chóp

.S ABC

.

A.

3

11

6

a

V =

. B.

3

11

4

a

V =

. C.

3

13

12

a

V =

. D.

3

11

12

a

V =

.

Lời giải

Chọn C

Do đáy là tam giác đều nên gọi

I

là trung điểm cạnh

BC

, khi đó

AI

là đường cao của tam giác

đáy. Theo định lý Pitago ta có

2

3

42

aa

AI a= − =

, và

2 2 3 3

3 3.2 3

aa

AO AI= = =

.

Trong tam giác

SOA

vuông tại

O

ta có

2

11

4

3

aa

SO a= − =

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 18

Vậy thể tích khối chóp

.S ABC

là

3

1 1 3 11 11

..

3 2 2 12

3

a a a

Va==

.

Câu 24: Cho khối chóp tứ giác đều có tất cả các cạnh bằng

2a

. Thể tích của khối chóp đã cho bằng

A.

3

22

3

a

. B.

3

8

3

a

. C.

3

82

3

a

. D.

3

42

3

a

.

Lời giải

Chọn D

Gọi hình chóp tứ giác đều có tất cả các cạnh bằng

2a

là

.S ABCD

và

I

tâm của đáy ta có:

SA SC BA BC DA DC= = = = =

SAC BAC DAC  =  = 

;;SAC BAC DAC   

lần lượt

vuông tại

,,S B D

.

I

là trung điểm của

AC

suy ra

11

2 . 2 2

22

SI AC a a= = =

( )

3

2

.

1 1 4 2

. 2 . 2

3 3 3

S ABCD ABCD

a

V S SI a a= = =

Câu 25: Cho hình chóp đều

.S ABCD

có cạnh đáy bằng

a

và cạnh bên tạo với đáy một góc

60

. Thể

tích của hình chóp đều đó là

A.

3

6

a

. B.

3

6

a

. C.

3

2

a

. D.

3

6

2

a

.

Lời giải

Chọn A

Gọi

( )

O AC BD SO ABCD=   ⊥

.

Ta có:

( )

(

)

( )

,,SC ABCD SC OC SCO==

60SCO = 

Xét tam giác vuông

SOC

ta có:

tan60

SO

OC

=

3

3 . 3

2

a

SO OC a = = =

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

19 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

2

ABCD

Sa=

Thể tích của hình chóp đều là:

3

2

1 1 3 6

. . . .

3 3 2 6

ABCD

a

V SO S a a= = =

.

Câu 26: Cho hình chóp đều

.S ABCD

đáy là hình vuông cạnh

a

. Biết

60SBD =

. Tính thể tích khối

chóp

.S ABCD

.

A.

3

23

3

a

. B.

3

6

a

. C.

3

6

3

a

. D.

3

46

3

a

.

Lời giải

Chọn B

Gọi

O

tâm của hình vuông

ABCD

.

Hình chóp

.S ABCD

đều nên

( )

SO ABCD⊥

.

Hình vuông

ABCD

có cạnh bằng

a

2=BD a

.

Ta có

SBD

là tam giác đều nên

36

.2

22

SO a a==

.

Thể tích khối chóp

.S ABCD

là

3

2

6

11

3

6

3

6

2

=  =   =

ABCD

a

V SO S a a

.

Câu 27: Cho hình chóp tứ giác đều

.S ABCD

có cạnh đáy bằng

a

và mặt bên tạo với mặt phẳng đáy một

góc

0

60

. Tính thể tích

V

của khối chóp

.S ABCD

.

A.

3

6

2

=

a

V

. B.

3

6

3

=

a

V

. C.

3

2

=

a

V

. D.

3

6

=

a

V

.

Lời giải

Chọn D

Ta có:

2

=

ABCD

Sa

.

Gọi

M

là trung điểm

BC

, góc giữa mặt bên

()SBC

và

()ABCD

là

SMO

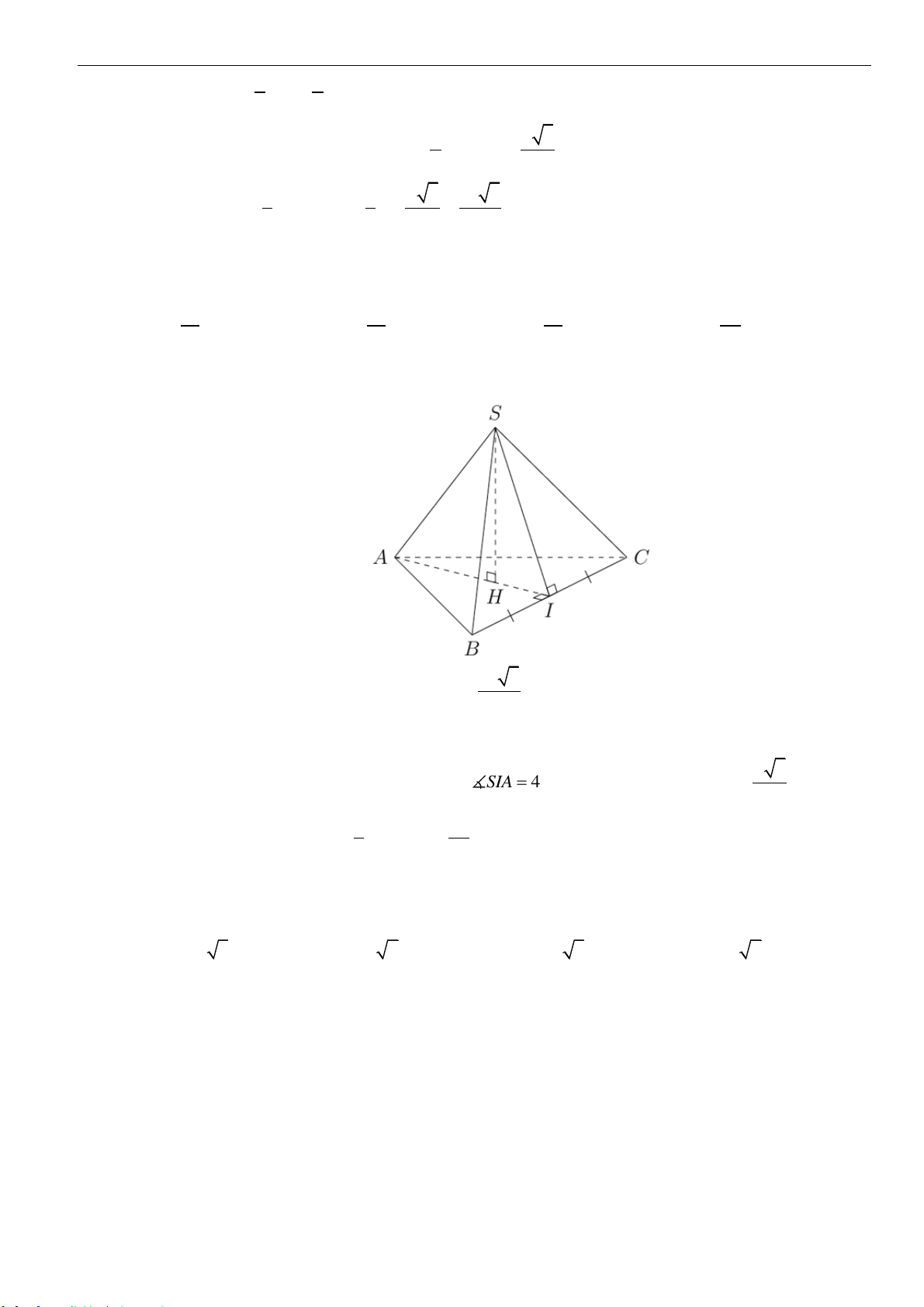
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 20

Ta có

1

.

22

==

a

OM AB

Chiều cao

SO

:

0

3

.tan .tan60

22

= = =

aa

SO OB SBO

.

Vậy

3

2

.

1 1 3 3

. . . .

3 3 2 6

= = =

S ABCD ABCD

aa

V S SO a

.

Câu 28: Cho hình chóp tam giác đều

.S ABC

có cạnh đáy bằng

a

và mặt bên tạo với đáy một góc

0

45

.

Tính thể tích của khối chóp

.S ABC

?

A.

3

8

a

. B.

3

12

a

. C.

3

4

a

. D.

3

24

a

.

Lời giải

Chọn D

Do đáy là tam giác đều cạnh

a

nên

2

3

4

ABC

a

S =

.

Gọi

H

là trọng tâm tam giác

ABC

ta có

( )

SH ABC⊥

Gọi

I

là trung điểm cạnh

BC

khi đó góc

45

o

SIA =

.Ta có

3

tan45 .

6

o

a

SH HI==

.

Vậy thể khối chóp là:

3

1

..

3 24

ABC

a

V SH S==

Câu 29: Cho khối chóp đều

.S ABCD

có

6AC a=

và góc tạo bởi hai mặt phẳng

( )

SAB

và

( )

SCD

bằng

0

60

. Thể tích khối chóp đã cho bằng:

A.

3

108 3a

. B.

3

96a

. C.

3

36 3a

. D.

3

27 6a

.

Lời giải

Chọn B

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

21 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Gọi

O AC BD=

và

,MN

lần lượt là trung điểm

,AB CD

.

Do

6 3 2

2

AC

AC a AB a=  = =

. Đồng thời

( ) ( )

SAB SCD d AB CD=

Dễ dàng chứng minh

SM AB⊥

và

SN CD⊥

(do

,SAB SCD

cân tại

S

).

Suy ra

( ) ( ) ( )

0

, ; 60SAB SCD SM SN==





.

Từ đó suy ra

SMN

đều hay

3 3 3 6

2 2 2

MN AB a

SO = = =

.

Vậy

( )

2

3

.

1 1 3 6

. . . 3 2 9 6

3 3 2

S ABCD ABCD

a

V SO S a a= = =

.

Câu 30: Cho khối chóp đều

.S ABCD

có

4AC a=

, hai mặt phẳng

()SAB

và

()SCD

vuông góc với

nhau. Thể tích của khối chóp đã cho bằng

A.

3

16 2

3

a

. B.

3

82

3

a

. C.

3

16a

D.

3

16

3

a

.

Lời giải

Chọn B

Gọi

,,M O N

lần lượt là trung điểm của

,,AB AC CD

nên

,AB SM CD SN⊥⊥

.

Qua

S

dựng đường thẳng

//Sx AB

.

Vì

( )

//

AB SAB

CD SCD

AB CD















nên

( ) ( )

// //SAB SCD Sx AB CD=

.

d

N

M

O

D

C

B

A

S

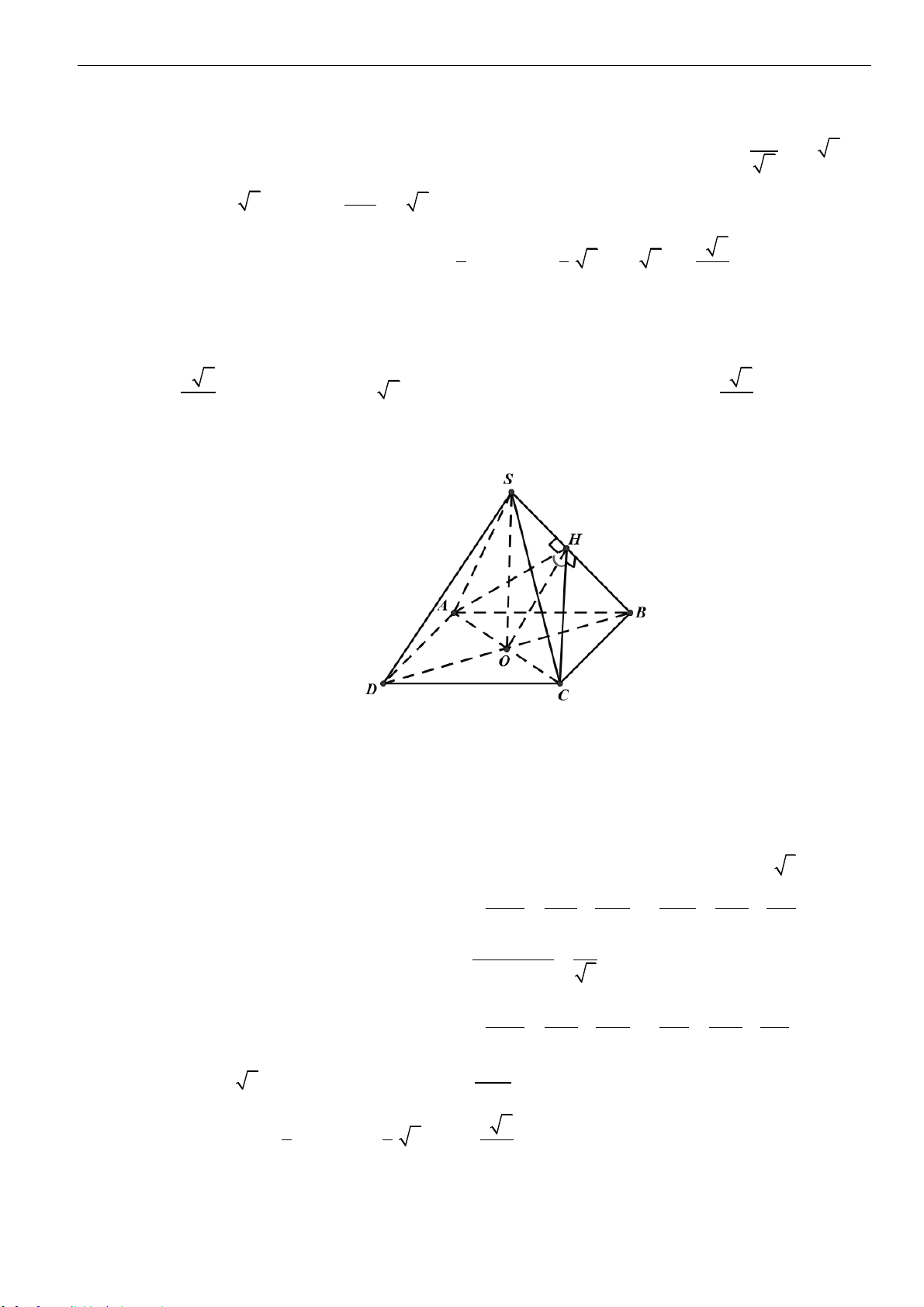
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 22

Ta có

( )

90

Sx SM

Sx SMN MSN

Sx SN



⊥



 ⊥  =



⊥



.

Hình chóp

.S ABCD

đều

ABCD

là hình vuông, có

4AC a=

22

2

AC

AB BC a = = =

22MN a=

2

MN

SO a = =

.

Vậy thể tích khối chóp

.S ABCD

là

( )

2

3

11

. . . 2 . 2 2

33

82

3

ABCD

V SO S a a a= = =

.

Câu 31: Cho khối chóp tứ giác đều

.S ABCD

có

4AC a=

, hai mặt phẳng

( )

SAB

và

( )

SBC

tạo với nhau

một góc

0

60

. Thể tích của khối chóp đã cho bằng

A.

3

22

3

a

B.

3

22a

. C.

3

16a

. D.

3

82

3

a

.

Lời giải

Chọn D

Gọi

O AC BD=

vì

.S ABCD

chóp tứ giác đều nên

( )

SO ABCD⊥

Kẻ đường cao

AH

của tam giác

SAB

, suy ra

SB AH

SB CH

⊥





⊥



Nên góc giữa hai mặt phẳng

( )

SAB

và

( )

SBC

là góc giữa

AH

và

CH

0

60=

Trường hợp 1:

0

60AHC =

khi đó, tam giác

AHC

đều cạnh

4AC a=

nên

23HO a=

Ta có

SOB

vuông tại O và

OH SB⊥

nên

2 2 2 2 2 2

1 1 1 1 1 1

12 4OH SO OB a SO a

= +  = +

(vô lý)

Trường hợp 2:

0

120AHC =

khi đó,

( )

2

3

tan

OC a

HO

OHC

==

Ta có

SOB

vuông tại O và

OH SB⊥

nên

2 2 2 2 2 2

1 1 1 3 1 1

44OH SO OB a SO a

= +  = +

Nên

2SO a=

. Mà diện tích đáy

2

3

8

2

ABCD

AC

Sa==

.

Do đó,

33

.

1 1 8 2

. . 2 .8

3 3 3

S ABCD ABCD

V SO S a a a= = =

.

Câu 32: Cho hình chóp đều

.S ABC

có cạnh đáy bằng

.a

Gọi E, F lần lượt là trung điểm của các cạnh

SB, SC. Biết rằng mặt phẳng

( )

AEF

vuông góc với mặt phẳng

( )

.SBC

Thể tích khối chóp

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

23 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

.S ABC

bằng

A.

3

5

24

a

. B.

3

5

8

a

. C.

3

5

12

a

. D.

3

5

16

a

.

Lời giải

Chọn A

Gọi

N

là trung điểm của

BC

,

O

là tâm đường tròn đáy.

Gọi

H

là giao điểm của

EF

và

SN

, tam giác

AEF

là tam giác cân tại

A

nên

AH EF⊥

Vì

( ) ( )

AEF SBC⊥

nên ta có

( )

AH SBC AH SN⊥  ⊥

.

Suy ra tam giác

SAN

cân tại

A

.

Khi đó

3

2

a

SA AN==

.

Ta lại có

3

a

AO =

22

3 15

4 3 6

a a a

SO SA AO = − = − =

.

Câu 33: Cho hình chóp tam giác đều

.S ABC

có cạnh bên bằng

2cm

, các điểm

,DE

lần lượt là trung

điểm của

,SA SC

, đồng thời

AE

vuông góc với

BD

. Thể tích khối chóp

.S ABC

bằng

A.

3

4 21

cm

27

. B.

3

4 21

cm

7

. C.

3

4 21

cm

3

. D.

3

4 21

cm

9

.

Lời giải

Chọn A

Gọi

M

trung điểm

SE



//DM AE

. Theo giả thiết

.BD AE BD DM⊥  ⊥

Đặt

( )

0AB x x=

.

2 2 2 2

2 2 2

2

2 4 2

BA BS SA x

BD BE AE

++

= = = − =

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 24

2

22

12

,

48

x

DM AE

+

==

2 2 2 2

2

S9

2 4 4

B BE SE x

BM

++

= − =

.

Tam giác

BDM

vuông tại

D

:

2 2 2

222

2 2 9

2 8 4

x x x

BD DM BM

+ + +

+ =  + =

26

3

x AB = =

.

Gọi

N

trung điểm

BC

,

O

trọng tâm tam giác

ABC

.

Tam giác

ABC

đều cạnh

26

3

cm

nên

22

2 2 2

33

AO AB BN= − =

cm

và

2

3 2 3

43

ABC

x

S ==

( )

2

cm

.

Vì

.S ABC

là hình chóp đều nên

()SO ABC⊥

.Ta có

22

8 2 7

4

93

SO SA AO= − = − =

( )

cm

.

1 1 2 7 2 3 4 21

. . .

3 3 3 3 27

S ABC ABC

V SO S= = =

( )

3

cm

.

Câu 34: Cho hình chóp tứ giác đều

.S ABCD

, đáy tâm

O

,

3SA SB SC SD a= = = =

. Gọi

,MN

lần

lượt là trung điểm cạnh

,CD AB

. Biết khoảng cách từ

M

đến

( )

SNC

bằng

510

51

a

. Tính thể

tích khối chóp

.S ABCD

.

A.

3

10

6

a

. B.

3

10

2

a

. C.

3

5

2

a

. D.

3

5

6

a

.

Lời giải

Chọn A

Ta có

//AN MC

AN MC





=



AMCN

là hình bình hành.

Do đó

( )

/ / / /AM CN AM SCN

.

Từ đó suy ra

( )

; ; 2 ;d M SCN d A SCN d O SCN==

Kẽ

OH CN⊥

tại

H

mà

SO CN⊥

. Suy ra

( ) ( )

1CN SHO⊥

.

Kẽ

OK SH⊥

tại

K

( )

2

.

Từ

( ) ( )

13OK CN⊥

.

Từ

( )( ) ( ) ( )

( )

2 3 ;OK SCN d O SCN OK ⊥  =

.

(Có thể sử dụng tứ diện vuông

.O SCE

)

Đặt

0AB x=

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

25 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Gọi

E CN OB=

. Khi đó

E

là trọng tâm

ABC

. Do đó

1 1 2

3 6 6

x

OE OB BD= = =

.

Xét

ACE

vuông tại

O

có

2 2 2

1 1 1

OH OE OC

=+

.

Xét

SOH

vuông tại

O

có:

2 2 2 2 2 2

1 1 1 1 1

xa

OK OH SO OH SC OC

= + = +  =

−

.

2

2 2 2

10

3

22

aa

SO SC CO a= − = − =

.

Vậy

3

2

.

1 1 10 10

..

3 3 2 6

S ABCD ABCD

aa

V SO S a= = =

.

Câu 35: Cho hình chóp đều

.S ABC

có đáy

ABC

là tam giác đều cạnh

.a

Gọi

,E

F

lần lượt là trung

điểm của các cạnh

,SB

.SC

Biết mặt phẳng

( )

AEF

vuông góc với mặt phẳng

( )

.SBC

Thể tích

khối chóp

.S ABC

bằng

A.

3

5

.

8

a

B.

3

.

24

a

C.

3

5

.

24

a

D.

3

15

.

27

a

Lời giải

Chọn C

Gọi

M

là trung điểm

,BC

O

là trọng tâm tam giác

.ABC

Suy ra

( )

.SO ABC⊥

Gọi

SN EF

N SM EF

AN EF

⊥



=  



⊥



nên

( ) ( )

0

, 90 .AEF SBC SNA==

Xét tam giác

,SAM

có

AN

là đường trung tuyến và cũng là đường cao nên tam giác

SAM

cân

tại

A

3

.

2

a

SA AM = =

Tam giác vuông

,SAO

có

22

5

.

23

a

SO SA AO= − =

Vậy

3

.

15

..

3 24

S ABC ABC

a

V S SO



==

Câu 36: Cho hình chóp tam giác đều

.S ABC

có cạnh

2AB a=

. Các cạnh bên tạo với đáy một góc

60

.

Thể tích của khối chóp

.S ABC

bằng

A.

3

23a

. B.

3

23

3

a

. C.

43

. D.

3

43

3

a

.

Lời giải

Chọn B

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 26

Gọi

H

là trọng tâm của tam giác

ABC

và

E

là trung điểm của cạnh

BC

.

Vì hình chóp tam giác đều

.S ABC

nên

( )

SH ABC⊥

.

Các cạnh bên tạo với đáy một góc

60

nên

60SAH SBH SCH= = = 

.

Ta có:

2 2 2 3 2 3

.

3 3 2 3

aa

AH AE= = =

.

23

tan tan60 . 2

3

SH a

SAH SH a

AH

=  =  =

.

( )

2

3

.

23

1 1 2 3

. . . .2

3 3 4 3

S ABC ABC

a

V S SH a a



= = =

.

Câu 37: Xét khối tứ diện đều

ABCD

có cạnh

AB x=

. Với giá trị nào của

x

thì thể tích khối tứ diện

ABCD

bằng

3

3a

A.

26xa=

. B.

6xa=

. C.

2x =

. D.

32xa=

.

Lời giải

Chọn B

Gọi

M

là trung điểm

CD

,

O

là trọng tâm

.BCD

ABO

vuông tại

O

có

2 2 3 3

;.

3 3 2 3

xx

AB x BO BM= = = =

Suy ra

22

6

.

3

x

AO AB BO= − =

2

3

.

4

BCD

x

S



=

3

12

. 3 6 .

3 12

ABCD BCD

x

V S AO a x a



= = =  =

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

27 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 38: Cho hình chóp đều

.S ABCD

với

O

là tâm đáy. Khoảng cách từ

O

đến mặt bên bằng 1 và góc

giữa mặt bên với đáy bằng

0

45

. Thể tích của khối chóp

.S ABCD

bằng

A.

42

3

V =

. B.

82

3

V =

. C.

23V =

. D.

43

3

V =

.

Lời giải

Chọn B

Gọi

I

là trung điểm của

, 2 .CD OI CD CD OI ⊥ =

Kẻ

OH SI⊥

tại

( ) ( )

( )

, 1.H OH SCD d O SCD OH ⊥  = =

Ta có

( ) ( )

( )

( ) ( )

( )

0

, , , 45 .

,

SCD ABCD CD

SI SCD SI CD SCD ABCD SI OI SIO

OI ABCD OI CD

=





 ⊥  = = =





⊥



Xét tam giác vuông

0

1

2 2 2 2.

sin45

sin

OH

HIO OI CD OI

SIO

 = = =  = =

Ta có

SIO

là tam giác vuông cân tại

2.O SO OI = =

Vậy

( )

2

.

1 1 8 2

. 2 2 . 2 .

3 3 3

S ABCD

V CD SO= = =

Câu 39: Cho khối chóp đều

.S ABCD

có

2AB a=

. Gọi

,MN

lần lượt là trung điểm

,SC SD

, hai mặt

phẳng

( )

AMN

và

( )

SCD

vuông góc với nhau. Thể tích của khối chóp đã cho bằng

A.

3

4

3

3a

. B.

3

43a

. C.

3

8

3

a

D.

3

4

3

2a

.

Lời giải

Chọn A

Gọi

,,P Q R

lần lượt là trung điểm của

,,AB CD MN

, ta có

,,S R Q

thẳng hàng.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 28

Ta có

( ) ( )

AMN SCD MN=

,

( )

PR AMN

,

PR MN⊥

nên

( )

PR SCD PR SQ⊥  ⊥

.

Tam giác

PSQ

có

PR

vừa là trung tuyến, vừa là đường cao nên

PSQ

cân tại P.

Ta được

2SP PQ a==

;

22

3SO SP OP a= − =

.

Vậy thể tích khối chóp

.S ABCD

là

( )

2

3

1 1 3

. . . 3. 2

33

4

ABCD

V SO S a a

a

= = =

Câu 40: Cho khối chóp tam giác đều

.S ABC

có cạnh đáy bằng

2a

. Gọi

,MN

lần lượt là trung điểm các

cạnh

,SB SC

. Biết mặt phẳng

( )

AMN

vuông góc với mặt phẳng

( )

SBC

. Thể tích của khối chóp

.S ABC

bằng:

A.

3

5

.

3

a

B.

3

5.a

C.

3

5

.

9

a

D.

3

3 5.a

Lời giải

Chọn A

Gọi

O

là trọng tâm giác đều

ABC

. Vì

.S ABC

là chóp tam giác đều nên

SO

là chiều cao.

Gọi

E

là trung điểm của

MN

.

SE

cắt

BC

tại

D

suy ra

E

là trung điểm của

SD

. Trong tam

giác

SAD

có

AE

là đường trung tuyến ứng với cạnh

( )

1.SD

Tam giác

SMN

cân tại

S

nên

SD MN⊥

.

Ta có

( ) ( )

2.

SD MN

MN AMN SBC SD AMN AE SD

AMN SBC



⊥



=  ⊥  ⊥





⊥



Từ

( )

1

và

( )

2

suy ra tam giác

SAD

cân tại

A

nên

( )

3 2 2 3

2 3 ;

2 3 3

SA AD a a AO AD a= = = = =

.

Tam giác

SAO

vuông tại

O

có:

( )

2

22

2 3 15

3

33

SO SA AO a a a



= − = − =





.

Diện tích tam giác

ABC

bằng

( )

2

3

23

4

aa=

.

Vậy thể tích của khối chóp

.S ABC

bằng:

23

1 15 5

. 3 . .

3 3 3

a a a=

Câu 41: Cho hình chóp tứ giác đều

.S ABCD

có cạnh đáy bằng

a

, tâm của đáy là

O

. Gọi

M

và

N

lần

lượt là trung điểm của

SA

và

BC

. Biết góc giữa đường thẳng

MN

và mặt phẳng

( )

ABCD

bằng

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

29 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

0

60

. Tính thể tích khối chóp

.S ABCD

.

A.

3

10

6

a

. B.

3

30

2

a

. C.

3

30

6

a

. D.

3

10

3

a

Lời giải

Chọn C

Gọi

H

là trung điểm

//AO MH SO

( )

MH ABCD⊥

. Khi đó góc giữa

MN

và

( )

ABCD

là

MNH

.

Ta có

2 2 0

2 . .cos45HN CN CH CN CH= + −

10

4

a

=

.

Suy ra

0

10 30

.tan60 . 3

44

aa

MH HN= = =

30

2

a

SO MH = =

.

Do đó thể tích khối chóp

3

2

.

1 1 30 30

. . . .

3 3 2 6

S ABCD ABCD

aa

V SO S a= = =

.

Câu 42: Cho khối chóp đều

.S ABC

có cạnh đáy bằng

a

, hai mặt phẳng

( )

SAC

và

( )

SBC

vuông góc

với nhau. Thể tích khối chóp đã cho bằng

A.

3

2

24

a

. B.

3

8

2a

. C.

3

2

5

1

a

. D.

3

5

4

a

.

Lời giải

Chọn A

Gọi

O

là tâm của

ABC

suy ra

()SO ABC⊥

Gọi

N

là trung điểm của

AB

, ta được

( )

AB SNC AB SC⊥  ⊥

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 30

Dựng

, NM SC M SC⊥

. Suy ra

( )

ABM SC⊥

Ta có

( )

( ) ( )

22

SAC SBC

AB a

SAC SBC SC AM BM MN

ABM SC



⊥



 =  ⊥  = =





⊥



Đặt

SO x=

.

Trong tam giác

SNC

ta có

22

36

..

2 2 3 6 6

..

a a a a a

xSN x x xO C MN SC=  =  = =+

Vậy

23

.

1 1 2

.

3 3 6 4 24

63

S ABC ABC

aa

VS

a

SO



= =   =

.

Câu 43: Cho hình chóp tứ giác đều

.S ABCD

có cạnh đáy bằng

a

. Gọi

M

,

N

lần lượt là trung điểm

của

SA

và

CD

. Cho biết

MN

tạo với mặt đáy một góc bằng

30

. Tính thể tích khối chóp

.S ABCD

.

A.

3

30

18

a

. B.

3

15

3

a

. C.

3

5

12

a

. D.

3

15

5

a

.

Lời giải

Chọn A

Gọi

O AC BD=

, ta có

( )

SO ABCD⊥

.

Gọi

H

là trung điểm

OA

, ta có

//MH SO

( )

MH ABCD⊥

.

Do đó

( )

,MN ABCD

( )

,MN NH=

MNH=

30=

.

Ta có:

22

2

31

44

NH AD CD

   

=+

   

   

2

5

8

a=

10

4

a

NH=

.

tan

MH

MNH

NH

=

10

4

MH

a

=

3

=

30

12

a

MH=

.

Mặt khác:

30

2

6

a

SO MH==

.

Vậy thể tích khối chóp

.S ABCD

là:

1

..

3

ABCD

V S SO=

2

1 30

..

36

a

a=

3

30

18

a

=

.

Câu 44: Cho hình chóp đều

.S ABCD

có cạnh đáy bằng

a

, góc giữa hai mặt phẳng

( )

SBC

và

( )

SCD

bằng

0

60

. Tính thể tích khối chóp

.S ABCD

theo

a

.

A.

3

2

a

. B.

3

6

a

. C.

3

2

12

a

. D.

3

2

4

a

.

Lời giải

Chọn B

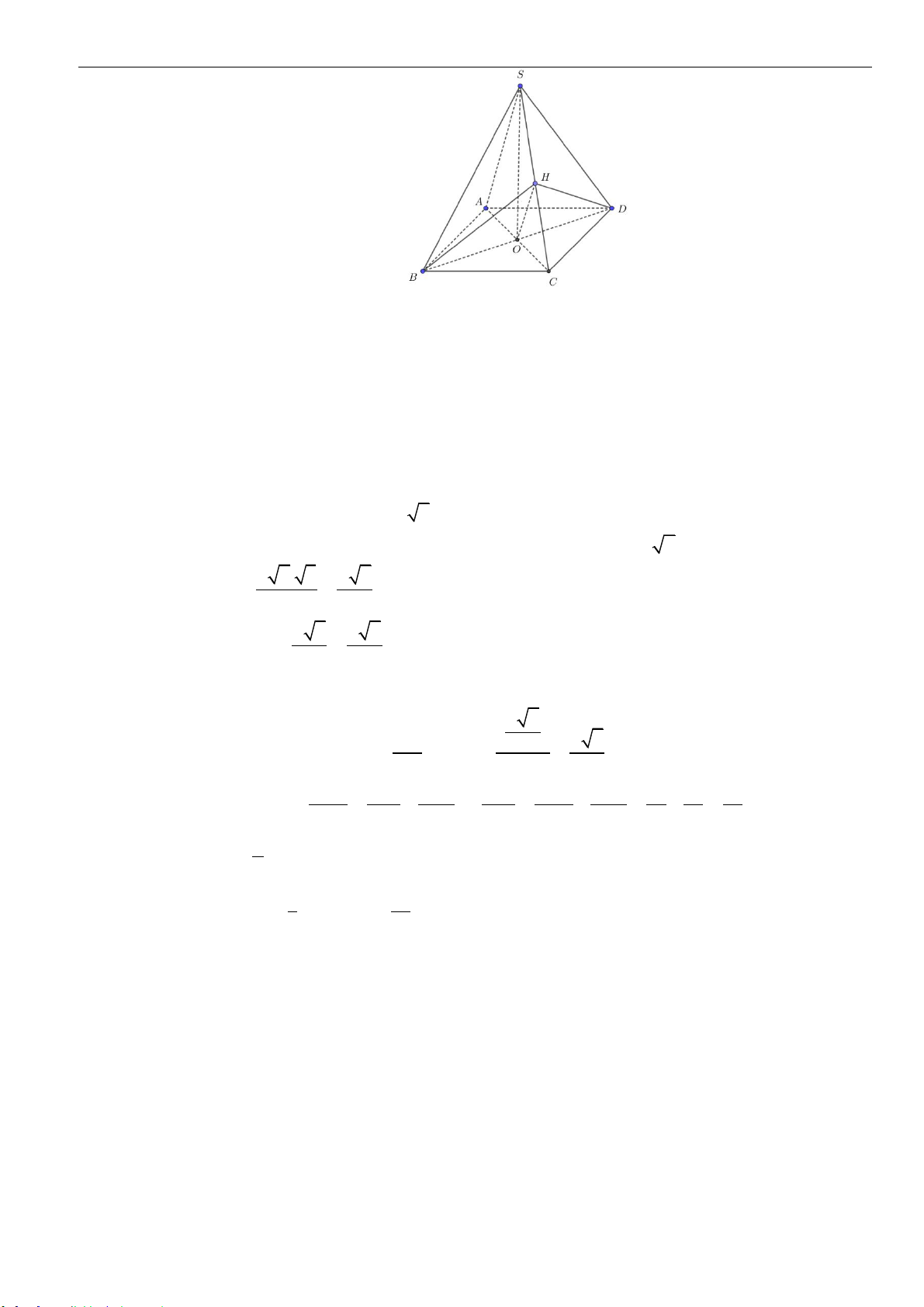
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

31 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Gọi

O

là tâm của hình vuông. Do

.S ABCD

là hình chóp đều nên

( )

SO ABCD⊥

.

Ta có:

,BD SO BD AC⊥⊥

nên

( )

BD SAC⊥

.

Trong tam giác

SBC

, dựng

BH SC⊥

. Do

( )

BD SAC⊥

nên

BD SC⊥

.

Khi đó

( )

SC BDH⊥

nên

SC DH⊥

.

Vậy

( ) ( )

( )

,,SBC SCD BH HD=

.

Ta có

BSC DSC = 

nên

BH DH=

do đó tam giác

HBD

cân tại

H

.

Nhận thấy:

BD OH⊥

và

2BD a=

.

TH1:

0

60BHD =

nên tam giác

BHD

là tam giác đều cạnh bằng

2a

.

Do đó

2. 3 6

22

aa

OH ==

.

Nhận thấy:

62

22

aa

OH OC=  =

vô lí (vì tam giác

HOC

vuông tại

H

).

TH2:

0

120BHD =

.

Xét tam giác

BHO

:

0

2

6

2

tan

tan60 6

a

BO a

BHO HO

HO

=  = =

.

Xét tam giác

OSC

:

2 2 2 2 2 2 2 2 2

1 1 1 1 1 1 6 2 4

OH SO OC SO OH OC a a a

= +  = − = − =

Suy ra

2

a

SO =

.

Khi đó:

3

.

1

..

36

S ABCD ABCD

a

V SO S==

.

Câu 45: Cho khối chóp đều

.S ABCD

có

6AC a=

. Gọi

,MN

lần lượt là trung điểm cạnh

SB

và

SD

.

Biết

( )

AMC

và

( )

CMN

cùng vuông góc nhau. Tính thể tích khối chóp đã cho.

A.

3

72a

. B.

3

108a

. C.

3

36a

. D.

3

216a

.

Lời giải

Chọn C

Gọi

O AC BD=

. Dễ thấy

( ) ( )

SO SAC SBD=

và

( ) ( )

MN AMN CMN=

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 32

Ta có :

MC NC=

(2 đường trung tuyến của 2 tam giác bằng nhau

SBC

và

SCD

)

Gọi

I

là trung điểm

MN IC MN⊥

.

Tương tự ta có

AM AN AI MN=  ⊥

.

Vậy

( ) ( ) ( )

0

, ; 90AMN CMN IA IC IA IC= =  ⊥





3

2

AC

IO a = =

.

Mặt khác

I

là trung điểm

SO

do

MN SO I=

với

MN

là đường trung bình

SBD

Suy ra

26SO OI a==

.

Vậy

2

3

.

1 1 6

. . .6 . 36

33

2

S ABCD ABCD

a

V SO S a a



= = =





.

Câu 46: Cho khối chóp đều

.S ABCD

có

4AC a=

, hai mặt phẳng

( )

SAB

và

( )

SCD

vuông góc với

nhau. Thể tích khối chóp đã cho bằng

A.

3

16 2

3

a

. B.

3

82

3

a

. C.

3

16a

. D.

3

16

3

a

.

Lời giải

Chọn B

Gọi

O

là tâm hình vuông suy ra

( )

SO ABCD⊥

Ta có

( ) ( )

// //SAB SCD Sx AB CD=

Gọi

I

là trung điểm của

AB

, suy ra

( )

SI AB SI Sx SI SCD SI SD⊥  ⊥  ⊥  ⊥

4 2 2 10AC a AD a DI a=  =  =

Đặt

22

2SD x SI x a=  = −

. Ta có hệ thức

2 2 2 2 2 2

2 10 6 6x a x a x a x a− + =  =  =

Từ đó ta tính được

2SO a=

.

Vậy

( )

2

3

.

1 8 2

. 2. 2 2

33

S ABCD

V a a a==

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

33 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 47: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác đều cạnh

1

, biết khoảng cách từ

A

đến

( )

SBC

là

6

4

, từ

B

đến

( )

SCA

là

15

10

, từ

C

đến

( )

SAB

là

30

20

và hình chiếu vuông góc

H

của

S

xuống đáy nằm trong tam giác

ABC

. Tính thể tích khối chóp

.S ABC

V

.

A.

1

12

. B.

1

36

. C.

1

24

. D.

1

48

Lời giải

Chọn D

Gọi

,,M N P

lần lượt là hình chiếu của

H

lên các cạnh

,,AC BC AB

.

Đặt

.

1 3 3

..

3 4 12

S ABC

h

SH h V h=  = =

.

Ta có

( )

.

26

3 30

2 : 10

2 20

;

SAB S ABC

SAB

SV

h

AP S h

AB

d C SAB

= = = = =

Tương tự, tính được

2,HM h HN h==

22

3PH SP SH h = − =

Ta có

( )

1

2

ABC HAB HAC HBC

S S S S HP HM HN= + + = + +

33

3

4 12

hh =  =

Vậy

.

3 3 1

.

12 12 48

S ABC

V ==

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

1 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Dạng 5: Tổng hợp về thể tích khối chóp

Câu 1: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Diện tích đáy và chiều cao của khối

lần lượt

S

và

h

. Tính thể tích của khối chóp

.S ABC

là

A.

1

3

Sh

. B.

1

6

Sh

. C.

2

3

Sh

. D.

Sh

.

Lời giải

Chọn B

Ta có:

.

1 1 1 1

.

2 2 3 6

SABC S ABCD

V V Sh Sh= = =

.

Câu 2: Cho hình chóp

.S ABC

có đáy là tam giác đều cạnh

2a

và có thể tích bằng

3

3a

. Tính chiều cao

h

của hình chóp đã cho.

A.

33

2

a

h =

. B.

3

a

h =

. C.

3ha=

. D.

23ha=

.

Lời giải

Chọn C

Tam giác

ABC

đều cạnh

2a

có diện tích

( )

2

23

3

4

ABC

a

Sa==

.

Thể tích chối chóp

.S ABC

là:

1

..

3

ABC

V h S=

.

Suy ra chiều cao

h

của hình chóp đã cho:

3

2

3 3 3

3

ABC

Va

ha

S

a

= = =

.

Câu 3: Khối chóp

.S ABCD

có đáy là hình vuông cạnh bằng

2a

, chân đường cao trùng với trung điểm

H

của

AB

, mặt bên

( )

SCD

tạo với mặt đáy một góc

0

30

. Gọi

M

là trung điểm của

SC

. Thể

tích khối chóp

.H BCM

là

A.

3

2

3

a

. B.

3

8

a

. C.

3

9

a

. D.

3

6

3

a

.

Lời giải

Chọn C

VÍ DỤ MINH HỌA

B

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 2

Ta có

.

. . .

.

1 1 1

2 2 8

M HBC

M HBC S HBC S ABCD

S HBC

V

MC

V V V

V SC

= =  = =

.

Gọi

K

là trung điểm của

CD

. Khi đó

( ) ( )

( )

0

, 30SCD ABCD SKH==

.

Ta có

( )

3

2

0

..

2 1 1 2 3

.tan30 . . 2 .

8 3 9

33

H BCM M HBC

a a a

SH HK V V a= =  = = =

.

Câu 4: Cho hình chóp

.S ABC

có

3AB a=

,

4BC a=

,

5CA a=

, các mặt bên cùng tạo với đáy một góc

60

, hình chiếu vuông góc của

S

lên mặt phẳng

( )

ABC

thuộc miền trong tam giác

ABC

. Tính

thể tích khối chóp

.S ABC

.

A.

3

23a

. B.

3

63a

. C.

3

12 3a

. D.

3

22a

Lời giải

Chọn A

Gọi

I

là hình chiếu của

S

trên mặt phẳng

( )

ABC

;

F

,

E

,

P

lần lượt là hình chiếu của

I

trên

,,AB BC CA

. Suy ra

60SFI SEI SPI= = = 

FI EI PI r = = =

I

là tâm đường tròn nội

tiếp tam giác

ABC

, bán kính

r

.

Gọi

p

là nửa chu vi tam giác

ABC

, ta có

345

6

22

AB BC CA a a a

pa

+ + + +

= = =

.

Ta có :

2 2 2 2 2 2

9 16 25AB BC a a a AC+ = + = =

nên tam giác

ABC

vuông tại

B

Do đó

2

11

. 3 .4 6

22

ABC

S BA BC a a a



= = =

và

2

6

ABC

S

a

ra

pa



= = =

.

Tam giác vuông

SFI

có :

0

.tan60 .tan60 3SI IF r a= =  =

.

Thể tích khối chóp

.S ABC

là:

23

.

11

. . 3.6 2 3

33

S ABC ABC

V SI S a a a



= = =

.

P

E

F

A

B

I

S

C

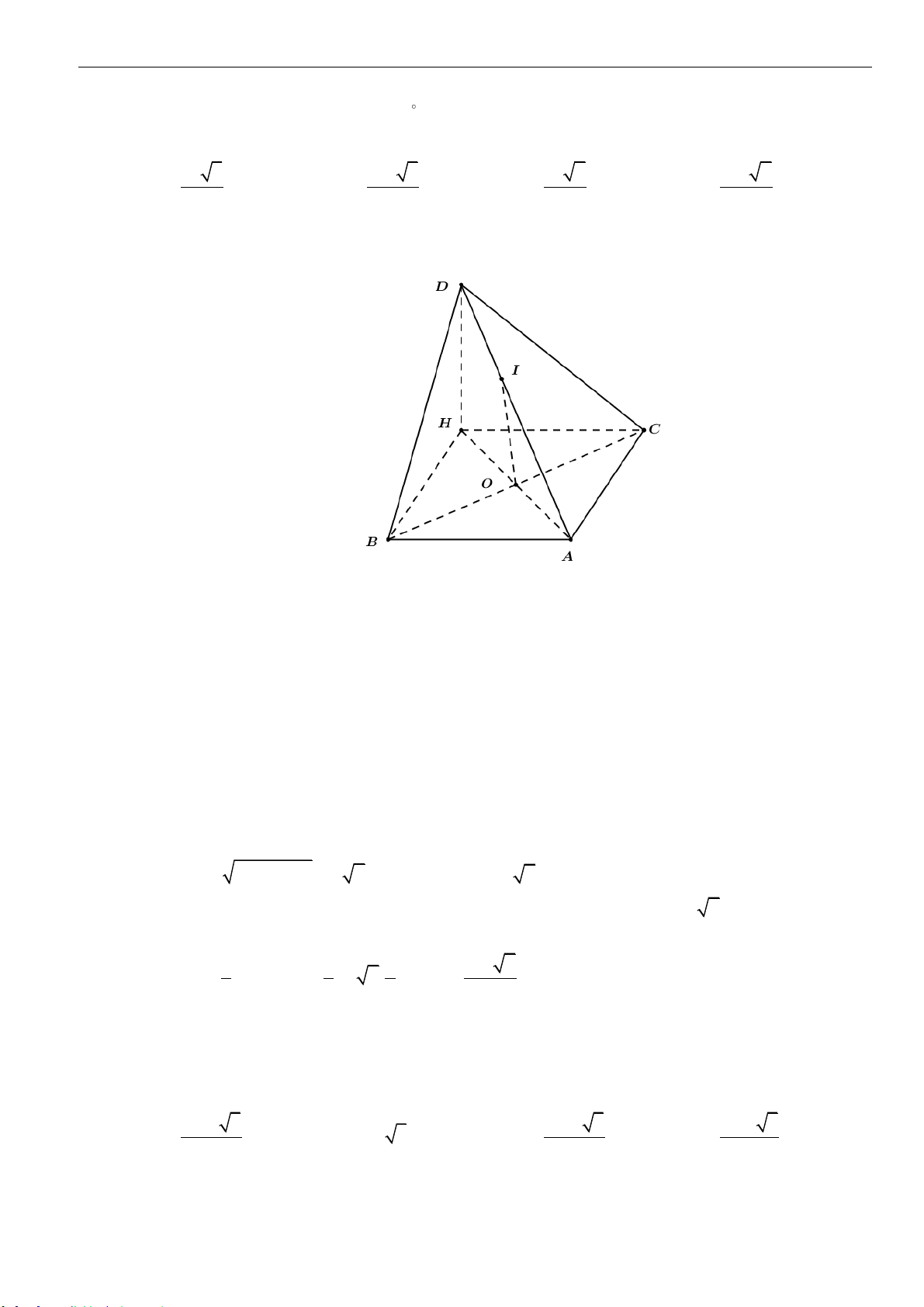
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

3 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 5: Cho tứ diện

ABCD

có

ABC

,

ABD

và

ACD

là các tam giác vuông tương ứng tại

,AB

và

C

.

Góc giữa

AD

và

( )

ABC

bằng

45

;

AD BC⊥

và khoảng cách giữa

AD

và

BC

bằng

a

. Tính

thể tích khối tứ diện

ABCD

.

A.

3

6

a

. B.

3

43

3

a

. C.

3

2

6

a

. D.

3

42

3

a

.

Lời giải

Chọn D

Dựng

( )

DH ABC⊥

. Vì

( )

DH AB

AB BDH AB BH

AB BD

⊥



 ⊥  ⊥



⊥



Tương tự

( )

DH AC

AC CDH AC CH

AC CD

⊥



 ⊥  ⊥



⊥



.

Tứ giác

ABHC

có

90A B C= = = 

suy ra

ABHC

là hình chữ nhật.

( )

BC AD

BC AHD BC AH

BC DH

⊥



 ⊥  ⊥



⊥



suy ra

ABHC

là hình vuông.

Kẻ

OI AD⊥

( )

,d BC AD IO a = =

;

( )

, 45AD ABC DAH= = 

.

OAI

vuông tại

I

có

45OAI =

suy ra

OAI

cân tại

I

AI IO a = =

22

2OA AI IO a = + =

2 2 2AH OA a = =

.

DHA H⊥

có

45DAH =

suy ra

DHA

cân tại

H

22DH AH a = =

ABC

vuông cân tại

A

2AB AC a = =

3

1 1 1 4 2

. 2 2. .2 .2

3 3 2 3

ABCD ABC

a

V DH S a a a= = =

.

Câu 6: Cho tứ diện

ABCD

có

AD

vuông góc với mặt phẳng

( )

ABC

. Biết

3AD a=

,

2AB a=

,

4AC a=

và

60BAC =

. Gọi

,HK

lần lượt là hình chiếu của

B

lên

AC

và

CD

. Đường thẳng

HK

cắt

AD

tại

E

. Thể tích khối tứ diện

BCDE

bằng

A.

3

52 3

9

a

. B.

3

3a

. C.

3

26 3

9

a

. D.

3

19 3

6

a

.

Lời giải

Chọn C

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 4

Theo bài ra

( )

BH AC

BH ACD BH CD

BH AD

⊥



 ⊥  ⊥



⊥



.

Mà

( )

CD BE

BK CD CD BHK

CD EK

⊥



⊥  ⊥ 



⊥



.

Ta có

HKC DAC∽

.KC CH AC CH

KC

AC CD CD

 =  =

( )

1

Ta có

DEK DCA∽

.DE DK DC DK

DE

DC DA DA

 =  =

( )

2

Vì tam giác

ABH

vuông tại

H

nên

.cos 2 .cos60AH AB A a a= =  =

.

Mà

43AC AH CH CH AC AH a a a= +  = − = − =

.

Vì tam giác

ACD

vuông tại

A

nên

( ) ( )

22

3 4 5CD AC AD a a a= + = + =

.

Từ

( )

1

suy ra

4 .3 12 12 13

5

5 5 5 5

a a a a a

KC DK DC KC a

a

= =  = − = − =

.

Từ

( )

2

suy ra

13

5.

13

5

33

a

DE

a

==

1 1 13 26

. . .4 .

2 2 3 3

DEC

aa

S AC DE a



 = = =

.

( )

3

1 1 26 26 3

. . . 3 .

3 3 3 9

BCDE DCE

aa

V BH S a = = =

.

Câu 7: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thoi cạnh bằng

a

. Biết rằng

, , 3,SA a SA AD SB a AC a= ⊥ = =

. Thể tích khối chóp

.S ABCD

bằng.

A.

3

2

a

. B.

3

2

3

a

. C.

3

2

6

a

. D.

3

6

2

a

.

Lời giải

Chọn C

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

5 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Gọi

23O AC BD BD BO a=   = =

. Ta có

22

2SD SA AD a= + =

Suy ra:

2 2 2 2 2 2 2

2

3 2 3 7

2 4 2 4 4

SB SD BD a a a a

SO

++

= − = − =

.

Lại có:

2 2 2 2 2 2 2

2

7

3

2 4 2 4 4

SA SC AC a SC a a

SO SC a

++

= − = − =  =

.

Xét

SCD

vuông tại

D

vì

2 2 2

SC SD DC=+

và

AS AD AC==

nên hình chiếu của

A

lên

( )

SCD

là điểm

H

trung điểm

SC

.

Do đó,

2 3 3

. . . .

1 1 2 3 2

. . . . 2

3 3 2 2 12 6

A SDC S ADC SDC S ABCD S ADC

a a a a

V V AH S V V



= = = =  = =

.

Câu 8: Cho khối chóp

.S ABCD

có đáy là hình vuông cạnh bằng

2

. Tam giác

SAB

là tam giác đều, tam

giác

SCD

vuông tại

S

(tham khảo hình vẽ bên). Tính thể tích

V

của khối chóp đã cho.

A.

43

3

V =

. B.

23V =

. C.

83

3

V =

. D.

23

3

V =

.

Lời giải

Chon D

Gọi

,MN

lần lượt là trung điểm

,AB CD

( )

1MN AB⊥

Do

SAB

đều nên

( )

2SM AB⊥

, từ

( ) ( )

1 , 2

suy ra

( ) ( ) ( )

AB SMN SMN ABCD⊥  ⊥

Kẻ

SH MN⊥

( )

SH ABCD⊥

.

2 2 2

3, 2, 1SM MN SN SM SN MN= = =  + = 

SMN

vuông tại

S

Khi đó:

.3

2

SM SN

SH

MN

==

.

Thể tích khối chóp

.S ABCD

là

1 2 3

.

33

ABCD

V SH S==

.

Câu 9: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thoi, hai đường chéo

23AC a=

,

2BD a=

và

cắt nhau tại

O

, hai mặt phẳng

( )

SAC

và

( )

SBD

cùng vuông góc với mặt phẳng

ABCD

. Biết

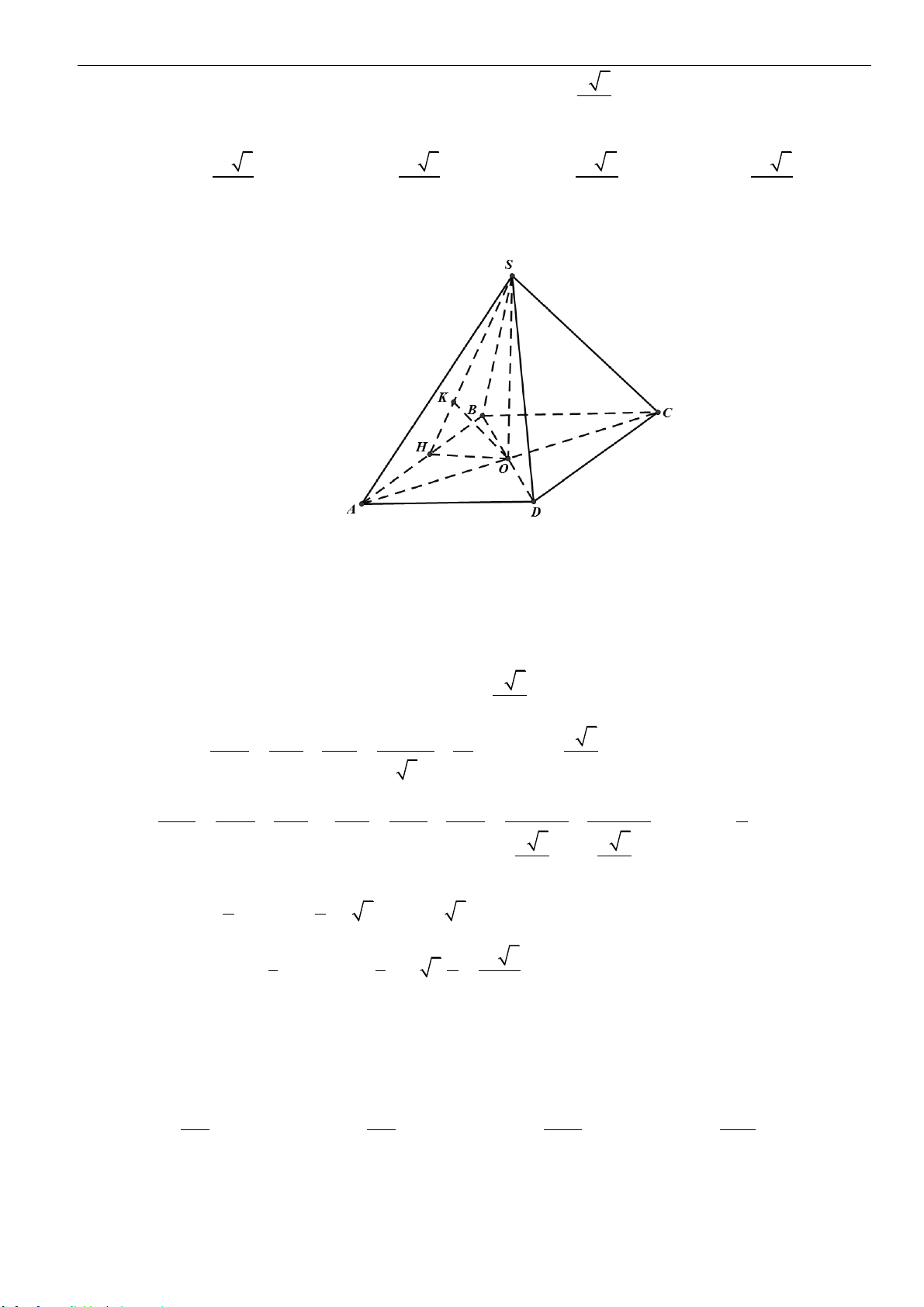
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 6

khoảng cách từ điểm

O

đến mặt phẳng

( )

SAB

bằng

3

4

a

. Tính thể tích

V

của khối chóp

.S ABCD

.

A.

3

12

a

V =

. B.

3

6

a

V =

. C.

3

2

6

a

V =

. D.

3

a

V =

.

Lời giải

Chọn D

Ta có

( ) ( )

( )

SAC ABCD

SBD ABCD SO ABCD

SAC SBD SO

⊥





⊥  ⊥





=



.

Kẻ

OH AB⊥

tại

H

và

OK SH⊥

tại

K

.

Suy ra

( ) ( )

( )

3

,

4

a

OK SAB d O SAB OK⊥  = =

.

Lại có

( )

2 2 2 2 2

1 1 1 1 1

3

OH OA OB a

a

= + = +

nên

3

2

a

OH =

.

2 2 2 2 2 2 2 2

1 1 1 1 1 1 1 1

33

42

OK OH OS OS OK OH

aa

= +  = − = −

   

   

   

nên

2

a

SO =

.

2

11

. . .2 3.2 2 3

22

ABCD

S AC BD a a a= = =

Vậy

3

2

.

1 1 3

. . .2 3.

3 3 2 3

S ABCD ABCD

aa

V SO S a= = =

.

Câu 10: Cho hình chóp tam giác

.S ABC

có

2SA a=

và

SA

tạo với mặt phẳng

( )

ABC

góc

30

. Tam giác

ABC

vuông cân tại

B

,

G

là trọng tâm tam giác

ABC

. Hai mặt phẳng

( )

SGB

và

( )

SGC

cùng

vuông góc với mặt phẳng đáy. Tính thể tích của khối chóp

.S ABC

theo

a

.

A.

3

9

10

a

. B.

3

9

40

a

. C.

3

27

10

a

. D.

3

81

10

a

.

Lời giải

Chọn A

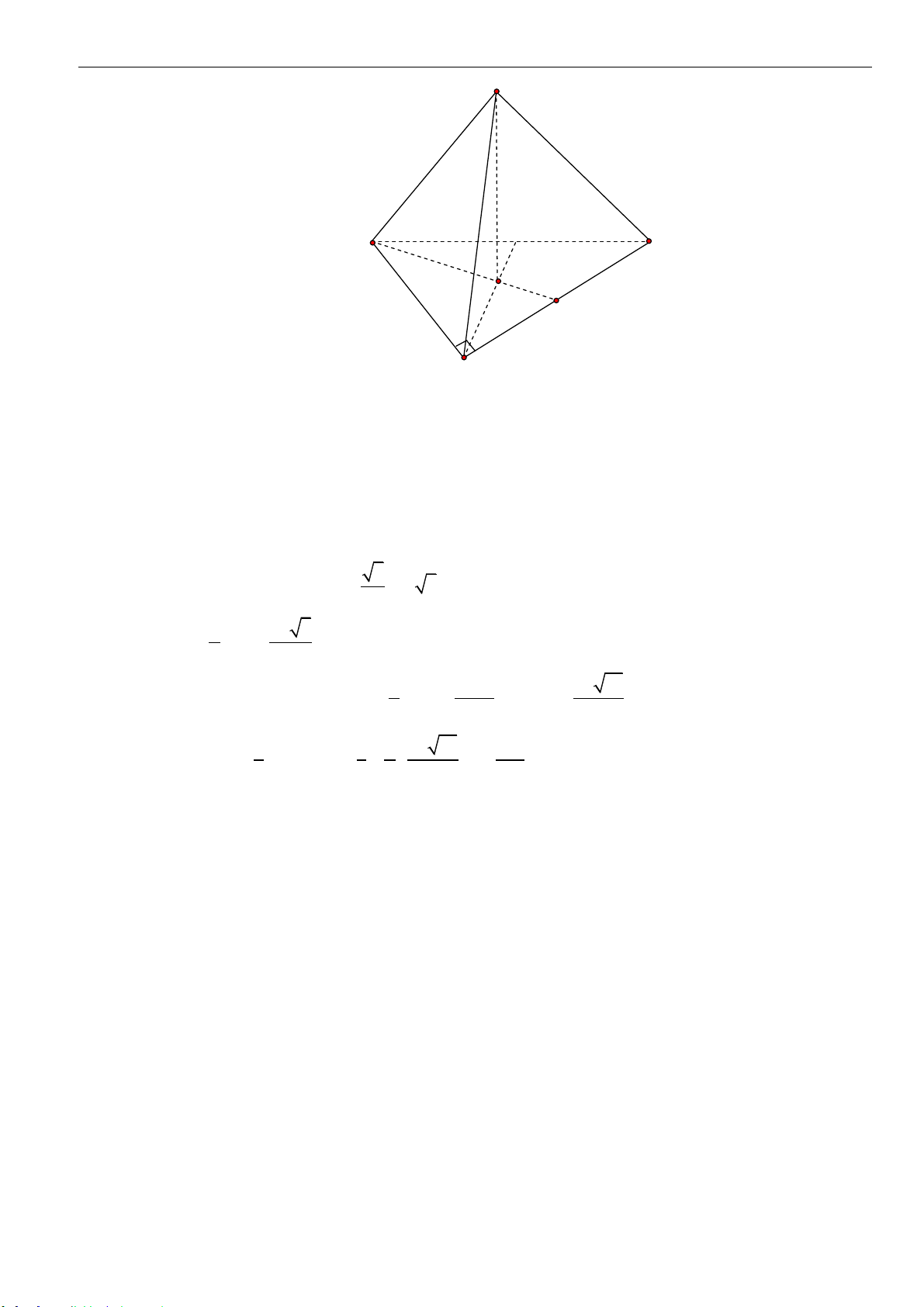
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

7 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Ta có

( ) ( )

( )

SGB ABC

SGC ABC SG ABC

SGB SGC SG

⊥





⊥  ⊥





=



.

Suy ra hình chiếu của

SA

lên

( )

ABC

là

AG

.

Do đó

( )

0

, , 30SA ABC SA AG SAG= = =

.

Nên

3

.cos30 2 . 3

2

AG SA a a=  = =

.

3 3 3

22

a

AM AG==

Suy ra

2

2 2 2 2

5 27

44

a

AB BM AM AB+ =  =

3 15

5

a

AB=

.

Vậy

2

3

1 1 1 3 15 9

..

3 3 2 5 10

SABC ABC

aa

V SG S a





= = =





.

S

G

C

B

A

M

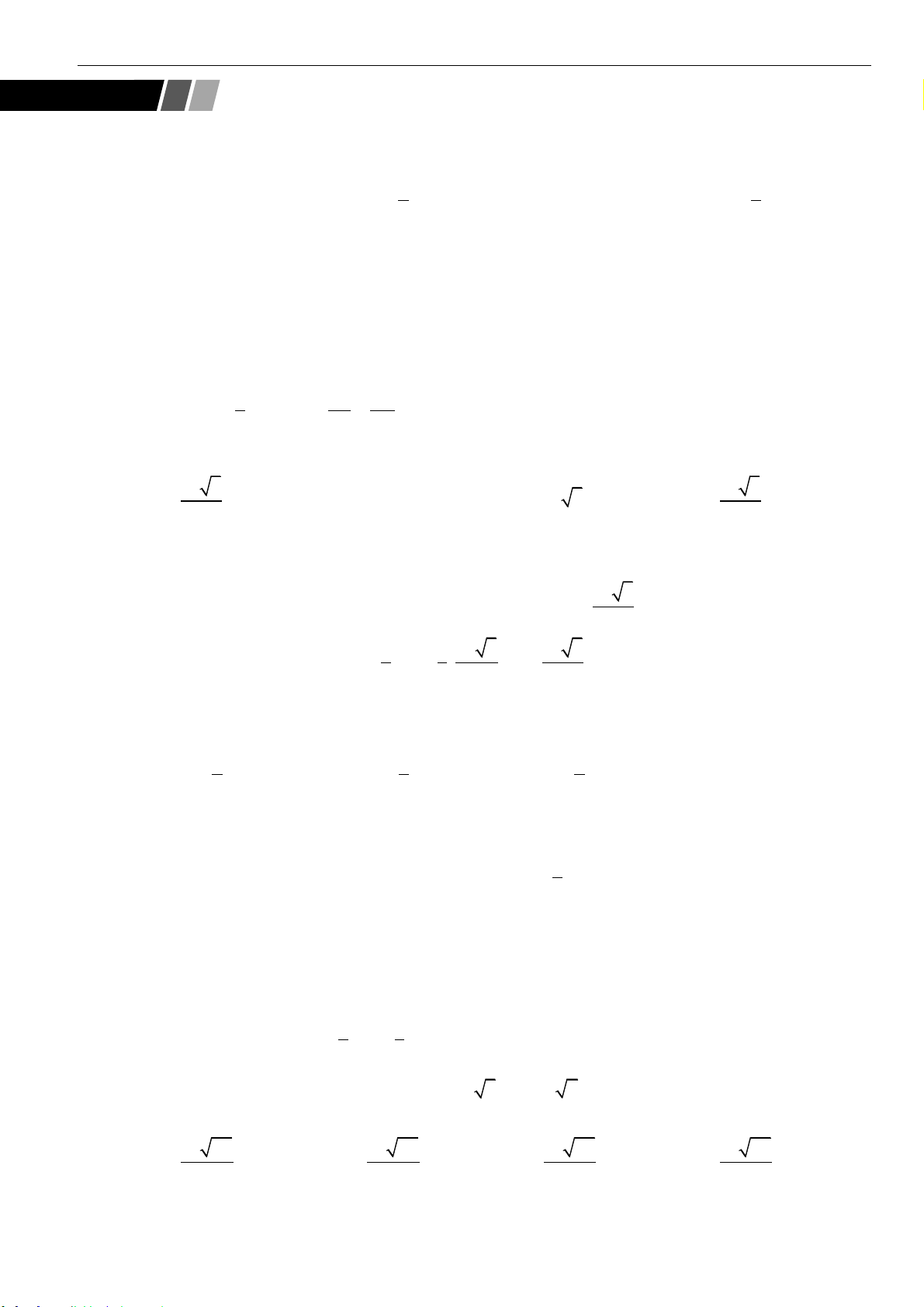
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 8

Câu 1: Cho khối chóp có diện tích đáy

B

và chiều cao

h

. Thể tíc

V

của khối chóp đã cho được tính

theo công thức nào dưới đây?

A.

V Bh=

. B.

2

3

V Bh=

. C.

3V Bh=

. D.

1

3

V Bh=

.

Lời giải

Chọn D

Câu 2: Thể tích của khối chóp tam giác bằng

6

, diện tích đáy bằng

2

. Chiều cao của khối chóp bằng?

A.

18

. B.

1

. C.

3

. D.

9

.

Lời giải

Chọn D

Ta có

1 3 3.6

. 9.

32

V

V B h h

B

=  = = =

Câu 3: Tính thể tích khối chóp có đáy là tam giác đều cạnh

a

và chiều cao của khối chóp bằng

3a

.

A.

3

4

a

. B.

3

a

. C.

3

3a

. D.

3

12

a

.

Lời giải

Chọn B

Ta có đáy là tam giác đều cạnh

a

nên diện tích đáy là

2

3

4

a

S =

.

Vậy thể tích khối chóp là

23

1 1 3 3

. . .3

3 3 4 4

aa

V S h a= = =

.

Câu 4: Cho khối chóp có diện tích đáy

B

và chiều cao

h

. Thể tích

V

của khối chóp đã cho được tính

theo công thức vào dưới đây?

A.

1

2

V Bh=

. B.

1

3

V Bh=

. C.

4

3

V Bh=

. D.

V Bh=

.

Lời giải

Chọn B

Thể tích của khối chóp được tính bởi công thức:

1

3

V Bh=

.

Câu 5: Cho khối chóp có diện tích đáy

5S =

, chiều cao

3h =

. Thể tích khối chóp đã cho bằng

A.

5

. B.

12

. C.

15

. D.

35

.

Lời giải

Chọn A

Thể tích khối chóp:

11

. .5.3 5

33

V S h= = =

.

Câu 6: Cho hình chóp

.S ABC

có

, 3, 2, 2 .AB a BC a AC a SA SB SC a= = = = = =

Tính thể tích khối

chóp

..S ABC

A.

3

26

24

a

. B.

3

26

12

a

. C.

3

26

4

a

. D.

3

26

8

a

.

Lời giải

Chọn B

BÀI TẬP TRẮC NGHIỆM

C

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

9 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Gọi

M

là trung điểm của

BC

, do tam giác

ABC

vuông tại

A

nên

M

là tâm đường tròn ngoại

tiếp tam giác

ABC

. Mà

2SA SB SC a= = =

nên

( )

SM ABC⊥

. Xét tam giác

SMA

vuông tại

M

:

22

2 2 2 2

3 13 13

4

4 4 2

a a a

SM SA AM a SM= − = − =  =

.

Vậy

3

.

1 1 1 13 26

. . . . . 2.

3 2 6 2 12

S ABC

aa

V AB AC SM a a= = =

Câu 7: Cho khối chóp

.S ABCD

có

( )

SA ABCD⊥

, đáy

ABCD

là hình thang,

//AB CD

,

,2SA AD DC a BC a= = = =

. Tam giác

SBC

vuông tại

C

, tam giác

SCD

vuông tại

D

. Thể

tích khối chóp đã cho bằng

A.

3

2a

. B.

3

4

3

a

. C.

3

2

3

a

. D.

3

1

2

a

.

Lời giải

Chọn D

Ta có:

CD SA

CD AD

CD SD

⊥



⊥



⊥



.

Ta lại có

AD DC a==

nên

ADC

vuông cân tại

D

.

Suy ra

2AC a=

.

Ta có:

CB SA

CB AC

CB SC

⊥



⊥



⊥



.

Suy ra

ABC

vuông cân tại

C

nên

22AB BC a==

.

Thể tích khối chóp đã cho là

3

1 1 1 2

..

3 3 2 3 2 2

ABCD

AB DC a a a

V SA S a AD a a

++

=  =  =  =

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 10

Câu 8: Cho hình chóp

.S ABCD

,có

AC

vuông góc với

BD

và

3cmAC =

,

4cmBD =

.Khoảng cách từ

điểm

S

đến mặt phẳng

( )

ABC

bằng

9cm

. Thể tích khối chóp

.S ABCD

bằng

A.

3

36cm

. B.

3

18cm

. C.

3

54cm

. D.

3

6cm

.

Lời giải

Chọn B

Do

AC BD

nên

2

1

. 6 ( )

2

ABCD

S AC BD cm

.

Suy ra:

3

1

( ,( )). 18( )

3

SABCD ABCD

V d S ABC S cm

.

Câu 9: Cho hình chóp

.S ABC

có tất cả các mặt bên cùng hợp với đáy một góc

60 .

Biết rằng mặt phẳng

đáy là tam giác

ABC

đều cạnh

.a

Tính thể tích khối chóp đã cho.

A.

3

.

24

a

B.

3

.

8

a

C.

3

.

12

a

D.

3

.

4

a

Lời giải

Chọn A

Gọi

,MN

lần lượt là trung điểm của

,,BC AB AM CN

là 2 đường trung tuyến của

ABC

đồng thời là 2 đường phân giác của

.ABC

Gọi

 

AM CN H H = 

là tâm đường tròn nội tiếp

( )

.ABC SH ABC  ⊥

Do đó

( ) ( )

(

)

, 60 .SBC ABC SMH= = 

Mà

ABC

đều cạnh

2

3

4

ABC

a

aS



=

và

3

.

36

AM a

HM ==

Xét

SHM

vuông tại

H

có

tan tan60 .

2

3

6

SH SH a

SMH SH

HM

a

=   =  =

Vậy thể tích của khối chóp

.S ABC

là

23

.

1 1 3 3

. . . . .

3 3 4 2 24

S ABC ABC

a a a

V S SH



= = =

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

11 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 10: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

. Hình chiếu vuông góc của đỉnh

S

lên đáy

()ABCD

là trọng tâm của tam giác

ABD

. Biết góc tạo bởi cạnh

SC

với đáy bằng

60



. Thể tích khối chóp

.S ABC

bằng:

A.

3

4

a

. B.

3

2

3

a

. C.

3

6

a

. D.

3

a

.

Lời giải

Chọn D

Nếu gọi

O

là giao điểm của hai đường chéo đáy

ABCD

và

H

là chân đường cao hạ từ đỉnh

S

xuống đáy thì ta có:

1 1 1 1 2 2 2

3 6 6 2 3 3

a

HO AO AC HC HO OC AC AC AC= =  = + = + = =

Góc tạo bởi

SC

và đáy

()ABCD

là:

60SCH



=

và

SHC

vuông tại

H

, suy ra:

23

tan60 tan60 2

3

a

SH h HC a



= =  = =

Diện tích tam giác

ABC

là:

2

1

22

ABC

a

S AB BC=  =

Thể tích khối chóp

.S ABC

là:

23

11

2

3 3 2 3

SABC ABC

aa

V S SH a=  =   =

.

Câu 11: Cho hình chóp

.S ABC

có các cạnh bên

,,SA SB SC

tạo với đáy các góc bằng nhau và bằng

60

. Biết

13 , 14AB a AC a==

và

15BC a=

. Tính thể tích

V

của khối chóp

.S ABC

.

A.

3

455 3

6

Va=

. B.

3

455 3Va=

. C.

3

455 3

3

a

. D.

3

455 3

2

Va=

.

Lời giải

Chọn D

Gọi

H

là hình chiếu của

S

trên mặt phẳng

( )

ABC

( )

SH ABC⊥

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 12

Khi đó ta có

( )

,

SAH SA ABC

SBH SB ABC

SCH SC ABC



=



=





=





. Theo giả thiết thì

60SAH SBH SCH= = = 

.

Suy ra

SHA SHB SHC =  = 

HA HB HC = =

H

là tâm đường tròn ngoại tiếp

ABC

và

bán kính đường tròn ngoại tiếp tam giác là

R HA HB HC= = =

.

Nửa chu vi tam giác

ABC

là

13 14 15

21

22

AB BC AC a a a

pa

+ + + +

= = =

.

Diện tích tam giác

ABC

là

( )( )( )

2

84

ABC

S p p AB p BC p AC a



= − − − =

.

Lại có

..

4

ABC

AB BC AC

S

R



=

2

. . 13 .14 .15 65

4 4.84 8

AB BC AC a a a a

R HA HB HC

Sa

 = = = = = =

.

Xét

SHA

vuông tại

H

có

65 65 3

.tan .tan60

88

aa

SH HA SAH= =  =

.

Thể tích khối chóp

.S ABC

là

3

2

1 1 65 3 455 3

. . . .84

3 3 8 2

ABC

aa

V SH S a



= = =

.

Câu 12: Cho hình chóp

.S ABC

có đáy là tam giác đều cạnh bằng

a

, tam giác

SAB

cân tại

S

và thuộc

mặt phẳng vuông góc với mặt phẳng

( )

ABC

, góc giữa hai mặt phẳng

( )

SCA

và

( )

SCB

bằng

0

60

. Gọi

H

là trung điểm của đoạn

AB

. Trong các mệnh đề sau, mệnh đề nào đúng:

A. Thể tích khối chóp

.S ABC

bằng

3

2

16

a

. B. Thể tích khối chóp

.B SHC

bằng

3

2

16

a

.

C. Thể tích khối chóp

.S AHC

bằng

3

2

64

a

. D. Không tồn tại hình chóp đã cho.

Lời giải

Chọn C

Tam giác

SAB

thuộc mặt phẳng vuông góc với mặt phẳng

( )

ABC

( )

SH ABC⊥

, từ đó suy

ra đường cao của hình chóp

.S AHC

là

SH

Kẻ

( )

AK SC SC AKB⊥  ⊥

SC KB⊥

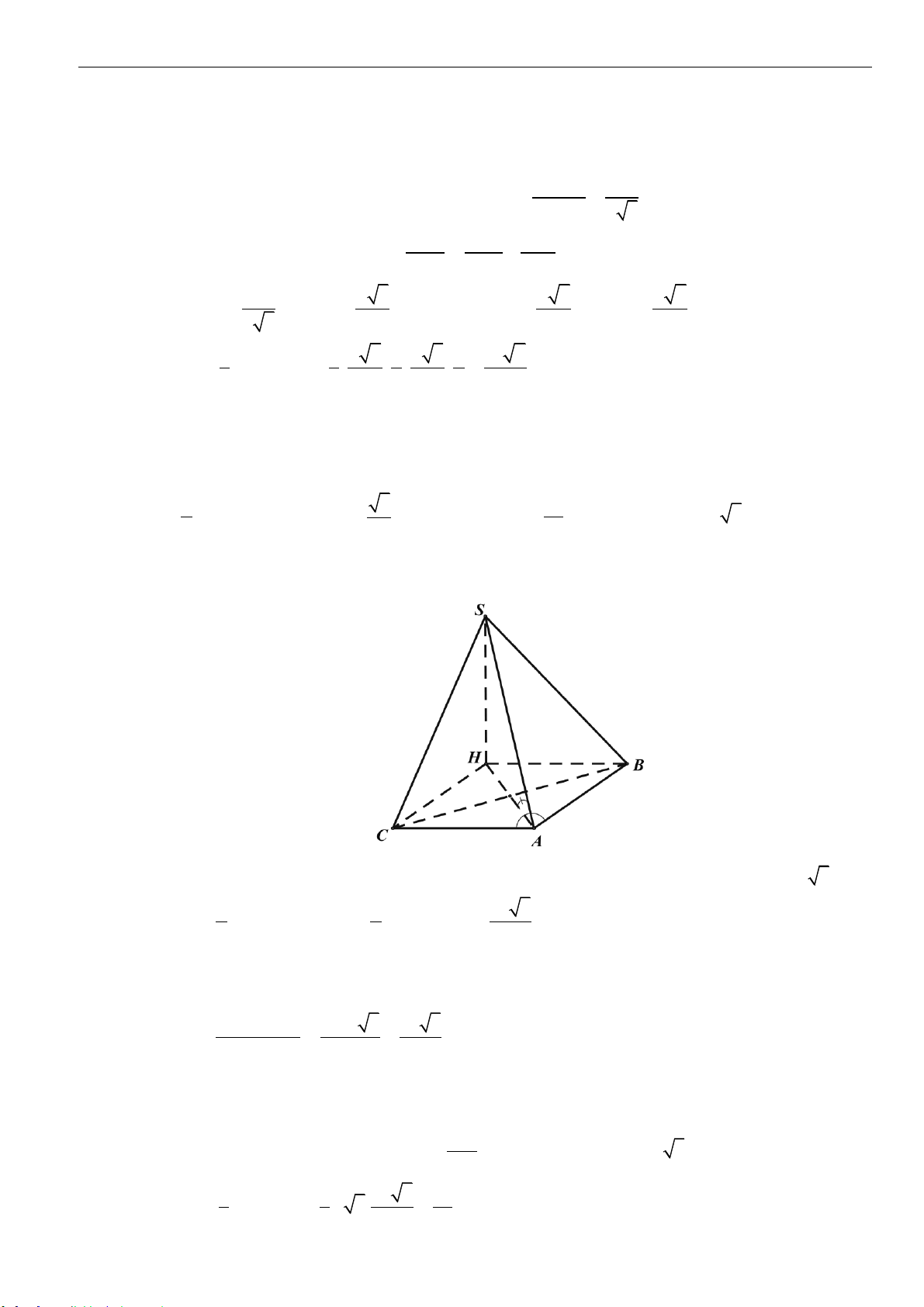
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

13 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

( ) ( )

( )

0

; ; 60SAC SBC KA KB = =

0

60

120

AKB



=





=



Nếu

0

60AKB =

thì dễ thấy

KAB

đều

KA KB AB AC = = =

(vô lí). Vậy

0

120AKB =

khi đó

KAB

cân tại

K

và

0

60AKH =

0

tan60

23

AH a

KH = =

Trong

SHC

vuông tại

H

ta có

2 2 2

1 1 1

KH HC HS

=+

thay

23

a

KH =

và

3

2

a

HC =

vào ta được

6

8

a

SH =

. Vậy

6

8

a

h =

.

3

.

1 1 6 1 3 2

. . . . . .

3 3 8 2 2 2 64

S AHC AHC

a a a a

V SH dt



= = =

.

Câu 13: Cho khối chóp

.S ABC

có đáy

ABC

là tam giác cân đỉnh

A

,

120BAC =

và

AB a=

. Các cạnh

bên

,,SA SB SC

bằng nhau và góc giữa

SA

với mặt phẳng đáy bằng

60

. Thể tích khối chóp đã

cho bằng

A.

3

4

a

. B.

3

4

a

. C.

3

4

a

. D.

3

3a

.

Lời giải

Chọn C

Ta có

2 2 2 2 2 2

2. . .cos 2. . .cos120 3 3BC AB AC AB AC BAC a a a a a BC a= + − = + −  =  =

.

2

1 1 3

. .sin . .sin120

2 2 4

ABC

a

S AB AC BAC a a



= =  =

.

Khối chóp

.S ABC

có

,,SA SB SC

bằng nhau. Gọi

( )

SH ABC⊥

nên

H

là tâm của đáy

H

là tâm đường tròn ngoại tiếp

ABC HA R  =

.

2

. . . . 3 3

4 4 4

ABC

AB AC BC a a a a

S R a

RR



= = =  =

.

Ta có

( )

SH ABC⊥

hình chiếu của

SA

lên mặt phẳng

( )

ABC

là

AH

60SAH = 

là góc giữa

SA

và mặt phẳng đáy.

Xét

SHA

vuông ở

H

có:

tan tan60 . 3

SH

SAH SH AH a

AH

=  =  =

.

23

.

1 1 3

. 3.

3 3 4 4

S ABC ABC

aa

V SH S a



= = =

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 14

Câu 14: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thoi, có

0

3, 60AC a ABC==

. Biết rằng

SA SC=

,

SB SD=

và khoảng cách từ

A

mặt phẳng

( )

SBC

bằng

6

2

a

. Tính thể tích khối chóp

.S ABC

bằng:

A.

3

36

8

a

. B.

3

96

16

a

. C.

3

3 15

40

a

. D.

3

36

16

a

.

Lời giải

Chọn D

Gọi

O

là giao điểm của 2 đường chéo

,AC BD

. Khi đó

( )

SO ABCD⊥

.

Dựng

,AK OI

lần lượt vuông góc với

BC

. Dựng

OH SI⊥

tại

H

.

Vì

0

3, 60AC a ABC==

nên tam giác

ABC

đều.

Ta có

( )

BC OI

BC SOI BC OH

BC SO

⊥



 ⊥  ⊥



⊥



.

Lại có

( )

OH SI OH SBC⊥  ⊥

( )

,d O SBC OH=

.

Mặt khác

( )

16

;;

24

a

d A SBC d O SBC OH= = =

,

3. 3 3 3

2 2 4

a a a

AK OI= =  =

.

Nên

2 2 2 2 2

1 1 1 16 16 3 2

6 9 4

a

SO

SO OH OI a a

= − = −  =

.

Thể tích khối chóp

( )

2

3

.

33

1 1 3 2 3 6

. . .

3 3 4 4 16

S ABC ABC

a

aa

V S SO



= = =

.

Câu 15: Cho tứ diện

MNPQ

. Biết rằng mặt phẳng

()MNP

vuông góc với mặt phẳng

()NPQ

, đồng thời

MNP

và

NPQ

là 2 tam giác đều cạnh

4a

. Tính theo

a

thể tích

V

của khối tứ diện

MNPQ

.

A.

3

24 3Va=

. B.

3

24Va=

. C.

3

83Va=

. D.

3

8Va=

.

Lời giải

Chọn D

4a

H

M

N

P

Q

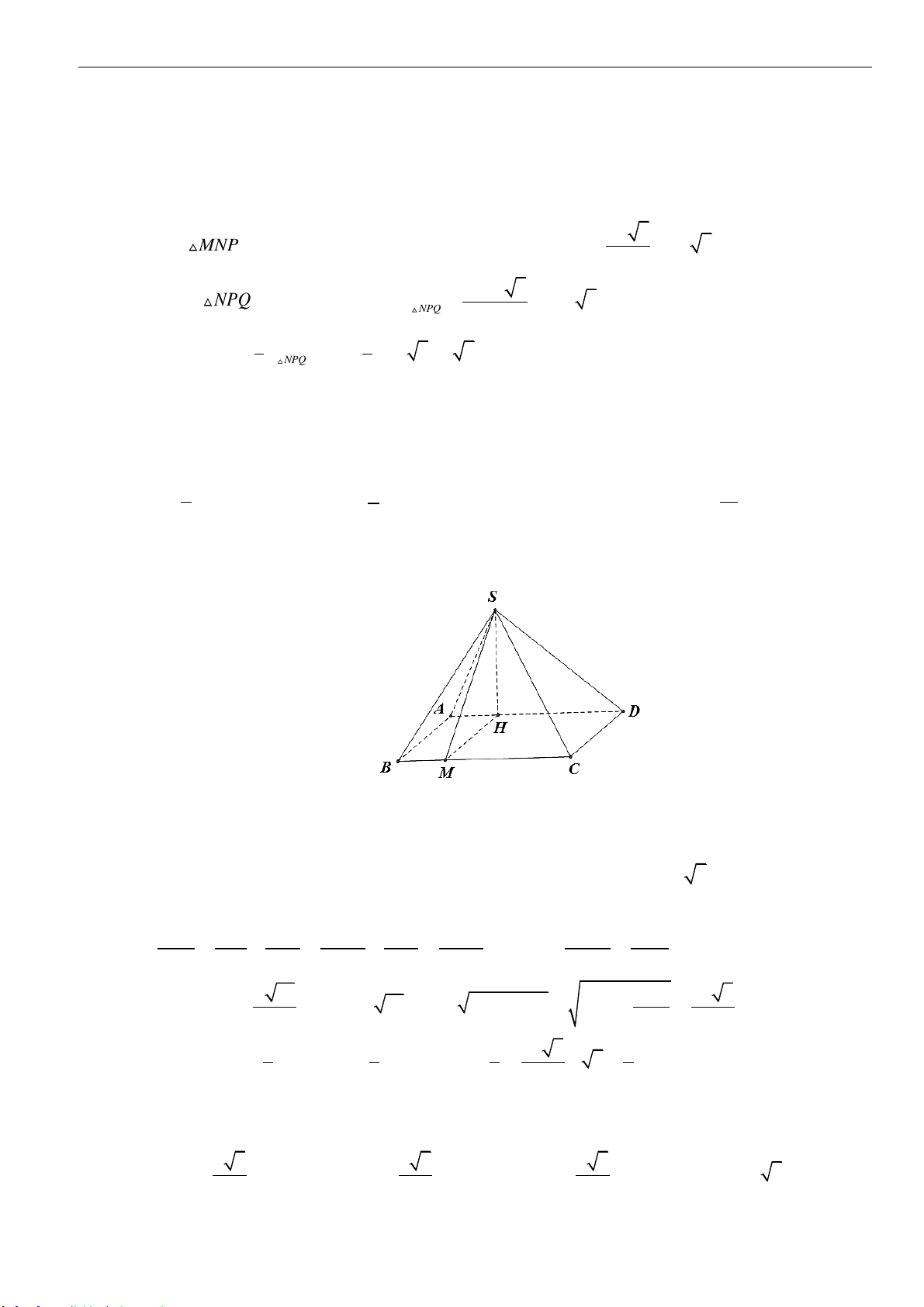
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

15 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Trong mặt phẳng

()MNP

dựng

MH NP⊥

và

MH NP H=

.

Ta có

( ) ( )

MNP NPQ NP

MNP NPQ

MH NP

=





⊥





⊥



()MH NPQ⊥

MH

là chiều cao tứ diện

MNPQ

.

Xét

MNP

: ta có

MH

là đường cao tam giác đều

43

23

2

a

MH a = =

.

Ta có

NPQ

là tam giác đều

2

(4 ) 3

43

4

NPQ

a

Sa = =

.

Vậy

23

11

. .4 3.2 3 8 .

33

MNPQ NPQ

V S MH a a a= = =

.

Câu 16: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật, tam giác

SAD

vuông tại

S

và nằm

trong mặt phẳng vuông góc với mặt phẳng đáy. Biết

,2AB a SA SD==

và mặt phẳng

( )

SBC

tạo với mặt phẳng đáy một góc

60

. Thể tích khối chóp

.S ABCD

bằng

A.

3

5

2

a

. B.

3

2

a

. C.

3

5a

. D.

3

15

2

a

.

Lời giải

Chọn A

Kẻ

( )

SH AD SH ABCD⊥  ⊥

. Kẻ

HM BC⊥

ta có góc giữa mặt phẳng

( )

SBC

và mặt

phẳng đáy là góc

60SMH =

.

Ta có

MH AB a==

. Xét tam giác

SMH

, ta có

.tan60 3SH MH a=  =

.

Mà tam giác

SAD

vuông tại

S

nên ta có

22

2

2 2 2 2 2 2

1 1 1 1 1 5 5 15

4 4 4 4

SH a

SD

SH SA SD SD SD SD

= + = + =  = =

Suy ra

2

2 2 2

15 15 5 3

15, 15

2 4 2

a a a

SD SA a AD SA SD a=  = = + = + =

.

Vậy

3

.

1 1 1 5 3 5

. . . . . . . . 3

3 3 3 2 2

S ABCD ABCD

a

V S SH AB AD SH a a a= = = =

.

Câu 17: Cho hình chóp

.S ABCD

có đáy là hình vuông cạnh

2

,

SAB

đều,

SCD

vuông tại

S

.Tính thể

tích

V

của khối chóp

.S ABCD

.

A.

23

3

V =

. B.

83

3

V =

. C.

43

3

V =

. D.

23V =

.

Lời giải

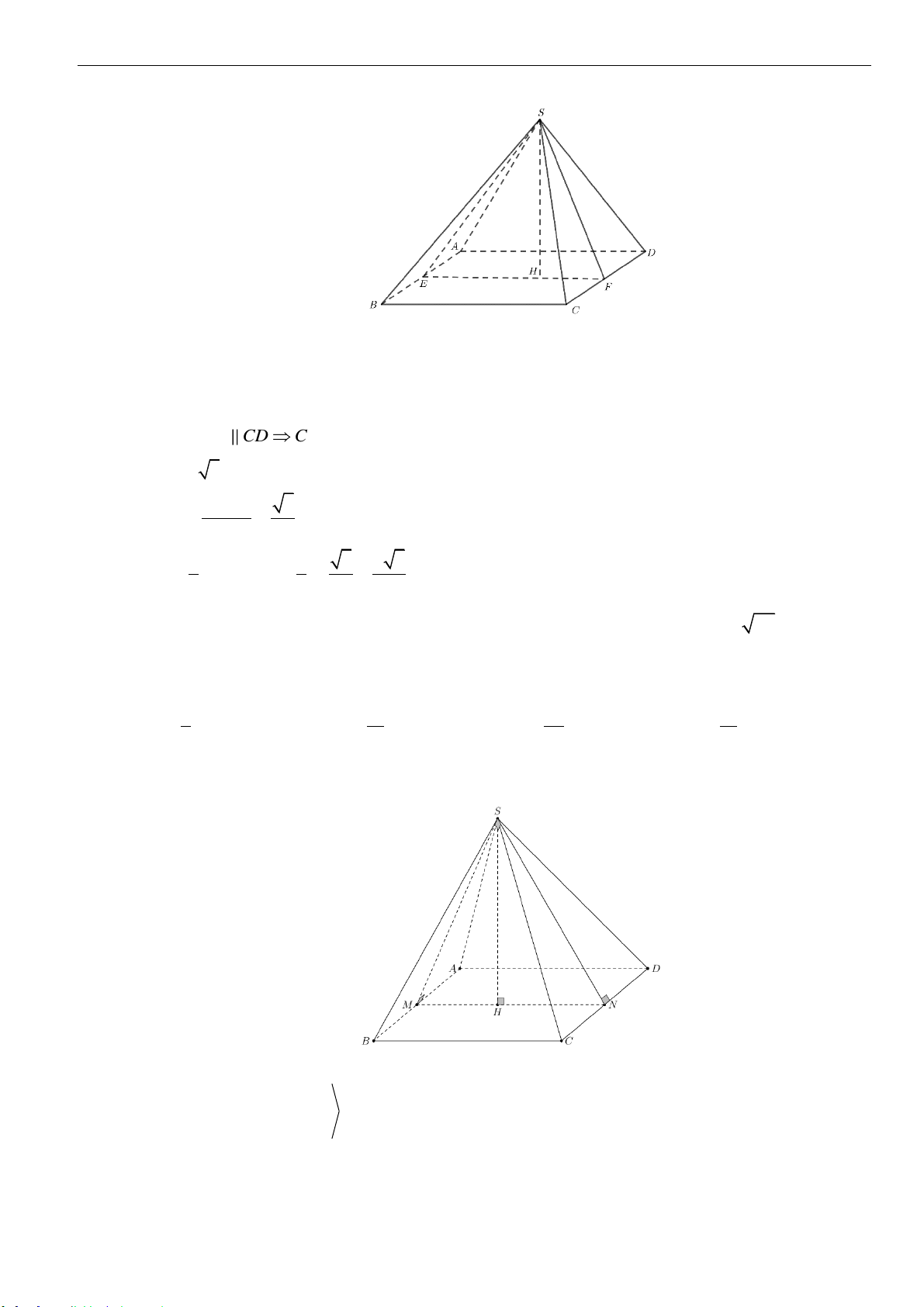
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 16

Chọn A

Gọi

,EF

lần lượt là trung điểm của

,AB CD

và

H

là hình chiếu của

S

lên đường thẳng

EF

.

( )

AB SE

AB SEF

AB EF

⊥



⊥



⊥



( )

AB SH

SH ABCD

EF SH

⊥



  ⊥



⊥



.

Ta có

( )

AB CD CD SEF CD SF SCD ⊥  ⊥  

vuông cân tại

S

.

2 2 2

3, 1, 2SE SF EF EF SE SF SEF= = =  = +  

vuông tại

S

.

.3

2

SE SF

SH

EF

==

.

1 1 3 2 3

. .4.

3 3 2 3

ABCD

V S SH= = =

.

Câu 18: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật,

1AB =

,

20AD =

,

SA SB=

,

SC SD=

. Biết mặt phẳng

( )

SAB

và

( )

SCD

vuông góc nhau đồng thời tổng diện tích của hai

tam giác

SAB

và

SCD

bằng

3

. Thể tích khối chóp

.S ABCD

bằng

A.

8

3

. B.

13

6

. C.

26

3

. D.

13

2

.

Lời giải

Chọn A

Gọi

M

,

N

lần lượt là trung điểm của các cạnh

AB

,

CD

.

Do

( ) ( )

//

S SAB SCD

SAB SCD d

AB CD



  =

với

//

Sd

d AB









.

Do

SAB

cân tại

S

nên

SM AB SM d⊥  ⊥

.

Mà

( ) ( )

SAB SCD⊥

nên

( )

SM SCD SM SN⊥  ⊥

và

( ) ( )

SMN ABCD⊥

.

Kẻ

( )

SH MN SH ABCD⊥  ⊥

.

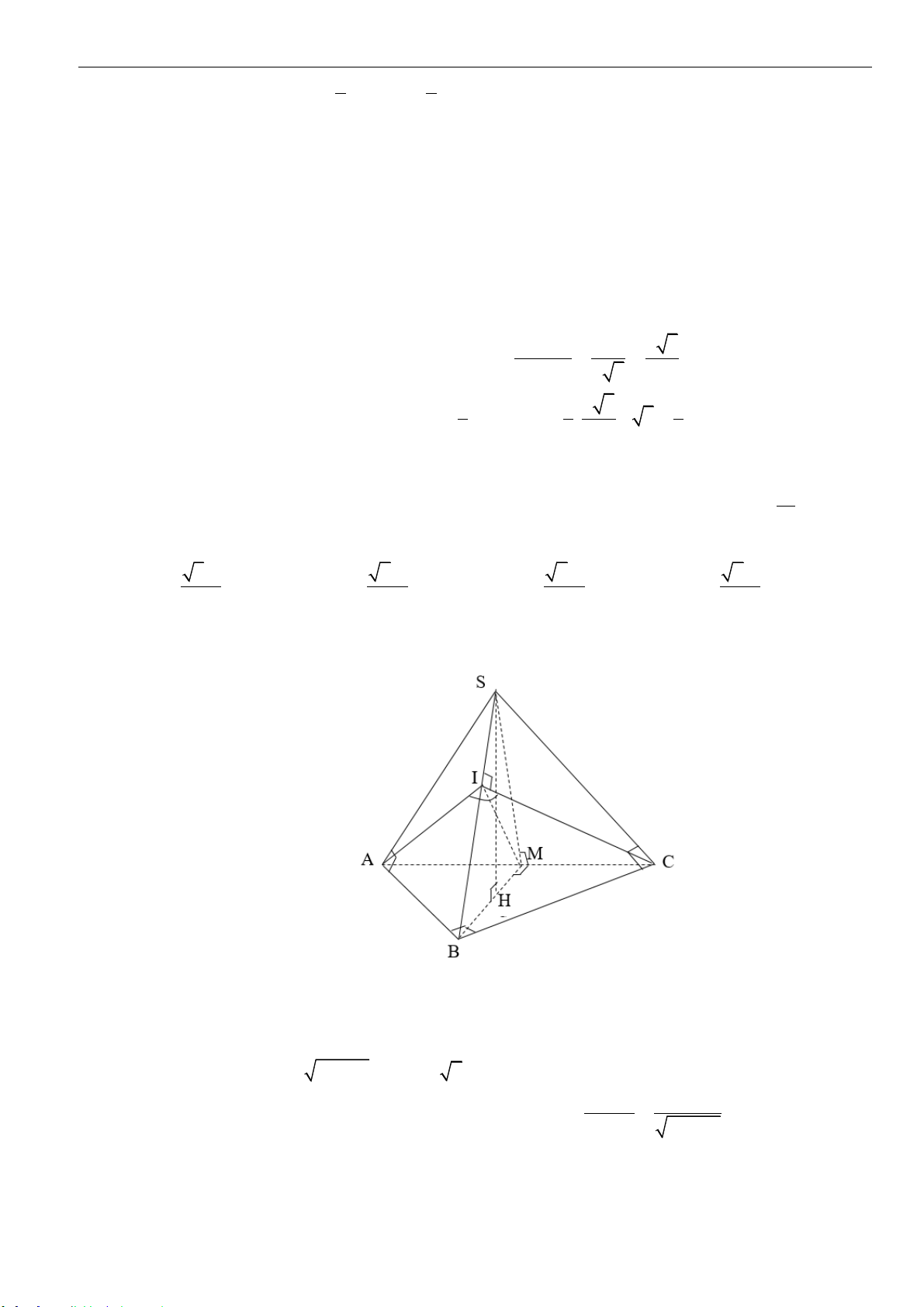
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

17 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Do

( ) ( )

11

3 . . . . 3 6 6 1

22

SAB SCD

S S SM AB SN CD AB SM SN SM SN



+ =  + =  + =  + =

.

Do

SMN

vuông tại

S

nên ta có:

( )

2 2 2 2 2 2 2 2

20 2SM SN MN SM SN AD SM SN+ =  + =  + =

.

Từ và ta có

( )

2

22

4

2

8

20

2. 20

6

4

.

2

.

SM

SM SN

SN

SM SN

SM

SM SN SM SN

SN

SM SN



=







+=



+=







  

  



=

+







=

+=

−



=







=



.

Trong

SMN

ta có

. 8 4 5

..

5

25

SM SN

SH MN SM SN SH

MN

=  = = =

.

Vậy thể tích khối chóp

.S ABCD

là

1 1 4 5 8

. . . .2 5

3 3 5 3

ABCD

V SH S= = =

.

Câu 19: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông cân tại

B

và

BA BC a==

,

SA AB⊥

và

SC CB⊥

. Biết góc giữa hai mặt phẳng

( )

SAB

và

( )

SBC

là



thỏa mãn

9

cos

16



=

Thể tích

khối chóp

.S ABC

bằng

A.

3

5

18

a

. B.

3

7

9

a

. C.

3

7

6

a

. D.

3

7

18

a

.

Lời giải

Chọn D

Xét hai tam giác vuông

SAB

và

SCB

, có

BA BC=

,có

SB

chung. Nên

SAB SCB = 

.

Gọi

CI

là đường cao của

SCB

thì

AI

cũng là đường cao của

SAB

. Suy ra góc giữa hai mặt

phẳng

( )

SAB

và

( )

SBC

là góc giữa

AI

và

CI

.

Đặt

22

SA x SB a x=  = +

,

2AC a=

.

Trong tam giác vuông

SAB

, có:

22

.

..

AB SA ax

AB SA AI SB AI IC

SB

ax

=  = = =

+

.

Xét 2 trường hợp:

TH1: Góc giữa

AI

và

CI

bằng góc

AIC



=

.

Áp dụng định cosin cho tam giác

AIC

ta có:

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 18

2 2 2 2 2 2

2 2 2 2

2 2 2 2 2 2

9

2 . .cos 2a 2 .

16

a x a x a x

AC AI CI AI CI

a x a x a x



= + −  = + −

+ + +

2 2 2

16a 16 7xx + =

.

TH2: Góc giữa

AI

và

CI

bằng góc bù của góc

AIC

. Suy ra

9

cos

16

AIC =−

Áp dụng định cosin cho tam giác

AIC

ta có:

2 2 2 2 2 2

2 2 2 2

2 2 2 2 2 2

9

2 . .cos 2a 2 .

16

a x a x a x

AC AI CI AI CI

a x a x a x



= + −  = + +

+ + +

2 2 2 2 2

4a 5a

16a 16 25

33

x x x SB a x + =  =  = + =

.

Cách 1:

Do

SAB SCB SA SC =   =

, suy ra

SAC

cân tại

S

.

Gọi

M

là trung điểm

AC

thì

( ) ( ) ( )

,SM AC BM AC AC SBM ABC SBM⊥ ⊥  ⊥  ⊥

.

22

7

52

a

IM AI AM= − =

,

12

22

a

BM AC==

Gọi

H

là hình chiếu của

S

lên

( )

ABC

thì

SH

thuộc

( )

SBM

.

Xét tam giác

SBM

, có các đường cao là

,SH MI

nên ta có:

57

.

.7

3

52

..

3

a2

2

aa

SB IM a

SH BM SB IM SH

BM

=  = = =

.

Diện tích tam giác

ABC

bằng

2

1

2

a

. Vậy

23

.

1 1 7 1 7

. . .

3 3 3 2 18

S ABC ABC

a

V SH dt a a



= = =

.

Cách 2:

Ta có:

4

5

a

AI IC==

.

22

3

.

1 1 5 1 1 5 1 4 9 7

. . . . sin . 1

3 3 3 2 3 3 2 5 16 18

S ABC AIC

a a a

V SB S AI IC AIC a



   

= = = − − =

   

   

Câu 20: Cho tứ diện

ABCD

có

=AB a

,

5=AC a

,

90DAB CBD= = 

,

135ABC =

. Biết góc giữa

hai mặt phẳng

( )

ABD

và

( )

BCD

bằng

30

. Thể tích khối tứ diện

ABCD

bằng

A.

3

2

a

. B.

3

32

a

. C.

3

23

a

. D.

3

6

a

.

Lời giải

Chọn D

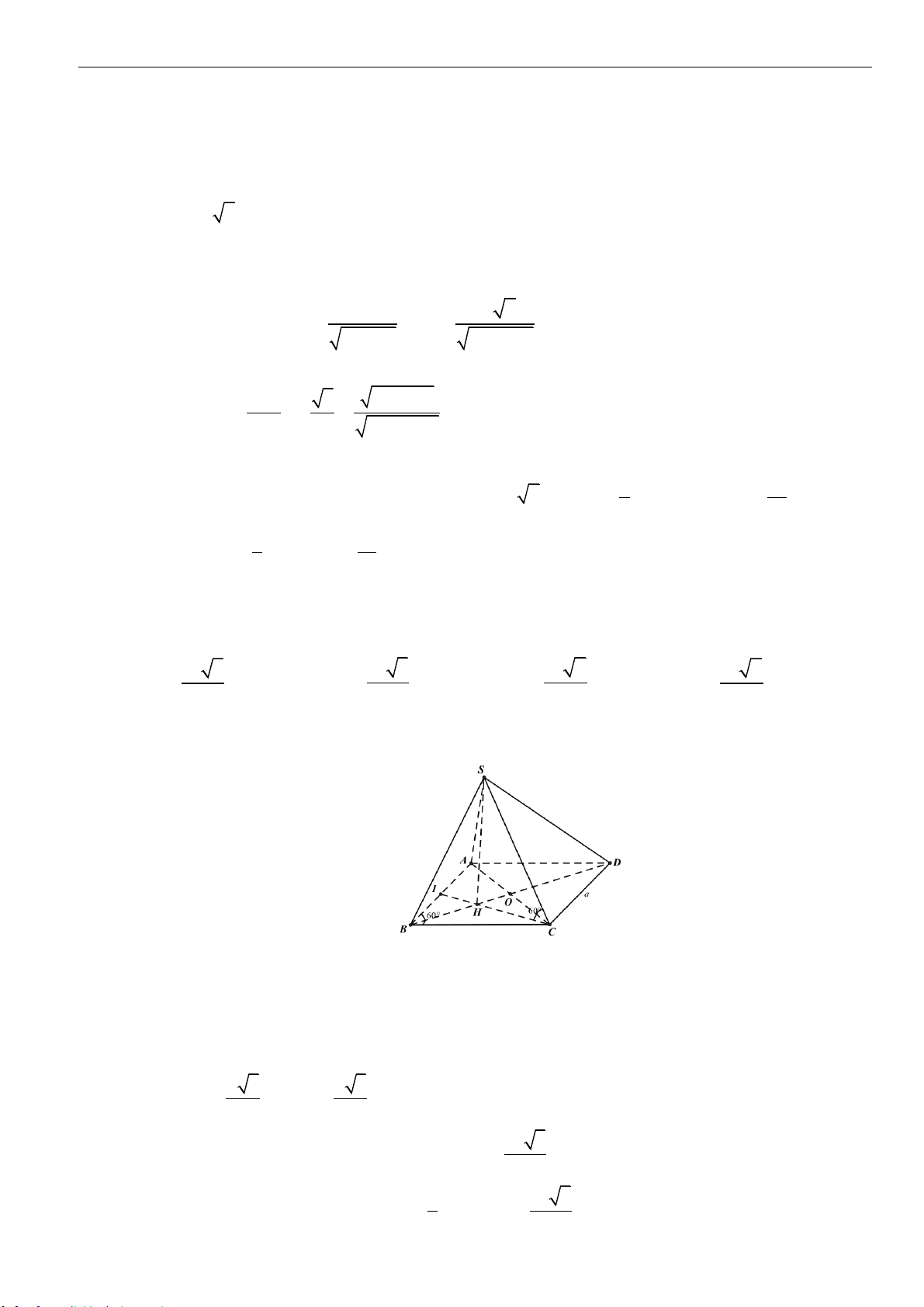
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

19 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Gọi

H

là hình chiếu vuông góc của

D

trên mặt phẳng

( )

ABC

.

Ta có:

( )

BA DA

BA DHA BA AH

BA DH

⊥



 ⊥  ⊥



⊥



. Tương tự:

⊥BC BH

.

Tam giác

ABH

vuông tại

A

và

45ABH ABH=   

vuông cân tại

A AH AB a = =

và

2HB a=

.

Dựng

HM

vuông góc với

DA

tại

M

và dựng

HN

vuông góc với

DB

tại

N

.

Suy ra

( )

HM DAB⊥

và

( ) ( ) ( )

( )

, , 30⊥  = = = HN DBC DBA DBC HM HN MHN

.

Đặt

2 2 2 2

2

;

2

ax ax

DH x HM HN

a x a x

=  = =

++

.

Trong tam giác

HMN

vuông tại

M

ta có

22

32

cos

2

22

+

=  =  =  =

+

HM a x

MHN x a DH a

HN

ax

.

Theo định lí cosin ta có:

2

2 2 2

1

2 . .cos135 2 . .sin135

22

= + −   =  =  =

ABC

a

AC AB BC AB BC BC a S AB BC

.

Vậy

3

1

.

36



==

ABCD ABC

a

V DH S

.

Câu 21: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thoi cạnh

a

và

60ABC =

. Biết

SA SB SC==

và góc giữa mặt bên

( )

SCD

và mặt đáy bằng

60

. Thể tích của khối chóp

.S ABCD

bằng

A.

3

2

a

. B.

3

6

a

. C.

3

2

a

. D.

3

2

6

a

.

Lời giải

Chọn B

Ta có

60ABC =

suy ra tam giác

ABC

là tam giác đều.

Gọi

H

là trọng tâm của tam giác

ABC

suy ra

( )

SH ABCD⊥

.

Gọi

I

là trung điểm của

AB

IH AB IH CD ⊥  ⊥

.

Hay

60SCH =

.

Mà

33

tan

23

aa

CI HC SH HC SCH a=  =  = =

.

Diện tích hình thoi

ABCD

là

2

3

2

ABCD ABC

a

SS==

.

Thể tích khối chóp

.S ABCD

là

3

13

.

36

ABCD

a

V S SH==

.

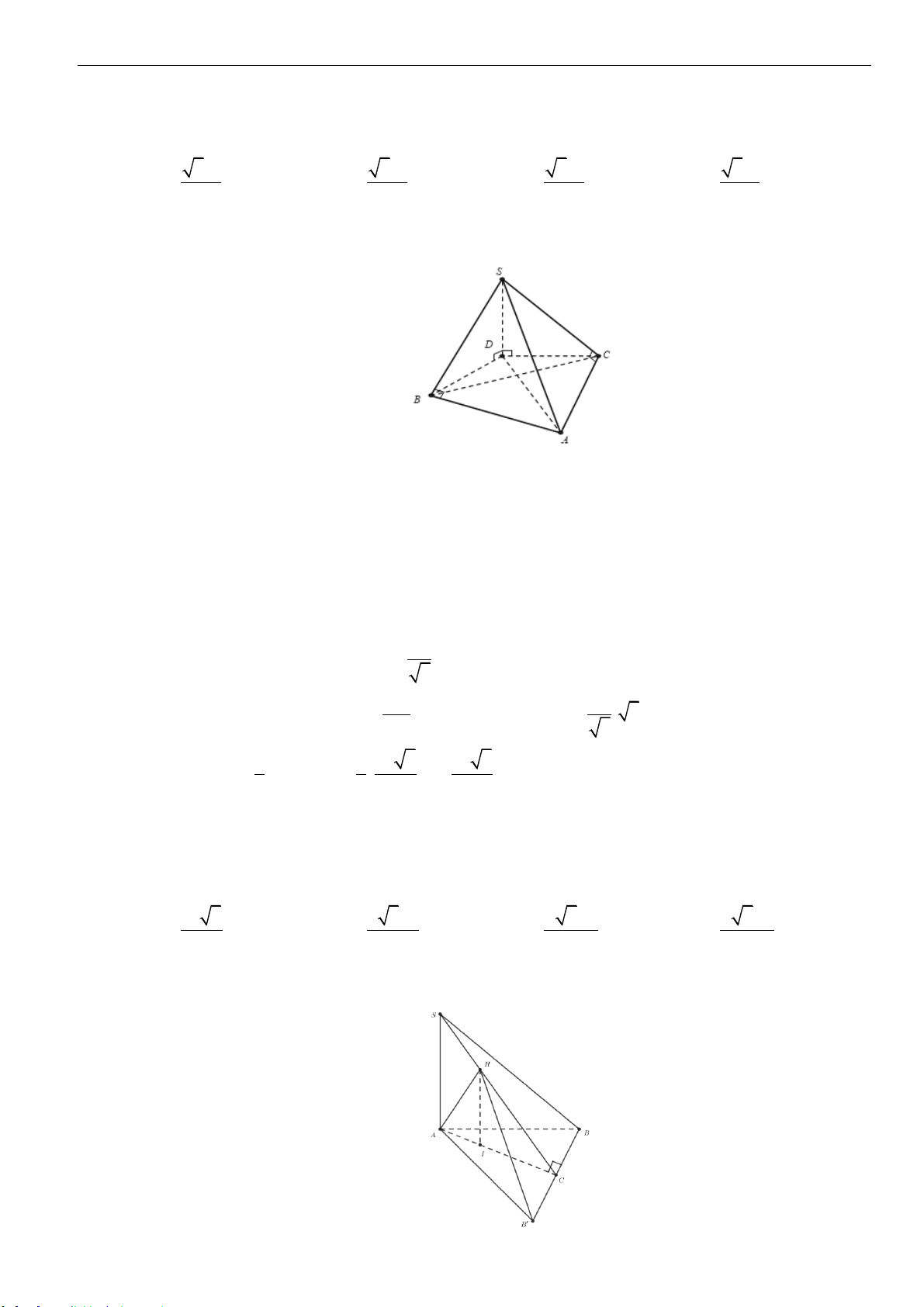
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 20

Câu 22: Cho hình chóp

.S ABC

có đáy là tam giác

ABC

đều cạnh

a

, tam giác

SBA

vuông tại

B

, tam

giác

SAC

vuông tại

C

. Biết góc giữa hai mặt phẳng

( )

SAB

và

( )

ABC

bằng

60

. Thể tích khối

chóp

.S ABC

bằng

A.

3

8

a

. B.

3

12

a

. C.

3

6

a

. D.

3

4

a

.

Lời giải

Chọn B

Gọi

D

là hình chiếu của

S

lên mặt phẳng

( )

ABC

, suy ra

( )

SD ABC⊥

.

Ta có

SD AB⊥

và

()SB AB gt⊥

, suy ra

( )

AB SBD BA BD⊥  ⊥

.

Tương tự có

AC DC⊥

hay tam giác

ACD

vuông ở

C

.

Dễ thấy

SBA SCA = 

(cạnh huyền và cạnh góc vuông), suy ra

SB SC=

. Từ đó ta chứng minh

được

SBD SCD = 

nên cũng có

DB DC=

.

Vậy

DA

là đường trung trực của

BC

, nên cũng là đường phân giác của góc

BAC

.

Ta có

30DAC =

, suy ra

3

a

DC =

. Ngoài ra góc giữa hai mặt phẳng

( )

SAB

và

( )

ABC

là

60SBD =

, suy ra

tan tan . 3

3

SD a

SBD SD BD SBD a

BD

=  = = =

.

Vậy

23

.

1 1 3 3

. . . .

3 3 4 12

S ABC ABC

aa

V S SD a



= = =

.

Câu 23: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông tại

C

, cạnh

SA

vuông góc với mặt đáy

và

2SA AB a==

,

30CAB =

. Gọi

H

là hình chiếu vuông góc của

A

trên

SC

,

B



là điểm đối

xứng của

B

qua mặt phẳng

( )

SAC

. Thể tích của khối chóp

.H AB B



bằng

A.

3

7

a

. B.

3

63

7

a

. C.

3

43

7

a

. D.

3

23

7

a

.

Lời giải

Chọn D

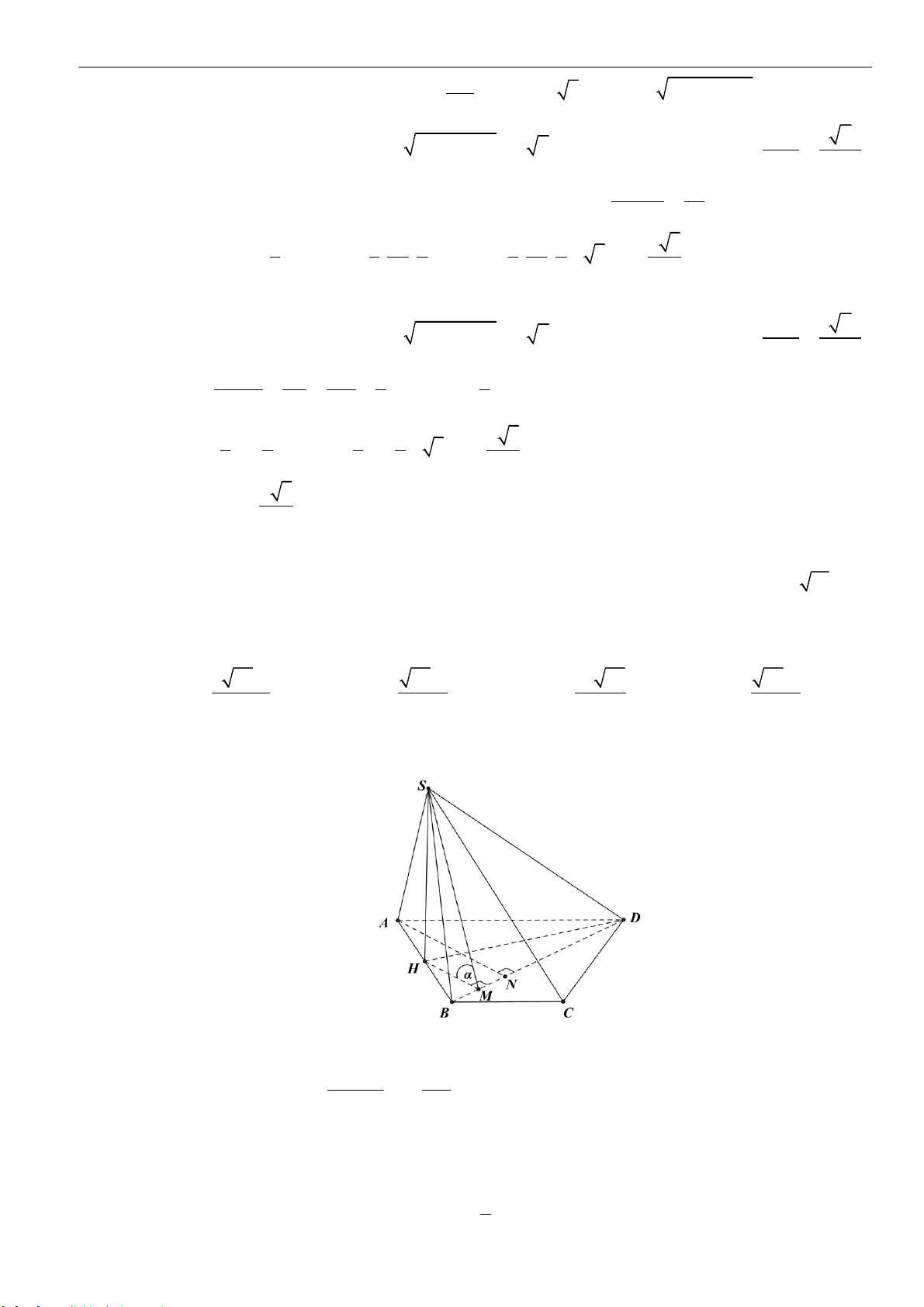
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

21 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Trong tam giác

ABC

ta có

cos 3

AC

CAB AC a

AB

=  =

và

22

BC AB AC a= − =

.

Trong tam giác

SAC

ta có

22

7SC SA AC a= + =

và

2

37

.

7

AC a

HC SC AC HC

SC

=  = =

Trong tam giác

SAC

kẻ

MI AC⊥

tại

I

. Khi đó ta có

.6

7

SA HC a

HI

SC

==

.

Ta có

3

.

1 1 6 1 1 6 1 2 3

. . . . . . . 3.2

3 3 7 2 3 7 2 7

H AB B AB B

aa

V HI S AC BB a a a







= = = =

.

Cách 2:

Trong tam giác

SAC

ta có

22

7SC SA AC a= + =

và

2

37

.

7

AC a

HC SC AC HC

SC

=  = =

Ta có :

.

..

.

33

77







= = =  =

H AB B

H AB B S AB B

S AB B

V

HI HC

VV

V SA SC

.

3

.

1 1 1 1 4 3

. . . .2 . . 3.2

3 2 3 2 6



= = =

S AB B

V SA AC BB a a a a

.

Vậy

3

.

23

7



=

H AB B

Va

.

Câu 24: Cho hình chóp

.S ABCD

có đáy là hình thang vuông tại

A

và

B

. Hình chiếu vuông góc của

S

trên mặt phẳng

( )

ABCD

trùng với trung điểm của

.AB

Biết

,AB a=

2,BC a=

10.BD a=

Góc

giữa hai mặt phẳng

( )

SBD

và mặt phẳng đáy là

30 .

Tính thể tích

V

của khối chóp

.S ABCD

theo

.a

A.

3

3 30

2

a

V =

B.

3

30

4

a

V =

C.

3

30

24

a

V =

D.

3

30

8

a

V =

Lời

giải

Chọn C

Xét

ABD

vuông ở

2 2 2 2

9 3 .A AD BD AB a AD a = − =  =

Diện tích đáy:

2

3 2 5

22

ABCD

a a a

Sa

+

=  =

Góc giữa hai mặt phẳng

( )

SBD

và mặt phẳng đáy

( )

ABCD

là

30



=

Từ

H

kẻ

( )

30HM BD BD SHM SMH⊥  ⊥  = 

là góc giữa

( )

SBD

và

( )

ABCD

Từ

A

kẻ

//AN BD MH AN⊥

và

1

.

2

MH AN=

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 22

Xét

ABD

vuông ở

A

có

2 2 2 2 2 2

1 1 1 1 1 10 3

99

10

a

AN

AN AB AD a a a

= + = + =  =

3

2 10

a

MH=

Xét

SHM

vuông ở

H

có

3 1 3

tan .tan30

2 10 3 2 30

SH a a

SMH SH MH

MH

=  =  =  =

.

23

311 03

.

33

23

4

0

5

22

S ABCD ABCD

a

V SH

aa

S  =  = = 

Câu 25: Cho khối chóp tứ giác đều

.S ABCD

có

22BD a=

, gọi

M

là trung điểm của

DC

, góc giữa

SM

và mặt phẳng

( )

ABCD

bằng

0

60

. Thể tích

V

của khối chóp

.S ABCD

bằng,

A.

3

33

2

a

V =

B.

3

42

3

a

V =

C.

3

43

3

a

V =

D.

3

6

a

V =

Lời giải

Chọn C

Gọi

O

là tâm của đáy. Vì

.S ABCD

là hình chóp đều nên

( )

SO ABCD⊥

và

ABCD

là hình

vuông.

Ta có

( )

SM ABDC M

SO ABCD O

=







⊥=





, suy ra góc giữa

SM

và mặt phẳng

( )

ABCD

là

0

60SMO =

.

Gọi cạnh của hình vuông

ABCD

là

x

. Có

1

22

x

OM BC==

,

0

3

tan60

2

x

SO OM==

.

2

ABCD

Sx=

Lại có

22BD a=

,

ABCD

là hình vuông nên

2 2 2 2x a x a=  =

. Suy ra

3SO a=

,

2

4

ABCD

Sa=

Thể tích khối chóp

.S ABCD

là

3

2

.

1 1 4 3

. 3.4

3 3 3

S ABCD ABCD

a

V SO S a a= == =

.

Câu 26: Cho hình chóp tứ giác đều

.S ABCD

có cạnh đáy bằng

a

, tâm của đáy là

O

. Gọi

M

và

N

lần

lượt là trung điểm của

SA

và

BC

. Biết góc giữa đường thẳng

MN

và mặt phẳng

( )

ABCD

bằng

0

60

. Tính thể tích khối chóp

.S ABCD

.

A.

3

10

6

a

B.

3

30

2

a

C.

3

30

6

a

D.

3

10

3

a

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

23 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Lời giải

Chọn C

Gọi

H

là trung điểm

AO

. Khi đó góc giữa

MN

và

( )

ABCD

là

MNH

.

Ta có

2 2 0

2 . .cos45HN CN CH CN CH= + −

10

4

a

=

.

Suy ra

0

10 30

.tan60 . 3

44

aa

MH HN= = =

.

Do đó

30

2

a

SO MH==

.

3

2

.

1 30 30

.

3 2 6

S ABCD

a

V a a==

.

Câu 27: Cho hình chóp

.S ABCD

với đáy

ABCD

là hình thang vuông tại

A

và

D

, đáy nhỏ của hình

thang là

CD

, cạnh bên

15SC a=

. Tam giác

SAD

là tam giác đều cạnh

2a

và nằm trong mặt

phẳng vuông góc với đáy hình chóp. Gọi

H

là trung điểm cạnh

AD

, khoảng cách từ

B

tới mặt

phẳng

( )

SHC

bằng

26a

. Tính thể tích

V

của khối chóp

.S ABCD

.

A.

3

46Va=

. B.

3

12 6Va=

. C.

3

86Va=

. D.

3

24 6Va=

.

Lời giải

Chọn A

Theo giả thiết ta có

( ) ( )

( )

,

SAD ABCD AD

SH ABCD

SH AD SH SAD

⊥=





⊥



⊥





.

Ta có

22

3SH SD DH a= − =

,

2 2 2 2

15 3 2 3HC SC SH a a a= − = − =

,

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 24

2 2 2 2

12 11CD HC HD a a a= − = − =

.

Ta có

( )

BF HC

BF SHC

BF SH

⊥



⊥



⊥



nên

( )

, 2 6d B SHC BF a==

.

2

11

. .2 3 .2 6 6 2

22

HBC

S BF HC a a a= = =

.

Đặt

AB x=

nên

1

..

22

AHB

a

S AH AB x==

;

2

1 11

.

22

CDH

a

S DH DC==

,

( )

1

11

2

ABCD

S CD AB AD a x a= + = +

.

AHB ABCD CDH BHC

S S S S= − −

( ) ( )

2

11

. 11 6 2 12 2 11

22

aa

x a x a a x a = + − −  = −

.

( )

2

11 12 2 11 12 2

ABCD

S a a a a= + − =

.

Vậy

23

.

11

. . 3.12 2 4 6

33

S ABCD ABCD

V SH S a a a= = =

.

Câu 28: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật, tam giác

SAB

đều và nằm trong mặt

phẳng vuông góc với đáy, biết khoảng cách giữa hai đường thẳng

SB

và

CD

bằng

a

và

0

30BDC =

. Tính thể tích của khối chóp

.S ABCD

.

A.

3

33

2

a

. B.

3

6

9

a

. C.

3

6

a

. D.

3

2

a

.

Lời giải

Chọn D

Gọi

H

là trung điểm của

AB

. Có

SH AB⊥

mà

( ) ( )

SAB ABCD

SAB ABCD AB

⊥







=





Nên

( )

SH ABCD⊥

và có

//CD AB

( )

//CD SAB

( ) ( )

( )

, , ,d SB CD d CD SAB d C SAB = =

Ta có:

( )

CB AB

CB SAB

CB SH

⊥



⊥



⊥



( )

,d C SAB CB a = =

Có

0

tan tan30

BC a

BDC

CD CD

=  =

3CD a=

.

Tam giác

SAB

đều có

SH

là đường cao

33

3.

22

a

SH a = =

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

25 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Thể tích

.S ABCD

:

.

1

.

3

S ABCD ABCD

V SH S=

3

1 3 3

. . . 3

3 2 2

aa

aa==

.

Câu 29: Cho khối chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật, tam giác

SAB

cân tại

S

và nằm trong

mặt phẳng vuông góc với

( )

ABCD

. Biết

2,BD a AB a==

, khoảng cách giữa

AB

và

SD

bằng

2a

. Tính thể tích khối chóp

.S ABCD

.

A.

3

a

. B.

3

32a

. C.

3

2

3

a

. D.

3

2a

.

Lời giải

Chọn D

Gọi

H

là trung điểm

AB

. Do tam giác

SAB

cân tại

S

và nằm trong mặt phẳng vuông góc với

( )

ABCD

nên

( )

SH AB SH ABCD SH CD⊥  ⊥  ⊥

.

Gọi

M

là trung điểm

CD

, do

,SH CD HM CD⊥⊥

nên

( ) ( ) ( )

CD SHM SHM SCD⊥  ⊥

.

Dựng

( )

HK SM HK SCD⊥  ⊥

.

Vì

( ) ( ) ( )

( )

// , , , 2AB SCD d AB SD d AB SCD d H SCD HK a = = = =

.

( )

2

2 2 2

23AD BD AB a a a HM= − = − = =

.

Vì

SHM

vuông tại

H

nên:

( ) ( )

22

2 2 2 2

1 1 1 1 1 1

6

23

SH a

HK SH HM SH

aa

= +  = +  =

Vậy:

3

.

1 1 1

. . . . 6. . 3 2

3 3 3

S ABCD ABCD

V SH S SH AB AD a a a a= = = =

.

Câu 30: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật,

AB a=

,

2BC a=

.

SA

vuông góc với

mặt phẳng đáy. Biết khoảng cách giữa hai đường thẳng

BD

và

SC

bằng

23

31

a

. Tính thể tích

của khối chóp

.S ABCD

.

A.

3

3a

. B.

3

a

. C.

3

23

3

a

. D.

3

23a

Lời giải

Chọn C

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 26

Đặt

,0SA x x=

Gọi

O

là tâm hình chữ nhật và

M

là trung điểm

SA

, ta có:

( )

// //SC MO SC BMD

.

Do đó

( )

,d SC BD

( )

,d SC BMD=

( )

,d S BMD=

( )

,d A BMD h==

Ta có:

,,AM AB AD

đôi một vuông góc nên

2 2 2 2 2 2 2 2 2 2

1 1 1 1 4 1 1 31 4 4

3

4 12 3

xa

h AM AB AD x a a a x a

= + + = + + =  =  =

Thể tích khối chóp

.S ABCD

là:

3

1 1 2 3

. . . 3. .2

3 3 3

SABCD ABCD

a

V SAS a a a= = =

.

Câu 31: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

. Gọi

;MN

lần lượt là trung điểm

của

AB

và

AD

;

H

là giao điểm của

CN

và

DM

. Biết

SH

vuông góc với mặt phẳng

( )

ABCD

và khoảng cách giữa hai đường thẳng

DM

và

SC

bằng

2 57

19

a

. Tính thể tích khối

chóp

.S ABCD

?

A.

3

a

. B.

3

6

9

a

. C.

3

a

. D.

3

33a

.

Lời giải

Chọn C

Ta có:

ADM DCN = 

(c – g – c).

90 .

 =  + = + =

 =  ⊥

ADM DCN ADM CDM DCN CDM

DHC DM HC

Ta có:

( )

.

HC DM

DM SHC

SH DM

⊥



⊥



⊥



Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

27 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Trong

( )

SHC

; kẻ

HK SC⊥

(

K SC

); mà

( )

DM SHC DM HK⊥  ⊥

.

HK

là đoạn vuông góc chung của hai đường thẳng

DM

và

SC

.

( )

2 57

;.

19

a

d DM SC HK = =

Xét

CDN

vuông tại

D

; đường cao

DH

có:

2 2 2

2

2 2 2

2

25

..

5

2

DC DC a a

DC HC CN HC

CN

DN DC

a

=  = = = =

+



+





Xét

SHC

vuông tại

H

; đường cao

HK

có:

22

2 2 2 2

1 1 1 1 1 1

3.

2 57 2 5

19 5

= +  = +  =

   

   

   

SH a

HK SH HC SH

aa

Thể tích của khối chóp

.S ABCD

:

3

2

1 1 3

. . . . 3

3 3 3

= = =

ABCD

a

V S SH a a

(đvtt).

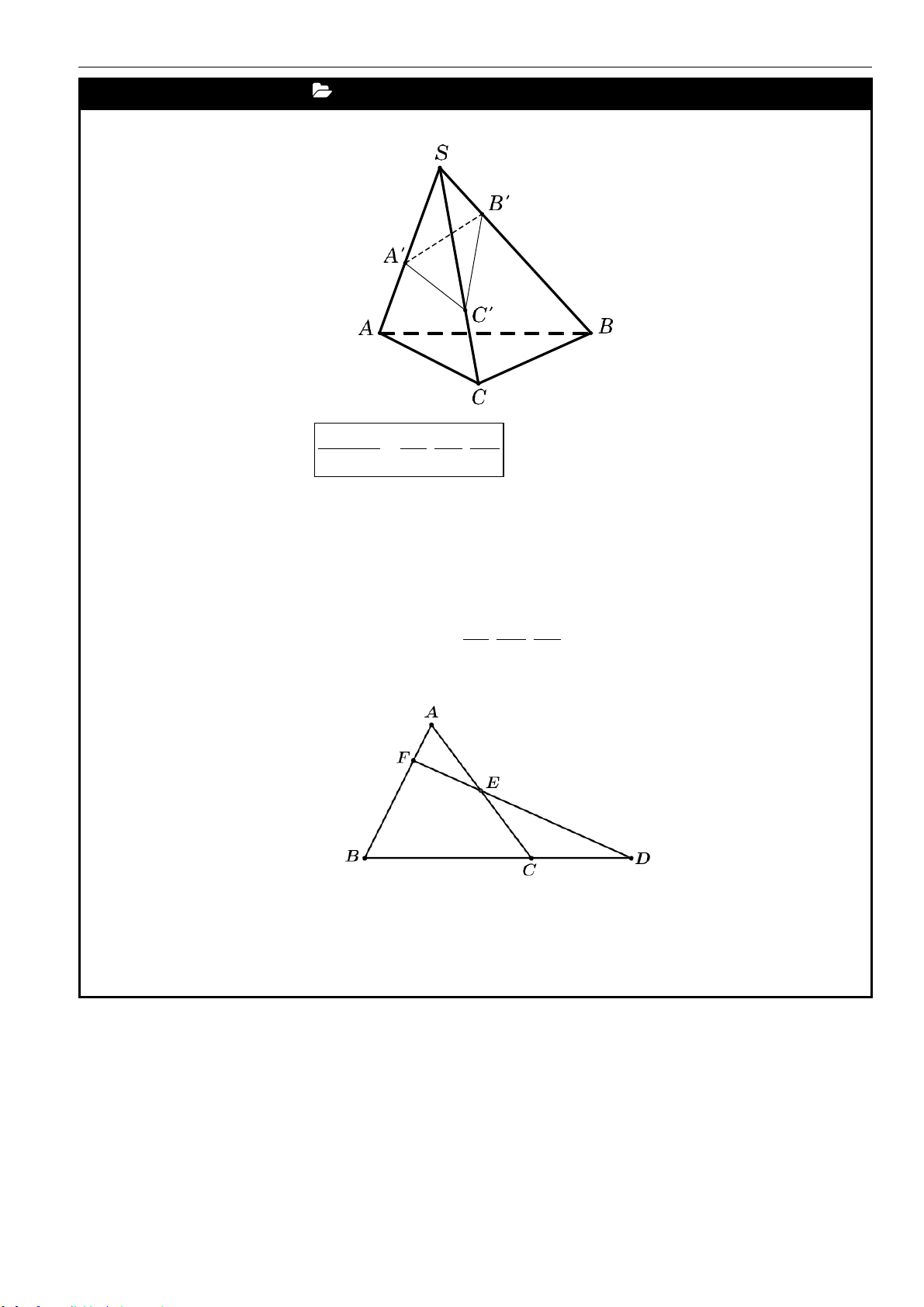
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

1 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Dạng 6: Tỷ số thể tích khối chóp

Cho khối chóp

.S ABC

và

,,A B C

  

là các điểm tùy ý lần lượt thuộc

,,SA SB SC

, ta có:

Công thức tỉ số thể tích:

. ' ' '

.

' ' '

..

S A B C

S ABC

V

SA SB SC

V SA SB SC

=

(hay gọi là công thức Simson)

Phương pháp này được áp dụng khi khối chóp không xác đinh được chiều cao một cách dễ dàng

hoặc khối chóp cần tính là một phần nhỏ trong khối chóp lớn và cần chú ý đến một số điều kiện sau:

▪ Hai khối chóp phải cùng chung đỉnh.

▪ Đáy hai khối chóp phải là tam giác.

▪ Các điểm tương ứng nằm trên các cạnh tương ứng.

Định lý Menelaus: Cho ba điểm thẳng hàng

. . 1

FA DB EC

FB DC EA

=

với

DEF

là một đường thẳng cắt ba

đường thẳng

,,BC CA AB

lần lượt tại

,,D E F

.

Chú ý: (Áp dụng cho khối chóp với mọi đáy)

▪ Hai hình chóp có cùng chiều cao thì tỉ số thể tích chính là tỉ số diện tích đáy tương ứng.

▪ Hai hình chóp có cùng diện tích đáy thì tỉ số thể tích chính là tỉ số đường cao tương ứng.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 2

Câu 1: Cho khối tứ diện

ABCD

có thể tích

V

và điểm

E

trên cạnh

AB

sao cho

3AE EB=

. Khi đó

thể tích khối tứ diện

EBCD

bằng

A.

3

V

. B.

5

V

. C.

4

V

. D.

2

V

.

Lời giải

Chọn C

Vì

1

3

4

AE EB EB AB=  =

. Ta có

1

44

EBCD

ABCD

V

EB V

V

V AB

= =  =

.

Câu 2: Cho hình chóp

.S ABC

. Gọi

M

,

N

,

P

lần lượt là trung điểm của

SA

,

SB

,

SC

. Tỉ số

.

S ABC

S MNP

V

bằng

A.

3

2

. B. 8. C.

1

8

. D. 6.

Lời giải

Chọn B

Ta có

.

. . 2.2.2 8

S ABC

S MNP

V

SA SB SC

V SM SN SP

= = =

.

Câu 3: Cho hình chóp

.S ABCD

có đáy là hình bình hành. Gọi

G

là trọng tâm tam giác

SAB

và

,MN

lần lượt là trung điểm của

,SC SD

. Biết thể tích khối chóp

.S ABCD

là

V

, tính thể tích khối

chóp

.S GMN

.

A.

8

V

. B.

4

V

. C.

6

V

. D.

12

V

.

Lời giải

Chọn D

Gọi

K

là trung điểm

AB

, ta có :

VÍ DỤ MINH HỌA

B

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

3 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

..

11

2 2 2

KCD ABCD S KCD S ABCD

V

S S V V



=  = =

.

Mặt khác:

.

..

.

1 1 2 1 1

. . . .

2 2 3 6 6 12

S MNG

S MNG S CDK

S CDK

V

SN SM SG V

VV

V SD SC SK

= = =  = =

.

Câu 4: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông cân tại

,,A AB a SA=

vuông góc với đáy,

góc hợp bởi

SB

và đáy bằng

60

. Gọi

,HK

lần lượt là hình chiếu vuông góc của

A

trên các

đường thẳng chứa cạnh

,SB SC

. Gọi

12

,VV

lần lượt là thể tích các khối đa diện

SAHK

và

ABCKH

. Tỉ số

1

2

V

bằng

A.

7

9

. B.

7

16

. C.

9

7

. D.

9

16

.

Lời giải

Chọn C

Ta có

3, 2 ,SA a SB SC a SH SK= = = =

.

Nên

24

11

2

99

.

16 7

V SH SK SH SA V

V SB SC SB SB V

   

= = = =  =

   

   

Câu 5: Cho khối tứ diện

ABCD

có thể tích

V

. Gọi

, , ,M N P Q

lần lượt là trung điểm các cạnh

AB

,

AC

,

BC

,

AD

. Tính thể tích tứ diện

MNPQ

theo

V

.

A.

3

8

V

. B.

4

V

. C.

8

V

. D.

12

V

.

Lời giải

Chọn C

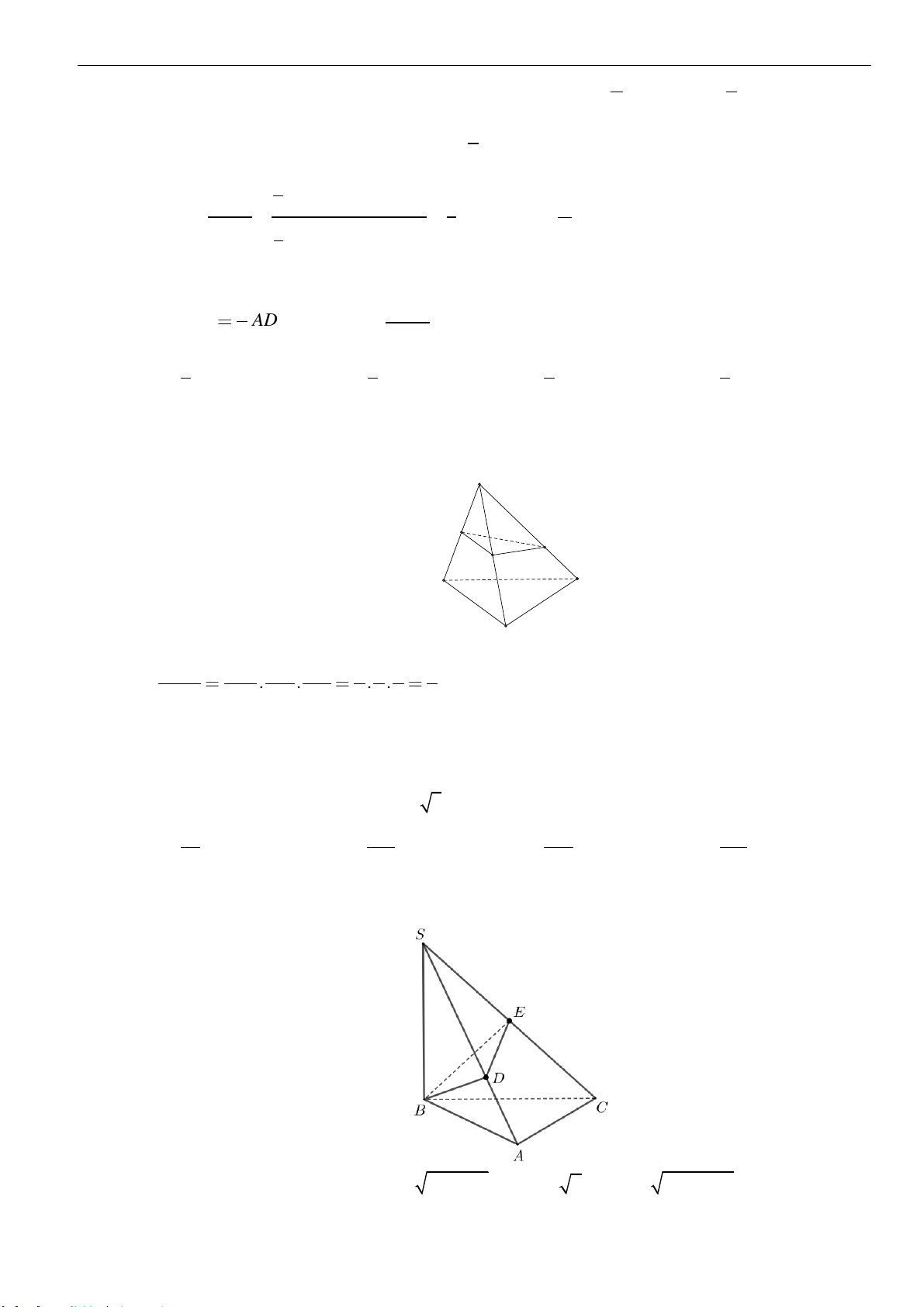
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 4

Ta có tam giác

MNP

đồng dạng với tam giác

CBA

theo tỉ số

1

2

nên

1

4

MNP ABC

SS



=

.

Q

là trung điểm

AD

nên

1

( ;( )) ( ;( ))

2

d Q ABC d D ABC=

.

Do đó

1

. ( ;( ))

1

3

1

8

. ( ;( ))

3

MNP

MNPQ

ABCD

ABC

S d Q ABC

V

S d D ABC



==

hay

8

MNPQ

V

V =

.

Câu 6: Cho tứ diện

ABCD

. Gọi

,M

N

là trung điểm của

,,AB AC

lấy điểm

P

thuộc cạnh

AD

sao

cho

2

3

AP AD

. Khi đó tỉ số

AMNP

ABCD

V

bằng

A.

1

.

6

B.

1

.

8

C.

1

.

3

D.

1

.

4

Lời giải

Chọn A

1 1 2 1

. . . .

2 2 3 6

AMNP

ABCD

V

AM AN AP

V AB AC AD

Câu 7: Cho hình chóp

.S ABC

có đáy là tam giác

ABC

vuông cân tại

,A

12=SB

,

SB

vuông góc với

mặt phẳng

( )

ABC

. Gọi

, DE

lần lượt là các điểm thuộc các đoạn

, SA SC

sao cho

2 , ==SD DA ES EC

. Biết

23=DE

, hãy tính thể tích khối chóp

.B ACED

.

A.

96

5

. B.

144

5

. C.

288

5

. D.

192

5

.

Lời giải

Chọn D

Đặt

0= = AB AC x

. Ta có

2

144=+SA x

;

2

2 2 144=  = +BC x SC x

.

P

N

M

A

B

C

D

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

5 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Định lý hàm số cos:

2 2 2 2 2 2

cos

2 . 2 .

+ − + −

==

SA SC AC SD SE ED

ASC

SASC SD SE

( ) ( )

22

2 2 2

41

144 2 144 12

144 2 144

94

21

.

32

+ + + −

=

xx

x x x

SA SC

( ) ( )

2 2 2

4 3 12 5

2 288 144 2 144 36

3 4 5

 + = + + + −  =x x x x

.

Vậy

2

. . .

2 2 1 2 1 12 5 192

1 . . . . .12

3 3 3 9 2 5 5



= − = = = =





B ACED S ABC S ABC ABC

SD SE

V V V S SB

SA SC

.

Câu 8: Cho hình chóp

.S ABCD

có đáy là hình vuông cạnh

a

,

SA

vuông góc với đáy, côsin góc hợp

bởi

SD

và mặt phẳng đáy

( )

ABCD

bằng

1

3

. Gọi

E

;

F

lần lượt là hình chiếu của

A

lên

SB

;

SD

. Mặt phẳng

( )

AEF

chia khối chóp thành hai phần. Tính thể tích phần khối chóp không

chứa đỉnh

S

:

A.

3

2

9

a

V =

. B.

3

2

4

a

V =

. C.

3

22

9

a

V =

. D.

3

2

6

a

V =

.

Lời giải

Chọn C

Dễ thấy

SAB SAD = 



AE AF=



SE SF

SA SB

=



//EF BD

Do

( )

SA ABCD⊥

nên

AD

là hình chiếu của

SD

lên mặt phẳng

( )

ABCD



( )

1

cos ; cos

3

AD

SD ABCD SDA

SD

= = =



33SD AD a==



( )

2

2 2 2

32SA SD AD a a a AC= − = − = =



Tam giác

SAC

vuông cân tại

A

Trong

( )

ABCD

: gọi

O AC BD=

. Trong

( )

SBD

: gọi

I SO EF=

Trong

( )

SAC

: gọi

M SC AI=

. Lại có:

SA BC

AB BC

⊥





⊥





( )

BC SAB⊥



BC AE⊥

Mà

AE SB⊥



( )

AE SBC⊥



AE SC⊥

( )

1

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 6

SA CD

AD CD

⊥





⊥





( )

CD SAD⊥



CD AF⊥

Mà

AF SD⊥



( )

AF SCD⊥



AF SC⊥

( )

2

Từ

( )

1

và

( )

2



( )

SC AEF⊥



SC AM⊥



M

là trung điểm

SC



I

là trọng tâm tam

giác

SAC



2

3

SE SF

SA SB

==



23

3

a

SE SF==

Ta có:

1

..

3

SAEM

SABC

V

SA SE SM

V SA SB SC

==



.

11

36

SAEM SABC S ABCD

V V V==

1

..

3

SAMF

SACD

V

SA SM SF

V SA SC SD

==



.

11

36

SAMF SACD S ABCD

V V V==



..

1

3

S AEMF SAEM SAMF S ABCD

V V V V= + =



3

. . .

2 2 1 2 3

..

3 3 3 9

S ABCD S AEMF S ABCD ABCD

a

V V V V SAS= − = = =

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

7 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 1: Cho khối chóp

.S ABC

có thể tích

V

. Các điểm

A



,

B



,

C



tương ứng là trung điểm các cạnh

SA

,

SB

,

SC

. Thể tích khối chóp

.S A B C

  

bằng

A.

8

V

. B.

2

V

. C.

4

V

. D.

16

V

.

Lời giải

Chọn A

Áp dụng định lý Sim-son ta có:

1

..

8

SA B C

SABC

V

SA SB SC

V SA SB SC

  

==

8

SA B C

V

  

=

.

Câu 2: Cho khối chóp

.S ABC

có thể tích

V

. Gọi

,MN

lần lượt là trung điểm của

SA

và

BC

. Tính

thể tích khối chóp

.M ANC

theo

V

.

A.

8

V

. B.

6

V

C.

12

V

. D.

4

V

.

Lời giải

Chọn D

( )

.

,

1 1 1

..

2 2 4 4

,

M ANC ANC

M ANC

S ABC ABC

d M ANC

VS

V

VS

d S ABC





= = =  =





.

Câu 3: Cho tứ diện

MNPQ

. Gọi

,IJ

và

K

lần lượt là trung điểm của

,MN MP

và

MQ

(tham khảo hình

vẽ). Tỉ số thể tích

MIJK

MNPQ

V

là:

BÀI TẬP TRẮC NGHIỆM

C

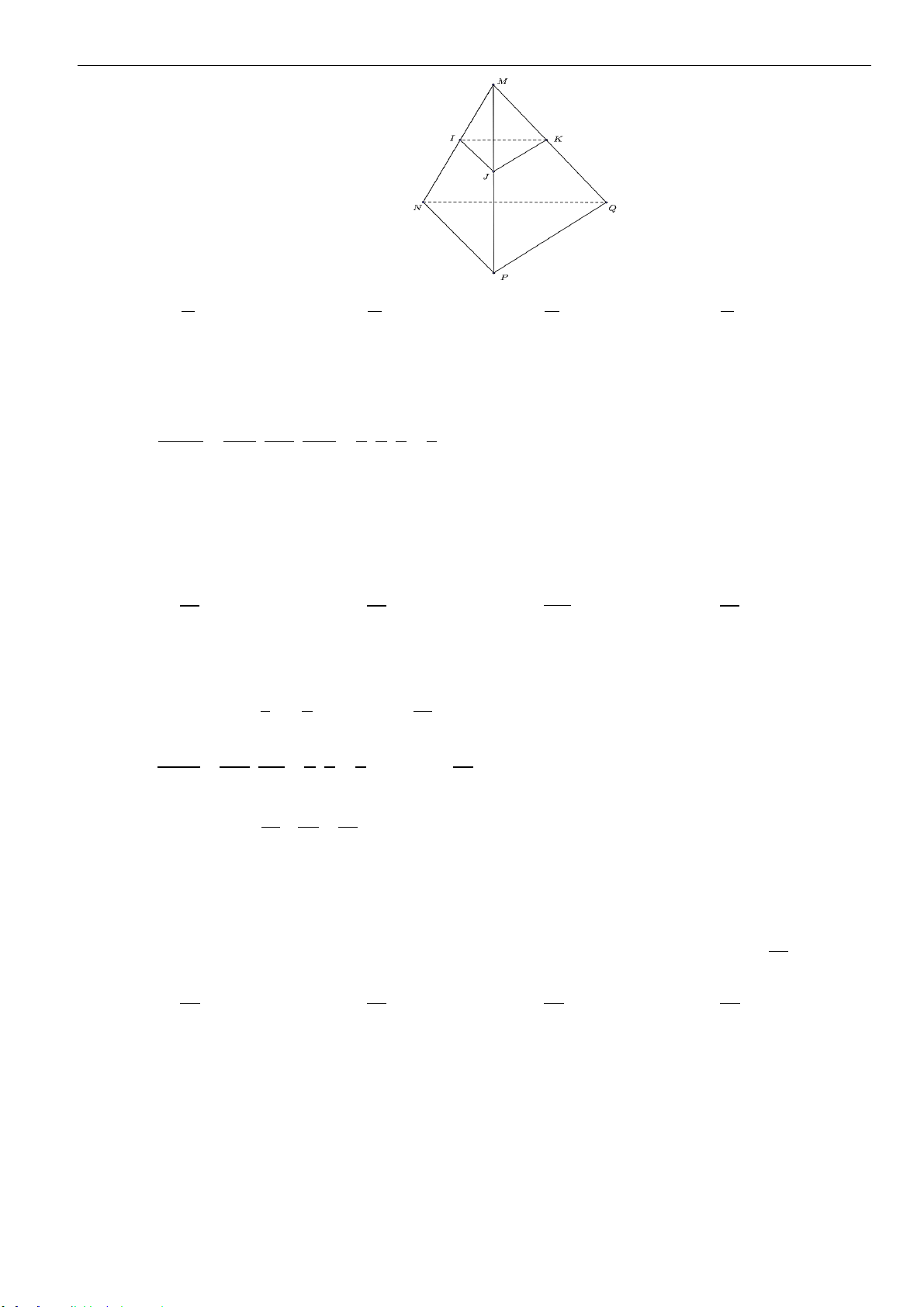
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 8

A.

1

8

. B.

1

4

. C.

1

6

. D.

1

3

.

Lời giải

Chọn A

Vì

,IJ

và

K

lần lượt là trung điểm của

,MN MP

và

MQ

nên theo công thức tỉ số thể tích ta có

1 1 1 1

. . . . .

2 2 2 8

MIJK

MNPQ

V

MI MJ MK

V MN MP MQ

= = =

Câu 4: Cho hình chóp

SABC

có đáy là tam giác cân tại

,A AB a=

và góc

A

bằng

0

30

. Cạnh bên

2SA a=

và

( )

SA ABC⊥

. Gọi

,MN

lần lượt là trung điểm của các cạnh

SB

và

SC

. Khi đó thể

tích khối đa diện có các đỉnh

, , , ,A B C M N

bằng

A.

3

4

a

. B.

3

12

a

. C.

3

8

a

. D.

3

8

a

.

Lời giải

Chọn D

Ta có

3

0

11

.2 . . .sin30

3 2 6

SABC

a

V a a a==

.

3

1 1 1

..

2 2 4 24

SAMN

SABC

V

SM SN a

V

V SB SC

= = =  =

.

Vậy

3 3 3

6 24 8

AMNBC

a a a

V = − =

Câu 5: Cho khối chóp

.S ABC

. Trên ba cạnh

,,SA SB SC

lần lượt lấy ba điển

,,A B C

  

sao cho

2 , 3 , 4SA SA SB SB SC SC

  

= = =

. Mặt phẳng

( )

ABC

  

chia khối chóp thành hai khối. Gọi

V

và

V



lần lượt là thể tích các khối đa diện

.S A B C

  

và

.ABC A B C

  

. Khi đó tỉ số

V



là:

A.

1

59

. B.

1

12

. C.

1

23

. D.

1

24

.

Lời giải

Chọn C

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

9 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Ta có

.

11

..

24 23

S ABC

V SA SB SC V

  

= =  =



.

Câu 6: Cho tứ diện

ABCD

. Các điểm

,,M N P

lần lượt thuộc các cạnh

,,AB AC AD

sao cho

, 2 , 3 .MA MB NA NC PA PD

Biết thể tích khối tứ diện

AMNP

bằng

V

thì khối tứ diện

ABCD

tính theo

V

có giá trị là

A.

6.V

B.

4.V

C.

8.V

D.

12 .V

Lời giải

Chọn B

Ta có:

1 2 3

,,

2 3 4

AM AB AN AC AP AD

1 2 3

..

. . 1

2 3 4

4.

. . . . 4

AMNP

ABCD

ABCD ABCD

AB AC AD

V

V AM AN AP

VV

V V AB AC AD AB AC AD

Câu 7: Cho hình chóp

.S ABCD

. Gọi

, , ,A B C D

   

theo thứ tự là trung điểm của

, , ,SA SB SC SD

. Tính

tỉ số thể tích của hai khối chóp

.S A B C D

   

và

.S ABCD

.

A.

1

16

. B.

1

4

. C.

1

8

. D.

1

2

.

Lời giải

Chọn C

Ta có

..

11

;

88

S A B C S A C D

S ABC S ACD

VV

     

==

.

Khi đó

( )

. . . . . .

11

88

S A B C D S A B C S A C D S ABC S ACD S ABCD

V V V V V V

         

= + = + =

Câu 8: Cho lăng trụ tam giác

.ABC A B C

  

. Biết diện tích mặt bên

( )

ABB A



bằng

15

, khoảng cách từ

C

đến mặt phẳng

( )

ABB A



bằng

6

. Thể tích khối lăng trụ

.ABC A B C

  

bằng

A.

60

. B.

45

. C.

90

. D.

30

Lời giải

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 10

Chọn B

Ta có

( )

. '. .

1

3 3 3. . . ;

3

ABC A B C A ABC C A AB A AB

V V V S d C ABB A

    



= = =

=

15

.6 45

2

=

.

Câu 9: Cho khối tứ diện

ABCD

có thể tích

V

và điểm

E

thỏa mãn

3EA EB=−

. Khi đó thể tích khối

tứ diện

EBCD

bằng

A.

2

V



B.

3

V



C.

5

V



D.

4

V



Lời giải

Chọn D

Từ giả thiết

3EA EB=−

ta suy ra điểm

E

trên đoạn

AB

thỏa

3

4

AE

AB

=

.

31

1 1 1

44

.

4

EBCD AECD AECD

EBCD

V V V V

AE

V V V AB

V

−

= = − = − = − =

=

Câu 10: Cho khối chóp

.S ABC

có đáy

ABC

là tam giác đều cạnh

a

,

2SA a=

và vuông góc với mặt

phẳng

( )

ABC

. Trên cạnh

,SB SC

lần lượt lấy các điểm

,MN

sao cho

12

,

23

SM SN

SB SC

==

(tham

khảo hình vẽ). Thể tích của khối chóp

.S AMN

bằng

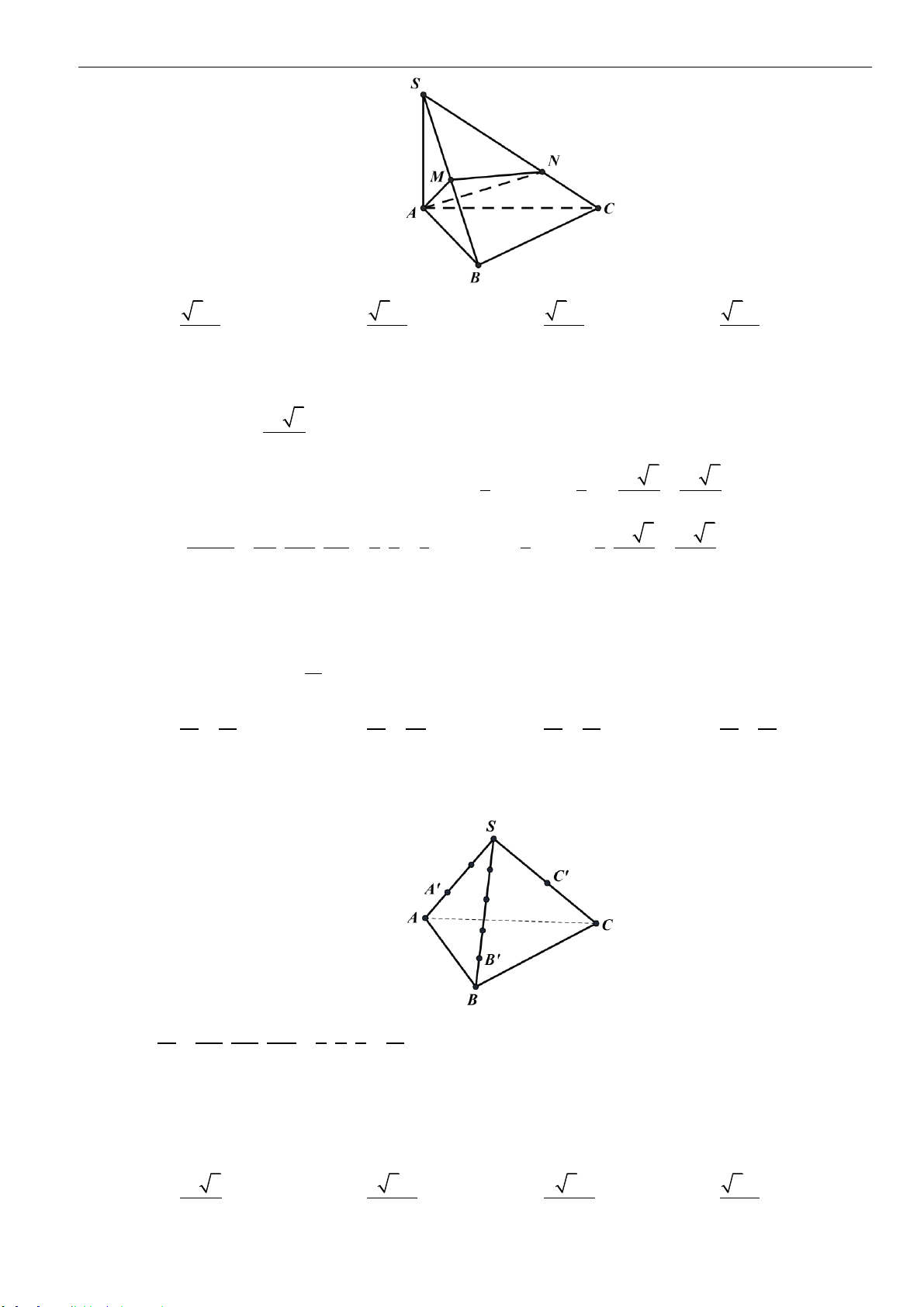
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

11 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

A.

3

36

a

. B.

3

9

a

. C.

3

18

a

. D.

3

a

.

Lời giải

Chọn C

Ta có

2

3

4

ABC

a

S



=

.

Thể tích của khối chóp

.S ABC

là:

23

.

1 1 3 3

. .2 .

3 3 4 6

S ABC ABC

aa

V SAS a



= = =

.

Mà

33

.

..

.

1 2 1 1 1 3 3

. . . .

2 3 3 3 3 6 18

S AMN

S AMN S ABC

S ABC

V

SA SM SN a a

VV

V SA SB SC

= = =  = = =

Câu 11: Cho hình chóp

.S ABC

, trên các cạnh

,,SA SB SC

lần lượt lấy các điểm

,,A B C

  

sao cho

2 , 4 ,SA AA SB BB SC CC

     

= = =

. Gọi

1

V

là thể tích khối chóp

.S A B C

  

,

2

V

là thể tích khối

chóp

.S ABC

. Tính

1

2

V

A.

1

2

4

15

V

=

. B.

1

2

1

24

V

=

. C.

1

2

8

15

V

=

. D.

1

2

1

16

V

=

.

Lời giải

Chọn A

1

2

2 4 1 4

. . . . .

3 5 2 15

V

SA SB SC

V SA SB SC

  

= = =

Câu 12: Cho hình chóp

.S ABC

có

SA

vuông góc với đáy,

3=SA a

, đáy

ABC

là tam giác đều cạnh bằng

a

.

,,M N P

lần lượt là trùng điểm của các cạnh bên

,,SA SB SC

. Tính thể tích khối đa diện

MNP ABC

.

A.

3

8

a

. B.

3

33

16

a

. C.

3

73

32

a

. D.

3

6

a

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 12

Lời giải

Chọn C

Diện tích tam giác

ABC

là

2

3

4

=

ABC

a

S

.

Thể tích của khối chóp

.S ABC

là

23

.

1 3 . 3 3

3 4 4

==

S ABC

a a a

V

.

Ta có

..

. . . . .

.

17

..

8 8 8

= =  =  = − =

S MNP S ABC

S MNP MNP ABC S ABC S MNP S ABC

S ABC

VV

SM SN SP

V V V V V

V SA SB SC

.

Vậy

33

.

7 3 7 3

8 4 32

==

MNP ABC

aa

V

.

Câu 13: Cho khối chóp

.S ABC

. Trên ba cạnh

,,SA SB SC

lần lượt lấy ba điểm

’, ,A B C



sao cho

2 , 4 , 5SA SA SB SB SC SC

  

= = =

. Tính tỉ số

. ' ' '

.

S A B C

S ABC

V

A.

1

10

. B.

1

40

. C.

1

8

. D.

1

20

.

Lời giải

Chọn B

2 , 4 , 5SA SA SB SB SC SC

  

= = =

1 1 1

,,

2 4 5

SA SB SC

  

 = = =

.

. ' ' '

.

1 1 1 1

. . . .

2 4 5 40

S A B C

S ABC

V SA SB SC

  

= = =

.

Câu 14: Cho hình chóp

.S ABC

, gọi

,,M N P

lần lượt là trung điểm của cạnh

,,SA SB SC

. Biết thể tích

khối chóp

.S MNP

bằng

5

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

13 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Khi đó thể tích của khối đa diện

.MNP ABC

bằng:

A.

40

. B.

10

. C.

35

. D.

25

.

Lời giải

Chọn C

Ta có

.

..

.

1

. . 8. 40

8

S MNP

S ABC S MNP

S ABC

V SM SN SP

VV

V SA SB SC

= =  = =

.

Khi đó

. . .

40 5 35

MNP ABC S ABC S MNP

V V V= − = − =

.

Câu 15: Cho hình chóp tứ giác

.S ABCD

có đáy

ABCD

là hình bình hành tâm

I

. Gọi

1

V

,

2

V

lần lượt là

thể tích của khối chóp

.S ABI

và

.S ABCD

. Khẳng định nào sau đây đúng?

A.

1

2

1

6

V

=

. B.

1

2

1

2

V

=

. C.

1

2

1

8

V

=

. D.

1

2

1

4

V

=

.

Lời giải

Chọn D

.

1

2.

1 1 1 1

. . . .

2. 2 2 2 4

B SAI

B SAD

V

BS BA BI

V V BS BA BD

= = = =

.

Câu 16: Cho tứ diện đều

ABCD

có cạnh bằng

a

. Gọi

,,M N P

lần lượt là trung điểm của các cạnh

,,AB AC AD

và điểm

O

tùy ý trên mặt phẳng

()BCD

. Thể tích tứ diện

OMNP

bằng

A.

3

2

96

a

. B.

3

2

24

a

. C.

3

2

48

a

. D.

3

2

36

a

.

Lời giải

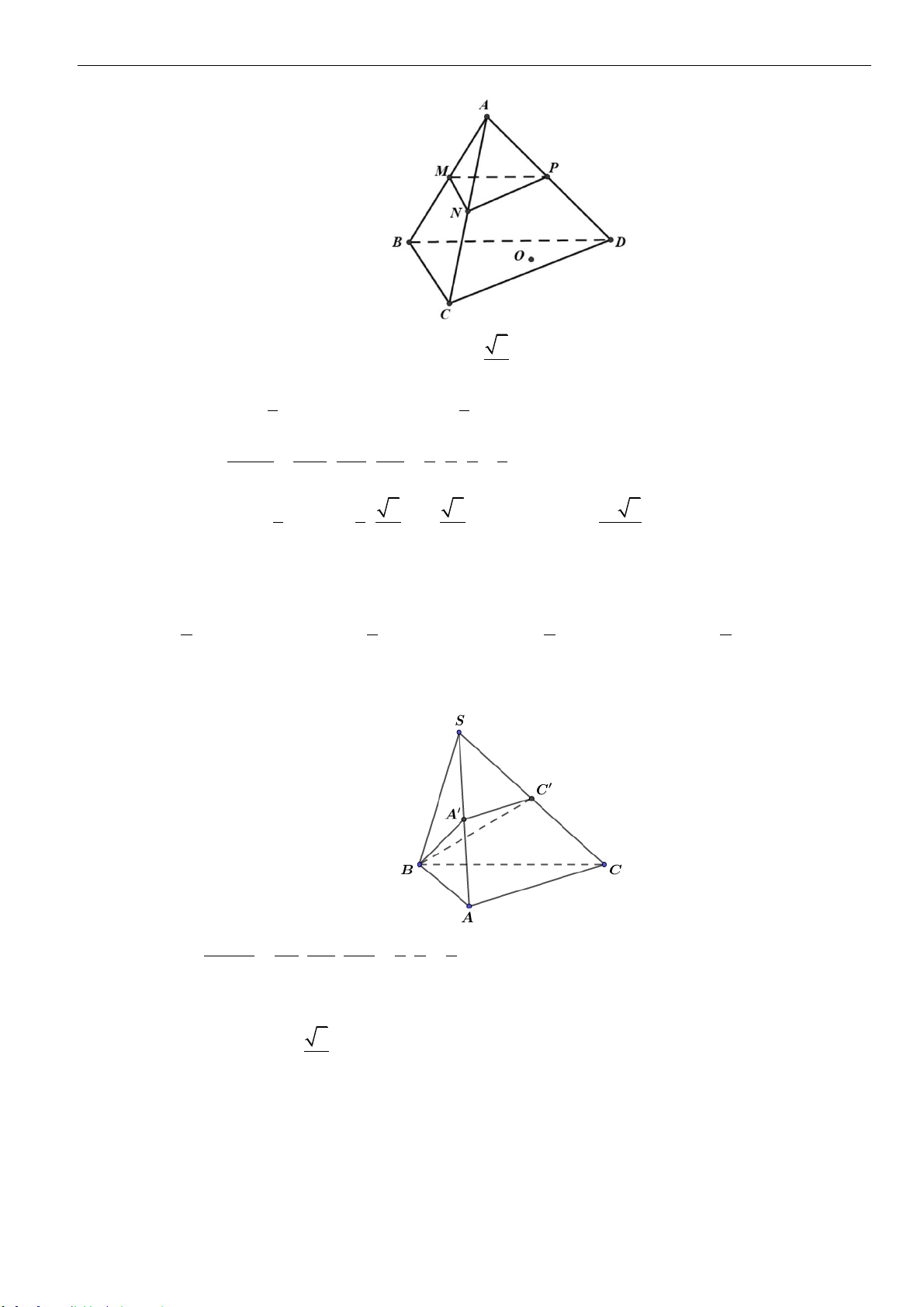
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 14

Chọn A

Thể tích của tứ diện đều

ABCD

là

3

.

12

2

A BCD

Va=

Ta có

( )

..

,

11

33

,

PO MNP MNP A MNMN P

V d O MNP S d A MNP S V



=   ==

Mà ta có

.

1 1 1 1

2 2 2 8

A MNP

A BCD

V

AM AN AP

V AB AC AD

   = = =

Suy ra

3

..

3

22

1

11

8 8 92 6

A MNP A BCD

VV a a=== 

. Vậy

3

.

2

96

O MNP

V

a

=

.

Câu 17: Cho khối chóp

.S ABC

. Gọi

'A

,

'C

lần lượt là trung điểm của

SA

và

SC

. Khi đó tỉ số thể tích

của hai khối chóp

. ' 'S BA C

và

.S ABC

bằng

A.

1

2

. B.

1

3

. C.

1

4

. D.

1

6

.

Lời giải

Chọn C

Ta có

. ' '

.

' ' 1 1 1

. . .

2 2 4

S BA C

S BAC

V

SB SA SC

V SB SA SC

= = =

.

Câu 18: Cho khối tứ diện đều

ABCD

có cạnh bằng

a

. Gọi

M

là điểm trên cạnh

AB

sao cho thể tích

khối

AMCD

bằng

3

2

18

a

. Phát biểu nào sau đây đúng?

A.

32MA MB=

. B.

3MA MB=

. C.

3MA MB=

. D.

2MA MB=

.

Lời giải

Chọn D

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

15 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

3

22

2

12 3

AMCD

ABCD

V

a AM

V MA MB

AB V

=  = =  =

.

Câu 19: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành và

M

là trung điểm cạnh bên

SC

.

Gọi

()P

là mặt phẳng chứa

AM

và song song với

BD

, mặt phẳng

()P

cắt

SB

và

SD

lần lượt

tại

B



và

D



. Tính tỷ số

.

S AB MD

S ABCD

V



.

A.

1

6

. B.

1

3

. C.

3

4

. D.

2

3

.

Lời giải

Chọn B

Trong

( )

SAC

gọi

I SO AM I SO=   

và

I AM

Mà

( )

SO SBD

nên suy ra

( )

I SBD

Trong

( )

SBD

vẽ đường thẳng đi qua

I

và song song với

BD

, cắt cạnh

SB

,

SD

lần lượt tại

'B

và

'D

Từ đó suy ra

( )

/ / ' 'BD AB MD

Xét

SAC

ta có

AM

và

SO

là đường trung tuyến mà

AM SO I=

Từ đó suy ra

I

là trọng tâm

SAC

suy ra

2

3

SI

SO

=

.

Xét

SBO

có

' / /B I BO

ta có

'2

3

SI SB

SO SB

==

Chứng minh tương tự

'2

3

SI SD

SO SD

==

. Ta có

. ' ' . ' . 'S AB MD S AB M S AMD

V V V=+

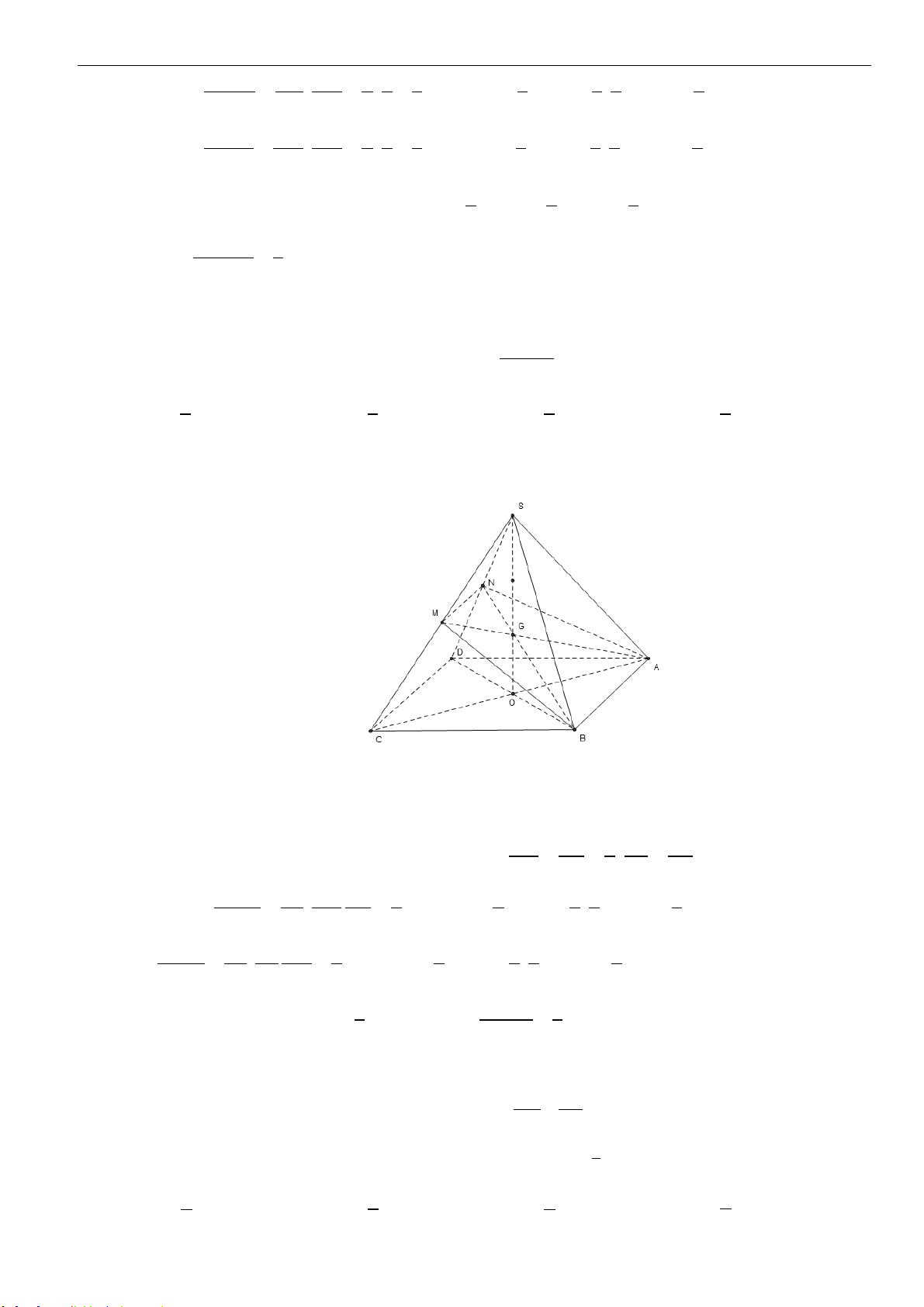
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 16

Ta có

.'

. ' . . .

.

' 2 1 1 1 1 1 1

. . .

3 2 3 3 3 2 6

S AB M

S AB M S ABC S ABCD S ABCD

S ABC

V

SB SM

V V V V

V SB SC

= = =  = = =

Ta có

.'

. ' . . .

.

' 2 1 1 1 1 1 1

. . .

3 2 3 3 3 2 6

S AMD

S AMD S ABC S ABCD S ABCD

S ABC

V

SD SM

V V V V

V SD SC

= = =  = = =

Từ đó suy ra

. ' ' . ' . ' . . .

1 1 1

6 6 3

S AB MD S AB M S AMD S ABCD S ABCD S ABCD

V V V V V V= + = + =

Vậy

. ' '

.

1

3

S AB MD

S ABCD

V

=

.

Câu 20: Cho hình chóp đều

.S ABCD

. Mặt phẳng

( )

P

chứa

AB

và đi qua trọng tâm

G

của tam giác

SAC

cắt

,SC SD

lần lượt tại

,MN

. Tỉ lệ

.

S ABMN

S ABCD

V

T

V

=

có giá trị là

A.

1

.

2

B.

3

.

8

C.

1

.

4

D.

3

.

4

Lời giải

Chọn B

Gọi

O AC BD=

. Mà

.S ABCD

là chóp đều nên

ABCD

là hình vuông

O

là trung điểm của

,AC BD



G

là trọng tâm của tam giác

SAC

thì

G

cũng là của tam giác

SBD

.

,MN

lần lượt là trung điểm của

,SC SD

1

;1

2

SM SN SB SD

SC SD SB SD

 = = = =

Ta có:.

.

. . . .

.

1 1 1 1 1

. . .

4 4 4 2 8

S AMN

S AMN S ACD S ABCD S ABCD

S ACD

V

SA SM SN

V V V V

V SA SC SD

= =  = = =

.

. . . .

.

1 1 1 1 1

. . .

2 2 2 2 4

S ABM

S ABM S ABC S ABCD S ABCD

S ABC

V

SA SB SM

V V V V

V SA SB SC

= =  = = =

. . . .

3

8

S ABMN S AMN S ABM S ABCD

V V V V= + =



.

3

.

8

S ABMN

S ABCD

V

T

V

==

Câu 21: Cho hình chóp

.S ABCD

có thể tích bằng

2

và đáy

ABCD

là hình bình hành. Lấy các điểm

,MN

lần lượt thuộc các cạnh

,SB SD

thỏa mãn

( )

01

SM SN

kk

SB SD

= =  

. Mặt phẳng

( )

AMN

cắt

cạnh

SC

tại

P

. Biết khối chóp

.S AMPN

có thể tích bằng

1

3

, khi đó giá trị của

k

bằng

A.

1

2

. B.

1

3

. C.

2

3

. D.

1

4

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

17 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Lời giải

Chọn A

Gọi

;;O AC BD I MN SO P AI SC=  =  = 

. Ta có:

( )

.

1

.*

2

S AMPN

S ABCD

V

SP SM SN

V SC SB SD



=+





Mà

1

2

SC SB SD SP k

SP SM SN SC k

+ = +  =

−

Do đó:

( )

2

1

11

2

* . .2 6 2 0

2

6 2 2

3

k TM

k

k k k

k

k KTM



=



 =  + − = 



−



=





. Vậy

1

2

k =

Câu 22: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông tâm

O

. Gọi

H

và

K

lần lượt là trung

điểm của

,SB SD

. Tỷ số thể tích

.

AOHK

S ABCD

V

bằng

A.

1

12

. B.

1

6

. C.

1

8

. D.

1

4

.

Lời giải

Chọn C

Gọi

. . 1 2

, , .

S ABCD S ABD AOHK

V V V V V V= = =

Ta có:

1

. . .

SAHK

V

SH SK SH SK

VV

V SB SD SB SD

=  =

;

1

. . .

BHAO

V

BH BO BH BO

VV

V BS BD BS BD

=  =

;

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 18

1

. . .

DAOK

V

DK DO DK DO

VV

V DS DB DS DB

=  =

Ta lại có

( )

2 1 1 1 1 1

. . . . . .

SAHK BHAO DAOK

SH SK BH BO DK DO

V V V V V V V V V

SB SD BS BD DS DB



= − + + = − + +





1 1 1 1 1 1 1

1 1 1 1 1 1 3 1 1 1 1

. . . . . . .

2 2 2 2 2 2 4 4 4 2 8

V V V V V V V V V



= − + + = − = = =





Vậy tỷ số thể tích

2

.

1

.

8

AOHK

S ABCD

V

VV

==

Câu 23: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật. Mặt phẳng

( )



đi qua

,AB

và trung

điểm

M

của

SC

. Mặt phẳng

( )



chia khối chóp đã cho thành hai phần có thể tích lần lượt là

12

,VV

với

12

VV

. Tính tỉ số

1

2

V

.

A.

1

2

1

4

V

=

. B.

1

2

3

8

V

=

. C.

1

2

5

8

V

=

. D.

1

2

3

5

V

=

.

Lời giải

Chọn D

Gọi

( )

N SD



=

||MN CD

, suy ra

N

là trung điểm của

SD

.

Ta có

1,

SA

a

SA

==

1,

SB

b

SB

==

2,

SC

c

SM

==

2

SD

d

SN

==

.

Suy ra

.

4

S ABMN

S ABCD

V

a b c d

V abcd

+ + +

=

1 1 2 2 3

4.1.1.2.2 8

+ + +

==

.

5

8

ABCDMN

S ABCD

V

=

Vậy

1.S ABMN

VV=

,

2 ABCDMN

VV=

và

1

2

3

5

V

=

.

Câu 24: Cho hình chóp tứ giác

.S ABCD

đáy là hình bình hành có thể tích bằng

V

. Lấy điểm

B



,

D



lần lượt là trung điểm của cạnh

SB

và

SD

. Mặt phẳng qua

( )

AB D



cắt cạnh

SC

tại

C



. Khi

đó thể tích khối chóp

.S AB C D

  

bằng

A.

3

V

B.

2

3

V

. C.

3

V

. D.

6

V

.

Lời giải

Chọn D

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

19 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Gọi

O

là giao điểm của hai đường chéo

AC

và

BD

thì

SO B D H



=

. Khi đó

H

là trung

điểm của

SO

và

C AH SO



=

.

Trong mặt phẳng

( )

SAC

: Ta kẻ

( )

//d AC

và

AC



cắt

( )

d

tại

K

. Khi đó áp dụng tính đồng

dạng của các tam giác ta có:

1

OH OA

SK OA

SH SK

= =  = 

1

2

SK

AC

=

;

1

2

SK SC

AC CC



= = 



1

3

SC



=

.

Vì

. . .

1

.

22

S ABD S BCD S ABCD

V

V V V= = =

nên ta có

.

1

4

S AB D

S ABD

V

SA SB SD

V SA SB SD



=   = 

.

1

8

S AB D

VV



=

và

.

1

4

S B C D

S BCD

V

SB SC SD SC

V SB SC SD SC

  

   

=   =  

.

8

S B C D

SC V

V

SC

  



=

.

Suy ra

. . .

1

8 8 8 6

S AB C D S AB D S B C D

SC V V SC V

V V V V

SC SC

       





= + = +  = + =





.

Lưu ý : Có thể sử dụng nhanh công thức

SA SC SB SD

+ = +

   

Câu 25: Cho hình chóp

.S ABCD

có đáy là hình thang vuông tại

A

và

B

.

2,AB BC a==

4AD a=

.

Mặt phẳng

( )



đi qua

A

và trung điểm các cạnh

SB

,

SC

chia khối chóp

.S ABCD

thành hai

khối đa diện. Gọi

V

là thể tích khối đa diện chứa đỉnh

S

,

V



là thể tích khối đa diện không chứa

đỉnh

S

. Tỉ số

V



bằng

A.

5

12

. B.

5

7

. C.

7

12

. D.

7

5

.

Lời giải

Chọn B

Ta có:

MN

là đường trung bình của tam giác

SBC

/ / / /MN BC AD

.

Mặt phẳng

( )



đi qua

A

và chứa

//MN BC

nên

( ) ( )

ABCD AD



=

.

Do đó thiết diện của hình chóp

.S ABCD

khi cắt bởi mặt phẳng

( )



là hình thang

AMND

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 20

Ta có:

1

..

21

2

1

42

..

2

ABC

ACD

AB BC

S BC a

S AD a

AB AD



= = = =

..

11

33

22

33

ABC ABCD S ABC S ABCD

ACD ABCD S ACD S ABCD

S S V V





==









==





.

. . . . . .

. . .

11

. . .

42

1 1 1 2 5

4 3 2 3 12

S AMN S AND S ABC S ACD S ABC S ACD

S ABCD S ABCD S ABCD

SM SN SN

V V V V V V V

SB SC SC

V V V

= + = + = +

   

= + =

   

   

..

7

12

S ABCD S ABCD

V V V V



 = − =

. Do đó,

5

7

V

=



.

Câu 26: Cho khối chóp tứ giác đều

.S ABCD

có cạnh đáy

AB a=

, cạnh bên

2SA a=

. Gọi

M

và

N

lần

lượt là trung điểm

,SA SC

. Mặt phẳng

( )

BMN

cắt

SD

tại

K

.

Thể tích khối chóp

.S MNK

bằng

A.

3

14

112

a

. B.

3

14

84

a

. C.

3

14

12

a

. D.

3

14

144

a

.

Lời giải

Chọn D

Gọi

I MN SO=

, suy ra

I

là trung điểm

SO

.

Gọi

K BI SD=

, suy ra

()K BMN SD=

Áp dụng định lí Menelaus trong tam giác

SOD

, cát tuyến

BIK

.

11

. . 1 . . 1 2

21

BO IS KD KD KD

BD IO KS KS KS

=  =  =

.

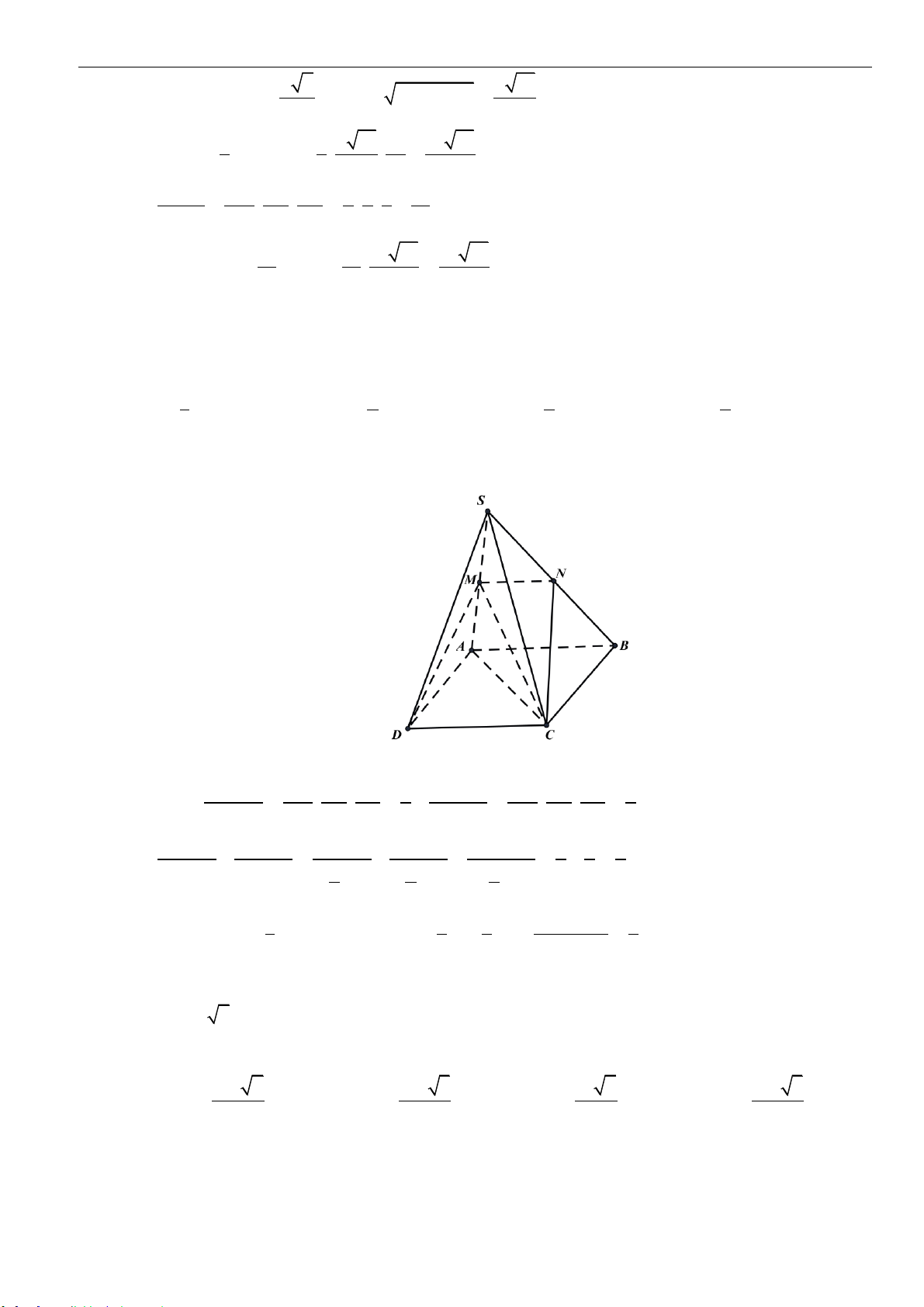
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

21 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

22

2 14

22

aa

AB a OA SO SA OA=  =  = − =

.

23

.

1 1 14 14

. . . .

3 3 2 2 12

S ACD ACD

a a a

V SO S= = =

.

1 1 1 1

. . . .

2 2 3 12

S MNK

S ACD

V

SM SN SK

V SA SC SD

= = =

.

Vậy

33

..

1 1 14 14

.

12 12 12 144

S MNK S ACD

aa

VV= = =

.

Câu 27: Cho hình chóp

.S ABCD

có đáy là hình bình hành. Gọi

,MN

là trung điểm của

,.SA SB

Mặt

phẳng

()MNCD

chia hình chóp đã cho thành hai phần. Tỉ số thể tích hai phần là (số bé chia số

lớn).

A.

3

5

. B.

3

4

. C.

1

3

. D.

4

5

.

Lời giải

Chọn A

Giả sử thể tích của khối chóp

.S ABCD

là

.V

Ta có

.

1

. . ;

2

S MDC

S ADC

V

SM SD SC

V SA SD SC

==

.

1

. . ;

4

S MNC

S ABC

V

SM SN SC

V SA SB SC

==

. . . . .

..

1 1 3

1 1 1

2 4 4

2 2 2

S MDC S MNC S MDC S MNC S MNCD

S ADC S ABC

V V V V V

VV

V V V

+ = + = = + =

.

3 3 5 3

.

8 8 8 5

S MNCD

S MNCD MNABCD

MNABCD

V

V V V V V V

V

 =  = − =  =

Câu 28: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

,

SA

vuông góc với đáy,

2SA a=

. Gọi

, BD



lần lượt là hình chiếu vuông góc của

A

lên

, SB SD

. Mặt phẳng

( )

AB D



cắt

SC

tại

C



. Thể tích khối chóp

.S AB C D

  

là

A.

3

22

3

a

V =

. B.

3

23

3

a

V =

. C.

3

2

9

a

V =

. D.

3

23

9

a

V =

.

Lời giải

Chọn C

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 22

Ta có thể tích khối chóp

.S ABCD

là

3

2

.

1 1 2

. . . . 2

3 3 3

S ABCD ABCD

a

V S SA a a= = =

.

Do đó

3

. . .

12

26

S ABC S ADC S ABCD

a

V V V= = =

.

( )

BC AB

BC SAB BC AB

BC SA

⊥





 ⊥  ⊥



⊥



AB SB

AB SC

AB BC



⊥





⊥





⊥



Tương tự ta chứng minh được

AD SC



⊥

, từ đó suy ra

( )

SC AB D



⊥

và suy ra

SC AC



⊥

.

Xét tam giác

SAB

vuông tại

A

, đường cao

AB



:

2 2 2

2

2 2 2 2 2

22

..

23

SB SA SA a

SA SB SB

SB SB SA AB a a



=  = = = =

++

Tương tự

2

3

SD SA

SD SD



==

.

2 2 2

2 2 2 2 2

21

2 2 2

SC SA SA a

SC SC SA AC a a



= = = =

++

.

Ta có

33

.

..

.

2 1 1 1 1 2 2

. . 1. . .

3 2 3 3 3 6 18

S AB C

S AB C S ABC

S ABC

V

SA SB SC a a

VV

V SA SB SC



= = =  = = =

.

Tương tự

3

.

2

18

S AD C

a

V



=

.

Vậy

3 3 3

. . .

2 2 2

18 18 9

S AB C D S AB C S AD C

a a a

V V V

      

= + = + =

.

Câu 29: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Gọi

,M

N

lần lượt là trung điểm

của các cạnh

,SA

SD

. Mặt phẳng

( )



chứa

MN

cắt các cạnh

,SB

SC

lần lượt tại

,Q

P

. Đặt

SQ

x

SB

=

,

1

V

là thể tích khối chóp

.,S MNPQ

V

là thể tích khối chóp

.S ABCD

. Tìm

x

để

1

2

VV=

.

A.

1

2

x =

. B.

2x =

. C.

1 41

4

x

−+

=

. D.

1 33

4

x

−+

=

.

Lời giải

Chọn D

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

23 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Vì

,MN

lần lượt là trung điểm của

,SA SD

nên

//MN AD

. Mà

//AD BC

, dẫn đến

//MN BC

.

Ta có

( ) ( )

; // // .

//

SBC PQ

SP SQ

MN BC SBC PQ BC MN x

SC SB

MN BC



=





    = =







Đặt

11

2; ; ; 2

SA SB SC SD

a b c d

SM SQ x SP x SN

= = = = = = = =

. Khi đó

.

1

.

11

22

.

11

4

4.2. . .2

S MQPN

S ABCD

V

a b c d

xx

V abcd V

xx

+++

+ + +

=  =

Do

1

2

VV=

nên:

2

1 33

2

1

4

2

2 4 0

16

13

4

x

V

x

xx

V

x



−+

=

+



=  + − = 



−−

=





Vì

0x 

nên

1 33

4

x

−+

=

.

Câu 30: Cho tứ diện

ABCD

, trên các cạnh

BC

,

BD

,

AC

lần lượt lấy các điểm

M

,

N

,

P

sao cho

3BC BM=

,

3

2

BD BN=

,

2AC AP=

. Mặt phẳng

( )

MNP

chia khối tứ diện

ABCD

thành hai

phần có thể tích là

1

V

,

2

V

. Tính tỉ số

1

2

V

.

A.

1

2

26

13

V

=

. B.

1

2

26

19

V

=

. C.

1

2

3

19

V

=

. D.

1

2

15

19

V

=

.

Lời giải

Chọn B

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 24

Gọi

ABCD

VV=

,

I MN CD=

,

Q IP AD=

ta có

( )

Q AD MNP=

.

Thiết diện của tứ diện

ABCD

được cắt bởi mặt phẳng

( )

MNP

là tứ giác

MNQP

.

Áp dụng định lí Menelaus trong các tam giác

BCD

và

ACD

ta có:

. . 1

NB ID MC

ND IC MB

=

1

4

ID

IC

=

và

. . 1

ID PC QA

IC PA QD

=

4

QA

QD

=

.

Áp dụng bài toán tỉ số thể tích của hai khối chóp tam giác, ta có:

ANPQ

ANCD

V

.

AP AQ

AC AD

=

2

5

=

2

5

ANPQ ANCD

VV=

2

15

V=

. Suy ra

.

12

3 15

N PQDC

V V V=−

1

5

V=

.

và

CMNP

CBNA

V

.

CM CP

CB CA

=

1

3

=

1

3

CMNP CBNA

VV=

2

9

V=

.

Suy ra

2.

19

45

N PQDC CMNP

V V V V= + =

.

Do đó

12

V V V=−

26

45

V=

. Vậy

1

2

26

19

V

=

.

Câu 31: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật

, 3,AB a AD a SA a= = =

và

SA

vuông góc với mặt phẳng

( )

ABCD

. Gọi

,HK

lần lượt là hình chiếu vuông góc của

A

lên

,SB SD

. Mặt phẳng

( )

AHK

cắt

SC

tại điểm

P

. Thể tích của khối

.S AHPK

là:

A.

3

40

a

. B.

3

120

a

. C.

3

60

a

. D.

3

30

a

.

Lời giải

Chọn A

Thế tích khối chóp

3

.

13

. . 3.

33

S ABCD

a

V a a a==

và

3

. . .

13

26

S ABC S ACD S ABCD

a

V V V= = =

.

Ta có trong tam giác vuông

SAB

vuông tại

A

và

AH SB⊥

ta được

2

1

2

SH SA

SB SB

==

.

Tương tự, trong tam giác vuông

SAD

vuông tại

A

và

AK SD⊥

ta được

2

1

4

SK SA

SD SD

==

.

Trong mặt phẳng

( )

ABCD

có

AC BD O=

, trong

()SBD

có

SO HK I=

và

AI SC P=

ta có

P

là giao điểm của

( )

AKH

với

SC

.

Ta có công thức

1

241

5

SB SD SA SC SC SP

SH SK SA SP SP SC

+ = +  + = +  =

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

25 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Từ đây ta có

.

1

..

10

S AHP

S ABC

V

SA SH SP

V SA SB SC

==

suy ra

3

..

13

10 60

S AHP S ABC

a

VV==

.

Tương tự

.

1

..

20

S AKP

S ADC

V

SA SK SP

V SA SD SC

==

suy ra

3

..

13

20 120

S AKP S ADC

a

VV==

.

Do vậy

3 3 3

. . .

3 3 3

60 120 40

S AHPK S AHP S AKP

a a a

V V V= + = + =

.

Câu 32: Cho hình chóp

.S ABCD

có đáy là hình bình hành tâm

O

. Gọi

,EF

lần lượt là trung điểm của

,SA SC

và

G

là trọng tâm của tam giác

ABC

. Mặt phẳng

( )

EFG

chia khối chóp

.S ABCD

thành hai phần có thể tích lần lượt là

12

,VV

với

1

V

là thể tích khối đa diện chứa đỉnh

S

. Tỉ số

1

2

V

bằng

A.

1

2

31

59

=

V

. B.

1

2

31

49

=

V

. C.

1

2

25

59

=

V

. D.

.

25

49

=

O AEMF

V

.

Lời giải

Chọn A

Đặt

.

=

S ABCD

VV

.

Vẽ đường thẳng qua

G

và song song với

AC

cắt các đường thẳng

, , ,AD AB BC CD

lần lượt tại

, , ,M H I N

.Gọi

J

là giao điểm của

SO

và

EF

,

K

là giao điểm của

GJ

và

SD

.

Thiết diện tạo bởi mặt phẳng

( )

EFG

và hình chóp

.S ABCD

là ngũ giác

EKFIH

.

Ta chứng minh được:

,,K E M

thẳng hàng và

,,K F N

thẳng hàng;

J

là trung điểm của

SO

.

Theo định lý Menelaus, ta có:

1

. . 1 .1. 1 4

4

=  =  =

GO JS KD KD KD

GD JO KS KS KS

( )

,

4

5

,





 = =





d K ABCD

DK

DS

d S ABCD

Vì

AC

//

MN

nên

4

3

= = =

DM DN DG

DA DC DO

Ta có:

1

. .sin

8

2

29

. .sin

= = =

DMN DMN

ABCD ACD

DM DN ADC

SS

DA DC ADC

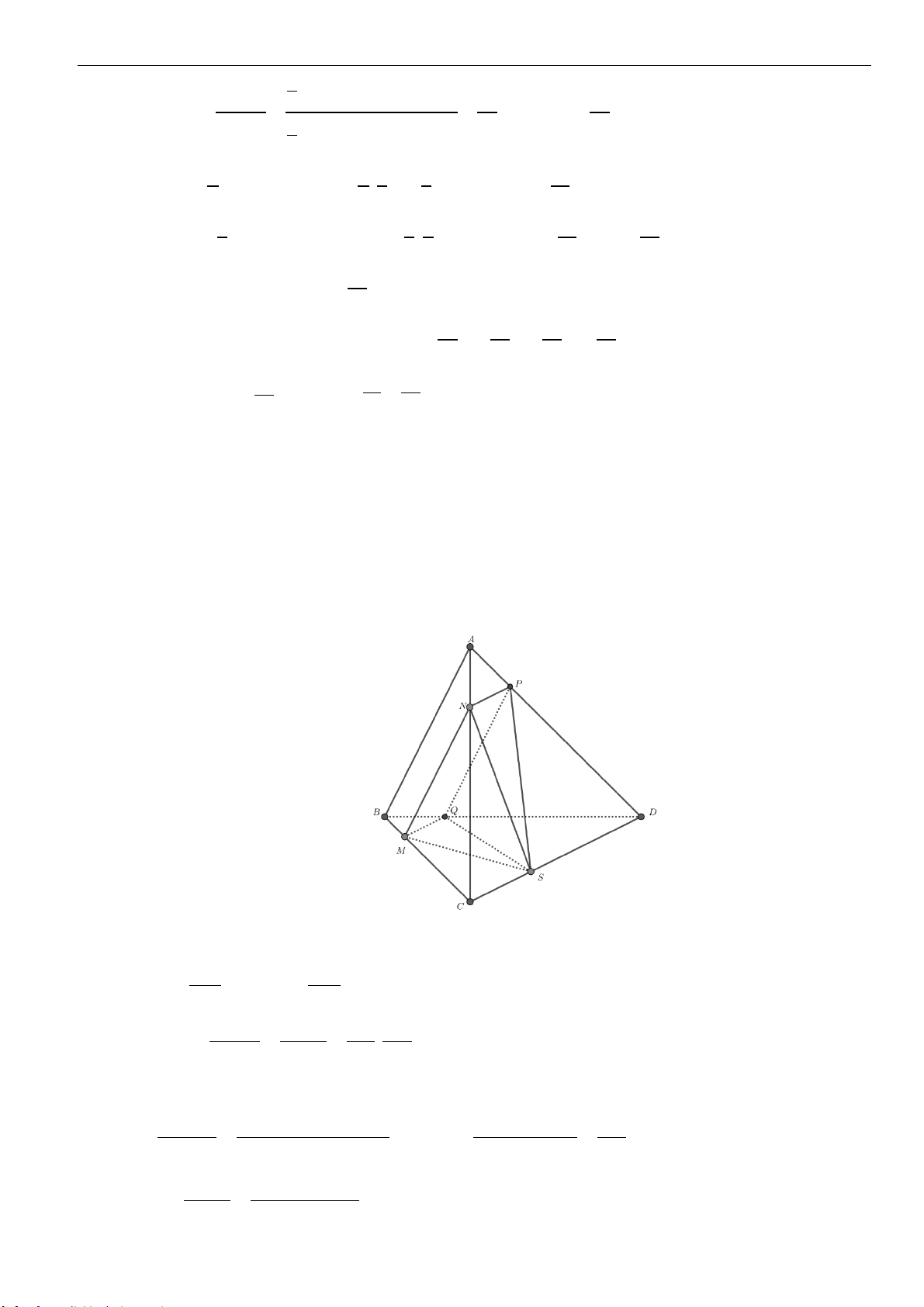
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 26

Suy ra:

( )

.

1

,.

32 32

3

1

45 45

,.

3





= =  =





DMN

K DMN

S ABCD

ABCD

d K ABCD S

V

VV

V

d S ABCD S

1 1 1 1 1

. . .sin . . .sin

2 2 3 3 18

= = =

CIN ABCD

S CI CN ICN DA DC ADC S

( ) ( )

.

1 1 1 1 1

. , . . , .

3 3 2 18 36

= = =

   

   

F CIN CIN ABCD

V d F ABCD S d S ABCD S V

Tương tự, ta có:

.

1

36

=

E AMH

VV

Suy ra:

2 . . .

32 1 1 59

45 36 36 90

= − − = − − =

K DMN F CIN E AMH

V V V V V V V V

12

31

90

= − =V V V V

. Suy ra:

1

2

31

59

=

V

.

Câu 33: Cho tứ diện

ABCD

có thể tích là

3

27cm

. Điểm

M

di động trên

BC

(

M

khác

,BC

), điểm

S

di động trên đường thẳng

CD

. Một mặt phẳng qua

M

song song với hai đường thẳng

,AB CD

đồng thời cắt

,,AC AD BD

lần lượt tại

,,N P Q

. Gọi

V

là thể tích của khối chóp

.S MNPQ

. Khi

,MN

thay đổi thì thể tích lớn nhất của

V

bằng

A.

12

. B.

18

. C.

4

. D.

8

.

Lời giải

Chọn D

Nhận xét:

( )

. . .

//

S MNPQ C MNPQ ABCD C PQD ANPBMQ

CS MNPQ V V V V V = = − +

Đặt

01

CM BM

xx

CB BC

=   = −

.

Ta có:

.

22

.

. .27

C PQD PQD

CPQD

C ABD ABD

VS

DP DQ

x V x

V S DA DB



= = =  =

.

Ta có:

..ANPBMQ N ABQP N BMQ

V V V=+

( )

.

,.

ABQP

N ABQP

C ABD ABD

d N ABD S

V

V d C ABD S

=

, trong đó

( )

,

1

,

d N ABD

AN

x

d C ABD AC

= = −

Và

2

1

ABQP ABD PQD

ABD ABD

S S S

x

SS



−

= = −

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

27 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Suy ra

( )

.

22

.

,.

1 1 1 1 .27

,.

ABQP

N ABQP

C ABD ABD

d N ABD S

V

x x V x x

V d C ABD S

= = − −  = − −

Ta có:

( )

2

.

,.

. . 1

,.

BMQ

N BMQ

A BCD BCD

d N BCD S

V

CN BM BQ

xx

V d A BCD S CA BC BD



= = = −

( )

2

.

1 .27

N BMQ

V x x = −

Nên

( )

2

..

1 1 .27 1 .27

ANPBMQ N ABQP N BMQ

V V V x x x x= + = − − + −

Vậy ta được:

( )

. . .S MNPQ C MNPQ ABCD C PQD ANPBMQ

V V V V V= = − +

( )

2

2 2 3 2

..

27 27 1 1 .27 1 .27 54 54

S MNPQ S MNPQ

V x x x x x V x x



 = − + − − + −  = − +



Xét:

( ) ( ) ( )

( )

3 2 2

0

54 54 , 0; ' 162 108 ; ' 0

2

3

x loai

f x x x x f x x x f x

x

=





= − +  = − + = 



=





Từ bảng biến thiên suy ra thể tích lớn nhất là

8V =

.

Câu 34: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

,

SA

vuông góc với mặt phẳng

( )

ABCD

. Góc giữa hai mặt phẳng

( )

SBD

và

( )

ABCD

bằng

60

. Gọi

M

là điểm đối xứng

của

C

qua

B

và

N

là trung điểm của

SC

. Mặt phẳng

( )

MND

chia khối chóp

.S ABCD

thành hai khối đa diện, trong đó khối đa diện chứa đỉnh

S

có thể tích

1

V

, khối đa diện còn lại có

thể tích

2

V

. Tính tỉ số

2

1

V

A.

2

1

7

5

V

=

. B.

2

1

7

9

V

=

. C.

2

1

9

7

V

=

. D.

2

1

5

7

V

=

.

Lời giải

Chọn D

Goi

O AC BD=

,

K MN SB=

,

I MD AB=

. Khi đó

I

là trung điểm của

AB

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 28

Góc giữa hai mặt phẳng

( )

SBD

và

( )

ABCD

bằng

60

60SOA = 

.

26

.tan60 . 3

22

aa

SA AO =  = =

.

Thể tích khối chóp

.S ABCD

bằng:

1

.

3

ABCD

V SA S=

3

2

1 6 6

..

3 2 6

aa

a==

.

Thể tích khối chóp

.N MCD

bằng thể tích khối chóp

.N ABCD

, gọi thể tích này là

V



thì:

3

16

2 12

a

VV



==

.

Chú ý rằng

11

. . 1

23

NS MC KB KB

KB SB

NC MB KS KS

=  =  =

.

Gọi thể tích khối chóp

KMIB

là

V



thì:

23

1 1 1 6 6

. . . .

3 3 9 2 4 72

MBI

a a a

V SA S



= = =

.

Khi đó:

3 3 3

2

6 6 5 6

12 72 72

a a a

V V V

 

= − = − =

;

3 3 3

12

6 5 6 7 6

6 72 72

a a a

V V V= − = − =

.

Vậy

2

1

5

7

V

=

.

Câu 35: Cho khối chóp

.S ABCD

có đáy

ABCD

là hình bình hành, có thể tích

3

24cm

. Gọi

E

là trung

điểm của

SC

. Một mặt phẳng chứa

AE

cắt các cạnh

SB

và

SD

lần lượt tại

M

và

N

. Tìm

giá trị nhỏ nhất của thể tích khối chóp

.S AMEN

.

A.

3

9cm

. B.

3

8 cm

. C.

3

6 cm

. D.

3

7 cm

.

Lời giải

Chọn B

Gọi

O

là tâm của hình bình hành

ABCD

.

Trong mặt phẳng

( )

SAC

, gọi

I

là giao điểm của

AE

và

SO

. Ta có

,SO AE

là 2 đường

trung tuyến của

SAC

nên

I

là trọng tâm của tam giác

SAC

.

Suy ra

2

3

SI

SO

=

hay

3

2

SO

SI

=

.

Ta có

. . 3

BO SD DO SB SO SB SD

BD SN DB SM SI SM SN

+ =  + =

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

29 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Mà

2.

SB SD SB SD

SM SN SM SN

+

nên

3 2 .

SB SD

SM SN



hay

.4

.9

SM SN

SB SD



.

1 1 . 1 4 1

. . .2. .2.

2 4 . 4 9 3

S AMEN

S ABCD

V

SA SE SM SN SM SN

V SA SC SB SD SB SD



= +   =





.

3

..

11

. .24 8 cm

33

S AMEN S ABCD

VV  = =

.

Dấu đẳng thức xảy ra khi

//

SM SN

MN BD

SB SD

=

.

Vậy thể tích khối chóp

.S AMEN

đạt giá trị nhỏ nhất bằng

3

8 cm

khi

//MN BD

.

Câu 36: Cho hình chóp

.S ABC

thỏa mãn

, 2 , 60 , 90SA a SB SC a ASB ASC= = = =  = 

và

1

cos

23

BSC =

. Thể tích khối chóp đã cho là:

A.

3

26

9

a

V =

. B.

3

2

6

a

V =

. C.

3

6

4

a

V =

. D.

3

23

3

a

V =

.

Lời giải

Chọn A

Trên cạnh

,SB SC

lấy điểm

,EF

tương ứng sao cho

,3SE a SF a==

. Gọi

D

là trung điểm

của

AF

. Ta có:

22

2AF SA SF a AD a= + =  =

và

SAE

đều.

Xét tam giác

SEF

, ta có:

2 2 2 2 2 2

1

2 . cos 3 2. . 3 3 3

23

EF SE SF SE SF ESF a a a a a EF a= + − = + − =  =

.

Do vậy:

2 2 2 2

4AF a AE EF AEF= = +  

vuông tại

E 

1

2

ED AF a==

. Khi đó tứ diện

SAED

là tứ diện đều.

Gọi

M

là trung điểm của

ED

và

H

là trọng tâm của

( )

AED SH AED  ⊥

. Ta có:

3

22

.

3 3 6 1 1 3 6 2

. . .

2 3 3 3 2 2 3 12

S AED

a a a a a a

AM AH SH SA AH V a=  =  = − =  = =

Mặt khác

3

..

2

22

6

AEF AED S AEF S AED

a

S S V V=  = =

. Ta lại có:

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 30

33

.

..

.

3 3 4 4 2 2 6

. . . .

2 2 4 6 9

33

S AEF

S ABC S AEF

S ABC

V

SE SF a a a a

VV

V SB SC a a

= = =  = = =

.

Câu 37: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật. Một mặt phẳng thay đổi luôn song

song với mặt phẳng chứa đa giác đáy và cắt các cạnh bên

SA

,

SB

,

SC

,

SD

lần lượt tại

I

,

J

,

K

,

L

. Gọi

E

,

F

,

G

,

H

lần lượt là hình chiếu vuông góc của

I

,

J

,

K

,

L

lên mặt phẳng

( )

ABCD

. Thể tích khối đa diện

.IJKL EFGH

đạt giá trị lớn nhất khi

SI a

SA b

=

(

,*a b N

,

a

b

là

phân số tối giản). Giá trị biểu thức

22

T a b=+

bằng

A.

10T =

. B.

5T =

. C.

13T =

. D.

25T =

.

Lời giải

Chọn C

Theo đề bài ta suy ra được

.IJKL EFGH

là hình hộp chữ nhật. Do đó:

.

..

IJKL EFGH

V IE IJ IL=

.

Gọi

SI

x

SA

=

( )

01x

. Ta có:

( )

1

,

IE AI

x

AS

d S ABCD

= = −



( ) ( )

( )

1,IE x d S ABCD=−

.

IJ SI

x

AB SA

==



.IJ x AB=

.

IL SI

x

AD SA

==



.IL x AD=

.

Vậy

( ) ( )

( )

2

.

1 , . .

IJKL EFGH

V x x d S ABCD AB AD=−



( )

2

..

1 .3

IJKL EFGH S ABCD

V x x V=−

.

Xét hàm số

( )

2

1y x x=−

,

( )

01x



2

32y x x



= − +

. Có

( )

0

2

3

xl

y

xn

=







=



=





Bảng biến thiên:

Vậy thể tích khối đa diện

.IJKL EFGH

đạt giá trị lớn nhất khi

2

3

SI

SA

=



2a =

,

3b =

.



22

13T a b= + =

.

Câu 38: Cho hình chóp

.S ABCD

có đáy là hình bình hành, gọi

G

là trọng tâm tam giác

SAD

, mặt

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

31 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

phẳng

( )



chứa

BG

và song song với

AC

cắt

,,SA SD SC

lần lượt tại

,,A D C

  

. Tỉnh số

.

S A BC D

S ABCD

V

  

bằng

A.

3

8

. B.

9

20

. C.

5

16

. D.

117

128

.

Lời giải

Chọn B

Nhắc lại công thức tỉ số thể tích liên quan khối chóp tứ giác:

Cho hình chóp tứ giác

.S ABCD

. Một mặt phẳng

( )



cắt các cạnh

SA

,

SB

,

SC

,

SD

lần lượt

tại

A



,

B



,

C



,

D



.

Đặt

SA

x

SA



=

,

SB

y

SB



=

,

SC

z

SC



=

,

SD

t

SD



=

. Khi đó ta có:

.

1 1 1 1

4

1 1 1 1

S A B C D

S ABCD

V

xyzt

V x y z t

x z y t

   





= + + +













+ = +





.

Gọi

M

là trung điểm

AD

; gọi

N

là giao điểm của

BM

và

AC

; gọi

I

là giao điểm của

SN

và

BG

.

Dễ thấy:

( ) ( )

( )

//

SAC A C

AC





=











//AC A C





và

I A C





.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 32

Theo đề bài:

G

là trọng tâm

SAD

1

3

MG

MS

=

.

AMN CNB∽

1

2

MN AM

BN CB

 = =

1

3

MN

MB

=

.

Suy ra

//GN SB

và

1

3

GN

SB

=

1

3

AA IN GN

SA SI SB



 = = =



.

Do đó

3

4

SA SC



==

.

Áp dụng công thức trên, ta được:

SD SB SA SC

+ = +

  

SD SA SC SB

 = + −

  

4 4 5

1

3 3 3

= + − =

.

Suy ra

3

5

SD



=

.

Vậy

.

S A BC D

S ABCD

V

  

3 3 3

.1. .

4 4 5

.1

4 3 3 3



= + + +





9

20

=

.

Câu 39: Cho hình chóp tứ giác đều

.S ABCD

có đáy là hình vuông tâm

O

, cạnh đáy bằng

2a

, góc giữa

hai mặt phẳng

( )

SAB

và

( )

ABCD

bằng

o

45

. Gọi

M

,

N

,

P

lần lượt là trung điểm của

SA

,

SB

và

AB

. Thể tích khối tứ diện

DMNP

bằng

A.

3

6

a

. B.

3

12

a

. C.

3

2

a

. D.

3

4

a

.

Lời giải

Chọn A

Dễ thấy

OP

là đường trung bình trong

ABC

nên

2

BC

OP a==

.

Mặt khác góc giữa hai mặt phẳng

( )

SAB

và

( )

ABCD

bằng góc

SPO

và bằng

o

45

.

Xét

SPO

vuông tại

O

, có

o

45SPO =

SPO

vuông cân tại

O

, suy ra

SO OP a==

.

Thể tích khối chóp

.S ABCD

bằng

.S ABCD

V =

1

..

3

ABCD

SO S =

2

1

. .4

3

aa

3

4

3

a

=

.

Suy ra

.S ABD

V =

3

.

12

23

S ABCD

a

V =

.

Xét

SAB

với

MN

,

NP

,

PM

là các đường trung bình, suy ra

1

4

MNP

SAB

S

=

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

33 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Ta có

.

D MNP

S ABD

V

=

( )

1

.d , .

1

3

1

4

.d , .

3

MNP

SAB

D SAB S

=

.

Vậy

..

1

.

4

D MNP S ABD

VV=

33

12

.

4 3 6

aa

==

.

Câu 40: Cho lăng trụ

. ' ' 'ABC A B C

có thể là

V

. Gọi

M

là điểm nằm trên cạnh

'BB

sao cho

2 3 'MB MB=

, điểm

N

nằm trên cạnh

AA'

sao cho

4'AN NA=

, điểm

P

nằm trên cạnh

'CC

sao cho

3'CP C P=

. Các đường thẳng

NM

và

PM

cắt các cạnh

''AB

và

''CB

lần lượt tại

H

và

K

. Hãy tính theo

V

thể tích của khối tứ diện

'MB HK

.

A.

16

105

V

. B.

6

35

V

. C.

4

15

V

. D.

2

7

V

.

Lời giải

Chọn A

Ta có

2

2 3 ' ' '

5

MB MB M B BB=  =

,

4

4 ' NA' '

5

AN NA AA=  =

3

3 ' ' '

4

CP C P C P CC=  =

Vì

'/ / 'MB A N

nên

' ' 1

' ' '

' ' 2

HB B M

HB A B

HA A N

= =  =

'/ /C'PMB

nên

' ' 8 ' 8

KC' C'P 15 ' ' 7

KB B M KB

BC

= =  =

( ) ( )

, ' ', 'd H KC d A KC=

Khi đó:

'

' 'C'

'8

' ' 7

HKB

AB

S

KB

S B C



==

Ta có

( )

; ' '

'2

'5

B; ' '

d M A B C

MB

BB

d A B C

==

( )

. ' ' ' ' '

1 1 2 8 16

. ; ' .S . B; ' . .S

3 3 5 7 105

M KHB HKB A C B

V d M HKB d HKB V



= = =

Câu 41: Cho tứ diện

ABCD

. Hai điểm

,MN

lần lượt di động trên hai đoạn thẳng

BC

và

BD

sao cho

2. 3. 10

BC BD

BM BN

+=

. Gọi

12

,VV

lần lượt là thể tích của các khối tứ diện

ABMN

và

ABCD

. Tìm

giá trị nhỏ nhất của

1

2

.

V

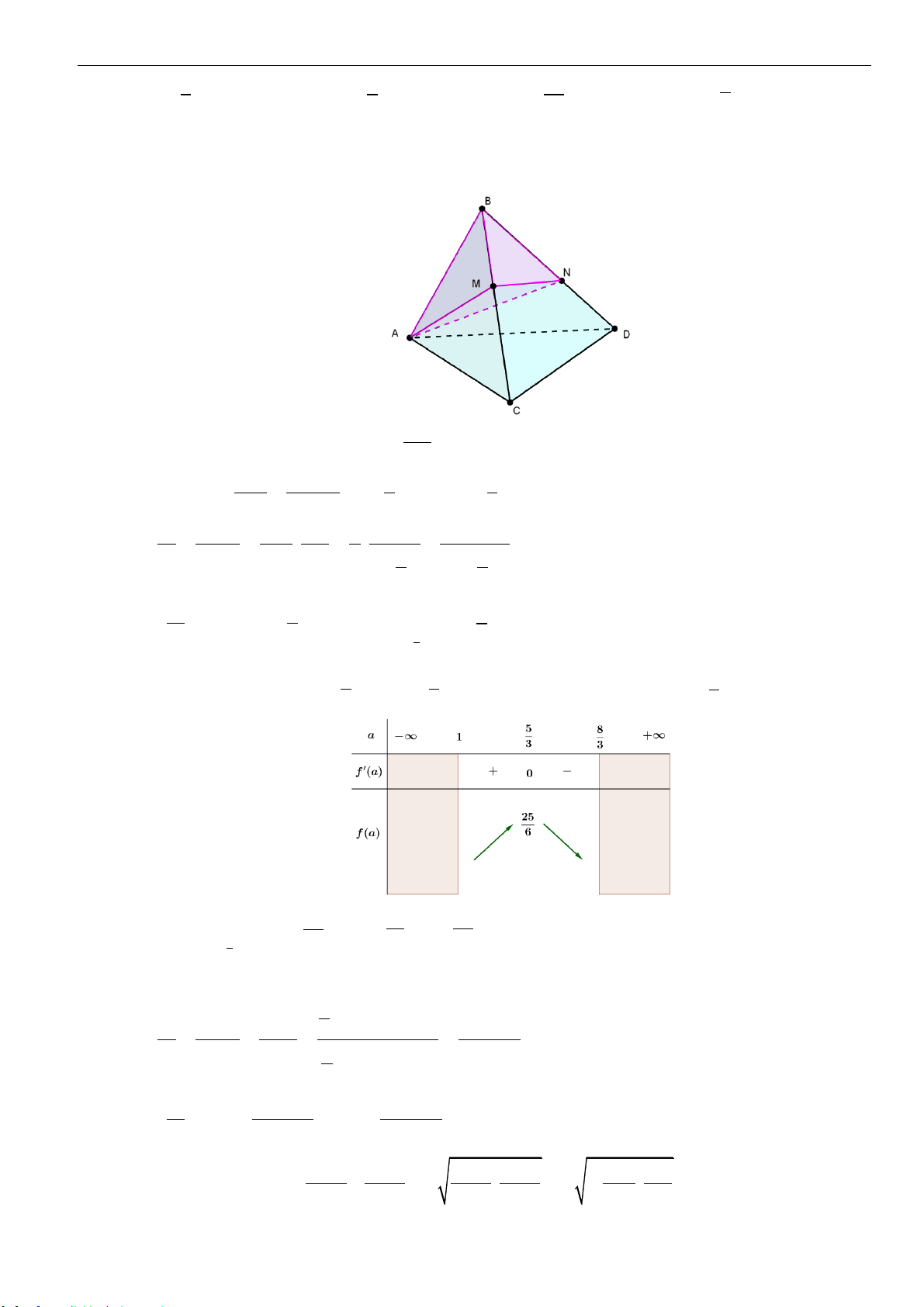
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 34

A.

3

.

8

B.

2

.

7

C.

6

.

25

D.

5

.

8

Lời giải

Chọn C

Cách 1

Vì

,M BC N BD

nên ta đặt

( )

1

BD

aa

BN

=

.

Suy ra

10 3 3 8

1 5 1 .

2 2 3

BC a

aa

BM

−

 = = −   

1

2

1 1 1

..

33

55

22

ABMN

ABCD

V

BM BN

V V BC BD a

a a a

= = = =

−−

.

2

1

2

min

3

5

2

max

V

aa

V



−





. Tìm

2

8

1;

3

5

2

max a a









−





.

Xét hàm số

( )

2

38

5 , 1;

23

f a a a a



= − 





;

( ) ( )

5

' 5 3 ; ' 0 .

3

f a a f a a= − =  =

Suy ra

( )

8

1;

3

25

max .

6

fa







=

Vậy

1

2

min

6

.

25

V



=





Cách 2

1

2

1

. . .sin

.

2

1

.

. . .sin

2

ABMN BMN

ABCD BCD

BM BN B

VS

V

BM BN

V V S BC BD

BC BD B

= = = =

.

1

min

2

min

..

.

..

max

V

BM BN BC BD

V BC BD BM BN



   





   

   



Theo giả thiết;

2. 3. 2. 3.

10 2. . 2. 6. .

BC BD BC BD BC BD

BM BN BM BN BM BN

= +  =

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

35 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

. . 25

5 6. .

. . 6

BC BD BC BD

BM BN BM BN

   

Do đó

1

2

min

6

.

25

V



=





Đẳng thức xảy ra

2. 3. 2

.

5

3

2. 3. 10 .

5

BC BD

BM BC

BM BN

BC BD

BN BD

BM BN



==









+ = =





.

Câu 42: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông cân tại

B

,

AB a=

,

AB SA⊥

,

BC SC⊥

. Gọi

,MN

lần lượt là trung điểm của

SC

,

AC

. Góc giữa hai mặt phẳng

( )

BMN

và

( )

SAB

là



thỏa mãn

5

cos

3



=

. Thể tích khối chóp

.S BMN

bằng bao nhiêu?

A.

3

24

a

. B.

3

a

. C.

3

12

a

. D.

3

6

a

.

Lời giải

Chọn C

Gọi H là hình chiếu vuông góc của S lên mặt phẳng (ABC).

Ta có:

BA SH

BA HA

BA SA

⊥



⊥



⊥



;

BC SH

BC HC

BC SC

⊥



⊥



⊥



. Suy ra tứ giác

HABC

là hình vuông.

Gọi K là trung điểm HC; P là trung điểm BC; E là trung điểm NH; trong mặt phẳng (MKE) kẻ

KQ ME⊥

()Q ME

. Khi đó:

( ) ( )

( );( ) ( );( )BMN SAB BMN PMN



=  = 

, vì

( ) / /( )PMN SAB

( )

;( ) ( ;( )d P BMN d K PMN KQ==

, vì

//KP HB

.

( )

;

2

a

d P MN PN==

;

52

cos sin

33



=  =

.

Ta có:

( )

( ) ( )

;( )

2

sin ;( ) ; .sin .

; 2 3 3

d P BMN

aa

d P BMN d P MN

d P MN



=  = = =

.

Xét tam giác MKE vuông tại K có:

2 2 2 2

1 1 1 1

KM a

KM KQ KE a

= − =  =

2SH a=

.

Có:

2 3 3

. . .

1 1 1

. . .2 .

3 3 2 3 2 6

S ABC ABC S BNC S ABC

a a a

V SH S a V V= = =  = =

.

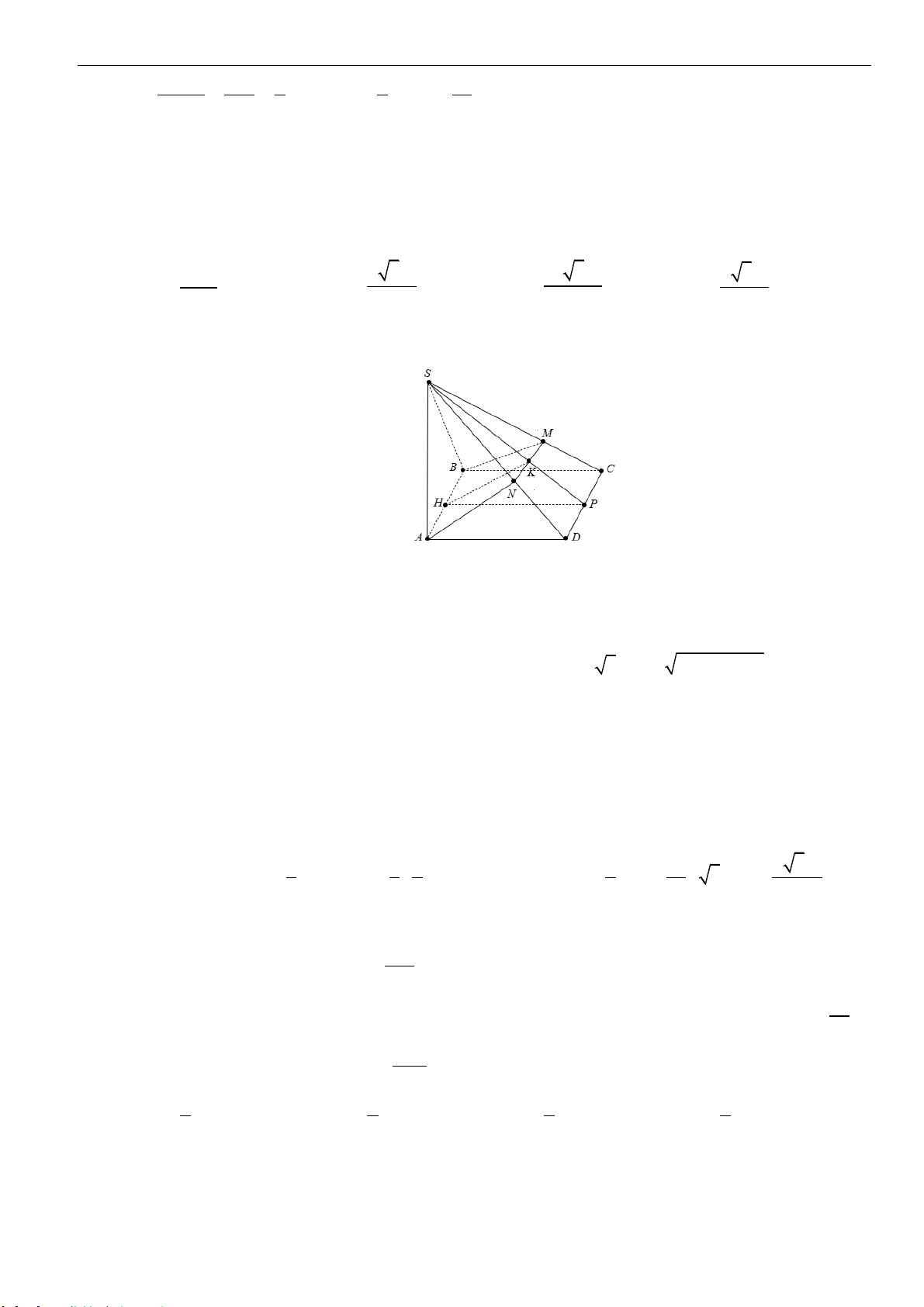
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 36

3

.

..

.

11

2 2 12

S BNM

S BNM S BNC

S BNC

V

SM a

VV

V SC

= =  = =

.

Câu 43: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

2a

. Hình chiếu vuông góc của

S

với mặt phẳng đáy là trung điểm cạnh

AB

và

( )

SCD

tạo với đáy một góc

0

60

. Mặt phẳng chứa

AB

và vuông góc với

( )

SCD

cắt

,SC SD

lần lượt tại

M

và

N

. Thể tích của khối chóp

.S ABMN

bằng

A.

3

21

4

a

. B.

3

73

2

a

. C.

3

21 3

4

a

. D.

3

73

4

a

.

Lời giải

Chọn D

Gọi

H

là trung điểm của cạnh

( )

AB SH ABCD⊥

. Gọi

P

là trung điểm của

CD

.

Suy ra

( )

CD HP

CD SHP

CD SH

⊥



⊥



⊥



. Do vậy :

( ) ( )

( )

0 0 2 2

, 60 .tan60 2 3; 4SCD ABCD SPH SH HP a SP SH HP a= =  = = = + =

.

Kẻ

( ) ( ) ( )

HK SP HK SCD ABK SCD⊥  ⊥  ⊥ 

( ) ( )

ABCD ABK

.

Mặt khác

( )

( ) ( )

//

/ / / /

AB CD

AB ABMN ABMN SCD MN CD AB

CD SCD





   =









nên

MN

là đường thẳng

đi qua

K

và song song với

CD

.

Ta có :

( )

3

.

1 1 1 1 3 7 3

. . . 2 3 .3 .

3 3 2 6 2 4

S ABMN ABMN

aa

V V SK AB MN HK SK a a a

   

= = + = + =

   

   

Câu 44: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành và có thể tích là

V

. Gọi

M

là một

điểm trên cạnh

AB

sao cho

MA

x

AB

=

,

01x

. Mặt phẳng

( )



qua

M

và song song với

( )

SBC

chia khối chóp

.S ABCD

thành hai phần, trong đó phần chứa điểm

A

thể tích bằng

4

27

V

. Tính giá trị của biểu thức

1

x

P

x

−

=

+

.

A.

1

2

. B.

1

5

. C.

1

3

. D.

3

5

.

Lời giải

Chọn A

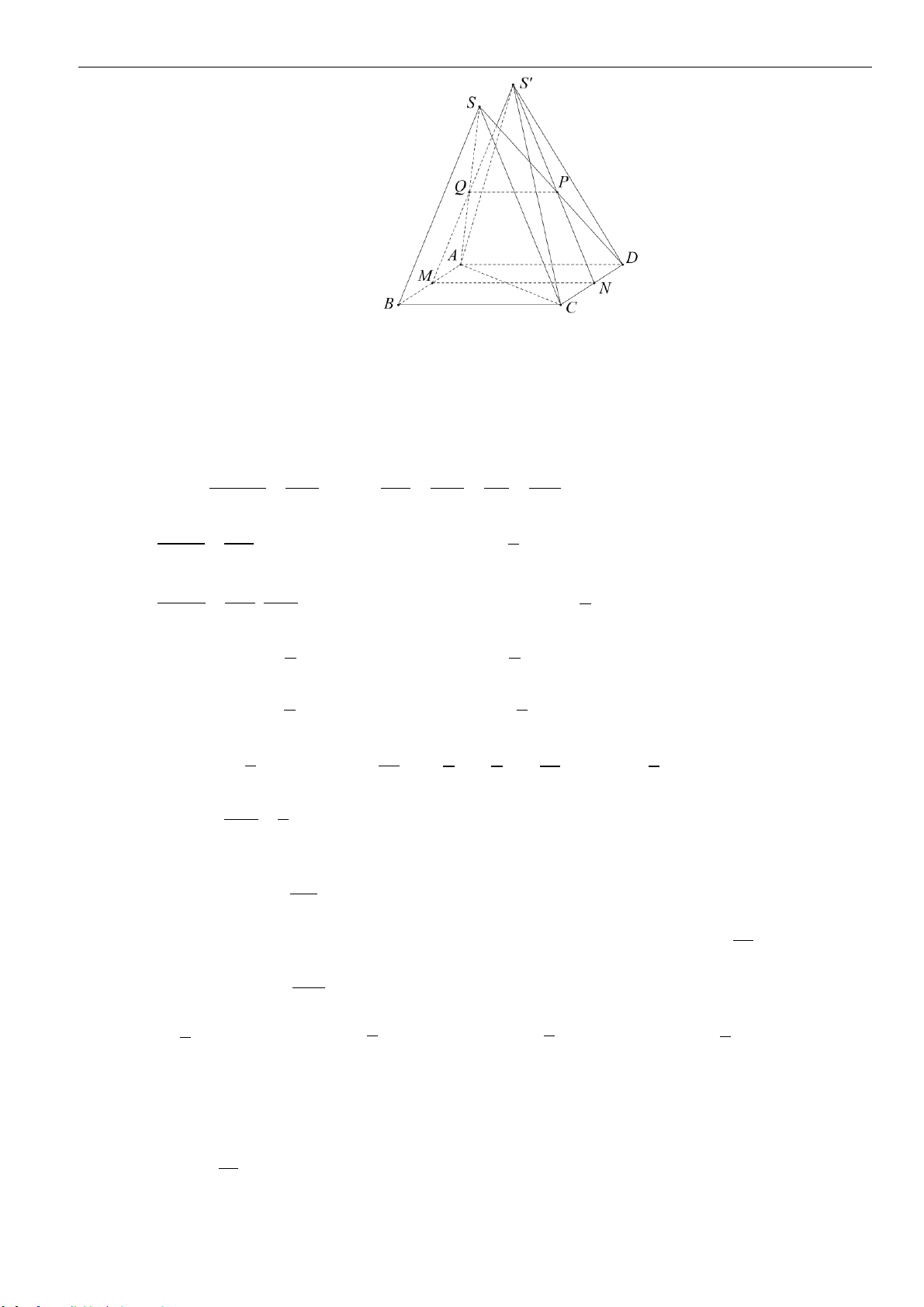
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

37 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Trong

( )

ABCD

, kẻ

//MN BC

,

N CD

. Trong

( )

SAB

, kẻ

//MQ SB

,

Q SA

.

Trong

( )

SAD

, kẻ

//QP AD

,

P SD

. Dễ thấy thiết diện là hình thang

MNPQ

.

Gọi

S MQ NP



=

, suy ra

SS



là giao tuyến của

( )

SAB

và

( )

SCD

,

// //SS AB CD



.

Suy ra

( )

;;d S ABCD d S ABCD



=

.

Ta có:

.

S AMND

S ABCD

V

AM

x

V AB



==

và

1

S P S Q SQ BM

x

S N S M SA AB



= = = = −



.

1

S PDA

S NAD

V

SP

x

V S N



= = −



( )

..

1

S PDA S NAD

V x V



 = −

( )

.

1

2

S MNDA

xV



=−

.

( )

2

.

.1

S PQA

S NMA

V

S P S Q

x

V S N S M





= = −



( ) ( )

22

. . .

1

11

2

S PQA S NMA S MNDA

V x V x V

  

 = − = −

.

Suy ra

( ) ( )

2

..

1

1 1 .

2

S PQDA S MNDA

V x x V





= − + −



( )

2

.

1

32

2

S MNDA

x x V



= − +

( )

2

.

1

1 3 2

2

PQMNDA S MNDA

V x x V





 = − − +





( )

2

.

1

1 3 2

2

S ABCD

x x x V



= − − +





Gt

( )

2

14

1 3 2

2 27

x x x



 − − + =





32

1 3 4

0

2 2 27

xx − + − =

1

3

x=

.

Vậy

11

12

x

P

x

−

==

+

.

Câu 45: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành có thể tích là

V

. Gọi

M

là một điểm

trên

AB

sao cho

,0 1

MA

xx

AB

=  

. Mặt phẳng

( )



qua

M

và song song với

( )

SBC

chia khối

chóp

.S ABCD

thành hai phần, trong đó phần chứa điểm

A

có thể tích bằng

4

27

V

. Tính giá trị

của biểu thức

1

x

P

x

−

=

+

.

A.

1

2

. B.

1

5

C.

1

3

. D.

3

5

Lời giải

Chọn A

Mặt phẳng

( )



được dựng thành mặt phẳng

( )

MEGF

Khi đó:

. . . . .

4

27

F AME G ADE E AFG F AMED E AFG

V V V V V V= + + = +

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 38

( )

. . . .

.

,

44

..

27 27

,

F AMED E AGF E AGF G AED

AMED

ABCD E AGD

d F ABCD

V V V V

S

V V S V V

d S ABCD

 = +  = +

( )

2 2 2

.

2 2 3 2

4 1 4 1 4 1

. . . . . . .

27 2 7 2 27 2

1

3

4 1 1 3 4

1 . . 0 2,97

27 2 2 2 27

0,3

AGF F AMED

AGD

SV

AM AM FG SF

x x x x

AB AB S V AD SA

xn

x x x x x x l

xl



 = +  = +  = +



=



 = + −  − + =  



−





11

12

x

PP

x

−

 =  =

+

.

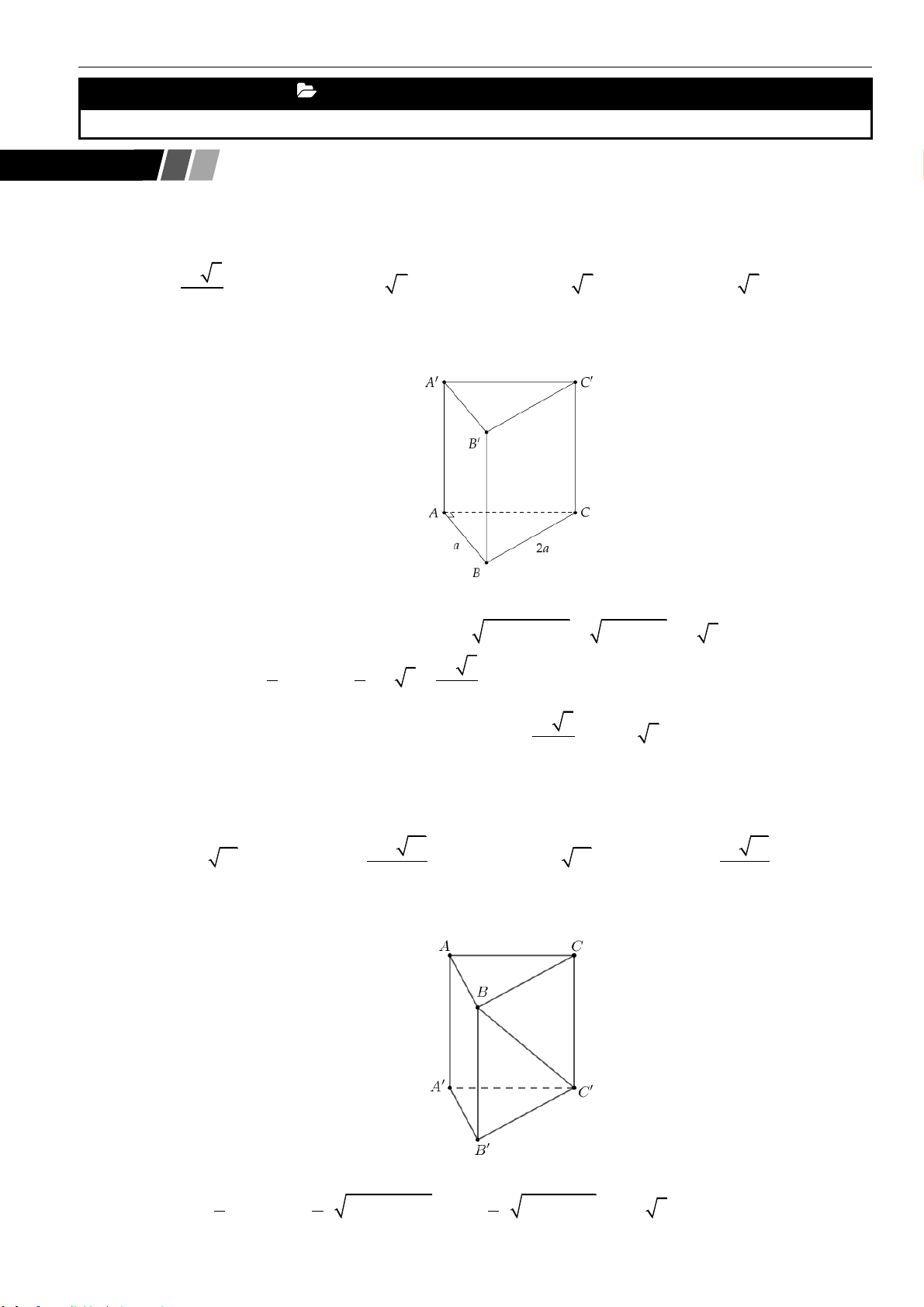
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

1 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Dạng 7: Thể tích khối lăng trụ đứng

Câu 1: Lăng trụ đứng

.ABC A B C

  

có đáy

ABC

là tam giác vuông tại

A

,

2BC a=

,

AB a=

. Mặt bên

BB C C



là hình vuông. Khi đó thể tích lăng trụ là

A.

3

a

. B.

3

2a

. C.

3

23a

. D.

3

3a

.

Lời giải

Chọn D

Vì

BB C C



là hình vuông nên

2BB BC a



==

.

Vì tam giác

ABC

vuông tại

A

nên

2 2 2 2

43AC BC AB a a a= − = − =

.

Ta có

2

1 1 3

. . . 3

2 2 2

ABC

a

S AB AC a a



= = =

.

Vậy thể tích của lăng trụ đứng là

2

3

. .2 3

2

ABC

a

V S BB a a





= = =

.

Câu 2: Cho hình lăng trụ đứng

.ABC A B C

  

có đáy

ABC

là tam giác vuông tại

C

,

3AB a=

,

2BC a=

. Góc giữa

BC



và mặt phẳng

( )

ABC

bằng

60

. Tính thể tích khối lăng trụ đó.

A.

3

2 15a

. B.

3

2 15

3

a

. C.

3

15a

. D.

3

15

3

a

.

Lời giải

Chọn A

Tam giác

ABC

vuông tại

C

nên diện tích:

2 2 2 2 2

1 1 1

9 4 2 5

2 2 2

ABC

S CA CB AB BC BC a a a a=   =  −  =  −  =

.

VÍ DỤ MINH HỌA

B

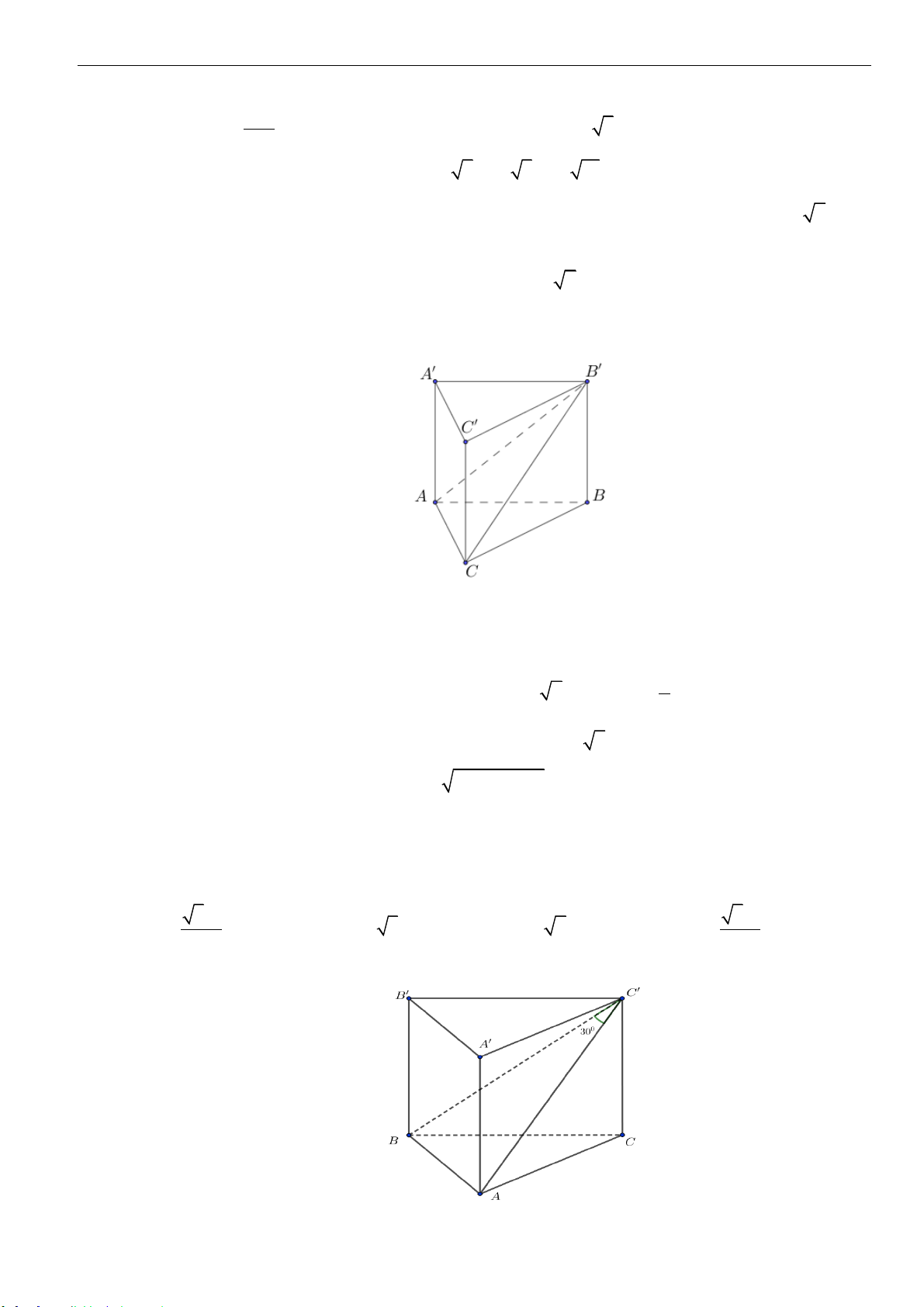
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 2

Góc giữa

BC



và

( )

ABC

là góc

60C BC



=

. Tam giác

CC B



vuông tại

C

nên

tan tan 2 tan60 2 3

CC

C BC CC BC C BC a a

BC



  

=  =  =   =

.

Thể tích khối lăng trụ

23

5 2 3 2 15

ABC

V S CC a a a



=  =  =

.

Câu 3: Cho khối lăng trụ đứng

.ABC A B C

  

có đáy

ABC

là tam giác vuông cân tại

, 2 2.C BC =

Góc

giữa đường thẳng

AB



và mặt phẳng

( )

BCC B



bằng

30 .

Thể tích của khối lăng trụ đã cho bằng

A.

12

. B.

4

. C.

42

. D.

16

.

Lời giải

Chọn D

Ta có

( )

,AC BC AC CC AC BCC B

  

⊥ ⊥  ⊥

.

Mà

( ) ( )

( )

, 30AB BCC B B AB BCC B AB C

       

 =  = = 

.

Tam giác

ABC

vuông cân tại

C

nên

22AC BC==

và

1

. 4.

2

ABC

S CACB



==

.

Tam giác

AC B



vuông tại

,C

có

.cot 2 6.B C AC AB C



==

Tam giác

CBB



vuông tại

22

4B BB B C BC



 = − =

. Vậy

.

. 16.

ABC A B C ABC

V S BB

  





==

Câu 4: Cho khối lăng trụ đứng

.ABC A B C

  

có đáy là tam giác

ABC

vuông tại

A

,

AC a=

,

60ACB =

. Đường thẳng

BC



tạo với mặt phẳng

( )

A C CA



một góc

30

. Tính thể tích khối

lăng trụ đã cho.

A.

3

2

a

. B.

3

23a

. C.

3

6a

. D.

3

a

.

Lời giải

Chọn C

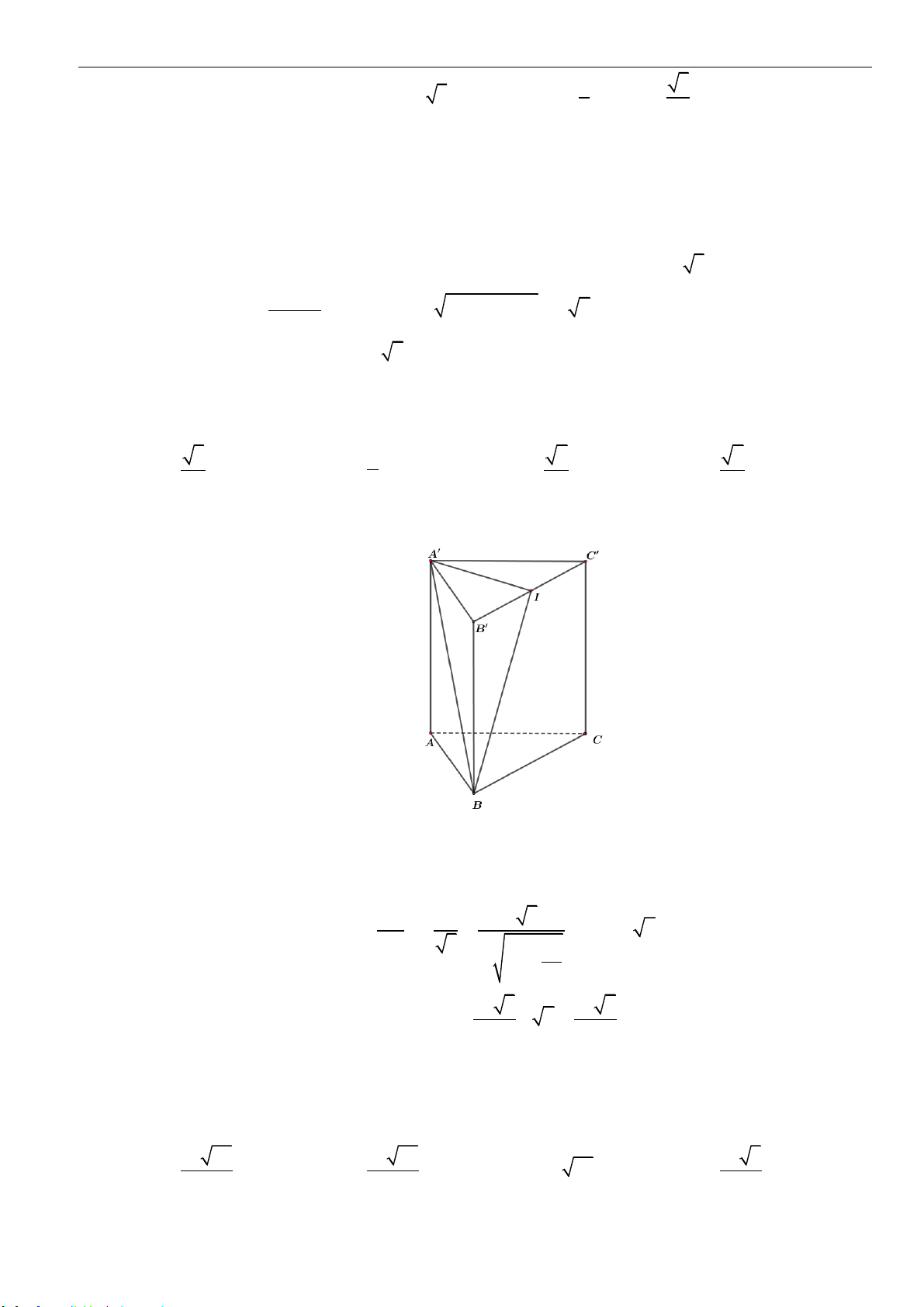
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

3 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Theo giả thiết,

.tan60 3AB AC a=  =

. Suy ra

2

13

.

22

ABC

S AB AC a



==

Mặt khác:

( )

AB AC

AB A C CA

AB AA

⊥





⊥





⊥



AC





là hình chiếu vuông góc của

BC



trên

( )

A C CA



.

Suy ra

( )

, , 30BC A C CA BC AC BC A

     

= = = 

.

Do

( )

AB A C CA



⊥

nên

AB AC ABC



⊥  

vuông tại

A

có

3AB a=

,

30BC A



=

.

Khi đó,

22

3 2 2

tan30

AB

AC a CC AC AC a

  

= =  = − =



.

Vậy

3

.

.6

ABC A B C ABC

V S CC a

  





==

.

Câu 5: Cho khối lăng trụ tam giác đều

.ABC A B C

  

có

AB a=

, góc giữa đường thẳng

AB



và mặt

phẳng

( )

BCC B



bằng

30

. Thể tích khối lăng trụ đã cho bằng

A.

3

2

a

. B.

3

4

a

. C.

3

6

12

a

. D.

3

6

4

a

.

Lời giải

Chọn D

Gọi

I

là trung điểm của

B C A I B C

    

⊥

.

Khi đó

( ) ( )

( )

, , 30

A I B C

A I BB C C A B BB C C A B BI A BI

A I BB

  

⊥



       

 ⊥  = = = 





⊥



Đặt

h BB



=

. Ta có

2

13

tan30 2

3

2.

4

A I a

ha

BI

a

h



 =  =  =

+

Suy ra thể tích khối lăng trụ đã cho là

23

36

.2

44

aa

Va==

.

Câu 6: Cho hình hộp đứng

.ABCD A B C D

   

có đáy

ABCD

là hình vuông. Gọi

S

là tâm hình vuông

A B C D

   

. Gọi

M

và

N

lần lượt là trung điểm của

SA

và

BC

. Biết rằng, nếu

MN

tạo với mặt

phẳng

( )

ABC D

một góc bằng

0

60

và

AB a=

thì thể tích khối chóp

.S ABC

bằng

A.

3

30

12

a

. B.

3

30

3

a

. C.

3

30a

. D.

3

2

a

.

Lời giải

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 4

Chọn A

Gọi

I

là tâm của đáy

ABCD

suy ra

( )

SI ABCD⊥

.

Kẻ

( )

MH ABCD⊥

//NH SI

,

1

2

NH SI=

và

H

là trung điểm của đoạn

AI

đồng thời suy ra

( )

, 60MN ABCD MNH= = 

.

Xét tam giác

HC N

có

22

3 3 3 2

4 4 4

a

HC AC AB BC= = + =

;

1

22

a

CN BC==

;

45HCN =

,

theo định lý côsin ta có

2 2 2 2

5

2 . .cos

8

HN HC CN HC CN HCN a= + − =

10

4

a

HN=

.

Do đó

10 30

.tan .tan60

44

aa

MH HN MNH= =  =

30

2

a

SI HM = =

.

Lại có diện tích của tam giác

ABC

là

2

1

.

22

ABC

a

S AB BC==

.

Vậy

3

.

1 30

..

3 12

S ABC ABC

a

V SI S==

.

Câu 7: Cho lăng trụ đứng

.ABC A B C

  

có đáy

ABC

là tam giác đều cạnh bằng

2.a

Biết diện tích tam

giác

A BC



bằng

2

23a

. Tính thể tích khối lăng trụ

.ABC A B C

  

.

A.

3

93a

. B.

3

63a

. C.

3

33a

D.

3

3a

Lời giải

Chọn C

Thể tích khối lăng trụ

.ABC A B C

  

bằng

.

ABC

S AA



.

a

60

0

H

N

M

I

S

A'

B'

C'

D'

A

D

C

B

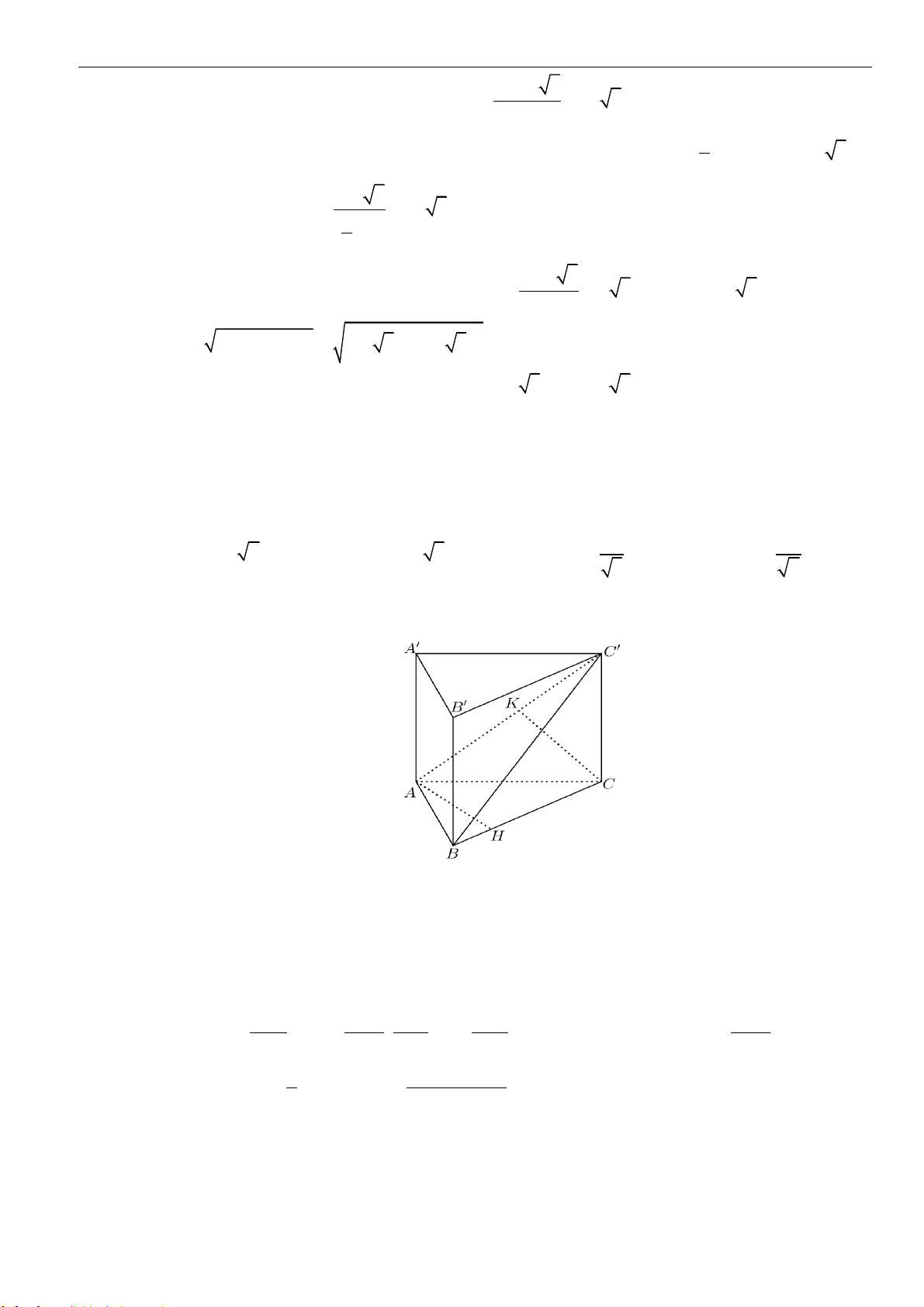
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

5 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Vì tam giác

ABC

đều nên có diện tích bằng

( )

2

23

3

4

a

a=

.

Gọi

H

là trung điểm cạnh

BC

. Tam giác

A BC



cân tại

A



nên

2

1

. . 2 3

2

A BC

S BC A H a



==

.

Với

2

23

2 2 3

1

.2

2

a

BC a A H a

a



=  = =

.

Xét tam giác

A AH



vuông tại

A

có cạnh

( )

23

3

2

a

AH a==

và

23A H a



=

, suy ra

( ) ( )

22

2 3 3 3 .AA A H AH a a a



= − = − =

Vậy thể tích khối lăng trụ

.ABC A B C

  

bằng:

23

3.3 3 3a a a=

Câu 8: Cho lăng trụ đứng

.ABC A B C

  

có đáy

ABC

là tam giác vuông tại

A

. Khoảng cách từ đường

thẳng

AA



đến mặt phẳng

( )

BCC B



bằng khoảng cách từ điểm

C

đến mặt phẳng

( )

ABC



và

cùng bằng

1

. Góc giữa hai mặt phẳng

( )

ABC



và

( )

ABC

bằng



. Tính

tan



khi thể tích khối

lăng trụ

.ABC A B C

  

nhỏ nhất.

A.

tan 2



=

. B.

tan 3



=

. C.

1

tan

3



=

. D.

1

tan

2



=

.

Lời giải

Chọn D

Gọi

H

là hình chiếu vuông góc của

A

lên

BC

, khi đó

( )

,1d A BCC B AH



==

.

Gọi

K

là hình chiếu vuông góc của

C

lên

AC



, do

( )

AB ACCA AB CK



⊥  ⊥

khi đó

( )

CK ABC



⊥

hay

( )

,1d C ABC CK



==

.

Ta có

( ) ( )

( )

,ABC ABC CAC





==

.

Ta có

22

1 1 1 1 1

; ; 1 1 sin cos

sin cos cos

AC CC AB

AB AC



  



= = = − = − =  =

.

Vậy

.

2

11

..

2

2sin .cos

ABC A B C

V AB AC CC



  



==

.

Thể tích khối lăng trụ

.ABC A B C

  

nhỏ nhất hhi

( )

22

sin .cos sin 1 sin

   

=−

đạt giá trị lớn

nhất

Đặt

( )

sin , 0;1tt



=

.

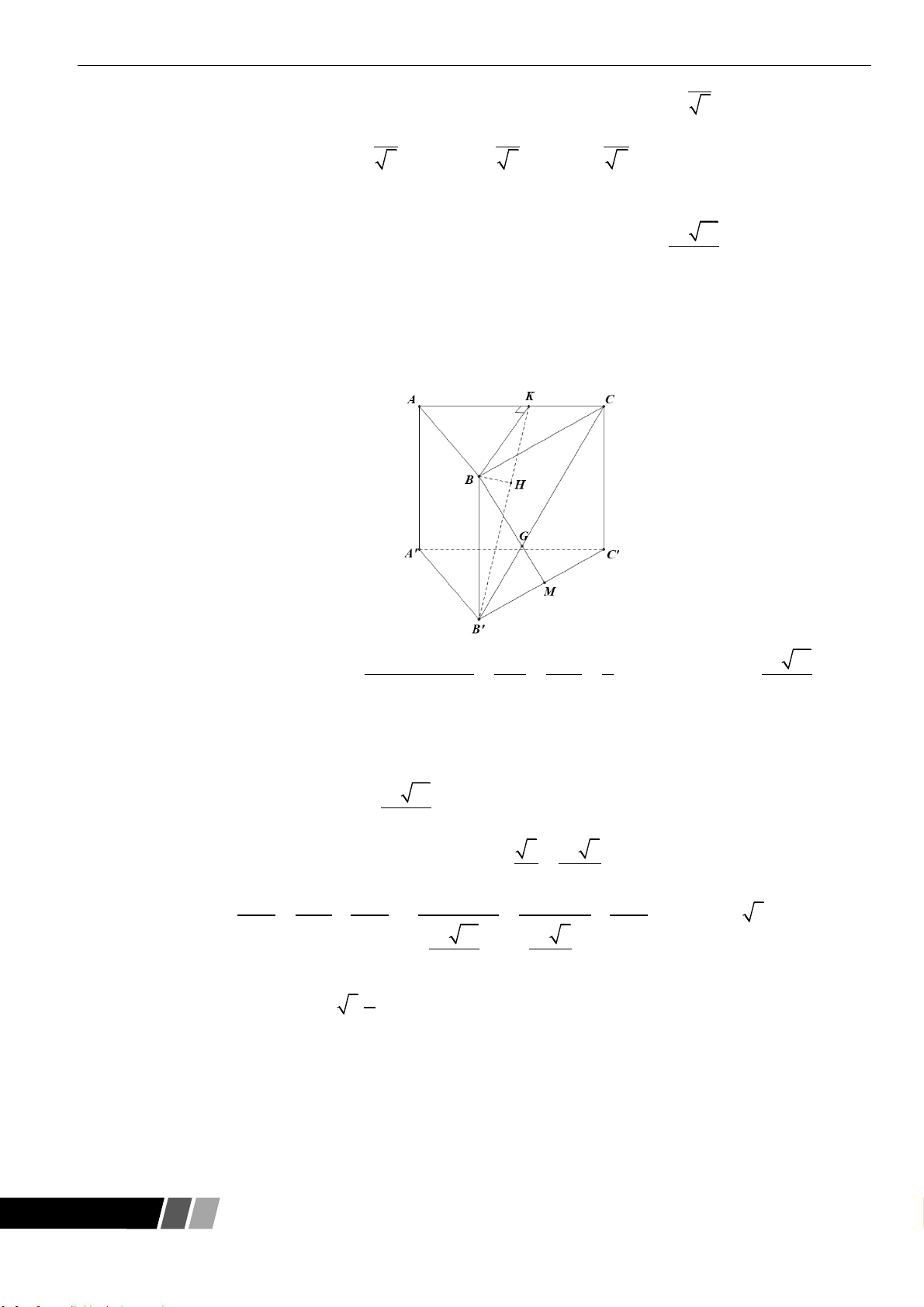
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 6

Xét

( )

3

f t t t= − +

trên

( )

0;1

, ta có

( ) ( )

2

1

3 1 0

3

f t t f t t



= − +  =  =

.

Vậy

( )

ft

đạt GTLN khi

1

3

t =

hay

11

sin tan

32



=  =

.

Câu 9: Cho khối lăng trụ đứng

.ABC A B C

  

có

60BAC =

,

3AB a=

và

4AC a=

. Gọi

M

là trung

điểm của

BC



, biết khoảng các từ

M

đến mặt phẳng

( )

B AC



bằng

3 15

10

a

. Thể tích khối lăng

trụ bằng

A.

3

4a

B.

3

27a

C.

3

7a

D.

3

9a

Lời giải

Chọn B

Gọi

B C BM G



=

, ta có:

( )

;

1 3 15

;

; 2 5

d M B AC

MG B M a

d B B AC

d B B AC BG BC



= = =  =



.

Kẻ

BK AC⊥

, mà

AC BB



⊥

nên

( ) ( ) ( )

AC BB K B AC BB K

  

⊥  ⊥

.

( ) ( )

B AC BB K B K

  

=

, trong mp

( )

B BK



kẻ

BH B K



⊥

, khi đó:

( )

BH B AC



⊥

.

Do đó:

( )

3 15

;

5

a

d B B AC BH



==

.

AKB

vuông tại

K

nên

3 3 3

.sin60 3 .

22

o

a

BK AB a= = =

.

Mặt khác:

2 2 2 2 2 2

1 1 1 1 1 1

33

3 15 3 3

52

BB a

BH BK BB BB

aa



= +  = +  =



   

   

   

.

Vậy

3

1

. 3 3. .3 .4 .sin60 27

2

o

ABC

V BB S a a a a





= = =

.

BÀI TẬP TRẮC NGHIỆM

C

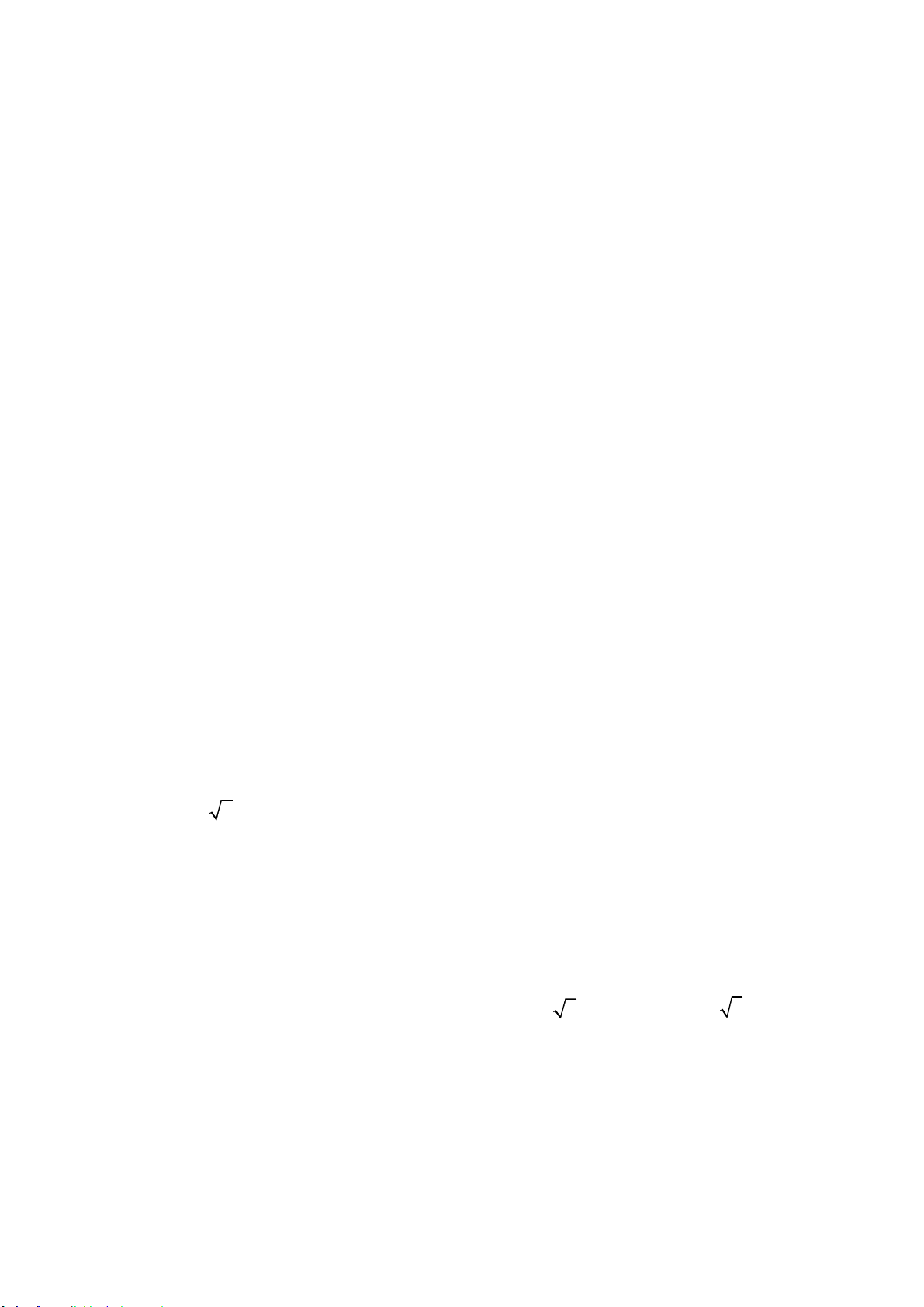
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

7 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 1: Một khối lăng trụ có thể tích bằng

V

, diện tích mặt đáy bằng

S

. Chiều cao của khối lăng trụ đó

bằng

A.

S

V

. B.

3V

S

. C.

V

S

. D.

3

S

V

.

Lời giải

Chọn C

Gọi

h

là chiều cao của khối lăng trụ.

Ta có thể tích khối lăng trụ là

.

V

V S h h

S

=  =

.

Câu 2: Thể tích khối hộp chữ nhật có các kích thước 2, 3, 4 là

A.

6

. B.

8

. C.

72

. D.

24

.

Lời giải

Chọn D

Ta có: thể tích khối hộp chữ nhật ba kích thước

a

,

b

,

c

là

..V a b c=

.

Vậy thể tích khối hộp chữ nhật cần tìm là:

2.3.4 24V ==

.

Câu 3: Cho khối lăng trụ có diện tích đáy bằng 5 và chiều cao bằng 3. Thể tích của khối lăng trụ đã cho

bằng

A.

45

. B.

24

. C.

5

. D.

15

.

Lời giải

Chọn D

Thể tích khối lăng trụ là:

5.3 15V ==

.

Câu 4: Khối lăng trụ có diện tích đáy là

2

6 cm

và có chiều cao là

3 cm

thì có thể tích

V

là

A.

3

6 cmV =

. B.

3

108 cmV =

. C.

3

54 cmV =

. D.

3

18 cmV =

.

Lời giải

Chọn D

Ta có

3.6 18V ==

.

Câu 5: Khối hộp chữ nhật có cách kích thước lần lượt là

, 2 , 3a a a

có thể tích bằng

A.

3

32

5

a

. B.

3

6a

. C.

3

2a

. D.

2

6a

.

Lời giải

Chọn B

3

.2 .3 6V a a a a==

.

Câu 6: Cho khối hộp chữ nhật

. ' ' ' 'ABCD A B C D

có

1 , ' 3 , 2= = =AB m AA m BC m

. Thể tích của khối

hộp đã cho bằng

A.

3

3m

. B.

3

6m

. C.

3

35m

. D.

3

5m

.

Lời giải

Chọn B

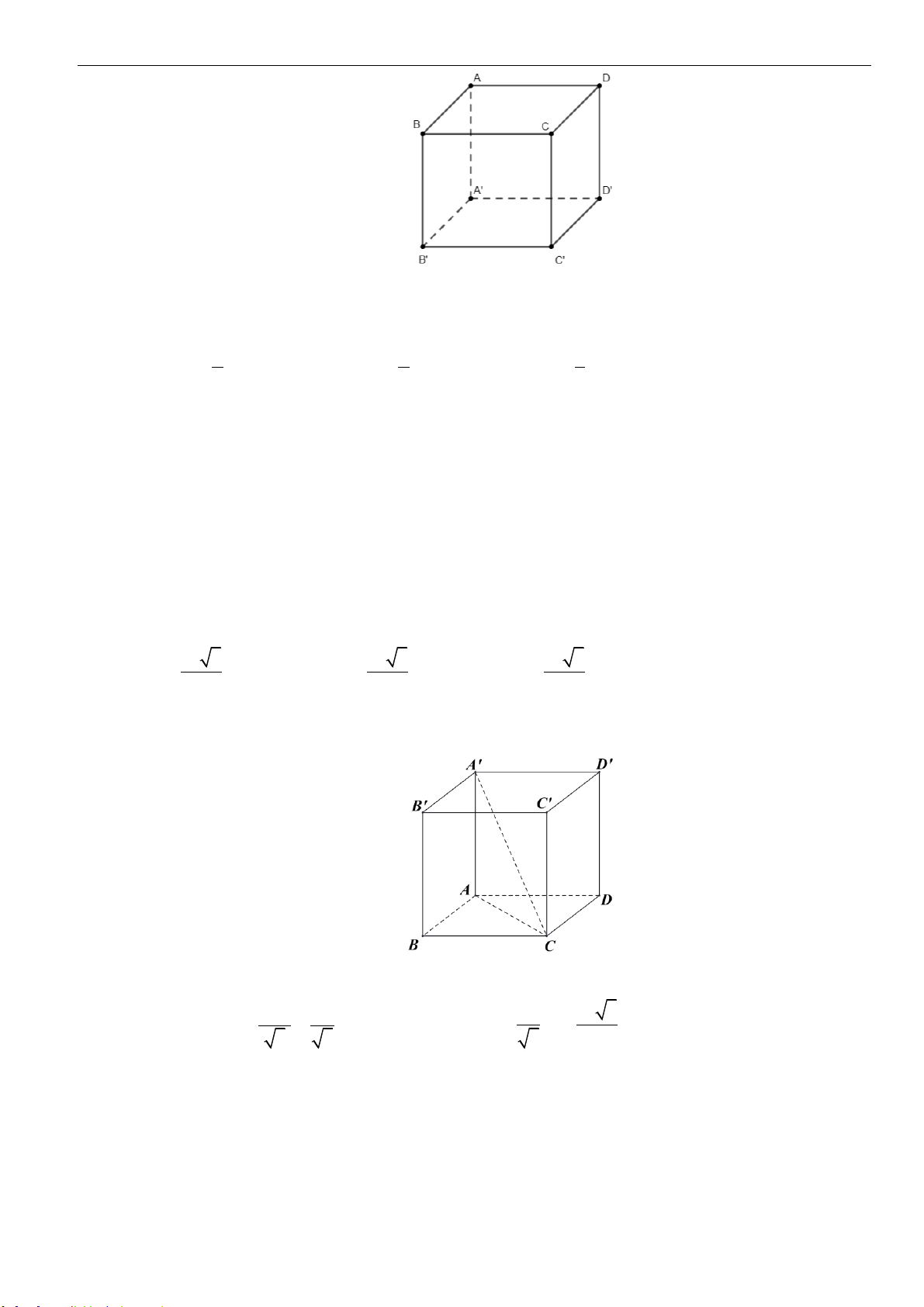
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 8

Thể tích của khối hộp đã cho là:

3

'. '. . 6= = =

ABCD

V AA S AA AB BC m

.

Câu 7: Thể tích khối lăng trụ có diện tích đáy bằng

B

và chiều cao bằng

h

là

A.

4

.

3

V B h=

. B.

1

.

2

V B h=

. C.

1

.

3

V B h=

. D.

.V B h=

.

Lời giải

Chọn D

Ta có

.V B h=

.

Câu 8: Cho khối hộp chữ nhật có ba kích thước là

4,5,6

. Thể tích của khối hộp đã cho bằng:

A.

120

. B.

80

. C.

40

. D.

60

.

Lời giải

Chọn A

Thể tích khối hộp chữ nhật là:

4.5.6 120V ==

.

Câu 9: Khối lập phương

.ABCD A B C D

   

có độ dài đoạn

A C a



=

. Thể tích khối đó là

A.

3

.

9

a

B.

3

.

6

a

C.

3

.

3

a

D.

3

.a

Lời giải

Chọn A

Ta có:

2 2 2 2 2 2 2

3A C AA AC AA AB BC AB

  

= + = + + =

.

Suy ra:

33

A C a

AB



==

. Do đó:

3

.

3

9

3

ABCD A B C D

aa

V

   



==





.

Câu 10: Cho khối lăng trụ đứng

. ' ' 'ABC A B C

có

'BB a=

, đáy

ABC

là tam giác vuông tại

A

và

2 , 3AB a AC a==

. Tính thể tích

V

của khối lăng trụ đã cho.

A.

3

.a

B.

3

6.a

C.

3

3.a

D.

3

2.a

Lời giải

Chọn C

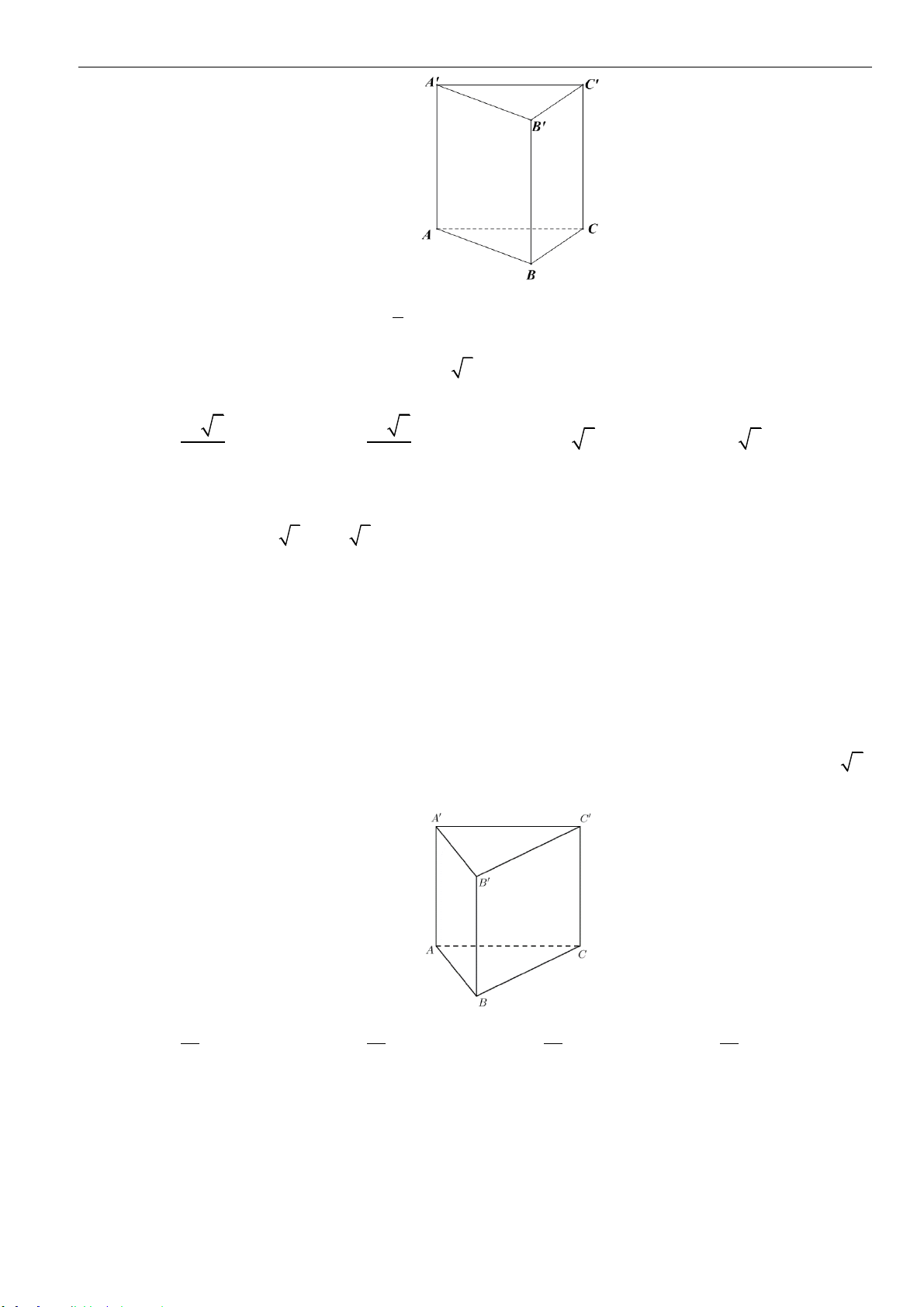
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

9 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Ta có:

3

.

1

. . .2 .3 3

2

ABC A B C ABC

V BB S a a a a

  



= = =

.

Câu 11: Cho khối lăng trụ có diện tích đáy

2

3Ba=

và chiều cao

ha=

. Thể tích của khối lăng trụ đã

cho bằng

A.

3

4

a

. B.

3

a

. C.

3

33a

. D.

3

3a

.

Lời giải

Chọn D

Ta có

23

. 3 . 3V B h a a a= = =

.

Câu 12: Cho một hình hộp chữ nhật có 3 kích thước bằng 12,15 và 20. Tính thể tích của hình hộp chữ

nhật đó.

A.

3600V =

. B.

1800V =

. C.

60V =

. D.

2880V =

.

Lời giải

Chọn A

Thể tích của hình hộp chữ nhật đó là

. . 12.15.20 3600V a b c= = =

.

Câu 13: Cho khối lăng trụ đứng

.ABC A B C

  

có đáy

ABC

là tam giác vuông cân tại

B

. Biết

2C A a



=

và

45AC C



=

(tham khảo hình vẽ). Thể tích của khối lăng trụ đã cho bằng

A.

3

6

a

. B.

3

12

a

. C.

3

4

a

. D.

3

2

a

.

Lời giải

Chọn C

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 10

Trong

ACC





có

2

.sin 2.

2

AC AC AC C a a



= = =

;

2

.cos 2.

2

CC AC AC C a a

  

= = =

.

Trong

BAC

có

2 2 2 2 2

2

AC a

AC BA BC AC BA BA= +  =  = =

.

Thể tích của khối lăng trụ là

23

2

.

11

. . . . .

2 2 2 4

ABC A B C ABC

aa

V CC S CC BA a

  





= = = =

.

Câu 14: Cho lăng trụ đứng

.ABC A B C

  

có đáy là tam giác đều cạnh bằng

2

. Mặt phẳng

()AB C



tạo

với mặt đáy bằng

45



. Thể tích lăng trụ

.ABC A B C

  

bằng

A.

3

B.

42

C.

6

D.

22

Lời giải

Chọn A

Xét

()AB C



và

()ABC

  

: Gọi

M

là trung điểm của

BC



, vì tam giác

ABC

  

đều nên

A M B C

  

⊥

, mặt khác lăng trụ

.ABC A B C

  

là lăng trụ đứng nên

AA B C

  

⊥

. Do đó

()AA M B C

  

⊥

. Vậy

(( ),( )) 45AB C A B C AMA



     

==

.

Tam giác

AA M



vuông tại

A



và có

45AMA





=

nên vuông cân tại

A



do đó

23

3

2

AA A M



= = =

;

2

2 . 3

3

4

ABC

S

  

==

Suy ra

.

. 3. 3 3

ABC A B C A B C

V AA S

     



= = =

.

Câu 15: Cho hình lăng trụ đứng

.ABC A B C

  

có tất cả các cạnh bằng

a

. Tính thể tích

V

của khối lăng

trụ

.ABC A B C

  

.

A.

3

2

a

V =

. B.

3

2

3

a

V =

. C.

3

2

a

V =

. D.

3

4

a

V =

.

Lời giải

Chọn D

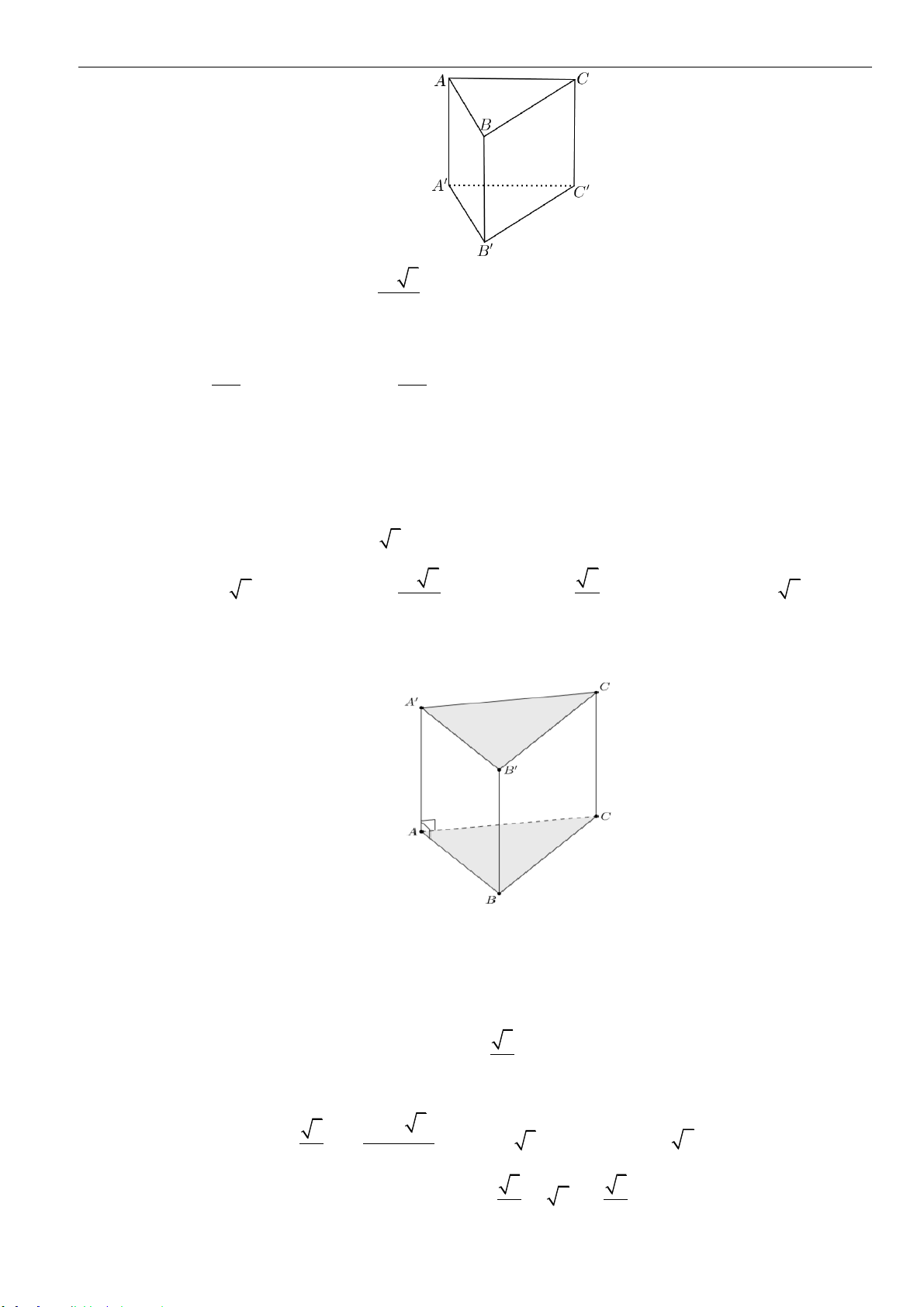
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

11 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Ta có

3

.

3

.

4

ABC A B C ABC

a

V S AA

  





==

.

Câu 16: Một khối lăng trụ có chiều cao bằng

2a

và diện tích đáy bằng

2

2a

. Tính thể tích khối lăng trụ.

A.

3

4

3

a

V =

. B.

3

2

3

a

V =

. C.

3

2aV =

. D.

3

4Va=

.

Lời giải

Chọn D

Áp dụng công thức tính thể tích hình lăng trụ

23

2 2 4V S h a a a=  =  =

.

Câu 17: Cho khối lăng trụ tam giác đều, cạnh bên có độ dài gấp hai lần cạnh đáy. Biết tổng diện tích các

mặt của khối lăng trụ là

( )

2

12 3 a+

. Tính theo

a

thể tích

V

của khối lăng trụ đã cho

A.

3

6Va=

. B.

3

6

3

a

V =

. C.

3

6

8

Va=

. D.

3

26Va=

.

Lời giải

Chọn A

Đặt độ dài một cạnh của tam giác đều

ABC

là

x

. Do độ dài của cạnh bên của hình lăng trụ gấp

hai lần cạnh đáy nên hình chữ nhật

ABB A



có

;2AB x AA x



==

.Diện tích xung quanh của khối

lăng trụ là

2

1

3. .2 6S x x x==

Diện tích hai đáy của khối lăng trụ là

2

3

2.

4

Sx=

Tổng diện tích các mặt của trụ tam giác đều là

( )

2 2 2 2

12

12 3

3

6 12 3

22

S S S x x x a

+

= + = + = = +

. Suy ra

2.xa=

Diện tích một đáy của khối lăng trụ là

( )

2

33

.2

42

ABC

S a a==

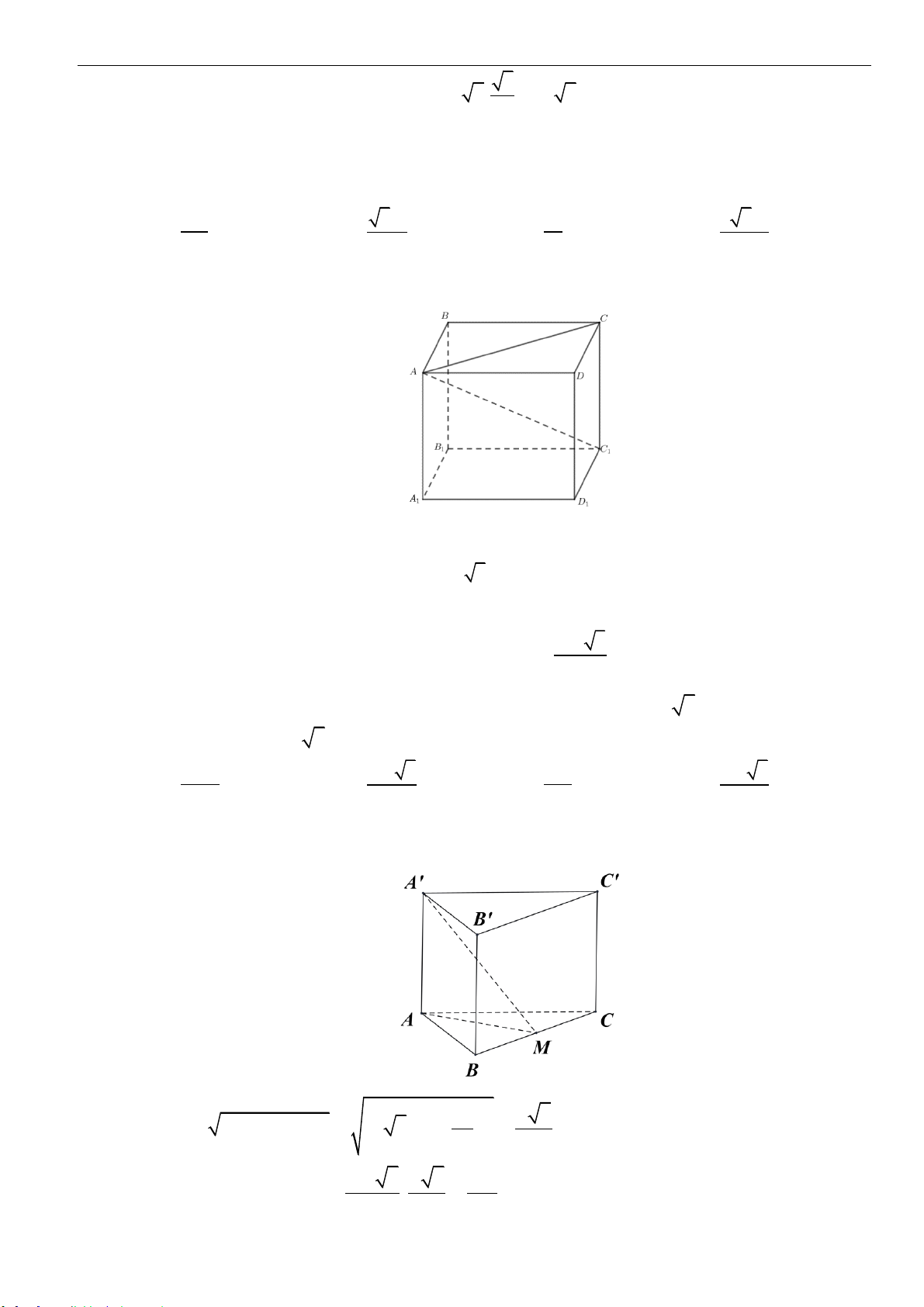
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 12

Thể tích khối lăng trụ

23

3

. 2. 2. 6

2

ABC

V AA S a a a



= = =

.

Câu 18: Cho khối hộp đứng

1 1 1 1

.ABCD A B C D

có đáy

ABCD

là hình thoi cạnh

a

,

120

o

ABC =

, đường

thẳng

1

AC

tạo với mặt phẳng

( )

ABC D

một góc

60

o

. Tính thể tích khối hộp đã cho

A.

3

2

a

B.

3

2

a

C.

3

2

a

D.

3

33

2

a

Lời giải

Chọn D

Ta có

( ) ( )

(

)

1 1 1

, 60

o

CC ABCD AC ABCD C AC⊥  = =

;

2 2 2

2 . . 3AC BA BC BA BC cosABC a= + − =

.

Xét tam giác vuông

1

ACC

, có:

11

.tan 3CC AC C AC a==

.

Vậy

1 1 1 1

3

. 1 1

3 . 3

. . .sin120 .

2

o

ABCD A B C D ABCD

a

V S CC BA BC CC= = = 

Câu 19: Cho lăng trụ đứng

.ABC A B C

  

có đáy

ABC

là tam giác đều cạnh

3a

. Gọi

M

là trung điểm

của

BC

,

3A M a



=

. Thể tích khối lăng trụ

.ABC A B C

  

bằng

A.

3

27

8

a



B.

3

93

8

a



C.

3

9

8

a



D.

3

33

8

a



Lời giải

Chọn C

( )

2

22

33

3.

22

aa

AA A M AM a





= − = − =





23

.

3 3 3 9

..

4 2 8

ABC A B C ABC

a a a

V S AA

  





= = =

.

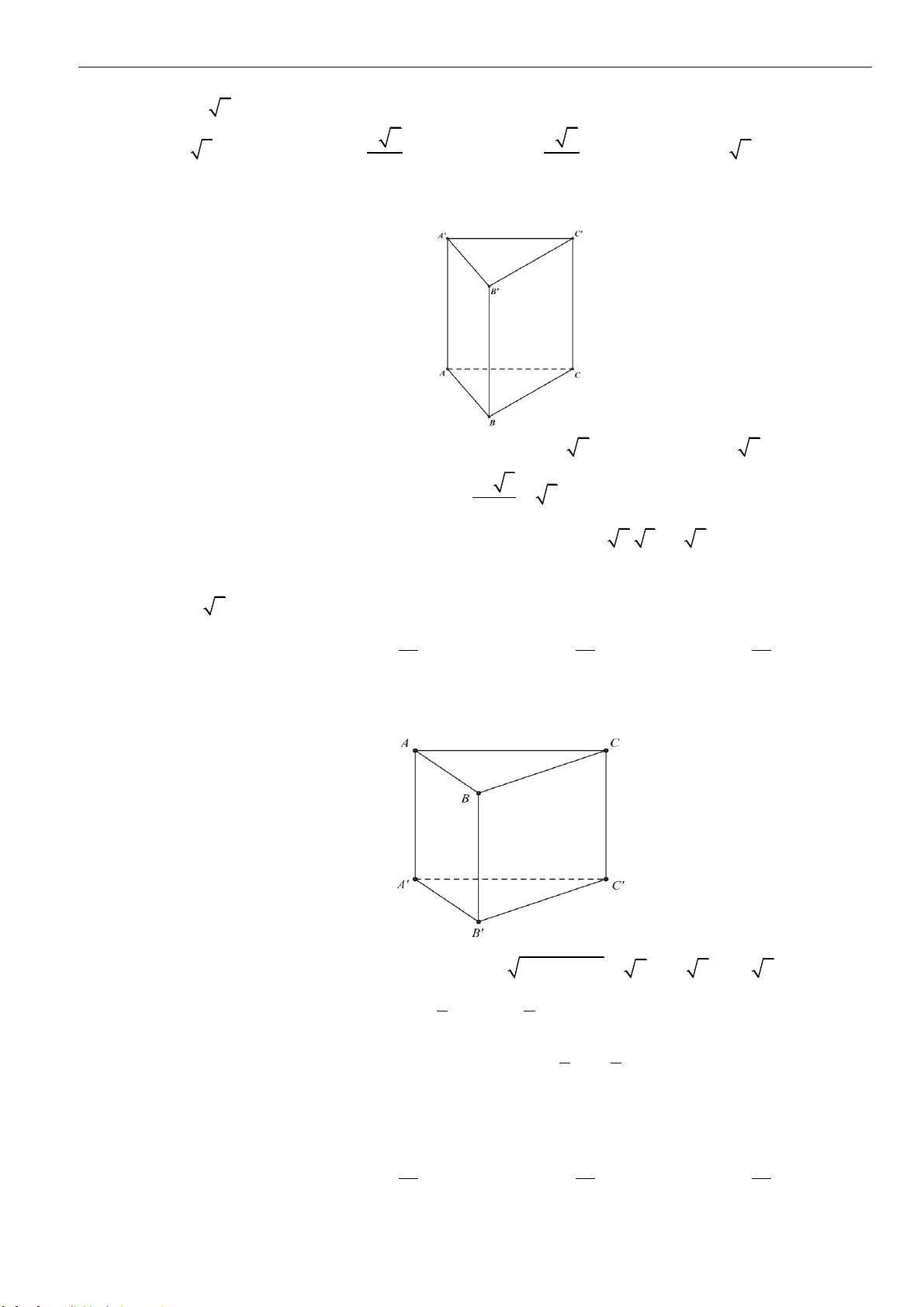
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

13 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 20: Cho hình lăng trụ tam giác đều

. ' ' 'ABC A B C

có cạnh đáy bằng

2

, một mặt bên có diện tích

bằng

42

. Thể tích khối lăng trụ đã cho bằng

A.

2 6.

B.

46

.

3

C.

26

.

3

D.

4 6.

Lời giải

Chọn A

Mặt bên

''AB B A

có diện tích là

''

'. 4 2 '.2 ' 2 2.

ABB A

S AA AB AA AA=  =  =

Tam giác

ABC

là tam giác đều

2

2 . 3

3.

4

ABC

S = =

Vậy thể tích khối lăng trụ

. ' ' 'ABC A B C

là

'. 2 2. 3 2 6.

ABC

V AA S= = =

Câu 21: Cho khối lăng trụ đứng

.ABC A B C

  

có

BB a



=

, đáy

ABC

là tam giác vuông cân tại

B

và

2AC a=

. Thể tích

V

của khối lăng trụ đã cho là

A.

3

Va=

. B.

3

a

V =

. C.

3

6

a

V =

. D.

3

2

a

V =

.

Lời giải

Chọn D

Ta có

ABC

vuông vuông cân tại

B

nên

22

2AC AB BC a= + =

22AB a=

AB a=

BC a=

suy ra

2

11

.

22

ABC

S AB BC a



==

.

Vậy thể tích khối lăng trụ là:

23

.

11

..

22

ABC A B C ABC

V BB S a a a

  



= = =

.

Câu 22: Cho khối lăng trụ đứng

.ABC A B C

  

có

BB a



=

, đáy

ABC

là tam giác vuông cân tại

B

và

BA BC a==

. Tính theo

a

thể tích

V

của khối lăng trụ đã cho.

A.

3

Va=

. B.

3

2

a

V =

. C.

3

a

V =

. D.

3

6

a

V =

.

Lời giải

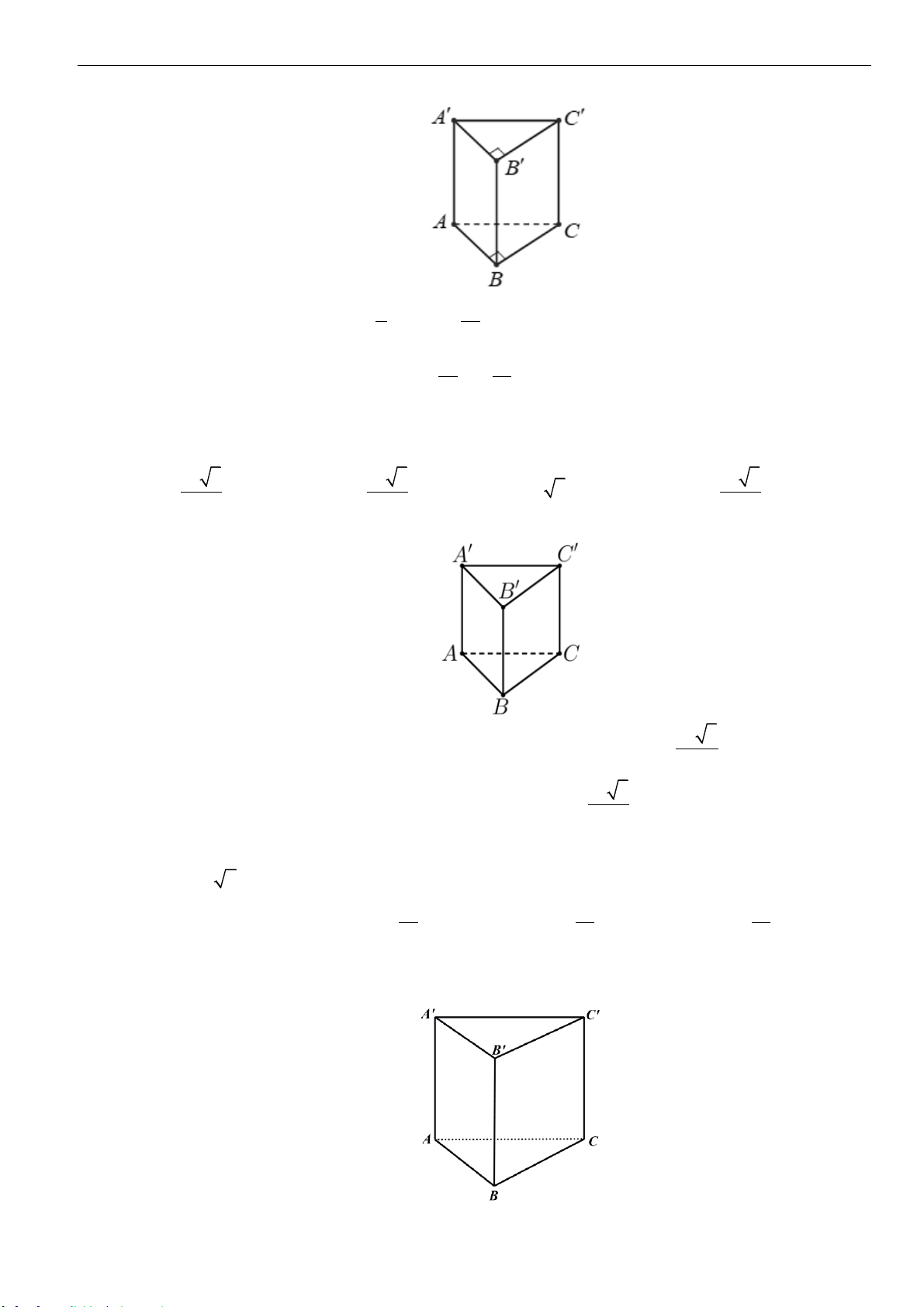
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 14

Chọn B

Ta có diện tích đáy là

2

1

.

22

ABC

a

S BA BC==

.

Thể tích khối lăng trụ là

23

..

22

ABC

aa

V S h a= = =

.

Câu 23: Cho khối lăng trụ đứng

.ABC A B C

  

có đáy là tam giác đều cạnh

a

và

AA 2a



=

. Thể tích của

khối lăng trụ đã cho bằng

A.

3

.

3

a

. B.

3

.

6

a

. C.

3

3a

. D.

3

.

2

a

Lời giải

Chiều cao của lăng trụ:

AA 2a



=

. Diện tích tam giác đều:

2

3

.

4

a

S

ABC

=



Vậy thể tích khối lăng trụ:

3

..

.

2

a

V S AA

ABC

ABC A B C



==

  



.

Câu 24: Cho khối lăng trụ đứng

.ABC A B C

  

có

BB a



=

, đáy

ABC

là tam giác vuông cân tại

B

và

2AC a=

. Tính thể tích

V

của khối lăng trụ đã cho.

A.

3

Va=

. B.

3

a

V =

. C.

3

2

a

V =

. D.

3

6

a

V =

.

Lời giải

Chọn C

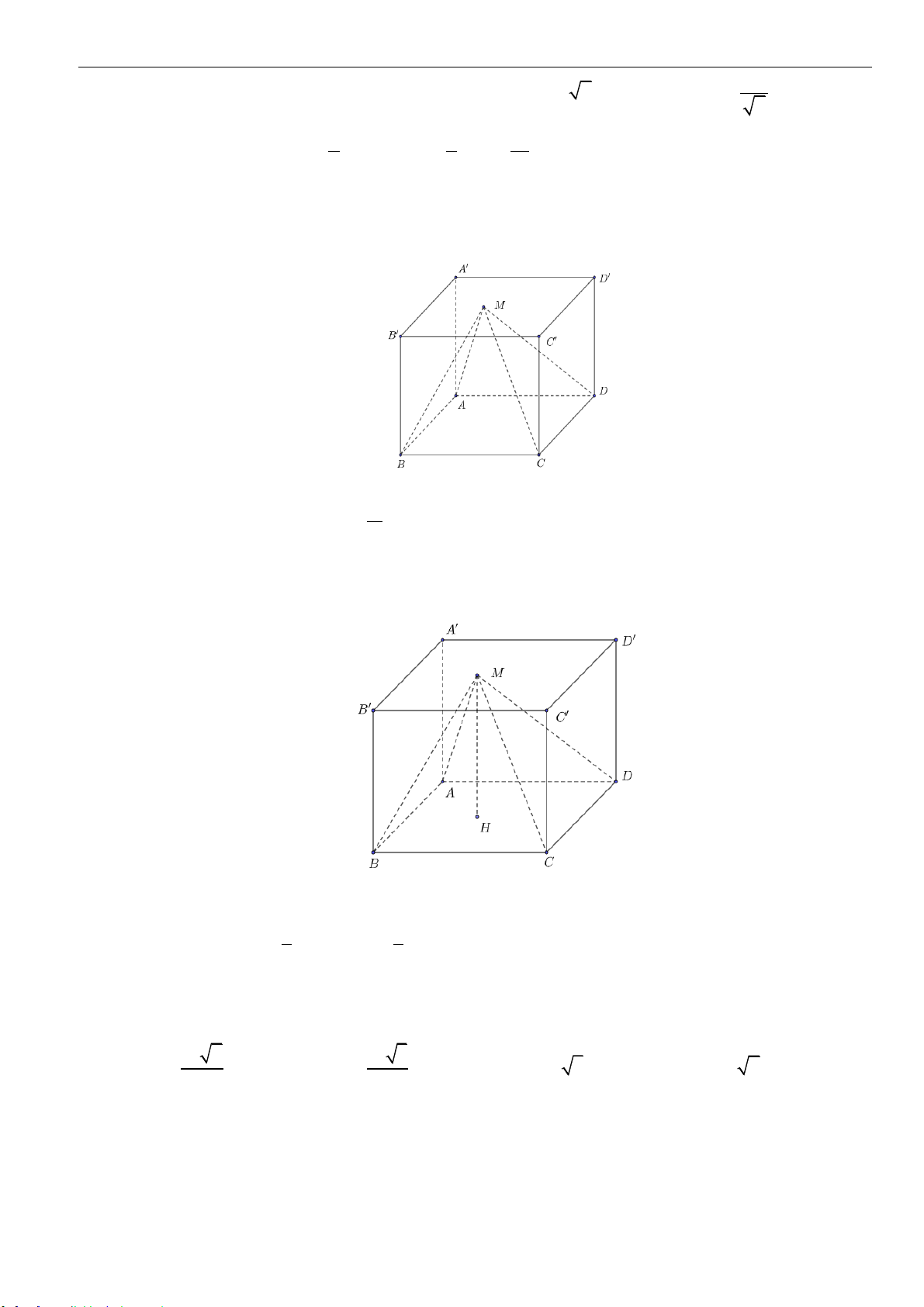
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

15 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Tam giác

ABC

là tam giác vuông cân tại

B

và

2AC a=

suy ra

2

AC

AB BC a= = =

.

Khi đó

3

2

11

. . . .

2 2 2



= = = =

ABC

a

V S BB AB BC BB a a

.

Câu 25: Cho hình lập phương

.ABCD A B C D

   

cạnh

3a

. Gọi

M

là một điểm trên mặt phẳng

( )

A B C D

   

(tham khảo hình vẽ). Thể tích khối chóp

.M ABCD

.

A.

3

9a

. B.

3

a

. C.

3

3a

. D.

3

8a

.

Lời giải

Chọn A

Do

M

thuộc mặt phẳng

( )

A B C D

   

nên

( )

,( ) 3d M ABCD MH AA a



= = =

.

Vì thế

23

.

11

. . .3 .9 9

33

M ABCD ABCD

V MH S a a a= = =

.

Câu 26: Cho lăng trụ đứng

. ' ' 'ABC A B C

có đáy

ABC

là tam giác vuông cân tại

B

và

2AC a=

, biết

rằng

( )

'A BC

hợp với đáy

( )

ABC

một góc

45

o

.Thể tích lăng trụ là:

A.

3

2

a

. B.

3

a

. C.

3

3a

. D.

3

2a

.

Lời giải

Chọn D

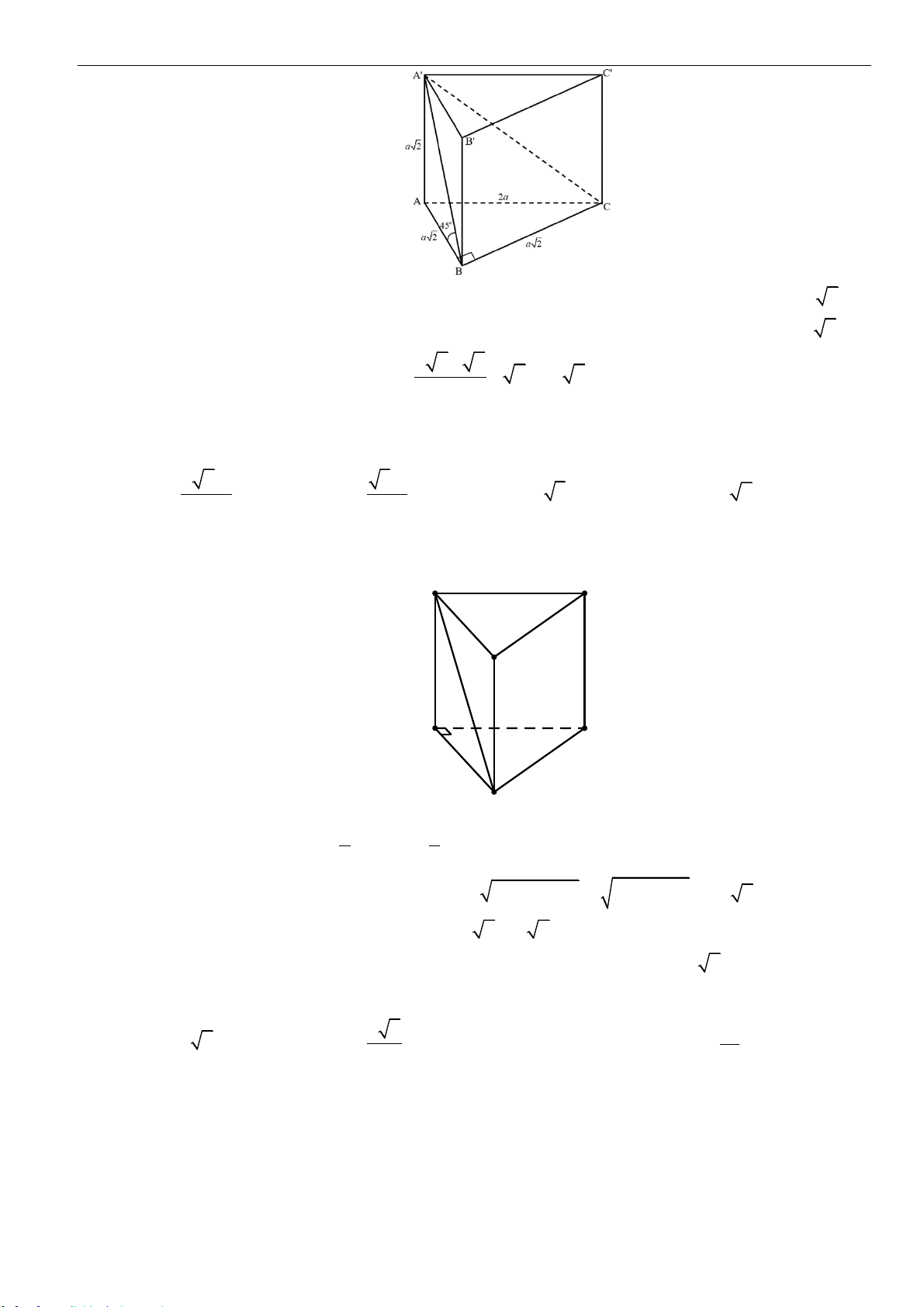
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 16

Do tam giác ABC vuông cân tại B, độ dài cạnh huyền

2AC a=

nên ta có :

2BA BC a==

Góc tạo bởi mặt phẳng

( ' )A BC

và đáy

()ABC

là góc

' 45

o

A BA =

do đó:

'2AA AB a==

Vậy thể tích lăng trụ là:

3

2. 2

. . 2 2.

2

aa

V B h a a= = =

Câu 27: Cho hình lăng trụ đứng

.ABC A B C

  

có đáy là

ABC

vuông tại

A

, biết

AB a=

,

2AC a=

và

3A B a



=

. Thể tích của khối lăng trụ

.ABC A B C

  

bằng

A.

3

22

3

a

. B.

3

5

3

a

. C.

3

5a

. D.

3

22a

.

Lời giải

Chọn D

Diện tích đáy là

1

.

2

ABC

S AB AC



=

1

. .2

2

aa=

2

a=

.

Tam giác

ABA



vuông tại

A

nên có

22

AA A B AB



=−

( )

2

3aa=−

22a=

.

Thể tích cần tính là

.

ABC

V S AA





=

2

.2 2aa=

3

22a=

.

Câu 28: Cho khối hộp chữ nhật

. ' ' ' 'ABCD A B C D

có đáy là hình vuông,

22AC a=

, góc giữa hai mặt

phẳng

( )

'C BD

và

( )

ABCD

bằng

0

45

. Thể tích của khối hộp chữ nhật đã cho bằng:

A.

3

42a

. B.

3

42

3

a

. C.

3

32a

. D.

3

32

3

a

.

Lời giải

Chọn A

a

3a

2a

C'

B'

A

C

B

A'

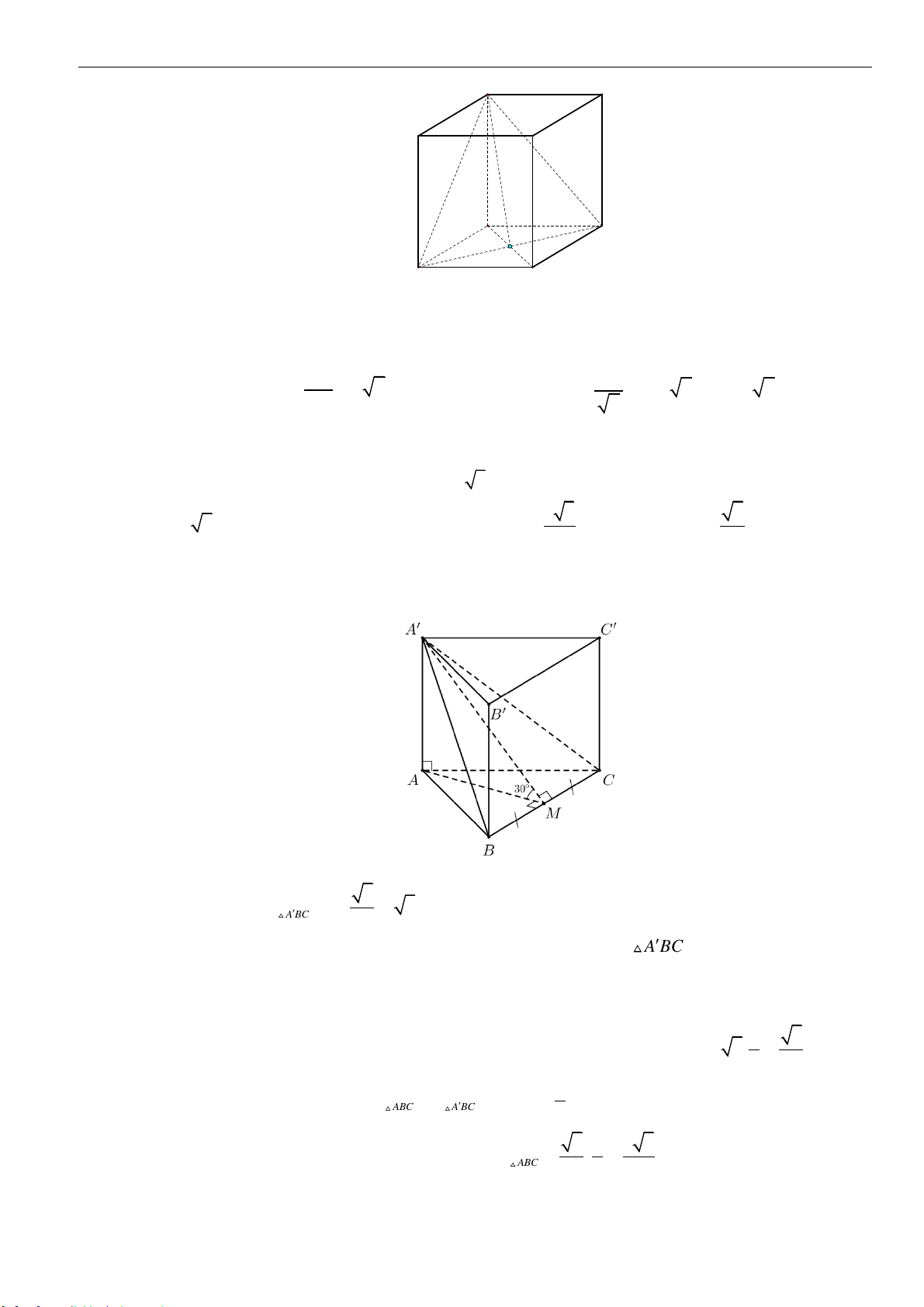
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

17 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Gọi

O

là tâm của hình vuông

ABCD

. Dễ thấy

AC BD⊥

tại

O

và

'BD CC⊥

Suy ra

( )

''BD ACC A⊥

'BD OC⊥

. Suy ra

( ) ( ) ( )

0

' , ', 45C BD ABCD OC OC==





.

Suy ra

'2

2

AC

CC OC a= = =

. Vậy,

2

23

. ' ' ' '

'. 2.4 4 2

2

ABCD A B C D

AC

V CC a a a



= = =





.

Câu 29: Cho lăng trụ đứng

.ABC A B C

  

. Biết rằng góc giữa hai mặt phẳng

( )

A BC



và

()ABC

là

30

,

tam giác

A B C



đều và có diện tích bằng

3

. Thể tích khối lăng trụ

.ABC A B C

  

bằng

A.

23

B. 6. C.

33

4

. D.

3

4

.

Lời giải

Chọn C

Đặt

2

3

32

4

A BC

BC x S x x



=  = =  =

.

Gọi

M

là trung điểm của

BC

suy ra

BC A M



⊥

(Do tam giác

A BC



đều).

Khi đó ta có:

BC A M

BC AM

BC AA



⊥



⊥





⊥



.

Vậy

( ) ( )

( )

o

13

; ; 30 .sin30 3.

22

A BC ABC A M AM A MA AA A M

    

= = =  =  = =

.

Áp dụng CT:

3

.cos .cos30

2

o

ABC A BC

S S S S





=  = =

.

Suy ra thể tích của lăng trụ là:

.

3 3 3 3

..

2 2 4

CABC A B C AB

V AA S

  



= = =

.

Câu 30: Cho lăng trụ đứng

.ABC A B C

  

. Biết rằng góc giữa hai mặt phẳng

( )

A BC



và

( )

ABC

là

30

,

O

C'

C

D'

B'

A'

A

B

D

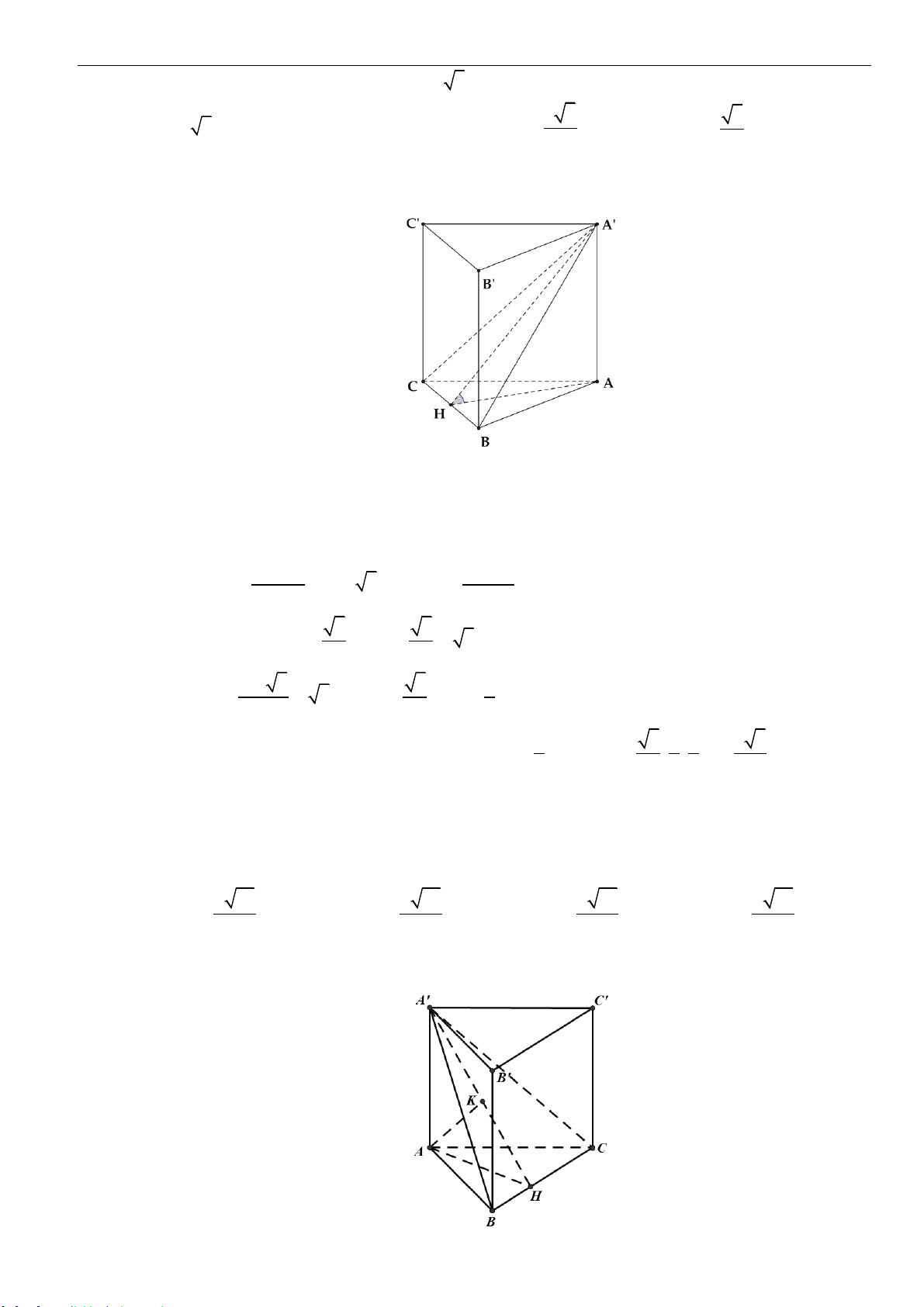
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 18

tam giác

A B C



đều và diện tích bằng

3

. Thể tích khối lăng trụ

.ABC A B C

  

bằng

A.

23

. B.

6

. C.

33

4

. D.

3

4

.

Lời giải

Chọn C

Trong

( )

ABC

vẽ

AH BC⊥

tại

H

.

Dễ thấy

( )

BC A AH BC A H



⊥  ⊥

nên

( ) ( )

( )

, , 30A BC ABC A H AH A HA

  

= = = 

.

Tam giác

A B C



đều có

AH



là đường cao nên đồng thời là đường trung tuyến.

Ta có

.3

tan30

AA

AH A A



==



và

2

sin30

AA

A H A A





==



.

Diện tích

2 2 2

33

3 4 2

44

A BC

S BC BC BC BC



=  =  =  =

.

Mà

3 3 3

3;

2 2 2

BC

A H A A AH



= =  = =

.

Thể tích khối lăng trụ

.

1 3 1 3 3 3

. . . . . . .2

2 2 2 2 4

ABC A B C ABC

V A A S A A AH BC

  





= = = =





.

Câu 31: Cho lăng trụ đứng

.ABC A B C

  

có đáy là tam giác

ABC

vuông tại

A

,

, 2AB a AC a==

. Góc

giữa hai mặt phẳng

( )

A B C



và

( )

ABC

bằng

60

. Thể tích

V

của khối lăng trụ

.ABC A B C

  

theo

a

.

A.

3

2 15

5

Va=

. B.

3

2 15

15

Va=

. C.

3

2 15

45

Va=

. D.

3

6 15

45

Va=

.

Lời giải

Chọn A

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

19 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Gọi

H

và

K

lần lượt là hình chiếu vuông góc của

A

trên

BC

và

( )

mp A BC



.

Khi đó:

( ) ( )

, 60ABC A BC AHK



= = 

. Theo giả thiết ta tính được

25

5

AH a=

.

Ta có:

15

.sin60

5

AK AH a=  =

và

2

.

2

cos60 2cos60

ABC

A BC

S

AB AC

Sa



= = =



33

..

1 2 15 2 15

..

3 15 5

A ABC A BC ABC A B C

V AK S a V a

    

 = =  =

Câu 32: Cho hình hộp

.ABCD A B C D

   

có đáy

ABCD

là hình thoi có cạnh bằng

a

và góc

0

60ABC =

.

Cạnh bên

2

3

a

AA



=

;

A



cách đều các đỉnh

,,A B C

. Tính theo

a

thể tích của khối hộp

.ABCD A B C D

   

.

A.

3

2

a

. B.

3

6

a

. C.

3

16 3a

. D.

3

83a

.

Lời giải

Chọn A

Ta có

ABCD

là hình thoi và

0

60ABC =

, suy ra

ABC

đều cạnh

a

.

Diện tích hình thoi

ABCD

là:

22

33

2 2. .

42

ABCD ABC

aa

SS



= = =

Gọi

G

là trọng tâm

ABC

, vẽ trục

Gx

vuông góc mp

( )

ABC

. Vì

A



cách đều các đỉnh

,,A B C

suy ra

( )

A Gx A G ABC



  ⊥

.

Xét

ABC

đều cạnh

a

, có

AM

là đường trung tuyến:

2 2 3 3

.

3 3 2 3

aa

AG AM= = =

.

Ta có:

( ) ( )

.A G ABC A G AG ABC



⊥  ⊥ 

Xét

AA G





vuông tại

G

, ta có:

2

22

23

.

3

aa

A G AA AG a





= − = − =





Thể tích của khối hộp

.ABCD A B C D

   

là

23

33

. . .

22

ABCD

aa

V S A G a



= = =

Câu 33: Cho hình lăng trụ đứng

.ABC A B C

  

có đáy là tam giác vuông cân đỉnh

A

, mặt bên là

BCC B



hình vuông, khoảng cách giữa

AB



và

CC



bằng

a

. Thể tích khối lăng trụ

.ABC A B C

  

là

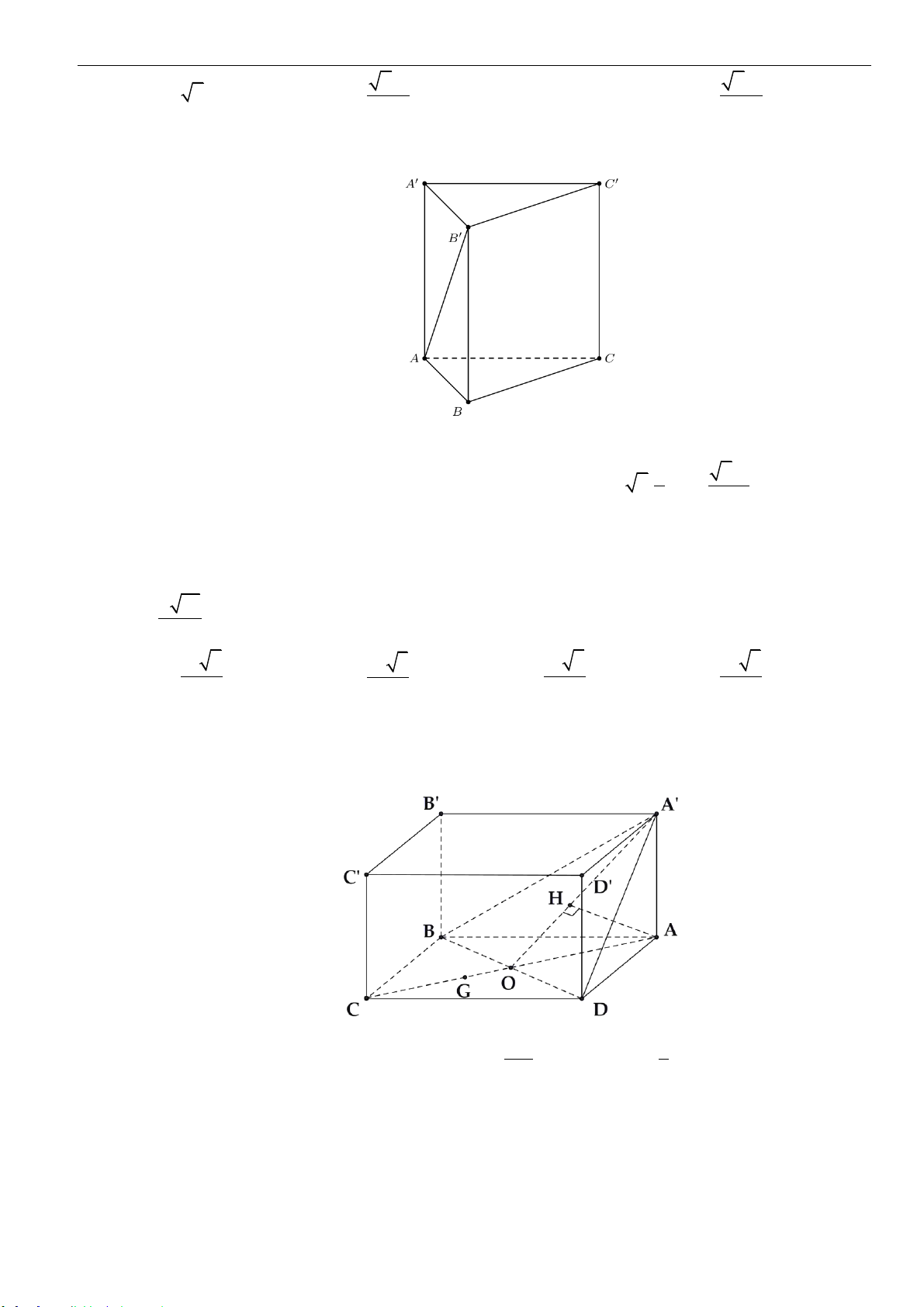
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 20

A.

3

2a

. B.

3

2

3

a

. C.

3

a

. D.

3

2

a

.

Lời giải

Chọn D

Theo giả thiết, ta có:

( ) ( )

( )

; , ,d CC AB d CC ABB A d C ABB A CA a

      

= = = =

.

Do đó, thể tích khối lăng trụ

.ABC A B C

  

là

3

2

12

. 2. .

22

ABC

a

V CC S a a





= = =

.

Câu 34: Cho hình hộp đứng

.ABCD A B C D

   

có đáy là hình thoi, góc

60BAD =

đồng thời

AA a



=

.

Gọi

G

là trọng tâm tam giác

BCD

. Biết rằng khoảng cách từ

G

đến mặt phẳng

( )

A BD



bằng

21

a

. Tính thể tích khối hộp

.ABCD A B C D

   

theo

a

.

A.

2

6

a



. B.

3

6

a



. C.

2

a



. D.

3

2

a



.

Lời giải

Chọn D

Gọi

O

là giao điểm của

AC

và

BD

.

Ta có

( )

AG A BD O



=

nên

( )

1

, , ,

3

GO

d G A BD d A A BD d A A BD

AO

  

==

.

Dễ thấy

( )

BD AA O



⊥

, trong

( )

AA O



vẽ

AH A O



⊥

tại

H

.

Khi đó

( ) ( )

( )

,

AH BD

AH A BD d A A BD AH

AH A O

⊥





 ⊥  =





⊥



.

Gọi

x

là cạnh hình thoi

ABCD

, ta có

60BAD =

nên

ABD

đều.

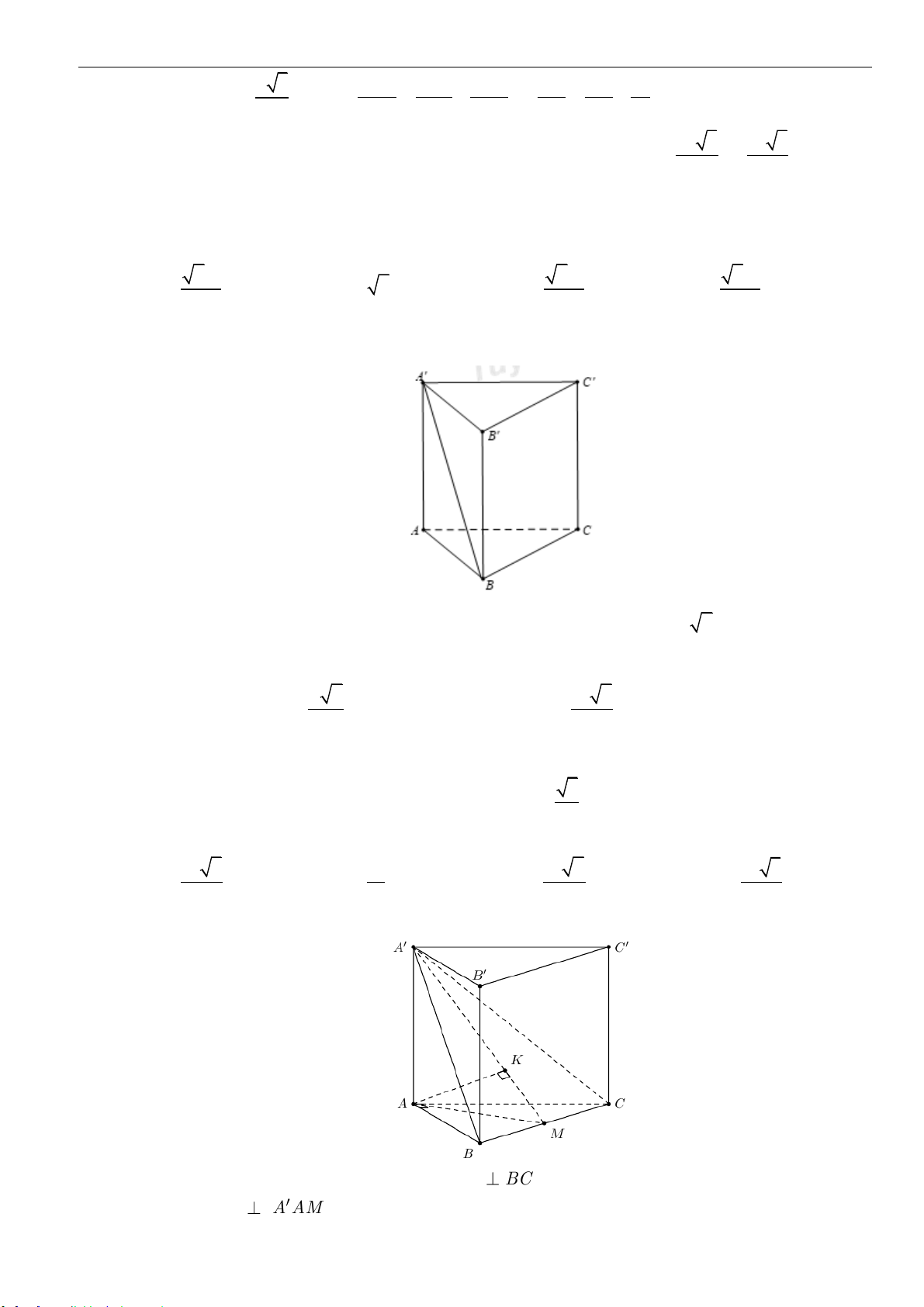
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

21 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Suy ra

3

2

x

AO =

, khi đó

2 2 2 2 2 2

1 1 1 7 4 1

33

xa

AH AO AA a x a

= +  = +  =



.

Thể tích khối hộp

.ABCD A B C D

   

là

2

.

33

. . 2.

42

ABCD A B C D ABCD

aa

V AA S a



   





= = =





.

Câu 35: Cho khối lăng trụ đứng

. ' ' 'ABC A B C

có đáy

ABC

là tam giác vuông cân tại

A

và

2aBC =

.

Góc giữa đường thẳng

'AB

với

( )

ABC

bằng

30

o

. Tính thể tích của khối lăng trụ đã cho?

A.

3

6

a

. B.

3

6a

. C.

3

6

9

a

. D.

3

6

3

a

Lời giải

Chọn D

Đáy

ABC

là tam giác vuông cân tại

A

và

2aBC =

. Nên

2

ABC

AB AC a S a= =  =

.

Góc giữa đường thẳng

'AB

với

( )

ABC

bằng

30

o

. Xét tam giác vuông

'A AB

có

6

' tan30 .

3

o

a

A A AB==

Vậy

3

. ' ' '

6

'.

3

ABC A B C ABC

a

V A A S==

.

Câu 36: Cho khối lăng trụ đứng

.ABC A B C

  

có đáy

ABC

là tam giác vuông cân tại

,A

AB a=

. Biết

khoảng cách từ

A

đến mặt phẳng

( )

A BC



bằng

3

a

. Tính thể tích của khối lăng trụ

..ABC A B C

  

A.

3

a

. B.

3

2

a

. C.

3

2

3

a

. D.

3

9

a

.

Lời giải

Gọi

M

là trung điểm của

BC

. Suy ra

AM BC

.

Khi đó

BC A AM

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 22

Trong

A BC

kẻ

AK A M

với

K A M

.

Khi đó

( ) ( )

( )

3

d,

3

a

AK A BC A A BC AK



⊥  = =

.

Trong

A AM

vuông tại

A

ta có

2

22

BC a

AM

;

3

a

AK =

.

Ta có

2 2 2 2 2 2 2 2 2 2

1 1 1 1 1 1 1 9 4 1

32

A A a

AK A A AM A A AK AM A A a a a



= +  = −  = − =  =

  

.

Vậy thể tích của khối lăng trụ

.ABC A B C

  

là

23

..

22

ABC

aa

V AA S a





= = =

(đvtt).

Câu 37: Cho hình hộp đứng

.ABCD A B C D

   

có đáy là hình vuông cạnh

a

, góc giữa mặt phẳng

( )

D AB



và mặt phẳng

( )

ABB A



bằng

30

. Thể tích khối hộp

.ABCD A B C D

   

bằng

A.

3

18

a

. B.

3

3a

. C.

3

a

. D.

3

9

a

.

Lời giải

Chọn B

Ta có

( ) ( )

( )

ABB A D AB AB

ADD A AB

  

=









⊥





nên góc giữa mặt phẳng

( )

D AB



và mặt phẳng

( )

ABB A



là

góc giữa

AD



và

AA



hay

30A AD



=

. Suy ra

3

tan30

AD

AA a





==



.

Ta có

2

.

ABCD

S a a a==

.

Vậy thể tích hình hộp là

23

.

. . 3 3

ABCD A B C D ABCD

V AA S a a a

   



= = =

.

Câu 38: Cho khối hộp chữ nhật

.ABCD A B C D

   

có

2AB a=

,

3BC a=

. Góc giữa hai mặt phẳng

( )

A B CD



và

( )

ABC D

bằng

45

. Thể tích khối hộp chữ nhật bằng

A.

3

12a

. B.

3

18 2a

. C.

3

18a

. D.

3

6 13a

.

Lời giải

Chọn C

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

23 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Ta có

.

ABCD

S AB BC=

2

2 .3 6a a a==

.

Lại có

( ) ( )

A B CD ABCD CD

B C CD

BC CD



=







⊥





⊥



, suy ra

( ) ( )

( )

, 45A B CD ABCD B CB

  

= = 

.

Tam giác

B CB



vuông tại

B

và

45B CB



=

nên

B CB





vuông cân tại

B

3BC B B a



 = =

.

Vậy

. ' ' ' '

.

ABCD A B C D ABCD

V S BB



==

23

6 .3 18a a a=

.

Câu 39: Cho khối lăng trụ đứng

.ABC A B C

  

có đáy là tam giác đều. Mặt phẳng

()A BC



tạo với đáy một

góc

30

và tam giác

A BC



có diện tích bằng

32

. Thể tích của khối lăng trụ đã cho bằng

A.

64 3

. B.

64 3

3

. C.

128

. D.

128

3

.

Lời giải

Chọn A

Gọi



là góc giữa mặt phẳng

( )

A BC



và

( )

ABC

. Gọi

M

là trung điểm của

BC

.

Khi đó

AM BC⊥

và

AA BC



⊥

.

Suy ra

( )

BC A AM BC A M



⊥  ⊥

. Ta có:

( ) ( )

A BC ABC BC

AM BC

A M BC



=





⊥







⊥



.

Suy ra góc

30A MA





= = 

. Ta có:

32

cos30

2

3

AM AM

A M AM

A M A M





=  =  =



.

Đặt

3

0

2

x

BC x AM=   =

và

23

.

2

3

x

A M x



==

.

Ta lại có:

11

43

. 32 . 8 4.

22

8

A BC

AM

S A M BC x x x A A

AM







=





=  =  =   =





=





Suy ra

2

83

.4 64 3.

4

.

ABC A B C ABC

V S AA

  





= = =

.

Câu 40: Cho khối lăng trụ đứng

. ' ' 'ABC A B C

có đáy là tam giác vuông tại

A

;

; 60AC b ACB= = 

.

Đường thẳng

'BC

tạo với mặt phẳng

( ' ' )AA C C

một góc

30

. Tính thể tích của khối lăng trụ

đã cho theo

b

.

A.

3

6

3

b

. B.

3

26b

. C.

3

6

b

. D.

3

6b

.

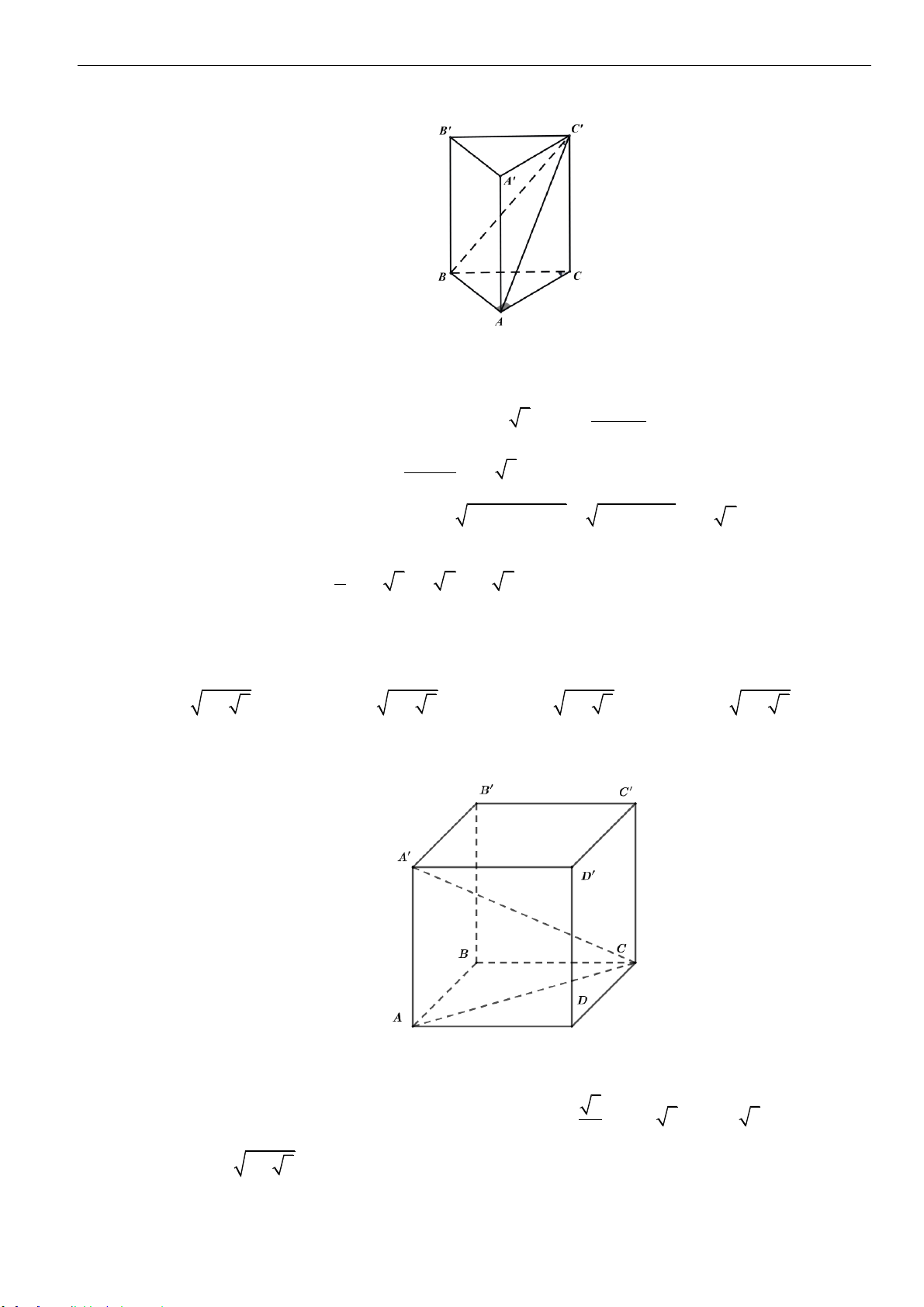
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 24

Lời giải

Chọn D

Ta có:

( )

'

''

BA AA

BA AA C C

BA AC

⊥



⊥



⊥



( )

'; ' ' ' 30BC AA C C BC A = = 

.

Xét tam giác

ABC

ta có:

tan60 3AB AC b=   =

;

2

cos60

AC

BC b==



.

Xét tam giác

'BAC

ta có:

' 2 3

sin30

AB

BC b==



.

Xét tam giác vuông

'BB C

ta có:

2 2 2 2

' ' ' ' 12 4 2 2BB BC B C b b b= − = − =

.

Vậy thể tích của khối lăng trụ đã cho là:

3

. ' ' '

1

' 3 2 2 6

2

ABC A B C ABC

V S BB b b b b=  =    =

.

Câu 41: Cho khối hộp đứng

.ABCD A B C D

   

có đáy là hình thoi cạnh đáy bằng

2cm

, góc

30BAD



=

,

góc giữa

AC



và mặt phẳng đáy bằng

45

. Thể tích khối hôp đã cho bằng

A.

4 2 3−

. B.

2 2 3+

. C.

2 2 3−

. D.

4 2 3+

.

Lời giải

Chọn D

Ta có:

30 150BAD ABC=   = 

.

Xét tam giác

ABC

, áp dụng định lý cosin ta có:

( )

2 2 2

3

2. . .Cos 4 4 2.2.2. 8 4 3 4(2 3)

2

AC AB BC AB BC ABC= + − = + + = + = +

.

( )

2 2 3AC cm = +

.

Vì

( ) ( )

1AA ABCD AA AC



⊥  ⊥

.

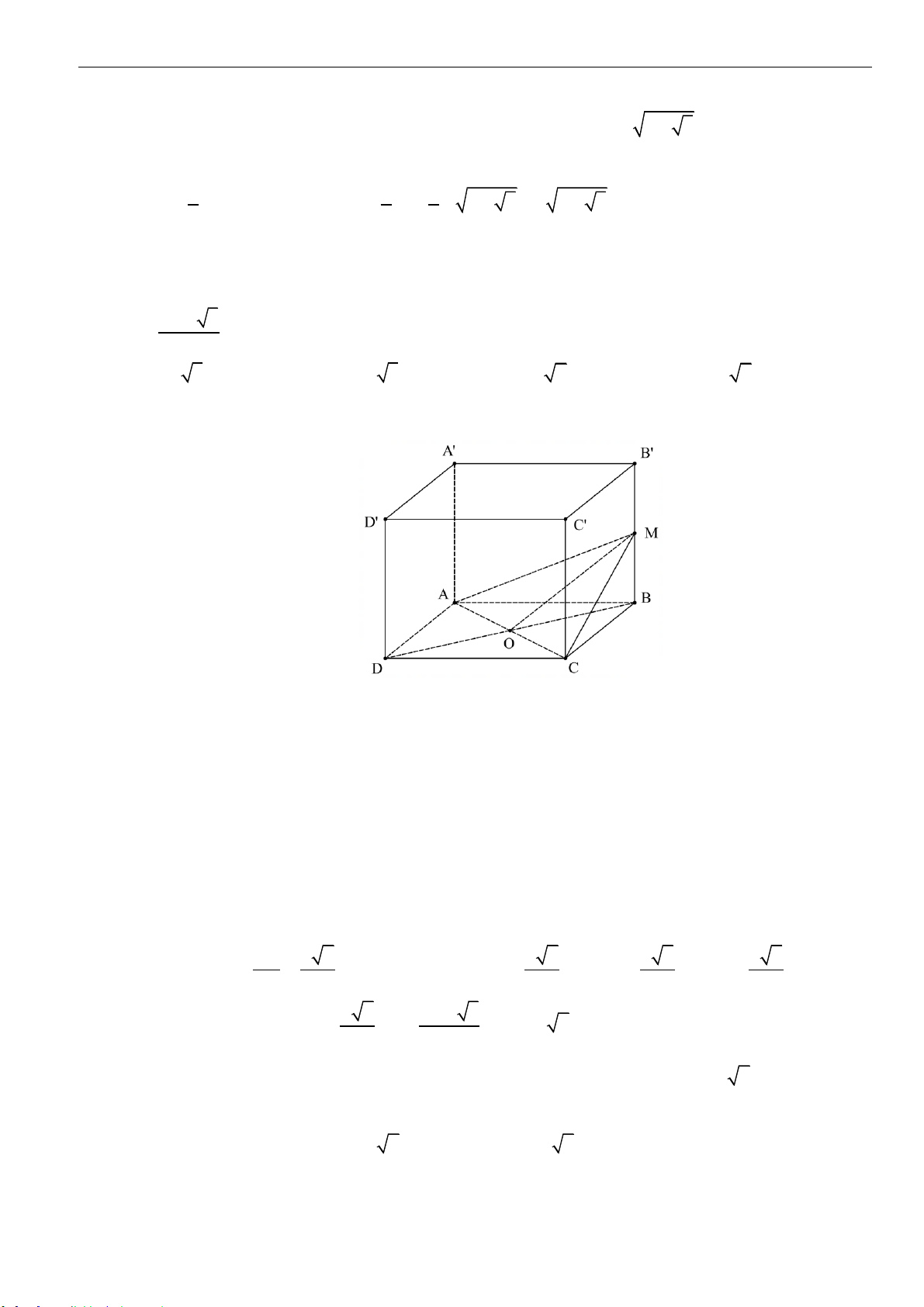
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

25 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Vì

( )

( ) ( )

, , 45 2A C ABCD A C AC A CA

  

= = = 

.

Từ

( )

1

và

( )

2

suy ra

A AC





vuông cân tại

A

( )

2 2 3AA AC cm



 = = +

.

. 2. .

ABCD A B C D ABCD ABD

V S AA S AA

   





==

( )

3

1 1 1

2. . . .sin30 . 2. .2.2. .2 2 3 4 2 3

2 2 2

AB AD AA cm



=  = + = +

.

Câu 42: Cho khối hộp chữ nhật

.ABCD A B C D

   

có đáy là hình vuông. Gọi

M

là trung điểm của

BB



,

góc giữa hai mặt phẳng

( )

MAC

và

( )

A B C D

   

bằng

0

30

. Thể tích của khối hộp chữ nhật bằng

3

32 3

3

a

. Tính độ dài cạnh hình vuông.

A.

3a

. B.

23a

. C.

2a

. D.

22a

.

Lời giải

Chọn D

Ta có:

( ) ( ) ( ) ( )

( )

( ) ( )

( )

0

/ / ; ; 30ABCD A B C D MAC A B C D MAC ABCD

       

→ = =

.

ABCD

là hình vuông

AC BD→⊥

tại

O

.

Ta có:

( )

AC BO

AC MBO AC MO

AC MB

⊥



 ⊥  ⊥



⊥



.

Ta có:

( ) ( )

( )

( ) ( )

( )

0

, ; , 30

,

MAC ABCD AC

MO MAC MO AC MAC ABCD MO BO MOB

BO ABCD BO AC

=





 ⊥  = = =





⊥



.

Đặt độ dài cạnh hình vuông là

( )

0xx

.

Ta có:

0

2 2 6 6

.tan .tan30

2 2 2 6 3

BD x x x x

OB MB OB MOB BB



= =  = = =  =

.

Ta có:

3

2

6 32 3

. . 2 2

33

ABCD

xa

V BB S x x a



= = =  =

.

Câu 43: Cho lăng trụ đứng

.ABCD A B C D

   

có đáy là hình chữ nhật,

,2CD a CB a==

, góc giữa hai

mặt phẳng

( )

'C BD

và

( )

ABC D

bằng

60

. Thể tích của khối hộp chữ nhật đã cho bằng

A.

3

2a

. B.

3

22a

. C.

3

32a

. D.

3

3a

.

Lời giải

Chọn A

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 26

Ta có

2

.2

ABCD

S CB CD a==

.

Kẻ

CH BD⊥

(1) kết hợp với

'C C BD⊥

suy ra

DB CH⊥

(2)

Từ (1),(2) suy ra

(( ' );( )) ( ' ; ) 'C BD ABCD C H CH C HC==

0

' 60C HC=

.

Xét tam giác

CBD

, ta có

2 2 2 2 2 2

1 1 1 1 1 3 2

2 2 3

CH a

CH CB CD a a a

= + = + =  =

.

Xét tam giác

'C CH

, ta có

0

'2

tan ' ' tan60 . 3. 2

3

CC

C HC CC CH a a

CH

=  = = =

.

Nên suy ra

23

. ' ' ' '

' . 2 . 2 2

ABCD A B C D ABCD

V C C S a a a= = =

.

Câu 44: Cho lăng trụ tam giác đều

.ABC A B C

  

có

2AA



=

, góc giữa đường thẳng

AB



và mặt phẳng

( )

AA C C



bằng

45

. Tính thể tích

V

của lăng trụ

.ABC A B C

  

.

A.

23V =

. B.

43V =

. C.

32V =

. D.

72V =

.

Lời giải

Chọn B

Gọi độ dài cạnh tam giác đều ABC là

x

và

I

là trung điểm AC.

Vì tam giác ABC đều nên

BI AC⊥

Mặt khác

BI AA



⊥

nên

()BI mp ACC A



⊥



( )

, , 45A B ACC A A B A I BA I

     

= = = 

(do tam giác

A BI



vuông tại I nên

90BA I





)

Khi đó

BA I





vuông cân tại I, suy ra

3

2

x

A I IB



==

,

2

x

AI =

Ta có

22

2 2 2

3

4 2 2

44

xx

A I AI AA x



− =  − =  =

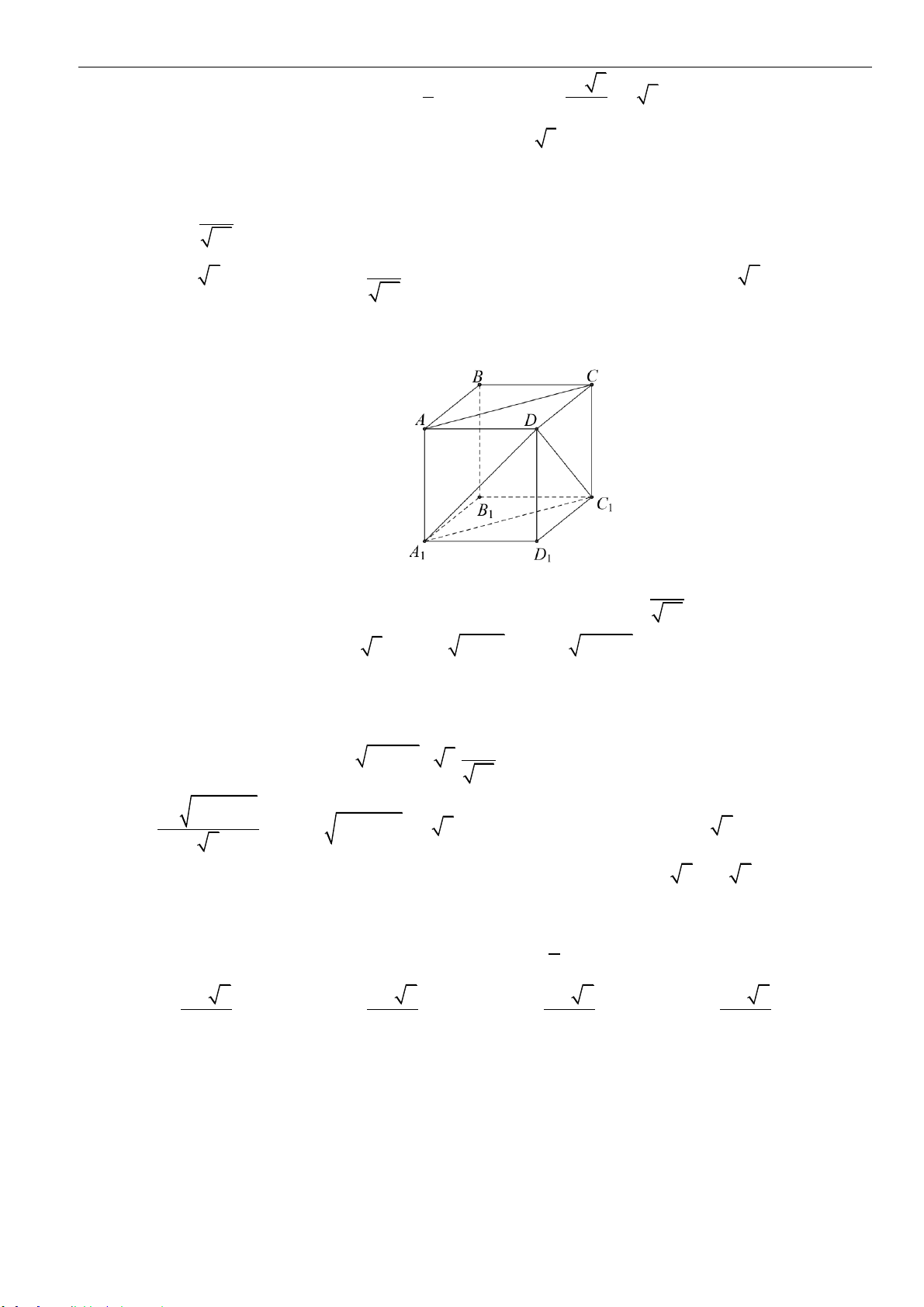
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

27 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Diện tích tam giác

ABC

là:

2

13

. .sin60 2 3

24

o

ABC

x

S AB AC= = =

Thể tích lăng trụ

.ABC A B C

  

là:

. 4 3

ABC

V AA S



==

.

Câu 45: Cho hình hộp chữ nhật

1 1 1 1

.ABCD A B C D

có

2AB =

,

4AD =

, cosin của góc giữa

AC

và

1

DA

bằng

4

30

. Tính thể tích khối hộp chữ nhật

1 1 1 1

.ABCD A B C D

.

A.

16 2

. B.

24

30

. C.

16

. D.

32 2

.

Lời giải

Chọn A

Vì

' '//A C AC

nên góc giữa

AC

và

1

DA

là

11

DAC

11

4

cos

30

DAC=

Đặt

x AA



=

, ta có:

25AC =

,

2

1

4DC x=+

,

2

1

16A D x=+

.

Áp dụng định lí cosin cho tam giác

11

A DC

ta có:

2 2 2

1 1 1 1 1 1 1 1 1

2. . .cosDC A D AC A D AC DAC= + −

.

2 2 2

4

4 16 20 2 16.2 5.

30

x x x + = + + − +

( )

2

16. 16

32 16 2 6

6

x

+

=  + =

22

16 24 8 2 2x x x + =  =  =

.

Thể tích khối hộp chữ nhật

1 1 1 1

.ABCD A B C D

:

. . 2.4.2 2 16 2V AB AD AA



= = =

Câu 46: Cho hình lăng trụ đứng

.ABC A B C

  

có đáy

ABC

là tam giác đều cạnh

a

. Khoảng cách từ tâm

O

của tam giác

ABC

đến mặt phẳng

( )

A BC



bằng

6

a

. Thể tích khối lăng trụ bằng

A.

3

32

4

a

. B.

3

32

8

a

. C.

3

32

28

a

. D.

3

32

16

a

Lời giải

Chọn D

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 28

Gọi

M

là trung điểm của

BC

và

H

là hình chiếu của

A

trên

'AM

.

Ta có

( )

BC AM

BC AA M BC AH

BC AA

⊥





 ⊥  ⊥





⊥



(1)

Mà

( )

2AH A M



⊥

Từ (1) và (2)

( )

,d A A BC AH



=

.

Ta có

( )

,

1

3

,

d O A BC

MO

MA

d A A BC



==



(do tính chất trọng tâm).

( )

, 3 ,

2

a

d A A BC d O A BC



 = =

2

a

AH=

.

Xét tam giác vuông

'A AM

:

2 2 2

1 1 1

AH AA AM

=+



2 2 2

1 4 4 3

3

22

a

AA

AA a a



 = −  =



.

Suy ra thể tích lăng trụ

.'ABC A B C



là:

23

3 3 3 2

..

4 16

22

ABC

a a a

V AA S





= = =

.

Câu 47: Cho khối hộp chữ nhật

.ABCD A B C D

   

có đáy là hình vuông cạnh

a

. Khoảng cách từ

A

đến

mặt phẳng

( )

A B CD



bằng

25

5

a

. Tính thể tích

V

của khối hộp chữ nhật đã cho.

A.

3

2.Va=

. B.

3

2

.

3

a

V =

. C.

3

2

V

a

=

. D.

3

32Va=

.

Lời giải

Chọn A

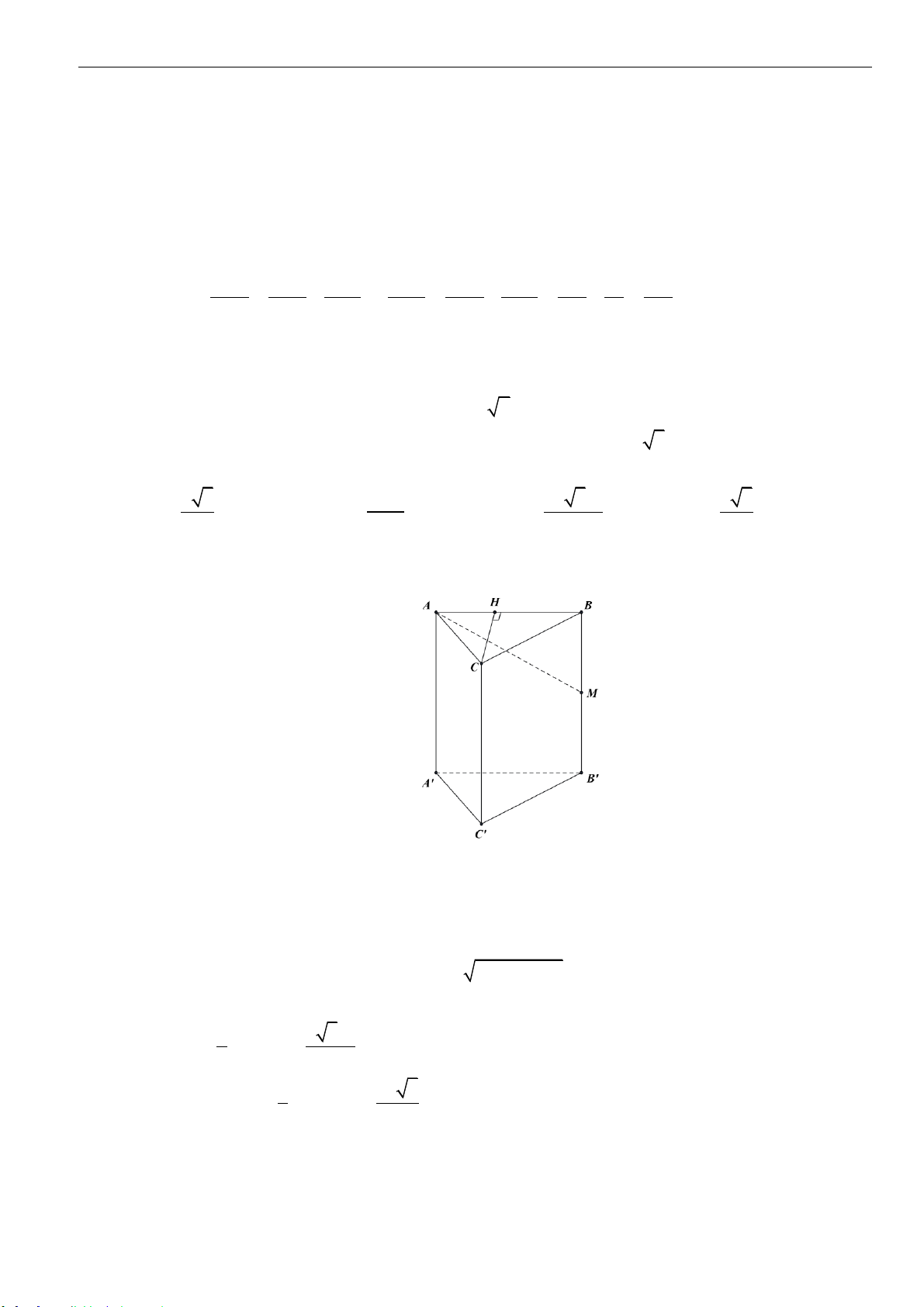
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

29 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Kẻ

AH AD



⊥

tại

H

.

Ta có

( )

AD

CD ADD A CD AH

D

CD

CD D

⊥



 ⊥  ⊥



⊥







Ta có

( )

D

A CD

AH A B C

AD

H

AH







⊥



⊥



⊥

tại

H

.

Vậy khoảng cách từ

A

đến mặt phẳng

( )

A B CD



là

AH

.

Tam giác

A AD



vuông tại

A

có

AH

là đường cao.

Suy ra

2 2 2 2 2 2 2 2 2

1 1 1 1 1 1 5 1 1

44AH AA AD AA AH AD a a a

= +  = − = − =



Vậy

2AA a



=

.

Suy ra

23

. 2 . .2

ABCD

V AA S a a a



===

.

Câu 48: Cho lăng trụ đứng

.ABC A B C

  

có

7, 30AC a ABC= = 

,

AB AA



=

. Gọi

M

là trung điểm

của

BB



, khoảng cách giữa hai đường thẳng

AM

và

CC



bằng

3a

. Thể tích của khối lăng trụ

đứng

.ABC A B C

  

là

A.

3

53

3

a

. B.

3

25

2

a

. C.

3

25 3

6

a

. D.

3

53

6

a

Lời giải

Chọn C

Gọi

H

là hình chiếu vuông góc của

C

trên

AB

.

Có

.ABC A B C

  

là hình lăng trụ đứng nên

( ) ( )

( )

,CH ABB A d C ABB A CH

   

⊥  =

( )

/ / / /CC BB CC ABB A

    



nên

( ) ( )

( )

, , ,d CC AM d CC ABB A d C ABB A CH

     

= = =

Tam giác

ACH

vuông tại

H

nên

22

2AH AC HC a= − =

Mặt khác,

0

.cot30 3 AA 5BH HC a AB a



= =  = =

2

1 5 3

.

22

ABC

a

S ABCH



==

.

Vậy

3

.

1 25 3

.

36

ABC A B C ABC

V AA S a

  



==

(đvtt).

Câu 49: Cho hình hộp đứng

.ABCD A B C D

   

có cạnh

2AA



=

, đáy

ABCD

là hình thoi với

ABC

là tam

giác đều cạnh bằng 4. Gọi

,,M N P

lần lượt là trung điểm của

,,B C C D DD

    

và

Q

thuộc cạnh

BC

sao cho

3QC QB=

. Tính thể tích tứ diện

MNPQ

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 30

A.

33

. B.

33

2

. C.

3

4

. D.

3

2

.

Lời giải

Chọn D

Gọi

I NP CC



=

;

K IQ B C



=

. Do

,NP

lần lượt là trung điểm của

,C D DD

  

nên

N

là

trung điểm của

IP

và

1

2

IC D P CC

  

==

. Suy ra:

( )

1

. , 1

3

MNPQ MNIQ IMQ

V V S d N IMQ



==

.

Theo giả thiết

ABC

  



đều nên

A M B C

  

⊥

, mà

A M B B



⊥

( do

.ABCD A B C D

   

là hình hộp

đứng). Suy ra:

( )

A M BB C C

  

⊥

.

Do đó:

( )

1 1 1

, , , 3

2 2 2

d N IMQ d D IMQ d A BCC B A M

    

= = = =

.

Ta có:

1

3

IK IC KC

IQ IC QC



= = =

3 1 1

;1

2 3 4

IQ

KC QC BC

KQ



 = = = =

.

Suy ra:

( ) ( )

3 3 3 3 3

. . . 2 1 .2

2 4 4 4 2

IMQ KMQ KMQ

IQ

S S S MK BB MC KC BB

KQ

  

   

= = = = − = − =

.

Vậy từ

( )

1

ta có:

1 3 3

. . 3

3 2 2

MNPQ

V ==

.

Câu 50: Cho lăng trụ đứng

.ABC A B C

  

có đáy là tam giác

ABC

là tam giác vuông cân tại

A

, cạnh

BC a=

. Gọi

M

là trung điểm của cạnh

AA



, biết hai mặt phẳng

()MBC

và

()MB C



vuông

góc với nhau, thể tích khối lăng trụ

.ABC A B C

  

bằng

A.

3

2

8

a

. B.

3

4

a

. C.

3

2

24

a

. D.

3

8

a

.

Lời giải

Chọn B

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

31 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Đặt

AA h



=

.

Ta có:

( ) ( )

;

/ /

M MBC MB C

BC MBC B C MB C

BC B C









   











( ) ( )

MBC MB C



  = 

, với



qua

M

và

/ / / / BC B C





.

Gọi

,IJ

lần lượt là trung điểm của

BC

và

BC



, khi đó

MI BC⊥

,

MJ B C



⊥

(vì các tam giác

MBC

và

MB C



cân tại

M

), hay

MI ⊥

,

MJ ⊥

.

Ta có:

( ) ( )

( )

( ) ( )

, ( );( ) ; 90

,

MBC MB C

MI MBC MI MBC MB C MI MJ

MJ MB C MJ



 = 







 ⊥   = = 







 ⊥ 



.

Ta có :

;

2

aa

AB AC AI= = =

;

22

44

ha

MI MJ MA AI= = + = +

.

Xét tam giác

MIJ

vuông cân tại

M

có:

22

2 2 2

2

22

ha

IJ MI h h a=  = +  =

.

Thể tích khối lăng trụ

.ABC A B C

  

là :

3

.

11

. . . . . . .

2 2 4

22

ABC A B C ABC

a a a

V S AA AB AC AA a

  



= = = =

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

1 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Dạng 8: Thể tích khối đa diện đều

Câu 1: Cho hình lăng trụ tam giác đều

.ABC A B C

  

có

,AB a=

góc giữa đường thẳng

AC



và mặt

phẳng

( )

ABC

bằng

45 .

Thể tích khối lăng trụ

.ABC A B C

  

bằng

A.

3

12

a

. B.

3

4

a

. C.

3

2

a

. D.

3

6

a

.

Lời giải

Chọn B

Ta có lăng trụ

.ABC A B C

  

đều nên

( ) ( )

( )

, 45AA ABC A C ABC CA C

   

⊥  = = 

.

.CC A C a



 = =

Lại có tam giác

ABC

đều cạnh

a

nên

2

3

.

4

ABC

a

S



=

Vậy

3

.

3

..

4

ABC A B C ABC

a

V S CC

  



==

Câu 2: Cho lăng trụ đều

.ABC A B C

  

có cạnh đáy bằng

a

,

AC



tạo với mặt phẳng

( )

ABC

góc

60

.

Tính thể tích của khối lăng trụ

.ABC A B C

  

theo

a

.

A.

3

4

a

. B.

3

12

a

. C.

3

4

a

. D.

3

4

a

.

Lời giải

Chọn D

Vì

( )

AA ABC



⊥

tại

A

nên

AC

là hình chiếu của

AC



trên

( )

ABC

.

Suy ra

( )

, , 60A C ABC A C AC A CA

  

= = = 

.tan60 3AA AC a



 =  =

.

Do đó

3

2

.

33

. 3. .

44

ABC A B C ABC

a

V AA S a a

  





= = =

.

VÍ DỤ MINH HỌA

B

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 2

Câu 3: Cho hình lăng trụ tam giác đều

. ' ' 'ABC A B C

có diện tích xung quanh bằng tổng diện tích hai

đáy và bằng

18 3

. Thể tích khối lăng trụ

. ' ' 'ABC A B C

tính theo đơn vị thể tích bằng

A.

18 3

. B.

27

. C.

36 3

. D.

64

.

Lời giải

Chọn B

Ta có

22

2

33

3 , 2 .

42

xq ñ

xx

S ax S= =  =

Mà

2

18 3

ñ

S =

do đó

2

3

18 3 36 6.

2

x

xx=  =  =

Khi đó:

3 3 .6 18

xq

S ax a a= = =

mà

18 3 18 18 3 3.

xq

S a a=  =  =

Vậy:

2

63

. . 3 27.

4

ñ

V S h= = =

Câu 4: Cho lăng trụ đứng

.ABC A B C

  

có đáy là tam giác đều cạnh

a

. Mặt phẳng

( )

AB C



tạo với mặt

phẳng

( )

ABC

một góc

60

. Thể tích khối lăng trụ

.ABC A B C

  

bằng

A.

3

2

a

. B.

3

33

4

a

. C.

3

8

a

. D.

3

33

8

a

.

Lời giải

Chọn D

Gọi

H

,

H



lần lượt là trung điểm của

BC

,

BC



.

Do lăng trụ đứng

.ABC A B C

  

có đáy là tam giác đều cạnh

a

nên

3

2

a

AH =

và

2

3

S

4

ABC

a

  



=

. Ta có:

( ) ( )

( )

, , 60AB C ABC AH AH H AH

   

= =  = 

.

Xét tam giác

H HA



vuông tại

H

có

33

tan60 .tan60 . 3

22

H H a

H H AH a

AH



 =  =  = =

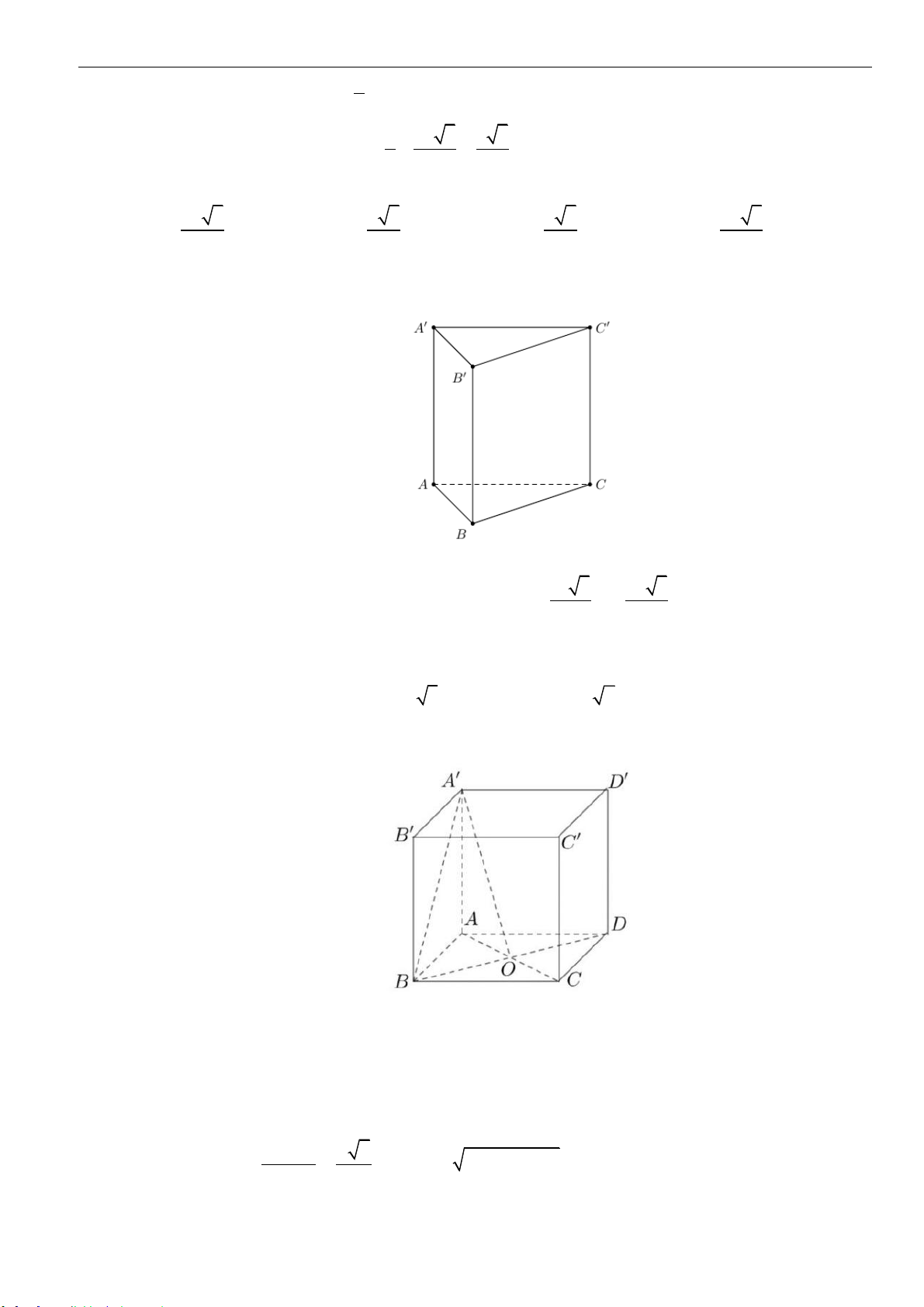
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

3 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

mà

A A H H



=

nên

3

2

A A a



=

.

Vậy

2

3

.

3 3 3 3

=AA.S .

2 4 8

ABC A B C A B C

a

V a a

     





==

.

Câu 5: Lăng trụ tam giác đều có độ dài tất cả các cạnh bằng

3

. Thể tích khối lăng trụ đã cho bằng

A.

27 3

4

. B.

93

8

. C.

93

2

. D.

27 3

12

.

Lời giải

Chọn A

Lăng trụ tam giác đều là lăng trụ đứng có đáy là tam giác đều.

Vậy thể tích khối lăng trụ đã cho là

2

3 3 27 3

. .3

44

ABC

V S AA





= = =

(đvtt).

Câu 6: Cho lăng trụ tứ giác đều

. ' ' ' 'ABCD A B C D

có cạnh đáy bằng

a

, góc giữa

'AB

và mặt phẳng

''A ACC

bằng

0

30

. Tính thể tích khối lăng trụ đã cho.

A.

3

Va=

. B.

3

3Va=

. C.

3

2Va=

. D.

3

2Va=

.

Lời giải

Chọn A

Gọi

O AC BD=

. Vì

( )

''

'

OB AC

OB A ACC

OB AA

⊥



⊥



⊥



Nên:

( )

0

' , ' ' ' ' 30A B ACC A BA O BA O=  =

Ta có:

0

6

'

2

tan30

OB a

AO==

22

''AA A O AO a = − =

Vậy

3

Va=

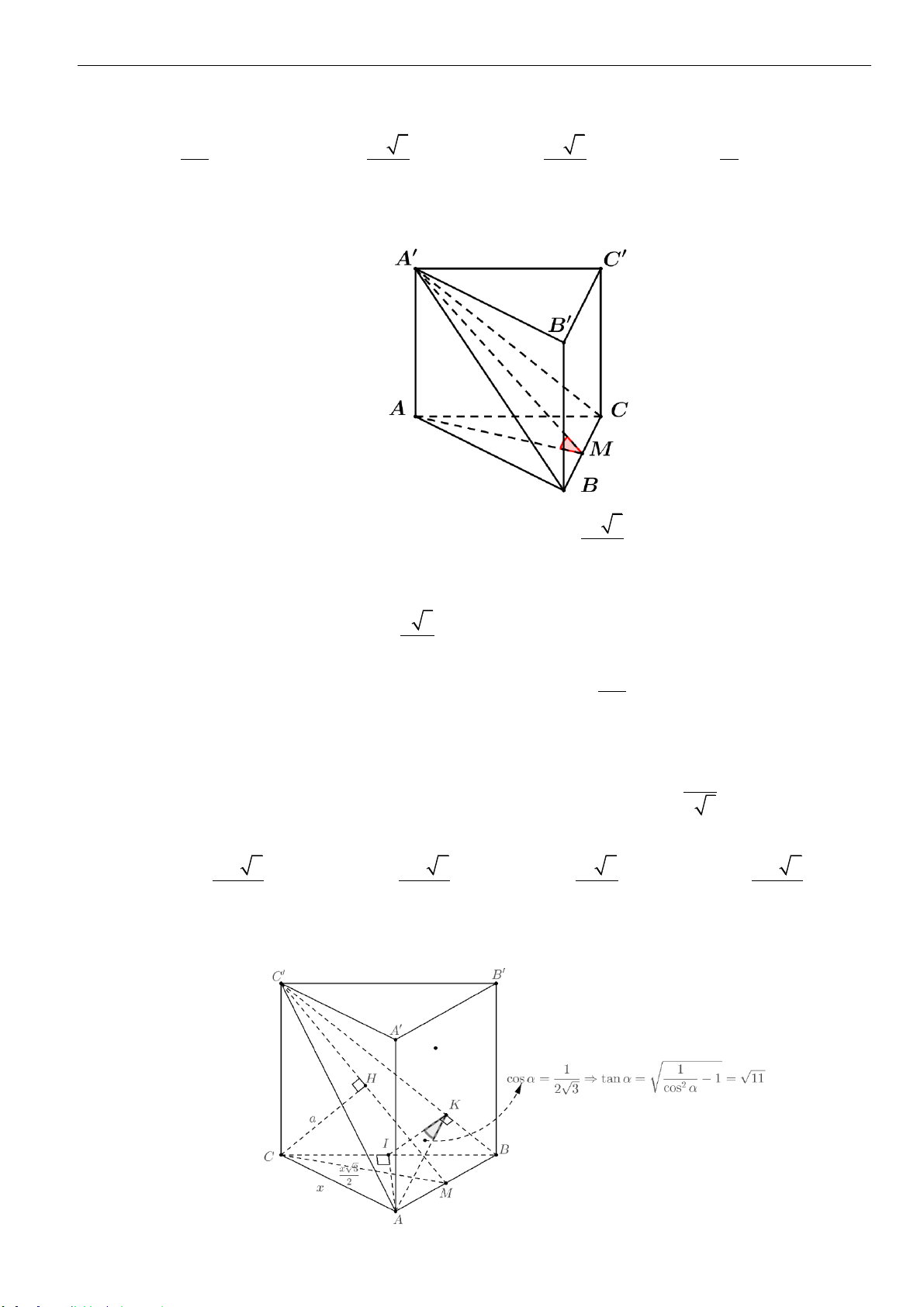
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 4

Câu 7: Cho lăng trụ tam giác đều

. ' ' 'ABC A B C

có cạnh đáy bằng

a

. Mặt phẳng

( )

'A BC

hợp với mặt

phẳng đáy một góc

0

45

. Tính thể tích khối lăng trụ

. ' ' 'ABC A B C

.

A.

3

8

a

B.

3

8

a

C.

3

4

a

D.

3

8

a

Lời giải

Chọn A

Vì đáy

ABC

là tam giác đều cạnh

a

nên diện tích bằng

2

3

4

a

.

Gọi

M

trung điểm

BC

, ta có

( ) ( )

( )

0

' , ' , ' 45A BC ABC A M AM A MA= = =

.

Xét

'A AM

ta có

3

'

2

a

AA AM==

.

Thể tích lăng trụ

. ' ' 'ABC A B C

là

3

. ' ' '

3

'.

8

ABC A B C ABC

a

V AA S==

Câu 8: Cho hình lăng trụ đều

.ABC A B C

  



Biết khoảng cách từ điểm

C

đến mặt phẳng

( )

ABC



bằng

,a

góc giữa hai mặt phẳng

( )

ABC



và

( )

BCCB



bằng



với

1

cos .

23



=

Tính thể tích khối

lăng trụ

.ABC A B C

  



A.

3

32

4

a

V =

. B.

3

2

8

3a

V =

. C.

3

2

a

V =

. D.

3

2

3a

V =

.

Lời giải

Chọn D

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

5 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Gọi

3

2

x

AB x CM=  =

, với

M

là trung điểm của

AB

.

Kẻ

( )

CH C M CH C AB



⊥  ⊥

( )

,'CH d C C AB a = =

2 2 2 2

2 2 2 2 2 2 2 2 2

1 1 1 1 4 3 4 3

'

' 3 3 3 4

x a a x

CC

CC CH CM a x a x x a

−

= − = − =  =

−

Gọi

I

là trung điểm của

BC

( )

AI BB C C



⊥

Ta có

( ) ( )

' ' ' 'C AB BB C C C B=

Kẻ

( ) ( )

( )

',

IK C B

IK C B C AB BB C C AKI

IA C B





⊥



  

⊥   = =





⊥



1

cos tan 11 11

23

AI

IK



=  =  =

2 2 2 2

2

2 2 2 2

'. 3 3

.:

' ' ' 2

3 4 3 4

IK BI CC BI a x x a x

IK x

CC BC BC

x a x a

=  = = +

−−

( )

22

3

43

ax

xa

=

−

2

11 11

AI AI

IK

=  =

( )

2 2 2 2

22

3 3 11

11. 1

4

3

43

x a x a

xa

 =  =

−

2 2 2 2 2

3 11 3 12 2x a a x a x a − =  =  =

( )

2

2 2 2 2

2 . 3

3

4

3 3 .4 6

2

3 4 3.4 4

ABC

a

Sa

a x a a a

h CC

x a a a



 = =









= = = =



−−



3

2

6 3 2

3.

22

aa

Va = =

.

Câu 9: Cho hình lăng trụ tam giác đều

.ABC A B C

  

có cạnh đáy bằng

a

. Đường thẳng

BC



tạo với mặt

phẳng

( )

ACC A



góc



thỏa mãn

cot 2



=

. Thể tích khối lăng trụ

.ABC A B C

  

bằng

A.

3

33

8

a

. B.

3

4 11

3

a

. C.

3

11

8

a

. D.

3

2 33

3

a

.

Lời giải

Chọn A

Kẻ

BH AC⊥

với

H AC

. Khi đó

( )

BH ACC A



⊥

và

H

là trung điểm

AC

.

Khi đó góc giữa đường thẳng

BC



với mặt phẳng

( )

ACC A



là góc giữa đường thẳng

BC



với

đường thẳng

HC



hay

HC B





=

.

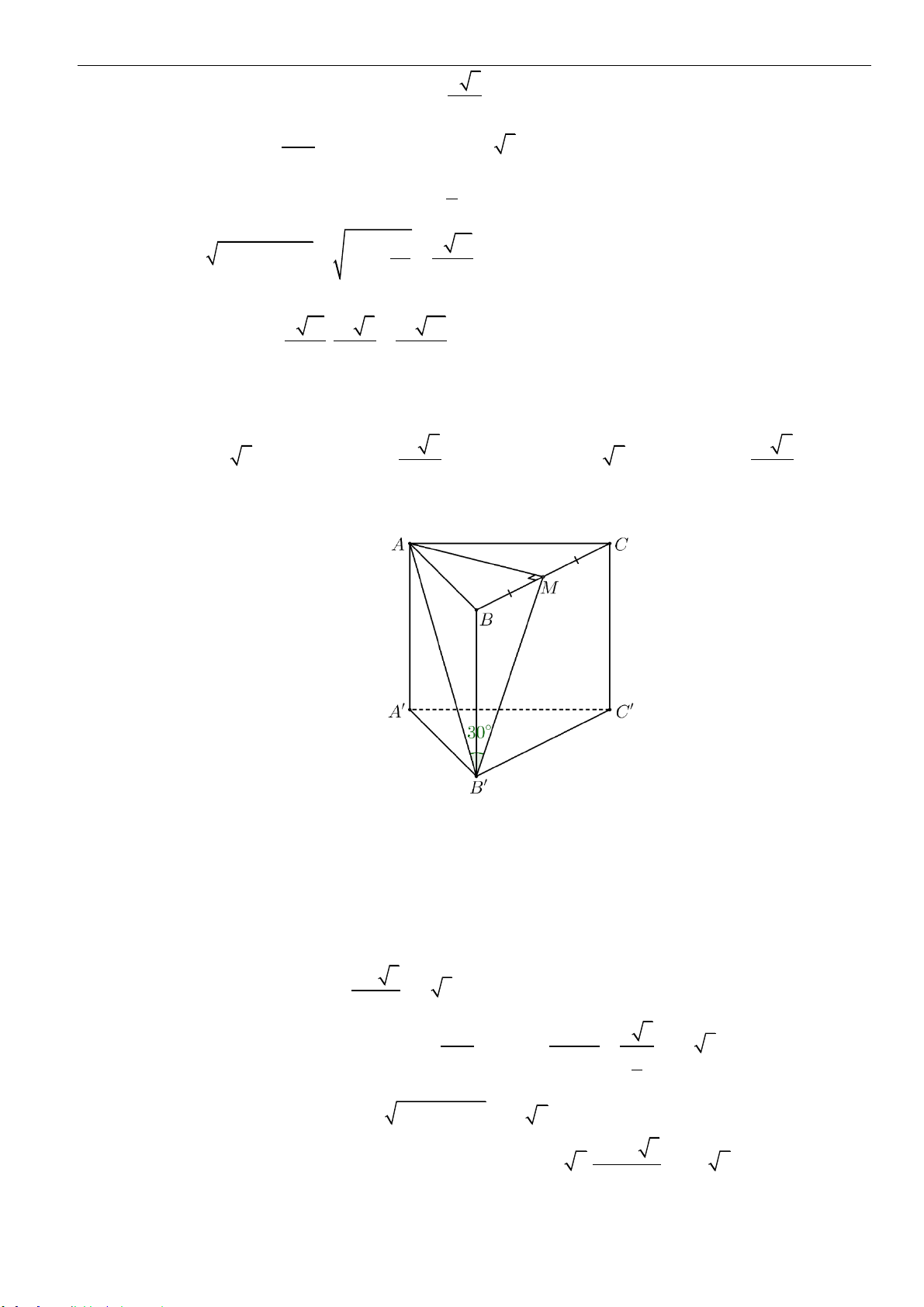
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 6

Trong

BHC





vuông tại

H

với

3

2

a

BH =

khi đó ta có

cot 2 2 2. 3

HC

HC B HC BH a

BH





=  =  = =

.

Trong

CHC





vuông tại

C

với

2

a

CH =

khi đó ta có

2

2 2 2

11

3

42

aa

CC HC CH a



= − = − =

.

Vậy thể tích khối lăng trụ

.ABC A B C

  

là

23

11 3 33

..

2 4 8

ABC

a a a

V CC S





= = =

(đvtt).

Câu 10: Cho hình lăng trụ tam giác đều

.ABC A B C

  

có

2,AB a=

đường thẳng

AB



tạo với mặt phẳng

( )

BCC B



một góc

30 .

Tính thể tích

V

của khối lăng trụ đã cho.

A.

3

6Va=

. B.

3

6

3

a

V =

. C.

3

26Va=

. D.

3

6

2

a

V =

.

Lời giải

Chọn C

Gọi

M

là trung điểm

.BC

Vì

ABC

đều nên

.AM BC⊥

Mà

AM BB



⊥

(do

.ABC A B C

  

là hình lăng trụ tam giác đều)

Suy ra

( )

.AM BB C C



⊥

Khi đó

BM



là hình chiếu của

AB



lên

( )

.BB C C



Suy ra

( )

, , 30 .AB BB C C AB B M AB M

     

= = = 

Vì

ABC

đều nên

3

3.

2

AB

AM a==

AB M





vuông tại

M

có

3

sin 2 3.

1

sin30

2

AM AM a

AB M AB a

AB



=  = = =





ABB





vuông tại

B

có

22

2 2.BB AB AB a



= − =

Thể tích của khối lăng trụ đã cho là

( )

2

3

23

. 2 2. 2 6

4

ABC

a

V BB S a a



= = =

(đvtt).

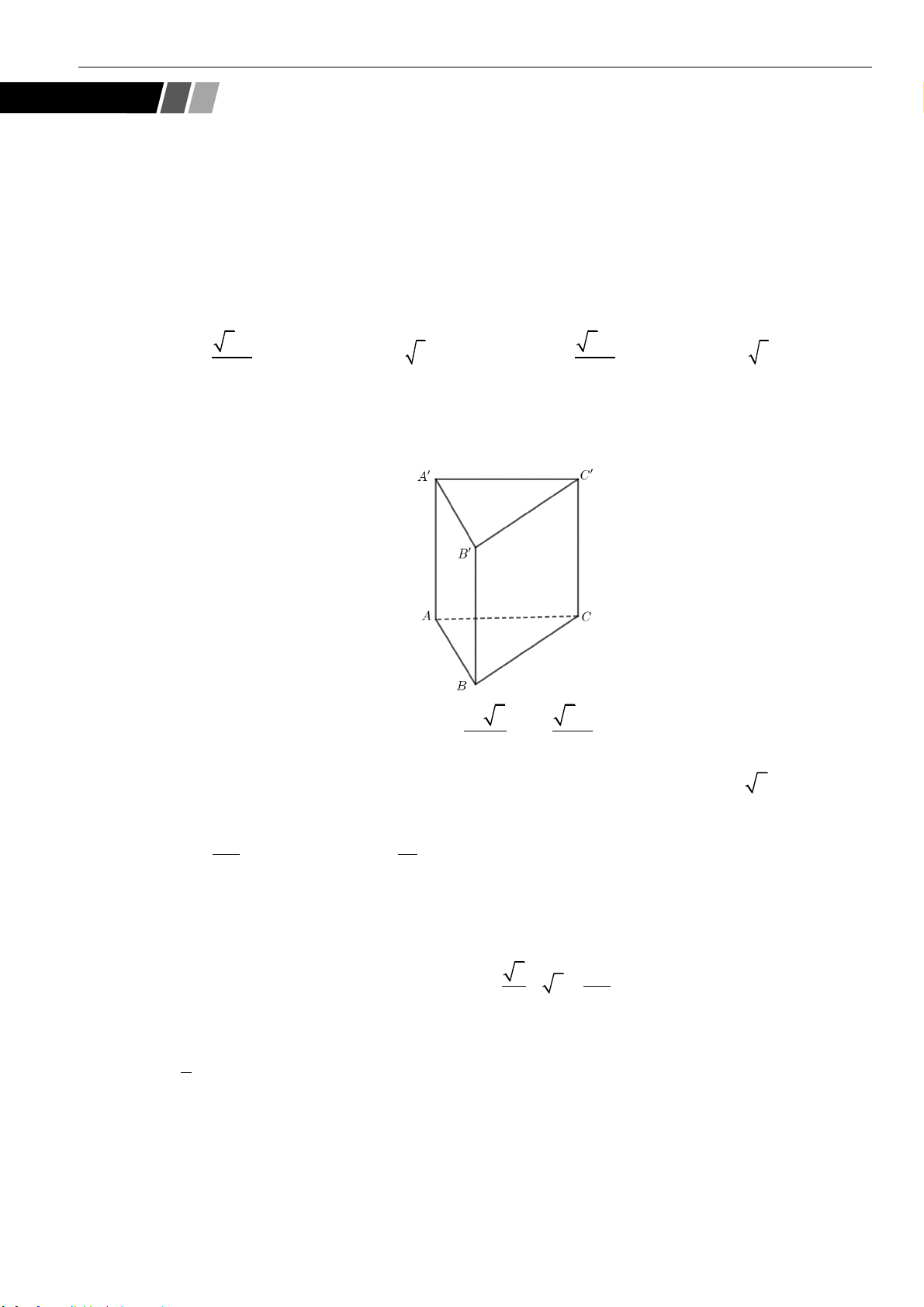
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

7 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 1: Thể tích

V

khối lập phương cạnh

3a

là

A.

3

81Va=

. B.

3

9Va=

. C.

3

Va=

. D.

3

27Va=

.

Lời giải

Chọn D

Thể tích

V

khối lập phương cạnh

3a

là

( )

3

3 27V a a==

.

Câu 2: Cho khối lăng trụ đứng

.ABC A B C

  

có tam giác

ABC

đều cạnh

a

và độ dài cạnh bên

2a

. Tính

thể tích

V

của khối lăng trụ

.ABC A B C

  

.

A.

3

4

a

V =

. B.

3

23Va=

. C.

3

2

a

V =

. D.

3

3Va=

.

Lời giải

Chọn C

Thể tích khối lăng trụ là

23

33

. .2

42

ABC

aa

V S AA a





= = =

.

Câu 3: Cho lăng trụ đều

. ' ' 'ABC A B C

có cạnh đáy bằng

2a

, độ dài cạnh bên bằng

3a

. Thể tích

V

của khối lăng trụ bằng

A.

3

4

a

V =

. B.

3

4

a

V =

. C.

3

Va=

. D.

3

3Va=

.

Lời giải

Chọn A

Theo tính chất lăng trụ tam giác đều, đáy là tam giác đều

ABC

và cạnh bên vuông góc với đáy.

Do đó áp dụng công thức

( )

3

2

33

. 2 . . 3 .

44

ABC

a

V S h a a



= = =

Câu 4: Thể tích khối lập phương có cạnh bằng

2

bằng

A.

8

3

. B.

4

. C.

6

. D.

8

.

Lời giải

Chọn D

Ta có

3

28V ==

.

Câu 5: Thể tích khối lập phương cạnh

2a

bằng

A.

3

32a

. B.

3

16a

. C.

3

64a

. D.

3

8a

.

BÀI TẬP TRẮC NGHIỆM

C

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 8

Lời giải

Chọn D

Thể tích khối lập phương cạnh

2a

bằng

( )

3

28aa=

.

Câu 6: Cho khối lập phương có thể tích bằng

64.

Cạnh của khối lập phương đã cho bằng

A.

4 2.

B.

4.

C.

32.

D.

8.

Lời giải

Chọn B

Gọi cạnh của khối lập phương là

.a

Ta có

3

64 4.V a a= =  =

Vậy cạnh của khối lập phương đã cho bằng

4.

Câu 7: Thể tích của một khối lập phương có cạnh bằng

1m

là

A.

3.Vm=

B.

3

1.Vm=

C.

3

1

.

3

Vm=

D.

2

1Vm=

Lời giải

Chọn B

Thể tích khối lập phường có cạnh bằng

1m

là:

33

11Vm==

Câu 8: Cho khối lăng trụ tứ giác đều có cạnh đáy bằng

a

, chiều cao bằng

2a

. Thể tích khối lăng trụ đã

cho bằng

A.

3

4a

. B.

3

4

3

a

. C.

3

2

3

a

. D.

3

2a

.

Lời giải

Chọn D

Ta có:

23

. .2 2V B h a a a= = =

.

Câu 9: Thể tích của khối lập phương cạnh 4a bằng

A.

3

16a

. B.

3

64a

. C.

3

4a

. D.

3

a

.

Lời giải

Chọn B

Thể tích của khối lập phương cạnh 4a là

( )

3

4 64V a a==

.

Câu 10: Thể tích khối lập phương có cạnh bằng 3 là

A.

36

. B.

9

. C.

27

. D.

81

.

Lời giải

Chọn C

Thể tích khối lập phương có cạnh bằng 3 là

3

3 27V ==

.

Chọn C

Câu 11: Cho khối lăng trụ đứng có chiều cao bằng

3

và đáy là tam giác đều có độ dài cạnh bằng

2

. Tính

thể tích khối lăng trụ đã cho

A.

3

. B.

33

. C.

3

. D.

6

.

Lời giải

Chọn B

Diện tích đáy bằng

2

23

3

4

B ==

.

Thể tích của khối lăng trụ là

. 3 3V B h

.

Câu 12: Thể tích khối lập phương cạnh

3a

bằng

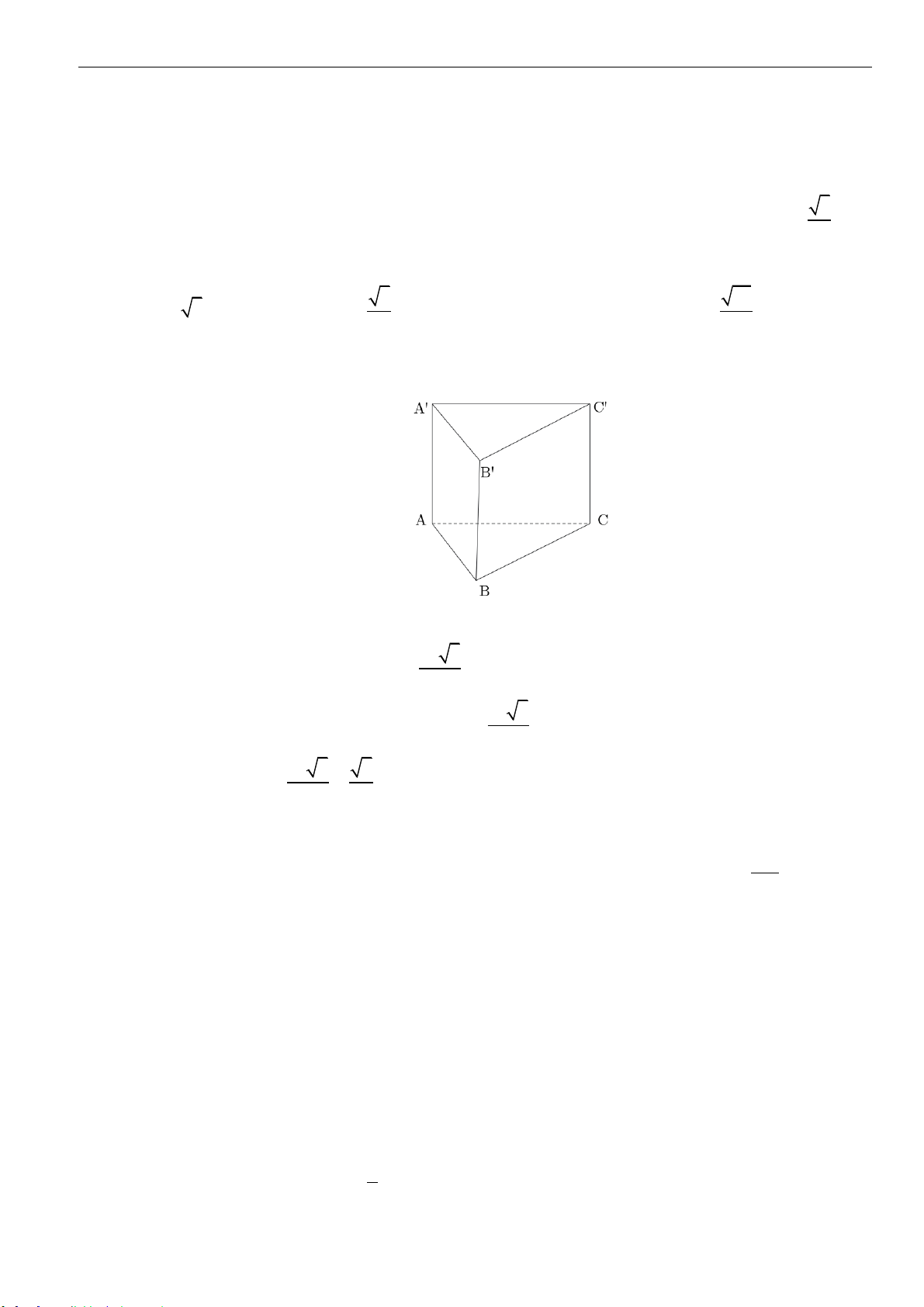
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

9 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

A.

3

3a

. B.

3

27a

. C.

3

a

. D.

3

9a

.

Lời giải

Chọn B

Thể tích khối lập phương

( )

3

3 27V a a==

.

Câu 13: Cho

( )

H

là lăng trụ tam giác đều có tất cả các cạnh bằng nhau, thể tích của

( )

H

bằng

3

4

. Độ

dài cạnh của khối lăng trụ

( )

H

là

A.

3

. B.

3

4

. C.

1

. D.

3

16

3

.

Lời giải

Chọn C

Gọi

a

là cạnh của hình lăng trụ.

Diện tích tam giác

ABC

là

2

3

4

ABC

a

S =

.

Thể tích của khối lăng trụ là

3

4

ABC

a

V S .AA



==

.

Theo bài ra ta có

3

33

11

44

a

aa=  =  =

.

Câu 14:

Khối lập phương có cạnh bằng

2a

thì có thể tích

V

là

A.

3

4Va=

. B.

3

Va=

. C.

3

8Va=

. D.

3

8

3

a

V =

.

Lời giải

Chọn C

Khối lập phương có cạnh bằng

2a

thì có thể tích

( )

3

28V a a==

.

Câu 15: Thể tích của khối lập phương cạnh

2

bằng

A.

6

. B.

8

. C.

2

. D.

4

.

Lời giải

Chọn B

Thể tích của khối lập phương cạnh

2

là:

3

28V ==

.

Câu 16: Khối lập phương đơn vị có thể tích bằng

A.

3

. B.

1

3

. C.

1

. D.

12

.

Lời giải

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 10

Chọn C

Khối lập phương đơn vị có thể tích bằng

1

.

Câu 17: Cho hình lăng trụ tứ giác đều có cạnh đáy bằng

2a

, cạnh bên bằng

5a

. Thể tích của khối

lăng trụ đó bằng

A.

3

25

9

a

. B.

3

5a

. C.

3

25a

. D.

3

25

3

a

.

Lời giải

Chọn C

Lăng trụ đã cho là lăng trụ tứ giác đều nên đáy là hình vuông cạnh bằng

2a

. Cạnh bên vuông

góc với mặt đáy.



Diện tích đáy của hình lăng trụ là

( )

2

22B a a==

.

Vậy thể tích của khối lăng trụ đã cho bằng

23

. 2 . 5 2 5.V B h a a a= = =

Câu 18: Cho lăng trụ tam giác đều có độ dài tất cả các cạnh bằng

3a

. Thể tích khối lăng trụ đã cho

bằng

A.

3

93

2

a

. B.

3

93

4

a

. C.

3

27 3

2

a

. D.

3

27 3

4

a

.

Lời giải

Chọn D

Diện tích đáy của hình lăng trụ là:

( )

2

3 9 3

3.

44

a

Ba==

.

Chiều cao của hình lăng trụ là:

3ha=

.

Thể tích khối lăng trụ là:

23

9 3 27 3

. .3

44

aa

V B h a= = =

.

Câu 19: Cho khối lăng trụ đều

. ' ' 'ABC A B C

có cạnh đáy bằng

a

, cạnh bên bằng

3a

. Thể tích của

khối lăng trụ bằng

A.

3

a

. B.

3

4

a

. C.

3

6

a

. D.

3

4

a

.

Lời giải

Chọn D

Diện tích đáy

2

3

4

ABC

a

S



=

.

Khối lăng trụ đều

. ' ' 'ABC A B C

có chiều cao bằng

'AA

.

Thể tích khối lăng trụ là:

23

. ' ' '

33

. ' . 3

44

ABC A B C ABC

aa

V S AA a



= = =

.

Câu 20: Thể tích của khối lập phương cạnh

2a

bằng

A.

3

.a

B.

3

8.a

C

.

31

.

4

a

D.

25

.

5

a

Lời giải

Chọn B

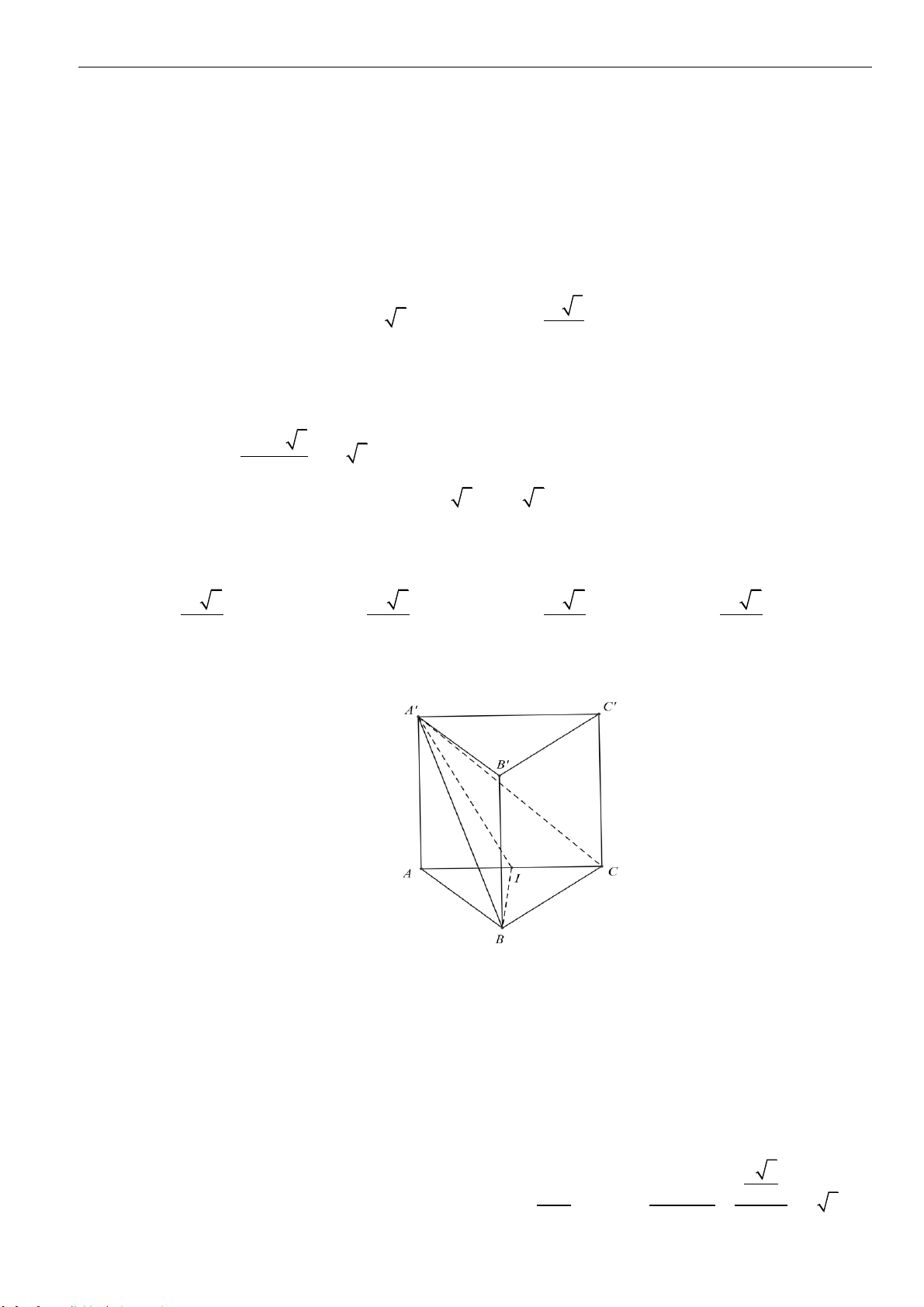
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

11 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Thể tích của khối lập phương:

( )

3

28V a a==

.

Câu 21: Thể tích của khối lập phương cạnh

3a

bằng

A.

3

3a

. B.

3

a

. C.

3

27a

. D.

3

9a

.

Lời giải

Chọn C

Thể tích của khối lập phương cạnh

3a

là

( )

3

3 27V a a==

.

Câu 22: Thể tích của khối lăng trụ đều có cạnh đáy bằng

2a

, cạnh bên bằng

a

là:

A.

3

8a

. B.

3

3a

. C.

3

a

. D.

3

2a

.

Lời giải

Chọn B

Thể tích của khối lăng trụ là

.V B h=

.

Ta có:

( )

2

23

3

4

a

Ba==

,

ha=

.

Vậy thể tích của khối lăng trụ là

23

3. 3.V a a a==

Câu 23: Cho lăng trụ tam giác đều

.ABC A B C

  

có cạnh đáy bằng

a

. Góc tạo bởi đường thẳng

AB



và

mặt phẳng

( )

AA C



bằng

0

30

. Thể tích khối lăng trụ bằng

A.

3

6

4

a

. B.

3

2

a

. C.

3

6

12

a

. D.

3

4

a

.

Lời giải

Chọn A

Gọi

I

là trung điểm của cạnh

AC

. Khi đó,

BI AC⊥

(do tam giác

ABC

đều).

Lại có,

( ) ( )

( )

' '

''

AA C C ABC

AA C C ABC AC

BI ABC

⊥





=









nên

( ) ( )

' ' 'BI AA C C BI AA C⊥  ⊥

. Do đó, góc tạo bởi đường thẳng

'AB

và mặt phẳng

( )

'AA C

chính là góc

0

' 30BA I =

.

Xét tam giác

'A BI

vuông tại

I

, ta có:

0

3

2

sin ' ' 3

' sin30

sin '

a

BI BI

BA I A B a

AB

BA I

=  = = =

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 12

22

' ' 2.AA A B AB a = − =

Ta có:

23

. ' ' '

36

. ' . 2 .

44

ABC A B C ABC

aa

V S AA a



= = =

Câu 24: Tính thể tích

V

của khối lập phương

.ABCD A B C D

   

biết

23AC a



=

.

A.

3

Va=

. B.

3

24 3Va=

. C.

3

8a

. D.

3

33Va=

.

Lời giải

Chọn D

Vì

.ABCD A B C D

   

là hình lập phương nên ta có

2 2 2 2 2 2 2

3AC AC CC AB BC CC AB

  

= + = + + =

( )

2

22

23

4

33

a

AC

AB a



 = = =

2AB a=

Vậy

( )

3

33

28V AB a a= = =

.

Câu 25: Cho hình lăng trụ tam giác đều

.ABC A B C

  

có

AB a=

, góc giữa đường thẳng

AC



và mặt

phẳng

( )

ABC

bằng

45

. Thể tích khối lăng trụ

.ABC A B C

  

bằng

A.

3

4

a

. B.

3

6

a

. C.

3

12

a

. D.

3

2

a

.

Lời giải

Chọn A

Ta có

( )

, 45A C ABC A CA



= = 

nên

AA C



vuông cân tại

A

suy ra

AA AC a



==

.

Vậy thể tích khối lăng trụ

.ABC A B C

  

là

23

33

.

44

aa

V Sh a= = =

.

Câu 26: Cho lăng trụ tam giác đều có độ dài tất cả các cạnh bằng

3

. Thể tích khối lăng trụ đã cho bằng

A.

9

4

. B.

3

4

. C.

9

12

. D.

3

8

.

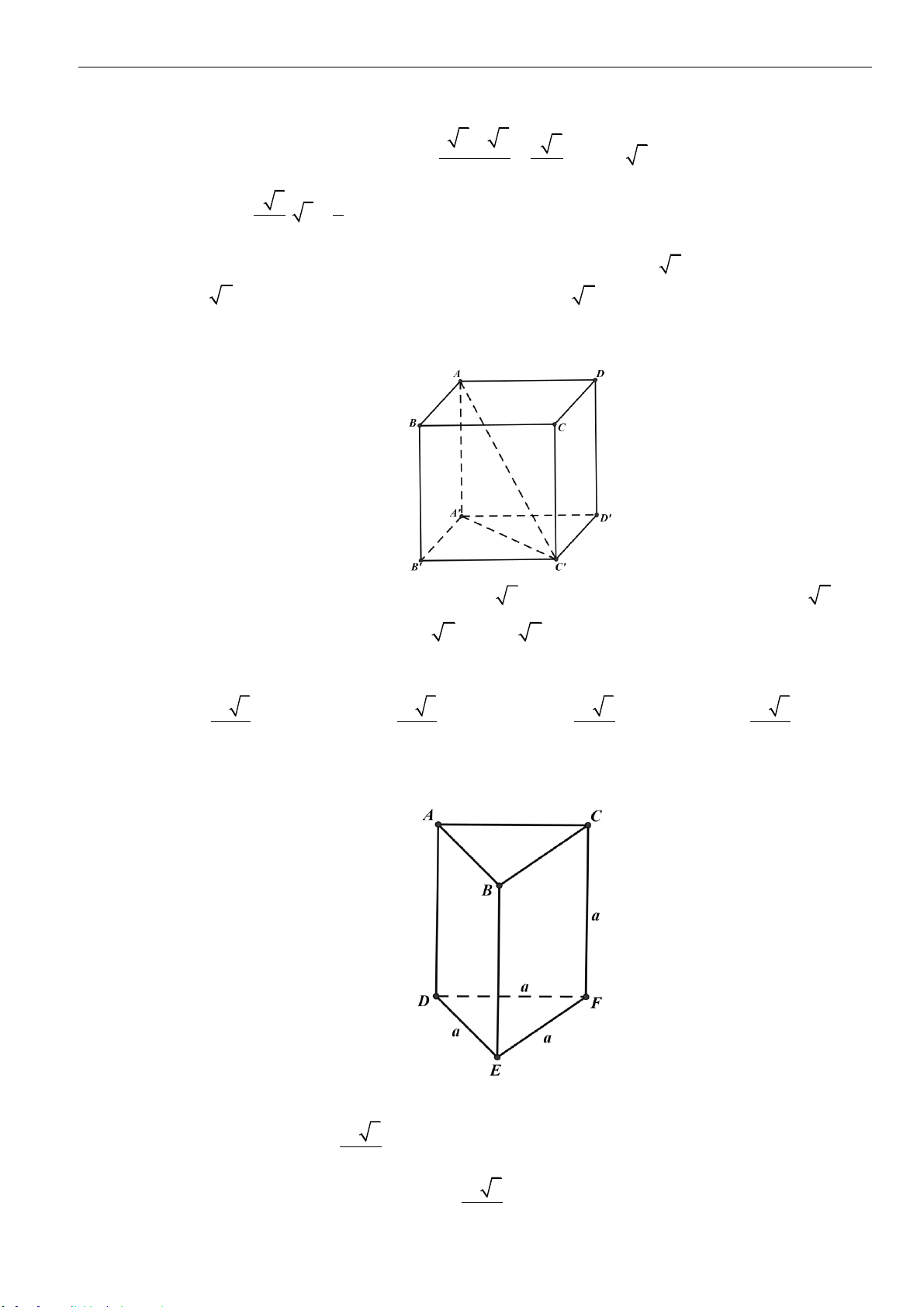
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

13 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Lời giải

Chọn A

Ta có

.

LT

V B h=

. Theo bài ra thì:

( )

2

33

44

B ==

và

3h =

Suy ra

3 3 9

.3

44

LT

V ==

.

Câu 27: Cho một khối lập phương

.ABCD A B C D

   

có đường chéo

6AC a



=

có thể tích là

A.

3

22a

. B.

3

a

. C.

3

66a

. D.

3

4a

.

Lời giải

Chọn A

Đường chéo của hình lập phương là

6AC a



=

nên khối lập phương có cạnh bằng

2a

. Do

đó, khối lập phương có thể tích là

( )

3

2 2 2aa=

.

Câu 28: Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng

a

.

A.

3

2

a

V =

. B.

3

4

a

V =

. C.

3

12

a

V =

. D.

3

6

a

V =

.

Lời giải

Chọn B

Gọi lăng trụ tam giác đều là

.ABC DEF

có các cạnh bằng

a

.

Diện tích đáy là

2

3

4

DEF

a

S



=

.

Thể tích khối lăng trụ là

3

.

4

DEF

a

V S CF



==

.

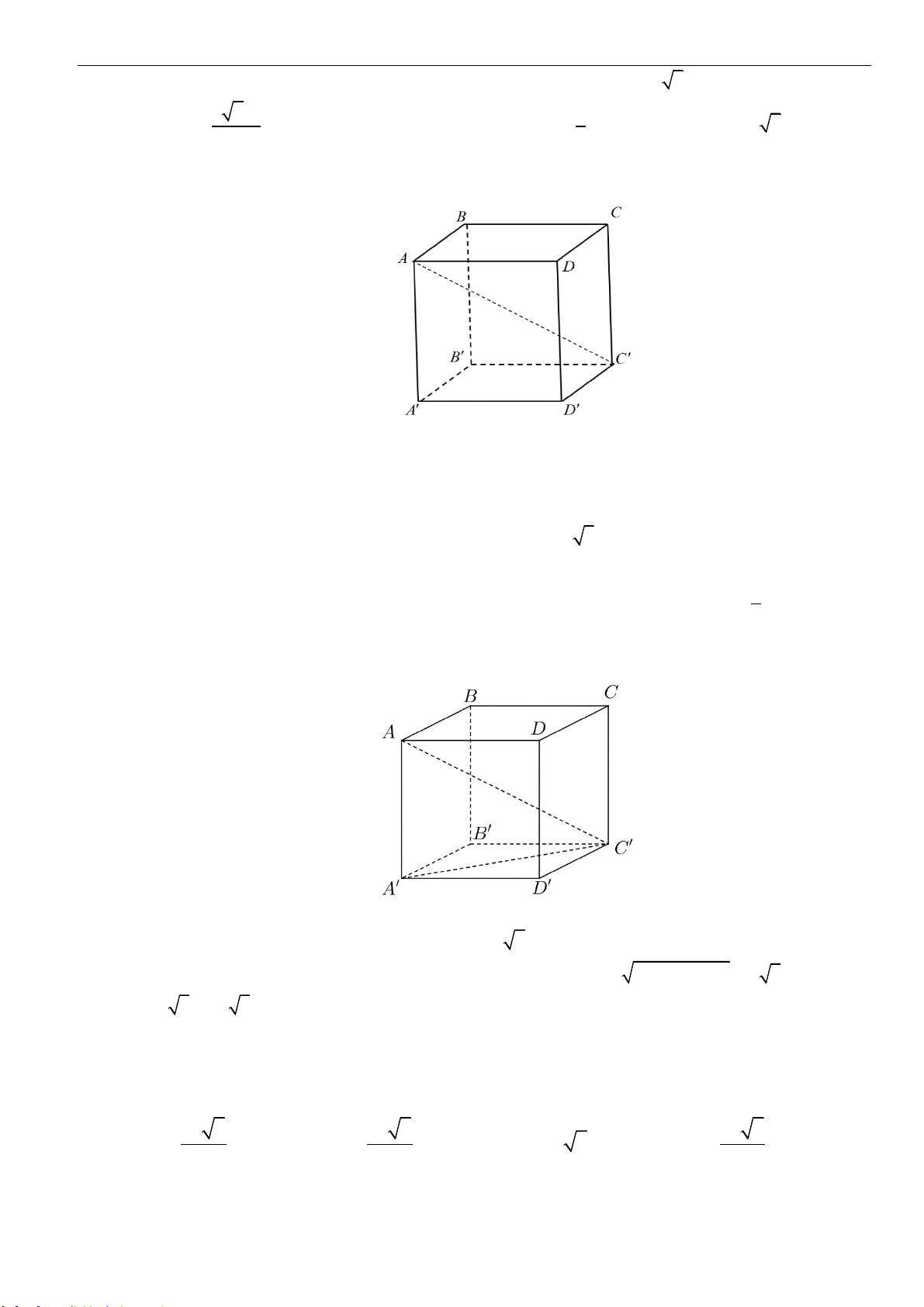
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 14

Câu 29: Tính thể tích

V

của khối lập phương

.ABCD A B C D

  

, biết

3AC a



=

A.

3

36

4

a

V =

. B.

3

Va=

. C.

3

1

3

Va=

. D.

3

33Va=

.

Lời giải

Chọn B

Gọi cạnh của hình lập phương là

x

, khi đó ta có:

2 2 2

AC AA A C

   

=+

2 2 2 2

AC AA AB BC



 = + +

2 2 2 2

3a x x x = + +

xa=

.

Vậy thể tích của hình lập phương là

3

Va=

.

Câu 30: Cho hình lập phương

.ABCD A B C D

   

có

23AC a



=

. Tính thể tích hình lập phương

.ABCD A B C D

   

.

A.

3

8Va=

. B.

3

4Va=

. C.

3

Va=

. D.

3

8

3

Va=

.

Lời giải

Chọn A

Gọi cạnh hình lập phương có độ dài

x

.

Xét tam giác

ABC

  

vuông tại

B



có

2A C x



=

.

Xét tam giác

AA C



vuông tại

A



có

22

3AC AA A C x

   

= + =

suy ra

3 2 3 2x a x a=  =

Vậy thể tích hình lập phương

.ABCD A B C D

   

là

3

8Va=

.

Câu 31: Cho khối lăng trụ tam giác đều

.ABC A B C

  

có

AB a=

và

' 2 .AA a=

Thể tích của khối lăng

trụ

.ABC A B C

  

bằng

A.

3

2

a

. B.

3

6

a

. C.

3

3a

. D.

3

12

a

.

Lời giải

Chọn A

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

15 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Diện tích

ABC

đều cạnh

AB a=

là:

2

3

4

ABC

a

S



=

.

Thể tích của khối lăng trụ đều

23

.

33

. 2 .

42

ABC A B C ABC

aa

V AA S a

  





= = =

.

Câu 32: Cho khối lăng trụ tam giác đều

.ABC A B C

  

, biết

AB a=

,

7AB a



=

. Thể tích

V

của khối lăng

trụ là

A.

3

32

4

a

V =

. B.

3

4

a

V =

. C.

3

33

4

a

V =

. D.

3

a

V =

.

Lời giải

Chọn A

Ta có

( ) ( )

( )

2

22

2

76AA AB A B a a a

   

= − = − =

.

Diện tích đáy

ABC

là

2

3

4

ABC

a

S =

.

Thể tích khối lăng trụ là

23

.

3 3 2

. 6.

44

ABC A B C ABC

aa

V AA S a

  



= = =

.

Câu 33: Cho lăng trụ tam giác đều

.ABC A B C

  

có cạnh bên bằng

2a

. Đáy

ABC

nội tiếp đường tròn

bán kính

Ra=

. Tính thể tích khối lăng trụ đã cho.

A.

3

33

2

a

. B.

3

3a

. C.

3

2

a

. D.

3

2

a

.

Lời giải

Chọn A

Gọi

M

là trung điểm

,BC N

là trung điểm của

AB

và

.I AM CN=

Đặt

AB x=

.

Đáy

ABC

là tam giác đều và nội tiếp đường tròn bán kính

Ra=

nên

AI a=

, suy ra

33

.

22

AM AI a==

I

N

M

C'

B'

A

C

B

A'

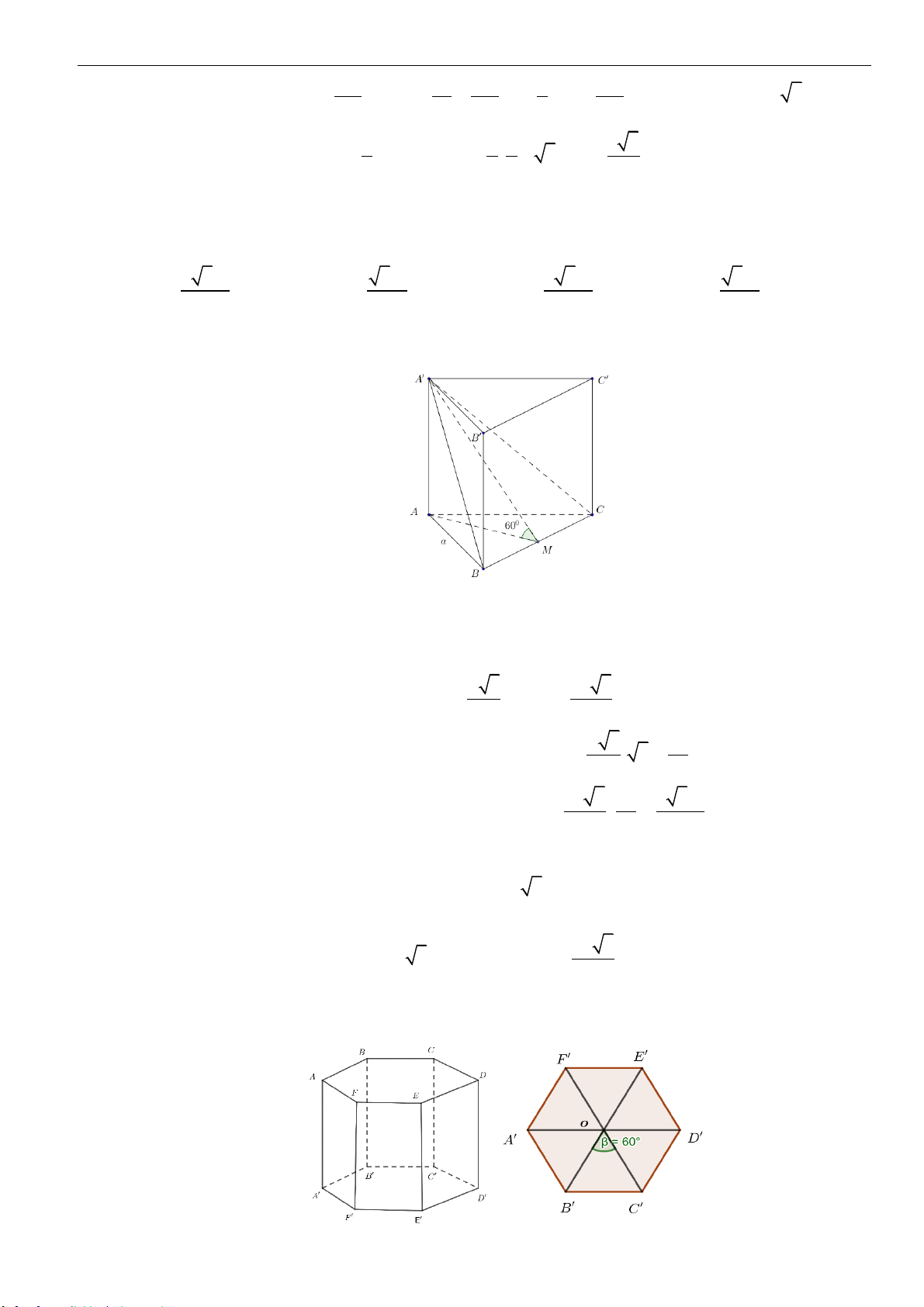
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 16

Khi đó,

2

22

2 2 2

3

2 4 4

BC x x

AM AB x





= − = − =







2

33

24

x

a





=







22

3xa=

.

Vậy

3

.

1 1 3 3 3

. . . . . 3 .2 .

2 2 2 2

ABC A B C ABC

V S AA AM BC AA a a a a

  



= = = =

Câu 34: Cho hình lăng trụ đều

.ABC A B C

  

, đáy là tam giác đều cạnh

a

góc giữa hai mặt phẳng

( )

A BC



và

( )

ABC

bằng

60



. Thể tích của khối lăng trụ

.ABC A B C

  

bằng

A.

3

33

4

a

. B.

3

4

a

. C.

3

33

8

a

. D.

3

8

a

.

Lời giải

Chọn C

Gọi

M

là trung điểm của

BC

, ta có

AM BC⊥

Mặt khác

.ABC A B C

  

là lăng trụ đều nên

AA BC



⊥

Suy ra

A M BC



⊥

, góc giữa hai hai mặt phẳng

( )

A BC



và

( )

ABC

là

60A MA



=

Tam giác

ABC

đều cạnh

a

, ta có

3

2

a

AM =

;

2

3

4

ABC

a

S =

.

Tam giác

A AM



vuông tại

A

, ta có

33

.tan60 . 3

22

aa

AA AM



=  = =

.

Thể tích khối lăng trụ

.ABC A B C

  

là

23

3 3 3 3

.

4 2 8

ABC

a a a

V S AA





= =  =

.

Câu 35: Cho hình lăng trụ lục giác đều

.ABCDEF A B C D E F

     

có cạnh đáy bằng

a

, biết thể tích của

khối lăng trụ

.ABCDEF A B C D E F

     

là

3

33Va=

. Tính chiều cao

h

của khối lăng trụ

.ABCDEF A B C D E F

     

.

A.

2ha=

. B.

3ha=

. C.

23

3

a

h =

. D.

ha=

.

Lời giải

Chọn A

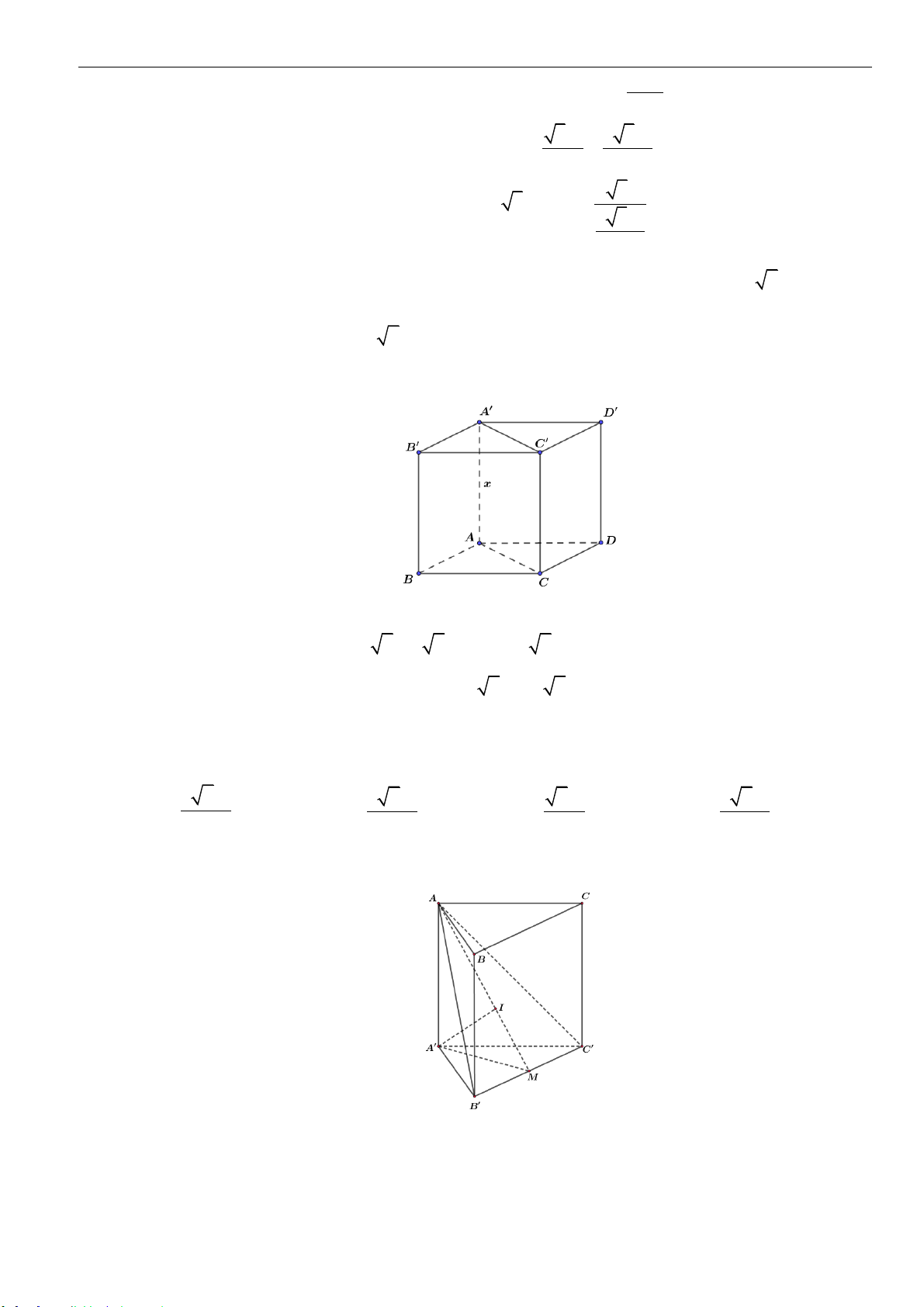
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

17 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Do

.ABCDEF A B C D E F

     

là lăng trụ đều nên ta có:

360

60

6

B OC





= = 

.

Suy ra

B OC





đều cạnh

a

22

3 3 3

66

42

A B C D E F B OC

aa

SS

       



= =  =

.

Thể tích của khối lăng trụ:

3

2

33

. 3 3 2

33

2

A B C D E F

a

V h S a h a

a

     

= =  = =

.

Câu 36: Cho khối lập phương

. ' ' ' 'ABCD A B C D

có diện tích mặt chéo

''ACC A

bằng

2

22a

. Thể tích

của khối lập phương

. ' ' ' 'ABCD A B C D

bằng

A.

3

2a

. B.

3

22a

. C.

3

a

. D.

3

8a

.

Lời giải

Chọn B

Gọi

x

là cạnh của hình lập phương

( )

0x 

.

Ta có

2

''

. ' . 2 2 2 2

ACC A

S AC AA x x a x a= = =  =

.

Vậy thể tích của khối lập phương là

( )

3

2 2 2V a a==

.

Câu 37: Cho khối lăng trụ đều

.ABC A B C

  

có cạnh đáy bằng

2a

. Khoảng cách từ điểm

A



đến mặt

phẳng

( )

AB C



bằng

a

. Thể tích khối lăng trụ đã cho là

A.

3

32

2

a

. B.

3

32

8

a

. C.

3

2

a

. D.

3

32

6

a

.

Lời giải

Chọn A

Gọi

M

là trung điểm của

BC



và

I

là hình chiếu của

A



lên

AM

. Khi đó ta có

( )

B C A M

B C A MA B C A I

B C A A

  

⊥



     

 ⊥  ⊥



  

⊥



(1)

Mà

( )

2AM A I



⊥

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 18

Từ (1) và (2) suy ra

( )

A I AB C

  

⊥

( )

,d A AB C A I a

   

 = =

.

Xét tam giác vuông

2 2 2

1 1 1 6

:

2

a

AA M AA

A I AA A M



= +  =

  



Thể tích khối lăng trụ đã cho là

2

6 4 3

..

24

ABC

aa

V AA S





= = =

3

32

2

a

.

Câu 38: Cho hình lập phương

.ABCD A B C D

   

có khoảng cách giữa hai đường thẳng

AB



và

BD

bằng

23

.

3

a

Thể tích của khối lập phương

.ABCD A B C D

   

bằng

A.

3

8a

. B.

3

36

4

a

. C.

3

33a

. D.

3

a

.

Lời giải

Chọn A

Gọi

O

là giao điểm của

BD

và

AC

.

Ta có:

BD AC

BD CC

AC CC C

⊥







⊥







=



( )

BD ACC A



⊥

.

Trong

( )

ACC A



: Từ

C

hạ

'CH C O⊥

tại

H

Khi đó ta có:

'

CH BD

CH C O

C O BD O

⊥







⊥





=



( )

'CH BDC⊥

Ta lại có:

( )

//AB DC BDC

  



và

( )

''AB BDC

( )

//AB BDC





( ) ( )

( )

;;d AB BD d AB BDC

  

=

( )

;d A BDC



=

( )

,d C BDC



=

CH=

23

3

a

=

.

Đặt cạnh hình lập phương là

x

2

CC x

x

CO



=









=





Khi đó

2 2 2

1 1 1

'CH CC CO

=+

2 2 2

3 1 2

4a x x

 = +

2

3

x

=

22

4xa=

2xa=

.

Do đó thể tích của khối lập phương là

( )

3

28aa=

.

Câu 39: Cho hình lăng trụ đều

.ABC A B C

  

có cạnh đáy bằng

23

3

a

. Đường thẳng

BC



tạo với mặt

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

19 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

phẳng

( )

ACC A



góc



thỏa mãn

cot 2



=

. Thể tích khối lăng trụ

.ABC A B C

  

bằng

A.

3

4

11

3

a

. B.

3

1

11

9

a

. C.

3

1

11

3

a

. D.

3

2

11

3

a

.

Lời giải

Chọn C

Gọi

H

là trung điểm cạnh

AC

.

Do tam giác

ABC

đều nên

BH AC⊥

và

2 3 3

.

32

a

BH a==

.

Ta có:

BH AC⊥

,

BH AA



⊥

(do

( )

AA ABC



⊥

) suy ra

( )

BH ACC A



⊥

.

Do đó:

( )

,,BC ACC A BC HC BC H

     

==



=

.

Xét tam giác vuông

HBC



:

cot .cot 2

CH

C H BH a

BH



=  = =



.

Áp dụng định lí Pitago trong tam giác vuông

CHC



:

2

2 2 2

3 33

4

93

aa

CC C H CH a



= − = − =

Thể tích khối lăng trụ:

.

1 1 2 3 33

. . . . . . .

2 2 3 3

ABC A B C ABC

aa

V S CC BH AC CC a

  



= = =

3

1

11

3

a=

.

Câu 40: Cho lăng trụ tứ giác đều

.ABCD A B C D

   

. Biết khoảng cách và góc giữa hai đường thẳng

AC

và

DC



lần lượt là

21

7

a

và



,

2

cos

4



=

. Tính thể tích lăng trụ

.ABCD A B C D

   

A.

3

21

6

a

. B.

3

7

2

a

. C.

3

15

2

a

. D.

3

3a

.

Lời giải

Chọn D

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 20

Gọi

x

,

y

lần lượt chiều dài cạnh đáy của hình vuông và chiều cao của lăng trụ đều.

Vì

AB



//

DC



nên ta có góc

( ) ( )

,,AC DC AC AB CAB



  

= = =

.

Xét tam giác cân

B AC



tại

B



:

2 2 2

2

2 . .cos

2

AB

B C AB AC AB AC AC





  

= + −  =

Suy ra

22

2

23

2

x x y y x= +  =

.

Diện tích của tam giác

ACB



:

2

1 1 7 7

. . .sin . 2.2 .

2 2 8 2

ACB

S AC AB x x x





= = =

.

Thể tích của khối chóp

.B ACD



là

3

2

. . .

1 1 1 3

. . . 3

2 6 6 6

B ACD B ABCD ABCD A B C D

x

V V V x x

     

= = = =

Mặt khác

AB



//

DC



suy ra khoảng cách

( ) ( )

( )

21

, , ,

7

a

d AC DC d DC B AC d D B AC

   

= = =

Suy ra

( )

32

.

1 3 1 7 21

. . , . .

3 6 3 2 7

B ACD B AC

x x a

V S d D B AC x a







=  =  =

Vậy thể tích của khối lăng trụ là

23

.

. 3 3

ABCD A B C D

V x x a

   

==

Câu 41: Cho hình lăng trụ đều

.ABC A B C

  

. Biết cosin góc giữa hai mặt phẳng

( )

ABC



và

( )

BCC B



bằng

1

23

và khoảng cách từ điểm C đến mặt phẳng

( )

ABC



bằng

a

. Thể tích khối lăng trụ

.ABC A B C

  

bằng:

A.

3

32

8

a

. B.

3

2

a

. C.

3

32

4

a

. D.

3

32

2

a

.

Lời giải

Chọn D

Đặt

,AB x AA y



==

,

0, 0xy

. Gọi M, N lần lượt là trung điểm của BC và

AB

. Kẻ

CH C N



⊥

tại H và

AK C B



⊥

tại K.

Ta có:

( )

3

,(

2

x

d A BCC B AM



==

,

2

2 2 2 2 2

31

34

42

x

C N CC CN y x y



= + = + = +

.

2 2 2 2

C B CC BC x y



= + = +

AC B





cân tại

C



22

34

1 1 .

. . . .

22

2

AC B

x x y

C N AB

S AK C B C N AB AK

CB

xy



+



 = =  = =



+

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

21 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

( )

22

,( )

3.

sin ( ),( )

,

34

d A BCC B

xy

AM

ABC BCC B

d A BC AK

xy



+

  

 = = =



+

( )

2

22

3.

16

1 3 8 1

4

23

34

xy

x

x y y

xy

+



 − =  =  =





+

Mặt khác:

( )

2 2 2 2 2

22

.3

,( 3 4 3 2

34

CC CN xy

d C ABC CH a a x y x y

CN

xy



= = = =  + =



+

Thay

( )

1

và

( )

2

ta tìm được

6

2

a

x a y=  =

.

Vậy

( )

2

3

.

23

6 3 2

..

4 2 2

ABC A B C ABC

a

aa

V S AA

  



= = =

.

Câu 42: Cho khối bát diện đều có cạnh

a

. Gọi

, , ,M N P Q

lần lượt là trọng tâm của các tam giác

, , ,SAB SBC SCD SDA

; gọi

, , ,M N P Q

   

lần lượt là trọng tâm của các tam giác

, , ,S AB S BC S CD S DA

   

(như hình vẽ dưới). Thể tích của khối lăng trụ

.MNPQ M N P Q

   

là

A.

3

2

72

a

. B.

3

22

81

a

. C.

3

2

24

a

. D.

3

22

27

a

.

Lời giải

Chọn D

Gọi

O AC BD=

;

,IJ

lần lượt là trung điểm của

,AB BC

.

Do

,MN

lần lượt là trọng tâm của các tam giác

,SAB SBC

nên ta có

2 1 2

AC=

3 3 3

a

MN IJ==

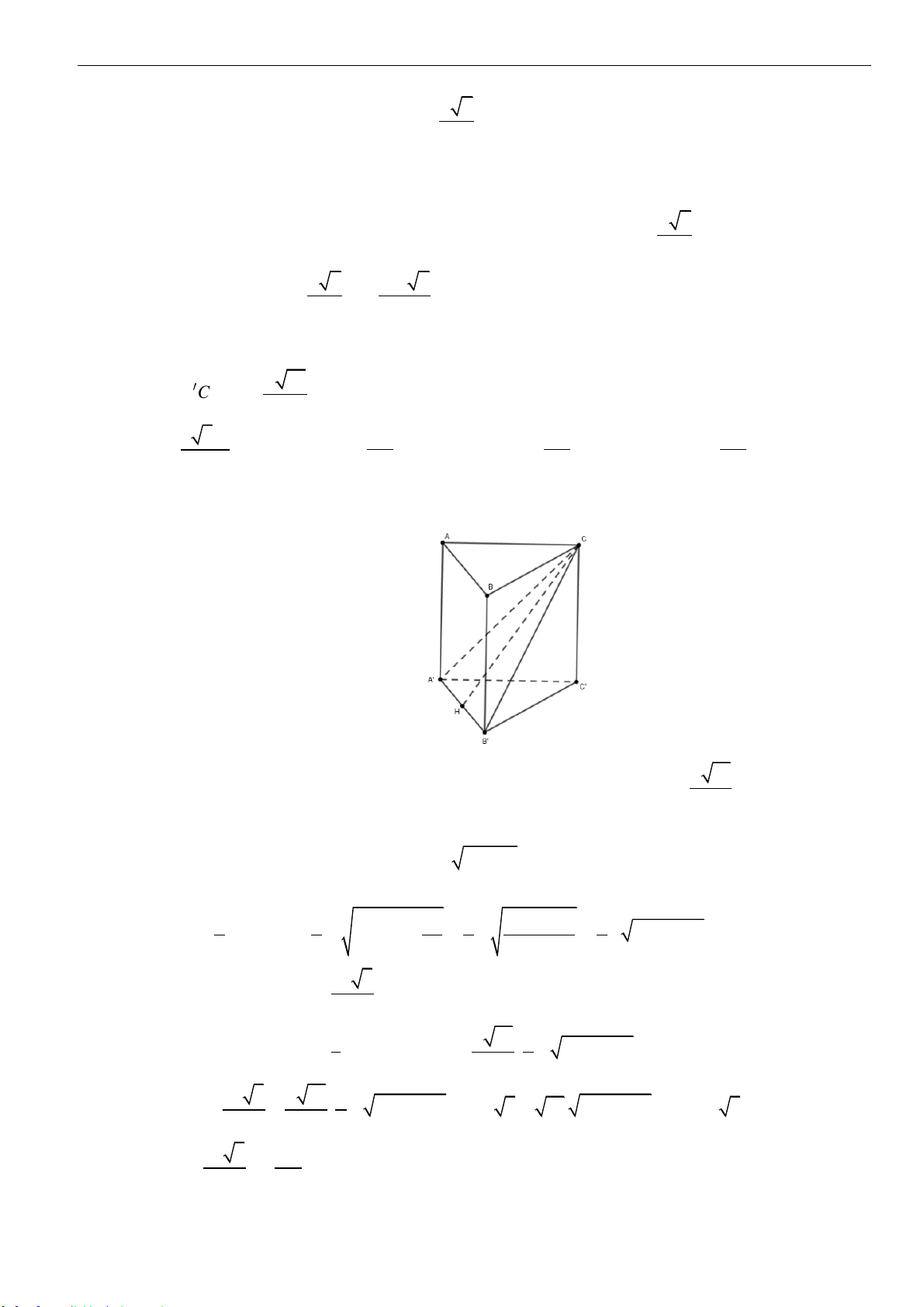
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 22

Do

SABCDS



là bát diện đều nên hoàn toàn tương tự ta có tất cả các cạnh còn lại của của khối

lăng trụ

.MNPQ M N P Q

   

cũng bằng

2

3

a

.

Mặt khác

AC BD⊥

, mà

//AC//PQ,MQ// //NPMN BD

nên

MNPQ

là hình vuông.

Tương tự ta có tất cả các mặt còn lại của lăng trụ

.MNPQ M N P Q

   

cũng là hình vuông.

Suy ra lăng trụ

.MNPQ M N P Q

   

là hình lập phương có cạnh bằng

2

3

a

.

Vậy

3

.

2 2 2

3 27

MNPQ M N P Q

aa

V

   



==





.

Câu 43: Cho hình lăng trụ đều

.ABC A B C

  

có cạnh đáy

a

; biết khoảng cách giữa hai đường thẳng

AB

và

AC

bằng

15

5

a

. Thể tích của khối lăng trụ

.ABC A B C

  

tính theo

a

bằng:

A.

3

33

8

a

. B.

3

2

a

. C.

3

8

a

. D.

3

4

a

.

Lời giải

Chọn D

Ta có

( )

,

,,

15

/ / / /

5

AB A C

AB A B C B A B C

a

AB A B AB A B C d d d



   

  = = =

Đặt

0AA x



=

.

Tam giác

CA B



cân tại

C

,

22

CA CB a x



= = +

.

Diện tích tam giác

CA B



là

2 2 2

2 2 2 2

1 1 1 3 4 1

. . . . 3 4

2 2 4 2 4 4

CA B

a a x

S CH A B a a x a a a x



+



= = + − = = +

Thể tích lăng trụ

( )

2

3

.1

4

a

Vx=

Lại có

( )

22

.

,

1 15 1

3 3. . . . 3 4

3 5 4

B A B C A B C

B A B C

a

V V d S a a x

   



= = = +

.

Do đó

2

2 2 2 2

3 15 1

. . . 3 4 5 3 15. 3 4 3

4 5 4

aa

x a a x x a x x a= +  = +  =

.

23

33

.

44

aa

Vx==

.

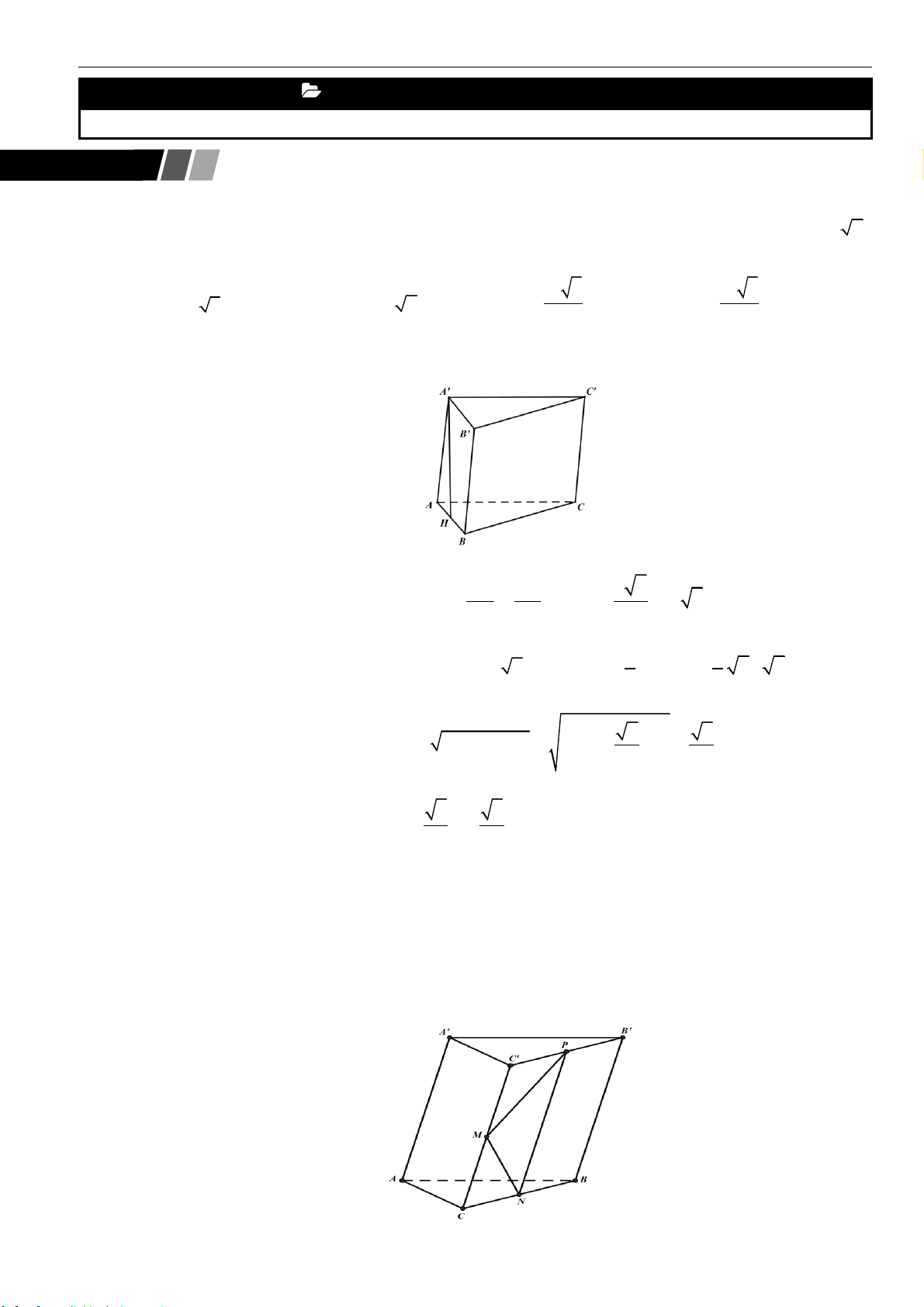
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

1 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Dạng 9: Thể tích khối lăng trụ xiên

Câu 1: Cho hình lăng trụ

. ' ' 'ABC A B C

có đáy

ABC

là tam giác vuông cân tại

B

và

2AC a=

. Hình

chiếu vuông góc của

'A

trên mặt phẳng

( )

ABC

là trung điểm

H

của cạnh

AB

và

'2AA a=

. Thể tích của khối lăng trụ đã cho bằng?

A.

3

3a

. B.

3

22a

. C.

3

6

2

a

. D.

3

6

a

.

Lời giải

Chọn C

Xét tam giác vuông cân

ABC

:

22

sin45 2

22

o

AB AB

AB a a

AC a

= =  = =

Mà tam giác

ABC

vuông cân nên

2AB BC a==

và

2

11

. 2 . 2

22

ABC

S AB BC a a a



= = =

.

Xét tam giác vuông

'AA H

:

2

2 2 2

26

' ' 2

22

A H AA AH a a a



= − = − =





.

Khi đó:

23

. ' ' '

66

. ' . .

22

ABC A B C ABC

V S A H a a a



= = =

Câu 2: Cho khối lăng trụ

.ABC A B C

  

có thể tích bằng

( )

3

18 cm

. Gọi

,,M N P

theo thứ tự là trung

điểm các cạnh

,,CC BC B C

  

. Khi đó thể tích

V

của khối chóp

.A MNP



là

A.

( )

3

9 cm

. B.

( )

3

3 cm

. C.

( )

3

12 cm

. D.

( )

3

6 cm

.

Lời giải

Chọn B

VÍ DỤ MINH HỌA

B

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 2

Ta có

3

..

2

12

3

A CBB C ABC A B C

V V cm

     

==

. Lại có

1

4

MNP BCC B

SS





=

( )

3

''

1

,.

11

3

1

44

,.

3

MNP

A MNP

A MNP A B C CB

A B C CB

BCC B

d A BCC B S

V

V V cm

V

d A BCC B S





   

  

 = =  = =

  

.

Câu 3: Cho lăng trụ

.ABC A B C

  

có đáy

ABC

là tam giác vuông tại

B

và

A A A B A C

  

==

. Biết rằng

,3AB a BC a==

và mặt phẳng

( )

A BC



tạo với mặt phẳng đáy một góc

60

. Thể tích khối

lăng trụ

.ABC A B C

  

bằng?

A.

3

4

a

. B.

3

2

a

C.

3

a

. D.

3

4

a

Lời giải

Chọn A

Gọi

H

là trung điểm của

AC

, vì tam giác

ABC

vuông tại

B

nên

H

là tâm đường tròn ngoại

tiếp của tam giác

ABC

.

Ta có:

A A A B A C

HA HB HC

  

==





==



( )

A H ABC



⊥

.

Kẻ

HM BC⊥

( ) ( )

(

)

; 60A BC ABC A MH



 = = 

.

Diện tích tam giác

ABC

:

2

13

.

22

ABC

a

S AB BC==

.

Xét tam giác vuông

A HM



có:

13

.tan60 .tan60

22

a

A H HM AB



=  =  =

.

Thể tích khối lăng trụ

.ABC A B C

  

:

23

3 3 3

..

2 2 4

ABC

a a a

V A H S



= = =

.

Câu 4: Cho lăng trụ tam giác

.ABC A B C

  

có đáy là tam giác đều cạnh

a

. Hình chiếu vuông góc của

A



trên mặt phẳng

( )

ABC

trùng với trọng tâm tam giác

ABC

. Biết khoảng cách giữa

AA



và

BC

bằng

3

4

a

. Khi đó thể tích khối lăng trụ là

A.

3

12

a

. B.

3

6

a

. C.

3

a

. D.

3

24

a

.

Lời giải

Chọn A

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

3 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Do tam giác

ABC

đều có trọng tâm

G

và

( )

'A G ABC⊥

nên

.A ABC



là hình chóp đều.

Gọi

H

là trung điểm của

BC

, khi đó

AH BC⊥

và

3

2

a

AH =

23

33

a

AG AH = =

.

Gọi

K

là hình chiếu vuông góc của

H

trên

AA



HK AA



⊥

( )

1

.

Lại có

( )

BC A HA



⊥

mà

( )

HK A HA





nên

BC HK⊥

( )

2

.

Từ

( )

1

và

( )

2

suy ra

HK

là đoạn vuông góc chung của

BC

và

AA



. Do đó

( )

3

,

4

a

d AA BC HK



==

. Đặt

A A A B A C x

  

= = =

, khi đó

2

3

a

A G x



=−

.

Ta có

22

2 2 2

3 3 2

2 . . . . 4

4 3 2 3 3

A HA

a a a a a

S HK AA A G AH x x x x x









= =  = −  = −  =





.

Khi đó

22

2

3

,

3 3 4

ABC

a a a

A G x S





= − = =

.

ABC A B C ABC

V A G S

  





=

2

3

.

34

aa

=

3

12

a

=

.

Câu 5: Cho hình lăng trụ

.ABC A B C

  

có đáy là tam giác đều cạnh

a

. Hình chiếu vuông góc của

A



xuống

mặt phẳng

( )

ABC

là trung điểm

H

của đoạn

AB

. Mặt bên

()AA C C



tạo với đáy 1 góc

45

.

Tính thể tích khối lăng trụ

.ABC A B C

  

.

A.

3

33

16

a

. B.

3

8

a

. C.

3

16

a

. D.

3

33

8

a

.

Lời giải

Chọn C

Gọi

,IK

lần lượt là trung điểm các đoạn

AC

và

AI

.

Do tam giác

ABC

đều nên

BI AC⊥

.

HK

là đường trung bình của tam giác

ABI

nên

HK AC⊥

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 4

Mặt khác

( )

A H ABC



⊥

A H AC



⊥

. Từ đó

( )

AC A HK



⊥

suy ra góc giữa mặt phẳng

( )

ABC

và mặt phẳng

()AA C C



là góc

45A KH A KH



 = 

.

Tam giác

A KH



vuông cân tại

H

3

24

BI a

A H HK



 = = =

.

Mà

2

3

4

ABC

a

S =

.Vậy

3

.

3

.

16

ABC A B C ABC

a

V A H S

  



==

.

Câu 6: Cho hình lăng trụ

.ABC A B C

  

có đáy

ABC

là tam giác đều cạnh

a

, hình chiếu vuông góc của

A



trên

( )

ABC

là trung điểm của cạnh

AB

, góc giữa đường thẳng

AC



với mặt phẳng đáy bằng

60

. Thể tích khối lăng trụ

.ABC A B C

  

bằng

A.

3

2

4

a

. B.

3

33

4

a

. C.

3

4

a

. D.

3

33

8

a

.

Lời giải

Chọn D

Gọi

H

là trung điểm cạnh

AB

. Vì hình chiếu vuông góc của

A



trên

( )

ABC

là trung điểm của

cạnh

AB

nên

( )

A H ABC



⊥

, do đó

CH

là hình chiếu vuông góc của

AC



trên mặt phẳng

( )

ABC

.

Suy ra

( )

, , 60A C ABC A C HC A CH

  

= = = 

.

Xét tam giác vuông

A HC



vuông tại

H

, ta có

( )

33

.tan . 3

22

a

A H CH A CH a



= = =

.

Khi đó

.

ABC A B C ABC

V A H S

  





=

2

33

.

24

a

a=

3

33

8

a

=

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

5 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 1: Cho khối lăng trụ có thể tích

45V =

và diện tích đáy

9B =

. Chiều cao của khối lăng trụ đã cho

bằng

A.

20

. B.

10

. C.

15

. D.

5

.

Lời giải

Chọn D

Thể tích của khối lăng trụ

45

.5

9

V

V B h h

B

=  = = =

.

Câu 2: Một lăng trụ có diện tích đáy bằng 5 và chiều cao bằng 6 có thể tích bằng.

A.

12

. B.

30

. C.

10

. D.

18

.

Lời giải

Chọn B

. 5.6 30.V B h= = =

Câu 3: Một khối lăng trụ có diện tích đáy

5B =

và chiều cao

6h =

. Thể tích của khối lăng trụ đó bằng

A.

25

. B.

10

. C.

15

. D.

30

.

Lời giải

Chọn D

Thể tích khối lăng trụ đã cho là

. 5.6 30V B h= = =

(đvtt).

Câu 4: Cho khối lăng trụ có đáy là hình vuông cạnh

a

và chiều cao bằng

4a

. Thể tích của khối lăng

trụ đã cho bằng ?

A.

3

4a

. B.

3

16a

. C.

3

16

3

a

. D.

3

4

3

a

.

Lời giải

Chọn A

Ta có

2

,4

day

S a h a==

.

Thể tích khối lăng trụ đã cho bằng

23

. .4 4

lt day

V S h a a a===

.

Câu 5: Cho khối lăng trụ có diện tích đáy

B

và chiều cao

h

. Thể tích

V

của khối lăng trụ đã cho được

tính theo công thức nào dưới đây?

A.

1

3

V Bh=

. B.

4

3

V Bh=

. C.

6V Bh=

. D.

V Bh=

.

Lời giải

Chọn D

Ta có thể tích của khối lăng trụ có diện tích đáy

B

và chiều cao

h

là

V Bh=

.

Câu 6: Cho hình hộp

.ABCD A B C D

   

có đáy

ABCD

là hình chữ nhật tâm

O

. Hình chiếu vuông góc

của

A



lên

( )

ABCD

trùng với

O

. Biết

2AB a=

,

BC a=

, cạnh bên

AA



bằng

3

2

a

. Thể tích của

khối hộp

.ABCD A B C D

   

bằng

A.

3

2a

. B.

3

3a

. C.

3

4

3

a

. D.

3

2

a

.

Lời giải

Chọn A

BÀI TẬP TRẮC NGHIỆM

C

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 6

Từ giả thiết ta có

( )

A O ABCD



⊥

'O AOA⊥

Trong hình chữ nhật

22

:5ABCD AC AB BC a= + =

5

2

a

AO=

.

Trong tam giác vuông

22

:A AO A O A A AO

  

=−

22

95

44

aa

a= − =

.

Diện tích ABCD,

2

2 . 2

ABCD

S a a a==

.

Thể tích khối hôp là:

23

. 2 . 2

ABCD

V S A O a a a



= = =

.

Câu 7: Cho lăng trụ

.ABC A B C

  

có diện tích tam giác

A BC



bằng 4, khoảng cách từ

A

đến

BC

bằng

3, góc giữa hai mặt phẳng

( )

A BC



và

( )

ABC

  

bằng

30

. Thể tích khối lăng lăng trụ

.ABC A B C

  

bằng

A.

12

. B.

6

. C.

2

. D.

33

.

Lời giải

Chọn B

Gọi

,HK

lần lượt là hình chiếu vuông góc của

A

lên

BC

và

( )

A BC



.

Khi đó

( ) ( )

( )

( ) ( )

( )

3

, , 30 .sin30

2

A BC A B C A BC ABC AHK AK AH

    

= = =   =  =

.

Vậy

. . .

3 3 . 6

ABC A B C A ABC A A BC A BC

V V V AK S

     



= = = =

.

Câu 8: Cho khối lăng trụ

.ABCD A B C D

   

có đáy là hình thoi cạnh

a

,

120BAD =

, khoảng cách giữa

hai đường thẳng

BD



và

AC

bằng

2a

. Thể tích của khối lăng trụ đã cho bằng

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

7 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

A.

3

3a

. B.

3

6

a

. C.

3

2

a

. D.

3

a

.

Lời giải

Chọn A

Góc

120BAD =

suy ra tam giác

ABC

đều. Do đó diện tích hình thoi

ABCD

là

22

33

2.

42

aa

S ==

.

Mặt khác

( )

, , 2d A ABCD d B D AC a

  

==

. Suy ra thể tích khối lăng trụ là

2

3

2 . 3

2

a

V a a==

.

Câu 9: Cho khối lăng trụ tam giác

. ' ' 'ABC A B C

. Mặt bên

( )

''BCC B

có diện tích bằng 10, khoảng cách

từ

'A

đến mặt phẳng

( )

''BCC B

bằng 6. Tính thể tích khối lăng trụ đã cho.

A.

40

. B.

30

. C.

40

3

. D.

60

.

Lời giải

Chọn B

'. ' '

1

.6.10 20

3

A BCC B

V ==

'. . ' ' ' . ' ' ' '. ' '

1 3 3

.20 30

3 2 2

A ABC ABC A B C ABC A B C A BCC B

V V V V=  = = =

.

Câu 10: Cho hình lăng trụ

.ABC A B C

  

có đáy là tam giác đều cạnh

a

, góc giữa cạnh bên và mặt phẳng

đáy bằng

30



. Hình chiếu của

A



xuống mặt phẳng

( )

ABC

trùng với trung điểm của

BC

. Tính

thể tích khối lăng trụ

.ABC A B C

  

.

A.

3

24

a

. B.

3

8

a

. C.

3

8

a

. D.

3

4

a

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 8

Lời giải

Chọn C

Gọi

H

là trung điểm

BC

. Khi đó

( )

, , 30AA ABC AA BH A AH



  

= = =

.

Suy ra

31

.tan30 .

22

3

aa

A H AH





= = =

. Vậy

23

33

.

2 4 8

a a a

V ==

.

Câu 11: Một khối lăng trụ tam giác có đáy là tam giác đều cạnh 3, cạnh bên bằng

23

và tạo với mặt

phẳng đáy một góc

30 .

Khi đó thể tích khối lăng trụ là?

A.

9

.

4

B.

27 3

.

4

C.

27

.

4

D.

93

.

4

Lời giải

Chọn C

Gọi

H

là hình chiếu của

'C

trên mặt phẳng

()ABC

.

CH

là hình chiếu của

'CC

trên

()ABC

( )

;.



=CC ABC C CH

Bài ra

( )

; 30 30CC ABC C CH



=   = 

1 1 2 3

sin30 3.

2 2 2

CH

C H CC

CC





  = =  = = =



Do đó

.

ABC A B C ABC

V C H S

  



=

1 1 3 27

. . .sin60 3. .3.3. .

2 2 2 4

C H AB AC



=  = =

Câu 12: Cho khối lăng trụ tam giác

.ABC A B C

  

có đáy là tam giác đều cạnh

a

. Độ dài cạnh bên bằng

4

a

. Mặt phẳng

( )

BCC B



vuông góc với đáy và

30B BC



=

. Thể tích khối chóp

.ACC B



bằng

A.

3

2

a

. B.

3

12

a

. C.

3

18

a

. D.

3

6

a

.

Lời giải

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

9 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Chọn D

Ta có

( ) ( )

BCC B ABC



⊥

(theo giả thiết).

Hạ

( )

B H BC B H ABC



⊥  ⊥

và

30B BH B BC



= = 

.

Suy ra chiều cao của lăng trụ

.ABC A B C

  

là

.sin30 2h B H BB a



= = =

.

Do đáy là tam giác đều cạnh

a 

Diện tích đáy là

2

3

4

đáy

S

a

=

.

Thể tích của khối lăng trụ

.ABC A B C

  

là

23

33

. .2 .

42

đáyLT

aa

V h aS= = =

Thể tích khối chóp

.ACC B



là

3

13

.

36

LT

a

VV==

Câu 13: Cho khối lăng trụ

.ABCD A B C D

   

có đáy

ABCD

là hình thoi cạnh

a

,

60ABC =

. Chân đường

cao hạ từ

B



trùng với tâm

O

của đáy

ABCD

, góc giữa mặt phẳng

( )

BB C C



với đáy bằng

60

. Thể tích khối lăng trụ đã cho bằng

A.

3

33

8

a

. B.

3

23

9

a

. C.

3

32

8

a

. D.

3

4

a

.

Lời giải

Chọn A

ABCD

là hình thoi nên

AB BC=

. Lại có

60ABC =

nên

ABC

là tam giác đều cạnh

a

.

Diện tích đáy

ABCD

là

22

33

2. 2.

42

ABCD ABC

aa

SS= = =

.

Kẻ

OH BC⊥

Góc giữa mặt phẳng

( )

BB C C



với đáy khi đó là

60B HO



=

.

Ta có

22

2 2 2 2 2 2

1 1 1 1 1 4 4 16

3

33

44

aa

OH OB OC a a a

= + = + = + =

3

4

a

OH=

.

Theo giả thiết,

BO



là đường cao lăng trụ

.ABCD A B C D

   

.

A'

B'

C'

C

B

A

H

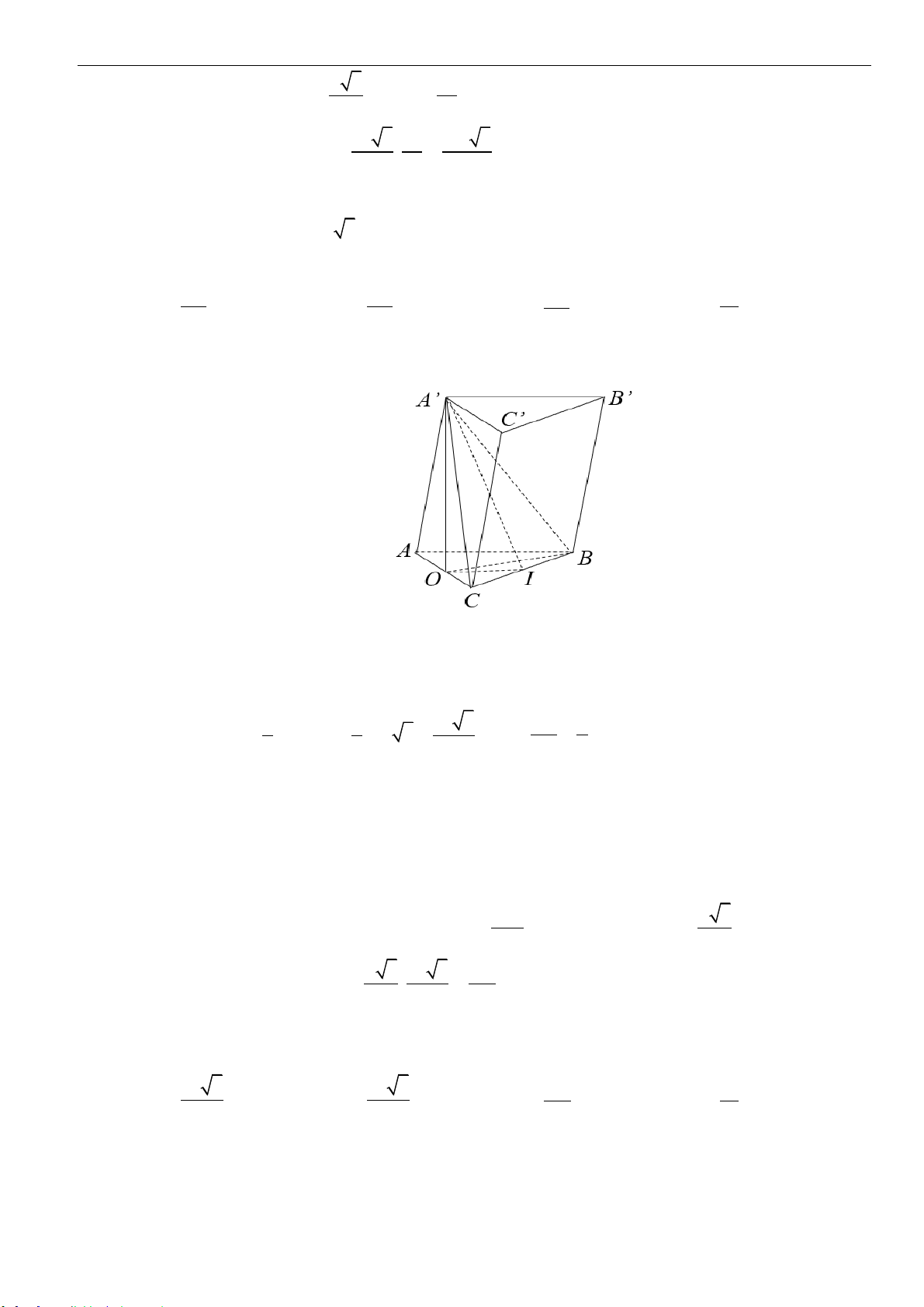
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 10

33

.tan tan60

44

aa

B O OH B HO



= =  =

.

23

.

3 3 3 3

..

2 4 8

ABCD A B C D ABCD

a a a

V S B O

   



= = =

.

Câu 14: Cho khối lăng trụ

.ABC A B C

  

có đáy

ABC

là tam giác vuông tại

B

và

A A A B A C

  

==

. Biết

rằng

AB a=

và

3BC a=

và mặt phẳng

( )

A BC



tạo với mặt phẳng đáy một góc bằng

60

.

Thể tích khối lăng trụ

.ABC A B C

  

bằng

A.

2

3

2

a

. B.

2

3

2

a

. C.

2

3

4

a

. D.

2

4

a

.

Lời giải

Chọn C

Gọi

,OI

lần lượt là trung điểm của đoạn

,AC BC

.

Nên

O

là tâm đường tròn ngoại tiếp tam giác

ABC

và

OI BC⊥

.

Do

A A A B A C

  

==

nên

( )

A O ABC



⊥

.

Ta có:

2

1 1 3

. . . . 3

2 2 2

ABC

a

S AB BC a a= = =

;

22

AB a

OI ==

( )

,A O BC OI BC BC A OI BC A I

  

⊥ ⊥  ⊥  ⊥

.

( ) ( )

( )

( ) ( )

( )

, , , 60

,

A BC ABC BC

A I A BC A I BC A BC ABC A I OI A IO

OI ABC OI BC



=





     

 ⊥  = = = 





⊥



.

Tam giác

A IO



vuông tại

O

nên

3

tan .tan60

2

A O a

A IO A O OI

OI





=  =  =

.

Vậy

23

.

3 3 3

..

2 2 4

ABC A B C ABC

a a a

V A O S

  



= = =

.

Câu 15: Cho hình lăng trụ

.

  

ABC A B C

có tất cả các cạnh bằng

a

, các cạnh bên tạo với đáy góc

60

.

Tính thể tích khối lăng trụ

.

  

ABC A B C

bằng

A.

3

24

a

. B.

3

8

a

. C.

3

8

a

. D.

3

8

a

.

Lời giải

Chọn C

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

11 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Kẻ

( ) ( )

( )

, 60 .

  

⊥  = = A H ABC A A ABC A AH

Xét

3

:sin60 .sin60 .

2



  

  =  =  =



A H a

AHA A H AA

AA

Thể tích khối lăng trụ

23

3 3 3

. : . . .

4 2 8



   

= = =

ABC

a a a

ABC A B C V S A H

Câu 16: Cho khối lăng trụ

.ABCD A B C D

   

có đáy

ABCD

là hình vuông cạnh

a

. Hình chiếu của

B



lên

( )

mp ABCD

trùng với giao điểm của

AC

và

BD

, biết góc giữa hai mặt phẳng

( )

ABA



và

( )

ABCD

bằng

60

. Tính thể tích khối lăng trụ

.ABCD A B C D

   

.

A.

3

a

. B.

3

6

a

. C.

3

2

a

. D.

3

6

2

a

.

Lời giải

Chọn C

Gọi

O

là giao điểm của

AC

và

BD

. Kẻ

OH AB⊥

. Theo giả thiết suy ra

60B HO



=

.

Ta có

3

.tan60

2

a

B O OH



=  =

. Khi đó:

3

2

.

33

.

22

ABCD A B C D

aa

Va

   

==

Câu 17: Cho hình lăng trụ tam giác

.ABC A B C

  

có đáy

ABC

là tam giác vuông tại

B

,

3 , 5AB a AC a==

, hình chiếu của

A



xuống mặt phẳng

( )

ABC

là trọng tâm tam giác

ABC

.

Biết mặt bên

ACC A



hợp với mặt đáy

ABC

  

một góc

0

60

, thể tích khối lăng trụ

.ABC A B C

  

là

A.

3

24 3

5

a

. B.

3

83

5

a

. C.

3

12 3

5

a

. D.

3

63

5

a

.

Lời giải

Chọn A

60

o

H

C'

B'

A'

C

B

A

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 12

( ) ( )

( )

( ) ( )

( )

,,ACC A A B C ACC A ABC

      

=

Kẻ

GH AC⊥

,

( )

A G AC AC A GH AC A H

  

⊥  ⊥  ⊥

Ta có:

( ) ( )

( )

0

, , 60

ACC A ABC AC

AC A H ACC A ABC A H GH A HG

AC GH



=





    

⊥  = = =





⊥



.

2 2 2 2

25 9 4BC AC AB a a a= − = − =

.

Kẻ

2 2 2 2 2 2

1 1 1 1 1 25 12

9 16 144 5

a

BK AC BK

BK AB BC a a a

⊥  = + = + =  =

.

Có

1 1 1 12 4

/ / .

3 3 3 5 5

GH MG a a

BK GH GH BK

BK MB

 = =  = = =

.

Tam giác

A HG



vuông tại

G

có:

0

4 4 3

tan tan60

55

A G a a

A HG A G

GH





=  = =

.

Vậy

3

.

1 4 3 24 3

. 3 .4 .

2 5 5

ABC A B C ABC

aa

V A G S a a

  



= = =

.

Câu 18: Cho khối hộp

.ABCD A B C D

   

có đáy

ABCD

là hình thoi cạnh

a

,

120ABC =

. Hình chiếu

vuông góc của

D



lên

( )

ABCD

trùng với giao điểm của

AC

và

BD

, góc giữa hai mặt phẳng

( )

ADD A



và

( )

A B C D

   

bằng

45

. Thể tích khối hộp đã cho bằng

A.

3

8

a

. B.

3

1

8

a

. C.

3

16

a

. D.

3

4

a

.

Lời giải

Chọn A

Gọi

O

là giao điểm của

AC

và

BD

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

13 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Ta có

( )

D O ABCD



⊥

và

( ) ( )

ADD A ABCD AD



=

. Dựng

OM AD⊥

tại

M

. Khi đó góc

giữa hai mặt phẳng

( )

ADD A



và

( )

ABCD

là

D MO



.

Vì

( )

A B C D

   

song song với

( )

ABCD

nên

45D MO



=

.

Do

120ABC =

nên

60BAC =

và do đó tam giác

ABD

đều.

Ta tính được

33

.sin60

2 2 4

aa

OM OD=  =  =

,

3

4

a

OD OM



==

.

Diện tích hình thoi

ABCD

là

2

3

. .sin120

2

ABCD

a

S a a=  =

.

Vậy thể tích khối hộp đã cho là

3

.

8

ABCD

a

V S OD



==

.

Câu 19: Cho lăng trụ

.ABCD A B C D

   

có đáy

ABCD

là hình chữ nhật tâm

O

và

AB a=

,

3AD a=

;

AO



vuông góc với đáy

( )

ABCD

. Cạnh bên

AA



hợp với mặt đáy

( )

ABCD

một góc

45

. Tính

theo

a

thể tích

V

của khối lăng trụ đã cho

A.

3

a

V =

. B.

3

6

a

V =

. C.

3

3Va=

. D.

3

6

2

a

V =

.

Lời giải

Chọn C

( )

A O ABCD

AA ABCD A



⊥









=







AO

là hình chiếu của

AA



trên

( )

ABCD

( )

, , 45AA ABCD AA AO A AO

  

 = = = 

.

( )

2

32AC a a a= + =

1

2

AO AC a = =

Tam giác

A AO



vuông cân tại

O

nên

A O AO a



==

.

( )

3

.

. . 3 . 3

ABCD A B C D ABCD

V S A O a a a a

   



= = =

(đvtt).

Câu 20: Cho hình lăng trụ

. ' ' ' 'ABCD A B C D

có đáy ABCD là hình thoi cạnh

2a

,

0

60ABC =

. Chân đường

cao hạ từ

'B

trùng với

O

của đáy

ABCD

, góc giữa mặt phẳng

( )

''BB C C

với đáy bằng

0

60

. Thể

tích lăng trụ bằng

A.

3

16 3

9

a

. B.

3

32a

. C.

3

33a

. D.

3

6a

.

Lời giải

Chọn C

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 14

Tam giác

ABC

có

2 , 60AB BC a ABC= = = 

ABC

đều cạnh

2a

22

3 2 2 3

ABC ABCD ABC

S a S S a



 =  = =

.

Gọi

I

là trung điểm của

BC

AI BC⊥

.

Gọi

K

là trung điểm của

CI

// OK AI

và

13

22

a

OK AI==

.

//

AI BC

AI OK

⊥







OK CB⊥

.

( ) ( )

( )

, , 60BCC B ABCD B K OK B KO

   

= = = 

.

Tam giác

B OK



vuông tại

O

:

3

.tan

2

a

B O OK B KO



==

.

3

.

. 3 3

ABCD A B C D ABCD

V B O S a

   



==

.

Câu 21: Cho hình lăng trụ

.ABC A B C

  

cạnh bên có độ dài bằng

4

,

BB



tạo với đáy góc

0

60

. Hình chiếu

vuông góc của

A



trên mặt phẳng

( )

ABC

trùng với trọng tâm

G

của tam giác

ABC

. Biết

khoảng cách từ điểm

A



đến các đường thẳng

BB



và

CC



bằng nhau và bằng

3

. Tính thể tích

khối lăng trụ

.ABC A B C

  

.

A.

18 3 

B.

93

C.

63

D.

12 3 

Lời giải

Chọn B

Gọi

,MM



lần lượt là trung điểm

BC

và

BC



.

Gọi

,HK



lần lượt là hình chiếu vuông góc của

A



lên

BB



và

CC



.

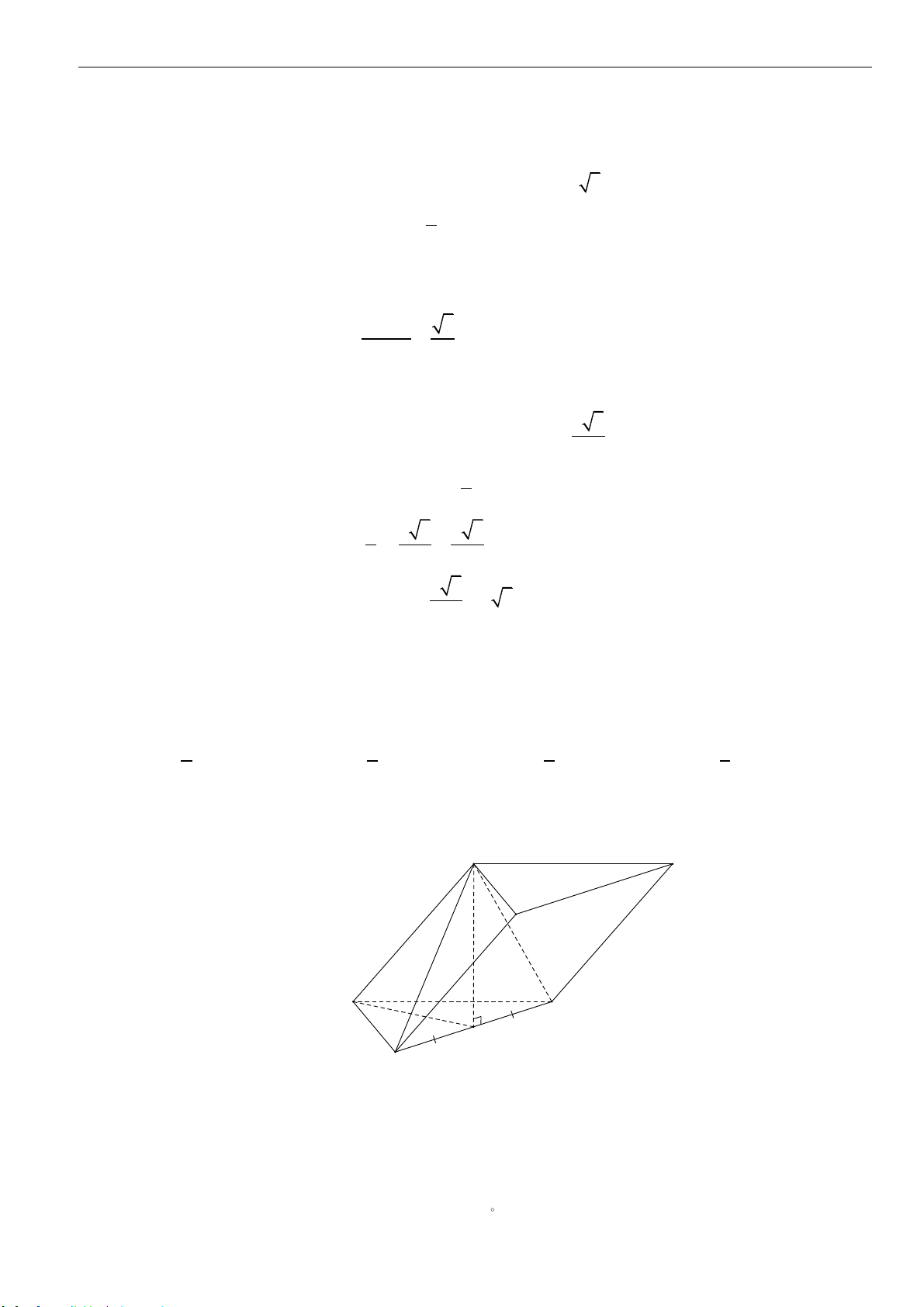
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

15 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

,HK

lần lượt là hình chiếu vuông góc của

A

lên

BB



và

CC



.

Khi đó

( )

;3d A BB A H

   

==

và

( )

;3d A CC A K

   

==

và

( )

AA A H K

   

⊥

.

Góc giữa

( )

0

, , 60BB ABC AA ABC A AG

  

= = =

.

Trong tam giác vuông

A AG



ta có

0

sin60 . 2 3A G AA



==

,

0

cos60 . 2AG AA



==

suy ra

3

2

AM AG==

Gọi

I MM H K

  

=

. Khi đó

I

là trung điểm

HK



.

Ta có

. ' ' ' ' ' '.ABC A B C A H K AHK

VV=

(vì

'. ' ' ' ' .A B C H K A BCHK

VV=

).

0

' ' '

' ' ' ' ' '

' ' '

3

. . cos30

2

A H K

A B C A H K

A B C

S

A G S AA S

S



=  = =

.

Góc giữa hai mặt phẳng

( ) ( )

( )

0

, ' 30A B C A H K M A I

      

==

.

Trong tam giác vuông

M IA



ta có

0

33

cos30 .

2

A I A M

  

==

.

Trong tam giác vuông

A IK



ta có

3

2

IK =

suy ra

23H K IK

  

==

.

Diện tích tam giác

' ' '

1 3 3 9 3

.3.

2 2 4

A H K

S ==

.

Thể tích lăng trụ

' ' '

93

. 4. 9 3

4

A H K

V AA S



= = =

.

Câu 22: Cho lăng trụ

. ' ' 'ABC A B C

có đáy tam giác

ABC

vuông tại

A

,

,2AB a BC a==

, biết hình

chiếu của

'A

lên mặt phẳng

( )

ABC

trùng với trung điểm của cạnh

BC

. Góc giữa

'AA

và mặt

phẳng

( )

ABC

bằng

0

60

. Khi đó thể tích của hình trụ

. ' ' 'ABC A B C

bằng:

A.

3

1

2

a

. B.

3

1

6

a

. C.

3

2

a

. D.

3

1

3

a

.

Lời giải

Chọn C

Gọi

I

là trung điểm của

BC

, theo giả thiết ta có

( )

AI ABC⊥

.

Hình chiếu của

AA



lên mặt phẳng đáy

( )

ABC

là

AI

.

Suy ra

( )

; ; 60AA ABC AA AI A AI

  

= = =

.

B'

C

B

A

C'

A'

I

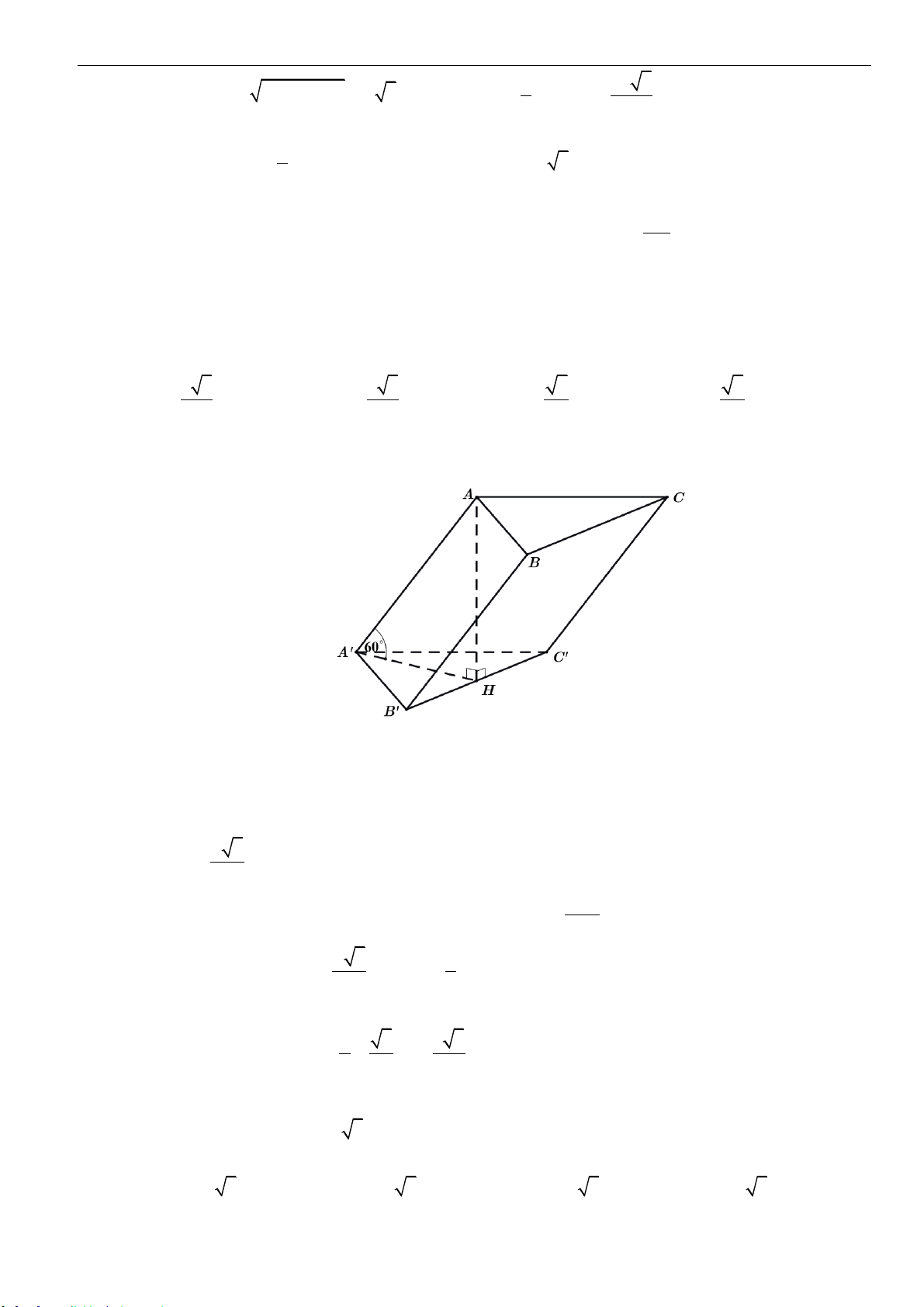
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 16

Ta có

22

3AC BC AB a= − =

; Do đó

2

13

..

22

ABC

a

S AB AC



==

.

Mặt khác,

1

2

AI BC a==

nên

.tan 3A I AI A AI a



==

.

Vậy thể tích khối lăng trụ

.ABC A'B'C'

là

3

.

3

.

2

ABC A'B'C' ABC

a

V S A I





==

.

Câu 23: Cho hình lăng trụ

.ABC A B C

  

có đáy là tam giác đều cạnh

a

. Hình chiếu vuông góc của

A

trên mặt phẳng

( )

ABC

  

trùng với trung điểm

H

của

BC



. Biết rằng góc giữa

AA



và mặt

phẳng

( )

ABC

  

bằng

60

. Thể tích của khối lăng trụ

.ABC A B C

  

bằng

A.

3

33

8

a

. B.

3

33

4

a

. C.

3

4

a

. D.

3

8

a

.

Lời giải

Chọn A

Vì hình chiếu vuông góc của

A

trên mặt phẳng

( )

ABC

  

trùng với trung điểm

H

của

BC



nên

( )

AH A B C

  

⊥

. Khi đó, góc giữa

AA



và mặt phẳng

( )

ABC

  

là

60AA H



=

.

Vì

ABC

  



là tam giác đều cạnh

a

và

H

là trung điểm của

BC



nên độ dài đường cao

3

2

a

AH



=

.

Xét trong tam giác

AHA



vuông tại

H

có

tan

AH

AA H

AH



=



nên

33

.tan .tan60

22

a

AH A H AA H a



= =  =

.

Vậy thể tích của khối lăng trụ

.ABC A B C

  

là

23

.

3 3 3 3

..

2 4 8

ABC A B C A B C

V AH S a a a

     



= = =

(đơn vị thể tích).

Câu 24: Cho lăng trụ

.ABC A B C

  

có đáy

ABC

là tam giác đều. Điểm

M

là trung điểm cạnh

AB

, tam

giác

MA C



đều cạnh

23a

và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối lăng trụ

.ABC A B C

  

là

A.

3

10 3a

. B.

3

43a

. C.

3

12 3a

. D.

3

83a

.

Lời giải

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

17 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Chọn C

Gọi

H

là trung điểm của

MC

.

Ta có

( ) ( )

( )

A H MC

A MC ABC A H ABC

A MC ABC MC





⊥





⊥  ⊥







=



.

Tam giác

MA C



đều cạnh

23a

23

3

MC a

A H a



=









=





Đặt

0AC x=

, vì tam giác

ABC

đều, suy ra

3

2 3 4

2

x

a x a=  =

.

Suy ra

02

1

. .sin60 4 3

2

ABC

S AB AC a==

. Do đó

3

.

. 12 3

ABC A B C ABC

V A H S a

  



==

.

Câu 25: Cho lăng trụ

.ABC A B C

  

có đáy là tam giác đều cạnh

a

. Hình chiếu vuông góc của điểm

A



lên mặt phẳng

( )

ABC

trùng với trọng tâm tam giác

ABC

. Biết khoảng cách giữa hai đường

thẳng

AA



và

BC

bằng

3

4

a

. Khi đó thể tích của khối lăng trụ là

A.

3

.

12

a

B.

3

.

6

a

C.

3

.

3

a

D.

3

.

24

a

Lời giải

Chọn A

Gọi

H

là trọng tâm tam giác

ABC

và

I

là trung điểm

.BC

Ta có:

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 18

( )

.

A H BC

AI BC BC A AI BC AA

A H AI H



⊥







⊥  ⊥  ⊥







=



Gọi

K

là hình chiếu vuông góc của

I

lên

AA



. Khi đó

IK

là đoạn vuông góc chung của

AA



và

BC

nên

( )

3

= , .

4

a

IK d AA BC



=

Xét tam giác vuông

AIK

vuông tại

K

có

3 3 1

= , 30 .

4 2 2

aa

IK AI IK AI KAI=  =  = 

Xét tam giác vuông

AA H



vuông tại

H

có

33

= .tan30 . .

3 3 3

aa

A H AH



 = =

Vậy

23

.

1 3 3

V ' . . .

3 4 3 12

ABC A B C ABC

a a a

AH S

  



= = =

Câu 26: Cho hình hộp có

3, 4, ' 5AB AD AA= = =

,

0

60''BAD DAA A AB= = =

.

Thể tích khối hộp đã cho là

A.

30 2

. B.

60

. C.

30

. D.

60 3

.

Lời giải

Chọn A

Ta có

..

6

ABCD A B C D A ABD

VV

    

=

.

Xét tứ diện

AA BD



, trên các cạnh

AD

và

AA



lần lượt lấy hai điểm

,MN

sao cho

3AM AN==

Khi đó tứ diện

ABMN

là tứ diện đều cạnh 3 nên

3 3

2 2 9 2

. .3

12 12 4

ABMN

V AB= = =

.

Ta có :

4 5 9 2

. . . . . 5 2

3 3 4

ABDA ABMN

AB AD AA

VV

AB AM AN



= = =

.

Vậy

..

6 6.5 2 30 2

ABCD A B C D A ABD

VV

    

= = =

.

Câu 27: Cho lăng trụ

.ABC A B C

  

có đáy

ABC

là tam giác vuông cân tại

A

. Mặt phẳng

( )

ACC A



vuông góc đáy,

2BC a=

và

C A C C CA



==

. Thể tích của khối lăng trụ

.ABC A B C

  

là

A.

3

12

a

. B.

3

2

a

. C.

3

3a

. D.

3

4

a

.

Lời giải

Chọn D

. ' ' ' 'ABCD A B C D

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

19 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Tam giác

ABC

vuông cân tại A nên

2

22

BC a

AB AC a= = = =

.

Ta có

C A C C CA



==

C AC





đều.

Gọi

CH



là đường cao của

C AC





3

2

a

CH



=

.

Ta có

( ) ( )

( ) ( ) ( )

ACC A ABC

ACC A ABC AC C H ABC

C H AC



⊥





  

 =  ⊥







⊥



.

3

.

1 3 3

. . .

2 2 4

ABC A B C ABC

a

V S C H a a a

  





= = =

Câu 28: Cho hình lăng trụ

.ABC A B C

  

có đáy là tam giác đều cạnh

.a

Hình chiếu của

A



lên mặt phẳng

( )

ABC

trùng với trung điểm cạnh

,AB

góc giữa

AA



và mặt đáy của hình lăng trụ đã cho bằng

60 .

Tính thể tích

V

của khối chóp

..A BCC B

  

A.

3

.

4

a

V =

B.

3

.

8

a

V =

C.

3

.

4

a

V =

D.

3

.

8

a

V =

Lời giải

Chọn A

Gọi

H

là trung điểm của

AB

Vì

( )

A H ABC



⊥

, nên

( )

3

, , 60 .tan60 .

2

a

AA ABC AA AH A AH A H AH

   

= = =  = =

23

.

3 3 3

. . .

4 2 8

ABC A B C ABC

a a a

V S A H

  





 = = =

3

. ' ' . . . . .

12

.

3 3 4

A BCC B ABC A B C A A B C ABC A B C ABC A B C ABC A B C

a

V V V V V V

              

 = − = − = =

Vậy

3

.

4

a

V =

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 20

Câu 29: Cho hình lăng trụ

.ABC A B C

  

có

AA AB AC

  

==

. Tam giác

ABC

vuông cân tại

A

có

2BC a=

. Khoảng cách từ

A



đến mặt phẳng

( )

BCC B



là

3

a

. Tính thể tích khối lăng trụ đã

cho.

A.

3

2

a

V =

. B.

3

2

6

a

V =

. C.

3

6

a

V =

. D.

3

a

V =

.

Lời giải

Chọn A

Gọi

H

là trung điểm

BC



. Vì tam giác

ABC

  

là tam giác vuông cân tại

A



nên

H

là tâm đường

tròn ngoại tiếp tam giác

ABC

  

.

Mặt khác

AA AB AC

  

==

, từ đó suy ra

,AH

cách đều 3 điểm

,,A B C

  

hay

( )

AH A B C

  

⊥

.

Gọi

I

là trung điểm của

BC

khi đó

( )

1AI BC⊥

Mà

B C AH



⊥

và

BC

//

BC



suy ra

( )

2BC AH⊥

Từ

( )

1

và

( )

2

ta suy ra

( ) ( ) ( )

BC AHI BCC B AHI



⊥  ⊥

theo giao tuyến là HI

( )

3

Kẻ

AK HI⊥

, ta được

( )

AK BCC B



⊥

hay

( )

3

,,

3

a

d A BCC B d A BCC B AK

    

= = =

Xét tam giác

AIH

vuông tại A, ta được

2 2 2 2 2 2

1 1 1 3 1 2 2

2

a

AH

AH AK AI a a a

= − = − =  =

Vậy thể tích khối lăng trụ

( )

3

2

2 1 2

.2

2 2 2

aa

Va=  =

.

Câu 30: Cho khối lăng trụ tam giác

. ' ' 'ABC A B C

có đáy

ABC

là tam giác đều. Biết

'AA AB a==

. Các

mặt bên

( ' )A AB

và

( ' )A AC

cùng hợp với đáy

()ABC

1 góc

0

60

. Thể tích khối lăng trụ

. ' ' 'ABC A B C

bằng?

A.

3

37

28

a

. B.

3

37

4

a

. C.

3

7

a

. D.

3

7

28

a

Lời giải

Chọn A

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

21 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Gọi

,KH

lần lượt là hình chiếu vuông góc của

'A

trên các cạnh

,AB AC

.

Vẽ đường cao

'AO

của khối lăng trụ (

()O ABC

).

Ta được

OK AB⊥

,

OH AC⊥

. Theo giả thiết ta có

0

' ' 60OKA OHA==

.

Suy ra

''A HO A KO OH OK =   =

. Do đó

AO

là phân giác góc

BAC

nên

0

30OAK =

. Đặt

AH AK x==

.

Ta có:

0 0 0

' .tan60 .tan30 .tan60A O OK AK AK x= = = =

.

( ) ( )

22

2 2 2

4

' ( ')

3

A O AA OA a x= − = −

.

Từ đó suy ra

2 2 2

4 21

37

x a x x a= −  =

.

Suy ra

23

. ' ' '

21 3 7

' . . 3

7 4 28

ABC A B C ABC

V A O S a a a= = =

.

Câu 31: Cho lăng trụ

.ABC A B C

  

có đáy là tam giác vuông cân tại

B

,

2AC a=

. Hình chiếu vuông góc

của

A



lên mặt phẳng

( )

ABC

là điểm

H

thuộc cạnh

AC

sao cho

1

3

AH AC=

. Mặt bên

( )

ABB A



tạo với đáy một góc

60

. Thể tích khối lăng trụ là

A.

3

9

a

. B.

3

6

9

a

. C.

3

6

3

a

. D.

3

a

.

Lời giải

Chọn C

Tam giác

ABC

vuông cân tại

B

,

2AC a=

. Do đó:

2AB BC a==

2

ABC

Sa



=

.

Ta có

( )

ABB A



tạo với đáy một góc

60

là

60A IH



=

, với

//IH BC

.

Suy ra

16

tan60 . 3

33

a

A H IH BC h



=  = = =

.

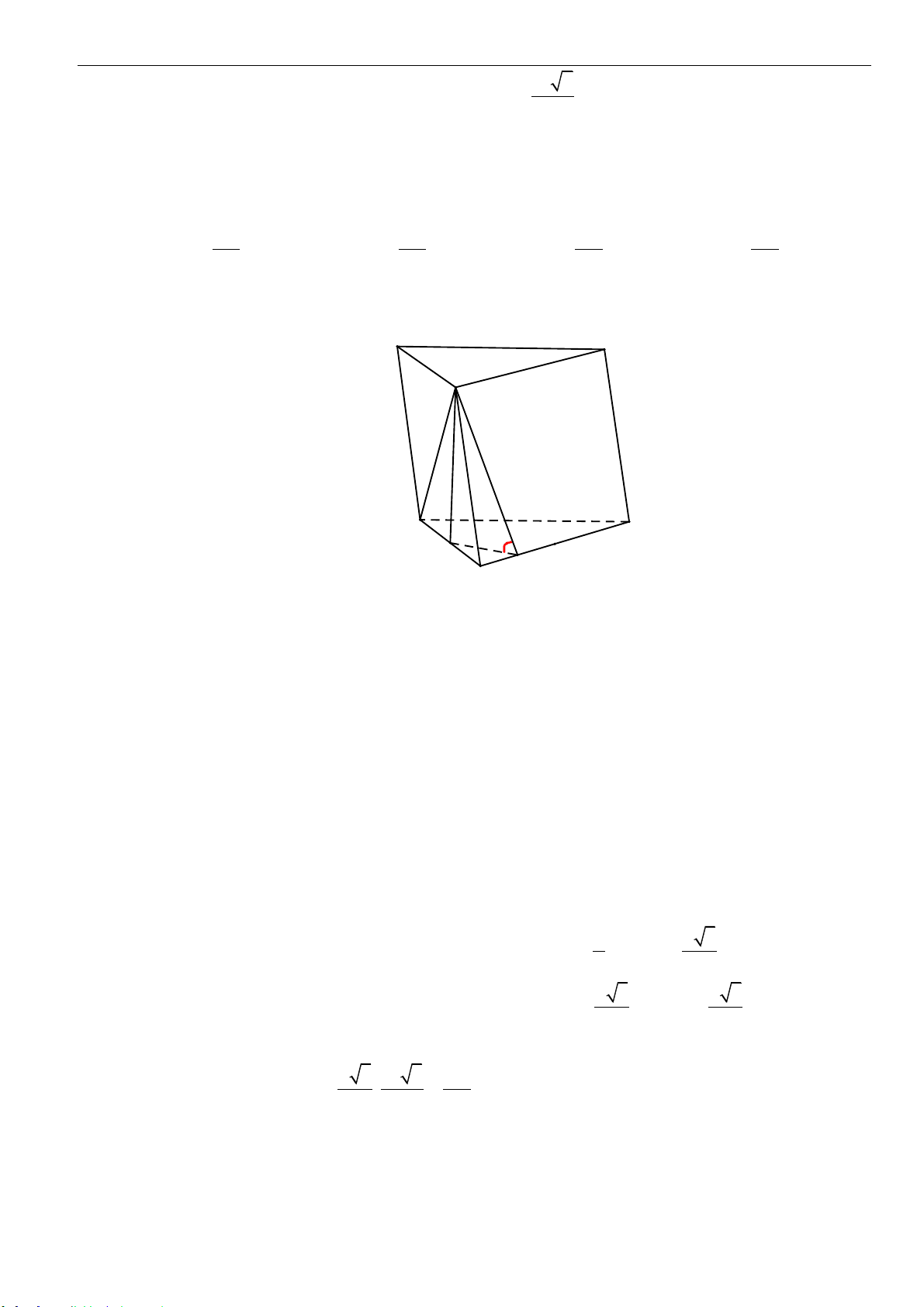
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 22

Vậy thể tích khối lăng trụ là:

3

.

6

.

3

ABC A B C ABC

a

V S h

  



==

.

Câu 32: Cho hình lăng trụ

.ABC A B C

  

có đáy

ABC

là tam giác đều cạnh là

a

. Tam giác

A AB



cân tại

A



và nằm trong mặt phẳng vuông góc với mặt đáy, mặt bên

( )



AA C C

tạo với mặt phẳng

( )

ABC

một góc

45



. Thể tích của khối lăng trụ

.ABC A B C

  

là

A.

3

32

a

V =

. B.

3

4

a

V =

. C.

3

8

a

V =

. D.

3

16

a

V =

.

Lời giải

Chọn D

Gọi

I

là trung điểm của

AB

.

Tam giác



A AB

cân tại

A



nên



⊥A I AB

.

Theo giả thiết, ta có

( ) ( )

( )

,

A BA ABC

A BA ABC AB

A I AB A I A BA





⊥





=





  

⊥



( )

A I ABC



⊥

.

Kẻ

⊥IM AC

.

Ta có

IM AC

A I AC

⊥







⊥



( )

A IM AC



⊥

A M AC



⊥

.

Lại có

( ) ( )

ACC A ABC AC

A M AC

IM AC





=





⊥





⊥



( ) ( )

(

)

( )

; ; 45ACC A ABC A M IM A MI

   

 = = = 

.

Xét tam giác

IAM

vuông tại

M

nên

3

.sin .sin60

24

aa

IM A I IAM



= =  =

.

Xét tam giác

A MI



vuông tại

I

nên

33

.tan .tan45

44

aa

A I IM A MI



= =  =

.

Thể tích của khối lăng trụ là

23

. ' ' '

3 3 3

..

4 4 16

ABC A B C ABC

a a a

V A I S





=  = =

Câu 33: Cho hình lăng trụ

.ABC A B C

  

có

A A A B A C

  

==

. Tam giác

ABC

vuông cân tại

A

có

2BC a=

. Hai mặt phẳng

()A ABB



và

()ABC



vuông góc nhau. Tính thể tích khối lăng trụ đã

cho.

M

I

B

A

C

A'

B'

C'

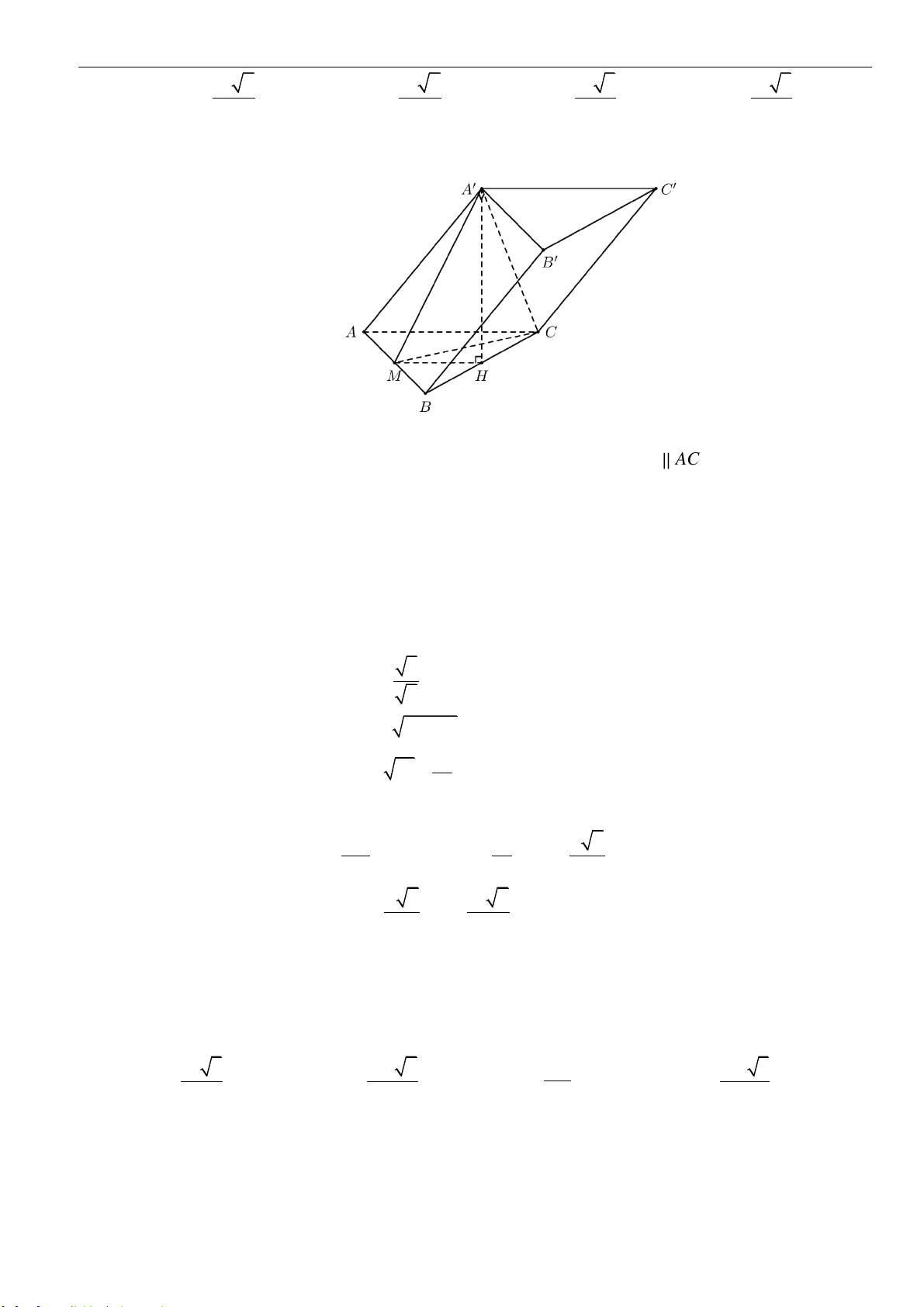
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

23 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

A.

3

2

a

V =

. B.

3

2

6

a

V =

. C.

3

2

a

V =

. D.

3

6

a

V =

.

Lời giải

Chọn A

Gọi

M

trung điểm

AB

.

Gọi

H

là trung điểm

BC

. Theo giả thiết có

()A H ABC



⊥

và

HM AC

.

Suy ra

AB HM

AB A M

AB A H

⊥





⊥





⊥



. (1)

Theo giả thiết

( ) ( )

) ( ) .

A B BA A B C

A B BA A B C A B

   

⊥





     

=



(2)

Từ (1), (2) suy ra

()A M CA B

  

⊥

hay

A M A C



⊥

.

Gọi

A H x



=

.

Xét tam giác

AMC

có

5

2

CM a=

.

Xét tam giác

A MH



có

22

A M x a



=+

.

Xét tam giác

A CM



có

2

a

AC x=+

.

Xét tam giác

A CM



vuông tại

A



có

22

2 2 2 2 2 2

52

.

2 2 2

a a a

CM A M A C x a x x



= +  = + + +  =

Vậy thể tích khối lăng trụ

3

2

22

aa

Va=  =

.

Câu 34: Cho hình hộp

. ' ' ' 'ABCD A B C D

,

0

2 , , 60AB a BC a ABC= = =

. Hình chiếu vuông góc của

điểm

'A

lên mặt phẳng

( )

ABCD

là trung điểm

O

của cạnh

AC

. Góc giữa hai mặt phẳng

( )

''ABB A

và

( )

ABCD

bằng

0

60

. Thể tích của hình hộp đã cho bằng

A.

3

2

a

. B.

3

37

4

a

. C.

3

2

a

. D.

3

33

4

a

.

Lời giải

Chọn D

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 24

Ta có

' ( )A O ABCD⊥

.

Từ

O

dựng

OH AB⊥

tại

H

, lại có

'A O AB⊥

nên

( ' )AB A OH⊥

suy ra góc giữa hai mặt

phẳng

( )

''ABB A

và

( )

ABCD

bằng

0

' 60A HO =

2

13

. . .sin 2 3.

22

ABC ABCD ABC

a

S AB BC B S S a= =  = =

Mà

( ) ( )

13

. . , , .

22

ABC

a

S AB d C AB d C AB=  =

Suy ra

( )

13

,.

24

a

OH d C AB==

Tam giác

'A OH

vuông tại

O

:

3

' .tan ' .

4

a

A O OH A HO==

Vậy thể tích hình hộp

. ' ' ' 'ABCD A B C D

là:

3

2

. ' ' ' '

3 3 3

' . . 3 .

44

ABCD A B C D ABCD

aa

V A O S a= = =

Câu 35: Cho hình lăng trụ

.ABCD A B C D

   

có đáy

ABCD

là hình thoi tâm

O

cạnh

a

,

60ABC =

.

Hình chiếu vuông góc của

A



lên mặt phẳng

ABCD

trùng với tâm

O

. Góc giữa mặt phẳng

( )

ADD A



và mặt đáy

( )

ABCD

bằng

60

. Tính thể tích lăng trụ

.ABCD A B C D

   

.

A.

3

4

a

. B.

3

4

a

. C.

3

33

8

a

. D.

3

8

a

.

Lời giải

Chọn C

Gọi

H

,

M

lần lượt là trung điểm

AD

,

AH

. Tam giác

ACD

đều nên

CH AD⊥

.

// OM CH

nên

OM AD⊥

.

Ta thấy

AD OM⊥

,

AD A O



⊥

nên

AD A M



⊥

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

25 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

( ) ( )

( )

,

ABCD ADD A AD

OM ABCD OM AD

A M ADD A A M AD



=





⊥





   

⊥



( ) ( )

(

)

, 60ABCD A B C D A MO

    

 = = 

.

3

2

a

CH =

13

24

a

OM CH = =

.

Tam giác

A OM



vuông tại

O

, ta có:

3

.tan60

4

a

A O OM



=  =

.

22

33

2 2.

42

ABCD ABC

aa

SS



= = =

;

23

.

3 3 3 3

.

2 4 8

ABCD A B C D

a a a

V

   

==

.

Câu 36: Cho hình lăng trụ

.ABCD A B C D

   

có đáy

ABCD

là hình chữ nhật tâm

O

có

2AB a=

,

4AC a=

và

A A A B A C

  

==

. Biết hai mặt phẳng

( )

A AC



và

( )

DA C



tạo với nhau góc

30

.

Tính thể tích khối lăng trụ đã cho.

A.

3

63a

. B.

3

12 2a

. C.

3

62a

. D.

3

12 3a

.

Lời giải

Chọn D

Vì

A A A B A C

  

==

và

ABCD

là hình chữ nhật tâm

O

nên

( )

A O ABCD



⊥

.

Ta có

( ) ( )

A AC DA C A C

    

=

( )

1

.

Vì

2OD OC CD a= = =

nên

DOC

đều. Gọi

M

là trung điểm

OC

.

DM AC⊥

, mà

DM A O



⊥

( )

DM A ACC



⊥

DM A C



⊥

.

Kẻ

MN A C



⊥

( )

2

(với

N

thỏa

1

4

A N A C

  

=

)

( )

A C MND



⊥

A C DN



⊥

( )

3

.

Từ

( )

1

,

( )

2

,

( )

3

suy ra

( ) ( )

(

)

( )

, , 30A AC DA C MN DN DNM

  

= = = 

.

Ta có

22

23AD AC AB a= − =

và

3

2

DM CD a==

.

3

tan

DM

A O MN a

MND



= = =

(vì

//MN A O



).

Khi đó thể tích khối lăng trụ

.ABCD A B C D

   

là:

3

.

. . 2 .2 3 .3 12 3

ABCD A B C D

V AB AD A O a a a a

   



= = =

.

Câu 37: Cho hình lăng trụ

.ABCD A B C D

   

có đáy là hình thang vuông tại

,AB

( )

//BC AD

, góc giữa hai

mặt phẳng

( )

ABCD

và

( )

AA B B



bằng

90

và

12, 16, 5BC AD CD= = =

,tam giác

ABA





CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 26

đều. Thể tích của khối lăng trụ đã cho là

A.

126 3

. B.

252

. C.

63 3

. D.

410

.

Lời giải

Chọn C

Trong mp

( )

ABCD

kẻ

CH

vuông góc với

AD

tại

H

.

Khi đó ta có

ABCH

là hình chữ nhật

Suy ra

12BC AH==

4HD=

Xét tam giác

CHD

vuông tại

H

ta có:

3HC AB==

Ta thấy

( ) ( )

ABCD AA B B AB



=

Kẻ

A I AB



⊥

Suy ra

( )

A I ABCD



⊥

(

I

là trung điểm của

AB

)

Tam giác

ABA





đều nên

33

2

AI



=

Vậy thể tích của khối lăng trụ đã cho là

( )

1

. . . . 63 3

2

ABCD

V S A I A I BC AD CH



= = + =

Câu 38: Lăng trụ tam giác

.ABC A B C

  

có đáy là tam giác đều cạnh

a

, góc giữa cạnh bên và mặt đáy

bằng

30

. Hình chiếu của

A



lên

( )

ABC

là trung điểm

I

của

BC

. Thể tích khối lăng trụ là

A.

3

12

a

. B.

3

6

a

. C.

3

2

a

. D.

3

8

a

.

Lời giải

Chọn D

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

27 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Ta có

( ) ( )

( )

, 30A AIA I ABC A A ABC

 

⊥  = = 

.

Do tam giác

ABC

đều nên

3

.sin6

2

0

a

AI AB==

.

Suy ra độ dài đường cao của lăng trụ là:

3

.tan30 .tan30

22

aa

A I AI



=  =  =

.

Ta lại có:

2

13

. .sin6

24

0

ABC

a

S AB AC= =

.

Vậy thể tích khối lăng trụ là:

23

33

..

4 2 8

ABC

a a a

V S A I



= = =

.

Câu 39: Cho lăng trụ tam giác

.ABC A B C

  

có đáy là tam giác đều cạnh

a

. Độ dài cạnh bên bằng

4a

.

Mặt phẳng

( )

BCC B



vuông góc với đáy và góc giữa hai đường thẳng

'AA

và

BC

bằng

0

30

.

Thể tích khối lăng trụ đã cho là

A.

3

9

a

. B.

3

a

. C.

3

6

a

. D.

3

2

a

.

Lời giải

Chọn D

Diện tích tam giác

ABC

là

2

3

4

ABC

a

S =

.

Giả sử tứ giác

''BCC B

có góc

B

nhọn.

Gọi

H

là hình chiếu của

B



trên

BC

. Từ giả thiết suy ra

( )

B H ABC



⊥

.

Ta có

( ) ( )

', ',AA BC BB BC==

'B BC

Diện tích tam giác

BB C



là

1

. .sin

2

BB C

S BB BC B BC





=

1

4 . .sin30

2

aa=

2

a=

.

Mặt khác

1

.

2

BB C

S B H BC



=

2

BB C

S

BH

BC



=

2

a

==

.

Thể tích khối lăng trụ

.ABC A B C

  

là

.

ABC

V B H S



=

2

3

2.

4

a

a=

3

2

a

=

.

Câu 40: Cho hình lăng trụ

.ABCD A B C D

   

có

ABCD

là hình chữ nhật. Tính thể tích khối lăng trụ đã

cho biết

A A A B A D

  

==

và

, 3, 2AB a AD a AA a



= = =

A.

3

3a

. B.

3

a

. C.

3

3a

. D.

3

33a

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 28

Lời giải

Chọn A

Gọi

H

là hình chiếu của

A



trên

( )

ABCD

. Vì

A A A B A D HA HB HD

  

= =  = =

H AC BD = 

;

22

2 2 2

3

4

AB AD

A H AA AH AA a

+

  

= − = − =

.

Vậy

23

.

. 3. 3 3

ABCD A B C D ABCD

V A H S a a a

   



= = =

.

Câu 41: Cho hình lăng trụ

.ABC A B C

  

có đáy là tam giác đều cạnh

a

. Hình chiếu vuông góc của điểm

A



lên mặt phẳng

( )

ABC

trùng với trọng tâm tam giác

ABC

. Biết khoảng cách giữa hai đường

thẳng

AA



và

BC

bằng

3

4

a

. Tính theo

a

thể tích

V

của khối lăng trụ

.ABC A B C

  

.

A.

3

6

a

V =

. B.

3

12

a

V =

. C.

3

a

V =

. D.

3

24

a

V =

.

Lời giải

Chọn B

Ta có

( )

A G ABC



⊥

nên

A G BC



⊥

;

BC AM⊥

( )

BC MAA



⊥

Trong mặt phẳng

( ')MAA

kẻ

MI AA



⊥

, mà

( ')BC MA A⊥

MI BC⊥

nên

( )

3

;

4

a

d AA BC IM



==

Trong mặt phẳng

( ')MAA

kẻ

GH AA



⊥

, ta có

2 2 3 3

.

3 3 4 6

AG GH a a

GH

AM IM

= =  = =

2 2 2

2 2 2 2

33

.

1 1 1 .

36

3

3 12

aa

AG HG a

AG

HG A G AG

AG HG a a



= +  = = =



−

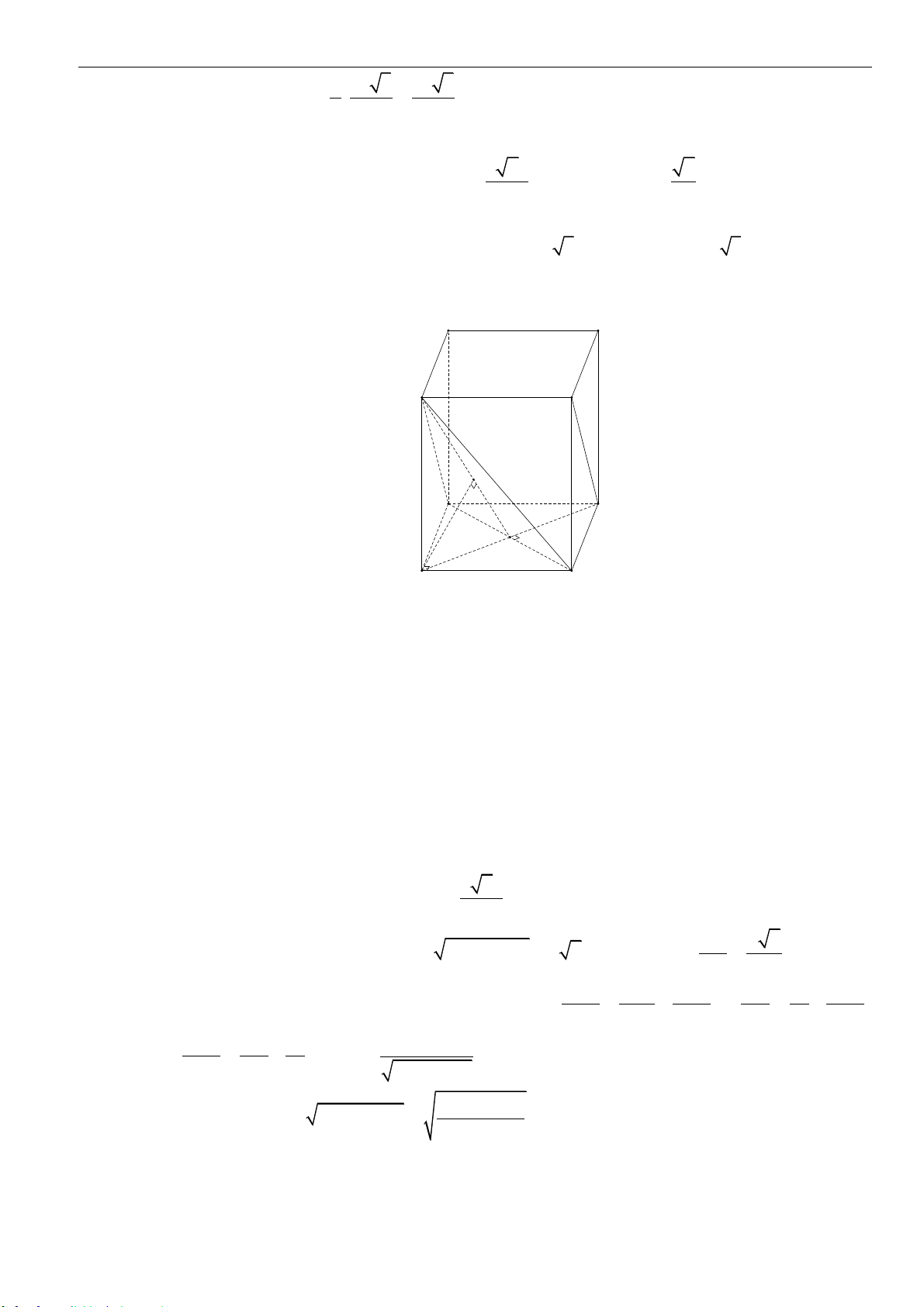
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

29 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

22

.

33

..

3 4 12

ABC A B C ABC

a a a

V A G S

  



= = =

( đvtt).

Câu 42: Cho hình lăng trụ tứ giác đều

.ABCD A B C D

   

có đáy là hình vuông; khoảng cách và góc giữa

hai đường thẳng

AC

và

DC



lần lượt bằng

37

7

a

và



với

2

cos

4



=

. Thể tích khối lăng trụ

đã cho bằng

A.

3

3a

. B.

3

9a

. C.

3

33a

. D.

3

3a

.

Lời giải

Chọn B

Ta có

.ABCD A B C D

   

là hình lăng trụ tứ giác đều nên

( )

BB ABCD



⊥

và

//DC AB



nên

( ) ( )

,,AC DC AC AB





==

.

Vì

BCC B



và

ABB A



là hai hình chữ nhật bằng nhau nên

''AB CB=

, suy ra

B AC





=

.

Lại có

//DC AB



( )

//DC AB C





( ) ( )

( )

, , , ,d AC DC d DC AB C d D AB C d B AB C

    

 = = =

.

Do

ABCD

là hình vuông nên

AC BD⊥

, mà

( )

BB ABCD BB AC



⊥  ⊥

.

Từ đó suy ra

( )

AC BDD B



⊥

.

Gọi

O AC BD=

, kẻ

BH B O



⊥

thì

( )

BH AB C



⊥

( )

7

,

37

,

a

BH d Dd B AB ACC C







===

.

Giả sử

( )

22

2

02

22

AC x

AB x x AC BD AB BC x AO BO=   = = + =  = = =

.

Tam giác

BB O



vuông tại

B

có

BH B O



⊥

nên

222

1 1 1

BH BO B B

=+



2 2 2

7 2 1

9a x B B

 = +



2 2 2

1 7 2

9B B a x

 = −



22

3

7 18

ax

BB

xa



=

−

.

Suy ra

4 2 2

22

79

7 18

x a x

B C AB BB AB

xa

−

  

= = + =

−

.

Tam giác

AB C



cân tại

B



và

O

là trung điểm của

AC

nên

B O AC



⊥

.

O

C'

B'

D'

C

A

D

B

A'

H

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 30

Suy ra

cos cos

AO

B AC

AB





==



4 2 2

22

2

4

79

7 18

x

x a x

xa

=

−

4 2 2

22

79

2

7 18

x a x

x

xa

−

=

−

4 2 2

2

22

79

4

7 18

x a x

x

xa

−

=

−

( )

4 2 2 2 2 2

7 9 4 7 18x a x x x a − = −

( )

2 2 2 2

7 9 4 7 18x a x a − = −

22

3xa=

.

Do đó

3BB a



=

,

22

3

ABCD

S AB a==

.

Vậy

3

.

.9

ABCD A B C D ABCD

V BB S a

   



==

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

1 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Dạng 10: Tỷ số thể tích khối lăng trụ

Câu 1: Cho khối lăng trụ tam giác

.ABC A B C

  

có thể tích

V

. Thể tích của khối chóp

.B ACC A



bằng

A.

2

3

V

. B.

1

3

V

. C.

1

2

V

. D.

3

4

V

.

Lời giải

Chọn A

Ta có:

( )

.

11

,.

33

B A B C A B C

V d B A B C S V

     

  

==

..

2

3

B ACC A B A B C

V V V V

    

 = − =

.

Câu 2: Cho hình hộp

.ABCD A B C D

   

. Tính tỷ số thể tích của khối tứ diện

BDA C



và khối hộp

.ABCD A B C D

   

.

A.

1

5

. B.

2

3

. C.

1

3

. D.

2

5

.

Lời giải

Chọn C

Gọi thể tích của khối hộp

.ABCD A B C D

   

là

V

.

Ta có:

. . . .

1

6

B A B C D A C D C BCD A ABD

V V V V V

       

= = = =

.

( )

. . . .

1

3

BDA C B A B C D A C D C BCD A ABD

V V V V V V V

         

 = − + + + =

.

Câu 3: Cho hình hộp

.ABCD A B C D

   

, gọi

,,M N P

lần lượt là trung điểm của các đoạn thẳng

,,AB A D B C

   

. Tỷ số thể tích của khối

MNPD



và khối hộp

.ABCD A B C D

   

bằng

A.

1

6

. B.

1

8

. C.

1

24

. D.

1

12

.

VÍ DỤ MINH HỌA

B

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 2

Lời giải

Chọn D

Ta có chiều cao của khối

MNPD



và khối hộp

.ABCD A B C D

   

bằng nhau, giả sử cùng bằng

h

.

Diện tích đáy của khối

MNPD



và khối hộp

.ABCD A B C D

   

lần lượt bằng:

A B C D

S

   

và

1

4

NPD A B C D

SS

    

=

. Nên

.

1 1 1 1 1

. . .

3 3 4 12 12

ABCD A B C D A B C D

MNPD NPD A B C D A B C D ABCD A B C D

V h S

V h S h S h S V

       

             

=







= = = =





Vậy tỷ số thể tích của khối

MNPD



và khối hộp

.ABCD A B C D

   

bằng

1

12

.

Câu 4: Cho khối hộp

. ' ' ' 'ABCD A B C D

có thể tích bằng

V

. Thể tích của khối tứ diện

''A BC D

bằng

A.

2

V

. B.

6

V

. C.

3

V

. D.

4

V

.

Lời giải

Chọn C

Ta có:

( )

1

,.

1 1 1

3

.

, . 3 2 6

ABD

A ABD

ABCD

d A ABCD S

V

V d A ABCD S



= = =



6

A ABD

V



=

.

Hoàn toàn tương tự

6

C BCD DA C D BA B C

V

V V V

      

= = =

( )

4.

63

A BC D A ABD C BCD DA C D BA B C

VV

V V V V V V V

         

 = − + + + = − =

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

3 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 1: Cho khối lăng trụ

.ABC A B C

  

có thể tích

V

và

M

là trung điểm của cạnh

AA



, thể tích khối

chóp

.M ABC

là

A.

6

V

. B.

4

V

. C.

2

V

. D.

3

V

.

Lời giải

Chọn A

Vì

M

là trung điểm cạnh

AA



nên

..

1

2

M ABC A ABC

VV



=

.

Mặt khác

..

11

33

A ABC ABC A B C

V V V

   

==

, vậy nên

..

1

26

M ABC A ABC

V

VV



==

.

Câu 2: Cho lăng trụ

.ABC A B C

  

biết diện tích mặt bên

( )

ABB A



bằng

15

, khoảng cách từ

C

đến mặt

phẳng

( )

ABB A



bằng

6

. Thể tích của khối lăng trụ

.ABC A B C

  

bằng

A.

60

. B.

45

. C.

90

. D.

30

.

Lời giải

Chọn B

Ta có

..

2

33

ABC A B C ABC A B C

C A B C C A B BA

VV

     

    

=  =

Ta có thể tích khối chóp

.C ABB A



bằng

( )

.

,

11

. .6.15 30

33

C ABB A ABB A

C ABB A

V d S

   



= = =

..

3

45

2

ABC A B C C A B BA

VV

    

 = =

.

BÀI TẬP TRẮC NGHIỆM

C

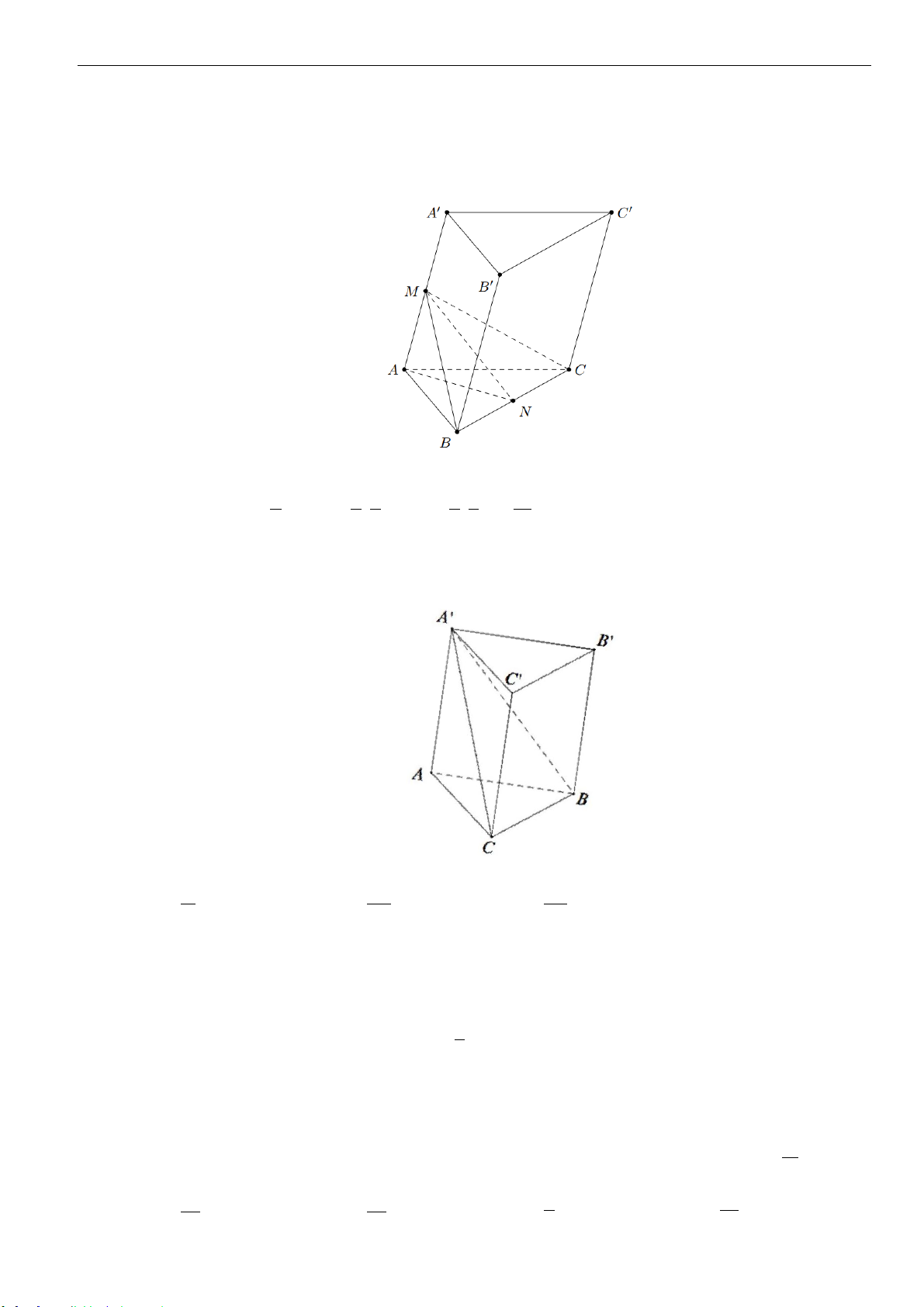
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 4

Câu 3: Cho lăng trụ

.ABC A B C

  

, gọi

M

,

N

lần lượt là trung điểm của cạnh

AA



và

BC

. Biết khối

tứ diện

AMNB

có thể tích là

3

3a

. Tính thể tích lăng trụ

.ABC A B C

  

.

A.

3

9a

. B.

3

12a

. C.

3

36a

. D.

3

18a

.

Lời giải

Chọn C

Gọi

V

là thể tích lăng trụ

.ABC A B C

  

Ta có

. . .

1 1 1 1 1 1

..

2 2 2 4 3 12

M ABN M ABC A ABC

V V V V V



= = = =

nên

3

12 36

AMNB

V V a==

.

Câu 4: Cho khối lăng trụ tam giác

.ABC A B C

  

. Biết thể tích của khối chóp

.A ABC



bằng

.V

Thể tích

khối lăng trụ

.ABC A B C

  

là

A.

.

3

V

B.

3

.

2

V

C.

2

.

3

V

D.

3.V

Lời giải

Chọn D

Thể tích khối lăng trụ là

( )

.

.,

ABC A B C ABC

V S d A ABC

  



=

Thể tích khối chóp

.A ABC



là

( )

.

1

.,

3

A ABC ABC

V S d A ABC V



==

Vậy

.

3.

ABC A B C

VV

  

=

Câu 5: Cho hình lăng trụ

.

  

ABC A B C

có thể tích bằng

V

. Gọi

M

là trung điểm cạnh



BB

, điểm

N

thuộc cạnh



CC

sao cho

2



=CN C N

. Khối chóp

.A BCNM

có thể tích là

1

V

. Tính

1

V

.

A.

7

12

. B.

5

18

. C.

1

3

. D.

7

18

.

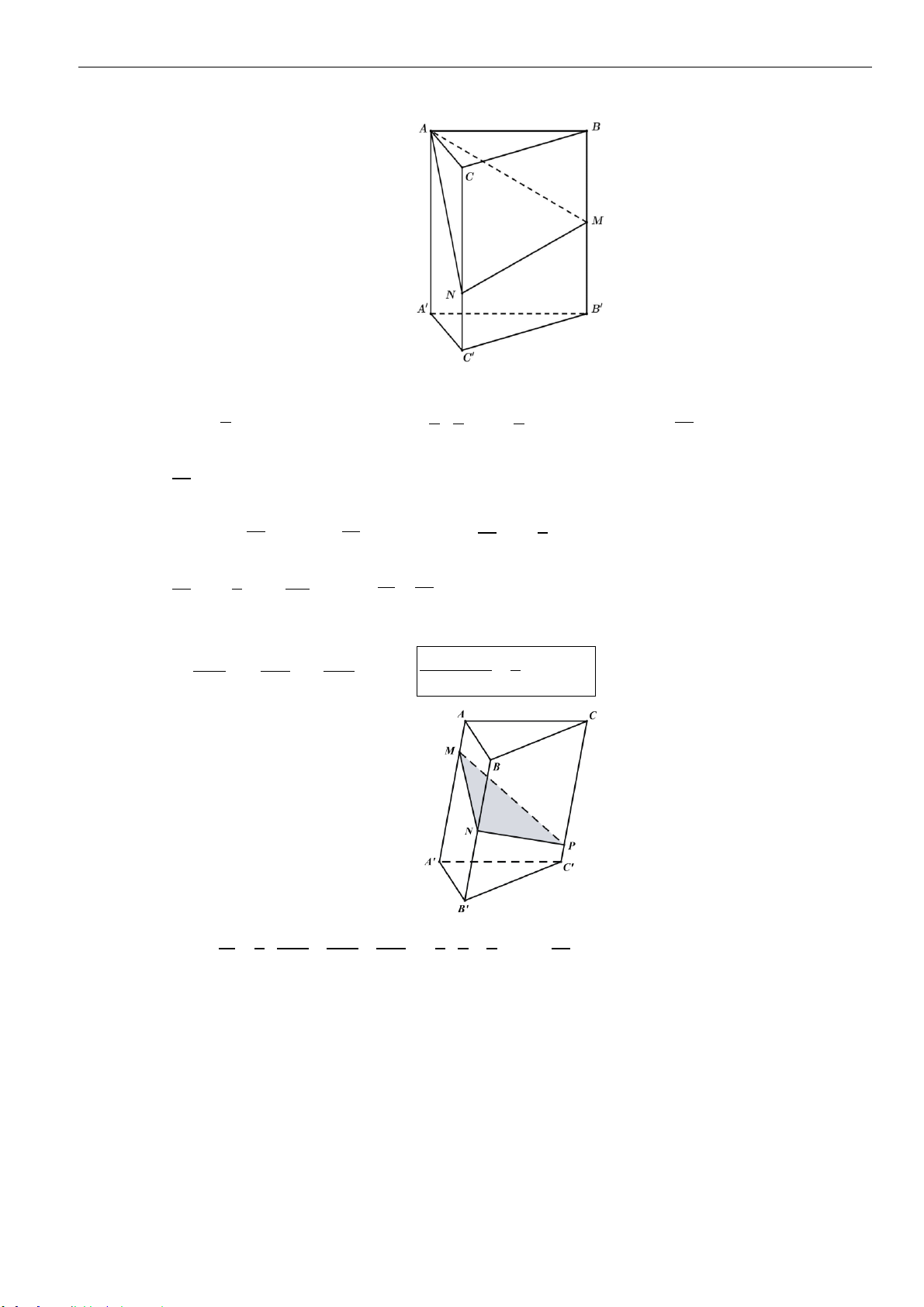
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

5 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Lời giải

Chọn D

Diện tích hình thang

BCNM

:

( ) ( )

1

.;

2

BCNM

S BM CN d B CC



=+

( )

1 1 2

.;

2 2 3

CC CC d B CC



  

=+





( )

7

. . ;

12

CC d B CC



=

7

12

BCC B

S



=

Khi đó:

( )

1 . .

77

12 12

A BCC B A A B C

V V V V

    

= = −

( )

71

. ; .

12 3

ABC

V d A A B C S

  



  

=−





7 1 7

12 3 18

V

VV



= − =





. Suy ra

1

7

18

V

=

Cách 2: Áp dụng công thức

Nếu

;;

AM BN CP

a b c

AA BB CC

= = =

  

thì

( )

.

1

3

ABC MNP

ABC A B C

V

abc

V

  

= + +

Khi đó:

1

1 1 2 1 7

0

3 3 3 2 18

V

CN BM AA

V CC BB AA

   

= + + = + + =

   



   

.

Câu 6: Cho khối hộp

.ABCD A B C D

   

có thể tích bằng

1

. Thể tích của khối tứ diện

ABC C



bằng

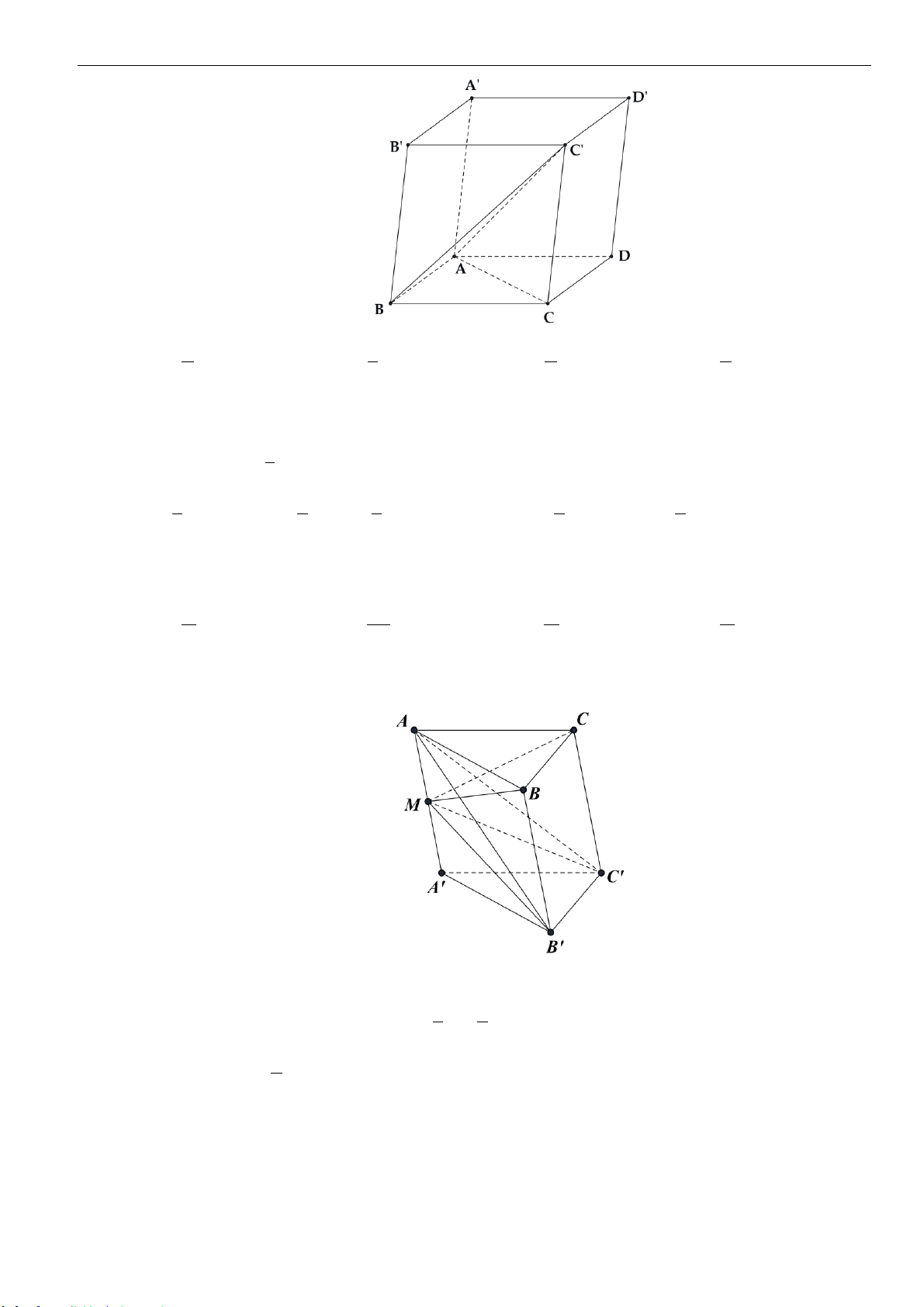
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 6

A.

2

3

. B.

1

3

. C.

1

2

. D.

1

6

.

Lời giải

Chọn D

Ta có

( )

1

. , .

3

ABC C ABC

V d C ABC S



=

( )

11

,.

32

ABCD

d C ABC S



=

( )

1

,.

6

ABCD

d C ABC S



=

.'

1

.

6

ABCD A B C D

V

  

=

1

6

=

.

Câu 7: Cho khối lăng trụ tam giác

.ABC A B C

  

có thể tích là

V

. Gọi

M

là trung điểm cạnh

AA



. Khi

đó thể tích khối chóp

.M BCC B



là

A.

2

V

. B.

2

3

V

. C.

3

V

. D.

6

V

.

Lời giải

Chọn B

Vì

( )

//AA BB C C

  

nên

( )

d , d ,M BB C C A BB C C

   

=

suy ra

..M BB C C A BB C C

VV

   

=

Mà

..

12

33

A BB C C ABC A B C AA B C

V V V V V V

       

= − = − =

Vậy

.

2

3

M BB C C

VV



=

.

Câu 8: Cho hình hộp

.ABCD A B C D

   

có

O AC BD=

. Với thể tích khối chóp

.A AOD



là

3

a

thì thể

tích khối hộp

.ABCD A B C D

   

là

A.

3

6a

. B.

3

12a

. C.

3

3a

. D.

3

4a

.

Lời giải

Chọn B

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

7 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Ta có:

( )

.

. , 4. . ,

ABCD A B C D ABCD AOD

V S d A ABCD S d A AOD

   





==

( )

3

.

1

4.3. . . , 12 12

3

AOD A AOD

S d A AOD V a







= = =

.

Câu 9: Cho hình lăng trụ đứng

. ' ' 'ABC A B C

. Gọi I là trung điểm BC. Tính tỉ số thể tích khối tứ diện

A’ABI và thể tích khối lăng trụ đã cho.

A.

1

4

. B.

1

12

. C.

1

6

. D.

1

3

.

Lời giải

Chọn C

Ta có:

. ' ' '

.'

ABC A B C ABC

V S AA=

và

'

1

.'

3

A ABI ABI

V S AA=

mặt khác

1

2

ABI ABC

SS=

Suy ra

'

. ' ' '

1 1 1

. ' . . '

1

3 3 2

. ' . ' 6

ABI ABC

A ABI

ABC A B C ABC ABC

S AA S AA

V

V S AA S AA

= = =

.

Câu 10: Cho khối lăng trụ tam giác

.ABC A B C

  

có thể tích

V

. Gọi

M

là trung điểm của

AA



,

N

là

trung điểm

AM

,

P

nằm trên

BB



sao cho

4BP B P



=

. Gọi thể tích khối đa diện

MNBCC P



là

1

V

. Tỉ số

1

V

bằng

A.

41

60

. B.

37

49

. C.

41

57

. D

2

3

.

Lời giải

Chọn A

Ta có

.

..

.

1 1 1

4 4 12

N ABC

N ABC A ABC

A ABC

V

NA

V V V

V A A



= =  = =



.

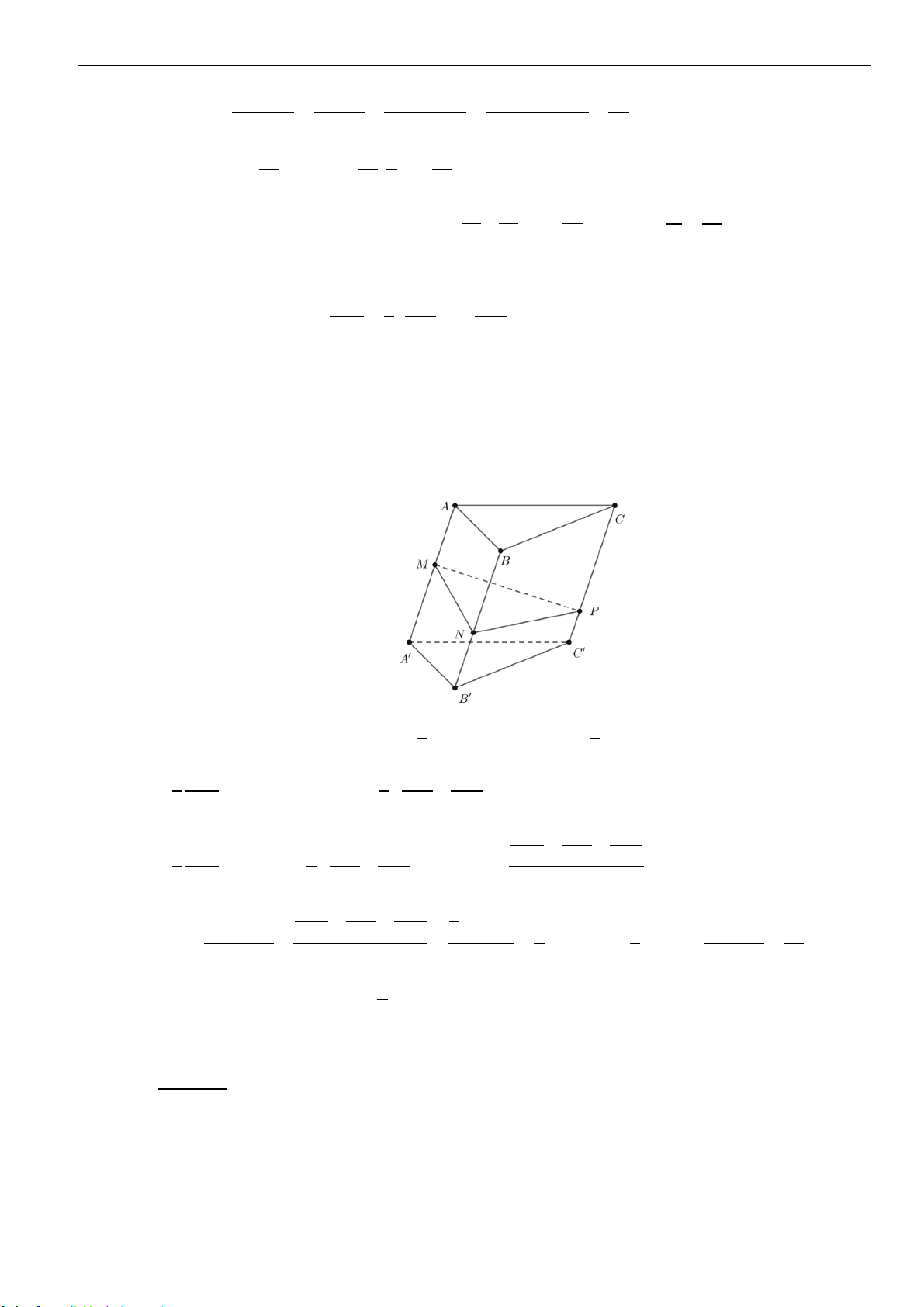
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 8

Mặt khác

.

11

7

25

2 20

C A B PM

A B PM

C A B BA A B BA

A A A A

V

S

A M B P

V S A A B B A A

  



    



+



+

= = = =

  

+

.

..

7 7 2 7

.

20 20 3 30

C A B PM C A B BA

V V V V

     

 = = =

.

Do đó

( )

1 . .

1 7 41

12 30 60

N ABC C A B PM

V V V V V V V

  



= − + = − + =





. Suy ra

1

41

60

V

=

.

Câu 11: Cho lăng trụ

. ' ' 'ABC A B C

có thể tích là

V

.

,,M N P

là các điểm lần lượt nằm trên các cạnh

', ', 'AA BB CC

sao cho

1

'3

AM

AA

=

,

'

BN

x

BB

=

,

'

CP

y

CC

=

. Biết thể tích khối đa diện

.ABC MNP

bằng

2

3

V

. Giá trị lớn nhất của

xy

bằng:

A.

17

21

. B.

25

36

. C.

5

24

. D.

9

16

.

Lời giải

Chọn B

Ta có

( )

. . .

11

,,

33

ABC MNP M ABC M NBCP ABC BNPC

V V V d M ABC S d M NBCP S= + = +

( )

''

11

', ,

3 ' 3 ' '

ABC BB C C

AM BN CP

d A ABC S d A NBCP S

AA BB CC



= + +





. ' ' ' . ' ' ' . ' ' '

11

' ' '

3 ' 3 ' ' 3

ABC A B C ABC A B C ABC A B C

AM BN CP

AA BB CC

V V V

AA BB CC

++



= + + =





Ta có

( )

2

.

. ' ' '

1

2 5 25

' ' ' 3

3 3 3 3 4 36

ABC MNP

ABC A B C

AM BN CP

xy

V

AA BB CC

x y xy

V

+ + + +

+

= = =  + =   =

.

Đẳng thức xảy ra khi

5

6

xy==

.

Câu 12: Cho lăng trụ

. ' ' 'ABC A B C

. Gọi

,MN

lần lượt là trung điểm của

'BB

và

'CC

. Tỉ số thể tích

. ' ' '

ABCMN

ABC A B C

V

là

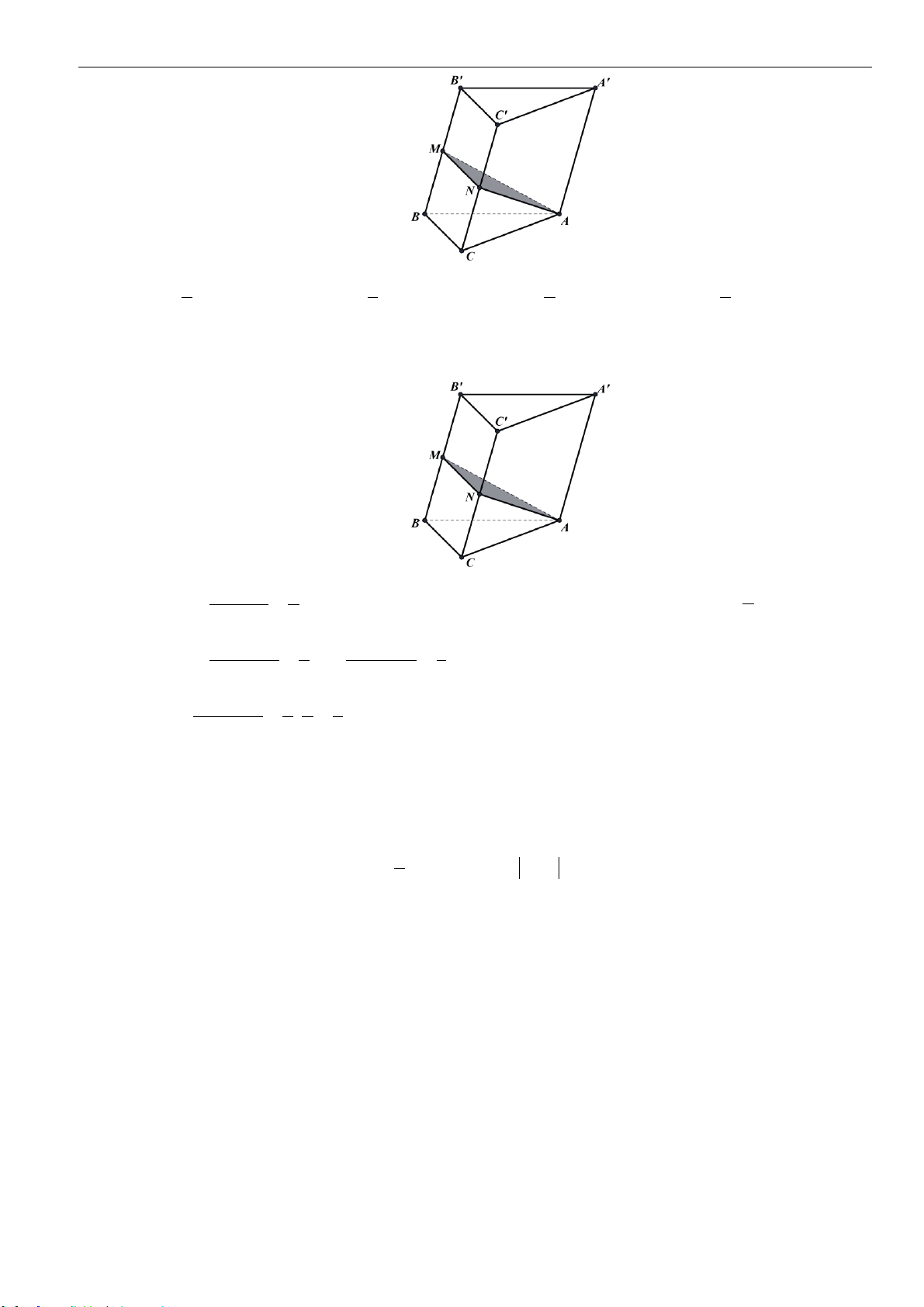
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

9 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

A.

1

6

. B.

1

3

. C.

1

2

. D.

2

3

.

Lời giải

Chọn B

Ta có:

. ' '

1

2

ABCMN

A BCC B

V

=

(hai hình chóp có chung đỉnh và đáy nhưng đáy này bằng

1

2

đáy kia).

Ta có:

. ' '

. ' ' '

2

3

A BCC B

ABC A B C

V

=

(vì

. ' ' '

1

3

A A B C

ABC A B C

V

=

)

Vậy

. ' ' '

1 2 1

..

2 3 3

ABCMN

ABC A B C

V

==

Câu 13: Cho hình lăng trụ tam giác

.ABC A B C

  

có thể tích là

V

và độ dài cạnh bên

6AA



=

đơn vị. Cho

điểm

1

A

thuộc cạnh

AA



sao cho

1

2AA =

. Các điểm

1

B

,

1

C

lần lượt thuộc cạnh

BB



,

CC



sao

cho

11

,BB x CC y==

, ở đó

,xy

là các số thực dương thỏa mãn

12.xy =

Biết rằng thể tích của

khối đa diện

1 1 1

.ABC A B C

bằng

1

.

2

V

Giá trị của

xy−

bằng

A.

3

. B.

4

. C.

1

. D.

0

.

Lời giải

Chọn C

Cách 1:

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 10

Gọi

,MN

lần lượt thuộc

BB



và

CC



sao cho

2.BM CN==

Khi đó ta có

1 1 1 1 1 1 1

..ABC A B C ABC A MN A MNC B

V V V=+

14

3 12

A BCC B

xy

VV

  

+−

=+

1 4 2

.

3 12 3

xy

VV

+−

= + 

Mặt khác theo giả thiết ta có

1 1 1

.

1

2

ABC A B C

VV=

nên suy ra

1 4 2 1

3 12 3 2

xy

V V V

+−

+  =

1 4 2 1

3 12 3 2

xy+−

 +  =

7xy + =

, kết hợp với

12.xy =

Ta có

3

4

x

y

=





=



hoặc

4

3

x

y

=





=



. Do đó

1.xy−=

Cách 2: Vận dụng công thức:

1 1 1

. . . .

2

6 6 6

3 3 18

ABC A B C ABC A B C ABC A B C ABC A B C

AA BB CC

xy

AA BB CC

V V V V

        



+ + + +



++



  

= = =









Giả thiết:

1 1 1

..

1 2 1

7

2 18 2

ABC A B C ABC A B C

xy

V V x y

  

++

=  =  + =

kết hợp với

12.xy =

Ta có

3

4

x

y

=





=



hoặc

4

3

x

y

=





=



. Do đó

1.xy−=

Câu 14: Cho hình lập phương

. ' ' ' 'ABCD A B C D

. Gọi

M

là điểm thuộc đoạn

'CC

thỏa mãn

'4CC CM=

. Mặt phẳng

( ' )AB M

chia khối lập phương thành hai phần có thể tích

1

V

và

2

V

.

Gọi

2

V

là phần có chứa điểm

B

. Tính tỉ số

1

2

V

k

V

=

.

A.

32

25

. B.

7

16

. C.

25

7

. D.

7

32

.

Lời giải

Chọn C

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

11 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Gọi

';K MB BC J AK CD=  = 

và

V

là thể tích của khối lập phương

. ' ' ' 'ABCD A B C D

.

Ta có

11

' ' ' 3 ' 4

CK CM KM KJ KC

B C MC KB KA KB

= =  = = =

.

Ta có

2 '. .B ABK K CMJ

V V V=−

;

.

.'

1 1 1 1

. . . .

' 4 4 4 64

K CMJ

K BB A

V

KC KM KJ

V KB KB KA

= = =

.

Suy ra

2 '.

63

64

B ABK

VV=

.

Ta có

1 1 4 2

( , ). ( , ).

2 2 3 3

ABK ABCD

S d A BK BK d A BK BC S



= = =

'.

2

9

B ABK

VV=

.

Suy ra

1

21

2

7 25 25

.

32 32 7

V

V V V V k

V

=  =  = =

Câu 15: Cho hình lăng trụ

.ABC A B C

  

. Gọi

M

,

N

,

P

lần lượt là các điểm thuộc các cạnh

AA



,

BB



,

CC



sao cho

2AM MA



=

,

2NB NB



=

,

PC PC



=

. Gọi

1

V

,

2

V

lần lượt là thể tích của hai khối

đa diện

ABCMNP

và

A B C MNP

  

. Tính tỉ số

1

2

V

.

A.

1

2

V

=

. B.

1

2

1

V

=

. C.

1

2

1

2

V

=

. D.

1

2

3

V

=

.

Lời giải

Chọn B

Gọi

V

là thể tích khối lăng trụ

.ABC A B C

  

. Ta có

1 . .M ABC M BCPN

V V V=+

.

( )

.

1 1 2 2

. , . . ,

3 3 3 9

M ABC ABC ABC

V S d M ABC S d A ABC V



= = =

.

( )

.

1 1 1 1

. , . . ,

3 3 3 9

M A B C A B C A B C

V S d M A B C S d A A B C V

        

     

= = =

.

J

K

M

C'

D'

A'

C

B

A

D

B'

V

ũ

V

ă

n

B

ắ

c

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 12

Do

BCC B



là hình bình hành và

2NB NB



=

,

PC PC



=

nên

7

5

B C PN BCPN

SS



=

.

Suy ra

..

7

5

M B C PN M BCPN

VV



=

, Từ đó

. . . .M ABC M BCPN M A B C M B C PN

V V V V V

    

= + + +

. . .

2 1 7 5

9 9 5 18

M BCPN M BCPN M BCPN

V V V V V V V = + + +  =

.

Như vậy

12

2 5 1 1

9 18 2 2

V V V V V V= + =  =

. Bởi vậy:

1

2

1

V

=

.

Câu 16: Cho khối lăng trụ tam giác

.ABC A B C

  

có thể tích

V

. Gọi

,,M N P

lần lượt là trung điểm của

các cạnh

;;A B BC CC

  

. Mặt phẳng

( )

MNP

chia khối lăng trụ đã cho thành

2

phần, phần chứa

điểm

B

có thể tích là

1

V

. Tỉ số

1

V

bằng

A.

61

144

. B.

37

144

. C.

49

144

. D.

25

144

.

Lời giải

Chọn C

Gọi

S

và

h

lần lượt là diện tích đáy và chiều cao của lăng trụ

.ABC A B C V Sh

  

=

.

Gọi

, , ,NP BB E NP B C F MF A C Q ME AB R

    

 =  =  =  =

Suy ra mặt phẳng

( )

MNP

cắt khối lăng trụ theo thiết diện là

MRNPQ

.

Ta có

BEPC



là hình bình hành

11

22

BE PC CC BB

  

 = = =

, tương tự ta có

BNFC



là hình

bình hành

11

22

C F BN BC B C

  

 = = =

.

Ta có :

1 3 1 3

. . .sin . . . .sin

2 4 2 4

MB F

S B M B F MB F A B B C A B C S



         

= = =

Khi đó :

( )

33

,,

22

d E A B C d B A B C h

     

==

( )

.

1 1 3 3 3

. , . . . .

3 3 2 4 8

E B MF B MF

V d E A B C S h S V



  

 = = =

Lại có

3

.

1 1 3 1

.

27 27 8 72

E BNR

E B FM

V

EB

V V V

V EB





= =  = =







Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

13 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Ta cũng có

.

1 1 1 1 1 3 1

. . . . .

3 3 2 18 18 8 48

F C PQ

F B EM

V

FC FP FQ

V V V

V FB FE FM



= = =  = =



.

Suy ra

( )

.

1 . .

49

144

E BNR

E B MF V F C PQ

V V V V V



= − + =

.

Vậy

1

49

144

V

=

.

Câu 17: Cho hình lập phương

. ' ' ' 'ABCD A B C D

. Gọi

,MN

lần lượt là trung điểm

''BA

và

'BB

. Mặt

phẳng

( )

P

đi qua

MN

và tạo với mặt phẳng

( )

''ABB A

một góc



sao cho

tan 2=

. Biết

( )

P

cắt các cạnh

'DD

và

DC

. Khi đó mặt phẳng

( )

P

chia khối lập phương thành hai phần,

gọi thể tích phần chứa điểm

A

là

1

V

và phần còn lại có thể tích

2

V

. Tỉ số

1

2

V

là

A.

1

2

1

V

=

. B.

1

2

V

=

. C.

1

2

1

3

V

=

. D.

1

2

1

2

V

=

.

Lời giải

Chọn A

Không mất tính tổng quát, giả sử độ dài cạnh của hình lập phương

. ' ' ' 'ABCD A B C D

là 1.

Gọi

,,QRI

lần lượt là trung điểm của các cạnh

, ', 'DC DD AA

.

Ta có

// // //QR MN D C A B



nên

, , ,M N Q R

đồng phẳng.

( ) ( )

''MNQR ABB A MN=

. Trong

( )

''ABB A

, ta có

IM MN⊥

.

( )

''RI ABB A RI MN⊥  ⊥

. Do đó,

( )

MN IMR MR MN⊥  ⊥

.

Suy ra

( ) ( )

( )

, ' ' ,MNQR ABB A IM MR RMI = = =

,

tan 2

RI

MI

 = =

. Như vậy, mặt phẳng

( )

P

chính là mặt phẳng

MNQR

.

Gọi

', , , ' 'T MN AA K MN AB P QK BC S RT A D=  =  =  = 

. Khi đó, thiết diện của khối

lập phương

. ' ' ' 'ABCD A B C D

cắt bởi mặt phẳng

( )

P

là lục giác

MNPQRS

.

1 . 'A MNPQRS AA MS ADRQ ABNP

V V V V V= + + +

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 14

2 '. ' ' ' ' 'C MNPQRS C D RS C CPQ C MNB

V V V V V= + + +

Dễ thấy

. '.A MNPQRS C MNPQRS

VV=

và

2

' ' ' ' ' '

1 1 1 1

.1.

3 2 2 24

AA MS ADRQ ABNP C D RS C CPQ C MNB

V V V V V V



= = = = = = =





.

Do đó,

1

12

2

1

V

VV

V

=  =

.

Câu 18: Cho khối hộp

. ' ' ' 'ABCD A B C D

, điểm

M

thuộc cạnh

'CC

sao cho

'3CC CM=

. Mặt phẳng

( )

'AB M

chia khối hộp thành hai khối đa diện.

1

V

là thể tích khối đa diện chứa đỉnh

'A

,

2

V

là

thể tích khối đa diện chứa đỉnh

B

. Tính tỉ số

1

2

V

?

A.

13

41

. B.

41

108

. C.

13

8

. D.

41

13

.

Lời giải

Chọn D

Gọi

'E B M BC=

,

F AE DC=

.

Gọi

V

là thể tích khối hộp

. ' ' ' '.ABCD A B C D

Ta có:

( )

''

. , ' '

ABB A

V S d C ABB A=

.

Ta có:

( )

. ' ' ' '

1 1 1 3 1

. , ' . . , ' '

3 3 2 2 4

E ABB ABB ABB A

V S d E ABB S d C ABB A V



= = =

.

. . ' . '

11

. . .

' 27 108

E FCM E ABB E ABB

EF EC EM

V V V V

EA EB EB

= = =

.

Suy ra:

2 . ' .

1 1 13

4 108 54

E ABB E FCM

V V V V V V= − = − =

. Và

12

13 41

54 54

V V V V V V= − = − =

.

Vậy:

1

2

41

13

V

=

.

Câu 19: Cho lăng trụ

.ABCD A B C D

   

có

ABCD

là hình thang đáy

,AB CD

sao cho

2AB CD=

. Gọi

,MN

lần lượt thuộc cạnh

,AA DD



sao cho

34

;

43

AM DN

MA ND

==



, mặt phẳng

( )

BMN

chia khối

lăng trụ thành hai khối đa diện, gọi

1

V

là thể tích của khối đa diện có chứa đỉnh

2

;AV

là thể tích

khối đa diện còn lại. Biết

1

2

V

a

Vb

=

. Giá trị của biểu thức

2ab+

bằng

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

15 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

A.

167

. B.

211

. C.

293

. D.

208

.

Lời giải

Chọn B

Gọi

,EE



lần lượt là trung điểm của

,AB A B



;

I BM EE



=

Ta có:

( ) ( )

//

BMN ECC E IK

BMN ADD A MN IK MN

ECC E ADD A



=







 = 





   



Ta lại có

1 1 3 3

3

2 2 14 14

7

EI EI EI EI

AM AA EE

AA

=  =  =  =





Mặt khác:

5

14

AM CK EI DN CK

AA CC EE DD CC

+ = +  =

    

.

..ADCE MNKI AECD MKN BEIKC

V V V=+

.

11

43

AECD A E C D ECBE C B

AM DN CK EI CK EI

VV

AA DD CC EE CC EE

      

   

= + + + + +

   

     

   

2 1 11 1 1 4 41

. . . .

3 4 7 3 3 7 126

V V V= + =

1

2

41

41, 85 2 211

85

V

a b a b

V

 =  = =  + =

Câu 20: Cho hình hộp

.ABCD A B C D

   

có thể tích bằng

V

. Điểm

M

là trung điểm cạnh

CC



. Mặt

phẳng

( )

P

chứa

AM



cắt các cạnh

,BB DD



lần lượt tại

,NP

chia khối hộp thành hai phần.

Thể tích phần chứa đỉnh

C



bằng

A.

2

V

. B.

3

V

. C.

6

V

. D.

4

V

.

Lời giải

Chọn D

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 16

Áp dụng công thức

1

2

4

A A C M

V

AA C C

V

  



+







=

. Ta có

1

0,

2

A A C M

AA C C

  

==



.

Khi đó:

1

20

1

2

44

V



+





==

.

Câu 21: Cho lăng trụ

.ABC A B C

  

có thể tích bằng

V

. Gọi

M

,

N

,

P

lần lượt là các điểm thuộc

AA



,

BB



,

AC



sao cho

1

2

AM B N C P

A M BN A P



= = =



. Gọi

Q

là trung điểm

BC

. Thể tích khối tứ diện

MNPQ

bằng

A.

2

9

V

. B.

1

3

V

. C.

2

7

V

. D.

2

3

V

.

Lời giải

Chọn A

Trong

( )

AA C C



, gọi

K MP CC



=

. Trong

( )

BB C C



, gọi

I NQ CC



=

.

Ta có:

( )

. . .

2 2 2

;;

3 3 3

MNPQ P MNQ K MNQ Q MNK

d P MNQ d K MNQ V V V V=  = = =

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

17 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

( )

. . .

1 1 1

;;

2 2 2

Q MNK I MNK M INK

d Q MNK d I MNK V V V=  = =

.

( )

. . . . .

11

;;

22

M INK A INK Q MNK A INK N AKI

d M INK d A INK V V V V V=  =  = =

.

( )

. . . . .

11

;;

22

N AKI B AKI Q MNK B AKI I ABK

d N AKI d B AKI V V V V V=  =  = =

.

( )

. . . . .

3 3 1 3 3

; ; .

2 2 2 2 4

I ABK C ABK Q MNK C ABK K ABC

d I ABK d C ABK V V V V V=  =  = =

.

( )

. . . . .

4 4 3 4 1

; ; .

3 3 4 3 3

K ABC C ABC Q MNK C ABC C ABC

d K ABC d C ABC V V V V V V

  



=  =  = = =

.

2 1 2

..

3 3 9

MNPQ

V V V==

Câu 22: Cho hình hộp

ABCD A B C D

   



có đáy

ABCD

là hình thoi tâm

O

, cạnh bằng

a

và

60BAC =

.

Gọi

, IJ

lần lượt là tâm của các mặt bên

, ABB A CDD C

   

. Biết

7

2

a

AI =

,

2AA a



=

và góc

giữa hai mặt phẳng

( ) ( )

,ABB A A B C D

     

bằng

60

. Tính theo

a

thể tích khối tứ diện

AOIJ

.

A. . B. . C. . D. .

Lời giải

Chọn C

Ta có

( )

2 2 2

2 2 2 2 2 2

2 4 3 3

24

A A AB A B

AI A B A A AB AI a A B a



+

  

= −  = + − =  =

Do

2 2 2

A B AB A A



+=

nên tam giác

A AB



vuông tại

B

2

3

2

A AB

a

S



=

Tam giác ABC đều cạnh a nên

2

3

4

ABC

a

S =

Theo đề

( ) ( )

(

)

, 60ABB A A B C D

     

=

, nên suy ra

3

2 sin60

3

38

..

A AB ABC

A ABC

SS

a

V

AB





==

( )

3

1 1 1 1 1 1 3

( ;( )). ;

3 3 2 2 4 4 32

AOIJ LAJ B AD B ABD A ABC

a

V d O IAJ S d B B AD S V V

  



= =   = = =

Câu 23: Cho lăng trụ

. ' ' '.ABC A B C

Điểm

M

thỏa mãn

1

.

2

B M B A

  

=−

,

D

là trung điểm của

'BB

và

E

là trung điểm của

AC



. Mặt phẳng

( )

MDE

chia khối lăng trụ

. ' ' 'ABC A B C

thành hai khối

3

33

64

a

3

48

a

3

32

a

3

192

a

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 18

đa diện có thể tích là

12

,VV

(

1

V

là thể tích khối đa diện chứa đỉnh

A

). Biết tỉ số

1

2

V

a

Vb

=

(

,ab

là

các số nguyên dương và

a

b

là phân số tối giản), tính

2ab+

.

A.

2 193ab+=

. B.

2 144ab+=

. C.

2 187ab+=

. D.

2 239ab+=

.

Lời giải

Chọn A

Gọi

''A B ME R=

.

Kéo dài

MD

cắt

,'AB AA

lần lượt tại

,PF

.

Gọi

EF AC Q=

.

Suy ra thiết diện là ngũ giác

ERDPQ

. Đặt

. ' ' 'ABC A B C

VV=

.

Ta có:

1 . ' . . 'F A EM F AQP M B DR

V V V V= − −

.

Ta có:

( ) ( )

' ' '

1 1 1 3 3

. ; . . . ; . .

2 2 2 2 4

A ME A B C

S d E A M A M d C A B A B S



      

= = =

Lại có

D

là trung điểm của

'BB

mà

1

.

2

B M B A

  

=−



P

là trung điểm của

AB

13

32

FA AP FA

FA A M AA



 = =  =

  

.

( )

'

.'

'

.'

' ' '

1

. ; ' ' ' .

1 ' 1 3 3 3 3

3

. . . .

3 ' 3 2 4 8 8

; ' ' ' .

A ME

F A ME

A ME

F A ME

A B C

d F A B C S

V

S

FA

VV

V AA S

d A A B C S

 = = = =  =

.

Ta có:

2

' ' ' '

'

1 1 1 1

'

9 9 12 12

APQ

APQ A ME A B C ABC

A ME

S

AP

APQ A ME S S S S

S A M



   = =  = = =







.

( )

.

1

. ; .

1 1 1 1 1 1

3

. . . .

3 ' 3 2 12 72 72

'; .

APQ

F APQ APQ

F APQ

ABC

d F ABC S

VS

FA

VV

V AA S

d A ABC S

 = = = =  =

Áp dụng định lí Mennelaus, ta có

' ' ' ' 2

. . 1

' ' ' ' 3

MA RB EC RB

MB RC EA RC

=  =

.

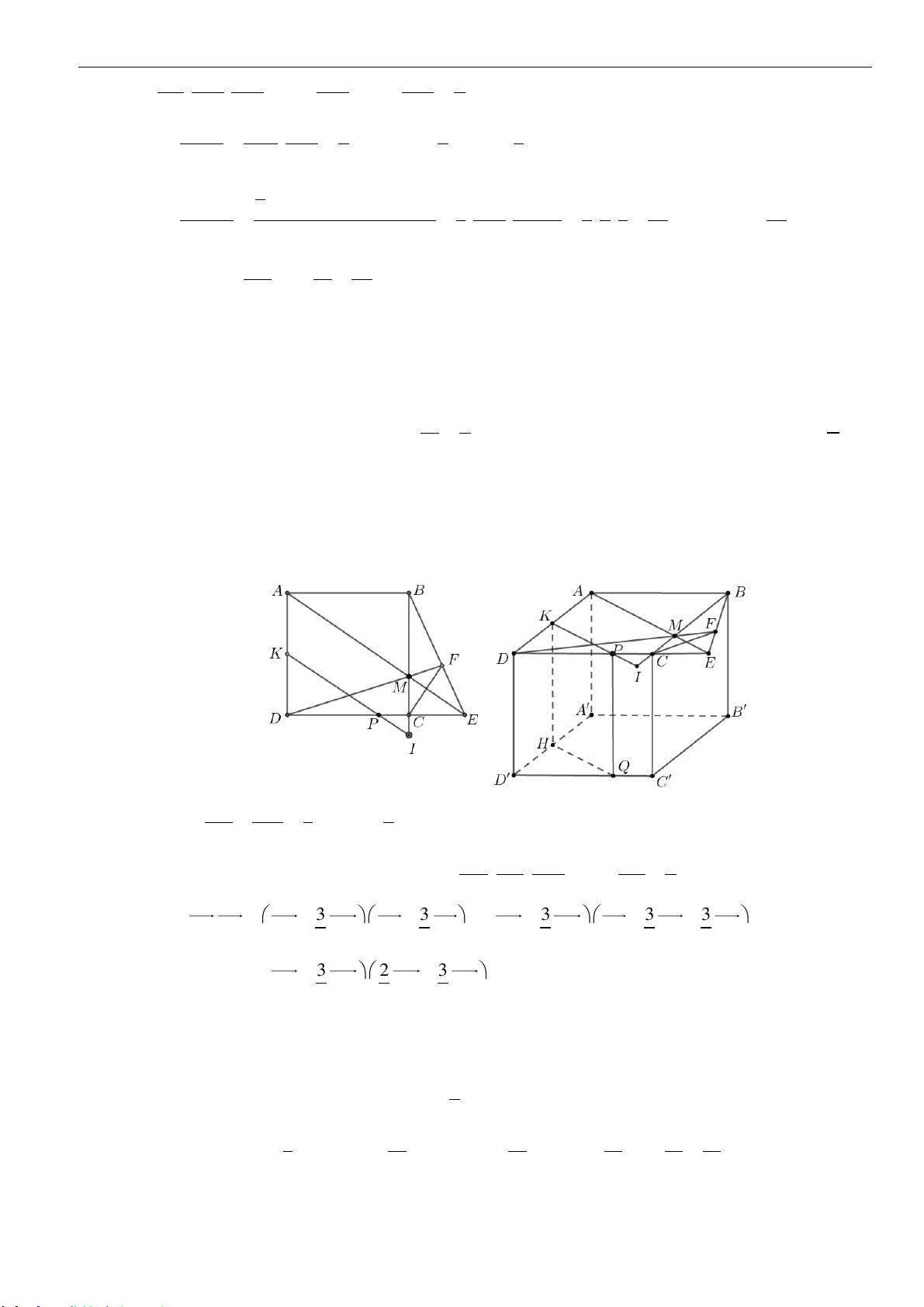
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

19 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

1

. . 1 1

2

CE BA RM RM RM

CA BM RE RE ME

=  =  =

.

'

' ' ' ' '

'

' 1 1 1

. . .

' 6 6 8

B RM

B RM A ME A B C

A ME

S MB RM

S S S

S MA ME

 = =  = =

( )

'

. ' '

.'

' ' ' ' ' '

1

. ; ' ' ' .

1 ' 1 1 1 1 1

3

. . . .

; ' ' ' . 3 ' 3 2 8 48 48

B RM

D B RM B RM

D B RM

A B C A B C

d D A B C S

V DB S

VV

V d B A B C S BB S

 = = = =  =

Suy ra

1

2

49 49

49, 95 2 193

144 95

V

V V a b a b

V

=  =  = =  + =

.

Câu 24: Cho hình lập phương

. ' ' ' 'ABCD A B C D

. Gọi

M

là một điểm trên cạnh

BC

sao cho

2BM MC=

,

E

là giao điểm của

AM

và

CD

,

F

là giao điểm của

DM

và

BE

. Mặt phẳng

( )



đi qua trung điểm của

''AD

và vuông góc với

CF

chia khối lập phương ra thành hai phần

có thể tích là

( )

1 2 1 2

,,V V V V

. Đặt

1

2

V

a

Vb

=

với

,ab

là các số nguyên dương và phân số

a

b

tối

giản. Giá trị

ab−

bằng

A.

7−

. B.

11−

. C.

10−

. D.

5−

.

Lời giải

Chọn C

Ta có

11

32

EC MC

CE CD

ED AD

= =  =

.

Theo định lý Menelaus trong

BCE

có

3

. . 1

4

DC EF BM EF

DE FB MC FB

=  =

.

Xét

33

.

27

AE CF AD DC CE EB

  

= + +

  

  

3 3 3

2 7 7

AD DC CE EC BC

  

= + + −

  

  

3 2 3

0

2 7 7

AD DC DC AD

  

= + − =

  

  

.

Vậy

AE CF⊥

.

Gọi

,HK

làn lượt là trung điểm của

' ',A D AD

và

// , // 'KP AM PQ CC

thì

( ) ( )

HKPQ





Gọi

1

3

2

KP BC I IM KA IC MC DP PC =  =  =  =

.

1

12

2

3 3 3 13 3

'. '. '.

8 16 16 16 13

DKP DAC ABCD

V

V DD S DD S DD S V V V

V

= = = =  =  =

.

Vậy

10ab− = −

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 20

Câu 25: Cho khối lăng trụ tam giác

.ABC A B C

  

có thể tích là

V

. Gọi

,IJ

lần lượt là trung điểm của

hai cạnh

AA



và

BB



. Khi đó thể tích khối đa diện

ABCIJC



bằng

A.

2

3

V

. B.

3

5

V

. C.

3

4

V

. D.

4

5

V

.

Lời giải

Chọn A

Có

.

1 1 1 1 2

1

3 3 2 2 3

ABC IJC

ABC A B C

V AI BJ CC

V AA BB CC



  



   

= + + = + + =

   

  

   

.

..

22

33

ABC IJC ABC A B C

V V V

   

 = =

.

Câu 26: Cho hình lăng trụ

.ABC A B C

  

. Gọi

,MN

lần lượt là trung điểm của

CC



và

BB



. Tính tỉ số

.

ABCMN

ABC A B C

V

  

.

A.

1

2

. B.

2

3

. C.

1

3

. D.

1

6

.

Lời giải

Chọn C

Đặt

.ABC A B C

VV

  

=

.

( )

..

1 1 1 2

.,

3 3 3 3

A A B C A B C A BCC B

V S d A A B C V V V V V

       

  

= =  = − =

.

( )

.

1 1 1 1 1 2 1

. , . . , .

3 3 2 2 2 3 3

ABCMN BCMN BCC B A BCC B

V S d A BCC B S d A BCC B V V V

   

= = = = =

.

Vậy

.

1

3

ABCMN

ABC A B C

V

  

=

.

J

I

B

C

A'

C'

B'

A

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

21 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 27: Cho hình lăng trụ tam giác

.ABC A B C

  

có thể tích là

V

. Gọi

M

là trung điểm

AA



và

N

là

trung điểm của

AB

. Mặt phẳng

( )

MNC



chia lăng trụ thành hai phần trong đó phần chứa đỉnh

A

có thể tích

V



. Thể tích của khối

V



theo

V

là

A.

11

25

VV



=

. B.

1

5

VV



=

. C.

13

36

VV



=

. D.

5

7

VV



=

.

Lời giải

Chọn C

Trong

( )

ABB A



, gọi

I MN A B



=

và

S MN BB



=

Trong

( )

BCC B



,gọi

E SC BC



=

.

Ta có

1

2

AI

AB



=



,

1

2

SB

BB

=



,

1

3

BE

BC

=

.

Gọi

h

là chiều cao và

S

là diện tích đáy của lăng trụ

V hS=

.

. . .A B C MNBE S B C I S BEN M A C I

V V V V

      

= − −

1 3 3 23

3 2 2 2 3.2 2 2 36

h S h S h S V



=  −  −  =





.

Suy ra

23 13

36 36

V

V V V



= − =

.

Câu 28: Cho hình lăng trụ

.'ABC A B C



có thể tích

V

. Gọi

M

là điểm nằm trên cạnh

BB



sao cho

23MB MB



=

, điểm

N

nằm trên cạnh

AA



sao cho

4AN NA



=

, điểm

P

nằm trên cạnh

CC



sao cho

3CP PC



=

. Các đường thẳng

NM

,

PM

lần lượt cắt các cạnh

AB



và

CB



lần lượt

tại

H

,

K

. Hãy tính theo

V

thể tích của khối tứ diện

MB HK



?

A.

16

105

V

. B.

6

35

V

. C.

4

15

V

. D.

2

7

V

.

Lời giải

Chọn A

Có

2

23

5

MB MB MB BB

  

=  =

,

4

5

AN NA NA AA

  

=  =

,

3

4

CP PC PC CC

  

=  =

.

Gọi

E

là hình chiếu của điểm

B

trên

( )

ABC

  

,

F

là hình chiếu của điểm

M

trên

( )

ABC

  

suy ra

B



,

F

,

E

thẳng hàng.

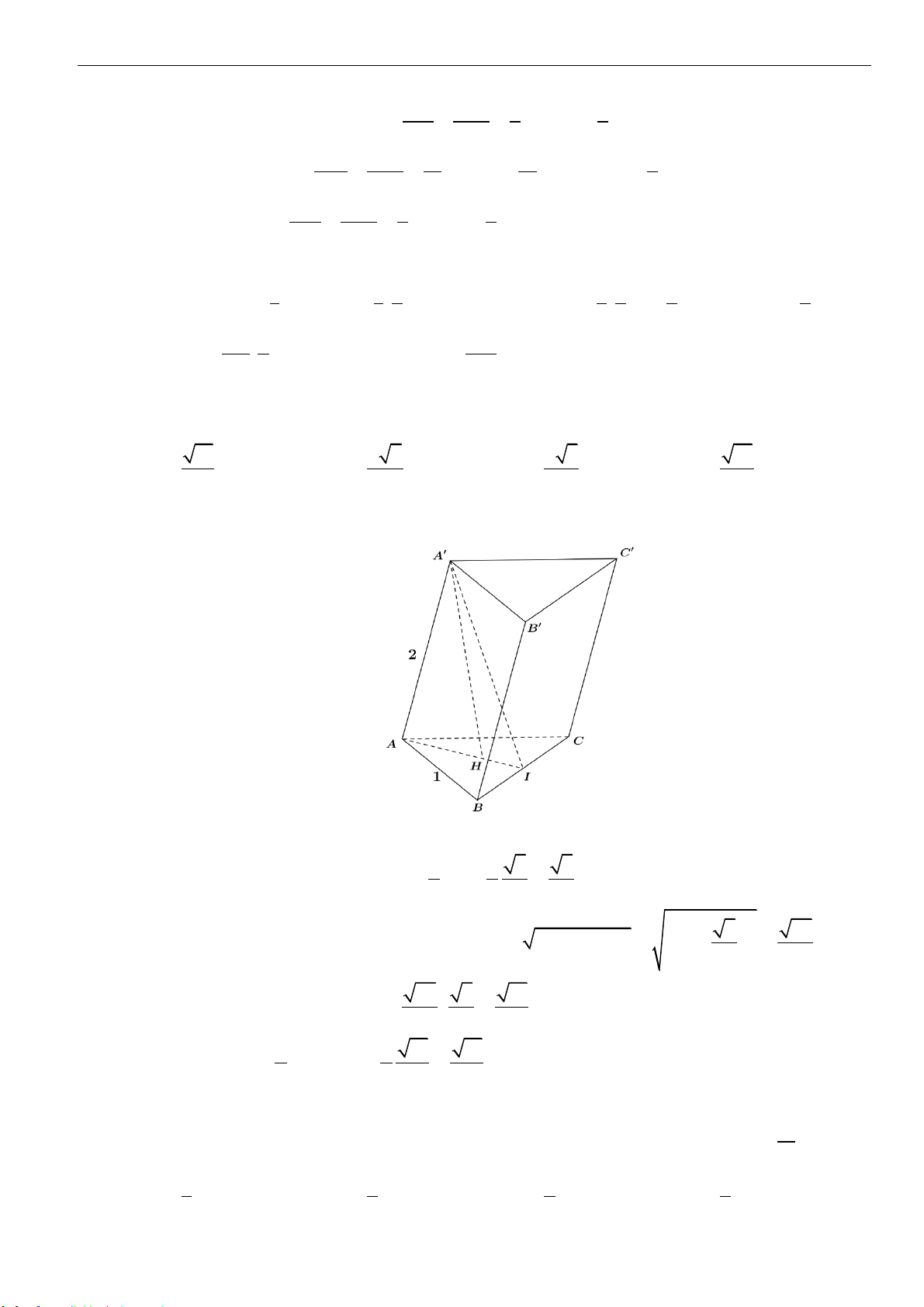
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 22

Xét hai tam giác

B MF



,

B BE



có góc

B



chung,

90

o

MFB BEB



==

suy ra hai tam giác

B MF



,

B BE



đồng dạng, ta có:

22

55

MF B M

MF BE

BE B B



= =  =



.

Vì

//BB CC



ta có:

8 8 8

'

15 15 7

KB B M

KB KC KB B C

KC C P



   

= =  =  =



.

//BB AA



ta có:

11

''

22

HB B M

HB HA HB A B

HA A N



  

= =  =  =



.

Góc

HB K A B C

   

=

(đối đỉnh).

Ta có:

1

.

3

MB HK B HK

V S MF



=

1 1 1 1 8 2

. . .sin . . . .sin .

3 2 3 2 7 5

B H B K HB K MF B A B C A B C BE

         

==

.

16 1 16

. . .sin .

105 2 105

MB HK

V

V B A B C A B C BE



      

==

.

Câu 29: Cho hình lăng trụ

.ABC A B C

  

có

.A ABC



là hình chóp tam giác đều, cạnh đáy

1AB =

, cạnh

bên

2AA



=

. Tính thể tích khối chóp

.A BB C C

  

.

A.

11

.

6

B.

26

.

3

C.

23

.

3

D.

15

3

.

Lời giải

Chọn A

Gọi

H

là tâm của tam giác

ABC

, suy ra

( )

A H ABC



⊥

.

Xét tam giác đều

ABC

, có

2 2 3 3

3 3 2 3

AH AI= = =

.

Tam giác

A AH





vuông tại

H

, suy ra :

2

2 2 2

3 33

2

33

A H AA AH





= − = − =





.

Suy ra

.

33 3 11

.

3 4 4

ABC A B C ABC

V A H S

  





= =  =

.

Vậy

..

2 2 11 11

3 3 4 6

A BB C C ABC A B C

VV

     

= = =

.

Câu 30: Cho khối lăng trụ

. ' ' 'ABC A B C

có

P

là trọng tâm tam giác

' ' 'A B C

và

Q

là trung điểm của

.BC

Gọi

12

,VV

lần lượt là thể tích hai khối tứ diện

'B PAQ

và

'A ABC

. Tính tỉ số

1

2

.

V

A.

1

3

. B.

2

3

. C.

1

6

. D.

1

2

.

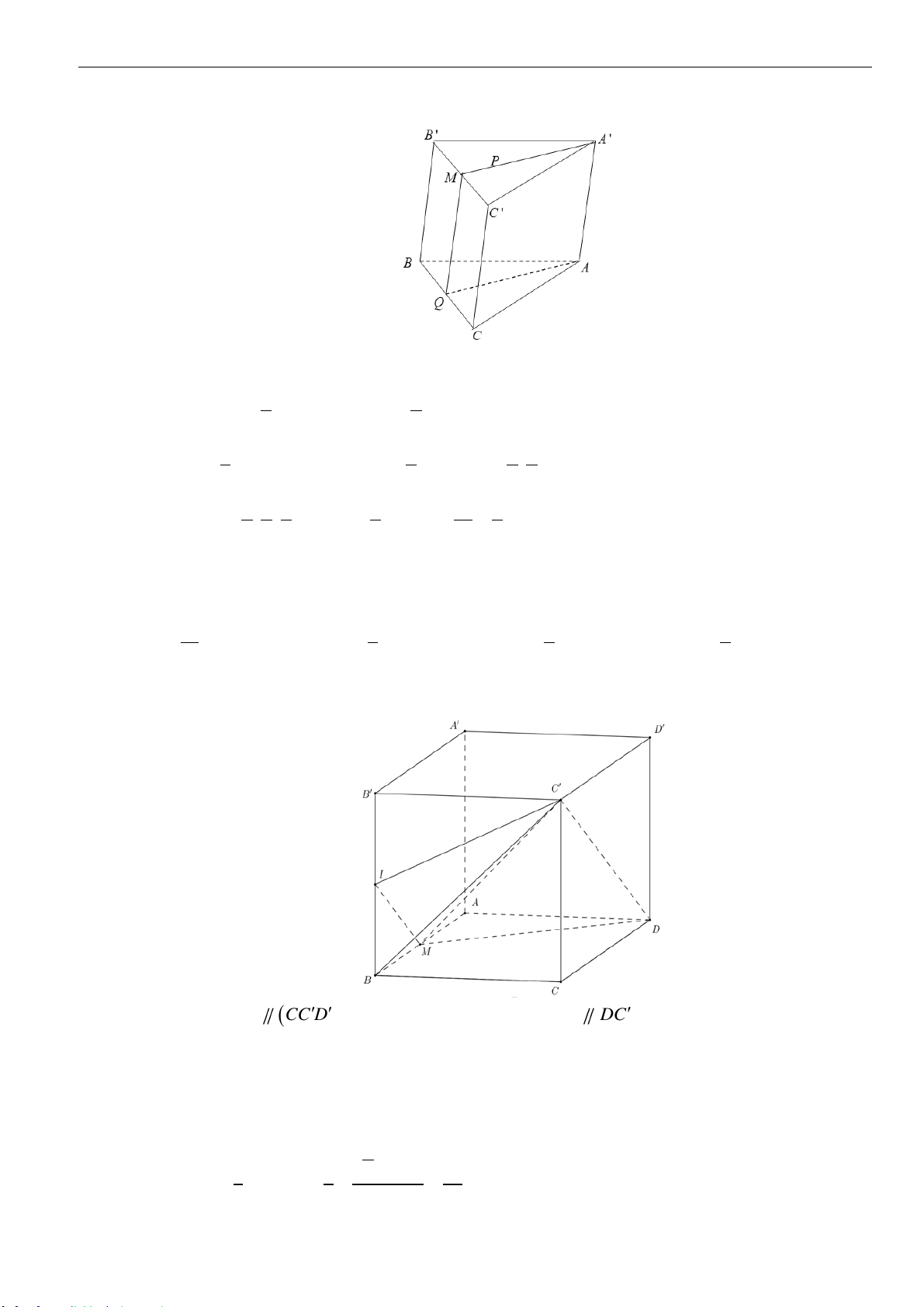
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

23 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Lời giải

Chọn D

Gọi

M

là trung điểm của

' ' , ,B C A M P

thẳng hàng.

Do đó

' ' '. '

11

.

22

PAQ AA MQ B PAQ B AA MQ

S S V V=  =

Dễ thấy

' ' ' . '. ' ' ' . ' ' '.

1 2 2 1

.

3 3 3 2

B ABQ B A M BAQ B AA MQ B A M BAQ A B C ABC

V V V V V=  = =

1

' ' '

2

1 2 1 1 1

. . .3

2 3 2 2 2

B PAQ A ABC A ABC

V

V V V

V

 = =  =

.

Câu 31: Cho hình lập phương

.ABCD A B C D

   

, gọi

I

là trung điểm của

BB



. Mặt phẳng

( )

DIC



chia

khối lập phương thành 2 phần. Tính tỷ số thể tích phần bé chia phần lớn.

A.

7

17

. B.

1

3

. C.

1

2

. D.

1

7

.

Lời giải

Chọn A

Do

( ) ( )

ABB A CC D D

   

nên

( ) ( )

DIC ABB A Ix DC

   

=

. Gọi

M Ix AB=

M

là

trung điểm của

AB

. Do đó, thiết diện của hình lập phương cắt bởi

( )

DIC



là tứ giác

DC IM



.

Và mặt phẳng

( )

DIC



chia khối lập phương thành 2 phần

.BIM CC D



và

.DD C IMAA B

   

.

Ta có,

. . .BIM CC D C BCDM C IMB

V V V

  

=+

.

3

.

11

2

..

3 3 2 4

C BCDM BCDM

a

aa

a

V a S a





+





= = =

.

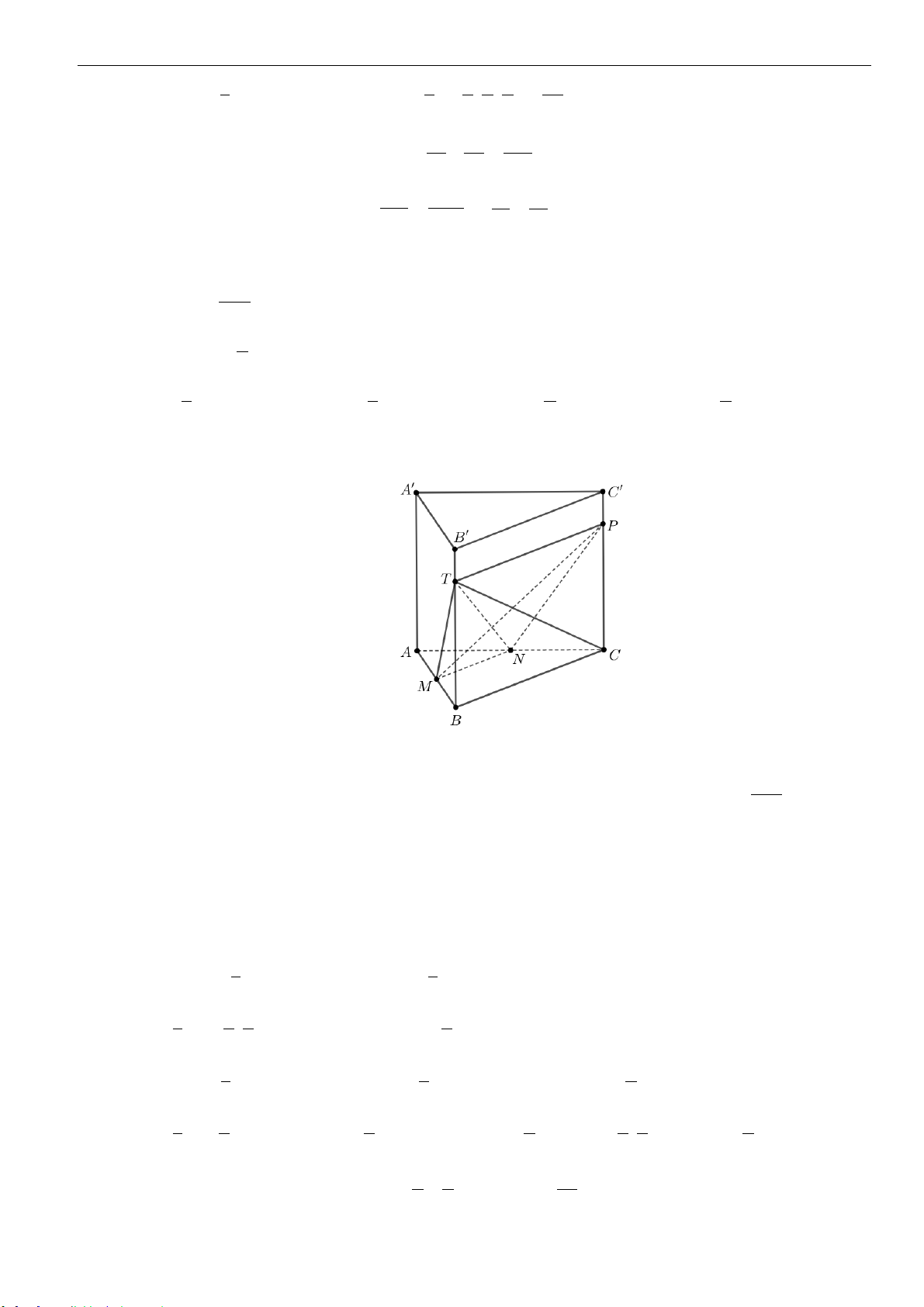
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 24

( )

3

.

1 1 1

. , . . . .

3 3 2 2 2 24

C IMB BIM

a a a

V a d C ABB A S a





  

= = =





3 3 3

1 . . .

7

4 24 24

BIM CC D C BCDM C IMB

a a a

V V V V

  

 = = + = + =

33

3

2 . 1

7 17

24 24

ABCD A B C D

aa

V V V a

   

 = − = − =

1

2

7

17

V

=

.

Câu 32: Cho lăng trụ tam giác

.

  

ABC A B C

.

,MN

lần lượt là trung điểm

,;AB AC P

thuộc đoạn



CC

sao cho

.=



CP

x

CC

Tìm

x

để mặt phẳng

( )

MNP

chia khối lăng trụ thành hai khối đa diện có tỉ lệ

thể tích là

1

2

.

A.

8

5

. B.

5

8

. C.

4

5

. D.

5

4

.

Lời giải

Chọn C

Ta có

( ) ( )

( )

( ) ( )

 

''

//

' ' / / / / 0;1

'

''

P MNP BB C C

MN BC

BT

MNP BB C C PT MN BC x

MN MNP

BB

BC BB C C







  =  = 











.

Thiết diện tạo bởi

( )

MNP

với khối lăng trụ

. ' ' 'ABC A B C

là hình tứ giác

MNPT

.

Ta có

( )

..

1

TPMNCB T BCNM N TPC

V V V=+

. Mà:

( )

( ) ( )

( )

.

11

. ; . ;

33

T BCNM BNCM ABC AMN

V S d T BCNM S S d T BCNM= = −

( )

. ' ' '

1 1 1

. 1 . . . ';

3 2 2 4

ABC ABC A B C

x

S x d B ABC V



= − =





( )

( ) ( )

( )

. ' ' ' '

1 1 1

. ; ' ' . ; ' '

3 3 2

N TPC TPC BB C C BTC B C PT

V S d N BB C C S S S d A BB C C= = − −

( ) ( )

( )

' ' . ' ' . ' ' ' . ' ' '

1 1 2

1 1 . ; ' ' .

3 2 2 4 4 3 6

BB C C A BCC B ABC A B C ABC A B C

x x x x

x S d A BB C C V V V



= − − − = = =





.

Thay vào

( )

1

, ta được

. ' ' ' . ' ' '

5

4 6 12

TPMNCB ABC A B C ABC A B C

x x x

V V V



= + =





.

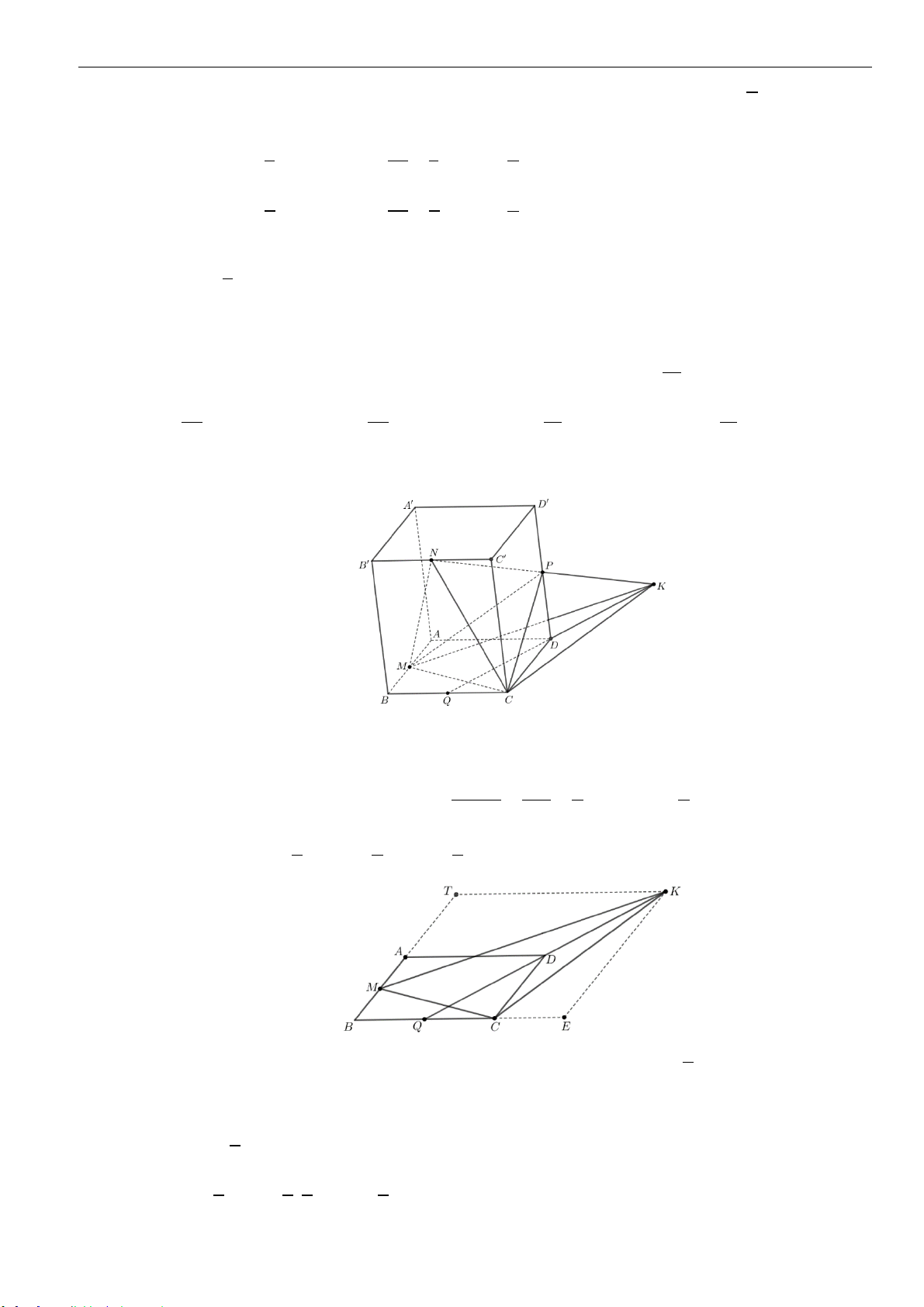
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

25 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Mặt phẳng

( )

MNP

chia khối lăng trụ thành hai khối đa diện có tỉ lệ thể tích là

1

2

( )

. ' ' '

1 5 1

4

3 12 3

5

2 5 2

8

3 12 3

4

TPMNCB ABC A B C

x

VV

x Nhan

x

VV

x Loai





==

=





  









==

=









.

Vậy

4

5

x =

thoả mãn yêu cầu bài toán.

Câu 33: Cho khối hộp

.ABCD A B C D

   

có thể tích

V

. Gọi

,,M N P

lần lượt là trung điểm của

AB

,

BC



DD



. Gọi thể tích khối tứ diện

CMNP

là

V



. Khi đó thể tích

V



bằng:

A.

1

64

. B.

3

64

. C.

1

16

. D.

3

16

.

Lời giải

Chọn D

Gọi

Q

là trung điểm

//BC NQ DD





.

Trong

( )

NQDD



: gọi

K QD NP=

. Suy ra

DP

là đường trung bình của

KNQ

.

Ta có

..CMNP K MNC K MPC

V V V V



= = −

. Mà

.

..

.

11

22

K MPC

K MPC K MNC

K MNC

V

KP

VV

V KN

= =  =

.

Nên

( )

. . . .

111

*

222

K MNC K MNC K MNC N KMC

V V V V V



= − = =

.

Dựng hình bình hành

TKEB

như hình vẽ. Khi đó

2TB AB=

và

3

2

EB BC=

.

Ta có

( )

1

KMC TKEB MBC CEK TMK

S S S S S= − − −

.

3

2. 3

2

TKEB ABCD ABCD

S S S==

;

1 1 1 1

.

2 2 2 4

MBC ABC ABCD ABCD

S S S S= = =

;

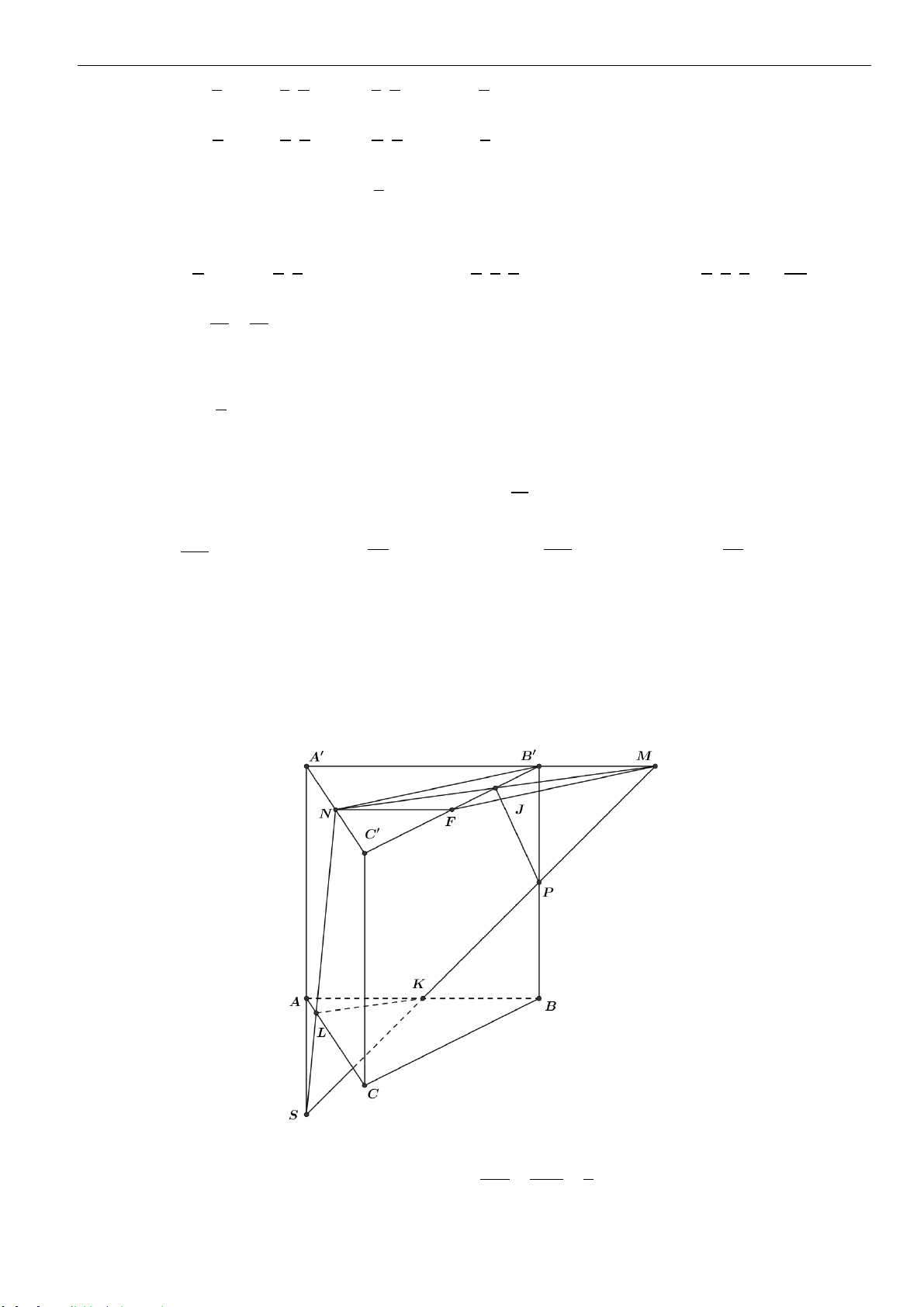
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 26

1 1 1 1 1 1

. . .3

3 3 2 3 2 2

CEK BEK TKEB ABCD ABCD

S S S S S= = = =

;

3 3 1 3 1 9

. . .3

4 4 2 4 2 8

TMK TBK TKEB ABCD ABCD

S S S S S= = = =

.

Thay vào

( )

1

ta đượ

9

8

KMC ABCD

SS=

.

Lại có

( )

;;d N KMC d A ABCD



=

. Do đó, từ

( )

*

ta có:

( )

.

1 1 1 1 1 9 1 1 9 3

. . ; . . . ; . .

2 2 3 2 3 8 2 3 8 16

N KMC KMC ABCD

V

V V S d N KMC S d A ABCD V



= = = = =

.

Suy ra

3

16

V



=

.

Câu 34: Cho lăng trụ tam giác đều

. ' ' 'ABC A B C

. Trên tia đối của tia

''BA

lấy điểm

M

sao cho

1

' ' '

2

B M B A=

. Gọi

,NP

lần lượt là trung điểm của

' ', 'A C BB

. Mặt phẳng

()MNP

chia khối

trụ

. ' ' 'ABC A B C

thành hai khối đa diện, trong đó khối đa diện có chứa đỉnh

'A

có thể tích

1

V

và

khối đa diện chứa đỉnh

'C

có thể tích

2

V

. Tỉ số

1

2

V

bằng

A.

95

144

. B.

97

59

. C.

49

144

. D.

49

95

.

Lời giải

Chọn D

Ta gọi:

, ', ;K MP AB S MP AA L NS AC=  =  = 

Khi đó thiết diện cần tìm chính là ngũ giác

NJPKL

chia hình lăng trụ

. ' ' 'ABC A B C

thành 2 phần

như hình vẽ. Cho

J

là trung điểm

BF

mà ta có:

/ / '

'

NF B M

B J JF

NF B M



=



=



Tương tự ta lại có thêm được:

MJ JN=

nên từ đó suy ra

'B NFM

là hình bình hành

Mặt khác:

'1

'

//

'3

AK KB

MP B P

SA BP B P

SA BP

MS A S

=



 = =  = =





Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

27 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Ta có:

.'

. ' . '

.'

' 1 1 1 1 1

. . . .

' 3 2 3 18 18

M PJB

M PJB M SNA

M SNA

V MP MJ MB

VV

V MS MN MA

= = =  =

Mặt khác: ta có

3

.

. . '

.'

1 1 1 1

..

' 3 ' 3 27 27

S ALK

S ALK S A NM

S A NM

SL SA V SK SA SL

VV

SN SA V SM SA SN



= =  = = =  =





Khi đó:

1 . ' . ' . . ' . '

1 1 49

1

18 27 54

S MNA M PJB S ALK M SNA M SNA

V V V V V V



= − − = − − =





Ta lại có:

. ' . ' . ' ' ' . ' ' ' 2 . ' ' ' 1 . ' ' '

49 49 3 49 95

.

54 54 8 144 144

S A NM M SNA ABC A B C ABC A B C ABC A B C ABC A B C

V V V V V V V V= = =  = − =

Vậy:

1

2

49

95

V

=

.

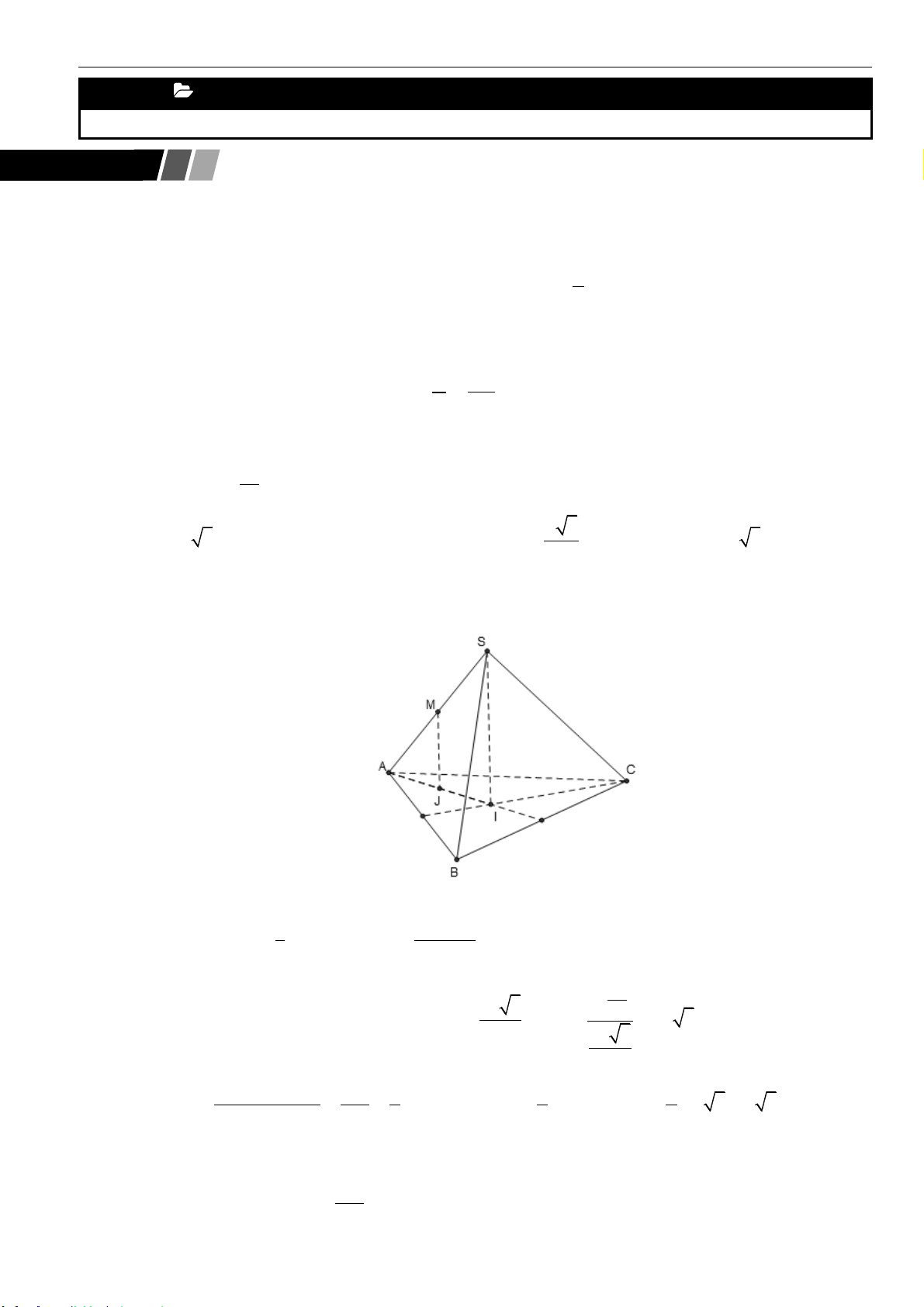
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

1 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Dạng 11: Góc, khoảng cách liên quan đến thể tích khối đa diện

Câu 1: Cho hình lăng trụ tứ giác

.ABCD A B C D

   

có đáy

ABCD

là hình vuông cạnh

a

và thể tích bằng

3

3a

. Tính chiều cao

h

của lăng trụ đã cho.

A.

ha=

. B.

9ha=

. C.

3

a

h =

. D.

3ha=

.

Lời giải

Chọn D

Thể tích khối lăng trụ

V

V Bh h

B

=  =

3

2

3

a

==

.

Câu 2: Cho khối chóp đều

.S ABC

có cạnh đáy bằng

a

. Gọi

M

là trung điểm

SA

. Biết thể tích khối

chóp bằng

3

2

a

, khoảng cách từ điểm

M

đến mặt phẳng

( )

ABC

bằng

A.

3a

. B.

3a

. C.

3

a

. D.

23a

.

Lời giải

Chọn A

Gọi

I

là trọng tâm tam giác

ABC

,

J

là trung điểm

AI

.

Ta có:

.

1

.

3

S ABC ABC

V SI S=

.

3.

S ABC

ABC

V

SI

S

=

.

Do tam giác

ABC

đều cạnh

a

nên

2

3

4

ABC

a

S =

3

2

3.

2

23

3

4

a

SI a

a

 = =

.

Lại có:

( )

;

1

S; 2

d M ABC

MA

d ABC SA

==

( )

11

; S; .2 3 3

22

d M ABC d ABC a a= = =

.

Câu 3: Lăng trụ

.ABC A B C

  

có đáy

ABC

là tam giác vuông cân tại

A

,

AB a=

, biết thể tích của lăng

trụ

.ABC A B C

  

là

3

4

3

a

V =

. Tính khoảng cách

h

giữa

AB

và

BC



.

VÍ DỤ MINH HỌA

B

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 2

A.

3

8

a

h =

. B.

2

3

a

h =

. C.

8

3

a

h =

. D.

3

a

h =

.

Lời giải

Chọn C

Ta có:

ABC

là tam giác vuông cân tại

A

,

AB a=

2

1

.

22

ABC

a

S AB AC



 = =

Vì

( )

// AB A B C

  

nên

( )

,h d AB B C



=

( )

,,d AB A B C d A A B C

     

==

.

h

là đường cao của lăng trụ

.ABC A B C

  

.

Khi đó

.

ABC

V h S



=

3

2

4

8

3

2

ABC

a

Va

h

S

a



 = = =

.

Câu 4: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

2.a

Tam giác

SAB

cân tại

S

và

( )

SAB

vuông góc với

( )

.ABCD

Giả sử thể tích của khối chóp

.S ABCD

bằng

3

4

.

3

a

Gọi



là

góc giữa đường thẳng

SC

và mặt phẳng

( )

.ABCD

Mệnh đề nào sau đây đúng?

A.

15

cos .

5



=

B.

6

cos .

6



=

C.

30

cos .

6



=

D.

35

cos .

5



=

Lời giải

Chọn C

Gọi

M

là trung điểm của

( ) ( )

( )

,.SA SM ABCD SC ABCD SCM ⊥  =

Ta có

.

3

1

..

3

S ABCD

S ABCD ABCD

ABCD

V

V S SM SM a

S

=  = =

Lại có

22

5 6 .MC BM BC a SC a= + =  =

Trong tam giác

SMC

vuông tại

M

, ta có

30

cos .

6

MC

SC



==

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

3 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 5: Cho hình chóp

SABCD

có đáy

ABCD

là hình vuông cạnh bằng

a

. Hình chiếu vuông góc của

đỉnh

S

lên đáy

()ABCD

là trọng tâm tam giác

ACD

và góc tạo bởi

SB

với đáy

()ABCD

bằng

30

o

. Thể tích khối chóp

SABD

bằng

A.

3

6

27

a

. B.

3

26

27

a

. C.

3

9

a

. D.

3

6

a

.

Lời giải

Chọn A

Gọi H là trọng tâm tam giác

ACD

. Từ giả thiết bài toán ta có

( )

DSH ABC⊥

và

0

30SBH =

Gọi O là giao điểm của

AC

và

DB

. Ta có

22

2 1 2 2 2

2

3 3 3 3 3

DH DO DB HB DB a a a= =  = = + =

.

Trong tam giác

SHB

vuông tại

H

có

2 1 2 6

.tan30 2.

39

3

o

a

SH HB a= = =

.

Suy ra

23

DD

1 1 2 6 6

. . .

3 3 9 2 27

SAB AB

a a a

V SH S



= = =

.

Câu 6: Cho hình chóp

.S ABC

có

,,SA SB SC

đôi một vuông góc với nhau và

SA a=

,

2SB a=

,

3SC a=

. Gọi

,,M N P

lần lượt là trung điểm của

,,AB BC CA

. Khoảng cách từ

M

đến mặt

phẳng

( )

SNP

.

A.

13

2

a

. B.

15

2

a

. C.

6

7

a

. D.

13

2

a

.

Lời giải

Chọn C

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 4

Thể tích khối chóp

.S ABC

:

3

.

11

. . . .2 .3

66

S ABC

V SASB SC a a a a= = =

.

Vì

,,M N P

lần lượt là trung điểm của

,,AB BC CA

nên

1

4

MNP ABC

SS



=

.

Vì

( )

,,S MNP S ABC

dd=

nên

3

.MNP .

1

.

44

S S ABC

a

VV==

.

Ta có

SBC

vuông tại

S

22

1 1 13

(2 ) (3 )

2 2 2

a

SN BC a a = = + =

.

Ta có

SAC

vuông tại

S

22

1 1 10

(3 )

2 2 2

a

SP AC a a = = + =

.

Ta có

NP

là đường trung bình của

ABC

22

1 1 5

(2 )

2 2 2

a

NP AB a a = = + =

.

Vậy

7

( )( )( )

8

SNP

a

S p p a p b p c



= − − − =

.

Xét hình chóp

.S MNP

có

( )

.

;( )

3

16

.

37

S MNP

S MNP SNP

M SNP

V

a

d h V S h h

S



=  =  = =

.

Câu 7: Cho hình hộp

.ABCD A B C D

   

có tất cả các cạnh đều bằng

a

và

0

60 .BAA DAA BAD



= = =

Gọi

G

là trọng tâm của tam giác

A BC



. Khoảng cách từ

G

đến mặt phẳng

( )

DA C



bằng

A.

22

66

a

. B.

4 11

11

a

. C.

2 11

11

a

. D.

22

.

11

a

Lời giải

Chọn D

Gọi

H

là trọng tâm tam giác

ABD

và

K

là trung điểm

.AD



Do

0

' ' 60BAA DAA BAD= = =

và

.A A A B A D AB AD BD a

  

= = = = = =

'A ABD

là tứ diện đều cạnh bằng

3

2

.

12

A ABD

a

aV



=



đường cao

6

',

3

a

AH=

3

..

2

.

12

D DA C D A C D A ABD

a

V V V

      

 = = =

Xét

' ',DA C

có

' , ' ' ' 3.A D a A C DC a= = =

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

5 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

( )

2

''

11 1 11

3 . .

2 2 2 4

DA C

a a a

C K a S A D C K





  

 = − =  = =





Do

G

là trọng tâm của tam giác

''A BC

và

//B O O D



( )

3

.

2

3.

3

22

12

, , , .

11

4

D DA C

DA C

a

V

a

d G DA C d B DA C d D DA C

S

a

  





       

 = = = = =

Vậy khoảng cách từ

G

đến mặt phẳng

( )

DA C



bằng

22

11

a

.

Câu 8: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

,

SA

vuông góc với đáy. Biết thể

tích khối chóp

.S ABCD

bằng

3

a

. Khoảng cách từ

D

đến mặt phẳng

()SBC

bằng

A.

2

a

. B.

3

2

a

. C.

2

a

. D.

2 39

13

a

.

Lời giải

Chọn B

Vì

SA

vuông góc với đáy nên ta có

3

.

2

3

3.

3

1

3

.3

3

S ABCD

S ABCD ABCD

ABCD

a

V

V SA S SA a

S

a

=  = = =

.

Ta có

AD

song song với mặt phẳng

()SBC

nên

d(D,( )) d(A,(SBC))SBC =

.

Lại có

( ) ( ) ( )

BC AB

BC SAB SAB SBC

BC SA

⊥



 ⊥  ⊥



⊥



theo giao tuyến

SB

Vẽ

()AH SB AH SBC⊥  ⊥

nên

( ,( ))AH d A SBC=

và

. 3. 3

22

SA AB a a a

AH

SB a

= = =

Vậy

3

d(D,( ))

2

a

SBC =

.

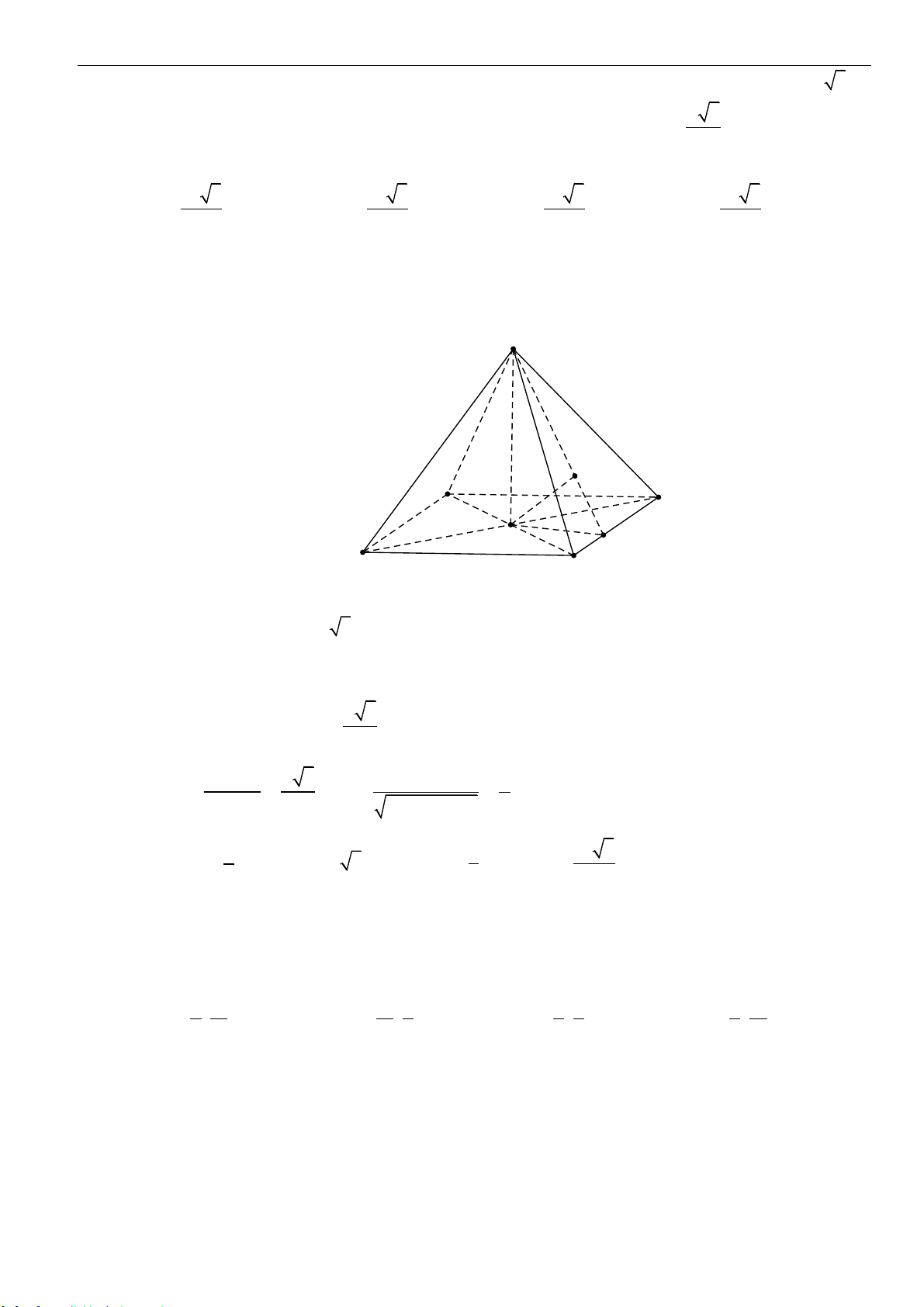
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 6

Câu 9: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thoi tâm

O

,

2AC a=

,

23BD a=

,

( )

SO ABCD⊥

. Biết khoảng cách từ

O

đến mặt phẳng

( )

SBC

bằng

3

4

a

. Tính thể tích của

khối chóp

.S ABCD

theo

a

.

A.

3

a

. B.

3

6

a

. C.

3

12

a

. D.

3

4

a

.

Lời giải

Chọn A

Ta có

OC a=

,

3BO a=

2BC a=

.

Kẻ

( ) ( ) ( )

,OG BC G BC OH SG H SG OH SBC⊥  ⊥   ⊥

( )

3

,

4

a

d O SBC OH = =

.

.3

2

OBOC a

OG

BC

==

,

22

.

2

OH OG a

SO

OG OH

==

−

.

2

1

. 2 3

2

ABCD

S AC BD a==

3

.

13

.

33

S ABCD ABCD

a

V SO S = =

.

Câu 10: Cho hình chóp tam giác

SABC

có đáy là tam giác đều cạnh

6

. Biết khoảng cách từ

B

đến mặt

phẳng

( )

SAC

bằng

3

; khoảng cách giữa hai đường thẳng

SB

và

AC

bằng

2

. Khoảng cách từ

điểm

S

đến mặt phẳng

( )

ABC

nằm trong khoảng nào dưới đây?

A.

5 11

;

48







. B.

11 3

;

82







. C.

75

;

84







. D.

3 13

;

28







.

Lời giải

Chọn A

O

B

A

D

C

S

G

H

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

7 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Dựng hình bình hành

ABDC

. Do

ABC

là tam giác đều nên

ABDC

là hình thoi.

Dựng

SI AC⊥

(

I AC

),

( )

SH ABC⊥

( )

H ABC

.

Gọi

IH BD K=

suy ra

( )

AC SIK⊥

và

( )

, 3 3IK d B AC==

.

Trong tam giác

SIK

, dựng

,IQ SK KP SI⊥⊥

với

,Q SK P SI

.

Ta có:

( )

AC KP

AC SIK

AC IQ

⊥



⊥



⊥



suy ra

( ) ( )

,KP SAC IQ SBD⊥⊥

.

Khi đó:

( )

,d K SAC KP=

mà

( )

,,d B SAC d K SAC=

nên

3KP =

;

( ) ( )

( )

, , ,d AC SB d AC SBD d I SBD IQ= = =

suy ra

2IQ =

.

Xét tam giác

SIK

:

3

..

2

SK PK

IQ SK SI PK

SI IQ

=  = =

.

Đặt

SI x=

suy ra

3

2

x

SK =

.

Ta có:

..SH IK SI PK=

. 3 3

3

33

SI PK x x

SH

IK

 = = =

Mặt khác

33IH HK IK+ = =

nên

2 2 2 2

33SI SH SK SH− + − =

2 2 2

2

3 9 3

33

9 4 9

x x x

x − + − =

6 69

33

36

xx

 + =

18 3

2 6 69

x=

+

Vậy

18

2 6 69

SH =

+

1,363

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 8

Câu 1: Thể tích của khối chóp tam giác bằng

6

, biết diện tích đáy bằng

2

. Chiều cao của khối chóp bằng

A.

18

. B.

1

. C.

3

. D.

9

.

Lời giải

Chọn D

Ta có

1 3 3.6

.9

32

V

V B h h

B

=  = = =

.

Câu 2: Cho hình chóp có thể tích

3

36V cm=

và diện tích đáy

2

6.B cm=

Chiều cao của khối chóp là

A.

72h cm=

. B.

18h cm=

. C.

6h cm=

. D.

1

2

h cm=

.

Lời giải

Chọn B

Ta có

1 3 3.36

. 18 .

36

V

V B h h h h cm

B

=  =  =  =

Câu 3: Cho khối lăng trụ

( )

H

có diện tích đáy bằng 4, thể tích bằng

4

3

. Tính chiều cao

h

của khối lăng

trụ.

A.

1h =

. B.

1

3

h =

. C.

3h =

. D.

9h =

.

Lời giải

Chọn B

Ta có thể tích của khối lăng trụ là

.V B h=

với

B

là diện tích đáy và

h

là chiều cao.

Do đó

41

:4

33

V

h

B

= = =

.

Câu 4: Cho khối chóp có thể tích

32V =

và đáy là hình vuông có cạnh bằng

4

. Chiều cao của khối chóp

đã cho bằng

A.

8

. B.

2

. C.

4

. D.

6

.

Lời giải

Chọn D

Ta có:

2

11

. 32 .4 . 6

33

V S h h h=  =  =

.

Câu 5: Khối chóp có thể tích bằng

144

và diện tích đáy bằng

12

thì chiều cao của nó bằng

A.

24

. B.

4

. C.

12

. D.

36

.

Lời giải

Chọn D

Ta có thể tích khối chóp

11

. 144 .12. 36

33

V B h h h=  =  =

.

Câu 6: Cho hình lăng trụ lục giác đều

.ABCDEF A B C D E F

     

có cạnh đáy bằng

a

, biết thể tích của khối

lăng trụ

.ABCDEF A B C D E F

     

là

3

33Va=

. Tính chiều cao

h

của khối lăng trụ lục giác đều

đó.

A.

3ha=

. B.

2ha=

. C.

23

3

a

h =

. D.

ha=

.

BÀI TẬP TRẮC NGHIỆM

C

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

9 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Lời giải

Chọn B

Diện tích đáy

22

3 3 3

6. .

42

S a a==

.

Chiều cao

2

V

ha

S

==

.

Câu 7: Cho khối chóp tam giác đều. Nếu tăng cạnh đáy lên hai lần và giảm chiều cao đi bốn lần thì thể

tích khối chóp đó sẽ

A. Không thay đổi. B. Giảm đi hai lần. C. Tăng lên hai lần. D. Giảm đi ba lần.

Lời giải

Chọn A

Gọi

0B 

là diện tích đáy của khối chóp, chiều cao là

0h 

. Khi đó

1

.

3

V B h=

.

Khi tăng cạnh đáy lên hai lần thì diện tích đáy tăng lên 4 lần

(vì

2

3

.

4

Ba=

( )

2

1

3

2 . 4

4

B a B = =

, với

a

là cạnh đáy của khối chóp ban đầu )

Tức là ta có

1

4BB=

.

Chiều cao giảm đi 4 lần, tức là

1

4

h

h =

.Khi đó

1 1 1

11

33

V B h Bh V= = =

.

Câu 8: Một hình lập phương có thể tích bằng

3

33a

thì cạnh của khối lập phương đó bằng

A.

3a

. B.

3a

. C.

33a

. D.

3

a

.

Lời giải

Chọn A

Gọi độ dài cạnh của hình lập phương là

( )

0xx

.

Ta có

33

3 3 3x a x a=  =

.

Câu 9: Khối lăng trụ có diện tích đáy bằng

2

20cm

và thể tích bằng

2

60cm

thì chiều cao bằng

A.

30cm

. B.

3cm

. C.

9cm

. D.

1cm

.

Lời giải

Chọn B

Áp dụng công thức

.

LT

V S h=

60

3

20

V

h cm

S

 = = =

Câu 10: Khối chóp có chiều cao bằng

7cm

và thể tích bằng

3

28cm

thì diện tích đáy bằng

A.

2

12cm

. B.

2

36cm

. C.

2

4cm

. D.

2

15cm

.

Lời giải

Chọn A

Ta có:

dd

13

.

3

V

V S h S

h

=  =

d

3.28

7

S = =

2

12cm

.

Câu 11: Cho hình lăng trụ tam giác

.ABC A B C

  

có các cạnh bên hợp với đáy những góc bằng

0

60

, đáy

ABC

là tam giác đều cạnh

a

và

A



cách đều

,,A B C

. Tính khoảng cách giữa hai đáy của hình lăng

trụ.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 10

A.

a

. B.

2a

. C.

3

2

a

. D.

2

3

a

.

Lời giải

Chọn A

Gọi

H

là trọng tâm tam giác đều

ABC

. Vì

A



cách đều

,,A B C

nên hình chiếu vuông góc của

đỉnh

A



là

H

cũng cách đều

,,A B C

. Khi đó khoảng cách giữa hai đáy chính là

.AH



Xét tam giác

AA H



có:

( )

0

90

2 2 3 3 3

. .tan60 . 3 .

3 3 2 3 3

, ' 60

H

a a a

AH AM A H AH a

AA ABC A AH





=





= = =  = = =









==











Vậy khoảng cách giữa hai đáy của hình lăng trụ là

.A H a



=

Câu 12: Cho khối chóp tam giác

.S ABC

có

BC a

và tam giác

ABC

vuông cân tại

B

. Biết thể tích khối

chóp đó bằng

3

6

a

. Khoảng cách từ

S

đến mặt phẳng

ABC

là

A.

3a

. B.

3

a

. C.

3

2

a

. D.

3a

.

Lời giải

Chọn A

Ta có

ABC

vuông cân tại

B

nên diện tích

ABC

là

2

1

22

ABC

a

S BC

.

Mà

.

1

. ,( )

3

S ABC ABC

V S d S ABC

Suy ra

3

.

2

3

3.

3

6

,( ) 3

2

S ABC

ABC

a

V

d S ABC a

a

S

.

Câu 13: Cho tứ diện đều cạnh

.a

Tính độ dài đường cao

h

của tứ diện đều.

A.

6

3

a

h =

. B.

6

2

a

h =

. C.

3

2

a

h =

. D.

3

a

h =

.

Lời giải

Chọn A

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

11 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Gọi

ABCD

là tứ diện đều cạnh

a

, đường cao là

AH

. Do

ABCD

là tứ diện đều nên

H

là tâm

đường tròn ngoại tiếp tam giác đều

BC D

và

2 2 3 3

3 3 2 3

aa

BH BE= = =

.

Áp dụng định lý pitago cho tam giác

ABH 

2 2 2 2

16

33

AH AB BH a a a= − = − =

.

Câu 14: Cho hình chóp

.S ABCD

có

ABCD

là hình thang vuông tại

A

và

D

,

AB AD a==

,

2CD a=

.

Hình chiếu của

S

lên mặt phẳng

( )

ABCD

trùng với trung điểm của

BD

. Biết thể tích tứ diện

SBCD

bằng

3

6

a

. Tính khoảng cách từ

A

đến mặt phẳng

( )

SBC

.

A.

3

2

a

. B.

2

6

a

. C.

3

6

a

. D.

6

4

a

.

Lời giải

Chọn D

Gọi

H

và

I

lần lượt là trung điểm của

BD

và

CD

;

K

là hình chiếu của

H

lên

SB

.

Tứ giác

ABID

có

//

90

AB DI

AB DI AD a

BAD





= = =





=



ABID

là hình vuông cạnh

a

BI a=

.

Do đó

1

2

BI CD=

BCD

vuông tại

B

BC BD⊥

.

Vì

ABID

là hình vuông nên

AH BD⊥

và

1

2

HB BD=

1

.AB. 2

2

=

2

a

=

.

Trong

( )

ABCD

ta có

B

C

D

A

E

H

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 12

AH BD

BC BD

⊥





⊥



//AH BC

( )

//AH SBC

( )

,,d A SBC d H SBC=

.

Khi đó

( )

SH BC vì SH ABCD

BD BC



⊥⊥





⊥





( )

BC SBD⊥

BC HK⊥

.

Ta có

HK BC

HK SB

⊥





⊥



( )

HK SBC⊥

( )

,d H SBC HK=

.

3

6

SBCD

a

V =

3

1

.

3

6

BCD

a

S SH



=

3

11

. . . .

32

6

a

BI CD SH=

6

2

a

SH=

.

Vì

SHB

vuông tại

H

và có

HK

là đường cao nên

2 2 2

1 1 1

HK SH HB

=+

22

2

1 1 16

6

62

22

a

aa

= + =

   

   

   

6

4

a

HK=

.

Vậy khoảng cách từ

A

đến mặt phẳng

( )

SBC

bằng

6

4

a

.

Câu 15: Cho hình lập phương

.ABCD A B C D

   

. Khoảng cách từ điểm

A

đến mặt phẳng

( )

A B D



là

A.

( )

.

3

,

ABCD A B C D

A BD

V

d A A BD

S

   



=

. B.

( )

.

,

ABCD A B C D

A BD

V

d A A BD

S

   



=

.

C.

( )

.

,

3

ABCD A B C D

A BD

V

d A A BD

S

   



=

. D.

( )

.

,

2

ABCD A B C D

A BD

V

d A A BD

S

   



=

.

Lời giải

Chọn D

Ta có

( )

.'

. . '

1

3.

3

6

,

2

ABCD A B C D

A A BD ABCD A B C D

A BD A BD A BD

V

VV

d A A BD

S S S

  

   

  



= = =

.

Câu 16: Cho khối chóp có đáy là tam giác đều cạnh

a

và có thể tích là

3

3Va=

. Chiều cao

h

của khối

chóp đã cho bằng

A.

10ha=

. B.

12 3ha=

. C.

10 3ha=

. D.

12ha=

.

Lời giải

Chọn D

Diện tích đáy của khối chóp là:

2

3

4

a

B=

.

Ta có:

3

2

1 3 3 3

12

3

4

Va

V Bh h a

B

a

=  = = =

.

Vậy chiều cao của khối chóp là:

12ha=

.

Câu 17: Cho hình tứ diện

ABCD

có

, 3,AB a CD a==

góc giữa hai đường thẳng

,AB CD

bằng

0

60 ,

thể

tích của khối tứ diện

ABCD

là

3

.a

Tính khoảng cách giữa hai đường thẳng

,.AB CD

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

13 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

A.

2

3

a

. B.

2a

. C.

3a

. D.

4a

.

Lời giải

Chọn D

Có

1

. . .sin( , )

6

ABCD

V ABCD h AB CD=

với

( , )h d AB CD=

(Bài tập SGK (cơ bản) trang 26) nên

3

6

4.

. .sin( , )

3

. 3.

2

ABCD

V

a

ha

AB CD AB CD

aa

= = =

Vậy khoảng cần tìm là

4.a

Câu 18: Cho khối chóp tứ giác có thể tích

3

2Va=

,

đáy là hình vuông có cạnh bằng

a

. Tính chiều cao khối

chóp.

A.

2a

. B.

6a

. C.

3a

. D.

a

.

Lời giải

Chọn B

Ta có

3

2

3 3.2

6

Va

ha

Ba

= = =

.

Câu 19: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

,

32SA a=

và

SA

vuông góc với

mặt phẳng

( )

ABC D

. Tính

tan

góc tạo bởi đường thẳng

SC

và mặt phẳng

( )

SAD

?

A.

19

. B.

3

. C.

1

3

. D.

19

.

Lời giải

Chọn A

Vì

ABCD

là hình vuông suy ra

(1)CD AD⊥

.

Mặt khác, theo giả thiết ta có

( )

SA ABCD⊥

nên

(2)SA CD⊥

.

Từ

(1)

và

(2)

suy ra

( )

CD SAD SD⊥

là hình chiếu của

SC

lên mặt phẳng

( )

SAD

Do đó

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 14

( ) ( )

,( ,SC SAD SC SD CSD==

.

Xét tam giác

SCD

vuông tại

D

, ta có:

( )

2 2 2

2

1 19

tan .

19

32

CD CD a

CSD

SD

SA AD

aa

= = = = =

+

Câu 20: Cho khối lăng trụ tam giác đều

. ' ' 'ABC A B C

có cạnh đáy bằng

2a

, chiều cao bằng

a

. Tính số đo

góc tạo bởi hai mặt phẳng

( )

''A B C

và

( )

ABC

?

A.

0

45

. B.

0

60

. C.

0

30

. D.

0

26 33'

.

Lời giải

Chọn C

Gọi

H

là trung điểm của

''BC

, do các tam giác

' ' ', ' 'A B C AB C

lần lượt cân đỉnh

'A

và

A

nên

''AH B C⊥

,

' ' ' 'A H B C⊥

nên

( ) ( )

( )

( ) ( )

( )

' ' , ' ' , ' ' ' , ' 'AB C ABC AB C A B C AH A H AHA= = =

Xét tam giác

'AHA

có

0

' 90 , ' 3A A H a==

và

'1

tan '

'

3

AA

AHA

AH

==

0

' 30AHA=

Câu 21: Một khối trụ có thể tích bằng

16 .



Nếu chiều cao khối trụ tăng lên hai lần và giữ nguyên bán kính

đáy thì được khối trụ mới có diện tích xung quanh bằng

16 .



Bán kính đáy của khối trụ ban đầu là

A.

1r =

. B.

4r =

. C.

3r =

. D.

8r =

.

Lời giải

Chọn B

Thể tích khối trụ:

2

16V r h



==

2

16

h

r

=

.

Nếu chiều cao khối trụ tăng lên hai lần và giữ nguyên bán kính đáy, suy ra:

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

15 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Diện tích xung quanh:

2

2.16

2 . 16Ar

r



==

2.2.16

4

16

r = =

.

Câu 22: Cho hình chóp tứ giác đều

.S ABCD

có đáy là hình vuông cạnh

a

. Gọi

M

là trung điểm của

SD

.

Khoảng cách từ

M

đến mặt phẳng

()SAC

bằng

A.

2

a

. B.

4

a

. C.

2

4

a

. D.

2

a

.

Lời giải

Chọn C

Do

.S ABCD

là hình chóp tứ giác đều nên

ABCD

là hình vuông.

Gọi

O

là tâm của hình vuông ta có

()SO ABCD⊥

.

Ta thấy rằng

DO AC⊥

và

SO OD⊥

nên

()DO SAC⊥

do đó

2

d( ;( )) .

2

a

D SAC DO==

Mà

M

là trung điểm của

SD

nên

12

d( ;( )) d( ;( )) .

24

a

M SAC D SAC==

Câu 23: Cho hình chóp

.S ABCD

có đáy là hình thang vuông tại

A

và

D

,

,2AB AD a CD a= = =

. Hình

chiếu của đỉnh

S

lên mặt

( )

ABC D

trùng với trung điểm của

BD

. Biết thể tích khối chóp

.S ABCD

bằng

3

2

.

2

a

Khoảng cách từ điểm

A

đến mặt phẳng

( )

SBC

bằng

A.

5

2

a

. B.

5

a

. C.

10

5

a

. D.

10

2

a

.

Lời giải

Chọn C

Gọi

O

,

M

lần lượt là trung điểm của

BD

,

DC

;

H

là hình chiếu của

O

trên

( )

1SB

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 16

Dễ thấy

ABMD

là hình vuông nhận

O

là tâm; tam giác

BDC

vuông tại

B

do

MB MC MD==

.

( )

2

13

22

ABCD

a

S AB CD AD= + =

;

23

.

12

..

3 2 2

S ABCD ABCD

aa

V SO S SO= = =

2SO a=

.

Ta có

( )

//BC d , d ,AM A SBC O SBC=

;

BC BD,SO⊥

( )

BC SBD⊥

( )

BC 2OH⊥

.

Từ

( ) ( )

1 , 2

( )

SBCOH⊥

( )

d,O SBC OH=

.

Xét tam giác vuông

BSO

có

1

2

a

OB BD==

,

2SO a=

22

.OS 10

5

OS

OB a

OH

OB

 = =

+

.

Vậy

( )

10

d,

5

a

A SBC =

.

Câu 24: Cho hình chóp tứ giác đều

.S ABCD

có cạnh đáy bằng

a

và thể tích bằng

3

23

a

. Tính góc giữa mặt

bên và mặt đáy của hình chóp

.S ABCD

.

A.

30

B.

45

C.

60

D.

75

Lời giải

Chọn C

Ta có

3

2

3.

1 3 3

23

.

32

ABCD

a

Va

V S SI SI

Sa

=  = = =

.

Gọi

M

là trung điểm

2

a

BC IM=

.

Ta có:

( ) ( )

( )

,,SBC ABCD SM IM SMI==

.

Lại có

3

2

tan 3 60

2

a

SI

SMI SMI

a

IM

= = =  = 

.

Câu 25: Cho hình chóp tứ giác đều

.S ABCD

,

O

là giao điểm của

AC

và

BD

. Biết mặt bên của hình chóp

là tam giác đều và khoảng cách từ

O

đến mặt bên là

a

. Tính thể tích khối chóp

.S ABCD

theo

a

.

A.

3

23a

. B.

3

43a

. C.

3

63a

. D.

3

83a

.

Lời giải

Chọn A

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

17 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Gọi

M

là trung điểm của

BC

. Vì mặt bên là tam giác đều nên

BC SM⊥

. Mặt khác

BC SO⊥

nên

( ) ( ) ( )

BC SOM SOM SBC⊥  ⊥

.

Gọi

H

là hình chiếu của

O

lên

SM

ta có

( )

OH SBC⊥

, do đó

( )

;d O SBC OH=

.

Đặt

AB x=

, ta có

SA x=

,

3

;

22

xx

SM OM==

;

2

2 2 2

2

x

SO SM OM= − =

.

Tam giác

SOM

vuông tại O có

OH

là đường cao nên

2 2 2

1 1 1 6

.

6

x

OH

OH SO OM

= +  =

Theo giả thiết

( )

;d O SBC OH a==

nên

6

x

a x a=  =

.

Từ đó suy ra

2

3; 6

ABCD

SO a S a==

. Thể tích khối chóp là

23

.

1

. 3.6 2 3

3

S ABCD

V a a a==

.

Câu 26: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thoi và thể tích bằng

2

. Gọi

,MN

lần lượt là các

điểm nằm trên

SB

và

SD

sao cho

SM SN

k

SB SD

==

. Mặt phẳng

( )

AMN

cắt cạnh

SC

tại

Q

. Tìm

giá trị của

k

để thể tích khối chóp

.S AMNQ

bằng

2

3

A.

2

3

k =

. B.

1

8

k =

. C.

1

4

k =

. D.

2

4

k =

.

Lời giải

Chọn A

Đặt

; ; 1 ;

SM SM SA SQ

k x k y z t

SB SB SA SC

= = = = = = =

1 1 2

1

2

SB SD SA SC SC SC k SQ k

SM SN SA SQ k k SQ SQ k SC k

−

+ = +  + = +  =  =

−

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 18

.

3

2

. .1.

1 1 1 1 2 1 1 2

2

. . 1 .2

4 3 4

42

4 3. . 3 2

23

S ABCD

k

kk

xyzt k

k

S AMNQ V

x y z t k k k

k

k k k

kk



−



−

= + + +  = + + +





 =  = −  =

−

Vậy

2

3

k =

Câu 27: Cho lăng trụ

.ABC A B C

có đáy là tam giác đều cạnh

a

, hình chiếu vuông góc của điểm

A

lên

mặt phẳng

ABC

trùng với trung điểm của đường trung tuyến

AM

trong

ABC

, biết thể tích

lăng trụ bằng

3

3a

16

. Tính khoảng cách giữa đường thẳng

AA

và

BC

.

A.

3

,

4

a

d AA BC

B

.

3

,

8

a

d AA BC

C

.

6

,

4

a

d AA BC

D.

6

,

2

a

d AA BC

Lời giải

Chọn C

Vì trung tuyến

AM

trong

ABC

đều cạnh

a

nên

3

2

a

AM

,

3

4

a

AO

.

2

3

4

ABC

a

S

;

A O ABC

.

Thể tích lăng trụ bằng

3

3a

16

nên

23

3 3a 3

.

4 16 4

aa

A O A O

.

Trong

AMA

kẻ

MK AA

.

Vì

BC AM

BC MK

BC A O

, do đó

,MK d AA BC

Ta có tam giác

'A AO

có

36

44

aa

AO A O A A

.

Mà

A O.AM 6

.A A A O.AM MK

A A 4

a

MK

.

Câu 28: Cho hình chóp

.S ABC

, có

==SA SB SC

, đáy là tam giác đều cạnh

a

. Biết thể tích khối chóp

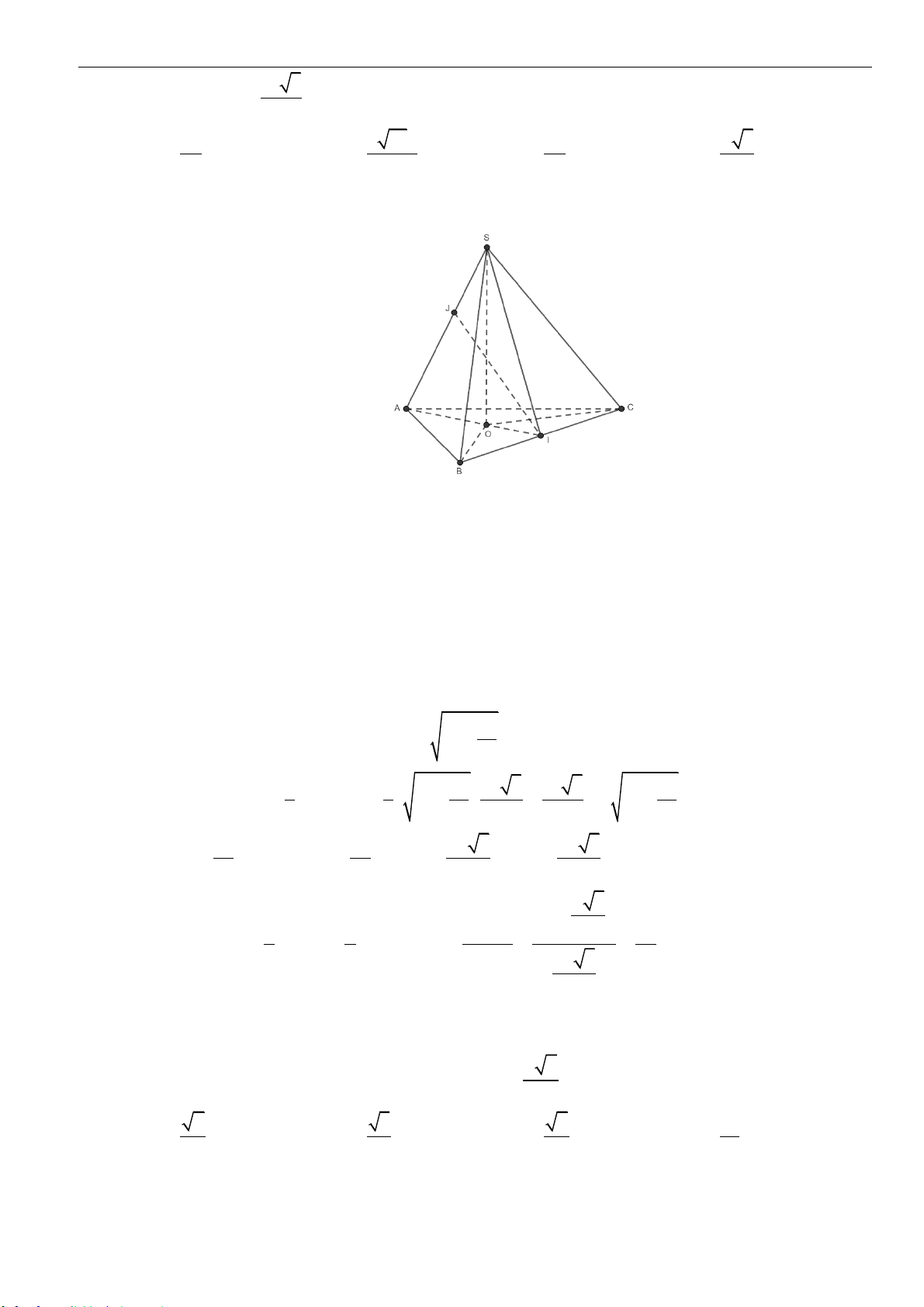
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

19 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

.S ABC

bằng

3

a

. Khoảng cách giữa hai đường thẳng

SA

và

BC

bằng

A.

4

7

a

. B.

3 13

13

a

. C.

6

7

a

. D.

3

4

a

.

Lời giải

Chọn C

Gọi

O

là hình chiếu vuông góc của

S

lên mặt phẳng

( )

ABC

. Suy ra

( )

⊥SO ABC

.

Mặt khác, vì

==SA SB SC

nên

==OA OB OC

. Vậy

O

là tâm của tam giác đều

ABC

.

Gọi

I

là trung điểm cạnh

BC

,

J

là hình chiếu vuông góc của

I

lên đường thẳng

SA

.

Khi đó

⊥BC AI

và

⊥IJ SA

.

Ta có:

( )

⊥



 ⊥  ⊥



⊥



BC SO

BC SAI BC IJ

BC AI

.

Vì

⊥IJ SA

tại

J

và

⊥IJ BC

tại

I

nên

IJ

là đoạn vuông góc chung của

SA

và

BC

.

Dẫn đến khoảng cách giữa hai đường thẳng

SA

và

BC

bằng độ dài đoạn thẳng

IJ

.

Đặt

= = =x SA SB SC

. Suy ra

2

3

=−

a

SO x

.

Thể tích

2 2 3 2

22

.

1 1 3 3

.4

3 3 3 4 3 3



= =  −  =  − =

S ABC ABC

a a a a

V SO S x x a

2

2 2 2 2

49 7 3 7 3

16

3 3 3 3

 − =  =  =  =

a a a

x a x a x SA

và

4=SO a

.

Ta có:

3

4

2

1 1 . 6

..

2 2 7

73

3

SAI

a

SO AI a

S SO AI SA IJ IJ

SA

a











= =  = = =







.

Câu 29: Cho khối chóp

.S ABCD

có đáy

ABCD

là hình thoi cạnh

,a

0

60ABC =

,

SA

vuông góc với đáy

và khoảng cách từ

A

đến mặt phẳng

( )

SBC

bằng

2

.

2

a

Thể tích của khối chóp

.S ABCD

bằng

A.

3

2

4

a

. B.

3

6

a

. C.

3

6

a

. D.

3

a

.

Lời giải

Chọn A

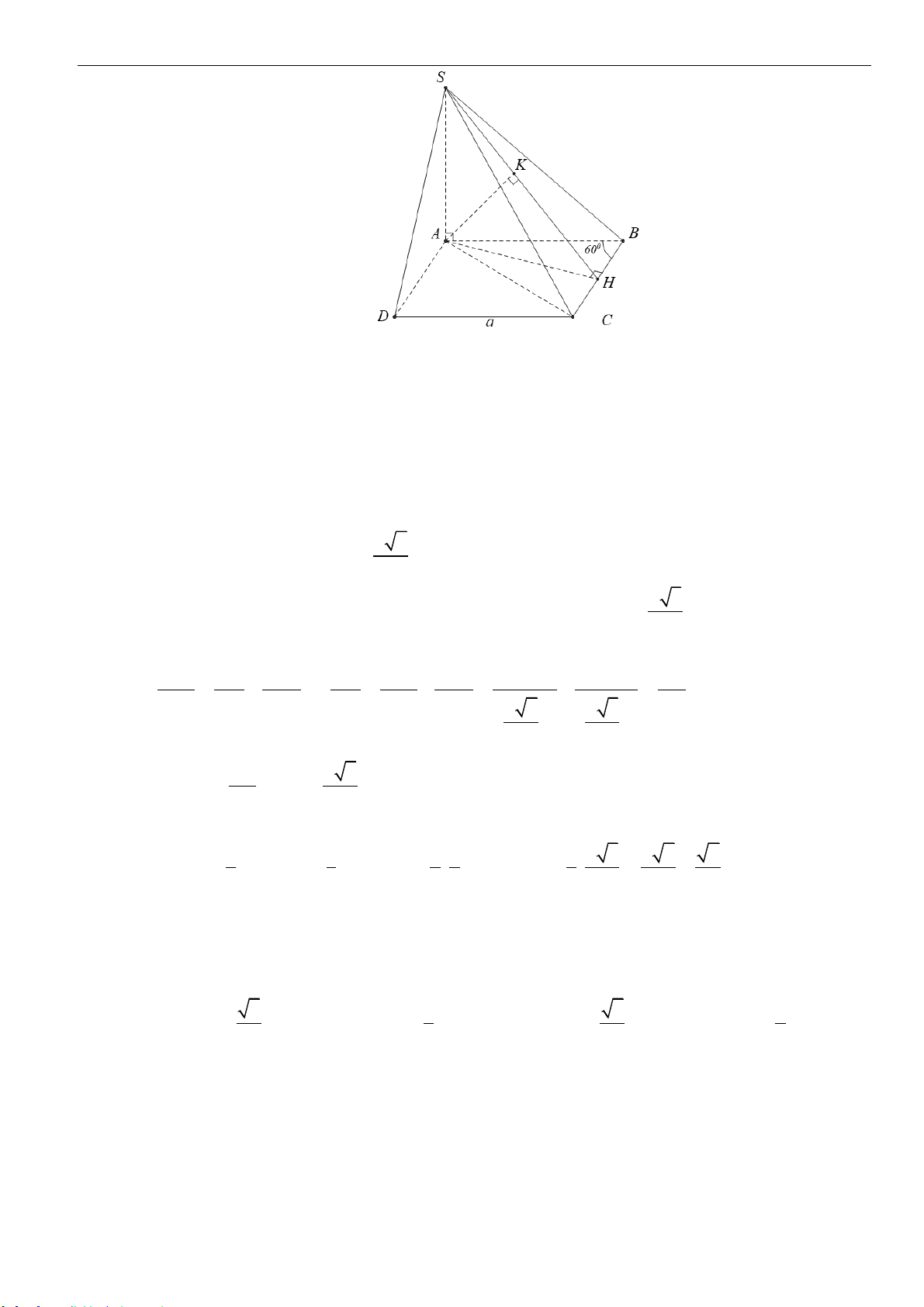
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 20

Ta có,

ABCD

là hình thoi cạnh

a

,

0

60ABC =

, nên

ABC

là tam giác đều cạnh

a

.

Gọi

H

là trung điểm của

BC

,

K

là hình chiếu vuông góc của

A

lên

SH

.

Ta có:

( )

Do

BC AH

BD

AB

A

C

C S SA ABC



⊥





⊥⊥







laø tam giaùc ñeàu

( )

BC SAH⊥

Ta lại có:

( )

Do

AK SH

AK BC BC SAH

⊥







⊥⊥





( )

AK SBC⊥

Do đó:

( )

2

,

2

a

d A SBC AK==

Xét

ABH

vuông tại

H

, ta có:

0

3

.sin .sin60

2

a

AH AB ABH a= = =

Xét

SAH

vuông tại

A

, ta có:

22

2 2 2 2 2 2 2

1 1 1 1 1 1 1 1 2

3

23

22

AK SA AH SA AK AH a

aa

= +  = − = − =

   

   

   

2

36

22

aa

SA SA =  =

Thể tích khối chóp

.S ABCD

là:

3

.

1 1 2 1 1 3 6 2

. . .2 . . . . . . . .

3 3 3 2 3 2 2 4

S ABCD ABCD ABC

aa

V S SA S SA AH BC SA a a= = = = =

Câu 30: Cho hình chóp

.S ABCD

có đáy là hình thang vuông tại

A

và

B

,

, 2AB BC AD AB==

. Biết

SA

vuông góc với mặt phẳng đáy,

2SA a=

và thể tích khối chóp

.S ABCD

bằng

3

3a

. Gọi



là góc

giữa hai mặt phẳng

( )

SCD

và

( )

ABCD

, tính

tan



.

A.

6

tan

2



=

. B.

1

tan

3



=

. C.

6

tan

3



=

. D.

2

tan

3



=

.

Lời giải

Chọn C

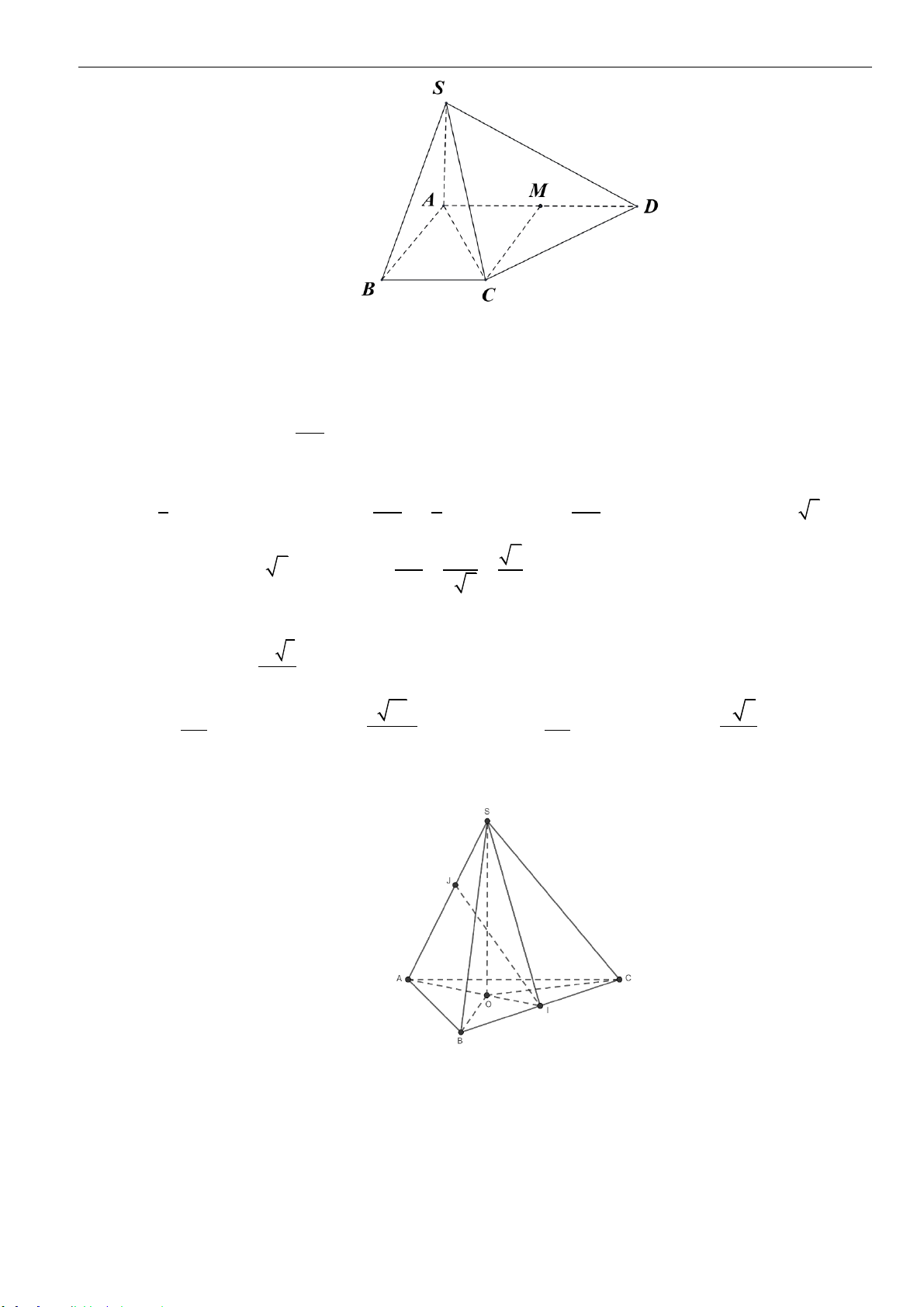
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

21 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Gọi

M

là trung điểm của

AD

. Khi đó các tam giác

,AMC

CM D

vuông cân tại

M

nên

AC CD⊥

.

Lại có:

CD SA⊥

suy ra

CD SC⊥

. Do đó

SCA



=

là góc giữa hai mặt phẳng

( )

SCD

và

( )

ABCD

,

tan

SA

AC



=

.

Ta có:

22

3 2 2

1 9 1 9

. . 3 ( ) 3 9 3.

3 2 2 2

ABCD ABCD

aa

S SA a S BC AD AB AB a AB a=  =  + =  =  =

Suy ra

6.AC a=

Vậy

26

tan .

3

6

SA a

AC

a



= = =

Câu 31: Cho hình chóp

.S AB C

, có

==SA SB SC

, đáy là tam giác đều cạnh

a

. Biết thể tích khối chóp

.S AB C

bằng

3

a

. Khoảng cách giữa hai đường thẳng

SA

và

BC

bằng

A.

4

7

a

. B.

3 13

13

a

. C.

6

7

a

. D.

3

4

a

.

Lời giải

Chọn C

Gọi

O

là hình chiếu vuông góc của

S

lên mặt phẳng

( )

ABC

. Suy ra

( )

⊥SO ABC

.

Mặt khác, vì

==SA SB SC

nên

==OA OB OC

. Vậy

O

là tâm của tam giác đều

ABC

.

Gọi

I

là trung điểm cạnh

BC

,

J

là hình chiếu vuông góc của

I

lên đường thẳng

SA

.

Khi đó

⊥BC AI

và

⊥IJ SA

.

Ta có:

( )

⊥



 ⊥  ⊥



⊥



BC SO

BC SAI BC IJ

BC AI

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 22

Vì

⊥IJ SA

tại

J

và

⊥IJ BC

tại

I

nên

IJ

là đoạn vuông góc chung của

SA

và

BC

.

Dẫn đến khoảng cách giữa hai đường thẳng

SA

và

BC

bằng độ dài đoạn thẳng

IJ

.

Đặt

= = =x SA SB SC

. Suy ra

2

3

=−

a

SO x

.

Thể tích

2 2 3 2

22

.

1 1 3 3

.4

3 3 3 4 3 3



= =  −  =  − =

S ABC ABC

a a a a

V SO S x x a

2

2 2 2 2

49 7 3 7 3

16

3 3 3 3

 − =  =  =  =

a a a

x a x a x SA

và

4=SO a

.

Ta có:

3

4

2

1 1 . 6

..

2 2 7

73

3

SAI

a

SO AI a

S SO AI SA IJ IJ

SA

a











= =  = = =







.

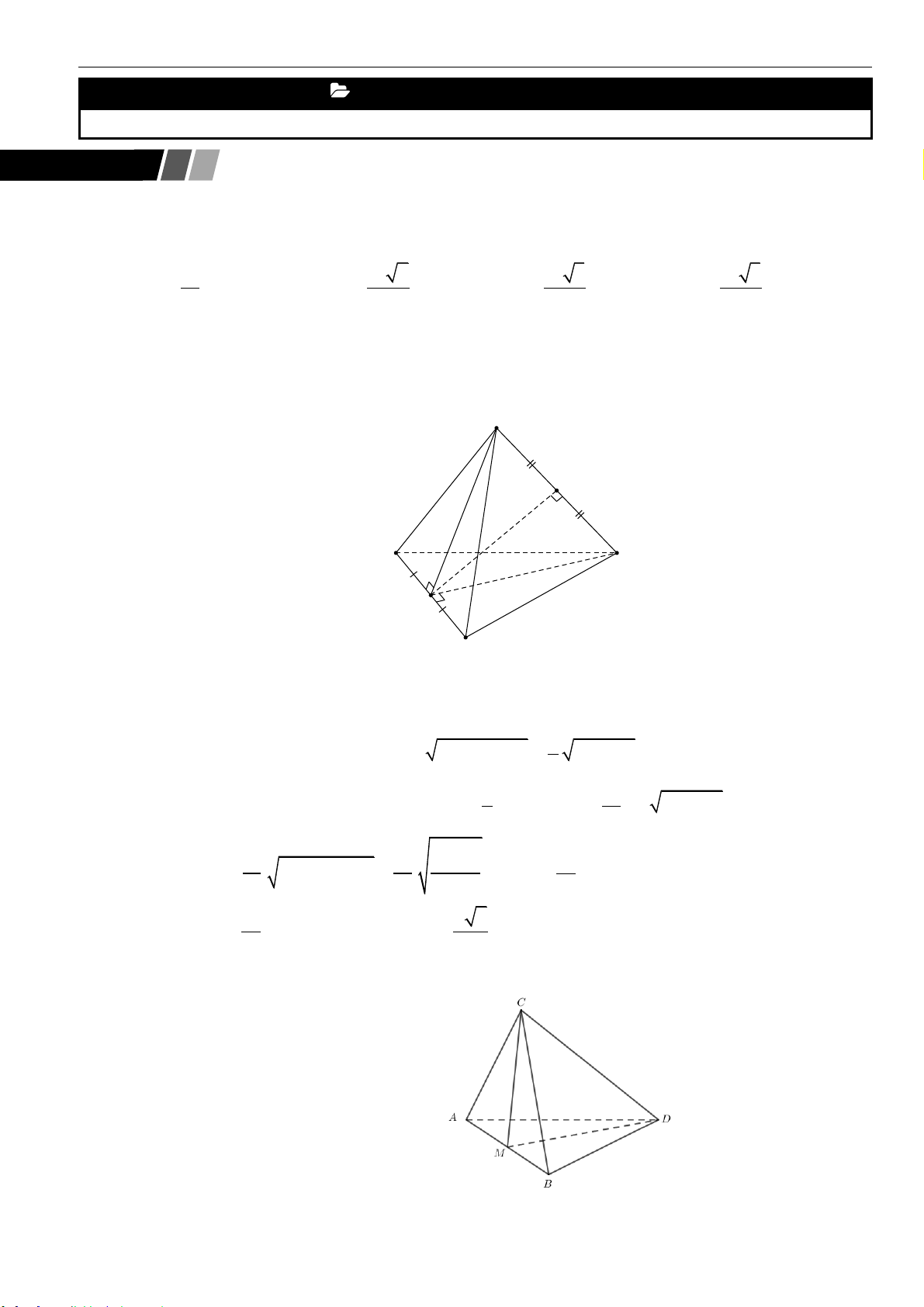
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

1 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Dạng 12: Cực trị khối đa diện

Câu 1: Cho tứ diện

ABCD

có

ABC

và

ABD

là các tam giác đều cạnh bằng

a

không đổi. Độ dài

CD

thay đổi. Tính giá trị lớn nhất đạt được của thể tích khối tứ diện

ABCD

.

A.

3

8

a

. B.

3

2

12

a

. C.

3

8

a

. D.

3

12

a

.

Lời giải

Chọn A

Cách 1.

Gọi

,MN

lần lượt là trung điểm của

,AB CD

ta có

MN

là đoạn vuông góc chung của

AB

và

CD

.

Đặt

CD x=

, với

0x 

ta có

2 2 2 2

1

3

2

MN CM CN a x= − = −

.

Khi đó, thể tích khối tứ diện

ABCD

là

22

11

. . . . 3

6 12

V AB CD MN a x a x= = −

.

Từ đó,

( )

2

2 2 2

3

. 3 .

12 12 4

a

aa

V x a x= − 

hay

3

8

a

V 

.

Vậy

3

max

8

a

V =

khi

2 2 2

6

3

2

a

x a x x= −  =

.

Cách 2.

x

N

M

C

A

B

D

VÍ DỤ MINH HỌA

B

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 2

Gọi

M

lần lượt là trung điểm của

AB

. Vì

ABC

và

ABD

là các tam giác đều cạnh bằng

a

nên

3

2

a

CM DM==

và

,CM AB DM AB⊥⊥

do đó

( )

AB CDM⊥

.

Thể tích khối tứ diện

ABCD

là

..

1 1 1 1

. . .sin . . .sin

3 2 3 2

A CDM B CDM

V V V AM CM DM CDM BM CM DM CDM= + = +

2

3

1 1 3

. . .sin . .

6 6 2 8

aa

AB CM DM CDM a



=  =





.

Vậy

3

max

8

a

V =

khi

22

6

2

a

CM DM CD CM DM⊥  = + =

.

Câu 2: Cho một hình lập phương

( )

H

và một hình lăng trụ tam giác đều

( )

L

có tổng độ dài các cạnh

bằng nhau. Tỷ lệ thể tích khối lăng trụ

( )

L

và khối lập phương

( )

H

tương ứng có giá trị lớn nhất

bằng

A.

16 3

27

. B.

17 3

24

. C.

32

27

. D.

83

9

.

Lời giải

Chọn A

Giả sử cạnh hình lập phương

( )

H

có độ dài bằng

a

và hình lăng trụ tam giác đều

( )

L

có độ dài

cạnh đáy bằng

x

và chiều cao bằng

y

.

Theo giả thiết ta có

12 6 3 4 2a x y a x y= +  = +

,

( )

; ; 0a x y 

.

Khối lăng trụ

( )

L

và khối lập phương

( )

H

có thể tích lần lượt là:

2

3

4

xy

và

3

a

.



Tỷ lệ thể tích khối lăng trụ

( )

L

và khối lập phương

( )

H

tương ứng bằng:

( )

2

23

33

3 4 2

33

2 , 0

4 4 2

x a x

x y x

T t t t

a a a

−

= = = − = 

.

Do:

4 2 4 2 2

x

a x y a x

a

= +    

.

Bảng biến thiên của

( )

23

3

2 , 0;2

2

f t t t t= − 

.

Vậy

16 3

27

MaxT =

.

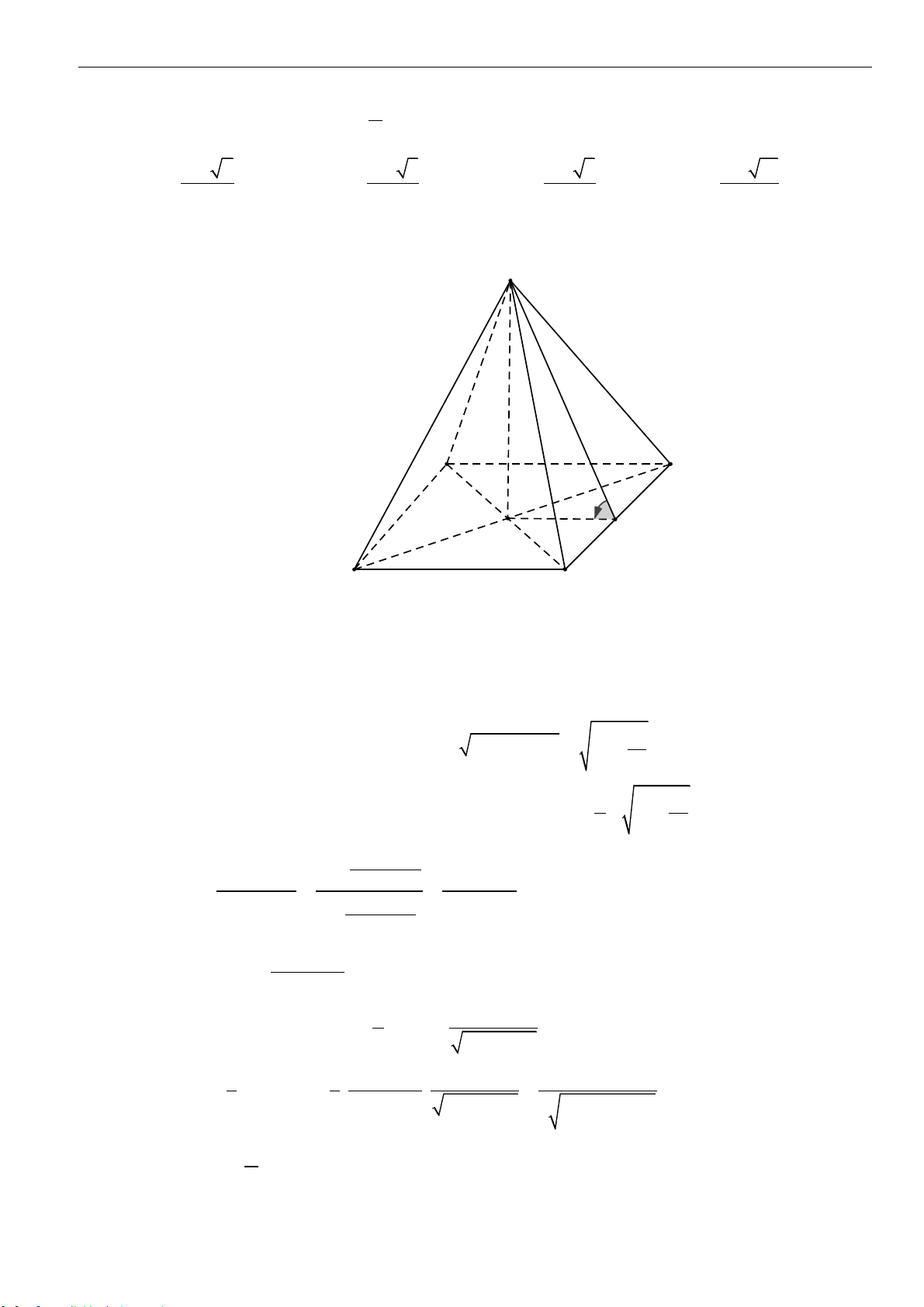
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

3 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 3: Cho hình chóp tứ giác đều

.S ABCD

có các cạnh bên bằng

a

, góc tạo bởi mặt phẳng bên và mặt

phẳng đáy là



với

0;

2













. Thể tích khối chóp

.S ABCD

đạt giá trị lớn nhất là

A.

3

47

.

49

a

B.

3

43

.

27

a

C.

3

23

.

9

a

D.

3

4 15

.

75

a

Lời giải

Gọi

O

là giao điểm của

AC

và

BD

( )

SO ABCD⊥

Gọi

M

là trung điểm

CD

( ) ( )

( )

,SCD ABCD SMO



 = =

Gọi độ dài một cạnh hình vuông là

x

Tam giác

SMC

vuông tại

M

có:

2

2 2 2

4

x

SM SC CM a= − = −

Tam giác

SOM

vuông tại

O

có:

.cosOM SM SMO=

2

.

24

xx

a cos



 = −

2

2 2 2

2

22

2

1

4.

4 cos 4

1 tan

1

1 cos 2 tan

1

1 tan

a

aa

x







+

 = = =

++

+

2

4

2 tan

ABCD

a

Sx



 = =

+

Ta có:

2

.tan

.tan .tan

2

2 tan

xa

SO OM SMO



= = =

+

( )

23

.

2

23

2

1 1 4 .tan 4 .tan

. . . .

3 3 2 tan

2 tan

3 2 tan

S ABCD ABCD

a a a

V S SO





= = =

+

Do

0; tan 0.

2







  





α

O

M

D

C

B

A

S

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 4

Thể tích khối chóp đạt giá trị lớn nhất khi

( )

3

2

4 .tan

.

3

2 tan

a



+

đạt giá trị lớn nhất.

Ta xét

( )

2

3

2

tan

2 tan

f



=

+

Áp dụng BĐT

AM GM−

cho ba số dương

222

tan 1 1

;;

2 tan 2 tan 2 tan





+++

ta có:

( )

22

3

222

2

tan tan 1 1

..

2 tan 2 tan 2 tan

2 tan

f









==

+++

+

3

2

222

1 tan 1 1 1

3 2 tan 2 tan 2 tan 27









 + + =





+++





( )

2

22

1 tan 1

tan 1

27 2 tan 2 tan 4

Maxf



  



=  =  =  =

++

Vậy

( )

33

.

3

4 4 3

27

3 2 1

S ABCD

aa

MaxV ==

+

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

5 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 1: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật

3, 2AB a SA SB SC SD a= = = = =

.

Giá trị lớn nhất của thể tích khối chóp

.S ABCD

bằng:

A.

3

13

12

a

. B.

3

13 2

12

a

. C.

3

13 6

12

a

. D.

3

13 3

12

a

.

Lời giải

Chọn D

Gọi

( )

0AD x x=

.

Ta có

2 2 2 2

11

33

22

AC x a AH AC x a= +  = = +

Khi đó:

2 2 2

22

3 13

4

4 4 4

x a x

SH a a

+

= − = −

.

Thể tích khối chóp

2 2 2

2

1 1 13 2 13

. . 3 . . . .

3 3 4 4 2 4 4

3

x a x a x

V B h a x a= = − = −

Đặt

( )

2 2 2

13

13 13

4 4 4

.

2 4 4 2 8

x a x

x a x a

fx

+−

= −  =

Thể tích lớn nhất của khối chóp

23

2 13 13 3

..

8 12

3

a a a

V ==

Câu 2: Cho hình chóp đều

.S ABCD

có cạnh bên bằng

a

, góc hợp bởi đường cao

SH

của hình chóp và

mặt bên bằng



. Tìm



để thể tích

.S ABCD

là lớn nhất.

A.

30

. B.

60

. C.

45

. D.

75

.

Lời giải

Chọn C

Vì

.S ABCD

là hình chóp đều có đường cao

SH

nên

H

là tâm của hình vuông

ABCD

.

BÀI TẬP TRẮC NGHIỆM

C

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 6

Vẽ

( )

⊥HE BC E BC

,

( )

⊥HF SE F SE

.

Ta chứng minh được

( )

⊥HF SBC

 SF

là hình chiếu vuông góc của

SH

lên

( )

SBC

( )

;;



 = = = =SH SBC SH SF FSH ESH

.

Đặt

=x BH

22

2 2 2 2

2

22



=

= = =







=−





= − = −



BD AB

AB x

x BH

SH a x

SH SB BH a x

.

Điều kiện:

22

0











   



−





x

xa

ax

.

Thể tích khối chóp

.S ABCD

là:

( )

2

2 2 2 2 2

1 1 2

. . 2

3 3 3

= = − = −

ABCD

V SH S a x x x a x

,

( )

0;xa

.

Xét hàm số

( ) ( )

2 2 2

2

, 0;

3

= − V x x a x x a

.

( )

22

2 2 3

3

−



=

−

x a x

Vx

ax

,

( )

22

2

0;

0 0;

22

3

0

33

2 3 0

2

0;

3



=



 = 





=   =   =



−=





= − 





x a a

xa

V x x a x a

ax

x a a

.

Bảng biến thiên của hàm

( )

Vx

trên

( )

0;a

:

Dựa vào bảng biến thiên, thể tích

V

đạt giá trị lớn nhất khi

22

33

=  =x a BH a

.

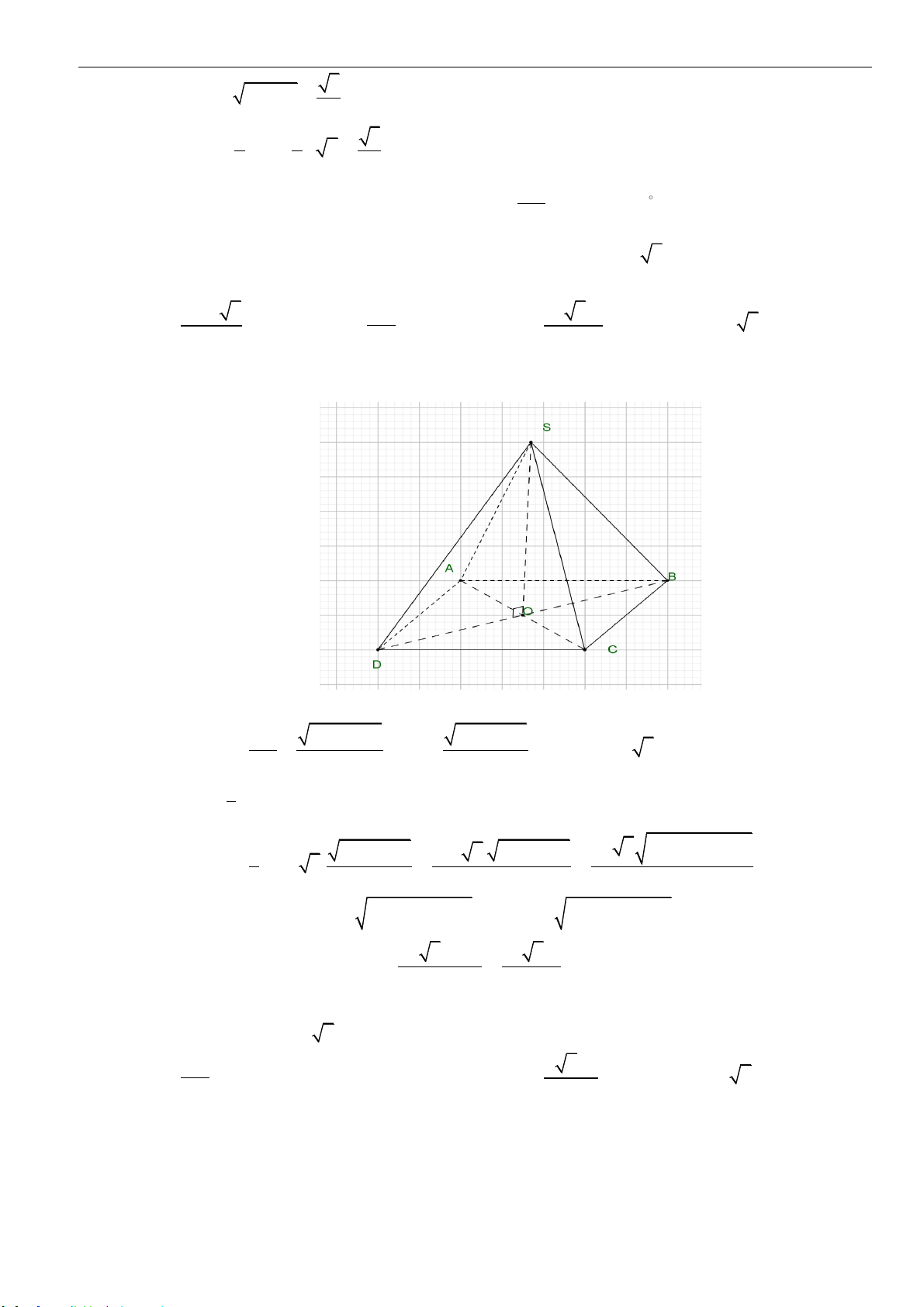
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

7 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

22

3

1 1 3

2

2 2 3



= − =









= = =





SH a x a

HE AB x a

.

Xét tam giác vuông

SHE

có

tan tan 1



= = =

HE

ESH

SH

45



=

.

Câu 3: Cho khối chóp

.S ABCD

, có đáy

là hình chữ nhật cạnh

25AB a=

và tất cả các cạnh bên của

hình chóp bằng

5a

. Thể tích lớn nhất của khối chóp đã cho bằng

A.

3

20 5

3

a

. B.

3

8

3

a

. C.

3

40 5

3

a

. D.

3

15 5a

.

Lời giải

Chọn C

Ta gọi độ dài cạnh

BC x=

,

0x 

.

Ta có:

22

20

22

BD x a

BO

+

==

;

22

80

2

ax

SO

−

=

;

2 . 5

ABCD

S a x=

;

.

1

..

3

S ABCD ABCD

V S SO=

( )

2 2 2

2 2 2 2

.

2 5 80

1 80 2 5. 80

.2 . 5.

3 2 6 6

S ABCD

a x a x

a x ax a x

V a x

−

−−

 = = =

(1).

Ta có:

( ) ( ) ( )

2 2 2 2 2 2 2 2 2 2

80 2 80 40 80x a x x a x a x a x+ −  −   −

(2).

Thế (2) vào (1), suy ra

23

.

2 5.40 40 5

63

S ABCD

a a a

V =

.

Câu 4: Cho khối chóp

.S ABCD

có đáy là hình bình hành, một cạnh của hình bình hành bằng

a

và các

cạnh bên đều bằng

2a

. Thể tích của khối chóp có giá trị lớn nhất là

A.

3

7

12

a

. B.

3

8a

. C.

3

26

3

a

. D.

3

26a

.

Lời giải

Chọn A

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 8

Gọi

H AC BD=

. Vì

SA SB SC SD= = =

nên

HA HB HC HD= = =

ABCD

là hình chữ nhật và

H

là hình chiếu vuông góc của

S

xuống

( )

ABCD

Giả sử

AB a=

. Đặt

AD x=

. Khi đó:

.

ABCD

S ax=

2 2 2 2

.

2 2 2

AC AB BC a x

AH

++

= = =

2 2 2 2

2 2 2

7

2.

42

a x a x

SH SA AH a

+−

= − = − =

Ta có

( )

2 2 2

2 2 2 2

.

3

.

7

1 1 7 7 1

. . . . . .

3 3 2 6 6 2

7

.

12

S ABCD ABCD

S ABCD

x a x

a x ax a x

V SH S ax a

a

V

+−

−−

= = = 



Dấu xảy ra khi

22

7x a x=−

hay

14

2

a

x =

.

Vậy thể tích của khối chóp có giá trị lớn nhất là

3

7

12

a

khi

14

2

a

x =

.

Câu 5: Cho khối chóp tứ giác đều

.S ABCD

có tất cả các cạnh đều bằng

1

. Gọi

,MN

lần lượt là các

điểm thuộc các cạnh

,BC CD

sao cho

1MN =

. Tìm giá trị nhỏ nhất của thể tích khối tứ diện

.S AMN

.

A.

42

24

−

. B.

3

12

. C.

2

12

. D.

12

+

.

Lời giải

Chọn A

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

9 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Hình chóp

.S ABCD

có đường cao

2

h =

.

Ta có

.

12

..

36

S AMC AMN AMN

V S h S



==

.

Thể tích khối tứ diện

.S AMN

đạt giá trị nhỏ nhất khi

AMN

S



nhỏ nhất.

Đặt

,x CM y NC==

1 , 1MB x DN y = − = −

Ta có

2

22

( ) 1

1

2

xy

x y xy

+−

+ =  =

Với

2 2 2

( ) 2( ) 1 2x y x y x y+  +   + 

.

Ta có

1 1 1

1 1 (1 ) . .(1 )

2 2 2

AMN ABM CMN ADN

S S S S x x y y

   

= − − − = − − − − −

1 . 1

1

2 2 2

x x y y−−

= − − −

2

1 ( ) 1

()

2 2 2

xy



+

= + − +





.

Đặt

2

1 1 1

4 2 4

AMN

t x y S t t



= +  = − + +

.

Tam giác có diện tích nhỏ nhất là

min

2 2 1

4

S

−

=

khi

2t =

.

Vậy thể tích nhỏ nhất của tứ diện

.S AMN

là

min

2 2 1 4 2

4 24

2

.

6

V

−−

==

.

Câu 6: Một tứ diện

ABCD

có

ABC

và

DBC

là hai tam giác đều cạnh

a

, cạnh

AD

thay đổi. Khi thể

tích tứ diện đạt giá trị lớn nhất, gọi



giữa hai mặt

( )

ADB

và

( )

ADC

. Tính

cos



.

A.

1

5

cos



=

. B.

5

7

cos



=

. C.

6

7

cos



=

. D.

1

5

cos



=

.

Lời giải

Chọn D

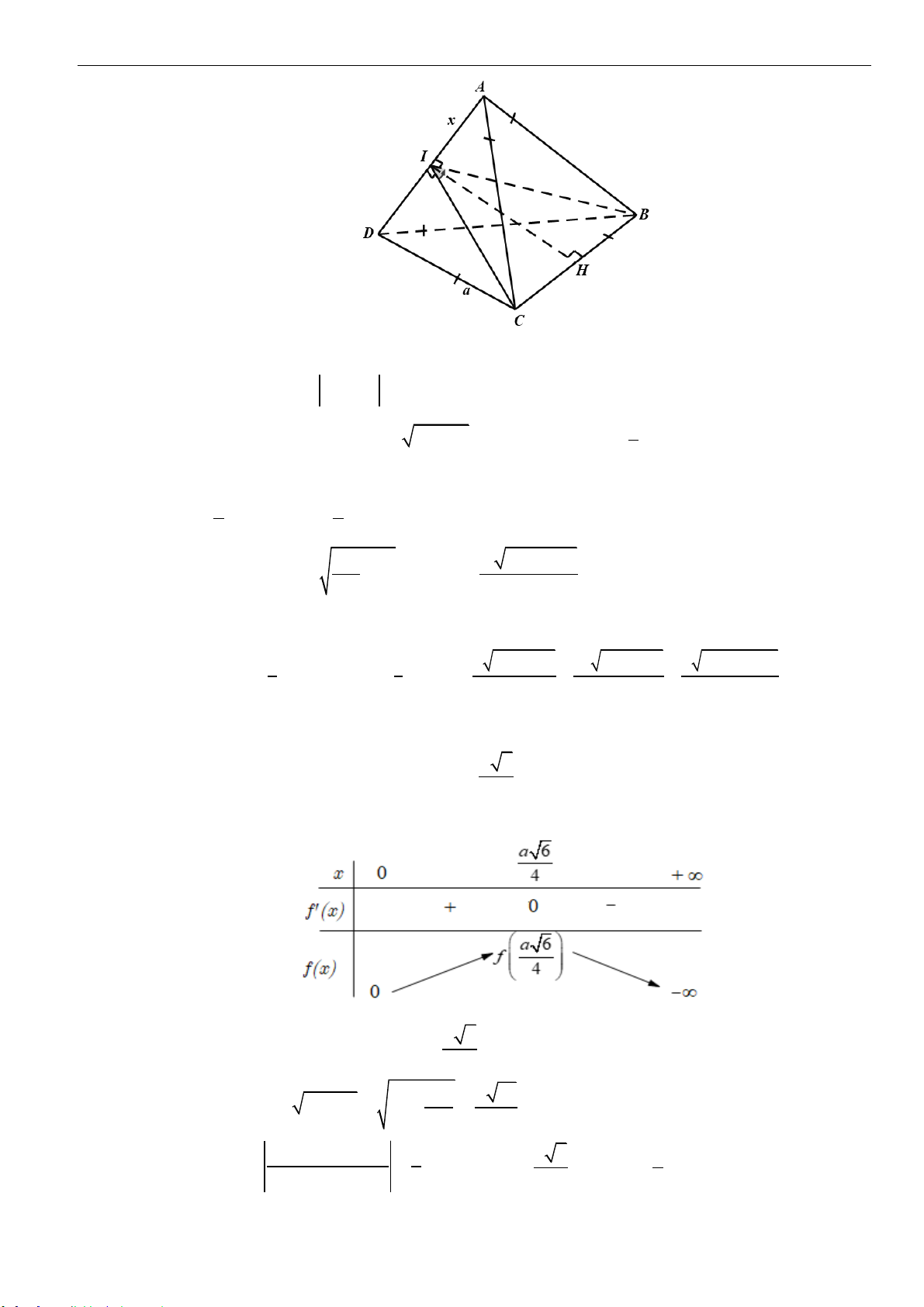
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 10

Gọi

I

là trung điểm của

AD

. Khi đó

AD IC⊥

và

AD IB⊥

. Suy ra góc



giữa hai mặt

( )

ADB

và

( )

ADC

thoả mãn

cos cosCIB



=

.

Đặt

( ) ( )

2 2 2 2

1

0 2. ( )sin 1

3

ABCD AICB

IA x x IC IB a x V V x a x



=   = = −  = = −

.

Ta có:

( )

2 2 2

22

11

. . .sin , .

22

3 . 3 4

( ).sin . sin 2

4

2

IBC

S IB IC d I BC BC

a a a x

a x a x

ax







==

−

 − = −  =

−

Từ

( )

1

và

( )

2

:

( )

2 2 2 2 2 2 4

2 2 2 2

22

1 1 3 4 3 4 3 4

2. ( )sin ( )

3 3 6 6

2

ABCD AICB

a a x ax a x a a x x

V V x a x x a x

ax



− − −

= = − = − = =

−

.

Xét hàm số:

( ) ( )

4 2 2

4 3 , 0f x x a x x= − + 

( ) ( )

32

6

16 6 ; 0

4

a

f x x a x f x x



 = − + =  =

.

Bảng biến thiên:

Vậy

ABCD

V

đạt giá trị lớn nhất khi

6

4

a

x =

.

Suy ra:

2

2 2 2

6 10

16 4

aa

IC IB a x a= = − = − =

.

Ta có:

2 2 2

1

2. . 5

IC IB CB

cos

IC IB



+−

==

(hoặc

2 6 1

sin cos

55



=  =

)

Câu 7: Cho lăng trụ

.ABC A B C

  

có thể tích là

V

.

M

,

N

,

P

là các điểm lần lượt nằm trên các cạnh

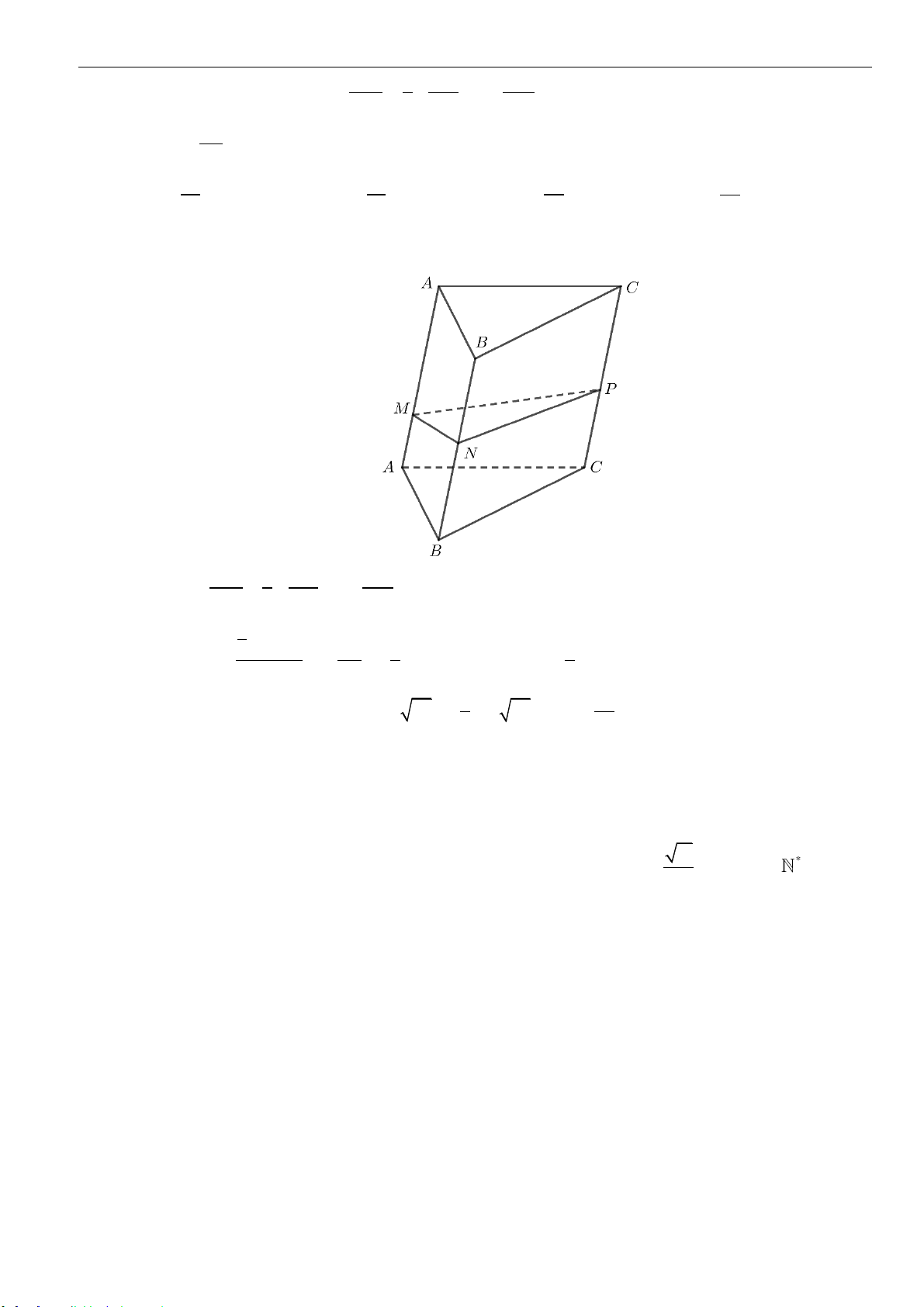
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

11 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

AA



,

BB



,

CC



sao cho

1

3

AM

AA

=



,

BN

x

BB

=



,

CP

y

CC

=



. Biết thể tích khối đa diện

.ABC MNP

bằng

2

3

V

. Giá trị lớn nhất của

.xy

bằng

A.

17

21

. B.

9

16

. C.

25

36

. D.

5

24

.

Lời giải

Chọn C

Ta có:

1

3

AM

AA

=



,

BN

x

BB

=



,

CP

y

CC

=



. Khi đó:

.

1

2

3

33

MNP ABC

xy

V

VV

++

==

15

2

33

x y x y + + =  + =

.

Áp dụng BĐT Cauchy:

2x y xy+

5 25

2

3 36

xy xy   

.

Câu 8: Trên cạnh

AD

của hình vuông

ABCD

cạnh

1

, người ta lấy điểm

M

sao cho

( )

01AM x x=  

và trên nửa đường thẳng

Ax

vuông góc với mặt phẳng chứa hình vuông,

người ta lấy điểm

S

với

SA y=

thỏa mãn

0y 

và

22

1xy+=

. Biết khi

M

thay đổi trên đoạn

AD

thì thể tích của khối chóp

.S ABCM

đạt giá trị lớn nhất bằng

m

n

với

*

,mn

và

,mn

nguyên tố cùng nhau. Tính

T m n=+

.

A.

11

. B.

17

. C.

27

. D.

35

.

Lời giải

Chọn A

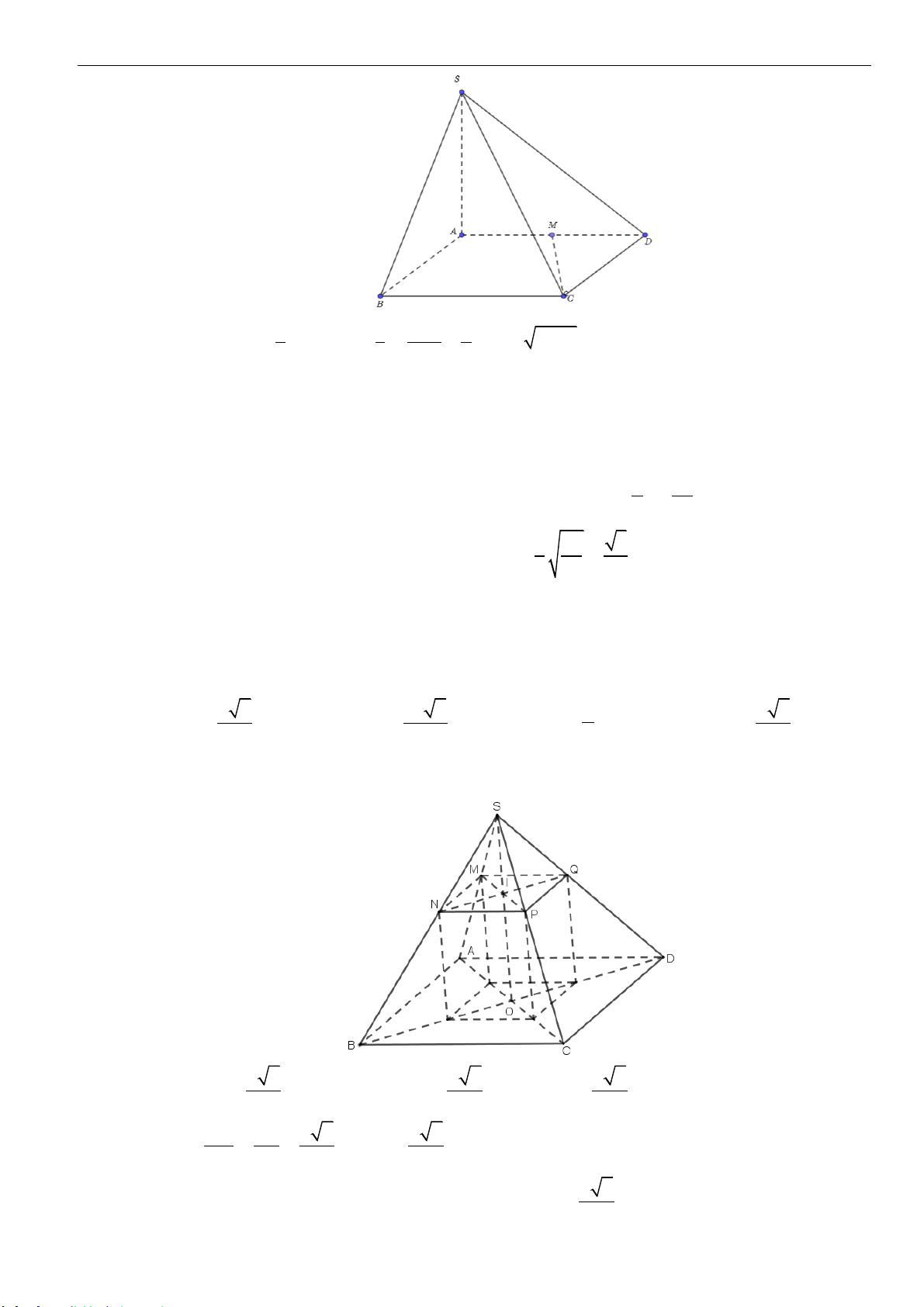
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 12

Ta có

( )

2

.

1 1 1 1

. . . 1 1

3 3 2 6

S ABCM ABCM

x

V SAS y x x

+

= = = + −

.

Xét

( ) ( )

( )

2

2 4 3

1 1 2 2 1f x x x x x x= + − = − − + +

trên

 

0;1

.

Có

( )

32

4 6 2f x x x



= − − +

;

( )

1

0

0.5

x

fx

x

=−





=



=



.

Lập bảng xét dấu của

( )

fx



trên

 

0;1

ta được

 

( )

0;1

1 27

max

2 16

f x f



==





.

Vậy thể tích lớn nhất của khối

.S ABCM

là

max

1 27 3

6 16 8

V ==

.

Câu 9: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng

a

. Gọi O là tâm của tứ giác ABCD

Một mẳng phẳng thay đổi và vuông góc với SO cắt các cạnh SO, SA, SB, SC, SD lần lượt tại I,

M, N, P, Q. Một hình trụ có một đáy nội tiếp tứ giác MNPQ và một đáy nằm trên hình vuông

ABCD

. Khi thể tích của khối trụ lớn nhất thì đội dài đoạn SI bằng

A.

2

a

SI =

. B.

32

2

a

SI =

. C.

3

a

SI =

. D.

2

3

a

SI =

.

Lời giải

Chọn D

Ta có

2

a

SO =

. Đặt

SI x=

,

2

0

2

a

x

. Suy ra

2

a

IO x=−

.

Ta có

22

.2

MP SI x x

MP AC x

AC SO a a

= =  = =

.

Đường tròn nội tiếp hình vuông MNPQ có bán kính

2

x

R =

.

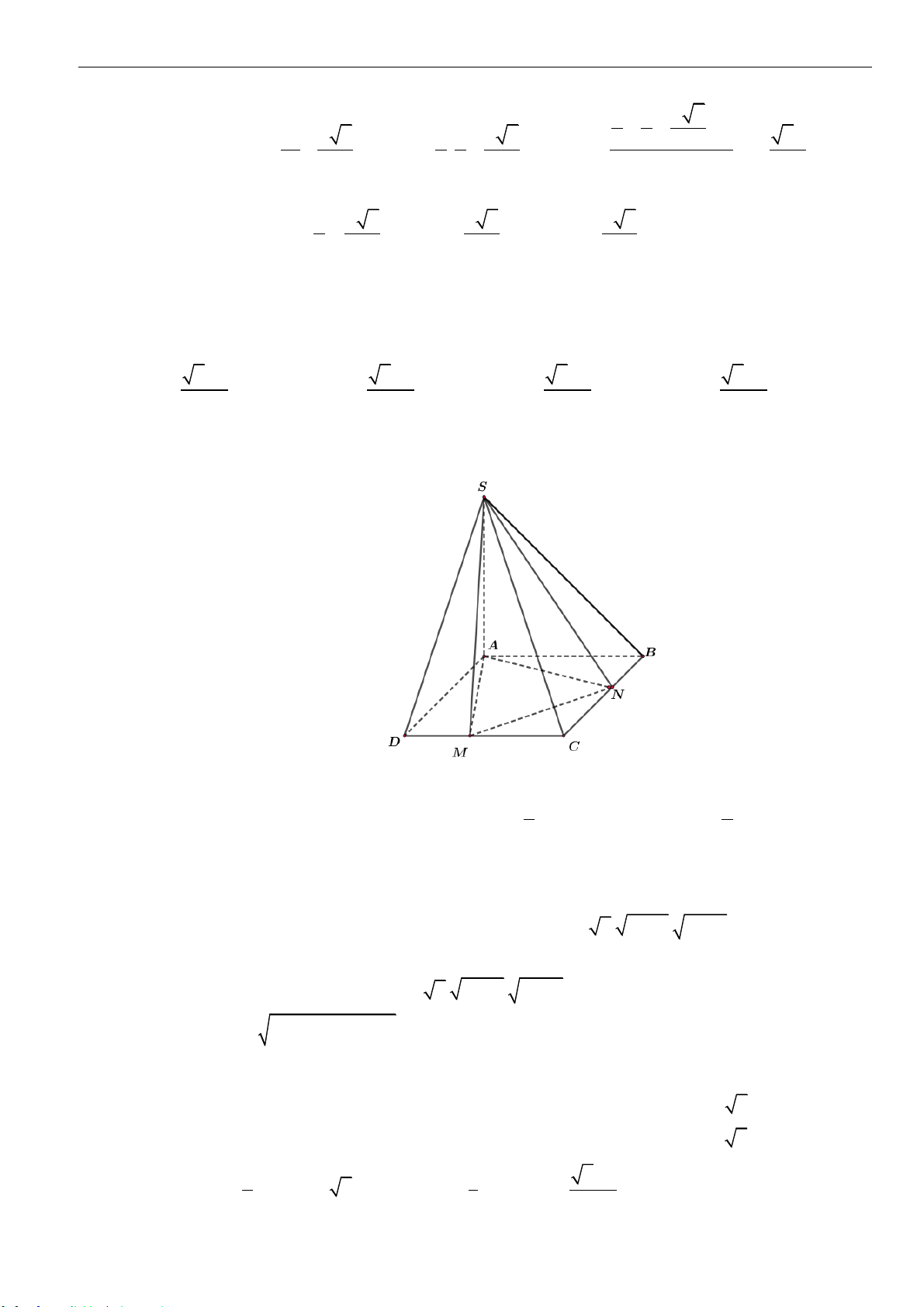
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

13 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Thể tích khối trụ có chiều cao SO và đáy là đường tròn nội tiếp tứ giác MNPQ là

3

2

2 2 2

. . . 2 . . . 2 .

2 2 2 2 2 3 54

x x a

x

x a x x a

V R IO x x



   



+ + −



   



= = − = −  =

   



   





.

Dấu

""=

xảy ra khi

22

2 2 3

x a a

xx= −  =

. Do đó

2

3

a

SI =

.

Câu 10: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông,

1AB =

, cạnh bên

1SA =

và vuông góc

với mặt phẳng đáy

( )

ABCD

. Kí hiệu

M

là điểm di động trên đoạn

CD

và

N

là điểm di động

trên đoạn

CB

sao cho

45MAN =

. Thể tích nhỏ nhất của khối chóp

.S AMN

là

A.

21

3

−

. B.

21

9

+

. C.

21

6

+

. D.

21

9

−

.

Lời giải

Chọn A

Đặt

( )

; 0 , 1DM x BN y x y= =  

Ta có

( )( ) ( )

11

1 1 1 1

22

AMN ABCD ABN ADM CMN

S S S S S x y x y xy

   

= − − − = − + + − − = −





Xét tam giác vuông

CMN

:

( ) ( ) ( )

22

2

1 1 1MN x y= − + −

.

Áp dụng định lí

cos

cho tam giác

AMN

:

( )

2 2 2 2 2 2 2

2. . .cos45 1 1 2. 1. 1 2MN AM AN AM AN x y x y= + −  = + + + − + +

Từ (1) và (2) suy ra

( ) ( )

( )( )

( )

22

2 2 2 2

2 2 2 2 2 2

1 1 1 1 2. 1. 1

2 2 2 1 1 1 4 3

x y x y x y

x y x y x y x y xy

− + − = + + + − + +

 + = + +  + = + −

Ta có

( )

22

24x y xy+

Từ (3) và (4) suy ra

( )

2

22

3 2 2

1 4 2 6 1 0

3 2 2

xy loai

x y xy xy xy xy

xy



+

+ −   − +  



−





( )

1

1 2 1

2

AMN

S xy



= −  −



.

1 2 1

..

33

S AMN AMN

V SA S



−

=

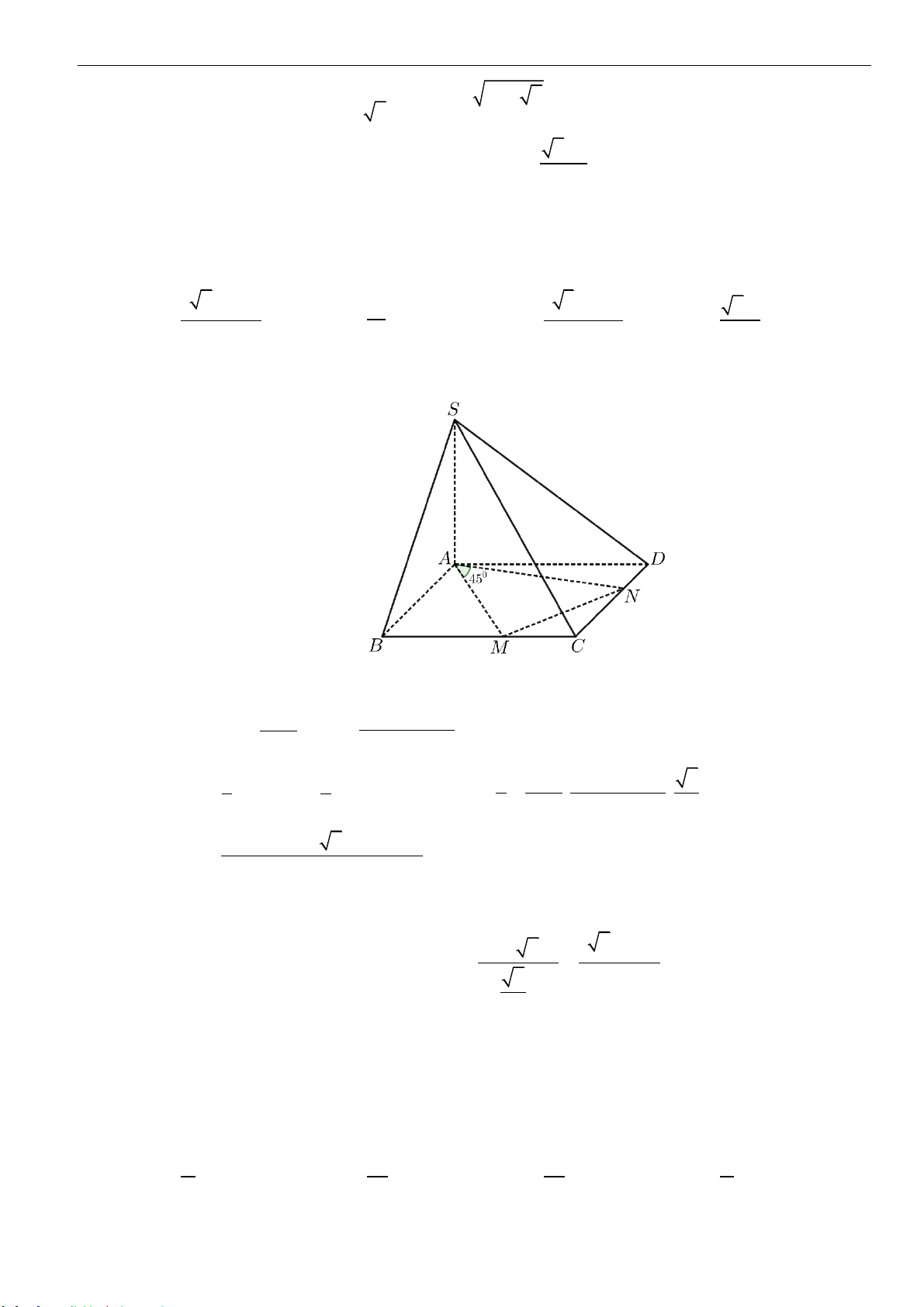
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 14

Dấu

""=

xảy ra

3 2 2

xy

=





 = = −



=−





Vậy thể tích nhỏ nhất của khối chóp

.S AMN

bằng

21

3

−

Câu 11: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh a,

SA a=

và

SA

vuông góc với mặt

phẳng đáy. Gọi

M

và

N

lần lượt là hai điểm di chuyển trên các cạnh

BC

và

DC

sao cho

45 .MAN =

Tìm giá trị nhỏ nhất của thể tích khối chóp

..S AMN

A.

( )

3

21

3

a−

. B.

3

6

a

. C.

( )

3

31

3

a−

. D.

3

2

3

a

.

Lời giải

Chọn A

Đặt

BAM α=

0

45NAD α = −

.

Ta có:

cos

a

AM

α

=

;

( )

cos 45

a

AN

α

=

−

.

. Δ

11

. . . .sin45

36

S AMN AMN

V SA S SA AM AN= = 

( )

12

. . .

6 cos cos 45 2

aa

a

αα

=

−

( )

3

.

2

6 cos45 cos 45 2

S AMN

a

V

α

=



+  −



.S AMN

V

đạt giá trị nhỏ nhất khi

( )

cos 45 2α−

đạt giá trị lớn nhất bằng

1



0

22,5α =

.

Vậy giá trị nhỏ nhất của

.S AMN

V

là

( )

3

.

21

2

3

2

61

2

S AMN

a

V

−

==



+





.

Câu 12: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành, có thể tích là

V

. Gọi

M

là trung

điểm của cạnh

SA

,

N

là điểm trên cạnh

SB

sao cho

3SN NB=

. Mặt phẳng

( )

P

thay đổi đi

qua các điểm

,MN

và cắt các cạnh

,SC SD

lần lượt tại hai điẻm phân biệt

,PQ

. Tìm giá trị lớn

nhất của thể tích khối chóp

.S MNPQ

.

A.

3

V

. B.

27

80

V

. C.

27

40

V

. D.

6

V

.

Lời giải

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

15 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Chọn C

Đặt

( )

; , 1

SC SD

k q k q

SP SQ

= = 

.

Vì bốn điểm

, , ,M N K Q

đồng phẳng nên ta có

SA SC SB SD

SM SP SN SQ

+ = +

.

Suy ra

42

2

33

k q q k+ = +  = +

.

Ta có

.

4 8 3

. . 2. .

3 3 8

S ABC

S MNP

V SA SB SC V

k k V

V SM SN SP k

= = =  =

.

. . 2. . 2

2

S ADC

S MQP

V SA SD SC V

q k qk V

V SM SQ SP qk

= = =  =

.

Suy ra

. . .

3 1 3 1

2

8 2 8

2

3

S MNPQ S MNP S MQP

V V V V V

k qk k

kk









= + = + = +









+





.

Để

MNPQ

V

lớn nhất khi và chỉ khi

( )

31

2

8

2

3

fk

k

kk

=+



+





đạt giá trị lớn nhất.

Ta có

( )

2

1

3

0, 1

8

3

k

f k k

k

kk

+



= − −   

+

. Suy ra

( ) ( )

27

1

40

Max f k f==

.

Suy ra

27

40

MNPQ

MaxV V=

.

Câu 13: Cho hình hộp chữ nhật

. ' ' ' 'ABCD A B C D

có diện tích toàn phần bằng 18 và độ dài đường chéo

' 18AC =

. Thể tích lớn nhất của khối hộp chữ nhật

. ' ' ' 'ABCD A B C D

là

A.

max

8V =

. B.

max

3V =

. C.

max

4V =

. D.

max

8V =

.

Lời giải

Chọn C

Gọi

,,a b c

là ba kích thước của hình hộp chữ nhật.

Theo giả thiết ta có: Diện tích toàn phần

( )

2 18 9.

tp

S ab bc ca ab bc ca= + + =  + + =

Độ dài đường chéo

2 2 2 2 2 2

' 18 18.AC a b c a b c= + + =  + + =

Từ đó:

( ) ( )

2

2 2 2

2 36a b c a b c ab bc ca+ + = + + + + + =

suy ra

6abc+ + =

.

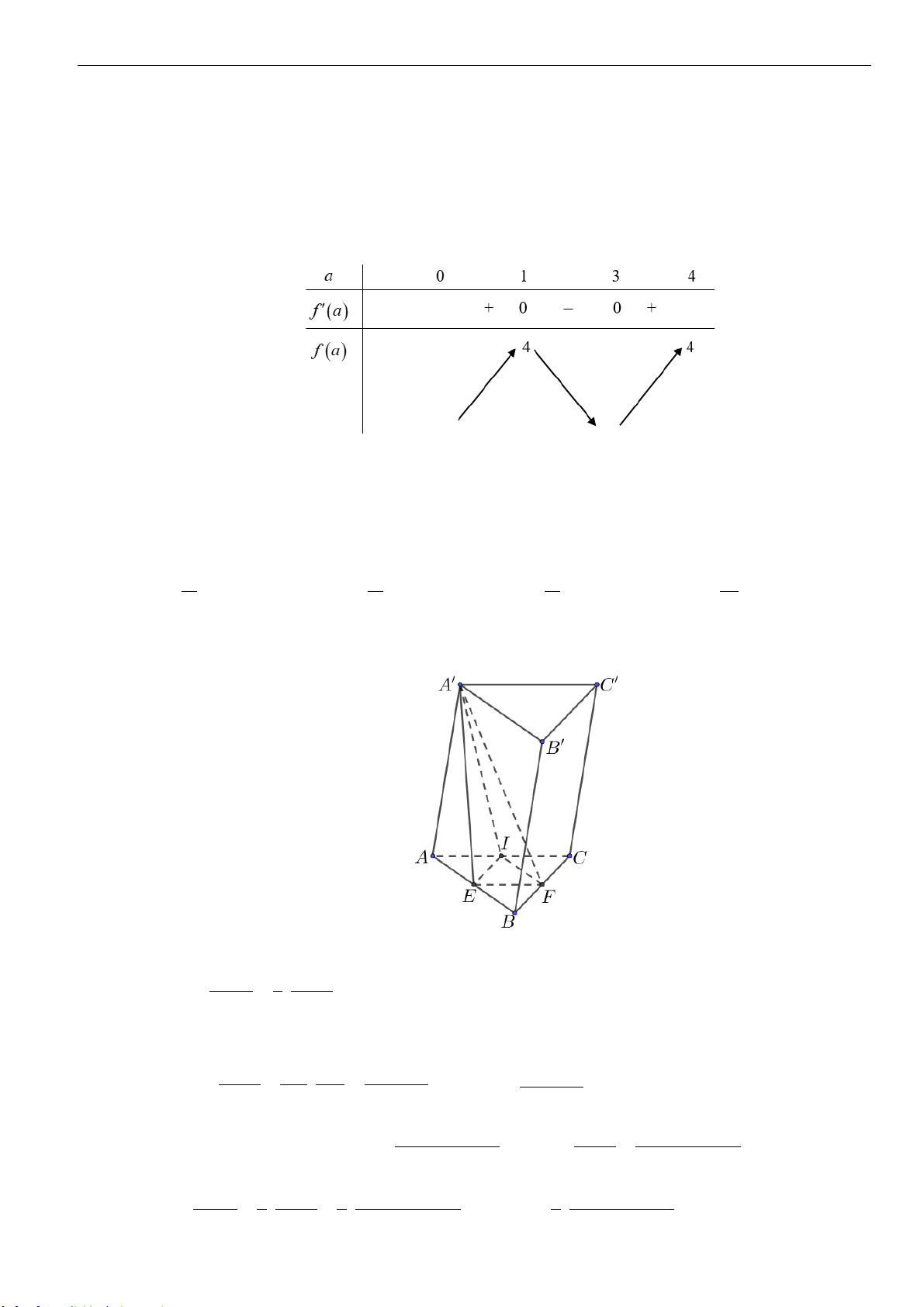
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 16

Ta có

( ) ( )

6 9 9 6b c a bc a b c a a+ = −  = − + = − −

.

Lại có:

( ) ( ) ( )

22

2

4 6 4 9 6 3 12 0 0 4.b c bc a a a a a a+   −  − −  −    





Tương tự ta cũng có

0 4 , 0 4bc   

.

Khi đó

.

Khảo sát hàm số

( )

32

69f a a a a= − +

với

04a

có

( )

2

3 12 9f a a a



= − +

Bảng biến thiên:

Vậy

max

4V =

. ( Bộ giá trị của

,,a b c

là

( )

4;1;1

và các hoán vị).

Câu 14: Cho hình lăng trụ

.ABC A B C

  

, có đáy là tam giác đều và thể tích bằng

V

. Gọi

,,E F I

là các

điểm lần lượt di động trên các cạnh

,,AB BC CA

sao cho

AE BF CI==

. Thể tích khối chóp

.A EFI



đạt giá trị nhỏ nhất bằng

A.

9

V

. B.

6

V

. C.

4

V

. D.

12

V

.

Lời giải

Chọn D

Tam giác

ABC

đều và

AE BF CI==

nên

AEI BFE CIF =  = 

suy ra

AEI BEF CFI

S S S

  

==

.

Ta có:

.

1

.

3

A EFI

EFI

ABC

V

S

VS





=

.

Gọi cạnh của tam giác

ABC

là

a

( )

0a 

,

( )

0AE BF CI x x a= = =  

.

Khi đó:

( )

2

.

AEI

ABC

x a x

S

AE AI

S AB AC a



−

==

( )

2

.

AEI ABC

x a x

SS

a



−

=

.

Suy ra:

2 2 2 2

22

3 3 3 3

3. .

EFI

EFI ABC AEI ABC

ABC

S

a ax x a ax x

S S S S

a S a



   



− + − +

= − =  =

Vậy

2 2 2 2

.

22

1 1 3 3 1 3 3

. . . .

3 3 3

A EFI

EFI

A EFI

ABC

V

S

a ax x a ax x

VV

V S a a









− + − +

= =  =

.

( )

32

9 6 6 9V abc a a a a a a= = − − = − +





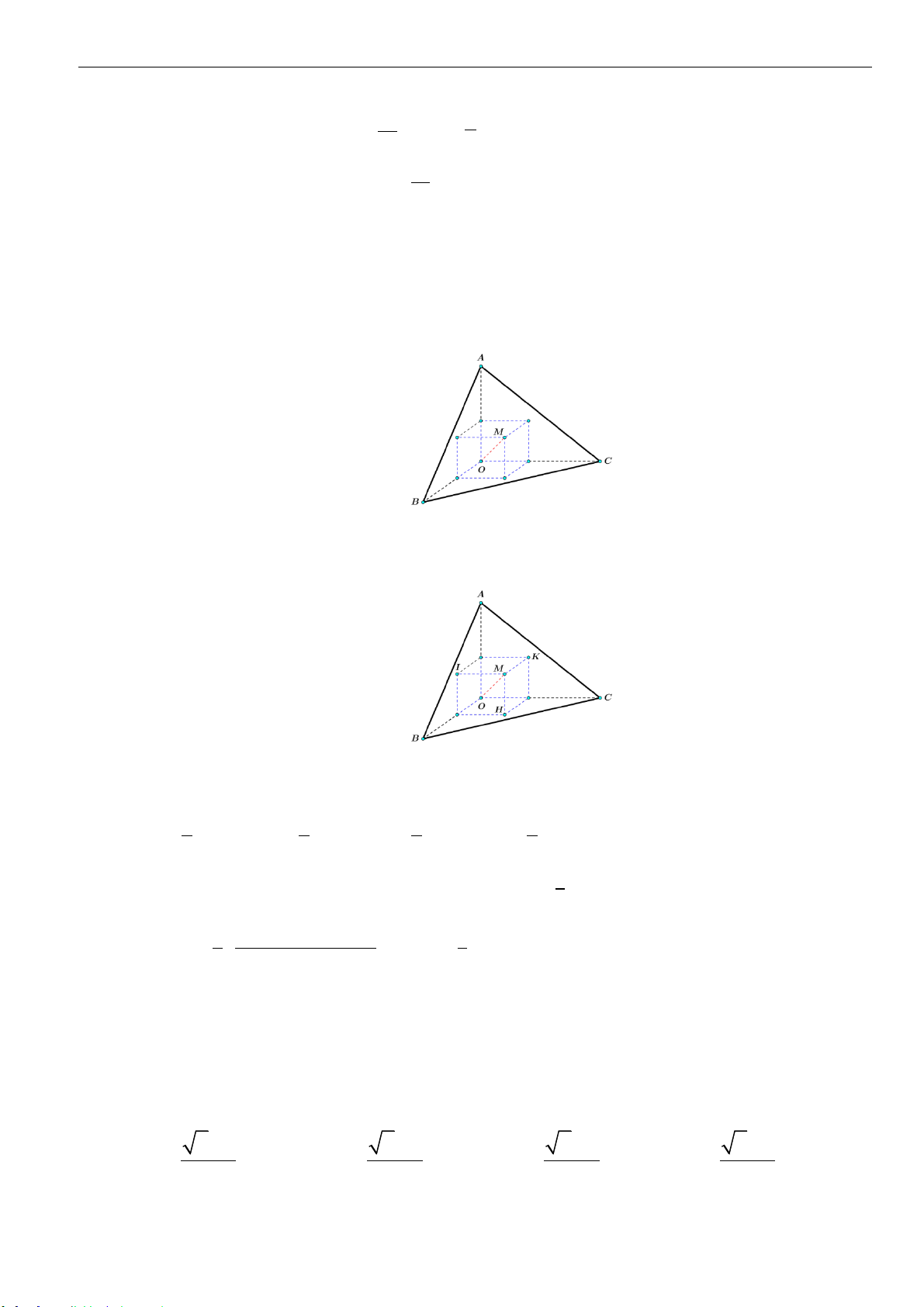
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

17 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

.A EFI

V



đạt giá trị nhỏ nhất khi và chỉ khi biểu thức

22

33a ax x−+

đạt giá trị nhỏ nhất trên

 

0;a

Ta có:

 

( )

2

22

0;

min 3 3

4

a

a ax x− + =

khi

2

a

x =

.

Vậy giá trị nhỏ nhất của

.A EFI

V



là

12

V

.

Câu 15: Một khối gỗ dạng hình chóp

.O ABC

CÓ

,,OA OB OC

đôi một vuông góc với nhau.

3 , 6 , 12OA cm OB cm OC cm= = =

. Trên mặt đáy

ABC

người ta đánh dấu một điểm

M

sau đó

người cắt gọt khối gỗ để thu được một khối hộp chữ nhật có

OM

là một đường chéo, đồng thời

hình hộp có ba mặt trên ba mặt bên của hình chóp (tham khảo hình vẽ). Khối hộp chữ nhật thu

được có thể tích lớn nhất bằng bao nhiêu?

A.

3

12 .cm

B.

3

36 .cm

C.

3

24 .cm

D.

3

8.cm

Lời giải

Chọn D

Gọi

,,I H K

lần lượt là hình chiếu của điểm

M

lên mp

( ) ( ) ( )

,,OAB OBC OCA

Ta có

. . . .O ABC M OAB M OBC M OCA

V V V V= + +

1 1 1 1

. . . . . . . . . . . .

6 6 6 6

OAOBOC MI OAOB MI OBOC MI OC OA = + +

4 2 12MI MH MK + + =

Khi đó thể tích khối hộp chữ nhật

( ) ( )

1

. . . 4 . 2

8

V MI MH MK MI MH MK==

3

1 4 2

83

MI MH MK

V

++









3

1

.4 8

8

VV   

Vậy

max

8V =

khi

4 2 1 , 4 , 2 .MI MH MK MI cm MH cm MK cm= =  = = =

Câu 16: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông,

1AB =

, cạnh bên

1SA =

và vuông

góc với mặt phẳng đáy

()ABCD

. Kí hiệu

M

là điểm di động trên đoạn

CD

và

N

là điểm di

động trên đoạn

CB

sao cho góc

MAN

bằng

45

. Thể tích nhỏ nhất của khối chóp

.S AMN

là

A.

21

3

−

. B.

21

9

+

. C.

21

6

+

. D.

21

9

−

.

Lời giải

Chọn A

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 18

Đặt

BAN



=

suy ra

45MAD



=  −

.

Khi đó

1

cos cos

AB

AN



==

và

( ) ( )

1

cos 45 cos 45

AD

AM



==

− −

.

Do đó diện tích tam giác

AMN

bằng

( )

1 2 1

. .sin45 .

2 4 cos .cos 45

AMN

B AM AN



=  =

−

.

Thể tích

.S AMN

bằng

( )

.

1 2 1

..

3 12 cos .cos 45

S AMN AMN

V B SA



==

−

.

Thể tích của khối chóp

.S AMN

nhỏ nhất khi

( )

cos .cos 45



−

lớn nhất.

Xét

( ) ( )

cos .cos 45f

  

=  −

trong đó

( )

0 ;45



  

.

Ta có

( ) ( )

sin 45 2f





=  −

;

( )

45

0

2

f







=  =

.

Bảng biến thiên

Từ bảng biến thiên ta có

 

( )

0 ;45

45 2 2

max

24

ff



  

+



==





.

Vậy thể tích nhỏ nhất của

.S AMN

bằng

.

2 1 2 1

.

12 3

22

4

S AMN

V

−

==

+

.

Vậy thể tích của khối chóp có giá trị lớn nhất là

3

7

12

a

khi

14

2

a

x =

.

Câu 17: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

,

SA

vuông góc với mặt đáy

( )

ABCD

và góc giữa

SC

với mặt phẳng

( )

SAB

bằng

30

. Gọi

M

là điểm di động trên cạnh

CD

và

H

là hình chiếu vuông góc của

S

lên đường thẳng

BM

. Khi điểm

M

di động trên

cạnh

CD

thì thể tích chóp

.S ABH

lớn nhất là

A.

3

2

15

a

V =

. B.

3

2

6

a

V =

. C.

3

2

8

a

V =

. D.

3

2

12

a

V =

.

Lời giải

Chọn D

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

19 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Ta có

( )

BC AB

BC SAB

BC SA

⊥



⊥



⊥



( )

3,, 0SC SAB SC SB BSC  = = =

.

Xét

SBC

vuông tại

B

, ta có

3.co 30tSB BC a= =

.

Xét

SBA

vuông tại

A

, ta có

2 222

32S aA SB aaAB = − ==−

.

Ta có

( )

BH SH

BH SAH BH AH

BH SA

⊥



 ⊥  ⊥



⊥



.

1 1 1

. . . . . .

3 3 2

S ABH ABH

V SA S SA HA HB==

.

Lại có

( )

2 2 2

11

..

22

AM GM

HA HB HA HB AB

−

 + =

23

.

1 1 1 2

. . . .

3 2 2 12

S ABH

V SA AB a  =

.

Dấu “=” xảy ra khi

HA HB AHB=  

vuông cân tại

H

, suy ra

45 MDABH =   

.

Vậy

3

.

2

max

12

S ABH

Va=

khi

MD

.

Câu 18: Cho tứ diện đều có cạnh bằng 3, điểm

M

thuộc miền trong đa diện, gọi

1 2 3 4

; ; ;d d d d

là khoảng

cách từ

M

đến 4 mặt của tứ diện. Tìm giá trị nhỏ nhất của

2222

1 2 3 4

P d d d d= + + +

?

A.

min

3

2

P =

. B.

min

3P =

. C.

min

3

2

P =

. D.

min

6P =

.

Lời giải

Chọn C

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 20

Gọi tứ diện đều là

ABCD

,

O

là trọng tâm tam giác

BCD

, chiều cao tứ diện là

,hI

là trung

điểm CD

Khi đó:

2

2 2 2 2

2 2 3

3 .3. 6.

3 3 2

h AO AB BO AB BI



= = − = − = − =





Ta có

ABCD MABC MBCD MACD MABD

V V V V V= + + +



1

MABC MBCD MACD

MABD

ABCD ABCD ABCD ABCD

V V V

V

V V V V

= + + +



3

1 2 4

1

d

d d d

h h h h

= + + +



1 2 3 4

6d d d d+ + + =

.

Theo bất đẳng thức Bunhiacopxki ta có:

( )

2 2 2 2 2

1 2 3 4 1 2 3 4

( ) 4.d d d d d d d d+ + +  + + +



( )

2

3

46

2

PP  

. Vậy

min

3

2

P =

.

Dấu “=” xảy ra



1 2 3 4

6

4

d d d d= = = =



M

là tâm mặt cầu ngoại tiếp tứ diện.

Câu 19: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh bằng

2

,

2SA =

và

SA

vuông góc

với mặt phẳng đáy

( )

ABCD

. Gọi

,MN

là hai điểm thay đổi trên hai cạnh

,AB AD

sao cho mặt

phẳng

( )

SMC

vuông góc với mặt phẳng

( )

SNC

. Biết rằng khi thể tích khối chóp

.S AMCN

đạt

giá trị nhỏ nhất thì biểu thức

2022 2021P AM AN a b a= − = −

với

,ab

. Tính

ab+

.

A.

4

. B.

5

. C.

6

. D.

2

.

Lời giải

Chọn B

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

21 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Đặt

,AM x AN y==

. Trong

( )

ABCD

, gọi

,,O AC BD E BD CM F BD CN=  =  = 

.

Gọi

H

là hình chiếu vuông góc của

O

trên

SC

, khi đó:

CHO

đồng dạng

CAS

( )

2

22

.2

2

3

2 2 2

HO CO CO AS

HO

AS CS CS

 =  = = =

+

.

Ta có:

( )

BD AC

BD SAC BD SC

BD SA

⊥



 ⊥  ⊥



⊥



.

Khi đó:

( )

SC OH SC HE

SC HBD

SC BD SC HF

⊥⊥



 ⊥ 



⊥⊥



.

Do đó:

( ) ( )

(

)

( )

, , 90SCM SCN HE HF= = 

hay

HE HF⊥

.

Ta có:

( ) ( )

11

4 .2. 2 .2. 2 4 2 2

22

AMCN ABCD BCM CDN

S S S S x y x y x y



= − − = − − − − = − + − + = +

.

Suy ra:

( )

.

12

.

33

S AMCN AMCN

V SA S x y= = +

.

Xét tam giác

HEF

vuông tại

H

, có đường cao

2

.OH OE OF=

( )

1

. Ta cần tính

,OE OF

.

Xét tam giác

OAB

với

EM OA C=

; theo định lí Menelaus, ta có:

12

. . 1 . . 1

2 2 4

AM BE OC x BE x

OE

MB EO AC x OE x

=  =  =

−−

. Tương tự:

2

4

y

OF

y

=

−

.

Thay

,OE OF

vừa tìm được vào

( )

1

:

( )( )

( )

22

3 16 4

3 4 4

xy

xy x y xy

xy

=  = − + +

−−

( )( )

2 2 8 2 2 12xy x y x y + + =  + + =

.

Ta có:

( ) ( ) ( ) ( )( )

( )

.

12

2 2 2 8

2 2 4 2 2 2 4 3 1

3 3 3 3

S AMCN

AM GM

V x y x y x y

−=





= + = + + + −  + + − = −





.

Do đó:

( )

.

min

8

31

3

S AMCN

V =−

. Dấu đẳng thức xảy ra khi và chỉ khi

2 2 12 2 3 2x y x y AM BN+ = + =  = = − = =

.

Vì vậy

2022 2021 2 3 2 2, 3P AM AN a b a a b= − = − = +  = =

. Ta có:

5ab+=

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 22

Câu 20: Cho hình chóp

.S ABC

có đáy là tam giác đều cạnh bằng 2,

SA

vuông góc với mặt phẳng chứa

đáy. Gọi

M

là trung điểm của

AB

và



là góc giữa đường thẳng

SM

và mặt phẳng

( )

SBC

.

Biết

6

sin

8



=

, hãy tìm giá trị lớn nhât của thể tích khối chóp

.S ABC

.

A.

3

. B.

4

3

. C.

1

. D.

1

3

.

Lời giải

Chọn C

Diện tích tam giác

ABC

là

3

ABC

S =

.

Gọi

K

là trung điểm của

BC

,

H

là hình chiếu vuông góc của

A

trên

( )

SK AH SBC⊥

.

( )

,d A SBC AH=

.

Gọi

I

là hình chiếu của

M

trên mặt phẳng

( ) ( )

( )

,SBC SM SBC MSI



 = =

.

Đặt

( )

,0SA x x=

2

1SM x = +

.

2 2 2 2

2

1 1 1 1 1 3

3

x

AH

AH AK SA x

x

= + = +  =

+

.

Vì

M

là trung điểm của

AB

nên

( )

2

1 1 3

,,

22

23

x

d M SBC d A SBC MI AH

x

 =  = =

+

.

Ta có:

6

sin

8

MI

SM



==

( )( )

2

22

2 2 2

3

6 3 6 1

23

8 4 8

31

1 3. 1

x

xx

x

xx

x x x

+

 =  =  =

++

+ + +

.

( )( )

2

4 2 2 4 2

22

2

1

4 3 8 4 3 0

8

31

3

x

x x x x x

xx

x

=



=

=  + + =  − + =  



++

=



.

Với

.

1 1 3

1 . .1. 3

3 3 3

S ABC ABC

x V SA S=  = = =

.

Với

.

11

3 . . 3. 3 1

33

S ABC ABC

x V SA S=  = = =

.

Vậy giá trị lớn nhất của thể tích của khối chóp

.S ABC

là

1V =

.

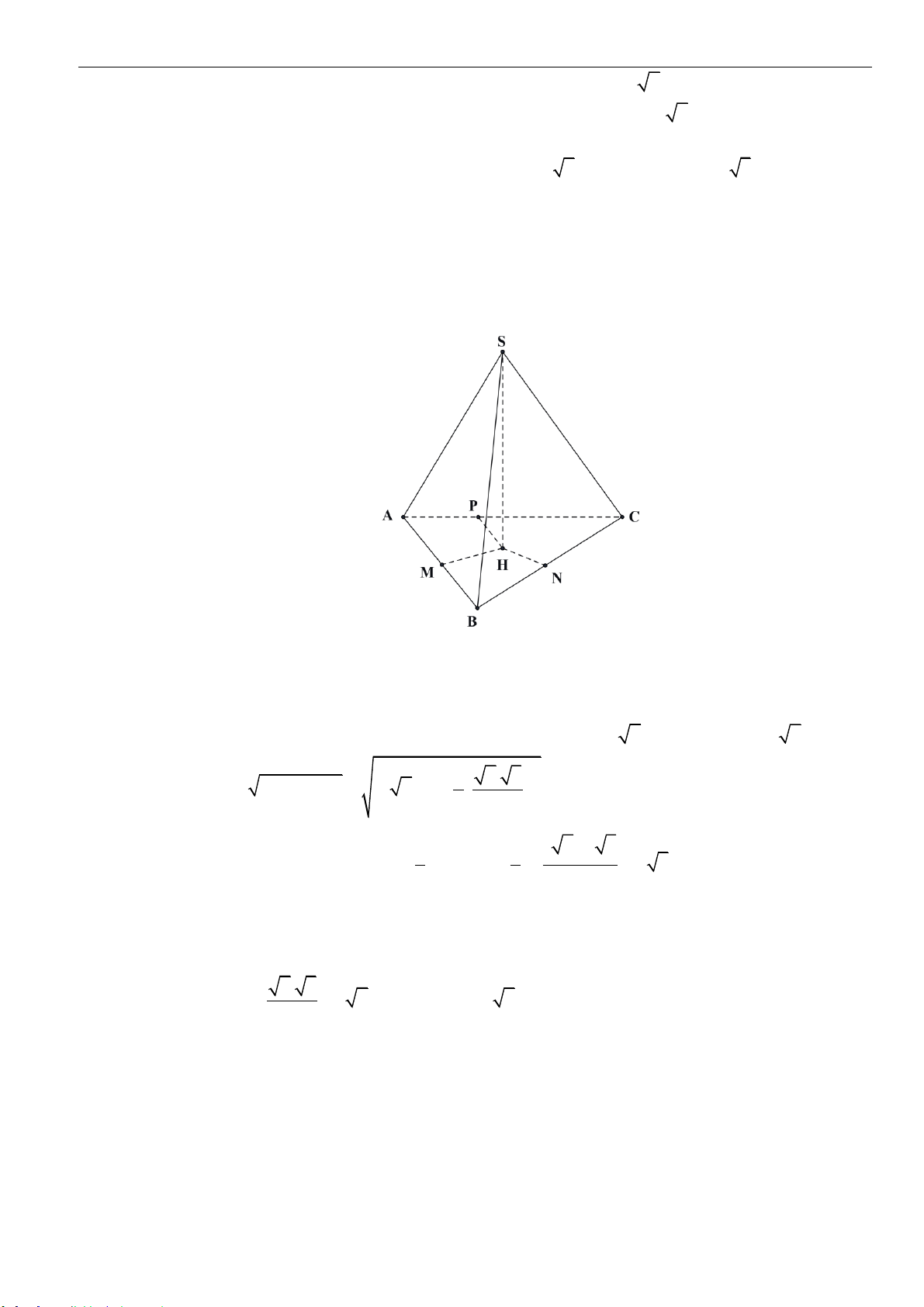
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

23 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Câu 21: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác đều cạnh bằng

6

. Biết rằng các mặt bên của

hình chóp có diện tích bằng nhau và một trong các cạnh bên bằng

32

. Tính thể tích nhỏ nhất

của khối chóp

.S ABC

A.

4

. B.

3

. C.

22

. D.

23

.

Lời giải

Chọn B

Gọi

H

là hình chiếu của

S

trên mặt phẳng đấy

( )

ABC

.

Gọi

M

,

N

,

P

lần lượt là hình chiếu của

H

trên

AB

,

BC

,

CA

. Do vậy

SM

,

SN

và

SP

là

đường cao của các mặt bên tương ứng.

Vì các mặt bên của hình chóp có cùng diện tích nên

SM SN SP==

. Do vậy

HM HN HP==

,

hay ta có

H

là tâm đường tròn nội tiếp hoặc bàng tiếp tam giác

ABC

.

Trường hợp 1:

H

là tâm đường tròn nội tiếp tam giác

ABC

.

Khi đó hình chóp

.S ABC

là hình chóp đều có cạnh đáy bằng

6

, cạnh bên bằng

32

.

Ta có

( )

2

22

2 6. 3

3 2 . 4

32

SH SA AH



= − = − =





.

Thể tích khối chóp

.S ABC

là

( )

2

6 . 3

11

. .4. 2 3

3 3 4

ABC

V SH S= = =

.

Trường hợp 2:

H

là tâm đường tròn bàng tiếp tam giác

ABC

.

Do tam giác

ABC

đều nên không mất tổng quát, giả sử

H

là tâm đường tròn bàng tiếp góc

A

của tam giác

ABC

.

Ta có

6. 3

2. 3 2

2

AH ==

và

6BH CH==

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 24

Nếu

32SA =

thì

22

0SH SA SH= − =

(vô lý).

Nếu

32SA 

thì

22

3 2 2 2SB SC SH SB BH= =  = − =

.

Thể tích khối chóp

.S ABC

là

( )

2

6 . 3

11

. .2 3. 3

3 3 4

ABC

V SH S= = =

.

Vậy thể tích nhỏ nhất của khối chóp

.S ABC

bằng

3

.

Câu 22: Cho hình chóp

.S ABC

có

4SA =

,

2AB =

,

1AC =

và

( )

SA ABC⊥

. Gọi

O

là tâm đường tròn

ngoại tiếp tam giác

ABC

. Mặt cầu tâm

O

, đi qua

A

và cắt các tia

SB

,

SC

lần lượt tại

D

và

E

. Khi độ dài đoạn thẳng

BC

thay đổi, giá trị lớn nhất của thể tích khối chóp

.S ADE

là

A.

64

85

. B.

8

3

. C.

4

3

. D.

256

255

.

Lời giải

Gọi

AM

là đường kính của mặt cầu tâm

O

và đi qua

A

.

Ta có

( )

MB AB

MB SAB MB AD

MB SA

⊥



 ⊥  ⊥



⊥



.

Mà

( )

AD DM AD SBM AD SB⊥  ⊥  ⊥

.

Áp dụng hệ thức lượng cho tam giác vuông ta có

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

25 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

2 2 2

2

2 2 2 2 2

44

.

4 2 5

SD SA SA

SD SB SA

SB SB SA AB

=  = = = =

++

.

Tương tự ta cũng có

2 2 2

2

2 2 2 2 2

4 16

.

4 1 17

SE SA SA

SE SC SA

SC SC SA AC

=  = = = =

++

.

Ta có

.

..

.

4 16 64 64

..

5 17 85 85

S ADE

S ADE S ABC

S ABC

V

SD SE

VV

V SB SC

= = =  =

, do đó

.S ADE

V

đạt giá trị lớn nhất khi

.S ABC

V

đạt giá trị lớn nhất.

Mà

.

1 1 1 1 1 4

. . . .sin . . .4.2.1 .

3 3 2 6 6 3

S ABC ABC

V SAS SA AB AC BAC SA AB AC= =  = =

Suy ra

.

64 4 256

..

85 3 255

S ADE

V =

Câu 23: Cho tam giác

OAB

đều cạnh

2a

. Trên đường thẳng

d

qua

O

và vuông góc với mặt phẳng

( )

OAB

lấy điểm

M

sao cho

OM x=

. Gọi

,EF

lần lượt là hình chiếu vuông góc của

A

trên

MB

và

OB

. Gọi

N

là giao điểm của

EF

với đường thẳng

d

. Tìm

x

sao cho tứ diện

ABMN

có thể tích nhỏ nhất.

A.

a

. B.

2a

. C.

2a

. D.

3a

.

Lời giải

Chọn B

Ta có

22

4.MA MB x a= = +

Gọi

C

là trung điểm của đoạn

22

3AB MC x a = +

.

Ta có

2 2 2 2 2

22

2 2 2 2 2 2

. 2 3 2 2

.

4 4 4

MC AB a x a x a a

AE ME MA AE BE

MB

x a x a x a

++

= =  = − =  =

+ + +

Vì tam giác

OAB

đều nên

F

là trung điểm của cạnh

OB

.

Theo định lí Menelaus, ta có:

2 2 2

22

2 2 2

. . 1 .

2

ON EM FB ON EB ON a a a

ON MN x

NM EB FO ON x EM ON x x a x x

=  =  =  =  = +

+ + +

Theo BĐT Cosi

2

2 2;

a

MN x a

x

 = + 

dấu bằng khi

2.xa=

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 26

Ta có

1

.

3

ABMN OAB

V MN S



=

Để thể tích

ABMN

V

đạt GTNN khi

MN

đạt GTNN

Theo chứng minh trên suy ra

2.xa=

Câu 24: Cho hình chóp

.S ABC

có

, 3, 60 .AB a BC a ABC



= = =

Hình chiếu vuông góc của

S

lên mặt

phẳng

()ABC

là một điểm thuộc cạnh

.BC

Góc giữa đường thẳng

SA

và mặt phẳng

()ABC

bằng

45



. Thể tích khối chóp

.S ABC

đạt giá trị nhỏ nhất bằng

A.

3

12

a

. B.

3

8

a

. C.

3

6

a

. D.

3

a

.

Lời giải

Chọn B

Giả sử

SH

là đường cao của hình chóp

.,S ABC

khi đó

H BC

.

Gọi

AK

là đường cao của tam giác

.ABC

Ta có

2

1 3 3

sin

2 4 2

ABC

S

aa

S AB BC ABC AK

BC

=   =  = =

.

Góc giữa đường thẳng

SA

và

()ABC

là

45 .SAH



=

Suy ra

SH AH=

.

Thể tích khối chóp

.S ABC

là

3

1

34

ABC

a

V S SH SH=  = 

.

Khi đó thể tích khối chóp

.S ABC

nhỏ nhất khi

AH

nhỏ nhất, điều này xảy ra khi

3

2

a

H K SH  =

. Vậy

3

.

3

8

S ABC

a

V =

.

Câu 25: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành, có thể tích là

V

. Gọi

M

là trung

điểm của cạnh

SA

,

N

là điểm trên cạnh

SB

sao cho

2SN NB=

. Mặt phẳng

( )

P

thay đổi đi

qua các điểm

,MN

và cắt các cạnh

,SC SD

lần lượt tại hai điểm phân biệt

,KQ

. Tìm giá trị

lớn nhất của thể tích khối chóp

.S MNKQ

.

A.

2

V

. B.

3

V

. C.

3

4

V

. D.

2

3

V

.

Lời giải

Chọn B

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

27 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Ta có hai công thức sau

Công thức thứ nhất

.

. ' ' '

..

S ABC

S A B C

V

SA SB SC

V SA SB SC

=

  

Công thức thứ hai cho hình chóp có đáy là hình bình hành

SA SC SB SD

+ = +

   

Mặt khác ta có theo công thức thứ nhất

( )

..

.

. . .

1 . . . . 1 1. 1. .

1

2 2 2 . . . . 2 3. 2. .

S MNKQ S MQK

S MNK

S ABCD S ABC S ADC

VV

V

SM SN SK SM SQ SK SK SQ SK

V V V SASB SC SA SD SC SC SD SC

   

= + = + = +

   

   

Và theo công thức thứ hai

31

2

22

SA SC SB SD SC SD

yx

SM SK SN SQ SK SQ

+ = +  + = +  = +

với

,

SC SD

xy

SK SQ

==

.

Khi đó thế lại

( )

1

ta được

.

2

.

1 1 1 1 1 1 2 1

2 3 2 2 3 2 1 6 3 3

S MNKQ

S ABCD

V

x

V x xy x x x x



+



= + = + = 



++



.

Xét hàm số

( )

2

63

x

fx

xx

+

=

+

, với

1x 

. Ta có

( )

2

6 24 6

0, 1

63

xx

f x x

xx

− − −



=   

+

nên hàm số

luôn nghịch biến trên nửa khoảng



)

1;+

.

Suy ra

( ) ( )

1 , 1f x f  

hay

( )

1

3

fx

,

1x

.

Vậy thể tích khối chóp

.S MNKQ

đạt giá trị lớn nhất bằng

3

V

, đạt được khi

KC

.

Câu 26: Cho tam giác đều

ABC

có cạnh bằng

1

. Gọi

d

là đường thẳng vuông góc với mặt phẳng

( )

ABC

tại

A

. Trên đường thẳng

d

lấy điểm

S

. Gọi

P

và

Q

lần lượt là trực tâm của tam giác

ABC

và

SBC

. Thể tích tứ diện

PQBC

lớn nhất bằng:

A.

1

144

. B.

3

144

. C.

1

48

. D.

6

72

.

Lời giải

Chọn A

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 28

Gọi

BI

là đường cao của tam giác

SBC

,

M

là trung điểm

BC

,

H

là chân đường vuông góc

hạ từ

Q

xuống

( )

BPC

. Suy ra

SM BC⊥

,

H AM

Đặt

( )

0SA x x=

, dễ có

2 2 2

3

4

SM SA AM x= + = +

, và

2

1

tan tan

3

2

4

MC

MBQ CSM

SM

x

= = =

+

Khi đó

2

1

.tan

3

4

MQ MB MBQ

x

==

+

,

2

sin

3

4

SA x

SMA

SM

x

==

+

Ta có

11

. .sin .

22

PQM

S PM MQ SMA QH PM==

2

43

x

QH

x

=

+

2

1 1 3

. . .

3 9 36 4 3

PQBC PBC ABC

x

V QH S QH S

x

= = =

+

31

144

36.2.2. 3

x

=

,

( )

0;x +

Dấu bằng xảy ra khi

3

2

x =

Hay thể tích tứ diện

PQBC

lớn nhất bằng

1

144

.

Câu 27: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông tại

C

,

2SA AB==

. Cạnh bên

SA

vuông góc với mặt phẳng đáy

( )

ABC

. Gọi

,HK

lần lượt là hình chiếu của

A

lên

SB

và

SC

. Tính thể tích lớn nhất

max

V

của khối chóp

.S AHK

.

A.

max

3

V =

. B.

max

3

6

V =

. C.

max

2

6

V =

. D.

max

2

3

V =

.

Lời giải

Chọn C

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

29 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Ta có

( )

SA AB

SA ABC

SA AC

⊥



⊥



⊥



.

Vì

2SA AB SAB= =  

vuông cân tại

A

H

là trung điểm của

AB

.

Đặt

AC x=

.

Trong tam giác vuông

SAC

ta có

2

22

4

.

4

SK SA

SA SK SC

SC

SC x

=  = =

+

.

Khi đó

.

..

2 2 2

.

1 4 2 2

. . .

2

4 4 4

S AHK

S AHK S ABC

S ABC

V

SH SK

VV

V SB SC

x x x

= = =  =

+ + +

( )

22

2

.

2 2 2

2

4

2 1 1 2 4 2

. .2. . . 4 . .

3 2 3 3

44

4

S AHK

xx

V x x

xx

x

−

 = − = =

++

+

.

Xét

( )

22

2

4

, 0;2

4

xx

Tx

x

−

=  

+

.

Đặt

( )

2

0;4t x t=  

.

Khi đó

( )

2

4

0;4

4

tt

T g t t

t

−

= =  

+

.

Ta có

( )

( ) ( )

3

16 12 4

0 0;4

3

4

t

g t g t t

t

−



=  =  = 

+

.

Khi đó ta có

( ) ( )

.

1 1 2 1 2

, 0;4

8 8 3 8 6

S AHK

g t t T V       =

.

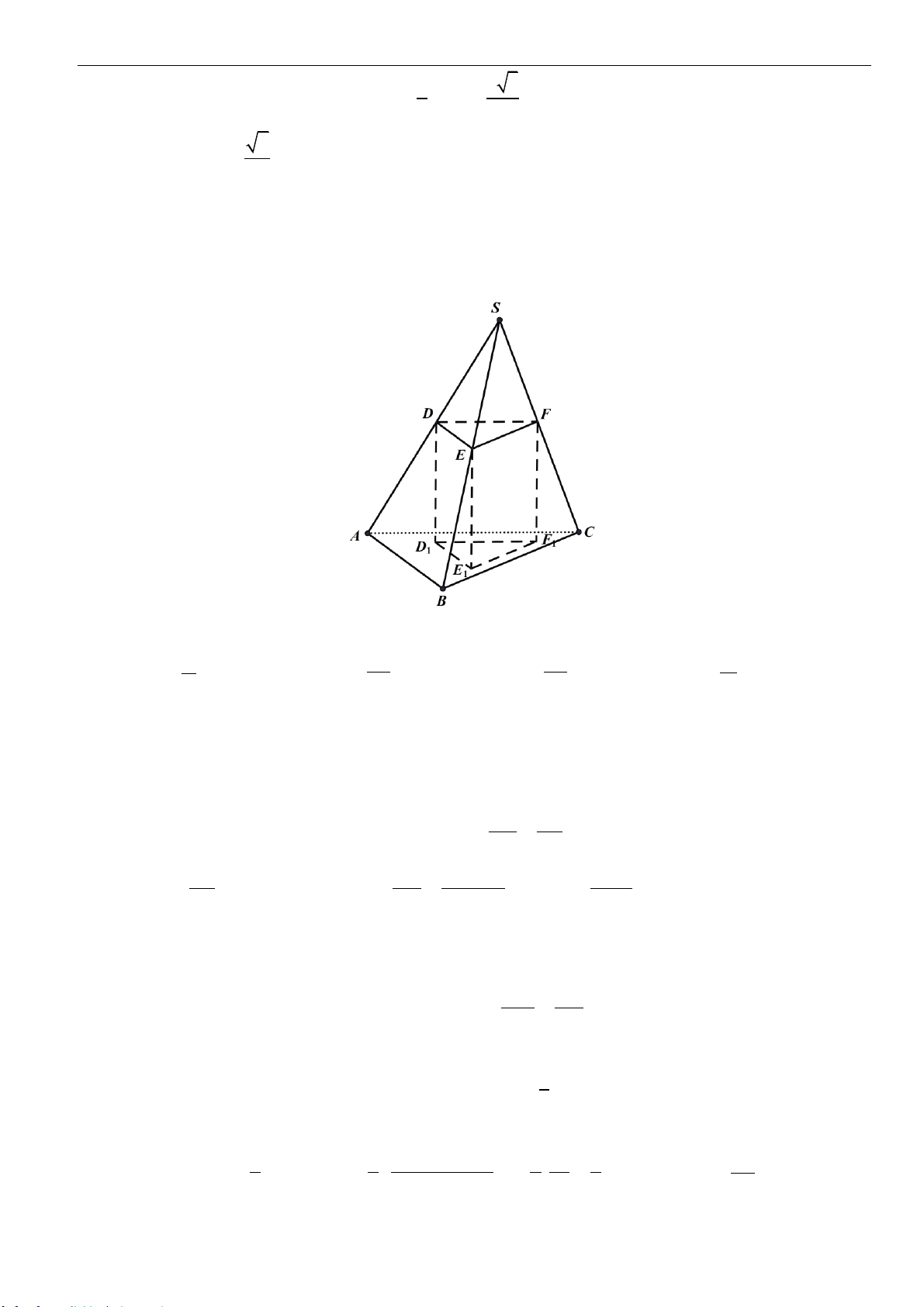
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 30

Dấu bằng xảy ra khi và chỉ khi

4 2 3

33

tx=  =

.

Vậy

max

2

.

6

V =

Câu 28: Cho hình chóp

.S ABC

. Mặt phẳng

()P

song song với đáy và cắt các cạnh

,,SA SB SC

lần lượt

,,D E F

. Gọi

1, 1 1

,,D E F

tương ứng là hình chiếu của

,,D E F

lên mặt phẳng đáy (tham khảo hình

vẽ)

V

là thể tích khối chóp

.S ABC

. Giá trị lớn nhất của thể tích khối đa diện

1 1 1

.DEF D E F

bằng

A.

6

V

. B.

4

9

V

. C.

2

3

V

. D.

12

V

.

Lời giải

Chọn B

Ta có: mặt phẳng

()P

song song với đáy và cắt các cạnh

,,SA SB SC

lần lượt

,,D E F

,,DE DF EF

song song với mặt phẳng

()ABC



Hai tam giác

ABC

và

DEF

theo tỉ số

DE SD

AB SA

=

Đặt

SD

x

SA

=

,

01x

. Khi đó

1

AD SA SD

x

SA SA

−

= = −

và

2

DEF

ABC

S

x

S



=

Do

1, 1 1

,,D E F

tương ứng là hình chiếu của

,,D E F

lên mặt phẳng đáy nên khối đa diện

1 1 1

.DEF D E F

là một hình lăng trụ đứng có chiều cao

1

DD

và đáy là

DEF

Gọi

h

là chiều cao của hình chóp

.S ABC

thì

1

1 (1 )

DD AD

x DD x h

h AS

= = −  = −

Thể tích khối đa diện

1 1 1

.DEF D E F

là:

1 1 1

2 3 2 3

.1

1

. (1 ). . 3( ). . . 3( )

3

DEF D E F DEF DEF ABC

V DD S x h S x x h S x x V

  

= = − = − = −

Áp dụng bất đẳng thức Cosi cho 3 số không âm, ta có:

3

23

3 3 2 2 3 8 4

3( ) . . (2 2 ) .

2 2 3 2 27 9

x x x

x x x x x

+ + −



− = −  = =





hay

1 1 1

.

4

9

DEF D E F

V

V 

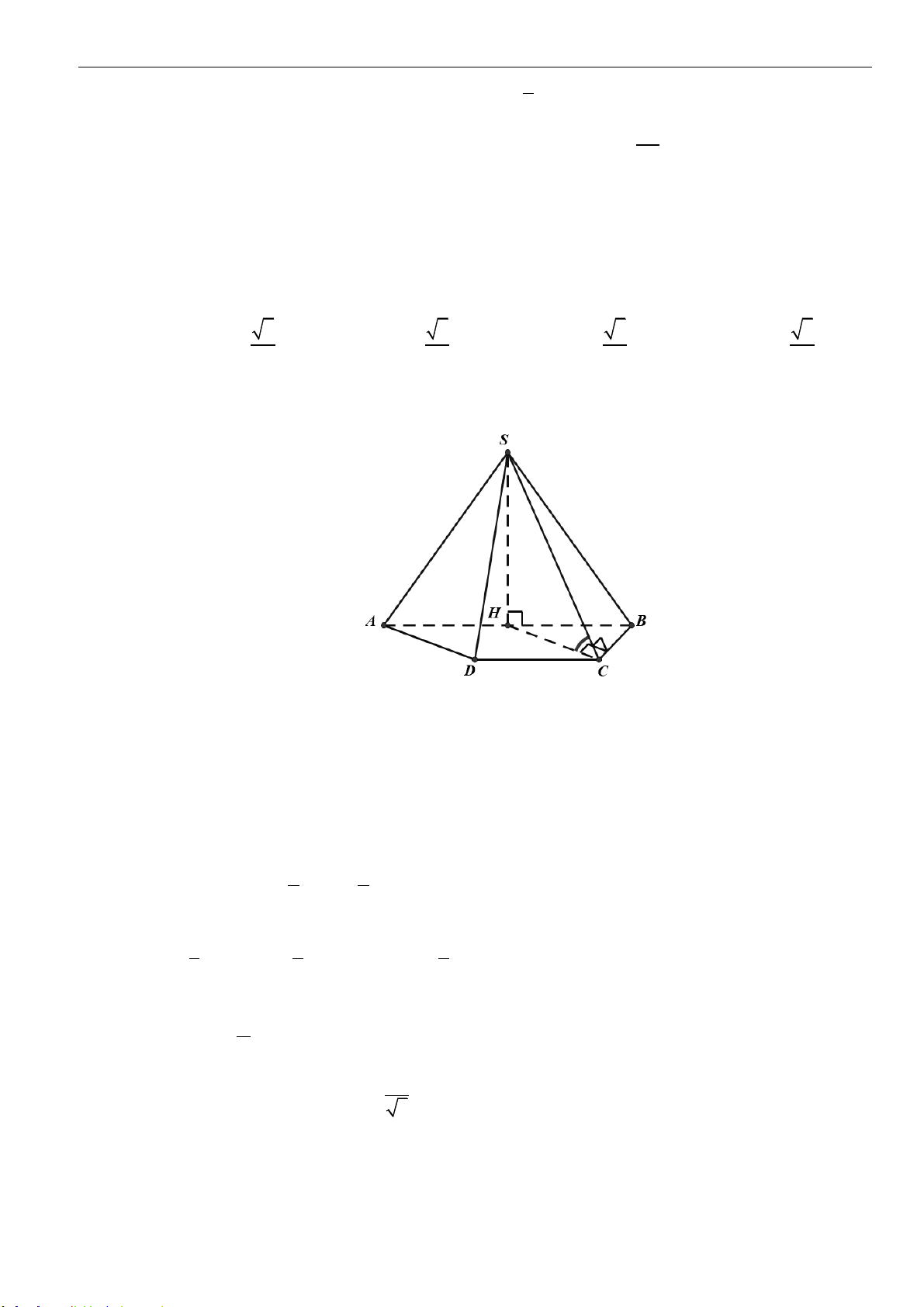
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

31 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Dấu

""=

xảy ra khi và chỉ khi

2

22

3

x x x= −  =

Vậy giá trị lớn nhất của thể tích khối đa diện

1 1 1

.DEF D E F

bằng

4

9

V

Câu 29: Cho hình chóp có đáy là hình thang,

// , 2 ,AB CD AB CD=

45ABC =

. Hình chiếu

vuông góc của đỉnh

S

lên mặt phẳng

( )

ABCD

là trung điểm của cạnh

AB

và

SC BC⊥

,

SC a=

. Gọi góc giữa hai mặt phẳng

( )

SBC

và

( )

ABCD

là



. Khi



thay đổi, tìm

cos



để

thể tích khối chóp

.S ABCD

có giá trị lớn nhất.

A.

6

cos

3



=−

. B.

6

cos

3



=

. C.

3

cos

3



=

. D.

6

cos

3



=

.

Lời giải

Chọn B

Gọi

H

là trung điểm của

AB

ta có

( )

SH ABCD⊥

suy ra

SH BC⊥

. Theo giả thiết

SC BC⊥

ta có

()BC SHC⊥

suy ra

BC HC⊥

, lại vì

45ABC =

nên tam giác

HBC

vuông cân tại

C

.

Từ trên ta cũng suy ra được góc giữa hai mặt phẳng

( )

SBC

và

( )

ABCD

là

SCH

do đó

.sinSH a



=

và

.cosCH a



=

.

Đáy

ABCD

là hình thang với

// , 2AB CD AB CD=

do vậy diện tích đáy được tính theo công thức

2 2 2

33

3 .cos

22

ABCD HCB

S S CH a





= = =

.

Ta có thể tích khối chóp

.S ABCD

được tính theo công thức

( )

3 2 3 3

1 1 1

. .cos .sin . sin sin

3 2 2

ABCD

V SH S a a

   

= = = −

.

Cách 1:

Do

0;

2













nên đặt

sin ,t



=

01t

, xét hàm số

( )

3

( ) , 0;1g t t t t= − 

ta có

2

( ) 1 3 ;g t t



=−

2

1 3 0

1

( ) 0

01

3

t

g t t

t



−=



=   =







. Khi đó ta có bảng biến thiên của

()gt

như sau

.S ABCD

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 32

Qua bảng ta thấy

( )

0;1

12

( ) max ( ) ( )

3 3 3

g t g g t g t



 =  





do đó thể tích của khối chóp lớn nhất

bằng

3

9

max

a

V =

đạt được khi

16

sin cos

3



=  =

.

Cách 2:

32

11

. .cos .sin

32

ABCD

V SH S a



==

Ta có:

2

2 2 2 3

2

3

cos cos cos sin 3

1 sin 3

2 2 2 9

AM GM

a

V

3

9

max

a

V =

đạt được khi

16

sin cos

3



=  =

.

Câu 30: Cho hình chóp

.S ABC

có đáy là tam giác đều cạnh bằng 2,

SA

vuông góc với mặt phẳng chứa

đáy. Gọi

M

là trung điểm của

AB

và

φ

là góc giữa đường thẳng

SM

và mặt phẳng

( )

SBC

.

Biết rằng

6

sinφ

8

=

, tìm giá trị lớn nhất của thể tích khối chóp

.S ABC

.

A.

3

. B.

4

3

. C. 1. D.

1

3

.

Lời giải

Chọn C

Vì đáy của khối chóp

.S ABC

là tam giác đều cạnh bằng 2 nên có diện tích

2

23

3

4

ABC

S ==

.

Đặt

SA a=

(

0a 

) là chiều cao của khối chóp

.S ABC

.

Do khối chóp

.S ABC

có diện tích đáy không đổi nên thể tích lớn nhất khi và chỉ khi chiều cao

lớn nhất, tức là ta đi tìm giá trị lớn nhất của

a

.

Gọi

I

là trung điểm của

BC

. Vì tam giác

ABC

đều, cạnh bằng 2 nên

23

3

2

AI BC

AI

⊥







==





.

Cách 1:

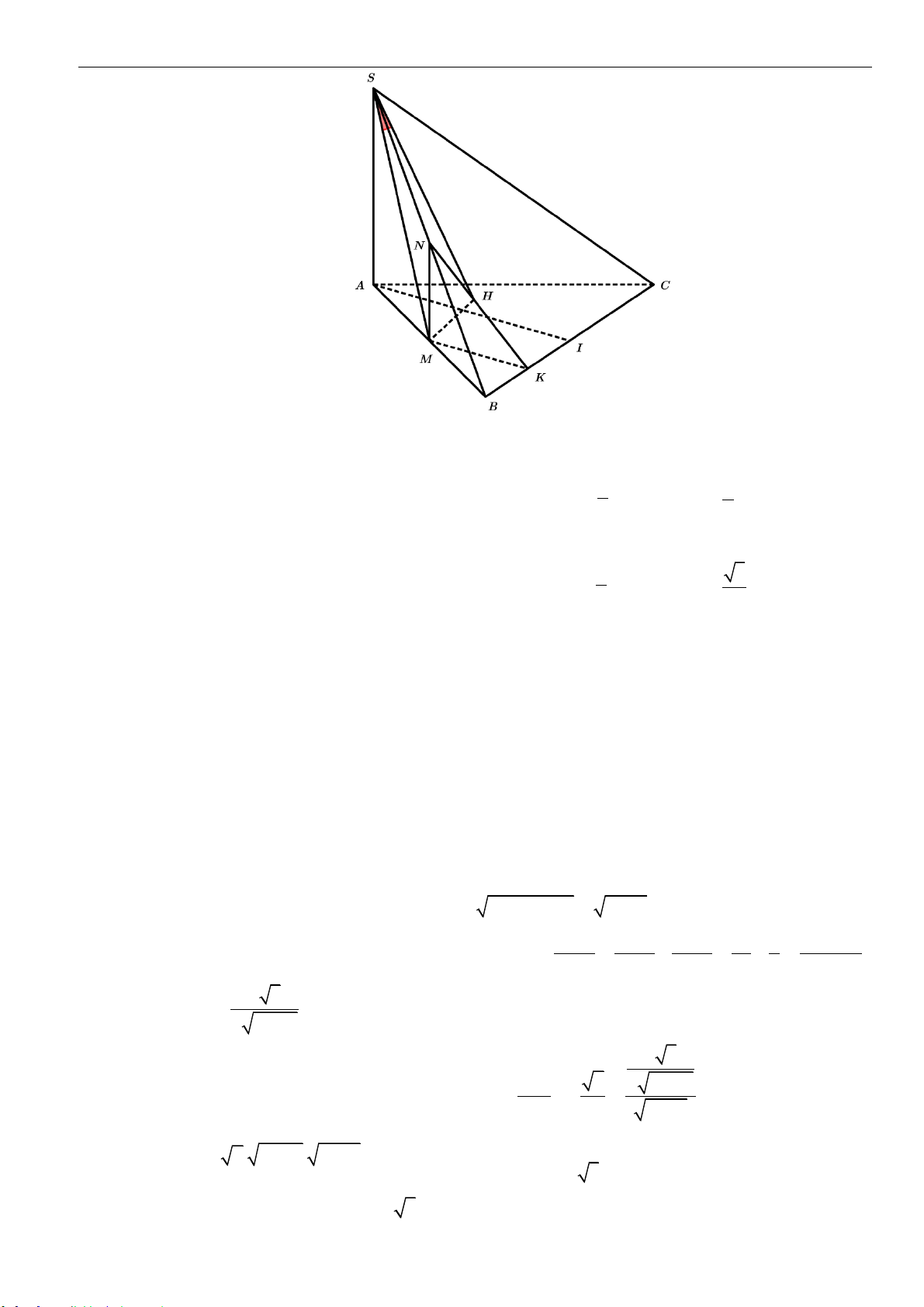
Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

33 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Gọi

N

,

K

lần lượt là trung điểm của

SB

và

IB

.

Xét tam giác

SAB

có

MN

là đường trung bình

1

2

//MN SA

MN SA









=





( )

2

MN ABC

a

MN

⊥









=





.

Xét tam giác

ABI

có

MK

là đường trung bình

1

2

//MK AI

MK AI









=





3

2

MK BC

MK

⊥









=





.

Trong mặt phẳng

( )

MNK

, kẻ

MH NK⊥

tại

H

.

Ta có

( )

Do

BC MK

BC MN MN ABC

⊥







⊥⊥





( )

BC MNK⊥

, mà

( )

MH MNK

do đó

BC MH⊥

.

Lại có

t¹ i MH NK H

MH BC

⊥





⊥



( )

MH SBC⊥

tại

H

.

Mặt khác

( )

t¹ i

SM SBC S

MH SBC H

=







⊥







SH

là hình chiếu của

SM

trên mặt phẳng

( )

SBC

( )

(

)

( )

,,φSM SBC SM SH MSH = = =

.

Xét tam giác

SAM

vuông tại

A

có

2 2 2

1SM SA AM a= + = +

.

Xét tam giác

MNK

vuông tại

M

, có

MH NK⊥

2

2 2 2 2 2

1 1 1 4 4 12 4

33

a

MH MN MK a a

+

 = + = + =

2

3

23

a

MH

a

=

+

.

Xét tam giác

SHM

vuông tại

H

có

2

3

6

23

sin

8

1

a

MH

a

MSH

SM

a

+

=  =

+

2 2 4 2

1

4 2. 3. 1 2 8 6 0

3

a

a a a a a

a

=



 = + +  − + = 



=



(Vì

0a 

).

Suy ra giá trị lớn nhất của

a

là

3

.

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 34

Vậy thể tích lớn nhất của khối chóp

.S ABC

là

max max

11

. . 3. 3 1

33

ABC

V S SA= = =

.

Cách 2:

Trong mặt phẳng

( )

SAI

, kẻ

AE SI⊥

tại

E

.

Ta có:

( )

V×

BC AI

BC SAI

BC SA SA ABC

⊥





⊥



⊥⊥





, mà

( )

AE SAI

suy ra

BC AE⊥

.

Lại có:

t¹ i AE SI E

AE BC

⊥





⊥



( )

AE SBC⊥

tại

E

( )

,d A SBC AE=

.

Xét tam giác

SAI

vuông tại

A

, có

AE SI⊥

2

2 2 2 2 2

1 1 1 1 1 3

33

a

AE SA AI a a

+

 = + = + =

2

3

a

AE

a

=

+

.

Gọi

H

là hình chiếu vuông góc của

M

trên mặt phẳng

( )

SBC

, thế thì

( )

,d M SBC MH=

.

Ta có:

( )

2

,

13

2

,

23

d A SBC

AB a

AM SBC B MH AE

MB

d M SBC

a

 =  = =  = =

+

.

Lại có:

( )

t¹ i

SM SBC S

MH SBC H

=







⊥







SH

là hình chiếu của

SM

trên mặt phẳng

( )

SBC

( )

(

)

( )

,,φSM SBC SM SH MSH = = =

.

Xét tam giác

SAM

vuông tại

A

có

2 2 2

1SM SA AM a= + = +

.

Xét tam giác

SHM

vuông tại

H

có

2

3

6

23

sin

8

1

a

MH

a

MSH

SM

a

+

=  =

+

2 2 4 2

1

4 2. 3. 1 2 8 6 0

3

a

a a a a a

a

=



 = + +  − + = 



=



(Vì

0a 

).

Suy ra giá trị lớn nhất của

a

là

3

.

Vậy thể tích lớn nhất của khối chóp

.S ABC

là

max max

11

. . 3. 3 1

33

ABC

V S SA= = =

.

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

35 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Cách 3:

Chọn hệ trục tọa độ

Oxyz

sao cho gốc

O

trùng với điểm

I

, chiều dương trục

Ox

cùng chiều

với

IA

, chiều dương trục

Oy

cùng chiều với

IB

, chiều dương trục

Oz

cùng chiều với

AS

.

Khi đó ta có tọa độ các điểm

( )

0;0;0I

,

( )

3;0;0A

,

( )

0;1;0B

,

( )

0; 1;0C −

,

( )

3;0;Sa

và

31

; ;0

22

M







.

31

;;

22

MS a



=−





,

( )

0;1;0IB =

,

( )

3;0;IS a=

.

Mặt phẳng

( )

SBC

có 1 vectơ pháp tuyến là

( )

, ;0; 3n IB IS a



= = −



.

Ta có:

( )

(

)

22

2 2 2

31

. .0 3

22

36

sinφ sin , cos ,

8

31

2 1. 3

. 0 3

44

aa

a

SM SBC MS n

aa

−−



= = = = =





++

+ + + +

2 2 4 2

1

4 2. 3. 1 2 8 6 0

3

a

a a a a a

a

=



 = + +  − + = 



=



(Vì

0a 

).

Suy ra giá trị lớn nhất của

a

là

3

.

Vậy thể tích lớn nhất của khối chóp

.S ABC

là

max max

11

. . 3. 3 1

33

ABC

V S SA= = =

.

Câu 31: Cho

,xy

là những số thực dương không đổi. Xét hình chóp

.S ABC

có

,SA x BC y==

và các

cạnh còn lại đều bằng 1. Khi thể tích khối chóp

.S ABC

đạt giá trị lớn nhất thì tích

.xy

bằng

A.

1

3

. B.

4

3

. C.

43

3

. D.

23

.

Lời giải

Chọn B

CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 36

Ta có: do

AB AC SB SC= = =

nên các tam giác

SBC

và

ABC

cân tại

,SA

. Gọi

,MN

lần

lượt là trung điểm

,BC SA

thì

()

BC SM

BC SAM

BC AM

⊥



⊥



⊥



. Từ đây ta hạ

,SH AM H AM⊥

Mà

( ( ))SH BC BC ASM⊥⊥

nên

()SH ABC⊥

Suy ra

2

1

4

y

AM =−

nên

2

1

. . 1

2 2 4

ABC

yy

S AM BC



= = −

Mặt khác vì

SM AM=

nên

SAM

cân tại

M

22

1

44

yx

MN AM AN = − = − −

Mà ta có:

22

2

1

.4

4

..

4

1

4

xy

x

MN SA x y

MN SA SH AM SH x

y

AM y

+

−

−−

=  = = =

−

Suy ra, ta có được

2 2 2 2

2 2 2

22

.

2

2 2 2 2

(4 )

1 1 4

. . . 1 4

3 3 4 2 4 12 12

1 4 2 3

12 3 27

S ABC ABC

x y x y

x y y y xy

V SH S x x y

y

x y x y



−−

= = − = − − =

−

+ + − −

=

Vậy

. max

23

27

S ABC

V =

khi và chỉ khi

2

2 2 2

2 2 4

42

3

33

x y x x y xy



= = −  = =  = =





.

Câu 32: Cho hình chóp

.S ABC

,

O

là trung điểm của

AB

. Điểm

M

di động trên cạnh

SB

. Đặt

SM

x

SB

=

. Mặt phẳng qua

A

,

M

song song với

OC

, cắt

SC

tại

N

. Thể tích khối chóp

ABMN

lớn nhất khi

A.

31x =−

. B.

1x =

. C.

35x =−

. D.

12x = − +

.

Lời giải

Chọn D

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

37 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Trong mặt phẳng

( )

SAB

, gọi

I

là giao điểm của

SO

và

AM

.

Mặt phẳng qua

,AM

, song song với

SO

, cắt

( )

SOC

theo giao tuyến là đường thẳng qua

I

,

đường thẳng đó cắt

SC

tại

N

.

Áp dụng định lý Menelauyt đối với tam giác

SOB

và bộ ba điểm thẳng hàng

,,A I M

ta có

2 2 2

1

1 1 1

SM BA OI SI SM BA x SN x NS x

MB AO IS OI MB AO x CN x CS x

  =  =  =  =  =

− − +

.

Thể tích khối chóp

( )

.

1

,

3

ABMN N ABM ABM

V V S d N ABM= =  

( ) ( )

( )

.

1 2 2

1 , 1

3 1 1

SAB S ABC

xx

x S d C SAB x V

xx

=  −  = −

++

( )

.

4

2 1 6

1

S ABC

xV

x



= − + − +



+



( )

..

4

2 2 1 6 6 4 2

1

S ABC S ABC

x V V

x



 − +  + = −



+



Do đó thể tích khối chóp

ABMN

lớn nhất bằng

( )

.

6 4 2

S ABC

V−

khi

( )

4

2 1 1 2 2 1

1

x x x

x

+ =  + =  = −

+

.

Câu 33: Cho hình chóp

.S ABC

có

SA x=

,

BC y=

,

1AB AC SB SC= = = =

. Thể tích khối chóp

.S ABC

lớn nhất khi

xy+

bằng

A.

3

. B.

2

3

. C.

4

3

. D.

43

.

Lời giải

Chọn C

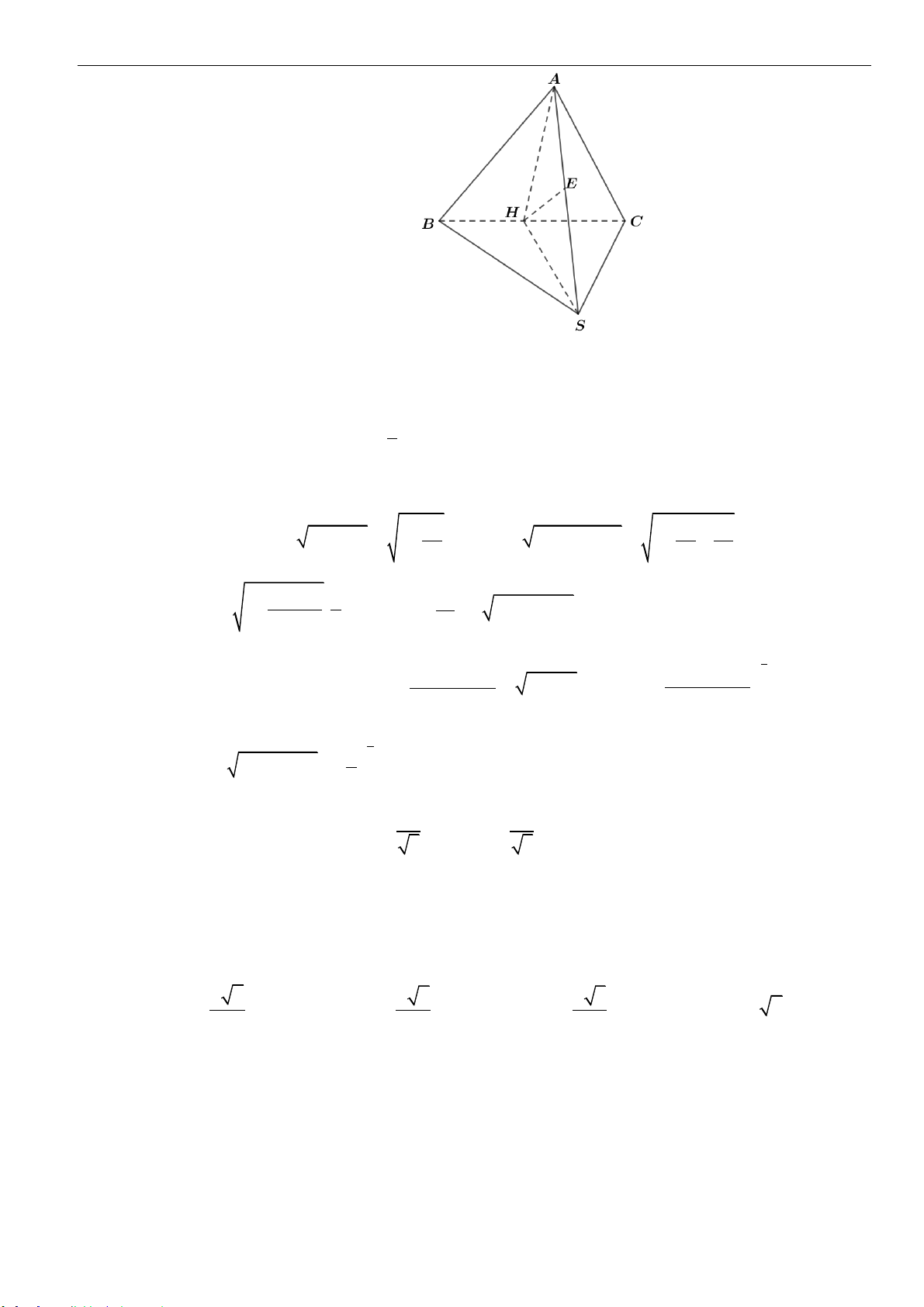
CHƯƠNG 02: THỂ TÍCH KHỐI ĐA DIỆN

TÀI LIỆU TOÁN 12 THPT | 38

Gọi

H

là trung điểm của

BC

khi đó:

( )

SH BC

BC SAH

AH BC

⊥



⊥



⊥



.

Ta có

. . .

1

.

3

S ABC B SAH C SAH SAH

V V V S BC= + =

Gọi

E

là trung điểm của

SA

HE AS⊥

Ta có

2

11

4

y

AH SH HC= = − = −

22

1

44

yx

HE AH AE = − = − −

22

1.

42

SAH

x y x

S

+

 = −

22

.

1

. . 4

12

S ABC

V xy x y = − −

.

Theo bất đăng thức Cô – si ta có:

2 2 2

3

2 2 2

3

abc

++



3

2 2 2

2

3

abc



++







Do đó

3

2

22

4

3

xy x y



− − 





. Dấu bằng xảy ra khi và chỉ khi:

2 2 2 2

2

4

3

x y x y x y= = − −  = =

4

3

xy + =

.

Câu 34: Cho tam giác

OAB

đều cạnh

2a

. Trên đường thẳng

d

qua

O

và vuông góc với mặt phẳng

( )

OAB

lấy điểm

M

sao cho

OM x=

. Gọi

,EF

lần lượt là hình chiếu vuông góc của

A

trên

MB

và

OB

. Gọi

N

là giao điểm của

EF

và

d

. Tìm

x

để thể tích tứ diện

ABMN

có giá trị nhỏ

nhất.

A.

2

=

a

x

. B.

6

12

=

a

x

. C.

3

2

=

a

x

. D.

2=xa

.

Lời giải

Chọn D

Phan Nhật Linh Nắm trọn các chuyên đề ôn thi THPT Quốc Gia

39 | Facebook tác giả: Phan Nhật Linh - SĐT: 0817.098.716

Vì tam giác

OAB

đều cạnh

2a

nên

F

là trung điểm của

OB

do đó

=OF a

. Ta có

( )

;⊥ ⊥  ⊥  ⊥AF OB AF MO AF MOB AF MB

mà

⊥MB AE

suy ra

( )

⊥MB AEF

. Do

đó

⊥MB EF

hay



OBM ONF

. Từ đó ta có

2

. 2 . 2

=  = = =

OB ON OBOF a a a

ON

OM OF OM x x

.

Thể tích

( )

2 2 2 3

2

1 1 4 3 2 3 2 6

. .2 2

3 3 4 3 3



= + = + = +  =





ABMN ABOM ABON OAB

a a a a

V V V S OM ON x a

x

Dấu bằng xảy ra khi

2

2=  =

a

x x a

x

.

Nắm trọn chuyên đề thể tích khối đa diện ôn thi THPT Quốc gia môn Toán

Chương 1: Khối đa diện 172 tài liệu

Toán 12 3.9 K tài liệu

Bình luận

Nắm trọn chuyên đề thể tích khối đa diện ôn thi THPT Quốc gia môn Toán