Ngân hàng câu hỏi số phức: Bài toán tìm số phức – Lê Bá Bảo Toán 12

Ngân hàng câu hỏi số phức: Bài toán tìm số phức – Lê Bá Bảo Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

15 8 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 4: Số phức

Môn: Toán 12

Thông tin:

27 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
SỐ PHỨC
LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ
BÀI TOÁN TÌM SỐ PHỨC
LUYỆN THI THPT QUỐC GIA
CẬP NHẬT TỪ ĐỀ THI MỚI NHẤT
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Ngân hàng câu hỏi:
CÁC BÀI TOÁN LIÊN QUAN ĐẾN TÌM SỐ PHỨC
NỘI DUNG ĐỀ BÀI
Câu 1: Cho số phức
z
thỏa mãn
2 . 3z i z i
. Mô đun của
z
bằng
A.
. B.
5
. C.
3
. D.
3
.
Câu 2: Cho số phức
z
thoả mãn
2 2 2 1z i z i
. Môđun của
z
bằng
A.
4
. B.
2
. C.
2
. D.
22
.
Câu 3: Cho số phức
0z
thỏa mãn
2
(4 7 ).z z i
Tính
.z
A.
65
. B.
56
. C.
65
. D.
56
.
Câu 4: Có bao nhiêu số phức
z
thỏa mãn
1 z z z
?
A.
0
. B.
1
. C.
4
. D.
3
.
Câu 5: Có bao nhiêu số phức
z
thỏa mãn
13
1?
z z i
z i z i



A.
0
. B.
1
. C.
2
. D.
4
.
Câu 6: Cho số phức
z
thỏa mãn
2z i z
. Mệnh đề nào dưới đây đúng?
A.
13
22
z
. B.
35
22
z
. C.
1
2
z
. D.
57
22
z
.
Câu 7: Có bao nhiêu số phức
z
thỏa mãn
3 2 3 ?z z i z
A. 1. B. 0. C. 2. D. Vô số.
Câu 8: Có bao nhiêu số phức
z
thỏa mãn đồng thời hai điều kiện sau:
10 2 2 14z i z i
và
1 10 5zi
?
A. 2. B. 0. C. 1. D. Vô số.
Câu 9: Có bao nhiêu số phức
z
thỏa mãn
1 2 4 3 2i z i
và
2
12z i zi
z
?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 10: Có bao nhiêu số phức z thỏa mãn
6 2 7z z i i i z
?
A. 1. B. 2. C. 3. D. 4.
Câu 11: Cho số phức
1
z
và
2
z
là hai nghiệm của phương trình:
6 3 2 6 9i iz z i
, thỏa mãn:
12
2zz
. Giá trị của biểu thức:
12
P z z
tương ứng bằng
A.
6
. B.
5
. C.
26
. D.
10
.
Câu 12: Cho số phức
1zi
. Biết rằng tồn tại các số phức
12
5,z a i z b
(trong đó
,ab
,
1b
)
thỏa mãn
1 2 1 2
33z z z z z z
. Tính
ba
.
A.
53ba
. B.
23ba
. C.
43ba
. D.
3 3.ba
Câu 13: Có bao nhiêu số phức
z
thỏa mãn đồng thời các điều kiện
2022 2023zi
và
2
z
là số
thuần ảo?
A.
1
. B.
0
. C.
4
. D.
2
.
Câu 14: Cho số phức
,z a bi a b
thỏa mãn
5z
và
2 1 2z i i
là một số thực. Tính
P a b
.
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
A.
5P
. B.
7P
. C.
8P
. D.
4P
.
Câu 15: Có bao nhiêu số phức
z
thỏa mãn
23zi
và
4 5 3zi i i
là số thực?
A.
1
. B.
0
. C.
2
. D.
3
.
Câu 16: Có bao nhiêu số phức
z
thỏa mãn
13z
và
24z i z i
là số thuần ảo?
A.
1
. B.
2
. C.
0
. D.
4
.
Câu 17: Có bao nhiêu số phức
z
thỏa mãn
2
( 2 )zi
là số thuần ảo và
( ) 2z i z
là số thực?
A.
1
. B.
0
. C.
2
. D.
4
.
Câu 18: Gọi
12
,zz
là hai trong các số phức
z
thỏa mãn
3 5 5zi
và
12
6zz
. Tìm môđun của số
phức
12
6 10z z i
.
A.
10
. B.
32
. C.
16
. D.
8
.
Câu 19: Gọi
S
là tập hợp các số thực
m
sao cho với mỗi
mS
có đúng một số phức thỏa mãn
4zm
và
6
z
z
là số thuần ảo. Tính tổng của các phần tử của tập
S
.
A. 0. B. 12. C. 6. D. 14.
Câu 20: Tập hợp các điểm biểu diễn số phức
z
thỏa mãn
2 1 2 z z z
trên mặt phẳng tọa độ là
một
A. đường thẳng. B. đường tròn. C. parabol. D. hypebol.
Câu 21: Cho số phức z thỏa mãn
3 1 3 z i z i
là một số thực. Biết rằng tập hợp các điểm biểu
diễn của
z
là một đường thẳng. Khoảng cách từ gốc tọa độ đến đường thẳng đó bằng
A.
42
. B.
0
. C.
22
. D.
32
.
Câu 22: Biết số phức
z
thỏa mãn điều kiện
3 3 1 5zi
*
. Tập hợp các điểm biểu diễn
z
tạo
thành 1 hình phẳng. Diện tích của hình phẳng đó bằng
A.
25 .
B.
9.
C.
4.
D.
16 .
Câu 23: Cho số phức
z
thỏa mãn
5z
. Biết rằng tập hợp các điểm biểu diễn số phức
23w i z i
là một đường tròn có bán kính bằng
r
. Tìm bán kính
r
.
A.
5
. B.
5
. C.
10
. D.
25
.
Câu 24: Cho số phức
z
thỏa mãn
1zi
. Trên mặt phẳng tọa độ
Oxy
, tập hợp các điểm biểu diễn
của số phức
w
thỏa mãn
23
1
zi
w
iz

là một đường tròn có bán kính bằng
A. 1. B.
5
. C.
25
. D.
20
.
Câu 25: Cho số phức
z
. Gọi
A
,
B
lần lượt là các điểm trong mặt phẳng
Oxy
biểu diễn các số phức
z
và
1 iz
. Tnh
z
biết diện tch tam giác
OAB
bằng
8
.
A.
4z
. B.
42z
. C.
2z
. D.
22z
.
Câu 26: Cho hai số phức
12
,zz
khác
0
, thỏa mãn
22
1 2 1 2
z z z z
.
,MN
lần lượt là hai điểm biểu diễn số
phức
12
,zz
trên mặt phẳng
Oxy
. Mệnh đề nào sau đây đúng?
A. Tam giác
OMN
nhọn và không đều. B. Tam giác
OMN
đều.
C. Tam giác
OMN
tù. D. Tam giác
OMN
vuông.
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Câu 27: Cho số phức
12
,zz
thỏa mãn
12
25zz
. Gọi
, MN
lần lượt là điểm biểu diễn hai số phức
12
,zz
trên mặt phẳng tọa độ. Biết
22MN
. Gọi
H
là đỉnh thứ tư của hình bình hành
OMHN
và
K
là trung điểm của
OM
. Tính
l KH
.
A.
32l
. B.
62l
. C.
41l
. D.
5l
.
Câu 28: Cho số phức
z
thỏa
1 2. 2 3z i z i
. Biết tập hợp các điểm biểu diễn số phức
w 1 . 2 3i z i
là một đường tròn. Bán knh đường tròn đó thuộc khoảng nào sau đây?
A.
1;2
. B.
3;4
. C.
2;3
. D.
0;1
.
Câu 29: Cho số phức
z
thỏa
1 2. 2 3z i z i
. Biết tập hợp các điểm biểu diễn số phức
w 1 . 2 3i z i
là một đường tròn. Bán knh đường tròn đó thuộc khoảng nào sau đây?
A.
1;2
. B.
3;4
. C.
2;3
. D.
0;1
.
Câu 30: Trong mặt phẳng tọa độ
Oxy
, gọi
H
là tập hợp các điểm biểu diễn hình học của số phức
z
thỏa mãn
12
4 3 2 2
zz
zi

. Diện tích của hình phẳng
H
là
A.
44
. B.
88
. C.
24
. D.
84
.
Câu 31: Xét các số phức
z
thỏa mãn
2
2
z
zi
là số thuần ảo. Biết rằng tập hợp các điểm biểu diễn các số
phức
z
luôn thuộc một đường tròn cố định. Bán kính của đường tròn đó bằng
A.
1
. B.
2
. C.
22
. D.
2
.
Câu 32: Trong mặt phẳng tọa độ
Oxy
, tập hợp điểm biểu diễn số phức
1
1
iz
w
z
là một đường tròn
có bán knh bằng
2
. Môđun của
z
thuộc tập nào dưới đây?
A.
1
;2
2



. B.
1
;2
2



. C.
2;2
. D.
1
;2
2



.
Câu 33: Cho hai số phức
,zw
thỏa mãn
23zw
,
2 3 5zw
và
34zw
. Tính giá trị biểu thức
..P z w z w
.
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 34: Có bao nhiêu số phức
z
thoả mãn
1 3 1z i z i
và
3
2
z
z
là một số thuần ảo?
A.
1
. B.
2
. C.
4
. D.
3
.
Câu 35: Có bao nhiêu số phức
z
thỏa mãn
2
3
20z i z
?
A.
4
. B.
3
. C.
2
. D.
6
.
Câu 36: Gọi
S
là tập hợp các số phức
z
thỏa mãn điều kiện
4
zz
. Số phần tử của
S
là
A.
7
. B.
6
. C.
5
. D.
4
.
Câu 37: Cho số phức
z
thỏa mãn
15z
,
1 1 5
17z
z
và
z
có phần ảo dương. Tìm tổng phần thực
và phần ảo của
z
.
A.
2
. B.
4
. C.
6
. D.
8
.
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Câu 38: Cho
z
là số phức có mô-đun bằng
2017
và
w
là số phức thỏa mãn
1 1 1
z w z w

. Mô đun của
số phức
w
là
A.
2015
. B.
0
. C.
1
. D.
2017
.
Câu 39: Cho số phức
,zw
khác 0 thỏa mãn
0zw
và
1 3 6
z w z w

. Khi đó
z
w
bằng
A. 3. B.
1
3
. C.
3
. D.
1
3
.
Câu 40: Gọi
S
là tập hợp các số phức
z
thỏa mãn
10z
. Gọi
12
,zz
là hai số phức thuộc
S
sao cho
1
2
z
z
là số thuần ảo. Gọi
,AB
lần lượt là các điểm biểu diễn số phức
12
,zz
. Diện tích
AOB
bằng
A.
25 3
. B.
50
. C.
25
. D.
50 3.
Câu 41: Có bao nhiêu số nguyên
m
để tồn tại 2 số phức
z
thoả mãn
12z m i z mi
và
3
| | ?
2
z
A. 5. B. 3. C. 4. D. 6.
Câu 42: Cho số phức
z
thay đổi thỏa mãn
14z z i
. Gọi
C
là đường cong tạo bởi tất cả các
điểm biểu diễn số phức
2 2 1z i i
khi
z
thay đổi. Tính diện tích
S
hình phẳng giới hạn
bởi đường cong
C
.
A.
57S
. B.
10 7S
. C.
5 14S
. D.
10 14S
.
Câu 43: Cho số phức
z
thỏa mãn
2
.z
1
2
z
z 
. Biết rằng tập hợp điểm biểu diễn số phức
1 2i 1z
là một đường tròn tâm I và bán kính R. Tìm I và R.
A.
I 0; 2 ,R 5
. B.
I 1; 4 ,R 10
.
C.
I 0;2 ,R 5
. D.
I 1; 4 ,R 10
.
Câu 44: Cho các số phức
1
z
,
2
z
thỏa mãn phương trình
2 3 5zi
và
12
6zz
. Biết rằng tập hợp
các điểm biểu diễn số phức
12
w z z
là một đường tròn. Tính bán knh đường tròn đó.
A.
8R
. B.
4R
. C.
22R
. D.
2R
.
Câu 45: Có bao nhiêu số phức
z
có phần thực và phần ảo đều là các số nguyên thỏa mãn
3 4 6z i z i z i z i
và
10z
?
A.
12
. B.
2
. C.
10
. D.
5
.
Câu 46: Gọi
S
là tập hợp các số phức
z
thỏa mãn
1 34z 
và
12z mi z m i
, (trong đó
m
). Gọi
1
z
,
2
z
là hai số phức thuộc
S
sao cho
12
zz
lớn nhất, khi đó giá trị của
12
zz
bằng
A.
2
. B.
10
. C.
2
. D.
130
.
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Câu 47: Cho số phức
2
3 ( 1) ,z m m i
với m là tham số thực thay đổi. Tập hợp các điểm biểu diễn
số phức z thuộc đường cong. Tính diện tích hình phẳng giới hạn bởi đường cong đó và trục
hoành.
A.
8
.
3
B.
4
.
3
C.
1
.
3
D.
2
.
3
Câu 48: Cho các số phức
12
,zz
thỏa mãn
1
6z
và
2
2z
. Gọi
,MN
lần lượt là các điểm biểu diễn
của các số phức
1
z
và
2
iz
. Biết
60MON 
. Tính
22
12
9T z z
.
A.
T
36 2
. B.
36 3T
. C.
24 3
. D. 18.
Câu 49: Gọi
S
là tập tất cả các giá trị thực của tham số
m
để tồn tại 4 số phức
z
thỏa mãn
2z z z z
và
2z z z z m
là số thuần ảo. Tổng các phần tử của
S
là
A.
21
B.
21
2
. C.
3
2
. D.
1
2
.
Câu 50: Cho số phức
z a bi
,ab
. Biết tập hợp các điểm
A
biểu diễn hình học số phức
z
là
đường tròn
C
có tâm
4;3I
và bán kính
3R
. Đặt
M
là giá trị lớn nhất,
m
là giá trị nhỏ
nhất của
4 3 1F a b
. Tính giá trị
Mm
.
A.
63Mm
. B.
48Mm
. C.
50Mm
. D.
41Mm
.
____________________HẾT____________________
Huế, 15h15’ Ngày 19 tháng 3 năm 2023
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
LỜI GIẢI CHI TIẾT
Câu 1: Cho số phức
z
thỏa mãn
2 . 3z i z i
. Mô đun của
z
bằng:
A.
. B.
5
. C.
3
. D.
3
.
Lời giải:
Đặt
z a bi
.
2 . 3 2 3 2 2 3z i z i a bi i a bi i a b i b a i
2 0 1
2 3 2
a b a
b a b




Suy ra:
22
5z a b
.
Câu 2: Cho số phức
z
thoả mãn
2 2 2 1z i z i
. Môđun của
z
bằng
A.
4
. B.
2
. C.
2
. D.
22
.
Lời giải:
,z x yi x y
.
Ta có:
2 2 2 1x yi i x yi i
2 2 2 2
4 4 4 4 2 2 1 2 1x x y y x x y y
22
4xy
.
Suy ra
22
2z x y
.
Câu 3: Cho số phức
0z
thỏa mãn
2
(4 7 ).z z i
Tính
.z
A.
65
. B.
56
. C.
65
. D.
56
.
Lời giải:
Ta có :
2
2 2 2 2
(4 7 ). (4 7 ) . . 4 7 4 7 65.z z i z z i z z i z
Câu 4: Có bao nhiêu số phức
z
thỏa mãn
1 z z z
?
A.
0
. B.
1
. C.
4
. D.
3
.
Lời giải:
Giả sử
z x yi
, xy
2 z x yi z z x
.
Bài ra ta có
22
22
1
1
1
1
1
21
2







xy
z
xy
zz
x
x
Với
2
1 1 3
1
2 4 2
x y y
.
Do đó có 4 số phức thỏa mãn là
1
13
22
zi
,
2
13
22
zi
,
3
13
22
zi
,
4
13
22
zi
.
Câu 5: Có bao nhiêu số phức
z
thỏa mãn
13
1?
z z i
z i z i



A.
0
. B.
1
. C.
2
. D.
4
.
Lời giải:
Gọi số phức
z a bi
với
,ab
.
Ta có
1
1
z
zi
1z z i
22
22
11a b a b
0ab
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
3
1
zi
zi
22
22
31a b a b
1b
Suy ra
1
1
a
b
. Vậy
1zi
Vậy có
1
số phức thỏa mãn yêu cầu bài toán.
Câu 6: Cho số phức
z
thỏa mãn
2z i z
. Mệnh đề nào dưới đây đúng?
A.
13
22
z
. B.
35
22
z
. C.
1
2
z
. D.
57
22
z
.
Lời giải:
Gọi
0zm
. Khi đó
2z i z
được viết lại thành
2m i z
.
Lấy module 2 vế ta có
2
2 2 2 4 2
2
11
. 2 1 2 1 2 2 0
2(VN)
mm
m i z m m m m m m
m

Do
0m
nên ta có
1m
, suy ra
1z
. Vậy
13
22
z
.
Câu 7: Có bao nhiêu số phức
z
thỏa mãn
3 2 3 ?z z i z
A. 1. B. 0. C. 2. D. Vô số.
Lời giải:
Gọi
,z a bi a b
Theo bài ra ta có
22
3 2 3 4 2 2 3z z i z a bi i a b
22
2 2 2
22
22
2 2 2
0
0
0
42
0
4
23
3
43
a
a
b
a a b
b
a a b
b a b
ab
b a b




Vậy có vô số số phức
z
thỏa mãn điều kiện đã cho.
Câu 8: Có bao nhiêu số phức
z
thỏa mãn đồng thời hai điều kiện sau:
10 2 2 14z i z i
và
1 10 5zi
?
A. 2. B. 0. C. 1. D. Vô số.
Lời giải:
Đặt
z a bi
với
,ab
.
Từ giả thiết
2 2 2 2
10 2 2 14 10 2 2 14z i z i a b a b
.
4
24 32 96 0 4
3
a b a b
.
Ta có:
2
22
2
4
1 10 5 1 10 25 5 20 100 25
3
z i a b b b b



.
2
25 100
100 0 6
93
b b b
.
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Suy ra
4a
. Vậy có một số phức thỏa mãn.
Câu 9: Có bao nhiêu số phức
z
thỏa mãn
1 2 4 3 2i z i
và
2
12z i zi
z
?
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải:
Ta có :
1 2 4 3 2 1 3 3i z i z i
.
Vậy tập hợp các điểm biểu diễn
z
thuộc đường tròn tâm
1
1; 3 ; 3IR
.
2 2 2
1 2 1 2 1 1 2 1z i zi i z i i z i
z z z
2
22
44
5. 1 5 1 0zz
zz
1
1
4 / 5
z
z
zl


Vậy tập hợp các điểm biểu diễn
z
thuộc đường tròn tâm
2
0;0 ; 1OR
.
Vì
12
10; 4IO R R
nên
1 2 1 2
R R IO R R
2 đường tròn cắt nhau tại 2 điểm phân biệt.
Câu 10: Có bao nhiêu số phức z thỏa mãn
6 2 7z z i i i z
?
A. 1. B. 2. C. 3. D. 4.
Lời giải:
Ta có:
6 2 7 7 6 2z z i i i z z z i z z i
(1).
Lấy môđun hai vế ta được:
2 2 2
2
7 1 6 2z z z z
.
Đặt:
;0t z t
ta được:
2 2 2
2
7 1 6 2t t t t
.
2 2 2 4 3 2 3 2
14 50 37 4 4 14 13 4 4 0 1 13 4 0(*)t t t t t t t t t t t t
.
Bấm máy tnh phương trình (*) có 3 nghiệm phân biệt dương.
Ứng với một giá trị t dương thế vào (1) ta tìm ra một số phức
62
7


z z i
z
zi
.
Vậy có 3 số phức z thỏa mãn.
Câu 11: Cho số phức
1
z
và
2
z
là hai nghiệm của phương trình:
6 3 2 6 9i iz z i
, thỏa mãn:
12
2zz
. Giá trị của biểu thức:
12
P z z
tương ứng bằng
A.
6
. B.
5
. C.
26
. D.
10
.
Lời giải:
Trước hết ta tìm quỹ tch điểm biểu diễn số phức
z
thỏa mãn giả thiết:
6 3 2 6 9 . 3 6 2 6 9 3 6 2 6 9 1i iz z i i z i z i z i z i
.
Đặt
z x iy
thay vào (1) ta được:
2 2 2 2
3 6 2 6 9 3 6 2 6 2 9x iy i x iy i x y x y
.
22
3 4 1xy
.
Như vậy điểm biểu diễn số phức
z
là đường tròn (C):
22
0
3 4 1x y z z R
.
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Trong đó:
0
34zi
và
1R
. Điểm I biểu diễn số phức
0
34zi
.
Gọi A là điểm biểu diễn số phức
1
z
và B là điểm biểu diễn số phức
2
z
khi đó ta có:
12
1; 2 2IA IB R AB z z R
. Suy ra AB là một đường kính của đường tròn (C).
Khi đó ta có I là trung điểm của AB tức là:
1 2 0
2 6 8z z z i
.
Suy ra:
12
10P z z
.
Câu 12: Cho số phức
1zi
. Biết rằng tồn tại các số phức
12
5,z a i z b
(trong đó
,ab
,
1b
)
thỏa mãn
1 2 1 2
33z z z z z z
. Tính
ba
.
A.
53ba
. B.
23ba
. C.
43ba
. D.
3 3.ba
Lời giải:
Ta có:
1 2 1 2
33z z z z z z
.
22
2
22
1 4 1 1
25 3 1 16
ab
b a a


22
2 2 2 2 2
1 1 15
23
1 2 1 1 1 3 1 1 1
15
ba
b b a a a b a


22
22
1 1 15
8 1 30 1 1 7 1 0
ba
b b a a
22
1 1 15
23
1
1
3
11
33
4
73
1
7
11
3
2
ba
a
ba
ba
b
ba






.
Câu 13: Có bao nhiêu số phức
z
thỏa mãn đồng thời các điều kiện
2022 2023zi
và
2
z
là số
thuần ảo?
A.
1
. B.
0
. C.
4
. D.
2
.
Lời giải:
Gọi
,,z a bi a b
.
2
2 2 2
2z a bi a b abi
là số thuần ảo nên
2 2 2 2
0a b a b
2022 2023zi
2
22
2022 2023 2022 2023a b i a b
2
2 4044 4045 0 1bb
Do
2. 4045 0
nên phương trình
1
luôn có hai nghiệm trái dấu hay
11
22
( 0)
1
( 0)
b b b
b b b


Với
1
bb
thì
2 2 2
1 1,2 1
a b a b
.
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Với
2
bb
thì
2 2 2
2 3,4 2
a b a b
Vậy có 4 số phức
z
cần tìm.
Câu 14: Cho số phức
,z a bi a b
thỏa mãn
5z
và
2 1 2z i i
là một số thực. Tính
P a b
.
A.
5P
. B.
7P
. C.
8P
. D.
4P
.
Lời giải:
Ta có:
22
5 25 1z a b
.
Mặt khác:
2 1 2 4 3 4 3 4 3z i i a bi i a b b a i
.
2 1 2z i i
là số thực nên
3
4 3 0
4
a
b a b
.
Thay vào
1
ta được
2
22
3
25 16 4 3 7
4
a
a a a b P



.
Câu 15: Có bao nhiêu số phức
z
thỏa mãn
23zi
và
4 5 3zi i i
là số thực?
A.
1
. B.
0
. C.
2
. D.
3
.
Lời giải:
Ta có:
23zi
nên
z
biểu diễn bởi
M
nằm trên đường tròn
C
, tâm
0; 2I
,
3R
.
Ta có:
4 5 3 4 5 4 5w zi i i y xi i i x i y
là số thực nên
w
biễu diễn
bởi điểm
A
nằm trên đường thẳng
50yd
.
Vì
2
25
;7
1
d I d R
nên đường thẳng
d
không cắt đường tròn
;IR
.
Vậy không có số phức
z
nào thỏa mãn yêu cầu bài toán.
Câu 16: Có bao nhiêu số phức
z
thỏa mãn
13z
và
24z i z i
là số thuần ảo?
A.
1
. B.
2
. C.
0
. D.
4
.
Lời giải:
Gọi
z x yi
với
,xy
.
Ta có
22
13 13 (1)z x y
.
Mà
22
2 4 2 4 2 8 ( 6 ).z i z i x yi i x yi i x y y x i
là số thuần ảo khi
22
5
2 8 0 13 2 8 0
2
x y y y y
.
Từ
5
2
y 
thay vào (1) ta được
33
2
33
2
x
x

.
Vậy có 2 số phức thoả yêu cầu bài toán.
Câu 17: Có bao nhiêu số phức
z
thỏa mãn
2
( 2 )zi
là số thuần ảo và
( ) 2z i z
là số thực?
A.
1
. B.
0
. C.
2
. D.
4
.
Lời giải:
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Đặt
z x yi
suy ra
2
2 2 2
2
2 2 2 2 2 2z i x yi i x y i x y x y i


Ta có
2
2zi
là số thuần ảo suy ra:
22
22
2
2
2 0 2 1
2
2
xy
yx
x y x y
xy
yx


22
( ) 2 2 1 2
2 1 2 1 2 2 2
z i z x yi i x yi x y i x yi
x x y y xy x y i x x y y x y i


Ta có
( ) 2z i z
là số thực suy ra:
2 2 0 2xy
Từ (1) và (2) suy ra hệ phương trình:
2
2
0
2
2 2 0
1
2
2
2
3
2 2 0 2
2 2 0 4
3
x
yx
y
yx
xy
yx
x
yx
xy
xy
y




Vậy có hai số phức
z
thỏa mãn yêu cầu bài toán.
Câu 18: Gọi
12
,zz
là hai trong các số phức
z
thỏa mãn
3 5 5zi
và
12
6zz
. Tìm môđun của số
phức
12
6 10z z i
.
A.
10
. B.
32
. C.
16
. D.
8
.
Lời giải:
Tập hợp điểm biểu diễn số phức
z
thỏa mãn
3 5 5zi
là đường tròn
C
tâm
3; 5I
bán
kính
5R
.
Gọi
,MN
lần lượt là điểm biểu diễn của số phức
12
,zz
suy ra
,MN
nằm trên đường tròn
C
.
Gọi
H
là trung điểm của
MN
suy ra
IH MN
.
Do
22
12
6 6 3 4z z MN MH NH IH IM MH
.
1 2 1 2
6 10 3 5 3 5
2 2 8.
z z i z i z i
IM IN IH IH
Câu 19: Gọi
S
là tập hợp các số thực
m
sao cho với mỗi
mS
có đúng một số phức thỏa mãn
4zm
và
6
z
z
là số thuần ảo. Tính tổng của các phần tử của tập
S
.
A. 0. B. 12. C. 6. D. 14.
Lời giải:
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Điều kiện:
6z
.
Giả sử
,z x yi x y
. Ta có
2
2
4 4 16z m x m yi x m y
(C).
Vậy (C) có tâm
;0Im
, bán kính
4R
.
Mặt khác:
2 2 2
2 2 2
6 6 6 6
6 6 6
1 1 1 1
6 6 6
6 6 6
x yi x
zy
i
z z x yi
x y x y x y
.
Khi đó
6
z
z
là số thuần ảo khi phần thực bằng 0 hay
2
2
66
10
6
x
xy


22
22
6 6 6 0 3 9x y x x y
C
.
Vậy:
C
có tâm
3;0I
, bán kính
3R
.
Do đó:
3 ;0 3II m II m

.
Có một số phức
z
thỏa mãn
C
và
C
tiếp xúc trong hoặc tiếp xúc ngoài.
4
31
1
2
12
10
37
7
4
m
m
II R R
m
S
m
m
II R R
m




.
Câu 20: Tập hợp các điểm biểu diễn số phức
z
thỏa mãn
2 1 2 z z z
trên mặt phẳng tọa độ là
một
A. đường thẳng. B. đường tròn. C. parabol. D. hypebol.
Lời giải:
Giả sử
z x yi
, xy
z x yi
2 z z x
.
Bài ra ta có
2
2
2 1 2 2 2 1 2 2 x yi x x y x
22
2 2 2 2 2
1 1 2 1 2 1 4 x y x x x y x x y x
.
Do đó tập hợp các điểm biểu diễn số phức
z
thỏa mãn
2 1 2 z z z
trên mặt phẳng tọa
độ là một parabol.
Câu 21: Cho số phức z thỏa mãn
3 1 3 z i z i
là một số thực. Biết rằng tập hợp các điểm biểu
diễn của
z
là một đường thẳng. Khoảng cách từ gốc tọa độ đến đường thẳng đó bằng
A.
42
. B.
0
. C.
22
. D.
32
.
Lời giải:
Đặt
,, z x yi x y
3 1 3 3 1 3
3 1 . 1 3
3 1 1 3 3 3 1 1


z i z i x yi i x yi i
x y i x y i
x x y y x y y x i
3 1 3 z i z i
là một số thực nên
3 3 1 1 0 x y y x
3 3 9 1 0 4 0 xy x y xy y x x y
.
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Suy ra tập các điểm biểu diễn của z là đường thẳng
có phương trình
40xy
.
Khoảng cách từ gốc tọa độ đến đường thẳng
:
4
; 2 2
2
dO
.
Câu 22: Biết số phức
z
thỏa mãn điều kiện
3 3 1 5zi
*
. Tập hợp các điểm biểu diễn
z
tạo
thành 1 hình phẳng. Diện tích của hình phẳng đó bằng
A.
25 .
B.
9.
C.
4.
D.
16 .
Lời giải:
Gọi
z x yi
với
,xy
3 1 1 3z i x y i
22
3 1 1 3z i x y
22
* 3 1 3 5xy
22
9 1 3 25xy
.
Gọi
1
C
là đường tròn
22
1 3 25xy
;
2
C
là đường tròn
22
1 3 9xy
Tập hợp các điểm biểu diễn
z
là hình vành khăn giới hạn bởi
1
C
và
2
C
và có diện tích
là
25 9 16S
.
Câu 23: Cho số phức
z
thỏa mãn
5z
. Biết rằng tập hợp các điểm biểu diễn số phức
23w i z i
là một đường tròn có bán kính bằng
r
. Tìm bán kính
r
.
A.
5
. B.
5
. C.
10
. D.
25
.
Lời giải:
Đặt
w x yi
, với
,xy
.
Ta có
23w i z i
23x yi i z i
3
2
x y i
z
i


.
Nên, từ
5z
ta có:
3
5
2
x y i
i

3
5
2
x y i
i


2
2
22
3
5
21
xy

2
2
35xy
2
2
3 25xy
.
Vậy, tập hợp điểm biểu diễn số phức
w
là đường tròn tâm
0; 3I
và bán kính
5r
.
Cách khác:
3
5 5 3 5 5
2
wi
z w i MI
i
với
M
và
I
là điểm biểu diễn
w
và
3i
r=5
Câu 24: Cho số phức
z
thỏa mãn
1zi
. Trên mặt phẳng tọa độ
Oxy
, tập hợp các điểm biểu diễn
của số phức
w
thỏa mãn
23
1
zi
w
iz

là một đường tròn có bán kính bằng
A. 1. B.
5
. C.
25
. D.
20
.
Lời giải:
Ta có
23
1
zi
w
iz

1 2 3z iw w i
23
1
wi
z
iw


.
Suy ra
1zi
23
1
1
wi
i
iw

24
1
1
i
iw


1 2 5iw
2 5 1wi
Giả sử
w x yi
, với
,xy
ta có
1
2
2
1 20xy
.
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Vậy tập hợp các điểm biểu diễn của số phức
w
là đường tròn có bán kính
25R
.
Câu 25: Cho số phức
z
. Gọi
A
,
B
lần lượt là các điểm trong mặt phẳng
Oxy
biểu diễn các số phức
z
và
1 iz
. Tnh
z
biết diện tch tam giác
OAB
bằng
8
.
A.
4z
. B.
42z
. C.
2z
. D.
22z
.
Lời giải:
Ta có:
A
,
B
lần lượt là các điểm trong mặt phẳng
Oxy
biểu diễn các số phức
z
và
1 iz
z OA
;
1 i z OB
.
1AB i z z iz z
.
OAB
có
OA OB
và
2 2 2
OA AB OB
OAB
vuông cân tại
A
.
Khi đó:
2
11
. 8 4
22
OAB
S OA AB z z
.
Câu 26: Cho hai số phức
12
,zz
khác
0
, thỏa mãn
22
1 2 1 2
z z z z
.
,MN
lần lượt là hai điểm biểu diễn số
phức
12
,zz
trên mặt phẳng
Oxy
. Mệnh đề nào sau đây đúng?
A. Tam giác
OMN
nhọn và không đều. B. Tam giác
OMN
đều.
C. Tam giác
OMN
tù. D. Tam giác
OMN
vuông.
Lời giải:
Cách 1:
22
1 2 1 2
z z z z
2
1 2 1 2
z z z z
2
1 2 1 2
.z z z z
2
.MN OM ON
1
Lại có:
22
1 2 1 2
z z z z
2
1 2 1 2
z z z z
2
1 2 1 2
.z z z z
2
.OM ON MN
2
Tương tự ta có:
2
.ON OM MN
3
Từ
2
và
3
ta có:
2
2
OM ON
OM ON
ON OM
.
4
Từ
1
và
4
ta có:
22
MN OM MN OM
.
Từ đó suy ra:
OM ON MN
.
Vậy
OMN
đều.
Cách 2: Ta có
2
2 2 2 2 2
1 2 1 2 1 1 2 2 1 2 2
13
00
24
z z z z z z z z z z z



.
1 2 2 1 2 2
1 3 1 3
0
2 2 2 2
z z iz z z iz
12
12
13
22
13
22
z i z
z i z










1
1 2 2
1 2 2
13
22
13
22
z z i z
z z i z








12
zz
2
z
MN ON
.
2
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Cũng từ
1
ta suy ra
12
z z OM ON
.
3
Từ
2
và
3
suy ra
OMN
đều.
Câu 27: Cho số phức
12
,zz
thỏa mãn
12
25zz
. Gọi
, MN
lần lượt là điểm biểu diễn hai số phức
12
,zz
trên mặt phẳng tọa độ. Biết
22MN
. Gọi
H
là đỉnh thứ tư của hình bình hành
OMHN
và
K
là trung điểm của
OM
. Tính
l KH
.
A.
32l
. B.
62l
. C.
41l
. D.
5l
.
Lời giải:
Giả sử
,z x yi x y
.
Ta có:
12
25zz
22
20xy
nên tập hợp điểm biểu diễn số phức là một đường tròn
tâm
O
bán kính
25R
. Khi đó điểm M, N nằm trên đường tròn tâm O bán kính
25R
.
Xét tam giác OMN:
Ta có:
2 2 2
4
cos
2 . 5
OM ON MN
MON
OM ON


.
Vì
180MON OMH
nên
4
cos
5
OMH 
.
Xét tam giác HNK có:
2 2 2
2 . .cosHK MH MK MH MK OMH
22
2 . .cosHK MH MK MH MK OMH
2
2
11
2 . .cos
22
ON OM ON OM OMH



2
2
1 1 4
2 5 .2 5 2.2 5. 2 5.
2 2 5
41
Câu 28: Cho số phức
z
thỏa
1 2. 2 3z i z i
. Biết tập hợp các điểm biểu diễn số phức
w 1 . 2 3i z i
là một đường tròn. Bán knh đường tròn đó thuộc khoảng nào sau đây?
A.
1;2
. B.
3;4
. C.
2;3
. D.
0;1
.
Lời giải:
Đặt
w x yi
;xy
Từ
w 1 . 2 3i z i
w 2 3 1 1 5
w
1 2 2
i i i
z
i



1
Theo giả thiết:
1 2. 2 3z i z i
1 2. 2 3z i z i
2
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Thay
1
vào
2
ta có:
13
.w 1 1 .w 3 8 w 3 2 11. 5
22
i
i i i i w i
Vậy diện tích hình tròn là
2
36SR


.
Câu 29: Cho số phức
z
thỏa
1 2. 2 3z i z i
. Biết tập hợp các điểm biểu diễn số phức
w 1 . 2 3i z i
là một đường tròn. Bán knh đường tròn đó thuộc khoảng nào sau đây?
A.
1;2
. B.
3;4
. C.
2;3
. D.
0;1
.
Lời giải:
Đặt
w x yi
;xy
Từ
w 1 . 2 3i z i
w 2 3 1 1 5
w
1 2 2
i i i
z
i



1
Theo giả thiết:
1 2. 2 3z i z i
1 2. 2 3z i z i
2
Thay
1
vào
2
ta có:
13
.w 1 1 .w 3 8 w 3 2 11. 5
22
i
i i i i w i
2 2 2
2
3 2 5 2 11x y x y
22
20 38 137
0
3 3 3
x y x y
Vậy tập hợp các điểm biểu diễn của số phức w là đường tròn tâm
10 19
;
33
I



, bán kính
52
3
R
.
Câu 30: Trong mặt phẳng tọa độ
Oxy
, gọi
H
là tập hợp các điểm biểu diễn hình học của số phức
z
thỏa mãn
12
4 3 2 2
zz
zi

. Diện tích của hình phẳng
H
là
A.
44
. B.
88
. C.
24
. D.
84
.
Lời giải:
x
y
D
6
O
A
B
I
3
4
M
Cách 1:
Trong mặt phẳng tọa độ
Oxy
, điểm biểu diễn số phức
z x yi
là điểm
;M x y
.
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Ta có
12
4 3 2 2
zz
zi

22
2 12
4 3 8
x
xy
22
6
6
4 3 8
x
x
xy

.
Hình phẳng
H
là hình tô đậm trên hình vẽ.
Ta có
22IA IB
,
2ID
và
22
2 2 4AB AD IA ID
, suy ra
2
AIB
.
Gọi
1
S
là diện tích hình quạt
AIB
. Ta có
2
1
1
2
4
SR


.
Diện tích tam giác
AIB
là
2
1
.4
2
S IA IB
.
Vậy diện tích hình phẳng
H
là
12
24
H
S S S
.
Cách 2:
Hình phẳng
H
được biểu thị là phần tô màu trên hình vẽ (kể cả bờ), là hình giới hạn bởi
đường tròn
C
có tâm
4;3I
, bán kính
22R
và đường thẳng
6x
.
Ta có
22
4 3 8xy
22
3 8 4yx
2
3 8 4yx
.
C
cắt đường thẳng
3y
tại 2 điểm có tọa độ
4 2 2;3
Gọi
0
S
là diện tích của hình phẳng giới hạn bởi các đường
2
3 8 4yx
,
3y
,
6x
,
4 2 2x 
.
Ta có
4 2 2
2
0
6
2. 2. 8 4 d 2,2831
H
S S x x
.
Câu 31: Xét các số phức
z
thỏa mãn
2
2
z
zi
là số thuần ảo. Biết rằng tập hợp các điểm biểu diễn các số
phức
z
luôn thuộc một đường tròn cố định. Bán kính của đường tròn đó bằng
A.
1
. B.
2
. C.
22
. D.
2
.
Lời giải:
Đặt
,,z a bi a b
. Gọi
;M a b
là điểm biểu diễn cho số phức
z
.
Ta có:
22
w
22
z a bi
z i a b i

2
2
22
2
a bi a b i
ab



2
2
2 2 2 2
2
a a b b a b ab i
ab



w
là số thuần ảo
2
2
2 2 0 1
20
a a b b
ab
Ta có
22
1 2 2 0a b a b
.
Suy ra
M
thuộc đường tròn tâm
1;1I
, bán kính
2R
.
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Câu 32: Trong mặt phẳng tọa độ
Oxy
, tập hợp điểm biểu diễn số phức
1
1
iz
w
z
là một đường tròn
có bán knh bằng
2
. Môđun của
z
thuộc tập nào dưới đây?
A.
1
;2
2



. B.
1
;2
2



. C.
2;2
. D.
1
;2
2



.
Lời giải:
Điều kiện
1z 
.
Đặt
,w x yi x y
, điểm
;M x y
là điểm biểu diễn số phức
w
trên mặt phẳng tọa độ
Oxy
. Đặt
2
.zt
Ta có
1
1 1 1 1
1
iz
w w z iz z w i w
z
.
1 1 1 1z w i w z x y i x yi
2 2 2 2
2 1 2 1t x y y x y x


22
1 2 2 1 0 2t x y x yt t
.
Do tập hợp điểm biểu diễn số phức
w
là một đường tròn có bán knh bằng
2
nên
1t
.
Khi đó
22
22
2 1 0
11
x y x yt
tt

.
Theo đề bài ta được
22
2
22
1
1 4 2 5 2 0
11
11
2
2
tz
t
tt
tt
tz

.
Câu 33: Cho hai số phức
,zw
thỏa mãn
23zw
,
2 3 5zw
và
34zw
. Tính giá trị biểu thức
..P z w z w
.
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải:
Đặt
22
;z a w b
với
;0ab
. Ta có:
2 3 2 2 9 . 2 . . 4. . 9 2 4 9.z w z w z w z z z w z w w w a P b
2 3 5 2 3 2 3 25 4. . 6 . . 9. . 25
4 6 9 25.
z w z w z w z z z w z w w w
a P b
3 4 3 3 16 . 3 . . 9. . 16 3 9 16.z w z w z w z z z w z w w w a P b
.
Vậy ta có hệ sau:
2 4 9 1
4 6 9 25 2.
3 9 16 1
a P b a
a P b P
a P b b





Do đó
2P
.
Câu 34: Có bao nhiêu số phức
z
thoả mãn
1 3 1z i z i
và
3
2
z
z
là một số thuần ảo?
A.
1
. B.
2
. C.
4
. D.
3
.
Lời giải:
Đặt
,z x yi x y
. Gọi
;M x y
là điểm biểu diễn của
z
.
1 3 1z i z i
2 2 2 2
1 3 1 1x y x y
20xy
.
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
2
2
3 . 2
33
22
2
x yi x yi
z x yi
z x yi
xy


22
22
22
65
.
22
x y x y
i
x y x y

.
3
2
z
z
là một số thuần ảo
22
2
2
2
6
0
2
z
x y x
xy


22
2
60
z
x y x

M
thuộc đường tròn
C
có tâm
1
;0
2
I



, bán kính
5
2
R
và
MD
.
5
,
22
d I R
nên
cắt
C
tại hai điểm phân biệt trong đó có điểm
D
.
Vậy có một số phức
z
thỏa yêu cầu bài toán.
Câu 35: Có bao nhiêu số phức
z
thỏa mãn
2
3
20z i z
?
A.
4
. B.
3
. C.
2
. D.
6
.
Lời giải:
Ta có
22
33
2 0 2z i z z i z
(*).
Lấy mô-đun hai vế có:
3
2 3 2
(*)
3
3
0
0
0
2 2 2
2
80
3




Thay
z
z
z
z i z z z z i
z
zi
zi
.
Câu 36: Gọi
S
là tập hợp các số phức
z
thỏa mãn điều kiện
4
zz
. Số phần tử của
S
là
A.
7
. B.
6
. C.
5
. D.
4
.
Lời giải:
Ta có:
4
(*)zz
4
zz
3
10zz
0
1
z
z
.
+)
0z
(*)
0
Thay
z
.
+)
1z
(*)
4
1
Thay
z
22
1 1 0zz
1
1
z
z
zi
zi


.
S
có 5 phần tử.
Câu 37: Cho số phức
z
thỏa mãn
15z
,
1 1 5
17z
z
và
z
có phần ảo dương. Tìm tổng phần thực
và phần ảo của
z
.
A.
2
. B.
4
. C.
6
. D.
8
.
Lời giải:
Gọi
z a bi
, , 0a b R b
.
Ta có
15z
2
2
1 25ab
22
2 24 1a b a
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
1 1 5
17z
z
1 1 5
17a bi a bi
22
25
17
a
ab
22
34
02
5
a b a
Trừ vế - vế của
1
cho
2
ta có
53ab
8ab
.
Câu 38: Cho
z
là số phức có mô-đun bằng
2017
và
w
là số phức thỏa mãn
1 1 1
z w z w

. Mô đun của
số phức
w
là
A.
2015
. B.
0
. C.
1
. D.
2017
.
Lời giải:
Ta có
1 1 1
z w z w

2
z w zw
22
0w wz z
3
2
z z i
w


.
Với
3
2
z z i
w

3
2
z z i
w


13
.
2
i
z

2017z
.
Với
3
2
z z i
w

3
2
z z i
w


13
.
2
i
z

2017z
.
Câu 39: Cho số phức
,zw
khác 0 thỏa mãn
0zw
và
1 3 6
z w z w

. Khi đó
z
w
bằng
A. 3. B.
1
3
. C.
3
. D.
1
3
.
Lời giải:
Với hai số phức
,zw
khác 0 thỏa mãn
w0z 
, ta có:
22
2
1 3 6 3 6
3 6 3 2 0
12
33
3 2. 1 0
12
33
wz
w z z w zw z zw w
z w z w zw z w
z
i
zz
w
ww
z
i
w



Suy ra
2
2
1 2 1
33
3
z
w







.
Câu 40: Gọi
S
là tập hợp các số phức
z
thỏa mãn
10z
. Gọi
12
,zz
là hai số phức thuộc
S
sao cho
1
2
z
z
là số thuần ảo. Gọi
,AB
lần lượt là các điểm biểu diễn số phức
12
,zz
. Diện tích
AOB
bằng
A.
25 3
. B.
50
. C.
25
. D.
50 3.
Lời giải:
Tập hợp các điểm biểu diễn số phức
z
là đường tròn
( ):C
;10O
. Suy ra
, ( )A B C
.
Từ giả thiết, ta đặt
11
22
,( ) 1
zz
mi m m m
zz
Ta có
12
10OA OB z z
,
2
2 1 2 2 2
1 10. 1 10 2AB z z z miz z mi m
.
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Suy ra
AOB
vuông tại
O
. Vậy
1
. 50
2
AOB
S OAOB

.
Câu 41: Có bao nhiêu số nguyên
m
để tồn tại 2 số phức
z
thoả mãn
12z m i z mi
và
3
| | ?
2
z
A. 5. B. 3. C. 4. D. 6.
Lời giải:
Đặt
,z a bi a b
. Theo giả thiết ta có
1 1 2
3
2
a m b i a b m i
a bi

2 2 2 2
22
1 1 2
9
4
a m b a b m
ab

2
22
2 2 4 2 3 0 1
9
2
4
m a m b m
ab

Phương trình
1
là phương trình đường thẳng, phương trình
2
là phương trình đường
tròn tâm
O
bán kính
3
2
R
.
Để tồn tại số phước
z
thoả mãn đề bài thì đường thẳng có phương trình
1
phải cắt đường
tròn có phương trình
2
Nghĩa là
,1d O R
2
22
3
3
2
2 2 4 2
m
mm

22
2
1 2 1m m m
42
5 6 2m m m
2
2
1 2 2 0m m m
1 3 1 3m
Vì
m
nên
2; 1;0;1;2m
.
Câu 42: Cho số phức
z
thay đổi thỏa mãn
14z z i
. Gọi
C
là đường cong tạo bởi tất cả các
điểm biểu diễn số phức
2 2 1z i i
khi
z
thay đổi. Tính diện tích
S
hình phẳng giới hạn
bởi đường cong
C
.
A.
57S
. B.
10 7S
. C.
5 14S
. D.
10 14S
.
Lời giải:
Đặt
21
2
2 1 2 1
2 2 1
5
1 2 1
2 1 2 1
x y i
x yi
z i z i
ii
z i i x yi
x yi x yi
zi
ii


Ta có:
2 2 2
2
1 4 2 1 5 4 5z z i x y x y
(1)
Gọi
;M x y
là điểm biểu diễn số phức
2 2 1z i i
khi
z
thay đổi.
12
2; 1 , 5;0FF
.
Từ (1) ta có:
12
45MF MF
.
Do đó quỹ tch điểm
M
là elip nhận
12
,FF
là hai tiêu điểm.
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
22
12
4 5 2 2 5
70
10
2
2 10
2
aa
b a c
F F c c
Vậy diện tích hình phẳng cần tìm là
5 14
C
S ab


.
Câu 43: Cho số phức
z
thỏa mãn
2
.z
1
2
z
z 
. Biết rằng tập hợp điểm biểu diễn số phức
1 2i 1z
là một đường tròn tâm I và bán kính R. Tìm I và R.
A.
I 0; 2 ,R 5
. B.
I 1; 4 ,R 10
.
C.
I 0;2 ,R 5
. D.
I 1; 4 ,R 10
.
Lời giải:
Gọi
i, ,x y x y
. Theo đề bài ta có
1 2i 1z
1i
1
1 2i 1 2i
xy
zz


Từ đó ta có:
2
.z
1
2
z
z 
2
1 i 1 i 1 i
1
1 . .
1 2i 2 1 2i 1 2i
x y x y x y
2
2
2
1 i 1
1
1.
1 2i 2 5
x y x y
22
22
21
1
.
5 2 5
x y x y

22
22
2 2 1x y x y


22
1 4 10xy
Vậy tập hợp các điểm biểu diễn số phức
là một đường tròn có tâm và bán kính là
I 1; 4 ;R 10
.
Câu 44: Cho các số phức
1
z
,
2
z
thỏa mãn phương trình
2 3 5zi
và
12
6zz
. Biết rằng tập hợp
các điểm biểu diễn số phức
12
w z z
là một đường tròn. Tính bán knh đường tròn đó.
A.
8R
. B.
4R
. C.
22R
. D.
2R
.
Lời giải:
Giả sử
A
,
B
lần lượt là các điểm biểu diễn số phức
1
z
,
2
z
trên mặt phẳng tọa độ
Oxy
. Theo
giả thiết ta có
A
,
B
thuộc đường tròn tâm
2;3I
, bán kính
5r
và
6AB
.
Gọi
M
là trung điểm của
AB
khi đó
M
cũng là điểm biểu diễn số phức
12
22
zz
w
u
.
Lại có
2
2 2 2 2
16 4
2
AB
IM IA AM r IM
.
Vậy
M
thuộc đường tròn tâm
2;3I
bán kính
'4r
.
Suy ra các điểm biểu diễn số phức
12
2w z z u
là một đường tròn bán kính
2 8.Rr
Câu 45: Có bao nhiêu số phức
z
có phần thực và phần ảo đều là các số nguyên thỏa mãn
3 4 6z i z i z i z i
và
10z
?
A.
12
. B.
2
. C.
10
. D.
5
.
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Lời giải:
Gọi
M
là điểm biểu diễn số phức
z
,
0; 1 , 0;3 , (0; 4), 0;6A B C D
.
Ta có
3 4 6z i z i z i z i MA MB MC MD
.
Theo bất đẳng thức tam giác ta có
10MC MD CD
.
Do đó
00
2 ( 5).MA MB MC MD a a
Vi vậy
M
thuộc hai elip
12
,EE
có cùng độ lớn là
0
2a
và tâm của hai elip này trùng nhau
tại
0;1I
là trung điểm của
,AB CD
. Do đó
10
12
20
0;1
0;1
Ma
M E E
Ma
Trường hợp 1:
0 0 0
0;1 10 1 10 5 9M a z a a
trường hợp này có 5 số
phức thỏa mãn.
Trường hợp 2:
0 0 0
0;1 10 1 10 5 12M a z a a
trường hợp này có 12 số
phức thỏa mãn.
Vậy có tổng 12 số phức thỏa mãn.
Câu 46: Gọi
S
là tập hợp các số phức
z
thỏa mãn
1 34z 
và
12z mi z m i
, (trong đó
m
). Gọi
1
z
,
2
z
là hai số phức thuộc
S
sao cho
12
zz
lớn nhất, khi đó giá trị của
12
zz
bằng
A.
2
. B.
10
. C.
2
. D.
130
.
Lời giải:
Đặt
z x yi
,
,xy
. Khi đó
1 34z 
2
2
1 34xy
;
12z mi z m i
2 1 2 2 3 0m x m y
.
Do đó tập hợp các điểm
M
biểu diễn số phức
z
là giao điểm của đường tròn
2
2
: 1 34C x y
và đường thẳng
:2 1 2 2 3 0d m x m y
.
Gọi
A
,
B
là hai điểm biểu diễn
1
z
và
2
z
. Suy ra
,C d A B
.
Mặt khác
12
2 2 34z z AB R
do đó
12
max 2 34 2 1;0z z AB R I d
.
Từ đó ta có
1
2
m 
nên
:3 5 3 0d x y
1
2
63
43
zi
zi

.
Vậy
12
2zz
.
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Câu 47: Cho số phức
2
3 ( 1) ,z m m i
với m là tham số thực thay đổi. Tập hợp các điểm biểu diễn
số phức z thuộc đường cong. Tính diện tích hình phẳng giới hạn bởi đường cong đó và trục
hoành.
A.
8
.
3
B.
4
.
3
C.
1
.
3
D.
2
.
3
Lời giải:
Điểm
2
3; 1M m m
biểu diễn số phức
2
31z m m i
nên ta có
2
3; 1x m y m
từ đó
2
2
3 1 6 8y x x x
.
Vậy điểm
M
thuộc đường Parabol
2
68y x x
.
Hoành độ giao điểm của và trục hoành là nghiệm phương trình
2
2
6 8 0
4
x
xx
x
Vậy diện tích hình phẳng giới hạn bởi và trục hoành là
4
2
2
4
6 8dx
3
S x x
.
Câu 48: Cho các số phức
12
,zz
thỏa mãn
1
6z
và
2
2z
. Gọi
,MN
lần lượt là các điểm biểu diễn
của các số phức
1
z
và
2
iz
. Biết
60MON 
. Tính
22
12
9T z z
.
A.
T
36 2
. B.
36 3T
. C.
24 3
. D. 18.
Lời giải:
Trong mặt phẳng tọa độ
Oxy
, gọi
,MN
lần lượt là điểm biểu diễn các số phức
1
z
và
2
iz
, gọi
,EF
lần lượt là các điểm biểu diễn các số phức
2
3iz
và
2
3iz
.
Theo bài ra ta có:
1
6z
nên tập hợp các điểm
M
là đường tròn tâm
O
, bán kính
6R
, gọi là đường tròn
1
C
;
2 2 2
2 . 2z iz i z
do đó tập hợp các điểm
N
biểu diễn số phức
2
iz
thuộc đường
tròn tâm
O
, bán kính
2r
, gọi là đường tròn
2
C
.
Lại thấy :
2
36iz
và
2
36iz
suy ra các điểm
E
,
F
thuộc đường tròn
1
C
.
Hơn nữa:
2
3iz
và
2
3iz
là các số phức đối nên
EF
là một đường kính của
1
C
.
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Mặt khác :
3OE ON
nên
N
nằm giữa
O
và
E
60MOE
, suy ra tam giác
MOE
là tam
giác đều cạnh bằng
6
và tam giác
MEF
vuông tại
M
.
- Khi đó :
2
2 2 2
1 2 1 2 1 2 1 2
9 3 3 . 3 .T z z z iz z iz z iz ME MF
.
- Nhận thấy:
2
6 . 3
. 2. 4. 4. 36 3
4
MEF MOE
ME MF S S

. Vậy
36 3T
.
Câu 49: Gọi
S
là tập tất cả các giá trị thực của tham số
m
để tồn tại 4 số phức
z
thỏa mãn
2z z z z
và
2z z z z m
là số thuần ảo. Tổng các phần tử của
S
là
A.
21
B.
21
2
. C.
3
2
. D.
1
2
.
Lời giải:
Đặt
,,z x yi x y
.
2 2 2 2 1z z z z x yi x y
. (1)
Đặt
2
2z z z z z m z z z m
.
z
là số thuần ảo nên có phần thực bằng 0. Tức là:
22
x y m
. (2)
Tập hợp các điểm
;M x y
thỏa mãn (1) là hình vuông tâm là gốc tọa
Để có 4 cặp số
;xy
thỏa mãn đồng thời (1) và (2) thì (2) phải là một đường tròn nội tiếp hoặc
ngoại tiếp hình vuông nói trên. Tức là
0m
và
1m
hoặc
2
2
m
1m
hoặc
1
2
m
Vậy tổng các phần tử của
S
là
3
2
.
Câu 50: Cho số phức
z a bi
,ab
. Biết tập hợp các điểm
A
biểu diễn hình học số phức
z
là
đường tròn
C
có tâm
4;3I
và bán kính
3R
. Đặt
M
là giá trị lớn nhất,
m
là giá trị nhỏ
nhất của
4 3 1F a b
. Tính giá trị
Mm
.
A.
63Mm
. B.
48Mm
. C.
50Mm
. D.
41Mm
.
Lời giải:
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Cách 1. Ta có phương trình đường tròn
22
: 4 3 9C x y
.
Do điểm
A
nằm trên đường tròn
C
nên ta có
22
4 3 9ab
.
Mặt khác
4 3 1 4 4 3 3 24F a b a b
24 4 4 3 3F a b
.
Ta có
2
22
22
4 4 3 3 4 3 4 3 25.9 255a b a b




.
15 4 4 3 3 15ab
15 24 15F
9 39F
.
Khi đó
39M
,
9m
.
Vậy
48Mm
.
Cách 2. Ta có
13
4 3 1
4
Fb
F a b a

2
22
2
22
13
4 3 9 4 6 9 9
4
25 2 3 3 225 0
Fb
a b b b
b F b F




2
2
3 3 25 5625FF
2
0 16 18 5625 0 9 39.F F F
____________________HẾT____________________
Huế, 15h15’ Ngày 19 tháng 3 năm 2023
| 1/27
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ SỐ PHỨC BÀI TOÁN TÌM SỐ PHỨC
 LUYỆN THI THPT QUỐC GIA
 CẬP NHẬT TỪ ĐỀ THI MỚI NHẤT
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Ngân hàng câu hỏi:
CÁC BÀI TOÁN LIÊN QUAN ĐẾN TÌM SỐ PHỨC NỘI DUNG ĐỀ BÀI Câu 1:
Cho số phức z thỏa mãn 2z  .
i z  3i . Mô đun của z bằng A. 5 . B. 5 . C. 3 . D. 3 . Câu 2:
Cho số phức z thoả mãn z  2  2i  2 z 1 i . Môđun của z bằng A. 4 . B. 2 . C. 2 . D. 2 2 . Câu 3:
Cho số phức z  0 thỏa mãn 2
z z (4  7i). Tính z . A. 65 . B. 56 . C. 65 . D. 56 . Câu 4:
Có bao nhiêu số phức z thỏa mãn z z z  1? A. 0 . B. 1. C. 4 . D. 3 . z 1 z  3i Câu 5:
Có bao nhiêu số phức z thỏa mãn  1? z i z i A. 0 . B. 1. C. 2 . D. 4 . Câu 6:
Cho số phức z thỏa mãn  z iz  2 . Mệnh đề nào dưới đây đúng? 1 3 3 5 1 5 7 A. z  . B.  z  . C. z  . D.  z  . 2 2 2 2 2 2 2 Câu 7:
Có bao nhiêu số phức z thỏa mãn 3z z  2  i 3 z ? A. 1. B. 0. C. 2. D. Vô số. Câu 8:
Có bao nhiêu số phức z thỏa mãn đồng thời hai điều kiện sau: z 10  2i z  2 14i và
z 110i  5 ? A. 2. B. 0. C. 1. D. Vô số. 2 Câu 9:
Có bao nhiêu số phức z thỏa mãn 1 iz  2  4i  3 2 và z
i  1 2zi ? z A. 0 . B. 1. C. 2 . D. 3 .
Câu 10: Có bao nhiêu số phức z thỏa mãn z z  6  i  2i  7  iz ? A. 1. B. 2. C. 3. D. 4.
Câu 11: Cho số phức z và z là hai nghiệm của phương trình: 6 3i iz  2z  6  9i , thỏa mãn: 1 2
z z  2 . Giá trị của biểu thức: P z z tương ứng bằng 1 2 1 2 A. 6 . B. 5 . C. 26 . D. 10 .
Câu 12: Cho số phức z  1  i . Biết rằng tồn tại các số phức z a  5i, z b (trong đó a,b  , b  1 ) 1 2
thỏa mãn 3 z z  3 z z z z . Tính b a . 1 2 1 2
A. b a  5 3 .
B. b a  2 3 .
C. b a  4 3 .
D. b a  3 3.
Câu 13: Có bao nhiêu số phức z thỏa mãn đồng thời các điều kiện z  2022i  2023 và 2 z là số thuần ảo? A. 1. B. 0 . C. 4 . D. 2 .
Câu 14: Cho số phức z a bia,b  thỏa mãn z  5 và z2  i1  2i là một số thực. Tính P a b .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia A. P  5 . B. P  7 . C. P  8 . D. P  4 .
Câu 15: Có bao nhiêu số phức z thỏa mãn z  2i  3 và  zi  4i  53i là số thực? A. 1. B. 0 . C. 2 . D. 3 .
Câu 16: Có bao nhiêu số phức z thỏa mãn z  13 và  z  2i z  4i là số thuần ảo? A. 1. B. 2 . C. 0 . D. 4 .
Câu 17: Có bao nhiêu số phức z thỏa mãn 2
(z  2i) là số thuần ảo và (z i)  z  2 là số thực? A. 1. B. 0 . C. 2 . D. 4 .
Câu 18: Gọi z , z là hai trong các số phức z thỏa mãn z  3  5i  5 và z z  6 . Tìm môđun của số 1 2 1 2
phức   z z  6 10i . 1 2 A.   10 . B.   32 . C.   16 . D.   8 .
Câu 19: Gọi S là tập hợp các số thực m sao cho với mỗi m S có đúng một số phức thỏa mãn z
z m  4 và
là số thuần ảo. Tính tổng của các phần tử của tập S . z  6 A. 0. B. 12. C. 6. D. 14.
Câu 20: Tập hợp các điểm biểu diễn số phức z thỏa mãn 2 z 1  z z  2 trên mặt phẳng tọa độ là một
A. đường thẳng.
B. đường tròn. C. parabol. D. hypebol.
Câu 21: Cho số phức z thỏa mãn  z  3  i z 1 3i là một số thực. Biết rằng tập hợp các điểm biểu
diễn của z là một đường thẳng. Khoảng cách từ gốc tọa độ đến đường thẳng đó bằng A. 4 2 . B. 0 . C. 2 2 . D. 3 2 .
Câu 22: Biết số phức z thỏa mãn điều kiện 3  z  3i 1  5 * . Tập hợp các điểm biểu diễn z tạo
thành 1 hình phẳng. Diện tích của hình phẳng đó bằng A. 25 . B. 9 . C. 4 . D. 16 .
Câu 23: Cho số phức z thỏa mãn z  5 . Biết rằng tập hợp các điểm biểu diễn số phức
w  2  iz  3i là một đường tròn có bán kính bằng r . Tìm bán kính r . A. 5 . B. 5 . C. 10 . D. 25 .
Câu 24: Cho số phức z thỏa mãn z i  1. Trên mặt phẳng tọa độ Oxy , tập hợp các điểm biểu diễn z  2  3i
của số phức w thỏa mãn w  1
là một đường tròn có bán kính bằng iz A. 1. B. 5 . C. 2 5 . D. 20 .
Câu 25: Cho số phức z . Gọi A , B lần lượt là các điểm trong mặt phẳng Oxy biểu diễn các số phức
z và 1 iz . Tính z biết diện tích tam giác OAB bằng 8 . A. z  4 . B. z  4 2 . C. z  2 . D. z  2 2 .
Câu 26: Cho hai số phức z , z khác 0 , thỏa mãn 2 2
z z z z . M , N lần lượt là hai điểm biểu diễn số 1 2 1 2 1 2
phức z , z trên mặt phẳng Oxy . Mệnh đề nào sau đây đúng? 1 2
A. Tam giác OMN nhọn và không đều.
B. Tam giác OMN đều.
C. Tam giác OMN tù.
D. Tam giác OMN vuông.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Câu 27: Cho số phức z , z thỏa mãn z z  2 5 . Gọi M , N lần lượt là điểm biểu diễn hai số phức 1 2 1 2
z , z trên mặt phẳng tọa độ. Biết MN  2 2 . Gọi H là đỉnh thứ tư của hình bình hành 1 2
OMHN và K là trung điểm của OM . Tính l KH . A. l  3 2 . B. l  6 2 . C. l  41 . D. l  5 .
Câu 28: Cho số phức z thỏa z 1 i  2.z  2  3i . Biết tập hợp các điểm biểu diễn số phức
w  1 i.z  2  3i là một đường tròn. Bán kính đường tròn đó thuộc khoảng nào sau đây? A. 1; 2 . B. 3; 4 . C. 2;3 . D. 0;  1 .
Câu 29: Cho số phức z thỏa z 1 i  2.z  2  3i . Biết tập hợp các điểm biểu diễn số phức
w  1 i.z  2  3i là một đường tròn. Bán kính đường tròn đó thuộc khoảng nào sau đây? A. 1; 2 . B. 3; 4 . C. 2;3 . D. 0;  1 .
Câu 30: Trong mặt phẳng tọa độ Oxy , gọi  H  là tập hợp các điểm biểu diễn hình học của số phức
z z 12  z thỏa mãn 
. Diện tích của hình phẳng  H  là
z  4  3i  2 2  A. 4  4 . B. 8  8 . C. 2  4 . D. 8  4 . z  2
Câu 31: Xét các số phức z thỏa mãn
là số thuần ảo. Biết rằng tập hợp các điểm biểu diễn các số z  2i
phức z luôn thuộc một đường tròn cố định. Bán kính của đường tròn đó bằng A. 1. B. 2 . C. 2 2 . D. 2 . 1  iz
Câu 32: Trong mặt phẳng tọa độ Oxy , tập hợp điểm biểu diễn số phức w  1 là một đường tròn z
có bán kính bằng 2 . Môđun của z thuộc tập nào dưới đây? 1   1   1  A.  ;2. B.  ; 2 . C.  2;  2 . D.  ;2.  2   2   2 
Câu 33: Cho hai số phức z, w thỏa mãn z  2w  3, 2z  3w  5 và z  3w  4. Tính giá trị biểu thức P  . z w  . z w . A. 1. B. 2 . C. 3 . D. 4 . z  3
Câu 34: Có bao nhiêu số phức z thoả mãn z 1 3i z 1 i và là một số thuần ảo? z  2 A. 1. B. 2 . C. 4 . D. 3 . 2
Câu 35: Có bao nhiêu số phức z thỏa mãn 3 z  2i z  0 ? A. 4 . B. 3 . C. 2 . D. 6 .
Câu 36: Gọi S là tập hợp các số phức z thỏa mãn điều kiện 4
z z . Số phần tử của S là A. 7 . B. 6 . C. 5 . D. 4 . 1 1 5
Câu 37: Cho số phức z thỏa mãn z 1 5 ,
và z có phần ảo dương. Tìm tổng phần thực z z 17
và phần ảo của z . A. 2 . B. 4 . C. 6 . D. 8 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 1 1 1
Câu 38: Cho z là số phức có mô-đun bằng 2017 và w là số phức thỏa mãn   . Mô đun của z w z w số phức w là A. 2015 . B. 0 . C. 1. D. 2017 . 1 3 6 z
Câu 39: Cho số phức z, w khác 0 thỏa mãn z w  0 và   bằng z w z  . Khi đó w w 1 1 A. 3. B. . C. 3 . D. . 3 3
Câu 40: Gọi S là tập hợp các số phức z thỏa mãn z  10 . Gọi z , z 1
2 là hai số phức thuộc S sao cho
z1 là số thuần ảo. Gọi ,
A B lần lượt là các điểm biểu diễn số phức z , z  1 2 . Diện tích AOB z2 bằng A. 25 3 . B. 50 . C. 25 . D. 50 3.
Câu 41: Có bao nhiêu số nguyên m để tồn tại 2 số phức z thoả mãn z m i z 1 2mi và 3 | z | ? 2 A. 5. B. 3. C. 4. D. 6.
Câu 42: Cho số phức z thay đổi thỏa mãn z 1  z i  4. Gọi C  là đường cong tạo bởi tất cả các
điểm biểu diễn số phức  z  2i2i  
1 khi z thay đổi. Tính diện tích S hình phẳng giới hạn
bởi đường cong C .
A. S  5 7 .
B. S  10 7 .
C. S  5 14 .
D. S  10 14 . 2 . z z
Câu 43: Cho số phức z thỏa mãn z 1 
. Biết rằng tập hợp điểm biểu diễn số phức 2
  1 2i z 1là một đường tròn tâm I và bán kính R. Tìm I và R. A. I 0; 2  ,R  5 . B. I 1; 4  ,R  10 .
C. I 0; 2, R  5 . D. I  1  ; 4  ,R  10 .
Câu 44: Cho các số phức z , z thỏa mãn phương trình z 2 3i 5 và z z 6 . Biết rằng tập hợp 1 2 1 2
các điểm biểu diễn số phức w z
z là một đường tròn. Tính bán kính đường tròn đó. 1 2 A. R 8 . B. R 4 . C. R 2 2 . D. R 2 .
Câu 45: Có bao nhiêu số phức z có phần thực và phần ảo đều là các số nguyên thỏa mãn
z i z  3i z  4i z  6i và z  10 ? A. 12. B. 2 . C. 10. D. 5 .
Câu 46: Gọi S là tập hợp các số phức z thỏa mãn z 1  34 và z 1 mi z m  2i , (trong đó m
). Gọi z , z là hai số phức thuộc S sao cho z z lớn nhất, khi đó giá trị của 1 2 1 2 z z bằng 1 2 A. 2 . B. 10 . C. 2 . D. 130 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Câu 47: Cho số phức 2
z m  3  (m  1)i, với m là tham số thực thay đổi. Tập hợp các điểm biểu diễn
số phức z thuộc đường cong. Tính diện tích hình phẳng giới hạn bởi đường cong đó và trục hoành. 8 4 1 2 A. . B. . C. . D. . 3 3 3 3
Câu 48: Cho các số phức z , z thỏa mãn z  6 và z  2 . Gọi M , N lần lượt là các điểm biểu diễn 1 2 1 2
của các số phức z và iz . Biết MON  60 . Tính 2 2
T z  9z . 1 2 1 2 A. T  36 2 . B. T  36 3 . C. 24 3 . D. 18.
Câu 49: Gọi S là tập tất cả các giá trị thực của tham số m để tồn tại 4 số phức z thỏa mãn
z z z z  2 và z z  2   z z  m là số thuần ảo. Tổng các phần tử của S là 2 1 3 1 A. 2 1 B. . C. . D. . 2 2 2
Câu 50: Cho số phức z a bi a,b   . Biết tập hợp các điểm A biểu diễn hình học số phức z là
đường tròn C  có tâm I 4;3 và bán kính R  3 . Đặt M là giá trị lớn nhất, m là giá trị nhỏ
nhất của F  4a  3b 1. Tính giá trị M m .
A. M m  63 .
B. M m  48 .
C. M m  50 .
D. M m  41.
____________________HẾT____________________
Huế, 15h15’ Ngày 19 tháng 3 năm 2023
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
LỜI GIẢI CHI TIẾT Câu 1:
Cho số phức z thỏa mãn 2z  .
i z  3i . Mô đun của z bằng: A. 5 . B. 5 . C. 3 . D. 3 . Lời giải:
Đặt z a bi .  a b  a  2z  .
i z  3i  2a bi  ia bi  3i  2a b i2b a  2 0 1 3i    
2b a  3 b   2 Suy ra: 2 2 z a b  5 . Câu 2:
Cho số phức z thoả mãn z  2  2i  2 z 1 i . Môđun của z bằng A. 4 . B. 2 . C. 2 . D. 2 2 .
Lời giải:
z x yi , x y   .
Ta có: x yi  2  2i  2 x yi 1 i  2 2 x x
y y    2 2 4 4 4 4
2 x  2x  1  y  2 y   1  2 2 x y  4. Suy ra 2 2 z x y  2 . Câu 3:
Cho số phức z  0 thỏa mãn 2
z z (4  7i). Tính z . A. 65 . B. 56 . C. 65 . D. 56 .
Lời giải: 2 Ta có : 2 2 2 2
z z (4  7i).  z
z (4  7i) .  z z . 4  7i z  4  7  65. Câu 4:
Có bao nhiêu số phức z thỏa mãn z z z  1? A. 0 . B. 1. C. 4 . D. 3 . Lời giải:
Giả sử z x yi x, y    z x yi z z  2x . 2 2 x y  2 2 1  z 1    x y 1  Bài ra ta có      1  z z 1   2x 1 x     2 1 1 3 Với 2 x  
  y 1  y   . 2 4 2 1 3 1 3 1 3 1 3
Do đó có 4 số phức thỏa mãn là z   i , z  
i , z   
i , z    i . 1 2 2 2 2 2 3 2 2 4 2 2 z 1 z  3i Câu 5:
Có bao nhiêu số phức z thỏa mãn  1? z i z i A. 0 . B. 1. C. 2 . D. 4 . Lời giải:
Gọi số phức z a bi với a, b  . z 1 2 2 Ta có
 1  z 1  z i  a   2 2
1  b a  b   1
a b  0 z i
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia z  3i  2 2 1 2
a  b   2 3
a  b   1  b  1 z ia 1 Suy ra 
. Vậy z  1 i b  1
Vậy có 1số phức thỏa mãn yêu cầu bài toán. Câu 6:
Cho số phức z thỏa mãn  z iz  2 . Mệnh đề nào dưới đây đúng? 1 3 3 5 1 5 7 A. z  . B.  z  . C. z  . D.  z  . 2 2 2 2 2 2 2 Lời giải:
Gọi z m  0 . Khi đó  z iz  2 được viết lại thành m iz  2 . Lấy module 2 vế ta có
m   m  
m i . z
2  m m 1  2  m m   2 1 1 2 2 2 4 2
1  2  m m  2  0   2 m  2  (VN) 1 3
Do m  0 nên ta có m  1, suy ra z  1. Vậy  z  . 2 2 Câu 7:
Có bao nhiêu số phức z thỏa mãn 3z z  2  i 3 z ? A. 1. B. 0. C. 2. D. Vô số. Lời giải:
Gọi z a bi  , a b 
Theo bài ra ta có z z    i
z abi  i  2 2 3 2 3 4 2 2 3 a b a  0    2 2 a 0
4a  2 a b b  0                2 2 2 b 0 2 2 4   2 3 a a b b a b      a b 4b  3  a b  2 2 3 2 2 2
Vậy có vô số số phức z thỏa mãn điều kiện đã cho. Câu 8:
Có bao nhiêu số phức z thỏa mãn đồng thời hai điều kiện sau: z 10  2i z  2 14i và
z 110i  5 ? A. 2. B. 0. C. 1. D. Vô số. Lời giải:
Đặt z a bi với a,b  . 2 2 2 2
Từ giả thiết z 10  2i z  2 14i   a 10  b   2  a   2 b 1  4 . 4  2
 4a  32b  96  0  a b  4 . 3 2 2 2  4 
Ta có: z 110i  5  a   1  b 10 2  25  b  5
b  20b 100  25   .  3  25 100 2  b
b 100  0  b  6 . 9 3
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Suy ra a  4 . Vậy có một số phức thỏa mãn. 2 Câu 9:
Có bao nhiêu số phức z thỏa mãn 1 iz  2  4i  3 2 và z
i  1 2zi ? z A. 0 . B. 1. C. 2 . D. 3 . Lời giải:
Ta có : 1 iz  2  4i  3 2  z 1 3i  3 .
Vậy tập hợp các điểm biểu diễn z thuộc đường tròn tâm I  1  ;  3 ; R  3. 1 2 z
i   zi    i 2 z  
i    i 2 1 2 1 2 1 1 2 z  1 i z z z 4  z  1 2 4  5. z  1  5 z 1  0    z  1 2 2 z zz  4  / 5  l
Vậy tập hợp các điểm biểu diễn z thuộc đường tròn tâm O0;0; R 1. 2
Vì IO  10; R R  4 nên R R IO R R 1 2 1 2 1 2
 2 đường tròn cắt nhau tại 2 điểm phân biệt.
Câu 10: Có bao nhiêu số phức z thỏa mãn z z  6  i  2i  7  iz ? A. 1. B. 2. C. 3. D. 4. Lời giải:
Ta có: z z  6  i  2i  7  iz z z  7  i  6 z   z  2i (1). 2 2 2
Lấy môđun hai vế ta được: zz   2 7
1  6 z    z  2 . 2 2 2
Đặt: t z ;t  0 ta được: t t   2 7
1  6t  t  2 . 2
t  2t t   2 4 3 2  t t
t t t t    t   3 2 14 50 37 4 4 14 13 4 4 0
1 t 13t  4  0(*) .
Bấm máy tính phương trình (*) có 3 nghiệm phân biệt dương.
6 z   z  2i
Ứng với một giá trị t dương thế vào (1) ta tìm ra một số phức z  . z  7  i
Vậy có 3 số phức z thỏa mãn.
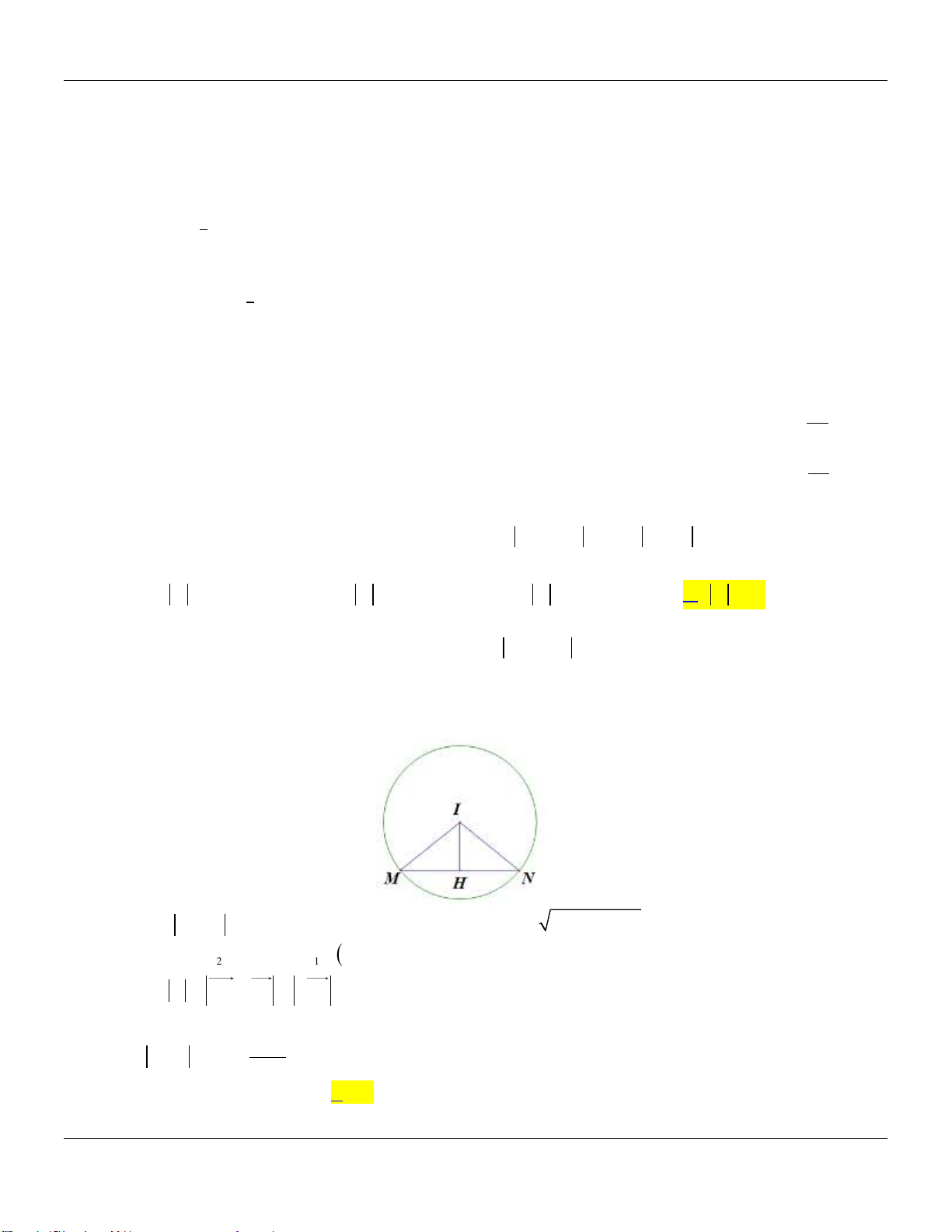
Câu 11: Cho số phức z và z là hai nghiệm của phương trình: 6 3i iz  2z  6  9i , thỏa mãn: 1 2
z z  2 . Giá trị của biểu thức: P z z tương ứng bằng 1 2 1 2 A. 6 . B. 5 . C. 26 . D. 10 . Lời giải:
Trước hết ta tìm quỹ tích điểm biểu diễn số phức z thỏa mãn giả thiết:
6 3i iz  2z  6  9i i . z  3 6i  2z  6  9i z  3 6i  2z  6  9i   1 .
Đặt z x iy thay vào (1) ta được:
x iy   i
x iy  i  x  2  y  2   x  2  y  2 3 6 2 6 9 3 6 2 6 2 9 .
 x  2  y  2 3 4 1. 2 2
Như vậy điểm biểu diễn số phức z là đường tròn (C):  x  
3   y  4 1  z z R . 0
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Trong đó: z  3  4i và R 1. Điểm I biểu diễn số phức z  3  4i . 0 0
Gọi A là điểm biểu diễn số phức z và B là điểm biểu diễn số phức z khi đó ta có: 1 2
IA IB R 1; AB z z  2  2R. Suy ra AB là một đường kính của đường tròn (C). 1 2
Khi đó ta có I là trung điểm của AB tức là: z z  2z  6  8i . 1 2 0
Suy ra: P z z 10. 1 2
Câu 12: Cho số phức z  1 i . Biết rằng tồn tại các số phức z a  5i, z b (trong đó a, b  , b  1) 1 2
thỏa mãn 3 z z  3 z z z z . Tính b a . 1 2 1 2
A. b a  5 3 .
B. b a  2 3 .
C. b a  4 3 .
D. b a  3 3. Lời giải:
Ta có: 3 z z  3 z z z z . 1 2 1 2 
 1 a2  4  b  2 2 1 1   
b a2  25  31 a2 16      b  2
1  1 a2  15   
b  2  b    a    a2    a2 23 1 2 1 1 1 3 1  b  2 1  1 a2  15      b   2
1  1 a2  15   8  b  2 1  30 b  
1 1 a  7 1 a2  0 
b  2   a2 1 1 15   2 3  a    b 1  1 a 1 1  3   
b a  3 3 4 .   7 3 7 b   b 1 1 a 1      3   2
Câu 13: Có bao nhiêu số phức z thỏa mãn đồng thời các điều kiện z  2022i  2023 và 2 z là số thuần ảo? A. 1. B. 0 . C. 4 . D. 2 . Lời giải:
Gọi z a bi,  , a b  .
z  a bi2 2 2 2
a b  2abi là số thuần ảo nên 2 2 2 2
a b  0  a b
z  2022i  2023  a  b  i
a  b  2 2 2 2022 2023 2022  2023 2
 2b  4044b  4045  0   1 Do 2. 4
 045  0 nên phương trình  
1 luôn có hai nghiệm trái dấu hay
  b b (b  0) 1 1 1  
b b (b  0)  2 2 Với b b
a b a   b 1 thì 2 2 2 1 1,2 1 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia Với b b
a b a   b 2 thì 2 2 2 2 3,4 2
Vậy có 4 số phức z cần tìm.
Câu 14: Cho số phức z a bia,b  thỏa mãn z  5 và z2  i1  2i là một số thực. Tính P a b . A. P  5 . B. P  7 . C. P  8 . D. P  4 . Lời giải: Ta có: 2 2
z  5  a b  25  1 .
Mặt khác: z 2  i1 2i  a bi4  3i  4a  3b  4b  3ai . 3a
z 2  i1 2i là số thực nên 4b  3a  0  b  . 4 2  3a  Thay vào   1 ta được 2 2 a
 25  a 16  a  4  b  3  P  7   .  4 
Câu 15: Có bao nhiêu số phức z thỏa mãn z  2i  3 và  zi  4i  53i là số thực? A. 1. B. 0 . C. 2 . D. 3 .
Lời giải:
Ta có: z  2i  3 nên z biểu diễn bởi M nằm trên đường tròn C , tâm I 0; 2 , R  3.
Ta có: w  zi  4i  53i  y xi  4i  5i  x  4  i y  5 là số thực nên w biễu diễn
bởi điểm A nằm trên đường thẳng y  5  0d  .  2   5
Vì d I ; d    
 7  R nên đường thẳng d không cắt đường tròn I ;R. 2 1
Vậy không có số phức z nào thỏa mãn yêu cầu bài toán.
Câu 16: Có bao nhiêu số phức z thỏa mãn z  13 và  z  2i z  4i là số thuần ảo? A. 1. B. 2 . C. 0 . D. 4 . Lời giải:
Gọi z x yi với x, y  . Ta có 2 2
z  13  x y  13 (1) .
Mà  z i z i   x yi ix yi i   2 2 2 4 2 4
x y  2 y  8  ( 6
x).i là số thuần ảo khi 5 2 2
x y  2 y  8  0  13  2 y  8  0  y   . 2  3 3 x  5 2 Từ y   thay vào (1) ta được  . 2  3 3 x    2
Vậy có 2 số phức thoả yêu cầu bài toán.
Câu 17: Có bao nhiêu số phức z thỏa mãn 2
(z  2i) là số thuần ảo và (z i)  z  2 là số thực? A. 1. B. 0 . C. 2 . D. 4 .
Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 2 2 2 2
Đặt z x yi suy ra  z i   x yi i  x    y   2 2 2 2 i  x  
y  2  2xy  2i
Ta có  z i2 2
là số thuần ảo suy ra:    x y   y x x y  2 2
2  0  x   y  22 2 2 2     x     y     1 2
y  x  2
(z i)  z  2   x yi i x yi  2  x   y  
1 i  x  2  yi    
xx  2  yy   1  xy  
x  2 y   1  i    2 2
x  2x y y    x  2y  2i
Ta có (z i)  z  2 là số thực suy ra: x  2y  2  0 2  x  2
y x  2         y  0 y x 2     1
x  2y  2  0        
Từ (1) và (2) suy ra hệ phương trình: 2 y x 2     x        x y      y x 2   3 2 2 0 2  
x  2y  2  0  4    y   3
Vậy có hai số phức z thỏa mãn yêu cầu bài toán.
Câu 18: Gọi z , z là hai trong các số phức z thỏa mãn z  3  5i  5 và z z  6 . Tìm môđun của số 1 2 1 2
phức   z z  6 10i . 1 2 A.   10 . B.   32 . C.   16 . D.   8 . Lời giải:
Tập hợp điểm biểu diễn số phức z thỏa mãn z  3  5i  5 là đường tròn C  tâm I 3; 5 bán kính R  5 .
Gọi M , N lần lượt là điểm biểu diễn của số phức z , z suy ra M , N nằm trên đường tròn C  . 1 2
Gọi H là trung điểm của MN suy ra IH MN . Do 2 2
z z  6  MN  6  MH NH  3  IH
IM MH  4 . 1 2
  z z  6 10i z  3 5i z  3 5i 1 2 1   2  
   IM IN  2IH  2IH  8.
Câu 19: Gọi S là tập hợp các số thực m sao cho với mỗi m S có đúng một số phức thỏa mãn z
z m  4 và
là số thuần ảo. Tính tổng của các phần tử của tập S . z  6 A. 0. B. 12. C. 6. D. 14.
Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Điều kiện: z  6 .
Giả sử z x yi x, y   . Ta có z m   x m yi    x m2 2 4 4
y  16(C).
Vậy (C) có tâm I m;0 , bán kính R  4 . z 6 6
6 x  6  yi 6 x  6 6 y Mặt khác: 1 1 1    i . z  6 z  6 x  6  yix 6 1 2  y
x 62  y x 62 2 2 2  y z 6 x  6 Khi đó
là số thuần ảo khi phần thực bằng 0 hay 1  0 z  6 x 62 2  y
 x  2  y  x     x  2 2 2 6 6 6 0 3
y  9 C .
Vậy: C có tâm I 3;0 , bán kính R  3 .
Do đó: II   3  m;0  II  m  3 .
Có một số phức z thỏa mãn  C  và C tiếp xúc trong hoặc tiếp xúc ngoài. m  4 
II  R R  1  m  3  1 m  2        S  12 .
II  R R  7  m  3  7 m 10   m  4 
Câu 20: Tập hợp các điểm biểu diễn số phức z thỏa mãn 2 z 1  z z  2 trên mặt phẳng tọa độ là một
A. đường thẳng.
B. đường tròn. C. parabol. D. hypebol. Lời giải:
Giả sử z x yi x, y    z x yi z z  2x . Bài ra ta có x   yi x   x  2 2 2 1 2 2 2
1  y  2x  2
 x  2  y  x  2 2 2 2 2 2 1 1
x  2x 1 y x  2x 1  y  4x .
Do đó tập hợp các điểm biểu diễn số phức z thỏa mãn 2 z 1  z z  2 trên mặt phẳng tọa độ là một parabol.
Câu 21: Cho số phức z thỏa mãn  z  3  i z 1 3i là một số thực. Biết rằng tập hợp các điểm biểu
diễn của z là một đường thẳng. Khoảng cách từ gốc tọa độ đến đường thẳng đó bằng A. 4 2 . B. 0 . C. 2 2 . D. 3 2 . Lời giải:
Đặt z x yi,  x, y  
z 3iz 13i  x yi 3ix yi 13i
  x  3   y  
1 i.  x  
1   y  3i    
  x  3 x   1   y  
1  y  3   x  3 y  3   y 1 x 1   i
z 3iz 13i là một số thực nên
x 3y 3 y  1x  1  0  xy 3x 3y 9 xy y x 1 0  x y  4  0.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Suy ra tập các điểm biểu diễn của z là đường thẳng  có phương trình x y  4  0 .
Khoảng cách từ gốc tọa độ đến đường thẳng  : d O  4 ;   2 2 . 2
Câu 22: Biết số phức z thỏa mãn điều kiện 3  z  3i 1  5 * . Tập hợp các điểm biểu diễn z tạo
thành 1 hình phẳng. Diện tích của hình phẳng đó bằng A. 25 . B. 9 . C. 4 . D. 16 .
Lời giải: 2 2
Gọi z x yi với x, y
z  3i 1  x 1  y  3i z 3i 1  x   1   y  3     2 2
x  2   y  2 * 3 1 3
 5  9  x   1
  y  3  25 . 2 2 2 2
Gọi C là đường tròn  x   1
  y  3  25; C là đường tròn x  
1   y  3  9 2  1 
 Tập hợp các điểm biểu diễn z là hình vành khăn giới hạn bởi C và C và có diện tích 2  1 
là S  25  9  16 .
Câu 23: Cho số phức z thỏa mãn z  5 . Biết rằng tập hợp các điểm biểu diễn số phức
w  2  iz  3i là một đường tròn có bán kính bằng r . Tìm bán kính r . A. 5 . B. 5 . C. 10 . D. 25 . Lời giải:
Đặt w x yi , với x, y  .
x   y  3i
Ta có w  2  iz  3i x yi  2  iz  3i z  2  . i
x   y  3i
x   y  3i
Nên, từ z  5 ta có:  5   5 2  i 2  i
x   y  32 2 
 5  x   y  2 2 3
 5  x   y  2 2 3  25. 2 2 2 1
Vậy, tập hợp điểm biểu diễn số phức w là đường tròn tâm I 0; 3
  và bán kính r  5 . w  3i
Cách khác: z  5 
 5  w  3i  5  MI  5 2 
với M và I là điểm biểu diễn i
w và 3i  r=5
Câu 24: Cho số phức z thỏa mãn z i  1. Trên mặt phẳng tọa độ Oxy , tập hợp các điểm biểu diễn z  2  3i
của số phức w thỏa mãn w  1
là một đường tròn có bán kính bằng iz A. 1. B. 5 . C. 2 5 . D. 20 .
Lời giải: z  2  3i w   i Ta có w
z 1iw  w  2  2 3 3i z  1 iz 1 . iw w   i 2   4i
Suy ra z i  2 3 1   i 1 
1  1 iw  2 5  w i  2 5   1 1 iw 1 iw
Giả sử w x yi , với x, y  ta có  
1  x   y  2 2 1  20 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Vậy tập hợp các điểm biểu diễn của số phức w là đường tròn có bán kính R  2 5 .
Câu 25: Cho số phức z . Gọi A , B lần lượt là các điểm trong mặt phẳng Oxy biểu diễn các số phức
z và 1 iz . Tính z biết diện tích tam giác OAB bằng 8 . A. z  4 . B. z  4 2 . C. z  2 . D. z  2 2 . Lời giải:
Ta có: A , B lần lượt là các điểm trong mặt phẳng Oxy biểu diễn các số phức z và
1iz z OA; 1iz OB .
AB  1 iz z iz z .
OAB có OA OB và 2 2 2
OA AB OB OAB  vuông cân tại A . 1 1 2 Khi đó: SO . A AB
z  8  z  4 . OAB 2 2
Câu 26: Cho hai số phức z , z khác 0 , thỏa mãn 2 2
z z z z . M , N lần lượt là hai điểm biểu diễn số 1 2 1 2 1 2
phức z , z trên mặt phẳng Oxy . Mệnh đề nào sau đây đúng? 1 2
A. Tam giác OMN nhọn và không đều.
B. Tam giác OMN đều.
C. Tam giác OMN tù.
D. Tam giác OMN vuông. Lời giải: Cách 1: 2 2
z z z z   z z  z z 1 2 2 1 2 1 2 1 2 2  z z  2
z . z MN OM .ON   1 1 2 1 2 Lại có: 2 2
z z z z 2
z z z  2 z
z z . z  2
z OM ON.MN 2 1 2  1 2  1 2 1 2 1 2 1 2 Tương tự ta có: 2
ON OM .MN 3 2 OM ON
Từ 2 và 3 ta có: 
OM ON . 4 2 ON OM Từ   1 và 4 ta có: 2 2
MN OM MN OM .
Từ đó suy ra: OM ON MN . Vậy OMN đều. 2  1  3 Cách 2: Ta có 2 2 2 2 2
z z z z z z z z  0  z zz  0 . 1 2 1 2 1 1 2 2  1 2  2  2  4   1 3  z    i z  1 2   1 3  1 3  2 2   
  z z
iz  z z iz   0    1 1 2 2 1 2 2     2 2 2 2     1 3 
z    iz 1 2    2 2      1 3 
z z     i z 1 2 2   2 2     
z z z MN ON . 2  1 2 2 1 3 
z z    iz 1 2 2    2 2   
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia Cũng từ  
1 ta suy ra z z OM ON . 3 1 2
Từ 2 và 3 suy ra OMN đều.
Câu 27: Cho số phức z , z thỏa mãn z z  2 5 . Gọi M , N lần lượt là điểm biểu diễn hai số phức 1 2 1 2
z , z trên mặt phẳng tọa độ. Biết MN  2 2 . Gọi H là đỉnh thứ tư của hình bình hành 1 2
OMHN và K là trung điểm của OM . Tính l KH . A. l  3 2 . B. l  6 2 . C. l  41 . D. l  5 .
Lời giải:
Giả sử z x yi x, y   .
Ta có: z z  2 5 2 2
x y  20 nên tập hợp điểm biểu diễn số phức là một đường tròn 1 2
tâm O bán kính R  2 5 . Khi đó điểm M, N nằm trên đường tròn tâm O bán kính R  2 5 . Xét tam giác OMN: 2 2 2
OM ON MN 4 Ta có: cos MON   . 2OM .ON 5 4
Vì MON OMH  180 nên cos OMH   . 5
Xét tam giác HNK có: 2 2 2
HK MH MK  2MH.MK.cos OMH 2   2 2
HK MH MK 2MH.MK.cosOMH 2 1 1  ON OM  
 2ON. OM.cosOMH  2  2   2 2  1  1  4   2 5  .2 5  2.2 5. 2 5.       41  2  2  5 
Câu 28: Cho số phức z thỏa z 1 i  2.z  2  3i . Biết tập hợp các điểm biểu diễn số phức
w  1 i.z  2  3i là một đường tròn. Bán kính đường tròn đó thuộc khoảng nào sau đây? A. 1; 2 . B. 3; 4 . C. 2;3 . D. 0;  1 . Lời giải:
Đặt w  x yi  ; x y  
  i  i   i
Từ w  1 i.z  2  w 2 3 1 1 5 3i z   w     1 1 i  2  2
Theo giả thiết: z 1 i  2.z  2  3i z 1 i  2.z  2  3i 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 1 i 3 Thay   1 vào 2 ta có: .w 
1i  1i.w 38i  w 3i  2w11.i 5 2 2
Vậy diện tích hình tròn là 2
S   R  36 .
Câu 29: Cho số phức z thỏa z 1 i  2.z  2  3i . Biết tập hợp các điểm biểu diễn số phức
w  1 i.z  2  3i là một đường tròn. Bán kính đường tròn đó thuộc khoảng nào sau đây? A. 1; 2 . B. 3; 4 . C. 2;3 . D. 0;  1 . Lời giải:
Đặt w  x yi  ; x y  
  i  i   i
Từ w  1 i.z  2  w 2 3 1 1 5 3i z   w     1 1 i  2  2
Theo giả thiết: z 1 i  2.z  2  3i z 1 i  2.z  2  3i 2 1 i 3 Thay   1 vào 2 ta có: .w 
1i  1i.w 38i  w 3i  2w11.i 5 2 2  20 38 137
x   y  2   x  2   y  2 2 3 2 5 2 11 2 2  x y x y   0 3 3 3 10 1  9 
Vậy tập hợp các điểm biểu diễn của số phức w là đường tròn tâm I ;   , bán kính  3 3  5 2 R  . 3
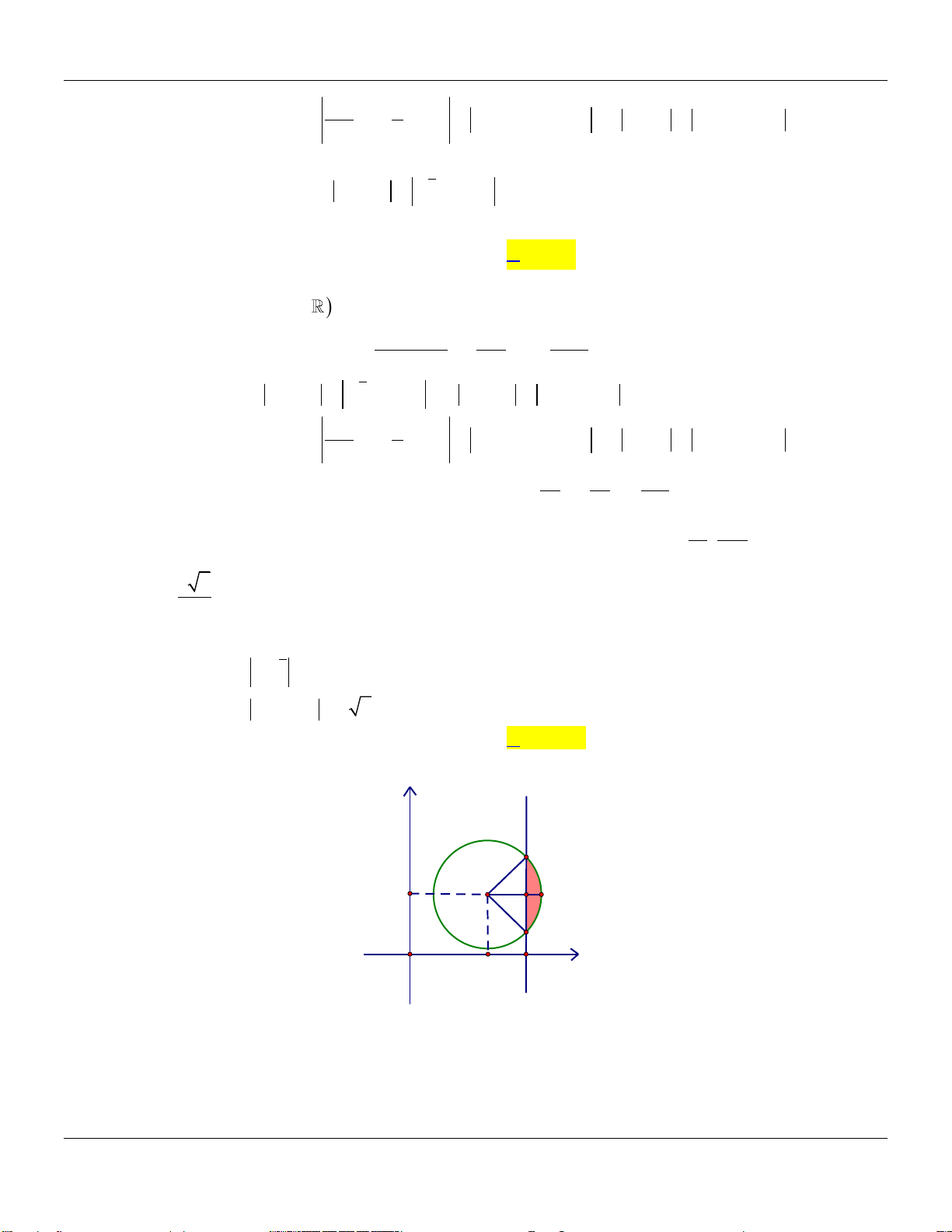
Câu 30: Trong mặt phẳng tọa độ Oxy , gọi  H  là tập hợp các điểm biểu diễn hình học của số phức
z z 12  z thỏa mãn 
. Diện tích của hình phẳng  H  là
z  4  3i  2 2  A. 4  4 . B. 8  8 . C. 2  4 . D. 8  4 .
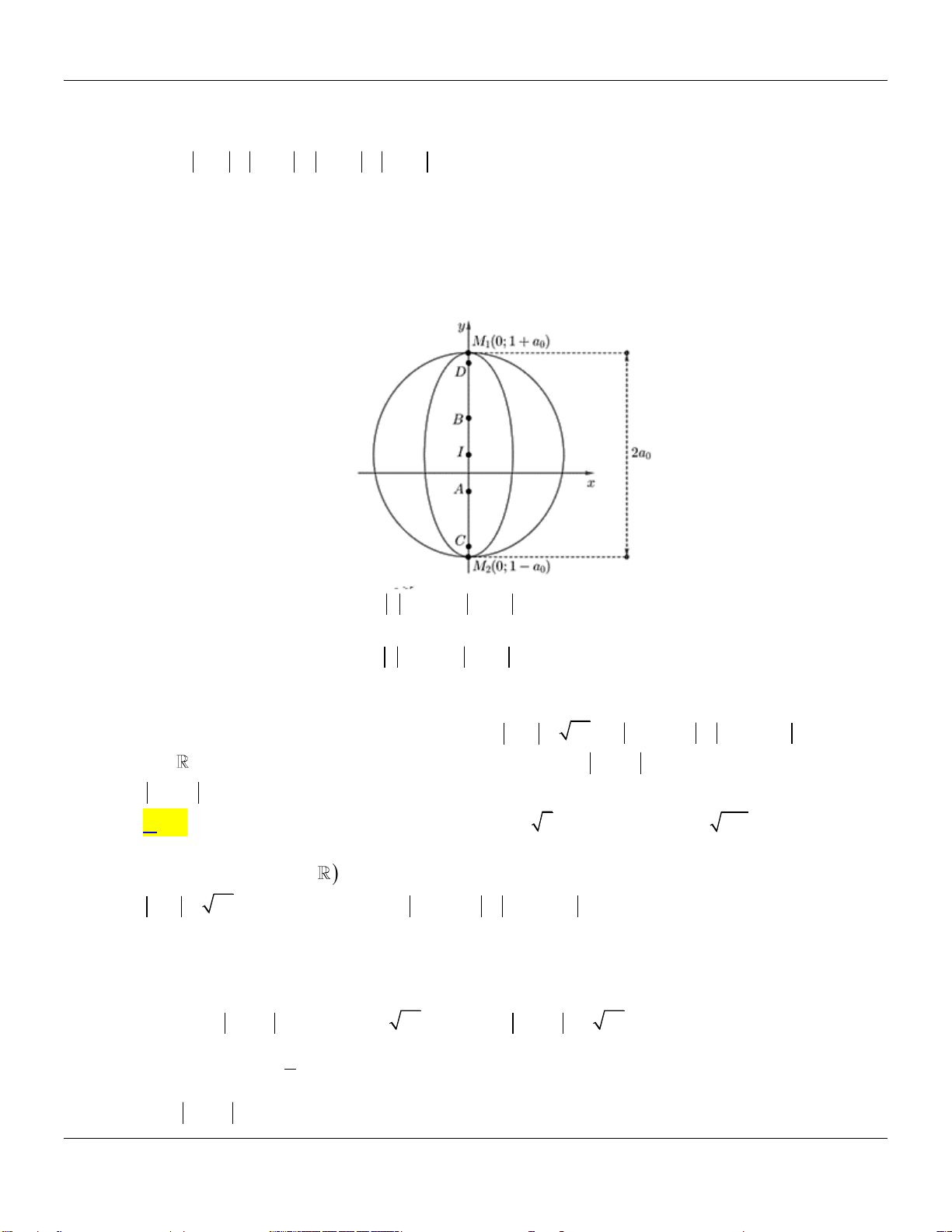
Lời giải: y A I 3 M D B x 6 O 4 Cách 1:
Trong mặt phẳng tọa độ Oxy , điểm biểu diễn số phức z x yi là điểm M  ; x y  .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia    x 6 z z  12   2x  12   Ta có     x  6  .  2 2
z  4  3i  2 2    x  4 
  y 3  8   x4 
2  y 32  8
Hình phẳng  H  là hình tô đậm trên hình vẽ. 
Ta có IA IB  2 2 , ID  2 và 2 2
AB  2 AD  2 IA ID  4 , suy ra AIB  . 2 1
Gọi S là diện tích hình quạt AIB . Ta có 2 S   R  2 . 1 1 4 1
Diện tích tam giác AIB là S I . A IB  4 . 2 2
Vậy diện tích hình phẳng  H  là S   S S  2  4 . H 1 2 Cách 2:
Hình phẳng  H  được biểu thị là phần tô màu trên hình vẽ (kể cả bờ), là hình giới hạn bởi
đường tròn C  có tâm I 4;3 , bán kính R  2 2 và đường thẳng x  6 . 2 2 2 2
Ta có  x  4   y  3  8   y  3  8   x  4  y    x  2 3 8 4 .
C cắt đường thẳng y  3tại 2 điểm có tọa độ 42 2;3
Gọi S là diện tích của hình phẳng giới hạn bởi các đường y    x  2 3 8 4
, y  3 , x  6 , 0 x  4  2 2 . 42 2 2 Ta có S  2.S  2. 8  x  4 dx  2, 2831  . H 0       6 z  2
Câu 31: Xét các số phức z thỏa mãn
là số thuần ảo. Biết rằng tập hợp các điểm biểu diễn các số z  2i
phức z luôn thuộc một đường tròn cố định. Bán kính của đường tròn đó bằng A. 1. B. 2 . C. 2 2 . D. 2 . Lời giải:
Đặt z a bi, a,b
. Gọi M a;b là điểm biểu diễn cho số phức z . z  2 a  2  bi
a  2bia b  2i   Ta có: w    z  2i a  b  2i
a  b  22 2
a a  2  b b  2  
 a  2b  2  abi  
a  b  22 2 a
 a  2  bb  2  0   1
w là số thuần ảo   a   b  22 2  0 Ta có   2 2
1  a b  2a  2b  0 .
Suy ra M thuộc đường tròn tâm I 1; 
1 , bán kính R  2 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 1  iz
Câu 32: Trong mặt phẳng tọa độ Oxy , tập hợp điểm biểu diễn số phức w  1 là một đường tròn z
có bán kính bằng 2 . Môđun của z thuộc tập nào dưới đây? 1   1   1  A.  ;2. B.  ; 2 . C.  2;  2 . D.  ;2.  2   2   2  Lời giải:
Điều kiện z  1  .
Đặt w x yi  ,
x y  , điểm M  ;
x y là điểm biểu diễn số phức w trên mặt phẳng tọa độ  2 1 iz Oxy . Đặt z
t. Ta có w
w1 z 1 iz zw i 1 w   1 1  . z  
1  z w i  1 w z x   y  
1 i  1 x yi 2 2 2 2
t x y  2y 1  x y  2x 1 2 2    t  
1 x y   2x  2yt t 1  0 2 .
Do tập hợp điểm biểu diễn số phức w là một đường tròn có bán kính bằng 2 nên t  1 . Khi đó   2 2 2 2
2  x y x yt  1  0 t 1 t  . 1     2 2 t 2 z 2  1   t   Theo đề bài ta được 2  
1  4  2t  5t  2  0       1 1 .  t 1  t 1 t   z   2 2
Câu 33: Cho hai số phức z, w thỏa mãn z  2w  3, 2z  3w  5 và z  3w  4. Tính giá trị biểu thức P  . z w  . z w . A. 1. B. 2 . C. 3 . D. 4 .
Lời giải: 2 2 Đặt z  ;
a w b với ; a b  0 . Ta có:
z  2w  3   z  2wz  2w  9  . z z  2 . z w  . z w  4. .
w w  9  a  2P  4b  9.
2z  3w  5  2z  3w2z  3w  25  4. . z z  6 . z w  . z w  9. . w w  25
 4a  6P  9b  25.
z  3w  4   z  3wz  3w 16  . z z  3 . z w  . z w  9. .
w w  16  a  3P  9b  16. .
a  2P  4b  9 a  1  
Vậy ta có hệ sau: 4a  6P  9b  25  P  2. Do đó P  2 .  
a  3P  9b  16 b  1   z  3
Câu 34: Có bao nhiêu số phức z thoả mãn z 1 3i z 1 i và là một số thuần ảo? z  2 A. 1. B. 2 . C. 4 . D. 3 . Lời giải:
Đặt z x yi x, y  . Gọi M x; y là điểm biểu diễn của z . 2 2 2 2
z 1 3i z 1 i   x  
1   y  3   x   1   y   1
x y  2  0 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia z  3 x yi  3
x 3 yi.x  2 yi 2 2      x y x 6 5y   .i . z  2 x yi  2  2 2 x  22 2  yx  2 2  yx  2 2  yz  2  z  3  z  2  là một số thuần ảo 2 2
  x y x  6   z  2   2 2
x y x  6  0   x  2 0 2 2  y   1  5
M thuộc đường tròn C  có tâm I ; 0 
, bán kính R  và M D.  2  2
d I  5 , 
R nên  cắt C tại hai điểm phân biệt trong đó có điểm D . 2 2
Vậy có một số phức z thỏa yêu cầu bài toán. 2
Câu 35: Có bao nhiêu số phức z thỏa mãn 3 z  2i z  0 ? A. 4 . B. 3 . C. 2 . D. 6 .
Lời giải: 2 2 Ta có 3 3 z  2i z  0  z  2  i z (*). Lấy mô-đun hai vế có: z  0 3  z  0 z   2 3 2 0 3 Thay (*) z  2
i z z  2 z      z  2  i . 3  z  2 
z  8i  0  z  3  i
Câu 36: Gọi S là tập hợp các số phức z thỏa mãn điều kiện 4
z z . Số phần tử của S là A. 7 . B. 6 . C. 5 . D. 4 .
Lời giải: z  0 4 3 Ta có: 4
z z (*)  z z z z   1  0   .  z  1  +) z  0 Thay (*)  z  0 . z  1  z 1 +) z  1 Thay (*) 4
 z  1   2 z   2 1 z   1  0    . z i  z i
S có 5 phần tử. 1 1 5
Câu 37: Cho số phức z thỏa mãn z 1 5 ,
và z có phần ảo dương. Tìm tổng phần thực z z 17
và phần ảo của z . A. 2 . B. 4 . C. 6 . D. 8 . Lời giải: Gọi z a bi a,b R,b 0 . Ta có z 1 5  a  2 2 1  b  25 2 2 a b 2a 24 1
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 1 1 5 1 1 5 2a 5 34 2 2 a b a 0 2 z z 17 a bi a bi 17 2 2 a b 17 5
Trừ vế - vế của 1 cho 2 ta có a 5 b 3 a b 8 . 1 1 1
Câu 38: Cho z là số phức có mô-đun bằng 2017 và w là số phức thỏa mãn   . Mô đun của z w z w số phức w là A. 2015 . B. 0 . C. 1. D. 2017 .
Lời giải: 1 1 1 z z i Ta có      2 z wzw 2 2
w wz z  3 0  w  . z w z w 2  
z z 3i 1 i 3  z z 3i Với w   w   z .  z  2017 . 2 2 2  
z z 3i 1 i 3  z z 3i Với w   w   z .  z  2017 . 2 2 2 1 3 6 z
Câu 39: Cho số phức z, w khác 0 thỏa mãn z w  0 và   bằng z w z  . Khi đó w w 1 1 A. 3. B. . C. 3 . D. . 3 3 Lời giải:
Với hai số phức z, w khác 0 thỏa mãn z  w  0 , ta có: 1 3 6 w  3z 6    
 w  3zz w 2 2
 6zw  3z  2zw w  0 z w z w zw z wz 1 2    2 iz   z w 3 3  3  2. 1  0        w   w   z 1 2    iw 3 3 2 2 z  1   2  1 Suy ra           . w  3  3   3
Câu 40: Gọi S là tập hợp các số phức z thỏa mãn z  10 . Gọi z , z 1
2 là hai số phức thuộc S sao cho
z1 là số thuần ảo. Gọi ,
A B lần lượt là các điểm biểu diễn số phức z , z  1 2 . Diện tích AOB z2 bằng A. 25 3 . B. 50 . C. 25 . D. 50 3. Lời giải:
Tập hợp các điểm biểu diễn số phức z là đường tròn (C) :  ; O 10. Suy ra , A B  (C) . z z
Từ giả thiết, ta đặt 1 1
mi,(m ) 
m m  1 z z 2 2
Ta có OA OB z z 10 , 2
AB z z z miz z 1  mi  10. 1  m  10 2 . 1 2 2 1 2 2 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 1 Suy ra A
OB vuông tại O . Vậy S O . A OB 50 A    . OB 2
Câu 41: Có bao nhiêu số nguyên m để tồn tại 2 số phức z thoả mãn z m i z 1 2mi và 3 | z | ? 2 A. 5. B. 3. C. 4. D. 6.
Lời giải:
 a m  b  
1 i  a  
1  b  2mi
Đặt z a bi  ,
a b  . Theo giả thiết ta có  3  a bi   2   2
a m2  b  2 1  a  2
1  b  2m2 
 2m  2a  4m  2b  3m  0    1     9  9 2 2 a b  2 2 a b  2  4  4 Phương trình  
1 là phương trình đường thẳng, phương trình 2 là phương trình đường 3
tròn tâm O bán kính R  . 2
Để tồn tại số phước z thoả mãn đề bài thì đường thẳng có phương trình   1 phải cắt đường
tròn có phương trình 2 2 3  m 3 2 2 Nghĩa là d  , O   1   R   2
m  m   1  2m   1
m 2  m 2 2 2 2 4 2 4 2
m  5m  6m  2  m  2  2 1
m  2m  2  0  1
  3  m  1 3
Vì m nên m 2  ;1;0;1;  2 .
Câu 42: Cho số phức z thay đổi thỏa mãn z 1  z i  4. Gọi C  là đường cong tạo bởi tất cả các
điểm biểu diễn số phức  z  2i2i  
1 khi z thay đổi. Tính diện tích S hình phẳng giới hạn
bởi đường cong C .
A. S  5 7 .
B. S  10 7 .
C. S  5 14 .
D. S  10 14 .
Lời giải: x yi
x  2   y   1 i z  2i   z i    
Đặt  z i i   2i 1 2i 1 2 2
1  x yi   x yi x  5  yiz 1  2i 1   2i 1 2i 1 2 2 2
Ta có: z   z i    x     y     x   2 1 4 2 1 5  y  4 5 (1) Gọi M  ;
x y là điểm biểu diễn số phức  z  2i2i   1 khi z thay đổi. F 2; 1  , F 5;0 . 1   2  
Từ (1) ta có: MF MF  4 5 . 1 2
Do đó quỹ tích điểm M là elip nhận F , F là hai tiêu điểm. 1 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
4 5  2a a  2 5  70 2 2       10 b a c 2
F F  2c  10  c  1 2  2
Vậy diện tích hình phẳng cần tìm là 
S   ab  5 14 . C 2 . z z
Câu 43: Cho số phức z thỏa mãn z 1 
. Biết rằng tập hợp điểm biểu diễn số phức 2
  1 2i z 1là một đường tròn tâm I và bán kính R. Tìm I và R. A. I 0; 2  ,R  5 . B. I 1; 4  ,R  10 .
C. I 0; 2, R  5 . D. I  1  ; 4  ,R  10 . Lời giải:
Gọi   x  i,
y x, y   . Theo đề bài ta có   1 2i z 1  1 x   1  i yz   z  1 2i 1 2i 2 . z z
Từ đó ta có: z 1  2  2 2 x   2 1  i y 1  x   1  i y x   1  i y
x  1 iy 1  x   2    1 y 1  . .  1  . 1 2i 2 1 2i 1 2i 1 2i 2 5
x   y  2 1  x  2 2 2 2 1  y   2 2 2 2 . 2
 x   y     x   2 2 2
1  y x 1  y  4 10 5 2 5      
Vậy tập hợp các điểm biểu diễn số phức  là một đường tròn có tâm và bán kính là I  1  ; 4  ;R  10 .
Câu 44: Cho các số phức z , z thỏa mãn phương trình z 2 3i 5 và z z 6 . Biết rằng tập hợp 1 2 1 2
các điểm biểu diễn số phức w z
z là một đường tròn. Tính bán kính đường tròn đó. 1 2 A. R 8 . B. R 4 . C. R 2 2 . D. R 2 . Lời giải:
Giả sử A , B lần lượt là các điểm biểu diễn số phức z , z trên mặt phẳng tọa độ Oxy . Theo 1 2 giả thiết ta có
A , B thuộc đường tròn tâm I 2;3 , bán kính r 5 và AB 6 . z z w
Gọi M là trung điểm của AB khi đó M cũng là điểm biểu diễn số phức 1 2 u . 2 2 2 AB Lại có 2 2 2 2 IM IA AM r 16 IM 4 . 2
Vậy M thuộc đường tròn tâm I 2;3 bán kính r ' 4 .
Suy ra các điểm biểu diễn số phức w z z
2u là một đường tròn bán kính R 2r 8. 1 2
Câu 45: Có bao nhiêu số phức z có phần thực và phần ảo đều là các số nguyên thỏa mãn
z i z  3i z  4i z  6i và z  10 ? A. 12. B. 2 . C. 10. D. 5 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia Lời giải:
Gọi M là điểm biểu diễn số phức z , A0;  1 , B0;  3 , C(0; 4  ), D0;6.
Ta có z i z  3i z  4i z  6i MA MB MC MD.
Theo bất đẳng thức tam giác ta có MC MD CD 10 .
Do đó MA MB MC MD  2a (a  5). 0 0
Vi vậy M thuộc hai elip E , E có cùng độ lớn là 2a và tâm của hai elip này trùng nhau 1   2  0 M 0;1 a 1 0 tại I 0; 
1 là trung điểm của A ,
B CD . Do đó M   E E   1   2   M 0;1  a  2  0 
Trường hợp 1: M 0;1 a z 10  1 a 10  5  a  9 trường hợp này có 5 số 0  0 0 phức thỏa mãn.
Trường hợp 2: M 0;1 a z 10  1 a 10  5  a 12trường hợp này có 12 số 0  0 0 phức thỏa mãn.
Vậy có tổng 12 số phức thỏa mãn.
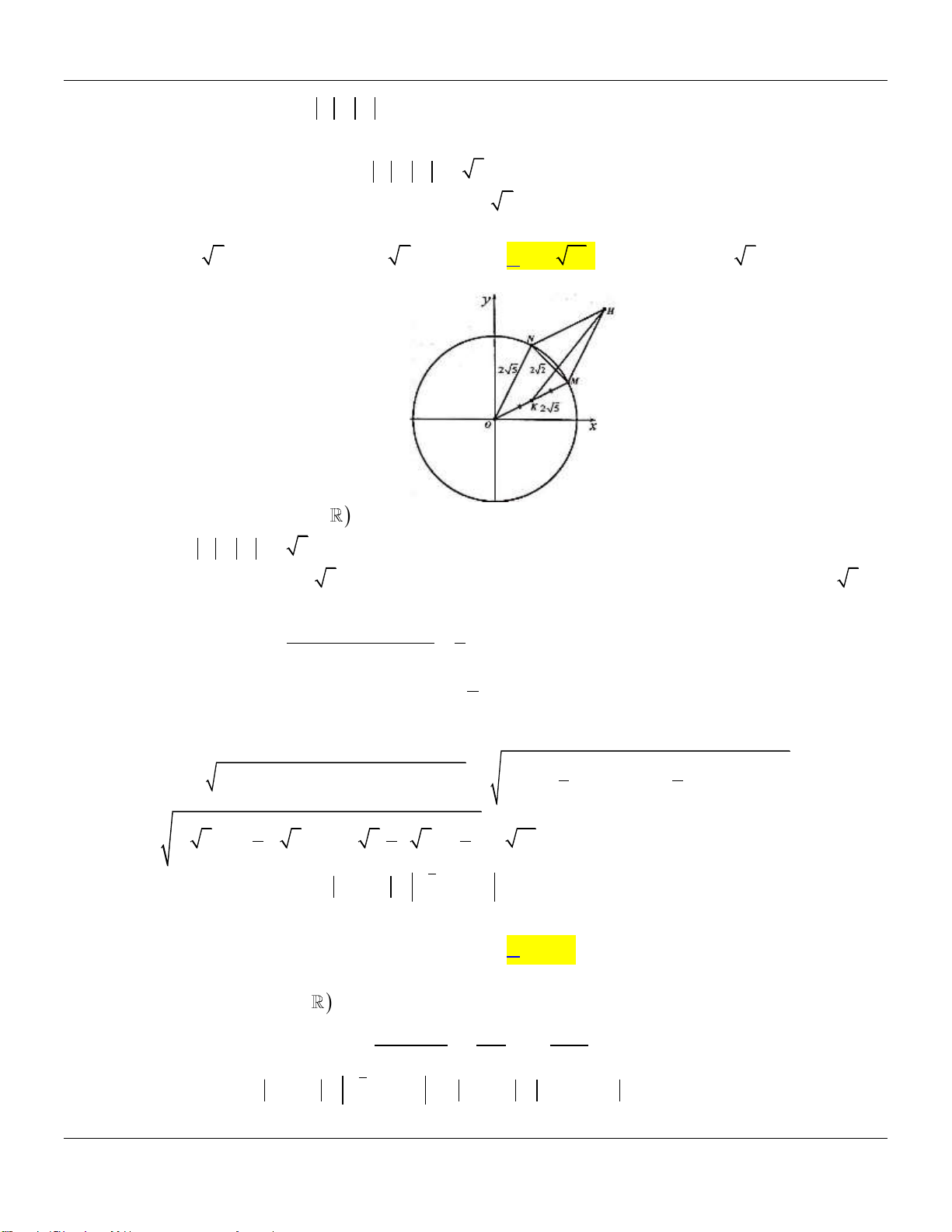
Câu 46: Gọi S là tập hợp các số phức z thỏa mãn z 1  34 và z 1 mi z m  2i , (trong đó m
). Gọi z , z là hai số phức thuộc S sao cho z z lớn nhất, khi đó giá trị của 1 2 1 2 z z bằng 1 2 A. 2 . B. 10 . C. 2 . D. 130 . Lời giải:
Đặt z x yi ,  x , y   . Khi đó z 1  34   x  2 2 1
y  34 ; z 1 mi z m  2i  2m  
1 x  2 2  my  3  0 .
Do đó tập hợp các điểm M biểu diễn số phức z là giao điểm của đường tròn
C x  2 2 : 1
y  34và đường thẳng d : 2m  
1 x  2 2  my  3  0 .
Gọi A , B là hai điểm biểu diễn z và z . Suy ra C   d   , AB . 1 2
Mặt khác z z AB  2R  2 34 do đó max z z  2 34  AB  2R I 1;0  d . 1 2   1 2 1
z  6  3i
Từ đó ta có m   nên d : 3x  5y  3  0 1   . 2 z  4   3i  2
Vậy z z  2 . 1 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Câu 47: Cho số phức 2
z m  3  (m  1)i, với m là tham số thực thay đổi. Tập hợp các điểm biểu diễn
số phức z thuộc đường cong. Tính diện tích hình phẳng giới hạn bởi đường cong đó và trục hoành. 8 4 1 2 A. . B. . C. . D. . 3 3 3 3 Lời giải:
Điểm M  2
m  3; m  
1 biểu diễn số phức z m    2 3 m   1 i nên ta có 2
x m  3; y m 1 từ đó y   x  2 2 3
1  x  6x  8 .
Vậy điểm M thuộc đường Parabol 2
y x  6x  8 .
Hoành độ giao điểm của và trục hoành là nghiệm phương trình x  2 2
x  6x  8  0   x  4 4 4
Vậy diện tích hình phẳng giới hạn bởi và trục hoành là 2 S
x  6x  8dx   . 3 2
Câu 48: Cho các số phức z , z thỏa mãn z  6 và z  2 . Gọi M , N lần lượt là các điểm biểu diễn 1 2 1 2
của các số phức z và iz . Biết MON  60 . Tính 2 2
T z  9z . 1 2 1 2 A. T  36 2 . B. T  36 3 . C. 24 3 . D. 18.
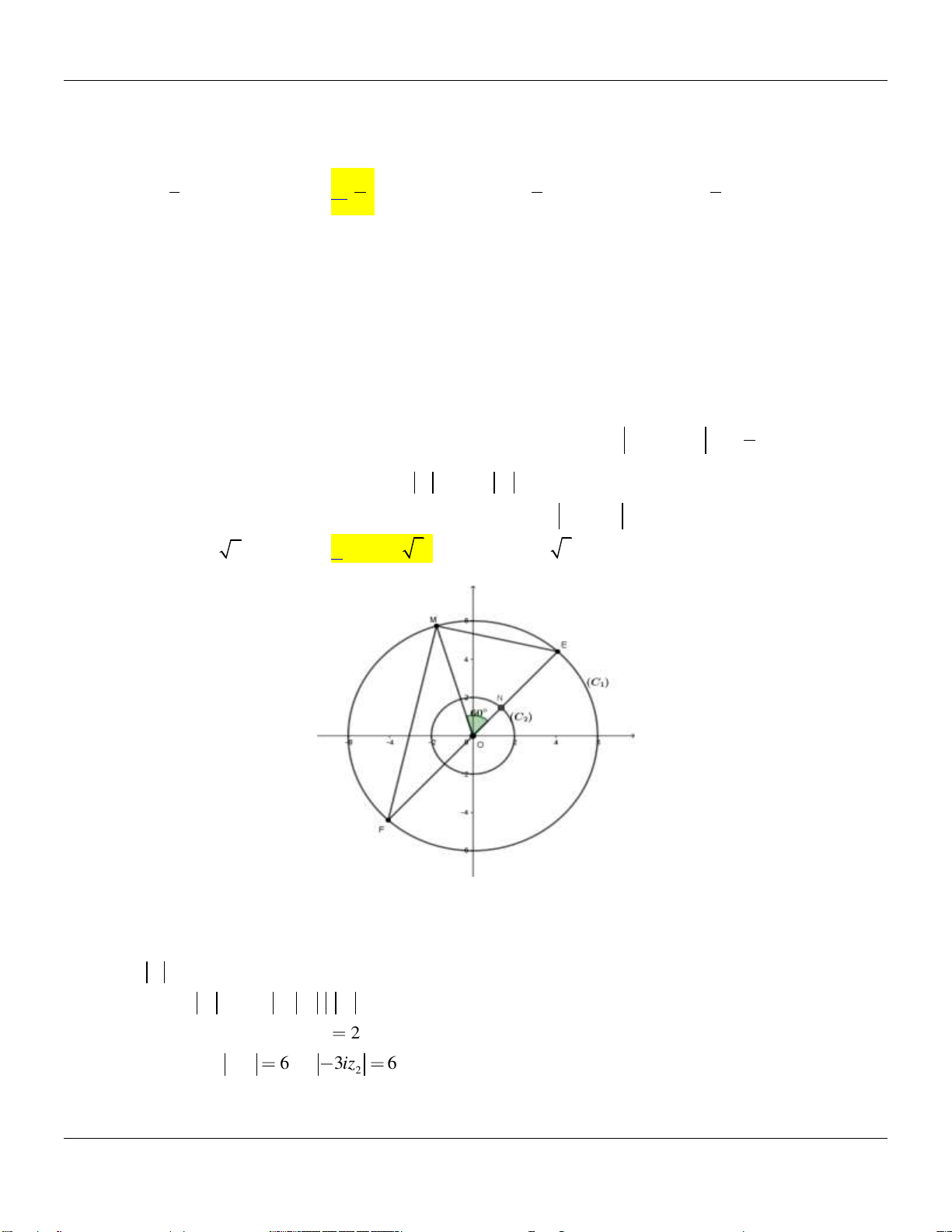
Lời giải:
Trong mặt phẳng tọa độ Oxy , gọi M , N lần lượt là điểm biểu diễn các số phức z và iz , gọi 1 2
E, F lần lượt là các điểm biểu diễn các số phức 3iz và 3iz . 2 2 Theo bài ra ta có:
z  6 nên tập hợp các điểm M là đường tròn tâm O , bán kính R  6 , gọi là đường tròn 1
C ; z  2  iz i . z  2do đó tập hợp các điểm N biểu diễn số phức iz thuộc đường 1  2 2 2 2
tròn tâm O , bán kính r
2 , gọi là đường tròn C . 2  Lại thấy : 3iz 6 và 3iz
6 suy ra các điểm E , F thuộc đường tròn C . 1  2 2
Hơn nữa: 3iz và 3iz là các số phức đối nên EF là một đường kính của C . 1  2 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Mặt khác : OE  3ON nên N nằm giữa O và E MOE  60 , suy ra tam giác MOE là tam
giác đều cạnh bằng 6 và tam giác MEF vuông tại M .
- Khi đó : T z  9z z  3iz 2 2 2 2
z  3iz . z  3iz ME.MF . 1 2 1 2 1 2 1 2 2 6 . 3
- Nhận thấy: ME.MF  2.S  4.S  4.
 36 3 . Vậy T  36 3 . MEF MOE 4
Câu 49: Gọi S là tập tất cả các giá trị thực của tham số m để tồn tại 4 số phức z thỏa mãn
z z z z  2 và z z  2   z z  m là số thuần ảo. Tổng các phần tử của S là 2 1 3 1 A. 2 1 B. . C. . D. . 2 2 2 Lời giải:
Đặt z x yi, x, y   .
z z z z  2  2x  2 yi  2  x y  1. (1)
Đặt z  z z    z z 2 2
m z z z m.
z là số thuần ảo nên có phần thực bằng 0. Tức là: 2 2
x y m . (2)
Tập hợp các điểm M  ;
x y  thỏa mãn (1) là hình vuông tâm là gốc tọa Để có 4 cặp số  ;
x y  thỏa mãn đồng thời (1) và (2) thì (2) phải là một đường tròn nội tiếp hoặc 2 1
ngoại tiếp hình vuông nói trên. Tức là m  0 và m  1hoặc m
m  1hoặc m  2 2 3
Vậy tổng các phần tử của S là . 2
Câu 50: Cho số phức z a bi a,b   . Biết tập hợp các điểm A biểu diễn hình học số phức z là
đường tròn C  có tâm I 4;3 và bán kính R  3 . Đặt M là giá trị lớn nhất, m là giá trị nhỏ
nhất của F  4a  3b 1. Tính giá trị M m .
A. M m  63 .
B. M m  48 .
C. M m  50 .
D. M m  41.
Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 2 2
Cách 1. Ta có phương trình đường tròn C  :  x  4   y  3  9 . 2 2
Do điểm A nằm trên đường tròn C  nên ta có a  4  b  3  9 .
Mặt khác F  4a  3b 1  4a  4  3b  3  24  F  24  4a  4  3b  3 . 2 2 2
Ta có  a    b      2 2 4 4 3 3
4  3  a  4  b  3   25.9  255   .  15
  4a  4  3b  3 15  15  F  24 15  9  F  39 .
Khi đó M  39 , m  9 .
Vậy M m  48 . F 1 3b
Cách 2. Ta có F  4a  3b 1  a  4 2   F   b
a  42  b  32 1 3 2  9 
 4  b  6b  9  9    4  2
 25b  23F  3 2
b F  225  0
   F  2 2 3 3  25F  5625 2   0  16
F 18F  5625  0  9  F  39.
____________________HẾT____________________
Huế, 15h15’ Ngày 19 tháng 3 năm 2023
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115