Ngân hàng câu hỏi số phức: Phương trình với hệ số thực – Lê Bá Bảo Toán 12

Ngân hàng câu hỏi số phức: Phương trình với hệ số thực – Lê Bá Bảo Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

34 17 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 4: Số phức

Môn: Toán 12

Thông tin:

32 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
SỐ PHỨC
LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ
PHƯƠNG TRÌNH VỚI HỆ SỐ THỰC
LUYỆN THI THPT QUỐC GIA
CẬP NHẬT TỪ ĐỀ THI MỚI NHẤT
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Ngân hàng câu hỏi:
PHƯƠNG TRÌNH VỚI HỆ SỐ THỰC
NỘI DUNG ĐỀ BÀI
Câu 1: Trên tập hợp các số phức, xét phương trình
1 1 6z a z a z
(
a
là tham số thực). Có
bao nhiêu giá trị của
a
để phương trình đó có hai nghiệm
,
2
z
thỏa mãn
22
12
42zz
?
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 2: Trên tập hợp số phức xét phương trình
22
2 2 1 0z mz m m
. Có bao nhiêu giá trị thực
của
m
để phương trình đã cho có 2 nghiệm
12
;zz
thoả mãn
12
2zz
?
A.
2
. B.
3
. C.
4
. D.
5
.
Câu 3: Biết phương trình
2
20z z m
(
m
là tham số thực) có một nghiệm là
1
13zi
. Gọi
2
z
là
nghiệm còn lại. Phần ảo của số phức
12
w2mz z
bằng
A.
36
. B.
24
. C.
36
. D.
8
.
Câu 4: Cho phương trình
2
2 6 8 0z mz m
. (
m
là tham số thực). Có bao nhiêu giá trị nguyên của
tham số
m
để phương trình có hai nghiệm phức phân biệt
12
,zz
thỏa mãn
1 1 2 2
z z z z
?
A.
4
. B.
1
. C.
3
. D.
2
.
Câu 5: Có bao nhiêu giá trị của tham số
m
để phương trình có nghiệm phức
0
z
thỏa mãn
0
26z 
?
A.
3.
B.
4.
C.
D.
2.
Câu 6: Trên tập hợp các số phức, xét phương trình
2
2 3 10 0z mz m
(
m
là tham số thực). Có bao
nhiêu giá trị nguyên của
m
để phương trình đó có hai nghiệm
12
,zz
không phải số thực thỏa
mãn
12
8zz
?
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 7: Trên tập số phức, xét phương trình
22
2 4 4 1 0z m z m m
,
m
là tham số thự C.
Có bao nhiêu giá trị
m
để phương trình đã cho có hai nghiệm phức phân biệt
12
,zz
thỏa điều
kiện
1 2 1 2 1
2z z z z z
.
A.
3
. B.
2
. C.
0
. D. 3.
Câu 8: Trên tập hợp các số phức, xét phương trình
22
2 2 1 4 5 0z m z m m
(
m
là tham số
thực). Có bao nhiêu giá trị của tham số
m
để phương trình có nghiệm
0
z
thoả mãn
22
00
1 4 4 5 3 10z m z m m
?
A.
1
. B.
2
. C.
4
.
D.
3
.
Câu 9: Trên tập số phức, xét phương trình
2
2 1 0 1z mz m
(
m
là tham số thực);
12
,zz
là hai
nghiệm phức của phương trình
1
;
,AB
lần lượt là điểm biểu diễn của hai nghiệm phức đó
trên mặt phẳng
Oxy
. Có bao nhiêu giá trị nguyên của
m
để
OAB
vuông tại
O
?
A.
2
. B.
1
. C.
3
. D.
4
.
Câu 10: Trên tập hợp số phức, xét phương trình
22
1
1 5 6 0(
4
z m z m m m
là tham số thực).
Có bao nhiêu số nguyên
[ 10;10]m
đề phương trình trên có hai nghiệm phức
12
,zz
thỏa
mãn
1 2 1 2
z z z z
?
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
A. 11. B. 10. C. 8. D. 9.
Câu 11: Trên tập số phức, cho phương trình
2
0 ( , )z az b a b
. Có bao nhiêu số phức
w
sao cho
phương trình đã cho có hai nghiệm là
1
(6 ) 2z i w i
và
2
( 5 ) | |z w i w
?
A. 4. B. 3. C. 6. D. 5.
Câu 12: Trên tập hợp các số phức, xét phương trình
2
2 8 12 0z mz m
. Có bao nhiêu giá trị
nguyên của
m
để phương trình đó có hai nghiệm phân biệt
12
,zz
thỏa mãn
12
?zz
A.
5
B.
6
. C.
3
. D.
4
.
Câu 13: Có bao nhiêu số nguyên
m
để phương trình
2
2 1 0z mz
có hai nghiệm phức phân biệt
12
,zz
thỏa mãn
12
3 3 ? zz
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 14: Có bao nhiêu số nguyên
a
để phương trình
22
30z a z a a
có hai nghiệm phức
12
,zz
thỏa mãn
1 2 1 2
z z z z
?
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 15: Cho số phức
w
và hai số thực
b
,
c
. Biết rằng
2w
và
34wi
là hai nghiệm của phương
trình
2
2022 0z bz c
. Tính giá trị biểu thức
P b c
bằng
A.
4044P 
. B.
8088P
. C.
4044P
. D.
8088P 
.
Câu 16: Trên tập các số phức, xét phương trình
2
80z mz m
(
m
là tham số thực). Có bao nhiêu
giá trị nguyên của tham số
m
để phương trình có hai nghiệm
12
,zz
phân biệt thỏa mãn
22
1 1 2 2
8z z mz m m z
?
A.
12
. B.
6
. C.
5
. D.
11
.
Câu 17: Biết phương trình
2
0,z az b a b
có một nghiệm là
1
3zi
và nghiệm còn lại là
2
z
.
Mô đun của số phức
2
a b z
bằng
A.
10
. B.
9
. C.
18
. D.
27
.
Câu 18: Cho số phức
w
và hai số thực
,ab
. Biết
1
2z w i
và
2
23zw
là hai nghiệm phức của
phương trình
2
0z az b
. Tính giá trị của
12
T z z
.
A.
2 13T
. B.
4 13T
. C.
2 97
3
T
. D.
2 85
3
T
.
Câu 19: Cho các số thực
,bc
sao cho phương trình
2
0z bz c
có hai nghiệm phức
12
;zz
với phần
thực là số nguyên và
thỏa mãn
1
3 2 1zi
và
12
22z i z
là số thuần ảo. Khi đó,
bc
bằng
A.
1
. B.
12
. C.
4
. D.
12
.
Câu 20: Gọi
1 2 3 4
, , ,z z z z
là
4
nghiệm phức của phương trình
42
4 4 0 z m z m
. Tìm tất cả các
giá trị m để
1 2 3 4
6 z z z z
.
A.
1m
. B.
2m
. C.
3m
D.
1m
.
Câu 21: Trên tập hợp các số phức, phương trình
2
0az bz
, với
,ab
có nghiệm
0
23zi
.
Biết rằng phương trình
2
0bz az
cũng có hai nghiệm phức
12
,zz
. Tính
12
S z z
.
A.
4
. B.
13
. C.
25
. D.
185
.
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Câu 22: Trên tập hợp các số phức, xét phương trình
22
4 2 0,z az b
(
,ab
là các tham số thực). Có
bao nhiêu cặp số thực
;ab
sao cho phương trình đó có hai nghiệm
12
,zz
thỏa mãn
12
2 3 3 ?z iz i
A.
4.
B.
1.
C.
2.
D.
3.
Câu 23: Trên tập số phức, cho phương trình
22
2 1 2 0z m z m m
. Có bao nhiêu tham số
m
để
phương trình đã cho có hai nghiệm phân biệt
12
;zz
thõa mãn
22
12
5zz
A.
1
. B.
0
. C.
2
. D.
4
.
Câu 24: Trên tập hợp số phức, xét phương trình
22
20z z m
(
m
là tham số thực). Có bao nhiêu
giá trị của
m
để phương trình đó có nghiệm
0
z
thỏa mãn điểm biểu diễn của
0
z
thuộc đường
E-lip có phương trình
2
2
1?
4

x
y
A.
2
. B.
3
. C.
4
. D.
1
.
Câu 25: Biết phương trình
22
20z mz m
(
m
là tham số thực) có hai nghiệm phức
12
,zz
. Gọi
,,A B C
lần lượt là điểm biểu diễn các số phức
12
,zz
và
0
zi
. Có bao nhiêu giá trị của tham
số
m
để diện tích tam giác
ABC
bằng 1?
A.
2
. B.
3
. C.
4
. D.
6
Câu 26: Trên tập hợp các số phức, xét phương trình
2
2 1 8 4 0z m z m
(
m
là tham số thực). Có
bao nhiêu giá trị nguyên của
m
để phương trình đã cho có hai nghiệm phân biệt
12
,zz
thỏa
mãn
22
1 1 2 2
2 8 2 8z mz m z mz m
?
A.
4
. B.
3
. C.
5
. D.
6
.
Câu 27: Tìm tổng các giá trị của số thực
a
sao cho phương trình
22
3 2 0z z a a
có nghiệm phức
0
z
thỏa
0
2z
.
A.
0
. B.
2
. C.
4
. D.
6
.
Câu 28: Trên tập hợp các số phức, gọi
S
là tổng các giá trị thực của
m
để phương trình
2
2 1 6 0mz m z m
có nghiệm
0
z
thỏa mãn
0
1z
. Tính
S
.
A.
3
. B.
4
. C.
1
. D.
2
.
Câu 29: Cho phương trình
22
20z az a
, với
a
là số thực dương. Gọi
12
,zz
là hai nghiệm phức của
phương trình, trong đó
1
z
có phần ảo dương. Biết rằng
1 2 1
2 10 2 7z z z i
. Khẳng định
nào sau đây đúng?
A.
13a
. B.
1a
. C.
58a
. D.
35a
.
Câu 30: Trên tập hợp các số phức, xét phương trình
22
2 2 1 4 5 0z m z m m
(
m
là tham số
thực). Có bao nhiêu giá trị của tham số
m
để phương trình có nghiệm
0
z
thoả mãn
0
3 10z 
?
A.
1
. B.
2
. C.
4
.
D.
3
.
Câu 31: Cho số phức
,zw
khác 0 thỏa mãn
0zw
và
2 3 4
z w z w

. Khi đó,
z
w
bằng
A.
2
. B.
6
3
. C.
3
. D.
2
3
.
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Câu 32: Tìm tất cả các giá trị thực của
a
sao cho phương trình
22
20z az a a
có hai nghiệm
phức có môđun bằng 1.
A.
1a 
. B.
1a
. C.
1a 
. D.
15
2
a

.
Câu 33: Trên tập số phức, xét phương trình
22
2 5 0z mz n
(với
m
,
n
là tham số thực). Có bao
nhiêu cặp số
( ; )mn
để phương trình đã cho có hai nghiệm phức
12
,zz
sao cho các điểm biểu
diễn của
1 2 3 4
, , 1, 5z z z z
là bốn đỉnh của một hình vuông?
A.
3
. B.
2
. C.
4
. D.
1
.
Câu 34: Trên tập hợp các số phức, xét phương trình
2
2 12 0z mz m
(
m
là tham số thực). Có bao
nhiêu giá trị nguyên của
m
để phương trình đó có hai nghiệm phân biệt
1
z
,
2
z
thỏa mãn
1 2 1 2
2z z z z
?
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 35: Cho phương trình
42
4 4 0z mz
trong tập số phức và
m
là tham số thực. Gọi
1 2 3 4
, , , z z z z
là bốn nghiệm của phương trình đã cho. Tìm tất cả các giá trị của
m
để
2222
1 2 3 4
4 4 4 4 324zzzz
.
A.
2
15
m
m

. B.
2
15
m
m

. C.
1
35
m
m

. D.
1
35
m
m

.
Câu 36: Cho các số thực
,bc
sao cho phương trình
2
0z bz c
có hai nghiệm phức
12
,zz
thỏa
mãn
1
4 3 1zi
và
2
8 6 4zi
. Mệnh đề nào sau đây đúng?
A.
5 12.bc
B.
5 4.bc
C.
5 4.bc
D.
5 12.bc
Câu 37: Cho phương trình
2
0z bz c
, có hai nghiệm
12
,zz
thỏa mãn
21
42z z i
. Gọi
,AB
là các
điểm biểu diễn các nghiệm của phương trình
2
2 4 0z bz c
. Tính độ dài đoạn
AB
.
A.
8 5.
B.
2 5.
C.
4 5.
D.
5.
Câu 38: Trên tập hợp các số phức, phương trình
2
2 2 3 0z a z a
(
a
là tham số thực) có
2
nghiệm
1
z
,
2
z
. Gọi
M
,
N
là điểm biểu diễn của
1
z
,
2
z
trên mặt phẳng tọa độ. Biết rằng có
2
giá trị của tham số
a
để tam giác
OMN
có một góc bằng
120
. Tổng các giá trị đó bằng bao
nhiêu?
A.
6
. B.
4
. C.
4
. D.
6
.
Câu 39: Trên tập hợp các số phức, xét phương trình
2
2z 2 0zm
(
m
là tham số thực). Gọi
là
tập hợp các giá trị của
m
để phương trình trên có hai nghiệm phân biệt được biểu diễn hình
học bởi hai điểm
, AB
trên mặt phẳng tọa độ sao cho diện tích tam giác
ABC
bằng
22
, với
1;1C
. Tổng các phần tử trong
bằng
A.
8
. B.
4
. C.
9
. D.
1
.
Câu 40: Biết rằng phương trình
2
20z az b
(,ab
là các số thực dương) có hai nghiệm phức liên
hợp
12
,zz
. Gọi
,,A B C
lần lượt là các điểm biểu diễn của số phức
12
2, ,w z z
. Tính giá trị của
4T b a
biết rằng ba điểm
,,A B C
tạo thành một tam giác vuông có diện tích bằng
9
.
A.
6
. B.
8
. C.
9
. D.
14
.
Câu 41: Trên tập hợp số phức, xét phương trình
22
2 20 0 1z az b
với
,ab
là các tham số
nguyên dương. Khi phương trình có hai nghiệm phân biệt
12
,zz
thỏa mãn:
12
3 7 5z iz i
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
thì giá trị của biểu thức
75ab
bằng
A.
19
. B.
17
. C.
32
. D.
40
.
Câu 42: Cho phương trình
2
40
c
xx
d
có hai nghiệm phức. Gọi
A
,
B
là hai điểm biểu diễn của
hai nghiệm đó trên mặt phẳng
Oxy
. Biết tam giác
OAB
đều, tính
2P c d
.
A.
18P
. B.
10P 
. C.
14P 
. D.
22P
.
Câu 43: Cho phương trình
42
4 4 0z mz
trong tập số phức và
m
là tham số thực. Gọi
1 2 3 4
, , ,z z z z
là bốn nghiệm của phương trình đã cho. Tìm tất cả các giá trị của
m
để
2222
1 2 3 4
4 4 4 4 324zzzz
.
A.
1;m
35m 
. B.
1;m
35m 
. C.
1;m
35m
. D.
1;m
35m
.
Câu 44: Tìm
m
để các nghiệm của phương trình sau đều là số ảo:
42
3 6 3 0m z z m
.
A.
3 3 2m
. B.
3 3 2m
. C.
3 2 3
.
3 3 2

m
m
D.
3 2 3m
.
Câu 45: Gọi
là tổng các số thực
m
thỏa mãn
32
7 16 12 3 0z z z mz m
có nghiệm phức
0
z
thỏa mãn
0
| | 2z
. Khẳng định nào dưới đây đúng?
A.
24S
. B.
25S
. C.
18S
. D.
16S
.
Câu 46: Trên tập hợp số phức cho phương trình
2
0z bz c
, với
,bc
. Biết rằng hai nghiệm của
phương trình có dạng
1
3zw
và
2
3 8 13z w i
với
w
là một số phức. Tính
bc
.
A.
9
. B.
10
. C.
11
. D.
12
.
Câu 47: Trên tập hợp các số phức, xét phương trình:
22
2 1 3 5 0z m z m m
(
m
là tham số
thực). Tính tổng các giá trị của
m
để phương trình trên có nghiệm
0
z
thỏa mãn
3
00
12 5 .zz
A.
9
. B.
12
. C.
10
. D.
8
.
Câu 48: Cho phương trình
2
0z bz c
có hai nghiệm
12
,zz
thỏa mãn
21
34z z i
. Gọi
,AB
là các
điểm biểu diễn các nghiệm của phương trình
2
2 4 0z bz c
. Tính độ dài đoạn
AB
.
A.
20.
B.
2 5.
C.
10.
D.
5.
Câu 49: Cho
m
là số thực, biết phương trình
2
2 9 0z mz
có hai nghiệm phức
12
,zz
. Có bao nhiêu
giá trị nguyên của
m
sao cho
1 2 2 1
16z z z z
?
A.
3
. B.
4
. C.
5
. D.
6
.
Câu 50: Gọi
S
là tập hợp tất cả các số thực
a
sao cho phương trình
2
( 2) 2 3 0z a z a
có hai
nghiệm phức
12
,zz
và các điểm biểu diễn của
12
,zz
cùng với gốc tọa độ
O
tạo thành một tam
giác có diện tích bằng 2. Số phần tử của
S
là?
A.
1
. B.
4
. C.
2
. D.
3
.
____________________HẾT____________________
Huế, 15h15’ Ngày 19 tháng 3 năm 2023
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
LỜI GIẢI CHI TIẾT
Câu 1: Trên tập hợp các số phức, xét phương trình
1 1 6z a z a z
(
a
là tham số thực). Có
bao nhiêu giá trị của
a
để phương trình đó có hai nghiệm
,
2
z
thỏa mãn
22
12
42zz
?
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải:
Ta có:
22
1 1 6 2 3 1 0z a z a z z a z a
1
có
6 10a
.
+ Trường hợp 1:
5
0
3
a
. Khi đó phương trình
1
có hai nghiệm thực
,
2
z
.
Suy ra
2
22
22
12
6 38
42 2 3 2 1 42 2 24 4 0
6 38
a
z z a a a a
a


.
Kết hợp với điều kiện
5
3
a 
, nhận
6 38a
.
+ Trường hợp 2:
5
0
3
a
. Khi đó phương trình
1
có hai nghiệm phức
,
2
z
thỏa
mãn
12
zz
.
Suy ra
22
2
1 2 1 1 2 2 1 2
22
42 42 21 22 0
22
a
z z z z z z z z a
a

.
Kết hợp với điều kiện
5
3
a 
, nhận
22a 
.
Vậy có
2
giá trị của
a
thỏa mãn.
Câu 2: Trên tập hợp số phức xét phương trình
22
2 2 1 0z mz m m
. Có bao nhiêu giá trị thực
của
m
để phương trình đã cho có 2 nghiệm
12
;zz
thoả mãn
12
2zz
?
A.
2
. B.
3
. C.
4
. D.
5
.
Lời giải:
TH1.
22
1
0 2 1 0 2 1 0
2
m m m m m
. Khi đó phương trình đã cho có 2
nghiệm thực.Theo định lý Vi-et ta có
12
2
12
21
. 2 1 2
z z m
z z m m

. Xét
12
12
12
23
2
24
zz
zz
z


.
Từ
1
và
3
ta có hệ phương trình
2
12
12
1
2
6
2
3
2 0 4
7
3
m
z
z z m
z z m
z



.
Thế
6
và
7
vào phương trình
2
ta được
22
9 6 2
24
. 2 1 18 9 0
33
9 6 2
m TM
mm
m m m m
m TM


.
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Từ
1
và
4
ta có hệ phương trình
2
12
12
1
2 10
2
20
49
zm
z z m
zz
zm




. Thế
9
và
10
vào
phương trình
2
ta được
22
2 4 2 1 9 2 1 0m m m m m m VN
.
TH2.
22
1
0 2 1 0 2 1 0
2
m m m m m
. Khi đó phương trình đã cho có 2
nghiệm phức phân biệt. Giả sử
12
z a bi z a bi
. Khi đó
2 2 2 2 2 2
12
0
2 2 0
0
a
z z a b a b a b
b
. Suy ra
12
00z z i
mẫu thuẫn
với điều kiện đề bài là phương trình có 2 nghiệm phân biệt. Trên tập hợp các số phức, xét
phương trình
2
2 1 3 0z m z m
(
m
là tham số thực).
Câu 3: Biết phương trình
2
20z z m
(
m
là tham số thực) có một nghiệm là
1
13zi
. Gọi
2
z
là
nghiệm còn lại. Phần ảo của số phức
12
w2mz z
bằng
A.
36
. B.
24
. C.
36
. D.
8
.
Lời giải:
Từ giả thiết
2 1 2
1 3 10 10z i z z m
.
Vậy phần ảo của số phức
12
w 10 2 10 1 3 2 1 3 8 36z z i i i
là
36
.
Câu 4: Cho phương trình
2
2 6 8 0z mz m
. (
m
là tham số thực). Có bao nhiêu giá trị nguyên của
tham số
m
để phương trình có hai nghiệm phức phân biệt
12
,zz
thỏa mãn
1 1 2 2
z z z z
?
A.
4
. B.
1
. C.
3
. D.
2
.
Lời giải:
Ta có
2
68mm
Trường hợp 1:
4
0
2
m
m
Khi đó phương trình đã cho có hai nghiệm thực phân biệt
12
,zz
và
22
1 1 2 2 1 2
z z z z z z
12
12
12
0 2 0 0
z z loai
z z m m tm
zz

Trường hợp 2:
0 2 4m
Khi đó phương trình đã cho có hai nghiệm phức phân biệt
12
,zz
1 1 2 2 1 2 1 1
..z z z z z z z z
( luôn đúng) mà
3mm
Vậy có 2 giá trị nguyên của tham số
m
thỏa mãn bài toán.
Câu 5: Có bao nhiêu giá trị của tham số
m
để phương trình có nghiệm phức
0
z
thỏa mãn
0
26z 
?
A.
3.
B.
4.
C.
D.
2.
Lời giải:
Xét phương trình
2
2 1 3 0 1z m z m
Ta có
2
2
1 3 2.m m m m
.
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Nếu
2
2
0 2 0
1
m
mm
m

thì phương trình
1
có nghiệm thực:
0
0
0
4
26
8
z
z
z

Với
0
4z
: thay vào
1
, được:
11
7
m
Với
0
8z 
: thay vào
1
, được:
83
17
m 
Nếu
2
0 2 0 2 1m m m
thì phương trình
1
có nghiệm phức
2
0
2
0
12
12
z m i m m
z m i m m
Khi đó
2
22
0
2 6 3 2 36 2 7 29 0z m m m m m
: Phương trình có hai
nghiệm phân biệt.
Vậy có 4 giá trị của tham số
m
để bài toán thỏa mãn.
Câu 6: Trên tập hợp các số phức, xét phương trình
2
2 3 10 0z mz m
(
m
là tham số thực). Có bao
nhiêu giá trị nguyên của
m
để phương trình đó có hai nghiệm
12
,zz
không phải số thực thỏa
mãn
12
8zz
?
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải:
Ta có
2
3 10mm
.
Phương trình không có nghiệm thực khi
2
0 3 10 0 2 5(1)m m m
.
Khi đó phương trình có hai nghiệm phân biệt
22
12
3 10. , 3 10.z m m m i z m m m i
Vậy
12
8 2 3 10 8 3 10 4z z m m
3 10 16 2mm
.
Kết hợp với điều kiện ta có
22m
. Vậy có 4 giá trị nguyên của
m
thỏa mãn.
Câu 7: Trên tập số phức, xét phương trình
22
2 4 4 1 0z m z m m
,
m
là tham số thự C.
Có bao nhiêu giá trị
m
để phương trình đã cho có hai nghiệm phức phân biệt
12
,zz
thỏa điều
kiện
1 2 1 2 1
2z z z z z
.
A.
3
. B.
2
. C.
0
. D. 3.
Lời giải:
Điều kiện để phương trình có hai nghiệm phức phân biệt trong đó
1
z
là nghiệm có phần ảo
âm là:
2
2
15
4 4 1 0 4 15 0
4
m m m m m
.
Khi đó:
22
1 2 1 2
2 2 4 2 4 1 2 10 10z z z z m m m m m
Và
1
4 4 15z b i m i m

Ta có:
2
2
1 2 1 2 1
2 2 10 10 4 4 15z z z z z m m m m
22
2 10 10 4 1m m m m
Vì
15
4
m
nên
2
4 1 0mm
, do đó:
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
2 2 2
2 2 2
11
2 10 10 4 1 3 14 11 0
1,
(*)
3
2 10 10 4 1 6 9 0
3
m m m m m m
mm
m m m m m m
m




Đối chiếu điều kiện
15
4
m
suy ra không có giá trị nào của
m
thỏa điều kiện bài toán.
Câu 8: Trên tập hợp các số phức, xét phương trình
22
2 2 1 4 5 0z m z m m
(
m
là tham số
thực). Có bao nhiêu giá trị của tham số
m
để phương trình có nghiệm
0
z
thoả mãn
22
00
1 4 4 5 3 10z m z m m
?
A.
1
. B.
2
. C.
4
.
D.
3
.
Lời giải:
Cách 1: Ta có
1m
.
Trường hợp 1:
1 0 1mm
.
Khi đó theo bài ra, phương trình đã cho có nghiệm thực
0
z
thoả mãn
0
0
0
7
3 10
13
z
z
z

.
Từ đó suy ra
22
2
2
7 2 2 1 7 4 5 0
13 2 2 1 13 4 5 0
m m m
m m m
2
2
4 33 63 0
4 47 143 0
mm
mm
3
21
4
m tm
m tm
.
Trường hợp 2:
1 0 1mm
.
Khi đó phương trình đã cho có hai nghiệm phức là
0
z
và
0
z
và thoả mãn
0
3 10z 
2
2
0 0 0 0 0
3 3 100 3 9 100 4 5 3.2 2 1 91 0z z z z z m m m
2
7 1601
8
4 7 97 0
7 1601
8
m tm
mm
m ktm


.
Vậy có 3 giá trị của tham số
m
thoả mãn yêu cầu bài toán.
Cách 2: Ta có
2
22
2 2 1 4 5 0 2 1 1 1z m z m m z m m
.
Trường hợp 1:
1 0 1mm
.
Khi đó
2 1 1
1
2 1 1
z m m
z m m
.
Theo bài ra, phương trình đã cho có nghiệm
0
z
thoả mãn
0
3 10z 
.
Do đó
3
2 2 1 10
21
2 2 1 10
4
m tm
mm
m tm
mm
.
Trường hợp 2:
1 0 1mm
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Khi đó
2 1 1
1
2 1 1
z m i m
z m i m
.
Theo bài ra, phương trình đã cho có nghiệm
0
z
thoả mãn
0
3 10z 
.
Do đó
22
2 2 1 10 4 8 4 1 100 4 7 97 0m i m m m m m m
7 1601
8
7 1601
8
m tm
m ktm


.
Vậy có 3 giá trị của tham số
m
thoả mãn yêu cầu bài toán.
Câu 9: Trên tập số phức, xét phương trình
2
2 1 0 1z mz m
(
m
là tham số thực);
12
,zz
là hai
nghiệm phức của phương trình
1
;
,AB
lần lượt là điểm biểu diễn của hai nghiệm phức đó
trên mặt phẳng
Oxy
. Có bao nhiêu giá trị nguyên của
m
để
OAB
vuông tại
O
?
A.
2
. B.
1
. C.
3
. D.
4
.
Lời giải:
Xét phương trình
2
2 1 0 1z mz m
Phương trình có hai nghiệm phức khi
2
1 5 1 5
0 1 0
22
m m m

*
Ta có các nghiệm
22
12
1; 1z m i m m z m i m m
,AB
lần lượt là điểm biểu diễn của hai nghiệm phức
12
,zz
nên
2
;1A m m m
;
2
;1B m m m
.
OAB
vuông tại
O
2
1
. 0 2 1 0 *
1
2
m
OAOB m m thõa mãn
m

.
Vậy chỉ có 1 giá trị nguyên
1m
thõa mãn yêu cầu.
Câu 10: Trên tập hợp số phức, xét phương trình
22
1
1 5 6 0(
4
z m z m m m
là tham số thực).
Có bao nhiêu số nguyên
[ 10;10]m
đề phương trình trên có hai nghiệm phức
12
,zz
thỏa
mãn
1 2 1 2
z z z z
?
A. 11. B. 10. C. 8. D. 9.
Lời giải:
Điều kiện
1 0 1mm
.
2
45mm
+ Trường hợp 1:
2
5
0 4 5 0
1
m
mm
m

phương trình có 2 nghiệm thực
12
,zz
Theo định lý Viet
2
12
1
56
4
.z mz m
.
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
22
1 2 1 2 1 2 1 2 1 2
04.z z z z z z z z z z
22
6
5 6 0 5 6 0
1
m
m m m m
m

Do
m
và
[ 10;10]m
nên số giá trị m thỏa mãn là
10 6 1 1 6
.
+ Trường hợp 2:
2
0 4 5 0 1 5m m m
.
phương trình có 2 nghiệm phức
12
,zz
1
2
22
1 2 1 2
2
2 1 2
2
6
5 6 0
1 4 5 1
3 4 0
14
z
m
z z z z
m
m
z
m
mzzm m m
m
m


Do
m
,
15m
và
[ 10;10]m
nên số giá trị m thỏa mãn là
0, 1, 2, 3m m m m
.
Vậy có 10 giá trị của m.
Câu 11: Trên tập số phức, cho phương trình
2
0 ( , )z az b a b
. Có bao nhiêu số phức
w
sao cho
phương trình đã cho có hai nghiệm là
1
(6 ) 2z i w i
và
2
( 5 ) | |z w i w
?
A. 4. B. 3. C. 6. D. 5.
Lời giải:
Trường hợp 1:
12
,zz
.
1
(6 ) 2 (6 )( ) 2z i w i i x yi i
là số thực nên
6 2 0xy
.
22
2
( 5 )| | [( 5) (1 ) ]z w i w x y x y i
là số thực nên
22
(1 ) 0y x y
.
Ta có hệ phương trình
22
6 2 0
4
4
1
(1 ) 0
xy
x
wi
y
y x y

.
Trường hợp 2:
12
,zz
. Khi đó phương trình đã cho có hai nghiệm là liên hợp với nhau.
12
(6 ) 2 ( 5 ) | | . 5 . ( | |)z z i w i w i w t w t t i t w
[( 6) ] 5 ( 2)w t i t t i
. (1)
2 2 2 2
( 6) 1 25 ( 2)t t t t


4 3 2
12 11 4 4 0t t t t
1
0,62079
10,967
t
t
t

.
Thay mỗi giá trị của
t
vào (1), ta được một số phức
w
tương ứng.
Vậy có tất cả 4 số phức
w
thoả mãn.
Câu 12: Trên tập hợp các số phức, xét phương trình
2
2 8 12 0z mz m
. Có bao nhiêu giá trị
nguyên của
m
để phương trình đó có hai nghiệm phân biệt
12
,zz
thỏa mãn
12
?zz
A.
5
B.
6
. C.
3
. D.
4
.
Lời giải:
Ta có:
2
2 8 12 0 *z mz m
thì
2
8 12mm
.
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
TH1:
2
6
0 8 12 0
2
m
mm
m
. Khi đó phương trình
*
có
2
nghiệm thực phân
biệt
12
,zz
và theo yêu cầu bài toán:
12
12
1 2 1 2
0 0
z z KTM
zz
z z z z m TM

TH2:
0 2 6m
. Phương trình
*
khi đó có
2
nghiệm
1,2
z m i
luôn thỏa
mãn
12
zz
. Nên:
3;4;5m
.
Vậy các giá trị
m
thỏa mãn là:
0;3;4;5m
.
Câu 13: Có bao nhiêu số nguyên
m
để phương trình
2
2 1 0z mz
có hai nghiệm phức phân biệt
12
,zz
thỏa mãn
12
3 3 ? zz
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải:
+) Với
2
10m
, phương trình
2
2 1 0z mz
có hai nghiệm phức liên hợp
12
,z a bi z a bi
.
Khi đó, hiển nhiên
2
2
12
3 3 3z a b z
.
+) Với
2
10m
, phương trình
2
2 1 0z mz
có hai nghiệm thực phân biệt
12
,zz
.
Đẳng thức
12
33zz
tương đương với
12
60zz
, điều này nghĩa là
2 6 0m
tức
3m
.
Tóm lại các số nguyên
m
cần tìm là
0, 3mm
.
Câu 14: Có bao nhiêu số nguyên
a
để phương trình
22
30z a z a a
có hai nghiệm phức
12
,zz
thỏa mãn
1 2 1 2
z z z z
?
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải:
Ta có
2
22
3 4 3 10 9a a a a a


Trường hợp 1:
2
5 2 13 5 2 13
0 3 10 9 0 *
33
a a a
Khi đó phương trình đã cho có hai nghiệm thực
12
,zz
, thỏa mãn
12
12
3
.
z z a
zz
Suy ra
1 2 1 2
z z z z
2
33aa
2
2
3 3 10 9a a a
2
0
4 4 0
1
a
aa
a

đều thỏa mãn
*
.
Trường hợp 2:
2
5 2 13
3
0 3 10 9 0 **
5 2 13
3
a
aa
a


Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Khi đó phương trình có hai nghiệm phức
12
,zz
, thỏa mãn
12
12
3
.
z z a
z z i
Suy ra
1 2 1 2
z z z z
2
33a i a
2
2
3 3 10 9a a a
2
1
2 16 18 0
9
a
aa
a

đều thỏa mãn
**
.
Vậy có 4 số nguyên a thỏa mãn yêu cầu bài toán.
Câu 15: Cho số phức
w
và hai số thực
b
,
c
. Biết rằng
2w
và
34wi
là hai nghiệm của phương
trình
2
2022 0z bz c
. Tính giá trị biểu thức
P b c
bằng
A.
4044P 
. B.
8088P
. C.
4044P
. D.
8088P 
.
Lời giải:
Nhận xét: Trong tập số phức, phương trình bậc hai
2
0az bz c
có hai nghiệm phức
12
,zz
thì
21
zz
.
Đặt
w x yi
, xy
. Vì
, bc
và phương trình
2
2022 0z bz c
có hai nghiệm là
1
2zw
,
2
34z w i
nên 2 nghiệm
12
,zz
là 2 nghiệm phức có phần ảo khác 0.
Do đó
21
2 3 4 2 3 4z z w w i x yi x yi i
2 3 1
2 3 4 3
4 3 1
x x x
x yi x y i
y y y



.
1
2
23
1
3 4 3
z w i
wi
z w i i
.
Theo định lý Viet:
12
22
2022
.
2022
b
zz
c
zz
, từ đó suy ra
6
6.2022
2022
8088
10.2022
10
2022
b
b
bc
cc



Vậy
8088P b c
.
Câu 16: Trên tập các số phức, xét phương trình
2
80z mz m
(
m
là tham số thực). Có bao nhiêu
giá trị nguyên của tham số
m
để phương trình có hai nghiệm
12
,zz
phân biệt thỏa mãn
22
1 1 2 2
8z z mz m m z
?
A.
12
. B.
6
. C.
5
. D.
11
.
Lời giải:
Ta có
2
4 32mm
là biệt thức của phương trình.
Trường hợp 1: Xét
2
8
0 4 32 0
4
m
mm
m

khi đó phương trình có hai nghiệm
thực phân biệt. Ta có
2
11
8z mz m
suy ra
22
1 2 1 2
88z mz m z z m m m
do đó
22
1 1 2 2
8z z mz m m z
22
12
88m m z m m z
(*).
Nếu
12
.0zz
thì
8 0 8mm
không thỏa mãn. Khi đó (*)
2
12
80mm
zz
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
2
12
80mm
zz

2
80
0
mm
m
hệ vô nghiệm.
Trường hợp 2: Xét
0 4 8m
khi đó phương trình có hai nghiệm phức phân biệt và
12
zz
, ta có
22
1 1 2 2
8z z mz m m z
22
12
88m m z m m z
2
1 33
2
80
1 33
2
m
mm
m
. Kết hợp điều kiện ta được
3;4;5;6;7m
.
Vậy có tất cả là
5
số nguyên cần tìm.
Câu 17: Biết phương trình
2
0,z az b a b
có một nghiệm là
1
3zi
và nghiệm còn lại là
2
z
.
Mô đun của số phức
2
a b z
bằng
A.
10
. B.
9
. C.
18
. D.
27
.
Lời giải:
Phương trình
2
0,z az b a b
có một nghiệm
1
3zi
thì nghiệm còn lại
2
3zi
.
Theo Vi-et ta có.
12
12
0
.9
z z a
a
z z b b


.
Vậy
2
9. 3 27a b z i
.
Câu 18: Cho số phức
w
và hai số thực
,ab
. Biết
1
2z w i
và
2
23zw
là hai nghiệm phức của
phương trình
2
0z az b
. Tính giá trị của
12
T z z
.
A.
2 13T
. B.
4 13T
. C.
2 97
3
T
. D.
2 85
3
T
.
Lời giải:
Vì
12
,zz
là 2 nghiệm phức của phương trình đã cho nên
12
21
zz
zz
2 2 3 2 4 4 6
2
3
3
2 3 2 2 3 2
w i w w i w
wi
w w i w w i





2
2
11
4 4 97
33
3 3 3
z i z



.
Mà
12
,zz
là 2 nghiệm phức của phương trình trên nên
12
97
3
zz
.
Vậy
2 97
3
T
.
Câu 19: Cho các số thực
,bc
sao cho phương trình
2
0z bz c
có hai nghiệm phức
12
;zz
với phần
thực là số nguyên và
thỏa mãn
1
3 2 1zi
và
12
22z i z
là số thuần ảo. Khi đó,
bc
bằng
A.
1
. B.
12
. C.
4
. D.
12
.
Lời giải:
Trường hợp 1: Nếu các nghiệm của phương trình là các số thực
;xy
thì
2
1
3 2 3 2 3 4 2 1z i x i x
mâu thuẫn với giả thiết.
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Trường hợp 2: Các nghiệm phức của phương trình không là các số thự C.
Giả sử
1 2 1
z x yi z z x yi
.
Khi đó
22
1
3 2 1 3 2 1 1z i x y
.
Lại có
12
2 2 2 . 2z i z x y i x yi
. 2 . 2 2 . 2 .x x y y x y xy i


là một số thuần ảo.
Suy ra
22
. 2 . 2 0 2 2 0 2x x y y x y x y
.
Giải hệ gồm
1
và
2
:
22
22
2
3 2 1
2
2 2 0
x
xy
y
x y x y


.
12
2 2 ; 2 2z i z i
.
Vì vậy theo Viet ta có:
12
12
2 2 2 2 4
4 8 12
. 2 2 . 2 2 8
z z b i i
bc
z z c i i
.
Câu 20: Gọi
1 2 3 4
, , ,z z z z
là
4
nghiệm phức của phương trình
42
4 4 0 z m z m
. Tìm tất cả các
giá trị m để
1 2 3 4
6 z z z z
.
A.
1m
. B.
2m
. C.
3m
D.
1m
.
Lời giải:
Ta có:
2
4 2 2 2
2
41
4 4 0 4 0
2

z
z m z m z z m
zm
Ta có:
n
n
zz
.
12
;zz
là nghiệm của phương trình
1
. Ta có:
12
42 zz
.
34
;zz
là nghiệm của phương trình
2
. Ta có:
34
z z m
.
Theo đề ra ta có:
1 2 3 4
6 2 4 6 1 1 z z z z m m m
.
Kết luận
1m
.
Câu 21: Trên tập hợp các số phức, phương trình
2
0az bz
, với
,ab
có nghiệm
0
23zi
.
Biết rằng phương trình
2
0bz az
cũng có hai nghiệm phức
12
,zz
. Tính
12
S z z
.
A.
4
. B.
13
. C.
25
. D.
185
.
Lời giải:
Phương trình
2
0az bz
, với
,ab
có nghiệm
0
23zi
khi và chỉ khi
2
2 5 4
2 3 2 3 0 2 5 3 4 0
4 0 13.
a b a
i a i b a b a i
ab



Khi đó phương trình
2
0bz az
trở thành
2
13 4 0zz
có hai nghiệm thực phân biệt
trái dấu
1,2
13
2
185
z
.
Suy ra
12
13 185 13 185 13 185 13 185
185
2 2 2 2
S z z
.
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Câu 22: Trên tập hợp các số phức, xét phương trình
22
4 2 0,z az b
(
,ab
là các tham số thực). Có
bao nhiêu cặp số thực
;ab
sao cho phương trình đó có hai nghiệm
12
,zz
thỏa mãn
12
2 3 3 ?z iz i
A.
4.
B.
1.
C.
2.
D.
3.
Lời giải:
Theo định lý Vi-ét, ta có:
12
2
12
4
2
z z a
z z b

.
Theo yêu cầu bài toán, phương trình đã cho có hai nghiệm
12
,zz
thỏa mãn
12
2 3 3z iz i
12
2 3 3 0z iz i
1 2 2 1
2 3 3 2 3 3 0z iz i z iz i
22
1 2 1 2 1 2
3 1 2 3 3 18 2 0z z i i z z i i z z
2
2
1 2 1 2
3 2 3 9 4 18 2 2 0b i a i i z z z z


2 2 2
3 2 3 9 4 18 2 16 2 2 0b i a i i a b


2
22
3 2 12 0
36 18 32 4 2 0
ba
a a b
2
2
24
36 18 32 16 0
ba
a a a
2
2
24
32 52 18 0
ba
aa
2
24
1
2
9
8
ba
a
a


2
1
;0
2
95
;
82
ab
ab
1
;0
2
.
9 10
;
82
ab
ab
Vậy có
3
cặp số thực
;ab
thỏa mãn bài toán.
Câu 23: Trên tập số phức, cho phương trình
22
2 1 2 0z m z m m
. Có bao nhiêu tham số
m
để
phương trình đã cho có hai nghiệm phân biệt
12
;zz
thõa mãn
22
12
5zz
A.
1
. B.
0
. C.
2
. D.
4
.
Lời giải:
Ta có:
2
2
1 2 4 1m m m m
TH1: YCBT
22
2
2
2
12
1 2 1 2
1
1
0
4
4
5
4 1 2 2 5
25
m
m
zz
m m m
z z z z




2
1
4
1
6 38
4
()
2
2 12 1 0
6 38
()
2
m
m
mL
mm
mN



TH2: Khi
1
0
4
m
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Phương trình đã cho có hai nghiệm phức
12
;zz
có dạng
12
,z a bi z a bi
với
1; 4 1a m b m
Khi đó:
22
2 2 2 2
12
2
5
5 2 2 5
2
2 14
()
5
2
1 4 1
2
2 14
()
2
z z a b a b
mN
mm
mL


Câu 24: Trên tập hợp số phức, xét phương trình
22
20z z m
(
m
là tham số thực). Có bao nhiêu
giá trị của
m
để phương trình đó có nghiệm
0
z
thỏa mãn điểm biểu diễn của
0
z
thuộc đường
E-lip có phương trình
2
2
1?
4

x
y
A.
2
. B.
3
. C.
4
. D.
1
.
Lời giải:
Xét phương trình
22
20z z m
có
2
1 m
.
Trường hợp 1:
0

1;1m
.
Phương trình có các nghiệm là
2
0
11zm
hoặc
2
0
11zm
.
Với
2
0
11zm
điểm biểu diễn thuộc E-lip
2
2
1
4
x
y
Do đó
2
2
1 1 4m
2
13mm
.
Với
2
0
11zm
điểm biểu diễn thuộc E-lip
2
2
1
4
x
y
Do đó
2
2
1 1 4m
2
1 1 0mm
.
Trường hợp này giá trị
0m
thỏa mãn.
Trường hợp 2:
0

; 1 1;m
.
Phương trình có các nghiệm là
2
0
11z i m
hoặc
2
0
11z i m
.
Điểm biểu diễn thuộc E-lip
2
2
1
4
x
y
Do đó
2
2
2
1
11
4
m
2
3
1
4
m
7
4
m
(thỏa mãn).
Trường hợp này giá trị
7
4
m
thỏa mãn.
Vậy có
3
giá trị của
m
thỏa mãn yêu cầu bài toán.
Câu 25: Biết phương trình
22
20z mz m
(
m
là tham số thực) có hai nghiệm phức
12
,zz
. Gọi
,,A B C
lần lượt là điểm biểu diễn các số phức
12
,zz
và
0
zi
. Có bao nhiêu giá trị của tham
số
m
để diện tích tam giác
ABC
bằng 1?
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
A.
2
. B.
3
. C.
4
. D.
6
Lời giải:
Ta có:
2 2 2
4 2 3 8m m m
Trường hợp 1:
2
2 6 2 6
0 3 8 0
33
mm
.
Khi đó, phương trình có hai nghiệm thực phân biệt là
12
,zz
.
Vì
,A B Ox
nên
22
2
1 2 1 2 1 2 1 2
4 3 8AB z z z z z z z z m
.
Mặt khác, ta có
0;1 ; 1C d C AB
.
2
1 3 8 2 3
. ; 1
2 2 3
ABC
m
S AB d C AB m n

.
Trường hợp 2:
2
26
3
0 3 8 0
26
3
m
m
m
.
Khi đó, phương trình có hai nghiệm phức liên hợp là
1,2
2
mi
z
.
Ta có:
22
12
3 8 3 8AB z z i m m
và
0;1C
.
Phương trình đường thẳng
AB
là
0
2
m
x 
nên
;
2
m
d C AB
.
Do đó,
2
2
2
4
38
1
. ; 1 2
4
24
(VN)
3
ABC
m
mm
S AB d C AB m
m

.
Vậy có 4 giá trị thực của tham số
m
thỏa mãn đề bài.
Câu 26: Trên tập hợp các số phức, xét phương trình
2
2 1 8 4 0z m z m
(
m
là tham số thực). Có
bao nhiêu giá trị nguyên của
m
để phương trình đã cho có hai nghiệm phân biệt
12
,zz
thỏa
mãn
22
1 1 2 2
2 8 2 8z mz m z mz m
?
A.
4
. B.
3
. C.
5
. D.
6
.
Lời giải:
Ta có
2
65mm
và
22
1 1 2 2
2 8 2 8z mz m z mz m
22
1 1 1 2 2 2
2 1 8 4 2 4 2 1 8 4 2 4z m z m z z m z m z
12
2 4 2 4zz
1
* Xét
5
0
1
m
m
. Khi đó PT có 2 nghiệm thực phân biệt
Nên
1
1 2 1 2
2 4 2 4 4 2 1 4 3z z z z m m
* Xét
0 1 5m
. Khi đó PT có 2 nghiệm phức phân biệt
12
,zz
liên hợp của nhau
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Nên
12
2 1, 2 1zz
cũng là hai số phức liên hợp của nhau. Suy ra
12
2 1 2 1zz
luôn thỏa
Vậy có 4 giá trị nguyên của tham số
m
thỏa mãn đề bài.
Câu 27: Tìm tổng các giá trị của số thực
a
sao cho phương trình
22
3 2 0z z a a
có nghiệm phức
0
z
thỏa
0
2z
.
A.
0
. B.
2
. C.
4
. D.
6
.
Lời giải:
Trường hợp 1:
0
z
. Khi đó
0
0
0
2
2
2
z
z
z


.
Nếu
0
2z
thì
2
2 10 0aa
không có nghiệm thực
a
.
Nếu
0
2z 
thì
2
13
2 2 0
13
a
aa
a


(1).
Trường hợp 2:
0
z
. Khi đó phương trình
22
3 2 0z z a a
có nghiệm phức
0
z
nên
0
z
cũng là nghiệm phức của phương trình.
Vì
0
2z
nên
2
0 0 0
.4z z z
.
Theo định lý Vi-ét, ta có:
2
2
00
2
.2
1
aa
z z a a
.
22
15
2 4 2 4 0
15
a
a a a a
a


(2).
Từ (1) và (2), ta có tổng các giá trị của số thực
a
thỏa yêu cầu bài toán là:
1 3 1 3 1 5 1 5 4
.
Câu 28: Trên tập hợp các số phức, gọi
S
là tổng các giá trị thực của
m
để phương trình
2
2 1 6 0mz m z m
có nghiệm
0
z
thỏa mãn
0
1z
. Tính
S
.
A.
3
. B.
4
. C.
1
. D.
2
.
Lời giải:
Xét phương trình
2
2 1 6 0mz m z m
.
Trường hợp 1:
0m 
Phương trình đã cho có dạng
2 6 0 3 3z z z
không
thõa mãn.
Trường hợp 2:
0m
Ta có
2
2
1 6 2 4 1m m m m m
.
Nếu:
2
22
2
0 2 4 1 0
22
2
m
mm
m
thì phương trình đã cho có hai nghiệm thực
0
z
là số thực. Theo bài ra, ta có
0
0
0
1
1
1
z
z
z


.
Với
0
1z
, ta có
2 2 6 0 4m m m m
(thỏa mãn ).
Với
0
1z 
, ta có
2 2 6 0 2m m m m
( thỏa mãn ).
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Nếu:
2
2 2 2 2
0 2 4 1 0
22
m m m

, thì phương trình đã cho có hai
nghiệm phức.
0
z
là nghiệm của phương trình đã cho
0
z
cũng là nghiệm của phương trình đã cho.
Áp dụng hệ thức viét, ta có
00
6
.
m
zz
m

mà
2
0 0 0
6
. 1 1 3
m
z z z m
m

(không
thõa mãn). Vậy
4; 2 2m m S
.
Câu 29: Cho phương trình
22
20z az a
, với
a
là số thực dương. Gọi
12
,zz
là hai nghiệm phức của
phương trình, trong đó
1
z
có phần ảo dương. Biết rằng
1 2 1
2 10 2 7z z z i
. Khẳng định
nào sau đây đúng?
A.
13a
. B.
1a
. C.
58a
. D.
35a
.
Lời giải:
Xét phương trình
22
20z az a
, với
0a
.
Ta có:
2 2 2
8 7 0a a a
,
0a
Suy ra phương trình có hai nghiệm phức
12
,zz
với
12
zz
và
2
7
2
a a i
z

.
Theo định lí Viét ta có:
12
2
12
.2
z z a
z z a
Khi đó:
1 2 1
2 10 2 7z z z i
22
1 2 2
2
22
2
2
7
10 2 7 2 10 2 7 2 . 10 2 7
2
5
10
57
2
10 2 7 4 2.
22
7
27
2
a a i
z a z i a az i a a i
a
a a i
i a a
a

Câu 30: Trên tập hợp các số phức, xét phương trình
22
2 2 1 4 5 0z m z m m
(
m
là tham số
thực). Có bao nhiêu giá trị của tham số
m
để phương trình có nghiệm
0
z
thoả mãn
0
3 10z 
?
A.
1
. B.
2
. C.
4
.
D.
3
.
Lời giải:
Cách 1: Ta có
1m
.
Trường hợp 1:
1 0 1mm
.
Khi đó theo bài ra, phương trình đã cho có nghiệm thực
0
z
thoả mãn
0
0
0
7
3 10
13
z
z
z

.
Từ đó suy ra
22
2
2
7 2 2 1 7 4 5 0
13 2 2 1 13 4 5 0
m m m
m m m
2
2
4 33 63 0
4 47 143 0
mm
mm
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
3
21
4
m tm
m tm
.
Trường hợp 2:
1 0 1mm
.
Khi đó phương trình đã cho có hai nghiệm phức là
0
z
và
0
z
và thoả mãn
0
3 10z 
2
2
0 0 0 0 0
3 3 100 3 9 100 4 5 3.2 2 1 91 0z z z z z m m m
2
7 1601
8
4 7 97 0
7 1601
8
m tm
mm
m ktm


.
Vậy có 3 giá trị của tham số
m
thoả mãn yêu cầu bài toán.
Cách 2: Ta có
2
22
2 2 1 4 5 0 2 1 1 1z m z m m z m m
.
Trường hợp 1:
1 0 1mm
.
Khi đó
2 1 1
1
2 1 1
z m m
z m m
.
Theo bài ra, phương trình đã cho có nghiệm
0
z
thoả mãn
0
3 10z 
.
Do đó
3
2 2 1 10
21
2 2 1 10
4
m tm
mm
m tm
mm
.
Trường hợp 2:
1 0 1mm
Khi đó
2 1 1
1
2 1 1
z m i m
z m i m
.
Theo bài ra, phương trình đã cho có nghiệm
0
z
thoả mãn
0
3 10z 
.
Do đó
22
2 2 1 10 4 8 4 1 100 4 7 97 0m i m m m m m m
7 1601
8
7 1601
8
m tm
m ktm


.
Vậy có 3 giá trị của tham số
m
thoả mãn yêu cầu bài toán.
Câu 31: Cho số phức
,zw
khác 0 thỏa mãn
0zw
và
2 3 4
z w z w

. Khi đó
z
w
bằng:
A.
2
. B.
6
3
. C.
3
. D.
2
3
.
Lời giải:
Với hai số phức
,zw
khác 0 thỏa mãn
0zw
, ta có:
22
2 3 4 2 3 4
2 3 4 3 2 0
wz
w z z w zw z zw w
z w z w zw z w

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
2
1 23
66
3 2 0
1 23
66
z
i
zz
w
ww
z
i
w
Suy ra
2
2
1 23 6
6 6 3
z
w







.
Câu 32: Tìm tất cả các giá trị thực của
a
sao cho phương trình
22
20z az a a
có hai nghiệm
phức có môđun bằng 1.
A.
1a 
. B.
1a
. C.
1a 
. D.
15
2
a

.
Lời giải:
Gọi
12
,zz
là hai nghiệm của phương trình
22
20z az a a
. Ta có
12
1zz
.
Theo định lí Viét, ta có
2
12
2z z a a
.
Lấy mô đun hai vế có
2 2 2
1 2 1 2
2 . 2 2 1z z a a z z a a a a
22
22
2 1 2 1 0
2 1 2 1 0
a a a a
a a a a





1
12
a
a

.
Với
1a
có phương trình thành
2
13
1 0 1
2
i
z z z z
1a
thỏa mãn.
Với
12a 
có phương trình thành
2
1 2 7 2 2
1 2 1 0
2
z z z
.
12a
không thỏa mãn.
Với
12a 
có phương trình thành
2
1 2 7 2 2
1 2 1 0
2
z z z
.
12a
không thỏa mãn. Vậy
1a
.
Câu 33: Trên tập số phức, xét phương trình
22
2 5 0z mz n
(với
m
,
n
là tham số thực). Có bao
nhiêu cặp số
( ; )mn
để phương trình đã cho có hai nghiệm phức
12
,zz
sao cho các điểm biểu
diễn của
1 2 3 4
, , 1, 5z z z z
là bốn đỉnh của một hình vuông?
A.
3
. B.
2
. C.
4
. D.
1
.
Lời giải:
Để phương trình có hai nghiệm phức khi và chỉ khi
22
50mn
.
Đặt
12
;,z a bi a b z a bi
.
Ta có bốn điểm
; , ; , 1;0 , 5;0A a b B a b C D
biểu diễn bốn số phức
1 2 3 4
, , 1, 5z z z z
lập
thành hình vuông. Suy ra
ACBD
là hình vuông nên
3
3;0
3
24
2
a
AB
a
b
b
AB CD




.
12
1
2
2
12
3
62
32
3
2 3 2
13 5
22
m
z z m
zi
a
b z i
z z n
n



.
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
12
1
2
2
12
3
62
32
3
2 3 2
13 5
22
m
z z m
zi
a
b z i
z z n
n



.
Vậy ta có hai cặp số
;mn
thỏa yêu cầu bài toán.
Câu 34: Trên tập hợp các số phức, xét phương trình
2
2 12 0z mz m
(
m
là tham số thực). Có bao
nhiêu giá trị nguyên của
m
để phương trình đó có hai nghiệm phân biệt
1
z
,
2
z
thỏa mãn
1 2 1 2
2z z z z
?
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải:
Phương trình đã cho có
2
12mm
.
Trường hợp 1:
2
4
0 12 0
3
m
mm
m

.
Khi đó, phương trình đã cho có hai nghiệm thực
1
z
,
2
z
phân biệt.
Do đó,
1 2 1 2
2z z z z
2
2
1 2 1 2
2z z z z
2 2 2 2
1 2 1 2 1 2 1 2
2 2 2z z z z z z z z
22
1 2 1 2 1 2 1 2 1 2
2 2 2 4z z z z z z z z z z


2
1 2 1 2 1 2
6 2 0z z z z z z
2
4 6 12 2 12 0m m m
Nếu
4m 
hoặc
3 12m
thì
22
6
4 8 12 0 2 24 0
4
m
m m m m
m

.
Nếu
12m
thì
22
4 4 12 0 12 0m m m m
.
Trường hợp 2:
2
0 12 0 4 3m m m
.
Khi đó, phương trình đã cho có hai nghiệm phân biệt
1
z
,
2
z
là hai số phức liên hợp:
2
12m i m m
và
2
12m i m m
.
Do đó,
1 2 1 2
2z z z z
2 2 2
2 12 2 12m m m m m
2
12 12m m m
0m
.
Vậy có 3 giá trị nguyên của tham số
m
thỏa mãn đề bài.
Câu 35: Cho phương trình
42
4 4 0z mz
trong tập số phức và
m
là tham số thực. Gọi
1 2 3 4
, , , z z z z
là bốn nghiệm của phương trình đã cho. Tìm tất cả các giá trị của
m
để
2222
1 2 3 4
4 4 4 4 324zzzz
.
A.
2
15
m
m

. B.
2
15
m
m

. C.
1
35
m
m

. D.
1
35
m
m

.
Lời giải:
Đặt
2
tz
, phương trình trở thành
2
4 4 0t mt
có hai nghiệm
12
, tt
.
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Ta có
12
12
4
.1
m
tt
tt
. Do vai trò bình đẳng, giả sử ta có
22
1 2 1
z z t
,
22
3 4 2
z z t
.
Yêu cầu bài toán
2
22
1 2 1 2 1 2
4 4 324 4 16 324t t t t t t


2
2
17 18 1
17 18
17 18 35
mm
m
mm



.
Câu 36: Cho các số thực
,bc
sao cho phương trình
2
0z bz c
có hai nghiệm phức
12
,zz
thỏa
mãn
1
4 3 1zi
và
2
8 6 4zi
. Mệnh đề nào sau đây đúng?
A.
5 12.bc
B.
5 4.bc
C.
5 4.bc
D.
5 12.bc
Lời giải:
Vì
12
,zz
là hai nghiệm phức của phương trình
2
0z bz c
nên
12
zz
Khi đó ta có
2 1 1
8 6 4 8 6 4 8 6 4.z i z i z i
Gọi
M
là điểm biểu diễn số phức
1
.z
M
vừa thuộc đường tròn
1
C
tâm
1
4; 3 ,I
bán kính
1
1R
và đường tròn
2
C
tâm
1
8; 6 ,I
bán kính
1
4R
12
.m C C
Ta có
22
1 2 1 2 1
4 3 5I I R R C
và
2
C
tiếp xúc ngoài.
Do đó có duy nhất 1 điểm
M
thỏa mãn, tọa độ điểm
M
là nghiệm của hệ
22
1
22
24
8 6 24 0
24 18 24 18
5
;
18
5 5 5 5
16 12 84 0
5
x
x y x y
M z i
x y x y
y






là nghiệm của
phương trình
2
0z bz c
2
24 18
55
zi
cũng là nghiệm của phương trình
2
0.z bz c
Áp dụng định lí Vi ét ta có
1 2 1 2
48 48
; . 36
55
z z b b z z c
Vậy
5 48 36 12.bc
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Câu 37: Cho phương trình
2
0z bz c
, có hai nghiệm
12
,zz
thỏa mãn
21
42z z i
. Gọi
,AB
là các
điểm biểu diễn các nghiệm của phương trình
2
2 4 0z bz c
. Tính độ dài đoạn
AB
.
A.
8 5.
B.
2 5.
C.
4 5.
D.
5.
Lời giải:
2
0z bz c
có hai nghiệm
12
,zz
thỏa mãn
21
42z z i
Xét
2 2 2
2
2 1 2 1 1 2
4 2 4 4 2 4 4 2z z i z z z z i b c i
Khi đó phương trình
2
2 4 0z bz c
có
2
2
4 2 4; 2
4 4 2 , ,
4 2 4;2
A
B
z b i A b
b c i b m ni m n
z b i B b
Vậy
22
4 4 2 2 4 5.AB b b
Câu 38: Trên tập hợp các số phức, phương trình
2
2 2 3 0z a z a
(
a
là tham số thực) có
2
nghiệm
1
z
,
2
z
. Gọi
M
,
N
là điểm biểu diễn của
1
z
,
2
z
trên mặt phẳng tọa độ. Biết rằng có
2
giá trị của tham số
a
để tam giác
OMN
có một góc bằng
120
. Tổng các giá trị đó bằng bao
nhiêu?
A.
6
. B.
4
. C.
4
. D.
6
.
Lời giải:
Vì
O
,
M
,
N
không thẳng hàng nên
1
z
,
2
z
không đồng thời là số thực, cũng không đồng
thời là số thuần ảo
1
z
,
2
z
là hai nghiệm phức, không phải số thực của phương trình
2
2 2 3 0z a z a
. Do đó, ta phải có
2
12 16 0aa
6 2 5; 6 2 5a
.
Khi đó, ta có
2
1
2
1
2 12 16
22
2 12 16
22
a a a
zi
a a a
zi


.
12
23OM ON z z a
và
2
12
12 16MN z z a a
.
Tam giác
OMN
cân nên
120MON 
2 2 2
cos120
2.
OM ON MN
OM ON

2
8 10 1
2 2 3 2
aa
a

2
6 7 0 3 2a a a
.
Suy ra tổng các giá trị cần tìm của
a
bằng
6
.
Câu 39: Trên tập hợp các số phức, xét phương trình
2
2z 2 0zm
(
m
là tham số thực). Gọi
là
tập hợp các giá trị của
m
để phương trình trên có hai nghiệm phân biệt được biểu diễn hình
học bởi hai điểm
, AB
trên mặt phẳng tọa độ sao cho diện tích tam giác
ABC
bằng
22
, với
1;1C
. Tổng các phần tử trong
bằng
A.
8
. B.
4
. C.
9
. D.
1
.
Lời giải:
Ta có:
2
2
2z 2 0 1 1 1z m z m
TH1. có hai nghiệm phức
1 0 1mm
.
Khi đó, phương trình có hai nghiệm phức
1
11z m i
;
2
11z m i
.
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Gọi
A
,
B
lần lượt là hai điểm biểu diễn của
1
z
;
2
z
trên mặt phẳng
Oxy
ta có:
1; 1Am
;
1; 1Bm
.
Ta có:
21AB m
;
; ; 1 2d C AB d C x
.
Khi đó
1
. ; 2 1 2 2 1.
2
ABC
S AB d C AB m m
TH2. có hai nghiệm thực phân biệt
1 0 1mm
.
Khi đó, phương trình có hai nghiệm
1
11zm
;
2
11zm
.
Gọi
A
,
B
lần lượt là hai điểm biểu diễn của
1
z
;
2
z
trên mặt phẳng
Oxy
ta có:
1 1 ;0Am
;
1 1 ;0Bm
.
Ta có:
21AB m
;
; ; 1d C AB d C Ox
.
Khi đó
1
. ; 1 2 2 9.
2
ABC
S AB d C AB m m
Vậy
1;9T 
nên tổng các phần tử
trong
bằng
8
.
Câu 40: Biết rằng phương trình
2
20z az b
(,ab
là các số thực dương) có hai nghiệm phức liên
hợp
12
,zz
. Gọi
,,A B C
lần lượt là các điểm biểu diễn của số phức
12
2, ,w z z
. Tính giá trị của
biểu thức
4T b a
biết rằng ba điểm
,,A B C
tạo thành một tam giác vuông có diện tích
bằng
9
.
A.
6
. B.
8
. C.
9
. D.
14
.
Lời giải:
Do phương trình
2
20z az b
(,ab
là các số thực dương) có hai nghiệm phức liên hợp
12
,zz
nên từ giả thiết ta gọi tọa độ các điểm biểu diễn cho các số phức
12
2, ,w z z
là
(2;0); ( ; ); ( ; )A B x y C x y
với
2, 0xy
(x 2;y); (x 2; y)AB AC
. Do
A
thuộc
Ox
,
,BC
đồi xứng qua
Ox
Nên theo giả thiết suy ra
ABC
là tam giác vuông cân tại
A
22
. 0 ( 2) 0 (1)AB AC x y
Mặt khác
1
.
2
ABC
S AB AC
22
1
9 ( 2)
2
xy


Từ và suy ra
53
13
xy
xy
Với
5, 3xy
ta tìm được
12
5 3 ; 5 3z i z i
.
Với
1, 3xy
ta tìm được
12
1 3 ; 1 3z i z i
suy ra
1; 10 6a b T
Câu 41: Trên tập hợp số phức, xét phương trình
22
2 20 0 1z az b
với
,ab
là các tham số
nguyên dương. Khi phương trình có hai nghiệm phân biệt
12
,zz
thỏa mãn:
12
3 7 5z iz i
thì giá trị của biểu thức
75ab
bằng
A.
19
. B.
17
. C.
32
. D.
40
.
Lời giải:
Nhận xét: Nếu
22
20 0ab
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Giả thiết
1
12
2
7
3 7 5
5
3
z
z iz i
z
. Suy ra
12
5
72
3
z z a
Suy ra:
22
20 0ab
Giải phương trình
1
ta có hai nghiệm
22
22
20
20
z a a b i
z a a b i
TH1:
22
1
2 2 2 2
12
22
2
20
3 7 5 3 20 3 20 7 5
20
z a a b i
z iz i a a b a a b i i
z a a b i
22
22
22
1
3 20 7
20 2
3 20 5
a
a a b
VN
ab
a a b



TH2:
22
1
2 2 2 2
12
22
2
20
3 7 5 3 20 3 20 7 5
20
z a a b i
z iz i a a b a a b i i
z a a b i
22
2
22
22
2
1
1
1
3 20 7
1
25 5
5
20 4
3 20 5
5( )
17( )
a
a
a
a a b
a
bb
b
ab
a a b
bl
bl


Suy ra
7 5 32ab
Cách 2 Nhận xét: Nếu
22
20 0ab
Giả thiết
1
12
2
7
3 7 5
5
3
z
z iz i
z
. Suy ra
12
5
72
3
z z a
Suy ra:
22
20 0ab
Giả thiết ta có:
11
1 2 1
2 1 2
21
3 7 5 3 7 5
3 7 5 1 2
3 7 5 1 2
3 7 5
z i i iz i
z iz i z i
z iz i z i
z iz i



Áp dụng viet suy ra
1
7 5 32
5
a
ab
b
.
Câu 42: Cho phương trình
2
40
c
xx
d
có hai nghiệm phức. Gọi
A
,
B
là hai điểm biểu diễn của
hai nghiệm đó trên mặt phẳng
Oxy
. Biết tam giác
OAB
đều, tính
2P c d
.
A.
18P
. B.
10P 
. C.
14P 
. D.
22P
.
Lời giải:
Ta có:
2
40
c
xx
d
có hai nghiệm phức
40
c
d
.
Khi đó, phương trình có hai nghiệm phức
1
2xi
;
2
2xi
.
Gọi
A
,
B
lần lượt là hai điểm biểu diễn của
1
x
;
2
x
trên mặt phẳng
Oxy
ta có:
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
2;A
;
2;B

.
Ta có:
2AB

;
4OA OB
.
Tam giác
OAB
đều khi và chỉ khi
2 4 4 4AB OA OB
4
3
. Vì
0

nên
4
3
hay
4 16
4
33
cc
dd
.
Từ đó ta có
16c
;
3d
.
Vậy:
2 22P c d
.
Câu 43: Cho phương trình
42
4 4 0z mz
trong tập số phức và
m
là tham số thự C. Gọi
1 2 3 4
, , ,z z z z
là bốn nghiệm của phương trình đã cho. Tìm tất cả các giá trị của
m
để
2222
1 2 3 4
4 4 4 4 324zzzz
.
A.
1;m
35m 
. B.
1;m
35m 
. C.
1;m
35m
. D.
1;m
35m
.
Lời giải:
Đặt
42
44f z z mz
.
Vì phương trình
0fz
có
4
nghiệm
1 2 3 4
, , ,z z z z
nên
42
1 2 3 4
4 4 4f z z mz z z z z z z z z
Ta có:
2
1 1 1
4 2 2z z i z i
2222
1 2 3 4
22
4 4 4 4 .
44
f i f i
zzzz
Mà
42
42
2 4 2 2 4 68 4
2 4 2 2 4 68 4
f i i m i m
f i i m i m
và
2222
1 2 3 4
4 4 4 4 324zzzz
Nên
2
68 4
324
16
m
1
35
m
m

.
Câu 44: Tìm
m
để các nghiệm của phương trình sau đều là số ảo:
42
3 6 3 0m z z m
.
A.
3 3 2m
. B.
3 3 2m
. C.
3 2 3
.
3 3 2

m
m
D.
3 2 3m
.
Lời giải:
* Nếu
3m
: Phương trình trở thành
2
6 6 0z z i
.
* Nếu
3m
: Đặt
z xi x
, phương trình
42
3 6 3 0 1m z z m
trở thành
42
3 6 3 0 2m x x m
.
Đặt
2
0t x t
, phương trình
2
trở thành
2
3 6 3 0 3m t t m
.
Phương trình
1
chỉ có nghiệm ảo
phương trình
2
chỉ có nghiệm thự C.
phương trình
3
có
2
nghiệm thực thỏa mãn:
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
12
0 tt
0
0
0
S
P


2
18 0
6
0
3
3
0
3
m
m
m
m


3 2 3 2
3
3
3
m
m
m
m


3 3 2m
.
Vậy
3 3 2m
thỏa mãn yêu cầu bài toán.
Câu 45: Gọi
là tổng các số thực
m
thỏa mãn
32
7 16 12 3 0z z z mz m
có nghiệm phức
0
z
thỏa mãn
0
| | 2z
. Khẳng định nào dưới đây đúng?
A.
24S
. B.
25S
. C.
18S
. D.
16S
.
Lời giải:
Ta có
32
7 16 12 3 0z z z mz m
2
3 4 4 0 1z z z m
2
3
2
z
zm

+ Với
0m
(1) 2zm
Ta có:
0
| 2 | 2
| | 2
| 2 | 2
m
z
m



0
16
m
m
+ Với
0m
(1) 2z i m
. Do đó
0
| | 4zm
Ta có:
0
| | 2 4 2zm
4 4 0mm
Vậy
0 16 16S
.
Câu 46: Trên tập hợp số phức cho phương trình
2
0z bz c
, với
,bc
. Biết rằng hai nghiệm của
phương trình có dạng
1
3zw
và
2
3 8 13z w i
với
w
là một số phức. Tính
bc
.
A.
9
. B.
10
. C.
11
. D.
12
.
Lời giải:
Gọi
w x yi
với
,xy
1
3 3 3z w x yi x yi
2
3 8 13 3( ) 8 13 3 13 3 8z w i x yi i x y i
12
,zz
là hai số phức liên hợp nên:
3 3 13
38
xx
yy
5
2
x
y

Khi đó
1
22zi
,
2
22zi
Ta có
12
12
4
.8
zz
zz
Suy ra
12
,zz
là nghiệm của phương trình:
2
4 8 0zz
Vậy
4 8 12bc
.
Câu 47: Trên tập hợp các số phức, xét phương trình:
22
2 1 3 5 0z m z m m
(
m
là tham số
thực). Tính tổng các giá trị của
m
để phương trình trên có nghiệm
0
z
thỏa mãn
3
00
12 5 .zz
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
A.
9
. B.
12
. C.
10
. D.
8
.
Lời giải:
Ta có
3
32
0 0 0 0 0 0 0 0
12 5 5 12 0 3 3 4 0 3z z z z z z z z
Đặt phương trình
22
2 1 3 5 0z m z m m
1
có
54m
TH1: xét
4
0 5 4 0
5
mm
khi đó
0
.z
Ta có
0
3z
0
0
3
3
z
z

Với
0
3z
thay vào
1
2
1
9 8 0
8
m
mm
m
Với
0
3z 
thay vào
1
2
3 20 0mm
pt vô nghiệm.
TH2: xét
4
0 5 4 0
5
mm
.
Khi đó phương trình
1
có hai nghiệm phức
10
zz
và
20
zz
thỏa mãn
2
22
0 0 0 0 1 2
1
3 9 . 9 . 9 3 5 9 3 4 0
4
m
z z z z z z m m m m
m

.
Với
1m 
thay vào
1
2
9 0 3z z i
thỏa mãn
Với
4m
không thỏa mãn điều kiện ban đầu.
Vậy có 3 giá trị
1
8
1
m
m
m

Nên tổng các giá trị của tham số
m
là 8.
Câu 48: Cho phương trình
2
0z bz c
có hai nghiệm
12
,zz
thỏa mãn
21
34z z i
. Gọi
,AB
là các
điểm biểu diễn các nghiệm của phương trình
2
2 4 0z bz c
. Tính độ dài đoạn
AB
.
A.
20.
B.
2 5.
C.
10.
D.
5.
Lời giải:
Phương trình
2
0z bz c
có hai nghiệm
12
,zz
thỏa mãn
21
34z z i
.
Theo định lý Viet ta có:
12
12
.
z z b
z z c
Xét
2 2 2
2
2 1 2 1 1 2
3 4 4 3 4 4 3 4z z i z z z z i b c i
Khi đó phương trình
2
2 4 0z bz c
có
2
2
3 4 3;4
4 3 4 , ,
3 4 3; 4
A
B
z b i A b
b c i b m ni m n
z b i B b
Vậy
22
3 3 4 4 10.AB b b
Câu 49: Cho
m
là số thực, biết phương trình
2
2 9 0z mz
có hai nghiệm phức
12
,zz
. Có bao nhiêu
giá trị nguyên của
m
sao cho
1 2 2 1
16z z z z
?
A.
3
. B.
4
. C.
5
. D.
6
.
Lời giải:
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
2
2 9 0 (*)z mz
có
2
9m
.
Phương trình
(*)
có hai nghiệm phức
12
,zz
thỏa mãn
1 2 2 1
16z z z z
nên
0 3 3m
.
Áp dụng định lý Vi-ét ta có,
1 2 1 2
2 , 9z z m z z
.
Ta có
1 2 1 2 1 2
93z z z z z z
và
1 1 2 2
,z z z z
.
1 2 2 1 1 2 1 2
.3 .3 3 6z z z z z z z z m
.
Theo đề,
1 2 2 1
8
16 6 16
3
z z z z m m
.
Kết hợp với điều kiện ta được
8
3
3
m
. Mà
m
nguyên nên
2; 1;0;1;2m
Vậy có
5
giá trị
m
thỏa mãn yêu cầu bài toán.
Câu 50: Gọi
S
là tập hợp tất cả các số thực
a
sao cho phương trình
2
( 2) 2 3 0z a z a
có hai
nghiệm phức
12
,zz
và các điểm biểu diễn của
12
,zz
cùng với gốc tọa độ
O
tạo thành một tam
giác có diện tích bằng 2. Số phần tử của
S
là?
A.
1
. B.
4
. C.
2
. D.
3
.
Lời giải:
Nếu
2
12
2 4 2 3 0 ,a a z z
là các số thực khi đó
12
( ), ( ) , ,M z N z Ox O M N
thẳng hàng.
Nếu
2
1 2 1 2 1 2
2 4 2 3 0 2 3a a z z z z z z a
.
Với
1 2 1 2
( ), ( )M z N z OM ON z z
và
2
22
1 2 1 2 1 2 1 2
( ) 4 4(2 3) (2 )MN z z z z z z z z a a
.
Tam giác
OMN
cân tại
O
. Do đó
2
2 2 2
11
. . 4
2 4 4
OMN
MN
S MN OM MN OM MN
.
Mà
2
OMN
S 
22
4
1
4(2 3) (2 ) (2 ) 2
10,369
4
a
a a a
a
.
Vậy có 2 số thực
a
thỏa mãn yêu cầu bài toán.
____________________HẾT____________________
Huế, 15h15’ Ngày 19 tháng 3 năm 2023
| 1/32
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ SỐ PHỨC
PHƯƠNG TRÌNH VỚI HỆ SỐ THỰC
 LUYỆN THI THPT QUỐC GIA
 CẬP NHẬT TỪ ĐỀ THI MỚI NHẤT
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Ngân hàng câu hỏi:
PHƯƠNG TRÌNH VỚI HỆ SỐ THỰC NỘI DUNG ĐỀ BÀI Câu 1:
Trên tập hợp các số phức, xét phương trình  z 1 a z 1 a  6z ( a là tham số thực). Có 2 2
bao nhiêu giá trị của a để phương trình đó có hai nghiệm z , z thỏa mãn z z  42 ? 1 2 1 2 A. 1. B. 2 . C. 3 . D. 4 . Câu 2:
Trên tập hợp số phức xét phương trình 2 2
z  2mz m  2m 1  0 . Có bao nhiêu giá trị thực
của m để phương trình đã cho có 2 nghiệm z ; z thoả mãn z  2 z ? 1 2 1 2 A. 2 . B. 3 . C. 4 . D. 5 . Câu 3: Biết phương trình 2
z  2z m  0 ( m là tham số thực) có một nghiệm là z  1
  3i . Gọi z là 1 2
nghiệm còn lại. Phần ảo của số phức w  mz  2z bằng 1 2 A. 36 . B. 24 . C. 36 . D. 8  . Câu 4: Cho phương trình 2
z  2mz  6m  8  0 . ( m là tham số thực). Có bao nhiêu giá trị nguyên của
tham số m để phương trình có hai nghiệm phức phân biệt z , z  1 2 thỏa mãn z z z z ? 1 1 2 2 A. 4 . B. 1. C. 3 . D. 2 . Câu 5:
Có bao nhiêu giá trị của tham số m để phương trình có nghiệm phức z thỏa mãn 0 z  2  6 ? 0 A. 3. B. 4. C. 1. D. 2. Câu 6:
Trên tập hợp các số phức, xét phương trình 2
z  2mz  3m 10  0 ( m là tham số thực). Có bao
nhiêu giá trị nguyên của m để phương trình đó có hai nghiệm z , z không phải số thực thỏa 1 2
mãn z z  8 ? 1 2 A. 1. B. 2 . C. 3 . D. 4 . Câu 7:
Trên tập số phức, xét phương trình 2
z  m   2 2
4 z m  4m 1  0 , m là tham số thự C.
Có bao nhiêu giá trị m để phương trình đã cho có hai nghiệm phức phân biệt z , z thỏa điều 1 2
kiện z z  2z z z . 1 2 1 2 1 A. 3 . B. 2 . C. 0 . D. 3. Câu 8:
Trên tập hợp các số phức, xét phương trình 2
z   m   2 2 2
1 z  4m  5m  0 ( m là tham số
thực). Có bao nhiêu giá trị của tham số m để phương trình có nghiệm z thoả mãn 0 2
z  1 4m 2
z  4m  5m  3  10 ? 0 0 A. 1. B. 2 . C. 4 . D. 3 . Câu 9:
Trên tập số phức, xét phương trình 2
z  2mz m  1  0  
1 ( m là tham số thực); z , z là hai 1 2
nghiệm phức của phương trình   1 ; ,
A B lần lượt là điểm biểu diễn của hai nghiệm phức đó
trên mặt phẳng Oxy . Có bao nhiêu giá trị nguyên của m để OAB vuông tại O ? A. 2 . B. 1. C. 3 . D. 4 . 1
Câu 10: Trên tập hợp số phức, xét phương trình 2 z m 1z   2
m  5m  6  0(m là tham số thực). 4
Có bao nhiêu số nguyên m [ 10
 ;10] đề phương trình trên có hai nghiệm phức z , z 1 2 thỏa
mãn z z z z ? 1 2 1 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia A. 11. B. 10. C. 8. D. 9.
Câu 11: Trên tập số phức, cho phương trình 2
z az b  0 (a, b  ) . Có bao nhiêu số phức w sao cho
phương trình đã cho có hai nghiệm là z  (6  i)  w  2i và z  (w  5  i) | w | ? 1 2 A. 4. B. 3. C. 6. D. 5.
Câu 12: Trên tập hợp các số phức, xét phương trình 2
z  2mz  8m 12  0 . Có bao nhiêu giá trị
nguyên của m để phương trình đó có hai nghiệm phân biệt z , z thỏa mãn z z ? 1 2 1 2 A. 5 B. 6 . C. 3 . D. 4 .
Câu 13: Có bao nhiêu số nguyên m để phương trình 2
z  2mz 1  0 có hai nghiệm phức phân biệt
z , z thỏa mãn z  3  z  3 ? 1 2 1 2 A. 1. B. 2 . C. 3 . D. 4 .
Câu 14: Có bao nhiêu số nguyên a để phương trình 2
z  a   2
3 z a a  0 có hai nghiệm phức
z , z thỏa mãn z z z z ? 1 2 1 2 1 2 A. 1. B. 2 . C. 3 . D. 4 .
Câu 15: Cho số phức w và hai số thực b , c . Biết rằng w  2 và 3w  4i là hai nghiệm của phương trình 2
2022z bz c  0 . Tính giá trị biểu thức P b c bằng A. P  4044  .
B. P  8088 .
C. P  4044 . D. P  8088  .
Câu 16: Trên tập các số phức, xét phương trình 2
z mz m  8  0 ( m là tham số thực). Có bao nhiêu
giá trị nguyên của tham số m để phương trình có hai nghiệm z , z 1 2 phân biệt thỏa mãn z  2
z mz    2
m m  8 z 1 1 2  2 ? A. 12. B. 6 . C. 5 . D. 11.
Câu 17: Biết phương trình 2
z az b  0 a ,b   có một nghiệm là z  3i và nghiệm còn lại là z . 1 2
Mô đun của số phức a bz bằng 2 A. 10 . B. 9 . C. 18 . D. 27 .
Câu 18: Cho số phức w và hai số thực a , b . Biết z w  2i và z  2w  3 là hai nghiệm phức của 1 2 phương trình 2
z az b  0 . Tính giá trị của T z z . 1 2 2 97 2 85
A. T  2 13 .
B. T  4 13 . C. T  . D. T  . 3 3
Câu 19: Cho các số thực b , c sao cho phương trình 2
z bz c  0 có hai nghiệm phức z ; z với phần 1 2
thực là số nguyên và thỏa mãn z  3  2i  1 và  z  2i z  2 là số thuần ảo. Khi đó, b c 1  2  1 bằng A. 1  . B. 12 . C. 4 . D. 12 .
Câu 20: Gọi z , z , z , z là 4 nghiệm phức của phương trình 4
z    m 2 4
z  4m  0 . Tìm tất cả các 1 2 3 4
giá trị m để z z z z  6 . 1 2 3 4
A. m  1.
B. m  2 .
C. m  3 D. m  1.
Câu 21: Trên tập hợp các số phức, phương trình 2
z az b  0 , với a, b
có nghiệm z  2  3i . 0
Biết rằng phương trình 2
z bz a  0 cũng có hai nghiệm phức z , z . Tính S z z . 1 2 1 2 A. 4 . B. 13 . C. 25 . D. 185 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Câu 22: Trên tập hợp các số phức, xét phương trình 2 2
z  4az b  2  0, ( a, b là các tham số thực). Có
bao nhiêu cặp số thực a;b  sao cho phương trình đó có hai nghiệm z , z 1 2 thỏa mãn
z  2iz  3  3i ? 1 2 A. 4. B. 1. C. 2. D. 3.
Câu 23: Trên tập số phức, cho phương trình 2
z  m   2 2
1 z m  2m  0 . Có bao nhiêu tham số m để
phương trình đã cho có hai nghiệm phân biệt z ; z thõa mãn 2 2 zz  5 1 2 1 2 A. 1. B. 0 . C. 2 . D. 4 .
Câu 24: Trên tập hợp số phức, xét phương trình 2 2
z  2z m  0 ( m là tham số thực). Có bao nhiêu
giá trị của m để phương trình đó có nghiệm z z
0 thỏa mãn điểm biểu diễn của 0 thuộc đường 2 x E-lip có phương trình 2  y 1? 4 A. 2 . B. 3 . C. 4 . D. 1.
Câu 25: Biết phương trình 2 2
z mz m  2  0 ( m là tham số thực) có hai nghiệm phức z , z 1 2 . Gọi ,
A B,C lần lượt là điểm biểu diễn các số phức z , z z i 1 2 và 0
. Có bao nhiêu giá trị của tham
số m để diện tích tam giác ABC bằng 1? A. 2 . B. 3 . C. 4 . D. 6
Câu 26: Trên tập hợp các số phức, xét phương trình 2
z  2m  
1 z  8m  4  0 ( m là tham số thực). Có
bao nhiêu giá trị nguyên của m để phương trình đã cho có hai nghiệm phân biệt z , z thỏa 1 2 mãn 2 2
z  2mz  8m z  2mz  8m ? 1 1 2 2 A. 4 . B. 3 . C. 5 . D. 6 .
Câu 27: Tìm tổng các giá trị của số thực a sao cho phương trình 2 2
z  3z a  2a  0 có nghiệm phức
z0 thỏa z  2 . 0 A. 0 . B. 2 . C. 4 . D. 6 .
Câu 28: Trên tập hợp các số phức, gọi S là tổng các giá trị thực của m để phương trình 2
mz  2m  
1 z m  6  0 có nghiệm z0 thỏa mãn z  1. Tính S . 0 A. 3 . B. 4  . C. 1. D. 2  .
Câu 29: Cho phương trình 2 2
z az  2a  0 , với a là số thực dương. Gọi z , z là hai nghiệm phức của 1 2
phương trình, trong đó z có phần ảo dương. Biết rằng 2z z z 10  2 7i . Khẳng định 1 2  1 1 nào sau đây đúng?
A. 1  a  3.
B. a 1 .
C. 5  a  8.
D. 3  a  5.
Câu 30: Trên tập hợp các số phức, xét phương trình 2
z   m   2 2 2
1 z  4m  5m  0 ( m là tham số
thực). Có bao nhiêu giá trị của tham số m để phương trình có nghiệm z thoả mãn 0 z  3  10 ? 0 A. 1. B. 2 . C. 4 . D. 3 . 2 3 4 z
Câu 31: Cho số phức z, w khác 0 thỏa mãn z w  0 và   . Khi đó, bằng z w z w w 6 2 A. 2 . B. . C. 3 . D. . 3 3
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Câu 32: Tìm tất cả các giá trị thực của a sao cho phương trình 2 2
z az  2a a  0 có hai nghiệm phức có môđun bằng 1. 1 5 A. a  1  . B. a 1. C. a  1  . D. a  . 2
Câu 33: Trên tập số phức, xét phương trình 2 2
z  2mz n  5  0 (với m , n là tham số thực). Có bao nhiêu cặp số ( ;
m n) để phương trình đã cho có hai nghiệm phức z , z sao cho các điểm biểu 1 2
diễn của z , z , z  1, z  5 là bốn đỉnh của một hình vuông? 1 2 3 4 A. 3 . B. 2 . C. 4 . D. 1.
Câu 34: Trên tập hợp các số phức, xét phương trình 2
z  2mz m 12  0 ( m là tham số thực). Có bao
nhiêu giá trị nguyên của m để phương trình đó có hai nghiệm phân biệt z z 1 , 2 thỏa mãn z z  2 z z ? 1 2 1 2 A. 1. B. 2 . C. 3 . D. 4 .
Câu 35: Cho phương trình 4 2
4z mz  4  0 trong tập số phức và m là tham số thực. Gọi z , z , z , z 1 2 3 4
là bốn nghiệm của phương trình đã cho. Tìm tất cả các giá trị của m để
 2z 4 2z 4 2z 4 2z 4  324 . 1 2 3 4  m  2 m  2  m 1 m  1  A.  . B.  . C.  . D.  . m  15  m  15 m  35  m  35
Câu 36: Cho các số thực b, c sao cho phương trình 2
z bz c  0 có hai nghiệm phức z , z thỏa 1 2
mãn z  4  3i  1 và z  8  6i  4 . Mệnh đề nào sau đây đúng? 1 2
A. 5b c  12.
B. 5b c  4.
C. 5b c  4.
D. 5b c  12.
Câu 37: Cho phương trình 2
z bz c  0 , có hai nghiệm z , z thỏa mãn z z  4  2i . Gọi , A B là các 1 2 2 1
điểm biểu diễn các nghiệm của phương trình 2
z  2bz  4c  0 . Tính độ dài đoạn AB . A. 8 5. B. 2 5. C. 4 5. D. 5.
Câu 38: Trên tập hợp các số phức, phương trình 2
z  a  2 z  2a  3  0 ( a là tham số thực) có 2
nghiệm z , z . Gọi M , N là điểm biểu diễn của z , z trên mặt phẳng tọa độ. Biết rằng có 2 1 2 1 2
giá trị của tham số a để tam giác OMN có một góc bằng 120 . Tổng các giá trị đó bằng bao nhiêu? A. 6 . B. 4  . C. 4 . D. 6  .
Câu 39: Trên tập hợp các số phức, xét phương trình 2
z  2z  m  2  0 ( m là tham số thực). Gọi T là
tập hợp các giá trị của m để phương trình trên có hai nghiệm phân biệt được biểu diễn hình học bởi hai điểm ,
A B trên mặt phẳng tọa độ sao cho diện tích tam giác ABC bằng 2 2 , với C 1; 
1 . Tổng các phần tử trong T bằng A. 8 . B. 4 . C. 9 . D. 1  .
Câu 40: Biết rằng phương trình 2
z  2az b  0 (a,b là các số thực dương) có hai nghiệm phức liên
hợp z , z . Gọi ,
A B, C lần lượt là các điểm biểu diễn của số phức w  2, z , z . Tính giá trị của 1 2 1 2
T b  4a biết rằng ba điểm ,
A B, C tạo thành một tam giác vuông có diện tích bằng 9 . A. 6 . B. 8  . C. 9 . D. 14 .
Câu 41: Trên tập hợp số phức, xét phương trình 2 2
z  2az b  20  0  
1 với a,b là các tham số
nguyên dương. Khi phương trình có hai nghiệm phân biệt z , z thỏa mãn: z  3iz  7  5i 1 2 1 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
thì giá trị của biểu thức 7a  5b bằng A. 19 . B. 17 . C. 32 . D. 40 . c
Câu 42: Cho phương trình 2 x  4x
 0 có hai nghiệm phức. Gọi A , B là hai điểm biểu diễn của d
hai nghiệm đó trên mặt phẳng Oxy . Biết tam giác OAB đều, tính P c  2d .
A. P  18 .
B. P  10 .
C. P  14 .
D. P  22 .
Câu 43: Cho phương trình 4 2
4z mz  4  0 trong tập số phức và m là tham số thực. Gọi z , z , z , z 1 2 3 4
là bốn nghiệm của phương trình đã cho. Tìm tất cả các giá trị của m để
 2z 4 2z 4 2z 4 2z 4  324 . 1 2 3 4 
A. m  1; m  35 .
B. m  1; m  35 .
C. m  1; m  35 .
D. m  1; m  35 .
Câu 44: Tìm m  để các nghiệm của phương trình sau đều là số ảo: m   4 2
3 z  6z m  3  0 .
3 2  m  3
A. 3  m  3 2 .
B. 3  m  3 2 . C.  .
D. 3 2  m  3 . 3  m  3 2
Câu 45: Gọi S là tổng các số thực m thỏa mãn 3 2
z  7z 16z 12  mz  3m  0 có nghiệm phức z 0
thỏa mãn | z | 2 . Khẳng định nào dưới đây đúng? 0 A. S  24 . B. S  25 . C. S  18 . D. S  16 .
Câu 46: Trên tập hợp số phức cho phương trình 2
z bz c  0 , với b, c
. Biết rằng hai nghiệm của
phương trình có dạng z w  3 và z  3w  8i 13 với w là một số phức. Tính b c . 1 2 A. 9 . B. 10 . C. 11. D. 12 .
Câu 47: Trên tập hợp các số phức, xét phương trình: 2
z  m   2 2
1 z m  3m  5  0 ( m là tham số
thực). Tính tổng các giá trị của m để phương trình trên có nghiệm z thỏa mãn 0 3 z 12  5 z . 0 0 A. 9 . B. 12 . C. 10 . D. 8 .
Câu 48: Cho phương trình 2
z bz c  0 có hai nghiệm z , z thỏa mãn z z  3  4i . Gọi , A B là các 1 2 2 1
điểm biểu diễn các nghiệm của phương trình 2
z  2bz  4c  0 . Tính độ dài đoạn AB . A. 20. B. 2 5. C. 10. D. 5.
Câu 49: Cho m là số thực, biết phương trình 2
z  2mz  9  0 có hai nghiệm phức z , z . Có bao nhiêu 1 2
giá trị nguyên của m sao cho z z z z  16 ? 1 2 2 1 A. 3 . B. 4 . C. 5 . D. 6 .
Câu 50: Gọi S là tập hợp tất cả các số thực a sao cho phương trình 2
z  (a  2)z  2a  3  0 có hai
nghiệm phức z , z và các điểm biểu diễn của z , z cùng với gốc tọa độ O tạo thành một tam 1 2 1 2
giác có diện tích bằng 2. Số phần tử của S là? A. 1. B. 4 . C. 2 . D. 3 .
____________________HẾT____________________
Huế, 15h15’ Ngày 19 tháng 3 năm 2023
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
LỜI GIẢI CHI TIẾT Câu 1:
Trên tập hợp các số phức, xét phương trình  z 1 a z 1 a  6z ( a là tham số thực). Có 2 2
bao nhiêu giá trị của a để phương trình đó có hai nghiệm z , z thỏa mãn z z  42 ? 1 2 1 2 A. 1. B. 2 . C. 3 . D. 4 . Lời giải:
Ta có:  z   a z   a 2
z z  a   2 1 1 6 2
3 z a 1  0  
1 có   6a 10 . 5
+ Trường hợp 1:   0  a   . Khi đó phương trình  
1 có hai nghiệm thực z , z . 3 1 2 a  6   38 2 2 2 Suy ra z z
 42  2a  3  2 2 a   2
1  42  2a  24a  4  0     . 1 2 a  6   38 5
Kết hợp với điều kiện a   , nhận a  6   38 . 3 5
+ Trường hợp 2:   0  a   . Khi đó phương trình  
1 có hai nghiệm phức z , z thỏa 3 1 2 mãn z z . 1 2   2 2 a 22 Suy ra 2 zz
 42  z z z z  42  z z  21  a  22  0   . 1 2 1 1 2 2 1 2 a   22 5
Kết hợp với điều kiện a   , nhận a   22 . 3
Vậy có 2 giá trị của a thỏa mãn. Câu 2:
Trên tập hợp số phức xét phương trình 2 2
z  2mz m  2m 1  0 . Có bao nhiêu giá trị thực
của m để phương trình đã cho có 2 nghiệm z ; z thoả mãn z  2 z ? 1 2 1 2 A. 2 . B. 3 . C. 4 . D. 5 . Lời giải: 1 TH1. 2
  0  m   2 m  2m  
1  0  2m 1  0  m
. Khi đó phương trình đã cho có 2 2
nghiệm thực.Theo định lý Vi-et ta có
z z  2m 1  z  2z 3 1 2   1 2   
. Xét z  2 z   . 2  1 2
z .z m  2m 1 2  z  2 4  1 2   1 2    2m z  6     2   z z 2m  3 Từ  
1 và 3 ta có hệ phương trình 1 2    . z  2z  0 4m  1 2 z  7 1    3
Thế 6 và 7 vào phương trình 2 ta được m  9  6 2 2 4 TM m m  2 2 .
m  2m 1  m 18m  9  0   . 3 3 m  9  6 2  TM
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
z z  2mz  2  m 10  1 2 2   Từ  
1 và 4 ta có hệ phương trình   
. Thế 9 và 10 vào z  2z  0  z  4m 9 1 2  1  
phương trình 2 ta được  m m 2 2 2 4
m  2m 1  9m  2m 1  0 VN  . 1 TH2. 2
  0  m   2 m  2m  
1  0  2m 1  0  m
. Khi đó phương trình đã cho có 2 2
nghiệm phức phân biệt. Giả sử z a bi z a bi . Khi đó 1 2 a  0 2 2 2 2 2 2 z  2 z
a b  2 a b a b  0  
. Suy ra z z  0  0i mẫu thuẫn 1 2 b   0 1 2
với điều kiện đề bài là phương trình có 2 nghiệm phân biệt. Trên tập hợp các số phức, xét phương trình 2
z  2 m  
1 z m  3  0 ( m là tham số thực). Câu 3: Biết phương trình 2
z  2z m  0 ( m là tham số thực) có một nghiệm là z  1
  3i . Gọi z là 1 2
nghiệm còn lại. Phần ảo của số phức w  mz  2z bằng 1 2 A. 36 . B. 24 . C. 36 . D. 8  . Lời giải:
Từ giả thiết  z  1
  3i z z 10  m 10. 2 1 2
Vậy phần ảo của số phức w  10z  2z  10 1   3i  2 1   3i  8   36i là 36 . 1 2     Câu 4: Cho phương trình 2
z  2mz  6m  8  0 . ( m là tham số thực). Có bao nhiêu giá trị nguyên của
tham số m để phương trình có hai nghiệm phức phân biệt z , z  1 2 thỏa mãn z z z z ? 1 1 2 2 A. 4 . B. 1. C. 3 . D. 2 . Lời giải: Ta có 2 
  m  6m  8 m  4 Trường hợp 1:    0   m  2
Khi đó phương trình đã cho có hai nghiệm thực phân biệt z , z    1 2 và 2 2 z z z z z z 1 1 2 2 1 2 z z loai 1 2    
z z  0  2m  0  m  0 tm 1 2   z  z  1 2 Trường hợp 2:
  0  2  m  4
Khi đó phương trình đã cho có hai nghiệm phức phân biệt z , z 1 2
z z z z z .z z .z ( luôn đúng) mà m  m  3 1 1 2 2 1 2 1 1
Vậy có 2 giá trị nguyên của tham số m thỏa mãn bài toán. Câu 5:
Có bao nhiêu giá trị của tham số m để phương trình có nghiệm phức z thỏa mãn 0 z  2  6 ? 0 A. 3. B. 4. C. 1. D. 2. Lời giải: Xét phương trình 2
z  2m  
1 z m  3  0   1
Ta có   m  2 2
1  m  3  m m  2. .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc giam  2  Nếu 2
  0  m m  2  0   thì phương trình   1 có nghiệm thực: m 1 z  4 0 z  2  6  0 z  8   0 11
Với z  4 : thay vào   1 , được: m  0 7 83
Với z  8 : thay vào   1 , được: m   0 17 Nếu 2
  0  m m  2  0  2
  m  1 thì phương trình   1 có nghiệm phức 2
z m 1i m m  2 0  2
z m 1 i m m  2  0 2
Khi đó z  2  6  m  3   2 m m  2 2
 36  2m  7m  29  0 : Phương trình có hai 0 nghiệm phân biệt.
Vậy có 4 giá trị của tham số m để bài toán thỏa mãn. Câu 6:
Trên tập hợp các số phức, xét phương trình 2
z  2mz  3m 10  0 ( m là tham số thực). Có bao
nhiêu giá trị nguyên của m để phương trình đó có hai nghiệm z , z không phải số thực thỏa 1 2
mãn z z  8 ? 1 2 A. 1. B. 2 . C. 3 . D. 4 . Lời giải: Ta có 2
  m  3m 10 .
Phương trình không có nghiệm thực khi 2
  0  m  3m 10  0  2   m  5(1) .
Khi đó phương trình có hai nghiệm phân biệt 2 2
z m  m  3m 10.i, z m  m  3m 10.i 1 2
Vậy z z  8  2 3m 10  8  3m 10  4  3m 10  16  m  2 . 1 2
Kết hợp với điều kiện ta có 2  m  2 . Vậy có 4 giá trị nguyên của m thỏa mãn. Câu 7:
Trên tập số phức, xét phương trình 2
z  m   2 2
4 z m  4m 1  0 , m là tham số thự C.
Có bao nhiêu giá trị m để phương trình đã cho có hai nghiệm phức phân biệt z , z thỏa điều 1 2
kiện z z  2z z z . 1 2 1 2 1 A. 3 . B. 2 . C. 0 . D. 3. Lời giải:
Điều kiện để phương trình có hai nghiệm phức phân biệt trong đó z là nghiệm có phần ảo 1 2 15
âm là:   m  4   2 m  4m   1  0  4
m 15  0  m  . 4
Khi đó: z z  2z z  2m  4  2 2 m  4m   2 1  2
m 10m 10 1 2 1 2 Và z b
   i   m  4  i 4  m 15 1 2 Ta có: 2
z z  2z z z  2
m 10m 10  m  4  4m 15 1 2 1 2 1     2 2  2
m 10m 10  m  4m 1 15 Vì m  nên 2
m  4m 1  0 , do đó: 4
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia  2 2 2 11  2
m 10m 10  m  4m 1
3m 14m 11  0 m  1, m   (*)      3 2 2 2  2
m 10m 10  m  4m 1
m  6m  9  0  m  3 15
Đối chiếu điều kiện m
suy ra không có giá trị nào của m thỏa điều kiện bài toán. 4 Câu 8:
Trên tập hợp các số phức, xét phương trình 2
z   m   2 2 2
1 z  4m  5m  0 ( m là tham số
thực). Có bao nhiêu giá trị của tham số m để phương trình có nghiệm z thoả mãn 0 2
z  1 4m 2
z  4m  5m  3  10 ? 0 0 A. 1. B. 2 . C. 4 . D. 3 . Lời giải:
Cách 1: Ta có   m 1.
Trường hợp 1: m 1  0  m  1. z  7
Khi đó theo bài ra, phương trình đã cho có nghiệm thực z thoả mãn 0 z  3  10  . 0 0 z  13   0 2 7  22m   2
1 7  4m  5m  0
Từ đó suy ra 132 22m 113 2
 4m  5m  0
m  3 tm 2
4m 33m  63  0     . 2 21  
4m  47m 143  0 m  tm  4
Trường hợp 2: m 1  0  m  1.
Khi đó phương trình đã cho có hai nghiệm phức là z và z và thoả mãn z  3  10 0 0 0
 z  3z  3 2
100  z  3z z  2
 9 100  4m  5m  3.2 2m 1  91  0 0 0 0 0 0    7  1601 m   tm 2 8
 4m  7m  97  0   .  7  1601 m   ktm  8
Vậy có 3 giá trị của tham số m thoả mãn yêu cầu bài toán. 2
Cách 2: Ta có 2
z   m   2 2 2
1 z  4m  5m  0   z  2m   1  m 1   1 .
Trường hợp 1: m 1  0  m  1.
z m   m  Khi đó   2 1 1 1   .
z  2m 1 m 1
Theo bài ra, phương trình đã cho có nghiệm z thoả mãn z  3  10 . 0 0  m  3 2  2  1 10 tm m m    Do đó  21   .
2m  2  m 1  10 m  tm   4
Trường hợp 2: m 1  0  m  1
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
z m   i m  Khi đó   2 1 1 1   .
z  2m 1 i m 1 
Theo bài ra, phương trình đã cho có nghiệm z thoả mãn z  3  10 . 0 0 Do đó 2 2
2m  2  i m 1  10  4m  8m  4  m 1  100  4m  7m  97  0  7  1601 m   tm 8   .  7  1601 m   ktm  8
Vậy có 3 giá trị của tham số m thoả mãn yêu cầu bài toán. Câu 9:
Trên tập số phức, xét phương trình 2
z  2mz m  1  0  
1 ( m là tham số thực); z , z là hai 1 2
nghiệm phức của phương trình   1 ; ,
A B lần lượt là điểm biểu diễn của hai nghiệm phức đó
trên mặt phẳng Oxy . Có bao nhiêu giá trị nguyên của m để OAB vuông tại O ? A. 2 . B. 1. C. 3 . D. 4 . Lời giải: Xét phương trình 2
z  2mz m  1  0   1 1  5 1  5
Phương trình có hai nghiệm phức khi 2
  0  m m 1  0   m  * 2 2 Ta có các nghiệm 2 2
z  m i m m 1; z  m i m m 1 1 2 , A B lần lượt là điểm biểu diễn của hai nghiệm phức z , z 1 2 nên A 2
m ; m m 1 ; B 2
m ;  m m 1 . m  1 OAB  vuông tại O  2 O .
A OB  0  2m m  1  0  1 thõa mãn *  . m    2
Vậy chỉ có 1 giá trị nguyên m  1 thõa mãn yêu cầu. 1
Câu 10: Trên tập hợp số phức, xét phương trình 2 z m 1z   2
m  5m  6  0(m là tham số thực). 4
Có bao nhiêu số nguyên m [ 10
 ;10] đề phương trình trên có hai nghiệm phức z , z 1 2 thỏa
mãn z z z z ? 1 2 1 2 A. 11. B. 10. C. 8. D. 9. Lời giải:
Điều kiện m 1  0  m  1. 2
  m  4m  5 m  5 + Trường hợp 1: 2
  0  m  4m  5  0  
phương trình có 2 nghiệm thực z , z  1 2 m  1  1
Theo định lý Viet z .z    2
m  5m  6 . 1 2  4
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 2 2
z z z z z zz z  4z .z  0 1 2 1 2 1 2 1 2 1 2  m  6 2
m  5m  6 2
 0  m  5m  6  0   m  1 
Do m  và m [ 10
 ;10] nên số giá trị m thỏa mãn là 10  6 11  6 . + Trường hợp 2: 2
  0  m  4m  5  0  1  m  5 .
phương trình có 2 nghiệm phức z , z 1 2 m  6 2     2 2 m 5m 6 0  2
z z z z z z
z z m 1 m  4m  5    m  1  1 2 1 2 1 2 1 2 2 
m  3m  4  0  1   m  4 
Do m  , 1  m  5 và m [ 10
 ;10] nên số giá trị m thỏa mãn là m  0, m  1, m  2, m  3 .
Vậy có 10 giá trị của m.
Câu 11: Trên tập số phức, cho phương trình 2
z az b  0 (a, b  ) . Có bao nhiêu số phức w sao cho
phương trình đã cho có hai nghiệm là z  (6  i)  w  2i và z  (w  5  i) | w | ? 1 2 A. 4. B. 3. C. 6. D. 5. Lời giải:
Trường hợp 1: z , z  . 1 2
z  (6  i)w  2i  (6  i)(x yi)  2i là số thực nên x  6 y  2  0 . 1 2 2
z  (w  5  i) | w |
x y [(x  5)  (1 y)i] là số thực nên 2 2
(1 y) x y  0 . 2
x  6y  2  0  x  4
Ta có hệ phương trình   
w  4  i . 2 2
(1 y) x y  0   y  1
Trường hợp 2: z , z
. Khi đó phương trình đã cho có hai nghiệm là liên hợp với nhau. 1 2
z z  (6  i)w  2i  (w  5  i) | w | t.w  5t t.i (t |  w |) 1 2  [
w (t  6)  i]  5t  (t  2)i . (1) 2 2 2 2
t (t  6) 1  25t  (t  2)   t 1  4 3 2
t 12t 11t  4t  4  0  t  0,62079  . t 10,967 
Thay mỗi giá trị của t vào (1), ta được một số phức w tương ứng.
Vậy có tất cả 4 số phức w thoả mãn.
Câu 12: Trên tập hợp các số phức, xét phương trình 2
z  2mz  8m 12  0 . Có bao nhiêu giá trị
nguyên của m để phương trình đó có hai nghiệm phân biệt z , z thỏa mãn z z ? 1 2 1 2 A. 5 B. 6 . C. 3 . D. 4 . Lời giải: Ta có: 2
z  2mz  8m 12  0 * thì 2
  m  8m 12 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc giam  6 TH1: 2
  0  m 8m 12  0  
. Khi đó phương trình * có 2 nghiệm thực phân m  2
z z KTM 1 2  
biệt z , z và theo yêu cầu bài toán: z z   1 2 1 2
z  z z z  0  m  0 TM  1 2 1 2  
TH2:   0  2  m  6 . Phương trình * khi đó có 2 nghiệm z m i  luôn thỏa 1,2
mãn z z . Nên: m 3; 4;  5 . 1 2
Vậy các giá trị m thỏa mãn là: m 0;3; 4;  5 .
Câu 13: Có bao nhiêu số nguyên m để phương trình 2
z  2mz 1  0 có hai nghiệm phức phân biệt
z , z thỏa mãn z  3  z  3 ? 1 2 1 2 A. 1. B. 2 . C. 3 . D. 4 . Lời giải: +) Với 2
  m 1  0 , phương trình 2
z  2mz 1  0 có hai nghiệm phức liên hợp
z a bi, z a bi . 1 2
Khi đó, hiển nhiên z  3  a  32 2
b z  3 . 1 2 +) Với 2
  m 1  0 , phương trình 2
z  2mz 1  0 có hai nghiệm thực phân biệt z , z . 1 2
Đẳng thức z  3  z  3 tương đương với z z  6  0 , điều này nghĩa là 2m  6  0 tức 1 2 1 2 m  3 .
Tóm lại các số nguyên m cần tìm là m  0, m  3 .
Câu 14: Có bao nhiêu số nguyên a để phương trình 2
z  a   2
3 z a a  0 có hai nghiệm phức
z , z thỏa mãn z z z z ? 1 2 1 2 1 2 A. 1. B. 2 . C. 3 . D. 4 . Lời giải: 2 Ta có     a      2a a 2 3 4  3
a 10a  9 5   2 13 5   2 13 Trường hợp 1: 2   0  3
a 10a  9  0   a  * 3 3
z z a  3 1 2 
Khi đó phương trình đã cho có hai nghiệm thực z , z , thỏa mãn  . 1 2 z z    1 2 
Suy ra z z z z a
   a  2 3 3   1 2 1 2     a 0 a  2 2 3  3
a 10a  9 2
 4a  4a  0   đều thỏa mãn * . a  1   5  2 13 a  3 Trường hợp 2: 2
  0  3a 10a  9  0   **  5  2 13 a   3
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
z z a  3 1 2 
Khi đó phương trình có hai nghiệm phức z , z , thỏa mãn  . 1 2
z z i   1 2 
Suy ra z z z z a
i   a  2 3 3   1 2 1 2     a 1 a  2 2 3
 3a 10a  9 2
 2a 16a 18  0  
đều thỏa mãn ** . a  9 
Vậy có 4 số nguyên a thỏa mãn yêu cầu bài toán.
Câu 15: Cho số phức w và hai số thực b , c . Biết rằng w  2 và 3w  4i là hai nghiệm của phương trình 2
2022z bz c  0 . Tính giá trị biểu thức P b c bằng A. P  4044  .
B. P  8088 .
C. P  4044 . D. P  8088  . Lời giải:
Nhận xét: Trong tập số phức, phương trình bậc hai 2
az bz c  0 có hai nghiệm phức z , z 1 2 thì z z . 1 2
Đặt w x yi x, y   . Vì b, c  và phương trình 2
2022z bz c  0 có hai nghiệm là
z w  2 , z  3w  4i nên 2 nghiệm z , z là 2 nghiệm phức có phần ảo khác 0. 1 2 1 2
Do đó z z w  2  3w  4i x yi  2  3 x yi  4i 1 2       
x   yi x    yx 2 3x x 1 2 3 4 3 i     .
y  4  3yy 1
z w  2  3 i 1
w 1 i   .
z  3w  4i  3  i  2  bb z z      6 1 2   2022  b   6  .2022 2022 Theo định lý Viet:  , từ đó suy ra   
b c  8088 cc  c 10.2022 z .z  10 2 2  2022 2022
Vậy P b c  8088 .
Câu 16: Trên tập các số phức, xét phương trình 2
z mz m  8  0 ( m là tham số thực). Có bao nhiêu
giá trị nguyên của tham số m để phương trình có hai nghiệm z , z 1 2 phân biệt thỏa mãn z  2
z mz    2
m m  8 z 1 1 2  2 ? A. 12. B. 6 . C. 5 . D. 11. Lời giải: Ta có 2
  m  4m  32 là biệt thức của phương trình. m  8
Trường hợp 1: Xét 2
  0  m  4m  32  0  
khi đó phương trình có hai nghiệm m  4  thực phân biệt. Ta có 2
z mz m  8 suy ra 2
z mz m z z
m 8  m m  8 do đó 1 2  1 2 2 1 1 z  2
z mz    2
m m  8 z 2 2
m m  8 z m m  8 z 1 1 2  2 1   2 (*). 2
m m  8  0 Nếu z .z  0       1 2 thì m 8 0 m
8 không thỏa mãn. Khi đó (*)   z z  1 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 2
m m  8  0 2      m m 8 0    hệ vô nghiệm. z  z  m  0 1 2
Trường hợp 2: Xét   0  4
  m  8 khi đó phương trình có hai nghiệm phức phân biệt và
z z , ta có z  2
z mz    2
m m  8 z 2 2
m m  8 z m m  8 z 1 1 2  1   1 2 2 2  1  33 m  2 2
m m  8  0  
. Kết hợp điều kiện ta được m 3  ;4;5;6;  7 .  1  33 m   2
Vậy có tất cả là 5 số nguyên cần tìm.
Câu 17: Biết phương trình 2
z az b  0 a ,b   có một nghiệm là z  3i và nghiệm còn lại là z . 1 2
Mô đun của số phức a bz bằng 2 A. 10 . B. 9 . C. 18 . D. 27 . Lời giải: Phương trình 2
z az b  0 a ,b   có một nghiệm z  3i thì nghiệm còn lại z  3i . 1 2
z z  aa  0 Theo Vi-et ta có. 1 2    .
z .z b b    9 1 2
Vậy a bz  9. 3  i  27 . 2  
Câu 18: Cho số phức w và hai số thực a , b . Biết z w  2i và z  2w  3 là hai nghiệm phức của 1 2 phương trình 2
z az b  0 . Tính giá trị của T z z . 1 2 2 97 2 85
A. T  2 13 .
B. T  4 13 . C. T  . D. T  . 3 3 Lời giải: z z
Vì z , z là 2 nghiệm phức của phương trình đã cho nên 1 2  1 2 z z  2 1
w  2i  2w 3
2w  4i  4w 6 2 2  4  4  97   
w  3  i 2
z  3 i z  3     .  1 1
2w  3  w  2i
2w 3  w  2i 3 3  3  3 97
Mà z , z là 2 nghiệm phức của phương trình trên nên z z  . 1 2 1 2 3 2 97 Vậy T  . 3
Câu 19: Cho các số thực b , c sao cho phương trình 2
z bz c  0 có hai nghiệm phức z ; z với phần 1 2
thực là số nguyên và thỏa mãn z  3  2i  1 và  z  2i z  2 là số thuần ảo. Khi đó, b c 1  2  1 bằng A. 1  . B. 12 . C. 4 . D. 12 . Lời giải:
Trường hợp 1: Nếu các nghiệm của phương trình là các số thực x ; y thì
z  3  2i   x  3  2i   x  32  4  2  1 mâu thuẫn với giả thiết. 1
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Trường hợp 2: Các nghiệm phức của phương trình không là các số thự C.
Giả sử z x yi z z x yi . 1 2 1 2 2
Khi đó z  3  2i  1  x  3  y  2 1 1 . 1      
Lại có  z  2i z  2  x y  2 i. x  2  yi 1  2          .
x x  2  .
y y  2   x  2. y  2  xy.i
 là một số thuần ảo.
Suy ra x x    y y   2 2 . 2 .
2  0  x y  2x  2 y  0 2 . 
 x  32   y  22 1 x  2  Giải hệ gồm   1 và 2 :    . 2 2       y  2 x y 2x 2 y 0
z  2  2i ; z  2  2i . 1 2
z z b
  2  2i  2  2i  4  1 2    
Vì vậy theo Viet ta có: 
b c  4  8  12 .
z . z c  2  2i . 2   2i  8  1 2    
Câu 20: Gọi z , z , z , z là 4 nghiệm phức của phương trình 4
z    m 2 4
z  4m  0 . Tìm tất cả các 1 2 3 4
giá trị m để z z z z  6 . 1 2 3 4
A. m  1.
B. m  2 .
C. m  3 D. m  1. Lời giải: 2 z  4  1 Ta có: 4
z  4  m 2
z  4m  0   2 z  4 2 z m    0   2 z   m 2 Ta có:  n n z z .
z ; z là nghiệm của phương trình  
1 . Ta có: z z  4   2 . 1 2 1 2
z ; z là nghiệm của phương trình 2 . Ta có: z z m . 3 4 3 4
Theo đề ra ta có: z z z z  6  2 m  4  6 
m  1  m  1. 1 2 3 4
Kết luận m  1.
Câu 21: Trên tập hợp các số phức, phương trình 2
z az b  0 , với a, b
có nghiệm z  2  3i . 0
Biết rằng phương trình 2
z bz a  0 cũng có hai nghiệm phức z , z . Tính S z z . 1 2 1 2 A. 4 . B. 13 . C. 25 . D. 185 . Lời giải: Phương trình 2
z az b  0 , với a, b
có nghiệm z  2  3i khi và chỉ khi 0       
i2  a  i  b   a b   a   2a b 5 a 4 2 3 2 3 0 2 5 3 4 i  0     a  4  0 b  13. Khi đó phương trình 2
z bz a  0 trở thành 2
z 13z  4  0 có hai nghiệm thực phân biệt 13   185 trái dấu z  . 1,2 2 1  3 185 1  3 185 1  3 185 13 185
Suy ra S z z      185 . 1 2 2 2 2 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Câu 22: Trên tập hợp các số phức, xét phương trình 2 2
z  4az b  2  0, ( a, b là các tham số thực). Có
bao nhiêu cặp số thực a;b  sao cho phương trình đó có hai nghiệm z , z 1 2 thỏa mãn
z  2iz  3  3i ? 1 2 A. 4. B. 1. C. 2. D. 3. Lời giải: z z  4  a
Theo định lý Vi-ét, ta có: 1 2  . 2 z z b  2  1 2
Theo yêu cầu bài toán, phương trình đã cho có hai nghiệm z , z 1 2 thỏa mãn
z  2iz  3  3i z  2iz  3  3i  0   z  2iz  3 3i z  2iz  3 3i  0 1 2  2 1  1 2 1 2  3
z z  1 2i3 3iz z  18i  2i  2 2 z z  0 1 2 1 2 1 2   3
 b  239i 4
a 18i  2i z z 2 2  2z z   0 1 2 1 2      2
b      i a 2
i i a    2 3 2 3 9 4 18 2 16 2 b  2  0   3    2
b  2 12a  0  2 2  b   2  4  a      b 2 4a    2 36
a 18  32a  4   2b 2  0 2 3
 6a 18  32a 16a  0 2 3
 2a  52a 18  0 2 b   2  4  a    1 1
a   ;b  0  1      a ;b 0  a   2   2   . 2    9 5   9 10 2 9         a ;b a ;ba      8 2 8 2  8
Vậy có 3 cặp số thực a;b  thỏa mãn bài toán.
Câu 23: Trên tập số phức, cho phương trình 2
z  m   2 2
1 z m  2m  0 . Có bao nhiêu tham số m để
phương trình đã cho có hai nghiệm phân biệt z ; z thõa mãn 2 2 zz  5 1 2 1 2 A. 1. B. 0 . C. 2 . D. 4 . Lời giải:
Ta có:   m  2   2 1
m  2m  4  m 1  1  1   0 m m     TH1: YCBT    4   4  2 2  zz  5     z z  2  2z z  5 4 m  2 1  2   2 1 2 m  2m  5 1 2 1 2   1 m   4 1   m   6  38   4  m  (L) 2 2
2m 12m1 0   6  38 m  (N )  2 TH2: Khi 1   0  m  4
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Phương trình đã cho có hai nghiệm phức z ; z có dạng z a bi, z a bi với 1 2 1 2
a  m 1;b  4m 1 Khi đó: 2 2 5 2 2 2 2 z
z  5  2a  2b  5  a b  1 2 2  2   14 m  (N )    m2 5 2 1  4m 1    2  2   14 m  (L)  2
Câu 24: Trên tập hợp số phức, xét phương trình 2 2
z  2z m  0 ( m là tham số thực). Có bao nhiêu
giá trị của m để phương trình đó có nghiệm z z
0 thỏa mãn điểm biểu diễn của 0 thuộc đường 2 x E-lip có phương trình 2  y 1? 4 A. 2 . B. 3 . C. 4 . D. 1. Lời giải: Xét phương trình 2 2
z  2z m  0 có 2    1 m . Trường hợp 1:    0  m 1  ;  1 .
Phương trình có các nghiệm là 2
z  1  1  m hoặc 2
z  1  1  m . 0 0 2 x Với 2
z  1  1  m điểm biểu diễn thuộc E-lip 2  y  1 0 4
Do đó    m 2 2 1 1  4 2
 1 m  3  m . 2 x Với 2
z  1  1  m điểm biểu diễn thuộc E-lip 2  y  1 0 4
Do đó    m 2 2 1 1  4 2
 1 m 1 m  0.
Trường hợp này giá trị m  0 thỏa mãn. Trường hợp 2:
  0  m ;    1  1;  .
Phương trình có các nghiệm là 2
z  1  i m 1 hoặc 2
z  1  i m 1 . 0 0 2 x
Điểm biểu diễn thuộc E-lip 2  y  1 4 2 2 1 Do đó   2  m 1 1 2 3  m   7 1  m   (thỏa mãn). 4 4 4 7
Trường hợp này giá trị  m   thỏa mãn. 4
Vậy có 3 giá trị của m thỏa mãn yêu cầu bài toán.
Câu 25: Biết phương trình 2 2
z mz m  2  0 ( m là tham số thực) có hai nghiệm phức z , z 1 2 . Gọi ,
A B,C lần lượt là điểm biểu diễn các số phức z , z z i 1 2 và 0
. Có bao nhiêu giá trị của tham
số m để diện tích tam giác ABC bằng 1?
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia A. 2 . B. 3 . C. 4 . D. 6 Lời giải: Ta có: 2   m   2 m   2 4 2  3  m  8  Trường hợp 1: 2 2 6 2 6
  0  3m  8  0   m  . 3 3
Khi đó, phương trình có hai nghiệm thực phân biệt là z , z 1 2 . 2 2 Vì ,
A B Ox nên AB z z   z z    z z  2
 4z z  3m  8 1 2 1 2 1 2 1 2 .
Mặt khác, ta có C0;  1  d  ; C AB 1 . 2 1  m   SAB d C AB    m   n . ABC    3 8 2 3 . ; 1   2 2 3  2 6  m  3 Trường hợp 2: 2
  0  3m  8  0   . 2  6 m   3 m i
Khi đó, phương trình có hai nghiệm phức liên hợp là z  . 1,2 2 Ta có: 2 2
AB z z i   3
m  8  3m  8 và C0;  1 . 1 2 m m
Phương trình đường thẳng AB là x
 0 nên d C; AB  . 2 2 2   2 m 4 1 m 3m  8  Do đó, SA . B d C AB     m   ABC   ;  1 2  . 2 4 2 4 m   (VN)  3
Vậy có 4 giá trị thực của tham số m thỏa mãn đề bài.
Câu 26: Trên tập hợp các số phức, xét phương trình 2
z  2m  
1 z  8m  4  0 ( m là tham số thực). Có
bao nhiêu giá trị nguyên của m để phương trình đã cho có hai nghiệm phân biệt z , z thỏa 1 2 mãn 2 2
z  2mz  8m z  2mz  8m ? 1 1 2 2 A. 4 . B. 3 . C. 5 . D. 6 . Lời giải: Ta có 2
  m  6m  5 và 2 2
z  2mz  8m z  2mz  8m 1 1 2 2 2
z  2m   2
1 z  8m  4  2z  4  z  2 m 1 z  8m  4  2z  4 1 1 1 2   2 2
 2z  4  2z  4   1 1 2 m  5 * Xét   0  
. Khi đó PT có 2 nghiệm thực phân biệt m 1 Nên  
1  2z  4   2z  4  z z  4
  2 m 1  4  m  3 1  2  1 2  
* Xét   0  1  m  5 . Khi đó PT có 2 nghiệm phức phân biệt z , z liên hợp của nhau 1 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Nên 2z 1, 2z 1cũng là hai số phức liên hợp của nhau. Suy ra 2z 1  2z 1 luôn thỏa 1 2 1 2
Vậy có 4 giá trị nguyên của tham số m thỏa mãn đề bài.
Câu 27: Tìm tổng các giá trị của số thực a sao cho phương trình 2 2
z  3z a  2a  0 có nghiệm phức
z0 thỏa z  2 . 0 A. 0 . B. 2 . C. 4 . D. 6 . Lời giải: z  2
Trường hợp 1: z    0 . Khi đó 0 z 2 . 0 z  2   0 Nếu z  2 a a   0 thì 2 2 10
0 không có nghiệm thực a . a  1 3 Nếu z  2 
a  2a  2  0   0 thì 2 (1). a 1 3
Trường hợp 2: z
z z a a z 0 . Khi đó phương trình 2 2 3 2
0 có nghiệm phức 0 nên z 0
cũng là nghiệm phức của phương trình. 2
Vì z  2 nên z .z z  4 . 0 0 0 0 2 a  2a
Theo định lý Vi-ét, ta có: 2 z .z   a  2a 0 0 . 1 a  1 5 2 2
a  2a  4  a  2a  4  0   (2). a  1 5
Từ (1) và (2), ta có tổng các giá trị của số thực a thỏa yêu cầu bài toán là:
1  3  1  3  1  5  1  5  4 .
Câu 28: Trên tập hợp các số phức, gọi S là tổng các giá trị thực của m để phương trình 2
mz  2m  
1 z m  6  0 có nghiệm z0 thỏa mãn z  1. Tính S . 0 A. 3 . B. 4  . C. 1. D. 2  . Lời giải: Xét phương trình 2
mz  2m  
1 z m  6  0 .
Trường hợp 1: m  0  Phương trình đã cho có dạng 2z  6  0  z  3   z  3 không thõa mãn.
Trường hợp 2: m  0 2 Ta có 
  m    mm   2 1
6  2m  4m  1.  2  2 m  2 Nếu: 2
  0  2m  4m 1  0  
thì phương trình đã cho có hai nghiệm thực  2  2  m   2 z 1  z  
0 là số thực. Theo bài ra, ta có 0 z 1 . 0 z  1   0 Với z  1         0
, ta có m 2m 2 m 6 0 m 4 (thỏa mãn ). Với z  1        0
, ta có m 2m 2 m 6 0 m 2 ( thỏa mãn ).
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia   Nếu: 2 2 2 2 2
  0  2m  4m 1  0   m
, thì phương trình đã cho có hai 2 2 nghiệm phức.
z0 là nghiệm của phương trình đã cho  z cũng là nghiệm của phương trình đã cho. 0 m  6 2 m  6
Áp dụng hệ thức viét, ta có z .z
z .z z 1 1  m  3 0 0 mà 0 0 0 (không m m
thõa mãn). Vậy m  4
 ;m  2  S  2  .
Câu 29: Cho phương trình 2 2
z az  2a  0 , với a là số thực dương. Gọi z , z là hai nghiệm phức của 1 2
phương trình, trong đó z có phần ảo dương. Biết rằng 2z z z 10  2 7i . Khẳng định 1 2  1 1 nào sau đây đúng?
A. 1  a  3.
B. a 1 .
C. 5  a  8.
D. 3  a  5. Lời giải: Xét phương trình 2 2
z az  2a  0 , với a  0 . Ta có: 2 2 2
  a 8a  7  a  0 , a   0
a a 7i
Suy ra phương trình có hai nghiệm phức z , z với  và z  . 1 2 z z 1 2 2 2
z z  a 1 2
Theo định lí Viét ta có:  2
z .z  2a  1 2
Khi đó: 2z z z 10  2 7i 1 2  1     z aa a 7i 2 2
z  10  2 7i  2a az  10  2 7i  2a  . a 10  2 7i 1 2 2 2 2 5a 10 2 2  5a a 7i  2 2   10  2 7i  
a  4  a  2. 2 2 2 a 7  2 7  2
Câu 30: Trên tập hợp các số phức, xét phương trình 2
z   m   2 2 2
1 z  4m  5m  0 ( m là tham số
thực). Có bao nhiêu giá trị của tham số m để phương trình có nghiệm z thoả mãn 0 z  3  10 ? 0 A. 1. B. 2 . C. 4 . D. 3 . Lời giải:
Cách 1: Ta có   m 1.
Trường hợp 1: m 1  0  m  1. z  7
Khi đó theo bài ra, phương trình đã cho có nghiệm thực z thoả mãn 0 z  3  10  . 0 0 z  13   0 2 7  22m   2
1 7  4m  5m  0 2
4m 33m  63  0 Từ đó suy ra   
132  22m   1 13 2
 4m  5m  0 2
4m  47m 143  0
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
m  3 tm   21  . m  tm  4
Trường hợp 2: m 1  0  m  1.
Khi đó phương trình đã cho có hai nghiệm phức là z và z và thoả mãn z  3  10 0 0 0
 z  3z  3 2
100  z  3z z  2
 9 100  4m  5m  3.2 2m 1  91  0 0 0 0 0 0    7  1601 m   tm 2 8
 4m  7m  97  0   .  7  1601 m   ktm  8
Vậy có 3 giá trị của tham số m thoả mãn yêu cầu bài toán. 2
Cách 2: Ta có 2
z   m   2 2 2
1 z  4m  5m  0   z  2m   1  m 1   1 .
Trường hợp 1: m 1  0  m  1.
z m   m  Khi đó   2 1 1 1   .
z  2m 1 m 1
Theo bài ra, phương trình đã cho có nghiệm z thoả mãn z  3  10 . 0 0  m  3 2  2  1 10 tm m m    Do đó  21   .
2m  2  m 1  10 m  tm   4
Trường hợp 2: m 1  0  m  1
z m   i m  Khi đó   2 1 1 1   .
z  2m 1 i m 1 
Theo bài ra, phương trình đã cho có nghiệm z thoả mãn z  3  10 . 0 0 Do đó 2 2
2m  2  i m 1  10  4m  8m  4  m 1  100  4m  7m  97  0  7  1601 m   tm 8   . 7  1601 m   ktm  8
Vậy có 3 giá trị của tham số m thoả mãn yêu cầu bài toán. 2 3 4 z
Câu 31: Cho số phức z, w khác 0 thỏa mãn z w  0 và   . Khi đó bằng: z w z w w 6 2 A. 2 . B. . C. 3 . D. . 3 3 Lời giải:
Với hai số phức z, w khác 0 thỏa mãn z w  0 , ta có: 2 3 4 2w  3z 4    
 2w 3zz w 2 2
 4zw  3z zw  2w  0 z w z w zw z w
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc giaz 1 23     2 iz   z w 6 6  3   2  0        w   w   z 1 23     iw 6 6 2 2 z  1   23  6 Suy ra           . w  6  6 3  
Câu 32: Tìm tất cả các giá trị thực của a sao cho phương trình 2 2
z az  2a a  0 có hai nghiệm phức có môđun bằng 1. 1 5 A. a  1  . B. a 1. C. a  1  . D. a  . 2 Lời giải:
Gọi z , z
z az a a    1
2 là hai nghiệm của phương trình 2 2 2 0 . Ta có z z 1. 1 2
Theo định lí Viét, ta có 2
z z  2a a . 1 2 Lấy mô đun hai vế có 2 2 2
z z  2a a z . z  2a a  2a a  1 1 2 1 2 2 2
2a a  1
a  2a 1  0 a  1       . 2 2
2a a  1 
a  2a 1  0 a  1 2  i
Với a 1 có phương trình thành 2 1 3
z z  1  0  z
z  1  a 1 thỏa mãn. 2 1  2  7  2 2
Với a  1  2 có phương trình thành 2
z  1 2 z 1  0  z  . 2
a  1 2 không thỏa mãn. 1  2  7  2 2
Với a  1  2 có phương trình thành 2
z  1 2 z 1  0  z  . 2
a  1 2 không thỏa mãn. Vậy a 1.
Câu 33: Trên tập số phức, xét phương trình 2 2
z  2mz n  5  0 (với m , n là tham số thực). Có bao nhiêu cặp số ( ;
m n) để phương trình đã cho có hai nghiệm phức z , z sao cho các điểm biểu 1 2
diễn của z , z , z  1, z  5 là bốn đỉnh của một hình vuông? 1 2 3 4 A. 3 . B. 2 . C. 4 . D. 1. Lời giải:
Để phương trình có hai nghiệm phức khi và chỉ khi 2 2
  m n  5  0 .
Đặt z a bi; a,b
z a bi . 1 2
Ta có bốn điểm A ; a b, B  ;
a b,C 1;0 , D 5;0 biểu diễn bốn số phức z , z , z  1, z  5 lập 1 2 3 4   3;0 ABa  3  a  3
thành hình vuông. Suy ra ACBD là hình vuông nên      . AB CD  2b  4 b    2  a  3 z  3 2i
z z  6  2  mm  3   1 1 2        2          b 2 z 3 2i z z 13 n 5  n  2  2 2 1 2 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc giaa  3 z  3 2i
z z  6  2  mm  3   1 1 2        2       b 2 z 3 2i
z z  13  n  5  n  2  2 2 1 2 .
Vậy ta có hai cặp số  ;
m n thỏa yêu cầu bài toán.
Câu 34: Trên tập hợp các số phức, xét phương trình 2
z  2mz m 12  0 ( m là tham số thực). Có bao
nhiêu giá trị nguyên của m để phương trình đó có hai nghiệm phân biệt z z 1 , 2 thỏa mãn z z  2 z z ? 1 2 1 2 A. 1. B. 2 . C. 3 . D. 4 . Lời giải:
Phương trình đã cho có 2
  m m 12 . m  4  Trường hợp 1: 2
  0  m m 12  0   . m  3
Khi đó, phương trình đã cho có hai nghiệm thực z z 1 , 2 phân biệt.
Do đó, z z  2 z z 1 2 1 2
  z z    2 z z 2 2 1 2 1 2 2 2
z z  2 z z  2 2 2
z z  2z z 1 2 1 2 1 2 1 2 
 z z 2  2z z  2 z z  2 z z 2  4z z  1 2 1 2 1 2 1 2 1 2  
  z z 2  6z z  2 z z  0 1 2 1 2 1 2 2
 4m  6m 12  2 m 12  0  m  6 
Nếu m  4 hoặc 3  m  12 thì  2
 4m 8m 12 2
 0  m  2m  24  0   . m  4
Nếu m  12 thì  2
m  m   2 4 4
12  0  m m 12  0 . Trường hợp 2: 2
  0  m m 12  0  4  m  3 .
Khi đó, phương trình đã cho có hai nghiệm phân biệt z z 1 ,
2 là hai số phức liên hợp: 2
m i m m 12 và 2
m i m m 12 .
Do đó, z z  2 z z 1 2 1 2 2  m   2
m m   2 2
12  2 m m 12 2
 m 12  m m 12  m  0 .
Vậy có 3 giá trị nguyên của tham số m thỏa mãn đề bài.
Câu 35: Cho phương trình 4 2
4z mz  4  0 trong tập số phức và m là tham số thực. Gọi z , z , z , z 1 2 3 4
là bốn nghiệm của phương trình đã cho. Tìm tất cả các giá trị của m để
 2z 4 2z 4 2z 4 2z 4  324 . 1 2 3 4  m  2 m  2  m 1 m  1  A.  . B.  . C.  . D.  . m  15  m  15 m  35  m  35 Lời giải: Đặt 2
t z , phương trình trở thành 2
4t mt  4  0 có hai nghiệm t , t . 1 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc giam t   t   Ta có 1 2 
4 . Do vai trò bình đẳng, giả sử ta có 2 2
z z t , 2 2
z z t . 1 2 1 3 4 2 t  .t 1  1 2 2 2
Yêu cầu bài toán  t  4 t  4
 324  t t  4 t t 16  324 1   2   1 2  1 2  2    m   m   m 172 17 18 1 2 18     . m 17  1  8 m  35
Câu 36: Cho các số thực b, c sao cho phương trình 2
z bz c  0 có hai nghiệm phức z , z thỏa 1 2
mãn z  4  3i  1 và z  8  6i  4 . Mệnh đề nào sau đây đúng? 1 2
A. 5b c  12.
B. 5b c  4.
C. 5b c  4.
D. 5b c  12. Lời giải:
Vì z , z là hai nghiệm phức của phương trình 2
z bz c  0 nên z z 1 2 1 2
Khi đó ta có z  8  6i  4  z  8  6i  4  z  8  6i  4. 2 1 1
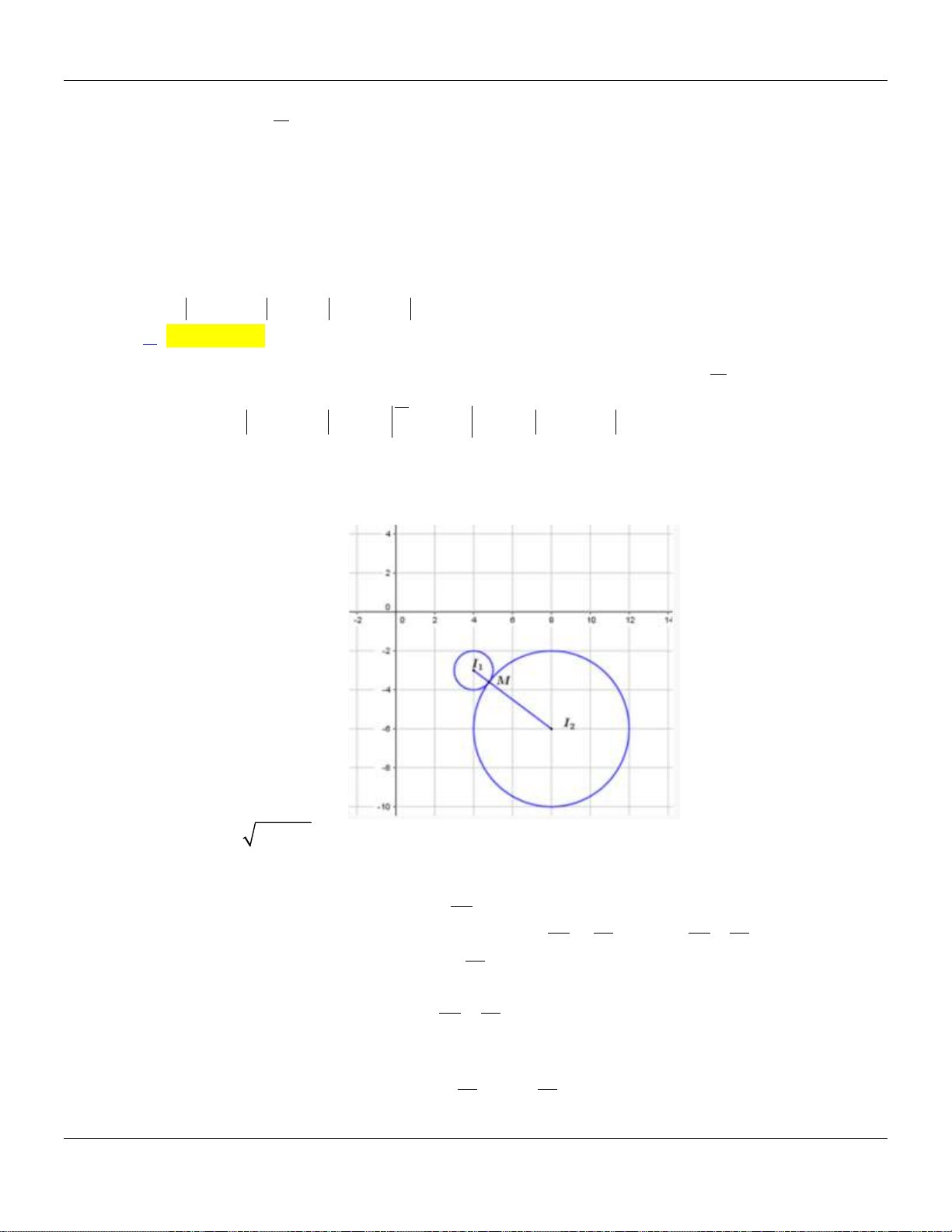
Gọi M là điểm biểu diễn số phức z . 1
M vừa thuộc đường tròn C tâm I 4; 3
 , bán kính R  1và đường tròn C tâm 2  1   1  1 I 8; 6
 , bán kính R  4  m C C . 1   2  1   1 Ta có 2 2 I I
4  3  5  R R C và C tiếp xúc ngoài. 2  1 2 1 2  1
Do đó có duy nhất 1 điểm M thỏa mãn, tọa độ điểm M là nghiệm của hệ  24  2 2 x
x y 8x  6y  24  0  5  24 18  24 18     M ;   z   i   là nghiệm của 1 2 2
x y 16x 12y  84  0 18   5 5  5 5 y    5 24 18 phương trình 2
z bz c  0  z  
i cũng là nghiệm của phương trình 2 5 5 2
z bz c  0. 48 48
Áp dụng định lí Vi ét ta có z z  b   b  
; z .z c  36 1 2 1 2 5 5
Vậy 5b c  48  36  12.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Câu 37: Cho phương trình 2
z bz c  0 , có hai nghiệm z , z thỏa mãn z z  4  2i . Gọi , A B là các 1 2 2 1
điểm biểu diễn các nghiệm của phương trình 2
z  2bz  4c  0 . Tính độ dài đoạn AB . A. 8 5. B. 2 5. C. 4 5. D. 5. Lời giải: 2
z bz c  0 có hai nghiệm z , z thỏa mãn z z  4  2i 1 2 2 1 2 2 2
Xét z z  4  2i   z z   4z z  4  2i 2
b  4c  4  2i 2 1 2 1 1 2   Khi đó phương trình 2
z  2bz  4c  0
z b  4  2i A b  4;2 2 A   có 2
  b  4c  4  2i  
b m ni,m,n 
z b  4  2i B b   B  4;2 2 2
Vậy AB  b  4  b  4  2  2  4 5.
Câu 38: Trên tập hợp các số phức, phương trình 2
z  a  2 z  2a  3  0 ( a là tham số thực) có 2
nghiệm z , z . Gọi M , N là điểm biểu diễn của z , z trên mặt phẳng tọa độ. Biết rằng có 2 1 2 1 2
giá trị của tham số a để tam giác OMN có một góc bằng 120 . Tổng các giá trị đó bằng bao nhiêu? A. 6 . B. 4  . C. 4 . D. 6  . Lời giải:
Vì O , M , N không thẳng hàng nên z , z không đồng thời là số thực, cũng không đồng 1 2
thời là số thuần ảo  z , z là hai nghiệm phức, không phải số thực của phương trình 1 2 2
z  a  2 z  2a  3  0 . Do đó, ta phải có 2
  a 12a 16  0  a 6 2 5; 6 2 5 . 2  2  a
a 12a 16 z   i 1  2 2 Khi đó, ta có  . 2  2  a
a 12a 16 z   i  1  2 2
OM ON z z  2a  3 và 2
MN z z  a 12a 16 . 1 2 1 2 2 2 2
OM ON MN 2 a  8a 10 1
Tam giác OMN cân nên MON  120   cos120    2OM .ON 22a  3 2 2
a  6a  7  0  a  3  2 .
Suy ra tổng các giá trị cần tìm của a bằng 6 .
Câu 39: Trên tập hợp các số phức, xét phương trình 2
z  2z  m  2  0 ( m là tham số thực). Gọi T là
tập hợp các giá trị của m để phương trình trên có hai nghiệm phân biệt được biểu diễn hình học bởi hai điểm ,
A B trên mặt phẳng tọa độ sao cho diện tích tam giác ABC bằng 2 2 , với C 1; 
1 . Tổng các phần tử trong T bằng A. 8 . B. 4 . C. 9 . D. 1  . Lời giải: 2 Ta có: 2
z  2z  m  2  0   z   1  m 1   1
TH1. có hai nghiệm phức  m 1  0  m  1 .
Khi đó, phương trình có hai nghiệm phức z  1 1 m i ; z  1 1 m i . 1 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Gọi A , B lần lượt là hai điểm biểu diễn của z ; z trên mặt phẳng Oxy 1 2 ta có:
A1; 1 m  ; B1; 1 m  .
Ta có: AB  2 1 m ; d C; AB  d C; x   1   2 . 1 Khi đó SA . B d C AB   m   m   ABC   ;  2 1 2 2 1. 2
TH2. có hai nghiệm thực phân biệt  m 1  0  m  1.
Khi đó, phương trình có hai nghiệm z  1 1 m ; z  1 1 m . 1 2
Gọi A , B lần lượt là hai điểm biểu diễn của z ; z trên mặt phẳng Oxy 1 2 ta có:
A1 1 m;0 ; B1 1 m;0 .
Ta có: AB  2 1 m ; d C; AB  d C;Ox  1 . 1 Khi đó SA . B d C AB   m
m  Vậy T   1  ; 
9 nên tổng các phần tử ABC   ;  1 2 2 9. 2 trong T bằng 8 .
Câu 40: Biết rằng phương trình 2
z  2az b  0 (a, b là các số thực dương) có hai nghiệm phức liên
hợp z , z . Gọi ,
A B, C lần lượt là các điểm biểu diễn của số phức w  2, z , z . Tính giá trị của 1 2 1 2
biểu thức T b  4a biết rằng ba điểm ,
A B, C tạo thành một tam giác vuông có diện tích bằng 9 . A. 6 . B. 8  . C. 9 . D. 14 . Lời giải: Do phương trình 2
z  2az b  0 (a, b là các số thực dương) có hai nghiệm phức liên hợp
z , z nên từ giả thiết ta gọi tọa độ các điểm biểu diễn cho các số phức w  2, z , z là 1 2 1 2 ( A 2; 0); B( ; x y);C( ;
x y) với x  2, y  0
AB  (x 2; y); AC  (x 2;  y) . Do A thuộc Ox , B, C đồi xứng qua Ox
Nên theo giả thiết suy ra ABC là tam giác vuông cân tại A 2 2  A .
B AC  0  (x  2)  y  0 (1) 1 Mặt khác SA . B AC ABC 2 1 2 2
 9  (x  2)  y    2
x  5  y  3  Từ và suy ra  x  1   y  3 
Với x  5, y  3 ta tìm được z  5  3i; z  5  3i . 1 2
Với x  1, y  3 ta tìm được z  1   3 ;i z  1
  3i suy ra a 1;b 10  T  6 1 2
Câu 41: Trên tập hợp số phức, xét phương trình 2 2
z  2az b  20  0  
1 với a,b là các tham số
nguyên dương. Khi phương trình có hai nghiệm phân biệt z , z thỏa mãn: z  3iz  7  5i 1 2 1 2
thì giá trị của biểu thức 7a  5b bằng A. 19 . B. 17 . C. 32 . D. 40 . Lời giải: Nhận xét: Nếu 2 2
  a b  20  0
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc giaz  7 1  5
Giả thiết z  3iz  7  5i   . Suy ra 7 
z z  2a  1 2 5 z   1 2 3 2  3 Suy ra: 2 2
  a b  20  0  2 2 z a
a b  20 i  Giải phương trình   1 ta có hai nghiệm  2 2 z a
a b  20 i   2 2 z a
a b  20 i  1 TH1: 2 2 
z  3iz  7  5i a  3 a b  20   2 2 3a
a b  20 i  7  5i 1 2 2 2 
z a a b  20 i 2   2 2
a  3 a b  20  7 a 1        VN 2 2 2 2
a b  20  2  3
a a b  20  5    2 2 z a
a b  20 i  1 TH2: 2 2 
z  3iz  7  5i a  3 a b  20   2 2 3a
a b  20 i  7  5i 1 2 2 2 
z a a b  20 i 2   a 1   2 2 a 1
a  3 a b  20  7 a 1     a 1 2    
 b  25  b  5   2 2 2 2
a b  20  4        b    5 3a a b 20 5 2  b 17(l) b  5  (l)
Suy ra 7a  5b  32
Cách 2 Nhận xét: Nếu 2 2
  a b  20  0 z  7 1  5
Giả thiết z  3iz  7  5i   . Suy ra 7 
z z  2a  1 2 5 z   1 2 3 2  3 Suy ra: 2 2
  a b  20  0
z  3iz  7  5i
z  3i 7 5i  3iz  7  5iz 1 2i 1 2 1  1  Giả thiết ta có: 1     
z  3iz  7  5i
z  3iz  7  5i z  1 2i 2 1   2 1 2 a 1 Áp dụng viet suy ra 
 7a  5b  32. b   5 c
Câu 42: Cho phương trình 2 x  4x
 0 có hai nghiệm phức. Gọi A , B là hai điểm biểu diễn của d
hai nghiệm đó trên mặt phẳng Oxy . Biết tam giác OAB đều, tính P c  2d .
A. P  18 .
B. P  10 .
C. P  14 .
D. P  22 . Lời giải: c c Ta có: 2 x  4x
 0 có hai nghiệm phức    4   0. d d
Khi đó, phương trình có hai nghiệm phức x  2 
 i ; x  2   i . 1 2
Gọi A , B lần lượt là hai điểm biểu diễn của x ; x trên mặt phẳng Oxy 1 2 ta có:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
A2;   ; B2;   .
Ta có: AB  2  ; OA OB  4   .
Tam giác OAB đều khi và chỉ khi AB OA OB  2   4    4   4   4 4 c 4 c 16
   . Vì   0 nên    hay 4      . 3 3 d 3 d 3
Từ đó ta có c  16 ; d  3 .
Vậy: P c  2d  22 .
Câu 43: Cho phương trình 4 2
4z mz  4  0 trong tập số phức và m là tham số thự C. Gọi z , z , z , z 1 2 3 4
là bốn nghiệm của phương trình đã cho. Tìm tất cả các giá trị của m để
 2z 4 2z 4 2z 4 2z 4  324 . 1 2 3 4 
A. m  1; m  35 .
B. m  1; m  35 .
C. m  1; m  35 .
D. m  1; m  35 . Lời giải:
Đặt f z 4 2
 4z mz  4 .
Vì phương trình f z   0 có 4 nghiệm z , z , z , z nên 1 2 3 4 f z 4 2
 4z mz  4  4z z z z z z z z 1   2   3   4  f 2i f 2  i Ta có: 2
z  4  z  2i
z  2i   2 z  4 2 z  4 2 z  4 2 z  4  . 1 2 3 4      1  1  1  4 4
 f 2i  42i4  m2i2  4  68 4m Mà  và  2 z  4 2 z  4 2 z  4 2 z  4  324 1 2 3 4   f   2  i  4 2
i4  m2i2  4  68  4m   m2 68 4 m  1  Nên 324    . 16 m  35
Câu 44: Tìm m  để các nghiệm của phương trình sau đều là số ảo: m   4 2
3 z  6z m  3  0 .
3 2  m  3
A. 3  m  3 2 .
B. 3  m  3 2 . C.  .
D. 3 2  m  3 . 3  m  3 2 Lời giải:
* Nếu m  3 : Phương trình trở thành 2
6z  6  0  z  i .
* Nếu m  3 : Đặt z xi x   , phương trình m   4 2
3 z  6z m  3  0   1 trở thành m   4 2
3 x  6x m  3  0 2 . Đặt 2
t x t  0 , phương trình 2 trở thành m   2
3 t  6t m  3  0 3 . Phương trình  
1 chỉ có nghiệm ảo  phương trình 2 chỉ có nghiệm thự C.
 phương trình 3 có 2 nghiệm thực thỏa mãn:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia   2 18   m  0    0  3  2  m  3 2   6 
0  t t  S  0    0       1 2 m 3 3 m 3 2 .  m  3   P  0     m  3 m 3   0       m  3 m 3
Vậy 3  m  3 2 thỏa mãn yêu cầu bài toán.
Câu 45: Gọi S là tổng các số thực m thỏa mãn 3 2
z  7z 16z 12  mz  3m  0 có nghiệm phức z 0
thỏa mãn | z | 2 . Khẳng định nào dưới đây đúng? 0 A. S  24 . B. S  25 . C. S  18 . D. S  16 . Lời giải: Ta có 3 2
z  7z 16z 12  mz  3m  0   z   2 3
z  4z  4  m  0  1 z  3  
z  22  m
+ Với m  0 (1)  z  2  m |  2  m | 2 m  0
Ta có: | z | 2    0  |  2  m | 2 m 16
+ Với m  0 (1)  z  2  i m . Do đó | z | 4  m 0
Ta có: | z | 2  4  m  2  4  m  4  m  0 0
Vậy S  0 16  16 .
Câu 46: Trên tập hợp số phức cho phương trình 2
z bz c  0 , với b, c
. Biết rằng hai nghiệm của
phương trình có dạng z w  3 và z  3w  8i 13 với w là một số phức. Tính b c . 1 2 A. 9 . B. 10 . C. 11. D. 12 . Lời giải:
Gọi w x yi với x, y
z w  3  x yi  3  x  3  yi 1
z  3w  8i 13  3(x yi)  8i 13  3x 13  3y  8 i 2  
x  3  3x 13  x  5 
z , z là hai số phức liên hợp nên:    1 2 y    3y 8 y  2 Khi đó z  2
  2i , z  2   2i 1 2 z z  4  Ta có 1 2  z .z  8  1 2
Suy ra z , z là nghiệm của phương trình: 2
z  4z  8  0 1 2
Vậy b c  4  8  12 .
Câu 47: Trên tập hợp các số phức, xét phương trình: 2
z  m   2 2
1 z m  3m  5  0 ( m là tham số
thực). Tính tổng các giá trị của m để phương trình trên có nghiệm z thỏa mãn 0 3 z 12  5 z . 0 0
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia A. 9 . B. 12 . C. 10 . D. 8 . Lời giải: 3 3 2 Ta có z
12  5 z z  5 z 12  0  z  3 z  3 z  4  0  z  3 0 0 0 0  0  0 0  0 Đặt phương trình 2
z  m   2 2
1 z m  3m  5  0  
1 có   5m  4 4 z  3
TH1: xét   0  5m  4  0  m
khi đó z  . Ta có z  3  0 0 0  5 z  3   0 m 1
Với z  3 thay vào   1  2
m  9m  8  0  0  m  8
Với z  3 thay vào   1  2
m  3m  20  0 pt vô nghiệm. 0 4
TH2: xét   0  5m  4  0  m  . 5
Khi đó phương trình  
1 có hai nghiệm phức z z và z z thỏa mãn 1 0 2 0    2 m 1 2 2 z  3  z
 9  z .z  9  z .z  9  m  3m  5  9  m  3m  4  0  . 0 0 0 0 1 2  m  4
Với m  1 thay vào   1  2
z  9  0  z  3i thỏa mãn
Với m  4 không thỏa mãn điều kiện ban đầu. m  1 m  8 Vậy có 3 giá trị  m  1  m
Nên tổng các giá trị của tham số là 8.
Câu 48: Cho phương trình 2
z bz c  0 có hai nghiệm z , z thỏa mãn z z  3  4i . Gọi , A B là các 1 2 2 1
điểm biểu diễn các nghiệm của phương trình 2
z  2bz  4c  0 . Tính độ dài đoạn AB . A. 20. B. 2 5. C. 10. D. 5. Lời giải: Phương trình 2
z bz c  0 có hai nghiệm z , z thỏa mãn z z  3  4i . 1 2 2 1
z z b  Theo định lý Viet ta có: 1 2 
z .z c  1 2 2 2 2
Xét z z  3  4i   z z   4z z  3  4i 2
b  4c  3 4i 2 1 2 1 1 2   Khi đó phương trình 2
z  2bz  4c  0
z b  3  4i A b  3;4 2 A   có 2
  b  4c  3 4i  
b m ni,m,n 
z b  3  4i B b    B  3; 4
Vậy AB  b   b  2    2 3 3 4 4  10.
Câu 49: Cho m là số thực, biết phương trình 2
z  2mz  9  0 có hai nghiệm phức z , z . Có bao nhiêu 1 2
giá trị nguyên của m sao cho z z z z  16 ? 1 2 2 1 A. 3 . B. 4 . C. 5 . D. 6 . Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 2
z  2mz  9  0 (*) có 2   m  9 .
Phương trình (*) có hai nghiệm phức z , z thỏa mãn z z z z  16 nên 1 2 1 2 2 1
  0  3  m  3 .
Áp dụng định lý Vi-ét ta có, z z  2 , m z z  9 . 1 2 1 2
Ta có z z z z
z z  9  3 và z z , z z . 1 2 1 2 1 2 1 1 2 2
z z z z z .3 z .3  3 z z  6m . 1 2 2 1 1 2  1 2  8
Theo đề, z z z z  16  6m  16  m  . 1 2 2 1 3 8
Kết hợp với điều kiện ta được 3
  m  . Mà m nguyên nên m 2  ; 1  ;0;1;  2 3
Vậy có 5 giá trị m thỏa mãn yêu cầu bài toán.
Câu 50: Gọi S là tập hợp tất cả các số thực a sao cho phương trình 2
z  (a  2)z  2a  3  0 có hai
nghiệm phức z , z và các điểm biểu diễn của z , z cùng với gốc tọa độ O tạo thành một tam 1 2 1 2
giác có diện tích bằng 2. Số phần tử của S là? A. 1. B. 4 . C. 2 . D. 3 . Lời giải:
Nếu   a  22  42a  3  0  z , z là các số thực khi đó M (z ), N (z ) Ox O, M , N 1 2 1 2 thẳng hàng. 2
Nếu   a  2  42a  3  0  z z z z z z  2a  3 . 1 2 1 2 1 2
Với M (z ), N (z )  OM ON z z và 1 2 1 2 2 2 2
MN z z z z
 (z z )  4z z  4(2a  3)  (2  a) . 1 2 1 2 1 2 1 2
Tam giác OMN cân tại O . Do đó 2 1 MN 1 2 2 2 SMN. OM
MN. 4OM MN . OMN 2 4 4 1 a  4 Mà S  2  2 2
4(2a  3)  (2  a) (2  a)  2  . OMN  4 a 10,369
Vậy có 2 số thực a thỏa mãn yêu cầu bài toán.
____________________HẾT____________________
Huế, 15h15’ Ngày 19 tháng 3 năm 2023
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115