Ôn tập giữa kì 2 Toán 12 năm 2022 – 2023 trường THPT Trần Phú – Hà Nội

Ôn tập giữa kì 2 Toán 12 năm 2022 – 2023 trường THPT Trần Phú – Hà Nội được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

58 29 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK2 Toán 12

Môn: Toán 12

Thông tin:

22 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
1
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
TRƯỜNG THPT TRẦN PHÚ-HOÀN KIẾM
NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HỌC KÌ II
Môn: Toán
Lớp: 12
Năm học 2022-2023
PHẦN 1: NGUYÊN HÀM –TÍCH PHÂN- ỨNG DỤNG CỦA TÍCH PHÂN
Câu 1. Hàm số
()Fx
là một nguyên hàm của hàm số
()fx
trên khoảng
K
nếu
A.
'() (), .F x fx x K=− ∀∈
B.
'() (), .fxFxxK= ∀∈
C.
'() (), .F x fx x K= ∀∈
D.
Câu 2. Họ nguyên hàm của hàm số
( )
cos 6fx x x= +
là
A.
2
sin 3xxC++
. B.
2
sin 3xxC− ++
. C.
2
sin 6x xC++
. D.
sin xC−+
.
Câu 3. Tìm nguyên hàm của hàm số
( )
2 1.
fx x
= −
A.
( )
(
)
2
2121 .
3
f x dx x x C
= − −+
∫
B.
( ) (
)
1
2121 .
3
f x dx x x C= − −+
∫
C.
( )
1
21 .
3
f x dx x C=− −+
∫
D.
( )
1
21 .
2
f x dx x C= −+
∫
Câu 4. Tìm nguyên hàm của hàm số
( )
2
2
2
fx x
x
= +
.
A.
( )
3
1
d
3
x
fx x C
x
= ++
∫
. B.
( )
3
2
d
3
x
fx x C
x
= −+
∫
.
C.
( )
3
1
d
3
x
fx x C
x
= −+
∫
. D.
( )
3
2
d
3
x
fx x C
x
= ++
∫
.
Câu 5. Tìm nguyên hàm của hàm số
( )
1
52
fx
x
=
−
.
A.
d1
ln 5 2
5 25
x
xC
x
= −+
−
∫
B.
d
ln 5 2
52
x
xC
x
= −+
−
∫
C.
d1
ln 5 2
52 2
x
xC
x
=− −+
−
∫
D.
d
5ln 5 2
52
x
xC
x
= −+
−
∫
Câu 6. Tìm nguyên hàm
( )
15
2
7 dxxx+
∫
?
A.
( )
16
2
1
7
2
xC++
B.
( )
16
2
1
7
32
xC− ++
C.
( )
16
2
1
7
16
xC++
D.
( )
16
2
1
7
32
xC++
Câu 7. Họ nguyên hàm của hàm số
3
(x) =
x
fe
là
A.
3 +
x
eC
. B.
3
1
3
+
x
eC
. C.
1
3
+
x
eC
. D.
3
3
+
x
eC
.
Câu 8. Đẳng thức nào trong các đẳng thức sau là sai?
A.
1
ln dxx C
x
= +
∫
. B.
2
1
d tan
cos
x xC
x
= +
∫
. C.
sin d cosxx x C=−+
∫
. D.
ed e
xx
xC= +
∫
.
2
Câu 9. Hàm số
( )
3
1
3
Fx x
=
là một nguyên hàm của hàm số nào sau đây trên
( )
;−∞ +∞
?
A.
( )
2
3fx x=
. B.
( )
3
fx x=
. C.
( )
2
fx x=
. D.
(
)
4
1
4
fx x=
.
Câu 10. Tìm nguyên hàm của hàm số
(
)
4
2
2x
fx
x
+
=
.
A.
( )
3
1
d
3
x
fx x C
x
= −+
∫
. B.
( )
3
2
d
3
x
fx x C
x
= ++
∫
.
C.
( )
3
1
d
3
x
fx x C
x
= ++
∫
. D.
( )
3
2
d
3
x
fx x C
x
= −+
∫
.
Câu 11. Họ nguyên hàm của hàm số
1
()
31
fx
x
=
−
trên khoảng
1
;
3

−∞


là:
A.
1
ln(3 1)
3
xC−+
B.
ln(1 3 )
xC−+
C.
1
ln(1 3 )
3
xC−+
D.
ln(3 x 1)
C−+
Câu 12. Trong các khẳng định sau, khẳng định nào sai?
A.
2 d 2 ln 2
xx
xC= +
∫
. B.
2
2
e
ed
2
x
x
xC= +
∫
.
C.
1
cos 2 d sin 2
2
xx x C
= +
∫
. D.
1
d ln 1
1
xxC
x
= ++
+
∫
( )
1
x
∀ ≠−
.
Câu 13. Hàm số
( )
2
x
Fx e
=
là nguyên hàm của hàm số nào trong các hàm số sau:
A.
2
() 2
x
f x xe=
. B.
2
2
() 1
x
f x xe= −
. C.
2
()
x
fx e=
. D.
2
()
2
x
e
fx
x
=
.
Câu 14. Tìm nguyên hàm của hàm số
( )
5
2018
2017
x
x
e
fx e
x
−

= −


.
A.
( )
4
2018
d 2017
x
fx x e C
x
= −+
∫
. B.
( )
4
2018
d 2017
x
fx x e C
x
= ++
∫
.
C.
( )
4
504,5
d 2017
x
fx x e C
x
= ++
∫
. D.
( )
4
504,5
d 2017
x
fx x e C
x
= −+
∫
.
Câu 15. Họ nguyên hàm của hàm số
2
2
cos
x
x
e
ye
x
−

= +


là
A.
2 tan
x
e xC++
B.
2 tan
x
e xC−+
C.
1
2
cos
x
eC
x
−+
D.
1
2
cos
x
eC
x
++
Câu 16. Hàm số
( )
Fx
là một nguyên hàm của hàm số
1
y
x
=
trên
( )
;0−∞
thỏa mãn
( )
20F −=
. Khẳng định
nào sau đây đúng?
A.
( ) ( )
ln ;0
2
x
Fx x
−

= ∀ ∈ −∞


B.
( ) ( )
ln ;0Fx x C x= + ∀ ∈ −∞
với
C
là một số thực bất kì.
3
C.
( ) ( )
ln ln 2 ;0Fx x x= + ∀ ∈ −∞
.
D.
( ) ( ) (
)
ln ;0Fx x C x= − + ∀ ∈ −∞
với
C
là một số thực bất kì.
Câu 17. Cho hàm số
( )
fx
xác định trên
{ }
\1R
thỏa mãn
( )
1
1
fx
x
′
=
−
,
( )
0 2017
f
=
,
(
)
2 2018f =
.
Tính
( ) ( )
31Sf f
= −−
.
A.
ln 4035S =
. B.
4
S =
. C.
ln 2S =
. D.
1S
=
.
Câu 18. Cho
(
)
Fx
là một nguyên hàm của hàm số
= +() 2
x
fx e x
thỏa mãn
( )
=
3
0
2
F
. Tìm
( )
Fx
A.
( )
=++
2
1
2
x
Fx e x
B.
( )
=++
2
5
2
x
Fx e x
C.
(
)
=++
2
3
2
x
Fx e x
D.
( )
= +−
2
1
2
2
x
Fx e x
Câu 19. Gọi
( )
Fx
là một nguyên hàm của hàm số
( )
2
x
fx
=
, thỏa mãn
( )
1
0
ln 2
F =
. Tính giá trị biểu
thức
( ) ( ) (
) (
)
0 1 ... 2018 2019TF F F F
= + ++ +
.
A.
2019
21
1009.
ln 2
T
+
=
. B.
2019.2020
2T =
C.
2019
21
ln 2
T
−
=
. D.
2020
21
ln 2
T
−
=
.
Câu 20. Tìm nguyên hàm
( )
Fx
của hàm số
( )
sin cosfx x x= +
thoả mãn
2
2
F
π

=


.
A.
( )
cos sin 3Fx x x
=−++
B.
( )
cos sin 1Fx x x
=−+−
C.
(
)
cos sin 1
Fx x x=−++
D.
( )
cos sin 3
Fx x x= −+
Câu 21. Biết
( )
Fx
là một nguyên hàm của hàm số
( )
2
tanfx x=
và
1
4
F
π

=


. Tính
4
F
π

−


.
A.
1
44
F
ππ

−=−


. B.
1
42
F
ππ

−=−


. C.
1
4
F
π

−=−


. D.
1
42
F
ππ

−=+


.
Câu 22. Tìm một nguyên hàm
( )
Fx
của hàm số
( ) ( )
2
1 sinfx x= +
biết
3
24
F
ππ

=


A.
( )
31
2 cos sin 2 .
24
Fx x x x=+−
B.
( )
31
2 cos sin 2 .
24
Fx x x x=−−
C.
( )
31
2 cos sin 2 .
24
Fx x x x=−+
D.
( )
31
2 cos sin 2 .
24
Fx x x x=++
Câu 23. Biết
( )
2x
Fx e x= +
là một nguyên hàm của hàm số
(
)
fx
trên R. Khi đó
( )
2f x dx
∫
bằng
A.
2
22 .
x
e xC++
B.
22
1
.
2
x
e xC++
C.
22
1
2.
2
x
e xC++
D.
22
4.
x
e xC++
Câu 24. Cho
( )
3
0
d4 2fx x x x C= ++
∫
. Tính
( )
2
dxf xIx=
∫
.
4
A.
62
2I xxC
=
++
. B.
10 6
10 6
xx
IC
=
++
C.
62
4
2
I x xC
=
++
. D.
2
12 2
Ix=
+
.
Câu 25. Tìm họ nguyên hàm của hàm số
( )
3
21
.e
+
=
x
fx x
.
A.
( )
3
3
1
d .e
3
+
= +
∫
x
x
fx x C
. B.
( )
3
1
d 3e
+
= +
∫
x
fx x C
.
C.
( )
3
1
de
+
= +
∫
x
fx x C
. D.
(
)
3
1
1
de
3
+
= +
∫
x
fx x C
.
Câu 26.
Nguyên hàm của
(
)
2
sin
sin 2 .
x
f x xe=
là
A.
2
2 sin 1
sin .
x
xe C
−
+
. B.
2
sin 1
2
sin 1
x
e
C
x
+
+
+
. C.
2
sin x
eC+
. D.
2
sin 1
2
sin 1
x
e
C
x
−
+
−
.
Câu 27. Tìm hàm số
( )
Fx
biết
( )
3
4
d
1
x
Fx x
x
=
+
∫
và
( )
01F =
.
A.
( )
( )
4
ln 1 1Fx x= ++
. B.
.
C.
( )
(
)
4
1
ln 1 1
4
Fx x= ++
. D.
(
)
( )
4
4 ln 1 1Fx x= ++
.
Câu 28. Biết
( )
( )
2017
2019
1
11
. ,1
1
1
b
x
x
dx C x
ax
x
−
−

= + ≠−

+

+
∫
với a, b ∈ N*. Mệnh đề nào sau đây đúng?
A.
2ab=
. B.
2ba=
. C.
2018ab=
. D.
2018ba=
.
Câu 29.
Nguyên hàm của
( )
1 ln
.ln
x
fx
xx
+
=
là:
A.
1 ln
d ln ln
.ln
x
x xC
xx
+
= +
∫
. B.
2
1 ln
d ln .ln
.ln
x
x x xC
xx
+
= +
∫
.
C.
1 ln
d ln ln
.ln
x
x x xC
xx
+
=++
∫
. D.
1 ln
d ln .ln
.ln
x
x x xC
xx
+
= +
∫
.
Câu 30. Nguyên hàm của hàm số
( )
3
31fx x= +
là
A.
( ) ( )
3
d 3131fx x x x C= + ++
∫
. B.
( )
3
d 31fx x x C= ++
∫
.
C.
( )
3
1
d 31
3
fx x x C= ++
∫
. D.
( ) ( )
3
1
d 3131
4
fx x x x C= + ++
∫
.
Câu 31. Cho hàm số
( )
ln 2
2.
x
fx
x
=
. Hàm số nào dưới đây không là nguyên hàm của hàm số
( )
fx
?
A.
( )
2
x
Fx C= +
B.
( )
( )
22 1
x
Fx C= −+
C.
( )
( )
22 1
x
Fx C= ++
D.
( )
1
2
x
Fx C
+
= +
Câu 32. Khi tính nguyên hàm
3
d
1
x
x
x
−
+
∫
, bằng cách đặt
1ux
= +
ta được?
5
A.
(
)
2
2 4duu
−
∫
. B.
(
)
2
4duu
−
∫
. C.
(
)
2
3duu
−
∫
. D.
( )
2
2 4duu u−
∫
.
Câu 33. Biết
( )
Fx
là một nguyên hàm của hàm số
sin
()
1 3cos
x
fx
x
=
+
và
2
2F
π

=


.Tính
( )
.0F
A.
1
(0) ln 2 2
3
F =−+
. B.
2
(0) ln 2 2
3
F
=−+
. C.
2
(0) ln 2 2
3
F
=−−
. D.
1
(0 ln 2 2
3
F =−−
.
Câu 34. Gọi
( )
Fx
là nguyên hàm của hàm số
( )
2
21
1
x
fx
x
x
= −
+
. Biết
( )
36F =
, giá trị của
( )
8F
là
A.
217
8
. B.
27
. C.
215
24
. D.
215
8
.
Câu 35. Cho hàm số
(
)
2
2
x
fx
x
=
+
. Họ tất cả các nguyên hàm của hàm số
( ) ( ) ( )
1.gx x f x
′
= +
là
A.
2
2
22
22
xx
C
x
+−
+
+
. B.
2
2
2
x
C
x
−
+
+
. C.
2
2
2
2
xx
C
x
++
+
+
. D.
2
2
22
x
C
x
+
+
+
.
Câu 36. Họ nguyên hàm của hàm số
(
) (
)
4 1 lnfx x x= +
là:
A.
22
2 ln 3x xx
+
. B.
22
2 lnx xx
+
C.
22
2 ln 3x xxC++
. D.
22
2 lnx xx C
++
.
Câu 37. Họ nguyên hàm của hàm số
( )
( )
21
x
fx x e= −
là
A.
( )
23−+
x
x eC
. B.
( )
23++
x
x eC
C.
(
)
21++
x
x eC
. D.
(
)
21−+
x
x eC
.
Câu 38. Cho hàm số
( )
fx
thỏa mãn
( )
1
2
25
= −f
và
( ) ( )
2
3
4
′
=


f x x fx
với mọi x ∈ R. Giá trị của
(
)
1
f
bằng
A.
391
400
−
B.
1
40
−
C.
41
400
−
D.
1
10
−
Câu 39. Cho hàm số
( )
y fx=
đồng biến và có đạo hàm liên tục trên R thỏa mãn
(
′()
)
2
=
(
)
.
,
∀x∈R và
( )
02f
=
. Khi đó
( )
2f
thuộc khoảng nào sau đây?
A.
( )
12;13 .
B.
( )
9;10 .
C.
(
)
11;12 .
D.
( )
13 14;.
Câu 40. Cho hàm số
( )
fx
thỏa mãn
( ) ( ) ( )
2
2
. 21f x fxf x x x
′ ′′
+ = −+


, ∀x∈R và
( ) ( )
0 03ff
′
= =
.
Giá trị của
( )
2
1f


bằng
A.
28
. B.
22
. C.
19
2
. D.
10
.
Câu 41. Biết
( )
3
2
d 6.fx x=
∫
Giá trị của
( )
3
2
2dfx x
∫
bằng.
A.
36
. B.
3
. C.
12
. D.
8
.
Câu 42. Biết
( )
2
Fx x=
là một nguyên hàm của hàm số
()fx
trên R. Giá trị của
[ ]
3
1
1 ()f x dx+
∫
bằng
6
A.
10
. B.
8
. C.
26
3
. D.
32
3
.
Câu 43. Biết
( )
3
2
f x dx 4=
∫
và
(
)
3
2
g x dx 1
=
∫
. Khi đó:
( ) ( )
3
2
f x g x dx

−

∫
bằng:
A.
3−
. B.
3
. C.
4
. D.
5
.
Câu 44. Biết
( )
1
0
f x 2x dx=2

+

∫
. Khi đó
( )
1
0
f x dx
∫
bằng :
A.
1
. B.
4
. C.
2
. D.
0
.
Câu 45. Khẳng định nào trong các khẳng định sau đúng với mọi hàm
f
,
g
liên tục trên
K
và
a
,
b
là
các số bất kỳ thuộc
K
?
A.
[ ]
() 2()d ()d+2 ()d
b bb
a aa
f x gx x f x x gx x+=
∫ ∫∫
. B.
( )d
()
d
()
( )d
b
b
a
b
a
a
fx x
fx
x
gx
gx x
=
∫
∫
∫
.
C.
[ ]
().()d ()d . ()d
b bb
a aa
f x gx x f x x gx x=
∫ ∫∫
. D.
2
2
()d= ()d
bb
aa
f x x fx x



∫∫
.
Câu 46. Cho
( )
2
2
d1fx x
−
=
∫
,
( )
4
2
d4
ft t
−
= −
∫
. Tính
( )
4
2
dfy y
∫
.
A.
5I
=
. B.
3
I = −
. C.
3I =
. D.
5I = −
.
Câu 47. Cho hàm số
( )
fx
liên tục trên
[ ]
0;10
thỏa mãn
( )
10
0
7
f x dx =
∫
,
( )
6
2
3f x dx =
∫
. Tính
( ) (
)
2 10
06
P f x dx f x dx
= +
∫∫
.
A.
10
P =
. B.
4P =
. C.
7P =
. D.
6P = −
.
Câu 48. Cho
f
,
g
là hai hàm liên tục trên đoạn
[ ]
1; 3
thoả:
( )
( )
3
1
3 d 10
f x gx x+=


∫
,
( ) ( )
3
1
2 d6f x gx x−=


∫
. Tính
( ) ( )
3
1
df x gx x+


∫
.
A. 7. B. 6. C. 8. D. 9.
Câu 49. Cho
( )
2
1
d2fx x
−
=
∫
và
( )
2
1
d1gx x
−
= −
∫
. Tính
( ) ( )
2
1
2 3dI x f x gx x
−

=+−
∫
.
A.
17
2
I =
B.
5
2
I =
C.
7
2
I =
D.
11
2
I =
Câu 50. Giả sử
4
0
2
sin 3
2
I xdx a b
π
= = +
∫
(a, b ∈Q). Khi đó giá trị của
ab−
là
A.
1
6
−
B.
1
6
−
C.
3
10
−
D.
1
5
7
Câu 51. Cho
(
)
2
0
3 2 1d 6
m
xx x−+ =
∫
. Giá trị của tham số m thuộc khoảng nào sau đây?
A.
( )
1; 2−
. B.
( )
;0−∞
. C.
( )
0; 4
. D.
( )
3;1−
.
Câu 52. Cho hàm số
()fx
. Biết
(0) 4f =
và f’(x) = 2cos
2
x + 3, ∀x ∈ R, khi đó
4
0
()f x dx
π
∫
bằng?
A.
2
88
8
ππ
++
. B.
2
82
8
ππ
++
. C.
2
68
8
ππ
++
. D.
2
2
8
π
+
.
Câu 53. Có bao nhiêu giá trị nguyên dương của
a
để
( )
0
2 3d 4
a
xx−≤
∫
?
A.
5
. B.
6
. C.
4
. D.
3
.
Câu 54. Có bao nhiêu số thực
b
thuộc khoảng
(
)
;3
ππ
sao cho
4 cos 2 1
b
xdx
π
=
∫
?
A. 8. B. 2. C. 4. D. 6.
Câu 55. Biết
( )
0
2
1
3 51 2
ln , ,
23
xx
I dx a b a b
x
−
+−
= =+∈
−
∫
. Khi đó giá trị của
4ab+
bằng
A.
50
B.
60
C.
59
D.
40
Câu 56. Tích phân
( )
2
1
2
0
1
d ln
1
x
I xa b
x
−
= = −
+
∫
trong đó
a
,
b
là các số nguyên. Tính giá trị của biểu thức
ab+
.
A.
1
. B.
0
. C.
1−
. D.
3
.
Câu 57. Biết
2
2
2
0
52
d ln 3 ln 5
43
xx
x ab c
xx
++
=++
++
∫
, Giá trị của
abc
bằng
A.
8−
. B.
10
−
. C.
12−
. D.
16
.
Câu 58. Cho
21
5
ln 3 ln 5 ln 7
4
dx
abc
xx
=++
+
∫
, với
,,abc
là các số hữu tỉ. Mệnh đề nào sau đây đúng?
A.
2ab c−=−
B.
2ab c+=−
C.
abc+=
D.
ab c−=−
Câu 59. Tính tích phân
2
2
1
21I x x dx= −
∫
bằng cách đặt
2
1ux= −
, mệnh đề nào dưới đây đúng?
A.
3
0
I udu=
∫
B.
2
1
1
2
I udu=
∫
C.
3
0
2I udu=
∫
D.
2
1
I udu=
∫
Câu 60. Giả sử tích phân
5
1
1
ln 3 ln 5
1 31
I dx a b c
x
= =++
++
∫
. Lúc đó
A.
5
3
abc++=
. B.
4
3
abc++=
. C.
7
3
abc++=
. D.
8
3
abc++=
.
Câu 61. Biết
1
ln
2
1 ln
e
x
dx a b
xx
= +
+
∫
với
,ab
là các số hữu tỷ. Tính
S ab= +
.
8
A.
1S =
. B.
1
2
S =
. C.
3
4
S =
. D.
2
3
S =
.
Câu 62. Cho tích phân
22
2
0
16 dI xx= −
∫
và
4sinxt=
. Mệnh đề nào sau đây đúng?
A.
( )
4
0
8 1 cos 2 dI tt
π
= +
∫
. B.
4
2
0
16 sin dI tt
π
=
∫
C.
( )
4
0
8 1 cos 2 dI tt
π
= −
∫
. D.
4
2
0
16 cos dI tt
π
= −
∫
.
Câu 63. Cho biết
7
3
3
2
0
d
1
=
+
∫
xm
x
n
x
với
m
n
là một phân số tối giản. Tính
7mn−
A.
0
. B.
1
. C.
2
. D.
91
.
Câu 64. Giả sử
64
3
1
d2
ln
3
x
I ab
xx
= = +
+
∫
với
,ab
là số nguyên. Khi đó giá trị
ab
−
là
A.
17−
. B. 5. C.
5−
. D.
17
.
Câu 65. Cho hàm số
( )
fx
có
( )
00f =
và
( )
2
cos cos 2 ,fx x x R
′
= ∀∈
. Khi đó
( )
0
dfx x
π
∫
bằng
A.
1042
225
. B.
208
225
. C.
242
225
. D.
149
225
.
Câu 66. Cho
2
2
0
cos 4
d ln
sin 5sin 6
x
xa
xx b
π
=
−+
∫
. Giá trị của
ab+
bằng
A.
0
. B.
1
. C.
4
. D.
3
.
Câu 67. Tính tích phân
2
4
4
0
sin
d
cos
x
Ix
x
π
=
∫
bằng cách đặt
tan
ux=
, mệnh đề nào dưới đây đúng?
A.
4
2
0
dI uu
π
=
∫
. B.
2
2
0
1
dIu
u
=
∫
. C.
1
2
0
dI uu= −
∫
. D.
1
2
0
dI uu=
∫
.
Câu 68. Biết
( )
ln 2
0
d1
ln ln ln
4e 3e
xx
x
I abc
c
−
=
+
= −+
+
∫
với
a
,
b
,
c
là các số nguyên dương.
Tính
2P abc= −+
.
A.
3P = −
. B.
1P = −
. C.
4P =
. D.
3P =
Câu 69. Cho
(
)
e
2
1
1 ln d e exxxa b c+ = ++
∫
với
a
,
b
,
c
là các số hữu tỷ. Mệnh đề nào dưới đây đúng?
A.
abc+=
B.
ab c+=−
C.
ab c−=
D.
ab c−=−
Câu 70. Biết rằng tích phân
( )
1
0
2+1ed= +.e
x
x x ab
∫
, tích
a.b
bằng
A.
15−
. B.
1−
. C. 1. D. 20.
9
Câu 71. Cho tích phân
2
2
1
ln
ln 2
xb
I dx a
xc
= = +
∫
với
a
là số thực,
b
và
c
là các số dương, đồng thời
b
c
là
phân số tối giản. Tính giá trị của biểu thức
23P a bc= ++
.
A.
6
P =
. B.
5P
=
. C.
6P = −
. D.
4P =
.
Câu 72. Cho hàm số
( )
fx
liên tục trên R và thỏa mãn
( )
1
5
d9fx x
−
=
∫
. Tích phân
( )
2
0
1 3 9dfx x−+


∫
bằng
A.
15
. B.
27
. C.
75
. D.
21
.
Câu 73. Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
0;10
thỏa mãn
( ) ( )
10 10
02
d 7, d 1
fx x fx x= =
∫∫
. Tính
( )
1
0
2dP f xx
=
∫
.
A.
6P
=
. B.
6
P = −
. C.
3P =
. D.
12P =
.
Câu 74. Cho
(
)
5
1
d 26I fx x
= =
∫
. Khi đó
( )
2
2
0
1 1d
J xfx x

= ++

∫
bằng
A.
15
. B.
13
. C.
54
. D.
52
.
Câu 75. Cho hàm số
()y fx=
liên tục trên R thỏa mãn
( )
9
1
4
fx
dx
x
=
∫
và
( )
2
0
sin cos 2.f x xdx
π
=
∫
Tích phân
3
0
()I f x dx=
∫
bằng
A.
8I =
. B.
6I =
. C.
4I =
. D.
10I =
.
Câu 76. Cho
( )
4
0
20 8d 1fx x=
∫
. Tính tích phân
( ) ( )
2
0
24d2I fx f x x= +−


∫
.
A.
0I =
. B.
2018I =
. C.
4036I =
. D.
1009I =
.
Câu 77. Cho hàm số
( )
fx
có đạo hàm liên tục trên R. Biết
( )
61f =
và
( )
1
0
6d 1xf x x =
∫
, khi đó
( )
6
2
0
dxf x x
′
∫
bằng
A.
107
3
. B.
34
. C.
24
. D.
36−
.
Câu 78. Cho
( )
fx
là hàm số có đạo hàm liên tục trên
[ ]
0;1
và
( )
1
1
18
f = −
,
( )
1
0
1
.d
36
xf x x
′
=
∫
. Giá trị
của
( )
1
0
d
fx x
∫
bằng
A.
1
12
−
. B.
1
36
. C.
1
12
. D.
1
36
−
.
10
Câu 79. Cho hàm số
(
)
fx
có
(
)
2
1fe=
và
( )
2
2
21
x
x
fx e
x
−
′
=
với mọi
x
khác
0
. Khi đó
( )
ln 3
1
dxf x x
∫
bằng
A.
2
6 e−
. B.
2
6
2
e−
. C.
2
9 e−
. D.
2
9
2
e−
.
Câu 80. Cho hàm số
()
y fx
=
có đạo hàm liên tục trên R và thỏa mãn
2
0
(2) 16, ( ) 4f f x dx
= =
∫
. Tính
1
0
(2 )I xf x dx
′
=
∫
.
A.
20
I
=
B.
7
I =
C.
12
I
=
D.
13I =
Câu 81. Gọi S là diện tích miền hình phẳng được tô đậm trong hình vẽ bên. Công thức tính S là
A.
( ) ( )
12
11
dd
S fx x fx x
−
= +
∫∫
. B.
( ) ( )
12
11
ddS fx x fx x
−
= −
∫∫
.
C.
( )
2
1
dS fx x
−
=
∫
. D.
( )
2
1
dS fx x
−
= −
∫
.
Câu 82. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số
32
3yx x
, trục hoành và hai đường thẳng
1x
,
4x
là
A.
53
4
B.
51
4
C.
49
4
D.
25
2
Câu 83. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số
1
2
x
y
x
, trục hoành và đường thẳng
2x
là
A.
3 2 ln 2
B.
3 ln 2
C.
3 2 ln 2
D.
3 ln 2
Câu 84. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
1
2
x
y
x
+
=
−
và các trục tọa độ Ox, Oy ta được:
ln 1
b
Sa
c
= +
. Chọn đáp án đúng
A.
8abc++=
B
0abc
++=
C
1abc++=
D.
10abc++=
Câu 85. Diện tích hình phẳng giới hạn bởi đường cong
lnyxx
, trục hoành và đường thẳng
xe
là
A.
2
1
2
e
B.
2
1
2
e
C.
2
1
4
e
D.
2
1
4
e
Câu 86. Cho hình thang cong
( )
H
giới hạn bởi các đường
e
x
y
=
,
0y =
,
0x =
,
ln 8x =
. Đường thẳng
xk=
( )
0 ln 8k<<
chia
( )
H
thành hai phần có diện tích là
1
S
và
2
S
. Tìm
k
để
12
SS=
.
A.
9
ln
2
k =
. B.
ln 4k =
. C.
2
ln 4
3
k =
. D.
ln 5k =
.
Câu 87. Tính diện tích miền hình phẳng giới hạn bởi các đường
2
2yx x= −
,
0y
=
,
10x = −
,
10x =
.
A.
2000
3
S =
. B.
2008S =
. C.
2008
3
S =
. D.
2000
.
Câu 88. Tính diện tích
S
của miền hình phẳng giới hạn bởi đồ thị của hàm số
( )
32
f x ax bx c=++
, các
đường thẳng
1x =
,
2x =
và trục hoành (miền gạch chéo) cho trong hình dưới đây.
O
x
y
2
1
1−
(
)
y fx
=
11
A.
51
8
S =
. B.
52
8
S =
. C.
50
8
S =
. D.
53
8
S
=
.
Câu 89. Cho hình phẳng
(
)
H
giới hạn bởi đồ thị của hai hàm số
( )
1
fx
và
( )
2
fx
liên tục trên đoạn
[ ]
;ab
và hai đường thẳng
xa
=
,
xb=
(tham khảo hình vẽ dưới). Công thức tính diện tích của hình
( )
H
là
A.
( ) ( )
12
d
b
a
S fx fx x= −
∫
. B.
( ) ( )
( )
12
d
b
a
S fx f x x= −
∫
.
C.
( ) ( )
12
d
b
a
S fx fx x= +
∫
. D.
( ) ( )
21
dd
bb
aa
S fxx fxx= −
∫∫
.
Câu 90. Hình phẳng (H) được giới hạn bởi đồ thị hai hàm số
2
2, 2yx x yx 
và hai đường thẳng
2; 3xx
. Diện tích của (H) bằng
A.
87
5
B.
87
4
C.
87
3
D.
87
5
Câu 91. Cho hình phẳng
( )
H
giới hạn bởi các đường
2
yx=
,
0y =
,
0x =
,
4x =
. Đường thẳng
yk
=
( )
0 16k<<
chia hình
( )
H
thành hai phần có diện tích
1
S
,
2
S
(hình vẽ).
Tìm
k
để
12
SS=
.
A.
8k =
. B.
4k
=
. C.
5k =
. D.
3k =
.
Câu 92. Diện tích hình phẳng được giới hạn bởi parabol
2
2yx
và đường thẳng
yx
là
A.
7
2
B.
9
4
C.
3
D.
9
2
Câu 93. Gọi (H) là hình phẳng được giới hạn bởi đồ thị hai hàm số
1 ,1
x
yexyex 
. Diện tích của
(H) bằng
A.
1
2
e
B.
2
2
e
C.
2
2
e
D.
1
2
e
Câu 94. Tính diện tích
S
của hình phẳng giới hạn bởi đồ thị hàm số
3
yx x= −
và đồ thị hàm số
2
y xx= −
.
O
x
y
a
1
c
2
c
b
( )
1
fx
(
)
2
fx
1
S
O
x
y
4
k
16
2
S
12
A.
13S =
. B.
81
12
S =
. C.
9
4
S =
. D.
37
12
S =
.
Câu 95. Cho
( )
H
là hình phẳng giới hạn bởi các đồ thị hàm số
ey =
,
e
x
y =
và
( )
1e 1yx
=−+
(tham khảo
hình vẽ bên).
Diện tích hình phẳng
(
)
H
là
A.
e1
2
S
+
=
. B.
3
e
2
S
= +
. C.
e1
2
S
−
=
. D.
1
e
2
S = +
.
Câu 96. Tích diện tích
S
của hình phẳng (phần gạch sọc) trong hình sau
A.
8
3
S
=
. B.
10
3
S =
. C.
11
3
S =
. D.
7
3
S =
.
Câu 97. Cho
(
)
H
là hình phẳng giới hạn bởi các đường
2yx=
;
22yx= −
và trục hoành. Tính diện tích
của
( )
H
.
A.
5
3
. B.
16
3
. C.
10
3
. D.
8
3
.
Câu 98. Cho
( )
H
là hình phẳng được tô đậm trong hình vẽ và được giới hạn bởi các đường có phương trình
2
10
3
y xx= −
,
khi 1
2 khi 1
xx
y
xx
−≤
=
−>
. Diện tích của
( )
H
bằng?
A.
11
6
. B.
13
2
. C.
11
2
. D.
14
3
.
Câu 99. Cho hình phẳng
( )
H
giới hạn bởi đồ thị hàm số
2
32yx x=−+ −
, trục hoành và hai đường thẳng
1x =
,
2
x =
. Quay
( )
H
xung quanh trục hoành được khối tròn xoay có thể tích là
A.
2
2
1
3 2dV xx x= −+
∫
. B.
2
2
2
1
3 2dV xx x= −+
∫
.
C.
( )
2
2
2
1
3 2dV xx x
π
= −+
∫
. D.
2
2
1
3 2dV xx x
π
= −+
∫
.
Câu 100. Cho hình phẳng (H) giới hạn bởi các đường
2
2xyx= −
, trục hoành, trục tung, đường thẳng
1x =
.
Tính thể tích V hình tròn xoay sinh ra bởi (H) khi quay (H) quanh trục Ox.
x
y
g
x
( )
=
x
2
f
x
( )
=
x
4
2
O
e
y
=
e
x
y =
O
x
1
e
y
O
x
1−
1
2
3
y
13
A.
8
15
V
π
=
B.
4
3
V
π
=
C.
15
8
V
π
=
D.
7
8
V
π
=
Câu 101. Cho hình phẳng
D
giới hạn bởi đường cong
e
x
y =
, trục hoành và các đường thẳng
0
x =
,
1x =
.
Khối tròn xoay tạo thành khi quay
D
quanh trục hoành có thể tích
V
bằng bao nhiêu?
A.
2
e1
2
V
−
=
. B.
( )
2
e1
2
V
π
+
=
. C.
( )
2
e1
2
V
π
−
=
. D.
2
e
2
π
.
Câu 102. Thể tích
V
của khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi đường tròn
(
)
(
)
2
2
: 31Cx y
+− =
xung quanh trục hoành là
A.
6V
π
=
. B.
3
6V
π
=
. C.
2
3V
π
=
. D.
2
6V
π
=
.
Câu 103. Cho hình phẳng trong hình (phần tô đậm) quay quanh trục hoành. Thể tích của khối tròn xoay tạo
thành được tính theo công thức nào?
A.
( ) ( )
22
12
d
b
a
V fx f x x

= −

∫
. B.
( )
( )
22
12
d
b
a
V fx fx x
π

= −

∫
.
C.
( ) ( )
22
21
d
b
a
V fx fx x
π

= −

∫
. D.
(
) (
)
2
12
d
b
a
V fx fx x
π
= −


∫
.
Câu 104. Cho hình phẳng
( )
D
được giới hạn bởi các đường
0x =
,
1x =
,
0y =
và
21yx
= +
. Thể tích
V
của khối tròn xoay tạo thành khi quay
( )
D
xung quanh trục
Ox
được tính theo công thức?
A.
1
0
2 1dV xx=π+
∫
. B.
(
)
1
0
2 1dV xx=π+
∫
. C.
( )
1
0
2 1dV xx= +
∫
. D.
1
0
2 1dV xx= +
∫
.
Câu 105. Thể tích khối tròn xoay khi quay hình phẳng
( )
H
giới hạn bởi
2
yx=
và
2yx= +
quanh trục
Ox
là
A.
72
10
π
(đvtt). B.
72
5
π
(đvtt). C.
81
10
π
(đvtt). D.
81
5
π
(đvtt).
Câu 106. Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số
e
x
y =
và các
đường thẳng
0
y =
,
0x =
và
1x =
được tính bởi công thức nào sau đây?
A.
1
2
0
ed
x
Vx
=
∫
. B.
2
1
0
ed
x
Vx
π
=
∫
. C.
2
1
0
ed
x
Vx=
∫
. D.
1
2
0
ed
x
Vx
π
=
∫
.
Câu 107. Tìm công thức tính thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi parabol
( )
2
: =Pyx
và đường thẳng
:2=dy x
quay xung quanh trục
Ox
.
A.
( )
2
2
2
0
2d
π
−
∫
x xx
. B.
22
24
00
4d d
ππ
−
∫∫
xx xx
.
C.
22
24
00
4d d
ππ
+
∫∫
xx xx
. D.
( )
2
2
0
2d
π
−
∫
xx x
.
Câu 108. Hình phẳng giới hạn bởi hai đồ thị
yx=
và
2
yx=
quay quanh trục tung tạo nên một vật thể tròn
xoay có thể tích bằng
A.
6
π
. B.
3
π
. C.
2
15
π
. D.
4
15
π
.
O
x
y
b
a
( )
1
fx
( )
2
fx
14
Câu 109. Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường
2
1
yx
= −
, y=0 quanh trục
Ox có kết quả dạng
a
b
π
. Khi đó a+b có kết quả là:
A. 11 B. 17 C. 31 D. 25
Câu 110. Cho hình
(
)
H
giới hạn bởi trục hoành, đồ thị của một Parabol và một đường thẳng tiếp xúc với
Parabol đó tại điểm
( )
2; 4A
, như hình vẽ bên. Thể tích vật thể tròn xoay tạo bởi khi hình
( )
H
quay quanh
trục
Ox
bằng
A.
16
15
π
. B.
32
5
π
. C.
2
3
π
. D.
22
5
π
.
Câu 111. Cho hình phẳng
( )
H
giới hạn bởi các đường
4xy =
,
0x =
,
1y =
và
4y
=
. Tính thể tích
V
của
khối tròn xoay tạo thành khi quay hình
(
)
H
quanh trục tung.
A.
8π
V
=
. B.
16π
V
=
. C.
10π
V
=
. D.
12π
V
=
.
Câu 112. Cho hình phẳng
( )
H
giới hạn bởi đồ thị hàm số
1
y
x
=
và các đường thẳng
0
y =
,
1x =
,
4x =
.
Thể tích
V
của khối tròn xoay sinh ra khi cho hình phẳng
( )
H
quay quanh trục
Ox
.
A.
2 ln 2π
. B.
3
4
π
. C.
3
4
1−
. D.
2 ln 2
.
Câu 113. Thể tích của khối tròn xoay thu được khi quay quanh trục
Ox
hình phẳng giới hạn bởi đồ thị hàm
số
e
x
yx=
, trục hoành và đường thẳng
1x
=
là:
A.
( )
2
e1
4
π
+
. B.
( )
2
1
e1
4
+
. C.
(
)
4
e1
4
π
−
. D.
( )
4
1
e1
4
−
.
Câu 114. Cho phần vật thể
( )
ℑ
giới hạn bởi hai mặt phẳng
có phương trình
0x =
và
2
x =
. Cắt phần vật thể
( )
ℑ
bởi mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
x
( )
02x≤≤
, ta được thiết diện là một tam
giác đều có độ dài cạnh bằng
2xx−
. Tính thể tích
V
của phần vật thể
( )
ℑ
.
A.
4
.
3
V =
B.
3
.
3
V =
C.
4 3.V =
D.
3.V =
Câu 115. Cho
( )
H
là hình phẳng giới hạn bởi parabol
2
yx
=
và đường tròn
22
2xy+=
(phần tô đậm
trong hình bên). Tính thể tích
V
của khối tròn xoay tạo thành khi quay
( )
H
quanh trục hoành.
A.
44
15
V
π
=
. B.
22
15
V
π
=
. C.
5
3
V
π
=
. D.
5
V
π
=
.
x
y
O
O
x
y
2
4
1
2
15
Câu 116. Cho phần vật thể
B
giới hạn bởi hai mặt phẳng có phương trình
0x =
và
3
x
π
=
. Cắt phần vật thể
B
bởi mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
x
0
3
x
π

≤≤


ta được thiết diện là một tam
giác vuông có độ dài hai cạnh góc vuông lần lượt là
2x
và
cos x
. Thể tích vật thể
B
bằng
A.
33
6
π
+
. B.
33
3
π
−
. C.
33
6
π
−
. D.
3
6
π
.
Câu 117. Tính thể tích
V
của vật thể tròn xoay sinh ra khi cho hình phẳng giới hạn bởi các đường
1
y
x
=
,
0y =
,
1x =
,
xa=
,
( )
1a >
quay xung quanh trục
Ox
.
A.
1
1V
a

= −


. B.
1
1V
a
π

= −


. C.
1
1V
a
π

= +


. D.
1
1V
a

= +


.
Câu 118. Cho hình phẳng
( )
H
giới hạn bởi các đường
2
yx=
,
2yx=
. Thể tích của khối tròn xoay được
tạo thành khi quay
( )
H
xung quanh trục
Ox
bằng:
A.
32
15
π
. B.
64
15
π
. C.
21
15
π
. D.
16
15
π
.
Câu 119. Tính thể tích
V
của vật tròn xoay tạo thành khi quay hình phẳng
( )
H
giới hạn bởi các đường
2
yx=
;
yx=
quanh trục
Ox
.
A.
9
10
V
π
=
. B.
3
10
V
π
=
. C.
10
V
π
=
. D.
7
10
V
π
=
.
Câu 120. Trong mặt phẳng tọa độ
Oxy
, gọi
( )
1
H
là hình phẳng giới hạn bởi các đường
2
4
x
y =
,
2
4
x
y = −
,
4x = −
,
4x =
và hình
( )
2
H
là hình gồm các điểm
( )
;xy
thỏa:
22
16xy+≤
,
( )
2
2
24xy+− ≥
,
( )
2
2
24xy++ ≥
.
Cho
( )
1
H
và
( )
2
H
quay quanh trục
Oy
ta được các vật thể có thể tích lần lượt là
1
V
,
2
V
. Đẳng thức nào sau
đây đúng?
A.
12
VV=
. B.
12
1
2
VV=
. C.
12
2VV=
. D.
12
2
3
VV=
PHẦN 2: HỆ TỌA ĐỘ TRONG KHÔNG GIAN
Câu 1. Trong không gian
Oxyz
, hình chiếu vuông góc của điểm
( )
2; 2;1M −
trên mặt phẳng
( )
Oxy
có
tọa độ là
A.
( )
2;0;1
. B.
( )
2; 2;0−
. C.
( )
0; 2;1−
. D.
( )
0;0;1
.
Câu 2. Trong không gian , hình chiếu vuông góc của điểm trên trục có tọa độ là
A. . B. . C. . D. .
Oxyz
( )
1; 2; 5A
Ox
( )
0; 2; 0
( )
0; 0; 5
( )
1;0;0
( )
0; 2; 5
16
Câu 3. Trong không gian
Oxyz
, hình chiếu vuông góc của điểm
(
)
3; 1; 1
M −
trên trục
Oz
có tọa độ là
A.
( )
3; 1; 0
−
. B.
(
)
0; 0;1
. C.
( )
0; 1; 0−
. D.
( )
3;0;0
.
Câu 4. Trong không gian với hệ trục tọa độ
Oxyz
cho điểm
(
)
;;M xyz
. Trong các mệnh đề sau, mệnh
đề nào đúng?
A. Nếu
M
′
đối xứng với
M
qua mặt phẳng
( )
Oxz
thì
( )
;;M xy z
′
−
.
B. Nếu
M
′
đối xứng với
M
qua
Oy
thì
( )
;;M xy z
′
−
.
C. Nếu
M
′
đối xứng với
M
qua mặt phẳng
(
)
Oxy
thì
( )
;;M xy z
′
−
.
D. Nếu
M
′
đối xứng với
M
qua gốc tọa độ
O
thì
(
)
2 ;2 ;0
M xy
′
.
Câu 5. Trong không gian
Oxyz
, tọa độ điểm đối xứng của
( )
M ;;
123
qua mặt phẳng
( )
Oyz
là
A.
( )
023;;
. B.
( )
123;;−−−
. C.
(
)
123;;−
. D.
(
)
12 3
;;
−
.
Câu 6. Trong không gian
Oxyz
, cho điểm
( )
2; 3; 5A −
. Tìm tọa độ
A
′
là điểm đối xứng với
A
qua trục
Oy
.
A.
( )
2;3;5A
′
. B.
( )
2;3;5A
′
−−
. C.
( )
2; 3; 5A
′
−−
. D.
( )
2;3;5A
′
−−−
.
Câu 7. Trong không gian
,Oxyz
cho hai điểm
(
)
1;1; 1A
−
và
( )
2; 3; 2B
. Vectơ
AB

có tọa độ là
A.
( )
1; 2; 3
B.
( )
1; 2; 3−−
C.
( )
3; 5;1
D.
( )
3; 4;1
Câu 8. Trong không gian với hệ toạ độ
Oxyz
, cho điểm
( )
2; 2;1A
. Tính độ dài đoạn thẳng
OA
.
A.
5OA =
B.
5OA
=
C.
3OA =
D.
9OA =
Câu 9. Trong không gian với hệ trục tọa độ
Oxyz
, cho ba vecto
( )
( )
(
)
1; 2;3 ; 2; 2; 1 ; 4; 0; 4
ab c
−−

. Tọa độ
của vecto
2d ab c=−+


là
A.
(
)
7; 0; 4
d
−−
B.
( )
7; 0; 4d −
C.
( )
7; 0; 4d −
D.
( )
7; 0; 4d
Câu 10. Trong không gian
Oxyz
, cho hai điểm
( )
1;2;1A −−
,
( )
1; 4; 3B
. Độ dài đoạn thẳng
AB
là
A.
2 13
B.
6
C.
3
D.
23
Câu 11. Trong không gian Oxyz, cho
(
) (
)
( )
2; 2; 0 , 2; 2; 0 , 2; 2; 2a bc−

. Giá trị của
abc++

bằng
A.
6.
B.
11
. C.
2 11
. D.
26
.
Câu 12. Trong không gian
Oxyz
, cho hai điểm
( )
2; 4; 3A −
và
(
)
2; 2;7B
. Trung điểm của đoạn thẳng
AB
có tọa độ là
A.
( )
4; 2;10−
B.
( )
1; 3; 2
C.
(
)
2; 6; 4
D.
( )
2; 1; 5−
Câu 13. Trong không gian với hệ tọa độ
Oxyz
, cho các điểm
( )
3; 4; 0A −
,
(
)
1;1; 3B −
,
( )
3,1, 0C
. Tìm tọa
độ điểm
D
trên trục hoành sao cho
AD BC=
.
A.
( )
6; 0; 0D
,
( )
12; 0; 0D
B.
( )
0; 0; 0D
,
( )
6; 0; 0D
C.
( )
2; 1; 0D −
,
( )
4; 0; 0D −
D.
( )
0; 0; 0D
,
( )
6; 0; 0D −
Câu 14. Trong không gian cho hệ trục toạ độ
Oxyz
, cho ba điểm
(
) ( ) ( )
1; 2;3 , 1; 2;5 , 0; 0;1ABC
−−
. Tìm
toạ độ trọng tâm
G
của tam giác
ABC
.
A.
( )
0; 0;3G
. B.
( )
0; 0; 9G
. C.
( )
1; 0; 3
G −
. D.
( )
0; 0;1G
.
Câu 15. Trong không gian
,Oxyz
cho vectơ
( ) ( )
2;2;4, 1;1;1.ab= −− = −
Mệnh đề nào dưới đây sai?
17
A.
( )
3; 3; 3ab+ = −−
B.
a
và
b
cùng phương C.
3
b =
D.
ab⊥
Câu 16. Trên mặt phẳng toạ độ
Oxy
, cho tam giác
ABC
biết
( )
1; 3A
,
( )
2; 2B −−
,
( )
3;1C
. Tính cosin góc
A
của tam giác.
A.
2
cos
17
A =
B.
1
cos
17
A
=
C.
2
cos
17
A = −
D.
1
cos
17
A
= −
Câu 17. Trong không gian
Oxyz
, góc giữa hai vectơ
i
và
(
)
3; 0; 1
u
= −
là
A.
120°
. B.
60
°
. C.
150°
. D.
30°
.
Câu 18. Trong không gian với hệ tọa độ
O
xyz
, cho vectơ
( )
3;0;1u =
và
( )
2;1;0v
=
. Tính tích vô hướng
.uv

.
A.
.8uv=

. B.
.6uv=

. C.
.0uv=

. D.
.6uv
= −

.
Câu 19. Trong không gian với hệ tọa độ
Oxyz
, cho tam giác
ABC
có
( )
1;0;0A
,
( )
0; 0;1B
,
( )
2;1;1C
.
Diện tích của tam giác
ABC
bằng:
A.
11
2
B.
7
2
C.
6
2
D.
5
2
Câu 20. Trong không gian
Oxyz
cho
2
véc tơ
2;1();1a = −
;
;;(1 )3mb =
. Tìm
m
để
(
)
; 90ab = °

.
A.
5m
= −
. B.
5m =
. C.
1m =
. D.
2m = −
Câu 21. Trong không gian với hệ trục tọa độ
Oxyz
, cho
(
)
2; 1;1
u = −
và
(
)
0; 3;vm= −−
. Tìm số thực
m
sao cho tích vô hướng
.1uv=

.
A.
4m
=
. B.
2m
=
. C.
3m
=
. D.
2
m
= −
.
Câu 22. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
( )
2;1; 2a
= −
và vectơ
( )
1; 0; 2b =
. Tìm tọa
độ vectơ
c
là tích có hướng của
a
và
b
.
A.
( )
2;6; 1c = −
. B.
( )
4;6; 1c = −
. C.
( )
4; 6; 1c = −−
. D.
( )
2; 6; 1c = −−
.
Câu 23. Trong không gian
Oxyz
, tọa độ một vectơ
n
vuông góc với cả hai vectơ
( )
1;1; 2a = −
,
( )
1; 0; 3b =
là
A.
( )
2; 3; 1−
. B.
( )
3; 5; 2−
. C.
( )
2;3;1−−
. D.
( )
3;5;1−−
.
Câu 24. Trong không gian với hệ trục tọa độ
Oxyz
, cho ba véctơ
( ) ( )
( )
1; 2; 1 , 3; 1; 0 , 1; 5; 2abc= −=− =−

.
Câu nào sau đây đúng?
A.
a
cùng phương với
b
. B.
a
,
b
,
c
không đồng phẳng.
C.
a
,
b
,
c
đồng phẳng. D.
a
vuông góc với
b
.
Câu 25. Trong hệ trục tọa độ
Oxyz
, cho bốn điểm
(1; 2; 0 )A −
,
(2; 0;3)B
,
( 2;1; 3)C −
và
(0;1;1)D
. Thể tích
khối tứ diện
ABCD
bằng:
A.
6
. B.
8
. C.
12
. D.
4
.
Câu 26. Trong không gian với hệ toạ độ
Oxyz
, cho
( )
1; 2; 3a = −
và
(
)
1;1; 1b = −
. Khẳng định nào sau đây
sai?
A.
3ab+=

. B.
.4
ab= −

. C.
5ab−=

. D.
( )
, 1; 4; 3ab

=−−


.
Câu 27. Trong không gian
,Oxyz
cho hai điểm
( ) ( )
1; 0; 1 , 1; 1; 2−−AB
. Diện tích tam giác
OAB
bằng
18
A.
11.
B.
6
.
2
C.
11
.
2
D.
6.
Câu 28. Trong không gian
Oxyz
, cho 4 điểm
(
)
2; 0; 2A
,
( )
1; 1; 2B −−
,
(
)
1;1; 0C −
,
( )
2; 1; 2D
−
. Thể tích của
khối tứ diện
ABCD
bằng
A.
42
3
. B.
14
3
. C.
21
3
. D.
7
3
.
Câu 29. Trong hệ trục tọa độ
Oxyz
, cho
( )
0; 0; 0O
,
( )
0; 1; 2A −
,
( )
1; 2; 1
B
,
( )
4; 3;Cm
. Tất cả giá trị của
m
để
4
điểm
,,,O ABC
đồng phẳng?
A.
14m =
. B.
14m
= −
. C.
7m
=
. D.
7m = −
.
Câu 30. Trong không gian
Oxyz
, cho hình chóp
.A BCD
có
( )
0; 1; 1 ,A −
( )
1;1; 2 ,B
(
)
1; 1; 0C −
và
(
)
0; 0;1 .D
Tính độ dài đường cao của hình chóp
.A BCD
.
A.
22
. B.
32
2
. C.
32
. D.
2
2
.
Câu 31. Trong không gian với hệ trục tọa độ, cho hình bình hành
ABCD
. Biết
( )
2 ; 1; 3A −
,
(
)
0; 2;5B −
và
(
)
1;1;3C
. Diện tích hình bình hành
ABCD
là
A.
2 87
. B.
349
2
. C.
349
. D.
87
.
Câu 32. Trong không gian với hệ tọa độ
Oxyz
, cho bốn điểm
( )
0;1;1A
,
( )
1; 0; 2B −
,
( )
1;1; 0C −
và điểm
( )
2; 1; 2D −
. Khi đó thể tích tứ diện
ABCD
là
A.
5
6
V =
. B.
5
3
V =
. C.
6
5
V =
. D.
3
2
V =
.
Câu 33. Trong không gian với hệ tọa độ
Oxyz
, cho các vectơ
( ) ( )
2; 1; 3 , 1; 3; 2am b n=−=−

. Tìm
,mn
để
các vectơ
,ab

cùng hướng.
A.
3
7;
4
mn
= = −
. B.
4; 3mn= = −
. C.
1; 0mn= =
. D.
4
7;
3
mn= = −
.
Câu 34. Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
( ) ( ) ( )
A2;1;5, 5;5;7, ;;1−−B M xy
. Với giá
trị nào của
,
xy
thì
,,ABM
thẳng hàng.
A.
4; 7= =xy
B.
4; 7=−=−xy
C.
4; 7= = −xy
D.
4; 7=−=xy
Câu 35. Trong không gian với hệ tọa độ
Oxyz
cho các véc tơ
22u i jk=−+

,
( )
; 2; 1v mm= +
với
m
là
tham số thực. Có bao nhiêu giá trị của
m
để
uv
=

.
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 36. Trong không gian với hệ tọa độ
Oxyz
, cho hình hộp
.ABCD A B C D
′′′′
có
( )
0; 0; 0A
,
( )
;0;0Ba
;
( )
0; 2 ; 0Da
,
( )
0; 0; 2Aa
′
với
0a ≠
. Độ dài đoạn thẳng
AC
′
là
A.
a
. B.
2 a
. C.
3 a
. D.
3
2
a
.
Câu 37. Trong không gian với hệ trục toạ độ
Oxyz
, cho
( )
2; 3;1a =

,
(
)
1; 5; 2b = −

,
(
)
4; 1; 3c = −

và
( )
3; 22; 5x = −

. Đẳng thức nào đúng trong các đẳng thức sau?
A.
23x a bc= −−
   
. B.
23x a bc=−++
   
.
19
C.
23x a bc= +−
   
. D.
23x a bc= −+
   
.
Câu 38. Trong không gian với hệ tọa độ
Oxyz
, cho tam giác
ABC
có
1; 2; 1A
,
2; 1; 3B
,
4; 7; 5C
. Gọi
;;D abc
là chân đường phân giác trong góc
B
của tam giác
ABC
. Giá trị của
2ab c
bằng
A.
5
. B.
4
. C.
14
. D.
15
.
Câu 39. Trong không gian với hệ tọa độ
Oxyz
cho ba điểm
( )
2; 3; 1M −
,
( )
1;1; 1N −
và
( )
1; 1; 2Pm−
. Tìm
m
để tam giác
MNP
vuông tại
N
.
A. B. C. D.
Câu 40. Trong không gian
Oxyz
cho các điểm
( ) ( ) ( )
5;1; 5 ; 4; 3; 2 ; 3; 2;1ABC−−
. Điểm
( )
;;I abc
là tâm
đường tròn ngoại tiếp tam giác
ABC
. Tính
2a bc++
?
A.
1
. B.
3.
C.
6.
D.
9.−
Câu 41. Trong không gian với hệ tọa độ
Oxyz
, cho véc tơ
( ) ( )
1;1; 2 , 1; 0;u vm=−=

. Tìm tất cả giá trị của
m
để góc giữa
u
,
v
bằng
45
°
.
A.
2m
=
. B.
26m = ±
. C.
26m = −
. D.
26m = +
.
Câu 42. Trong không gian
Oxyz
, cho các vec tơ
( )
5; 3; 2a = −
và
( )
; 1; 3bm m=−+
. Có bao nhiêu giá trị
nguyên dương của
m
để góc giữa hai vec tơ
a
và
b
là góc tù?
A.
2.
B.
3.
C.
1.
D.
5.
Câu 43. Trong không gian
Oxyz
, cho hai vectơ
u
và
v
tạo với nhau một góc
120°
và
2u =
,
5v =
. Tính
uv+

A.
19
. B.
5−
. C.
7
. D.
39
.
Câu 44. Trong hệ trục tọa độ
Oxyz
, cho tứ diện
ABCD
biết
( )
3; 2;Am−
,
( )
2;0;0B
,
( )
0;4;0C
,
( )
0;0;3D
. Tìm giá trị dương của tham số
m
để thể tích tứ diện bằng 8.
A.
8m =
. B.
4m
=
. C.
12m =
. D.
6m =
.
Câu 45. Trong không gian với hệ tọa độ
Oxyz
, cho
( ) ( )
1;1; 2 , 1; ; 2u v mm= =−−

. Khi
, 14uv

=


thì
A.
1m =
hoặc
11
5
m = −
B.
1m = −
hoặc
11
3
m = −
C.
1m =
hoặc
3m = −
D.
1m = −
Câu 46. Trong không gian với hệ trục tọa độ
Oxyz
, cho tứ diện
ABCD
có
( )
2; 1; 1−A
,
( )
3; 0; 1−B
,
( )
2; 1; 3−C
,
∈D Oy
và có thể tích bằng
5
. Tính tổng tung độ của các điểm
D
.
A.
6−
B.
2
C.
7
D.
4−
Câu 47. Trong không gian
Oxyz
, có tất cả bao nhiêu giá nguyên của
m
để
( ) ( )
2 22 2
2 2 2 1 3 50+ + + + − − + −=xyz m x m zm
là phương trình một mặt cầu?
A.
4
B.
6
C.
5
D.
7
Câu 48. Trong không gian
Oxyz
, xét mặt cầu
( )
S
có phương trình dạng
2 22
4 2 2 10 0x y z x y az a++−+ − + =
. Tập hợp các giá trị thực của
a
để
( )
S
có chu vi đường tròn lớn bằng
8π
là
A.
{ }
1;1 0
. B.
{ }
2; 10−
. C.
{ }
1;1 1−
. D.
{ }
1; 1 1−
.
2m =
6m = −
0m =
4m = −
20
Câu 49. Trong không gian với hệ trục tọa độ
Oxyz
, cho ba điểm
(
)
1;0;0
A
,
( )
0; 0; 3C
,
( )
0; 2; 0B
. Tập hợp
các điểm
M
thỏa mãn
222
MA MB MC= +
là mặt cầu có bán kính là:
A.
2R =
. B.
3
R =
. C.
3R
=
. D.
2
R
=
.
Câu 50. Trong không gian Oxyz, cho điểm
(1; 2;3)I
−
. Viết phương trình mặt cầu tâm I, cắt trục
Ox
tại hai
điểm
A
và
B
sao cho
23AB
=
A.
2 22
( 1) ( 2) ( 3) 16.xy z− ++ +− =
B.
2 22
( 1) ( 2) ( 3) 20.xy z− ++ +− =
C.
2 22
( 1) ( 2) ( 3) 25.xy z− ++ +− =
D.
2 22
( 1) ( 2) ( 3) 9.xy z− ++ +− =
Câu 51. Trong không gian với hệ toạ độ
Oxyz
, cho
( )
;0;0Aa
,
( )
0; ; 0Bb
,
(
)
0; 0;Cc
,
(
)
0abc ≠
. Khi đó
phương trình mặt phẳng
( )
ABC
là:
A.
1
xyz
abc
++=
. B.
1
xyz
bac
++=
.
C.
1
xyz
acb
++=
. D.
1
xyz
cba
++=
.
Câu 52. Trong không gian với hệ toạ độ
Oxyz
, cho mặt phẳng
(
)
:3 0xz
α
−=
. Tìm khẳng định đúng
trong các mệnh đề sau:
A.
( )
//Ox
α
. B.
( ) ( )
// xOz
α
.
C.
( )
//Oy
α
. D.
( )
Oy
α
⊃
.
Câu 53. Trong không gian với hệ toạ độ
Oxyz
. Mặt phẳng (P) là
3 20xz−+ − =
có phương trình song
song với:
A. Trục Oy. B. Trục Oz. C. Mặt phẳng Oxy. D. Trục Ox.
Câu 54. Trong không gian với hệ toạ độ
Oxyz
, cho mặt phẳng (P) có phương trình
3 2 10x yz+ −+=
.
Mặt phẳng (P) có một vectơ pháp tuyến là:
A.
(3; 2;1)
n
. B.
( 2; 3;1)
n −
. C.
(3; 2; 1)n −
. D.
(3;2;1)n
−−
.
Câu 55. Trong không gian với hệ toạ độ
Oxyz
, cho mặt phẳng (P) có phương trình
2 2 30
x yz− + −−=
.
Mặt phẳng (P) có một vectơ pháp tuyến là:
A.
(4; 4; 2)n −
. B.
( 2; 2; 3)n
−−
. C.
( 4; 4; 2)n −
. D.
(0; 0; 3)n −
.
Câu 56. Trong không gian với hệ toạ độ
Oxyz
, cho ba điểm
( )
1; 2; 1A −
,
( )
1;3;3
B −
,
( )
2; 4; 2C −
. Một
vectơ pháp tuyến
n
của mặt phẳng
( )
ABC
là:
A.
(
)
9; 4; 1n
= −
. B.
( )
9; 4;1n =
. C.
( )
4;9; 1n = −
. D.
( )
1; 9; 4n
= −
.
Câu 57. Trong không gian với hệ toạ độ
Oxyz
. Điểm nào sau đây thuộc mặt phẳng (P)
2 50xy− +−=
A.
( 2; 1; 0 )−
. B.
( 2; 1; 5)−−
. C.
(1;7;5)
. D.
( 2; 2; 5)−−
.
Câu 58. Trong không gian với hệ toạ độ
Oxyz
. Phương trình mặt phẳng (P) đi qua điểm
( 1; 2; 0 )A −
và
nhận
( 1; 0; 2)n −
là VTPT có phương trình là:
A.
2 50xy−+ −=
B.
2 50xz−+ − =
C.
2 50xy−+ −=
D.
2 10xz−+ −=
Câu 59. Trong không gian với hệ toạ độ
Oxyz
, cho ba điểm
( )
3;2;2A −−
,
( )
3; 2; 0B
,
( )
0; 2;1C
. Phương
trình mặt phẳng
( )
ABC
là:
A.
2360xyz−+=
. B.
4 2 30
yz
+ −=
. C.
3 2 10xy+ +=
. D.
2 30yz+−=
.
Câu 60. Trong không gian với hệ trục tọa độ
Oxyz
, cho hai điểm
)1;1;2
(
),
1;0;1( −− BA
. Phương trình mặt
phẳng trung trực của đoạn
AB
là:
21
A.
02 =−− yx
. B.
01 =+− yx
. C.
20xy−+=
. D.
02 =++− yx
.
Câu 61. Trong không gian với hệ toạ độ
Oxyz
. Mặt phẳng (P) đi qua các điểm
( 1;0;0)
A −
,
(0; 2; 0)B
,
(0; 0; 2)C −
có phương trình là:
A.
2 20
xyz− ++−=
. B.
2 20xyz− −−+=
.
C.
2 20
xyz− +−−=
. D.
2 20xyz− +−+=
.
Câu 62. Trong không gian với hệ trục toạ độ
Oxyz
, cho điểm
( )
2; 1; 3M −
và các mặt phẳng:
(
)
: 20
x
α
−=
,
( )
: 10y
β
+=
,
( )
: 30z
γ
−=
. Tìm khẳng định sai.
A.
( )
//Ox
α
. B.
( )
β
đi qua
M
. C.
( ) ( )
// xOy
γ
. D.
( ) ( )
βγ
⊥
.
Câu 63. Trong không gian với hệ trục toạ độ
Oxyz
. Phương trình mặt phẳng qua
( )
2; 5;1
A
và song song
với mặt phẳng
( )
Oxy
là:
A.
25 0x yz
+ +=
. B.
20x −=
. C.
50y −=
. D.
10z −=
.
Câu 64. Trong không gian với hệ trục toạ độ
Oxyz
. Mặt phẳng đi qua
( )
1; 4; 3M
và vuông góc với trục
Oy
có phương trình là:
A.
40y −=
. B.
10x
−=
.
C.
30z −=
. D.
430xyz++=
.
Câu 65. Trong không gian với hệ trục toạ độ
Oxyz
. Biết
,,ABC
là số thực khác
0
, mặt phẳng chứa trục
Oz
có phương trình là:
A.
0
Ax Bz C+ +=
. B.
0Ax By+=
C.
0By Az C+ +=
. D.
0Ax By C
+ +=
.
Câu 66. Trong không gian với hệ trục tọa độ
Oxyz
, cho các điểm
)6
;0;4
(),4
;0
;
5
(
),6;
2;1(
),3;
1;5
( DC
BA
.
Viết phương trình mặt phẳng qua
D
và song song với mặt phẳng
)(ABC
.
A.
0
10 =
−++
zy
x
. B.
09 =−++ zyx
.
C.
08 =−++ zyx
. D.
010
2 =
−++
zy
x
.
Câu 67. Trong không gian với hệ trục tọa độ
Oxyz
, cho các điểm
)6;0;4(),4;0;5(),6;2;1(),3;1;5( DCBA
.
Viết phương trình mặt phẳng chứa
AB
và song song với
CD
.
A.
2 5 18 0x yz+ +− =
. B.
063
2 =+
+− z
yx
.
C.
0
42 =
++− z
yx
. D.
90
xyz++−=
.
Câu 68. Trong không gian với hệ trục tọa độ
Oxyz
, gọi
)(P
là mặt phẳng chứa trục
Ox
và vuông góc
với mặt phẳng
03:)( =−++ zyxQ
. Phương trình mặt phẳng
)(P
là:
A.
0=+ zy
. B.
0=− zy
. C.
01 =−− zy
. D.
02 =− zy
.
Câu 69. Trong không gian với hệ trục tọa độ
Oxyz
. Phương trình của mặt phẳng chứa trục
Ox
và qua
điểm
( )
2; 3;1I −
là:
A.
30
yz+=
. B.
30xy+=
. C.
30yz−=
. D.
30yz+=
.
Câu 70. Trong không gian với hệ toạ độ
Oxyz
, cho ba điểm
2; 1; 1 , 1; 0; 4AB
và
0; 2; 1C

.
Phương trình mặt phẳng qua
A
và vuông góc với đường thẳng
BC
là:
A.
2 2 50xy z 
. B.
2 3 70xyz 
.
C.
2 5 50xyz 
. D.
2 5 50xyz 
.
Câu 71. Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt phẳng
( )
α
đi qua
( )
2; 1; 4A −
,
( )
3; 2; 1B −
và vuông góc với mặt phẳng
( )
: 2 30Qxy z++ −=
. Phương trình mặt phẳng
( )
α
là:
A.
5 3 4 90xyz+ − +=
. B.
3 5 21 0xyz+−+=
.
22
C.
2 30xy z++ −=
. D.
534 0xyz+−=
.
Câu 72. Trong không gian với hệ trục tọa độ
Oxyz
. Tọa độ giao điểm
M
của mặt phẳng
( )
:2 3 4 0P x yz+ +−=
với trục
Ox
là ?
A.
( )
0, 0, 4M
. B.
4
0, , 0
3
M



. C.
(
)
3,0,0M
. D.
( )
2, 0, 0M
.
Câu 73. Trong không gian với hệ toạ độ
Oxyz
, gọi
là mặt phẳng qua các hình chiếu của
5; 4; 3
A
lên các trục tọa độ. Phương trình của mặt phẳng
là:
A.
12 15 20 60 0xyz
B.
12 15 20 60 0xyz 
.
C.
0
543
xyz

. D.
60 0
543
xyz

.
Câu 74. Trong không gian với hệ toạ độ
Oxyz
, cho mặt phẳng
( )
α
đi qua hai điểm
5; 2; 0A
,
3; 4;1B
và có một vectơ chỉ phương là
1;1;1a
. Phương trình của mặt phẳng
(
)
α
là:
A.
5 9 14 0xy z

. B.
70xy
.
C.
591470xy z 
. D.
591470
xy z 
.
Câu 75. Trong không gian với hệ trục tọa độ
Oxyz
, có bao nhiêu mặt phẳng song song với mặt phẳng
( ): 6 0Pxyz++−=
và tiếp xúc với mặt cầu
12:)(
222
=++ zyxS
?
A. 2 B. Không có. C. 1. D. 3.
Câu 76. Trong không gian với hệ trục tọa độ
Oxyz
, cho hai mặt phẳng
( ) (
)
:3 1 4 2 0
xm y z
α
+ − + −=
,
( ) ( )
: 2 2 40nx m y z
β
+ + + +=
. Với giá trị thực của
,mn
bằng bao nhiêu để
( )
α
song song
( )
β
A.
3; 6mn= = −
. B.
3; 6mn
= =
. C.
3; 6mn=−=
D.
3; 6mn=−=−
.
Câu 77. Trong không gian với hệ trục tọa độ
Oxyz
, cho hai mặt phẳng
( ) ( )
: 1 20P x my m z+ + − +=
,
( )
:2 3 4 0Q xy z−+ −=
. Giá trị số thực
m
để hai mặt phẳng
(
) ( )
,PQ
vuông góc
A.
1m =
B.
1
2
m = −
C.
2m
=
D.
1
2
m =
Câu 78. Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt phẳng
( )
: 2 10Px yz
+ −+=
. Gọi mặt phẳng
( )
Q
là mặt phẳng đối xứng của mặt phẳng
( )
P
qua trục tung. Khi đó phương trình mặt phẳng
( )
Q
là ?
A.
2 10x yz+ −−=
B.
2 10x yz− −+=
C.
2 10x yz+ ++=
D.
2 10x yz− −−=
Câu 79. Trong không gian với hệ toạ độ
Oxyz
,
là mặt phẳng đi qua điểm
2; 1; 5A
và vuông góc
với hai mặt phẳng
:3 2 7 0P x yz 
và
:5 4 3 1 0Qx y z 
. Phương trình mặt
phẳng
là:
A.
2 50x yz

. B.
2 4 2 10 0xyz 
.
C.
2 4 2 10 0xyz 
. D.
2 50x yz 
.
Câu 80. Trong không gian với hệ toạ độ
Oxyz
, gọi
( )
α
là mặt phẳng qua
( )
1; 2; 3G
và cắt các trục
,,Ox Oy Oz
lần lượt tại các điểm
,,ABC
(khác gốc
O
) sao cho
G
là trọng tâm của tam giác
ABC
. Khi đó mặt phẳng
( )
α
có phương trình:
A.
3 6 2 18 0xyz+ ++=
. B.
6 3 2 18 0
xyz++−=
.
C.
2 3 90xy z++ −=
. D.
6 3 2 90xyz+ + +=
.
| 1/22
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HỌC KÌ II
TRƯỜNG THPT TRẦN PHÚ-HOÀN KIẾM Môn: Toán Lớp: 12
Năm học 2022-2023
PHẦN 1: NGUYÊN HÀM –TÍCH PHÂN- ỨNG DỤNG CỦA TÍCH PHÂN
Câu 1. Hàm số F(x) là một nguyên hàm của hàm số f (x) trên khoảng K nếu
A. F '(x) = − f (x), x ∀ ∈ K.
B. f '(x) = F(x), x ∀ ∈ K.
C. F '(x) = f (x), x ∀ ∈ K.
D. f '(x) = −F(x), x ∀ ∈ K.
Câu 2. Họ nguyên hàm của hàm số f (x) = cos x + 6x là A. 2
sin x + 3x + C . B. 2
−sin x + 3x + C . C. 2
sin x + 6x + C .
D. −sin x + C .
Câu 3. Tìm nguyên hàm của hàm số f (x) = 2x −1. 2 1 A. f
∫ (x)dx = (2x− )1 2x−1+C. B. f
∫ (x)dx = (2x− )1 2x−1+C. 3 3 C. f ∫ (x) 1 dx = −
2x −1 + C. D. f ∫ (x) 1 dx = 2x −1 + C. 3 2 Câu 4. 2
Tìm nguyên hàm của hàm số f (x) 2 = x + . 2 x 3 3 A. f ∫ (x) x 1 dx = + + C x 2 . B. f
∫ (x)dx = − +C. 3 x 3 x 3 3 C. f ∫ (x) x 1 dx = − + C x 2 . D. f
∫ (x)dx = + +C . 3 x 3 x
Câu 5. Tìm nguyên hàm của hàm số f (x) 1 = . 5x − 2 A. dx 1
= ln 5x − 2 + C ∫ B.
dx = ln 5x−2 +C 5x ∫ − 2 5 5x − 2 C. dx 1
= − ln 5x − 2 + C ∫ D.
dx = 5ln 5x−2 +C 5x ∫ − 2 2 5x − 2
Câu 6. Tìm nguyên hàm x(x + ∫ )15 2 7 dx ? A. 1 (x + 7)16 2 + C B. 1 − (x +7)16 2 + C C. 1 (x + 7)16 2 + C D. 1 (x + 7)16 2 + C 2 32 16 32
Câu 7. Họ nguyên hàm của hàm số 3 (x) = x f e là A. 3 x e + C . B. 1 3x e + C . C. 1 x e + C . D. 3 3 x e + C . 3 3
Câu 8. Đẳng thức nào trong các đẳng thức sau là sai? A. 1
ln xdx = + C ∫ . B.
1 dx = tanx+C x x = − x + C x x x = + C x ∫ . C. sin d cos 2 cos x ∫ . D. e d e ∫ . 1
Câu 9. Hàm số F (x) 1 3
= x là một nguyên hàm của hàm số nào sau đây trên ( ; −∞ +∞) ? 3 A. f (x) 2 1 = 3x . B. ( ) 3
f x = x . C. ( ) 2
f x = x . D. f (x) 4 = x . 4 4 Câu 10. x + 2
Tìm nguyên hàm của hàm số f (x) = . 2 x 3 x 1 3 x 2 A. f
∫ (x)dx = − +C . B. f
∫ (x)dx = + +C. 3 x 3 x 3 3 C. f ∫ (x) x 1 dx = + + C x 2 . D. f
∫ (x)dx = − +C . 3 x 3 x Câu 11. 1  1
Họ nguyên hàm của hàm số f (x) = trên khoảng  ;  −∞ là: 3x −1 3    1 1
A. ln(3x −1) + C
B. ln(1− 3x) + C
C. ln(1− 3x) + C
D. ln(3x−1) + C 3 3
Câu 12. Trong các khẳng định sau, khẳng định nào sai? 2x
A. 2xd = 2x x ln 2 + C ∫ . B. 2x e e dx = + C ∫ . 2 1 1 C. cos 2 d
x x = sin 2x + C ∫ . D.
dx = ln x +1 + C x ∀ ≠ − . 2 ∫ ( ) 1 x +1 Câu 13. Hàm số ( ) 2 x
F x = e là nguyên hàm của hàm số nào trong các hàm số sau: 2 x A. 2 ( ) = 2 x f x xe . B. 2 2 ( ) x
f x = x e −1. C. 2 ( ) x
f x = e . D. ( ) e f x = . 2x − x Câu 14.  
Tìm nguyên hàm của hàm số ( ) x 2018 = 2017 e f x e − . 5 x    A. ∫ ( ) 2018 d = 2017 x f x x e − + C . B. ∫ ( ) 2018 d = 2017 x f x x e + + C . 4 x 4 x C. ∫ ( ) 504,5 d = 2017 x f x x e + + C . D. ∫ ( ) 504,5 d = 2017 x f x x e − + C . 4 x 4 x − x Câu 15.  
Họ nguyên hàm của hàm số x = 2 e y e + là 2 cos x    A. 2 x
e + tan x + C B. 2 x
e − tan x + C C. x 1 2e − + C D. x 1 2e + + C cos x cos x
Câu 16. Hàm số F (x) là một nguyên hàm của hàm số 1 y = trên (− ;0 ∞ ) thỏa mãn F ( 2 − ) = 0 . Khẳng định x nào sau đây đúng?
A. ( ) ln −x F x  = x ∀ ∈(− ; ∞   0)  2 
B. F (x) = ln x +C x ∀ ∈( ;
−∞ 0) với C là một số thực bất kì. 2
C. F (x) = ln x + ln 2 x ∀ ∈(− ; ∞ 0) .
D. F (x) = ln(−x) + C x ∀ ∈( ;
−∞ 0) với C là một số thực bất kì.
Câu 17. Cho hàm số f (x) xác định trên R \{ }
1 thỏa mãn f ′(x) 1 =
, f (0) = 2017 , f (2) = 2018 . x −1
Tính S = f (3) − f (− ) 1 .
A. S = ln 4035 .
B. S = 4 .
C. S = ln 2 . D. S =1.
Câu 18. Cho F(x) là một nguyên hàm của hàm số ( ) = x
f x e + 2x thỏa mãn F ( ) 3
0 = . Tìm F (x) 2 A. ( ) = x F x e + 2 1 x + B. ( ) = x F x e + 2 5 x + 2 2 C. ( ) = x F x e + 2 3 x + D. ( ) = x F x e + 2 1 2 x − 2 2
Câu 19. Gọi F (x) là một nguyên hàm của hàm số ( ) 2x
f x = , thỏa mãn F ( ) 1 0 = . Tính giá trị biểu ln 2
thức T = F (0) + F ( )
1 +...+ F (2018) + F (2019) . 2019 2019 2020 A. 2 +1 T =1009. . B. 2019.2020 T = 2 C. 2 1 T − = . D. 2 1 T − = . ln 2 ln 2 ln 2
Câu 20. Tìm nguyên hàm  π
F (x) của hàm số f (x) = sin x + cos x thoả mãn F  =   2 .  2 
A. F (x) = −cos x + sin x + 3
B. F (x) = −cos x + sin x −1
C. F (x) = −cos x + sin x +1
D. F (x) = cos x −sin x + 3 Câu 21.  π  π
Biết F (x) là một nguyên hàm của hàm số f (x) 2 = tan x và F  =    1. Tính F −   .  4   4   π  π  π  π  π  π  π A. F − = −    1. B. F − = −   1. C. F − = 1 −   . D. F − = +   1.  4  4  4  2  4   4  2 Câu 22.  π  π
Tìm một nguyên hàm F (x) của hàm số f (x) = ( + x)2 1 sin biết 3 F =  2    4
A. F (x) 3 1
= x + 2cos x − sin 2 . x
B. F (x) 3 1
= x − 2cos x − sin 2 . x 2 4 2 4
C. F (x) 3 1
= x − 2cos x + sin 2 . x
D. F (x) 3 1
= x + 2cos x + sin 2 . x 2 4 2 4
Câu 23. Biết F (x) x 2
= e + x là một nguyên hàm của hàm số f (x) trên R. Khi đó f (2x)dx ∫ bằng A. x 2
2e + 2x + C. B. 1 2x 2
e + x + C. C. 1 2x 2
e + 2x + C. D. 2x 2
e + 4x + C. 2 2 Câu 24. Cho f ∫ (x) 3
dx = 4x + 2x + C 2
I = xf x dx 0 . Tính ∫ ( ) . 3 10 6 x x A. 6 2
I = 2x + x + C . B. I = + + C C. 6 2
I = 4x + 2x + C . D. 2
I =12x + 2 . 10 6
Câu 25. Tìm họ nguyên hàm của hàm số ( ) 3 2 1 .e + = x f x x . 3 A. f (x) x 3 1 dx .e + = + ∫ x C .
B. ∫ f (x) 3 x 1 dx 3e + = + C . 3 C. ( ) 3 1 d e + = + ∫ x f x x C . D. ( ) 1 3 1 d e + = + ∫ x f x x C . 3
Câu 26. Nguyên hàm của ( ) 2 sin = sin 2 . x f x x e là 2 sin x 1 + 2 sin x 1 − A. 2 2 sin 1 sin . x
x e − + C . B. e + C . C. 2 sin x e + C . D. e + C . 2 sin x +1 2 sin x −1 3
Câu 27. Tìm hàm số F (x) biết ( ) x F x = dx ∫ và F (0) =1. 4 x +1 1 3
A. F (x) = ( 4 ln x + ) 1 +1.
B. F (x) = ln ( 4 x + ) 1 + . 4 4 1
C. F (x) = ln ( 4 x + ) 1 +1.
D. F (x) = ( 4 4ln x + ) 1 +1. 4 (x − )2017 b Câu 28. 1 Biết 1  x −1 dx .  = + ∫   C , x ≠ 1
− với a, b ∈ N*. Mệnh đề nào sau đây đúng? (x + )2019 1 a x +1
A. a = 2b .
B. b = 2a .
C. a = 2018b .
D. b = 2018a . Câu 29. + x
Nguyên hàm của f (x) 1 ln = là: .xln x
A. 1+ ln xdx + = ln ln x + C ∫ . B. 1 ln x 2
dx = ln x .ln x + C .xln x ∫ . .xln x
C. 1+ ln xdx +
= ln x + ln x + C ∫ .
D. 1 ln xdx = ln .xln x + C .xln x ∫ . .xln x
Câu 30. Nguyên hàm của hàm số f (x) 3 = 3x +1 là A. f
∫ (x) x = ( x+ ) 3 d
3 1 3x +1 + C . B. f ∫ (x) 3
dx = 3x +1 + C . 1 1 C. f ∫ (x) 3 dx =
3x +1 + C . D. f
∫ (x)dx = (3x+ ) 3 1 3x +1 + C . 3 4
Câu 31. Cho hàm số f (x) x ln 2 = 2 .
. Hàm số nào dưới đây không là nguyên hàm của hàm số f (x) ? x A. ( ) = 2 x F x + C B. ( ) = 2(2 x F x − ) 1 + C C. ( ) = 2(2 x F x + ) 1 + C D. ( ) 1 2 x F x + = + C
Câu 32. Khi tính nguyên hàm x − 3 dx ∫
, bằng cách đặt u = x +1 ta được? x +1 4 A. ∫ ( 2
2 u − 4)du .
B. ∫( 2u − 4)du.
C. ∫( 2u − 3)du . D. u ∫ ( 2 2 u − 4)du . Câu 33. sin x
Biết F ( x) là một nguyên hàm của hàm số f (x) = và  π F  =
  2 .Tính F (0). 1+ 3cos x  2  1 2 2 1
A. F(0) = − ln 2 + 2 . B. F(0) = − ln 2 + 2.
C. F(0) = − ln 2 − 2 .
D. F(0 = − ln 2 − 2. 3 3 3 3
Câu 34. Gọi F (x) là nguyên hàm của hàm số f (x) 2x 1 = −
. Biết F (3) = 6, giá trị của F (8) là 2 x +1 x A. 217 . B. 27 . C. 215 . D. 215 . 8 24 8
Câu 35. Cho hàm số ( ) x f x =
. Họ tất cả các nguyên hàm của hàm số g (x) = (x + )
1 . f ′(x) là 2 x + 2 2 2
A. x + 2x − 2 − + + + + C .
B. x 2 + C . C. x x 2 +C .
D. x 2 + C . 2 2 x + 2 2 x + 2 2 x + 2 2 2 x + 2
Câu 36. Họ nguyên hàm của hàm số f (x) = 4x(1+ ln x) là: A. 2 2
2x ln x + 3x . B. 2 2
2x ln x + x C. 2 2
2x ln x + 3x + C . D. 2 2
2x ln x + x + C .
Câu 37. Họ nguyên hàm của hàm số ( ) = (2 − ) 1 x f x x e là A. (2 −3) x x e + C . B. (2 + 3) x x e + C C. (2 + ) 1 x x e + C . D. (2 − ) 1 x x e + C .
Câu 38. Cho hàm số f (x) thỏa mãn f ( ) 1 2 = −
và f ′(x) = x  f (x) 2 3 4
 với mọi x ∈ R. Giá trị của 25  f ( ) 1 bằng A. 391 − B. 1 − C. 41 − D. 1 − 400 40 400 10
Câu 39. Cho hàm số y = f (x) đồng biến và có đạo hàm liên tục trên R thỏa mãn (𝑓𝑓′(𝑥𝑥))2 = 𝑓𝑓(𝑥𝑥). 𝑒𝑒𝑥𝑥,
∀x∈R và f (0) = 2 . Khi đó f (2) thuộc khoảng nào sau đây? A. (12;13). B. (9;10). C. (11;12). D. (13 14 ; ).
Câu 40. Cho hàm số f (x) thỏa mãn  f ′  ( x) 2  + f
(x) f ′′(x) 2 .
= 2x − x +1, ∀x∈R và f (0) = f ′(0) = 3.
Giá trị của  f ( ) 2 1    bằng
A. 28 . B. 22 . C. 19 . D. 10. 2 3 3
Câu 41. Biết f
∫ (x)dx = 6. Giá trị của 2 f (x)dx ∫ bằng. 2 2
A. 36. B. 3. C. 12. D. 8. 3 Câu 42. Biết ( ) 2
F x = x là một nguyên hàm của hàm số f (x) trên R. Giá trị của ∫[1+ f (x)]dx bằng 1 5
A. 10. B. 8. C. 26 . D. 32 . 3 3 3 3 3
Câu 43. Biết f (x)dx = ∫ 4 và g(x)dx = ∫ 1. Khi đó:  ∫ f (x)−g(x) dx  bằng: 2 2 2 A. 3 − . B. 3 . C. 4 . D. 5. 1 1 Câu 44. Biết  ∫ f (x)+2x dx  =2 
. Khi đó ∫f (x)dx bằng : 0 0
A. 1. B. 4 . C. 2 . D. 0 .
Câu 45. Khẳng định nào trong các khẳng định sau đúng với mọi hàm f , g liên tục trên K và a , b là
các số bất kỳ thuộc K ? b f (x)dx b b b b ∫
A. ∫[ f (x)+ 2g(x)]dx = f (x)dx+2 g(x)dx ∫ ∫ . B. f (x)d a x = ∫ . g(x) b a a a a g(x)dx ∫a b b b 2 b b  
C. ∫[ f (x).g(x)]dx = f (x)dx . g(x)dx ∫ ∫ . D. 2 f (x)dx= ∫
f (x)dx ∫  . a a a aa  2 4 4 f
∫ (x)dx =1 f (t)dt = 4 − ∫ f ( y)dy ∫ Câu 46. Cho 2− , 2− . Tính 2 .
A. I = 5. B. I = 3 − .
C. I = 3 . D. I = 5 − . 10 6
Câu 47. Cho hàm số f (x) liên tục trên [0;10] thỏa mãn f
∫ (x)dx = 7 , f
∫ (x)dx = 3. Tính 0 2 2 10 P = f
∫ (x)dx+ f
∫ (x)dx. 0 6
A. P =10.
B. P = 4 .
C. P = 7 . D. P = 6 − .
Câu 48. Cho f , g là hai hàm liên tục trên đoạn [1; ] 3 thoả: 3 3 3  f
∫ (x)+3g(x) dx =10  , 2 f
∫ (x)− g(x) dx = 6  . Tính  f
∫ (x)+ g(x) dx  . 1 1 1
A. 7. B. 6. C. 8. D. 9. 2 2 2 f ∫ (x)dx = 2
g (x)dx = 1 − ∫
I = x + 2 f ∫ 
(x)−3g (x)dxCâu 49. Cho 1− và 1− . Tính 1 − . A. 17 I = B. 5 I = C. 7 I = D. 11 I = 2 2 2 2 π 4 Câu 50. Giả sử 2
I = sin 3xdx = a + b ∫
(a, b ∈Q). Khi đó giá trị của a − b là 2 0 A. 1 − B. 1 − C. 3 − D. 1 6 6 10 5 6 m Câu 51. Cho ∫( 2 3x − 2x + )
1 dx = 6. Giá trị của tham số m thuộc khoảng nào sau đây? 0 A. ( 1; − 2) . B. ( ;0 −∞ ). C. (0;4) . D. ( 3 − ; ) 1 . π 4
Câu 52. Cho hàm số f (x) . Biết f (0) = 4 và f’(x) = 2cos2x + 3, ∀x ∈ R, khi đó f (x)dx ∫ bằng? 0 2 π + 8π +8 2 π + 8π + 2 2 π + 6π +8 2 π + 2 A. . B. . C. . D. . 8 8 8 8
Câu 53. Có bao nhiêu giá trị nguyên dương của a a
để ∫ (2x − 3)dx ≤ 4 ? 0
A. 5. B. 6 . C. 4 . D. 3. b
Câu 54. Có bao nhiêu số thực b thuộc khoảng (π;3π ) sao cho 4cos2xdx =1 ∫ ? π
A. 8. B. 2. C. 4. D. 6. 0 2 Câu 55. Biết 3x + 5x −1 2 I =
dx = a ln + b, ∫
(a,b∈) . Khi đó giá trị của a + 4b bằng − − x 2 3 1
A. 50 B. 60 C. 59 D. 40 Câu 56. (x − )2 1 Tích phân 1 I =
dx = a − ln b ∫
trong đó a , b là các số nguyên. Tính giá trị của biểu thức 2 x +1 0 a + b .
A. 1. B. 0 . C. 1 − . D. 3. 2 2
Câu 57. Biết x + 5x + 2 dx = a + bln3+ cln5 ∫
, Giá trị của abc bằng 2 x + 4x + 3 0 A. 8 − . B. 10 − . C. 12 − . D. 16. 21 Câu 58. Cho dx
= a ln 3 + bln 5 + c ln 7 ∫
, với a,b,c là các số hữu tỉ. Mệnh đề nào sau đây đúng? 5 x x + 4
A. a − b = 2 − c
B. a + b = 2 − c
C. a + b = c
D. a − b = −c 2
Câu 59. Tính tích phân 2
I = 2x x −1dx ∫ bằng cách đặt 2
u = x −1, mệnh đề nào dưới đây đúng? 1 3 2 3 2 A. I = udu ∫ B. 1 I = udu I = 2 udu I = udu 2 ∫ C. ∫ D. ∫ 0 1 0 1 5
Câu 60. Giả sử tích phân 1 I =
dx = a + bln 3+ c ln 5 ∫ . Lúc đó + + 1 1 3x 1 5 7 8
A. a + b + c = . B. 4
a + b + c = .
C. a + b + c = .
D. a + b + c = . 3 3 3 3 e Câu 61. Biết ln x
dx = a + b 2 ∫
với a,b là các số hữu tỷ. Tính S = a + b . + 1 x 1 ln x 7 A. S =1. B. 1 S = . C. 3 S = . D. 2 S = . 2 4 3 2 2
Câu 62. Cho tích phân 2 I = 16 − x dx ∫
và x = 4sint . Mệnh đề nào sau đây đúng? 0 π π π π 4 4 4 4
A. I = 8∫(1+ cos2t)dt . B. 2 I = 16 sin d t t ∫
C. I = 8∫(1− cos2t)dt . D. 2 I = −16 cos d t t ∫ . 0 0 0 0 7 3 Câu 63. Cho biết d = ∫ x m x
với m là một phân số tối giản. Tính m − 7n 3 2 x n n 0 1+
A. 0 . B. 1. C. 2 . D. 91. 64 Câu 64. Giả sử dx 2 I = = a ln + b ∫
với a, blà số nguyên. Khi đó giá trị a − b là 3 x + x 3 1 A. 17 − . B. 5. C. 5 − . D. 17 . π
Câu 65. Cho hàm số f (x) có f (0) = 0 và f ′(x) 2
= cos xcos 2x,∀∈ R . Khi đó f
∫ (x)dx bằng 0 1042 208 242 149 A. . B. . C. . D. . 225 225 225 225 π 2 Câu 66. cos x 4 Cho dx = a ln ∫
. Giá trị của a + b bằng 2
sin x − 5sin x + 6 b 0
A. 0 . B. 1. C. 4 . D. 3. π 4 2
Câu 67. Tính tích phân sin x I = dx ∫
bằng cách đặt u = tan x , mệnh đề nào dưới đây đúng? 4 cos x 0 π 4 2 1 1 1 A. 2 I = u du ∫ . B. I = du ∫ . C. 2
I = − u du 2 I = u du 2 u ∫ . D. ∫ . 0 0 0 0 Câu 68. ln 2 dx 1 Biết I = =
a − b + c ∫
với a , b , c là các số nguyên dương. x −x (ln ln ln ) 0 e + 3e + 4 c
Tính P = 2a − b + c . A. P = 3 − . B. P = 1 − .
C. P = 4 . D. P = 3 e
Câu 69. Cho ∫(1+ xln x) 2 d
x = ae + be + c với a , b , c là các số hữu tỷ. Mệnh đề nào dưới đây đúng? 1
A. a + b = c
B. a + b = −c
C. a −b = c
D. a − b = −c 1
Câu 70. Biết rằng tích phân ∫(2 + )1ex x dx = a + .
b e, tích a.b bằng 0 A. 15 − . B. 1 − . C. 1. D. 20. 8 2 ln x b
Câu 71. Cho tích phân I = dx = + aln 2 ∫ 2
với a là số thực, là x c
b và c là các số dương, đồng thời b 1 c
phân số tối giản. Tính giá trị của biểu thức P = 2a + 3b + c . A. P = 6 .
B. P = 5. C. P = 6 − . D. P = 4 . 1 2
Câu 72. Cho hàm số f (x) liên tục trên R và thỏa mãn f
∫ (x)dx = 9 . Tích phân  f
∫ (1−3x)+9dx  5 − 0 bằng
A. 15. B. 27 . C. 75. D. 21. 10 10
Câu 73. Cho hàm số f (x) liên tục trên đoạn [0;10] thỏa mãn f
∫ (x)dx = 7, f
∫ (x)dx =1. Tính 0 2 1 P = f
∫ (2x)dx. 0
A. P = 6 . B. P = 6 − .
C. P = 3. D. P =12. 5 2
Câu 74. Cho I = f
∫ (x)dx = 26. Khi đó J = xf
∫  ( 2x + )1+1dx  bằng 1 0
A. 15. B. 13. C. 54. D. 52. π 9 f ( x ) 2
Câu 75. Cho hàm số y = f (x) liên tục trên R thỏa mãn dx = ∫
4 và f (sin x)cos xdx = ∫ 2. 1 x 0 3
Tích phân I = ∫ f (x)dx bằng 0
A. I = 8 .
B. I = 6.
C. I = 4 . D. I = 10 . 4 2 Câu 76. Cho f ∫ (x)dx = 20 8
1 . Tính tích phân I =  f
∫ (2x)+ f (4−2x)dx  . 0 0
A. I = 0.
B. I = 2018.
C. I = 4036 . D. I =1009. 1
Câu 77. Cho hàm số f (x) có đạo hàm liên tục trên R. Biết f (6) =1 và xf
∫ (6x)dx =1, khi đó 0 6 2 x f ′ ∫
(x)dx bằng 0 107 A. . B. 34. C. 24 . D. 36 − . 3 1
Câu 78. Cho f (x) là hàm số có đạo hàm liên tục trên [0; ]1 và f ( ) 1 1 = − , x f ′ ∫ (x) 1 . dx = . Giá trị 18 36 0 1
của f (x)dx ∫ bằng 0 A. 1 − . B. 1 . C. 1 . D. 1 − . 12 36 12 36 9 ln3 Câu 79. Cho hàm số 2x −1
f (x) có f ( ) 2
1 = e và f ′(x) 2x =
e với mọi x khác 0 . Khi đó xf (x)dx ∫ 2 x 1 bằng 2 6 − 2 9 − A. 2 6 − e e e . B. . C. 2 9 − e . D. . 2 2 2
Câu 80. Cho hàm số y = f (x) có đạo hàm liên tục trên R và thỏa mãn f (2) =16, f (x)dx = 4 ∫ . Tính 0 1 I = xf (2 ′ x)dx ∫ . 0
A. I = 20
B. I = 7
C. I =12 D. I =13
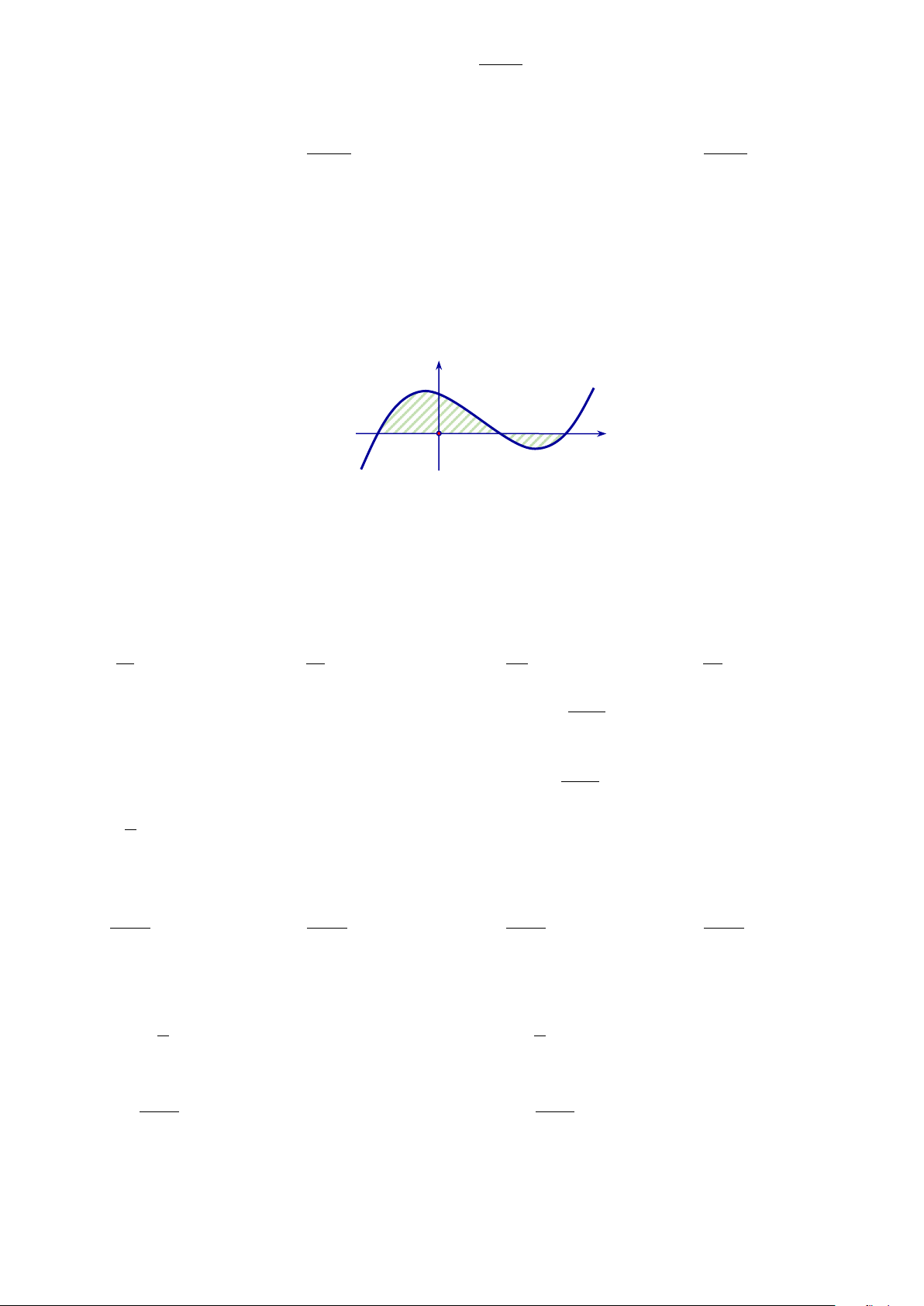
Câu 81. Gọi S là diện tích miền hình phẳng được tô đậm trong hình vẽ bên. Công thức tính S là y y = f (x) 1 − O 1 2 x 1 2 1 2 A. S = f
∫ (x)dx+ f
∫ (x)dx . B. S = f
∫ (x)dx− f
∫ (x)dx . 1 − 1 1 − 1 2 2 C. S = f
∫ (x)dx .
D. S = − f ∫ (x)dx . 1 − 1 −
Câu 82. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số 3 2
y x  3x , trục hoành và hai đường thẳng
x  1, x  4 là
A. 53 B. 51 C. 49 D. 25 4 4 4 2
Câu 83. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số x 1 y
, trục hoành và đường thẳng x  2 là x  2 A. 3 2ln 2 B. 3 ln 2 C. 3 2ln 2 D. 3 ln 2
Câu 84. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số x +1 y =
và các trục tọa độ Ox, Oy ta được: x − 2 = ln b S a
+1. Chọn đáp án đúng c
A. a + b + c = 8
B a + b + c = 0
C a + b + c =1
D. a + b + c =10
Câu 85. Diện tích hình phẳng giới hạn bởi đường cong y xln x , trục hoành và đường thẳng x e là 2 2 2 2
A. e 1
B. e 1
C. e 1
D. e 1 2 2 4 4
Câu 86. Cho hình thang cong (H ) giới hạn bởi các đường ex
y = , y = 0, x = 0 , x = ln8. Đường thẳng
x = k (0 < k < ln8) chia (H ) thành hai phần có diện tích là S và S . Tìm k để S = S . 1 2 1 2 A. 9 k = ln .
B. k = ln 4 . C. 2 k = ln 4 . D. k = ln 5 . 2 3
Câu 87. Tính diện tích miền hình phẳng giới hạn bởi các đường 2
y = x − 2x , y = 0, x = 10 − , x =10 . A. 2000 S = .
B. S = 2008 . C. 2008 S = . D. 2000 . 3 3
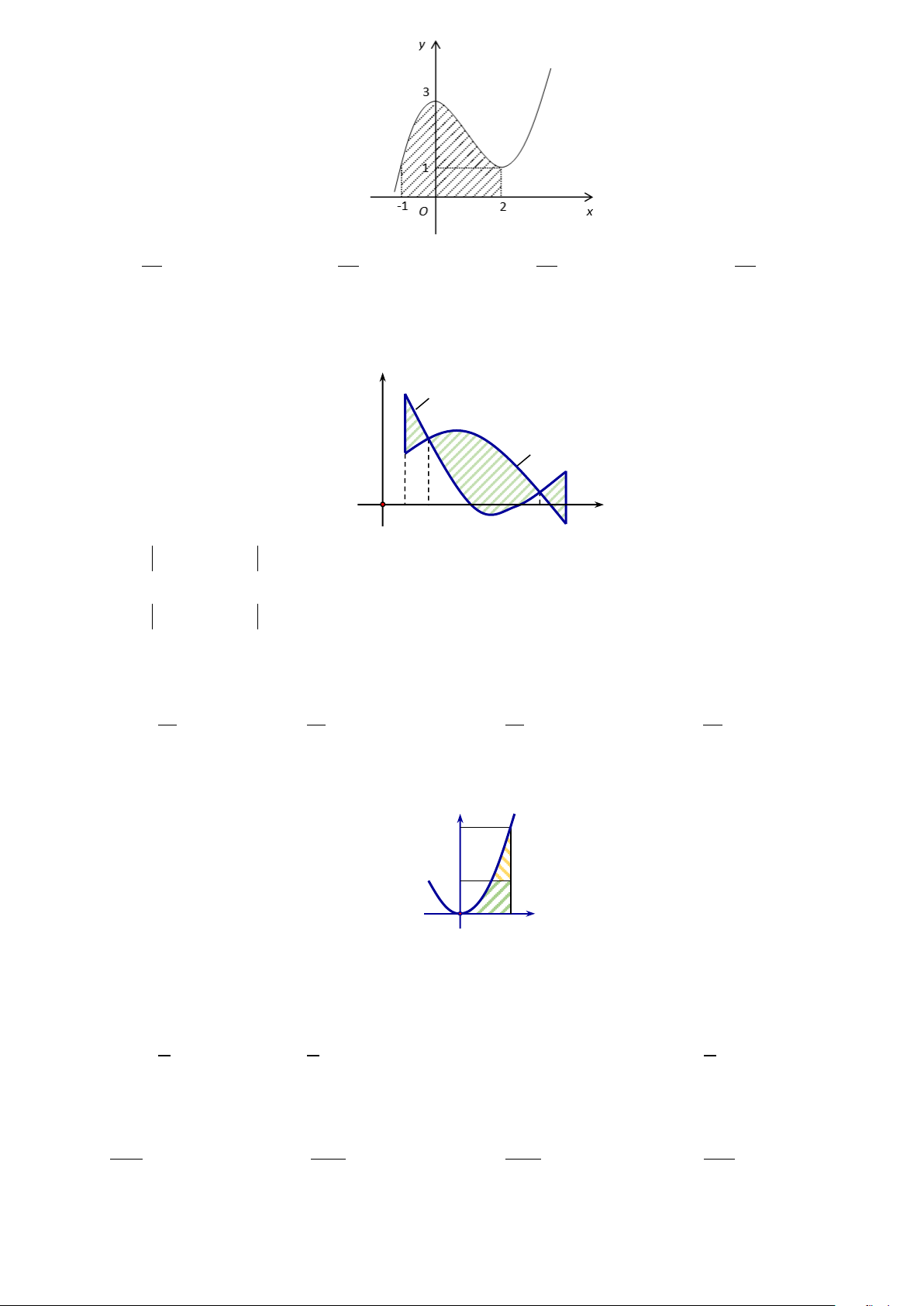
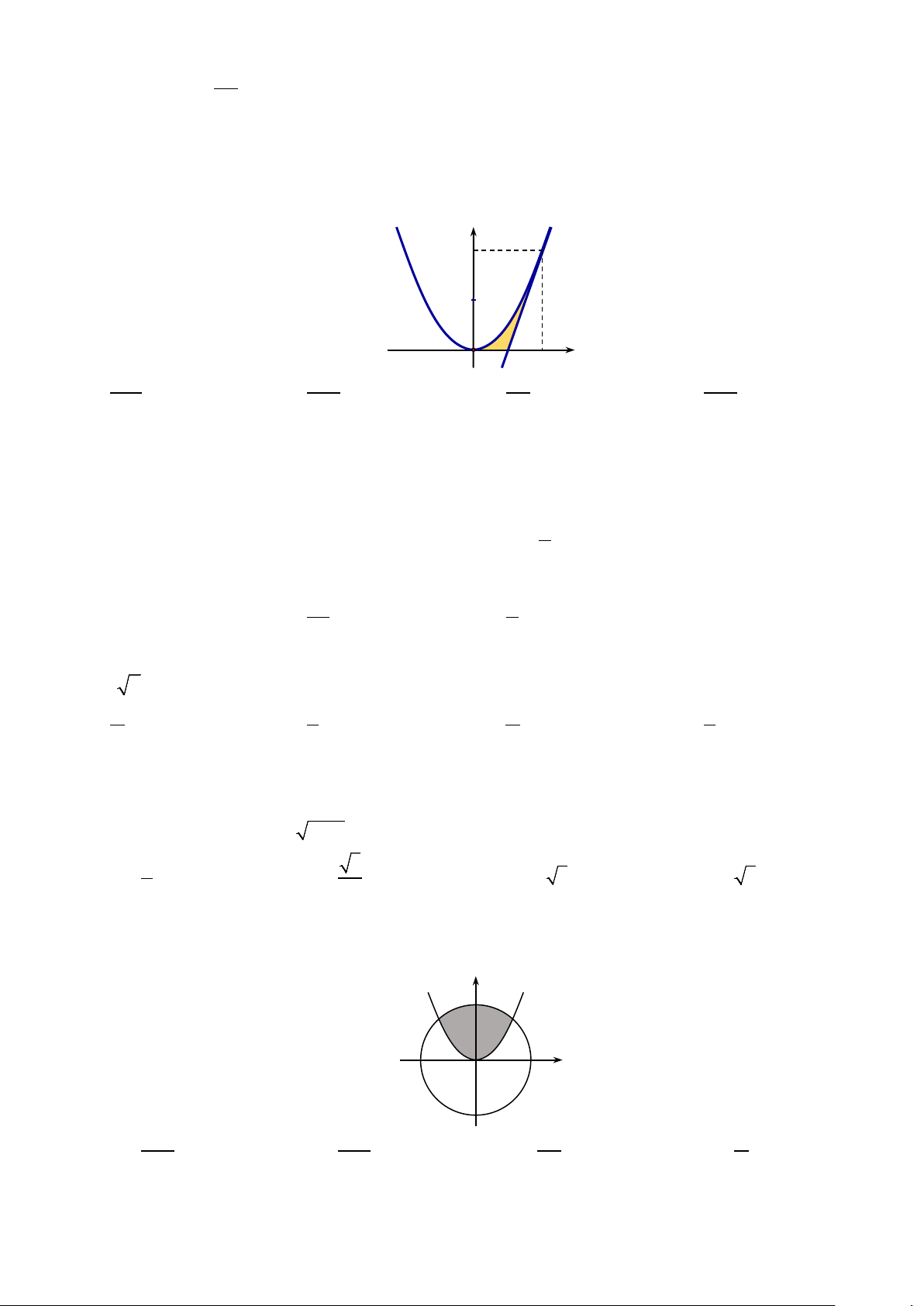
Câu 88. Tính diện tích S của miền hình phẳng giới hạn bởi đồ thị của hàm số ( ) 3 2
f x = ax + bx + c , các
đường thẳng x =1, x = 2 và trục hoành (miền gạch chéo) cho trong hình dưới đây. 10 A. 51 S = . B. 52 S = . C. 50 S = . D. 53 S = . 8 8 8 8
Câu 89. Cho hình phẳng (H ) giới hạn bởi đồ thị của hai hàm số f x và f x liên tục trên đoạn [ ; a b] 2 ( ) 1 ( )
và hai đường thẳng x = a , x = b (tham khảo hình vẽ dưới). Công thức tính diện tích của hình (H ) là y f x 1 ( ) f x 2 ( ) O a c c 1 2 b x b b
A. S = f x − f x dx ∫ .
S = ∫( f x − f x dx . 1 2 ) 1 ( ) 2 ( ) B. ( ) ( ) a a b b b
C. S = f x + f x dx ∫
S = f x dx − f x dx 1 ( ) 2 ( ) . D. ∫ 2 ( ) ∫ 1( ) . a a a
Câu 90. Hình phẳng (H) được giới hạn bởi đồ thị hai hàm số 2
y x x  2, y x  2 và hai đường thẳng x  2;
x  3. Diện tích của (H) bằng A. 87 B. 87 C. 87 D. 87 5 4 3 5
Câu 91. Cho hình phẳng (H ) giới hạn bởi các đường 2
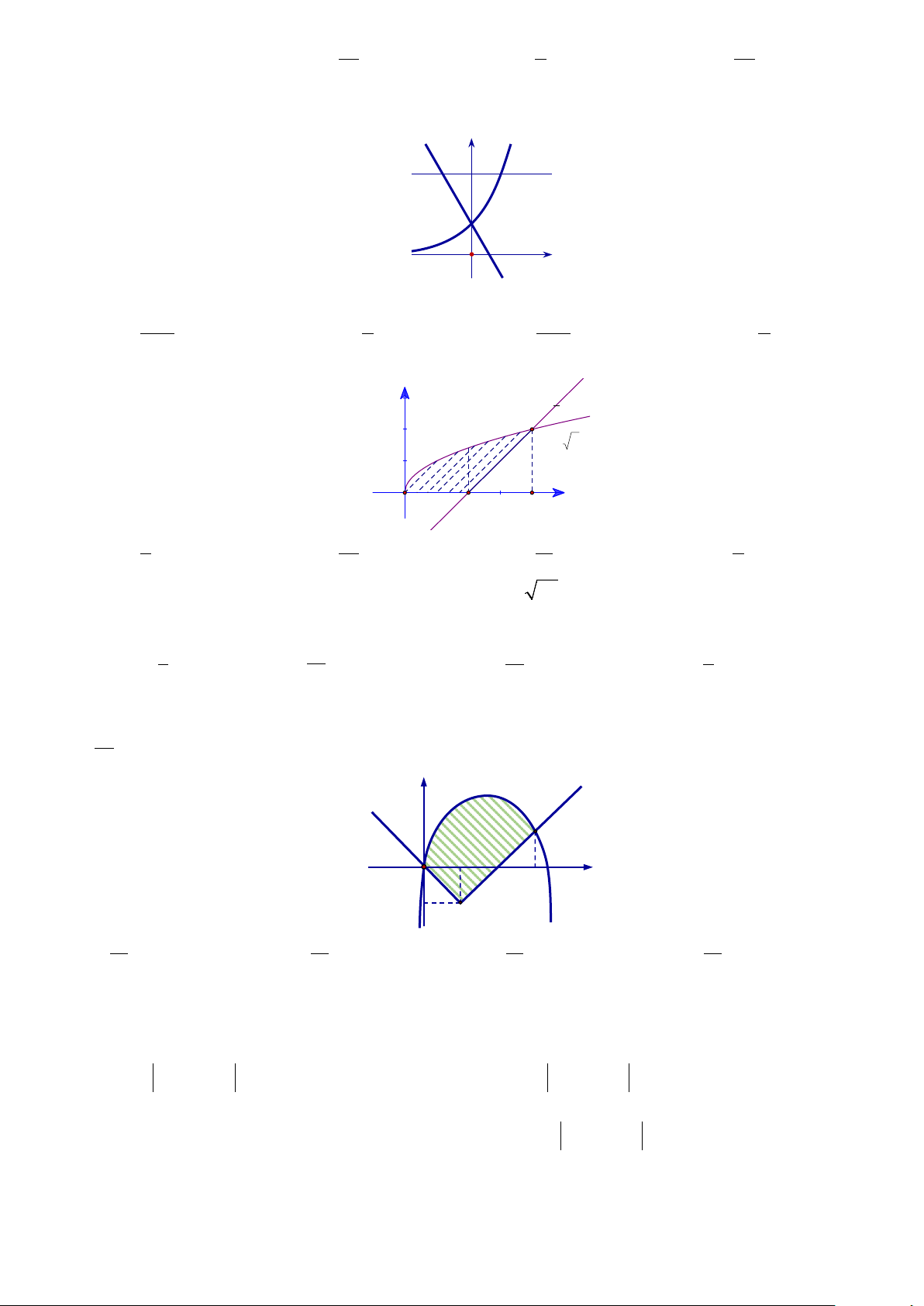
y = x , y = 0, x = 0 , x = 4 . Đường thẳng y = k
(0 < k <16) chia hình (H ) thành hai phần có diện tích S , S (hình vẽ). 1 2 y 16 S1 k S2 O 4 x
Tìm k để S = S . 1 2
A. k = 8.
B. k = 4 .
C. k = 5 . D. k = 3.
Câu 92. Diện tích hình phẳng được giới hạn bởi parabol 2
y  2  x và đường thẳng y  x là A. 7 B. 9 C. 3 D. 9 2 4 2
Câu 93. Gọi (H) là hình phẳng được giới hạn bởi đồ thị hai hàm số  1 x y
e x, y  1 
e x . Diện tích của (H) bằng
A. e 1 B. e  2
C. e  2 D. e 1 2 2 2 2
Câu 94. Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số 3
y = x − x và đồ thị hàm số 2
y = x − x . 11
A. S =13. B. 81 S = . C. 9 S = . D. 37 S = . 12 4 12
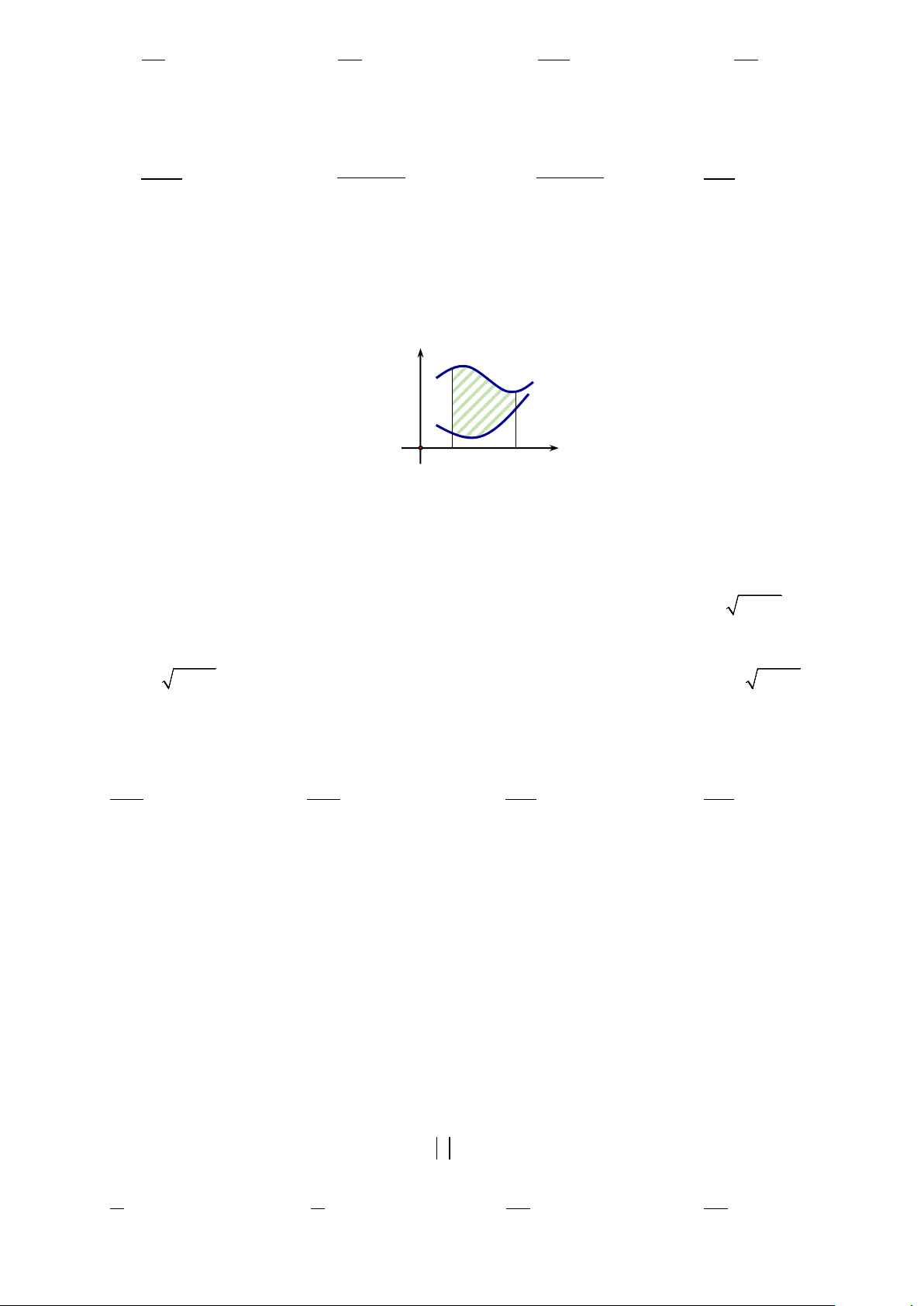
Câu 95. Cho (H ) là hình phẳng giới hạn bởi các đồ thị hàm số y = e , ex
y = và y = (1− e) x +1 (tham khảo hình vẽ bên). y e y = e ex y = 1 O x
Diện tích hình phẳng (H ) là A. e 1 S + = . B. 3 S = e + . C. e 1 S − = . D. 1 S = e + . 2 2 2 2
Câu 96. Tích diện tích S của hình phẳng (phần gạch sọc) trong hình sau y
g(x) = x 2 f(x) = x O 2 4 x A. 8 S = . B. 10 S = . C. 11 S = . D. 7 S = . 3 3 3 3
Câu 97. Cho (H ) là hình phẳng giới hạn bởi các đường y = 2x ; y = 2x − 2 và trục hoành. Tính diện tích của (H ) . A. 5 . B. 16 . C. 10 . D. 8 . 3 3 3 3
Câu 98. Cho (H ) là hình phẳng được tô đậm trong hình vẽ và được giới hạn bởi các đường có phương trình 10 −x khi x ≤1 2 y =
x − x , y = 
. Diện tích của (H ) bằng? 3
x − 2 khi x >1 y O 1 2 3 x 1 −
A. 11. B. 13 . C. 11. D. 14 . 6 2 2 3
Câu 99. Cho hình phẳng (H ) giới hạn bởi đồ thị hàm số 2
y = −x + 3x − 2 , trục hoành và hai đường thẳng
x =1, x = 2 . Quay (H ) xung quanh trục hoành được khối tròn xoay có thể tích là 2 2 A. 2
V = x − 3x + 2 dx ∫ . B. 2 2
V = x −3x + 2 dx ∫ . 1 1 2 2
C. V = π ∫(x −3x + 2)2 2 dx . D. 2
V = π x −3x + 2 dx ∫ . 1 1
Câu 100. Cho hình phẳng (H) giới hạn bởi các đường 2
y = x − 2x , trục hoành, trục tung, đường thẳng x =1.
Tính thể tích V hình tròn xoay sinh ra bởi (H) khi quay (H) quanh trục Ox. 12 A. 8π π π π V = B. 4 V = C. 15 V = D. 7 V = 15 3 8 8
Câu 101. Cho hình phẳng D giới hạn bởi đường cong ex
y = , trục hoành và các đường thẳng x = 0 , x =1.
Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu? 2 π ( 2e + )1 π ( 2e − )1 2 A. e 1 π V − = . B. V = . C. V = . D. e . 2 2 2 2
Câu 102. Thể tích V của khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi đường tròn (C) 2
: x + ( y −3)2 =1 xung quanh trục hoành là
A. V = 6π . B. 3
V = 6π . C. 2
V = 3π . D. 2 V = 6π .
Câu 103. Cho hình phẳng trong hình (phần tô đậm) quay quanh trục hoành. Thể tích của khối tròn xoay tạo
thành được tính theo công thức nào? y f x 1 ( ) f x 2 ( ) O a b x b b A. 2 V =  f ∫ (x) 2 − f x  dx 2 2 
V = π  f x − f x  dx 1 2 ( ) . B.
∫ 1 ( ) 2 ( ) . a a b b C. 2 V = π  f ∫ (x) 2 − f x  dx
V = π  f x − f x  dx 2 1 ( ) . D. ∫ ( ) ( ) 2 1 2  . a a
Câu 104. Cho hình phẳng (D) được giới hạn bởi các đường x = 0 , x =1, y = 0 và y = 2x +1 . Thể tích
V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức? 1 1 1 1
A. V = π 2x +1dx ∫ .
B. V = π (2x + ∫ )1dx .
C. V = (2x + ∫ )1dx . D. V = 2x +1dx ∫ . 0 0 0 0
Câu 105. Thể tích khối tròn xoay khi quay hình phẳng (H ) giới hạn bởi 2
y = x và y = x + 2 quanh trục Ox là
A. 72π (đvtt).
B. 72π (đvtt).
C. 81π (đvtt). D. 81π (đvtt). 10 5 10 5
Câu 106. Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số ex y = và các
đường thẳng y = 0 , x = 0 và x = 1 được tính bởi công thức nào sau đây? 1 1 1 1 A. 2 = e x V dx ∫ . B. 2 = π ex V dx ∫ . C. 2 = ex V dx ∫ . D. 2 = π e x V dx ∫ . 0 0 0 0
Câu 107. Tìm công thức tính thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi parabol (P) 2
: y = x và đường thẳng d : y = 2x quay xung quanh trục Ox . 2 2 2
A. π ∫(x −2x)2 2 dx . B. 2 4
π 4x dx −π x d ∫ ∫ x. 0 0 0 2 2 2 C. 2 4
π 4x dx +π x d ∫ ∫ x. D. π ( 2 2 − ∫ x x )dx . 0 0 0
Câu 108. Hình phẳng giới hạn bởi hai đồ thị y = x và 2
y = x quay quanh trục tung tạo nên một vật thể tròn
xoay có thể tích bằng
A. π . B. π . C. 2π . D. 4π . 6 3 15 15 13
Câu 109. Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường 2
y =1− x , y=0 quanh trục π
Ox có kết quả dạng a . Khi đó a+b có kết quả là: b
A. 11 B. 17 C. 31 D. 25
Câu 110. Cho hình (H ) giới hạn bởi trục hoành, đồ thị của một Parabol và một đường thẳng tiếp xúc với
Parabol đó tại điểm A(2;4) , như hình vẽ bên. Thể tích vật thể tròn xoay tạo bởi khi hình (H ) quay quanh trục Ox bằng y 4 2 O 1 2 x A. 16π . B. 32π . C. 2π . D. 22π . 15 5 3 5
Câu 111. Cho hình phẳng (H ) giới hạn bởi các đường xy = 4, x = 0 , y =1 và y = 4 . Tính thể tích V của
khối tròn xoay tạo thành khi quay hình (H ) quanh trục tung.
A. V = 8π .
B. V =16π .
C. V =10π . D. V =12π .
Câu 112. Cho hình phẳng (H ) giới hạn bởi đồ thị hàm số 1
y = và các đường thẳng y = 0, x =1, x = 4 . x
Thể tích V của khối tròn xoay sinh ra khi cho hình phẳng (H ) quay quanh trục Ox . A. 2πln 2 . B. 3π . C. 3 1 − . D. 2ln 2. 4 4
Câu 113. Thể tích của khối tròn xoay thu được khi quay quanh trục Ox hình phẳng giới hạn bởi đồ thị hàm số = ex y
x , trục hoành và đường thẳng x = 1 là: A. π ( 2e π + ) 1 . B. 1 ( 2e + ) 1 . C. ( 4e − ) 1 . D. 1 ( 4e − ) 1 . 4 4 4 4
Câu 114. Cho phần vật thể (ℑ) giới hạn bởi hai mặt phẳng có phương trình x = 0 và x = 2. Cắt phần vật thể
(ℑ) bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (0 ≤ x ≤ 2) , ta được thiết diện là một tam
giác đều có độ dài cạnh bằng x 2 − x . Tính thể tích V của phần vật thể (ℑ) . A. 4 V = . B. 3 V = .
C. V = 4 3. D. V = 3. 3 3
Câu 115. Cho (H ) là hình phẳng giới hạn bởi parabol 2
y = x và đường tròn 2 2
x + y = 2 (phần tô đậm
trong hình bên). Tính thể tích V của khối tròn xoay tạo thành khi quay (H ) quanh trục hoành. y x O A. 44π π π π V = . B. 22 V = . C. 5 V = . D. V = . 15 15 3 5 14 π
Câu 116. Cho phần vật thể B giới hạn bởi hai mặt phẳng có phương trình x = 0 và x = . Cắt phần vật thể 3  π
B bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ  x 0 ≤ x ≤ 
ta được thiết diện là một tam 3   
giác vuông có độ dài hai cạnh góc vuông lần lượt là 2x và cos x . Thể tích vật thể B bằng π π π π A. 3 + 3 − − . B. 3 3 . C. 3 3 . D. 3 . 6 3 6 6
Câu 117. Tính thể tích V của vật thể tròn xoay sinh ra khi cho hình phẳng giới hạn bởi các đường 1 y = , x
y = 0, x =1, x = a , (a > )
1 quay xung quanh trục Ox . A.  1 V 1  = −        . B. 1
V = 1− π . C. 1 V = 1+ π . D. 1 V = 1+ . a        a   a   a
Câu 118. Cho hình phẳng (H ) giới hạn bởi các đường 2
y = x , y = 2x . Thể tích của khối tròn xoay được
tạo thành khi quay (H ) xung quanh trục Ox bằng: A. 32π . B. 64π . C. 21π . D. 16π . 15 15 15 15
Câu 119. Tính thể tích V của vật tròn xoay tạo thành khi quay hình phẳng (H ) giới hạn bởi các đường 2
y = x ; y = x quanh trục Ox . A. 9π π π π V = . B. 3 V = . C. V = . D. 7 V = . 10 10 10 10 2 2
Câu 120. Trong mặt phẳng tọa độ Oxy , gọi (H là hình phẳng giới hạn bởi các đường x y = , x y = − , 1 ) 4 4 x = 4
− , x = 4 và hình (H là hình gồm các điểm ( ; x y) thỏa: 2 2 + ≤ , 2
x + ( y − 2)2 ≥ 4, 2 ) x y 16 2
x + ( y + 2)2 ≥ 4.
Cho (H và (H quay quanh trục Oy ta được các vật thể có thể tích lần lượt là 2 ) 1 )
V , V . Đẳng thức nào sau 1 2 đây đúng? A. V 1 2 = V .
B. V = V .
C. V = 2V .
D. V = V 1 2 1 2 2 1 2 1 2 3
PHẦN 2: HỆ TỌA ĐỘ TRONG KHÔNG GIAN
Câu 1. Trong không gian Oxyz , hình chiếu vuông góc của điểm M (2;− 2; )
1 trên mặt phẳng (Oxy) có tọa độ là A. (2;0; ) 1 .
B. (2;− 2;0) . C. (0;− 2; ) 1 . D. (0;0; ) 1 .
Câu 2. Trong không gian Oxyz , hình chiếu vuông góc của điểm A(1;2;5) trên trục Ox có tọa độ là A. (0;2;0) . B. (0;0;5) . C. (1;0;0) . D. (0;2;5) . 15
Câu 3. Trong không gian Oxyz , hình chiếu vuông góc của điểm M (3; 1; − )
1 trên trục Oz có tọa độ là A. (3; 1; − 0). B. (0;0; ) 1 . C. (0; 1; − 0) . D. (3;0;0).
Câu 4. Trong không gian với hệ trục tọa độ Oxyz cho điểm M (x; y; z) . Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu M ′đối xứng với M qua mặt phẳng (Oxz) thì M ′(x; y;−z) .
B. Nếu M ′đối xứng với M qua Oy thì M ′(x; y;−z) .
C. Nếu M ′đối xứng với M qua mặt phẳng (Oxy) thì M ′(x; y;−z) .
D. Nếu M ′đối xứng với M qua gốc tọa độ O thì M ′(2x;2y;0) .
Câu 5. Trong không gian Oxyz , tọa độ điểm đối xứng của M ( ; 1 ; 2 )
3 qua mặt phẳng (Oyz) là
A. (0;2;3) . B. ( 1 − ; 2 − ; 3 − ). C. ( 1
− ;2;3) .
D. (1;2; 3 − ) .
Câu 6. Trong không gian Oxyz , cho điểm A(2; 3
− ;5) . Tìm tọa độ A′ là điểm đối xứng với A qua trục Oy .
A. A′(2;3;5). B. A′(2; 3 − ; 5 − ). C. A′( 2 − ; 3 − ;5) . D. A′( 2 − ; 3 − ; 5 − ) . 
Câu 7. Trong không gian Oxyz, cho hai điểm A(1;1;− )
1 và B(2;3;2). Vectơ AB có tọa độ là A. (1; 2; 3) B. ( 1; − − 2; 3) C. (3;5; ) 1 D. (3;4; ) 1
Câu 8. Trong không gian với hệ toạ độ Oxyz , cho điểm A(2;2; )
1 . Tính độ dài đoạn thẳng OA.
A. OA = 5
B. OA = 5
C. OA = 3
D. OA = 9  
Câu 9. Trong không gian với hệ trục tọa độ Oxyz , cho ba vecto a (1;2;3);b (2;2;− ) 1 ;c (4;0; 4 − ) . Tọa độ   
của vecto d = a − b + 2c là     A. d ( 7 − ;0; 4 − ) B. d ( 7 − ;0;4) C. d (7;0; 4 − ) D. d (7;0;4)
Câu 10. Trong không gian Oxyz , cho hai điểm A(1; 2 − ;− )
1 , B(1;4;3) . Độ dài đoạn thẳng AB là A. 2 13 B. 6 C. 3 D. 2 3      
Câu 11. Trong không gian Oxyz, cho a( 2;
− 2;0),b(2;2;0),c(2;2;2) . Giá trị của a + b + c bằng
A. 6. B. 11.
C. 2 11 . D. 2 6 .
Câu 12. Trong không gian Oxyz , cho hai điểm A(2; 4;
− 3) và B(2;2;7) . Trung điểm của đoạn thẳng AB có tọa độ là A. (4; 2; − 10) B. (1;3;2) C. (2;6;4) D. (2; 1; − 5)
Câu 13. Trong không gian với hệ tọa độ Oxyz , cho các điểm A(3; 4 − ;0) , B( 1;
− 1;3) , C (3,1,0). Tìm tọa
độ điểm D trên trục hoành sao cho AD = BC .
A. D(6;0;0) , D(12;0;0)
B. D(0;0;0) , D(6;0;0) C. D( 2 − ;1;0), D( 4; − 0;0)
D. D(0;0;0) , D( 6; − 0;0)
Câu 14. Trong không gian cho hệ trục toạ độ Oxyz , cho ba điểm A(1; 2; − 3), B( 1 − ;2;5),C (0;0; ) 1 . Tìm
toạ độ trọng tâm G của tam giác ABC .
A. G(0;0;3) .
B. G (0;0;9) . C. G ( 1; − 0;3) . D. G (0;0; ) 1 .  
Câu 15. Trong không gian Oxyz, cho vectơ a = (2; 2 − ; 4 − ), b = (1; 1 − ; )
1 . Mệnh đề nào dưới đây sai? 16      
A. a + b = (3; 3 − ; 3 − )
B. a và b cùng phương C. b = 3
D. a ⊥ b
Câu 16. Trên mặt phẳng toạ độ Oxy , cho tam giác ABC biết A(1;3) , B(−2;−2), C (3;1) . Tính cosin góc
A của tam giác. A. 2 cos A = B. 1 cos A = C. 2 cos A = − D. 1 cos A = − 17 17 17 17  
Câu 17. Trong không gian Oxyz , góc giữa hai vectơ i và u = (− 3; 0; )1 là A. 120° . B. 60°. C. 150°. D. 30° .  
Câu 18. Trong không gian với hệ tọa độ Oxyz , cho vectơ u = (3;0 )
;1 và v = (2;1;0). Tính tích vô hướng  . u v .        
A. u.v = 8 . B. . u v = 6. C. . u v = 0 .
D. u.v = 6 − .
Câu 19. Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC có A(1;0;0), B(0;0; ) 1 , C (2;1 ) ;1 .
Diện tích của tam giác ABC bằng:
A. 11 B. 7 C. 6 D. 5 2 2 2 2    
Câu 20. Trong không gian Oxyz cho 2 véc tơ a = (2;1;− ) 1 ; b = ; (1 ; 3 )
m . Tìm m để ( ;ab) = 90° . A. m = 5 − .
B. m = 5 . C. m =1. D. m = 2 −  
Câu 21. Trong không gian với hệ trục tọa độ Oxyz , cho u = (2; 1; − ) 1 và v = (0; 3
− ;−m) . Tìm số thực m   sao cho tích vô hướng . u v =1.
A. m = 4 .
B. m = 2 .
C. m = 3 . D. m = 2 − .  
Câu 22. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a = (2;1; 2
− ) và vectơ b = (1;0;2). Tìm tọa   
độ vectơ c là tích có hướng của a và b .    
A. c = (2;6;− ) 1 .
B. c = (4;6;− ) 1 . C. c = (4; 6; − − ) 1 . D. c = (2; 6; − − ) 1 .   
Câu 23. Trong không gian Oxyz , tọa độ một vectơ n vuông góc với cả hai vectơ a = (1;1; 2 − ) , b = (1;0;3)
là A. (2;3; )1−. B. (3;5; 2 − ) . C. (2; 3 − ;− ) 1 . D. (3; 5 − ;− ) 1 .   
Câu 24. Trong không gian với hệ trục tọa độ Oxyz , cho ba véctơ a = (1;2;− ) 1 ,b = (3; 1; − 0),c = (1; 5 − ;2) .
Câu nào sau đây đúng?     
A. a cùng phương với b .
B. a ,b , c không đồng phẳng.     
C. a ,b , c đồng phẳng.
D. a vuông góc với b .
Câu 25. Trong hệ trục tọa độ Oxyz , cho bốn điểm (
A 1;− 2;0) , B(2;0;3) ,C( 2;
− 1;3) và D(0;1;1). Thể tích
khối tứ diện ABCD bằng:
A. 6 . B. 8 . C. 12. D. 4 .  
Câu 26. Trong không gian với hệ toạ độ Oxyz , cho a = (1; 2
− ;3) và b = (1;1;− )
1 . Khẳng định nào sau đây sai?        
A. a + b = 3 . B. . a b = 4 − .
C. a − b = 5 .
D. a,b = ( 1; − 4 − ;3)   .
Câu 27. Trong không gian Oxyz, cho hai điểm A(1;0;− ) 1 , B(1; 1;
− 2) . Diện tích tam giác OAB bằng 17
A. 11. B. 6 . C. 11 . D. 6. 2 2
Câu 28. Trong không gian Oxyz , cho 4 điểm A(2;0;2) , B(1; 1; − 2 − ) , C ( 1; − 1;0) , D( 2 − ;1;2) . Thể tích của
khối tứ diện ABCD bằng
A. 42 . B. 14 . C. 21 . D. 7 . 3 3 3 3
Câu 29. Trong hệ trục tọa độ Oxyz , cho O(0;0;0) , A(0;1; 2 − ), B(1;2; )
1 , C (4;3;m) . Tất cả giá trị của
m để 4 điểm O, ,
A B,C đồng phẳng?
A. m =14. B. m = 14 − .
C. m = 7 . D. m = 7 − .
Câu 30. Trong không gian Oxyz , cho hình chóp .
A BCD có A(0;1;− )
1 , B(1;1;2), C (1; 1; − 0) và D(0;0; )
1 . Tính độ dài đường cao của hình chóp . A BCD . A. 2 2 . B. 3 2 . C. 3 2 . D. 2 . 2 2
Câu 31. Trong không gian với hệ trục tọa độ, cho hình bình hành ABCD . Biết A(2;1;−3) , B(0;− 2;5) và
C (1;1;3) . Diện tích hình bình hành ABCD là A. 2 87 . B. 349 . C. 349 . D. 87 . 2
Câu 32. Trong không gian với hệ tọa độ Oxyz , cho bốn điểm A(0;1 ) ;1 , B( 1; − 0;2) , C ( 1; − 1;0) và điểm D(2;1; 2
− ) . Khi đó thể tích tứ diện ABCD là A. 5 V = . B. 5 V = . C. 6 V = . D. 3 V = . 6 3 5 2  
Câu 33. Trong không gian với hệ tọa độ Oxyz , cho các vectơ a = (2;m −1;3),b = (1;3; 2 − n). Tìm , m n để  
các vectơ a,b cùng hướng. 3
A. m = 7;n = − .
B. m = 4;n = 3 − .
C. m =1;n = 0 . D. 4 m = 7;n = − . 4 3
Câu 34. Trong không gian với hệ tọa độ Oxyz , cho ba điểm A(2; 1 − ;5), B(5; 5 − ;7), M ( ; x y; ) 1 . Với giá
trị nào của x, y thì ,
A B, M thẳng hàng.
A. x = 4; y = 7 B. x = 4; − y = 7 −
C. x = 4; y = 7 − D. x = 4; − y = 7     
Câu 35. Trong không gian với hệ tọa độ Oxyz cho các véc tơ u = 2i − 2 j + k , v = ( ; m 2;m + ) 1 với m là  
tham số thực. Có bao nhiêu giá trị của m để u = v .
A. 0 . B. 1. C. 2 . D. 3.
Câu 36. Trong không gian với hệ tọa độ Oxyz , cho hình hộp ABC . D A′B C ′ D
′ ′ có A(0;0;0) , B( ;0 a ;0) ;
D(0;2a;0) , A′(0;0;2a) với a ≠ 0 . Độ dài đoạn thẳng AC′ là 3
A. a . B. 2 a . C. 3 a . D. a . 2   
Câu 37. Trong không gian với hệ trục toạ độ Oxyz , cho a = (2;3; ) 1 , b = ( 1;
− 5;2) , c = (4;−1;3) và
x =( 3−;22;5). Đẳng thức nào đúng trong các đẳng thức sau?        
A. x = 2 a − 3 b − c . B. x = 2
− a + 3 b + c . 18        
C. x = 2 a + 3 b − c .
D. x = 2 a − 3 b + c .
Câu 38. Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC có A1;2;  1 , B2;1;  3 , C4;7;  5 . Gọi D ; a ;
b c là chân đường phân giác trong góc B của tam giác ABC . Giá trị của a b  2c bằng
A. 5. B. 4 . C. 14. D. 15.
Câu 39. Trong không gian với hệ tọa độ Oxyz cho ba điểm M (2;3;− ) 1 , N ( 1; − 1; )
1 và P(1;m −1;2) . Tìm
m để tam giác MNP vuông tại N .
A. m = 2 B. m = 6 − C. m = 0 D. m = 4 −
Câu 40. Trong không gian Oxyz cho các điểm A(5;1;5); B( 4;3;2); C ( 3 − ; 2 − ; ) 1 . Điểm I ( ; a ; b c) là tâm
đường tròn ngoại tiếp tam giác ABC . Tính a + 2b + c ?
A. 1. B. 3. C. 6. D. 9. −  
Câu 41. Trong không gian với hệ tọa độ Oxyz , cho véc tơ u = (1;1; 2
− ), v = (1;0;m). Tìm tất cả giá trị của m
để góc giữa u , v bằng 45° .
A. m = 2 .
B. m = 2 ± 6 .
C. m = 2 − 6 . D. m = 2 + 6 .  
Câu 42. Trong không gian Oxyz , cho các vec tơ a = (5;3; 2 − ) và b = ( ; m 1;
− m + 3) . Có bao nhiêu giá trị  
nguyên dương của m để góc giữa hai vec tơ a và b là góc tù?
A. 2. B. 3. C. 1. D. 5.    
Câu 43. Trong không gian Oxyz , cho hai vectơ u và v tạo với nhau một góc 120° và u = 2 , v = 5. Tính   u + v A. 19 . B. 5 − . C. 7 . D. 39 .
Câu 44. Trong hệ trục tọa độ Oxyz , cho tứ diện ABCD biết A(3;− 2;m), B(2;0;0), C (0;4;0) ,
D(0;0;3) . Tìm giá trị dương của tham số m để thể tích tứ diện bằng 8.
A. m = 8 .
B. m = 4 .
C. m =12. D. m = 6.    
Câu 45. Trong không gian với hệ tọa độ Oxyz , cho u = (1;1;2),v = ( 1; − ;
m m − 2) . Khi u,v = 14   thì A. m =1 hoặc 11 m = − B. m = 1 − hoặc 11 m = − 5 3
C. m =1 hoặc m = 3 − D. m = 1 −
Câu 46. Trong không gian với hệ trục tọa độ Oxyz , cho tứ diện ABCD có A(2;−1;1) , B(3;0;−1),
C (2;−1;3) , D ∈Oy và có thể tích bằng 5 . Tính tổng tung độ của các điểm D .
A. −6 B. 2 C. 7 D. −4
Câu 47. Trong không gian Oxyz , có tất cả bao nhiêu giá nguyên của m để 2 2 2
x + y + z + (m + ) x − (m − ) 2 2 2 2
1 z + 3m − 5 = 0 là phương trình một mặt cầu?
A. 4 B. 6 C. 5 D. 7
Câu 48. Trong không gian Oxyz , xét mặt cầu (S ) có phương trình dạng 2 2 2
x + y + z − 4x + 2y − 2az +10a = 0 . Tập hợp các giá trị thực của a để (S)có chu vi đường tròn lớn bằng 8π là A. {1;1 } 0 . B. {2; 1 − } 0 . C. { 1; − 1 } 1 . D. {1; 1 − } 1 . 19
Câu 49. Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm A(1;0;0), C (0;0;3), B(0;2;0) . Tập hợp
các điểm M thỏa mãn 2 2 2
MA = MB + MC là mặt cầu có bán kính là:
A. R = 2 .
B. R = 3 .
C. R = 3. D. R = 2 .
Câu 50. Trong không gian Oxyz, cho điểm I(1; 2;
− 3) . Viết phương trình mặt cầu tâm I, cắt trục Ox tại hai
điểm A và B sao cho AB = 2 3 A. 2 2 2
(x −1) + (y + 2) + (z −3) =16. B. 2 2 2
(x −1) + (y + 2) + (z −3) = 20. C. 2 2 2
(x −1) + (y + 2) + (z −3) = 25. D. 2 2 2
(x −1) + (y + 2) + (z −3) = 9.
Câu 51. Trong không gian với hệ toạ độ Oxyz , cho A( ;0 a ;0) , B(0; ;
b 0) , C (0;0;c) , (abc ≠ 0) . Khi đó
phương trình mặt phẳng ( ABC) là: A. x y z + + = 1. B. x y z + + = 1. a b c b a c C. x y z + + = 1. D. x y z + + = 1. a c b c b a
Câu 52. Trong không gian với hệ toạ độ Oxyz , cho mặt phẳng (α ) :3x − z = 0 . Tìm khẳng định đúng trong các mệnh đề sau:
A. (α ) / /Ox .
B. (α ) / / (xOz).
C. (α ) / /Oy .
D. (α ) ⊃ Oy .
Câu 53. Trong không gian với hệ toạ độ Oxyz . Mặt phẳng (P) là −x + 3z − 2 = 0 có phương trình song song với: A. Trục Oy. B. Trục Oz. C. Mặt phẳng Oxy. D. Trục Ox.
Câu 54. Trong không gian với hệ toạ độ Oxyz , cho mặt phẳng (P) có phương trình 3x + 2y − z +1= 0 .
Mặt phẳng (P) có một vectơ pháp tuyến là:     A. n(3;2;1) . B. n( 2 − ;3;1) . C. n(3;2; 1) − . D. n(3; 2 − ; 1 − ).
Câu 55. Trong không gian với hệ toạ độ Oxyz , cho mặt phẳng (P) có phương trình 2
− x + 2y − z − 3 = 0.
Mặt phẳng (P) có một vectơ pháp tuyến là:     A. n(4; 4; − 2) . B. n( 2; − 2; 3) − . C. n( 4; − 4;2) . D. n(0;0; 3) − .
Câu 56. Trong không gian với hệ toạ độ Oxyz , cho ba điểm A(1; 2 − ; ) 1 , B( 1 − ;3;3) , C (2; 4; − 2) . Một 
vectơ pháp tuyến n của mặt phẳng ( ABC) là:    
A. n = (9;4;− )
1 . B. n = (9;4; )
1 . C. n = (4;9;− ) 1 . D. n = ( 1; − 9;4) .
Câu 57. Trong không gian với hệ toạ độ Oxyz . Điểm nào sau đây thuộc mặt phẳng (P) 2
− x + y − 5 = 0 A. ( 2 − ;1;0) . B. ( 2 − ;1; 5 − ) . C. (1;7;5) . D. ( 2; − 2; 5 − ) .
Câu 58. Trong không gian với hệ toạ độ Oxyz . Phương trình mặt phẳng (P) đi qua điểm ( A 1; − 2;0) và  nhận n( 1;
− 0;2) là VTPT có phương trình là:
A. −x + 2y − 5 = 0 B. −x + 2z − 5 = 0 C. −x + 2y − 5 = 0 D. −x + 2z −1 = 0
Câu 59. Trong không gian với hệ toạ độ Oxyz , cho ba điểm A(3; 2 − ; 2
− ), B(3;2;0) , C (0;2; ) 1 . Phương
trình mặt phẳng ( ABC) là:
A. 2x − 3y + 6z = 0 . B. 4y + 2z − 3 = 0 . C. 3x + 2y +1 = 0. D. 2y + z − 3 = 0 .
Câu 60. Trong không gian với hệ trục tọa độ Oxyz , cho hai điểm ( A − ), 1 ; 0 ; 1 B(− ) 1 ; 1 ; 2 . Phương trình mặt
phẳng trung trực của đoạn AB là: 20
A. x − y − 2 = 0.
B. x − y +1 = 0.
C. x − y + 2 = 0 .
D. − x + y + 2 = 0 .
Câu 61. Trong không gian với hệ toạ độ Oxyz . Mặt phẳng (P) đi qua các điểm ( A 1 − ;0;0) , B(0;2;0), C(0;0; 2
− ) có phương trình là: A. 2
− x + y + z − 2 = 0 . B. 2
− x − y − z + 2 = 0 . C. 2
− x + y − z − 2 = 0 . D. 2
− x + y − z + 2 = 0 .
Câu 62. Trong không gian với hệ trục toạ độ Oxyz , cho điểm M (2; 1;
− 3) và các mặt phẳng:
(α ): x − 2 = 0, (β ): y +1= 0, (γ ): z −3 = 0 . Tìm khẳng định sai.
A. (α ) / /Ox . B. (β ) đi qua M . C. (γ ) / / (xOy). D. (β ) ⊥ (γ ).
Câu 63. Trong không gian với hệ trục toạ độ Oxyz . Phương trình mặt phẳng qua A(2;5; ) 1 và song song
với mặt phẳng (Oxy) là:
A. 2x + 5y + z = 0 . B. x − 2 = 0. C. y − 5 = 0. D. z −1 = 0 .
Câu 64. Trong không gian với hệ trục toạ độ Oxyz . Mặt phẳng đi qua M (1;4;3) và vuông góc với trục
Oy có phương trình là:
A. y − 4 = 0 . B. x −1 = 0 .
C. z − 3 = 0 .
D. x + 4y + 3z = 0.
Câu 65. Trong không gian với hệ trục toạ độ Oxyz . Biết ,
A B,C là số thực khác 0 , mặt phẳng chứa trục
Oz có phương trình là:
A. Ax + Bz + C = 0 .
B. Ax + By = 0
C. By + Az + C = 0.
D. Ax + By + C = 0 .
Câu 66. Trong không gian với hệ trục tọa độ Oxyz , cho các điểm A ), 3 ; 1 ; 5 ( B ; 1 ( 6 ; 2 ),C ; 0 ; 5 ( 4), D( 6 ; 0 ; 4 ).
Viết phương trình mặt phẳng qua D và song song với mặt phẳng (ABC).
A. x + y + z −10 = 0 .
B. x + y + z − 9 = 0.
C. x + y + z − 8 = 0 .
D. x + 2y + z −10 = 0 .
Câu 67. Trong không gian với hệ trục tọa độ Oxyz , cho các điểm A ), 3 ; 1 ; 5 ( B ; 1 ( 6 ; 2 ),C ; 0 ; 5 ( ), 4 D( ) 6 ; 0 ; 4 .
Viết phương trình mặt phẳng chứa AB và song song với CD .
A. 2x + 5y + z −18 = 0 .
B. 2x − y + 3z + 6 = 0.
C. 2x − y + z + 4 = 0 .
D. x + y + z − 9 = 0 .
Câu 68. Trong không gian với hệ trục tọa độ Oxyz , gọi (P) là mặt phẳng chứa trục Ox và vuông góc
với mặt phẳng (Q) : x + y + z − 3 = 0 . Phương trình mặt phẳng (P) là:
A. y + z = 0 .
B. y − z = 0 .
C. y − z −1 = 0 .
D. y − 2z = 0 .
Câu 69. Trong không gian với hệ trục tọa độ Oxyz . Phương trình của mặt phẳng chứa trục Ox và qua điểm I (2; 3 − ; ) 1 là:
A. 3y + z = 0.
B. 3x + y = 0 .
C. y − 3z = 0.
D. y + 3z = 0.
Câu 70. Trong không gian với hệ toạ độ Oxyz , cho ba điểm A2;1; 
1 , B1;0;4và C0;2;  1 .
Phương trình mặt phẳng qua A và vuông góc với đường thẳng BC là:
A. 2x y  2z 5  0 .
B. x2y 3z 7  0 .
C. x  2y 5z 5  0 .
D. x  2y 5z 5  0.
Câu 71. Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng (α ) đi qua A(2; 1; − 4) , B(3;2;− ) 1
và vuông góc với mặt phẳng (Q) : x + y + 2z −3 = 0 . Phương trình mặt phẳng (α ) là:
A. 5x + 3y − 4z + 9 = 0.
B. x + 3y − 5z + 21 = 0. 21
C. x + y + 2z − 3 = 0 .
D. 5x + 3y − 4z = 0 .
Câu 72. Trong không gian với hệ trục tọa độ Oxyz . Tọa độ giao điểm M của mặt phẳng
(P):2x +3y + z − 4 = 0 với trục Ox là ? A. M (0,0,4) . B. 4 M 0, ,0  . C. M (3,0,0) . D. M (2,0,0) . 3   
Câu 73. Trong không gian với hệ toạ độ Oxyz , gọi là mặt phẳng qua các hình chiếu của A5;4;  3
lên các trục tọa độ. Phương trình của mặt phẳng là:
A. 12x 15y  20z 60  0
B.12x 15y  20z 60  0 . C. x y z x y z    0 .
D.   60  0 . 5 4 3 5 4 3
Câu 74. Trong không gian với hệ toạ độ Oxyz , cho mặt phẳng (α) đi qua hai điểm A5;2;0,  B3;4; 
1 và có một vectơ chỉ phương là a1;1; 
1 . Phương trình của mặt phẳng (α) là:
A. 5x 9y14z  0 .
B. xy7  0 .
C. 5x 9y14z 7  0 .
D.5x9y14z 7  0 .
Câu 75. Trong không gian với hệ trục tọa độ Oxyz , có bao nhiêu mặt phẳng song song với mặt phẳng
(P) : x + y + z − 6 = 0 và tiếp xúc với mặt cầu (S) : 2 2 2
x + y + z =12? A. 2 B. Không có. C. 1. D. 3.
Câu 76. Trong không gian với hệ trục tọa độ Oxyz , cho hai mặt phẳng (α ) :3x + (m − )
1 y + 4z − 2 = 0 ,
(β ):nx +(m + 2) y + 2z + 4 = 0. Với giá trị thực của ,
m n bằng bao nhiêu để (α ) song song (β )
A. m = 3;n = 6 − .
B. m = 3;n = 6 . C. m = 3 − ;n = 6 D. m = 3 − ;n = 6 − .
Câu 77. Trong không gian với hệ trục tọa độ Oxyz , cho hai mặt phẳng (P) : x + my + (m − ) 1 z + 2 = 0 ,
(Q):2x − y +3z − 4 = 0 . Giá trị số thực m để hai mặt phẳng (P),(Q) vuông góc A. m =1 B. 1 m = − C. m = 2 D. 1 m = 2 2
Câu 78. Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng (P) : x + 2y − z +1= 0. Gọi mặt phẳng
(Q) là mặt phẳng đối xứng của mặt phẳng (P) qua trục tung. Khi đó phương trình mặt phẳng (Q) là ?
A. x + 2y − z −1 = 0
B. x − 2y − z +1 = 0
C. x + 2y + z +1 = 0
D. x − 2y − z −1 = 0
Câu 79. Trong không gian với hệ toạ độ Oxyz , là mặt phẳng đi qua điểm A2;1;  5 và vuông góc
với hai mặt phẳng P:3x2y z 7  0 và Q:5x4y 3z 1 0 . Phương trình mặt phẳng  là:
A. x  2y z 5  0 .
B. 2x4y2z 10  0 .
C. 2x  4y  2z 10  0.
D. x  2yz 5  0 .
Câu 80. Trong không gian với hệ toạ độ Oxyz , gọi (α ) là mặt phẳng qua G(1;2;3) và cắt các trục
Ox,Oy,Oz lần lượt tại các điểm ,
A B,C (khác gốc O ) sao cho G là trọng tâm của tam giác
ABC . Khi đó mặt phẳng (α ) có phương trình:
A.3x + 6y + 2z +18 = 0 .
B. 6x + 3y + 2z −18 = 0.
C. 2x + y + 3z − 9 = 0 .
D. 6x + 3y + 2z + 9 = 0 . 22