TRƯỜNG ĐẠI HỌC XÂY DỰNG HÀ NỘI
Trần Minh Tú – Bộ môn Sức bền Vật liệu – Đại học Xây dựng Nội dung ôn tập
I. CHƯƠNG 1 - BiỂU ĐỒ NỘI LỰC
II. CHƯƠNG 2 - THANH CHỊU KÉO (NÉN) ĐÚNG TÂM
III. CHƯƠNG 3 - TRẠNG THÁI ỨNG SUẤT VÀ CÁC THUYẾT BỀN
IV. CHƯƠNG 4 - ĐẶC TRƯNG HÌNH HỌC MẶT CẮT NGANG
V. CHƯƠNG 5 - THANH CHỊU XOẮN THUẦN TÚY
VI. CHƯƠNG 6 - THANH CHỊU UỐN Chương 1:
BiỂU ĐỒ NỘI LỰC
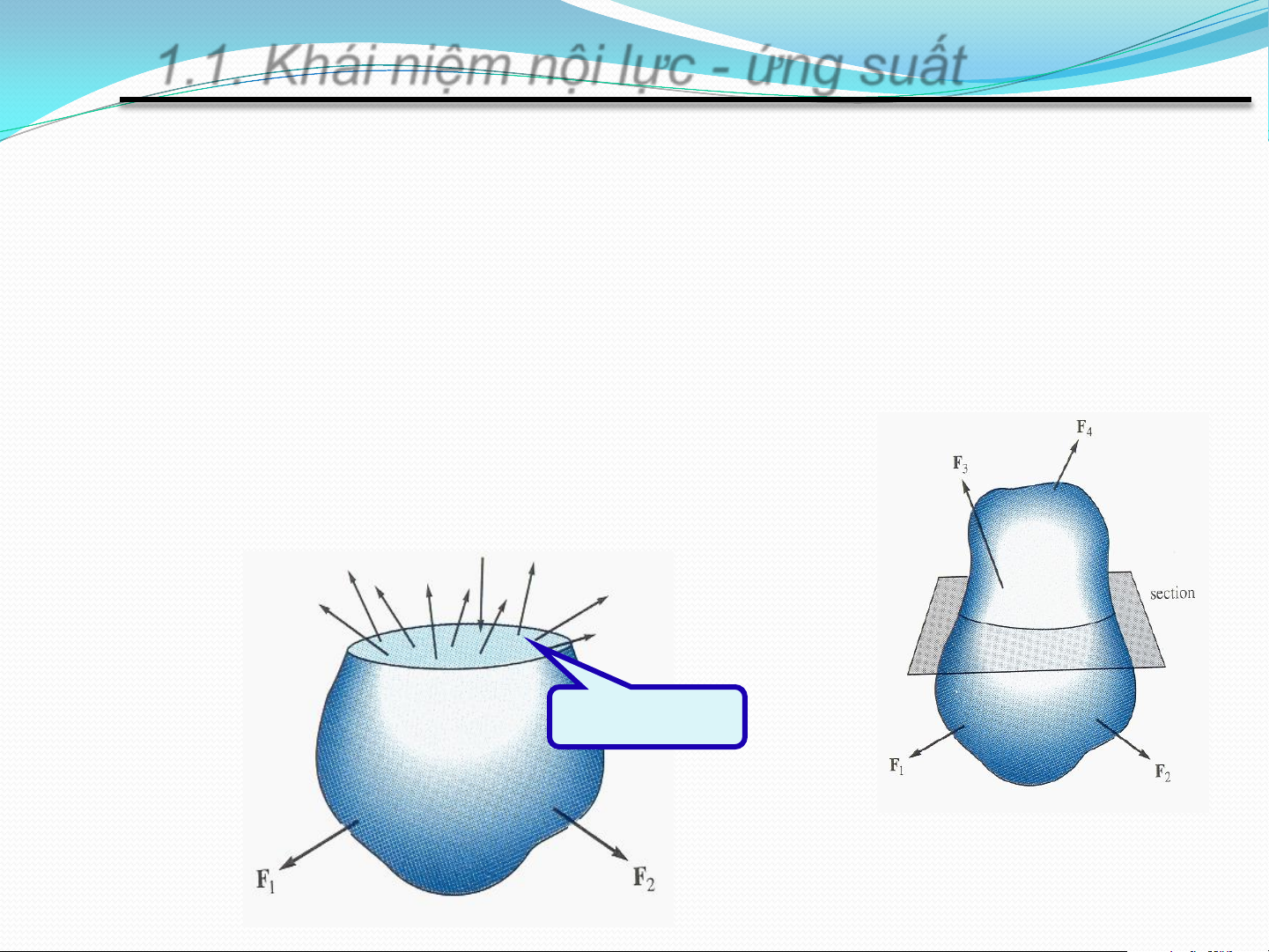
1.1. Khái niệm nội lực - ứng suất  Nội lực
 Lượng thay đổi lực tương tác giữa các phần tử vật chất
của vật thể khi chịu tác dụng của ngoại lực
 Khi có tác dụng ngoại lực => biến dạng => xuất hiện
nội lực chống lại sự biến dạng
 Nghiên cứu nội lực – PP mặt cắt
 Nội lực – lực phân bố trên mặt cắt Nội lực
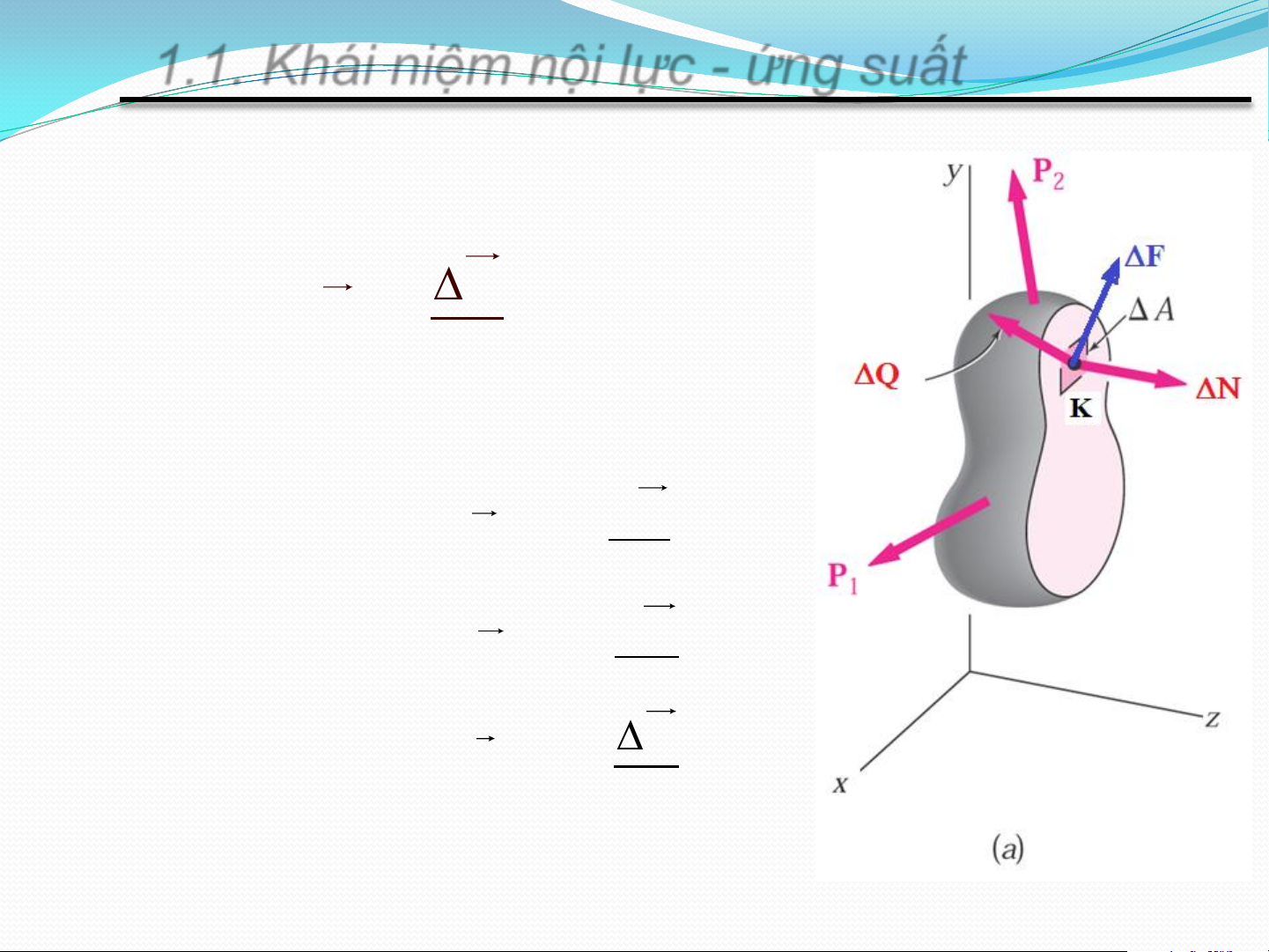
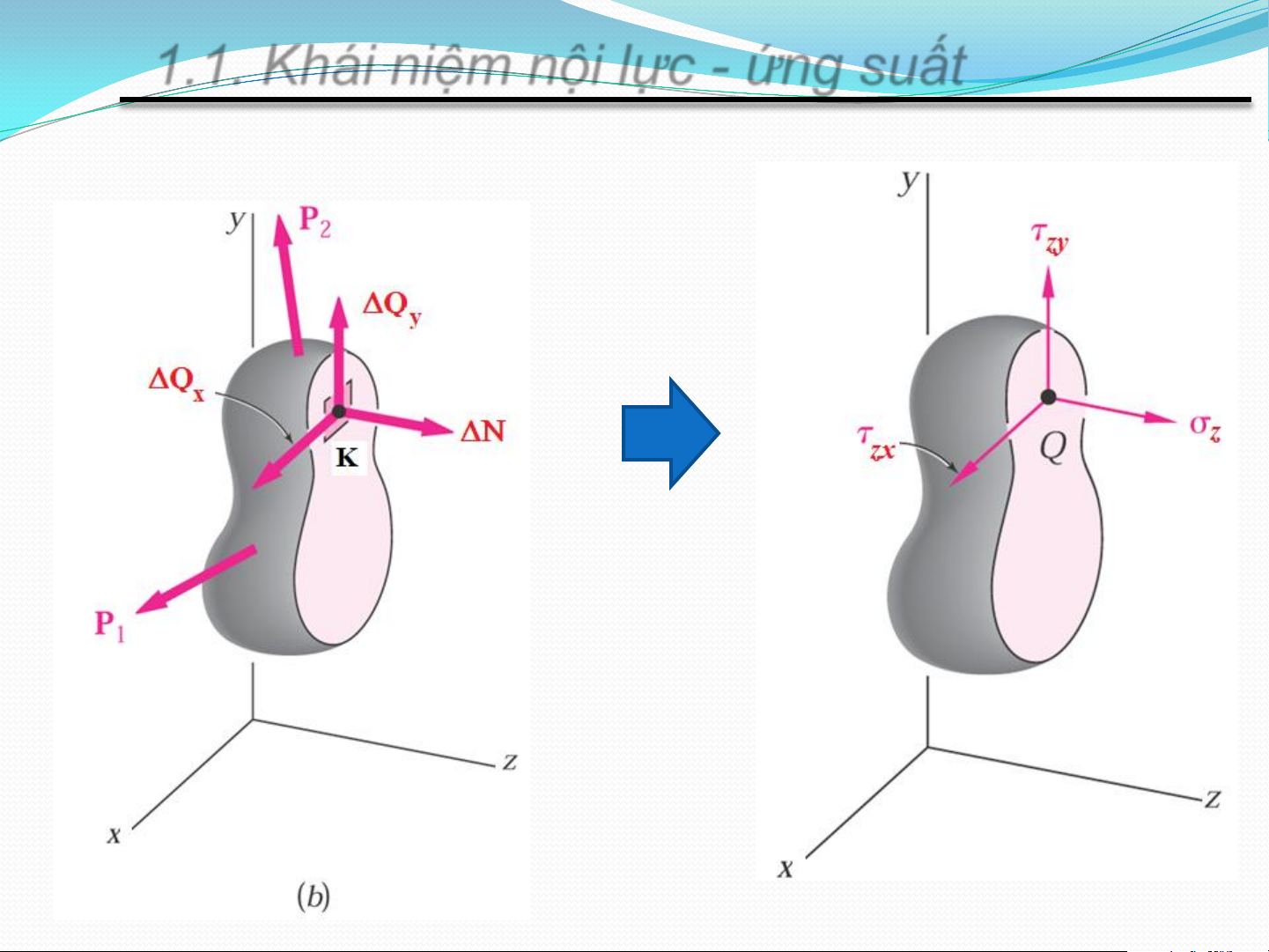
1.1. Khái niệm nội lực - ứng suất
• Ứng suất trung bình – Cường độ nội lực F p  tb A  • Ứ
ng suất tại điểm K thuộc mặt cắt F  Ứs toàn phần p  lim A  0  A  N
 Ứng suất pháp   lim A  0  A  Q  Ứng suất tiếp   lim A  0  A   Đơn vị: N/m2 (Pa)
1.1. Khái niệm nội lực - ứng suất
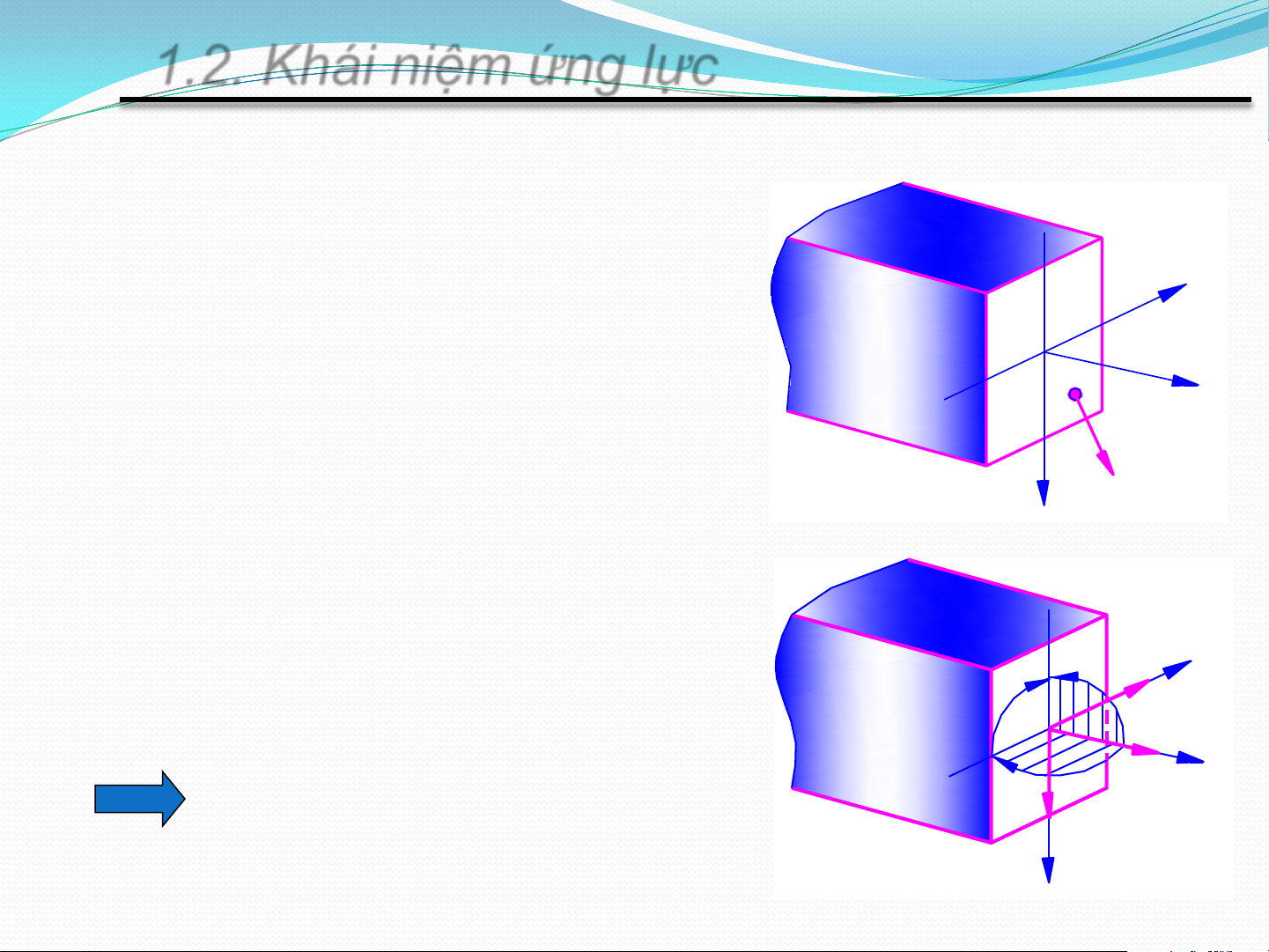
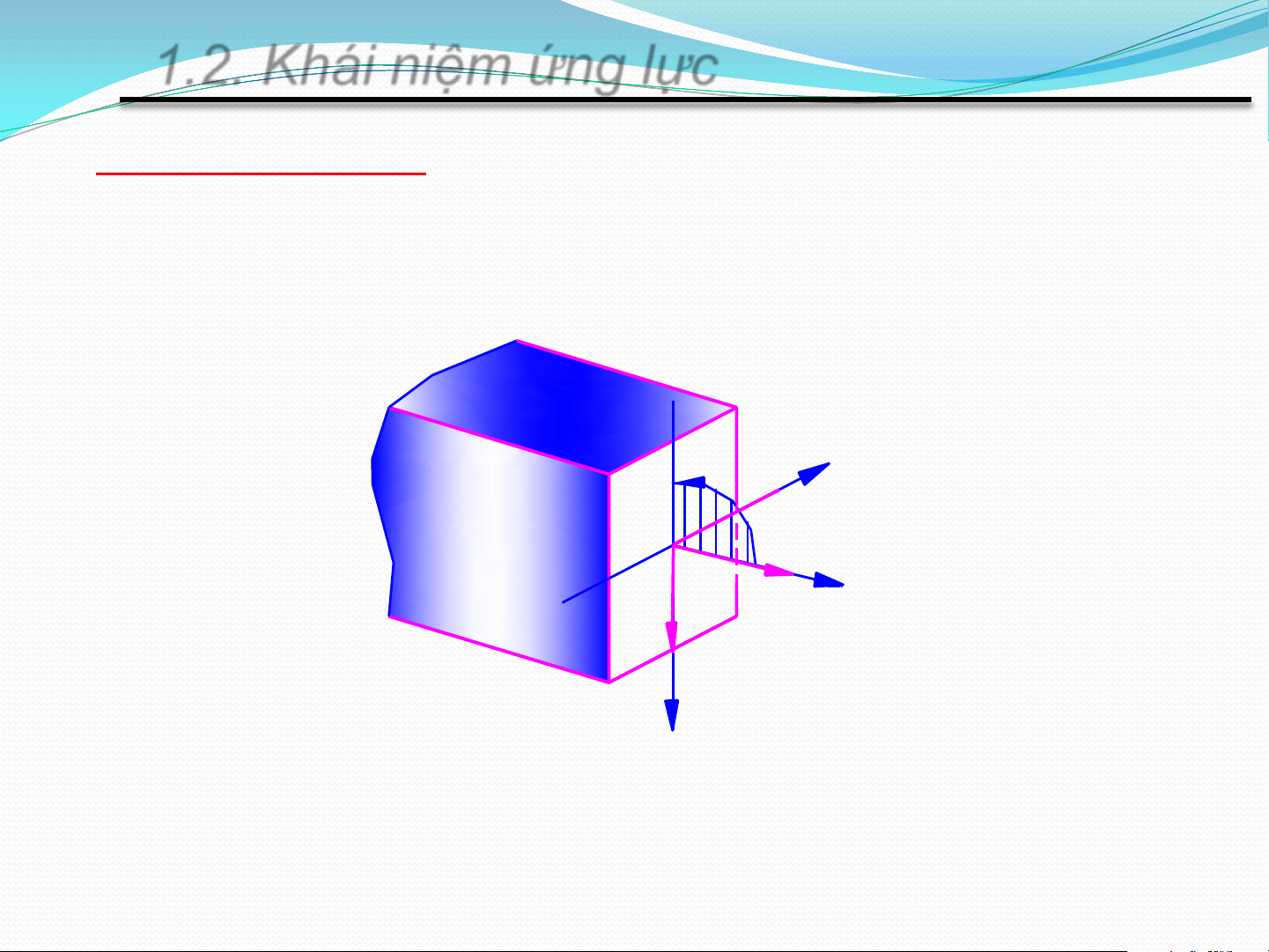
1.2. Khái niệm ứng lực
 Ứng lực R: Hợp lực nội lực trên mặt cắt ngang của x thanh O
 R: phương, chiều, điểm đặt K z
bất kỳ => dời về trọng tâm O R  N y z – lực dọc  Qx, Qy - lực cắt  M x M x, My – mô men uốn x Mz Q  M x z –mô men xoắn N z 6 ứng lực M Z y Qy y
1.2. Khái niệm ứng lực
• Bài toán phẳng: Ngoại lực nằm trong mặt phẳng đi
qua trục z (yOz) => Chỉ tồn tại các thành phần ứng
lực trong mặt phẳng này: Nz, Mx, Qy x Mx N z Z Qy y
• Nz - lực dọc; Qy - lực cắt; Mx – mô men uốn
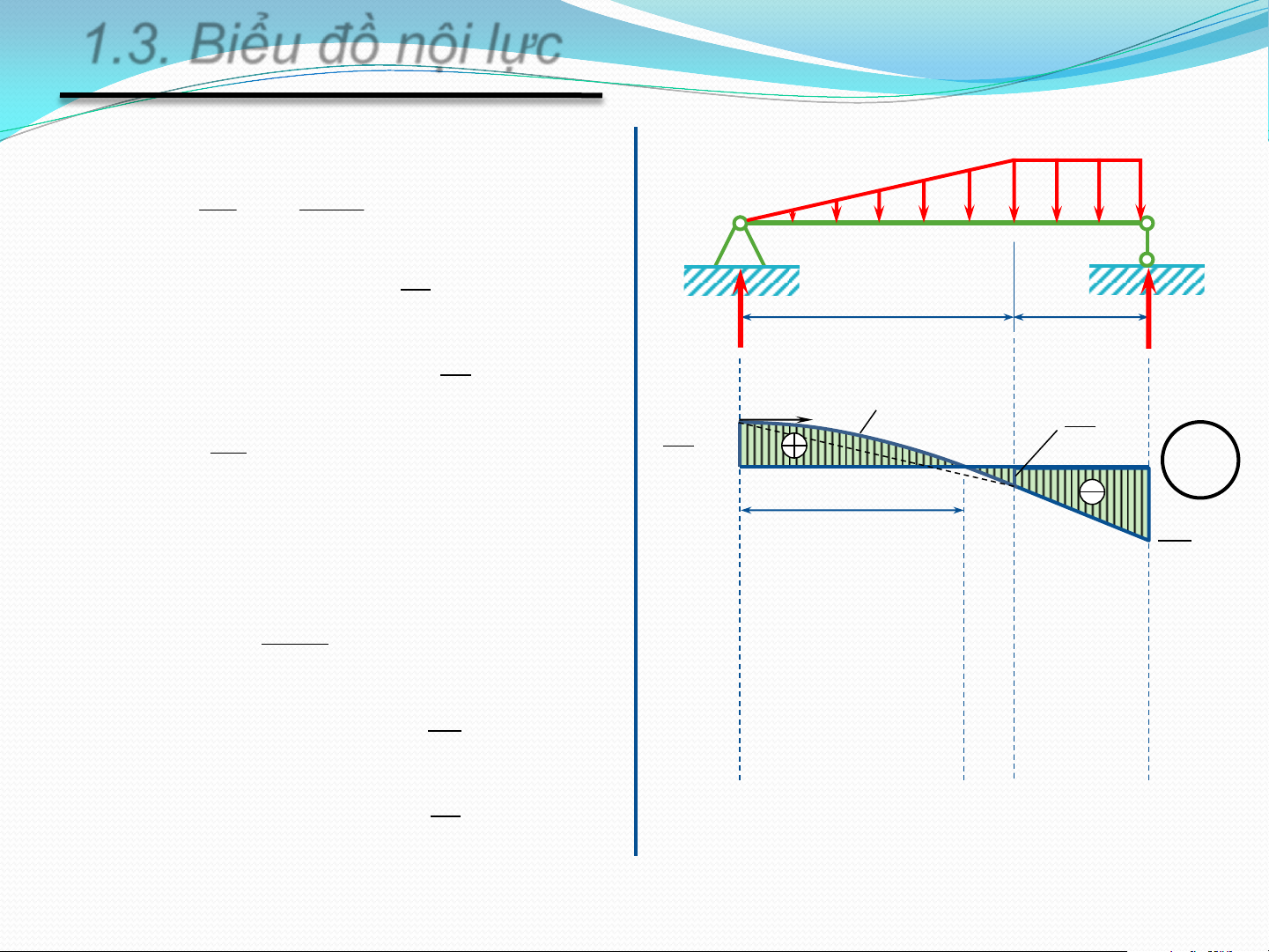
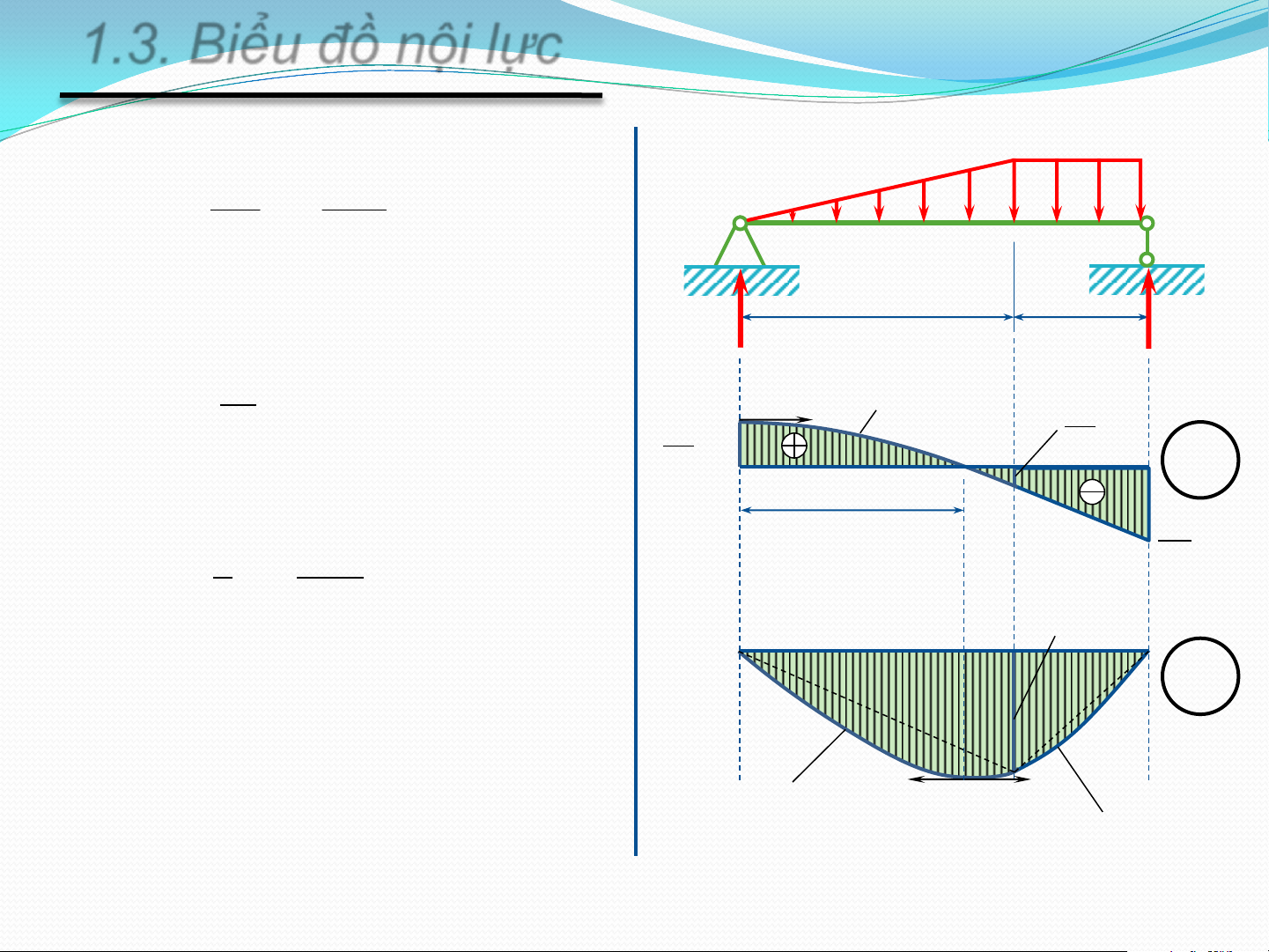
1.3. Biểu đồ nội lực
Để xác định các thành phần nội lực: PP MẶT CẮT
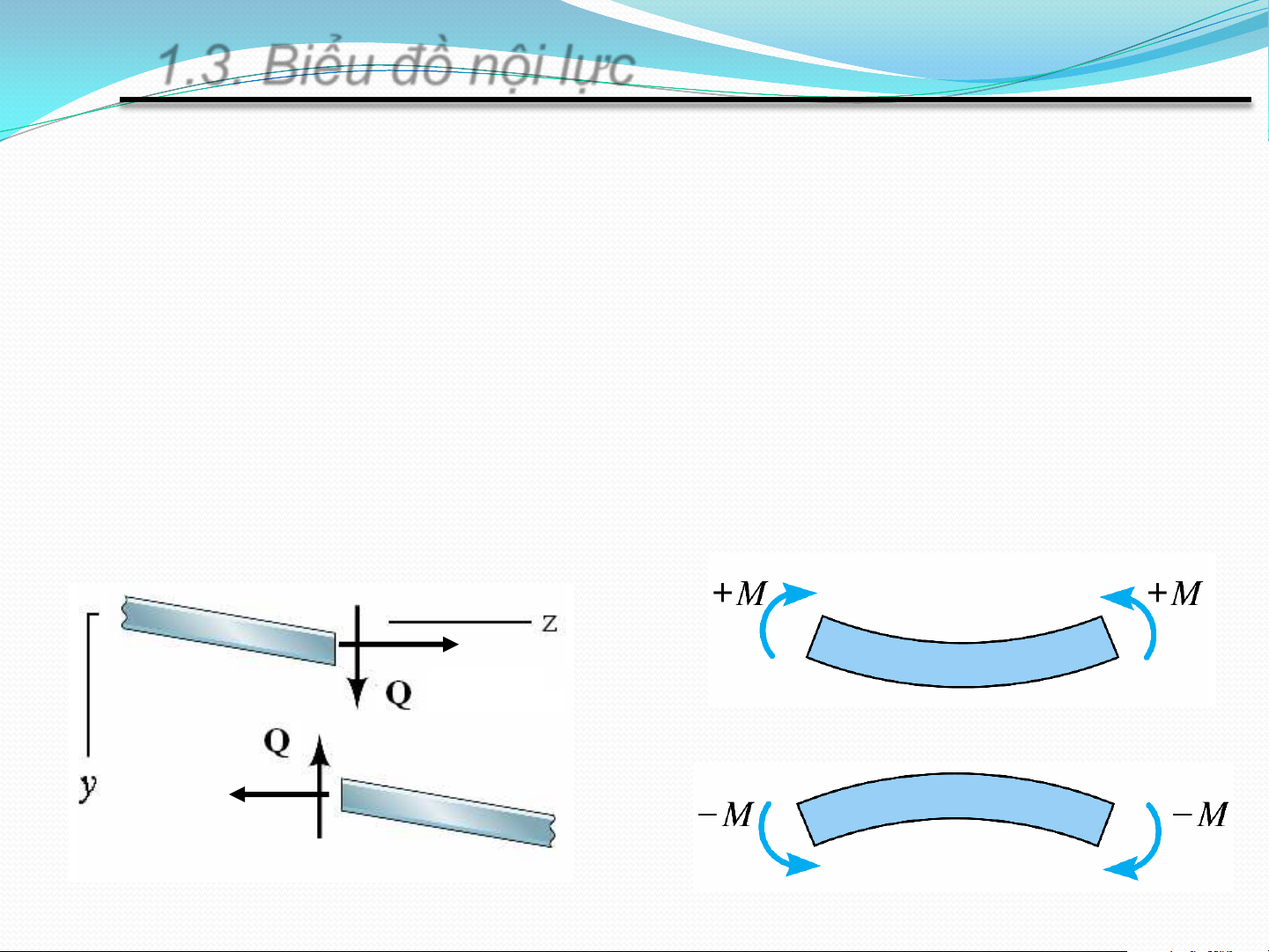
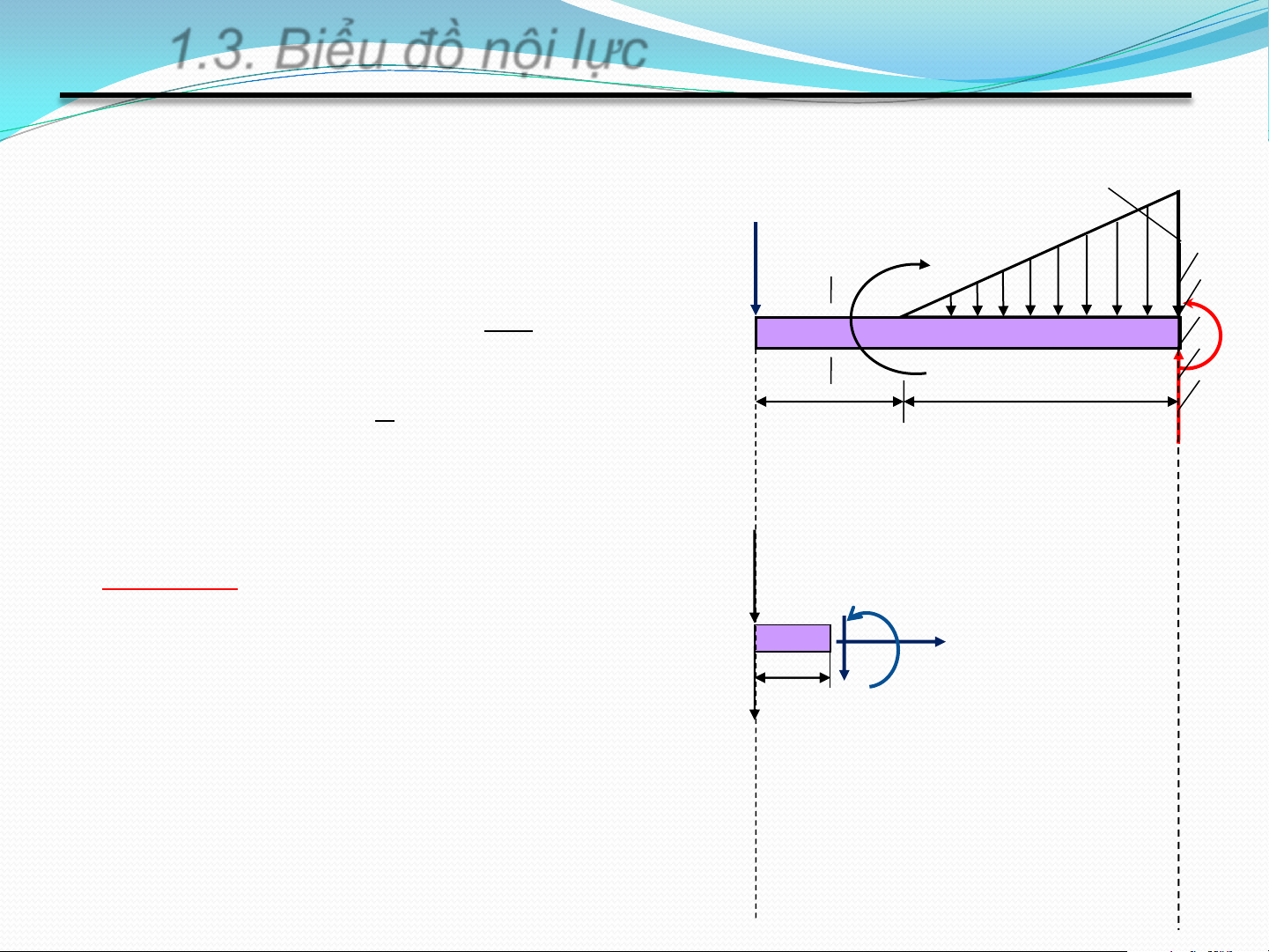
 Qui ước dấu các thành phần ứng lực
 Lực dọc: N>0 khi có chiều đi ra khỏi mặt cắt
 Lực cắt: Q>0 khi có chiều đi vòng quanh phần thanh
đang xét theo chiều kim đồng hồ
 Mô men uốn: M>0 khi làm căng các thớ dưới N N
1.3. Biểu đồ nội lực – PP mặt cắt biến thiên
Các bước vẽ biểu đồ nội lực a.
Xác định phản lực tại các liên kết
b. Phân đoạn thanh sao cho biểu thức của các
thành phần ứng lực trên từng đoạn là liên tục c.
Viết biểu thức xác định các thành phần ứng lực
N, Q, M theo toạ độ mặt cắt ngang bằng phương pháp mặt cắt
d. Vẽ biểu đồ cho từng đoạn căn cứ vào phương
trình nhận được từ bước (c) e.
Kiểm tra biểu đồ nhờ vào các nhận xét mang
tính trực quan, tính kinh nghiệm.
1.3. Biểu đồ nội lực
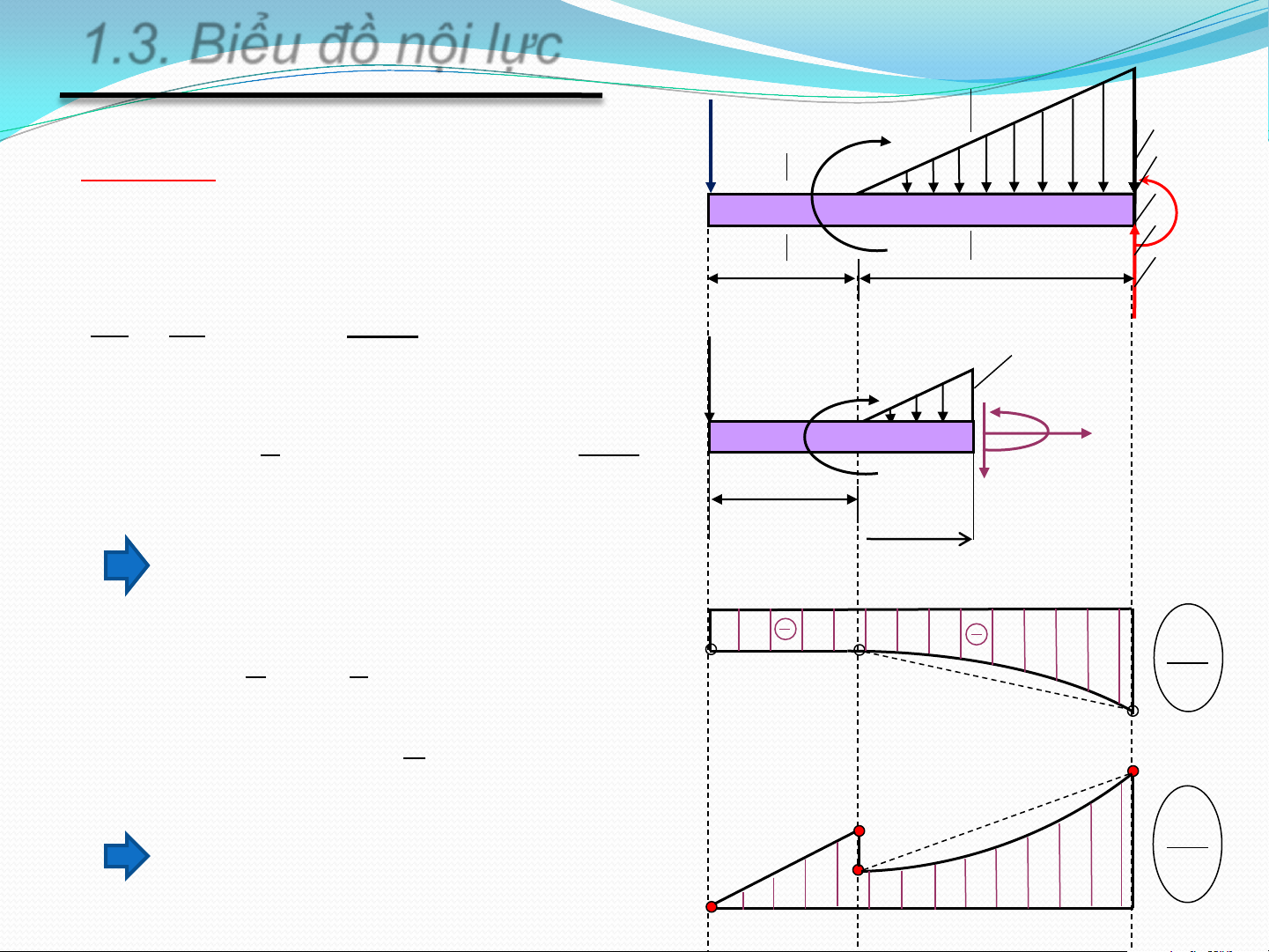
 Biểu đồ lực dọc, lực cắt vẽ theo qui ước và mang dấu N, Q z
 Biểu đồ mô men luôn vẽ về phía thớ căng z M
1.3. Biểu đồ nội lực NHẬN XÉT:
• Tại mặt cắt có lực tập trung thì biểu đồ lực cắt có bước
nhảy, độ lớn bước nhảy bằng giá trị lực tập trung. Xét từ
trái qua phải chiều bước nhảy cùng chiều lực tập trung.
• Tại mặt cắt có mô men tập trung thì biểu đồ mô men
có bước nhảy, độ lớn bước nhảy bằng giá trị mô men tập
trung. Xét từ trái qua phải nếu mô men quay thuận chiều
kim đồng hồ thì bước nhảy đi xuống.
• Tại mặt cắt có lực cắt bằng 0 thì biểu đồ mô men đạt cực trị.
• Biểu đồ mô men luôn có xu hướng “hứng” lực.
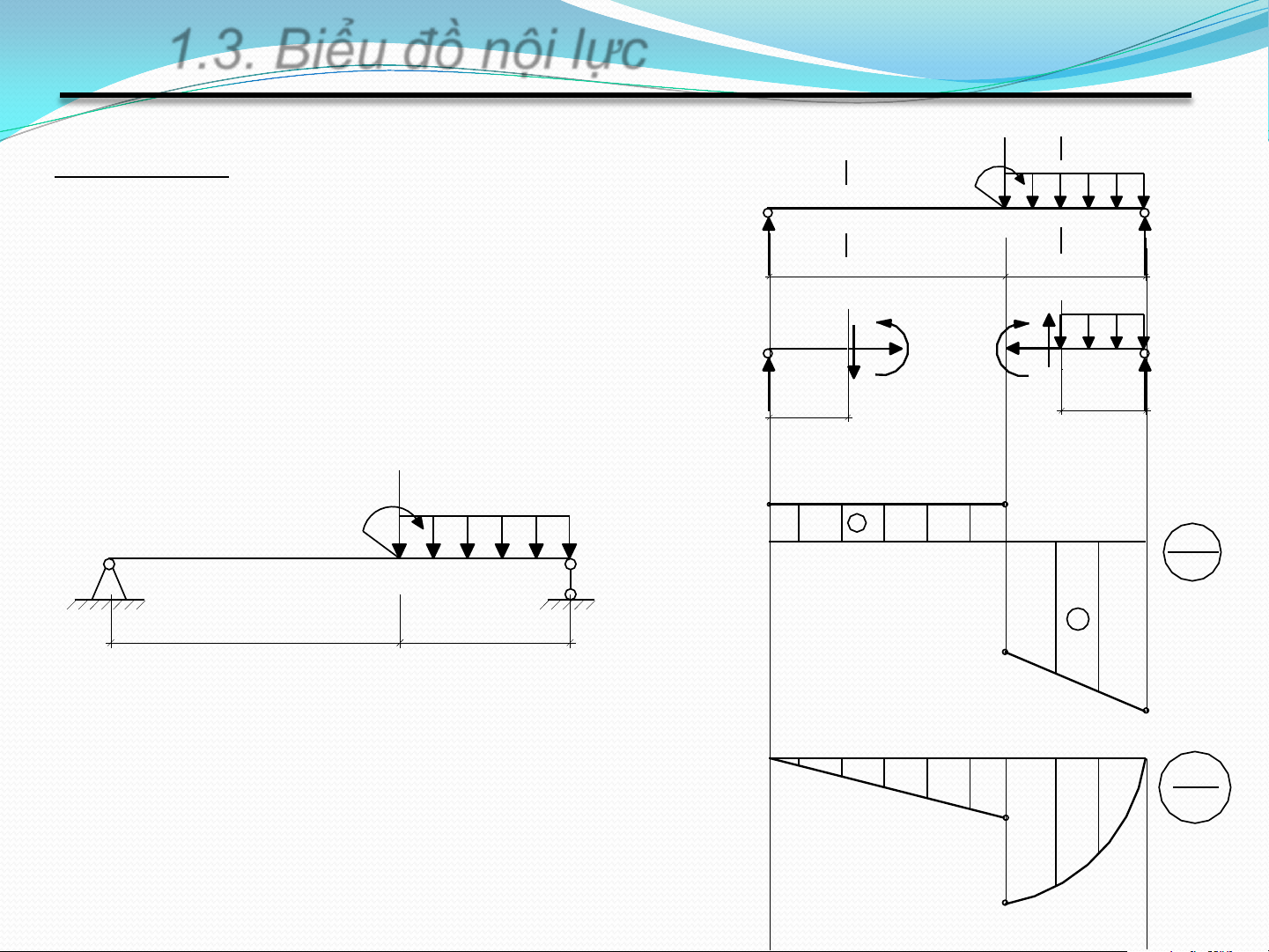
1.3. Biểu đồ nội lực F Ví dụ 1: Vẽ 2 các biểu đồ nội 1 Mo q
lực cho dầm chịu lực như B V 2 hình vẽ V C A 1 2a F a
Số liệu: a=1m; F=15 kN; M q 0= 9 M M kNm; q=6kNm N N V V Q C A Q Z1 Z2 F M q o 3 3 + Q kN _ 2a a 12 18 M kNm 6 15
1.3. Biểu đồ nội lực VÍ DỤ 2 1. Phản lực ngàm: q=15kN/m F=10kN M=5kNm
Y  F  q V  0 V 1015  25kN C C 1     M .  . BC M M M F AC q  0 C C C 3 A 1 B C 2
 M  5 10.315.  35kNm 1m 2m C V 3 C
2. Biểu đồ lực cắt và mô men uốn: F *Đoạn AB: M 1 Mặt cắt 1-1 : 0  z 1( ) 1 m N N1 N  0 1 1 z Q 1
Y Q  F  0Q  1  0 1 1 kN
M  M  F.z  0 M  1  0 1 1 1 1 1 z
1.3. Biểu đồ nội lực M=5kNm 2 F=10kN q=15kN/m *Đoạn BC: 1 M Mặt cắt 2-2 : 0  C z  2( ) 2 m A B C N  0 1 2 2 1m 2m V q z 15z C z 2  2  q  z q F z q 2 2 M M 2 2 1 15z2
Y  Q  F  q z  0Q  1  0  N 2 z 2 2 2 2 4 Q 2 1m z
z  0  Q  1  0 2 2 2 kN
z  2  Q  2  5 2 2 kN 0 0 Q 1 1 10 10
M  M  q .z . z  F. 1  0 2 z M z 2 2  2  kN 2 3 5 25 3  M  5  10  2 z2 z2 4 35 10
z  0  M  5  M 2 2 kN 5
z  2  M  3  5 kNm 2 2 kN 0 0
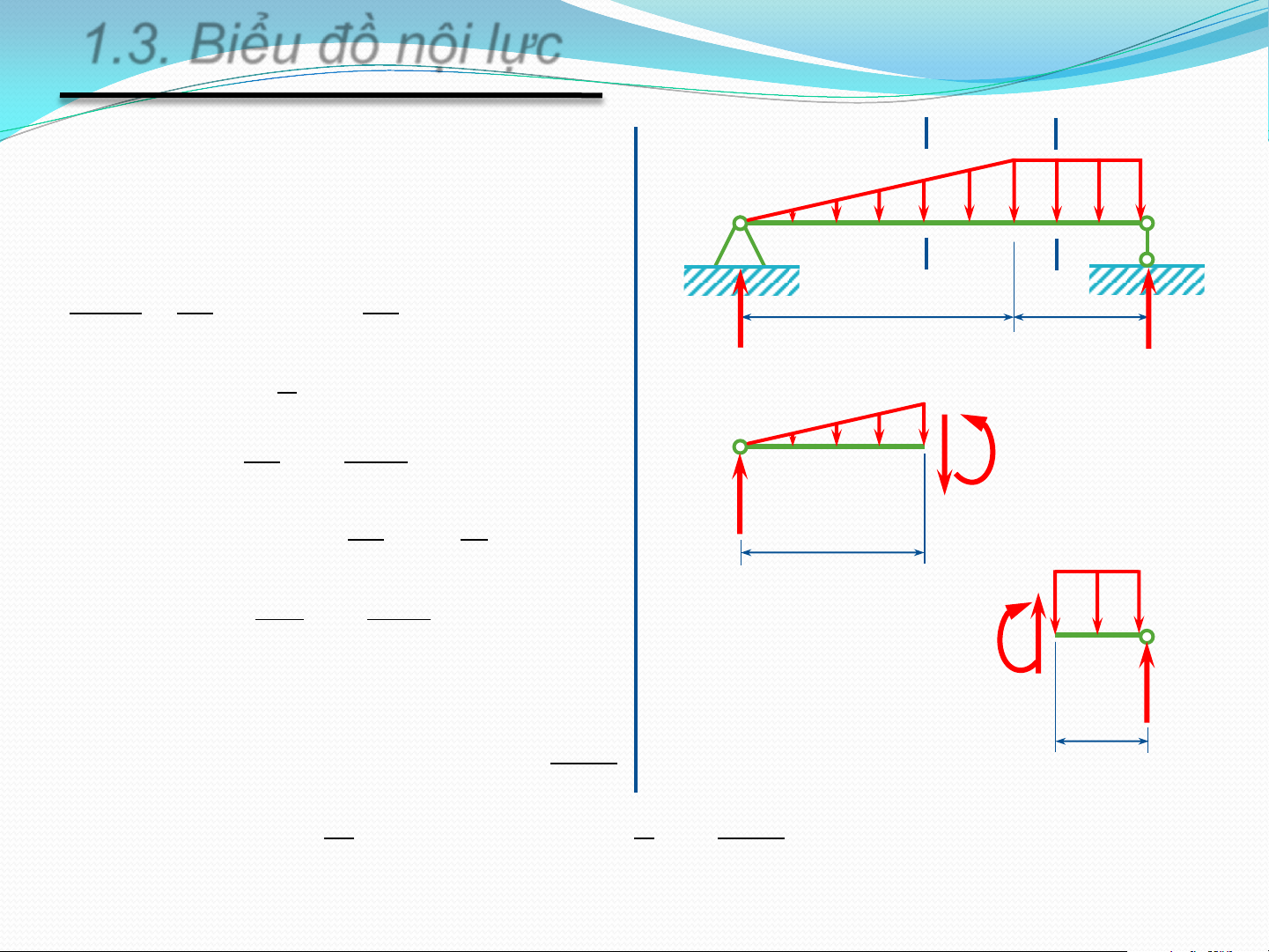
1.3. Biểu đồ nội lực q Ví dụ 2.4:
Vẽ biểu đồ các thành phần ứng lực A B
trên các mặt cắt ngang của thanh C
chịu tải trọng như hình vẽ. VA 2a a B V GIẢI: 1. Xác định phản lực a a
M V  a  qa   qa   B A   5 3   0 3 2 13  V  qa A 18
Y V V qa qa  0 A B 23  V  qa B 18
1.3. Biểu đồ nội lực 1 q 2
2. Cắt và xét từng phần thanh như hình vẽ A B
Đoạn AC: 0  z  2 1 a 1 C 2 q  1 z  1 z    q q  1 z  1 z V q 2a 2a A 2a a B V 1  q  1 z 
Y  Q V  q z  z  0 1 M A  1 1 2 1 q 13 2 qa     1 Q 1 z O 4a 18  q V 2  1 z  A 1 Q
M  M V z  z   0 O 1 A 1  1   4 q a  3 1 z q 13qa M 3 2  M    1 1 z 1 z 12a 18 O
Đoạn BC: 0  z  a 2 Q 2 B V 23
  Q qz V  0 qa Y    z 2 2 Q qz B 2 2 18 2 z q 23      0 qa M M qz V z
 M   z  z O 2  2  2 2 B 2 2 2 2 2 2 18
1.3. Biểu đồ nội lực q 3. Vẽ biểu đồ q 13 2  qa Q   z  0  z  2 1 1  1 a A B 4a 18 C  13
Q  Q z  0  qa  A 1  1   18  V  A 2a a B V 5 Q 
 Q z  2a   qa C 1  1   18 parabol 5 13 qa q     Parabol lồi qa Q ' 0 18 1 Q 2 18 y a
Q '  0  z  0   1 1 Q Q A 1,max 1,7 23 a qa 18
Q  0  z  1, 7 1 1 a 23  qa Q  qz  0   2 2  z2 a 18  23 Q  Q z  0   qa  B 2  2   18   5 Q 
 Q z  a   qa C 2  2   18
1.3. Biểu đồ nội lực q 3. Vẽ biểu đồ q 13 3  qa M   z  z 0  z  2 1 1 1  1 a A B 12a 18 C
M  M z  0  0  A 1  1    2 V
M  M z  2a  0,78 A qa  C 1  1  2a a B V q parabol M '   z  0 0  z  2 1 1 với a 5 2a 1 13 qa qa 18 Q
 Đường cong bậc 3 lồi 18 y 2
M '  0  z  1, 7a  M  0,82 1 1 1,max qa 1,7 23 a qa q 23 2 qa 18
 M   z  z 0   2 2 2  z2 a 2 18 2 0,78qa
M  M z  0  0  B 2  2   M  x
M  M z  a  qa  C   2 0,78 2 2
M '  q  0  2 Parabol lồi 2
M '  0  z  2, 56  đường bậc a a 0,82qa 2 2 3 parabol
 M2 không có cực trị trên [0,a]
1.4. Biểu đồ nội lực – PP vẽ theo điểm đặc biệt
 Cơ sở: Dựa vào mối liên hệ vi phân giữa Q, M và q(z) 2 d M dQ   q(z) 2 dz dz
 Biết tải trọng phân bố =>nhận xét dạng biểu đồ Q,
M => xác định số điểm cần thiết để vẽ được biểu đồ
 q=0 => Q=const => QA=? (hoặc QB)
M bậc 1 => MA=? và MB=?
 q=const => Q bậc 1 => QA=? QB=?
M bậc 2 => MA=?; MB=?; cực trị? tính lồi, lõm,..?