



















Preview text:
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 Điện thoại: 0946798489 ĐỀ Đ Ề SỐ S 2. 2 ÔN THI T ĐG Đ NL ĐHQ Đ G HÀ NỘI 20 2 2 0 1- 1 2 - 02 0 2 2
• |FanPage: Nguyễn Bảo Vương
A. TRẮC NGHIỆM KHÁCH QUAN (35 CÂU)
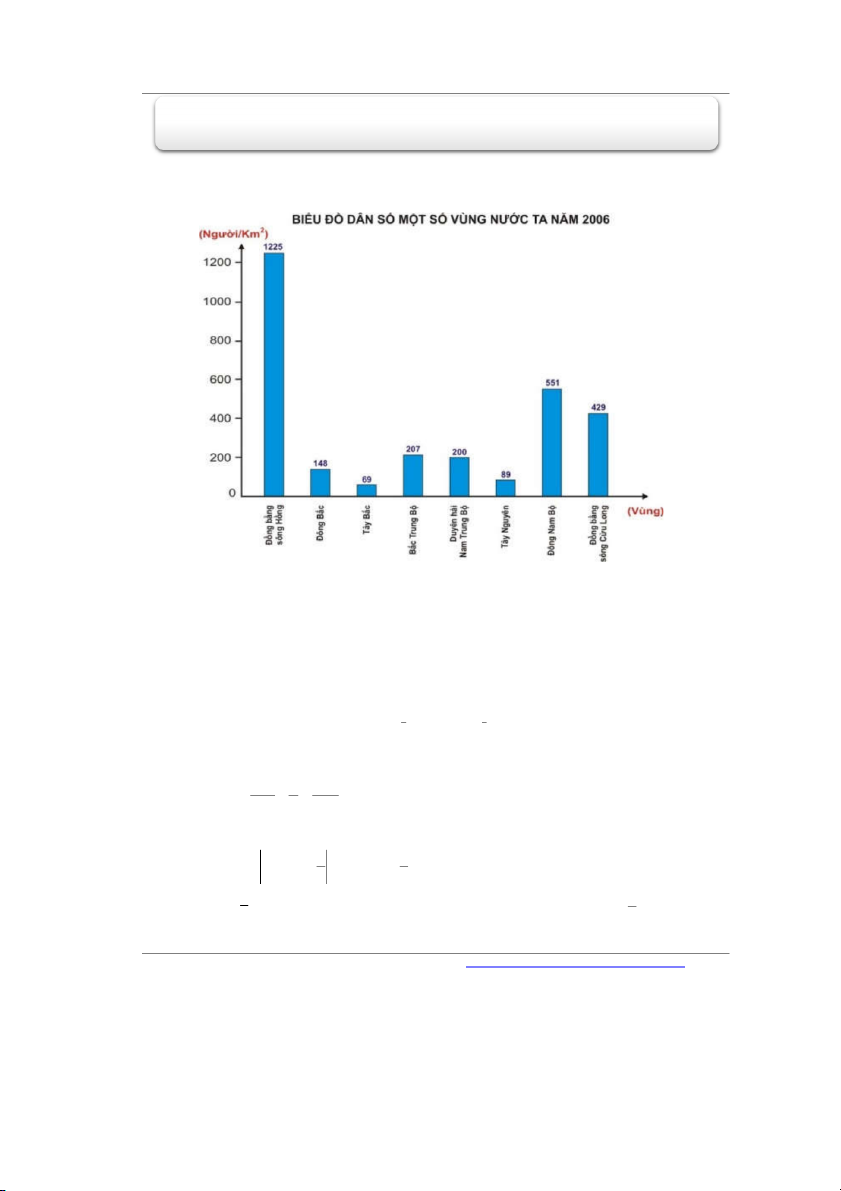
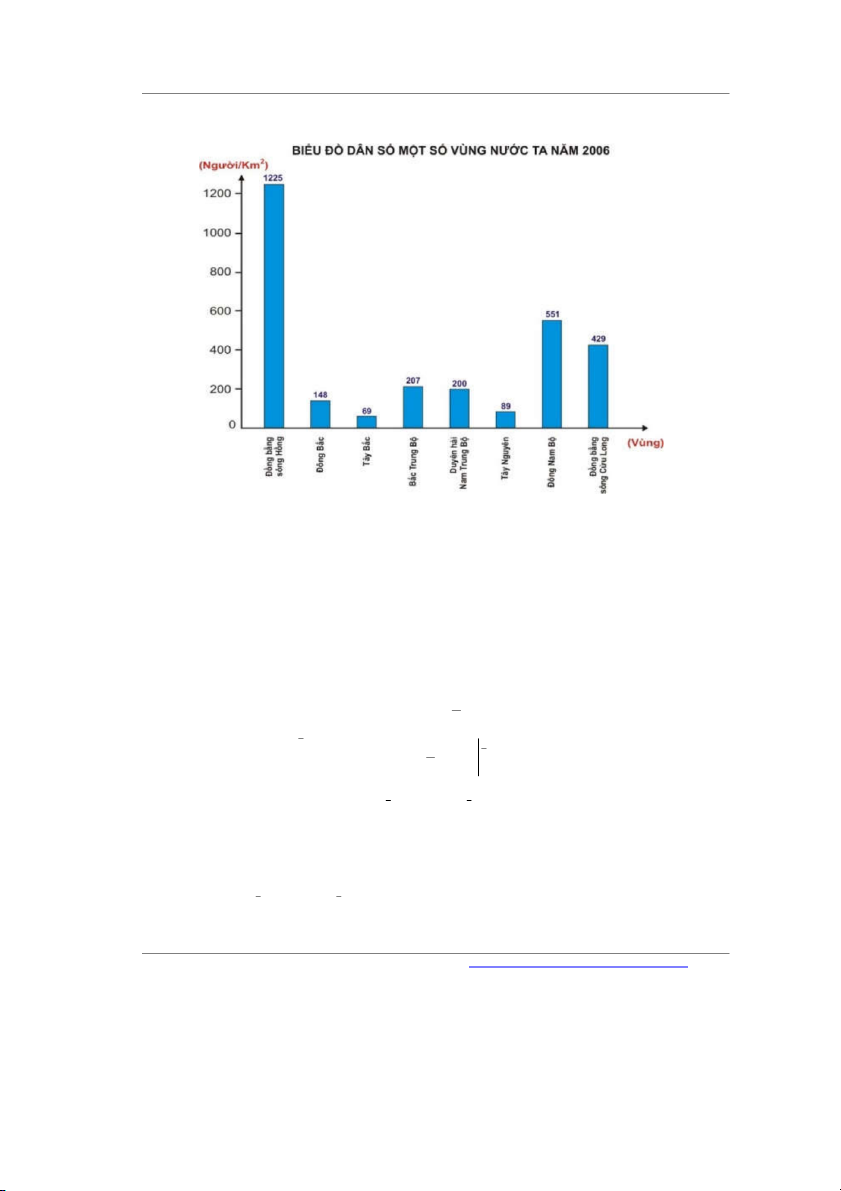
Câu 1. Người ta thống kê dân số một số vùng nước ta năm 2006 biểu diễn thành biểu đồ ở trên.
Vùng nào có dân số ít nhất? A. Tây Bắc. B. Tây Nguyên
C. Đồng Bằng Sông Hồng. D. Đồng Bắc
Câu 2. Một ô tô đang chạy đều với vận tốc a m / s thì người ta đạp phanh; từ thời điểm đó, ô tô
chuyển động chậm dần đều với vận tốc v t 5t a m / s , trong đó t là thời gian tính bằng
giây, kể từ lúc đạp phanh. Hỏi từ lúc đạp phanh đến lúc dừng hẳn ô tô di chuyển được 40 mét thì
vận tốc ban đầu a bằng bao nhiêu? A. a 25 . B. a 80 . C. a 20 . D. a 40 .
Câu 3. Tập nghiệm của bất phương trình log 2 x x log 2x 2 1 1 2 2 A. 1; .
B. 1;2 2; . C. 1; 2 . D. 1; 2 .
Câu 7. Trong không gian với hệ tọa độ Oxyz , gọi H hình chiếu vuông góc của M 2;0; 1 lên đường x 1 y z 2 thẳng :
. Tìm tọa độ điểm H . 1 2 1 A. H 2;2;3. B. H 0;2; 1 . C. H 1;0; 2 . D. H 1 ; 4 ;0 . 1 1 Câu 8. Tìm m để 2 4x 2m
x 2x mvới mọi x? 2 2 3 3 A. m . B. 2 m 3 C. m 3 . D. m . 2 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Câu 9. Có bao nhiêu giá trị nguyên m để phương trình dưới đây có nghiệm? 2 4sin x .cos x m 3 sin 2x cos 2 x 3 6 A. 5 B. 1 C. 3 D. 7 Câu 12. Cho f
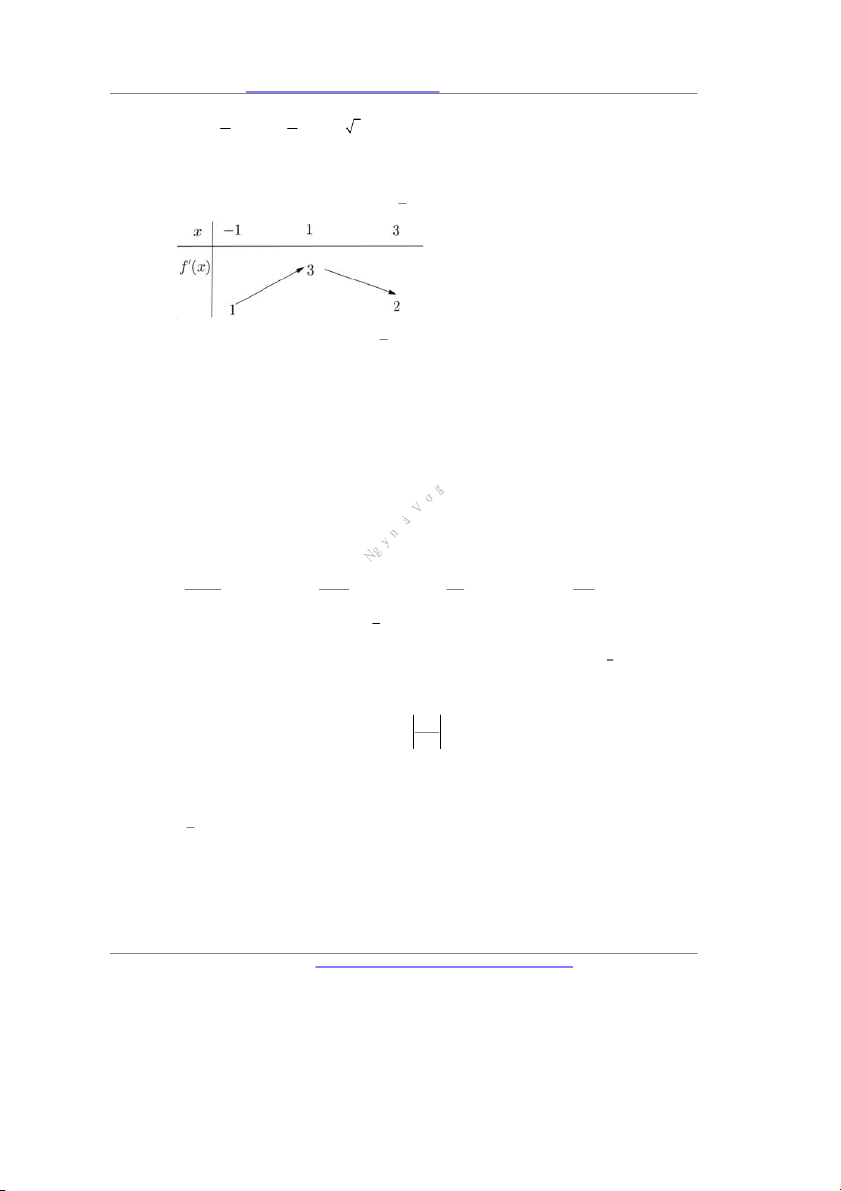
x mà hàm số y f 'x có bảng biến thiên như hình vẽ bên. Tất cả các giá trị của tham 1
số m để bất phương trình 2 m x f x 3
x nghiệm đúng với mọi x 0;3 3 là A. m f 3 B. m f 2 1 C. m f 0 D. m f 0 3
Câu 13. Một chất điểm thực hiện chuyển động thẳng trên trục Ox với vận tốc được cho bởi công thức vt 2
3t 4t (m / s), (t là thời gian). Biết rằng tại thời điểm bắt đầu của chuyển động, chất điểm
đang ở vị trí có tọa độ x 3. Tọa độ của chất điểm sau 1 giây chuyển động là ? A. x 9. B. x 4. C. x 5. D. x 6.
Câu 14. Một khách hàng có 100 triệu đồng gửi vào ngân hàng kì hạn 3 tháng với lãi suất 0.65% một
tháng theo phương thức lãi kép. Hỏi sau bao nhiêu quý thì vị khách này mới có số tiền lãi nhiều hơn số tiền gốc. A. 48 quý. B. 36 quý. C. 12 quý. D. 24 quý.
Câu 15. Số nghiệm của phương trình log x 4 3 là: 5 A. 3 . B. 1. C. 2 . D. 0 .
Câu 16. Gọi H là hình phẳng giới hạn bởi các đường 2
y x 1 và y 4x 2 . Khi đó thể tích khối tròn
xoay được sinh ra khi quay hình phẳng H quanh trục Ox là: 1016 248 4 224 A. . B. . C. . D. . 15 3 3 15 1
Câu 17. Giá trị lớn nhất của m để hàm số 3 2
y x mx 8 2m x m 3 đồng biến trên là? 3 A. m 6 B. m 2 C. m 2 D. m 4
Câu 18. Cho 2018 phức z a bi (trong đó a , b là các 2018 thực thỏa mãn 3z 4 5i z 1 7 11i . Tính ab . A. ab 6 . B. ab 6. C. ab 3 . D. ab 3 . z
Câu 19. Tập hợp điểm biểu diễn số phức z thỏa mãn 3 là đường nào? z i A. Một đường tròn. B. Một đường elip. C. Một đường thẳng. D. Một đường parabol.
Câu 20. Trong mặt phẳng tọa độ Oxy cho bốn điểm A3;-5,B-3;3 ,C -1;-2,D5;-10. Hỏi 1 G ;-3
là trọng tâm của tam giác nào dưới đây? 3 A. ABD. B. ABC . C. BCD . D. ACD .
Câu 21. Với giá trị nào của m thì phương trình sau đây là phương trình sau đây là phương trình của đường tròn 2 2 x y 2 m
2 x 4my 19m 6 0 ? A. m 1hoặc m 2. B. m 2 hoặc m 1. C. 1 m 2 . D. 2 m 1.
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Câu 22. Trong không gian với hệ tọa độ Oxyz cho điểm M 1; 2 ;
3 . Gọi A , B , C lần lượt là hình chiếu của M lên các trục x O x , y O y , z O
z . Phương trình mặt phẳng ABC là A. x y z 0 .
B. x 2y 3z 6 0 . 1 2 3
C. 6 x 3 y 2z 6 0 . D. 6 x3 y 2z 6 0 .
Câu 23. Cho tam giác ABC vuông cân tại A , AB 2a. Thể tích của khối tròn xoay tạo thành khi quay
tam giác ABC quanh cạnh AB bằng 3 4 a 3 3 a 3 8 a A. . B. 8 a 2 . C. . D. . 3 3 3 3
Câu 24. Hình trụ có thiết diện qua trục là hình vuông cạnh 2a. Một mặt cầu tiếp xúc với các đường sinh
của hình trụ và hai đáy của hình trụ. Tỉ số thể tích của khối trụ và khối cầu là. A. 4 . B. 2. C. 1 . D. 3 . 3 2 2
Câu 25. Cho hình lăng trụ ABC .A B C
có đáy là tam giác đều cạnh a . Hình chiếu vuông góc của A lên
mặt phẳng ABC trùng với trung điểm cạnh BC . Góc giữa BB và mặt phẳng ABC bằng
60. Tính thể tích khối lăng trụ ABC.A B C . 3 3 3 3 A. 3a 3 . B. 2 a 3 . C. a 3 . D. a 3 . 8 8 4 8
Câu 26. Cho tứ diện ABCD . Điểm M thuộc đoạn AC ( M khác A , M khác C ). Mặt phẳng đi
qua M song song với AB và AD . Thiết diện của với tứ diện ABCD là hình gì? A. Hình tam giác B. Hình bình hành C. Hình vuông D. Hình chữ nhật
Câu 27. Trong không gian Oxyz , cho điểm A 2 ;2; 2 , B3; 3
;3 . M là điểm thay đổi trong không MA 2 gian thỏa mãn
. Khi đó độ dài OM lớn nhất bằng? MB 3 A. 6 3. B. 5 3 . C. 5 3 . D. 12 3. 2 x 1 2t
Câu 28. Trong không gian với hệ tọa độ Oxyz cho đường thẳng d : y 2 4t . Hình chiếu song song z 3t x 1 y 6 z 2
của d lên mặt phẳng Oxz theo phương : có phương trình là 1 1 1 x 3 2t x 3 t x 1 2t x 3 2t A. y 0 . B. y 0 . C. y 0 . D. y 0 . z 1 4t z 1 2t z 5 4t z 1 t
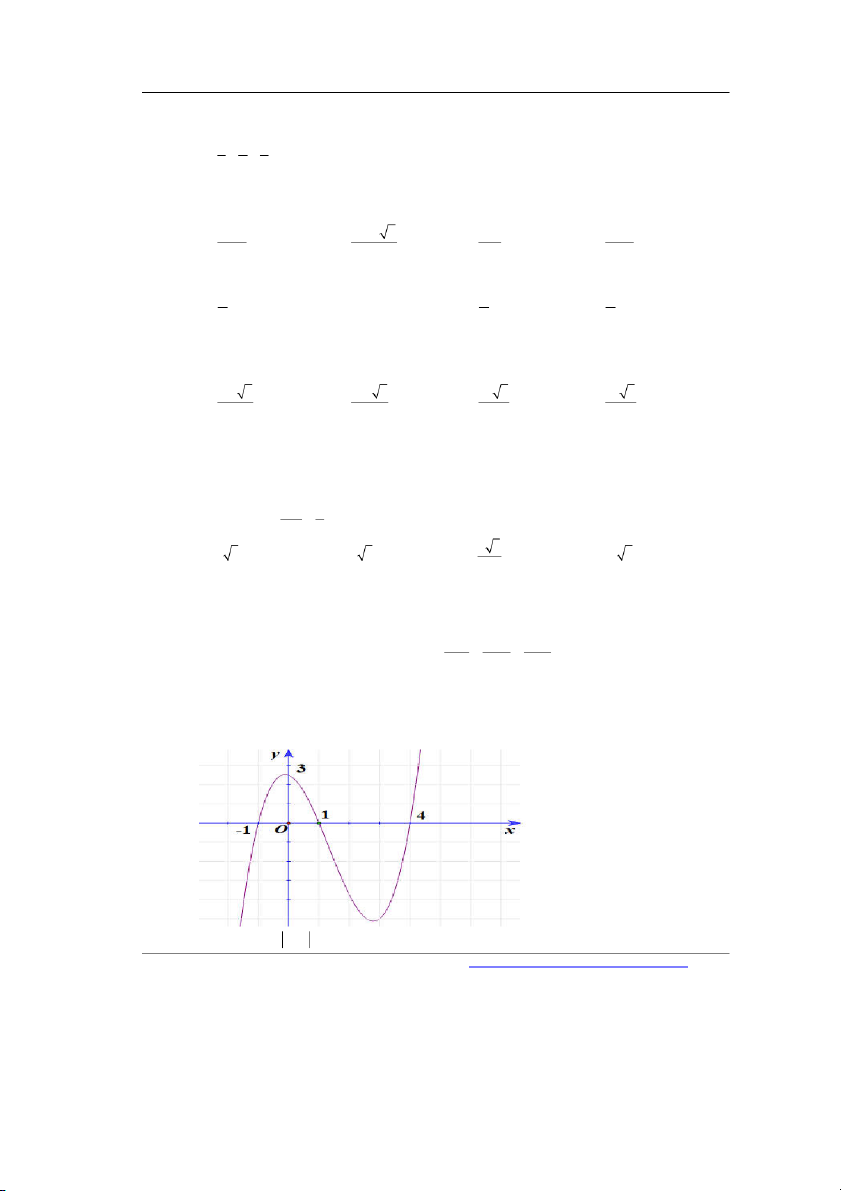
Câu 29. Cho hàm số f (x) liên tục và xác định trên , đồ thị hàm số y f (x) như hình vẽ dưới đây.
Hàm số y f 3 x có bao nhiêu điểm cực trị?
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/ A. 2. B. 5 . C. 4 . D. 1.
Câu 31. Cho hàm số f x 3 2
mx 3mx 3m
2 x m 2 với m là tham số thực. Có bao nhiêu giá trị
nguyên dương nhỏ hơn 10 của tham số m để hàm số g x f x có đúng 5 điểm cực trị ? A. 9. B. 10. C. 8. D. 11. 2
Câu 32. Cho phương trình: 2 x x + m 2 x x 2 – 2 3 2 3 – – 2
3 m 6m 0 . Tìm m để phương trình có nghiệm: A. m 2. B. m 4 . C. m 2 . D. m .
Câu 33. Cho hàm số f
x có đạo hàm liên tục trên và thỏa mãn các điều kiện sau: f 0 2 và 3
2x 1 f 'x xf x x,x . Tính tích phân I xf ( )xd .x 0 A. 5 I . B. 3 I . C. 3 I . D. 5 I . 2 2 2 2
Câu 34. Cho tập A 1, 2,3, 4,5,
6 . Trong các số tự nhiên gồm 6 chữ số được lập từ các chữ số thuộc tập
A , chọn ngẫu nhiên một số. Tính xác suất để trong số đó luôn xuất hiện 3 chữ số 2 , các chữ số
còn lại đôi một khác nhau. 55 35 25 45 A. . B. . C. . D. . 972 972 972 972
Câu 35. Cho khối lăng trụ ABC.A B C
có thể tích bằng 2020. Gọi M, N lần lượt là trung điểm của AA ;
BBvà điểm P nằm trên cạnh CC sao cho PC 3PC . Thể tích của khối đa diện lồi có các đỉnh là các điểm , A B,C, M , N, P bằng 2020 5353 2525 3535 A. . B. . C. . D. . 3 3 3 3 B. ĐIỀN KHUYẾT (15 CÂU) Câu 36. Cho hàm số 3 2
y x 3x 6x 1 (C). Viết phương trình tiếp tuyến của đồ thị (C) biết tung độ tiếp điểm bằng 9 Đáp án: …………..
Câu 37. Cho hàm số f x có f x x x 2x 3 3
2 ,x . Số điểm cực tiểu của hàm số đã cho là Đáp án: …………..
Câu 38. Khoảng cách từ điểm M 2 ; 4
;3 đến mặt phẳng P : 2 x– y 2 z – 3 0 là: Đáp án: …………..
Câu 39. Trong hộp có 5 quả cầu đỏ và 7 quả cầu xanh kích thước giống nhau. Lấy ngẫu nhiên 5quả cầu
từ hộp. Hỏi có bao nhiêu khả năng lấy được số quả cầu đỏ nhiều hơn số quả cầu xanh. Đáp án: ………….. f x 16
Câu 40. Cho hàm số y f x xác định trên thỏa mãn lim 12 .Tính giới hạn x2 x 2 3 5 f x 16 4 lim . 2 x2 x 2x 8 Đáp án: …………..
Câu 41. Biết rằng hàm số 2
y ax bx c a 0 đạt giá trị lớn nhất bằng 1 tại 3 x và tổng lập phương 4 2
các nghiệm của phương trình y 0 bằng 9. Tính P abc .
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 Đáp án: ………….. Câu 42. Cho hàm số 4 y mx m 2
1 x 2019 . Tìm tất cả các giá trị thực của tham số m để hàm số có ba điểm cực trị. Đáp án: …………..
Câu 43. Cho hàm số f x 3 2
ax bx cx 4 và 2
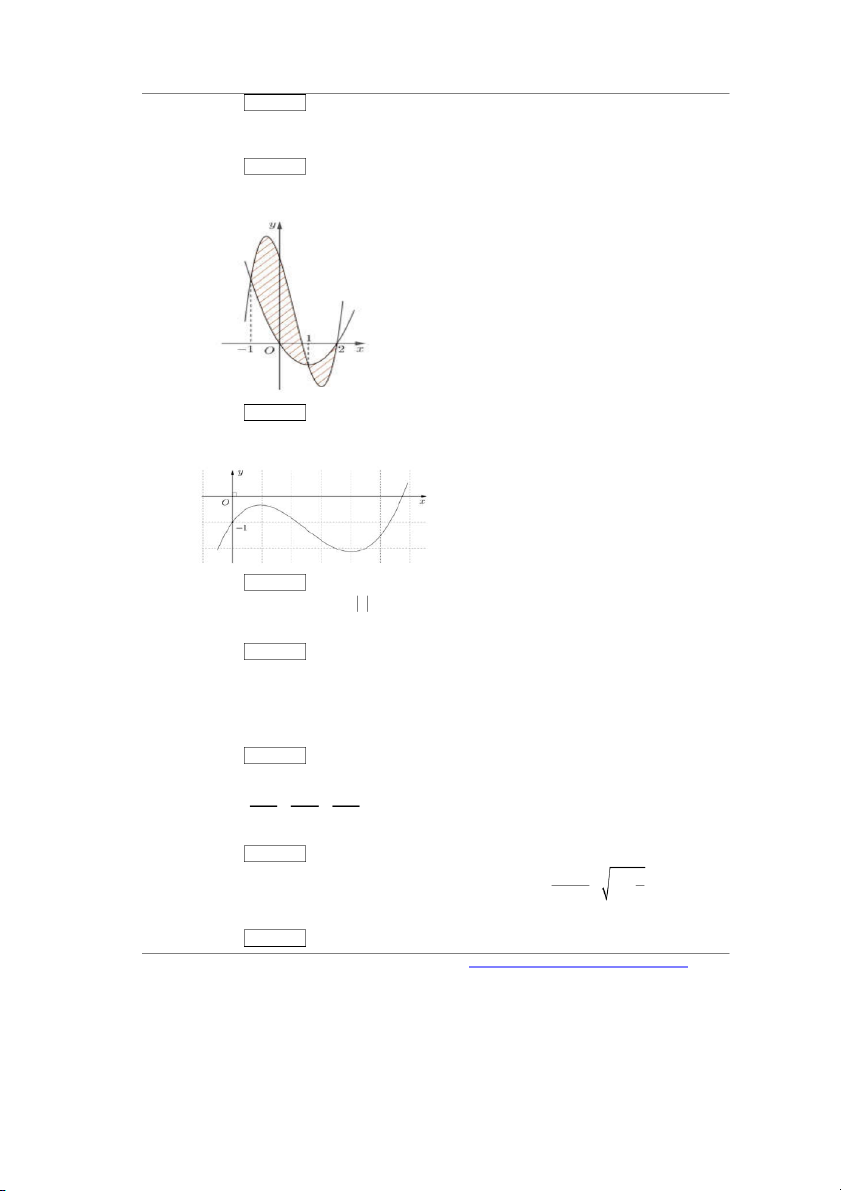
g x mx nx có đồ thị trong hình bên. Diện tích hình
phẳng giới hạn bởi đồ thị của hai hàm số trên (phần gạch chéo trong hình vẽ) bằng Đáp án: …………..
Câu 44. Cho hàm số bậc ba y f ( )
x có đồ thị là đường cong trong hình bên. Số nghiệm thực phân biệt của phương trình f 3 x f (x ) 1 0 là Đáp án: …………..
Câu 45. Cho các số phức z thỏa mãn z 2 . Biết rằng tập hợp các điểm biểu diễn các số phức
w 3 2i 2 i z là một đường tròn. Tính bán kính r của đường tròn đó. Đáp án: …………..
Câu 46. Cho hình vuông ABCD cạnh 4a , lấy H ,K lần lượt trên các cạnh AB , AD sao cho
BH 3HA AK 3KD. Trên đường thẳng vuông góc với mặt phẳng ABCD tại H lấy điểm S sao cho
SBH 30. Gọi E là giao điểm của CH và BK . Tính cosin của góc giữa hai đường thẳng SE và BC. Đáp án: …………..
Câu 47. Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng : 2x 2y z 4 0 và đường x 2 y 2 z 2 thẳng d : . Tam giác ABC có A 1;2;
1 , các điểm B, C nằm trên và 1 2 1
trọng tâm G nằm trên đường thẳng d . Tọa độ trung điểm M của BC là: Đáp án: ………….. 1 a
Câu 48. Cho các số thực a,b thỏa mãn a b 1. Biết rằng biểu thức P log đạt giá trị lớn log a a b ab nhất khi k
b a . Khi k thuộc khoảng nào sau đây: Đáp án: …………..
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Câu 49. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, mặt bên SAB là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Gọi H , M , O lần lượt là trung điểm các cạnh AB , SA, AC
và G là trọng tâm tam giác SB .
C Khoảng cách từ G đến mặt phẳng (HMO) bằng Đáp án: …………..
Câu 50. Cho khối chóp S.ABC có đáy là tam giác vuông tại , A AB 1, AC 2 .
Các mặt bên SBC , SCA , SAB lần lượt tạo với đáy các góc 90 ; ; sao cho
90 .Thể tích khối chóp S.ABC có giá trị lớn nhất bằng Đáp án: …………..
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 Lời giải tham khảo
A. TRẮC NGHIỆM KHÁCH QUAN (35 CÂU)
Câu 1. Người ta thống kê dân số một số vùng nước ta năm 2006 biểu diễn thành biểu đồ ở trên.
Vùng nào có dân số ít nhất? A. Tây Bắc. B. Tây Nguyên
C. Đồng Bằng Sông Hồng. D. Đồng Bắc Lời giải Chọn A
Câu 2. Một ô tô đang chạy đều với vận tốc a m / s thì người ta đạp phanh; từ thời điểm đó, ô tô chuyển
động chậm dần đều với vận tốc v t 5t a m / s, trong đó t là thời gian tính bằng giây, kể từ
lúc đạp phanh. Hỏi từ lúc đạp phanh đến lúc dừng hẳn ô tô di chuyển được 40 mét thì vận tốc ban đầu a bằng bao nhiêu? A. a 25 . B. a 80 . C. a 20 . D. a 40 . Lời giải Chọn C Khi ôtô dừng hẳn a v(t) 0 5 t a 0 t . 5 a 5 5 a
Theo đề bài: 40 5 t a 2 5 dt 40 t at a 20 . 0 2 0
Câu 3. Tập nghiệm của bất phương trình log 2 x x log 2x 2 1 1 2 2 A. 1; .
B. 1;2 2; . C. 1; 2 . D. 1;2. Lời giải Chọn D 2 2 x x 0 x x 0 Ta có: log 2 x x log 2x 2 1 1 2 2 x x x x x 2 2 2 2 3 2 0
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/ x 0
x 1 1 x 2 . 1 x 2
Vậy phương trình đã cho có tập nghiệm S 1;2 . x y 9
Câu 4. Hệ phương trình có nghiệm là: . x y 90 A. 15; 6 , –6;–1 5 . B. 15; 6 ,6;1 5 , –15;– 6 , –6;–1 5 . C. 15;6 , 6;15 .
D. –15; –6, –6; –15. Lời giải Chọn A
Ta có : y x 9 x x 9 90 2
x 9x 90 0 x 15; x 6
x 15 y 6 , x 6 y 15.
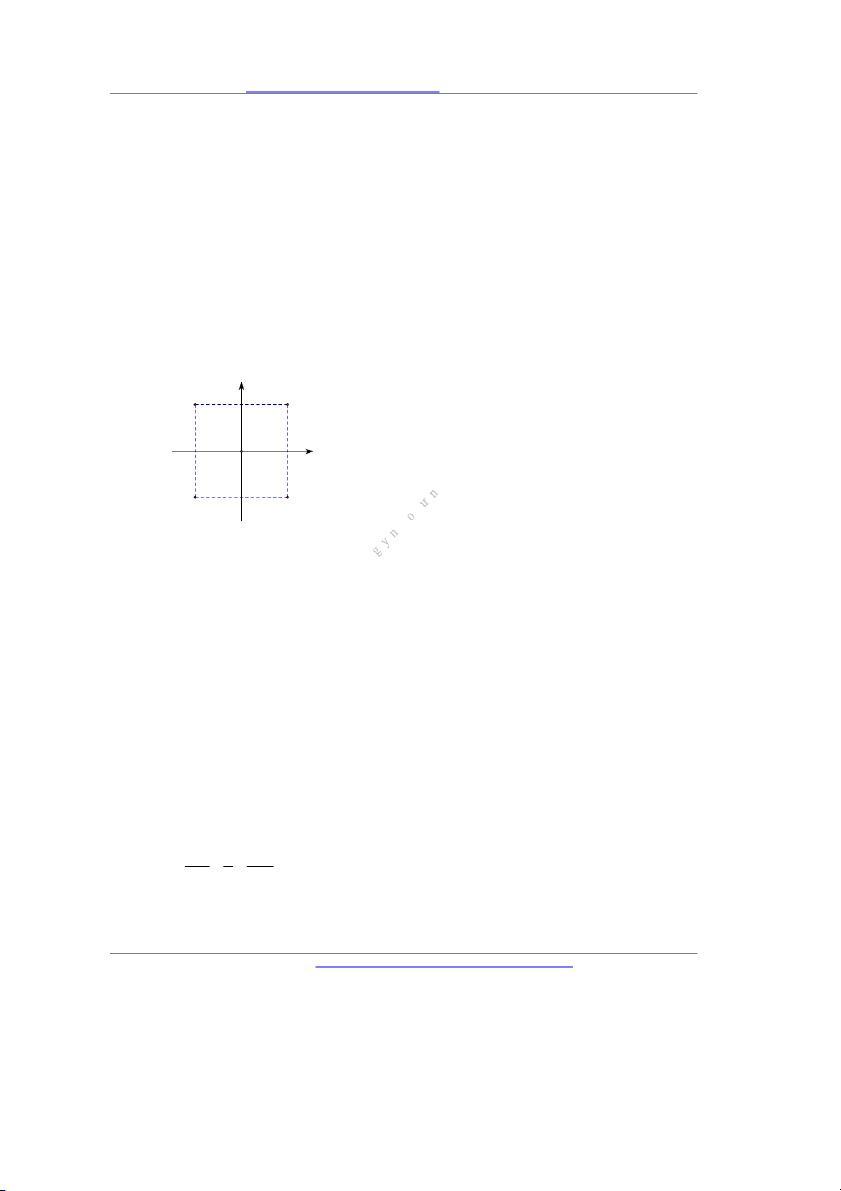
Câu 5. Cho các số phức z 1
2 ,i w 2 .i Điểm nào trong hình bên biểu diễn số phức z w ? A. Q B. M C. N D. P y N 1 P -1 0 1 x M Q -1 Lời giải Chọn D Ta có z w 1
2i 2 i 1 i . Vậy điểm biểu diễn số phức z w là điểm P 1;1 .
Câu 6. Trong không gian Oxyz , phương trình của mặt phẳng P đi qua điểm B2;1; 3 , đồng thời vuông
góc với hai mặt phẳng Q : x y 3z 0 , R : 2x y z 0 là
A. 4x 5y 3z 12 0 . B. 2x y 3z 14 0.
C. 4x 5y 3z 22 0 . D. 4x 5y 3z 22 0 . Lời giải Chọn C
Mặt phẳng Q : x y 3z 0 , R: 2 x y z 0 có các vectơ pháp tuyến lần lượt là
n 1;1;3 và n 2;1;1 . 2 1
Vì P vuông góc với hai mặt phẳng Q , R nên P có vectơ pháp tuyến là
n n , n 4;5; 3 . 1 2
Ta lại có P đi qua điểm B2;1;
3 nên P : 4 x 2 5 y 1 3 z 3 0
4x 5y 3z 22 0 .
Câu 7. Trong không gian với hệ tọa độ Oxyz , gọi H hình chiếu vuông góc của M 2;0; 1 lên đường thẳng x 1 y z 2 :
. Tìm tọa độ điểm H . 1 2 1 A. H 2;2;3. B. H 0;2;1. C. H 1;0;2. D. H 1 ; 4 ; 0 . Lời giải
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 Chọn C x 1 t
Ta có : y 2t t mà H H t1;2 ;t t 2 MH t1;2 ;t t 1 . z 2 t
Đường thẳng có một VTCP là u 1;2; 1 . Khi đó MH M . H u 0 t 1 4t t
1 0 t 0 H1;0;2 . 1 1 Câu 8. Tìm m để 2 4x 2m
x 2x m với mọi x ? 2 2 3 3 A. m . B. 2 m 3 C. m 3 . D. m . 2 2 Lời giải Chọn A 1 1 Ta thấy để 2 4 x 2m
x 2x m đúng với mọi x thì 2 1 x 2x m 0, x 2 2 2 1 1 3 Hay 2 x 2x , m x
1 m 0 m . 2 2 2
Câu 9. Có bao nhiêu giá trị nguyên m để phương trình dưới đây có nghiệm? 2 4sin x .cos x m 3 sin 2x cos 2 x 3 6 A. 5 B. 1 C. 3 D. 7 Lời giải Chọn A
Phương trình ban đầu tương đương với 2 2 sin 2x sin m 3 sin 2x cos 2 x 6 2 2 2 m 2
3 sin 2x cos 2x 2 m 3 sin 2x c os 2x cos 2x . 2 2 m 2 1 m ; 2
Phương trình ban đầu có nghiệm khi và chỉ khi 2 m 2 2 m 2 2 m 2 1 2
Câu 10. Người ta trồng 3240 cây theo một hình tam giác như sau: hàng thứ nhất trồng 1 cây, kể từ hàng
thứ hai trở đi số cây trồng mỗi hàng nhiều hơn 1 cây so với hàng liền trước nó. Hỏi có tất cả bao nhiêu hàng cây? A. 80 . B. 79 . C. 81. D. 82. Lời giải Chọn A
Giả sử trồng được n hàng cây n 1, n .
Số cây ở mỗi hàng lập thành cấp số cộng có u 1 và công sai d 1 . 1 Theo giả thiết:
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/ n 80 S n
3240 2u n 1 d 3240 2
n n 1 6480 n n 6480 0 1 n 2 n 8 1
So với điều kiện, suy ra: n 80 .
Vậy có tất cả 80 hàng cây. 2x 1
Câu 11. Họ nguyên hàm của hàm số f x
trên khoảng 2; là x 22 A. x 3 2ln 2 C . B. x 1 2ln 2 C . x 2 x 2 C. x 1 2ln 2 C . D. x 3 2ln 2 C . x 2 x 2 Lời giải 2 x 1 2 x 2 3 2 3 Ta có: f x . x 22 x 22 x 2 x 2 2 Khi đó: f x 2 x 1 2 3 3 dx dx dx 2 ln x 2 C . x 22 x 2 x 22 x 2
Trên khoảng 2; thì x 2 x 2. 2x 1 3 Vậy f x dx dx 2 l n x 2 C . x 22 x 2
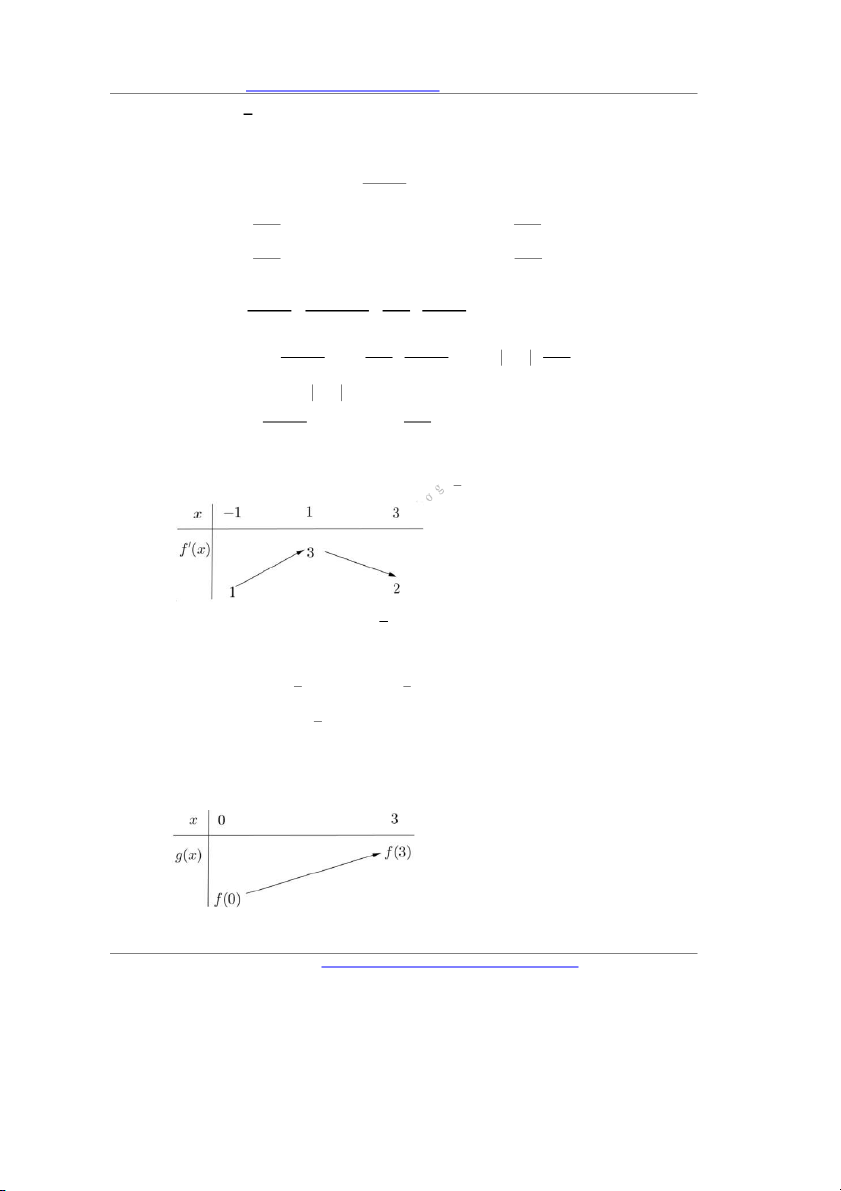
Câu 12. Cho f x mà hàm số y f 'x có bảng biến thiên như hình vẽ bên. Tất cả các giá trị của tham 1
số m để bất phương trình 2 m x f x 3
x nghiệm đúng với mọi x 0; 3 3 là A. m f 3 B. m f 2 1 C. m f 0 D. m f 0 3 Lời giải Chọn D 1 1 Ta có: 2 m x f x 3 x m f x 3 2 x x . 3 3 1
Xét hàm số g x f x 3 2 x x trên 0; 3 , có g x f x 2 ' ' x 2x . 3 g x f x 2 ' 0 ' 2x x x 0;3. Theo bảng biến thiên f ' x 1 , x 0; 3 , mà 2 2x x 1, x f x 2 ' 2 x x , x
0;3 nên ta có bảng biến thiên của g x trên 0; 3 :
Từ bảng biến thiên ta có m g x , x
0;3 m f 0
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Câu 13. Một chất điểm thực hiện chuyển động thẳng trên trục Ox với vận tốc được cho bởi công thức v t 2
3t 4t (m / s) , ( t là thời gian). Biết rằng tại thời điểm bắt đầu của chuyển động, chất điểm
đang ở vị trí có tọa độ x 3 . Tọa độ của chất điểm sau 1 giây chuyển động là ? A. x 9. B. x 4. C. x 5. D. x 6. Lời giải Chọn D
Chọn mốc thời gian khi chất điểm bắt đầu chuyển động là t 0 . 1
Khi đó quãng đường chất điểm di chuyển được trong thời gian 1 giây là s 2 3t 4tdt 3. 0
Vì tại thời điểm bắt đầu của chuyển động, chất điểm đang ở vị trí có tọa độ x 3 nên tọa độ của
chất điểm sau 1 giây chuyển động là x 3 3 6 .
Câu 14. Một khách hàng có 100 triệu đồng gửi vào ngân hàng kì hạn 3 tháng với lãi suất 0.65% một
tháng theo phương thức lãi kép. Hỏi sau bao nhiêu quý thì vị khách này mới có số tiền lãi nhiều hơn số tiền gốc. A. 48 quý. B. 36 quý. C. 12 quý. D. 24 quý. Lời giải Chọn B
Sau n quý thì ta có tổng số tiền cả vốn và lãi là 1 3 n T A r .
Với A : Số tiền ban đầu, r là lãi suất một tháng.
Số tiền lãi sau n quý là. 1 3 n T A A r 1 . Theo bài ra. T A A 1 3r n 1
A 1 3r n 2 n log 2 n 35,89 13 r .
Câu 15. Số nghiệm của phương trình log x 4 3 là: 5 A. 3. B. 1. C. 2 . D. 0 . Lời giải Chọn B
Ta có: log x 4 3 x 4 125 x 121 5
Câu 16. Gọi H là hình phẳng giới hạn bởi các đường 2
y x 1 và y 4x 2 . Khi đó thể tích khối tròn
xoay được sinh ra khi quay hình phẳng H quanh trục Ox là: A. 1016 . B. 248 . C. 4 . D. 224 . 15 3 3 15 Lời giải Chọn D x 1 3 224 2 2 2 2
x 1 4 x 2 x 4 x 3 0 2
V 4x 2 x 1 dx x 3 . 15 1 . 1
Câu 17. Giá trị lớn nhất của m để hàm số 3 2
y x mx 8 2
m x m 3 đồng biến trên là? 3 A. m 6 B. m 2 C. m 2 D. m 4 Lời giải Chọn C 2
y x 2mx 8 2m . Để hàm số đồng biến trên thì 2
y x 2mx 8 2m 0,x
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/ 1 a 0, m 3 4 m 2 . 2 m 2m 8 0 y'
Vậy giá trị lớn nhất của m là m 2.
Câu 18. Cho 2018 phức z a bi (trong đó a , b là các 2018 thực thỏa mãn 3z 4 5i z 1 7 11i. Tính ab . A. ab 6 . B. ab 6. C. ab 3 . D. ab 3 . Lời giải Chọn B
Ta có z a bi z a bi .
Khi đó 3z 4 5i z 1
7 11i 3 a bi 4 5i a bi 1 7 11i a
b a b a 5b 17 a 2 5 5 7 i 1 7 1 1i z 2 3i . 5a 7b 11 b 3 Vậy ab 6 . z
Câu 19. Tập hợp điểm biểu diễn số phức z thỏa mãn 3 là đường nào? z i A. Một đường tròn. B. Một đường elip. C. Một đường thẳng. D. Một đường parabol. Lời giải Chọn A
Gọi z x yi , x, y . z
3 z 3 z i x yi 3 x yi i x y x y 2 2 2 2 3 1 z i 9 9 2 2 x y y 0 . 4 8
Vậy tập hợp điểm biểu diễn số phức z là một đường tròn.
Câu 20. Trong mặt phẳng tọa độ Oxy cho bốn điểm A 3;- 5 , B -3; 3 , C -1;- 2 , D 5;-1 0 . Hỏi 1 G ;-3
là trọng tâm của tam giác nào dưới đây? 3 A. ABD . B. ABC . C. BCD . D. ACD . Lời giải Chọn C
Ta thấy BC 2;5 , BD 8; 1
3 nên chúng không cùng phương B,C , D là 3 đỉnh của một tam giác. x x x 3 1 5 1 B C D Mặt khác, ta lại có 3 3 3 y y y 3 2 1 0 B C D 3 3 3 1 VậyG ; 3
là trọng tâm của tam giác BCD 3
Câu 21. Với giá trị nào của m thì phương trình sau đây là phương trình sau đây là phương trình của đường tròn 2 2 x y 2 m
2 x 4my 19m 6 0 ? A. m 1hoặc m 2. B. m 2 hoặc m 1. C. 1 m 2 . D. 2 m 1. Lời giải
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 Chọn A Xét phương trình 2 2
x y 2m 2 x 4my 19m 6 0 . Để là phương trình đường tròn thì
Ta có a b c m 2 m2 2 2 m 2 2 2 19
6 5m 15m 10 0 m 1 hoặc m 2.
Câu 22. Trong không gian với hệ tọa độ Oxyz cho điểm M 1; 2 ;
3 . Gọi A , B , C lần lượt là hình chiếu của M lên các trục x O x , y O y , z O
z . Phương trình mặt phẳng ABC là A. x y z 0 . B. x 2 y 3z 6 0 . 1 2 3
C. 6 x 3 y 2z 6 0 . D. 6 x3 y 2z 6 0 . Lời giải Chọn D
Tọa độ hình chiếu của M lên các trục x O x , y O y, z O
z lần lượt là A 1; 0 ; , B0; 2 ; 0 , C 0; 0; 3 . x y z
Phương trình mặt phẳng ABC là: 1 hay 6x 3y 2z 6 0 . 1 2 3
Câu 23. Cho tam giác ABC vuông cân tại A , AB 2a . Thể tích của khối tròn xoay tạo thành khi quay
tam giác ABC quanh cạnh AB bằng 3 4 a 3 3 a 3 8 a A. . B. 8 a 2 . C. . D. . 3 3 3 3 Lời giải Chọn D B C A
Khi quay tam giác ABC quanh cạnh AB ta được một hình nón có bán kính đáy r 2a và chiều cao là h 2a .
Áp dụng công thức tính thể tích khối nón ta có 3 1 1 a2 2 8 a V r h 2 2a 3 3 3 .
Câu 24. Hình trụ có thiết diện qua trục là hình vuông cạnh 2a . Một mặt cầu tiếp xúc với các đường sinh
của hình trụ và hai đáy của hình trụ. Tỉ số thể tích của khối trụ và khối cầu là. A. 4 . B. 2. C. 1 . D. 3 . 3 2 2 Lời giải Chọn D
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/ A D O B C .
Do thiết diện đi qua trục của hình trụ là hình vuông cạnh 2a nên bán kính đáy, chiều cao của hình
trụ lần lượt là và mặt cầu nội tiếp khối trụ có bán kính là a. Thể tích khối trụ là: 2 3 V h..R 2..a . T Thể tích khối cầu là: 4 4 3 3 V R a . C 3 3 V 3
Tỉ số thể tích là T . V 2 C
Câu 25. Cho hình lăng trụ AB . C AB C
có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của A lên
mặt phẳng ABC trùng với trung điểm cạnh BC. Góc giữa BB và mặt phẳng ABC bằng
60 . Tính thể tích khối lăng trụ AB . C AB C . 3 3a 3 3 2a 3 3 a 3 3 a 3 A. . B. . C. . D. . 8 8 4 8 Lời giải Chọn A C' A' B' C H A 60° B .
Gọi H là trung điểm cạnh BC . Theo đề ra: A H ABC. AB 3 a 3 2 2 AB 3 a 3 AH . S v đ dt . A BC 2 2 4 4 AA', ABC A' AH Ta có: A' AH 60 . AA', ABC BB' ,ABC 60 3
Xét AAH vuông tại H : AH AH.tan 60 a. 2 3 Vậy 3a 3 V A H .S đvtt . ABC AB C ABC . 8
Câu 26. Cho tứ diện ABCD. Điểm M thuộc đoạn AC ( M khác A, M khác C ). Mặt phẳng đi
qua M song song với AB và AD . Thiết diện của với tứ diện ABCD là hình gì? A. Hình tam giác B. Hình bình hành C. Hình vuông D. Hình chữ nhật Lời giải Chọn A
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 A M D B P N C //AB Ta có
AB
C MN với MN //AB và N BC . AB ABC //AD Ta có
ADC MP với MP//AD và P CD . AD ADC
BCD NP .
Do đó thiết diện của với tứ diện ABCD là hình tam giác MNP .
Câu 27. Trong không gian Oxyz , cho điểm A 2;2; 2
, B 3; 3;3 . M là điểm thay đổi trong không MA 2 gian thỏa mãn
. Khi đó độ dài OM lớn nhất bằng? MB 3 5 3 A. 6 3. B. 5 3 . C. . D. 12 3. 2 Lời giải Chọn D .
Gọi M x; y; z . Ta có: MA 2 2 2
9 MA 4 MB 9 x 2 2 y 2 2 z 2 2 4 x 3 2 y 3 2 z 3 2 MB 3 2 2 2
x y z 12x 12y 12z 0 M mặt cầu S tâm I 6;6; 6 bán kính R 6 3. Khi đó OM
OI R 6 3 6 3 12 3 . max d O; I R x 1 2t Câu 28.
Trong không gian với hệ tọa độ Oxyz cho đường thẳng d :y 2 4t . Hình chiếu song song z 3 t x 1 y 6 z 2
của d lên mặt phẳng Oxz theo phương : có phương trình là 1 1 1 x 3 2t x 3 t x 1 2t x 3 2t A. y 0 . B. y 0 . C. y 0 . D. y 0 . z 1 4t z 1 2t z 5 4t z 1 t Lời giải
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/ Chọn B
Giao điểm của d và mặt phẳng Oxz là: M (5;0;5) . 0 x 1 2t
Trên d : y 2 4t chọn M bất kỳ không trùng với M (5;0;5) M 0 ; ví dụ: (1; 2;3) . Gọi A là z 3 t x1 y 6 z 2
hình chiếu song song của M lên mặt phẳng Oxz theo phương : . 1 1 1 x 1 y 6 z 2
+/ Lập phương trình d’ đi qua M và song song hoặc trùng với : . 1 1 1
+/ Điểm A chính là giao điểm của d’ và Oxz +/ Ta tìm được ( A 3;0;1) x 1 2t
Hình chiếu song song của d : y
2 4t lên mặt phẳng Oxz theo phương z 3 t x 1 y 6 z 2 :
là đường thẳng đi qua M (5;0;5) và ( A 3;0;1) . 1 1 1 0 x 3 t
Vậy phương trình là y 0 . z 1 2t
Câu 29. Cho hàm số f (x) liên tục và xác định trên , đồ thị hàm số y f (x) như hình vẽ dưới đây.
Hàm số y f 3 x có bao nhiêu điểm cực trị? A. 2 . B. 5 . C. 4 . D. 1. Lời giải Chọn B x 1 f x 0 x 1 x 4 Đặt g x f 3 x
g x x f x x 3 3 . 3 . f 3 x 3 x
Điều kiện của g x : x 3 .
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 x 2 3 x 1 x 4
gx 0 f 3 x 0 3 x 1 x 1 3 x 4 x 7
Bảng xét dấu g x :
Từ bảng xét dấu g x ta thấy hàm số y f 3 x đạt cực trị tại 5 điểm. Câu 30. 2 2 2
Trong không gian Oxyz , cho mặt cầu S : x
1 y2 z 3 1 2 và mặt phẳng
P : 2x 2y z 3 0 . Gọi Q là mặt phẳng song song với P và cắt S theo thiết diện là
đường tròn C sao cho khối nón có đỉnh là tâm của mặt cầu và đáy là hình tròn giới hạn bởi C
có thể tích lớn nhất. Phương trình của mặt phẳng Q là
A. 2x 2y z 6 0 hoặc 2x 2y z 3 0 . B. 2x 2y z 4 0 hoặc 2x 2y z 17 0 .
C. 2x 2y z 2 0 hoặc 2x 2y z 8 0. D. 2x 2y z 1 0 hoặc 2x 2y z 11 0. Lời giải Chọn D
Mặt cầu S có tâm I 1; 2
;3 và bán kính R 2 3 .
Gọi r là bán kính đường tròn C và H là hình chiếu của I lên Q . Đặt IH x ta có 2 2 r R x 2 12 x 1 1 1
Vậy thể tích khối nón tạo được là V .IH.S . . x 12 x 2 2 3 12x x . 3 C 3 3 Gọi f x 3
12x x với x 0;2 3. Thể tích nón lớn nhất khi f x đạt giá trị lớn nhất Ta có f x 2 12 3x f x 0 2
12 3x 0 x 2 x 2 . Bảng biến thiên :
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/ 1 16 Vậy V khi x IH 2. max 16 3 3
Mặt phẳng Q// P nên Q : 2x 2y z a 0 2.1 2 2 3 a a 11
Và d I;Q IH
2 a 5 6 . 2 2 2 2 2 1 a 1
Vậy mặt phẳng Q có phương trình 2x 2y z 1 0 hoặc 2x 2y z 11 0.
Câu 31. Cho hàm số f x 3 2
mx 3mx 3m 2 x m 2 với m là tham số thực. Có bao nhiêu giá trị
nguyên dương nhỏ hơn 10 của tham số m để hàm số g x f x có đúng 5 điểm cực trị ? A. 9. B. 10. C. 8. D. 11. Lời giải Chọn A
Hàm số g x f x 3 2
mx 3mx 3m 2x m 2 có 5 điểm cực trị
đồ thị hàm số f x 3 2
mx 3mx 3m 2 x m 2 cắt trục Ox tại 3 điểm phân biệt. phương trình 3 2
mx 3mx 3m 2x m 2 0 có 3 nghiệm phân biệt. Ta có 3 2
mx 3mx 3m 2x m 2 0 x 2
1 mx 2mx m 2 0 x 1 . h x 2
mx 2mx m 2 0 (2)
Yêu cầu bài toán phương trình 2 có hai nghiệm phân biệt khác 1 m 0 m 0 2
m m m 2 0 m 0 m 0. h 1 0 2 0
Vì m là số nguyên dương nhỏ hơn 10 nên m 1, 2,3,..., 9 .
Vậy có tất cả 9 giá trị m thỏa mãn yêu cầu bài toán. 2 Câu 32. 2 2 2
Cho phương trình: x – 2x
3 +2 3 – m x – 2x
3 m 6m 0. Tìm m để phương trình có nghiệm: A. m 2. B. m 4 . C. m 2 . D. m . Lời giải Chọn A Cách 1: Đặt 2
t x 2x 3 t 2. Ta có phương trình 2 2
t 2(3 m)t m 6m 0 (2)
Phương trình ban đầu có nghiệm khi PT (2) có nghiệm t 2.
Trường hợp 1: PT (2) có 2 nghiệm t m 1, t 2 thỏa mãn 2 1
t t2 . Khi đó ta tìm được 8 .
Trường hợp 2:: PT (2) có 2 nghiệm m 1
t , t2 thỏa mãn 1t 2 2t . Khi đó ta tìm được 2 8 Suy ra m 2. Cách 2: 2 2 2 2
(x 2x 3) 2(3 m)(x 2x 3) m 6m 0 (1) Đặt 2
t x 2x 3, t 0. Phương trình (1) trở thành: 2 2
t 2(3 m)t m 6m 0 . Ta có: 2 2
' (3 m) (m 6m) 9
Suy ta: t m; t m 6 . 1 2 + Với t m , suy ra: 2
x 2x 3 m 2. Xét parabol 2
y x 2x 3 (P) và đường thẳng 1 y m d .
Để (2) có nghiệm thì (P) và (d) phải có điểm chung.
Mà (P) có đỉnh I(1;2) và có bề lõm hướng lên nên m 2. (*)
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
+ Với t m 6 , suy ra: 2 2
x 2 x 3 m 6 x 2 x 9 m (3) 2 Xét parabol 2
y x 2x 9 (P ') và đường thẳng y m d ' .
Để (3) có nghiệm thì (P’) và (d’) phải có điểm chung. Mà (P’) có đỉnh (
I 1;8) và có bề lõm hướng lên nên m 8. (**)
Kết hợp (*) và (**) ta được m 2.
Câu 33. Cho hàm số f
x có đạo hàm liên tục trên và thỏa mãn các điều kiện sau: f 0 2 và 3
2x 1 f ' x xf x x,x . Tính tích phân I xf ( )xd .x 0 A. 5 I . B. 3 I . C. 3 I . D. 5 I . 2 2 2 2 Lời giải Ta có: 2
x 1 f ' x xf x x,x f ' x Suy ra: 2
x 1 f ' x x f x 1 x f x 2 1 x 1 f ' x Nên: x dx dx f x 1 ln 1 ln 2x 1 C. 2 f x 1 x 1 2 Do đó: f 1 ln 0 1 ln 2 0 1 C C 0. 2 f x 1 1 2 1 1 x 1
Khi đó: ln f x 1 ln 2 x 1 f x 1 . 2 2 x 1 f x 1 1 2 x 1 f x 1 1 2 x 1 f x 1 1 2 x 1 1
Vì f (0) 2 nên f x 1 2 x 1 3 3 3 3 3 1 x 1 Suy ra: I x 1 dx dx xdx d 2x 1 xdx 2 2 2 0 x 1 0 x 1 0 0 2 x 1 0 3 2 x 3 5 2 x 1 2 1 . 2 2 2 0
Câu 34. Cho tập A 1, 2,3, 4,5,
6 . Trong các số tự nhiên gồm 6 chữ số được lập từ các chữ số thuộc tập
A , chọn ngẫu nhiên một số. Tính xác suất để trong số đó luôn xuất hiện 3 chữ số 2 , các chữ số
còn lại đôi một khác nhau. 55 35 25 45 A. . B. . C. . D. . 972 972 972 972 Lời giải Chọn C Ta có: n 6 6 .
Gọi A là biến cố: “Chọn được số tự nhiên có 6 chữ số trong đó luôn có 3 chữ số 2 và các chữ số
còn lại đôi một khác nhau ”.
Chọn vị trí để xếp 3 chữ số 2 là: 3
C , chọn 3chữ số cho 3 vị trí còn lại là 3 A 6 5
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/ 3 3 n A C .A 25 Vậy n A 3 3 C .A P A 6 5 . 6 5 n 6 6 972
Câu 35. Cho khối lăng trụ AB . C A B C
có thể tích bằng 2020. Gọi M , N lần lượt là trung điểm của AA;
BB và điểm P nằm trên cạnh CC sao cho PC 3PC . Thể tích của khối đa diện lồi có các đỉnh là các điểm , A B,C, M , N, P bằng 2020 5353 2525 3535 A. . B. . C. . D. . 3 3 3 3 Lời giải Chọn D Giả sử V V 2020 . ABC .A B C 1 V 2 Ta có V d C ; ABC .S V . V C. ABC ABC C . 3 3 ABB A 3 1.d P ;ABC.SABC V d P ; ABC PC 3 1 P. ABC 3 Lại có V V . V 1 P ABC d C ABC CC C ABC .d . ; 4 4 . C ; ABC.S 3 A BC
1 .d P;ABBA.SABNM V Ta có P.ABNM 3 . V 1 C. ABBA .d ; C ABB A .S 3 ABBA 1 Mà d P; ABB A
d C; ABB A và S S . ABNM 2 ABB A V 1 1 Suy ra P.ABNM V V . P. V 2 ABNM C ABB A 3 . 7 3535 Vậy V V V V . ABC .MNP P .ABNM P .ABC 12 3
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 B. ĐIỀN KHUYẾT (15 CÂU) Câu 36. Cho hàm số 3 2
y x 3x 6x 1 (C). Viết phương trình tiếp tuyến của đồ thị (C) biết tung độ tiếp điểm bằng 9 Đáp án: ………….. Lời giải
Gọi M x ; y là tiếp điểm 0 0 Ta có: 2 y 3x 6x 6. Ta có: 3 2
y 9 x 3x 6x 8 0 x 1, x 2, x 4 . 0 0 0 0 0 0 0
x 4 y(x ) 18 . Phương trình tiếp tuyến là:y 18(x 4) 9 18x 81 0 0
x 1 y (x ) 9 . Phương trình tiếp tuyến là: y 9 (x 1) 9 9 x 0 0
x 2 y(x ) 18 . Phương trình tiếp tuyến là: . 0 0 y 18( x 2) 9 18 x 27 Câu 37. 2 3
Cho hàm số f x có f x x x 3 x
2 ,x . Số điểm cực tiểu của hàm số đã cho là Đáp án: ………….. Lời giải x 0 Ta có: f x 0 x 3 x 2
Ta có bảng xét dấu của f x
Vậy hàm số có 1 điểm cực tiểu
Câu 38. Khoảng cách từ điểm M 2 ; 4
;3 đến mặt phẳng P: 2 x– y 2 z – 3 0 là: Đáp án: ………….. Lời giải 2.(2) 4 2.3 3 d 1. 2 2 2 2 1 2
Câu 39. Trong hộp có 5 quả cầu đỏ và 7 quả cầu xanh kích thước giống nhau. Lấy ngẫu nhiên 5quả cầu
từ hộp. Hỏi có bao nhiêu khả năng lấy được số quả cầu đỏ nhiều hơn số quả cầu xanh. Đáp án: ………….. Lời giải
Lấy ngẫu nhiên 5quả cầu từ hộp 12 quả cầu, để số quả cẩu đỏ nhiều hơn số quả cầu xanh, những
trường hợp có thể xảy ra là
Trường hợp 1: 5 cầu đỏ Số khả năng: 5 C 1khả năng. 5
Trường hợp 1: 4 cầu đỏ, 1 cầu xanh Số khả năng: 4 1 C .C 35 khả năng. 5 7
Trường hợp 2: 3 cầu đỏ, 2 cầu xanh Số khả năng: 3 2 C .C 210 khả năng. 5 7
Áp dụng quy tắc cộng: có tất cả: 35 210 1 246 khả năng. f x 16
Câu 40. Cho hàm số y f x xác định trên thỏa mãn lim 12 .Tính giới hạn x 2 x 2 3 5 f x 16 4 lim . 2 x2 x 2x 8 Đáp án: ………….. Lời giải
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Theo giả thiết có lim f x 1
6 0 lim f x 1
6 0 lim f x 16 . x2 x2 x2 3 5 f x 16 4 5f x16 64 Ta có: lim lim 2 x 2 x 2x 8 x x 2 x 4 5f x16 2 2 4 5 f x 2 3 3 16 4 5 f x1 6 lim x x 2 x 4 5f x1 2 2 6 4 5 f x 2 3 3 16 4 f x 16 5 lim . x x 2
x 4 5f x 162 2 4 5f x 2 3 3 16 4 5 5 12. . 2 3 3 24 6
5.16 16 4 5.16 16 16
Câu 41. Biết rằng hàm số 2
y ax bx c a 0 đạt giá trị lớn nhất bằng 1 tại 3 x và tổng lập phương 4 2
các nghiệm của phương trình y 0 bằng 9. Tính P abc. Đáp án: ………….. Lời giải Hàm số b 2 y ax b x c
a 0 đạt giá trị lớn nhất bằng 1 tại 3 x nên ta có 3 a 0 và 4 2 2a 2 điểm 3 1 ; thuộc đồ thị 9 3 1 a b c . 2 4 4 2 4
Gọi x , x là hai nghiệm của phương trình y 0 . Theo giả thiết: 3 3 x x 9 1 2 1 2 3 b b c
x x 3 3x x x x Viet 9 3
9 . Từ đó ta có hệ: 1 2 1 2 1 2 a a a b 3 b 3 2 2 a a a 1 9 3 1 9 3 1 a b c a b c b 3 P abc 6. 4 2 4 4 2 4 c 2 3 c b b c 2 3 9 a a a a Câu 42. Cho hàm số 4 y mx m 2
1 x 2019. Tìm tất cả các giá trị thực của tham số m để hàm số có ba điểm cực trị. Đáp án: ………….. Lời giải m Ta có hàm số 4 y mx m 2
1 x 2019 có ba điểm cực trị m m 1 . 1 0 . m 0
Câu 43. Cho hàm số f 3 2
x ax bx cx 4 và 2
g x mx nx có đồ thị trong hình bên. Diện tích hình
phẳng giới hạn bởi đồ thị của hai hàm số trên (phần gạch chéo trong hình vẽ) bằng
Trang 22 Fanpage Nguyễn Bảo Vương
https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 Đáp án: ………….. Lời giải
Phương trình hoành độ giao điểm: 3 2 2
ax bx cx 4 mx nx 3 ax b 2 m x c n x 4 0 .
h x Vì h
x 0 có ba nghiệm x 1 , x 1 , x 2 nên hx a x 1 x 1 x 2 .
Ta có h 0 4 2a 4 a 2 .
Vậy h x 2x 1 x 1x 2 . 2 2 37
Diện tích hình phẳng S h x dx 2 2x 1 x 2 dx . 6 1 1
Câu 44. Cho hàm số bậc ba y f (x) có đồ thị là đường cong trong hình bên. Số nghiệm thực phân biệt của phương trình f 3 x f (x ) 1 0 là Đáp án: ………….. Lời giải x 0 3 f ( ) x 0 x f (x) 0 3
( ) 1 0 3 ( ) 3 1 ( ) 0 a f x f x f x f x x f x a f (x) (do x 0) 3 x 3 x f (x) b 0 b f ( ) x (do x 0) 3 x
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
f (x) 0 có một nghiệm dương x c . k Xét phương trình f ( ) x với x 0, k 0 . 3 x k Đặt g(x) f (x) . 3 x 3k g (x) f '(x) . 4 x 3k
Với x c , nhìn hình ta ta thấy f ( )
x 0 g(x) f (x) 0 4 x ( g ) x 0
có tối đa một nghiệm. g( ) c 0 Mặt khác g x ; c lim g(x)
và ( ) liên tục trên x g( )
x 0 có duy nhất nghiệm trên ; c . k
Với 0 x c thì f (x) 0 g( ) x 0 vô nghiệm. 3 x 3k
Với x 0 , nhìn hình ta ta thấy f (x) 0 g(x) f ( ) x 0 4 x ( g )
x 0 có tối đa một nghiệm. l im g( ) x 0 Mặt khác x 0
và g(x) liên tục trên ; 0. lim g( ) x x g( )
x 0 có duy nhất nghiệm trên ; 0. Tóm lại g( )
x 0 có đúng hai nghiệm trên \ 0 . a b
Suy ra hai phương trình f ( ) x , f( ) x
có 4 nghiệm phân biệt khác 0 và khác c. 3 x 3 x Vậy phương trình f 3
x f (x ) 1 0 có đúng 6 nghiệm.
Câu 45. Cho các số phức z thỏa mãn z 2 . Biết rằng tập hợp các điểm biểu diễn các số phức
w 3 2i 2 i z là một đường tròn. Tính bán kính r của đường tròn đó. Đáp án: ………….. Lời giải Gọi M x;
y là điểm biểu diễn của số phức w x yi x, y . i
Ta có: w i i w 3 2 3 2 2 z z . 2 i Theo đề bài ta có: w 3 2i w 3 2i w 3 2i z 2 2 2
2 w 3 2i 2 5 . 2 i 2 i 5
x y i
x 2 y 2
x 2 y 2 3 2 10 3 2 10 3 2 20 .
Vậy tập hợp các điểm biểu diễn của số phức w là đường tròn tâm I(3; 2 ) , bán kính R 20.
Câu 46. Cho hình vuông ABCD cạnh 4a , lấy H , K lần lượt trên các cạnh AB , AD sao cho
BH 3HA AK 3KD . Trên đường thẳng vuông góc với mặt phẳng ABCD tại H lấy điểm S sao cho
SBH 30 . Gọi E là giao điểm của CH và BK . Tính cosin của góc giữa hai đường thẳng SE và BC . Đáp án: …………..
Trang 24 Fanpage Nguyễn Bảo Vương
https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 Lời giải
Gọi I là hình chiếu vuông góc của E lên AB ta có A BK B CH .
ABK BCH HEB 90. S A H I B E K A I B H K D C E D C Ta có: SE BC SE EI cos ; cos ; cos SEI 3 , SH BH .tan 30 3a. a 3 . 3 2 HB HE HB 9 a 2 81a 2a 39 HE , 2 2 2 SE SH HE 3a . HC HB HC 5 25 5 2 HE HI HE 27 a 2 a a HI , 2 2 2 27 2 651 SI SH HI 3a . HB HE HB 25 25 25 a
Trong tam giác vuông SEI có: 2 2 36 EI SE SI 25 EI Vậy: 18 cosSEI . SE 5 39
Câu 47. Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng : 2x 2y z 4 0 và đường x 2 y 2 z 2 thẳng d : . Tam giác ABC có A 1;2;
1 , các điểm B , C nằm trên và 1 2 1
trọng tâm G nằm trên đường thẳng d . Tọa độ trung điểm M của BC là: Đáp án: ………….. Lời giải 3 3 7 3 7 Gọi
G t 2,2t 2, t 2 là trọng tâm. Vì AM AG M t ;3t 2; t . 2 2 2 2 2
Lại có M α t 1 M 2, 1 , 2 . 1 a
Câu 48. Cho các số thực a,b thỏa mãn a b 1. Biết rằng biểu thức P log đạt giá trị lớn log a a b ab nhất khi k
b a . Khi k thuộc khoảng nào sau đây:
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/ Đáp án: ………….. Lời giải 1 a Ta có P log
log ab 1 log b 1 log b 1 log b . log a a a a b a a ab Với k
b a suy ra P 1 k 1 k . 2 1 9 9
Đặt t 1 k k 1 suy ra 2
P t t 2 t . 2 4 4 9 1 1 1 3 Vậy P
t 1 k 1 k k . max 4 2 2 4 4
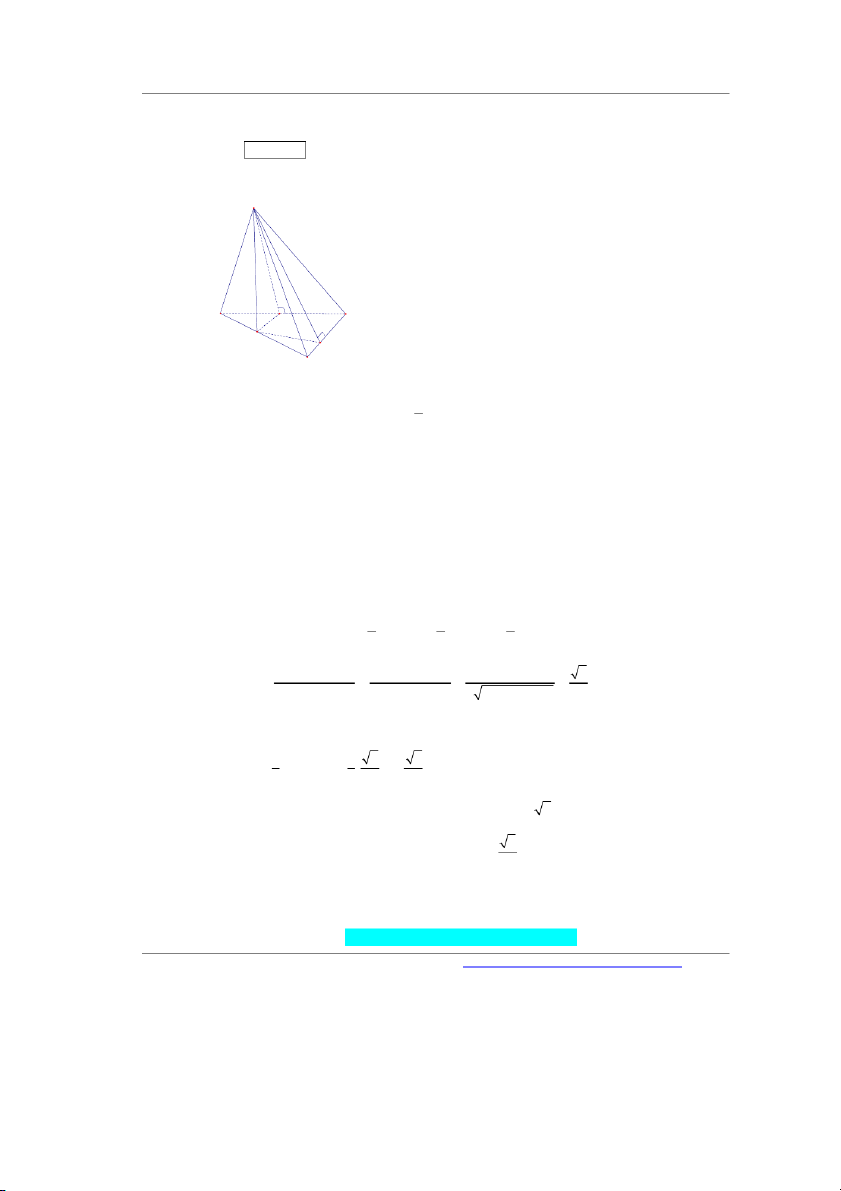
Câu 49. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, mặt bên SAB là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Gọi H , M , O lần lượt là trung điểm các cạnh AB, S , A AC
và G là trọng tâm tam giác SBC. Khoảng cách từ G đến mặt phẳng (HMO) bằng Đáp án: ………….. Lời giải
Dựng MK / /SH K AB , KI HO I HO , KJ MI J MI KJ HMO .
Chứng minh được SBC / / d G; d S; d ;
A 2d K; 2KJ. Tính được KI KH AH 3 1 a 3 a 3 SH a 3 .sin 60 . . , MK . 2 2 4 2 8 2 4 KI .KM a 15 Suy ra a a KJ . Vậy d G 15 15 ; 2KJ 2. . 2 2 20 KI KM 20 10
Câu 50. Cho khối chóp S.ABC có đáy là tam giác vuông tại , A AB 1, AC 2 .
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Các mặt bên SBC , SCA, SAB lần lượt tạo với đáy các góc 90 ;; sao cho
90 .Thể tích khối chóp S.ABC có giá trị lớn nhất bằng Đáp án: ………….. Lời giải S M B A H N C 1
Tam giác ABC vuông tại A S A . B AC 1. A BC 2
Gọi SH H BC là đường cao của SBC , theo giả thiết SBC ABC SH ABC . SMH SAB,ABC
Gọi M , N lần lượt là hình chiếu của S trên AB, AC SN H SAC,ABC S MH . S NH Ta có: 1 1 1 S
.SH .cot 2.SH .cot S S HM AB HN AC ABC AHB AHC . . . . 2 2 2 2 2 2 2 Do đó: SH
cot 2.cot 2.cot tan 2 2.cot . tan 2
(Vì 90 nên cot tan ) Vậy 1 1 2 2 V SH S . S ABC . . ABC . .1 . 3 3 2 6
Dấu bằng xảy ra khi 2cot tan 2
tan 2 tan 2 . 2
Vậy thể tích khối chóp .
S ABC có giá trị lớn nhất bằng . 6
• XEM THÊM ĐỀ CƯƠNG ÔN THI TẠI:
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
• https://www.nbv.edu.vn/2022/01/de-cuong-danh-gia-nang-luc-dhqg-ha-noi.html
Theo dõi Fanpage: Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Hoặc Facebook: Nguyễn Vương
https://www.facebook.com/phong.baovuong
Tham gia ngay: Nhóm Nguyễn Bào Vương (TÀI LIỆU TOÁN) https://www.facebook.com/groups/703546230477890/
Ấn sub kênh Youtube: Nguyễn Vương
https://www.youtube.com/channel/UCQ4u2J5gIEI1iRUbT3nwJfA?view_as=subscriber
Tải nhiều tài liệu hơn tại: https://www.nbv.edu.vn/
Trang 28 Fanpage Nguyễn Bảo Vương
https://www.facebook.com/tracnghiemtoanthpt489/




