Ôn thi đánh giá năng lực(Đề 7) | Trường đại học Quốc gia Hà Nội

Ôn thi đánh giá năng lực(Đề 7) | Trường đại học Quốc gia Hà Nội được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

91 46 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Đánh giá năng lực

Trường: Đại học Quốc gia Hà Nội

Thông tin:

28 trang 7 tháng trước

Tác giả:

Profile Kim Oanh
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 Điện thoại: 0946798489
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuong Trang 1
A. TRẮC NGHIỆM KHÁCH QUAN (35 CÂU)
Câu 1. Thống kê điểm môn toán trong một kì thi của 400 em học sinh thấy có 72 bài được điểm 5. Hỏi
giá trị tần suất của giá trị x
i
=5 là
A. B. C. D. 72% 36% 18% 10%
Câu 2. Một ô tô đang chạy với vận tốc
15 /m s
thì tăng tốc chuyển động nhanh dần với gia tốc
2
3 8 /a t m s
, trong đó
t
là khoảng thời gian tính bằng giây kể từ lúc tăng vận tốc. Hỏi sau
10
giây tăng vận tốc ô tô đi được bao nhiêu mét?
A.
246
. B.
250
. C.
150
. D.
180
.
Câu 3. Tập nghiệm của bất phương trình
3
log 1 1x
là
A.
;4 .

B.
1;4 .
C.
1;4 .
D.
;4 .

Câu 4. Hệ phương trinh:
1
5
1
5
y x
x
x y
y
. Có bao nhiêu cặp nghiệm
,x y
mà
x y
?
A.
3
. B.
4
. C.
1
. D.
2
.
Câu 5. Giả sử
A
,
B
theo thứ tự là điểm biểu diễn của số phức
1
z
,
2
z
. Khi đó độ dài của
AB
bằng
A.
1 2
z z
. B.
2 1
z z
. C.
2 1
z z
. D.
1 2
z z
.
Câu 6. Trong không gian
Oxyz
, cho hai điểm
2;1;0
A
,
B
. Mặt phẳng trung trực của đoạn
thẳng
AB
có phương trình là
A.
2 3 0x y z
. B.
2 2 0x y
.
C.
2 4x y z
. D.
2 3 0x y z
.
Câu 7. Trong không gian
Oxyz
, cho mặt phẳng
:3 2 6 0x y z
. Hình chiếu vuông góc của điểm
2; 1;0A
lên mặt phẳng
có tọa độ là
A.
2; 2;3
. B.
1;1; 1
. C.
1;1; 1
. D.
1;0;3
.
Câu 8. Bất phương trình
2 2
2
x x - 1
0
x + 5x + 6
có tập nghiệm là:
A.
2; 1 0;1
. B.
3; 2 1;1
.
C.
3; 2 1;1
. D.
3; 2 0;1
.
Câu 9. Có tất cả bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
3;3
để phương trình
2 2
2 cos 2 sin 2 1 0m x m x
có nghiệm.
A.
7
. B.
6
. C.
4
. D.
3
.
Câu 10. Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nửa diện tích
của mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng 1 bằng nửa diện tích của đế
tháp (có diện tích là
2
12288 m
). Tính diện tích mặt trên cùng.
A.
2
6m
. B.
2
12m
. C.
2
10m
. D.
2
8m
.
ĐỀ
ĐỀ
ĐỀ
ĐỀ ĐỀ
SỐ
SỐ
SỐ
SỐ SỐ
7.
7.
7.
7. 7.
Ô
Ô
Ô
ÔÔ
N
N
N
N N
THI
THI
THI
THITHI
ĐG
ĐG
ĐG
ĐGĐG
NL
NL
NL
NLNL
Đ
Đ
Đ
ĐĐ
HQ
HQ
HQ
HQHQ
G
G
G
GG
H
H
H
H H
À
À
À
À À
NỘ
NỘ
NỘ
NỘNỘ
I
I
I
I I
2
2
2
22
02
02
02
0202
1-2
1-2
1-2
1-21-2
0
0
0
00
22
22
22
2222
• |FanPage: Nguyễn Bảo Vương
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Trang 2 Fanpage Nguyễn Bảo Vương
https://www.facebook.com/tracnghiemtoanthpt489/
Câu 11. Họ các nguyên hàm của hàm số
2
1x
y
x
là:
A.
1
x
e C
x
. B.
1
ln x C
x
. C.
1
ln x C
x
. D.
1
ln x C
x
.
Câu 12. Cho hàm số
y f x
liên tục trên
R
và có đồ thị như hình vẽ dưới đây. Tập hợp tất cả các giá trị
thực của tham số
m
để phương trình
2
2 2 3 1f x x m
có nghiệm thuộc khoảng
0;1 .
A.
0;4
. B.
1;0
. C.
0;1
. D.
1
;1
3
Câu 13. Một vật chuyển động với vận tốc ban đầu
10m/s
thì tăng tốc chuyển động nhanh dần có gia tốc là
2
3a t t t
. Tính quãng đường vật đi được trong khoảng thời gian
12
giây kể từ khi vật bắt đầu
tăng tốc
A.
2712m
. B.
2160m
. C.
2736m
. D.
2592m
.
Câu 14. Một người có 58000000 đồng gửi tiết kiệm ngân hàng với kì hạn 1 tháng (theo hình thức lãi kép),
sau đúng 8 tháng thì lĩnh về được 61328000 đồng cả gốc và lãi. Tìm lãi suất hàng tháng.
A. B. 0, 6%/ tháng. 0, 8%/ tháng. 0, 5%/ tháng. 0, 7%/ tháng. C. D.
Câu 15. Nghiệm của phương trình
3
log 2 167 7
x
là
A.
2021x
. B.
2020x
. C.
1010x
. D.
2019x
.
Câu 16. Cho hình phẳng
H
giới hạn bởi đồ thị hàm số
1
1
y
x
và các đường thẳng
0y
,
0x
,
2x
. Tính thể tích
V
của khối tròn xoay sinh ra khi cho hình phẳng
H
quay quanh trục
Ox
.
A.
ln 3V
. B.
2
3
V
. C.
2
3
V
. D.
ln 3V
.
Câu 17. Có bao nhiêu giá trị nguyên của
m
thuộc đoạn
2018;2018
để hàm số
2 2
cot 2 cot 2 1
cot
x m x m
y
x m
nghịch biến trên
;
4 2
.
A.
0
. B.
2020
. C.
2019
. D.
2018
.
Câu 18. Xét số phức
z
thỏa mãn
10
1 2 2 . i z i
z
Mệnh đề nào dưới đây đúng?
A.
3
2.
2
z
B.
2.z
C.
1
.
2
z
D.
1 3
.
2 2
z
Câu 19. Tập hợp các điểm biểu diễn số phức z thỏa mãn
2 3
1
4
z i
z i
là.
A. Đường tròn tâm
2;3I
bán kính
1
. B. Đường tròn tâm
4 ;1I
bán kính
1
.
C. Đường thẳng
3 1 0x y
. D. Đường thẳng
3 1 0xy
.
Câu 20. Cho hai điểm
1;2A
và
4;6 .B
Tìm tọa độ điểm
M
trên trục
Oy
sao cho diện tích tam giác
MAB
bằng
1
?
A.
0;2 .
B.
0;0
và
4
0; .
3
C.
1;0 .
D.
4;0 .
Điện thoại: 0946798489 TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 3
Câu 21. Trong mặt phẳng toạ độ cho ba điểm
( 2;0), (8;0), (0;4)
A B C
. Tính bán kính đường tròn ngoại
tiếp tam giác.
A.
6
. B.
5
. C.
2 6
. D.
26
.
Câu 22. Cho
1;0;1
A
;
2;1;2
B
và
: 2 3 3 0
P x y z
. Viết phương trình mặt phẳng
Q
đi qua 2
điểm A,B và vuông góc
P
.
A.
: 2 2 0
Q x y z
. B.
: 2 2 0
Q x y z
.
C.
: 2 2 0
Q x y z
. D.
: 2 2 0
Q x y z
.
Câu 23. Hình chữ nhật
ABCD
có
6, 4
AB AD
. Gọi
, , , M N P Q
lần lượt là trung điểm bốn cạnh
, , , AB BC CD DA
. Cho hình chữ nhật
ABCD
quay quanh
QN
, khi đó tứ giác
MNPQ
tạo thành
vật tròn xoay có thể tích bằng:
A.
2
V
. B.
4
V
. C.
8
V
. D.
6
V
.
Câu 24. Xét hình trụ
T
có bán kính
R
, chiều cao
h
thoả mãn
2 3R h
.
N
là hình nón có bán kính
đáy
R
và chiều cao gấp đôi chiều cao của
T
. Gọi
1
S
và
2
S
lần lượt là diện tích xung quanh
của
T
và
N
, khi đó
1
2
S
S
bằng
A.
3
4
. B.
4
3
. C.
1
2
. D.
2
3
.
Câu 25.
Cho hình lăng trụ
. ' ' 'ABC A B C
có đáy
ABC
là tam giác vuông cân tại
B
và
2AC a
. Hình chiếu
vuông góc của
'A
trên mặt phẳng
ABC
là trung điểm
H
của cạnh
AB
và
' 2AA a
. Thể
tích của khối lăng trụ đã cho bằng?
A.
3
3
a
. B.
3
2 2
a
. C.
3
6
2
a
. D.
3
6
6
a
.
Câu 26. Cho tứ diện
ABCD
và điểm
M
ở trên cạnh
BC
. Mặt phẳng
qua
M
song song song với
AB
và
CD
. Thiết diện của
với tứ diện là hình gì?
A. Hình chữ nhật. Tứ giác lồi. Hình thang. B. C. D. Hình bình hành.
Câu 27. Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
2;2; 2
A
;
3; 3;3
B
. Điểm
M
trong
không gian thỏa mãn
2
3
MA
MB
. Khi đó độ dài
OM
lớn nhất bằng
A.
6 3
. B.
12 3
. C.
5 3
2
. D.
5 3
.
Câu 28. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
3 5 1
:
1 1 1
x y z
và mặt phẳng
: 2 3 4 0
P x y z
. Đường thẳng
d
nằm trong mặt phẳng
P
sao cho
d
cắt và vuông góc
với đường thẳng
.
A.
1;2;1
u
. B.
1;2;1
u
. C.
1; 2;1
u
. D.
1;2; 1
u
.
Câu 29. Cho hàm số
y f x
là hàm số bậc bốn. Hàm số
y f x
có đồ thị như hình vẽ.
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Trang 4 Fanpage Nguyễn Bảo Vương
https://www.facebook.com/tracnghiemtoanthpt489/
Số điểm cực tiểu của hàm số
2
2 2020g x f x x
là
A.
3
. B.
2
. C.
1
. D.
0
.
Câu 30. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 3 3 2 15 0P x y z
và ba điểm
1;2;0A
,
1; 1;3B
,
1; 1; 1C
. Điểm
0 0 0
( ; ; )M x y z thuộc
( )P
sao cho
2 2 2
2MA MB MC
nhỏ nhất. Giá trị
0 0 0
2 3x y z bằng
A.
10
. B.
11
. C.
5
. D.
15
.
Câu 31. Cho hàm số
y f x
có đồ thị như hình vẽ bên dưới. Tìm tất cả các giá trị thực của tham số
m
để
hàm số
g x f x m
có
5
điểm cực trị.
A.
1m
. B.
1m
. C.
1m
. D.
1m
.
Câu 32. Giá trị nào của
m
thì phương trình
2
3 2 3 1 0
m x m x m
có hai nghiệm phân biệt?
A.
3;5 m
. B.
5; m
.
C.
3m
. D.
; 3 5;  m
.
Câu 33. Cho hàm số
f x
liên tục trên đoạn
1;0
thỏa mãn
2
2 1 6 9 9f x f x x x
. Tính
0
2
d
2
x
xf x
bằng:
A.
13
3
. B.
74
3
. C.
26
3
. D.
2 2
3
.
Câu 34. Một lớp học có 30 học sinh nam và 10 học sinh nữ. Giáo viên chủ nhiệm cần chọn một ban cán sự
lớp gồm có 3 học sinh. Tính xác suất để ban cán sự lớp có cả nam và nữ.
A.
435
988
. B.
135
988
. C.
285
494
. D.
5750
9880
.
Câu 35. Cho lăng trụ tam giác
.ABC A B C
có chiều cao bằng
4
và diện tích đáy bằng
3
. Gọi
M
,
N
,
P
lần lượt là tâm của các mặt bên
ABB A
,
BCC B
và
CAA C
. Thể tích khối đa diện lồi có các
đỉnh là các điểm
A
,
B
,
C
,
M
,
N
,
P
bằng
Điện thoại: 0946798489 TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 5
A.
6
. B.
9
4
. C.
9
2
. D.
3
.
B. ĐIỀN KHUYẾT (15 CÂU)
Câu 36. Cho hàm số
2 4
3
x
y
x
có đồ thị là
(H)
. Phương trình tiếp tuyến tại giao điểm của
(H)
với trục
hoành là:
Đáp án: …………..
Câu 37. Cho hàm số
( )f x
có đạo hàm
2 5 7
'( ) ( 1) ( 2) ( 3)
f x x x x x
. Số điểm cực trị của hàm số đã cho là
Đáp án: …………..
Câu 38. Trong không gian
Oxyz
cho mặt phẳng
: 2 5 0
P x y z
và đường thẳng
1 2
:
2 1 3
x y z
. Gọi
A
là giao điểm của
và
P
; và
M
là điểm thuộc đường thẳng
sao cho
84
AM . Tính khoảng cách từ
M
đến mặt phẳng
P
.
Đáp án: …………..
Câu 39. Tổ của An và Cường có
7
học sinh. Số cách xếp
7
học sinh ấy theo hàng dọc mà An đứngđầu
hàng, Cường đứng cuối hàng là:
Đáp án: …………..
Câu 40. Cho
2
1
2
lim 14.
1
x
f x
x
Giới hạn của
1
3 2 2
lim
1
x
f x
x
là:
Đáp án: …………..
Câu 41. Cổng Arch tại thành phố St Louis của Mỹ có hình dạng là một parabol. Biết khoảng cách giữa hai
chân cổng bằng
162m
. Trên thành cổng, tại vị trí có độ cao
43m
so với mặt đất, người ta thả một
sợi dây chạm đất. Vị trí chạm đất của đầu sợi dây này cách chân cổng
A
một đoạn
10m
. Giả sử
các số liệu trên là chính xác
Gọi
h
là chiều cao của cổng. Hãy tính chiều cao của cổng.
Đáp án: …………..
Câu 42. Tìm tham số
m
để hàm số
3 2
1
2 2018
3
y x mx m x
không có cực trị.
Đáp án: …………..
Câu 43. Cho hàm số
4 2
3
y x x m
có đồ thị
m
C
, với
m
là tham số thực. Giả sử
m
C
cắt trục
Ox
tại
bốn điểm phân biệt như hình vẽ
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Trang 6 Fanpage Nguyễn Bảo Vương
https://www.facebook.com/tracnghiemtoanthpt489/
Gọi
1 2 3
, ,S S S
là diện tích các miền gạch chéo được cho trên hình vẽ. Biết tồn tại duy nhất giá trị
a
m
b
với
,a b
nguyên dương và
a
b
tối giản sao cho
1 3 2
S S S
. Đặt
T a b
. Mệnh đề nào
đúng ?
Đáp án: …………..
Câu 44. Cho hàm số
f x
xác định trên tập số thực và có đồ thị như hình vẽ bên dưới. Đặt
g x f f f x .
Số nghiệm của phương trình
' 0
g x
trên nửa khoảng
;2

là
Đáp án: …………..
Câu 45. Cho số phức
z
thỏa mãn điều kiện
3 4 2.z i
Trong mặt phẳng
Oxy
tập hợp điểm biểu diễn
số phức
2 1w z i
là hình tròn có diện tích
Đáp án: …………..
Câu 46. Cho hình lăng trụ tam giác đều
.ABC A B C
có cạnh đáy bằng
a
, cạnh bên
AA a
. Gọi
M
,
N
lần lượt là trung điểm của
BB
,
B C
. Lấy điểm
P
thuộc
A B
sao cho
4
a
PB
. Tính
tan
góc
giữa đường thẳng
AP
và mặt phẳng
MNP
Đáp án: …………..
Câu 47. Trong không gian với hệ tọa độ , cho 3 điểm Oxyz
1;2;3 , 0;1;1 , 1;0; 2
A B C
và mặt phẳng
: 2 0P x y z
. Gọi là điểm thuộc mặt phẳng ( ) sao cho giá trị của biểu thức M P
2 2 2
2 3T MA MB MC nhỏ nhất. Tính khoảng cách từ đến mặt phẳng M
:2 2 3 0
Q x y z
?
Đáp án: …………..
Câu 48. Cho các số thực dương
x
,
y
thỏa mãn
log 2 log log x y x y
. Tìm giá trị nhỏ nhất của biểu
thức
2
2
4
1 2
1
e .e
x
y
y
x
P
.
Đáp án: …………..
Điện thoại: 0946798489 TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 7
Câu 49. Cho hình chóp .
S ABCD
có đáy
ABCD
là hình thoi và
0
60
ABC
. Mặt bên
SAB
là tam giác
đều cạnh
a
, mặt phẳng
( )SAB
vuông góc với mặt phẳng
( )ABCD
. Kí hiệu
( , )d BC SD
là khoảng
cách giữa 2 đường thẳng
CD
và
SA
. Khẳng định nào sau đây đúng ?
Đáp án: …………..
Câu 50. Cho hình chóp
.
S ABC
có
SA SB SC a
,
60
ASB
,
90
BSC
,
120
CSA
. Gọi
,M N
lần lượt là các điểm trên cạnh
AB
và
SC
sao cho
CN AM
SC AB
. Khi khoảng cách giữa
M
và
N
nhỏ nhất, tính thể tích
V
của khối chóp
.
S AMN
.
Đáp án: …………..
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Trang 8 Fanpage Nguyễn Bảo Vương
https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải tham khảo
A. TRẮC NGHIỆM KHÁCH QUAN (35 CÂU)
Câu 1. Thống kê điểm môn toán trong một kì thi của 400 em học sinh thấy có 72 bài được điểm 5. Hỏi
giá trị tần suất của giá trị x
i
=5 là
A.72% B. 36% C. 18% D. 10%
Lời giải:
Chọn C
72
.100% 18%
400
Câu 2. Một ô tô đang chạy với vận tốc
15 /m s
thì tăng tốc chuyển động nhanh dần với gia tốc
2
3 8 /a t m s
, trong đó
t
là khoảng thời gian tính bằng giây kể từ lúc tăng vận tốc. Hỏi sau
10
giây tăng vận tốc ô tô đi được bao nhiêu mét?
A.
246
. B.
250
. C.
150
. D.
180
.
Lời giải
Chọn B
Ta có:
2
3
dt 3 8 dt = 8
2
t
v t a t t t C
.
Vận tốc khi ô tô bắt đầu tăng tốc là
15 /m s
:
0 15 15
v C
.
Vận tốc của ô tô là
2
3
8 15
2
t
v t t
.
Quãng đường ô tô đi được sau
10
giây kể từ lúc bắt đầu tăng tốc là
10 10
2
0 0
3
dt = 8 15 dt = 250 m
2
t
v t t
.
Câu 3. Tập nghiệm của bất phương trình
3
log 1 1
x
là
A.
;4 .

B.
1;4 .
C.
1;4 .
D.
;4 .

Lời giải
Chọn C
Bất phương trình tương đương
3
log 1 1 0 1 3 1 4.
x x x
Câu 4. Hệ phương trinh:
1
5
1
5
y x
x
x y
y
. Có bao nhiêu cặp nghiệm
,x y
mà
x y
?
A.
3
. B.
4
. C.
1
. D.
2
.
Lời giải
Chọn D
Điều kiện
0; 0
x y
Ta có
2
2
2
1
5
5 1
5 1
1
( )( ) 0
5 1
5
y x
x xy
x xy
x
x y x yy xy
x y
y
Do
x y
nên
2 2
1 1
;
5 1 4 1
2 2
1 1
( )( ) 0
;
2 2
x y
x xy x
x y x y y x
x y
Câu 5. Giả sử
A
,
B
theo thứ tự là điểm biểu diễn của số phức
1
z
,
2
z
. Khi đó độ dài của
AB
bằng
Điện thoại: 0946798489 TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 9
A.
1 2
z z
. B.
2 1
z z
. C.
2 1
z z
. D.
1 2
z z
.
Lời giải
Chọn C
Giả sử
1
z a bi
,
2
z c di
,
, , ,a b c d
.
Theo đề bài ta có:
;A a b
,
;B c d
2 2
AB c a d b
.
2 1
z z a c d b i
2 2
2 1
z z c a d b
.
Câu 6. Trong không gian
Oxyz
, cho hai điểm
2;1;0
A
,
B
. Mặt phẳng trung trực của đoạn thẳng
AB
có phương trình là
A.
2 3 0
x y z
. B.
2 2 0
x y
.
C.
2 4x y z
. D.
2 3 0
x y z
.
Lời giải
Chọn D
Gọi
M
là trung điểm của
AB
1;0;2
M
.
Mặt phẳng trung trực của đoạn thẳng
AB
có một véc tơ pháp tuyến là
2; 2;4
AB

Mặt phẳng trung trực của
AB
đi qua
1;0;2
M
và nhận
AB
làm véc tơ pháp tuyến nên phương
trình mặt phẳng là:
2 1 2 4 2 0
x y z
2 3 0
x y z
.
Câu 7. Trong không gian
Oxyz
, cho mặt phẳng
:3 2 6 0
x y z
. Hình chiếu vuông góc của điểm
2; 1;0
A
lên mặt phẳng
có tọa độ là
A.
2; 2;3
. B.
1;1; 1
. C.
1;1; 1
. D.
1; 0;3
.
Lời giải
Chọn C
:3 2 6 0
x y z
có vectơ pháp tuyến là
3; 2;1
n
.
Gọi
; ;H x y z
là hình chiếu của điểm
A
lên mặt phẳng
. Khi đó:
.AH k n
H

2; 1; 3; 2;1
3 2 6 0
x y z k
x y z
2 3
1 2
3 2 6 0
x k
y k
z k
x y z
2 3
1 2
3 2 6 0
x k
y k
z k
x y z
Giải hệ trên ta có:
1
x
;
1y
;
1
x
hay
1;1; 1
H
.
Câu 8. Bất phương trình
2 2
2
x x - 1
0
x + 5x + 6
có tập nghiệm là:
A.
2; 1 0;1
. B.
3; 2 1;1
.
C.
3; 2 1;1
. D.
3; 2 0;1
.
Lời giải
Chọn B
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Trang 10 Fanpage Nguyễn Bảo Vương
https://www.facebook.com/tracnghiemtoanthpt489/
Cho
2
0 0x x
2
1 0 1x x
2
3
5 6 0
2
x
x x
x
Lập bảng xét dấu ta được:
Dựa vào bảng xét dấu suy ra tập nghiệm bất phương trình đã cho là:
3; 2 1;1
S
.
Câu 9. Có tất cả bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
3;3
để phương trình
2 2
2 cos 2 sin 2 1 0m x m x
có nghiệm.
A.
7
. B.
6
. C.
4
. D.
3
.
Lời giải.
Chọn B
Phương trình
2
1 cos 2
2 . 2 sin 2 1 0
2
x
m m x
.
2 2
4 sin 2 2 cos 2 4m x m x m
.
Phương trình có nghiệm
2 2
2 2 2 2 2
16 2 4 12 12 1 1m m m m m m .
3;3
3; 2; 1;1;2;3
m
m
m
 
có
6
giá trị nguyên.
Câu 10. Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nửa diện tích
của mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng 1 bằng nửa diện tích của đế
tháp (có diện tích là
2
12288 m
). Tính diện tích mặt trên cùng.
A.
2
6m
. B.
2
12m
. C.
2
10m
. D.
2
8m
.
Lời giải
Chọn A
Ta nhận thấy diện tích các mặt trên của mỗi tầng lập thành 1 cấp số nhân với công bội
1
2
q
Số hạng đầu
1
12288u . Khi đó mặt trên cùng tầng 11 ứng với
12
u .
Do đó
11
12 1
.u u q
11
1
12288.
2
6
.
Câu 11. Họ các nguyên hàm của hàm số
2
1x
y
x
là:
A.
1
x
e C
x
. B.
1
ln x C
x
. C.
1
ln x C
x
. D.
1
ln x C
x
.
Lời giải
Chọn C
Điện thoại: 0946798489 TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 17
, 1;2;1u n
.
Đường thẳng
d
nằm trong mặt phẳng
P
sao cho
d
cắt và vuông góc với đường thẳng
nên
d
nhận
1; 2;1
d
u

làm vectơ chỉ phương.
Câu 29. Cho hàm số
y f x
là hàm số bậc bốn. Hàm số
y f x
có đồ thị như hình vẽ.
Số điểm cực tiểu của hàm số
2
2 2020g x f x x
là
A.
3
. B.
2
. C.
1
. D.
0
.
Lời giải
Chọn D
Từ đồ thị hàm số
y f x
ta thấy
1
0 1
3
x
f x x
x
.
Xét hàm số
2
2 2020g x f x x
.
2
2
1
. 2 2020 .
2 2020
x
g x f x x
x x
2
2
1
0 2 2020 . 0
2 2020
x
g x f x x
x x
2
2
2 2020 0
1
0
2 2020
f x x
x
x x
2
2
2
2 2020 1
2 2020 1
2 2020 3
1
x x
x x
x x
x
2
2
2
2 2020 1
2 2019 0
2 2011 0
1
x x vn
x x vn
x x vn
x
1x
.
Từ đồ thị hàm số
y f x
ta có:
3x
thì
0f x
.
Mà
2
2 2020 2019 3x x
nên
2
2 2019 0f x x
với
x
.
Bảng biến thiên
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Trang 18 Fanpage Nguyễn Bảo Vương
https://www.facebook.com/tracnghiemtoanthpt489/
Vậy hàm số
g x
chỉ có một cực đại.
Câu 30. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 3 3 2 15 0P x y z
và ba điểm
1; 2;0
A
,
1; 1;3
B
,
C
. Điểm
0 0 0
( ; ; )M x y z thuộc
( )P
sao cho
2 2 2
2MA MB MC
nhỏ nhất. Giá trị
0 0 0
2 3x y z bằng
A.
10
. B.
11
. C.
5
. D.
15
.
Lời giải
Chọn C
Xét điểm
I
thỏa
2 0IA IB IC
 
suy ra
1; 2; 2I
.
2 2 2
2MA MB MC
2 2 2
2
MI IA MI IB MI IC
    
2 2 2 2
2 2MI IA IB IC
.
2 2 2
2MA MB MC
nhỏ nhất khi và chỉ khi
MI
nhỏ nhất hay
M
là hình chiếu của
I
lên
( )P
.
Lúc đó, đường thẳng
MI
có phương trình
1 3
2 3
2 2
x t
y t
z t
suy ra
0
0
0
1 3
2 3
2 2
x t
y t
z t
.
Mà
0 0 0
3 3 2 15 0x y z
3 1 3 3 2 3 2 2 2 15 0
t t t
1t
.
0 0 0
2 3 2 1 3 3 2 3 2 2x y z t t t
6 t 5
.
Câu 31. Cho hàm số
y f x
có đồ thị như hình vẽ bên dưới. Tìm tất cả các giá trị thực của tham số
m
để
hàm số
g x f x m
có
5
điểm cực trị.
A.
1
m
. B.
1
m
. C.
1
m
. D.
1
m
.
Lời giải
Chọn A
Nhận xét: Hàm
g x f x m
là hàm số chẵn nên đồ thị đối xứng qua trục
0Oy x
là
một điểm cực trị của hàm số.
Ta có
.
x
g x f x m
x
với
0.x
theo do thi
1 1
0 0 .
1 1
f x
x m x m
g x f x m
x m x m
*
Để hàm số
g x
có
5
điểm cực trị
*
có
4
nghiệm phân biệt khác
0
Điện thoại: 0946798489 TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 19
1 0
1 0 1.
1 1
m
m m
m m
Câu 32. Giá trị nào của
m
thì phương trình
2
3 2 3 1 0
m x m x m
có hai nghiệm phân biệt?
A.
3;5
m
. B.
5;
m
.
C.
3
m
. D.
; 3 5;
 
m
.
Lời giải
Chọn C
Ta có:
2
3 2 3 1 0
m x m x m
có hai nghiệm phân biệt khi:
2
3 0
0
3
0
2 4 6 0,
m
a
m
m m m
.
Câu 33. Cho hàm số
f x
liên tục trên đoạn
1;0
thỏa mãn
2
2 1 6 9 9
f x f x x x
. Tính
0
2
d
2
x
xf x
bằng:
A.
13
3
. B.
74
3
. C.
26
3
. D.
2 2
3
.
Lời giải
Ta có:
2
2 1 6 9 9
f x f x x x
1 2 0 6 1 4
0 2 1 9 0 1
f f f
f f f
0 0 0
2 2
1 1 1
13
2 1 6 9 9 2 1 6 9 9
2
f x f x x x f x dx f x dx x x dx
Mà
0 0
1 1
1
f x dx f x dx
nên suy ra
0
1
13
6
f x dx
0
0 0 0 0
2 2 2 22
22
d 2 2 d 16 2 d 16 4 d
2 2 2 2 2 2 3
x x x x x x
xf x xf f x f x f
Câu 34. Một lớp học có 30 học sinh nam và 10 học sinh nữ. Giáo viên chủ nhiệm cần chọn một ban cán sự
lớp gồm có 3 học sinh. Tính xác suất để ban cán sự lớp có cả nam và nữ.
A.
435
988
. B.
135
988
. C.
285
494
. D.
5750
9880
.
Lời giải
Chọn C
Ta có
3
40
n C
.
Gọi
A
là biến cố: “3 học sinh trong ban cán sự lớp có cả nam và nữ”
1 2 2 1
30 10 30 10
. .n A C C C C
1 2 2 1
30 10 30 10
3
40
. .
15 285
26 494
C C C C
P A
C
Câu 35. Cho lăng trụ tam giác
.
ABC A B C
có chiều cao bằng
4
và diện tích đáy bằng
3
. Gọi
M
,
N
,
P
lần lượt là tâm của các mặt bên
ABB A
,
BCC B
và
CAA C
. Thể tích khối đa diện lồi có các
đỉnh là các điểm
A
,
B
,
C
,
M
,
N
,
P
bằng
A.
6
. B.
9
4
. C.
9
2
. D.
3
.
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Trang 20 Fanpage Nguyễn Bảo Vương
https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải
Chọn C
Ta có 3.4 12
.
V
ABC A B C
. Gọi
, ,I J K
lần lượt là trung điểm của
AA
,
BB
,
CC
.
6
.
V
ABC IJK
.
Áp dụng bài toán tỷ số thể tích ta có:
1
.
8
.
V
A IMP
V
A A B C
. .
1 1
8 2
A IMP A A B C
V V
Dễ thấy
. . .
1
2
A IMP B MNJ C NPK
V V V
.
Vậy
.
V
ABC MNP
3
. .
V V
ABC IJK A IMP
1 9
6 3.
2 2
.
B. ĐIỀN KHUYẾT (15 CÂU)
Câu 36. Cho hàm số
2 4
3
x
y
x
có đồ thị là
(H)
. Phương trình tiếp tuyến tại giao điểm của
(H)
với trục
hoành là:
Đáp án: …………..
Lời giải
Giao điểm của
(H)
với trục hoành là
(2; 0)A
. Ta có:
2
2
' '(2) 2
( 3)
y y
x
Phương trình tiếp tuyến cần tìm là
2( 2)y x
hay
2 4y x
.
Câu 37. Cho hàm số
( )f x
có đạo hàm
2 5 7
'( ) ( 1) ( 2) ( 3)f x x x x x
. Số điểm cực trị của hàm số đã cho là
Đáp án: …………..
Lời giải
Ta có
2 5 7
'( ) 0
( 1) ( 2) ( 3) 0
0
1
2
3
f x
x x x x
x
x
x
x
Bảng xét dấu
( )f x
x

0
1
2
3

'( )f x
0
0
0
0
Từ bảng xét dấu ta thấy
'( )f x
có
3
lần đổi dấu nên hàm số đã cho có
3
điểm cực trị.
K
J
I
P
N
M
A'
C'
B'
C
A
B
Điện thoại: 0946798489 TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 21
Câu 38. Trong không gian
Oxyz
cho mặt phẳng
: 2 5 0
P x y z
và đường thẳng
1 2
:
2 1 3
x y z
. Gọi
A
là giao điểm của
và
P
; và
M
là điểm thuộc đường thẳng
sao cho
84
AM . Tính khoảng cách từ
M
đến mặt phẳng
P
.
Đáp án: …………..
Lời giải
Ta có:
.
sin ,
.
P
P
u n
P
u n
 
 
3 21
14
6. 14
.
Gọi
H
là hình chiếu của điểm
M
lên mặt phẳng. Khi đó ta có tam giác
AMH
là tam giác
vuông tại
H
nên
sin , sin
MH
P MAH
MA
3
MH
.
Câu 39. Tổ của An và Cường có
7
học sinh. Số cách xếp
7
học sinh ấy theo hàng dọc mà An đứngđầu
hàng, Cường đứng cuối hàng là:
Đáp án: …………..
Lời giải
Chọn An đứng đầu hàng có
1
cách, chọn Cường đứng cuối hàng có
1
cách.
Sắp xếp
5
bạn còn lại có:
5
5! 120
P
cách.
Vậy có:
1.1.120 120
cách.
Câu 40. Cho
2
1
2
lim 14.
1
x
f x
x
Giới hạn của
1
3 2 2
lim
1
x
f x
x
là:
Đáp án: …………..
Lời giải
Ta có:
2
1
2
lim 14
1
x
f x
x
suy ra
1 2
f
Theo đề bài ta có:
21 1
2
1
3 2 2
3 2 4 1
lim lim
1
1 3 2 2
2 3 1
lim .
1
3 2 2
x x
x
f x f x x
x
x f x
f x x
x
f x
Ta có:
2
1
2
lim 14;
1
x
f x
x
1
3 1
3.2 3.2 3
lim
2 2 2
3 2 2 3 1 2 2
x
x
f x f
Suy ra:
1
3 2 2
3
lim 14. 21
1 2
x
f x
x
Câu 41. Cổng Arch tại thành phố St Louis của Mỹ có hình dạng là một parabol. Biết khoảng cách giữa hai
chân cổng bằng
162m
. Trên thành cổng, tại vị trí có độ cao
43m
so với mặt đất, người ta thả một
sợi dây chạm đất. Vị trí chạm đất của đầu sợi dây này cách chân cổng
A
một đoạn
10m
. Giả sử
các số liệu trên là chính xác
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Trang 22 Fanpage Nguyễn Bảo Vương
https://www.facebook.com/tracnghiemtoanthpt489/
Gọi
h
là chiều cao của cổng. Hãy tính chiều cao của cổng.
Đáp án: …………..
Lời giải
Chọn hệ trục tọa độ sao cho
,A O AB Ox
. Ta có:
0;0 , 162;0 , 10;43A O B M
.
Gọi phương trình parabol là:
2
y ax bx c .
Vì
, ,MA B
parabol ta có:
2
43
152
0
162 0
3483
162 162 0 10 43
76
100 10 43 0
0
a
c
a b
a b c a b b
a b c c
c
Vậy phương trình parabol là:
2
43 3483
152 76
y x x
. Do đó chiều cao của cổng là:
81 185,6
2
b
x h m
a
.
Câu 42. Tìm tham số
m
để hàm số
3 2
1
2 2018
3
y x mx m x
không có cực trị.
Đáp án: …………..
Lời giải
Ta có:
2
2 2y x mx m
Để hàm số đã cho không có cực trị khi phương trình
0
y
vô nghiệm hoặc có nghiệm kép hay
0
2
2 0m m
1 2m
.
Câu 43. Cho hàm số
4 2
3y x x m
có đồ thị
m
C
, với
m
là tham số thực. Giả sử
m
C
cắt trục
Ox
tại
bốn điểm phân biệt như hình vẽ
Gọi
1 2 3
, ,S S S
là diện tích các miền gạch chéo được cho trên hình vẽ. Biết tồn tại duy nhất giá trị
a
m
b
với
,a b
nguyên dương và
a
b
tối giản sao cho
1 3 2
S S S
. Đặt
T a b
. Mệnh đề nào
đúng ?
Đáp án: …………..
Lời giải
Điện thoại: 0946798489 TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 23
Giả sử
1
x
là nghiệm lớn nhất của phương trình
4 2
3 0x x m
.
Suy ra
4 2
3m x x
(1).
Vì
1
1 3 2
2 3 2 3
1 3
0
1
2 0 ( ). 0
2
x
S S S
S S S S f x dx
S S
Ta có
1 1
5 4
4 2 3 2
1 1
1 1 1 1
0 0
( ) ( 3 ) ( )
5 5
x x
x x
f x dx x x m dx x mx x x m
Do đó
4 4
2 2
1 1
1 1 1
( ) 0 0
5 5
x x
x x m x m
(2), vì
1
( 0)x
Từ (1), (2) suy ra:
4
2 4 2 4 2 2
1
1 1 1 1 1 1
5
3 0 4 10 0
5 2
x
x x x x x x
Suy ra:
4 2
1 1
5
3 5; 4
4
m x x a b
Vậy
9T a b
.
Câu 44. Cho hàm số
f x
xác định trên tập số thực và có đồ thị như hình vẽ bên dưới. Đặt
g x f f f x .
Số nghiệm của phương trình
' 0
g x
trên nửa khoảng
;2

là
Đáp án: …………..
Lời giải
Dựa vào đồ thị ta thấy:
1
0 ( 1; 0)
(2; 3)
x
f x x k
x a
;
0
' 0
2
x
f x
x
;2 ;2 ;2x f x f f x   
*
g x f f f x với
;2x 
' ' . ' . 'g x f x f f x f f f x
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Trang 24 Fanpage Nguyễn Bảo Vương
https://www.facebook.com/tracnghiemtoanthpt489/
0
0
2
0
0
2
1
2
2
' 0
0
0
0
' 0 ' 0 2 0
2
2
' 0
0
1
1
2
0
x
x
x
x
x
x
x
x
x
f x
f x
x k
f x
f x
g x f f x f x x
f x
f x
x b
f x k
f f f x
f f x
f x k
x e
f x
f x
f f x
x c
f x
x d
Vậy, phương trình
' 0g x
có
8
nghiệm thuộc khoảng
;2
.
Câu 45. Cho số phức
z
thỏa mãn điều kiện
3 4 2.z i
Trong mặt phẳng
Oxy
tập hợp điểm biểu diễn
số phức
2 1w z i
là hình tròn có diện tích
Đáp án: …………..
Lời giải
1
2 1
2
w i
w z i z
1
3 4 2 3 4 2 1 6 8 4 7 9 4 1
2
w i
z i i w i i w i
Giả sử
,w x yi x y
, khi đó
2 2
1 7 9 16x y
Suy ra tập hợp điểm biểu diễn số phức
w
là hình tròn tâm
7; 9
I
, bán kính
4.r
Vậy diện tích cần tìm là
2
.4 16 .S
Câu 46. Cho hình lăng trụ tam giác đều
.ABC A B C
có cạnh đáy bằng
a
, cạnh bên
AA a
. Gọi
M
,
N
lần lượt là trung điểm của
BB
,
B C
. Lấy điểm
P
thuộc
A B
sao cho
4
a
PB
. Tính
tan
góc
giữa đường thẳng
AP
và mặt phẳng
MNP
Đáp án: …………..
Lời giải
Điện thoại: 0946798489 TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 25
Gọi
H
,
K
lần lượt là trung điểm của
A B
.
Khi đó ta có
/ /
HB PM
,
HB AM
. Suy ra
AM MP
(1)
Mặt khác ta có
BC MK
,
BC AK
(vì
AK BCB
)
BC AMK
MN AM
(2)
Từ (1) và (2) suy ra
AM MNP
. Vậy góc giữa đường thẳng
AP
và mặt phẳng
MNP
là góc
APM
.
Ta có
2
2 2 2
5
2 2
a
AM AB MB a a
2 2
2 2
5
2 4 4
a a
MP B M B P a
Suy ra
tan 2
AM
APM
PM
.
Câu 47. Trong không gian với hệ tọa độ , cho 3 điểm Oxyz
1;2;3 , 0;1;1 , 1;0; 2
A B C
và mặt phẳng
: 2 0
P x y z
. Gọi là điểm thuộc mặt phẳng ( ) sao cho giá trị của biểu thức M P
2 2 2
2 3
T MA MB MC
nhỏ nhất. Tính khoảng cách từ đến mặt phẳng M
:2 2 3 0
Q x y z
?
Đáp án: …………..
Lời giải
Gọi
; ;I a b c
là điểm thỏa mãn
2 3 0
IA IB IC
  
.
Ta có
1 ; 2 ; 3 , ;1 ;1 , 1 ; ; 2
IA a b c IB a b c IC a b c
 
2
3
1 2 3 3 0 6 4
2
2 3 0 2 2 2 3 0 6 4
3
3 2 2 6 3 0 6 1
1
6
a
a a a a
IA IB IC b b b b b
c c c c
c
 
2 2 1
; ;
3 3 6
I
.
Ta chứng minh được
2 2 2 2
6 2 3
T MI IA IB IC
. Do đó đạt T GTNN khi
MI
đạt GTNN
M
là hình chiếu vuông góc của trên mặt phẳng ( ). I P
K
M
N
P
H
C
B
A
B'
C'
A'
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có
2
3
2
:
3
1
6
x t
MI y t
z t
,
2 2 1 19 19
; ; , 3 0
3 3 6 6 18
M MI M t t t M P t t
7 7 22
3
7 7 11 91
9 18 9
; ; ;
18 18 9 3 54
M d M Q
.
Câu 48. Cho các số thực dương
x
,
y
thỏa mãn
log 2 log log
x y x y
. Tìm giá trị nhỏ nhất của biểu
thức
2
2
4
1 2
1
e .e
x
y
y
x
P
.
Đáp án: …………..
Lời giải
Từ
log 2 log log log 2
x y x y xy x y xy
.
Biến đổi
2
2 2 2
2 2
2 2
2
4
4 2 1 4 2 1 1
1 2 2 1 1
1 1
e .e e .e e e
x
x x y
x y
y y
y y x
y y x
x x
P
.
Áp dụng BĐT Bunhiacopski ta có
2
2
2
2
2 1 1
2 1 1 2
x
y x
y x y
y x
2 2
2
2
2
2 2
2 1 1 2 2 4 2 2
x x
y
x y
y
y x x y x y
.
Áp dụng BĐT Côsi ta có
2 2 .2
xy x y x y
2 2
8
x y xy
8
xy
2 8
x y
.
Khi đó
2
2
8
4 2 2 5
x y
x y
2
5 2 32 2 64
20 2 2
x y x y
x y
2 8 5 2 8
0
20 2 2
x y x y
x y
2
2
8
4 2 2 5
x y
x y
2
2
8
2
2 1 1 5
x
y
y x
8
5
e
P .
Dấu “
” xảy ra
4
x
,
2
y
8
5
min e
P .
Câu 49. Cho hình chóp .
S ABCD
có đáy
ABCD
là hình thoi và
0
60
ABC
. Mặt bên
SAB
là tam giác
đều cạnh
a
, mặt phẳng
( )SAB
vuông góc với mặt phẳng
( )ABCD
. Kí hiệu
( , )d BC SD
là khoảng
cách giữa 2 đường thẳng
CD
và
SA
. Khẳng định nào sau đây đúng ?
Đáp án: …………..
Lời giải
Điện thoại: 0946798489 TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 27
Gọi
M
là trung điểm
AB
. Ta được
SM ABCD
Ta có
//AAC D
nên
, ,
d BC SD d BC SAD
, 2 ,
d B SAD d M SAD
.
Vì
ABCD
là hình thoi và
0
60
ABC
nên
ABC
đều cạnh
a
.
Kẻ
MF AD
;
MH SF
. Ta có
( )
AF SMF AF MH
(1).
Ta lại có
MH SF
(2).
Từ (1), (2) suy ra
MH SAD
.
Xét tam giác
MFA
, ta có:
3
Sin
4
MF a
FAM MF
MA
.
Xét tam giác
SFA
, ta có:
2 22 2 2 2
1 1 1 1 1 20 15
3 3
3 10
4 16
a
MH
a aMH SM MF a
.
Vậy
15
, 2
5
a
d BC SD MH
.
Câu 50. Cho hình chóp
.
S ABC
có
SA SB SC a
,
60
ASB
,
90
BSC
,
120
CSA
. Gọi
,M N
lần lượt là các điểm trên cạnh
AB
và
SC
sao cho
CN AM
SC AB
. Khi khoảng cách giữa
M
và
N
nhỏ nhất, tính thể tích
V
của khối chóp
.
S AMN
.
Đáp án: …………..
Lời giải
Dựng
//MK AC
K BC
;
//
MI SB I SA
.
Khi đó:
cos ; cos ; .
AM AI NC
x IN MK AC SB IM MK
AB SA SC
Ta có
.
cos ;
.
AC SB
AC SB
AC SB

và
3,
AC a SB a
Lại có
2
. . . . . .cos120 . cos90
2
a
AC SB AS SC SB AS SB SC SB AS SB SC SB
       
A
D
B
C
S
F
M
H
I
K
S
C
B
A
M
N
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
2
2
3
2
. cos ,
2 6
3
a
a
AC SB AC SB
a

3
cos
6
IMK
hay
3
cos
6
IMK
.
TH1:
3
cos
6
IMK
Ta có
2
2 2 2 2 2 2 2 2
3 3
2 . . 3 1 2 . 3 1 .
6 6
MN MI MK MI MK a x a x a x a x
2
2 2
3 1 1
a x x x x
2
2
2
5 11 11
3
6 12 12
a
a x
.
Do đó
2
min
11 5
12 6
a
MN x
.
Vậy
3 3
2 1 5 5 2
. . .
12 6 6 432
SAMN
SAMN
SABC
V
SN AM
V a a
V SC AB
.
TH2:
3
cos
6
IMK
Ta có
2
2 2 2 2 2 2 2 2
3 3
2 . . 3 1 2 . 3 1 .
6 6
MN MI MK MI MK a x a x a x a x
2
2 2
3 1 1
a x x x x
2
2
2
7 11 11
5
10 20 20
a
a x
.
Do đó
2
min
11 7
20 10
a
MN x
Vậy
3
2 3 7 7 2
. . .
12 10 10 400
SAMN
SAMN
SABC
V
SN AM
V a
V SC AB
.
• XEM THÊM ĐỀ CƯƠNG ÔN THI TẠI:
• https://www.nbv.edu.vn/2022/01/de-cuong-danh-gia-nang-luc-dhqg-ha-noi.html
Theo dõi Fanpage: Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Hoặc Facebook: Nguyễn Vương https://www.facebook.com/phong.baovuong
Tham gia ngay: Nhóm Nguyễn Bào Vương (TÀI LIỆU TOÁN) https://www.facebook.com/groups/703546230477890/
Ấn sub kênh Youtube: Nguyễn Vương
https://www.youtube.com/channel/UCQ4u2J5gIEI1iRUbT3nwJfA?view_as=subscriber
Tải nhiều tài liệu hơn tại: https://www.nbv.edu.vn/
| 1/28
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 Điện thoại: 0946798489 ĐỀ Đ Ề SỐ S 7. 7 ÔN THI T ĐG Đ NL ĐHQG H À NỘI I202 0 1- 1 2 - 022 2
• |FanPage: Nguyễn Bảo Vương
A. TRẮC NGHIỆM KHÁCH QUAN (35 CÂU)
Câu 1. Thống kê điểm môn toán trong một kì thi của 400 em học sinh thấy có 72 bài được điểm 5. Hỏi
giá trị tần suất của giá trị xi =5 là A. 72% B. 36% C. 18% D. 10%
Câu 2. Một ô tô đang chạy với vận tốc 15 m / s thì tăng tốc chuyển động nhanh dần với gia tốc a  t   2
3 8 m / s  , trong đó t là khoảng thời gian tính bằng giây kể từ lúc tăng vận tốc. Hỏi sau
10 giây tăng vận tốc ô tô đi được bao nhiêu mét? A. 246 . B. 250 . C. 150 . D. 180.
Câu 3. Tập nghiệm của bất phương trình log x 1 1 là 3   A. ;  4 . B. 1;4 . C. 1;4. D.  ;4.  1  y  5x x
Câu 4. Hệ phương trinh: 
. Có bao nhiêu cặp nghiệm x, y mà x  y ? 1   x  5y  y A. 3 . B. 4 . C. 1. D. 2 . 
Câu 5. Giả sử A , B theo thứ tự là điểm biểu diễn của số phức bằng 1
z , z . Khi đó độ dài của 2 AB A. z  . B.  . C.  . D.  . 1 z 2 z2 1 z 2 z 1 z 1 z z2
Câu 6. Trong không gian Oxyz , cho hai điểm A2;1;0  , B0; 1
 ;4 . Mặt phẳng trung trực của đoạn
thẳng AB có phương trình là
A. x  y  2z 3  0 . B. 2x  y  2  0 . C. 2x  y  z  4 .
D. x  y  2z 3  0 .
Câu 7. Trong không gian Oxyz , cho mặt phẳng   :3x 2y  z  6  0. Hình chiếu vuông góc của điểm A 2; 1
 ;0 lên mặt phẳng   có tọa độ là A. 2; 2  ;3 . B. 1;1; 1   . C.  1  ;1;  1 . D. 1;0;3. 2 x  2 x -  1 Câu 8. Bất phương trình  0 có tập nghiệm là: 2 x + 5x + 6 A.  2; 1 0;1       . B.     .     3;  2 1;1   C.  3  ; 2    1  ;1. D.  3  ; 2   0;1.
Câu 9. Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn  3  ;  3 để phương trình  2 m   2
2 cos x  2msin 2x 1  0 có nghiệm. A. 7 . B. 6 . C. 4 . D. 3.
Câu 10. Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nửa diện tích
của mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng 1 bằng nửa diện tích của đế tháp (có diện tích là 2
12288 m ). Tính diện tích mặt trên cùng. A. 2 6m . B. 2 12m . C. 2 10m . D. 2 8m .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/ x 1
Câu 11. Họ các nguyên hàm của hàm số y  là: 2 x 1 1 1 x 1 A. e   C . B. ln x   C . C. ln x  C . D. ln x   C . x x x x
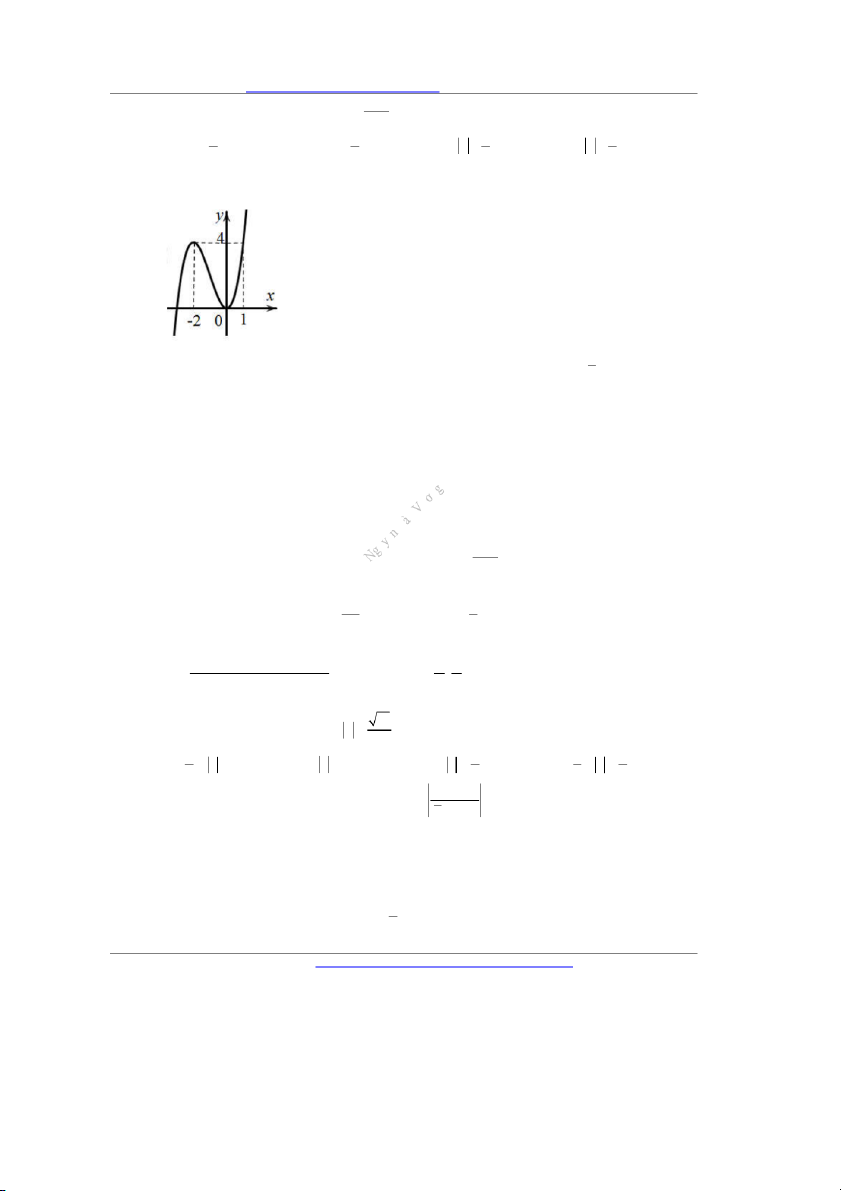
Câu 12. Cho hàm số y  f  x liên tục trên R và có đồ thị như hình vẽ dưới đây. Tập hợp tất cả các giá trị
thực của tham số m để phương trình f  2
x  2x  2  3m 1 có nghiệm thuộc khoảng 0;  1 .  1 A. 0;4 . B.  1  ;0. C.   0;1  ;1  . D.    3   
Câu 13. Một vật chuyển động với vận tốc ban đầu 10m/s thì tăng tốc chuyển động nhanh dần có gia tốc là a t  2
 t  3t . Tính quãng đường vật đi được trong khoảng thời gian 12 giây kể từ khi vật bắt đầu tăng tốc A. 2712m . B. 2160m . C. 2736m. D. 2592m.
Câu 14. Một người có 58000000 đồng gửi tiết kiệm ngân hàng với kì hạn 1 tháng (theo hình thức lãi kép),
sau đúng 8 tháng thì lĩnh về được 61328000 đồng cả gốc và lãi. Tìm lãi suất hàng tháng. A. 0, 6%/ tháng. B. 0, 8%/ tháng. C. 0, 5%/ tháng. D. 0, 7%/ tháng.
Câu 15. Nghiệm của phương trình log 2x 167  7 là 3   A. x  2021. B. x  2020 . C. x  1010 . D. x  2019. 1
Câu 16. Cho hình phẳng  H giới hạn bởi đồ thị hàm số y 
và các đường thẳng y  0, x  0 , x  1
x  2 . Tính thể tích V của khối tròn xoay sinh ra khi cho hình phẳng  H  quay quanh trục Ox . 2 2 A. V   ln 3 . B. V  . C. V  . D. V  ln 3. 3 3
Câu 17. Có bao nhiêu giá trị nguyên của m thuộc đoạn  2  018;201  8 để hàm số 2 2 cot x  2m cotx  2m  1     y  nghịch biến trên ; . cot   x  m  4 2  A. 0 . B. 2020. C. 2019. D. 2018.
Câu 18. Xét số phức z thỏa mãn   i 10 1 2 z 
 2  .i Mệnh đề nào dưới đây đúng? z 3 1 1 3 A.  z  2. B. z  2. C. z  . D.  z  . 2 2 2 2 z 2 3
Câu 19. Tập hợp các điểm biểu diễn số phức z thỏa mãn i 1  là. z 4  i
A. Đường tròn tâm I 2;3 bán kính 1.
B. Đường tròn tâm I 4 ;  1 bán kính 1. C. Đường thẳng 3x  1 y  0 . D. Đường thẳng 3x 1 y  0 .
Câu 20. Cho hai điểm A1;2 và B4;6. Tìm tọa độ điểm M trên trục Oy sao cho diện tích tam giác MAB bằng 1 ?  4 A. 0;2. B. 0;0 và 0; .  C. 1;  0 . D. 4;0. 3  
Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Câu 21. Trong mặt phẳng toạ độ cho ba điểm ( A 2  ;0), (
B 8;0), C(0; 4) . Tính bán kính đường tròn ngoại tiếp tam giác. A. 6 . B. 5. C. 2 6 . D. 26 . A1; 0;  1 B 2;1; 2 
 P: x2 y3 z 3  0 Q Câu 22. Cho ; và
. Viết phương trình mặt phẳng đi qua 2 P điểm A,B và vuông góc .
A. Q : x  2y  z  2  0 .
B. Q: x  2 y  z  2  0 .
C. Q : x  2y  z  2  0. D.  
Q : x 2 y z 2  0 .
Câu 23. Hình chữ nhật ABCD có AB  6, AD  4. Gọi M , N , P, Q lần lượt là trung điểm bốn cạnh
AB, BC, CD, DA . Cho hình chữ nhật ABCD quay quanh QN , khi đó tứ giác MNPQ tạo thành
vật tròn xoay có thể tích bằng: A. V  2 . B. V  4 . C. V 8 . D. V  6 .
Câu 24. Xét hình trụ T  có bán kính R , chiều cao h thoả mãn R  2h 3 . N  là hình nón có bán kính
đáy R và chiều cao gấp đôi chiều cao của T  . Gọi S và S lần lượt là diện tích xung quanh 2  1 của  S
T  và N  , khi đó 1 bằng S 2 3 4 1 2 A. . B. . C. . D. . 4 3 2 3 Câu 25. Cho hình lăng trụ AB .
C A' B 'C 'có đáy ABC là tam giác vuông cân tại B và AC  2a . Hình chiếu
vuông góc của A ' trên mặt phẳng ABC  là trung điểm H của cạnh AB và AA'  a 2 . Thể
tích của khối lăng trụ đã cho bằng? 3 3 A. a 6 a 6 3 a 3. B. 3 2a 2 . C. . D. . 2 6
Câu 26. Cho tứ diện ABCD và điểm M ở trên cạnh BC . Mặt phẳng   qua M song song song với
AB và CD . Thiết diện của   với tứ diện là hình gì? A. Hình chữ nhật. B. Tứ giác lồi. C. Hình thang. D. Hình bình hành.
Câu 27. Trong không gian với hệ tọa độ Oxyz , cho hai điểm  A 2;2;  2 ; B3; 3  ;3 . Điểm M trong MA 2 không gian thỏa mãn
 . Khi đó độ dài OM lớn nhất bằng MB 3 5 3 A. 6 3 . B. 12 3 . C. . D. 5 3 . 2   
Câu 28. Trong không gian với hệ tọa độ x y z Oxyz , cho đường thẳng 3 5 1  :   và mặt phẳng 1 1 1
P: x 2 y 3z 4  0 . Đường thẳng d nằm trong mặt phẳng P sao cho d cắt và vuông góc với đường thẳng  .     A. u 1;2;  1 . B. u   1  ;2;  1 . C. u   1  ; 2  ;1 . D. u  1; 2;  1 .
Câu 29. Cho hàm số y  f x là hàm số bậc bốn. Hàm số y  f x có đồ thị như hình vẽ.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Số điểm cực tiểu của hàm số g x   f  2 x  2x  2020  là A. 3. B. 2. C. 1. D. 0 .
Câu 30. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) : 3x  3y  2z 15  0 và ba điểm A 1; 2; 0, B 1; 1  ;3  ,C1; 1  ;   1 . Điểm M (x ; y ; z ) thuộc (P) sao cho 0 0 0 2 2 2
2MA  MB  MC nhỏ nhất. Giá trị 2x  3  bằng 0 y0 z0 A. 10 . B. 11. C. 5 . D. 15 .
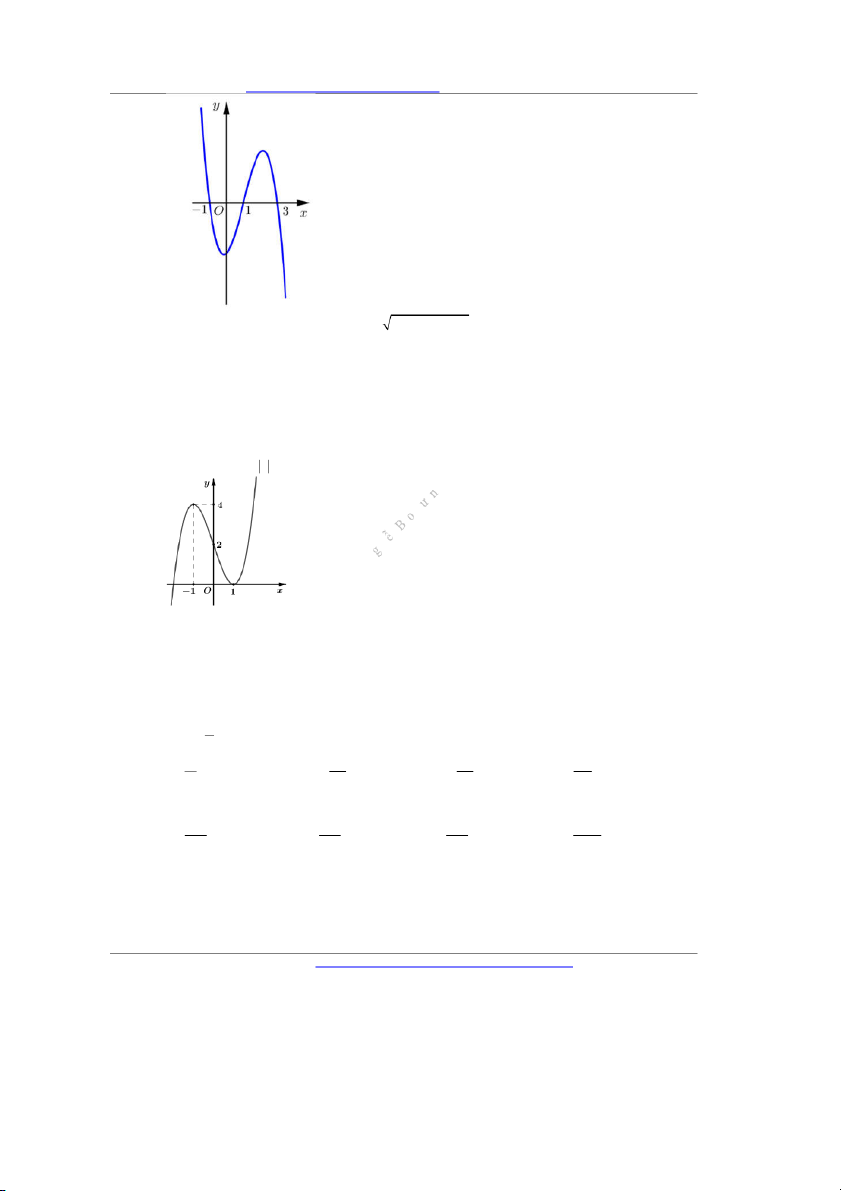
Câu 31. Cho hàm số y  f  
x có đồ thị như hình vẽ bên dưới. Tìm tất cả các giá trị thực của tham số m để hàm số g  x  f  x   m có 5 điểm cực trị. A. m  1. B. m  1  . C. m 1. D. m  1.
Câu 32. Giá trị nào của m thì phương trình  m  2 3 x  2 m 
3 x m1  0 có hai nghiệm phân biệt? A. m   3  ;5 . B. m   5;   . C. m  3. D. m   ;  3   5; .
Câu 33. Cho hàm số f x liên tục trên đoạn  1  ; 
0 thỏa mãn f  x  f  x    2 2 1 6x 9x9. Tính 0  x  xf  dx   bằng:  2  2   A. 13 . B. 74  . C. 26  . D. 2 2 . 3 3 3 3
Câu 34. Một lớp học có 30 học sinh nam và 10 học sinh nữ. Giáo viên chủ nhiệm cần chọn một ban cán sự
lớp gồm có 3 học sinh. Tính xác suất để ban cán sự lớp có cả nam và nữ. 435 135 285 5750 A. . B. . C. . D. . 988 988 494 9880
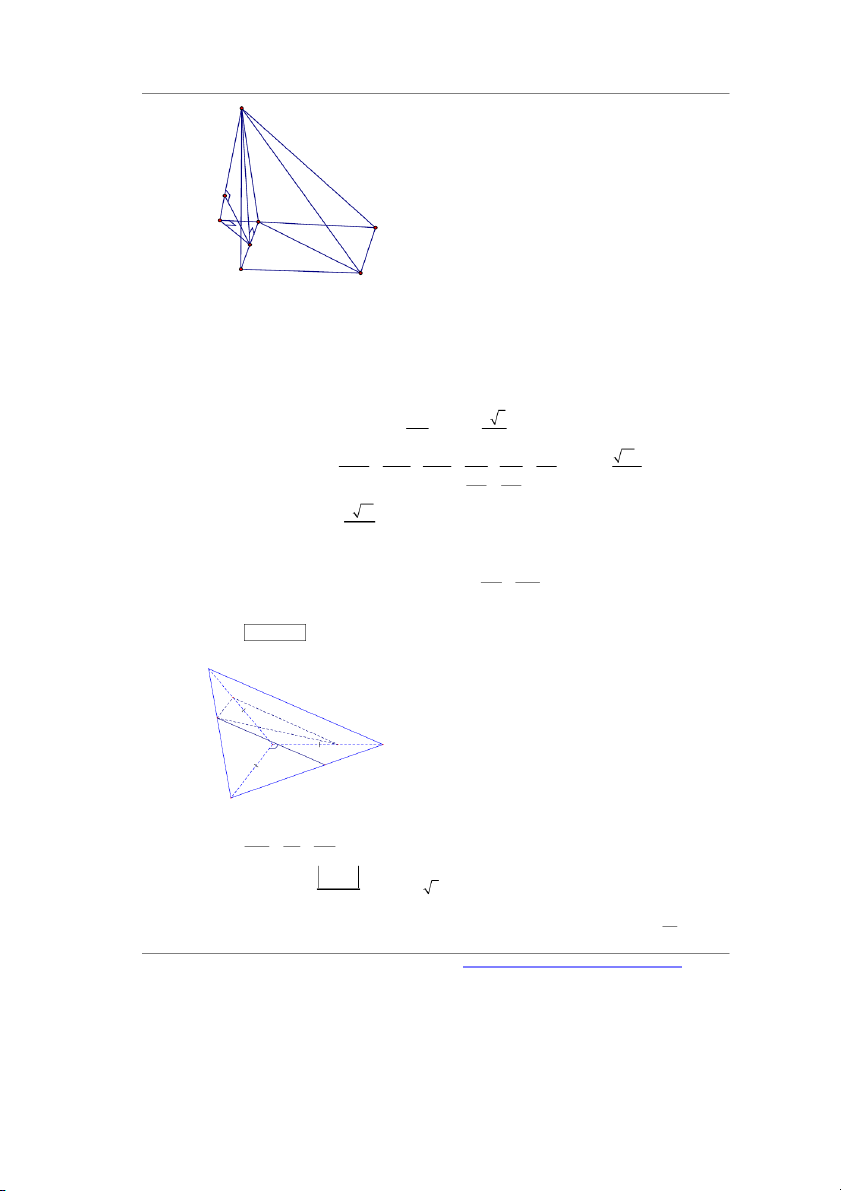
Câu 35. Cho lăng trụ tam giác ABC.ABC có chiều cao bằng 4 và diện tích đáy bằng 3 . Gọi M , N , P
lần lượt là tâm của các mặt bên ABBA , BCC B   và CAA C
  . Thể tích khối đa diện lồi có các
đỉnh là các điểm A , B , C , M , N , P bằng
Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 9 9 A. 6 . B. . C. . D. 3. 4 2 B. ĐIỀN KHUYẾT (15 CÂU) 2 x4 Câu 36. Cho hàm số y 
có đồ thị là (H). Phương trình tiếp tuyến tại giao điểm của (H) với trục x  3 hoành là: Đáp án: ………….. Câu 37. Cho hàm số f ( ) x có đạo hàm 2 5 7 f '( ) x  (
x x 1) ( x  2) ( x  3) . Số điểm cực trị của hàm số đã cho là Đáp án: …………..
Câu 38. Trong không gian Oxyz cho mặt phẳng P  :x  y  2z  5  0 và đường thẳng x 1 y  2 z  :  
. Gọi A là giao điểm của  và P ; và M là điểm thuộc đường thẳng  2 1 3
sao cho AM  84 . Tính khoảng cách từ M đến mặt phẳng P . Đáp án: …………..
Câu 39. Tổ của An và Cường có 7 học sinh. Số cách xếp 7 học sinh ấy theo hàng dọc mà An đứngđầu
hàng, Cường đứng cuối hàng là: Đáp án: ………….. f  x 2 3 f  x 2 2 Câu 40. Cho lim  14. Giới hạn của lim là: 2 x 1  1 x x 1  x 1 Đáp án: …………..
Câu 41. Cổng Arch tại thành phố St Louis của Mỹ có hình dạng là một parabol. Biết khoảng cách giữa hai
chân cổng bằng 162m . Trên thành cổng, tại vị trí có độ cao 43m so với mặt đất, người ta thả một
sợi dây chạm đất. Vị trí chạm đất của đầu sợi dây này cách chân cổng A một đoạn 10 m . Giả sử
các số liệu trên là chính xác
Gọi h là chiều cao của cổng. Hãy tính chiều cao của cổng. Đáp án: ………….. 1
Câu 42. Tìm tham số m để hàm số 3 2 y 
x  mx   m  2 x  2018 không có cực trị. 3 Đáp án: ………….. Câu 43. Cho hàm số 4 2
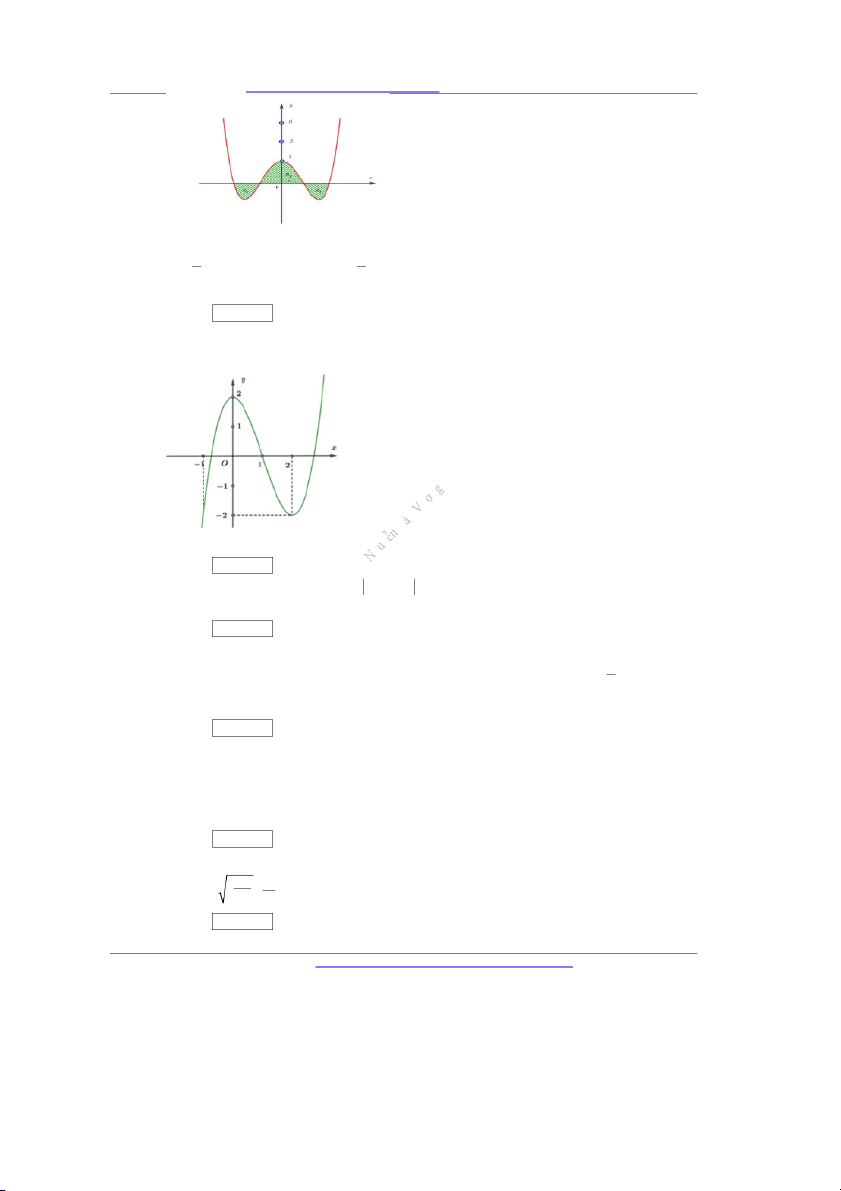
y  x  3x  m có đồ thị C
, với m là tham số thực. Giả sử C cắt trục Ox tại m  m 
bốn điểm phân biệt như hình vẽ
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/ Gọi S , S , 1 2 3
S là diện tích các miền gạch chéo được cho trên hình vẽ. Biết tồn tại duy nhất giá trị a m 
với a,b nguyên dương và a tối giản sao cho S  S  S . Đặt   . Mệnh đề nào 1 3 2 T a b b b đúng ? Đáp án: …………..
Câu 44. Cho hàm số f  
x xác định trên tập số thực và có đồ thị như hình vẽ bên dưới. Đặt
g x   f  f  f x  .
Số nghiệm của phương trình g 'x  0 trên nửa khoảng  ;  2 là Đáp án: …………..
Câu 45. Cho số phức z thỏa mãn điều kiện z  3  4i  2. Trong mặt phẳng Oxy tập hợp điểm biểu diễn
số phức w  2z  1 i là hình tròn có diện tích Đáp án: …………..
Câu 46. Cho hình lăng trụ tam giác đều AB . C A B  C
  có cạnh đáy bằng a , cạnh bên AA  a. Gọi M , N a
lần lượt là trung điểm của BB , B C
  . Lấy điểm P thuộc A B
  sao cho PB  . Tính tangóc 4
giữa đường thẳng AP và mặt phẳng MNP  Đáp án: …………..
Câu 47. Trong không gian với hệ tọa độ Oxyz, cho 3 điểm A 1;2;  3 ,B 0;1; 
1 ,C 1;0; 2 và mặt phẳng
P :x  y z  20 . Gọi M là điểm thuộc mặt phẳng (P) sao cho giá trị của biểu thức 2 2 2 T  MA  2MB  3MC
nhỏ nhất. Tính khoảng cách từ M đến mặt phẳng
Q:2x  y 2z 3 0 ? Đáp án: …………..
Câu 48. Cho các số thực dương x, y thỏa mãn log x  2y  log x  log y. Tìm giá trị nhỏ nhất của biểu 2 2 x 4 y thức 12 y 1 e .e   x P . Đáp án: …………..
Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Câu 49. Cho hình chóp S.ABCD có đáy ABCD là hình thoi và  0
ABC  60 . Mặt bên SAB là tam giác
đều cạnh a , mặt phẳng (SAB) vuông góc với mặt phẳng (ABCD) . Kí hiệu d(BC, SD) là khoảng
cách giữa 2 đường thẳng CD và SA . Khẳng định nào sau đây đúng ? Đáp án: …………..
Câu 50. Cho hình chóp S.ABC có SA  SB  SC  a ,  ASB  60 ,  BSC  90 ,  CSA 120 . Gọi M , N
lần lượt là các điểm trên cạnh AB và SC sao cho CN AM 
. Khi khoảng cách giữa M và N SC AB
nhỏ nhất, tính thể tích V của khối chóp S .AMN . Đáp án: …………..
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/ Lời giải tham khảo
A. TRẮC NGHIỆM KHÁCH QUAN (35 CÂU)
Câu 1. Thống kê điểm môn toán trong một kì thi của 400 em học sinh thấy có 72 bài được điểm 5. Hỏi
giá trị tần suất của giá trị xi =5 là A.72% B. 36% C. 18% D. 10% Lời giải: Chọn C 72 .100%  18% 400
Câu 2. Một ô tô đang chạy với vận tốc 15 m / s thì tăng tốc chuyển động nhanh dần với gia tốc a  t   2
3 8 m / s , trong đó t là khoảng thời gian tính bằng giây kể từ lúc tăng vận tốc. Hỏi sau
10 giây tăng vận tốc ô tô đi được bao nhiêu mét? A. 246 . B. 250 . C. 150. D. 180 . Lời giải Chọn B 2 3
Ta có:      dt  3 8dt = t v t a t t 8t  C . 2
Vận tốc khi ô tô bắt đầu tăng tốc là 15 m / s : v0  15  C  15 . 2 3
Vận tốc của ô tô là   t v t   8t  15 . 2
Quãng đường ô tô đi được sau 10 giây kể từ lúc bắt đầu tăng tốc là 10 10 2     3  dt = t v t 8t 1  5 dt = 250   m .  2 0 0 
Câu 3. Tập nghiệm của bất phương trình log x 1 1 là 3  A.  ;  4 . B. 1;4. C. 1;4. D.  ;  4. Lời giải Chọn C
Bất phương trình tương đương log x 1 1  0  x 1 3  1 x  4. 3  1  y5x x
Câu 4. Hệ phương trinh: 
. Có bao nhiêu cặp nghiệm  x, y mà x  y ? 1   x 5 y y A. 3. B. 4 . C. 1. D. 2 . Lời giải Chọn D
Điều kiện x  0; y  0 1  y 5x  2 2  x 5  x  xy 1 5  x  xy 1 Ta có      2 1     5 y  xy 1 (x y)(x y)  0 x 5 y y  1 1 x  ; 2 2    5   1  4  1 y x xy x  Do 2 2 x  y nên      (  x  y)(x  y)  0  y  x  1 1 x  ; y   2 2 
Câu 5. Giả sử A , B theo thứ tự là điểm biểu diễn của số phức bằng 1
z , z . Khi đó độ dài của 2 AB
Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 A. z  z . B. z  z . C. z  z . D. z  z . 1 2 2 1 2 1 1 2 Lời giải Chọn C
Giả sử z  a  bi , z  c  di ,  a,b, c, d  . 1 2 Theo đề bài ta có: 2 2
A a;b, B c;d   AB   c  a  d  b . 2 2 z            . 2 z 1 z  c  a  d  2 1 z a c  d b i b
Câu 6. Trong không gian Oxyz , cho hai điểm A2;1;0 , B 0; 1;
 4 . Mặt phẳng trung trực của đoạn thẳng AB có phương trình là
A.  x y2 z3  0 . B. 2x y 2  0 . C. 2x  y  z  4 . D. x  y 2z 3 0 . Lời giải Chọn D
Gọi M là trung điểm của AB  M 1;0;2 . 
Mặt phẳng trung trực của đoạn thẳng AB có một véc tơ pháp tuyến là AB   2  ; 2;4 
Mặt phẳng trung trực của AB đi qua M 1;0;2 và nhận AB làm véc tơ pháp tuyến nên phương
trình mặt phẳng là: 2x   1  2y  4 z   2  0  x   y  2z 3  0.
Câu 7. Trong không gian Oxyz , cho mặt phẳng  :3x 2 y z 6  0 . Hình chiếu vuông góc của điểm  A 2; 1
 ;0 lên mặt phẳng   có tọa độ là A. 2; 2  ;3 . B. 1;1; 1   . C.  1  ;1;  1 . D. 1;0;  3 . Lời giải Chọn C 
 :3x 2y z 6 0 có vectơ pháp tuyến là n  3;2; 1 . Gọi H  ;
x y; z là hình chiếu của điểm A lên mặt phẳng   . Khi đó: x 2 3k x  2 3k      AH  k.n
x  2;y 1;z  k 3; 2  ;  1 y 1   2  k  y  1 2k         H    3x  2y  z  6  0  z  k  z  k  3  x  2y  z  6 0  3x 2y z 6 0 
Giải hệ trên ta có: x  1; y 1; x  1 hay H  1;1;  1 . 2 x  2 x - 1 Câu 8. Bất phương trình  0 có tập nghiệm là: 2 x + 5x + 6 A.  2; 1 0;1         . B. 3;    .    2 1;1     C.  3  ;  2  1  ;  1 . D.  3  ;  2   0;  1 . Lời giải Chọn B
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/ Cho 2 x  0  x  0 2 x  1 0  x   1 x   3 2 x 5x 6 0      x  2 
Lập bảng xét dấu ta được:
Dựa vào bảng xét dấu suy ra tập nghiệm bất phương trình đã cho là: S  3; 2  1;1       .  
Câu 9. Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn  3
 ;3 để phương trình  2 m   2
2 cos x  2m sin 2x 1  0 có nghiệm. A. 7. B. 6 . C. 4 . D. 3 . Lời giải. Chọn B 1 cos 2 Phương trình   2 x m  2 .  2m sin 2x 1  0 . 2  m x  2 m   2 4 sin 2 2 cos 2x  m  4. 2 2 Phương trình có nghiệm 2  m   2 m     2 m   2 2 16 2
4  12m  12  m  1  m 1 . m   
 m  3;2;1;1;2;3   có 6 giá trị nguyên. m 3;3    
Câu 10. Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nửa diện tích
của mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng 1 bằng nửa diện tích của đế tháp (có diện tích là 2
12288 m ). Tính diện tích mặt trên cùng. A. 2 6m . B. 2 12m . C. 2 10m . D. 2 8m . Lời giải Chọn A 1
Ta nhận thấy diện tích các mặt trên của mỗi tầng lập thành 1 cấp số nhân với công bội q  2
Số hạng đầu u  12288 . Khi đó mặt trên cùng tầng 11 ứng với 1 1 u . 2 11 Do đó  1 11  u  u . 12288.  6. 12 1 q   2  x 1 
Câu 11. Họ các nguyên hàm của hàm số y là: 2 x 1 1 1 x 1 A. e   C . B. ln x   C . C. ln x  C . D. ln x   C . x x x x Lời giải Chọn C
Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022   u  , n   1  ;2;1   .
Đường thẳng d nằm trong mặt phẳng  
P sao cho d cắt và vuông góc với đường thẳng  nên  d nhận u  1; 2;  1 làm vectơ chỉ phương. d
Câu 29. Cho hàm số y  f x  là hàm số bậc bốn. Hàm số y  f x có đồ thị như hình vẽ.
Số điểm cực tiểu của hàm số g  x  f  2x  2x  2020  là A. 3. B. 2. C. 1. D. 0. Lời giải Chọn D  x  1  Từ đồ thị hàm số 
y  f  x ta thấy f  x   0  x  1  .  x  3 
Xét hàm số g  x  f  2x  2x  2020 .  g  x  x 1  .f   2 x  2x  2020 . 2  x  2x  2020 
g  x   0  f   x 1 2 x  2x  2020 .  0 2 x  2x  2020 2      2  x 2x 2020  1  vn   x 2x 2020 1 f      2 x  2x  2020  0 2  2  x  2x 2019   0 v   x  2x  2020  1   n   x  1. x 1     0 2  2 x  2x  2020  3  x  2x 2011  0 v  n 2  x  2x 2020   x   1  x  1
Từ đồ thị hàm số y  f  x ta có: x  3 thì f  x 0 . Mà 2
x  2x  2020  2019  3 nên f  2
x  2x  2019   0 với x . Bảng biến thiên
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Vậy hàm số g x chỉ có một cực đại.
Câu 30. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) : 3x  3y  2z 15  0 và ba điểm A1; 2;  0 , B1; 1  ;3 ,C 1; 1  ; 1  . Điểm M (x ; y ; z ) thuộc (P) sao cho 0 0 0 2 2 2
2MA  MB  MC nhỏ nhất. Giá trị 2x  3  bằng 0 y0 z0 A. 10 . B. 11. C. 5 . D. 15 . Lời giải Chọn C    
Xét điểm I thỏa 2IA IB  IC  0 suy ra I1;2;  2 .   2   2   2 2 2 2 2MA  MB  MC  
2 MI  IA MI  IB MI  IC 2 2 2 2
 2MI  2IA  IB  IC . 2 2 2
2MA  MB  MC nhỏ nhất khi và chỉ khi MI nhỏ nhất hay M là hình chiếu của I lên (P) . x   1 3t x  1  3 0 t  
Lúc đó, đường thẳng MI có phương trình y  2 3t suy ra y  2 3 . 0 t   z  2    2t z  2   2  0 t
Mà 3x  3y  2z 15  0   3 1 3t   3 2 3t  
2 2 2t 15  0  t 1 . 0 0 0
2x  3y  z  2 1 3t  3 2  3t  2   2  6   5. 0 0 0      t t
Câu 31. Cho hàm số y  f  
x có đồ thị như hình vẽ bên dưới. Tìm tất cả các giá trị thực của tham số m để hàm số g  x  f  x   m có 5 điểm cực trị. A. m  1  . B. m  1. C. m 1. D. m 1. Lời giải Chọn A
Nhận xét: Hàm g x  f  x  m là hàm số chẵn nên đồ thị đối xứng qua trục Oy  x  0 là
một điểm cực trị của hàm số. Ta có   x g x 
. f   x m  với x  0. x          x m x m
g x  0  f   x m  1 1 theo do thi f    0 x    . *  x  m  1   x  1 m 
Để hàm số g x  có 5 điểm cực trị  * có 4 nghiệm phân biệt khác 0
Trang 18 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 1 m  0   1 m  0  m  1. 1 m  1  m
Câu 32. Giá trị nào của m thì phương trình  m  2 3 x  2 m 
3 x m1  0 có hai nghiệm phân biệt? A. m   3  ;  5 . B. m5;  . C. m  3. D. m ;    3 5; . Lời giải Chọn C Ta có: m  2
3 x  2m 3 x m1  0 có hai nghiệm phân biệt khi:  a  0 m  3  0     m 3. 2     0 2m   4m 6 0, m  
Câu 33. Cho hàm số f x liên tục trên đoạn  1
 ;0 thỏa mãn f x  fx  2 2 1  6x 9x9. Tính 0  x  xf  d    x bằng:  2   2 A. 13 . B. 74  . C. 26  . D. 2 2 . 3 3 3 3 Lời giải f    1 2f 06 f    1 4
Ta có: f  x f x  2 2 1  6x 9x9     f  02f   1 9 f    0 1    0 0 0 f x2 f x  13 2
1 6x 9x9 f xdx2 f x 1  dx  2 6x 9x9dx    2 1  1  1  0 0 0 13 Mà f   x dx  f  x    
1dx nên suy ra f xdx  6 1  1  1  0 0 0 0 0  x   x   x   x   x  x 22 xf  dx  2 xf  2 f dx 16  2 f dx 16 4 f d       2   2   2   2   2            2 3 2  2 2 2 2
Câu 34. Một lớp học có 30 học sinh nam và 10 học sinh nữ. Giáo viên chủ nhiệm cần chọn một ban cán sự
lớp gồm có 3 học sinh. Tính xác suất để ban cán sự lớp có cả nam và nữ. 435 135 285 5750 A. . B. . C. . D. . 988 988 494 9880 Lời giải Chọn C Ta có n 3  C . 40
Gọi A là biến cố: “3 học sinh trong ban cán sự lớp có cả nam và nữ” n A 1 2 2 1  C .C C .C 30 10 30 10 1 2 2 1 C . C  C . C 15 285 P A 30 10 30 10    3 C 26 494 40
Câu 35. Cho lăng trụ tam giác AB .
C A B C có chiều cao bằng 4 và diện tích đáy bằng 3. Gọi M , N , P
lần lượt là tâm của các mặt bên ABBA , BCC B
  và CAAC . Thể tích khối đa diện lồi có các
đỉnh là các điểm A , B , C , M , N , P bằng 9 9 A. 6 . B. . C. . D. 3 . 4 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/ Lời giải Chọn C C A B P K I N M J C' A' B' Ta có V  3.4  12 I J K AB . C ABC
. Gọi , , lần lượt là trung điểm của AA , BB , CC. V  6 . AB . C IJK V . 1 1 1
Áp dụng bài toán tỷ số thể tích ta có: A IMP   V  V  A .IMP A .    V 8 A B C . 8 2 A AB C   1 Dễ thấy    . A V .IMP B V .MNJ C V .NPK 2 1 9 Vậy V  V  3V  6 3.  . ABC.MNP AB . C IJK . A IMP 2 2 B. ĐIỀN KHUYẾT (15 CÂU) 2 x 4 Câu 36. Cho hàm số y 
có đồ thị là (H) . Phương trình tiếp tuyến tại giao điểm của (H) với trục x  3 hoành là: Đáp án: ………….. Lời giải 2 
Giao điểm của (H) với trục hoành là ( A 2; 0) . Ta có: y'   y'(2)  2  2 (x  3)
Phương trình tiếp tuyến cần tìm là y  2(x  2) hay y  2x  4 .
Câu 37. Cho hàm số f (x) có đạo hàm 2 5 7
f '(x)  x(x 1) (x  2) (x  3) . Số điểm cực trị của hàm số đã cho là Đáp án: ………….. Lời giải Ta có f '( ) x  0 2 5 7
 x (x  1) (x  2) (x  3)  0  x  0  x  1  x  2  x   3 Bảng xét dấu f (x) x  0 1 2 3  f '(x)  0  0  0  0 
Từ bảng xét dấu ta thấy f '(x) có 3 lần đổi dấu nên hàm số đã cho có 3 điểm cực trị.
Trang 20 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Câu 38. Trong không gian Oxyz cho mặt phẳng P :x  y  2z  5  0 và đường thẳng x 1 y  2 z  :  
. Gọi A là giao điểm của  và P ; và M là điểm thuộc đường thẳng  2 1 3
sao cho AM  84 . Tính khoảng cách từ M đến mặt phẳng P . Đáp án: ………….. Lời giải   u n 3 21 Ta có:    P  . sin , P      . u . n 6. 14 14  P
Gọi H là hình chiếu của điểm M lên mặt phẳng. Khi đó ta có tam giác AMH là tam giác vuông tại H nên     sin ,  sin MH P MAH   MH 3 . MA
Câu 39. Tổ của An và Cường có 7 học sinh. Số cách xếp 7 học sinh ấy theo hàng dọc mà An đứngđầu
hàng, Cường đứng cuối hàng là: Đáp án: ………….. Lời giải
Chọn An đứng đầu hàng có 1 cách, chọn Cường đứng cuối hàng có 1 cách.
Sắp xếp 5 bạn còn lại có: P  5! 120 cách. 5
Vậy có: 1.1.120  120 cách. f  x 2 3 f x 2  2 lim  14. lim Câu 40. Cho 2 x 1  1 x Giới hạn của x 1  x 1 là: Đáp án: ………….. Lời giải Ta có: f   x  2 lim 14 suy ra f 1  2 2 x 1  1x Theo đề bài ta có: 3 f  x  2  2
3f  x  2 4 x  1 lim  lim x 1  x 1 x  1   2 x   1  3f x  2   2  f  x 2 3 x  1      lim .  2 x1  1  x 3 f  x  2  2    f   x 2 3   x1    Ta có: lim 1  4; 3.2 3.2 3 lim    2 x1 1  x x 1  3 f x  2  2 3 f 1 2  2 2 2 2 3 f  x  2  2  3  Suy ra: lim 14.  2    1 x 1  x 1  2 
Câu 41. Cổng Arch tại thành phố St Louis của Mỹ có hình dạng là một parabol. Biết khoảng cách giữa hai
chân cổng bằng 162m . Trên thành cổng, tại vị trí có độ cao 43m so với mặt đất, người ta thả một
sợi dây chạm đất. Vị trí chạm đất của đầu sợi dây này cách chân cổng A một đoạn 10 m . Giả sử
các số liệu trên là chính xác
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Gọi h là chiều cao của cổng. Hãy tính chiều cao của cổng. Đáp án: ………….. Lời giải
Chọn hệ trục tọa độ sao cho A  O, AB  Ox . Ta có: A  O 0;0, B 162;0, M 10;43 .
Gọi phương trình parabol là: 2 y  ax  bx  c .  43 a    152 c  0 162a  b  0     3483 Vì , A , B M  parabol ta có: 2 162 a  162b  c  0  10a   b  43  b   76 1  00a 10b c 43 c  0        c   0  43 3483
Vậy phương trình parabol là: 2 y   x 
x . Do đó chiều cao của cổng là: 152 76 b x    81  h 185,6m . 2 a 1
Câu 42. Tìm tham số m để hàm số 3 2 y 
x  mx   m 2 x 2018 không có cực trị. 3 Đáp án: ………….. Lời giải Ta có: 2
y  x  2mx  m  2
Để hàm số đã cho không có cực trị khi phương trình y  0 vô nghiệm hoặc có nghiệm kép hay    0 2
 m  m  2  0  1   m  2. Câu 43. Cho hàm số 4 2
y  x  3x  m có đồ thị C
, với m là tham số thực. Giả sử C cắt trục Ox tại m  m 
bốn điểm phân biệt như hình vẽ Gọi S , S , 1
2 S là diện tích các miền gạch chéo được cho trên hình vẽ. Biết tồn tại duy nhất giá trị 3 a m 
với a,b nguyên dương và a tối giản sao cho   . Đặt   . Mệnh đề nào 1 S S3 S2 T a b b b đúng ? Đáp án: ………….. Lời giải
Trang 22 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 Giả sử    . 1
x là nghiệm lớn nhất của phương trình 4 2 x 3x m 0 Suy ra 4 2 m  x  3x (1). 1    1 x S S S Vì 1 3 2 
 S  2S  S  S  0  f (x).dx  0 2 3 2 3   S  S 2 1 3 0 1 x 1 x 5 4 Ta có 4 2 1 x 3 1 x 2
f (x)dx  (x  3x  m)dx   x  mx  x (  x  m)   1 1 1 1 5 5 0 0 4 4 x x Do đó 1 2 1 2 x (  x  ) m  0 
 x  m  0 (2), vì (x  0) 1 1 1 5 5 1 4 x 5 Từ (1), (2) suy ra: 1 2 4 2 4 2 2  x  x 3 x 0  4  x 1  0 x 0   1 1 1 1 1 1 x 5 2 5 Suy ra: 4 2 m   x  3x   a  5; b  4 1 1 4 Vậy T  a  b  9 .
Câu 44. Cho hàm số f  
x xác định trên tập số thực và có đồ thị như hình vẽ bên dưới. Đặt
g x   f  f  f x  .
Số nghiệm của phương trình g ' x  0 trên nửa khoảng  ;  2  là Đáp án: ………….. Lời giải  x  1 x 
Dựa vào đồ thị ta thấy:  f  x 0  x  k (  1  ; 0)  ; f x 0 '  0   x  2    x  a (2; 3) x  ;
 2 f x  ;  
2  f  f x  ;  2 * g  x  f  f  f   x  với x  ;   2
g ' x  f 'x. f ' f x. f '  f  f  x
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/ x  0 x  0  x  x  2 0  x  0    x  2 x  2   x  1 x  2    f 'x  0        f x  0  0      0 x  k f x f x 
g ' x  0   f ' f  x  0             f  x f x  2   f x  x 0 2  2      
f ' f  f x   0    f   f x  f x  k x b  0 f  x  k  x  e       f   f x  f x  1  2 f   x  1   0 x  c f x  x d 
Vậy, phương trình g 'x  0 có 8 nghiệm thuộc khoảng   ;   2 .
Câu 45. Cho số phức z thỏa mãn điều kiện z  3  4i  2. Trong mặt phẳng Oxy tập hợp điểm biểu diễn
số phức w  2z  1 i là hình tròn có diện tích Đáp án: ………….. Lời giải w 1   2 1 i w z  i  z  2 w 1  3 4  2 i z i 
 3 4i  2  w 1 i  6 8i  4  w  7  9i  4   1 2 Giả sử 2 2
w  x  yi x, y   , khi đó 1  x  7    y  9  16
Suy ra tập hợp điểm biểu diễn số phức w là hình tròn tâm I 7;  9 , bán kính r  4.
Vậy diện tích cần tìm là 2 S  .4 16 .
Câu 46. Cho hình lăng trụ tam giác đều AB .
C ABC có cạnh đáy bằng a , cạnh bên AA  a . Gọi M , N a
lần lượt là trung điểm của BB , B C
  . Lấy điểm P thuộc A B
  sao cho PB  . Tính tangóc 4
giữa đường thẳng AP và mặt phẳng MNP  Đáp án: ………….. Lời giải
Trang 24 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 C' A' H P N B' M C A K B
Gọi H , K lần lượt là trung điểm của AB .
Khi đó ta có HB / /PM , HB  AM . Suy ra AM  MP (1)
Mặt khác ta có BC  MK , BC  AK (vì AK  BCB)
 BC   AMK   MN  AM (2)
Từ (1) và (2) suy ra AM  MNP  . Vậy góc giữa đường thẳng AP và mặt phẳng MNP là góc  APM . 2  a Ta có 2 2 2 5 AM  AB  MB  a   a  2    2 2 2  a   a  5 2 2 MP  B M   B P     a  2   4      4 Suy ra  tan AM APM   2. PM
Câu 47. Trong không gian với hệ tọa độ Oxyz, cho 3 điểm A1;2;  3 ,B 0;1; 
1 ,C 1;0; 2 và mặt phẳng
P:x y z 2 0. Gọi M là điểm thuộc mặt phẳng (P) sao cho giá trị của biểu thức 2 2 2 T  MA  2MB  3MC
nhỏ nhất. Tính khoảng cách từ M đến mặt phẳng
Q:2 x  y 2 z 3 0 ? Đáp án: ………….. Lời giải     Gọi I  ; a ;
b c là điểm thỏa mãn IA 2IB 3IC 0.   
Ta có IA 1 a;2 b;3c ,IB  a;1 b;1 c ,IC 1 a;b; 2c   2 a   3 1
  a 2 a 3 3a 0 6  a 4         2  2 2 1  IA  2IB  3IC  0  2
 b  2 2b 3b  0  6  b  4  b   I ; ;  . 3     3 3 6  3 c 2 2c 6 3c 0 6c 1             1 c   6 Ta chứng minh được 2 2 2 2
T  6MI  IA  2IB  3IC . Do đó T đạt GTNN khi MI đạt GTNN  M
là hình chiếu vuông góc của I trên mặt phẳng (P).
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/  2 x   t  3   2  2 2 1 19 19
Ta có MI : y  t , M M  I M t  ;t  ;t  , M     P 3  t  0  t   3   3 3 6 6 18  1 z   t  6 7 7 22    3  7 7 11   M  ;  ;   d M;Q 9 18 9 91     .  18 18 9  3 54
Câu 48. Cho các số thực dương x , y thỏa mãn log x 2y  log x log y. Tìm giá trị nhỏ nhất của biểu 2 2 x 4 y thức 12 y 1 e .e   x P . Đáp án: ………….. Lời giải
Từ log x  2y   log x  log y  log xy  x  2y  xy . 2  x  2 2 2 2   2 2 x x 2 x y y y  2  y 4   Biến đổi 1 2y 1  4 2 y   1 x x 1   4 2 y   1 x 1  2y 1 x  1 P  e .e  e .e e e .
Áp dụng BĐT Bunhiacopski ta có 2  2 2 x     x  x      2     2  y  2  y  2   x 2  2 2  y  y x  y   x   2 2 1 1             y     .  2y  1 x 1    2   2 y 1 x 1 x  2 y  2 4x  2y  2    
Áp dụng BĐT Côsi ta có xy  x  2y  2 . x 2y 2 2
 x y  8xy  xy  8  x  2 y  8 .  2 x  y2 2
5 x 2 y 32 x 2 y 64 x 2y   8 5   x  2y 8 Khi đó 8      0 4 x 2 y 2 5 20 x  2 y  2 20x 2y 2 2  x   x y2 2 8   2  2 y 8 8       5  P  e . 4 x 2 y 2 5 2 y 1  x 1  5 8
Dấu “ ” xảy ra  x  4 , y  2 5  min P  e .
Câu 49. Cho hình chóp S.ABCD có đáy ABCD là hình thoi và  0
ABC 60 . Mặt bên SAB là tam giác
đều cạnh a , mặt phẳng (SAB) vuông góc với mặt phẳng (ABCD) . Kí hiệu d (BC, SD) là khoảng
cách giữa 2 đường thẳng CD và SA. Khẳng định nào sau đây đúng ? Đáp án: ………….. Lời giải
Trang 26 Fanpage Nguyễn Bảo Vương 
 https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 S H A F D M B C
Gọi M là trung điểm AB. Ta được SM   ABCD
Ta có AC //AD nên d BC ,SD   d BC ,SAD  d ,
B SAD   2 d M,  SAD .
Vì ABCD là hình thoi và  0 ABC  60 nên A  BC đều cạnh a .
Kẻ MF  AD ; MH  SF. Ta có AF  (SMF)  AF  MH (1). Ta lại có MH  SF (2).
Từ (1), (2) suy ra MH  SAD . Xét tam giác MF a MFA , ta có:  3 Sin FAM   MF  . MA 4 1 1 1 1 1 20 15 Xét tam giác a SFA , ta có:       MH  . 2 2 2 2 2 2 MH SM MF 3a 3a 3a 10 4 16 Vậy d  BC SD a 15 ,  2MH  . 5   
Câu 50. Cho hình chóp S.ABC có SA  SB  SC  a , ASB  60 , BSC  90 , CSA 120 . Gọi M , N
lần lượt là các điểm trên cạnh AB và SC sao cho CN AM 
. Khi khoảng cách giữa M và N SC AB
nhỏ nhất, tính thể tích V của khối chóp S.AMN . Đáp án: ………….. Lời giải A I M S C N K B
Dựng MK//AC K BC ; MI //SB I S  A. Khi đó: AM AI NC  
 x  IN  MK  cos AC;SB  cos IM ; MK . AB SA SC   A . C SB Ta có cos AC; SB  và AC  a 3, SB  a A . C SB          Lại có     2 . .  .  .  . .cos120  . cos 90 a AC SB AS SC SB AS SB SC SB AS SB SC SB    2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/ 2 a 2   a  AC SB   AC SB 3 2 . cos ,    3  cos IMK  hay  3 cos IMK   . 2 2 a 3 6 6 6 TH1:  3 cosIMK  6 Ta có 2 2 2 3 2 2 2 MN  MI  MK  MI MK  a x  a   2 2 2 x  a x a   3 2 . . 3 1 2 . 3 1 x . 6 6 2 2 a  x 31 x2 x 1 x        2 2  5 11   11 2  3 a a  x      .   6  12 12   2 11a 5 Do đó MN    . min x 12 6 V SN AM 2 1 5 5 2 Vậy SAMN 3 3  . V  a . .  a . SAMN V SC AB 12 6 6 432 SABC TH2:  3 cosIMK   6  3  3 Ta có 2 2 2 2 2 2
MN  MI  MK 2MI.MK. 
  a x 3a 1  x 2 2 2 2a x . 3a x 1  .  6  6    a  x    2 2 2 3 1 x  x x 1     2 2  7 11   11 2 a  a 5 x       .   10  20 20   2 11a 7 Do đó MN    min x 20 10 V SN AM 2 3 7 7 2 Vậy SAMN 3  .  V  a . .  . SAMN V SC AB 12 10 10 400 SABC
• XEM THÊM ĐỀ CƯƠNG ÔN THI TẠI:
• https://www.nbv.edu.vn/2022/01/de-cuong-danh-gia-nang-luc-dhqg-ha-noi.html
Theo dõi Fanpage: Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Hoặc Facebook: Nguyễn Vương 
 https://www.facebook.com/phong.baovuong
Tham gia ngay: Nhóm Nguyễn Bào Vương (TÀI LIỆU TOÁN)  https://www.facebook.com/groups/703546230477890/
Ấn sub kênh Youtube: Nguyễn Vương
 https://www.youtube.com/channel/UCQ4u2J5gIEI1iRUbT3nwJfA?view_as=subscriber
Tải nhiều tài liệu hơn tại: https://www.nbv.edu.vn/
Trang 28 Fanpage Nguyễn Bảo Vương 
 https://www.facebook.com/tracnghiemtoanthpt489/