Ôn thi đánh giá năng lực(Đề 9) | Trường đại học Quốc gia Hà Nội

Ôn thi đánh giá năng lực(Đề 9) | Trường đại học Quốc gia Hà Nội được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

93 47 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Đánh giá năng lực

Trường: Đại học Quốc gia Hà Nội

Thông tin:

27 trang 7 tháng trước

Tác giả:

Profile Kim Oanh
Trang 1
A. TRẮC NGHIỆM KHÁCH QUAN (35 CÂU)
Câu 1. Có 100 học sinh tham dự kì thi học sinh giỏi Hóa (thang điểm 20). Kết quả như sau:
Điểm
9
10
11
12
13
14
15
16
17
18
19
Tần số
1
1
3
5
8
13
19
24
14
10
2
Số trung vị là:
A.
15
e
M
B.
15,50
e
M
C.
16
e
M
D.
16,5
e
M
Câu 2. Gọi
h t cm
là mực nước ở bồn chứa sau khi bơm nước được giây. Biết rằng t
3
1
8
5
h t t
và lúc đầu bồn không có nước Tìm mức nước ở bồn sau khi bơm nước được 6 giây (làm tròn đến .
kết quả hàm phần trăm).
A.
2,33 cm
. B.
5,06 cm
. C.
3,33 cm
. D.
2,66 cm
.
Câu 3. Tập nghiệm của phương trình
2
2
log 2 1
x x
là :
A.
1
B.
0
C.
0;1
D.
1;0
Câu 4. Cho hệ phương trình:
2 2
2 2
3 4 2 17
16
x xy y
y x
. Hệ thức biểu diễn
x
theo
y
rút ra từ hệ phương
trình là?
A.
5
13
x y
hay
3
5
x y
B.
3
2
y
x
hay
3
2
y
x
.
C.
1
2
y
x
hay
1
2
y
x
. D.
2
2
y
x
hay
2
2
y
x
.
Câu 5. Cho hai số phức
1
1 3z i
,
2
4 6z i
có các điểm biểu diễn trên mặt phẳng tọa độ lần lượt là
hai điểm và M
N
. Gọi
z
là số phức mà có điểm biểu diễn là trung điểm của đoạn
MN
. Hỏi
z
là
số phức nào trong các số phức dưới đây?
A.
3 9
2 2
z i
. B.
3 9z i
. C.
1 3z i
. D.
5 3
2 2
z i
.
Câu 6. Phương trình mặt phẳng đi qua
1;1; 2A
, song song với
: 2 2 1 0x y z
là
A.
2 2 5 0x y z
. B.
2 2 1 0x y z
.
C.
2 2 2 0x y z
. D.
2 2 0x y z
.
Câu 7. Trong không gian
Oxyz
, tọa độ điểm đối xứng của điểm
0 ;1; 2M
qua mặt phẳng
0x y z
là:
A.
2 ; 1; 0
. B.
0 ; 1; 2
. C.
0;1; 2
. D.
2; 1; 0
.
Câu 8. Bất phương trình 2 1 3 2x x có tổng năm nghiệm nguyên nhỏ nhất là
A.
20
. B.
15
. C.
5
. D.
10
.
Câu 9.
Nghiệm của phương trình lượng giác
2
2sin 3sin 1 0x x
thõa điều kiện
0
2
x
là:
A.
6
x
. B.
5
6
x
. C.
3
x
. D.
2
x
.
ĐỀ
ĐỀ
ĐỀ
ĐỀ ĐỀ
SỐ
SỐ
SỐ
SỐ SỐ
9.
9.
9.
9. 9.
ÔN
ÔN
ÔN
ÔN ÔN
THI
THI
THI
THI THI
ĐGN
ĐGN
ĐGN
ĐGNĐGN
L
L
L
L L
ĐHQ
ĐHQ
ĐHQ
ĐHQĐHQ
G
G
G
G G
HÀ
HÀ
HÀ
HÀ HÀ
NỘ
NỘ
NỘ
NỘNỘ
I
I
I
I I
202
202
202
202202
1-2
1-2
1-2
1-21-2
02
02
02
0202
2
2
2
22
• |FanPage: Nguyễn Bảo Vương
Trang 2
Câu 10. Sinh nhật bạn của An vào ngày
tháng năm. An muốn mua một món quà sinh nhật cho bạn nên
quyết định bỏ ống heo
100
đồng vào ngày
01
tháng
01
năm
2016
, sau đó cứ liên tục ngày sau
hơn ngày trước
100
đồng. Hỏi đến ngày sinh nhật của bạn, An đã tích lũy được bao nhiêu tiền ?
(thời gian bỏ ống heo tính từ ngày
01
tháng
năm
2016
đến ngày
30
tháng
4
năm
2016
).
A.
714.000
đồng. B.
750.300
đồng. C.
738.100
đồng. D.
726.000
đồng.
Câu 11. Cho một nguyên hàm của hàm số
1
1
x
f x
x
là
F x
và
0 3
F
. Khi đó
F x
bằng:
A.
2ln 1 3
x x
. B.
2ln 1 3
x x
.
C.
2ln 1 3
x x
. D.
2
2
3
1
x
x
.
Câu 12. Tìm tất cả các giá trị thực của tham số
m
sao cho bất phương trình:
3
3
1
3 2x mx
x
nghiệm
đúng
1x
?
A.
3
2
m
. B.
1 3
3 2
m
. C.
2
3
m
. D.
2
3
m
.
Câu 13. Một chất điểm
A
xuất phát từ
O
, chuyển động thẳng với vận tốc biến thiên theo thời gian bởi
quy luật
2
1 58
/
120 45
v t t t m s
, trong đó
t
(giây) là khoảng thời gian tính từ lúc
A
bắt đầu
chuyển động. Từ trạng thái nghỉ, một chất điểm
B
cũng xuất phát từ
O
, chuyển động thẳng
cùng hướng với
A
nhưng chậm hơn
3
giây so với
A
và có gia tốc bằng
2
/a m s
(
a
là hằng
số). Sau khi
B
xuất phát được
15
giây thì đuổi kịp
A
. Vận tốc của
B
tại thời điểm đuổi kịp
A
bằng
A.
25 /m s
B.
36 /m s
C.
30 /m s
D.
21 /m s
Câu 14. Hiện tại dân số ở Hà Nội là
7,55
triệu người với tốc độ tăng dân số
2%
một năm và dân số
Thành phố Hồ Chí Minh là
8,15
triệu người với tốc dộ tăng dân số
1,5%
một năm. Hỏi ít nhất
sau bao nhiêu năm nữa thì số dân Hà Nội vượt số dân Thành phố Hồ Chí Minh.
A.
16
năm. B.
20
năm. C.
18
năm. D.
17
năm.
Câu 15. Tìm nghiệm của phương trình
2
log 5 4
x
A.
13
x
. B.
11
x
. C.
3
x
. D.
21
x
.
Câu 16. Thể tích của vật tròn xoay có được khi quay hình phẳng giới hạn bởi đồ thị hàm
tany x
, trục
Ox
, đường thẳng
0
x
, đường thẳng
3
x
quanh trục
Ox
là:
A.
2
3
3
V
. B.
2
3
3
V
. C.
3
3
V
. D.
3
3
V
.
Câu 17. Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
9
mx
y
x m
nghịch biến trên từng
khoảng xác định
A.
3 3
m
. B.
3 3
m
C.
3 3
m
. D.
3 3
m
.
Câu 18. Cho số phức
z a bi
,
,a b
thỏa mãn
1 3 0z i z i
. Tính
3S a b
.
A.
7
3
S
. B.
5
S
. C.
5
S
. D.
7
3
S
.
Câu 19. Trong mặt phẳng phức, tập hợp các điểm
M
biểu diễn số phức
z
thỏa mãn điều kiện
3 4z z i
là?
A. Parabol
2
4y x
. B. Đường tròn
2 2
4 0
x y
.
C. Elip
2 2
1
4 2
x y
. D. Đường thẳng
6 8 25 0
x y
.
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 3
Câu 20.
Cho đường thẳng
2 3
:
1 2
x t
y t
. Hoành độ hình chiếu của
4;5
M
trên
gần nhất với số nào
sau đây?
A.
1,5
. B.
1,2
. C.
1,3
. D.
.
Câu 21. Đường tròn
2 2
3 3 6 9 9 0
x y x y
có bán kính bằng bao nhiêu?
A.
5
2
. B.
5
. C.
25
2
. D.
25
4
.
Câu 22. Trong không gian hệ tọa độ
Oxyz
, cho
1;2; 1
A
;
1;0;1
B
và mặt phẳng
: 2 1 0
P x y z
. Viết phương trình mặt phẳng
Q
qua
,A B
và vuông góc với
P
A.
:3 0
Q x y z
B.
:2 3 0
Q x y
C.
: 0
Q x z
D.
: 0
Q x y z
Câu 23. Cho một hình nón đỉnh
S
có chiều cao bằng
8cm
, bán kính đáy bằng
6cm
. Cắt hình nón đã cho
bởi một mặt phẳng song song với mặt phẳng chứa đáy được một hình nón
N
đỉnh
S
có đường
sinh bằng
4cm
. Tính thể tích của khối nón
N
.
A.
3
768
cm
125
V
B.
3
786
cm
125
V
C.
3
2304
cm
125
V
D.
3
2358
cm
125
V
Câu 24. Một cái cột có hình dạng như hình bên (gồm một khối nón và một khối trụ ghép lại). Chiều cao đo
được ghi trên hình, chu vi đáy là. Thể tích của cột bằng
A.
3
52000 p
cm
. B.
3
13000 p
cm
. C.
3
5000p
cm
. D.
3
15000 p
cm
.
Câu 25. Cho lăng trụ tam giác
.
ABC A B C
có đáy là tam giác đều cạnh
a
. Độ dài cạnh bên bằng
4a
.
Mặt phẳng
BCC B
vuông góc với đáy và
30
B BC
. Thể tích khối chóp
.
ACC B
là:
A.
3
3
6
a
. B.
3
3
12
a
. C.
3
3
18
a
. D.
3
3
2
a
.
Câu 26. Cho tứ diện
ABCD
. Gọi
H
là một điểm nằm trong tam giác
ABC
,
là mặt phẳng đi qua
H
song song với
AB
và
CD
. Mệnh đề nào sau đây đúng về thiết diện của
của tứ diện?
A. Thiết diện là hình bình hành. Thiết diện là hình chữ nhật. B.
C. Thiết diện là hình vuông. Thiết diện là hình thang cân. D.
Câu 27. Trong hệ tọa độ
O
xyz
, cho điểm
2;1;3
A
, mặt phẳng
( ) : 2 2 3 0
x y z
và mặt cầu
2 2 2
( ) : 6 4 10 2 0
S x y z x y z
. Gọi
là đường thẳng đi qua
A
, nằm trong mặt phẳng
( )
và cắt
( )S
tại hai điểm
,M N
. Độ dài đoạn
MN
nhỏ nhất là:
A.
2 30
. B.
30
. C.
30
2
. D.
3 30
2
.
Câu 28. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
: 2 4 0
P x y z
và đường thẳng
1 2
:
2 1 3
x y z
d
. Lập phương trình đường thẳng
nằm trong mặt phẳng
P
, đồng thời cắt
và vuông góc với đường thẳng
d
.
Trang 4
A.
1 1 1
5 2 3
x y z
. B.
1 1 1
5 1 2
x y z
.
C.
1 1 1
5 1 3
x y z
. D.
1 3 1
5 1 3
x y z
.
Câu 29. Cho hàm số bậc bốn
y f x
có đồ thị như hình vẽ dưới đây
Số điểm cực trị của hàm số
2
3
x
g x f e
là
A.
6
. B.
5
. C.
4
. D.
3
.
Câu 30. Trong không gian với hệ trục tọa độ
Oxyz
, cho
1;1;1 ,A
2;1; 1 ,B
0;4; 6C
. Điểm
M
di
chuyển trên trục
Ox
. Tìm tọa độ
M
để
P MA MB MC

có giá trị nhỏ nhất.
A.
1;0;0
. B.
1; 0;0
. C.
2;0;0
. D.
2;0;0
.
Câu 31. Cho hàm số
4 3 2
bx cx dx ef x ax
.
f x
có đồ thị như hình vẽ
Tập tất cả các giá trị của
e
để đồ thị hàm số
f x
có số điểm cực trị lớn nhất là
A.
9
0;
4
. B.
9
;0
4
. C.
9
;0
4
. D.
9
0;
4
.
Câu 32. Cho phương trình
2
1 4 4 0x x mx
.Phương trình có ba nghiệm phân biệt khi:
A.
3
4
m
. B.
3
4
m
. C.
m
. D.
0m
.
Câu 33. Cho hàm số
f x
liên tục trên tập
Biết
2 0f
và
2 4 2
3 1 ' 3 2 2 2 3 2 1, .x f x x x xf x x
Giá trị của
5
2
f x dx
bằng
A.
1953
4
. B.
651
4
. C.
3
4
. D.
9
4
.
Câu 34. Từ
12
học sinh gồm
5
học sinh giỏi,
4
học sinh khá,
3
học sinh trung bình, giáo viên muốn
thành lập
4
nhóm làm
4
bài tập lớn khác nhau, mỗi nhóm có
3
học sinh. Tính xác suất để nhóm
nào cũng có học sinh giỏi và học sinh khá.
A.
72
385
. B.
114
385
. C.
36
385
. D.
18
385
.
Câu 35. Cho khối tứ diện đều
ABCD
có thể tích là
V
. Gọi
, , ,M N P Q
lần lượt là trung điểm của
, , ,AC AD BD BC
. Thể tích khối chóp
.A MNPQ
là
A.
12
V
. B.
3
V
. C.
6
V
. D.
4
V
.
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 5
B. ĐIỀN KHUYẾT (15 CÂU)
Câu 36. Cho hàm số
3 2
6 7 5y x x x có đồ thị
C
. Phương trình tiếp tuyến với đồ thị
C
tại điểm
có hoành độ bằng
2
là:
Đáp án: …………..
Câu 37. Hàm số
y f x
có đạo hàm trên
và đồ thị hàm số
y f x
như hình bên.
Hàm số
y f x
có bao nhiêu điểm cực đại.
Đáp án: …………..
Câu 38. Trong không gian với hệ tọa độ
Oxyz
, cho
1; 0;0
A
,
0; 2;0
B
và
0;0;3
C
. Tính khoảng
cách
d
từ điểm
O
đến mặt phẳng
ABC
.
Đáp án: …………..
Câu 39. Từ các số của tập
0,1,2,3, 4,5,6
A
có thể lập được bao nhiêu số chẵn gồm 5 chữ số đôi một
khác nhau trong đó có hai chữ số lẻ và hai chữ số lẻ đứng cạnh nhau.
Đáp án: …………..
Câu 40.
Cho hàm số
y f x
liên tục trên
và thỏa mãn
2
2 1 2 1,f x f x x x x
Tính
0
2 2
lim
x
f x f
x
.
Đáp án: …………..
Câu 41. Một kĩ sư thiết kế cây cầu treo bắt ngang dòng sông ( như hình vẽ). Ở hai bên dòng sông, kĩ sư
thiết kế hai cột trụ đỡ
'AA
và
'BB
có độ cao
30m
và bên trên có bắt một dây truyền có dạng
Parabol
ACB
để đỡ nền cầu. Hai đầu của dây truyền được gắn chặt vào hai điểm
A
và
B
. Để
chịu sức nặng của cây cầu và các phương tiện giao thông thì ở khoảng giữa cầu phải đặt thêm dây
cáp treo thẳng đứng nối nền cầu với dây truyền. Biết khoảng cách giữa các dây cáp treo và hai cột
trụ là bằng nhau và dây cáp có độ dài ngắn nhất là
5OC m
. Khoảng cách
' ' 200A B m
. Chiều
dài các cáp treo còn lại là
Đáp án: …………..
Câu 42. Để hàm số
3 2
2 3 1 6 2y x m x m x
đạt cực đại và cực tiểu thì:
Đáp án: …………..
Trang 6
Câu 43. Trong mặt phẳng
Oxy
cho
H
là hình phẳng giới hạn bởi parabol
2
4
y x
và trục hoành.
Đường thẳng
2 2
x k k
chia
H
thành hai phần
1
H
,
2
H
như hình vẽ.
Biết rằng diện tích hình
1
H
gấp
20
7
lần diện tích của hình
2
H
, hỏi giá trị
k
bằng bao nhiêu?
Đáp án: …………..
Câu 44. Cho hàm số
3 2
4
f x x x m
. Có bao nhiêu giá trị nguyên của tham số
5;5
m
để phương
trình
2
2
1
2
f f x f x
f x f x
có
9
nghiệm phân biệt?
Đáp án: …………..
Câu 45. Cho số phức
z
thỏa mãn
3 4 2
z i
và
2 1-w z i
. Trong mặt phẳng phức, tập hợp điểm
biểu diễn số phức
w
là đường tròn tâm
I
, bán kính
R
. Tìm tâm
I
, bán kính
R
.
Đáp án: …………..
Câu 46. Cho hình hộp chữ nhật
.
ABCD A B C D
có đáy
ABCD
là hình vuông cạnh bằng
2 2
,
4
AA
.
Tính góc giữa đường thẳng
A C
với mặt phẳng
AA B B
.
Đáp án: …………..
Câu 47. Trong không gian
Oxyz
, cho
3;1; 2
A
,
3; 1;0
B
và mặt phẳng
: 3z 14 0
P x y
. Điểm
M
thuộc mặt phẳng
P
sao cho
MAB
vuông tại
. Tính khoảng cách từ điểm
đến mặt
phẳng
Oxy
.
Đáp án: …………..
Câu 48. Cho
,a b
thỏa mãn các điều kiện
2 2
1
a b
và
2 2
log 1
a b
a b
. Giá trị lớn nhất của biểu
thức
2 4 3
P a b
là
Đáp án: …………..
Câu 49. Cho hình lăng trụ đứng
.
ABC A B C
có đáy là tam giác
ABC
đều cạnh
,a
3,
AA a
M
là
trung điểm của
CC
. Tính khoảng cách từ điểm
C
đến mặt phẳng
.A BM
Đáp án: …………..
Câu 50. Cho chóp
.
S ABCD
có
SA x
và tất cả các cạnh còn lại đều bằng
1
.Tìm
x
để thể tích của khối
chóp
.
S ABCD
đạt giá trị lớn nhất
Đáp án: …………..
Lời giải tham khảo
A. TRẮC NGHIỆM KHÁCH QUAN (35 CÂU)
Câu 1. Có 100 học sinh tham dự kì thi học sinh giỏi Hóa (thang điểm 20). Kết quả như sau:
Điểm
9
10
11
12
13
14
15
16
17
18
19
x
y = 4 - x
2
H
1
H
2
O
x = k
4
2
-2
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 7
Tần số
1
1
3
5
8
13
19
24
14
10
2
Số trung vị là:
A.
15
e
M
B.
15,50
e
M
C.
16
e
M
D.
16,5
e
M
Lời giải:
Chọn B ta thấy N=100 chăn nên số trung vị là:
15 16
15,5
2
e
M
Câu 2. Gọi
h t cm
là mực nước ở bồn chứa sau khi bơm nước được
t
giây. Biết rằng
3
1
8
5
h t t
và
lúc đầu bồn không có nước Tìm mức nước ở bồn sau khi bơm nước được 6 giây (làm tròn đến kết .
quả hàm phần trăm).
A.
2,33
cm
. B.
5,06
cm
. C.
3,33
cm
. D.
2,66
cm
.
Lời giải
Chọn D
6
4
6 6
3
3
0 0
0
1 1 3
d 8d . 8 2,66.
5 5 4
h t h t t t t t
.
Câu 3. Tập nghiệm của phương trình
2
2
log 2 1
x x
là :
A.
1
B.
0
C.
0;1
D.
1;0
Lời giải
Chọn C
2 2
2
0
log 2 1 2 2
1
x
x x x x
x
Câu 4. Cho hệ phương trình:
2 2
2 2
3 4 2 17
16
x xy y
y x
. Hệ thức biểu diễn
x
theo
y
rút ra từ hệ phương trình
là?
A.
5
13
x y
hay
3
5
x y
B.
3
2
y
x
hay
3
2
y
x
.
C.
1
2
y
x
hay
1
2
y
x
. D.
2
2
y
x
hay
2
2
y
x
.
Lời giải
Chọn A
Ta có :
2 2
2 2
3 4 2 17
16
x xy y
y x
2 2 2 2
3 4 2 17
x xy y y x

2 2
65 64 15 0
x xy y
13 5 5 3 0
x y x y
5
13
x y
hay
3
5
x y
.
Câu 5. Cho hai số phức
1
1 3z i
,
2
4 6z i
có các điểm biểu diễn trên mặt phẳng tọa độ lần lượt là hai
điểm
M
và
N
. Gọi
z
là số phức mà có điểm biểu diễn là trung điểm của đoạn
MN
. Hỏi
z
là số
phức nào trong các số phức dưới đây?
A.
3 9
2 2
z i
. B.
3 9z i
. C.
1 3z i
. D.
5 3
2 2
z i
.
Lời giải
Chọn A
Ta có
1; 3
M
,
4; 6
N
. Suy ra trung điểm
I
của
MN
là
3 9
;
2 2
.
Trang 8
Do đó
I
là điểm biểu diễn của số phức
3 9
2 2
z i
.
Câu 6. Phương trình mặt phẳng đi qua
1;1; 2
A
, song song với
: 2 2 1 0
x y z
là
A.
2 2 5 0
x y z
. B.
2 2 1 0
x y z
.
C.
2 2 2 0
x y z
. D.
2 2 0
x y z
.
Lời giải
Chọn A
Ta có phương trình mặt phẳng ở dạng:
2 2 0 1 .
x y z C C
1;1; 2
A
thuộc mặt phẳng khi
1 2.1 2 2 0 5
C C
(thỏa mãn).
Vậy phương trình mặt phẳng cần tìm:
2 2 5 0
x y z
.
Câu 7. Trong không gian
Oxyz
, tọa độ điểm đối xứng của điểm
0 ;1; 2
M
qua mặt phẳng
0
x y z
là:
A.
2 ; 1; 0
. B.
0 ; 1; 2
. C.
0;1; 2
. D.
2; 1;0
.
Lời giải
Chọn D
Đường thẳng
d
đi qua điểm
0 ;1; 2
M
và vuông góc với mặt phẳng
0
x y z
có phương
trình là
1
2
x t
y t
z t
.
Tọa độ giao điểm
I
của đường thẳng
d
và mặt phẳng
0
x y z
thỏa mãn hệ
1
2
0
x t
y t
z t
x y z
1
1
0
1
t
x
y
z
1; 0 ;1
I
Gọi
M
đối xứng với
0 ;1; 2
M
qua mặt phẳng
0
x y z
nên
I
là trung điểm
M M
2 2
2 1
2 0
M I M
M I M
M I M
x x x
y y y
z z z
2 ; 1; 0
M
Câu 8. Bất phương trình
2 1 3 2x x
có tổng năm nghiệm nguyên nhỏ nhất là
A.
20
. B.
. C.
5
. D.
10
.
Lời giải
Chọn B
Bất phương trình đã cho
2
2 1 0
3 2 0
2 1 3 2
x
x
x x
2
2
3
9 14 5 0
x
x x
2
3
1
5
9
x
x
x
1x
.
Do đó năm nghiệm nguyên nhỏ nhất là
1;2;3;4;5
. Vậy tổng năm nghiệm là
1 2 3 4 5 15
.
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 9
Câu 9. Nghiệm của phương trình lượng giác
2
2sin 3sin 1 0
x x
thõa điều kiện
0
2
x
là:
A.
6
x
. B.
5
6
x
. C.
3
x
. D.
2
x
.
Lời giải
Chọn A
2
1
2sin 3sin 1 0 .
1
2
sinx
x x
sinx
Thay
6
x
vào
1
2
0
2
sinx
x
thỏa mãn.
Câu 10. Sinh nhật bạn của An vào ngày
01
tháng năm. An muốn mua một món quà sinh nhật cho bạn nên
quyết định bỏ ống heo
100
đồng vào ngày
01
tháng
01
năm
2016
, sau đó cứ liên tục ngày sau
hơn ngày trước
100
đồng. Hỏi đến ngày sinh nhật của bạn, An đã tích lũy được bao nhiêu tiền ?
(thời gian bỏ ống heo tính từ ngày
01
tháng
01
năm
2016
đến ngày
30
tháng
4
năm
2016
).
A.
714.000
đồng. B.
750.300
đồng. C.
738.100
đồng. D.
726.000
đồng.
Lời giải
Chọn C
Số ngày bạn An để dành tiền (thời gian bỏ ống heo tính từ ngày
01
tháng
năm
2016
đến ngày
tháng
4
năm
2016
) là
31 29 31 30 121
ngày.
Số tiền bỏ ống heo ngày đầu tiên là:
1
100
u
.
Số tiền bỏ ống heo ngày thứ hai là:
2
100 1.100
u
.
Số tiền bỏ ống heo ngày thứ ba là:
3
100 2.100
u
.
…
Số tiền bỏ ống heo ngày thứ
n
là:
1
1
n
u u n d
100 1 100
n
100n
.
Số tiền bỏ ống heo ngày thứ
121
là:
121
100.121
u
12100
.
Sau
121
ngày thì số tiền An tích lũy được là tổng của
121
số hạng đầu của cấp số cộng có số hạng
đầu
1
100
u
, công sai
100
d
.
Vậy số tiền An tích lũy được là
121 1 121
121
2
S u u
121
100 12100
2
738100
đồng.
Câu 11. Cho một nguyên hàm của hàm số
1
1
x
f x
x
là
F x
và
0 3
F
. Khi đó
F x
bằng:
A.
2ln 1 3
x x
. B.
2ln 1 3
x x
.
C.
2ln 1 3
x x
. D.
2
2
3
1
x
x
.
Lời giải
Chọn A
Ta có:
1 2
d d 1 d 2ln 1
1 1
x
f x x x x x x C
x x
.
Khi đó
2ln 1
F x x x C
.
Do
0 3
F
nên
0 0 2 ln 0 1 3 3
F C C
.
Vậy
2ln 1 3
F x x x
.
Câu 12. Tìm tất cả các giá trị thực của tham số
m
sao cho bất phương trình:
3
3
1
3 2x mx
x
nghiệm
đúng
1x
?
Trang 10
A.
3
2
m
. B.
1 3
3 2
m
. C.
2
3
m
. D.
2
3
m
.
Lời giải
Chọn C
Bpt
3 2
3 4
1 1 2
3 2, 1 3 , 1mx x x m x f x x
x
x x
.
Ta có
5 2 5 2 2
4 2 24 2 4 2
2 2 2 0
f x x x
x x x x x
suy ra
f x
tăng.
Ycbt
1
2
3 , 1 min 1 2 3
3
x
f x m x f x f m m
Câu 13. Một chất điểm
A
xuất phát từ
O
, chuyển động thẳng với vận tốc biến thiên theo thời gian bởi
quy luật
2
1 58
/
120 45
v t t t m s
, trong đó
t
(giây) là khoảng thời gian tính từ lúc
A
bắt đầu
chuyển động. Từ trạng thái nghỉ, một chất điểm
B
cũng xuất phát từ
O
, chuyển động thẳng
cùng hướng với
A
nhưng chậm hơn
3
giây so với
A
và có gia tốc bằng
2
/a m s
(
a
là hằng
số). Sau khi
B
xuất phát được
15
giây thì đuổi kịp
A
. Vận tốc của
B
tại thời điểm đuổi kịp
A
bằng
A.
25 /m s
B.
36 /m s
C.
30 /m s
D.
21 /m s
Lời giải
Chọn C
Thời điểm chất điểm
B
đuổi kịp chất điểm
A
thì chất điểm
B
đi được
15
giây, chất điểm
A
đi
được
18
giây.
Biểu thức vận tốc của chất điểm
B
có dạng
d
B
v t a t at C
mà
0 0
B
v
nên
B
v t at
.
Do từ lúc chất điểm
A
bắt đầu chuyển động cho đến khi chất điểm
B
đuổi kịp thì quãng đường
hai chất điểm đi được bằng nhau. Do đó
18 15
2
0 0
1 58 225
d d 225 . 2
120 45 2
t t at t a a
Vậy, vận tốc của chất điểm
B
tại thời điểm đuổi kịp
A
bằng
2.15 30 /
B
v t m s
.
Câu 14. Hiện tại dân số ở Hà Nội là
7,55
triệu người với tốc độ tăng dân số
2%
một năm và dân số
Thành phố Hồ Chí Minh là
8,15
triệu người với tốc dộ tăng dân số
1,5%
một năm. Hỏi ít nhất
sau bao nhiêu năm nữa thì số dân Hà Nội vượt số dân Thành phố Hồ Chí Minh.
A.
16
năm. B.
20
năm. C.
18
năm. D.
17
năm.
Lời giải
Chọn A
Số dân của Hà Nội sau
n
năm là
1
7, 55 1 0, 02
n
X
7,55. 1,02
n
.
Số dân của thành phố Hồ Chí Minh sau
n
năm là
2
8,15 1 0, 015
n
X
8,15. 1,015
n
.
1 2
X X
7,55. 1,02 8,15. 1.015
n n
1,02 8,15
1,015 7,55
n
1,02
1,015
8,15
log
7,55
n
15,56
.
Vậy sau ít nhất
16
năm.
Câu 15. Tìm nghiệm của phương trình
2
log 5 4
x
A.
13
x
. B.
11
x
. C.
3
x
. D.
21
x
.
Lời giải
Chọn D
+) Điều kiện
5 0 5
x x
.
+)
4
5 2 21
pt x x
(tmđk)
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 11
Câu 16. Thể tích của vật tròn xoay có được khi quay hình phẳng giới hạn bởi đồ thị hàm
tany x
, trục
Ox
, đường thẳng
0
x
, đường thẳng
3
x
quanh trục
Ox
là:
A.
2
3
3
V
. B.
2
3
3
V
. C.
3
3
V
. D.
3
3
V
.
Lời giải
Chọn B
Thể tích của vật tròn xoay là:
3
2
0
tan dV x x
3
2
0
1
1 d
cos
x
x
3
0
tan
x x
tan
3 3
2
3
3
.
Câu 17. Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
9
mx
y
x m
nghịch biến trên từng
khoảng xác định
A.
3 3
m
. B.
3 3
m
C.
3 3
m
. D.
3 3
m
.
Lời giải
Chọn D
ĐKXĐ:
x m
Ta có
2
2
9
m
y
x m
, hàm số nghịch biến trên từng khoảng xác định
0
y x m
2
9 0 3 3
m m
.
Câu 18. Cho số phức
z a bi
,
,a b
thỏa mãn
1 3 0z i z i
. Tính
3S a b
.
A.
7
3
S
. B.
5
S
. C.
5
S
. D.
7
3
S
.
Lời giải
Chọn C
Ta có :
1 3 0z i z i
2 2
1 3 0
a bi i i a b
2 2
1 3 0a b a b i
2 2
1 0
3 0
a
b a b
2
1
1 3
a
b b
2
2
1
3
1 3
a
b
b b
1
4
3
a
b
.
Vậy
3S a b
1 4 5
.
Câu 19. Trong mặt phẳng phức, tập hợp các điểm
M
biểu diễn số phức
z
thỏa mãn điều kiện
3 4z z i
là?
A. Parabol
2
4y x
. B. Đường tròn
2 2
4 0
x y
.
C. Elip
2 2
1
4 2
x y
. D. Đường thẳng
6 8 25 0
x y
.
Lời giải
Chọn D
Đặt
,z x yi x y
và
;M x y
là điểm biểu diễn của z.
Ta có
2 2
3 4 3 4 3 4
z x y
z i x iy i x y i
.
2 2
3 4 3 4
z i x y
.
Vậy
2 2
2 2
3 4 3 4 6 8 25 0
z z i x y x y x y
.
Trang 12
Câu 20.
Cho đường thẳng
2 3
:
1 2
x t
y t
. Hoành độ hình chiếu của
4;5
M
trên
gần nhất với số nào
sau đây?
A.
1,5
. B.
1,2
. C.
1,3
. D.
1,1
.
Lời giải.
Chọn A
Gọi
H
là hình chiếu của
M
trên
. Ta có:
2 3 ;1 2 , 2 3 ; 4 2 .H H t t MH t t

Đường thẳng
có vectơ chỉ phương là
3; 2
u
.
2 20 17
. 0 3 2 3 2 4 2 0 13 2 0 ; .
13 13 13
MH u MH u t t t t H
 
Câu 21. Đường tròn
2 2
3 3 6 9 9 0
x y x y
có bán kính bằng bao nhiêu?
A.
5
2
. B.
5
. C.
25
2
. D.
25
4
.
Lời giải
Chọn D
2 2 2 2
3 3 6 9 9 0 2 3 3 0.
x y x y x y x y
Đường tròn có tâm
3
1; ,
2
I
bán kính
9 5
1 3 .
4 2
R
Câu 22. Trong không gian hệ tọa độ
Oxyz
, cho
1;2; 1
A
;
1;0;1
B
và mặt phẳng
: 2 1 0
P x y z
. Viết phương trình mặt phẳng
Q
qua
,A B
và vuông góc với
P
A.
:3 0
Q x y z
B.
:2 3 0
Q x y
C.
: 0
Q x z
D.
: 0
Q x y z
Lời giải
Chọn C
2; 2;2 2 1;1; 1 , 1;1; 1
AB u

1;2; 1
P
n
, 1;0;1
Q P
n AB n
  
Vậy
: 0
Q x z
.
Câu 23. Cho một hình nón đỉnh
S
có chiều cao bằng
8cm
, bán kính đáy bằng
6cm
. Cắt hình nón đã cho
bởi một mặt phẳng song song với mặt phẳng chứa đáy được một hình nón
N
đỉnh
S
có đường
sinh bằng
4cm
. Tính thể tích của khối nón
N
.
A.
3
768
cm
125
V
B.
3
786
cm
125
V
C.
3
2304
cm
125
V
D.
3
2358
cm
125
V
Lời giải
Chọn A
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 13
Đường sinh của hình nón lớn là:
l SB
2 2
h r
2 2
8 6
10cm
.
Gọi
2
l
,
2
r
,
2
h
lần lượt là đường sinh, bán kính đáy và chiều cao của hình nón
N
.
2
4cm
l SK
Ta có:
SOB
và
SIK
đồng dạng nên:
4 2
10 5
SI IK SK
SO OB SB
.
2 2 2
4 2
10 5
h r l
h r l
2
2
2 16
5 5
2 12
.
5 5
h h
r r
.
Thể tích khối nón
N
là:
2
( ) 2 2
1
. . .
3
N
V r h
2
1 12 16
. . .
3 5 5
3
768
cm
125
.
Câu 24. Một cái cột có hình dạng như hình bên (gồm một khối nón và một khối trụ ghép lại). Chiều cao đo
được ghi trên hình, chu vi đáy là. Thể tích của cột bằng
A.
3
52000 p
cm
. B.
3
13000 p
cm
. C.
3
5000p
cm
. D.
3
15000 p
cm
.
Lời giải
Chọn D
Gọi
R
là bán kính đường tròn đáy của hình nón và hình trụ.
Theo đề:
10 3
2 20 3
p
R p R
.
Thể tích khối trụ là
2
2
1 1
10 3 12000
.40
p p
V R h
Thể tích khối nón là
2
2
2 2
1 1 10 3 3000
.10
3 3
p p
V R h
Thể tích của cột là
12000 3000 15000p p p
V
.
Câu 25. Cho lăng trụ tam giác
.
ABC A B C
có đáy là tam giác đều cạnh
a
. Độ dài cạnh bên bằng
4a
.
Mặt phẳng
BCC B
vuông góc với đáy và
30
B BC
. Thể tích khối chóp
.
ACC B
là:
A.
3
3
6
a
. B.
3
3
12
a
. C.
3
3
18
a
. D.
3
3
2
a
.
(N)
K
M
I
O
B
S
Trang 14
Lời giải
Chọn A
Gọi
H
là hình chiếu của
B
trên
BC
. Từ giả thiết suy ra:
B H ABC
.
1
. .sin
2
BB C
S BB BC B BC
1
4 . .sin30
2
a a
2
a
.
Mặt khác:
1
.
2
BB C
S B H BC
2
BB C
S
B H
BC
2
2
2
a
a
a
.
.
LT ABC
V B H S
2
3
2 .
4
a
a
3
3
2
a
.
. .
1
2
A CC B A CC B B
V V
1 2 1
.
2 3 3
LT LT
V V
3
1 3
.
3 2
a
3
3
6
a
.
Câu 26. Cho tứ diện
ABCD
. Gọi
H
là một điểm nằm trong tam giác
ABC
,
là mặt phẳng đi qua
H
song song với
AB
và
CD
. Mệnh đề nào sau đây đúng về thiết diện của
của tứ diện?
A. Thiết diện là hình bình hành. Thiết diện là hình chữ nhật. B.
C. Thiết diện là hình vuông. D. Thiết diện là hình thang cân.
Lời giải
Chọn A
Qua
H
kẻ đường thẳng
d
song song
AB
và cắt
,
BC AC
lần lượt tại
,M N
.
Từ
N
kẻ
NP
song song vớ
CD P CD
. Từ
P
kẻ
PQ
song song với
AB Q BD
.
Ta có
MN
//
PQ
//
AB
suy ra
, , ,M N P Q
đồng phẳng và
AB
//
MNPQ
.
Suy ra
MNPQ
là thiết diện của
và tứ diện.
Vậy tứ diện là hình bình hành.
a
C'
A'
B'
C
B
A
H
4a
P
Q
M
N
H
A
D
C
B
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 15
Câu 27. Trong hệ tọa độ
Oxyz
, cho điểm
2;1;3A
, mặt phẳng
( ) : 2 2 3 0x y z
và mặt cầu
2 2 2
( ) : 6 4 10 2 0S x y z x y z . Gọi
là đường thẳng đi qua
A
, nằm trong mặt phẳng
( )
và cắt
( )S
tại hai điểm
,M N
. Độ dài đoạn
MN
nhỏ nhất là:
A. 2 30 . B. C. 30 .
30
2
. D.
3 30
2
.
Lời giải
Chọn A
+ Mặt cầu
( )S
có tâm
3;2;5
I
và bán kính
6R
.
Ta có:
( ),A
6IA R nên
( ) ( ) ( )S C
và
A
nằm trong mặt cầu
( )S
.
Suy ra: Mọi đường thẳng
đi qua
A
, nằm trong mặt phẳng
( )
đều cắt
( )S
tại hai điểm
,M N
.
(
,M N
cũng chính là giao điểm của
và)
( )C
.
+ Vì
( , )d I IA
nên ta có:
2 2 2 2
2 ( , ) 2 2 30
MN R d I R IA
.
Dấu
" "
xảy ra khi
A
là điểm chính giữa dây cung
MN
.
Vậy độ dài đoạn
MN
nhỏ nhất là
MN
bằng 2 30 .
Câu 28. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
: 2 4 0
P x y z
và đường thẳng
1 2
:
2 1 3
x y z
d
. Lập phương trình đường thẳng
nằm trong mặt phẳng
P
, đồng thời cắt
và vuông góc với đường thẳng
d
.
A.
1 1 1
5 2 3
x y z
. B.
1 1 1
5 1 2
x y z
.
C.
1 1 1
5 1 3
x y z
. D.
1 3 1
5 1 3
x y z
.
Lời giải
Chọn C
Giao điểm của
d
với
P
là
1;1;1H
.
đi qua
H
và nhận
;

p d
u n u
làm véc tơ chỉ phương
1 1 1
5; 1; 3 :
5 1 3
x y z
u
.
Câu 29. Cho hàm số bậc bốn
y f x
có đồ thị như hình vẽ dưới đây
Số điểm cực trị của hàm số
2
3
x
g x f e
là
A.
6
. B.
5
. C.
4
. D.
3
.
Trang 16
Lời giải
Chọn D
Do
y f x
là hàm số bậc bốn nên là hàm số liên tục và có đạo hàm luôn xác định tại mọi điểm
x
.
Theo đồ thị hàm số ta có được
0
f x
;0
0;4
4;
x a
x b
x c


.
Mặt khác
2 2
2 . . 3
x x
g x x e f e
.
Do đó
2 2
2
0
0 2 . 3 0
3 0
x x
x
x
g x x e f e
f e
2
2
2
0
3 ;0
3 0; 4
3 4;
x
x
x
x
e a
e b
e c


.
Xét hàm số
2
3
x
h x e
.
Ta có
2
2
x
h x xe
;
0 0
h x x
. Từ đó ta có bảng biến thiên của hàm số
y h x
Từ bảng biến thiên ta thấy phương trình
2
3
x
e a
,
2
3
x
e b
vô nghiệm; còn hai đồ thị hàm số
y h x
và
y c
cắt nhau tại hai điểm phân biệt có hoành độ khác
0
do đó phương trình
2
3
x
e c
có hai nghiệm phân biệt khác
0
.
Vậy hàm số
2
3
x
g x f e
có ba điểm cực trị.
Câu 30. Trong không gian với hệ trục tọa độ
Oxyz
, cho
1;1;1 ,
A
2;1; 1 ,
B
0;4;6
C
. Điểm
di
chuyển trên trục
Ox
. Tìm tọa độ
M
để
P MA MB MC
có giá trị nhỏ nhất.
A.
1;0;0
. B.
1;0;0
. C.
2;0;0
. D.
2;0;0
.
Lời giải
Chọn A
Gọi
;0;0 ,M x Ox x
.
Khi đó
1 ;1;1 , 2 ;1; 1 , ;4;6
MA x MB x MC x
.
3 3 ;6;6
MA MB MC x
.
2 2
2 2 2
3 3 6 6 9 18 81 9 1 72 72
P MA MB MC x x x x
  
.
để
P MA MB MC
 
có giá trị nhỏ nhất khi và chỉ khi
1x
.
Vậy tọa độ
1;0;0 .
M
.
Câu 31. Cho hàm số
4 3 2
bx cx dx e
f x ax
.
f x
có đồ thị như hình vẽ
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 17
Tập tất cả các giá trị của
e
để đồ thị hàm số
f x
có số điểm cực trị lớn nhất là
A.
9
0;
4
. B.
9
;0
4
. C.
9
;0
4
. D.
9
0;
4
.
Lời giải
Chọn D
Từ đồ thị
f x
ta có
3 3 4 2
1 3
3 3 dx
4 2
xf x x f x x x x ex
Ta thấy
f x
là hàm bậc bốn trùng phương đạt cực đại tại
0x
và đạt cực tiểu tại 2 điểm
3x và 3x .
Đồ thị hàm số
f x
có số điểm cực trị lớn nhất là 7 điểm cực trị khi
3
0 0
0
f
f
0
9
0;
9
4
4
e
e
e
Câu 32. Cho phương trình
2
1 4 4 0x x mx
.Phương trình có ba nghiệm phân biệt khi:
A.
3
4
m
. B.
3
4
m
. C.
m
. D.
0m
.
Lời giải
Chọn B
Phương trình có 3 nghiệm phân biệt khi
2
4 4 0x mx
có 2 nghiệm phân biệt khác 1
2
4 4 0
4 3 0
m
m
3
4
m
.
Câu 33. Cho hàm số
f x
liên tục trên tập
Biết
2 0f
và
2 4 2
3 1 ' 3 2 2 2 3 2 1, .x f x x x xf x x
Giá trị của
5
2
f x dx
bằng
A.
1953
4
. B.
651
4
. C.
3
4
. D.
9
4
.
Lời giải
Ta có:
Trang 18
2 4 2
2
2
2
2 2
'
3 1 ' 3 2 2 2 3 2 1
3 1 ' 3 2 2 3 2
1, ..
1
3 2 3 2
1 . 1
1 1
x f x x x xf x
x f x xf x
x
x
f x f x
x C
x x
Cho
0
x
từ
1
2 3
2
0
0 0 3 2 1
1 1
f
C C C f x x x x x
.
Ta có:
5 1 1
4 2
3
2 0 0
1
9
3 3 2 3 3
0
4 2 4
x x
f x dx f x dx x x dx
.
Câu 34. Từ
12
học sinh gồm
5
học sinh giỏi,
4
học sinh khá,
3
học sinh trung bình, giáo viên muốn
thành lập
4
nhóm làm
4
bài tập lớn khác nhau, mỗi nhóm có
3
học sinh. Tính xác suất để nhóm
nào cũng có học sinh giỏi và học sinh khá.
A.
72
385
. B.
114
385
. C.
36
385
. D.
18
385
.
Lời giải
Chọn C
3 3 3
12 9 6
. .
15400
4!
C C C
n
Gọi
:A
“
4
nhóm có cả học sinh giỏi và khá”
Để có
4
nhóm có cả học sinh giỏi và khá ta chia các nhóm như sau:
+ Một nhóm có
2
giỏi,
1
khá.
+ Ba nhóm có
1
giỏi,
1
khá,
1
trung bình.
Cách chọn nhóm có
2
giỏi,
1
khá:
2 1
5 4
.C C
Cách xếp vị trí
3
học sinh giỏi và
3
học sinh khá vào ba nhóm còn lại:
3!
Cách xếp
3
học sinh trung bình vào ba nhóm còn lại là
3!
Suy ra
2 1
5 4
. .3!.3! 1440
n A C C
Vậy
1440 36
15400 385
n A
P A
n
.
Câu 35. Cho khối tứ diện đều
ABCD
có thể tích là
V
. Gọi
, , ,M N P Q
lần lượt là trung điểm của
, , ,AC AD BD BC
. Thể tích khối chóp
.
A MNPQ
là
A.
12
V
. B.
3
V
. C.
6
V
. D.
4
V
.
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 19
Lời giải
Chọn D
Cách 1:
Ta có:
1
. .
4
AMNP
ACDP
V AM AN AP
V AC AD AP
.
Mà
1
2
ACDP
ABCD
V
V
.
Vậy
.
1 1 1 1
2 2. 2. . .
4 4 2 4 4
A MNPQ AMNP ACDP ABCD ABCD
V
V V V V V
.
Cách 2:
Ta có:
.
2
A MNPQ APMQ
V V
(do
MNPQ
là hình thoi).
Mà
APMQ BPMQ
V V
(do
//AB MQ
) nên
.
2
A MNPQ BPMQ
V V
.
Vì
P
là trung điểm của
BD
nên
1
, ,
2
d P ABC d D ABC
và
1
4
BQM ABC
S S
.
Nên
1
, .
3
BPMQ BQM
V d P ABC S
1 1 1
. , .
3 2 4
ABC
d D ABC S
1 1
. , .
8 3
ABC
d D ABC S
8
V
.
Suy ra
4
AMNPQ
V
V
.
B. ĐIỀN KHUYẾT (15 CÂU)
Câu 36. Cho hàm số
3 2
6 7 5y x x x có đồ thị
C
. Phương trình tiếp tuyến với đồ thị
C
tại điểm
có hoành độ bằng
2
là:
Đáp án: …………..
Trang 20
Lời giải
Ta có
0 0
2 3x y
2
' 3 12 7 '(2) 5y x x y
Phương trình tiếp tuyến với đồ thị
C
tại điểm
(2;3)M
là
' 2 2 3 5( 2) 3y y x x
hay
5 13y x
Câu 37. Hàm số
y f x
có đạo hàm trên
và đồ thị hàm số
y f x
như hình bên.
Hàm số
y f x
có bao nhiêu điểm cực đại.
Đáp án: …………..
Lời giải
Từ đồ thị hàm số
y f x
, ta có
0f x
có 4 nghiệm phân biệt
1 2 3 4
, , ,x x x x như hình vẽ.
Ta có bảng biến thiên của hàm số
y f x
là:
Từ đó suy ra hàm số
y f x
có 2 điểm cực đại.
Câu 38. Trong không gian với hệ tọa độ
Oxyz
, cho
1;0;0
A
,
0; 2;0
B
và
0;0;3
C
. Tính khoảng
cách
d
từ điểm
O
đến mặt phẳng
ABC
.
Đáp án: …………..
Lời giải
Phương trình
: 1 6 3 2 6 0
1 2 3
x y z
ABC x y z
.
2
2 2
6
6
,
7
6 3 2
d O ABC
.
Câu 39. Từ các số của tập
0,1,2,3, 4,5,6
A
có thể lập được bao nhiêu số chẵn gồm 5 chữ số đôi một
khác nhau trong đó có hai chữ số lẻ và hai chữ số lẻ đứng cạnh nhau.
Đáp án: …………..
Lời giải
Vì có 3 số lẻ là 1,3,5, nên ta tạo được 6 cặp số kép:
13,31,15,51,35,53
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 21
Gọi A là tập các số gồm 4 chữ số được lập từ
0,13,2, 4,6
X
.
Gọi
1 2 3
, ,A A A
tương ứng là số các số tự nhiên lẻ gồm 4 chữ số khác nhau được lập từ các chữ số
của tập
0,13, 2, 4,6
X
và 13 đứng ở vị trí thứ nhất, thứ hai và thứ ba.
Ta có:
3
1 4 2 3
24; 3.3.2 18
A A A A
nên
24 2.18 60
A
Vậy số các số cần lập là:
6.60 360
số.
Câu 40.
Cho hàm số
y f x
liên tục trên
và thỏa mãn
2
2 1 2 1,f x f x x x x
Tính
0
2 2
lim
x
f x f
x
.
Đáp án: …………..
Lời giải
Đặt
2
u x
ta có:
0 2
2 2 2
lim lim 2
2
x u
f x f f u f
f
x u
.
Đặt
1 1t x x t
ta có:
2
2 1 2 1,f x f x x x x
2
2
2 1 1 2 1 1 4 2f t f t t t t t
2
2 1 4 2
f x f x x x
2
.
Từ
1
và
2
ta được:
2
8 4 2 8
2 4
3 3
x x x
f x f x f
.
Cách 2
Đặt
2
u x
ta có:
0 2
2 2 2
lim lim 2
2
x u
f x f f u f
f
x u
.
Từ điều kiện
2
2 1 2 1,f x f x x x x
ta suy ra hàm
f x
có dạng
2
ax bx c
Từ đó ta có:
2
2 2
2 1 2 2 2 1 1 3 2 3
f x f x ax bx c a x b x c ax b a x c a b
Đồng nhất hai vế, ta được hệ phương trình
1
3
3 1
8
2 2
3
3 1
4
3
a
a
b a b
c a b
c
Vậy
2
8 4 2 8
2 4
3 3
x x x
f x f x f
.
Câu 41. Một kĩ sư thiết kế cây cầu treo bắt ngang dòng sông ( như hình vẽ). Ở hai bên dòng sông, kĩ sư
thiết kế hai cột trụ đỡ
'AA
và
'BB
có độ cao
30m
và bên trên có bắt một dây truyền có dạng
Parabol
ACB
để đỡ nền cầu. Hai đầu của dây truyền được gắn chặt vào hai điểm
A
và
B
. Để
chịu sức nặng của cây cầu và các phương tiện giao thông thì ở khoảng giữa cầu phải đặt thêm dây
cáp treo thẳng đứng nối nền cầu với dây truyền. Biết khoảng cách giữa các dây cáp treo và hai cột
trụ là bằng nhau và dây cáp có độ dài ngắn nhất là
5OC m
. Khoảng cách
' ' 200A B m
. Chiều
dài các cáp treo còn lại là
Trang 22
Đáp án: …………..
Lời giải
Chọn hệ trục tọa độ
Oxy
như hình vẽ.
Parabol
P
có dạng:
2
y ax b .
Ta có:
1
(100,30)
10000 30
400
5C(0;5)
5
B P
a b
a
b
P
b
.
Do đó Parabol
P
:
2
1
5
400
y x
.
Vậy chiều dài các cáp treo còn lại lần lượt là:
6.56 ,11.25 ,19.06m m m
.
Câu 42. Để hàm số
3 2
2 3 1 6 2y x m x m x
đạt cực đại và cực tiểu thì:
Đáp án: …………..
Lời giải
0
y
có
2
nghiệm phân biệt
=
2
( 3) 0 3m m
.
Câu 43. Trong mặt phẳng
Oxy
cho
H
là hình phẳng giới hạn bởi parabol
2
4y x và trục hoành.
Đường thẳng
2 2x k k
chia
H
thành hai phần
1
H
,
2
H
như hình vẽ.
Biết rằng diện tích hình
1
H
gấp
20
7
lần diện tích của hình
2
H
, hỏi giá trị
k
bằng bao nhiêu?
x
y = 4 - x
2
H
1
H
2
O
x = k
4
2
-2
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 23
Đáp án: …………..
Lời giải
Diện tích hình
2
H
là
2
2
3 3
2
2
16
4 d 4 4
3 3 3
k
k
x k
S x x x k
.
Diện tính hình
1
H
là
2
3 3
2
1 2
2
32 16 16
4 d 4 4
3 3 3 3 3
k k
S x x S k k
.
Theo đề bài ta có:
1 2
20
7
S S
3 3
16 20 16
4 4
3 3 7 3 3
k k
k k
3
9 108 208
0
7 7 21
k k
.
2
3
105 1
3
k
k
. So với điều kiện
2 2
k
nhận
2
3
k
.
Câu 44. Cho hàm số
3 2
4
f x x x m
. Có bao nhiêu giá trị nguyên của tham số
5;5
m
để phương
trình
2
2
1
2
f f x f x
f x f x
có
9
nghiệm phân biệt?
Đáp án: …………..
Lời giải
3 2
4
f x x x m
Đặt
f x t
;
f x t
có
3
nghiệm phân biệt
256
;
27
t m m
khi đó
2
2
1
2
f f x f x
f x f x
trở thành
2
2
2
1 0
*
2
2
f t t
f t t
t
t t
t
.
Yêu cầu bài toán dẫn đến
2
f t t
có
3
nghiệm phân biệt
256
;
27
0; 2
t m m
t t
hay
3 2
5 0
t t m
có
3
nghiệm phân biệt
256
;
27
0, 2
t m m
t t
3 2
5
h t t t m
Ta có
2
0
0 3 10 0
10
3
t
h t t t
t
.
Trang 24
để (1) có
9
nghiệm phân biệt thì
3 2
10 256
3 27
0
4 5
256
4 5
0
27
5 0
5 21
0 0 5
256
2
0
27
2 0
5;5
m
h m
m
m
h m
m m m
h m m
h m
h
m
m
m
m
.
thử lại thấy
5
m
thỏa mãn.
Câu 45. Cho số phức
z
thỏa mãn
3 4 2
z i
và
2 1-w z i
. Trong mặt phẳng phức, tập hợp điểm
biểu diễn số phức
w
là đường tròn tâm
I
, bán kính
R
. Tìm tâm
I
, bán kính
R
.
Đáp án: …………..
Lời giải
Giả sử
,z x yi x y
.
Từ giả thuyết
2 2
3 4 2 3 4 2 3 4 4 *
z i x yi i x y
.
Từ
2 1 2 1 2 1 2 1w z i x yi i x y i
.
Giả sử
,w a bi a b
. Ta có
1
2 1
2
2 1 2 1
2 1 1
2
a
x
x a
a bi x y i
y b b
y
.
Thay
,x y
vào phương trình
, ta có
2 2
2 2
1 1
3 4 4 7 9 16
2 2
a b
a b
.
Suy ra
w
chạy trên đường tròn tâm
7; 9
I
, bán kính
4R
.
Câu 46. Cho hình hộp chữ nhật
.
ABCD A B C D
có đáy
ABCD
là hình vuông cạnh bằng
2 2
,
4
AA
.
Tính góc giữa đường thẳng
A C
với mặt phẳng
AA B B
.
Đáp án: …………..
Lời giải
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 25
Ta có
CB AA B B
tại
B
. Khi đó
A B
là hình chiếu của
A C
lên mặt phẳng
AA B B
.
Vậy góc tạo bởi đường thẳng
A C
và mặt phẳng
AA B B
là góc
CA B
.
Khi đó
2
2
2 2 1
tan ' 30
3
4 2 2
BC
CA B CA B
A B
.
Câu 47. Trong không gian
Oxyz
, cho
3;1;2
A
,
3; 1;0
B
và mặt phẳng
: 3z 14 0
P x y
. Điểm
thuộc mặt phẳng
P
sao cho
MAB
vuông tại
M
. Tính khoảng cách từ điểm
M
đến mặt
phẳng
Oxy
.
Đáp án: …………..
Lời giải
Tam giác
MAB
vuông tại
M
, suy ra
M
thuộc mặt cầu
S
đường kính
2 11
AB
.
Xét vị trí tương đối của
P
và
S
, ta có
( )P
tiếp xúc
S
.
Lại vì
M P
nên
M
là tiếp điểm của
P
và
S
, hay
là hình chiếu của tâm của mặt cầu
S
trên
P
,
S
có tâm là trung điểm
0;0;1
I
của đoạn
AB
.
Đường thẳng
IM
qua
0;0;1
I
và nhận vectơ pháp tuyến của mặt phẳng
P
làm véctơ chỉ
phương
: ( )
1 3
x t
IM y t t
z t
( ; ;1 3 )M M t t t
3(1 3 ) 14 0 11. 11 1M P t t t t t
1;1;4
M
: 0
Oxy z
Suy ra:
4
( , ) 4
1
d M Oxy
.
Câu 48. Cho
,a b
thỏa mãn các điều kiện
2 2
1
a b
và
2 2
log 1
a b
a b
. Giá trị lớn nhất của biểu
thức
2 4 3
P a b
là
Đáp án: …………..
Lời giải.
Do
2 2
1
a b
và
2 2
log 1
a b
a b
nên
2 2
2 2
1 1 1
2 2 2
a b a b a b
(1)
O
B'
C'
A'
D'
D
A
C
B
Trang 26
Ta có:
1 1 3
2 2
2 2 2
a b a b
(2)
Áp dụng bất đẳng thức Bunhiacốpski cho hai dãy số
1 1
,
2 2
a b
và
1,2
ta có:
2
2 2
2 2
1 1 1 1
(1 2 ) 2
2 2 2 2
a b a b
2 2 2
1 1 3
5 2
2 2 2
a b a b
(3)
Từ (1) và (3)
Ta có:
2
1 3 3 10
5. 2 2 2 4 3 10
2 2 2 2
a b a b a b
Dấu
'' ''
xảy ra khi và chỉ khi
2 2
1 1
5 10
2 2
10
1 2
5 2 10
1 1 1
10
2 2 2
a b
a
b
a b
Câu 49. Cho hình lăng trụ đứng
.
ABC A B C
có đáy là tam giác
ABC
đều cạnh
,a
3,
AA a
M
là
trung điểm của
CC
. Tính khoảng cách từ điểm
C
đến mặt phẳng
.A BM
Đáp án: …………..
Lời giải
Gọi
E AC A M
, vì
M
là trung điểm của
CC
nên dễ thấy
C
là trung điểm của
AE
.
Ta có,
, ,
d C A BM d C A BM
1
,
2
d A A BM
Áp dụng định lí cosin cho
ABE
ta có:
2 2 2 2
2. . .cos60
3 3.
BE AB AE AB AE a BE a
Xét tam giác
ABE
có
2 2 2
AB BE AE ABE
vuông tại
.B AB BE
Kẻ
1
AH A B
, khi đó
, (2)
BE AB BE AA BE ABA BE AH
Từ (1) và (2) ta có
,
d A A BM AH
Lại có
2 2 2 2 2 2
1 1 1 1 1 4 3
3 3 2
a
AH
AH AB AA a a a
Vậy
1 3
; .
2 4
a
d C A BM AH
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 27
Câu 50. Cho chóp
.
S ABCD
có
SA x
và tất cả các cạnh còn lại đều bằng
1
.Tìm
x
để thể tích của khối
chóp
.
S ABCD
đạt giá trị lớn nhất
Đáp án: …………..
Lời giải
Tứ giác
ABCD
có các cạnh bằng nhau nên
ABCD
là hình thoi do đó
AC
cắt
BD
tại trung điểm
O
của mỗi đường và
AC
đường trung trực của đoạn thẳng
BD
.
Gọi
H
là hình chiếu của điểm
S
trên mặt phẳng
ABCD
Ta có:
1
SB SD HB HD
suy ra
H
thuộc đường trung trực
AC
của đoạn thẳng
BD
.
Xét hai tam giác cân
SBD
và
CBD
có
1
SB SD CB CD
;
BD
chung
Suy ra:
SBD BCD SO OC
SAC
có đường trung tuyến
1
2
SO AC SAC
vuông tại
S
khi đó:
2 2 2
1
AC SA SC x
và
2
.
. .
1
SA SC x
SH AC SA SC SH
AC
x
Trong tam giác vuông
OBC
2 2
2 2 2
1 3
1 3 0 3
4 2
x x
OB BC OC BD x x
Diện tích
2 2
1 1 1
. . . . 3
3 6 6
S ABCD ABCD
V S SH AC BD SH x x
Áp dụng bất đẳng thức cauchy có
2 2
2 2
3 3
3
2 2
x x
x x
Dấu bằng xảy ra khi:
2 2
6
3 0; 3
2
x x x
Vậy thể tích chóp
.
S ABCD
lớn nhất bằng
1
4
khi
6
2
x
• XEM THÊM ĐỀ CƯƠNG ÔN THI TẠI:
• https://www.nbv.edu.vn/2022/01/de-cuong-danh-gia-nang-luc-dhqg-ha-noi.html
Theo dõi Fanpage: Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Hoặc Facebook: Nguyễn Vương https://www.facebook.com/phong.baovuong
Tham gia ngay: Nhóm Nguyễn Bào Vương (TÀI LIỆU TOÁN)
https://www.facebook.com/groups/703546230477890/
Ấn sub kênh Youtube: Nguyễn Vương
https://www.youtube.com/channel/UCQ4u2J5gIEI1iRUbT3nwJfA?view_as=subscriber
Tải nhiều tài liệu hơn tại: https://www.nbv.edu.vn/
| 1/27
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

ĐỀ Đ Ề SỐ S 9. 9 ÔN THI T HI ĐGN Đ L ĐHQ Đ G HÀ NỘI I20 2 2 0 1- 1 2 - 02 0 2
• |FanPage: Nguyễn Bảo Vương
A. TRẮC NGHIỆM KHÁCH QUAN (35 CÂU)
Câu 1. Có 100 học sinh tham dự kì thi học sinh giỏi Hóa (thang điểm 20). Kết quả như sau: Điểm 9 10 11 12 13 14 15 16 17 18 19 Tần số 1 1 3 5 8 13 19 24 14 10 2 Số trung vị là: A. M 15 M  M  M  e B. 15,50 e C. 16 e D. 16,5 e 1
Câu 2. Gọi h t  cm là mực nước ở bồn chứa sau khi bơm nước được t giây. Biết rằng ht  3  t  8 5
và lúc đầu bồn không có nước. Tìm mức nước ở bồn sau khi bơm nước được 6 giây (làm tròn đến
kết quả hàm phần trăm). A. 2,33cm . B. 5,06 cm . C. 3,33cm. D. 2,66 cm.
Câu 3. Tập nghiệm của phương trình log  2 x  x  2  1 là : 2  A.   1 B.   0 C. 0;  1 D.  1  ;0 2 2 3  x  4xy  2y 17
Câu 4. Cho hệ phương trình: 
. Hệ thức biểu diễn x theo y rút ra từ hệ phương 2 2  y  x  16  trình là? 5 3 y  3 y 3 A. x  y hay x  y B. x  hay x  . 13 5 2 2 y 1 y 1 y  2 y  2 C. x  hay x  . D. x  hay x  . 2 2 2 2
Câu 5. Cho hai số phức z  1 3i, z  4
  6i có các điểm biểu diễn trên mặt phẳng tọa độ lần lượt là 1 2
hai điểm M và N . Gọi z là số phức mà có điểm biểu diễn là trung điểm của đoạn MN . Hỏi zlà
số phức nào trong các số phức dưới đây? 3 9 5 3 A. z    i . B. z  3  9i . C. z  1  3i . D. z   i . 2 2 2 2
Câu 6. Phương trình mặt phẳng đi qua A1;1; 2
  , song song với   : x 2y 2z 1 0 là
A. x  2y  2z  5  0 . B. x  2y  2z 1  0 .
C. x  2y  2z  2  0 . D. x  2y  2z  0 .
Câu 7. Trong không gian Oxyz , tọa độ điểm đối xứng của điểm M  0;1;2 qua mặt phẳng x yz 0 là: A. 2;1;0  . B. 0 ;  1;  2 . C. 0;1;  2 . D. 2; 1;0.
Câu 8. Bất phương trình 2x 1  3x  2 có tổng năm nghiệm nguyên nhỏ nhất là A. 20. B. 15 . C. 5 . D. 10 . 
Câu 9. Nghiệm của phương trình lượng giác 2
2sin x 3sin x 1  0 thõa điều kiện 0  x  là: 2  5   A. x  . B. x  . C. x  . D. x  . 6 6 3 2 Trang 1
Câu 10. Sinh nhật bạn của An vào ngày 01 tháng năm. An muốn mua một món quà sinh nhật cho bạn nên
quyết định bỏ ống heo 100 đồng vào ngày 01 tháng 01 năm 2016 , sau đó cứ liên tục ngày sau
hơn ngày trước 100 đồng. Hỏi đến ngày sinh nhật của bạn, An đã tích lũy được bao nhiêu tiền ?
(thời gian bỏ ống heo tính từ ngày 01 tháng 01 năm 2016 đến ngày 30 tháng 4 năm 2016 ). A. 714.000 đồng. B. 750.300 đồng. C. 738.100 đồng. D. 726.000 đồng. 
Câu 11. Cho một nguyên hàm của hàm số f  x x 1 
là F  x và F 0   3 . Khi đó F  x bằng: x 1 A. x  2ln x 1  3 . B. x  2ln x 1  3 . 2 C. x  2ln  x   1  3 . D. x   3 .  x 2 1 1
Câu 12. Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình: 3 x 3mx 2   nghiệm 3 x đúng x  1 ? 3 1 3 2 2 A. m  . B.   m  . C. m  . D. m  . 2 3 2 3 3
Câu 13. Một chất điểm A xuất phát từ O , chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật v t 1 58 2  t 
t m / s , trong đó t (giây) là khoảng thời gian tính từ lúc A bắt đầu 120 45
chuyển động. Từ trạng thái nghỉ, một chất điểm B cũng xuất phát từ O , chuyển động thẳng
cùng hướng với A nhưng chậm hơn 3 giây so với A và có gia tốc bằng a 2 m / s  ( a là hằng
số). Sau khi B xuất phát được 15 giây thì đuổi kịp A . Vận tốc của B tại thời điểm đuổi kịp A bằng A. 25 m / s  B. 36 m / s  C. 30 m / s  D. 21m / s 
Câu 14. Hiện tại dân số ở Hà Nội là 7,55 triệu người với tốc độ tăng dân số 2% một năm và dân số
Thành phố Hồ Chí Minh là 8,15 triệu người với tốc dộ tăng dân số 1,5% một năm. Hỏi ít nhất
sau bao nhiêu năm nữa thì số dân Hà Nội vượt số dân Thành phố Hồ Chí Minh. A. 16 năm. B. 20 năm. C. 18 năm. D. 17 năm.
Câu 15. Tìm nghiệm của phương trình log x 5  4 2   A. x  13. B. x  11. C. x  3 . D. x  21.
Câu 16. Thể tích của vật tròn xoay có được khi quay hình phẳng giới hạn bởi đồ thị hàm y  tan x , trục 
Ox , đường thẳng x  0 , đường thẳng x  quanh trục Ox là: 3 2  2    A. V   3  . B. V   3 . C. V  3  . D. V  3  . 3 3 3 3 mx 9
Câu 17. Tìm tất cả các giá trị thực của tham số m sao cho hàm số y  nghịch biến trên từng x m khoảng xác định A. 3   m  3 . B. 3   m  3 C. 3 m  3 . D. 3  m  3 .
Câu 18. Cho số phức z  a  bi , a,b  thỏa mãn z 1 3i  z i  0. Tính S  a  3b. 7 7 A. S   . B. S  5. C. S  5 . D. S  . 3 3
Câu 19. Trong mặt phẳng phức, tập hợp các điểm M biểu diễn số phức z thỏa mãn điều kiện z  z  3  4i là? A. Parabol 2 y  4x . B. Đường tròn 2 2 x  y  4  0 . 2 2 C. Elip x y   1 .
D. Đường thẳng 6x 8 y 25  0. 4 2 Trang 2 x   2 3t Cho đường thẳng  :
. Hoành độ hình chiếu của M 4;5 trên  gần nhất với số nào Câu 20. y  1  2t sau đây? A. 1,5. B. 1,2 . C. 1,3 . D. 1,1 . Câu 21. Đường tròn 2 2 3x 3y 6x 9y 9
0 có bán kính bằng bao nhiêu? 5 25 25 A. . B. 5 . C. . D. . 2 2 4
Câu 22. Trong không gian hệ tọa độ Oxyz , cho A1;2;  1 ; B 1  ;0;1 và mặt phẳng
 P:x 2 y z1 0 . Viết phương trình mặt phẳng Q qua ,
A B và vuông góc với P 
A. Q :3x  y  z  0 B. Q :2x  y 3 0 C. Q :x z 0
D. Q  : x  y  z  0
Câu 23. Cho một hình nón đỉnh S có chiều cao bằng 8cm , bán kính đáy bằng 6cm . Cắt hình nón đã cho
bởi một mặt phẳng song song với mặt phẳng chứa đáy được một hình nón N  đỉnh S có đường
sinh bằng 4cm . Tính thể tích của khối nón N . 768 786 2304 2358 A. 3 V   cm B. 3 V   cm C. 3 V   cm D. 3 V   cm 125 125 125 125
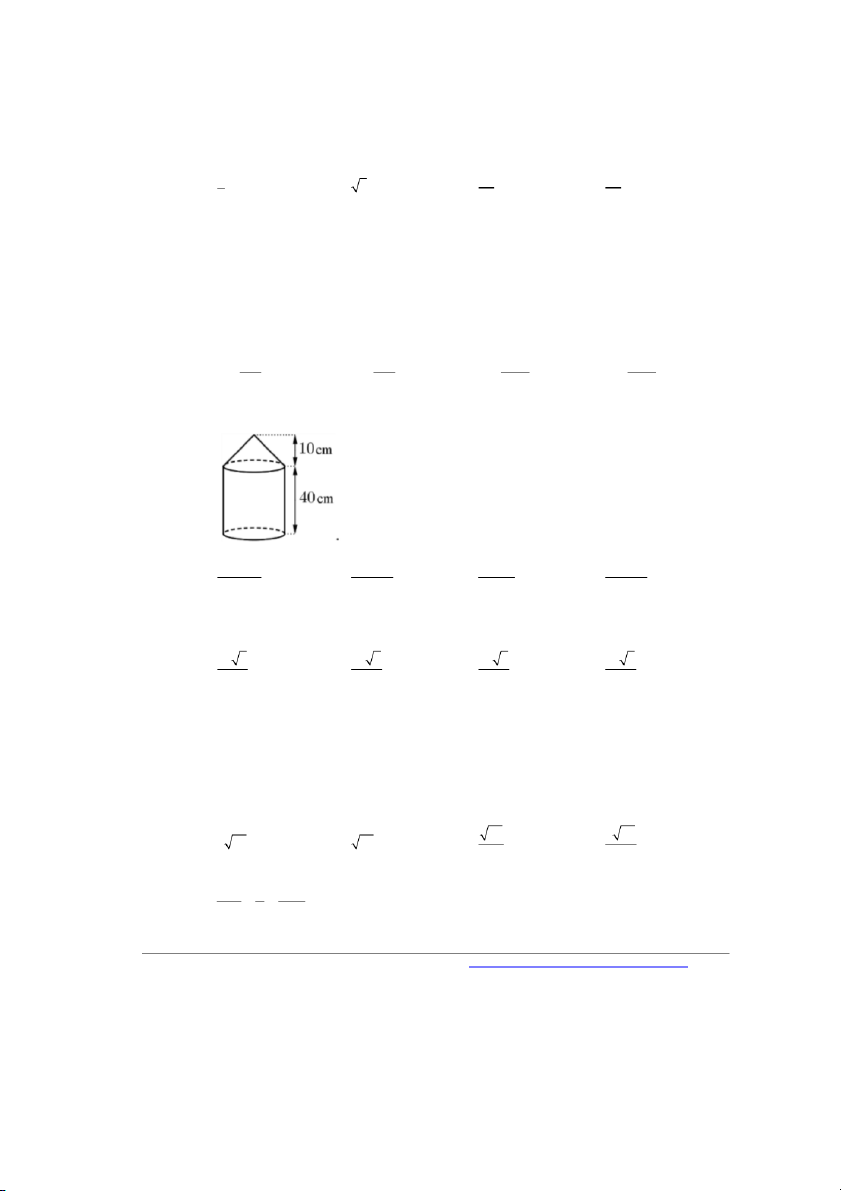
Câu 24. Một cái cột có hình dạng như hình bên (gồm một khối nón và một khối trụ ghép lại). Chiều cao đo
được ghi trên hình, chu vi đáy là. Thể tích của cột bằng 52000 13000 5000 15000 A. p 3 p p p cm . B. 3 cm . C. 3 cm . D. 3 cm .
Câu 25. Cho lăng trụ tam giác AB . C AB C
  có đáy là tam giác đều cạnh a . Độ dài cạnh bên bằng 4a . Mặt phẳng BCC B
  vuông góc với đáy và  B B
 C  30 . Thể tích khối chóp . A CCB là: 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 6 12 18 2
Câu 26. Cho tứ diện ABCD . Gọi H là một điểm nằm trong tam giác ABC ,   là mặt phẳng đi qua H
song song với AB và CD. Mệnh đề nào sau đây đúng về thiết diện của   của tứ diện?
A. Thiết diện là hình bình hành.
B. Thiết diện là hình chữ nhật.
C. Thiết diện là hình vuông.
D. Thiết diện là hình thang cân.
Câu 27. Trong hệ tọa độ Oxyz , cho điểm A2;1;3, mặt phẳng () : 2x  2y  z  3  0 và mặt cầu 2 2 2 ( )
S : x  y  z  6 x 4 y 10 z 2  0 . Gọi  là đường thẳng đi qua A , nằm trong mặt phẳng
() và cắt (S) tại hai điểm M , N . Độ dài đoạn MN nhỏ nhất là: 30 3 30 A. 2 30 . B. 30 . C. . D. . 2 2
Câu 28. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P  :x  2y  z  4  0 và đường thẳng x 1  y z 2 d :  
. Lập phương trình đường thẳng  nằm trong mặt phẳng P  , đồng thời cắt 2 1 3
và vuông góc với đường thẳng d .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3 x  1 y  1 z  1 x 1  y 1  z 1  A.   . B.   . 5 2 3 5 1  2 x 1  y 1  z 1  x 1  y 3 z 1  C.   . D.   . 5 1  3  5 1  3
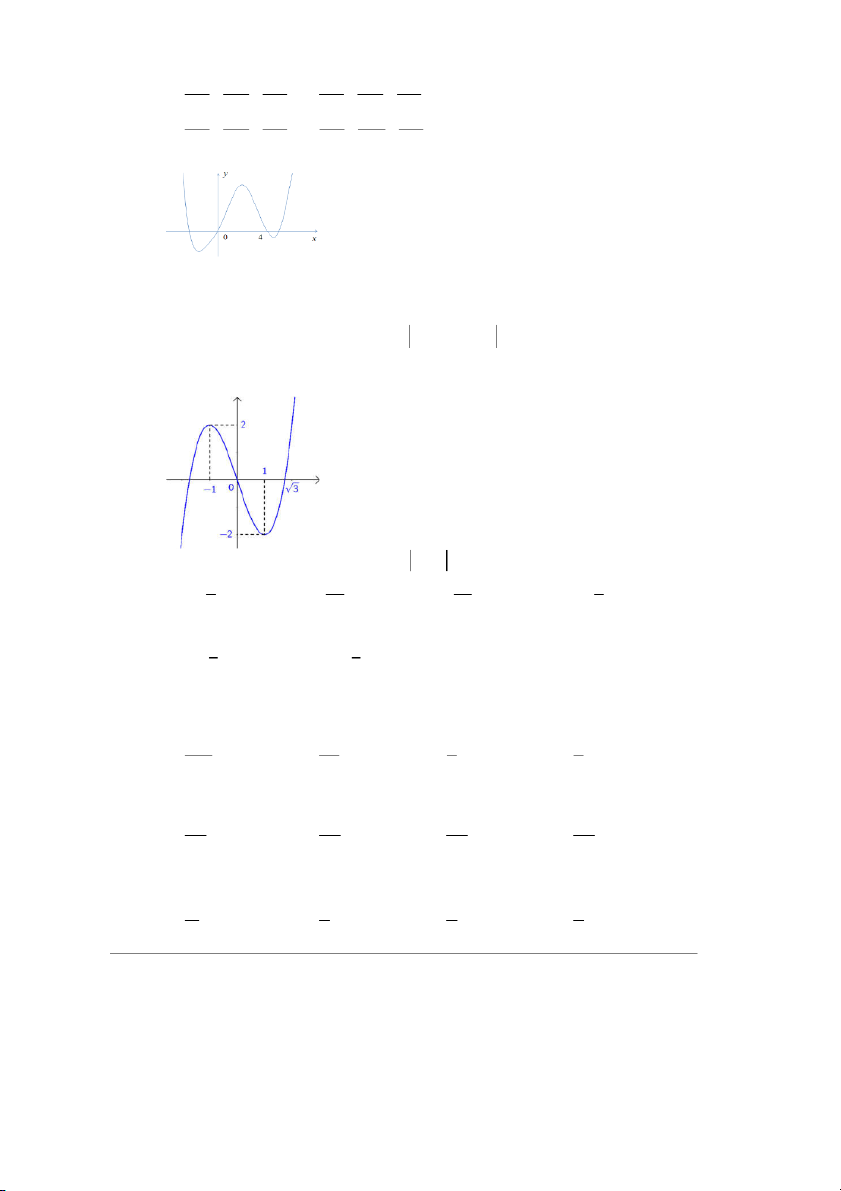
Câu 29. Cho hàm số bậc bốn y  f  x có đồ thị như hình vẽ dưới đây
Số điểm cực trị của hàm số     2x g x f e 3 là A. 6 . B. 5 . C. 4 . D. 3 .
Câu 30. Trong không gian với hệ trục tọa độ Oxyz , cho A 1;1;1, B 2;1; 1, C 0;4;6  . Điểm M di   
chuyển trên trục Ox . Tìm tọa độ M để P  MA  MB  MC có giá trị nhỏ nhất. A. 1;0;0 . B.  1  ; 0;0 . C. 2;0;0  . D.  2  ;0;0  .
Câu 31. Cho hàm số f  x 4 3 2
 ax  bx  cx  dx  e . f x có đồ thị như hình vẽ
Tập tất cả các giá trị của e để đồ thị hàm số f  x có số điểm cực trị lớn nhất là  9  9   9   9  A. 0;  . B. ;0 . C. ;0 . D. 0; . 4         4     4   4 
Câu 32. Cho phương trình  x    2
1 x  4mx  4  0 .Phương trình có ba nghiệm phân biệt khi: 3 3 A. m  . B. m   . C. m   . D. m  0 . 4 4 Câu 33. Cho hàm số f   x liên tục trên tập  Biết f 2  0 và 5
 2x   f  x   4 2 3 1 ' 3
2  x  2x  2xf 3x  2 1,x  .  Giá trị của f   x dx  bằng 2 A. 1953 . B. 651. C. 3 . D. 9 . 4 4 4 4
Câu 34. Từ 12 học sinh gồm 5 học sinh giỏi, 4 học sinh khá, 3 học sinh trung bình, giáo viên muốn
thành lập 4 nhóm làm 4 bài tập lớn khác nhau, mỗi nhóm có 3 học sinh. Tính xác suất để nhóm
nào cũng có học sinh giỏi và học sinh khá. 72 114 36 18 A. . B. . C. . D. . 385 385 385 385
Câu 35. Cho khối tứ diện đều ABCD có thể tích là V . Gọi M , N, P,Q lần lượt là trung điểm của AC, A , D B ,
D BC . Thể tích khối chóp . A MNPQ là V V V V A. . B. . C. . D. . 12 3 6 4 Trang 4 B. ĐIỀN KHUYẾT (15 CÂU) Câu 36. Cho hàm số 3 2
y  x  6x  7x  5 có đồ thị C  . Phương trình tiếp tuyến với đồ thị C  tại điểm
có hoành độ bằng 2 là: Đáp án: …………..
Câu 37. Hàm số y  f  
x có đạo hàm trên  và đồ thị hàm số y  f  x như hình bên. Hàm số y  f  
x có bao nhiêu điểm cực đại. Đáp án: …………..
Câu 38. Trong không gian với hệ tọa độ Oxyz , cho A1; 0; 0 , B 0;2;0 và C 0;0;3. Tính khoảng
cách d từ điểm O đến mặt phẳng ABC  . Đáp án: …………..
Câu 39. Từ các số của tập A  0,1, 2,3, 4,5, 
6 có thể lập được bao nhiêu số chẵn gồm 5 chữ số đôi một
khác nhau trong đó có hai chữ số lẻ và hai chữ số lẻ đứng cạnh nhau. Đáp án: …………..
Câu 40. Cho hàm số y  f x liên tục trên  và thỏa mãn f x  f   x 2 2 1  x  2x 1, x    Tính f  x   2  f   2 lim . x 0  x Đáp án: …………..
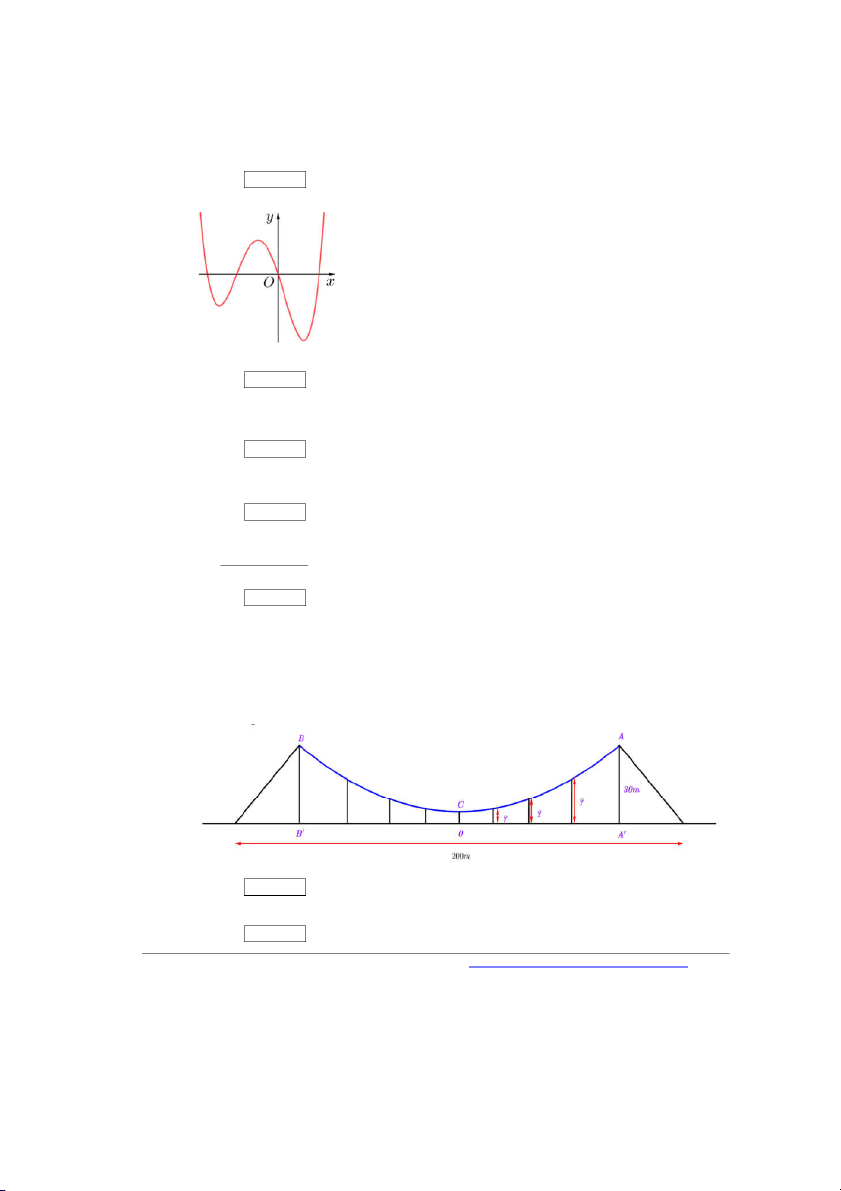
Câu 41. Một kĩ sư thiết kế cây cầu treo bắt ngang dòng sông ( như hình vẽ). Ở hai bên dòng sông, kĩ sư
thiết kế hai cột trụ đỡ AA' và BB' có độ cao 30m và bên trên có bắt một dây truyền có dạng
Parabol ACB để đỡ nền cầu. Hai đầu của dây truyền được gắn chặt vào hai điểm A và B . Để
chịu sức nặng của cây cầu và các phương tiện giao thông thì ở khoảng giữa cầu phải đặt thêm dây
cáp treo thẳng đứng nối nền cầu với dây truyền. Biết khoảng cách giữa các dây cáp treo và hai cột
trụ là bằng nhau và dây cáp có độ dài ngắn nhất là OC  5m. Khoảng cách A'B '  200m . Chiều
dài các cáp treo còn lại là Đáp án: ………….. Câu 42. Để hàm số 3 y  x   m   2 2 3 1 x   6 m  
2 x đạt cực đại và cực tiểu thì: Đáp án: …………..
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
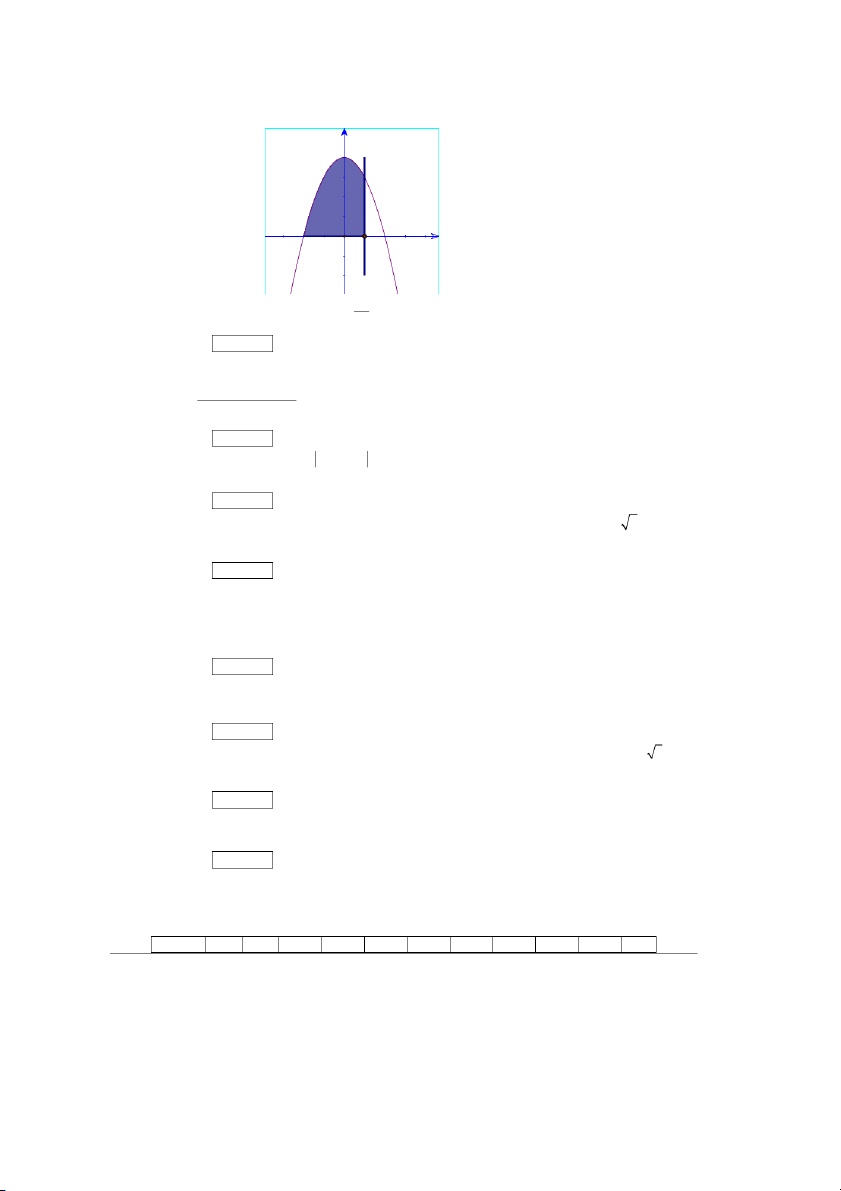
Câu 43. Trong mặt phẳng Oxy cho H  là hình phẳng giới hạn bởi parabol 2
y  4 x và trục hoành.
Đường thẳng x  k 2  k  2 chia H  thành hai phần H ,  như hình vẽ. 2 H  1  y x = k 4 y = 4 - x2 H1 H2 -2 O 2 x 20
Biết rằng diện tích hình  gấp
lần diện tích của hình H , hỏi giá trị 2  1 H  k bằng bao nhiêu? 7 Đáp án: …………..
Câu 44. Cho hàm số f x 3 2
 x  4x  m. Có bao nhiêu giá trị nguyên của tham số m 5  ;5 để phương
f  f x 2 f   x trình
 1 có 9 nghiệm phân biệt? 2 f x   2 f  x Đáp án: …………..
Câu 45. Cho số phức z thỏa mãn z 3 4 i 2 và w
2z 1- i . Trong mặt phẳng phức, tập hợp điểm
biểu diễn số phức w là đường tròn tâm I , bán kính R . Tìm tâm I , bán kính R . Đáp án: …………..
Câu 46. Cho hình hộp chữ nhật ABC . D AB C  D
  có đáy ABCD là hình vuông cạnh bằng 2 2 , AA  4 .
Tính góc giữa đường thẳng AC với mặt phẳng  AABB . Đáp án: ………….. A 3;1; 2 B  3  ; 1  ;0 
P : x  y  3z 14  0
Câu 47. Trong không gian Oxyz , cho , và mặt phẳng . Điểm P M thuộc mặt phẳng
sao cho MAB vuông tại M . Tính khoảng cách từ điểm M đến mặt phẳng Oxy . Đáp án: ………….. Câu 48. Cho ,
a b  thỏa mãn các điều kiện 2 2 a  b  1 và log
a  b  1. Giá trị lớn nhất của biểu 2 2   a b
thức P  2a 4b 3 là Đáp án: …………..
Câu 49. Cho hình lăng trụ đứng ABC.ABC có đáy là tam giác A
 BC đều cạnh a, AA  a 3, M là
trung điểm của CC . Tính khoảng cách từ điểm C đến mặt phẳng  A B  M . Đáp án: …………..
Câu 50. Cho chóp S.ABCD có SA  x và tất cả các cạnh còn lại đều bằng 1 .Tìm x để thể tích của khối
chópS .ABCD đạt giá trị lớn nhất Đáp án: ………….. Lời giải tham khảo
A. TRẮC NGHIỆM KHÁCH QUAN (35 CÂU)
Câu 1. Có 100 học sinh tham dự kì thi học sinh giỏi Hóa (thang điểm 20). Kết quả như sau: Điểm 9 10 11 12 13 14 15 16 17 18 19 Trang 6 Tần số 1 1 3 5 8 13 19 24 14 10 2 Số trung vị là: A. M 15 M  M  M  e B. 15,50 e C. 16 e D. 16,5 e Lời giải: 15 16 
Chọn B ta thấy N=100 chăn nên số trung vị là: M   15,5 e 2 Câu 2. Gọi 1
h t  cm là mực nước ở bồn chứa sau khi bơm nước được t giây. Biết rằng h t  3  t  8 và 5
lúc đầu bồn không có nước. Tìm mức nước ở bồn sau khi bơm nước được 6 giây (làm tròn đến kết quả hàm phần trăm). A. 2,33 cm  . B. 5,06 cm . C. 3,33 cm. D. 2,66 cm  . Lời giải Chọn D 6 h t  h  t 1 1 3 dt  t  8dt  .   t 84 6 6 3 3  2,66. . 0 0 5 5 4 0
Câu 3. Tập nghiệm của phương trình log  2 x  x  2  1 là : 2  A.   1 B.   0 C. 0;  1 D.  1  ;  0 Lời giải Chọn C x  log  0 2 x  x   2
2  1 x x  2  2  2 x  1 2 2 3  x 4  xy 2  y 17 
Câu 4. Cho hệ phương trình: 
. Hệ thức biểu diễn x theo y rút ra từ hệ phương trình 2 2  y  x  16  là? 5 3 y 3 y  3 A. x  y hay x  y B. x  hay x  . 13 5 2 2 y 1  y 1  y  2 y 2 C. x  hay x  . D. x  hay x  . 2 2 2 2 Lời giải Chọn A Ta có : 2 2 3  x 4  xy 2  y 17      2 2 x  xy  y   2 2 3 4 2 17 y  2 2
x   65x  64xy  15y  0 2 2 y  x 16    5 3
13x  5y 5x 3 y  0  x  y hay x  y . 13 5
Câu 5. Cho hai số phức z  1 3i , z  4
  6i có các điểm biểu diễn trên mặt phẳng tọa độ lần lượt là hai 1 2
điểm M và N . Gọi z là số phức mà có điểm biểu diễn là trung điểm của đoạn MN . Hỏi z là số
phức nào trong các số phức dưới đây? 3 9 5 3 A. z    i . B. z  3  9 . C. z  1  3 . D. z   i . 2 2 i i 2 2 Lời giải Chọn A  3 9 Ta có  M 1;3 , N  4  ; 6
 . Suy ra trung điểm I của MN là  ;  . 2 2   
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Do đó I là điểm biểu diễn của số phức 3 9 z    i . 2 2
Câu 6. Phương trình mặt phẳng đi qua A1;1; 2
 , song song với  : x  2 y  2z 1  0 là
A. x  2y  2z 5  0 . B. x  2y  2z 1  0 .
C. x  2 y  2z  2  0 . D. x  2y  2z  0 . Lời giải Chọn A
Ta có phương trình mặt phẳng ở dạng: x 2 y 2 z C 0 C   1 .
A1;1;2 thuộc mặt phẳng khi 1 2.12 2
   C  0  C  5  (thỏa mãn).
Vậy phương trình mặt phẳng cần tìm: x 2y 2z 5 0 .
Câu 7. Trong không gian Oxyz , tọa độ điểm đối xứng của điểm M  0;1; 
2 qua mặt phẳng x y z  0 là: A. 2; 1;0 . B. 0 ;  1;  2  . C. 0;1;  2  . D. 2; 1;0 . Lời giải Chọn D
Đường thẳng d đi qua điểm M  0;1; 
2 và vuông góc với mặt phẳng x y z  0 có phương  x  t
trình là  y  1 t .  z   2  t
Tọa độ giao điểm I của đường thẳng d và mặt phẳng x y z  0 thỏa mãn hệ  x  t t   1    y  1 t  x  1     I 1;0 ;1 z  2  t  y  0   x  y  z 0   z  1 
Gọi M  đối xứng với M  0;1; 
2 qua mặt phẳng x  y  z  0 nên I là trung điểm M M   x      2x x 2 M I M   y  
   M 2 ; 1; 0   2 y y 1 M I M  z      2z z 0 M I M
Câu 8. Bất phương trình 2x 1  3x  2 có tổng năm nghiệm nguyên nhỏ nhất là A. 20 . B. 15 . C. 5 . D. 10 . Lời giải Chọn B  2 x  2  x 1  0  2   3 x  
Bất phương trình đã cho   3  x  2  0   3  x 1  x 1.  2   2  9  x 14x  5  0 x 1   5  3x 22 x   9
Do đó năm nghiệm nguyên nhỏ nhất là 1;2;3;4; 
5 . Vậy tổng năm nghiệm là 12345 15. Trang 8 
Câu 9. Nghiệm của phương trình lượng giác 2 2sin x 3sin x 1
  0 thõa điều kiện 0  x  là: 2     A. x  . B. 5 x  . C. x  . D. x  . 6 6 3 2 Lời giải Chọn A  1  sinx  1 sinx   2   2sin 2 x 3sin x 1 0      1. Thay  vào thỏa mãn.  x  sinx  6   2 0   x   2
Câu 10. Sinh nhật bạn của An vào ngày 01 tháng năm. An muốn mua một món quà sinh nhật cho bạn nên
quyết định bỏ ống heo 100 đồng vào ngày 01 tháng 01 năm 2016 , sau đó cứ liên tục ngày sau
hơn ngày trước 100 đồng. Hỏi đến ngày sinh nhật của bạn, An đã tích lũy được bao nhiêu tiền ?
(thời gian bỏ ống heo tính từ ngày 01 tháng 01 năm 2016 đến ngày 30 tháng 4 năm 2016 ). A. 714.000 đồng. B. 750.300 đồng. C. 738.100 đồng. D. 726.000 đồng. Lời giải Chọn C
Số ngày bạn An để dành tiền (thời gian bỏ ống heo tính từ ngày 01 tháng 01 năm 2016 đến ngày
30 tháng 4 năm 2016 ) là 31 29  31 30 121 ngày.
Số tiền bỏ ống heo ngày đầu tiên là: u  100 . 1
Số tiền bỏ ống heo ngày thứ hai là: u  100 1.100. 2
Số tiền bỏ ống heo ngày thứ ba là: u 1  00 2.100 . 3 …
Số tiền bỏ ống heo ngày thứ n là: u  u  n 1 d  100 n 1100 100n. n 1  
Số tiền bỏ ống heo ngày thứ 121 là: u  100.121 12100. 121
Sau 121 ngày thì số tiền An tích lũy được là tổng của 121 số hạng đầu của cấp số cộng có số hạng
đầu u  100 , công sai d 100 . 1
Vậy số tiền An tích lũy được là 121 121   
100 12100  738100 đồng. 1 S 21  1u 1u21 2 2 
Câu 11. Cho một nguyên hàm của hàm số f  x x 1 
là F  x và F 0   3. Khi đó F  x bằng: x 1 A. x 2ln x 1  3. B. x  2ln x  1  3. 2 C. x 2ln  x  1  3. D. x   3 . x 12 Lời giải Chọn A  Ta có:   f  x x 1 2 dx  dx  1 dx  x  2ln x 1  C    . x 1   x 1  
Khi đó F  x  x  2ln x  1 C .
Do F 0   3 nên F0  0  2ln 0 1  C  3  C  3. Vậy F  x  x 2 ln x 1  3 . 1
Câu 12. Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình: 3 x 3mx  2   nghiệm 3 x đúng x  1 ?
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9 3 1 3 2 2 A. m  . B.   m  . C. m  . D. m  . 2 3 2 3 3 Lời giải Chọn C Bpt 3 1 2 1 2  3mx  x 
 2,x  1 3m x 
  f  x,x  1. 3 4 x x x Ta có  f    4 2 4 2 4 2 2 x  2x    2 2x  
 0 suy ra f  x tăng. 5 2 x x  5x  2 2 x x Ycbt  f x   m x    f x     2 3 , 1 min f 1  2  3m   m x1 3
Câu 13. Một chất điểm A xuất phát từ O , chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật vt 1 2 58  t 
t  m / s , trong đó t (giây) là khoảng thời gian tính từ lúc A bắt đầu 120 45
chuyển động. Từ trạng thái nghỉ, một chất điểm B cũng xuất phát từ O , chuyển động thẳng
cùng hướng với A nhưng chậm hơn 3 giây so với A và có gia tốc bằng a 2 m / s  (a là hằng
số). Sau khi B xuất phát được 15 giây thì đuổi kịp A . Vận tốc của B tại thời điểm đuổi kịp A bằng A. 25 m / s  B. 36 m / s C. 30m / s D. 21 m / s Lời giải Chọn C
Thời điểm chất điểm B đuổi kịp chất điểm A thì chất điểm B đi được 15 giây, chất điểm A đi được 18 giây.
Biểu thức vận tốc của chất điểm B có dạng v t   d a t  at  C  mà v  nên v t  at . B   B 0  0 B
Do từ lúc chất điểm A bắt đầu chuyển động cho đến khi chất điểm B đuổi kịp thì quãng đường
hai chất điểm đi được bằng nhau. Do đó 18 1 58 15 2  225 t  dt  atdt  225  a.  a  2     0 0  120 45 2
Vậy, vận tốc của chất điểm B tại thời điểm đuổi kịp A bằng v t  2.15 3  0 m / s . B 
Câu 14. Hiện tại dân số ở Hà Nội là 7,55 triệu người với tốc độ tăng dân số 2% một năm và dân số
Thành phố Hồ Chí Minh là 8,15 triệu người với tốc dộ tăng dân số 1,5% một năm. Hỏi ít nhất
sau bao nhiêu năm nữa thì số dân Hà Nội vượt số dân Thành phố Hồ Chí Minh. A. 16 năm. B. 20 năm. C. 18 năm. D. 17 năm. Lời giải Chọn A
Số dân của Hà Nội sau n năm là 7, 55 1 0, 02 n n X    7,55 .1,02 . 1  
Số dân của thành phố Hồ Chí Minh sau n n năm là 8,15 1 0, 015 n X    8,15. 1,015  . 2   1,02 n   8,15   8,15 
7,55.1,02n 8,15.1.015n      n  log 15,56 . 1 X X2 1,015      7,55 1,02  7,55 1,015  Vậy sau ít nhất 16 năm.
Câu 15. Tìm nghiệm của phương trình log x 5  4 2   A. x  13. B. x  11. C. x  3 . D. x  21. Lời giải Chọn D
+) Điều kiện x 5  0  x  5 . +) 4
pt  x  5  2  x  21 (tmđk) Trang 10
Câu 16. Thể tích của vật tròn xoay có được khi quay hình phẳng giới hạn bởi đồ thị hàm y  tan x , trục 
Ox , đường thẳng x  0 , đường thẳng x quanh trục Ox là: 3 2  2    A. V  3  . B. V  3  . C. V  3  . D. V  3  . 3 3 3 3 Lời giải Chọn B
Thể tích của vật tròn xoay là:   3 3      2  2  1  V   tan xdx   1 dx 
   tanx  x 3   tan    3  . 2     cos  0  3 3  3 0 0 x mx 9
Câu 17. Tìm tất cả các giá trị thực của tham số m sao cho hàm số y  nghịch biến trên từng x  m khoảng xác định A. 3   m 3 . B. 3   m  3 C. 3  m  3. D. 3   m  3 . Lời giải Chọn D ĐKXĐ: x  m 2 m  9 Ta có y  
, hàm số nghịch biến trên từng khoảng xác định y 0 x  m x m 2 2
 m  9  0  3  m  3.
Câu 18. Cho số phức z  a  bi , a,b  thỏa mãn z 1 3i  z i  0 . Tính S  a  3b. 7 7 A. S   . B. S  5. C. S  5  . D. S  . 3 3 Lời giải Chọn C Ta có : 2 2 2 2
z 1 3i  z i  0  a bi  1 3i i a b  0  a 1 b  3 a b i  0  a  1    a  1  0 a 1  a  1          b 3   4 . 2 2 b   3 a  b  0  2  1 b  b  3   b    1   b   b 32 2  3 Vậy S  a  3b  1   4  5  .
Câu 19. Trong mặt phẳng phức, tập hợp các điểm M biểu diễn số phức z thỏa mãn điều kiện z  z  3  4i là? A. Parabol 2 y  4x . B. Đường tròn 2 2 x  y  4  0 . 2 2 C. Elip x y   1 .
D. Đường thẳng 6x 8y 25  0. 4 2 Lời giải Chọn D
Đặt z  x  yi x, y  
 và M  x; y  là điểm biểu diễn của z. 2 2  z  x  y Ta có  .
z  3 4i  x iy  3 4i  x   3  y  4i 
 z   i  x  2   y  2 3 4 3 4 .
Vậy z  z   i  x  y  x  2  y  2 2 2 3 4 3 4  6x 8y 25  0 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11 x  2  3t Cho đường thẳng : 
. Hoành độ hình chiếu của M 4;5 trên  gần nhất với số nào Câu 20. y  1  2t sau đây? A. 1,5 . B. 1,2 . C. 1,3 . D. 1,1. Lời giải. Chọn A
Gọi H là hình chiếu của M trên  . Ta có: 
H    H  2  3t;1  2t , MH   2   3t; 4  2t. 
Đường thẳng có vectơ chỉ phương là u 3; 2   .      
MH  u  MH u     t    t  2 20 17 . 0 3 2 3
2 4 2  0  13t  2  0  t   H ; . 13  13 13   Câu 21. Đường tròn 2 2 3x 3y 6x 9y 9
0 có bán kính bằng bao nhiêu? 5 25 25 A. . B. 5 . C. . D. . 2 2 4 Lời giải Chọn D 2 2 2 2 3 x 3 y 6 x 9 y 9 0 x y 2 x 3 y 3 0. 3 9 5 Đường tròn có tâm I 1; , R 1 3 . 2 bán kính 4 2
Câu 22. Trong không gian hệ tọa độ Oxyz , cho  A 1;2;  1 ; B 1  ;0;1 và mặt phẳng
P:x 2y  z 1 0 . Viết phương trình mặt phẳng Q qua ,
A B và vuông góc với P 
A. Q :3x  y  z  0 B. Q:2 x  y 3  0 C. Q :x z  0
D. Q : x y z  0 Lời giải Chọn C   AB   2; 2  ;2  2  1;1;  1 ,u  1;1;  1  n  1;2;1 P       n
 AB,n   1;0;       1 Q P 
Vậy Q: x  z  0 .
Câu 23. Cho một hình nón đỉnh S có chiều cao bằng 8cm , bán kính đáy bằng 6cm . Cắt hình nón đã cho
bởi một mặt phẳng song song với mặt phẳng chứa đáy được một hình nón N  đỉnh S có đường
sinh bằng 4cm . Tính thể tích của khối nón N  . 768 786 2304 2358 A. 3 V   cm B. 3 V   cm C. 3 V   cm D. 3 V   cm 125 125 125 125 Lời giải Chọn A Trang 12 S (N) M K I A O B
Đường sinh của hình nón lớn là: l  SB 2 2  h  r 2 2  8  6  10cm . Gọi l , N . 2 2 r , 2
h lần lượt là đường sinh, bán kính đáy và chiều cao của hình nón   l  SK  4 cm 2 SI IK SK 4 2 Ta có: SOB và S  IK đồng dạng nên:     . SO OB SB 10 5  2 16 h  h  h r l 4 2 2  2 2 2      5 5   . h r l 10 5 2 12  r  .  2 r  5 5 1 2 1 12  16 768
Thể tích khối nón N là: 2 V  . .r .  .. . 3   cm . ( h N ) 2 2   3 3  5  5 125
Câu 24. Một cái cột có hình dạng như hình bên (gồm một khối nón và một khối trụ ghép lại). Chiều cao đo
được ghi trên hình, chu vi đáy là. Thể tích của cột bằng 52000 13000 5000 15000 A. p 3 p p p cm . B. 3 cm . C. 3 cm . D. 3 cm . Lời giải Chọn D
Gọi R là bán kính đường tròn đáy của hình nón và hình trụ. 10 3 Theo đề: p 2 R 20 3 p R . 2 10 3p 12000 Thể tích khối trụ là 2 V R h .40 p 1 1 2 1 1 10 3p 3000 Thể tích khối nón là 2 R h .10 p V 2 2 3 3 12000 p 3000 p 15000 Thể tích của cột là p V .
Câu 25. Cho lăng trụ tam giác AB .
C A BC có đáy là tam giác đều cạnh a . Độ dài cạnh bên bằng 4a . Mặt phẳng BCC B
  vuông góc với đáy và  B B
 C  30 . Thể tích khối chóp . A CCB là: 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 6 12 18 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13 Lời giải Chọn A B' C' A' 4a B C H a A
Gọi H là hình chiếu của B trên BC . Từ giả thiết suy ra: B H   ABC . 1  1 S  BB .BC.sin B B  C  4 . a . a sin 30 2  a . BB C  2 2 1 2S 2 2a Mặt khác: S  B . H BC BB C  B H      2a . BB C  2 BC a 2 a 3 3 a 3 V  B H  .S  2 . a  . LT ABC 4 2 1 1 2 1 3 1 a 3 3 a 3 V  V  . V  V  .  . A .CC B   A . 2 CC B  B  2 3 LT 3 LT 3 2 6
Câu 26. Cho tứ diện ABCD. Gọi H là một điểm nằm trong tam giác ABC ,   là mặt phẳng đi qua H
song song với AB và CD. Mệnh đề nào sau đây đúng về thiết diện của   của tứ diện?
A. Thiết diện là hình bình hành.
B. Thiết diện là hình chữ nhật.
C. Thiết diện là hình vuông.
D. Thiết diện là hình thang cân. Lời giải Chọn A A N P H B C M Q D
Qua H kẻ đường thẳng d  song song AB và cắt BC, AC lần lượt tại M, N .
Từ N kẻ NP song song vớ CD  P CD. Từ P kẻ PQ song song với AB Q BD .
Ta có MN // PQ // AB suy ra M , N, ,
P Q đồng phẳng và AB //  MNPQ .
Suy ra MNPQ là thiết diện của   và tứ diện.
Vậy tứ diện là hình bình hành. Trang 14
Câu 27. Trong hệ tọa độ Oxyz , cho điểm A2;1;3 , mặt phẳng ( ) : 2x  2 y  z 3  0 và mặt cầu 2 2 2
(S) : x  y  z  6x  4y 10z  2  0 . Gọi  là đường thẳng đi qua A , nằm trong mặt phẳng
( ) và cắt (S) tại hai điểm M , N . Độ dài đoạn MN nhỏ nhất là: 30 3 30 A. 2 30 . B. 30 . C. . D. . 2 2 Lời giải Chọn A
+ Mặt cầu (S) có tâm I 3; 2;  5 và bán kính R  6.
Ta có: A ( ), IA  6  R nên (S)  ( )  (C) và A nằm trong mặt cầu (S) .
Suy ra: Mọi đường thẳng  đi qua A , nằm trong mặt phẳng () đều cắt (S) tại hai điểm M , N .
( M , N cũng chính là giao điểm của  và) (C).
+ Vì d(I, )  IA nên ta có: 2 2 2 2
MN  2 R  d (I , )  2 R  IA  2 30 .
Dấu "  " xảy ra khi A là điểm chính giữa dây cung MN .
Vậy độ dài đoạn MN nhỏ nhất là MN bằng 2 30 .
Câu 28. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P  :x  2y  z  4  0 và đường thẳng x 1 y z  2 d :  
. Lập phương trình đường thẳng  nằm trong mặt phẳng   P , đồng thời cắt 2 1 3
và vuông góc với đường thẳng d . x 1  y 1  z 1  x 1 y 1 z 1 A.   . B.   . 5 2 3 5 1  2 x 1  y 1  z 1  x 1  y 3 z 1  C.   . D.   . 5 1  3  5 1  3 Lời giải Chọn C
Giao điểm của d với P  là H 1;1;  1 .      đi qua H và nhận u  n ; u  làm véc tơ chỉ phương   p d   x y z  u       .    1 1 1 5; 1; 3 : 5 1  3 
Câu 29. Cho hàm số bậc bốn y  f  x có đồ thị như hình vẽ dưới đây
Số điểm cực trị của hàm số     2x g x f e 3 là A. 6 . B. 5. C. 4 . D. 3 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15 Lời giải Chọn D
Do y  f  x là hàm số bậc bốn nên là hàm số liên tục và có đạo hàm luôn xác định tại mọi điểm x   . x  a    ;  0 
Theo đồ thị hàm số ta có được f x 0  x  b  0;4  .  x c 4;   Mặt khác    2 x    2 2 . . x g x x e f e  3 .  x  0  x   0 2 x
 e  3  a ;0 Do đó g x  2  0  2 . x x e f  2x  e 3  0     .  2 f   2x e  3  0 x  e  3  b  0;4  2x  e  3  c  4; Xét hàm số   2 x h x  e  3 . Ta có   2  2 x h x
xe ; h x  0 x 0 . Từ đó ta có bảng biến thiên của hàm số y  h x 2 2
Từ bảng biến thiên ta thấy phương trình x e  3  a , x
e  3 b vô nghiệm; còn hai đồ thị hàm số
y  h x và y  c cắt nhau tại hai điểm phân biệt có hoành độ khác 0 do đó phương trình 2 x
e  3  c có hai nghiệm phân biệt khác 0 .
Vậy hàm số     2x g x f e   3 có ba điểm cực trị.
Câu 30. Trong không gian với hệ trục tọa độ Oxyz , cho A1;1;1, B2;1; 
1 , C 0;4;6 . Điểm M di   
chuyển trên trục Ox . Tìm tọa độ M để P  MA MB MC có giá trị nhỏ nhất. A. 1;0;0. B.  1  ;0;0. C. 2;0;0 . D.  2  ;0;0  . Lời giải Chọn A Gọi M  x;0;  0 Ox, x    .    Khi đó MA  1 ; x 1;  1 ,MB  2 x;1;  1 ,MC  x;4;6.   
MA MB  MC  3 3 ; x 6; 6  .    P  MA  MB  MC    x2    x  x   x  2 2 2 2 3 3 6 6 9 18 81 9 1  72  72 .   
để P  MA MB MC có giá trị nhỏ nhất khi và chỉ khi x 1 .
Vậy tọa độ M 1;0;0. .
Câu 31. Cho hàm số f x  4 3 2
 ax  bx  cx  dx  e . f  x có đồ thị như hình vẽ Trang 16
Tập tất cả các giá trị của e để đồ thị hàm số f  
x có số điểm cực trị lớn nhất là  9   9    9   9  A. 0;  . B. ;0 . C. ;0 . D. 0; . 4         4     4   4  Lời giải Chọn D 1 3 Từ đồ thị f   x ta có f   x 3
 x  3x  f  x   3x  3x 4 2 dx  x  x  e 4 2
Ta thấy f x là hàm bậc bốn trùng phương đạt cực đại tại x  0 và đạt cực tiểu tại 2 điểm x   3 và x  3 .  f 0  0 Đồ thị hàm số  f  
x có số điểm cực trị lớn nhất là 7 điểm cực trị khi  f    3  0 e   0   9   9  e 0;   e   4   4
Câu 32. Cho phương trình x   2
1 x  4mx  4  0 .Phương trình có ba nghiệm phân biệt khi: 3 3 A. m  . B. m   . C. m   . D. m  0 . 4 4 Lời giải Chọn B
Phương trình có 3 nghiệm phân biệt khi 2
x  4mx  4  0 có 2 nghiệm phân biệt khác 1 2 4m  4  0  3   m   . 4m  3 0 4 Câu 33. Cho hàm số f x liên tục trên tập  Biết f 2  0 và 5
 2x   f  x   4 2 3 1 ' 3
2  x  2x  2xf  3x   2 1, x
  . Giá trị của f  x dx  bằng 2 A. 1953 . B. 651 . C. 3 . D. 9 . 4 4 4 4 Lời giải Ta có:
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17 3 2x   1 f '3x  4 2
2  x  2 x  2 xf 3x  2  1 3 2 x  
1 f '3x2 2xf 3 x 2   1,x .  .  x  2 2 1  f 3x 2 ' f 3x  2     1  x C . 1 2 2   x 1  x 1    f 2 0 Cho x  0 từ1 
 0C   C C  0 f 3x  2  x 2 x   3 1  x  x . 1 1 5 1 1 4 2  x x  1 Ta có: f   xdx 3 f  3x 2dx 3  9 3 x   xdx 3    . 4 2    0 4 2 0 0
Câu 34. Từ 12 học sinh gồm 5 học sinh giỏi, 4 học sinh khá, 3 học sinh trung bình, giáo viên muốn
thành lập 4 nhóm làm 4 bài tập lớn khác nhau, mỗi nhóm có 3 học sinh. Tính xác suất để nhóm
nào cũng có học sinh giỏi và học sinh khá. A. 72 . B. 114 . C. 36 . D. 18 . 385 385 385 385 Lời giải Chọn C 3 3 3 C .C .   12 9 6 C n    15400 4!
Gọi A: “4 nhóm có cả học sinh giỏi và khá”
Để có 4 nhóm có cả học sinh giỏi và khá ta chia các nhóm như sau:
+ Một nhóm có 2 giỏi, 1 khá.
+ Ba nhóm có 1 giỏi, 1 khá, 1 trung bình.
Cách chọn nhóm có 2 giỏi, 1 khá: 2 1 C .C 5 4
Cách xếp vị trí 3 học sinh giỏi và 3 học sinh khá vào ba nhóm còn lại: 3!
Cách xếp 3 học sinh trung bình vào ba nhóm còn lại là 3! Suy ra n  2 1 A  C .C .3!.3! 1440 5 4 n A 1440 36 Vậy P A      . n   15400 385
Câu 35. Cho khối tứ diện đều ABCD có thể tích là V . Gọi M , N, ,
P Q lần lượt là trung điểm của AC, A , D B ,
D BC . Thể tích khối chóp . A MNPQ là A. V . B. V . C. V . D. V . 12 3 6 4 Trang 18 Lời giải Chọn D Cách 1: V AM AN AP 1 Ta có: AMNP  . .  . V AC AD AP 4 ACDP V 1 Mà ACDP  . V 2 ABCD 1 1 1 1 V Vậy V  2V  2. V  2. . .V  V  . A .MNPQ AMNP 4 ACDP 4 2 ABCD 4 ABCD 4 Cách 2: Ta có: V  2 (do . V MNPQ là hình thoi). A MNPQ APMQ Mà V  V (do AB // MQ ) nên V  2V . APMQ BPMQ A .MNPQ BPMQ 1 1
Vì P là trung điểm của BD nên d P, ABC   d D,ABC  và S  S . 2 BQM 4 ABC 1 1 1 1 1 1 V Nên V  d P ABC S  . d D,ABC  . S  . d , D  ABC .S  . BPMQ  ,  . 3 BQM 3 2 4 ABC 8 3 ABC 8 V Suy ra V  . AMNPQ 4 B. ĐIỀN KHUYẾT (15 CÂU) Câu 36. Cho hàm số 3 2
y  x  6x  7 x  5 có đồ thị C  . Phương trình tiếp tuyến với đồ thị C  tại điểm
có hoành độ bằng 2 là: Đáp án: …………..
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19 Lời giải Ta có x  2  y  3 0 0 2
y '  3x 12x  7  y '(2)  5 
Phương trình tiếp tuyến với đồ thị C  tại điểm M (2;3) là
y  y ' 2  x  2  3  5(x  2)  3hay y  5x  13
Câu 37. Hàm số y  f  x có đạo hàm trên  và đồ thị hàm số y  f x  như hình bên.
Hàm số y  f x  có bao nhiêu điểm cực đại. Đáp án: ………….. Lời giải
Từ đồ thị hàm số y  f  x , ta có f 
x  0 có 4 nghiệm phân biệt x , x , x , 1 2 3 x như hình vẽ. 4
Ta có bảng biến thiên của hàm số y  f  x là:
Từ đó suy ra hàm số y  f x có 2 điểm cực đại.
Câu 38. Trong không gian với hệ tọa độ Oxyz , cho A1;0;0, B0; 2
 ;0  và C 0;0;3. Tính khoảng
cách d từ điểm O đến mặt phẳng ABC . Đáp án: ………….. Lời giải Phương trình   x y z ABC : 
  1 6x  3y  2z  6  0 . 1 2 3 6 6 d O, ABC   .   2 2 2 7 6 3  2
Câu 39. Từ các số của tập A   0,1, 2,3, 4,5, 
6 có thể lập được bao nhiêu số chẵn gồm 5 chữ số đôi một
khác nhau trong đó có hai chữ số lẻ và hai chữ số lẻ đứng cạnh nhau. Đáp án: ………….. Lời giải
Vì có 3 số lẻ là 1,3,5, nên ta tạo được 6 cặp số kép: 13,31,15,51,35,53 Trang 20
Gọi A là tập các số gồm 4 chữ số được lập từ X 0,13, 2, 4,  6 . Gọi A , A , 1 2 3
A tương ứng là số các số tự nhiên lẻ gồm 4 chữ số khác nhau được lập từ các chữ số
của tập X 0,13, 2, 4, 
6 và 13 đứng ở vị trí thứ nhất, thứ hai và thứ ba. Ta có: 3
A  A  24; A  A  3.3.2  18 nên A  24  2.18  60 1 4 2 3
Vậy số các số cần lập là: 6.60  360 số.
Câu 40. Cho hàm số y  f x liên tục trên  và thỏa mãn f   x  f   x 2 2 1
 x  2x 1,x  Tính f  x   2  f   2 lim . x0 x Đáp án: ………….. Lời giải f  x   2  f   2 f u   f   2
Đặt u  x  2 ta có: lim  lim  f   2 . x 0 u 2 x u 2
Đặt t  1 x  x  1 t ta có: f  x  f    2 2
1 x  x  2x 1,x   1
 f  t  f t    t2    t 2 2 1 1 2 1 1  t  4t  2  f    x  f   2 2 1
x  x  4x  2 2 . Từ   1 và 2 ta được: 2    f  x x 8x 4   f x 2x 8   f 2 4 . 3 3 Cách 2 f x  2  f 2 f u   f 2
Đặt u  x  2 ta có: lim  lim  f 2. x 0  u 2 x  u 2
Từ điều kiện f x  f   x  2 2 1  x 2x 1  , x
   ta suy ra hàm f x có dạng 2 ax  bx  c Từ đó ta có:
f  x  f   x  ax  bx  c  a   x2 2  b   x 2 2 1 2 2 2 1 1
 c  3ax  b  2a x  3c  a  b  1 a   3 3  a  1    8
Đồng nhất hai vế, ta được hệ phương trình b   2a  2  b   3 3  c a b 1        4 c    3 2 x  8x  4 2x  8 Vậy f x   f  x   f  2 4 . 3 3
Câu 41. Một kĩ sư thiết kế cây cầu treo bắt ngang dòng sông ( như hình vẽ). Ở hai bên dòng sông, kĩ sư
thiết kế hai cột trụ đỡ AA' và BB' có độ cao 30m và bên trên có bắt một dây truyền có dạng
Parabol ACB để đỡ nền cầu. Hai đầu của dây truyền được gắn chặt vào hai điểm Avà B . Để
chịu sức nặng của cây cầu và các phương tiện giao thông thì ở khoảng giữa cầu phải đặt thêm dây
cáp treo thẳng đứng nối nền cầu với dây truyền. Biết khoảng cách giữa các dây cáp treo và hai cột
trụ là bằng nhau và dây cáp có độ dài ngắn nhất là OC  5m. Khoảng cách A' B '  200m . Chiều
dài các cáp treo còn lại là
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21 Đáp án: ………….. Lời giải
Chọn hệ trục tọa độ Oxy như hình vẽ. Parabol P có dạng: 2 y  ax  b .  B    P 1 (100,30) 1  0000a  b  30 a  Ta có:    400 . C(0;5)    P  b   5 b   5 1 Do đó Parabol  2 P  : y  x  5. 400
Vậy chiều dài các cáp treo còn lại lần lượt là: 6.56m,11.25m,19.06m . Câu 42. Để hàm số 3 y  x  m   2 2 3
1 x  6 m  2 x đạt cực đại và cực tiểu thì: Đáp án: ………….. Lời giải
y  0 có 2 nghiệm phân biệt   = 2 (m  3)  0  m  3.
Câu 43. Trong mặt phẳng Oxy cho H  là hình phẳng giới hạn bởi parabol 2
y  4  x và trục hoành.
Đường thẳng x  k 2  k  2 chia  H thành hai phần H , H như hình vẽ. 2 1  y x = k 4 y = 4 - x2 H1 H2 -2 O 2 x 20
Biết rằng diện tích hình  gấp
lần diện tích của hình  , hỏi giá trị 2 H  1 H  k bằng bao nhiêu? 7 Trang 22 Đáp án: ………….. Lời giải 2 2 3 3  x  16 Diện tích hình  k H là S   2 4  x dx  4  x     4  . 2  2  k 3 3 3   k k 2 3 3 32 16  k  16 Diện tính hình  k H là S    2 4  x dx S     4k     4  . 1  1  2 k 3  3 3  3 3 2 3 3 16 k 20 16  Theo đề bài ta có: 20 9 108 208    4k     4 k  3  k  k   0 . 1 S S2 k 7  3 3 7  3 3  7 7 21  2 k   3   . So với điều kiện 2   k  2 nhận 2 k  .   105 1 3 k   3
Câu 44. Cho hàm số f x 3 2
 x  4x  m. Có bao nhiêu giá trị nguyên của tham số m  5  ;5 để phương
f  f x  2 f  x trình
 1 có 9 nghiệm phân biệt? 2 f  x  2f  x Đáp án: ………….. Lời giải f x 3 2  x 4x  m Đặt f x  t ;  256 
f x  t có 3nghiệm phân biệt t m ;m  27     f t 2  t   *
f  f x  2 f x f t   2t  khi đó  1 trở thành  1  t   0 . 2 f  x  2 f  x 2 t  2t t  2    256  t  m  ;m
Yêu cầu bài toán dẫn đến   2 
f t  t có 3nghiệm phân biệt   27  t  0; t  2   256  t   m  ;m hay 3 2 
t 5t  m  0 có 3nghiệm phân biệt   27   t  0, t  2 h t  3 2  t 5t  m t   0 Ta có h t 2 0 3t 10t 0        10 .  t   3
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23 1  0 256  m   3 27  h  m  0   256  4  m 5 h m  0 4   m 5  3 2   27  m 5m m  0      5  21
để (1) có 9 nghiệm phân biệt thì h0  0    256   m  m 5 . h m   0 2      h2  0  27    m     5  ;5 m m      m   
thử lại thấy m  5 thỏa mãn.
Câu 45. Cho số phức z thỏa mãn z 3 4 i 2 và w
2z 1- i . Trong mặt phẳng phức, tập hợp điểm
biểu diễn số phức w là đường tròn tâm I , bán kính R . Tìm tâm I , bán kính R . Đáp án: ………….. Lời giải Giả sử z x yi x, y . Từ giả thuyết 2 2 z 3 4i 2 x yi 3 4i 2 x 3 y 4 4 * . Từ w 2z 1 i 2 x yi 1 i 2x 1 2y 1 i . a 1 2 1 x x a Giả sử 2 w a bi a, b . Ta có a bi 2x 1 2y 1 i . 2 y 1 b b 1 y 2 2 2 a 1 b 1 Thay 2 2
x, y vào phương trình * , ta có 3 4 4 a 7 b 9 16 . 2 2
Suy ra w chạy trên đường tròn tâm I 7; 9 , bán kính R 4 .
Câu 46. Cho hình hộp chữ nhật ABC . D AB C  D
  có đáy ABCD là hình vuông cạnh bằng 2 2 , AA  4 .
Tính góc giữa đường thẳng AC với mặt phẳng  AABB . Đáp án: ………….. Lời giải Trang 24 B' C' A' D' B C O A D
Ta có CB   AABB tại B . Khi đó AB là hình chiếu của AC lên mặt phẳng AA B  B  .
Vậy góc tạo bởi đường thẳng AC và mặt phẳng AA B  B   là góc  CA B . BC 2 2 1 Khi đó   tan ' CA B     CAB  30 . A B    2 2 3 4 2 2 A 3;1;2 B  3  ; 1  ;0 
P: x y3z 14  0
Câu 47. Trong không gian Oxyz , cho , và mặt phẳng . Điểm P  M thuộc mặt phẳng
sao cho MAB vuông tại M . Tính khoảng cách từ điểm M đến mặt phẳng Oxy . Đáp án: ………….. Lời giải
Tam giác MAB vuông tại M , suy ra M thuộc mặt cầu S  đường kính AB  2 11.
Xét vị trí tương đối của P và S , ta có (P) tiếp xúc S  .
Lại vì M  P  nên M là tiếp điểm của P và S  , hay M là hình chiếu của tâm của mặt cầu
S trên P , S có tâm là trung điểm I 0;0;1 của đoạn AB .
Đường thẳng IM qua I 0;0;1 và nhận vectơ pháp tuyến của mặt phẳng  P làm véctơ chỉ phương x  t   IM : y t (t ) z 13t 
M    M (t;t;1  3t )
M  P   t  t  3(1 3t) 14  0  11.t  11 t  1  M  1;1;  4 Oxy : z  0 Suy ra: d M Oxy 4 ( , )  4 . 1 Câu 48. Cho ,
a b thỏa mãn các điều kiện 2 2 a  b  1 và log
a  b  1. Giá trị lớn nhất của biểu 2 2   a b 
thức P  2a 4b 3 là Đáp án: ………….. Lời giải. 2 2  1   1  1 Do 2 2 a  b  1 và log a b  1 nên 2 2         (1) 2 2   a b a b  a   b  a  b  2  2 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25  1   1   3 Ta có: a 2b  a   2 b   (2)  2   2      2 1 1
Áp dụng bất đẳng thức Bunhiacốpski cho hai dãy số a  ,b  và 1,2 ta có: 2 2 2 2 2  1   1    1   1  2 2 2  1 1       3 2 2    a   b       (1  2 )  a   2 b   5 a   b        a  2b  2 2  2   2              2   2    2  (3) Từ (1) và (3) 2 Ta có: 1  3  3 10 5.  a  2b  a  2b    2a  4b 3  10 2  2    2 2  1 1 a  b   5   10 2 2  a   
Dấu '  ' xảy ra khi và chỉ khi 10 1 2    2 2   5  2 10  1   1  1 b  a b           10   2   2  2
Câu 49. Cho hình lăng trụ đứng ABC.ABC có đáy là tam giác A
 BC đều cạnh a, AA  a 3, M là
trung điểm của CC . Tính khoảng cách từ điểm C đến mặt phẳng  A B  M . Đáp án: ………….. Lời giải Gọi E  AC  A M
 , vì M là trung điểm của CC nên dễ thấy C là trung điểm của AE. 1
Ta có, d C, ABM   d C, ABM   d  A , ABM   2
Áp dụng định lí cosin cho ABE ta có: 2 2 2 2
BE  AB  AE  2.AB.AE.cos60  3a  BE  a 3. Xét tam giác ABE có 2 2 2 AB  BE  AE  A
 BE vuông tại B  AB  BE. Kẻ AH  A B   
1 , khi đó BE  AB, BE  AA  BE   ABA   BE  AH (2)
Từ (1) và (2) ta có d A, A B  M   AH 1 1 1 1 1 4 a 3 Lại có       AH  2 2 2 2 2 2 AH AB AA a 3 a 3a 2
Vậy d C  ABM  1 a 3 ;  AH  . 2 4 Trang 26
Câu 50. Cho chóp S.ABCD có SA  x và tất cả các cạnh còn lại đều bằng 1.Tìm x để thể tích của khối
chópS.ABCD đạt giá trị lớn nhất Đáp án: ………….. Lời giải
Tứ giác ABCDcó các cạnh bằng nhau nên ABCD là hình thoi do đó AC cắt BD tại trung điểm
O của mỗi đường và AC đường trung trực của đoạn thẳng BD .
Gọi H là hình chiếu của điểmS trên mặt phẳng  ABCD
Ta có: SB  SD 1  HB  HD suy ra H thuộc đường trung trực AC của đoạn thẳng BD .
Xét hai tam giác cân SBD và CBD có SB SD CB CD 1 ; BD chung
Suy ra:  SBD   BCD  SO  OC 1
 SAC có đường trung tuyến SO  AC  SAC vuông tạiS 2 S . khi đó: 2 2 2 A SC x
AC  SA  SC  1 x và SH .AC  SA.SC  SH   2 AC 1 x Trong tam giác vuông OBC 2 2   2 2 x 1 3 x 2 OB  BC  OC  1 
 BD  3 x 0  x  3 4 2 1 1 1 Diện tích 2 V  S SH  AC BD SH  x  x S ABCD . ABCD. . .  2 3  3 6 6 x  3 x 3
Áp dụng bất đẳng thức cauchy có x 3 x  2 2 2 2   2 2 6 Dấu bằng xảy ra khi: 2 2 x  3  x  x  0; 3 2 1 6
Vậy thể tích chóp S.ABCD lớn nhất bằng khi x  4 2
• XEM THÊM ĐỀ CƯƠNG ÔN THI TẠI:
• https://www.nbv.edu.vn/2022/01/de-cuong-danh-gia-nang-luc-dhqg-ha-noi.html
Theo dõi Fanpage: Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Hoặc Facebook: Nguyễn Vương https://www.facebook.com/phong.baovuong
Tham gia ngay: Nhóm Nguyễn Bào Vương (TÀI LIỆU TOÁN) https://www.facebook.com/groups/703546230477890/
Ấn sub kênh Youtube: Nguyễn Vương
https://www.youtube.com/channel/UCQ4u2J5gIEI1iRUbT3nwJfA?view_as=subscriber
Tải nhiều tài liệu hơn tại: https://www.nbv.edu.vn/
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27