Phần 1: cơ sở lý thuyết và thống kê - Công nghệ thông tin | Đại học Hoa Sen
Phần 1: cơ sở lý thuyết và thống kê - Công nghệ thông tin | Đại học Hoa Sen được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem
Môn: Công nghệ thông tin (asf-1243)
Trường: Đại học Hoa Sen
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
Phần 1: CƠ SỞ LÝ THUYẾT 1. Thống kê
Thống kê là một hệ thống các phương pháp bao gồm nhiều lĩnh vực khác nhau: thu
nhập, tổng hợp, trình bày số liệu, tính toán các đặc trưng của đối tượng nghiên cứu
nhằm phục vụ cho quá trình phân tích, dự đoán và ra quyết định phản ánh hiện tượng
kinh tế - xã hội, tự nhiên và kỹ thuật.
Thống kê có hai lĩnh vực: - Thông kê mô tả - Thống kê suy diễn
Đây là một môn học toán ứng dụng và là hệ thống các phương pháp được sử dụng để
nghiên cứu. Một quá trình mô hình thống kê sẽ được nghiên cứu. Nó đề cập tới tất cả
các khía cạnh bao gồm việc lập kế hoạch, thu thập dữ liệu mẫu cho các cuộc khảo sát và thí nghiệm. 2. Quy trình thống kê
1- Xác định mục đích, đối tượng cần nghiên cứu
2- Lập câu hỏi để nghiên cứu
3- Tạo bảng hỏi, điều tra thống kê
4- Tổng hợp, xử lý và phân tích dữ liệu
5- Giải thích kết quả và dự đoán xu hướng
6- Trình bày, báo cáo và truyền đạt kết quả.
3. Các phương pháp thống kê được sử dụng 3.1 Trung bình mẫu
Bằng bình phương giữa tổng giá trị tất cả các phần tử và tổng số phần tử. Bao gồm
trung bình cộng đơn giản (trung bình tổng thể, trung bình mẫu) và trung bình cộng có
trọng số (trường hợp đặc biệt của trung bình cộng đơn giản khi giá trị X xuất hiện nhiều lần)
Trong phân tích dữ liệu, cũng như trong cuộc sống hàng ngày, chúng ta thưởng nói
đến chiều cao trung bình, thu nhập trung binh, vân vân. Đó chính là trung bình mẫu. - Trung bình mẫu: = -
Trung bình cộng có trọng số: Là trường hợp đặc biệt của trung bình cộng đơn
giản khi giá trị Xi xuất hiện nhiều lần.
= với là số phần tử của mẫu.
3.2 Phương sai (Variance)
Phương sai mẫu là số trung bình cộng của bình phương các độ lệch giữa đường biến
và số trung bình cộng của lượng biến đó. - Phương sai mẫu : = - Phương sai hiệu chỉnh
: Được sử dụng trong thống kê suy diễn như ước lượng, kiểm định. 3.3 Độ lệch mẫu
Là độ lệch trung bình của tất cả các lượng biến so với giá trung bình, sử dụng để so
sánh độ phân tán của nhiều tổng thể trong từng trường hợp đơn vị giống nhau hoặc
giá trị trung bình bằng nhau. -
Độ lệch chuẩn của mẫu: s = -
Độ lệch mẫu hiệu chỉnh: S = 3.4 Mode (Mo)
Mốt là giá trị xuất hiện nhiều nhất trong một dãy sôs, kí hiệu là Mo.
Cách xác định theo từng trường hợp: -
Trường hợp dữ liệu không phân nhóm: Mốt có giá trị tần số lớn nhất. -
Trường hợp dữ liệu phân nhóm có khoảng cách đều nhau: trước mắt cần phải
xác định nhóm chứa mốt là nhóm có giá trị tần số lớn nhất. Giá trị của mốt
được xác định gần chính xác bằng công thức: M0 = XMomin + hMo x 3.5 Trung vị (Median)
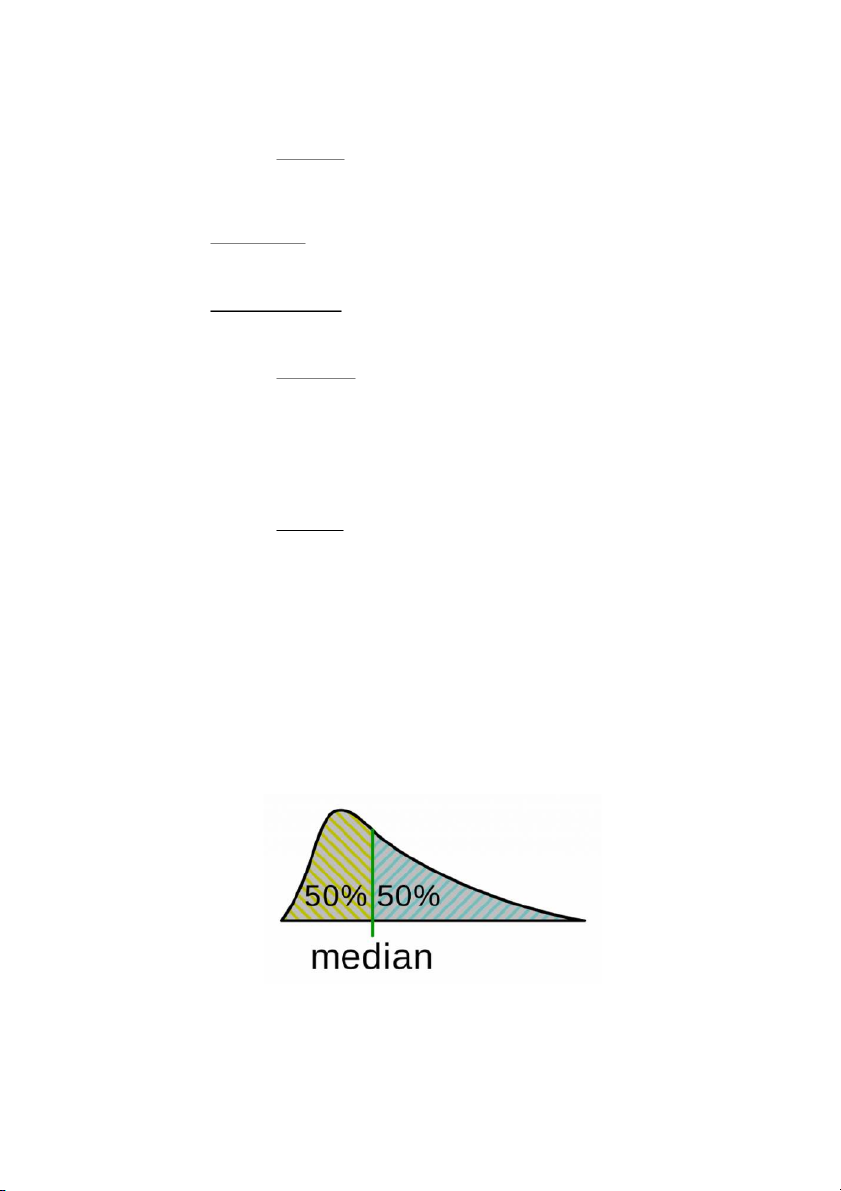
Trung vị (Me) là giá trị đứng giữa trong một danh sách các giá trị được sắp xếp theo thứ tự tăng dần.
Cách xác định trung vị: -
Trường hợp n là số lẻ:
(trung vị là giá trị đứng giữa, tại vị trí thứ trong dãy các giá trị tăng dần) -
Trường hợp n là số chẵn:
(trung vị là trung bình cộng của hai giá tị đứng giữa trong dãy số) -
Trường hợp mẫu phân nhóm:
(trung vị thuộc nhóm tần số tích lũy vào đủ )
Đặc điểm của trung vị: -
Là trị số duy nhất có thể xác định được trong một dãy số -
Là đặc trưng đo lường khuynh hướng tập trung không bị ảnh hưởng bởi các giá trị đột biến -
Có thể tính cho các dữ liệu sử dụng thang đo tỉ lệ, khoảng, thứ bậc.
3.6 Ước lượng giá trị trung bình một tổng thể:
Tổng thể có thể phân phối chuẩn và giá trị trung bình chưa biết và cần ước lượng với độ tin cậy cho trước. Phương pháp
B1: Tính n, , độ lệch mẫu hiệu chỉnh S
B2: Có 2 trường hợp để tính định lượng trung bình tổng thể: TH1: Đã biết phương sai
Độ chính xác được tính bởi công thức
TH2: Chưa biết phương sai (trong trường hợp này chia làm 2 phương pháp nhỏ phụ thuộc vào n) -
Nếu thì độ chính xác (tổng thể có phân phối bất kì) -
Nếu cỡ mẫu thì độ chính xác (tổng thể có thể phân phối chuẩn)
(trong đó có phân phối Student với bâc tự do) B3: Tính sai số B4: Kết luận:
3.7 Kiểm định trung bình tổng thể trên một mẫu
Kiểm định giả thuyết với mức ý nghĩa cho trước và là một giá trị cụ thể. Có 2 trường hợp:
TH1: Đã biết phương sai của tổng thể có phân phối chuẩn
Giá trị kiểm định được tính bởi công thức
Quy tắc quyết định: Bác bỏ ở mức ý nghĩa nếu
Ta nhận thấy có sự liên hệ giữa ước lượng và kiểm định giả thuyết, cụ thể giả thuyết
H0 bị bác bỏ với mức ý nghĩa khi và chỉ khi khoảng tin cậy (với độ tin cậy của không chứa trị số
TH2: Chưa biết phương sai của tổng thể n
- Với mẫu kích thước có và tổng thể có phân phối bất kì thì
- Với mẫu kích thước có và tổng thể có phân phối chuẩn thì giá trị kiểm định
Quy tắc quyết định: Bác bỏ ở mức ý nghĩa nếu , trong đó có phân phối Student với bậc tự do.
Chú ý: Khi giar thuyết đã bị bã bỏ thì cần so sánh trung bình mẫu với Với ta kết luận Với ta kết luận
Giá trị p (p-value) là mức ý nghĩa nhỏ nhất mà ở đó giả thuyết bị bác bỏ. Được xem
như mức ý nghĩa tiêu chuẩn, gắn liền với từng trường hợp cụ thể.
Nếu thì chấp nhận , nếu thì bác bỏ
3.8 Kiểm định tỉ lệ tổng thể trên một mẫu
Giả sử tổng thể gồm hai loại phần tử là có tính chất T và không có tính chất T Ta đưa ra giả thuyết
: Tỉ lệ các phần tử có tính chất T của tổng thể là , ta cần kiểm định xem giả thuyết đó
là đúng hay sai với mức ý nghĩa cho trước Phương pháp
- Lấy mẫu định tính gồm phần tử của tổng thể, ta tính được mẫu
- Từ mức ý nghĩa , tra bảng hàm số Laplace, ta tìm được số sao cho
- Tính giá trị kiểm định:
- So sánh : Nếu thì chấp nhận . Nếu thì bác bỏ .