























Preview text:
PHÂN LOẠI DẠNG VÀ
PHƯƠNG PHÁP GIẢI NHANH TẬP 01 HÌNH CHÓP
Biên Hòa – ��y 10 ��ng 07 năm 2017
TÀI LIỆU LƯU HÀNH NỘI BỘ
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
Phần 01 : HÌNH CHÓP – KHỐI CHÓP
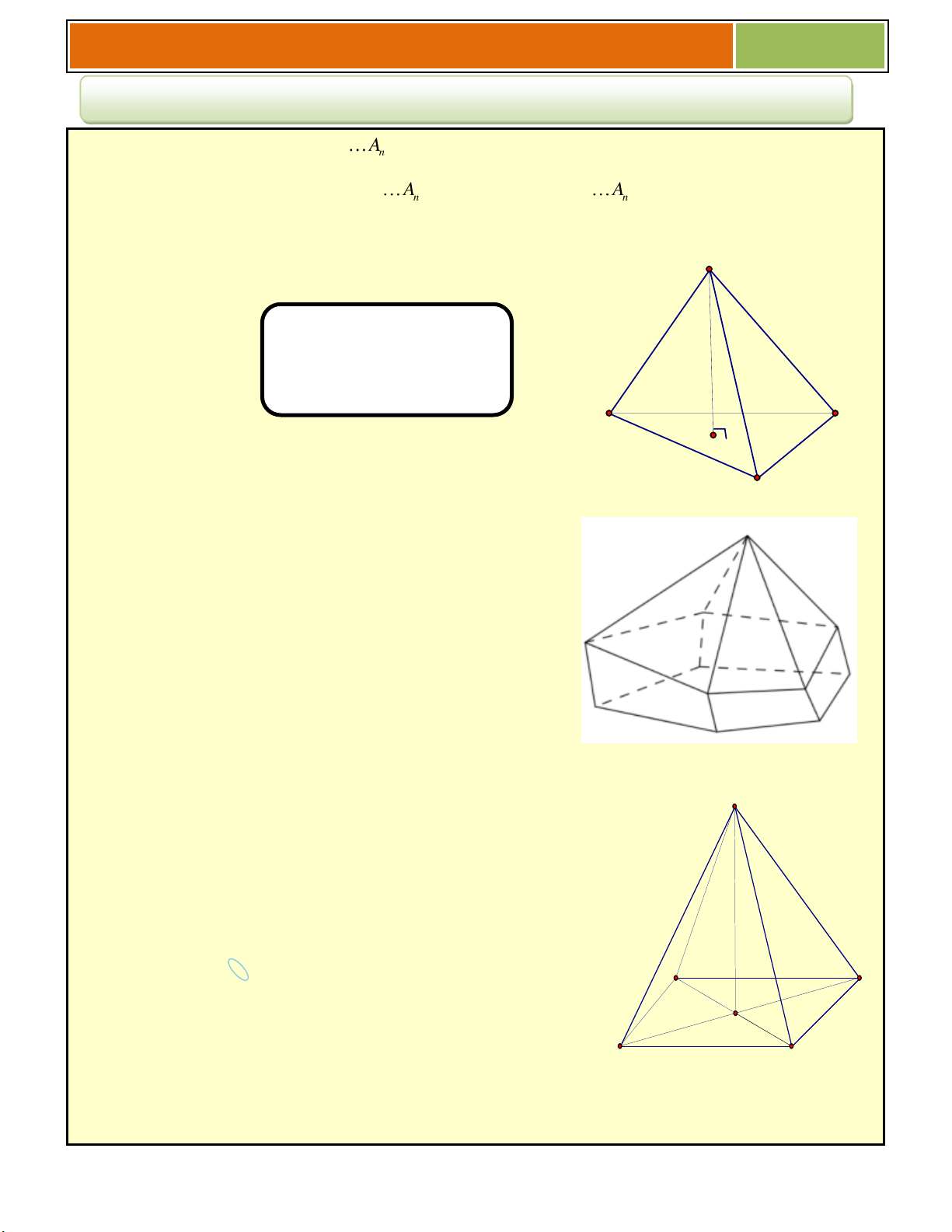
1. Định nghĩa : Cho đa giác A A
A và điểm S nằm ngoài mặt phẳng chứa đa giác đó . 1 2 n
Hình gồm n tam giác và đa giác A A
A là hình chóp S. A A A . 1 2 n 1 2 n
• Tứ diện là hình chóp tam giác . S
• Tứ diện đều là hình chóp tam giác có tất cả các cạnh bằng nhau
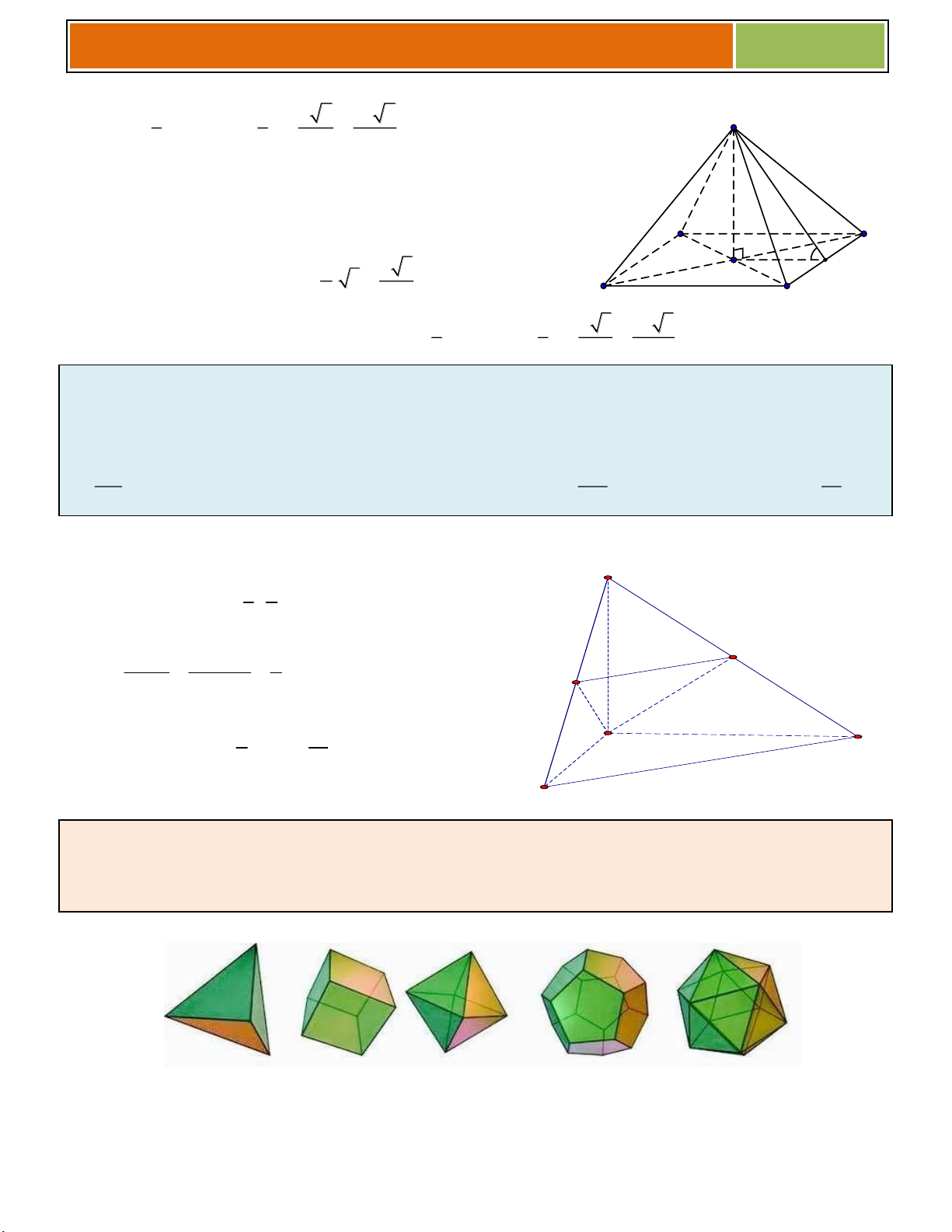
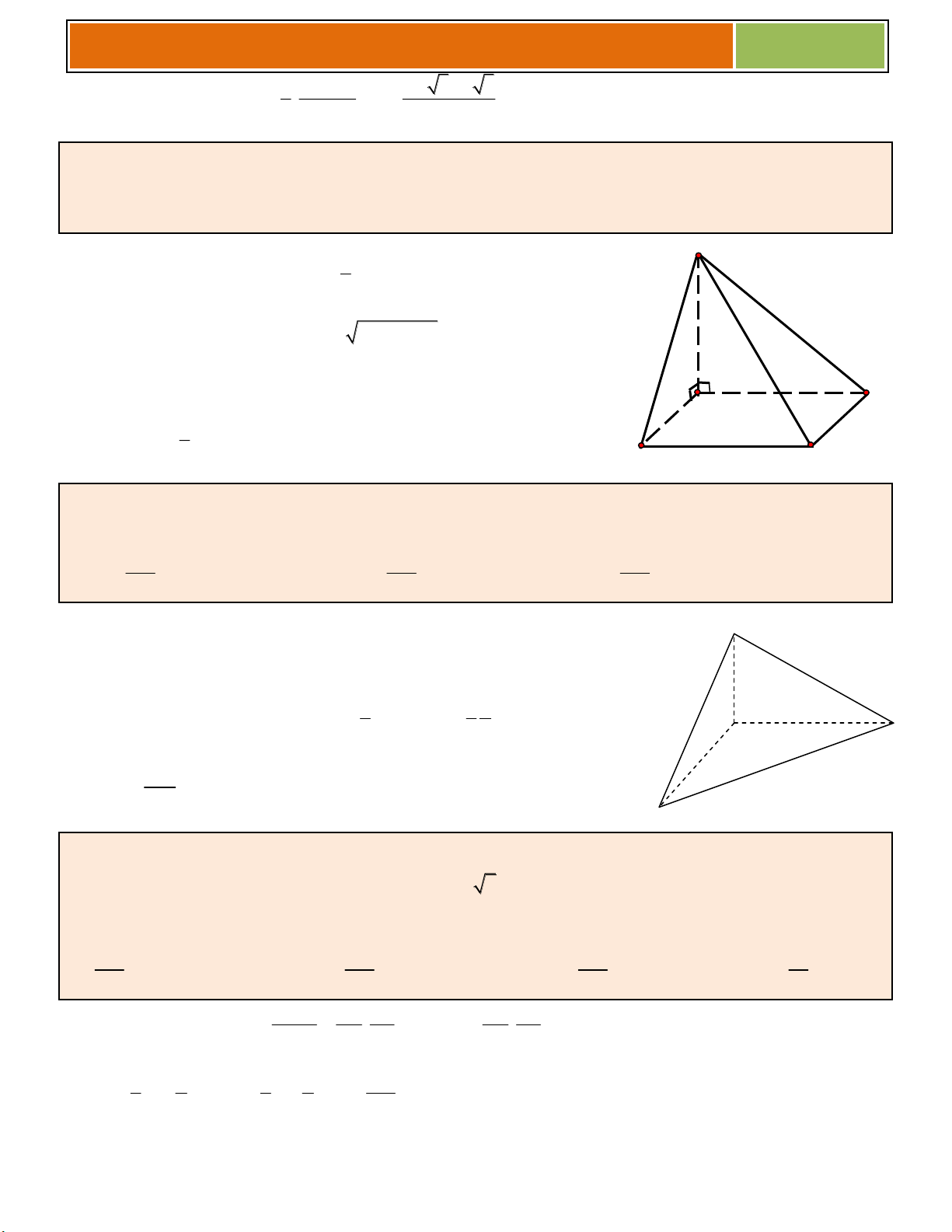
+ Thể tích khối chóp h C A H
S là diện tích đa giác đáy, h : là đường cao của hình chóp B
Ví dụ : (Trích đề minh họa lần 3 – BGD-ĐT):
Hình đa diện trong hình vẽ bên có bao nhiêu mặt . A. 6 . B. 10 . C. 12 . D. 11. 2. Hình chóp đều : S
• Hình chóp đều là hình chóp có đáy là đa giác đều và các cạnh bên bằng nhau .
• Hình chóp đều khi và chỉ khi đáy của nó là đa giác đều và
đường cao của nó qua tâm của đáy
( tâm đường tròn ngoại tiếp , nội tiếp ) A B
• Hình chóp đều khi và chỉ khi đáy của nó là đa giác đều và O D
các cạnh bên tạo với đáy các góc bằng nhau . C
Gv cần file word xin liên hệ trực tiếp qua zalo – facebook – sđt : 0914449230 1
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
HÌNH VẼ MỘT SỐ HÌNH CHÓP ĐẶT BIỆT
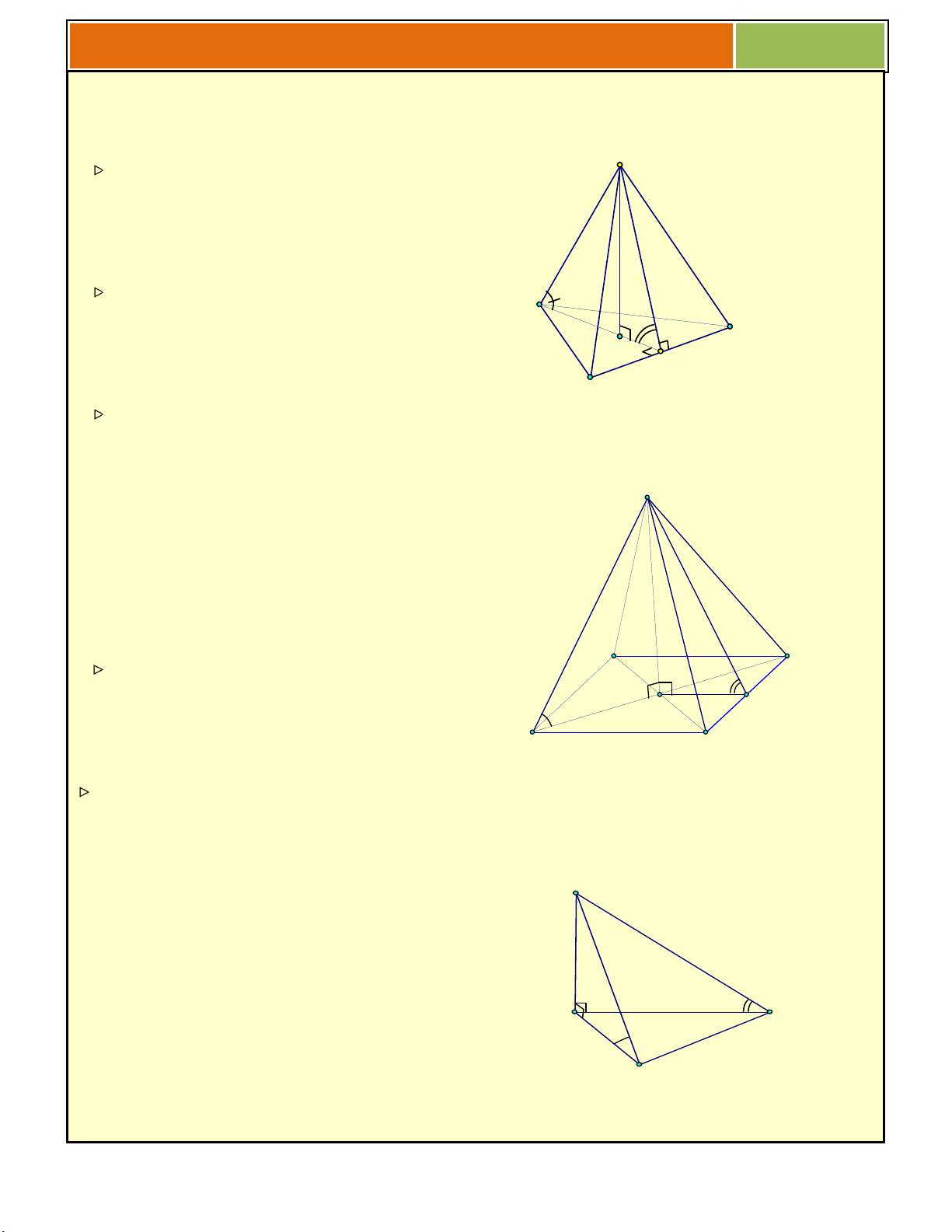
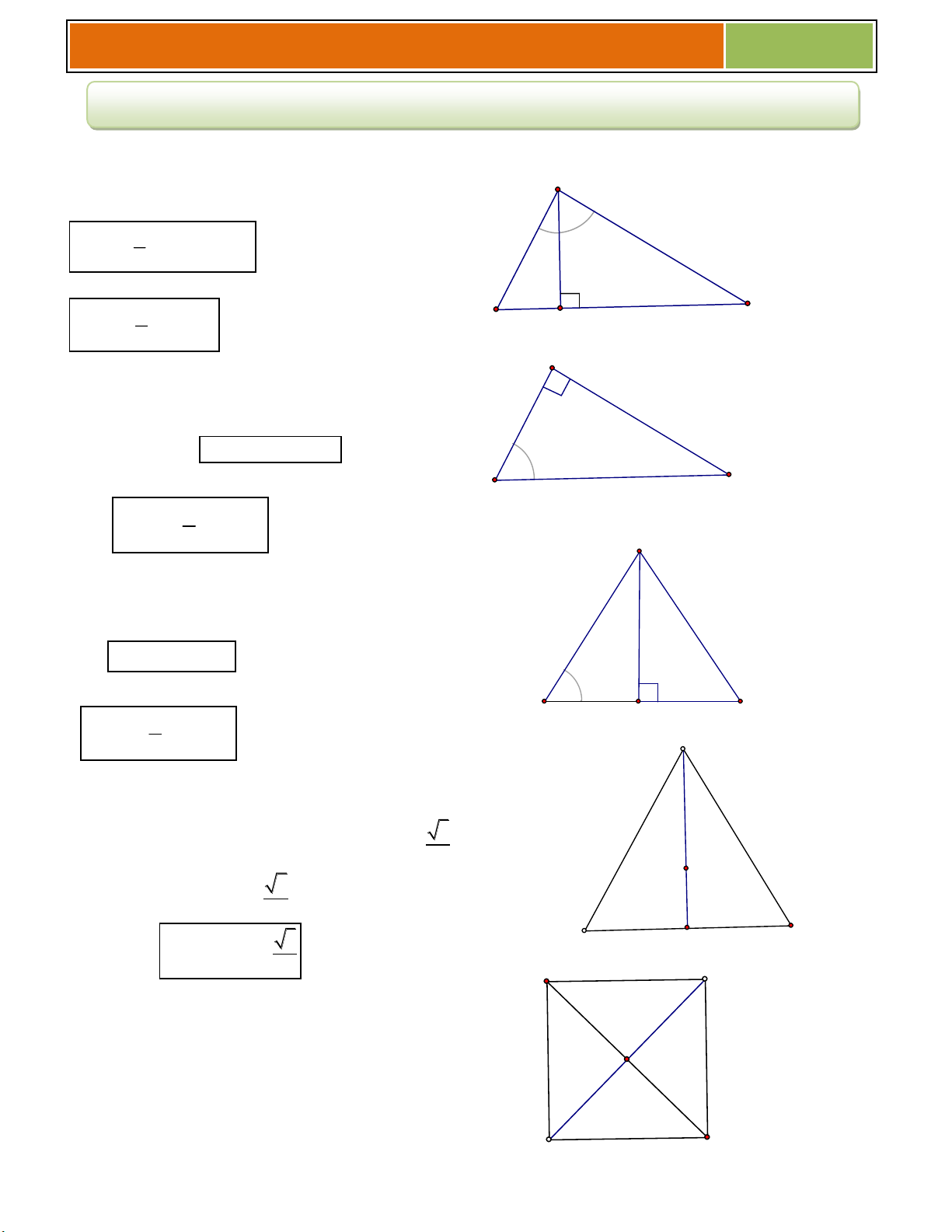
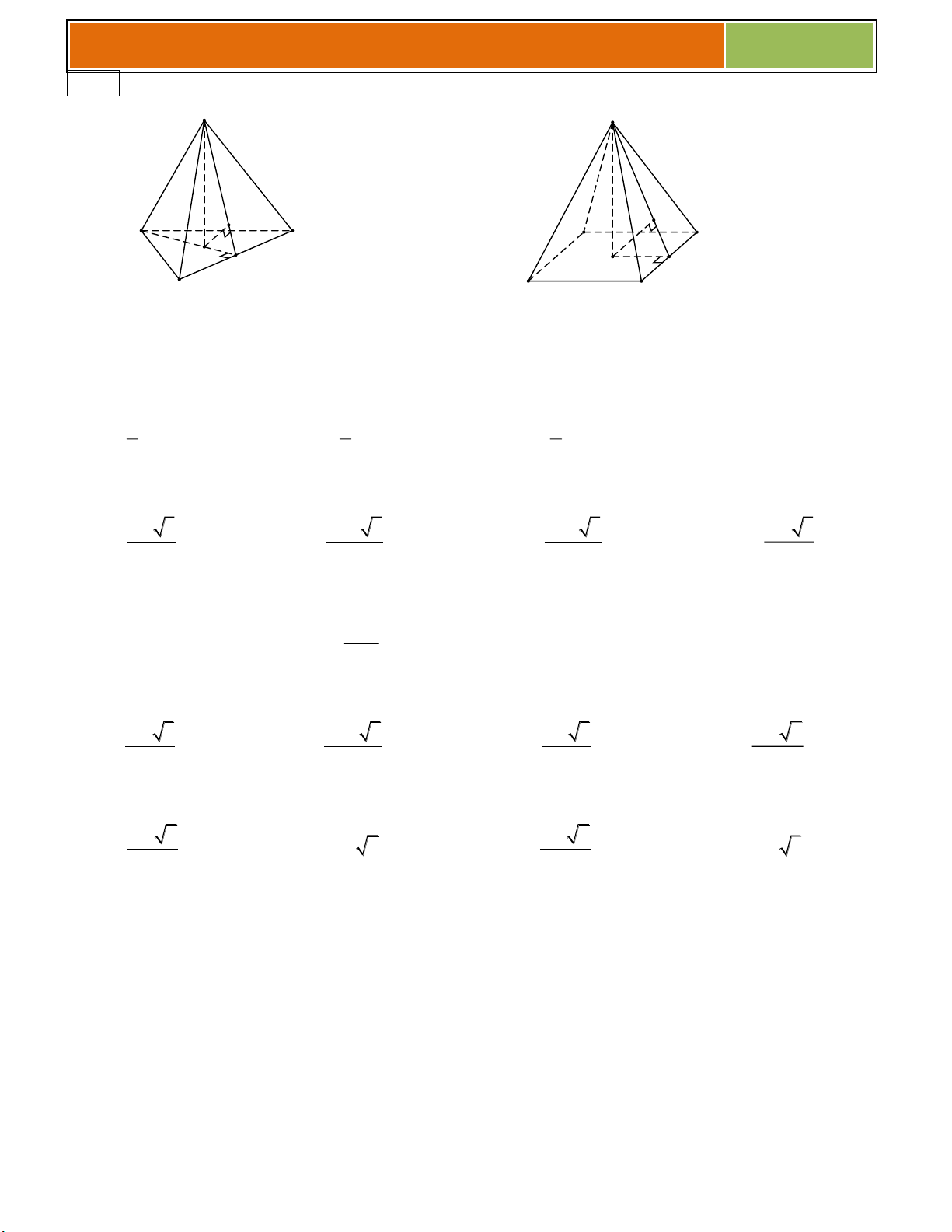
Hình chóp tam giác đều S
Hình chóp tam giác đều: Đáy là tam giác đều
Các mặt bên là những tam giác cân h
Đặc biệt: Hình tứ diện đều có: A C Đáy là tam giác đều H
Các mặt bên là những tam giác đều I B Cách vẽ:
Vẽ đáy ABC Vẽ trung tuyến AI Dựng trọng tâm H Vẽ SH (ABC)
Ta có: SH là chiều cao của hình chóp S
Góc giữa cạnh bên và mặt đáy là: SAH .
Góc mặt bên và mặt đáy là: SIH
Hình chóp tứ giác đều A D
Hình chóp tứ giác đều: Đáy là hình vuông I H B C
Các mặt bên là những tam giác cân Cách vẽ: Vẽ đáy ABCD
Dựng giao điểm H của hai đường chéo AC & BD S Vẽ SH (ABCD) Ta có:
SH là chiều cao của hình chóp A C
Góc giữa cạnh bên và mặt đáy là: SAH . B
Góc mặt bên và mặt đáy là: SIH 2
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
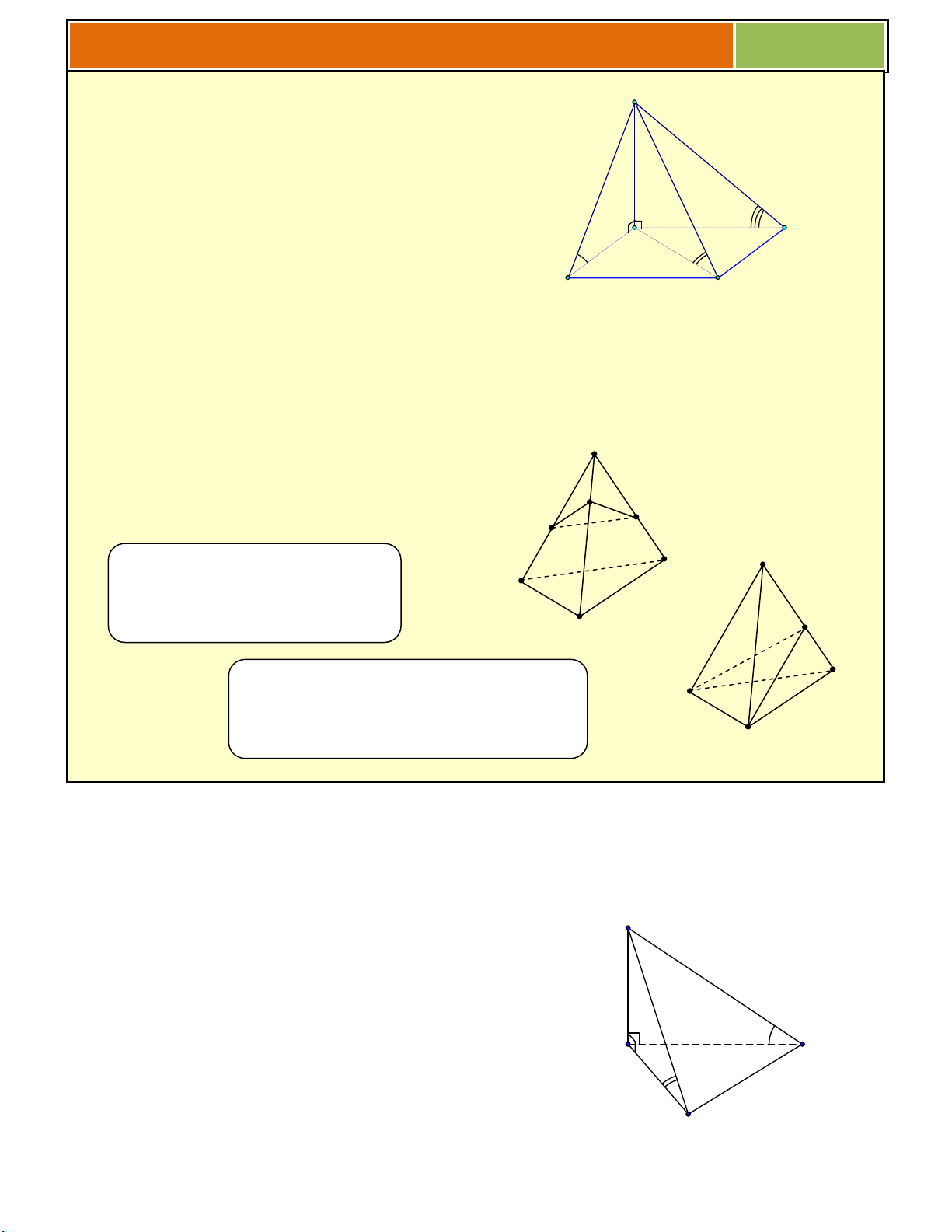
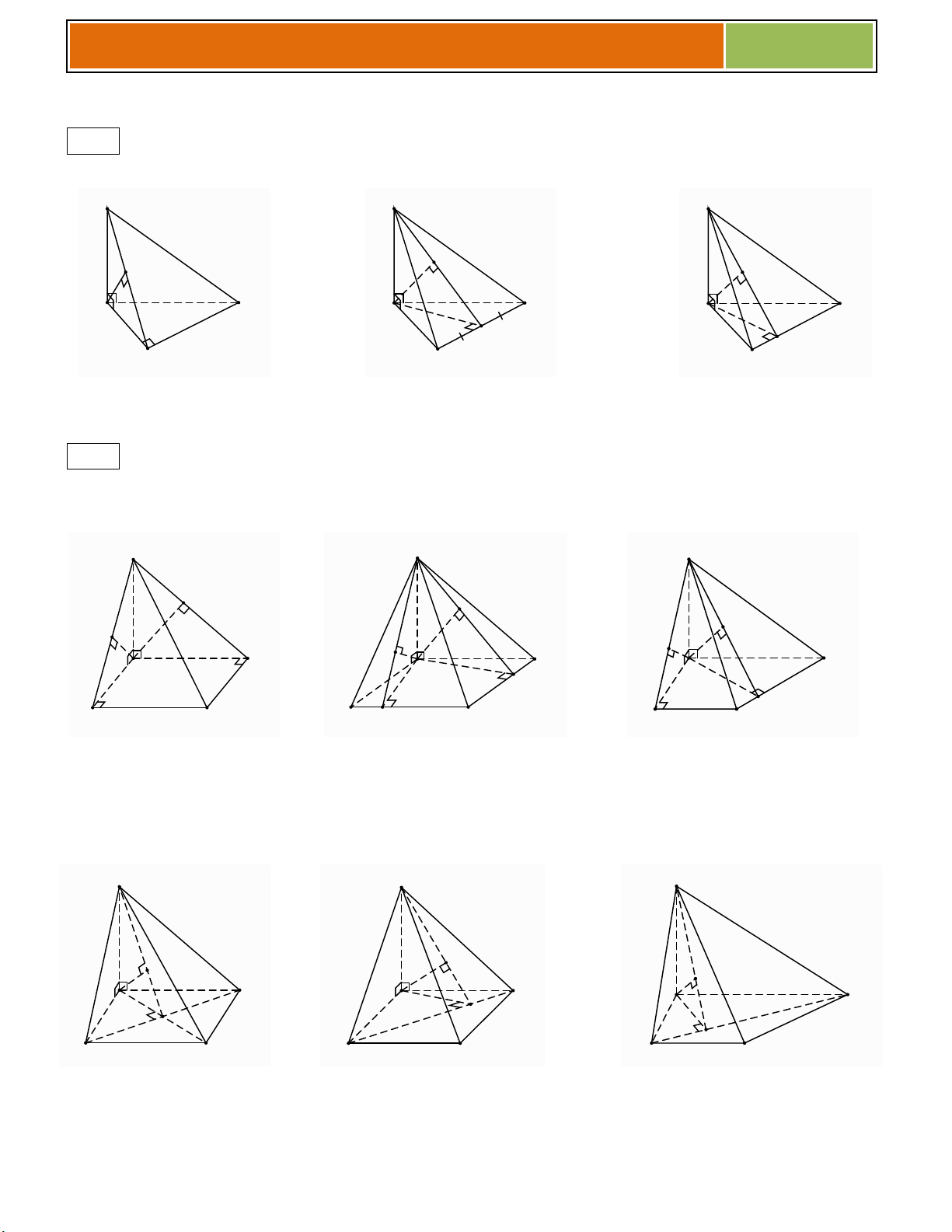
Hình chóp có cạnh bên vuông góc với đáy S
Loại 1 : đáy là tam giác ABC SA (ABC)
Góc giữa cạnh bên SB và mặt đáy là: SBA A D
Góc giữa cạnh bên SC và mặt đáy là: SCA B C
Loại 2 : đáy là hình vuông ABCC SA (ABCD)
Góc giữa cạnh bên SB và mặt đáy là: SBA
Góc giữa cạnh bên SC và mặt đáy là: SCA S
Góc giữa cạnh bên SD và mặt đáy là: SDA B' TỈ SỐ THỂ TÍCH C' A' C S A M B C
MSC, ta có : A B
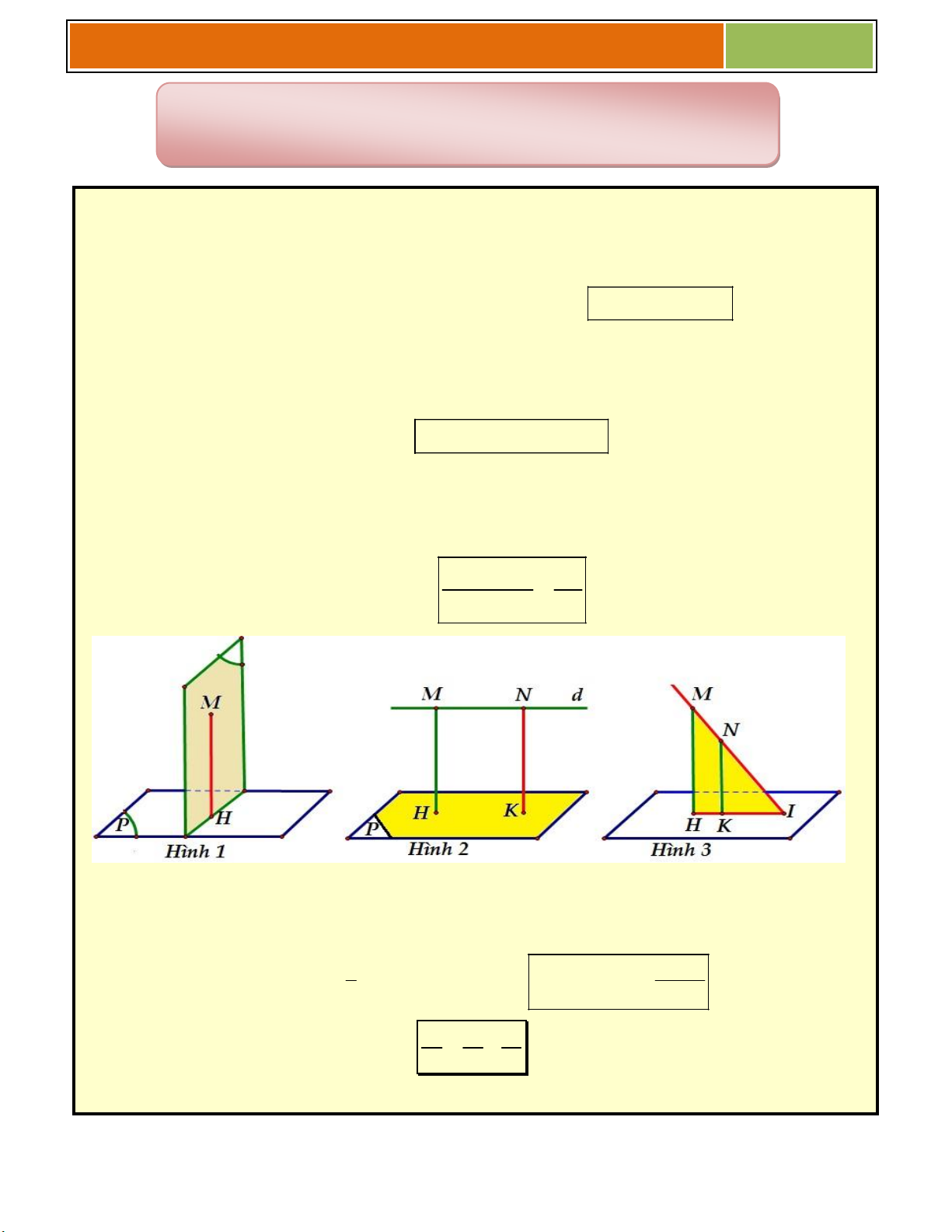
TỔNG HỢP LẠI MỘT SỐ HÌNH CƠ BẢN HAY GẶP TRONG ĐỀ THI (SƢU TẦM) HÌNH 1
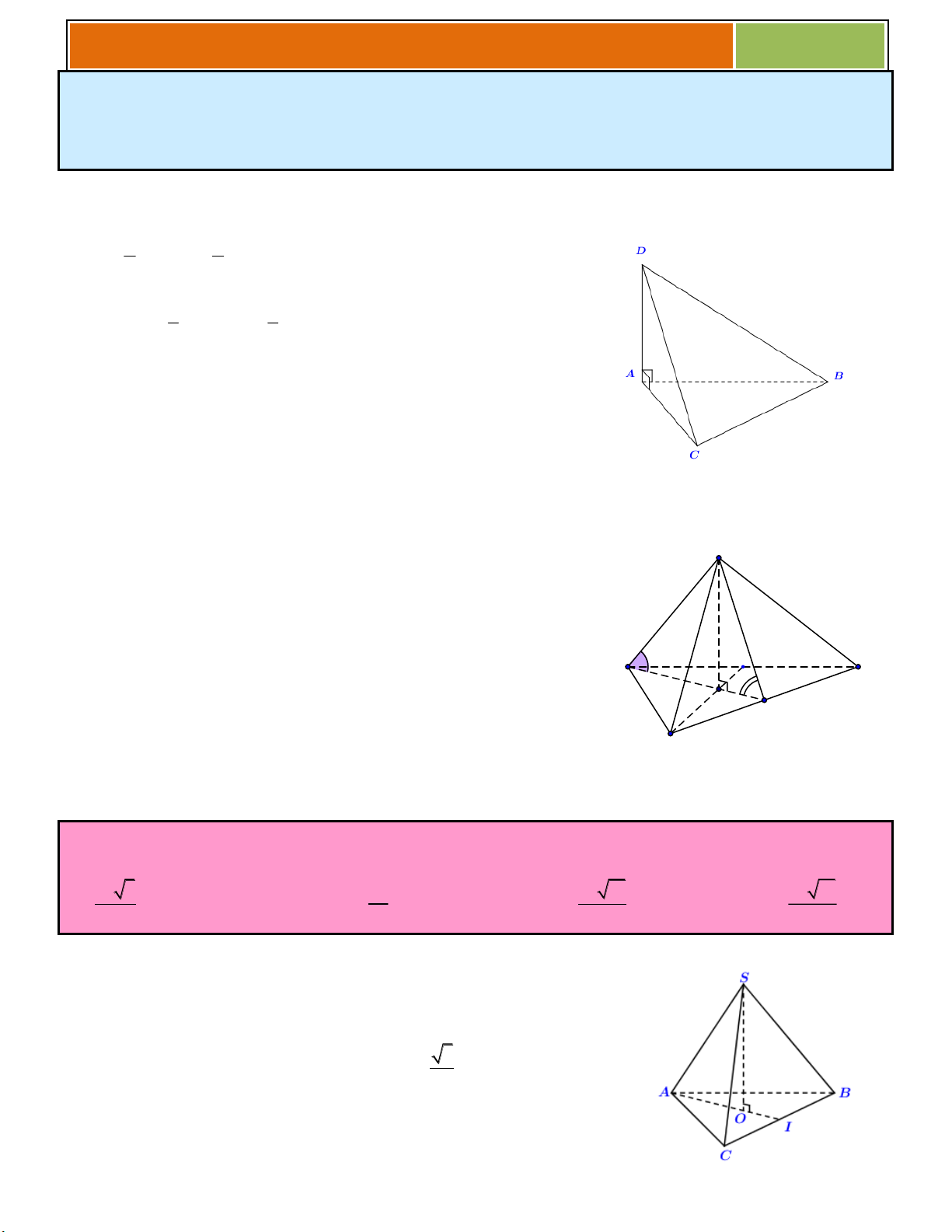
Hình chóp S.ABC, SA vuông góc với đáy S
Đáy là tam giác ABC . Đường cao SA . Cạnh bên S ,
B SC, SA . S A , B S
AC là các tam giác vuông tại A . A C
Góc giữa cạnh SB với đáy ABC là góc SBA.
Góc giữa cạnh SC với đáy ABC là góc SCA . B 3
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
Ví dụ minh họa Hình 1 : Cho tứ diện ABCD có cạnh AD vuông góc mới mặt phẳng ABC,
AC AD 4a , AB 3a , BC 5a . Thể tích khối tứ diện ABCD là A. 3 4a . B. 3 3a . C. 3 8a . D. 3 6a .
Hƣớng dẫn giải :Ta có 2 2 2 2 2 2
BC 25a 16a 9a AC AB nên ABC
vuông tại A . 1 1 2 S A . B AC .3 .
a 4a 6a . ABC 2 2 1 1 Vậy 2 3 V .A . D S .4 .
a 6a 8a . Chọn C ABCD 3 ABC 3 HÌNH 2
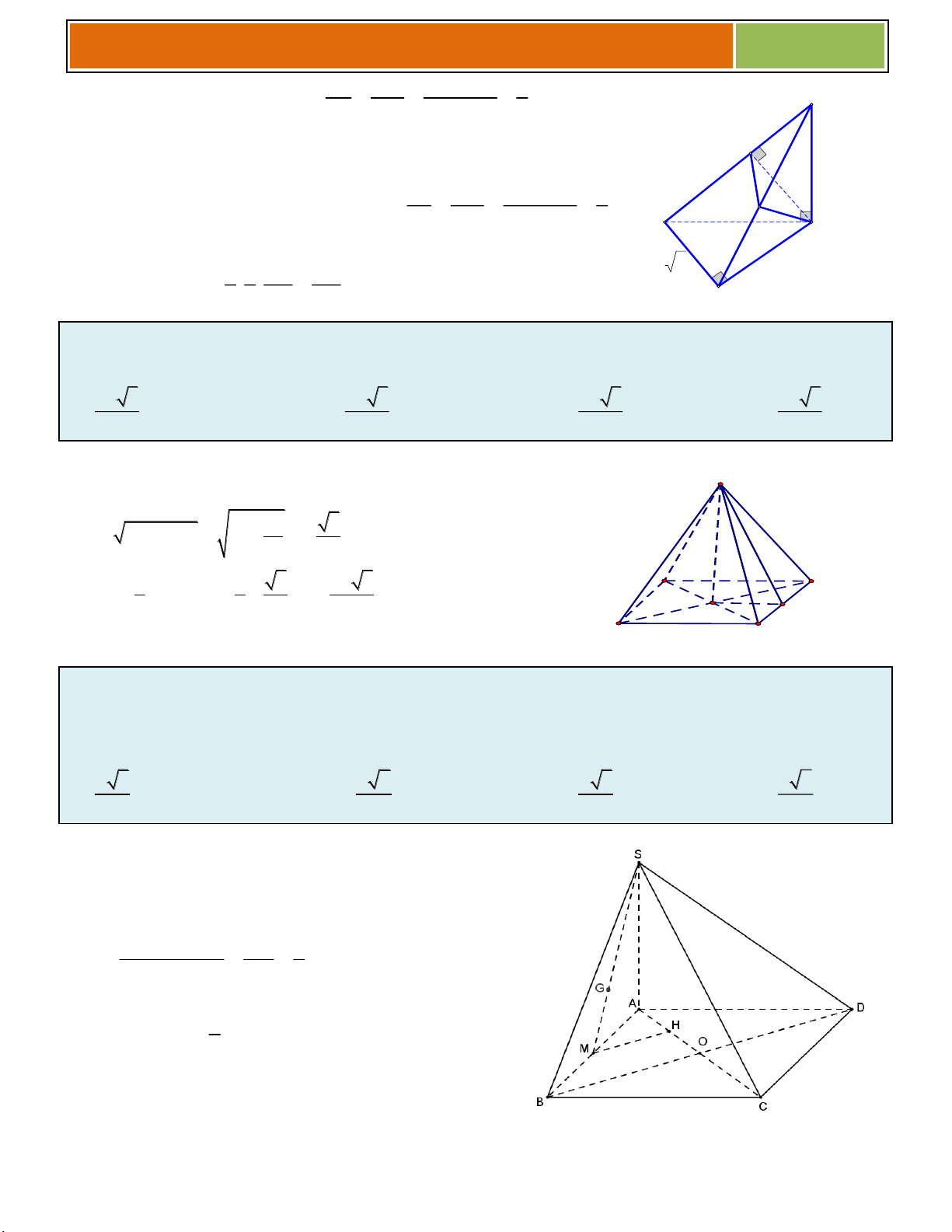
Hình chóp tam giác đều S.ABC S
Đáy là tam giác đều ABC .
Đường cao SG , với G là trọng tâm tam giác ABC . Cạnh bên S , A S ,
B SC hợp với đáy một góc bằng nhau. A C
Góc giữa cạnh bên với đáy bằng SAG (hoặc SCG, SBG ). G M Mặt bên SA ,
B SBC, SCA hợp với đáy một góc bằng nhau. B
Góc giữa mặt bên với đáy là góc SMG .
Ví dụ minh họa Hình 2 : Cho hình chóp đều S.ABC có SA 2a ; AB a . Thể tích khối chóp S.ABC là. 3 a 3 3 a 3 a 11 3 a 11 A. . B. . C. . D. . 12 12 12 4
Hƣớng dẫn giải :
Gọi I là trung điểm của BC , O là trọng tâm tam giác ABC . 3
Ta có tam giác ABC đều cạnh a nên 2 S a . ABC 4 4
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018 3 2 3 AI a ; AO AI a . 2 3 3 2 a 33
Xét tam giác SAO vuông tại O có 2 2 2 SO
SA AO 4a a . 3 3 1 1 33 3 11
Vậy thể tích khối chóp S.ABC là 2 3 V S . O S . . a a a . Chọn C S . ABC 3 ABC 3 3 4 12 HÌNH 3
Hình chóp S.ABCD, có đáy ABCD là hình chữ nhật (hoặc hình vuông)
và SA vuông góc với đáy
Đáy là hình chữ nhật (hình vuông) ABCD . S Đường cao SA . Cạnh bên S ,
B SC, S , D SA . A B S A , B S AC, S
AD là các tam giác vuông tại A .
Góc giữa cạnh SB với đáy ABCD là góc SBA. D C
Góc giữa cạnh SC với đáy ABCD là góc SCA .
Góc giữa cạnh SD với đáy ABCD là góc SDA .
Ví dụ minh họa Hình 3 : Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB a .
Cạnh bên SA vuông góc với mặt phẳng đáy, SC tạo với mặt phẳng đáy một góc 0 45 và
SC 2a 2 . Thể tích khối chóp S.ABCD bằng: 3 a 3 2a 3 2a 3 3 a 3 A. . B. . C. . D. . 3 3 3 3
Hƣớng dẫn giải :
Vì SA ABCD suy ra AC là hình chiếu vuông góc của
SC lên ABCD SC ABCD o , SCA 45 . 2 S
AC vuông tại A có: o
SA AC SC.sin 45 2 2 . a 2a . 2 A
BC vuông tại B có: 2 2 2 2 BC
AC AB 4a a 3a . 5
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018 2 S A . B BC . a a 3 3a . ABCD 1 1 2 3 Vậy 2 3 V S . A S .2 . a 3a a . Chọn C S . ABCD 3 ABCD 3 3 HÌNH 4
Hình chóp tứ giác đều S.ABCD
Đáy là hình vuông ABCD . S
Đường cao SO , với O là giao điểm của AC và BD . Cạnh bên S , A S ,
B SC, SD hợp với đáy một góc bằng nhau. A B
Góc giữa cạnh bên với đáy bằng SBO (hoặc SA , O SC , O SDO ) M O Mặt bên SA ,
B SBC, SCA hợp với đáy một góc bằng nhau. D C
Góc giữa mặt bên với đáy là góc SMG
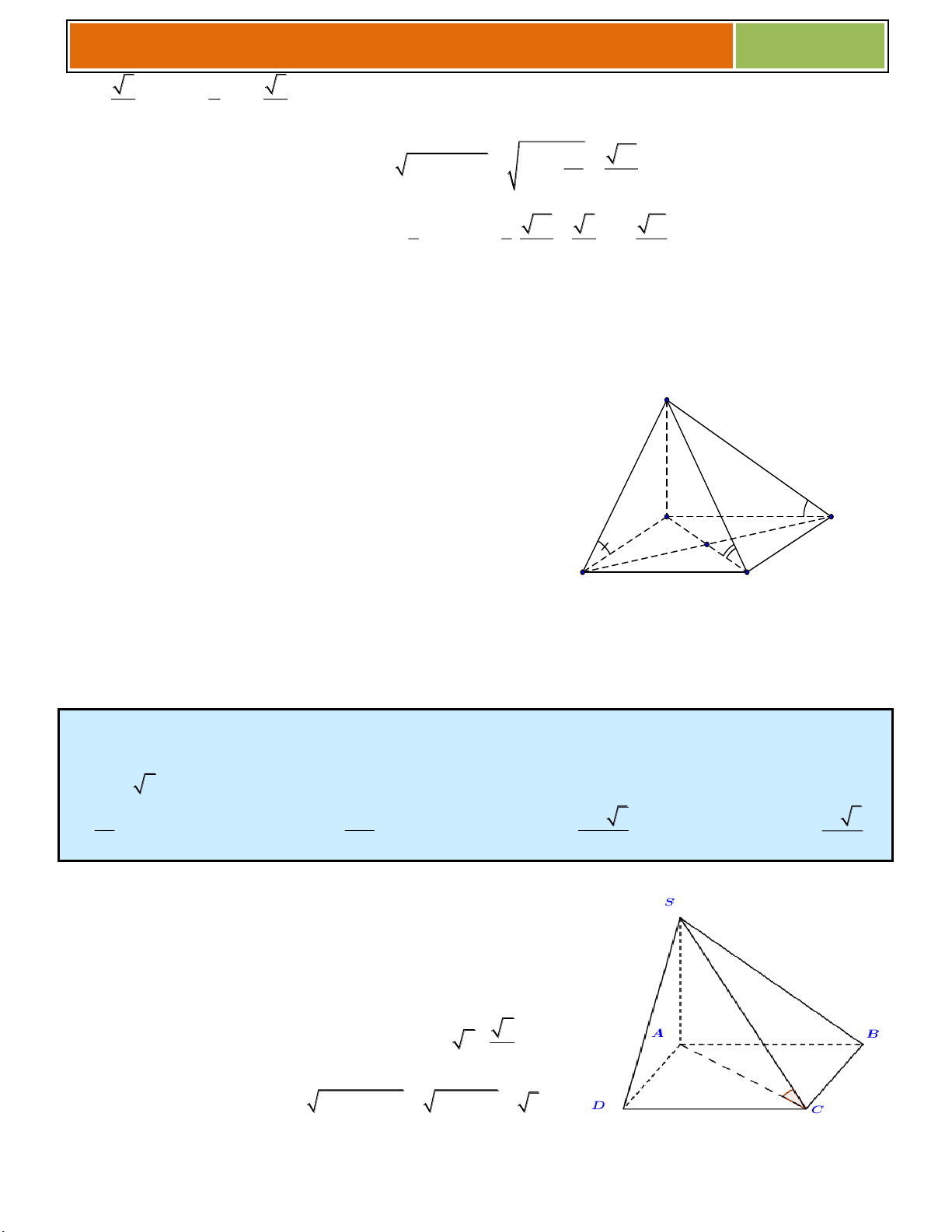
Ví dụ minh họa Hình 4 (THPT Chuyên Lê Thánh Tông – Quảng Nam): Một hình chóp tứ giác
đều có góc tạo bởi mặt bên và mặt đáy bằng 60 và diện tích xung quanh bằng 2
8a . Tính diện tích
S của mặt đáy hình chóp. A. 2 S 4a 3 . B. 2 S 2a 3 . C. 2 S 4a . D. 2 S 2a .
Hƣớng dẫn giải :
Gọi H là trung điểm của AB .
Vì S.ABCD là hình chóp tứ giác đều nên SH AB . O H AB
SAB; ABCD SH;OH SHO (1). Trong S
OH vuông tại O , có OH SH 2.OH AB cos 60
Diện tích xung quanh của hình chóp 2 S 4.S
2.SH.AB 2AB xp SAB Mà 2 S 8a nên 2 2
2AB 8a AB 2a xq 6
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
Vậy diện tích đáy của mặt chóp là 2 2
S AB 4a . Chọn C B\ I TẬP MINH HỌA
PHƯƠNG PHÁP CHUNG TÍNH THỂ TÍCH KHỐI ĐA DIỆN
Phƣơng pháp trực tiếp: Sử dụng trực tiếp công thức PHƢƠNG PH[ P TÍNH THỂ TÍCH KHỐI ĐA DIỆN
Tính thể tích bằng cách chia nhỏ
Phƣơng pháp gián tiếp
Tính thể tích bằng cách bổ sung
Tính thể tích bằng tỉ số thể tích
Bài 1. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB , a AC 2 .
a Cạnh bên SA
vuông góc với ABCD . Tính thể tích khối chóp S.ABCD trong các trường hợp sau: a) Biết SA 3 . a
b) Biết SB a 5 .
c) Biết góc giữa SC với mặt đáy bằng o 60 . Hƣớng dẫn giải S a) 2 2 2 2 BC
AC AB 4a a a 3. Diện tích đáy: 2 S A . B BC a 3 ABCD 3a
Đường cao: SA 3a a A B
Thể tích khối chóp S.ABCD là: 2a 1 1 D 2 3 V .S .SA .a 3.3a a 3. C S.ABCD 3 ABCD 3 S a 5 b) Diện tích đáy 2 S A . B BC a 3 ABCD Đường cao 2 2 2 2
SA SB AB 5a a 2 . a a A B
Thể tích khối chóp S.ABCD là: 2a S 1 1 2 2 3 3 D V .S .SA .a 3.2a a . C S.ABCD ABCD 3 3 3 a c) Diện tích đáy 2 S A . B BC a 3 A ABCD B 60o 2a
Góc giữa SC với ABCD bằng góc o SCA 60 D C 7
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018 SA S AC vuông tại o
A tan SCA
SA AC.tan 60 2 3 . a AC
Thể tích khối chóp S.ABCD là: 1 1 2 3 V .S .SA .a 3.2 3a 2a . S.ABCD 3 ABCD 3
Bài 2. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và góc giữa SC với ABC bằng o
60 . Tính thể tích khối chóp S.ABC . Hƣớng dẫn giải 2 S a 3 S . SCG ABC
Góc giữa SC với đáy bằng o 60 4 a 3 2 a 3 a 3 CK CG . 2 3 2 3 S
GC vuông tại G , suy ra: 60o A C o SG o a 3 tan 60 SG C . G tan 60 . 3 . a G CG 3 K
Thể tích khối chóp S.ABC là: B 2 3 1 1 a 3 3a . V S .SG . .a ABC 3 3 4 12
Bài 3. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng .
a Tính thể tích khối chóp S.ABCD
trong các trường hợp sau:
a) Biết cạnh bên SB a 2 .
b) Biết góc giữa cạnh bên SB với đáy bằng o 45 .
c) Biết góc giữa mặt bên SBC với đáy bằng o 60 . Hƣớng dẫn giải S
a) Diện tích đáy ABCD là 2 S a . ABCD a 2 BD a 2
ABCD là hình vuông BD a 2 BO 2 2 a 2 A B a a S BO vuông tại 2 2 2 6 O SO SB OB 2a . 2 2 O
Thể tích khối chóp S.ABCD là: D C 3 1 1 a 6 a 6 S 2 V S .SO .a . . S.ABCD ABCD 3 3 2 6
b) Diện tích đáy ABCD là 2 S a . ABCD A 45o a B
Góc giữa SB với đáy bằng góc o SBO 45 O a Đường cao o 2 D SO B . O tan 45 . C 2 8
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
Thể tích khối chóp S.ABCD là: 3 1 1 a 2 a 2 S 2 V S .SO .a . . S.ABCD ABCD 3 3 2 6
c) Diện tích đáy ABCD là 2 S a . ABCD a A
Góc giữa mặt bên SBC với đáy bằng góc o SIO 60 B 600 a a I Đường cao o 3 SO I . O tan 60 . 3 . O 2 2 D C 3 1 1 a 3 a 3
Thể tích khối chóp S.ABCD là: 2 V S .SO .a . . S.ABCD ABCD 3 3 2 6
Bài 4. (THPT Chuyên Lê Khiết – Quảng Ngãi) Cho khối tứ diện OABC với OA,OB ,OC vuông
góc từng đôi một và OA a , OB 2a , OC 3a . Gọi M , N lần lượt là trung điểm của hai cạnh
AC, BC . Thể tích của khối tứ diện OCMN tính theo a bằng. 3 3a 3 2a 3 a A. . B. 3 a . C. . D. . 4 3 4 Hƣớng dẫn giải C 1 1 Ta có thể tích 3 V O .
A OB .OC a (đvtt). OABC 3 2 V CM .CN 1 3a N Ta có: OCMN V C . A CB 4 M OCAB 3 1 a 2a Vậy thể tích V V (đvtt). Chọn D O B OCMN 4 OABC 4 a A
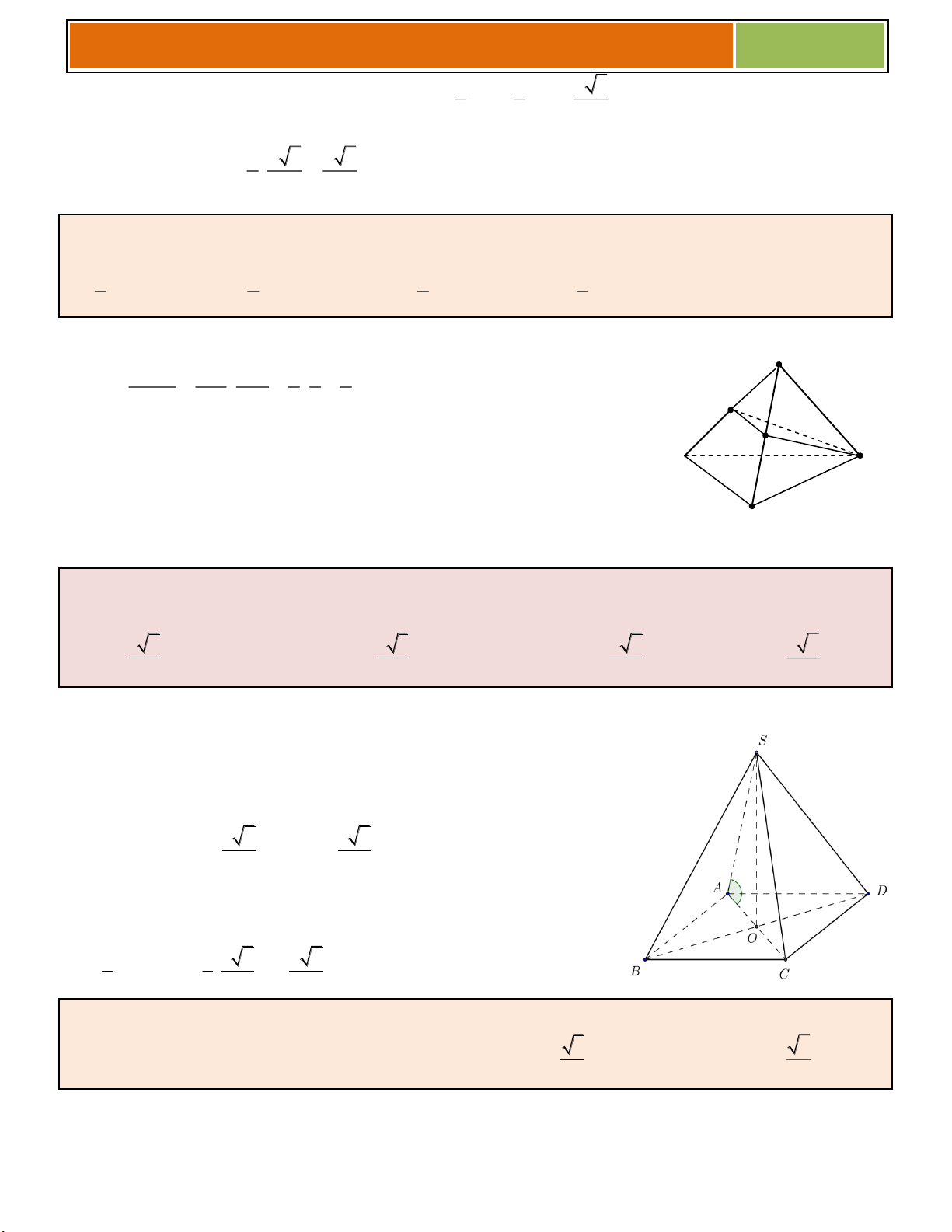
Bài 5. (THPT Chuyên Lê Khiết – Quảng Ngãi) hối đa diện nào sau đây có các mặt không phải là tam giác đều A. Bát diện đều. B. h thập diện đều. C. Tứ diện đều. D. Thập nh diện đều. Hƣớng dẫn giải
Bát diện đều có 8 mặt là các tam giác đều. Nh thập diện đều có 20 mặt là các tam giác đều.
Tứ diện đều có 4 mặt là các tam giác đều. 9
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
Thập nh diện đều có 12 mặt là các ngũ giác đều. Chọn D
Bài 6. (THPT Chuyên Tuyên Quang) hối Cho khối chóp S.ABC , trên ba cạnh S , A S , B SC lần 1 1 1
lượt lấy ba điểm A , B , C sao cho S A SA , S B
SB , SC SC . Gọi V và V lần lượt là thể 3 3 3 V
tích của các khối chóp S.ABC và S. A
B C . hi đó tỉ số là V 1 1 1 1 A. . B. . C. . D. . 3 27 9 6 V S A S B SC H 1 1 1 1
ƣớng dẫn giải: Ta có . . . . Chọn B V SA SB SC 3 3 3 27
Bài 7. (THPT Chuyên Tuyên Quang) Cho hình chóp đều S.ABCD có chiều cao bằng a 2 và độ
dài cạnh bên bằng a 6 . Tính thể tích khối chóp S.ABCD . 3 8a 2 3 10a 2 3 8a 3 3 10a 3 A. . B. . C. . D. . 3 3 3 3
Hƣớng dẫn giải: Ta có 2 2
BO SA SO 2a . Vậy BD 4a , suy ra AB 2a 2 . 3 1 1 8a 2 Vậy 2 V S .SO AB .SO Chọn A 3 ABCD 3 3
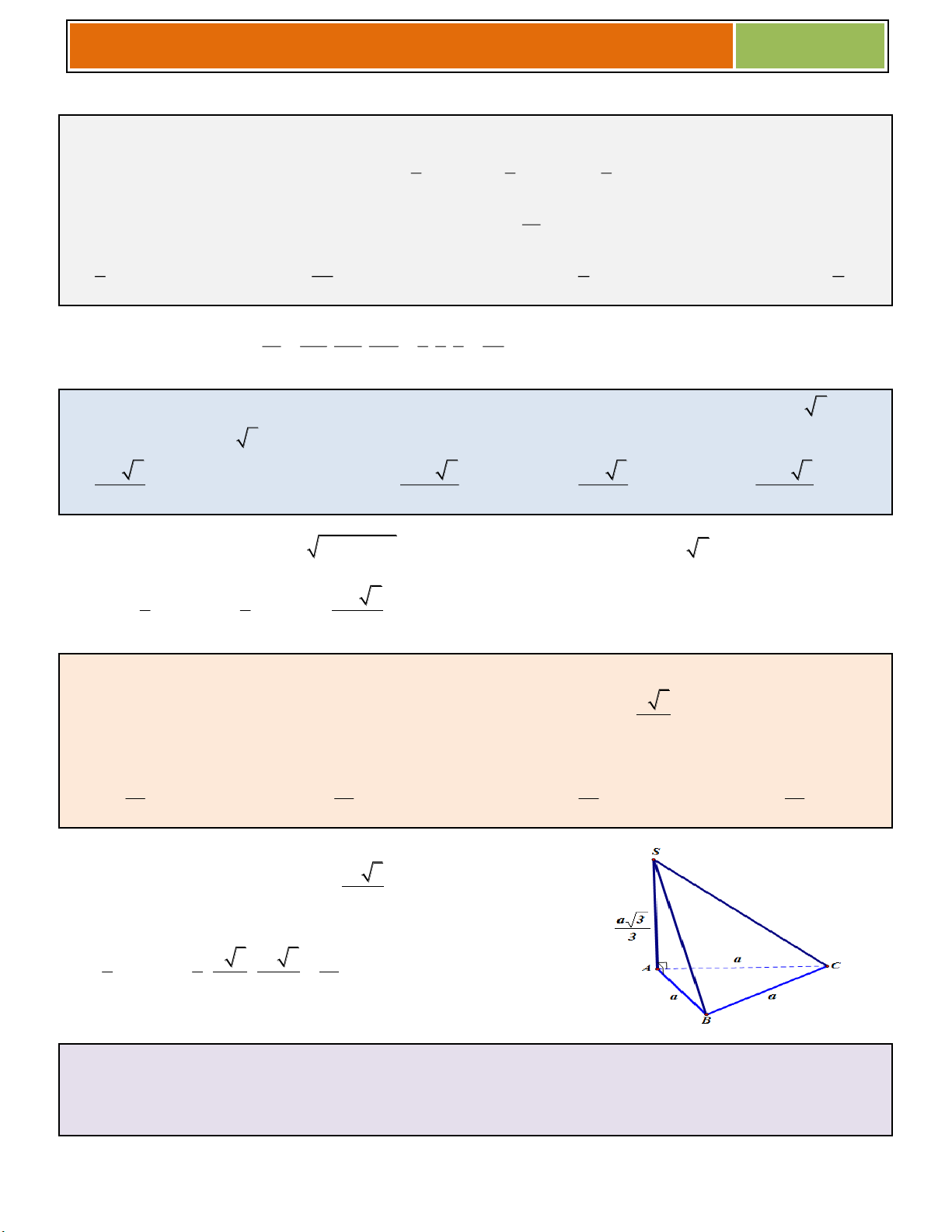
Bài 8. (THPT Chuyên Lê Thánh Tông – Quảng Nam) Cho hình chóp S.ABC có đáy ABC là tam a 3
giác đều cạnh a . Cạnh SA vuông góc với mặt phẳng ABC và SA
. Tính thể tích V của 3
khối chóp S.ABC . 3 a 3 a 2 a 3 a A. V . B. V . C. V . D. V . 8 12 4 6 Hƣớng dẫn giải: 2 a 3 Vì ABC
đều cạnh a S . ABC 4
Vậy thể tích của khối chóp S.ABC là 2 3 1 1 a 3 a 3 a V S . A S . Chọn B 3 ABC 3 3 4 12
Bài 9. (THPT Chuyên Lê Thánh Tông – Quảng Nam) Cho hình chóp S.ABC . Gọi M là trung điểm
cạnh SA và N là điểm trên cạnh SC sao cho SN 3NC . Tính tỉ số k giữa thể tích khối chóp . A BMN
và thể tích khối chóp S.ABC . 10
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018 3 2 1 3 A. k . B. k . C. k . D. k . 8 5 3 4 Hƣớng dẫn giải S
Ta có: M là trung điểm SA nên V V . A BMN S.BMN M V SM SN 1 3 3
Ta có: S.BMN . . . N V SA SC 2 4 8 S .BAC A C V 3 Vậy: A.BMN k . Chọn A V 8 S .BAC B
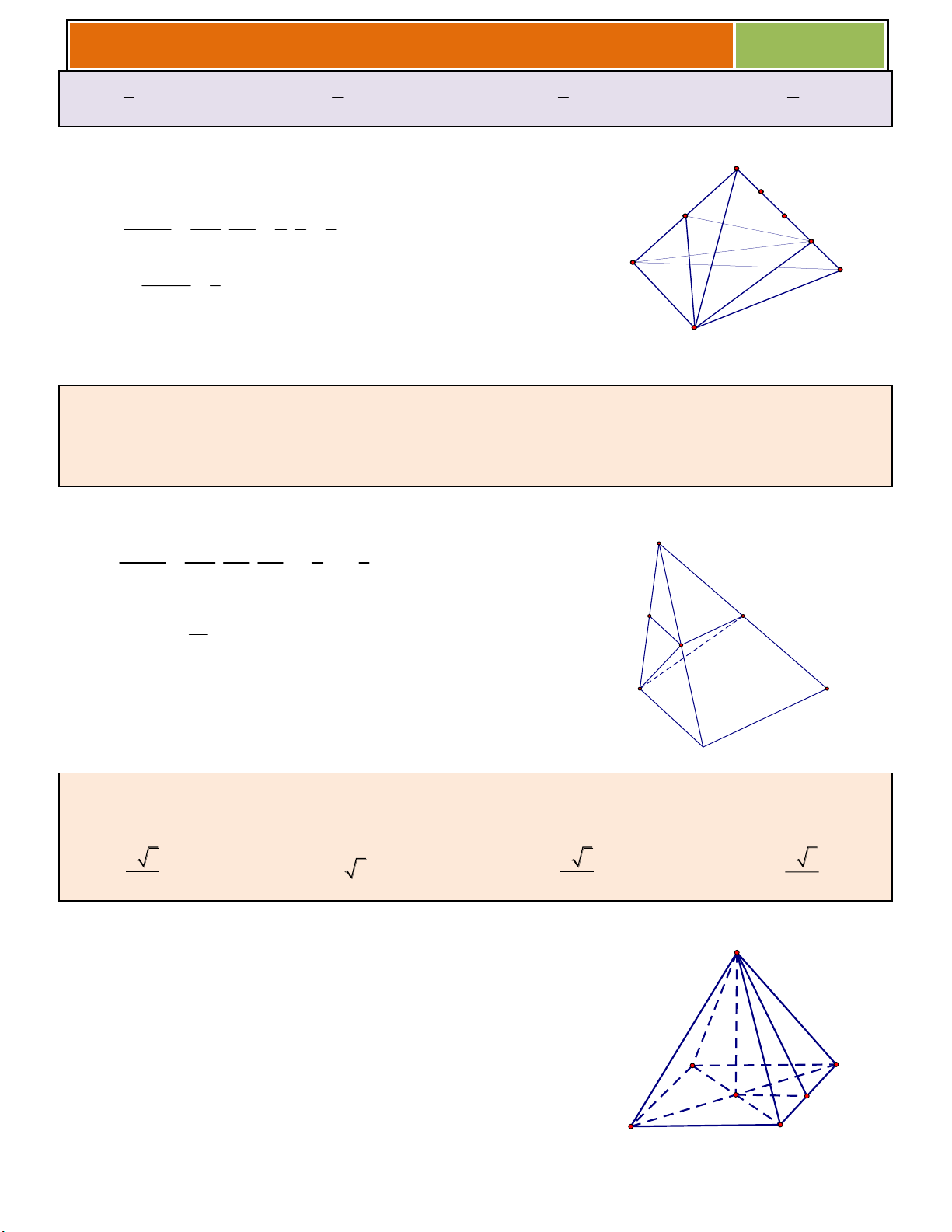
Bài 10. (THPT Chuyên Ngoại Ngữ – Hà Nội) Cho khối chóp S.ABC có thể tích bằng 16. Gọi M ,
N , P lần lượt là trung điểm của các cạnh SA , SB , SC . Tính thể tích V của khối tứ diện AMNP . A. V 2 . B. V 6 . C. V 4 . D. V 8 .
Hƣớng dẫn giải: 3 V SM SN SP 1 1 S Ta có S.MNP . . V SA SB SC 2 8 S . ABC M P 16 Do đó V 2 . S .MNP 8 N A C
Do M là trung điểm SA , ta có d( , A (MN )
P ) d(S, (MNP)) Suy ra V V 2 . Chọn A. AMNP S.MNP B
Bài 11. (THPT Chuyên Ngoại Ngữ – Hà Nội) Tính thể tích V của khối chóp tứ giác đều có cạnh
đáy bằng 2a , góc giữa mặt bên và mặt đáy bằng 60 . 2 3 4 3 4 3 A. 3 V a . B. 3 V 4 3a . C. 3 V a . D. 3 V a . 3 2 3 Hƣớng dẫn giải: S
Gọi G là trung điểm của đoạn CD , dễ thấy CD
SG SCD CD
GO ABCD . SCD
ABCD CD D Suy ra G
SCD, ABCD SGO 60 O B C 11
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018 SO
Vậy, trong tam giác vuông SGO , ta có tan 60
SO a 3 . OG 1 1 4 3
Vậy thể tích khối chóp là 2 3 V .S . O S a 34a a Chọn D. SABCD 3 ABCD 3 3
Bài 12. (THPT Chuyên Thái Bình) Cho hình chóp đều S.ABCD , đáy ABCD là hình vuông cạnh a ,
các cạnh bên tạo với đáy góc 45 . Diện tích toàn phần của hình chóp trên theo a là A. 2 2 3a . B. 2 3 1 a . C. 2 4a . D. 2 3 1 a . Hƣớng dẫn giải:
Gọi O là tâm của hình vuông ABCD . hi đó SO ABCD .
Suy ra OB là hình chiếu của SB trên ABCD nên góc giữa SB và ABCD là o SBO 45 . BO BO 2 2 Ta có o cos 45 SB a : a o SB cos 45 2 2
Suy ra SB SA SC SD a
hay SAB , SBC , SCD , SDA là các tam giác đều cạnh a .
Diện tích toàn phần của hình chóp S.ABCD là S S S S S S S AB S BC S CD S DA ABCD 2 2 2 2 a 3 a 3 a 3 a 3 2
a 1 3 2 a . Chọn D. 4 4 4 4
Bài 13. (THPT Chuyên Phan Bội Châu– Nghệ An) Cho khối chóp S.ABC có đáy là tam giác
vuông tại A , SB ABC, AB a , ACB 30 , góc giữa đường thẳng SC và mặt phẳng ABC là
60 . Tính thể tích V của khối chóp S.ABC theo . a 3 3a A. 3 V 3a . B. 3 V a . C. 3 V 2a . D. V . 2 S
Hƣớng dẫn giải: Ta có tam giác ABC vuông tại A và 0 0
ACB 30 ABC 60 ; AB a BC 2a .
Vì SB ABC góc giữa SC và ABC chính là góc 0 SCB 60 . 600
Vậy đường cao của hình chóp 0 SB B .
C tan 60 2 3a C B 600 a A 12
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018 1 A . B AC . a a 3.a2 3 Thể tích hình chóp là 3 V . .SB a Chọn B. 3 2 6
Bài 14. (THPT Chuyên Phan Bội Châu– Nghệ An) Cho khối chóp S.ABCD có đáy là hình chữ
nhật, SA ABCD,
AB 3a , AD 2a , SB 5 .
a Tính thể tích V của khối chóp S.ABCD theo . a A. 2 V 8a . B. 3 V 24a . C. 3 V 10a . D. 3 V 8a . S H 1
ƣớng dẫn giải: Ta có: V .S . A S S . ABCD 3 ABCD 5a
Xét tam giác vuông SAB có: 2 2
SA SB AB 4a Và 2 S A .
B AD 6a (ñvdt) 3a ABCD A B 2a 1 ên 2 3 V .4 .
a 6a 8a (ñvtt) Chọn D. S . ABCD 3 D C
Bài 15. (THPT Chuyên Phan Bội Châu– Nghệ An) Cho tứ diện ABCD có AB, AC, AD đôi một
vuông góc với nhau, AB , a AC , b AD .
c Tính thể tích V của khối tứ diện ABCD theo a , b , c abc abc abc A. V . B. V . C. V . D. V abc . 2 6 3 B H AB AC
ƣớng dẫn giải: Có :
AB ACD AB AD
Thể tích tứ diện ABCD là : 1 V 1 1 S .AB AC.A . D AB ABCD 3 ACD 3 2 D A abc Hay V Chọn B. 6 C
Bài 16. (THPT Chuyên ĐH Vinh– Lần 3) Cho hình chóp S.ABC có SC 2a và SC ABC. Đáy
ABC là tam giác vuông cân tại B và có AB a 2 . Mặt phẳng đi qua C và vuông góc với ,
SA cắt S ,
A SB lần lượt tại ,
D E . Tính thể tích khối chóp S.CDE . 3 4a 3 2a 3 2a 3 a A. . B. . C. . D. . 9 3 9 3 V SD SE SD SE
Hƣớng dẫn giải : Ta có S.CDE . V . .V . S .CDE S.CAB V SA SB SA SB S .CAB 3 1 1 1 1 2a 2 V .S . C B . A BC .2 . a .2a . S.CAB 3 2 3 2 3 13
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018 2 2 SD SC 4a 1 Xét S AC ta có 2 SC S . D SA . S 2 2 2 SA SA 4a 4a 2 D
Ta có AB SBC AB CE CE SAB CE SB . 2a 2 2 SE SC 4a 2 Tương tự xét S BC ta có 2 SC S . E SB . E 2 2 2 A SB SB 4a 2a 3 C 3 3 a 2 1 2 2a 2a Vậy suy ra V . . . Chọn C S .CEF 2 3 3 9 B
Bài 17. (THPT Nguyễn Bỉnh Khiêm– Quảng Nam) Cho hình chóp tứ giác đều có cạnh đáy bằng
x . Diện tích xung quanh gấp đôi diện tích đáy. hi đó thể tích của khối chóp bằng: 3 x . 3 3 x . 3 3 x . 3 3 x . 3 A. . B. . C. . D. . 6 2 12 3 Hƣớng dẫn giải 2 S
x ; S 4.S 2SI.x ABCD xq SCD S
Theo yêu cầu bài toán thì 2
2SI.x x SI x 2 x 3 2 2 2 SO SI OI x x 4 2 3 1 1 3 x . 3 A D 2 V S . O S .x .x SABCD Chọn A 3 ABCD 3 2 6 O I B C
Bài 18. (THPT Chuyên Thái Nguyên) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh
a, SA và vuông góc với mặt phẳng đáy. Tính khoảng cách từ trọng tâm G của tam giác SAB đến
mặt phẳng SAC. a 3 a 2 a 3 a 2 A. . B. . C. . D. . 6 6 2 4
Hƣớng dẫn giải: Gọi M là trung điểm của AB
và gọi AC cắt BD tại O .
d G,SAC SG 2 Ta có
d M ,SAC SM 3
d G SAC 2 ,
d M,SAC . 3
Gọi H là hình chiếu của M trên AC . 14
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018 a
hi đó MH SAC nên d M SAC 1 1 2 ,
MH BO BD . 2 4 4 a a
Vậy d G SAC 2 2 2 , . . Chọn B. 3 4 6
Bài 19. (THPT Đặng Thúc Hứa – Nghệ An) Cho tứ diện ABCD. Gọi B' và C ' lần lượt là trung
điểm của AB và AC . Tính tỉ số thể tích của khối tứ diện AB 'C ' D và khối tứ diện ABCD . 1 1 1 1 A. . B. . C. . D. . 4 2 6 8 Hƣớng dẫn giải: A V AB AC 1 1 1 Ta có: AB C D . V AB AC 2 2 4 ABCD C B C D B
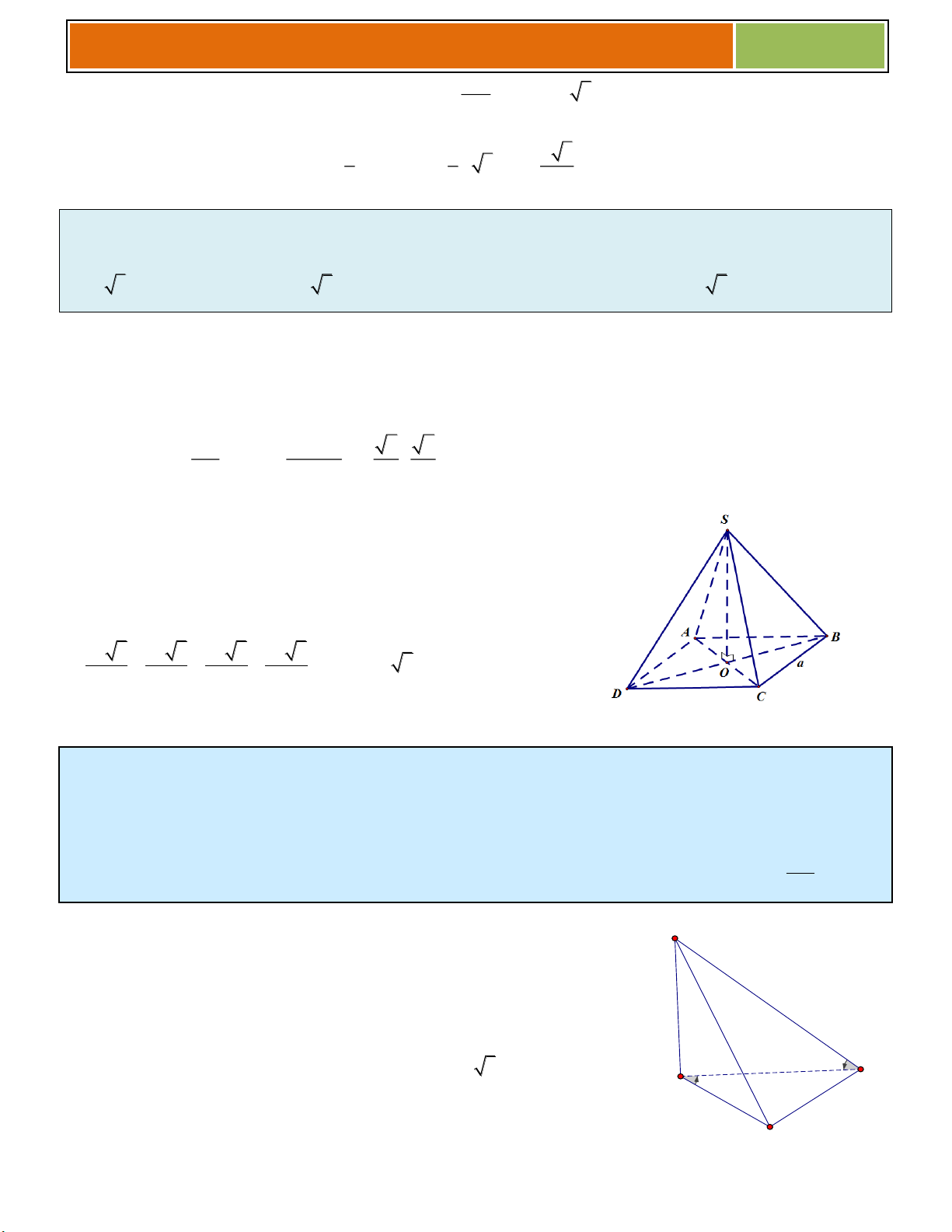
Bài 20. (THPT Lƣơng Thế Vinh – Hà Nội) Cho hình chóp tứ giác đều S.ABCD có đáy là hình
vuông cạnh 3 . Cạnh bên tạo với đáy một góc 60 . Tính thể tích V . 9 2 9 3 9 6 3 6 A. V . B. V . C. V . D. V . 2 2 2 2
Hƣớng dẫn giải : Gọi O là giao của AC và BD suy ra
SO ABCD . Trong tam giác SAO có 3 2 3 6 SO O . A tan SAO .tan 60 . 2 2 Diện tích đáy là 2 S AB 9. ABCD 1 1 3 6 9 6 V S . O S . .9 . Chọn C 3 ABCD 3 2 2
Bài 21. (THPT Lƣơng Thế Vinh – Hà Nội) Thể tích của khối tứ diện đều cạnh 1 là 3 2 A. V 1. B. V 1. C. V . D. V . 12 12
Hƣớng dẫn giải : 15
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018 Cách 1:
+ Gọi I là trung điểm CD , H là tâm đường tròn ngoại tiếp ABC
, ta có: AH (BC ) D . 2 3 + Ta có: BH BI . A 3 3 6 2 2 AH AB BH . 3 1 1 6 3 2 Vậy V AH.S . . . ABCD 3 BCD 3 3 4 12 B D Cách 2: H I
Có thể cho học sinh nhớ công thức: Thể tích khối tứ diện đều cạnh 3 a 2 2 C a là V
, thay a 1 ta được V . 12 12 Chọn D
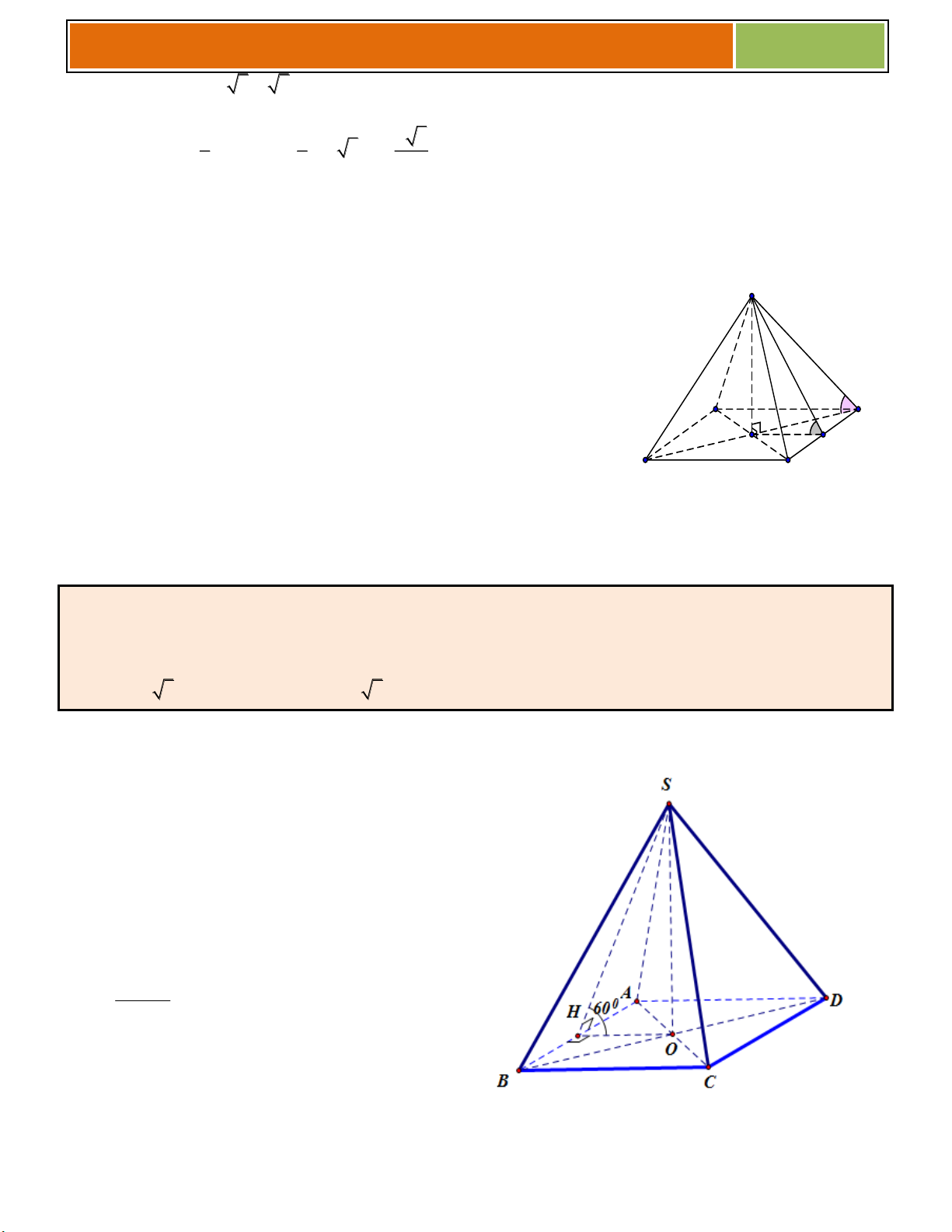
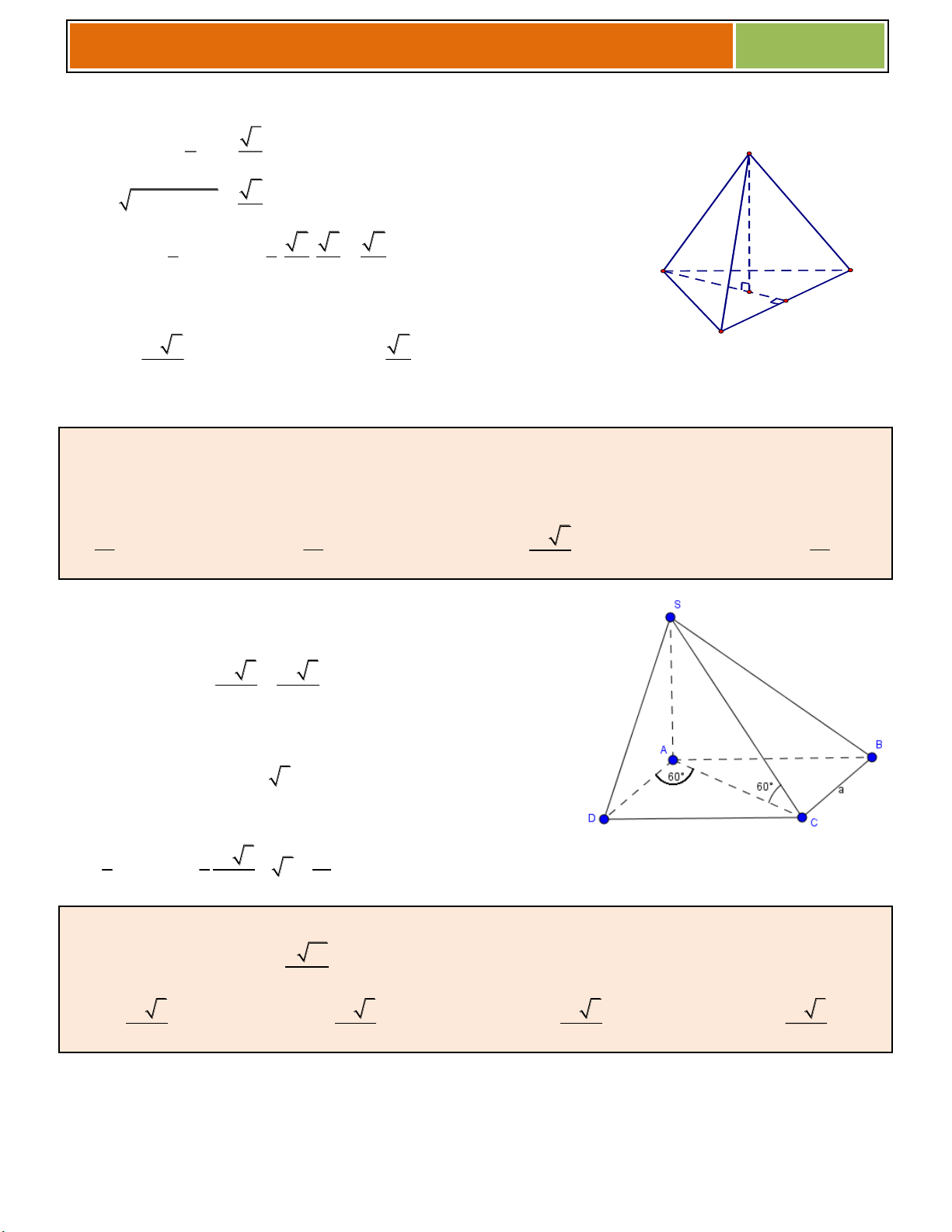
Bài 22. (THPT Lê Hồng Phong – Khánh Hòa) Hình chóp tứ giác S.ABCD có đáy là hình thoi cạnh
bằng a , góc BAC 60 , SA vuông góc với đáy, góc giữa SC và đáy bằng 60 . Thể tích hình chóp
S.ABCD bằng 3 a 3 a 3 a 3 3 a A. . B. . C. . D. . 2 6 2 3
Hƣớng dẫn giải :
Đáy là hình thoi cạnh a và có góc BAC 60 nên ABC đều , 2 2 a 3 a 3 S 2S 2. ACBD A BC 4 2
Góc giữa SC và đáy bằng 60 nên góc SCA 60 Suy ra SA tan 60 . AC 3.a
Vậy thể tích hình chóp S.ABCD là : 2 3 1 1 a 3 a V S .SA .a 3 Chọn A 3 ABCD 3 2 2
Bài 23. (THPT Hoàng Hoa Thám – Khánh Hòa) Cho hình chóp tam giác đều S.ABC có cạnh đáy a 21
bằng a và cạnh bên bằng
. Tính theo a thể tích khối chóp S.ABC . 6 3 a 3 3 a 3 3 a 3 3 a 3 A. V . B. V . C. V . D. V . 8 12 24 6
Hƣớng dẫn giải Gọi G là trọng tâm ABC 16
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018 a 3 a 2 2 AG
SG SA AG 3 2 2 3 1 a 3 a a 3 V . . 3 4 2 24 Chọn C.
Bài 24. (THPT Hoàng Hoa Thám – Khánh Hòa) Cho hình chóp tứ giác đều S.ABCD có cạnh đáy
bằng 1, cạnh bên hợp với mặt đáy một góc 0
60 . Tính khoảng cách từ O đến mặt phẳng SBC . 1 2 7 42 A. . B. . C. . D. . 2 2 2 14 Hƣớng dẫn giải
SC ABCD 0 ; SCO 60 , 2 6 0 OC
SO OC tan 60 2 2
Gọi I là trung điểm BC, kẻ OH SI tại H
OH SBC d ;
O SBC OH 1 1 1 42 OH . Chọn D. 2 2 2 OH OI SO 14
Bài 25. (THPT ISCHOOL NHA TRANG – Khánh Hòa) Cho khối chóp tứ giác đều có cạnh đáy
bằng a và cạnh bên bằng a 3 . Tính thể tích V của khối chóp đó theo a . 3 a 2 3 a 2 3 a 10 3 a A. V . B. V . C. V . D. V . 3 6 6 2
Hƣớng dẫn giải Gọi O là giao điểm của AC và BD . S a 2 a 10 Ta có AO 2 2
SO SA AO 2 2 A D 3 1 a 10 Do đó V S . O S Chọn C. S . ABCD 3 ABCD 6 O B C 17
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
Bài 26. (THPT ISCHOOL NHA TRANG – Khánh Hòa) Cho hình chóp S.ABCD có đáy ABCD là
hình vuông cạnh a , hình chiếu vuông góc của S trên mặt phẳng ABCD trùng với trung điểm
của cạnh AD ; M là trung điểm đoạn thẳng CD ; cạnh bên SB hợp với đáy một góc O 60 . Tính
thể tích V của khối chóp S.ABM . 3 a 15 3 a 15 3 a 15 3 a 15 A. V . B. V . C.V . D. V . 3 4 6 12 Hƣớng dẫn giải a 5 Ta có: 2 2 BH AB AH S 2 a 15 O
SH BH tan 60 2 A B 1 1 2 S S a A BM 2 ABCD 2 H D C 3 M 1 a 15 V SH.S . Chọn D. S . ABM 3 ABM 12
Bài 27. Cho khối chóp S.ABCD , hỏi hai mặt phẳng SAC và SBD chia khối chóp S.ABCD thành mấy khối chóp A. 4. B. 3. C. 5. D. 2.
Hƣớng dẫn giải : Gọi O là giao điểm của AC và BD .
Mặt phẳng SAC và SBD chia khối chóp S.ABCD thành 4
khối chóp, là các khối chóp sau S.ABO , S.ADO , S.CDO , S.BCO . Chọn A
Bài 28. Cho hình chóp S.ABC có tam giác SAB đều cạnh a, tam giác ABC cân tại C . Hình chiếu
của S lên ABC là trung điểm của cạnh AB ; góc hợp bởi cạnh SC và mặt đáy là 30o . Thể tích
khối chóp S.ABC tính theo a là 3 a 3 3 a 2 3 a 3 3 a 3 A. V . B. V . C. V . D. V . 4 8 2 8 2 a 3
Hƣớng dẫn giải : S . SAB 4 S 18
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook) A a 30 C a H B
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
Gọi H là trung điểm AB . CH AB
CH (SAB) . CH SH ( vi
` SH ( ABC) CH ) a 3 SH SH a o 3 2 tan 30 HC HC tan 30o 3 2 3 2 3 1 1 a 3 3a a 3 V S .HC . . . SABC 3 SAB 3 4 2 8 Chọn D.
Bài 29. Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh x . Góc tạo bởi mặt 4 bên và mặt đáy bằng 0
45 . Biết thể tích của khối chóp S.ABCD bằng 3
a , biểu thức thể hiện mối 3
liên hệ giữa x và a là A. x a . B. x 2a . C. x 4a . D. x a 2 .
Hƣớng dẫn giải :Gọi H là tâm của hình vuông ABCD .
Và K là trung điểm của BC . Suy ra BC SHK .
hi đó SBC ABCD 0 ,
SK, KH SKH 45 . x Suy ra S
HK vuông cân tại H nên SH HK . 2 3 1 1 4a Ta có 2 V .SH.S .SH.x S .ABCD 3 ABCD 3 3 3 1 x 4a 2 3 3 . .x
x 8a x 2a . Chọn B. 3 2 3 19
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
C]U H ỎI TRẮC NGHIỆM
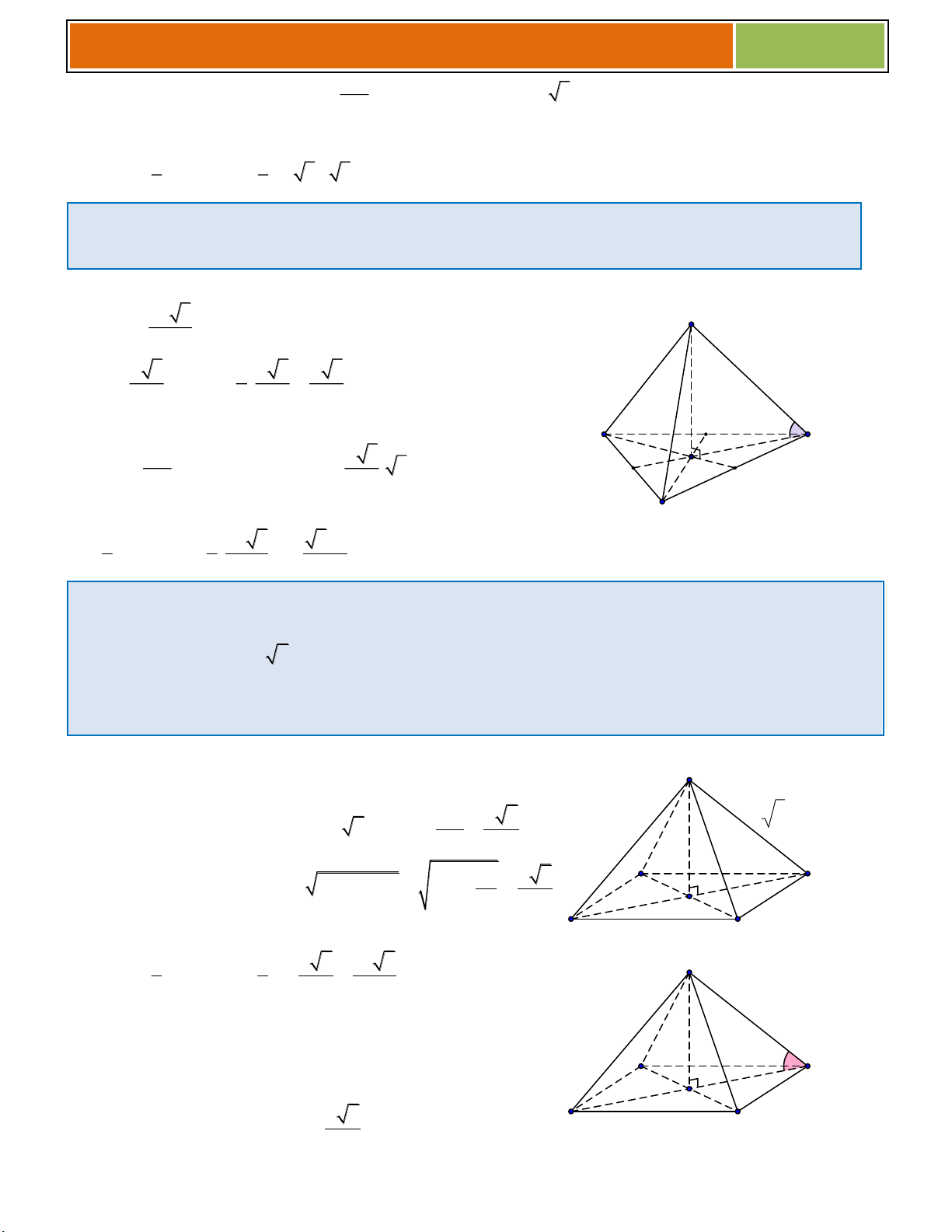
Câu 01 : Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng nhau và bằng a thì thể
tích V của khối chóp là 3 a 6 3 a 2 3 a 5 3 a 6 A. B. C. D. 9 6 3 2 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Vận dụng 1 : Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng nhau và bằng 3a thì
thể tích V của khối chóp là
Vận dụng 2 : Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng nhau và bằng a 5
thì thể tích V của khối chóp là
Vận dụng 3 : Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng nhau và bằng 2a 7
thì thể tích V của khối chóp là
Vận dụng 4 : Một hình chóp tứ giác đều có tất cả các cạnh bằng 6. Thể tích cả khối chóp này gần
bằng số nào dưới đây nhất? A. 46 B. 48 C. 52 D. 50
Vận dụng 5 (Trích đề thi thử Chuyên Hạ Long – 2017) : Cho hình chóp tứ giác đều có cạnh đáy
bằng cạnh bên và bằng 2 .
a Tính thể tích khối chóp đã cho. 3 a 2 3 4a 2 3 a 3 3 a 2 A. . B. . C. . D. . 4 3 12 6
Câu 02 (TRƢỜNG AMSTERDAM – Giữa học kì 1) : Thể tích khối tứ diện đều cạnh a là 3 3 3 A. a a a 2 B. C. D. 3 a 3 2 3 12 20
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Vận dụng 1 : Thể tích khối tứ diện đều cạnh 2a là
Vận dụng 2 : Thể tích khối tứ diện đều cạnh 4a là Vận dụng 3 : a 2
Thể tích khối tứ diện đều cạnh là 2
Câu 03 : a/ Cho tứ diện OABC có O , A O ,
B OC đôi một vuông góc, OA 1, OB 1, OC 2 . Khoảng
cách từ O đến mặt phẳng ABC là 1 2 10 A. . B. 1. C. . D. . 3 3 5
b/ Cho tứ diện ABCD có A ,
B AC, AD đôi một vuông góc và AC AB a , AD a 2 . Khoảng
cách từ A đến BCD là a 10 a 5 a 2 a 10 A. . B. . C. . D. . 2 2 5 5
c/ (THPT lục Ngạn Số 3) : Cho tứ diện OABC có O , A O ,
B OC đôi một vuông góc.
OA 3,OB 4,OC 5. Tính khoảng cách từ O đến ( ABC) ? 60 30 60 12 A. . B. . C. . D. . 469 91 769 61
d/ (THPT Minh Hà – Giữa kì 1) : Cho hình chóp S.ABC có A ,
B AC, SA đôi một vuông góc với nhau,
AB 2a , AC 4a , SA 6a . Tính thể tích V của khối chóp S.ABCD . A. 3 V 8a B. 3 V 48a C. 3 V 72a D. 3 V 24a
e/ (THPT Chuyên Quốc Học Huế) : Cho khối chóp .
O ABC có ba cạnh OA , OB , OC đôi một
vuông góc với nhau. Biết OA 1, OB 2 và thể tích của khối chóp .
O ABC bằng 3 . Tính OC . 3 9 A. . B. . C. 9 . D. 3 . 2 2 21
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 04 : a/ Cho hình chóp đều S.ABC có SA 2 ;
a AB a . Thể tích khối chóp S.ABC là: 3 a 3 3 a 11 3 3a 2 3 a 3 A. B. C. D. 12 12 2 214
b/ Hình đa diện nào dưới đây không có tâm đối xứng ? A. Tứ diện đều. B. Bát diện đều. C. Hình lập phương.
D. Lăng trụ lục giác đều
c/ (TRƢỜNG AMSTERDAM – Giữa học kì 1) : Cho hình chóp S.ABCD có đáy ABCD là hình
vuông cạnh a và SA (ABC ) D , SA 2 .
a Thể tích của khối chóp S.ABC là 3 3 3 3 A. a a 2a a B. C. D. 4 3 5 6 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 22
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
Câu 05 : Khối chóp S.ABC có thể tích bằng 120. M là trung điểm của SC và là trung điểm của
BM. Thể tích khối chóp N.ABC bằng bao nhiêu A. 30 B. 40 C. 60 D. hông tính được. ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. Câu 06
a/ (Trích đề thi thử Chuyên Hạ Long – 2017) : Cho hình chóp S.ABCD có đáy là hình vuông cạnh
bằng a, cạnh bên SA vuông góc với mặt phẳng đáy SA a 3. Tính thể tích khối chóp S.BC . D 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 3 6 4 2
b/ (Trích đề thi thử Chuyên Lê Hồng Phong – 2017) : Đáy của hình chóp S.ABCD là một hình
vuông cạnh a . Cạnh bên SA vuông góc với mặt phẳng đáy và có độ dài là a . Thể tích khối tứ
diện S.BCD bằng: 3 a 3 a 3 a 3 a A. . B. . C. . D. . 4 8 3 6 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 07 : a/ Một hình chóp tam giác có các cạnh bên đều bằng 12; cạnh đáy bằng 6, 8, 10. Thể tích
của khối chóp này bằng bao nhiêu A. 8 119 B.12 119 C.16 119 ; D. hông tính được. 23
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
b/ Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a và thể tích bằng 3
a . Tính chiều cao h của hình chóp đã cho. 3a 3a 3a A. h . B. h . C. h . D. h 3a . 6 2 3
c/ Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâmO , độ dài cạnh đáy bằng a, góc
BAC 60 . SO vuông góc mặt phẳng ABCD và SO a 6 . Tính thể tích khối chóp S.ABC ? 3 a 2 3 3a 2 3 a 2 3 3a 2 A. B. C. D. 4 2 2 4 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 08 : a/ Cho khối chóp S.ABC có SA ABC, tam giác ABC vuông tại B , AB , a AC a 3.
Tính thể tích khối chóp S.ABC biết rằng SB a 5 3 a 2 3 a 6 3 a 6 3 a 15 A. B. C. D. 3 4 6 6 24
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
b/ (Chuyên KHTN – 2017) : Cho hình chóp S.ABCD có đáy là hình vuông cạnh a . Cạnh bên SA
vuông góc với mặt phẳng đáy, cạnh bên SC tạo với mặt phẳng SAB một góc 30 . Thể tích của khối chóp đó bằng 3 a 3 3 a 2 3 a 2 3 a 2 A. . B. . C. . D. . 3 4 2 3
c/ (Chuyên Thái Bình – 2017) : Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a , SA
vuông góc với mặt phẳng đáy ABCD . Biết góc giữa SC và mặt phẳng ABCD bằng 0 60 ,tính thể
tích khối chóp S.ABCD . 3 3a 3 2a 3 6a A. . B. 3 3a . C. . D. . 6 3 3
d/ (THPT Lục Ngạn số 3 – Bắc Ninh – 2017) : Hình chóp S.ABCD có đường cao là SA , đáy hình
chữ nhật, AB 3 ,
a BC 4a , góc giữa SC và mặt phẳng đáy bằng 0
45 . Thể tích khối chóp S.ABCD là 3 12a A. . B. 3 20a . C. 3 10a . D. 3 10 2a . 5
e/ (THPT Lục Ngạn số 3 – Bắc Ninh – 2017) : Cho hình chóp S.ABC có đáy ABC là tam giác đều
cạnh 2a 3 . SA vuông góc với mặt phẳg đáy, SB tạo với đáy góc 0
60 . Thể tích khối chóp S.ABC là: 13 3 a 3 3 a 3 31 3 a A. B. C. 6 3 a 3 D. 4 4 4 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 25
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 09 (THPT Lục Ngạn số 3 – Bắc Ninh) : Cho khối chóp S.ABC có đáy ABC là tam giác đều
cạnh a . Hai mặt bên SAB và SAC cùng vuông góc với đáy. Tính thể tích khối chóp biết 3 2a 6 3 a 6 3 a 3 3 a 3 SC a 3 : A. B. C. D. 9 12 4 2 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 10 : Cho hình chóp SABC có SB = SC = BC = CA = a . Hai mặt (ABC) và (ASC) cùng vuông
góc với (SBC). Thể tích khối chóp là 3 a 3 3 a 3 3 a 3 3 a 2 A. B. C. D. 12 4 6 12 26
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 11 : Cho hình chóp SA BC có đáy ABC là tam giác vuông cân tại B với AC = a biết SA vuông
góc với đáy ABC và SB hợp với mặt đáy một góc 60o. Thể tích khối chóp là 3 a 6 3 a 3 3 a 6 3 a 6 A. B. C. D. 24 24 8 48 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 12 : a/ Cho hình chóp SABC có đáy ABC là tam giác đều cạnh a biết SA vuông góc với đáy
ABC và (SBC) hợp với đáy (ABC) một góc 60o. Thể tích khối chóp là 3 a 3 3 a 3 3 a 3 a 3 A. B. C. D. 8 12 4 4
b/ (THPT Lục Ngạn số 3) : Cho hình chóp S.ABCD đáy ABCD là hình vuông có cạnh a và SA
vuông góc đáy ABCD và mặt bên SCD hợp với đáy một góc 60o. Tính thể tích hình chóp S.ABCD . 3 2a 3 3 a 3 3 a 3 A. . B. . C. . D. 3 a 3 . 3 3 6 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 27
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 13 : a/ Cho hình chóp SABCD có đáy ABCD là hình vuông có cạnh a và SA vuông góc đáy
ABCD và mặt bên (SCD) hợp với đáy một góc 60o. Tính thể tích khối chóp S.ABCD 3 a 3 3 2a 3 3 a 3 A. B. C. D. 3 a 3 3 3 6
b/ (THPT Chuyên Lê hồng Phong – 2017) : Cho hình chóp S.ABC có đáy là tam giác đều cạnh
bằng a , SA vuông góc với đáy, mặt phẳng SBC tạo với đáy một góc 45 . Tính thể tích khối chóp S.ABC . 3 a 3 2a 3 3a 3 a A. . B. . C. . D. . 8 6 18 27 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 28
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
Câu 14 : Cho khối chóp S.ABCD có đay ABCD là hình chữa nhật tâm O , AC 2AB 2 , a SA
vuông góc với đáy. Tính thể tích khối chóp biết SD a 5 3 a 5 3 a 15 3 a 6 A. B. C. 3 a 6 D. 3 3 3 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 15 : Cho khối chóp S.ABCD có đáy là hình vuông cạnh a . Hai mặt phẳng SAB,SAD cùng
vuông góc với đáy. Tính thể tích khối chóp biết SC a 3 3 a 3 3 a 3 3 a A. B. C. 3 a D. 9 3 3 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 16 : Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật AD 2 ,
a AB a . Gọi H là trung
điểm của AD , biết SH ABCD . Tính thể tích khối chóp biết SA a 5 . 3 2a 3 3 4a 3 3 4a 3 2a A. B. C. D. 3 3 3 3 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 29
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
Câu 17 : Cho khối chóp S.ABCD có đáy là hình vuông cạnh 2a . Gọi H là trung điểm cạnh AB
biết SH ABCD . Tính thể tích khối chóp biết tam giác SAB đều 3 2a 3 3 4a 3 3 a 3 a A. B. C. D. 3 3 6 3 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
Câu 18 : a/ Cho hình chóp tứ giác đều S.ABCD có cạnh bên bằng a và tạo với đáy một góc 600. Thể 3 a 6 3 a 2 3 a 6 3 a 6 tích khối chóp là A. B. C. D. 9 12 6 3
b/ (THPT Lê Quý Đôn – Bình Phƣớc) : Cho khối chóp đều S.ABCD . BD a 6 , góc giữa cạnh bên và mặt đáy bằng 0
60 . Thể tích khối chóp S.ABCD là: 30
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018 3 a 2 3 3a 2 3 3a 6 3 2a 3 A. B. C. D. 2 2 2 2 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 19 : Cho hình chóp tứ giác đều S.ABCD có cạnh bên bằng a và mặt bên hợp với đáy góc 300 . Thể tích khối chóp là 3 a 2 3 a 2 3 a 3 3 a 3 A. B. C. D. 18 12 18 9
b/ (THPT Chuyên Lê Quý Đôn – Bình Định) : Cho hình chóp tứ giác đều có cạnh đáy bằng a và
mặt bên tạo với đáy một góc 0
45 . Thể tích khối chóp tứ giác đều bằng: 3 a 3 a 3 4a 3 2a A. B. C. D. 6 9 3 3 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 20 (Đề minh họa lần 01) : Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh
a , cạnh bên SA vuông góc với mặt phẳng đáy và SA a 2 . Tính thể tích V của khối chóp S.ABCD : 3 a 2 3 2a 2 A. V B. V C. 3 V 2a D. 3 V a 6 4 3 31
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 21 : a/ Cho hình chóp tam giác đều có cạnh đáy là a và cạnh bên hợp với cạnh đáy góc 300. Thể 3 a 2 3 a 3 3 a 3 3 a 3
tích của khối chóp là A. B. C. D. 6 9 12 36
b/ (THPT Chuyên Lê Quý Đôn – Bình Định) : Cho hình chóp tứ giác đều S.ABCD có cạnh đáy 3 a
bằng a, thể tích khối chóp bằng
. Tính góc giữa cạnh bên và mặt phẳng đáy. 3 2 A. 0 30 B. 0 60 C. 0 75 D. 0 45 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 32
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
Câu 22 : Cho hình chóp tam giác đều có cạnh đáy là a . Khoảng cách từ một đỉnh của đáy đến mặt a 2 bên đối diện là
. Thể tích của khối chóp là 2 3 a 2 3 a 3 3 a 3 3 a 3 A. B. C. D. 24 9 12 36 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 23 : Cho hình chóp S.ABC có mặt bên SBC là tam giác đều cạnh a. Cạnh bên SA vuông góc
với mặt phẳng đáy. Biết 0
BAC 120 . Thể tích của khối chóp này là 3 a 2 3 a 3 3 a 3 3 a 2 A. B. C. D. 24 9 12 36 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 24 : Cho hình chóp S.ABCD có SA vuông góc với mặt đáy và đáy ABCD là hình vuông cạnh
a, góc giữa hai mặt phẳng (SBD) và (ABCD) là 600 . Thể tích của khối chóp là 3 a 2 3 a 6 3 a 11 3 a 2 A. B. C. D. 24 6 6 36 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 33
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 25 : Cho tứ diện ABCD có thể tích bằng 12 và G là trọng tâm tam giác BCD. Tính thể tích V của khối chóp . A GBC . A. V 3 . B. V 4 . C. V 6 . D. V 5 . ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 26 : Đáy của một hình chóp S.ABCD là một hình vuông cạnh a. Cạnh bên SA vuông góc với
đáy và có độ dài bằng a. Thể tích khối tứ diện S.BCD bằng 3 a 3 a 3 a 3 a A. B. C. D. 4 2 6 8 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 27 : Cho hình chóp S.ABC đáy là tam giác vuông cân tại A, BC = 2a. Hình chiếu vuông góc
của S lên (ABC) trùng với trung điểm BC, mặt phẳng (SAC) tạo với (ABC) góc 600 .
Thể tích khối chóp S.ABC theo a. 3 a 3 a 6 3 a 3 A. B. Đáp án khác C. D. 4 6 8 34
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 28 : Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, SC
tạo với đáy một góc 450. Tính theo a thể tích của khối chóp S.ABCD 3 a 2 3 a 2 3 a 2 A. B. Đáp án khác C. D. 6 3 5 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 29 : Cho khối chóp S.ABC có đáy là tam giác vuông tại B. Cạnh SA vuông góc với đáy, góc
ACB = 600, BC = a , SA = a. 3 . Gọi M là trung điểm của cạnh SB Tính thể tích khối tứ diện M.ABC 3 a 2 3 a 3 a 2 3 a 2 A. B. C. D. 6 4 3 5 35
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 30 : a/ Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A , mặt bên SBC là tam
giác đều cạnh a và mặt phẳng SBC vuông góc với mặt đáy. Tính theo a thể tích khối chóp S.ABC . 3 a 3 3 a 3 2 a 3 2 a 3 A. . B. . C. . D. . 24 8 24 8
b/ (THPT Chuyên Lê hồng Phong – 2017) : Cho hình chóp S.ABC có đáy ABC là tam giác đều;
mặt bên SAB nằm trong mặt phẳng vuông góc với mặt phẳng đáy và tam giác SAB vuông tại S ,
SA a 3 , SB a . Tính thể tích khối chóp S.ABC . 3 a 3 a 3 a 3 a A. . B. . C. . D. . 3 2 4 6 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 36
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 31 (THPT Lục Ngạn 1 – Bắc Ninh) : Cho hình chóp S.ABCD có đáy ABCD là hình vuông
cạnh 2a 3 , mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Thể tích
của khối chóp S.ABCD là: A. 3 12a B.14a 3 C. 3 15a D. 3 17a ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. Câu 32 : 3a
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SD = , hình chiếu vuông 2
góc của S trên mặt phẳng (ABCD) là trung điểm của cạnh AB. Tính theo a thể tích khối chóp S.ABCD 3 a 3 a 3 3 a 3 a 3 A. B. C. D. 3 24 6 12 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 33 : Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB a, AD 2a . Cạnh bên
SA vuông góc với đáy, góc giữa SD với đáy bằng 0
60 .Tính theo a thể tích khối chóp S.ABCD . 37
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018 3 3 3 4a 3 a 3 a 3 a 3 A. B. C. D. 3 24 6 12 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 34 : Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB a, AD 2a . Cạnh bên
SA vuông góc với đáy, góc giữa SD với đáy bằng 0
60 .Tính theo a khoảng cách từ điểm C đến
mặt phẳng SBD 3 a 3 a 3 a 3 a 3 A. B. C. D. 3 2 6 12 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. < <<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 35 : Cho hình chóp tứ giác đều có cạnh đáy bằng a. Diện tích xung quanh gấp đôi diện tích
đáy . hi đó thể tích của hình chóp bằng ? 3 a 3 3 a 3 3 a 3 3 a 3 A. B. C. D. 12 3 2 6 38
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 36 (THPT Nguyễn Bỉnh Khiêm – Bình Định) : Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại ,
B AB a, BC a 3, SA vuông góc với mặt phẳng đáy. Biết góc giữa SC và ABC bằng 0
60 . Thể tích khối chóp S.ABC bằng: 3 a 3 A. 3 3a . B. 3 a 3 . C. 3 a . D. . 3 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 37 : a/ Trong các hình dưới đây hình nào là khối đa diện A. . B. . C. . D. .
b/ Khối chóp tam giác đều SABC với cạnh đáy bằng a, cạnh bên bằng 2a có thể tích là: 3 a 3 3 a 11 3 a 11 3 a A. B. C. D. 12 11 12 11 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 39
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
Câu 38 : a/ Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt đáy. BC 9m , AB 10m,
AC 17m . Biết thể tích khối chóp S.ABC bằng 3 72m
. Tính khoảng cách h từ điểm A đến mặt phẳng (SBC) . 24 42 18 A. h m . B. h m . C. h 34m . D. h m . 5 5 5
b/ Cho hình chóp tam giác có đường cao bằng 100 cm và các cạnh đáy bằng 20 cm, 21 cm, 29 cm.
Thể tích của hình chóp đó bằng : A. 3 6000cm B. 3 6213cm C. 3 7000cm D. 3 7000 2cm ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 39 : Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , AB a . Cạnh bên
SA a 2 , hình chiếu của điểm S lên mặt phẳng đáy trùng với trung điểm của cạnh huyền AC .
a/ Chọn đáp án đúng 6 A. a SM B. ∆SAC cân 3 2 a C. ∆SAC đều D. S ABC 4
b/ Thể tích khối chóp S.ABC theo a là 3 a 6 3 a 6 3 a 6 3 a A. B. C. D. 12 6 8 11 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 40
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 40 (TRƢỜNG AMSTERDAM – Giữa học kì 1) : a/ Cho khối chóp S.ABCD có thể tích V với
đáy ABCD là hình bình hành. Gọi E, F lần lượt là trung điểm của các cạnh AB và AD. Thể tích của
khối chóp S.AECF là: V V V V A. B. C. D. 2 4 3 5
b/ Cho hình chóp tam giác S.ABC có M, N lần lượt là trung điểm của các cạnh SA và SB. Tỉ số V 1 1 1 1 S .CMN là: A. B. C. D. V 3 8 2 4 S .CAB ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. Câu 41
a/ (Đề thi THPT Quốc gia 2017) : Cho khối chóp S.ABC có SA vuông góc với đáy, SA 4 , AB 6,
BC 10 và CA 8 . Tính thể tích V của khối chóp S.ABC . A. V 24 . B. V 32 . C. V 192. D. V 40 .
b/ (TRƢỜNG AMSTERDAM – Giữa học kì 1) : Cho hình tứ diện ABCD có DA BC 5,
AB 3, AC 4. Biết DA vuông góc với mặt phẳng (ABC). Thể tích của khối tứ diện ABCD là: A. V 10 B. V 20 C. V 30 D. V 60 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 41
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 42 : Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a tâm O , SA vuông góc với
mặt phẳng ABCD và SA a .
a/ Chọn đáp án đúng 3 a A. 2 S a B. V ABCD S . ABCD 3
C. góc giữa SC và đáy là SCA D. Cả A, B, C đều đúng.
b/ Tan của góc giữa SC với mặt phẳng SAD . 2 A. 1 B. C. 2 D. 3 2 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 43 : Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a . Cạnh bên SA vuông
góc với đáy, SB hợp với mặt đáy một góc 60 .
a/ Thể tích của khối chóp S.ABCD theo a là 3 a 3 3 a 3 A. V B. V S . ABCD 3 S . ABCD 6 3 a 3 C. V D. Cả A, B, C đều sai S . ABCD 8 42
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
b/ Khoảng cách từ điểm D đến mặt phẳng SBC a a
A. d D SBC 3 , .
B. d D SBC 3 , . 4 3 a
C. d D SBC 3 , D. d ,
D SBC a 2 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 44 : Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Cạnh SA vuông góc với
đáy, góc giữa SC với đáy bằng 0 60 .
a/ Thể tích của khối chóp S.ABCD là 3 a 3 3 a 6 3 a 6 3 a 2 3 A. B. C. D. 6 3 4 9
b/ Gọi I là trung điểm của đoạn thẳng SB . Tính khoảng cách từ điểm S đến mặt phẳng ADI . a 41 a 42 a 3 a 21 A. . B. . C. D. . 7 7 7 7 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 43
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
Câu 45 (đề minh họa lần 3 – BGD-ĐT) : Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA
vuông góc với mặt đáy, SD tạo với mặt phẳng (SAB) một góc bằng 0
30 . Tính thể tích V của khối chóp S.ABCD. 3 6a 3 6a 3 3a A. V B. 3 V 3a C. V D. V 18 3 3 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 46 : Cho hình chóp tam giác đều S.ABC có đáy ABC là tam giác đều cạnh a . Góc giữa mặt bên với mặt đáy bằng 0 60 .
a/ Thể tích khối chóp S.ABC . 3 9a 3 7a 3 5a 3 a 3 A. B. C. D. 2 2 2 24
b/ Gọi M , N lần lượt là hai điểm trên cạnh S ,
A SC sao cho AM 2SM , CN 2SN . Tính thể tích
khối chóp S.BMN 3 3a 3 3 a 3 3 3a 2 3 a 3 A. B. C. D. 2 216 2 214 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 44
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
Câu 47 : Cho hình chóp S.ABCD đáy là hình vuông, Tam giác SAB đều và nằm trong mặt phẳng
vuông góc với đáy. Biết diện tích của tam giác SAB là 2
9 3 cm . Thể tích khối chóp S.ABCD là: A. V 3 36 3 cm B. V 3 50 3 cm C. V 3 9 3 cm D. V 3 72 3 cm ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. Câu 48 :
a/ Cho hình chóp S.ABC có SA = SB = SC. Phát biểu nào sau đây là đúng.
A. Hình chóp S.ABC là hình chóp đều.
B. Hình chiếu của S trên (ABC) là tâm đường tròn ngoại tiếp tam giác ABC
C. Hình chiếu của S trên (ABC) là trung điểm của cạnh BC
D. Hình chiếu của S trên (ABC) là trọng tâm của tam giác AB
b/ Cho khối chóp S.ABCD có đáy là hình vuông cạnh a và có tâm O , h là chiều cao của khối chóp. Xét các mệnh đề: Thể tích khối chóp 2
S.ABCD :V a .h 1 (I) 1 Thể tích khối chóp 2
S.AOB :V a .h (II) 2 12 Mệnh đề nào đúng A. (I) đúng, (II) sai B. (I) sai, (II) đúng
C. Cả (I) và (II) đều đúng
D. Cả (I) và (II) đều sai. ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 45
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
Câu 49 : Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB 5 3 dm, AD 1 2 3 dm, SA (
ABCD) . Góc giữa SC và đáy bằng 0 30 . Thể tích khối chóp S.ABCD. A. 3 780 dm B. 3 800 dm C. 3 860 dm D. 3 900 dm ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. Câu 50 :
a/ Cho tứ diện ABCD có thể tích của khối ABCD bằng 126, hai tam giác ABC và ABD có diện
tích cùng bằng 21. M là một điểm thuộc cạnh CD và d1, d2 là khoảng cách từ M tới mặt phẳng
(ABC) và (ABD). Giá tr (d1 + d2) bằng: A. 18 B. 20 C. 22 D. 24
b/ Cho khối chóp S.ABC , trên ba cạnh S , A S ,
B SC lần lượt lấy ba điểm A', B ' và C ' sao cho: 1 1 1 SA' S ; A SB ' SB và SC '
SC . Tỉ số thể tích giữa khối tứ diện S.A' B 'C ' và S.ABC bằng 5 6 7 1 1 1 107 A. B. C. D. . 420 630 210 210 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 46
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
Câu 51 : Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Diện tích toàn phần của hình chóp là: 3 A. 2 1 2 a B. 2 1 3 a C. 2 1 a D. 2 1 2 3 a 2 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 52 : Cho hình chóp S.ABCD đáy là hình bình hành. Gọi M là trung điểm của SA. Mặt phẳng
(MBC) chia khối chóp thành hai phần. Tỉ số thể tích của hai phần trên và dưới là: 3 3 5 A. B. C. 1 D. 8 5 8 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 53 (Đề thi THPTQG 2017) : Cho hình chóp đều S.ABCD có độ dài cạnh đáy bằng . Gọi là
trọng tâm tam giácSAC . Mặt phẳng chứa AB và đi qua G cắt các cạnh SC, SD lần lượt tại M và
N . Biết mặt bên của hình chóp tạo với đáy một góc bằng
. Thể tích khối chóp S.ABMN bằng: 3 a 3 3 3a 3 3 a 3 3 a 3 A. . B. . C. . D. . 8 16 4 16 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 47
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 54 : Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a , đường cao của hình chóp bằng
a 3 . Góc giữa mặt bên và đáy bằng 2 A. 0 30 B. 0 60 C. 0 45 D. Đáp án khác ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
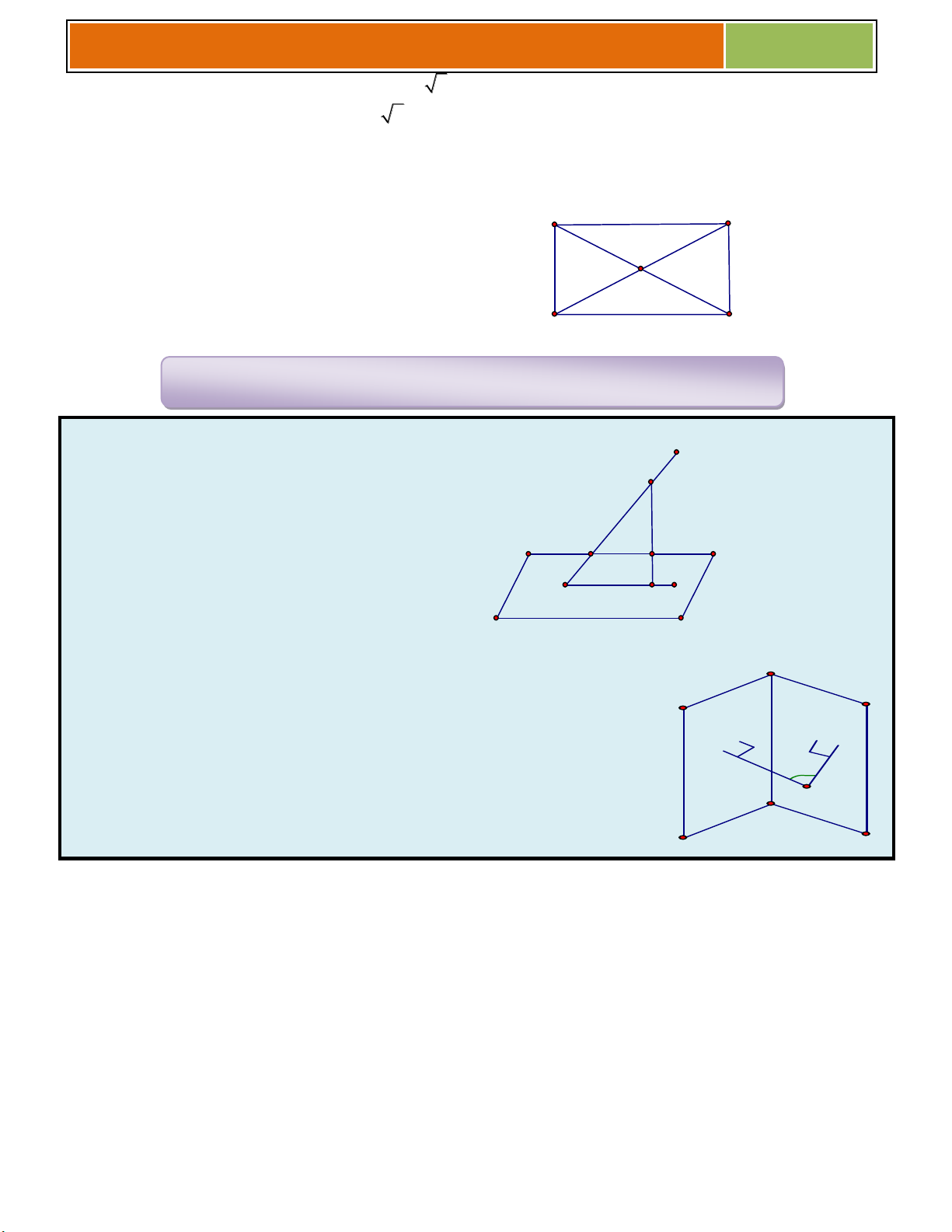
Câu 55 : Trong mặt phẳng (P) cho tam giác ABC, trên đường thẳng (d) vuông góc với (P) tại A, lấy
hai điểm M, N khác phía đối với (P) sao cho (MBC) (NC )
B . Trong các công thức 1 1 1 (I). V N . B S ;
(II). V MN.S ;
(III). V MC.S , 3 MBC 3 ABC 3 NBC
thể tích tứ diện MNBC có thể được tính bằng công thức nào ? A. I B. II C. III D. Cả A, B, C 48
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 56 : Cho hình chóp S.ABCD có tất cả các cạnh bằng nhau. Chứng minh rằng SABCD là chóp 3 9a 2
tứ giác đều. Tính cạnh của hình chóp này khi thể tích của nó bằng V 2 A. a B. 2a C. 3a D. 4a ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 57 : Cho hình chóp tứ giác đều có mặt bên hợp với đáy một góc 45o và khoảng cách từ chân
đường cao của chóp đến mặt bên bằng a. Tính thể tích hình chóp 3 a 3 3 a 5 3 8a 3 A. B. C. D. 3 3a 3 3 2 3 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 58 : Cho hình chóp tam giác đều có đường cao h và mặt bên có góc ở đỉnh bằng 60o.
Tính thể tích hình chóp. 49
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018 3 h 3 3 h 3 h 3 3 h 2 A. B. C. D. 8 4 3 12
Câu 45 : Cho hình chóp tứ giác đều SABCD có cạnh đáy a và o
ASB 60 . Tính thể tích hình chóp 3 a 2 3 a 2 3 a 3 3 a 3 A. B. C. D. 6 3 3 6 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 59 (Đề thi THPTQG 2017) : Cho khối chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông a 2
góc vơi đáy và khoảng cách từ A đến mặt phẳng SBC bằng
. Tính thể tích của khối chóp 2 3 a 3 a 3 3a đã cho A. . B. . C. 3 a . D. . 2 3 9 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 50
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
Câu 60 : Cho hình chóp S.ABC có đáy là tam giác cân tại A, AB = AC = a, 0
BAC 120 . Mặt bên
(SAB) là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính theo a thể tích khối chóp S.ABC 3 a 3 a A. B. 3 a C. D. 3 2a 8 2 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 61 : Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc với
mặt phẳng đáy, góc giữa SC và mặt phẳng đáy bằng 600
a/ Chọn đáp án đúng A. 0 SCA 60 B. SA a 6 3 a 6 C. V D. Cả A, B, C đều đúng S.ABCD 3
b/ Gọi M và N lần lượt là trung điểm của SB và SD. Tỉ số thể tích của hai khối chóp S.AMN và S.ABD. V 2 V 2 A. S.AMN B. S.AMN V 8 V 3 S . ABD S . ABD V 2 C. S.AMN D. Đáp án khác V 9 S . ABD ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 51
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 62 : Cho hình chóp S.ABC có AB = 6a, AC = 8a, BC = 10a ; mặt bên (SBC) là tam giác đều và
vuông góc với đáy. Thể tích khối chóp này là A. 3 25a 3 B. 3 20a 3 C. 3 40a 3 D. Đáp án khác ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 63 : Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a. Cạnh bên SA vuông góc với 6
đáy và SA a . 2
a/ Khoảng cách x từ điểm A đến mp(SBC) 2 3 A. x a B. x a C. x a 3 D. x 2a 2 2
b/ Thể tích khối chóp S.ABC 3 a 2 3 a 3 3 a 2 3 a 3 A. B. C. D. 2 2 8 8
c/ Diện tích tam giác SBC. 2 a 2 2 a 3 3 2 a 3 A. B. C. 2 a D. 8 2 4 8 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 52
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 64 (THPT Chuyên Thái Bình – 2017): Một kim t tháp ở Ai C p được ây d ng vào khoảng
2500 trước Công nguyên. im t tháp này là một khối chóp tứ giác đều có chiều cao150 m , cạnh
đáy dài 220 m . Diện tích ung quanh của kim t tháp này là: A. 2 2200 346 m . B. 2 4400 346 m . C. 3 2420000 m . D. 2 1100 346 m ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 65 : Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a , góc 0
BAD 120 . Cạnh bên
SA vuông góc với đáy ABCD và SD tạo với đáy ABCD một góc 0 60 .Thể tích khối chóp S.ABCD . 3 a 3 a 2 A. 3 3 a B. C. 3 2a D. 2 4 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 53
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
Câu 66 : Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và S.ABC , AC 2a. Hình
chiếu vuông góc của đỉnh S trên mặt đáy là trung điểm H của đoạn thẳng AC và SH a 3 .
Thể tích khối chóp S.ABC . 3 a 3 a 2 A. 3 3 a B. C. 3 2a D. 2 4 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 67 : Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a , tam giác SAB cân tại S
và nằm trong mặt phẳng vuông góc với mặt đáy, SA 2a .
a/ Thể tích khối chóp S.ABCD . 3 a 3 a 15 3 a 15 A. 3 3 a B. C. D. 6 5 6
b/ Gọi I là trung điểm của AB . Khoảng cách từ I đến mặt phẳng SAC là a 465 a 465 a 465 A. B. C. a 465 D. 62 6 4 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 54
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
Câu 68 (Đề minh họa lần 01) : Cho tứ diện ABCD có các cạnh A ,
B AC và AD đôi một vuông góc với
nhau: AB 6a ,AC 7a và AD 4a . Gọi M,N,P tương ứng là các trung điểm các cạnh BC,C , D DB
Tính thể tích V của tứ diện AMNP. 7 28 A. 3 V a B. 3 V 14a C. 3 V a D. 3 V 7a 2 3 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 69 : Một hình chóp tứ giác đều có tổng diện tích các mặt bên bằng 72, mặt bên tạo với đáy một góc bằng o
60 . Thể tích khối chóp này gần bằng số nào dưới đây nhất? A. 60 B. 62 C. 64 D. 66 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 70 : Một hình chóp tứ giác đều có đường cao bằng 5, khoảng cách hai trọng tâm của hai mặt
bên kề nhau bằng 4. Thể tích khối chóp này bằng: 55
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018 A. 100 B. 110 C. 120 D. không tính được ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 71 : Cho hình chóp S.ABCD có đáy là hình chữ nh t, AB ; a D A
2a;SA a 3 . M là điểm a 3 trên SA sao cho AM . V ? 3 S.BCM 3 2a 3 3 2a 3 3 a 3 3 a 3 A. B. C. D. 9 5 6 9 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 56
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
Câu 72 : Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O. Gọi H và K lần lượt là trung V
điểm của SB, SD. Tỷ số thể tích A.OHK bằng VS.ABCD 1 1 1 1 A. B. C. D. 8 6 4 12 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 73 : Cho khối lăng trụ có thể tích V, chiều cao h, diện tích đáy là S. Diện tích đáy tính theo S là
bao nhiêu nếu giữ nguyên thể tích V và chiều cao h tăng lên 3 lần? 1 1 A. S B. 3S C. S D. S 2 3 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 74 : Cho hình chóp S.ABC có đáy là tam giác vuông tại A, AC a . Tam giác ∆SAB đều cạnh 2 2 a 39
và nằm trong mp vuông góc với đáy. Biết a Δ S SAB
. Khoảng cách từ C đến mp(SAB): 16 a 39 a 39 a 39 A. B. C. a 39 D. 12 2 13 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 57
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 75 : Cho hình chóp SABCD có ABCD là hình thang vuông tại A và D thỏa mãn AB = 2AD =
2CD và SA (ABCD). Gọi O = AC BD. hi đó góc hợp bởi SB và mặt phẳng (SAC) là: A. BSO B. BSC C. DSO D. BSA ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 76 : Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân đỉnh C, cạnh góc vuông bằng a. 1
Mặt phẳng (SAB) vuông góc đáy. Biết diện tích tam giác SAB bằng 2
a . hi đó, chiều cao hình 2 chóp bằng a a a A. a B. C. D. 2 3 2 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 77 : a/ Cho hình chóp tam giác S.ABC với S , A S ,
B SC đôi một vuông góc và SA SB SC a .
hi đó, thể tích khối chóp trên bằng: 58
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018 3 a 3 a 3 a 3 2a A. B. C. D. 6 9 3 3
b/ Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc giữa mặt bên và mặt đáy bằng 450. Gọi M,
N, P lần lượt là trung điểm của SA, SB và CD. Thể tích khối tứ diện AMNP bằng 3 a 3 a 3 a 3 2a A. B. C. D. 36 18 48 9
c/ Cho hình chóp S.ABC có SA ABC . Tam giác ABC vuông tại A và SA , a AB ,
b AC c . Khi
đó thể tích hình chóp bằng: 1 1 1 A. abc B. abc C. abc D. abc . 2 3 6
d/ Cho tứ diện O.ABC có OA, OB, OC đôi một vuông góc và có độ dài lần lượt là 1cm, 2cm, 3cm.
hi đó khoảng cách từ O đến mp(ABC) là 11 7 6 5 A. cm B. cm C. cm D. cm . 6 6 7 6 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 78 : Kim T Tháp ở Ai C p có hình dáng của khối đa diện nào sau đây
A. Khối chóp tam giác đều B. Khối chóp tứ giác C. Khối chóp tam giác
D. Khối chóp tứ giác đều
Câu 79 : Thể tích khối chóp có diện tích đáy là 3B và chiều cao h là: 1 1 A. V Bh B. V Bh C. V Bh D. V 3Bh 3 2
Câu 80 : Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất: A. Hai mặt. B. Ba mặt. C. Bốn mặt. D. Năm mặt. Câu 81 : 1
Cho một khối chóp có thể tích bằng V . Khi giảm diện tích đa giác đáy uống lần thì 3
thể tích khối chóp lúc đó bằng: V V V V A. B. C. D. 9 6 3 27 59
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
Câu 82 : Cho khối tứ diện ABCD. Lấy một điểm M nằm giữa A và B, một điểm N nằm giữa C và
D. Bằng hai mặt phẳng MCD và NAB ta chia khối tứ diện đã cho thành bốn khối tứ diện: A. AMCN, AMND, AMCD, BMCN B. AMCD, AMND, BMCN, BMND C. AMCD, AMND, BMCN, BMND D. BMCD, BMND, AMCN, AMDN
Câu 83 : Cho khối chóp S.ABC, trên ba cạnh SA, SB, SC lần lượt lấy ba điểm A’, B’, C’ sao cho 1 1 1 SA' = SA ; SB' = SB ; SC' =
SC . Gọi V và V’ lần lượt là thể tích của các khối chóp S.ABC và 2 3 4 V
S.A’B’C’. hi đó tỉ số là: V 1 1 A. 12 B. C. 24 D. 12 24
Câu 84 : Cho hình chóp tam giác đều có cạnh đáy bằng a và mặt bên hợp với đáy góc α. hi đó
chiều cao của hình chóp bằng a A. 2 a 9 tan 3 B. 2 9 tan 3 6 a C. 2 9 tan 3 D. 2 a 9 tan 3 6 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 60
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
Câu 85 : Cho khối chóp S.ABC. Gọi M, N lần lượt là trung điểm SA và SB. Tỉ số thể tích của hai
khối chóp S.ACN và S.BCM là : 1 A. 12 B. C. 1 D. hông ác định được 4
Câu 86 : Cho tứ diện S.ABC có các cạnh SA, SB, SC đôi một vuông góc với nhau và AB 5
, BC 6,CA 7 . hi đó thể tích tứ diện S.ABC bằng 210 95 A. 210 B. C. D. 95 3 3 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 87 : Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a. SA vuông góc với mặt đáy và
SA = 3a. Gọi M, N lần lượt là hình chiếu vuông góc của A lên SB và SC. Thể tích khối chóp A.BCNM theo a là 3 19 3a 3 19 3a 3 3a 3 2a A. B. C. D. 200 400 200 200 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 61
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
Câu 88 : Cho tứ diện ABCD có cạnh AD vuông góc với mp (ABC); AC = AD = 4cm; AB = 3cm ; BC = 5cm.
a/ Khoảng cách từ điểm A đến mp (BCD) là 34 6 17 6 34 6 34 A. B. C. D. 34 34 17 34
b/ Thể tích khối tứ diện ABCD là A. 6 B. 7 C. 8 D. 9 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 89 : a/ Cho hình chóp tam giác O.ABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau
và OA = a, OB = b, OC = c. Độ dài đường cao OH của hình chóp bằng ac bc A. B. 2 2 2 2 2 2
a b b c c a 2 2 2 2 2 2
a b b c c a abc ab C. D. 2 2 2 2 2 2
a b b c c a 2 2 2 2 2 2
a b b c c a
b/ Cho tứ diện OABC biết OA, OB, OC đôi một vuông góc. OA = 3, OB = 4 và V 6 O.ABC .Khoảng
cách từ O đến mặt phẳng (ABC) là: 1 2 1 1 A. B. C. D. 3 3 27 9
c/ Cho tứ diện O.ABC có OA, OB, OC đôi một vuông góc và có độ dài lần lượt là 1cm, 2cm, 3cm.
hi đó thể tích V (cm3) của tứ diện là một nghiệm của phương trình : 62
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018 A. 2 V 25 0 B. 2
V 5V 6 0 C. 2
V 5V 6 0 D. 2
V V 3 0 .
d/ Cho hình chóp tam giác SABC có đáy là tam giác đều cạnh 2a , có SA vuông góc với (ABC). Để 3 a 3
thể tích của khối chóp SABC là
thì góc giữa hai mặt phẳng (SBC) và (ABC) là 2 A. 600 B. 450 C. 300 D. Đáp án khác ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 90 : Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D với AD CD a ,
AB = 3a. Cạnh bên SA vuông góc với mặt đáy và cạnh bên SC tạo với đáy một góc 450. Tính thể
tích khối chóp S.ABCD theo a. 3 2 2a 3 2 3a 3 2a 3 2 3a A. B. C. D. 3 5 6 3 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 91 : Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B, SA vuông góc với đáy, với
AB = 3a, SA = 4a. khoảng cách từ điểm A tới mp(SBC) là: 12a 2a 21 2a 21 12a A. B. C. D. 5 12 7 25 63
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 92 : Cho hình chóp tam giác đều SABC , AB a . H là tr c tâm tam giác ABC, SH a 2 . Thể V 3 3 a 6 3 3
tích khối chóp SABC là V, khi đó : A. B. C. D. 3 a 2 12 12 24 16 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 93 : Cho tứ diện ABCD. Gọi B' và C ' lần lượt là trung điểm của AB và AC .
hi đó tỉ số thể tích của khối tứ diện ABCD và khối tứ diện AB 'C ' D bằng bao nhiêu? 1 1 1 1 A. B. C. D. . 2 4 6 8 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 94 : Cho hình chóp S.ABCD . Gọi A', B',C',D' lần lượt là trung điểm của S , A S ,
B SC, SD . Trong
các kết quả sau, kết quả nào đúng? Tỉ số thể tích của hai khối chóp S.A' B 'C ' D' và S.ABCD bằng: 64
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018 1 1 1 1 A. B. C. D. . 2 4 6 8 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 95 : Cho hình hộp ABC .
D A' B 'C ' D ' . Trong các mệnh đề sau, mệnh đề nào đúng? Tỉ số thể
tích của khối tứ diện ACBB ' và khối hộp ABC .
D A' B 'C ' D ' bằng: 1 1 1 1 A. B. C. D. . 2 3 4 6 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 96 : Cho hình chóp tứ giác đều S.ABCD . Biết AB a và góc giữa hai mặt bên và mặt đáy
bằng a . hi đó, thể tích của khối chóp bằng 3 a tan 3 a tan 3 a tan 3 a cot A. B. C. D. . 6 3 2 6 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 97 : Cho hình chóp SABC có đáy ABC là tam giác đều cạnh a biết SA vuông góc với đáy ABC
và (SBC) hợp với đáy (ABC) một góc 60o. Thể tích khối chóp SABC là: 65
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018 3 a 3 3 a 3 3 a 3 2 a 3 A. B. C. D. 12 4 6 8 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
Câu 98 : Cho khối chóp tam giác S.ABC có đáy là tam giác vuông tại A , các cạnh bên
SA = SB = SC = 3a và AB = 3a, AC = 4a, Thể tích của khối chóp S.ABC bằng 3 a 3 3 a 3 A. B. C. 3 3a 11 D. 3 6a 11 12 4 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
Câu 99 : Cho hình chóp tứ giác S.ABCD có đáy là hình vuông cạnh a ; cạnh bên SA vuông góc
với mặt phẳng đáy, đường thẳng SD tạo với (ABC) một góc 45 . Tính khoảng cách h từ điểm B
đến mặt phẳng (SCD) 2a 6a a 2a .A. h . B. h . C. h . D. h . 2 3 3 3 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 66
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 100 : Cho hình chóp tứ giác S.ABC có BC 15a , AB 8a, AC 17a ; mặt bên (SAB) nằm
trong mặt phẳng vuông góc với đáy. Biết thể tích khối chóp S.ABC bằng 3 2017a . Tính khoảng
cách h từ điểm C đến mặt phẳng (SAB) . 120 113 A. h 15a . B. h a . C. h 4a . D. h a . 17 10 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<< Câu 101 : 1
Biết thể tích của khối tứ diện đều là 3
a và diện tích của một mặt của nó bằng 2 a . Tính 3
chiều cao của khối tứ diện đều đó . 1 1 A .9a B. a C. 3a D. a 9 3
Cho khối chóp có là diện tích của mặt đáy khối chóp, h là chiều cao của khối chóp. Thể tích của khối chóp là: 1 1 A. .h B. .h C. 3.h D. .h 3 2 Câu 102 : a 6
Cho biết khối tứ diện đều có cạnh đáy bằng a sẽ có đường cao bằng 3
Như thế, nếu một khối tứ diện đều có thể tích bằng 18 2 thì đường cao của nó bằng: A. 6 B. 2 6 C. 3 6 D. Đáp số khác. 67
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Câu 103 : Cho hình chóp S.ABC có đáy ABC và tam giác vuông tại B với BC = 4a, AB = 3a. Mặt
phẳng (SBC) vuông góc với mặt đáy (ABC). Biết SB = 2a 3 và 0 SBC 30
Thể tích của khối chóp S.ABC là 3 2a 2 3 a 3 A. B. C. 3 2a 3 D. 3 2a 5 7 3
Câu 104 : Cho tứ diện ABCD có I là trung điểm của BC, diện tích tam giác ADI bằng 38, khoảng
cách từ điểm B đến mặt phẳng (ADI) bằng 6. Thể tích của khối tứ diện ABCD bằng bao nhiêu? A. 150 B. 152 C. 158 D. hông tính được. ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<< 68
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
HỆ THỐNG CÁC KIẾN THỨC CƠ BẢN
TAM GIÁC
Diện tích của tam giác A * 1 S .A . B A . C sin A h ABC 2 1 C * S .BC.AH B H ABC 2 A
Các tam giác đặc biệt : b
Tam giác vuông : c + Định lý pitago: 2 2 2
BC AB AC
+ Diện tích tam giác vuông: a C B 1 S .A . B AC ABC 2 A
Tam giác cân:
+ Đường cao AH cũng là đường trung tuyến
+ Tính đường cao và diện tích
AH BH.tan B B C 1 H S .BC.AH ABC A 2
Tam giác đều 3
+ Đường cao của tam giác đều h AM A . B 2 3 G
( đường cao h = cạnh x 2 ) C B 3 M + Diện tích : 2 S (AB) . ABC 4 A B
TỨ GIÁC Hình vuông + Diện tích hình vuông : 2 S (AB) O ABCD
( Diện tích bằng cạnh bình phương) D C 69
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
+ Đường chéo hình vuông AC BD A . B 2
( đường chéo hình vuông bằng cạnh x 2 ) + OA = OB = OC = OD Hình chữ nhật
+ Diện tích hình vuông : S A . B AD A B ABCD
( Diện tích bằng dài nhân rộng)
+ Đường chéo hình chữa nhật bằng nhau và O OA = OB = OC = OD D C
CÁC CÁCH XÁC ĐỊNH GÓC Cách xác định góc
Góc giữa đường thẳng A và mặt phẳng (P): a
+ Tìm hình chiếu a’ của a lên mặt phẳng (P)
+ Khi đó góc giữa a và (P) là góc giữa a và a’ a' P
Góc giữa hai mặt phẳng (P) và (Q) :
+ Xác định giao tuyến d của (P) và (Q)
+ Tìm trong (P) đường thẳng a (d),
trong mặt phẳng (Q) đường thẳng b (d) b a
+ Khi đó góc giữa (P) và (Q) là góc giữa hai đường thẳng a và b P Q 70
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
CÁC CÁCH XÁC ĐỊNH KHOẢNG CÁCH
TỪ MỘT ĐIỂM M ĐẾN MP(P) M
►Cách 1: Tìm một mặt phẳng : (xem hình 1) P
P
Ke MH tai H MH Ptai H d M;
P MH MH M d
►Cách 2: Tìm một đường thẳngd : (xem hình 2) d / / P H d
d M;P d N;P
(đổi khoảng cách, QUY VỀ khoảng cáchcủa điểm khác khác dễ tính hơn) M d
►Cách 3: Tìm một đường thẳngd : (xem hình 3) d P I
d M ; P MI N d d N; P NI
►Cách 4: Ứng dụng “thể tích” để tính khoảng cách. 1 V V d S;
ABC S
d S; ABC ABC 3 SABC SABC 3 SABC 1 1 1
+ Hệ thức liên hệ trong tam giác vuông: 2 2 2 h b c với ,
b c là hai cạnh kề góc vuông, h - chiều cao từ góc vuông lên cạnh huyền tương ứng 71
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
ỨNG DỤNG VÀO HÌNH HỌC CỤ THỂ
Loại 1 Hình chóp tam giác S.ABC có cạnh bên SA (ABC) . Xét 3 trường hợp:
ABC vuông tại B
ABC cân tại A (hoặc đều)
ABC không cân tại A S S S H H H A C A C A C I I B B B d ,
A (SBC) AH d ,
A (SBC) AH d ,
A (SBC) AH
(Nếu SA (ABC) và ABC vuông tại A thì H là trực tâm của SBC )
Loại 2 Hình chóp tứ giác S.ABCD có cạnh bên SA (ABC )
D . Xét các trường hợp:
Đáy là hình chữ nhật
Đáy là hình hình hành
Đáy là hình thang vuông (hoặc hình vuông) (hoặc hình thoi)
(tại A và B ) S S S K T K H H D H D D A A A F I B C B E C B C d ,
A (SBC) AH d ,
A (SBC) AH d ,
A (SBC) AH d ,
A (SBC) AK d ,
A (SBC) AT d ,
A (SBC) AK Đáy là hình vuông
Đáy là hình chữ nhật Đáy là hình thang (hoặc hình thoi)
(hoặc hình bình hành thường)
(tại A và B ) S S S H H T D A D A A D I O I B C B C B C d , A (SB ) D AH d , A (SB ) D AH d , A (SB ) D AT 72
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018
Loại 3 Hình chóp tam giác đều
hình chóp tứ giác đều S S H H A C A D O O B B C d ,
O (SBC) OH d , O (SC ) D OH
TÍNH CÁC ĐẠI LƯỢNG HÌNH HỌC
Câu 1: Diện tích của tam giác ABC vuông tại A là: 1 1 1 A. S BC.AB B. S A . B AC C. S BC.AC D. S A . C AB 2 2 2
Câu 2: Diện tích của tam giác đều ABC là: AB 3 2 AB 3 2 AB 3 BC 3 A. S B. S C. S D. S 4 2 4 4
Câu 3: Diện tích của hình vuông ABCD là: 1 2 AB A. S A . B AC B. S C. S AB D. 2 S CD 2 2
Câu 4: Đường cao của tam giác đều ABC là: BC 3 2 AB 3 AB 3 BC 2 A. h B. h C. h D. h 2 2 4 3
Câu 5: Đường chéo của hình vuông ABCD là: BC 2 AB 2 A. d B. d AC 2 C. d D. d BC 3 2 3
Câu 6: Diện tích của hình thoi ABCD là: AC.BD 2 AB A. 2 S AB B. S C. S A . C BD D. S 2 2
Câu 7: Cho tam giác ABC vuông tại A, tanC là: AB AB AC BC A. tan C B. tan C C. tan C D. tan C BC AC AB AB
Câu 8: Cho tam giác ABC vuông tại B, sinA là: 73
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018 BC AC AB AC A. sin A B. sin A C. sin A D. sin A AC BC AC AB
XÁC ĐỊNH CHIỀU CAO
Câu 1: Cho hình chóp S.ABCD có (SAB) và (SAD) cùng vuông góc (ABCD) , đường cao là A. SB B. SA C. SC D. SD
Câu 2: Cho hình chóp S.ABCD đáy là hình vuông cạch a, M là trung điểm của AB,mặt phẳng SAB
là tam giác đều vuông góc với đáy. Đường cao là: A. SA B. SB C. SC D. SM
Câu 3: Cho hình chóp đều S.ABC gọi G là trọng tâm của tam giác ABC,đường cao là: A. SB B. SA C. SG D. SC
Câu 4: Cho hình chóp S.ABC gọi I thuộc BC, hình chiếu vuông góc S lên mặt đáy trùng với I, đường cao là A. SI B. SA C. SC D. SB
Câu 5: Cho lăng trụ đứng ABC.A’B’C’ đường cao là A. AB B. AB’ C. AC’ D. A’A.
Câu 6: Cho lăng trụ ABCD .A’B’C’D’ hình chiếu vuông góc A’ lên ABCD trùng với trung I điểm AC, đường cao là A. A’A B. A’B C. A’ I D. A’C XÁC ĐỊNH GÓC
Câu 1: Cho hình chóp S.ABCD có SA vuông góc với đáy góc giữa SC là đáy là . A SBA . B SAC . C SDA . D SCA
Câu 2: Cho hình chóp S.ABCD có ABCD là tứ giác đều tâm O và (SAB) và (SAD) cùng vuông góc
(ABCD) , góc giữa (SBD)và đáy là: . A SCO . B SOC . C SOA . D SCA
Câu 3: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. SA ABCD, SA a. Tính góc giữa SD và (ABCD) A. 0 30 B. 0 60 C. 0 45 D. arctan2
Câu 4: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. SA ABCD, SA a. Tính góc giữa SB và (SAD) 74
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018 A. 0 60 B. 0 30 C. 0 45 D. 0 90
Câu 5: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. SA ABCD, SA a. Tính góc giữa SC và (SAB) 2 A. 0 45 B. arctan C. 0 30 D. 0 60 2 KHOẢNG CÁCH
Câu 1: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. SA ABCD, SA a. Tính d S , A CD 2 3 A.
a B. a C. a D. a 2 2 4
Câu 2: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. SA ABCD, SA a. Tính d , B SCD 3 3 2 A. a B. a C. a 2 D. a 4 2 2
Câu 3: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. SA ABCD, SA a. Tính d B , D SC 6 3 3 6 A. a B. a C. a D. a 6 4 2 4 KHỐI ĐA DIỆN
Câu 1: Hãy chọn cụm từ (hoặc từ) cho dưới đây để sau khi điền nó vào chỗ trống mệnh đề sau
trở thành mệnh đề đúng:
“Số cạnh của một hình đa diện luôn …………..…… số mặt của hình đa diện ấy.” A. bằng B. nhỏ hơn hoặc bằng C. nhỏ hơn D. lớn hơn
Câu 2: Hãy chọn cụm từ (hoặc từ) cho dưới đây để sau khi điền nó vào chỗ trống mệnh đề sau
trở thành mệnh đề đúng:
“Số cạnh của một hình đa điện luôn ……………… số đỉnh của hình đa diện ấy.” A. bằng B. nhỏ hơn C. nhỏ hơn hoặc bằng D. lớn hơn 75
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – THỂ TÍCH HÌNH CHÓP 2018 CHÓP ĐỀ Trường hợp
Công thức tính nhanh 2 x 2 h b chop B 3 bê =b 2 2 2
x . 3b x V chop 12 S . x tan h chop 3 B 3 x .tan : V b chop b 12 . x tan h chop h 2 3 B A 3 x .tan : V C chop 24 x H 2 x h . x I chop B 3 Đ 3 2.x V chop 12 2 x 2 h b chop 2 x. B 2 2 2 bê =b x . 4b 2x V chop S 6 2. . x tan h chop 2 B 3 b 2.x .tan : V chop b 6 . x tan h chop 2 B A 3 D x .tan : V chop 6 x 2.x h I H chop 2 B C Đ : b = x 3 2.x x V chop 6
Gv cần file word xin liên hệ trực tiếp qua zalo – facebook – sđt : 0914449230 76
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)




