Phân tích dữ liệu | Bài tập nhóm môn một số kiến thức cơ bản về toán và thống kê

lOMoAR cPSD| 44985297
TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN lOMoAR cPSD| 44985297 -------***-------
PHÂN TÍCH DỮ LIỆU
Bài tập nhóm: Một số kiến thức cơ bản về toán và thống kê
Lớp học phần: Phân tích dữ liệu_01
Nhóm thực hiện: Nhóm 2 Họ và tên Mã Sinh viên 1) Bùi Huy Hoàng 11212331
2) Nguyễn Thị Hồng Duyên 11201045
3) Lê Anh Dũng 11204882 4) Quán Minh Dương 11211633 5) Trần Ngọc Đạt
11200764 6) Ninh Quỳnh Giao 11211840 7) Trần Thu Hải 11216935
8) Trần Thị Hiền 11212179 9) Vũ Đức Hiếu 11205303 Hà Nội 2023
MỘT SỐ KIẾN THỨC CƠ BẢN VỀ TOÁN VÀ THỐNG KÊ A.
KIẾN THỨC TOÁN Khái niệm về ma trận
Ma trận cấp , ký hiệu: là một bảng số xếp theo dòng và cột:
Trong đó được gọi là phần tử thuộc dòng i cột j của ma trận A. Ví dụ: 2 | Page lOMoAR cPSD| 44985297
là một ma trận cấp 2 x 3. Đối chiếu với ký hiệu tổng quát thì các phần tử của A là:
1. Ma trận chuyển vị -
Một ma trận chuyển vị của ma trận A, ký hiệu A’, là ma trận cấp có các
cột chính là các dòng tương ứng của A. -
Phép biến đổi ma trận A thành ma trận A’ được gọi là phép chuyển vị ma trận.
- Một số tính chất của ma trận chuyển vị bao gồm: + (A+B)’ = A’+B’ + (A’)’ = A + (kA)’ = kA’ + (AB)’ = B’A' -
Nếu xoay các dòng của A thành các cột (các cột thành các dòng) với thứ
tựtương ứng ta được một ma trận cấp m x n: -
Nếu gọi a’ij là phần tử thuộc dòng i cột j của ma trận chuyển vị A’ thì ta có:
a’ij = aij (i = 1, 2, …, n; j = 1, 2, ..., m) Ví dụ: 2. Ma trận vuông
- Ma trận vuông là ma trận có số dòng và số cột bằng nhau. Một ma trận có số
dòng và số cột bằng nhau và bằng n được gọi là ma trận vuông cấp n.
- Dạng tổng quát của ma trận vuông cấp n:
Các phần tử trên đường chéo chính
Các phần từ nằm trên đường chéo phụ
- Vị trí của các phần tử aij so với đường chéo chính được xác định theo chỉ số i, j như sau
+ aij thuộc đường chéo chính khi và chỉ khi i = j
+ aij nằm phía trên đường chéo chính khi và chỉ khi i < j
+ aij nằm phía dưới đường chéo chính khi và chỉ khi i > j
- Bất kỳ hai ma trận vuông có cùng một bậc có thể được cộng và nhân với nhau. lOMoAR cPSD| 44985297 Ví dụ
3. Ma trận đối xứng
- Một ma trận đối xứng là một ma trận vuông mà ma trận chuyển vị của nó
bằng chính nó. Nói cách khác, nếu A là một ma trận đối xứng, thì ma trận chuyển vị của A sẽ bằng A.
- Một số tính chất của ma trận đối xứng bao gồm:
+ Các phần tử của ma trận A bằng các phần tử
+ Tổng hai ma trận đối xứng cũng là một ma trận đối xứng.
+ Tích của một ma trận đối xứng với một ma trận khác không nhất thiết là
một ma trận đối xứng. - VD:
Ma trận => Ma trận chuyển vị
=> Ma trận A là ma trận đối xứng 4. Ma trận chéo
- Ma trận chéo là ma trận vuông có tất cả các phần tử nằm ngoài đường chéo
chính bằng 0. Đường chéo chính là đường chéo từ góc trên bên trái đến góc dưới bên phải của ma trận. - VD: Ma trận chéo
- Trong ma trận này, tất cả các phần tử nằm ngoài đường chéo chính (các phầntử
không thuộc các vị trí (i, i)) đều bằng 0. Các phần tử trên đường chéo chính có
thể là bất kỳ giá trị nào.
- Một số tính chất của ma trận chéo bao gồm:
+ Tổng hai ma trận chéo là một ma trận chéo.
+ Tích của một ma trận chéo với một ma trận khác có thể không còn là ma trận chéo nữa.
- Trường hợp đặt biệt, Khi , ma trận đường chéo được gọi là ma trận vô hướng.
5. Ma trận đơn vị -
Ma trận đường chéo có tất cả các phần tử thuộc đường chéo chính bằng 1
đượcgọi là ma trận đơn vị. Mỗi cấp ma trận vuông có một ma trận đơn vị được ký hiệu bằng chữ E: 4 | Page lOMoAR cPSD| 44985297 -
Trong ma trận đơn vị, các phần tử tại vị trí (i, i) (các phần tử trên đường
chéochính) đều bằng 1, và các phần tử còn lại đều bằng 0. -
Ma trận đơn vị có tính chất đặc biệt là khi nhân một ma trận bất kỳ với
ma trậnđơn vị, ta sẽ thu được ma trận ban đầu.
6. Ma trận trực giao
- Ma trận trực giao là một loại ma trận vuông, với các phần tử là số thực hoặc
không phức tạp, mà khi chuyển vị (hoán đổi hàng và cột) của nó bằng với ma
trận nghịch đảo của nó. Điều này có nghĩa là tích của ma trận ban đầu với ma
trận chuyển vị của nó là ma trận đơn vị.
+ A là ma trận trực giao khi AT= A-1
+ A’ .A= A. A’ = I (I là ma trận đơn vị) Ví dụ:
7. Hạng của ma trận
7.1. Định nghĩa và các tính chất cơ bản
- Định thức con cấp k của ma trận : Cho A là ma trận cấp m x n; k là số tự nhiên 1
≤ k ≤ min{m, n}. Chọn ra k dòng và k cột bất kỳ của A. Các phần tử thuộc giao của k
dòng, k cột này tạo thành ma trận vuông cấp k, gọi là ma trận con cấp k của ma trận A.
Định thức của ma trận con cấp k này gọi là một định thức con cấp k của A.
7.1.1 Định nghĩa hạng của ma trận
Cho A là ma trận cấp m x n khác không.
Hạng của ma trận A là số tự nhiên r, 1 ≤ r ≤ min{m, n} thỏa mãn các điều kiện sau :
1. Tồn tại ít nhất một định thức con cấp r của ma trận A khác 0.
2. Mọi định thức con cấp lớn hơn r ( nếu có) của ma trận A đều bằng0). lOMoAR cPSD| 44985297
Tức là, hạng của ma trận A ≠ O chính là cấp cao nhất của các định thức con
khác không của ma trận A.
Hạng của ma trận A ký hiệu là r(A) hoặc rank(A).
Quy ước : Hạng của ma trận O là 0.
7.1.2 Các tính chất cơ bản về hạng của ma trận
1. Hạng của ma trận không thay đổi qua phép chuyển vị, tức là rank At = rank A
2. Nếu A là ma trận vuông cấp n thì : rank A = n ⇔ det A ≠ 0 rank A < n ⇔ det A = 0
Nếu xảy ra trường hợp đầu, ta nói A là ma trận vuông không suy biến. Nếu
xảy ra trường hợp thứ hai, ta nói A là ma trận vuông suy biến.
3. Nếu A, B là các ma trận cùng cấp thì :
rank(A + B) ≤ rank A + rank B
4. Cho A, B là các ma trận sao cho tồn tại tích AB. Khi đó :
rank(AB) ≤ min{rankA, rankB};
Nếu A là ma trận vuông không suy biến thì rank{AB} = rankB.
7.2 Tìm hạng của ma trận bằng phương pháp định thức
- Từ định nghĩa hạng của ma trận ta có thể suy ra các bước để tìm hạng của ma
trận A cấp m x n (A ≠ O)
+ Bước 1: Tìm một định thức con cấp k khác 0 của A. Số k càng lớn càng
tốt. Giả sử định thức con cấp k khác không là Dk .
+ Bước 2: Xét tất cả các định thức con cấp k + 1 của A bao quanh Dk Xảy ra 3 khả năng sau : 1.
Không có một định thức con cấp k + 1 nào của A. Khả năng
nàyxảy ra khi và chỉ khi k = min{m, n}. Khi đó, rank A =k = min{m, n}. Thuật toán kết thúc. 2.
Tất cả các định thức con cấp k+1 của A chứa định thức con Dk
đều bằng 0. Khi đó, rankA=k. Thuật toán kết thúc. 3.
Tồn tại một định thức con cấp k + 1 của A là Dk+1 bao quanh
Dk thì ta lại chuyển sang xét các định thức k + 2 bao quanh Dk+1 ( nếu có). 6 | Page lOMoAR cPSD| 44985297
Lặp lại quá trình này sau một số hữu hạn bước ta sẽ xác định được hạng của ma trận.
Ví dụ : Tìm hạng của ma trận: Giải
Vì là ma trận cỡ 3 x 5 nên chỉ có thể có các định thức con cấp 3 trở xuống
+ Xét định thức con cấp 3
Vì hàng 3 bằng tổng của hàng 1 và 2 => Các định thức cấp 3 đều = 0 (tính chất 6) => r(A) < 3 + Xét định thức cấp 2
7.3 Tìm hạng của ma trận bằng phương pháp sử dụng các phép biến đối sơ
cấp (Phương pháp Gause)
Một vài khái niệm cần nhớ
7.3.1 Ma trận bậc thang
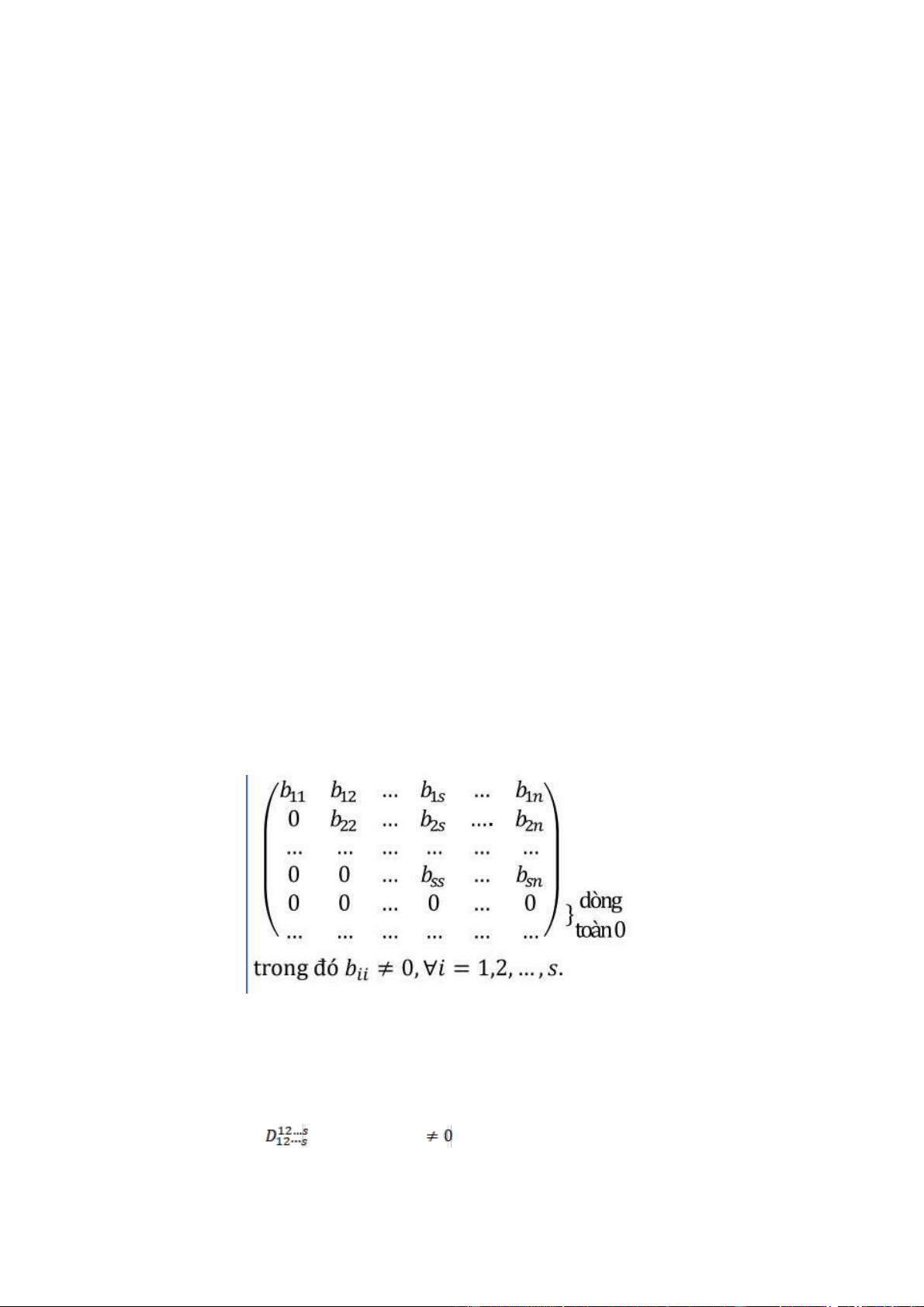
- Xét ma trận bậc thang có dạng :
Nếu xóa đi các dòng gồm tất cả các phần tử bằng 0 phía dưới dòng thứ s(nếu
có) thì hạng của ma trận trên không thay đổi ( do mỗi dòng đó biểu diễn tuyến
tính qua các dòng còn lại). Mặt khác ta thấy ma trận trên có một định thức cấp s khác 0 : = b11b22 ... bss lOMoAR cPSD| 44985297
Điều này chứng tỏ hạng của ma trận trên bằng s.
Tức là, hạng của ma trận bậc thang bằng số dòng khác không của nó.
7.3.2 Phép biến đổi sơ cấp trên ma trận
- Ba phép biến đổi sau gọi là phép biến đổi sơ cấp trên các dòng của ma trận:
1. Đổi chỗ 2 dòng cho nhau
2. Nhân 1 dòng cho 1 số khác 0
3. Cộng vào một dòng tích của dòng khác với 1 số khác 0.
- Tương tự, bằng cách thay dòng thành cột, ta có 3 phép biến đổi sơ cấp trên cáccột của ma trận.
7.3.3 Tìm hạng của ma trận bằng phương pháp sử dụng các phép biến đổi sơ cấp
- Nội dung của phương pháp này dựa trên hai nhận xét khá đơn giản sau: 1.
Các phép biến đổi sơ cấp không làm thay đổi hạng của ma trận. 2.
Một ma trận khác O bất kỳ đều có thể đưa về dạng bậc thang sau
một sốhữu hạn các phép biến đổi sơ cấp trên dòng.
- Như vậy, muốn tìm hạng của ma trận A, ta dùng các phép biến đổi sơ cấp đểđưa
A về dạng bậc thang, do nhận xét (1), hạng của A bằng hạng của ma trận bậc
thang, và ta đã biết hạng của ma trận bậc thang chính bằng số dòng khác không của nó. Xét ma trận : + Bước 1:
Bằng cách đổi chỗ 2 dòng cho nhau ( nếu cần), ta giả sử a11 ≠ 0.
Nhân dòng (1) với , cộng vào dòng (2),
Nhân dòng (1) với - , cộng vào dòng (3),
Nhân dòng (1) với - , cộng vào dòng (n).
Ta nhận được ma trận: 8 | Page lOMoAR cPSD| 44985297 + Bước 2 : Xét ma trận :
Nếu B = O hoặc B có dạng bậc thang thì A1 là ma trận bậc thang, thuật toán
kết thúc. Trong trường hợp ngược lại, tiếp tục lặp lại bước 1 cho ma trận B.
Cần chú ý rằng ma trận B có ít hơn ma trận A 1 dòng và 1 cột. Do đó, sau một
số hữu hạn bước lặp, B sẽ là ma trận không hoặc ma trận bậc thang. Khi đó thuật toán sẽ kết thúc. 7.4 Ví dụ
Tìm hạng của ma trận : lOMoAR cPSD| 44985297 Giải Vậy rank A = 3
7.5 Hạng của ma trận phụ hợp
Cho A = ( aij) n x n (n > 2) là ma trận vuông cấp n, khi đó : 1. r(A) = n ⇔ r(A*) = n ;
2. r(A) ≤ n - 2 ⇔ r(A*) = 0 ; 3. r(A) = n - 1 ⇔ r(A*) = 1 10 | Page lOMoAR cPSD| 44985297 Ví dụ :
7.6 Hạng của ma trận tổng và tích
Định lý : Cho 2 ma trận A và B :
1. r( A + B ) ≤ r(A) + r(B) ;
2. r(AB) ≤ min { r(A) ; r(B) } ( r(AB) ≤ r(A) ; r(AB) ≤ r(B) )
Ví dụ : Cho A = ( aij) 5 x 3 a, Tìm ma
trận phụ hợp của A x A’ b, Tìm ma trận
phụ hợp của ( -3AA’)2017 Giải
a, A5x3 . A’3x5 = AA’5x5 => r(AA’) ≤ r(A) ≤ 3
=> Tất cả các định thức con cấp 4 của ma trận AA’ bằng 0. Vậy (AA’)* = 0
b, r [ (-3AA’)2017] ≤ r(AA’) ≤ r(A) ≤ 3.
=> [ (-3AA’)2017]* = O5x5
7.7 Khảo sát hạng của hệ vectơ
Cho hệ m vectơ n chiều X1 , X2, …, Xm. Gọi A là ma trận nhận X1 , X2, …, Xm 11 |
Downloaded by Ho Thi Thu Trang (23a4010661@hvnh.edu.vn) lOMoAR cPSD| 44985297
theo thứ tự đó làm các dòng. Khi đó, r { X1 , X2, …, Xm } = r(A) : Page
1. Khi r { X1 , X2, …, Xm } = m khi và chỉ khi hệ vectơ X1 , X2, …, Xm độc lập tuyến tính;
2. Khi r { X1 , X2, …, Xm } < m khi và chỉ khi hệ vectơ X1 , X2, …, Xm phụ thuộc tuyến tính. 12 |
Downloaded by Ho Thi Thu Trang (23a4010661@hvnh.edu.vn) lOMoAR cPSD| 44985297 Page 13 |
Downloaded by Ho Thi Thu Trang (23a4010661@hvnh.edu.vn)