










Preview text:
PHIẾU BÀI TẬP TOÁN 9 - CHƯƠNG IV Năm học 2024-2025
A. TÓM TẮT LÝ THUYẾT
Kiến thức cần nhớ
I. Khái niệm tỉ số lượng giác của góc nhọn
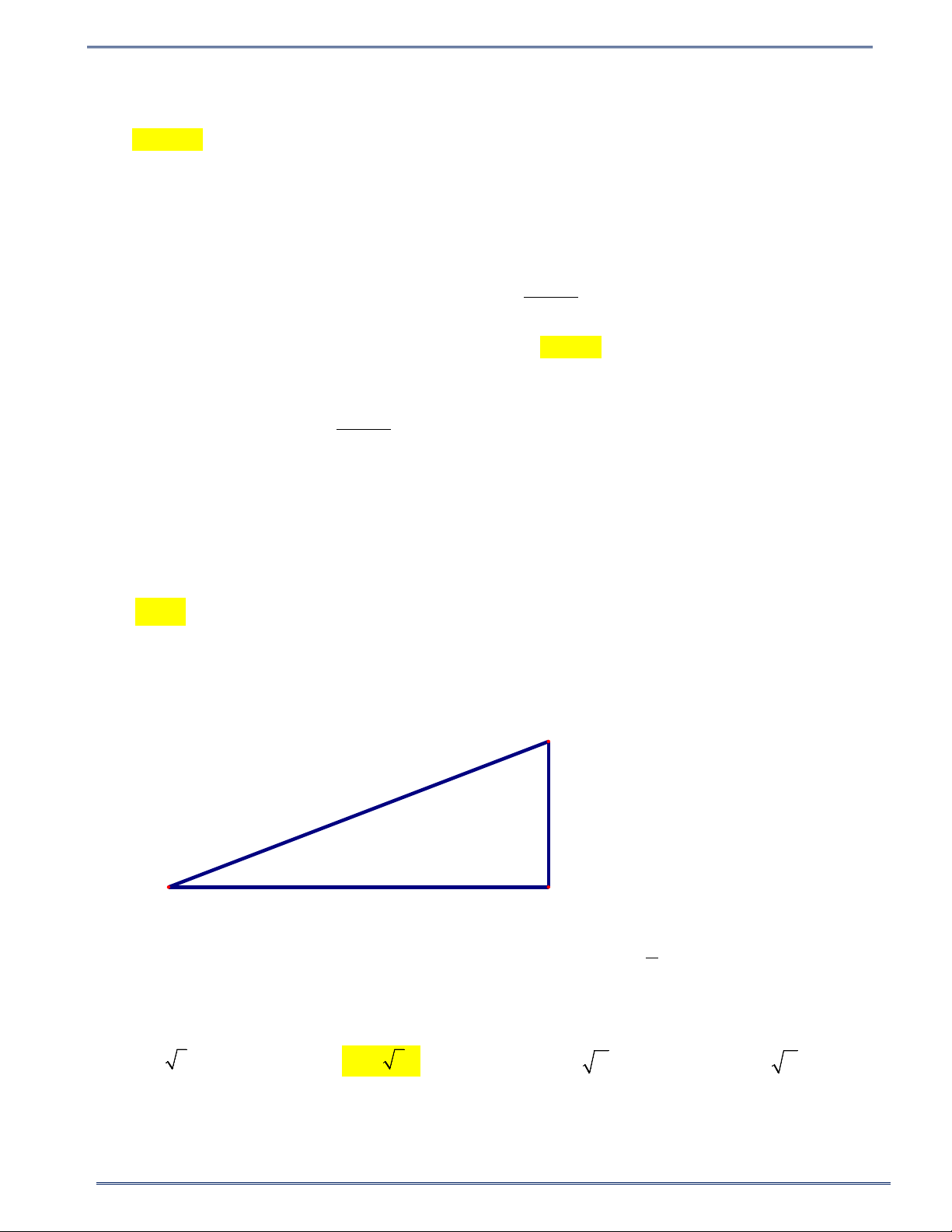
Cho tam giác ABC vuông tại A , với góc nhọn B thì:
Cạnh BC là cạnh huyền.
Cạnh AC là cạnh đối và cạnh AB là cạnh kề. A Cạnh kề Cạnh đối B Cạnh huyền C
Khi đó, ta có 4 tỉ số lượng giác của góc nhọn B như sau: sin AC B =
(tỉ số cạnh đối và cạnh kề) cos AB B =
(tỉ số cạnh kề và cạnh huyền) BC BC tan AC B =
(tỉ số cạnh đối và cạnh kề) cot AB B =
(tỉ số cạnh kề và cạnh đối) AB AC
Chú ý: Giá trị sin và cos của một góc nhọn luôn nhỏ hơn 1 (vì trong tam giác vuông, cạnh huyền là cạnh lớn nhất).
II. Tỉ số lượng giác của hai góc phụ nhau
Cho tam giác ABC vuông tại A . Khi đó, góc B và gócC là hai góc phụ nhau. A B C Định lí:
Nếu hai góc phụ nhau thì sin góc này bằng cos góc kia và tan góc này bằng cot góc kia.
sin B = cosC cos B = sinC tan B = cotC cot B = tanC
Chú ý: Một số công thức biến đổi α α
sin2α + cos2α = 1 tanα.cotα = 1 sin tanα = cos cotα = cosα sinα 1 Đại số 9
PHIẾU BÀI TẬP TOÁN 9 - CHƯƠNG IV Năm học 2024-2025
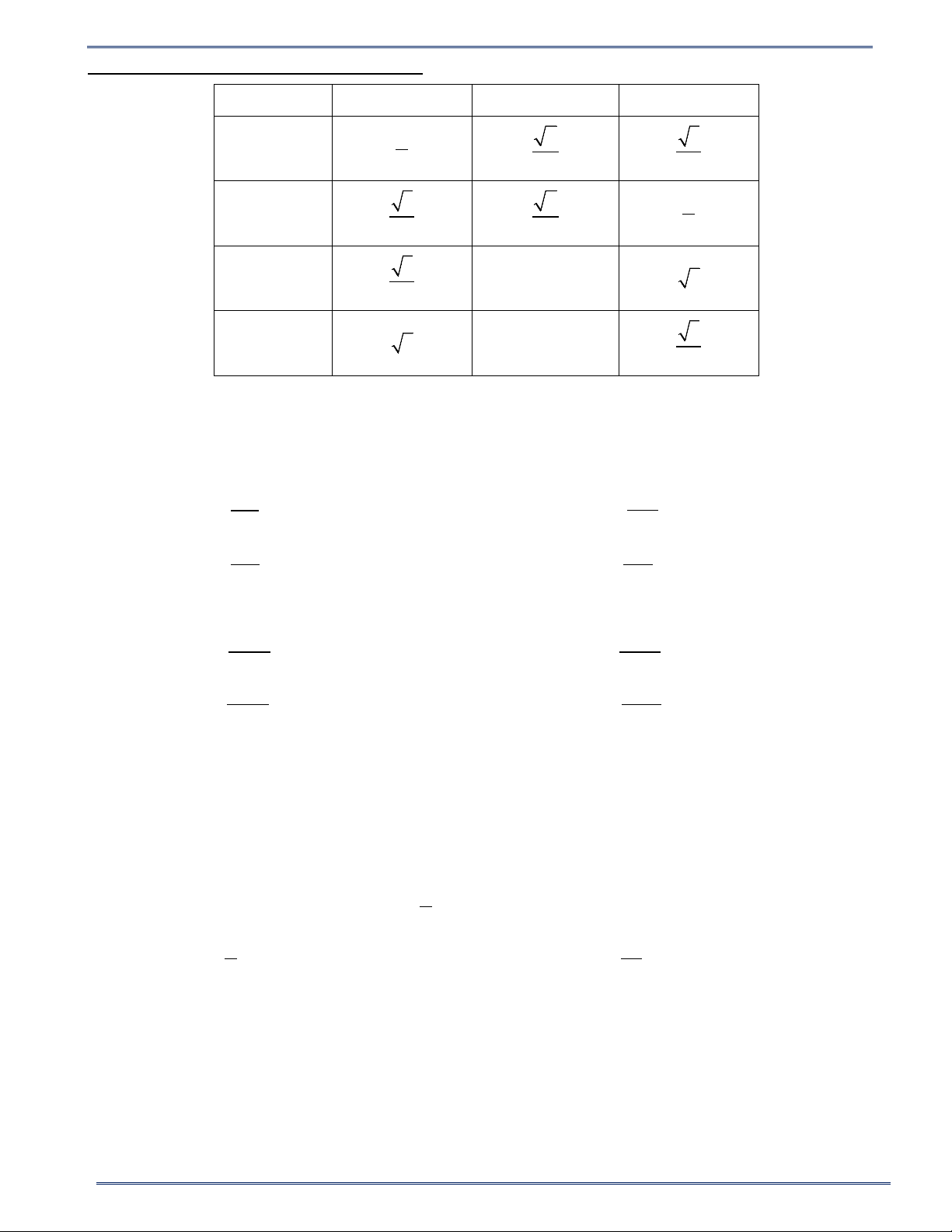
Bảng tỉ số lượng giác của các góc đặc biệt: 30° 45° 60° sinα 1 2 3 2 2 2 1 cosα 3 2 2 2 2 tanα 3 1 3 3 cotα 3 1 3 3
A. BÀI TẬP TRẮC NGHIỆM
I – MỨC ĐỘ NHẬN BIẾT
Câu 1: Cho tam giác ABC vuông tại A có góc nhọn C bằng α Khi đó cosα bằng A. cos AB α = B. cos AC α = BC BC C. cos AB α = D. cos AC α = AC AB
Câu 2: Cho α là góc nhọn bất kì. Khẳng định đúng là A. 1 cosα = B. 1 sinα = tanα tanα C. 1 cotα = D. 1 cotα = tanα sinα
Câu 3: Cho tam giác vuông có góc α là góc nhọn. Khẳng định sai là
A. Tỉ số giữa cạnh đối và cạnh huyền được gọi là cosin của góc α , kí hiệu cos α
B. Tỉ số giữa cạnh kề và cạnh huyền được gọi là cosin của góc α , kí hiệu cos α
C. Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc α , kí hiệu tan α
D. Tỉ số giữa cạnh kề và cạnh đối được gọi là cosin của góc α , kí hiệu cot α
Câu 4: Cho α là góc nhọn bất kì có 1
tanα = , khi đó cotα bằng: 7 A. 1 cotα = B. 1 cotα − = 7 7 C. cotα = 7 D. cotα = 7 −
Câu 5: Cho α; β là hai góc nhọn phụ nhau, khi đó:
A. sinα =cos β
B. sinα =cot β
C. sinα = tan β D. cosα =cot β
Câu 6: Tỉ số lượng giác của góc nào lớn hơn tỉ số lượng giác của góc 45°? A. sin 25° B. cos 25° C. cos30° D. tan 50° 2 Đại số 9
PHIẾU BÀI TẬP TOÁN 9 - CHƯƠNG IV Năm học 2024-2025
Câu 7: Tỉ số lượng giác của góc nào nhỏ hơn tỉ số lượng giác của góc 45°? A. cos55° B. sin 75° C. cot 30° D. tan 40°
II – MỨC ĐỘ THÔNG HIỂU
Câu 8: Cho tam giác ABC vuông tại A Khi đó, trong các khẳng định sau, khẳng định nào đúng? AB cosC A. =
B. sin B = cosC AC cos B
C. sin B = tan C
D. tan B = cosC
Câu 9: Cho tam giác ABC vuông tại C có AC =1c ,
m BC = 2cm . Tính tỉ số lượng giác sinB, cosB 1 2 3 5 2 5 A. sin B = ;cos B = B. sin B = ;cos B = 3 3 5 5 1 2 2 5 5
C. sin B = ;cos B = D. sin B = ;cos B = 2 5 5 5
Câu 10: Cho tam giác ABC vuông tại C có AC =1,2c ,
m BC = 0,9cm .Tính các tỉ số lượng giác sinB, cosB
A. sin B = 0,6; cos B = 0,8 B. sin B = 0,8; cos B = 0,6
C. sin B = 0,4; cos B = 0,8 D. sin B = 0,6; cos B = 0,4
Câu 11: Cho tam giác ABC, vuông tại A có AB = 3; AC = 4.Chọn khẳng định sai? AC 4 AB 3 A. sin B = = B. cos B = = BC 5 BC 5 AC 4 AC 4 C. tan B = = D. cot B = = AB 3 BC 5
Câu 12: Cho tam giác ABC vuông tại A, có B = 34° Khi đó: A. sin = sin34 AB B ° = B. cos = cos34 AB B ° = BC BC C. tan = tan 34 AC B ° = D. cot = cot 34 AC B ° = BC AB
Câu 13: Không dùng MTBT, tính giá trị của biểu thức M = sin 35 12 ° '− sin 20 25
° ' ( làm tròn đến chữ số thập phân thứ ba ) A. M = 0,15 B. M = 0,154 C. M = 0,23 D. M = 0,228
Câu 14: Không dùng MTBT, tìm độ đo của góc nhọn x (làm tròn đến phút) của cot x =1,254 A. x ≈ 51 25 ° ' B. x ≈ 51 52 ° ' C. x ≈ 38 34 ° ' D. x ≈ 38 43 ° '
Câu 15: Không dùng MTBT, tính giá trị của biểu thức K = tan 76° − cot14° A. K = 0 B. K =1 C. K = 2 D. K = 3
Bài 16: Không dùng MTBT, tính giá trị của biểu thức sin 32 I ° = cos58° 3 Đại số 9
PHIẾU BÀI TẬP TOÁN 9 - CHƯƠNG IV Năm học 2024-2025 A. I = 4 B. I = 2 C. I =1 D. I = 3
III – MỨC ĐỘ VẬN DỤNG
Câu 17: Một cái thang dài 6m, được đặt tạo với mặt đất một góc 60°, vậy chân thang cách tường bao nhiêu mét? A. 3m B. 3,2 m C. 7,8m D. 0,4m
Câu 18. Một mảnh vườn hình chữ nhật có chiều dài là 30m , góc giữa đường chéo và chiều dài của mảnh
vườn là 30° . Tính chiều rộng của mảnh vườn hình chữ nhật đó. A. 20 3m B. 10 3m C. 10 6 m D. 20 6 m
Câu 19: Một máy bay đang bay ở độ cao 12km , khi hạ cánh xuống mặt đất, đường đi của máy bay tạo với
mặt đất một góc nghiêng α . Nếu cách sân bay 320km máy bay bắt hạ cánh thì góc nghiêng α làm tròn đến phút) là A. α ≈ 87 51 ° ' B. α ≈ 87 52 ° ' C. α ≈ 2 9' ° D. α ≈ 2 8' °
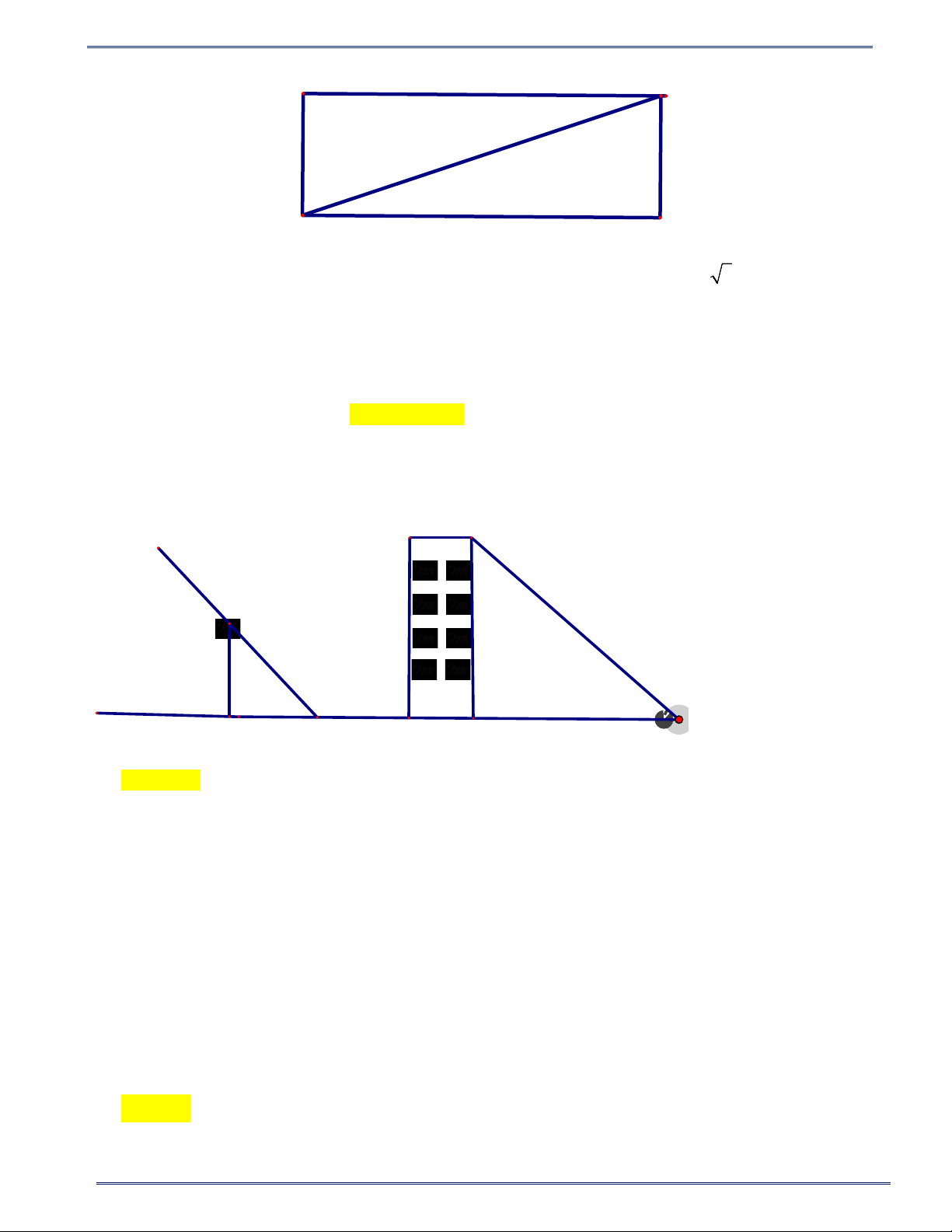
Câu 20: Một cột đèn cao 7m có bóng trên mặt đất dài 4m , gần đó có một tòa nhà cao tầng có bóng trên mặt
đất dài 80m ( hình vẽ ). Em hãy cho biết tòa nhà đó có bao nhiêu tầng, biết rằng mỗi tầng cao 2m 7m α 4m 80m A. 80 tầng B. 75 tầng C. 70 tầng D. 60 tầng
IV – MỨC ĐỘ VẬN DỤNG CAO
Câu 21: Một học sinh dùng giác kế, đứng cách chân cột cờ 10m rồi chỉnh mặt ngắm cao bằng mắt của mình
để xác định góc “ nâng “ ( góc tạo bởi tia sáng đi thẳng từ cột cờ với mắt tạo với phương nằm ngang). Khi
đó góc nâng đo được là 31° , biết khoảng cách từ mặt sân đến mắt học sinh đó bằng 1,5m , tính chiều cao
cột cờ ( kết quả làm tròn đến một chữ số thập phân ) A. 6,0m
B. 16,6m C. 7,5m D. 5,0m
Câu 22: Tính chiều cao của một ngọn núi ( làm tròn đến mét ), biết tại hai điểm A, B cách nhau 500m,
người ta nhìn thấy đỉnh núi với góc nâng lần lượt là 34 ,° 38°
A. Chiều cao ngọn núi là 2667,7m
B. Chiều cao ngọn núi là 2647,7m
C. Chiều cao ngọn núi là 2467,7m
D. Chiều cao ngọn núi là 2447,7m
Câu 23: Trên một quả đồi có một cái tháp cao 100m , từ đỉnh B và chân C của tháp nhìn điểm A ở chân
đồi dưới các góc tương ứng bằng 60°và 30° so với phương nằm ngang. Chiều cao h của quả đồi là70°
A. h = 50m
B. h = 45m
C. h = 52m
D. h = 47m 4 Đại số 9
PHIẾU BÀI TẬP TOÁN 9 - CHƯƠNG IV Năm học 2024-2025
Câu 24: Từ nhà bạn An đến trường học, bạn phải đi đò qua một khúc sông rộng đến điểm A ( bờ bên kia)
rồi từ A đi bộ đến trường tại điểm D ( ở hình bên ) Thực tế, do nước chảy nên chiếc đò bị dòng nước đẩy
xiên một góc đưa bạn tới điểm C ( bờ bên kia ) Từ C bạn An đi bộ đến trường theo đường CD mất thời gian
gấp đôi khi đi từ A đến trường theo đường AD. Độ dài quãng đường CD là (giả sử vận tốc đi bộ của bạn
An không thay đổi ( chuyển động thẳng đều ) kết quả làm tròn đến hàng đơn vị ) A. 190m B. 220m C. 200m D. 210m
Câu 25: Nhà bạn Bình có gác lửng cao so với nền nhà là 3m. Ba của bạn Bình cần đặt một thang đi lên gác,
biết khi đặt thang phải để thang tạo được với mặt đất một góc 70° thì đảm bảo sự an toàn khi sử dụng. Với
kiến thức đã học, Bình hãy giúp Ba của mình tính chiều dài thang là bao nhiêu mét để sử dụng ( kết quả làm
tròn đến chữ số thập phân thứ hai) A. 4,24 B. 2,34 C. 2,43 D. 3,19
B. CÁC DẠNG TỰ LUẬN
Dạng 1. Tính tỉ số lượng giác của góc nhọn, tính cạnh, tính góc. Phương pháp giải
Vận dụng các tỉ số lượng giác của góc B và các công thức biến đổi (xem ở phần lý thuyết trên).
Bài 1. Cho tam giác ABC vuông tạiC có BC =1,2 , m AC = 0,9 .
m Tính các tỉ số lượng giác của góc B . Từ đó
suy ra tỉ số lượng giác của góc A .
Bài 2. Cho tam giác ABC vuông tại A , đường cao AH . Hãy tính sin B và sinC trong các trường hợp sau
(làm tròn kết quả đến chữ số thập phân thứ 4): a) AB =13c ; m BH = 0,5d . m b) AH = 3c ; m CH = 4c . m
Bài 3. Cho tam giác ABC có AB = a 5;BC = a 3; AC = a 2.
a) Chứng minh tam giác ABC là tam giác vuông.
b) Tính các tỉ số lượng giác của góc B . Từ đó suy ra tỉ số lượng giác của góc A .
Bài 4. Cho tam giác ABC vuông tại A . Hãy tính các tỉ số lượng giác của góc C biết rằng: cosC = 0,6.
Bài 5. Cho tam giác ABC vuông tại A , 5 AB = 5c ,
m cot B = . Tính độ dài các đoạn thẳng AC và BC. 8
Dạng 2. Sắp thứ tự dãy các tỉ số lượng giác và tính giá trị biểu thức Phương pháp giải
Để sắp xếp thứ tự dãy các tỉ số lượng giác cho trước, ta cần làm được hai bước sau:
Bước 1: Đưa về các tỉ số lượng giác trong các bài toán cùng loại bằng cách sử dụng tính chất:
“Nếu hai góc phụ nhau thì sin góc này bằng cos góc kia, tan góc này bằng cot góc kia”.
Bước 2: Với hai góc nhọn α, β , ta có: 5 Đại số 9
PHIẾU BÀI TẬP TOÁN 9 - CHƯƠNG IV Năm học 2024-2025
sinα < sin β ⇔ α < β;
cosα < cos β ⇔ α > β;
tanα < tan β ⇔ α < β;
cotα < cot β ⇔ α > β .
Bài 1. Không dùng bảng số và máy tính, hãy so sánh: a) sin 20°vàsin 70 .° b) cos60° vàcos70 .° c) tan 73 20 ° ′ và tan 45 .° d) cot 20° vàcot 37 40 ° .′
Bài 2. Sắp xếp các tỉ số lượng giác sau theo thứ tự
a) Từ bé đến lớn: tan 42 ,°cot 71 ,° tan 38 ,°cot 69 15 ° ,′ tan 28 .°
b) Từ lớn đến bé: cos67 ,°sin 56 ,°cos63 41 ° ,′sin 74 ,°cos85 .°
Bài 3. Tính giá trị các biểu thức sau:
a) A = sin 23° − cos67 ;°
b) B = cos34° − sin 56 ;°
c) C = tan18° − cot 72 ;° d) 2 2
D = sin 10° + cos 10 ;° e) 2 2
E = sin 60° + sin 30 ;°
f) F = cos 25° − sin 65 ;°
g) G = tan 40° − cot 50 ;° h) 1 H = .tan 2 .° cot 2°
Bài 4. Tính giá trị các biểu thức sau: a) sin 60 .°cos30° A = ;
b) B = sin 30° − 2cos60° + tan 45 ;° 2.cot 45°
c) C = sin 45° + cot 60 .°cos30 ;°
d) D = cot 44 .°cot 45 .°cot 46 ;° e) 3.cot 60° E ° = ; f) cos60 1 F = + ; 2 2cos 60° −1 1+ sin 60° tan 30° g) 2 2 3
G =10 − sin 45° + 3cos 60° − 5cos 45 ;°
h) H = tan 45 .°cos30 .°cot 30 .°
Bài 5. Không dùng bảng số và máy tính, hãy tính:
a) A = sin10° + sin10° − cos50° − cos80 ;° b) 2 2 2 2
B = cos 15° + cos 55° + cos 35° + cos 75 ;° c) 2 2
C = cos 81° + cos 9° − 5.cot 62 .°cot 28 ;° d) 2 2 2 2 2 2
D = cos 20° + cos 30° + cos 40° + cos 50° + cos 60° + cos 70 ;° e) 2 2 2 2 2
E = sin 5° + sin 25° + sin 45° + sin 65° + sin 85 .° f) 2 2 8.cot 35
F 12.tan 32 .tan 58 sin 51 sin 39 ° = ° ° + ° + ° − ; tan 55° g) 2 2 cot 22
G sin 50 sin 40 tan 28 cot 62 ° = ° + ° − ° + ° − ; tan 68° h) 2 2sin 37° 2
H = cot13 .°cot 77° − sin 26° − − sin 64 .° 3cos53°
Dạng 3.Toán thực tế 6 Đại số 9
PHIẾU BÀI TẬP TOÁN 9 - CHƯƠNG IV Năm học 2024-2025 Phương pháp giải
Vận dụng các tỉ số lượng giác của góc B và các công thức biến đổi (xem ở phần lý thuyết trên)
để giải các bài toán thực tế.
Bài 1. Vào thời điểm các tia nắng mặt trời tạo với mặt đất một góc A
60 ,° bóng của một cái tháp trên mặt đất dài 20m (hình vẽ bên).
Tính chiều cao của tháp. (Kết quả làm tròn đến số thập phân thứ hai) 60° C 20 m B
Bài 2. Để đo chiều cao của một tháp, không thể trèo lên đỉnh, người ta dùng thước dài, thước đo góc và đèn
laser để thực hiện thao đó thu được kết quả như hình vẽ. Hãy tính chiều cao của tháp. A 20 m 40° C B
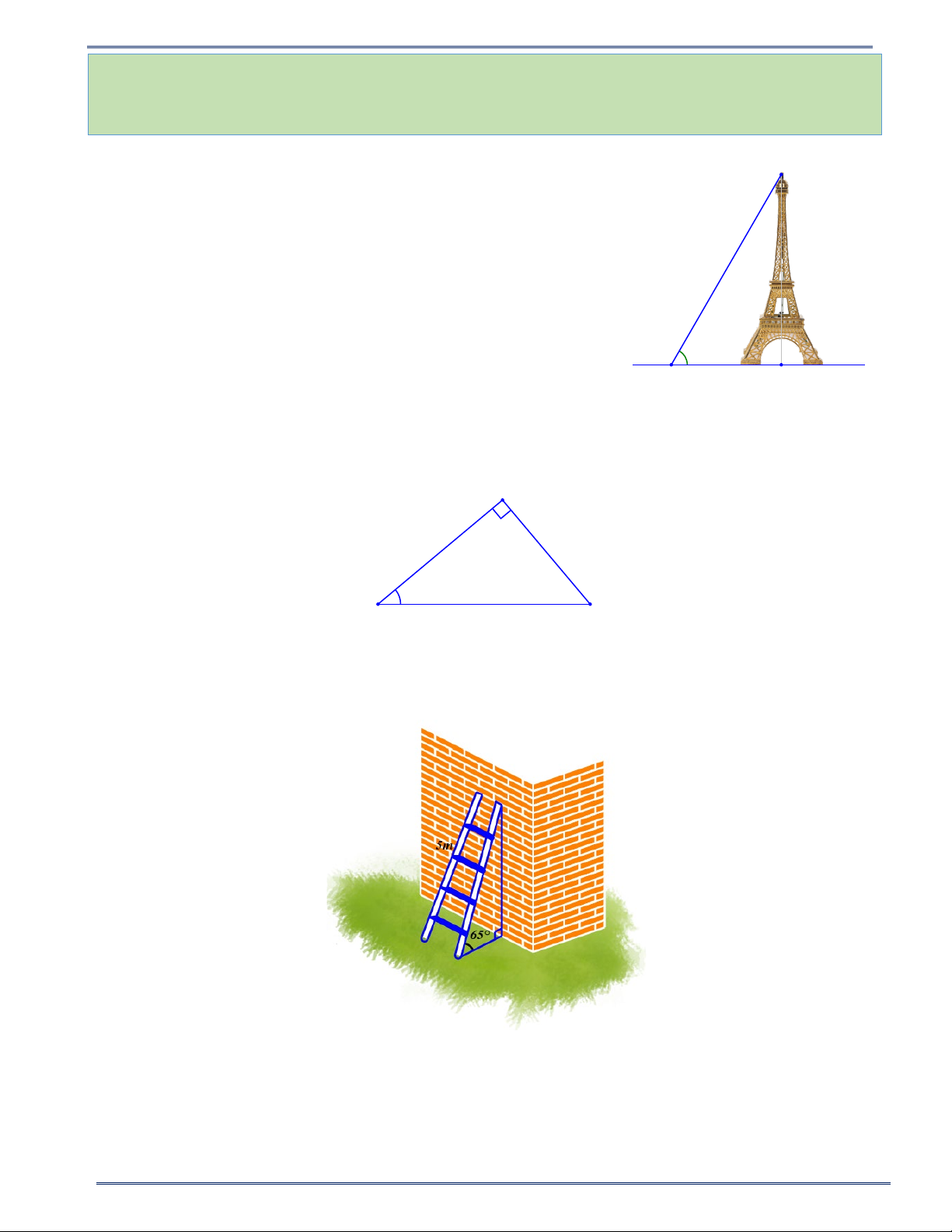
Bài 3. Đặt một chiếc thang dài 5mét vào bức tường như hình vẽ, để người trèo thang được an toàn, theo
kinh nghiệm người ta đặt chiếc thang đó tạo với mặt đất góc 65. Hỏi khi đó chiếc thang đạt độ cao bao nhiêu?
Bài 4. Trong một buổi luyện tập, một tàu ngầm ở trên mặt biển bắt đầu lặn xuống và di chuyển theo một
đường thẳng tạo với mặt nước biển một góc 0 21 . (Hình 30) 7 Đại số 9
PHIẾU BÀI TẬP TOÁN 9 - CHƯƠNG IV Năm học 2024-2025 21° Hình 30
a) Khi tàu chuyển động theo hướng đó và đi được 250m thì tàu ở độ sâu bao nhiêu so với mặt nước
(làm tròn đến hàng đơn vị).
b) Giả sử tốc độ trung bình của tàu là 9km/h thì sau bao lâu (tính từ lúc bắt đầu lặn) tàu ở độ sâu 200
mét (cách mặt nước biển 200m) (làm tròn đến phút).
Bài 5. Một khúc sông rộng khoảng 250 .
m Một chiếc đò chèo qua sông bị dòng nước đẩy lệch đi một góc
40°. Hỏi con đò phải đi thêm bao nhiêu mét nữa so với dự định ban đầu để qua được khúc sông ấy? 8 Đại số 9
PHIẾU BÀI TẬP TOÁN 9 - CHƯƠNG IV Năm học 2024-2025
C. ĐÁP ÁN BÀI TẬP TRẮC NGHIỆM:
BẢNG ĐÁP ÁN BÀI TẬP TRẮC NGHIỆM 1 2 3 4 5 6 7 8 9 10 B C D C A D D C C B 11 12 13 14 15 16 17 18 19 20 D D B A C B A B B A 21 22 23 24 25 C C A C D HƯỚNG DẪN
Câu 1: Cho tam giác ABC vuông tại A có góc nhọn C bằng α Khi đó cosα bằng A. cos AB α = B. cos AC α = BC BC C. cos AB α = D. cos AC α = AC AB HƯỚNG DẪN
Chọn B, theo định nghĩa tỉ số lượng giác trong tam giác vuông.
Câu 2: Cho α là góc nhọn bất kì. Khẳng định đúng là A. 1 cosα = B. 1 sinα = tanα tanα C. 1 cotα = D. 1 cotα = tanα sinα HƯỚNG DẪN
Chọn C, theo định nghĩa tỉ số lượng giác trong tam giác vuông.
Câu 3: Cho tam giác vuông có góc α là góc nhọn. Khẳng định sai là
A. Tỉ số giữa cạnh đối và cạnh huyền được gọi là cosin của góc α , kí hiệu cos α
B. Tỉ số giữa cạnh kề và cạnh huyền được gọi là cosin của góc α , kí hiệu cos α
C. Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc α , kí hiệu tan α
D. Tỉ số giữa cạnh kề và cạnh đối được gọi là cosin của góc α , kí hiệu cot α HƯỚNG DẪN
Chọn D, theo định nghĩa tỉ số lượng giác trong tam giác vuông.
Câu 4: Cho α là góc nhọn bất kì có 1
tanα = , khi đó cotα bằng: 7 A. 1 cotα = B. 1 cotα − = 7 7 9 Đại số 9
PHIẾU BÀI TẬP TOÁN 9 - CHƯƠNG IV Năm học 2024-2025 C. cotα = 7 D. cotα = 7 − HƯỚNG DẪN
Chọn C, theo tính chất tỉ số lượng giác trong tam giác vuông
Câu 5: Cho α; β là hai góc nhọn phụ nhau, khi đó:
A. sinα =cos β
B. sinα =cot β
C. sinα = tan β D. cosα =cot β HƯỚNG DẪN
Chọn A theo tính chất tỉ số lượng giác trong tam giác vuông
Câu 6: Tỉ số lượng giác của góc nào lớn hơn tỉ số lượng giác của góc 45°? A. sin 25° B. cos 25° C. cos30° D. tan 50° HƯỚNG DẪN
Chọn D theo tính chất tỉ số lượng giác trong tam giác vuông
Câu 7: Tỉ số lượng giác của góc nào nhỏ hơn tỉ số lượng giác của góc 45°? A. cos55° B. sin 75° C. cot 30° D. tan 40° HƯỚNG DẪN
Chọn D theo tính chất tỉ số lượng giác trong tam giác vuông
II – MỨC ĐỘ THÔNG HIỂU
Câu 8: Cho tam giác ABC vuông tại A. Khi đó, trong các khẳng định sau, khẳng định nào đúng? AB cosC A. =
B. sin B = cosC AC cos B
C. sin B = tan C
D. tan B = cosC HƯỚNG DẪN
Chọn C, theo tính chất tỉ số lượng giác trong tam giác vuông
Câu 9: Cho tam giác ABC vuông tại C có AC =1c ,
m BC = 2cm . Tính tỉ số lượng giác sinB, cosB 1 2 3 5 2 5 A. sin B = ;cos B = B. sin B = ;cos B = 3 3 5 5 1 2 2 5 5
C. sin B = ;cos B = D. sin B = ;cos B = 2 5 5 5 HƯỚNG DẪN 10 Đại số 9
PHIẾU BÀI TẬP TOÁN 9 - CHƯƠNG IV Năm học 2024-2025
Theo định lý Pytago, tính được AB= 5cm AC 5 BC 2 5 sin B = = ;cos B = = AB 5 AB 5
Câu 10: Cho tam giác ABC vuông tại C có AC =1,2c ,
m BC = 0,9cm .Tính các tỉ số lượng giác sinB, cosB
A. sin B = 0,6; cos B = 0,8
B. sin B = 0,8; cos B = 0,6
C. sin B = 0,4; cos B = 0,8
D. sin B = 0,6; cos B = 0,4 HƯỚNG DẪN
Theo định lý Pytago, tính được AB=1,5cm
Theo tỉ số lượng giác, ta có: sin B = 0,8; cos B = 0,6
Câu 11: Cho tam giác ABC, vuông tại A có AB = 3; AC = 4.Chọn khẳng định sai? AC 4 AB 3 A. sin B = = B. cos B = = BC 5 BC 5 AC 4 AC 4 C. tan B = = D. cot B = = AB 3 BC 5 HƯỚNG DẪN AB 3
Vì theo tỉ số lượng giác trong tam giác vuông: cot B = = AC 4
Câu 12: Cho tam giác ABC vuông tại A, có B = 34° Khi đó: A. sin = sin34 AB B ° = B. cos = cos34 AB B ° = BC BC C. tan = tan 34 AC B ° = D. cot = cot 34 AC B ° = BC AB HƯỚNG DẪN
Chọn B, theo định nghĩa tỉ số lượng giác của góc nhọn trong tam giác vuông
Câu 13. Dùng MTBT, tính giá trị của biểu thức M = sin 35 12 ° '− sin 20 25
° ' ( làm tròn đến chữ số thập phân thứ ba ) A. M = 0,15 B. M = 0,154 C. M = 0,23 D. M = 0,228 HƯỚNG DẪN Bấm máy tính
Câu14. Dùng MTBT, tìm độ đo của góc nhọn x ( làm tròn đến phút) của cot x =1,254 A. x ≈ 51 25 ° ' B. x ≈ 51 52 ° ' C. x ≈ 38 34 ° ' D. x ≈ 38 43 ° ' HƯỚNG DẪN 11 Đại số 9
PHIẾU BÀI TẬP TOÁN 9 - CHƯƠNG IV Năm học 2024-2025 Bấm máy tính
Câu 15. Không dùng MTBT, tính giá trị của biểu thức K = tan 76° − cot14° A. K = 0 B. K =1 C. K = 2 D. K = 3 HƯỚNG DẪN
Vì tan 76° = cot14° nên K = tan 76° − cot14° = 0
Bài 16. Không dùng MTBT, tính giá trị của biểu thức sin 32 I ° = cos58° A. I = 4 B. I = 2 C. I =1 D. I = 3 HƯỚNG DẪN
Vì sin 32° = cos58° nên sin 32° =1 cos58°
III – MỨC ĐỘ VẬN DỤNG
Câu 17: Một cái thang dài 6m, được đặt tạo với mặt đất một góc 60°, vậy chân thang cách tường bao nhiêu mét? A. 3m B. 3,2 m C. 7,8m D. 0,4m HƯỚNG DẪN
Theo đề ta có hình vẽ minh họa sau : B 60° C A
Chân thang cách tường số mét là : 1
AC = BC.cos60° = 6.cos60° = 6. = 3(m) 2
Câu 18. Một mảnh vườn hình chữ nhật có chiều dài là 30m , góc giữa đường chéo và chiều dài của mảnh
vườn là 30° . Tính chiều rộng của mảnh vườn hình chữ nhật đó. A. 20 3m B. 10 3m C. 10 6 m D. 20 6 m HƯỚNG DẪN 12 Đại số 9
PHIẾU BÀI TẬP TOÁN 9 - CHƯƠNG IV Năm học 2024-2025 B 30m C 30° A D
Chiều rộng của mảnh vườn hình chữ nhật là : AB = BC.tan C = 30.tan 30° =10 3
Câu 19: Một máy bay đang bay ở độ cao 12km , khi hạ cánh xuống mặt đất, đường đi của máy bay tạo với
mặt đất một góc nghiêng α . Nếu cách sân bay 320km máy bay bắt hạ cánh thì góc nghiêng α ( làm tròn đến phút ) là A. α ≈ 87 51 ° ' B. α ≈ 87 52 ° ' C. α ≈ 2 9' ° D. α ≈ 2 8' ° HƯỚNG DẪN
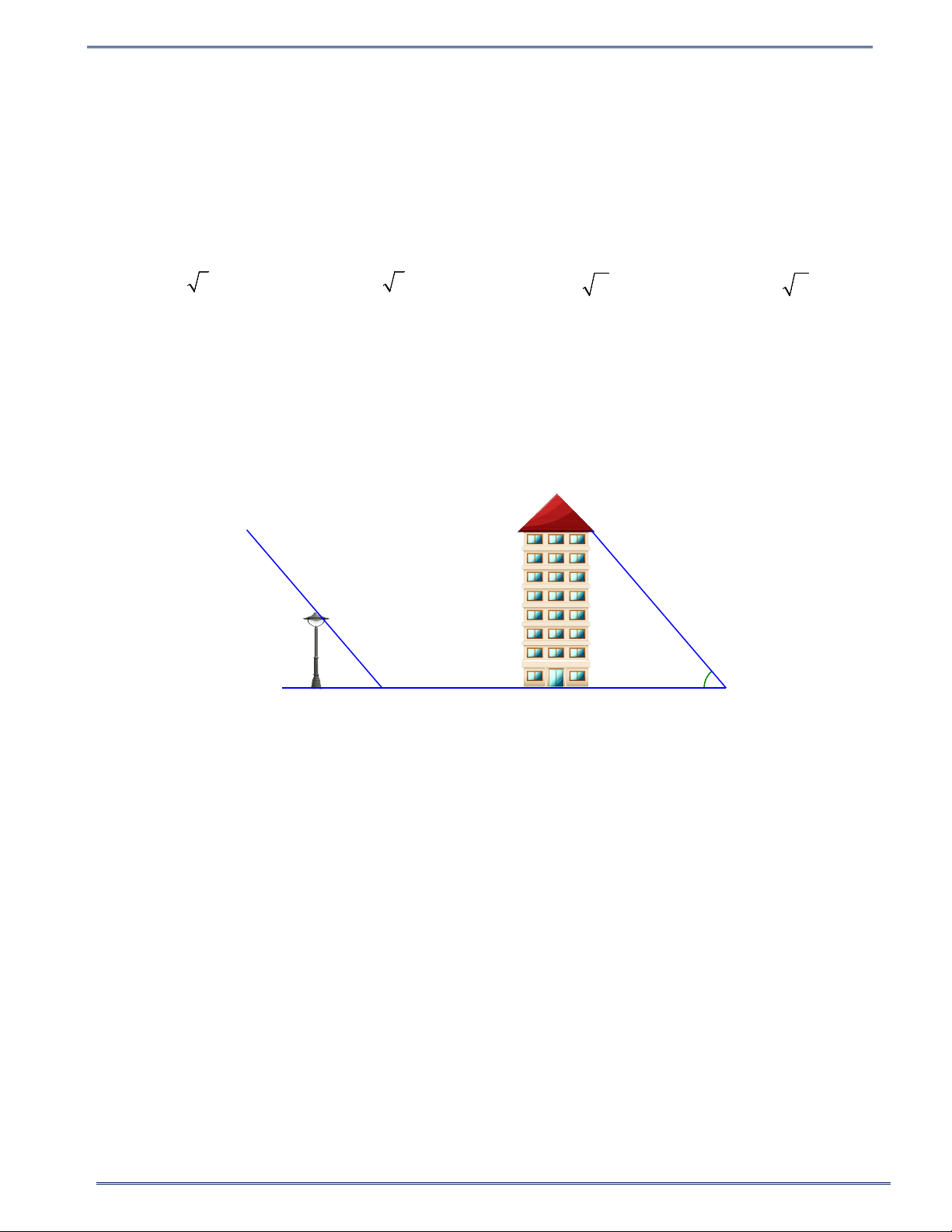
Câu 20: Một cột đèn cao 7m có bóng trên mặt đất dài 4m , gần đó có một tòa nhà cao tầng có bóng trên
mặt đất dài 80m ( hình vẽ ). Em hãy cho biết tòa nhà đó có bao nhiêu tầng, biết rằng mỗi tầng cao 2m 7m α 4m 80m A. 80 tầng B. 75 tầng C. 70 tầng D. 60 tầng HƯỚNG DẪN
IV – MỨC ĐỘ VẬN DỤNG CAO
Câu 21: Một học sinh dùng giác kế, đứng cách chân cột cờ 10m rồi chỉnh mặt ngắm cao bằng mắt của mình
để xác định góc “ nâng “ ( góc tạo bởi tia sáng đi thẳng từ cột cờ với mắt tạo với phương nằm ngang). Khi
đó góc nâng đo được là 31° , biết khoảng cách từ mặt sân đến mắt học sinh đó bằng 1,5m , tính chiều cao
cột cờ ( kết quả làm tròn đến một chữ số thập phân ) A. 6,0m
B. 16,6m C. 7,5m D. 5,0m HƯỚNG DẪN 13 Đại số 9
PHIẾU BÀI TẬP TOÁN 9 - CHƯƠNG IV Năm học 2024-2025
Câu 22: Tính chiều cao của một ngọn núi ( làm tròn đến mét ), biết tại hai điểm A, B cách nhau 500m,
người ta nhìn thấy đỉnh núi với góc nâng lần lượt là 34 ,° 38°
A. Chiều cao ngọn núi là 2667,7m
B. Chiều cao ngọn núi là 2647,7m
C. Chiều cao ngọn núi là 2467,7m
D. Chiều cao ngọn núi là 2447,7m HƯỚNG DẪN
Câu 23: Trên một quả đồi có một cái tháp cao 100m , từ đỉnh B và chân C của tháp nhìn điểm A ở chân
đồi dưới các góc tương ứng bằng 60°và 30° so với phương nằm ngang. Chiều cao h của quả đồi là70°
A. h = 50m
B. h = 45m
C. h = 52m
D. h = 47m HƯỚNG DẪN
Câu 24: Từ nhà bạn An đến trường học, bạn phải đi đò qua một khúc sông rộng đến điểm A ( bờ bên kia)
rồi từ A đi bộ đến trường tại điểm D ( ở hình bên ) Thực tế, do nước chảy nên chiếc đò bị dòng nước đẩy
xiên một góc đưa bạn tới điểm C ( bờ bên kia ) Từ C bạn An đi bộ đến trường theo đường CD mất thời
gian gấp đôi khi đi từ A đến trường theo đường AD. Độ dài quãng đường CD là
( giả sử vận tốc đi bộ của bạn An không thay đổi ( chuyển động thẳng đều ) kết quả làm tròn đến hàng đơn vị ) A. 190m B. 220m C. 200m D. 210m HƯỚNG DẪN
Câu 25: Nhà bạn Bình có gác lửng cao so với nền nhà là 3m. Ba của bạn Bình cần đặt một thang đi lên
gác, biết khi đặt thang phải để thang tạo được với mặt đất một góc 70° thì đảm bảo sự an toàn khi sử
dụng. Với kiến thức đã học, Bình hãy giúp Ba của mình tính chiều dài thang là bao nhiêu mét để sử dụng (
kết quả làm tròn đến chữ số thập phân thứ hai) A. 4,24 B. 2,34 C. 2,43 D. 3,19 14 Đại số 9
PHIẾU BÀI TẬP TOÁN 9 - CHƯƠNG IV Năm học 2024-2025 HƯỚNG DẪN
D. HƯỚNG DẪN GIẢI CHI TIẾT CÁC DẠNG BÀI TỰ LUẬN
Dạng 1.Tính tỉ số lượng giác của góc nhọn, tính cạnh, tính góc. Phương pháp giải
Vận dụng các tỉ số lượng giác của góc B và các công thức biến đổi (xem ở phần lý thuyết trên).
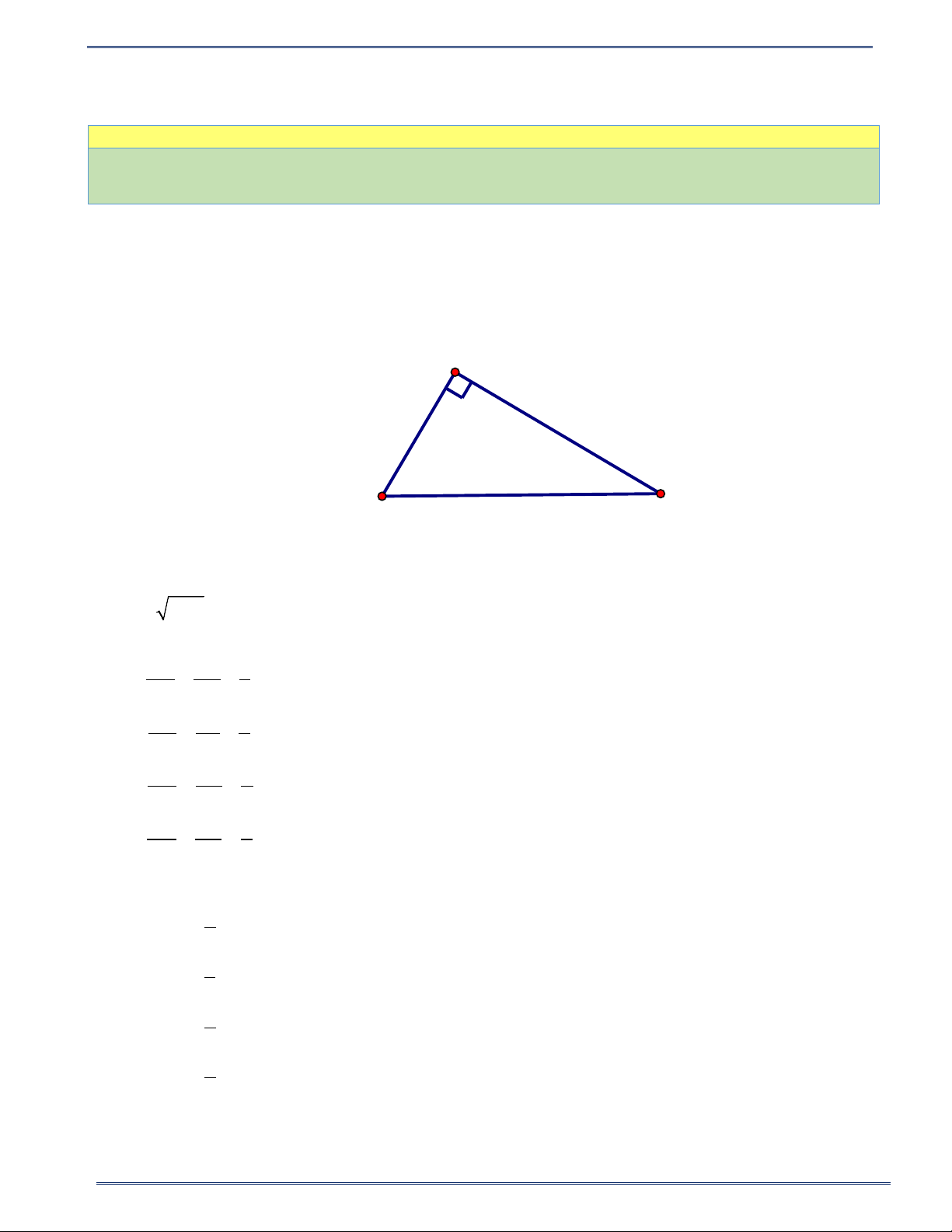
Bài 1. Cho tam giác ABC vuông tại C có BC =1,2 , m AC = 0,9 .
m Tính các tỉ số lượng giác của góc B . Từ
đó suy ra tỉ số lượng giác của góc A . Lời giải C 1,2m 0,9m A B
Áp dụng định lý Py-ta-go trong tam giác ABC vuông tại A , ta có: 2 2 2 2 2
AB = AC + BC = 0,9 +1,2 = 2,25
⇒ AB = 2,25 =1,5(m). Ta có: AC 0,9 3 sin B = = = ; AB 1,5 5 BC 1,2 4 cos B = = = ; AB 1,5 5 AC 0,9 3 tan B = = = ; BC 1,2 4 BC 1,2 4 cot B = = = . AC 0,9 3 Vì +
A B = 90° là hai góc phụ nhau, nên ta có: 4
sin A = cos B = ; 5 3
cos A = sin B = ; 54
tan A = cot B = ; 3 3
cot A = tan B = . 4
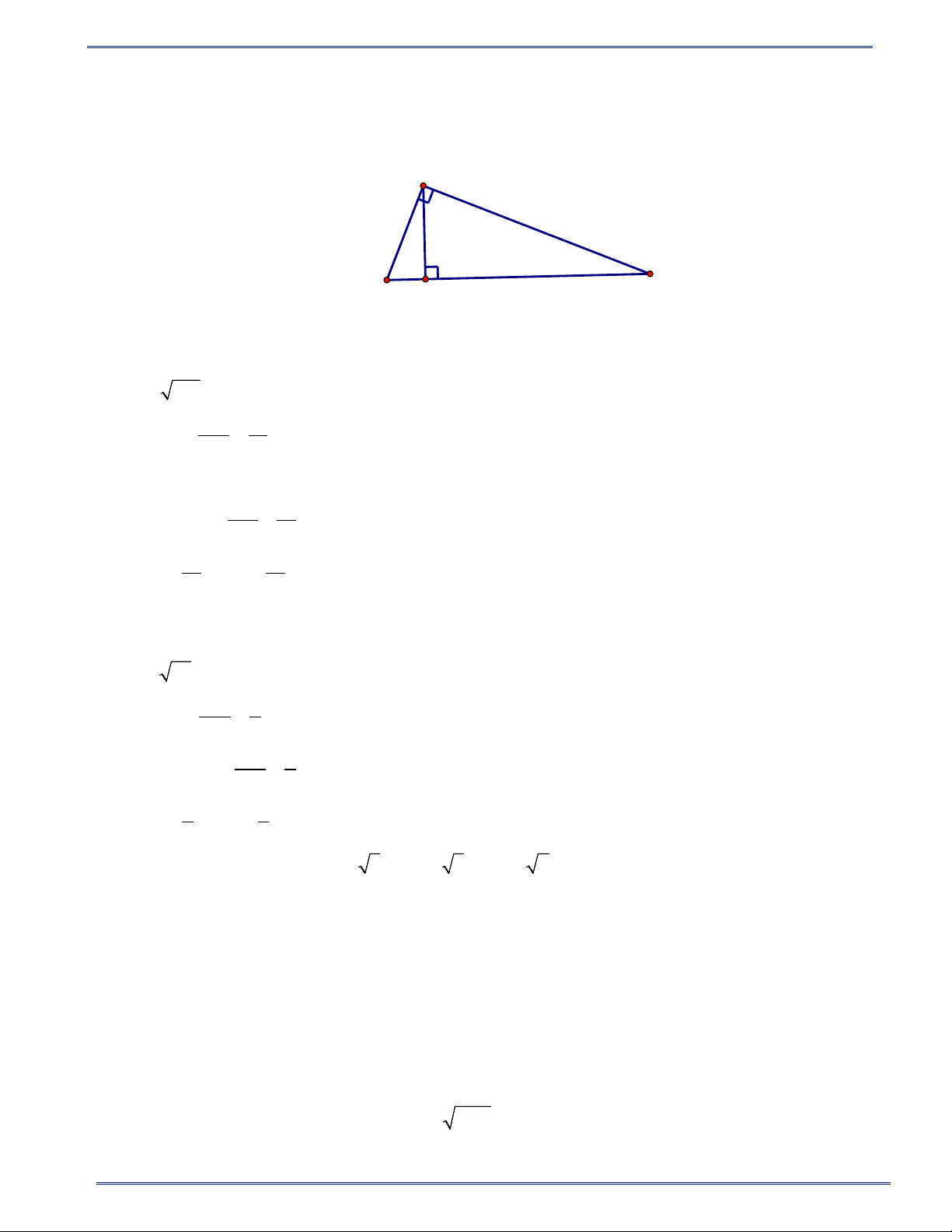
Bài 2. Cho tam giác ABC vuông tại A, đường cao AH. Hãy tính sin B và sinC trong các trường hợp sau
(làm tròn kết quả đến chữ số thập phân thứ 4): 15 Đại số 9
PHIẾU BÀI TẬP TOÁN 9 - CHƯƠNG IV Năm học 2024-2025 a) AB =13c ; m BH = 0,5d . m b) AH = 3c ; m CH = 4c . m Lời giải A B C H
a) BH = 0,5dm = 5c . m
Áp dụng định lý Py-ta-go trong A
∆ BH vuông tại H , ta có: 2 2 2 2 2
AH = AB − BH =13 −5 =169 − 25 =144
⇒ AH = 144 =12(cm). Ta có: AH 12 sin B = = AB 13 Vì +
B C = 90° là 2 góc phụ nhau BH 5
⇒ sinC = cos B = = AB 13 Vậy 12 5
sin B = ;sinC = . 13 13
b) Áp dụng định lý Py-ta-go trong A
∆ HC vuông tại H , ta có: 2 2 2 2 2
AC = AH + CH = 3 + 4 = 25
⇒ CH = 25 = 5(cm). Ta có: AH 3 sinC = = . AC 5 Mà CH 4 sin B = cosC = = AC 5 Vậy 4 3
sin B = ;sinC = . 5 5
Bài 3. Cho tam giác ABC có AB = a 5;BC = a 3; AC = a 2.
a) Chứng minh tam giác ABC là tam giác vuông.
b) Tính các tỉ số lượng giác của góc B . Từ đó suy ra tỉ số lượng giác của góc A . Lời giải a) Ta có: 2 2 2 AB = 5 ; a BC = 3 ; a AC = 2 . a mà 2 2 2
AB = 5a = AC + BC (theo định lý Py-ta-go đảo) ⇒ A
∆ BC vuông tạiC . b) Ta có: 2 2 2 2 2
AB = AC + CB = 0,9 +1,2 = 2,25 ⇒ AB = 2,25 =1,5(m). 16 Đại số 9
PHIẾU BÀI TẬP TOÁN 9 - CHƯƠNG IV Năm học 2024-2025 AC 0,9 3 ⇒ sin B = = = ; AB 1,5 5 CB 1,2 4 cos B = = = ; AB 1,5 5 AC 0,9 3 tan B = = = ; CB 1,2 4 CB 1,2 4 cot B = = = . AC 0,9 3
Vì góc A và góc B là hai phụ nhau, nên ta có: 4
sin A = cos B = ; 5 3
cos A = sin B = ; 54
tan A = cot B = ; 3 3
cot A = tan B = . 4
Bài 4. Cho tam giác ABC vuông tại A. Hãy tính các tỉ số lượng giác của góc C biết rằng cosC = 0,6. Lời giải Ta có: 2 2 2 2
+)sin C + cos C =1⇒ sinC = 1− cos C = 1− 0,6 = 0,8. sinC 0,8 4 +) tanC = = = cosC 0,6 3 1 1 3 ⇒ cotC = = = . tanC 4 4 3
Bài 5. Cho tam giác ABC vuông tại A , 5 AB = 5c ,
m cot B = . Tính độ dài các đoạn thẳng AC và BC . 8 Lời giải Ta có: AB AB 5 cot B = ⇒ AC = = = 8(cm). AC cot B 58
Áp dụng định Pytago trong tam giác ABC vuông tại A , ta có: 2 2 2 2 2
BC = AB + AC = 5 + 8 = 89 ⇒ BC = 89(cm).
Dạng 2. Sắp thứ tự dãy các tỉ số lượng giác và tính giá trị biểu thức Phương pháp giải
Để sắp xếp thứ tự dãy các tỉ số lượng giác cho trước, ta cần làm được hai bước sau:
Bước 1: Đưa về các tỉ số lượng giác trong các bài toán cùng loại bằng cách sử dụng
tính chất: “Nếu hai góc phụ nhau thì sin góc này bằng cos góc kia, tan góc này bằng cot góc kia”. 17 Đại số 9
PHIẾU BÀI TẬP TOÁN 9 - CHƯƠNG IV Năm học 2024-2025
Bước 2: Với hai góc nhọn α, β, ta có:
sinα < sin β ⇔ α < β;
cosα < cos β ⇔ α > β;
tanα < tan β ⇔ α < β;
cotα < cot β ⇔ α > β.
Bài 1. Không dùng bảng số và máy tính, hãy so sánh: a)sin 20° và sin 70 .° b) cos60° và cos70 .° c) tan 73 20 ° ′ và tan 45 . ° d) cot 20° và cot37 40 ° .′ Lời giải
a) Vì α = 20° < β = 70° ⇒ sin 20° < sin 70 .°
b) Vì α = 60° < β = 70° ⇒ cos60° > cos70 .° c) Vì α = 73 20
° ′ < β = 45° ⇒ tan 73 20 ° ′ < tan 45 .°
d) Vì α = 20° < β = 37 40
° ′ ⇒ cot 20° > cot37 40 ° .′
Bài 2. Sắp xếp các tỉ số lượng giác sau theo thứ tự
a) Từ bé đến lớn: tan 42 ,°cot 71 ,°tan38 ,°cot 69 15 ° ,′tan 28 .°
b) Từ lớn đến bé: cos67 ,°sin56 ,°cos63 41 ° ,′sin 74 ,°cos85 .° Lời giải
a) Các tỉ số lượng giác sắp xếp từ bé đến lớn là: cot 71° < cot 69 15
° ′ < tan 28° < tan 42° < tan 71 . °
b) Các tỉ số lượng giác sắp xếp từ lớn đến bé là: sin 74° > sin56° > cos63 41
° ′ > cos67° > cos85 . °
Bài 3. Tính giá trị các biểu thức sau:
a) A = sin 23° − cos67 ;°
b) B = cos34° − sin56 ;°
c)C = tan18° − cot 72 ;° d) 2 2
D = sin 10° + sin 80 ;° e) 2 2
E = sin 60° + sin 30 ;°
f) F = cos25° − sin 65 ;°
g)G = tan 40° − cot50 ;° h) 1 H = .tan88 .° cot 2° Lời giải
a) A = sin 23° − cos67° = sin 23° − sin 23° =1−1 = 0.
b) B = cos34° − sin56° = cos34° − cos34° =1−1 = 0.
c) C = tan18° − cot 72° = tan18° − tan18° =1−1 = 0. d) 2 2 2 2
D = sin 10° + sin 80° = sin 10° + cos 10° =1. e) 2 2 2 2
E = sin 60° + sin 30° = sin 60° + cos 60° =1.
f) F = cos25° − sin 65° = cos25° − cos25° = 0.
g) G = tan 40° − cot50° = tan 40 .°cot 40° =1. h) 1 1 H = .tan88° = .cot 2° =1. cot 2° cot 2°
Bài 4. Tính giá trị các biểu thức sau: a) sin 60 .cos30 A ° ° = ;
b) B = sin30° − 2cos60° + tan 45 ;° 2.cot 45°
c) C = sin 45° + cot 60 .°cos30 ;°
d) D = cot 44 .°cot 45 .°cot 46 ;° 18 Đại số 9
PHIẾU BÀI TẬP TOÁN 9 - CHƯƠNG IV Năm học 2024-2025 e) 3.cot 60 E ° = ; f) cos60 1 F ° = + ; 2 2cos 60° −1 1+ sin 60° tan30° g) 2 2 3
G =10 − sin 45° + 3cos 60° − 5cos 45 ;°
h) H = tan 45 .°cos30 .°cot30 .° Lời giải 3 3 3 . a) sin 60 .cos30 2 2 4 3 A ° ° = = = = 2.cot 45° 2.1 2 8 Vậy 3 A = . 8 b) 1 1 1
B = sin 30° − 2cos60° + tan 45° = − 2. +1 = . 2 2 2 Vậy 1 B = . 2 2 3 1 6
c)C = sin 45° + cot 60 .°cos30° = + . = . 2 3 2 12 6 Vậy C = . 12
d) D = cot 44 .°cot 45 .°cot 46° = cot 44 .°cot 45 .°tan 44° =1.cot 45° =1.1 =1. Vậy D =1. 3 3. e) 3.cot 60 3 3 E ° = = = = 2 − 3. 2 2 2cos 60° −1 1 1 − − 1 2. 1 2 2 Vậy E = 2 − 3. 1 1+ f) cos60° 1 2 F = + =
+ cot 30° = 6 − 3 3 + 3 = 6 − 2 3. 1+ sin 60° tan 30° 3 1+ 2 Vậy F = 6 − 2 3. 2 3 2 g) 2 2 3 2 1 2 41− 5 2
G =10 − sin 45° + 3cos 60° − 5cos 45° =10 − + 3. − 5. = . 2 2 2 4 41 5 2 Vậy G − = . 4 3 3
h) H = tan 45 .°cos30 .°cot 30° =1. . 3 = . 2 2 Vậy 3 H = . 2
Bài 5. Không dùng bảng số và máy tính, hãy tính:
a) A = sin10° + sin 40° − cos50° − cos80 ;° b) 2 2 2 2
B = cos 15° + cos 55° + cos 35° + cos 75 ;° 19 Đại số 9
PHIẾU BÀI TẬP TOÁN 9 - CHƯƠNG IV Năm học 2024-2025 c) 2 2
C = cos 81° + cos 9° − 5.cot 62 .°cot 28 ;° d) 2 2 2 2 2 2
D = cos 20° + cos 30° + cos 40° + cos 50° + cos 60° + cos 70 ;° e) 2 2 2 2 2
E = sin 5° + sin 25° + sin 45° + sin 65° + sin 85 .° f) 2 2 8.cot35
F 12.tan32 .tan58 sin 51 sin 39 ° = ° ° + ° + ° − ; tan55° g) 2 2 cot 22
G sin 50 sin 40 tan 28 cot 62 ° = ° + ° − ° + ° − ; tan 68° h) 2 2sin37° 2
H = cot13 .°cot 77° − sin 26° − − sin 64 .° 3cos53° Lời giải
a) A = sin10° + sin 40° − cos50° − cos80° = sin10° + sin 40° − sin 40° − sin10°
= (sin10° − sin10°) − (sin 40° + sin 40°) = 0 Vậy A = 0. b) 2 2 2 2 2 2 2 2
B = cos 15° + cos 55° + cos 35° + cos 75° = sin 75° + cos 55° + sin 55° + cos 75° = ( 2 2 ° + °) + ( 2 2 sin 75 cos 75 cos 55° + sin 55°) =1+1= 2 Vậy B = 2. c) 2 2 2 2
C = cos 81° + cos 9° −5.cot 62 .°cot 28° = sin 9° + cos 9° −5.cot 62 .°tan 62° =1−5.1 = 4. − Vậy C = 4. − d) Ta có: 2 2 2 2 2 2
D = cos 20° + cos 30° + cos 40° + cos 50° + cos 60° + cos 70° 2 2 2 2 2 2
= sin 70° + sin 60° + sin 50° + cos 50° + cos 60° + cos 70° = ( 2 2 sin 70° + cos 70°) + ( 2 2 sin 60° + cos 60°) + ( 2 2 sin 50° + cos 50°) =1+1+1 = 3 Vậy D = 3. e) Ta có: 2 2 2 2 2
E = sin 5° + sin 25° + sin 45° + sin 65° + sin 85° 2 2 2 2 2 = ° + ° + ° + ° + ° = ( 2 2 ° + °) + ( 2 2 ° + °) 2
cos 85 cos 65 sin 45 sin 65 sin 85 cos 85 sin 85 cos 65 sin 65 + sin 45° 2 2 =1+1+ = 2 + 2 2 2 Vậy E = 2 + . 2 f) 2 2 8.cot 35
F 12.tan 32 .tan 58 sin 51 sin 39 ° = ° ° + ° + ° − tan 55° 2 2 8.cot 35
12.tan 32 .cot 32 sin 51 cos 51 ° = ° ° + ° + ° − =12.1+1−8 = 5 cot 35° Vậy F = 5. g) 2 2 cot 22
G sin 50 sin 40 tan 28 cot 62 ° = ° + ° − ° + ° − tan 68° 2 2 tan 68 cos 40 sin 40 cot 62 cot 62 ° = ° + ° − ° + ° − =1−1 = 0 tan 68° 20 Đại số 9




