Phương pháp chuẩn hóa trong số phức – Phạm Minh Tuấn Toán 12

Phương pháp chuẩn hóa trong số phức – Phạm Minh Tuấn Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

37 19 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 4: Số phức

Môn: Toán 12

Thông tin:

6 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
PHƯƠNG PHÁP CHUẨN HÓA TRONG SỐ PHỨC
Ví dụ 1: Cho số phức
0z a bi
sao cho z không phải là số thực và
3
1
z
w
z
là số
thực. Tính
2
2
1
z
z
.
A.
1
21a
C.
1
32a
B.
2
2a
D.
1
22a
Lời giải:
Chuẩn hóa: : Vì w là số thực nên ta chọn
Suy ra
22
22
0,6624 0,5623
11
0
2 1 2.0,6624 1
1 1 0,6624 0,5623
zi
a
zi

Vậy đáp án là A
Ví dụ 2: Cho hai số phức
,zw
khác 0 và thỏa mãn
2z w z w
. Gọi a, b lần lượt là
phần thực và phần ảo của số phức
z
u
w
. Tính
22
?ab
A.
1
2
C.
1
8
B.
7
2
D.
1
4
Lời giải:
Chuẩn hóa:
1w
. Theo đề ta có:
2
2 2 2
22
2
2
14
12
1 15 1 15 1
8 8 8 8 4
11
11
x y x y
zz
z i u i a b
z
xy




_________________________________________________________________________________
_________________________________________________________________________________
Phương pháp CHUẨN HÓA trong số phức
Tác giả: Phạm Minh Tuấn - TOANMATH.com
Ví dụ 3: Cho hai số phức
,zw
khác 0 và thỏa mãn
5z w z w
. Gọi a, b lần lượt là
phần thực và phần ảo của số phức
.u z w
. Tính
22
?ab
A.
1
50
C.
1
100
B.
1
25
D.
1
10
Lời giải:
Chuẩn hóa:
1w
. Theo đề ta có:
2
2 2 2
22
2
2
1 25
15
1 3 11 1 3 11 1
50 50 50 50 25
11
11
x y x y
zz
z i u i a b
z
xy




Ví dụ 4: Cho
z ,z ,z
1 2 3
là các số phức thoả mãn
1 2 3
1z z z
và
1 2 3
1z z z
. Biểu
thức
2 1 2 1 2 1
1 2 3
nnn
P z z z

,
n
nhận giá trị nào sao đây?
A. 1 B. 0
C.
1
D. 3
Lời giải:
Chuẩn hóa:
1 2 3
1, 1, ,n z z i z i
Suy ra đáp áp A
Ví dụ 5: Cho
z ,z ,z
1 2 3
là các số phức thoả mãn
z z z
1 2 3
1
. Khẳng định nào sau đây
là đúng?
A.
z z z z z z z z z
1 2 3 1 2 2 3 3 1
B.
z z z z z z z z z
1 2 3 1 2 2 3 3 1
C.
z z z z z z z z z
1 2 3 1 2 2 3 3 1
D.
z z z z z z z z z
1 2 3 1 2 2 3 3 1
Lời giải:
Chuẩn hóa:
1 2 3
, , 1z i z i z
suy ra đáp án A
_________________________________________________________________________________
_________________________________________________________________________________
Phương pháp CHUẨN HÓA trong số phức
Tác giả: Phạm Minh Tuấn - TOANMATH.com
Ví dụ 6: Cho ba số phức
1 2 3
,,z z z
thỏa mãn
1 2 3
1z z z
và
1 2 3
0z z z
. Tính giá trị
của biểu thức
222
1 2 3
P z z z
.
A.
0
B.
1
C.
1
D.
2
Lời giải:
Chuẩn hóa:
1 2 3
1 3 1 3
, , 1
2 2 2 2
z i z i z
Suy ra
0P
Ví dụ 7: Cho các số phức
1 2 3
,,z z z
thỏa mãn đồng thời hai điều kiện
1 2 3
1999z z z
và
1 2 3
0z z z
. Tính
1 2 2 3 3 1
1 2 3
z z z z z z
P
z z z


.
A.
1999P
C.
999,5P
B.
2
1999P
D.
5997P
Lời giải:
Chuẩn hóa:
2
1 2 3
1999; 1999; 1 1999 1z z z i
suy ra
1999P
Ví dụ 8: Cho các số phức
, , ,a b c z
thỏa
2
0az bz c
0a
. Gọi
1
z
và
2
z
lần lượt là hai
nghiệm của phương trình bậc hai đã cho. Tính giá trị của biểu thức
2
22
1 2 1 2 1 1
2P z z z z z z


A.
2
c
P
a
C.
4
c
P
a
B.
c
P
a
D.
1
.
2
c
P
a
Lời giải:
Chuẩn hóa:
1
2
13
22
14
13
22
zi
a b c P
zi
. Đáp án C thỏa
4P
_________________________________________________________________________________
_________________________________________________________________________________
Phương pháp CHUẨN HÓA trong số phức
Tác giả: Phạm Minh Tuấn - TOANMATH.com
Ví dụ 9: Nếu z không phải là số thực đồng thời
1
zz
có phần thực bằng 4 thì môđun
của z là?
A.
1
8
C.
1
12
B.
1
6
D.
1
16
Lời giải:
Thử đáp án:
Đáp án A:
Với
1
8
z
, chọn
1 17
9 72
xy
, do đó
1 17
9 72
zi
Thay z vào ta được
1
4 4 17i
zz

( thỏa yêu cầu đề bài có phần thưc bằng 4 )
Vậy đáp án là A
Ví dụ 10: Nếu hai số thức
12
,zz
thỏa mãn
12
1zz
và
12
.1zz
thì số phức
12
12
1
zz
w
zz
có phần ảo bằng?
A.
0
C.
1
B.
1
D. Lớn hơn 1
Lời giải:
Chuẩn hóa:
1
zi
;
2
1z
do đó
1
1
1 .1
i
w
i

suy ra phần ảo của w bằng 0
Vậy đáp án là A
_________________________________________________________________________________
_________________________________________________________________________________
Phương pháp CHUẨN HÓA trong số phức
Tác giả: Phạm Minh Tuấn - TOANMATH.com
Ví dụ 11: Cho số phức
z a bi
,ab
thỏa mãn điều kiện
2
42zz
. Đặt
22
8 12P b a
. Mệnh đề nào sau đây đúng?
A.
2
2Pz
C.
2
2
2Pz
B.
2
4Pz
D.
2
2
4Pz
Lời giải:
Ta có:
2
2 2 2 2 2 2 2
4 2 4 4 4z z a b a b a b
Chọn
2
22
0 4 4 1 3b a a a i
suy ra
1
13
3
a
zi
b

. Thay a, b vào
P
ta được
4P
Thay
13zi
vào đáp án C ta được kết quả là 4. Vậy đáp án là C
Ví dụ 12: Cho các số phức
12
,0zz
,ab
thỏa mãn điều kiện
1 2 1 2
2 1 1
z z z z

. Tính
giá trị của biểu thức
12
21
zz
P
zz

.
A.
2
2
C.
3
B.
2
D.
32
2
Lời giải:
Chuẩn hóa:
12
22
11
1 2 0,5 0,5
1
z z i
zz
1 0,5 0,5 3 2
0,5 0,5 1 2
i
P
i


_________________________________________________________________________________
_________________________________________________________________________________
Phương pháp CHUẨN HÓA trong số phức
Tác giả: Phạm Minh Tuấn - TOANMATH.com
Ví dụ 13: Cho số phức
0z a bi
sao cho z không phải là số thực và
2
1
z
w
z
là số
thực. Tính
2
1
z
z
.
A.
1
5
C.
1
2
B.
1
3
D. 1
Lời giải:
Chuẩn hóa: Vì w là số thực nên ta chọn
2
1 1 0,5 0,5 3
1
z
w z i
z
Suy ra
22
0,5 0,5 3
1
2
1
1 0,5 0,5 3
i
z
z
i


Ví dụ 14: Cho hai số phức
12
,zz
thỏa mãn điều kiện
1 2 1 2
1z z z z
. Tính giá trị
của biểu thức
22
12
21
zz
P
zz

A.
1
C.
2
B.
1 i
D.
1 i
Lời giải:
Chuẩn hóa:
1
2
13
22
1
13
22
zi
P
zi

_________________________________________________________________________________
_________________________________________________________________________________
Phương pháp CHUẨN HÓA trong số phức
Tác giả: Phạm Minh Tuấn - TOANMATH.com
| 1/6
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Phương pháp CHUẨN HÓA trong số phức
_________________________________________________________________________________
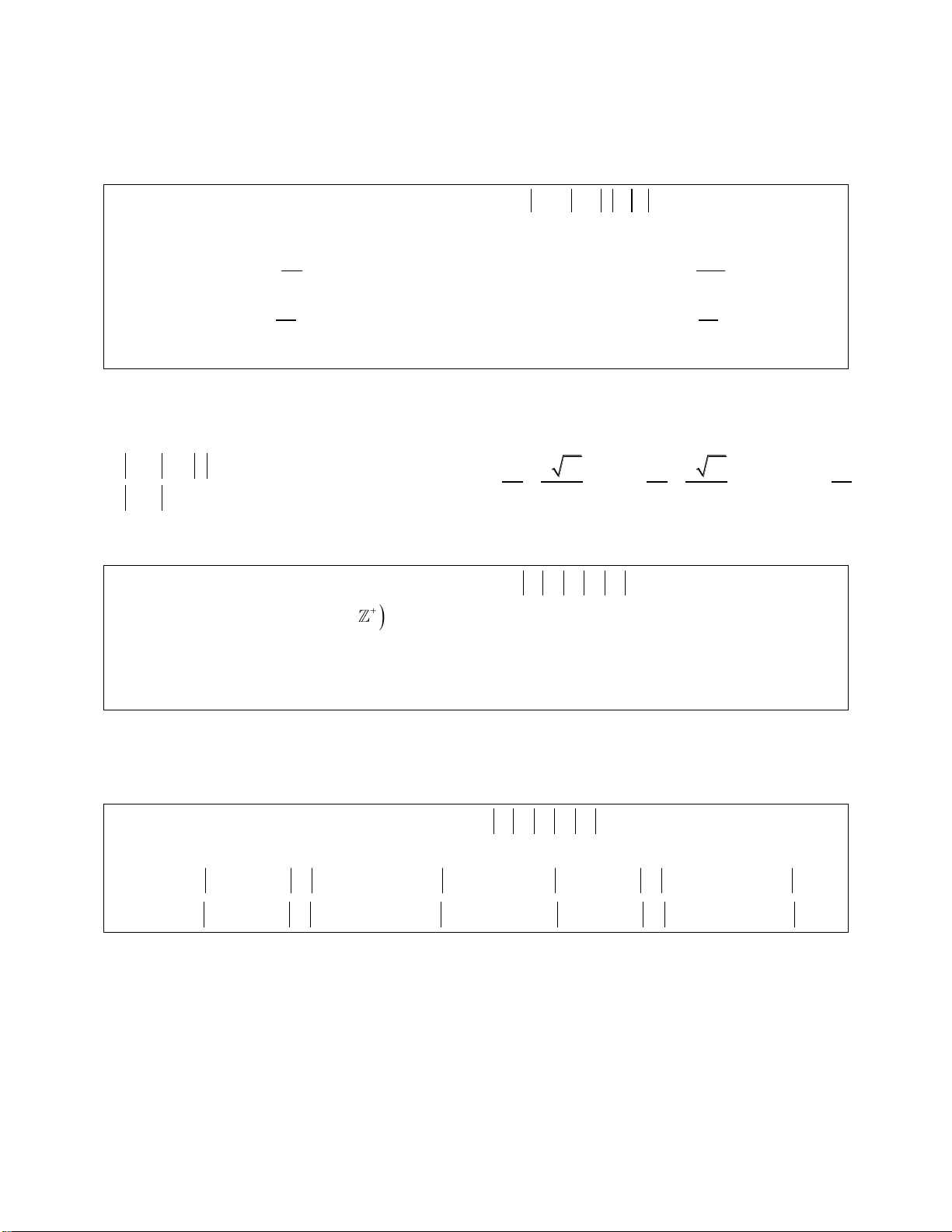
PHƯƠNG PHÁP CHUẨN HÓA TRONG SỐ PHỨC z
Ví dụ 1: Cho số phức z a bi  0 sao cho z không phải là số thực và w  là số 3 1  z 2 z thực. Tính . 2 1  z 1 1 A. C. 2a  1 3a  2 2 1 B. D. a  2 2a  2 Lời giải: z
Chuẩn hóa: : Vì w là số thực nên ta chọn w  1 
 1 z  0,6624  0,5623i 3 1 z 2 2 z 1 0,6624  0, 5623i 1 Suy ra     0 2 2 2a  1 2.0,6624     1 1 z 1 0,6624 0, 5623i Vậy đáp án là A
Ví dụ 2: Cho hai số phức z,w khác 0 và thỏa mãn z w  2 z w . Gọi a, b lần lượt là z
phần thực và phần ảo của số phức u  . Tính 2 2 a b  ? w 1 1 A. C. 2 8 7 1 B. D. 2 4 Lời giải:
Chuẩn hóa: w  1 . Theo đề ta có:   z 1   2 zx  2 2 1  y  4 2 2 x y  1 15 1 15 2 2 1     z   i u  
i a b z  1   1  x  2 2 8 8 8 8 4 1  y  1
_________________________________________________________________________________
Tác giả: Phạm Minh Tuấn - TOANMATH.com
Phương pháp CHUẨN HÓA trong số phức
_________________________________________________________________________________
Ví dụ 3: Cho hai số phức z,w khác 0 và thỏa mãn z w  5 z w . Gọi a, b lần lượt là
phần thực và phần ảo của số phức u  . z w . Tính 2 2 a b  ? 1 1 A. C. 50 100 1 1 B. D. 25 10 Lời giải:
Chuẩn hóa: w  1 . Theo đề ta có:   z 1   5 zx  2 2 1  y  25 2 2 x y  1 3 11 1 3 11 2 2 1     z   i u  
i a b z  1   1  x  2 2 50 50 50 50 25 1  y  1
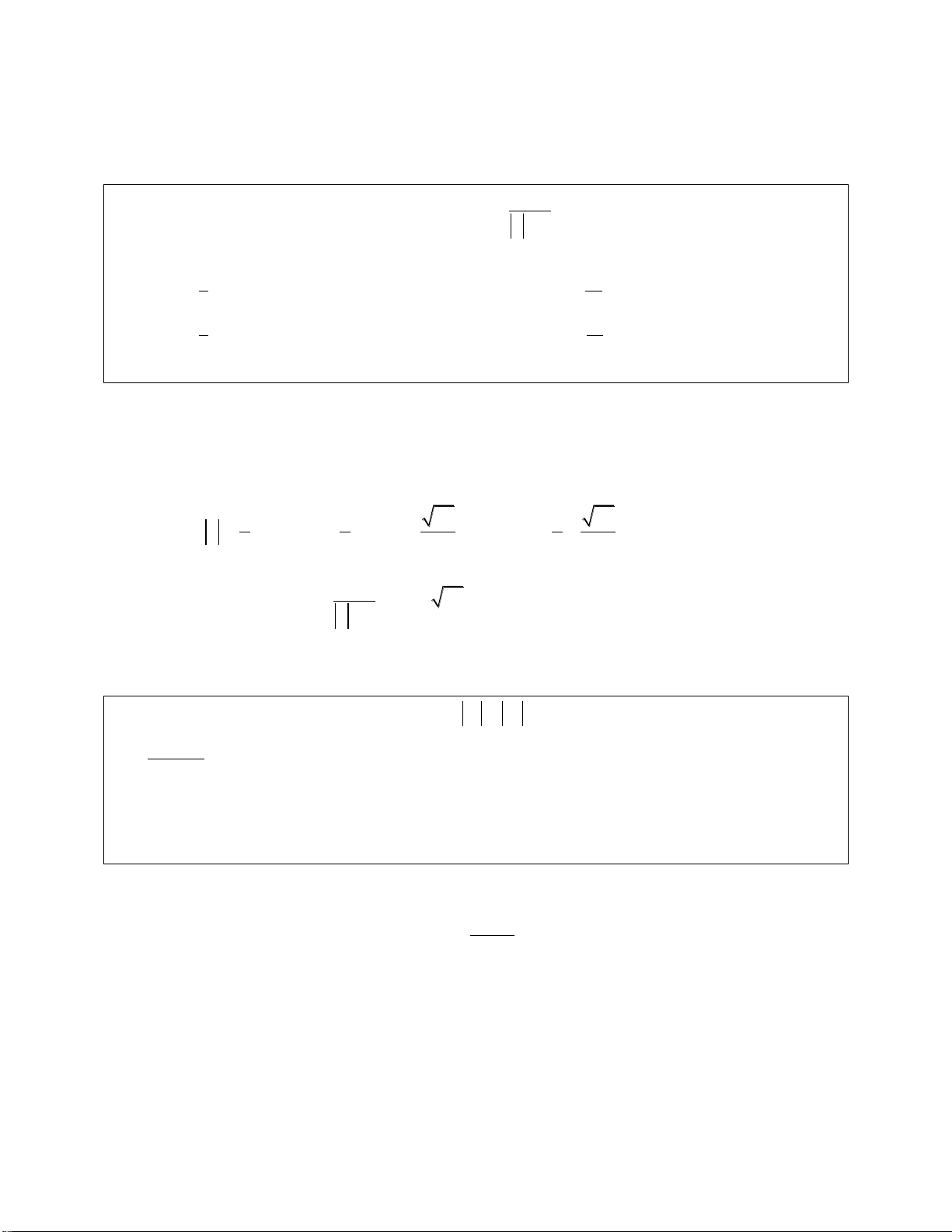
Ví dụ 4: Cho z ,z ,z là các số phức thoả mãn z z z  1 và z z z  1. Biểu 1 2 3 1 2 3 1 2 3 thức 2n1 2n1 2n1 P zzz , n  
 nhận giá trị nào sao đây? 1 2 3 A. 1 B. 0 C. 1  D. 3 Lời giải:
Chuẩn hóa: n  1, z  1, z i, z i  Suy ra đáp áp A 1 2 3
Ví dụ 5: Cho z ,z ,z là các số phức thoả mãn z z z  1. Khẳng định nào sau đây 1 2 3 1 2 3 là đúng?
A. z z z z z z z z z
B. z z z z z z z z z 1 2 3 1 2 2 3 3 1 1 2 3 1 2 2 3 3 1
C. z z z z z z z z z
D. z z z z z z z z z 1 2 3 1 2 2 3 3 1 1 2 3 1 2 2 3 3 1 Lời giải:
Chuẩn hóa: z i, z i
 ,z  1 suy ra đáp án A 1 2 3
_________________________________________________________________________________
Tác giả: Phạm Minh Tuấn - TOANMATH.com
Phương pháp CHUẨN HÓA trong số phức
_________________________________________________________________________________
Ví dụ 6: Cho ba số phức z ,z ,z thỏa mãn z z z  1 và z z z  0 . Tính giá trị 1 2 3 1 2 3 1 2 3 của biểu thức 2 2 2
P z z z . 1 2 3 A. 0 B. 1  C. 1 D. 2 Lời giải: 1 3 1 3
Chuẩn hóa: z   i, z   i, z  1  Suy ra P  0 1 2 3 2 2 2 2
Ví dụ 7: Cho các số phức z ,z ,z thỏa mãn đồng thời hai điều kiện z z z  1999 1 2 3 1 2 3
z z z z z z
và z z z  0 . Tính 1 2 2 3 3 1 P  . 1 2 3
z z z 1 2 3 A. P  1999 C. P  999,5 B. P  2 1999 D. P  5997 Lời giải: Chuẩn hóa: 2
z  1999; z  1
 999; z  1 i 1999 1 suy ra P  1999 1 2 3
Ví dụ 8: Cho các số phức a,b,c, z thỏa 2
az bz c  0 a  0 . Gọi z và z lần lượt là hai 1 2
nghiệm của phương trình bậc hai đã cho. Tính giá trị của biểu thức 2 2 2
P z z
z z  2  z z  1 2 1 2  1 1  c c A. P  2 C. P  4 a a c 1 c B. P  D. P  . a 2 a Lời giải:  1 3 z    i 1  Chuẩn hóa: 2 2
a b c  1  
P  4 . Đáp án C thỏa P  4  1 3 z    i  2  2 2
_________________________________________________________________________________
Tác giả: Phạm Minh Tuấn - TOANMATH.com
Phương pháp CHUẨN HÓA trong số phức
_________________________________________________________________________________ 1
Ví dụ 9: Nếu z không phải là số thực đồng thời
có phần thực bằng 4 thì môđun z z của z là? 1 1 A. C. 8 12 1 1 B. D. 6 16 Lời giải: Thử đáp án: Đáp án A: 1 1 17 1 17 Với z  , chọn x   y   , do đó z   i 8 9 72 9 72 1 Thay z vào ta được
 4  4 17i ( thỏa yêu cầu đề bài có phần thưc bằng 4 ) z z Vậy đáp án là A
Ví dụ 10: Nếu hai số thức z , z thỏa mãn z z  1 và z .z  1  thì số phức 1 2 1 2 1 2 z z 1 2 w  1 có phần ảo bằng? z z 1 2 A. 0 C. 1 B. 1  D. Lớn hơn 1 Lời giải: i  1
Chuẩn hóa: z i ; z  1 do đó w
 1 suy ra phần ảo của w bằng 0 1 2 1  . i 1 Vậy đáp án là A
_________________________________________________________________________________
Tác giả: Phạm Minh Tuấn - TOANMATH.com
Phương pháp CHUẨN HÓA trong số phức
_________________________________________________________________________________
Ví dụ 11: Cho số phức z a bi a,b  thỏa mãn điều kiện 2
z  4  2 z . Đặt P   2 2
8 b a  12 . Mệnh đề nào sau đây đúng?
A. P   z  2 2
C. P   z  2 2 2
B. P   z  2 4
D. P   z  2 2 4 Lời giải: 2 Ta có: 2 z   z   2 2 a b   2 2  a b   2 2 4 2 4 4 4 a b  a   1
Chọn b   a  2 2 2 0 4
 4a a  1 i 3 suy ra z  1 i 3   . Thay a, b vào P b  3 ta được P  4
Thay z  1 i 3 vào đáp án C ta được kết quả là 4. Vậy đáp án là C 2 1 1
Ví dụ 12: Cho các số phức z , z  0 a,b  thỏa mãn điều kiện   . Tính 1 2 z z z z 1 2 1 2 z z
giá trị của biểu thức 1 2 P   . z z 2 1 2 A. C. 3 2 3 2 B. 2 D. 2 Lời giải: 1 1
Chuẩn hóa: z  1  2    z  0  ,5  0,5i 1 2 z z  1 2 2 1 0  ,5  0,5i 3 2 P    0  ,5  0,5i 1 2
_________________________________________________________________________________
Tác giả: Phạm Minh Tuấn - TOANMATH.com
Phương pháp CHUẨN HÓA trong số phức
_________________________________________________________________________________ z
Ví dụ 13: Cho số phức z a bi  0 sao cho z không phải là số thực và w  là số 2 1  z z thực. Tính . 2 1  z 1 1 A. C. 5 2 1 B. D. 1 3 Lời giải: z
Chuẩn hóa: Vì w là số thực nên ta chọn w  1 
 1 z  0,5  0,5 3i 2 1 z 0, 5  0, 5 3i z 1 Suy ra   2 2  2 1 z 1  0, 5  0, 5 3i
Ví dụ 14: Cho hai số phức z , z thỏa mãn điều kiện z z z z  1 . Tính giá trị 1 2 1 2 1 2 2 2
z   z  của biểu thức 1 2 P        z   z 2 1  A. 1  C. 2 B. 1 i D. 1 i Lời giải:  1 3 z   i 1  Chuẩn hóa: 2 2   P  1   1 3 z    i  2  2 2
_________________________________________________________________________________
Tác giả: Phạm Minh Tuấn - TOANMATH.com