Phương pháp Đirichlê và ứng dụng – Nguyễn Hữu Điển

Nguyên lý những cái lồng và các chú thỏ đã được biết đến từ rất lâu. Ngay trong chương trình phổ thông cơ sở chúng ta cũng đã làm quen với phương pháp giải toán này. Thực ra nguyên lý này mang tên nhà bác học người Đức Pête Gutxtap Legien Dirichlet (1805 – 1859).

72 36 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

NGUY

ÊN H

U ÐIÊ

PHU

NG PH

AP ÐIRICHLÊ

NG D

UNG

A XU

ÂT B

AN KHOA H

OC V

A K

Y THU

ÂT

A N

ÔI - 1999

I N

OI Ð

ÂU

Nguyên l

y nh

ng c

ai lô

ng v

a c

ac ch

u th

c biê

dê

n t

râ

lâu. Ngay trong chu

ng tr

ınh phô

thông co

ung ta c

ung

a l

quen v

i phu

ng ph

ap gi

ai to

an n

ay. Th

c ra nguyên l

y n

ay mang

tên nh

a b

ac h

oc ngu

i Ð

c Pête Gutxtap Legien Dirichlet (1805-

1859). Nguyên l

y ph

at biê

u râ

n gi

an: Nê

u ch

ung ta nhô

t th

o v

ac lô

ng m

a sô

lô

ıt ho

n sô

o, th

ı thê

ao c

ung c

o m

ôt lô

ng nhô

ıt

nhâ

t hai con th

ı b

ang nguyên l

n gi

an nhu

ây h

ang lo

at c

ac b

ai to

c gi

ai.

Cuô

n s

ach

c biên so

an l

ai theo t

ng ch

dê

o liên quan

dê

nguyên l

y, m

ôi c

ach gi

ai trong v

ı d

u c

ua t

ng chu

ng l

ap d

ung

diê

n h

ınh nguyên l

y Ðirichlê. B

ai t

âp gi

ai tru

c c

o liên quan

dê

n b

ai sau nên câ

n lu

y khia

oc s

ach. V

i mong muô

n c

ung b

ao lu

ân m

ôt phu

ng ph

ap ch

ng minh to

an h

oc v

a hy v

ong cung

câ

p m

ôt t

ai li

êu bô

ıch cho c

ac thâ

y cô gi

ao v

a c

ac em h

oc sinh ham

mê t

ım t

oi trong to

an h

oc, t

ac gi

a m

anh d

an biên so

an cuô

n s

ach

ay. Do kh

a n

ang v

a th

i gian c

on h

an chê

, cuô

n s

ach ch

ac ch

không tr

anh kh

oi thiê

u s

ot. Ch

ung tôi mong

c s

ong g

kiê

n c

oc gi

a. Thu

y xin g

i vê

a xuâ

t b

an Khoa h

oc v

a K

thu

ât - 70 Trâ

n Hu

ng Ð

ao, H

a N

ôi.

4 L

i n

dâ

ac gi

a xin chân th

anh c

am o

n PGS-TSKH Ð

ô Hô

ng Tân

ong g

op nhiê

y kiê

n qu

ı b

au trong qu

a tr

ınh ho

an ch

ınh b

ao.

ac gi

CHU

NG 1

NGUYÊN L

Y ÐIRICHLÊ V

A V

I D

1.1. Nguyên l

y Ðirichlê

Nguyên l

y Ðirichlê nhiê

u khi ngu

i ta g

oi l

a ¨Nguyên l

y nh

an k

eo¨. Ðây l

a m

ôt nguyên l

y râ

n gi

an,

ac bi

êt c

o nhiê

ng d

ung trong c

ac l

ınh v

c kh

ac nhau c

ua to

an h

oc. D

ung nguyên

y n

ay ngu

i ta d

ê d

ang ch

ng minh tô

n t

ai m

ôt

dô

i tu

ng v

i t

ınh

châ

t x

inh. D

ang

n gi

an nhâ

t c

o thê

at biê

u nhu

Nê

u c

o m v

ât

˘at v

ao n c

ai ng˘an k

eo v

a m > n th

ı c

ıt nhâ

t m

ôt

ng˘an k

eo ch

ıt nhâ

t hai v

ât.

Tuy r

ang v

i nguyên l

y n

ay ngu

i ta ch

ı ch

ng minh

c s

tô

ai m

a không

a ra

c phu

ng ph

ap t

ım

c v

ât c

u thê

, nhu

trong th

c tê

nhiê

u b

ai to

an ta ch

ı câ

n ch

ı ra s

tô

n t

ai l

u rô

Nguyên l

y Ðirichlê l

a m

ôt

inh l

y vê

âp h

p h

u h

an. Ph

at biê

ınh x

ac nguyên l

y n

ay nhu

Cho A v

a B l

a hai t

âp h

p không r

ông c

o sô

phâ

n t

an, m

a sô

ng phâ

n t

ua A l

n ho

n sô

ng phâ

n t

B. Nê

u v

i m

ôt qui t

ac n

dâ

y, m

ôi phâ

n t

ua A cho tu

ng v

i m

ôt phâ

n t

B, th

ı tô

n t

ai hai phâ

n t

ac nhau c

ua A

a ch

ung tu

ng v

i c

ung m

ôt phâ

n t

ua B.

Ðê

ê hiê

u ta c

cho r

ang c

ac phâ

n t

ua t

âp B l

a ¨Nh

ng ng

6 Chu

ng 1. Nguyên l

y Ðirichlê v

a v

ı d

eo¨ v

a c

ac phâ

n t

ua A

at v

ao c

ac ng

an k

eo c

ua n

o. Trong

at biê

u c

ua nguyên l

y trên c

ac phâ

n t

u h

c t

ınh b

ang

sô

nhiên, v

ı v

ây Nguyên l

y Ðirichlê c

o liên quan m

ât thiê

t t

i t

âp

p sô

nhiên v

a c

ac t

ınh châ

t c

ua t

âp h

p sô

ay.

1.2. V

ı d

. 1.1. Ðê

y ni

êm 20 n˘am ng

ay gi

ai ph

ong Miê

n Nam, t

ai m

ôt th

anh

phô

ngu

i ta tô

c buô

i l

ê g

˘ap m

˘at nh

ng ngu

i 20 tuô

i. Ng

ay 30

ang 4 n˘am

o trong buô

i g

˘ap m

˘at c

o 400 thanh niên. Ch

ng minh

˘ang c

ıt nhâ

t hai ngu

i trong sô

ngu

i t

i d

ung chung m

ôt ng

sinh.

i gi

ai. N

am 1995 c

o 365 ng

ay. Ch

ung ta coi m

ôi ng

ay nhu

ôt

an k

eo v

anh sô

dê

n 365 (ng

an k

eo cuô

i c

ung l

a ng

ay 31

ang 12 n

am 1995). Ch

ung ta

at nh

ng thanh niên c

o ng

ay sinh

ng v

ao c

ac ng

an k

o. Nhu

ng sô

thanh niên

dê

n d

ê l

n sô

an k

eo, theo nguyên l

y Ðirichlê c

ıt nhâ

t hai ngu

at v

ao c

ung m

ôt ng

an k

eo. Ðiê

o c

o ngh

ıa l

a h

o sinh c

ung m

ôt

ay.

. 1.2. Trong sinh h

oc ngu

i ta biê

t r

˘ang sô

oc trên

dâ

u c

ua m

ôi ngu

không qu

a 200.000 c

ai. Ch

ng minh r

˘ang trong sô

ngu

i c

ua th

anh

phô

a n

ôi, v

i sô

dân ho

n 2.000.000, c

ıt nhâ

t 11 ngu

i c

o c

ung sô

oc.

i gi

ai. Ch

ung ta x

et 200.000 ng

an k

anh sô

dê

199.999. Ch

ung ta ¨

at¨ m

ôi ngu

i dân H

a n

ôi v

ao m

ôt ng

an k

a sô

oc b

ang sô

ua ng

an k

eo. Gi

a s

không c

o 11 ngu

o c

ung sô

oc, nhu

ây m

ôi ng

an c

o nhiê

u nhâ

t l

a 10 ngu

i c

o c

ung

sô

oc, do

o sô

dân H

a n

ôi nhiê

u nhâ

t l

a 200.000×10=2.000.000,

1.2. V

ı d

u 7

diê

u n

ay không

ung v

i gi

a thiê

t l

a sô

dân H

a n

ôi l

n ho

n 2 tri

êu.

. 1.3. Ba mu

i h

oc sinh l

am b

ai viê

t ch

ınh t

a. M

ôt trong sô

oc sinh

o b

i 14 l

ôi, c

on c

ac h

oc sinh kh

ac m

˘ac l

ôi

ıt ho

n. Ch

ng minh r

˘ang

ıt nhâ

t ba ngu

i m

˘ac sô

ôi b

˘ang nhau.

i gi

ai. Ch

ung ta x

et 15 ng

an k

anh sô

dê

n 14. Ch

ung

ta ¨

at¨ m

ôi h

oc sinh v

ao m

ôt ng

an k

eo mang sô

ung b

ang sô

ôi

ua h

oc sinh n

ay. Nê

u không c

o ba h

oc sinh n

ao c

o sô

ôi b

ang nhau,

ı trong m

ôi ng

an mang sô

0,1,2,. . . ,13 s

e c

o nhiê

u nhâ

t hai h

sinh. Khi

o sô

ng c

ua nh

ng h

oc sinh n

ay nhiê

u nhâ

t l

a 28. Nê

thêm v

o h

oc sinh m

ac 14 l

ôi (trong ng

an k

eo sô

14) ch

ung ta s

ân

c nhiê

u nhâ

t 29 h

oc sinh viê

t ch

ınh t

diê

u n

ay d

ân

dê

vô l

y v

diê

u ki

ên

a cho.

. 1.4. Ch

ng minh r

˘ang trong m

ôi nh

om b

an 5 ngu

i c

ıt nhâ

t hai

ngu

i c

o c

ung sô

ng ngu

i quen gi

a nh

ng ngu

i trong nh

dos.

ng minh r

˘ang c

ung kê

t lu

ân nhu

ây v

i nh

om b

an c

o sô

anh viên bâ

t k

i gi

ai. Ch

ung ta x

et n

am ng

an k

eo,

anh sô

dê

n 4. M

ôi ngu

tham d

at v

ao ng

an k

eo mang sô

ung v

i sô

ngu

i trong

om m

a ngu

o quen.

a) Nê

u c

o m

ôt ngu

i không quen ai c

a trong sô

ng ngu

on l

ai, th

ı ng

an sô

4 l

a trô

ng (v

ı ngu

c l

ai th

ı c

a hai ng

an 0 v

a 4

dê

u không trô

ng, d

ân

dê

n vô l

y). Nhu

ây, m

ôi ngu

i trong sô

ngu

at v

ao c

ac ng

an mang sô

0,1,2,3 v

i sô

ng 4 ng

an.

nguyên l

y Ðirichlê suy ra

ıt nhâ

t c

o hai ngu

trong m

ôt ng

an,

hay l

a, h

o c

o chung sô

ng ngu

i quen.

8 Chu

ng 1. Nguyên l

y Ðirichlê v

a v

ı d

b) Nê

u m

oi ngu

i c

ıt nhâ

t m

ôt ngu

i quen, m

ôi ngu

i s

at v

ao c

ac ng

an mang sô

1,2,3,4, v

i sô

ng 4 ng

an. Phâ

n c

on l

ap d

ung nguyên l

y Ðirichlê.

. 1.5. Trong m

ôt gi

ai b

ong

a tham d

ôi. M

ôi c

˘ap hai

ôi ph

dâ

u v

i nhau. Ch

ng minh r

˘ang t

ai m

ôi th

diê

m c

ua gi

ai c

ıt nhâ

ôi c

o sô

ân

dâ

u nhu

nhau.

i gi

ai. Ch

ung ta x

et 16 ng

an k

anh sô

dê

n 15. Ch

y r

ang

15 l

a sô

ng l

n nhâ

t c

ac tr

ân b

ong m

a m

ôi

ôi c

o thê

dâ

u t

ai th

diê

dang x

et. H

at m

ôi

ôi b

ong v

ao ng

an k

eo mang sô

ang

sô

ac tr

ân m

ôi

dâ

dê

n th

diê

o. Ch

ung ta nh

ân ra r

ang

ac ng

an 0 v

a 15 không thê

dô

ng th

i không trô

c v

a nhu

ây

o thê

ap d

ung nguyên l

y Ðirichlê.

. 1.6. Trên tr

dâ

t sô

ng ho

n 5 t

y ngu

i, biê

t r

˘ang không qu

a 1% sô

trên m

ôt tr˘am tuô

i. Ch

ng minh r

˘ang

ıt nhâ

t c

o hai ngu

i sinh c

ung

ôt giây

dô

ng hô

i gi

ai. Theo du

ng l

ich hi

ên h

anh 100 n

am c

ıt ho

n 37000 ng

ay.

ôi ng

ay c

o 24 gi

, m

ôi gi

o 3600 giây. Khi

o 100 n

am c

ıt ho

3,33 t

y giây. T

diê

u ki

ên ch

ung ta t

ım

c nh

ng ngu

i trên tr

dâ

t không qu

a 100 tuô

ıt nhâ

t l

a 99% t

5 t

y ngu

i ngh

ıa l

ıt nhâ

o 4,9 t

y. Vi

êc c

on l

ap d

ung nguyên l

y Ðirichlê:

at 4,9 t

y ngu

ao 3,33 t

y ng

an k

eo.

. 1.7. Trong th

i gian k

eo d

ai m

ôt n˘am h

oc m

ôt h

oc sinh gi

ıt nhâ

ôt b

ai t

âp m

ôi ng

ay. Ðê

anh c˘ang th

˘ang h

oc sinh gi

ai h

ang tuâ

không qu

a 12 b

ai t

âp. Ch

ng minh r

˘ang trong th

i gian k

eo d

ai liên

uc m

ôt sô

ay h

oc sinh n

ay ph

ai gi

ung 20 b

ai t

âp m

ôi ng

ay.

1.2. V

ı d

u 9

i gi

ai. Ch

ung ta k

y hi

êu a

a sô

ng b

ai t

âp h

oc sinh

a gi

trong ng

dâ

u tiên, a

a sô

ng b

ai t

âp

a gi

ai trong hai ng

dâ

u, a

a sô

ng b

ai t

âp

a gi

ai trong ba ng

dâ

u, v

a v.v. a

a sô

ng b

ai t

âp

a gi

ai trong 77 ng

dâ

u (11 tuâ

n). Theo gi

thiê

t a

≤ 11.12 = 132. Ch

ung ta x

et t

âp h

p c

ac sô

nhiên

M = {a

, a

, . . . , a

, a

+ 20, a

+ 20, . . . , a

+ 20}. N

a 154 phâ

n t

a sô

n nhâ

t trong ch

ung l

a a

+ 20 ≤ 152.

Theo nguyên l

y Ðirichlê trong M c

ıt nhâ

t hai sô

ang nhau. Nhu

ac sô

, a

, . . . , a

a ho

an to

an kh

ac nhau. suy ra tô

n t

ai a

a a

= a

+ 20, l < k ≤ 77. Nhu

ây a

− a

= 20,

diê

u n

o ngh

ıa l

a t

ay th

l + 1

dê

n ng

ay th

k h

oc sinh n

ay ph

ai gi

ung 20 b

ai.

. 1.8. Trong m

ôt khu t

âp thê

sô

ng 123 ngu

i. Tô

ng sô

tuô

i c

ua h

a 3813. Ch

ng minh r

˘ang c

o thê

on 100 ngu

i sô

khu t

âp thê

ay, m

a tô

ng sô

tuô

i c

ua h

o không nh

o ho

n 3100.

i gi

ai. Ch

ung ta h

ay ch

on 100 ngu

i nhiê

u tuô

i nhâ

t v

a gi

a s

tô

ng sô

tuô

i c

ua h

o nh

o ho

n 3100. Khi

o ngu

i tr

e nhâ

t trong sô

ngu

c ch

on l

a 3100:100=31 tuô

i. M

at kh

ac ngu

i n

ay không

e ho

n 23 ngu

i c

on l

ai theo c

ach ch

on. Khi

o tô

ng sô

tuô

i c

ua 23

ngu

i n

ay không l

n ho

n 23.31=713. Suy ra tô

ng sô

tuô

i c

ua tâ

t c

oi ngu

i sô

ng trong t

âp thê

o ho

n 3100+713=3813 d

ân

dê

vô l

. 1.9. N˘am c

˘ap v

chô

ng tô

c m

ôt buô

i g

˘ap m

˘at. Khi g

˘ap nhau h

˘at tay nhau, nhu

ng không ai t

˘at tay ngu

i trong gia

ınh m

ınh

a ngu

i m

a chô

ng m

ınh (ho

˘ac v

ınh)

a b

˘at tay rô

i. C

ung không

ai b

˘at tay c

ung m

ôt ngu

i hai lâ

n. Sau cu

ôc g

˘ap ch

uc m

ng ban

dâ

ôt ngu

an ông tên l

a H

ung h

oi tâ

t c

a nh

ng ngu

i c

o m

˘at, kê

10 Chu

ng 1. Nguyên l

y Ðirichlê v

a v

ı d

ınh, l

a h

a b

˘at tay

c bao nhiêu lâ

n. H

o nh

ân thâ

y r

˘ang ch

ın

ngu

c h

dê

u tr

a l

i c

ac con sô

ac nhau. Nhu

ây v

ua H

ung

a b

˘at tay bao nhiêu lâ

i gi

ai. M

ôi m

ôt ngu

i kh

ach b

at tay không qu

a 8 lâ

n. V

ı câu tr

a l

ua 9 ngu

i l

a c

ac sô

ac nhau nên c

ac sô

o ph

ai l

a 0,1,2,3,4,5,6,7

a 8. Ngu

i b

at tay 8 lâ

n ph

ai l

a v

(ho

ac chô

ng) c

ua ngu

i không

at tay lâ

n n

ao (nê

u ngu

c l

ai th

ı ngu

o không b

at tay 8 lâ

n m

nhiê

u nhâ

t ch

ı l

a 7 lâ

n thôi). Tu

ng t

nhu

ây ngu

i b

at tay 7 lâ

o ngu

i v

(ho

ac chô

ng) b

at tay m

ôt lâ

n, ngu

i b

at tay 6 lâ

n c

ngu

i v

(ho

ac chô

ng) b

at tay 2 lâ

n, ngu

i b

at tay 5 lâ

n c

o ngu

i v

(ho

ac chô

ng) b

at tay 3 lâ

n. Ch

ı c

on l

ai m

ôt ngu

i duy nhâ

t b

at tay

4 lâ

o ch

ınh l

a ngu

i v

ua H

ung.

. 1.10. M

ôt câu chuy

ên cô

ıch kê

ai r

˘ang: M

ôt lâ

n vua H

ung vu

18 c

o m

i c

ac quan trong triê

u h

op ngô

i quanh m

ôt c

ai b

an tr

on. Theo

ênh c

ua vua, m

ôt c

ân thâ

a viê

t tên c

ua m

ôi quan trên b

an tru

chiê

c ghê

a ông ta ph

ai ngô

i. C

ac quan trong triê

u không

c b

tru

c nên h

a ngô

i không theo s

˘ap xê

inh m

a chiê

m ch

ô m

ôt

ach bâ

t k

y. Ch

ng minh r

˘ang ông c

ân thâ

n c

o thê

quay chiê

c b

an sao

cho

ıt nhâ

t c

o hai ông quan ngô

ung v

i tr

ı tên c

ua m

ınh ?

i gi

ai. Ð

at sô

ng c

ac quan l

a n. Khi

o m

at b

an c

o n tr

ang th

ai,

i c

ac tr

ang th

ai n

dô

i di

ên v

i c

ac quan l

a biê

dê

tên n

Ngo

ai ra v

i m

ôi m

ôt ông quan ch

ı c

o m

ôt tr

ang th

ai, m

a khi ngô

ung th

ı ông â

dô

i di

ên v

i ch

ınh tên c

ua m

ınh trên biê

dê

an.

Ngh

ıa l

a, nê

u m

ôi tr

ang th

ai c

ua b

an (v

ı b

an c

o thê

xoay

c) ta

cho tu

ng v

i m

ôt sô

ang sô

ng c

ac quan ngô

ung v

i tr

tên m

ınh, th

ı tô

ng c

ua tâ

t c

a nh

ng sô

ân

c (m

oi tr

ang th

an) s

e không nh

o ho

n n. Nhu

ng m

ôt tr

ang th

dâ

u tiên c

ua s

1.3. B

ai t

âp 11

xê

p b

an cho tu

ng v

i 0 (không ai ngô

ung ch

ô ). Nê

u gi

a s

trong n −1 tr

ang th

ai m

at b

an c

on l

ai tu

ng v

i sô

o ho

n 2

c l

a ch

ı c

o sô

1 ho

ac 0), th

ı tô

ng c

ua n sô

ân

c s

e nh

o ho

diê

o không thê

c. Suy ra t

n − 1 tr

ang th

ai m

at b

an c

ai c

ıt nhâ

t m

ôt tr

ang th

ai m

a hai ngu

i s

dô

i di

ên v

i ch

ınh tên

ua m

ınh.

1.3. B

ai t

âp

. 1.11. Trong sân cung

ên nh

a vua h

ôi h

op 2n(n ≥ 2) ông quan,

ôi ông quan

a quen biê

t không

ıt ho

n n ông c

o m

at t

o. Ch

minh r

ang ngu

i xê

p b

an tr

on c

o thê

xê

c m

ôi b

an 4 ngu

i sao

cho m

ôi ngu

ng gi

a hai ngu

i quen c

ua m

ınh.

. 1.12. M

ôt khu r

ng thông c

o d

ang h

ınh vuông m

ôi chiê

u 1km.

Trong r

ng c

o 4500 cây thông, cây to nhâ

t c

ng k

ınh 0,5m.

ng minh r

ang trong khu r

ng c

ıt nhâ

t 60 m

anh

dâ

t, di

ên t

ıch

ôi m

anh 200m

, không c

o m

ôt cây thông n

ao.

. 1.13. Trong m

ôt gi

a s

ach c

o 25 ng

an. Ta thâ

y c

o m

ôt ng

an ch

10 cuô

n, c

on c

ac ng

an kh

ac ch

a sô

ach

ıt ho

n. Ch

ng minh r

ang

ıt nhâ

t ba ng

an s

ach ch

a c

ung sô

ach nhu

nhau (kê

a nh

an không c

o s

ach).

. 1.14. T

ai m

ôt th

anh phô

biê

n xe ôtô

anh sô

ang tô

ai rô

dê

n d

ay sô

. Ch

ng minh r

ang trên m

ôt

ng c

o 11 chiê

c ôtô

di qua th

ı bao gi

ung c

o hai chiê

c ôtô c

o c

ung ch

sô

ân c

ung.

. 1.15. M

ôt chiê

c hô

c b

oc b

i 4 tr

am chuyê

n tiê

p s

ong

thông tin. Gi

a hai tr

am ngu

i ta xây d

ng c

ac trung tâm ph

at s

ong

a nh

ân s

ong,

ng s

ong bao ph

u l

n nhâ

t l

ng tr

on c

o tâm

12 Chu

ng 1. Nguyên l

y Ðirichlê v

a v

ı d

trung tâm v

di qua hai tr

am. Ch

ng minh r

ang v

i bô

n trung tâm

an gi

a c

ua t

ng c

ap tr

am th

ı to

an b

ô m

at hô

c ph

ong thông tin.

CHU

NG 2

Ô H

2.1. Ph

ep chia sô

nhiên

Trong c

ac ph

ep t

ınh trên sô

nguyên: c

ông, tr

, nhân, chia, th

ep chia l

a râ

ac bi

êt. Ph

ep chia c

o h

ang lo

at t

ınh châ

t m

a tâ

t c

ac ph

ep t

ınh c

on l

ai không c

o. V

ı d

u c

ac ph

ep to

dê

u th

c hi

ên

i sô

c, nhu

ng riêng ph

ep chia cho sô

0 th

ı không

c. Ph

chia không ch

ac bi

êt v

i ph

ep chia cho 0. V

i c

ac ph

ep t

ınh c

ông,

, nhân trên sô

nguyên cho ta sô

nguyên, nhu

ng v

i ph

ep chia th

ınh châ

o không c

ung v

ı không ph

ai l

uc n

ao ta c

ung nh

ân

c sô

nguyên sau ph

ep chia. Nh

ng d

i bi

êt c

ua ph

ep chia m

trong to

an h

oc xây d

ng h

an m

ôt l

y thuyê

t vê

ep chia nh

ng sô

nguyên. Nh

ng v

ı d

u v

a b

ai t

âp chu

ng n

ay c

o liên quan m

ât thiê

a ph

ep chia v

a nguyên l

y Ðirichlê, nên ch

ung ta nh

ac l

inh

ngh

ıa ph

ep chia:

Cho a v

a b l

a nh

ng sô

nguyên, v

i b > 0. Ch

ung ta n

oi r

ang a

chia hê

t cho b, k

y hi

êu l

a b|a, khi tô

n t

ai m

ôt sô

nguyên q sao cho

ang th

c sau

ung a = b q.

ung ta thu

ng g

oi sô

a l

a b

ôi c

ua b, ho

ac b l

a u

c c

ua a. Sô

oi l

a thu

ng sô

ua ph

ep chia a cho b. Trong ph

at biê

inh ngh

ıa

trên, nê

u không tô

n t

ai m

ôt sô

q n

ao c

a, th

ı ch

ung ta n

oi r

ang a

14 Chu

ng 2. Sô

không chia hê

t cho b v

a k

y hi

êu l

a b 6 |a.

inh ngh

ıa ch

ung ta d

ê d

ang ch

ng minh

c c

ac t

ınh châ

1) V

i m

oi sô

nguyên a > 0 ch

ung ta c

o a|a, Ph

ep chia hê

t c

ınh ph

an x

2) Nê

u b|a v

a a|c th

ı b|c- ph

ep chia hê

t c

o t

ı nh b

ac câ

3) Nê

u b|a v

a b|c, th

ı b|(ac).

4) Nê

u a, b, m, n l

a nh

ng sô

nguyên v

a nê

u c|a v

a c|b, th

c|(ma + nb).

inh l

y sau

dây gi

vai tr

o quan tr

ong cho ph

ep chia m

ôt sô

nguyên cho m

ôt sô

nguyên.

i hai sô

nguyên bâ

t k

y a v

a b sao cho b > 0, tô

n t

ai duy

nhâ

t nh

ng sô

nguyên q v

a r th

oa m

an a = bq + r v

a 0 ≤ r < b.

on râ

t nhiê

u t

ınh châ

t kh

ac c

ua sô

nguyên c

ung nhu

sô

nhu

ng ch

ung ta không

di theo hu

ng n

ay, m

a ch

ı d

ung c

ac t

ınh châ

ua sô

oc v

a Nguyên l

y Ðirichlê

dê

ai c

ac b

ai to

an.

2.2. V

ıd

. 2.1. Cho k l

a m

ôt sô

nhiên, A l

a t

âp h

p gô

m k + 1 sô

nhiên.

ng minh r

˘ang c

ıt nhâ

t m

ôt hi

êu hai phâ

n t

trong A chia hê

cho k.

i gi

ai. G

oi a

, a

, . . . , a

k+1

a c

ac phâ

n t

ua A, c

on b

, b

, . . . , b

k+1

a nh

ng sô

ua ph

ep chia c

ac sô

trên cho k. Khi

o a

+ b

, a

= kc

+ b

, . . . , a

k+1

= kc

k+1

+ b

k+1

i c

ac sô

nguyên

, c

, . . . , c

k+1

sao cho 0 ≤ b

≤ k − 1, 0 ≤ b

≤ k − 1, . . . , 0 ≤

k+1

≤ k −1. M

ôt phâ

n t

bâ

t k

y a

thu

ôc A cho tu

ng v

i sô

2.2. V

ıd

u 15

ua n

o.G

oi t

âp h

p c

ac sô

a B. Nhu

ây, m

ôi phâ

n t

ua A

at tu

ng v

i m

ôt phâ

n t

ua t

âp h

p B, gô

m tâ

t c

a c

sô

nguyên t

dê

n k − 1. Nhu

ng sô

ng phâ

n t

ua A theo gi

thiê

t l

a k + 1, c

on B c

o sô

ng k. Theo nguyên l

y Ðirichlê suy ra

tô

n t

ai hai phâ

n t

ac nhau c

ua A c

o c

ung sô

. Ðiê

o ngh

ıa l

tô

n t

ai hai ch

ı sô

ac nhau s v

a t v

i a

= kc

+ b

a a

= kc

+ b

sau khi tr

di cho nhau ta

c a

− a

= k(c

−c

. 2.2. Cho A m

ôt t

âp h

p bâ

t k

y gô

m 101 sô

nhiên, m

ôi sô

không

n ho

n 200. Ch

ng minh r

˘ang trong A c

ıt nhâ

t hai sô

a m

ôt sô

ay chia hê

t cho sô

kia.

i gi

ai. M

ôi sô

a c

ua A c

o thê

biê

u di

ên du

i d

ang a = 2

b v

i k l

sô

nguyên không âm, c

on b l

a m

ôt sô

e. V

i m

ôi sô

a thu

ôc A cho

ng v

i sô

b trong s

biê

u di

ên

trên. B

ang c

ach n

ay, m

ôi

phâ

n t

a c

ua A

at tu

ng v

i m

ôt phâ

n t

ua t

âp h

p B

gô

m c

ac sô

e gi

a 1 v

a 200. Nhu

ng t

âp h

p B ch

ı c

o 100 phâ

n t

ây sô

phâ

n t

ua A l

n ho

n sô

phâ

n t

ua B. Ta c

o thê

ap d

ung

nguyên l

y Ðirichlê, suy ra tô

n t

ai hai phâ

n t

ac nhau a

a a

thu

ôc A m

a ch

ung tu

ng v

i c

ung m

ôt sô

ua t

âp h

p B. Ngh

ıa

a, a

= 2

b, a

= 2

b v

a nê

u k

< k

, th

ı sô

chia hê

t cho a

. 2.3. Cho M l

a t

âp h

p bâ

t k

y gô

m 75 sô

nhi

ên m

a m

ôi sô

không

n ho

n 100. Ch

ng minh r

˘ang v

i m

ôi sô

nhiên l nh

o ho

n ho

˘ac

˘ang 49 tô

n t

ai hai phâ

n t

ua M c

o hi

êu l

a l.

i gi

ai. G

oi c

ac phâ

n t

ua M l

a x

, x

, . . . , x

. K

y hi

êu A l

a t

âp

p c

ac sô

nhiên t

dê

n 150. V

i m

ôi sô

1, 2, 3 . . . , 75 cho tu

ng v

i c

ac sô

, x

, . . . , x

, c

on c

ac sô

76, 77, 78, . . . 150 lâ

n lu

ng v

i x

+ l, x

+ l, . . . , x

+ l. V

ı x

≤ 100(m = 1, 2, . . . , 75) v

16 Chu

ng 2. Sô

l ≤ 49 th

ı x

+ l < 150. Suy ra m

ôi phâ

n t

ua A tu

ng v

ôt phâ

n t

ua B gô

m nh

ng sô

nhiên t

dê

n 149. V

ı sô

phâ

ua A l

n ho

n sô

phâ

n t

ua B, theo nguyên l

y Ðirichlê tô

n t

hai phâ

n t

ac nhau c

ua A, m

a ch

ung tu

ng v

i c

ung m

ôt

phâ

n t

ua B . Nhu

ng v

i c

ac gi

a tr

i kh

ac nhau c

ua m t

dê

n 75

c cho tu

ng v

i c

ac gi

a tr

i kh

ac nhau c

ua x

dê

n x

trong

B. Tu

ng t

ac gi

a tr

i c

ua m

kho

ang 76

dê

n 150 tu

ng v

ac gi

a tr

i kh

ac nhau trong kho

ang c

on l

ai. T

o suy ra tô

n t

ai x

a x

= x

+ l, ngh

ıa l

a x

− x

= l.

. 2.4. Cho k ≥ 1 v

a n ≥ 1 l

a nh

ng sô

nhiên v

a A l

a t

âp h

p gô

( k −1 )n + 1 sô

nguyên du

ng, m

ôi sô

dê

u nh

o ho

n ho

˘ac b

˘ang kn.

ng minh r

˘ang

ıt nhâ

t c

o m

ôt phâ

n t

ua A c

o thê

biê

u di

ên nhu

tô

ng c

ua k phâ

n t

trong A.

i gi

ai. V

i k = 1 b

ai to

an hiê

n nhiên l

ung, ch

ung ta gi

a thiê

k ≥ 2. K

y hi

êu m l

a sô

o nhâ

t thu

ôc A. D

ê thâ

y r

ang m ≤ n v

tô

n t

ung n − m sô

thu

ôc A m

a ch

ung l

n ho

n m nhu

ng không

t qu

a kn.

Ðê

ng minh b

ai to

an ch

ung ta t

ım hai sô

x v

a y thu

ôc A sao

cho x = y + (k − 1)m; ngh

ıa l

a biê

u di

ên m

ôt sô

o thu

ôc A

anh tô

ng k sô

ang thu

ôc A trong

o c

o k −1 sô

ang b

ang m. Ch

câ

n t

ım sô

x thu

ôc A m

a x > (k −1)m v

a x − (k − 1)m thu

ôc A.

ât v

ây, trong kho

ang ∆ = ((k − 1)m, kn] c

o kn − (k − 1)m =

k(n − m) + m sô

nguyên. V

ı k ≥ 2, nên (k −1)m ≥ m, theo nh

ân

et ban

dâ

u suy ra c

o nhiê

u nhâ

t n − m sô

trong ∆ không thu

ôc A.

Ðiê

u n

ay ngh

ıa l

a A ch

ıt nhâ

t s = k(n − m) + m − (n − m) =

( k − 1) (n − m) + m sô

. Nhu

ng s ≥ n, v

ı (k − 2)(n − m) ≥ 0. G

, a

, . . . , a

thu

ôc A, v

i (k − 1)m < a

≤ kn, i = 1, 2, . . . , s. Khi

2.2. V

ıd

u 17

ng hi

êu a

−(k −1)m, a

−(k −1)m, . . . , a

−(k −1)m l

a nh

sô

nguyên kh

ac nhau trong kho

ang [1, kn]. Nê

u m

ôt sô

o trong

ung không thu

ôc A, th

ı theo nguyên l

y Ðirichlê ch

ung ta nh

ân

c s ≤ n −1, v

ı ngo

ai A c

ung n −1 sô

trong kho

ang n

ay. Nhu

ây tr

ai v

i bâ

ang th

a ch

ng minh s ≥ n. Suy ra tô

n t

ai m

ôt

êu a

−( k −1)m thu

ôc A.

. 2.5. Ch

ng minh r

˘ang t

n + 1 sô

ng kh

ac nhau nh

o ho

n 2n, c

thê

c ba sô

sao cho tô

ng hai sô

trong ch

ung b

˘ang sô

ba.

i gi

ai. K

y hi

êu 0 < a

< a

< . . . < a

n+1

a nh

ng sô

a cho.

ung ta x

et c

ac hi

êu sô

− a

, a

− a

, . . . , a

n+1

− a

a c

ac sô

, a

. . . , a

n+1

. V

ı tâ

t c

a c

ac sô

dê

u nh

o ho

n 2n nên c

ac sô

trên

ı n

am trong kho

ang 1, 2, . . . , 2n −1. Nhu

ây ch

ung ta s

e t

ım

ôt sô

om th

nhâ

t b

ang m

ôt sô

om th

hai: a

− a

= a

suy ra a

= a

+ a

. 2.6. Ch

ng minh r

˘ang v

i m

ôt sô

bâ

t k

y n tô

n t

ai m

ôt sô

o d

ang

111 . . . 000

| {z }

n ch

sô

a chia hê

t cho n.

i gi

ai. Ch

ung ta x

et nh

ng sô

1, 11, 111, . . . , 111 . . . 111

| {z }

n ch

sô

a nh

sô

khi chia d

ay sô

trên cho n. V

ı d

ay sô

a cho gô

m n phâ

, nên nh

ng sô

ng kh

ac nhau khi chia ch

ung cho n c

o sô

ng n − 1. C

o thê

a thiê

t không c

o m

ôt sô

ao trong d

ay trên

chia hê

t cho n v

ı nê

u ngu

c l

ai th

ı b

ai to

c gi

ai. Khi

e c

o hai sô

trong ch

ung, v

ı d

u 111 . . . 111

| {z }

k ch

sô

a 111 . . . 111

| {z }

l ch

sô

, l > k,

a khi chia ch

ung cho n s

e cho c

ung m

ôt sô

. Do

o l − k =

18 Chu

ng 2. Sô

111 . . . 000

| {z }

(l-k ch

sô

1, k ch

sô

e chia hê

t cho n.

. 2.7. Cho p l

a sô

nguyên tô

n ho

n 5. Ch

ng minh r

˘ang tô

n t

ai m

ôt

sô

o d

ang 111 . . . 111 m

a chia hê

t cho p.

i gi

ai. Ta x

et d

ay sô

1, 11, 111, . . . , 111 . . . 1

| {z }

(p ch

sô

)

. Nê

u trong d

ay trên

không c

o sô

ao chia hê

t cho p, th

ı ta cho tu

ng m

ôi sô

i sô

ua ph

ep chia. T

âp h

p c

ac sô

ı c

o 1, 2, . . . , p −1 gô

m p −1

phâ

n t

ı 0 không thê

o trong t

âp n

ay). Nhu

ng v

ı ch

ung ta c

o p

sô

ang trên, nên theo nguyên l

y Ðirichlê tô

n t

ai hai sô

o c

ung

sô

. Gi

a s

ac sô

o l

a 111 . . . 1

| {z }

(m ch

sô

)

a 111 . . . 1

| {z }

( n ch

sô

)

i m > n. Khi

o 1 ≤ n < m ≤ p. V

ây

111 . . . 1

| {z }

(m ch

sô

)

− 111 . . . 1

| {z }

(n ch

sô

)

= 111 . . . 000

| {z }

(m-n ch

sô

1, n ch

sô

= 111 . . . 1

| {z }

(m-n ch

sô

)

.10

ıch n

ay chia hê

t cho p v

ı (p, 10) = 1, suy ra 111 . . . 1

| {z }

(m-n ch

sô

chia hê

t cho p v

a n

o c

ung n

am trong d

trên. M

a 1 ≤ m −n ≤ p

mâu thu

ân v

i gi

a thiê

t không c

o sô

ao trong d

ay chia hê

t cho p.

. 2.8. (Ðê

thi Olympic to

an thê

i lâ

n th

14) Cho M l

a t

âp h

p bâ

y gô

m 10 sô

nhiên, m

ôi sô

không l

n ho

n 100. Ch

ng minh r

˘ang

tô

n t

ai hai t

âp h

p con c

ua M m

a tô

ng c

ua c

ac phâ

n t

trong ch

ung

˘ang nhau.

2.2. V

ıd

u 19

i gi

ai. C

o thê

ng minh nê

u tô

n t

ai hai t

âp th

oa m

an kê

t lu

ân

ua b

ai to

an, th

ı ta c

o thê

c hai t

âp con c

o c

ung t

ınh châ

y nhu

ng không giao nhau. Th

ât v

ây, Cho X, Y l

a hai t

âp con c

ua M

o tô

ng c

ac phâ

n t

ang nhau. Ch

ung ta k

y hi

êu X

gô

m c

ac phâ

ua X m

a không thu

ôc Y. Tu

ng t

nhu

ây Y

gô

m c

ac phâ

ua Y m

a không thu

ôc X. R

o r

ang X

a Y

o tô

ng c

ac phâ

ang nhau m

a không giao nhau. G

oi A l

a t

âp h

p m

oi t

âp h

con không r

ông c

ua M. Sô

ng phâ

n t

ua A l

a 2

−1 = 1023.

ung ta x

et tô

ng S c

ac phâ

n t

ua m

ôt t

âp h

p con nhu

ây, r

ang S ≤ 91 + 92 + ··· + 100 < 10.100 = 1000. Nhu

ây tô

n t

không qu

a 1000 tô

ng kh

ac nhau. K

y hi

êu B l

a t

âp h

p tâ

t c

a c

tô

ng nhu

ây. Do

o sô

ng phâ

n t

ua B nh

n 1000 v

a nh

n sô

ng phâ

n t

ua A. Ð

at tu

ng m

ôi phâ

n t

ua t

âp h

A v

i tô

ng c

ac phâ

n t

ua n

o. Ta thâ

y r

ang c

o thê

ap d

ung nguyên

y Ðirichlê

dây. Suy ra tô

n t

ıt nhâ

t hai t

âp h

p con kh

ac nhau c

ung m

ôt tô

ng c

ac phâ

n t

. 2.9. (Ðê

thi h

oc sinh gi

oi to

an Câ

p II to

an quô

c 1983) Ch

ng minh

˘ang trong c

ac sô

nhiên thê

ao c

ung c

o sô

k sao cho 1983

−1 chia

hê

t cho 10

i gi

ai. Cho k lâ

y gi

a tr

i t

dê

n 10

+ 1 rô

i thay v

ao biê

u th

1983

− 1 s

e nh

ân

c 10

+ 1 gi

a tr

i kh

ac nhau. Chia 10

+ 1 sô

a nh

ân

trên cho 10

, s

c nhiê

u nhâ

t l

a 10

sô

. Do

theo nguyên l

y Ðirichlê ph

ai c

ıt nhâ

t hai sô

cho c

ung m

ôt sô

a s

o l

a sô

1983

− 1 v

a 1983

− 1(m > n). Thê

ı ( 1983

−

1) − ( 1983

−1) chia hê

t cho 10

a (1983

−1) − (1983

−1) =

(1983

−1983

) = 1983

(1983

m−n

−1). Nhu

ng 1983 v

a 10

nguyên

tô

ung nhau, do v

ây ph

ai c

o (1983

m−n

− 1) chia hê

t cho 10

. Sô

k = m −n th

oa m

diê

u ki

ên

dâ

u b

ai.

20 Chu

ng 2. Sô

. 2.10. Ch

ng minh r

˘ang tô

n t

ai nh

ng sô

nguyên a, b v

a c, không

dô

ng th

i b

˘ang 0 v

a gi

a tr

i tuy

êt

dô

i c

ua m

ôi sô

không qu

a 1000000,

oa m

an |a + b

√

2 + c

√

3| < 10

−11

i gi

ai. Ð

at S l

a t

âp h

p c

ua 10

sô

c r + s

√

2 + t

√

3 v

i m

r, s, t thu

ôc {0, 1, 2, . . . , 10

− 1} v

at d = (1 +

√

2 +

√

3d)10

Khi

o m

ôi x trong S

dê

u n

am trong kho

ang 0 ≤ x < d. Chia

an n

ay th

anh 10

−1 phâ

n b

ang nhau, m

ôi

an nh

o c

ô d

e =

−1

. Theo nguyên l

y Ðirichlê tô

n t

ai hai sô

trong 10

sô

ua S n

am trong c

ung m

ôt

an nh

o. Hi

êu c

ua hai sô

ay k

y hi

êu l

a + b

√

2 + c

√

o ch

ınh l

a c

ac sô

a, b, c v

ı e <

= 10

−11

2.3. B

ai t

âp

. 2.11. Cho A l

a t

âp h

p bâ

t k

y gô

m 201 sô

nhiên, m

ôi sô

không

t qu

a 300. Ch

ng minh r

ang A ch

ıt nhâ

t hai sô

, m

a t

y sô

ung l

a l

uy th

a b

âc ba.

. 2.12. Cho k l

a sô

nhiên bâ

t k

y, c

on a v

a b l

a nh

ng sô

nguyên

sao cho a ≤ b v

a b −a < 2k −2. Ch

ng minh r

ang nê

u M l

a t

âp h

k sô

nhiên n

am trong kho

ang [a, b], v

a l l

a sô

nhiên th

oa m

1 ≤ l ≤ 2k + a − b − 2, th

ı c

ıt nhâ

t m

ôt hi

êu nh

ng phâ

n t

M tr

ung v

i l.

. 2.13. Cho d

ây sô

, a

, . . . , a

, m

a m

ôi phâ

n t

c t

i sô

1 v

a, sô

2, trong

o c

ıt nhâ

t 21 sô

c t

ao b

i c

ac sô

ng minh r

ang tô

n t

ai m

ôt sô

phâ

n t

liên tiê

p c

ua d

ay c

o tô

ang

ung 20.

. 2.14. Ch

ng minh r

ang tô

n t

ai m

ôt sô

nhiên n, sao cho sô

2.3. B

ai t

âp 21

111 . . . 1

| {z }

(n ch

sô

)

chia hê

t cho 139. (B

ai to

an c

ung nê

u ta thay 139

ang m

ôt sô

nguyên tô

ung nhau v

i 10).

. 2.15. Ch

ng minh r

ang trong m

oi sô

ao b

i 100 ch

sô

N tô

n t

ôt sô

chia hê

t cho 1967.

. 2.16. Ch

ng minh r

ang bao gi

ung t

ım

c sô

19971997. . . 19970. . . 0 chia hê

t cho 1998.

. 2.17. Ch

ng minh r

ang c

o m

ôt sô

nhiên chia hê

t cho 1997, m

bô

n ch

sô

cuô

i c

ung c

ua n

o l

a 1998.

. 2.18. Ch

ng minh r

ang nê

u c

ac sô

nguyên m v

a n nguyên tô

ung

nhau th

ı t

ım

c sô

nhiên k sao cho m

−1 chia hê

t cho n.

22 Chu

ng 2. Sô

CHU

NG 3

AY S

3.1. Nguyên l

y Ðirichlê cho d

ay sô

vô h

Trong phâ

n n

ay ch

ung ta x

et nguyên l

y Ðirichlê du

i d

ang:

Nê

u c

o h

u h

an nh

ng ng

an k

eo m

a ch

ung ta

at vô h

ng v

ât v

o, th

ıt nhâ

t c

o m

ôt ng

an k

eo ch

a vô h

ng v

ât

a c

ung ta d

ê c

o c

am tu

ng r

ang nguyên l

y n

ay l

a hiê

n nhiên nên

ıt ch

dê

n n

o. B

ang ph

an ch

ng c

o thê

ng minh nguyên l

y n

ung. Trong sô

oc, t

âp h

p c

o liên quan

dê

n vô h

an phâ

n t

ây sô

. Ch

ung ta biê

t râ

t nhiê

u d

ay sô

ep nhu

ay câ

p sô

ông, d

câ

p sô

nhân, d

ay c

ac sô

nguyên tô

, ho

ac d

ay Fibonaxi,. . . Chu

ay ch

ung ta ch

ı quan tâm

dê

ap d

ung

diê

u ph

at biê

u trên

dê

ac b

ai to

an liên quan

dê

n d

ây sô

. Nh

ng t

âp vô h

an trong c

ac b

an du

dây ta x

et nhu

ac d

ay sô

3.2. V

ı d

. 3.1. X

et d

ay sô

6, 6

, 6

, . . . , 6

, . . . v

a viê

t 4 ch

sô

cuô

i c

ung

ua c

ac sô

ay 0006, 0036, 0216, 1296, 7776, . . .. Ch

ng minh r

˘ang b

˘at

dâ

u t

ôt sô

o d

ây v

a l

âp l

a d

ây tuâ

n ho

an.

i gi

ai. V

ı tô

n t

ai h

u h

an sô

ng (10

) c

ach ch

on kh

ac nhau

24 Chu

ng 3. D

ay sô

ac sô

o 4 ch

sô

, nên trong d

a cho ch

ac ch

an t

ım

c hai

ach ch

on c

o c

ung 4 ch

sô

cuô

i. C

o ngh

ıa l

a t

ım

c hai sô

a n

+ t m

a v

i ch

ung th

ı 6

a 6

+t+1

o c

ung 4 ch

sô

cuô

+t+1

− 6

= 10

.6k). N

oi chung, ch

sô

a 6

n+t

i bâ

t k

n > n

e c

o c

ung 4 ch

sô

cuô

i ( 6

n+t

−6

= 10

n−n

. 3.2. (Ðê

thi To

an Olympic quô

c tê

lâ

n 17 n˘am 1975) Cho

, a

, . . . , a

, . . . l

a d

ay t˘ang ng

˘at c

ac sô

nhiên. Ch

ng minh r

˘ang

vô h

an c

ac phâ

n t

ua d

ây trên c

o thê

biê

u di

ên du

i d

ang

= xa

+ ya

dây x v

a y l

a nh

ng sô

nguyên du

ng v

a p 6= q.

i gi

ai. Nê

u a

= 1 kê

t lu

ân c

ua b

ai to

an l

a hiê

n nhiên. Th

ât v

ây,

i m

oi n ≥ 3 sô

ang a

o biê

u di

ên d

ang a

= a

n−1

+ (a

n−1

) = 1.a

n−1

+ (a

− a

n−1

).a

o t

ınh châ

t mong muô

n. Ch

ung ta

e ch

ng minh tô

n t

ai ch

ı sô

p l

n ho

n 1 sao cho vô h

an c

ac sô

ang

ua d

a cho c

o thê

viê

t du

i d

ang xa

+ ya

i c

ac sô

nguyên

ng th

ıch h

p x v

a y. M

ôi sô

ang c

ua d

ay ta

at tu

ng v

sô

ua n

o khi chia ch

ınh n

o cho a

. T

âp h

p tâ

t c

a c

ac sô

ang

ua d

ay l

a vô h

an, c

on tâ

t c

a c

ac kh

a n

ang c

ua sô

khi chia c

ac sô

ang cho a

a h

u h

an. Ðiê

o ch

ng t

o r

ang vô h

an phâ

n t

, a

, . . . , a

, . . . , v

i n

< n

< . . . < n

< . . .

cho c

ung m

ôt sô

r khi chia cho a

. Không mâ

t t

ınh tô

ng qu

ta gi

a thiê

t n

> 1, v

ı trong tru

ng h

p ngu

c l

ai ta x

et c

ac sô

, a

, . . . , a

, . . . c

ung l

a d

ay vô h

an v

a cho c

ung sô

r khi chia

cho a

. V

i m

oi k = 1, 2, . . . tô

n t

ai sô

nguyên du

ng x

sao cho a

+ r. Khi

o a

− a

= (x

+ r) − (x

+ r) = (x

− x

suy ra v

i m

oi k ≥ 2 ta c

ang th

c a

= a

+ (x

− x

1.a

+ (x

− x

. Ngh

ıa l

a, nh

ng sô

, a

, . . . , a

, . . . ., c

o biê

ên v

a c

ac t

ınh châ

t nhu

ai to

oi h

oi. Th

ât v

ây, ch

ı sô

1 v

a n

3.2. V

ı d

u 25

ac nhau v

ı theo c

ach ch

on trên n

c s

n ho

n 1. Ch

ı c

on ph

ang

inh r

ang sô

− x

a sô

nguyên du

ng v

i k ≥ 2,

diê

ung v

ı t

< n

suy ra x

< x

. 3.3. Cho sô

nhiên bâ

t k

y k. Ch

ng minh r

˘ang tô

n t

ai sô

nguyên tô

p v

a m

ôt d

ay sô

nhiên t˘ang ng

˘at a

, a

, . . . , a

, . . . sao cho tâ

t c

a c

phâ

n t

ua d

ay p + ka

, p + ka

, . . . , p + ka

, . . . l

a nh

ng sô

nguyên

tô

i gi

ai. K

y hi

êu P l

a t

âp h

p tâ

t c

a c

ac sô

nguyên tô

. V

i m

i = 0, 1, . . . , k − 1 k

y hi

êu P

a t

âp h

p c

ac sô

nguyên tô

a khi

chia cho k c

o sô

i. D

ê thâ

y r

ang m

oi sô

nguyên tô

am trong m

ôt

trong c

ac t

âp h

p P

, P

, . . . , P

k−1

. B

i v

ı sô

nguyên tô

a vô h

an,

ây

ıt nhâ

t ph

ai c

o m

ôt trong sô

ac t

âp h

p P

, P

, . . . , P

k−1

vô h

an sô

nguyên tô

. Gi

a s

a vô h

an sô

a k

y hi

êu p l

a phâ

o nhâ

t c

ua n

o. Khi

o m

oi sô

x thu

ôc P

o d

ang x = p + ka v

ôt sô

nhiên a. Lâ

y x

, x

, . . . l

a c

ac phâ

n t

ua P

xê

p theo

n dâ

n. V

i m

oi sô

nhiên n

at a

− p

. D

ê thâ

y r

ang

sô

nguyên tô

p v

a d

ay a

, a

, . . . , a

, . . . c

o t

ınh châ

t mong muô

. 3.4. Cho f l

da th

c k

dô

i sô

i h

ê sô

nguyên v

a a

, a

, . . . , a

, . . . l

ay nh

ng sô

nguyên th

oa m

an h

ê th

c a

n+1

= f (a

, . . . , a

n−k+1

i m

oi sô

nguyên n, k m

a n ≥ k. Ch

ung ta x

et sô

ng bâ

t k

y m

a v

i m

oi n = 1, 2, . . .. K

y hi

êu

a sô

không âm nh

o nhâ

t c

theo mô

dun m. Ch

ng minh r

˘ang d

ay a

, a

, . . . , a

, . . . . l

a d

tuâ

n ho

an.

i gi

ai. Ch

ung ta s

e s

ung kh

ang

inh sau: Nê

u g l

da th

dô

i sô

i h

ê sô

nguyên v

a x

, x

, . . . , x

, y

, . . . , y

a c

ac sô

nguyên sao cho x

≡ y

(mod m), x

≡ y

(mod m), . . . , x

≡ y

(mod m), th

ı g(x

, x

, . . . , x

) ≡ g(y

, y

, . . . , y

) (mod m) .

26 Chu

ng 3. D

ay sô

oi sô

ang c

ua d

ay b

ang m

ôt trong c

ac sô

, a

, . . . , a

, . . .

0, 1, . . . , m −1. Ch

ung ta x

et c

ac b

ô s

ap th

gô

m k phâ

n t

, a

, . . . , a

), (a

, a

, . . . , a

k+1

), . . . , (a

, a

n+1

. . . , a

n+k−1

)..

o tâ

t c

a vô h

an b

ô s

ap nhu

ây, nhu

ng sô

ng c

ac b

ô k sô

( α

, α

, . . . , α

), v

i 0 ≤ α

≤ m − 1, i = 1, 2 . . . , k l

a h

u h

ang m

theo l

y thuyê

t tô

p). Theo nguyên l

y Ðirichlê tô

n t

ai hai

ı sô

i v

a j, i < j sao cho

= a

, a

i +1

= a

j+1

, . . . , a

i +k−1

= a

j+k−1

ac l

≡ y

(mod m), x

≡ y

(mod m) , . . . , x

≡ y

(mod m).

dây suy ra d

ay a

, a

, . . . , a

. . . l

a tuâ

n ho

an (chu k

y c

ua n

a u

c sô

ua j − i). Th

ât v

ây, v

ı f l

da th

c v

i h

ê sô

nguyên nên

theo c

ach ch

ng minh trên ch

ung ta c

f (a

i +k−1

, a

i +k−2

, . . . , a

) ≡ f (a

j+k−1

, a

j+k−2

, . . . , a

) (mod m)

=⇒ a

i +k

≡ a

j+k

(mod m) ho

ac l

i +k

≡ a

j+k

. Biê

dô

i m

ôt ch

ut d

thâ

y r

ang v

i m

oi n ≥ i ta c

ang th

c sau a

n+(i−j)

≡ a

. 3.5. Cho d

ay x

, x

, . . . , x

, . . . .

c x

inh theo công th

c sau

= 1, x

= 0, x

= 2, x

n+1

= 2x

n−1

+ x

n−2

, n ≥ 3.

ng minh r

˘ang v

i m

oi sô

nhiên m tô

n t

ai hai phâ

n t

liên tiê

ua d

ay m

a ch

ung

dê

u chia hê

t cho m.

i gi

ai. Công th

c hô

i quy trên c

o thê

viê

t l

n−2

= x

n+1

−2x

n−1

(3.1)

o ch

ı ra r

ang d

ay c

o kh

a n

ang ph

at triê

n vê

ıa tr

ai, t

a x

inh x

i n ≤ 0. V

ı d

u v

i n = 2, 1, 0 ch

ung ta nh

ân

c x

= 0, x

−1

= 0, x

−2

= 1. Nhu

uc 3.4 ch

ı ra r

ang d

3.2. V

ı d

u 27

, x

, . . . , x

, . . . gô

m nh

ng sô

ng x

, x

, . . . , x

, . . . theo

môdd un m, l

a d

ay tuâ

n ho

an. T

công th

c (3.1) suy ra m

ôi

phâ

n t

ua d

ay {x

} v

a suy ra c

a {

} x

inh duy nhâ

t t

phâ

n t

tru

c n

o. Khi

o nê

u ( r

, r

, . . . , r

) l

a phâ

n chu k

y c

ua d

, x

, . . . , x

, . . . th

ı phâ

n n

ay s

e chuyê

ông tuâ

n ho

an vê

ıa tr

ua d

ay . . . , x

−3

, x

−2

, x

−1

, x

, . . . v

a s

e c

o d

ang

. . . , r

, r

, . . . , r

, r

, . . . , r

, r

, . . . , r

. . . (3.2)

Bây gi

ta ch

y r

ang x

−1

= x

= 0, suy ra x

−1

= x

= 0. T

(3.2)

suy ra r

ang d

ay c

ac sô

theo môdd un m ch

a vô sô

ap phâ

n t

liên tiê

p b

ang không. N

oi c

ach kh

ac tô

n t

ai vô sô

ac c

ap sô

liên tiê

ua d

ay x

, x

, . . . , x

, . . . m

a m

ôi phâ

n t

trong c

dê

u chia hê

t cho

. 3.6. D

ay sô

Fibonaxi

inh ngh

ıa b

˘ang c

˘ang th

c F

= 1, F

n+2

= F

n+1

+ F

, n ≥ 1. Ch

ng minh r

˘ang

ıt nhâ

t m

ôt trong

1.000.000.000 phâ

n t

dâ

u tiên c

ua d

ay chia hê

t cho 10.000.

i gi

ai. Tu

ng t

nhu

3.5 ch

ung ta x

et c

ac sô

ua c

ac sô

trong d

a cho khi chia cho 10.000. K

y hi

êu sô

ı th

k khi chia cho 10 000 l

a r

. Khi

o th

ı r

= 1, r

1, r

= 2, r

= 3, . . . . . . .r

= r

k−1

+ r

k−2

. R

o r

ang c

o 10.000 sô

ac nhau do

o c

o 10000

= 100000000 (tr

am tri

êu) c

ap sô

ac nhau. X

et 100000001 c

ap sô

, r

), (r

, r

), (r

, r

) . . .

. . . (r

100000001

, r

100000002

). Theo nguyên l

y Ðirichlê trong sô

ay c

ıt

nhâ

t 2 c

ap sô

ung nhau, t

c l

a t

ım

c hai sô

n v

a p v

i n, p

dê

u nh

o ho

n 100000002,n nh

o ho

n p sao cho r

= r

, r

n+1

= r

p+1

Nhu

ng nê

u biê

t sô

ua tô

ng hai sô

a sô

ua m

ôt sô

ı sô

kia c

ung t

ınh

c. V

ı v

ây ta c

o r

n−1

= r

p−1

, r

n−2

= r

p−2

, . . . .

cho

dê

n khi r

= 1 = r

p−n+2

, r

= 1 = r

p−n+1

, Áp d

ung công th

28 Chu

ng 3. D

ay sô

sô

hô

i qui

trên ta c

o r

p−n

= 0 v

i p − n ≤ 100000001 − 1 =

100000000. Ngh

ıa l

a sô

i tr

ı p −n s

e th

oa m

diê

u ki

ên b

ra, chia hê

t cho 10 000.

. 3.7. (Ð

inh l

y Fecma) Nê

u m

ôt sô

nguyên tô

p không chia hê

t sô

nguyên a, th

˘ang th

c sau

ung a

p−1

≡ 1( mod p).

i gi

ai. Ch

ung ta ch

ng minh m

ênh

dê

tô

ng qu

at ho

n. Cho m > 1

a sô

nhiên bâ

t k

y v

a a l

a sô

nguyên tô

ung nhau v

i m. Ch

ung

ta x

et d

ay nh

ng l

uy th

a liên tiê

p c

ua a

, a

, . . . (3.3)

a k

y hi

êu

, r

, . . . (3.4)

a nh

ng sô

ng c

ua (3.3) khi chia cho m, ngh

ıa l

≡ r

(mod m), 1 ≤ r

≤ m −1.

Khi

o sô

ng c

ac sô

trong (3.3) l

a vô h

an, c

on nh

ng sô

(3.4)

ı c

o thê

ân nh

ng gi

a tr

i trong 1, 2, 3, . . . , m −1 nên sô

ng l

u h

an. Suy ra theo nguyên l

y Ðirichlê, gi

a nh

ng sô

e c

ıt nhâ

t hai sô

ung nhau; n

oi c

ach kh

ac tô

n t

ai hai ch

ı sô

i v

a j v

i 6= j sao cho r

= r

. Khi

o ch

ung ta c

o a

≡ a

( mod m). Theo gi

thiê

t (a, m) = 1, v

i i 6= j ch

ung ta nh

ân

c a

i −j

≡ 1( mod m).

ung ta c

o kê

t lu

ân tô

n t

ai sô

nhiên l sao cho

ang th

c sau

dây

ung:

≡ 1 (mod m) (3.5)

- Sô

l trong (3.5) không x

inh duy nhâ

t, th

âm ch

ı c

on tô

n t

vô sô

sô

nhiên l th

oa m

an (3.5).

- Trong tru

ng h

p m = p l

a sô

nguyên tô

, Fecma t

ım ra l c

o thê

on l

a sô

p −1.

3.2. V

ı d

u 29

-Tru

ng h

p m bâ

t k

y th

ı O

le ch

ng minh r

ang l c

o thê

on l

am ch

ı sô

ua m (ch

ung ta không xem x

et vâ

dê

dây,

ôc

a c

o thê

ım trong bâ

t c

cuô

n s

ach sô

oc n

ao).

. 3.8. Cho x

, x

, . . . l

a d

ây vô h

an c

ac sô

nguyên v

a k l

a m

ôt sô

nhiên bâ

t k

y. Ch

ng minh r

˘ang tô

n t

ai d

ây sô

gô

m nh

ng phâ

n t

liên tiê

p c

ua d

ây, m

a tô

ng c

ua ch

ung chia hê

t cho k.

i gi

ai. Ch

ung ta c

o thê

i h

an l

ai, gi

a m

oi b

ô k phâ

n t

liên

tiê

p c

ua d

ây c

o thê

c m

ôt sô

phâ

n t

o t

ınh châ

t mong

muô

n. Ðê

n gi

an ta xem x

et k phâ

n t

dâ

u tiên x

, x

, . . . , x

ung ta x

et tô

= x

, S

= x

+ x

, S

= x

+ x

, . . . , S

= x

+ x

+ ···+ x

Nê

u m

ôt tô

ng n

o trong sô

trên chia hê

t cho k, th

ı b

ai to

ai. Ngu

c l

ai, c

ac sô

, S

, . . . , S

o sô

ng k) khi chia cho k

c c

ac sô

1, 2, 3, . . . , k −1. T

nguyên l

y Ðirichlê suy ra c

o m

ôt

ap ch

ı sô

i v

a j, 1 ≤ i < j ≤ k, m

a c

ac tô

ng S

a S

cho c

ung m

ôt sô

khi chia cho k. Khi

o tô

ng c

ac phâ

n t

liên tiê

p x

i +1

, x

n+2

, . . . , x

ua d

a cho chia hê

t cho k, v

ı x

i +1

+ x

n+2

+ ··· + x

= S

− S

. 3.9. Cho d

ay vô h

an c

ac ch

sô

. Ch

ng minh r

˘ang v

i m

oi sô

nhiên n, nguyên tô

ung nhau v

i 10, trong d

ay vô h

an trên tô

n t

ôt nh

om ch

sô

liên tiê

p, m

a sô

ao b

i c

ac ch

sô

trong nh

om (viê

theo th

ı sô

ng tru

c) chia hê

t cho n.

i gi

ai. Cho d

ay c

ac ch

sô

, a

, . . . , a

, . . .. Ch

ung ta x

et c

ac sô

, A

= a

, . . . , A

= a

n−1

. . . a

, . . . , A

n+1

= a

n+1

. . . a

ı sô

ng nh

ng sô

ay l

a n + 1, c

on sô

ng kh

a n

ang c

ua sô

khi chia ch

ung cho n l

a n, nên theo nguyên l

y Ðirichlê tô

n t

ıt nhâ

30 Chu

ng 3. D

ay sô

hai sô

cho c

ung m

ôt sô

ta k

y hi

êu ch

ung l

a A

, ( i < j). Khi

o hi

êu A

− A

chia hê

t cho n. Hay n

oi c

ach kh

− A

= a

. . . a

− a

. . . a

= a

. . . a

i −1

.10

j−i+1

ı (n, 10) = 1, nên a

. . . a

i −1

chia hê

t cho n.

. 3.10. Cho k l

a sô

nguyên du

ng bâ

t k

y v

, x

, . . . , x

, . . .

, y

, . . . , y

, . . .

a nh

ng chu

ôi sô

nguyên bâ

t k

y. Ch

ng minh r

˘ang tô

n t

ai vô sô

˘ap

ı sô

(i, j), v

i i < j sao cho m

ôi tô

i +1

+ x

n+2

+ ··· + x

; y

i +1

+ y

n+2

+ ··· + y

dê

u chia hê

t cho k.

i gi

ai. Ch

ı câ

n ch

ng minh r

ang trong b

ô sô

phâ

n t

liên tiê

ua 2 d

ây trên c

o thê

c tô

ng v

i t

ınh châ

a ch

ı ra. V

ı v

ây

ung ta ch

ı quan tâm

dê

n k

phâ

n t

dâ

u tiên c

ua c

ac chu

ôi

a cho.

ang c

ach tô

ng qu

at h

oa c

ach gi

ai b

ai to

an 3.8, lâ

y tô

= x

, S

= x

+ x

, S

= x

+ x

, . . . , S

= x

+ x

+ ···+ x

= y

, T

= y

+ y

, T

= y

+ y

, . . . , T

= y

+ y

+ ···+ y

i m

ôi m = 1, 2, 3, . . . , k

at tu

ng c

ap (S

, T

) v

i c

(RS

, RT

) c

ua nh

ng sô

, khi chia S

a T

cho k. V

ı RS

a RT

a m

ôt trong c

ac sô

0, 1, 2, . . . , k − 1, nên tô

p tâ

t c

ac d

ang kh

ac nhau (RS

, RT

) l

a không qu

a k

. Nê

u tô

n t

ôt ch

ı sô

m, sao cho (RS

, RT

) tr

ung v

i (0, 0), th

ı m

oi tô

= x

+ x

+ ···+ x

a T

= y

+ y

+ ···+ y

dê

u chia hê

t cho

k. V

ı nê

u không nhu

ây, th

ı c

ac c

ap sô

(RS

, RT

), m = 1, 2, . . . .., k

o nhiê

u nhâ

t l

a k

− 1 kh

a n

ang kh

ac nhau. Nhu

ng sô

3.3. B

ai t

âp 31

ng c

ap sô

ay l

a k

suy ra c

ıt nhâ

t hai trong ch

ung b

ang

nhau. N

oi c

ach kh

ac, tô

n t

ai hai ch

ı sô

i v

a j, sao cho 1 ≤ i <

j ≤ k

a (RS

, RT

) = (RS

, RT

). Trong tru

ng h

p n

ay m

ôi sô

i +1

+ x

n+2

+ ··· + x

= S

− S

; y

i +1

+ y

n+2

+ ··· + y

= T

− T

dê

u chia hê

t cho k.

y: Ðây l

a b

ai to

an tô

ng qu

at h

oa b

ai to

an 3.8. M

ông kê

a n

ay c

ac b

an h

ay xem v

a l

am b

ai tâp 3.15.

3.3. B

ai t

âp

. 3.11. C

o tô

n t

ai lu

y th

a c

ua sô

3 m

a c

ac ch

sô

cuô

i c

ung c

ua n

a 0001 không ?

. 3.12. Cho F l

a t

âp h

u h

an nh

ng sô

nguyên du

ng v

a x

, x

, . . .

, x

, . . . v

a y

, y

, . . . , y

, . . . l

a hai d

ây vô h

an nh

ng phâ

n t

thu

ôc

F. Ch

ng minh r

ang tô

n t

ai nh

ng ch

ı sô

i v

a j, i < j sao cho t

ıch

ua x

i +1

, x

i +2

, . . . , x

a y

i +1

, y

i +2

, . . . , y

a m

ôt sô

o l

uy th

a b

âc k.

. 3.13. Cho u

, u

, . . . , u

, . . . l

a d

ay nh

ng sô

nguyên x

inh b

ang

công th

c u

= 39, u

= 45, u

n+2

= u

n+1

− u

( n ≥ 1). Ch

ng minh

ang 1986 chia hê

t cho vô sô

ng phâ

n t

trong d

ay n

ay.

. 3.14. Cho k l

a m

ôt sô

nhiên. D

ay x

, x

, . . . , x

, . . . th

oa m

an c

ang th

c x

= 0, x

= 1 v

a x

n+1

− x

n−1

) v

i m

oi n ≥ 1.

ng minh r

ang gi

a nh

ng sô

, x

, . . . , x

1986

tô

n t

ai hai sô

ıch c

ua ch

ung chia hê

t cho tich 19.86.

. 3.15. Cho k l

a sô

nguyên du

ng v

, x

, . . . , x

, . . .

, x

, . . . , x

, . . .

32 Chu

ng 3. D

ay sô

. . . . . . . . . . . . . . .

, x

, . . . , x

, . . .

a s d

ay sô

nguyên. Khi

o tô

n t

ai vô h

an c

ac c

ap ch

ı sô

(i, j), v

i < j sao cho c

ac tô

ng sau

dây

i +1

+ x

i +2

+ ··· + x

i +1

+ x

i +2

+ ··· + x

. . . . . . . . . . . . . . . . . . . . .

i +1

+ x

i +2

+ ··· + x

dê

u chia hê

t cho k.

CHU

NG 4

INH H

4.1. V

ı d

Trong sô

ac b

ai to

an h

ınh h

oc trong to

an h

oc tô

p c

o m

ôt l

ai to

an gi

ai b

ang phu

ng ph

ap Ðirichlê râ

t thu

ân ti

ên v

a r

o r

ang.

oc c

o thê

ım thâ

y nh

ng c

ach gi

ai kh

ac, nhu

ng v

ı m

ıch

chuyên

dê

phu

ng ph

ap ch

ung ta

dang x

et nên ch

ung ta ch

ı kh

at c

ac v

ı d

u sau.

. 4.1. Trong h

ınh vuông v

i c

anh 1

n v

c ch

on 101

diê

m. Ch

minh r

˘ang c

o n˘am

diê

m trong c

diê

a ch

on c

o thê

u b

on b

an k

ınh

i gi

ai. Chia h

ınh vuông ra ra 25 h

ınh vuông con c

o c

anh 0,2.

ng h

ınh vuông n

ay c

o sô

ng 25 v

a v

ı tâ

t c

a sô

diê

a ch

a 101, th

ıt nhâ

t c

o m

ôt h

ınh vuông nh

o ch

ıt nhâ

t 5

diê

m. M

an k

ınh

ng tr

on ngo

ai tiê

p h

ınh vuông nh

o b

ang

√

. 4.2. Ch

ng minh r

˘ang trong m

oi khô

da di

ên lô

i tô

n t

ıt nhâ

t hai

˘at c

o c

ung sô

anh.

i gi

ai. K

y hi

êu F l

a m

at c

o sô

anh l

n nhâ

t c

ua khô

da di

ên. Nê

sô

anh c

ua F l

a k, th

ı khô

da di

ên c

ıt nhâ

t k + 1 m

at (v

ı c

o k m

34 Chu

ng 4. H

ınh h

o c

anh chung v

i F), c

on sô

ng c

ac c

anh c

ua m

ôi m

at l

a m

ôt

trong c

ac sô

3, 4, . . . , k. Theo nguyên l

y Ðirichlê c

ıt nhâ

t hai m

o c

ung sô

anh.

. 4.3. Trong phâ

n trong c

ua m

ôt h

ınh tr

on v

ng k

ınh 5

n v

ngu

i ta ch

on bâ

t k

y 10

diê

m. Ch

ng minh r

˘ang

ıt nhâ

t c

o hai

diê

trong c

diê

a ch

on c

o kho

ang c

ach nh

o ho

n 2.

i gi

ai. Chia

ng tr

E D

ınh 4.1:

anh 8 r

e qu

at b

ang nhau

i g

tâm m

ôi r

e qu

at l

a d

ng tr

dô

tâm C

i b

an k

ınh 1. K

êu C

, C

, . . . , C

a nh

ınh t

am r

e qu

at tr

phâ

n m

ng tr

on C

chiê

m. C

o thê

ng minh

c bâ

t c

hai

diê

m n

thu

ôc m

ôt trong ch

ın h

ınh

trên

dê

u c

o kho

ang c

ach nh

n 2. Th

ât v

ây, nê

u hai

diê

m ro

i v

ng tr

dô

ng tâm th

kho

ang c

ach gi

a ch

ung nh

o ho

n 2. Gi

a s

hai

diê

m A v

a B ro

ao m

ôt CDEF trong sô

am r

e qu

at. Trên b

an k

ınh OC v

a OD lâ

ng hai

diê

m A

a B

sao cho OA

= OA; OB

= OB, ngh

ıa

a AB ≤ A

(theo

inh l

y h

am cosin, b

i v

[

AOB ≤

Ðê

y r

ang A

≤ max{A

D, A

E}. Th

ât v

ây

diê

m B

am trong

an th

ang t

ao b

i h

ınh chiê

u H c

ua A

trên OD v

ıt nhâ

t m

ôt

trong hai

diê

m D, E, ch

ang h

diê

m D. B

i v

ây h

ınh chiê

u HD

ng xiên A

D không b

e ho

n h

ınh chiê

u HB

ua A

trên

OD. Ngh

ıa l

a A

≤ A

D. C

ung ch

ng minh nhu

trên ta c

4.1. V

ı d

u 35

≤ max{DF, DC}, EA

≤ max{EF, EC}. T

anh gi

< CD

= OC

+ OD

−2.OC.OD. cos 45

= 2

−

√

< 3, 75 < 4

= FD

= OF

+ OD

−2OF.OD. cos 45

= 1 +

−

√

< 7, 25 −

5.1, 4

= 3, 75 < 4,

c AB ≤ A

≤ max{DF, DC, EF, EC} < 2.

. 4.4. Gi

a s

ôi

diê

m trong m

ôt m

˘at ph

˘ang

c so

n b

˘ang m

ôt trong

hai mâ

o v

a xanh. Ch

ng minh r

˘ang c

o m

ôt h

ınh ch

ât n

trong m

˘at ph

˘ang m

a bô

ınh c

ua n

o c

ung mâ

i gi

ai. D

ê thâ

y theo nguyên l

ınh 4.2:

Ðirichlê, m

ôt t

âp bâ

t k

y 7

diê

a so

n m

ôt trong hai mâ

u th

ıt

nhâ

t c

o 4

diê

m c

ung mâ

u. Trên

ôt

ng th

ang c

o 7

diê

m th

ung ta ph

ai c

o 4

diê

m th

ang

ang c

ung mâ

u, gi

a s

o l

, P

o c

ung mâ

o. Ta

chiê

u nh

diê

m n

ay xuô

ng hai

ng th

ang song song v

a ch

ung t

ao ra (Q

, Q

) v

a (R

, R

) tu

ng v

, P

). Nh

diê

m n

ay t

ao ra m

ôt sô

ınh ch

ât, ch

ung

ta ch

dê

n c

ac h

ınh ch

ât c

ınh l

a P

, i = 1, 2, 3, 4. Nhu

ây

nê

u 2

diê

m bâ

t k

y c

ua Q l

o th

ı ta c

o kê

t qu

a m

ôt h

ınh vuông

ınh c

ung mâ

u. Tu

ng t

cho c

diê

m R. Nê

dô

i không c

diê

m Q v

a R th

oa m

an tru

ng h

p trên th

ı c

o 3 (ho

36 Chu

ng 4. H

ınh h

diê

m Q n

o v

a 3

diê

m R n

o c

ung mâ

u xanh. Nhu

trong b

ô ba nhu

ây ph

ai c

o c

dôi t

ao ra h

ınh ch

ât v

i c

ınh mâ

u xanh trong sô

diê

m Q v

a R.

. 4.5. Gi

a s

ôt b

an c

ınh ch

ât c

o 4x7 ô vuông

c so

den

˘ac tr

˘ang. Ch

ng minh r

˘ang v

i c

ach so

n mâ

u bâ

t k

y, trong b

an c

luôn tô

n t

ai h

ınh ch

ât gô

m c

ac ô vuông, m

a bô

n ô

oc l

a c

ac ô

ung mâ

i gi

ai. Ch

ung ta ch

ınh 4.3:

minh cho b

ai to

an b

an c

3 × 7. M

âu so

n mâ

u c

thê

xâ

y ra v

i b

an c

o d

ang t

dê

n 8. Gi

ôt trong sô

ac c

ôt

thu

ôc d

ang 1. B

ai to

an s

c ch

ng minh nê

u tâ

a nh

ng c

ôt c

on l

ai trong

6 c

ôt thu

ôc c

ac d

ang 1, 2,

3, 4. Nhu

ây gi

a s

tâ

t c

ac c

ôt c

on l

ai thu

ôc d

ang

5, 6, 7, ho

ac 8. Khi

o theo nguyên l

y Ðirichlê hai trong sô

au c

ôt

o hai c

ôt c

ung m

ôt d

ang v

a nhu

ây b

ai to

an c

ung

c ch

minh. Ch

ng minh ho

an to

an tu

ng t

nê

u m

ôt c

o d

ang 8. Gi

không c

o c

ôt n

ao trong 7 c

ôt c

o d

ang 1 ho

ac 8. Nhu

ây ta c

o 7

ôt v

i 6 d

ang. Theo nguyên l

y Ðirichlê c

o hai c

ôt c

ung d

ang v

a b

c ch

ng minh

dâ

. 4.6. N˘am

diê

m A, B, C, D, E n

˘am trong m

ôt m

˘at ph

˘ang v

a t

ua ch

ung l

a c

ac sô

nguyên. Ch

ng minh r

˘ang trong sô

ng tam

4.1. V

ı d

u 37

ac m

ınh c

ua n

o l

a ba

diê

m n

o trong c

diê

m n

ay, c

ıt nhâ

ba tam gi

ac v

i di

ên t

ıch l

a c

ac sô

nguyên.

i gi

ai. Ta c

o thê

ng minh r

ang nê

u m

ôt trong c

ac t

ô c

ınh tam gi

a cho thay

dô

i m

ôt sô

an, th

ı di

ên t

ıch c

ua tam

ac c

ung thay

dô

i m

ôt sô

nguyên. M

ôt c

ach tô

ng qu

at ho

n ta c

o thê

ang

inh nê

u c

ac t

ınh c

ua m

ôt tam gi

ac thay

dô

i m

ôt sô

an, th

ı di

ên t

ıch c

ua n

o c

ung thay

dô

i m

ôt sô

nguyên. V

ı v

ây, nê

ên t

ıch c

ua tam gi

ac m

i nh

ân

c l

a sô

nguyên, th

ı di

ên t

ıch

tam gi

ac ban

dâ

u c

ung l

a sô

nguyên (h

ay v

e h

ınh v

a ch

ng minh).

ı nh

ng t

ô c

ua c

diê

a cho A, B, C , D, E l

a nh

ng sô

nguyên, sau khi thêm v

ao c

ac t

ô n

ay nh

ng sô

an th

ıch h

ı m

ôi t

ô s

e ch

ı nh

ân c

ac gi

a tr

i 0 v

a 1. Do

o m

oi 5

diê

a cho

ao nên b

i c

diê

m (0, 0), ( 0, 1), (1, 0), (1, 1). Áp d

ung nguyên l

Ðirichlê suy ra

ıt nhâ

t hai

diê

m trong c

diê

m A, B, C, D, E biê

dô

anh c

ung m

ôt

diê

m trong {(0, 0), (0, 1), (1, 0), (1, 1 )}. Gi

a s

o l

A, B. Ch

ung ta s

e kh

ang

inh di

ên t

ıch c

ac tam gi

ac ABC, ABD v

ABE l

a nh

ng sô

nguyên. Th

ât v

ây, c

ac tam gi

ac n

ay b

i biê

n th

anh

an th

ang (do A v

a B biê

n th

anh c

ung m

ôt

diê

m) nên di

ên t

ıch

anh c

ua ch

ung b

ang 0. V

ây tru

c khi biê

dô

i, di

ên t

ıch c

ua ch

ung

ai l

a sô

nguyên.

. 4.7. Trong m

ôt m

˘at ph

˘ang cho m

ôt t

âp h

p A c

o n

diê

m (n ≥ 2),

ôt sô

˘ap

diê

c nô

i v

i nhau b

˘ang

an th

˘ang. Ch

ng minh

˘ang trong A c

ıt nhâ

t hai

diê

c nô

i v

i c

ung sô

ng c

diê

ac thu

ôc A.

i gi

ai. V

i m

diê

m bâ

t k

y a thu

ôc A ch

ung ta k

y hi

êu S(a) l

sô

ng nh

diê

m c

ua A m

a a nô

i th

anh

an th

ang. B

ai to

muô

n kh

ang

inh r

ang tô

n t

ai hai

diê

m kh

ac nhau a

a a

ua A

38 Chu

ng 4. H

ınh h

a S(a

) = S(a

). Ch

ung ta thâ

y ngay r

ang 0 ≤ S(a) ≤ n − 1 v

oi phâ

n t

a thu

ôc A. M

at kh

ac, c

ung không tô

n t

ai nh

diê

a x

thu

ôc A, m

a S (x

) = n − 1 v

a S (x

) = 0. B

i v

diê

u n

o ngh

ıa l

diê

m x

nô

i v

i tâ

t c

a c

diê

m c

on l

ai c

ua A, c

on x

không nô

i v

diê

m n

ao c

ua A,

ân

dê

n vô l

y. C

ac sô

nguyên t

dê

n n −1 c

o sô

ng l

a n. V

ı 0 v

a n −1 không

dô

ng th

i l

a gi

a tr

ua S nên S nh

ân nhiê

u nhâ

t l

a n −1 gi

a tr

i. B

ai to

c gi

ai suy

ra t

nguyên l

y Ðirichlê.

. 4.8. Cho

da gi

dê

u 100 c

anh n

ôi tiê

p trong

ng tr

on k. M

ôi

ınh

c g

an m

ôt trong c

ac sô

1, 2, . . . , 49. Ch

ng minh r

˘ang trên k

tô

n t

ai hai cung AB v

a CD v

i c

ac t

ınh châ

t sau:

a) C

diê

m A, B, C v

a D l

ınh c

da gi

dê

a cho.

b) C

ac dây cung AB v

a CD song song v

i nhau

c) Nê

u A, B, C v

a D c

o nh

an tu

ng l

a c

ac sô

a, b, c, d th

ı a + b =

c + d.

i gi

ai. Trong

ng tr

on k c

ınh 4.4:

ung 50

ng k

ınh kh

ac nhau m

diê

m cuô

i c

ng k

ınh l

a m

ôt

ınh c

da gi

dê

u 100 c

anh

cho. Nê

u PQ l

a m

ôt trong sô

ınh

o v

dir nh P

c g

an nh

p, c

on Q v

i nh

an q th

ınh PQ tu

ng v

i sô

nguyên

|p − q|. R

o r

ang, 0 ≤ |p − q| ≤ 48.

ang c

ach n

ay m

ôi

ng k

ınh

et (tô

ng sô

o 50 tâ

t c

c cho

ng v

i m

ôt trong c

ac sô

0, 1, 2, . . . , 48. Suy ra c

ıt nhâ

t hai

4.1. V

ı d

u 39

ng k

ınh

at tu

ng v

i c

ung m

ôt sô

Ta k

y hi

êu

o l

a AB v

a CD , c

on c

ınh

c g

an tu

ac nh

an a, b, c, d. Không mâ

t t

ınh tô

ng qu

at ch

ung ta c

o thê

thiê

t c ≤ a v

a b ≤ d. Khi

o dây cung AC v

a BD c

o c

ac t

ınh châ

mong muô

n. Th

ât v

ây, v

ng k

ınh AC ch

ung ta

at tu

ng v

i a − c, c

on BD

ng v

i d − b v

a nh

ng sô

ay b

ang nhau,

ung ta nh

ân

c a − c = d − b hay l

a a + b = c + d. Ngo

ai ra,

ac ABCD l

a h

ınh vuông, nên AB song song v

i CD (th

âm ch

AB = CD).

. 4.9. Tâ

t c

a c

diê

m trong m

ôt m

˘at ph

˘ang

c bôi b

i n mâ

ac nhau. Cho tru

c 2

− 1

ng tr

dô

ng tâm kh

ac nhau

, k

, . . . , k

−1

. Trong c

ng tr

on d

ng b

an k

ınh tu

, OA

, . . . , OA

−1

sao cho m

ôi c

˘ap b

an k

ınh không c

diê

chung n

ao kh

ac ngo

ai O. Ch

ng minh r

˘ang tô

n t

ai m

ôt

ng tr

, i = 1, 2, . . . , 2

−1 sao cho trên n

o v

a trên b

an k

ınh OA

ua n

o c

diê

m tu

ng X

a Y

, m

a ch

ung

c bôi c

ung m

ôt mâ

u v

không tr

ung v

i O v

a A

i gi

ai. K

y hi

êu c

ac mâ

a cho l

a c

, c

, . . . , c

. Ch

ung ta s

e t

ınh

sô

ng c

ac tô

p kh

ac nhau c

ua c

ac mâ

u m

a v

i ch

ung c

o thê

bôi mâ

u c

diê

m trên m

ôt h

ınh ph

ang. M

oi t

âp con kh

ac trô

, i

, . . . , i

}, 1 ≤ k ≤ n c

ua t

âp h

p N = {1, 2, . . . , n} tu

i tô

p mâ

u {c

, c

, . . . , c

}. R

o r

ang nh

ng t

âp con kh

ac trô

ac nhau c

ua N b

ang c

ach n

ay tu

ng v

i nh

ng tô

p mâ

ac nhau. Ngo

ai ra, m

oi tô

p mâ

u {c

, c

, . . . , c

} c

o thê

ân

c nh

xây d

ng t

âp con kh

ac trô

ng {i

, i

, . . . , i

}. Suy ra, tô

ng mâ

u c

, c

, . . . , c

a v

i ch

ung c

o thê

bôi c

diê

m m

ôt h

ınh

ang l

a tu

ng m

ôt - m

ôt v

i nh

ng t

âp h

p con kh

ac trô

40 Chu

ng 4. H

ınh h

ua N = {1, 2, . . . , n}. Ngh

ıa l

a sô

ac tô

p kh

ac nhau c

ua mâ

ang sô

ac t

âp h

p con kh

ac trô

ng c

ua N, c

o tâ

t c

a 2

−1 t

âp h

nhu

ây.

Tru

c tiên ch

ung ta gi

a thiê

t r

ang tô

n t

ng tr

on k

, i =

1, 2, . . . , 2

− 1 m

a muô

n bôi k

ın n

o ph

ai d

ung tâ

t c

a c

ac mâ

, c

, . . . , c

. Khi

o ch

ung ta ch

diê

m bâ

t k

y Y

diê

m trong

ua b

an k

ınh OA

. Gi

a s

c bôi b

ang mâ

u c

. Nhu

ng trên k

ıt nhâ

t m

ôt

diê

m X

c bôi c

ung mâ

u nhu

ây, v

ı m

oi mâ

a cho

dê

u b

at g

ap trên k

; v

ây b

ai to

c gi

ai trong tru

ng h

p gi

a thiê

ay. Ta x

et tru

ng h

p c

on l

ai: Gi

a s

không c

ng tr

on n

ao m

diê

m c

ua n

c bôi mâ

u v

i to

an b

ô tô

p c

, c

, . . . , c

Khi

o c

o tâ

t c

a 2

−2 kh

a n

ang tô

p mâ

u, v

i n

o c

diê

bôi cho c

ng tr

on k

, k

, . . . , k

−1

. B

i v

ı 2

−1 > 2

−2 nên

o hai

ng tr

on k

a k

, i < j trên n

o s

e c

o c

ung m

ôt tô

p mâ

a s

o b

an k

ınh l

n ho

n k

. K

y hi

êu Y

diê

m c

at c

ua OA

. Trong tru

ng h

o Y

am trên k

a v

ı nh

diê

m c

ua k

c bôi v

i c

ung m

ôt tô

p mâ

u, trên k

diê

m X

c bôi

ung mâ

u v

i Y

. 4.10. Tô

ng c

ô d

ai m

ôt sô

vecto

trong m

˘at ph

˘ang l

a 4. Ch

minh r

˘ang t

ng vecto

ay c

o thê

on m

ôt sô

vecto

a tô

ai c

ua ch

ung l

n ho

n 1.

i gi

ai. Ch

ung ta

a v

ao h

ê t

ô v

a x

et vecto

ai di

ên nh

vecto

a cho t

diê

m gô

c. Ch

ung ta chiê

u nh

ng vecto

ay xuô

uc t

ô Ox v

a Oy. V

ı m

ôi vecto

ô d

ai nh

o ho

n tô

ng c

ua c

ô d

ai h

ınh chiê

u c

ua n

o xuô

ng hai tr

uc;nên tô

ô d

ai c

ua tâ

t c

ınh chiê

u c

ua c

ac vecto

n ho

n 4. Khi

o trên

ıt nhâ

t m

ôt trong

4 n

a tr

uc c

ua h

ê t

ô tô

ô d

ai c

ua h

ınh chiê

u s

e l

n ho

n 1,

4.2. B

ai t

âp 41

diê

o c

o ngh

ıa l

a tô

ng c

ô d

ai c

ua nh

ng vecto

ng s

n ho

n 1. (

ô d

ai h

ınh chiê

a l

n ho

n th

ı tâ

t nhiên

ô d

ai vecto

ung l

n ho

n.)

4.2. B

ai t

âp

. 4.11. Trong h

ınh vuông v

i c

anh 1

n v

i cho 112

diê

m. Ch

minh r

ang

ıt nhâ

t hai trong sô

o c

o kho

ang c

ach nh

o ho

. 4.12. (Ðê

thi To

an Olympic quô

c tê

lâ

n th

25 n

am 1984) Trong

at ph

ang cho hai

diê

m kh

ac nhau O v

a A. V

i m

ôi

diê

m X thu

ôc

at ph

ang kh

ac O ch

ung ta k

y hi

êu a(X) l

do b

ang radian

ua g

oc AOX,

do theo chiê

u ngu

c kim

dô

ng hô

dê

n OX

(0 ≤ a(X) ≤ 2). C

on c(X) l

ng tr

on tâm O v

a b

an k

ınh c

ai OX +

a(X)

. Cho tru

c b

ô h

u h

an mâ

u v

a m

ôi

diê

m trong m

ang

c bôi b

ang 1 trong sô

o. Ch

ng minh r

ang tô

n t

diê

i a(X

) > 0 v

a trên

ng tr

on c(X

) c

ıt nhâ

t 1

diê

bôi c

ung mâ

u v

i X

. 4.13. Trong m

at ph

ang cho n

diê

m, n ≥ 7, sao cho kho

ang c

ach

ôi c

diê

m gi

a ch

ung l

a kh

ac nhau. M

ôi m

ôt

diê

c nô

i v

diê

m gâ

n n

o nhâ

t. Ch

ng minh r

ang không c

diê

m n

c nô

i nhiê

u ho

n 5

diê

m kh

ac.

. 4.14. Ch

ng minh r

ang trong m

ôt h

ınh tr

on b

an k

ınh 1, không

thê

c qu

a n

diê

m m

a kho

ang c

ach gi

a hai

diê

m m

ôt

n ho

n 1.

. 4.15. Ngu

i ta qu

ang 120 h

ınh vuông c

o k

ıch thu

c 1 ×1 v

ao m

ôt

ınh ch

ât k

ıch thu

c20 ×25. Ch

ng minh r

ang v

i m

oi c

ach s

42 Chu

ng 4. H

ınh h

xê

p c

ac h

ınh vuông th

trong h

ınh ch

ât v

ân c

on ch

ô trô

dê

at m

ôt h

ınh tr

ng k

ınh 1.

CHU

NG 5

ÔNG NGUYÊN L

Y ÐIRICHLÊ

5.1. Nguyên l

y Ðirichlê m

ông

Cho A l

a t

âp h

u h

an nh

ng phâ

n t

, k

y hi

êu s(A) l

a sô

ac phâ

n t

thu

ôc A. Nguyên l

y Ðirichlê c

o thê

ông nhu

Nê

u A v

a B l

a nh

ng t

âp h

p h

u h

an v

a s(A) > k.s(B),

dây k l

a m

ôt sô

nhiên n

o v

a nê

u m

ôi phâ

n t

ua A cho

ng v

i m

ôt phâ

n t

o c

ua B, th

ı tô

n t

ıt nhâ

t k + 1

phâ

n t

ua A m

a ch

ung tu

ng v

i c

ung m

ôt phâ

n t

ât v

ây, tru

ng h

p k = 1 l

a nguyên l

y Ðirichlê m

a ta

a x

trong c

ac b

ai t

âp t

dâ

u t

i gi

. Ðê

ng minh m

ênh

dê

trên ch

ung

ta gi

a s

ôi phâ

n t

ua B ch

ı tu

ng v

i nhiê

u nhâ

t k phâ

n t

ua A. Khi

o s(A) ≤ k.s(B) tr

ai v

i gi

a thiê

t s(A) > k.s(B).

y. Ngay t

ng chu

dâ

u nguyên l

y n

c s

ung v

i c

ach ch

ng minh tu

ng t

nhu

trên. Ðê

tiê

p t

uc hiê

u sâu

thêm nguyên l

ang m

i ch

ung ta x

et m

ôt lo

at b

ai to

diê

ınh.

44 Chu

ng 5. M

ông nguyên l

y Ðirichlê

5.2. V

ı d

. 5.1. Trong m

ôt h

ınh vuông c

o c

anh b

˘ang 1 ta ch

on bâ

t k

y 51

diê

ng minh r

˘ang

ıt nhâ

t c

o ba

diê

m trong sô

o n

˘am trong m

ôt h

ınh

vuông c

o c

anh 0,2.

i gi

ai. Ch

ung ta chia h

ınh vuông th

anh 25 h

ınh vuông con c

anh 0,2 b

ang c

ng th

ang song song v

i c

ac c

anh c

ua h

ınh

vuông.Nê

u gi

a su

ang m

ôi h

ınh vuông v

a nh

ân

c ch

a không

a 2

diê

m th

ı tâ

t c

a c

diê

m trong h

ınh vuông l

n s

e c

o sô

diê

nhiê

u nhâ

t l

a 2 ×25 = 50 d

ân

dê

n vô l

. 5.2. Tâ

t c

a 9 c

anh v

a 27

ng ch

eo c

ua m

ôt h

ınh ch

da gi

ınh

c bôi so

n: m

ôt sô

bôi so

o, c

on l

ai bôi so

n xanh. Ch

minh r

˘ang tô

n t

ai ba

ınh c

ua h

ınh ch

op, m

a ch

ung l

a nh

ınh

ua m

ôt h

ınh tam gi

ac v

i c

ac c

anh

c so

n c

ung m

ôt mâ

i gi

ai. 9 c

anh bên c

ua h

ınh ch

c so

n b

ang hai mâ

u. V

ı 9 >

4.2, t

nguyên l

y m

ông trên suy ra

ıt nhâ

t c

o 5 c

anh bên

c bôi

ung m

ôt mâ

u. Gi

a s

o l

a SA

, SA

c bôi c

ung

mâ

dây S l

ınh h

ınh ch

op. Không

anh hu

ng t

i kê

t lu

ân

ai to

an ch

ung ta gi

a s

diê

m A

, A

c s

ap xê

theo chiê

u ngu

c kim

dô

ng hô

. Ít nhâ

t m

ôt trong c

ac c

anh c

ua ng

ac l

ng ch

eo c

da gi

ay; gi

a s

o l

a A

. Ch

ung ta

et tam gi

ac A

. Nh

ng c

anh c

ua n

o l

a c

ng ch

eo c

ay (do c

ach xê

p trên) v

a suy ra ch

ung

c bôi so

n.Nê

u tâ

t c

ac c

anh A

, A

a mâ

u xanh th

ı b

ai to

a gi

ai xong.

Tru

ng h

p ngu

c l

ai m

ôt trong c

ac c

anh A

, A

a mâ

o, gi

a s

o l

a A

. Khi

o c

ac c

anh c

ua tam gi

ac SA

a mâ

5.2. V

ı d

u 45

. 5.3. Ch

ng minh r

˘ang trong m

da gi

ac lô

i v

i sô

anh ch

˘an tô

ng ch

eo không song song v

i m

ôt c

anh n

ao c

da gi

ac.

i gi

ai. B

ang qui n

ap ta c

o thê

k−1

ınh 5.1:

ng minh

c m

da gi

ac v

i n

anh c

n(n −3)

ng ch

eo.

Bây gi

ung ta x

da gi

ac lô

i bâ

y P c

o 2k c

anh v

i k(≥ 2) l

a m

ôt sô

nguyên.

a s

ôi

ng ch

eo c

ua P song song v

i m

ôt c

anh n

ua P. Khi

o m

ôi

ng ch

eo d c

o thê

cho tu

ng v

i c

anh song

song v

i d. K

y hi

êu s l

a sô

ng ch

eo ch

ung ta c

s =

2k(2k − 3)

= k(2k −3)

= 2k(k −2) + k > (k −2).2k.

Nhu

ây theo nguyên l

y Ðirichlê m

ông suy ra tô

n t

ai k − 1

ng ch

eo d

, d

, . . . , d

k−1

da gi

ac P m

a ch

ung tu

ng v

ung m

ôt c

anh a c

da gi

ac, ngh

ıa l

a a, d

, d

, . . . , d

k−1

song song

i nhau. Suy ra c

ng ch

eo d

, d

, . . . , d

k−1

ung n

am trong

ôt n

a m

at ph

ang x

inh b

i c

anh a v

ı P l

da gi

ac lô

i (h

ınh v

e).

Ngo

ai ra d

, d

, . . . , d

k−1

a a l

a nh

an th

ang kh

ac nhau v

a b

ı sô

ng c

ua ch

ung l

a k, m

ôi

ınh c

da gi

ac P l

diê

dâ

u c

ôt

an n

o trong ch

ung. Không

anh hu

dê

n kê

t qu

a ch

minh ta gi

a thiê

t d

an xa nhâ

dô

i v

i a trong c

ng ch

, d

, . . . , d

k−1

. Khi

o t

y lu

ân trên suy ra r

ang

da gi

ac P n

an b

ô trong m

ôt n

a m

at ph

ang x

inh b

i d

. Ðiê

u n

ay tr

ai v

ınh lô

i c

da gi

ac P.

. 5.4. Trong m

˘at ph

˘ang cho 6

diê

m. M

ôi

an th

˘ang nô

i t

ng c

˘ap

46 Chu

ng 5. M

ông nguyên l

y Ðirichlê

diê

c bôi mâ

o ho

˘ac xanh. Ch

ng minh r

˘ang ba

diê

m trong sô

diê

m l

ınh c

ua m

ôt tam gi

ac, m

a c

ac c

anh c

ua n

c bôi c

ung

ôt mâ

i gi

ai. K

y hi

êu A l

a m

ôt trong c

diê

a cho v

a x

et n

ang, c

ınh chung l

a A. Nh

an th

ang n

c so

n hai

mâ

u v

a v

ı 5=2.2+1, suy ra t

nguyên l

y Ðirichlê m

ông ch

ung

ta c

ıt nhâ

t ba

an c

ung mâ

u. Gi

a s

o l

a AB

, AB

mâ

xanh. Nê

u m

ôt v

an th

ang B

, B

a xanh th

ı tô

n t

ôt tam gi

ac v

i ba c

anh xanh v

a c

ınh l

a A. Nê

u ba

an th

ang

, B

o, th

ı m

ôt tam gi

ac th

oa m

dê

a ra l

ac c

anh

dê

u mâ

o).

. 5.5. Cho d

ay vô h

an c

ac sô

nhiên u

, u

, . . . , u

, . . .

c x

inh

theo công th

c sau u

= 3, u

n+1

= (n + 1)u

− n + 1, n = 1, 2, . . ..

Cho n sô

nhiên bâ

t k

y v

a t

âp h

p M gô

m u

diê

m sao cho không

o ba

diê

m n

ao th

˘ang h

ang. M

ôi

an th

˘ang nô

i hai

diê

m kh

ac nhau

trong M

c bôi so

n b

˘ang m

ôt trong n mâ

a cho. Khi

o tô

n t

ai 3

diê

m trong M l

ınh c

ua m

ôt tam gi

dô

ng mâ

i gi

ai. Ch

ng minh b

ang qui n

ap theo n. V

i n = 1 ch

ung ta c

= 3 v

a kê

t lu

ân l

a hiê

n nhiên. V

i n = 2 t

công th

c t

ınh

= 6,

dây l

a tru

ng h

p ta

a ch

ng minh

ai trên. Gi

a s

an v

i u

diê

m v

a c

an th

ang nô

c bôi b

i n mâ

u, c

o m

ôt

tam gi

ac v

i c

ac c

anh c

ung mâ

u. Bây gi

ta x

et u

n+1

diê

m bâ

t k

y, m

ng nô

i gi

a ch

ung

c bôi b

ang n + 1 mâ

u: c

, c

, . . . , c

n+1

. Lâ

A l

a m

ôt trong c

diê

m trên. Ðiê

m n

ay c

o thê

nô

i v

i c

diê

m c

c u

n+1

− 1

an th

ang bôi mâ

u. M

at kh

ac do công th

c hô

qui u

n+1

−1 = (n + 1)(u

−1) + 1, nhu

ây theo nguyên l

y Ðirichlê

ông

ıt nhâ

t u

an th

ang c

o chung

ınh A

c bôi c

ung mâ

5.2. V

ı d

u 47

a s

, AB

, . . . , AB

c bôi c

ung mâ

u, ch

ang h

an mâ

u c

ng kh

a n

ang c

o thê

xâ

y ra nhu

a) Nê

u m

ôt trong c

an th

ang nô

i gi

a c

diê

m B

, B

, . . .

, B

theo t

ng c

c bôi b

ang mâ

u c

ı tô

n t

ai tam gi

dô

mâ

u c

ınh A. C

ac c

anh c

ua tam gi

ac n

ay so

n mâ

u c

b) Không c

o m

ôt

an n

ao trong c

an th

ang nô

i gi

a c

diê

m B

, B

, . . . , B

c so

n mâ

u c

. Khi

ap d

ung qui n

ap to

oc cho nh

diê

m B

, B

, . . . , B

. Ðiê

u n

ay c

o thê

c v

ı tâ

t c

an th

ang

a nô

c bôi so

n n mâ

u c

, c

, . . . c

n+1

. Trong

tru

ng h

p n

ay ta c

ung d

ân

dê

n kê

t lu

ân tô

n t

ai m

ôt tam gi

dô

mâ

. 5.6. Cho sô

ang c

ua d

ay u

inh ngh

ıa nhu

ai tru

c. T

âp

p nh

ng sô

nhiên t

dê

n u

−1

c phân chia b

˘ang phu

ap bâ

t k

y v

ao n t

âp h

p con, m

a t

dôi m

ôt không c

o phâ

n t

chung. Ch

ng minh r

˘ang tô

n t

ai hai sô

ua c

ung m

ôt t

âp h

p con, m

tô

ng c

ua ch

ung c

ung n

˘am trong t

âp h

p con n

ay ; ho

˘ac l

a tô

n t

ai m

ôt

sô

trong m

ôt t

âp h

p con n

o, m

a sau khi nhân

dôi v

ân thu

ôc t

âp

p con n

ay.

i gi

ai. K

y hi

êu nh

ng t

âp h

p con

a cho l

a l

a A

, A

, . . . , A

ung ta x

et t

âp h

p bâ

t k

y M gô

m u

diê

m, m

a ch

ung

anh

sô

ang phu

ng ph

ap n

o trong c

ac sô

0, 1, 2, . . . , u

−1. Ch

ung

ta bôi mâ

u nh

an th

ang nô

i c

diê

m trong M b

ang n mâ

, c

, . . . , c

theo c

ach sau: Ðo

an th

ang nô

i c

diê

m th

i v

a j, v

i > j

c so

n b

ang mâ

u c

khi v

a ch

ı khi hi

êu i − j thu

ôc t

âp h

. Theo b

ai to

an tru

c 5.5 ba

diê

m n

o c

ua M l

ınh c

ua m

ôt

tam gi

ac c

ung mâ

u. Gi

a s

diê

m n

ay l

a i, j , k v

a i > j > k. Khi

o c

ac sô

i − j, j −k v

a i − k = (i − j) + (j − k) n

am trong c

ung m

ôt

48 Chu

ng 5. M

ông nguyên l

y Ðirichlê

âp h

p A

a ch

ung c

o c

ac t

ınh châ

t ta câ

n t

ım.

. 5.7. Trong m

˘at ph

˘ang cô

inh h

ê t

ô O xy. Ch

ung ta x

et t

âp h

R gô

m nh

diê

m v

i t

ô (x, y),

dây x, y l

a nh

ng sô

nguyên

a 1 ≤ x ≤ 12, 1 ≤ y ≤ 10. M

ôi

diê

m n

c so

n b

˘ang m

ôt mâ

˘ang, xanh ho

˘ac

o. Ch

ng minh r

˘ang tô

n t

ai h

ınh ch

ât c

o c

anh song song v

i c

ac tr

uc t

ô, m

ınh c

ua n

o l

a nh

diê

m c

c so

n c

ung m

ôt mâ

i gi

ai. Trong ch

ng minh ta d

ung hai kh

ang

inh sau:

a) Nê

u X l

a t

âp h

u h

an v

i n phâ

n t

, th

ı sô

ng t

âp h

p con

ua X gô

m c

ac c

ap phâ

n t

{x, y}, v

i x ∈ X , y ∈ X l

n(n −1)

b) M

oi sô

ng bâ

t k

y x

, x

, . . . , x

dê

u th

oa m

an bâ

ang

+ x

+ ··· + x

≥ (

+ x

+ ··· + x

)

Dâ

u b

ang ch

ı xâ

y ra khi x

= x

= . . . = x

ai b

ai to

dang x

et, v

ı tô

ng sô

diê

m ta x

et l

a 120, nên

ıt nhâ

t c

o 40

diê

c bôi c

ung mâ

u, gi

a s

a mâ

o. V

i m

ôi

i = 1, 2, . . . , 12 ch

ung ta k

y hi

êu l

ng th

ang

di qua

diê

m (i , 0)

a song song v

i tr

uc Oy. Nê

u trên l

o n

diê

o, i = 1, 2, . . . , 12,

+ n

+ ··· + n

≥ 40. Ngo

ai ra t

diê

m c

o thê

ao ra c

ac c

dôi

c s

ap c

o sô

( n

−1)

. Ngh

ıa l

a v

i m

ôi i = 1, 2, . . . , 12

tô

n t

ung

( n

−1)

ap sô

nguyên {j

, j

} th

oa m

an 1 ≤ j

≤

10, 1 ≤ j

≤ 10 v

a c

diê

m {i, j

} v

a {i, j

} l

o. M

at kh

ac sô

ua tâ

t c

a c

ap nh

ng sô

nguyên {j

, j

} v

i 1 ≤ j

≤ 10, 1 ≤ j

≤ 10

5.2. V

ı d

u 49

ang

10( 10 −1)

= 45. Ch

ung ta ph

ai ch

ng minh r

ang tô

ng c

ac sô

( n

−1)

( n

−1)

, . . . ,

( n

−1)

n ho

n 45. T

o suy ra tô

n t

ai nh

ng ch

ı sô

ac nhau i

a i

1 ≤ i

< i

≤ 12 v

a c

ap sô

nguyên {j

, j

} v

i 1 ≤ j

≤ 10, 1 ≤ j

≤

10 sao cho 4

diê

m {i

, j

}, {i

, j

}, {i

, j

}, {i

, j

} l

o. B

i nh

diê

m n

ay l

ınh c

ua h

ınh ch

ât v

i c

ac c

anh song song v

i tr

ô, nhu

ây b

ai to

c ch

ng minh.

Nhu

ây, ta ch

ı c

on ph

ai ch

ng minh

S =

( n

−1)

( n

−1)

+ ··· +

( n

−1)

> 45

ung bâ

ang th

c b)

S =

((n

−

)

−

) +

((n

−

)

−

) + ··· +

((n

−

)

−

)

((n

−

)

+ ( n

−

)

+ ··· + (n

−

)

) −12

≥

.12(

( n

−

) + (n

−

) + ··· + (n

−

)

−

((n

+ n

+ ··· + n

) −12

)

−

≥

(40 −6)

−

> 45

ı n

+ n

+ ··· + n

≥ 40.

. 5.8. (B

ai thi Olympic to

an quô

c tê

lâ

n th

20, 1978) M

ôt h

ôi to

oc bao gô

m c

ac th

anh viên

6 nu

c. Danh s

ach c

ac h

ôi viên gô

1978 ngu

anh sô

ao danh t

dê

n 1978. Ch

ng minh r

˘ang

tô

n t

ıt nhâ

t m

ôt h

ôi viên c

o sô

ao danh gâ

dôi sô

ao danh c

50 Chu

ng 5. M

ông nguyên l

y Ðirichlê

ôt h

ôi viên kh

ac c

ung nu

c, ho

˘ac b

˘ang tô

ng hai sô

ao danh c

ua hai

ôi viên c

ung m

ôt nu

c v

i m

ınh.

i gi

ai. T

329.6 < 1978 suy ra m

ôt trong c

ac nu

c (k

y hi

êu l

A) c

o không

ıt ho

n 330

ai biê

u trong h

ôi v

a ch

ung ta c

o thê

viê

sô

ao danh a

< a

< . . . < a

330

< . . . Ch

ung ta x

et nh

ng hi

êu

= a

330

− a

, i = 1, 2, . . . 329. Nê

u c

o m

ôt sô

o tr

ung v

i a

(sô

ao danh c

ua m

ôt

daj i biê

u c

ua A) th

ı ch

ung ta c

o a

330

= a

+ a

ai to

a ch

ng minh xong. Nê

u x

6= a

i m

oi i, j, th

ı sô

sô

ao danh c

ua m

ôt sô

a i biê

u thu

ôc 5 nu

c c

on l

ai. Bây gi

ı 65.5 < 329 , th

ıt nhâ

t c

o m

ôt trong n

am nu

c n

ay (k

y hi

êu l

B) s

e c

o không

ıt ho

n 66 th

anh viên, m

a sô

ao danh c

ua h

o l

ôt trong c

ac sô

, x

, . . . , x

329

. Cho c

ac sô

o l

a b

< b

. . . < b

< . . . v

i b

= x

, i = 1, 2, . . . , 66. Ch

ung ta l

ai x

et hi

êu

= b

− b

, i = 1, 2, . . . , 65 Nê

u m

ôt hi

êu n

o tr

ung v

i sô

danh b

ua m

ôt

ai biê

u c

ua B th

ı b

= b

+ b

. Nê

u v

i hai sô

a k n

o ch

ung ta c

o y

= a

, th

ı a

= b

− b

= x

− x

330

−a

−(a

330

−a

) = a

−a

ac l

a a

= a

+ a

. Nê

u hai

tru

ng h

p trên không xâ

y ra, th

ı nh

ng sô

ay s

e l

a sô

ao danh

ai biê

u 4 nu

c c

on l

ai v

a suy ra

ıt nhâ

t m

ôt trong c

ac nu

c n

o sô

ôi viên

ıt nhâ

t l

a 17 v

i sô

ao danh y

. Tiê

p t

uc qu

a tr

ınh

nhu

ây v

a l

ap l

ai l

y lu

ân trên ch

ung ta c

o kê

t lu

ân c

ua b

ai to

an.

. 5.9. (Ðê

thi To

an vô

ich nu

c Anh, 1978) M

ôt h

ınh l

âp phu

ng c

anh b

˘ang 15 ch

a 11.000

diê

m. Ch

ng minh r

˘ang c

o m

ôt h

ınh câ

an k

ınh b

˘ang

n v

i ch

ıt nhâ

t 6

diê

m trong sô

11.000

diê

cho.

i gi

ai. Chia m

ôi c

anh c

ua h

ınh l

âp phu

ng th

anh 13 phâ

n b

ang

nhau, thê

ı h

ınh l

âp phu

ng ban

dâ

c chia th

anh 13

= 2187

5.2. V

ı d

u 51

ınh l

âp phu

ng nh

o. V

ı h

ınh l

âp phu

ng ban

dâ

u ch

a 11.000

diê

m, nên tô

n t

ai m

ôt h

ınh l

âp phu

ng nh

o ch

ıt nhâ

t 6

diê

ê thâ

y c

anh c

ua h

ınh l

âp phu

ng nh

o l

, do

o b

an k

ınh h

ınh

câ

u ngo

ai tiê

p h

ınh l

âp phu

ng nh

o l

a r =

)

675

169

676

169

√

4 = 1. V

ây: Tô

n t

ai m

ôt h

ınh câ

u b

an k

ınh 1 ch

ıt

nhâ

t 6

diê

m trong 11.000

diê

a cho.

. 5.10. Trong m

at ph

ang cho m

ôt sô

u h

diê

m, m

ôt sô

trong

ung

c nô

i l

ai b

ang

an th

ang. Ch

ung ta n

oi r

ang m

ôt d

, e

, . . . , e

oan th

ang

c nô

i l

a m

ôt dây chuyê

n, nê

oi c

an th

ang liê

n nhau e

a e

i +1

o chung m

ôt

dâ

u m

ut,

i = 1, 2, . . . , m −1. Sô

ng m nh

an th

ang trong dây chuyê

oi l

ô d

ai c

ua n

o. Ch

ung ta x

et b

ai to

an:

Cho n

diê

m, t

diê

m n

ay d

ng nh

an th

˘ang, sô

˘ang

a d

ng l

a q. Gi

a s

an th

˘ang

anh sô

ôt c

ach

bâ

t k

y b

˘ang c

ac sô

1, 2, . . . , q. Khi

o trong c

ach t

ao h

ınh nhu

ây tô

ai m

ôt dây chuyê

n v

ô d

ai nh

o nhâ

t l

, trên dây chuyê

n n

ac sô

ng v

i nh

an th

˘ang th

anh phâ

n l

âp nên m

ôt d

ay sô

˘at.

i gi

ai. G

oi G l

a câ

u h

ınh bâ

t k

y c

ua nh

diê

m v

an th

ang,

a ch

ung

anh sô

ang sô

nhiên nhu

dê

a ra. V

i m

v thu

ôc G ch

ung ta k

y hi

êu L

( v) l

ô d

ai c

ua dây chuyê

n d

ai nhâ

trong G, m

a n

o b

dâ

u t

v v

a gi

am dâ

n. B

ang phu

ng ph

ap qui

ap ch

ung ta s

e ch

ng minh bâ

ang th

c sau

c th

oa m

( v

) + L

( v

) + ··· + L

( v

) ≥ 2q (5.1)

52 Chu

ng 5. M

ông nguyên l

y Ðirichlê

dây v

, v

, . . . , v

a tâ

t c

a c

diê

m thu

ôc G. Kê

t lu

ân ph

ai ch

minh suy ra t

(5.1) theo nguyên l

y Ðirichlê m

ông: M

ôt trong

ac sô

( v

), L

( v

), . . . , L

( v

) l

n ho

ac b

ang

, nhu

ây

tô

n t

ai dây chuyê

n v

i t

ınh châ

a ch

ı ra. Do

o ch

ı c

on ph

ai ch

minh (5.1)

c th

oa m

an v

i n

diê

m c

ua G v

a q

an th

ang

anh sô

nhu

mô t

dâ

u b

ai. B

ang qui n

ap v

i q = 1 bâ

ang

c (5.1) l

a hiê

n nhiên. Gi

a s

(5.1) th

oa m

an cho m

oi câ

u h

ınh

i q − 1

an th

ang v

a ch

ung ta xem x

et câ

u h

ınh v

i n

diê

m v

an th

ang. Nê

an th

ang k

y hi

êu l

a q nô

i v

i hai

diê

m v

ı ch

ung ta b

an th

ang n

ay v

a nh

ân

c câ

u h

ınh G

ua n

diê

m v

a q − 1

an th

ang. V

i câ

u h

ınh n

ay theo qui n

ap ch

ung ta

o L

( v

) + L

( v

) + ··· + L

( v

) ≥ 2( q − 1). Bây gi

ung ta

diê

m v

. Dây chuyê

n gi

am dâ

n xuâ

t ph

at t

ô d

ai L

( v

a nh

an th

ang trong dây chuyê

n n

c k

y hi

êu b

i nh

sô

o trong d

ây 1, 2, . . . , q − 1. Nê

u nô

i thêm v

ao dây chuyê

ôt

an th

ang c

o k

y hi

êu q ch

ung ta s

e nh

ân

c dây chuyê

am v

diê

dâ

u v

a v

ô d

ai L

( v

) + 1. Theo

inh ngh

ıa

ua L

( v

) ch

ung ta c

o L

( v

) ≥ L

( v

) + 1. B

ang m

ôt c

ach ch

minh ho

an to

an tu

ng t

ung ta c

ung ch

ng minh

c L

( v

) ≥

( v

) + 1. M

at kh

ac, L

( v

) = L

( v

) v

i m

diê

m v

thu

ôc G

a n

o kh

ac v

a v

. Suy ra, L

( v

) + L

( v

) + ··· + L

( v

) ≥

( v

) + L

( v

) + ··· + L

( v

) + 2 ≥ 2(q − 1) + 2 = 2q.

5.3. B

ai t

âp

. 5.11. (Ðê

thi vô

ich Áo - Balan, 1978) Cho 1978 t

âp h

p, m

ôi

âp h

p c

o 40 phâ

n t

. Biê

t r

ang hai t

âp h

p bâ

t k

y c

ung m

ôt

phâ

n t

chung. Ch

ng minh r

ang, tô

n t

ai m

ôt phâ

n t

thu

ôc tâ

t c

1978 t

âp h

p trên.

5.3. B

ai t

âp 53

. 5.12. Ch

ng minh r

ang m

oi t

âp h

p ch

a 55 sô

c t

âp

p sô

{1, 2, 3, . . . , 100} ch

a hai sô

a hi

êu c

ua ch

ung b

ang 9.

. 5.13. Cho n l

a sô

nhiên. Cho n t

âp h

p con A

, A

, . . . , A

at ph

ang v

i t

ınh châ

t: v

i m

oi i = 1, 2, . . . , n tô

n t

ai n + 1 ph

inh tiê

n sao cho c

anh c

ua A

qua c

ac ph

ep t

inh tiê

n t

dôi m

ôt

không c

diê

m chung. Ch

ng minh r

ang tô

n t

ai m

ôt

diê

m trên m

ang, không n

am trong bâ

t c

âp h

p A

ao, i = 1, 2, . . . , n.

. 5.14. Trong phâ

n trong c

ua m

ôt tam gi

dê

u v

i c

anh d

ai 15

i, ch

ung ta ch

on b

ang phu

ng ph

ap bâ

t k

y 111

diê

m. Ch

ng minh

ang tô

n t

ai h

ınh tr

on v

ng k

ınh

√

3, m

a n

o ph

ıt nhâ

t 3

diê

trong sô

diê

a ch

trên.

. 5.15. (Ðê

thi vô

ich Quô

c gia Bungari, 1977) Trong m

ôt nh

ngu

i, hai ngu

i X v

a Y g

oi l

a quen nhau gi

an tiê

p, nê

u h

o tr

tiê

p quen nhau, ho

ac l

a nê

u tô

n t

ai m

ôt dây truyê

n nh

ng ngu

, Z

, . . . , Z

sao cho X v

a Z

quen nhau, Z

a Z

quen nhau,...

, Z

a Y quen nhau. Cho biê

t nh

o gô

m 134 ngu

i, c

on gi

ôi nh

om nh

o 8 ngu

i t

a biê

ıt nhâ

t c

o hai ngu

i quen

an tiê

p. Ch

ng minh r

ang c

o m

ôt nh

om nh

o 12 ngu

i trong nh

ngu

a biê

t, m

a m

oi c

ap hai ngu

i trong nh

om nh

o n

dê

u quen

nhau gi

an tiê

54 Chu

ng 5. M

ông nguyên l

y Ðirichlê

CHU

NG 6

AI T

ÂP S

Ô H

OC NÂNG CAO

6.1. Ð

inh l

y co

an c

ua sô

Trong l

y thuyê

t sô

oc co

o m

ôt

inh l

y co

an:

oi sô

nhiên l

n ho

n m

ôt

dê

u c

o thê

phân t

ıch ra t

ıch c

ac th

sô

nguyên tô

a phân t

ıch

o l

a duy nhâ

t nê

u ta không

dê

n th

ua c

ac th

a sô

Cho p

, p

, . . . , p

a nh

ng sô

nguyên tô

ac nhau. Trong

chu

ng n

ay ch

ung ta x

et m

ôt sô

kê

t lu

ân vê

vê

âp h

p M c

ac sô

nhiên m

a n

o c

o thê

phân t

ıch ra c

ac th

a sô

am trong

, p

, . . . , p

}. M

oi sô

x c

ua M c

o thê

biê

u di

ên du

i d

ang

x = p

. . . p

dây α

, α

, . . . , α

a c

ac sô

nguyên không âm.

6.2. V

ı d

. 6.1. T

âp h

p M ch

on m

ôt c

ach bâ

t k

y 2

+ 1 sô

. Ch

ng minh

˘ang tô

n t

ai hai sô

trong t

âp v

a ch

on m

a t

ıch c

ua ch

ung l

a m

ôt sô

ınh phu

ng.

i gi

ai. Nh

ân x

et r

ang m

ôt sô

nhiên x = p

. . . p

a sô

ınh phu

ng khi v

a ch

ı khi tâ

t c

a c

ac sô

dê

u ch

an. Ch

ung ta

56 Chu

ng 6. B

ai t

âp sô

oc nâng cao

biê

u di

ên m

oi sô

a ch

on v

i d

ang

trên v

a cho tu

ng v

i b

n-sô

( α

, α

, . . . , α

dây α

, α

, . . . , α

a c

ac sô

ua c

ac sô

ng α

, α

, . . . , α

khi chia cho 2. R

o r

ang α

= 0 ho

ac α

= 1

i m

oi i = 1, 2, . . . , n. V

ây (α

, α

, . . . , α

) l

a b

ô xê

p th

n sô

gô

sô

0 v

a 1. Theo l

y thuyê

t tô

p, tâ

t c

a n-b

ô nhu

ây c

o sô

a 2

, c

on c

ac sô

dang x

et c

o sô

ng l

a 2

+ 1. Nhu

ây

ıt nhâ

o 2 sô

trong ch

ung c

o c

ung b

ô s

ap xê

p gô

m sô

0 v

a sô

1 giô

nhau. Gi

a s

ac sô

o l

a x = p

. . . p

a y = p

. . . p

ung c

o (α

, α

, . . . , α

) = (β

, β

, . . . , β

). Ð

ang th

c sau c

ung c

ngh

ıa l

a α

= β

, i = 1, 2, . . . , n . Do

o c

ac sô

u α

a β

o c

ung

ınh ch

an l

e nhu

nhau v

i bâ

t k

y i = 1, 2, . . . , n. Khi

o α

+ β

, . . . , α

+ β

, l

a c

ac sô

an v

a theo nh

ân x

et ban

dâ

u t

ıch

xy = (p

. . . p

)(p

. . . p

) = p

+β

. . . p

+β

ung

a sô

ınh phu

ng.

. 6.2. Ch

ng minh r

˘ang gi

a n + 1 sô

trong t

âp ho

p M c

o thê

c m

ôt v

ai sô

a t

ıch c

ua ch

ung l

a m

ôt sô

ınh phu

ng.

i gi

ai. Cho x

, x

, . . . , x

a nh

ng sô

bâ

t k

y c

ua M. V

i m

ôi t

âp

con kh

ac trô

ng {i

, i

, . . . , i

} c

ua t

âp h

p {1, 2, . . . n + 1}, ch

ung ta

et c

ac x

, x

, . . . , x

(tâ

t nhiên sô

ay c

ung thu

ôc M). Biê

u di

ên c

sô

ay theo d

ang chuâ

n v

a m

ôi t

âp h

p con {i

, i

, . . . , i

} cho tu

ng v

i n-b

ô (α

, α

, . . . , α

) ,

dây α

, α

, . . . , α

a c

ac sô

u tu

ng α

, α

, . . . , α

khi chia cho 2. Nhu

ng sô

ng t

âp con kh

ac r

ông c

ua {1, 2, . . . , n + 1} l

a 2

n+1

− 1, c

on sô

ng c

ac n-b

ô s

ap gô

m nh

ng sô

0 v

a 1 l

a 2

. Suy ra tô

n t

ai nh

âp h

p con kh

ac trô

ng kh

ac nhau {i

, i

, . . . , i

} v

a {j

, j

, . . . , j

}

ua {1, 2, . . . , n + 1}, m

a ch

ung tu

ng v

i c

ung m

ôt n-b

ô s

ap c

ng sô

. Ðiê

u n

ay c

o ngh

ıa l

a nê

u x

. . . x

= p

. . . p

a x

. . . x

= p

. . . p

ı c

ac sô

u α

a β

o c

ung t

ınh

6.2. V

ı d

u 57

an l

e v

i i = 1, 2, . . . , k. Ðiê

u n

ay c

o ngh

ıa l

a t

ıch c

ua nh

sô

, x

, . . . , x

, x

, . . . , x

a ch

ınh phu

ng. Nê

u {i

, i

, . . . , i

}

a {j

, j

, . . . , j

} không c

o phâ

n t

chung, th

ı b

ai to

c gi

ai.

Tru

ng h

p ngu

c l

ai, trong P = x

. . . x

ap l

ung

ng sô

, m

a s thu

ôc {i

, i

, . . . , i

} v

a {j

, j

, . . . , j

}. Ch

ung ta

ai tr

trong P tâ

t c

a c

ac nh

ng x

nhu

ây v

a nh

ân

c t

ıch c

ai sô

trong sô

, x

, . . . , x

n+1

a n

ung l

a ch

ınh phu

ng.

. 6.3. Ch

ng minh r

˘ang gi

a m

oi 3.2

+ 1 sô

âp h

p M c

o thê

c 4 sô

a t

ıch c

ua ch

ung l

a l

uy th

a b

âc bô

n c

ua m

ôt sô

i gi

ai. V

ı 3.2

+ 1 > 2

+ 1 gi

a nh

ng sô

a ch

on theo b

ai 6.1

o hai sô

a t

ıch c

ua ch

ung l

a m

ôt sô

ınh phu

ng. T

ach hai sô

trên ra th

ı c

on l

ai 3.2

−1 sô

ap d

ung tiê

p 6.1 cho hai sô

a m

ıch c

ua ch

ung l

a sô

ınh phu

ng. Ch

ung ta c

o thê

ap l

ai qu

a tr

ınh

ıt nhâ

(3.2

−1) − (2

+ 1)

= 2

+ 1 lâ

n. Gi

a s

ung ta nh

ân

c 2

+ 1 c

ap (x

, y

), (x

, y

), . . . , v

i x

a c

ac sô

ınh phu

ng,

i = 1, 2, . . . , 2

+ 1. Ch

y r

ang theo c

ach ch

on trên th

ı c

ac c

ap sô

, y

), (x

, y

), . . . , (x

, y

) t

dôi m

ôt kh

ac nhau. Ðê

dây

suy ra c

ac sô

√

, . . . ,

√

a nh

ng sô

nguyên v

thu

ôc M. Khi

ap d

ung m

ôt lâ

n n

a 6.1 ch

ı ra r

ang t

ıch c

ua hai sô

o trong ch

ung l

a ch

ınh phu

ng. Nhu

ây x

= t

ngh

ıa l

ıch c

ua 4 sô

dôi m

ôt kh

ac nhau x

, y

, x

, y

a l

uy th

a b

âc bô

ua m

ôt sô

. 6.4. Cho p l

a m

ôt sô

nguyên tô

e v

a a

, a

, . . . , a

p+1

a nh

ng sô

nhiên kh

ac nhau nh

o ho

n p. Ch

ng minh r

˘ang v

i m

oi sô

nhiên

r nh

o ho

n p, tô

n t

ai hai sô

o thê

˘ang nhau) a

a a

, m

a t

ıch c

ung khi chia cho p c

o sô

ung l

a r.

58 Chu

ng 6. B

ai t

âp sô

oc nâng cao

i gi

ai. Áp d

ung m

ôt

inh l

y trong l

y thuyê

t sô

: Nê

u a v

a b

a hai sô

nguyên tô

ung nhau, th

ı tô

n t

ai m

ôt sô

nguyên x sao cho

ax ≡ 1 (mod b).

i m

ôi i = 1, 2, . . . ,

p + 1

, c

ac sô

a p l

a nguyên tô

ung

nhau, v

ı 1 ≤ a

≤ p − 1 v

a p l

a sô

nguyên tô

. Áp d

ung

inh l

y v

at biê

u trên, tô

n t

ai c

ac sô

nguyên b

, b

, . . . , b

p+1

sao cho v

i m

i = 1, 2, . . . ,

p+1

ang th

c sau

dê

u th

oa m

≡ 1 (mod p) (6.1)

ung ta x

et d

ay sô

, a

, . . . , a

p+1

, rb

, . . . , rb

p+1

. Ch

ung ta c

tâ

t c

a p + 1 sô

sao cho

ıt nhâ

t hai sô

trong ch

ung khi chia cho p

o c

ung m

ôt sô

. Theo gi

a thiê

t c

ac sô

, a

, . . . , a

p+1

ac nhau

an to

an v

a nh

o ho

n p. Suy ra sô

ua ch

ung theo môdd un p

a kh

ac nhau. V

ı r l

a sô

nguyên tô

ung nhau v

i p, nên d

ê d

ang

ng minh

c r

ang c

ac sô

, rb

, . . . , rb

p+1

cho sô

an to

ac nhau khi chia cho p. Ngh

ıa l

a ch

ı tô

n t

ai hai ch

ı sô

i v

a j sao

cho a

≡ rb

(mod p). T

(6.1) ch

ung ta nh

ân

c a

≡ rb

≡

r.1 ≡ r (mod p).

. 6.5. Bô

dê

Tue: Cho n l

a sô

nhiên l

n ho

n 1 v

a a l

a sô

nguyên

tô

ung nhau v

i n. Khi

o tô

n t

ai c

ac sô

nguyên x v

a y, m

a ch

ung

oa m

an phu

ng tr

ınh ax ≡ y ( mod n) v

a c

ac bâ

t phu

ng tr

ınh

1 ≤ x ≤ [

√

n], 1 ≤ |y| ≤ [

√

n].

i gi

ai. Ch

ung ta x

et tâ

t c

a c

ac sô

o d

ang au −v,

dây u v

a v ch

ôc l

âp nhau trong c

ac sô

0, 1, 2, . . . , [

√

n]. Sô

ng tâ

t c

a c

ac sô

a ([

√

n] + 1)

. Suy ra sô

ay l

n ho

n n v

ı ([

√

n] + 1)

> (

√

= n.

i c

ung n sô

ac nhau theo mô

dun n, nên tô

n t

ai hai c

sô

ac nhau (u

, v

), (u

, v

) t

ac sô

nguyên sao cho 1 ≤ u

≤

6.2. V

ı d

u 59

[

√

n], 1 ≤ v

≤ [

√

n], i = 1, 2 v

a au

− v

≡ au

− v

(mod n).

ê d

ang ch

ng minh

c v

ac v

. Th

ât v

ây, nê

u ngu

c l

ai th

≡ au

(mod n),suy ra u

≡ u

(mod n), do a l

a sô

nguyên tô

ung nhau v

i n. M

at kh

ac, u

, u

a c

ac sô

nhiên nh

o ho

n n. Nhu

ây

ang th

c sau c

ung ch

ı c

o m

ôt kh

a n

ang duy nhâ

t u

= u

. Do

o c

ap (u

, v

), (u

, v

) tr

ung nhau, tr

ai v

i c

ach ch

on trên. Nhu

ây

a u

ung ph

ai kh

ac nhau. C

o thê

a thiê

t u

> u

a không

anh hu

dê

n kê

t qu

a ch

ng minh. Bây gi

at x = u

−u

, y =

− v

. T

o suy ra 1 ≤ x ≤ [

√

n], 1 ≤ |y| ≤ [

√

n] v

a ax ≡ y

(mod n).

. 6.6. Áp d

ung bô

dê

Tue: M

oi sô

nguyên tô

ang 4k + 1 c

o thê

biê

ên du

i d

ang tô

ng b

ınh phu

ng c

ua hai sô

nguyên.

i gi

ai. Ch

ung ta ch

ng minh kh

ang

inh sau: Nê

u p = 4k + 1 l

a sô

nguyên tô

, th

ı phu

ng tr

ınh x

≡ −1 (mod p) c

o nghi

êm. Th

ât v

ây,

ı p l

a sô

nguyên tô

, theo

inh l

y Wilson, (p −1)! ≡ −1 (mod p).

Ngo

ai ra p −1 ≡ −1 (mod p), p −2 ≡ −2 (mod p), . . . , p −

p+1

≡

p+1

(mod p). Suy ra,

−1 ≡ (p −1)! = 1.2 . . . .

(p −1)

(p + 1)

≡ (−1

)(−2

) . . . (−(

p −1

)

= (−1)

p−1

(1.2 . . .

p −1

)

= (−1)

((

p −1

) !)

= ((

p −1

) !)

(mod p).

Nhu

ây a = (

p −1

) ! l

a nghi

êm c

ua phu

ng tr

ınh trên. V

ı a

+ 1

chia hê

t cho p nên a l

a nguyên tô

ung nhau v

i p . Bây gi

ung bô

dê

Tue cho hai sô

a v

a p. Tô

n t

ai c

ac sô

nguyên x v

a y m

60 Chu

ng 6. B

ai t

âp sô

oc nâng cao

1 ≤ x ≤ [

√

p], 1 ≤ |y| ≤ [

√

p] v

a ax ≡ y (mod p). Khi

o a

≡ y

(mod p), nhu

ây x

≡ −y

(mod p), v

ı a

≡ −1 (mod p). T

suy ra x

+ y

chia hê

t cho p. M

at kh

ac 1 ≤ x

≤ p, 1 ≤ y

≤ p. Ta

thâ

y r

ang x

= p v

a y

= p không thê

xâ

y ra v

ı p l

a sô

nguyên tô

, suy

ra 0 < x

+ y

< 2p v

a v

ı x

+ y

chia hê

t cho p, nên x

+ y

= p.

y: Tu

ng t

, ch

ng minh r

ang m

oi sô

p, sao cho phu

ınh x

≡ −2 (mod p) c

o nghi

êm,

dê

u c

o thê

biê

u di

ên du

i d

ang

p = x

+ 2y

i x, y l

a c

ac sô

nguyên.

. 6.7. (Ðê

thi To

an Olympic quô

c tê

lâ

n 18 n˘am 1976) Cho h

ê p

phu

ng tr

ınh v

i q = 2p â

+ a

+ ··· + a

= 0

. . . . . . . . . . . . . . . . . . . . .

+ a

+ ··· + a

= 0

Tâ

t c

a c

ac h

ê sô

thu

ôc t

âp ho

p {−1, 0, 1}. Ch

ng minh r

˘ang tô

n t

nghi

êm (x

, x

, . . . , x

) c

ua h

ê, m

a n

o th

oa m

a) tâ

t c

a x

(j = 1, 2, . . . , q) l

a nhu

ng sô

nguyên;

ıt nhâ

t c

o m

ôt j(j = 1, 2, . . . , q) m

a x

≤ 0;

c) v

i m

oi j(j = 1, 2, . . . , q) ta luôn c

o x

≤ q;

i gi

ai. X

et b

ô (x

, x

, . . . , x

) gô

m nh

ng sô

nguyên bâ

t k

y, m

ung th

oa m

an |x

| ≤ p, |x

| ≤ p, . . . , |x

| ≤ p. B

i v

ı tâ

t c

a c

ê sô

ua h

ê phu

ng tr

ınh ch

ı l

a -1,0 ho

ac 1, v

i vi

êc thay c

ac â

, x

, . . . , x

ung ta nh

ân

c gi

a tr

i c

ua m

ôi phu

ng tr

ınh n

trong kho

ang [−pq, pq]. Th

ât v

ây, v

i m

ôi i = 1, 2, . . . , p ch

ung ta

o |a

+ a

+ ··· + a

i q

| ≤ |x

| + |x

| + ··· + |x

| ≤ pq . Suy

ra, nê

u thay nh

ng â

n trong tâ

t c

a phu

ng tr

ınh c

ua h

ê tu

6.2. V

ı d

u 61

i x

, x

, . . . , x

e nh

ân

c b

ô p sô

nguyên ( y

, y

, . . . , y

). Tâ

a nh

ng sô

dê

u n

am trong kho

ang [−pq, pq]. Trong kho

ang

ay c

ung 2pq + 1 sô

nguyên. Suy ra gi

a nh

ng b

ô s

ap xê

p phâ

n t

nhu

trên c

o (2pq + 1)

ô xê

p kh

ac nhau. M

at kh

sô

ng nh

ng b

ô xê

p q-phâ

n t

, x

, . . . , x

) m

a |x

| ≤ p

i j = 1, 2, . . . q, l

a (2p + 1)

. D

ê thâ

y r

ang t

q = 2p suy ra

(2p + 1)

> (2pq + 1)

. Theo nguyên l

y Ðirichlê tô

n t

ai hai b

ô q-

sô

nguyên (x

, x

, . . . , x

) v

a (x

, x

, . . . , x

) kh

ac nhau m

a ch

ung

oa m

an |x

| ≤ p, |x

| ≤ p v

i j = 1, 2, . . . q v

a sau khi thê

ê phu

ng tr

ınh cho c

ung m

ôt b

ô p sô

nguyên (y

, y

, . . . , y

). Ð

= x

−x

, x

= x

−x

, . . . , x

= x

−x

. R

o r

ang (x

, x

, . . . , x

)

a nghi

êm c

ua h

ê phu

ng tr

ınh v

a x

a c

ac sô

nguyên v

i m

j = 1, 2, . . . , q. V

ı (x

, x

, . . . , x

) v

a (x

, x

, . . . , x

) l

a hai b

ô q sô

an to

an kh

ac nhau, th

ıt nhâ

t m

ôt trong c

ac sô

ac không.

Cuô

i c

ung v

i m

oi j = 1, 2, . . . , q ch

ung ta c

o |x

| = |x

− x

| ≤

|+ |x

| ≤ p + p = 2p = q. Nhu

ây ( x

, x

, . . . , x

) l

a nghi

êm c

ê phu

ng tr

ınh c

o t

ınh châ

t mong muô

. 6.8. (Ðê

thi To

an Olympic quô

c tê

lâ

n 28 n˘am 1987) Cho

, x

, . . . , x

a nh

ng sô

c v

a x

+ x

+ ···+ x

= 1. Ch

ng minh

˘ang v

i m

ôi sô

nguyên k, k ≥ 2, tô

n t

ai nh

ng sô

nguyên a

, a

, . . . , a

không

dô

ng th

i b

˘ang không sao cho |a

| ≤ k − 1, i = 1, 2, . . . , n v

oa m

an bâ

t phu

ng tr

ınh sau |a

+ a

+ ··· + a

| ≤

(k−1)

√

−1

i gi

ai. Ch

ung ta s

ung bâ

ang th

c Cosi-Buniakovski-Svars

|α

+ |α

+ ··· + |α

| ≤

+ ··· + α

+ ··· + β

dus ng v

i m

oi sô

c α

, α

, . . . α

, β

, . . . , β

. Dâ

u b

ang xâ

y ra

khi v

a ch

ı khi tô

n t

ai m

ôt sô

λ sao cho α

= λβ

, α

= λβ

. . . , α

λβ

62 Chu

ng 6. B

ai t

âp sô

oc nâng cao

Bây gi

ung ta x

et c

ac sô

= −

k−1

, y

= −

k−1

+ 1, . . . ,

k−1

= −

k−1

+ (k −1) =

k−1

Sô

ng c

ua ch

ung l

a k v

a hi

êu t

ap trong ch

ung l

a nh

ng sô

nguyên, m

a gi

a tr

i tuy

êt

dô

i c

ua n

không qu

a k − 1. M

ôi b

ô s

ap xê

p n-th

anh phâ

n β = (b

, b

, . . . , b

dây b

a m

ôt sô

o trong y

, y

, . . . , y

i m

oi i = 1, 2, . . . , n,

ung ta

at tu

ng v

i m

ôt sô

= b

+ b

+ ··· + b

bâ

ang th

c Cosi

= b

+ b

+ ··· + b

≤

+ b

+ ··· + b

+ x

+ ··· + x

+ b

+ ··· + b

Nhu

ng |b

| ≤

k−1

i m

oi i = 1, 2, . . . , n sao cho

| ≤

+ b

+ ··· + b

≤

k −1

√

ac l

a −

k−1

√

n ≤ S

≤

k−1

√

n. Theo phu

ng ph

ap n

ay n-b

ô β =

( b

, b

, . . . , b

dây b

a m

ôt trong c

ac sô

, y

, . . . , y

k−1

i m

i = 1, 2, . . . , n,

at tu

ng v

i m

ôt sô

= b

+ b

··· + b

trong

an ∆ = [−

k−1

√

k−1

√

n]. Sô

ng n-b

ap xê

p l

a k

. Chia ∆ ra k

− 1

an nh

o v

ô d

k−1

−1

√

n. T

nguyên l

y Ðirichlê suy ra tô

n t

ai hai n-b

ô β = (b

, b

, . . . , b

) v

γ = (c

, c

, . . . , c

), m

a nh

ng sô

= b

+ b

+ ··· + b

a S

= c

+ c

+ ··· + c

ng v

i ch

ung n

am trong

ung m

ôt

an nh

o. Ð

at a

= b

− c

= b

− c

, . . . , a

= b

−

. D

ê kiê

m tra

c a

, a

.., a

oa m

diê

u ki

ên

a cho. Th

ât

ây, v

i m

oi i = 1, 2, . . . , n sô

= b

− c

a hi

êu c

ua hai sô

o trong y

, y

, . . . , y

k−1

nhu

a n

trên v

a l

a sô

nguyên không

t qu

a k − 1. V

ı hai n-b

ô trên kh

ac nhau ho

an to

an th

ıt nhâ

ôt trong c

ac sô

= b

− c

ac không. Ngo

ai ra, |b

+ b

6.2. V

ı d

u 63

···+ b

| = |x

( b

−c

) + x

( b

−c

) + ···+ x

( b

−c

) | = |S

−

| ≤

k−1

−1

√

. 6.9. Ch

ng minh r

˘ang m

ôi b

ô gô

m 11 sô

c kh

ac nhau trong

kho

ang [1,1000] c

o thê

c hai sô

x v

a y, m

a ch

ung th

oa m

bâ

˘ang th

c sau

0 < x −y < 3

√

xy (6.2)

i gi

ai. Ch

ung ta x

et c

an b

âc ba c

ua c

ac sô

trong b

ô sô

a cho

, x

, . . . , x

diê

u ki

ên

a cho suy ra 1 ≤

√

≤ 10, i =

1, 2, . . . , 11. Ch

ung ta chia kho

ang [1,10] ra mu

i phâ

n b

ang nhau.

Khi

o, c

ıt nhâ

t m

ôt trong hai sô

√

, . . . ,

√

am trong

ung m

ôt

an nh

o. Nê

u c

ac sô

o l

√

, i 6= j v

a x

> x

ung ta c

0 <

√

−

≤

< 1. (6.3)

Nhu

ây, 0 < (

√

−

√

)

< 1, kê

t h

p v

i (6.3) ta c

o 0 < x

−

< 1 + 3

√

(

√

−

√

) < 1 + 3

√

y: B

ai to

an không c

ung v

i b

ô 10 sô

c trong kho

ang

[1,1000]. Ph

an v

ı d

u: b

ô sô

, 2

, . . . , 10

. nê

u i 6= j v

a i > j ch

ung

ta c

o (i − j)

≥ 1, nhu

ây i

+ ij + j

≥ 1 + 3ij. Ngh

ıa l

a i − j =

(i − j)(i

+ ij + j

) ≥ 1 + 3ij.

ang th

c xâ

y ra khi i = j + 1.

. 6.10. Cho 7 sô

c bâ

t k

y. Ch

ng minh r

˘ang gi

a ch

ung c

o thê

c hai sô

, ch

˘ang h

an x v

a y, sao cho

0 ≤

x − y

1 + xy

≤

√

i gi

ai. C

ac sô

a cho k

y hi

êu l

a x

, x

, . . . , x

. M

ıch c

ua ch

ung

ta l

a biê

u di

ên m

oi sô

i d

ang x

= tg α

dây α

a m

ôt sô

trong kho

ang (−

), i = 1, 2, . . . , 7. Ch

ung ta chia

an n

ay ra

64 Chu

ng 6. B

ai t

âp sô

oc nâng cao

an con c

ô d

ai b

ang nhau, ngh

ıa l

a b

ang

. D

ê d

ang thâ

ang

ıt nhâ

t c

o hai sô

trong α

, α

, . . . , α

ung n

am trong m

ôt

coni

o. Nê

u ch

ung ta k

y hi

êu c

ac sô

o l

a α

, α

≥ α

, th

ı t

suy ra 0 ≤ α

−α

≤

. V

ı h

am sô

tg l

a t

ang trong kho

ang (−

suy ra

0 ≤ tg(α

−α

) =

tg α

−tg α

1 + tg α

tg α

− x

1 + x

≤ tg

√

y: B

ang c

ach gi

ai c

ua hai b

ai t

âp n

ay ch

ung ta c

o thê

ang

ao ra m

ôt lo

at b

ai to

an tu

ng t

, m

a v

i c

ach gi

ai b

ınh thu

ng kh

a gi

ai quyê

6.3. B

ai t

âp

. 6.11. (Ðê

thi To

an Olympic quô

c tê

lâ

n 26 n

am 1985). Cho t

âp

p M gô

m 1985 sô

nhiên, không c

o sô

ao c

o u

c sô

n ho

26. Ch

ng minh r

ang t

ng phâ

n t

ua M c

o thê

c 4

sô

dôi m

ôt kh

ac nhau m

a t

ıch c

ua ch

ung l

a l

uy th

a b

âc 4 c

ôt sô

nguyên. (kê

t lu

ân

ung v

i t

âp h

p gô

m 3.2

+ 1 = 1537 sô

a nh

ng u

c sô

ua ch

ung không qu

a 23).

. 6.12. Cho bô

n sô

ng bâ

t k

y. Ch

ng minh r

ang c

o hai sô

trong

bô

n sô

o, ch

ang h

an x v

a y, th

oa m

an bâ

t phu

ng tr

ınh sau

0 ≤

x − y

1 + x + y + 2xy

≤ 2 −

√

. 6.13. Ch

ng minh r

ang m

ôt sô

nhiên c

o thê

biê

u di

ên th

anh

tô

ng b

ınh phu

ng c

ua hai sô

nguyên khi v

a ch

ı khi, trong phân t

ıch

ra d

ang ch

ınh t

ac c

ua n

o, c

ac th

a sô

nguyên tô

ang 4k + 3

dê

u c

sô

u ch

an.

6.3. B

ai t

âp 65

. 6.14. Ch

ng minh r

ang t

k + 1 sô

, m

a ch

ung nh

o ho

n 2k, luôn

luôn c

o thê

c hai sô

a t

y sô

ua ch

ung l

a m

ôt l

uy th

ua 2.

. 6.15. Cho n l

a m

ôt sô

e. Ch

ng minh r

ang t

( n − 1)

+ 1 sô

nguyên bâ

t k

y c

o thê

c n sô

sao cho tô

ng c

ua ch

ung chia

hê

t cho n.

66 Chu

ng 6. B

ai t

âp sô

oc nâng cao

CHU

NG 7

AI T

ÂP D

ÂY S

Ô NÂNG CAO

7.1. V

ı d

. 7.1. Cho d

ay Fibonaxi u

= u

= 1, u

= u

n−1

+ u

n−2

. V

i m

oi sô

nguyên du

ng m, th

ı gi

a nh

ng sô

ang t

dâ

u d

ây

dê

n sô

ang th

−1 tô

n t

ai m

ôt sô

ang chia hê

t cho m.

i gi

ai. Ch

ung ta k

y hi

êu k l

a phâ

n du

ua sô

k cho m. Ch

ung ta

et c

ac c

ap phâ

n du

ua d

ay Fibonaxi khi chia cho m:

( u

, u

). (u

, u

), (u

, u

), . . . , (u

, u

n+1

), . . . (7.1)

Nê

u ch

ung ta qui

inh hai c

ap (a

, b

) v

a (a

, b

) l

a b

ang nhau khi

= b

a a

= b

, th

ı sô

tâ

t c

a kh

a n

ang c

ua c

ac c

ap phâ

n du

khi chia cho m l

a m

. V

ı thê

ung ta lâ

y m

+ 1 sô

ang

dâ

u tiên

ua d

ay (7.1) th

ı trong ch

ung ph

ai c

o hai c

ap tr

ung nhau,( theo

nguyên l

y Ðirichlê ) v

a t

o c

ac c

ap sau l

ap l

ai. Gi

a s

ap (u

, u

k+1

)

a c

dâ

u tiên l

ap l

ai trong (7.1). Ch

ung ta s

e ch

ng minh r

ang

ap n

ay b

ang c

ap (1, 1). Th

ât v

ây, gi

a s

ngu

c l

ai, ngh

ıa l

a c

dâ

u tiên l

ap l

ai l

a (

, u

k+1

), v

i k > 1. Khi

o ch

ung ta s

e t

ım

c trong (7.1) m

ôt c

ap (u

, u

l+1

), (l > k), m

a n

o b

ang (u

, u

k+1

)

. Nhu

ây u

l−1

= u

l+1

− u

a u

k−1

= u

k+1

− u

, do u

l+1

= u

k+1

= u

, nên phâ

n du

ua u

l−1

a u

k−1

khi chia cho m c

ung b

ang

nhau, ngh

ıa l

l−1

= u

k−1

. T

o suy ra (u

k−1

, u

) = (u

l−1

, u

), v

ây

68 Chu

ng 7. B

ai t

âp d

ây sô

nâng cao

ap (u

k−1

, u

am trong d

ay (7.1) tru

c c

a (u

, u

k+1

). Ðiê

o n

lên r

ang (u

, u

k+1

) không ph

ai c

ap l

dâ

u tiên, tr

ai v

i gi

a thiê

at ra. Ngh

ıa l

a k > 1 không thê

ay ra, v

ây k = 1.

Nhu

ây c

ap (1, 1) l

a c

dâ

u tiên l

ap l

ai trong (7.1). Gi

a s

ap l

ai t lâ

n (1 < t < m

+ 1). ho

ac l

a (u

, u

t+1

) = (1, 1). Ngh

ıa l

a u

t+1

khi chia cho m cho phâ

n du

ung l

a 1, v

ây hi

êu c

ua ch

ung

chia hê

t cho m. Nhu

ng u

t+1

−u

= u

t−1

. Nhu

ây sô

ang th

t −1

ua d

ay Fibonaxi s

e chia hê

t cho m.

. 7.2. Gi

a s

a v

a x l

a c

ac sô

nhiên th

c s

n ho

n 1 v

a (x, a −1) =

1. D

ay sô

vô h

an {u

}

c x

inh nhu

= ax

− a + 1, n = 1, 2, . . .

ng minh r

˘ang trong d

ay sô

oi trên ch

a vô h

an sô

dôi m

ôt nguyên

tô

ung nhau.

i gi

ai. Gi

a thiê

t ph

an ch

ng trong d

ay sô

ı c

o h

u h

an sô

, u

, . . . , u

dôi m

ôt nguyên tô

ung nhau.

at q = u

. . . u

. X

et (q + 1) sô

sau a, ax, ax

, . . . , ax

. Theo

nguyên l

y Ðirichlê tô

n t

ai hai sô

nguyên r, s sao cho 0 ≤ r < s ≤ q

≡ ax

(mod q) =⇒ ax

− ax

≡ 0 (mod q) hay

(1 − x

s−r

) ≡ 0 (mod q) (7.2)

Theo gi

a thiê

t ta c

o (x, a −1) = 1, nên suy ra

(ax

, u

) = 1, ∀j = 1, 2, . . . , k. (7.3)

(7.3) suy ra

(ax

, q) = 1. (7.4)

7.1. V

ı d

u 69

(7.2) v

a (7.4) c

o x

s−r

≡ 1 (mod q) =⇒ x

s−r

= lq + 1 v

i l ∈ N.

et sô

k+j

= ax

s−r

− a + 1. V

ây

k+j

= a(lq + 1) − a + 1 = qal + 1. (7.5)

(7.5) ta c

( u

k+j

, u

) = 1, ∀j = 1, 2, . . . , k. (7.6)

ê th

c (7.6) ch

ng t

o r

ang luôn c

o thê

bô

sung thêm v

ao b

ô sô

q = u

. . . u

ac sô

i, m

a b

ô sô

ay v

ân th

oa m

diê

u ki

ên:

bâ

t k

y hai sô

ao c

ung nguyên tô

ung nhau. Ðiê

u n

ay c

o ngh

ıa l

trong d

ay {u

}

a cho c

o vô h

an sô

dôi m

ôt nguyên tô

ung nhau.

. 7.3. Cho {u

} l

a d

ay c

ac sô

nhiên t˘ang dâ

n: u

< u

< . . .

a th

oa m

diê

u ki

ên u

= 1, u

n+1

≤ 2n, v

i m

oi n l

a sô

nhiên.

ng minh r

˘ang v

i m

oi sô

nhiên n tô

n t

ai c

ac sô

ang u

a u

ua d

ay sao cho u

−u

= n.

i gi

ai. Gi

a s

n ∈ N l

a sô

nhiên cho tru

c. T

a thiê

t suy ra

ôi sô

ang u

, u

, . . . , u

n+1

không vu

t qu

a 2n. X

et t

âp h

p 2n sô

nhiên sau {1, 2, . . . , 2n}. Ch

ung ta chia t

âp h

p n

ay ra l

am n c

(1, n + 1), (2, n + 2 ), . . . , (n, 2n). Do t

âp h

p trên ch

a không

ıt ho

( n + 1) phâ

n t

ua d

ay {u

}

a cho (v

ı n

oi riêng u

, u

, . . . , u

n+1

thu

ôc t

âp h

p â

y), v

ây theo nguyên l

y Ðirichlê tô

n t

ai hai sô

ang

ac nhau u

a u

ua d

ay thu

ôc v

ao m

ôt c

ap ( gi

a s

> u

Nhu

ng hi

êu sô

ua m

ôi c

dê

u b

ang n, nên ch

ung ta c

o u

−u

= n.

. 7.4. Cho {u

}, k = 1, 2, . . . , n l

a d

ay sô

nhiên sao cho

1 ≤ u

≤ u

≤ . . . ≤ u

a u

+ u

+ ··· + u

= 2n

70 Chu

ng 7. B

ai t

âp d

ây sô

nâng cao

ng minh r

˘ang nê

u n ch

˘an v

a u

6= n + 1, th

ı t

ay trên luôn ch

c m

ôt d

ay con m

a tô

ng c

ac sô

ang c

ua d

ay con

o b

˘ang n.

i gi

ai. Ð

at S

= u

+ u

+ ···+ u

, k = 1, 2, 3, . . . , n. X

et n + 2 sô

{0, u

−u

, S

, . . . , S

} Theo nguyên l

y Ðirichlê th

ıt nhâ

t hai sô

khi chia cho n c

o c

ung phâ

n du

. V

ây, ch

ı c

o 4 kh

a n

ang sau

dây:

1) (u

−u

) chia hê

t cho n.

Do u

+ u

+ ··· + u

≥ n u

=⇒ 2n ≥ nu

=⇒ u

≤ 2

a) Nê

u u

= 2 th

ı t

1 ≤ u

≤ u

≤ . . . ≤ u

a u

+ u

+ ···+

= 2n suy ra u

= u

= . . . = u

= 2. Do n ch

an nên n = 2m v

ây

+ u

+ ··· + u

= 2m = n

b) Nê

u u

< 2 th

ı t

− u

chia hê

t cho n, suy ra u

= 1 ho

a u

= 1 + n ( do u

nguyên nên u

= 1 v

a 1 ≤ u

≤ 2n suy ra

c kê

t lu

ân trên). Nhu

ng u

6= n + 1 suy ra u

= 1. M

at kh

1 ≤ u

≤ u

≤ . . . ≤ u

ây th

ı u

= u

= . . . = u

n−1

= 1. Suy ra

+ u

+ ··· + u

= n, vô l

Nhu

ây trong tru

ng h

p n

ay, ta ch

ı ra tô

n t

ai d

ay con u

, u

, . . . , u

sao cho u

+ u

+ ··· + u

= n v

i m =

2) S

−S

, (j > i) chia hê

t cho n.

Ta c

o S

−S

= u

i +1

+ u

i +2

+ ···+ u

. R

o r

ang vê

ai c

ang

c trên c

ıt nhâ

t m

ôt sô

ang m

a u

≥ 1, ∀k = 1, 2, . . . , n, suy ra

−S

≥ 1. M

at kh

ac c

ung hi

êu trên nê

u không

u c

ac phâ

n t

ay th

ı bao gi

ta c

ung c

o S

− S

< u

+ u

+ ··· + u

≤ 2n − 1.

o cuô

i c

ung ta c

o 1 ≤ S

− S

< u

+ u

+ ··· + u

≤ 2n − 1

a S

− S

chia hê

t cho n.

diê

u n

ay ch

ı xâ

y ra khi S

− S

= n ho

a u

i +1

+ u

i +2

+ ··· + u

= n.

3) S

chia hê

t cho n.

7.1. V

ı d

u 71

Ta c

o 1 ≤ S

≤ S

n−1

= 2n − u

< 2n m

a S

chia hê

t cho n, suy

ra S

= n ho

ac l

a u

+ u

+ ··· + u

chia hê

t cho n.

4) S

a u

− u

cho c

ung phâ

n du

khi chia cho n, v

i k n

o, 1 ≤ k ≤ n − 1. Suy ra S

− (u

− u

) |n =⇒ (u

+ u

+ ··· +

+ u

) |n. M

a u

+ u

+ ··· + u

+ u

≤ 2n − u

< 2n. Suy ra

+ u

+ ··· + u

+ u

= n.

om l

ai luôn luôn ch

c d

ay con m

a tô

ng c

ua ch

ung b

ang

. 7.5. Cho d

ay sô

nguyên u

, u

, . . . , u

i n ≥ 2. Ch

ng minh r

˘ang

tô

n t

ai d

ay con u

, u

, . . . , u

trong

o 1 ≤ k

< k

< . . . < k

≤ n

sao cho u

+ u

+ ··· + u

chia hê

t cho n.

i gi

ai. X

et (n + 1) sô

0, u

, u

+ u

, u

+ u

, . . . , u

+ u

+ ··· + u

Chia c

ac sô

ay cho n, th

ı ch

ung cho nhiê

u nhâ

t n sô

. Theo

nguyên l

y Ðirichlê tô

n t

ai hai sô

cho c

ung sô

, gi

a s

o l

a u

+ ··· + u

a u

+ u

+ ··· + u

(0 ≤ j < k ≤ n). C

o ngh

ıa

a sô

( u

+ u

+ ··· + u

) − (u

+ u

+ ··· + u

) chia hê

t cho n.

ac l

a u

j+1

+ u

j+2

+ ··· + u

chia hê

t cho n. D

ay con ph

ai t

ım l

j+1

, u

j+2

, . . . , u

. 7.6. Cho d

ay Fibonaxi 1, 2, 3, 5, 8,. . . .Ð

˘at f (n) = 1985

1956n

+ 1960 Ch

ng minh r

˘ang tô

n t

ai vô h

an sô

ang u

ua d

Fibonaxi, sao cho f (u

) |1989

i gi

ai. Ð

at h(n) = 4n

+ 33 n + 29 =⇒ h(n) = 1989(n

+ n + 1) −

f (n). T

o suy ra f (n)|1989 ⇐⇒ h(n)|1989.

72 Chu

ng 7. B

ai t

âp d

ây sô

nâng cao

et d

ay sô

} sau

dây, trong



= −1, v

= 1

n+1

= v

+ v

n+1

, n = 1, 2, . . .

oi c

ach kh

ac d

ay {v

} l

a d

ay sinh ra b

i d

ay Fibonaxi {u

} :

1, 1, 2, 3, 5, . . . b

ang c

ach thêm v

ao tru

c d

ay n

ay ba sô

ang -1, 1, 0.

oi r

a phâ

n du

trong ph

ep chia v

cho 1989(i = 0, 1, 2, . . .).

Nhu

ây ta c

o 0 ≤ r ≤ 1988. X

et d

ay c

ac c

ap sô

dây

, r

), (r

, r

), (r

, r

), . . . .

ı m

ôi c

ap r

ı nh

ân m

ôt trong 1989 gi

a tr

i, v

ây sô

ac c

ap kh

nhau tô

da l

a 1989

. T

o theo nguyên l

y Ðirichlê th

ı trong 1989

1 c

dâ

u tiên

ıt nhâ

t c

o hai c

ap tr

ung nhau. Gi

a s

hai c

ap â

y l

, r

p+1

), (r

p+q

, r

p+q+1

), p, q ∈ N

Ðiê

u â

y c

o ngh

ıa l

a r

= r

p+1

, r

p+q

= r

p+q+1

. Theo c

ach x

inh

ay, ta c

p−1

= v

p+1

−v

=⇒ r

p−1

= r

p+1

−r

ngt

, ta c

p+q−1

= v

p+q+1

−v

p+q

=⇒ r

p+q−1

= r

p+q+1

−r

p+q

o suy ra r

p−1

= r

p+q−1

. Tu

ngt

, ta c

p−2

= r

p+q−2

. . . . . . .

= r

q+2

= r

q+1

= r

, r

= r

q+1

a v

n+1

= v

+ v

n+1

suy ra r

= r

i +q

, ∀i =

0, 1, 2, . . .. Do v

ây r

= r

= . . . = r

, ∀k ≥ 1, suy

7.1. V

ı d

u 73

ra h(v

) = 1989.A + h(−1) = 1989.A. Nhu

ng ∀k = 1, 2, 3 . . . v

dê

u l

a sô

Fibonaxi suy ra c

o vô sô

sô

ang v

ua d

ay Fibonaxi m

f (v

) |1989.

. 7.7. Cho d

ay sô

} x

inh nhu

= 20, u

= 100, v

a u

n+1

= 4u

+ 5u

n−1

−1976, n = 1, 2, . . .

ng minh r

˘ang tô

n t

ıt nhâ

t m

ôt sô

ua d

ay sô

chia hê

t cho 1996.

i gi

ai. Ð

at u

= 1996p

+ q

, ∀n = 1, 2, . . . trong

o p

, q

a c

sô

nguyên v

a 0 ≤ q

≤ 1995. X

et d

ay sô

( q

, q

), (q

, q

), . . . , (q

, q

n+1

), . . .

ı d

ay n

ay vô h

an m

a sô

ac sô

a h

u h

an nên tô

n t

ai hai sô

nhiên l, m ( gi

a s

m > l) sao cho (q

, q

l+1

) = (q

, q

m+1

) hiê

theo ngh

ıa q

= q

a q

l+1

= q

m+1

. Ch

ung ta s

e ch

ng minh r

ang

l−1

= q

m−1

. Th

ât v

ây,

5(u

m−1

−u

l−1

) = (u

m+1

−4u

+ 1976) − (u

l+1

−4u

+ 1976)

= (u

m+1

−u

l+1

) −4 (u

−u

) (7.7)

Do u

= 1996p

+ q

, nên t

(7.7) c

5(u

m−1

−u

l−1

) = 1996(p

m+1

− p

l+1

) −(q

m+1

−q

l+1

) −

−4[1996 (p

− p

) −( q

−q

)] (7.8)

Thay nh

ng gi

a tr

i b

ang nhau v

ao ((7.8) ta

dê

5(u

m−1

−u

l−1

) = 1996[(p

m+1

− p

l+1

) −4(q

−q

)] (7.9)

(7.9) suy ra 5(u

m−1

−u

l−1

) |1996, m

a (5, 1996) = 1 =⇒ (u

m−1

−

l−1

) |1996 =⇒ 1996(p

m−1

− p

l−1

) + (q

m−1

−q

l−1

) |1996

=⇒ (q

m−1

−q

l−1

) |1996. (7.10)

74 Chu

ng 7. B

ai t

âp d

ây sô

nâng cao

Do 0 ≤ q

m−1

≤ 1995, 0 ≤ q

l−1

≤ 1995

=⇒ −1995 ≤ q

m−1

−q

l−1

≤ 1995 (7.11)

(7.10) v

a (7.11) suy ra (q

m−1

− q

l−1

) = 0 hay q

m−1

= q

l−1

ng t

ung ta c

ung c

o thê

dê

n q

m−2

= q

l−2

a c

tiê

p t

nhu

thê

dê

= q

+ ( m −1) v

a q

= q

+ ( m −l) (7.12)

Ta ch

ng minh r

ang u

m−l

ınh l

a sô

ang c

ua d

ay m

a chia hê

t cho

1996. Th

ât v

ây theo c

ach x

inh d

ay, ta c

m−l

= u

m−l+2

−4u

m−l+1

+ 1976

= 1996p

m−l+2

+ q

m−l+2

−4(1996p

m−l+1

+ q

m−l+1

) + 1996

= 1996(p

m−l+2

+ 4p

m+l+1

) + (q

m−l+2

+ 4q

m−l+1

) + 1996

Thay (7.12) v

ang th

c trên ta c

m−l

= 1996(p

m−l+2

−4p

m−l+1

) + (q

−4q

) + 1996. (7.13)

= 20 =⇒ u

= 0.1996 + 20 =⇒ q

= 20

= 100 =⇒ u

= 0.1996 + 100 =⇒ q

= 100

ây t

(7.13) suy ra

m−l

= 1996(p

m−l+2

−4p

m−l+1

) + 1996. (7.14)

Do p

m−l+2

a p

m−l+1

a sô

nguyên, v

ây t

(7.14) suy ra 5u

m−l

|1996

a ( 5, 1996) = 1 suy ra u

m−l

|1996.

. 7.8. Cho d

ay sô

nhiên u

, u

, . . . , u

n+1

sao cho 1 ≤ u

< u

. . . < u

n+1

≤ 2n . Ch

ng minh r

˘ang tô

n t

ai hai sô

nhiên i v

a j sao

cho u

chia hê

t cho u

, (j > i).

i gi

ai. K

y hi

êu v

a u

c sô

e l

n nhâ

t c

ua u

ng, ngh

ıa l

= 2

, v

i v

e v

a sô

nhiên p

o (i = 1, 2, . . . , n + 1).

7.1. V

ı d

u 75

Do 1 ≤ u

< u

< . . . < u

n+1

≤ 2n suy ra v

i m

oi i = 1, 2, . . . , n + 1

ta c

o v

< 2n . X

et (n + 1) sô

e v

, v

, . . . , v

n+1

. C

ac sô

e n

dê

ng v

a nh

o ho

n 2n. nên sô

ng c

ua ch

ung b

ang n. V

ây theo

nguyên l

y Ðirichlê tô

n t

ai hai sô

i, j sao cho 1 ≤ i < j ≤ n + 1 m

= v

. Theo c

ach

at trên th

ı u

= 2

a u

= 2

. Nhu

< u

suy ra 2

< 2

, m

a v

= v

. Suy ra 2

< 2

. Do p

, p

ac sô

nguyên du

ng nên 2

chia hê

t cho 2

. Ngh

ıa l

a u

chia hê

cho u

. 7.9. (Ðê

thi To

an Olympic Quô

c tê

lâ

n th

13) D

ay sô

}, n =

2, 3, 4, . . . x

inh nhu

sau u

= 2

−3. Ch

ng minh r

˘ang d

ay sô

a m

ôt t

âp vô h

an c

ac phâ

n t

, sao cho bâ

t k

y hai sô

ao c

ua t

âp

p n

ay c

ung nguyên tô

ung nhau.

i gi

ai. Ta ch

ng minh b

ang quy n

ap. Gi

a thiê

a xây d

k phâ

n t

ua d

= 2

−3, u

= 2

−3, . . . , u

= 2

−3

a v

i m

oi i 6= j, th

ı (u

, u

) = 1, v

i 1 ≤ i, j ≤ k,

dây 2 = n

< . . . < n

ung ta s

e xây d

ng sô

k+1

= 2

k+ 1

−3 nguyên tô

ung nhau

i c

ac sô

, u

, . . . , u

ang c

ach sau

dây: Ð

at l = u

. . . u

. X

( l + 1 ) sô

, 2

, . . . 2

Khi chia c

ac sô

ay cho l ta

c m

ôt t

âp h

gô

m l sô

. V

ây theo nguyên l

y Ðirichlê c

ıt nhâ

t hai sô

cho ta

ung phâ

n du

. Gi

a s

hai sô

o l

a 2

, (s > r). Bây gi

on sô

sao cho pl = 2

−2

= 2

r−s

−1). Do l l

a sô

e nên 2

không chia

hê

t cho l . M

at kh

ac (2

, 2

r−s

) = 1 suy ra (2

r−s

−1) chia hê

t cho l.

Ðiê

u n

ay ngh

ıa l

a tô

n t

ai sô

nhiên q sao cho 2

r−s

−1 = ql, suy ra

r−s+2

−3 = 4.2

r−s

−3 = 4 (ql + 1) −3 = 4ql + 1.

76 Chu

ng 7. B

ai t

âp d

ây sô

nâng cao

at u

k+1

= 2

r−s+2

− 3 = ql. Do u

k+1

= 4ql + 1 v

a l =

. . . u

, suy ra u

k+1

> u

Do u

k+1

= 4q l + 1, suy ra (u

k+1

, 1) = 1. Do

o (u

k+1

, u

) = 1 v

oi i = 1, 2, . . . , k.

Nhu

ây khi

a xây d

c d

ay con u

, u

, . . . , u

oa m

diê

u ki

ên

dâ

u b

ai, th

ı s

e xây du

c d

ay con m

i u

, u

, . . . , u

k+1

ung c

o t

ınh châ

t â

y. Theo nguyên l

y qui n

ap ch

ung ta xây d

c d

ay con vô h

an u

, u

, . . . , u

, . . . . c

ua d

a cho c

o t

ınh châ

Bâ

t c

ap phâ

n t

ao c

ua d

ay con â

y c

ung nguyên tô

ung nhau.

. 7.10. Cho u

a u

a hai sô

nguyên du

ng nguyên tô

ung nhau.

ay sô

} x

inh v

i u

, u

a hai sô

ang

dâ

u tiên, c

on khi n =

2, 3, . . . ta x

inh

n+1

= u

n−1

+ 1

ng minh r

˘ang v

i m

oi i > 1 tô

n t

ai j > i sao cho u

chia hê

t cho

i gi

ai. Lâ

y i > 1 t

y, v

a p l

a u

c sô

nguyên tô

ua u

. Xây d

ay sô

} nhu



0 ≤ v

≤ p − 1

≡ u

(mod p)

Ta c

ung c

o v

n+1

= v

n−1

+ 1 (mod p), ∀n = 2, 3 . . . V

ı c

ac c

( v

, v

n−1

) l

a vô h

an, m

a v

ı nh

ân h

u h

an gi

a tr

i suy ra {v

}

ai l

a d

ay tuâ

n ho

an t

ôt l

uc n

o. Ta câ

n ch

ng minh r

ang

tô

n t

ai sô

nguyên du

ng k

> 0 sao cho

i +k

= 0. (7.15)

et hai kh

a n

ang sau

7.1. V

ı d

u 77

1) Gi

a s

ay {v

} tuâ

n ho

an t

i chu k

y T, trong

o s > i.

Ta c

s+1

= v

s−1

+ 1 = v

s+T+1

= v

s+T

s+T−1

+ 1 (mod p)

s−1

= v

s+T

s+T−1

(mod p). (7.16)

a) Nê

u v

= v

s+T

≡ 0 (mod p), th

ı v

= v

s+T

= 0, do 0 ≤ v

≤

p − 1, ∀n. Khi

o ch

ı vi

êc ch

on k

= s − i, Suy ra v

i +k

= v

= 0,

ây (7.15)

ung.

b) Nê

u v

= v

s+T

6= 0, th

ı t

(7.16) c

o v

s−1

= v

s+T−1

. Suy ra

} tuâ

n ho

an không ph

ai b

dâ

u t

diê

u n

ay mâu thu

ân v

ach ch

on s.Kh

a n

ang n

ay không xâ

y ra.

om l

ai h

ê th

c (7.15)

ung trong tru

ng h

p 1).

2) Nê

u s ≤ i th

ı h

ê th

c (7.15) hiê

n nhiên

ung. Ta c

o v

i +1

≡

i +1

(mod p) ≡ u

i −1

+ 1 (mod p) v

ây v

≡ u

(mod p) nhu

do p l

a u

c nguyên tô

ua u

suy ra v

≡ 0 (mod p), nhu

ây v

i +1

≡

1 (mod p) hay l

a v

i +1

= 1.

ngt

, do v

i +k

= 0 suy ra v

i +k

= 1. Nhu

ây suy ra {v

}

ung tuâ

n ho

an v

i chu k

y k

c l

a v

i m

oi l nguyên du

ng, ta c

i +l.k

= 0. (7.17)

Ngh

ıa l

a u

i +l.k

chia hê

t cho p.

Nhu

ây v

i m

oi u

c nguyên tô

p c

ua u

ta xây d

c sô

sao cho (7.17)

ung.

oi m l

a b

ôi sô

chung nh

o nhâ

t c

ua tâ

t c

a c

ac sô

, theo (7.3)

suy ra v

i +lm

= 0 v

i m

oi l nguyên du

ng. Suy ra u

i +lm

chia hê

t cho

tâ

t c

a c

ac u

c sô

nguyên tô

ua u

. T

c l

a u

i +lm

chia hê

t cho u

oi sô

nguyên du

ng l. Lâ

y j = i + lm, ta c

diê

u ph

ai ch

ng minh.

78 Chu

ng 7. B

ai t

âp d

ây sô

nâng cao

7.2. B

ai t

âp

. 7.11. Nê

u ba sô

nguyên tô

c s

n ho

n 3 l

âp th

anh m

ôt câ

sô

ông th

ı công sai c

ua ch

ung chia hê

t cho 6.

. 7.12. cho f (n) l

a h

am x

inh trên t

âp c

ac sô

nguyên du

ng nhu

sau: nê

u n = a

. . . a

, th

ı f (n) = (a

+ a

+ ··· + a

)

1998

. V

i m

ôi

sô

nguyên du

ng n, l

âp d

ay vô h

an u

( n), i = 1, 2, . . . nhu

( n) = f ( f (. . . f (n)i lâ

n f

| {z }

ng minh r

ang v

i m

oi n nguyên du

ng, tô

n t

ai p sao cho d

( n), i = p, p + 1, . . . l

a d

ay tuâ

n ho

an.

. 7.13. Cho u

, u

, . . . , u

a d

ay sô

y gô

m n sô

ang. Ch

minh r

ang luôn luôn tr

ıch

c m

ôt d

ay con sao cho nê

u g

oi S l

tô

ng c

ac phâ

n t

ua d

ay con â

y, th

ı S kh

ac v

i sô

nguyên gâ

n nhâ

ôt lu

ng không vu

t qu

n + 1

. 7.14. Ch

ng minh r

ang nê

u nh

ng sô

nguyên a v

a m nguyên tô

ung nhau, th

ı tô

n t

ai m

ôt sô

nhiên n m

a t

ıch na chia cho m cho

sô

CHU

NG 8

Ô TH

C V

I T

ÂP TR

U M

ÂT

8.1. T

âp tr

u m

ât

Trên

ng th

ang th

c ch

ung ta thu

ng quan tâm t

i kh

ai ni

êm

ôt kho

ang (m

ôt

an th

ang), ta c

o thê

hiê

u m

ôt kho

ang trên

ng th

ang th

c l

a t

âp h

p tâ

t c

a c

ac sô

c n

am gi

a hai

diê

a cho. Nhu

ây hai

diê

dê

inh m

ôt kho

ang c

o thê

am trong

ac n

am ngo

ai kho

ang

o ;

dây l

a xuâ

t ph

at c

ua kh

ai ni

êm

ong,

,..

anh gi

ai t

ıch, gi

ai t

ıch h

am trong to

an h

oc cao câ

p. Nhu

dây ta không quan tâm

diê

o, m

a ch

ı quan tâm t

i c

ac kh

êm sau

dây v

i quan

diê

m kiê

n th

c so

câ

p. V

i a, b l

a sô

c, k

êu [a,b] l

a kho

ang

c t

ınh c

a hai

diê

dâ

u a, b v

a g

oi l

a kho

ang

ong. Kho

ang m

c k

y hi

êu l

a (a, b), không lâ

y hai

diê

dâ

a, b. Ngo

ai ra ta c

on x

et kho

ang n

ong (n

a m

) do vi

êc ta ch

lâ

y m

ôt trong hai

diê

dâ

u a ho

ac b,v

ı d

u nhu

[a, b) ho

ac (a, b]. M

ôt

kho

ang trong t

âp sô

c g

oi l

a suy tho

ai nê

u n

o ch

ı l

a m

ôt

diê

c l

a khi hai

diê

dâ

u tr

ung nhau).

ôt t

âp h

p A c

ua sô

c g

oi l

a tr

u m

ât, nê

u m

oi kho

ang

không suy tho

dê

u ch

a m

ôt sô

phâ

n t

ua A.

ôt v

ı d

u d

ê thâ

y l

a t

âp h

p sô

u t

y gô

m c

ac sô

o thê

biê

ên nhu

ôt thu

ng c

ua hai sô

nguyên v

a t

âp h

p sô

vô t

y gô

80 Chu

ng 8. Sô

c v

i t

âp tr

u m

ât

ng sô

không ph

ai l

a sô

u t

dê

u l

a nh

ng t

âp tr

u m

ât trong

âp sô

Ngu

i ta c

on m

ông kh

ai ni

êm tr

u m

ât cho m

ôt kho

ang trên

ng th

ang th

c. Cho ∆ l

a m

ôt kho

ang bâ

t k

y trên

ng th

ang

c. Ch

ung ta g

oi t

âp h

p B gô

m nh

ng sô

c l

a tr

u m

ât trong

∆, nê

u v

i m

oi kho

ang con không suy tho

ai c

ua ∆

dê

u ch

a nh

phâ

n t

ua B. R

o r

ang t

âp h

p c

ac sô

u t

y tr

u m

ât trong m

kho

ang; v

a t

âp h

p c

ac sô

vô t

y c

ung c

o t

ınh châ

t â

ng k

y hi

êu hay

c d

ung: v

i m

oi sô

c x, k

y hi

êu [x] l

sô

nguyên l

n nhâ

t không vu

t qu

a x, {x} l

a sô

x − [x]; [x] v

a {x}

oi l

a phâ

n nguyên v

a phâ

n th

âp phân c

ua sô

x. T

inh ngh

ıa c

thê

thâ

y ngay 0 ≤ x − [x] < 1. Ðê

hiê

u r

o ho

n kh

ai ni

êm tr

u m

ât

trong phâ

n n

ay ta x

et m

ôt lo

at b

ai to

an c

o liên quan v

a c

ach s

ung

nguyên l

y Ðirichlê

dê

ng minh

dinh l

y co

an Kronecker.

8.2. V

ı d

. 8.1. Nê

u m

ôt t

âp h

p A c

ua sô

c l

a tr

u m

ât v

a r l

a sô

c kh

không, th

ı t

âp h

p gô

m tâ

t c

a t

ıch sô

{ra} v

i a ch

ay trong A c

ung l

âp tr

u m

ât.

i gi

ai. C

o hai tru

ng h

p xâ

y ra: r > 0 v

a r < 0. V

ı c

ach ch

minh ho

an to

an tu

ng t

nên ta ch

ı x

et tru

ng h

dâ

u. Cho x v

y l

a hai sô

c v

a x < y. Khi

a theo gi

a thiê

t A l

a t

âp

u m

ât, th

ı tô

n t

ai phâ

n t

a thu

ôc A sao cho

< a <

. Suy ra

x < ar < y. Nhu

ây m

oi kho

ang m

(x, y) ch

a sô

ang ra v

i a

thu

ôc A.

. 8.2. (Ð

inh l

y Kronecker) V

i m

oi sô

vô t

y α, t

âp h

p tâ

t c

a c

ac sô

8.2. V

ı d

u 81

ang mα + n l

a t

âp tr

u m

ât,

dây m v

a n l

a nh

ng sô

nguyên bâ

t k

i gi

ai. Câ

n ph

ai ch

ng minh r

ang m

oi kho

ang không suy tho

∆ ch

a nh

diê

m d

ang mα + n. Ch

ung ta chia kho

ang [0,1] ra

anh m

ôt sô

u h

an kho

ang con ∆

, ∆

, . . . , ∆

ô d

ai c

ua m

ôi

kho

ang con nh

o ho

ô d

ai c

ua ∆. Ch

y r

ang v

i m

oi sô

a tô

n t

ôt sô

nguyên n, sao cho sô

a + n n

am trong kho

ang [0,1]. Suy ra

i m

oi sô

nguyên m c

o thê

cho tu

ng v

i m

ôt sô

ang mα + n,

a n

o n

am trong kho

ang [0,1]. Nhu

an th

ang [0,1]

c chia

ra h

u h

an kho

ang nh

o. Suy ra tô

n t

ai nh

ng sô

nguyên m, m

, n, n

i m 6= m

a nh

ng sô

mα + n v

a m

α + n

am trong c

ung m

ôt

kho

ang nh

o ∆

. Do

o kho

ang c

ach gi

a hai

diê

m n

ay nh

o ho

ai c

ua ∆. Ch

ung ta c

ung thâ

y không thê

xâ

y ra mα + n = m

α + n

ı t

ang th

c n

ay suy ra α =

−n

m −m

a l

ai l

a m

ôt sô

u t

y, tr

i gi

a thiê

Nhu

ây ch

ung ta kh

ang

inh r

ang sô

( m −m

) α + (n −n

) kh

không v

a c

o gi

a tr

i tuy

êt

dô

i nh

o ho

n ∆. T

o suy ra m

ôt sô

c sô

ua n

o, c

ung c

o d

ang mα + n, s

e n

am trong kho

ang ∆.

. 8.3. Cho α l

a m

ôt sô

vô t

y du

ng. Khi

o t

âp h

p tâ

t c

a sô

o d

ang

mα −n l

a t

âp tr

u m

ât,v

i m v

a n l

a nh

ng sô

nhiên bâ

t k

i gi

ai. Kê

t lu

ân c

ua b

ai n

ay m

anh ho

inh l

y trên v

ı n

o kh

ang

inh m

ôt t

âp sô

c nh

o ho

n t

âp mô t

a trong

dij nh l

o c

ung tr

ât.

Cho kho

ang không suy tho

ai ∆ n

bên ph

ai sô

không v

a c

ô d

ai e > 0. Không

anh hu

dê

n kê

t qu

a ch

ng minh c

o thê

thiê

t e < 1. Ngo

ai ra ta c

o thê

on sô

nhiên k sao cho k ≥

. T

8.1 v

a 8.2 suy ra t

âp c

ac sô

kpα + kq v

i p v

a q l

a c

ac sô

nguyên bâ

82 Chu

ng 8. Sô

c v

i t

âp tr

u m

ât

y, l

a t

âp tr

u m

ât. Ngh

ıa l

a tô

n t

ai c

ac sô

nguyên p v

a q th

oa m

0 < kp α + kq < e. (8.1)

ung ta s

e ch

ı ra r

ang gi

a nh

ng c

ap sô

nguyên (p, q) trong (8.1)

o nh

ng c

ap m

a p > 0. Th

ât v

ây, tru

ng h

p p = 0 không thê

xâ

ra v

ı t

(8.1) suy ra 0 < kq < e, mâu thu

ân v

diê

u ta

a biê

t l

a kq

a sô

nguyên v

a e < 1. Do v

ây ch

ı c

on ph

ai ch

ng minh cho tru

p p < 0. Trong tru

ng h

p n

ay sô

o d

ang kpsα + kqt v

i s, t l

ng sô

nguyên bâ

t k

y, t

ao th

anh t

âp tr

u m

ât. T

(8.1) suy ra tô

ai sô

nguyên s v

a t sao cho

0 < kp sα + kqt < kpα + kq. (8.2)

Nê

u s < 0, th

ı kps > 0 v

a ch

ng minh l

ung. V

ı thê

ta ch

ı x

s ≥ 0. T

(8.1) v

a (8.2) suy ra

0 < kp (1 − s)α + kq − kpt < e. (8.3)

ı v

i s = 0 bâ

ang th

c (8.2) không thê

xâ

y ra, nên s > 0. Nhu

i v

ı s l

a sô

nguyên, th

ı t

s > 0 suy ra s ≥ 1. T

ai v

ı ((8.3) không

thê

xâ

y ra v

i s = 1, t

bâ

ang th

c cuô

i c

ung l

ai suy ra s > 1.

Nhu

ây kp(1 − s) > 0. Ðiê

o c

o ngh

ıa l

a tô

n t

ai c

ac sô

nguyên p

a q th

oa m

an (8.1) v

a p > 0. T

(8.1) suy ra

kq < e −kpα < e − p

α = e(1 − p) ≤ 0

ây kq < 0. Theo c

ach n

ay (8.1)

a vê

ang 0 < mα −n < e,

dây m v

a n l

a nh

ng sô

nhiên. B

i v

ı e l

ô d

ai c

ua∆, t

bâ

ang th

c cuô

i c

ung suy ra m

ôt u

c sô

o c

ua mα − n, c

ung c

ang n

ay, s

e n

am trong ∆. Tu

ng t

ung ch

ng minh

c khi ∆

bên tr

ai sô

không.

. 8.4. Cho α l

a sô

vô t

y bâ

t k

y. Khi

o t

âp h

p nh

ng sô

ang {αn},

i n l

a sô

nhiên bâ

t k

y, l

a t

âp tr

u m

ât trong kho

ang (0,1).

8.2. V

ı d

u 83

i gi

ai. Câ

n ph

ai ch

ng minh r

ang m

oi kho

ang con không suy

biê

n (a, b) c

ua (0,1) ch

a sô

o d

ang {αn} v

i m

ôt sô

nhiên

n n

o. Ch

ung ta ch

ng minh cho tru

ng h

p khi α l

a m

ôt sô

ng. Theo b

ai 8.3 nh

ng sô

o d

ang nα − m v

i n, m l

a c

ac sô

nhiên, t

ao th

anh t

âp tr

u m

ât. Ngh

ıa l

a tô

n t

ai nh

ng sô

nhiên

m v

a n th

oa m

an 0 ≤ a < nα − m < b < 1. Nhu

ng t

inh ngh

ıa

[α n] suy ra 0 ≤ nα − [nα] < 1. Ch

ung ta nh

ân

c hi

êu hai sô

nguyên m v

a [nα] th

oa m

an −1 < m − [nαm] < 1,

diê

u n

ay ch

xâ

y ra khi m − [nαm] = 0, do

o m = [nα]. T

(8.1) ch

ı ra r

ang sô

{n α} = nα − [nα] n

am trong kho

ang (a, b). V

i α > 0, ch

ung ta

ng minh xong.

Tru

ng h

p α < 0. Khi

o −α > 0 v

a t

ai 8.3 suy ra tô

n t

ng sô

nhiên m v

a n, th

oa m

an −1 ≤ −b < n(−α) − m <

−a ≤ 0. Nhân c

ac vê

i -1 ch

ung ta nh

ân

c 0 ≤ a < nα − m <

b ≤ 1. Nhu

ây d

ê d

ang t

ınh ra m = −[nα] v

a {nα} n

am trong

kho

ang (a, b).

. 8.5. T

âp h

p tâ

t c

a c

ac sô

ang {log n} v

i n l

a sô

nhiên bâ

t k

a t

âp tr

u m

ât trong (0,1).

i gi

ai. Ch

ung ta c

o thê

ng minh m

ông ho

n m

ôt ch

ut: t

âp

p c

ac sô

ang {n log 2} v

i n l

a sô

nhiên bâ

t k

y, l

a t

âp tr

u m

ât

trong (0,1).

Ðê

at m

ıch n

ay ch

ung ta ch

ng minh log 2 l

a m

ôt sô

vô

y. Th

ât v

ây, trong tru

ng h

p ngu

c l

ai th

ı tô

n t

ai hai sô

nhiên

p v

a q, m

a log 2 =

, ngh

ıa l

a 2 = 10

. L

uy th

ang th

c cuô

ung v

i q ch

ung ta nh

ân

c 2

= 2

. Ðiê

u n

ay tr

inh l

an c

ua sô

oc vê

êc phân t

ıch ra th

a sô

nguyên tô

. Nhu

ây

84 Chu

ng 8. Sô

c v

i t

âp tr

u m

ât

log 2 th

c s

a m

ôt sô

vô t

y. Áp d

ung 8.4 suy ra t

âp c

ac sô

o d

ang

{n log 2 } l

a tr

u m

ât trong (0,1).

at kh

ac, theo t

ınh châ

t c

ua logarit, log 2

= n log 2 v

i m

n = 1, 2, . . .

. 8.6. Cho m l

a sô

nguyên, n l

a sô

nguyên không âm. T

âp h

p tâ

t c

ac sô

o d

ang

a t

âp tr

u m

ât.

i gi

ai. Do c

ac b

ai to

an trên, ch

ung ta ch

ı câ

n ch

ng minh r

ang

âp h

p sô

ang

i m, n l

a nh

ng sô

nguyên du

ng, l

a tr

u m

ât

trong kho

ang (0, +∞). Ðiê

o c

o ngh

ıa l

a v

i m

oi c

ap sô

a, b(a < b) tô

n t

ai nh

ng sô

nhiên m v

a n th

oa m

an a <

< b.

Sau khi logarit h

oa c

ap bâ

ang th

c n

ay theo co

sô

2, ch

ung ta

ân

c c

ap bâ

ang th

c tu

ng log

a < m log

3 − n <

log

b. C

ach ch

ng minh tu

ng t

nhu

8.5 cho thâ

y log

3 l

a vô t

Khi

inh l

y Kronecker ch

ı ra r

ang trong

an (log

a, log

b) ch

sô

o d

ang {m log

3 − n}.

. 8.7. T

âp h

p tâ

t c

a c

ac sô

ang c

ua d

ay x

inh b

˘ang công th

[log n]+1

, n = 1, 2, 3 . . ., l

a tr

u m

ât trong kho

ang (

, 1) .

i gi

ai. Lâ

y hai sô

c a v

a b sao cho

≤ a < b ≤ 1. Câ

n ph

ng minh r

ang tô

n t

ai sô

nhiên n, th

oa m

an a <

[log n]+1

b. Sau khi logarit h

oa bâ

ang th

c trên v

i co

sô

10 ch

ung ta

ân

c bâ

ang th

c tu

ng 1 + log a < log n −[log n] =

{log n} < 1 + log b. Nhu

ng kho

ang m

i c

dâ

u m

ut 1 + log a

a 1 + log b r

o r

ang n

am trong kho

ang (0, 1). Ðiê

u n

ay gi

ai th

ıch t

sao tô

n t

ai m

ôt sô

nhiên n th

oa m

an bâ

ang th

c sau c

ung, b

8.2. V

ı d

u 85

ı theo 8.5 t

âp h

p c

ac sô

o d

ang {log n} l

a tr

u m

ât trong (0, 1).

Nhu

ây th

ı a < x

< b,

diê

u ta câ

n ch

ng minh.

. 8.8. Ch

ng minh r

˘ang tô

n t

ai vô h

an nh

ng sô

uy th

a c

ua 2, m

khi viê

t theo co

sô

10 ch

ung luôn luôn b

˘at

dâ

u b

˘ang 8975.

i gi

ai. M

ôt sô

dâ

u b

ang nh

om sô

8975 khi v

a ch

ı khi v

ôt sô

nhiên n n

o, nh

ang th

c sau

c th

oa m

8975.10

≤ 2

< 8976.10

. Nhu

ach gi

ai c

ac b

ai tru

c ch

ung ta

logarit h

oa bâ

ang th

c trên v

a nh

ân

c c

ac bâ

ang th

c tu

ng log 8975 ≤ m log 2 − n < log 8976. T

ai v

ı log 2 l

a m

ôt sô

vô

y, nên nh

ng sô

o d

ang m log 2 − n v

i n, m l

a nh

ng sô

nhiên

ao th

anh m

ôt t

âp tr

u m

ât. Ðiê

u n

ay c

o ngh

ıa l

a tô

n t

ai vô sô

ap sô

nhiên m v

a n th

oa m

an c

ac bâ

ang th

c sau c

ung, suy ra c

ung

oa m

an c

ac bâ

ang th

c tru

o. Ch

y b

ai to

an c

ung khi

thay co

sô

hai b

ang co

sô

10 c

ua logarit v

a sô

8975 c

o thê

thay b

ang

ôt tô

p sô

bâ

t k

y, ch

ng minh

diê

u n

ay d

anh cho b

oc.

. 8.9. V

i m

oi sô

nhiên n, k

y hi

êu x

a ch

sô

dâ

u tiên c

sô

(trong c

ach viê

t v

i co

sô

10). Ch

ng minh r

˘ang d

ay sô

, x

, . . . , x

, . . . không ph

ai l

a d

ây tuâ

n ho

an.

i gi

ai. Gi

a s

ngu

c l

ai l

a tô

n t

ai nh

ng sô

nguyên du

ng k v

d sao cho x

= x

k+d

= x

k+2d

= . . . = x

k+nd

= . . . N

oi c

ach kh

, 2

k+d

, 2

k+2d

, . . . , 2

k+nd

, . . . c

o c

ung ch

sô

daah u tiên trong c

ach

viê

t v

i co

sô

10. Bâ

y gi

ung ta kh

ang

inh r

ang m

oi sô

nhiên

N c

o thê

biê

u di

ên du

i d

ang N = 10

log N

= 10

[log N]+{log N}

[log N]

.10

{log N}

. V

ı 0 ≤ {log N} < 1, nên 1 ≤ 10

{log N}

< 10, suy

ra ch

sô

dâ

u tiên c

ua N tr

ung v

i phâ

n nguyên c

ua c

ua sô

{log N}

Ðê

dây suy ra tô

n t

ai m

ôt ch

sô

s, 1 ≤ s ≤ 9, th

oa m

an bâ

ang

86 Chu

ng 8. Sô

c v

i t

âp tr

u m

ât

c sau: s ≤ 10

{log 2

k+nd

}

< s + 1 v

i n = 0, 1, 2, . . .. Sau khi logarit

ang th

c trên ch

ung ta c

o log s ≤ {(k + nd) log 2} < log(s +

1) . Ðiê

u n

ay ngh

ıa l

a tâ

t c

a c

ac sô

o d

ang {(k + nd) log 2}, n =

0, 1, 2, . . . n

am trong kho

ang [log s, log(s + 1)). D

ê d

ang ch

ng minh

ang t

âp h

p nh

ng sô

ay tr

u m

ât trong

an (0,1). Ðiê

o tr

i kê

t lu

ân : tô

n t

ai t

âp con m

an (0,1) không c

diê

chung v

i [log s, log(s + 1)). Nhu

ây

diê

u gi

a s

ngu

c l

ai l

a sai.

. 8.10. H

ay t

ım trong

an th

˘ang [0, π], tâ

t c

a sô

c t th

oa m

bâ

t phu

ng tr

ınh cos nt ≥ cos t v

i m

oi sô

nhiên n.

i gi

ai. - Ch

ung ta s

e ch

ng minh r

ang nê

u t c

o t

ınh châ

a nêu

trong b

ai to

an th

ı t

y sô

a m

ôt sô

u t

y. Th

ât v

ây gi

a s

sô

vô t

y. Khi

o t 6= π ; Không mâ

t t

ınh tô

ng qu

at ch

ung ta c

o thê

a thiê

t r

ang 0 ≤ t < π. V

2π

a sô

vô t

y du

ng, theo

inh l

Kronecker tô

n t

ai nh

ng sô

nhiên m v

a n, th

oa m

an bâ

t phu

ınh

2π

< m

2π

−n < 1 −

2π

, hay l

a t < mt −2nπ < 2π − t. T

ınh châ

t c

ua h

am cos trong

an [0, 2π] ch

ung ta suy ra cos mt =

cos(mt − 2nπ) < cos t. Ðiê

u n

ay tr

ai v

i c

ach ch

on t, do v

ây t

y sô

a sô

u t

Nhu

ây t c

o thê

biê

u di

ên du

i d

ang t =

2π,

dây p v

a q l

ng sô

nguyên tô

ung nhau v

a 0 ≤ p ≤ q (t

ai v

ı 0 ≤ t ≤ 2π ).

Nê

u q l

a sô

an, th

ı n =

a sô

nhiên v

a ngo

ai ra p l

a sô

e, v

ı p

a q l

a nguyên tô

ung nhau. V

ı v

ây cos t ≤ cos nt = cos pπ = −1,

o suy ra cos t = −1 v

a t = π. R

o r

ang π th

oa m

an tâ

t c

a c

diê

u ki

ên

a cho.

ung ta ch

ı c

on ph

ai x

et tru

ng h

p q l

a sô

e. C

o thê

8.3. B

ai t

âp 87

minh r

ang v

i m

oi n = 1, 2, . . . cos nt b

ang m

ôt sô

o trong d

ây

dây

1 = cos 0.

2π

, cos 1.

2π

, cos 2.

2π

, . . . , cos((q −1)

2π

). (8.4)

ât v

ây, nê

u n = sq + r,

dây 0 ≤ r ≤ q −1, th

ı cos nt = cos(sqt +

rt) = cos(2psπ + rt) = cos rt. Nê

u q = 2k + 1 l

a m

ôt sô

e, th

ı sô

o nhâ

t trong (8.4) l

a c

ac sô

cos

2k + 1

2π v

a cos

k + 1

2k + 1

2π. Lâ

t =

2k + 1

2π, 0 ≤ t ≤ π, c

o t

ınh châ

t mong muô

n, ch

ung ta s

ng minh khi

o p = k. Ðê

at m

ıch n

ay ch

ı câ

n ch

ı ra r

ang

tô

n t

ai m

ôt sô

nguyên du

ng n m

a cos nt = cos

2k + 1

2π. Th

ât v

ây:

ı 2k + 1 v

a p l

a nh

ng sô

nguyên tô

ung nhau tô

n t

ai nh

ng sô

nguyên m v

a n th

oa m

an 0 ≤ n ≤ 2k + 1 v

a (2k + 1) m + pn = k. T

ang th

c sau c

ung suy ra 2mπ + nt =

2k + 1

2π. Suy ra cos nt =

cos

2k + 1

2π. D

ê d

ang thâ

y r

ang nh

ng sô

o d

ang

2k + 1

2π v

k + 1

2k + 1

2π, k = 0, 1, 2, . . . l

a nghi

êm c

ua b

ai to

an. Kê

t lu

ân cuô

i c

ung

a nh

ng gi

a tr

i c

ua t ph

ai t

ım l

a t = π v

2k + 1

2π,

k + 1

2k + 1

2π, v

k = 0, 1, 2 . . . . . .

8.3. B

ai t

âp

. 8.11. Cho a, b, c l

a nh

ng sô

c sao cho [an] + [bn] = [cn] v

oi sô

nhiên n. Ch

ng minh r

ang

ıt nhâ

t m

ôt trong c

ac sô

a, b l

nguyên.

. 8.12. Cho α l

a m

ôt sô

u t

y. Ch

ng minh r

ang t

âp h

p c

ac sô

ang {αn}, n = 1, 2, . . . không tr

u m

ât trong kho

ang ( 0, 1).

88 Chu

ng 8. Sô

c v

i t

âp tr

u m

ât

. 8.13. Ch

ng minh r

ang v

i m

ôt sô

vô t

y bâ

t k

y α v

a m

ôt sô

u t

bâ

t k

y β, t

âp h

p sô

o d

ang {αn + β}, n = 1, 2, . . . l

a tr

u m

ât trong

kho

ang ( 0, 1).

. 8.14. Ch

ng minh r

ang t

âp h

p sô

ang {

√

n} v

i n l

a sô

nhiên

a t

âp tr

u m

ât trong kho

ang (0,1).

CHU

NG 9

NG D

UNG KH

AC C

NGUYÊN L

Y ÐIRICHLE

9.1. Xâ

p x

ı m

ôt sô

. 9.1. Cho x l

a m

ôt sô

c, c

on n l

a m

ôt sô

nhiên. Khi

o tô

n t

ng sô

nguyên p v

a q th

oa m

an 1 ≤ q ≤ n v



x −



≤

. (9.1)

i gi

ai. Ch

ung ta x

et nh

ng sô

kx − [kx](k = 0, 1, 2, . . . , n ). Ch

ung

gô

m n + 1 sô

a n

am trong kho

ang [0, 1]. Ch

ung ta chia kho

ang [0, 1]

ra n kho

ang con b

ang nhau ∆

, ∆

, . . . , ∆

ô d

ai c

ua m

ôi kho

ang

ay b

ang

. Theo nguyên l

y Ðirichlê tô

n t

ai hai sô

ac nhau k v

a l

am trong 0, 1, 2, . . . , n, sao cho nh

ng sô

kx − [kx] v

a lx − [lx] n

trong c

ung m

ôt kho

ang con th

m. Do

o kho

ang c

ach gi

a ch

ung

không qu

, t

c l

kx − [kx] − (lx − [lx])

≤

, hay l

( k − l)x − ([kx] − [lx])

≤

. (9.2)

i v

ı k 6= l, không

anh hu

dê

n kê

t qu

a ch

ng minh ta c

o thê

a thiê

t r

ang k > l. B

i v

ı ngo

ai ra c

on c

o 0 ≤ k ≤ n, 0 ≤ l ≤ n,

nên 1 ≤ k −l ≤ n. Ta

at q = k −l v

a p = [kx] −[lx]. Khi

o p v

a q

90 Chu

ng 9. Nh

ng d

ung kh

ac c

ua nguyên l

y Ðirichle

a nh

ng sô

nguyên v

a th

oa m

an 1 ≤ q ≤ n. V

i c

ach d

at n

ay (9.2)

a vê

ang |qx − p| ≤

, t

dây chia hai vê

cho q ta c

o (9.1).

. 9.2. V

i m

oi sô

c x tô

n t

ai vô h

an sô

nhiên q, v

i m

ôi q tô

ai sô

nguyên p, sao cho ch

ung th

oa m

an bâ

˘ang th



x −



≤

. (9.3)

i gi

ai. Nê

u x l

a sô

u t

y, t

c l

a x =

i r l

a sô

nguyên v

a s l

sô

nhiên, th

ı kê

t lu

ân c

ua b

ai to

an l

ung, v

ı c

o thê

at p = mr

a q = ms v

i sô

nhiên bâ

t k

y m. V

i tâ

t c

a c

ach ch

on p v

a q nhu

ây (9.3)

c th

oa m

an, v

ı vê

ai luôn luôn b

ang không. Nhu

ây

ı c

on ph

ai x

et tru

ng h

p x l

a sô

vô t

y. Gi

a s

ı c

o h

u h

an sô

nhiên q, m

a v

i ch

ung tô

n t

ai sô

nguyên p th

oa m

an (9.3), k

êu ch

ung l

a q

, q

, . . . , q

. V

i bâ

t k

y λ = 1, 2, . . . , l k

y hi

êu p

a sô

nguyên th

oa m



x −



≤



x −



i m

oi sô

nguyên p. V

ı sô

x l

a vô t

y, m

oi gi

a tr

i tuy

êt

dô

ıa tr

bâ

ang th

c trên l

a du

ng, sô

ng gi

a tr

i tuy

êt

dô

i n

ay l

a h

an. V

ı v

ây tô

n t

ai sô

nhiên n, sao cho



x −



, (λ =

1, 2, . . . , l).

Theo b

ai tru

c s

e tô

n t

ai sô

nhiên q v

a sô

nguyên p, sao cho

(9.1) th

oa m

an v

a 1 ≤ q ≤ n. Nhu

ng khi



x −



≤

, suy ra q = q

i m

ôt sô

λ = 1, 2, . . . , l T

ng bâ

ang th

trên suy ra



x −



≤



x −



≤

. Nhu

ây

ı thê

9.1. Xâ

p x

ı m

ôt sô

c 91

q < 1,

diê

u n

ay không thê

c v

ı q l

a sô

nhiên. Ta nh

ân

diê

u vô l

. 9.3. V

i m

oi c > 2 bâ

˘ang th



√

2 −



≤

. (9.4)

ung ch

ı v

i h

u h

an c

˘ap sô

nguyên p v

a sô

nhiên q.

i gi

ai. Ch

ung ta ch

ng minh bâ

ang th

c sau l

ung



√

2 −



≤

√

. (9.5)

i m

oi sô

nguyên p v

a v

i m

oi sô

nhiên q. V

≤ 1, bâ

ang

c (9.5) tâ

t nhiên th

oa m

an, khi



√

2 −



√

. Nhu

ây ch

câ

n x

et tru

ng h



√

2 −



≤

√

. Nhu

ng khi

√

2 −

√

≤

√

2 +

√

suy ra

0 <

< 2

√

2. (9.6)

at kh



√

2 −



√

2 −



√

2 +



√

2 +



− p



√

2 −



. (9.7)

Nhu

ng sô

− p

a sô

ac không, v

√

2 l

a m

ôt sô

vô t

y. Ngo

ra n

o l

a sô

nguyên nên |2q

− p

| ≥ 1 . T

(9.7) suy ra



√

2 −



≥



√

2 +



a c

ung v

i (9.6) cho ta (9.5).

92 Chu

ng 9. Nh

ng d

ung kh

ac c

ua nguyên l

y Ðirichle

a s

bâ

ang th

c (9.4)

ung v

i m

ôt c

ap sô

(p, q) n

o. T

(9.4) v

a (9.5) suy ra

ang th

√

≤

c−2

. V

ı c > 2 bâ

ang th

ay ch

ung cho h

u h

an sô

nhiên q. V

i m

ôi sô

q nhu

ây ch

o nhiê

u nhâ

t hai sô

nguyên p, v

i ch

ung th

oa m

an bâ

ang th

(9.4). Ngh

ıa l

a (9.4) ch

ı th

oa m

an cho h

u h

an c

ap sô

p v

a q.

. 9.4. Nê

u D l

a sô

nhiên bâ

t k

y, không l

a sô

ınh phu

ng, th

ı tô

ai vô h

an c

ac c

˘ap sô

nhiên (x, y), l

a nghi

êm c

ua bâ

t phu

ng tr

ınh

− Dy

| ≤ 1 + 2

√

D. (9.8)

i gi

ai. Theo b

ai 9.2 ta biê

t r

ang tô

n t

ai vô h

an c

ap sô

(x, y) t

nhiên, sao cho



−

√



≤

. (9.9)

at kh

ac bâ

ang th

c sau l

ung



√



(

−

√

D) + 2

√



≤



−

√



+ 2

√

Suy ra v

i m

ôi c

ap (x, y) ta c



√



≤

+ 2

√

Nhu

ây, v

i c

ach ch

on bâ

t k

y c

ap (x, y), sao cho th

oa m

an (9.9)

ung ta nh

ân

− Dy

| = |x − y

√

D|.|x + y

√

≤

(

+ 2

√

Dy) ≤

+ 2

√

D ≤ 1 + 2

√

Ðiê

u n

a ch

ng minh r

ang bâ

t phu

ng tr

ınh (9.8) c

o vô h

nghi

êm trong t

âp h

p sô

nhiên.

9.1. Xâ

p x

ı m

ôt sô

c 93

. 9.5. Nê

u D l

a sô

nhiên bâ

t k

y, không l

a sô

ınh phu

ng, th

phu

ng tr

ınh x

− Dy

= 1 c

ıt nhâ

t m

ôt nghi

êm nguyên (u, v) v

v 6= 0.

i gi

ai. Ch

ung ta x

et tâ

t c

a c

ac c

ap (x , y) sô

nhiên, m

a n

o th

an −1 − 2

√

D ≤ x

− Dy

≤ 1 + 2

√

D. Theo b

ai 9.4 c

o vô sô

sô

nhiên th

oa m

an bâ

ang th

c trên, Nhu

ng biê

u th

c x

−Dy

ı c

o h

u h

an gi

a tr

i v

ı ch

ung l

a c

ac sô

nguyên trong

an (−1 −

√

D, 1 + 2

√

D). Ngh

ıa l

a tô

n t

ai m

ôt sô

nguyên k, sao cho phu

ınh x

−Dy

= k c

o vô h

an nghi

êm t

nhiên (x, y). R

o r

ang k 6= 0,

ı nê

u ngu

c l

ai th

ı d

ân

dê

n mâu thu

ân do sô

√

D không thê

biê

ên du

i d

ang h

u t

√

D =

. Gi

a nh

ng c

ap n

ay c

o thê

ıt

nhâ

t hai c

ap kh

ac nhau (x

, y

) v

a (x

, y

) m

a ch

ung th

oa m

≡ x

(mod |k|), y

≡ y

(mod |k|). (9.10)

ât v

ây,ch

ı câ

n ch

ı ra tâ

t c

a c

ac kh

a n

ang c

ua c

ac c

ap sô

theo

mô

dun |k| c

o sô

ng h

u h

an. C

o ngh

ıa l

a tô

n t

ai nh

ng c

ap kh

nhau nh

ng sô

nhiên (x

, y

) v

a (x

, y

), m

a x

− Dy

= x

−

= k v

a th

oa m

an d

ang th

c (9.10).

ung ta x

ang th

−y

√

D)(x

+ y

√

D) = (x

−y

D) + (x

− x

(9.11)

(9.10) ch

ung ta c

−y

D ≡ x

− Dy

≡ k ≡ 0 (mod |k|),

− x

≡ x

− x

≡ 0 (mod |k|).

Khi

o tô

n t

ai sô

nguyên u v

a v, sao cho x

−y

D = ku, x

−

= kv. V

ı v

ây (9.11) c

o thê

viê

t th

anh

−y

√

D)(x

+ y

√

D) = k(u + v

√

D).

94 Chu

ng 9. Nh

ng d

ung kh

ac c

ua nguyên l

y Ðirichle

Nhân t

ng sô

ang v

i nhau trong c

ang th

c sau c

ung ch

ung ta

ân

= (x

− Dy

)(x

− Dy

) = k

( u

− Dv

o suy ra u

−Dv

= 1, ngh

ıa l

a c

ap (u, v) l

a nghi

êm c

ua phu

ınh.

ı c

on ph

ai ch

ng minh v 6= 0. Nê

u gi

a thiê

t ngu

c l

ai, ch

ung

ta s

e c

o x

= y

D = |k| v

a x

= x

. Khi

|k|y

= |(x

−y

D| = |y

−y

D| = y

−Dy

| = |k|y

dây, v

ı k 6= 0 ch

ı c

o kh

a n

ang khi y

= y

. Ðiê

u n

ay không thê

xâ

y ra v

ı (x

, y

) kh

ac (x

, y

) , c

on t

= y

suy ra x

= x

. 9.6. Cho x

, x

, . . . , x

a nh

ng sô

c v

a N l

a sô

nhiên. Khi

tô

n t

ai nh

ng sô

nguyên p

, p

, . . . , p

, q sao cho 1 ≤ q ≤ N



−



≤

, (9.12)

i m

oi i = 1, 2, . . . , n.

i gi

ai. Ch

ung ta ch

ng minh b

ai to

an cho tru

ng h

p n = 2. V

tru

ng h

p n l

n ho

n 2 ch

ng minh ho

an to

an tu

ng t

a d

anh

cho b

oc. Nhu

ây cho x

a x

a nh

ng sô

c, c

on N l

a sô

nhiên. Ch

ung ta s

e ch

ng minh r

ang tô

n t

ai nh

ng sô

nguyên p

, p

a q v

i 1 ≤ q ≤ N

a th

oa m



−



−



. (9.13)

ung ta cô

inh h

ê t

ô trong m

at ph

ang v

a x

et h

ınh vuông Q

i c

ınh (0, 0), ( 1, 0), (1, 1) v

a (0, 1) nhu

ınh v

e. Chia Q ra N

ınh vuông nh

o b

ang nhau v

i c

anh l

ang c

ng th

ang

song song v

i tr

uc t

ô (trong h

ınh v

e ta chia v

i N=7).

9.1. Xâ

p x

ı m

ôt sô

c 95

Bây gi

ung ta ch

dê

n c

ap sô

o d

ang (qx

− [qx

], qx

−

[qx

]),

dây q nh

ân nh

ng gi

a tr

i nguyên 0, 1, 2, . . . , N

. V

ı 0 ≤

− [qx

] < 1, i = 1, 2, . . . , N

ôi c

ap nhu

vây c

o thê

coi nhu

ôt c

ap t

ô c

diê

m trong h

ınh vuông Q. B

ang c

ach

o m

ôi sô

0, 1, 2, . . . , N

ao ra m

ôt

diê

m tu

ng trong h

ınh vuông Q , sô

ng c

ac sô

o l

a N

+ 1. Nhu

ng Q

c chia ra N

ınh vuông

o, suy ra tô

n t

ai hai sô

nguyên kh

ac nhau q

, q

trong

an [0, N],

diê

m tu

ng v

i ch

ung c

o c

ac t

ô (q

− [q

], q

−

]), (q

− [q

], q

− [q

]) v

a c

ung n

am trong m

ôt h

ınh

vuông nh

o v

i c

anh

. Ðiê

o c

o ngh

ıa l

|(q

−[q

]) − (q

−[q

])| ≤

|(q

−[q

]) − (q

−[q

])| ≤

. (9.14)

Không mâ

t t

ınh tô

ng qu

at c

o thê

a thiê

t q

> q

. Nê

at q =

− q

, p

= [q

] − [q

], p

= [q

] − [q

] th

ı bâ

ang th

(9.14) c

o d

ang

|qx

− p

| ≤

, |qx

− p

| ≤

. (9.15)

ung ta thâ

y r

ang 1 ≤ q ≤ N

, v

ı 1 ≤ q

< p

≤ N

. Chia hai vê

ua (9.15) cho q ch

ung ta nh

ân

c (9.13).

Hai b

ai to

an du

dây liên quan t

i m

ôt t

ınh châ

t m

a ta

a ch

minh

chu

ng 2. Ðê

ông t

ınh châ

t n

ay ch

ung ta

a v

inh

ngh

ıa.

Nê

u a

, a

, . . . , a

2n+1

a 2n + 1 sô

c (n ≥ 1). Ch

ung ta n

oi r

ang

ay n

ay c

o t

ınh châ

t P, nê

u bâ

t k

y 2n sô

trong ch

ung c

o thê

chia

am hai nh

om, m

ôi nh

om n sô

, sao cho tô

ng c

ua c

ac sô

trong hai

om b

ang nhau.

96 Chu

ng 9. Nh

ng d

ung kh

ac c

ua nguyên l

y Ðirichle

. 9.7. Ch

ng minh r

˘ang m

oi b

ô 2n + 1 sô

gô

m nh

ng sô

nguyên

ng c

o t

ınh châ

t P, th

ı tâ

t c

a c

ac sô

dê

u b

˘ang nhau.

i gi

ai. Ch

ng minh b

ang qui n

ap theo sô

n nhâ

t c

ua d

ây sô

Nê

u sô

n nhâ

t b

ang 1 th

ı tâ

t c

a c

ac sô

on l

ai c

ung

dê

u l

a 1, nên

ai to

a gi

ai. Bây gi

a s

kê

t lu

ân

ung v

i m

oi b

ô 2n+1 sô

nguyên du

ng m

a m

ôi sô

không vu

t qu

a k, k ≥ 2 v

a c

o t

ınh châ

t P.

Lâ

y p

, p

, . . . , p

2n+1

a b

ô sô

nguyên du

ng c

o t

ınh châ

t P v

a m

ôi sô

không vu

t qu

a k + 1. T

diê

u ki

ên b

ai to

an suy ra p

, p

, . . . , p

2n+1

o c

ung t

ınh ch

an l

a) Nê

u p

, p

, . . . , p

2n+1

a c

ac sô

an, ch

ung ta x

et c

ac sô

, . . . ,

2n+1

. Ch

ung ta thâ

y ngay ch

ung c

o t

ınh châ

P. Ngo

ai ra m

oi sô

không vu

t qu

a k v

ı p

≤ k + 1 v

i m

oi i =

1, 2, . . . , 2n + 1. B

ang qui n

ap suy ra

= . . . =

2n+1

.Ngh

ıa

a p

= p

= . . . = p

2n+1

b) Nê

u p

, p

, . . . , p

2n+1

a c

ac sô

e, ch

ung ta ch

ng b

ang qui

ap cho d

ay p

−1, p

−1, . . . , p

2n+1

−1. Ch

ung c

o t

ınh châ

P v

a không vu

t qu

a k, ch

ung ta nh

ân

c p

−1 = p

−1 = . . . =

2n+1

−1. Ngh

ıa l

a p

= p

= . . . = p

2n+1

. 9.8. Ch

ng minh r

˘ang m

oi b

ô 2n+1 sô

gô

m nh

ng sô

c du

o t

ınh châ

t P, th

ı tâ

t c

a c

ac sô

dê

u b

˘ang nhau.

i gi

ai. - Hiê

n nhiên r

ang nê

u c

ac sô

, a

, . . . , a

2n+1

o t

ınh châ

P v

a q l

a sô

c bâ

t k

y, th

ı c

ac sô

, qa

, . . . , qa

2n+1

ung c

o t

ınh

châ

t P.

Bây gi

cho x

, x

, . . . , x

2n+1

a nh

ng sô

c du

ng v

i t

ınh

châ

t P. Nê

u tâ

t c

a c

ac sô

a h

u t

y th

diê

u kh

ang

inh c

ua b

ai to

suy ra không kh

o. Th

ât v

ây, k

y hi

êu q l

a b

ôi sô

chung nh

o nhâ

t c

9.1. Xâ

p x

ı m

ôt sô

c 97

âu sô

ac sô

trên. Khi

o qx

, qx

, . . . , qx

2n+1

a nh

ng sô

nguyên

ng c

o t

ınh châ

t P, theo c

ach ch

ng minh b

ai tru

c ch

ung ta c

= qx

= . . . = qx

2n+1

. V

ı v

ây x

= x

= . . . = x

2n+1

. Ch

ı c

ai ch

ng minh tru

ng h

p c

o trong d

ây x

, x

, . . . , x

2n+1

ôt sô

vô t

y. Nhu

ng theo kê

t qu

a c

ua b

ai 9.6 tô

n t

ai sô

nhiên q, v

a c

sô

nguyên du

ng p

, p

, . . . , p

2n+1

oa m

−

| <

2n+1

, i = 1, 2, . . . , n. (9.16)

Tru

ng h

p riêng, tô

n t

ai p

, p

, . . . , p

2n+1

, q v

i q > (2n)

2n+1

ung th

oa m

an |qx

− p

| ≤

2n+1

, i = 1, 2, . . . , n.

at α

= qx

− p

, i = 1, 2, . . . , 2n + 1. Nhu

phâ

dâ

u kh

ang

inh

ang qx

, qx

, . . . , qx

2n+1

o t

ınh châ

t P. Ch

ung ta s

e ch

ng minh

ang p

, p

, . . . , p

2n+1

ung c

o t

ınh châ

t P. Ch

on 2n sô

trong

o, v

u nhu

, p

, . . . , p

. V

ı qx

, qx

, . . . , qx

o t

ınh châ

t P, không

mâ

t t

ınh tô

ng qu

at ch

ung ta lâ

ang th

c qx

+ qx

+ ··· + qx

n+1

+ qx

n+2

+ ··· + qx

, khi

o (p

+ α

) + (p

+ α

) + ··· +

+ α

) = (p

n+1

+ α

n+1

) + (p

n+2

+ α

n+2

) + ··· + (p

+ α

ung ta viê

t l

+ p

+ ··· + p

− p

n+1

− p

n+2

−··· − p

= α

n+1

+ α

n+2

+ ··· + α

−α

−··· − α

. (9.17)

Vê

bên tr

ang th

c trên l

a sô

nguyên nên sô

α = α

n+1

n+2

+ ··· + α

− α

− ··· − α

ung l

a sô

nguyên. Nhu

|α

| ≤

2n+1

, i = 1, 2, . . . , n. Do

o |α| ≤ |α

n+1

| + |α

n+2

| + ··· +

|α

| + |α

| + ··· + |α

| <

2n+1

< 1, v

ı q > (2n)

2n+1

. Khi

98 Chu

ng 9. Nh

ng d

ung kh

ac c

ua nguyên l

y Ðirichle

o α = 0 v

a t

ang th

c tru

o ta c

o p

+ p

+ ··· + p

n+1

+ p

n+2

+ ··· + p

Nhu

ây ch

ung ta kh

ang

inh

c nh

sô

nguyên p

, p

, . . . p

2n+1

o t

ınh châ

t P. Ch

ung ta c

o thê

kê

t lu

ân

c p

= p

= . . . = p

2n+1

c châ

dê

dây ch

ung ta

a ch

ng minh

c :

Nê

u p

, p

, . . . , p

2n+1

, q l

a nh

ng sô

nguyên th

oa m

an (9.16) v

q > (2n)

2n+1

ı p = p

= p

= . . . = p

2n+1

. Suy ra (9.16) c

o d

ang

−

| <

2n+1

, i = 1, 2, . . . , 2n + 1

Trong 9.6 ch

ung ta kh

ang

inh r

ang tô

n t

ai vô h

an sô

nhiên q

oa m

an (9.16). Không mâ

t t

ınh tô

ng qu

at ch

ung ta gi

a thiê

t r

ang

ng sô

o l

a q

< q

< . . . < q

< . . .,

dây q

> (2n)

2n+1

. Trong

tru

ng h

p n

ay v

i m

oi k tô

n t

ai sô

nguyên p

sao cho

−

| <

2n+1

, i = 1, 2, . . . , 2n + 1. (9.18)

ı lim

2n+1

= 0 khi k tiê

n t

i vô c

ung, t

(9.18) suy ra lim

khi k tiê

n t

i vô c

ung, v

i m

oi i = 1, 2, . . . , 2n + 1. Nhu

ng m

ôi d

sô

c không c

o nhiê

u ho

n m

ôt gi

i h

an, suy ra x

= x

= . . . =

2n+1

. 9.9. Ch

ng minh r

˘ang trong t

am sô

, m

ôi sô

o ba ch

sô

, bao gi

ung ch

c hai sô

o ba ch

sô

dê

khi gh

ep l

ai ta

c m

ôt sô

chia hê

t cho 7.

i gi

ai. Khi mang t

am sô

chia cho 7 th

ı thê

ao c

ung c

o hai sô

ung sô

(nguyên l

y Ðirichlê ). Gi

a s

hai sô

o l

ab c v

a αβγ . Hiê

9.2. B

ai t

âp 99

nhiên abcαβγ = 1000abc + αβγ. T

ach ch

on ta c

o abc = 7m + r

a αβγ = 7n + r v

i 0 ≤ r < 7 v

a m, n, r l

a c

ac sô

nhiên. V

ây abcαβγ = 1000(7m + r) + (7n + r) = 7(1000m + n) + 1001.r =

7( 1000m + n + 143.r).

. 9.10. Cho a, b, c, d l

a c

ac sô

nguyên. Ch

ng minh r

˘ang t

ıch c

ua c

êu b − a, c − a, d − a, d − c, b − d v

a c − b chia hê

t cho 12.

i gi

ai. Câ

n ch

ng minh t

ıch: P = (b −a)(c −a)(d −a) (d −c)( d −

b)(c − b) chia hê

t cho 12=4.3. Ch

ung ta biê

t r

ang m

ôt sô

nguyên

bâ

t k

y khi chia cho 4 th

ı ch

ı c

o c

ac sô

0, 1, 2, 3.

Trong bô

n sô

a, b, c, d cho tru

c nê

u c

o hai sô

khi chia cho 4 m

o c

ung sô

ı hi

êu c

ua ch

ung s

e chia hê

t cho 4. Nê

u không c

hai sô

ao khi chia cho 4 cho c

ung sô

ı trong bô

n sô

ai c

hai sô

an v

a hai sô

e. V

ı hi

êu c

ua hai sô

an c

ung nhu

êu c

hai sô

dê

u l

a sô

an nên P chia hê

t cho 4.

at kh

ac trong bô

n sô

a, b, c, d luôn t

ım

c hai sô

khi chia cho

3 th

ı c

o c

ung sô

(nguyên l

y Ðirichlê ). Do

o hi

êu c

ua ch

ung chia

hê

t cho 3, suy ra P chia hê

t cho 3. T

om l

ai P chia hê

t cho 12=4.3.

9.2. B

ai t

âp

. 9.11. Cho x l

a m

ôt sô

c, c

on n l

a m

ôt sô

nhiên. Khi

o tô

n t

ng sô

nguyên p v

a q th

oa m

an 1 ≤ q ≤ n v



x −



≤

( n + 1)q

. 9.12. Cho x

, x

, . . . , x

a nh

ng sô

c v

a n l

a sô

nhiên. Khi

o tô

n t

ai nh

ng sô

nguyên p

, p

, . . . , p

, q không

dô

ng th

i b

ang

0, sao cho ta c

o q

≤ n (µ = 1, 2, . . . , m) v

+ q

+ ··· + q

− p| ≤

( n + 1)

100 Chu

ng 9. Nh

ng d

ung kh

ac c

ua nguyên l

y Ðirichle

. 9.13. Ch

ng minh r

ang v

i m

oi c

ap sô

nguyên p v

a q > 0 ta

dê

o bâ

ang th

c sau



√

2 −



≥

√

3 −

√

. 9.14. Ch

ng minh r

ang v

i m

oi c

ap sô

nguyên p v

a q > 0 ta

dê

o bâ

ang th

c sau



√

3 −



≥

√

. 9.15. Cho m, n v

a s l

a nh

ng sô

nguyên v

a α l

a nghi

êm c

ua phu

ınh b

âc hai mx

+ nx + s = 0, (m 6= 0). Ch

ng minh r

ang nê

u α l

sô

vô t

y, th

ı tô

n t

ai m

ôt sô

ng c th

oa m



α −



≥

i m

ôi

ap sô

nguyên p v

a q > 0.

CHU

NG 10

NGUYÊN L

Y ÐIRICHLÊ

CHO DI

ÊN T

ICH

10.1. Ph

at biê

u nguyên l

y Ðirichlê cho di

ên t

ıch

Trong chu

ng n

ay ch

ung ta x

et nh

ng t

âp h

p trên m

at ph

ang,

ng ph

ep to

an trên c

ac t

âp h

p nê

u c

ac b

an chu

a quen biê

t c

thê

xem

ınh cuô

i s

ach. Ch

ung ta quan tâm t

i c

ac kh

ai ni

êm

dây:

ôt t

âp h

p trong m

at ph

ang g

oi l

a b

i ch

an, khi tô

n t

ai m

ôt

ınh tr

on ch

a to

an b

ô c

diê

m c

ua t

âp h

o. Khi không tô

n t

ôt h

ınh tr

on n

ao nhu

trên th

ı t

âp h

o g

oi l

a t

âp h

p không b

an. V

ı d

u nhu

ôt

da gi

ac lô

i l

a t

âp b

i ch

an c

on n

a m

at ph

ang l

âp h

p không b

i ch

an. D

ê d

ang ch

ng minh

c c

ac t

ınh châ

t sau

ua nh

ng t

âp h

p b

i ch

1. H

p v

a giao c

ua h

u h

an nh

ng t

âp b

i ch

an l

a m

ôt t

âp b

an. Hi

êu c

ua hai t

âp b

i ch

an l

a m

ôt t

âp b

i ch

an.

2. M

ôt t

âp h

p con c

ua m

ôt t

âp b

i ch

an l

a m

ôt t

âp b

i ch

an. M

ôt

âp h

p ch

a m

ôt t

âp h

p con không b

i ch

an th

ı n

o c

ung không b

an.

ôt

diê

m P g

oi l

diê

m biên c

ua t

âp h

p A trong m

at ph

ang,

102 Chu

ng 10. Nguyên l

y Ðirichlê cho di

ên t

ıch

nê

u m

oi h

ınh tr

on tâm t

ai P c

o ch

a nh

diê

m thu

ôc A v

a c

diê

m không thu

ôc A.T

âp h

p tâ

t c

a c

diê

m biên c

ua A g

a biên c

ua A v

a k

y hi

êu l

a K(A). V

ı d

u biên c

ua h

ınh tr

on l

on v

i c

ung tâm v

a b

an k

ınh. V

ı d

ac bi

êt v

a t

ınh châ

t biên c

âp h

p nhu

3. Cho t

âp h

p A gô

m to

an b

ô nh

diê

m c

o t

ô h

u t

trong m

ôt h

ınh vuông v

i t

ô c

dir nh (0, 0), (0, 1), (1, 0), (1, 1).

ê d

ang thâ

y r

ang biên c

ua A l

a to

an b

ô h

ınh vuông n

oi trên.

4. V

i m

oi t

âp h

p A gô

m c

diê

m trong m

at ph

ang

dê

u c

công th

c sau K(K(A)) ⊂ K(A).

5. M

oi c

ap t

âp h

p bâ

t k

y trong m

at ph

ang

dê

u th

oa m

an c

công th

c sau

K(A ∪ B) ⊂ K(A) ∪K(B)

K(A ∩ B) ⊂ K(A) ∩K(B)

K(A\B) ⊂ K(A) ∪ K(B)

ôt

diê

m P g

oi l

diê

m trong c

ua t

âp h

p A nh

diê

m trong

at ph

ang, khi tô

n t

ai h

ınh tr

on tâm P m

a n

o n

am tr

on trong A.

inh ngh

ıa n

ay thâ

y ngay l

a m

diê

m trong c

ua t

âp h

p A

dê

thu

ôc A. Ðiê

u ngu

c l

ai không

ung: trong v

ı d

u 3

trên t

âp h

p A

không c

o m

ôt

diê

m trong n

ao. Ta thâ

y ngay

6. M

ôt

diê

m thu

ôc A l

diê

m trong c

ua A khi v

a chi khi n

o không

diê

m biên c

ua A. Ðiê

u n

ay gi

ai th

ıch t

ai sao nh

diê

m trong

ua h

ınh tr

on không n

am trên

ng tr

on.

Ðê

ai tr

ac t

âp h

ac bi

êt, ch

ung ta

a v

ao m

ôt kh

ai ni

êm

ac chu

ng cho l

p t

âp h

p không

ac bi

êt trong m

at ph

ang : M

ôt

âp h

p b

i ch

an c

diê

m trong m

at ph

ang g

oi l

a bê

at, khi biên

ua n

o không ch

diê

m trong (c

ua biên).

ı d

u c

ac h

ınh tr

on ho

da gi

dê

u l

a bê

at trong m

at ph

ang.

10.1. Ph

at biê

u nguyên l

y Ðirichlê cho di

ên t

ıch 103

Nhu

ng trong v

ı d

u 3 t

âp h

p A không l

a bê

at. B

ang c

ach d

ung

inh ngh

ıa vê

âp h

p v

a c

inh ngh

ıa trong phâ

n trên ch

ung

ta ch

ng minh

7. Nê

u A v

a B l

a hai bê

at, nh

ng t

âp h

p A ∪ B, A ∩ B v

A\B c

ung l

a nh

ng bê

at trong m

at ph

ang.

8. Nê

u A, B v

a C l

a c

ac bê

at v

a A không c

o chung

diê

m trong

i B v

a v

i C, th

ı A không c

diê

m trong chung v

i B ∪C.

ôt trong nh

inh l

y co

an trong h

ınh h

oc ph

ang, nhiê

u khi

phô

thông ch

ung ta công nh

ân nhu

ôt tiên

dê

9. M

oi bê

at A nh

diê

m trong m

at ph

ang c

o thê

cho tu

ng v

i m

ôt sô

c không âm S(A) sao cho

a) S(∆) = 1, v

i ∆ l

a m

ôt h

ınh vuông c

o c

anh l

a 1;

b) Nê

u A v

a B l

a hai bê

at không c

diê

m trong chung, th

S(A ∪ B) = S(A) + S(B).

ep cho tu

ng S v

i c

ac t

ınh châ

t trên

c x

inh m

ôt

ach duy nhâ

Cho bê

at A bâ

t k

y, sô

S(A) g

oi l

a di

ên t

ıch c

ua A. Nh

ng m

c x

et trong c

ac tru

ng phô

thông l

a h

ınh ch

ât, tam gi

ac,

ınh tr

on,. . . v

a sô

S(A) theo

inh ngh

ıa trên tr

ung v

i kh

ai ni

êm

ên t

ıch c

ua c

ac h

ınh n

ay. V

i c

ach tr

u tu

ng h

oa kh

ai ni

êm di

ên

ıch ch

ung ta d

ê d

ang kh

ao s

at t

ınh châ

t vê

ên t

ıch c

ua c

ac h

ınh.

a) v

a b) ch

ung ta c

o thê

ê d

ang ch

ng minh

10. Nê

u A v

a B l

a nh

ng bê

at v

a A ⊂ B, th

ı S(A\B) =

S(A) − S(B) .

11. Nê

u A

, A

, . . . , A

a c

ac bê

at t

dôi m

ôt không c

diê

m trong chung, th

ı S(A

∪ A

∪ . . . ∪ A

) = S(A

) + S(A

) +

104 Chu

ng 10. Nguyên l

y Ðirichlê cho di

ên t

ıch

··· + S(A

Nguyên l

y Ðirichlê cho di

ên t

ıch: Nê

u A l

a m

ôt bê

˘at, c

, A

, . . . , A

a c

ac bê

˘at sao cho A

⊂ A(i = 1, 2, . . . , n) v

S(A) < S(A

) + S(A

) + ··· + S(A

), th

ıt nhâ

t c

o hai bê

˘at

trong sô

ac bê

˘at trên c

o m

ôt

diê

m trong chung.

ung nhu

nguyên l

dâ

u tiên, ch

ung ta c

ung c

o thê

thâ

diê

ay l

a hiê

n nhiên v

a ch

ng minh

c. Th

ât v

ây, Gi

a s

không c

ap n

ao trong nh

ng m

a cho c

diê

m trong chung. Khi

o theo

ang

inh 11. ta c

o S(A

∪A

∪. . . ∪ A

) = S(A

) + S(A

) + ···+

S(A

). M

at kh

ac A

⊂ A(i = 1, 2, . . . , n) suy ra A

∪A

∪. . . ∪ A

⊂

A, t

o c

o S(A

∪ A

∪. . . ∪ A

) ⊂ S(A). Thô

ng nhâ

t c

ac bâ

ang

c l

ai ch

ung ta c

o S(A) < S(A), d

ân t

i vô l

o thê

thâ

y r

ang nguyên l

y trên bao tr

um nguyên l

y Ðirichlê

cho nh

ng t

âp h

u h

an. Ngo

ai ra nguyên l

y Ðirichlê trên c

o thê

thê

oa cho nh

ng l

p bê

at thông d

ung trong chu

ng tr

ınh phô

thông v

a c

ac kh

ai ni

êm

ô d

ai, thê

ıch c

ung c

o c

ung t

ınh châ

t nhu

ai ni

êm di

ên t

ıch

trên. Do

o ch

ung ta c

o thê

at biê

u nguyên

y Ðirichlê theo c

ac phu

an kh

ac nhau.

12.Cho nh

an th

˘ang ∆

, ∆

, . . . , ∆

˘am trong

an ∆ v

tô

ô d

ai c

ua ∆

, ∆

, . . . , ∆

n ho

ô d

ai c

ua ∆. Khi

ıt nhâ

t c

hai trong sô

an th

˘ang ∆

, ∆

, . . . , ∆

diê

m chung.

13. Cho nh

da di

ên P

, P

, . . . , P

˘am trong

da di

ên P v

a tô

thê

ıch c

ua P

, P

, . . . , P

n ho

n thê

ıch c

ua P. Khi

ıt nhâ

t c

o hai

trong sô

da di

ên P

, P

, . . . P

diê

m chung.

14. Cho nh

ng cung c

, c

, . . . , c

˘am trên

ng tr

on c v

a tô

ô d

ai c

ua c

, c

, . . . , c

n ho

ô d

ng tr

on c. Khi

ıt nhâ

t c

hai trong sô

ng cung c

, c

, . . . c

diê

m chung.

10.2. V

ı d

u 105

Tâ

t c

a c

ac ph

at biê

u 12, 13, 14 ch

ung ta

dê

u g

oi l

a nguyên l

Ðirichlê v

a b

oc c

o thê

ng minh

c c

ac nguyên l

y n

ay.

10.2. V

ı d

. 10.1. Cho M l

a m

ôt

da gi

ac lô

i v

i di

ên t

ıch S v

a chu vi P. Ch

minh r

˘ang

a) M c

o thê

c m

ôt h

ınh tr

on v

i b

an k

ınh l

n ho

;

b) B

an k

ınh c

ua c

ac h

ınh tr

on n

˘am trong M không qu

i gi

ai. a) Ch

ung ta d

ng trên m

ôi c

anh

da gi

ac M m

ôt h

ınh ch

ât chiê

u cao h =

, nhu

ınh 10.1.

h =

ınh 10.1:

ınh 10.2:

ng h

ınh ch

ât n

ay c

o nh

diê

m chung gi

a ch

ung; n

chung m

ôt sô

ınh ch

ât không n

am tr

on trong M. Ch

ung ta c

thê

ınh to

an tô

ng di

ên t

ıch c

ua c

ac h

ınh ch

ât n

ay l

a S. Nhu

ây

phâ

n c

ua M b

i c

ac h

ınh ch

ât ph

u ph

ai c

o di

ên t

ıch nh

o ho

n S.

Ðiê

u n

ay ch

ı ra r

ang tô

n t

ai m

ôt

diê

m O c

ua M không thu

ôc

106 Chu

ng 10. Nguyên l

y Ðirichlê cho di

ên t

ıch

ınh ch

ât n

ao c

a. Nhu

ây c

o ngh

ıa l

a kho

ang c

ach t

dê

ac c

anh c

ua M ph

ai l

n ho

n h =

. Ta lâ

y O l

a tâm h

ınh tr

on b

ınh R >

, h

ınh tr

on n

ay s

e n

am tr

on trong M.

b) Cho h

ınh tr

on C tâm O b

an k

ınh R n

am trong M. Ch

ung ta x

ac tam gi

ac m

a hai

ınh c

ua n

o l

a hai

ınh liên tiê

p c

ua t

ac, c

ınh th

ba l

a tâm h

ınh tr

on O. Ðu

ng cao h

a t

O xuô

ng c

ac c

anh

ua tam gi

ac n

ay l

n ho

n R. T

dây suy ra tô

ng c

ac di

ên t

ıch c

ung b

ang S v

a không nh

o ho

n P.R. Suy ra R ≤

ınh 10.2).

. 10.2. Trong không gian cho 30 vecto

ac không. Ch

ng minh r

˘ang

trong sô

o c

o hai vecto

a g

oc gi

a ch

ung nh

o ho

n 45

i gi

ai. C

o thê

a thiê

t r

ang tâ

t c

ınh 10.3:

ecto

o chung

diê

dâ

u O. Lâ

y OA

ôd

ai b

ang 1 trên vecto

nhâ

ung ta d

ng h

ınh n

ınh O v

uc OA, m

a g

ınh l

a 45

. B

an s

c ch

ng minh nê

u ch

ung

ta ch

ı ra r

ang

ıt nhâ

t hai trong sô

ınh n

on (

c xây du

ng theo c

ach

trên

ng v

i 30 vecto

a cho) c

diê

trong chung (h

ınh 10.3).

ung ta x

et h

ınh câ

u S v

i tâm

O v

a b

an k

ınh 1. M

ôi lâ

n d

ng h

ınh n

on c

at m

at câ

u S m

ôt h

ınh

i di

ên t

ıch δ

a c

o thê

ınh to

c. Ta c

ung thâ

y r

ang

hai h

ınh n

on c

diê

m trong chung khi v

a chi khi nh

ng phâ

trên m

at câ

u c

ung ph

ai c

diê

m trong chung. T

diê

u n

ay v

10.2. V

ı d

u 107

nguyên l

y Ðirichlê ch

ung ta ch

ı câ

n thiê

t kiê

m tra tô

ng di

ên t

ıch

ua 30 h

ınh trên m

at câ

u l

n ho

n di

ên t

ıch m

at câ

u (b

ang 4π).

ung ta c

o δ

= 2π



1 −cos



= 2π

1 −

2 +

√

. V

ây

30.2π

1 −

2 +

√

> 4π tu

ng v

2 +

√

ac l



167

225



. 10.3. Nê

u m

ôt bê

˘at A trong m

˘at ph

˘ang th

oa m

diê

u ki

ên

S(A) > 1. th

ı n

o luôn luôn ch

ıt nhâ

t hai

diê

m trong (x

, y

) m

a hi

êu x

− x

a y

−y

a nh

ng sô

nguyên.

i gi

ai. Qua m

ôi

diê

m (m, n) v

2 3

−1

−2−3

ınh 10.4:

ô nguyên ch

ung ta k

e c

ng th

ang

ng v

ng th

ang

ngang (h

ınh 10.4).

ung ta s

e t

c lu

diê

m v

i t

oa d

ô nguyên.

i nguyên chia m

at ph

ang ra c

ınh vuông b

ang nhau, m

ôi h

ınh

vuông c

o di

ên t

ıch l

a 1. Ch

y r

ang

ôi h

ınh vuông c

o thê

xê d

ich

dê

ung v

i m

ôt h

ınh vuông kh

ac, ch

ı c

o kh

ac l

a t

ô c

ua h

ınh vuông

i chuyê

dê

n c

ung l

a c

ac sô

nguyên.

ung ta ch

on m

ôt h

ınh vuông trong lu

i nguyên l

am gô

c cô

inh rô

i d

ich chuyê

n m

oi h

ınh vuông vê

ınh vuông gô

c. Nhu

ây

ng phâ

n c

ua A n

am trong c

ac h

ınh vuông kh

ac nhau

dê

u chuyê

vê

ınh vuông gô

c (h

ınh v

e). Tô

ng c

ua di

ên t

ıch c

ua c

ac phâ

108 Chu

ng 10. Nguyên l

y Ðirichlê cho di

ên t

ıch

ang di

ên t

ıch c

ua A v

a suy ra l

n ho

n 1. Suy ra

ıt nhâ

t hai trong

sô

ac phâ

n n

am trong h

ınh vuông d

ich

dê

n s

e c

diê

m trong chung

, y

). Trong t

âp A ban

dâ

u th

diê

m (x

, y

) tu

ng v

i hai

diê

m kh

ac nhau (x

, y

) v

a (x

, y

) m

a x

−x

, y

−y

, x

−x

, y

−

a c

ac sô

nguyên. Nhu

ây th

ı x

−x

a y

−y

ung l

a sô

nguyên.

. 10.4. Cho A l

a t

âp h

p lô

i v

a b

i ch

˘an nh

diê

m trong m

˘at

˘ang, c

on P

, P

a nh

diê

m thu

ôc A. G

oi A

a t

âp

p nh

ân t

A sau m

ôt ph

ep t

inh tiê

n c

diê

m theo vecto

(i =

1, 2, 3, 4, 5). Ch

ng minh r

˘ang

ıt nhâ

t c

o hai t

âp h

p trong sô

(i = 1, 2, 3, 4, 5) c

diê

m chung.

i gi

ai. Ch

ung ta chia ra hai

Q Q

ınh 10.5:

tru

ng h

p A c

o thê

o ho

o thê

không c

diê

m trong.

1. Tru

ng h

p A c

diê

trong. K

y hi

êu A

a t

âp h

a n

o nh

ân

c t

A, sau

khi t

ông ph

ep v

i t

tâm

a h

ê sô

i t

2. Khi

công th

c sau

ung A

⊂ A

ınh 10.5).

ât v

ây, nê

u Q ∈ A v

a Q

anh c

ua Q qua ph

ep t

inh tiê

n theo

vecto

−−→

(xem h

ınh v

e), th

ı P

Q l

a h

ınh b

ınh h

anh. K

y hi

êu

a trung

diê

m c

ua P

. R

o r

ang Q

∈ A, v

ı Q v

a P

a phâ

n t

ua A v

a A lô

i. M

at kh

ac P

= 2P

a v

ı A

anh c

ua A qua

ep v

i t

tâm P

a h

ê sô

2, nên

diê

m Q

am trong t

âp h

p A

Nhu

ây m

ôi tâp trong c

ac t

âp A

am trong A

. Ðô

ng th

i m

ôi t

âp

10.2. V

ı d

u 109

ua A

dô

ng d

ang v

i A v

a suy ra S(A

) = S(A). Do

S(A

) + S(A

) = 5S(A). (10.1)

Nhu

ng t

âp h

p A

dô

ng d

ang v

i A v

i h

ê sô

2. Suy ra

S(A

) = 4S(A). (10.2)

at kh

ac A c

diê

m trong, v

ı thê

S(A) > 0. Ngh

ıa l

a t

(10.1) v

(10.2) suy ra S(A

) + S (A

) > S(A

Nhu

ây trong tru

ng h

p 1 b

ai to

c suy ra t

nguyên l

Ðirichlê cho di

ên t

ıch.

2. Tru

ng h

p A không c

diê

m trong, A s

e n

am trên m

ôt

ang. Th

ât v

ây, nê

ıt nhâ

t ba

diê

m n

am trên m

ôt

ng th

ang, do

ınh châ

t lô

i A ch

a to

an b

ô h

ınh tam gi

ac v

ınh l

a c

diê

ay, suy ra A c

diê

m trong. Nhu

ng t

âp lô

i, b

i ch

an trên m

ôt

ang ch

ınh l

an th

ang trên du

ng th

ang n

ay. Phâ

n c

on l

ai l

ân tu

ng t

nhu

phâ

n trên. Nhu

ng trong tru

ng h

p trên

ang ch

ı câ

n 3

diê

m v

a nguyên l

y Ðirichlê vê

ô d

ai.

. 10.5. (Ð

inh l

y Minkovski) Cho A l

a t

âp h

diê

m trong m

˘at ph

˘ang

o t

ınh châ

t lô

i, b

i ch

˘an v

dô

i x

ng qua gô

c t

ô v

a S(A) > 4. Khi

o A ch

a nh

diê

m trong kh

diê

m gô

c v

i t

ô nguyên.

i gi

ai. T

ac d

ung lên A ph

ep v

i t

tâm l

a gô

c t

ô v

a h

ê sô

Nhu

ây ch

ung ta nh

ân

c A

dô

ng d

ang v

i A v

a c

o k

ıch thu

ang n

a k

ıch thu

c c

ua A. Suy ra S(A

) =

S(A) > 1. Theo b

10.13 suy ra A

ıt nhâ

t hai

diê

m kh

ac nhau (x

, y

) v

a (x

, y

a c

ac hi

êu x

−x

a y

−y

a nguyên. V

ı t

âp h

p A

dô

i x

ng qua

gô

c t

ô nên t

âp h

p A

ung v

ây. Ðiê

o gi

ai th

ıch r

ang

diê

( −x

, −y

) thu

ôc A

. V

ı A lô

i nên A

ung lô

i. Do

o trung

diê

110 Chu

ng 10. Nguyên l

y Ðirichlê cho di

ên t

ıch

ua c

diê

m m

ut (−x

, −y

) v

a (x

, y

) c

ung thu

ôc A

a c

o t

(

− x

−y

). Nhân t

ô n

ay v

i 2 th

c t

ô c

ua m

ôt

diê

m thu

ôc A. Nhu

ây (x

−x

, y

−y

) thu

ôc A. Ðiê

m ta t

ım

ac gô

c t

ô v

a c

o t

ô nguyên v

a l

diê

m trong c

ua t

âp A.

. 10.6. Nê

u A l

a m

ôt bê

˘at,

, A

, . . . , A

. (10.3)

a nh

ng bê

˘at v

a th

oa m

an A

⊂ A(i = 1, 2, . . . , n), c

on k l

a sô

nhiên m

k.S(A) < S (A

) + S(A

) + ··· + S(A

). (10.4)

ıt nhâ

t k + 1 trong sô

ng bê

˘at trên c

o m

ôt

diê

m trong chung.

i gi

ai. Ch

ung ta ch

ng minh b

ang qui n

ap,Tru

ng h

p k = 1

a nguyên L

y Ðirichlê

a ch

ng minh

trên. Bây gi

a s

ai to

ung cho k, ch

ung ta ph

ai ch

ng minh n

o c

ung

ung cho k + 1.

Ta cô

inh m

ôt k v

a c

o bâ

ang th

( k + 1)S(A) < S(A

) + S(A

) + ··· + S(A

). (10.5)

ung ta s

e ch

ı ra r

ang v

i (10.5) tô

n t

ai m

ôt

diê

m l

diê

m trong c

k + 2 t

âp h

p c

ua (10.3). Do A

⊂ A(µ = 1, 2, . . . , n), nên S(A

) ≤

S(A), t

o suy ra S(A

) + S(A

) + ··· + S(A

) ≤ nS(A). T

bâ

ang th

c sau c

ung v

a (10.5) ch

ung ta c

o (k + 1)S(A) < nS(A) suy

ra k + 1 < n. V

ı v

ây

n ≥ k + 2. (10.6)

Tô

n t

diê

m chung cho

ıt nhâ

t k + 2 t

âp h

p (10.3)

c ch

minh b

ang qui n

ap theo n. T

(10.4) suy ra (10.5), v

ây ta ph

ai b

dâ

u t

k + 2. Nhu

ây viê

t l

( k + 1)S(A) < S(A

) + S(A

) + ··· + S(A

k+2

). (10.7)

10.2. V

ı d

u 111

Câ

n ph

ai ch

ng minh tô

n t

diê

m m

a n

o l

diê

m trong c

ua A

, A

. . . , A

k+2

. Lâ

= A

k+2

( µ = 1, 2, . . . , k + 1) (10.8)

= A

∩ A

k+2

( µ = 1, 2, . . . , k + 1) (10.9)

= A\A

k+2

(10.10)

= A

k+2

. (10.11)

o r

ang A

⊂ A

a A

⊂ A

( µ = 1, 2, . . . , k + 1) . V

ı c

o tâ

t c

a k + 1

âp h

p A

, t

bao h

am th

c trên suy ra

( k + 1)S(A

) ≥ S(A

) + S(A

) + ··· + S(A

k+1

). (10.12)

Nê

u lâ

y (10.7) tr

di (10.12) ch

ung ta nh

ân

( k + 1)S(A

) < S(A

k+2

) + S(A

) + ··· + S(A

k+1

(10.13)

ı S(A) − S(A

) = S(A

) v

a S(A

) − S(A

) = S(A

) do (10.8)-

(10.11) nên t

(10.13),(10.9) v

a (10.11) suy ra

kS(A

k+2

) < S(A

∩ A

k+2

) + S(A

∩ A

k+2

) + ··· + S(A

k+1

∩ A

k+2

(10.14)

(10.14) v

a gi

a thiê

ung cho k theo qui n

ap suy ra A

∩

k+2

, A

∩ A

k+2

, . . . , A

k+1

∩ A

k+2

diê

m trong chung,

diê

u n

o ngh

ıa l

a t

âp h

p A

, A

, . . . , A

k+2

diê

m trong chung. Nhu

ây

i n = k + 2 t

(10.5) suy ra

ıt nhâ

t k + 2 t

âp h

p t

(10.3) c

diê

m trong chung.

Bây gi

ung ta gi

a thiê

t v

i m

ôt n ≥ k + 2 t

(10.5) suy ra

ıt nhâ

t k + 2 t

âp h

p t

(10.3) c

diê

m trong chung v

a s

e ph

ai kê

ân r

ang t

( k + 1)S(A) < S(A

) + S(A

) + ··· + S(A

) + S(A

n+1

). (10.15)

112 Chu

ng 10. Nguyên l

y Ðirichlê cho di

ên t

ıch

suy ra c

ıt nhâ

t k + 2 t

âp h

p trong d

ây A

, A

, . . . , A

n+1

diê

trong chung. Th

ât v

ây, ch

ung ta

= A

n+1

, (µ = 1, 2, . . . , n). (10.16)

= A

∩ A

n+1

, (µ = 1, 2, . . . , n) (10.17)

= A\A

n+1

(10.18)

= A

n+1

. (10.19)

ı A

∪ A

= A

, A

∩ A

= ∅(µ = 1, 2, . . . , n) v

a A

∪ A

A, A

∩ A

= ∅ nên

S(A

) + S(A

) = S(A

), (µ = 1, 2, . . . , n) (10.20)

S(A

) + S(A

) = S(A). (10.21)

ung ta s

e ch

ng minh m

ôt trong c

ac bâ

ang th

c sau l

ung

( k + 1)S(A

) < S(A

) + S(A

) + ··· + S(A

) (10.22)

ac l

kS(A

) < S(A

) + S(A

) + ··· + S(A

). (10.23)

ât v

ây, trong tru

ng h

p ngu

c l

ai ch

ung ta s

e c

o (k + 1)S(A

) ≥

S(A

) + S(A

) + ··· + S(A

) v

a kS(A

) ≥ S(A

) + S(A

) + ··· +

S(A

) C

ông hai vê

ai v

a do (10.20), (10.21) ch

ung ta nh

ân

S(A

) + kS(A) ≥ S(A

) + S(A

) + ··· + S(A

). (10.24)

ông hai vê

(10.24) v

i S(A

) v

a t

(10.19), (10.21) ch

ung ta nh

ân

( k + 1)S(A) ≥ S(A

) + S(A

) + ··· + S(A

)

Nhu

diê

u n

ay tr

ai v

i (10.15). Do

o trong hai bâ

ang th

(10.22) v

a (10.23) ph

ai c

ıt nhâ

t m

ôt c

ung.

10.2. V

ı d

u 113

a s

(10.22)

ung. Theo gi

a thiê

t qui n

dô

i v

i n t

(10.22)

suy ra

ıt nhâ

t k + 2 t

âp h

p trong d

ây A

, A

, . . . , A

diê

m trong

chung. T

(10.16) suy ra r

ang kê

t lu

ân trên c

ung

ung cho d

ây

(10.3).

a s

(10.23)

ung. T

a thiê

t qui n

dô

i v

i k suy ra k + 1

âp h

p trong A

, A

, . . . , A

diê

m chung v

a c

ung v

i (10.17) ch

ra r

ang tô

n t

ai m

ôt

diê

m m

a n

o l

diê

m trong c

ua k + 1 t

âp h

p t

(10.3) v

a c

ua A

n+1

Nhu

ây t

(10.15) suy ra k + 2 t

âp h

p trong d

ay A

, A

. . . , A

n+1

diê

m trong chung. Suy ra kê

t lu

ân

ung v

i n + 1. T

phu

ng ph

ap qui n

ap bây gi

ai suy ra, v

i m

oi n, v

i (10.5) tô

ai m

ôt

diê

m m

a n

o l

diê

m trong c

ıt nhâ

t k + 2 t

âp h

p trong

(10.3).

y. Trong ch

ng minh

inh l

y d

ung phu

ng ph

ap qui n

theo k. Nhu

di t

c k sang k + 1 ta l

ai d

ung phu

ng ph

ap qui

ap theo n. V

i ch

ng minh qui n

ap theo n t

c n sang n + 1 ta

ai d

ung bu

c k tru

o v

a n.

. 10.7. Trong m

ôt h

ınh vuông c

o c

anh l

1 ch

a m

ôt sô

ng tr

on, Tô

ô d

ai c

ung l

a 10. Ch

ng minh r

˘ang tô

n t

ai m

ôt

ng th

˘ang, m

a n

o c

˘at

ıt nhâ

t 4 trong nh

ng tr

on n

ay.

i gi

ai. (H

ınh 10.6) Ch

ung ta ch

on m

ôt

anh h

ınh vuông rô

i chiê

u vuông g

oc c

ınh 10.6:

ng tr

on xuô

ng c

anh

114 Chu

ng 10. Nguyên l

y Ðirichlê cho di

ên t

ıch

ê thâ

y r

ang h

ınh chiê

u c

ua m

ôt

ng tr

on b

an k

ınh R l

a m

ôt

an th

ang c

ô d

ai 2R. V

ı v

ây trên c

anh h

ınh vuông

a ch

on s

o nh

an th

ang chiê

u xuô

ng v

i tô

ôd

ai l

Nhu

> 3 = 3.1, theo nguyên l

y Ðirichlê suy ra c

o m

ôt

diê

m M n

o thu

ôc AB l

diê

m trong chung c

ua 4

an th

ang

chiê

u xuô

ng. Khi

ng th

ang

di qua

diê

m M vuông g

oc v

i AB

e c

at 4

ng tr

on.

. 10.8. M

ôt sô

cung n

˘am trên

ng tr

on v

i b

an k

ınh 1

c so

xanh. Tô

ô d

ai c

ua c

ac cung mâ

u xanh l

n ho

n π. Ch

ng minh

˘ang v

i m

ôi

ng k

ınh d c

ng tr

on tô

n t

ai dây cung song song

i d, m

a hai

dâ

u c

ua dây cung

c so

n xanh.

i gi

ai. (H

ınh 10.7) Không mâ

ınh 10.7:

ınh tô

ng qu

at ch

ung ta gi

a thiê

ac cung bôi so

n không c

diê

chung. Cho d l

ng k

ınh bâ

t k

ng tr

on k v

a c l

a m

ôt trong

ac cung

c bôi mâ

u. Trên

on k ta t

ao ra cung c

ang c

ach

lâ

dô

i x

ng c qua

ng k

ınh d

vuông g

oc v

i d.

ê thâ

y cung c

cho c

ung

ô d

i cung c. Ta l

am nhu

ây v

i m

oi cung c

on l

ai th

ı trên k nh

ân

ôt h

ê cung c

o tô

ô d

ai l

n ho

n 2π. Nhu

ô d

ai c

ua k l

a 2π,

nhu

ây theo nguyên l

y Ðirichlê c

ıt nhâ

t hai cung trong h

ê n

ay c

diê

m chung.

10.2. V

ı d

u 115

Nhu

ng ch

ung ta

a gi

a thiê

trên nh

ng cung d

ang c t

dôi

không c

diê

m chung,

diê

o c

ung

ung cho c

ac cung c

. Khi

tô

n t

ai m

ôt cung bôi so

n c

diê

m chung A v

i cung c

dô

i x

i cung c

qua d

. R

o r

ang dây cung

di qua A v

a song song v

i d c

ınh châ

t mong muô

n v

ı m

ôt

dâ

, c

dâ

u kia

. 10.9. Trong h

ınh tr

on b

an k

ınh 1 ngu

i ta tô so

n m

ôt sô

dây cung.

ng minh r

˘ang nê

u m

ng k

ınh c

˘at nhiê

u nhâ

t k dây cung, th

tô

ô d

ai c

ua tâ

t c

a c

ac dây cung

a tô so

n nh

o ho

n πk.

i gi

ai. Lâ

y c l

a m

ôt dây cung bâ

t k

y trong h

ınh tr

on C

a cho v

a γ

a cung nh

o trong hai cung do c t

ao ra. K

y hi

êu γ

a cung

dô

i x

i γ qua tâm c

ua h

ınh tr

on. R

o r

ang m

ôt

ng k

ınh c

ua C c

at dây

cung c khi v

a ch

ı khi c

o hai

dâ

u m

ut n

am trong γ v

a γ

a s

ang tô

ô d

ai nh

ng dây cung

a k

e l

n ho

ang πk. Khi

o tô

ô d

ai tâ

t c

a c

ac cung d

ang γ l

n ho

n πk.

ung

ung nhu

ây cho tô

ô d

ai c

ac cung d

ang γ

. Suy ra tô

ô d

ai c

ua c

ac cung d

ang γ

ac γ l

a l

n ho

n 2πk. V

ô d

ai c

ng tr

on C l

a 2π, t

nguyên l

y Ðirichlê m

ông suy ra tô

n t

ıt

nhâ

t m

ôt

diê

m thu

ôc C, m

a n

o n

am trên

ıt nhâ

t k + 1 cung c

o d

ang

γ ho

ac γ

. Nê

u t

diê

m chung n

ay ta k

ng k

ınh c

ua C,th

ı n

o c

ıt nhâ

t k + 1 dây cung

a cho,

diê

u n

ay tr

ai v

diê

u ki

ên trong

dâ

ai. V

ây

diê

u kh

ang

inh c

ua b

ai to

an l

ung.

. 10.10. M

ôt t

âp h

p M l

a h

p c

ua m

ôt sô

an th

˘ang n

˘am trong

kho

ang [0, 1]. Biê

t r

˘ang kho

ang c

ach gi

a hai

diê

m bâ

t k

y c

ua M

không b

˘ang 0,1. Ch

ng minh r

˘ang tô

ô d

ai c

ua nh

an t

nên M không vu

t qu

a) 0, 55;

b) 0, 5.

116 Chu

ng 10. Nguyên l

y Ðirichlê cho di

ên t

ıch

i gi

ai. a) Ch

ng minh b

ang ph

an ch

ng. Gi

a s

tô

ng S c

ai nh

an th

ang t

ao nên M l

n ho

n 0,55. Ch

ung ta x

et t

âp N

ân

c t

M b

ang c

ach c

ông m

ôi

an th

ang c

ua M v

i 0,1. T

diê

u ki

ên c

ua b

ai to

an suy ra M v

a N không c

diê

m chung. Ngo

ra tô

ô d

ai c

ua N b

ang S nên l

n ho

n 0,55. D

ê thâ

y hai t

âp h

M v

a N n

am trong

an [0;1,1]. V

ı 2.S > 2.0, 55 = 1, 1, t

nguyên

y Ðirichlê suy ra M v

a N c

diê

m chung,

diê

u n

ay d

ân t

i vô l

b) Gi

a s

ô d

ai c

ua tâ

t c

a c

an trong M l

n ho

n 0,5. Ch

ung

ta chia

an [0,1] th

anh 10 phâ









, . . . ,



, 1



. K

êu M

a phâ

n c

ua M n

am trong



i + 1



, i = 0, 1, . . . , 9

a S

a tô

ô d

ai c

an th

ang tao ra M

. B

ang c

ach t

inh

tiê

n th

ıch h

p ch

ung ta chuyê

n m





, . . . ,



, 1







. K

y hi

êu M

anh c

ua M

i i = 2, 3, 4 . . . , 9. V

S = S

+ S

+ ··· + S

> 0, 5 = 5.0, 1, t

nguyên l

y Ðirichlê

ông suy ra c

ıt nhâ

t 6 t

âp h

p trong M

, M

, . . . , M

diê

chung. Ðiê

u n

ay c

o ngh

ıa l

a m

ôt sô

o trong





a kê

a c

ua 6

diê

m kh

ac nhau x

, x

, . . . , x

ua M tr

di tu

ng sô

ang

, . . . ,

dây k

a m

ôt sô

o trong

0, 1, 2, . . . , 9, i = 1, 2, . . . 6. D

ê d

ang thâ

y r

ang

ıt nhâ

t c

o hai trong c

sô

, k

, . . . , k

a liên tiê

p (

ap d

ung nguyên l

y Ðirichlê). V

ı d

u nhu

= k

+ 1. V

ı x

−

= x

−

, nên x

− x

= (k

− k

) =

diê

u n

ân

dê

n vô l

10.3. B

ai t

âp 117

10.3. B

ai t

âp

. 10.11. Cho n l

a m

ôt sô

nhiên bâ

t k

y, c

on A l

a m

ôt bê

trong m

at ph

ang, m

a s(A) > n. Khi

o tô

n t

ai n + 1

diê

m trong

ac nhau (x

, y

) (i = 1, 2, . . . , n + 1) c

ua A, m

a hi

êu x

− x

−y

(i, j = 1, 2, . . . , n + 1) l

a nh

ng sô

nguyên.

. 10.12. Nê

u v

i m

ôt bê

at A trong m

at ph

ang v

a m

ôt sô

nguyên

ng k th

oa m

an S(A) < k, th

ı tô

n t

ai m

ôt ph

ep t

inh tiê

n sao cho

anh c

ua A qua ph

ep t

inh tiê

n n

ay ch

a nhiê

u nhâ

t k − 1

diê

m v

ô nguyên.

. 10.13. Cho A l

a t

âp h

p lô

dô

i x

ng qua gô

c t

ô trong m

ang, n l

a sô

nhiên v

a S(A) > 4n. Khi

o A ch

ıt nhâ

t 2n + 1

diê

m trong kh

ac nhau v

i t

ô nguyên.

. 10.14. Nê

u A l

a t

âp h

p lô

i, b

i ch

an,

dô

i x

ng qua gô

c t

ô v

o di

ên t

ıch b

ang 615, th

ı A ch

ıt nhâ

t 307

diê

m m

a kho

ang c

ach

a m

oi c

ap trong ch

ung l

n ho

ac b

ang 1.

. 10.15. Cho F l

a t

âp h

p lô

i, b

i ch

an nh

diê

m c

ua m

at ph

ang.

ung ta g

ô h

u hi

êu c

ua t

âp h

p F l

a kho

ang c

ach nh

o nhâ

a hai

ng th

ang song song

hai ph

ıa c

ua t

âp h

p F. Ch

minh r

ang nê

u trong m

ôt t

âp h

p lô

i, b

i ch

an v

ô h

u hi

êu d c

a m

ôt sô

âp h

p con m

a tô

ô h

u hi

êu c

ua ch

ung l

n ho

kd, th

ı tô

n t

ng th

ang, m

a n

o c

ıt nhâ

t k + 1 t

âp h

p con n

trên.

118 Chu

ng 10. Nguyên l

y Ðirichlê cho di

ên t

ıch

CHU

NG 11

AN H

OC TÔ

11.1. V

ı d

. 11.1. (Ðê

thi To

an Olympic Quô

c tê

,1972) Cho t

âp h

p gô

m 10 sô

o hai ch

sô

. Ch

ng minh r

˘ang t

âp h

o c

ıt nhâ

t hai t

âp h

p con

không giao nhau, m

a tô

ng nh

ng phâ

n t

trong ch

ung b

˘ang nhau.

i gi

ai. Nê

u c

o hai t

âp h

p con giao nhau m

a tô

ng trong ch

ung

ang nhau th

ı ch

ung ta c

o thê

o nh

ng phâ

n t

chung

di. Khi

on l

ai hai t

âp không giao nhau v

a tô

ng c

ac phâ

n t

ua ch

ung v

ân

ang nhau.

ung ta t

ınh c

o bao nhiêu t

âp h

p con không r

ông c

ua m

ôt t

âp

p c

o mu

i phâ

n t

. Sô

ng nh

ng t

âp h

p con ch

ı ch

a 1 phâ

o 10 ho

ac l

a C

. Sô

ng nh

ng t

âp h

p con ch

a 2 phâ

n t

a C

. Sô

ng nh

ng t

âp h

p con ch

a 3 phâ

n t

a C

,. . . Suy ra

tô

ng sô

ng c

ac t

âp h

p con l

+ C

+ ··· + C

= (1 + 1)

= 1023

Ðiê

u ki

ên b

ai ra l

a 10 sô

a cho không l

n ho

n 99. V

ây tô

ng c

ac sô

trong m

ôi t

âp h

p con không vu

t qu

a 99.10 = 990, nhu

ây

sô

ng nh

ng tô

ng kh

ac nhau nhiê

u nhâ

t l

a 990. Theo nguyên l

Ðirichlê trong sô

1023 t

âp h

p con c

ua t

âp h

p gô

m 10 sô

e c

ıt

nhâ

t hai t

âp m

a tô

ng c

ac phâ

n t

trong ch

ung ph

ai b

ang nhau.

120 Chu

ng 11. To

an h

oc tô

. 11.2. Cho 15 b

ai to

an tr

˘ac nghi

êm,

anh sô

dê

n 15, m

ôi b

ı c

o hai kh

a n˘ang tr

a l

i :

ung ho

˘ac sai. C

o 1600 th

ı sinh tham gia

thi, nhu

ng không c

o ai tr

a l

ung 2 b

ai liê

n nhau. Ch

ng minh r

˘ang

ıt nhâ

t hai th

ı sinh tr

a l

i to

an b

ô 15 b

ai h

êt nhu

nhau.

i gi

ai. B

ai l

am c

ua m

ôi th

ı sinh tu

ng v

i m

ôt d

ay 15 phâ

n t

ôi phâ

n t

ac l

a Ð (

ung) ho

ac l

a S (sai). Theo gi

a thiê

t không

o d

ay n

ao c

o 2 phâ

n t

kê

nhau l

a Ð, Ð, nên sô

tô

da c

ac phâ

n t

SS trong d

ay l

a 8.

Ta nh

ân thâ

y v

i m

ôi 0 ≤ k ≤ 8 th

ı sô

ac d

ay c

ung k phâ

Ð l

a C

15−k+1

= C

16−k

i v

ı m

ôi m

ôt d

ay nhu

thê

i c

ach

at k tâ

m b

ıa gi

a 15 − k quyê

n s

ach: c

o tâ

t c

a 16 − k v

i tr

dê

at b

ıa, kê

a hai

dâ

u c

ua chô

ng s

ach

o).

ây l

a sô

ac d

ay c

o t

ınh châ

t nêu trên l

∑

k=0

16−k

= 1 + 15 + 91 + 286 + 495 + 462 + 210 + 36 + 1

= 1597 < 1600

Ðiê

u n

ay ch

ng t

o r

ang ph

ai c

ıt nhâ

t 2 th

ı sinh c

o c

ac câu tr

a l

êt nhu

nhau.

. 11.3. Trong m

ôt h

ınh 9 c

anh

dê

u c

o m

ôt

ınh

c tô mâ

u tr

˘ang

on c

ınh kh

c tô

den. Ch

ng minh r

˘ang tô

n t

ai hai tam gi

phân bi

êt to

˘ang (di

ên t

ıch b

˘ang nhau) m

a c

ınh c

ua m

ôi tam

c tô c

ung m

ôt mâ

i gi

ai. T

ınh

c tô mâ

u th

ıt nhâ

t c

ung c

o 5

ınh

c tô

ung m

ôt mâ

u. Gi

a s

o l

a mâ

u tr

ang. N

am mâ

u tr

ang t

ao th

anh

5.4.3

2.3

= 10 tam gi

ac phân bi

êt c

ung m

ôt mâ

u tr

ang. Ðê

y r

ang

11.1. V

ı d

u 121

ep quay m

ôt g

2kπ

( k = 0, 1, . . . , 8) xung quanh tâm O c

ınh 9 c

anh

dê

u không

anh hu

dê

n t

âp M c

ınh c

ua h

ınh 9

anh n

ay. V

ı thê

sau khi quay m

ôi tam gi

ac trong 10 tam gi

ac trên

ôt g

2kπ

(0 ≤ k ≤ 8 ) xung quanh O ta

c 10.9 = 90 tam gi

ınh trong t

âp h

p M. Tâ

t c

a ch

ung không thê

phân bi

êt v

ı sô

tam gi

ac kh

ac nhau c

ınh trong t

âp h

p M b

ang C

2.8.7

2.3

78 < 90.

Nhu

ây ta t

ım

c hai tam gi

ac tr

ang ∆

a ∆

sau m

ôt v

ep quay tr

ung v

i c

ung m

ôt tam gi

ac ∆. Lu

y l

a hai tam gi

ac ∆

a ∆

a phân bi

êt. Th

ât thê

, hai tam gi

ac nhu

nhau không thê

c sau khi quay t

ôt tam gi

ac.

ı m

ôi tam gi

ac ∆

a ∆

e tr

ung v

i tam gi

ac ∆ sau khi quay,

nên t

tam gi

ac ∆

ang m

ôt ph

ep quay ta c

o thê

ân

c tam

ac ∆

(ch

ang h

an c

ac ph

ep quay ∆

→ ∆, ∆ → ∆

). V

ây ∆

a ∆

a hai tam gi

ac ph

ai t

ım.

. 11.4. Trên m

˘at ph

˘ang c

o n h

ınh. Gi

a s

... i

, l

a di

ên t

ıch phâ

giao c

ua c

ac h

ınh th

, . . . , i

, c

on S l

a di

ên t

ıch phâ

n m

˘at ph

˘ang b

u b

i c

ac h

ınh

o. K

y hi

êu M

a tô

ng tâ

t c

a c

ac S

... i

, t

c l

a tô

ên t

ıch c

ua tâ

t c

a c

ac h

ınh c

o thê

o l

a giao c

ua k h

ınh

a cho. Ch

minh r

˘ang

a) S = M

− M

+ M

−. . . − (−1)

n+1

b) S ≥ M

− M

+ M

−. . . − (−1)

n+1

i m ch

˘an v

S ≤ M

− M

+ M

−. . . − (−1)

n+1

i m l

i gi

ai. a) K

y hi

êu C

a sô

ach ch

on k phâ

n t

n phâ

n t

, ta

o nh

i th

c Niuto

n (x + y)

∑

k=0

n−k

. K

y hi

êu D

a di

ên

122 Chu

ng 11. To

an h

oc tô

ıch phâ

n m

at ph

ang b

i ph

u b

ung m h

ınh. Phâ

n m

at ph

ang

gô

m nh

ng m

anh, m

ôi m

anh b

i ph

u b

i m h

ınh x

inh n

Khi t

ınh M

ên t

ıch m

ôi m

anh nhu

ây, s

c t

ınh C

lâ

n, b

i v

m h

ınh c

o thê

c C

giao c

ua k h

ınh. Do

= C

+ C

k+1

+ ··· + C

Suy ra M

− M

+ M

− ··· + (−1)

n+1

= C

+ ( C

− C

··· + (C

−C

+ C

−···)D

= D

+ D

+ ··· + D

i v

ı do nh

i th

c Niuto

n C

−C

+ 3m −···−(−1)

= (−1 +

−C

+ C

−··· − (−1)

) + 1 = (1 − 1)

+ 1 = 1

Cuô

i c

ung ch

ung ta lu

y r

ang S = D

+ D

+ ··· + D

b) T

phâ

n a) ta c

S −(M

− M

+ ··· + (−1)

m+1

) =

= (−1)

m+2

m+1

+ ( −1)

m+3

m+2

+ ··· + (−1)

n+1

∑

i =1

((−1)

m+2

m+1

+ ··· + (−1)

n+1

(Ta qui u

c nê

u k > i th

ı C

= 0. Do

o ta ch

ı câ

n ph

ai ch

ng minh

ang:

m+1

−C

m+2

+ C

m+3

−. . . − (−1)

m+n+1

≥ 0 v

i i ≤ n.

ang th

c (x + y)

= (x + y)

i −1

(x + y) suy ra

ang th

= C

i −1

j−1

+ C

i −1

m+1

−C

m+2

+ C

m+3

−. . . − (−1)

m+n+1

= C

i −1

+ C

i −1

m+1

−C

i −1

m+2

+ C

i −1

m+3

−. . .

+(−1)

m+n+1

i −1

n−1

+ ( −1)

m+n+1

i −1

= C

i −1

±C

i −1

Cuô

i c

ung ch

ı câ

n lu

y r

ang C

i −1

= 0 v

i i ≤ n.

11.1. V

ı d

u 123

. 11.5. M

ôt c

ao di

ên t

ıch b

˘ang 1 c

o 5 miê

ng v

a, m

a di

ên t

ıch c

ôi miê

ng v

a không nh

o ho

n 0,5. Ch

ng minh r

˘ang luôn t

ım

c hai

miê

ng v

a c

o di

ên t

ıch phâ

n chung c

ua ch

ung không nh

o ho

n 0,2.

i gi

ai. Gi

a s

ên t

ıch c

ao b

ang M, di

ên t

ıch phâ

n giao c

ua c

miê

ng v

a th

, . . . , i

ang S

... i

, c

on M

∑

... i

. T

ai trên suy

ra M − M

+ M

− M

+ M

− M

≥ 0, b

i v

ı M ≥ S. C

ac bâ

ang

c tu

ng t

o thê

c viê

t không ch

ı cho c

a c

ao, m

a c

on cho

ng miê

ng v

a. Nê

u ta coi miê

ng v

a S

nhu

ôt c

ao v

i c

ac miê

a S

, S

ı ta

c S

−

∑

1ij

−

∑

1ijk

+ S

12345

≥

0. C

ông c

ac bâ

ang th

c nhu

ây cho tâ

t c

a 5 miê

ng v

a, ta

− 2M

+ 3M

− 4M

+ 5M

≥ 0 (h

ang t

... i

o trong c

bâ

ang th

c cho c

ac miê

ng v

a i

. . . i

, nên trong tô

ng tâ

t c

a c

bâ

ang th

c n

o c

o h

ê sô

k). C

ông c

ac bâ

ang th

c 3(M − M

− M

+ M

− M

) ≥ 0 v

a M

−2M

+ 3M

−4M

+ 5M

≥ 0,

c 3M − 2M

+ M

− M

+ 2M

≥ 0. C

ông v

o bâ

ang

c M

−2M

≥ 0, (

c suy ra t

12345

o trong tâ

t c

a c

ac S

c l

a M

≥ 5M

≥ 2M

), ta

c 3M − 2M

+ M

≥ 0, t

c l

≥ 2M

−3M ≥ 5 −3 = 2. B

i v

ı t

5 miê

ng v

a c

o thê

10 c

ap, nên di

ên t

ıch giao c

ua m

ôt trong sô

ac c

o không nh

≥ 0, 2.

. 11.6. (Ðê

thi To

an vô

ich CHLB Ð

c, 1979) Gi

a s

ôi

diê

m c

˘at ph

˘ang

c tô b

˘ang 1 trong n mâ

u (n l

a sô

nhiên cho tru

c).

ng minh r

˘ang tô

n t

ai m

ôt h

ınh ch

ât v

i c

ınh

c tô c

ung

ôt mâ

i gi

ai. Ta thiê

t l

âp trong m

at ph

ang m

ôt h

ê to

ô Ðê

ac vuông

oc tu

y v

a ch

y t

diê

m nguyên (i, j) v

i 1 ≤ i ≤ n + 1 v

124 Chu

ng 11. To

an h

oc tô

1 ≤ j ≤ n

n+1

+ 1. Vi

êc tô mâ

u kê

theo th

n + 1

diê

m trên m

ôi

ong c

o n

n+1

ach kh

ac nhau (m

ôi

diê

m c

o n c

ach tô). Do

o c

ıt nhâ

t l

a 2 d

ong trong sô

n+1

+ 1 d

ong

c tô mâ

u giô

ng nhau

(ngh

ıa l

a hai d

ong giô

ng nhau vê

mâ

u s

ac tô

diê

m th

nhâ

diê

hai,. . . ,

diê

m th

n + 1 ch

ang h

an t

ınh t

ai qua ph

ai). Gi

a s

hai d

ong â

y l

a d

ong nh

diê

m c

o to

ô k v

a m; ngh

ıa l

a v

i m

ôi

i ∈ {1, 2, . . . , n} c

diê

m (i, k) v

a (i, m) c

o c

ung m

ôt mâ

u. B

i v

ı c

o n mâ

u nên trong sô

n + 1

diê

m trên d

ong c

diê

m c

o tung

ô k

at c

ıt nhâ

t hai

diê

m c

o c

ung mâ

u, ch

ang h

an,

o l

a 2

diê

(a, k) v

a (b, k). Khi

o h

ınh ch

ât v

i c

ınh (a, k), (b, k), (b, m)

a (a, m) c

o 4

ınh c

ung mâ

. 11.7. Cho 1000

diê

m trên m

˘at ph

˘ang M

, M

, . . . , M

1000

. Ch

minh r

˘ang trên bâ

t c

ng tr

on b

an k

ınh 1 n

ao ta

dê

u t

ım

c m

ôt

diê

m S sao cho tô

ng kho

ang c

ach t

dê

n c

diê

m M

, M

, . . . , M

1000

không nh

o ho

n 1000.

i gi

ai. Gi

a s

a S

a hai

diê

m tu

dô

i tâm c

ng tr

T b

an k

ınh 1. Ta c

o S

= 2, v

ây S

+ S

≥ S

= 2;

+ S

≥ 2;. . . ; S

1000

+ S

1000

≥ 2. V

ı thê

( S

) + (S

+ S

) + ··· + (S

1000

+ S

1000

) = ( S

+ ··· + S

1000

) + (S

+ S

+ ··· + S

1000

) ≥ 2000.

ıt nhâ

t m

ôt trong hai

diê

m S

a S

ac ch

an tho

a m

ai ra l

a tô

ng kho

ang c

ach t

dê

n c

diê

m M

, M

, . . . , M

1000

không nh

o ho

n 1000.

. 11.8. Cho 37

diê

m phân bi

êt trong không gian c

o to

o l

a nh

sô

nguyên sao cho không c

o ba

diê

m n

ao th

˘ang h

ang. Ch

ng minh

˘ang ta c

o thê

on 3

diê

m m

a to

ô giao

diê

m c

ac trung tuyê

n c

tam gi

ac t

ao th

anh

dê

u l

a sô

nguyên.

11.1. V

ı d

u 125

i gi

ai. V

i m

ôi

diê

m x ; y; z c

o to

ô l

a nh

ng sô

nguyên (

diê

nguyên) ta cho tu

ng c

ac sô

z l

a nh

ng sô

ua ph

chia c

ac sô

x; y; z cho 3. V

x nh

ân không qu

a 3 gi

a tr

i nên

ıt nhâ

13 trong sô

diê

m c

o c

ung gi

a tr

i (nê

u không, thê

ı sô

diê

không l

n ho

n 12.3=36). Tu

ng t

, c

o không

ıt ho

n 5 trong 13

diê

o c

o gi

a tr

y nhu

nhau.

Thê

ı giao

diê

m c

ac trung tuyê

n c

ua tam gi

ac c

ınh (x

, y

, z

, y

, z

) v

a (x

, y

, z

) c

o to

+ x

; y

+ y

; z

+ z

Nê

ı c

ac sô

a y

a nguyên c

sô

ı nguyên khi v

a ch

ı khi z

+ z

≡ 0 ( mod 3). Trong

tru

ng h

p b

ai ra ta ch

on ra 5

diê

m m

a tâ

t c

a sô

x b

ang nhau v

a tâ

a sô

y b

ang nhau. Nê

u trong c

diê

m n

ay ta t

ım

c ba

diê

m m

ac sô

z nh

ân c

ac gi

a tr

i 0; 1; 2 th

ı v

i c

diê

o ta c

+ z

≡

≡ 0 + 1 + 2 ≡ 0( mod 3)

Nê

u không c

o nh

diê

m n

ay th

ı sô

z v

i 5

diê

a ch

on s

e nh

ân

không qu

a 2 gi

a tr

i, do

o ta t

ım

c 3

diê

m m

a gi

a tr

z nh

ân c

ung

ôt gi

a tr

i m

a sô

ng v

i n

o l

a sô

nguyên.

. 11.9. Trên m

˘at ph

˘ang cho 7

ng th

˘ang trong

o không c

o hai

ng th

˘ang n

ao song song. Ch

ng minh r

˘ang ta t

ım

c hai trong

ng th

˘ang n

oi trên m

a g

oc gi

a ch

ung nh

o ho

n 26

i gi

ai. Ta h

ay t

inh tiê

n tâ

t c

a 7

ng th

ang

a cho sao cho ch

ung

di qua m

ôt

diê

m cô

inh O. Ta s

c 7

ng th

ang chia g

dâ

ınh O th

anh 14 phâ

n. V

ı thê

ôt trong c

ac g

oc t

ao th

anh nh

360

= 25

< 26

(nê

u tâ

t c

a c

ac g

dê

u b

ang nhau th

ı m

ôi

126 Chu

ng 11. To

an h

oc tô

oc không l

n ho

n 26

). Nhu

ng g

oc gi

a hai

ng th

ang c

at nhau

ang g

oc gi

a hai

ng th

ang ban

dâ

. 11.10. Cho A l

a m

ôt t

âp c

ac sô

nguyên v

a x l

a m

ôt sô

nguyên bâ

y. T

âp h

p x + A = {x + a|a ∈ A} g

oi l

a t

inh tiê

n c

ua A x

inh

i x. Hay n

oi c

ach kh

ac t

âp h

p x + A gô

m c

ac phâ

n t

ua A c

ông

thêm v

i c

ung m

ôt sô

x. Ch

ung ta n

oi r

ang m

ôt t

âp h

p nh

ng sô

nguyên l

a k-nh

o nhâ

t, nê

u tô

n t

ai k t

âp t

inh tiê

n c

ua A, m

a ch

ung

dôi không c

diê

m chung. V

ı d

u: m

oi t

âp sô

u h

an l

a k-nh

nhâ

t v

i m

oi sô

nguyên du

ng k. C

ung c

o t

âp vô h

an l

a k-nh

o nhâ

nhu

ay k + 1, (k + 1)

, . . . , (k + 1)

, . . . Nhu

ng ch

ung ta ch

ng minh

kê

t lu

ân sau:

Cho n l

a sô

nhiên. Khi

o t

âp h

p nh

ng sô

nguyên không thê

biê

ên nhu

p c

ua n t

âp h

p (n + 1)-nh

o nhâ

i gi

ai. Ch

ung ta gi

a s

ngu

c l

ai: tô

n t

ai nh

ng t

âp h

p (n + 1)-

o nhâ

t A

, A

, . . . , A

sao cho m

ôi sô

nguyên thu

ôc m

ôt trong

ng t

âp h

p n

ay. Theo

inh ngh

ıa c

ua t

âp (n + 1)-nh

o nhâ

t v

oi i = 1, 2, . . . , n tô

n t

ai n + 1 sô

nguyên a

i,1

, a

i,2

, . . . , a

i, n+ 1

sao cho

i 1 ≤ r ≤ n + 1, 1 ≤ s ≤ n + 1 v

a r 6= s nh

ng ph

ep t

inh tiê

+ A

a a

i s

+ A

không c

diê

m chung. K

y hi

êu N l

a t

âp h

tâ

t c

a n-b

ô s

ap th

, j

, . . . , j

)

dây j

, j

, . . . , j

ôc l

âp nh

ân

ac gi

a tr

i 1, 2, . . . , n, n + 1. V

i m

ôi n-b

ô a = (j

, j

, . . . , j

) t

cho tu

ng v

i m

ôt sô

nguyên x

= a

+ a

+ ··· + a

. B

ı ch

ung ta

a gi

a thiê

t t

âp h

p nh

ng sô

nguyên l

a h

p c

ua c

âp h

p A

, A

, . . . , A

, m

ôi sô

thu

ôc m

ôt t

âp n

o trong d

âp h

p trên. Ngo

ai ra sô

phâ

n t

ua N l

a (n + 1)

(

dây l

a t

ınh tô

p).T

nguyên l

y Ðirichle m

ông ch

ung ta c

ıt nhâ

t m

ôt trong

ac t

âp A

, A

, . . . , A

a nh

ng sô

ang x

ıt nhâ

( n + 1)

11.2. B

ai t

âp 127

ô a t

Không mâ

t t

ınh tô

ng qu

at ch

ung ta gi

a thiê

t A

o t

ınh châ

trên. Ch

ung ta x

et tâ

t c

a c

ac phâ

n t

α c

ua N m

a sô

thu

ôc A

ung gô

ıt nhâ

( n + 1)

phâ

n t

. Nê

u α = (j

, j

, . . . , j

) l

a m

ôt

phâ

n t

trong ch

ung, th

ı ch

ung ta cho tu

ng v

i (n − 1)-b

ap α

= (j

, j

, . . . , j

). V

ı 1 ≤ j

≤ n + 1 v

i m

oi µ = 2, 3, . . . , n,

theo t

ınh châ

t tô

p v

i α

o nhiê

u nhâ

t (n + 1)

n−1

a n

ang.

bâ

ang th

( n + 1)

> (n + 1)

n−1

suy ra

ıt nhâ

t c

o hai n-b

α = (j

, j

, . . . , j

), β = (k

, k

, . . . , k

) ho

an to

an kh

ac nhau, m

∈ A

, x

∈ A

, tu

ng v

i c

ung m

ôt (n −1)-b

ô.

ung ta c

o thê

om t

at ng

an g

on nhu

sau: tô

n t

ai hai b

ô kh

nhau α = (j

, j

, . . . , j

) v

a β = (k

, k

, . . . , k

) thu

ôc N, m

a x

∈

, x

∈ A

, j

6= k

a j

= k

, j

= k

, . . . , j

= k

. Nhu

ng, x

+ a

+ ··· + a

= a

+ a

+ ··· + a

nhu

ng v

ı j

= k

i m

ôi µ = 2, 3, . . . n ch

ung ta c

o x

− x

= a

− a

ac l

+ x

= a

+ x

. Khi

o sô

x = a

+ x

= a

+ x

thu

ôc v

âp h

p a

+ A

a a

+ A

. Suy ra t

âp t

inh tiê

n A

inh b

ac sô

a a

diê

m chung,

diê

o tr

ai v

i gi

a thiê

t khi b

dâ

u ch

ng minh.

11.2. B

ai t

âp

. 11.11. a) Trong h

ınh vuông di

ên t

ıch 6

at ba

da gi

ac di

ên t

ıch

3. Ch

ng minh r

ang trong sô

o luôn t

ım

c hai

da gi

ac m

a di

ên

ıch phâ

n chung c

ua ch

ung không nh

o ho

n 1.

b) Trong h

ınh vuông di

ên t

ıch 5

at 9

da gi

ac di

ên t

ıch 1. Ch

minh r

ang trong sô

o luôn t

ım

c hai

da gi

ac m

a di

ên t

ıch phâ

128 Chu

ng 11. To

an h

oc tô

chung c

ua ch

ung không nh

o ho

. 11.12. S

diê

c s

ap xê

p trên m

at ph

ang sao cho ba

diê

bâ

t k

y l

ınh c

ua m

ôt tam gi

ac m

a c

ac c

anh c

ô d

ai kh

ac nhau.

ng minh r

ang c

anh nh

o nhâ

t c

ua m

ôt trong c

ac tam gi

dô

i l

a c

anh l

n nhâ

t c

ua m

ôt tam gi

ac kh

ac.

. 11.13. Cho P

, P

, . . . , P

a bâ

diê

m trong không gian, trong

không c

o bô

diê

m n

dô

ng ph

ang. Tô mâ

u m

ôi

an P

(i < j)

i m

ôt trong hai mâ

o ho

den. Ch

ng minh r

ang c

o hai tam

n s

ac không c

o chung c

anh.

. 11.14. C

o hai

ıa

dê

c chia th

anh 1998 h

ınh qu

at b

ang nhau,

a trên m

ôi

ıa tô m

ôt c

ach bâ

t k

y (b

ang m

ôt mâ

u) 200 h

ınh qu

at.

ıa

at chô

ng lên nhau v

a quay m

ôt

ıa theo nh

ng g

a b

ôi c

360

1998

. Ch

ng minh r

ang tô

n t

ıt nhâ

t 94 v

i tr

ı c

o không

a 20 h

ınh qu

c so

n tr

ung nhau.

. 11.15. Trên m

at ph

ang cho n

ng th

ang t

dôi không song

song v

i nhau. Ch

ng minh r

ang g

oc gi

a hai

ng th

ang n

trong sô

o không l

n ho

180

CHU

NG 12

ÔT S

Ô B

AI T

ÂP H

INH H

OC KH

12.1. V

ı d

. 12.1. Trong h

ınh ch

ât 3x4

˘at 6

diê

m. Ch

ng minh r

˘ang trong

sô

o luôn t

ım

c hai

diê

m c

o kho

ang c

ach gi

a ch

ung không l

√

i gi

ai. Chia h

ınh ch

ât ra l

ınh 12.1:

5 h

ınh nhu

ınh 12.1. Trong m

ôt

trong sô

ac h

ınh

o s

e c

ıt nhâ

diê

m, v

a kho

ang c

ach gi

a hai

diê

o s

e không l

n ho

√

. 12.2. Trên m

˘at ph

˘ang c

o 25

diê

m, biê

t r

˘ang trong 3

diê

m bâ

t k

trong sô

o luôn c

o 2

diê

m c

ach nhau nh

o ho

n 1. Ch

ng minh r

˘ang

tô

n t

ai h

ınh tr

on b

an k

ınh 1 ch

a không

ıt ho

n 13

diê

a cho.

i gi

ai. Gi

a s

A l

a m

ôt

diê

a cho. Nê

u tâ

t c

a c

diê

m c

on l

am trong h

ınh tr

on S

tâm A b

an kinh 1 th

ı ta không câ

n ph

ng minh g

ı thêm. Gi

a s

o m

ôt

diê

m B trong sô

a cho n

ngo

ng tr

on S

c l

a AB > 1. X

et h

ınh tr

on S

tâm B b

an k

ınh

1. Trong sô

diê

m A, B, C trong

o C l

diê

a cho bâ

t k

y luôn

o hai

diê

m c

ach nhau nh

o ho

n 1, ho

n n

o không thê

a 2

diê

130 Chu

ng 12. M

ôt sô

ai t

âp h

ınh h

oc kh

A v

a B. Do

o c

ac h

ınh tr

on S

a S

a tâ

t c

a c

diê

a cho,

c l

a m

ôt trong hai h

ınh tr

o ch

a không

ıt ho

n 13

diê

a cho.

. 12.3. Bên trong

ng tr

on b

an k

ınh n

˘at 4n

an th

˘ang c

ô d

1. Ch

ng minh r

˘ang c

o thê

e m

ôt

ng th

˘ang song song ho

˘ac vuông

oc v

ng th

˘ang l cho tru

c v

a c

˘at

ıt nhâ

t 2

an th

˘ang

a cho.

i gi

ai. Gi

a s

ng th

ang bâ

t k

y vuông g

oc v

i l. K

y hi

êu

ô d

ai c

ac h

ınh chiê

u c

an th

ang th

i lên c

ng th

ang l

a l

a a

a b

ng. B

i v

ô d

ai c

ua m

ôi

an th

ang b

ang

1, nên a

+ b

≥ 1. Do

o (a

+ ··· + a

) + (b

+ ··· + b

) ≥ 4n.

Không mâ

t t

ınh tô

ng qu

at gi

a s

+ ···+ a

) ≥ (b

+ ···+ b

Khi

o a

+ ···+ a

≥ 2n. Tâ

t c

a c

an th

ang

a cho

dê

chiê

u xuô

an th

ang c

ô d

ai 2n, b

i v

ı ch

ung

dê

u n

am trong

ng tr

on b

an k

ınh n. Nê

u nhu

ac h

ınh chiê

u c

ua c

an th

ang

a cho lên

ng th

ang l không c

diê

m chung, th

ı s

e c

o bâ

ang

c a

+ ···+ a

< 2n. Do

o trên l ph

ai c

o m

ôt

diê

m b

i c

diê

ıt nhâ

t hai trong sô

an th

ang

a cho chiê

u lên

o. Ðu

vuông g

oc v

i l t

diê

o s

e c

ıt nhâ

t hai

an th

ang

a cho.

. 12.4. Trên do

an th

˘ang c

ô d

ai 1 ta tô m

ôt sô

an th

˘ang sao

cho kho

ang c

ach gi

a hai

diê

c tô bâ

t k

y không b

˘ang 0,1. Ch

minh r

˘ang tô

ô d

ai c

ac do

an th

˘ang

c tô không l

n ho

n 0,5.

i gi

ai. Chia

an th

ang ra l

am 10

an th

ang c

ô d

ai 0,1,

ung theo m

ôt c

ôt v

a chiê

u ch

ung xuô

ng m

ôt

an th

ang nhu

ây.

i v

ı kho

ang c

ach gi

a hai

diê

c tô bâ

t k

y không b

ang 0,1,

nên c

diê

c tô c

ua c

an th

ang c

anh nhau không thê

ung

chiê

u xuô

ng 1

diê

m. Do

o không c

diê

m n

ao c

o thê

a h

ınh chiê

12.1. V

ı d

u 131

ua c

diê

c tô c

ua nhiê

u ho

n 5

an th

ang. Suy ra tô

ô d

ai c

ac h

ınh chiê

u c

ua c

an th

ang

c tô không l

n ho

5.0, 1 = 0, 5.

. 12.5. Ch

ng minh r

˘ang nê

u m

ôt

ng th

˘ang l n

˘am trong m

˘at

˘ang c

ua tam gi

ac ABC v

a không

di qua

ınh n

ao c

ua tam gi

ı n

o c

˘at không qu

a hai c

anh c

ua tam gi

a cho.

i gi

ai. K

y hi

êu α v

a α l

a hai n

a m

at ph

ang do l chia m

at ph

ang

ua tam gi

ac ABC. M

ôi

ınh A, B v

a C n

am trong m

ôt n

a m

ang trên. Theo nguyên l

y Ðirichlê

ıt nhâ

t m

ôt trong hai n

a m

ang trên, ch

ang h

an nhu

α, ch

a hai

ınh c

ua tam gi

ac ABC,

ang h

an nhu

A v

a B. Khi

ng th

ang l không c

an th

ang

AB, ngh

ıa l

a n

o không c

at m

ôt trong ba c

anh c

ua tam gi

ac ABC .

. 12.6. Nh

diê

m trong m

˘at ph

˘ang

c so

n b

˘ang m

ôt trong ba

mâ

u. Ch

ng minh r

˘ang luôn t

ım

c hai

diê

m c

ung mâ

u c

ach nhau

ung b

˘ang 1.

i gi

ai. Gi

a s

hai

diê

m bâ

t k

y c

ach nhau 1

dê

c tô b

ang c

mâ

u kh

ac nhau. X

et tam gi

dê

u ABC c

o c

anh b

ang 1. Tâ

t c

a c

ınh c

ua n

c tô b

ang c

ac mâ

u kh

ac nhau. Gi

a s

diê

m A

dô

ng v

i A qua

ng th

ang BC. B

i v

ı A

B = A

C = 1, nên

diê

o mâ

u kh

ac v

i mâ

u c

ua B v

a C, t

c l

a n

c tô c

ung m

ôt mâ

diê

m A. C

ac l

âp lu

ân

o th

c châ

a ch

ı ra r

ang nê

u AA

√

ı c

diê

m A v

a A

tô c

ung m

ôt mâ

u. Do

o tâ

t c

a c

diê

m n

trên

ng tr

on tâm A b

an k

ınh

√

3 c

o c

ung m

ôt mâ

u. R

o r

ang trên

ng tr

o luôn t

ım

c hai

diê

m c

o kho

ang c

ach gi

a ch

ung

ang 1. Ta

c mâu thu

ân, v

ây luôn t

ım

c hai

diê

m c

ung mâ

o kho

ang c

ach gi

a ch

ung b

ang 1.

132 Chu

ng 12. M

ôt sô

ai t

âp h

ınh h

oc kh

. 12.7. Cho 11

diê

m kh

ac nhau trong h

ınh câ

u thê

ıch V. Ch

minh r

˘ang qua tâm c

ua h

ınh câ

u c

o thê

ng hai m

˘at ph

˘ang sao cho

ung c

˘at h

ınh câ

u th

anh m

ôt "miê

ng" v

i thê

ıch

, m

a phâ

n trong

ua n

o không ch

a trong phâ

n trong bâ

t c

ôt

diê

m n

a cho.

i gi

ai. Chia h

ınh câ

u ra hai b

an câ

u b

ang m

ôt m

at ph

ang

di qua

tâm v

a hai

diê

m t

diê

a cho. M

ôt b

an câ

u ch

a trong phâ

trong nhiê

u nhâ

t l

a 4

diê

m t

diê

m c

on l

ai. Chia n

a h

ınh câ

ang hai m

at ph

ang, m

a m

ôi m

at ph

ang

di qua tâm h

ınh câ

u v

hai

diê

m trong 4

diê

m c

on l

ai. Nhu

ây n

a h

ınh câ

u chia th

anh 3

"miê

ng" không ch

a m

ôt

diê

m n

ao bên trong.

ıt nhâ

t thê

ıch c

ôt miê

ng l

n ho

thê

ıch c

ua b

an h

ınh câ

. 12.8. Cho khô

da di

ên lô

i P

o 9

ınh A

, A

, . . . , A

y hi

êu

, P

, .., P

a nh

da di

ên

c t

ao th

anh b

i c

ac ph

ep t

inh tiê

ng theo c

ac vecto

−−−→

, . . . ,

−−−→

. Ch

ng minh r

˘ang

ıt nhâ

2 trong sô

da di

ên trên c

ıt nhâ

t m

ôt

diê

m chung.

i gi

ai. X

et h

ınh

da di

ên P l

anh c

ua P

qua ph

ep v

i t

tâm A

a h

ê sô

2. Ta s

e ch

ng minh r

ang 9

da di

ên

dê

u n

am trong P. Th

ât

ây, cho A

, A

∗

, . . . , A

∗

a c

ınh c

da di

ên P. Ch

ung ta s

e ch

minh, ch

ang h

an nhu

am trong P. Ðê

ng minh

diê

o ch

ung

ta ch

y t

i ph

ep t

inh tiê

−−−→

chuyê

n c

diê

m A

, A

, . . . , A

i c

diê

m A

, A

∗

, A

, . . . , A

dây A

a trung

diê

m c

∗

Tô

ng thê

ıch c

ua c

da di

ên P

, P

, . . . , P

am trong P b

ang

9V,

dây V l

a thê

ıch c

da di

ên P

, c

on thê

ıch c

da di

ên P

ang 8V. Suy ra

ıt nhâ

t c

o hai

da di

ên c

diê

m chung (nguyên l

Ðirichlê cho thê

ıch.

12.1. V

ı d

u 133

. 12.9. Trong h

ınh câ

ng k

ınh 3

˘at m

ôt sô

ınh câ

u m

a tô

ng k

ınh c

ua ch

ung b

˘ang 25 (nh

ng h

ınh câ

u n

ay c

o thê

giao

nhau). Ch

ng minh r

˘ang v

i m

oi m

˘at ph

˘ang tô

n t

ai m

ôt m

˘at ph

˘ang

song song v

i n

o v

a c

˘at

ıt nhâ

t 9 h

ınh câ

u con.

i gi

ai. Ch

ung ta x

et h

ınh chiê

u c

ac h

ınh câ

u lên

ng th

ang

vuông g

oc v

i m

at ph

ang

a cho. H

ınh câ

u l

n chiê

u v

ao m

ôt

ang c

ô d

ai 3, c

on c

ac h

ınh câ

u con chiê

u v

ao c

an th

ang

o c

o tô

ng 25. Gi

a s

không c

o m

ôt m

at ph

ang n

ao nhu

dê

ai ra,

ngh

ıa l

a m

oi m

at ph

ang song song v

i m

at ph

ang

a cho ch

ı c

at 8

ınh câ

u nh

o. khi

o m

ôi

diê

m trong

an th

ang

ô d

ai 3 ch

ı thu

ôc

nhiê

u nhâ

t l

a 8

an th

ang h

ınh chiê

u c

ua nh

ng h

ınh câ

u nh

o. Suy

ra tô

ng c

ua ch

ung không qu

a 24. Nh

ân

c s

vô l

. 12.10. Trong h

ınh vuông c

anh 1

n v

i c

o m

ôt

ng gâ

p kh

uc L

không t

˘a v

ô d

ai l

n ho

n 1000. Ch

ng minh r

˘ang tô

n t

ai m

ôt

ng th

˘ang m song song v

i c

anh h

ınh vuông v

a c

˘at

ng L t

ai ho

500

diê

i gi

ai. Gi

a s

ô d

ai m

at th

i c

ng gâ

p kh

uc, a

a b

ô d

ai h

ınh chiê

u c

ua n

o lên c

ac c

anh c

ua h

ınh vuông. Khi

≤ a

+ b

. Suy ra

1000 = l

+ ··· + l

≤ (a

+ ··· + a

) + (b

+ ··· + b

)

c l

a ho

ac a

+ ··· + a

≥ 500 ho

ac l

a b

+ ··· + b

≥ 500. Nê

tô

ô d

ai h

ınh chiê

u c

ua c

ac m

at lên m

ôt c

anh

ô d

ai 1 không nh

n 500, th

ı theo nguyên l

y Ðirichlê cho

ô d

an th

ang ph

ai c

diê

m chung cho ho

n 500 h

ınh chiê

u c

ua c

ac m

at gâ

p kh

uc, t

c l

ng vuông g

oc k

e t

diê

m chung

o s

e c

ng gâ

p kh

uc t

ıt

nhâ

t 500

diê

134 Chu

ng 12. M

ôt sô

ai t

âp h

ınh h

oc kh

12.2. B

ai t

âp

. 12.11. Cho A l

a t

âp h

p nh

diê

m trên m

ôt m

at câ

u v

a c

o di

ên

ıch l

n ho

n n

a di

ên t

ıch m

at câ

u. Ch

ng minh r

ang A ch

ıt nhâ

ôt c

diê

m m

a n

o l

a 2

daah u

ng k

ınh c

ua qu

a câ

. 12.12. Ta g

oi h

ınh ch

âp l

a h

ınh t

ao b

i c

ng ch

eo c

ınh vuông c

anh 1. Ch

ng minh r

ang trong h

ınh tr

on b

an k

ınh 100

ı c

o thê

c m

ôt sô

u h

an c

ac ch

âp không c

at nhau.

. 12.13. Trên m

at ph

ang cho

diê

m O. H

oi c

o thê

at trên m

at ph

ang

5 h

ınh tr

on không ph

diê

m O sao cho m

oi tia xuâ

t ph

at t

O c

không

ıt ho

n hai h

ınh tr

c hay không ? (c

dây c

o ngh

ıa l

diê

m chung).

. 12.14. Nh

diê

m trong m

at ph

ang

c so

n b

ang m

ôt trong

hai mâ

u. Ch

ng minh r

ang luôn t

ım

c hai

diê

m c

ung mâ

u c

ach

nhau

ung b

ang 1.

CHU

NG 13

ÔT S

Ô Ð

Ê THI VÔ Ð

ICH

ng b

ai to

an thi vô

ich c

ac nu

c l

a c

ac b

ai to

diê

n h

ınh cho

êc v

ân d

ung tr

ı thông minh, s

ang t

dê

ai. N

oi h

oc sinh

ai n

c c

ac kiê

n th

c co

an v

ng ch

ac v

a hiê

u thâ

ao.

Ðê

ai c

ac b

ai to

an thi vô

ich ph

ai v

ân d

ung cao t

ınh phân t

ıch

a tô

ng h

p c

ac kiê

n th

c to

an h

oc. Râ

t nhiê

u b

ai to

an thi vô

ich

ac nu

c c

o m

ôt phâ

n gi

ai s

ung nguyên l

y Ðirichlê, c

ac chu

tru

c ta

a g

ap m

ôt sô

ai. Ðê

thu

ân ti

ên cho b

doj c muô

n tham

dâ

u vê

dê

ay tôi ch

ep l

ai v

a thô

ng kê ra

dây c

dê

thi vô

ich c

ac nu

c ch

u yê

u trong cuô

n s

ach [4] v

a m

ôt sô

tuyê

âp kh

ac. Nhu

ng v

ı t

ai li

êu tham kh

ao c

o h

an, phâ

n su

u tâ

m c

ua tôi

ac ch

an chu

dâ

u mong c

ac b

oc bô

sung v

a cho

y kiê

ôi b

ai trong chu

ng n

ay k

em theo tên nu

c v

a n

am k

y thi vô

ich

. 13.1. (Anh, 1966) Ch

ng minh r

˘ang t

52 sô

nguyên bâ

t k

y luôn

o thê

c ra hai sô

a tô

ng ho

˘ac hi

êu c

ua ch

ung chia hê

t cho

100.

i gi

ai. Tâ

t c

a c

ac sô

trong ph

ep chia cho 100,

c chia th

anh

ng nh

om nhu

sau: {0}, {1; 99}, {2; 98}, . . . , {49, 51}, {50}. V

ı c

tâ

t c

a 51 nh

om, m

a l

ai c

o 52 sô

, nên theo nguyên l

y Ðirichlê gi

136 Chu

ng 13. M

ôt sô

dê

thi vô

ich

ung ph

ai c

o hai sô

a c

ac sô

trong ph

ep chia cho 100 ro

i v

ôt nh

om. Hai sô

ay l

a hai sô

câ

n t

ım v

ı nê

u sô

ua ch

ung b

ang

nhau th

ı hi

êu c

ua ch

ung chia hê

t cho 100, c

on nê

u sô

ua ch

ung

ac nhau th

ı tô

ng c

ua ch

ung chia hê

t cho 100.

. 13.2. (Anh, 1970) Ch

ng minh r

˘ang t

âp h

p tu

y gô

m n sô

nhiên luôn t

ach ra

c m

ôt t

âp h

p con (kh

ac r

ông) ch

a c

ac sô

tô

ng c

ua ch

ung chia hê

t cho n.

i gi

ai. Gi

a s

i m

ôt t

âp h

p n

o ch

a c

ac sô

, a

, . . . , a

không tho

a m

an kh

ang

inh c

ua b

ai to

an. Khi

o không c

o sô

trong c

ac sô

= a

, S

= a

+ a

, . . . , S

= a

+ a

+ ··· + a

chia hê

t cho n. V

ı sô

ac sô

ac không trong ph

ep chia cho

n l

a n − 1, nên theo nguyên l

y Ðirichlê t

ım

c hai sô

a S

(1 ≤ i < j ≤ n) c

o c

ung sô

. Suy ra hi

êu S

−S

= a

i −1

+ ··· + a

chia hê

t cho n,

diê

u n

ay mâu thu

ân v

i gi

a s

oi trên v

a kh

ang

inh c

ua b

ai to

c ch

ng minh.

. 13.3. (Anh, 1976) Gi

a s

trong t

âp h

p h

u h

an X ch

on ra 50 t

âp

p con A

, . . . , A

sao cho m

ôi t

âp h

p con ch

a ho

n m

ôt n

a phâ

ua t

âp X. Ch

ng minh r

˘ang c

o thê

ım

c t

âp h

p con B ⊂ X

a không nhiê

u ho

n 5 phâ

n t

a c

ıt nhâ

t m

ôt phâ

n t

chung cho

ac t

âp h

p A

, A

, . . . A

i gi

ai. Gi

a s

sô

ac phâ

n t

ua t

âp X b

ang n. M

ôi t

âp h

p con

c ch

on A

, . . . , A

a không

ıt ho

phâ

n t

, c

o ngh

ıa l

tô

ng sô

ac phâ

n t

ua tâ

t c

a c

ac t

âp n

ay vu

t qu

a 50.

= 25.n.

Theo nguyên l

y Ðirichlê tô

n t

ai m

ôt phâ

n t

ua X thu

ôc không

ıt

137

n 26 t

âp con

a ch

on. Tu

ng t

ta ch

ng minh v

i gi

a tr

i bâ

t k

k < 50 gi

a c

ac t

âp A

, A

, . . . , A

o thê

on ra không

ıt ho





+ 1 t

âp h

p ch

a c

ung m

ôt phâ

n t

. Ta lâ

y phâ

n t

ua m

ôt

âp h

p X m

a n

o thu

ôc không

ıt ho

n 26 t

âp (phâ

n t

ay s

e l

a m

ôt

trong 5 phâ

n t

ua t

âp h

p B). Ta lo

ai ra 26 t

âp m

a ch

a phâ

n t

a x

et. Khi

o t

ım

c 1 phâ

n t

thu

ôc

ıt nhâ

t 13 t

24 t

âp c

on l

ai.

Ta l

ai lo

ai 13 t

âp n

ay ra, khi

o gi

a 11 t

âp c

on l

ai t

ım

c 1 phâ

thu

ôc không

ıt ho

n 6 trong sô

ac t

âp h

p. Ðô

i v

i 5 t

âp h

p c

ai t

ım

c 1 phâ

n t

thu

ôc không

ıt ho

n 3 trong sô

ung. V

a cuô

ung tô

n t

ai m

ôt phâ

n t

thu

ôc hai t

âp cuô

i c

ung. Nhu

ây ta t

ım

c không nhiê

u ho

n 5 phâ

n t

ua t

âp X (c

o thê

ıt ho

n v

ı m

ôt v

phâ

n t

e tr

ung nhau), ch

ung s

e t

ao th

anh t

âp B. Ngo

ai ra m

ôt t

âp

bâ

t k

y t

, . . . , A

ıt nhâ

t m

ôt trong c

ac phâ

n t

. 13.4. (Ba Lan, 1979) Khi chia c

ac sô

nhiên a

, a

, . . . , a

cho sô

nhiên m n

o, nh

ân

c c

ac sô

ac nhau,

dô

ng th

i n >

ng minh r

˘ang v

i m

oi sô

k ∈ Z tô

n t

ai c

ac sô

i, j ∈ {1, 2, . . . , n}

(không nhâ

t thiê

t kh

ac nhau) sao cho sô

+ a

−k chia hê

t cho m.

i gi

ai. X

et 2n sô

, a

, . . . , a

, k − a

, . . . , k −a

. V

ı 2n > m,

nên c

o 2 trong c

ac sô

o c

ung sô

trong ph

ep chia cho m. Theo

diê

u ki

ên b

ai to

an, c

ac sô

, a

, . . . , a

, c

o sô

ac nhau trong

ep chia cho m, nên c

ac sô

k − a

, k − a

, . . . , k − a

ung c

o sô

ac nhau. Do

o c

ap sô

o sô

ang nhau ch

ı c

o thê

a hai sô

ang a

a k − a

i i, j n

o. Khi

o hi

êu c

ua ch

ung a

+ a

− k

chia hê

t cho m.

. 13.5. (Ba Lan, 1977) Ch

ng minh r

˘ang v

i m

oi gi

a tr

i a, b ∈ R v

e > 0, tô

n t

ai c

ac sô

k, m ∈ Z v

a n ∈ N tho

a m

an c

ac bâ

˘ang th

138 Chu

ng 13. M

ôt sô

dê

thi vô

ich

|na − k| < e v

a |nb − m| < e.

i gi

ai. Cho sô

nguyên N >

a v

i m

ôi c

ap x, y ∈ [0; 1] ta thay

thê

ang c

ap u, v tho

a m

an u = [Nx], v = [Ny] , khi

o nê

u v

i hai

ap (x

, y

), (x

, y

) tu

ng v

i m

ôt c

ap duy nhâ

t (u, v) th

− x

| =



( u + {Nx

}) −

( v + {Nx

})



|{Nx

}−{Nx

}| <

< e

a tu

ng t

ta c

o |y

− y

| < e. V

ı u, v ∈ {0, . . . , N −1}, nên c

o tâ

a N

ap (u, v) kh

ac nhau. X

et t

âp h

p N

+ 1 c

ap gi

a tr

x = {la}, y = {lb} v

i l = 0, 1, . . . , N

Theo nguyên l

y Ðirichlê c

ıt nhâ

t hai c

ap (gi

a s

i l = i v

l = j, i > j) t

âp h

p n

ay tu

ng c

ung m

ôt c

ap (u, v). Do

i k

y hi

êu

n = i − j, k = [ia] −[ja], m = [ib] − [jb]

ta nh

ân

c c

ac bâ

ang th

c câ

n ch

ng minh :

|na − k| = |(ia − [ia]) − (ja − [ja])| = |{ia} − {ja}| < e,

|n b − m| = |(ib − [ib]) − (jb − [jb] )| = |{ib} − {jb}| < e.

. 13.6. (B

ı, 1977) Trong h

ınh tr

on c

o b

an k

ınh n ∈ N c

o 4n

˘ang

dê

u c

ô d

ai b

˘ang 1. Ch

ng minh r

˘ang nê

u c

o m

ôt

ng th

˘ang

cho tru

c th

ı t

ım

c m

ôt

ng th

˘ang kh

ac, ho

˘ac song song, ho

˘ac

vuông g

oc v

ng th

˘ang n

ay v

a c

˘at

ıt nhâ

t hai

an th

˘ang n

oi trên.

i gi

ai. Ðê

y r

ang tô

ô d

ai hai h

ınh chiê

u c

ua m

ôi m

ôt

ang lên

ng th

ang l v

ng th

ang l

, vuông g

oc v

i n

o, không

139

e ho

n 1. Th

ât v

ây, nê

u vecto

a c

ô d

ai l

a 1 song song v

ang n

o, c

on c

ac vecto

x v

a y l

a c

ac h

ınh chiê

u c

ua vecto

a lên

ng th

ang l v

a l

ı a = x + y, suy ra |x| + |y| ≥ |a| = 1. Nhu

ô d

ai c

ac h

ınh chiê

u c

an th

ang b

ang |x| v

a |y| do

o tô

ng c

ung c

ung không b

e ho

n 1. D

ân

dê

n tô

ô d

ai h

ınh chiê

u c

ua tâ

a c

an th

ang không b

e ho

n 4n. B

i v

ây t

hai

ng th

ang l

a l

o thê

c m

ôt

ng th

ang, tô

ô d

ai c

ua h

ınh chiê

an th

ang trên n

o không b

e ho

n 2n (nguyên l

y Ðirichlê). V

ı tâ

a c

an th

ang

c s

ap xê

p trong h

ınh tr

on b

an k

ınh n, nên h

ac h

ınh chiê

u c

ua ch

ung trên

ng th

ang bâ

t k

y c

ô d

ai b

e ho

2n. Suy ra trên

ng th

ang

c ch

on t

ım

c 1

diê

m thu

ôc v

ınh chiê

u c

ıt nhâ

t hai

an th

ang (Nguyên l

y Ðirichlê cho

ang). Ðu

ng th

ang

di qua

diê

m n

ay vuông g

oc v

ng th

ang

c ch

on, s

e c

ıt nhâ

t hai

an th

ang n

ay. V

ng th

ang n

ac vuông g

oc v

i, ho

ac song song v

ng th

ang l, th

ı n

o tho

diê

u ki

ên b

ai to

an.

. 13.7. (Bungari (

dê

thi ch

ôi tuyê

n),1973) Cho a

, a

, . . . , a

ng sô

nguyên kh

ac nhau trong kho

ang [100,200], m

a ch

ung tho

an a

+ a

+ ···+ a

≥ 11100. Ch

ng minh r

˘ang gi

a nh

ng sô

ıt nhâ

t m

ôt sô

, m

a viê

t n

ang th

âp phân c

ıt nhâ

t hai ch

sô

giô

ng nhau.

i gi

ai. Ch

ung ta l

âp danh s

ach c

ac sô

trong kho

ang [100,200], m

ung viê

ê th

âp phân

ıt nhâ

t c

o hai ch

sô

ung nhau.: 100,

101, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 121, 122,

131, 133, 141, 144, 151, 155, 161, 166, 171, 177, 181, 188, 191,

199, 200. Tô

ng c

ua tâ

t c

a c

ac sô

trên l

a 4050. M

at kh

ac tô

ng tâ

t c

ac sô

nguyên trong kho

ang [100,200] l

a 15150. Nê

u trong nh

sô

a cho a

, a

, . . . , a

không c

o sô

ao trong danh s

ach trên, th

140 Chu

ng 13. M

ôt sô

dê

thi vô

ich

+ a

+ ··· + a

< 15150 − 4050 = 11100,

diê

u n

ay vô l

y. Ngh

ıa

a trong c

ac sô

, a

, . . . , a

ıt nhâ

t m

ôt sô

viê

sô

i c

ıt

nhâ

t hai ch

sô

ung nhau.

. 13.8. (Bungari,1973) Trong m

ôt thu

ên c

o 20000 cuô

n s

ach,

ung

c xê

p v

ao nh

ng gi

a s

ach sao cho m

ôi gi

a s

ach c

ıt nhâ

ôt quyê

n ho

˘ac nhiê

u nhâ

t 199 cuô

n s

ach. Ch

ng minh r

˘ang

ıt nhâ

o hai gi

a s

ach c

o c

ung sô

ng s

ach.

i gi

ai. Gi

a s

ngu

c l

ai. Nê

u trong thu

ên c

o n gi

a s

ach v

a ch

ung

anh sô

dê

n n, th

ı r

o r

ang l

a n ≤ 199. Ch

ung ta k

y hi

êu a

a sô

cuô

n s

ach

at lên gi

a s

ach th

i, ch

ung ta s

e c

o 1 ≤ a

≤

199. khi

o t

diê

u ki

ên a

6= a

i i 6= j, ch

ung ta nh

ân

20000 = a

+ a

+ ··· + a

≤ 1 + 2 + ··· + 199 = 19900 < 20000

diê

u n

ay vô l

y. Suy ra c

ıt nhâ

t hai gi

a s

ach, trên ch

ung ch

a c

ung

sô

ach.

. 13.9. (Bungari, 1983) T

ım h

ınh vuông c

o k

ıch thu

c b

e nhâ

dê

trong h

ınh vuông

o c

o thê

˘ap xê

p 5 h

ınh tr

on b

an k

ınh b

˘ang 1, sao

cho không c

o 3 h

ınh tr

on n

ao trong ch

ung c

diê

m trong chung.

i gi

ai. Gi

a s

ınh vuông ABCD

ınh 13.1:

o tâm O v

a c

anh a, ch

a 5 h

ınh

on không c

at nhau v

dê

u c

an k

ınh b

ang 1, khi

o c

ac tâm

ua ch

ung n

am trong h

ınh vuông

o tâm O v

a c

anh b

ang

a −2 (

dây A

//AB ).

ng th

ang nô

i t

ac trung

diê

m c

ua c

ac c

anh

dô

i di

ên c

ınh vuông A

chia h

ınh vuông

o th

anh bô

n h

ınh vuông

141

ôt trong ch

ung

ıt nhâ

t c

ung c

o hai trong sô

ac tâm (Nguyên

y Ðirichlê). Khi

o kho

ang c

ach gi

a hai tâm n

ay m

ôt m

at không

n ho

ng ch

eo h

ınh vuông b

e, m

at kh

ac không b

e ho

n 2. Do

ây c

2 ≤ OA

√

2 =

a −2

√

suy ra a ≥ 2

√

2 + 2.

Cuô

i c

ung, nê

u a = 2

√

2 + 2 v

a tâm c

ua c

ac h

ınh tr

on l

a c

diê

m O, A

, B

, C

, D

ı tâ

t c

a c

diê

u ki

ên nêu trên

c tho

an. Nhu

ây c

anh c

ua h

ınh vuông câ

n t

ım l

a 2

√

2 + 2.

. 13.10. (Nam Tu

, 1977) Cho tru

c 20 sô

nhiên a

< a

< . . . <

không vu

t qu

a 70. Ch

ng minh r

˘ang gi

a c

ac hi

êu a

−a

(j > k)

luôn t

ım

ıt nhâ

t 4 hi

êu b

˘ang nhau.

i gi

ai. Gi

a s

ang

inh c

ua b

ai to

an l

a sai. Khi

o gi

a 19 sô

nhiên a

− a

, a

− a

, . . . , a

− a

không c

o 4 sô

ao b

ang nhau.

o gi

a ch

ung m

ôi sô

1, 2, 3, 4, 5, 6 c

o m

at không qu

a 3 lâ

Suy ra c

o m

ôt trong 19 sô

o ph

ai l

n ho

n 6 (nê

u không th

ı sô

sô

không l

n ho

n 6 s

e nhiê

u ho

n 18), c

o 3 trong 18 sô

on l

ai ph

n ho

n 5, 3 trong 15 sô

on l

ai ph

ai l

n ho

n 4,. . . Do

o tô

ng c

ung (a

−a

) + (a

−a

) + ···+ (a

−a

) ≥ 7 + 3( 6 + 5 + 4 +

3 + 2 + 1) = 70 không thê

ang a

− a

≤ 70 −1 = 69. Mâu thu

ân

a ch

ng minh kh

ang

inh c

ua b

ai to

an.

. 13.11. (Nam Tu

, 1981) T

âp h

p c

ac sô

{1, 2, . . . , 100}

c chia

am 7 t

âp h

p con. Ch

ng minh r

˘ang

ıt nhâ

ôt trong c

ac t

âp h

con â

y t

ım

c ho

˘ac 4 sô

a, b, c, d sao cho a + b = c + d, ho

˘ac ba sô

e, f , g sao cho e + f = 2g.

i gi

ai. Ðê

y r

ang c

ıt nhâ

t m

ôt trong 7 t

âp h

p con ch

a không

ıt ho

n 15 sô

(trong tru

ng h

p ngu

c l

ai, tâ

t c

a c

ac t

âp h

p con

142 Chu

ng 13. M

ôt sô

dê

thi vô

ich

a không nhiê

u ho

n 7.14 = 98 sô

). M

ôi c

ap sô

a > b c

ua t

âp h

con n

at tu

ng v

i hi

êu a − b. Khi

o ta nh

ân

không

ıt ho

n C

= 15

= 105 hi

êu, trong sô

o ph

ai c

o c

ac hi

êu

ang nhau (v

ı c

ac hi

êu nh

ân

c không qu

a 99 gi

a tr

i kh

ac nhau

1, 2,. . . ,99). Gi

a s

i hai c

ap sô

a > b, c > d ta c

ang th

a − b = c − d(a 6= c, b 6= d). Khi

o a + d = b + c. Nê

u a = d

(ho

ac b = c,

ang th

c kh

ac không thê

xâ

y ra), th

ı c + b = 2a (ho

a + d = 2b).

. 13.12. (Nam tu

,1977) Ch

ng minh r

˘ang di

ên t

ıch c

ua h

ınh vuông

bâ

t k

y n

˘am trong tam gi

ac, không l

n ho

n n

a di

ên t

ıch c

ua tam gi

i gi

ai. (H

ınh 13.2) Ta ch

ınh 13.2:

minh kh

ang

inh tô

ng qu

at ho

n :

ên t

ıch c

ua h

ınh b

ınh h

anh bâ

y KLMN n

trong tam gi

ABC không l

n ho

n n

a di

ên t

ıch

ua tam gi

Ðê

y r

ang m

ôi m

ôt

ng th

ang

KL v

a MN c

at hai c

anh c

ua tam

ac ABC (c

o thê

ınh tam gi

ac), ngh

ıa l

a c

o 2 trong 4 giao

diê

am trên 1 c

anh theo nguyên l

y Ðirichlê. Ch

ang h

an,

ng th

ang

KL v

a MN c

at BC lâ

n lu

a N

. Trên c

anh AB, AC v

a BC

on c

diê

m D, E v

a F sao cho L

, M

a giao

diê

m c

ua DE v

i KL

a MN tho

a m

an:

= KL; L

//K

dô

ng th

i BF//BD

Khi

o h

ınh b

ınh h

anh KLMN v

a K

ng cao b

ang

nhau

dê

das y chung, c

on c

ac h

ınh b

ınh h

anh BDEF v

a K

143

ay DE không b

e ho

ay L

a hai

ng cao h

a t

D v

a L

xuô

ng BF b

ang nhau. B

i v

ây c

o: S

KLMN

= S

≤ S

BDEF

. Gi

AE = x.AC, khi

o EC = (1 − x)AC, c

ac tam gi

ac ABC , ADE

a EFC

dô

ng d

ang v

i nhau nên ta c

BDEF

= S

ABC

−S

ADE

−S

EFC

= S

ABC

− x

ABC

−(1 − x)

ABC

= 2x(1 − x)S

ABC

≤

ABC

ı x( 1 − x) ≤

i x lâ

y gi

a tr

i bâ

t k

y, nên S

KLMN

≤

ABC

. 13.13. (Nam tu

, 1972) Ðô

i v

i m

ôi gi

a tr

i n ∈ N, h

ay t

ım sô

k l

nhâ

t (k ∈ N) tho

a m

an t

ınh châ

t sau: Trong t

âp h

p gô

m n phâ

n t

o thê

on ra k t

âp h

p con kh

ac nhau, sao cho hai t

âp h

p con bâ

dê

u c

o t

âp giao kh

ac r

ông.

i gi

ai. Cô

inh phâ

n t

ua t

âp h

p X = {a

, a

, . . . , a

} v

a ch

et c

ac t

âp h

p con ch

a phâ

n t

.Sô

ac t

âp h

p nhu

ây b

ang sô

ac t

âp h

p con c

ua t

âp h

p {a

, . . . , a

}, ngh

ıa l

a b

ang 2

n−1

. Suy ra

k ≥ 2

n−1

. M

at kh

ac gi

a s

a ch

c ho

n 2

n−1

âp con c

ua X. Ta

chia tâ

t c

a c

ac t

âp con c

ua X th

anh 2

n−1

c t

ao b

i 1 t

âp con

ua X v

a phâ

n b

u c

ua n

o. Theo nguyên l

y Ðirichlê c

ıt nhâ

t 2 t

âp

con

a ch

on t

ao th

anh m

ôt c

ap, suy ra ch

ung không giao nhau. V

ây

k = 2

n−1

. 13.14. (M

y, 1983) Trên tr

uc sô

lâ

y m

ôt kho

ang c

ô d

( n ∈

N). Ch

ng minh r

˘ang kho

ang n

ay c

o ch

a nhiê

u ho

n + 1

phân sô

tô

i gi

an d

ang

, trong

o p, q ∈ Z, 1 ≤ q ≤ n.

144 Chu

ng 13. M

ôt sô

dê

thi vô

ich

i gi

ai. Gi

a thiê

t r

ang trong m

ôt kho

ang n

o c

ô d

, ch

nhiê

u ho

n + 1

phân sô

tô

i gi

, v

i q ∈ {1; 2; . . . ; n}. Ta s

ng minh r

ang gi

a c

ac m

âu sô

ua c

ac phân sô

ay luôn t

ım

c hai m

âu sô

a m

âu sô

ay chia hê

t cho m

âu sô

kia. Th

ât v

ây

ta biê

u di

ên c

ac m

âu sô

i d

ang 2

.s v

i s l

a sô

e, r ∈ Z

. Sô

ac sô

e kh

ac nhau gi

a c

ac sô

1, 2, 3, . . . , n b

ang



n + 1



( ngh

ıa

ıt ho

n sô

ac m

âu sô

dang x

et), suy ra luôn t

ım

c hai m

âu sô

q = 2

.s v

a q

= 2

a s = s

a r = r

. Khi

o c

o m

ôt m

âu

sô

chia hê

t cho m

âu sô

kia, hay q

= kq. Nhu

ây gi

a c

ac phân sô

c hai sô

ac nhau d

ang

, v

i kq ≤ n. Khi



−



ı c

a hai n

am trong kho

ang c

ô d

. Do

o km − l = 0, v

ı trong

tru

ng h

p ngu

c l

ai th



−



|km −l|

≥

a do

o km = l v

, ngh

ıa l

a hai phân sô

c ch

on tr

ung

nhau.

. 13.15. (Vi

êt nam, 1976) Ch

ng minh r

˘ang tô

n t

ai vô sô

ac sô

ang 5

( n ∈ N), m

a trong c

ac biê

u di

ên th

âp phân c

ua m

ôi sô

o c

không

ıt ho

n 1976 ch

sô

ng liên tiê

i gi

ai. Ta ch

ng minh r

ang v

i m

oi k ∈ N tô

n t

ai vô sô

ac sô

m ∈ N tho

a m

diê

u ki

ên 5

= 1 (mod 2

145

ât v

ây, gi

a c

ac sô

, 5

, . . . , 5

luôn t

ım

c hai sô

(p > q) c

o c

ung sô

trong ph

ep chia cho 2

. Khi

o hi

êu c

ung 5

− 5

= 5

p−q

− 1) chia hê

t cho 2

nghi

a l

a sô

p−q

− 1

a tâ

t c

a c

ac sô

o d

ang 5

r(p−q)

−1 (r ∈ N)

dê

u chia hê

t cho 2

Nhu

ây v

i m

ôi gi

a tr

i m = r(p − q), r ∈ N, ta c

o 5

≡ 1

(mod 2

), t

o 5

m+k

≡ 5

(mod 10

) ngh

ıa l

a k ch

sô

ân c

ung

ua 5

m+k

ung v

i k ch

sô

ân c

ung c

ua 5

. Gi

a s

sô

k tho

a m

> 10

1976

a không nhiê

u ho

n k − 1976 ch

sô

. Do

o gi

a k

sô

ân c

ung c

ua sô

m+k

ı c

o k −1976 ch

sô

ac không, c

1976 ch

sô

on l

ai (liên tiê

p nhau) b

ang 0.

. 13.16. (Ti

êp kh

˘ac, 1979) Trên m

ôt

ng th

˘ang c

o n

+ 1(n ∈ N)

an th

˘ang. Ch

ng minh r

˘ang, ho

˘ac l

a gi

a ch

ung c

o thê

on n + 1

dôi m

ôt không c

˘at nhau, ho

˘ac l

a t

ım

c n + 1

an th

˘ang n

o c

diê

m chung.

i gi

ai. Ta

inh hu

ng bên tr

ai cho

ng th

ang khi n

oi r

ang m

ôt

an n

bên tr

an th

ang kh

ac, nê

dâ

u m

ut bên tr

ai c

an th

ang th

nhâ

t n

bên tr

dâ

u m

ut bên tr

ai c

ang th

hai. M

ôi

an th

ang

anh sô

ang m

ôt sô

ng t

ac sô

1, 2, . . . , n b

ang c

ach sau:

c th

nhâ

an th

ang

ân c

ung bên tr

ai cho tu

ng sô

1. Sau

o m

ôi bu

c tiê

p theo

ta l

ai ch

on trong sô

an th

ang chu

anh sô

an t

ân c

ung

bên tr

ai v

at cho n

o sô

ng, kh

ac v

i c

ac sô

ua nh

ang giao v

i n

o (

anh sô

). Nê

dê

n bu

c n

dâ

y, ta ch

an th

ang, nhu

dô

i v

i n

o không ch

c sô

, th

diê

u n

ay c

o ngh

ıa l

a n

o giao v

i n

an th

ang n

am bên tr

ai n

o v

a c

ng sô

ac nhau. Trong tru

ng h

p n

dâ

u m

ut tr

ai c

ang

c ch

on thu

ôc v

ao n + 1

an th

ang. Nê

c â

146 Chu

ng 13. M

ôt sô

dê

thi vô

ich

ang cuô

i c

ung

anh sô

ı theo nguyên l

y Ðirichlê

ıt nhâ

ôt trong n sô

ng v

i nhiê

u ho

n n

an th

ang, m

a c

an th

ang

o v

i c

ac sô

ıch h

p, không giao nhau.

. 13.17. (Rumani, 1978) C

ac h

am sô

f , g, h : N → N tho

a m

an ba

diê

u ki

ên sau:

a) H

am h(n) không nh

ân gi

a tr

i n

ao t

ai nhiê

u ho

n m

ôt

diê

m n ∈ N.

b) T

âp h

p gi

a tr

i h

am sô

g(n) l

a N.

c) f (n) ≡ g(n ) − h(n) + 1, n ∈ N.

ng minh r

˘ang

dô

ng nhâ

t th

c f (n) ≡ 1, n ∈ N, l

ung.

i gi

ai. Ta ch

ng minh

dô

ng nhâ

t th

c g(n) ≡ h(n) (n ∈ N) . T

o v

diê

u ki

ên b) s

e d

ân

dê

n f (n) ≡ g(n) −h(n) + 1 ≡ 1, n ∈ N.

i bâ

t k

y n ∈ N c

h(n) = g(n) + 1 − f (n) ≤ g (n)

ı f (n) ≥ 1. Gi

a s

ang,

dô

i v

i gi

a tr

i n

o n ∈ N

ang th

g(n) = h(n) không

ung, khi

o h(n) < g(n) = k. Theo

diê

u ki

ên

b) ta t

ım c

ac sô

, n

, . . . , n

k−1

∈ N,

dê

sao cho g(n

) = i khi i =

1, . . . , k −1. B

i v

ây m

ôi sô

trong k sô

h(n

), h( n

), . . . , h(n

k−1

), h( n)

thu

ôc v

ao t

â p h

p {1, 2, . . . , k − 1}, do

o theo nguyên l

y Ðirichlê

am sô

h(n) nh

ân gi

a tr

i n

o nhiê

u ho

n m

ôt lâ

diê

u n

ay tr

diê

u ki

ên a).Kh

ang

inh

c ch

ng minh.

. 13.18. (M

y (N

u U

c), 1979) Ch

ng minh r

˘ang c

ınh c

ua n-gi

dê

u c

o di

ên t

ıch b

e nhâ

t (n > 3) n

ôi tiê

p trong m

ôt n-gi

ac cho tru

ung v

i trung

diê

m c

ac c

anh c

ua n-gi

ac cho tru

i gi

ai. (H

ınh 13.3) Gi

a s

n-gi

dê

u B

, . . . , B

o di

ên t

ıch S

ôi tiê

p trong n-gi

dê

u A

, . . . , A

ên t

ıch S

147

Khi

o nê

u ch

ung không tr

ung nhau th

ı trên m

ôi m

ôt c

anh A

i +1

i i = 1, 2, . . . , n (A

n+1

= A

) c

o m

ôt

ınh B

c x

inh

trên c

anh â

y. Th

ât v

ây, trong tru

ng h

p ngu

c l

ai theo nguyên l

Ðirichlê

ıt nhâ

t c

o m

ôt c

anh, ch

ang h

an A

, ch

a hai

diê

m B

a B

o (

dê

inh, gi

a s

> A

), khi

diê

m B

(

∆A

) c

o thê

am trên c

anh A

a A

ng (v

ı n >

an A

a A

ng ch

eo, m

a không l

a c

anh c

ua n-gi

, . . . , A

), ngh

ıa l

a B

= A

a B

= A

. Ta ch

ng minh r

ang

= A

= . . . = A

ât v

ây tam gi

ac B

a tam gi

ac B

ang nhau, v

= 180

n −2

= 180

−

= 180

−

a B

= B

. B

i v

ây A

= A

. Ta c

ung ch

ng minh tu

ang th

c c

on l

ai. Ð

ai lu

= S

−S

−. . . − S

= S

−nS

ân gi

a tr

i nh

o nhâ

t, khi di

ên t

ıch tam gi

ac B

n nhâ

t. Gi

= a, A

= x, khi

ai lu

sin

(a − x)x. sin

(

−(x −

)

) sin

ân gi

a tr

i l

n nhâ

t khi x =

, ngh

ıa l

a A

= B

. 13.19. (CHLB Ð

c, 1978) M

ôt b

ô gô

m n

con tem cho

i (n>2) mang

ac nh

an hi

êu "1","2","3",. . . ,"n". M

ôi lo

ai nh

an hi

êu c

o n con tem. H

148 Chu

ng 13. M

ôt sô

dê

thi vô

ich

o thê

xê

p tâ

t c

a c

ac con tem â

y th

anh m

ôt d

ay tho

a m

an c

diê

u ki

ên

sau không : v

i m

oi x ∈ {1, 2, . . . , n} gi

a m

ôt con tem mang nh

êu "x" v

a con tem mang nh

an hi

êu "x" tiê

p theo luôn c

o v

ung x

con tem mang nh

an hi

êu kh

ac "x" ?

i gi

ai. Trong m

ôi

an n

am gi

ınh 13.3:

hai con tem liên tiê

p v

i nh

an "n"

dê

u c

o n con tem. C

o n-1

an nhu

ây do

o sô

tem

a con tem

dâ

u tiên mang nh

an hi

êu "n" v

a con

tem cuô

i c

ung v

i c

ung nh

an hi

êu

o c

ông v

i hai con tem v

a n

oi l

( n − 1)n + n, ngh

ıa l

a n

con tem.

ây con tem

dâ

u tiên v

a con tem

cuô

i c

ung trong d

dê

u ph

ai c

ung mang nh

an hi

êu "n".

Trong sô

n con tem v

i nh

an "n-1" ph

ai c

o (theo nguyên l

Ðirichlê)

ıt nhâ

t hai con tem c

ung n

am trong

ıt nhâ

t m

ôt

trong sô

n-1

an kê

trên. Nhu

ng khi

a hai con tem n

ı c

o nhiê

u nhâ

t l

a n-2 con tem;

diê

o mâu thu

ân v

i t

ınh châ

ua d

ay.

. 13.20. (CHLB Nga 1972) Ch

ın

ng th

˘ang c

ung c

o t

ınh châ

t l

ôi

ng th

˘ang chia h

ınh vuông th

anh hai t

ac c

o t

y sô

ên t

ıch

˘ang

. Ch

ng minh r

˘ang c

ıt nhâ

t ba

ng th

˘ang trong sô

o c

ung

di qua m

ôt

diê

i gi

ai. (H

ınh 13.4) C

ng th

ang

a cho không thê

at c

anh kê

nhau c

ua h

ınh vuông ABCD, b

i v

ı nê

u thê

không thê

c hai t

ac, m

a l

a tam gi

ac v

a ng

u gi

ac. Gi

a s

ôt

149

ang c

at c

ac c

anh BC v

a AD t

ai c

diê

m M v

a N. C

ac h

ınh thang

ABMN v

a CDNM c

o c

ng cao b

ang nhau do

o t

y sô

ên

ıch c

ua ch

ung b

ang t

y sô

ng trung b

ınh, t

c l

a MN chia

an th

ang nô

i trung

diê

m c

ua c

ac c

anh AB v

a CD theo t

y sô

Tô

ng sô

diê

m chia c

ng trung b

ınh c

ua h

ınh vuông theo t

sô

a 4 (H

ınh v

e). B

i sô

ng th

ang

a cho l

a 9 v

dê

u ph

qua m

ôt trong sô

diê

m n

oi trên, nên c

o m

ôt

diê

m thu

ôc

ıt nhâ

t 3

ng th

ang.

ınh 13.4:

150 Chu

ng 13. M

ôt sô

dê

thi vô

ich

CHU

NG 14

AI T

ÂP T

. 14.1. M

ôt h

ınh l

âp phu

ng c

o c

anh b

ang 15 ch

a 11.000

diê

ng minh r

ang c

o m

ôt h

ınh câ

u b

an k

ınh b

ang 1 ch

ıt nhâ

t 6

diê

m trong sô

diê

a cho.

. 14.2. Cho F = {a

, a

, . . . , a

} l

a t

âp h

p h

u h

an nh

ng sô

nguyên du

ng v

a x

, x

, . . . , x

, . . . . . . l

a d

ay vô h

an, m

oi phâ

n t

o n

am trong F, ngh

ıa l

a tr

ung v

i m

ôt sô

o trong a

, a

, . . . , a

. Ch

ng minh r

ang v

i m

oi sô

nguyên du

ng bâ

t k

y tô

n t

ai m

ôt sô

phâ

n t

liên tiê

p c

ua d

ay, m

a t

ıch c

ua ch

ung l

a l

uy th

a c

ua m

ôt sô

nguyên n

. 14.3. Cho 5

diê

m P

, P

trong phâ

n trong c

ua m

ôt h

ınh

vuông c

o c

anh 1

n v

i. K

y hi

êu d

a kho

ang c

ach gi

a hai

diê

a P

. Ch

ng minh r

ang

ıt nhâ

t c

o m

ôt trong sô

ac kho

ang c

ach

a c

diê

m nh

o ho

√

. 14.4. Trong m

ôt h

ınh vuông c

o c

anh 50

n v

i , ngu

i ta k

gâ

p kh

uc sao cho m

diê

m trên c

anh h

ınh vuông c

o kho

ang c

ach

o ho

n 1

dê

ng gâ

p kh

uc. Ch

ng minh r

ang

ô d

ai c

ua c

ng gâ

p kh

uc l

n ho

n 1248.

. 14.5. Cho A l

a m

ôt

da gi

ac lô

i v

i di

ên t

ıch S v

a chu vi P, c

on r

152 Chu

ng 14. B

ai t

âp t

a sô

c du

ng. K

y hi

êu M l

a t

âp h

p tâ

t c

a c

diê

m trong m

ang, sao cho v

i m

ôi

diê

m R c

ua M tô

n t

ai m

ôt

diê

m Q thu

ôc A

a kho

ang c

ach gi

a R v

a Q nh

o ho

n ho

ac b

ang r. H

ay t

ım di

ên

ıch c

ua h

ınh M.

. 14.6. Trong h

ınh vuông c

o c

anh b

ang 70, ngu

i ta n

em ba h

ınh

ât v

i k

ıch thu

c 20x10, 25x15 v

a 30x30 v

a ba h

ınh tr

on b

ınh 5. Ch

ng minh r

ang trong h

ınh vuông c

o thê

ich chuyê

n m

ôt

ınh tr

on b

an k

ınh 5 sao cho n

o không c

o nh

diê

m trong chung

i 5 h

ınh

a cho.

. 14.7. Trong m

at ph

ang cho m

ôt

ng gâ

p kh

uc A

. . . A

ınh tr

on b

an k

ınh r, tâm h

ınh tr

on chuyê

ông trên

ng gâ

uc n

ay. Cho L l

ô d

ai c

ng gâ

p kh

uc, c

on F l

a h

ınh sinh

ra b

i s

chuyê

ông c

ua h

ınh tr

on trên

ng gâ

p kh

uc. Ch

minh bâ

ang th

c S(F) ≤ 2Lr + πr

. 14.8. T

âp h

p M l

a h

p m

ôt sô

u h

an nh

an th

ang n

trong (0,1). Kho

ang c

ach gi

a m

ôt sô

diê

m trong M không b

ang δ

dây 0 ≤ δ ≤ 1 . Ch

ng minh r

ang tô

ô d

ai c

ua nh

ang m

a ch

ung t

ao nên M, không vu

t qu

[

] + 1

δ v

a s

anh

a n

ay l

a ch

ınh x

ac.

. 14.9. Trên

ng tr

on b

an k

ınh 1 cho n

diê

m P

, P

, . . . , P

a t

âp

p A t

ao b

i m

ôt sô

u h

an cung không c

at nhau, m

a tô

ô d

ua ch

ung l

a l(A). Ch

ng minh r

ang

a) Nê

u l(A) >

2kπ

, (k = 1, 2, . . . , n − 1), th

ı c

o thê

quay t

âp

p A trên

ng tr

on sao cho

anh c

ua n

o ch

ıt nhâ

t k + 1

diê

trong d

ây P

, P

, . . . , P

153

b) Nê

u l(A) <

2kπ

, (k = 1, 2, . . . , n − 1), th

ı c

o thê

quay t

âp

p A trên

ng tr

on sao cho

anh c

ua n

o ch

a nhiê

u nhâ

t k −1

diê

m trong d

ây P

, P

, . . . , P

. 14.10. Cho t

âp h

p A nh

diê

m trên m

ôt m

at câ

u v

i di

ên t

ıch

n ho

n n

a di

ên t

ıch c

ua m

at câ

u. Ch

ng minh r

ang A ch

ıt nhâ

hai

dâ

u m

ôt

ng k

ınh c

ua h

ınh câ

. 14.11. K

y hi

êu N

, N

, . . . , N

a nh

ng t

âp h

p, m

a ch

ung c

c sau khi nh

ınh c

ua m

ôt lu

i nguyên

c t

ông b

i n

ep t

inh tiê

n, A l

a m

ôt bê

at v

a k l

a sô

nhiên sao cho 1 ≤ k ≤

n −1. Ch

ng minh r

ang

a) Nê

u S(A) >

ı c

o thê

inh tiê

n t

âp h

p A sao cho

anh c

o ch

ıt nhâ

t k + 1

diê

m trong l

a nh

ınh c

ua N

, N

, . . . , N

b) Nê

u S(A) <

ı c

o thê

inh tiê

n t

âp h

p A sao cho

anh c

ua n

o ch

a nhiê

u nhâ

t k − 1

diê

m trong l

a nh

ınh c

, N

, . . . , N

. 14.12. Trong h

ınh vuông v

i c

anh 1

n v

i d

ng gâ

p kh

sao cho m

ng th

ang song song v

i c

anh h

ınh vuông c

gâ

p kh

uc không qu

a m

ôt

diê

m. Ch

ng minh r

ang

ô d

ai c

gâ

p kh

uc nh

o ho

n 2.

. 14.13. Trong m

ôt m

at ph

ang cho 6

diê

m. Nh

an th

ang nô

ac c

diê

c so

n mâ

o ho

ac xanh. Ch

ng minh r

ang v

ach t

ao h

ınh nhu

ây tô

n t

ıt nhâ

t hai h

ınh tam gi

ac c

o c

ac c

anh

ung mâ

u. (c

o thê

hai tam gi

ac kh

ac mâ

u nhau).

154 Chu

ng 14. B

ai t

âp t

CHU

NG 15

I GI

AI V

A G

15.1. L

i gi

ai v

a g

y chu

ng 1

. 1.11. L

i gi

ai: Nê

u tâ

t c

a c

ac ông quan

dê

u quen nhau th

ı vi

êc

xê

p b

an bô

n ngu

i nhu

dê

ra không c

o g

ı kh

o kh

an. Gi

a c

o ông A

a ông B không quen nhau. T

2n −2 ông quan c

on l

ai c

ung nhu

a B c

ıt nhâ

t n ngu

i quen. V

ı n + n = 2n = (2n − 2 ) + 2, th

ı tô

ai hai ông C v

a D, m

a h

o quen A c

ung nhu

B. Khi

o ngu

i xê

o thê

xê

p A

dô

i di

ên B v

a gi

a h

o l

a C

dô

i di

ên D.

. 1.12. G

y: Chia m

ôt c

anh h

ınh vuông th

anh 48

an m

ôi

20m, kho

ang c

ach gi

a 2

an l

a 0,6m, hai

hai

dâ

u d

5,9m. (V

ây 48.20m+47.0,6m+2.5,9m =1000m=1km). C

anh thu

hai chia ra l

am 95

an, kho

a ng c

ach hai

an l

a 0,52m, hai

dâ

u d

ai 0,56m ( v

ây 95.10m+94.0,52m+20,56m= 1000m=1km).

Nhu

ây c

o 48.95=4560 m

anh c

o di

ên t

ıch 200m

a sô

cây ch

ı c

4500, nên c

ıt nhâ

t 60 ô nhu

ây không c

o cây n

ao.

. 1.13. G

y: Ta nh

om c

ac ng

an c

o c

ung sô

ach v

anh dâ

u t

0,1,. . . ,9 (c

ac ng

an ch

a sô

ach

ıt ho

n 10) v

a m

ôt ng

an c

o 10 cuô

a s

không c

o ba ng

an ch

a c

ung sô

ach, th

ı trong c

ac nh

om ta

anh dâ

u c

ıt ho

n ba ng

an c

o c

ung sô

ach (nhiê

u nhâ

t l

a 2), v

ây

156 Chu

ng 15. L

i gi

ai v

a g

ı v

i 10 nh

om trên 10.2=20 ng

an s

ach c

ông v

i m

ôt ng

an 10 cuô

a không cho ta sô

an s

ach l

a 25, d

ân

dê

n vô l

. 1.14. G

y: Ta lâ

y sô

ua ôtô chia cho 10 th

c sô

0, 1, 2, 3,

4, 5, 6, 7, 8, 9. V

ı c

o 11 sô

a 10 sô

ı theo nguyên l

y Ðirichlê

o hai sô

o c

ung sô

. Nhu

ây hi

êu c

ua hai sô

chia hê

t cho 10

ngh

ıa l

a n

o c

ung m

ôt ch

sô

ân c

ung.

. 1.15. L

i gi

ai: G

oi c

ac tr

am chuyê

n tiê

p l

a A, B, C, D, c

ac h

ınh

on v

ng k

ınh l

a c

ng nô

i gi

a c

ac tr

am l

a v

ung bao ph

ua m

ôt trung tâm ph

at s

ong. Ch

ung ta c

o 4 h

ınh tr

on nhu

ây v

ai ch

ng minh r

ang m

ôt

diê

m M bâ

t k

y n

am trong t

ac c

ua 4

dê

c ph

u b

ıt nhâ

t m

ôt h

ınh tr

on. Th

ât v

ây, nê

diê

m M

am trong h

ınh tr

ng k

ınh AB th

ı g

oc AMB ph

ai l

a t

u ho

ang 90

. Ta nô

i M v

i c

ac tr

am A, B, C, D, t

ao ra bô

n g

dô

i v

ac c

anh t

ac. Tô

ng c

ua bô

n g

oc n

ay l

a 360

. Nhu

ây

ıt nhâ

t c

ôt g

oc t

u ho

ac c

ung l

am l

a b

ang 90

. V

ây M thu

ôc m

ôt h

ınh tr

a t

ai M nh

ın c

anh c

ua t

ac du

i m

ôt g

oc t

15.2. L

i gi

ai v

a g

y chu

ng 2

. 2.11. G

y: Áp d

ung Phu

ng ph

ap b

ai 2.2.

. 2.12. G

y: Áp d

ung phu

ng ph

ap b

ai 2.4

. 2.13. G

y: Ð

at b

= a

+ a

+ ··· + a

, k = 1, 2, . . . , 41 v

ung b

ai t

âp trên.

. 2.14. G

y: Nhu

ai 2.8, nê

u M l

a sô

nguyên tô

ung nhau v

10, th

ı t

chia hê

t c

ua l − k =

111 . . . 11.10k cho M, suy ra sô

15.2. L

i gi

ai v

a g

y chu

ng 2 157

111 . . . 11

| {z }

(k-l ch

sô

chia hê

t cho M.

. 2.15. G

y: D

ung phu

ng ph

ap b

ai 2.8. H

ay x

et d

N, NN, NNN, . . . , NNN . . . N

| {z }

(1968 ch

sô

)

. 2.16. L

i gi

ai: Ta viê

t 1998 sô

1997, 19971997, . . .

, 1997 . . . 1997

| {z }

sô

1997 l

˘ap 1998 lâ

. V

a x

et c

ac sô

trong ph

ep chia m

ôi

ôt sô

o cho 1998. R

o r

ang không m

ôt sô

ao trong c

ac sô

a viê

chia hê

t cho 1998 (v

ı 1998 l

a sô

an, m

a c

ac sô

a viê

t l

a l

e), nhu

ây, c

ac sô

ua ph

ep chia

dê

u kh

ac không, v

ı sô

ac sô

n ho

sô

ac sô

o 1998 sô

a sô

ac sô

a 1997), nên t

ım

hai sô

o sô

nhu

nhau, hi

êu c

ua hai sô

o c

o d

ang câ

n t

ım v

chia hê

t cho 1998.

. 2.17. L

i gi

ai: Ta x

et 1997 sô

ang 1998, 19981998,. . . . Sô

cuô

ung trong c

ac sô

ay t

ao th

anh t

1997 nh

om trong bô

n ch

sô

9, 9, 8. Ho

ac m

ôt trong c

ac sô

ay chia hê

t cho 1997 (v

ây,

o l

a sô

ai t

ım), ho

ac t

ım

c hai sô

nhu

nhau trong ph

ep chia cho

1997. Khi

o hi

êu c

ua ch

ung c

o d

ang 19981998 . . . 1998.10

a chia

hê

t cho1997. V

ı 10

a 1997 nguyên tô

ung nhau nên nhân t

nhâ

t, ngh

ıa l

a sô

19981998. . . 1998, chia hê

t cho 1997.

. 2.18. L

i gi

ai: Trong n + 1 sô

m, m

, . . . , m

n+1

ım

c hai sô

o sô

nhu

nhau trong ph

ep chia cho n. Khi

o hi

êu c

ua ch

ung

chia hê

t cho n. Gi

a s

− m

= a.n ho

ac m

( m

l−t

− 1) = a.n. V

( m, n) = 1 nên (m

, n) = 1, ngh

ıa l

a, m

l−t

− 1 chia hê

t cho n. V

ây

l−t

−1 l

a sô

ai t

ım.

158 Chu

ng 15. L

i gi

ai v

a g

15.3. L

i gi

ai v

a g

y chu

ng 3

. 3.11. L

i gi

ai: Ta x

et 10

ac lu

y th

a kh

ac nhau c

ua 3: 3, 3

, 3

, . . . , 3

a c

ac sô

ua ph

ep chia m

ôi lu

y th

o cho 10

. M

ôi

sô

cho m

ôt sô

ac không khi chia cho 10

; sô

ac sô

không l

a 10

−1; sô

ac sô

a 10

. Do

o, t

ım

c hai lu

y th

a kh

nhau 3

a 3

o sô

nhu

nhau trong ph

ep chia cho 10

, ngh

ıa l

−3

= 10

.l ho

ac 3

m−n

−1) = 10

.l. V

ı 3

a 10

nguyên tô

ung nhau nên 3

m−n

−1 chia hê

t cho 10

ac 3

m−n

−1 = 10

.k. T

o suy ra 3

m−n

= 10

.k + 1. Nhu

ây, tr

a l

i: c

o thê

. 3.12. G

y: L

y lu

ân nhu

ai 3.10.

. 3.13. G

y: Ch

y u

= 1986,

ap d

ung phu

ng ph

ap b

ai 3.4.

. 3.14. G

y: L

y lu

ân nhu

trong 3.4. Ch

ng minh r

ang v

i m

oi sô

nhiên m

ıt nhâ

t m

ôt trong c

ac sô

, x

, . . . , chia hê

t cho m. Sau

o d

at m = 38 v

a m = 43.

. 3.15. G

y: Tu

ng t

nhu

3.8 ta x

et b

ô xê

p s-phâ

n t

ng sô

ng. D

ê thâ

y r

ang tô

n tai nh

ng ch

ı sô

i v

a j sao cho

1 ≤ i < j ≤ k

a m

ôi tô

ng trên

dê

u chia hê

t cho k.

15.4. L

i gi

ai v

a g

y chu

ng 4

. 4.11. G

y: Quanh m

ôi

diê

a cho v

ng tr

on b

an k

ınh

. 4.12. G

y: B

ai to

an suy ra t

ai 4.9.

. 4.13. L

i gi

ai: Gi

a s

tô

n tai

diê

m X t

diê

a cho m

a n

o nô

c v

i 6

diê

m X

, X

. Khi

o c

an th

ang XX

15.4. L

i gi

ai v

a g

y chu

ng 4 159

a XX

c d

ng theo m

ôt trong hai c

ach sau

dây (th

c ra c

o c

ach

ba nhu

ng l

a h

ê qu

a c

ua (b) khi ta

dô

i ch

ı sô

)

(a) Nê

u X l

diê

m gâ

n nhâ

dê

n X

a A

, th

ı XX

< X

, ngh

ıa l

a trong tam gi

ac XX

o c

anh X

a l

nhâ

(b) Nê

u X

gâ

diê

m X nhâ

t, c

on X gâ

diê

m X

nhâ

t, th

< XX

< X

ung ta c

ung c

o c

anh X

a l

n nhâ

t trong

tam gi

ac XX

Suy ra

> 60

. Ch

ng minh ho

an to

an tu

ng t

, ch

ung ta

ung c

n ho

n 60

diê

ay không thê

c v

ı tô

ng c

ac g

oc n

ay ph

ai b

ang 360

. Nhu

ây,

ôi

diê

m ch

ı nô

c nhiê

u nhâ

t v

i 5

diê

m thôi.

. 4.14. L

i gi

ai: Ta chia h

ınh tr

on th

anh 6 h

ınh qu

at b

ang nhau (c

ınh t

ai tâm h

ınh tr

on). Khi

o t

ai m

ôi m

ôt h

ınh qu

at, không c

o qu

ôt

diê

m ro

i v

ao (b

i v

ı kho

ang c

ach gi

a hai

diê

m bâ

t k

y trong m

ôt

ınh qu

at không l

n ho

n 1). Nê

u t

ai m

ôi h

ınh qu

at c

o m

ôt

diê

m th

ta c

o thê

ım

c hai

diê

m m

a g

oc gi

a c

ac b

an k

ınh vecto

ung không l

n ho

n 60

a do

o kho

ang c

ach gi

a ch

ung không

n ho

n 1. Do v

ây, c

o thê

on không qu

a 5

diê

. 4.15. L

i gi

ai: Ta thay m

ôi h

ınh vuông b

ang m

ôt h

ınh l

n ho

n gi

an b

i m

ôt

ng c

ach biên c

ua h

ınh vuông m

ôt kho

ang

(

ay gô

m bô

an th

ang

n v

i v

a bô

n cung tr

on c

o b

an k

ınh

ôi m

ôt h

ınh nhu

thê

o di

ên t

ıch b

ang 3 +

, c

on 120 h

ınh

"viê

n ra" s

e ph

u m

ôt di

ên t

ıch không qu

a 120.(3 +

) = 360 + 30π.

Ta bao vây biên c

ua h

ınh ch

ât

a cho b

ang m

ôt d

ai c

o chiê

160 Chu

ng 15. L

i gi

ai v

a g

ông

. Di

ên t

ıch c

ua d

ai b

ang 44. Nhu

ây, di

ên t

ıch tô

ng c

ông

ua d

ai v

a tâ

t c

a c

ac h

ınh

c viê

n ra b

ang 360 + 30π + 44 =

404 + 30π < 404 + 94, 5 < 500, t

c l

a b

e ho

n di

ên t

ıch c

ua h

ınh

ât (S = 20.25 = 500). Do

o, trong h

ınh ch

ât c

diê

m O

không b

i ph

u b

i d

ai v

a c

ac h

ınh vuông

c viê

n ra. Ngh

ıa l

diê

m O c

ach bien c

ua h

ınh ch

ât v

a c

ach m

oi h

ınh vuông m

ôt

kho

ang l

n ho

. H

ınh tr

on b

an k

ınh

o tâm t

ai O l

a h

ınh tr

câ

n t

ım.

15.5. L

i gi

ai v

a g

y chu

ng 5

. 5.11. L

i gi

ai: X

et m

ôt t

âp A bâ

t k

y t

1978 t

âp. V

ı n

o giao v

1977 t

âp c

on l

ai, v

ı v

ây tô

n t

ai phâ

n t

a ∈ A , thu

ôc không

ıt ho

n 50

âp h

p n

ay (th

ât v

ây nê

u m

ôi m

ôt t

40 phâ

n t

ua t

âp A thu

ôc

không nhiê

u ho

n 49 t

âp, th

ı tâ

t c

a c

o không nhiê

u ho

n 40.49 = 1960

âp kh

ac A,

diê

u n

ay không

ung). V

ây phâ

n t

a thu

ôc c

ac t

âp

p A, A

, . . . , A

. Ta s

e ch

ng minh n

o s

e thu

ôc t

âp bâ

t k

y B t

1978 t

âp. Th

ât v

ây không c

o hai t

âp n

ao t

ac t

âp A, A

, . . . , A

a c

o phâ

n t

chung kh

ac v

i a (v

ı hai t

âp bâ

t k

y giao nhau ch

ı c

ôt phâ

n t

chung). Gi

a s

a ∈ B. Khi

o t

âp B c

o v

i m

ôi t

âp

A, A

, . . . , A

ôt phâ

n t

chung kh

ac v

i a, suy ra t

âp B c

o không

ıt ho

n 51 phâ

n t

diê

u n

ay không thê

c. Suy ra phâ

n t

a thu

ôc

tâ

t c

a c

ac t

âp h

. 5.12. L

i gi

ai: M

ôt sô

chia cho 9 th

ı c

o c

ac phâ

n du

{0, 1, 2, . . . , 8}.

Theo nguyên l

y Dirichlê m

ông, trong 55 sô

on ra th

ıt nhâ

t c

ôt nh

om 7 sô

khi chia cho 9 cho c

ung phâ

n du

(nê

u ngu

c l

ai th

ac nh

om ch

ı c

o 6 phâ

n t

ây 6.9=54 m

a ta lâ

y ra nh

ng 55 sô

ung ta k

y hi

êu c

ac sô

o l

a a

, a

, . . . , a

. V

ı a

i +1

≡ a

(mod 9),

15.6. L

i gi

ai v

a g

y chu

ng 6 161

nên a

i +1

− a

∈ {9, 18, . . .}. Ch

ung ta ph

ai ch

ng minh r

ang a

i +1

−

= 9 v

i m

ôt i n

o. Gi

a s

ngu

c l

ai, v

i m

oi i, a

i +1

− a

≥ 18,

diê

u n

ay ngh

ıa l

a a

− a

≥ 6.8 = 108. Ðiê

u n

ay không thê

c v

− a

< 100. Nhu

ây gi

a hai phâ

n t

ua a

, a

, . . . , a

o hai

sô

a hi

êu c

ua ch

ung ph

ai b

ang 9.

. 5.13. G

y: C

ach ch

ng minh nhu

ai 5.10.

. 5.14. L

i gi

ai: (B

an t

e lâ

y h

ınh ) Ch

ung ta xây d

ng lu

i gô

ng h

ınh l

uc gi

ac c

o c

anh

√

. M

ôi h

ınh l

uc gi

ac c

o thê

u b

ng tr

on v

i b

an k

ınh

√

3. C

o thê

ınh to

c sô

ng l

ac m

a ch

ung c

diê

m chung v

i tam gi

dê

a cho l

a 1 + 2 +

3 + ··· + 10 = 55. V

ı 111 = 55 × 2 + 1, nên c

o m

ôt l

uc gi

ac trong

i trên ch

ıt nhâ

t 3

diê

m trong sô

111

diê

a ch

on. Nhu

ây

ng tr

on bao l

uc gi

ac n

ay c

o t

ınh châ

a nêu.

. 5.15. L

i gi

ai: K

y hi

êu A

, A

, . . . , A

a sô

ng ngu

i l

n nhâ

a bâ

t c

hai ngu

i n

ao c

ung không quen nhau gi

an tiê

p. T

diê

ên b

ai ra k ≤ 7. M

ôi ngu

i c

on l

ai trong nh

om quen gi

an tiê

ıt

nhâ

t m

ôt ngu

i trong A

, A

, . . . , A

(tru

ng h

p ngu

c l

ai ch

ung

ta c

o nhiê

u ho

n k ngu

i, m

a hai ngu

i không quen nhau gi

an tiê

p).

ôt trong sô

, A

, . . . , A

ıt nhâ

t 20 ngu

i quen gi

an tiê

p, v

nê

u không

ung nhu

ây, ch

ung ta s

e nh

ân

c tô

ng sô

ng ngu

nhiê

u nhâ

t l

a 7.19 = 133 < 134. C

on l

ai kh

ang

inh r

ang tâ

t c

ng ngu

i quen gi

an tiê

p qua c

ung m

ôt ngu

i l

a quen gi

an tiê

15.6. L

i gi

ai v

a g

y chu

ng 6

. 6.11. G

y: Ðây l

a tru

ng h

p riêng c

ua b

ai 6.1 v

a b

ai 6.2.

162 Chu

ng 15. L

i gi

ai v

a g

. 6.12. G

y: Sô

a cho l

a x

, x

a y

= 1 +

, i = 1, 2, 3, 4.

ı câ

n ch

ng minh r

ang hai sô

dâ

y trong y

, y

oa m

0 ≤

−y

1 + 2y

≤ 2 −

√

3. Phâ

n c

on l

ai tu

ng t

nhu

2.6.

. 6.13. L

i gi

ai: V

inh l

y Fecma ch

ng minh

c r

ang nê

u m

ôt

sô

nguyên tô

p c

o d

ang 4k + 3 chia hê

t cho tô

ng a

+ b

dây

a, b l

a nh

ng sô

nguyên, th

ı p chia hê

t cho t

ng sô

a v

a b. H

ung c

ang th

c sau 2 = 1

+ 1

, k

+ b

) = (ka)

+ (kb)

+ b

)(a

+ b

) = (a

+ b

)

+ (a

− a

)

. 6.14. L

i gi

ai: Cho tu

ng m

ôi sô

i c

an b

âc hai c

ua ch

ınh

o. Nhu

ây khi phân t

ıch ra m

ôi sô

ng v

i c

an b

âc hai c

sô

e. M

a sô

tâ

t c

a c

ac sô

e nh

o ho

n 2k l

a k. V

ây theo nguyên l

Ðirichlê c

o hai sô

trong k + 1 sô

o c

ung phâ

n c

an sô

e, do

o t

y sô

ua n

o s

e l

a l

uy th

a c

ua 2.

. 6.15. L

i gi

ai: Nê

u gi

a c

ac sô

a cho c

o n sô

a khi chia cho n

ung cho nh

ng phâ

n du

ac nhau. Tô

ng c

ua ch

ung s

e chia hê

cho n, v

ı n l

a sô

e. Trong tru

ng h

p ngu

c l

ai,

ap d

ung nguyên l

Ðirichlê.

15.7. L

i gi

ai v

a g

y chu

ng 7

. 7.11. L

i gi

ai: Ch

ung ta thâ

y r

ang m

oi sô

nguyên tô

c s

n 3

dê

u c

o d

ang 6n + 1 ho

ac 6n + 5. V

ı ba sô

nguyên tô

n ho

3 l

âp th

anh m

ôt câ

p sô

ông, nên theo nguyên l

y Ðirichlê ph

ai c

ıt

nhâ

t hai sô

ung d

ang, t

c l

a hi

êu hai sô

o chia hê

t cho 6. G

oi d l

công sai c

ua câ

p sô

ông, th

ı hi

êu c

ua hai sô

y ho

ac l

a d, ho

ac l

15.7. L

i gi

ai v

a g

y chu

ng 7 163

2d. Nhu

thê

ac l

a d|6 ho

ac 2d|6. Ch

y công sai d l

a hi

êu c

ua hai

sô

nguyên tô

n ho

n 3, nên n

o l

a sô

an. Nhu

thê

ı d|3 v

a d|2 suy

ra d|6.

. 7.12. L

i gi

ai: Ta luôn c

o lim

m→+∞

1998

= ∞. N

oi c

ach kh

ac tô

n t

sô

nguyên du

ng m

sao cho ∀m ≥ m

1998

> 9

1998

. X

et m

ôt

sô

nguyên du

ng n bâ

t k

y v

a n c

o k

sô

n = a

. . . a

. Tru

p n

ay ta c

ung ch

> (9k

)

1998

a N > m

(15.1)

u thê

o thê

lâ

y N = max{[1998lg(9k

)] + 1, m

+ 1})

- Ch

ung ta s

e ch

ng minh

( n) < 10

i m

oi i = 1, 2, . . . (15.2)

ât v

ây, ta s

e ch

ng minh b

ang qui n

ap.

1) V

i i = 1 ta c

o u

( n) = (k

+ ··· + k

)

1998

≤ (9k

)

1998

< 10

(do (15.1)). V

ây (15.2)

ung khi i = 1.

2. Gi

a s

(15.2)

ung v

i i = k, ngh

ıa l

a u

( n) < 10

. Ta c

k+1

( n) = f (u

( n)). Theo gi

a thiê

t qui n

ap th

ı u

( n) < 10

. do

( n) c

o không qu

a N ch

sô

, t

c l

a u

( n) c

o d

ang

( n) = a

. . . a

i p ≤ N

Theo

inh ngh

ıa th

k+1

( n) = (a

+ a

+ ··· + a

)

1998

≤ (9N)

1998

. (15.3)

Do N > m

ây t

(1) suy ra

> (9N)

1998

. (15.4)

(15.3) v

a (15.4) suy ra

k+1

( n) < 10

164 Chu

ng 15. L

i gi

ai v

a g

ây (15.2)

ung v

i i = k + 1. Theo nguyên l

y qui n

ap th

ı (15.2)

ung v

i m

oi i = 1, 2, . . ..

- D

ay vô h

an c

ac sô

nguyên du

ng {u

( n)}, i = 1, 2, . . . b

i ch

i 10

nên theo nguyên l

y Ðirichlê ph

ai tô

n t

ai hai ch

ı sô

p < q

sao cho

( n) = u

( n) =⇒ u

p+k

( n) = u

q+k

( n), ∀k

oi c

ach kh

ac d

ay u

( n), i = p, p + 1, .. l

a d

ay tuâ

n ho

an v

i chu k

( n), u

p+1

( n), . . . , u

p+q+1

( n).

. 7.13. L

i gi

ai: Cho a l

a m

ôt sô

y, th

ı {a} = a −[a] g

oi l

a phâ

e c

ua sô

dây k

y hi

êu [a] l

a phâ

n nguyên c

ua sô

a. Xây d

ng d

i nhu

= {u

}

= {u

+ u

}

. . . .

= {u

+ u

+ ··· + u

}

o r

ang v

i m

oi k = 1, 2, . . . , n ta c

o 0 ≤ v

< 1.

Chia [0, 1) ra l

am n + 1 t

âp h

p nhu

∆

= [0,

n + 1

); ∆

= [

n + 1

); . . . ; ∆

= [

n + 1

, 1)

ı c

o c

ac kh

a n

ang sau xâ

y ra

1. Ho

ac tô

n t

ai k m

a v

∈ ∆

∪∆

n+1

- Nê

u v

∈ ∆

, t

c l

a 0 ≤ {u

+ u

+ ··· + u

} <

n + 1

. Ð

= u

+ u

+ ··· + u

:⇒ 0 ≤ {S} <

n + 1

⇔ [ S] ≤ S < [S] +

n + 1

. (15.5)

15.7. L

i gi

ai v

a g

y chu

ng 7 165

ây [S] l

a sô

nguyên gâ

n S nhâ

t, nên t

(15.5) suy ra

diê

u ph

ng minh.

-Nê

u v

∈ ∆

c l

n + 1

≤ {u

+ u

+ ··· + u

} < 1 hay l

n + 1

≤ {S} < 1 ⇔

n + 1

≤ S −[ S] < 1 hay l

n + 1

+ [S ] ≤ S < [S] + 1. (15.6)

(15.6) suy ra [S] + 1 l

a sô

nguyên gâ

n S nhâ

t v

a kh

ac n

o m

ôt

ng ≤ [S] + 1 − ([S] +

n + 1

) =

n + 1

2. Ho

ac l

a c

ac sô

, v

, . . . , v

6∈ ∆

∪ ∆

, v

ây v

, v

, . . . , v

∈

∪

n−1

i =1

∆

. Theo nguyên l

y Ðirichlê tô

n t

ai v

, v

, k > l, thu

ôc c

ung m

ôt

âp h

p ∆

o, 1 ≤ j ≤ n −1.

Ðiê

o c

o ngh

ıa l

n + 1

≤ {u

+ u

+ ··· + u

} <

j + 1

n + 1

≤ {u

+ u

+ ··· + u

} <

j + 1

n + 1

at S

= u

+ u

+ ··· + u

a S

= u

+ u

+ ··· + u

ta c

n + 1

≤ S

−[S

] <

j + 1

n + 1

⇒ [ S

] +

n + 1

≤ S

< [S

] +

j + 1

n + 1

≤ S

−[S

] <

j + 1

n + 1

⇒ [ S

] +

n + 1

≤ S

< [S

] +

j + 1

n + 1

] −[S

] −

n + 1

≤ S

−S

≤ [S

] −[S

] +

n + 1

] −[S

] −

n + 1

≤ u

l+1

+ u

l+2

+ ··· + u

≤ [S

] −[S

] +

n + 1

Nhu

ây d

ay con u

l+1

+ u

l+2

+ ··· + u

o sô

nguyên gâ

n nhâ

t l

] −[S

] v

ô l

êch không qu

n + 1

om l

ai, trong m

oi tru

ng h

p ta

dê

u c

o tô

n t

ai d

ay con tho

an yêu câ

dê

ra.

166 Chu

ng 15. L

i gi

ai v

a g

. 7.14. L

i gi

ai: X

et d

ây sô

= 1a = a, p

= 2a, p

= 3a,. . . ,

m−1

= (m − 1)a. K

y hi

êu q

, q

, . . . , q

m−1

a c

ac sô

ua d

ây trên chia cho m. V

ı theo

diê

u ki

ên b

ai to

an a v

a m l

a nguyên

tô

ung nhau, th

ı tâ

t c

a c

ac sô

trên

dê

u kh

ac không. Nê

u m

ôt

trong c

ac sô

ang 1 th

ı b

ai to

c gi

ai. Nê

u tâ

t c

a c

ac sô

dê

u kh

ac 1. Khi

o m

ôi sô

trong m − 1 sô

, q

, . . . , q

− 1

ang m

ôt trong m − 2 sô

2, 3, . . . , m − 1. Theo nguyên l

y Ðirichlê

ıt nhâ

t hai sô

trong q

, q

, . . . , q

m−1

ang nhau, ch

ang h

an nhu

= q

, i < j. T

o suy ra sô

(j − i)a = p

− p

chia hê

t cho m,

diê

u n

ay không thê

xâ

y ra. S

vô l

y n

ay do gi

a thiê

t không m

ôt sô

trong q

, q

, . . . , q

m−1

ang 1, do

o suy ra

ıt nhâ

t m

ôt trong c

sô

ai b

ang 1.

15.8. L

i gi

ai v

a g

y chu

ng 8

. 8.11. L

i gi

ai: Tru

c tiên ch

ung ta s

e ch

ng minh a + b = c. T

bâ

ang th

c 0 ≤ an −[an] < 1 suy ra |

[an]

−a| <

i m

oi n ≥ 1

sao cho lim

n→∞

[an]

= a. Ch

ung ta c

ung c

o bâ

ang th

c tu

ng t

cho b v

a c. Ch

ung ta lâ

y gi

i h

an c

ang th

[an]

[b n]

[c n]

a nh

ân

c a + b = c.

at a = [a] + α, b = [b] + β

dây 0 ≤ α < 1, 0 ≤ β < 1. Khi

[an] + [bn] = [([a] + α)n ] + [([b] + β)n] = [a]n + [b]n + [ αn] + [βn],

[(a + b)n] = [([a] + [b] + α + β)n] = [a]n + [b]n + [(α + β)n].

Nhu

ây b

ai to

an c

o thê

at l

ai nhu

sau: Ch

ng minh r

ang nê

u a

a b l

a nh

ng sô

trong kho

ang [0, 1) m

a ch

ung tho

a m

ang th

[an] + [bn] = [(a + b)n] (15.7)

i m

oi sô

nhiên n, th

ıt nhâ

t m

ôt trong hai sô

o b

ang 0.

15.8. L

i gi

ai v

a g

y chu

ng 8 167

a s

a 6= 0 v

a b 6= 0. Ch

ung ta s

e ch

ng minh tô

n t

ai sô

nhiên n sao cho

ang th

c (15.7) không

ung. Không mâ

t t

ınh tô

at ch

ung ta c

o thê

a thiê

t r

ang a + b < 1, v

ı nê

u ngu

c l

ai th

(15.7) s

e không

ung th

âm ch

ı v

i n = 1.

a) Ch

ung ta x

et tru

ng h

p a v

a b l

a nh

ng sô

u t

y. Khi

o c

thê

biê

u di

ên ch

ung du

i d

ang a =

dây A, B v

a N l

a nh

sô

nguyên v

a tho

a m

an 0 < A < N, 0 < B < N. D

ê d

ang kiê

m tra

ang (15.7) không tho

a m

an v

i n = N − 1. Th

ât v

ây,

[a(N −1)] = [aN − a] = [A − a] = A + [−a] = A −1,

[b (N − 1)] = [bN −b] = [B − b] = B + [−b] = B −1,

[(a + b)(N −1)] = [A + B − (a + b)] = A + B − [a + b]

= A + B −1

Nhu

ây [a(N − 1)] + [b(N −1)] 6= [(a + b) (N − 1)].

b) Ch

ung ta x

et tru

ng h

p m

ôt trong c

ac sô

a v

a b l

a sô

vô t

ung ta s

e ch

ı ra r

ang c

o m

ôt sô

nhiên n, m

{an} + {bn} ≥ 1. (15.8)

Khi

ang th

c (15.8) s

e suy ra không thê

o (15.7).

a s

a l

a m

ôt sô

vô t

y, theo b

ai 8.1 t

âp h

p nh

ng sô

{an}, n =

1, 2, . . . l

a tr

u m

ât trong kho

ang (0, 1). K

y hi

êu k l

a sô

nhiên l

nhâ

t m

a a + kb < 1. Khi

o tô

n t

ai sô

nhiên n m

a + kb < {an} < 1. (15.9)

Nê

u {bn} ≥ b, th

ı t

inh ngh

ıa c

ua k suy ra

{an} + {bn} > (a + kb) + b = a + (k + 1)b ≥ 1

hay n

oi c

ach kh

ac tô

n t

ai sô

nhiên n m

ang th

c (15.8)

ung.

168 Chu

ng 15. L

i gi

ai v

a g

Nê

u {bn} < b, th

ı v

i vi

êc thêm 1 − b v

ao c

ac vê

ua bâ

ang

c 0 ≤ {bn} < b, ch

ung ta nh

ân

1 − b ≤ b(n −1) − [bn] + 1 < 1

Ðiê

o c

o ngh

ıa l

a [b(n − 1)] = [bn] − 1 v

a {b( n − 1)} ≥ 1 − b.

Ngo

ai ra, tu

ng t

(15.9) suy ra

kb < a(n −1) − [an] < 1 − a < 1

ı thê

[a(n −1)] = [an] v

a {a(n −1)} > kb. Nhu

ng khi

{a(n −1)} + {b(n −1)} > kb + (1 −b) = 1 + (k −1)b ≥ 1,

ı k ≥ 1. Trong tru

ng h

p n

ay (15.8)

ung cho sô

nhiên n −1.

Nhu

ây d

ân

dê

n vô l

y khi m

ôt trong c

ac sô

a v

a b l

a sô

vô t

. 8.12. G

y: Ch

y r

ang {n} ch

ı c

o thê

ân h

u h

an gi

a tr

. 8.13. G

y: L

y lu

ân tu

ng t

nhu

8.4.

. 8.14. G

y: X

et c

ac sô

o d

ang n = 2k

ap d

ung 8.4.

15.9. L

i gi

ai v

a g

y chu

ng 9

. 9.11. G

y: X

et c

ac sô

kx − [kx](k = 0, 1, 2, . . . , n) v

a sô

1, chia

an [0,1] ra n + 1 phâ

n, phâ

n c

on l

ap d

ung phu

ng ph

ay.

. 9.12. G

y: V

i m

ôi c

ach ch

on nh

ng sô

, q

, . . . q

tô

n t

ai sô

nguyên p, v

i n

o 0 ≤ q

+ q

+ ··· + q

− p < 1. Bây gi

chia

an [0,1] ra (n + 1)

an con b

ang nhau.

15.10. L

i gi

ai v

a g

y chu

ng 10 169

. 9.13. G

y: H

ay x

et hai tru

ng h



√

2 −



√

3 −

√

2 v



√

2 −



≤

√

3 −

√

. 9.14. G

y: Tu

ng t

ai trên.

. 9.15. G

y: Gi

a thiê

t v

i m

oi p v

a q th

oa m

|mp

+ npq + sq

| ≥ 1.

15.10. L

i gi

ai v

a g

y chu

ng 10

. 10.11. L

i gi

ai: Ðây l

a s

tô

ng qu

at h

oa b

ai 10.3. C

ach ch

minh ho

an to

an tu

ng t

. Ch

ung ta c

ung t

ao ra lu

i v

i c

ac h

ınh

vuông c

o di

ên t

ıch 1. Sau

o lâ

y m

ôt h

ınh vuông l

am gô

c rô

i t

inh

tiê

n c

ac h

ınh vuông c

o ch

a c

ac m

anh c

ua A vê

ınh vuông gô

Nhu

ây tô

ng di

ên t

ıch nh

ng phâ

n t

inh tiê

n c

ua A s

e l

n ho

n n.

Theo nguyên l

y Ðirichlê m

ông cho di

ên t

ıch suy ra c

ıt nhâ

n + 1 trong sô

ng phâ

n c

ua A

a t

inh tiê

n t

i h

ınh vuông gô

diê

m chung (x

, y

). Nh

diê

m t

ac h

ınh vuông nh

o ban

dâ

inh tiê

dê

diê

m n

ay c

o to

ô l

a (x

, y

) (i = 1, 2, . . . , n + 1), m

− x

a y

−y

(i, j = 1, 2, . . . , n + 1) l

a nh

ng sô

nguyên.

. 10.12. L

i gi

ai: Ch

ung ta x

et h

ınh vuông V, m

a n

o ch

a bê

at A

a c

o c

anh v

ô d

ai n nguyên. Ð

at B = V\A. Ch

ung ta thâ

y ngay

S(V) = n

a S(A) < k, do

o S(B) > n

− k . Bây gi

ap d

ung b

10.11. V

ı thê

B c

o thê

inh tiê

n sao cho n

o ch

ıt nhâ

t n

− k + 1

diê

m v

i to

ô nguyên. K

y hi

êu A

, V

, B

a c

anh c

ua ph

ep t

inh

tiê

n trên c

ua A, V, B tu

ng. R

o r

ang B

= V

. Ch

ung ta s

ng minh r

ang A

a nhiê

u nhâ

t k −1

diê

m v

i to

ô nguyên.

170 Chu

ng 15. L

i gi

ai v

a g

ât v

ây, Gi

a s

ngu

c l

ai ch

ung ta c

o k

diê

m v

i to

ô nguyên

trong A

. V

ı theo c

ach d

ng trên B

ıt nhâ

t n

− k + 1

diê

trong v

i to

ô nguyên v

a B

⊂ V

, A

⊂ V

, A

∩ B

= ∅, Khi

ınh vuông V

ıt nhâ

t n

+ 1

diê

m v

i to

ô nguyên,

diê

u n

không thê

xâ

y ra, d

ân

dê

n vô l

. 10.13. L

i gi

ai: C

ung nhu

ai 10.5 t

ac d

ung lên A ph

ep v

i t

tâm t

ai gô

c t

ô v

a h

ê sô

, ch

ung ta nh

ân

c t

âp h

p m

i A

ı S(A) > 4n nên S(A

) > n. Theo nguyên l

y Ðirichlê m

ông

cho di

ên t

ıch A

ıt nhâ

t n + 1

diê

m kh

ac nhau (x

, y

) (i =

1, 2, . . . , n + 1) m

a x

− x

a y

−y

a nh

ng sô

nguyên.

ung ta x

da gi

ac lô

i nh

o nhâ

t ch

a tâ

t c

a c

diê

m trên. D

ang thâ

y r

ang m

ôi

ınh c

da gi

ac l

a m

ôt trong c

diê

m (x

, y

ınh c

da gi

ac không thu

ôc trong

an n

ao m

a hai

dâ

u l

diê

m n

am trong

da gi

ac. V

ı thê

trong nh

diê

m (x

, y

) tô

ai m

ôt

diê

m m

a không n

am trong

an th

ang nô

i hai

diê

m trong

âp h

diê

a ch

on. Gi

a s

diê

o l

a (x

, y

). C

ung theo b

10.5 cho ta n

diê

m kh

ac nhau v

a kh

diê

m gô

c to

ô, v

i to

nguyên (x

− x

, y

− y

), i = 2, 3, . . . , n + 1,

dê

u n

am trong A. V

ınh

dô

i x

ng nên c

diê

m (x

− x

, y

− y

), i = 2, 3, . . . , n + 1,

ung thu

ôc A.

ung ta s

e ch

ng minh nh

diê

m x

inh theo c

ach trên l

ac nhau t

dôi m

ô t. Th

ât v

ây, gi

a s

ngu

c l

ai ch

ung ta c

− x

, y

−y

) = (x

− x

, y

−y

)

i hai ch

ı sô

o i, j m

a i, j = 2, 3, . . . , n + 1. V

ı v

ây x

) v

a y

( y

+ y

). Nê

u i = j th

ı (x

, y

) = (x

, y

), vô l

y v

15.11. L

i gi

ai v

a g

y chu

ng 11 171

1 6= j. Nê

u i 6= j, th

ı (x

, y

) l

a trung

diê

m c

an th

ang nô

i hai

diê

m (x

, y

) v

a (x

, y

diê

u n

ay không thê

c theo c

ach ch

on.

ng minh trên ch

ı ra r

ang A ch

ıt nhâ

t 2n

diê

m kh

ac nhau

a kh

ac gô

c to

ô, c

o to

ô nguyên. Nhu

diê

m gô

c to

ô c

ung

am trong t

âp A v

a c

o to

ô nguyên, suy ra kê

t lu

ân c

ua b

ai to

an.

. 10.14. G

Ap d

ung b

ai t

âp 10.13.

. 10.15. G

y: C

ach ch

ng minh tu

ng t

10.9.

15.11. L

i gi

ai v

a g

y chu

ng 11

. 11.11. a) T

ai 11.3 suy ra 6 = 9 − (S

+ S

) + S

123

, t

a S

+ S

= 3 + S

123

≥ 3. Do

o m

ôt trong c

ac sô

, S

không nh

o ho

n 1.

b) L

i gi

ai: T

ai 11.3 suy ra 5 ≥ 9 − M

, t

c l

a M

≥ 4. B

i v

da gi

ac c

o thê

c 9.

= 36 c

ap, di

ên t

ıch phâ

n chung c

ôt sô

ac c

o không nh

o ho

≥

. 11.12. L

i gi

ai: G

oi M

, M

, . . . , M

a 6

diê

a cho. Trong m

ôi

tam gi

ac M

ta tô c

anh l

n nhâ

t b

ang mâ

o. Kê

t qu

a s

e l

ôt

an th

ang M

o c

on c

ac c

anh kh

ac s

e không

o. Ch

ı câ

ng minh r

ang tô

n t

ai m

ôt tam gi

ac c

ınh l

a c

diê

a cho v

ba c

anh

c tô mâ

o. Th

ât v

ây, c

anh l

n nhâ

t c

ua tam gi

ac nhu

thê

dô

ng th

i l

a c

anh nh

o nhâ

t c

ua tam gi

ac kh

ac v

ı n

c tô mâ

o. T

ôi

diê

a cho xuâ

t ph

at 5

an th

ang nô

i n

o v

i c

diê

on l

ai. V

ây ho

ıt nhâ

t c

o 3 trong nh

an th

ang n

c tô

mâ

o, ho

ıt nhâ

t c

o 3

an v

ân không

c tô mâ

172 Chu

ng 15. L

i gi

ai v

a g

Nê

u t

diê

m M

xuâ

t ph

at 3

c tô mâ

o (ch

ang h

, M

) th

ı trong ∆M

ıt nhâ

t c

o m

ôt c

anh (l

nhâ

c tô mâ

o, gi

a s

o l

an M

. Thê

ı trong

∆M

tâ

t c

a c

ac c

anh

dê

c tô mâ

Nê

u t

diê

m M

xuâ

t ph

ıt nhâ

t 3

an không

c tô mâ

o (ch

ang h

an 3

an M

, M

) th

ı ta x

et 3 tam gi

, M

. Trong m

ôi tam gi

ac n

ıt nhâ

t c

ôt c

anh

c tô mâ

o, nhu

ng c

anh không ch

ınh M

. V

ây

an M

, M

c tô mâ

o, t

c l

a 3 c

anh c

∆M

dê

u mâ

. 11.13. L

i gi

ai: Tru

c hê

t ta nh

ân x

et c

ıt nhâ

t m

ôt tam gi

ac (B

ai 5.4). Gi

a s

a tam gi

n s

ac, ch

ang h

o. Ðê

riêng P

ta c

on l

ai 6

diê

m v

a ta l

ai c

o m

ôt tam gi

n s

ac không

o P

ınh (B

ai 5.4). Nê

u tam gi

ac n

ay không ch

a c

anh P

c kê

t qu

a, thê

ı c

o m

ôt

diê

m th

sao cho P

ung

a tam gi

o. Tu

ng t

dê

riê

n P

a P

c P

a P

sao cho

a P

a tam gi

Tru

c hê

t ta x

et kh

a n

angl

a 3

diê

m P

, P

a P

không phân bi

êt.

Trong tru

ng h

p n

ay m

ôt trong ch

ung t

ao th

anh v

i P

ôt

ınh t

ên. C

on l

ai 3

diê

m. Nê

u c

ac c

anh gi

a m

ôt trong ba

diê

on l

o v

a 2

ınh c

ua h

ınh t

ên l

o ta s

c hai tam gi

o v

i 2 c

anh r

i nhau, m

ôt tam gi

ac c

o m

ôt

ınh m

i v

a m

ôt c

anh

ua t

ên v

a tam gi

ac kia trên t

ên. Nê

u không, m

ôi

diê

m c

ıt

nhâ

t c

anh

o thu

ôc t

ên. Nhu

thê

ıt nhâ

t m

ôt

ınh c

ua t

ên

nô

i v

i c

a 3

ınh c

on l

ai b

ang c

anh mâ

den. Nê

u c

ap n

ao trong 3

nô

i b

ang c

anh

den th

ı ta c

o m

ôt tam gi

den v

a m

ôt

o. Nê

u không

c hai tam gi

o c

ınh r

i nhau.

15.12. L

i gi

ai v

a g

y chu

ng 12 173

ây ta c

o thê

a s

ang ba

diê

m P

, P

a P

a phân bi

êt. Nê

diê

m, P

a P

c nô

i b

ang c

anh

o th

ı ta

c hai tam gi

a P

. Nê

u không th

ı P

a P

cho theo th

ôt tam gi

o v

a m

ôt tam gi

den.

. 11.14. L

i gi

ai: Lâ

y 1998

ıa

c tô giô

ng nhu

ıa th

hai c

ung ta v

at chô

ng tâ

t c

a ch

ung lên

ıa th

nhâ

t sao cho ch

ung

o tâ

t c

a c

ac v

i tr

ı c

o thê

(nhu

khi quay). Khi

o trên m

ôi h

ınh qu

ıa th

nhâ

t c

o 200 h

ınh qu

at,

c tô, t

c l

a c

o tâ

t c

a 200

ap h

ınh qu

c tô tr

ung nhau. Gi

a s

o n v

i tr

ı c

ıa th

hai c

o không

ıt ho

n 21 c

ap h

ınh qu

c tô tr

ung nhau. Khi

sô

ac h

ınh qu

c tô tr

ung nhau không nh

o ho

n 21n. Do

21n ≤ 200

, t

c l

a n ≤ 1904, 8. B

i v

ı n l

a sô

nguyên, nên n ≤ 1904.

Suy ra c

ıt nhâ

t 1998 −1904 = 94 v

i tr

ı c

o không qu

a 20 c

ap h

ınh

c tô tr

ung nhau.

. 11.15. G

y: Ch

ng minh ho

an to

an nhu

ai 11.2.

15.12. L

i gi

ai v

a g

y chu

ng 12

. 12.11. L

i gi

ai: Lâ

y A

∗

a nh

diê

m trên m

at câ

dô

i x

ng qua

tâm c

ua qu

a câ

u t

diê

m c

ua t

âp h

p A . Theo gi

a thiê

t tô

ên t

ıch c

ua A v

a A

∗

n ho

n di

ên t

ıch m

at câ

u. Theo nguyên l

Ðirichlê cho di

ên t

ıch ch

ung c

diê

m chung. V

ây

diê

m chung

o v

diê

dô

i x

ng c

ua n

o l

a c

diê

dê

u thu

ôc A t

ao ra

ng k

ınh

a câ

. 12.12. L

i gi

ai: V

i m

ôi h

ınh ch

âp ta x

et h

ınh tr

on c

o tâm t

tâm ch

âp v

a b

an k

ınh b

ang

√

. Ta ch

ng minh r

ang nê

u hai

174 Chu

ng 15. L

i gi

ai v

a g

ınh tr

o c

at nhau th

ı hai ch

âp c

ung s

e c

at nhau. Kho

ang

ach gi

a hai tâm c

ua h

ınh tr

on b

ang nhau v

a c

at nhau không l

n hai lâ

n b

an k

ınh c

ua ch

ung, do

o kho

ang c

ach gi

a tâm c

ac ch

âp tu

ng v

i ch

ung không l

n ho

√

. X

et h

ınh ch

ât x

inh b

i c

ac c

anh c

ua h

ınh ch

âp th

nhâ

t v

a tâm c

âp th

hai. S

e c

o m

ôt c

anh c

ua ch

âp th

hai

di qua h

ınh

ât

o, do

o s

e c

at ch

âp th

nhâ

t, b

i v

ô d

ai c

ua c

anh

ang

√

, c

ô d

ng ch

eo h

ınh ch

ât không l

n ho

√

o r

ang trong h

ınh tr

on b

an k

ınh 100 ch

ı c

o thê

c m

ôt

sô

u h

an c

ac h

ınh tr

on b

an k

ınh

√

không c

at nhau.

. 12.13. L

i gi

ai: C

o thê

. Gi

a s

O l

a tâm c

ua ng

u gi

dê

u ABCDE.

Khi

o c

ac h

ınh tr

on n

ôi tiê

p trong c

ac g

oc AOC, BOD, COE, DOA,

EOB c

o t

ınh châ

a nêu.

. 12.14. L

i gi

ai: X

et m

ôt tam gi

dê

u c

o c

anh b

ang 1. Tâ

t c

a 3

ınh c

ua n

o không thê

c tô b

ang c

ac mâ

u kh

ac nhau, do

o ph

o hai

diê

m c

ung mâ

u, v

a kho

ang c

ach gi

ung b

ang 1.

U L

UC A

ÂP H

P V

ANH X

A.1. T

âp h

p v

a To

an t

trên t

âp h

Khi ch

ung ta coi m

ôt

dô

i tu

ng a n

o l

a m

ôt phâ

n t

ua t

âp

p A, th

ı k

y hi

êu l

a a ∈ A, c

on khi a không l

a phâ

n t

ua A th

ı k

êu l

a a 6∈ A .

ôt t

âp h

p A g

oi l

a t

âp h

p con c

ua t

âp h

p B, khi m

oi phâ

ua t

âp h

p A l

a phâ

n t

ua t

âp h

p B, K

y hi

êu l

a A ⊂ B ho

B ⊃ A. Ngh

ıa l

a t

a ∈ A suy ra a ∈ B ho

ac l

a t

a 6∈ B suy ra

a 6∈ A.

âp h

p r

ông không c

o m

ôt phâ

n t

ao, k

y hi

êu l

a ∅. M

dô

ng x

dê

u không n

am trong t

âp h

p r

ông x 6∈ ∅ . T

âp h

p r

ông

dê

u n

am trong m

oi t

âp h

p, ngh

ıa l

a ∅ ⊂ A, v

i m

oi A.

Hai t

âp h

p A v

a B tr

ung nhau khi ch

ung c

o c

ung c

ac phâ

n t

nhu

nhau, k

y hi

êu A = B. Tu

ng , A = B khi v

a ch

ı khi t

a ∈ A suy ra a ∈ B v

a t

a ∈ B suy ra a ∈ A ho

ac A ⊂ B v

a B ⊂ A.

Cho A

, A

, . . . , A

a m

ôt sô

u h

an nh

ng t

âp h

p. H

p c

ng t

âp h

p trên l

a m

ôt t

âp h

p gô

m tâ

t c

a c

ac phâ

n t

a n

thu

ôc v

ao m

ôt trong c

ac t

âp h

p A

, A

, . . . , A

. H

p c

ua c

ac t

âp

p A

, A

, . . . , A

, k

y hi

êu l

a A

∪ A

∪. . . ∪ A

. C

u thê

, a ∈ A

∪

∪. . . ∪ A

ngh

ıa l

a tô

n t

ai m

ôt ch

ı sô

i trong {1, 2, . . . , n } sao cho

175

176 Chu

ng A. T

âp h

p v

Anh x

a ∈ A

Cho A

, A

, . . . , A

a m

ôt sô

u h

an nh

ng t

âp h

p. Giao

ua nh

ng t

âp h

p trên l

a m

ôt t

âp h

p gô

m c

ac phâ

n t

o n

am trong m

oi t

âp h

p A

, A

, . . . , A

. Giao c

ua c

ac t

âp h

, A

, . . . , A

y hi

êu l

a A

∩ A

∩. . . ∩ A

. C

u thê

, a ∈ A

∩ A

∩

. . . ∩ A

ngh

ıa l

a v

i m

oi ch

ı sô

i trong {1, 2, . . . , n} ta c

o a ∈ A

êu c

ua hai t

âp h

p A v

a B l

a m

ôt t

âp h

p, k

y hi

êu A\B, gô

ng phâ

n t

a c

o t

ınh châ

t a ∈ A v

a a 6∈ B.

A.2. Qui n

ap to

an h

oc v

a B

ai to

an tô

Trong t

âp h

p sô

nhiên, c

ung v

i nguyên l

y Ðirichlê c

on m

ôt

nguyên l

y qui n

ap to

an h

oc c

ung hay

c s

ung. D

ang

n gi

ua phu

ng ph

ap qui n

ap to

an h

oc nhu

Cho m

ôt d

ay nh

diê

u kh

˘ang

inh

, K

, . . . , K

, . . . (A.1)

o t

ınh châ

t sau:

a)K

a kh

˘ang

inh

ung.

b) V

i m

ôi sô

nhiên n,nê

u K

a kh

˘ang

inh

dus ng th

ı suy ra

n+1

ung l

a kh

˘ang

inh

ung.

Khi

o tâ

t c

a c

ac kh

˘ang

inh trong d

ay (A.1)

dê

ung.

diê

u ki

ên a)

am b

ao cho K

ung, sau

ap d

ung b)

cho K

ung

ung, tiê

p t

ap d

ung b) cho K

ung

ung v

a tiê

p t

a tr

ınh

o v

i m

oi n. Ðê

minh h

oa ch

ung ta ch

ng minh m

ôt

inh

y vê

tô

p m

a râ

t hay

ap d

ung trong cuô

n s

ach n

ay:

oi t

âp h

p h

u h

an v

i n phâ

n t

ung 2

âp h

p con t

ao b

ac phâ

n t

ac nhau c

ua n

A.3.

Anh x

a trên t

âp h

p 177

i m

oi sô

n ch

ung ta k

y hi

êu

diê

u kh

ang

inh trên b

ang K

Nhu

ây ch

ung ta s

e nh

ân

c d

ay (A.1). V

i n = 1 kh

ang

inh

ung, v

ı m

oi t

âp h

p c

o m

ôt phâ

n t

ung hai t

âp h

p con,

o l

âp r

ông v

a ch

ınh t

âp ( m

ôt phâ

n t

)

dos . V

ây (A.1) c

o t

ınh châ

a).

Bây gi

ung ta ph

ai ch

ng minh b)

ung. Ngh

ıa l

a cho n l

ôt sô

nhiên bâ

t k

y v

a kh

ang

inh K

ung t

c l

a m

oi t

âp h

p c

n phâ

n t

ung 2

âp h

p con. Câ

n ph

ai ch

ng minh r

ang K

n+1

dus ng. Ch

ung ta x

et S l

a t

âp h

p c

o n + 1 phâ

n t

a s l

a m

ôt

phâ

n t

ua n

o. Ch

ung ta chia nh

ng t

âp h

p con c

ua S l

am hai l

p a

gô

m tâ

t c

a c

ac t

âp h

p con c

ua S không ch

a s. L

p a

gô

tâ

t c

a c

ac t

âp h

p con c

ua S ch

a s. Nh

ng t

âp h

p con thu

ôc l

p a

a t

âp h

p con c

ua m

ôt t

âp h

p n phâ

n t

, m

a n

o nh

ân t

S sau

khi b

di phâ

n t

s. Theo gi

a thiê

t qui n

ap sô

ng t

âp h

p con c

ung l

a 2

. M

at kh

ac c

ac t

âp h

p con c

ua l

p a

a tu

ng 1-1

i v

i c

ac t

âp h

p con c

ua S

. Th

ât v

ây, m

oi t

âp h

p con Z ch

a s

ua S ta cho tu

ng v

i t

âp h

p con Z

ua S

ang c

ach t

ta b

i phâ

n t

s. Ngh

ıa l

a sô

ng t

âp h

p con c

ua S trong l

p a

ung v

i sô

ng t

âp h

p con c

ua S

a b

ang 2

. Do

o tâ

t c

a t

âp

p con c

ua S l

a 2

+ 2

= 2

n+1

. Nhu

ây ch

ung ta

a ch

ng minh,

i m

oi n, t

dus ng suy ra K

n+1

dus ng. Ch

ung ta ch

ng minh

c (A.1) c

o t

ınh châ

t b). Suy ra tâ

t c

a c

ac kh

ang

inh

dê

ung.

A.3.

Anh x

a trên t

âp h

ng kh

ai ni

êm sô

phâ

n t

ua m

ôt t

âp h

p n

ay l

n ho

n sô

phâ

n t

ua m

ôt t

âp h

p kia, ngu

i ta xây d

ng kh

ai ni

êm

anh x

dê

ai th

ıch v

a ch

ınh x

ac h

oa trong khi ch

ng minh.

178 Chu

ng A. T

âp h

p v

Anh x

ung ta n

oi r

ang cho m

ôt

anh x

a f : A → B t

âp h

p A v

âp h

p B, khi m

oi phâ

n t

a thu

ôc A cho tu

ng v

i m

ôt phâ

f (a) thu

ôc B. Phâ

n t

f (a) g

oi l

a gi

a tr

i c

anh x

a f v

i phâ

a c

ua A. C

o thê

ı ra nhiê

u v

ı d

u nhu

anh x

a sô

nhiên v

ao sô

an, v

i m

oi n cho tu

ng v

i 2n,. . . .

Ngu

i ta c

a ra m

ôt sô

ınh châ

t c

anh x

a: M

ôt

anh x

f : A → B g

oi l

anh, nê

u t

f (a

) = f (a

)(a

, a

∈ A) suy ra

= a

. N

oi c

ach kh

ac f l

anh khi m

oi phâ

n t

ac nhau c

A cho tu

ng v

i nh

ng phâ

n t

ac nhau c

ua B.

ôt

anh x

a f : A → B g

oi l

a to

anh, nê

u v

i m

oi phâ

n t

ua b c

ua B tô

n t

ai phâ

n t

a thu

ôc A sao cho f (a) = b. C

o nhiê

u v

u vê

anh x

a lo

ai n

ay, nhu

ep chiê

u lên tr

uc to

ô c

ua m

diê

trong m

at ph

ang.

ôt

anh x

a f : A → B g

oi l

a song

anh, khi n

dô

ng th

i l

anh v

a to

anh. Nê

u f : A → B l

a song

anh, th

ı v

i m

oi phâ

n t

ua B tô

n t

ai duy nhâ

t phâ

n t

a thu

ôc A sao cho f (a) = b.

Cho song

anh f : A → B. Nê

u ch

ung ta

at g(b) = a khi

o f (a) = b, ch

ung ta nh

ân

anh x

a g : B → A g

oi l

anh

a ngu

c c

ua f v

a k

y hi

êu l

a f

−1

= g. Nhu

ây f ( f

−1

( b)) = b v

−1

( f (a)) = a v

i m

oi a thu

ôc A v

a b thu

ôc B.

Cho hai

anh x

a f : A → B v

a g : B → C, c

o thê

ao ra

anh x

h : A → C b

ang công th

c h(a) = f (g(a)). K

y hi

êu h = g ◦ f .

AI LI

ÊU THAM KH

[1] Tuyê

n t

âp 30 n˘am t

ap ch

ı To

an h

oc v

a Tuô

i tr

e, NXBGD, 1997.

[2] 255 b

ai to

an sô

oc ch

on l

oc, V.D. Th

uy, T. C. Th

anh, N. N.

am, S

GD H

a tây, 1993

[3] 10000 B

ai to

an so

câ

p - D

ay sô

a gi

i h

an, Phan Huy Kh

ai,

NXB H

a n

ôi, 1997.

[4] C

dê

thi vô

ich to

an c

ac nu

c, Xv. Cônhiagin, G.A.Tônôian,

If. Saru

gin, NXB GD 1996.

[5] C

ac b

ai to

an h

ınh h

oc ph

˘ang, V.V. Praxolov, T

âp II, NXB H

ong 1997.

[6] Zadatri Vsesaiun

c matematitreskii olimpiada, N.B. Vasilev,

A.A. Egorov, Maskova- Nauka 1988.

[7] Matematichskii akvarium V. A. Uphnarovskii, Kishinev " shti-

insa" 1987.(Tiê

ng Nga).

[8] Problem-Solving Through Problems, Loren C. Larson, Spring-

Verlag, 1983.

[9] Princil na Dirichle, Ivan Prodanov, "Narodna Prosveta", Sophia

1988 (Tiê

ng Bungari).

179

180 M

uc l

[10] Zadachi da idvu

nklasna Rabota po matematika,

R.Rusev, K.Bankov, Sv. Slavchev, "Narodna Prosveta", Sophia

1986 (Tiê

ng Bungari).

[11] Sbornhik ot Zadachi za Matematicheski Olympiadi,

St. Budurov, V. Phlorov, "Narodna Prosveta", Sophia 1966

(Tiê

ng Bungari).

ÔI DUNG

i n

dâ

u.. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

Chu

ng 1. Nguyên l

y Ðirichlê v

a v

ı d

u . . . . . . . . . . . . . . . . . . . . . . 5

1.1. Nguyên l

y Ðirichlê . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

1.2. V

ı d

u. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6

1.3. B

ai t

âp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11

Chu

ng 2. Sô

oc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13

2.1. Ph

ep chia sô

nhiên . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13

2.2. V

ıd

u . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14

2.3. B

ai t

âp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20

Chu

ng 3. D

ay sô

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23

3.1. Nguyên l

y Ðirichlê cho d

ay sô

vô h

an. . . . . . . . . . . . . . . . . . 23

3.2. V

ı d

u . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23

3.3. B

ai t

âp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31

Chu

ng 4. H

ınh h

oc. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33

4.1. V

ı d

u . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33

4.2. B

ai t

âp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41

Chu

ng 5. M

ông nguyên l

y Ðirichlê. . . . . . . . . . . . . . . . . . . . . 43

5.1. Nguyên l

y Ðirichlê m

ông . . . . . . . . . . . . . . . . . . . . . . . . . . . 43

5.2. V

ı d

u . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44

181

182 N

ÔI DUNG

5.3. B

ai t

âp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52

Chu

ng 6. B

ai t

âp sô

oc nâng cao . . . . . . . . . . . . . . . . . . . . . . . . 55

6.1. Ð

inh l

y co

an c

ua sô

oc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55

6.2. V

ı d

u . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55

6.3. B

ai t

âp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64

Chu

ng 7. B

ai t

âp d

ây sô

nâng cao . . . . . . . . . . . . . . . . . . . . . . . . 67

7.1. V

ı d

u . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67

7.2. B

ai t

âp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78

Chu

ng 8. Sô

c v

i t

âp tr

u m

ât . . . . . . . . . . . . . . . . . . . . . . . . . 79

8.1. T

âp tr

u m

ât. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79

8.2. V

ı d

u . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80

8.3. B

ai t

âp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87

Chu

ng 9. Nh

ng d

ung kh

ac c

ua nguyên l

y Ðirichle. . 89

9.1. Xâ

p x

ı m

ôt sô

c . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89

9.2. B

ai t

âp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 99

Chu

ng 10. Nguyên l

y Ðirichlê cho di

ên t

ıch . . . . . . . . . . . . . 101

10.1. Ph

at biê

u nguyên l

y Ðirichlê cho di

ên t

ıch . . . . . . . . . . 101

10.2. V

ı d

u. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105

10.3. B

ai t

âp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 117

Chu

ng 11. To

an h

oc tô

p. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 119

11.1. V

ı d

u. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 119

11.2. B

ai t

âp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 127

Chu

ng 12. M

ôt sô

ai t

âp h

ınh h

oc kh

ac . . . . . . . . . . . . . . . . 129

12.1. V

ı d

u. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 129

uc l

uc 183

12.2. B

ai t

âp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 134

Chu

ng 13. M

ôt sô

dê

thi vô

ich . . . . . . . . . . . . . . . . . . . . . . . . 135

Chu

ng 14. B

ai t

âp t

ai . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 151

Chu

ng 15. L

i gi

ai v

a g

y . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 155

15.1. L

i gi

ai v

a g

y chu

ng 1. . . . . . . . . . . . . . . . . . . . . . . . . . . 155

15.2. L

i gi

ai v

a g

y chu

ng 2. . . . . . . . . . . . . . . . . . . . . . . . . . . 156

15.3. L

i gi

ai v

a g

y chu

ng 3. . . . . . . . . . . . . . . . . . . . . . . . . . . 158

15.4. L

i gi

ai v

a g

y chu

ng 4. . . . . . . . . . . . . . . . . . . . . . . . . . . 158

15.5. L

i gi

ai v

a g

y chu

ng 5. . . . . . . . . . . . . . . . . . . . . . . . . . . 160

15.6. L

i gi

ai v

a g

y chu

ng 6. . . . . . . . . . . . . . . . . . . . . . . . . . . 161

15.7. L

i gi

ai v

a g

y chu

ng 7. . . . . . . . . . . . . . . . . . . . . . . . . . . 162

15.8. L

i gi

ai v

a g

y chu

ng 8. . . . . . . . . . . . . . . . . . . . . . . . . . . 166

15.9. L

i gi

ai v

a g

y chu

ng 9. . . . . . . . . . . . . . . . . . . . . . . . . . . 168

15.10. L

i gi

ai v

a g

y chu

ng 10 . . . . . . . . . . . . . . . . . . . . . . . . 169

15.11. L

i gi

ai v

a g

y chu

ng 11 . . . . . . . . . . . . . . . . . . . . . . . . 171

15.12. L

i gi

ai v

a g

y chu

ng 12 . . . . . . . . . . . . . . . . . . . . . . . . 173

u l

uc A. T

âp h

p v

Anh x

a .. . . . . . . . . . . . . . . . . . . . . . . . . . . 175

A.1. T

âp h

p v

a To

an t

trên t

âp h

p. . . . . . . . . . . . . . . . . . . . . 175

A.2. Qui n

ap to

an h

oc v

a B

ai to

an tô

p . . . . . . . . . . . . . . . . . 176

A.3.

Anh x

a trên t

âp h

p . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 177

uc l

uc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 180

NGUY

ÊN H

U ÐIÊ

PHU

NG PH

AP ÐIRICHLÊ V

NG D

UNG

Ebook 1.0 c

ua cuô

n s

ach nguyên gô

c t

an in, c

ac b

an tham

ao, cho

y kiê

n sai s

ot v

a l

i khuyên t

ai b

an. M

oi liên h

ac gi

a: Nguy

ên H

u Ðiê

Ði

ên tho

ai: 0989061951

Email: huudien@vnu.edu.vn

Web: http://nhdien.wordpress.com

iu tr

ach nhi

êm xuâ

t b

an: TÔ Ð

ANG H

Biên t

âp v

a s

a b

an in: Ð

Ô PH

ınh bâ

y v

a chê

an: H

U ÐIÊ

N, PH

U LINH

ınh bâ

y b

ıa: HU

NG LAN

A XU

ÂT B

AN KHOA H

OC V

A K

Y THU

ÂT

70 TR

ÂN HU

NG Ð

AO - H

A N

ÔI

6.6T7.3

KHKT −98

290 - 4-98

In 1000 b

an khô

14, 5 ×20, 5 t

ai Công ty In Công Ðo

an Vi

êt Nam

191 So

n Tây - Ðô

ng Ða - H

a N

ôi. Giâ

y ph

ep XB sô

: 290-22/4/98.

In xong v

a n

ôp lu

u chiê

u th

ang 1 n

am 1999.

Bấm Tải xuống để xem toàn bộ.

| 1/184

| | Tải xuống

Preview text:

, , NGUY˜ ÊN H ˜ UU ÐIÊN , , PHUONG PH´ AP ÐIRICHLÊ , V` A ´ UNG D .UNG , NH` A XU´
ÂT BAN KHOA H .OC V`A K˜Y THU .ÂT H` A N .ÔI - 1999 , L ` OI N ´ OI Ð ` ÂU , , , , , Nguyên l´ y nh˜ ung c´ ai lô`ng v` a c´ ac ch´ u tho ¯ d˜ a ¯
du .oc biê´t ¯dê´n t`u râ´t , , , , ,,
lâu. Ngay trong chuong tr`ınh phô thông co so ch´ ung ta c˜ ung ¯ d˜ a l` am , , , , , quen v´ oi phuong ph´ ap giai to´ an n`
ay. Th .uc ra nguyên l´y n`ay mang , , , tên nh` a b´
ac h .oc ngu`oi Ð´uc Pête Gutxtap Legien Dirichlet (1805- , , , , 1859). Nguyên l´ y ph´ at biêu râ´t ¯ don gian: Nê´u ch´ ung ta nhô´t tho v` ao , , , c´ ac lô`ng m`
a sô´lô`ng ´ıt hon sô´tho, th`ı thê n` ao c˜ ung c´
o m .ôt lô`ng nhô´t ´ıt , nhâ´t hai con tho. , , , , Chı b` ˘ ang nguyên l´ y ¯
don gian nhu v .ây h`ang lo.at c´ac b`ai to´an ¯d˜a , , , ¯ du .oc giai. , , , , Cuô´n s´ ach ¯
du .oc biên so.an l.ai theo t`ung chu ¯dê`c´o liên quan ¯dê´n , , , , , nguyên l´ y, m˜ ôi c´
ach giai trong v´ı d .u cua t`ung chuong l`a ´ap d .ung , , , , ¯ diên h`ınh nguyên l´ y Ðirichlê. B`
ai t .âp giai tru´oc c´o liên quan ¯dê´n b`ai , , , giai sau nên câ`n luu ´ y khia ¯
d .oc s´ach. V´oi mong muô´n c`ung b.an ¯d .oc , , , ,
thao lu .ân m .ôt phuong ph´ap ch´ung minh to´an h .oc v`a hy v .ong cung ,
câ´p m .ôt t`ai li.êu bô ´ıch cho c´ac thâ`y cô gi´ao v`a c´ac em h .oc sinh ham , mê t`ım t` oi trong to´
an h .oc, t´ac gia m.anh d.an biên so.an cuô´n s´ach , , n` ay. Do kha n˘ ang v` a th` oi gian c`
on h .an chê´, cuô´n s´ach ch´˘ac ch´˘an , , , , không tr´ anh khoi thiê´u s´ ot. Ch´ ung tôi mong ¯ du .oc s .u ¯d´ong g´op ´y , , , ,, , kiê´n cua ¯
d .oc gia. Thu g´op ´y xin gui vê`Nh`a xuâ´t ban Khoa h .oc v`a K˜y ,
thu .ât - 70 Trâ`n Hung Ð.ao, H`a N .ôi. 3 , 4 L` oi n´ oi ¯ dâ`u , , , T´ ac gia xin chân th` anh cam on PGS-TSKH Ð˜ ô Hô`ng Tân ¯ d˜ a ¯ d .oc , , v` a ¯ d´ ong g´ op nhiê`u ´ y kiê´n qu´ı b´ au trong qu´ a tr`ınh ho` an chınh ban , thao. , T´ ac gia , , CHUONG 1 NGUYÊN L ´ Y ÐIRICHLÊ V ` A V´I D .U 1.1. Nguyên l´ y Ðirichlê , , , Nguyên l´ y Ðirichlê nhiê`u khi ngu`
oi ta g .oi l`a ¨Nguyên l´y nh˜ung , , ng˘ an k´ eo¨. Ðây l`
a m .ôt nguyên l´y râ´t ¯don gian, ¯d.˘ac bi.êt c´o nhiê`u , ´, ,
ung d .ung trong c´ac l˜ınh v .uc kh´ac nhau cua to´an h .oc. D`ung nguyên , , , , , , l´ y n` ay ngu` oi ta d˜ ê d` ang ch´
ung minh tô`n t .ai m .ôt ¯dô´i tu .ong v´oi t´ınh , , , , , châ´t x´ ac ¯
d.inh. D.ang ¯don gian nhâ´t c´o thê ph´at biêu nhu sau: Nê´u c´
o m v .ât ¯d .˘at v`ao n c´ai ng˘an k´eo v`a m > n th`ı c´o ´ıt nhâ´t m.ôt , ng˘ an k´eo ch´
ua ´ıt nhâ´t hai v .ât. , , , , , , , , Tuy r` ˘ ang v´ oi nguyên l´ y n` ay ngu`oi ta chı ch´ ung minh ¯ du .oc s .u tô`n , , , , , , , , ,
t .ai m`a không ¯dua ra ¯du .oc phuong ph´ap t`ım ¯du .oc v.ât c .u thê, nhung , , , , ,
trong th .uc tê´nhiê`u b`ai to´an ta chı câ`n chı ra s .u tô`n t.ai l`a ¯du rô`i. , , , Nguyên l´ y Ðirichlê l`
a m .ôt ¯d.inh l´y vê`t.âp h .op h˜uu h.an. Ph´at biêu , ch´ınh x´ ac nguyên l´ y n` ay nhu sau: , ,, , Cho A v` a B l`
a hai t .âp h .op không r˜ông c´o sô´ phâ`n tu h˜uu , , ,, , , , , , ,, ,
h .an, m`a sô´ lu .ong phâ`n tu cua A l´on hon sô´ lu .ong phâ`n tu cua , ,, , , , B. Nê´u v´
oi m .ôt qui t´˘ac n`ao ¯dâ´y, m˜ôi phâ`n tu cua A cho tuong , , , ´, , , , ung v´
oi m .ôt phâ`n tu B, th`ı tô`n t .ai hai phâ`n tu kh´ac nhau cua A , , , , ,, , m` a ch´ ung tuong ´ ung v´ oi c`
ung m .ôt phâ`n tu cua B. , , , ,, , , Ðê d˜ ê hiêu ta c´ u cho r` ˘ ang c´
ac phâ`n tu cua t .âp B l`a ¨Nh˜ung ng˘an , , 6 Chuong 1. Nguyên l´ y Ðirichlê v` a v´ı d .u ,, , , , , k´ eo¨ v` a c´ ac phâ`n tu cua A ¯
du .oc ¯d.˘at v`ao c´ac ng˘an k´eo cua n´o. Trong , , ,, , , , ph´ at biêu cua nguyên l´ y trên c´ ac phâ`n tu h˜
uu h .an ¯du .oc t´ınh b`˘ang , ,
sô´t .u nhiên, v`ı v.ây Nguyên l´y Ðirichlê c´o liên quan m.ât thiê´t t´oi t.âp , , , ,
h .op sô´t .u nhiên v`a c´ac t´ınh châ´t cua t.âp h .op sô´n`ay. 1.2. V´ı d .u , , ,
. 1.1. Ðê ky ni.êm 20 n˘am ng`ay giai ph´ong Miê`n Nam, t .ai m.ôt th`anh , , , , , , , , , phô´ ngu` oi ta tô ch´ uc buôi l˜
ê g .˘ap m .˘at nh˜ung ngu`oi 20 tuôi. Ng`ay 30 , , th´ ang 4 n˘ am ¯ d´
o trong buôi g .˘ap m .˘at c´o 400 thanh niên. Ch´ung minh , , , , , , r` ˘ ang c´
o ´ıt nhâ´t hai ngu` oi trong sô´ ngu` oi t´
oi d .u c`ung chung m.ôt ng`ay sinh. , , , L` oi giai. N˘ am 1995 c´ o 365 ng` ay. Ch´ ung ta coi m˜ ôi ng` ay nhu m .ôt , ng˘ an k´ eo v` a ¯ d´ anh sô´ t` u 1 ¯ dê´n 365 (ng˘ an k´ eo cuô´i c` ung l` a ng` ay 31 , th´ ang 12 n˘ am 1995). Ch´ ung ta ¯
d .˘at nh˜ung thanh niên c´o ng`ay sinh , , , , , , tuong ´ ung v` ao c´ ac ng˘ an k´ eo ¯ d´ o. Nhung sô´thanh niên ¯ dê´n d .u l˜ê l´on , , , , , hon sô´ ng˘ an k´ eo, theo nguyên l´ y Ðirichlê c´ o ´ıt nhâ´t hai ngu` oi ¯ du .oc ¯
d .˘at v`ao c`ung m .ôt ng˘an k´eo. Ðiê`u ¯d´o c´o ngh˜ıa l`a h .o sinh c`ung m .ôt ng` ay. J , , , , ,
. 1.2. Trong sinh h .oc ngu`oi ta biê´t r`˘ang sô´t´oc trên ¯dâ`u cua m˜ôi ngu`oi , , , , không qu´ a 200.000 c´ ai. Ch´ ung minh r` ˘ ang trong sô´ ngu` oi cua th` anh , , , , phô´H`
a n .ôi, v´oi sô´dân hon 2.000.000, c´o ´ıt nhâ´t 11 ngu`oi c´o c`ung sô´ t´ oc. , , , , , L` oi giai. Ch´ ung ta x´ et 200.000 ng˘ an k´ eo ¯
du .oc ¯d´anh sô´ t`u 0 ¯dê´n , , 199.999. Ch´ ung ta ¨¯
d .˘at¨ m˜ôi ngu`oi dân H`a n .ôi v`ao m .ôt ng˘an k´eo , , , , ,, , , m` a sô´ t´ oc b` ˘ ang sô´ th´
u t .u cua ng˘an k´eo. Gia su không c´o 11 ngu`oi , , , c´ o c` ung sô´t´
oc, nhu v .ây m˜ôi ng˘an c´o nhiê`u nhâ´t l`a 10 ngu`oi c´o c`ung sô´t´ oc, do ¯ d´ o sô´dân H`
a n .ôi nhiê`u nhâ´t l`a 200.000×10=2.000.000, 1.2. V´ı d .u 7 , , , , ¯ diê`u n` ay không ¯ d´ ung v´ oi gia thiê´t l` a sô´ dân H` a n .ôi l´on hon 2 tri.êu. J , , ,
. 1.3. Ba muoi h .oc sinh l`am b`ai viê´t ch´ınh ta. M.ôt trong sô´h.oc sinh , , ¯ d´
o b.i 14 l˜ôi, c`on c´ac h.oc sinh kh´ac m´˘ac l˜ôi ´ıt hon. Ch´ung minh r`˘ang , , c´ o ´ıt nhâ´t ba ngu` oi m´ ˘ ac sô´l˜ ôi b` ˘ ang nhau. , , , , , L` oi giai. Ch´ ung ta x´ et 15 ng˘ an k´ eo ¯
du .oc ¯d´anh sô´t`u 0 ¯dê´n 14. Ch´ung ta ¨¯
d .˘at¨ m˜ôi h .oc sinh v`ao m .ôt ng˘an k´eo mang sô´ ¯d´ung b`˘ang sô´ l˜ôi ,
cua h .oc sinh n`ay. Nê´u không c´o ba h .oc sinh n`ao c´o sô´l˜ôi b`˘ang nhau, , th`ı trong m˜ ôi ng˘ an mang sô´t` u 0,1,2,. . . ,13 s˜ e c´ o nhiê`u nhâ´t hai h .oc , , , , sinh. Khi ¯ d´
o sô´lu .ong cua nh˜ung h .oc sinh n`ay nhiê`u nhâ´t l`a 28. Nê´u thêm v` ao ¯ d´
o h .oc sinh m´˘ac 14 l˜ôi (trong ng˘an k´eo sô´14) ch´ung ta s˜e , , ,
nh .ân ¯du .oc nhiê`u nhâ´t 29 h .oc sinh viê´t ch´ınh ta, ¯diê`u n`ay d˜ân ¯dê´n , ,
s .u vô l´y v´oi ¯diê`u ki.ên ¯d˜a cho. J , , , . 1.4. Ch´ ung minh r` ˘ ang trong m˜ ôi nh´
om b .an 5 ngu`oi c´o ´ıt nhâ´t hai , , , , , , , , , , ngu` oi c´ o c`
ung sô´lu .ong ngu`oi quen gi˜ua nh˜ung ngu`oi trong nh´om ¯dos. , , , , , Ch´ ung minh r` ˘ ang c`
ung kê´t lu .ân nhu v .ây v´oi nh´om b .an c´o sô´ lu.ong th` anh viên bâ´t k` y. , , , , , L` oi giai. Ch´ ung ta x´ et n˘ am ng˘ an k´ eo, ¯ d´ anh sô´t` u 0 ¯ dê´n 4. M˜ ôi ngu` oi , , , , , ,
tham d .u ¯du .oc ¯d.˘at v`ao ng˘an k´eo mang sô´ tr`ung v´oi sô´ ngu`oi trong , , nh´ om m` a ngu` oi ¯ d´ o quen. , , , , , , a) Nê´u c´
o m .ôt ngu`oi không quen ai ca trong sô´ nh˜ung ngu`oi , , , c`
on l .ai, th`ı ng˘an sô´ 4 l`a trô´ng (v`ı ngu .oc l.ai th`ı ca hai ng˘an 0 v`a 4 , , , ¯ dê`u không trô´ng, d˜ ân ¯ dê´n vô l´
y). Nhu v .ây, m˜ôi ngu`oi trong sô´ 5 , , , , , , , ngu` oi ¯
du .oc ¯d.˘at v`ao c´ac ng˘an mang sô´ 0,1,2,3 v´oi sô´ lu .ong 4 ng˘an. , , , ,, T` u nguyên l´
y Ðirichlê suy ra ´ıt nhâ´t c´ o hai ngu` oi o trong m .ôt ng˘an, , , , , hay l`
a, h .o c´o chung sô´lu .ong ngu`oi quen. , , 8 Chuong 1. Nguyên l´ y Ðirichlê v` a v´ı d .u , , , , , , , ,
b) Nê´u m .oi ngu`oi c´o ´ıt nhâ´t m .ôt ngu`oi quen, m˜ôi ngu`oi s˜e ¯du .oc , , , ¯
d .˘at v`ao c´ac ng˘an mang sô´1,2,3,4, v´oi sô´lu .ong 4 ng˘an. Phâ`n c`on l.ai ´
ap d .ung nguyên l´y Ðirichlê. J , , ,
. 1.5. Trong m .ôt giai b´ong ¯d´a tham d .u 16 ¯d.ôi. M˜ôi c .˘ap hai ¯d.ôi phai , , , , , , ¯ dâ´u v´ oi nhau. Ch´ ung minh r` ˘
ang t .ai m˜ôi th`oi ¯diêm cua giai c´o ´ıt nhâ´t , 2 ¯
d .ôi c´o sô´tr .ân ¯d˜a ¯dâ´u nhu nhau. , , , L` oi giai. Ch´ ung ta x´ et 16 ng˘ an k´ eo ¯ d´ anh sô´t` u 0 ¯ dê´n 15. Ch´ u ´ y r` ˘ ang , , , , , 15 l`
a sô´lu .ong l´on nhâ´t c´ac tr.ân b´ong m`a m˜ôi ¯d .ôi c´o thê ¯dâ´u t.ai th`oi , ¯ diêm ¯ dang x´ et. H˜ ay ¯
d .˘at m˜ôi ¯d .ôi b´ong v`ao ng˘an k´eo mang sô´ b`˘ang , , sô´c´
ac tr .ân m`a ¯d .ôi ¯d˜a ¯dâ´u ¯dê´n th`oi ¯diêm ¯d´o. Ch´ung ta nh.ân ra r`˘ang , , , , , c´ ac ng˘ an 0 v` a 15 không thê ¯ dô`ng th` oi không trô´ng ¯ du .oc v`a nhu v.ây , c´ o thê ´
ap d .ung nguyên l´y Ðirichlê. J , , , ,
. 1.6. Trên tr´ ai ¯
dâ´t sô´ng hon 5 ty ngu` oi, biê´t r` ˘ ang không qu´ a 1% sô´ng , , , ,
trên m .ôt tr˘am tuôi. Ch´ung minh r`˘ang ´ıt nhâ´t c´o hai ngu`oi sinh c`ung
m .ôt giây ¯dô`ng hô`. , , , , , L`
oi giai. Theo duong l.ich hi.ên h`anh 100 n˘am c´o ´ıt hon 37000 ng`ay. , , , M˜ ôi ng` ay c´ o 24 gi` o, m˜ ôi gi` o c´ o 3600 giây. Khi ¯ d´ o 100 n˘ am c´ o ´ıt hon , , , , , , , 3,33 ty giây. T` u ¯
diê`u ki .ên ch´ung ta t`ım ¯du .oc nh˜ung ngu`oi trên tr´ai , , , , , ¯ dâ´t không qu´ a 100 tuôi ´ıt nhâ´t l` a 99% t` u 5 ty ngu` oi ngh˜ıa l` a ´ıt nhâ´t , , , , c´
o 4,9 ty. Vi .êc c`on l.ai ´ap d .ung nguyên l´y Ðirichlê: ¯d.˘at 4,9 ty ngu`oi , v` ao 3,33 ty ng˘ an k´ eo. J , , . 1.7. Trong th` oi gian k´eo d`
ai m .ôt n˘am h.oc m.ôt h.oc sinh giai ´ıt nhâ´t , , ,
m .ôt b`ai t .âp m˜ôi ng`ay. Ðê tr´anh c˘ang th˘ang h.oc sinh giai h`ang tuâ`n , , không qu´ a 12 b`
ai t .âp. Ch´ung minh r`˘ang trong th`oi gian k´eo d`ai liên , ,
t .uc m.ôt sô´ng`ay h.oc sinh n`ay phai giai ¯d´ung 20 b`ai t .âp m˜ôi ng`ay. 1.2. V´ı d .u 9 , , , , , L` oi giai. Ch´ ung ta k´
y hi .êu a1 l`a sô´ lu .ong b`ai t.âp h .oc sinh ¯d˜a giai , , , trong ng` ay ¯
dâ`u tiên, a2 l`a sô´ lu .ong b`ai t.âp ¯d˜a giai trong hai ng`ay , , , ¯
dâ`u, a3 l`a sô´ lu .ong b`ai t.âp ¯d˜a giai trong ba ng`ay ¯dâ`u, v`a v.v. a77 , , , , l`
a sô´ lu .ong b`ai t.âp ¯d˜a giai trong 77 ng`ay ¯dâ`u (11 tuâ`n). Theo gia , ,
thiê´t a77 ≤ 11.12 = 132. Ch´ung ta x´et t .âp h .op c´ac sô´ t .u nhiên
M = {a1, a2, a3, . . . , a77, a1 + 20, a2 + 20, a3 + 20, . . . , a77 + 20}. N´o , ,, , ch´ ua 154 phâ`n tu v` a sô´ l´ on nhâ´t trong ch´ ung l` a a77 + 20 ≤ 152. , Theo nguyên l´ y Ðirichlê trong M c´ o ´ıt nhâ´t hai sô´b` ˘ ang nhau. Nhung c´
ac sô´ a1, a2, a3, . . . , a77 l`a ho`an to`an kh´ac nhau. suy ra tô`n t .ai ak v`a ,
al m`a ak = al + 20, l < k ≤ 77. Nhu v .ây ak − al = 20, ¯diê`u n`ay , , , , , c´ o ngh˜ıa l` a t` u ng` ay th´ u l + 1 ¯ dê´n ng` ay th´ u k h .oc sinh n`ay phai giai ¯ d´ ung 20 b` ai. J , , , , , ,
. 1.8. Trong m .ôt khu t .âp thê sô´ng 123 ngu`oi. Tông sô´ tuôi cua h.o , , , , ,, , l` a 3813. Ch´ ung minh r` ˘ ang c´
o thê ch .on 100 ngu`oi sô´ng o khu t .âp thê , , , , , n` ay, m`
a tông sô´tuôi cua h .o không nho hon 3100. , , , , , , ,, L` oi giai. Ch´ ung ta h˜
ay ch .on 100 ngu`oi nhiê`u tuôi nhâ´t v`a gia su , , , , , , , ,
tông sô´ tuôi cua h .o nho hon 3100. Khi ¯d´o ngu`oi tre nhâ´t trong sô´ , , , , , , , ngu` oi ¯
du .oc ch .on l`a 3100:100=31 tuôi. M.˘at kh´ac ngu`oi n`ay không , , , , , , , tre hon 23 ngu`oi c`
on l .ai theo c´ach ch .on. Khi ¯d´o tông sô´tuôi cua 23 , , , , , , , , ngu` oi n` ay không l´
on hon 23.31=713. Suy ra tông sô´tuôi cua tâ´t ca , , , , ,
m .oi ngu`oi sô´ng trong t.âp thê nho hon 3100+713=3813 d˜ân ¯dê´n vô l´ y. J , , , , . 1.9. N˘
am c .˘ap v.o chô`ng tô ch´uc m.ôt buôi g .˘ap m .˘at. Khi g .˘ap nhau h.o , , , , b´ ˘
at tay nhau, nhung không ai t .u b´˘at tay ngu`oi trong gia ¯d`ınh m`ınh , , , v` a ngu` oi m`
a chô`ng m`ınh (ho .˘ac v.o m`ınh) ¯d˜a b´˘at tay rô`i. C˜ung không , , , ai b´ ˘ at tay c`
ung m .ôt ngu`oi hai lâ`n. Sau cu.ôc g .˘ap ch´uc m`ung ban ¯dâ`u, , , , , , , , , ,
m .ôt ngu`oi ¯d`an ông tên l`a H`ung hoi tâ´t ca nh˜ung ngu`oi c´o m .˘at, kê ca , , 10 Chuong 1. Nguyên l´ y Ðirichlê v` a v´ı d .u , , ,
v .o m`ınh, l`a h.o ¯d˜a b´˘at tay ¯du.oc bao nhiêu lâ`n. H.o nh .ân thâ´y r`˘ang ch´ın , , , , , , , , , , ngu` oi ¯
du .oc hoi ¯dê`u tra l`oi c´ac con sô´kh´ac nhau. Nhu v .ây v.o cua H`ung ¯ d˜ a b´ ˘
at tay bao nhiêu lâ`n? , , , , , , L` oi giai. M˜
ôi m .ôt ngu`oi kh´ach b´˘at tay không qu´a 8 lâ`n. V`ı câu tra l`oi , , , , cua 9 ngu`oi l` a c´ ac sô´kh´ ac nhau nên c´ ac sô´ ¯ d´ o phai l` a 0,1,2,3,4,5,6,7 , , , , , , , v` a 8. Ngu` oi b´ ˘ at tay 8 lâ`n phai l`
a v .o (ho.˘ac chô`ng) cua ngu`oi không , , , , b´ ˘ at tay lâ`n n`
ao (nê´u ngu .oc l.ai th`ı ngu`oi ¯d´o không b´˘at tay 8 lâ`n m`a , , , , , , , nhiê`u nhâ´t chı l`
a 7 lâ`n thôi). Tuong t .u nhu v.ây ngu`oi b´˘at tay 7 lâ`n , , , , , c´ o ngu`
oi v .o (ho.˘ac chô`ng) b´˘at tay m .ôt lâ`n, ngu`oi b´˘at tay 6 lâ`n c´o , , , , , , , , ngu`
oi v .o (ho.˘ac chô`ng) b´˘at tay 2 lâ`n, ngu`oi b´˘at tay 5 lâ`n c´o ngu`oi v .o , , ,
(ho .˘ac chô`ng) b´˘at tay 3 lâ`n. Chı c`on l.ai m .ôt ngu`oi duy nhâ´t b´˘at tay , , , , 4 lâ`n, ¯ d´ o ch´ınh l` a ngu` oi v .o cua H`ung. J , , , ,
. 1.10. M .ôt câu chuy.ên cô t´ıch kê l .ai r`˘ang: M.ôt lâ`n vua H`ung vuong , 18 c´ o m` oi c´
ac quan trong triê`u h .op ngô`i quanh m.ôt c´ai b`an tr`on. Theo , , , ,
l.ênh cua vua, m.ôt c .ân thâ`n ¯d˜a viê´t tên cua m˜ôi quan trên b`an tru´oc , , , chiê´c ghê´ m`
a ông ta phai ngô`i. C´
ac quan trong triê`u không ¯ du .oc b´ao , , tru´
oc nên h .o ¯d˜a ngô`i không theo s´˘ap xê´p ¯d˜a ¯d.inh m`a chiê´m ch˜ô m.ôt , , c´ ach bâ´t k` y. Ch´ ung minh r` ˘
ang ông c .ân thâ`n c´o thê quay chiê´c b`an sao , cho ´ıt nhâ´t c´
o hai ông quan ngô`i ¯ d´
ung v.i tr´ı tên cua m`ınh ? , , , , L`
oi giai. Ð .˘at sô´lu .ong c´ac quan l`a n. Khi ¯d´o m.˘at b`an c´o n tr.ang th´ai, , , , v´ oi c´
ac tr .ang th´ai n`ay ¯dô´i di.ên v´oi c´ac quan l`a biên ¯dê` tên n`ao ¯d´o. , , Ngo` ai ra v´ oi m˜
ôi m .ôt ông quan chı c´o m .ôt tr.ang th´ai, m`a khi ngô`i , , , ¯ d´ ung th`ı ông â´y ¯
dô´i di .ên v´oi ch´ınh tên cua m`ınh trên biên ¯dê` s˜˘an. , , , , Ngh˜ıa l` a, nê´u m˜
ôi tr .ang th´ai cua b`an (v`ı b`an c´o thê xoay ¯du .oc) ta , , , , , , cho tuong ´ ung v´
oi m .ôt sô´ b`˘ang sô´ lu .ong c´ac quan ngô`i ¯d´ung v.i tr´ı , , , , , ,
tên m`ınh, th`ı tông cua tâ´t ca nh˜
ung sô´ nh .ân ¯du .oc (m .oi tr.ang th´ai , , , , b` an) s˜
e không nho hon n. Nhung m .ôt tr.ang th´ai ¯dâ`u tiên cua s´˘ap 1.3. B` ai t .âp 11 , , , , , ,, xê´p b` an cho tuong ´ ung v´ oi 0 (không ai ngô`i ¯ d´ ung ch˜ ô ). Nê´u gia su , , , , , ,
trong n − 1 tr .ang th´ai m.˘at b`an c`on l.ai tuong ´ung v´oi sô´ nho hon 2 , , , , , , , , (t´ uc l` a chı c´
o sô´ 1 ho .˘ac 0), th`ı tông cua n sô´nh.ân ¯du .oc s˜e nho hon , , , , n, ¯ diê`u ¯ d´ o không thê ¯
du .oc. Suy ra t`u n − 1 tr.ang th´ai m.˘at b`an c`on , , ,
l .ai c´o ´ıt nhâ´t m .ôt tr.ang th´ai m`a hai ngu`oi s˜e ¯dô´i di.ên v´oi ch´ınh tên , cua m`ınh. J 1.3. B ` ai t .âp
. 1.11. Trong sân cung ¯
di .ên nh`a vua h .ôi h .op 2n(n ≥ 2) ông quan, , , m˜ ôi ông quan ¯ d˜
a quen biê´t không ´ıt hon n ông c´ o m .˘at t.ai ¯d´o. Ch´ung , , , , , , , minh r` ˘ ang ngu`oi xê´p b` an tr` on c´ o thê xê´p ¯
du .oc m˜ôi b`an 4 ngu`oi sao , , , , , , , cho m˜ ôi ngu` oi ¯ d´ ung gi˜ua hai ngu` oi quen cua m`ınh. ,
. 1.12. M .ôt khu r`ung thông c´o d.ang h`ınh vuông m˜ôi chiê`u 1km. , , , Trong r` ung c´
o 4500 cây thông, cây to nhâ´t c´ o ¯ du` ong k´ınh 0,5m. , , , Ch´ ung minh r` ˘ ang trong khu r` ung c´ o ´ıt nhâ´t 60 manh ¯ dâ´t, di .ên t´ıch , m˜ ôi manh 200m2, không c´ o m .ôt cây thông n`ao. ,
. 1.13. Trong m .ôt gi´a s´ach c´o 25 ng˘an. Ta thâ´y c´o m .ôt ng˘an ch´ua , , , 10 cuô´n, c` on c´ ac ng˘ an kh´ ac ch´ ua sô´ s´ ach ´ıt hon. Ch´ ung minh r` ˘ ang , , , , , c´ o ´ıt nhâ´t ba ng˘ an s´ ach ch´ ua c` ung sô´ s´ ach nhu nhau (kê ca nh˜ ung ng˘ an không c´ o s´ ach). , , , , ,
. 1.14. T .ai m .ôt th`anh phô´ biên xe ôtô ¯du .oc ¯d´anh sô´ b`˘ang tô h .op , , , , , ch˜ u c´ ai rô`i ¯ dê´n d˜ ay sô´. Ch´ ung minh r` ˘
ang trên m .ôt ¯do.an ¯du`ong c´u , , c´ o 11 chiê´c ôtô ¯ di qua th`ı bao gi` o c˜ ung c´ o hai chiê´c ôtô c´ o c` ung ch˜ u sô´t .ân c`ung. , , , ,, ,
. 1.15. M .ôt chiê´c hô` l´on ¯du .oc b .oc boi 4 tr.am chuyên tiê´p s´ong , , , , thông tin. Gi˜
ua hai tr .am ngu`oi ta xây d .ung c´ac trung tâm ph´at s´ong , , , , , , ,, v`
a nh .ân s´ong, ¯du`ong s´ong bao phu l´on nhâ´t l`a ¯du`ong tr`on c´o tâm o , , 12 Chuong 1. Nguyên l´ y Ðirichlê v` a v´ı d .u , , trung tâm v` a ¯
di qua hai tr .am. Ch´ung minh r`˘ang v´oi bô´n trung tâm ,, , , , , , , o c´ ac ¯
do .an gi˜ua cua t`ung c.˘ap tr.am th`ı to`an b .ô m.˘at hô` s˜e ¯du .oc phu s´ ong thông tin. , , CHUONG 2 S ´ Ô H .OC , 2.1. Ph ´ ep chia sô´ t .u nhiên , Trong c´ ac ph´
ep t´ınh trên sô´ nguyên: c .ông, tr`u, nhân, chia, th`ı, ph´ ep chia l` a râ´t ¯
d .˘ac bi.êt. Ph´ep chia c´o h`ang lo.at t´ınh châ´t m`a tâ´t ca , c´ ac ph´ ep t´ınh c`
on l .ai không c´o. V´ı d .u c´ac ph´ep to´an ¯dê`u th .uc hi.ên , , , , , , v´ oi sô´0 ¯
du .oc, nhung riêng ph´ep chia cho sô´0 th`ı không ¯du .oc. Ph´ep , , , chia không chı ¯
d .˘ac bi.êt v´oi ph´ep chia cho 0. V´oi c´ac ph´ep t´ınh c .ông, , , , tr`
u, nhân trên sô´nguyên cho ta sô´nguyên, nhung v´ oi ph´ ep chia th`ı , t´ınh châ´t ¯ d´ o không c` on ¯ d´ ung v`ı không phai l´ uc n` ao ta c˜ ung nh .ân , , , , , ¯
du .oc sô´nguyên sau ph´ep chia. Nh`o nh˜ung d.i bi.êt cua ph´ep chia m`a , , , trong to´
an h .oc xây d .ung h˘an m .ôt l´y thuyê´t vê` ph´ep chia nh˜ung sô´ , , , nguyên. Nh˜
ung v´ı d .u v`a b`ai t.âp chuong n`ay c´o liên quan m.ât thiê´t , gi˜ ua ph´ ep chia v` a nguyên l´ y Ðirichlê, nên ch´ ung ta nh´ ˘ ac l .ai ¯d.inh ngh˜ıa ph´ ep chia: , , Cho a v`a b l`a nh˜ ung sô´ nguyên, v´ oi b > 0. Ch´ ung ta n´ oi r` ˘ ang a
chia hê´t cho b, k´y hi .êu l`a b|a, khi tô`n t.ai m .ôt sô´ nguyên q sao cho , , ¯ d˘ ang th´ uc sau ¯ d´ ung a = bq. , , , , , , Ch´ ung ta thu`
ong g .oi sô´ a l`a b.ôi cua b, ho.˘ac b l`a u´oc cua a. Sô´q , , , ,
g .oi l`a thuong sô´ cua ph´ep chia a cho b. Trong ph´at biêu ¯d.inh ngh˜ıa ,
trên, nê´u không tô`n t .ai m .ôt sô´ q n`ao ca, th`ı ch´ung ta n´oi r`˘ang a , , 14 Chuong 2. Sô´h .oc
không chia hê´t cho b v`a k´y hi .êu l`a b 6 |a. , , , , T` u ¯
d.inh ngh˜ıa ch´ung ta d˜ê d`ang ch´ung minh ¯du .oc c´ac t´ınh châ´t sau , 1) V´
oi m .oi sô´ nguyên a > 0 ch´ung ta c´o a|a, Ph´ep chia hê´t c´o , t´ınh phan x .a.
2) Nê´u b|a v`a a|c th`ı b|c- ph´ep chia hê´t c´ o t´ı nh b´ ˘ ac câ`u.
3) Nê´u b|a v`a b|c, th`ı b|(ac). ,
4) Nê´u a, b, m, n l`a nh˜ung sô´ nguyên v`a nê´u c|a v`a c|b, th`ı c|(ma + nb). ,
Ð.inh l´y sau ¯dây gi˜u vai tr`o quan tr .ong cho ph´ep chia m .ôt sô´
nguyên cho m .ôt sô´nguyên. , V´
oi hai sô´ nguyên bâ´t k` y a v`
a b sao cho b > 0, tô`n t .ai duy , , nhâ´t nh˜
ung sô´ nguyên q v` a r thoa m˜ an a = bq + r v`
a 0 ≤ r < b. , , , C`
on râ´t nhiê`u t´ınh châ´t kh´ ac cua sô´ nguyên c˜ ung nhu sô´ th .uc , , , , nhung ch´ ung ta không ¯ di theo hu´ ong n` ay, m` a chı d` ung c´ ac t´ınh châ´t , , ,
cua sô´h .oc v`a Nguyên l´y Ðirichlê ¯dê giai c´ac b`ai to´an. 2.2. V´ıd .u , , ,
. 2.1. Cho k l`
a m .ôt sô´t .u nhiên, A l`a t .âp h.op gô`m k + 1 sô´t .u nhiên. , ,, Ch´ ung minh r` ˘ ang c´
o ´ıt nhâ´t m .ôt hi.êu hai phâ`n tu trong A chia hê´t cho k. , , ,, , L`
oi giai. G .oi a1, a2, . . . , ak+1 l`a c´ac phâ`n tu cua A, c`on b1, b2 , . . . , bk+1 , , , l` a nh˜ ung sô´ du cua ph´ ep chia c´ ac sô´ trên cho k. Khi ¯ d´ o a1 = ,
kc1 + b1, a2 = kc2 + b2, . . . , ak+1 = kck+1 + bk+1,v´oi c´ac sô´ nguyên
c1, c2, . . . , ck+1 sao cho 0 ≤ b1 ≤ k − 1, 0 ≤ b2 ≤ k − 1, . . . , 0 ≤ ,, , , , ,
bk+1 ≤ k − 1. M .ôt phâ`n tu bâ´t k`y as thu .ôc A cho tuong ´ung v´oi sô´ 2.2. V´ıd .u 15 , , , , , ,, ,
du bs cua n´o.G .oi t.âp h .op c´ac sô´du l`a B. Nhu v.ây, m˜ôi phâ`n tu cua A , , , , , , ,, , , , ¯
du .oc ¯d.˘at tuong ´ung v´oi m .ôt phâ`n tu cua t.âp h .op B, gô`m tâ´t ca c´ac , , , , ,, , , sô´ nguyên t` u 0 ¯
dê´n k − 1. Nhung sô´ lu .ong phâ`n tu cua A theo gia , , thiê´t l` a k + 1, c` on B c´
o sô´ lu .ong k. Theo nguyên l´y Ðirichlê suy ra ,, , ,
tô`n t .ai hai phâ`n tu kh´ac nhau cua A c´o c`ung sô´du. Ðiê`u ¯d´o ngh˜ıa l`a, , ,
tô`n t .ai hai chı sô´kh´ac nhau s v`a t v´oi as = kcs + bs v`a at = kct + bs , , , sau khi tr` u ¯ di cho nhau ta ¯
du .oc at − as = k(ct − cs). J , ,
. 2.2. Cho A m .ôt t .âp h.op bâ´t k`y gô`m 101 sô´t .u nhiên, m˜ôi sô´không , , , l´ on hon 200. Ch´ ung minh r` ˘ ang trong A c´
o ´ıt nhâ´t hai sô´ m` a m .ôt sô´ n`
ay chia hê´t cho sô´kia. , , , , , , , , L` oi giai. M˜ ôi sô´ a cua A c´ o thê biêu di˜ ên du´ oi d .ang a = 2kb v´oi k l`a , , sô´ nguyên không âm, c`
on b l`a m .ôt sô´ le. V´oi m˜ôi sô´ a thu .ôc A cho , , , , , , ,, tuong ´ ung v´
oi sô´ b trong s .u biêu di˜ên o trên. B`˘ang c´ach n`ay, m˜ôi ,, , , , , , , , ,, , , phâ`n tu a cua A ¯
du .oc ¯d.˘at tuong ´ung v´oi m .ôt phâ`n tu cua t.âp h .op B , , , , , ,, gô`m c´ ac sô´le gi˜ ua 1 v`
a 200. Nhung t .âp h .op B chı c´o 100 phâ`n tu v`ı ,, , , , ,, , ,
v .ây sô´ phâ`n tu cua A l´on hon sô´ phâ`n tu cua B. Ta c´o thê ´ap d .ung ,, nguyên l´
y Ðirichlê, suy ra tô`n t .ai hai phâ`n tu kh´ac nhau a1 v`a a2 , , , , , ,
thu .ôc A m`a ch´ung tuong ´ung v´oi c`ung m .ôt sô´cua t.âp h .op B. Ngh˜ıa l`
a, a1 = 2k1b, a2 = 2k2b v`a nê´u k1 < k2, th`ı sô´ a2 chia hê´t cho a1. J , ,
. 2.3. Cho M l`
a t .âp h.op bâ´t k`y gô`m 75 sô´t .u nhi.ên m`a m˜ôi sô´không , , , , , , , l´ on hon 100. Ch´ ung minh r` ˘ ang v´ oi m˜
ôi sô´ t .u nhiên l nho hon ho .˘ac ,, , b` ˘
ang 49 tô`n t .ai hai phâ`n tu cua M c´o hi.êu l`a l. , , ,, , L`
oi giai. G .oi c´ac phâ`n tu cua M l`a x1, x2, . . . , x75. K´y hi.êu A l`a t.âp , , , , , ,
h .op c´ac sô´t .u nhiên t`u 1 ¯dê´n 150. V´oi m˜ôi sô´1, 2, 3 . . . , 75 cho tuong ´, , , , ung v´ oi c´
ac sô´ x1, x2, . . . , x75, c`on c´ac sô´ 76, 77, 78, . . . 150 lâ`n lu .ot ´, , ung v´
oi x1 + l, x2 + l, . . . , x75 + l. V`ı xm ≤ 100(m = 1, 2, . . . , 75) v`a , , 16 Chuong 2. Sô´h .oc ,, , , , , ,
l ≤ 49 th`ı xm + l < 150. Suy ra m˜ôi phâ`n tu cua A tuong ´ ung v´ oi ,, , , , ,
m .ôt phâ`n tu cua B gô`m nh˜ung sô´t .u nhiên t`u 1 ¯dê´n 149. V`ı sô´phâ`n ,, , , , ,, , tu cua A l´
on hon sô´ phâ`n tu cua B, theo nguyên l´y Ðirichlê tô`n t .ai ,, , , , , , hai phâ`n tu kh´ ac nhau cua A, m`a ch´ ung tuong ´ ung v´ oi c` ung m .ôt ,, , , , , , phâ`n tu cua B. Nhung v´ oi c´ ac gi´
a tr.i kh´ac nhau cua m t`u 1 ¯dê´n 75 , , , , , , , ¯
du .oc cho tuong ´ung v´oi c´ac gi´a tr.i kh´ac nhau cua x1 ¯dê´n x75 trong , , , , ,, , , , , ,
B. Tuong t .u c´ac gi´a tr.i cua m o khoang 76 ¯dê´n 150 tuong ´ung v´oi , , c´ ac gi´
a tr.i kh´ac nhau trong khoang c`on l.ai. T`u ¯d´o suy ra tô`n t.ai xm v`
a xn m`a xm = xn + l, ngh˜ıa l`a xm − xn = l. J , , ,
. 2.4. Cho k ≥ 1 v` a n ≥ 1 l` a nh˜
ung sô´t .u nhiên v`a A l`a t .âp h.op gô`m , , , ,
(k − 1)n + 1 sô´nguyên duong, m˜ ôi sô´n` ay ¯
dê`u nho hon ho .˘ac b`˘ang kn. , ,, , , , , Ch´ ung minh r` ˘ ang ´ıt nhâ´t c´
o m .ôt phâ`n tu cua A c´o thê biêu di˜ên nhu , , ,,
tông cua k phâ`n tu trong A. , , , , , L` oi giai. V´
oi k = 1 b`ai to´an hiên nhiên l`a ¯ d´ ung, ch´ ung ta gia thiê´t ,
k ≥ 2. K´y hi .êu m l`a sô´ nho nhâ´t thu .ôc A. D˜ê thâ´y r`˘ang m ≤ n v`a , , ,
tô`n t .ai ¯d´ung n − m sô´ thu .ôc A m`a ch´ung l´on hon m nhung không , , vu .ot qu´a kn. , , Ðê ch´ ung minh b` ai to´ an ch´
ung ta t`ım hai sô´ x v`a y thu .ôc A sao ,
cho x = y + (k − 1)m; ngh˜ıa l`a biêu di˜ên m .ôt sô´ n`ao ¯d´o thu .ôc A , , th`
anh tông k sô´h .ang thu .ôc A trong ¯d´o c´o k − 1 sô´h.ang b`˘ang m. Chı
câ`n t`ım sô´ x thu .ôc A m`a x > (k − 1)m v`a x − (k − 1)m thu .ôc A. ,
Th .ât v.ây, trong khoang ∆ = ((k − 1)m, kn] c´o kn − (k − 1)m =
k(n − m) + m sô´ nguyên. V`ı k ≥ 2, nên (k − 1)m ≥ m, theo nh .ân x´ et ban ¯ dâ`u suy ra c´
o nhiê`u nhâ´t n − m sô´ trong ∆ không thu .ôc A. , Ðiê`u n` ay ngh˜ıa l` a A ch´
ua ´ıt nhâ´t s = k(n − m) + m − (n − m) = ,
(k − 1)(n − m) + m sô´. Nhung s ≥ n, v`ı (k − 2)(n − m) ≥ 0. G .oi ,
a1, a2, . . . , as thu .ôc A, v´oi (k − 1)m < ai ≤ kn, i = 1, 2, . . . , s. Khi ¯d´o 2.2. V´ıd .u 17 , , nh˜
ung hi .êu a1 − (k − 1)m, a2 − (k − 1)m, . . . , as − (k − 1)m l`a nh˜ung , sô´nguyên kh´
ac nhau trong khoang [1, kn]. Nê´u m .ôt sô´n`ao ¯d´o trong ch´
ung không thu .ôc A, th`ı theo nguyên l´y Ðirichlê ch´ung ta nh.ân , , , , ¯
du .oc s ≤ n − 1, v`ı ngo`ai A c´o ¯d´ung n − 1 sô´trong khoang n`ay. Nhu , , , ,
v .ây tr´ai v´oi bâ´t ¯d˘ang th´uc ¯d˜a ch´ung minh s ≥ n. Suy ra tô`n t.ai m .ôt
hi .êu ai − (k − 1)m thu .ôc A. J , , , , , , . 2.5. Ch´ ung minh r` ˘ ang t`
u n + 1 sô´duong kh´
ac nhau nho hon 2n, c´ o , , , , ,
thê ch .on ¯du.oc ba sô´sao cho tông hai sô´trong ch´ung b`˘ang sô´th´u ba. , , , L` oi giai. K´
y hi .êu 0 < a1 < a2 < . . . < an+1 l`a nh˜ung sô´ ¯d˜a cho. Ch´ ung ta x´ et c´
ac hi .êu sô´ a2 − a1, a3 − a1, . . . , an+1 − a1 v`a c´ac sô´ , , ,
a2, a3 . . . , an+1. V`ı tâ´t ca c´ac sô´ n`ay ¯
dê`u nho hon 2n nên c´ac sô´ trên , , , , , chı n` ˘
am trong khoang 1, 2, . . . , 2n − 1. Nhu v .ây ch´ung ta s˜e t`ım ¯du .oc ,, , ,, ,
m .ôt sô´o nh´om th´u nhâ´t b`˘ang m .ôt sô´o nh´om th´u hai: ak − a1 = al, suy ra ak = a1 + al. J , , . 2.6. Ch´ ung minh r` ˘ ang v´
oi m .ôt sô´ bâ´t k`y n tô`n t .ai m.ôt sô´ c´o d .ang 111 . . . 000 m`
a chia hê´t cho n. | {z } , n ch˜ u sô´ , , , , L` oi giai. Ch´ ung ta x´
et nh˜ung sô´ 1, 11, 111, . . . , 111 . . . 111 v`a nh˜ung | {z } , n ch˜ u sô´ , sô´ du khi chia d˜
ay sô´ trên cho n. V`ı d˜ay sô´ ¯ d˜ a cho gô`m n phâ`n ,, , , , , tu, nên nh˜ ung sô´ du duong kh´ ac nhau khi chia ch´ ung cho n c´ o sô´ , , , ,
lu .ong n − 1. C´o thê gia thiê´t không c´o m .ôt sô´ n`ao trong d˜ay trên , , , , ,
chia hê´t cho n v`ı nê´u ngu .oc l.ai th`ı b`ai to´an ¯d˜a ¯du .oc giai. Khi ¯d´o s˜ e c´ o hai sô´ trong ch´
ung, v´ı d .u 111 . . . 111 v`a 111 . . . 111, l > k, | {z } , | {z } , k ch˜ u sô´ l ch˜ u sô´ , m` a khi chia ch´ ung cho n s˜e cho c`
ung m .ôt sô´ du. Do ¯d´o l − k = , , 18 Chuong 2. Sô´h .oc 111 . . . 000 s˜ e chia hê´t cho n. J | {z } , , (l-k ch˜ u sô´1, k ch˜ u sô´0) , , ,
. 2.7. Cho p l` a sô´nguyên tô´l´ on hon 5. Ch´ ung minh r` ˘ ang tô`n t .ai m.ôt sô´c´
o d .ang 111 . . . 111 m`a chia hê´t cho p. , , L` oi giai. Ta x´ et d˜
ay sô´1, 11, 111, . . . , 111 . . . 1 . Nê´u trong d˜ay trên | {z } , (p ch˜ u sô´) , , , , không c´ o sô´ n`
ao chia hê´t cho p, th`ı ta cho tuong ´ ung m˜ ôi sô´ v´ oi sô´ , , , , , du cua ph´
ep chia. T .âp h .op c´ac sô´du chı c´o 1, 2, . . . , p − 1 gô`m p − 1 ,, , ,
phâ`n tu (v`ı 0 không thê c´
o trong t .âp n`ay). Nhung v`ı ch´ung ta c´o p ,,
sô´ o d .ang trên, nên theo nguyên l´y Ðirichlê tô`n t.ai hai sô´ c´o c`ung , , ,, , sô´du. Gia su c´ ac sô´ ¯ d´ o l` a 111 . . . 1 v` a 111 . . . 1 v´ oi m > n. Khi | {z } , | {z } , (m ch˜ u sô´) ( n ch˜ u sô´) ¯ d´ o 1 ≤ n < m ≤ p. V .ây 111 . . . 1 − 111 . . . 1 = 111 . . . 000 | {z } , | {z } , | {z } , , (m ch˜ u sô´) (n ch˜ u sô´) (m-n ch˜ u sô´1, n ch˜ u sô´0) = 111 . . . 1 .10n | {z } , (m-n ch˜ u sô´) T´ıch n`
ay chia hê´t cho p v`ı (p, 10) = 1, suy ra 111 . . . 1 | {z } , (m-n ch˜ u sô´1) ,, chia hê´t cho p v`a n´ o c˜ ung n` ˘ am trong d˜ ay o trên. M` a 1 ≤ m − n ≤ p , , mâu thu˜ ân v´ oi gia thiê´t không c´ o sô´ n` ao trong d˜ ay chia hê´t cho p. J , , ,
. 2.8. (Ðê` thi Olympic to´ an thê´gi´ oi lâ`n th´ u 14) Cho M l` a t .âp h.op bâ´t , , , , k`
y gô`m 10 sô´ t .u nhiên, m˜ôi sô´không l´on hon 100. Ch´ung minh r`˘ang , , , , ,,
tô`n t .ai hai t .âp h.op con cua M m`a tông cua c´ac phâ`n tu trong ch´ung b` ˘ ang nhau. 2.2. V´ıd .u 19 , , , , , L` oi giai. C´ o thê ch´
ung minh nê´u tô`n t .ai hai t.âp thoa m˜an kê´t lu.ân , , , , cua b` ai to´ an, th`ı ta c´
o thê ch .on ¯du .oc hai t.âp con c´o c`ung t´ınh châ´t , ,
â´y nhung không giao nhau. Th .ât v.ây, Cho X, Y l`a hai t.âp con cua M , ,, c´ o tông c´ ac phâ`n tu b` ˘ ang nhau. Ch´ ung ta k´
y hi .êu X1 gô`m c´ac phâ`n ,, , , , , ,
tu cua X m`a không thu .ôc Y. Tuong t .u nhu v.ây Y1 gô`m c´ac phâ`n ,, , ,
tu cua Y m`a không thu .ôc X. R˜o r`ang X1 v`a Y1 c´o tông c´ac phâ`n ,, , , tu b` ˘ ang nhau m`
a không giao nhau. G .oi A l`a t.âp h .op m .oi t.âp h .op , , , ,, , con không r˜
ông cua M. Sô´ lu .ong phâ`n tu cua A l`a 210 − 1 = 1023. , ,, , , , Ch´ ung ta x´
et tông S c´ac phâ`n tu cua m .ôt t.âp h .op con nhu v.ây, r˜o , r`
ang S ≤ 91 + 92 + · · · + 100 < 10.100 = 1000. Nhu v .ây tô`n t.ai , , , không qu´ a 1000 tông kh´ ac nhau. K´
y hi .êu B l`a t.âp h .op tâ´t ca c´ac , , , , ,, , ,, , ,
tông nhu v .ây. Do ¯d´o sô´ lu .ong phâ`n tu cua B nho hon 1000 v`a nho , , , ,, , , , , ,, , ,
hon sô´lu .ong phâ`n tu cua A. Ð.˘at tuong ´ung m˜ôi phâ`n tu cua t.âp h .op , , ,, , , A v´ oi tông c´ ac phâ`n tu cua n´ o. Ta thâ´y r` ˘ ang c´ o thê ´ ap d .ung nguyên ,, , l´ y Ðirichlê o ¯
dây. Suy ra tô`n t .ai ´ıt nhâ´t hai t.âp h .op con kh´ac nhau c´o , ,, c`
ung m .ôt tông c´ac phâ`n tu. J , ,
. 2.9. (Ðê` thi h .oc sinh gioi to´an Câ´p II to`an quô´c 1983) Ch´ung minh , r` ˘ ang trong c´
ac sô´t .u nhiên thê´n`ao c˜ung c´o sô´k sao cho 1983k − 1 chia hê´t cho 105. , , , , , L`
oi giai. Cho k lâ´y gi´a tr.i t`u 1 ¯dê´n 105 + 1 rô`i thay v`ao biêu th´uc , ,
1983k − 1 s˜e nh .ân ¯du .oc 105 + 1 gi´a tr.i kh´ac nhau. Chia 105 + 1 sô´ , ,, , , , v`
ua nh .ân o trên cho 105, s˜e ¯du .oc nhiê`u nhâ´t l`a 105 sô´ du. Do ¯d´o , , theo nguyên l´ y Ðirichlê phai c´
o ´ıt nhâ´t hai sô´ cho c` ung m .ôt sô´ du. , ,, Gia su ¯ d´ o l`
a sô´ 1983m − 1 v`a 1983n − 1(m > n). Thê´ th`ı (1983m −
1) − (1983n − 1) chia hê´t cho 105 m`
a (1983m − 1) − (1983n − 1) = ,
(1983m − 1983n) = 1983n(1983m−n − 1). Nhung 1983 v` a 105 nguyên , tô´ c`
ung nhau, do v .ây phai c´o (1983m−n − 1) chia hê´t cho 105. Sô´ , k = m − n thoa m˜ an ¯ diê`u ki .ên ¯dâ`u b`ai. J , , 20 Chuong 2. Sô´h .oc , , . 2.10. Ch´ ung minh r` ˘
ang tô`n t .ai nh˜ung sô´ nguyên a, b v`a c, không , , ¯ dô`ng th` oi b` ˘ ang 0 v` a gi´
a tr.i tuy.êt ¯dô´i cua m˜ôi sô´ không qu´a 1000000, , √ √ thoa m˜
an |a + b 2 + c 3| < 10−11. , , , , , √ √ , L`
oi giai. Ð .˘at S l`a t.âp h .op cua 1018 sô´ th .uc r + s 2 + t 3 v´oi m .oi √ √
r, s, t thu .ôc {0, 1, 2, . . . , 106 − 1} v`a ¯d.˘at d = (1 + 2 + 3d)106. , Khi ¯ d´ o m˜ ôi x trong S ¯ dê`u n` ˘
am trong khoang 0 ≤ x < d. Chia , ¯
do .an n`ay th`anh 1018 − 1 phâ`n b`˘ang nhau, m˜ôi ¯do.an nho c´o ¯d .ô d`ai d e = . Theo nguyên l´
y Ðirichlê tô`n t .ai hai sô´ trong 1018 sô´ 1018 − 1 , , , cua S n`˘am trong c`
ung m .ôt ¯do.an nho. Hi.êu cua hai sô´n`ay k´y hi.êu l`a √ √ 107 a + b 2 + c 3 ¯ d´ o ch´ınh l` a c´ ac sô´ a, b, c v`ı e < = 10−11. J 1018 2.3. B ` ai t .âp , , . 2.11. Cho A l`
a t .âp h .op bâ´t k`y gô`m 201 sô´t .u nhiên, m˜ôi sô´không , , , , , ,
vu .ot qu´a 300. Ch´ung minh r`˘ang A ch´ua ´ıt nhâ´t hai sô´, m`a ty sô´cua , ch´ ung l` a l˜ uy th` ua b .âc ba. , , . 2.12. Cho k l`
a sô´ t .u nhiên bâ´t k`y, c`on a v`a b l`a nh˜ung sô´nguyên , ,
sao cho a ≤ b v`a b − a < 2k − 2. Ch´ ung minh r` ˘ ang nê´u M l`a t .âp h .op , , , ,
k sô´ t .u nhiên n`˘am trong khoang [a, b], v`a l l`a sô´t .u nhiên thoa m˜an , ,, ,
1 ≤ l ≤ 2k + a − b − 2, th`ı c´
o ´ıt nhâ´t m .ôt hi.êu nh˜ung phâ`n tu cua , M tr` ung v´ oi l. ,, , , , . 2.13. Cho d˜
ây sô´ a1, a2, a3, . . . , a41, m`a m˜ôi phâ`n tu chı ¯ du .oc t.ao ,, , , , ,, boi sô´1 v` a, sô´2, trong ¯ d´ o c´
o ´ıt nhâ´t 21 sô´chı ¯ du .oc t.ao boi c´ac sô´1. , ,, , , Ch´ ung minh r` ˘
ang tô`n t .ai m .ôt sô´ phâ`n tu liên tiê´p cua d˜ay c´o tông b` ˘ ang ¯ d´ ung 20. , , . 2.14. Ch´ ung minh r` ˘
ang tô`n t .ai m .ôt sô´ t .u nhiên n, sao cho sô´ 2.3. B` ai t .âp 21 111 . . . 1 chia hê´t cho 139. (B` ai to´ an c` on ¯ d´ ung nê´u ta thay 139 | {z } , (n ch˜ u sô´) , b` ˘
ang m .ôt sô´nguyên tô´c`ung nhau v´oi 10). , ,, , . 2.15. Ch´ ung minh r` ˘
ang trong m .oi sô´t.ao boi 100 ch˜u sô´ N tô`n t.ai
m .ôt sô´chia hê´t cho 1967. , , , , . 2.16. Ch´ ung minh r` ˘ ang bao gi`o c˜ ung t`ım ¯ du .oc sô´
19971997. . . 19970. . . 0 chia hê´t cho 1998. , , . 2.17. Ch´ ung minh r` ˘ ang c´
o m .ôt sô´t .u nhiên chia hê´t cho 1997, m`a , , bô´n ch˜u sô´cuô´i c` ung cua n´ o l` a 1998. , . 2.18. Ch´ ung minh r` ˘ ang nê´u c´
ac sô´nguyên m v`a n nguyên tô´c` ung , , , nhau th`ı t`ım ¯
du .oc sô´t .u nhiên k sao cho mk − 1 chia hê´t cho n. , , 22 Chuong 2. Sô´h .oc , , CHUONG 3 D ˜ AY S ´ Ô 3.1. Nguyên l´ y Ðirichlê cho d˜ ay sô´ vô h .an , , Trong phâ`n n` ay ch´ ung ta x´ et nguyên l´ y Ðirichlê du´ oi d .ang: , , Nê´u c´ o h˜
uu h .an nh˜ung ng˘an k´eo m`a ch´ung ta ¯d .˘at vô h .an , , nh˜
ung v .ât v`ao ¯d´o, th`ı ´ıt nhâ´t c´o m .ôt ng˘an k´eo ch´ua vô h .an , nh˜
ung v .ât ¯d˜a c´o. , ,,, , Ch´ ung ta d˜ ê c´ o cam tuong r` ˘ ang nguyên l´ y n` ay l` a hiên nhiên nên , , , , ´ıt ch´ u ´ y ¯ dê´n n´ o. B` ˘ ang phan ch´ ung c´ o thê ch´ ung minh nguyên l´ y n` ay , ,, l` a ¯ d´
ung. Trong sô´ h .oc, t.âp h .op c´o liên quan ¯dê´n vô h.an phâ`n tu l`a , d˜ ây sô´. Ch´
ung ta biê´t râ´t nhiê`u d˜ ay sô´ ¯
d .ep nhu d˜ay câ´p sô´c .ông, d˜ay , , câ´p sô´ nhân, d˜ ay c´
ac sô´ nguyên tô´, ho .˘ac d˜ay Fibonaxi,. . . Chuong , , , , n` ay ch´ ung ta chı quan tâm ¯ dê´n ´
ap d .ung ¯diê`u ph´at biêu trên ¯dê giai , c´ ac b` ai to´ an liên quan ¯ dê´n d˜ ây sô´. Nh˜
ung t .âp vô h.an trong c´ac b`ai , , , to´ an du´ oi ¯ dây ta x´ et nhu c´ ac d˜ ay sô´. 3.2. V´ı d .u , . 3.1. X´et d˜
ay sô´ 6, 62, 63, 64, 65, . . . , 6n, . . . v` a viê´t 4 ch˜ u sô´ cuô´i c` ung , , cua c´ ac sô´ n`
ay 0006, 0036, 0216, 1296, 7776, . . .. Ch´ ung minh r` ˘ ang b´ ˘ at , , ¯ dâ`u t`
u m .ôt sô´n0 n`ao ¯d´o d˜ây v`ua l .âp l`a d˜ây tuâ`n ho`an. , , , , , L`
oi giai. V`ı tô`n t .ai h˜uu h.an sô´ lu .ong (104) c´ach ch .on kh´ac nhau , , 24 Chuong 3. D˜ ay sô´ , , , c´ ac sô´ c´ o 4 ch˜ u sô´, nên trong d˜ ay ¯ d˜ a cho ch´ ˘ ac ch´ ˘ an t`ım ¯ du .oc hai , , , c´
ach ch .on c´o c`ung 4 ch˜u sô´ cuô´i. C´o ngh˜ıa l`a t`ım ¯du .oc hai sô´ n0 , , v`
a n0 + t m`a v´oi ch´ung th`ı 6n0 v`a 6n0+t+1 c´o c`ung 4 ch˜u sô´ cuô´i , ,
(6n0+t+1 − 6n0 = 104.6k). N´ oi chung, ch˜ u sô´ 6n v`a 6n+t v´ oi bâ´t k` y ,
n > n0 s˜e c´o c`ung 4 ch˜u sô´cuô´i (6n+t − 6n = 104.6n−n0). J
. 3.2. (Ðê` thi To´
an Olympic quô´c tê´ lâ`n 17 n˘ am 1975) Cho , ,
a1, a2, . . . , an, . . . l`a d˜ay t˘ang ng .˘at c´ac sô´ t .u nhiên. Ch´ung minh r`˘ang ,, , , , , ,
vô h .an c´ac phâ`n tu an cua d˜ây trên c´o thê biêu di˜ên du´oi d .ang ,, , , ,
an = xap + yaq,o ¯dây x v`a y l`a nh˜ung sô´nguyên duong v`a p 6= q. , , , , L`
oi giai. Nê´u a1 = 1 kê´t lu .ân cua b`ai to´an l`a hiên nhiên. Th.ât v.ây, , , v´
oi m .oi n ≥ 3 sô´ h.ang an c´o biêu di˜ên d.ang an = an−1 + (an +
an−1) = 1.an−1 + (an − an−1).a1 c´o t´ınh châ´t mong muô´n. Ch´ung ta , , , , s˜ e ch´
ung minh tô`n t .ai chı sô´ p l´on hon 1 sao cho vô h.an c´ac sô´h.ang , , , , , cua d˜ ay ¯ d˜ a cho c´ o thê viê´t du´
oi d .ang xap + ya1 v´oi c´ac sô´ nguyên , , , , , , , ,
duong th´ıch h .op x v`a y. M˜ôi sô´ h.ang cua d˜ay ta ¯d.˘at tuong ´ung v´oi , , , , sô´ du cua n´ o khi chia ch´ınh n´
o cho a1. T .âp h .op tâ´t ca c´ac sô´ h.ang , , , , , cua d˜ ay l`
a vô h .an, c`on tâ´t ca c´ac kha n˘ang cua sô´du khi chia c´ac sô´ , , , ,,
h .ang cho a1 l`a h˜uu h.an. Ðiê`u ¯d´o ch´ung to r`˘ang vô h.an phâ`n tu ,
an , a , . . . , a , . . . , v´oi n 1 n2 nk
1 < n2 < . . . < nk < . . . , , cho c`
ung m .ôt sô´ du r khi chia cho a1. Không mâ´t t´ınh tông qu´at , , , , , ,
ta gia thiê´t n1 > 1, v`ı trong tru`ong h .op ngu .oc l.ai ta x´et c´ac sô´ , an , a , . . . , a , . . . c˜ ung l` a d˜ ay vô h r khi chia 2 n3 nk .an v` a cho c` ung sô´ du , , ,
cho a1. V´oi m .oi k = 1, 2, . . . tô`n t.ai sô´nguyên duong xk sao cho an = k xka1 + r. Khi ¯ d´ o an − a = (x k n1
k a1 + r) − (x1 a1 + r) = (xk − x1)a1 , , , suy ra v´
oi m .oi k ≥ 2 ta c´o ¯d˘ang th´uc an = a + (x k n1 k − x1)a1 = , , 1.an + (x
ng sô´ a , a , . . . , a , . . . ., c´ o biêu 1 k − x1)a1. Ngh˜ ıa l` a, nh˜ u n2 n3 nk , , , di˜ ên v` a c´ ac t´ınh châ´t nhu b` ai to´ an ¯ d`
oi hoi. Th .ât v.ây, chı sô´ 1 v`a n1 3.2. V´ı d .u 25 , , , , , , kh´ ac nhau v`ı theo c´
ach ch .on trên n1 th .uc s .u l´on hon 1. Chı c`on phai , , , , kh˘ ang ¯
d.inh r`˘ang sô´ xk − x1 l`a sô´ nguyên duong v´oi k ≥ 2, ¯diê`u ¯d´o , ¯ d´ ung v`ı t`
u n1 < nk suy ra x1 < xk. J , ,
. 3.3. Cho sô´t .u nhiên bâ´t k`y k. Ch´ung minh r`˘ang tô`n t .ai sô´nguyên tô´ , , p v`
a m .ôt d˜ay sô´t .u nhiên t˘ang ng .˘at a1, a2, . . . , an, . . . sao cho tâ´t ca c´ac ,, , , phâ`n tu cua d˜
ay p + ka1, p + ka2, . . . , p + kan, . . . l`a nh˜ung sô´nguyên tô´. , , , , , L` oi giai. K´
y hi .êu P l`a t.âp h .op tâ´t ca c´ac sô´ nguyên tô´. V´oi m .oi ,
i = 0, 1, . . . , k − 1 k´y hi .êu Pi l`a t.âp h .op c´ac sô´ nguyên tô´ m`a khi , chia cho k c´
o sô´du i. D˜ê thâ´y r`˘ang m .oi sô´nguyên tô´n`˘am trong m .ôt , ,, trong c´
ac t .âp h .op P0, P1, P2, . . . , Pk−1. Boi v`ı sô´nguyên tô´l`a vô h.an, , , ,
v .ây ´ıt nhâ´t phai c´o m .ôt trong sô´c´ac t.âp h .op P0, P1, P2, . . . , Pk−1 ch´ua , ,, ,
vô h .an sô´nguyên tô´. Gia su Pi ch´ua vô h.an sô´v`a k´y hi.êu p l`a phâ`n ,, , , , tu nho nhâ´t cua n´ o. Khi ¯ d´
o m .oi sô´x thu .ôc Pi c´o d.ang x = p + ka v´oi , ,, ,
m .ôt sô´ t .u nhiên a. Lâ´y x1, x2, x3, . . . l`a c´ac phâ`n tu cua Pi xê´p theo , , , , , x th´ u t n − p .u l´ on dâ`n. V´
oi m .oi sô´t .u nhiên n ¯d.˘at an = . D˜ ê thâ´y r` ˘ ang k
sô´nguyên tô´ p v`a d˜ay a1, a2, . . . , an, . . . c´o t´ınh châ´t mong muô´n. J , , . 3.4. Cho f l` a ¯ da th´ uc k ¯ dô´i sô´v´
oi h.ê sô´nguyên v`a a1, a2, . . . , an, . . . l`a , , , d˜ ay nh˜
ung sô´ nguyên thoa m˜
an h.ê th´uc an+1 = f (a,a2, . . . , an−k+1), , , , v´
oi m .oi sô´ nguyên n, k m`a n ≥ k. Ch´ung ta x´et sô´ duong bâ´t k`y m , , , , v` a v´
oi m .oi n = 1, 2, . . .. K´y hi.êu an l`a sô´ du không âm nho nhâ´t cua ,
an theo mô ¯dun m. Ch´ ung minh r` ˘ ang d˜
ay a1, a2, a3, . . . , an, . . . . l`a d˜ay tuâ`n ho` an. , , ,, , , L` oi giai. Ch´ ung ta s˜
e su d .ung kh˘ang ¯d.inh sau: Nê´u g l`a ¯da th´uc , k ¯ dô´i sô´ v´
oi h .ê sô´ nguyên v`a x1, x2, . . . , xk, y1, y2, . . . , yk l`a c´ac sô´
nguyên sao cho x1 ≡ y1 (mod m), x2 ≡ y2 (mod m), . . . , xk ≡ yk
(mod m), th`ı g(x1, x2, . . . , xk) ≡ g(y1, y2, . . . , yk) (mod m). , , 26 Chuong 3. D˜ ay sô´ ,
M .oi sô´ h.ang cua d˜ay b`˘ang m .ôt trong c´ac sô´ a1, a1, a3, . . . , an, . . . , , ,, 0, 1, . . . , m − 1. Ch´ ung ta x´ et c´
ac b .ô s´˘ap th´u t .u gô`m k phâ`n tu
(a1, a2, . . . , ak), (a2, a3, . . . , ak+1), . . . , (an, an+1 . . . , an+k−1).. , , , , , C´
o tâ´t ca vô h .an b .ô s´˘ap nhu v.ây, nhung sô´ lu .ong c´ac b .ô k sô´ , ,
(α1, α2, α3, . . . , αk), v´oi 0 ≤ αi ≤ m − 1, i = 1, 2 . . . , k l`a h˜uu h .an , , (b` ˘
ang mk theo l´y thuyê´t tô h .op). Theo nguyên l´y Ðirichlê tô`n t.ai hai ,
chı sô´ i v`a j, i < j sao cho
ai = aj, ai+1 = aj+1, . . . , ai+k−1 = aj+k−1 ho .˘ac l`a
x1 ≡ y1 (mod m), x2 ≡ y2 (mod m) , . . . , xk ≡ yk (mod m). , , T` u ¯ dây suy ra d˜
ay a1, a2, a3, . . . , an . . . l`a tuâ`n ho`an (chu k`y cua n´o , , , , , l` a u´
oc sô´ cua j − i). Th .ât v.ây, v`ı f l`a ¯da th´uc v´oi h.ê sô´ nguyên nên , theo c´ ach ch´ ung minh trên ch´ ung ta c´ o
f (ai+k−1, ai+k−2, . . . , ai) ≡ f (aj+k−1, aj+k−2, . . . , aj) (mod m) ,
=⇒ ai+k ≡ aj+k (mod m) ho .˘ac l`a ai+k ≡ aj+k. Biê´n ¯dôi m .ôt ch´ut d˜ê , , , thâ´y r` ˘ ang v´
oi m .oi n ≥ i ta c´o ¯d˘ang th´uc sau an+(i−j) ≡ an. J , , , . 3.5. Cho d˜
ay x1, x2, . . . , xn, . . . . ¯du .oc x´ac ¯d.inh theo công th´uc sau
x1 = 1, x2 = 0, x3 = 2, xn+1 = 2xn−1 + xn−2, n ≥ 3. , , , ,, Ch´ ung minh r` ˘ ang v´
oi m .oi sô´ t .u nhiên m tô`n t .ai hai phâ`n tu liên tiê´p , cua d˜ ay m` a ch´ ung ¯
dê`u chia hê´t cho m. , , , , L`
oi giai. Công th´ uc hô`i quy trên c´ o thê viê´t l .ai xn−2 = xn+1 − 2xn−1 (3.1) , , , , , T` u ¯ d´ o chı ra r` ˘ ang d˜ ay c´ o kha n˘ ang ph´ at triên vê` ph´ıa tr´ ai, t´ uc , , l` a x´ ac ¯
d.inh xn v´oi n ≤ 0. V´ı d .u v´oi n = 2, 1, 0 ch´ung ta nh.ân , , , , ¯
du .oc x0 = 0, x−1 = 0, x−2 = 1. Nhu m .uc 3.4 chı ra r`˘ang d˜ay 3.2. V´ı d .u 27 , , , , ,
x1, x2, . . . , xn, . . . gô`m nh˜ung sô´du tuong ´ung x1, x2, . . . , xn, . . . theo , ,
môdd un m, l`a d˜ay tuâ`n ho`an. T`u công th´ uc (3.1) suy ra m˜ ôi ,, , , , phâ`n tu cua d˜
ay {xn} v`a suy ra ca {xn} x´ac ¯ d.inh duy nhâ´t t`u 3 ,, , , , phâ`n tu tru´ oc n´ o. Khi ¯ d´
o nê´u (r1, r2, . . . , rk) l`a phâ`n chu k`y cua d˜ay ,
x1, x2, . . . , xn, . . . th`ı phâ`n n`ay s˜e chuyên ¯
d .ông tuâ`n ho`an vê`ph´ıa tr´ai , cua d˜
ay . . . , x−3, x−2, x−1, x0, x1, x2, . . . v`a s˜e c´o d .ang
. . . , r1, r2, . . . , rk, r1, r2, . . . , rk, r1, r2, . . . , rk . . . (3.2) , , Bây gi` o ta ch´ u ´ y r` ˘
ang x−1 = x0 = 0, suy ra x−1 = x0 = 0. T`u (3.2) , , ,, suy ra r` ˘ ang d˜ ay c´
ac sô´ du theo môdd un m ch´ ua vô sô´ c .˘ap phâ`n tu liên tiê´p b` ˘ ang không. N´ oi c´ ach kh´
ac tô`n t .ai vô sô´c´ac c.˘ap sô´liên tiê´p , ,, cua d˜
ay x1, x2, . . . , xn, . . . m`a m˜ôi phâ`n tu trong c .˘ap ¯dê`u chia hê´t cho m. J , , , , . 3.6. D˜ ay sô´ Fibonaxi ¯
du .oc ¯d.inh ngh˜ıa b`˘ang c´ac ¯d˘ang th´uc F1 = ,
F2 = 1, Fn+2 = Fn+1 + Fn, n ≥ 1. Ch´ ung minh r` ˘
ang ´ıt nhâ´t m .ôt trong ,, ,
1.000.000.000 phâ`n tu ¯ dâ`u tiên cua d˜
ay chia hê´t cho 10.000. , , , , , , , , L`
oi giai. Tuong t .u nhu 3.5 ch´ung ta x´et c´ac sô´ du cua c´ac sô´ , , ,, trong d˜ ay ¯ d˜ a cho khi chia cho 10.000. K´
y hi .êu sô´ du ¯d´ung o v.i , tr´ı th´
u k khi chia cho 10 000 l`a rk. Khi ¯ d´ o th`ı r1 = 1, r2 =
1, r3 = 2, r4 = 3, . . . . . . .rk = rk−1 + rk−2. R˜o r`ang c´o 10.000 sô´ , du kh´ ac nhau do ¯ d´ o c´
o 100002 = 100000000 (tr˘am tri .êu) c.˘ap sô´ , , du kh´ ac nhau. X´
et 100000001 c .˘ap sô´ du (r1, r2), (r2, r3), (r3, r4) . . .
. . . (r100000001, r100000002). Theo nguyên l´y Ðirichlê trong sô´ n`ay c´o ´ıt , , , ,
nhâ´t 2 c .˘ap sô´ tr`ung nhau, t´uc l`a t`ım ¯du .oc hai sô´ n v`a p v´oi n, p , , , , ¯
dê`u nho hon 100000002,n nho hon p sao cho rn = rp, rn+1 = rp+1. , , , , , ,
Nhung nê´u biê´t sô´ du cua tông hai sô´ v`
a sô´ du cua m .ôt sô´ th`ı sô´ , , , du kia c˜ ung t´ınh ¯
du .oc. V`ı v.ây ta c´o rn−1 = rp−1, rn−2 = rp−2, . . . . , cho ¯
dê´n khi r2 = 1 = rp−n+2, r1 = 1 = rp−n+1, Áp d .ung công th´uc , , 28 Chuong 3. D˜ ay sô´ , ,, ,
sô´ du hô`i qui o trên ta c´
o rp−n = 0 v´oi p − n ≤ 100000001 − 1 = , ,, , 100000000. Ngh˜ıa l` a sô´ ¯ d´
ung o v.i tr´ı p − n s˜e thoa m˜an ¯diê`u ki.ên b`ai ra, chia hê´t cho 10 000. J
. 3.7. (Ð.inh l´y Fecma) Nê´u m.ôt sô´ nguyên tô´ p không chia hê´t sô´ , ,
nguyên a, th`ı ¯ d˘ ang th´ uc sau ¯ d´
ung ap−1 ≡ 1( mod p). , , , , , L` oi giai. Ch´ ung ta ch´
ung minh m .ênh ¯dê` tông qu´at hon. Cho m > 1 , , l`
a sô´ t .u nhiên bâ´t k`y v`a a l`a sô´ nguyên tô´ c`ung nhau v´oi m. Ch´ung , , , ta x´ et d˜ ay nh˜ung l˜ uy th` ua liên tiê´p cua a a1, a2, a3, . . . (3.3) v` a k´ y hi .êu r1, r2, r3, . . . (3.4) , , , , , , l` a nh˜ ung sô´du tuong ´
ung cua (3.3) khi chia cho m, ngh˜ıa l`a
ak ≡ rk (mod m), 1 ≤ rk ≤ m − 1. , , , ,, Khi ¯ d´
o sô´ lu .ong c´ac sô´ trong (3.3) l`a vô h.an, c`on nh˜ung sô´ o (3.4) , , , , , chı c´
o thê nh .ân nh˜ung gi´a tr.i trong 1, 2, 3, . . . , m − 1 nên sô´lu .ong l`a , , , , h˜
uu h .an. Suy ra theo nguyên l´y Ðirichlê, gi˜ua nh˜ung sô´du rk s˜e c´o , , ´ıt nhâ´t hai sô´ tr` ung nhau; n´ oi c´ ach kh´
ac tô`n t .ai hai chı sô´ i v`a j v´oi, i 6= j sao cho ri = rj. Khi ¯ d´ o ch´ ung ta c´ o ai ≡ aj( mod m). Theo gia , , , thiê´t (a, m) = 1, v´ oi i 6= j ch´
ung ta nh .ân ¯du .oc ai−j ≡ 1( mod m). , , , Ch´ ung ta c´
o kê´t lu .ân tô`n t.ai sô´t .u nhiên l sao cho ¯d˘ang th´uc sau ¯ dây ¯ d´ ung: al ≡ 1 (mod m) (3.5)
- Sô´ l trong (3.5) không x´ac ¯
d.inh duy nhâ´t, th.âm ch´ı c`on tô`n t.ai , ,
vô sô´sô´t .u nhiên l thoa m˜an (3.5). , , , , - Trong tru`
ong h .op m = p l`a sô´nguyên tô´, Fecma t`ım ra l c´o thê ch .on l`a sô´ p − 1. 3.2. V´ı d .u 29 , , , , , , -Tru`
ong h .op m bâ´t k`y th`ı Ole ch´ung minh r`˘ang l c´o thê ch .on l`a , , ,, h` am chı sô´ cua m (ch´ ung ta không xem x´ et vâ´n ¯ dê` n` ay o ¯ dây, ¯ d .ôc , , , gia c´ o thê t`ım trong bâ´t c´ u cuô´n s´ ach sô´h .oc n`ao). J
. 3.8. Cho x1, x2, x3, . . . l`a d˜
ây vô h .an c´ac sô´ nguyên v`a k l`a m.ôt sô´ , , , ,,
t .u nhiên bâ´t k`y. Ch´ung minh r`˘ang tô`n t .ai d˜ây sô´gô`m nh˜ung phâ`n tu , , , liên tiê´p cua d˜ ây, m` a tông cua ch´
ung chia hê´t cho k. , , , , , ,, L` oi giai. Ch´ ung ta c´ o thê gi´
oi h .an l.ai, gi˜ua m .oi b .ô k phâ`n tu liên , , , , ,, tiê´p cua d˜ ây c´
o thê ch .on ¯du .oc m .ôt sô´ phâ`n tu c´o t´ınh châ´t mong , , , ,, muô´n. Ðê ¯ don gian ta xem x´ et k phâ`n tu ¯
dâ`u tiên x1, x2, x3, . . . , xk. , Ch´ ung ta x´ et tông
S1 = x1, S2 = x1 + x2, S3 = x1 + x2 + x3, . . . , Sk = x1 + x2 + · · · + xk , , ,
Nê´u m .ôt tông n`ao ¯d´o trong sô´trên chia hê´t cho k, th`ı b`ai to´an ¯du .oc , , , , ,
giai. Ngu .oc l.ai, c´ac sô´ S1, S2, . . . , Sk (c´o sô´ lu .ong k) khi chia cho k , , , , ¯
du .oc c´ac sô´du 1, 2, 3, . . . , k − 1. T`u nguyên l´y Ðirichlê suy ra c´o m .ôt , ,
c .˘ap chı sô´i v`a j, 1 ≤ i < j ≤ k, m`a c´ac tông Si v`a Sj cho c`ung m .ôt sô´ , , ,, du khi chia cho k. Khi ¯ d´ o tông c´
ac phâ`n tu liên tiê´p xi+1, xn+2, . . . , xj , cua d˜ ay ¯ d˜
a cho chia hê´t cho k, v`ı xi+1 + xn+2 + · · · + xj = Sj − Si. J , , , , . 3.9. Cho d˜
ay vô h .an c´ac ch˜u sô´. Ch´ung minh r`˘ang v´oi m.oi sô´ t .u ,
nhiên n, nguyên tô´ c` ung nhau v´ oi 10, trong d˜
ay vô h .an trên tô`n t .ai , ,, ,
m .ôt nh´om ch˜u sô´liên tiê´p, m`a sô´t .ao boi c´ac ch˜u sô´trong nh´om (viê´t , , , , , , , theo th´
u t .u chı sô´l´on ¯d´ung tru´oc) chia hê´t cho n. , , , L` oi giai. Cho d˜ ay c´ ac ch˜
u sô´ a1, a2, . . . , an, . . .. Ch´ung ta x´et c´ac sô´
A1 = a1, A2 = a2a1, . . . , An = anan−1 . . . a1, . . . , An+1 = an+1 . . . a1. , , , , , , , ,
V`ı sô´lu .ong nh˜ung sô´n`ay l`a n + 1, c`on sô´lu .ong kha n˘ang cua sô´du khi chia ch´
ung cho n l`a n, nên theo nguyên l´y Ðirichlê tô`n t .ai ´ıt nhâ´t , , 30 Chuong 3. D˜ ay sô´ , hai sô´cho c`
ung m .ôt sô´du ta k´y hi.êu ch´ung l`a Ai v`a Aj, (i < j). Khi ¯ d´
o hi .êu Aj − Ai chia hê´t cho n. Hay n´oi c´ach kh´ac
Aj − Ai = aj . . . a1 − ai . . . a1 = aj . . . ai−1.10j−i+1
v`ı (n, 10) = 1, nên aj . . . ai−1 chia hê´t cho n. J , , . 3.10. Cho k l`
a sô´nguyên duong bâ´t k` y v` a x1, x2, . . . , xn, . . . y1, y2, . . . , yn, . . . , , l` a nh˜ ung chu˜
ôi sô´ nguyên bâ´t k` y. Ch´ ung minh r` ˘
ang tô`n t .ai vô sô´ c .˘ap , , ,
chı sô´ (i, j), v´
oi i < j sao cho m˜ ôi tông
xi+1 + xn+2 + · · · + xj; yi+1 + yn+2 + · · · + yj ¯
dê`u chia hê´t cho k. , , , , ,, L`
oi giai. Chı câ`n ch´ ung minh r` ˘
ang trong b .ô sô´ k2 phâ`n tu liên tiê´p , , , , , , , cua 2 d˜ ây trên c´
o thê ch .on ¯du .oc tông v´oi t´ınh châ´t ¯d˜a chı ra. V`ı v.ây , ,, , ch´ ung ta chı quan tâm ¯ dê´n k2 phâ`n tu ¯ dâ`u tiên cua c´ ac chu˜ ôi ¯ d˜ a cho. , , , B` ˘ ang c´ ach tông qu´ at h´ oa c´ ach giai b` ai to´ an 3.8, lâ´y tông
S1 = x1, S2 = x1 + x2, S3 = x1 + x2 + x3, . . . , Sk2 = x1 + x2 + · · · + xk2
T1 = y1, T2 = y1 + y2, T3 = y1 + y2 + y3, . . . , Tk2 = y1 + y2 + · · · + yk2 , , , , , V´ oi m˜ ôi m = 1, 2, 3, . . . , k2 ¯
d .˘at tuong ´ung c.˘ap (Sm, Tm) v´oi c.˘ap , , ,
(RSm, RTm) cua nh˜ung sô´ du, khi chia Sm v`a Tm cho k. V`ı RSm , , , v`
a RTm l`a m .ôt trong c´ac sô´ 0, 1, 2, . . . , k − 1, nên tô h .op tâ´t ca c´
ac d .ang kh´ac nhau (RSm, RTm) l`a không qu´a k2. Nê´u tô`n t.ai , , ,
m .ôt chı sô´ m, sao cho (RSm, RTm) tr`ung v´oi (0, 0), th`ı m .oi tông
Sm = x1 + x2 + · · · + xm v`a Tm = y1 + y2 + · · · + ym ¯ dê`u chia hê´t cho ,
k. V`ı nê´u không nhu v .ây, th`ı c´ac c.˘ap sô´(RSm, RTm), m = 1, 2, . . . .., k2 , , , , c´ o nhiê`u nhâ´t l`
a k2 − 1 kha n˘ang kh´ac nhau. Nhung sô´ lu .ong 3.3. B` ai t .âp 31 , nh˜
ung c .˘ap sô´ n`ay l`a k2 suy ra c´o ´ıt nhâ´t hai trong ch´ung b`˘ang , nhau. N´ oi c´ ach kh´
ac, tô`n t .ai hai chı sô´ i v`a j, sao cho 1 ≤ i < , , , j ≤ k2 v`
a (RSi, RTi) = (RSj, RTj). Trong tru`ong h .op n`ay m˜ôi sô´
xi+1 + xn+2 + · · · + xj = Sj − Si; yi+1 + yn+2 + · · · + yj = Tj − Ti ¯ dê`u chia hê´t cho k. J , ,, Ch´ u ´ y: Ðây l` a b` ai to´ an tông qu´ at h´ oa b` ai to´ an 3.8. Mo r .ông kê´t , qua n` ay c´
ac b .an h˜ay xem v`a l`am b`ai tâp 3.15. 3.3. B ` ai t .âp , , , , . 3.11. C´
o tô`n t .ai lu˜y th`ua cua sô´3 m`a c´ac ch˜u sô´cuô´i c`ung cua n´o l` a 0001 không ? , , , , . 3.12. Cho F l`
a t .âp h˜uu h.an nh˜ung sô´nguyên duong v`a x1, x2, . . . , ,,
, xn, . . . v`a y1, y2, . . . , yn, . . . l`a hai d˜ây vô h .an nh˜ung phâ`n tu thu .ôc , , , F. Ch´ ung minh r` ˘
ang tô`n t .ai nh˜ung chı sô´ i v`a j, i < j sao cho t´ıch , ,
cua xi+1, xi+2, . . . , xj v`a yi+1, yi+2, . . . , yj l`a m .ôt sô´c´o l˜uy th`ua b.âc k. ,
. 3.13. Cho u1, u2, . . . , un, . . . l`a d˜ay nh˜ung sô´nguyên x´ac ¯ d.inh b`˘ang , , công th´ uc u1 = 39, u2 = 45, un+2 = u2 − u ng minh n+1 n(n ≥ 1). Ch´ u , ,, r` ˘
ang 1986 chia hê´t cho vô sô´nh˜ ung phâ`n tu trong d˜ ay n` ay. , , . 3.14. Cho k l`
a m .ôt sô´t .u nhiên. D˜ay x1, x2, . . . , xn, . . . thoa m˜an c´ac , , 1 , ¯ d˘ ang th´ uc x0 = 0, x1 = 1 v`a xn = (x i m .oi n ≥ 1. k n+1 − xn−1) v´ o , , , Ch´ ung minh r` ˘ ang gi˜ ua nh˜
ung sô´ x1, x2, . . . , x1986 tô`n t .ai hai sô´ m`a , t´ıch cua ch´
ung chia hê´t cho tich 19.86. , , . 3.15. Cho k l` a sô´nguyên duong v` a x11, x12, . . . , x1n, . . . x21, x22, . . . , x2n, . . . , , 32 Chuong 3. D˜ ay sô´ . . . . . . . . . . . . . . . xs1, xs2, . . . , xsn, . . . , , l`
a s d˜ay sô´ nguyên. Khi ¯ d´
o tô`n t .ai vô h.an c´ac c.˘ap chı sô´ (i, j), v´oi , i < j sao cho c´ ac tông sau ¯ dây x1 + + · · · + i+1 x1i+2 x1j x2 + + · · · + i+1 x2i+2 x2j
. . . . . . . . . . . . . . . . . . . . . xs + + · · · + i+1 xsi+2 xsj ¯ dê`u chia hê´t cho k. , , CHUONG 4 H`INH H .OC 4.1. V´ı d .u , , , Trong sô´c´ ac b` ai to´
an h`ınh h .oc trong to´an h .oc tô h .op c´o m .ôt l´op , , , b` ai to´ an giai b` ˘ ang phuong ph´
ap Ðirichlê râ´t thu .ân ti.ên v`a r˜o r`ang. , , , ,
B .an ¯d .oc c´o thê t`ım thâ´y nh˜ung c´ach giai kh´ac, nhung v`ı m .uc ¯d´ıch , , , , chuyên ¯ dê` phuong ph´ ap ch´ ung ta ¯ dang x´ et nên ch´ ung ta chı khao s´ at c´ ac v´ı d .u sau. , , , , , ,
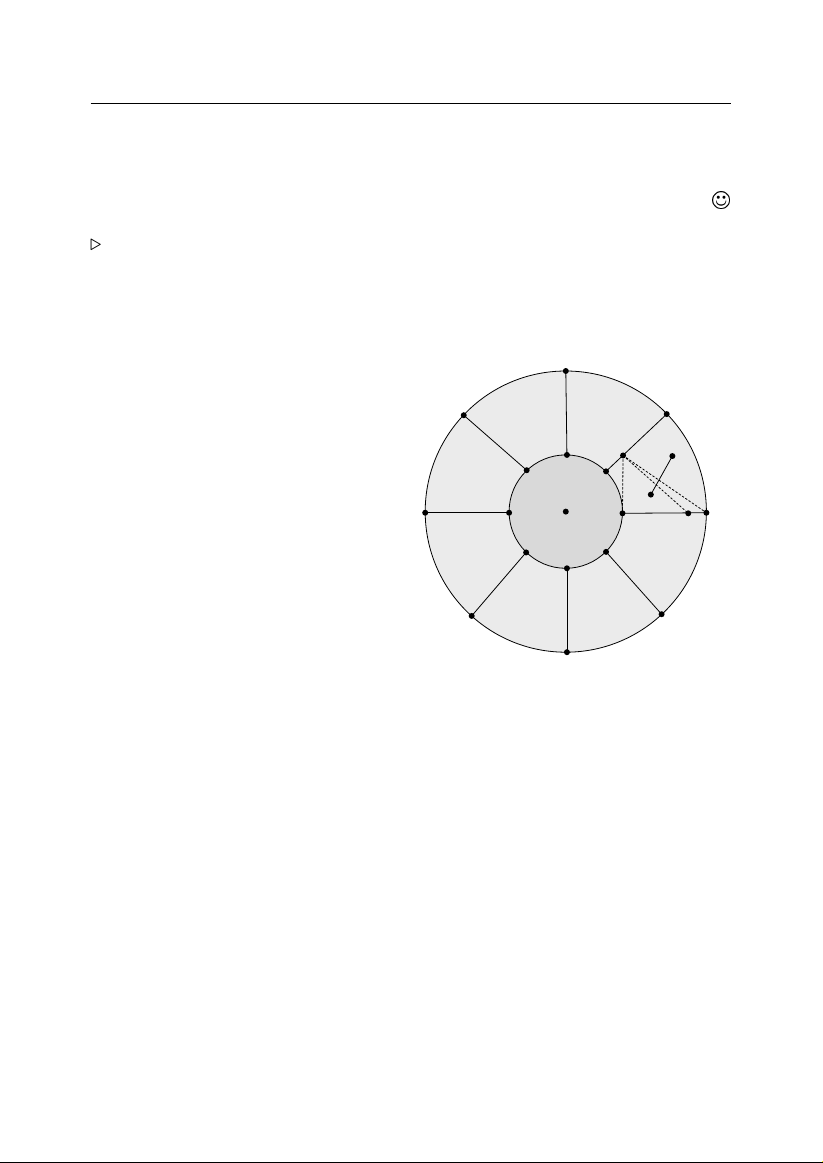
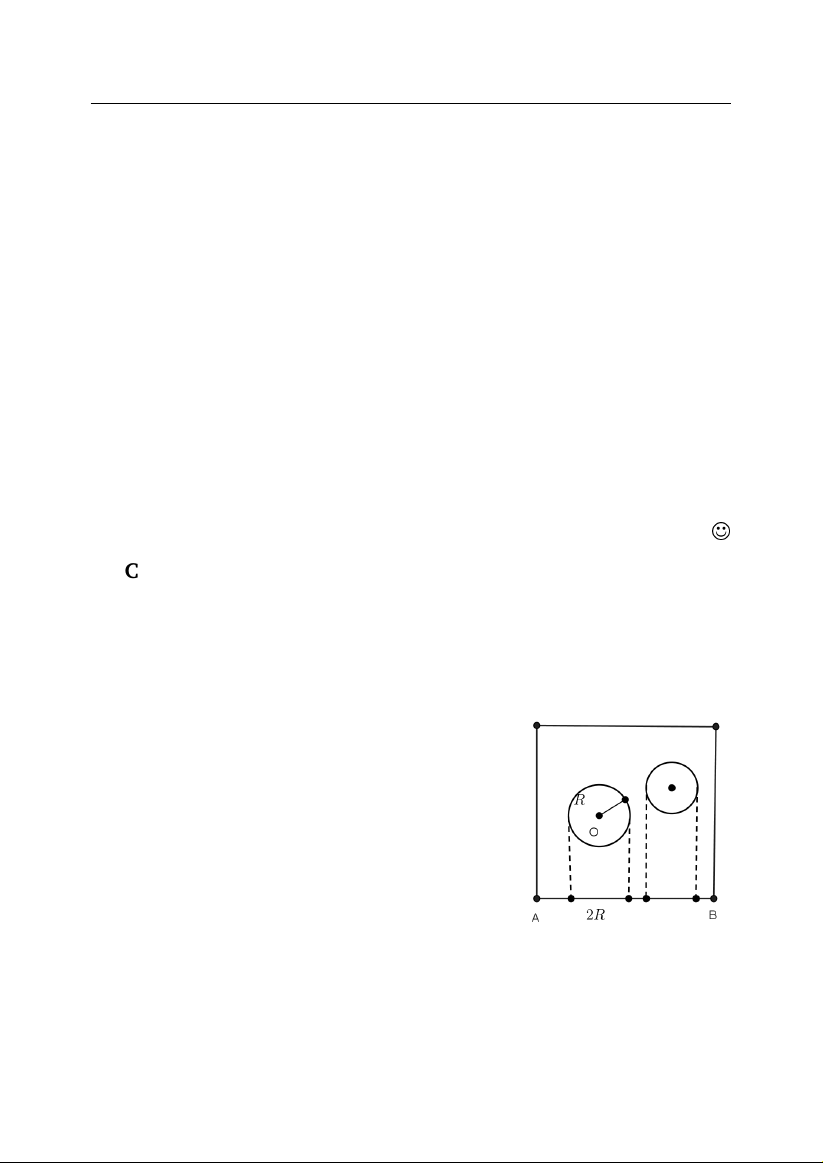
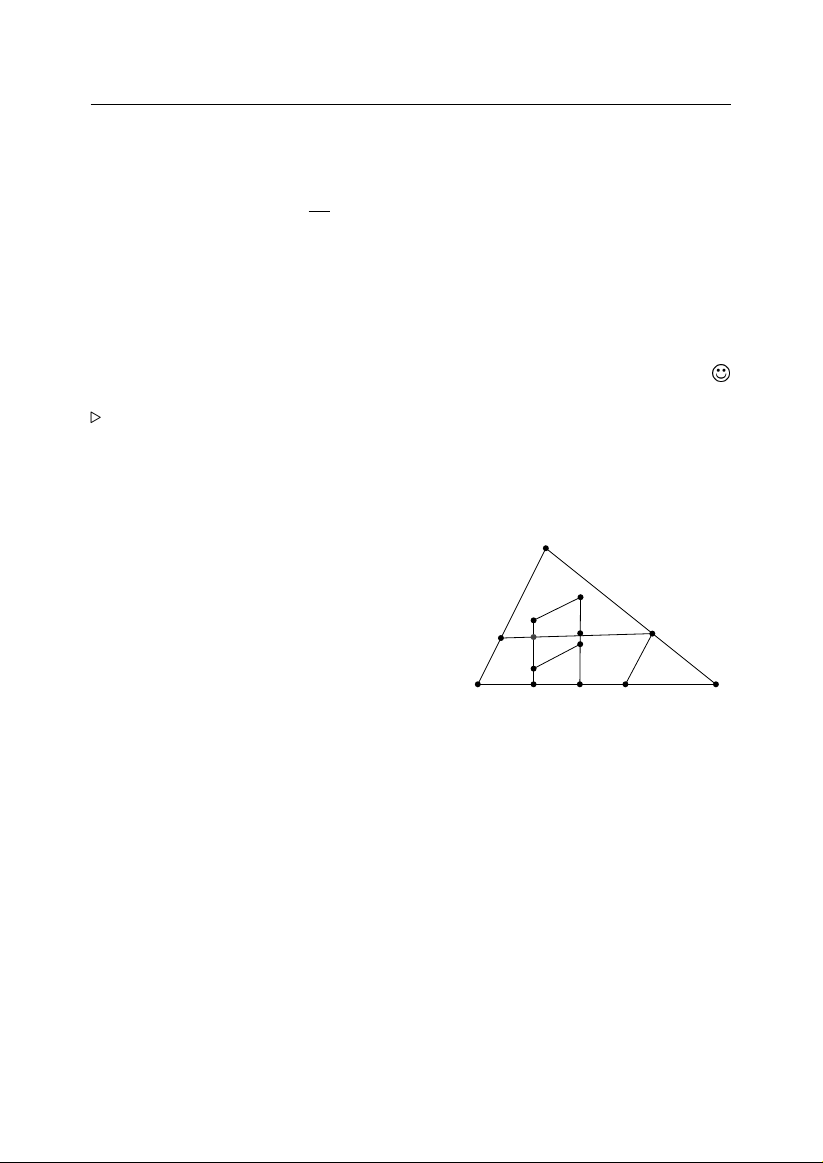
. 4.1. Trong h`ınh vuông v´
oi c .anh 1 ¯don v.i ¯du.oc ch.on 101 ¯diêm. Ch´ung , , , , ,, , , minh r` ˘ ang c´ o n˘ am ¯ diêm trong c´ ac ¯ diêm ¯ d˜
a ch .on c´o thê phu boi ¯du`ong 1 tr` on b´ an k´ınh . 7 , , L`
oi giai. Chia h`ınh vuông ra ra 25 h`ınh vuông con c´ o c .anh 0,2. , , , , , Nh˜ ung h`ınh vuông n` ay c´
o sô´ lu .ong 25 v`a v`ı tâ´t ca sô´ ¯diêm ¯d˜a ch .on , , , l` a 101, th`ı ´ıt nhâ´t c´
o m .ôt h`ınh vuông nho ch´ua ´ıt nhâ´t 5 ¯diêm. M`a , , , 1 1 b´ an k´ınh ¯ du` ong tr`
on ngo .ai tiê´p h`ınh vuông nho b`˘ang √ < . J 5 5 7 , . 4.2. Ch´ ung minh r` ˘
ang trong m .oi khô´i ¯da di.ên lô`i tô`n t .ai ´ıt nhâ´t hai
m .˘at c´o c`ung sô´c .anh. , , , , L` oi giai. K´
y hi .êu F l`a m.˘at c´o sô´c.anh l´on nhâ´t cua khô´i ¯da di.ên. Nê´u ,
sô´c .anh cua F l`a k, th`ı khô´i ¯da di.ên c´o ´ıt nhâ´t k + 1 m.˘at (v`ı c´o k m.˘at , , 34 Chuong 4. H`ınh h .oc , , , , c´
o c .anh chung v´oi F), c`on sô´ lu .ong c´ac c.anh cua m˜ôi m.˘at l`a m .ôt trong c´
ac sô´ 3, 4, . . . , k. Theo nguyên l´y Ðirichlê c´ o ´ıt nhâ´t hai m .˘at c´ o c` ung sô´c .anh. J , , , , ,
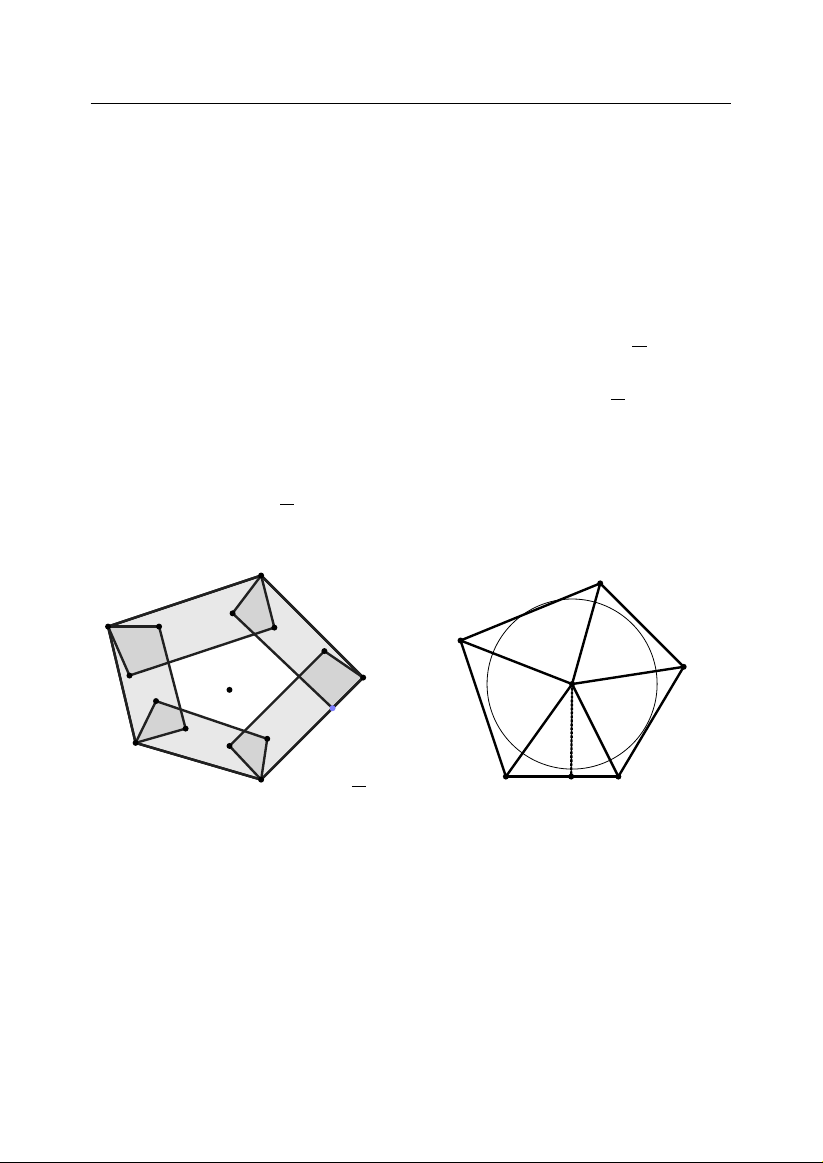
. 4.3. Trong phâ`n trong cua m .ôt h`ınh tr`on v´oi ¯du`ong k´ınh 5 ¯don v.i, , , , , , ngu`
oi ta ch .on bâ´t k`y 10 ¯diêm. Ch´ung minh r`˘ang ´ıt nhâ´t c´o hai ¯diêm , , , , trong c´ ac ¯ diêm ¯ d˜
a ch .on c´o khoang c´ach nho hon 2. , , , , L` oi giai. Chia ¯ du` ong tr` on , th` anh 8 re qu .at b`˘ang nhau , C , 9 , , C C 2 v´ oi g´ oc o tâm m˜ ôi re qu .at l`a A1 , , , B 450 v`
a d .ung ¯du`ong tr`on ¯dô`ng C F 8 , A C tâm C i b´ an k´ınh 1. K´ y 3 1 v´ o E D ,
hi .êu C2, C3, . . . , C9 l`a nh˜ung O B1 , , , C h`ınh t` u t´ am re qu 7 ¯ di C1 .at tr` u , , phâ`n m` a ¯ du` ong tr` on C1 ¯ d˜ a C , 4 , chiê´m. C´ o thê ch´ ung minh C , 6 , , , C5 ¯
du .oc bâ´t c´u hai ¯diêm n`ao
thu .ôc m .ôt trong ch´ın h`ınh , , H`ınh 4.1: trên ¯ dê`u c´ o khoang c´ ach nho , , , , ,
hon 2. Th .ât v.ây, nê´u hai ¯diêm roi v`ao ¯du`ong tr`on ¯dô`ng tâm th`ı , , , , , ,, , , khoang c´ ach gi˜ ua ch´ ung nho hon 2. Gia su hai ¯ diêm A v`a B roi , v`
ao m .ôt CDEF trong sô´ t´am re qu.at. Trên b´an k´ınh OC v`a OD lâ´y , , , , tuong ´ ung hai ¯
diêm A1 v`a B1 sao cho OA1 = OA; OB1 = OB, ngh˜ıa ,, l` a AB ≤ A1B1 (theo ¯
d.inh l´y h`am cosin, boi v`ı [ AOB ≤ \ A1OB1). , , Ðê ´ y r` ˘
ang A1B1 ≤ max{A1D, A1E}. Th .ât v.ây ¯diêm B1 n`˘am trong , ,, , ¯
do .an th˘ang t.ao boi h`ınh chiê´u H cua A1 trên OD v`a ´ıt nhâ´t m .ôt , , , ,, trong hai ¯
diêm D, E, ch˘ang h .an ¯diêm D. Boi v.ây h`ınh chiê´u HD , , , , , cua ¯ du`
ong xiên A1D không b´e hon h`ınh chiê´u HB1 cua A1B1 trên , , OD. Ngh˜ıa l`
a A1B1 ≤ A1D. C˜ung ch´ung minh nhu trên ta c´o 4.1. V´ı d .u 35 , ,
DA1 ≤ max{DF, DC}, EA1 ≤ max{EF, EC}. T`u s .u ¯d´anh gi´a
EF2 < CD2 = OC2 + OD2 − 2.OC.OD. cos 450 √ 25 25 2 = 2 − < 3, 75 < 4 4 4 v` a
EC2 = FD2 = OF2 + OD2 − 2OF.OD. cos 450 √ 25 5 2 5.1, 4 = 1 + − < 7, 25 − = 3, 75 < 4, 4 2 2 , , ta ¯
du .oc AB ≤ A1B1 ≤ max{DF, DC, EF, EC} < 2. J , ,, , , , , ,
. 4.4. Gia su m˜ ôi ¯
diêm trong m .ôt m .˘at ph˘ang ¯du.oc son b`˘ang m.ôt trong , , , hai mâ`u ¯ do v` a xanh. Ch´ ung minh r` ˘ ang c´
o m .ôt h`ınh ch˜u nh .ât n`ao ¯d´o , , ,
trong m .˘at ph˘ang m`a bô´n ¯dınh cua n´o c`ung mâ`u. , , L` oi giai. D˜ ê thâ´y theo nguyên l´ y , P1 P2 P3 P4
Ðirichlê, m .ôt t.âp bâ´t k`y 7 ¯diêm , m`
a son m .ôt trong hai mâ`u th`ı´ıt , Q1 Q2 Q3 Q4 nhâ´t c´ o 4 ¯ diêm c` ung mâ`u. Trên , , , ,
m .ôt ¯du`ong th˘ang c´o 7 ¯diêm th`ı R R 1 2 R3 R4 , , , ch´ ung ta phai c´ o 4 ¯ diêm th˘ ang , ,, h` ang c` ung mâ`u, gia su ¯ d´ o l` a , H`ınh 4.2:
P1, P2, P3, P4 c´o c`ung mâ`u ¯ do. Ta , , , , , , , , chiê´u nh˜ ung ¯ diêm n` ay xuô´ng hai ¯ du` ong th˘ ang song song v´ oi ¯ du` ong , , , , , ch´ ua ch´
ung t .ao ra (Q1, Q2, Q3, Q4) v`a (R1, R2, R3, R4) tuong ´ung v´oi , , , (P1, P2, P3, P4). Nh˜ung ¯ diêm n`
ay t .ao ra m .ôt sô´h`ınh ch˜u nh.ât, ch´ung , , , ta ch´ u ´ y ¯ dê´n c´ ac h`ınh ch˜
u nh .ât c´o ¯dınh l`a Pi, i = 1, 2, 3, 4. Nhu v.ây , , , , nê´u 2 ¯ diêm bâ´t k` y cua Q l`a ¯ do th`ı ta c´
o kê´t qua m .ôt h`ınh vuông , , , , , PiPjQjQi c´o ¯ dınh c`
ung mâ`u. Tuong t .u cho c´ac ¯diêm R. Nê´u ¯dô`ng , , , , , , th` oi không c´ o ¯
diêm Q v`a R thoa m˜an tru`ong h .op trên th`ı c´o 3 (ho.˘ac , , 36 Chuong 4. H`ınh h .oc , , , , hon) ¯ diêm Q n`ao ¯ d´ o v` a 3 ¯ diêm R n`ao ¯ d´ o c´ o c` ung mâ`u xanh. Nhung , , , ,
trong b .ô ba nhu v.ây phai c´o c.˘ap ¯dôi t.ao ra h`ınh ch˜u nh.ât v´oi c´ac , , ¯
dınh mâ`u xanh trong sô´c´ ac ¯ diêm Q v`a R. J , ,, , , , , ,
. 4.5. Gia su m .ôt b`an c`o h`ınh ch˜u nh .ât c´o 4x7 ô vuông ¯du.oc son ¯den , , , ,
ho .˘ac tr´˘ang. Ch´ung minh r`˘ang v´oi c´ach son mâ`u bâ´t k`y, trong b`an c`o , ,,
luôn tô`n t .ai h`ınh ch˜u nh .ât gô`m c´ac ô vuông, m`a bô´n ô o g´oc l`a c´ac ô c` ung mâ`u. , , , L` oi giai. Ch´ ung ta ch´ ung, minh cho b` ai to´ an b` an c` o , 3 × 7. M˜ âu son mâ`u c´ o , , , , thê xây ra v´ oi b` an c` o n` ay , , c´ o d .ang t`u 1 ¯dê´n 8. Gia ,,
su m .ôt trong sô´ c´ac c .ôt
thu .ôc d.ang 1. B`ai to´an s˜e , , , ¯
du .oc ch´ung minh nê´u tâ´t , , ca nh˜ ung c .ôt c`on l.ai trong
6 c .ôt thu .ôc c´ac d.ang 1, 2, , , ,, ,
3, 4. Nhu v .ây gia su tâ´t ca H`ınh 4.3: c´
ac c .ôt c`on l.ai thu .ôc d.ang
5, 6, 7, ho .˘ac 8. Khi ¯d´o theo nguyên l´y Ðirichlê hai trong sô´ s´au c .ôt , , , , c´
o hai c .ôt c`ung m .ôt d.ang v`a nhu v.ây b`ai to´an c˜ung ¯du .oc ch´ung , , , , , minh. Ch´ ung minh ho` an to`
an tuong t .u nê´u m .ôt c .ôt c´o d.ang 8. Gia ,, , su không c´
o c .ôt n`ao trong 7 c .ôt c´o d.ang 1 ho.˘ac 8. Nhu v.ây ta c´o 7 ,
c .ôt v´oi 6 d.ang. Theo nguyên l´y Ðirichlê c´o hai c .ôt c`ung d.ang v`a b`ai , , , , to´ an ¯
du .oc ch´ung minh ¯dâ`y ¯du. J , , . 4.6. N˘ am ¯
diêm A, B, C, D, E n` ˘
am trong m .ôt m .˘at ph˘ang v`a t.oa ¯d.ô , , , cua ch´ ung l` a c´ ac sô´ nguyên. Ch´ ung minh r` ˘ ang trong sô´ nh˜ ung tam 4.1. V´ı d .u 37 , , , , gi´ ac m` a ¯ dınh cua n´ o l` a ba ¯ diêm n` ao ¯ d´ o trong c´ ac ¯ diêm n` ay, c´ o ´ıt nhâ´t , ba tam gi´ ac v´
oi di.ên t´ıch l`a c´ac sô´nguyên. , , , , , L` oi giai. Ta c´ o thê ch´ ung minh r` ˘
ang nê´u m .ôt trong c´ac t .oa ¯d .ô cua , , , c´ ac ¯ dınh tam gi´ ac ¯ d˜ a cho thay ¯
dôi m .ôt sô´ch˜˘an, th`ı di.ên t´ıch cua tam , , , , gi´ ac c˜ ung thay ¯
dôi m .ôt sô´nguyên. M .ôt c´ach tông qu´at hon ta c´o thê , , , , kh˘ ang ¯
d.inh nê´u c´ac t .oa ¯d .ô ¯dınh cua m .ôt tam gi´ac thay ¯dôi m .ôt sô´ , , ch˜ ˘
an, th`ı di .ên t´ıch cua n´o c˜ung thay ¯dôi m .ôt sô´nguyên. V`ı v.ây, nê´u , , , ,
di .ên t´ıch cua tam gi´ac m´oi nh.ân ¯du .oc l`a sô´ nguyên, th`ı di.ên t´ıch , tam gi´ ac ban ¯ dâ`u c˜ ung l` a sô´nguyên (h˜ ay v˜ e h`ınh v` a ch´ ung minh). , , , , V`ı nh˜
ung t .oa ¯d .ô cua c´ac ¯diêm ¯d˜a cho A, B, C, D, E l`a nh˜ung sô´ , , nguyên, sau khi thêm v` ao c´
ac t .oa ¯d .ô n`ay nh˜ung sô´ch˜˘an th´ıch h .op, , , th`ı m˜
ôi t .oa ¯d .ô s˜e chı nh.ân c´ac gi´a tr.i 0 v`a 1. Do ¯d´o m .oi 5 ¯diêm ¯d˜a cho ,, ,
t .ao nên boi c´ac ¯diêm (0, 0), (0, 1), (1, 0), (1, 1). Áp d .ung nguyên l´y , , ,
Ðirichlê suy ra ´ıt nhâ´t hai ¯ diêm trong c´ ac ¯ diêm A, B, C, D, E biê´n ¯ dôi , , ,, th` anh c`
ung m .ôt ¯diêm trong {(0, 0), (0, 1), (1, 0), (1, 1)}. Gia su ¯d´o l`a , A, B. Ch´ ung ta s˜ e kh˘ ang ¯
d.inh di.ên t´ıch c´ac tam gi´ac ABC, ABD v`a , ABE l` a nh˜
ung sô´ nguyên. Th .ât v.ây, c´ac tam gi´ac n`ay b.i biê´n th`anh , , ¯
do .an th˘ang (do A v`a B biê´n th`anh c`ung m .ôt ¯diêm) nên di.ên t´ıch , , , , , , anh cua ch´ ung b` ˘
ang 0. V .ây tru´oc khi biê´n ¯dôi, di.ên t´ıch cua ch´ung , phai l` a sô´nguyên. J , , ,
. 4.7. Trong m .ôt m .˘at ph˘ang cho m.ôt t .âp h.op A c´o n ¯diêm (n ≥ 2), , , , , , ,
m .ôt sô´ c .˘ap ¯diêm ¯du.oc nô´i v´oi nhau b`˘ang ¯do .an th˘ang. Ch´ung minh , , , , , , , r` ˘ ang trong A c´ o ´ıt nhâ´t hai ¯ diêm ¯
du .oc nô´i v´oi c`ung sô´lu.ong c´ac ¯diêm kh´ ac thu .ôc A. , , , , L` oi giai. V´
oi m .oi ¯diêm bâ´t k`y a thu .ôc A ch´ung ta k´y hi.êu S(a) l`a , , , , , ,
sô´ lu .ong nh˜ung ¯diêm cua A m`a a nô´i th`anh ¯do.an th˘ang. B`ai to´an , , , muô´n kh˘ ang ¯
d.inh r`˘ang tô`n t.ai hai ¯diêm kh´ac nhau a1 v`a a2 cua A , , 38 Chuong 4. H`ınh h .oc , m`
a S(a1) = S(a2). Ch´ung ta thâ´y ngay r`˘ang 0 ≤ S(a) ≤ n − 1 v´oi ,, , ,
m .oi phâ`n tu a thu .ôc A. M.˘at kh´ac, c˜ung không tô`n t.ai nh˜ung ¯diêm ,,
x1 v`a x2 thu .ôc A, m`a S(x1) = n − 1 v`a S(x2) = 0. Boi v`ı ¯diê`u n`ay , , , , , c´ o ngh˜ıa l` a ¯
diêm x1 nô´i v´oi tâ´t ca c´ac ¯ diêm c` on l .ai cua A, c`on x2 , , , , không nô´i v´ oi ¯ diêm n` ao cua A, ¯ d˜ ân ¯ dê´n vô l´ y. C´ ac sô´ nguyên t` u 0 , , , ¯ dê´n n − 1 c´
o sô´ lu .ong l`a n. V`ı 0 v`a n − 1 không ¯dô`ng th`oi l`a gi´a tr.i , , , ,
vua S nên S nh .ân nhiê`u nhâ´t l`a n − 1 gi´a tr.i. B`ai to´an ¯du .oc giai suy , ra t` u nguyên l´ y Ðirichlê. J , , . 4.8. Cho ¯ da gi´ ac ¯
dê`u 100 c .anh n.ôi tiê´p trong ¯du`ong tr`on k. M˜ôi , , , , ¯ dınh ¯
du .oc g´an m.ôt trong c´ac sô´ 1, 2, . . . , 49. Ch´ung minh r`˘ang trên k ,
tô`n t .ai hai cung AB v`a CD v´oi c´ac t´ınh châ´t sau: , , , a) C´ ac ¯ diêm A, B, C v` a D l` a ¯ dınh cua ¯ da gi´ ac ¯ dê`u ¯ d˜ a cho. , b) C´
ac dây cung AB v`
a CD song song v´ oi nhau , , ,
c) Nê´u A, B, C v` a D c´ o nh˜ an tuong ´ ung l` a c´
ac sô´ a, b, c, d th`ı a + b = c + d. , , , , L`
oi giai. Trong ¯ du` ong tr` on k c´ o , , ¯ d´ ung 50 ¯ du` ong k´ınh kh´ ac nhau m` a D C , , , , ¯ diêm cuô´i cua ¯ du` ong k´ınh l` a m .ôt , , ¯ dınh cua ¯ da gi´ ac ¯ dê`u 100 c .anh ¯d˜a , ,
cho. Nê´u PQ l`a m .ôt trong sô´¯du`ong , , k´ınh ¯ d´ o v` a ¯ dir nh P ¯ du .oc g´an nh˜an , , , p, c` on Q v´ oi nh˜ an q th`ı ¯ du` ong , , , , k´ınh PQ tuong ´ ung v´ oi sô´ nguyên B A
|p − q|. R˜o r`ang, 0 ≤ |p − q| ≤ 48. , , B` ˘ ang c´ ach n` ay m˜ ôi ¯ du` ong k´ınh ¯ d˜ a H`ınh 4.4: , , , , x´ et (tông sô´ c´ o 50 tâ´t ca) ¯ du .oc cho , , , , tuong ´ ung v´
oi m .ôt trong c´ac sô´ 0, 1, 2, . . . , 48. Suy ra c´o ´ıt nhâ´t hai 4.1. V´ı d .u 39 , , , , , , , , ¯ du` ong k´ınh ¯
du .oc ¯d.˘at tuong ´ung v´oi c`ung m .ôt sô´. , , , , , , Ta k´
y hi .êu ¯d´o l`a AB v`a CD, c`on c´ac ¯dınh ¯du .oc g´an tuong ´ung , , , c´ ac nh˜
an a, b, c, d. Không mâ´t t´ınh tông qu´at ch´ ung ta c´ o thê gia
thiê´t c ≤ a v`a b ≤ d. Khi ¯ d´ o dây cung AC v`a BD c´ o c´ ac t´ınh châ´t , , , , ,
mong muô´n. Th .ât v.ây, v´oi ¯du`ong k´ınh AC ch´ung ta ¯d˜a ¯d.˘at tuong ´, , , , , ung v´ oi a − c, c` on BD ´ ung v´
oi d − b v`a nh˜ung sô´ n`ay b`˘ang nhau, , , ch´
ung ta nh .ân ¯du .oc a − c = d − b hay l`a a + b = c + d. Ngo`ai ra, , , t´ u gi´
ac ABCD l`a h`ınh vuông, nên AB song song v´ oi CD (th .âm ch´ı AB = CD). J , , , , , ,,
. 4.9. Tâ´t ca c´ ac ¯
diêm trong m .ôt m .˘at ph˘ang ¯du.oc bôi boi n mâ`u , , , , kh´ ac nhau. Cho tru´ oc 2n − 1 ¯ du` ong tr` on ¯ dô`ng tâm kh´ ac nhau , , , , , ,
k1, k2, . . . , k2n−1. Trong c´ac ¯du`ong tr`on d .ung b´an k´ınh tuong ´ung ,
OA1, OA2, . . . , OA2n−1 sao cho m˜
ôi c .˘ap b´an k´ınh không c´o ¯diêm , , , chung n` ao kh´ ac ngo` ai O. Ch´ ung minh r` ˘
ang tô`n t .ai m.ôt ¯du`ong tr`on ,
ki, i = 1, 2, . . . , 2n − 1 sao cho trên n´o v`a trên b´an k´ınh OAi cua n´o c´o , , , , , , , nh˜ ung ¯ diêm tuong ´
ung Xi v`a Yi, m`a ch´ung ¯du .oc bôi c`ung m.ôt mâ`u v`a ,
Yi không tr`ung v´oi O v`a Ai. , , L` oi giai. K´
y hi .êu c´ac mâ`u ¯d˜a cho l`a c1, c2, . . . , cn. Ch´ung ta s˜e t´ınh , , , , , , ,
sô´ lu .ong c´ac tô h .op kh´ac nhau cua c´ac mâ`u m`a v´oi ch´ung c´o thê , , bôi mâ`u c´ ac ¯
diêm trên m .ôt h`ınh ph˘ang. M .oi t.âp con kh´ac trô´ng , , , , ,
{i1, i2, . . . , ik}, 1 ≤ k ≤ n cua t.âp h .op N = {1, 2, . . . , n} tuong ´ung , , , , v´
oi tô h .op mâ`u {ci , c , . . . , c }. R˜o r`ang nh˜ung t 1 i2 ik .âp con kh´ ac trô´ng , , , , , , , , kh´
ac nhau cua N b`˘ang c´ach n`ay tuong ´ ung v´ oi nh˜ ung tô h .op mâ`u , , , kh´ ac nhau. Ngo`
ai ra, m .oi tô h .op mâ`u {ci , c , . . . , c } c´o thê nh 1 i2 ik .ân , , , , , , ¯
du .oc nh`o xây d .ung t.âp con kh´ac trô´ng {i1, i2, . . . , ik}. Suy ra, tô h .op , , , , nh˜
ung mâ`u c1, c2, . . . , cn m`a v´oi ch´ung c´o thê bôi c´ac ¯ diêm m .ôt h`ınh , , , , , , , ph˘ ang l` a tuong ´
ung m .ôt - m .ôt v´oi nh˜ung t.âp h .op con kh´ac trô´ng , , 40 Chuong 4. H`ınh h .oc , , , ,
cua N = {1, 2, . . . , n}. Ngh˜ıa l`a sô´ c´ac tô h .op kh´ac nhau cua mâ`u , , , , b` ˘ ang sô´ c´
ac t .âp h .op con kh´ac trô´ng cua N, c´o tâ´t ca 2n − 1 t.âp h .op , nhu v .ây. , , , , , Tru´ oc tiên ch´ ung ta gia thiê´t r` ˘
ang tô`n t .ai ¯du`ong tr`on ki, i = , , 1, 2, . . . , 2n − 1 m` a muô´n bôi k´ın n´ o phai d` ung tâ´t ca c´ ac mâ`u , , c1, c2, . . . , cn. Khi ¯ d´ o ch´
ung ta ch .on ¯diêm bâ´t k`y Yi l`a ¯diêm trong , , ,, , , , cua b´ an k´ınh OAi. Gia su Yi ¯
du .oc bôi b`˘ang mâ`u c1. Nhung trên ki c´o , , , ,
´ıt nhâ´t m .ôt ¯diêm Xi, ¯du .oc bôi c`ung mâ`u nhu v.ây, v`ı m .oi mâ`u ¯d˜a cho , , , , , , , ¯ dê`u b´ ˘
at g .˘ap trên ki; v.ây b`ai to´an ¯du .oc giai trong tru`ong h .op gia thiê´t , , , , ,, , , n` ay. Ta x´ et tru`
ong h .op c`on l.ai: Gia su không c´o ¯du`ong tr`on n`ao m`a , , , , , , , , nh˜ ung ¯ diêm cua n´ o ¯
du .oc bôi mâ`u v´oi to`an b .ô tô h .op c1, c2, . . . , cn. , , , , , , , , Khi ¯ d´ o c´
o tâ´t ca 2n − 2 kha n˘ang tô h .op mâ`u, v´oi n´o c´ac ¯diêm ¯du .oc , , ,, bôi cho c´ ac ¯ du` ong tr`
on k1, k2, . . . , k2n−1 . Boi v`ı 2n − 1 > 2n − 2 nên , , , , c´ o hai ¯ du` ong tr`
on ki v`a kj, i < j trên n´o s˜e c´o c`ung m .ôt tô h .op mâ`u. , ,, , , , ,
Gia su ki c´o b´an k´ınh l´on hon kj. K´y hi.êu Yi l`a ¯diêm c´˘at cua OAi v`a , , , , , ,
kj. Trong tru`ong h .op ¯d´o Yi n`˘am trên kj v`a v`ı nh˜ung ¯diêm cua ki v`a , , , , , , , , kj ¯
du .oc bôi v´oi c`ung m .ôt tô h .op mâ`u, trên ki c´o ¯diêm Xi ¯du .oc bôi , c` ung mâ`u v´ oi Yi. J , , , , ,
. 4.10. Tông cua ¯
d .ô d`ai m.ôt sô´ vecto trong m .˘at ph˘ang l`a 4. Ch´ung , , , , , , minh r` ˘ ang t` u nh˜ ung vecto n` ay c´
o thê ch .on m.ôt sô´ vecto m`a tông ¯d.ô , , , d` ai cua ch´ ung l´ on hon 1. , , , , , L` oi giai. Ch´ ung ta ¯ dua v`
ao h .ê t .oa ¯d .ô v`a x´et vecto ¯d.ai di.ên nh˜ung , , , , vecto ¯ d˜
a cho t .ai ¯diêm gô´c. Ch´ung ta chiê´u nh˜ung vecto n`ay xuô´ng , , , , ,
tr .uc t .oa ¯d .ô Ox v`a Oy. V`ı m˜ôi vecto c´o ¯d .ô d`ai nho hon tông cua c´ac , , , , ¯
d .ô d`ai h`ınh chiê´u cua n´o xuô´ng hai tr .uc;nên tông ¯d .ô d`ai cua tâ´t ca , , , , h`ınh chiê´u cua c´ ac vecto l´ on hon 4. Khi ¯ d´
o trên ´ıt nhâ´t m .ôt trong ,, , , , , ,
4 nua tr .uc cua h.ê t .oa ¯d .ô tông ¯d .ô d`ai cua h`ınh chiê´u s˜e l´on hon 1, 4.2. B` ai t .âp 41 , , , , , , , , ¯ diê`u ¯ d´ o c´ o ngh˜ıa l` a tông cua ¯
d .ô d`ai cua nh˜ung vecto tuong ´ung s˜e , , , , , l´ on hon 1. (¯
d .ô d`ai h`ınh chiê´u ¯d˜a l´on hon th`ı tâ´t nhiên ¯d .ô d`ai vecto , , c˜ ung l´ on hon.) J 4.2. B ` ai t .âp , , , ,
. 4.11. Trong h`ınh vuông v´
oi c .anh 1 ¯don v.i cho 112 ¯diêm. Ch´ung , , , 2 minh r` ˘
ang ´ıt nhâ´t hai trong sô´ ¯ d´ o c´ o khoang c´ ach nho hon . 15 , . 4.12. (Ðê` thi To´
an Olympic quô´c tê´ lâ`n th´ u 25 n˘ am 1984) Trong , , , ,
m .˘at ph˘ang cho hai ¯diêm kh´ac nhau O v`a A. V´oi m˜ôi ¯diêm X thu .ôc ,
m .˘at ph˘ang kh´ac O ch´ung ta k´y hi.êu a(X) l`a ¯d .ô ¯do b`˘ang radian , , , , cua g´ oc AOX, ¯
do theo chiê`u ngu .oc kim ¯dô`ng hô` t`u OA ¯dê´n OX , , (0 ≤ a(X) ≤ 2). C` on c(X) l`a ¯ du` ong tr`
on tâm O v`a b´an k´ınh c´ o ¯ d .ô a(X) , , , , d` ai OX + . Cho tru´
oc b .ô h˜uu h.an mâ`u v`a m˜ôi ¯diêm trong m.˘at OX , , , , , ph˘ ang ¯
du .oc bôi b`˘ang 1 trong sô´ ¯d´o. Ch´ung minh r`˘ang tô`n t.ai ¯diêm , , , , , ,
X1 v´oi a(X1) > 0 v`a trên ¯ du` ong tr`
on c(X1) c´o ´ıt nhâ´t 1 ¯ diêm ¯ du .oc , bôi c` ung mâ`u v´ oi X1. , , ,
. 4.13. Trong m .˘at ph˘ang cho n ¯diêm, n ≥ 7, sao cho khoang c´ach , , , , , , m˜
ôi c .˘ap ¯diêm gi˜ua ch´ung l`a kh´ac nhau. M˜ôi m .ôt ¯diêm ¯du .oc nô´i v´oi , , , , , ¯ diêm gâ`n n´ o nhâ´t. Ch´ ung minh r` ˘ ang không c´ o ¯ diêm n` ao ¯ du .oc nô´i , , , v´ oi nhiê`u hon 5 ¯ diêm kh´ ac. , . 4.14. Ch´ ung minh r` ˘
ang trong m .ôt h`ınh tr`on b´an k´ınh 1, không , , , , , , ,
thê ch .on ¯du .oc qu´a n˘am ¯diêm m`a khoang c´ach gi˜ua hai ¯diêm m .ôt , , l´ on hon 1. , , , , . 4.15. Ngu` oi ta qu˘ ang 120 h`ınh vuông c´ o k´ıch thu´ oc 1 × 1 v`ao m .ôt , , , , , h`ınh ch˜
u nh .ât k´ıch thu´oc20 × 25. Ch´ung minh r`˘ang v´oi m .oi c´ach s´˘ap , , 42 Chuong 4. H`ınh h .oc ,, , , xê´p c´
ac h`ınh vuông th`ı o trong h`ınh ch˜
u nh .ât v˜ân c`on ch˜ô trô´ng ¯dê , , ¯
d .˘at m .ôt h`ınh tr`on ¯du`ong k´ınh 1. , , CHUONG 5 ,,
MO R .ÔNG NGUYÊN L´Y ÐIRICHLÊ ,, 5.1. Nguyên l´ y Ðirichlê mo r .ông , , ,, , ,
Cho A l`a t .âp h˜uu h.an nh˜ung phâ`n tu, k´y hi.êu s(A) l`a sô´ lu .ong ,, , ,, , c´
ac phâ`n tu thu .ôc A. Nguyên l´y Ðirichlê c´o thê mo r .ông nhu sau: , , , ,, Nê´u A v` a B l` a nh˜
ung t .âp h .op h˜uu h .an v`a s(A) > k.s(B), o , ,, , ¯ dây k l`
a m .ôt sô´ t .u nhiên n`ao ¯d´o v`a nê´u m˜ôi phâ`n tu cua A cho , , , , ,, , tuong ´ ung v´
oi m .ôt phâ`n tu n`ao ¯d´o cua B, th`ı tô`n t .ai ´ıt nhâ´t k + 1 ,, , , , , , ,, ,
phâ`n tu cua A m` a ch´ ung tuong ´ ung v´ oi c`
ung m .ôt phâ`n tu cua B , , ,
Th .ât v.ây, tru`ong h .op k = 1 l`a nguyên l´y Ðirichlê m`a ta ¯d˜a x´et , , , , , trong c´ ac b`
ai t .âp t`u ¯dâ`u t´oi gi`o. Ðê ch´ung minh m.ênh ¯dê`trên ch´ung , ,, ,, , , , , , , ,, ta gia su m˜
ôi phâ`n tu cua B chı tuong ´ ung v´ oi nhiê`u nhâ´t k phâ`n tu , , , cua A. Khi ¯ d´ o s(A) ≤ k.s(B) tr´ai v´
oi gia thiê´t s(A) > k.s(B). , , , , , , ,, Ch´ u ´ y. Ngay t` u nh˜ ung chuong ¯ dâ`u nguyên l´ y n` ay ¯ d˜ a ¯ du .oc su , , , , , , , ,
d .ung v´oi c´ach ch´ung minh tuong t .u nhu trên. Ðê tiê´p t .uc hiêu sâu ,, , , thêm nguyên l´
y o d .ang m´oi ch´ung ta x´et m .ôt lo.at b`ai to´an ¯diên h`ınh. , , ,, 44
Chuong 5. Mo r .ông nguyên l´y Ðirichlê 5.2. V´ı d .u ,
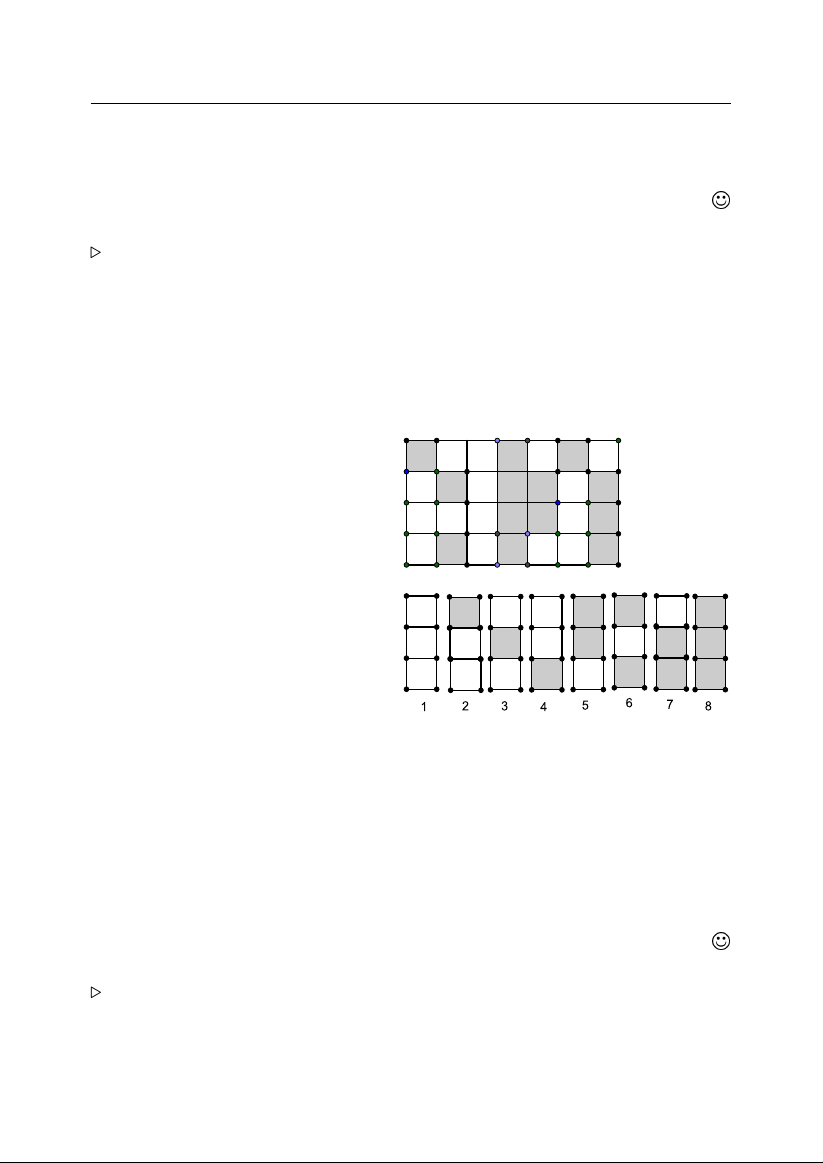
. 5.1. Trong m .ôt h`ınh vuông c´o c .anh b`˘ang 1 ta ch.on bâ´t k`y 51 ¯diêm. , , Ch´ ung minh r` ˘ ang ´ıt nhâ´t c´ o ba ¯ diêm trong sô´ ¯ d´ o n` ˘ am trong m .ôt h`ınh vuông c´ o c .anh 0,2. , , L` oi giai. Ch´ ung ta chia h`ınh vuông th` anh 25 h`ınh vuông con c´ o , , , , ,
c .anh 0,2 b`˘ang c´ac ¯du`ong th˘ang song song v´oi c´ac c.anh cua h`ınh , , , , , , vuông.Nê´u gia su r` ˘ ang m˜ ôi h`ınh vuông v`
ua nh .ân ¯du .oc ch´ua không , , , , , qu´ a 2 ¯ diêm th`ı tâ´t ca c´ ac ¯ diêm trong h`ınh vuông l´ on s˜ e c´ o sô´ ¯ diêm nhiê`u nhâ´t l` a 2 × 25 = 50 d˜ân ¯ dê´n vô l´ y. J , , , ,
. 5.2. Tâ´t ca 9 c .anh v`a 27 ¯du`ong ch´eo cua m.ôt h`ınh ch´op ¯d´ay ¯da gi´ac , , , , , , , , 9 ¯ dınh ¯
du .oc bôi son: m.ôt sô´ bôi son ¯do, c`on l .ai bôi son xanh. Ch´ung , , , , minh r` ˘
ang tô`n t .ai ba ¯dınh cua h`ınh ch´op, m`a ch´ung l`a nh˜ung ¯dınh , , , , ,
cua m .ôt h`ınh tam gi´ac v´oi c´ac c .anh ¯du.oc son c`ung m.ôt mâ`u. , , , , , , L`
oi giai. 9 c .anh bên cua h`ınh ch´op ¯du .oc son b`˘ang hai mâ`u. V`ı 9 > , ,, , , 4.2, t` u nguyên l´
y mo r .ông trên suy ra ´ıt nhâ´t c´o 5 c.anh bên ¯du .oc bôi , ,, , , c`
ung m .ôt mâ`u. Gia su ¯d´o l`a SA1, SA2, SA3, SA4, SA5 ¯du .oc bôi c`ung , ,, , , ,,, , mâ`u ¯ do, o ¯ dây S l`a ¯ dınh h`ınh ch´ op. Không anh huong t´ oi kê´t lu .ân , ,, , , , b` ai to´ an ch´ ung ta gia su c´ ac ¯ diêm A1, A2, A3, A4, A5 ¯ du .oc s´˘ap xê´p , , ,
theo chiê`u ngu .oc kim ¯dô`ng hô`. Ít nhâ´t m .ôt trong c´ac c.anh cua ng˜u , , , , ,, gi´ ac l` a ¯ du` ong ch´ eo cua ¯ da gi´ ac ¯ d´ ay; gia su ¯ d´ o l` a A1A2. Ch´ung ta , , , , , x´ et tam gi´
ac A1A2A4. Nh˜ung c .anh cua n´o l`a c´ac ¯du`ong ch´eo cua ¯da , , , , gi´ ac ¯ d´ ay (do c´ ach xê´p trên) v` a suy ra ch´ ung ¯
du .oc bôi son.Nê´u tâ´t ca , c´
ac c .anh A1A2, A2A4, A4A1 l`a mâ`u xanh th`ı b`ai to´an ¯d˜a giai xong. , , , , , Tru`
ong h .op ngu .oc l.ai m .ôt trong c´ac c.anh A1A2, A2A4, A4A1 l`a mâ`u , , ,, , ¯ do, gia su ¯ d´ o l` a A1A2. Khi ¯ d´ o c´
ac c .anh cua tam gi´ac SA1A2 l`a mâ`u , ¯ do. J 5.2. V´ı d .u 45 , , . 5.3. Ch´ ung minh r` ˘
ang trong m .oi ¯da gi´ac lô`i v´oi sô´ c .anh ch˜˘an tô`n , , , ,
t .ai ¯du`ong ch´eo không song song v´oi m.ôt c .anh n`ao cua ¯da gi´ac. , , , d1 L` oi giai. B` ˘
ang qui n .ap ta c´o thê d˜ê , , , , d2 ch´ ung minh ¯
du .oc m .oi ¯da gi´ac v´oi n n(n − 3) , , c .anh c´o ¯ du` ong ch´ eo. 2 dk−1 , Bây gi` o ch´ ung ta x´ et ¯ da gi´ ac lô`i bâ´t , k` y P c´
o 2k c .anh v´oi k(≥ 2) l`a m .ôt sô´ a nguyên. H`ınh 5.1: , ,, , , , , Gia su m˜ ôi ¯ du`ong ch´ eo cua P song song v´ oi m .ôt c.anh n`ao ¯d´o , , , , , , , , cua P. Khi ¯ d´ o m˜ ôi ¯ du` ong ch´ eo d c´ o thê cho tuong ´ ung v´ oi c .anh song , , , song v´
oi d. K´y hi .êu s l`a sô´c´ac ¯du`ong ch´eo ch´ung ta c´o 2k(2k − 3) s = = k(2k − 3) 2
= 2k(k − 2) + k > (k − 2).2k. , ,,
Nhu v .ây theo nguyên l´y Ðirichlê mo r .ông suy ra tô`n t.ai k − 1 , , , , , , , ¯ du` ong ch´
eo d1, d2, . . . , dk−1 cua ¯da gi´ac P m`a ch´ung tuong ´ung v´oi , c`
ung m .ôt c.anh a cua ¯da gi´ac, ngh˜ıa l`a a, d1, d2, . . . , dk−1 song song , , , v´ oi nhau. Suy ra c´ ac ¯ du` ong ch´
eo d1, d2, . . . , dk−1 c`ung n`˘am trong ,, , ,,
m .ôt nua m.˘at ph˘ang x´ac ¯d.inh boi c.anh a v`ı P l`a ¯da gi´ac lô`i (h`ınh v˜e). , , ,, Ngo`
ai ra d1, d2, . . . , dk−1 v`a a l`a nh˜ung ¯do .an th˘ang kh´ac nhau v`a boi , , , , , , ,
v`ı sô´ lu .ong cua ch´ung l`a k, m˜ôi ¯dınh cua ¯da gi´ac P l`a ¯diêm ¯dâ`u cua , ,,, , ,
m .ôt ¯do.an n`ao ¯d´o trong ch´ung. Không anh huong ¯dê´n kê´t qua ch´ung , , , , minh ta gia thiê´t d1 l`a ¯
do .an xa nhâ´t ¯dô´i v´oi a trong c´ac ¯du`ong ch´eo , d1, d2, . . . , dk−1. Khi ¯ d´ o t` u l´
y lu .ân trên suy ra r`˘ang ¯da gi´ac P n`˘am ,, , ,, , to`
an b .ô trong m .ôt nua m.˘at ph˘ang x´ac ¯d.inh boi d1. Ðiê`u n`ay tr´ai v´oi , t´ınh lô`i cua ¯ da gi´ ac P. J , , , ,
. 5.4. Trong m .˘at ph˘ang cho 6 ¯diêm. M˜ôi ¯do .an th˘ang nô´i t`ung c .˘ap , , ,, 46
Chuong 5. Mo r .ông nguyên l´y Ðirichlê , , , , , , ¯ diêm ¯
du .oc bôi mâ`u ¯do ho .˘ac xanh. Ch´ung minh r`˘ang ba ¯diêm trong sô´ , , , , , , c´ ac ¯ diêm l` a ¯
dınh cua m .ôt tam gi´ac, m`a c´ac c .anh cua n´o ¯du.oc bôi c`ung m .ôt mâ`u. , , , L` oi giai. K´
y hi .êu A l`a m .ôt trong c´ac ¯diêm ¯d˜a cho v`a x´et n˘am ¯do.an , , , , , , , th˘ ang, c´ o ¯ dınh chung l` a A. Nh˜ung ¯
do .an th˘ang n`ay ¯du .oc son hai , ,, mâ`u v` a v`ı 5=2.2+1, suy ra t` u nguyên l´
y Ðirichlê mo r .ông ch´ung , ,, ta c´ o ´ıt nhâ´t ba ¯
do .an c`ung mâ`u. Gia su ¯d´o l`a AB1, AB2, AB3 mâ`u ,
xanh. Nê´u m .ôt v`ai ¯do.an th˘ang B1B2, B2B3, B3B1 l`a xanh th`ı tô`n t.ai , , ,
m .ôt tam gi´ac v´oi ba c.anh xanh v`a c´o ¯dınh l`a A. Nê´u ba ¯do.an th˘ang , , B1B2, B2B3, B3B1 l`a ¯
do, th`ı m .ôt tam gi´ac thoa m˜an ¯dê` to´an ¯d˜a ra l`a ,
B1B2B3 (c´ac c .anh ¯dê`u mâ`u ¯do). J , , , . 5.5. Cho d˜
ay vô h .an c´ac sô´t .u nhiên u1, u2, . . . , un, . . . ¯du.oc x´ac ¯d.inh , theo công th´
uc sau u1 = 3, un+1 = (n + 1)un − n + 1, n = 1, 2, . . .. , , ,
Cho n sô´ t .u nhiên bâ´t k`y v`a t .âp h.op M gô`m un ¯diêm sao cho không , , , , c´ o ba ¯ diêm n` ao th˘ ang h` ang. M˜ ôi ¯
do .an th˘ang nô´i hai ¯diêm kh´ac nhau , , , trong M ¯
du .oc bôi son b`˘ang m.ôt trong n mâ`u ¯d˜a cho. Khi ¯d´o tô`n t .ai 3 , , , ¯ diêm trong M l` a ¯
dınh cua m .ôt tam gi´ac ¯dô`ng mâ`u. , , , , L` oi giai. Ch´ ung minh b` ˘
ang qui n .ap theo n. V´oi n = 1 ch´ung ta c´o , , , , , ,
u1 = 3 v`a kê´t lu .ân l`a hiên nhiên. V´oi n = 2 t`u công th´uc t´ınh ¯du .oc , , , , ,, , ,, u2 = 6, ¯ dây l` a tru`
ong h .op ta ¯d˜a ch´ung minh o b`ai trên. Gia su b`ai , , , , , ,, to´ an v´ oi un ¯ diêm v` a c´ ac ¯
do .an th˘ang nô´i ¯du .oc bôi boi n mâ`u, c´o m .ôt , , , tam gi´ ac v´ oi c´
ac c .anh c`ung mâ`u. Bây gi`o ta x´et un+1 ¯diêm bâ´t k`y, m`a , , , , , ¯ du`ong nô´i gi˜ ua ch´ ung ¯
du .oc bôi b`˘ang n + 1 mâ`u: c1, c2, . . . , cn+1. Lâ´y , , , , , A l`
a m .ôt trong c´ac ¯diêm trên. Ðiêm n`ay c´o thê nô´i v´oi c´ac ¯diêm c`on , , , ,
l .ai ¯du .oc un+1 − 1 ¯do.an th˘ang bôi mâ`u. M.˘at kh´ac do công th´uc hô`i ,
qui un+1 − 1 = (n + 1)(un − 1) + 1, nhu v .ây theo nguyên l´y Ðirichlê ,, , , , ,
mo r .ông ´ıt nhâ´t un ¯do.an th˘ang c´o chung ¯dınh A ¯du .oc bôi c`ung mâ`u. 5.2. V´ı d .u 47 , ,, , , ,
Gia su AB1, AB2, . . . , ABu ¯ du c bôi c` ung mâ`u, ch˘ ang h n .o .an mâ`u c1. , , , , , Nh˜ ung kha n˘ ang c´ o thê xây ra nhu sau: , , ,
a) Nê´u m .ôt trong c´ac ¯do.an th˘ang nô´i gi˜ua c´ac ¯diêm B1, B2, . . . , , , , Bu theo t`ung c c bôi b` ˘ ang mâ`u c n .˘ ap ¯ du .o 1 th`
ı tô`n t .ai tam gi´ac ¯dô`ng , , , mâ`u c´ o ¯
dınh A. C´ac c .anh cua tam gi´ac n`ay son mâ`u c1. , , b) Không c´
o m .ôt ¯do.an n`ao trong c´ac ¯do.an th˘ang nô´i gi˜ua c´ac , , , , ¯ diêm B1, B2, . . . , Bu ¯ du c son mâ`u c n .o 1. Khi ¯ d´ o ´ ap d .ung qui n.ap to´an , , , , , ,
h .oc cho nh˜ung ¯diêm B1, B2, . . . , Bu . Ðiê`u n`ay c´o thê ¯du c v`ı tâ´t ca n .o , , , , c´ ac ¯
do .an th˘ang ¯d˜a nô´i ¯du .oc bôi son n mâ`u c2, c3, . . . cn+1. Trong , , , tru`
ong h .op n`ay ta c˜ung d˜ân ¯dê´n kê´t lu.ân tô`n t.ai m .ôt tam gi´ac ¯dô`ng mâ`u. J , , , , , ,
. 5.6. Cho sô´ h .ang cua d˜ay un ¯du.oc ¯d.inh ngh˜ıa nhu b`ai tru´oc. T .âp , , , , , , , ,
h .op nh˜ung sô´ t .u nhiên t`u 1 ¯dê´n un − 1 ¯du.oc phân chia b`˘ang phuong , , ,, ph´ ap bâ´t k` y v`
ao n t .âp h.op con, m`a t`ung ¯dôi m.ôt không c´o phâ`n tu , , , chung. Ch´ ung minh r` ˘
ang tô`n t .ai hai sô´cua c`ung m.ôt t .âp h.op con, m`a , , , tông cua ch´ ung c˜ ung n` ˘
am trong t .âp h.op con n`ay ; ho .˘ac l`a tô`n t .ai m.ôt ,
sô´ trong m .ôt t .âp h.op con n`ao ¯d´o, m`a sau khi nhân ¯dôi v˜ân thu.ôc t .âp , h .op con n`ay. , , , , L` oi giai. K´
y hi .êu nh˜ung t.âp h .op con ¯d˜a cho l`a l`a A1, A2, . . . , An. , , , , Ch´ ung ta x´
et t .âp h .op bâ´t k`y M gô`m un ¯diêm, m`a ch´ung ¯du .oc ¯d´anh , , sô´ b` ˘ ang phuong ph´ ap n` ao ¯ d´ o trong c´
ac sô´ 0, 1, 2, . . . , un − 1. Ch´ung , , , ta bôi mâ`u nh˜ ung ¯
do .an th˘ang nô´i c´ac ¯diêm trong M b`˘ang n mâ`u , , , ,
c1, c2, . . . , cn theo c´ach sau: Ðo .an th˘ang nô´i c´ac ¯diêm th´u i v`a j, v´oi , , , , , i > j ¯
du .oc son b`˘ang mâ`u ck khi v`a chı khi hi.êu i − j thu .ôc t.âp h .op , , , , , ,
Ak. Theo b`ai to´an tru´oc 5.5 ba ¯ diêm n` ao ¯ d´ o cua M l`a ¯ dınh cua m .ôt , ,, , tam gi´ ac c` ung mâ`u. Gia su c´ ac ¯ diêm n` ay l`
a i, j, k v`a i > j > k. Khi ¯ d´ o c´
ac sô´i − j, j − k v`a i − k = (i − j) + (j − k) n`˘am trong c` ung m .ôt , , ,, 48
Chuong 5. Mo r .ông nguyên l´y Ðirichlê ,
t .âp h .op As v`a ch´ung c´o c´ac t´ınh châ´t ta câ`n t`ım. J , ,
. 5.7. Trong m .˘at ph˘ang cô´¯d.inh h.ê t.oa ¯d.ô Oxy. Ch´ung ta x´et t .âp h.op , , , ,, , R gô`m nh˜ ung ¯ diêm v´
oi t .oa ¯d.ô (x, y), o ¯dây x, y l`a nh˜ung sô´ nguyên , , , , v`
a 1 ≤ x ≤ 12, 1 ≤ y ≤ 10. M˜ ôi ¯ diêm n` ay ¯
du .oc son b`˘ang m.ôt mâ`u , , , tr´ ˘
ang, xanh ho .˘ac ¯do. Ch´ung minh r`˘ang tô`n t .ai h`ınh ch˜u nh .ât c´o c´ac , , , , , ,
c .anh song song v´oi c´ac tr .uc t.oa ¯d.ô, m`a ¯dınh cua n´o l`a nh˜ung ¯diêm cua , , , R ¯
du .oc son c`ung m.ôt mâ`u. , , , , L`
oi giai. Trong ch´ ung minh ta d` ung hai kh˘ ang ¯ d.inh sau: , , ,, , , ,
a) Nê´u X l`a t .âp h˜uu h.an v´oi n phâ`n tu, th`ı sô´lu .ong t.âp h .op con , ,, , n(n − 1)
cua X gô`m c´ac c .˘ap phâ`n tu {x, y}, v´oi x ∈ X, y ∈ X l`a . 2 , , , ,
b) M .oi sô´ duong bâ´t k`y x1, x2, . . . , xn ¯dê`u thoa m˜an bâ´t ¯d˘ang , th´ uc x2 + x2 + · · · + x2 1 2 n x
≥ ( 1 + x2 + · · · + xn )2 2 2 , , Dâ´u b` ˘
ang chı xây ra khi x1 = x2 = . . . = xn. ,, , ,
Tro l .ai b`ai to´an ¯dang x´et, v`ı tông sô´c´ac ¯diêm ta x´et l`a 120, nên , , , , ,, , , ´ıt nhâ´t c´ o 40 ¯ diêm ¯
du .oc bôi c`ung mâ`u, gia su l`a mâ`u ¯do. V´oi m˜ôi , , , , i = 1, 2, . . . , 12 ch´ ung ta k´
y hi .êu li l`a ¯du`ong th˘ang ¯di qua ¯diêm (i, 0) , , , v` a song song v´
oi tr .uc Oy. Nê´u trên li c´o ni ¯diêm ¯do, i = 1, 2, . . . , 12, , , ,
n1 + n2 + · · · + n12 ≥ 40. Ngo`ai ra t`u ni ¯ diêm c´ o thê t .ao ra c´ac c.˘ap , , , , n , ¯ dôi ¯ du i (ni − 1) .oc s´ ˘ ap c´ o sô´lu .ong . Ngh˜ıa l` a v´ oi m˜ ôi i = 1, 2, . . . , 12 2 n , tô`n t i (ni − 1) .ai ¯ d´ ung c .˘ap sô´ nguyên {j oa m˜ an 1 ≤ j 2 1, j2} th 1 ≤ , , , ,
10, 1 ≤ j2 ≤ 10 v`a c´ac ¯
diêm {i, j1} v`a {i, j2} l`a ¯
do. M .˘at kh´ac sô´lu .ong , , , ,
cua tâ´t ca c .˘ap nh˜ung sô´nguyên {j1, j2} v´oi 1 ≤ j1 ≤ 10, 1 ≤ j2 ≤ 10 5.2. V´ı d .u 49 10(10 − 1) , , , b` ˘ ang = 45. Ch´ ung ta phai ch´ ung minh r` ˘ ang tông c´ ac sô´ 2 n1(n1 − 1) n n
, 2(n2 − 1) , . . . , 12(n12 − 1) 2 2 2 , , , , , , l´ on hon 45. T` u ¯ d´
o suy ra tô`n t .ai nh˜ung chı sô´kh´ac nhau i1 v`a i2 v´oi ,
1 ≤ i1 < i2 ≤ 12 v`a c .˘ap sô´nguyên {j1, j2} v´oi 1 ≤ j1 ≤ 10, 1 ≤ j2 ≤ , , ,, , 10 sao cho 4 ¯
diêm {i1, j1}, {i1, j2}, {i2, j1}, {i2, j2} l`a ¯ do. Boi nh˜ ung , , , , , , ¯ diêm n` ay l` a ¯ dınh cua h`ınh ch˜
u nh .ât v´oi c´ac c.anh song song v´oi tr .uc , , , ,
t .oa ¯d .ô, nhu v.ây b`ai to´an ¯du .oc ch´ung minh. , , , ,
Nhu v .ây, ta chı c`on phai ch´ung minh n n n
S = 1(n1 − 1) + 2(n2 − 1) + · · · + 12(n12 − 1) > 45 2 2 2 ,, , ,
Su d .ung bâ´t ¯d˘ang th´uc b) 1 1 1 1 1 1 1 1 1 S = ((n )2 − ) + ((n )2 − ) + · · · + ((n )2 − ) 2 1 − 2 4 2 2 − 2 4 2 12 − 2 4 1 1 1 1 1 = ((n )2 + (n )2 + · · · + (n )2) − 12 2 1 − 2 2 − 2 12 − 2 8 1 1 1 1
(n1 − ) + (n2 − ) + · · · + (n12 − ) 3 ≥ .12( 2 2 2 )2 − 2 12 2 1 1 3 = ((n )2 − 24
1 + n2 + · · · + n12) − 12 2 2 1 3 342 3 ≥ (40 − 6)2 − = − > 45 24 2 24 2
v`ı n1 + n2 + · · · + n12 ≥ 40. J , . 5.8. (B` ai thi Olympic to´
an quô´c tê´ lâ`n th´
u 20, 1978) M .ôt h.ôi to´an ,, , ,
h .oc bao gô`m c´ac th`anh viên o 6 nu´oc. Danh s´ach c´ac h.ôi viên gô`m , , , , , , 1978 ngu` oi ¯
du .oc ¯d´anh sô´b´ao danh t`u 1 ¯dê´n 1978. Ch´ung minh r`˘ang ,
tô`n t .ai ´ıt nhâ´t m.ôt h.ôi viên c´o sô´ b´ao danh gâ´p ¯dôi sô´ b´ao danh cua , , ,, 50
Chuong 5. Mo r .ông nguyên l´y Ðirichlê , , , ,
m .ôt h.ôi viên kh´ac c`ung nu´oc, ho .˘ac b`˘ang tông hai sô´b´ao danh cua hai , , ,
h .ôi viên c`ung m.ôt nu´oc v´oi m`ınh. , , , , , L` oi giai. T`
u 329.6 < 1978 suy ra m .ôt trong c´ac nu´oc (k´y hi.êu l`a , , , A) c´ o không ´ıt hon 330 ¯
d .ai biêu trong h .ôi v`a ch´ung ta c´o thê viê´t , sô´ b´
ao danh a1 < a2 < . . . < a330 < . . . Ch´ung ta x´et nh˜ung hi.êu ,
xi = a330 − ai, i = 1, 2, . . . 329. Nê´u c´o m .ôt sô´ xi n`ao ¯d´o tr`ung v´oi aj , , , (sô´b´
ao danh cua m .ôt ¯daj i biêu cua A) th`ı ch´ung ta c´o a330 = ai + aj, , , b` ai to´ an ¯ d˜ a ch´
ung minh xong. Nê´u xi 6= aj v´oi m .oi i, j, th`ı sô´ xi l`a , , , , , sô´ b´
ao danh cua m .ôt sô´ ¯d.a i biêu thu .ôc 5 nu´oc c`on l.ai. Bây gi`o, , ,
v`ı 65.5 < 329 , th`ı ´ıt nhâ´t c´
o m .ôt trong n˘am nu´oc n`ay (k´y hi.êu l`a , , B) s˜ e c´ o không ´ıt hon 66 th` anh viên, m` a sô´ b´ ao danh cua h .o l`a
m .ôt trong c´ac sô´ x1, x2, . . . , x329. Cho c´ac sô´ ¯d´o l`a b1 < b2 < b3 < ,
. . . < b66 < . . . v´oi bi = xn , i = 1, 2, . . . , 66. Ch´ung ta l i .ai x´ et hi .êu ,
yi = b66 − bi, i = 1, 2, . . . , 65 Nê´u m .ôt hi.êu n`ao ¯d´o tr`ung v´oi sô´b´ao , , , ,
danh bj cua m .ôt ¯d.ai biêu cua B th`ı b66 = bi + bj. Nê´u v´oi hai sô´ i v` a k n`ao ¯ d´ o ch´ ung ta c´
o yi = ak, th`ı ak = b66 − bi = xn − x = 66 ni a330 − an − (a ) = a − a ho = a + a 66 330 − ani ni n66 .˘ ac l` a ani n66 k. Nê´u hai , , , , , tru`
ong h .op trên không xây ra, th`ı nh˜ung sô´ n`ay s˜e l`a sô´ b´ao danh , , , , , , cua ¯
d .ai biêu 4 nu´oc c`on l.ai v`a suy ra ´ıt nhâ´t m .ôt trong c´ac nu´oc n`ay , c´
o sô´ h .ôi viên ´ıt nhâ´t l`a 17 v´oi sô´ b´ao danh yi. Tiê´p t .uc qu´a tr`ınh , ,
nhu v .ây v`a l.˘ap l.ai l´y lu.ân trên ch´ung ta c´o kê´t lu.ân cua b`ai to´an. J , , , ,
. 5.9. (Ðê` thi To´ an vô ¯
d.ich nu´oc Anh, 1978) M.ôt h`ınh l .âp phuong c´o , , ,
c .anh b`˘ang 15 ch´ua 11.000 ¯diêm. Ch´ung minh r`˘ang c´o m.ôt h`ınh câ`u , , , , b´ an k´ınh b` ˘ ang ¯
don v.i ch´ua ´ıt nhâ´t 6 ¯diêm trong sô´ 11.000 ¯diêm ¯d˜a cho. , , , , , L`
oi giai. Chia m˜
ôi c .anh cua h`ınh l.âp phuong th`anh 13 phâ`n b`˘ang , , , ,
nhau, thê´ th`ı h`ınh l .âp phuong ban ¯dâ`u ¯du .oc chia th`anh 133 = 2187 5.2. V´ı d .u 51 , , , , , ,
h`ınh l .âp phuong nho. V`ı h`ınh l.âp phuong ban ¯dâ`u ch´ua 11.000 , , , , , , ¯
diêm, nên tô`n t .ai m .ôt h`ınh l.âp phuong nho ch´ua ´ıt nhâ´t 6 ¯diêm. , , , , 15 D˜
ê thâ´y c .anh cua h`ınh l.âp phuong nho l`a , do ¯ d´ o b´ an k´ınh h`ınh 13r r , , , 1 15 1 675
câ`u ngo .ai tiê´p h`ınh l.âp phuong nho l`a r = 3( )2 = < 2 13 2 169 1 r 676 1 √ , =
4 = 1. V .ây: Tô`n t.ai m .ôt h`ınh câ`u b´an k´ınh 1 ch´ua ´ıt 2 169 2 , , nhâ´t 6 ¯ diêm trong 11.000 ¯ diêm ¯ d˜ a cho. J , , ,
. 5.10. Trong m .˘at ph˘ang cho m .ôt sô´ h˜uu h.an ¯diêm, m .ôt sô´ trong , , , ch´ ung ¯
du .oc nô´i l.ai b`˘ang ¯do.an th˘ang. Ch´ung ta n´oi r`˘ang m .ôt d˜ay , , , ,
e1, e2, . . . , em t`u c´ac ¯
d .oan th˘ang ¯du .oc nô´i l`a m .ôt dây chuyê`n, nê´u ,
m .oi c.˘ap ¯do.an th˘ang liê`n nhau ei v`a ei+1 c´o chung m .ôt ¯dâ`u m´ut, , , , ,
i = 1, 2, . . . , m − 1. Sô´lu .ong m nh˜ung ¯do.an th˘ang trong dây chuyê`n ,
g .oi l`a ¯d .ô d`ai cua n´o. Ch´ung ta x´et b`ai to´an: , , , , , , , , Cho n ¯ diêm, t` u c´ ac ¯ diêm n`
ay d .ung nh˜ung ¯do .an th˘ang, sô´ lu.ong ¯do .an , , , ,, , , , , th˘ ang ¯ d˜
a d .ung l`a q. Gia su nh˜ung ¯do .an th˘ang ¯du.oc ¯d´anh sô´m.ôt c´ach , bâ´t k` y b` ˘ ang c´
ac sô´ 1, 2, . . . , q. Khi ¯ d´ o trong c´
ach t .ao h`ınh nhu v .ây tô`n , , 2q
t .ai m.ôt dây chuyê`n v´oi ¯d.ô d`ai nho nhâ´t l`a
, trên dây chuyê`n n` ay n , , , , , c´ ac sô´ ´ ung v´ oi nh˜ ung ¯
do .an th˘ang th`anh phâ`n l .âp nên m.ôt d˜ay sô´giam ng .˘at. , , , , , , L`
oi giai. G .oi G l`a câ´u h`ınh bâ´t k`y cua nh˜ung ¯diêm v`a ¯do.an th˘ang, , , , , , m` a ch´ ung ¯
du .oc ¯d´anh sô´b`˘ang sô´t .u nhiên nhu ¯dê` b`ai ¯d˜a ra. V´oi m .oi ,
v thu .ôc G ch´ung ta k´y hi.êu LG(v) l`a ¯d .ô d`ai cua dây chuyê`n d`ai nhâ´t , , , , trong G, m`a n´ o b´ ˘ at ¯ dâ`u t`
u v v`a giam dâ`n. B`˘ang phuong ph´ap qui , , , , , ,
n .ap ch´ung ta s˜e ch´ung minh bâ´t ¯d˘ang th´uc sau ¯du .oc thoa m˜an
LG(v1) + LG(v2) + · · · + LG(vn) ≥ 2q (5.1) , , ,, 52
Chuong 5. Mo r .ông nguyên l´y Ðirichlê ,, , , , , o ¯
dây v1, v2, . . . , vn l`a tâ´t ca c´ac ¯
diêm thu .ôc G. Kê´t lu.ân phai ch´ung , ,, minh suy ra t` u (5.1) theo nguyên l´
y Ðirichlê mo r .ông: M .ôt trong , , 2q , c´
ac sô´ LG(v1), LG(v2), . . . , LG(vn) l´on hon ho .˘ac b`˘ang , nhu v .ây n , , , , ,
tô`n t .ai dây chuyê`n v´oi t´ınh châ´t ¯d˜a chı ra. Do ¯d´o chı c`on phai ch´ung , , , , , , , , , minh (5.1) ¯
du .oc thoa m˜an v´oi n ¯diêm cua G v`a q ¯do.an th˘ang ¯du .oc , , ,, , , ¯ d´ anh sô´ nhu mô ta o ¯ dâ`u b` ai. B` ˘
ang qui n .ap v´oi q = 1 bâ´t ¯dang , , , ,, , th´ uc (5.1) l`
a hiên nhiên. Gia su (5.1) thoa m˜ an cho m .oi câ´u h`ınh , , , , v´ oi q − 1 ¯
do .an th˘ang v`a ch´ung ta xem x´et câ´u h`ınh v´oi n ¯diêm v`a , , , , q ¯
do .an th˘ang. Nê´u ¯do.an th˘ang k´y hi.êu l`a q nô´i v´oi hai ¯diêm vi v`a , , , , , vj th`ı ch´ung ta bo ¯
do .an th˘ang n`ay v`a nh.ân ¯du .oc câ´u h`ınh G0 cua n , , , ¯ diêm v` a q − 1 ¯
do .an th˘ang. V´oi câ´u h`ınh n`ay theo qui n.ap ch´ung ta , c´
o LG0(v1) + LG0(v2) + · · · + LG0(vn) ≥ 2(q − 1). Bây gi`o ch´ung ta , , , x´ et ¯
diêm vj. Dây chuyê`n giam dâ`n xuâ´t ph´at t`u xj c´o ¯ d .ô d`ai LG0(vj), , , , , ,, , v` a nh˜ ung ¯
do .an th˘ang trong dây chuyê`n n`ay ¯du .oc k´y hi.êu boi nh˜ung sô´ n` ao ¯ d´ o trong d˜
ây 1, 2, . . . , q − 1. Nê´u nô´i thêm v`ao dây chuyê`n , , ,
m .ôt ¯do.an th˘ang c´o k´y hi.êu q ch´ung ta s˜e nh.ân ¯du .oc dây chuyê`n , , , , giam v´ oi ¯ diêm ¯ dâ`u vi v`a v´oi ¯
d .ô d`ai LG0(vj) + 1. Theo ¯d.inh ngh˜ıa , ,
cua LG(vi) ch´ung ta c´o LG(vi) ≥ LG0(vj) + 1. B`˘ang m .ôt c´ach ch´ung , , , , , , minh ho` an to`
an tuong t .u ch´ung ta c˜ung ch´ung minh ¯du .oc LG(vj) ≥ , , L0 (v i m m v G i ) + 1. M .˘ at kh´ ac, LG(vk) = LG0(vk) v´o .oi ¯ diê k thu . ôc G m` a n´ o kh´
ac vi v`a vj. Suy ra, LG(v1) + LG(v2) + · · · + LG(vn) ≥
LG0 (v1) + LG0 (v2) + · · · + LG0 (vn) + 2 ≥ 2(q − 1) + 2 = 2q. J 5.3. B ` ai t .âp ,
. 5.11. (Ðê` thi vô ¯
d.ich Áo - Balan, 1978) Cho 1978 t.âp h .op, m˜ôi , ,, ,
t .âp h .op c´o 40 phâ`n tu. Biê´t r`˘ang hai t.âp h .op bâ´t k`y c´o ¯d´ung m .ôt ,, , ,, , phâ`n tu chung. Ch´ ung minh r` ˘
ang, tô`n t .ai m .ôt phâ`n tu thu .ôc tâ´t ca , 1978 t .âp h .op trên. 5.3. B` ai t .âp 53 , , , , , , . 5.12. Ch´ ung minh r` ˘
ang m .oi t.âp h .op ch´ua 55 sô´ch .on ¯du .oc t`u t.âp , , ,
h .op sô´{1, 2, 3, . . . , 100} ch´ua hai sô´m`a hi.êu cua ch´ung b`˘ang 9. , , , . 5.13. Cho n l`
a sô´t .u nhiên. Cho n t.âp h .op con A1, A2, . . . , An cua , , ,
m .˘at ph˘ang v´oi t´ınh châ´t: v´oi m .oi i = 1, 2, . . . , n tô`n t.ai n + 1 ph´ep , , ,
t.inh tiê´n sao cho c´ac anh cua Ai qua c´ac ph´ep t.inh tiê´n t`ung ¯dôi m .ôt , , , không c´ o ¯ diêm chung. Ch´ ung minh r` ˘
ang tô`n t .ai m .ôt ¯diêm trên m.˘at , , , ph˘ ang, không n` ˘ am trong bâ´t c´
u t .âp h .op Ai n`ao, i = 1, 2, . . . , n. , , ,
. 5.14. Trong phâ`n trong cua m .ôt tam gi´ac ¯dê`u v´oi c.anh d`ai 15 ¯don , , , ,
v.i, ch´ung ta ch .on b`˘ang phuong ph´ap bâ´t k`y 111 ¯diêm. Ch´ung minh , , , √ , , r` ˘
ang tô`n t .ai h`ınh tr`on v´oi ¯du`ong k´ınh 3, m`a n´o phu ´ıt nhâ´t 3 ¯diêm , , ,, trong sô´nh˜ ung ¯ diêm ¯ d˜ a ch .on o trên.
. 5.15. (Ðê` thi vô ¯
d.ich Quô´c gia Bungari, 1977) Trong m .ôt nh´om , , , , , ngu` oi, hai ngu`
oi X v`a Y g .oi l`a quen nhau gi´an tiê´p, nê´u h .o tr .uc , , ,
tiê´p quen nhau, ho .˘ac l`a nê´u tô`n t.ai m .ôt dây truyê`n nh˜ung ngu`oi
Z1, Z2, . . . , Zp sao cho X v`a Z1 quen nhau, Z1 v`a Z2 quen nhau,... , , ,
, Zp v`a Y quen nhau. Cho biê´t nh´om ¯ d´ o gô`m 134 ngu`oi, c` on gi˜ ua , , , , , , m˜ ôi nh´ om nho 8 ngu`oi t`u nh´ om ¯ d˜ a biê´t ´ıt nhâ´t c´ o hai ngu` oi quen , , , , gi´ an tiê´p. Ch´ ung minh r` ˘ ang c´
o m .ôt nh´om nho 12 ngu`oi trong nh´om , , , , , ngu` oi ¯ d˜ a biê´t, m`
a m .oi c.˘ap hai ngu`oi trong nh´om nho n`ay ¯dê`u quen nhau gi´ an tiê´p. , , ,, 54
Chuong 5. Mo r .ông nguyên l´y Ðirichlê , , CHUONG 6 B ` AI T .ÂP S ´ Ô H .OC NÂNG CAO , , ,
6.1. Ð.inh l´y co ban cua sô´ h .oc , ,, , , Trong l´
y thuyê´t sô´h .oc co so c´o m .ôt ¯d.inh l´y co ban: , , , , ,
M .oi sô´t .u nhiên l´on hon m.ôt ¯dê`u c´o thê phân t´ıch ra t´ıch c´ac th`ua , , sô´ nguyên tô´ v` a phân t´ıch ¯ d´ o l`
a duy nhâ´t nê´u ta không ¯ dê ´ y ¯ dê´n th´ u , , ,
t .u cua c´ac th`ua sô´. ,
Cho p1, p2, . . . , pn l`a nh˜ung sô´ nguyên tô´ kh´ac nhau. Trong , , , , chuong n` ay ch´ ung ta x´
et m .ôt sô´ kê´t lu.ân vê` vê` t.âp h .op M cua , , , c´
ac sô´ t .u nhiên m`a n´o c´o thê phân t´ıch ra c´ac th`ua sô´ n`˘am trong , , , , ,
{p1, p2, . . . , pn}. M .oi sô´ x cua M c´o thê biêu di˜ên du´oi d.ang
x = pα1 pα2 . . . pαn 1 2 n
,,o ¯dây α1,α2,. . .,αn l`a c´ac sô´nguyên không âm. 6.2. V´ı d .u , , , . 6.1. T`
u t .âp h.op M ch.on m.ôt c´ach bâ´t k`y 2n + 1 sô´. Ch´ung minh , , r` ˘
ang tô`n t .ai hai sô´ trong t .âp v`ua ch.on m`a t´ıch cua ch´ung l`a m.ôt sô´ , , ch´ınh phuong. , , , L`
oi giai. Nh .ân x´et r`˘ang m .ôt sô´ t .u nhiên x = pα1 pα2 . . . pαn 1 2 n l` a sô´ , , , , ch´ınh phuong khi v` a chı khi tâ´t ca c´ ac sô´ m˜ u ¯ dê`u ch˜ ˘ an. Ch´ ung ta , , 56 Chuong 6. B` ai t .âp sô´h .oc nâng cao , , ,, , , , , biêu di˜
ên m .oi sô´ ¯d˜a ch .on v´oi d.ang o trên v`a cho tuong ´ung v´oi b .ô ,, , ,
n-sô´ (α1, α2, . . . , αn), o ¯
dây α1, α2, . . . , αn l`a c´ac sô´ du cua c´ac sô´ m˜u , , , tuong ´
ung α1, α2, . . . , αn khi chia cho 2. R˜o r`ang αi = 0 ho .˘ac αi = 1 , , , v´
oi m .oi i = 1, 2, . . . , n. V.ây (α1, α2, . . . , αn) l`a b .ô xê´p th´u t .u n sô´gô`m , , , , , , sô´ 0 v` a 1. Theo l´
y thuyê´t tô h .op, tâ´t ca n-b .ô nhu v.ây c´o sô´ lu .ong , , , l` a 2n, c` on c´ ac sô´ ta ¯ dang x´ et c´
o sô´ lu .ong l`a 2n + 1. Nhu v.ây ´ıt nhâ´t c´ o 2 sô´ trong ch´ ung c´ o c`
ung b .ô s´˘ap xê´p gô`m sô´ 0 v`a sô´ 1 giô´ng , ,, , nhau. Gia su c´ ac sô´ ¯ d´ o l`
a x = pα1 pα2 . . . pαn pβ2 . . . pβn i 1 2 n v` a y = pβ1 1 2 n v´ o , , ch´ ung c´
o (α1, α2, . . . , αn) = (β , , . . . , ). Ð˘ ang th´ uc sau c` ung c´ o 1 β2 βn ngh˜ıa l`
a αi = β , i = 1, 2, . . . , n . Do c´ o c` ung i ¯ d´ o c´ ac sô´ m˜ u αi v`a βi , , , t´ınh ch˜ ˘ an le nhu nhau v´ oi bâ´t k` y i = 1, 2, . . . , n. Khi ¯ d´ o α1 + β1,
α2 + β2, . . . , αn + βn, l` a c´ ac sô´ ch˜ ˘ an v`
a theo nh .ân x´et ban ¯dâ`u t´ıch
xy = (pα1 pα2 . . . pαn pβ2 . . . pβn
pα2+β2 . . . pαn+βn 1 2 n )( pβ1 1 2 n ) = pα1+β1 1 2 n ¯ d´ ung , , l` a sô´ch´ınh phuong. J , , , , . 6.2. Ch´ ung minh r` ˘ ang gi˜
ua n + 1 sô´ trong t .âp hop M c´o thê ch.on , , , , , ¯
du .oc m.ôt v`ai sô´m`a t´ıch cua ch´ung l`a m.ôt sô´ch´ınh phuong. , , , , , L`
oi giai. Cho x1, x2, . . . , xn l`a nh˜ung sô´ bâ´t k`y cua M. V´oi m˜ôi t .âp , , con kh´
ac trô´ng {i1, i2, . . . , ik} cua t .âp h .op {1, 2, . . . n + 1}, ch´ung ta , x´ et c´
ac xi , x , . . . , x (tâ´t nhiên sô´n`ay c˜ung thu u di˜ ên c´ ac 1 i2 ik .ôc M). Biê , , , , sô´n`
ay theo d .ang chuân v`a m˜ôi t.âp h .op con {i1, i2, . . . , ik} cho tuong , , ´, , , , ung v´
oi n-b .ô (α1, α2, . . . , αn) , o ¯dây α1, α2, . . . , αn l`a c´ac sô´ du cua , , , , , , c´ ac sô´ m˜ u tuong ´
ung α1, α2, . . . , αn khi chia cho 2. Nhung sô´ lu .ong , , nh˜
ung t .âp con kh´ac r˜ông cua {1, 2, . . . , n + 1} l`a 2n+1 − 1, c`on sô´ , , , ,
lu .ong c´ac n-b .ô s´˘ap gô`m nh˜ung sô´0 v`a 1 l`a 2n. Suy ra tô`n t.ai nh˜ung ,
t .âp h .op con kh´ac trô´ng kh´ac nhau {i1, i2, . . . , ik} v`a {j1, j2, . . . , jl} , , , , , ,
cua {1, 2, . . . , n + 1}, m`a ch´ ung tuong ´ ung v´ oi c` ung m .ôt n-b .ô s´˘ap cua , , nh˜ ung sô´ du. Ðiê`u n` ay c´ o ngh˜ıa l`
a nê´u xi x . . . x = pα1 pα2 . . . pαn 1 i2 ik 1 2 n v`
a xj x . . . x = pβ1 pβ2 . . . pβn 1 j2 jk 1 2 n th`ı c´ ac sô´ m˜
u αi v`a βi c´o c`ung t´ınh 6.2. V´ı d .u 57 , , , , ch˜ ˘ an le v´
oi i = 1, 2, . . . , k. Ðiê`u n`ay c´ o ngh˜ıa l` a t´ıch cua nh˜ ung , ,
sô´ xi , x , . . . , x , x , x , . . . , x l`a ch´ınh phuong. Nê´u {i 1 i2 ik j1 j2 jk 1, i2, . . . , ik} ,, , , , v`
a {j1, j2, . . . , jl} không c´o phâ`n tu chung, th`ı b`ai to´an ¯ d˜ a ¯ du .oc giai. , , , , , Tru`
ong h .op ngu .oc l.ai, trong P = xi x . . . x x x . . . x l 1 i2 ik j1 j2 jk .˘ ap l .ai ¯d´ung , nh˜
ung sô´ xs, m`a s thu .ôc {i1, i2, . . . , ik} v`a {j1, j2, . . . , jl}. Ch´ung ta , , , , , , ,
lo .ai tr`u trong P tâ´t ca c´ac nh˜ung xs nhu v.ây v`a nh.ân ¯du .oc t´ıch cua , , v`
ai sô´trong sô´ x1, x2, . . . , xn+1 m`a n´o ¯ d´ ung l` a ch´ınh phuong. J , , , , , . 6.3. Ch´ ung minh r` ˘ ang gi˜
ua m .oi 3.2n + 1 sô´ t`u t .âp h.op M c´o thê , , , , ,
ch .on ¯du.oc 4 sô´m`a t´ıch cua ch´ung l`a l˜uy th`ua b .âc bô´n cua m.ôt sô´. , , , , L`
oi giai. V`ı 3.2n + 1 > 2n + 1 gi˜ua nh˜ung sô´ ¯ d˜ a ch .on theo b`ai 6.1 , , , c´ o hai sô´ m` a t´ıch cua ch´ ung l`
a m .ôt sô´ ch´ınh phuong. T´ach hai sô´ , trên ra th`ı c`
on l .ai 3.2n − 1 sô´v`a ´ap d .ung tiê´p 6.1 cho hai sô´n˜ua m`a , , , , t´ıch cua ch´ ung l` a sô´ch´ınh phuong. Ch´ ung ta c´
o thê l .˘ap l.ai qu´a tr`ınh (3.2n − 1) − (2n + 1) , ,, n` ay ´ıt nhâ´t = 2n + 1 lâ`n. Gia su ch´ ung ta nh .ân 2 , , , , , ¯
du .oc 2n + 1 c.˘ap (x1, y1), (x2, y2), . . . , v´oi xiyi l`a c´ac sô´ch´ınh phuong, i = 1, 2, . . . , 2n + 1. Ch´ u ´ y r` ˘ ang theo c´
ach ch .on trên th`ı c´ac c.˘ap sô´ ,
(x1, y1), (x2, y2), . . . , (x2n+1, y2n+1) t`ung ¯
dôi m .ôt kh´ac nhau. Ðê´n ¯dây √ √ √ , suy ra c´ ac sô´
x1y1, x2y2, . . . , x2n+1y2n+1 l`a nh˜ung sô´nguyên v`a , , ,
thu .ôc M. Khi ¯d´o ´ap d .ung m .ôt lâ`n n˜ua 6.1 chı ra r`˘ang t´ıch cua hai sô´ , , , n` ao ¯ d´ o trong ch´ ung l`
a ch´ınh phuong. Nhu v .ây xiyixjyj = t4 ngh˜ıa l`a , , , t´ıch cua 4 sô´t` ung ¯
dôi m .ôt kh´ac nhau xi, yi, xj, yj l`a l˜uy th`ua b.âc bô´n , cua m .ôt sô´. J , , , . 6.4. Cho p l`
a m .ôt sô´nguyên tô´le v`a a1, a2, . . . , a p+1 l`a nh˜ung sô´t .u 2 , , , , , nhiên kh´ ac nhau nho hon p. Ch´ ung minh r` ˘ ang v´
oi m .oi sô´ t .u nhiên , , , ,
r nho hon p, tô`n t .ai hai sô´ (c´o thê b`˘ang nhau) ai v`a aj, m`a t´ıch cua , ch´ ung khi chia cho p c´ o sô´du ¯ d´ ung l` a r. , , 58 Chuong 6. B` ai t .âp sô´h .oc nâng cao , , , ,, L`
oi giai. Áp d .ung m .ôt ¯d.inh l´y trong l´y thuyê´t sô´ co so: Nê´u a v`a b l` a hai sô´ nguyên tô´ c`
ung nhau, th`ı tô`n t .ai m .ôt sô´nguyên x sao cho ax ≡ 1 (mod b). , p + 1 V´ oi m˜ ôi i = 1, 2, . . . , , c´ ac sô´ a 2 i v` a p l`a nguyên tô´ c` ung ,
nhau, v`ı 1 ≤ ai ≤ p − 1 v`a p l`a sô´ nguyên tô´. Áp d .ung ¯d.inh l´y v`ua , , ph´
at biêu trên, tô`n t .ai c´ac sô´nguyên b1, b2, . . . , b p+1 sao cho v´oi m .oi 2 , , , i = 1, 2, . . . , p+1 c´ ac ¯ d˘ ang th´ uc sau ¯ dê`u thoa m˜ an 2 aibi ≡ 1 (mod p) (6.1) Ch´ ung ta x´ et d˜
ay sô´ a1, a2, . . . , a p+1 , rb1, rb2, . . . , rb p+1 . Ch´ung ta c´o 2 2 ,
tâ´t ca p + 1 sô´ sao cho ´ıt nhâ´t hai sô´ trong ch´ ung khi chia cho p , , c´ o c`
ung m .ôt sô´ du. Theo gia thiê´t c´ac sô´ a1, a2, . . . , a p+1 kh´ac nhau 2 , , , , ho` an to` an v`
a nho hon p. Suy ra sô´ du cua ch´ ung theo môdd un p , l` a kh´
ac nhau. V`ı r l`a sô´ nguyên tô´ c` ung nhau v´ oi p, nên d˜ê d`ang , , , , ch´ ung minh ¯
du .oc r`˘ang c´ac sô´rb1, rb2, . . . , rb p+1 cho sô´du ho`an to`an 2 , , kh´
ac nhau khi chia cho p. Ngh˜ıa l`a chı tô`n t .ai hai chı sô´ i v`a j sao , , ,
cho ai ≡ rbj (mod p). T`u (6.1) ch´ung ta nh .ân ¯du .oc aiaj ≡ rbjaj ≡ r.1 ≡ r (mod p). J , , , , . 6.5. Bô ¯
dê` Tue: Cho n l`
a sô´ t .u nhiên l´on hon 1 v`a a l`a sô´ nguyên , tô´ c` ung nhau v´ oi n. Khi ¯ d´
o tô`n t .ai c´ac sô´ nguyên x v`a y, m`a ch´ung , , , , , thoa m˜
an phuong tr`ınh ax ≡ y (mod n) v` a c´
ac bâ´t phuong tr`ınh √ √
1 ≤ x ≤ [ n], 1 ≤ |y| ≤ [ n]. , , , ,, L` oi giai. Ch´ ung ta x´ et tâ´t ca c´ ac sô´c´
o d .ang au − v, o ¯dây u v`a v ch.ay √ , , , ¯
d .ôc l.âp nhau trong c´ac sô´0, 1, 2, . . . , [ n]. Sô´lu .ong tâ´t ca c´ac sô´ ¯d´o √ , , √ √ l`
a ([ n] + 1)2 . Suy ra sô´n`ay l´
on hon n v`ı ([ n] + 1)2 > ( n)2 = n. ,, , Boi c´ o ¯ d´
ung n sô´ du kh´ac nhau theo mô¯
dun n, nên tô`n t .ai hai c.˘ap , sô´ kh´
ac nhau (u1, v1), (u2, v2) t`u c´ac sô´ nguyên sao cho 1 ≤ ui ≤ 6.2. V´ı d .u 59 √ √
[ n], 1 ≤ vi ≤ [ n], i = 1, 2 v`a au1 − v1 ≡ au2 − v2 (mod n). , , , , , D˜ ê d` ang ch´ ung minh ¯
du .oc v1 kh´ac v2. Th.ât v.ây, nê´u ngu .oc l.ai th`ı
au1 ≡ au2 (mod n),suy ra u1 ≡ u2 (mod n), do a l`a sô´ nguyên tô´ , , , , , c` ung nhau v´
oi n. M .˘at kh´ac, u1, u2 l`a c´ac sô´t .u nhiên nho hon n. Nhu , , , ,
v .ây ¯d˘ang th´uc sau c`ung chı c´o m .ôt kha n˘ang duy nhâ´t u1 = u2. Do , , ¯ d´
o c .˘ap (u1, v1), (u2, v2) tr`ung nhau, tr´ai v´oi c´ach ch .on trên. Nhu v.ây , , ,
u1 v`a u2 c˜ung phai kh´ac nhau. C´o thê gia thiê´t u1 > u2 m`a không , ,,, , , , anh huong ¯ dê´n kê´t qua ch´ ung minh. Bây gi` o ta ¯ d .˘at x = u1 − u2, y = , √ √ v1 − v2. T`u ¯ d´
o suy ra 1 ≤ x ≤ [ n], 1 ≤ |y| ≤ [ n] v`a ax ≡ y (mod n). J , , ,
. 6.6. Áp d .ung bô ¯dê` Tue: M.oi sô´ nguyên tô´ d .ang 4k + 1 c´o thê biêu , , , , , , di˜ ên du´
oi d .ang tông b`ınh phuong cua hai sô´nguyên. , , , , L` oi giai. Ch´ ung ta ch´ ung minh kh˘ ang ¯
d.inh sau: Nê´u p = 4k + 1 l`a sô´ , ,
nguyên tô´, th`ı phuong tr`ınh x2 ≡ −1 (mod p) c´ o nghi .êm. Th.ât v.ây,
V`ı p l`a sô´ nguyên tô´, theo ¯
d.inh l´y Wilson, (p − 1)! ≡ −1 (mod p). Ngo`
ai ra p − 1 ≡ −1 (mod p), p − 2 ≡ −2 (mod p), . . . , p − p+1 ≡ 2 p+1 (mod p). Suy ra, 2 (p − 1) (p + 1)
−1 ≡ (p − 1)! = 1.2 . . . . 2 2 p − 1 ≡ (−11)(−21) . . . (−( )2) 2 p−1 p − 1 p − 1 = (−1) 2 (1.2 . . . )2 = (−1)2k(( )!)2 2 2 p − 1 = (( )!)2 (mod p). 2 , p − 1 , , , Nhu v .ây a = ( )! l`
a nghi .êm cua phuong tr`ınh trên. V`ı a 2 2 + 1 , ,
chia hê´t cho p nên a l`a nguyên tô´ c` ung nhau v´ oi p. Bây gi`o ta ´ap ,
d .ung bô ¯dê` Tue cho hai sô´ a v`a p. Tô`n t.ai c´ac sô´nguyên x v`a y m`a , , 60 Chuong 6. B` ai t .âp sô´h .oc nâng cao √ √
1 ≤ x ≤ [ p], 1 ≤ |y| ≤ [ p] v` a ax ≡ y (mod p). Khi ¯ d´ o a2x2 ≡ y2 , ,
(mod p), nhu v .ây x2 ≡ −y2 (mod p), v`ı a2 ≡ −1 (mod p). T`u ¯d´o
suy ra x2 + y2 chia hê´t cho p. M .˘at kh´ac 1 ≤ x2 ≤ p, 1 ≤ y2 ≤ p. Ta , , thâ´y r` ˘
ang x2 = p v`a y2 = p không thê xây ra v`ı p l`a sô´nguyên tô´, suy
ra 0 < x2 + y2 < 2p v`a v`ı x2 + y2 chia hê´t cho p, nên x2 + y2 = p. J , , , , , , Ch´ u ´
y: Tuong t .u, ch´ung minh r`˘ang m .oi sô´ p, sao cho phuong , , , ,
tr`ınh x2 ≡ −2 (mod p) c´
o nghi .êm, ¯dê`u c´o thê biêu di˜ên du´oi d.ang , p = x2 + 2y2 v´
oi x, y l`a c´ac sô´nguyên.
. 6.7. (Ðê` thi To´
an Olympic quô´c tê´ lâ`n 18 n˘ am 1976) Cho h.ê p , , , , phuong tr`ınh v´ oi q = 2p ân
a11x1 + a12x2 + · · · + a1qxq = 0
. . . . . . . . . . . . . . . . . . . . .
ap1x1 + ap2x2 + · · · + apqxq = 0 , , , Tâ´t ca c´
ac h.ê sô´aij thu.ôc t .âp hop {−1, 0, 1}. Ch´ung minh r`˘ang tô`n t .ai , ,
nghi.êm (x1, x2, . . . , xq) cua h.ê, m`a n´o thoa m˜an , ,
a) tâ´t ca xj(j = 1, 2, . . . , q) l`a nhung sô´nguyên; b) ´ıt nhâ´t c´
o m .ôt j(j = 1, 2, . . . , q) m`a xj ≤ 0; , c) v´
oi m .oi j(j = 1, 2, . . . , q) ta luôn c´o xj ≤ q; , , , L` oi giai. X´
et b .ô (x1, x2, . . . , xq) gô`m nh˜ung sô´ nguyên bâ´t k`y, m`a , ,, , ch´ ung thoa m˜
an |x1| ≤ p, |x2| ≤ p, . . . , |xq| ≤ p. Boi v`ı tâ´t ca c´ac , , , , , ,
h .ê sô´ cua h.ê phuong tr`ınh chı l`a -1,0 ho.˘ac 1, v´oi vi.êc thay c´ac ân , , , , ,
x1, x2, . . . , xq ch´ung ta nh .ân ¯du .oc gi´a tr.i cua m˜ôi phuong tr`ınh n`˘am , ,
trong khoang [−pq, pq]. Th .ât v.ây, v´oi m˜ôi i = 1, 2, . . . , p ch´ung ta c´
o |ai1x1 + ai2x2 + · · · + aiqxq| ≤ |x1| + |x2| + · · · + |xq| ≤ pq. Suy , , , , , , , , , ra, nê´u thay nh˜
ung ân trong tâ´t ca phuong tr`ınh cua h .ê tuong ´ung 6.2. V´ı d .u 61 , , , v´
oi x1, x2, . . . , xq s˜e nh .ân ¯du .oc b .ô p sô´ nguyên (y1, y2, . . . , yp). Tâ´t , , , , ca nh˜ ung sô´ n` ay ¯ dê`u n` ˘
am trong khoang [−pq, pq]. Trong khoang , , n` ay c´ o ¯ d´
ung 2pq + 1 sô´ nguyên. Suy ra gi˜ua nh˜ung b .ô s´˘ap xê´p ,, , ,, p phâ`n tu nhu o trên c´
o (2pq + 1)p b .ô xê´p kh´ac nhau. M.˘at kh´ac , , , ,,
sô´ lu .ong nh˜ung b .ô xê´p q-phâ`n tu (x1, x2, . . . , xq) m`a |xj| ≤ p , , v´
oi j = 1, 2, . . . q, l`a (2p + 1)q. D˜ê thâ´y r`˘ang t`u q = 2p suy ra
(2p + 1)q > (2pq + 1)p. Theo nguyên l´y Ðirichlê tô`n t .ai hai b .ô q- sô´ nguyên (x0 , x0 , x00 1 2, . . . , x0q) v`
a (x001 2 , . . . , x00q) kh´ac nhau m`a ch´ung , , thoa m˜ an |x0| ≤ p, |x00| ≤ p v´
oi j = 1, 2, . . . q v`a sau khi thê´ v`ao j j , ,
h .ê phuong tr`ınh cho c`ung m .ôt b .ô p sô´ nguyên (y1, y2, . . . , yp). Ð.˘at x1 = x0 − x00, x − x00 − x00 1 1 2 = x02 2 , . . . , xq = x0q q . R˜ o r` ang (x1, x2, . . . , xq) , , , , l`
a nghi .êm cua h.ê phuong tr`ınh v`a xj l`a c´ac sô´ nguyên v´oi m .oi
j = 1, 2, . . . , q. V`ı (x0 , x0 , x00 1 2, . . . , x0q) v`
a (x001 2 , . . . , x00q) l`a hai b .ô q sô´ ho` an to` an kh´
ac nhau, th`ı ´ıt nhâ´t m .ôt trong c´ac sô´ xj kh´ac không. , Cuô´i c` ung v´
oi m .oi j = 1, 2, . . . , q ch´ung ta c´o |xj| = |x0 − x00| ≤ j j , ,
|x0| + |x00| ≤ p + p = 2p = q. Nhu v ua j j .ây (x1, x2, . . . , xq) l` a nghi .êm c , ,
h .ê phuong tr`ınh c´o t´ınh châ´t mong muô´n. J
. 6.8. (Ðê` thi To´
an Olympic quô´c tê´ lâ`n 28 n˘ am 1987) Cho , , ,
x1, x2, . . . , xn l`a nh˜ung sô´th .uc v`a x2 + x2 + · · · + x2 ng minh 1 2 n = 1. Ch´ u , , r` ˘ ang v´ oi m˜
ôi sô´nguyên k, k ≥ 2, tô`n t .ai nh˜ung sô´nguyên a1, a2, . . . , an , không ¯ dô`ng th` oi b` ˘
ang không sao cho |ai| ≤ k − 1, i = 1, 2, . . . , n v`a , √ , , thoa m˜
an bâ´t phuong tr`ınh sau |a n
1 x1 + a2 x2 + · · · + an xn| ≤ (k−1) kn−1 , , ,, , , L` oi giai. Ch´
ung ta su d .ung bâ´t ¯d˘ang th´uc Cosi-Buniakovski-Svars q q | 2 2
α1β1 + |α2β2 + · · · + |αn βn| ≤ α + · · · + + · · · + 1 α2n β1 β2n , , , , ¯ dus ng v´
oi m .oi sô´th .uc α1, α2, . . . αn, β1, β2, . . . , βn. Dâ´u b`˘ang xây ra , khi v`
a chı khi tô`n t .ai m .ôt sô´λ sao cho α1 = λβ1, α2 = λβ2 . . . , αn = λβn. , , 62 Chuong 6. B` ai t .âp sô´h .oc nâng cao , Bây gi` o ch´ ung ta x´ et c´ ac sô´ y0 = − k−1, y + 1, . . . , 2 1 = − k−1 2 , , , ,
yk−1 = − k−1 + (k − 1) = k−1 Sô´lu ng cua ch´ung l`a k v`a hi ng 2 2 .o .êu t` u , ,
c .˘ap trong ch´ung l`a nh˜ung sô´ nguyên, m`a gi´a tr.i tuy.êt ¯dô´i cua n´o không qu´ a k − 1. M˜
ôi b .ô s´˘ap xê´p n-th`anh phâ`n β = (b1, b2, . . . , bn), ,, , o ¯
dây bi l`a m .ôt sô´n`ao ¯d´o trong y1, y2, . . . , yn v´oi m .oi i = 1, 2, . . . , n, , , , , ch´ ung ta ¯
d .˘at tuong ´ung v´oi m .ôt sô´ S = b β
1 x1 + b2 x2 + · · · + bn xn. , , , T` u bâ´t ¯ d˘ ang th´ uc Cosi S = b β
1 x1 + b2 x2 + · · · + bn xn q q ≤ b2 + b2 + · · · + b2 x2 + x2 + · · · + x2 1 2 n 1 2 n q = b2 + b2 + · · · + b2 1 2 n , , Nhung |bi| ≤ k−1 v´oi m 2
.oi i = 1, 2, . . . , n sao cho q k − 1 √ |S | ≤ b2 + b2 + · · · + b2 ≤ n β 1 2 n 2 √ √ , ,
ho .˘ac l`a − k−1 n ≤ S ≤ k−1 n. Theo phuong ph´ap n`ay n-b 2 β 2 .ô β = ,, , (b1, b2, . . . , bn), o ¯
dây bi l`a m .ôt trong c´ac sô´ y0, y1, . . . , yk−1 v´oi m .oi , , , , , , i = 1, 2, . . . , n, ¯
du .oc ¯d.˘at tuong ´ung v´oi m .ôt sô´ S = b β 1 x1 + b2 x2 + √ √ , , , , · · · + bnxn trong ¯
do .an ∆ = [− k−1 n, k−1 n]. Sô´ lu ng n-b c 2 2 .o .ô ¯ du .o , , √ , s´ ˘ ap xê´p l` a kn. Chia ∆ ra kn − 1 ¯
do .an nho v´oi ¯d .ô d`ai k−1 n. T` u kn−1 nguyên l´
y Ðirichlê suy ra tô`n t .ai hai n-b .ô β = (b1, b2, . . . , bn) v`a ,
γ = (c1, c2, . . . , cn), m` a nh˜ung sô´ S = b β
1 x1 + b2 x2 + · · · + bn xn , , , , v` a S = c ong ´ ung v´ oi ch´ ung n` ˘ am trong γ
1 x1 + c2 x2 + · · · + cn xn tu , c`
ung m .ôt ¯do.an nho. Ð.˘at a1 = b1 − c1,a2 = b2 − c2, . . . , an = bn − , , , , cn. D˜ê kiêm tra ¯
du .oc a1, a2.., an thoa m˜an ¯diê`u ki.ên ¯d˜a cho. Th.ât , ,
v .ây, v´oi m .oi i = 1, 2, . . . , n sô´ ai = bi − ci l`a hi.êu cua hai sô´ n`ao , ,, ¯ d´
o trong y0, y1, . . . , yk−1 nhu ¯d˜a n´oi o trên v`a l`a sô´ nguyên không , ,
vu .ot qu´a k − 1. V`ı hai n-b .ô trên kh´ac nhau ho`an to`an th`ı ´ıt nhâ´t
m .ôt trong c´ac sô´ ai = bi − ci kh´ac không. Ngo`ai ra, |b1x1 + b2x2 + 6.2. V´ı d .u 63
· · · + bnxn| = |x1(b1 − c1) + x2(b2 − c2) + · · · + xn(bn − cn)| = |S − β √ S | ≤ k−1 n. J γ kn−1 , , . 6.9. Ch´ ung minh r` ˘ ang m˜
ôi b .ô gô`m 11 sô´ th .uc kh´ac nhau trong , , , , , khoang [1,1000] c´
o thê ch .on ¯du.oc hai sô´ x v`a y, m`a ch´ung thoa m˜an , , bâ´t ¯ d˘ ang th´ uc sau √ 0 < x − y < 3 3 xy (6.2) , , , L` oi giai. Ch´ ung ta x´ et c˘
an b .âc ba cua c´ac sô´ trong b .ô sô´ ¯d˜a cho , √ x1, x2, . . . , x11 T`u ¯
diê`u ki .ên ¯d˜a cho suy ra 1 ≤ 3 xi ≤ 10, i = , , , 1, 2, . . . , 11. Ch´
ung ta chia khoang [1,10] ra mu` oi phâ`n b` ˘ ang nhau. √ √ √ Khi ¯ d´ o, c´
o ´ıt nhâ´t m .ôt trong hai sô´ 3 x1, 3 x2, . . . , 3 x11 n`˘am trong , √ √ c`
ung m .ôt ¯do.an nho. Nê´u c´ac sô´ ¯d´o l`a 3 xi v`a 3 xj, i 6= j v`a xi > xj, ch´ ung ta c´ o √ 9 0 < 3 xi − 3 pxj ≤ < 1. (6.3) √ √ 10 , , ,
Nhu v .ây, 0 < ( 3 xi − 3 xj)3 < 1, kê´t h .op v´oi (6.3) ta c´o 0 < xi − √ √ √ √
xj < 1 + 3 3 xixj( 3 xi − 3 xj) < 1 + 3 3 xixj. J , , , Ch´ u ´ y: B` ai to´ an không c` on ¯ d´ ung v´
oi b .ô 10 sô´th .uc trong khoang ,
[1,1000]. Phan v´ı d .u: b .ô sô´13, 23, . . . , 103. nê´u i 6= j v`a i > j ch´ung , ta c´
o (i − j)3 ≥ 1, nhu v .ây i2 + ij + j2 ≥ 1 + 3ij. Ngh˜ıa l`a i − j = , , ,
(i − j)(i2 + ij + j2) ≥ 1 + 3ij. ¯ d˘ ang th´ uc xây ra khi i = j + 1. , , , ,
. 6.10. Cho 7 sô´ th .uc bâ´t k`y. Ch´ung minh r`˘ang gi˜ua ch´ung c´o thê , , ,
ch .on ¯du.oc hai sô´, ch˘ang h .an x v`a y, sao cho √ x − y 3 0 ≤ ≤ . 1 + xy 3 , , , L` oi giai. C´ ac sô´ ¯ d˜ a cho k´
y hi .êu l`a x1, x2, . . . , x7. M .uc ¯d´ıch cua ch´ung , , , ,, ta l` a biêu di˜
ên m .oi sô´ du´oi d.ang xi = tg αi, o ¯dây αi l`a m .ôt sô´ , π trong khoang (− π , ), i = 1, 2, . . . , 7. Ch´ ung ta chia ¯ do .an n`ay ra 2 2 , , 64 Chuong 6. B` ai t .âp sô´h .oc nâng cao π s´ au ¯
do .an con c´o ¯d .ô d`ai b`˘ang nhau, ngh˜ıa l`a b`˘ang . D˜ ê d` ang thâ´y 6 r` ˘ ang ´ıt nhâ´t c´
o hai sô´ trong α1, α2, . . . , α7 c`ung n`˘am trong m .ôt ¯do.an , coni ¯ d´ o. Nê´u ch´ ung ta k´
y hi .êu c´ac sô´ ¯d´o l`a αi v`a αj, αi ≥ αj, th`ı t`u ¯d´o ,
suy ra 0 ≤ αi − αj ≤ π . V`ı h`am sô´tg l`a t˘ang trong khoang (− π , π ), 6 2 2 suy ra √
tg αi − tg αj xi − xj π 3
0 ≤ tg(αi − αj) = = ≤ tg = .
1 + tg αi tg αj 1 + xixj 6 3 J , , , Ch´ u ´ y: B` ˘ ang c´ ach giai cua hai b`
ai t .âp n`ay ch´ung ta c´o thê s´ang , , , , , , ,
t .ao ra m .ôt lo.at b`ai to´an tuong t .u, m`a v´oi c´ach giai b`ınh thu`ong kh´o , , , m` a giai quyê´t ¯ du .oc. 6.3. B ` ai t .âp . 6.11. (Ðê` thi To´
an Olympic quô´c tê´ lâ`n 26 n˘ am 1985). Cho t .âp , , , , , ,
h .op M gô`m 1985 sô´ t .u nhiên, không c´o sô´ n`ao c´o u´oc sô´ l´on hon , , , ,, , , , , 26. Ch´ ung minh r` ˘ ang t` u nh˜ung phâ`n tu cua M c´ o thê ch .on ¯du .oc 4 , , , , sô´ t` ung ¯
dôi m .ôt kh´ac nhau m`a t´ıch cua ch´ung l`a l˜uy th`ua b.âc 4 cua , ,
m .ôt sô´nguyên. (kê´t lu.ân ¯d´ung v´oi t.âp h .op gô`m 3.29 + 1 = 1537 sô´ , , , , m` a nh˜ ung u´ oc sô´cua ch´ ung không qu´ a 23). , , ,
. 6.12. Cho bô´n sô´duong bâ´t k` y. Ch´ ung minh r` ˘ ang c´ o hai sô´trong , , , , bô´n sô´ ¯ d´ o, ch˘
ang h .an x v`a y, thoa m˜an bâ´t phuong tr`ınh sau x − y √ 0 ≤ ≤ 2 − 3. 1 + x + y + 2xy , , , , . 6.13. Ch´ ung minh r` ˘
ang m .ôt sô´ t .u nhiên c´o thê biêu di˜ên th`anh , , , , ,
tông b`ınh phuong cua hai sô´nguyên khi v`
a chı khi, trong phân t´ıch , ,
ra d .ang ch´ınh t´˘ac cua n´o, c´ac th`ua sô´nguyên tô´d.ang 4k + 3 ¯dê`u c´o sô´m˜ u ch˜ ˘ an. 6.3. B` ai t .âp 65 , , , , . 6.14. Ch´ ung minh r` ˘ ang t` u k + 1 sô´, m`a ch´ ung nho hon 2k, luôn , , , , , , luôn c´
o thê ch .on ¯du .oc hai sô´ m`a ty sô´ cua ch´ung l`a m .ôt l˜uy th`ua , cua 2. , , , . 6.15. Cho n l`
a m .ôt sô´ le. Ch´ung minh r`˘ang t`u (n − 1)2 + 1 sô´ , , , , , nguyên bâ´t k` y c´
o thê ch .on ¯du .oc n sô´ sao cho tông cua ch´ung chia hê´t cho n. , , 66 Chuong 6. B` ai t .âp sô´h .oc nâng cao , , CHUONG 7 B ` AI T .ÂP D ˜ ÂY S ´ Ô NÂNG CAO 7.1. V´ı d .u , . 7.1. Cho d˜
ay Fibonaxi u1 = u2 = 1, un = un−1 + un−2. V´oi m .oi sô´ , , , , , ,
nguyên duong m, th`ı gi˜ ua nh˜
ung sô´ h .ang t`u ¯dâ`u d˜ây ¯dê´n sô´h .ang th´u
m2 − 1 tô`n t .ai m.ôt sô´h .ang chia hê´t cho m. , , , , L` oi giai. Ch´ ung ta k´
y hi .êu k l`a phâ`n du cua sô´ k cho m. Ch´ung ta , , x´ et c´
ac c .˘ap phâ`n du cua d˜ay Fibonaxi khi chia cho m:
(u1, u2).(u2, u3), (u3, u4), . . . , (un, un+1), . . . (7.1) Nê´u ch´ ung ta qui ¯
d.inh hai c.˘ap (a1, b1) v`a (a2, b2) l`a b`˘ang nhau khi , , , ,
a1 = b1 v`a a2 = b2, th`ı sô´ tâ´t ca kha n˘ang cua c´ac c .˘ap phâ`n du khi chia cho m l` a m2. V`ı thê´ ch´
ung ta lâ´y m2 + 1 sô´ h .ang ¯dâ`u tiên , , cua d˜ ay (7.1) th`ı trong ch´ ung phai c´
o hai c .˘ap tr`ung nhau,( theo , , ,, nguyên l´ y Ðirichlê ) v` a t` u ¯ d´ o c´
ac c .˘ap sau l.˘ap l.ai. Gia su c.˘ap (uk, uk+1) , l`
a c .˘ap ¯dâ`u tiên l.˘ap l.ai trong (7.1). Ch´ung ta s˜e ch´ung minh r`˘ang , ,, , ,
c .˘ap n`ay b`˘ang c.˘ap (1, 1). Th.ât v.ây, gia su ngu .oc l.ai, ngh˜ıa l`a c.˘ap , ¯
dâ`u tiên l .˘ap l.ai l`a (uk, uk+1), v´oi k > 1. Khi ¯d´o ch´ung ta s˜e t`ım , , ¯
du .oc trong (7.1) m .ôt c.˘ap (ul, ul+1), (l > k), m`a n´o b`˘ang (uk, uk+1) ,
. Nhu v .ây ul−1 = ul+1 − ul v`a uk−1 = uk+1 − uk, do ul+1 = uk+1 v`a , ,
ul = uk, nên phâ`n du cua ul−1 v`a uk−1 khi chia cho m c˜ung b`˘ang , nhau, ngh˜ıa l`
a ul−1 = uk−1. T`u ¯d´o suy ra (uk−1, uk) = (ul−1, ul), v.ây , , 68 Chuong 7. B`
ai t .âp d˜ây sô´nâng cao , , ,
c .˘ap (uk−1, uk)n`˘am trong d˜ay (7.1) tru´oc ca (uk, uk+1). Ðiê`u ¯d´o n´oi , , , lên r` ˘
ang (uk, uk+1) không phai c .˘ap l.˘ap l.ai ¯dâ`u tiên, tr´ai v´oi gia thiê´t , , ¯
d .˘at ra. Ngh˜ıa l`a k > 1 không thê xay ra, v.ây k = 1. , , ,,
Nhu v .ây c.˘ap (1, 1) l`a c.˘ap ¯dâ`u tiên l.˘ap l.ai trong (7.1). Gia su n´o
l .˘ap l.ai t lâ`n (1 < t < m2 + 1). ho.˘ac l`a (ut, ut+1) = (1, 1). Ngh˜ıa l`a ut , , v`
a ut+1 khi chia cho m cho phâ`n du c`ung l`a 1, v .ây hi.êu cua ch´ung , , ,
chia hê´t cho m. Nhung ut+1 − ut = ut−1. Nhu v .ây sô´h.ang th´u t − 1 , cua d˜ ay Fibonaxi s˜ e chia hê´t cho m. J , ,, , , , , ,
. 7.2. Gia su a v` a x l` a c´
ac sô´t .u nhiên th .uc s .u l´on hon 1 v`a (x, a − 1) = , , , 1. D˜
ay sô´vô h .an {un} ¯du.oc x´ac ¯d.inh nhu sau
un = axn − a + 1, n = 1, 2, . . . , , Ch´ ung minh r` ˘ ang trong d˜ ay sô´n´ oi trên ch´
ua vô h .an sô´¯dôi m.ôt nguyên tô´c` ung nhau. , , , , , , , L`
oi giai. Gia thiê´t phan ch´ ung trong d˜ ay sô´ chı c´ o h˜ uu h .an sô´ ui , u , . . . , u ¯ dôi m 1 i2 ik .ôt nguyên tô´c` ung nhau.
Ð .˘at q = ui u . . . u . X´et (q + 1) sô´ sau a, ax, ax2, . . . , axq. Theo 1 i2 ik nguyên l´
y Ðirichlê tô`n t .ai hai sô´ nguyên r, s sao cho 0 ≤ r < s ≤ q v` a axr ≡ axs (mod q) =⇒ axr − axs ≡ 0 (mod q) hay axr(1 − xs−r) ≡ 0 (mod q) (7.2) , Theo gia thiê´t ta c´
o (x, a − 1) = 1, nên suy ra
(axr, ui ) = 1, ∀j = 1, 2, . . . , k. (7.3) j , T` u (7.3) suy ra (axr, q) = 1. (7.4) 7.1. V´ı d .u 69 , , T` u (7.2) v` a (7.4) c´
o xs−r ≡ 1 (mod q) =⇒ xs−r = lq + 1 v´ oi l ∈ N. X´ et sô´ ui = axs−r − a + 1. V k+j .ây ui
= a(lq + 1) − a + 1 = qal + 1. (7.5) k+j , T` u (7.5) ta c´ o (ui , u ) = 1, ∀j = 1, 2, . . . , k. (7.6) k+j ij , , , , ,
H .ê th´uc (7.6) ch´ung to r`˘ang luôn c´o thê bô sung thêm v`ao b .ô sô´ , ,
q = ui u . . . u c´ac sô´ m´oi, m`a b oa m˜ an ¯ diê`u ki 1 i2 ik .ô sô´ n` ay v˜ ân th .ên: bâ´t k` y hai sô´ n` ao c˜ ung nguyên tô´ c` ung nhau. Ðiê`u n` ay c´ o ngh˜ıa l` a trong d˜ ay {un} ¯ d˜ a cho c´
o vô h .an sô´ ¯dôi m .ôt nguyên tô´ c`ung nhau. J ,
. 7.3. Cho {un} l`a d˜ay c´ac sô´t .u nhiên t˘ang dâ`n: u1 < u2 < u3 < . . . , , , v` a thoa m˜ an ¯
diê`u ki.ên u1 = 1, un+1 ≤ 2n, v´oi m.oi n l`a sô´ t .u nhiên. , , , Ch´ ung minh r` ˘ ang v´
oi m .oi sô´ t .u nhiên n tô`n t .ai c´ac sô´ h .ang up v`a uq , cua d˜
ay sao cho up − uq = n. , , , ,, , , , , , L`
oi giai. Gia su n ∈ N l`a sô´ t .u nhiên cho tru´oc. T`u gia thiê´t suy ra , , , m˜
ôi sô´ h .ang u1, u2, . . . , un+1 không vu .ot qu´a 2n. X´et t.âp h .op 2n sô´ , ,
t .u nhiên sau {1, 2, . . . , 2n}. Ch´ung ta chia t.âp h .op n`ay ra l`am n c.˘ap , , ,
(1, n + 1), (2, n + 2), . . . , (n, 2n). Do t .âp h .op trên ch´ua không ´ıt hon ,, , (n + 1) phâ`n tu cua d˜ ay {un} ¯ d˜ a cho (v`ı n´
oi riêng u1, u2, . . . , un+1 ¯ d˜ a ,
thu .ôc t.âp h .op â´y), v.ây theo nguyên l´y Ðirichlê tô`n t.ai hai sô´ h.ang , , ,, kh´
ac nhau up v`a uq cua d˜ay thu .ôc v`ao m .ôt c.˘ap ( gia su up > uq). , ,
Nhung hi .êu sô´cua m˜ôi c.˘ap ¯dê`u b`˘ang n, nên ch´ung ta c´o up − uq = n. J ,
. 7.4. Cho {uk}, k = 1, 2, . . . , n l`a d˜ay sô´t .u nhiên sao cho
1 ≤ u1 ≤ u2 ≤ . . . ≤ un v`a u1 + u2 + · · · + un = 2n , , 70 Chuong 7. B`
ai t .âp d˜ây sô´nâng cao , , Ch´ ung minh r` ˘
ang nê´u n ch˜ ˘ an v`
a un 6= n + 1, th`ı t`u d˜ay trên luôn ch .on , , , , ra ¯
du .oc m.ôt d˜ay con m`a tông c´ac sô´h .ang cua d˜ay con ¯d´o b`˘ang n. , , L`
oi giai. Ð .˘at Sk = u1 + u2 + · · · + uk, k = 1, 2, 3, . . . , n. X´et n + 2 sô´
{0, u1 − un, S1, S2, . . . , Sn} Theo nguyên l´y Ðirichlê th`ı´ıt nhâ´t hai sô´ , , , khi chia cho n c´ o c`
ung phâ`n du. V .ây, chı c´o 4 kha n˘ang sau ¯dây:
1) (u1 − un) chia hê´t cho n.
Do u1 + u2 + · · · + un ≥ nu1 =⇒ 2n ≥ nu1 =⇒ u1 ≤ 2 ,
a) Nê´u u1 = 2 th`ı t`u 1 ≤ u1 ≤ u2 ≤ . . . ≤ un v`a u1 + u2 + · · · +
un = 2n suy ra u1 = u2 = . . . = un = 2. Do n ch˜˘an nên n = 2m v .ây
u1 + u2 + · · · + um = 2m = n ,
b) Nê´u u1 < 2 th`ı t`u u1 − un chia hê´t cho n, suy ra un = 1 ho .˘ac l`
a un = 1 + n ( do u1 nguyên nên u1 = 1 v`a 1 ≤ un ≤ 2n suy ra , , , ¯
du .oc kê´t lu.ân trên). Nhung un 6= n + 1 suy ra un = 1. M.˘at kh´ac
1 ≤ u1 ≤ u2 ≤ . . . ≤ un v .ây th`ı u2 = u3 = . . . = un−1 = 1. Suy ra
u1 + u2 + · · · + un = n, vô l´y. , , , , ,
Nhu v .ây trong tru`ong h .op n`ay, ta chı ra tô`n t.ai d˜ay con u1, u2 , n
, . . . , um sao cho u1 + u2 + · · · + um = n v´oi m = . 2
2) Sj − Si, (j > i) chia hê´t cho n. , , , Ta c´
o Sj − Si = ui+1 + ui+2 + · · · + uj. R˜o r`ang vê´phai cua ¯d˘ang , th´ uc trên c´
o ´ıt nhâ´t m .ôt sô´h.ang m`a uk ≥ 1, ∀k = 1, 2, . . . , n, suy ra , ,, ,
Sj − Si ≥ 1. M .˘at kh´ac c˜ung hi.êu trên nê´u không ¯du c´ac phâ`n tu cua , d˜ ay th`ı bao gi` o ta c˜ ung c´
o Sj − Si < u1 + u2 + · · · + un ≤ 2n − 1. Do ¯ d´ o cuô´i c` ung ta c´
o 1 ≤ Sj − Si < u1 + u2 + · · · + un ≤ 2n − 1 , , m`
a Sj − Si chia hê´t cho n. ¯ diê`u n`
ay chı xây ra khi Sj − Si = n ho .˘ac l`
a ui+1 + ui+2 + · · · + uj = n. 3) Si chia hê´t cho n. 7.1. V´ı d .u 71 Ta c´
o 1 ≤ Si ≤ Sn−1 = 2n − un < 2n m`a Si chia hê´t cho n, suy
ra Si = n ho .˘ac l`a u1 + u2 + · · · + ui chia hê´t cho n. , ,
4) Sk v`a u1 − un cho c`ung phâ`n du khi chia cho n, v´oi k n`ao ¯ d´
o, 1 ≤ k ≤ n − 1. Suy ra Sk − (u1 − un)|n =⇒ (u2 + u3 + · · · +
uk + un)|n. M`a u2 + u3 + · · · + uk + un ≤ 2n − u1 < 2n. Suy ra
u2 + u3 + · · · + uk + un = n. , , , , T´
om l .ai luôn luôn ch .on ¯du .oc d˜ay con m`a tông cua ch´ung b`˘ang n. J , , . 7.5. Cho d˜
ay sô´ nguyên u1, u2, . . . , un v´oi n ≥ 2. Ch´ ung minh r` ˘ ang
tô`n t .ai d˜ay con uk , u , . . . , u trong ¯d´o 1 ≤ k 1 k2 km
1 < k2 < . . . < km ≤ n
sao cho u2 + u2 + · · · + u2 chia hê´t cho n. k1 k2 km , , L` oi giai. X´ et (n + 1) sô´
0, u21, u21 + u22, u21 + u22 + u23, . . . , u21 + u22 + · · · + u2n , Chia c´ ac sô´ n` ay cho n, th`ı ch´
ung cho nhiê`u nhâ´t n sô´ du. Theo , , ,, nguyên l´
y Ðirichlê tô`n t .ai hai sô´ cho c`ung sô´ du, gia su ¯d´o l`a u2 + 1 u2 + · · · + u2 v` a u2 + u2 + · · · + u2( 2 0 ≤ j < k ≤ n). C´ o ngh˜ıa j 1 2 k l`
a sô´ (u2 + u2 + · · · + u2) − (u2 + u2 + · · · + u2) chia hê´t cho n. 1 2 j 1 2 k ,
Ho .˘ac l`a uj+1 + uj+2 + · · · + uk chia hê´t cho n. D˜ay con phai t`ım l`a uj+1, uj+2, . . . , uk. J . 7.6. Cho d˜
ay Fibonaxi 1, 2, 3, 5, 8,. . . .Ð .˘at f (n) = 19852 + , , 1956n2 + 1960 Ch´ ung minh r` ˘
ang tô`n t .ai vô h .an sô´ h .ang uk cua d˜ay
Fibonaxi, sao cho f (uk)|1989 , , L`
oi giai. Ð .˘at h(n) = 4n2 + 33n + 29 =⇒ h(n) = 1989(n2 + n + 1) − , f (n). T` u ¯ d´
o suy ra f (n)|1989 ⇐⇒ h(n)|1989. , , 72 Chuong 7. B`
ai t .âp d˜ây sô´nâng cao X´ et d˜ ay sô´ {vn} sau ¯ dây, trong ¯ d´ o v0 = −1, v1 = 1
vn+1 = vn + vn+1, n = 1, 2, . . . ,, N´ oi c´ ach kh´ ac d˜
ay {vn} l`a d˜ay sinh ra boi d˜ay Fibonaxi {un} : , , 1, 1, 2, 3, 5, . . . b` ˘ ang c´ ach thêm v` ao tru´ oc d˜ ay n` ay ba sô´h .ang -1, 1, 0. ,
G .oi ri l`a phâ`n du trong ph´ep chia vi cho 1989(i = 0, 1, 2, . . .). ,
Nhu v .ây ta c´o 0 ≤ r ≤ 1988. X´et d˜ay c´ac c.˘ap sô´sau ¯dây
(r0, r1), (r1, r2), (r2, r3), . . . . , V`ı m˜
ôi c .˘ap ri chı nh.ân m .ôt trong 1989 gi´a tr.i, v.ây sô´ c´ac c.˘ap kh´ac , nhau tô´i ¯ da l` a 19892. T`u ¯ d´ o theo nguyên l´
y Ðirichlê th`ı trong 19892 + , ,,
1 c .˘ap ¯dâ`u tiên ´ıt nhâ´t c´o hai c.˘ap tr`ung nhau. Gia su hai c.˘ap â´y l`a
(rp, rp+1), (rp+q, rp+q+1), p, q ∈ N Ðiê`u â´y c´ o ngh˜ıa l`
a rp = rp+1, rp+q = rp+q+1. Theo c´ach x´ac ¯ d.inh d˜ ay, ta c´ o
vp−1 = vp+1 − vp =⇒ rp−1 = rp+1 − rp , , , Tuongt .u, ta c´o
vp+q−1 = vp+q+1 − vp+q =⇒ rp+q−1 = rp+q+1 − rp+q , , , , T` u ¯ d´
o suy ra rp−1 = rp+q−1. Tuongt .u, ta c´o rp−2 = rp+q−2 . . . . . . . r2 = rq+2 r1 = rq+1 r0 = rq , T`
u r0 = rq, r1 = rq+1 v`a vn+1 = vn + vn+1 suy ra ri = ri+q, ∀i =
0, 1, 2, . . .. Do v .ây r0 = rq = r2q = r3q = . . . = rkq, ∀k ≥ 1, suy 7.1. V´ı d .u 73 ,
ra h(vkq) = 1989.A + h(−1) = 1989.A. Nhung ∀k = 1, 2, 3 . . . vkq , ¯ dê`u l` a sô´ Fibonaxi suy ra c´
o vô sô´ sô´ h .ang vkq cua d˜ay Fibonaxi m`a f (vkq)|1989. J , . 7.7. Cho d˜
ay sô´ {un} x´ac ¯d.inh nhu sau
u1 = 20, u2 = 100, v`a un+1 = 4un + 5un−1 − 1976, n = 1, 2, . . . , , Ch´ ung minh r` ˘
ang tô`n t .ai ´ıt nhâ´t m.ôt sô´cua d˜ay sô´chia hê´t cho 1996. , , L`
oi giai. Ð .˘at un = 1996pn + qn, ∀n = 1, 2, . . . trong ¯d´o pn, qn l`a c´ac sô´nguyên v`
a 0 ≤ qn ≤ 1995. X´et d˜ay sô´
(q1, q2), (q2, q3), . . . , (qn, qn+1), . . . , V`ı d˜ ay n`
ay vô h .an m`a sô´ c´ac sô´ qi l`a h˜uu h.an nên tô`n t.ai hai sô´ , , ,, ,
t .u nhiên l, m ( gia su m > l) sao cho (ql, ql+1) = (qm, qm+1) hiêu ,
theo ngh˜ıa ql = qm v`a ql+1 = qm+1. Ch´ung ta s˜e ch´ung minh r`˘ang
ql−1 = qm−1. Th .ât v.ây,
5(um−1 − ul−1) = (um+1 − 4um + 1976) − (ul+1 − 4ul + 1976)
= (um+1 − ul+1) − 4(um − ul) (7.7) ,
Do uk = 1996pk + qk, nên t`u (7.7) c´o
5(um−1 − ul−1) = 1996(pm+1 − pl+1) − (qm+1 − ql+1)−
− 4[1996(pm − pl) − (qm − ql)] (7.8) , Thay nh˜ ung gi´
a tr.i b`˘ang nhau v`ao ((7.8) ta ¯di ¯dê´n
5(um−1 − ul−1) = 1996[(pm+1 − pl+1) − 4(qm − ql)] (7.9) , T`
u (7.9) suy ra 5(um−1 − ul−1)|1996, m`a (5, 1996) = 1 =⇒ (um−1 −
ul−1)|1996 =⇒ 1996(pm−1 − pl−1) + (qm−1 − ql−1)|1996 =⇒ (qm−1 − ql−1)|1996. (7.10) , , 74 Chuong 7. B`
ai t .âp d˜ây sô´nâng cao
Do 0 ≤ qm−1 ≤ 1995, 0 ≤ ql−1 ≤ 1995
=⇒ −1995 ≤ qm−1 − ql−1 ≤ 1995 (7.11) , T` u (7.10) v`
a (7.11) suy ra (qm−1 − ql−1) = 0 hay qm−1 = ql−1. , , , , ,
Tuong t .u ch´ung ta c˜ung c´o thê ¯di ¯dê´n qm−2 = ql−2 v`a c´u tiê´p t .uc , nhu thê´ ¯ di ¯ dê´n
q2 = q2 + (m − 1) v`a q1 = q1 + (m − l) (7.12) , , Ta ch´ ung minh r` ˘
ang um−l ch´ınh l`a sô´h .ang cua d˜ay m`a chia hê´t cho
1996. Th .ât v.ây theo c´ach x´ac ¯d.inh d˜ay, ta c´o
5um−l = um−l+2 − 4um−l+1 + 1976
= 1996pm−l+2 + qm−l+2 − 4(1996pm−l+1 + qm−l+1) + 1996
= 1996(pm−l+2 + 4pm+l+1) + (qm−l+2 + 4qm−l+1) + 1996 , , Thay (7.12) v` ao ¯ d˘ ang th´ uc trên ta c´ o
5um−l = 1996(pm−l+2 − 4pm−l+1) + (q2 − 4q1) + 1996. (7.13) Do
u1 = 20 =⇒ u1 = 0.1996 + 20 =⇒ q1 = 20
u2 = 100 =⇒ u2 = 0.1996 + 100 =⇒ q2 = 100 , V .ây t`u (7.13) suy ra
5um−l = 1996(pm−l+2 − 4pm−l+1) + 1996. (7.14) ,
Do pm−l+2 v`a pm−l+1 l`a sô´nguyên, v.ây t`u (7.14) suy ra 5um−l|1996 m`
a (5, 1996) = 1 suy ra um−l|1996. J , . 7.8. Cho d˜
ay sô´ t .u nhiên u1, u2, . . . , un+1 sao cho 1 ≤ u1 < u2 < , ,
. . . < un+1 ≤ 2n . Ch´ ung minh r` ˘
ang tô`n t .ai hai sô´t .u nhiên i v`a j sao
cho uj chia hê´t cho ui, (j > i). , , , , , , , , , , L` oi giai. K´
y hi .êu vi l`a u´oc sô´le l´on nhâ´t cua ui tuong ´ung, ngh˜ıa l`a , , ,
ui = 2pi.vi , v´oi vi le v`a sô´ t .u nhiên pi n`ao ¯d´o (i = 1, 2, . . . , n + 1). 7.1. V´ı d .u 75 ,
Do 1 ≤ u1 < u2 < . . . < un+1 ≤ 2n suy ra v´oi m .oi i = 1, 2, . . . , n + 1 , , ta c´
o vi < 2n . X´et (n + 1) sô´ le v1, v2, . . . , vn+1. C´ac sô´ le n`ay ¯ dê`u , , , , , , , duong v`
a nho hon 2n. nên sô´ lu .ong cua ch´ung b`˘ang n. V.ây theo nguyên l´
y Ðirichlê tô`n t .ai hai sô´ i, j sao cho 1 ≤ i < j ≤ n + 1 m`a , vi = vj. Theo c´ach ¯
d .˘at trên th`ı ui = 2pivi v`a uj = 2pjvj. Nhung
ui < uj suy ra 2pi vi < 2pj vj, m`a vi = vj. Suy ra 2pi < 2pj. Do pi, pj l`a , , c´
ac sô´ nguyên duong nên 2pj chia hê´t cho 2pi. Ngh˜ıa l`a uj chia hê´t cho ui. J ,
. 7.9. (Ðê` thi To´
an Olympic Quô´c tê´ lâ`n th´ u 13) D˜ ay sô´ {un}, n = , , 2, 3, 4, . . . x´ ac ¯
d.inh nhu sau un = 2n − 3. Ch´ung minh r`˘ang d˜ay sô´n`ay , ,, , ch´
ua m .ôt t .âp vô h .an c´ac phâ`n tu, sao cho bâ´t k`y hai sô´ n`ao cua t .âp ,
h .op n`ay c˜ung nguyên tô´c`ung nhau. , , , , , , , L` oi giai. Ta ch´ ung minh b` ˘
ang quy n .ap. Gia thiê´t ¯d˜a xây d .ung ¯du .oc ,, , k phâ`n tu cua d˜ ay
u1 = 2n1 − 3, u2 = 2n2 − 3, . . . , uk = 2nk − 3 , , ,, m` a v´
oi m .oi i 6= j, th`ı (uj, ui) = 1, v´oi 1 ≤ i, j ≤ k, o ¯dây 2 = n1 < n2 < . . . < nk. , Ch´ ung ta s˜
e xây d .ung sô´ uk+1 = 2nk+1 − 3 nguyên tô´c`ung nhau , v´ oi c´
ac sô´ u1, u2, . . . , uk b`˘ang c´ach sau ¯
dây: Ð .˘at l = u1.u2 . . . uk. X´et , , ,
(l + 1) sô´20, 21, . . . 2l Khi chia c´ ac sô´ n` ay cho l ta ¯ du .oc m .ôt t.âp h .op ,
gô`m l sô´ du. V .ây theo nguyên l´y Ðirichlê c´o ´ıt nhâ´t hai sô´ cho ta , , ,, , c`
ung phâ`n du. Gia su hai sô´ ¯ d´ o l`
a 2r v`a 2s, (s > r). Bây gi`o ch .on sô´ p ,
sao cho pl = 2r − 2s = 2s(2r−s − 1). Do l l`a sô´le nên 2s không chia
hê´t cho l . M .˘at kh´ac (2r, 2r−s) = 1 suy ra (2r−s − 1) chia hê´t cho l. , Ðiê`u n` ay ngh˜ıa l`
a tô`n t .ai sô´t .u nhiên q sao cho 2r−s − 1 = ql, suy ra
2r−s+2 − 3 = 4.2r−s − 3 = 4(ql + 1) − 3 = 4ql + 1. , , 76 Chuong 7. B`
ai t .âp d˜ây sô´nâng cao
Ð .˘at uk+1 = 2r−s+2 − 3 = ql. Do uk+1 = 4ql + 1 v`a l =
u1.u2 . . . uk, suy ra uk+1 > uk. ,
Do uk+1 = 4ql + 1, suy ra (uk+1, 1) = 1. Do ¯d´o (uk+1, ui) = 1 v´oi m .oi i = 1, 2, . . . , k. , , , , ,
Nhu v .ây khi ¯d˜a xây d .ung ¯du .oc d˜ay con u1, u2, . . . , uk thoa m˜an , , , , , ¯
diê`u ki .ên ¯dâ`u b`ai, th`ı s˜e xây du .ong ¯du .oc d˜ay con m´oi u1, u2, . . . , uk, ,
uk+1 c˜ung c´o t´ınh châ´t â´y. Theo nguyên l´y qui n .ap ch´ung ta xây d .ung , , , ¯
du .oc d˜ay con vô h.an u1, u2, . . . , un, . . . . cua d˜ay ¯d˜a cho c´o t´ınh châ´t: , ,, , Bâ´t c´
u c .˘ap phâ`n tu n`ao cua d˜ay con â´y c˜ung nguyên tô´ c`ung nhau. J , ,
. 7.10. Cho u1 v`a u2 l`a hai sô´ nguyên duong nguyên tô´ c`ung nhau. , D˜
ay sô´ {un} x´ac ¯d.inh v´oi u1, u2 l`a hai sô´ h .ang ¯dâ`u tiên, c`on khi n = 2, 3, . . . ta x´ ac ¯ d.inh un+1 = unun−1 + 1 , , Ch´ ung minh r` ˘ ang v´
oi m .oi i > 1 tô`n t .ai j > i sao cho uj chia hê´t cho ui. , , , , , , L`
oi giai. Lâ´y i > 1 t` uy ´ y, v` a p l`a u´
oc sô´ nguyên tô´ cua ui. Xây d .ung , d˜ ay sô´ {vn} nhu sau 0 ≤ vn ≤ p − 1 vn ≡ un (mod p) Ta c˜ ung c´
o vn+1 = vnvn−1 + 1 (mod p), ∀n = 2, 3 . . . V`ı c´ac c .˘ap , ,
(vn, vn−1) l`a vô h .an, m`a vn chı nh.ân h˜uu h.an gi´a tr.i suy ra {vn} , , , phai l` a d˜ ay tuâ`n ho` an t`
u m .ôt l´uc n`ao ¯d´o. Ta câ`n ch´ung minh r`˘ang , ,
tô`n t .ai sô´nguyên duong kp > 0 sao cho vi+k = 0. (7.15) p , X´ et hai kha n˘ ang sau 7.1. V´ı d .u 77 , ,, , , 1) Gia su d˜
ay {vn} tuâ`n ho`an t`u vs v´oi chu k`y T, trong ¯ d´ o s > i. Ta c´ o
vs+1 = vsvs−1 + 1 = vs+T+1 = vs+Tvs+T−1 + 1 (mod p)
vsvs−1 = vs+Tvs+T−1 (mod p). (7.16)
a) Nê´u vs = vs+T ≡ 0 (mod p), th`ı vs = vs+T = 0, do 0 ≤ vn ≤ , p − 1, ∀n. Khi ¯ d´
o chı vi .êc ch .on kp = s − i, Suy ra vi+k = v p s = 0, v .ây (7.15) ¯d´ung. ,
b) Nê´u vs = vs+T 6= 0, th`ı t`u (7.16) c´o vs−1 = vs+T−1. Suy ra , , ,
{vn} tuâ`n ho`an không phai b´˘at ¯ dâ`u t` u vs ¯ diê`u n` ay mâu thu˜ ân v´ oi , , c´
ach ch .on s.Kha n˘ang n`ay không xây ra. , , , , T´
om l .ai h.ê th´uc (7.15) ¯d´ung trong tru`ong h .op 1). , ,
2) Nê´u s ≤ i th`ı h .ê th´uc (7.15) hiên nhiên ¯d´ung. Ta c´o vi+1 ≡ ,
ui+1 (mod p) ≡ uiui−1 + 1 (mod p) v .ây vi ≡ ui (mod p) nhung , , , , do p l`a u´
oc nguyên tô´cua ui suy ra vi ≡ 0 (mod p), nhu v .ây vi+1 ≡ 1 (mod p) hay l` a vi+1 = 1. , , , ,
Tuongt .u, do vi+k = 0 suy ra v v p i+kp+1 = 1. Nhu .ây suy ra {vn} , , , , , c˜ ung tuâ`n ho` an v´ oi chu k`
y kp t´uc l`a v´oi m .oi l nguyên duong, ta c´o vi+l.k = 0. (7.17) p Ngh˜ıa l` a ui+l.k chia hê´t cho p. p , , , , , , , ,
Nhu v .ây v´oi m .oi u´oc nguyên tô´ p cua ui ta xây d .ung ¯du .oc sô´kp sao cho (7.17) ¯ d´ ung. , , ,
G .oi m l`a b .ôi sô´ chung nho nhâ´t cua tâ´t ca c´ac sô´ kp, theo (7.3) , , ,
suy ra vi+lm = 0 v´oi m .oi l nguyên duong. Suy ra ui+lm chia hê´t cho , , , , , , tâ´t ca c´ ac u´
oc sô´ nguyên tô´ cua ui. T´uc l`a ui+lm chia hê´t cho ui v´oi , , , ,
m .oi sô´nguyên duong l. Lâ´y j = i + lm, ta c´o ¯diê`u phai ch´ung minh. J , , 78 Chuong 7. B`
ai t .âp d˜ây sô´nâng cao 7.2. B ` ai t .âp , , , ,
. 7.11. Nê´u ba sô´ nguyên tô´ th .uc s .u l´on hon 3 l.âp th`anh m .ôt câ´p ,
sô´c .ông th`ı công sai cua ch´ung chia hê´t cho 6. , , , . 7.12. cho f (n) l` a h` am x´ ac ¯
d.inh trên t.âp c´ac sô´nguyên duong nhu ,
sau: nê´u n = a1a2 . . . ak, th`ı f (n) = (a1 + a2 + · · · + ak)1998. V´oi m˜ôi , , ,
sô´nguyên duong n, l .âp d˜ay vô h.an ui(n), i = 1, 2, . . . nhu sau
ui(n) = f ( f (. . . f (n)i lâ`n f | {z } , , , , Ch´ ung minh r` ˘ ang v´
oi m .oi n nguyên duong, tô`n t.ai p sao cho d˜ay
ui(n), i = p, p + 1, . . . l`a d˜ay tuâ`n ho`an. ,
. 7.13. Cho u1, u2, . . . , un l`a d˜ay sô´ t`uy ´y gô`m n sô´ h .ang. Ch´ung , , minh r` ˘ ang luôn luôn tr´ıch ¯
du .oc m .ôt d˜ay con sao cho nê´u g .oi S l`a , ,, , , tông c´ ac phâ`n tu cua d˜
ay con â´y, th`ı S kh´ac v´ oi sô´ nguyên gâ`n nhâ´t , , , , 1
m .ôt lu .ong không vu .ot qu´a . n + 1 , , . 7.14. Ch´ ung minh r` ˘
ang nê´u nh˜ung sô´ nguyên a v`a m nguyên tô´ , c`
ung nhau, th`ı tô`n t .ai m .ôt sô´t .u nhiên n m`a t´ıch na chia cho m cho , sô´du 1. , , CHUONG 8 , , S ´ Ô TH .UC V ´ OI T .ÂP TR`U M .ÂT 8.1. T .âp tr`u m .ât , , , , , , , Trên ¯ du` ong th˘
ang th .uc ch´ung ta thu`ong quan tâm t´oi kh´ai ni.êm , , , , ,
m .ôt khoang (m .ôt ¯do.an th˘ang), ta c´o thê hiêu m .ôt khoang trên , , , , , , , , , ¯ du` ong th˘
ang th .uc l`a t.âp h .op tâ´t ca c´ac sô´ th .uc n`˘am gi˜ua hai ¯diêm , , , , , ¯ d˜
a cho. Nhu v .ây hai ¯diêm ¯dê x´ac ¯d.inh m .ôt khoang c´o thê n`˘am trong , ,
ho .˘ac n`˘am ngo`ai khoang ¯d´o ; ¯dây l`a xuâ´t ph´at cua kh´ai ni.êm ¯d´ong, ,, ,, , , , mo,.. o ng`
anh giai t´ıch, giai t´ıch h` am trong to´ an h .oc cao câ´p. Nhung ,, , , o ¯ dây ta không quan tâm ¯ diê`u ¯ d´ o, m` a chı quan tâm t´ oi c´ ac kh´ ai , , , , , ,
ni .êm sau ¯dây v´oi quan ¯diêm kiê´n th´uc so câ´p. V´oi a, b l`a sô´th .uc, k´y , , , , , ,
hi .êu [a,b] l`a khoang ¯du .oc t´ınh ca hai ¯diêm ¯dâ`u a, b v`a g .oi l`a khoang , ,, , , , ¯ d´ ong. Khoang mo ¯
du .oc k´y hi.êu l`a (a, b), không lâ´y hai ¯diêm ¯dâ`u , ,, ,, ,, , a, b. Ngo` ai ra ta c` on x´ et khoang nua ¯ d´
ong (nua mo ) do vi .êc ta chı , ,
lâ´y m .ôt trong hai ¯diêm ¯dâ`u a ho.˘ac b,v´ı d .u nhu [a, b) ho.˘ac (a, b]. M .ôt , , , ,
khoang trong t .âp sô´ th .uc g .oi l`a suy tho´ai nê´u n´o chı l`a m .ôt ¯diêm , , (t´ uc l` a khi hai ¯ diêm ¯ dâ`u tr` ung nhau). , , , ,
M .ôt t .âp h .op A cua sô´ th .uc g .oi l`a tr`u m .ât, nê´u m .oi khoang , ,, , không suy tho´ ai ¯ dê`u ch´
ua m .ôt sô´phâ`n tu cua A. , , , , ,
M .ôt v´ı d .u d˜ê thâ´y l`a t.âp h .op sô´ h˜uu ty gô`m c´ac sô´ c´o thê biêu , , , , , , di˜
ên nhu m .ôt thuong cua hai sô´ nguyên v`a t.âp h .op sô´ vô ty gô`m , , , , 80
Chuong 8. Sô´th .uc v´oi t.âp tr`u m.ât , , , , , nh´ ung sô´ không phai l` a sô´ h˜ uu ty ¯ dê`u l` a nh˜ ung t .âp tr`u m.ât trong , t .âp sô´th .uc. , , ,, , Ngu` oi ta c`
on mo r .ông kh´ai ni.êm tr`u m.ât cho m .ôt khoang trên , , , , , , , , ¯ du` ong th˘
ang th .uc. Cho ∆ l`a m .ôt khoang bâ´t k`y trên ¯du`ong th˘ang , , , ,
th .uc. Ch´ung ta g .oi t.âp h .op B gô`m nh˜ung sô´ th .uc l`a tr`u m.ât trong , , ∆ , , , , nê´u v´
oi m .oi khoang con không suy tho´ai cua ∆ ¯dê`u ch´ua nh˜ung ,, , , , , phâ`n tu cua B. R˜ o r`
ang t .âp h .op c´ac sô´ h˜uu ty tr`u m.ât trong m .oi , , , khoang; v`
a t .âp h .op c´ac sô´vô ty c˜ung c´o t´ınh châ´t â´y. , , , , , Nh˜ung k´
y hi .êu hay ¯du .oc d`ung: v´oi m .oi sô´th .uc x, k´y hi.êu [x] l`a , , , sô´ nguyên l´
on nhâ´t không vu .ot qu´a x, {x} l`a sô´ x − [x]; [x] v`a {x} , ,
g .oi l`a phâ`n nguyên v`a phâ`n th.âp phân cua sô´ x. T`u ¯d.inh ngh˜ıa c´o , , , ,
thê thâ´y ngay 0 ≤ x − [x] < 1. Ðê hiêu r˜ o hon kh´ ai ni .êm tr`u m.ât ,, trong phâ`n n` ay ta x´
et m .ôt lo.at b`ai to´an c´o liên quan v`a c´ach su d .ung , , , , nguyên l´ y Ðirichlê ¯ dê ch´ ung minh ¯ dinh l´ y co ban Kronecker. 8.2. V´ı d .u , , , ,
. 8.1. Nê´u m .ôt t .âp h.op A cua sô´th .uc l`a tr`u m .ât v`a r l`a sô´th .uc kh´ac , , ,
không, th`ı t .âp h.op gô`m tâ´t ca t´ıch sô´{ra} v´oi a ch .ay trong A c˜ung l`a t .âp tr`u m .ât. , , , , , , , L` oi giai. C´ o hai tru`
ong h .op xây ra: r > 0 v`a r < 0. V`ı c´ach ch´ung , , , , , , , minh ho` an to`
an tuong t .u nên ta chı x´et tru`ong h .op ¯dâ`u. Cho x v`a , x y , y l`
a hai sô´ th .uc v`a x < y. Khi ¯d´o < v`
a theo gia thiê´t A l`a t .âp r r ,, x y tr`
u m .ât, th`ı tô`n t.ai phâ`n tu a thu .ôc A sao cho < a < . Suy ra r r , , ,, , ,
x < ar < y. Nhu v .ây m .oi khoang mo (x, y) ch´ua sô´ d.ang ra v´oi a thu .ôc A. J , , , ,
. 8.2. (Ð.inh l´y Kronecker) V´oi m.oi sô´vô ty α, t .âp h.op tâ´t ca c´ac sô´c´o 8.2. V´ı d .u 81 ,, ,
d .ang mα + n l`a t .âp tr`u m .ât, o ¯dây m v`a n l`a nh˜ung sô´nguyên bâ´t k`y. , , , , , L`
oi giai. Câ`n phai ch´ ung minh r` ˘
ang m .oi khoang không suy tho´ai , , ∆ , , ch´ ua nh˜ ung ¯
diêm d .ang mα + n. Ch´ung ta chia khoang [0,1] ra , , , th`
anh m .ôt sô´h˜uu h.an khoang con ∆1, ∆2, . . . , ∆k m`a ¯d .ô d`ai cua m˜ôi , , , , , khoang con nho hon ¯
d .ô d`ai cua ∆. Ch´u ´y r`˘ang v´oi m .oi sô´ a tô`n t.ai ,
m .ôt sô´nguyên n, sao cho sô´ a + n n`˘am trong khoang [0,1]. Suy ra , , , , , , v´
oi m .oi sô´nguyên m c´o thê cho tuong ´ung v´oi m .ôt sô´d.ang mα + n, , , , , , m` a n´ o n` ˘
am trong khoang [0,1]. Nhung ¯
do .an th˘ang [0,1] ¯du .oc chia , , , , ra h˜
uu h .an khoang nho. Suy ra tô`n t.ai nh˜ung sô´nguyên m, m1, n, n1, , , v´
oi m 6= m1 v`a nh˜ung sô´ mα + n v`a m1α + n1 n`˘am trong c`ung m .ôt , , , , , , , khoang nho ∆i. Do ¯ d´ o khoang c´ ach gi˜ ua hai ¯ diêm n` ay nho hon ¯ d .ô , , , d`
ai cua ∆. Ch´ung ta c˜ung thâ´y không thê xây ra mα + n = m1α + n1, , , , n , , v`ı t` u ¯ d˘ ang th´ uc n` ay suy ra 1 − n α = m`
a l .ai l`a m .ôt sô´h˜uu ty, tr´ai m − m1 , , v´ oi gia thiê´t. , ,
Nhu v .ây ch´ung ta kh˘ang ¯d.inh r`˘ang sô´(m − m1)α + (n − n1) kh´ac , , , , , không v` a c´ o gi´
a tr.i tuy.êt ¯dô´i nho hon ∆. T`u ¯d´o suy ra m .ôt sô´u´oc sô´ , , cua n´ o, c˜ ung c´
o d .ang mα + n, s˜e n`˘am trong khoang ∆. J , , , , , . 8.3. Cho α l`
a m .ôt sô´vô ty duong. Khi ¯d´o t .âp h.op tâ´t ca sô´c´o d .ang , , , mα − n l`
a t .âp tr`u m .ât,v´oi m v`a n l`a nh˜ung sô´t .u nhiên bâ´t k`y. , , , , , L`
oi giai. Kê´t lu .ân cua b`ai n`ay m.anh hon ¯d.inh l´y trên v`ı n´o kh˘ang , , , , ¯
d.inh m .ôt t.âp sô´th .uc nho hon t.âp mô ta trong ¯dij nh l´y ¯d´o c˜ung tr`u m .ât. , ,, , Cho khoang không suy tho´
ai ∆ n`˘am o bên phai sô´ không v`a c´o , ,,, , , , , ¯
d .ô d`ai e > 0. Không anh huong ¯dê´n kê´t qua ch´ung minh c´o thê gia , , ,
thiê´t e < 1. Ngo`ai ra ta c´
o thê ch .on sô´t .u nhiên k sao cho k ≥ e . T`u α , 8.1 v`
a 8.2 suy ra t .âp c´ac sô´kpα + kq v´oi p v`a q l`a c´ac sô´nguyên bâ´t , , , , 82
Chuong 8. Sô´th .uc v´oi t.âp tr`u m.ât , k` y, l`
a t .âp tr`u m.ât. Ngh˜ıa l`a tô`n t.ai c´ac sô´nguyên p v`a q thoa m˜an
0 < kpα + kq < e. (8.1) , , , Ch´ ung ta s˜ e chı ra r` ˘ ang gi˜ ua nh˜
ung c .˘ap sô´nguyên (p, q) trong (8.1) , , , , , , c´ o nh˜
ung c .˘ap m`a p > 0. Th.ât v.ây, tru`ong h .op p = 0 không thê xây , , ra v`ı t`
u (8.1) suy ra 0 < kq < e, mâu thu˜ân v´ oi ¯ diê`u ta ¯ d˜ a biê´t l` a kq , , , , , l` a sô´ nguyên v`
a e < 1. Do v .ây chı c`on phai ch´ung minh cho tru`ong , , , , ,
h .op p < 0. Trong tru`ong h .op n`ay sô´ c´o d.ang kpsα + kqt v´oi s, t l`a , , nh˜ ung sô´ nguyên bâ´t k`
y, t .ao th`anh t.âp tr`u m.ât. T`u (8.1) suy ra tô`n
t .ai sô´nguyên s v`a t sao cho
0 < kpsα + kqt < kpα + kq. (8.2) , ,
Nê´u s < 0, th`ı kps > 0 v`a ch´
ung minh l .ai ¯d´ung. V`ı thê´ ta chı x´et , s ≥ 0. T`u (8.1) v` a (8.2) suy ra
0 < kp(1 − s)α + kq − kpt < e. (8.3) , , , , , , V`ı v´ oi s = 0 bâ´t ¯ d˘ ang th´
uc (8.2) không thê xây ra, nên s > 0. Nhung ,, ,
boi v`ı s l`a sô´ nguyên, th`ı t`u s > 0 suy ra s ≥ 1. T .ai v`ı ((8.3) không , , , , , , thê xây ra v´ oi s = 1, t`u bâ´t ¯ d˘ ang th´ uc cuô´i c` ung l .ai suy ra s > 1. ,
Nhu v .ây kp(1 − s) > 0. Ðiê`u ¯d´o c´o ngh˜ıa l`a tô`n t.ai c´ac sô´nguyên p , , v`
a q thoa m˜an (8.1) v`a p > 0. T`u (8.1) suy ra e
kq < e − kpα < e − p α = e(1 − p) ≤ 0 α , , ,
V .ây kq < 0. Theo c´ach n`ay (8.1) ¯du .oc ¯dua vê`d.ang 0 < mα − n < e, ,, , , ,, , , o ¯
dây m v`a n l`a nh˜ung sô´ t .u nhiên. Boi v`ı e l`a ¯d .ô d`ai cua∆, t`u bâ´t , , , , , ¯ d˘ ang th´ uc cuô´i c`
ung suy ra m .ôt u´oc sô´n`ao ¯d´o cua mα − n, c˜ung c´o , , , , , ,
d .ang n`ay, s˜e n`˘am trong ∆. Tuong t .u c˜ung ch´ung minh ¯du .oc khi ∆ ,, n` ˘ am o bên tr´ ai sô´không. J , , , . 8.4. Cho α l`
a sô´ vô ty bâ´t k` y. Khi ¯ d´
o t .âp h.op nh˜ung sô´d .ang {αn}, , , , v´ oi n l`
a sô´t .u nhiên bâ´t k`y, l`a t .âp tr`u m .ât trong khoang (0,1). 8.2. V´ı d .u 83 , , , , , L`
oi giai. Câ`n phai ch´ ung minh r` ˘
ang m .oi khoang con không suy , , , , biê´n (a, b) cua (0,1) ch´ ua sô´ c´
o d .ang {αn} v´oi m .ôt sô´ t .u nhiên , , , , n n` ao ¯ d´ o. Ch´ ung ta ch´ ung minh cho tru`
ong h .op khi α l`a m .ôt sô´ , , , , , duong. Theo b` ai 8.3 nh˜ ung sô´ c´
o d .ang nα − m v´oi n, m l`a c´ac sô´t .u , ,
nhiên, t .ao th`anh t.âp tr`u m.ât. Ngh˜ıa l`a tô`n t.ai nh˜ung sô´ t .u nhiên , , , m v`
a n thoa m˜an 0 ≤ a < nα − m < b < 1. Nhung t`u ¯ d.inh ngh˜ıa , ,
[αn] suy ra 0 ≤ nα − [nα] < 1. Ch´
ung ta nh .ân ¯du .oc hi.êu hai sô´ , ,
nguyên m v`a [nα] thoa m˜an −1 < m − [nαm] < 1, ¯ diê`u n` ay chı , , ,
xây ra khi m − [nαm] = 0, do ¯ d´
o m = [nα]. T`u (8.1) chı ra r`˘ang sô´ , ,
{nα} = nα − [nα] n`˘am trong khoang (a, b). V´oi α > 0, ch´ ung ta ¯ d˜ a , ch´ ung minh xong. , , , , Tru`
ong h .op α < 0. Khi ¯d´o −α > 0 v`a t`u b`ai 8.3 suy ra tô`n t.ai , , , nh˜
ung sô´ t .u nhiên m v`a n, thoa m˜an −1 ≤ −b < n(−α) − m < , , ,
−a ≤ 0. Nhân c´ac vê´v´oi -1 ch´
ung ta nh .ân ¯du .oc 0 ≤ a < nα − m < ,
b ≤ 1. Nhu v .ây d˜ê d`ang t´ınh ra m = −[nα] v`a {nα} n`˘am trong , khoang (a, b). J , , , ,
. 8.5. T .âp h.op tâ´t ca c´ac sô´d .ang {log n} v´oi n l`a sô´t .u nhiên bâ´t k`y l`
a t .âp tr`u m .ât trong (0,1). , , , , ,, , L` oi giai. Ch´ ung ta c´ o thê ch´
ung minh mo r .ông hon m .ôt ch´ut: t.âp , , ,
h .op c´ac sô´d.ang {n log 2} v´oi n l`a sô´t .u nhiên bâ´t k`y, l`a t.âp tr`u m.ât trong (0,1). , , Ðê ¯
d .at m .uc ¯d´ıch n`ay ch´ung ta ch´ung minh log 2 l`a m .ôt sô´ vô , , , , , , ,
ty. Th .ât v.ây, trong tru`ong h .op ngu .oc l.ai th`ı tô`n t.ai hai sô´ t .u nhiên p p , , , p v` a q, m`a log 2 = , ngh˜ıa l` a 2 = 10 q . L˜ uy th` ua ¯ d˘ ang th´ uc cuô´i q , , , c` ung v´ oi q ch´
ung ta nh .ân ¯du .oc 2q = 2p.5p. Ðiê`u n`ay tr´ai ¯d.inh l´y , , , , ,
co ban cua sô´ h .oc vê` vi.êc phân t´ıch ra th`ua sô´ nguyên tô´. Nhu v.ây , , , , 84
Chuong 8. Sô´th .uc v´oi t.âp tr`u m.ât , , ,
log 2 th .uc s .u l`a m .ôt sô´vô ty. Áp d .ung 8.4 suy ra t.âp c´ac sô´c´o d.ang {n log 2} l`a tr` u m .ât trong (0,1)., ,
M .˘at kh´ac, theo t´ınh châ´t cua logarit, log 2n = n log 2 v´oi m .oi n = 1, 2, . . . J , , . 8.6. Cho m l` a sô´ nguyên, n l`
a sô´ nguyên không âm. T .âp h.op tâ´t ca m c´ ac sô´c´ o d .ang l` a t .âp tr`u m .ât. 2n , , , , L` oi giai. Do c´ ac b` ai to´ an trên, ch´ ung ta chı câ`n ch´ ung minh r` ˘ ang , 3m , , , , t .âp h .op sô´d.ang v´
oi m, n l`a nh˜ung sô´ nguyên duong, l`a tr` u m .ât 2n , , , ,
trong khoang (0, +∞). Ðiê`u ¯ d´ o c´ o ngh˜ıa l` a v´ oi m .oi c.˘ap sô´ duong , , , 3m
a, b(a < b) tô`n t .ai nh˜ung sô´t .u nhiên m v`a n thoa m˜an a < < b. 2n , , , Sau khi logarit h´
oa c .˘ap bâ´t ¯d˘ang th´uc n`ay theo co sô´ 2, ch´ung ta , , , , , , , ,
nh .ân ¯du .oc c.˘ap bâ´t ¯d˘ang th´uc tuong ¯duong log a < m log 3 − n < 2 2 , , , , , , log b. C´ ach ch´
ung minh tuong t nhu 8.5 cho thâ´y log 3 l`a vô ty. 2 .u 2 , , Khi ¯ d´ o ¯
d.inh l´y Kronecker chı ra r`˘ang trong ¯do.an (log a, log b) ch´ua 2 2 sô´c´ o d .ang {m log 3 − n}. J 2 , , , ,
. 8.7. T .âp h.op tâ´t ca c´ac sô´ h .ang cua d˜ay x´ac ¯d.inh b`˘ang công th´uc n , 1 xn = , n = 1, 2, 3 . . ., l` a tr` u m .ât trong khoang ( , 1). 10[log n]+1 10 , , , 1 , L`
oi giai. Lâ´y hai sô´ th .uc a v`a b sao cho ≤ a < b ≤ 1. Câ`n phai 10 , , , n ch´ ung minh r` ˘
ang tô`n t .ai sô´ t .u nhiên n, thoa m˜an a < < 10[log n]+1 , , , , b. Sau khi logarit h´ oa bâ´t ¯ d˘ ang th´ uc trên v´ oi co sô´ 10 ch´ ung ta , , , , , , , ,
nh .ân ¯du .oc bâ´t ¯d˘ang th´uc tuong ¯duong 1 + log a < log n − [log n] = , , ,, ,
{log n} < 1 + log b. Nhung khoang mo v´oi c´ac ¯ dâ`u m´ ut 1 + log a , , v` a 1 + log b r˜ o r` ang n` ˘
am trong khoang (0, 1). Ðiê`u n`ay giai th´ıch t .ai , , , , ,,
sao tô`n t .ai m .ôt sô´t .u nhiên n thoa m˜an bâ´t ¯d˘ang th´uc sau c`ung, boi 8.2. V´ı d .u 85 ,
v`ı theo 8.5 t .âp h .op c´ac sô´ c´o d.ang {log n} l`a tr`u m.ât trong (0, 1). , ,
Nhu v .ây th`ı a < xn < b, ¯diê`u ta câ`n ch´ung minh. J , , , , . 8.8. Ch´ ung minh r` ˘
ang tô`n t .ai vô h .an nh˜ung sô´l˜uy th`ua cua 2, m`a ,
khi viê´t theo co sô´10 ch´ ung luôn luôn b´ ˘ at ¯ dâ`u b` ˘ ang 8975. , , , , L`
oi giai. M .ôt sô´ 2m b´˘at ¯dâ`u b`˘ang nh´om sô´ 8975 khi v`a chı khi v´oi , , , , , , ,
m .ôt sô´ t .u nhiên n n`ao ¯d´o, nh˜ung ¯d˘ang th´uc sau ¯du .oc thoa m˜an , , , ,
8975.10n ≤ 2m < 8976.10n. Nhu c´ ach giai c´ ac b` ai tru´ oc ch´ ung ta , , , , , , , , logarit h´ oa bâ´t ¯ d˘ ang th´ uc trên v`
a nh .ân ¯du .oc c´ac bâ´t ¯d˘ang th´uc tuong , , ¯
duong log 8975 ≤ m log 2 − n < log 8976. T .ai v`ı log 2 l`a m .ôt sô´ vô , , , , , ty, nên nh˜ ung sô´ c´
o d .ang m log 2 − n v´oi n, m l`a nh˜ung sô´t .u nhiên
t .ao th`anh m .ôt t.âp tr`u m.ât. Ðiê`u n`ay c´o ngh˜ıa l`a tô`n t.ai vô sô´c.˘ap sô´ , , , ,
t .u nhiên m v`a n thoa m˜an c´ac bâ´t ¯d˘ang th´uc sau c`ung, suy ra c˜ung , , , , , thoa m˜ an c´ ac bâ´t ¯ d˘ ang th´ uc tru´ oc ¯ d´ o. Ch´ u ´ y b` ai to´ an c` on ¯ d´ ung khi , , , , thay co sô´hai b` ˘ ang co sô´10 cua logarit v` a sô´8975 c´ o thê thay b` ˘ ang , , ,
m .ôt tô h .op sô´bâ´t k`y, ch´ung minh ¯diê`u n`ay d`anh cho b.an ¯d .oc. J , , , , . 8.9. V´
oi m .oi sô´ t .u nhiên n, k´y hi.êu xn l`a ch˜u sô´ ¯dâ`u tiên cua , , ,
sô´ 2n (trong c´ ach viê´t v´ oi co sô´ 10). Ch´ ung minh r` ˘ ang d˜ ay sô´ ,
x1, x2, . . . , xn, . . . không phai l`a d˜ ây tuâ`n ho` an. , , , ,, , , , , , L`
oi giai. Gia su ngu .oc l.ai l`a tô`n t.ai nh˜ung sô´ nguyên duong k v`a
d sao cho xk = xk+d = xk+2d = . . . = xk+nd = . . . N´oi c´ach kh´ac ,
2k, 2k+d, 2k+2d, . . . , 2k+nd, . . . c´ o c` ung ch˜ u sô´ ¯ daah u tiên trong c´ ach , , , , , viê´t v´ oi co sô´10. Bâ`y gi` o ch´ ung ta kh˘ ang ¯
d.inh r`˘ang m .oi sô´t .u nhiên , , , , N c´ o thê biêu di˜ ên du´
oi d .ang N = 10log N = 10[log N]+{log N} =
10[log N].10{log N}. V`ı 0 ≤ {log N} < 1, nên 1 ≤ 10{log N} < 10, suy , , , , , ra ch˜ u sô´ ¯ dâ`u tiên cua N tr` ung v´
oi phâ`n nguyên cua cua sô´10{log N}. , , , Ðê´n ¯
dây suy ra tô`n t .ai m .ôt ch˜u sô´ s, 1 ≤ s ≤ 9, thoa m˜an bâ´t ¯d˘ang , , , , 86
Chuong 8. Sô´th .uc v´oi t.âp tr`u m.ât , , th´
uc sau: s ≤ 10{log 2k+nd} < s + 1 v´
oi n = 0, 1, 2, . . .. Sau khi logarit , , h´ oa ¯ d˘ ang th´ uc trên ch´ ung ta c´
o log s ≤ {(k + nd) log 2} < log(s + , 1). Ðiê`u n` ay ngh˜ıa l` a tâ´t ca c´ ac sô´ c´ o d .ang {(k + nd) log 2}, n = , , 0, 1, 2, . . . n` ˘
am trong khoang [log s, log(s + 1)). D˜ê d`ang ch´ ung minh , , r` ˘
ang t .âp h .op nh˜ung sô´ n`ay tr`u m.ât trong ¯do.an (0,1). Ðiê`u ¯d´o tr´ai , ,, , , v´
oi kê´t lu .ân : tô`n t.ai t.âp con mo cua ¯do.an (0,1) không c´o ¯diêm , , , ,, , , chung v´
oi [log s, log(s + 1)). Nhu v .ây ¯diê`u gia su ngu .oc l.ai l`a sai. J , , , , . 8.10. H˜ ay t`ım trong ¯
do .an th˘ang [0, π], tâ´t ca sô´ th .uc t thoa m˜an , , , ,
bâ´t phuong tr`ınh cos nt ≥ cos t v´
oi m .oi sô´t .u nhiên n. , , , L` oi giai. - Ch´ ung ta s˜ e ch´ ung minh r` ˘ ang nê´u t c´ o t´ınh châ´t ¯ d˜ a nêu , t , , , ,, t trong b` ai to´ an th`ı ty sô´ l`
a m .ôt sô´ h˜uu ty. Th.ât v.ây gia su l` a π π , , , sô´ vô ty. Khi ¯ d´
o t 6= π ; Không mâ´t t´ınh tông qu´at ch´ ung ta c´ o thê , t , , , gia thiê´t r` ˘
ang 0 ≤ t < π. V`ı l` a sô´ vô ty duong, theo ¯ d.inh l´y 2π , , , , ,
Kronecker tô`n t .ai nh˜ung sô´ t .u nhiên m v`a n, thoa m˜an bâ´t phuong t t t , tr`ınh < m − n < 1 − , hay l`
a t < mt − 2nπ < 2π − t. T`u 2π 2π 2π , t´ınh châ´t cua h` am cos trong ¯
do .an [0, 2π] ch´ung ta suy ra cos mt = , ,
cos(mt − 2nπ) < cos t. Ðiê`u n` ay tr´ ai v´ oi c´
ach ch .on t, do v.ây ty sô´ t , , l` a sô´h˜ uu ty. π , , , , , p ,,
Nhu v .ây t c´o thê biêu di˜ên du´oi d.ang t = 2π, o ¯dây p v`a q l`a q , nh˜ ung sô´ nguyên tô´ c` ung nhau v`
a 0 ≤ p ≤ q (t .ai v`ı 0 ≤ t ≤ 2π ). q , ,
Nê´u q l`a sô´ch˜˘an, th`ı n = l`
a sô´t .u nhiên v`a ngo`ai ra p l`a sô´le, v`ı p 2 v` a q l`a nguyên tô´ c`
ung nhau. V`ı v .ây cos t ≤ cos nt = cos pπ = −1, , , , t` u ¯ d´
o suy ra cos t = −1 v`a t = π. R˜ o r`
ang π thoa m˜an tâ´t ca c´ac ¯ diê`u ki .ên ¯d˜a cho., , , , , , , , Ch´ ung ta chı c` on phai x´ et tru`
ong h .op q l`a sô´ le. C´o thê ch´ung 8.3. B` ai t .âp 87 , minh r` ˘ ang v´
oi m .oi n = 1, 2, . . . cos nt b`˘ang m .ôt sô´n`ao ¯d´o trong d˜ây sau ¯ dây 2π 2π 2π 2π 1 = cos 0. , cos 1. , cos 2. , . . . , cos((q − 1) ). (8.4) q q q q ,,
Th .ât v.ây, nê´u n = sq + r, o ¯dây 0 ≤ r ≤ q − 1, th`ı cos nt = cos(sqt + ,
rt) = cos(2psπ + rt) = cos rt. Nê´u q = 2k + 1 l` a m .ôt sô´ le, th`ı sô´ , k k + 1 nho nhâ´t trong (8.4) l` a c´ ac sô´ cos 2π v` a cos 2π. Lâ´y 2k + 1 2k + 1 p t =
2π, 0 ≤ t ≤ π, c´
o t´ınh châ´t mong muô´n, ch´ ung ta s˜ e 2k + 1 , , , , ch´ ung minh khi ¯ d´ o p = k. Ðê ¯
d .at m .uc ¯d´ıch n`ay chı câ`n chı ra r`˘ang , , k
tô`n t .ai m .ôt sô´nguyên duong n m`a cos nt = cos 2π. Th .ât v.ây: 2k + 1 , ,
v`ı 2k + 1 v`a p l`a nh˜ung sô´ nguyên tô´ c`
ung nhau tô`n t .ai nh˜ung sô´ , ,
nguyên m v`a n thoa m˜an 0 ≤ n ≤ 2k + 1 v`a (2k + 1)m + pn = k. T`u , , k ¯ d˘ ang th´ uc sau c` ung suy ra 2mπ + nt = 2π. Suy ra cos nt = 2k + 1 k , k cos 2π. D˜ê d` ang thâ´y r` ˘ ang nh˜ ung sô´ c´ o d .ang 2π v` a 2k + 1 2k + 1 k + 1 ,
2π, k = 0, 1, 2, . . . l`
a nghi .êm cua b`ai to´an. Kê´t lu.ân cuô´i c`ung 2k + 1 , , , k k + 1 , l` a nh˜ ung gi´
a tr.i cua t phai t`ım l`a t = π v`a 2π, 2π, v´ oi 2k + 1 2k + 1 k = 0, 1, 2 . . . . . . J 8.3. B ` ai t .âp , , , . 8.11. Cho a, b, c l` a nh˜
ung sô´ th .uc sao cho [an] + [bn] = [cn] v´oi , ,
m .oi sô´t .u nhiên n. Ch´ung minh r`˘ang ´ıt nhâ´t m .ôt trong c´ac sô´ a, b l`a nguyên. , , , ,
. 8.12. Cho α l`
a m .ôt sô´h˜uu ty. Ch´ung minh r`˘ang t.âp h .op c´ac sô´c´o ,
d .ang {αn}, n = 1, 2, . . . không tr`u m.ât trong khoang (0, 1). , , , , 88
Chuong 8. Sô´th .uc v´oi t.âp tr`u m.ât , , , , , . 8.13. Ch´ ung minh r` ˘ ang v´
oi m .ôt sô´vô ty bâ´t k`y α v`a m .ôt sô´h˜uu ty , bâ´t k`
y β, t .âp h .op sô´c´o d.ang {αn + β}, n = 1, 2, . . . l`a tr`u m.ât trong , khoang (0, 1). , , √ , , . 8.14. Ch´ ung minh r` ˘
ang t .âp h .op sô´d.ang { n} v´oi n l`a sô´t .u nhiên , l`
a t .âp tr`u m.ât trong khoang (0,1). , , CHUONG 9 , , , NH˜ UNG ´ UNG D .UNG KH ´AC CUA NGUYÊN L ´ Y ÐIRICHLE , ,
9.1. Xâ´p xı m .ôt sô´ th .uc , ,
. 9.1. Cho x l`
a m .ôt sô´th .uc, c`on n l`a m.ôt sô´t .u nhiên. Khi ¯d´o tô`n t .ai , , nh˜
ung sô´nguyên p v` a q thoa m˜
an 1 ≤ q ≤ n v` a p 1 x − ≤ . (9.1) q nq , , , L` oi giai. Ch´ ung ta x´ et nh˜
ung sô´ kx − [kx](k = 0, 1, 2, . . . , n). Ch´ ung , ,
gô`m n + 1 sô´v`a n`˘am trong khoang [0, 1]. Ch´ ung ta chia khoang [0, 1] , , ,
ra n khoang con b`˘ang nhau ∆1, ∆2, . . . , ∆n v`a ¯ d .ô d`ai cua m˜ôi khoang 1 n` ay b` ˘ ang . Theo nguyên l´
y Ðirichlê tô`n t .ai hai sô´kh´ac nhau k v`a l n , n` ˘
am trong 0, 1, 2, . . . , n, sao cho nh˜ung sô´kx − [kx] v`a lx − [lx] n`˘am , , , , trong c`
ung m .ôt khoang con th´u m. Do ¯d´o khoang c´ach gi˜ua ch´ung 1 , 1 không qu´ a , t´ uc l`
a |kx − [kx] − (lx − [lx])| ≤ , hay l` a n n 1
|(k − l)x − ([kx] − [lx])| ≤ . (9.2) n ,, , ,,, , , ,
Boi v`ı k 6= l, không anh huong ¯ dê´n kê´t qua ch´ ung minh ta c´ o thê , ,, gia thiê´t r` ˘
ang k > l. Boi v`ı ngo`ai ra c` on c´
o 0 ≤ k ≤ n, 0 ≤ l ≤ n,
nên 1 ≤ k − l ≤ n. Ta ¯
d .˘at q = k − l v`a p = [kx] − [lx]. Khi ¯d´o p v`a q , , , , , 90 Chuong 9. Nh˜ ung ´
ung d .ung kh´ac cua nguyên l´y Ðirichle , , , l` a nh˜ ung sô´ nguyên v` a thoa m˜ an 1 ≤ q ≤ n. V´ oi c´ ach d .˘at n`ay (9.2) , 1 , ¯
dua vê` d .ang |qx − p| ≤ , t`u ¯dây chia hai vê´cho q ta c´o (9.1). J n , , , , . 9.2. V´
oi m .oi sô´ th .uc x tô`n t .ai vô h .an sô´ t .u nhiên q, v´oi m˜ôi q tô`n , , ,
t .ai sô´nguyên p, sao cho ch´ung thoa m˜an bâ´t ¯d˘ang th´uc. p 1 x − ≤ . (9.3) q q2 , , , , , r , L`
oi giai. Nê´u x l`a sô´ h˜uu ty, t´ uc l` a x = v´
oi r l`a sô´ nguyên v`a s l`a s , , ,
sô´ t .u nhiên, th`ı kê´t lu.ân cua b`ai to´an l`a ¯d´ung, v`ı c´o thê ¯d.˘at p = mr , , , , , v` a q = ms v´
oi sô´t .u nhiên bâ´t k`y m. V´oi tâ´t ca c´ach ch .on p v`a q nhu , , , ,
v .ây (9.3) ¯du .oc thoa m˜an, v`ı vê´tr´ai luôn luôn b`˘ang không. Nhu v.ây , , , , , , , ,, , , chı c` on phai x´ et tru`
ong h .op x l`a sô´ vô ty. Gia su chı c´o h˜uu h.an sô´ , , ,
t .u nhiên q, m`a v´oi ch´ung tô`n t.ai sô´ nguyên p thoa m˜an (9.3), k´y ,
hi .êu ch´ung l`a q1, q2, . . . , ql. V´oi bâ´t k`y λ = 1, 2, . . . , l k´y hi.êu p l`a sô´ λ , nguyên thoa m˜ an p p λ x − ≤ x − q q λ λ , , ,, v´
oi m .oi sô´nguyên p. V`ı sô´x l`a vô ty, m .oi gi´a tr.i tuy.êt ¯dô´i o ph´ıa tr´ai , , , , , , bâ´t ¯ d˘ ang th´ uc trên l` a duong, sô´ nh˜ ung gi´
a tr.i tuy.êt ¯dô´i n`ay l`a h˜uu , 1 p h λ
.an. V`ı v .ây tô`n t .ai sô´ t .u nhiên n, sao cho < x − , (λ = n qλ 1, 2, . . . , l). , , , Theo b` ai tru´ oc s˜
e tô`n t .ai sô´ t .u nhiên q v`a sô´ nguyên p, sao cho , , p 1 1 (9.1) thoa m˜ an v` a 1 ≤ q ≤ n. Nhung khi ¯ d´ o x − ≤ ≤ = q qn qq 1 , , , , , , suy ra q = q v´
oi m .ôt sô´λ = 1, 2, . . . , l T`u nh˜ung bâ´t ¯d˘ang th´uc q2 λ 1 p p 1 , 1 1 trên suy ra < λ x − ≤ x − ≤ . Nhu v .ây < v`ı thê´ n q q nq n nq λ , ,
9.1. Xâ´p xı m .ôt sô´th .uc 91 , , , , , , q < 1, ¯ diê`u n` ay không thê ¯
du .oc v`ı q l`a sô´ t .u nhiên. Ta nh.ân ¯du .oc ¯ diê`u vô l´ y. J , , , . 9.3. V´
oi m .oi c > 2 bâ´t ¯d˘ang th´uc √ p 1 2 − ≤ . (9.4) q qc , , , , ¯ d´ ung chı v´ oi h˜
uu h .an c .˘ap sô´nguyên p v`a sô´t .u nhiên q. , , , , , L` oi giai. Ch´ ung ta ch´ ung minh bâ´t ¯ d˘ ang th´ uc sau l` a ¯ d´ ung √ p 1 √ 2 − ≤ . (9.5) q 3 2q2 , , , 1 , v´
oi m .oi sô´ nguyên p v`a v´oi m .oi sô´ t .u nhiên q. V`ı ≤ 1, bâ´t ¯ d˘ ang q2 , , √ p 1 , , th´
uc (9.5) tâ´t nhiên thoa m˜ an, khi √ 2 − > . Nhu v .ây chı q 3 2 , , , √ p 1 , √ 1 câ`n x´ et tru` ong h .op √ √ 2 − ≤ . Nhung khi ¯ d´ o 2 − ≤ q 3 2 3 2 p √ 1 ≤ 2 + √ suy ra q 3 2 p √ 0 < < 2 2. (9.6) q M .˘at kh´ac √ p √ p 2 − . 2 + √ p q q 2q2 − p2 2 − = = . (9.7) √ √ q p p 2 + q2 2 − q q , √ ,
Nhung sô´ 2q2 − p2 l`a sô´ kh´ac không, v`ı 2 l` a m .ôt sô´ vô ty. Ngo`ai , √ p ra n´ o l`
a sô´nguyên nên |2q2 − p2| ≥ 1 . T`u (9.7) suy ra 2 − ≥ q 1 , v` a c` ung v´ oi (9.6) cho ta (9.5). √ p q2 2 + q , , , , , 92 Chuong 9. Nh˜ ung ´
ung d .ung kh´ac cua nguyên l´y Ðirichle , ,, , , , , Gia su bâ´t ¯ d˘ ang th´ uc (9.4) ¯ d´ ung v´
oi m .ôt c.˘ap sô´(p, q) n`ao ¯d´o. T`u , , 1 1 , , (9.4) v` a (9.5) suy ra ¯ d˘ ang th´ uc √ ≤ . V`ı c > 2 bâ´t ¯ d˘ ang th´ uc 3 2 qc−2 , , , , , , n` ay chı ¯ d´ ung cho h˜
uu h .an sô´ t .u nhiên q. V´oi m˜ôi sô´ q nhu v.ây chı , , , , c´
o nhiê`u nhâ´t hai sô´ nguyên p, v´ oi ch´ ung thoa m˜ an bâ´t ¯ d˘ ang th´ uc , , , (9.4). Ngh˜ıa l` a (9.4) chı thoa m˜ an cho h˜ uu h .an c.˘ap sô´ p v`a q. J , , ,
. 9.4. Nê´u D l`
a sô´t .u nhiên bâ´t k`y, không l`a sô´ch´ınh phuong, th`ı tô`n , , , ,
t .ai vô h .an c´ac c .˘ap sô´t .u nhiên (x, y), l`a nghi.êm cua bâ´t phuong tr`ınh sau √ |x2 − Dy2| ≤ 1 + 2 D. (9.8) , , , L` oi giai. Theo b` ai 9.2 ta biê´t r` ˘
ang tô`n t .ai vô h.an c.˘ap sô´ (x, y) t .u nhiên, sao cho x √ 1 − D ≤ . (9.9) y y2 , ,
M .˘at kh´ac bâ´t ¯d˘ang th´uc sau l`a ¯d´ung x √ x √ √ x √ √ + D = ( − D) + 2 D ≤ − D + 2 D. y y y , Suy ra v´ oi m˜ ôi c .˘ap (x, y) ta c´o x √ 1 √ + D ≤ + 2 D. y y2 , , ,
Nhu v .ây, v´oi c´ach ch .on bâ´t k`y c.˘ap (x, y), sao cho thoa m˜an (9.9) , , ch´ ung ta nh .ân ¯du .oc √ √
|x2 − Dy2| = |x − y D|.|x + y D| 1 1 √ 1 √ √ ≤ ( + 2 Dy) ≤ + 2 D ≤ 1 + 2 D. y y y2 , , , Ðiê`u n` ay ¯ d˜ a ch´ ung minh r` ˘
ang bâ´t phuong tr`ınh (9.8) c´ o vô h .an , ,
nghi .êm trong t.âp h .op sô´t .u nhiên. J , ,
9.1. Xâ´p xı m .ôt sô´th .uc 93 , , ,
. 9.5. Nê´u D l`
a sô´ t .u nhiên bâ´t k`y, không l`a sô´ ch´ınh phuong, th`ı , , ,
phuong tr`ınh x2 − Dy2 = 1 c´
o ´ıt nhâ´t m .ôt nghi.êm nguyên (u, v) v´oi v 6= 0. , , , , , L` oi giai. Ch´ ung ta x´ et tâ´t ca c´
ac c .˘ap (x, y) sô´t .u nhiên, m`a n´o thoa √ √ m˜
an −1 − 2 D ≤ x2 − Dy2 ≤ 1 + 2 D. Theo b`ai 9.4 c´ o vô sô´ c .˘ap , , , , , , ,
sô´t .u nhiên thoa m˜an bâ´t ¯d˘ang th´uc trên, Nhung biêu th´uc x2 − Dy2 , , chı c´
o h˜uu h .an gi´a tr.i v`ı ch´ung l`a c´ac sô´ nguyên trong ¯do.an (−1 − √ √ , , 2 D, 1 + 2 D). Ngh˜ıa l`
a tô`n t .ai m .ôt sô´nguyên k, sao cho phuong , tr`ınh x2 − Dy2 = k c´
o vô h .an nghi.êm t .u nhiên (x, y). R˜o r`ang k 6= 0, , , √ , ,
v`ı nê´u ngu .oc l.ai th`ı d˜ân ¯dê´n mâu thu˜ân do sô´ D không thê biêu , , , , √ x , , , di˜ ên du´ oi d .ang h˜uu ty D = . Gi˜ ua nh˜
ung c .˘ap n`ay c´o thê ch .on ´ıt y ,
nhâ´t hai c .˘ap kh´ac nhau (x1, y1) v`a (x2, y2) m`a ch´ung thoa m˜an
x1 ≡ x2 (mod |k|), y1 ≡ y2 (mod |k|). (9.10) , , , , , ,
Th .ât v.ây,chı câ`n chı ra tâ´t ca c´ac kha n˘ang cua c´ac c.˘ap sô´ du theo , , , , mô¯ dun |k| c´
o sô´lu .ong h˜uu h.an. C´o ngh˜ıa l`a tô`n t.ai nh˜ung c.˘ap kh´ac , , nhau nh˜
ung sô´ t .u nhiên (x1, y1) v`a (x2, y2), m`a x2 − Dy2 = x2 − 1 1 2 , , , Dy2 = k v` a thoa m˜ an d˘ ang th´ uc (9.10). 2 , , Ch´ ung ta x´ et ¯ d˘ ang th´ uc √ √
(x1 − y1 D)(x2 + y2 D) = (x1x2 − y1y2D) + (x1y2 − x2y1). (9.11) , T` u (9.10) ch´ ung ta c´ o x1x2 − y1y2D ≡ x2 − ≡ 1 Dy21 k ≡ 0 (mod |k|),
x1y2 − x2y1 ≡ x1y1 − x1y1 ≡ 0 (mod |k|). Khi ¯ d´
o tô`n t .ai sô´nguyên u v`a v, sao cho x1x2 − y1y2D = ku, x1y2 − ,
x2y1 = kv. V`ı v .ây (9.11) c´o thê viê´t th`anh √ √ √
(x1 − y1 D)(x2 + y2 D) = k(u + v D). , , , , , 94 Chuong 9. Nh˜ ung ´
ung d .ung kh´ac cua nguyên l´y Ðirichle , , , , Nhân t`
ung sô´h .ang v´oi nhau trong c´ac ¯d˘ang th´uc sau c`ung ch´ung ta , , nh .ân ¯du .oc k2 = (x2 − − 1 Dy21)(x22 Dy22) = k2(u2 − Dv2), , , , , t` u ¯ d´
o suy ra u2 − Dv2 = 1, ngh˜ıa l`a c .˘ap (u, v) l`a nghi.êm cua phuong tr`ınh. , , , , , , Chı c` on phai ch´
ung minh v 6= 0. Nê´u gia thiê´t ngu .oc l.ai, ch´ung ta s˜ e c´
o x1x2 = y1y2D = |k| v`a x1y2 = x2y1. Khi ¯ d´ o |k|y2 = |(x1y2)x2 − y1y2 − − | 2 D| = |y1 x2 2 y1y22D| = y1|x22 Dy22 = |k|y1 , , , , t` u ¯ dây, v`ı k 6= 0 chı c´ o kha n˘
ang khi y1 = y2. Ðiê`u n`ay không thê , ,
xây ra v`ı (x1, y1) kh´ac (x2, y2) , c`on t`u y1 = y2 suy ra x1 = x2. J , , ,
. 9.6. Cho x1, x2, . . . , xn l`a nh˜ung sô´th .uc v`a N l`a sô´t .u nhiên. Khi ¯d´o ,
tô`n t .ai nh˜ung sô´nguyên p1, p2, . . . , pn, q sao cho 1 ≤ q ≤ Nn v`a p 1 i xi − ≤ , (9.12) q Nq , v´
oi m .oi i = 1, 2, . . . , n. , , , , , , , L` oi giai. Ch´ ung ta ch´ ung minh b` ai to´
an cho tru`ong h .op n = 2. V´oi , , , , , , , , ,
tru`ong h .op n l´on hon 2 ch´ung minh ho`an to`an tuong t .u v`a d`anh , , , ,
cho b .an ¯d .oc. Nhu v.ây cho x1 v`a x2 l`a nh˜ung sô´th .uc, c`on N l`a sô´t .u , , nhiên. Ch´ ung ta s˜ e ch´ ung minh r` ˘
ang tô`n t .ai nh˜ung sô´nguyên p1, p2 , , v` a q v´
oi 1 ≤ q ≤ N2 v`a thoa m˜an p 1 p 1 1 2 x1 − < , x2 − < . (9.13) q Nq q Nq , Ch´ ung ta cô´ ¯
d.inh h.ê t .oa ¯d .ô trong m.˘at ph˘ang v`a x´et h`ınh vuông Q , , , v´ oi c´ ac ¯
dınh (0, 0), (1, 0), (1, 1) v`a (0, 1) nhu h`ınh v˜e. Chia Q ra N2 , , 1 , , , h`ınh vuông nho b` ˘ ang nhau v´ oi c .anh l`a b` ˘ ang c´ ac ¯ du` ong th˘ ang N , , song song v´
oi tr .uc t .oa ¯d .ô (trong h`ınh v˜e ta chia v´oi N=7). , ,
9.1. Xâ´p xı m .ôt sô´th .uc 95 , Bây gi` o ch´ ung ta ch´ u ´ y ¯
dê´n c .˘ap sô´ c´o d.ang (qx1 − [qx1], qx2 − ,, , [qx2]), o ¯
dây q nh .ân nh˜ung gi´a tr.i nguyên 0, 1, 2, . . . , N2. V`ı 0 ≤ , , ,
qxi − [qxi] < 1, i = 1, 2, . . . , N2 m˜ôi c .˘ap nhu vây c´o thê coi nhu , ,
m .ôt c.˘ap t .oa ¯d .ô cua ¯diêm trong h`ınh vuông Q. B`˘ang c´ach ¯d´o m˜ôi sô´ , , , ,
0, 1, 2, . . . , N2 t .ao ra m .ôt ¯diêm tuong ´ung trong h`ınh vuông Q , sô´ , , , , ,
lu .ong c´ac sô´ ¯d´o l`a N2 + 1. Nhung Q ¯du .oc chia ra N2 h`ınh vuông ,
nho, suy ra tô`n t .ai hai sô´nguyên kh´ac nhau q1, q2 trong ¯do.an [0, N], , , , , , m` a ¯ diêm tuong ´ ung v´ oi ch´ ung c´ o c´
ac t .oa ¯d .ô (q1x1 − [q1x1], q1x2 −
[q1x2]), (q2x1 − [q2x1], q2x2 − [q2x2]) v`a c`ung n`˘am trong m .ôt h`ınh , , 1 vuông nho v´ oi c .anh . Ðiê`u ¯ d´ o c´ o ngh˜ıa l` a N 1
|(q1x1 − [q1x1]) − (q1x2 − [q1x2])| ≤ , N 1
|(q2x1 − [q2x1]) − (q2x2 − [q2x2])| ≤ . (9.14) , , , N
Không mâ´t t´ınh tông qu´ at c´
o thê gia thiê´t q1 > q2. Nê´u ¯ d .˘at q = , ,
q1 − q2, p1 = [q1x1] − [q2x1], p2 = [q1x2] − [q2x2] th`ı bâ´t ¯ d˘ ang th´ uc (9.14) c´ o d .ang 1 1 |qx1 − p1| ≤ , |qx . (9.15) N 2 − p2| ≤ N Ch´ ung ta thâ´y r` ˘
ang 1 ≤ q ≤ N2, v`ı 1 ≤ q2 < p1 ≤ N2. Chia hai vê´ , , , cua (9.15) cho q ch´
ung ta nh .ân ¯du .oc (9.13). J , , , , Hai b` ai to´ an du´ oi ¯ dây liên quan t´
oi m .ôt t´ınh châ´t m`a ta ¯d˜a ch´ung ,, , , , ,, ,
minh o chuong 2. Ðê mo r .ông t´ınh châ´t n`ay ch´ung ta ¯dua v`ao ¯d.inh ngh˜ıa. ,
Nê´u a1, a2, . . . , a2n+1 l`a 2n + 1 sô´th .uc (n ≥ 1). Ch´ung ta n´oi r`˘ang , d˜ ay n` ay c´
o t´ınh châ´t P, nê´u bâ´t k` y 2n sô´ trong ch´ ung c´ o thê chia , , l` am hai nh´ om, m˜ ôi nh´
om n sô´, sao cho tông cua c´ac sô´ trong hai nh´ om b` ˘ ang nhau. , , , , , 96 Chuong 9. Nh˜ ung ´
ung d .ung kh´ac cua nguyên l´y Ðirichle , , . 9.7. Ch´ ung minh r` ˘
ang m .oi b.ô 2n + 1 sô´ gô`m nh˜ung sô´ nguyên , , , duong c´
o t´ınh châ´t P, th`ı tâ´t ca c´ ac sô´ ¯ dê`u b` ˘ ang nhau. , , , , , L` oi giai. Ch´ ung minh b` ˘
ang qui n .ap theo sô´ l´on nhâ´t cua d˜ây sô´. , , Nê´u sô´ l´ on nhâ´t b` ˘ ang 1 th`ı tâ´t ca c´ ac sô´ c`
on l .ai c˜ung ¯dê`u l`a 1, nên , , , ,, , b` ai to´ an ¯ d˜ a giai. Bây gi`
o gia su kê´t lu .ân ¯d´ung v´oi m .oi b .ô 2n+1 sô´ , , , , nguyên duong m` a m˜
ôi sô´không vu .ot qu´a k, k ≥ 2 v`a c´o t´ınh châ´t P. , ,
Lâ´y p1, p2, . . . , p2n+1 l`a b .ô sô´nguyên duong c´o t´ınh châ´t P v`a m˜ôi sô´ , , ,
không vu .ot qu´a k + 1. T`u ¯diê`u ki.ên b`ai to´an suy ra p1, p2, . . . , p2n+1 , c´ o c` ung t´ınh ch˜ ˘ an le.
a) Nê´u p1, p2, . . . , p2n+1 l`a c´ac sô´ ch˜˘an, ch´ung ta x´et c´ac sô´ p1 p p , 2 , . . . ,
2n+1 . Ch´ung ta thâ´y ngay ch´ung c˜ung c´o t´ınh châ´t 2 2 2 , , , P. Ngo`
ai ra m .oi sô´ không vu .ot qu´a k v`ı pi ≤ k + 1 v´oi m .oi i = p p p 1, 2, . . . , 2n + 1. B` ˘ ang qui n 1 2 2n+1 .ap suy ra = = . . . = .Ngh˜ıa 2 2 2 l` a p1 = p2 = . . . = p2n+1. , ,
b) Nê´u p1, p2, . . . , p2n+1 l`a c´ac sô´ le, ch´ung ta ch´ung b`˘ang qui
n .ap cho d˜ay p1 − 1, p2 − 1, . . . , p2n+1 − 1. Ch´ung c˜ung c´o t´ınh châ´t , , , , P v`
a không vu .ot qu´a k, ch´ung ta nh.ân ¯du .oc p1 − 1 = p2 − 1 = . . . =
p2n+1 − 1. Ngh˜ıa l`a p1 = p2 = . . . = p2n+1. J , , , , , . 9.8. Ch´ ung minh r` ˘
ang m .oi b.ô 2n+1 sô´ gô`m nh˜ung sô´ th .uc duong , c´
o t´ınh châ´t P, th`ı tâ´t ca c´ ac sô´ ¯ dê`u b` ˘ ang nhau. , , , L`
oi giai. - Hiên nhiên r` ˘ ang nê´u c´
ac sô´ a1, a2, . . . , a2n+1 c´o t´ınh châ´t , P v`
a q l`a sô´ th .uc bâ´t k`y, th`ı c´ac sô´ qa1, qa2, . . . , qa2n+1 c˜ung c´o t´ınh châ´t P. , , , , , , Bây gi`
o cho x1, x2, . . . , x2n+1 l`a nh˜ung sô´ th .uc duong v´oi t´ınh , , , , ,
châ´t P. Nê´u tâ´t ca c´ ac sô´ l` a h˜ uu ty th`ı ¯ diê`u kh˘ ang ¯ d.inh cua b`ai to´an , , suy ra không kh´
o. Th .ât v.ây, k´y hi.êu q l`a b .ôi sô´chung nho nhâ´t cua , ,
9.1. Xâ´p xı m .ôt sô´th .uc 97 , m˜ âu sô´ c´ ac sô´ trên. Khi ¯ d´
o qx1, qx2, . . . , qx2n+1 l`a nh˜ung sô´ nguyên , , , , , duong c´ o t´ınh châ´t P, theo c´ ach ch´ ung minh b` ai tru´ oc ch´ ung ta c´ o ,
qx1 = qx2 = . . . = qx2n+1. V`ı v .ây x1 = x2 = . . . = x2n+1. Chı c`on , , , , , phai ch´ ung minh tru`
ong h .op c´o trong d˜ây x1, x2, . . . , x2n+1 m .ôt sô´ , , , , ,
vô ty. Nhung theo kê´t qua cua b`
ai 9.6 tô`n t .ai sô´ t .u nhiên q, v`a c´ac , , ,
sô´nguyên duong p1, p2, . . . , p2n+1 thoa m˜an p 1 |x i i − | < , i = 1, 2, . . . , n. (9.16) q 1 q1+ 2n+1 , , , , Tru`
ong h .op riêng, tô`n t.ai p1, p2, . . . , p2n+1, q v´oi q > (2n)2n+1 v`a , 1 ch´ ung thoa m˜ an |qxi − pi| ≤ , i = 1, 2, . . . , n. 1 q 2n+1 , ,
Ð .˘at αi = qxi − pi, i = 1, 2, . . . , 2n + 1. Nhu phâ`n ¯dâ`u kh˘ang ¯d.inh , r` ˘
ang qx1, qx2, . . . , qx2n+1 c´o t´ınh châ´t P. Ch´ung ta s˜e ch´ung minh r` ˘
ang p1, p2, . . . , p2n+1 c˜ung c´o t´ınh châ´t P. Ch .on 2n sô´ trong ¯d´o, v´ı ,
d .u nhu p1, p2, . . . , p2n . V`ı qx1, qx2, . . . , qx2n c´o t´ınh châ´t P, không , , , mâ´t t´ınh tông qu´ at ch´ ung ta lâ´y ¯ d˘ ang th´
uc qx1 + qx2 + · · · + qxn =
qxn+1 + qxn+2 + · · · + qx2n, khi ¯ d´
o (p1 + α1) + (p2 + α2) + · · · +
(pn + αn) = (pn+1 + αn+1) + (pn+2 + αn+2) + · · · + (p2n + α2n). Ch´ ung ta viê´t l .ai
p1 + p2 + · · · + pn − pn+1 − pn+2 − · · · − p2n =
= αn+1 + αn+2 + · · · + α2n − α1 − α2 − · · · − αn. (9.17) , , Vê´ bên tr´ ai ¯ d˘ ang th´ uc trên l`
a sô´ nguyên nên sô´ α = αn+1 + ,
αn+2 + · · · + α2n − α1 − α2 − · · · − αn c˜ ung l` a sô´ nguyên. Nhung 1 |αi| ≤ , i = 1, 2, . . . , n. Do ¯ d´ o | 1
α| ≤ |αn+1| + |αn+2| + · · · + q 2n+1 2n
|α2n| + |α1| + |α2| + · · · + |αn| <
< 1, v`ı q > (2n)2n+1. Khi 1 q 2n+1 , , , , , 98 Chuong 9. Nh˜ ung ´
ung d .ung kh´ac cua nguyên l´y Ðirichle , , , , , ¯ d´ o α = 0 v`a t`u ¯ d˘ ang th´ uc tru´ oc ¯ d´ o ta c´ o p1 + p2 + · · · + pn = , , , , ,
pn+1 + pn+2 + · · · + p2n Nhu v .ây ch´ung ta kh˘ang ¯d.inh ¯du .oc nh˜ung ,
sô´ nguyên p1, p2, . . . p2n+1 c´o t´ınh châ´t P. Ch´ung ta c´o thê kê´t lu .ân , , ¯ du .oc p1 = p2 = . . . = p2n+1 , , , ,
Th .uc châ´t ¯dê´n ¯dây ch´ung ta ¯d˜a ch´ung minh ¯du .oc : , ,
Nê´u p1, p2, . . . , p2n+1, q l`a nh˜ung sô´ nguyên thoa m˜an (9.16) v`a
q > (2n)2n+1 th`ı p = p1 = p2 = . . . = p2n+1. Suy ra (9.16) c´o d .ang p 1 |xi − | < , i = 1, 2, . . . , 2n + 1 q 1 q1+ 2n+1 , , Trong 9.6 ch´ ung ta kh˘ ang ¯
d.inh r`˘ang tô`n t.ai vô h.an sô´ t .u nhiên q , , , thoa m˜
an (9.16). Không mâ´t t´ınh tông qu´ at ch´ ung ta gia thiê´t r` ˘ ang , ,, nh˜ ung sô´ ¯ d´ o l`
a q1 < q2 < . . . < qk < . . ., o ¯ dây q1 > (2n)2n+1. Trong , , , , tru`
ong h .op n`ay v´oi m .oi k tô`n t.ai sô´nguyên pk sao cho p 1 |x k i − | < , i = 1, 2, . . . , 2n + 1. (9.18) q 1 k 1+ q 2n+1 k 1 , , p V`ı lim = 0 khi k tiê´n t´ oi vô c` ung, t` u (9.18) suy ra lim k = 1 1+ qk q 2n+1 k , , ,
xi khi k tiê´n t´oi vô c`ung, v´oi m .oi i = 1, 2, . . . , 2n + 1. Nhung m˜ôi d˜ay , , ,
sô´ th .uc không c´o nhiê`u hon m .ôt gi´oi h.an, suy ra x1 = x2 = . . . = x2n+1. J , , , . 9.9. Ch´ ung minh r` ˘ ang trong t´ am sô´, m˜ ôi sô´ c´ o ba ch˜ u sô´, bao gi` o , , , , , , c˜
ung ch .on ¯du.oc hai sô´ c´o ba ch˜u sô´ v`a ¯dê khi gh´ep l .ai ta ¯du.oc m.ôt sô´ chia hê´t cho 7. , , , L`
oi giai. Khi mang t´
am sô´ chia cho 7 th`ı thê n` ao c˜ ung c´ o hai sô´ c´ o , , ,, , c` ung sô´du (nguyên l´
y Ðirichlê ). Gia su hai sô´ ¯ d´ o l` a abc v`a αβγ. Hiên 9.2. B` ai t .âp 99 ,
nhiên abcαβγ = 1000abc + αβγ. T`u c´ach ch .on ta c´o abc = 7m + r , , v` a αβγ = 7n + r v´
oi 0 ≤ r < 7 v`a m, n, r l`a c´ac sô´ t .u nhiên. V`ı
v .ây abcαβγ = 1000(7m + r) + (7n + r) = 7(1000m + n) + 1001.r = 7(1000m + n + 143.r). J , ,
. 9.10. Cho a, b, c, d l` a c´ ac sô´ nguyên. Ch´ ung minh r` ˘ ang t´ıch cua c´ ac
hi.êu b − a, c − a, d − a, d − c, b − d v`a c − b chia hê´t cho 12. , , , L`
oi giai. Câ`n ch´
ung minh t´ıch: P = (b − a)(c − a)(d − a)(d − c)(d −
b)(c − b) chia hê´t cho 12=4.3. Ch´ ung ta biê´t r` ˘ ang m .ôt sô´ nguyên , , bâ´t k`
y khi chia cho 4 th`ı chı c´ o c´ ac sô´du 0, 1, 2, 3. , ,
Trong bô´n sô´ a, b, c, d cho tru´ oc nê´u c´ o hai sô´ khi chia cho 4 m` a , , c´ o c`
ung sô´ du th`ı hi .êu cua ch´ung s˜e chia hê´t cho 4. Nê´u không c´o , , hai sô´ n` ao khi chia cho 4 cho c`
ung sô´ du th`ı trong bô´n sô´ phai c´ o , , , , hai sô´ ch˜ ˘ an v`
a hai sô´ le. V`ı hi .êu cua hai sô´ch˜˘an c˜ung nhu hi.êu cua , hai sô´le ¯ dê`u l` a sô´ch˜ ˘ an nên P chia hê´t cho 4. , ,
M .˘at kh´ac trong bô´n sô´a, b, c, d luôn t`ım ¯du .oc hai sô´khi chia cho , , 3 th`ı c´ o c` ung sô´du (nguyên l´ y Ðirichlê ). Do ¯ d´ o hi .êu cua ch´ung chia
hê´t cho 3, suy ra P chia hê´t cho 3. T´
om l .ai P chia hê´t cho 12=4.3. J 9.2. B ` ai t .âp , , . 9.11. Cho x l`
a m .ôt sô´th .uc, c`on n l`a m .ôt sô´t .u nhiên. Khi ¯d´o tô`n t.ai , , p 1 nh˜
ung sô´nguyên p v`a q thoa m˜an 1 ≤ q ≤ n v`a x − ≤ . q (n + 1)q , , ,
. 9.12. Cho x1, x2, . . . , xm l`a nh˜ung sô´th .uc v`a n l`a sô´t .u nhiên. Khi , , ¯ d´
o tô`n t .ai nh˜ung sô´ nguyên p1, p2, . . . , pn, q không ¯dô`ng th`oi b`˘ang 0, sao cho ta c´ o q ≤ n( µ
µ = 1, 2, . . . , m) v` a 1
|q1x1 + q2x2 + · · · + qmxm − p| ≤ . (n + 1)m , , , , , 100 Chuong 9. Nh˜ ung ´
ung d .ung kh´ac cua nguyên l´y Ðirichle , , . 9.13. Ch´ ung minh r` ˘ ang v´
oi m .oi c.˘ap sô´nguyên p v`a q > 0 ta ¯dê`u √ √ , , √ p 3 − 2 c´ o bâ´t ¯ d˘ ang th´ uc sau 2 − ≥ . q q2 , , . 9.14. Ch´ ung minh r` ˘ ang v´
oi m .oi c.˘ap sô´nguyên p v`a q > 0 ta ¯dê`u , , √ p 1 c´ o bâ´t ¯ d˘ ang th´ uc sau √ 3 − ≥ . q 3 3q2 , , , , . 9.15. Cho m, n v`
a s l`a nh˜ung sô´nguyên v`a α l`a nghi .êm cua phuong ,
tr`ınh b .âc hai mx2 + nx + s = 0, (m 6= 0). Ch´ung minh r`˘ang nê´u α l`a , , , , p c , sô´ vô ty, th`ı tô`n t
.ai m .ôt sô´ duong c thoa m˜ an α − ≥ v´ oi m .ôi q q2
c .˘ap sô´nguyên p v`a q > 0. , , CHUONG 10 NGUYÊN L ´ Y ÐIRICHLÊ CHO DI .ÊN T´ICH , 10.1. Ph ´ at biêu nguyên l´
y Ðirichlê cho di .ên t´ıch , , , , , Trong chuong n` ay ch´ ung ta x´ et nh˜
ung t .âp h .op trên m.˘at ph˘ang, , , , nh˜ ung ph´ ep to´ an trên c´
ac t .âp h .op nê´u c´ac b.an chua quen biê´t c´o , ,, ,
thê xem o Ph .u ¯d´ınh cuô´i s´ach. Ch´ung ta quan tâm t´oi c´ac kh´ai ni.êm sau ¯ dây: , ,
M .ôt t.âp h .op trong m.˘at ph˘ang g .oi l`a b.i ch .˘an, khi tô`n t.ai m .ôt , , , , h`ınh tr` on ch´ ua to`
an b .ô c´ac ¯diêm cua t.âp h .op ¯d´o. Khi không tô`n t.ai , , ,
m .ôt h`ınh tr`on n`ao nhu trên th`ı t.âp h .op ¯d´o g .oi l`a t.âp h .op không b.i , ,, ,
ch .˘an. V´ı d .u nhu m .ôt ¯da gi´ac lô`i l`a t.âp b.i ch.˘an c`on nua m.˘at ph˘ang l`a , , , ,
t .âp h .op không b.i ch.˘an. D˜ê d`ang ch´ung minh ¯du .oc c´ac t´ınh châ´t sau , , , cua nh˜ ung t .âp h .op b.i ch.˘an , , , ,
1. H .op v`a giao cua h˜uu h.an nh˜ung t.âp b.i ch.˘an l`a m .ôt t.âp b.i ,
ch .˘an. Hi.êu cua hai t.âp b.i ch.˘an l`a m .ôt t.âp b.i ch.˘an. , ,
2. M .ôt t.âp h .op con cua m .ôt t.âp b.i ch.˘an l`a m .ôt t.âp b.i ch.˘an. M .ôt , , ,
t .âp h .op ch´ua m .ôt t.âp h .op con không b.i ch.˘an th`ı n´o c˜ung không b.i ch .˘an. , , , , ,
M .ôt ¯diêm P g .oi l`a ¯
diêm biên cua t .âp h .op A trong m.˘at ph˘ang, , , 102 Chuong 10. Nguyên l´
y Ðirichlê cho di .ên t´ıch , , , ,
nê´u m .oi h`ınh tr`on tâm t.ai P c´o ch´ua nh˜ung ¯diêm thu .ôc A v`a ca , , , , , , nh˜ ung ¯
diêm không thu .ôc A.T.âp h .op tâ´t ca c´ac ¯diêm biên cua A g .oi , , , , l`
a biên cua A v`a k´y hi .êu l`a K(A). V´ı d .u biên cua h`ınh tr`on l`a ¯du`ong , , tr` on v´ oi c` ung tâm v` a b´
an k´ınh. V´ı d .u ¯d.˘ac bi.êt v`a t´ınh châ´t biên cua , , t .âp h .op nhu sau: , , , , ,
3. Cho t .âp h .op A gô`m to`an b .ô nh˜ung ¯diêm c´o t .oa ¯d .ô h˜uu ty ,
trong m .ôt h`ınh vuông v´oi t .oa ¯d .ô c´ac ¯dir nh (0, 0), (0, 1), (1, 0), (1, 1). , D˜ ê d` ang thâ´y r` ˘
ang biên cua A l`a to`an b .ô h`ınh vuông n´oi trên. , , , , 4. V´
oi m .oi t.âp h .op A gô`m c´ac ¯diêm trong m.˘at ph˘ang ¯dê`u c´o , công th´ uc sau K(K(A)) ⊂ K(A). , , ,
5. M .oi c.˘ap t.âp h .op bâ´t k`y trong m.˘at ph˘ang ¯dê`u thoa m˜an c´ac , công th´ uc sau K(A ∪ B) ⊂ K(A) ∪ K(B) K(A ∩ B) ⊂ K(A) ∩ K(B) K(A\B) ⊂ K(A) ∪ K(B) , , , , , ,
M .ôt ¯diêm P g .oi l`a ¯
diêm trong cua t .âp h .op A nh˜ung ¯diêm trong ,
m .˘at ph˘ang, khi tô`n t.ai h`ınh tr`on tâm P m`a n´o n`˘am tr .on trong A. , , , , T` u ¯
d.inh ngh˜ıa n`ay thâ´y ngay l`a m .oi ¯diêm trong cua t.âp h .op A ¯dê`u , , ,, ,
thu .ôc A. Ðiê`u ngu .oc l.ai không ¯d´ung: trong v´ı d .u 3 o trên t.âp h .op A , không c´
o m .ôt ¯diêm trong n`ao. Ta thâ´y ngay , , ,
6. M .ôt ¯diêm thu .ôc A l`a ¯diêm trong cua A khi v`a chi khi n´o không , , , , , l` a ¯
diêm biên cua A. Ðiê`u n`ay giai th´ıch t .ai sao nh˜ung ¯diêm trong , , , cua h`ınh tr` on không n` ˘ am trên ¯ du` ong tr` on. , , , ,
Ðê lo .ai tr`u c´ac t.âp h .op ¯d.˘ac bi.êt, ch´ung ta ¯dua v`ao m .ôt kh´ai ni.êm , , , , ¯
d .˘ac chung cho l´op t.âp h .op không ¯d.˘ac bi.êt trong m.˘at ph˘ang : M .ôt , , ,
t .âp h .op b.i ch.˘an c´ac ¯diêm trong m.˘at ph˘ang g .oi l`a bê` m .˘at, khi biên , , , , cua n´ o không ch´ ua ¯ diêm trong (cua biên). ,
V´ı d .u c´ac h`ınh tr`on ho.˘ac ¯da gi´ac ¯dê`u l`a bê`m.˘at trong m.˘at ph˘ang. , 10.1. Ph´ at biêu nguyên l´
y Ðirichlê cho di .ên t´ıch 103 , ,
Nhung trong v´ı d .u 3 t.âp h .op A không l`a bê` m.˘at. B`˘ang c´ach d`ung , c´ ac ¯
d.inh ngh˜ıa vê` t.âp h .op v`a c´ac ¯d.inh ngh˜ıa trong phâ`n trên ch´ung , , , ta ch´ ung minh ¯ du .oc , ,
7. Nê´u A v`a B l`a hai bê` m .˘at, nh˜ung t.âp h .op A ∪ B, A ∩ B v`a , , A\B c˜ ung l` a nh˜
ung bê` m .˘at trong m.˘at ph˘ang. ,
8. Nê´u A, B v`a C l`a c´ac bê` m .˘at v`a A không c´o chung ¯diêm trong , , , , v´ oi B v`a v´ oi C, th`ı A không c´ o ¯ diêm trong chung v´ oi B ∪ C. , , , ,
M .ôt trong nh˜ung ¯d.inh l´y co ban trong h`ınh h .oc ph˘ang, nhiê`u khi ,, , , o phô thông ch´
ung ta công nh .ân nhu m .ôt tiên ¯dê`: , , , , , ,
9. M .oi bê` m.˘at A nh˜ung ¯diêm trong m.˘at ph˘ang c´o thê cho tuong ´, , , ung v´
oi m .ôt sô´th .uc không âm S(A) sao cho ,
a) S(∆) = 1, v´oi ∆ l`a m .ôt h`ınh vuông c´o c.anh l`a 1; ,
b) Nê´u A v`a B l`a hai bê` m .˘at không c´o ¯diêm trong chung, th`ı S(A ∪ B) = S(A) + S(B). , , , , , , Ph´ ep cho tuong ´ ung S v´ oi c´ ac t´ınh châ´t trên ¯ du .oc x´ac ¯d.inh m .ôt c´ ach duy nhâ´t. , ,
Cho bê`m .˘at A bâ´t k`y, sô´S(A) g .oi l`a di.ên t´ıch cua A. Nh˜ung m.˘at , , , , , , ¯ d˜ a ¯
du .oc x´et trong c´ac tru`ong phô thông l`a h`ınh ch˜u nh.ât, tam gi´ac, , h`ınh tr` on,. . . v` a sô´ S(A) theo ¯
d.inh ngh˜ıa trên tr`ung v´oi kh´ai ni.êm , , , , ,
di .ên t´ıch cua c´ac h`ınh n`ay. V´oi c´ach tr`uu tu .ong h´oa kh´ai ni.êm di.ên , , t´ıch ch´ ung ta d˜ ê d` ang khao s´
at t´ınh châ´t vê` di .ên t´ıch cua c´ac h`ınh. , , , , , T` u a) v` a b) ch´ ung ta c´ o thê d˜ ê d` ang ch´ ung minh ¯ du .oc: ,
10. Nê´u A v`a B l`a nh˜ung bê` m .˘at v`a A ⊂ B, th`ı S(A\B) = S(A) − S(B). ,
11. Nê´u A1, A2, . . . , An l`a c´ac bê` m .˘at t`ung ¯dôi m .ôt không c´o , ¯
diêm trong chung, th`ı S(A1 ∪ A2 ∪ . . . ∪ An) = S(A1) + S(A2) + , , 104 Chuong 10. Nguyên l´
y Ðirichlê cho di .ên t´ıch · · · + S(An). Nguyên l´
y Ðirichlê cho di .ên t´ıch: Nê´u A l`a m.ôt bê` m.˘at, c`on
A1, A2, . . . , An l`a c´ac bê` m .˘at sao cho Ai ⊂ A(i = 1, 2, . . . , n) v`a
S(A) < S(A1) + S(A2) + · · · + S(An), th`ı ´ıt nhâ´t c´o hai bê` m .˘at , trong sô´c´
ac bê` m .˘at trên c´o m.ôt ¯diêm trong chung. , , C˜ ung nhu nguyên l´ y ¯ dâ`u tiên, ch´ ung ta c˜ ung c´ o thê thâ´y ¯ diê`u , , , , , ,, n` ay l` a hiên nhiên v` a ch´ ung minh ¯
du .oc. Th.ât v.ây, Gia su không c´o , ,
c .˘ap n`ao trong nh˜ung m.˘at ¯d˜a cho c´o ¯diêm trong chung. Khi ¯d´o theo , kh˘ ang ¯
d.inh 11. ta c´o S(A1 ∪ A2 ∪ . . . ∪ An) = S(A1) + S(A2) + · · · +
S(An). M .˘at kh´ac Ai ⊂ A(i = 1, 2, . . . , n) suy ra A1 ∪ A2 ∪ . . . ∪ An ⊂ , , A, t` u ¯ d´ o c´
o S(A1 ∪ A2 ∪ . . . ∪ An) ⊂ S(A). Thô´ng nhâ´t c´ac bâ´t ¯ d˘ ang , , th´
uc l .ai ch´ung ta c´o S(A) < S(A), d˜ân t´oi vô l´y. , C´ o thê thâ´y r` ˘ ang nguyên l´ y trên bao tr` um nguyên l´ y Ðirichlê , , , cho nh˜
ung t .âp h˜uu h.an. Ngo`ai ra nguyên l´y Ðirichlê trên c´o thê c .u , , , , , , thê h´ oa cho nh˜ ung l´
op bê` m .˘at thông d .ung trong chuong tr`ınh phô , , thông v` a c´ ac kh´
ai ni .êm ¯d .ô d`ai, thê t´ıch c˜ung c´o c`ung t´ınh châ´t nhu ,, , , kh´
ai ni .êm di.ên t´ıch o trên. Do ¯d´o ch´ung ta c´o thê ph´at biêu nguyên , , l´ y Ðirichlê theo c´ ac phuong ´ an kh´ ac nhau. , , 12.Cho nh˜ ung ¯
do .an th˘ang ∆1, ∆2, . . . , ∆n n`˘am trong ¯do .an ∆ v`a , , , , , tông ¯
d .ô d`ai cua ∆1, ∆2, . . . , ∆n l´on hon ¯d.ô d`ai cua ∆. Khi ¯d´o ´ıt nhâ´t c´o , , , hai trong sô´nh˜ ung ¯
do .an th˘ang ∆1, ∆2, . . . , ∆n c´o ¯diêm chung. , , 13. Cho nh˜ ung ¯
da di.ên P1, P2, . . . , Pn n`˘am trong ¯da di.ên P v`a tông , , , , , ,
thê t´ıch cua P1, P2, . . . , Pn l´on hon thê t´ıch cua P. Khi ¯d´o ´ıt nhâ´t c´o hai , , trong sô´nh˜ ung ¯
da di.ên P1, P2, . . . Pn c´o ¯diêm chung. , , , , 14. Cho nh˜
ung cung c1, c2, . . . , cn n`˘ am trên ¯ du` ong tr` on c v` a tông , , , , , ¯
d .ô d`ai cua c1, c2, . . . , cn l´on hon ¯d.ô d`ai ¯du`ong tr`on c. Khi ¯d´o ´ıt nhâ´t c´o , , hai trong sô´nh˜
ung cung c1, c2, . . . cn c´o ¯diêm chung. 10.2. V´ı d .u 105 , , Tâ´t ca c´ ac ph´ at biêu 12, 13, 14 ch´ ung ta ¯ dê`u g .oi l`a nguyên l´y , , , , Ðirichlê v`
a b .an ¯d .oc c´o thê ch´ung minh ¯du .oc c´ac nguyên l´y n`ay. 10.2. V´ı d .u , ,
. 10.1. Cho M l`
a m .ôt ¯da gi´ac lô`i v´oi di.ên t´ıch S v`a chu vi P. Ch´ung minh r` ˘ ang , , , , , , , S a) M c´ o thê phu ¯
du .oc m.ôt h`ınh tr`on v´oi b´an k´ınh l´on hon ; P , S b) B´ an k´ınh cua c´ ac h`ınh tr` on n` ˘
am trong M không qu´ a . P , , , , L` oi giai. a) Ch´
ung ta d .ung trên m˜ôi c.anh ¯da gi´ac M m .ôt h`ınh ch˜u S ,
nh .ât chiê`u cao h = , nhu h`ınh 10.1. P M M O H C S h = P H`ınh 10.1: H`ınh 10.2: , , , , , Nh˜ ung h`ınh ch˜
u nh .ât n`ay c´o nh˜ung ¯diêm chung gi˜ua ch´ung; n´oi ,
chung m .ôt sô´h`ınh ch˜u nh.ât không n`˘am tr .on trong M. Ch´ung ta c´o , , , , , thê t´ınh to´
an tông di .ên t´ıch cua c´ac h`ınh ch˜u nh.ât n`ay l`a S. Nhu v.ây , , , , , ,
phâ`n cua M b.i c´ac h`ınh ch˜u nh.ât phu phai c´o di.ên t´ıch nho hon S. , , , Ðiê`u n` ay chı ra r` ˘
ang tô`n t .ai m .ôt ¯diêm O cua M không thu .ôc , , 106 Chuong 10. Nguyên l´
y Ðirichlê cho di .ên t´ıch , , , , , h`ınh ch˜
u nh .ât n`ao ca. Nhu v.ây c´o ngh˜ıa l`a khoang c´ach t`u O ¯dê´n , , , , S c´
ac c .anh cua M phai l´on hon h = . Ta lâ´y O l`a tâm h`ınh tr`on b´an P S k´ınh R > , h`ınh tr` on n` ay s˜ e n` ˘ am tr .on trong M. P b) Cho h`ınh tr`
on C tâm O b´an k´ınh R n`˘am trong M. Ch´ ung ta x´ et , , , , , c´ ac tam gi´ ac m` a hai ¯ dınh cua n´ o l` a hai ¯ dınh liên tiê´p cua t´ u gi´ ac, c` on , , , , , ¯ dınh th´ u ba l` a tâm h`ınh tr`
on O. Ðu`ong cao h .a t`u O xuô´ng c´ac c.anh , , , , , , cua tam gi´ ac n` ay l´ on hon R. T`u ¯ dây suy ra tông c´ ac di .ên t´ıch cua , , S ch´ ung b` ˘
ang S v`a không nho hon P.R. Suy ra R ≤ (H`ınh 10.2). P J , ,
. 10.2. Trong không gian cho 30 vecto kh´ ac không. Ch´ ung minh r` ˘ ang , , , , trong sô´ ¯ d´ o c´ o hai vecto m` a g´ oc gi˜ ua ch´ ung nho hon 450. , , , , , L` oi giai. C´ o thê gia thiê´t r` ˘ ang tâ´t ca , , v´ ecto c´ o chung ¯ diêm ¯ dâ`u O. Lâ´y OA , , , A v´ oi ¯
d .ôd`ai b`˘ang 1 trên vecto th´u nhâ´t. , , , Ch´
ung ta d .ung h`ınh n´on ¯dınh O v´oi ,, , 450 J
tr .uc OA, m`a g´oc o ¯dınh l`a 450. B`ai , , , O to´ an s˜ e ¯
du .oc ch´ung minh nê´u ch´ung , ta chı ra r` ˘
ang ´ıt nhâ´t hai trong sô´ 30 , , , , h`ınh n´ on (¯ du .oc xây duong theo c´ach , , , , trên ´ ung v´ oi 30 vecto ¯ d˜ a cho) c´ o ¯ diêm trong chung (h`ınh 10.3). , H`ınh 10.3: Ch´ ung ta x´ et h`ınh câ`u S v´ oi tâm , O v` a b´ an k´ınh 1. M˜
ôi lâ`n d .ung h`ınh n´on c´˘at m.˘at câ`u S m .ôt h`ınh , , , , v´
oi di .ên t´ıch δ1 m`a c´o thê t´ınh to´an ¯du .oc. Ta c˜ung thâ´y r`˘ang , , hai h`ınh n´ on c´ o ¯ diêm trong chung khi v` a chi khi nh˜ ung phâ`n , , ,
trên m .˘at câ`u c˜ung phai c´o ¯diêm trong chung. T`u ¯diê`u n`ay v`a 10.2. V´ı d .u 107 , , , nguyên l´ y Ðirichlê ch´
ung ta chı câ`n thiê´t kiêm tra tông di .ên t´ıch , , ,
cua 30 h`ınh trên m .˘at câ`u l´on hon di.ên t´ıch m.˘at câ`u (b`˘ang 4π). √ p ! π 2 + 2 Ch´ ung ta c´
o δ1 = 2π 1 − cos = 2π 1 − . V .ây 8 2 √ √ p ! p 2 + 2 , , , , , 2 + 2 14 30.2π 1 − > 4π tuong ¯ duong v´ oi < 2 2 15 1 167 2 ho .˘ac l`a < . J 2 225 , ,
. 10.3. Nê´u m .ôt bê` m .˘at A trong m .˘at ph˘ang thoa m˜an ¯diê`u ki.ên , ,
S(A) > 1. th`ı n´o luôn luôn ch´ ua ´ıt nhâ´t hai ¯ diêm trong (x1, y1), ,
(x2, y2) m`a hi.êu x2 − x1 v`a y2 − y1 l`a nh˜ung sô´nguyên. , , , , L` oi giai. Qua m˜ ôi ¯ diêm (m, n) v´ oi , y
t .oa ¯d .ô nguyên ch´ung ta ke c´ac , , , , , , , ¯ du` ong th˘ ang ¯ d´ ung v` a ¯ du`ong th˘ ang ngang (h`ınh 10.4). , , , , Ch´ ung ta s˜ e t .ao ¯du .oc lu´oi −3 −2 −1 0 1 2 3 x , , , nh˜ ung ¯ diêm v´ oi t .oa d .ô nguyên. , , , Lu´
oi nguyên chia m .˘at ph˘ang ra c´ac h`ınh vuông b` ˘ ang nhau, m˜ ôi h`ınh vuông c´
o di .ên t´ıch l`a 1. Ch´u ´y r`˘ang , H`ınh 10.4: m˜ ôi h`ınh vuông c´ o thê xê d.ich ¯dê´n , , , tr` ung v´
oi m .ôt h`ınh vuông kh´ac, chı c´o kh´ac l`a t .oa ¯d .ô cua h`ınh vuông , , m´ oi chuyên ¯ dê´n c˜ ung l` a c´ ac sô´nguyên. , , Ch´
ung ta ch .on m .ôt h`ınh vuông trong lu´oi nguyên l`am gô´c cô´ , , ¯
d.inh rô`i d.ich chuyên m .oi h`ınh vuông vê` h`ınh vuông gô´c. Nhu v.ây , , , nh˜
ung phâ`n cua A n`˘am trong c´ac h`ınh vuông kh´ac nhau ¯ dê`u chuyên , , ,
vê` h`ınh vuông gô´c (h`ınh v˜
e). Tông cua di .ên t´ıch cua c´ac phâ`n ¯d´o , , 108 Chuong 10. Nguyên l´
y Ðirichlê cho di .ên t´ıch , , , b` ˘
ang di .ên t´ıch cua A v`a suy ra l´on hon 1. Suy ra ´ıt nhâ´t hai trong , sô´c´ ac phâ`n n` ˘
am trong h`ınh vuông d.ich ¯dê´n s˜e c´o ¯diêm trong chung , , , , ,
(x0, y0). Trong t .âp A ban ¯dâ`u th`ı ¯diêm (x0, y0) tuong ´ung v´oi hai , ¯ diêm kh´
ac nhau (x1, y1) v`a (x2, y2) m`a x1 − x0, y1 − y0, x2 − x0, y2 − ,
y0 l`a c´ac sô´nguyên. Nhu v .ây th`ı x2 − x1 v`a y2 − y1 c˜ung l`a sô´nguyên. J , , ,
. 10.4. Cho A l`
a t .âp h.op lô`i v`a b.i ch .˘an nh˜ung ¯diêm trong m .˘at , , , ph˘ ang, c`
on P1, P2, P3, P4, P5 l`a nh˜ung ¯diêm thu .ôc A. G.oi Ai l`a t .âp , , , ,
h .op nh .ân t`u A sau m.ôt ph´ep t.inh tiê´n c´ac ¯diêm theo vecto P1Pi(i = , , 1, 2, 3, 4, 5). Ch´ ung minh r` ˘ ang ´ıt nhâ´t c´
o hai t .âp h.op trong sô´ c´ac ,
Ai(i = 1, 2, 3, 4, 5) c´o ¯diêm chung. , , L` oi giai. Ch´ ung ta chia ra hai , , , , Q Qi tru`
ong h .op A c´o thê c´o ho.˘ac , , c´ o thê không c´ o ¯ diêm trong. Q00 , , , , 1. Tru` ong h .op A c´o ¯diêm , trong. K´ y hi .êu A0 l`a t.âp h .op, , , , m` a n´ o nh c t` u A, sau P P .ân ¯ du .o 1 i , khi t´ ac ¯ d .ông ph´ep v.i t .u tâm H`ınh 10.5: ,
P1 v`a h.ê sô´ v.i t .u 2. Khi ¯d´o , công th´ uc sau ¯ d´ ung Ai ⊂ A0 (h`ınh 10.5). , ,
Th .ât v.ây, nê´u Q ∈ A v`a Qi l`a anh cua Q qua ph´ep t.inh tiê´n theo , −−→
vecto P1Pi (xem h`ınh v˜e), th`ı P1PiQiQ l`a h`ınh b`ınh h`anh. K´y hi.êu , , ,, Q00 l` a trung ¯
diêm cua P1Qi. R˜o r`ang Q00 ∈ A, v`ı Q v`a Pi l`a phâ`n tu , , ,
cua A v`a A lô`i. M .˘at kh´ac P1Qi = 2P1Q00 v`a v`ı A0 l`a anh cua A qua , , , ph´
ep v.i t .u tâm P1 v`a h.ê sô´ 2, nên ¯diêm Qi n`˘am trong t.âp h .op A0. , ,
Nhu v .ây m˜ôi tâp trong c´ac t.âp Ai n`˘am trong A0. Ðô`ng th`oi m˜ôi t.âp 10.2. V´ı d .u 109 , , cua Ai ¯
dô`ng d .ang v´oi A v`a suy ra S(Ai) = S(A). Do ¯d´o
S(A1) + S(A2) + S(A3) + S(A4) + S(A5) = 5S(A). (10.1) , , , ,
Nhung t .âp h .op A0 ¯dô`ng d.ang v´oi A v´oi h.ê sô´2. Suy ra S(A0) = 4S(A). (10.2) , ,
M .˘at kh´ac A c´o ¯diêm trong, v`ı thê´ S(A) > 0. Ngh˜ıa l`a t`u (10.1) v`a
(10.2) suy ra S(A1) + S(A2) + S(A3) + S(A4) + S(A5) > S(A0). , , , , , , ,
Nhu v .ây trong tru`ong h .op 1 b`ai to´an ¯du .oc suy ra t`u nguyên l´y
Ðirichlê cho di .ên t´ıch. , , , , , , 2. Tru`
ong h .op A không c´o ¯diêm trong, A s˜e n`˘am trên m .ôt ¯du`ong , , , , , th˘
ang. Th .ât v.ây, nê´u ´ıt nhâ´t ba ¯diêm n`˘am trên m .ôt ¯du`ong th˘ang, do , , , , t´ınh châ´t lô`i A ch´ ua to`
an b .ô h`ınh tam gi´ac v´oi ¯dınh l`a c´ac ¯diêm , , , , n` ay, suy ra A c´ o ¯
diêm trong. Nhung t .âp lô`i, b.i ch.˘an trên m .ôt ¯du`ong , , , , , th˘ ang ch´ınh l` a ¯
do .an th˘ang trên du`ong th˘ang n`ay. Phâ`n c`on l.ai l´y , , , , , , , , , ,
lu .ân tuong t .u nhu phâ`n trên. Nhung trong tru`ong h .op trên ¯du`ong , , , th˘ ang chı câ`n 3 ¯ diêm v` a nguyên l´ y Ðirichlê vê` ¯ d .ô d`ai. J , , ,
. 10.5. (Ð.inh l´y Minkovski) Cho A l`a t .âp h.op ¯diêm trong m .˘at ph˘ang , c´
o t´ınh châ´t lô`i, b.i ch .˘an v`a ¯dô´i x´ung qua gô´c t.oa ¯d.ô v`a S(A) > 4. Khi , , , , , ¯ d´ o A ch´ ua nh˜ ung ¯ diêm trong kh´ ac ¯ diêm gô´c v´
oi t .oa ¯d.ô nguyên. , , , L` oi giai. T´
ac d .ung lên A ph´ep v.i t .u tâm l`a gô´c t .oa ¯d .ô v`a h.ê sô´ 1. 2 , , , , , ,
Nhu v .ây ch´ung ta nh.ân ¯du .oc A0, ¯dô`ng d.ang v´oi A v`a c´o k´ıch thu´oc ,, , , , 1 b` ˘ ang nua k´ıch thu´ oc cua A. Suy ra S(A0) = S(A) > 1. Theo b` ai 4 , , 10.13 suy ra A0 ch´ ua ´ıt nhâ´t hai ¯ diêm kh´ ac nhau (x1, y1) v`a (x2, y2), , , m` a c´
ac hi .êu x2 − x1 v`a y2 − y1 l`a nguyên. V`ı t.âp h .op A ¯dô´i x´ung qua , , ,
gô´c t .oa ¯d .ô nên t.âp h .op A0 c˜ung v.ây. Ðiê`u ¯d´o giai th´ıch r`˘ang ¯diêm ,
(−x1, −y1) thu .ôc A0. V`ı A lô`i nên A0 c˜ung lô`i. Do ¯d´o trung ¯diêm , , 110 Chuong 10. Nguyên l´
y Ðirichlê cho di .ên t´ıch , , cua c´ ac ¯ diêm m´
ut (−x1, −y1) v`a (x2, y2) c˜ung thu .ôc A0 v`a c´o t .oa ¯d .ô x y , , , ,
( 2 − x1 , 2 − y1 ). Nhân t .oa ¯d .ô n`ay v´oi 2 th`ı ¯du .oc t .oa ¯d .ô cua m .ôt 2 2 , , , , , ¯
diêm thu .ôc A. Nhu v.ây (x2 − x1, y2 − y1) thu .ôc A. Ðiêm ta t`ım ¯du .oc , , kh´
ac gô´c t .oa ¯d .ô v`a c´o t .oa ¯d .ô nguyên v`a l`a ¯diêm trong cua t.âp A. J
. 10.6. Nê´u A l` a m .ôt bê` m .˘at, A1, A2, . . . , An. (10.3) , , , l` a nh˜
ung bê` m .˘at v`a thoa m˜an Ai ⊂ A(i = 1, 2, . . . , n), c`on k l`a sô´t .u nhiên m` a
k.S(A) < S(A1) + S(A2) + · · · + S(An). (10.4) , ,
th`ı´ıt nhâ´t k + 1 trong sô´nh˜
ung bê` m .˘at trên c´o m.ôt ¯diêm trong chung. , , , , , , L` oi giai. Ch´ ung ta ch´ ung minh b` ˘
ang qui n .ap,Tru`ong h .op k = 1 ¯d´o , ,, , , ,, l` a nguyên L´ y Ðirichlê ¯ d˜ a ch´ ung minh o trên. Bây gi` o gia su b` ai to´ an , , ¯ d˜ a ¯ d´ ung cho k, ch´ ung ta phai ch´ ung minh n´ o c˜ ung ¯ d´ ung cho k + 1. , , Ta cô´ ¯
d.inh m .ôt k v`a c´o bâ´t ¯d˘ang th´uc
(k + 1)S(A) < S(A1) + S(A2) + · · · + S(An). (10.5) , , , , , Ch´ ung ta s˜ e chı ra r` ˘ ang v´
oi (10.5) tô`n t .ai m .ôt ¯diêm l`a ¯diêm trong cua , ,
k + 2 t .âp h .op cua (10.3). Do A ⊂ A( ) ≤ µ
µ = 1, 2, . . . , n), nên S(Aµ , , S(A), t` u ¯ d´
o suy ra S(A1) + S(A2) + · · · + S(An) ≤ nS(A). T`u bâ´t , , ¯ d˘ ang th´ uc sau c` ung v` a (10.5) ch´ ung ta c´ o (k + 1)S(A) < nS(A) suy ra k + 1 < n. V`ı v .ây n ≥ k + 2. (10.6) , , , , ,
Tô`n t .ai ¯diêm chung cho ´ıt nhâ´t k + 2 t.âp h .op (10.3) ¯du .oc ch´ung , , minh b` ˘
ang qui n .ap theo n. T`u (10.4) suy ra (10.5), v.ây ta phai b´˘at , , ¯ dâ`u t`
u k + 2. Nhu v .ây viê´t l.ai
(k + 1)S(A) < S(A1) + S(A2) + · · · + S(Ak+2). (10.7) 10.2. V´ı d .u 111 , , , , , Câ`n phai ch´
ung minh tô`n t .ai ¯diêm m`a n´o l`a ¯diêm trong cua A1, A2, . . . , Ak+2. Lâ´y A0 = A \A µ µ
k+2(µ = 1, 2, . . . , k + 1) (10.8) A00 = A ∩ A µ µ
k+2(µ = 1, 2, . . . , k + 1) (10.9) v` a A0 = A\Ak+2 (10.10) A00 = Ak+2. (10.11) , R˜ o r` ang A0 ⊂ A0 v`a A0 ⊂ A00( a k + 1 µ µ
µ = 1, 2, . . . , k + 1) . V` ı c´ o tâ´t c , , ,
t .âp h .op A0 , t`u bao h`am th´uc trên suy ra µ
(k + 1)S(A0) ≥ S(A01) + S(A02) + · · · + S(A0 ) k+1 . (10.12) , , , Nê´u lâ´y (10.7) tr` u ¯ di (10.12) ch´ ung ta nh .ân ¯du .oc
(k + 1)S(A00) < S(Ak+2) + S(A001) + S(A002) + · · · + S(A00 ) k+1 . (10.13)
V`ı S(A) − S(A0) = S(A00) v`a S(A ) − S(A0 ) = S(A00) do (10.8)- µ µ µ , (10.11) nên t` u (10.13),(10.9) v` a (10.11) suy ra
kS(Ak+2) < S(A1 ∩ Ak+2) + S(A2 ∩ Ak+2) + · · · + S(Ak+1 ∩ Ak+2). (10.14) , , T` u (10.14) v` a gia thiê´t ¯ d´
ung cho k theo qui n .ap suy ra A1 ∩ ,
Ak+2, A2 ∩ Ak+2, . . . , Ak+1 ∩ Ak+2 c´o ¯ diêm trong chung, ¯ diê`u n` ay , , , c´ o ngh˜ıa l`
a t .âp h .op A1, A2, . . . , Ak+2 c´o ¯diêm trong chung. Nhu v.ây , , , , v´
oi n = k + 2 t`u (10.5) suy ra ´ıt nhâ´t k + 2 t .âp h .op t`u (10.3) c´o , ¯ diêm trong chung. , , , , Bây gi` o ch´ ung ta gia thiê´t v´
oi m .ôt n ≥ k + 2 t`u (10.5) suy ra , , , ,
´ıt nhâ´t k + 2 t .âp h .op t`u (10.3) c´o ¯diêm trong chung v`a s˜e phai kê´t , lu .ân r`˘ang t`u
(k + 1)S(A) < S(A1) + S(A2) + · · · + S(An) + S(An+1). (10.15) , , 112 Chuong 10. Nguyên l´
y Ðirichlê cho di .ên t´ıch , , suy ra c´
o ´ıt nhâ´t k + 2 t .âp h .op trong d˜ây A1, A2, . . . , An+1 c´o ¯diêm
trong chung. Th .ât v.ây, ch´ung ta ¯d.˘at A0 = A \A µ µ n+1, (µ = 1, 2, . . . , n). (10.16) A00 = A ∩ A µ µ n+1, (µ = 1, 2, . . . , n) (10.17) v` a A0 = A\An+1 (10.18) A00 = An+1. (10.19)
V`ı A0 ∪ A0 = A0 , A0 ∩ A00 = ∅( µ µ µ µ µ
µ = 1, 2, . . . , n) v` a A0 ∪ A00 = A, A0 ∩ A00 = ∅ nên S(A0 ) + S(A00) = S(A ), ( µ µ µ µ = 1, 2, . . . , n) (10.20) v` a S(A0) + S(A00) = S(A). (10.21) , , , Ch´ ung ta s˜ e ch´
ung minh m .ôt trong c´ac bâ´t ¯d˘ang th´uc sau l`a ¯d´ung
(k + 1)S(A0) < S(A01) + S(A02) + · · · + S(A0n) (10.22) ho .˘ac l`a
kS(A00) < S(A001) + S(A002) + · · · + S(A00n). (10.23) , , , , ,
Th .ât v.ây, trong tru`ong h .op ngu .oc l.ai ch´ung ta s˜e c´o (k + 1)S(A0) ≥
S(A0 ) + S(A0 ) + · · · + S(A0 ) + S(A00) + · · · + 1 2 n) v` a kS(A00) ≥ S(A001 2 , ,
S(A00n) C .ông hai vê´l.ai v`a do (10.20), (10.21) ch´ung ta nh.ân ¯du .oc
S(A0) + kS(A) ≥ S(A1) + S(A2) + · · · + S(An). (10.24) , ,
C .ông hai vê´(10.24) v´oi S(A00) v`a t`u (10.19), (10.21) ch´ung ta nh.ân , , ¯ du .oc
(k + 1)S(A) ≥ S(A1) + S(A2) + · · · + S(An) , , , , Nhung ¯ diê`u n` ay tr´ ai v´ oi (10.15). Do ¯ d´ o trong hai bâ´t ¯ d˘ ang th´ uc , (10.22) v` a (10.23) phai c´
o ´ıt nhâ´t m .ôt c´ai ¯d´ung. 10.2. V´ı d .u 113 , ,, , , , Gia su (10.22) ¯ d´
ung. Theo gia thiê´t qui n .ap ¯dô´i v´oi n t`u (10.22) , ,
suy ra ´ıt nhâ´t k + 2 t .âp h .op trong d˜ây A0 , A0 m trong 1 2, . . . , A0n c´ o ¯ diê , chung. T` u (10.16) suy ra r` ˘
ang kê´t lu .ân trên c˜ung ¯d´ung cho d˜ây (10.3). , ,, , , , Gia su (10.23) ¯ d´ ung. T`
u gia thiê´t qui n .ap ¯dô´i v´oi k suy ra k + 1 , , , , t .âp h .op trong A00, A00 m chung v` a c` ung v´ oi (10.17) chı 1 2 , . . . , A00 n c´ o ¯ diê , , , , , ra r` ˘
ang tô`n t .ai m .ôt ¯diêm m`a n´o l`a ¯diêm trong cua k + 1 t.âp h .op t`u , , (10.3) v` a ca cua An+1. , , ,
Nhu v .ây t`u (10.15) suy ra k + 2 t.âp h .op trong d˜ay A1, A2, , , , . . . , An+1 c´o ¯
diêm trong chung. Suy ra kê´t lu .ân ¯d´ung v´oi n + 1. T`u , , , , , phuong ph´
ap qui n .ap bây gi`o l.ai suy ra, v´oi m .oi n, v´oi (10.5) tô`n , , , ,
t .ai m .ôt ¯diêm m`a n´o l`a ¯diêm trong cua ´ıt nhâ´t k + 2 t.âp h .op trong (10.3). J , , , Ch´ u ´ y. Trong ch´ ung minh ¯
d.inh l´y d`ung phuong ph´ap qui n.ap , , , , , , theo k. Nhung ¯ di t` u bu´
oc k sang k + 1 ta l .ai d`ung phuong ph´ap qui , , , , ,
n .ap theo n. V´oi ch´ung minh qui n.ap theo n t`u bu´oc n sang n + 1 ta , , , ,
l .ai d`ung bu´oc k tru´oc ¯d´o v`a n.
. 10.7. Trong m .ôt h`ınh vuông c´o c .anh l`a , , , , , 1 ch´
ua m .ôt sô´ ¯du`ong tr`on, Tông ¯d.ô d`ai cua , ch´ ung l` a 10. Ch´ ung minh r` ˘ ang tô`n t .ai m.ôt , , , , ¯ du` ong th˘ ang, m` a n´ o c´ ˘
at ´ıt nhâ´t 4 trong nh˜ ung , , ¯ du` ong tr` on n` ay. , , L`
oi giai. (H`ınh 10.6) Ch´ ung ta ch .on m .ôt H`ınh 10.6:
c .anh h`ınh vuông rô`i chiê´u vuông g´oc c´ac , , ¯ du` ong tr` on xuô´ng c .anh ¯d´o. , , 114 Chuong 10. Nguyên l´
y Ðirichlê cho di .ên t´ıch , , , D˜ ê thâ´y r` ˘
ang h`ınh chiê´u cua m .ôt ¯du`ong tr`on b´an k´ınh R l`a m .ôt , ¯
do .an th˘ang c´o ¯d .ô d`ai 2R. V`ı v.ây trên c.anh h`ınh vuông ¯d˜a ch .on s˜e , , , , 10 c´ o nh˜ ung ¯
do .an th˘ang chiê´u xuô´ng v´oi tông ¯d .ôd`ai l`a . π , 10 Nhung
> 3 = 3.1, theo nguyên l´y Ðirichlê suy ra c´ o m .ôt π , , , , ¯ diêm M n`ao ¯ d´
o thu .ôc AB l`a ¯diêm trong chung cua 4 ¯do.an th˘ang ¯d˜a , , , , , chiê´u xuô´ng. Khi ¯ d´ o ¯ du` ong th˘ ang ¯ di qua ¯ diêm M vuông g´ oc v´ oi AB , , s˜ e c´ ˘ at 4 ¯ du` ong tr` on. J , , , , , ,
. 10.8. M .ôt sô´ cung n`˘am trên ¯du`ong tr`on v´oi b´an k´ınh 1 ¯du.oc son , , , , , xanh. Tông ¯
d .ô d`ai cua c´ac cung mâ`u xanh l´on hon π. Ch´ung minh , , , , , , r` ˘ ang v´ oi m˜ ôi ¯ du` ong k´ınh d cua ¯ du` ong tr`
on tô`n t .ai dây cung song song , , , , , v´ oi d, m` a hai ¯ dâ`u cua dây cung ¯ du .oc son xanh. , , L`
oi giai. (H`ınh 10.7) Không mâ´t C , , A t´ınh tông qu´ at ch´ ung ta gia thiê´t , , c´ ac cung bôi son không c´ o ¯ diêm , , d chung. Cho d l`a ¯ du` ong k´ınh bâ´t k` y , , cua ¯ du` ong tr` on k v`a c l`a m .ôt trong , , , , c´ ac cung c bôi mâ`u. Trên ` ong d0 ¯ du .o ¯ du tr`
on k ta t .ao ra cung c0 b`˘ang c´ach , , , lâ´y ¯ dô´i x´ ung c qua ¯ du` ong k´ınh d0 k A0 , vuông g´ oc v´ oi d. C0 H`ınh 10.7: D˜ ê thâ´y cung c0 cho c` ung ¯ d .ô d`ai , , , , , v´
oi cung c. Ta l`am nhu v .ây v´oi m .oi cung c`on l.ai th`ı trên k nh.ân ¯du .oc , , , , ,
m .ôt h.ê cung c´o tông ¯d .ô d`ai l´on hon 2π. Nhung ¯d .ô d`ai cua k l`a 2π, ,
nhu v .ây theo nguyên l´y Ðirichlê c´o ´ıt nhâ´t hai cung trong h.ê n`ay c´o , ¯ diêm chung. 10.2. V´ı d .u 115 , , ,, , , Nhung ch´ ung ta ¯ d˜
a gia thiê´t o trên nh˜ung cung d .ang c t`ung ¯dôi , không c´ o ¯ diêm chung, ¯ diê`u ¯ d´ o c˜ ung ¯ d´ ung cho c´ ac cung c0. Khi ¯ d´ o , , , ,
tô`n t .ai m .ôt cung bôi son c1 c´o ¯diêm chung A v´oi cung c0 , ng 2 ¯ dô´i x´ u , , v´
oi cung c2 qua d0. R˜o r`ang dây cung ¯ di qua A v`a song song v´ oi d c´ o ,, ,,
t´ınh châ´t mong muô´n v`ı m .ôt ¯dâ`u o c1, c`on ¯dâ`u kia o c2. J , , ,
. 10.9. Trong h`ınh tr` on b´ an k´ınh 1 ngu`
oi ta tô son m .ôt sô´dây cung. , , , Ch´ ung minh r` ˘
ang nê´u m .oi ¯du`ong k´ınh c´˘at nhiê`u nhâ´t k dây cung, th`ı , , , , , , tông ¯
d .ô d`ai cua tâ´t ca c´ac dây cung ¯d˜a tô son nho hon πk. , , L`
oi giai. Lâ´y c l`a m .ôt dây cung bâ´t k`y trong h`ınh tr`on C ¯d˜a cho v`a γ , , l`
a cung nho trong hai cung do c t 0 .ao ra. K´
y hi .êu γ l`a cung ¯dô´i x´ung , , , , , v´
oi γ qua tâm cua h`ınh tr` on. R˜ o r`
ang m .ôt ¯du`ong k´ınh cua C c´˘at dây , cung c khi v`a chı khi c´ o hai ¯ dâ`u m´ ut n` ˘ am trong 0 γ v` a γ . , ,, , , , , , Gia su r` ˘ ang tông ¯
d .ô d`ai nh˜ung dây cung ¯d˜a ke l´on hon ho.˘ac , , , , b` ˘ ang πk. Khi ¯ d´ o tông ¯
d .ô d`ai tâ´t ca c´ac cung d.ang γ l´on hon πk. , , , C˜ ung ¯ d´ ung nhu v 0 .ây cho tông ¯
d .ô d`ai c´ac cung d.ang γ . Suy ra tông , , , , ¯ d 0 .ô d` ai cua c´
ac cung d .ang γ ho.˘ac γ l`a l´on hon 2πk. V`ı ¯d .ô d`ai cua , , , ,, ¯ du` ong tr`
on C l`a 2π, t`u nguyên l´y Ðirichlê mo r .ông suy ra tô`n t.ai ´ıt ,
nhâ´t m .ôt ¯diêm thu .ôc C, m`a n´o n`˘am trên ´ıt nhâ´t k + 1 cung c´o d.ang , , , 0 , , , γ ho .˘ ac γ . Nê´u t`u ¯ diêm chung n` ay ta ke ¯ du` ong k´ınh cua C,th`ı n´ o c´ ˘ at ,
´ıt nhâ´t k + 1 dây cung ¯ d˜ a cho, ¯ diê`u n` ay tr´ ai v´ oi ¯ diê`u ki .ên trong ¯dâ`u , , b`
ai. V .ây ¯diê`u kh˘ang ¯d.inh cua b`ai to´an l`a ¯d´ung. J , , , ,
. 10.10. M .ôt t .âp h.op M l`a h.op cua m.ôt sô´ ¯do .an th˘ang n`˘am trong , , , , ,
khoang [0, 1]. Biê´t r` ˘ ang khoang c´ ach gi˜ ua hai ¯ diêm bâ´t k` y cua M , , , , không b` ˘ ang 0,1. Ch´ ung minh r` ˘ ang tông ¯
d .ô d`ai cua nh˜ung ¯do .an t .ao , ,
nên M không vu .ot qu´a a) 0, 55; b) 0, 5. , , 116 Chuong 10. Nguyên l´
y Ðirichlê cho di .ên t´ıch , , , , , , ,, , , L` oi giai. a) Ch´ ung minh b` ˘ ang phan ch´ ung. Gia su tông S cua ¯ d .ô , , , , d` ai nh˜ ung ¯
do .an th˘ang t.ao nên M l´on hon 0,55. Ch´ung ta x´et t.âp N , , , , , , ,
nh .ân ¯du .oc t`u M b`˘ang c´ach c .ông m˜ôi ¯do.an th˘ang cua M v´oi 0,1. T`u , , ¯
diê`u ki .ên cua b`ai to´an suy ra M v`a N không c´o ¯diêm chung. Ngo`ai , , , , , ra tông ¯
d .ô d`ai cua N b`˘ang S nên l´on hon 0,55. D˜ê thâ´y hai t.âp h .op , M v` a N n`˘am trong ¯
do .an [0;1,1]. V`ı 2.S > 2.0, 55 = 1, 1, t`u nguyên , , l´
y Ðirichlê suy ra M v`a N c´ o ¯ diêm chung, ¯ diê`u n` ay d˜ ân t´ oi vô l´ y. , ,, , , , , b) Gia su ¯
d .ô d`ai cua tâ´t ca c´ac ¯do.an trong M l´on hon 0,5. Ch´ung 1 1 2 9 ta chia ¯
do .an [0,1] th`anh 10 phâ`n 0, , , , . . . , , 1 . K´y 10 10 10 10 , i i + 1
hi .êu Mi l`a phâ`n cua M n`˘am trong ¯do.an , , i = 0, 1, . . . , 9 10 10 , , v` a Si l`a tông ¯
d .ô d`ai c´ac ¯do.an th˘ang tao ra Mi. B`˘ang c´ach t.inh , , 1 2 9
tiê´n th´ıch h .op ch´ung ta chuyên m .oi ¯do.an , , . . . , , 1 10 10 10 , 1 , , , t´ oi 0, . K´ y hi .êu M0 l`a anh cua M i i = 2, 3, 4 . . . , 9. V`ı 10 i i v´ o ,
S = S1 + S2 + · · · + S10 > 0, 5 = 5.0, 1, t`u nguyên l´y Ðirichlê ,, , ,
mo r .ông suy ra c´o ´ıt nhâ´t 6 t.âp h .op trong M0, M0 , . . . , M0 c´o m 1 9 ¯ diê 1 chung. Ðiê`u n` ay c´ o ngh˜ıa l`
a m .ôt sô´ n`ao ¯d´o trong 0, l` a kê´t 10 , , , , , , , , qua cua 6 ¯ diêm kh´
ac nhau x1, x2, . . . , x6 cua M tr`u ¯ di tuong ´ ung , k k k ,, nh˜ ung sô´ d 1 2 6 .ang , , . . . , , o ¯ dây k 10 10 10 i l`
a m .ôt sô´ n`ao ¯d´o trong
0, 1, 2, . . . , 9, i = 1, 2, . . . 6. D˜ê d` ang thâ´y r` ˘ ang ´ıt nhâ´t c´ o hai trong c´ ac,
sô´ k1, k2, . . . , k6 l`a liên tiê´p (´ap d .ung nguyên l´y Ðirichlê). V´ı d .u nhu k k 1 k 1 2 2 = k1 + 1. V` ı x1 − = x , nên x , 10 2 − 10 2 − x1 = (k2 − k1) = 10 ¯ diê`u n` ay ¯ d˜ ân ¯ dê´n vô l´ y. J 10.3. B` ai t .âp 117 10.3. B ` ai t .âp , . 10.11. Cho n l`
a m .ôt sô´ t .u nhiên bâ´t k`y, c`on A l`a m .ôt bê` m.˘at , ,
trong m .˘at ph˘ang, m`a s(A) > n. Khi ¯d´o tô`n t.ai n + 1 ¯diêm trong , kh´
ac nhau (xi, yi) (i = 1, 2, . . . , n + 1) cua A, m`a hi.êu xi − xj v`a ,
yi − yj(i, j = 1, 2, . . . , n + 1) l`a nh˜ung sô´nguyên. , , . 10.12. Nê´u v´
oi m .ôt bê`m.˘at A trong m.˘at ph˘ang v`a m .ôt sô´nguyên , , ,
duong k thoa m˜an S(A) < k, th`ı tô`n t .ai m .ôt ph´ep t.inh tiê´n sao cho , , , , ,
anh cua A qua ph´ep t.inh tiê´n n`ay ch´ua nhiê`u nhâ´t k − 1 ¯diêm v´oi t .oa ¯d .ô nguyên. , , . 10.13. Cho A l`
a t .âp h .op lô`i, ¯dô´i x´ung qua gô´c t .oa ¯d .ô trong m.˘at , , , ph˘
ang, n l`a sô´t .u nhiên v`a S(A) > 4n. Khi ¯d´o A ch´ua ´ıt nhâ´t 2n + 1 , , ¯ diêm trong kh´ ac nhau v´ oi t .oa ¯d .ô nguyên. , , . 10.14. Nê´u A l`
a t .âp h .op lô`i, b.i ch.˘an, ¯dô´i x´ung qua gô´c t .oa ¯d .ô v`a , , , c´
o di .ên t´ıch b`˘ang 615, th`ı A ch´ua ´ıt nhâ´t 307 ¯diêm m`a khoang c´ach , , , gi˜
ua m .oi c.˘ap trong ch´ung l´on hon ho.˘ac b`˘ang 1. , , , , , . 10.15. Cho F l`
a t .âp h .op lô`i, b.i ch.˘an nh˜ung ¯diêm cua m.˘at ph˘ang. , , , , , Ch´
ung ta g .oi ¯d .ô h˜uu hi.êu cua t.âp h .op F l`a khoang c´ach nho nhâ´t , , , , ,, , , , gi˜ ua hai ¯ du` ong th˘
ang song song o hai ph´ıa cua t .âp h .op F. Ch´ung , , , minh r` ˘
ang nê´u trong m .ôt t.âp h .op lô`i, b.i ch.˘an v´oi ¯d .ô h˜uu hi.êu d c´o , , , , , , , ch´
ua m .ôt sô´ t.âp h .op con m`a tông ¯d .ô h˜uu hi.êu cua ch´ung l´on hon , , , ,
kd, th`ı tô`n t .ai ¯du`ong th˘ang, m`a n´o c´˘at ´ıt nhâ´t k + 1 t.âp h .op con n´oi trên. , , 118 Chuong 10. Nguyên l´
y Ðirichlê cho di .ên t´ıch , , CHUONG 11 , , TO ´ AN H .OC TÔ H .OP 11.1. V´ı d .u ,
. 11.1. (Ðê` thi To´
an Olympic Quô´c tê´,1972) Cho t .âp h.op gô`m 10 sô´ , , , , c´ o hai ch˜ u sô´. Ch´ ung minh r` ˘
ang t .âp h.op ¯d´o c´o ´ıt nhâ´t hai t .âp h.op con , , ,, không giao nhau, m` a tông nh˜
ung phâ`n tu trong ch´ ung b` ˘ ang nhau. , , , , L`
oi giai. Nê´u c´
o hai t .âp h .op con giao nhau m`a tông trong ch´ung , , , ,, b` ˘ ang nhau th`ı ch´ ung ta c´ o thê bo nh˜ ung phâ`n tu chung ¯ di. Khi ¯ d´ o , ,, , c`
on l .ai hai t.âp không giao nhau v`a tông c´ac phâ`n tu cua ch´ung v˜ân b` ˘ ang nhau. , , Ch´ ung ta t´ınh c´
o bao nhiêu t .âp h .op con không r˜ông cua m .ôt t.âp , , , ,, , , , , , ,
h .op c´o mu`oi phâ`n tu. Sô´lu .ong nh˜ung t.âp h .op con chı ch´ua 1 phâ`n ,, , , , , , ,, tu c´
o 10 ho .˘ac l`a C1 . Sô´ lu ng nh˜ung t p con ch´ ua 2 phâ`n tu 10 .o .âp h .o , , , , , ,, l` a C2 . Sô´lu ng nh˜ung t p con ch´ ua 3 phâ`n tu l` a C3 ,. . . Suy ra 10 .o .âp h .o 10 , , , ,
tông sô´lu .ong c´ac t.âp h .op con l`a C110 + C210 + C3 + · · · + = ( 10 C10 10 1 + 1)10 = 1023 , , , ,
Ðiê`u ki .ên b`ai ra l`a 10 sô´ ¯d˜a cho không l´on hon 99. V.ây tông cua , , , , c´ ac sô´ trong m˜
ôi t .âp h .op con không vu .ot qu´a 99.10 = 990, nhu v.ây , , , ,
sô´ lu .ong nh˜ung tông kh´ac nhau nhiê`u nhâ´t l`a 990. Theo nguyên l´y , , ,
Ðirichlê trong sô´ 1023 t .âp h .op con cua t.âp h .op gô`m 10 sô´ s˜e c´o ´ıt , ,, ,
nhâ´t hai t .âp m`a tông c´ac phâ`n tu trong ch´ung phai b`˘ang nhau. J , , , , 120 Chuong 11. To´ an h .oc tô h .op ,
. 11.2. Cho 15 b` ai to´ an tr´ ˘
ac nghi.êm, ¯d´anh sô´ t`u 1 ¯dê´n 15, m˜ôi b`ai , , , , chı c´ o hai kha n˘ ang tra l` oi : ¯ d´
ung ho .˘ac sai. C´o 1600 th´ı sinh tham gia , , , , thi, nhung không c´ o ai tra l` oi ¯ d´ ung 2 b` ai liê`n nhau. Ch´ ung minh r` ˘ ang , , , c´
o ´ıt nhâ´t hai th´ı sinh tra l` oi to`
an b .ô 15 b`ai h.êt nhu nhau. , , , , , , , ,, L` oi giai. B` ai l` am cua m˜ ôi th´ı sinh tuong ´ ung v´ oi m .ôt d˜ay 15 phâ`n tu, ,, , m˜
ôi phâ`n tu ho .˘ac l`a Ð (¯d´ung) ho.˘ac l`a S (sai). Theo gia thiê´t không ,, ,, c´ o d˜ ay n` ao c´ o 2 phâ`n tu kê` nhau l` a Ð, Ð, nên sô´ tô´i ¯ da c´ ac phâ`n tu SS trong d˜ ay l` a 8. ,
Ta nh .ân thâ´y v´oi m˜ôi 0 ≤ k ≤ 8 th`ı sô´ c´ac d˜ay c´o ¯d´ung k phâ`n ,, ,, , , , , , tu Ð l`
a C15−k+1 = C16−k (boi v`ı m˜ ôi m thê´ tuong ¯ duong k k .ôt d˜ ay nhu , , , , v´ oi c´ ach ¯
d .˘at k tâ´m b`ıa gi˜ua 15 − k quyên s´ach: c´o tâ´t ca 16 − k v.i tr´ı , , , , ¯ dê ¯
d .˘at b`ıa, kê ca hai ¯dâ`u cua chô`ng s´ach ¯d´o).
V .ây l`a sô´c´ac d˜ay c´o t´ınh châ´t nêu trên l`a 8
∑ C16−k = 1 + 15 + 91 + 286 + 495 + 462 + 210 + 36 + 1 k k=0 = 1597 < 1600 , , , , , Ðiê`u n` ay ch´ ung to r` ˘ ang phai c´
o ´ıt nhâ´t 2 th´ı sinh c´ o c´ ac câu tra l` oi , h .êt nhu nhau. , , ,
. 11.3. Trong m .ôt h`ınh 9 c .anh ¯dê`u c´o m.ôt ¯dınh ¯du.oc tô mâ`u tr´˘ang , , , , c` on c´ ac ¯ dınh kh´ ac ¯
du .oc tô ¯den. Ch´ung minh r`˘ang tô`n t .ai hai tam gi´ac , , ,
phân bi.êt to`an ¯d˘ang (di.ên t´ıch b`˘ang nhau) m`a c´ac ¯dınh cua m˜ôi tam , , gi´ ac ¯
du .oc tô c`ung m.ôt mâ`u. , , , , , , , , , L` oi giai. T` u 9 ¯ dınh ¯
du .oc tô mâ`u th`ı´ıt nhâ´t c˜ung c´o 5 ¯dınh ¯du .oc tô , ,, c`
ung m .ôt mâ`u. Gia su ¯d´o l`a mâ`u tr´˘ang. N˘am mâ`u tr´˘ang t.ao th`anh 5.4.3 , C5 = = 10 tam gi´ ac phân bi ´ y r` ˘ ang 3 .êt c`
ung m .ôt mâ`u tr´˘ang. Ðê 2.3 11.1. V´ı d .u 121 2kπ , ph´ ep quay m .ôt g´oc
(k = 0, 1, . . . , 8) xung quanh tâm O cua 9 , ,,, , ,
h`ınh 9 c .anh ¯dê`u không anh huong ¯dê´n t.âp M c´ac ¯dınh cua h`ınh 9
c .anh n`ay. V`ı thê´ sau khi quay m˜ôi tam gi´ac trong 10 tam gi´ac trên 2kπ , , m .ôt g´oc
(0 ≤ k ≤ 8) xung quanh O ta ¯ du .oc 10.9 = 90 tam gi´ac 9 , , , , c´ o ¯
dınh trong t .âp h .op M. Tâ´t ca ch´ung không thê phân bi.êt v`ı sô´ , , 2.8.7 tam gi´ ac kh´ ac nhau c´ o ¯
dınh trong t .âp h .op M b`˘ang C5 = = 3 2.3 78 < 90. , , ,
Nhu v .ây ta t`ım ¯du .oc hai tam gi´ac tr´˘ang ∆1 v`a ∆2 sau m .ôt v`ai , , ph´ ep quay tr` ung v´ oi c`
ung m .ôt tam gi´ac ∆. Luu ´y l`a hai tam gi´ac ∆1 , , v`
a ∆2 l`a phân bi.êt. Th.ât thê´, hai tam gi´ac nhu nhau không thê c´o , , , ¯
du .oc sau khi quay t`u m .ôt tam gi´ac. , V`ı m˜ ôi tam gi´
ac ∆1 v`a ∆2 s˜e tr`ung v´oi tam gi´ac ∆ sau khi quay, , , , , nên t` u tam gi´
ac ∆1 b`˘ang m .ôt ph´ep quay ta c´o thê nh.ân ¯du .oc tam , gi´
ac ∆2 (ch˘ang h .an c´ac ph´ep quay ∆1 → ∆, ∆ → ∆2). V.ây ∆1 v`a ∆2 , l` a hai tam gi´ ac phai t`ım. J , , ,,
. 11.4. Trên m .˘at ph˘ang c´o n h`ınh. Gia su Si , l` a di 1 ...ik .ên t´ıch phâ`n , , , giao cua c´ ac h`ınh th´
u i1, . . . , ik, c`on S l`a di.ên t´ıch phâ`n m .˘at ph˘ang b.i , ,, , , , , phu boi c´ ac h`ınh ¯ d´ o. K´
y hi.êu Mk l`a tông tâ´t ca c´ac Si , t´ uc l` a tông 1 ...ik , , , , ,
di.ên t´ıch cua tâ´t ca c´ac h`ınh c´o thê c´o l`a giao cua k h`ınh ¯d˜a cho. Ch´ung minh r` ˘ ang
a) S = M1 − M2 + M3 − . . . − (−1)n+1Mn ,
b) S ≥ M1 − M2 + M3 − . . . − (−1)n+1Mn v´oi m ch˜˘ an v` a , ,
S ≤ M1 − M2 + M3 − . . . − (−1)n+1Mn v´oi m le. , , ,, , ,, L` oi giai. a) K´
y hi .êu Cn l`a sô´ c´ach ch u t` u n phâ`n tu, ta k .on k phâ`n t , , c´
o nh.i th´uc Niuton (x + y)n = ∑nk=0 Cnxkyn−k. K´y hi k .êu Dm l` a di .ên , , , , 122 Chuong 11. To´ an h .oc tô h .op , , ,, ,
t´ıch phâ`n m .˘at ph˘ang b.i phu boi ¯d´ung m h`ınh. Phâ`n m.˘at ph˘ang ¯d´o , , , , ,, gô`m nh˜ ung manh, m˜
ôi manh b.i phu boi m h`ınh x´ac ¯d.inh n`ao ¯d´o. , , , , ,,
Khi t´ınh Mk di.ên t´ıch m˜ôi manh nhu v.ây, s˜e ¯du .oc t´ınh Cm lâ`n, boi v`ı k , , , , , t` u m h`ınh c´
o thê t .ao ¯du .oc Cm giao cua k h`ınh. Do ¯d´o k Mk = CkkDk + Ck+1D k k+1 + · · · + Cn k Dn
Suy ra M1 − M2 + M3 − · · · + (−1)n+1 = C1D − C2)D 1 1 + (C2 1 2 2 +
· · · + (Cn − Cn + Cn − · · · )D 1 2 3 n = D1 + D2 + · · · + Dn ,, , ,
boi v`ı do nh.i th´uc Niuton Cm − Cm + 3m − · · · − (−1)mCm 1 2 m = (−1 +
Cm − Cm + Cm − · · · − (−1)mCm 1 2 3 m ) + 1 = (1 − 1)m + 1 = 1 , Cuô´i c` ung ch´ ung ta luu ´ y r` ˘
ang S = D1 + D2 + · · · + Dn. , b) T` u phâ`n a) ta c´ o
S − (M1 − M2 + · · · + (−1)m+1Mm) =
= (−1)m+2 Mm+1 + (−1)m+3Mm+2 + · · · + (−1)n+1Mn n
= ∑((−1)m+2Cim+ + · · · + (− 1 1)n+1Cin)Di i=1 , , , , , (Ta qui u´
oc nê´u k > i th`ı Ci = 0. Do ¯ d´ o ta chı câ`n phai ch´ ung minh k r` ˘ ang: , Ci − Ci + Ci
− . . . − (−1)m+n+1Ci ≥ 0 v´oi i ≤ n. m+1 m+2 m+3 n , , , , , T` u ¯ d˘ ang th´
uc (x + y)i = (x + y)i−1(x + y) suy ra ¯ d˘ ang th´ uc Ci = Ci−1 + Ci−1. j j−1 j Do ¯ d´ o Ci − − m+1 Cim+2 + Cim+3 . . . − (−1)m+n+1Cin = = Ci−1 − − m + Ci−1 Ci−1 + Ci−1 . . . m+1 m+2 m+3
+(−1)m+n+1Ci−1 + (−1)m+n+1Ci−1 ± Ci−1 n−1 n = Ci−1 m n , , , Cuô´i c` ung chı câ`n luu ´ y r` ˘ ang Ci−1 n = 0 v´ oi i ≤ n. J 11.1. V´ı d .u 123 ,
. 11.5. M .ôt c´ai ´ao di.ên t´ıch b`˘ang 1 c´o 5 miê´ng v´a, m`a di.ên t´ıch cua , , , , , m˜ ôi miê´ng v´
a không nho hon 0,5. Ch´ ung minh r` ˘ ang luôn t`ım ¯ du .oc hai , , , miê´ng v´ a c´
o di.ên t´ıch phâ`n chung cua ch´ung không nho hon 0,2. , , , ,, , L`
oi giai. Gia su di .ên t´ıch c´ai ´ao b`˘ang M, di.ên t´ıch phâ`n giao cua c´ac , , miê´ng v´ a th´ u i1, . . . , ik b`˘ang Si , c` on M . T` u b` ai trên suy 1 ...ik k = ∑ Si1...ik ,, ,
ra M − M1 + M2 − M3 + M4 − M5 ≥ 0, boi v`ı M ≥ S. C´ac bâ´t ¯ d˘ ang , , , , , , , , , th´
uc tuong t .u c´o thê ¯du .oc viê´t không chı cho ca c´ai ´ao, m`a c`on cho , , , t` ung miê´ng v´ a. Nê´u ta coi miê´ng v´
a S1 nhu m .ôt c´ai ´ao v´oi c´ac miê´ng , , v´
a S12, S13, S14, S15 th`ı ta ¯
du .oc S1 − ∑ S1i + ∑ S1ij − ∑ S1ijk + S12345 ≥ , , , , , ,
0. C .ông c´ac bâ´t ¯d˘ang th´uc nhu v.ây cho tâ´t ca 5 miê´ng v´a, ta ¯du .oc ,,
M1 − 2M2 + 3M3 − 4M4 + 5M5 ≥ 0 (h .ang tu Si c´ o trong c´ ac 1 ...ik , , , , bâ´t ¯ d˘ ang th´ uc cho c´ ac miê´ng v´
a i1 . . . ik, nên trong tông tâ´t ca c´ac , , , , bâ´t ¯ d˘ ang th´ uc n´ o c´
o h .ê sô´ k). C .ông c´ac bâ´t ¯d˘ang th´uc 3(M − M1 +
M2 − M3 + M4 − M5) ≥ 0 v`a M1 − 2M2 + 3M3 − 4M4 + 5M5 ≥ 0, , , , ta ¯
du .oc 3M − 2M1 + M2 − M4 + 2M5 ≥ 0. C .ông v`ao ¯d´o bâ´t ¯d˘ang , , , , , th´ uc M4 − 2M5 ≥ 0, (¯
du .oc suy ra t`u S12345 c´o trong tâ´t ca c´ac Si1i2i3i4 , , , , t´ uc l` a M4 ≥ 5M5 ≥ 2M5), ta ¯
du .oc 3M − 2M1 + M2 ≥ 0, t´uc l`a ,, , , , ,
M2 ≥ 2M1 − 3M ≥ 5 − 3 = 2. Boi v`ı t`u 5 miê´ng v´a c´o thê t .ao ¯du .oc , ,
10 c .˘ap, nên di.ên t´ıch giao cua m .ôt trong sô´ c´ac c.˘ap ¯d´o không nho , M hon 2 ≥ 0, 2. J 10 , , ,, , ,
. 11.6. (Ðê` thi To´ an vô ¯
d.ich CHLB Ð´uc, 1979) Gia su m˜ôi ¯diêm cua , , , , , ,
m .˘at ph˘ang ¯du.oc tô b`˘ang 1 trong n mâ`u (n l`a sô´ t .u nhiên cho tru´oc). , , , , , , Ch´ ung minh r` ˘
ang tô`n t .ai m.ôt h`ınh ch˜u nh .ât v´oi c´ac ¯dınh ¯du.oc tô c`ung m .ôt mâ`u. , , , L`
oi giai. Ta thiê´t l .âp trong m.˘at ph˘ang m .ôt h.ê to.a ¯d .ô Ðê` c´ac vuông , , , g´ oc tu` y ´ y v` a ch´ u ´ y t´ oi ¯ diêm nguyên (i, j) v´ oi 1 ≤ i ≤ n + 1 v`a , , , , 124 Chuong 11. To´ an h .oc tô h .op , , , ,
1 ≤ j ≤ nn+1 + 1. Vi .êc tô mâ`u kê theo th´u t .u n + 1 ¯diêm trên m˜ôi , d` ong c´ o nn+1 c´ach kh´ac nhau (m˜ ôi ¯ diêm c´ o n c´ach tô). Do ¯ d´ o c´ o , , ´ıt nhâ´t l` a 2 d` ong trong sô´ nn+1 + 1 d` ong ¯ du .oc tô mâ`u giô´ng nhau ,, , , , (ngh˜ıa l` a hai d`
ong giô´ng nhau vê` mâ`u s´ ˘ ac tô o ¯ diêm th´ u nhâ´t, ¯ diêm , , , , , , , ,, th´ u hai,. . . ,¯ diêm th´
u n + 1 ch˘ang h .an t´ınh t`u tr´ai qua phai). Gia su , , , hai d` ong â´y l` a d` ong nh˜ ung ¯ diêm c´
o to .a ¯d .ô k v`a m; ngh˜ıa l`a v´oi m˜ôi , ,, i ∈ {1, 2, . . . , n} c´ ac ¯ diêm (i, k) v`a (i, m) c´ o c` ung m .ôt mâ`u. Boi v`ı , , , chı c´
o n mâ`u nên trong sô´ n + 1 ¯ diêm trên d` ong c´ ac ¯ diêm c´ o tung , , , ¯
d .ô k ´˘at c´o ´ıt nhâ´t hai ¯diêm c´o c`ung mâ`u, ch˘ang h.an, ¯d´o l`a 2 ¯diêm , , , (a, k) v` a (b, k). Khi ¯ d´ o h`ınh ch˜
u nh .ât v´oi c´ac ¯dınh (a, k), (b, k), (b, m) , v` a (a, m) c´ o 4 ¯ dınh c` ung mâ`u. J , , ,
. 11.7. Cho 1000 ¯
diêm trên m .˘at ph˘ang M1, M2, . . . , M1000. Ch´ung , , , , , minh r` ˘ ang trên bâ´t c´ u ¯ du` ong tr` on b´ an k´ınh 1 n` ao ta ¯ dê`u t`ım ¯ du .oc m.ôt , , , , , ¯
diêm S sao cho tông khoang c´ ach t` u S ¯ dê´n c´ ac ¯
diêm M1, M2, . . . , M1000 , , không nho hon 1000. , , , ,, , , , , L`
oi giai. Gia su S1 v`a S2 l`a hai ¯ diêm tu` y ´ y ¯ dô´i tâm cua ¯ du` ong tr` on T b´ an k´ınh 1. Ta c´
o S1S2 = 2, v .ây S1M1 + S2M2 ≥ S1S2 = 2;
S1M2 + S2M2 ≥ 2;. . . ; S1M1000 + S2M1000 ≥ 2. V`ı thê´ (S1M1 +
S2M1) + (S1M2 + S2M1) + · · · + (S1M1000 + S2M1000) = (S1M1 +
S1M2 + · · · + S1M1000) + (S2M1 + S2M2 + · · · + S2M1000) ≥ 2000. , , Do ¯ d´
o ´ıt nhâ´t m .ôt trong hai ¯diêm S1 v`a S2 ch´˘ac ch´˘an thoa m˜an , , , , b` ai ra l` a tông khoang c´ ach t` u n´ o ¯ dê´n c´ ac ¯ diêm M1, M2, . . . , M1000 , , không nho hon 1000. J , ,
. 11.8. Cho 37 ¯
diêm phân bi.êt trong không gian c´o to .a ¯d.o l`a nh˜ung , , ,
sô´ nguyên sao cho không c´ o ba ¯ diêm n` ao th˘ ang h` ang. Ch´ ung minh , , , , r` ˘ ang ta c´
o thê ch .on 3 ¯diêm m`a to .a ¯d.ô giao ¯diêm c´ac trung tuyê´n cua tam gi´
ac t .ao th`anh ¯dê`u l`a sô´nguyên. 11.1. V´ı d .u 125 , , , , , , L` oi giai. V´ oi m˜ ôi ¯ diêm x; y; z c´
o to .a ¯d .ô l`a nh˜ung sô´ nguyên (¯diêm , , , , , , nguyên) ta cho tuong ´ ung c´
ac sô´ ¯x; ¯y; ¯z l`a nh˜ung sô´ du cua ph´ep chia c´
ac sô´ x; y; z cho 3. V`ı ¯x nh .ân không qu´a 3 gi´a tr.i nên ´ıt nhâ´t , , 13 trong sô´37 ¯ diêm c´ o c` ung gi´
a tr.i (nê´u không, thê´th`ı sô´c´ac ¯diêm , , , , , , , không l´
on hon 12.3=36). Tuong t .u, c´o không´ıt hon 5 trong 13 ¯diêm , ¯ d´ o c´ o gi´ a tr.i ¯y nhu nhau. , , , Thê´ th`ı giao ¯ diêm c´ ac trung tuyê´n cua tam gi´ ac c´ o ¯ dınh (x1, y1, z1),
(x2, y2, z2) v`a (x3, y3, z3) c´o to .a ¯d .ô x y z x 1 + x2 + x3 1 + y2 + y3 1 + z2 + z3 0 = ; y ; z 3 0 = 3 0 = 3
Nê´u ¯x1 = ¯x2 = ¯x3 v`a ¯y1 = ¯y2 = ¯y3 th`ı c´ac sô´ x0 v`a y0 l`a nguyên c`on , ,
sô´ z0 chı nguyên khi v`a chı khi z1 + z2 + z3 ≡ 0( mod 3). Trong , , , , , tru`
ong h .op b`ai ra ta ch .on ra 5 ¯diêm m`a tâ´t ca sô´ ¯x b`˘ang nhau v`a tâ´t , , , , ,
ca sô´ ¯y b`˘ang nhau. Nê´u trong c´ac ¯ diêm n` ay ta t`ım ¯ du .oc ba ¯diêm m`a , , c´
ac sô´ ¯z nh .ân c´ac gi´a tr.i 0; 1; 2 th`ı v´oi c´ac ¯diêm ¯d´o ta c´o
z1 + z2 + z3 ≡ ¯z1 + ¯z2 + ¯z3 ≡ 0 + 1 + 2 ≡ 0( mod 3) , , , , Nê´u không c´ o nh˜ ung ¯ diêm n` ay th`ı sô´ ¯z v´ oi 5 ¯ diêm ¯ d˜ a ch .on s˜e nh.ân , , , không qu´ a 2 gi´
a tr.i, do ¯d´o ta t`ım ¯du .oc 3 ¯diêm m`a gi´a tr.i ¯z nh.ân c`ung , ,
m .ôt gi´a tr.i m`a sô´z0 ´ung v´oi n´o l`a sô´nguyên. J , , , ,
. 11.9. Trên m .˘at ph˘ang cho 7 ¯du`ong th˘ang trong ¯d´o không c´o hai , , , , , , ¯ du` ong th˘ ang n` ao song song. Ch´ ung minh r` ˘ ang ta t`ım ¯ du .oc hai trong , , , , , , 7 ¯ du` ong th˘ ang n´ oi trên m` a g´ oc gi˜ ua ch´ ung nho hon 260. , , , , , , L` oi giai. Ta h˜
ay t.inh tiê´n tâ´t ca 7 ¯du`ong th˘ang ¯d˜a cho sao cho ch´ung , , , , , , c` ung ¯
di qua m .ôt ¯diêm cô´ ¯d.inh O. Ta s˜e ¯du .oc 7 ¯du`ong th˘ang chia g´oc , , ¯ dâ`y ¯
dınh O th`anh 14 phâ`n. V`ı thê´ m .ôt trong c´ac g´oc t.ao th`anh nho , 3600 5 , hon = 250 < 260 (nê´u tâ´t ca c´ ac g´ oc ¯ dê`u b` ˘ ang nhau th`ı m˜ ôi 14 7 , , , , 126 Chuong 11. To´ an h .oc tô h .op , , , , , , , g´ oc không l´ on hon 260). Nhung g´ oc gi˜ ua hai ¯ du` ong th˘ ang c´ ˘ at nhau , , , , b` ˘ ang g´ oc gi˜ ua hai ¯ du` ong th˘ ang ban ¯ dâ`u. J . 11.10. Cho A l`
a m .ôt t.âp c´ac sô´nguyên v`a x l`a m .ôt sô´nguyên bâ´t , , k`
y. T .âp h .op x + A = {x + a|a ∈ A} g .oi l`a t.inh tiê´n cua A x´ac ¯d.inh ,, , ,, , bo i x. Hay n´ oi c´ ach kh´
ac t .âp h .op x + A gô`m c´ac phâ`n tu cua A c .ông , , , thêm v´ oi c`
ung m .ôt sô´ x. Ch´ung ta n´oi r`˘ang m .ôt t.âp h .op nh˜ung sô´ , , nguyên l`
a k-nho nhâ´t, nê´u tô`n t .ai k t.âp t.inh tiê´n cua A, m`a ch´ung , , , , t` ung ¯ dôi không c´ o ¯
diêm chung. V´ı d .u: m .oi t.âp sô´h˜uu h.an l`a k-nho , , , , nhâ´t v´
oi m .oi sô´nguyên duong k. C˜ung c´o t.âp vô h.an l`a k-nho nhâ´t , , , nhu d˜
ay k + 1, (k + 1)2, . . . , (k + 1)n, . . . Nhung ch´ ung ta ch´ ung minh kê´t lu .ân sau: , , , , , Cho n l`
a sô´t .u nhiên. Khi ¯d´o t .âp h.op nh˜ung sô´nguyên không thê biêu , , , , , di˜
ên nhu h .op cua n t .âp h.op (n + 1)-nho nhâ´t. , , , ,, , , , , L` oi giai. Ch´
ung ta gia su ngu .oc l.ai: tô`n t.ai nh˜ung t.âp h .op (n + 1)- ,
nho nhâ´t A1, A2, . . . , An sao cho m˜ôi sô´ nguyên thu .ôc m .ôt trong , , , , , nh˜
ung t .âp h .op n`ay. Theo ¯d.inh ngh˜ıa cua t.âp (n + 1)-nho nhâ´t v´oi
m .oi i = 1, 2, . . . , n tô`n t.ai n + 1 sô´nguyên ai,1, ai,2, . . . , ai,n+1 sao cho , , v´
oi 1 ≤ r ≤ n + 1, 1 ≤ s ≤ n + 1 v`a r 6= s nh˜ung ph´ep t.inh tiê´n , ,
air + Ai v`a ais + Ai không c´o ¯ diêm chung. K´ y hi .êu N l`a t.âp h .op , , , ,,
tâ´t ca n-b .ô s´˘ap th´u t .u (j1, j2, . . . , jn) o ¯dây j1, j2, . . . , jn ¯d .ôc l.âp nh.ân , , c´ ac gi´
a tr.i 1, 2, . . . , n, n + 1. V´oi m˜ôi n-b .ô a = (j1, j2, . . . , jn) t`u N , , , , ,, cho tuong ´ ung v´
oi m .ôt sô´ nguyên xa = a1j + a + · · · + a . Boi 1 2j2 njn , , , , , v`ı ch´ ung ta ¯ d˜
a gia thiê´t t .âp h .op nh˜ung sô´ nguyên l`a h .op cua c´ac ,
t .âp h .op A1, A2, . . . , An, m˜ôi sô´ xa thu .ôc m .ôt t.âp n`ao ¯d´o trong d˜ay , ,, , ,
t .âp h .op trên. Ngo`ai ra sô´phâ`n tu cua N l`a (n + 1)n (¯dây l`a t´ınh tô , , ,,
h .op).T`u nguyên l´y Ðirichle mo r .ông ch´ung ta c´o ´ıt nhâ´t m .ôt trong , , , (n + 1)n c´
ac t .âp A1, A2, . . . , An ch´ua nh˜ung sô´ d.ang xa v´oi ´ıt nhâ´t n 11.2. B` ai t .âp 127 , b .ô a t`u N. , ,
Không mâ´t t´ınh tông qu´ at ch´
ung ta gia thiê´t A1 c´o t´ınh châ´t , ,, , trên. Ch´ ung ta x´ et tâ´t ca c´
ac phâ`n tu α cua N m`a sô´ x thu α .ôc A1. (n + 1)n ,, Ch´ ung gô`m ´ıt nhâ´t
phâ`n tu. Nê´u α = (j n 1, j2, . . . , jn) l` a m .ôt ,, , , , , phâ`n tu trong ch´ ung, th`ı ch´ ung ta cho tuong ´ ung v´ oi (n − 1)-b .ô , s´ ˘ ap 0
α = (j2, j3, . . . , jn). V`ı 1 ≤ j ≤ n + 1 v´oi m µ
.oi µ = 2, 3, . . . , n, , , , , theo t´ınh châ´t tô h 0 .op v´ oi α c´
o nhiê`u nhâ´t (n + 1)n−1 kha n˘ang. , , , (n + 1)n T` u bâ´t ¯ d˘ ang th´ uc
> (n + 1)n−1 suy ra ´ıt nhâ´t c´ o hai n-b .ô n
α = (j1, j2, . . . , jn), β = (k1, k2, . . . , kn) ho` an to` an kh´ ac nhau, m` a , , , , x ∈ A ∈ A ong ´ ung v´ oi c` ung m α 1, xβ 1, tu .ôt (n − 1)-b .ô. , , Ch´ ung ta c´ o thê t´ om t´ ˘ at ng´ ˘
an g .on nhu sau: tô`n t.ai hai b .ô kh´ac
nhau α = (j1, j2, . . . , jn) v`a β = (k1, k2, . . . , kn) thu .ôc N, m`a x ∈ α , A1, x ∈ A ng, x = β 1, j1 6= k1 v`
a j2 = k2, j3 = k3, . . . , jn = kn. Nhu α , a1j + a + · · · + a x = a + a + · · · + a nhung v`ı j = k 1 2j2 njn β 1k1 2k2 nkn µ µ , v´ oi m˜
ôi µ = 2, 3, . . . n ch´ ung ta c´ o x − x = a − a ho α β 1j1 1k1 .˘ ac l` a a1k + x = a + x . Khi ¯ d´ o sô´ x = a + x = a + x thu 1 α 1j1 β 1k1 α 1j1 β .ôc v` ao , ,, t .âp h .op a1k + A + A oi 1 1 v` a a1j1
1. Suy ra t .âp t.inh tiê´n A1 x´ ac ¯ d.inh b , , , c´ ac sô´ a1k v`a a c´ o ¯ diêm chung, ¯ diê`u ¯ d´ o tr´ ai v´ oi gia thiê´t khi b´ ˘ at 1 1j1 , ¯ dâ`u ch´ ung minh. J 11.2. B ` ai t .âp
. 11.11. a) Trong h`ınh vuông di .ên t´ıch 6 ¯d.˘at ba ¯da gi´ac di.ên t´ıch , , , 3. Ch´ ung minh r` ˘ ang trong sô´ ¯ d´ o luôn t`ım ¯
du .oc hai ¯da gi´ac m`a di.ên , , , t´ıch phâ`n chung cua ch´ ung không nho hon 1. ,
b) Trong h`ınh vuông di .ên t´ıch 5 ¯d.˘at 9 ¯da gi´ac di.ên t´ıch 1. Ch´ung , , minh r` ˘ ang trong sô´ ¯ d´ o luôn t`ım ¯
du .oc hai ¯da gi´ac m`a di.ên t´ıch phâ`n , , , , 128 Chuong 11. To´ an h .oc tô h .op , , , 1 chung cua ch´ ung không nho hon . 9 , , , , , . 11.12. S´ au ¯ diêm ¯
du .oc s´˘ap xê´p trên m.˘at ph˘ang sao cho ba ¯diêm , , bâ´t k` y l` a ¯
dınh cua m .ôt tam gi´ac m`a c´ac c.anh c´o ¯d .ô d`ai kh´ac nhau. , , , Ch´ ung minh r` ˘
ang c .anh nho nhâ´t cua m .ôt trong c´ac tam gi´ac ¯dô`ng , , , th` oi l`
a c .anh l´on nhâ´t cua m .ôt tam gi´ac kh´ac. , ,
. 11.13. Cho P1, P2, . . . , P7 l`a bây ¯
diêm trong không gian, trong ¯ d´ o , , không c´ o bô´n ¯ diêm n` ao ¯ dô`ng ph˘ ang. Tô mâ`u m˜ ôi ¯ do .an PiPj (i < j) , , , v´
oi m .ôt trong hai mâ`u ¯do ho.˘ac ¯den. Ch´ung minh r`˘ang c´o hai tam , gi´ ac ¯ don s´ ˘ ac không c´ o chung c .anh. , , . 11.14. C´ o hai ¯ d˜ıa ¯ dê`u ¯
du .oc chia th`anh 1998 h`ınh qu.at b`˘ang nhau, v` a trên m˜ ôi ¯
d˜ıa tô m .ôt c´ach bâ´t k`y (b`˘ang m .ôt mâ`u) 200 h`ınh qu.at. , , , C´ ac ¯ d˜ıa ¯
du .oc ¯d.˘at chô`ng lên nhau v`a quay m .ôt ¯d˜ıa theo nh˜ung g´oc , 3600 , l` a b .ôi cua . Ch´ ung minh r` ˘
ang tô`n t .ai ´ıt nhâ´t 94 v.i tr´ı c´o không 1998 , , , qu´
a 20 h`ınh qu .at ¯du .oc son tr`ung nhau. , , , , ,
. 11.15. Trên m .˘at ph˘ang cho n ¯du`ong th˘ang t`ung ¯dôi không song , , , , , , song v´ oi nhau. Ch´ ung minh r` ˘ ang g´ oc gi˜ ua hai ¯ du` ong th˘ ang n` ao ¯ d´ o , , 1800 trong sô´ ¯ d´ o không l´ on hon . n , , CHUONG 12 M .ÔT S ´ Ô B ` AI T .ÂP H`INH H .OC KH ´AC 12.1. V´ı d .u , , ,
. 12.1. Trong h`ınh ch˜
u nh .ât 3x4 ¯d .˘at 6 ¯diêm. Ch´ung minh r`˘ang trong , , , , , , sô´ ¯ d´ o luôn t`ım ¯
du .oc hai ¯diêm c´o khoang c´ach gi˜ua ch´ung không l´on , √ hon 5. , , , L`
oi giai. Chia h`ınh ch˜u nh .ât ra l`am ,
5 h`ınh nhu h`ınh 12.1. Trong m .ôt trong sô´ c´ ac h`ınh ¯ d´ o s˜ e c´ o ´ıt nhâ´t , , , 2 ¯ diêm, v` a khoang c´ ach gi˜ ua hai , , , √ ¯ diêm ¯ d´ o s˜ e không l´ on hon 5. J H`ınh 12.1: , , ,
. 12.2. Trên m .˘at ph˘ang c´o 25 ¯diêm, biê´t r`˘ang trong 3 ¯diêm bâ´t k`y , , , , trong sô´ ¯ d´ o luôn c´ o 2 ¯ diêm c´
ach nhau nho hon 1. Ch´ ung minh r` ˘ ang , , ,
tô`n t .ai h`ınh tr`on b´an k´ınh 1 ch´ua không ´ıt hon 13 ¯diêm ¯d˜a cho. , , , ,, , , , L`
oi giai. Gia su A l`a m .ôt ¯diêm ¯d˜a cho. Nê´u tâ´t ca c´ac ¯diêm c`on l.ai , n` ˘ am trong h`ınh tr`
on S1 tâm A b´an kinh 1 th`ı ta không câ`n phai , , ,, , ch´
ung minh g`ı thêm. Gia su c´
o m .ôt ¯diêm B trong sô´ ¯d˜a cho n`˘am , , , ngo` ai ¯ du` ong tr`
on S1 t´uc l`a AB > 1. X´et h`ınh tr`on S2 tâm B b´an k´ınh , , 1. Trong sô´ c´ ac ¯ diêm A, B, C trong ¯ d´ o C l`a ¯ diêm ¯ d˜ a cho bâ´t k` y luôn , , , , , , , c´ o hai ¯ diêm c´ ach nhau nho hon 1, hon n˜ ua ¯ d´ o không thê l` a 2 ¯ diêm , , 130
Chuong 12. M .ôt sô´b`ai t.âp h`ınh h .oc kh´ac , , , A v` a B. Do ¯ d´ o c´ ac h`ınh tr`
on S1 v`a S2 ch´ua tâ´t ca c´ac ¯ diêm ¯ d˜ a cho, , , , , t´ uc l`
a m .ôt trong hai h`ınh tr`on ¯d´o ch´ua không ´ıt hon 13 ¯diêm ¯d˜a cho. J , , ,
. 12.3. Bên trong ¯ du` ong tr` on b´ an k´ınh n ¯
d .˘at 4n ¯do .an th˘ang c´o ¯d.ô d`ai , , , , , , 1. Ch´ ung minh r` ˘ ang c´
o thê ke m .ôt ¯du`ong th˘ang song song ho .˘ac vuông , , , , , , , g´ oc v´ oi ¯ du` ong th˘ ang l cho tru´ oc v` a c´ ˘ at ´ıt nhâ´t 2 ¯
do .an th˘ang ¯d˜a cho. , , , ,, , , , , L`
oi giai. Gia su l1 l`a ¯ du` ong th˘ ang bâ´t k` y vuông g´ oc v´ oi l. K´y hi .êu , , , , , , ¯
d .ô d`ai c´ac h`ınh chiê´u cua ¯do.an th˘ang th´u i lên c´ac ¯du`ong th˘ang l , , , ,, , , v`
a l1 l`a ai v`a bi tuong ´ung. Boi v`ı ¯
d .ô d`ai cua m˜ôi ¯do.an th˘ang b`˘ang 1, nên ai + bi ≥ 1. Do ¯ d´
o (a1 + · · · + a4n) + (b1 + · · · + b4n) ≥ 4n. , , ,,
Không mâ´t t´ınh tông qu´
at gia su (a1 + · · · + a4n) ≥ (b1 + · · · + b4n). , , , , Khi ¯ d´
o a1 + · · · + a4n ≥ 2n. Tâ´t ca c´ac ¯
do .an th˘ang ¯d˜a cho ¯dê`u ¯du .oc , ,, chiê´u xuô´ng ¯
do .an th˘ang c´o ¯d .ô d`ai 2n, boi v`ı ch´ung ¯dê`u n`˘am trong , , , , , ¯ du` ong tr` on b´
an k´ınh n. Nê´u nhu c´ac h`ınh chiê´u cua c´ac ¯ do .an th˘ang , , , , , ¯ d˜ a cho lên ¯ du` ong th˘ ang l không c´ o ¯ diêm chung, th`ı s˜ e c´ o bâ´t ¯ d˘ ang , , , , th´
uc a1 + · · · + a4n < 2n. Do ¯ d´ o trên l phai c´
o m .ôt ¯diêm b.i c´ac ¯diêm , , , ,
cua ´ıt nhâ´t hai trong sô´ c´ ac ¯
do .an th˘ang ¯d˜a cho chiê´u lên ¯d´o. Ðu`ong , , , vuông g´ oc v´
oi l t .ai ¯diêm ¯d´o s˜e c´˘at ´ıt nhâ´t hai ¯do.an th˘ang ¯d˜a cho. J , ,
. 12.4. Trên do .an th˘ang c´o ¯d.ô d`ai 1 ta tô m.ôt sô´ ¯do .an th˘ang sao , , , , , , cho khoang c´ ach gi˜ ua hai ¯ diêm ¯
du .oc tô bâ´t k`y không b`˘ang 0,1. Ch´ung , , , , , , minh r` ˘ ang tông ¯
d .ô d`ai c´ac do .an th˘ang ¯du.oc tô không l´on hon 0,5. , , , , L` oi giai. Chia ¯
do .an th˘ang ra l`am 10 ¯do.an th˘ang c´o ¯d .ô d`ai 0,1, ¯d.˘at , , ch´
ung theo m .ôt c .ôt v`a chiê´u ch´ung xuô´ng m .ôt ¯do.an th˘ang nhu v.ây. ,, , , , , , Boi v`ı khoang c´ ach gi˜ ua hai ¯ diêm ¯
du .oc tô bâ´t k`y không b`˘ang 0,1, , , , , , , nên c´ ac ¯ diêm ¯
du .oc tô cua c´ac ¯do.an th˘ang c.anh nhau không thê c`ung , , , chiê´u xuô´ng 1 ¯ diêm. Do ¯ d´ o không c´ o ¯ diêm n` ao c´ o thê l` a h`ınh chiê´u 12.1. V´ı d .u 131 , , , , , , , , cua c´ ac ¯ diêm ¯
du .oc tô cua nhiê`u hon 5 ¯do.an th˘ang. Suy ra tông , , , , , , ¯
d .ô d`ai c´ac h`ınh chiê´u cua c´ac ¯do.an th˘ang ¯du .oc tô không l´on hon 5.0, 1 = 0, 5. J , , , , . 12.5. Ch´ ung minh r` ˘
ang nê´u m .ôt ¯du`ong th˘ang l n`˘am trong m .˘at , , , , ph˘ ang cua tam gi´ ac ABC v` a không ¯ di qua ¯ dınh n` ao cua tam gi´ ac ¯ d´ o, , th`ı n´ o c´ ˘ at không qu´
a hai c .anh cua tam gi´ac ¯d˜a cho. , , ,, , , L` oi giai. K´
y hi .êu α v`a α l`a hai nua m.˘at ph˘ang do l chia m.˘at ph˘ang , , ,, cua tam gi´ ac ABC. M˜ ôi ¯
dınh A, B v`a C n`˘am trong m .ôt nua m.˘at , ,, ph˘ ang trên. Theo nguyên l´
y Ðirichlê ´ıt nhâ´t m .ôt trong hai nua m.˘at , , , , , , ph˘ ang trên, ch˘
ang h .an nhu α, ch´ua hai ¯dınh cua tam gi´ac ABC, , , , , , , ch˘
ang h .an nhu A v`a B. Khi ¯d´o ¯du`ong th˘ang l không c´˘at ¯do.an th˘ang , AB, ngh˜ıa l` a n´ o không c´ ˘
at m .ôt trong ba c.anh cua tam gi´ac ABC. J , , , , , , . 12.6. Nh˜ ung ¯
diêm trong m .˘at ph˘ang ¯du.oc son b`˘ang m.ôt trong ba , , , , mâ`u. Ch´ ung minh r` ˘ ang luôn t`ım ¯
du .oc hai ¯diêm c`ung mâ`u c´ach nhau ¯ d´ ung b` ˘ ang 1. , , , ,, , , , L`
oi giai. Gia su hai ¯ diêm bâ´t k` y c´ ach nhau 1 ¯ dê`u ¯ du .oc tô b`˘ang c´ac , mâ`u kh´ ac nhau. X´ et tam gi´ ac ¯ dê`u ABC c´
o c .anh b`˘ang 1. Tâ´t ca c´ac , , , , , ,, , ¯ dınh cua n´ o ¯
du .oc tô b`˘ang c´ac mâ`u kh´ac nhau. Gia su ¯diêm A1 ¯dô´i , , , , , ,, , x´ ung v´ oi A qua ¯ du` ong th˘
ang BC. Boi v`ı A1B = A1C = 1, nên ¯ diêm , , , , ,
A1 c´o mâ`u kh´ac v´oi mâ`u cua B v`a C, t´uc l`a n´o ¯ du .oc tô c`ung m .ôt mâ`u , , , , √ v´ oi ¯
diêm A. C´ac l .âp lu.ân ¯d´o th .uc châ´t ¯d˜a chı ra r`˘ang nê´u AA1 = 3, , , , th`ı c´ ac ¯
diêm A v`a A1 tô c`ung m .ôt mâ`u. Do ¯d´o tâ´t ca c´ac ¯diêm n`˘am , , √ trên ¯ du`ong tr` on tâm A b´an k´ınh 3 c´ o c`
ung m .ôt mâ`u. R˜o r`ang trên , , , , , , , ¯ du` ong tr` on ¯ d´ o luôn t`ım ¯
du .oc hai ¯diêm c´o khoang c´ach gi˜ua ch´ung , , , , , b` ˘ ang 1. Ta ¯
du .oc mâu thu˜ân, v.ây luôn t`ım ¯du .oc hai ¯diêm c`ung mâ`u , , c´ o khoang c´ ach gi˜ua ch´ ung b` ˘ ang 1. J , , 132
Chuong 12. M .ôt sô´b`ai t.âp h`ınh h .oc kh´ac , , ,
. 12.7. Cho 11 ¯ diêm kh´
ac nhau trong h`ınh câ`u thê t´ıch V. Ch´ ung , , , , minh r` ˘
ang qua tâm cua h`ınh câ`u c´
o thê d .ung hai m .˘at ph˘ang sao cho , , V ch´ ung c´ ˘ at h`ınh câ`u th`
anh m .ôt "miê´ng" v´oi thê t´ıch , m` a phâ`n trong 6 , , , , cua n´ o không ch´
ua trong phâ`n trong bâ´t c´
u m .ôt ¯diêm n`ao ¯d˜a cho. , , , L`
oi giai. Chia h`ınh câ`u ra hai b´ an câ`u b` ˘
ang m .ôt m.˘at ph˘ang ¯di qua , , , , tâm v` a hai ¯ diêm t` u c´ ac ¯ diêm ¯ d˜
a cho. M .ôt b´an câ`u ch´ua trong phâ`n , , , ,, trong nhiê`u nhâ´t l` a 4 ¯ diêm t` u c´ ac ¯ diêm c`
on l .ai. Chia nua h`ınh câ`u , , b` ˘
ang hai m .˘at ph˘ang, m`a m˜ôi m.˘at ph˘ang ¯di qua tâm h`ınh câ`u v`a , , , ,, hai ¯ diêm trong 4 ¯ diêm c`
on l .ai. Nhu v.ây nua h`ınh câ`u chia th`anh 3 , , , , "miê´ng" không ch´
ua m .ôt ¯diêm n`ao bên trong. ´ıt nhâ´t thê t´ıch cua , , 1 , , m .ôt miê´ng l´on hon thê t´ıch cua b´ an h`ınh câ`u. J 3 ,
. 12.8. Cho khô´i ¯
da di.ên lô`i P1 c´o 9 ¯dınh A1, A2, . . . , A9.K´y hi.êu , , , ,,
P2, P3, .., P9 l`a nh˜ung ¯da di.ên ¯du.oc t .ao th`anh boi c´ac ph´ep t.inh tiê´n , , , , −−−→ −−−→ , tuong ´ ung theo c´
ac vecto A1A2, . . . , A1A9. Ch´ ung minh r` ˘ ang ´ıt nhâ´t , 2 trong sô´9 ¯
da di.ên trên c´o ´ıt nhâ´t m.ôt ¯diêm chung. , , , , , L` oi giai. X´ et h`ınh ¯
da di .ên P l`a anh cua P1 qua ph´ep v.i t .u tâm A1 , v`
a h .ê sô´2. Ta s˜e ch´ung minh r`˘ang 9 ¯da di.ên ¯dê`u n`˘am trong P. Th.ât , , , v .ây, cho A1, A∗ l` a c´ ac ınh cua ng 2 , . . . , A∗ 9 ¯ d ¯
da di .ên P. Ch´ung ta s˜e ch´u , , , , minh, ch˘
ang h .an nhu P2 n`˘am trong P. Ðê ch´ung minh ¯diê`u ¯d´o ch´ung , −−−→ , , ta ch´ u ´ y t´ oi ph´
ep t.inh tiê´n A1A2 chuyên c´ac ¯diêm A1, A2, . . . , A9 , , ,, , , t´ oi c´ ac ¯ diêm A2, A∗ , o l` a trung m cua 2 , A03, . . . , A09 ¯ dây A0i ¯ diê ¯ do .an A∗ A∗). 2 i , , , Tông thê t´ıch cua c´ ac ¯
da di .ên P1, P2, . . . , P9 n`˘am trong P b`˘ang ,, , , , , 9V, o ¯ dây V l`a thê t´ıch cua ¯
da di .ên P1, c`on thê t´ıch cua ¯da di.ên P , b` ˘
ang 8V. Suy ra ´ıt nhâ´t c´ o hai ¯
da di .ên c´o ¯diêm chung (nguyên l´y , Ðirichlê cho thê t´ıch. J 12.1. V´ı d .u 133 , , ,
. 12.9. Trong h`ınh câ`u ¯ du` ong k´ınh 3 ¯
d .˘at m.ôt sô´ h`ınh câ`u m`a tông , , , , , ¯ du` ong k´ınh cua ch´ ung b` ˘ ang 25 (nh˜ ung h`ınh câ`u n` ay c´ o thê giao , , , , nhau). Ch´ ung minh r` ˘ ang v´
oi m .oi m .˘at ph˘ang tô`n t .ai m.ôt m .˘at ph˘ang , song song v´ oi n´ o v` a c´ ˘
at ´ıt nhâ´t 9 h`ınh câ`u con. , , , , , L` oi giai. Ch´ ung ta x´ et h`ınh chiê´u c´ ac h`ınh câ`u lên ¯ du` ong th˘ ang , , , vuông g´ oc v´
oi m .˘at ph˘ang ¯d˜a cho. H`ınh câ`u l´on chiê´u v`ao m .ôt ¯do.an , , th˘ ang c´ o ¯
d .ô d`ai 3, c`on c´ac h`ınh câ`u con chiê´u v`ao c´ac ¯do.an th˘ang , , , ,, , , nho c´ o tông 25. Gia su không c´
o m .ôt m.˘at ph˘ang n`ao nhu ¯dê` b`ai ra, , , , , ngh˜ıa l`
a m .oi m.˘at ph˘ang song song v´oi m.˘at ph˘ang ¯d˜a cho chı c´˘at 8 , , , , h`ınh câ`u nho. khi ¯ d´ o m˜ ôi ¯ diêm trong ¯
do .an th˘ang ¯d .ô d`ai 3 chı thu .ôc , , , , nhiê`u nhâ´t l` a 8 ¯
do .an th˘ang h`ınh chiê´u cua nh˜ung h`ınh câ`u nho. Suy , , , , , ra tông cua ch´ ung không qu´
a 24. Nh .ân ¯du .oc s .u vô l´y. J , , ,
. 12.10. Trong h`ınh vuông c .anh 1 ¯don v.i c´o m.ôt ¯du`ong gâ´p kh´uc L , , , , ,
không t .u c´˘a v´oi ¯d.ô d`ai l´on hon 1000. Ch´ung minh r`˘ang tô`n t .ai m.ôt , , , , , , , ¯ du` ong th˘
ang m song song v´
oi c .anh h`ınh vuông v`a c´˘at ¯du`ong L t .ai hon , 500 ¯ diêm. , , , ,, , , , , L`
oi giai. Gia su li l`a ¯
d .ô d`ai m´˘at th´u i cua ¯du`ong gâ´p kh´uc, ai v`a bi , , l` a ¯
d .ô d`ai h`ınh chiê´u cua n´o lên c´ac c.anh cua h`ınh vuông. Khi ¯d´o li ≤ ai + bi. Suy ra
1000 = l1 + · · · + ln ≤ (a1 + · · · + an) + (b1 + · · · + bn) , T´ uc l`
a ho .˘ac a1 + · · · + an ≥ 500 ho.˘ac l`a b1 + · · · + bn ≥ 500. Nê´u , , , tông ¯
d .ô d`ai h`ınh chiê´u cua c´ac m´˘at lên m .ôt c.anh ¯d .ô d`ai 1 không nho , , ,
hon 500, th`ı theo nguyên l´ y Ðirichlê cho ¯
d .ô d`ai ¯do.an th˘ang phai c´o , , , , ¯
diêm chung cho hon 500 h`ınh chiê´u cua c´ ac m´ ˘ at gâ´p kh´ uc, t´ uc l` a , , , , , , , ¯ du` ong vuông g´ oc ke t` u ¯ diêm chung ¯ d´ o s˜ e c´ ˘ at ¯ du` ong gâ´p kh´ uc t .ai ´ıt , nhâ´t 500 ¯ diêm. J , , 134
Chuong 12. M .ôt sô´b`ai t.âp h`ınh h .oc kh´ac 12.2. B ` ai t .âp , , , . 12.11. Cho A l`
a t .âp h .op nh˜ung ¯diêm trên m .ôt m.˘at câ`u v`a c´o di.ên , , ,, , , t´ıch l´
on hon nua di .ên t´ıch m.˘at câ`u. Ch´ung minh r`˘ang A ch´ua ´ıt nhâ´t , , , , ,
m .ôt c.˘ap ¯diêm m`a n´o l`a 2 ¯daah u ¯du`ong k´ınh cua qua câ`u. , ,, , , ,
. 12.12. Ta g .oi h`ınh ch˜u th.âp l`a h`ınh t.ao boi c´ac ¯du`ong ch´eo cua ,
h`ınh vuông c .anh 1. Ch´ung minh r`˘ang trong h`ınh tr`on b´an k´ınh 100 , , , , , , chı c´ o thê ¯
d .˘at ¯du .oc m .ôt sô´h˜uu h.an c´ac ch˜u th.âp không c´˘at nhau. , , , , ,
. 12.13. Trên m .˘at ph˘ang cho ¯diêm O. Hoi c´o thê ¯d.˘at trên m.˘at ph˘ang , , , 5 h`ınh tr` on không phu ¯
diêm O sao cho m .oi tia xuâ´t ph´at t`u O c´˘at , , , ,,
không ´ıt hon hai h`ınh tr` on ¯
du .oc hay không ? (c´˘at o ¯dây c´o ngh˜ıa l`a , c´ o ¯ diêm chung). , , , , , , . 12.14. Nh˜ ung ¯
diêm trong m .˘at ph˘ang ¯du .oc son b`˘ang m .ôt trong , , , , hai mâ`u. Ch´ ung minh r` ˘ ang luôn t`ım ¯
du .oc hai ¯diêm c`ung mâ`u c´ach nhau ¯ d´ ung b` ˘ ang 1. , , CHUONG 13 M .ÔT S ´ Ô Ð`Ê THI VÔ Ð.ICH , , , , Nh˜ ung b` ai to´ an thi vô ¯
d.ich c´ac nu´oc l`a c´ac b`ai to´an ¯diên h`ınh cho , , ,
vi .êc v.ân d .ung tr´ı thông minh, s´ang t.ao ¯dê giai. N´o ¯d`oi hoi h .oc sinh , , , , , , , , phai n´ ˘ am ¯
du .oc c´ac kiê´n th´uc co ban v˜ung ch´˘ac v`a hiêu thâ´u ¯d´ao. , , , Ðê giai c´ ac b` ai to´ an thi vô ¯
d.ich phai v.ân d .ung cao t´ınh phân t´ıch , , , v`
a tông h .op c´ac kiê´n th´uc to´an h .oc. Râ´t nhiê`u b`ai to´an thi vô ¯d.ich , , , ,, , , c´ ac nu´ oc c´
o m .ôt phâ`n giai su d .ung nguyên l´y Ðirichlê, c´ac chuong , , , tru´ oc ta ¯ d˜
a g .˘ap m .ôt sô´b`ai. Ðê thu.ân ti.ên cho b.an ¯doj c muô´n tham , , , khao ¯ dâ`y ¯ du vê` chu ¯ dê` n` ay tôi ch´
ep l .ai v`a thô´ng kê ra ¯dây c´ac ¯dê` , , , , thi vô ¯
d.ich c´ac nu´oc chu yê´u trong cuô´n s´ach [4] v`a m .ôt sô´ tuyên , , , ,
t .âp kh´ac. Nhung v`ı t`ai li.êu tham khao c´o h.an, phâ`n suu tâ`m cua tôi , , , ch´ ˘ ac ch´ ˘ an chua ¯ dâ`y ¯ du mong c´
ac b .an ¯d .oc bô sung v`a cho ´y kiê´n. , , , , M˜ ôi b` ai trong chuong n` ay k` em theo tên nu´ oc v` a n˘ am k` y thi vô ¯ d.ich , , nu´ oc ¯ d´ o. , ,
. 13.1. (Anh, 1966) Ch´ ung minh r` ˘ ang t`
u 52 sô´ nguyên bâ´t k` y luôn , , , , , c´
o thê ch .on ¯du.oc ra hai sô´m`a tông ho .˘ac hi.êu cua ch´ung chia hê´t cho 100. , , , , , , L`
oi giai. Tâ´t ca c´ ac sô´du trong ph´ ep chia cho 100, ¯ du .oc chia th`anh , , t` ung nh´
om nhu sau: {0}, {1; 99}, {2; 98}, . . . , {49, 51}, {50}. V`ı c´ o , , tâ´t ca 51 nh´ om, m`
a l .ai c´o 52 sô´, nên theo nguyên l´y Ðirichlê gi˜ua , , 136
Chuong 13. M .ôt sô´ ¯dê` thi vô ¯d.ich , , , ch´ ung phai c´ o hai sô´ m` a c´ ac sô´ du trong ph´ ep chia cho 100 roi v` ao , ,
m .ôt nh´om. Hai sô´n`ay l`a hai sô´câ`n t`ım v`ı nê´u sô´du cua ch´ung b`˘ang , , ,
nhau th`ı hi .êu cua ch´ung chia hê´t cho 100, c`on nê´u sô´du cua ch´ung , , kh´ ac nhau th`ı tông cua ch´ ung chia hê´t cho 100. J , , , ,
. 13.2. (Anh, 1970) Ch´ ung minh r` ˘ ang t`
u t .âp h.op tu`y ´y gô`m n sô´ t .u , , , , nhiên luôn t´ ach ra ¯
du .oc m.ôt t .âp h.op con (kh´ac r˜ông) ch´ua c´ac sô´m`a , , tông cua ch´
ung chia hê´t cho n. , , , ,, , , , L`
oi giai. Gia su v´
oi m .ôt t.âp h .op n`ao ¯d´o ch´ua c´ac sô´a1, a2, . . . , an m`a , , , không thoa m˜ an kh˘ ang ¯
d.inh cua b`ai to´an. Khi ¯d´o không c´o sô´ n`ao trong c´ ac sô´
S1 = a1, S2 = a1 + a2, . . . , Sn = a1 + a2 + · · · + an ,
chia hê´t cho n. V`ı sô´ c´ ac sô´ du kh´ ac không trong ph´ ep chia cho , , n l`
a n − 1, nên theo nguyên l´y Ðirichlê t`ım ¯ du .oc hai sô´ Si v`a Sj , (1 ≤ i < j ≤ n) c´ o c`
ung sô´du. Suy ra hi .êu Sj − Si = ai−1 + · · · + aj , , ,, , chia hê´t cho n, ¯ diê`u n` ay mâu thu˜ ân v´ oi gia su n´ oi trên v` a kh˘ ang , , , , ¯
d.inh cua b`ai to´an ¯du .oc ch´ung minh. J , ,, , ,
. 13.3. (Anh, 1976) Gia su trong t .âp h.op h˜uu h .an X ch.on ra 50 t .âp , , , , ,,
h .op con A1, . . . , A50 sao cho m˜ôi t .âp h.op con ch´ua hon m.ôt nua phâ`n ,, , , , , , ,
tu cua t .âp X. Ch´ung minh r`˘ang c´o thê t`ım ¯du.oc t .âp h.op con B ⊂ X , , ,, ,, ch´
ua không nhiê`u hon 5 phâ`n tu v` a c´
o ´ıt nhâ´t m .ôt phâ`n tu chung cho , c´
ac t .âp h.op A1, A2, . . . A50. , , , ,, ,, , , L`
oi giai. Gia su sô´ c´
ac phâ`n tu cua t .âp X b`˘ang n. M˜ôi t.âp h .op con , , , , n ,, ¯
du .oc ch .on A1, . . . , A50 ch´ua không ´ıt hon phâ`n tu, c´ o ngh˜ıa l` a 2 , ,, , , , , n tông sô´ c´ ac phâ`n tu cua tâ´t ca c´
ac t .âp n`ay vu .ot qu´a 50. = 25.n. 2 ,, , Theo nguyên l´
y Ðirichlê tô`n t .ai m .ôt phâ`n tu cua X thu .ôc không ´ıt 137 , , , , , ,
hon 26 t .âp con ¯d˜a ch .on. Tuong t .u ta ch´ung minh v´oi gi´a tr.i bâ´t k`y , , , k < 50 gi˜ua c´
ac t .âp Ai , A , . . . , A c´o thê ch n 1 i2 ik .on ra không ´ıt ho k , , ,, ,, ,
+ 1 t .âp h .op ch´ua c`ung m .ôt phâ`n tu. Ta lâ´y phâ`n tu cua m .ôt 2 , , ,,
t .âp h .op X m`a n´o thu .ôc không ´ıt hon 26 t.âp (phâ`n tu n`ay s˜e l`a m .ôt ,, , , , ,,
trong 5 phâ`n tu cua t .âp h .op B). Ta lo.ai ra 26 t.âp m`a ch´ua phâ`n tu , , ,, , ¯ d˜ a x´ et. Khi ¯ d´ o t`ım ¯
du .oc 1 phâ`n tu thu .ôc ´ıt nhâ´t 13 t`u 24 t.âp c`on l.ai. , , ,
Ta l .ai lo.ai 13 t.âp n`ay ra, khi ¯d´o gi˜ua 11 t.âp c`on l.ai t`ım ¯du .oc 1 phâ`n ,, , , , ,
tu thu .ôc không ´ıt hon 6 trong sô´c´ac t.âp h .op. Ðô´i v´oi 5 t.âp h .op c`on , , ,, ,
l .ai t`ım ¯du .oc 1 phâ`n tu thu .ôc không ´ıt hon 3 trong sô´ch´ung. V`a cuô´i ,, , c`
ung tô`n t .ai m .ôt phâ`n tu thu .ôc hai t.âp cuô´i c`ung. Nhu v.ây ta t`ım , , , ,, , , , ¯
du .oc không nhiê`u hon 5 phâ`n tu cua t.âp X (c´o thê ´ıt hon v`ı m .ôt v`ai ,, phâ`n tu s˜ e tr` ung nhau), ch´ ung s˜
e t .ao th`anh t.âp B. Ngo`ai ra m .ôt t.âp , , ,, bâ´t k` y t`
u A1, . . . , A50 ch´ua ´ıt nhâ´t m .ôt trong c´ac phâ`n tu ¯d´o. ,
. 13.4. (Ba Lan, 1979) Khi chia c´
ac sô´ t .u nhiên a1, a2, . . . , an cho sô´ , , , , , m
t .u nhiên m n`ao ¯d´o, nh .ân ¯du.oc c´ac sô´du kh´ac nhau, ¯dô`ng th`oi n > . 2 , , Ch´ ung minh r` ˘ ang v´
oi m .oi sô´ k ∈ Z tô`n t .ai c´ac sô´ i, j ∈ {1, 2, . . . , n}
(không nhâ´t thiê´t kh´
ac nhau) sao cho sô´ ai + aj − k chia hê´t cho m. , , L` oi giai. X´
et 2n sô´a1, a2, . . . , an, k − a1, k − a2, . . . , k − an. V`ı 2n > m, , nên c´ o 2 trong c´ ac sô´ ¯ d´ o c´ o c` ung sô´du trong ph´ ep chia cho m. Theo , ¯
diê`u ki .ên b`ai to´an, c´ac sô´ a1, a2, . . . , an, c´o sô´ du kh´ac nhau trong, ph´
ep chia cho m, nên c´ac sô´ k − a1, k − a2, . . . , k − an c˜ung c´o sô´du , , , kh´ ac nhau. Do ¯ d´
o c .˘ap sô´c´o sô´du b`˘ang nhau chı c´o thê l`a hai sô´c´o , ,
d .ang ai v`a k − aj v´oi i, j n`ao ¯d´o. Khi ¯d´o hi.êu cua ch´ung ai + aj − k chia hê´t cho m. J , ,
. 13.5. (Ba Lan, 1977) Ch´ ung minh r` ˘ ang v´
oi m .oi gi´a tr.i a, b ∈ R v`a , , ,
e > 0, tô`n t .ai c´
ac sô´ k, m ∈ Z v`
a n ∈ N thoa m˜ an c´ ac bâ´t ¯ d˘ ang th´ uc , , 138
Chuong 13. M .ôt sô´ ¯dê` thi vô ¯d.ich
|na − k| < e v`a |nb − m| < e. , , 1 , L`
oi giai. Cho sô´ nguyên N > v` a v´ oi m˜
ôi c .˘ap x, y ∈ [0; 1] ta thay e , , thê´ b` ˘
ang c .˘ap u, v thoa m˜an u = [Nx], v = [Ny], khi ¯d´o nê´u v´oi hai , , , ,
c .˘ap (x1, y1), (x2, y2) tuong ´ung v´oi m .ôt c.˘ap duy nhâ´t (u, v) th`ı 1 1 |x 1 − x2| = (u + {Nx1}) − (v + {Nx2}) = N N 1 1 = |{Nx < e N 1} − {N x2}| < N , , , v`
a tuong t .u ta c´o |y1 − y2| < e. V`ı u, v ∈ {0, . . . , N − 1}, nên c´o tâ´t , ,
ca N2 c .˘ap (u, v) kh´ac nhau. X´et t.âp h .op N2 + 1 c.˘ap gi´a tr.i , x = {la}, y = {lb} v´ oi l = 0, 1, . . . , N2 , ,, , Theo nguyên l´ y Ðirichlê c´
o ´ıt nhâ´t hai c .˘ap (gia su v´oi l = i v`a , , , , ,
l = j, i > j) t`u t .âp h .op n`ay tuong ´ung c`ung m .ôt c.˘ap (u, v). Do ¯d´o, , v´ oi k´ y hi .êu
n = i − j, k = [ia] − [ja], m = [ib] − [jb] , , , , ,
ta nh .ân ¯du .oc c´ac bâ´t ¯d˘ang th´uc câ`n ch´ung minh :
|na − k| = |(ia − [ia]) − (ja − [ja])| = |{ia} − {ja}| < e,
|nb − m| = |(ib − [ib]) − (jb − [jb])| = |{ib} − {jb}| < e. J ,
. 13.6. (Bı, 1977) Trong h`ınh tr` on c´ o b´
an k´ınh n ∈ N c´ o 4n ¯ do .an , , , , , th˘ ang ¯ dê`u c´ o ¯
d .ô d`ai b`˘ang 1. Ch´ung minh r`˘ang nê´u c´o m.ôt ¯du`ong th˘ang , , , , , , , cho tru´ oc th`ı t`ım ¯
du .oc m.ôt ¯du`ong th˘ang kh´ac, ho .˘ac song song, ho .˘ac , , , , , vuông g´ oc v´ oi ¯ du` ong th˘ ang n` ay v` a c´ ˘ at ´ıt nhâ´t hai ¯
do .an th˘ang n´oi trên. , , , , , L` oi giai. Ðê ´ y r` ˘ ang tông ¯
d .ô d`ai hai h`ınh chiê´u cua m˜ôi m .ôt ¯do.an , , , , , , , , th˘ ang lên ¯ du`ong th˘ ang l v`a ¯ du` ong th˘ ang l0, vuông g´ oc v´ oi n´ o, không 139 , , , b´
e hon 1. Th .ât v.ây, nê´u vecto a c´o ¯d .ô d`ai l`a 1 song song v´oi ¯do.an , , , , th˘ ang n` ao ¯ d´ o, c` on c´
ac vecto x v`a y l`a c´ac h`ınh chiê´u cua vecto a lên , , , , ¯ du` ong th˘
ang l v`a l0 th`ı a = x + y, suy ra |x| + |y| ≥ |a| = 1. Nhung , , , , ¯
d .ô d`ai c´ac h`ınh chiê´u cua ¯do.an th˘ang b`˘ang |x| v`a |y| do ¯d´o tông cua , , , ch´ ung c˜ ung không b´ e hon 1. D˜ ân ¯ dê´n tông ¯
d .ô d`ai h`ınh chiê´u cua tâ´t , , , , , , , , ca c´ ac ¯
do .an th˘ang không b´e hon 4n. B´oi v.ây t`u hai ¯du`ong th˘ang l , , , , , , , , v` a l0 c´
o thê ch .on ¯du .oc m .ôt ¯du`ong th˘ang, tông ¯d .ô d`ai cua h`ınh chiê´u , , c´ ac ¯
do .an th˘ang trên n´o không b´e hon 2n (nguyên l´y Ðirichlê). V`ı tâ´t , , , , , ca c´ ac ¯
do .an th˘ang ¯du .oc s´˘ap xê´p trong h`ınh tr`on b´an k´ınh n, nên h .op , , , , , c´ ac h`ınh chiê´u cua ch´ ung trên ¯ du` ong th˘ ang bâ´t k` y c´ o ¯ d .ô d`ai b´e hon , , , , , , , , 2n. Suy ra trên ¯ du` ong th˘ ang ¯
du .oc ch .on t`ım ¯du .oc 1 ¯diêm thu .ôc v`ao , ,
h`ınh chiê´u cua ´ıt nhâ´t hai ¯
do .an th˘ang (Nguyên l´y Ðirichlê cho ¯do.an , , , , , , , , , th˘ ang). Ðu` ong th˘ ang ¯ di qua ¯ diêm n` ay vuông g´ oc v´ oi ¯ du` ong th˘ ang , , , , , , ¯
du .oc ch .on, s˜e c´˘at ´ıt nhâ´t hai ¯do.an th˘ang n`ay. V`ı ¯du`ong th˘ang n`ay , , , , , ,
ho .˘ac vuông g´oc v´oi, ho.˘ac song song v´oi ¯du`ong th˘ang l, th`ı n´o thoa m˜ an ¯ diê`u ki .ên b`ai to´an. J ,
. 13.7. (Bungari (¯
dê` thi ch .on ¯d.ôi tuyên),1973) Cho a1, a2, . . . , an l`a , , , nh˜ ung sô´nguyên kh´
ac nhau trong khoang [100,200], m` a ch´ ung thoa , , , m˜
an a1 + a2 + · · · + an ≥ 11100. Ch´ ung minh r` ˘ ang gi˜ ua nh˜ ung sô´n` ay ,, , c´
o ´ıt nhâ´t m .ôt sô´, m`a viê´t n´o o d .ang th .âp phân c´o ´ıt nhâ´t hai ch˜u sô´ giô´ng nhau. , , , L` oi giai. Ch´
ung ta l .âp danh s´ach c´ac sô´trong khoang [100,200], m`a ,, , ch´
ung viê´t o h .ê th.âp phân ´ıt nhâ´t c´o hai ch˜u sô´ tr`ung nhau.: 100,
101, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 121, 122,
131, 133, 141, 144, 151, 155, 161, 166, 171, 177, 181, 188, 191, , , , , ,
199, 200. Tông cua tâ´t ca c´ ac sô´ trên l`
a 4050. M .˘at kh´ac tông tâ´t ca , , c´
ac sô´ nguyên trong khoang [100,200] l` a 15150. Nê´u trong nh˜ ung sô´ ¯ d˜
a cho a1, a2, . . . , an không c´o sô´ n`ao trong danh s´ach trên, th`ı , , 140
Chuong 13. M .ôt sô´ ¯dê` thi vô ¯d.ich
a1 + a2 + · · · + an < 15150 − 4050 = 11100, ¯ diê`u n` ay vô l´ y. Ngh˜ıa ,, , , , l` a trong c´
ac sô´ a1, a2, . . . , an c´o ´ıt nhâ´t m .ôt sô´viê´t o co sô´mu`oi c´o ´ıt , nhâ´t hai ch˜u sô´tr` ung nhau. J ,
. 13.8. (Bungari,1973) Trong m .ôt thu vi.ên c´o 20000 cuô´n s´ach, , , , ch´ ung ¯
du .oc xê´p v`ao nh˜ung gi´a s´ach sao cho m˜ôi gi´a s´ach c´o ´ıt nhâ´t , ,
m .ôt quyên ho .˘ac nhiê`u nhâ´t 199 cuô´n s´ach. Ch´ung minh r`˘ang ´ıt nhâ´t , , c´ o hai gi´ a s´ ach c´ o c`
ung sô´lu .ong s´ach. , , , ,, , , , L`
oi giai. Gia su ngu .oc l.ai. Nê´u trong thu vi.ên c´o n gi´a s´ach v`a ch´ung , , , ¯
du .oc ¯d´anh sô´t`u 1 ¯dê´n n, th`ı r˜o r`ang l`a n ≤ 199. Ch´ung ta k´y hi.êu ai , , , l` a sô´ cuô´n s´ ach ¯
du .oc ¯d.˘at lên gi´a s´ach th´u i, ch´ung ta s˜e c´o 1 ≤ ai ≤ ,, , , , 199. khi ¯ d´ o tu ¯
diê`u ki .ên ai 6= aj v´oi i 6= j, ch´ung ta nh.ân ¯du .oc
20000 = a1 + a2 + · · · + an ≤ 1 + 2 + · · · + 199 = 19900 < 20000 , ¯ diê`u n` ay vô l´ y. Suy ra c´ o ´ıt nhâ´t hai gi´ a s´ ach, trên ch´ ung ch´ ua c` ung sô´s´ ach. J , , ,
. 13.9. (Bungari, 1983) T`ım h`ınh vuông c´ o k´ıch thu´ oc b´e nhâ´t, ¯ dê , trong h`ınh vuông ¯ d´ o c´ o thê s´ ˘ ap xê´p 5 h`ınh tr` on b´ an k´ınh b` ˘ ang 1, sao , cho không c´ o 3 h`ınh tr` on n` ao trong ch´ ung c´ o ¯ diêm trong chung. , , , ,, A B L`
oi giai. Gia su h`ınh vuông ABCD A1 B1 , c´
o tâm O v`a c .anh a, ch´ua 5 h`ınh O tr` on không c´ ˘ at nhau v` a ¯ dê`u c´ o D1 C1 b´ an k´ınh b` ˘ ang 1, khi ¯ d´ o c´ ac tâm , D C cua ch´ ung n` ˘ am trong h`ınh vuông
A1B1C1D1 c´o tâm O v`a c .anh b`˘ang H`ınh 13.1: ,, a − 2 (o ¯ dây A1B1//AB ). , , , , , , , C´ ac ¯ du` ong th˘ ang nô´i t` u c´ ac trung ¯ diêm cua c´ ac c .anh ¯dô´i di.ên cua
h`ınh vuông A1B1C1D1 chia h`ınh vuông ¯ d´ o th` anh bô´n h`ınh vuông 141 , ,,
nho, o m .ôt trong ch´ung´ıt nhâ´t c˜ung c´o hai trong sô´c´ac tâm (Nguyên , , l´ y Ðirichlê). Khi ¯ d´ o khoang c´ ach gi˜ ua hai tâm n` ay m .ôt m.˘at không , , , , , l´ on hon ¯ du` ong ch´ eo h`ınh vuông b´
e, m .˘at kh´ac không b´e hon 2. Do v .ây c´o A √ a − 2 √ 2 ≤ OA 1 B1 1 = 2 = 2 √ 2 2 suy ra a ≥ 2 2 + 2. √ , Cuô´i c`
ung, nê´u a = 2 2 + 2 v`a tâm cua c´ac h`ınh tr` on l` a c´ ac , , , , , ¯
diêm O, A1, B1, C1, D1 th`ı tâ´t ca c´ac ¯
diê`u ki .ên nêu trên ¯du .oc thoa , , √ m˜
an. Nhu v .ây c.anh cua h`ınh vuông câ`n t`ım l`a 2 2 + 2. J , , , ,
. 13.10. (Nam Tu, 1977) Cho tru´
oc 20 sô´ t .u nhiên a1 < a2 < . . . < , , , ,
a20 không vu .ot qu´a 70. Ch´ung minh r`˘ang gi˜ua c´ac hi.êu aj − ak(j > k) , , luôn t`ım ¯
du .oc ´ıt nhâ´t 4 hi.êu b`˘ang nhau. , , , ,, , , , , L`
oi giai. Gia su kh˘ ang ¯
d.inh cua b`ai to´an l`a sai. Khi ¯d´o gi˜ua 19 sô´t .u
nhiên a20 − a19, a19 − a18, . . . , a2 − a1 không c´o 4 sô´n`ao b`˘ang nhau. , Do ¯ d´ o gi˜ ua ch´ ung m˜ ôi sô´ 1, 2, 3, 4, 5, 6 c´
o m .˘at không qu´a 3 lâ`n. , , , Suy ra c´
o m .ôt trong 19 sô´ ¯d´o phai l´on hon 6 (nê´u không th`ı sô´c´ac , , , , sô´ không l´ on hon 6 s˜ e nhiê`u hon 18), c´ o 3 trong 18 sô´ c` on l .ai phai , , , , , , , l´ on hon 5, 3 trong 15 sô´ c`
on l .ai phai l´on hon 4,. . . Do ¯d´o tông cua ch´
ung (a20 − a19) + (a19 − a18) + · · · + (a2 − a1) ≥ 7 + 3(6 + 5 + 4 + , 3 + 2 + 1) = 70 không thê b` ˘
ang a20 − a1 ≤ 70 − 1 = 69. Mâu thu˜ân , , , , ,
nh .ân ¯du .oc ¯d˜a ch´ung minh kh˘ang ¯d.inh cua b`ai to´an. J , , , ,
. 13.11. (Nam Tu, 1981) T .âp h.op c´ac sô´ {1, 2, . . . , 100} ¯du.oc chia , , ,, , l`
am 7 t .âp h.op con. Ch´ung minh r`˘ang ´ıt nhâ´t o m.ôt trong c´ac t .âp h.op , , con â´y t`ım ¯
du .oc ho .˘ac 4 sô´ a, b, c, d sao cho a + b = c + d, ho .˘ac ba sô´
e, f , g sao cho e + f = 2g. , , , , , L` oi giai. Ðê ´ y r` ˘ ang c´
o ´ıt nhâ´t m .ôt trong 7 t.âp h .op con ch´ua không , , , , , , , ,
´ıt hon 15 sô´ (trong tru`ong h .op ngu .oc l.ai, tâ´t ca c´ac t.âp h .op con , , 142
Chuong 13. M .ôt sô´ ¯dê` thi vô ¯d.ich , , , , ch´
ua không nhiê`u hon 7.14 = 98 sô´). M˜
ôi c .˘ap sô´ a > b cua t.âp h .op , , , , , , , , con n` ay ¯
du .oc ¯d.˘at tuong ´ung v´oi hi.êu a − b. Khi ¯d´o ta nh.ân ¯du .oc , 14 , không ´ıt hon C2 = 15 = 105 hi ai c´ o c´ ac hi 15 .êu, trong sô´ ¯ d´ o ph .êu 2 , , b` ˘ ang nhau (v`ı c´
ac hi .êu nh.ân ¯du .oc không qu´a 99 gi´a tr.i kh´ac nhau , ,, , , , 1, 2,. . . ,99). Gia su v´
oi hai c .˘ap sô´ a > b, c > d ta c´o ¯d˘ang th´uc
a − b = c − d(a 6= c, b 6= d). Khi ¯ d´ o a + d = b + c. Nê´u a = d , , , ,
(ho .˘ac b = c, ¯d˘ang th´uc kh´ac không thê xây ra), th`ı c + b = 2a (ho.˘ac a + d = 2b). J , , ,
. 13.12. (Nam tu,1977) Ch´ ung minh r` ˘
ang di.ên t´ıch cua h`ınh vuông , , ,, , bâ´t k` y n` ˘ am trong tam gi´ ac, không l´
on hon nua di.ên t´ıch cua tam gi´ac ¯ d´ o. , , , L`
oi giai. (H`ınh 13.2) Ta ch´ ung A , , , minh kh˘ ang ¯ d.inh tông qu´at hon : , M
di .ên t´ıch cua h`ınh b`ınh h`anh bâ´t , L , k`
y KLMN n`˘am o trong tam gi´ac E L M1 F 1 , , ,, N ABC không l´ on hon nua di .ên t´ıch K , C B cua tam gi´ ac ¯ d´ o. K N 1 1 , , , , Ðê ´ y r` ˘ ang m˜ ôi m .ôt ¯du`ong th˘ang , H`ınh 13.2: KL v`
a MN c´˘at hai c .anh cua tam , ,, , , gi´ ac ABC (c´ o thê o ¯ dınh tam gi´ ac), ngh˜ıa l` a c´ o 2 trong 4 giao ¯ diêm , , , , n` ˘
am trên 1 c .anh theo nguyên l´y Ðirichlê. Ch˘ang h.an, ¯du`ong th˘ang , , ,, KL v`
a MN c´˘at BC lâ`n lu .ot o K1 v`a N1. Trên c.anh AB, AC v`a BC , , , ,
ch .on c´ac ¯diêm D, E v`a F sao cho L1, M1 l`a giao ¯diêm cua DE v´oi KL , v` a MN thoa m˜an: , K1L1 = KL; L1M1//K1N1 ¯ dô`ng th` oi BF//BD , , Khi ¯ d´ o h`ınh b`ınh h` anh KLMN v`a K1L1M1N1 c´o ¯ du`ong cao b` ˘ ang nhau ¯ dê´n ¯ das y chung, c` on c´ ac h`ınh b`ınh h` anh BDEF v`a K1L1M1N1 143 , , , , c´ o ¯ d´ ay DE không b´e hon ¯ d´ ay L1M1 v`a hai ¯ du` ong cao h .a t`u D v`a L1 ,, ,
xuô´ng BF b`˘ang nhau. Boi v .ây c´o: SKLMN = SK ≤ S a 1 L1 M1 N1 BDEF. Gi ,, su AE = x.AC, khi ¯ d´
o EC = (1 − x)AC, c´ac tam gi´ac ABC, ADE , v` a EFC ¯
dô`ng d .ang v´oi nhau nên ta c´o: SBDEF = SABC − SADE − SEFC
= SABC − x2SABC − (1 − x)2SABC 1 = 2x(1 − x)SABC ≤ S 2 ABC. 1 , 1 V`ı x(1 − x) ≤ v´
oi x lâ´y gi´a tr.i bâ´t k`y, nên S S 4 KLMN ≤ 2 ABC. J , , ,
. 13.13. (Nam tu, 1972) Ðô´i v´ oi m˜ ôi gi´
a tr.i n ∈ N, h˜ay t`ım sô´k l´on , , ,,
nhâ´t (k ∈ N) thoa m˜
an t´ınh châ´t sau: Trong t .âp h.op gô`m n phâ`n tu , , , c´
o thê ch .on ra k t .âp h.op con kh´ac nhau, sao cho hai t .âp h.op con bâ´t k` y ¯ dê`u c´
o t .âp giao kh´ac r˜ông. , , ,, , , , L`
oi giai. Cô´ ¯
d.inh phâ`n tu ai cua t.âp h .op X = {a1, a2, . . . , an} v`a chı , , ,, , , x´ et c´
ac t .âp h .op con ch´ua phâ`n tu a1.Sô´c´ac t.âp h .op nhu v.ây b`˘ang sô´ , , , c´
ac t .âp h .op con cua t.âp h .op {a2, . . . , an}, ngh˜ıa l`a b`˘ang 2n−1. Suy ra , ,, , , , ,
k ≥ 2n−1. M .˘at kh´ac gia su ¯d˜a ch .on ¯du .oc hon 2n−1 t.âp con cua X. Ta , , , , ,, chia tâ´t ca c´
ac t .âp con cua X th`anh 2n−1 c.˘ap ¯du .oc t.ao boi 1 t.âp con , , cua X v`a phâ`n b` u cua n´ o. Theo nguyên l´ y Ðirichlê c´ o ´ıt nhâ´t 2 t .âp con ¯ d˜
a ch .on t.ao th`anh m .ôt c.˘ap, suy ra ch´ung không giao nhau. V.ây k = 2n−1. J , 1 . 13.14. (M˜
y, 1983) Trên tr .uc sô´ lâ´y m.ôt khoang c´o ¯d.ô d`ai (n ∈ n , , , , n + 1 N). Ch´ ung minh r` ˘ ang khoang n` ay c´ o ch´ ua nhiê`u hon phân sô´ 2 , p
tô´i gian d .ang , trong ¯d´o p, q ∈ Z, 1 ≤ q ≤ n. q , , 144
Chuong 13. M .ôt sô´ ¯dê` thi vô ¯d.ich , , , , 1 , L`
oi giai. Gia thiê´t r` ˘
ang trong m .ôt khoang n`ao ¯d´o c´o ¯d .ô d`ai , ch´ua n , n + 1 , p , nhiê`u hon phân sô´ tô´i gian , v´
oi q ∈ {1; 2; . . . ; n}. Ta s˜e 2 q , , , ch´ ung minh r` ˘ ang gi˜ ua c´ ac m˜ âu sô´ cua c´ ac phân sô´ n` ay luôn t`ım , , ¯
du .oc hai m˜âu sô´ m`a m˜âu sô´ n`ay chia hê´t cho m˜âu sô´ kia. Th.ât v.ây , , , , , ta biêu di˜ ên c´ ac m˜ âu sô´ du´
oi d .ang 2r.s v´oi s l`a sô´ le, r ∈ Z+. Sô´ , , n + 1 c´ ac sô´ le kh´ ac nhau gi˜ ua c´
ac sô´ 1, 2, 3, . . . , n b`˘ang ( ngh˜ıa 2 , , , l` a ´ıt hon sô´ c´ ac m˜ âu sô´ ¯ dang x´ et), suy ra luôn t`ım ¯ du .oc hai m˜âu sô´ q = 2r.s v`
a q1 = 2r1s1 m`a s = s1 v`a r = r1. Khi ¯ d´ o c´ o m .ôt m˜âu , , sô´ chia hê´t cho m˜
âu sô´ kia, hay q1 = kq. Nhu v .ây gi˜ua c´ac phân sô´ , , m l ,
ch .on ¯du .oc hai sô´kh´ac nhau d.ang v` a , v´ oi kq ≤ n. Khi ¯ d´ o q kq m l 1 − < , q kq n , , 1 v`ı ca hai n` ˘ am trong khoang c´ o ¯
d .ô d`ai . Do ¯d´o km − l = 0, v`ı trong n , , , , , tru` ong h .op ngu .oc l.ai th`ı m l |km − l| 1 1 − = ≥ ≥ , q kq kq kq n l km , , v` a do ¯ d´ o km = l v`a = , ngh˜ıa l` a hai phân sô´ ¯ du .oc ch .on tr`ung kq kq nhau. J ,
. 13.15. (Vi.êt nam, 1976) Ch´ung minh r`˘ang tô`n t .ai vô sô´ c´ac sô´ c´o , ,
d .ang 5n(n ∈ N), m`a trong c´ac biêu di˜ên th .âp phân cua m˜ôi sô´ ¯d´o c´o , , ,
không ´ıt hon 1976 ch˜ u sô´0 ¯ d´ ung liên tiê´p. , , , , L` oi giai. Ta ch´ ung minh r` ˘ ang v´
oi m .oi k ∈ N tô`n t.ai vô sô´ c´ac sô´ , m ∈ N thoa m˜ an ¯
diê`u ki .ên 5m = 1 (mod 2k). 145 , , ,
Th .ât v.ây, gi˜ua c´ac sô´ 50, 51, . . . , 52k luôn t`ım ¯du .oc hai sô´ 5p v`a , , 5q(p > q) c´ o c` ung sô´ du trong ph´ ep chia cho 2k. Khi ¯ d´ o hi .êu cua ch´
ung 5p − 5q = 5q(5p−q − 1) chia hê´t cho 2k nghi˜a l`a sô´ 5p−q − 1 , v` a tâ´t ca c´ ac sô´c´
o d .ang 5r(p−q) − 1 (r ∈ N) ¯dê`u chia hê´t cho 2k. , ,
Nhu v .ây v´oi m˜ôi gi´a tr.i m = r(p − q), r ∈ N, ta c´o 5m ≡ 1 , , (mod 2k), t`u ¯ d´
o 5m+k ≡ 5k (mod 10k) ngh˜ıa l`a k ch˜u sô´ t .ân c`ung , , , , , ,, , cua 5m+k tr` ung v´
oi k ch˜u sô´ t .ân c`ung cua 5k. Gia su sô´ k thoa m˜an , , , , 2k > 101976 ch´
ua không nhiê`u hon k − 1976 ch˜u sô´. Do ¯ d´ o gi˜ ua k , , , , ch˜
u sô´t .ân c`ung cua sô´5m+k chı c´o k − 1976 ch˜u sô´kh´ac không, c`on , 1976 ch˜u sô´c`
on l .ai (liên tiê´p nhau) b`˘ang 0. J , , ,
. 13.16. (Ti.êp kh´˘ac, 1979) Trên m.ôt ¯du`ong th˘ang c´o n2 + 1(n ∈ N) , , , , ¯
do .an th˘ang. Ch´ung minh r`˘ang, ho .˘ac l`a gi˜ua ch´ung c´o thê ch.on n + 1 , , , ¯
do .an ¯dôi m.ôt không c´˘at nhau, ho .˘ac l`a t`ım ¯du.oc n + 1 ¯do .an th˘ang n`ao , ¯ d´ o c´ o ¯ diêm chung. , , , , , , , L` oi giai. Ta ¯
d.inh hu´ong bên tr´ai cho ¯du`ong th˘ang khi n´oi r`˘ang m .ôt ,, , , ¯
do .an n`˘am o bên tr´ai ¯do.an th˘ang kh´ac, nê´u ¯dâ`u m´ut bên tr´ai cua , , ,, , ¯
do .an th˘ang th´u nhâ´t n`˘am o bên tr´ai ¯dâ`u m´ut bên tr´ai cua ¯do.an , , , , , , , th˘ ang th´ u hai. M˜ ôi ¯
do .an th˘ang ¯du .oc ¯d´anh sô´ b`˘ang m .ôt sô´ tuong , , ´, , , , , , ung t` u c´
ac sô´1, 2, . . . , n b`˘ang c´ach sau: o bu´ oc th´ u nhâ´t ¯ do .an th˘ang ,, , , , , ,
o t .ân c`ung bên tr´ai cho tuong ´ung sô´ 1. Sau ¯d´o m˜ôi bu´oc tiê´p theo , , ,
ta l .ai ch .on trong sô´nh˜ung ¯do.an th˘ang chua ¯d´anh sô´, ¯do.an t.ân c`ung , , , , , , bên tr´ ai v` a ¯
d .˘at cho n´o sô´tuong ´ung, kh´ac v´oi c´ac sô´cua nh˜ung ¯do.an , , , , , , th˘ ang giao v´ oi n´ o (¯ d˜ a ¯
du .oc ¯d´anh sô´). Nê´u ¯dê´n bu´oc n`ao ¯dâ´y, ta ch .on , , , , , , , , , ¯
du .oc ¯do.an th˘ang, nhung ¯dô´i v´oi n´o không ch .on ¯du .oc sô´ th´u t .u, th`ı , , ¯ diê`u n` ay c´ o ngh˜ıa l` a n´ o giao v´ oi n ¯
do .an th˘ang n`˘am bên tr´ai n´o v`a c´o , , , , , nh˜ ung sô´ kh´ ac nhau. Trong tru`
ong h .op n`ay ¯dâ`u m´ut tr´ai cua ¯do.an , , , , ,, , , th˘ ang ¯
du .oc ch .on thu .ôc v`ao n + 1 ¯do.an th˘ang. Nê´u o bu´oc â´y, ¯do.an , , 146
Chuong 13. M .ôt sô´ ¯dê` thi vô ¯d.ich , , , th˘ ang cuô´i c` ung ¯
du .oc ¯d´anh sô´ th`ı theo nguyên l´y Ðirichlê ´ıt nhâ´t , , , , ,
m .ôt trong n sô´´ung v´oi nhiê`u hon n ¯do.an th˘ang, m`a c´ac ¯do.an th˘ang , , , , ¯ d´ o v´ oi c´ ac sô´th´
u t .u th´ıch h .op, không giao nhau. J ,
. 13.17. (Rumani, 1978) C´ ac h`
am sô´ f , g, h : N → N thoa m˜ an ba ¯ diê`u ki.ên sau: , , a) H`
am h(n) không nh .ân gi´a tr.i n`ao t .ai nhiê`u hon m.ôt ¯diêm n ∈ N. ,
b) T .âp h.op gi´a tr.i h`am sô´ g(n) l`a N.
c) f (n) ≡ g(n) − h(n) + 1, n ∈ N. , , Ch´ ung minh r` ˘ ang ¯ dô`ng nhâ´t th´
uc f (n) ≡ 1, n ∈ N, l` a ¯ d´ ung. , , , , , L` oi giai. Ta ch´ ung minh ¯ dô`ng nhâ´t th´ uc g(n) ≡ h(n) (n ∈ N). T` u ¯ d´ o v` a ¯
diê`u ki .ên b) s˜e d˜ân ¯dê´n f (n) ≡ g(n) − h(n) + 1 ≡ 1, n ∈ N. , V´ oi bâ´t k` y n ∈ N c´ o
h(n) = g(n) + 1 − f (n) ≤ g(n) , ,, , , ,
v`ı f (n) ≥ 1. Gia su r`˘ang, ¯ dô´i v´ oi gi´
a tr.i n`ao ¯d´o n ∈ N ¯d˘ang th´uc g(n) = h(n) không ¯ d´ ung, khi ¯ d´ o h(n) < g(n) = k. Theo ¯ diê`u ki .ên , b) ta t`ım c´
ac sô´ n1, n2, . . . , nk−1 ∈ N, ¯dê sao cho g(ni) = i khi i = ,,
1, . . . , k − 1. Boi v .ây m˜ôi sô´trong k sô´h(n1), h(n2), . . . , h(nk−1), h(n) ,
thu .ôc v`ao t.â p h .op {1, 2, . . . , k − 1}, do ¯d´o theo nguyên l´y Ðirichlê , h`
am sô´ h(n) nh .ân gi´a tr.i n`ao ¯d´o nhiê`u hon m .ôt lâ`n, ¯diê`u n`ay tr´ai , , , , , v´ oi ¯
diê`u ki .ên a).Kh˘ang ¯d.inh ¯d˜a ¯du .oc ch´ung minh. J , , , , , , . 13.18. (M˜ y (N˜ uu U´ oc), 1979) Ch´ ung minh r` ˘ ang c´ ac ¯ dınh cua n-gi´ ac , , ¯ dê`u c´
o di.ên t´ıch b´e nhâ´t (n > 3) n.ôi tiê´p trong m.ôt n-gi´ac cho tru´oc, , , , , , tr` ung v´ oi trung ¯ diêm c´
ac c .anh cua n-gi´ac cho tru´oc. , , , ,, L`
oi giai. (H`ınh 13.3) Gia su n-gi´ac ¯
dê`u B1, . . . , Bn c´o di.ên t´ıch SB
n .ôi tiê´p trong n-gi´ac ¯dê`u A1, . . . , An di.ên t´ıch SA. 147 Khi ¯ d´ o nê´u ch´ ung không tr` ung nhau th`ı trên m˜ ôi m .ôt c.anh Ai Ai+1 , , , , v´
oi i = 1, 2, . . . , n (An+1 = A1) c´o m .ôt ¯dınh Bi ¯du .oc x´ac ¯d.inh , , , , ,
trên c .anh â´y. Th.ât v.ây, trong tru`ong h .op ngu .oc l.ai theo nguyên l´y , , , Ðirichlê ´ıt nhâ´t c´
o m .ôt c.anh, ch˘ang h.an A1A2, ch´ua hai ¯diêm B1 , , ,, , ,, v` a B2 ¯ d´ o (¯ dê x´ ac ¯
d.inh, gia su A1B2 > A1B1), khi ¯d´o ¯diêm Bn (o , ∆ , , ,
A1A2An) c´o thê n`˘am trên c .anh A2A3 v`a A1An tuong ´ung (v`ı n > , , , 3, ¯
do .an A1A3 v`a A2An l`a ¯du`ong ch´eo, m`a không l`a c.anh cua n-gi´ac ,
A1, . . . , An), ngh˜ıa l`a B1 = A1 v`a B2 = A2. Ta ch´ung minh r`˘ang A1B1 = A2B2 = . . . = AnBn
Th .ât v.ây tam gi´ac B1A2B2 v`a tam gi´ac B2A3B3 b`˘ang nhau, v`ı \ B1A2B2 = \ B2A3B3 = \ B1B2B3 = 1800 n − 2 n \ A2B1B2 = 1800 − \ B1A2B2 − \ A2B2B1 = 1800 − \ B1B2B3 − \ A2B2B1 = \ A2B2B3 ,, , , , v`
a B1B2 = B2B3. Boi v .ây A2B2 = A3B3. Ta c˜ung ch´ung minh tuong , , , , ,
t .u c´ac ¯d˘ang th´uc c`on l.ai. Ð.ai lu .ong SB = SA − SB − S − . . . − S = S 1 A2 B2 B2 A3B3 Bn A1B1 A − nSB1 A2B2 , , ,
nh .ân gi´a tr.i nho nhâ´t, khi di.ên t´ıch tam gi´ac B1A2B2 l´on nhâ´t. Gia ,, , , su A1A2 = a, A1B1 = x, khi ¯ d´ o ¯ d .ai lu .ong 1 1 SB = B (a − x)x. sin \ B 1 A2 B2 2 1 A2.A2B2 sin \ B1A2B2 = 2 1 A2 B2 1 a2 a = ( − (x − )2) sin \ B 2 4 2 1 AB2 , a
nh .ân gi´a tr.i l´on nhâ´t khi x = , ngh˜ıa l`a A 2 1 B1 = B1 A2. J , ,
. 13.19. (CHLB Ð´
uc, 1978) M .ôt b.ô gô`m n2 con tem choi (n>2) mang , c´ ac nh˜
an hi.êu "1","2","3",. . . ,"n". M˜ôi lo .ai nh˜an hi.êu c´o n con tem. Hoi , , 148
Chuong 13. M .ôt sô´ ¯dê` thi vô ¯d.ich , , , c´
o thê xê´p tâ´t ca c´ ac con tem â´y th`
anh m .ôt d˜ay thoa m˜an c´ac ¯diê`u ki.ên , , sau không : v´
oi m .oi x ∈ {1, 2, . . . , n} gi˜ua m.ôt con tem mang nh˜an ,
hi.êu "x" v`a con tem mang nh˜an hi.êu "x" tiê´p theo luôn c´o v`ua ¯d´ung x con tem mang nh˜ an hi.êu kh´ac "x" ? , , , L`
oi giai. Trong m˜ ôi ¯ do .an n`˘am gi˜ua A3 , A B 2 2 hai con tem liên tiê´p v´ oi nh˜ an "n", B B 1 3 ¯ dê`u c´ o n con tem. C´ o n-1 ¯ do .an nhu , A A 1 4 , ,
v .ây do ¯d´o sô´ tem o gi˜ua con tem B4 ¯ dâ`u tiên mang nh˜ an hi .êu "n" v`a con , A5 tem cuô´i c` ung v´ oi c` ung nh˜ an hi .êu , , ¯ d´
o c .ông v´oi hai con tem v`ua n´oi l`a (n − 1)n + n, ngh˜ıa l` a n2 con tem. V H`ınh 13.3: .ây con tem ¯ dâ`u tiên v` a con tem , cuô´i c` ung trong d˜ ay ¯ dê`u phai c` ung mang nh˜ an hi .êu "n". , , Trong sô´ n con tem v´ oi nh˜ an "n-1" phai c´ o (theo nguyên l´ y
Ðirichlê) ´ıt nhâ´t hai con tem c` ung n` ˘
am trong ´ıt nhâ´t m .ôt ¯do.an , , ,, , trong sô´ n-1 ¯
do .an kê trên. Nhung khi ¯d´o o gi˜ua hai con tem n`ay , , chı c´ o nhiê`u nhâ´t l` a n-2 con tem; ¯ diê`u ¯ d´ o mâu thu˜ ân v´ oi t´ınh châ´t , cua d˜ ay. J , , ,
. 13.20. (CHLB Nga 1972) Ch´ın ¯ du` ong th˘ ang c` ung c´ o t´ınh châ´t l` a , , , , , m˜ ôi ¯ du` ong th˘
ang chia h`ınh vuông th` anh hai t´ u gi´ ac c´
o ty sô´ di.ên t´ıch 2 , , , , b` ˘ ang . Ch´ ung minh r` ˘ ang c´ o ´ıt nhâ´t ba ¯ du` ong th˘ ang trong sô´ ¯ d´ o c` ung 3 , ¯ di qua m .ôt ¯diêm. , , , , , , L`
oi giai. (H`ınh 13.4) C´ ac ¯ du` ong th˘ ang ¯ d˜ a cho không thê c´ ˘ at c´ ac , ,, ,
c .anh kê` nhau cua h`ınh vuông ABCD, boi v`ı nê´u thê´ không thê t.ao , , , , ,, , , ra ¯
du .oc hai t´u gi´ac, m`a l`a tam gi´ac v`a ng˜u gi´ac. Gia su m .ôt ¯du`ong 149 , , th˘ ang c´ ˘ at c´
ac c .anh BC v`a AD t.ai c´ac ¯diêm M v`a N. C´ac h`ınh thang , , , ABMN v` a CDNM c´ o c´ ac ¯ du` ong cao b` ˘ ang nhau do ¯ d´ o ty sô´ di .ên , , , , , t´ıch cua ch´ ung b` ˘ ang ty sô´ c´ ac ¯ du` ong trung b`ınh, t´ uc l` a MN chia , , , , ¯
do .an th˘ang nô´i trung ¯diêm cua c´ac c.anh AB v`a CD theo ty sô´ 2. 3 , , , , , , Tông sô´c´ ac ¯ diêm chia c´ ac ¯ du`
ong trung b`ınh cua h`ınh vuông theo ty ,, , , , , sô´ 2 l` a 4 (H`ınh v˜ e). Boi sô´ ¯ du` ong th˘ ang ¯ d˜ a cho l` a 9 v` a ¯ dê`u phai ¯ di 3 , ,
qua m .ôt trong sô´4 ¯diêm n´oi trên, nên c´o m .ôt ¯diêm thu .ôc ´ıt nhâ´t 3 , , , ¯ du` ong th˘ ang. M C B D A N H`ınh 13.4: , , 150
Chuong 13. M .ôt sô´ ¯dê` thi vô ¯d.ich , , CHUONG 14 , , B ` AI T .ÂP T .U GIAI , , , ,
. 14.1. M .ôt h`ınh l.âp phuong c´o c.anh b`˘ang 15 ch´ua 11.000 ¯diêm. , , Ch´ ung minh r` ˘ ang c´
o m .ôt h`ınh câ`u b´an k´ınh b`˘ang 1 ch´ua ´ıt nhâ´t 6 , , , ¯ diêm trong sô´nh˜ ung ¯ diêm ¯ d˜ a cho. , , ,
. 14.2. Cho F = {a1, a2, . . . , al} l`a t .âp h .op h˜uu h.an nh˜ung sô´ , , ,, , nguyên duong v`
a x1, x2, . . . , xn, . . . . . . l`a d˜ay vô h .an, m .oi phâ`n tu cua , n´ o n` ˘ am trong F, ngh˜ıa l`a tr` ung v´
oi m .ôt sô´n`ao ¯d´o trong a1, a2, . . . , al , , , , . Ch´ ung minh r` ˘ ang v´
oi m .oi sô´ nguyên duong bâ´t k`y tô`n t.ai m .ôt sô´ ,, , , , ,
phâ`n tu liên tiê´p cua d˜ ay, m` a t´ıch cua ch´ ung l` a l˜ uy th` ua cua m .ôt sô´ nguyên n` ao ¯ d´ o. , , . 14.3. Cho 5 ¯
diêm P1, P2, P3, P4, P5 trong phâ`n trong cua m .ôt h`ınh , , , , vuông c´
o c .anh 1 ¯don v.i. K´y hi.êu dij l`a khoang c´ach gi˜ua hai ¯diêm , ,
Pi v`a Pj. Ch´ung minh r`˘ang ´ıt nhâ´t c´o m .ôt trong sô´c´ac khoang c´ach √ , , , , 2 gi˜ ua c´ ac ¯ diêm nho hon . 2 , , , , , ,
. 14.4. Trong m .ôt h`ınh vuông c´o c.anh 50 ¯don v.i , ngu`oi ta ke ¯du`ong , , gâ´p kh´
uc sao cho m .oi ¯diêm trên c.anh h`ınh vuông c´o khoang c´ach , , , , , , , nho hon 1 ¯ dê´n ¯ du`ong gâ´p kh´ uc. Ch´ ung minh r` ˘ ang ¯ d .ô d`ai cua cua , , , , ¯ du` ong gâ´p kh´ uc l´ on hon 1248. , . 14.5. Cho A l`
a m .ôt ¯da gi´ac lô`i v´oi di.ên t´ıch S v`a chu vi P, c`on r , , , , 152 Chuong 14. B` ai t .âp t .u giai , , , , , , l`
a sô´ th .uc duong. K´y hi.êu M l`a t.âp h .op tâ´t ca c´ac ¯diêm trong m.˘at , , , , , ph˘ ang, sao cho v´ oi m˜ ôi ¯
diêm R cua M tô`n t .ai m .ôt ¯diêm Q thu .ôc A , , , , m` a khoang c´
ach gi˜ua R v`a Q nho hon ho .˘ac b`˘ang r. H˜ay t`ım di.ên , t´ıch cua h`ınh M. , ,
. 14.6. Trong h`ınh vuông c´
o c .anh b`˘ang 70, ngu`oi ta n´em ba h`ınh , , , , ch˜
u nh .ât v´oi k´ıch thu´oc 20x10, 25x15 v`a 30x30 v`a ba h`ınh tr`on b´an , , , k´ınh 5. Ch´ ung minh r` ˘ ang trong h`ınh vuông c´ o thê d.ich chuyên m .ôt , , h`ınh tr` on b´ an k´ınh 5 sao cho n´ o không c´ o nh˜ ung ¯ diêm trong chung , v´ oi 5 h`ınh ¯ d˜ a cho. , , ,
. 14.7. Trong m .˘at ph˘ang cho m .ôt ¯du`ong gâ´p kh´uc A1A2 . . . An v`a , , , h`ınh tr` on b´ an k´ınh r, tâm h`ınh tr` on chuyên ¯ d .ông trên ¯du`ong gâ´p , , , kh´ uc n` ay. Cho L l`a ¯
d .ô d`ai cua ¯du`ong gâ´p kh´uc, c`on F l`a h`ınh sinh ,, , , , , , ,
ra boi s .u chuyên ¯d .ông cua h`ınh tr`on trên ¯du`ong gâ´p kh´uc. Ch´ung , , minh bâ´t ¯ d˘ ang th´
uc S(F) ≤ 2Lr + πr2 . , , , , ,
. 14.8. T .âp h .op M l`a h .op m .ôt sô´h˜uu h.an nh˜ung ¯do.an th˘ang n`˘am , , , trong (0,1). Khoang c´ ach gi˜
ua m .ôt sô´ ¯diêm trong M không b`˘ang δ ,, , , , , , o ¯
dây 0 ≤ δ ≤ 1 . Ch´ ung minh r` ˘ ang tông ¯ d .ô d`ai cua nh˜ung ¯do.an , " # , , [ 1 ] + 1 , th˘ ang m` a ch´
ung t .ao nên M, không vu .ot qu´a δ δ v` a s .u ¯d´anh 2 gi´ a n` ay l` a ch´ınh x´ ac. , , , . 14.9. Trên ¯ du` ong tr` on b´ an k´ınh 1 cho n ¯
diêm P1, P2, . . . , Pn v`a t .âp , ,, , ,
h .op A t.ao boi m .ôt sô´h˜uu h.an cung không c´˘at nhau, m`a tông ¯d .ô d`ai , , cua ch´ ung l` a l(A). Ch´ ung minh r` ˘ ang 2kπ , a) Nê´u l(A) >
, (k = 1, 2, . . . , n − 1), th`ı c´ o thê quay t .âp n , , , , , , ,
h .op A trên ¯du`ong tr`on sao cho anh cua n´o ch´ua ´ıt nhâ´t k + 1 ¯diêm trong d˜ ây P1, P2, . . . , Pn . 153 2kπ , b) Nê´u l(A) <
, (k = 1, 2, . . . , n − 1), th`ı c´ o thê quay t .âp n , , , , , ,
h .op A trên ¯du`ong tr`on sao cho anh cua n´o ch´ua nhiê`u nhâ´t k − 1 , ¯ diêm trong d˜ ây P1, P2, . . . , Pn . , , , ,
. 14.10. Cho t .âp h .op A nh˜ung ¯diêm trên m .ôt m.˘at câ`u v´oi di.ên t´ıch , , ,, , , , l´
on hon nua di .ên t´ıch cua m.˘at câ`u. Ch´ung minh r`˘ang A ch´ua ´ıt nhâ´t , , , hai ¯
dâ`u m .ôt ¯du`ong k´ınh cua h`ınh câ`u. , , . 14.11. K´
y hi .êu N1, N2, . . . , Nn l`a nh˜ung t.âp h .op, m`a ch´ung c´o , , , , , , , , , ,, ¯
du .oc sau khi nh˜ung ¯dınh cua m .ôt lu´oi nguyên ¯du .oc t´ac ¯d .ông boi n , ph´
ep t.inh tiê´n, A l`a m .ôt bê` m.˘at v`a k l`a sô´t .u nhiên sao cho 1 ≤ k ≤ , n − 1. Ch´ ung minh r` ˘ ang k , , , , a) Nê´u S(A) > th`ı c´
o thê t.inh tiê´n t.âp h .op A sao cho anh cua r , , , , , n´ o ch´ ua ´ıt nhâ´t k + 1 ¯ diêm trong l` a nh˜ ung ¯ dınh cua N1, N2, . . . , Nn. k , , b) Nê´u S(A) < th`ı c´
o thê t.inh tiê´n t.âp h .op A sao cho r , , , , , , , anh cua n´ o ch´ ua nhiê`u nhâ´t k − 1 ¯ diêm trong l` a nh˜ ung ¯ dınh cua N1, N2, . . . , Nn . , , , , ,
. 14.12. Trong h`ınh vuông v´
oi c .anh 1 ¯don v.i d .ung ¯du`ong gâ´p kh´uc , , , , , ,
sao cho m .oi ¯du`ong th˘ang song song v´oi c.anh h`ınh vuông c´˘at ¯du`ong , , , , , gâ´p kh´ uc không qu´
a m .ôt ¯diêm. Ch´ung minh r`˘ang ¯d .ô d`ai cua ¯du`ong , , gâ´p kh´ uc nho hon 2. , , , ,
. 14.13. Trong m .ôt m.˘at ph˘ang cho 6 ¯diêm. Nh˜ung ¯do.an th˘ang nô´i , , , , , , , c´
ac c .˘ap ¯diêm ¯du .oc son mâ`u ¯do ho.˘ac xanh. Ch´ung minh r`˘ang v´oi , c´
ach t .ao h`ınh nhu v.ây tô`n t.ai ´ıt nhâ´t hai h`ınh tam gi´ac c´o c´ac c.anh , c` ung mâ`u. (c´ o thê hai tam gi´ ac kh´ ac mâ`u nhau). , , , , 154 Chuong 14. B` ai t .âp t .u giai , , CHUONG 15 , , , L ` OI GIAI V ` A G .OI ´Y , , , , , 15.1. L` oi giai v ` a g .oi ´y chuong 1 , , , . 1.11. L` oi giai: Nê´u tâ´t ca c´ ac ông quan ¯ dê`u quen nhau th`ı vi .êc , , , , xê´p b` an bô´n ngu` oi nhu ¯ dê` ra không c´ o g`ı kh´ o kh˘ an. Gia c´ o ông A , , v`
a ông B không quen nhau. T`u 2n − 2 ông quan c` on l .ai c˜ung nhu A , , v` a B c´
o ´ıt nhâ´t n ngu`oi quen. V`ı n + n = 2n = (2n − 2) + 2, th`ı tô`n , , ,
t .ai hai ông C v`a D, m`a h .o quen A c˜ung nhu B. Khi ¯d´o ngu`oi xê´p ¯d.˘at , , c´ o thê xê´p A ¯
dô´i di .ên B v`a gi˜ua h .o l`a C ¯dô´i di.ên D. ,
. 1.12. G .oi ´y: Chia m .ôt c.anh h`ınh vuông th`anh 48 ¯do.an m˜ôi ¯do.an , , ,, 20m, khoang c´ ach gi˜ ua 2 ¯
do .an l`a 0,6m, hai ¯do.an o hai ¯dâ`u d`ai,
5,9m. (V .ây 48.20m+47.0,6m+2.5,9m =1000m=1km). C.anh thu , hai chia ra l` am 95 ¯
do .an, khoa ng c´ach hai ¯do.an l`a 0,52m, hai ¯do.an ¯ dâ`u d`
ai 0,56m ( v .ây 95.10m+94.0,52m+20,56m= 1000m=1km). , , ,
Nhu v .ây c´o 48.95=4560 manh c´o di.ên t´ıch 200m2 m`a sô´cây chı c´o , 4500, nên c`
on ´ıt nhâ´t 60 ô nhu v .ây không c´o cây n`ao. , ,
. 1.13. G .oi ´y: Ta nh´om c´ac ng˘an c´o c`ung sô´ s´ach v`a ¯d´anh dâ´u t`u , , 0,1,. . . ,9 (c´ ac ng˘ an ch´ ua sô´s´ ach ´ıt hon 10) v`
a m .ôt ng˘an c´o 10 cuô´n. , ,, , Gia su không c´ o ba ng˘ an ch´ ua c` ung sô´ s´ ach, th`ı trong c´ ac nh´ om ta , ¯ d´ anh dâ´u c´ o ´ıt hon ba ng˘ an c´ o c` ung sô´ s´ ach (nhiê`u nhâ´t l` a 2), v .ây , , , , , 156 Chuong 15. L` oi giai v` a g .oi ´y , , th`ı v´ oi 10 nh´ om trên 10.2=20 ng˘ an s´
ach c .ông v´oi m .ôt ng˘an 10 cuô´n , n˜ ua không cho ta sô´ng˘ an s´ ach l` a 25, d˜ ân ¯ dê´n vô l´ y. , , , , ,
. 1.14. G .oi ´y: Ta lâ´y sô´cua ôtô chia cho 10 th`ı ¯du .oc sô´du 0, 1, 2, 3, , 4, 5, 6, 7, 8, 9. V`ı c´ o 11 sô´ m`
a 10 sô´ du th`ı theo nguyên l´ y Ðirichlê , , , c´ o hai sô´ c´ o c`
ung sô´ du. Nhu v .ây hi.êu cua hai sô´ chia hê´t cho 10 , ngh˜ıa l` a n´ o c´ o c`
ung m .ôt ch˜u sô´t.ân c`ung. , , , . 1.15. L`
oi giai: G .oi c´ac tr.am chuyên tiê´p l`a A, B, C, D, c´ac h`ınh , , , , , , , tr` on v´ oi ¯ du` ong k´ınh l` a c´ ac ¯ du` ong nô´i gi˜ ua c´ ac tr .am l`a v`ung bao phu , ,
cua m .ôt trung tâm ph´at s´ong. Ch´ung ta c´o 4 h`ınh tr`on nhu v.ây v`a , , , , , phai ch´ ung minh r` ˘
ang m .ôt ¯diêm M bâ´t k`y n`˘am trong t´u gi´ac cua 4 , , , ,, ,
tr .am ¯dê`u ¯du .oc phu boi ´ıt nhâ´t m .ôt h`ınh tr`on. Th.ât v.ây, nê´u ¯diêm M , , , n` ˘ am trong h`ınh tr` on ¯ du` ong k´ınh AB th`ı g´ oc AMB phai l`a t` u ho .˘ac , , b` ˘ ang 900. Ta nô´i M v´ oi c´
ac tr .am A, B, C, D, t.ao ra bô´n g´oc ¯dô´i v´oi , , , , c´
ac c .anh t´u gi´ac. Tông cua bô´n g´oc n`ay l`a 3600. Nhu v.ây ´ıt nhâ´t c´o
m .ôt g´oc t`u ho.˘ac c`ung l´˘am l`a b`˘ang 900. V.ây M thu .ôc m .ôt h`ınh tr`on , , , , m`
a t .ai M nh`ın c.anh cua t´u gi´ac du´oi m .ôt g´oc t`u. , , , , , 15.2. L` oi giai v ` a g .oi ´y chuong 2 , , ,
. 2.11. G .oi ´y: Áp d .ung Phuong ph´ap b`ai 2.2. , , ,
. 2.12. G .oi ´y: Áp d .ung phuong ph´ap b`ai 2.4 ,
. 2.13. G .oi ´y: Ð.˘at bk = a1 + a2 + · · · + ak, k = 1, 2, . . . , 41 v`a ´ap d .ung b`ai t.âp trên. , , ,
. 2.14. G .oi ´y: Nhu b`ai 2.8, nê´u M l`a sô´ nguyên tô´ c`ung nhau v´oi , , , 10, th`ı t`
u s .u chia hê´t cua l − k = 111 . . . 11.10k cho M, suy ra sô´ , , , , , 15.2. L` oi giai v` a g .oi ´y chuong 2 157 111 . . . 11 chia hê´t cho M. | {z } , (k-l ch˜ u sô´1) , , ,
. 2.15. G .oi ´y: D`ung phuong ph´ap b`ai 2.8. H˜ay x´et d˜ay
N, NN, NNN, . . . , NNN . . . N . | {z } , (1968 ch˜ u sô´) , , . 2.16. L` oi giai: Ta viê´t 1998 sô´ 1997, 19971997, . . . , , 1997 . . . 1997 . V` a x´ et c´ ac sô´ du trong ph´ ep chia m˜ ôi | {z }
sô´1997 l .˘ap 1998 lâ`n
m .ôt sô´ ¯d´o cho 1998. R˜o r`ang không m .ôt sô´n`ao trong c´ac sô´ ¯d˜a viê´t , ,
chia hê´t cho 1998 (v`ı 1998 l` a sô´ ch˜ ˘ an, m` a c´ ac sô´ ¯ d˜ a viê´t l` a le), nhu , , , ,
v .ây, c´ac sô´ du cua ph´ep chia ¯dê`u kh´ac không, v`ı sô´ c´ac sô´ l´on hon , , , , sô´ c´ ac sô´ du (c´ o 1998 sô´ m` a sô´ c´ ac sô´ du l` a 1997), nên t`ım ¯ du .oc , , , hai sô´ c´
o sô´ du nhu nhau, hi .êu cua hai sô´ ¯d´o c´o d.ang câ`n t`ım v`a chia hê´t cho 1998. , , . 2.17. L` oi giai: Ta x´
et 1997 sô´ d .ang 1998, 19981998,. . . . Sô´ cuô´i , , c` ung trong c´ ac sô´ n`
ay t .ao th`anh t`u 1997 nh´om trong bô´n ch˜u sô´1,
9, 9, 8. Ho .˘ac m .ôt trong c´ac sô´n`ay chia hê´t cho 1997 (v.ây, ¯d´o l`a sô´ , , , , ,
phai t`ım), ho .˘ac t`ım ¯du .oc hai sô´ du nhu nhau trong ph´ep chia cho , 1997. Khi ¯ d´
o hi .êu cua ch´ung c´o d.ang 19981998 . . . 1998.104m v`a chia ,, ,
hê´t cho1997. V`ı 104m v`a 1997 nguyên tô´c` ung nhau nên nhân tu th´ u nhâ´t, ngh˜ıa l`
a sô´19981998. . . 1998, chia hê´t cho 1997. , , , , . 2.18. L`
oi giai: Trong n + 1 sô´ m, m2, . . . , mn+1 t`ım ¯ du .oc hai sô´ , , , c´ o sô´ du nhu nhau trong ph´ ep chia cho n. Khi ¯ d´ o hi .êu cua ch´ung , ,,
chia hê´t cho n. Gia su ml − mt = a.n ho .˘ac mt(ml−t − 1) = a.n. V`ı
(m, n) = 1 nên (mt, n) = 1, ngh˜ıa l`
a, ml−t − 1 chia hê´t cho n. V .ây , ml−t − 1 l` a sô´phai t`ım. , , , , , 158 Chuong 15. L` oi giai v` a g .oi ´y , , , , , 15.3. L` oi giai v ` a g .oi ´y chuong 3 , , , , . 3.11. L` oi giai: Ta x´
et 104 c´ac lu˜y th`ua kh´ac nhau cua 3: 3, 32, 33 , , , , . . . , 3104 v` a c´ ac sô´ du cua ph´ ep chia m˜ ôi lu˜ y th` ua ¯ d´ o cho 104. M˜ ôi , ,
sô´ cho m .ôt sô´ du kh´ac không khi chia cho 104; sô´ c´ac sô´ du kh´ac , , , không l`
a 104 − 1; sô´c´ac sô´l`a 104. Do ¯ d´ o, t`ım ¯ du .oc hai lu˜y th`ua kh´ac , , nhau 3m v`a 3n c´ o sô´ du nhu nhau trong ph´ ep chia cho 104, ngh˜ıa l`a
3m − 3n = 104.l ho .˘ac 3n(3m−n − 1) = 104.l. V`ı 3n v`a 104 nguyên tô´, c`
ung nhau nên 3m−n − 1 chia hê´t cho 104 ho .˘ac 3m−n − 1 = 104.k. T`u , , , , ¯ d´
o suy ra 3m−n = 104.k + 1. Nhu v .ây, tra l`oi: c´o thê. , ,
. 3.12. G .oi ´y: L´y lu.ân nhu b`ai 3.10. , , ,
. 3.13. G .oi ´y: Ch´u ´y u3 = 1986, ´ap d .ung phuong ph´ap b`ai 3.4. , , , ,
. 3.14. G .oi ´y: L´y lu.ân nhu trong 3.4. Ch´ung minh r`˘ang v´oi m .oi sô´ ,
t .u nhiên m ´ıt nhâ´t m .ôt trong c´ac sô´ x1, x2, . . . , chia hê´t cho m. Sau ¯ d´ o d .˘at m = 38 v`a m = 43. , , , , , ,, ,
. 3.15. G .oi ´y: Tuong t .u nhu 3.8 ta x´et b .ô xê´p s-phâ`n tu nh˜ung sô´ , , , , , , du tuong ´ ung. D˜ ê thâ´y r` ˘ ang tô`n tai nh˜ ung chı sô´ i v`a j sao cho , 1 ≤ i < j ≤ ks v` a m˜ ôi tông trên ¯ dê`u chia hê´t cho k. , , , , , 15.4. L` oi giai v ` a g .oi ´y chuong 4 , , , , 1
. 4.11. G .oi ´y: Quanh m˜ôi ¯diêm ¯d˜a cho v˜e ¯du`ong tr`on b´an k´ınh . 15 , ,
. 4.12. G .oi ´y: B`ai to´an suy ra t`u b`ai 4.9. , , , ,, , , , . 4.13. L` oi giai: Gia su tô`n tai ¯ diêm X t`u c´ac ¯ diêm ¯ d˜ a cho m` a n´ o nô´i , , , , , ¯
du .oc v´oi 6 ¯diêm X1, X2, X3, X4, X5, X6. Khi ¯d´o c´ac ¯do.an th˘ang XX1 , , , , , 15.4. L` oi giai v` a g .oi ´y chuong 4 159 , , , , v` a XX2 ¯
du .oc d .ung theo m .ôt trong hai c´ach sau ¯dây (th .uc ra c´o c´ach , , , , , , th´ u ba nhung l`
a h .ê qua cua (b) khi ta ¯dôi chı sô´) , (a) Nê´u X l`a ¯ diêm gâ`n nhâ´t ¯
dê´n X1 v`a A2, th`ı XX1 < X1X2 v`a ,
XX2 < X1X2, ngh˜ıa l`a trong tam gi´ac XX1X2 c´o c .anh X1X2 l`a l´on nhâ´t. , , (b) Nê´u X1 gâ`n ¯ diêm X nhâ´t, c` on X gâ`n ¯ diêm X2 nhâ´t, th`ı ,
XX1 < XX2 < X1X2ch´ung ta c˜ung c´o c .anh X1X2 l`a l´on nhâ´t trong tam gi´ ac XX1X2 , , , , Suy ra \
X1XX2 > 600. Ch´ung minh ho`an to`an tuong t .u, ch´ung ta , , c˜ ung c´ o \ X2XX3, \ X3XX4, \ X4XX5, \ X5XX6, \ X6XX1 l´on hon 600, ¯ diê`u , , , , , , n` ay không thê ¯
du .oc v`ı tông c´ac g´oc n`ay phai b`˘ang 3600. Nhu v.ây, , , , , , , m˜ ôi ¯ diêm chı nô´i ¯
du .oc nhiê`u nhâ´t v´oi 5 ¯diêm thôi. , , . 4.14. L` oi giai: Ta chia h`ınh tr` on th`
anh 6 h`ınh qu .at b`˘ang nhau (c´o , ¯
dınh t .ai tâm h`ınh tr`on). Khi ¯d´o t.ai m˜ôi m .ôt h`ınh qu.at, không c´o qu´a , , ,, , , ,
m .ôt ¯diêm roi v`ao (boi v`ıkhoang c´ach gi˜ua hai ¯diêm bâ´t k`y trong m .ôt , , ,
h`ınh qu .at không l´on hon 1). Nê´u t.ai m˜ôi h`ınh qu.at c´o m .ôt ¯diêm th`ı , , , , , , , ta c´ o thê t`ım ¯
du .oc hai ¯diêm m`a g´oc gi˜ua c´ac b´an k´ınh vecto cua , , , , ch´ ung không l´ on hon 600 v`a do ¯ d´ o khoang c´ ach gi˜ ua ch´ ung không , , , , l´
on hon 1. Do v .ây, c´o thê ch .on không qu´a 5 ¯diêm. , , , , , . 4.15. L` oi giai: Ta thay m˜ ôi h`ınh vuông b` ˘
ang m .ôt h`ınh l´on hon gi´oi ,, , , , , 1 , ,
h .an boi m .ôt ¯du`ong c´ach biên cua h`ınh vuông m .ôt khoang (¯ du`ong 2 , , 1 n` ay gô`m bô´n ¯
do .an th˘ang ¯don v.i v`a bô´n cung tr`on c´o b´an k´ınh ). 2 , π , , M˜
ôi m .ôt h`ınh nhu thê´c´o di.ên t´ıch b`˘ang 3 + , c`on 120 h`ınh ¯d˜a ¯du .oc 4 , π "viê`n ra" s˜
e phu m .ôt di.ên t´ıch không qu´a 120.(3 + ) = 360 + 30π. 4 , , ,
Ta bao vây biên cua h`ınh ch˜u nh .ât ¯d˜a cho b`˘ang m .ôt dai c´o chiê`u , , , , , 160 Chuong 15. L` oi giai v` a g .oi ´y 1 , , , ,
r .ông . Di.ên t´ıch cua dai b`˘ang 44. Nhu v.ây, di.ên t´ıch tông c .ông 2 , , , , , cua dai v` a tâ´t ca c´ ac h`ınh ¯
du .oc viê`n ra b`˘ang 360 + 30π + 44 = , , ,
404 + 30π < 404 + 94, 5 < 500, t´ uc l` a b´
e hon di .ên t´ıch cua h`ınh , , , ch˜
u nh .ât (S = 20.25 = 500). Do ¯d´o, trong h`ınh ch˜u nh.ât c´o ¯diêm O , ,, , , ,
không b.i phu boi dai v`a c´ac h`ınh vuông ¯d˜a ¯du .oc viê`n ra. Ngh˜ıa l`a , , , ¯
diêm O c´ach bien cua h`ınh ch˜u nh .ât v`a c´ach m .oi h`ınh vuông m .ôt , , , 1 1 khoang l´ on hon . H`ınh tr` on b´ an k´ınh c´
o tâm t .ai O l`a h`ınh tr`on 2 2 câ`n t`ım. , , , , , 15.5. L` oi giai v ` a g .oi ´y chuong 5 , , , , . 5.11. L` oi giai: X´
et m .ôt t.âp A bâ´t k`y t`u 1978 t.âp. V`ı n´o giao v´oi ,, ,
1977 t .âp c`on l.ai, v`ı v.ây tô`n t.ai phâ`n tu a ∈ A, thu .ôc không ´ıt hon 50 , , ,, ,
t .âp h .op n`ay (th.ât v.ây nê´u m˜ôi m .ôt t`u 40 phâ`n tu cua t.âp A thu .ôc , , ,
không nhiê`u hon 49 t .âp, th`ı tâ´t ca c´o không nhiê`u hon 40.49 = 1960 ,,
t .âp kh´ac A, ¯diê`u n`ay không ¯d´ung). V.ây phâ`n tu a thu .ôc c´ac t.âp , , ,
h .op A, A1, . . . , A50. Ta s˜e ch´ung minh n´o s˜e thu .ôc t.âp bâ´t k`y B t`u ,
1978 t .âp. Th.ât v.ây không c´o hai t.âp n`ao t`u c´ac t.âp A, A1, . . . , A50 ,, , , l` a c´ o phâ`n tu chung kh´ ac v´
oi a (v`ı hai t .âp bâ´t k`y giao nhau chı c´o ,, , ,, ,
m .ôt phâ`n tu chung). Gia su a ∈ B. Khi ¯d´o t.âp B c´o v´oi m˜ôi t.âp ,, ,
A, A1, . . . , A50 m .ôt phâ`n tu chung kh´ac v´oi a, suy ra t.âp B c´o không , ,, , , , ,, ´ıt hon 51 phâ`n tu, ¯ diê`u n` ay không thê ¯
du .oc. Suy ra phâ`n tu a thu .ôc , , tâ´t ca c´ ac t .âp h .op. , , , . 5.12. L`
oi giai: M .ôt sô´chia cho 9 th`ıc´o c´ac phâ`n du {0, 1, 2, . . . , 8}. ,, Theo nguyên l´
y Dirichlê mo r .ông, trong 55 sô´ch .on ra th`ı´ıt nhâ´t c´o , , ,
m .ôt nh´om 7 sô´khi chia cho 9 cho c`ung phâ`n du (nê´u ngu .oc l.ai th`ı , ,, , c´ ac nh´ om chı c´
o 6 phâ`n tu v .ây 6.9=54 m`a ta lâ´y ra nh˜ung 55 sô´). Ch´ ung ta k´
y hi .êu c´ac sô´ ¯d´o l`a a1, a2, a3, . . . , a7. V`ı ai+1 ≡ ai (mod 9), , , , , , 15.6. L` oi giai v` a g .oi ´y chuong 6 161 , ,
nên ai+1 − ai ∈ {9, 18, . . .}. Ch´ung ta phai ch´ung minh r`˘ang ai+1 − , , ,, , , ,
ai = 9 v´oi m .ôt i n`ao ¯d´o. Gia su ngu .oc l.ai, v´oi m .oi i, ai+1 − ai ≥ 18, , , , ¯ diê`u n` ay ngh˜ıa l`
a a7 − a1 ≥ 6.8 = 108. Ðiê`u n`ay không thê ¯ du .oc v`ı , , ,, ,
a7 − a1 < 100. Nhu v .ây gi˜ua hai phâ`n tu cua a1, a2, a3, . . . , a7 c´o hai , , sô´m`
a hi .êu cua ch´ung phai b`˘ang 9. , , ,
. 5.13. G .oi ´y: C´ach ch´ung minh nhu b`ai 5.10. , , , , , , . 5.14. L`
oi giai: (B .an t .u v˜e lâ´y h`ınh ) Ch´ung ta xây d .ung lu´oi gô`m √ , 3 , , ,, nh˜
ung h`ınh l .uc gi´ac c´o c.anh . M˜
ôi h`ınh l .uc gi´ac c´o thê phu boi √ 2 , , , , , , , , ¯ du` ong tr` on v´ oi b´ an k´ınh 3. C´ o thê t´ınh to´ an ¯ du .oc sô´ lu .ong l .uc , , gi´ ac m` a ch´ ung c´ o ¯ diêm chung v´ oi tam gi´ ac ¯ dê`u ¯ d˜ a cho l` a 1 + 2 +
3 + · · · + 10 = 55. V`ı 111 = 55 × 2 + 1, nên c´ o m .ôt l .uc gi´ac trong , , , , , , lu´ oi trên ch´ ua ´ıt nhâ´t 3 ¯ diêm trong sô´ 111 ¯ diêm ¯ d˜ a ch .on. Nhu v.ây , , ¯ du` ong tr`
on bao l .uc gi´ac n`ay c´o t´ınh châ´t ¯d˜a nêu. , , , , , , , . 5.15. L` oi giai: K´
y hi .êu A1, A2, . . . , Ak l`a sô´ lu .ong ngu`oi l´on nhâ´t , , , , m` a bâ´t c´ u hai ngu` oi n` ao c˜ ung không quen nhau gi´ an tiê´p. T` u ¯ diê`u , ,
ki .ên b`ai ra k ≤ 7. M˜ôi ngu`oi c`on l.ai trong nh´om quen gi´an tiê´p ´ıt , , , , , , ,
nhâ´t m .ôt ngu`oi trong A1, A2, . . . , Ak (tru`ong h .op ngu .oc l.ai ch´ung , , , , , ta c´
o nhiê`u hon k ngu`oi, m`a hai ngu`oi không quen nhau gi´an tiê´p). , ,
M .ôt trong sô´ A1, A2, . . . , Ak c´o ´ıt nhâ´t 20 ngu`oi quen gi´an tiê´p, v`ı , , , , , , , , nê´u không ¯ d´
ung nhu v .ây, ch´ung ta s˜e nh.ân ¯du .oc tông sô´lu .ong ngu`oi , , nhiê`u nhâ´t l` a 7.19 = 133 < 134. C`
on l .ai kh˘ang ¯d.inh r`˘ang tâ´t ca , , , , , nh˜ ung ngu` oi quen gi´ an tiê´p qua c`
ung m .ôt ngu`oi l`a quen gi´an tiê´p. , , , , , 15.6. L` oi giai v ` a g .oi ´y chuong 6 , , , , ,
. 6.11. G .oi ´y: Ðây l`a tru`ong h .op riêng cua b`ai 6.1 v`a b`ai 6.2. , , , , , 162 Chuong 15. L` oi giai v` a g .oi ´y , 1
. 6.12. G .oi ´y: Sô´ ¯d˜a cho l`a x1, x2, x3, x4 v`a yi = 1 + , i = 1, 2, 3, 4. xi , , , Chı câ`n ch´ ung minh r` ˘ ang hai sô´n` ao ¯
dâ´y trong y1, y2, y3, y4 thoa m˜an y √ i − yj , , , , 0 ≤ ≤ 2 − 3. Phâ`n c` on l .ai tuong t .u nhu 2.6. 1 + 2yiyj , , , , , , . 6.13. L` oi giai: V´ oi ¯
d.inh l´y Fecma ch´ung minh ¯du .oc r`˘ang nê´u m .ôt , ,, sô´ nguyên tô´ p c´
o d .ang 4k + 3 chia hê´t cho tông a2 + b2, o ¯dây , , a, b l` a nh˜
ung sô´ nguyên, th`ı p chia hê´t cho t`ung sô´ a v`a b. H˜ay , , d` ung c´ ac ¯ d˘ ang th´
uc sau 2 = 12 + 12, k2(a2 + b2) = (ka)2 + (kb)2, (a2 + b2)(a2 + b2) = (a 1 1 2 2
1 a2 + b1b2)2 + (a1b2 − a2b1)2. , , , , , , , . 6.14. L` oi giai: Cho tuong ´ ung m˜ ôi sô´ v´ oi c˘ an b .âc hai cua ch´ınh , , , , , , n´
o. Nhu v .ây khi phân t´ıch ra m˜ôi sô´ tuong ´ung v´oi c˘an b.âc hai cua , , , , , sô´ le. M` a sô´ tâ´t ca c´
ac sô´ le nho hon 2k l`a k. V .ây theo nguyên l´y , , Ðirichlê c´
o hai sô´trong k + 1 sô´c´ o c` ung phâ`n c˘ an sô´le, do ¯ d´ o ty sô´ , , , cua n´ o s˜ e l` a l˜ uy th` ua cua 2. , , , . 6.15. L` oi giai: Nê´u gi˜ ua c´ ac sô´ ¯ d˜ a cho c´ o n sô´ m`a khi chia cho n , , , , ch´ ung cho nh˜ ung phâ`n du kh´ ac nhau. Tông cua ch´ ung s˜ e chia hê´t , , , , , ,
cho n, v`ı n l`a sô´ le. Trong tru`ong h .op ngu .oc l.ai, ´ap d .ung nguyên l´y Ðirichlê. , , , , , 15.7. L` oi giai v ` a g .oi ´y chuong 7 , , , , , . 7.11. L` oi giai: Ch´ ung ta thâ´y r` ˘
ang m .oi sô´ nguyên tô´ th .uc s .u l´on , , , hon 3 ¯ dê`u c´
o d .ang 6n + 1 ho.˘ac 6n + 5. V`ı ba sô´ nguyên tô´ l´on hon ,
3 l .âp th`anh m .ôt câ´p sô´c .ông, nên theo nguyên l´y Ðirichlê phai c´o ´ıt , nhâ´t hai sô´c`
ung d .ang, t´uc l`a hi.êu hai sô´ ¯d´o chia hê´t cho 6. G .oi d l`a , ,
công sai cua câ´p sô´ c .ông, th`ı hi.êu cua hai sô´ â´y ho.˘ac l`a d, ho.˘ac l`a , , , , , 15.7. L` oi giai v` a g .oi ´y chuong 7 163 , ,
2d. Nhu thê´ ho .˘ac l`a d|6 ho.˘ac 2d|6. Ch´u ´y công sai d l`a hi.êu cua hai , , , sô´nguyên tô´l´ on hon 3, nên n´ o l` a sô´ch˜ ˘
an. Nhu thê´v`ı d|3 v`a d|2 suy ra d|6. , , 10m . 7.12. L` oi giai: Ta luôn c´ o lim
= ∞. N´oi c´ach kh´ac tô`n t .ai m→+∞ 1998 , , 10m
sô´ nguyên duong m0 sao cho ∀m ≥ m0 th`ı > 91998. X´et m .ôt 1998 , , , , ,
sô´nguyên duong n bâ´t k`y v`a n c´
o k0 ch˜u sô´n = a1a2 . . . ak . Tru`ong 0 , , ,
h .op n`ay ta c˜ung ch .on ¯du .oc
10N > (9k0)1998 v`a N > m0 (15.1) , ,
(c .u thê c´o thê lâ´y N = max{[1998lg(9k0)] + 1, m0 + 1}) , - Ch´ ung ta s˜ e ch´ ung minh ,
ui(n) < 10N v´oi m .oi i = 1, 2, . . . (15.2) ,
Th .ât v.ây, ta s˜e ch´ung minh b`˘ang qui n.ap. , 1) V´ oi i = 1 ta c´
o u1(n) = (k1 + · · · + k0)1998 ≤ (9k0)1998 < 10N
(do (15.1)). V .ây (15.2) ¯d´ung khi i = 1. , ,, , 2. Gia su (15.2) ¯ d´ ung v´
oi i = k, ngh˜ıa l`a uk(n) < 10N. Ta c´o ,
uk+1(n) = f (uk(n)). Theo gia thiê´t qui n .ap th`ı uk(n) < 10N. do ¯d´o , ,
uk(n) c´o không qu´a N ch˜u sô´, t´uc l`a uk(n) c´o d .ang ,
uk(n) = a1a2 . . . ap v´oi p ≤ N Theo ¯ d.inh ngh˜ıa th`ı
uk+1(n) = (a1 + a2 + · · · + ap)1998 ≤ (9N)1998. (15.3) ,
Do N > m0 v .ây t`u (1) suy ra 10N > (9N)1998. (15.4) , T` u (15.3) v` a (15.4) suy ra uk+1(n) < 10N. , , , , , 164 Chuong 15. L` oi giai v` a g .oi ´y ,
V .ây (15.2) ¯d´ung v´oi i = k + 1. Theo nguyên l´y qui n.ap th`ı (15.2) , ¯ d´ ung v´ oi m .oi i = 1, 2, . . .. , , - D˜
ay vô h .an c´ac sô´ nguyên duong {ui(n)}, i = 1, 2, . . . b.i ch.˘an ,, , ,
boi 10N nên theo nguyên l´y Ðirichlê phai tô`n t .ai hai chı sô´ p < q sao cho
up(n) = uq(n) =⇒ up+k(n) = uq+k(n), ∀k , N´ oi c´ ach kh´ ac d˜
ay ui(n), i = p, p + 1, .. l`a d˜ay tuâ`n ho`an v´oi chu k`y
up(n), up+1(n), . . . , up+q+1(n). , , . 7.13. L`
oi giai: Cho a l`a m .ôt sô´tu`y ´y, th`ı {a} = a − [a] g .oi l`a phâ`n , , ,, , , le cua sô´ a, o ¯ dây k´
y hi .êu [a] l`a phâ`n nguyên cua sô´a. Xây d .ung d˜ay , , m´ oi nhu sau v1 = {u1} v2 = {u1 + u2} . . . . vn = {u1 + u2 + · · · + un} , R˜ o r` ang v´
oi m .oi k = 1, 2, . . . , n ta c´o 0 ≤ vk < 1. , ,
Chia [0, 1) ra l`am n + 1 t .âp h .op nhu sau ∆ 1 1 2 n 0 = [0, ); ∆ , ); . . . ; ∆ , 1) n + 1 1 = [ n + 1 n + 1 n = [ n + 1 , , , Chı c´ o c´ ac kha n˘ ang sau xây ra
1. Ho .˘ac tô`n t.ai k m`a vk ∈ ∆0 ∪ ∆n+1: , 1
- Nê´u vk ∈ ∆0, t´uc l`a 0 ≤ {u1 + u2 + · · · + uk} < . Ð .˘at n + 1 1
Sk = u1 + u2 + · · · + uk :⇒ 0 ≤ {S} < n + 1 1 ⇔ [S] ≤ S < [S] + . (15.5) n + 1 , , , , , 15.7. L` oi giai v` a g .oi ´y chuong 7 165 , ,
V .ây [S] l`a sô´ nguyên gâ`n S nhâ´t, nên t`u (15.5) suy ra ¯diê`u phai , ch´ ung minh. , n -Nê´u vk ∈ ∆n t´uc l`a ≤ {u n + 1
1 + u2 + · · · + uk} < 1 hay l` a n n ≤ {S} < 1 ⇔ ≤ S − [S] < 1 hay l`a n + 1 n + 1 n + [S] ≤ S < [S] + 1. (15.6) n + 1 , T`
u (15.6) suy ra [S] + 1 l`a sô´ nguyên gâ`n S nhâ´t v`a kh´ac n´ o m .ôt , , n 1 lu .ong ≤ [S] + 1 − ([S] + ) = . n + 1 n + 1
2. Ho .˘ac l`a c´ac sô´ v1, v2, . . . , vn 6∈ ∆0 ∪ ∆n, v.ây v1, v2, . . . , vn ∈ ∪n−1∆ i=1 i. Theo nguyên l´
y Ðirichlê tô`n t .ai vk, vl, k > l, thu .ôc c`ung m .ôt ,
t .âp h .op ∆j n`ao ¯d´o, 1 ≤ j ≤ n − 1. Ðiê`u ¯ d´ o c´ o ngh˜ıa l` a j j + 1 ≤ {u n + 1
1 + u2 + · · · + ul } < n + 1 j j + 1 ≤ {u n + 1
1 + u2 + · · · + uk} < n + 1
Ð .˘at Sk = u1 + u2 + · · · + uk v`a Sl = u1 + u2 + · · · + ul ta c´o j j + 1 j j + 1 ≤ S ⇒ [S ≤ S n + 1 k − [Sk] < n + 1 k] + n + 1 k < [Sk] + n + 1 j j + 1 j j + 1 ≤ S ⇒ [S ≤ S n + 1 l − [Sl ] < n + 1 l ] + n + 1 l < [Sl ] + n + 1 1 1 [Sk] − [Sl] − ≤ S n + 1
k − Sl ≤ [Sk] − [Sl ] + n + 1 1 1 [Sk] − [Sl] − ≤ u n + 1
l+1 + ul+2 + · · · + ul ≤ [Sk] − [Sl ] + n + 1 ,
Nhu v .ây d˜ay con ul+1 + ul+2 + · · · + ul c´o sô´ nguyên gâ`n nhâ´t l`a , 1 [Sk] − [Sl] v´oi ¯ d .ô l.êch không qu´a . n + 1 , , , , T´
om l .ai, trong m .oi tru`ong h .op ta ¯dê`u c´o tô`n t.ai d˜ay con thoa m˜ an yêu câ`u ¯ dê` ra. , , , , , 166 Chuong 15. L` oi giai v` a g .oi ´y , , . 7.14. L` oi giai: X´ et d˜
ây sô´ p1 = 1a = a, p2 = 2a, p3 = 3a,. . . , , , , ,
pm−1 = (m − 1)a. K´y hi.êu q1, q2, . . . , qm−1 l`a c´ac sô´ du tuong ´ung , cua d˜
ây trên chia cho m. V`ı theo ¯
diê`u ki .ên b`ai to´an a v`a m l`a nguyên , , tô´ c` ung nhau, th`ı tâ´t ca c´ ac sô´ du trên ¯ dê`u kh´ ac không. Nê´u m .ôt , , , , , trong c´ ac sô´ du b` ˘ ang 1 th`ı b`ai to´an ¯ d˜ a ¯
du .oc giai. Nê´u tâ´t ca c´ac sô´ , , du ¯ dê`u kh´ ac 1. Khi ¯ d´ o m˜
ôi sô´ trong m − 1 sô´ du q1, q2, . . . , qm − 1 b` ˘
ang m .ôt trong m − 2 sô´ 2, 3, . . . , m − 1. Theo nguyên l´y Ðirichlê , , c´
o ´ıt nhâ´t hai sô´ trong q1, q2, . . . , qm−1 b`˘ang nhau, ch˘ang h .an nhu , qi = qj, i < j. T` u ¯ d´
o suy ra sô´ (j − i)a = pj − pi chia hê´t cho m, , , , , ¯ diê`u n`
ay không thê xây ra. S .u vô l´y n`ay do gia thiê´t không m .ôt sô´ ,
du trong q1, q2, . . . , qm−1 b`˘ang 1, do ¯ d´
o suy ra ´ıt nhâ´t m .ôt trong c´ac , , sô´du phai b` ˘ ang 1. , , , , , 15.8. L` oi giai v ` a g .oi ´y chuong 8 , , , , , , . 8.11. L` oi giai: Tru´ oc tiên ch´ ung ta s˜ e ch´ ung minh a + b = c. T`u , , [an] 1 , bâ´t ¯ d˘ ang th´
uc 0 ≤ an − [an] < 1 suy ra | − a| < v´ oi m .oi n ≥ 1 n n [an] , , , , , sao cho limn→∞ = a. Ch´ ung ta c˜ ung c´ o bâ´t ¯ d˘ ang th´ uc tuong t .u n , , , , [an] [bn] [cn] cho b v`a c. Ch´ ung ta lâ´y gi´ oi h .an cua ¯d˘ang th´uc + = n n n , , v` a nh .ân ¯du .oc a + b = c. ,,
Ð .˘at a = [a] + α, b = [b] + β o ¯dây 0 ≤ α < 1, 0 ≤ β < 1. Khi ¯d´o
[an] + [bn] = [([a] + α)n] + [([b] + β)n] = [a]n + [b]n + [αn] + [βn],
[(a + b)n] = [([a] + [b] + α + β)n] = [a]n + [b]n + [(α + β)n]. , , , ,
Nhu v .ây b`ai to´an c´o thê ¯d.˘at l.ai nhu sau: Ch´ung minh r`˘ang nê´u a , , , , , v`
a b l`a nh˜ung sô´trong khoang [0, 1) m`a ch´ ung thoa m˜ an ¯ d˘ ang th´ uc [an] + [bn] = [(a + b)n] (15.7) , , v´
oi m .oi sô´t .u nhiên n, th`ı´ıt nhâ´t m .ôt trong hai sô´ ¯d´o b`˘ang 0. , , , , , 15.8. L` oi giai v` a g .oi ´y chuong 8 167 , ,, , , Gia su a 6= 0 v`a b 6= 0. Ch´ ung ta s˜ e ch´
ung minh tô`n t .ai sô´ t .u , , , nhiên n sao cho ¯ d˘ ang th´ uc (15.7) không ¯ d´
ung. Không mâ´t t´ınh tông , , , , qu´ at ch´ ung ta c´ o thê gia thiê´t r` ˘
ang a + b < 1, v`ı nê´u ngu .oc l.ai th`ı , (15.7) s˜ e không ¯ d´
ung th .âm ch´ı v´oi n = 1. , , , , , , a) Ch´ ung ta x´ et tru`
ong h .op a v`a b l`a nh˜ung sô´h˜uu ty. Khi ¯d´o c´o , , , , A B ,, , thê biêu di˜ ên ch´ ung du´ oi d .ang a = , , o ¯ dây A, B v`a N l`a nh˜ung N N , , sô´ nguyên v` a thoa m˜
an 0 < A < N, 0 < B < N. D˜ê d`ang kiêm tra , , r` ˘ ang (15.7) không thoa m˜ an v´ oi n = N − 1. Th .ât v.ây,
[a(N − 1)] = [aN − a] = [A − a] = A + [−a] = A − 1,
[b(N − 1)] = [bN − b] = [B − b] = B + [−b] = B − 1,
[(a + b)(N − 1)] = [A + B − (a + b)] = A + B − [a + b] = A + B − 1 ,
Nhu v .ây [a(N − 1)] + [b(N − 1)] 6= [(a + b)(N − 1)]. , , , , b) Ch´ ung ta x´ et tru`
ong h .op m .ôt trong c´ac sô´ a v`a b l`a sô´ vô ty. , , Ch´ ung ta s˜ e chı ra r` ˘ ang c´
o m .ôt sô´t .u nhiên n, m`a {an} + {bn} ≥ 1. (15.8) , , , Khi ¯ d´ o ¯ d˘ ang th´ uc (15.8) s˜ e suy ra không thê c´ o (15.7). , ,, , , ,
Gia su a l`a m .ôt sô´vô ty, theo b`ai 8.1 t.âp h .op nh˜ung sô´{an}, n = , , , 1, 2, . . . l` a tr`
u m .ât trong khoang (0, 1). K´y hi.êu k l`a sô´ t .u nhiên l´on , nhâ´t m` a a + kb < 1. Khi ¯ d´
o tô`n t .ai sô´t .u nhiên n m`a a + kb < {an} < 1. (15.9) , ,
Nê´u {bn} ≥ b, th`ı t`u ¯ d.inh ngh˜ıa cua k suy ra
{an} + {bn} > (a + kb) + b = a + (k + 1)b ≥ 1 , , , hay n´ oi c´ ach kh´
ac tô`n t .ai sô´t .u nhiên n m`a ¯d˘ang th´uc (15.8) ¯d´ung. , , , , , 168 Chuong 15. L` oi giai v` a g .oi ´y , , , Nê´u {bn} < b, th`ı v´
oi vi .êc thêm 1 − b v`ao c´ac vê´ cua bâ´t ¯d˘ang , , , th´ uc 0 ≤ {bn} < b, ch´ ung ta nh .ân ¯du .oc
1 − b ≤ b(n − 1) − [bn] + 1 < 1 Ðiê`u ¯ d´ o c´ o ngh˜ıa l`
a [b(n − 1)] = [bn] − 1 v`a {b(n − 1)} ≥ 1 − b. , , , , Ngo`
ai ra, tuong t .u t`u (15.9) suy ra
kb < a(n − 1) − [an] < 1 − a < 1 ,
v`ı thê´ [a(n − 1)] = [an] v`a {a(n − 1)} > kb. Nhung khi ¯ d´ o
{a(n − 1)} + {b(n − 1)} > kb + (1 − b) = 1 + (k − 1)b ≥ 1, , , , ,
v`ı k ≥ 1. Trong tru`ong h .op n`ay (15.8) ¯d´ung cho sô´ t .u nhiên n − 1. , ,
Nhu v .ây d˜ân ¯dê´n vô l´y khi m .ôt trong c´ac sô´ a v`a b l`a sô´vô ty. , , , ,
. 8.12. G .oi ´y: Ch´u ´y r`˘ang {n} chı c´o thê nh.ân h˜uu h.an gi´a tr.i. , , , , ,
. 8.13. G .oi ´y: L´y lu.ân tuong t .u nhu 8.4. ,
. 8.14. G .oi ´y: X´et c´ac sô´c´o d.ang n = 2k2 v`a ´ap d .ung 8.4. , , , , , 15.9. L` oi giai v ` a g .oi ´y chuong 9 ,
. 9.11. G .oi ´y: X´et c´ac sô´ kx − [kx](k = 0, 1, 2, . . . , n) v`a sô´ 1, chia , , ¯
do .an [0,1] ra n + 1 phâ`n, phâ`n c`on l.ai ´ap d .ung phuong ph´ap ¯do.an n` ay. , , ,
. 9.12. G .oi ´y: V´oi m˜ôi c´ach ch .on nh˜ung sô´ q1, q2, . . . qn tô`n t.ai sô´ , , nguyên p, v´ oi n´
o 0 ≤ q1x1 + q2x2 + · · · + qmxm − p < 1. Bây gi`oi chia ¯
do .an [0,1] ra (n + 1)m ¯do.an con b`˘ang nhau. , , , , , 15.10. L` oi giai v` a g .oi ´y chuong 10 169 , , , , √ p √ √ . 9.13. G .oi ´ y: H˜ ay x´ et hai tru` ong h .op 2 − > 3 − 2 v` a q √ p √ √ 2 − ≤ 3 − 2 q , , , ,
. 9.14. G .oi ´y: Tuong t .u b`ai trên. , , , ,
. 9.15. G .oi ´y: Gia thiê´t v´oi m .oi p v`a q thoa m˜an |mp2 + npq + sq2| ≥ 1. , , , , , 15.10. L` oi giai v ` a g .oi ´y chuong 10 , , , , , . 10.11. L` oi giai: Ðây l`
a s .u tông qu´at h´oa b`ai 10.3. C´ach ch´ung , , , , , , minh ho` an to`
an tuong t .u. Ch´ung ta c˜ung t.ao ra lu´oi v´oi c´ac h`ınh vuông c´
o di .ên t´ıch 1. Sau ¯d´o lâ´y m .ôt h`ınh vuông l`am gô´c rô`i t.inh , , , tiê´n c´ ac h`ınh vuông c´ o ch´ ua c´
ac manh cua A vê` h`ınh vuông gô´c. , , , , , ,
Nhu v .ây tông di.ên t´ıch nh˜ung phâ`n t.inh tiê´n cua A s˜e l´on hon n. ,, Theo nguyên l´
y Ðirichlê mo r .ông cho di.ên t´ıch suy ra c´o ´ıt nhâ´t , , ,
n + 1 trong sô´ nh˜ung phâ`n cua A ¯ d˜
a t.inh tiê´n t´oi h`ınh vuông gô´c , , , , , c´ o ¯
diêm chung (x0, y0). Nh˜ung ¯ diêm t` u c´ ac h`ınh vuông nho ban ¯ dâ`u ,
t.inh tiê´n ¯dê´n ¯diêm n`ay c´o to.a ¯d .ô l`a (xi, yi) (i = 1, 2, . . . , n + 1), m`a ,
xi − xj v`a yi − yj (i, j = 1, 2, . . . , n + 1) l`a nh˜ung sô´nguyên. , , , . 10.12. L` oi giai: Ch´ ung ta x´ et h`ınh vuông V, m`a n´ o ch´ ua bê`m .˘at A , v` a c´
o c .anh v´oi ¯d .ô d`ai n nguyên. Ð.˘at B = V\A. Ch´ung ta thâ´y ngay , S(V) = n2 v` a S(A) < k, do ¯ d´
o S(B) > n2 − k. Bây gi`o ´ap d .ung b`ai , , 10.11. V`ı thê´ B c´
o thê t.inh tiê´n sao cho n´o ch´ua ´ıt nhâ´t n2 − k + 1 , , , , ¯ diêm v´
oi to .a ¯d .ô nguyên. K´y hi.êu A1, V1, B1 l`a c´ac anh cua ph´ep t.inh , , , ,
tiê´n trên cua A, V, B tuong ´ ung. R˜ o r`
ang B1 = V1\A1. Ch´ung ta s˜e , , , , ch´ ung minh r` ˘
ang A1 ch´ua nhiê`u nhâ´t k − 1 ¯ diêm v´ oi to .a ¯d .ô nguyên. , , , , , 170 Chuong 15. L` oi giai v` a g .oi ´y , ,, , , , ,
Th .ât v.ây, Gia su ngu .oc l.ai ch´ung ta c´o k ¯diêm v´oi to.a ¯d .ô nguyên , , ,
trong A1. V`ı theo c´ach d .ung trên B1 ch´ua ´ıt nhâ´t n2 − k + 1 ¯diêm , trong v´
oi to .a ¯d .ô nguyên v`a B1 ⊂ V1, A1 ⊂ V1, A1 ∩ B1 = ∅, Khi ¯d´o , , ,
h`ınh vuông V1 ch´ua ´ıt nhâ´t n2 + 1 ¯ diêm v´
oi to .a ¯d .ô nguyên, ¯diê`u n`ay , , không thê xây ra, d˜ ân ¯ dê´n vô l´ y. , , , , , . 10.13. L` oi giai: C˜ ung nhu b` ai 10.5 t´
ac d .ung lên A ph´ep v.i t .u v´oi , , , ,
tâm t .ai gô´c t.a ¯d .ô v`a h.ê sô´ 1, ch´ung ta nh.ân ¯du .oc t.âp h .op m´oi A0. 2 ,,
V`ı S(A) > 4n nên S(A0) > n. Theo nguyên l´y Ðirichlê mo r .ông , ,
cho di .ên t´ıch A0 ch´ua ´ıt nhâ´t n + 1 ¯diêm kh´ac nhau (xi, yi) (i = , 1, 2, . . . , n + 1) m`
a xi − xj v`a yi − yj l`a nh˜ung sô´nguyên. , , , , Ch´ ung ta x´ et ¯ da gi´ ac lô`i nho nhâ´t ch´ ua tâ´t ca c´ ac ¯ diêm trên. D˜ ê , , , d` ang thâ´y r` ˘ ang m˜ ôi ¯ dınh cua ¯ da gi´ ac l`
a m .ôt trong c´ac ¯diêm (xi, yi). , , , Nh˜ ung ¯ dınh cua ¯ da gi´
ac không thu .ôc trong ¯do.an n`ao m`a hai ¯dâ`u l`a , , , , nh˜ ung ¯ diêm n` ˘ am trong ¯ da gi´ ac. V`ı thê´trong nh˜ ung ¯ diêm (xi, yi) tô`n , , ,
t .ai m .ôt ¯diêm m`a không n`˘am trong ¯do.an th˘ang nô´i hai ¯diêm trong , , , ,, ,
t .âp h .op ¯diêm ¯d˜a ch .on. Gia su ¯diêm ¯d´o l`a (x1, y1). C˜ung theo b`ai , , , 10.5 cho ta n ¯ diêm kh´ ac nhau v` a kh´ ac ¯
diêm gô´c to .a ¯d .ô, v´oi to.a ¯d .ô
nguyên (xi − x1, yi − y1), i = 2, 3, . . . , n + 1, ¯ dê`u n` ˘ am trong A. V`ı , , t´ınh ¯ dô´i x´ ung nên c´ ac ¯ diêm (x1 − xi, y1 − yi), i = 2, 3, . . . , n + 1, c˜ ung thu .ôc A. , , , Ch´ ung ta s˜ e ch´ ung minh nh˜ ung ¯ diêm x´ ac ¯ d.inh theo c´ach trên l`a , , ,, , , kh´ ac nhau t` ung ¯
dôi m .ô t. Th.ât v.ây, gia su ngu .oc l.ai ch´ung ta c´o
(xi − x1, yi − y1) = (x1 − xj, y1 − yj) , , 1 v´ oi hai chı sô´n` ao ¯ d´
o i, j m`a i, j = 2, 3, . . . , n + 1. V`ı v .ây x1 = (x 2 i + 1 xj) v`a y1 = (y 2 i + yj). Nê´u i = j th`
ı (x1, y1) = (xj, yj), vô l´y v`ı , , , , , 15.11. L` oi giai v` a g .oi ´y chuong 11 171 , , ,
1 6= j. Nê´u i 6= j, th`ı (x1, y1) l`a trung ¯ diêm cua ¯ do .an th˘ang nô´i hai , , , , ¯
diêm (xi, yi) v`a (xj, yj), ¯ diê`u n` ay không thê ¯ du .oc theo c´ach ch .on. , , , , Ch´ ung minh trên chı ra r` ˘ ang A ch´ ua ´ıt nhâ´t 2n ¯ diêm kh´ ac nhau , , v` a kh´
ac gô´c to .a ¯d .ô, c´o to.a ¯d .ô nguyên. Nhung ¯diêm gô´c to.a ¯d .ô c˜ung , n` ˘
am trong t .âp A v`a c´o to.a ¯d .ô nguyên, suy ra kê´t lu.ân cua b`ai to´an. ,
. 10.14. G .oi ´y: ´Ap d .ung b`ai t.âp 10.13. , , , , ,
. 10.15. G .oi ´y: C´ach ch´ung minh tuong t .u 10.9. , , , , , 15.11. L` oi giai v ` a g .oi ´y chuong 11 , , . 11.11. a) T` u b`
ai 11.3 suy ra 6 = 9 − (S12 + S23 + S13) + S123, t´uc l`
a S12 + S23 + S13 = 3 + S123 ≥ 3. Do ¯ d´
o m .ôt trong c´ac sô´S12, S23, S13 , , không nho hon 1. , , , , ,, b) L` oi giai: T` u b`
ai 11.3 suy ra 5 ≥ 9 − M2, t´uc l`a M2 ≥ 4. Boi v`ı , , , , 8 , t` u 9 ¯ da gi´ ac c´
o thê t .ao ¯du .oc 9. = 36 c.˘ap, di.ên t´ıch phâ`n chung cua 2 , , M 1 m 2 .ôt sô´c´
ac c .˘ap ¯d´o không nho hon ≥ . 36 9 , , , . 11.12. L`
oi giai: G .oi M1, M2, . . . , M6 l`a 6 ¯diêm ¯d˜a cho. Trong m˜ôi , , , tam gi´
ac Mi Mj Mk ta tô c .anh l´on nhâ´t b`˘ang mâ`u ¯do. Kê´t qua s˜e l`a , , , ,
m .ôt ¯do.an th˘ang Mr Ms l`a ¯do c`on c´ac c.anh kh´ac s˜e không ¯do. Chı câ`n , , , ch´ ung minh r` ˘
ang tô`n t .ai m .ôt tam gi´ac c´o ¯dınh l`a c´ac ¯diêm ¯d˜a cho v`a , , , , , ,
ba c .anh ¯du .oc tô mâ`u ¯do. Th.ât v.ây, c.anh l´on nhâ´t cua tam gi´ac nhu , , , , , thê´ ¯ dô`ng th` oi l`
a c .anh nho nhâ´t cua tam gi´ac kh´ac v`ı n´o ¯du .oc tô mâ`u , , , , , , ¯ do. T` u m˜ ôi ¯ diêm ¯ d˜ a cho xuâ´t ph´ at 5 ¯
do .an th˘ang nô´i n´o v´oi c´ac ¯diêm , , , , c`
on l .ai. V.ây ho.˘ac ´ıt nhâ´t c´o 3 trong nh˜ung ¯do.an th˘ang n`ay ¯du .oc tô , , , , mâ`u ¯
do, ho .˘ac ´ıt nhâ´t c´o 3 ¯do.an v˜ân không ¯du .oc tô mâ`u ¯do. , , , , , 172 Chuong 15. L` oi giai v` a g .oi ´y , , , , , , Nê´u t` u ¯ diêm M1 xuâ´t ph´at 3 ¯
do .an ¯du .oc tô mâ`u ¯do (ch˘ang h.an ,
M1M2, M1M3, M1M4) th`ı trong ∆M2M3M4 ´ıt nhâ´t c´o m .ôt c.anh (l´on , , , , ,, nhâ´t) ¯
du .oc tô mâ`u ¯do, gia su ¯d´o l`a ¯do.an M2M3. Thê´ th`ı trong , , ∆ , ,
M1M2M3 tâ´t ca c´ac c .anh ¯dê`u ¯du .oc tô mâ`u ¯do. , , , , Nê´u t` u ¯
diêm M1 xuâ´t ph´at ´ıt nhâ´t 3 ¯
do .an không ¯du .oc tô mâ`u , , ¯ do (ch˘
ang h .an 3 ¯do.an M1M2, M1M3, M1M4) th`ı ta x´et 3 tam gi´ac
M1M2M3, M1M2M4, M1M3M4. Trong m˜ôi tam gi´ac n`ay ´ıt nhâ´t c´o , , , , , ,
m .ôt c.anh ¯du .oc tô mâ`u ¯do, nhung c.anh không ch´ua ¯dınh M1. V.ây , , , , , 3 ¯
do .an M2M3, M2M4, M3M4 ¯du .oc tô mâ`u ¯do, t´uc l`a 3 c.anh cua , ∆M2M3M4 ¯dê`u mâ`u ¯do. , , , , , . 11.13. L` oi giai: Tru´
oc hê´t ta nh .ân x´et c´o ´ıt nhâ´t m .ôt tam gi´ac ¯don , ,, , , , , s´ ˘ ac (B`
ai 5.4). Gia su P1P2P3 l`a tam gi´ac ¯ don s´ ˘ ac, ch˘ ang h .an ¯do. Ðê , ,
riêng P1 ta c`on l .ai 6 ¯diêm v`a ta l.ai c´o m .ôt tam gi´ac ¯don s´˘ac không , , c´ o P1 l`a ¯ dınh (B` ai 5.4). Nê´u tam gi´ ac n` ay không ch´ ua c .anh P2P3 th`ı , , , , , , ta ¯
du .oc kê´t qua, thê´th`ı c´o m .ôt ¯diêm th´u tu P0 sao cho P0 P 1 1 2 P3 c˜ ung , , , , , , , l` a tam gi´ ac ¯
do. Tuong t .u ¯dê riê`n P2 v`a P3 ta ¯du .oc P0 v`a P0 sao cho 2 3 , P1P0 P l` a tam gi´ ac o. 2 3 v` a P1P2P03 ¯ d , , , , Tru´ oc hê´t ta x´ et kha n˘ angl` a 3 ¯
diêm P0, P0 v`a P0 không phân bi 1 2 3 .êt. , , , , Trong tru`
ong h .op n`ay m .ôt trong ch´ung t.ao th`anh v´oi P1P2P3 m .ôt , , , , h`ınh t´
u di .ên. C`on l.ai 3 ¯diêm. Nê´u c´ac c.anh gi˜ua m .ôt trong ba ¯diêm , , , , , , c`
on l .ai ¯d´o v`a 2 ¯dınh cua h`ınh t´u di.ên l`a ¯do ta s˜e ¯du .oc hai tam gi´ac , , , , , ¯ do v´
oi 2 c .anh r`oi nhau, m .ôt tam gi´ac c´o m .ôt ¯dınh m´oi v`a m .ôt c.anh , , , , cua t´
u di .ên v`a tam gi´ac kia trên t´u di.ên. Nê´u không, m˜ôi ¯diêm c´o ´ıt , , , , , ,
nhâ´t c .anh ¯do thu .ôc t´u di.ên. Nhu thê´c´o ´ıt nhâ´t m .ôt ¯dınh cua t´u di.ên , , , nô´i v´ oi ca 3 ¯ dınh c`
on l .ai b`˘ang c.anh mâ`u ¯den. Nê´u c.˘ap n`ao trong 3 , nô´i b` ˘
ang c .anh ¯den th`ı ta c´o m .ôt tam gi´ac ¯den v`a m .ôt ¯do. Nê´u không , , , , , ta ¯
du .oc hai tam gi´ac ¯do c´o ¯dınh r`oi nhau. , , , , , 15.12. L` oi giai v` a g .oi ´y chuong 12 173 , , ,, ,
V .ây ta c´o thê gia su r`˘ang ba ¯diêm P0, P0 v`a P0 l`a phân bi 1 2 3 .êt. Nê´u , , , , , , , 2 ¯ diêm, P0 v`a P0, c nô´i b` ˘ ang c o th`ı ta c hai tam gi´ ac o 1 2 ¯ du .o .anh ¯ d ¯ du .o ¯ d , , P1P2P3 v`a P0 P0 P P0 P0 cho theo th´ u t 1 2 3. Nê´u không th` ı P1P2P3 v`a P01 2 3 .u ,
m .ôt tam gi´ac ¯do v`a m .ôt tam gi´ac ¯den. , , , , , , , . 11.14. L` oi giai: Lâ´y 1998 ¯ d˜ıa ¯
du .oc tô giô´ng nhu ¯d˜ıa th´u hai cua , , ch´ ung ta v` a ¯
d .˘at chô`ng tâ´t ca ch´ung lên ¯d˜ıa th´u nhâ´t sao cho ch´ung , , , c´ o tâ´t ca c´
ac v.i tr´ı c´o thê (nhu khi quay). Khi ¯d´o trên m˜ôi h`ınh qu.at , , , , , , cua ¯ d˜ıa th´ u nhâ´t c´
o 200 h`ınh qu .at, ¯du .oc tô, t´uc l`a c´o tâ´t ca 2002 , , , ,, , ,
c .˘ap h`ınh qu.at ¯du .oc tô tr`ung nhau. Gia su c´o n v.i tr´ı cua ¯d˜ıa th´u , , , hai c´
o không ´ıt hon 21 c .˘ap h`ınh qu.at ¯du .oc tô tr`ung nhau. Khi ¯d´o , , , , sô´ c´
ac h`ınh qu .at ¯du .oc tô tr`ung nhau không nho hon 21n. Do ¯d´o , ,, 21n ≤ 2002, t´ uc l`
a n ≤ 1904, 8. Boi v`ı n l`a sô´nguyên, nên n ≤ 1904. Suy ra c´
o ´ıt nhâ´t 1998 − 1904 = 94 v.i tr´ı c´o không qu´a 20 c.˘ap h`ınh , ,
qu .at ¯du .oc tô tr`ung nhau. , , ,
. 11.15. G .oi ´y: Ch´ung minh ho`an to`an nhu b`ai 11.2. , , , , , 15.12. L` oi giai v ` a g .oi ´y chuong 12 , , , , , . 12.11. L`
oi giai: Lâ´y A∗ l`a nh˜ung ¯
diêm trên m .˘at câ`u ¯dô´i x´ung qua , , , , , , , , , tâm cua qua câ`u t` u nh˜ ung ¯
diêm cua t .âp h .op A. Theo gia thiê´t tông , , ,
di .ên t´ıch cua A v`a A∗ l´on hon di.ên t´ıch m.˘at câ`u. Theo nguyên l´y , ,
Ðirichlê cho di .ên t´ıch ch´ung c´o ¯diêm chung. V.ây ¯diêm chung ¯d´o v`a , , , , , , ¯ diêm ¯ dô´i x´ ung cua n´ o l`
a c .˘ap ¯diêm ¯dê`u thu .ôc A t.ao ra ¯du`ong k´ınh , qua câ`u. , , , , . 12.12. L` oi giai: V´ oi m˜
ôi h`ınh ch˜u th .âp ta x´et h`ınh tr`on c´o tâm t.ai , 1 , tâm ch˜
u th .âp v`a b´an k´ınh b`˘ang √ . Ta ch´ung minh r`˘ang nê´u hai 2 2 , , , , , 174 Chuong 15. L` oi giai v` a g .oi ´y , , h`ınh tr` on ¯ d´ o c´ ˘ at nhau th`ı hai ch˜
u th .âp c˜ung s˜e c´˘at nhau. Khoang , , , c´ ach gi˜ ua hai tâm cua h`ınh tr` on b` ˘ ang nhau v` a c´ ˘ at nhau không l´ on , , , , , hon hai lâ`n b´ an k´ınh cua ch´ ung, do ¯ d´ o khoang c´ ach gi˜ ua tâm cua , , , , , , , 1 , c´ ac ch˜
u th .âp tuong ´ung v´oi ch´ung không l´on hon √ . X´et h`ınh ch˜u 2 ,, , , , ,
nh .ât x´ac ¯d.inh boi c´ac c´anh cua h`ınh ch˜u th.âp th´u nhâ´t v`a tâm cua , , , , , ch˜
u th .âp th´u hai. S˜e c´o m .ôt c´anh cua ch˜u th.âp th´u hai ¯di qua h`ınh , , , ,, , ch˜
u nh .ât ¯d´o, do ¯d´o s˜e c´˘at ch˜u th.âp th´u nhâ´t, boi v`ı ¯d .ô d`ai cua c´anh 1 , , , , , 1 b` ˘ ang √ , c` on ¯
d .ô d`ai ¯du`ong ch´eo h`ınh ch˜u nh.ât không l´on hon √ . 2 2 , , , , R˜ o r` ang trong h`ınh tr` on b´ an k´ınh 100 chı c´ o thê ¯ d .˘at ¯du .oc m .ôt , 1 sô´h˜
uu h .an c´ac h`ınh tr`on b´an k´ınh √ không c´˘at nhau. 2 2 , , , , ,, , . 12.13. L` oi giai: C´
o thê. Gia su O l`a tâm cua ng˜ u gi´ ac ¯ dê`u ABCDE. Khi ¯ d´ o c´ ac h`ınh tr`
on n .ôi tiê´p trong c´ac g´oc AOC, BOD, COE, DOA, EOB c´ o t´ınh châ´t ¯ d˜ a nêu. , , , . 12.14. L` oi giai: X´
et m .ôt tam gi´ac ¯dê`u c´o c.anh b`˘ang 1. Tâ´t ca 3 , , , , , , ¯ dınh cua n´ o không thê ¯
du .oc tô b`˘ang c´ac mâ`u kh´ac nhau, do ¯d´o phai , , , c´ o hai ¯ diêm c` ung mâ`u, v` a khoang c´ ach gi˜ u ch´ ung b` ˘ ang 1. PH .U L .UC A , T .ÂP H .OP V `A ´ANH X .A , ,, ,
A.1. T .âp h .op v`a To´an tu trên t .âp h .op. , , ,, , Khi ch´
ung ta coi m .ôt ¯dô´i tu .ong a n`ao ¯d´o l`a m .ôt phâ`n tu cua t.âp , ,, ,
h .op A, th`ı k´y hi.êu l`a a ∈ A, c`on khi a không l`a phâ`n tu cua A th`ı k´y hi .êu l`a a 6∈ A. , , , ,
M .ôt t.âp h .op A g .oi l`a t .âp h .op con cua t.âp h .op B, khi m .oi phâ`n ,, , , ,, , ,
tu cua t .âp h .op A l`a phâ`n tu cua t.âp h .op B, K´y hi.êu l`a A ⊂ B ho.˘ac , , B ⊃ A. Ngh˜ıa l` a t`
u a ∈ A suy ra a ∈ B ho .˘ac l`a t`u a 6∈ B suy ra a 6∈ A. , ,,
T .âp h .op r˜ông không c´o m .ôt phâ`n tu n`ao, k´y hi.êu l`a ∅. M .oi ¯dô´i , , ,
tu .ong x ¯dê`u không n`˘am trong t.âp h .op r˜ông x 6∈ ∅ . T.âp h .op r˜ông , , ¯ dê`u n` ˘
am trong m .oi t.âp h .op, ngh˜ıa l`a ∅ ⊂ A, v´oi m .oi A. , ,,
Hai t .âp h .op A v`a B tr`ung nhau khi ch´ung c´o c`ung c´ac phâ`n tu , , , , , , , nhu nhau, k´
y hi .êu A = B. Tuong ¯duong , A = B khi v`a chı khi t`u , a ∈ A suy ra a ∈ B v` a t`
u a ∈ B suy ra a ∈ A ho .˘ac A ⊂ B v`a B ⊂ A. , , , , ,
Cho A1, A2, . . . , An l`a m .ôt sô´ h˜uu h.an nh˜ung t.âp h .op. H .op cua , , , , ,, nh˜
ung t .âp h .op trên l`a m .ôt t.âp h .op gô`m tâ´t ca c´ac phâ`n tu m`a n´o , , ,
thu .ôc v`ao m .ôt trong c´ac t.âp h .op A1, A2, . . . , An. H .op cua c´ac t.âp , ,
h .op A1, A2, . . . , An , k´y hi.êu l`a A1 ∪ A2 ∪ . . . ∪ An. C .u thê, a ∈ A1 ∪ ,
A2 ∪ . . . ∪ An ngh˜ıa l`a tô`n t .ai m .ôt chı sô´i trong {1, 2, . . . , n} sao cho 175 , , , 176 Chuong A. T .âp h .op v`a ´ Anh x .a a ∈ Ai. , , ,
Cho A1, A2, . . . , An l`a m .ôt sô´ h˜uu h.an nh˜ung t.âp h .op. Giao , , , , ,, cua nh˜
ung t .âp h .op trên l`a m .ôt t.âp h .op gô`m c´ac phâ`n tu m`a , , , n´ o n` ˘
am trong m .oi t.âp h .op A1, A2, . . . , An. Giao cua c´ac t.âp h .op ,
A1, A2, . . . , An k´y hi.êu l`a A1 ∩ A2 ∩ . . . ∩ An. C .u thê, a ∈ A1 ∩ A2 ∩ , ,
. . . ∩ An ngh˜ıa l`a v´oi m .oi chı sô´i trong {1, 2, . . . , n} ta c´o a ∈ Ai. , , ,
Hi .êu cua hai t.âp h .op A v`a B l`a m .ôt t.âp h .op, k´y hi.êu A\B, gô`m , ,, nh˜ ung phâ`n tu a c´
o t´ınh châ´t a ∈ A v`a a 6∈ B. , ,
A.2. Qui n .ap to´an h .oc v`a B`ai to´an tô h .op , , ,
Trong t .âp h .op sô´t .u nhiên, c`ung v´oi nguyên l´y Ðirichlê c`on m .ôt , , ,, , , nguyên l´
y qui n .ap to´an h .oc c˜ung hay ¯du .oc su d .ung. D.ang ¯don gian , , , , cua phuong ph´
ap qui n .ap to´an h .oc nhu sau: , ,
Cho m .ôt d˜ay nh˜ung ¯diê`u kh˘ang ¯d.inh K1, K2, . . . , Kn, . . . (A.1) c´ o t´ınh châ´t sau: ,
a)K1 l`a kh˘ang ¯d.inh ¯d´ung. , , , b) V´ oi m˜
ôi sô´ t .u nhiên n,nê´u Kn l`a kh˘ang ¯d.inh ¯dus ng th`ı suy ra ,
Kn+1 c˜ung l`a kh˘ang ¯d.inh ¯d´ung. , , Khi ¯ d´ o tâ´t ca c´ ac kh˘ ang ¯
d.inh trong d˜ay (A.1) ¯dê`u ¯d´ung. , , Ch´ u ´ y: ¯
diê`u ki .ên a) ¯dam bao cho K1 ¯d´ung, sau ¯d´o ´ap d .ung b) cho K2 c˜ung ¯ d´
ung, tiê´p t .uc ´ap d .ung b) cho K3 c˜ung ¯d´ung v`a tiê´p t .uc , , , qu´ a tr`ınh ¯ d´ o v´
oi m .oi n. Ðê minh h .oa ch´ung ta ch´ung minh m .ôt ¯d.inh , , l´
y vê` tô h .op m`a râ´t hay ´ap d .ung trong cuô´n s´ach n`ay: , , , ,, , ,,
M .oi t .âp h.op h˜uu h .an v´oi n phâ`n tu c´o ¯d´ung 2n t .âp h.op con t .ao boi ,, , c´ ac phâ`n tu kh´ ac nhau cua n´ o. , A.3. ´ Anh x .a trên t.âp h .op 177 , , V´
oi m .oi sô´ n ch´ung ta k´y hi.êu ¯diê`u kh˘ang ¯d.inh trên b`˘ang Kn. , , , , ,
Nhu v .ây ch´ung ta s˜e nh.ân ¯du .oc d˜ay (A.1). V´oi n = 1 kh˘ang ¯d.inh , ,, , ¯ d´
ung, v`ı m .oi t.âp h .op c´o m .ôt phâ`n tu c´o ¯d´ung hai t.âp h .op con, ¯d´o l`a ,,
t .âp r˜ông v`a ch´ınh t.âp ( m .ôt phâ`n tu ) ¯dos . V.ây (A.1) c´o t´ınh châ´t a). , , , Bây gi` o ch´ ung ta phai ch´ ung minh b) ¯ d´ ung. Ngh˜ıa l` a cho n l`a , , , ,
m .ôt sô´t .u nhiên bâ´t k`y v`a kh˘ang ¯d.inh Kn ¯d´ung t´uc l`a m .oi t.âp h .op c´o ,, , , , n phâ`n tu c´ o ¯ d´
ung 2n t .âp h .op con. Câ`n phai ch´ung minh r`˘ang Kn+1 , ,, l` a ¯ dus ng. Ch´ ung ta x´
et S l`a t .âp h .op c´o n + 1 phâ`n tu v`a s l`a m .ôt ,, , , , , , phâ`n tu cua n´ o. Ch´ ung ta chia nh˜
ung t .âp h .op con cua S l`am hai l´op: , , , , , , L´
op a1 gô`m tâ´t ca c´ac t .âp h .op con cua S không ch´ua s. L´op a2 gô`m , , , , , , , tâ´t ca c´
ac t .âp h .op con cua S ch´ua s. Nh˜ung t.âp h .op con thu .ôc l´op a1 , , , ,, , l`
a t .âp h .op con cua m .ôt t.âp h .op n phâ`n tu S1, m`a n´o nh.ân t`u S sau , ,, , , , , , khi bo ¯
di phâ`n tu s. Theo gia thiê´t qui n .ap sô´lu .ong t.âp h .op con cua , , , , , , n´ o ¯ d´ ung l`
a 2n. M .˘at kh´ac c´ac t.âp h .op con cua l´op a2 l`a tuong ´ung 1-1 , , , , , , v´ oi v´ oi c´
ac t .âp h .op con cua S1. Th.ât v.ây, m .oi t.âp h .op con Z ch´ua s , , , , , , , , cua S ta cho tuong ´ ung v´
oi t .âp h .op con Z1 cua S1 b`˘ang c´ach t`u Z , ,, , , , , , ta bo ¯
d.i phâ`n tu s. Ngh˜ıa l`a sô´lu .ong t.âp h .op con cua S trong l´op a2 , , , , , , tr` ung v´
oi sô´ lu .ong t.âp h .op con cua S1 v`a b`˘ang 2n. Do ¯d´o tâ´t ca t.âp , , , ,
h .op con cua S l`a 2n + 2n = 2n+1. Nhu v.ây ch´ung ta ¯d˜a ch´ung minh, , , , v´
oi m .oi n, t`u Kn ¯dus ng suy ra Kn+1 ¯dus ng. Ch´ung ta ch´ung minh , , , , ¯
du .oc (A.1) c´o t´ınh châ´t b). Suy ra tâ´t ca c´ac kh˘ang ¯d.inh ¯dê`u ¯d´ung. J , A.3. ´ Anh x .a trên t .âp h .op , , ,, , , , , T` u nh˜ ung kh´
ai ni .êm sô´phâ`n tu cua m .ôt t.âp h .op n`ay l´on hon sô´ ,, , , , , ,
phâ`n tu cua m .ôt t.âp h .op kia, ngu`oi ta xây d .ung kh´ai ni.êm ´anh x.a , , , ¯ dê giai th´ıch v` a ch´ınh x´ ac h´ oa trong khi ch´ ung minh. , , , 178 Chuong A. T .âp h .op v`a ´ Anh x .a , , Ch´ ung ta n´ oi r` ˘
ang cho m .ôt ´anh x .a f : A → B t`u t.âp h .op A v`ao , ,, , , , ,
t .âp h .op B, khi m .oi phâ`n tu a thu .ôc A cho tuong ´ung v´oi m .ôt phâ`n ,, ,, , ,
tu f (a) thu .ôc B. Phâ`n tu f (a) g .oi l`a gi´a tr.i cua ´anh x.a f v´oi phâ`n ,, , , , , , tu a cua A. C´
o thê chı ra nhiê`u v´ı d .u nhu ´anh x.a sô´t .u nhiên v`ao sô´ , , , , , ch˜ ˘ an, v´
oi m .oi n cho tuong ´ung v´oi 2n,. . . . , , , , Ngu` oi ta c` on ¯
dua ra m .ôt sô´ t´ınh châ´t cua ´anh x.a: M .ôt ´anh x.a , ,
f : A → B g .oi l`a ¯don ´anh, nê´u t`u f (a1) = f (a2)(a1, a2 ∈ A) suy ra , ,, ,
a1 = a2. N´oi c´ach kh´ac f l`a ¯ don ´
anh khi m .oi phâ`n tu kh´ac nhau cua , , , , , ,, , A cho tuong ´ ung v´ oi nh˜ ung phâ`n tu kh´ ac nhau cua B. , ,,
M .ôt ´anh x.a f : A → B g .oi l`a to`an ´anh, nê´u v´oi m .oi phâ`n tu , , ,,
cua b cua B tô`n t .ai phâ`n tu a thu .ôc A sao cho f (a) = b. C´o nhiê`u v´ı , , ,
d .u vê` ´anh x.a lo.ai n`ay, nhu ph´ep chiê´u lên tr .uc to.a ¯d .ô cua m .oi ¯diêm , trong m .˘at ph˘ang. , ,
M .ôt ´anh x.a f : A → B g .oi l`a song ´anh, khi n´o ¯dô`ng th`oi l`a ¯don , ,, ´ anh v` a to` an ´
anh. Nê´u f : A → B l`a song ´anh, th`ı v´ oi m .oi phâ`n tu b , ,,
cua B tô`n t .ai duy nhâ´t phâ`n tu a thu .ôc A sao cho f (a) = b. Cho song ´ anh f : A → B. Nê´u ch´ ung ta ¯ d .˘at g(b) = a khi ¯d˜a , , c´ o f (a) = b, ch´
ung ta nh .ân ¯du .oc ´anh x.a g : B → A g .oi l`a ´anh , , , ,
x .a ngu .oc cua f v`a k´y hi.êu l`a f −1 = g. Nhu v.ây f ( f −1(b)) = b v`a , f −1( f (a)) = a v´
oi m .oi a thu .ôc A v`a b thu .ôc B. , Cho hai ´
anh x .a f : A → B v`a g : B → C, c´o thê t.ao ra ´anh x.a , h : A → C b`˘ ang công th´
uc h(a) = f (g(a)). K´y hi .êu h = g ◦ f . , T ` AI LI .ÊU THAM KHAO , , ,
[1] Tuyên t .âp 30 n˘am t .ap ch´ı To´an h.oc v`a Tuôi tre, NXBGD, 1997. [2] 255 b` ai to´
an sô´ h .oc ch.on l.oc, V.D. Th .uy, T. C. Th`anh, N. N. ,, Ð .am, So GD H`a tây, 1993 , , , [3] 10000 B` ai to´ an so câ´p - D˜ ay sô´ v` a gi´
oi h .an, Phan Huy Khai, NXB H` a n .ôi, 1997. , , [4] C´ ac ¯ dê` thi vô ¯
d.ich to´an c´ac nu´oc, Xv. Cônhiagin, G.A.Tônôian, , If. Sarugin, NXB GD 1996. , , [5] C´ ac b` ai to´
an h`ınh h .oc ph˘ang, V.V. Praxolov, T.âp II, NXB Hai ph` ong 1997. , [6] Zadatri Vsesaiun´
uc matematitreskii olimpiada, N.B. Vasilev,
A.A. Egorov, Maskova- Nauka 1988.
[7] Matematichskii akvarium V. A. Uphnarovskii, Kishinev " shti- insa" 1987.(Tiê´ng Nga).
[8] Problem-Solving Through Problems, Loren C. Larson, Spring- Verlag, 1983.
[9] Princil na Dirichle, Ivan Prodanov, "Narodna Prosveta", Sophia 1988 (Tiê´ng Bungari). 179 180 M .uc l .uc ,
[10] Zadachi da idvunklasna Rabota po matematika,
R.Rusev, K.Bankov, Sv. Slavchev, "Narodna Prosveta", Sophia 1986 (Tiê´ng Bungari).
[11] Sbornhik ot Zadachi za Matematicheski Olympiadi,
St. Budurov, V. Phlorov, "Narodna Prosveta", Sophia 1966 (Tiê´ng Bungari). N .ÔI DUNG , L` oi n´ oi ¯
dâ`u . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 , , Chuong 1. Nguyên l´ y Ðirichlê v`
a v´ı d .u . . . . . . . . . . . . . . . . . . . . . . 5 1.1. Nguyên l´
y Ðirichlê . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
1.2. V´ı d .u. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 1.3. B`
ai t .âp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 , ,
Chuong 2. Sô´ h .oc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 , 2.1. Ph´
ep chia sô´t .u nhiên . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
2.2. V´ıd .u . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 2.3. B`
ai t .âp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20 , , Chuong 3. D˜
ay sô´. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23 3.1. Nguyên l´ y Ðirichlê cho d˜
ay sô´vô h .an. . . . . . . . . . . . . . . . . . 23
3.2. V´ı d .u . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23 3.3. B`
ai t .âp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31 , ,
Chuong 4. H`ınh h .oc. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
4.1. V´ı d .u . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33 4.2. B`
ai t .âp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41 , , ,,
Chuong 5. Mo r .ông nguyên l´y Ðirichlê. . . . . . . . . . . . . . . . . . . . . 43 ,, 5.1. Nguyên l´
y Ðirichlê mo r .ông . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
5.2. V´ı d .u . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44 181 182 N .ÔI DUNG 5.3. B`
ai t .âp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52 , , Chuong 6. B`
ai t .âp sô´h .oc nâng cao . . . . . . . . . . . . . . . . . . . . . . . . 55 , , ,
6.1. Ð.inh l´y co ban cua sô´h .oc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55
6.2. V´ı d .u . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55 6.3. B`
ai t .âp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64 , , Chuong 7. B`
ai t .âp d˜ây sô´nâng cao . . . . . . . . . . . . . . . . . . . . . . . . 67
7.1. V´ı d .u . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67 7.2. B`
ai t .âp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78 , , , ,
Chuong 8. Sô´ th .uc v´oi t .âp tr`u m .ât . . . . . . . . . . . . . . . . . . . . . . . . . 79
8.1. T .âp tr`u m.ât . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79
8.2. V´ı d .u . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80 8.3. B`
ai t .âp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87 , , , , , Chuong 9. Nh˜ ung ´
ung d .ung kh´ac cua nguyên l´y Ðirichle . . 89 , ,
9.1. Xâ´p xı m .ôt sô´th .uc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89 9.2. B`
ai t .âp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 99 , , Chuong 10. Nguyên l´
y Ðirichlê cho di .ên t´ıch . . . . . . . . . . . . . 101 , 10.1. Ph´ at biêu nguyên l´
y Ðirichlê cho di .ên t´ıch . . . . . . . . . . 101
10.2. V´ı d .u . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105 10.3. B`
ai t .âp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 117 , , , , Chuong 11. To´
an h .oc tô h .op. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 119
11.1. V´ı d .u . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 119 11.2. B`
ai t .âp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 127 , ,
Chuong 12. M .ôt sô´b`ai t .âp h`ınh h .oc kh´ac . . . . . . . . . . . . . . . . 129
12.1. V´ı d .u . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 129 M .uc l .uc 183 12.2. B`
ai t .âp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 134 , ,
Chuong 13. M .ôt sô´ ¯dê` thi vô ¯d.ich . . . . . . . . . . . . . . . . . . . . . . . . 135 , , , , Chuong 14. B`
ai t .âp t .u giai . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 151 , , , , , Chuong 15. L` oi giai v`
a g .oi ´y . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 155 , , , , , 15.1. L`oi giai v`
a g .oi ´y chuong 1. . . . . . . . . . . . . . . . . . . . . . . . . . . 155 , , , , , 15.2. L` oi giai v`
a g .oi ´y chuong 2. . . . . . . . . . . . . . . . . . . . . . . . . . . 156 , , , , , 15.3. L` oi giai v`
a g .oi ´y chuong 3. . . . . . . . . . . . . . . . . . . . . . . . . . . 158 , , , , , 15.4. L` oi giai v`
a g .oi ´y chuong 4. . . . . . . . . . . . . . . . . . . . . . . . . . . 158 , , , , , 15.5. L` oi giai v`
a g .oi ´y chuong 5. . . . . . . . . . . . . . . . . . . . . . . . . . . 160 , , , , , 15.6. L` oi giai v`
a g .oi ´y chuong 6. . . . . . . . . . . . . . . . . . . . . . . . . . . 161 , , , , , 15.7. L` oi giai v`
a g .oi ´y chuong 7. . . . . . . . . . . . . . . . . . . . . . . . . . . 162 , , , , , 15.8. L` oi giai v`
a g .oi ´y chuong 8. . . . . . . . . . . . . . . . . . . . . . . . . . . 166 , , , , , 15.9. L` oi giai v`
a g .oi ´y chuong 9. . . . . . . . . . . . . . . . . . . . . . . . . . . 168 , , , , , 15.10. L` oi giai v`
a g .oi ´y chuong 10 . . . . . . . . . . . . . . . . . . . . . . . . 169 , , , , , 15.11. L` oi giai v`
a g .oi ´y chuong 11 . . . . . . . . . . . . . . . . . . . . . . . . 171 , , , , , 15.12. L` oi giai v`
a g .oi ´y chuong 12 . . . . . . . . . . . . . . . . . . . . . . . . 173 ,
Ph .u l .uc A. T .âp h .op v`a ´Anh x .a . . . . . . . . . . . . . . . . . . . . . . . . . . . . 175 , ,, ,
A.1. T .âp h .op v`a To´an tu trên t.âp h .op. . . . . . . . . . . . . . . . . . . . . 175 , ,
A.2. Qui n .ap to´an h .oc v`a B`ai to´an tô h .op . . . . . . . . . . . . . . . . . 176 , A.3. ´
Anh x .a trên t.âp h .op . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 177
M .uc l .uc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 180 , , NGUY˜ ÊN H ˜ UU ÐIÊN , , , PHUONG PH´ AP ÐIRICHLÊ V` A ´ UNG D .UNG , , , c Ebook 1.0 cua cuô´n s´ ach nguyên gô´c t` u ban in, c´ ac b .an tham , , , khao, cho ´ y kiê´n sai s´ ot v` a l` oi khuyên t´ ai ban. M .oi liên h.ê , , , T´ ac gia: Nguy˜ ên H˜ uu Ðiên Ði .ên tho.ai: 0989061951 Email: huudien@vnu.edu.vn
Web: http://nhdien.wordpress.com , ,
Ch.iu tr´ach nhi.êm xuâ´t ban: TÔ Ð˘ANG HAI ,, , Biên t .âp v`a sua ban in: Ð ˜ Ô PH ´ U , , , Tr`ınh bâ`y v` a chê´ban: H˜ UU ÐIÊN, PH ` U LINH , , Tr`ınh bâ`y b`ıa: HUONG LAN , NH` A XU´
ÂT BAN KHOA H .OC V`A K˜Y THU .ÂT , 70 TR` ÂN HUNG Ð .AO - H`A N .ÔI 6.6T7.3 290 - 4-98 KHKT − 98 , ,
In 1000 ban khô 14, 5 × 20, 5 t .ai Công ty In Công Ðo`an Vi.êt Nam ,
191 Son Tây - Ðô´ng Ða - H`
a N .ôi. Giâ´y ph´ep XB sô´: 290-22/4/98. , , In xong v`
a n .ôp luu chiêu th´ang 1 n˘am 1999.
Document Outline

Lời nói đầu
Nguyên lý Đirichlê và ví dụ
- Nguyên lý Đirichlê
- Ví dụ
- Bài tập
Số học
- Phép chia số tự nhiên
- Vídụ
- Bài tập
Dãy số
- Nguyên lý Đirichlê cho dãy số vô hạn
- Ví dụ
- Bài tập
Hình học
- Ví dụ
- Bài tập
Mở rộng nguyên lý Đirichlê
- Nguyên lý Đirichlê mở rộng
- Ví dụ
- Bài tập
Bài tập số học nâng cao
- Định lý cơ bản của số học
- Ví dụ
- Bài tập
Bài tập dẫy số nâng cao
- Ví dụ
- Bài tập
Số thực với tập trù mật
- Tập trù mật
- Ví dụ
- Bài tập
Những ứng dụng khác của nguyên lý Đirichle
- Xấp xỉ một số thực
- Bài tập
Nguyên lý Đirichlê cho diện tích
- Phát biểu nguyên lý Đirichlê cho diện tích
- Ví dụ
- Bài tập
Toán học tổ hợp
- Ví dụ
- Bài tập
Một số bài tập hình học khác
- Ví dụ
- Bài tập
Một số đề thi vô địch
Bài tập tự giải
Lời giải và gợi ý
- Lời giải và gợi ý chương 1
- Lời giải và gợi ý chương 2
- Lời giải và gợi ý chương 3
- Lời giải và gợi ý chương 4
- Lời giải và gợi ý chương 5
- Lời giải và gợi ý chương 6
- Lời giải và gợi ý chương 7
- Lời giải và gợi ý chương 8
- Lời giải và gợi ý chương 9
- Lời giải và gợi ý chương 10
- Lời giải và gợi ý chương 11
- Lời giải và gợi ý chương 12
Tập hợp và Ánh xạ
- Tập hợp và Toán tử trên tập hợp.
- Qui nạp toán học và Bài toán tổ hợp
- Ánh xạ trên tập hợp
- Mục lục

Phương pháp Đirichlê và ứng dụng – Nguyễn Hữu Điển

Thông tin :

Tài liệu liên quan:

Tổng hợp kiến thức Đại số THCS

Cấu trúc đề thi vào 10 năm 2023 tỉnh Tỉnh Bà Rịa - Vũng Tàu

Cấu trúc đề thi tuyển sinh lớp 10 tỉnh Thái Nguyên năm 2023 - 2024

Cấu trúc đề thi vào lớp 10 năm 2023 - 2024 tỉnh Thanh Hóa

Cấu trúc đề thi vào 10 tỉnh Quãng Ngãi năm 2023 - 2024