Phương Pháp Giải Hệ Thức Giữa Các Tỉ Số Lượng Giác Toán 9

Chuyên đề 4: HỆ THỨC GIỮA CÁC TỈ SỐ LƯỢNG GIÁC CỦA CÁC GÓC  VÀ 2 (0    45) A. Đặt vấn đề
Trong chuyên đề này ta sẽ thiết lập các hệ thức liên hệ giữa các tỉ số lượng giác của góc  và góc 2 .
Nhờ đó mà ta tính được các tỉ số lượng giác của góc  khi biết tỉ số lượng giác của góc 2 và ngược lại B. Một số ví dụ
Ví dụ 1. Cho   45 , chứng minh rằng sin2 = 2sin cos
Áp dụng: Cho sin = 0,6 tính sin2 Giải
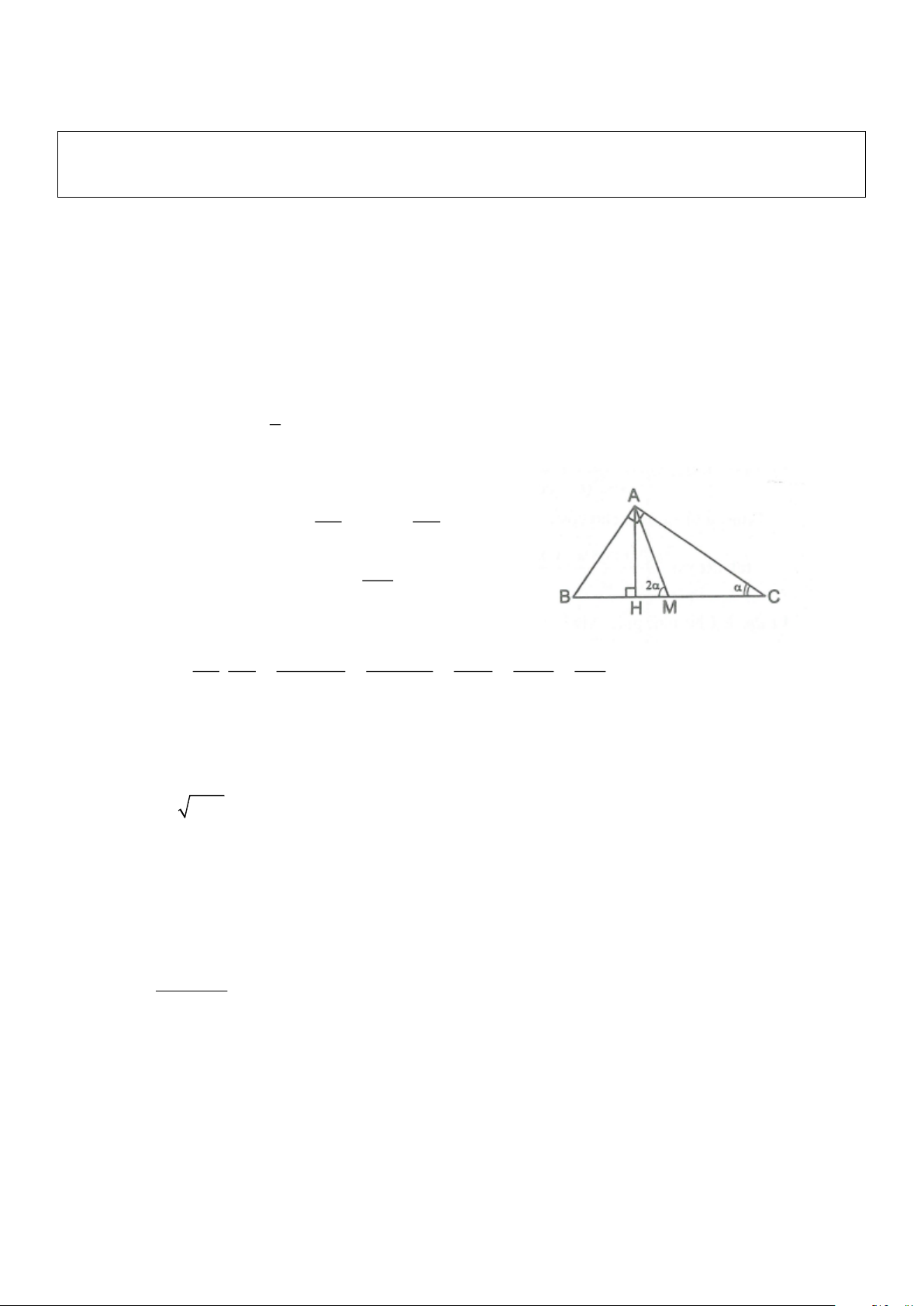
Xét ABC vuông tại A, C  45
Vẽ đường cao AH và đường trung tuyến AM. 1
Khi đó MA = MB = MC = BC 2
Ta có AMC cân tại M, do đó AMB = 2C = 2  AB AC
ABC vuông tại A, ta có sin = ; cos = BC BC AH
Xét AHM vuông tại H, ta có sin2 = ( ) 1 AM Ta có AB AC 2.A . B AC 2A . H BC 2AH 2AH AH 2sin .  cos = 2 . = = = = = (2) 2 2 BC BC BC BC BC 2AM AM Từ ( )
1 và (2) suy ra sin2 = 2sin cos
Áp dụng: Nếu sin = 0,6 thì  = −  = − ( )2 2 2 cos 1 sin 1 0,6 = 0,64
Do đó cos = 0,64 = 0,8. Vậy sin2 = 2sin .  cos = 2.0,6.0,8 = 0,96
Nhận xét: Việc xét ABC vuông tại A là để có sin và cos . Việc vẽ đường trung tuyến AM là để
xuất hiện 2 . Vẽ thêm đường cao AH để có thể tính sin2
Ví dụ 2. Cho   45 . Chứng minh các hệ thức sau: a) 2 2 cos2 = cos  − sin  2tan b) tan2 = 2 1− tan  Giải a) Ta có  = −  = − (  )2 2 2 2 2 cos 2 1 sin 2 1 2sin cos =1− 4sin  cos  = (  + )2 2 2 2 2 cos sin − 4sin  cos  4 2 2 4
= cos  − 2sin  cos  + sin  = (  − )2 2 2 cos sin Trang 1 Do đó:  = (  − )2 2 2 cos2 cos sin 2 2 = cos  − sin 
Vì   45 nên sin  cos (xem bài 2.26). Vậy 2 2 cos2 = cos  − sin 
Lưu ý: Tiếp tục biến đổi các hệ thức trên ta được các hệ thức sau 2 2 2  −  =  − ( 2 − ) 2 cos sin cos 1 cos = 2cos  −1 2 2  −  = ( 2 − ) 2 2 cos sin 1 sin − sin  = 1− 2sin  Vậy 2 2 2 2
cos2 = cos  − sin  = 2cos  − 1= 1− 2sin  sin2 2sin cos b) Ta có tan2 = = cos2 2 2 cos  − sin  Chia cả tử và mẫu cho 2 cos  ta được: 2 2
2sin cos cos  − sin  2sin 2tan tan2 = : = : ( 2 1− tan ) = 2 2 cos  cos  cos 2 1− tan 
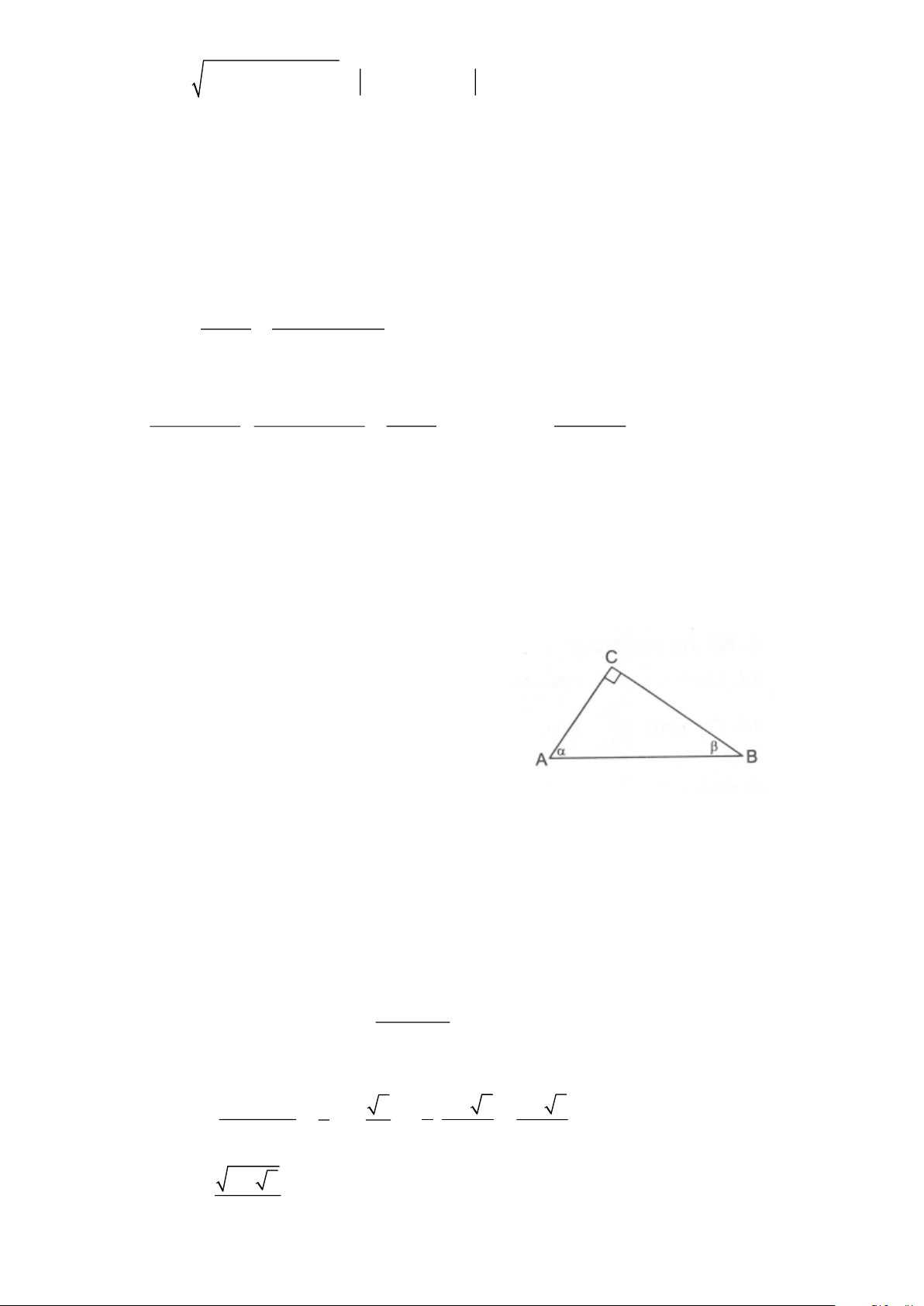
Ví dụ 3. Cho tam giác ABC vuông tại C, A =  , B =  với    . Chứng minh rằng: (  + )2 sin sin = 1+ sin2 Giải
ABC vuông tại C nên A + B = 90
Mặt khác, A  Bnên A =   45
Ta có  +  = 90 nên sin = cos Do đó (  + )2 = (  + )2 sin sin sin cos 2 2 = sin  + cos  + 2sin .
 cos = 1+ sin2
Ví dụ 4. Không dùng máy tính hoặc bảng số hãy tính: sin22 3  0 , cos22 3  0 , tan22 3  0 Giải
 Tìm hướng giải Vì 22 3
 0 bằng một nửa của góc 45 , nên ta dùng công thức tỉ số lượng giác của góc nhân đôi để giải.
 Trình bày lời giải −  • 1 cos2 Ta có 2 cos2 = 1− 2sin  2  sin  = 2 Với  = 22 3
 0 , 2 = 45 ta được: 1 cos45   − − 2 −  1 2 1 2 2 sin 2  2 3  0 = = 1−  = 2 2 . = 2 2  2    2 2 4 2 − 2 Suy ra sin22 3  0 = 2 Trang 2 +  • 1 cos2 Ta có 2 cos2 = 2cos  −1 2  cos  = 2 Với  = 22 3
 0 , 2 = 45 ta được: 1+ cos45   1 2 + 2 + cos22 3  0 = 1 2 = 1+  = 2 2 . = 2 2  2    2 2 4 + Suy ra   = 2 2 cos22 30 2   − + 2 2 2 ( 2 − − )1 • sin22 30 2 2 2 2 tan22 3  0 = = : = = cos22 3  0 2 2 2 + 2 2 ( 2 + ) 1 ( − )2 2 1 = = 2 −1 1
C. Bài tập vận dụng
4.1. Cho 0    45 , chứng minh rằng 1+ sin2 = sin + cos 24 4.2. Cho sin = 25 a) sin2  b) sin 2
4.3. Không dùng máy tính hoặc bảng số, hãy tính: sin15 , cos15 , tan15
4.4. Không dùng máy tính hoặc bảng số, hãy tính: sin75 , cos75 , tan75
4.5. Không dùng máy tính hoặc bảng số, hãy tính: sin67 3  0 , cos67 3  0 , tan67 3  0
4.6. Không dùng máy tính hoặc bảng số, hãy tính: a) cos36
b) Từ đó hãy tính cos72, cos18 , sin72 , sin18
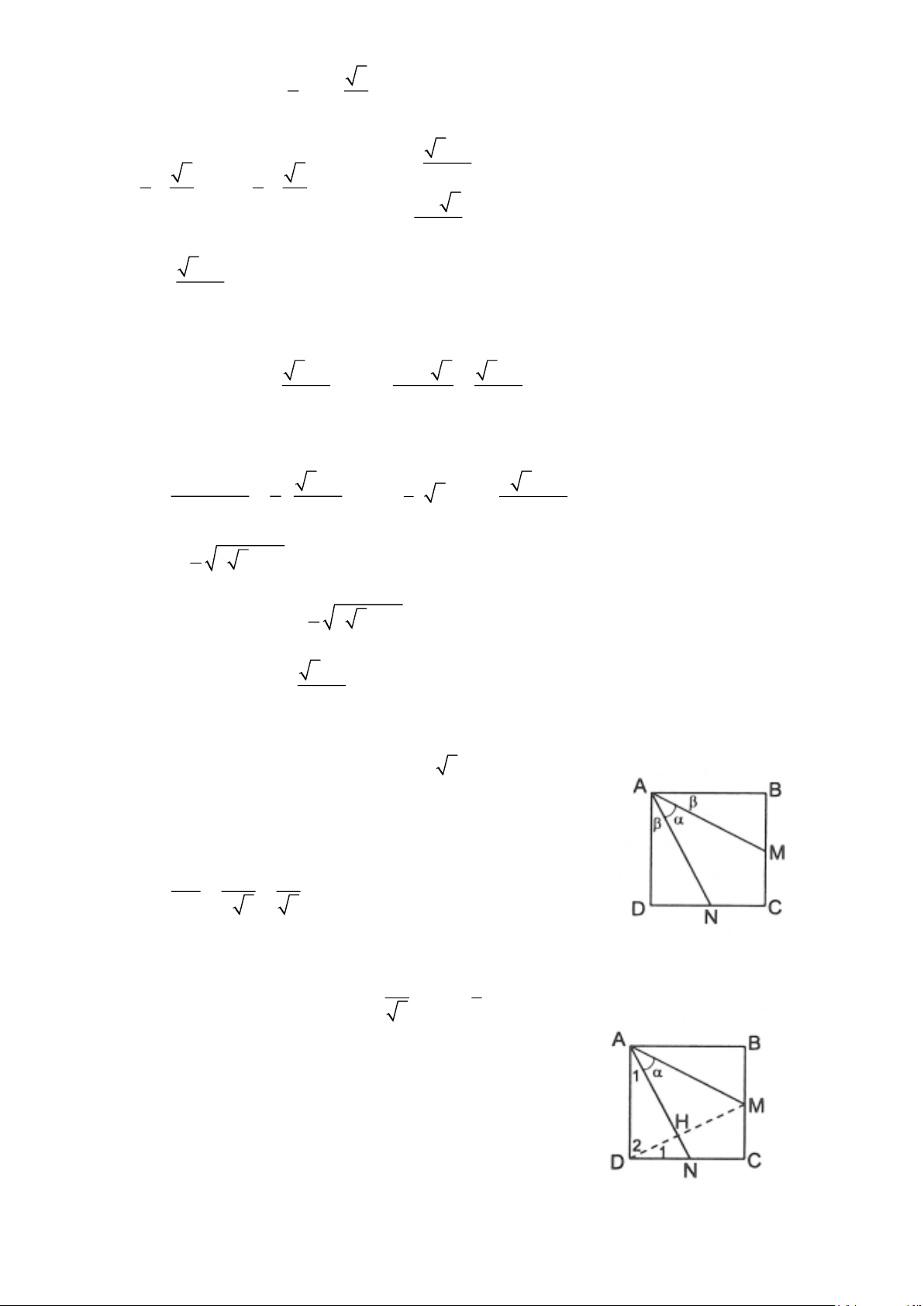
4.7. Cho hình vuông ABCD. Gọi M, N lần lượt là trung điểm của BC và CD. Đặt MAN =  , tính sin
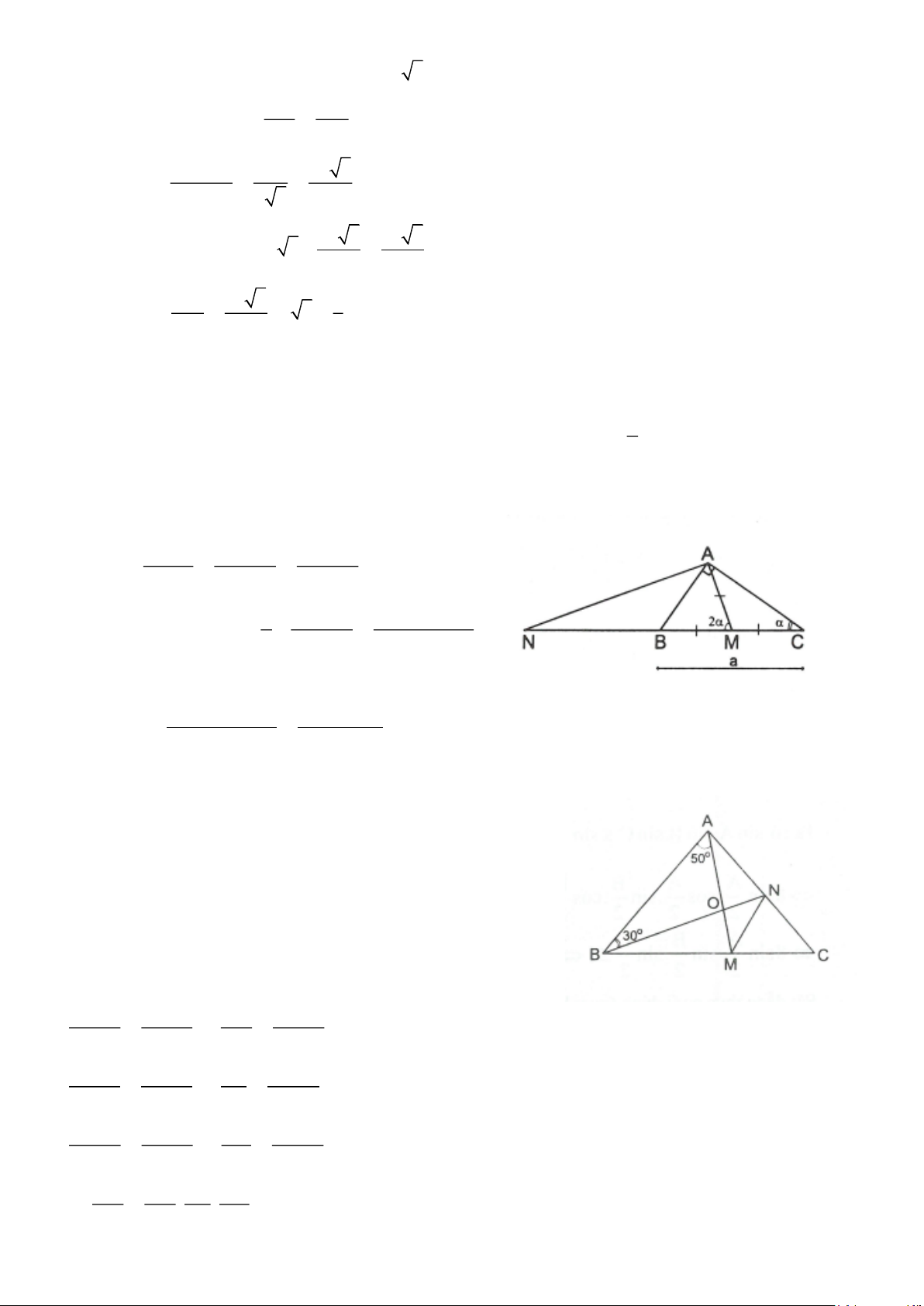
4.8. Cho tam giác ABC vuông tại A, BC = a , C =   45 . Vẽ đường trung tuyến AM. Qua A vẽ một 2 a cos
đường thẳng vuông góc với AM cắt đường thẳng BC tại N. Chứng minh rằng: CN = 2 2cos  −1
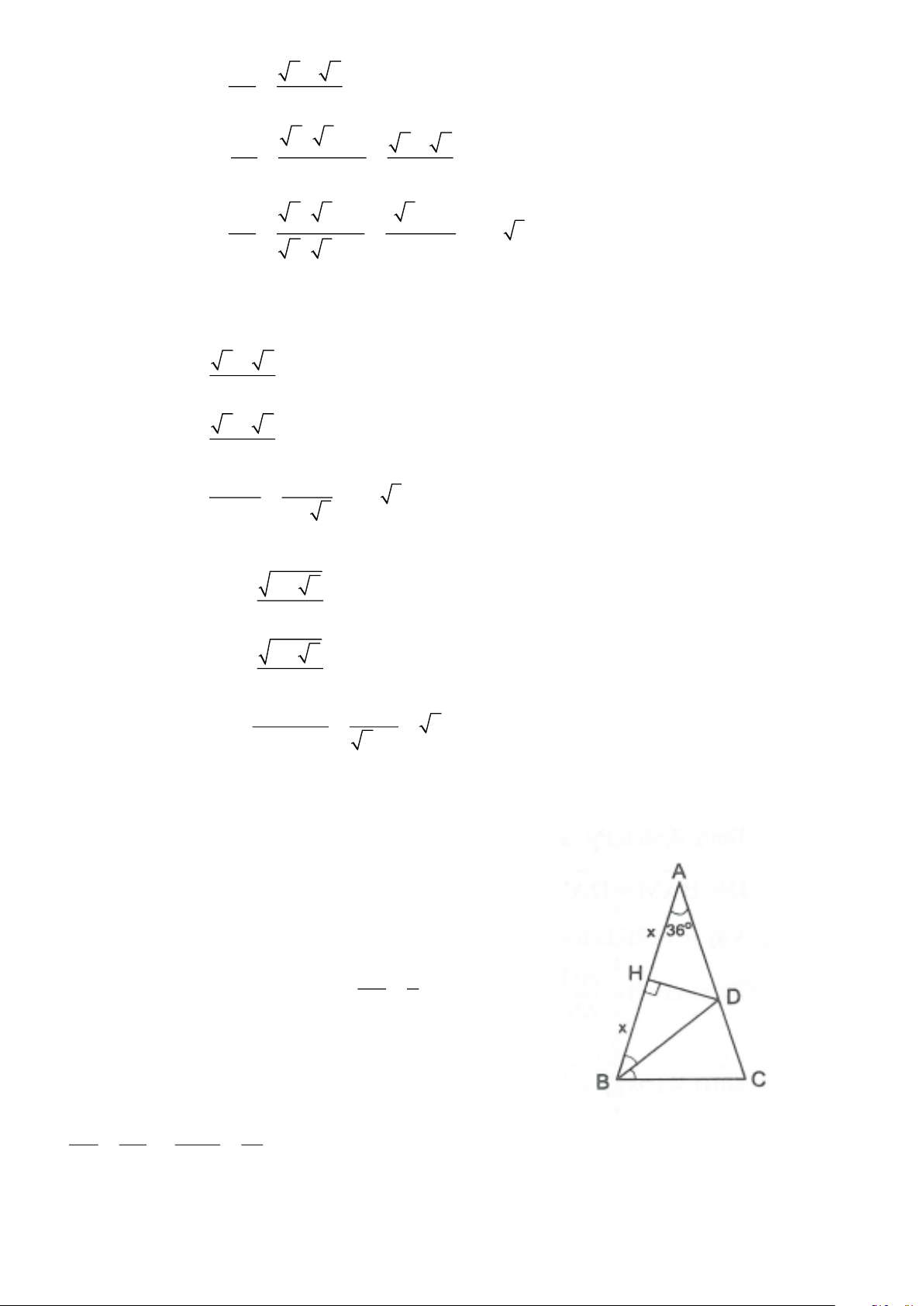
4.9. Cho tam giác ABC cân tại A, A = 80 . Trên cạnh BC lấy điểm M, trên cạnh AC lấy điểm N sao cho
BAM = 50, ABN = 30 . Gọi O là giao điểm của AM và BN. Chứng minh rằng MON là tam giác cân
4.10. Cho tam giác ABC nhọn. Chứng minh rằng: B + C C + A A + B sin . A sin . B sinC  sin .sin .sin 2 2 2 Trang 3
HƯỚNG DẪN GIẢI - ĐÁP SỐ 4.1. Ta có 1+ sin2 2 2 = sin  + cos + 2sin .  cos = (  + )2 sin cos Do đó 1+ sin2 = (  + )2 sin cos = sin + cos
Ta có sin + cos  0 nên 1+ sin2 = sin + cos 4.2. 2  24  49 a) Ta có 2 2 sin  + cos  = 1 2  cos  = 1− =  25   625 49 7 Do đó cos = = 625 25 24 7 336 Vậy sin2 = 2sin .  cos = 2. . = 25 25 625  b) Từ công thức 2
cos2 = 1− 2sin  suy ra 2 cos = 1− 2sin 2  1− cos    3 Do đó 2 sin = 7 9 = 1− : 2 = . Vậy sin = 2 2  25   25 2 5 1− cos2 4.3. Ta có 2 cos2 = 1− 2sin  2  sin  = 2
Với  = 15 , 2 = 30 ta được:   − − ( 3− )2 1− cos30 1 3 2 3 4 2 3 2 sin 15 = = 1−  : 2 = = = 2  2  4 8 8   3 −1 3 −1 6 − 2 2 ( )2 Do đó sin 15 = = = 8 2 2 4
Với  = 15 , 2 = 30 ta được: 1+ cos30   + + ( + )2 3 1 3 2 3 4 2 3 2 cos 15 = = 1+  : 2 = = = 2  2  4 8 8   ( + )2 3 1 3 + 1 6 + 2 Do đó cos15 = = = 8 2 2 4 sin15 2 ( 3 − ) 1 ( 3− )2 6 − 2 6 + 2 1 4 − 2 3 Ta có tan15 = = : = = = = 2 − 3 cos15 4 4 2 ( 3 + ) 1 2 2 Trang 4
Cách giải khác: Tính trực tiếp theo định nghĩa tỉ số lượng giác.
• Cách thứ nhất
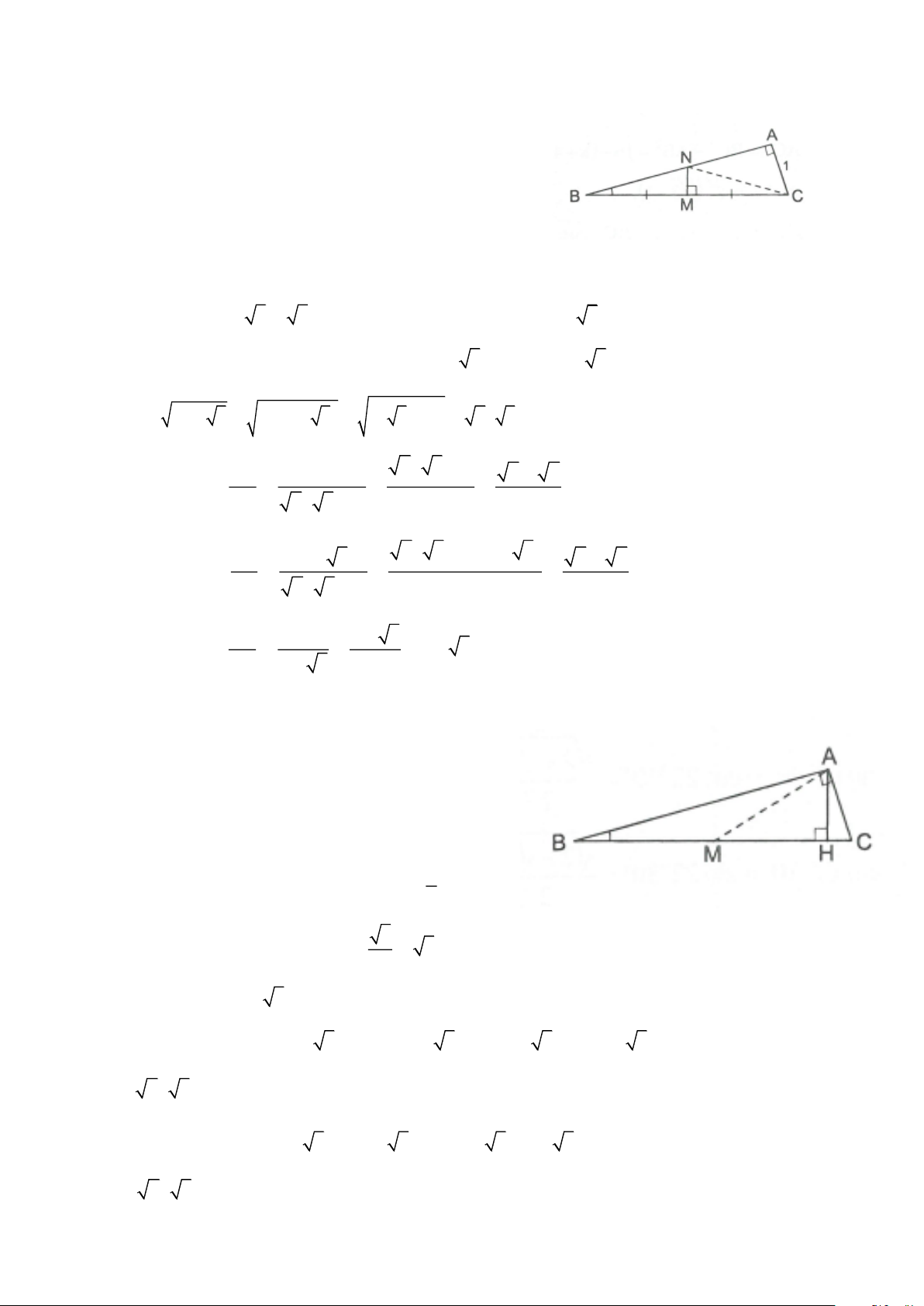
Xét ABC vuông tại A, B = 15 , AC = 1
Để tính sin B, cosB, tan B ta cần phải biết AB, BC
Vẽ đường trung trực của BC cắt AB tại N.
NBCcân tại N. Ta có ANC = 2B = 30
Xét ANC vuông tại A có ANC = 30 , nên NC = 2AC = 2 AN = A .
C cot 30 = 1. 3 = 3 ; AB = AN + NB = AN + NC = 2 + 3
Xét ABC vuông tại A có BC = AB + AC = ( + )2 2 2 2 2 2 3 + 1 = 8+ 4 3 2
Do đó BC = 8+ 4 3 = 2(4+ 2 3) = 2( 3 + ) 1 = 2 ( 3 + ) 1 AC 2 ( 3 − ) 1 1 6 − 2
Vậy sin15 = sin B = = = = BC 2 ( 3 + ) 1 2.2 4 AB 2 + ( 3− )1(2+ 3 2 3 ) 6 + 2 cos15 = cosB = = = = BC 2 ( 3 + ) 1 4 4 AC − tan15 = tan B = 1 2 3 = = = 2 − 3 AB 2 + 3 1
• Cách thứ hai
Xét ABC vuông tại A, B = 15 , BC = 4
Vẽ đường trung tuyến AM và đường cao AH.
Ta có MA = MB = MC = 2
MAB cân tại M, AMC = 2B = 30 1
Xét AMH vuông tại H, AMC = 30 nên AH = AM = 1 2 3 Ta có HM = A .
M cosM = 2.cos30 = 2. = 3 2
Suy ra HB = HM + MB = 3 + 2 2 2 Ta có 2 2 2
AB = AH + HB 2
= 1 + ( 3 + 2) = 8+ 4 3 = 2(4+ 2 3) = 2(2+ 3)  AB = 2 ( 3 + ) 1 2 2 2
AC = BC − AB = − ( + ) = − = ( − ) = ( − )2 16 8 4 3 8 4 3 2 4 2 3 2 3 1  AC = 2 ( 3 − ) 1 Trang 5 AC 6 − 2
Vậy sin15 = sin B = = BC 4 2 AB ( 3+ )1 6+ 2 cos15 = cosB = = = BC 4 4 AC ( − ) ( − )2 2 3 1 3 1 tan15 = tan B = = = = − AB 2 ( 3 + ) 2 3 1 2
4.4. Dùng kết quả bài 4.3 ta được: 6 + 2 sin75 = cos15 = 4 6 − 2 cos75 = sin15 = 4 1 1 tan75 = cot15 = = = 2 + 3 tan15 2 − 3
4.5. Dùng kết quả ví dụ 4 ta được: 2 + 2 sin67 3  0 = cos22 3  0 = 2 2 − 2 cos67 3  0 = sin22 3  0 = 2 1 1 tan67 3  0 = cot 22 3  0 = = = 2 +1 tan22 3  0 2 −1 4.6.
a) Vẽ ABC cân tại A, A = 36 , BC = 1. Khi đó B = C = 72 Vẽ đường phân giác BD
Dễ thấy các tam giác BCD, ABD là những tam giác cân.
Do đó AD = BD = BC = 1. Vẽ DH ⊥ AB thì HA = HB
Ta đặt HA = HB = x AH x
Xét ADH vuông tại H, ta có cosA = = AD 1 Do đó cos36 = x
Xét ABC có AB = AC = 2x ; CD = 2x − 1
Vì BD là đường phân giác nên: DA AB 1 2x =  = DC AC 2x −1 1 Trang 6 2 2  1   5  2
 4x − 2x −1 = 0  2x − −     = 0 2  2       5 + 1   x = (chän) 1 5  1 5   4 2x − − 2x − +  = 0    2 2  2 2      1− 5 x =  0 (lo¹i)  4 5 + 1 Vậy cos36 = 4 b) Vận dụng hệ thức 2
cos2 = 2cos  −1 ta được 2  5 +1 6 + 2 5 5 −1 2
cos72 = 2cos 36 −1 = 2.  −1 = =  4  8 4  
Cũng vận dụng hệ thức trên ta được 2 cos36 = 2cos 18 −1 2 cos36 + 1 1  5 + 1  + 2  1 2 5 10 cos 18 = =  + 1 = ( 5 + ) 5 = 2 2  4    8 16 1 Do đó cos18 = 2 5 +10 4 1
Từ đó suy ra sin72 = cos18 = 2 5 + 10 4 5 −1 sin18 = cos72 = 4
4.7. Ta đặt AB = 2athì BM = DN = a
Dùng định lí Py-ta-go ta tính được AM = AN = a 5
Đặt BAM = DAN =  , khi đó  = 90 − 2
Vậy  và 2 là hai góc phụ nhau AD 2a 2 Ta có cos = = = AN a 5 5 2  2  3 2
sin = cos2 = 2cos  −1 = 2. −1=    5  5 Cách giải khác
Gọi H là giao điểm của AN với DM A  ND = D  MC( . c .
g c) . Suy ra A = D 1 1
Ta có D + D = 90 nên A + D = 90 1 2 1 2
Suy ra AH ⊥ DH Trang 7
Ta đặt AB = 2a thì DN = a, DM = AM = a 5 D  HN  D  DH DN CM ( . g g)  = DC DM D . C DN 2 . a a 2a 5 Suy ra DH = = = DM a 5 5 2a 5 3a 5
Do đó HM = DM − DH = a 5 − = 5 5 HM 3a 5 3 Ta có sin = = : a 5 = AM 5 5 4.8.  a
ABC vuông cân tại A, AM là đường trung tuyến nên AM = MB = MC = 2
AMC cân tại M  AMN = 2
Xét AMN vuông cân ta có AM = MN.cos2 AM 2AM a  MN = = = cos2 2cos2 2cos2 a a a(cos2 + ) 1
Ta có CN = CM + MN = + = 2 2cos2 2cos2 Vì 2 cos2 = 2cos  −1 nên 2 cos2 + 1 = 2cos  2 2 . a 2cos  . a cos  Do đó CN = = 2( 2 2cos  − ) 2 1 2cos  −1
4.9. ABC cân tại A, A = 80 nên B = C = 50
Ta có BMA = 180 − (50 + 50) = 80
CBN = 50 − 30 = 20
ANB = NBC + C = 20 + 50 = 70
CAM = 80 − 50 = 30
Áp dụng định lí sin vào các tam giác OBM, OAB, OAN ta được: OM OB OM sin20 =  = sin20 sin80 OB sin80 OB OA OB sin50 =  = sin50 sin30 OA sin30 OA ON OA sin70 =  = sin70 sin30 ON sin30 OM OM OB OA Vì = . . nên: ON OB OA ON Trang 8 OM sin20 sin50 sin70 sin20 .  cos40 .  cos20 = . . = ON sin80 sin30 sin30 1 1 sin80 .  . 2 2 2sin20 .  cos20 .  2cos40 sin40 .  2cos40 sin80 = = = = 1 sin80 sin80 sin80
Suy ra OM = ON do đó MON cân tại O A A B B C C
4.10. Ta có sin A = 2sin .cos ; sin B = 2sin cos ; sinC = 2sin cos 2 2 2 2 2 2 B + C 180 − A  A  A sin = sin = sin 90 − = cos 2 2  2    2 C + A 180 − B  B  B sin = sin = sin 90 − = cos 2 2  2    2 A + B 180 − C  C  C sin = sin = sin 90 − = cos 2 2  2    2 B + C C + A A + B Ta có sin . A sin . B sinC  sin .sin .sin 2 2 2 A A B B C C A B C
 8sin .cos .sin .cos .sin .cos  cos .cos .cos 2 2 2 2 2 2 2 2 2 A B C  A B C 8sin .sin .sin  1 1  sin .sin .sin  2 2 2 2 2 2 8
Bất đẳng thức cuối đúng (xem bài 2.8). Do đó bất đẳng thức đã cho là đúng. Trang 9