Phương Pháp Giải Hình 9 Tỉ Số Lượng Giác Của Góc Nhọn

Bài 2. TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN
A. KIẾN THỨC TRỌNG TÂM 1. Định nghĩa
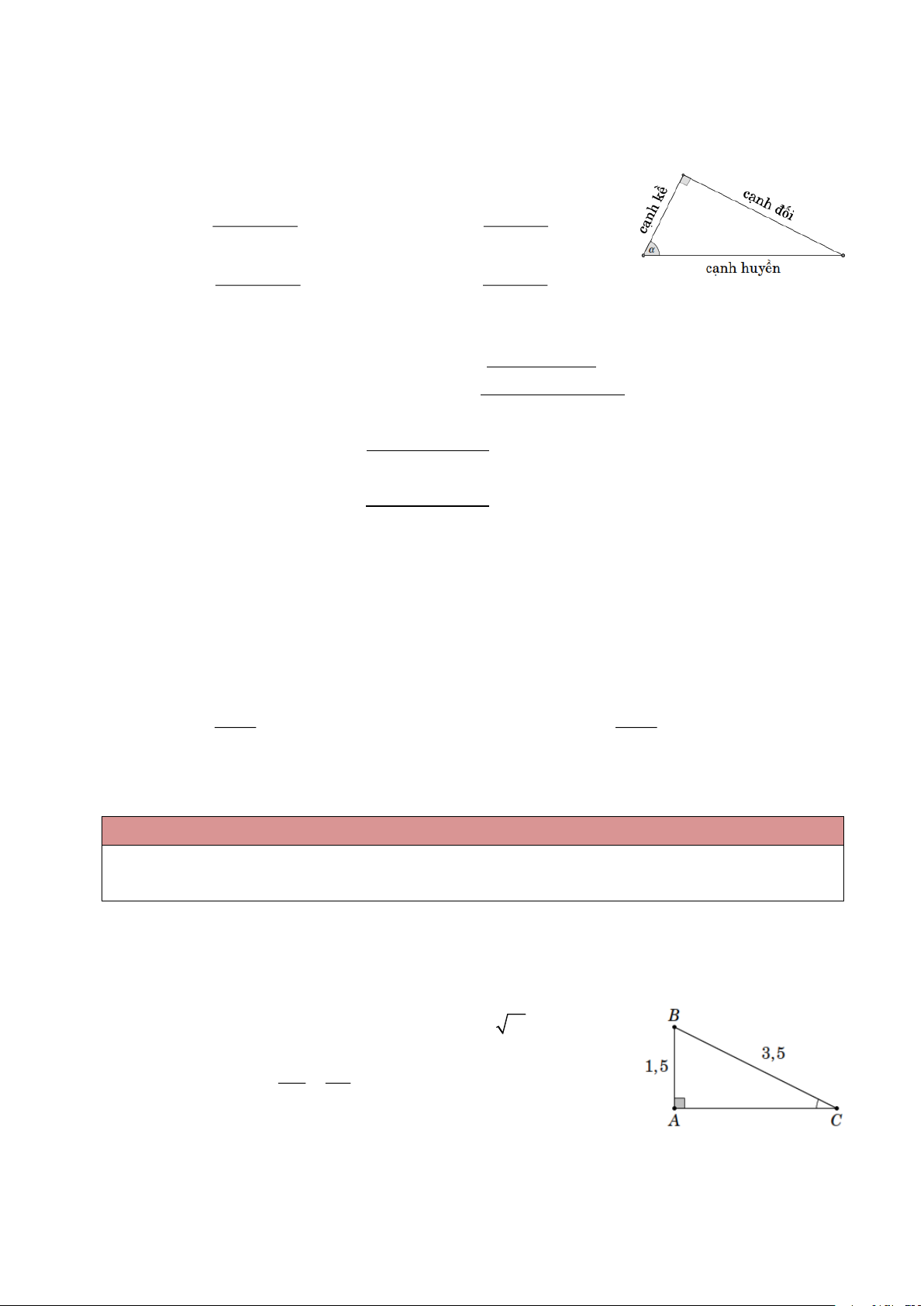
▪ Với  là góc nhọn trong tam giác vuông ta có canh doi canh doi ▪ sin = ; ▪ tan = ; canh huyen canh ke canh ke canh ke ▪ cos = ; ▪ cot = . canh huyen canh doi Cách ghi nhớ
“Tìm sin lấy đối chia huyền,
Cô-sin hai cạnh kề huyền chia nhau,
Còn tang thì phải tính sao?
Đối trên kề dưới chia nhau ra liền,
Cô-tang cũng dễ ăn tiền,
Kề trên đối dưới chia liền bạn ơi!”
2. Một số hệ thức và tính chất cơ bản
▪ Với hai góc nhọn ,  và  +  = 90 thì
sin = cos ; cos = sin ; tan = tan ; cot = cot  .
Với góc nhọn  (0    90) , ta có
▪ 0  sin  1;0  cos  1 .
▪ Nếu  tăng thì sin và tan tăng; còn cos và cot giảm. sin cos ▪ tan = ; ▪ cot = ; cos sin ▪ tan  cot = 1; ▪ 2 2 sin  + cos  = 1 .
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Tính tỉ số lượng giác của góc nhọn trong tam giác vuông khi biết độ dài hai cạnh
▪ Bước 1: Tính độ dài cạnh thứ ba theo định lý Py-ta-go (nếu cần).
▪ Bước 2: Tính các tỉ số lượng giác của góc nhọn theo yêu cầu đề bài.
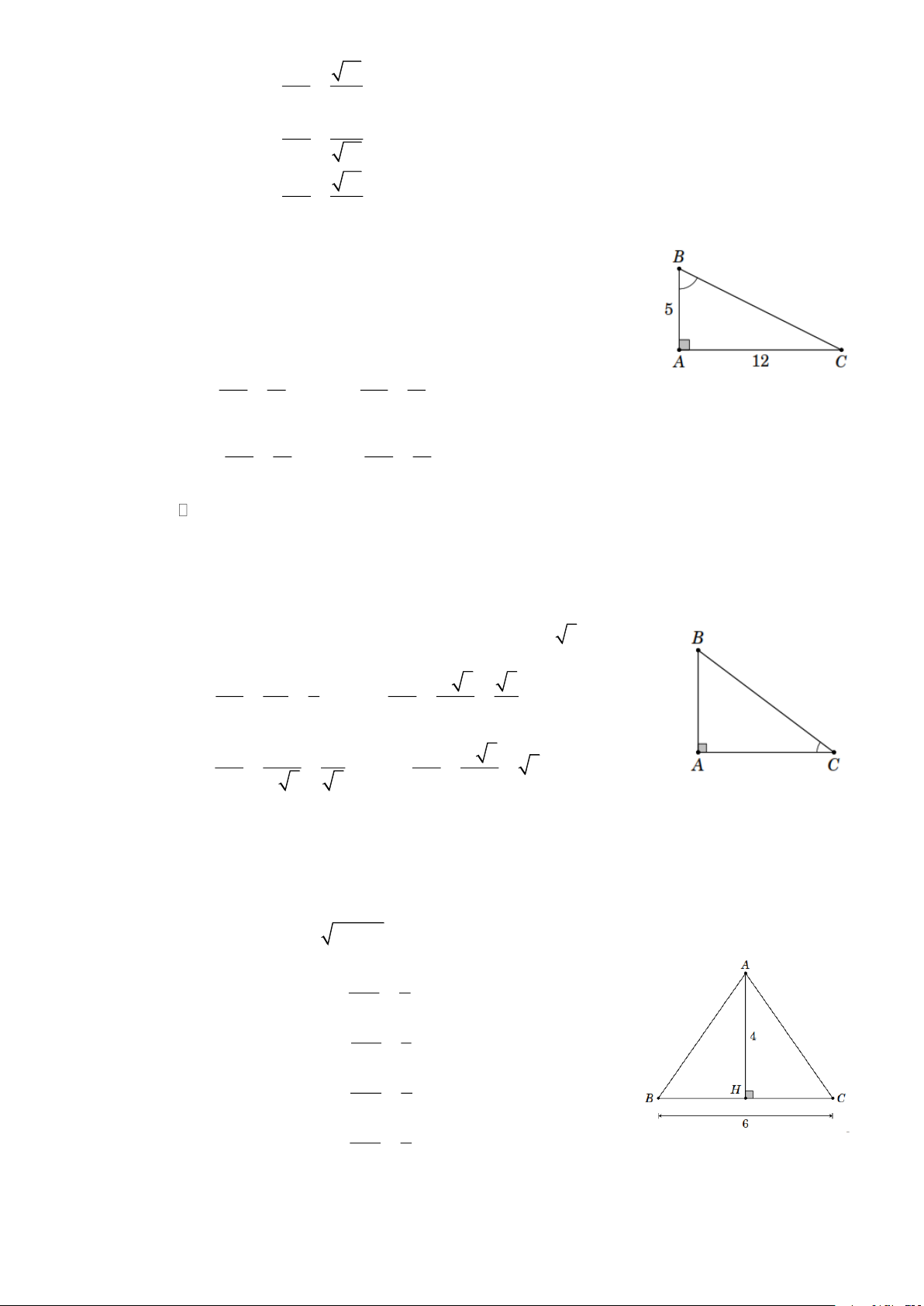
Ví dụ 1. Tam giác ABC vuông tại A , AB = 1,5 ; BC = 3,5 . Tính tỉ số lượng giác của góc C rồi
suy ra các tỉ số lượng giác của góc B . Lời giải Ta có 2 2 2 2 2
AC = BC − AB = 3,5 −1,5 = 10  AC = 10 . AB 1,5
Do đó cos B = sin C = =  0,4286 BC 3,5 Trang 1 AC 10 sin B = cosC = =  0,9035 BC 3,5 AB 1,5 cot B = tan C = =  0, 4743 AC 10 AC 10 tan B = cot C = =  2,1082 AB 1,5
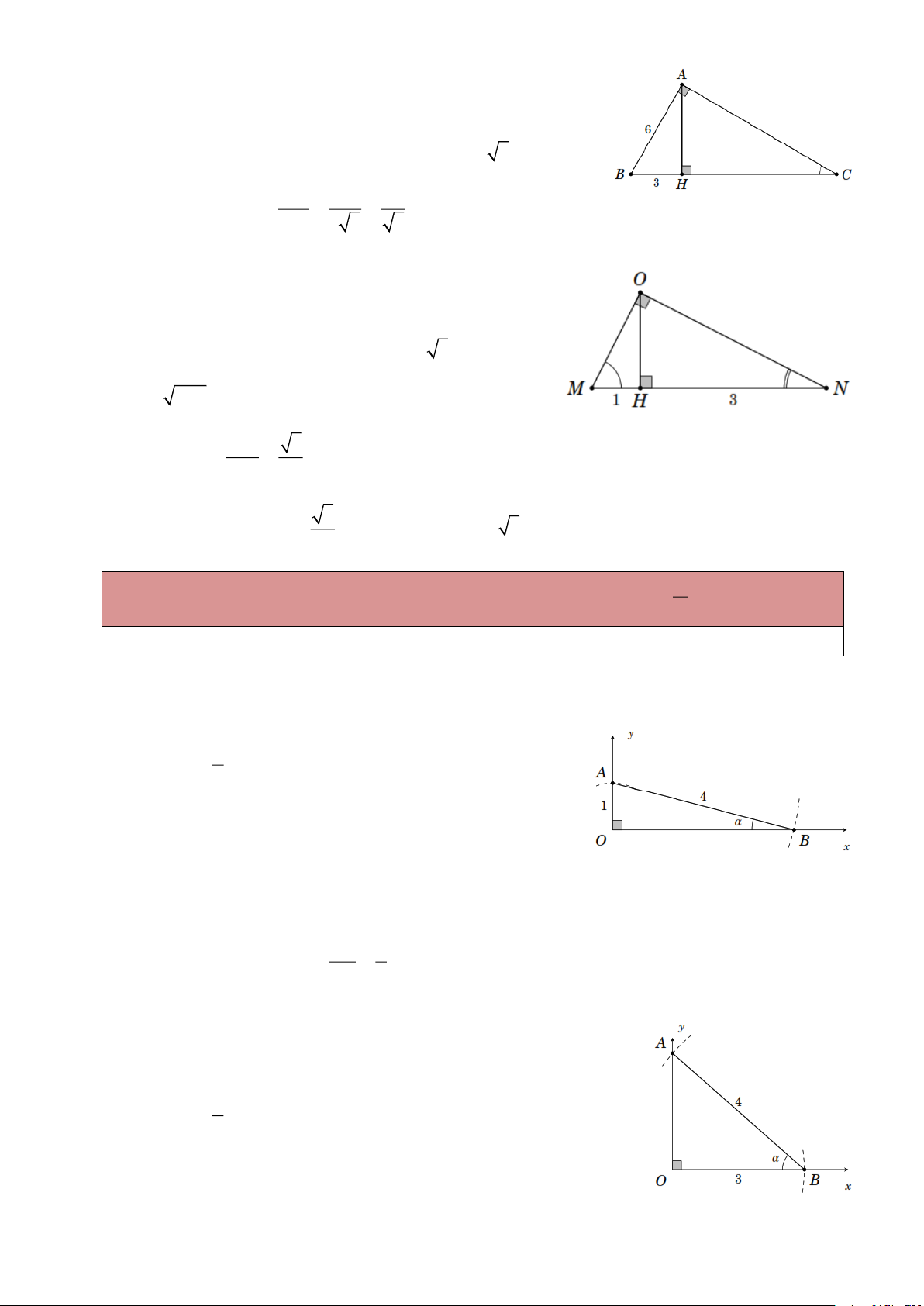
Ví dụ 2. Tính tỉ số lượng giác của góc B trong hình bên. Lời giải Ta có 2 2 2 2 2
BC = AB + AC = 5 +12 = 169  BC = 13 . AC 12 AB 5 Do đó sin B = = ; cos B = = ; BC 13 BC 13 AC 12 AB 5 tan B = = ; cot B = = . AB 5 AC 12
Ví dụ 3. ABC vuông tại A có BC = 2AB . Tính các tỉ số lượng giác của góc C . Lời giải
Ta đặt AB = m thì BC = 2m , suy ra 2 2 2 2 2 2
AC = BC − AB = 4m − m = 3m  AC = m 3 . AB m 1 AC m 3 3 Ta có sin C = = = ;cosC = = = ; BC 2m 2 BC 2m 2 AB m 1 AC m 3 tan C = = = ;cot C = = = 3 . AC m 3 3 AB m
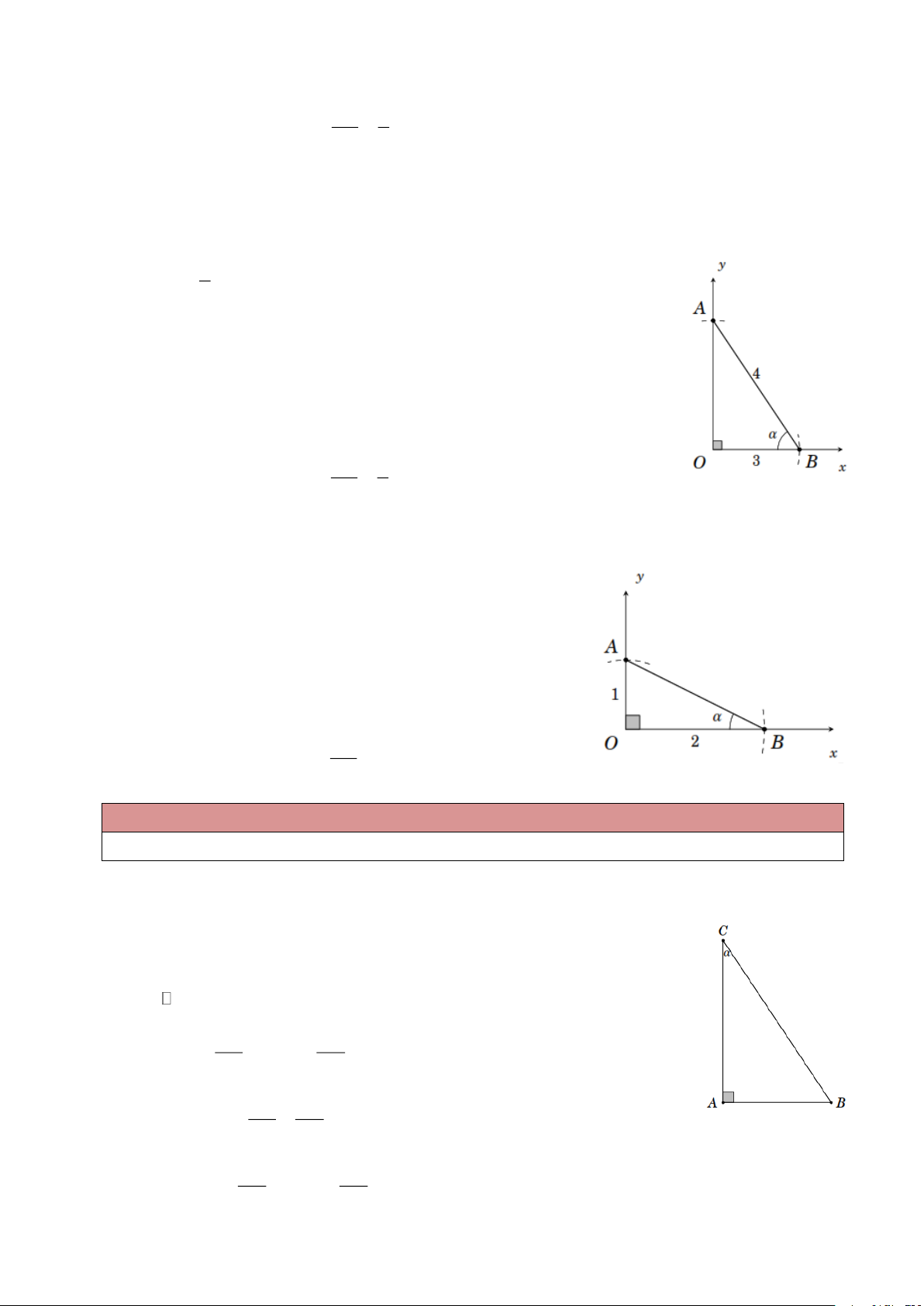
Ví dụ 4. Tam giác ABC cân tại A , có BC = 6 , đường cao AH = 4 . Tính các tỉ số lượng giác của góc B . Lời giải
Ta có BH = 6 : 2 = 3 ; 2 2
AB = 4 + 3 = 5 . Do đó AH 4 sin B = = = 0,8; AB 5 BH 3 cos B = = = 0,6; AB 5 AH 4 tan B = = ; AB 3 BH 3 cot B = = = 0,75. AH 4 Trang 2
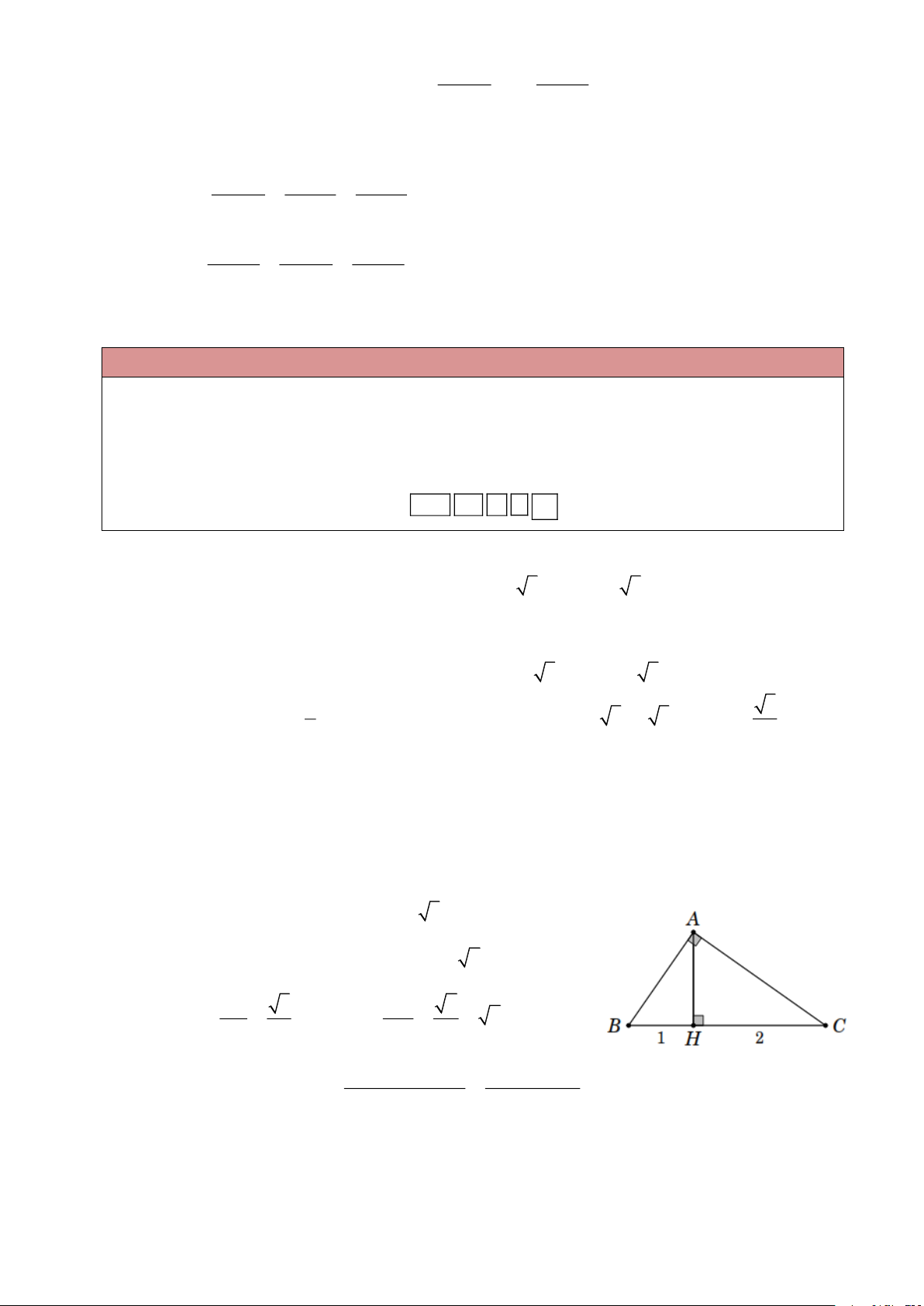
Ví dụ 5. Tính tan C trong hình bên. Lời giải Ta có 2 2 2 2 2
AH = AB − BH = 6 − 3 = 27  AH = 3 3 . BH 3 1
Do đó tan C = cot B = = = . AH 3 3 3
Ví dụ 6. Tính sin M + cos N trong hình bên. Lời giải Ta có 2
OH = HM  HN = 13 = 3  OH = 3 ; OM = 1+ 3 = 2 . OH 3 Do đó sin M = = . OM 2 3
Mặt khác cos N = sin M =
nên sin M + cos N = 3 . 2 m
Dạng 2: Dựng góc nhọn  khi biết tỉ số lượng giác của góc nhọn đó bằng . n
▪ Dựng một tam giác vuông có cạnh là m và n rồi vận dụng định nghĩa để nhận ra góc  .
Ví dụ 7. Dựng góc  , biết sin = 0, 25. Lời giải 1 Ta có 0, 25 = . 4
Dựng góc vuông xOy ;
Trên cạnh Ox đặt OA = 1; Dựng đường tròn ( ;
A 4) cắt cạnh Oy tại B .  OA 1 
Khi đó ABO =  vì sin = =   .  AB 4 
Ví dụ 8. Dựng góc  , biết cos = 0,75 . Lời giải 3 Ta có 0,75 = . 4
Dựng góc vuông xOy ;
Trên cạnh Oy đặt OB = 3 ; Trang 3
Dựng đường tròn (B; 4) cắt cạnh Ox tại A .  OB 3 
Khi đó ABO =  vì cos = =   .  AB 4 
Ví dụ 9. Dựng góc  , biết tan = 1,5 . Lời giải 3 Ta có 1,5 = . 2
Dựng góc vuông xOy ;
Trên cạnh Ox đặt OA = 3;
Trên cạnh Oy đặt OB = 2 .  OA 3 
Khi đó ABO =  vì tan = =   .  OB 2 
Ví dụ 10. Dựng góc  , biết cot = 2 . Lời giải
Dựng góc vuông xOy ;
Trên cạnh Ox đặt OA = 1;
Trên cạnh Oy đặt OB = 2 .  OB 
Khi đó ABO =  vì cot = = 2   .  OA 
Dạng 3: Chứng minh hệ thức lượng giác
▪ Sử dụng định nghĩa và một số hệ thức lượng giác cơ bản để chứng minh.
Ví dụ 11. Cho góc nhọn  . Chứng minh rằng a) sin  tan ; b) cos  cot . Lời giải
a) Xét ABC vuông tại A , ˆ C =  (hình bên). AB AB Ta có sin = ; tan = . BC AC AB AB
Vì BC  AC nên  , suy ra sin  tan . BC AC AC AC b) Ta có cos = ; cot = . BC AB Trang 4 AC AC
Vì BC  AB nên  , suy ra cos  cot . BC AB
Ví dụ 12. Chứng minh các hệ thức 1 1 a) 2 1+ tan  = ; b) 2 1+ cot  = . 2 cos  2 sin  Lời giải 2 2 2  sin  cos  + sin  1 a) 2 1+ tan  = 1+ = =   . 2 2  cos  cos  cos  2 2 2  cos  sin  + cos  1 b) 2 1+ cot  =1+ = =   . 2 2  sin  sin  sin 
Ví dụ 13. Chứng minh rằng 1+ cos sin tan +1 1+ cot a) = ; b) = . sin 1− cos tan −1 1− cot Lời giải 1+ cos sin a) Ta có 2 =
 (1− cos)(1+ cos) = sin  sin 1− cos 2 2 2 2
 1− cos  = sin   sin  = sin  .
Đẳng thức cuối cùng đúng nên đẳng thức đã cho là đúng. tan +1 1+ cot b) Xét vế trái T = ; vế phải P = . tan −1 1− cot  1   1
 1+ cot 1− cot 1+ cot T = +1 : −1 = : =      cot   cot  cot cot 1− cot
Rõ ràng T = P .
Ví dụ 14. Chứng minh rằng 2 2 2 2
tan  − sin  = tan  sin  . Lời giải Ta biến đổi vế trái 2  sin  ( 2 2 1− cos sin  ) 2 2 sin  sin  2 2 2 2 2
T = tan  − sin  = − sin  = = = tan  sin  2 2 2 cos  cos  cos 
Ta thấy vế trái bằng vế phải. 2 2 1− 4sin  cos 
Ví dụ 15. Chứng minh rằng = sin + cos . 2 ( )2 (sin −cos) Lời giải Trang 5 Xét vế trái
(1− 2sin cos)(1+ 2sin cos) T = 2 (sin − cos) ( 2 2
sin  + cos  − 2sin cos )( 2 2
sin  + cos  + 2sin cos ) = 2 (sin − cos ) 2 2
(sin − cos ) (sin + cos ) = 2 (sin − cos ) 2 = (sin + cos)
Ta thấy vế trái đúng bằng vế phải.
Dạng 4: Biết một giá trị lượng giác của góc nhọn, tính các tỉ số lượng giác khác của góc đó
▪ Vận dụng các hệ thức cơ bản đã học.
Ví dụ 16. Cho biết sin = 0,6 ; tính cos , tan , cot . Lời giải Ta có 2 2
cos = 1− sin  = 1− (0,6) = 0,8 sin 0,6 cos 0,8 4 tan = = = 0,75;cot = = = . cos 0,8 sin 0,6 3 2
Ví dụ 17. Cho biết cos = ; tính sin , tan , cot . 3 Lời giải 2 Ta có 2 2 5 sin 1 cos    = − = 1− =    3  3 sin 5 2 5 cos 2 5 2 tan = = : = ;cot = = : = . cos 3 3 2 sin 3 3 5 1
Ví dụ 18. Cho biết tan =
, tính cot , sin , cos . 3 Lời giải 1 1 2 1  1  2 Ta có cot = =1: = 3 ; 2 = 1+ tan  = 1+ =   . tan 3 cos  3  3 2 3  3  1 Do đó cos = ; 2
sin = 1− cos  = 1−   = . 2  2  2  
Ví dụ 19. Cho biết cot x = 2 , tính tan x , sin x , cos x . Lời giải Trang 6 1 1 1 Ta có tan x = = ; 2 2
= 1+ cot x = 1+ 2 = 5 . cot x 2 sin x 1 2   Do đó sin x = ; 2 1 2
cos x = 1− sin x = 1− =   . 5  5  5
Dạng 5: Tính giá trị lượng giác với các góc đặc biệt (không dùng máy tính hoặc bảng số)
▪ Căn cứ vào bảng giá trị lượng giác của các góc đặc biệt 30; 45;60 .
▪ Căn cứ vào tỉ số lượng giác của hai góc phụ nhau.
▪ Căn cứ vào các hệ thức lượng giác cơ bản.
Ví dụ 20. Tính giá trị của biểu thức a) 2   3 M 4cos 45 3 cot 30 16cos 60 = + − ; 2sin 30 − sin 60 b) N = . 2 cos 30 − cos 60 Lời giải 2 3     a) 2   3  2 1
M = 4 cos 45 + 3 cot 30 −16 cos 60 = 4   + 3  3 −16 = 2 + 3 − 2 = 3     . 2    2  1 3 3   2 − 1− 2sin 30 − sin 60 b) 2 2 2 N = = = = = 4 − 2 3 . 2   2 cos 30 − cos 60 3 1  3  1 −   − 4 2 2 2  
Ví dụ 21. Tính giá trị của biểu thức a) 2  2  2  2 P sin 30 sin 40 sin 50 sin 60 = − − + ; b) 2  2  2  2  2 Q cos 25 cos 35 cos 45 cos 55 cos 65 = − + − + . Lời giải a) 2  2  2  2 P sin 30 sin 40 sin 50 sin 60 = − − + = ( 2  2
sin 30 + sin 60 ) −( 2  2 sin 40 + sin 50 ) = ( 2  2
sin 30 + cos 30 ) −( 2  2 sin 40 + cos 40 ) =1−1 = 0 b) 2  2  2  2  2 Q cos 25 cos 35 cos 45 cos 55 cos 65 = − + − + Trang 7 = ( 2  2 cos 25 + cos 65 ) − ( 2  2 cos 35 + cos 55 ) 2 + cos 45 2 = (   2  2  + )−( 2  2  + ) 2 cos 25 sin 25 cos 35 sin 35 +    2    1 1 = 1−1+ = 2 2
Ví dụ 22. Tính giá trị của biểu thức sau với 0 0  90   : 2    2 2
A = cos  − tan 60 + cot 45 − 2sin 30 + cos   tan  . Lời giải 2    2 2
A = cos  − tan 60 + cot 45 − 2sin 30 + cos   tan  1 2 2 2
= cos  + cos   tan  − 3 +1− 2 2 2 = cos  ( 2 1+ tan  ) − 3 +1−1 2 1 = cos   − 3 2 cos  = 1− 3.
Ví dụ 23. Rút gọn các biểu thức sau với 0  90   a) 4 4 2 2
B = sin  + cos  + 2sin  cos  ; b) 6 6 2 2
C = sin  + cos  + 3sin  cos  . Lời giải a) B =  +  +   = (  +  )2 4 4 2 2 2 2 sin cos 2sin cos sin cos =1 . 6 6 2 2
C = sin  + cos  + 3sin  cos  b) 6 6 2 2
= sin  + cos  + 3sin  cos  ( 2 2 sin  + cos  ) = (sin  + cos  )3 2 2 = 1 2 2 sin  − cos 
Ví dụ 24. Cho biểu thức A == . 1+ 2sin cos sin − cos
a) Chứng minh rằng A = ; sin + cos 2
b) Tính giá trị của A , biết tan = . 3 Lời giải 2 2 sin  − cos 
(sin − cos)(sin + cos) sin − cos a) A = = = . 2 1+ 2sin cos (sin + cos) sin + cos Trang 8
b) Chia cả tử và mẫu của A cho cos ta được sin cos 2 − −1   tan −1 1 cos cos 3 A = = = = − . sin cos tan +1 2 5 + +1 cos cos 3
Dạng 6: So sánh các tỉ số lượng giác mà không dùng máy tính hoặc bảng số ▪
Ví dụ 25. Sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần
a) sin 70,cos30,cos 40,sin 51 ;
b) cos 34,sin 57,cot 32 . Lời giải a) Ta có cos 30 sin 60 = ; cos 40 sin 50 = .
Vì sin 50 sin 51 sin 60 sin 70   
nên cos 40 sin 51 cos30 sin 70    . b) Ta có cos34 sin 56 = ; cot 32 tan 58 = .
Vì sin 56 sin 57 sin 58 tan 58   
nên cos34 sin 57 cot 32   .
Ví dụ 26. Sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần
a) cot 40,sin 40,cot 43, tan 42 ;
b) tan 52,cot 63, tan 72,cot 31,sin 27 . Lời giải a) Ta có cot 40 tan 50 = ; cot 43 tan 47 = .
Vì sin 40 tan 40 tan 42 tan 47 tan 50     nên sin 40 tan 42 cot 43 cot 40    . b) Ta có cot 63 tan 27 = ; cot 31 tan 59 = .
Vì sin 27 tan 27 tan 52 tan 59 tan 72    
nên sin 27 cot 63 tan 52 cot 31 tan 72     .
Ví dụ 27. Cho 25  50  
, hãy sắp xếp các tỉ số lượng giác sau theo thứ tự giảm dần:
sin; cos( 40 ); tan ( 10 + + ). Lời giải Vì 25  50   nên  10  50 +   − .
Mặt khác góc 50 − phụ với góc a 40 + .
Ta có tan ( 10 ) sin( 10 ) sin sin(50 +  +   − ) ,
do đó tan ( 10 ) sin cos( 40 +   + ). Trang 9 sin 50 cot 70
Ví dụ 28. So sánh hai số m và n , biết m = ; n = . cos 65 tan 35 Lời giải sin 50 sin 50 sin 25 Ta có m = =  =1; (1) cos 65 sin 25 sin 25 cot 70 tan 20 tan 35 n = =  =1. (2) tan 35 tan 35 tan 35
Từ (1) và ( 2 ) suy ra m  n .
Dạng 7: Tìm góc nhọn  thỏa đẳng thức cho trước
▪ Sử dụng các hệ thức lượng giác cơ bản để biến đổi về dạng cơ bản
▪ Dùng MTBT hoặc bảng giá trị lượng giác các góc đặc biệt để tìm.
Cách dùng MTBT tìm  khi biết sin (tương tự đối với cos và tan )
Nếu sin = m thì bấm các phím sau shift sin m = ' ' .
Ví dụ 29. Tìm góc nhọn x , biết a) 4sin x −1 = 1;
b) 2 3 − 3tan x = 3 . Lời giải a) 4sin x −1 = 1 b) 2 3 − 3tan x = 3 1  3
4sin x = 2  sin x =
 −3tan x = 3 − 2 3  tan x = 2 3
 sin x = sin 30  x = 30 .  
 tan x = tan 30  x = 30 . C. BÀI TẬP VẬN DỤNG
Bài 1. Cho hình bên. Tính sin C và tan B . Lời giải Ta có 2
AB = BC  BH = 31 suy ra AB = 3 . Tương tự 2
AH = BH CH = 1 2 suy ra AH = 2 . AB 3 AH 2 Do đó sin C = = và tan B = = = 2 . BC 3 BH 1 2 1− 2cos  sin − cos
Bài 2. Chứng minh đẳng thức = . 1+ 2sin cos sin + cos Lời giải Ta có Trang 10 2 2 2 2 2 2 1− 2cos 
cos  + sin  − 2cos  sin  − cos  = = 2 2 1+ 2sin cos
cos  + sin  + 2sin cos (cos +sin )2 (
sin − cos )(sin + cos ) sin − cos = = . (cos +sin )2 sin + cos
Vậy đẳng thức được chứng minh.
Bài 3. Cho góc nhọn  . 1
a) Biết cos = , hãy tính sin và tan . 3
b) Biết tan = 2 , hãy tính sin và cos . Lời giải 1 a) Do 2 2
cos  + sin  = 1 mà cos = nên 3  2 2 2 sin =  1  2 2 8 3
+ sin  = 1 sin  =      3  9  2 2 sin = −  3 2 2
vì  là góc nhọn nên sin  0 do đó sin = . 3 2 2 sin Mặt khác 3 tan = = = 2 2 . cos 1 3  1 cos = 1 1 1  5 b) Do 2
=1+ tan  mà tan = 2 nên 2 =1+ 2 suy ra 2 cos  =   . 2 cos  2 cos  5  1 cos = −  5 1
Vì  là góc nhọn nên cos  0 do đó cos = . 5
Bài 4. Không dùng máy tính hoặc bảng số, hãy
a) Tính giá trị của biểu thức 2  2  2  2  2  2 M sin 20 cos 30 sin 40 sin 50 cos 60 sin 70 = + − − + + .
b) Sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần sin 41 ; cos 58 ; cot 49 ; cos 75 ; sin 25 . Lời giải a) Ta có 2  2 (   ) 2 sin 70 sin 90 20 cos 20 = − = . Trang 11 Tương tự 2  2 (   ) 2 sin 50 sin 90 40 cos 40 = − = và 2  2 (   ) 2 cos 60 cos 90 30 sin 30 = − = . Do đó 2  2  2  2  2  2 M
= sin 20 + cos 30 − sin 40 − cos 40 + sin 60 + cos 20 = ( 2  2 sin 20 + cos 20 ) + ( 2  2
cos 30 + sin 30 ) − ( 2  2
sin 40 + cos 40 ) =1+1−1 =1. b) Ta có cos58 sin 32 = , cos 49 sin 41 = và cos 75 sin 25 = .
Mà sin 25 sin 32 sin 41   mà cos 49 cot 49  nên sin 25 cos 75 cos 58 sin 41 cos 49 cot 49 . =   = 
Vậy sin 25 cos 75 cos58 sin 41 cot 49 . =   
Bài 6. Cho tam giác nhọn ABC , độ dài các cạnh BC , CA , AB lần lượt bằng a , b , c . a b c a) Chứng minh rằng = = . sin A sin B sin C
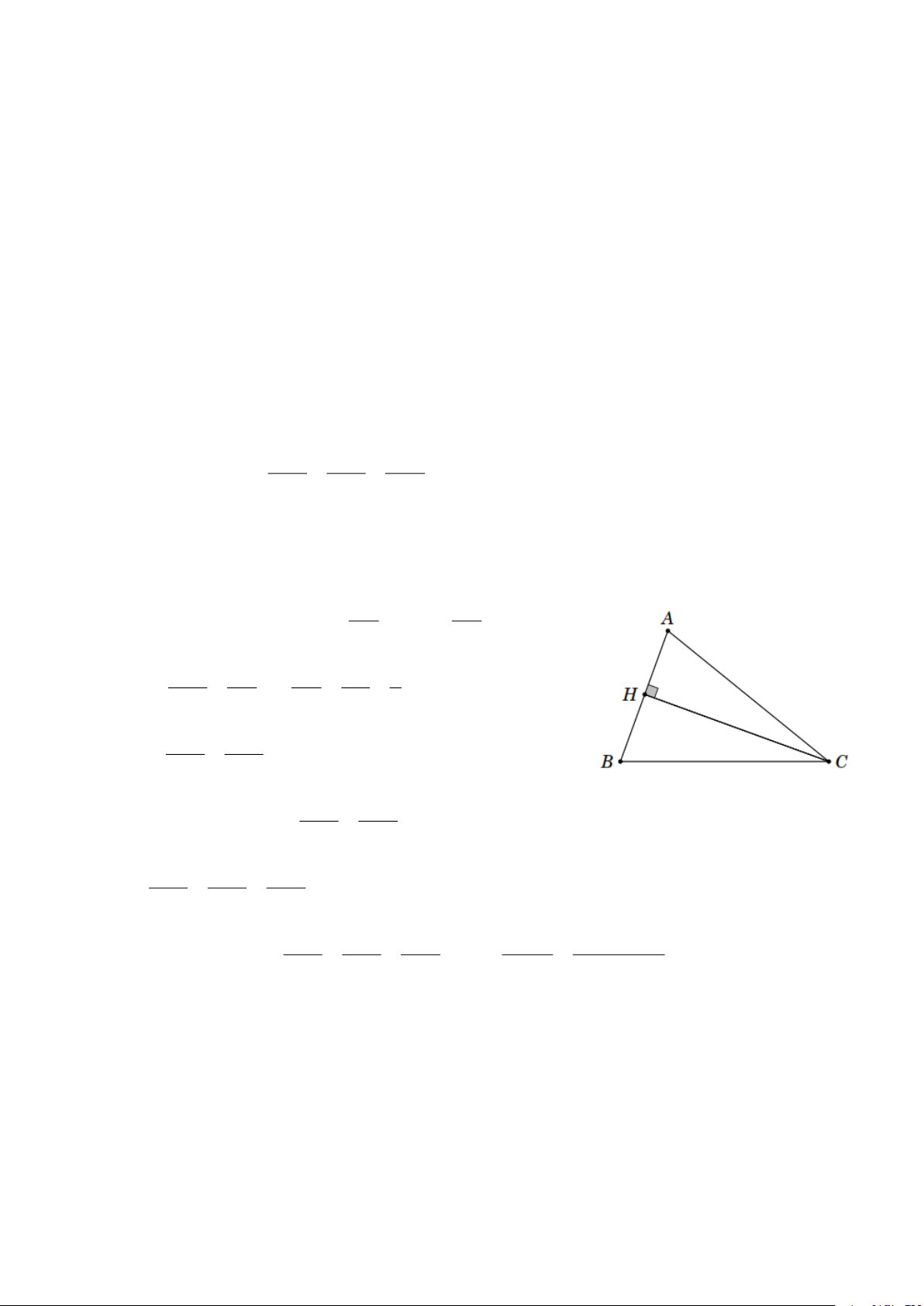
b) Chứng minh rằng nếu a + b = 2c thì sin A + sin B = 2sin C . Lời giải CH CH
a) Kẻ CH ⊥ AB . Ta có sin A = ; sin B = . AC BC sin A CH CH BC a Do đó = và = = . sin B AC BC AC b a b Suy ra = . sin A sin B b c b) Chứng minh tương tự = . sin B sin C a b c Vậy = = . sin A sin B sin C a b c 2c a + b Theo chứng minh trên = = suy ra = . sin A sin B sin C 2sin C sin A + sin B
Vì a + b = 2c thì sin A + sin B = 2sin C . --- HẾT --- Trang 12