Phương pháp phần bù tính thể tích khối đa diện phức tạp – Vương Thanh Bình Toán 12

PHƢƠNG PHÁP PHẦN BÙ
TÍNH THỂ TÍCH KHỐI ĐA DIỆN PHỨC TẠP
Tác giả: Vương Thanh Bình
Bản Full đáp án tại Facebook: https://www.facebook.com/ThanhBinhKami
Link video full miễn phí tại : http://moon.vn/Pro/1/228
Mọi góp ý và bài tập liên quan đến phương pháp vui lòng Inbox Facebook A-LÝ THUYẾT CHUNG
1) Khái niệm khối đa diện phức tạp : Là khối đa diện không cơ bản ( không phải chóp tam
giác, chóp tứ giác, hình lăng trụ, hình hộp, hình lập phương ... ) Hoặc cơ bản nhưng khó tính
chiều cao và diện tích đáy.
2) Ý tƣởng : Ta sẽ xây dựng khối đa diện phức tạp H  nằm trong khối chóp cơ bản  A . Ví
dụ dụ khối chóp  A gồm khối đa diện phức tạp  H  và khối chóp cơ bản  B khi đó
V  V V H A B
3) Các dạng thƣờng gặp : +) Dạng 1: (Cơ bản) A  H  B  V  V V H A B
+) Dạng 2: (Nâng cao) A  H  B  C V  V V  B H A B C
+) Dạng 3: (Sao) A  H  B  C  D V  V V V V H A B C D
4) Kiến thức liên quan :
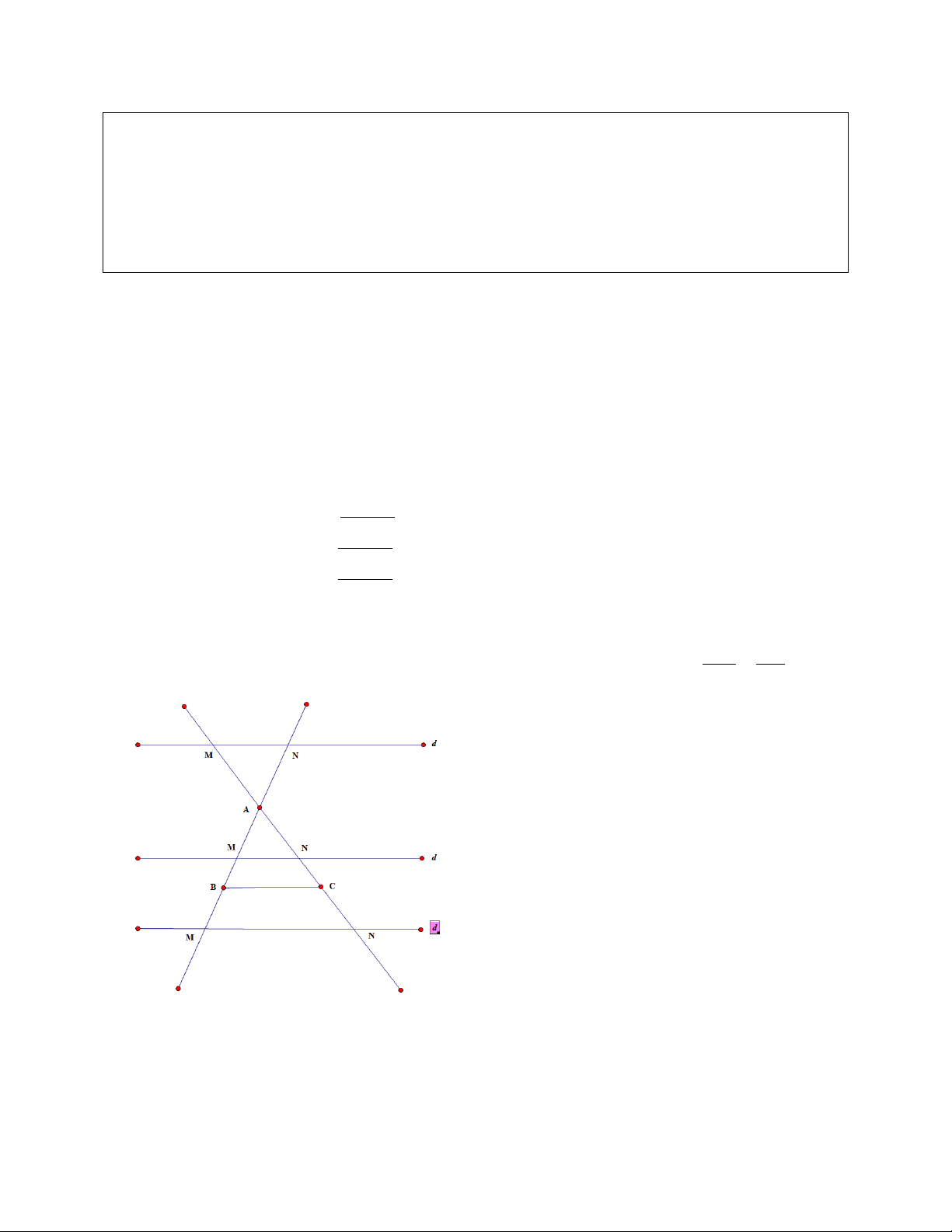
4.1. Định lý Talet: Cho tam giác ABC , đường thẳng d song song với BC đồng thời cắt các AM AN cạnh A ,
B AC hoặc các đường kéo dài của 2 cạnh này tại M , N thì ta có tỉ lệ :  AB AC
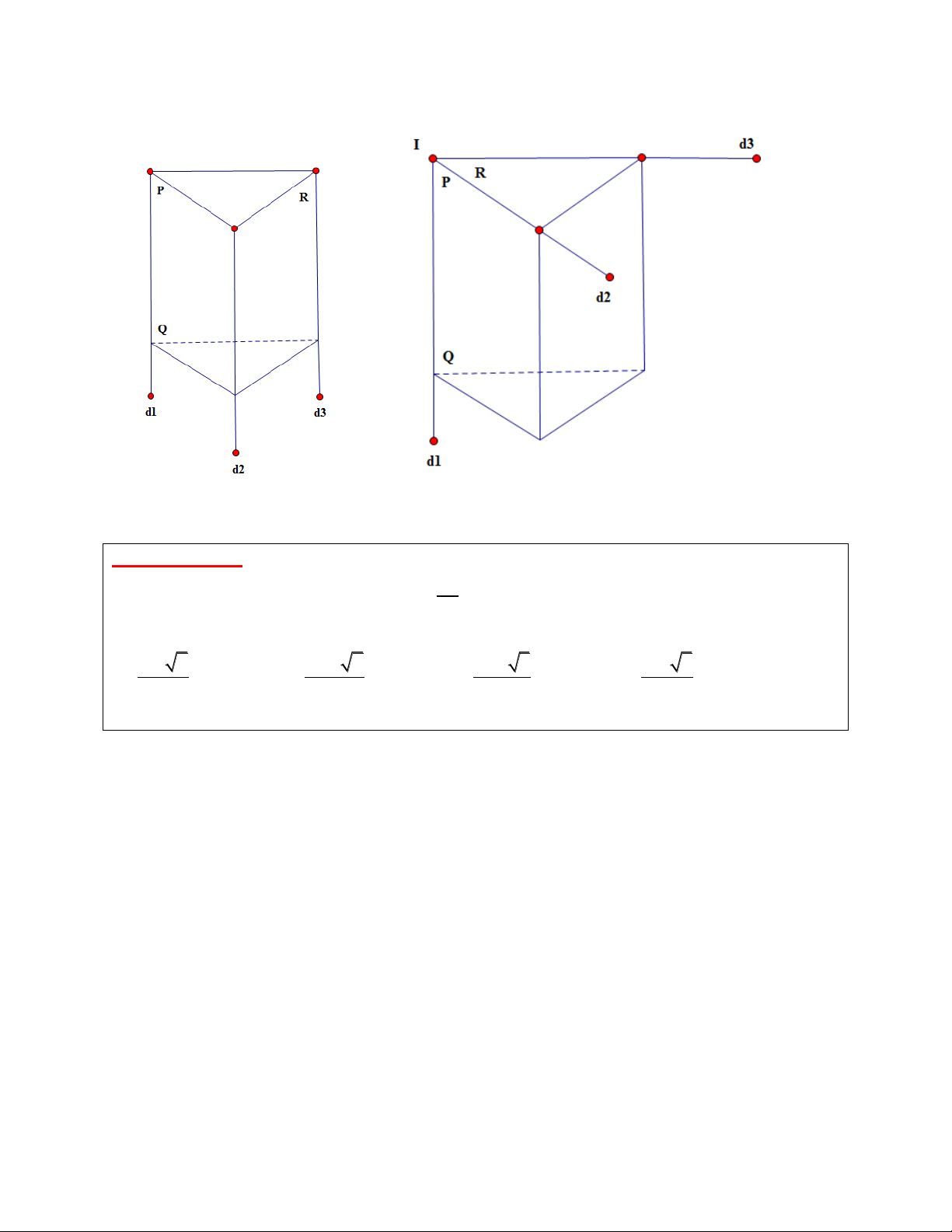
4.2. Định lý 3 đƣờng giao tuyến: Cho 3 mặt phẳng P,Q,R giao nhau theo 3 giao tuyến
d , d , d thì 3 giao tuyến này một là đôi một song song hai là đồng quy. 1 2 3 DẠNG 1:  V
V V H  A B
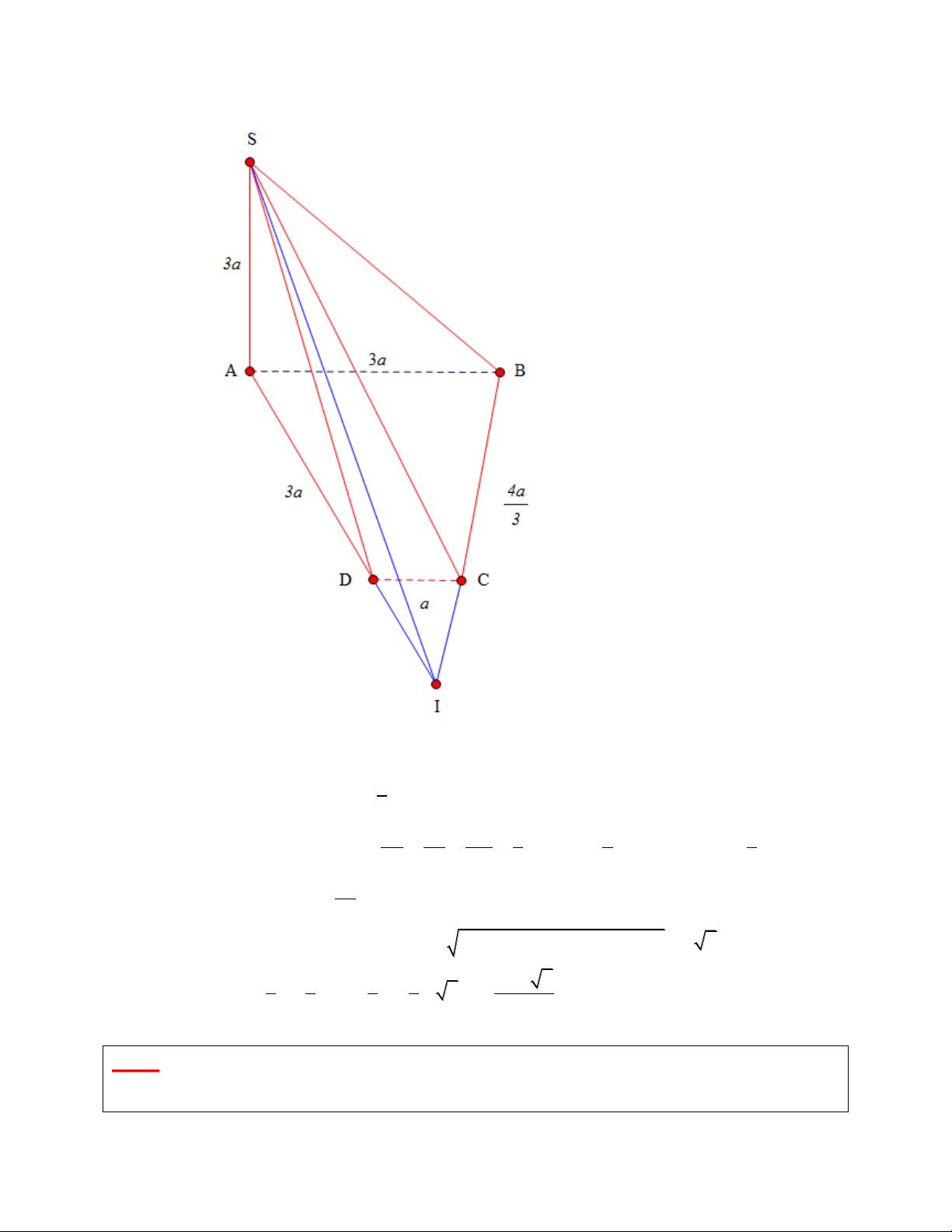
Ví dụ minh họa: Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn AB  3a , đáy nhỏ 4a
CD  a , cạnh bên AD  2a, BC 
. Chiều cao SA  3a . Tính thể tích của khối chóp 3 S.ABCD 3 8a 2 3 16a 2 3 11a 3 3 7a 5 A. B. C. D. 3 9 9 9
 Phân tích ý tƣởng
+) Để tính thể tích khối chóp S.ABCD ta phải tính được diện tích đáy ABCD là một
hình thang rất khó tính diện tích ( Vì không phải hình thang cân, không phải hình thang
vuông và chiều cao trong hình thang khó tính được )
+) Trong trường hợp này ta sẽ sử dụng phƣơng pháp phần bù tính thể tích
Ta xây dựng khối chóp S.ABCD nằm trong khối chóp S.IAB khi đó  V V V S.ABCD S.IAB S.ICD
Đương nhiên ta phải chọn sao cho khối chóp S.IAB và khối chóp S.ICD đều dễ dàng tính được thể tích.  Giải
+) Kéo dài AD và BC cắt nhau tại I. Khi đó 1 V V V  S . A S  S S .ABCD S.IAB S.ICD         3 IAB ICD ID IC CD 1 8
+) Theo định lý Talet ta có:    1  S  S hay S  S IA IB AB 3 ICD 9 IAB ABCD 9 IAB 4a
+) Từ AD  2a, BC 
dễ tính được IA  3 , a IB  2a . 3
+) Theo định lý Herong ta có: S
 p p  IA p  IB p  IC 2  2 2a IAB 3 1 8 1 8 16 a 2 Vậy 2 V  S . A S  .3 . a .2 2a  ABCD 3 9 IAB 3 9 9
BÀI TẬP TƢƠNG TỰ
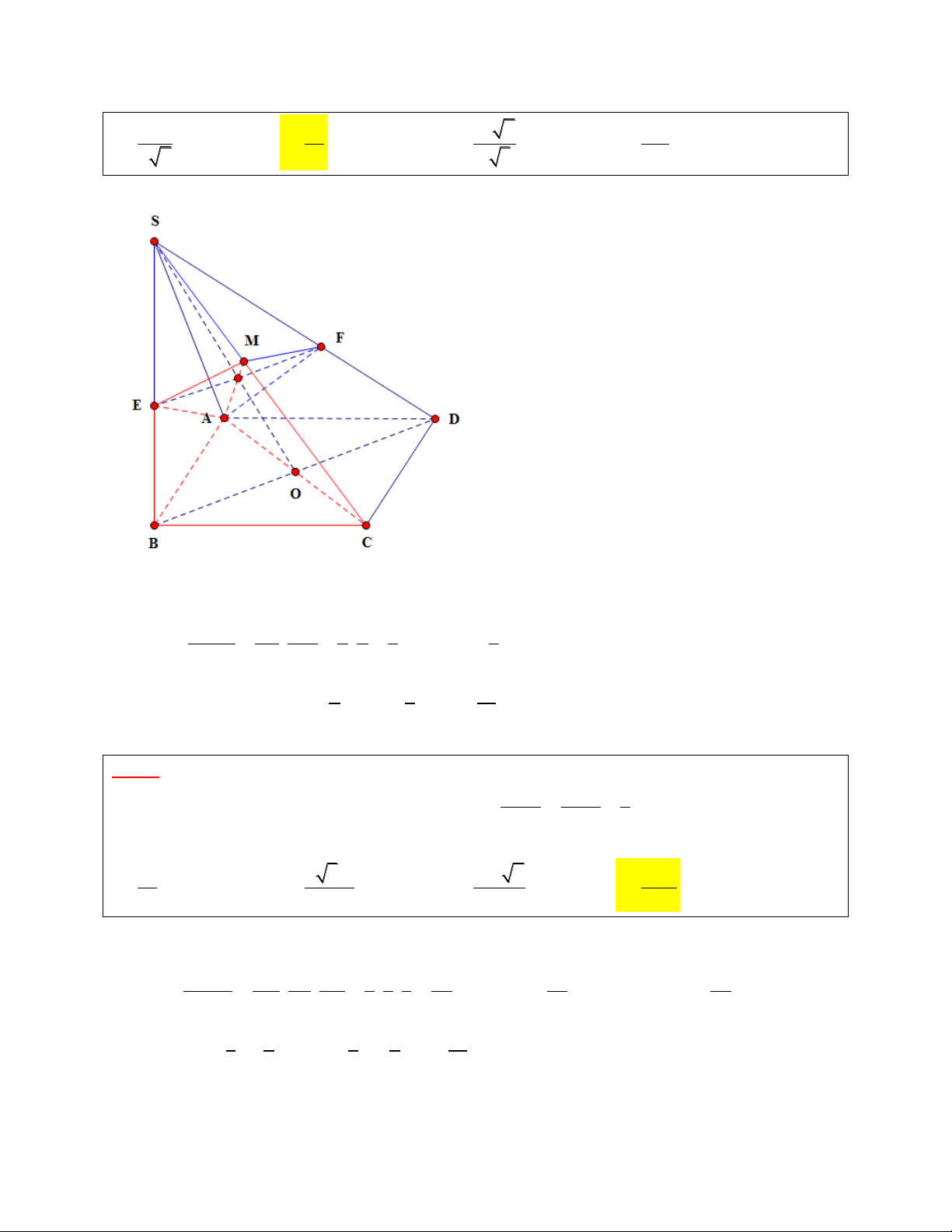
Bài 1: Cho hình chóp S.ABCD có thể tích là 3
a đáy ABCD là hình bình hành tâm O. Mặt phẳng
  qua AM và song song với BD cắt SB, SD tại E và F. Tính thể tích của khối đa diện AEMCB 3 a 3 a 3 a 2 3 5a A. B. C. D. 2 2 3 2 3 14 GIẢI
+) Ta xây dựng khối đa diện AEMCB nằm trong khối chóp S.ABC. Khi đó: V V V AEMCB S.ABC S.AEM V SE SM 2 1 1 1
+) Ta có: S.AEM  .  .  V  V S .AEM S . V SB SC 3 2 3 3 ABC S. ABC 3 2 1 a  V  V V  V  V  AEMCB S .ABC S .AEM S . 3 ABC 3 ABCD 3
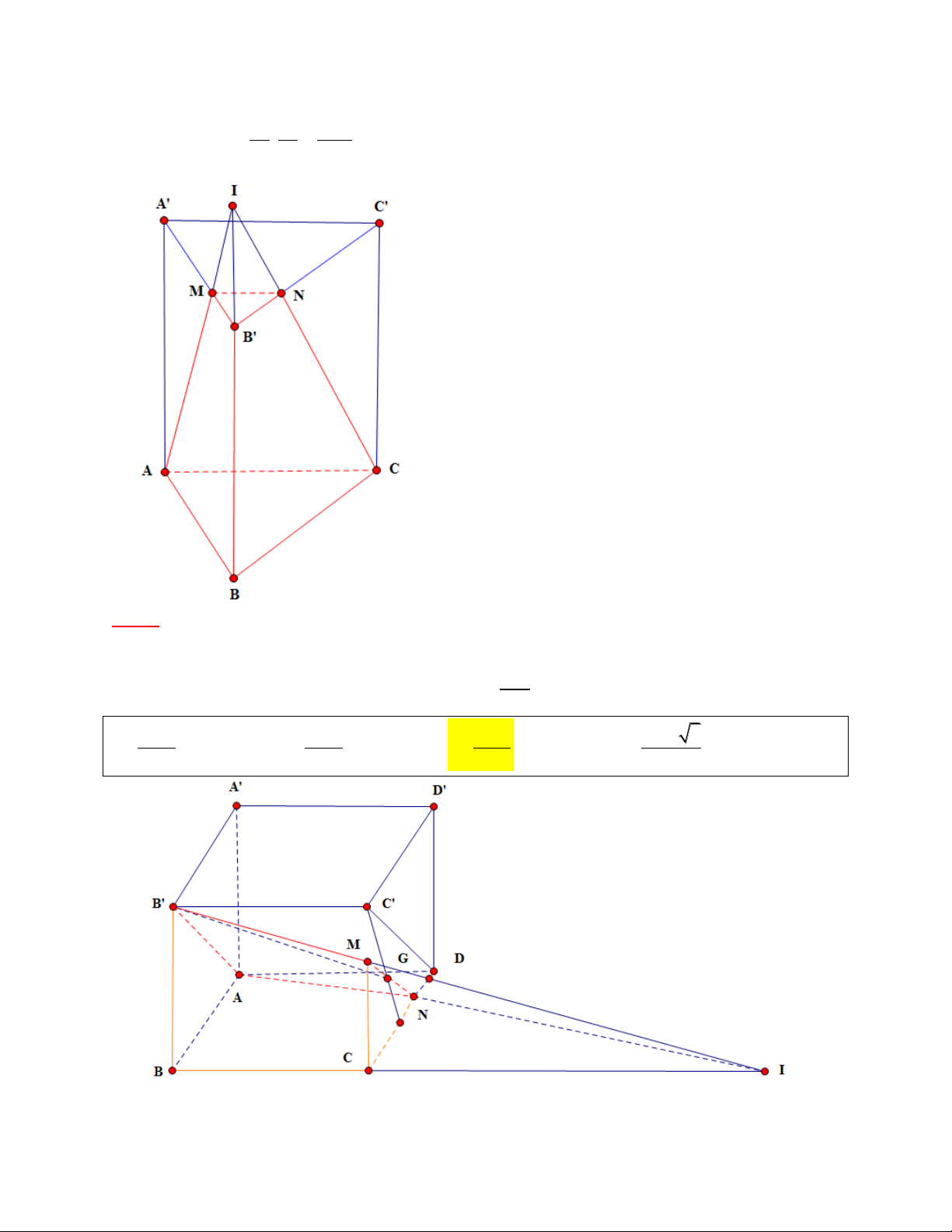
Bài 2: Cho lăng đứng AB .
C A' B 'C ' có đáy ABC là tam giác vuông cân, AB  BC  a cạnh bên B ' M B ' N 1
AA'  2a . Gọi M và N là 2 điểm thỏa mãn sao cho 
 . Tính thể tích khối đa điện BA' B 'C ' 3 B ' MNCBA 3 a 3 4 3a 3 9a 2 3 13a A. B. C. D. 2 15 28 27 GIẢI
+) Ta xây dựng khối đa diện B ' MNCBA nằm trong khối chóp tam giác I.ABC V IM IN IB ' 1 1 1 1 1 26
+) Ta có I.B'MN  . .  . .   V  V V  V V IA IC IB 3 3 3 27 IB 'MN IABC B 'MNCBA I . 27 27 ABC I .ABC 3 1 1 1 1 a +) Mà V  I . B B . A BC  .3 . a . . a a  I .ABC 3 2 3 2 2 3 3 26 a 13a +) Vậy V  .  B 'MNCBA 27 2 27
Bài 3: Cho hình hộp chữ nhật ABC .
D A' B 'C ' D' có AB  3 , a AD  4 ,
a AA'  3a . Gọi G là
trọng tâm tam giác CC ' D . Măt phẳng chứa B 'G và song song với C ' D chia khối hộp thành 2  V H 
phần. Gọi  H  là khối đa diện chứa C . Tính tỉ số
với V là thể tích khối hộp đã cho. V 3 25a 3 57a 3 38a 3 23a 3 A. B. C. D. 2 5 3 4
+) Khối đa diện  H  chứa C là: CMNABB'
+) Ta xây dựng khối đa diện  H  nằm trong khối chóp I.ABB ' Khi đó V  V V H I .BB' A ICMN 1 1 1 1 +) Tính 3 V  I . B
BB '.BA  .12 . a .3 .
a 3a  18a I .BB ' A 3 2 3 2 V 8 19 38 +) Tính ICMN 3  V  V  a H IBB ' V 27 27 A 3 IBB ' A DẠNG 2:  V
V V V H  A B C
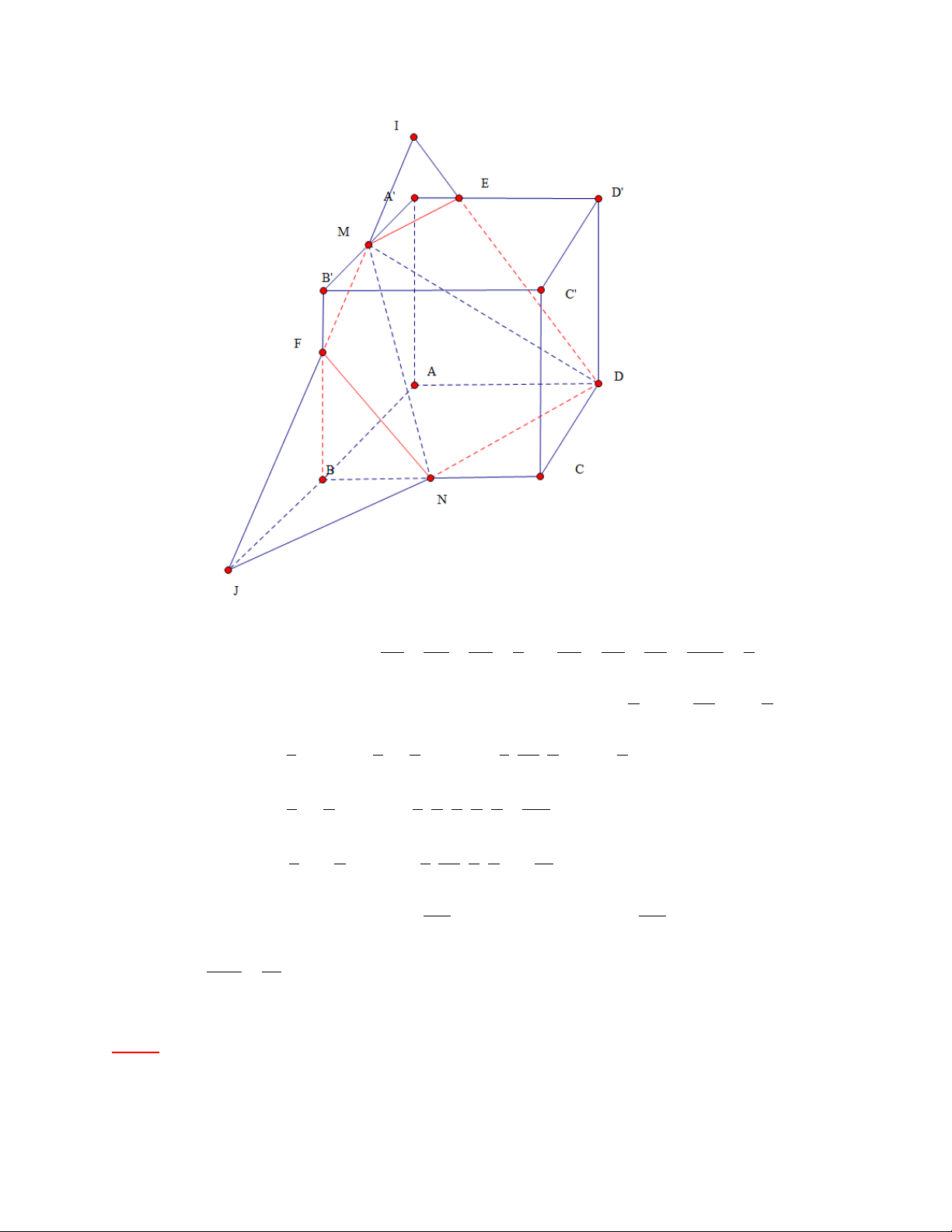
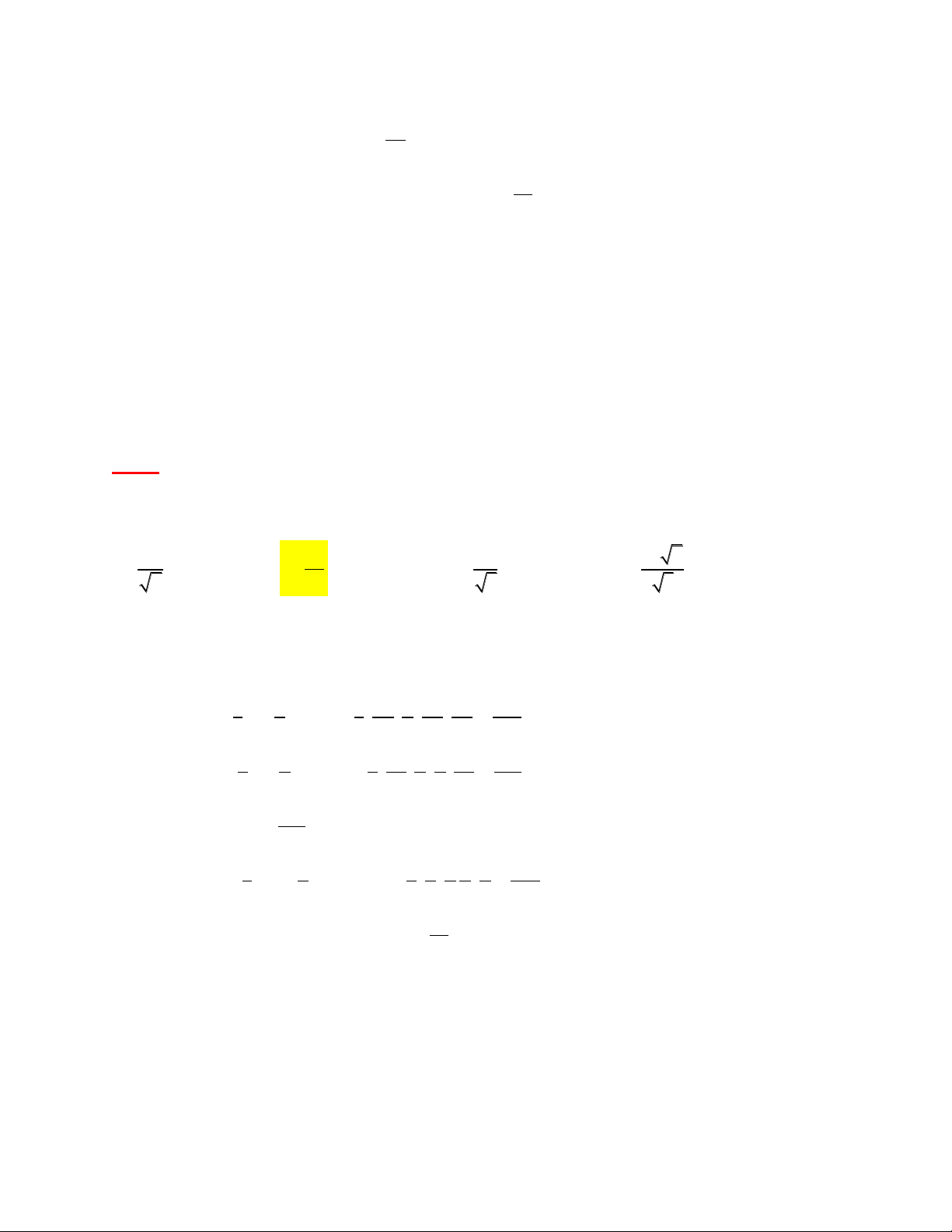
Ví dụ minh họa: [THPT THĂNG LONG 2016] Cho hình lập phương ABC .
D A' B 'C ' D ' cạnh a
có M và N lần lượt là trung điểm A' B ', BC . Mặt phẳng  DMN  chia hình lập phương thành 2  V 1 H 
phần. Khối đa diện đỉnh A kí hiệu là  H , phần còn lại kí hiệu là  H . Tính tỉ số 2  1   V H2 37 55 2 1 A. B. C. D. 48 89 3 2
 Phân tích tƣ duy
+) Nhìn vào hình vẽ ta thấy mặt phẳng  DMN  chia khối lập phương thành 2 khối đa
diện trong đó khối đa diện  H là ABNDENF và phần còn lại 1 
+) Khối đa diện  H cực kì phức tạp (không phải chóp, không phải lăng trụ, không phải 1 
hộp...) nên việc tính toán là rất phức tạp
+) Để dễ tính ta sẽ sử dụng phƣơng pháp phần bù tính thể tích khối đa diện phức tạp
Ta sẽ đi xây dựng khối đa diện  H nằm trong khối đa diện dễ tính I.ADJ 1  Khi đó  V V V V H I .ADJ IANE FBNJ 1   Giải +) Theo đị JB JN JF 1 IA' IN IE A' N 1 nh lý Talet ta có:    và     JA JD JI 2 IA IJ ID AJ 4 a a a
Từ đó ta có thể tích được hết các đoạn thẳng ví dụ như: 2 JB  ; BF  , IA  ... 2 3 4 1 1 1 1 4a 1 4 +) Tính 3 V  I . A S  I . A .A . D AJ  . . .2 . a a  a IADJ 3 ADJ 3 2 3 3 2 9 3 1 1 1 a 1 a a a +) Tính V  I . A
AE.AN  . . . .  IANE 3 2 3 3 2 4 2 144 3 1 1 1 2a 1 a a +) Tính V  .F . B BN.BJ  . . . .a  FBNJ 3 2 3 3 2 2 18 55 89 Vậy 3 3 3  V  V V V  a  V  a V  a H I .ADJ IANE FBNJ H H 2   1 1  144 144  V H 55 1  Vậy   V 89 H2 
BÀI TẬP TƢƠNG TỰ
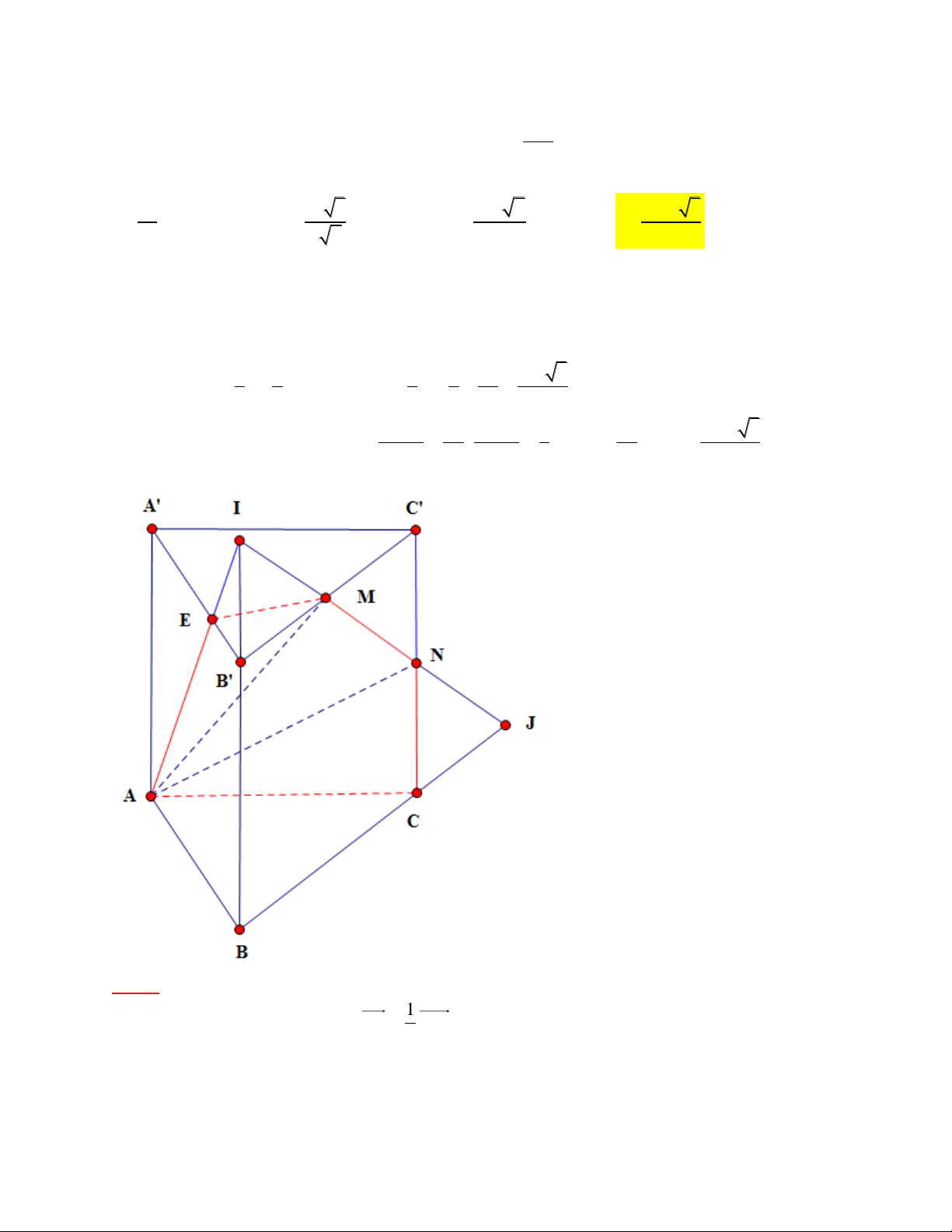
Bài 1: Cho hình lăng trụ đều AB .
C A' B 'C ' cạnh đáy là a, cạnh bên là 2a . Gọi M và N lần lượt
là trung điểm của các cạnh B 'C ',CC ' . Mặt phẳng  AMN  chia khối lăng trụ thành 2 khối đa  V H 
diện. Gọi  H  là khối đa diện chứa đỉnh B. Tính tỉ số
với V là thể tích của khối lăng trụ V đều. 3 a 3 a 3 3 7a 2 3 23a 3 A. B. C. D. 3 4 2 15 72 GIẢI
+) Khối đa diện chứa đỉnh B là B'MEABCN (khối đa diện H )
+) Ta xây dựng khối đa diện H nằm trong khối chóp I.ABJ Khi đó: V V V V H I .ABJ I .EB 'M N .ACJ 3 1 1 1 1 3a 3a 3 +) Tính 0 V  I . B B . A BJ sin 60  .3 . a . a  I . ABJ 3 2 3 2 2 8 3 V 1 V 1 23 23a 3
+) Theo công thức tỉ số thể tích thì IEB'M N .  , ACJ  V  V  H I . V 27 V 9 27 ABC 72 IABC I . ABC
Bài 2: Cho hình lập phương ABC .
D A' B 'C ' D ' cạnh a. Gọi M và N lần lượt là trung điểm 1
A' B ', A' D ' và điểm P thỏa mãn CP 
CC ' . Mặt phẳng MNP chia khối lập phương thành 2 4
khối đa diện. Gọi  H là khối đa diện chứa đỉnh C'. Gọi  H là khối đa diện còn lại. Tính tỉ 2  1  V số H1 VH2 3 a 3 4a 3 25a 41 A. B. C. D. 3 a 4 25 96 155 GIẢI
+) Khối đa diện chứa đỉnh C ' là : PFB'MND'EC' là khối đa diện  H 1 
+) Ta xây dựng khối đa diện  H trong chóp . P C ' IJ 1 
Khi đó: V  V V V 1 H P.C ' IJ E.D'IN F .B'MJ 3 1 1
1 3a 1 3a 3a 9a +) Tính V
 PC '. CI.CJ  . . . .  P.C ' IJ 3 2 3 4 2 2 2 32 3 1 25 25a
+) Theo công thức tỉ số thể tích thì: V  V  V V  V  E.D ' IN F .B 'MJ P.CIJ H P.C ' 27 27 IJ 96 DẠNG 3:  V
V V V V H  A B C D
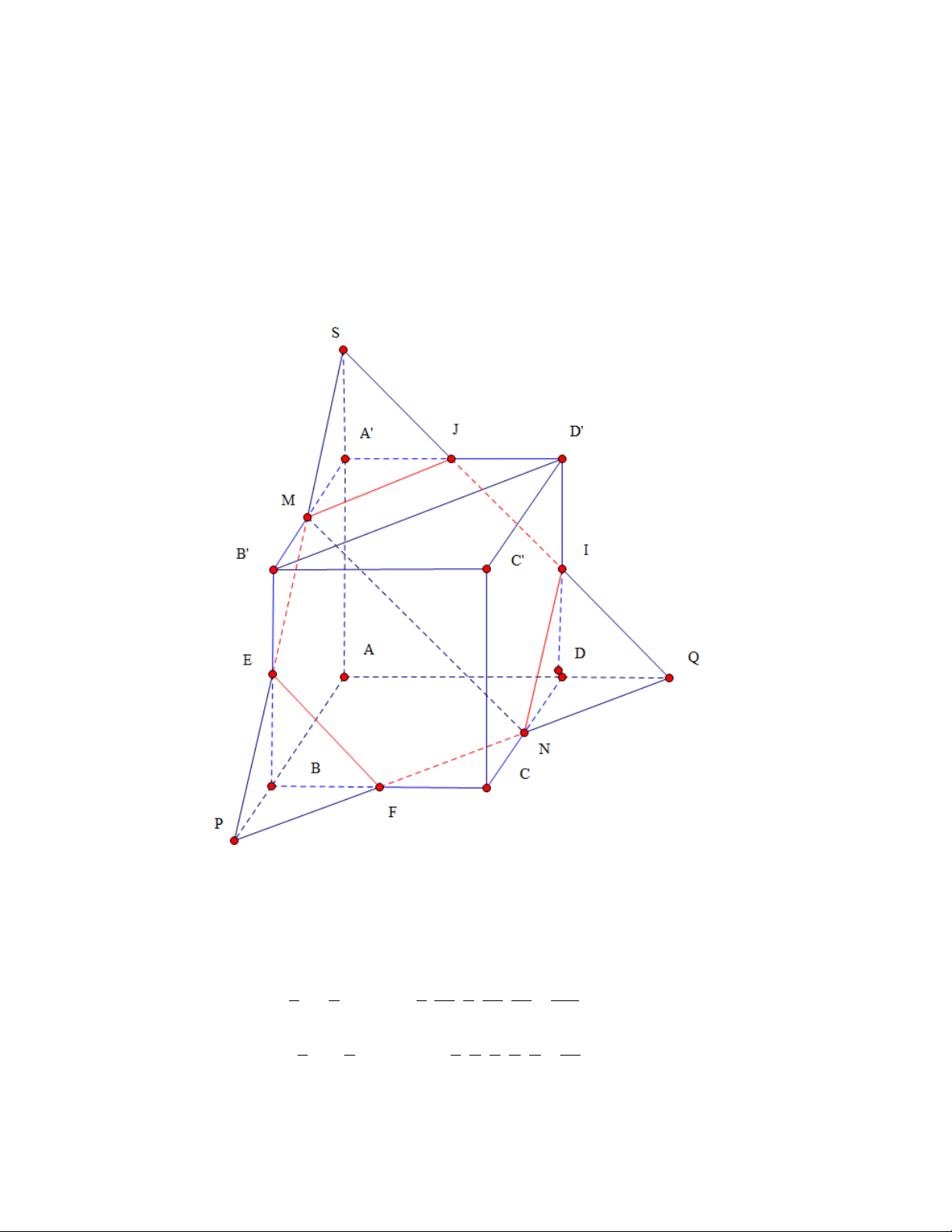
Ví dụ minh họa: Cho hình lập phương ABC .
D A' B 'C ' D ' cạnh a, có M và N là trung điểm của
A' B ' và CD . Mặt phẳng   qua MN và song song với B ' D ' chia khối đa điện thành 2 phần.
Tính thể tích của khối đa diện chứa đỉnh A. 3 a 3 2a 3 3a 3 4a A. B. C. D. 2 3 5 7
 Phân tích ý tƣởng
+) Xác định thiết diện và ta xác định được khối đa diện chứa A là A'MJINFEBA (ta gọi
đây là khối đa diện H )
+) Đến dạng 3 thì chắc chúng ta đã quen với ý tưởng: Nếu tính thể tích 1 khối đa diện
phức tạp ta sẽ sử dụng phương pháp phần bù
+) Vậy ta sẽ xây dựng khối đa diện H nằm trong khối chóp tam giác S.APQ (dễ tính thể tích) và  V V V V V H  S.APQ S.A'MJ E.BPF IDNQ  Giải +) Ta có  V V V V V H  S.APQ S.A'MJ E.BPF IDNQ
+) Sử dụng tính chất của quan hệ song song và định lý Talet ta dễ dàng tính được độ dài
các đoạn thẳng SA', A'J, ID.... 3 1 1
1 3a 1 3a 3a 9a +) Tính V  S . A A . P AQ  . . . .  SAPQ 3 2 3 2 2 2 2 16 3 1 1 1 a 1 a a a +) Tính V
 SA'. A'M.A' J  . . . .  S. A'MJ 3 2 3 2 2 2 2 48 3 +) Tương tự a V  V  E.BPF IDNQ 48 3 a +) Vậy  V V V V V  H  S.APQ S .A 'MJ E .BPF IDNQ 2  Bình luận
+) Bài này còn 1 cách làm nhanh nữa là dựa và tính chất đối xứng của 2 khối đa diện tạo
thành bởi mặt phẳng   ta thấy thể tích của 2 khối đa diện này đều bằng nhau và bằng 1
nửa thể tích khối lập phương.
+) Do dạng này khá phức tạp nên ví dụ minh họa tác giả đã cố tính cho các bạn tỉ số rất
đẹp (toàn là trung điểm ) nên mới sinh ra cách đặc biệt kia.
+) Nếu các bạn muốn bài toán mang tính chất tổng quát hơn. Tác giả sẽ sửa lại vị trí điểm
thuộc cạnh A'D' như trong bài tập tự luyện số 2 thì bài toán sẽ căng thẳng hơn rất nhiều.
BÀI TẬP TƢƠNG TỰ
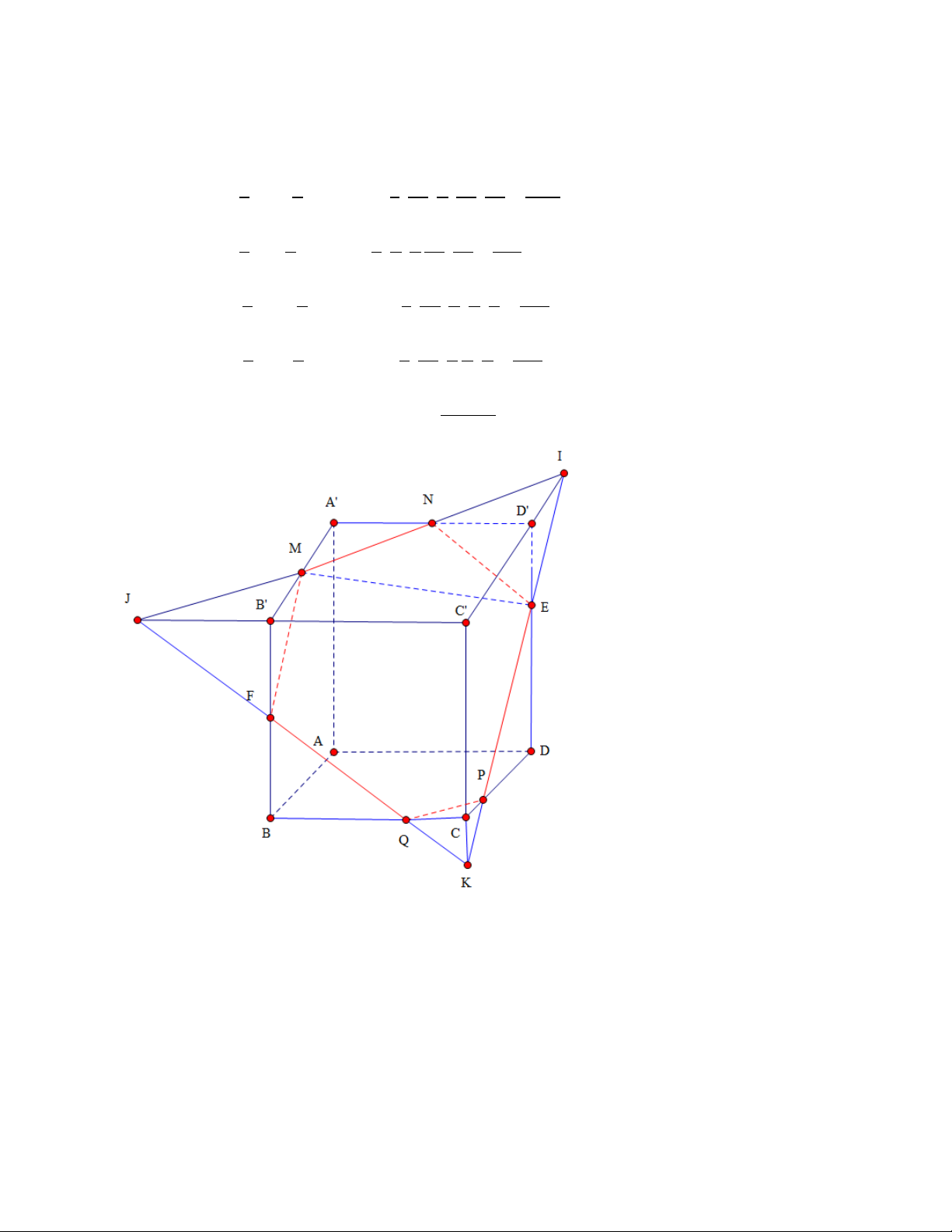
Bài 1: Cho hình lập phương ABCD.A'B'C'D' cạnh a. M, N là trung điểm A' B ',CD . H là điểm
thuộc cạnh A' D ' sao cho HA'  3HD ' . Mặt phẳng  HMN  chia khối chóp thành 2 đa diện.
Tính thể tích khối đa diện chứa điểm C. 3 a 3 a 3 a 3 a 2 A. B. C. D. 2 2 3 3 GIẢI
+) Khối đa diện chứa điểm C là CNFEB'C'D'HMG gọi tắt là hình  H  +) Ta có:  V V V V V H  J .CIA JCNF GD' IH EB'MA 1 1
1 7a 1 7a 7a 343 +) Tính 3 V  JC. C . A CI  . . . .  a J .CIA 3 2 3 4 2 4 6 576 3 1 1
1 3a 1 a 3a 3a +) Tính V
 JC. CN.CF  . . . .  J .CNF 3 2 3 4 2 2 4 64 3 +) Tương tự 3a V  E. AB 'M 64 3 1 1 1 a 1 a a a +) Tính V
 .GD'. .D' I.D' H  . . .  G.D ' HI 3 2 3 4 2 4 6 576 3 a Vậy  V V V V V  H  J .CIA JCNF GD 'IH EB 'MA 2
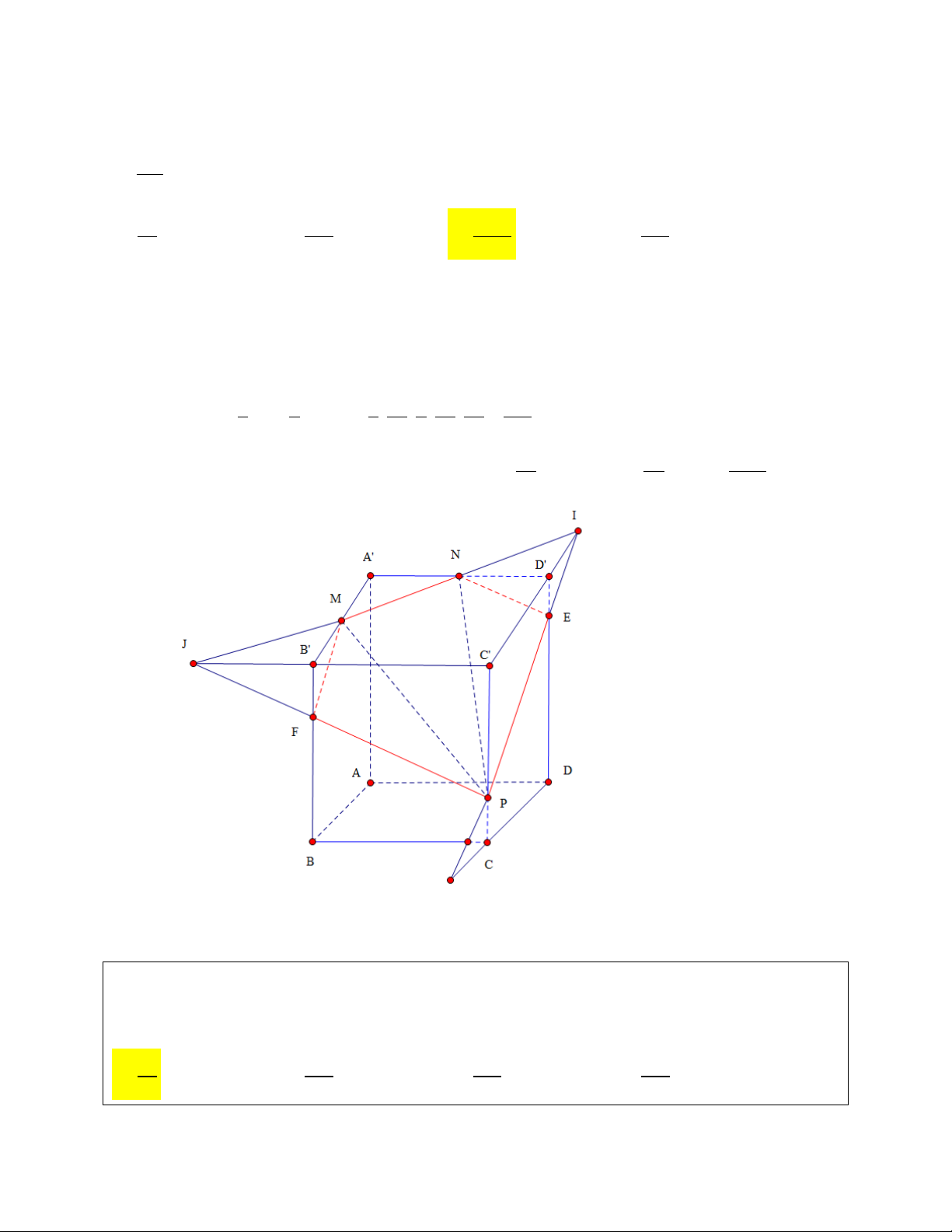
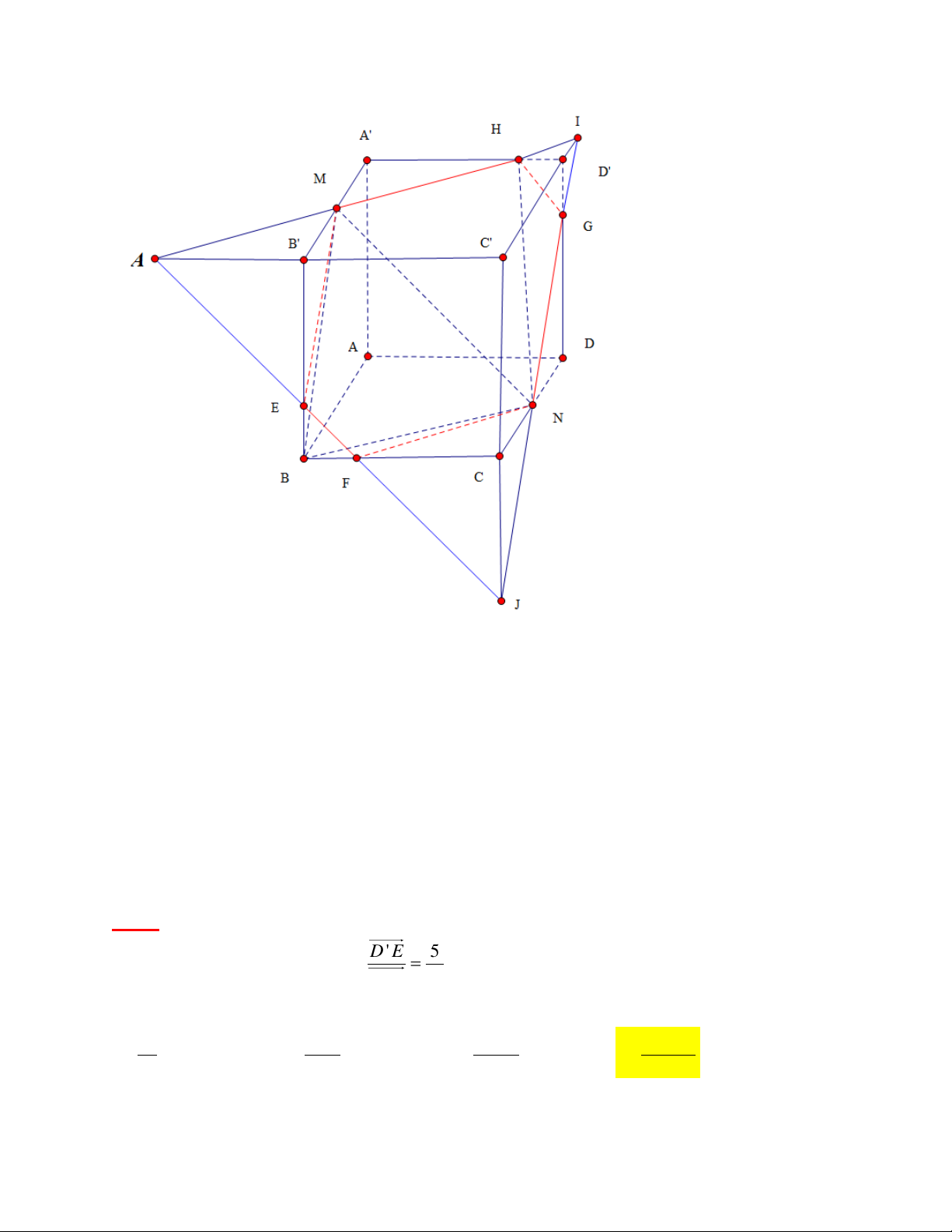
Bài 2: Cho hình lập phương ABC .
D A' B 'C ' D ' cạnh a . Gọi M và N lần lượt là trung điểm của D ' E 5
A' B ', A' D ' . E là điểm thỏa mãn 
. Mặt phẳng MNE chia khối lập phương thành 2 D ' D 12
khối đa diện. Gọi  H  là khối đa diện chứa đỉnh C ' . Tính thể tích khối đa điện  H  3 a 3 15a 3 154a 3 1549a A. B. C. D. 3 37 365 3600 GIẢI
+) Khối đa diện chứa đỉnh C' là EPCQFMND'C'B' (khối da diện H )
+) Ta có: V  V V V V H K .C ' IJ K .CPQ E.D' IN F .B 'MJ 3 1 1
1 5a 1 3a 3a 15a +) Tính V
 KC '. C ' I.C ' J  . . . .  K .C ' IJ 3 2 3 4 2 2 2 32 3 1 1
1 a 1 3a 3a 3a +) Tính V  KC. C . P CQ  . . .  K .CPQ 3 2 3 4 2 10 10 800 3 1 1 1 5a 1 a a 5a +) Tính V
 .ED'. D' I.D' N  . . . .  K .D ' IN 3 2 3 12 2 2 2 288 3 1 1 1 5a 1 a a 5a +) Tính V
 FB '. B 'M.B ' J  . . .  F .B 'MJ 3 2 3 12 2 2 2 288 3 1549a Vậy V  V V V V  H K .C ' IJ K.CPQ . E ' D IN . F ' B MJ 3600