Phương pháp tọa độ hóa trong không gian Toán 12
Phương pháp tọa độ hóa trong không gian Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Chủ đề: Chương 3: Phương pháp tọa độ trong không gian
Môn: Toán 12
Thông tin:
Tác giả:
Thông tin :
Chủ đề:
Chương 3: Phương pháp tọa độ trong không gian
Môn:
Tác giả:
Tài liệu liên quan:
Preview text:
HÌNH HỌC 12. CHƯƠNG III
PHƯƠNG PHÁP TỌA ĐỘ HÓA TRONG KHÔNG GIAN
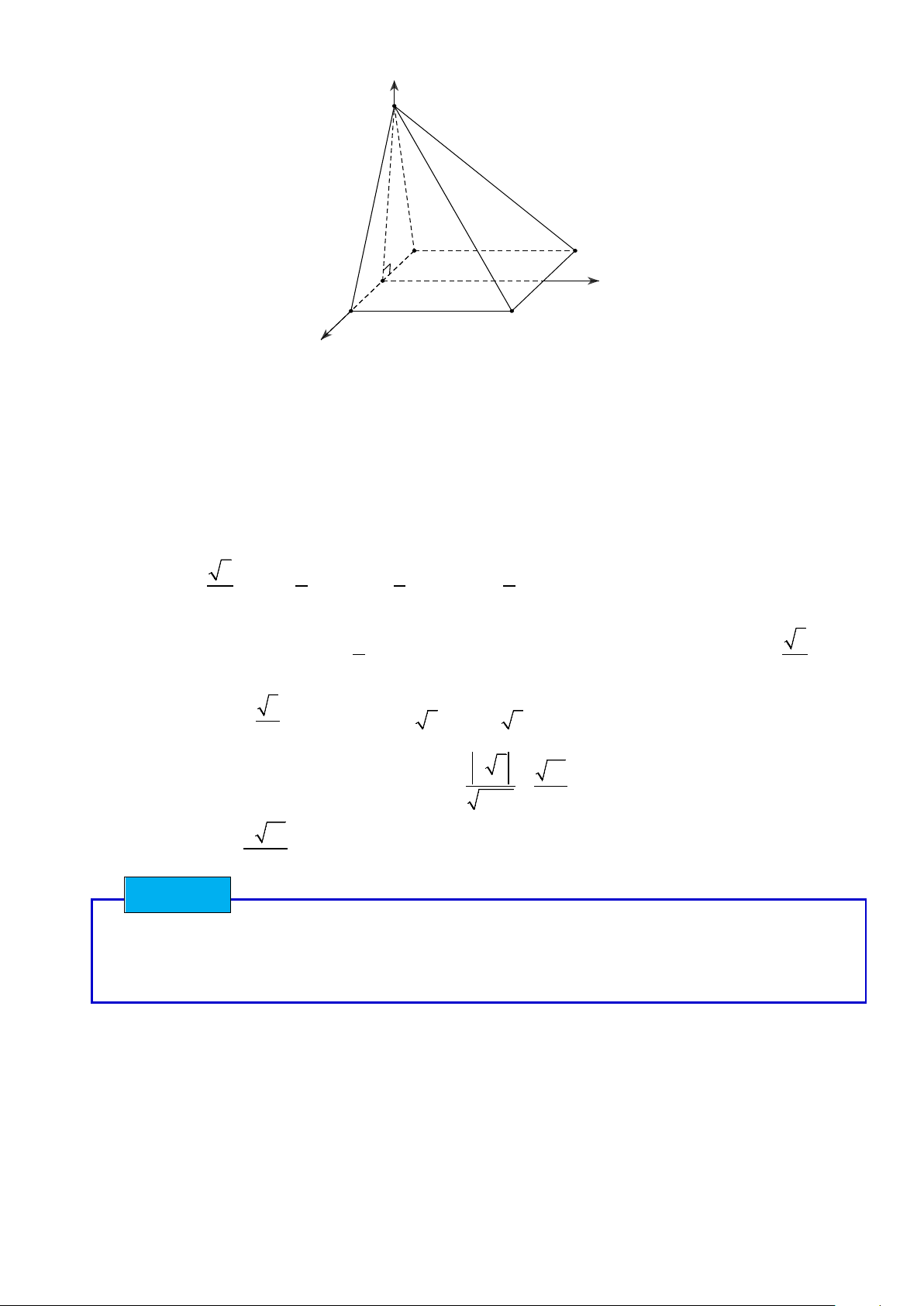
DẠNG 1. GẮN HỆ TRỤC TỌA ĐỘ VÀO CÁC HÌNH ĐA DIỆN CÓ SẴN MÔ HÌNH TAM DIỆN VUÔNG Phương pháp
Bước 1: Chọn hệ trục toạ độ Oxyz thích hợp. Trong đó gốc tọa độ là giao điểm chung của ba
đường đôi một vuông góc với nhau, các tia Ox,Oy,Oz lần lượt nằm trên ba đường đó.
Bước 2: Xác định các toạ độ điểm toạ độ của các véc tơ có liên quan.
Bước 3: Sử dụng các kiến thức về toạ độ để giải quyết các bài toán có liên quan.
Loại 1. Hình chóp có đáy là tam giác Ví DỤ 1
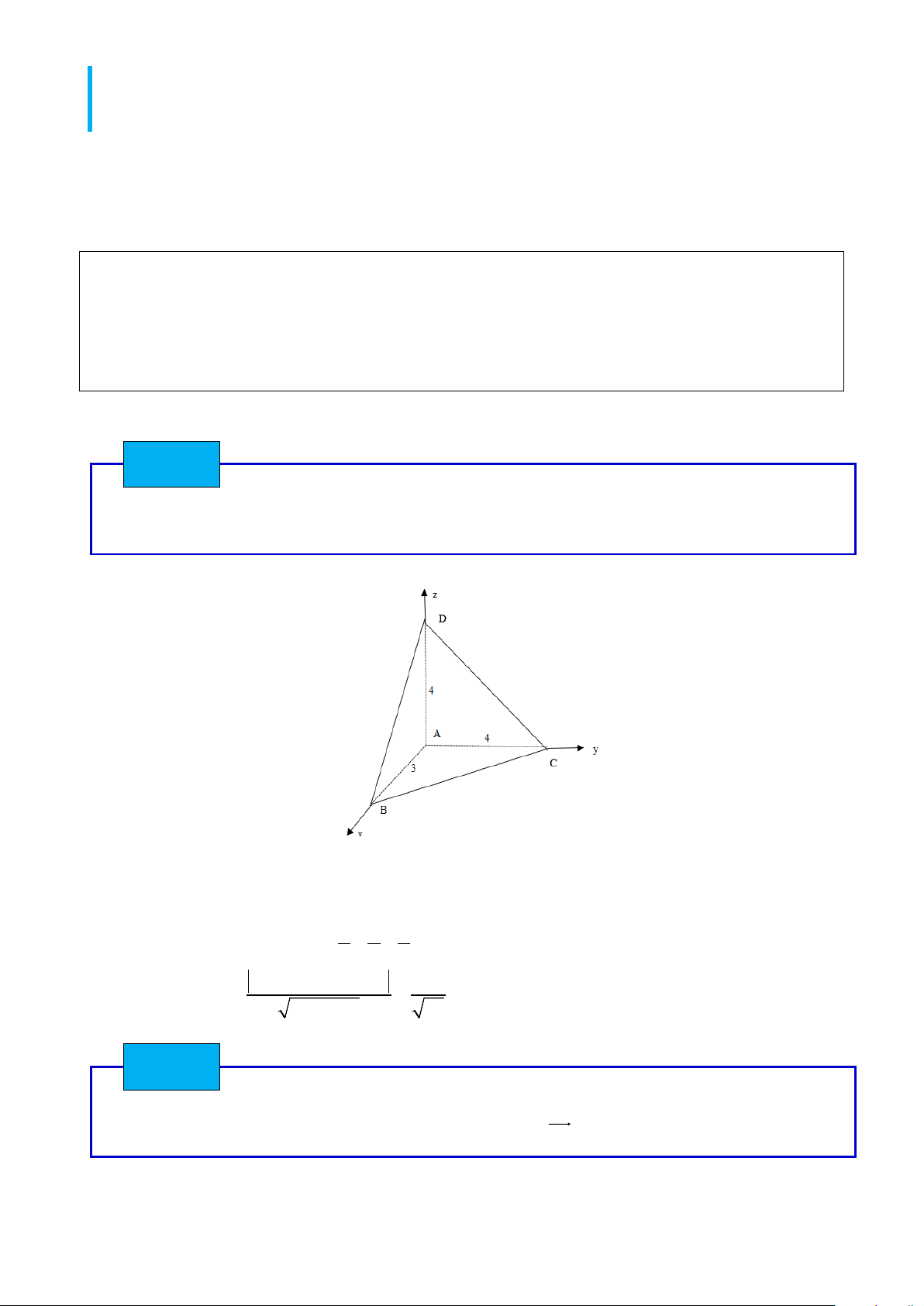
Cho tứ diện ABCD có AD ⊥ ( ABC) , AC = AD = 4(cm); AB = 3(cm); BC = 5(cm) . Tính khoảng
cách từ A đến mặt phẳng (BCD) .
Tam giác ABC có AB = 3, AC = 4, BC = 5 nên tam giác ABC vuông tại A . Do đó tứ diện ABCD
có ba cạnh AB, AC, AD đôi một vuông góc.
Chọn hệ trục như hình vẽ. Khi đó: A(0;0;0), B(3;0;0),C (0;4;0), D(0;0;4)
Phương trình mặt phẳng ( ): x y z BCD
+ + = 1 ⇔ 4x + 3y + 3z −12 = 0 . 3 4 4 + + −
Vậy d ( A (BCD)) 4.0 3.0 3.0 12 12 , = = . 16 + 9 + 9 34 Ví DỤ 2
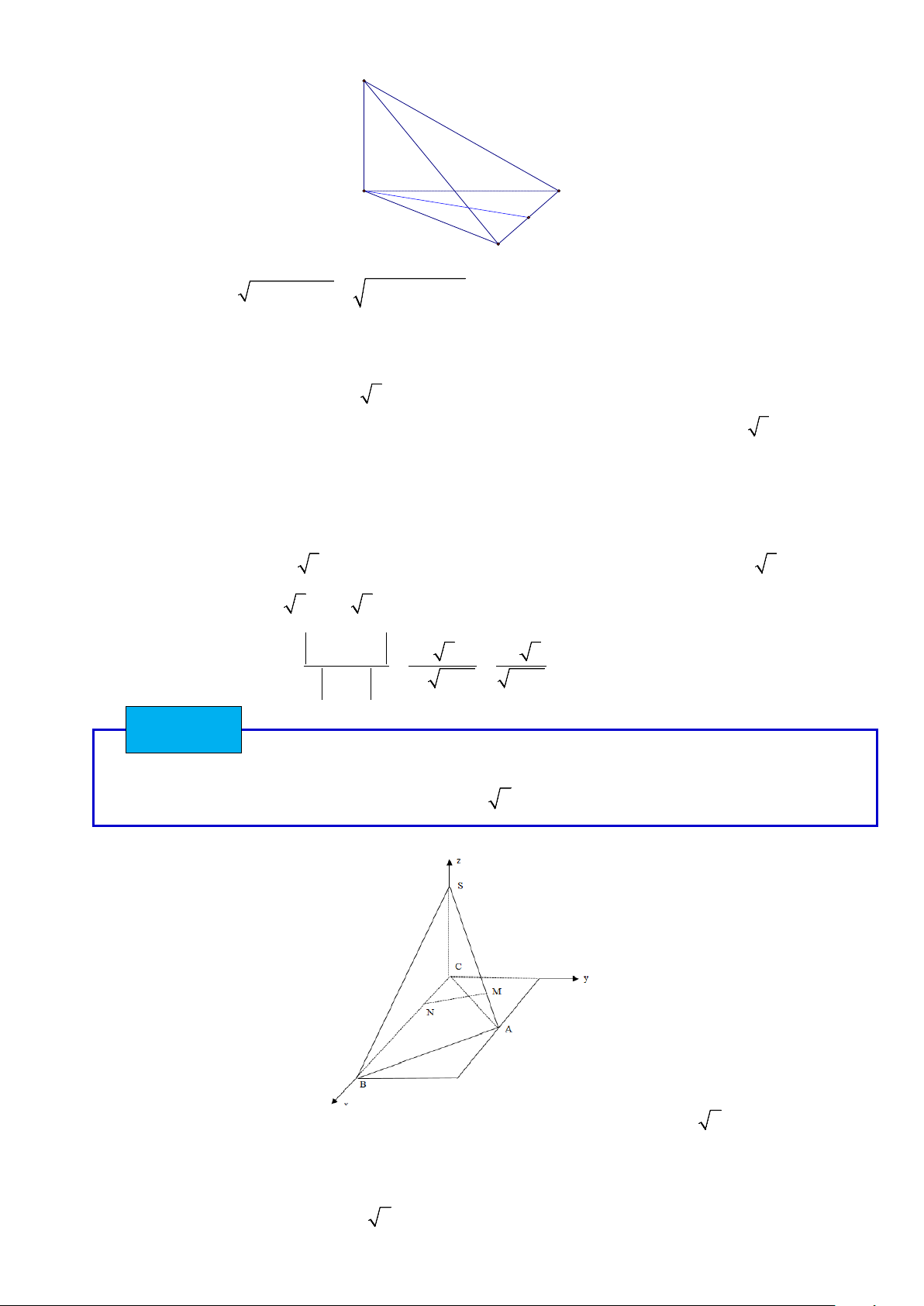
Cho hình chóp O.ABC có ba cạnh OA,OB,OC đôi một vuông góc và OA = OB = OC = a
Gọi M là trung điểm cạnh AB .Tính góc tạo bởi hai vectơ BC và OM .
Chọn hệ trục toạ độ Oxyz như hình vẽ ta có (0;0;0), (0; ;0),B(a;0;0),C(0;0; ), (a ; a O A a a M ;0) 2 2 Ta có : = (−a ;0;a) ; = (a ; a BC OM ;0) 2 2 2 −a
BC.OM 2 1
0
⇒ cos(BC,OM ) = =
= − ⇒ (BC,OM ) =120 | BC |.| OM | a 2 2 . a 2. 2
Loại 2. Hình chóp có đáy là hình thang . Ví DỤ 3
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D , AB = 2a,CD = DA = a . Cạnh
bên SA = 2a và vuông góc với đáy ABCD . Tính cosin của góc giữa hai mặt phẳng (SBC) và (SCD). Giải : S A B D C
Chọn hệ trục tọa độ Oxyz sao cho A ≡ O(0;0;0), D(a;0;0), B(0;2a;0),S (0;0;2a) , thì C ( ; a ;0 a )
Ta có SB = (0;2a; 2 − a),SC = ( ; a ; a 2 − a),SD = ( ; a 0; 2
− a), SB SC = ( 2 2 2 , 2 − a ; 2 − a ; 2 − a ), SC SD = ( 2 2 , 2
− a ;0;−a ). Suy ra mặt phẳng (SBC) có véc tơ pháp tuyến n = 1;1;1 1 ( ), mặt phẳng
(SCD)có véc tơ pháp tuyến n = 2;0;1 2 ( ). 3 3
Ta có cos((SBC),(SCD)) = cos(n ,n = = 1 2 ) . 3. 5 15 Ví DỤ 4
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D , AB = 2a,CD = DA = a . Cạnh
bên SA = 2a và vuông góc với đáy ABCD . Tính khoảng cách giữa hai đường thẳng BD, SC . S A B D C
Chọn hệ trục tọa độ Oxyz sao cho A ≡ O(0;0;0), D(a;0;0), B(0;2a;0),S (0;0;2a) , thì C ( ; a ;0 a ) Ta có BD = ( ; a 2 − ;
a 0),SC = ( ;a ;a 2
− a),SB = (0;2 ; a 2
− a) , BD SC = ( 2 2 2 ,
4a ;2a ;3a ) ,
BD, SC SB 3 3
BD, SC SB = 2 − a 2a 2a , 2
BD, SC = 29a
. Suy ra d (BD,SC) = = = 2 BD, SC 29a 29 Ví DỤ 5
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D , AB = 2a,CD = DA = a . Cạnh
bên SA = 2a và vuông góc với đáy ABCD . Gọi M là trung điểm SD , G là trọng tâm tam giác S
∆ BC . Tính thể tích khối tứ diện ACMG S M G A B D C
Chọn hệ trục tọa độ Oxyz sao cho A ≡ O(0;0;0), D(a;0;0), B(0;2a;0),S (0;0;2a) , thì C ( ; a ;0 a ) a a 2 ;0; , ; ; a M a G a . 2 3 3 a a a
Ta có AM = a AC = (a a ) 2 ;0; , ; ;0 , AG = ;a; 3
⇒ AM , AC AG = a 2 3 3 3
⇒ ( ) 1 = , a V ACMG AM AC AG = 6 6 .
Loại 3. Hình chóp có đáy là hình vuông, hình chữ nhật. Ví DỤ 6
Cho hình chóp S.ABCD , đáy ABCD là hình vuông cạnh a , SA vuông góc với mặt phẳng ( ABCD)
; M , N hai điểm nằm trên hai cạnh BC , CD. Đặt BM = x , DN = y (0 < x, y < a). Xác định hệ thức
liên hệ giữa x và y để hai mặt phẳng (SAM ) và (SMN ) vuông góc với nhau? Lời giải S A D N B M C
Tọa độ hóa với O ≡ A, Ox ≡ AD , Oy ≡ AB , Oz ≡ AS .
Đặt SA = z > 0 , ta có S (0;0; z) , M ( ; x a;0) , N ( ; a y;0) . AS = (0;0; z) Do đó
⇒ AS; AM = (−az; xz;0) . AM ( ;xa;0) = SM = ( ; x a;− z)
⇒ SM ; SN = ( 2
yz − az; xz − az; xy − a ) . SN = ( ; a y;−z)
Mặt phẳng (SAM ) nhận AS; AM = (−az; xz;0) là một VTPT.
Mặt phẳng (SMN ) nhận SM SN = ( 2 ;
yz − az; xz − az; xy − a ) là một VTPT.
Ta có (SAM ) ⊥ (SMN ) ⇔ AS; AM .SM;SN = 0
⇔ az (az − yz) + xz ( xz − az) = ⇔ a (a − y) + x( x − a) 2 2 0
= 0 ⇔ x + a = a ( x + y) . Ví DỤ 7
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với đáy,
AB = a, AD = 2a,SA = 3a . Gọi M, N lần lượt là hình chiếu của A lên SB, SD và P là giao điểm
của SC với mặt phẳng ( AMN ) . Tính thể tích khối chóp S.AMPN . Lời giải z S P N M A y D B x C
Chọn hệ trục tọa độ như hình vẽ.
Ta có tọa độ các điểm A(0;0;0), B(a;0;0), D(0;2a;0),C (a;2a;0),S (0;0;3a) .
Suy ra SB = (a;0;−3a),SD = (0;2a;−3a),SC = (a;2a;−3a).
x = a + t
Phương trình SB : y = 0 . z = − 3t
⇒ M (a + t;0;−3t) ⇒ AM = (a + t;0;−3t) . 9a 3a Mà . 0 ( ) 9 0 a AM SB AM SB a t t t − ⊥ ⇒ = ⇔ + + = ⇒ = ⇒ M ;0; . 10 10 10 18a 12a
Tương tự vậy ta tìm được N 0; ; . 13 13 2 27a
Suy ra n = AM , AN = − 1;2;−3 1 ( ) 65 .
Do đó ta có phương trình của ( AMN ) : x + 2y − 3z = 0. x = t
Phương trình SC : y = 2t
nên tọa độ điểm P là nghiệm của hệ z = 3a − 3t x = t y = 2t 9a 9a 15a 9a 9a 15 , , ; ; a x y z P ⇒ = = = ⇒ . y 2t 14 7 14 14 7 14 =
x + 2y − 3z = 0 2 27a 2 27a
Ta có: AM , AP = − (1;2;− )3 AN, AP = 1;2; 3 − 70 , ( ) 91 2 1 621 14.a Suy ra S =
AM AP + AN AP = a AMPN , ,
và d (S,( AMN )) 9 2 1820 = . 14 2 3 1 9a 621 14.a 1863. Vậy a V = = S AMPN . . . . 3 14 1820 1820 Ví DỤ 8
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA = 2a và vuông góc với
mặt phẳng đáy. Gọi M là trung điểm cạnh SD . Tính tan của góc tạo bởi hai mặt phẳng ( AMC) và (SBC). Lời giải
Chọn hệ trục tọa độ và chuẩn hóa cho a =1 sao cho A(0;0;0) , B(0;1;0), D(1;0;0) , S (0;0;2) 1
Ta có M là trung điểm SD ⇒ M ;0;1 , C (1;1;0) . 2 1 AM ;0;1 = 1
, AC = (1;1;0) , AM , AC = 1; − 1; có một vtpt 2 ⇒ ( AMC) 2 n = ( 2; − 2; ) 1 SB = (0;1; 2 − ) , SC = (1;1; 2
− ) , SB,SC = (0;2; ) 1
⇒ (SBC) có một vtpt k = (0;2; ) 1 n.k 5
Gọi α là góc giữa hai mặt phẳng ( AMC) và (SBC) thì cosα = = n . n 3 1 2 5 Do tanα > 0 nên tanα = −1 = . 2 cos α 5 Ví DỤ 9
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a , AD = a 2, SA = a và SA vuông
góc với mặt phẳng ( ABCD) . Gọi M , N lần lượt là trung điểm của AD và SC , I là giao điềm của
BM và AC . Tính thề tích khối tứ diện ANIB . Lời giải
Chọn hệ trục tọa độ Oxyz sao cho O ≡ A, tia Ox chứa B , tia Oy chứa D và tia Oz chứa S . Khi đó: ( ) ( ) ( ) ( ) (
) a 2 a a 2 0;0;0 , ;0;0 , ; 2;0 , 0; 2;0 , 0;0; , 0; ;0, ; ; a A B a C a a D a S a M N . 2 2 2 2 (
) a a 2 = ;0;0 , = ; ; a AB a AN . 2 2 2
Ta có ∆ IAM đồng dạng với ∆ ICB (góc-góc) a a 2 Suy ra: IC BC = = 2 ⇒ IC = 2
− IA . Từ đây tìm được I ; ;0 . IA AM 3 3 a a 2 2 2 AI = a 2 a ;
;0 , AN, AI = ; ;0 . 3 3 6 6 3 3
1 1 a 2 a 2
Thể tích khối tứ diện ANIB là V
= AN AI AB = ⋅ = ANIB , . . 6 6 6 36 Ví DỤ 10
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 2 , SA = 2 và SA vuông góc với
mặt phẳng đáy ( ABCD) . Gọi M , N là hai điểm thay đổi trên hai cạnh AB , AD sao cho mặt phẳng ( 1 1
SMC) vuông góc với mặt phẳng (SNC) . Tính tổng T = +
khi thể tích khối chóp S.AMCN 2 2 AN AM
đạt giá trị lớn nhất. Lời giải
Chọn hệ trục tọa độ Oxyz sao cho A(0;0;0) , B(2;0;0) , D(0;2;0) , S (0;0;2) .
Suy ra C (2;2;0). Đặt AM = x , AN = y , x, y ∈[0;2], suy ra M ( ;0
x ;0) , N (0; y;0) . SM = ( ;x0; 2 − ), SC = (2;2; 2
− ), SN = (0; y; 2 − ).
⇒ n = SM , SC = 4;2x − 4;2x , n = SN, SC = 4 − 2y; 4 − ; 2 − y . 2 ( ) 1 ( )
Do(SMC) ⊥ (SNC)nên n .n = 0 ⇔ 4 4 − 4y − 4 2x − 4 − 4xy = 0 1 2 ( ) ( )
⇔ xy + 2( x + y) = 8 . 8 − 2x − ⇔ y =
, do y ≤ 2 nên 8 2x ≤ 2 ⇔ x ≥1. x + 2 x + 2 S = S − S − S = − − x −
− y = x + y . AMCN ABCD BMC DNC 4 (2 ) (2 ) 2 1 2 2
8 − 2x 2 x + 8 Do đó V = SA S =
x + y = x + = S AMCD . . AMCN ( ) . 3 3 3 x 2 + 3 x + 2 2 2 x +8 2 2 x + 4x − 8 Xét f (x) = f ′ x = 3 với , ( ) . x x ∈[1;2] + 2 3 (x + 2)2 f ′(x) 2
= 0 ⇔ x + 4x − 8 = 0 ⇔ x = 2 − + 2 3 ; x = 2 − − 2 3 (loại).
Lập BBT ta suy ra max f (x) = f ( ) 1 = f (2) = 2 . [0;2] x =1 y = 2 1 1 1 1 5 Vậy maxV = ⇔ ⇒ T = + = + = S AMCN 2 . . 2 2 2 2 x = 2 AM AN x y 4 y =1
Loại 4. Lăng trụ đứng tam giác Ví DỤ 11
Cho hình lăng trụ đứng ABC. A′B C
′ ′ có mặt đáy ABC là tam giác vuông tại A có AB = 3, AC = 4 và
AA' = 2 . Tính cosin góc giữa hai vectơ AB ' và BC . Bài giải
Chọn hệ trục toa độ như hình vẽ. Khi đó ta có:
A(0;0;0) , B (3;0;0) , C (0;4;0) , B '(3;0;2) .
Ta có: AB ' = (3;0;2), BC = ( 3 − ;4;0) . Khi đó : ( − + + AB BC) AB '.BC 3.( 3) 0.4 2.0 9 13 cos ',
= = = − . 2 2 2 AB ' . BC 3 + 0 + 2 . ( 3 − )2 2 2 65 + 4 + 0 Ví DỤ 12
Cho hình lăng trụ đứng ABC.A' B'C ' có mặt đáy ABC là tam giác vuông tại B có AB =1, AC = 3
và A'B = 2 . Gọi M là trung điểm của AC . Tính khoảng cách từ M đến ( A' BC) . Bài giải
Chọn hệ trục toa độ như hình vẽ. Ta có: 2 2 2 2
AA' = A' B − AB = 2 −1 = 3 . 2 2 2
BC = AC − AB = 3 −1 = 2 . Khi đó ta có: 2 1
B (0;0;0) , A(0;1;0) , C ( 2 ;0;0) , A'(0;1; 3) , M ; ;0 . 2 2
Ta có: BA' = (0;1; 3),BC = ( 2;0;0) .
⇒ BA'∧ BC = (0; 6;− 2) .
Khi đó phương trình ( A'BC) là 3y − z = 0 . 3 2
Suy ra d (M ( A BC)) 3 , ' = = . 2 4 Ví DỤ 13
Cho hình lăng trụ tam giác đều ABC.A' B'C ' có cạnh bên 2a , góc tạo bởi A' B và mặt đáy là O 60 .
Gọi M là trung điểm BC .Tính cosin góc tạo bởi hai đường thẳng A'C và AM . Bài giải 2a 2a BC a
Ta có: AB = AC = BC = = ⇒ MC = = tan 60o . 3 2 3 AB 3 AM = = a . 2
Chọn hệ trục tọa độ như hình vẽ. Khi đó: a
M (0;0;0) , A(0;a;0) , C
;0;0 , A'(0;a;2a) . 3 4a Ta có : ' a A C ; a; 2a = − − ⇒ A'C = . 3 3
AM = (0;− a;0) ⇒ AM = a .
A′C.AM 3
Khi đó có cos( A′C, AM ) = = . A′C AM 4 Ví DỤ 14
Cho hình lăng trụ đứng ABC.A' B'C ' với đáy ABC là tam giác vuông tại C có AB = 8cm , 0
BAC = 60 , diện tích tam giác A'CC ' là 2
10cm . Tính tang của góc tạo bởi hai mặt phẳng (C AB ′ ) và ( ABC). Bài giải Ta có : sin 60o BC = ⇒ = sin 60o BC AB = 4 3 . AB 2 2
A'C ' = AC = AB − BC = 4 . 1 S 2 = S A ∆ 'CC ' ⇔ CC ' = = 5. ∆ CC A C A CC '. ' ' ' ' 2 A'C '
Chọn hệ trục toa độ như hình vẽ.
Khi đó ta có : C (0;0;0) , A(0;4;0), B(4 3;0;0) , C '(0;0;5).
Ta có : ( ABC) ≡ (Oxy) ⇒ Phương trình ( ABC) là z = 0.
Lại có C ' A = (0;4;− 5) , C 'B = (4 3;0;−5) .
⇒ C ' A ∧ C 'B = ( 20 − ;− 20 3;−16 3) = 4 − (5;5 3;4 3) . Suy ra (C A
′ B) có VTPT là n = (5;5 3;4 3) và (ABC) có VTPT là n′ = (0;0; )1 n n′ Khi đó
( C A′B) (ABC)) . 2 3 cos , = = . n n 37 1 5 3 Mà: 2 1+ tan α = ⇒ tan C A ′ B , ABC = . 2 ( ) ( )) cos α 6
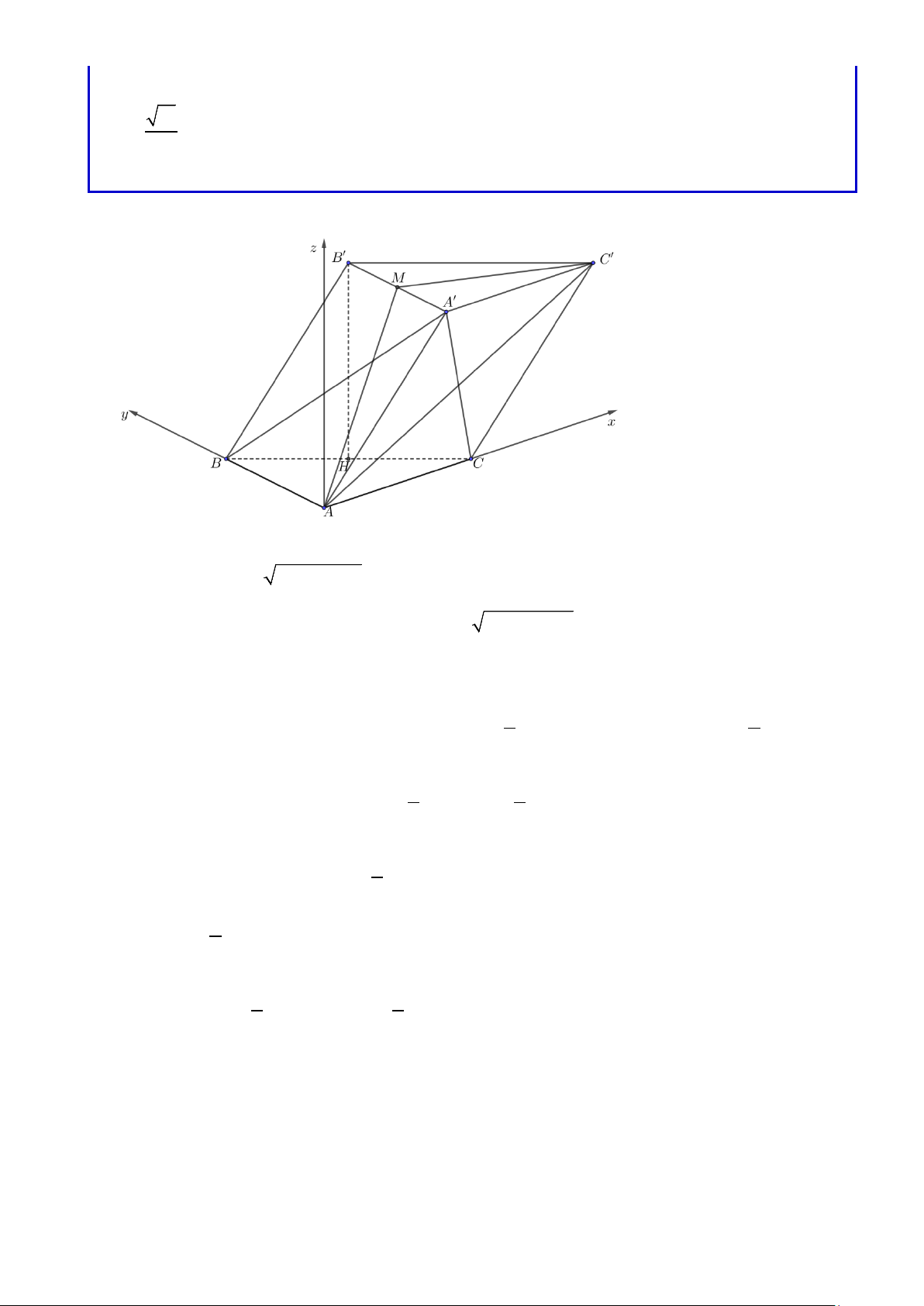
Loại 5. Lăng trụ đứng tứ giác Ví DỤ 15
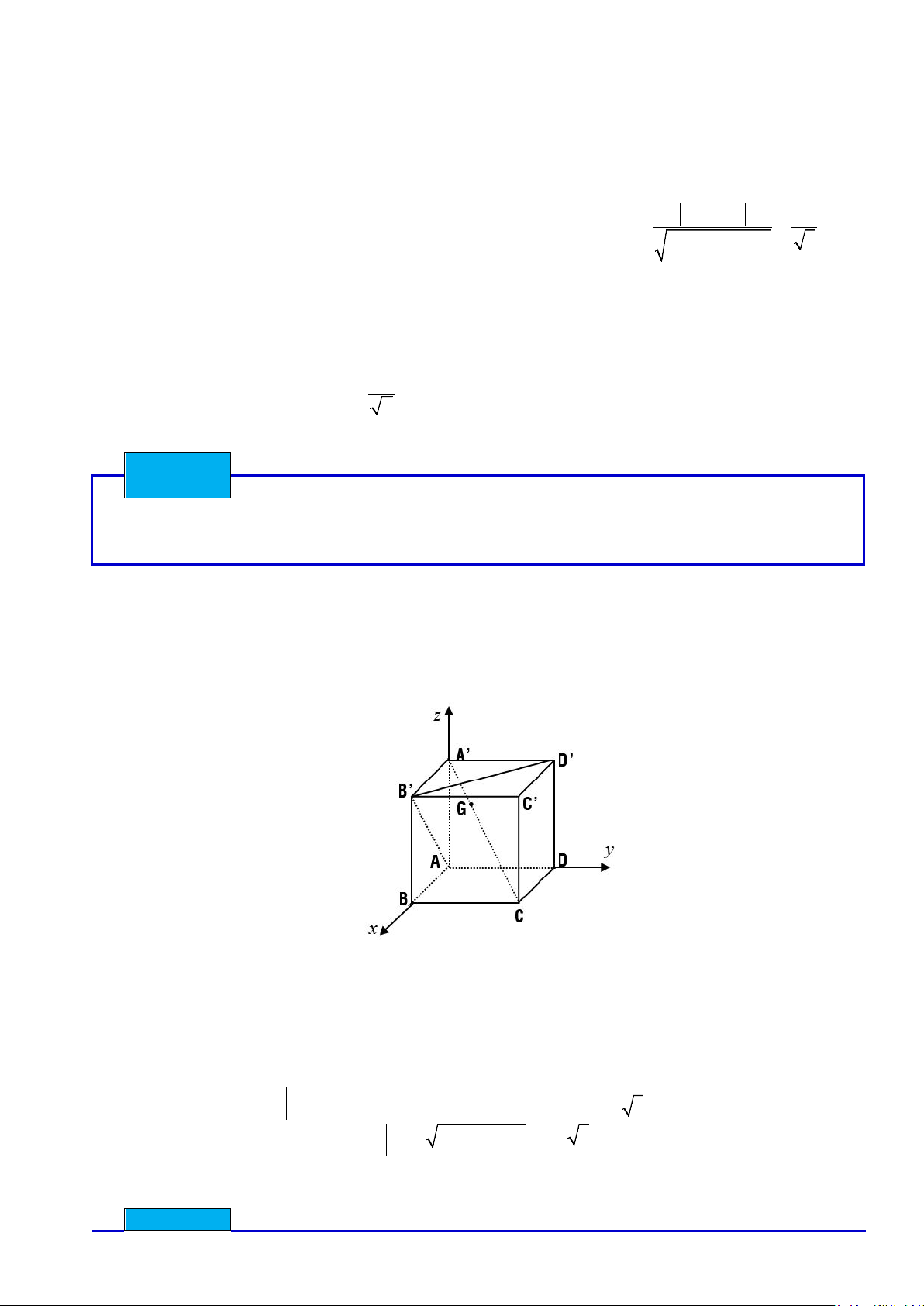
Cho hình lập phương ABC . D A′B C ′ D
′ ′ có cạnh bằng a .
a. Chứng minh rằng giao điểm của đường chéo A′C và mặt phẳng (AB D
′ )′ là trọng tâm của tam giác AB D ′ ′ .
b.Tìm khoảng cách giữa hai mặt phẳng (AB D ′ )′ và (C B ′ D)
c.Tìm cosin của góc tạo bởi hai mặt phẳng (DA′C) và (ABB A ′ )′
( Dựa SGK Hình 12, trang 112, Văn Như Cương chủ biên, NXBGD 2000 ) Bài giải
Chọn hệ trục toạ độ Đề các vuông góc Oxyz như sau : O ≡ ( A ) 0 ;0 ;0 ; A (′0;0;a) B(a ) 0;
0; ; B (′ ;a0;a) ; C( ; a a 0 ; ) ; C (′ ; a ; a a) ; D( ; 0 a ) 0
; ; D (′0;a;a).
a. Gọi G là trọng tâm của tam giác AB D ′ ′ . Đường thẳng
A′C nhận véc tơ chỉ phương là u =
− và qua A′ nên phương trình A C (1;1; 1) ' x = t đường
A'C là y = t (t ∈ ) . z = a − t
Véc tơ pháp tuyến của mặt phẳng (AB D ′ )′ là 2 2 2
n = AB ', AD ' = (−a ;−a ;a ) hay 1 n = (1;1; 1 − ) 1
Phương trình tổng quát của mặt phẳng (AB D
′ )′ x + y − z = 0
Gọi G = A′C ∩ (AB D
′ )′ . Toạ độ giao điểm G của đường thẳng A′C và mặt phẳng (AB D ′ )′ a x = t x = 3 y = t a a a 2a là nghiệm của hệ ⇔ y =
⇒ G ; ; (1)
z = a − t 3 3 3 3
x + y − z = 0 2a z = 3 x + A x + B xD a x = ' ' = G 3 3 y + A y + B yD a Mặt khác : y = ' ' = G (2) 3 3 z + A z + B zD a ' ' 2 z = = G 3 3
Từ (1), (2) ta có giao điểm G của đường chéo A'C và mặt phẳng (AB D
′ )′ là trọng tâm của tam giác AB D ′ ′ .
b. Tính d ((AB D ′ ), ′ (C B ′ D))
Véc tơ pháp tuyến của mặt phẳng (C B ′ D) là 2 2 2 n = C B
′ ,C′D = (a ;a ;−a ) hay 2 n = (1;1; 1 − ) . 2
Phương trình tổng quát của mặt phẳng (C B
′ D) là x + y − z − a = 0 .
Phương trình tổng quát của mặt phẳng (AB D
′ )′ là x + y − z = 0 . a + 0 − 0 ⇒ ( a AB D ′ ′) / / (C B
′ D) ⇒ d ((AB D ′ )′,(C BD ′
)) = d (B,(AB D ′ )′) = = . + + (− )2 2 2 3 1 1 1
c. Tính cos((DA′C),(ABB A ′ )′)
Oy ⊥ (ABB' A')
nên véc tơ pháp tuyến của (ABB' '
A ) là j = (0 ; 1 ; 0) . Vectơ pháp tuyến của ( ' DA C) là 2 2 n
= DA',DC = (0;a ;a ) hay . 3 n = (0;1;1) 3 ( DA C ABB A ) 1 cos ( ' ),( ' ') = . 2 Do đó ( DA C ABB A ) 0 ( ' ),( ' ') = 45 . Ví DỤ 16
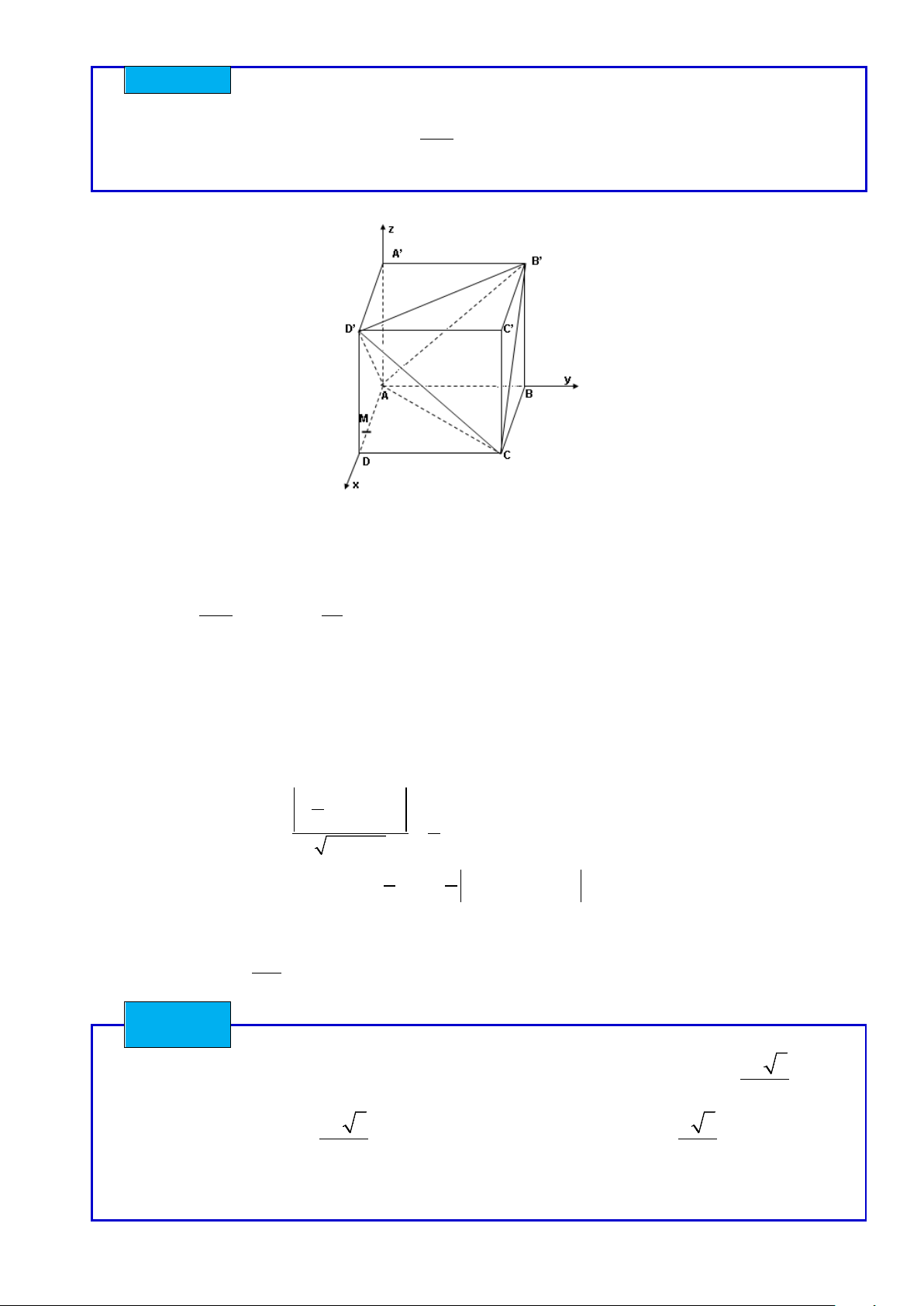
Cho hình lập phương ABC . D '
A B'C'D' có cạnh bằng a .
Chứng minh hai đường chéo B'D'và A'B của hai mặt bên là hai đường thẳng chéo nhau. Tìm
khoảng cách giữa hai đường thẳng chéo nhau B'D' và A'B . Bài giải
Chọn hệ trục toạ độ Đề các vuông góc Oxyz như sau : O ≡ ( A ) 0 ;0 ;0
, A (′0;0;a), B(a;0;0) , B (′ ;
a 0;a) , C(a;a ) 0 ; , C (′ ; a ;
a a) , D(0;a;0),
D (′0;a;a). Ta có B D ′ ′ = (− ; a ; a 0) , A′B = ( ;
a 0;−a) , BB′ = (0;0;a) nên
2 2 2 B D
′ ,′ A′B = (−a ;−a ;−a ) , 3 B D
′ ,′ A′B BB′ = −a ≠ 0
⇒ ba vectơ B D
′ ;′ A′B, BB′ không đồng phẳng. Hay B D
′ ′ và A′B chéo nhau. Khoảng
cách giữa hai đường là
′ ′ ′ ′ 3 3
[B D , A B].BB d (B D ′ ′ A′B) a a a 3 , = = = = . 4 4 4 2 [B D ′ ,′ A′B] a + a + a a 3 3 Ví DỤ 17
Cho hình hộp chữ nhật ABC . D A′B C ′ D
′ ′ có cạnh AB = a , AD = 2a và AA′ = a .
a. Gọi M là điểm nằm trong AD sao cho AM = 3. Tính khoảng cách từ M đến (AB C ′ ) . MD
b. Tính thể tích tứ diện (AB D ′ C ′ ) . Bài giải
a) Chọn hệ trục toạ độ Đề các vuông góc Oxyz như sau : (
A 0;0;0); A (′0;0;a); B( ; 0 a 0
; ); B (′0;a;a) C(2 ; a ; a 0) ; C (2 ′ ; a ; a a) ; D(2 ;0 a ;0); D (′2 ;
a 0;a) . Vì M là điểm nằm trong AD sao cho AM = 3 nên 3 ( a M ;0;0) . MD 2
Véc tơ pháp tuyến của mặt phẳng (AB C ′ ) 2 2 2 n
= AB ,′ AC = (−a ;2a ; 2 − a ) hay (AB'C) n = (1; 2 − ;2) (AB'C) .
Phương trình tổng quát của mặt phẳng (AB C
′ ) là x − 2y + 2z = 0.
Do đó khoảng cách từ M đến mặt phẳng (AB C ′ ) là: 3. a − 2.0 + 2.0 2 ( ,( ′ )) a d M AB C = = . 1+ 4 + 4 2
b) Theo công thức 1 1 V = = ′ ′ . ′ ′ V AB AD AC AB D C hop , . 6 6 Mà AD′ = (2 ;
a 0;a); AB′ = (0;a;a); AC = (2a;a;a). 3 2a ⇒ V = ′ ′ dvdt AB D C ( ) 3 . Ví DỤ 18 2a 5
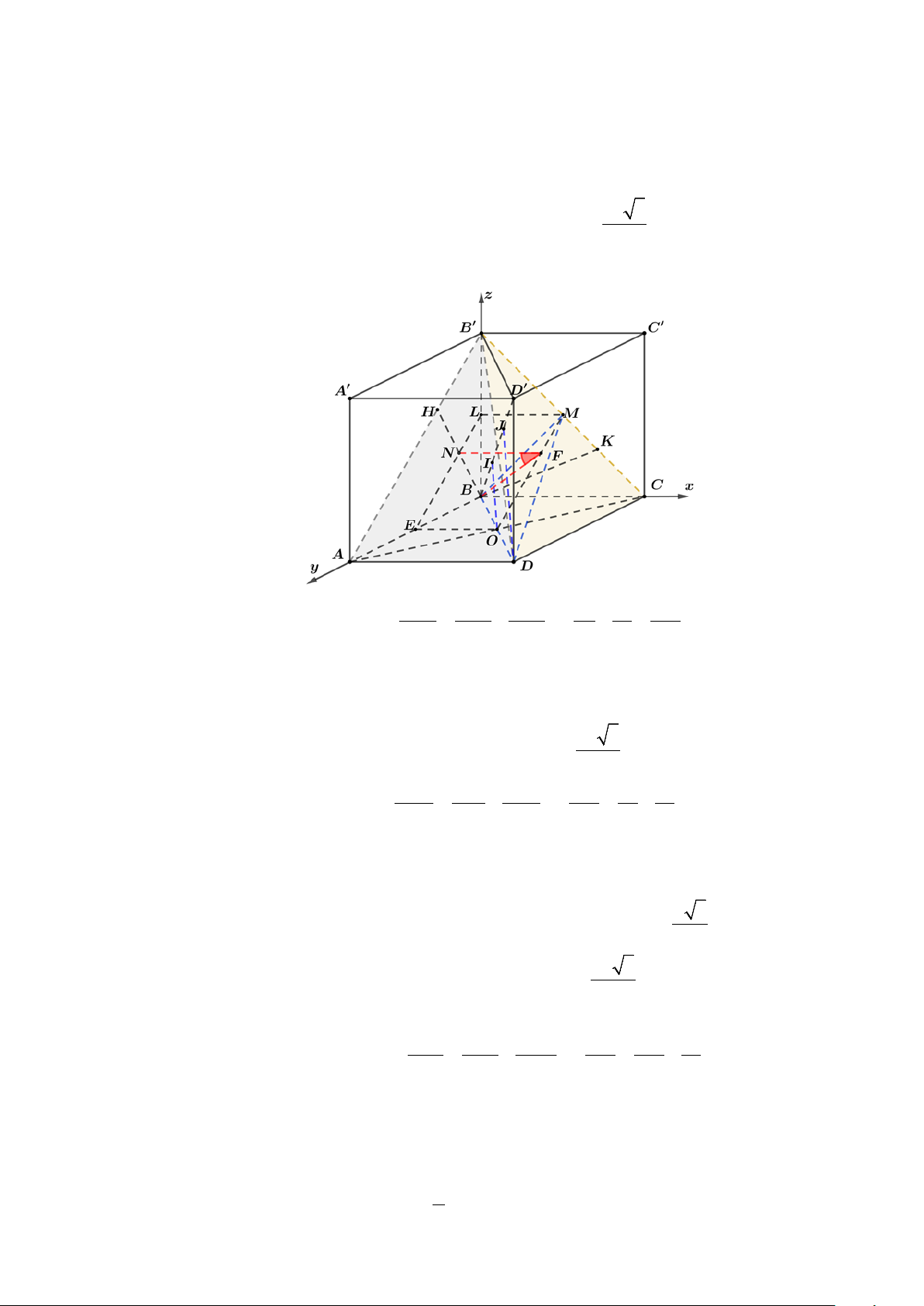
Cho hình hộp chữ nhật ABC . D ′ A ′ B C′ ′
D . Biết khoảng cách giữa AB và B C ′ bằng , khoảng 5 2a 5 a 3
cách giữa BC và A ′ B bằng , khoảng cách giữa . Gọi 5 AC và B ′ D bằng 3 M là trung điểm ′
B C . Tính tan của góc tạo bởi hai mặt phẳng ( BMD) và ( B A ′ D) . Lời giải
Đặt BA x, BC y, ′ = =
BB = z . Gọi O là tâm ABCD . Ta có AB //( ′
B DC) ⇒ d (AB, ′
B C) = d (AB,( ′
B DC)) = d (B,( ′ B DC)) .
Ta dễ dàng chứng minh được (B D ′ C) ⊥ (BB C ′ C
′ ) và cắt nhau theo giao tuyến ′ B C . a Kẻ BK ⊥ B C
′ ⇒ BK ⊥ (B D
′ C), hay d ( AB B C ′ ) 2 5 , = BK = . 5 Xét ′ 1 1 1 1 1 5
∆BB C vuông tại B , ta có = + ⇔ + = (1) . 2 2 ′2 2 2 2 BK BC BB y z 4a Lại có BC //( ′
B AD) ⇒ d (BC, A ′
B ) = d (BC,( ′
B AD)) = d (B,( ′ B AD)) .
Ta dễ dàng chứng minh được (B A ′ D) ⊥ (BB A
′ ′A) và cắt nhau theo giao tuyến A ′ B . Kẻ a
BH ⊥ AB′ ⇒ BH ⊥ (B A
′ D) , hay d (BC AB′) 2 5 , = BH = . 5 Xét 1 1 1 5 1 1 ∆B ′
B A vuông tại B , ta có = + ⇔ = + (2) . 2 2 2 2 2 2 BH BA B ′ B 4a x z
Từ (1) và (2) , suy ra x = y , hay ABCD là hình vuông.
Ta dễ dàng chứng minh AC ⊥ (B ′ B ′
D D) . Kẻ OI ⊥ B ′
D , suy ra AC ⊥ OI , hay OI là
đoạn vuông góc chung của AC và ′ BD , suy ra ( ′) 3 , = = a d AC BD OI . 3 Trong (B ′ B ′
D D) , kẻ DJ / /OI(J 2 3 ∈ BD) ⇒ = 2 = a DJ OI
( vì OI là đường trung 3 bình ∆B ′ DD ). Xét 1 1 1 3 1 1 ∆B ′
DD vuông tại D , ta có = + ⇔ = + (3) ′ . 2 2 2 2 2 2 DJ BD DD 4a 2x z
Giải (2),(3) ta được x = a, z = 2a .
Chọn hệ trục tọa độ Oxyz như hình vẽ với : B(0;0;0), B′(0;0;2), C (1;0;0) , A(0;1;0) , D(1;1;0) , 1
M là trung điểm B C
′ , suy ra M ;0;1 . 2 +) Ta có B A ′ = (0;1; 2 − ), B D ′ = (1;1; 2 − ) , B′ , A B D ′ = (0;− 2;− ) 1 . Suy ra mặt phẳng ( ′
B AD) có một véctơ pháp tuyến là n = (0;2; ) 1 . 1 1
+) Ta có BM = ;0;1 , BD = (1;1;0), BM , BD = 1; − 1; . 2 2
Suy ra mặt phẳng (BMD) có một véctơ pháp tuyến là n′ = ( 2; − 2; ) 1 .
Gọi α là góc tạo bởi hai mặt phẳng (BMD) và (B A ′ D), ta có: | . n n′ | 5 5 2 2 5 cosα = = = ⇒ sinα = ⇒ tanα = . | n | ⋅ n′ 5.3 3 3 5
DẠNG 2. GẮN HỆ TRỤC TỌA ĐỘ VÀO CÁC HÌNH ĐA DIỆN CÓ SẴN MÔ HÌNH TAM DIỆN VUÔNG
Dạng toán : Cho tứ diện ABCD có BCD là tam giác vuông tại C , AB ⊥ (BCD) . Cách dựng : A B D C
Ta dựng hệ trục tọa độ Oxyz sao cho C ≡ O, D∈Ox , B ∈Oy , Oz qua C và vuông góc với (BCD)
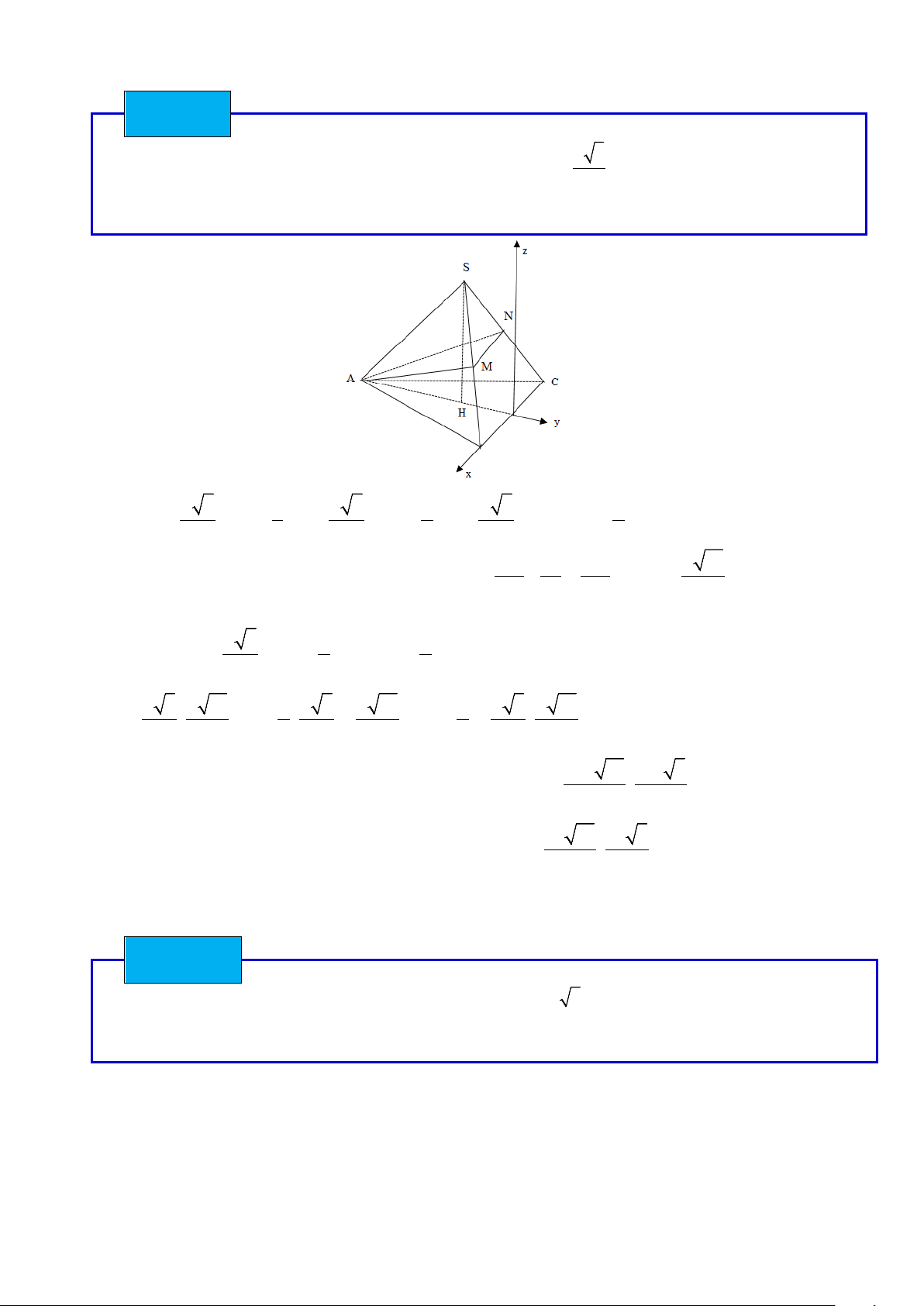
Loại 1. Tứ diện có một cạnh vuông góc với mặt đáy Ví DỤ 19
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và cạnh AB = 3 .a Cạnh bên
SA = a 6 và vuông góc với mặt phẳng đáy. Tính khoảng cách giữa hai đường thẳng chéo nhau AB và SC . Lời giải S A C B
Chọn hệ trục tọa độ sao cho: A(0; 3a; 0) , B(0; 0; 0) , C (3a; 0; 0), S (0; 3 ;a a 6) . Khi đó BA = (0; 3 ;
a 0), suy ra AB có một vectơ chỉ phương u = (0; 3a; 0)
SC = (3 ;a −3 ;a − a 6), suy ra SC có một vectơ chỉ phương v = (3 ;a −3 ;a − a 6) . Suy ra u v = ( 2 2 , 3
− a 6; 0; − 9a )
u, v.BC 3
Khi đó d ( AB SC) 9a 6 3a 10 ; = = = 2 u, v 3a 15 5 Ví DỤ 20
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và cạnh AB = 3a, BC = 4a . Tam giác
SAB vuông cân tại A và SA vuông góc với mặt phẳng đáy. Tính khoảng cách giữa hai đường thẳng
chéo nhau AC và SB . Lời giải S A C B
Ta có SA = AB = 3a (do tam giác SAB vuông cân tại A ).
Chọn hệ trục tọa độ sao cho: A(0; 3a; 0) , B(0; 0; 0) , C (4 ;
a 0; 0) , S (0; 3a; 3a) . Khi đó AC = (4 ; a −3 ;
a 0) , suy ra AC có một vectơ chỉ phương u = (4a; −3a; 0) BS = (0; 3 ;
a 3a), suy ra SB có một vectơ chỉ phương v = (0; 3a; 3a). Suy ra u v = ( 2 2 2 , 9
− a ; −12a ; 12a )
u, v.BA 3
Khi đó d ( AB SC) 36a 12a 41 ; = = = 2 u, v 3a 41 41 Ví DỤ 21
Cho hình chóp S.ABC có SA ⊥ ( ABC), đáy ABC là tam giác vuông tại B và cạnh AB = 3a,
BC = 4a . Góc tạo bởi SC và ( ABC) là 0
60 . Tính khoảng cách giữa hai đường thẳng chéo nhau AM
và SC với M là trung điểm BC . Lời giải S A C M B Ta có 2 2
AC = AB + BC = (3a)2 + (4a)2 = 5a
Mà AC là hình chiếu của SC và ( ABC) nên (SC ( ABC)) (SC AC) , , SCA 60° = = = (do
tam giác SAC vuông tại A ). Khi đó SA AC.tan 60° = = 5a 3 .
Chọn hệ trục tọa độ sao cho: A(0; 3a; 0) , B(0; 0; 0) , C (4 ;
a 0; 0) , S (0; 3 ; a 5a 3) .
M là trung điểm BC nên M (2a; 0; 0) Khi đó
AM = (2 ;a −3 ;a 0), suy ra AM có một vectơ chỉ phương u = (2 ;a −3 ;a 0)
SC = (4a; −3a; −5a 3), suy ra SB có một vectơ chỉ phương v = (4 ;a −3a; −5a 3) . Suy ra u v = ( 2 2 2 ,
15 3a ; 10 3a ; 6a )
u, v.AC 3
Khi đó d ( AB SC) 30 3a 30 3 ; = = = a . 2 u, v a 1011 1011 Ví DỤ 22
Cho hình chóp S.ABC có SC ⊥ ( ABC) . Tam giác ABC vuông tại A , các điểm M , N lần lượt thuộc ,
SA BC sao cho AM = CN. Biết SC = CA = AB = a 2 . Tìm giá trị nhỏ nhất của đoạn MN ?
Chọn hệ trục tọa độ như hình vẽ, ta có : A( ; a ;0 a ), B(2 ;0
a ;0),C (0;0;0), S (0;0;a 2).
x = a − t
Phương trình đường thẳng
SA: y = a − t z = 2t
Gọi M (a −t ;a −t ; 2t ∈S ,
A t ∈ 0;a .Ta có: AM = ( t − ; t
− ; 2t ⇒ AM = 2t . 0 0 0 ) 0 0 0 ) 0 [ ] 0
Vì N ∈ BC : NC = AM nên
N (2t ;0;0) ⇒ MN = (3t − a;t − a;− 2t ) 2 2
⇒ MN =12t −8at + 2a ,t ∈ 0;a . 0 0 0 0 0 0 0 [ ] a 6
Suy ra giá trị nhỏ nhất của MN = khi 2a 3 t = . 0 3 Ví DỤ 23
Cho tứ diện ABCD có BC = 3, CD = 4, = =
ABC BCD ADC = 90° ,
(AD,BC) =60°. Tính Cosin của
góc giữa hai mặt phẳng ( ABC) và ( ACD)
Gọi H là chân đường cao của tứ diện ABCD . BC ⊥ AB Ta có:
⇒ BC ⊥ HB .(1) BC ⊥ AH C D ⊥ AD Lại có:
⇒ CD ⊥ HD .(2) C D ⊥ AH Mà BCD = 90° .
Từ đây ta suy ra HBCD là hình chữ nhật. Mặt khác: (AD BC) = (AD HD) = , ,
ADH = 60°. Suy ra: AH = HD tan 60° = 3 3 .
Chọn hệ trục Oxyz ≡ H.DBA như hình vẽ.
Ta có: H (0;0;0) , A(0;0;3 3), B(0;4;0) , D(3;0;0),C(3;4;0)
AD = (3;−0;−3 3) , AC = (3;4;−3 3), AB = (0;4;−3 3) . Gọi
n , n lần lượt là một véc tơ pháp tuyến của ( ABC) và ( ABD). 1 2
Suy ra: n = AB, AC = 0;− 9 3;−12 ; n = AD, AC = 12 3;0;12 . 2 ( ) 1 ( ) n .n 0.12 3 − 9 3.0 −12.12 2 43
Vậy cos(( ABC),( ADC)) 1 2 = = = n . n 2 2 2 2 2 2 43 1 2 0 + ( 9 − 3) +( 12 − ) . (12 3) + 0 +(12)
Loại 2. Chóp tam giác đều Ví DỤ 24 a 3
Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên bằng
. Gọi M , N lần lượt là trung điểm 2
của SB, SC . Chứng minh rẳng: ( AMN ) ⊥ (SBC). a 3 1 a 3 2 a 3 a Ta có OA = ,OH = OA = , AH = OA = ,OB = OC = . 2 3 6 3 3 2 2 2 2 a a a a
Tam giác SAH vuông tại H nên 2 2 2 3 5 15
SH = SA − AH = − = ⇒ SH = . 4 3 12 6
Chọn hệ trục như hình vẽ. Ta có: ( ) a 3 0;0;0 , 0; ;0, a
;0;0, a O A B C ;0;0 − − 2 2 2 a 3 a 15
a a 3 a 15 a a 3 a 15 S 0;− , , M ; ,− , N − ;− , . 6 6 4 12 12 4 12 12 2 2
−a 15 5a 3
Mặt phẳng ( AMN ) có vec tơ pháp tuyến n = AM , AN = 0; ; 1 . 24 24 2 2 a 15 a 3
Mặt phẳng (SBC) có vec tơ pháp tuyến n = SB,SC = 0; ; 2 . 6 6 Khi đó
n .n = 0 ⇒ n ⊥ n . Vậy ( AMN ) ⊥ (SBC) . 1 2 1 2 Ví DỤ 25
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a 3 , mặt bên SAB là tam giác cân với
ASB =120° và nằm trong mặt phẳng vuông góc với đáy. Gọi M là trung điểm của SC
và N là trung điểm của MC . Tính khoảng cách giữa hai đường thẳng AM , BN . z S M N C A y H B x
Gọi H là trung điểm AB .
Vì (SAB) ⊥ ( ABC) nên SH ⊥ ( ABC) .
Chọn hệ trục tọa độ Oxyz , với O ≡ H , HB ≡ Ox , HC ≡ Oy , HS ≡ Oz . Ta có : AH 2 2
HC = AC − AH = 3a ; SH = = a . tan ASH 3a a 9a a
H (0;0;0) , S (0;0;a) , A(−a 3;0;0), B(a 3;0;0), C (0;3a;0) , M 0; ; , N 0; ; 2 2 4 4 3 2 2 2 3; a ; a AM a ⇒ = 9a a 3a 3 3a 15 3a , BN = − a 3; ;
, AM , BN = − ;− ; . 2 2 4 4 4 4 4 3
3 3a
AM , BN .AB 2 2 237a
Khoảng cách giữa AN, BN là : d ( AM , BN ) = = = . 2 AM , BN 711a 79 4 Ví DỤ 26
Cho hình chóp tam giác đều S.ABC có độ dài cạnh đáy là a . Gọi M , N lần lượt là trung điểm của
cạnh SB và SC . Tính theo a diện tích tam giác AMN biết mặt phẳng ( AMN ) vuông góc với mặt
phẳng (SBC) . Lời giải
Gọi O là hình chiếu của S trên ( ABC), ta suy ra O là trọng tâm tam giác ABC . Gọi I là trung a 3 a 3 a 3
điểm của BC , ta có AI = . Suy ra OA = ,OI = 2 3 6
Ta chọn hệ trục tọa độ Oxyz như hình vẽ với O trùng với gốc tọa độ. Đặt SO = h , khi đó ta được a 3 a 3
O(0;0;0) , S (0;0;h) , A ;0;0 , I − ;0;0 . 3 6 a 3 a a 3 a a 3 a h a 3 a h Suy ra B − ; ;0 , C − ;− ;0 , M − ; ; , N − ;− ; . 6 2 6 2 12 4 2 12 4 2 Ta có
5a 3 a h 5a 3 a h a 3 a
a 3 a AM = − ; ; , AN = − ;− ; , SB = −
; ;−h , SC = − ;− ;−h . 12 4 2 12 4 2 6 2 6 2 2 ah 5a 3 2 a 3 Suy ra = = ( n AM AN = n SB,SC = − ; ah 0; AMN ) , ;0; và . 4 24 (SBC) 6
(AMN) ⊥ (SBC) ⇔ 2 2 4 2 a h 15a 2 5a ( n ). ( n ) = 0 ⇔ − + = 0 ⇔ h = AMN SBC 4 144 12 2 1 a 10 2 ⇒ S = = a 10 S = ∆ AM AN AMN , . Vậy . 2 16 A ∆ MN 16 Ví DỤ 27
Cho hình chóp tam giác đều S.ABC có SA = 2a , AB = a . Gọi M là trung điểm cạnh BC . Tính
khoảng cách từ M tới mặt phẳng (SAB) . Lời giải
Gọi O là hình chiếu của S trên ( ABC), ta suy ra O là trọng tâm tam giác ABC . a 3 a 3 a 3
Do M là trung điểm BC nên AM = . Suy ra OA = và OM = . 2 3 6 2 Xét tam giác a a
SOA vuông tại O , ta có 2 2 2 33
SO = SA − OA = 4a − = . 3 3
Ta chọn hệ trục tọa độ Oxyz như hình vẽ với O trùng với gốc tọa độ, khi đó ta được: a 3 a 33 a 3 O (0;0;0) , A ;0;0 , S 0; 0; , M − ;0;0 . 3 3 6 a 3 a a 3 a Suy ra B − ; ;0 , C − ;− ;0 6 2 6 2 a 3
a 33 a 3 a a 33 Ta có SA = ;0;− , SB = − ; ;− 3 3 6 2 3 2 2 2
a 33 a 11 a 3 Suy ra = ( n SA SB = . SAB) ; ; ; 6 2 6 33 11 3 a 11
Phương trình măt phẳng (SAB) là x + y + z − = 0 . 6 2 6 6 33 −a 3 a 11 ⋅ − 6 6 6 a 165
Suy ra d (M ,(SAB)) = = . 33 11 3 30 + + 36 4 36 Ví DỤ 28
Cho hình chóp tam giác đều .
A BCD có AB = a 3 , BC = a . Gọi M là trung điểm cạnh CD . Tính
khoảng cách giữa hai đường thẳng BM và AD . Lời giải
Gọi O là hình chiếu của A trên (BCD) , ta suy ra O là trọng tâm tam giác BCD . a 3 a 3 a 3
Do M là trung điểm CD nên BM = . Suy ra OB = và OM = . 2 3 6 2 Xét tam giác a a
AOB vuông tại O , ta có 2 2 2 2 6
AO = AB − OB = 3a − = . 3 3
Ta chọn hệ trục tọa độ Oxyz như hình vẽ với O trùng với gốc tọa độ, khi đó ta được: a 3 2a 6 a 3
O (0;0;0) , B ;0;0 , A0; 0; , M − ;0;0 . 3 3 6 a 3 a a 3 a Suy ra D − ; ;0 , C − ;− ;0 6 2 6 2 a 3
a 3 a 2a 6 a 3 2a 6 Ta có BM = − ;0;0, AD = − ; ;− , AB = ;0;− 2 6 2 3 3 3 2 2 a a Suy ra 2 3 35
BM , AD = 0;−a 2;−
⇒ BM , AD = 4 4 3
a 2
BM , AD.AB 2a 70
Khi đó d (BM AD) 2 , = = = . 2 BM, AD a 35 35 4
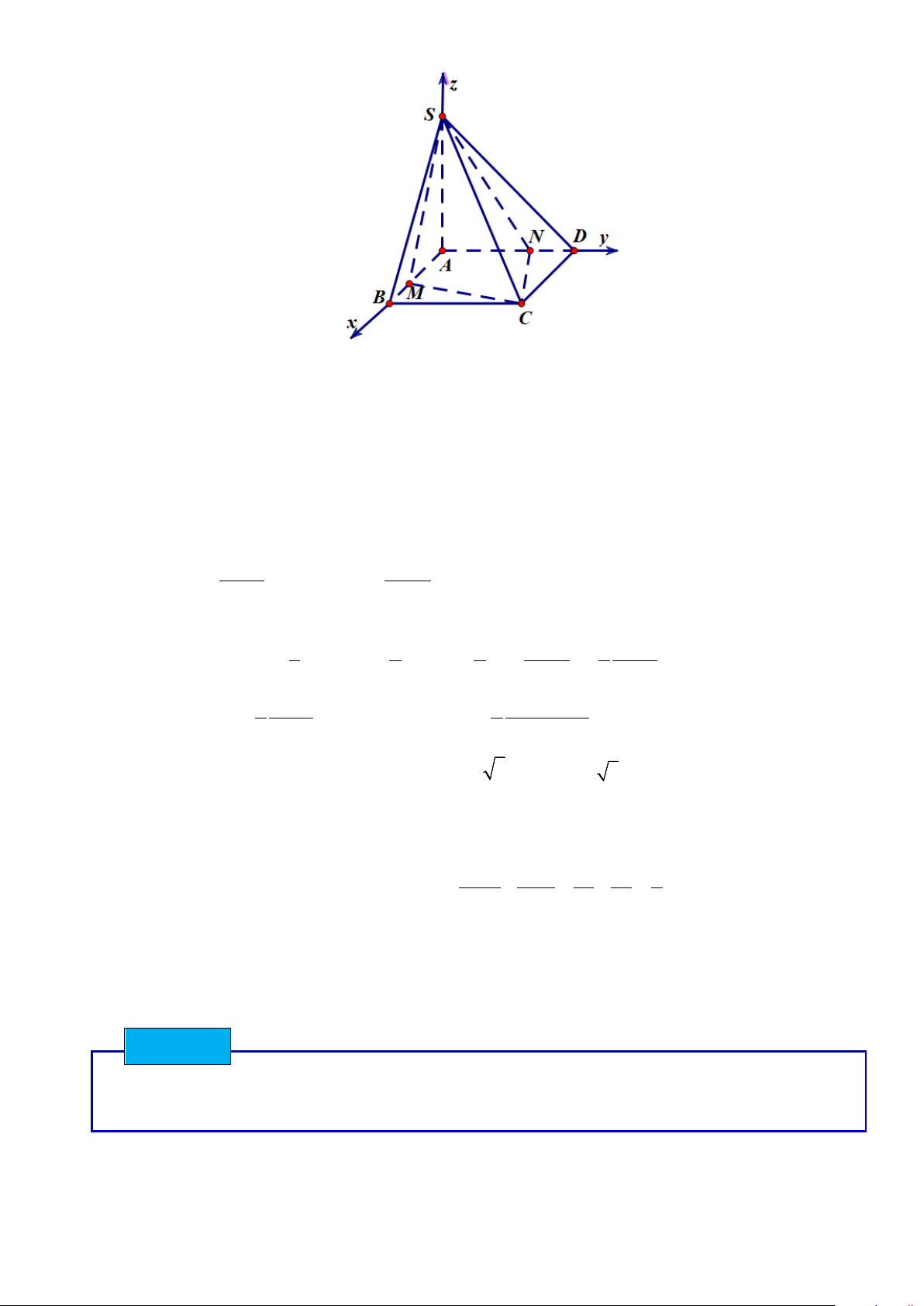
Loại 3. Chóp tứ giác đều hoặc chóp có đáy là hình thoi, đường cao SO. Ví DỤ 29
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a , Gọi N, M lần lượt là trung điểm của
DC và BC , K là điểm trên cạnh BC sao cho BK = 4KM , tính theo a khoảng cách hai đường thẳng
SK và BN . Lời giải S A D N O B C K M 2 2 a 2
SO = SA −OA = 2
Chọn hệ trục tọa độ Oxyz sao cho OM ≡ Ox , ON ≡ Oy ,OS ≡ Oz a 2 a a a a a Khi đó S 0;0; ; K ;− ;0 ; B ;− ;0 ; N 0; ;0 2 2 10 2 2 2
a a a 2 a 2 2 2
a 2 a 2 9a
Suy ra SK = ;− ;− ; BN −
;a;0 nên n = SK,BN = ; ; 2 10 2 2 2 4 20
a a 2 SN = 0; ;− 2 2 2 . n SN a ( , ) 10 2 2a
d SK BN = = = . SK, BN 331 331 20 Ví DỤ 30
Cho hình chóp tứ giác đều S.ABCD có SA = 2a ; AB = a . Gọi N, M lần lượt là trung điểm của DC
và BC , tính cosin góc giữa hai đường thẳng SM và MN . Lời giải S A D N O B K M C 2 2 a 14
SO = SA − OA = 2
Chọn hệ trục tọa độ Oxyz sao cho OM ≡ Ox , ON ≡ Oy ,OS ≡ Oz a 14 a a Khi đó S 0;0;
; M ;0;0 ; N 0; ;0 2 2 2 a
a 14 a a Suy ra SM = ;0;− ; MN − ; ;0 2 2 2 2 SM.MN (SM MN) 30 cos ,
= = SM . MN 30 Ví DỤ 31
Cho hình chóp tứ giác đều S.ABCD có AB = a . Tính cosin của góc giữa hai mặt phẳng (SCD) và
(SBC) biết góc giữa cạnh bên và mặt đáy bằng o 60 . S A α B D O C Lời giải
Góc giữa SB và mặt đáy là góc 0 SBO = 60 a 6 SO = tan 60.OB = 2
Chọn hệ trục tọa độ Oxyz sao cho OC ≡ Ox , OB ≡ Oy ,OS ≡ Oz . a 6
a 2 a 2 a 2 Khi đó S 0;0; ; B0; ;0 ;C ;0;0 ; D0;− ;0 2 2 2 2 2 2 2 − 3a 3a a
Suy ra vectơ pháp tuyến của mặt phẳng (SBC)là n = SB,SC = ;− ;− 2 2 2 2 2 2 3a 3a a
Vectơ pháp tuyến của mặt phẳng (SDC) là a = SD,SC = ;− ; 2 2 2 . n a 1
Do đó cosin góc giữa hai mặt phẳng trên là cosα = = . n . a 7
Loại 4. Hình chóp có đáy là hình vuông (chữ nhật) và mặt bên vuông góc với đáy. Ví DỤ 32
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a , SA = a; SB = a 3 và mặt phẳng
(SAB) vuông góc với mặt phẳng đáy. Gọi M,N lần lượt là trung điểm của các cạnh AB,BC . Tính
theo a thể tích của khối chóp S.BMDN và tính cosin của góc giữa hai đường thẳng SM , DN . Lời giải
Gọi H là hình chiếu của S lên AB ⇒ SH ⊥ ( ABCD) . 2 SA a a Ta có: 2 2 2 3
SA + SB = AB ⇒ SA ⊥ SB ⇒ AH = = , SH = . AB 2 2
Chọn hệ trục tọa độ như hình vẽ, ta có tọa độ các điểm: z S M A D y B H N C x A( ) B( a
) D( a ) C ( a a ) a a a 3
0;0;0 , 2 ;0;0 , 0;2 ;0 , 2 ;2 ;0 , H ;0;0,S ;0;
, M (a;0;0), N (2a;a;0) . 2 2 2 Ta có 1 2 S = = = 2 2 2 ⇒ S
= a − a = a . BNDM 4 2 2 ∆ S∆ a a a ADM CDN .2 2 3 1 1 a 3 a 3
Thể tích khối chóp S.BMDN : 2 V = SH.S = a = BMDN . .2 . 3 3 2 3 a a 3 Vì SM = ;0;−
, DN = (2a;−a;0) 2
⇒ SM.DN = a . 2 2 2 SM.DN a 5
Vậy cos(SM , DN ) = = = .
DM.DN a.a 5 5 Ví DỤ 33
Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều cạnh a và nằm
trong mặt phẳng vuông góc với ( ABCD) . Tính khoảng cách từ A đến (SCD) theo a . Lời giải z S A D y O B x C
Gọi O là trung điểm của AB . Ta có : (
SAB) ∩( ABCD) = AB (
SAB) ⊥ ( ABCD)
⇒ SO ⊥ ( ABCD) . SO ⊥ AB
Không mất tính tổng quát, đặt a =1.
Chọn hệ trục (Oxyz) như hình vẽ. 3 1 1 1 Ta có : S 0;0; , A −
;0;0 , C ;1;0 , D− ;1;0 . 2 2 2 2 1 3
Mặt phẳng (SCD) đi qua điểm C ;1;0 và có một vectơ pháp tuyến n = SC ,SD = 0; ;1 2 2 3 nên có phương trình :
( y − )1+ z = 0 ⇔ + − = . 2 3y 2z 3 0 −
Khoảng cách từ A đến (SCD) là: d ( A (SCD)) 3 21 , = = . 3+ 4 7 a
Vậy d ( A (SCD)) 21 , = . 7 Ví DỤ 34
Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều cạnh a và
nằm trong mặt phẳng vuông góc với ( ABCD) . Tính côsin của góc tạo bởi hai mặt phẳng (SAB) và (SCD). Lời giải z S A D y O B x C
Gọi O là trung điểm của AB . Ta có : (
SAB) ∩( ABCD) = AB (
SAB) ⊥ ( ABCD)
⇒ SO ⊥ ( ABCD) . SO ⊥ AB
Không mất tính tổng quát, đặt a =1.
Chọn hệ trục (Oxyz) như hình vẽ. 3 1 1 1 1 Ta có : S 0;0; , A −
;0;0 , B ;0;0 , C ;1;0 , D− ;1;0 . 2 2 2 2 2
Mặt phẳng (SAB) có phương trình y = 0 ⇒ j = (0;1;0) . 3
Mặt phẳng (SCD) có một vectơ pháp tuyến n = SC , SD = 0; ;1 2 j ⋅n
Cosin của góc tạo bởi hai mặt phẳng (SAB) và (SCD) là : ((SAB) (SCD)) 21 cos , = = . j ⋅ n 7 Ví DỤ 35
Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều cạnh a và
nằm trong mặt phẳng vuông góc với ( ABCD) . Tính khoảng cách giữa hai đường thẳng AD và SC theo a . Lời giải z S A D y O B x C
Gọi O là trung điểm của AB . Ta có : (
SAB) ∩( ABCD) = AB (
SAB) ⊥ ( ABCD)
⇒ SO ⊥ ( ABCD) . SO ⊥ AB
Không mất tính tổng quát, đặt a =1.
Chọn hệ trục (Oxyz) như hình vẽ. 3 1 1 1 Ta có : S 0;0; , A −
;0;0 , C ;1;0 , D− ;1;0 . 2 2 2 2
Khoảng cách giữa hai đường thẳng AD và SC là:
AD, SC ⋅ AC d ( AD SC) 3 , = = . AD, SC 2 a Vậy d ( AD SC) 3 , = . 2
Loại 5. Lăng trụ xiên. Ví DỤ 36 Cho lăng trụ ABC . D A B C D có đáy A 1 1 1 1
ABCD là hình vuông cạnh a . Hình chiếu vuông góc của 1
lên ( ABCD) trùng với giao điểm của AC và BD. Tính khoảng cách từ điểm B đến mặt phẳng 1 ( A BD . 1 )
Chọn hệ trục toạ độ sao cho tâm O là gốc toạ độ , OA là trục Ox, OB là trục Oy, OA1 là trục Oz a 2 ⇒ A ;0;0 2
Vì mp( A BD ≡ mp(Oy;Oz) ≡ mp(Oyz) nên mp( A BD có phương trình: x = 0 1 ) 1 ) Khi đó : a 2 a 2
d(B ;(A BD)) = d( ; A (A BD)) = = 1 1 1 2 2 Ví DỤ 37
Cho hình lăng trụ ABC.A′B C
′ ′ có tất cả các cạnh bằng a và hình chiếu vuông góc của A′ trên mặt
phẳng ( ABC) trùng với trung điểm H của BC . Tính khoảng cách h giữa 2 đường thẳng AA′ và BC .
Ta có : d(AA';BC) = d(AA';(BCC'B')) = d( ;
A (BCC'B')
Chọn hệ trục sao cho H (0;0;0) như hình vẽ Khi đó : a 3 a a a ( A
;0;0) , B(0;− ;0) , C(0; ;0) , A'(0;0; ) 2 2 2 2
a 3 a
⇒ BC = (0;a;0), BB' = AA' = − ;0; 2 2 2 2 2
VTPT của mp(BCC’B’) : a a 3 = , ' = ;0; a n BC BB = (1;0; 3) 2 2 2
⇒ Phương trình mp(BCC’B’) : x + 3z = 0 a 3 Vậy 2 a 3 d(AA';BC) = d( ;
A (BCC 'B') = = 2 4 Ví DỤ 38
Cho hình lăng trụ ABC.A′B C
′ ′ có A .′ABC là tứ diện đều cạnh a . Gọi M , N lần lượt là trung
điểm của AA′ và BB′ . Tính tan của góc giữa hai mặt phẳng ( ABC) và (CMN ) .
Gọi O là trung điểm của AB . Gắn hệ trục tọa độ sao cho O(0;0;0)
như hình và không mất tính tổng quát ta chọn a =1, khi đó ta có: 1 A ;0;0 1 3 3 , B− ;0;0 , C 0; ;0 , H 0; ;0 2 2 2 6 6 A′H = 3 6 ⇒ A′0; ; 3 6 3 3 6
Ta có AB = A′B′ ⇒ B′ 1; − ;
. Dễ thấy ( ABC) có vtpt n = 0;0;1 1 ( ). 6 3 1 3 6 3 − 3 6
M là trung điểm AA′ ⇒ M ; ; , ⇒ N ; ; 4 12 6
N là trung điểm BB′ 4 12 6 − MN = ( 1 − ;0;0) 1 5 3 6 , CM = ; ; 4 12 6 6 5 3 3
⇒ (CMN ) có vtpt n = 0; ; = (0;2 2;5) 2 6 12 12 5 1 2 2 cosϕ = ⇒ tanϕ = −1 = 33 2 cos ϕ 5 Ví DỤ 39
Cho hình lăng trụ tam giác ABC.A′B C
′ ′ có đáy là tam giác ABC vuông tại A , AB = 3 , AC = 4 , 61 AA′ = . Hình chiếu của là trung điểm cạnh 2
B′ lên mặt phẳng ( ABC)
BC , M là trung điểm cạnh
A′B′ . Tính cosin của góc tạo bởi mặt phẳng ( AMC′) và mặt phẳng ( A′BC)
Gọi H là trung điểm BC . Ta có: 2 2
BC = AB + AC = 5 Xét tam giác B B
′ H vuông tại H : 2 2 B H
′ = BB′ − BH = 3 .
Chọn hệ trục tọa độ Oxyz có A trùng với O như hình vẽ 3 3
Với A(0;0;0) , B(0;3;0) ,C (4;0;0) ⇒ H 2; ;0 là trung điểm ⇒ B ′2; ;3 2 BC 2
3 3
Do BB′ = AA′ = CC′ ⇒ A ′ 2;− ;3 ;C ′6;− ;3 ⇒ M (2;0;3) 2 2 AM = (2;0;3) 3
; AC ′= 6;−
;3 nên vectơ pháp tuyến (MAC′) là n
= AM , AC′ 2 (MAC′) 9 ;12; 3 = − 2 9 A B 2; ; 3 ′ = − − 3 ; A′C = 2; ; 3
− nên vectơ pháp tuyến ′ là n 2 ( A BC) 2 (A′BC)
= A′B, A′C = ( 9; − 1 − 2; 1 − 2)
Gọi ϕ là góc tạo bởi mặt phẳng ( AMC′) và mặt phẳng( A′BC) . 9 n n .( 9 − ) +12.( 12 − ) − 3.( 12 − ) MAC . ( ) (A BC) 33 cosϕ ′ ′ = 2 = = . n 2 3157 ′ n MAC . ( ) (A′BC) 9 2 +12 + ( 3 − )2 . ( 9 − )2 + ( 12 − )2 + ( 12 − )2 2