Rút gọn biểu thức đại số và các bài toán liên quan

Bài toán rút gọn biểu thức đại số và các bài toán liên quan là dạng câu hỏi không thể thiếu trong các đề thi tuyển sinh vào lớp 10 môn Toán, đây là bài toán không khó, học sinh có thể làm tốt bài toán này nếu nắm vững các công thức biến đổi. Mời bạn đọc đón xem.

20 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 9

Môn: Toán 9

Thông tin:

32 trang 3 tháng trước

Tác giả:

Profile Hà Việt Anh
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 1
RÚT GỌN BIỂU THỨC ĐẠI SỐ
VÀ CÁC BÀI TOÁN LIÊN QUAN
A-LÝ THUYẾT
1. Kiến thức 6, 7, 8 quan trọng cần nhớ
a. Tính chất về phân số ( phân thức):
.
(
0, 0)
.
A
M A
M B
B
M B
b. Những hằng đẳng thức đáng nhớ
(A + B)
2
= A
2
+ 2AB + B
2
(A - B)
2
= A
2
- 2AB + B
2
A
2
- B
2
= (A - B)(A + B)
(A + B)
3
= A
3
+ 3A
2
B + 3AB
2
+ B
3
A - B)
3
= A
3
- 3A
2
B + 3AB
2
- B
3
A
3
+ B
3
= (A + B)(A
2
- AB + B
2
)
A
3
- B
3
= (A - B)(A
2
+ AB + B
2
)
2. Các kiến thức về căn bậc hai
Nếu a ≥ 0, x ≥ 0,
a
= x  x
2
= a
Để
A
có nghĩa
0
A
2
A A
.AB
A B
( với
0; 0)
A B
A A
B
B
( với
A
B
2
A
B A B
( với
0)
B
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 2
2
A
B A B
( với
0; 0)
A B
2
A B A B
( với
0; 0)
A B
A
AB
B B
( với
0
; 0)
AB
B
A A B
B
B
( với
0
)
B
2
( )C C A B
A B
A B
( với
2
0; A B )
A
( )C C A B
A B
A B
( với
0
; 0
A
B
)
v
à
A
B
3. CÁC DẠNG BÀI TẬP VỀ RÚT GỌN BIỂU THỨC ĐẠI SỐ VÀ CÁC BÀI TOÁN CÓ
LIÊN QUAN
Xét biểu thức A với biến số x
Dạng 1. Rút gọn biểu thức
- Ngoài việc rèn kỹ năng thực hiện các phép tính trong bài toán rút gọn. Học sinh hay quên
hoặc thiếu điều kiện xác định của biến x ( ĐKXĐ gồm điều kiện để các căn thức bậc hai có
nghĩa, các mẫu thức khác 0 và biểu thức chia (nếu có) khác 0)
Dạng 2. Tính giá trị của biểu thức A khi
x
= m
( với m là số hoặc biểu thức chứa x)
- Nếu m là biểu thức chứa căn
x m
( bằng số), trước tiên phải rút gọn; nếu m là biểu thức
có dạng căn trong căn thường đưa về hằng đẳng thức để rút gọn; nếu m là biểu thức ta
phải đi giải phương trình tìm x.
- Trước khi tính giá trị của biểu thức A, học sinh thường quên xét xem m có thỏa mãn
ĐKXĐ hay không rồi mới được thay vào biểu thức dã rút gọn để tính.
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 3
Ví dụ minh họa : Cho
1
x
A
x
, điều kiện
0
, 1.
x
x
a) Tính giá trị của biểu thức
A
khi
9.
x
b) Tính giá trị của biểu thức
A
khi
3
2 2.
x
c) Tính giá trị của biểu thức
A
biết x thỏa mãn phương trình
2
5
4 0
x
x
.
Hướng dẫn giải
a) Có
3
3
9 3
3 1 2
x x A
b) Có
2
3 2 2 2 1
x
2
2 1 2 1 2 1
x
2 1 2 2
2
2
A
c) Có
2
1
5 4 0
4
x
x x
x
. Kết hợp điều kiên:
0, 1.
x x
1x
(loại) và
4
x
(thỏa mãn)
Với
4
x
2
2
2
2
1
x
A
.
Dạng 3. Tìm giá trị của biến x để
A
k
( với k là hằng số hoặc là biểu thức chứa x)
- Thực chất đây là việc giải phương trình.
- Học sinh thường quên khi tìm được giá trị của x không xét xem giá trị x dó có thỏa mãn
ĐKXĐ của A hay không.
Ví dụ minh họa: Cho
1
2
x
A
x
, điều kiện xác định
0
, 4
x
x
.
a) Tìm x biết
2.
A
b) Tìm x biết
4 1
4
x
A
.
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 4
Hướng dẫn giải
a) Có
2A
1
2 1 2 4 3
2
x
x x x
x
(vô lí)
không tồn tại x để
2.
A
b) Có
4 1 1 4 1
4 4 4 9 2
4 4
2
x x x
A x x x
x
4 5 6 0 2 4 3 0
x x x x
4
2
9
3
16
4
x
x
x
x
Kết hợp điều kiện
0
, 4
x
x
4
x
( loại) và
9
16
x
( thỏa mãn)
Vậy
9
16
x
thì
4 1
4
x
A
.
Dạng 4. Tìm giá trị của biến x để
A
k
( hoặc
A
k
,
A
k
,
A
k
,…) trong đó k là hằng số
hoặc là biểu thức chứa x.
- Thực chất đây là việc giải bất phương trình.
- Học sinh thường mắc sai lầm khi giải bất phương trình thường dùng tích chéo hoặc sử
dụng một số phép biến đổi sai.
Ví dụ minh họa: Cho
2
3
x
A
x
, điều kiện xác định
0
, 9
x
x
.
a) Tìm x để
1A
.
b) Tìm x để
2A
.
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 5
Hướng dẫn giải
a) Để
1A
2 2 2 3
1 1 0 0
3 3 3
x x x x
x x x
5
0
3x
Mà
5 0
3 0 9.
x x
Kết hợp điều kiện
0
, 9
x
x
0
9
x
Vậy
0 9
x
thì
1A
.
b) Để
2A
2 2 2 2 6
2 2 0 0
3 3 3
x x x x
x x x
8
0
3
x
x
TH1:
8 0 8 64
9 64
9
3 0 3
x x x
x
x
x x
.
TH2:
8 0 8 64
9
3 0 3
x x x
x
x x
(vô lí)
loại
Vậy
9
64
x
thì
2A
.
Dạng 5. So sánh biểu thức A với một số hoặc một biểu thức.
- Thực chất đây là việc đi xét hiệu của biểu thức A với một số hoặc một biểu thức rồi so
sánh hiệu đó với số 0.
Ví dụ minh họa: Cho
2 1
1
x
A
x
, điều kiện xác định
0.
x
a) So sánh
A
với 2.
b) So sánh
A
với 1.
Hướng dẫn giải
a) Xét hiệu
2 1 2 1 2 2 1
2 2
1 1 1
x x x
A
x x x
Có
0
x
0 1 0
x x
và
1
0
1
0
1x
2
0 2
A
A
.
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 6
b) Xét hiệu
2 1 2 1 1
1 1
1 1 1
x x x x
A
x x x
Có
0
x
0
x
và
1 0
x
0
1
x
x
1
0 1
A
A
.
Dạng 6. Chứng minh biểu thức
A k
( hoặc
A k
,
A k
,
A k
) với k là một số.
- Thực chất đây là việc đưa về chứng minh đẳng thức hoặc bất đẳng thức. Ta xét hiệu
A
k
rồi xét dấu biểu thức.
Ví dụ minh họa: Cho
3
2
x
A
x
, điều kiện
0.
x
Chứng minh
1A
.
Hướng dẫn giải
Cách 1:
Có
3 1
1
2 2
x
A
x x
.
Có
0 0
x x
1
0
2x
1
1 1
2x
hay
1A
.
Cách 2:
Xét hiệu
1
1
2
A
x
. Có
0 0
x x
1
0
2x
với mọi
0.
x
1
0
A
hay
1A
.
Dạng 7. Tìm giá trị của biến x là số nguyên, số tự nhiên để biểu thức A có giá trị nguyên
- Cách làm: chia tử thức cho mẫu thức, rồi tìm giá trị của biến x để mẫu thức là ước của
phần dư (một số)
- Học sinh thường quên kết hợp với điều kiên xác định của biểu thức.
Ví dụ minh họa: Cho
3
2
x
A
x
, điều kiện xác định
0
, 4, 9
x
x x
.Tìm x nguyên để
A
có giá trị nguyên
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 7
Hướng dẫn giải
Có
3 5
1
2 2
x
A
x x
. Để
A
nhận giá trị nguyên
5
2
x
là số nguyên
2
x
là ước của 5
2 1; 1;5; 5
x
2
x
1 -1 5 -5
x
3 1 7 -3
x
9 (loại) 1 (thỏa mãn) 49(thỏa mãn) loại
Vậy
1;49
x
thì
A
có giá trị nguyên
Dạng 8. Tìm giá trị của biến x là số thực, số bất kì để biểu thức A có giá trị nguyên
- Học sinh thường nhầm lẫn cách làm của dạng này với dạng tìm giá trị của biến x là số
nguyên, số tự nhiên để biểu thức A có giá trị nguyên.
- Cách làm: sử dụng ĐKXĐ để xét xem biểu thức A nằm trong khoảng giá trị nào, rồi tính
giá trị của biểu thức A và từ đó tìm giá trị của biến x.
Ví dụ minh họa : Cho
2 1
2
x
A
x
, điều kiện xác định
0.
x
Tìm x để
A
có giá trị nguyên.
Hướng dẫn giải
Cách 1:
Có
2 1 5
2
2 2
x
A
x x
Có
0 0
x x
2 0
x
5
0
2x
5
2 2
2x
2A
Lại có
0 0
x x
5 5 5 1
2 2 2
2 2
2 2
x
x x
1
2
A
Vậy
1
2
2
A
mà
0;1
A A
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 8
+) Với
0
A
2 1 1 1
0 2 1 0
2 4
2
x
x x x
x
+)Với
1A
2 1
1 2 1 2 3 9
2
x
x x x x
x
Vậy
1
;
9
4
x
thì
A
có giá trị nguyên.
Cách 2:
2 1
2 2 1 2 1 2
2
x
A A x x A x A
x
Dễ thấy
2A
không là nghiệm của phương trình
2A
2
1
2
A
x
A
Vì
0 0
x x
2 1
0
2
A
A
Th1:
1
2
1 0
2
2
0
2
A
A
A
A
(vô lí)
Loại
Th2:
1
2
1 0
1
2
2
2 0
2
2
A
A
A
A
A
Vậy
1
2
2
A
mà
0
;1
A
A
+) Với
0
A
2 1 1 1
0 2 1 0
2 4
2
x
x x x
x
+)Với
1A
2 1
1 2 1 2 3 9
2
x
x x x x
x
Vậy
1
;
9
4
x
thì
A
có giá trị nguyên.
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 9
Dạng 9. Tìm giá trị của tham số để phương trình hoặc bất phương trình có nghiệm
- Học sinh cần biết cách tìm điều kiện để phương trình hoạc bất phương trình có nghiệm.
+ Học sinh đưa biểu thức chưa căn về dạng bậc hai sử dụng điều kiện để phương trình bậc
hai có nghiệm
+Cô lập tham số
m
, tìm miền giá trị của vế chứa biến
x
rồi suy ra điều kiện để phương
trình có nghiệm thì biể thức chứa tham số
m
nằm trong miền giá trị của vế chứa biến
x
Ví dụ minh họa 1: Cho
A
x x
, điều kiện xác định
0
; 1
x
x
. Tìm m để phương trình
A m
có nghiệm
x
.
Hướng dẫn giải
Có
A m
1
1
4
4
x
x m x x m
2
1
1
2 4
x
m
.
Do
0
x
2
1
1
2
4
x
2
1
1
0 0
2
4
x m
Vì
0
; 1
x
x
1
x
2 2
x x m
Vậy
0
; 2
m
m
thì phương trình
A
m
có nghiệm
x
.
Ví dụ minh họa 2: Cho
3 1
x x
A
x
, điều kiện xác định
1
0
;
9
x
x
. Tìm m để phương
trình
A
m
có nghiệm
x
.
Hướng dẫn giải
Có
A
m
(1 3 ) 0
3 1
x x
m x m x m
x
(1)
Đặt
t x
, có
1
0
;
9
x
x
1
0
;
3
t
t
2
(1) (1 3 ) 0
t m t m
(2)
Vì
1
a
khác 0
(2) luôn là phương trình bậc hai
Ta có:
2
2
(1 3 ) 4 9 10 1
m m m m
(1) Có nghiệm khi (2) có ít nhất một nghiệm
0t
và
1
3
t
TH1: Phương trình (2) có nghiệm khi t = 0
m = 0
TH2: Phương trình (2) có nghiệm kép
1
0;
3
t t
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 10
1
0
9
1
m
m
Với
1
m
1t
(thỏa mãn)
Với
1
9
m
4
3
t
(không thỏa mãn)
TH3: Phương trình (2) có hai nghiệm trái dấu và
1
3
t
2
0
0
0
4
1
1
0
(1 3 ). 0
9
3 3
ac
m
m
m m
TH4: Phương trình (2) có hai nghiệm phân biệt cùng dương
( 1)(9 1) 0
1
1 3 0 0
9
0
m
m
m m
m
Kết hợp điều kiện lại
1
0
9
m
hoặc m = 1
Ví dụ minh họa 3: Cho
x
A
x 1
, điều kiện xác định
0
x
. Tìm m để phương trình
A
m
có nghiệm.
Hướng dẫn giải
Ta có:
A
m
x
m
x 1
m
. x m x
1 m x m
(1)
+) TH1: Nếu
m
1
thì phương trình (1) có
0.
x 1
(vô lý)
+) TH2: Nếu
m
1
thì phương trình (1) có
m
x
1 m
(2)
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 11
Vì
0 0
x x
=> Để phương trình
A
m
có nghiệm thì phương trình (2) cần có
m
0
1
m
(3)
Vì
x
0 m 0
x 1
Từ (3) suy ra
1
m 0 m 1
Vậy với
0 m 1
thì phương trình
A m
có nghiệm.
Dạng 10. Tìm giá trị của biến x để
A
A
(hoặc
;
;...)
A
A A A
- Nếu
A
< 0
A
A
- Nếu
A
0
A
A
Ví dụ minh họa: Cho
1x
A
x
, điều kiện xác định
0
x
. Tìm
x
biết
a)
A
A
b)
A
A
Hướng dẫn giải
a) Có
A
< 0
A
A
1
0
x
x
Mà
0
x
0
x
1
0
x
x
1 0 1x x
.
Kết hợp điều kiện ta có
0
1
x
thì
A
A
b) Có
A
0
A
A
1
0
x
x
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 12
Mà
0
x
0
x
1
0
x
x
1 0 1x x
.
Vậy
1x
thì
A A
Dạng 11. Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức A.
- Học sinh cần biết cách tìm cực trị của phân thức ở một số dạng tổng quát.
- Học sinh cần đưa biểu thức rút gọn A về một trong những dạng sau để tìm cực trị:
+ Tử thức và mẫu thức là một số hoặc là một biểu thức có dấu xác định trong tập
ĐKXĐ
+ Biến đổi biểu thức A thành một hằng đẳng thức có chứa biến x.
+ Biến đổi biểu thức A thành một tổng của hai (hoặc nhiều) số dương rồi áp dụng bất
đẳng thức Cô – si hoặc một vài bất đẳng thức phụ.
- Học sinh thường mắc sai lầm khi chỉ chứng minh biểu thức
A k
( hoặc
A k
) chưa chỉ
ra dấu bằng nhưng đã kết luận cực trị của biểu thức A.
Ví dụ minh họa: Cho
2
1
x
A
x
, điều kiện xác định
0
x
.
a) Tìm giá trị lớn nhất của A.
b) Đặt
3 4 .B x x A
. Tìm giá trị nhỏ nhất của
B
.
c) Đặt 1
C x A
. Tìm giá trị nhỏ nhất của
C
.
Hướng dẫn giải
a) Có
2 1
1
1 1
x
A
x x
.
Vì
0
x
0
x
1 1
x
1
1
1
x
1
1 2
1x
2A
.
Vậy giá trị lớn nhất của
A
bằng 2. Dấu “=” xẩy ra khi và chỉ khi
0
x
.
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 13
b) Có
2
3 4 . 1 4 . 4 2 2 8
1
x
B x x A x x x x x x
x
2
2 1 9 1 9
x x x
.
Có
2 2
1 0 1 9 9 9
x x B
.
Vậy giá trị nhỏ nhất của B là
9
. Dấu “=” xẩy ra
2
1 0 1 1x x x
.
c) Có
1 1
1 2 1 1
1 1
C x A x x
x x
Có
0
x
0
x
1 0
x
và
1
0
1x
Áp dụng bât đẳng thức Cô – si với 2 số dương
1x
và
1
1x
ta có:
1 1
1 2 1 .
1 1
x x
x x
1 1
1 2 1 1 3 3.
1 1
x x C
x x
Vậy giá trị nhỏ nhất của C bằng 3.
Dấu “=” xẩy ra khi và chỉ khi
1x
=
1
1x
2
1 1 1 1 0
x x x
.
Dạng 12: Tìm giá trị lớn nhất, giá trị nhỏ nhất của
A
khi
x
N
.
+ Học sinh chú ý bài toán thường cho dưới dạng điều kiện xác định
,
x a x b
trong đó
a
b
. Ta phải tính giá trị với
x
là các số tự nhiện thuộc
;a
b
và trường hợp
x
là số tự
nhiên lớn hơn
b
.
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 14
Ví dụ minh họa: Cho
1
x
A
x
, điều kiện xác định
0
; 1
x
x
.Với
x
và
1x
Tìm giá trị lớn nhất của biểu thức
.A
Hướng dẫn giải
Ta có:
1
1
1 1
x
A
x x
Với
x
và
1x
, ta xét các trường hợp:
TH1.
0
x
thì
0
A
.
TH2. Nếu
2
x
thì
1 2 1
x
Do đó:
2 2 1
1 1 2
1
1 2 2
2 1
1 2 1 2 1
A
x
Dấu “=” xảy ra khi
2
x
.
So sánh các trường hợp của
P
, ta thấy:
m
ax 2 2
P
khi và chỉ khi
2
x
.
B. BÀI TẬP
Bài 1. Cho các biểu thức :
2
1
x
A
x x x
và
1
1
B
x
( với x > 0; x
1)
1. Tính giá trị của biểu thức B khi
9
x
2. Đặt
:C A B
, rút gọn biểu thức C
3. Tìm giá trị của x để
3
C
4. So sánh C với
1
4
5. Chứng minh
2
C
6. Tìm x nguyên để biểu thức C có giá trị nguyên
7. Tìm giá trị nhỏ nhất của biểu thức C
8. Tìm các giá trị của m để nghiệm x thoản mãn bất phương trình :
. 3
x C x m
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 15
Hướng dẫn giải
1. Với
9
x
(thỏa mãn ĐKXĐ) thay vào biểu thức B, ta được :
1 1
8
9 1
B
Vậy khi
9
x
thì giá trị của biểu thức
1
8
B
2. Đặt
:C
A B
, rút gọn biểu thức C
2 1
( ) :
1 1
x
C
x x x x
2
1
C
( ) :
1 ( 1) 1
x
x x x x
2
(
) 2 1
.
1
(
1)
x
x
C
x
x
( 2)( 1)
(
1)
x x
C
x x
2
x
C
x
3. ĐKXĐ: x > 0; x
1
Để
3
C
2
3
2 3
0
3 2 0 (*)
x
x
x x
x x
x x
Giải phương trình (*) ta suy ra được :
1x
( loại) và
4
x
( thỏa mãn ĐKXĐ)
Vậy để
3
C
thì
4
x
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 16
4. Xét hiệu
1 2 1 4 8
4 4
4
x x x
C
x x
2
1
127
2
4 16
4
x
x
Vì
2
1
2 0
4
x
với mọi x nên
2
1
127
2 0
4
16
x
Vì
0
x
nên
0
x
suy ra
4 0
x
Suy ra
2
1
127
2
4 16
0
4
x
x
. Do đó
1
4
C
5. Xét hiệu
2
1
1
2 2 2
2 2
x
x x x
C
x x x
Vì
2
1 0
x
với mọi x nên
2
1 1 0
x
Vì
0
x
nên
0
x
, suy ra
2
1
1
0
x
x
. Do đó
2
C
6. ĐKXĐ: x > 0; x
1
Ta có :
2 2
x
C x
x x
Để giá trị của biểu thức C nguyên thì
2
x
x
nguyên
Suy ra
2
Z x
x
là ước của 2
Từ đó
x
nhận các giá trị 1 ; 2 nên x nhận các giá trị
1x
(loại) và
4
x
( TMĐK)
Khi đó với
4
x
thì C có giá trị là 3
Vậy với
4
x
thì biểu thức C có giá trị nguyên
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 17
7. Ta có :
2 2
x
C x
x x
Áp dụng bất đẳng thức Cô – si với hai số dương
x
và
2
x
, ta được :
2
2 2
x
x
m
in
2
2
A
Dấu “ = ” xảy ra
2
2
x x
x
( thỏa mãn ĐKXĐ)
Vậy giá trị nhỏ nhất
m
in
2
2 2
A
x
8. Ta có :
. 3
x C x m
Suy ra :
1 0
x x m
1 0
x x m
1
5
0
4 4
x x m
2
1 5
0
2
4
x m
2
1
5
2 4
x
m
Vì
0
x
nên
0
x
, suy ra
2
1
1
2
4
x
Suy ra
2
1
1 5
4 2 4
x m
1
5
1
4 4
m
m
Vậy với
1
m
thì x thoản mãn bất phương trình :
. 3
x C x m
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 18
Bài 2. Cho các biểu thức :
3
9 3 2
1
:
9
6
2 3
x
x x x x
M
x
x x x x
và
4 8
3
x
N
x
(với
0
; 4; 9)
x
x x
1. Rút gọn biểu thức M
2. Tìm x để
M
M
3. Đặt
.Q
M N
, tìm các giá trị của x để biểu thức Q có giá trị nguyên.
Hướng dẫn giải
1. Rút gọn biểu thức M
2
2
3
9 3 2
1 :
9
6 2 3
3
3 9 3 3 2
:
3
3 2 3
2 3
3
.
3
2
3
2
x x x x x
M
x
x x x x
x x x x x
M
x x x x
x x
M
x
x
M
x
2. ĐKXĐ :
0
; 4; 9
x
x x
Để
0
M M M
3
0
2
2 0
2
4
x
x
x
x
Kết hợp với ĐKXĐ:
0
x
, suy ra
0
4
x
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 19
Vậy với
0
4
x
thì
M
M
3. ĐKXĐ :
0
; 4; 9
x
x x
3 4 8 12
. .
2 3 3
x
Q M N
x x x
Vì
12
0 0 0
3
x x
x
Vì
1 1 12
0 0 3 3 4
3
3 3
x x x
x x
Do đó:
0
4
Q
Mà
Q Z
, suy ra
1
; 2; 3; 4
Q
TH1:
12
1 1 3 12 9 81
3
Q x x x
x
( thỏa mãn ĐKXĐ)
TH2:
12
2 2 3 6 3 9
3
Q x x x
x
( loại)
TH3:
12
3 3 3 4 1 1
3
Q x x x
x
( thỏa mãn ĐKXĐ)
TH4:
12
4 4 3 3 0 0
3
Q x x x
x
( thỏa mãn ĐKXĐ)
Vậy để biểu thức Q có giá trị nguyên thì
0
; 1; 81
x
Bài 3. Cho biểu thức
1 1 3 1
1
1 1
x x x
A
x
x x
với
0, 1x x
1) Rút gọn biểu thức
A
.
2) Tính giá trị của
A
khi
9
x
.
3) Tìm giá trị của
x
để
1
2
A
.
4) Tìm các giá trị nguyên của
x
để
A
nhận giá trị nguyên.
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 20
5) Tìm
m
để phương trình
2
mA x
có hai nghiệm phân biệt.
6) Tính các giá trị của
x
để
1A
.
7) Tính giá trị nhỏ nhất của biểu thức
A
.
Hướng dẫn giải
1)
1 1 3 1
1
1 1
x x x
A
x
x x
0
; 1
x
x
2
2
1
1 3 1
1
1
x
x x
A
x
x
2
1 2 1 3 1
1
1
x
x x x x
A
x
x
2 3 1
1 1
2 1 1
1
1
2 1
1
x x
A
x x
x x
A
x x
x
A
x
2) Thay
9
x
(TMĐK) vào
A
ta được:
2 9 1 5
4
9 1
A
Vậy với
9
x
thì
5
4
A
3) ĐKXĐ:
0
, 1
x
x
1 2 1 1
2 2
1
x
A
x
4 2 1x x
3 3
x
1x
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 21
1x
(Không thỏa mãn)
Vậy không có giá trị của x để
1
2
A
4) ĐKXĐ:
0
, 1
x
x
Ta có:
2
1 3
2 1 3
2
1
1 1
x
x
A
x
x x
Để
A
nhận giá trị nguyên thì
3
1x
nhận giá trị nguyên
3
3 1 1
x x U
3
3; 1;3;1
U
Ta có bảng sau:
1x
3
1
1
3
x
4
2
0
2
x
0
4
ĐK - - TM TM
Vậy
0; 4
x
thì
A
nhận giá trị nguyên
5) ĐKXĐ:
0
, 1
x
x
Để
. 2
m A x
2 1
. 2
1
x
m x
x
2 2
m x m x x
2 1 2 0
x m x m
(1)
Đặt
0; t 1
t x t
ta có phương trình:
2
1 2 1 2 0 *
t m x m
Phương trình (1) có hai nghiệm phân biệt khi phương trình (2) có hai nghiệm phân
biệt khác 1 và
2
1
0
t t
0
0
0
0
P
S
a b c
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 22
2
2
4
9 0
2 1 4. 2 0
2
2 0
2
1
2
1 0
2
1 (2 1) 2 0
2
m m
m m
m
m
m
m
m
m m
m
Vậy với
2
m
thì pt (1) có 2 nghiệm phân biệt
6) ĐKXĐ:
0
, 1
x
x
Để
2 1
1 1
1
x
A
x
2 1 1
0
1
x x
x
2
0
1
x
x
Ta có :
0x x
ĐKXĐ
1
1
Đ
x
ĐKX
x
2
0
1
2 0
2
4
x
x
x
x
x
Kết hợp với điều kiện ta có
0 4; 1x x
Vậy với
0
4; 1
x
x
thì
1A
7) ĐKXĐ:
0
, 1
x
x
3
2
1
A
x
0
; 1
x
x
Ta có:
0 1 1
x x
3 3
3 2 2 3 1
1 1
A
x x
Dấu “ = “ xảy ra
0
0
x
x
(TMĐK)
Vậy GTNN của
A
là
1
khi
0
x
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 23
Bài 4. Cho biểu thức
1
1
:
1
1 1
x
x
B
x x x x x
với
0
, 1
x
x
1) Rút gọn B
2) Tính giá trị của B khi
3 2 2 3 2 2.
x
3) Tìm x để
B x
4) Với x >1, hãy so sánh
B
với
B
Hướng dẫn giải
1)
1
1
:
1
1
1
1
x x
B
x x x
x x x
1
1
.
1
1 1
x
x x x x
B
x
x
x x
1
1
x
B
x
2)
3 2 2 3 2 2
x
2
2
2 1 2 1 2 1 2 1 2
Thay x = 2 (TMĐK) vào B ta được
2
2
1
2 1
3 2 2
1
2
1
B
.
Vậy khi
3 2 2 3 2 2
x thì
3
2 2
B
3) ĐKXĐ:
0, 1x x
2
1
1
1
2 1 0
1 2 0
B x
x
x
x
x x x
x x
x
1 2 1 2 0
x x
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 24
2
1 2
1 2
1 2
3 2 2
x L
x
x
x
4) Xét hiệu
1
B B B B
CÁCH 1
+) Ta có :
1
0
x
B B
có nghĩa
+) Xét
1 2
1 1 0
1 1
x
B
x x
1
1
B
B
+) Ta có :
(
1) 0
B
B B B
B
B
CÁCH 2
+) Ta có:
1
1 1 0
x
x x
Mà
1 0
x
1
0 0 0 1
1
x
B B
x
+) Lại có:
2 9 3 2 1
5 6 2 3
x x x
B
x x x x
1 1 1 2
1 1
1 1 1
x x x
B
x x x
Mà
2
1 0 0
1
x
x
1 0
1 1 0
B
B B
Mà
0
B
1 0
1 0 2
B
B
Từ (1) và (2)
1 0
B B
0
B
B
B B
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 25
Bài 5. Cho biểu thức
2 9 3 2 1
5 6 2 3
x x x
C
x x x x
với
0
, 4, 9
x
x x
1) Rút gọn biểu thức C
2) Tính giá trị của x để C đạt giá trị lớn nhất
3) So sánh
1
C
với 1
Hướng dẫn giải
1)
2
9 3 2 1
2
3
2
3
x
x x
C
x
x
x x
2 9 3 3 2 1 2
2 3
x x x x x
C
x x
2 9 9 2 3 2
2 3
x x x x
C
x x
2
2 3
x x
C
x x
1
3
x
C
x
2) ĐKXĐ:
0
, 4, 9
x
x x
Để
m
ax
1
m
in
C
C
Ta có:
1 3 1 4 4
1
1 1 1
x x
C
x x x
Ta có:
0x
x
ĐKXĐ
1 1
1
1
1
x
x
4
4
1
4
1 3
1
x
x
1
3
1
3
C
C
ĐKXĐ
x
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 26
Dấu “ = ” xảy ra
0 0
x x
(TMĐK)
Vậy GTLN của C là
1
3
khi x = 0
3) Xét hiệu
1 3 4
1 1
1 1
x
C
x x
Ta có:
0x x
ĐKXĐ
1
1 0
4
0
1
1
1 0
1
1
x
x
C
Đ
x
C
ĐKX
C. BÀI TẬP TỰ LUYỆN
A. Đề bài
Bài 1 . Cho biểu thức
4
1
x
A
x
và
1
2 3
:
2
1 1
x
x
B
x
x x
Với
0, 1, 4
x x x
.
1) Tìm giá trị của
x
để
4.
A
2) Rút gọn biểu thức
B
3) Với các biểu thức
A
và
B
nói trên, hãy tìm giá trị nhỏ nhất của biểu thức
18
.A B
.
Bài 2. Cho hai biểu thức
2 1
1
x
A
x x
và
1
: 1 0; 1
1
1
1
x x
P x x
x
x x
1) Tính giá trị của biểu thức A với
16
x
2) Rút gọn biểu thức
P
.
3 ) Tìm giá trị lớn nhất của biểu thức
A
M
P
.
Bài 3. Cho hai biểu thức
4 2 13
0; 9
9
3 3
x x x
A x x
x
x x
và
5
0; 9
3
x
B x x
x
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 27
1) Tính giá trị của biểu thức B với
11
6 2
x
2) Rút gọn biểu thức
A
P
B
.
3) Tìm x để
1
9
P
.
Bài 4. Cho biểu thức
2
x
A
x
và
5 4
0; 1
1 2 2
x x
B x x
x x x x
1) Tính A khi
1
4
x
.
2) Rút gọn B.
3) Biết
A
P
B
. Hãy Chứng tỏ
P
P
với
1
x
.
Bài 5. Cho hai biểu thức
2 2 6 8
1 2 3 2
x x x
A
x x x x
và
4 13
1
x
B
x
0; 1; 4
x x x
1) Tính giá trị của biểu thức B với
36
x
2) Rút gọn biểu thức A.
3) Tìm giá trị lớn nhất của biểu thức
.P
A B
Bài 6.
Cho biểu thức
2
3
x
A
x
và
15
3 3
: , 0, 25.
25
5
5
x x
B x x
x
x x
1) Khi
3 3
9
5 2. 5 2,
x
Tính giá trị của
A.
2) Rút gọn biểu thức
B
.
3) Tìm
x
để
P A B
nhận giá trị nguyên.
Bài 7 . Cho hai biểu thức
2 1 1
; ( 0; 2)
4
2 2
x x
A B x x
x
x x x
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 28
1) Rút gọn B và tính
A
P
B
2) Tìm x để B = |B|
3) Tìm x thỏa mãn:
10 29 25
xP x x
Bài 8.
Cho biểu thức:
2 5
1
x
A
x
và
2 3 9 2
.
1
9
3
3 3
x x x x
B
x
x x
(với
0
, 9
x
x
)
1) Tính giá trị của
A
khi
19
8 3 19 8 3
x
2) Rút gọn
B
3) Gọi
.M
A B
. So sánh
M
và
M
Bài 9. Cho biểu thức
2
2 2 1
x x x x x
P
x x x x x x
với
0
, 1
x
x
.
1) Rút gọn biểu thức
P
.
2) Tìm giá trị của biểu thức
P
khi
3
2 2
x
.
3) Chứng minh rằng với mọi giá trị của
x
đề biểu thức
P
có nghĩa thì biểu thức
7
P
chỉ
nhận một giá trị nguyên.
Bài 10. Cho hai biểu thức
3
2 1 1
8
2
x x
U
x
x x x
với
0
x
và
4
x
.
1) Rút gọn biểu thức
.U
2) Tìm giá trị của
U
tại
14 6 5
x .
3) Tìm tất cả các giá trị của
x
để biểu thức
8K
U
có giá trị là số nguyên
Bài 11 . Cho hai biểu thức
4 3
x
A
x
và
10
4
2
x x
B
x
x
với
9
0
, 4, .
16
x
x x
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 29
1) Tính giá trị của biểu thức
A
khi
25.
x
2) Rút gọn biểu thức
.B
3) Tìm giá trị của
x
để
2 .B A
Bài 12. : Cho biểu thức
2
6 1
: 1
1 2 2 1
x
P
x x x x x
với
0
x
,
1x
,
4
x
.
1) Rút gọn
P
. 2) Tính
P
biết
3
2 2
x
. 3) Tìm
x
để
1
2
P
.
Bài 13. Cho biểu thức
3 2 1
,
9
1 3 3 3
x x
A B
x
x x x
với
0
, 9
x
x
.
1) Tính giá trị biểu thức
A
khi
4
9
x
.
2) Rút gọn
B
.
3) Cho
B
P
A
, tìm
x
để
3
P
.
Bài 14 . Cho biểu thức :
1 1
1 1
A
x x
và
3
2
1
(
2)( 1)
x
x x x
B
x
x
x
( với
0
; 1
x
x
)
1) Rút gọn và tính giá trị biểu thức A khi
4 2 3
x
2) Rút gọn biểu thức B
3) Đặt M = B : A , tìm
x
để
1
1
1
8
x
M
Bài 15. Cho biểu thức:
1 1 4
x x x x
P
x x x x x
và
1
1
x
Q
x
với
0
; 1
x
x
1) Tính giá trị của Q khi
2
5
x
.
2) Rút gọn biểu thức
.A P Q
.
3) Tìm các giá trị của
x
để
. 8
A x
.
Bài 16. Cho biểu thức
2
2
;
1
2 1
x x
A
x
x x
1x
B
x
với
0, 1x x
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 30
1) Tính giá trị của
B
khi
36
x
2) Chứng minh rằng
2
.
1
A B
x
3) Tìm
x
để
.
1 . 1
A
B A B
Bài 17. Cho hai biểu thức
12
1
x
A
x
và
3 1 1
:
1
1 1
B
x
x x
với
0
, 1
x
x
1) Tính giá trị của biểu thức
A
khi
9
x
.
2) Rút gọn biểu thức
B
.
3) Tìm giá trị nhỏ nhất của biểu thức
A
M
B
.
Bài 18. Cho hai biểu thức
2 3 2
2
x x
A
x
và
3
2
2
2
x
x x
B
x
với
0
x
và
4
x
.
1) Tính giá trị của
A
khi
4 2 3
x .
2) Tìm giá trị của
x
để
1B
A
.
3) Tìm giá trị nhỏ nhất của biểu thức
C
B A
.
Bài 19. Cho biểu thức
1 1 3 1
1
1 1
x x x
A
x
x x
với
0; 1x x
1) Rút gọn biểu thức
A
.
2) Tìm giá trị nguyên của
x
để
1.
A
3) Tìm
m
để phương trình
2
mA x
có hai nghiệm phân biệt
Bài 20.
Cho 2 biểu thức:
1 2
4
2
x
A
x
x
và
2
x
B
x
với
0
x
và
4
x
.
1) Tính giá trị biểu thức
B
khi
16
x
.
2) Rút gọn biểu thức
:M A B
.
3) Tìm các giá trị thực của
x
để
1M
.
Bài 21. Cho hai biểu thức
1
1
x
A
x
và
1
.
1
1
2 1
x
x x
B
x
x
x
với
0; 1x x
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 31
1) Tính giá trị của
A
khi
9
4
x
2) Rút gọn
B
.
3) Với
x
và
1x
, hãy tìm giá trị lớn nhất của biểu thức
.P A B
Bài 22. Cho hai biểu thức
1
2
x
A
x
và
6 2 2 1
3 2 2 1
x
B
x x x x
với
0; 1; 4
x x x
1) Tính giá trị của A khi
1
4
x
2) Rút gọn biểu thức M = A.B
3) Tìm m để phương trình
2
m
M
(m là tham số) có nghiệm.
Bài 23. Cho hai biểu thức
2
1 4 4 1 1
;
( 0; )
4
4
2 1 8 1 2 1
x x x
A B x x
x x x x x
1) Tính giá trị của A khi
1x
2) Chứng minh biểu thức
1
.
2 1
B
T
A
x
3)Với
1x
, tìm giá trị nhỏ nhất của
1
4
.
L
T
T
4) Tìm các giá trị nguyên của x để biểu thức
2 1
.
2 1
x
P T
x
nhận giá trị nguyên
dương.
Bài 24. Cho hai biểu thức
2
2
x
A
x
với
0
x
và
2 3 12
4
2 2
x
B
x
x x
với
0, 4
x x
1) Tính giá trị của biểu thức A khi
9
x
2) Rút gọn biểu thức B
3) Cho biểu thức
1
P
AB
. Với
,
x
tìm giá trị lớn nhất của P.
Bài 25. Cho hai biểu thức
1
2
x
A
x
và
20
2 3 2
:
25
5
5
x
x
B
x
x x
với
0, 25
x x
1) Khi
16
x
, tính giá trị của biểu thức A
2) Rút gọn biểu thức B
3) Tìm tất cả các giá trị nguyên của tham số m để phương trình
6
B
m
A
có nghiệm
Lê Trung – Uyên Vi Toán học là đam mê
Tài liệu tự hoc- luyện thi vào 10 Page 32
Bài 26. Cho hai biểu thức
1 1
4
2 2
x
P
x
x x
và
2
3
x
Q
x
với
0
; 4; 9
x
x x
1. Tính giá trị của biểu thức Q khi
64
x
2. Chứng minh
2
x
P
x
3. Với
x
Z
, tìm GTLN của biểu thức
.
1
K
Q P
| 1/32
| | Tải xuống

Có thể bạn quan tâm:

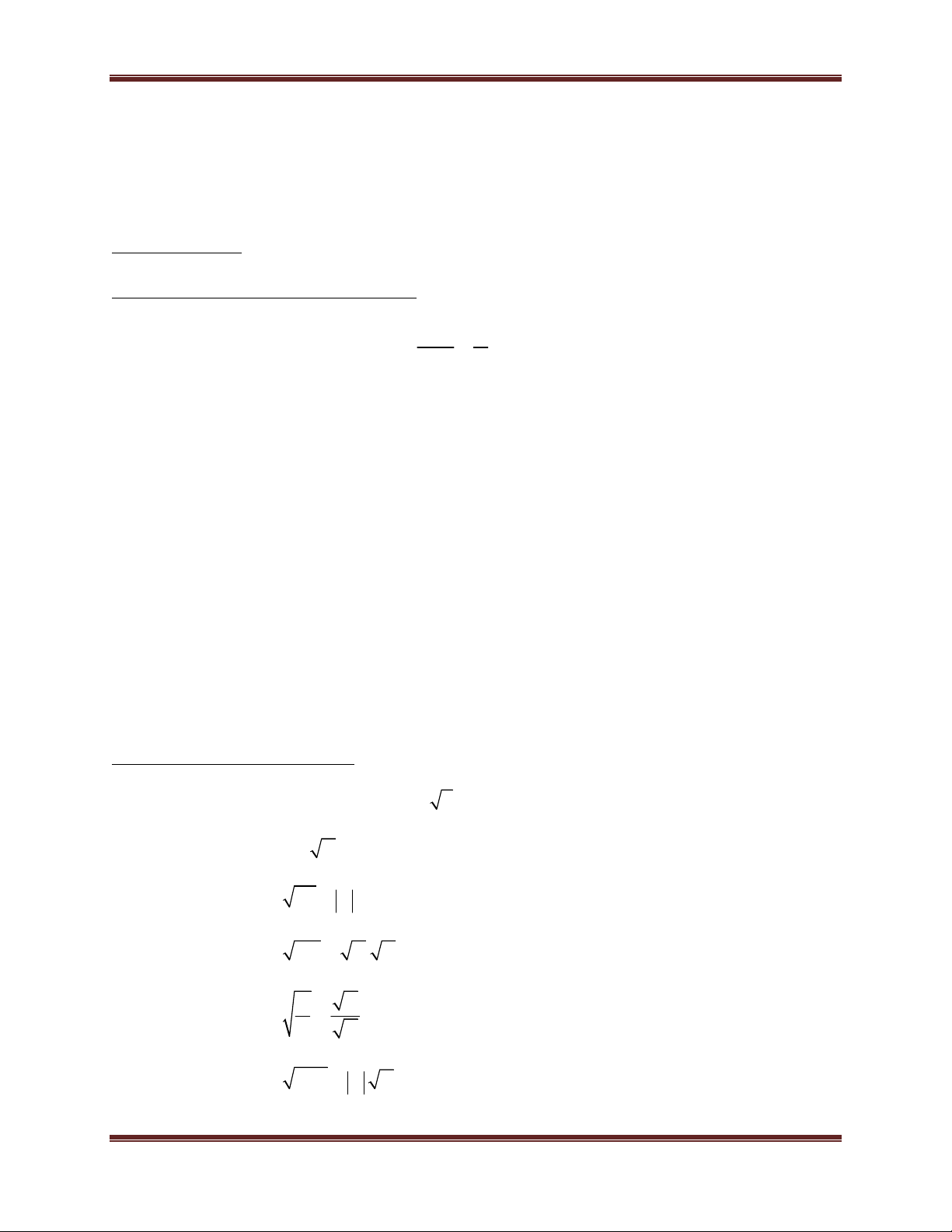
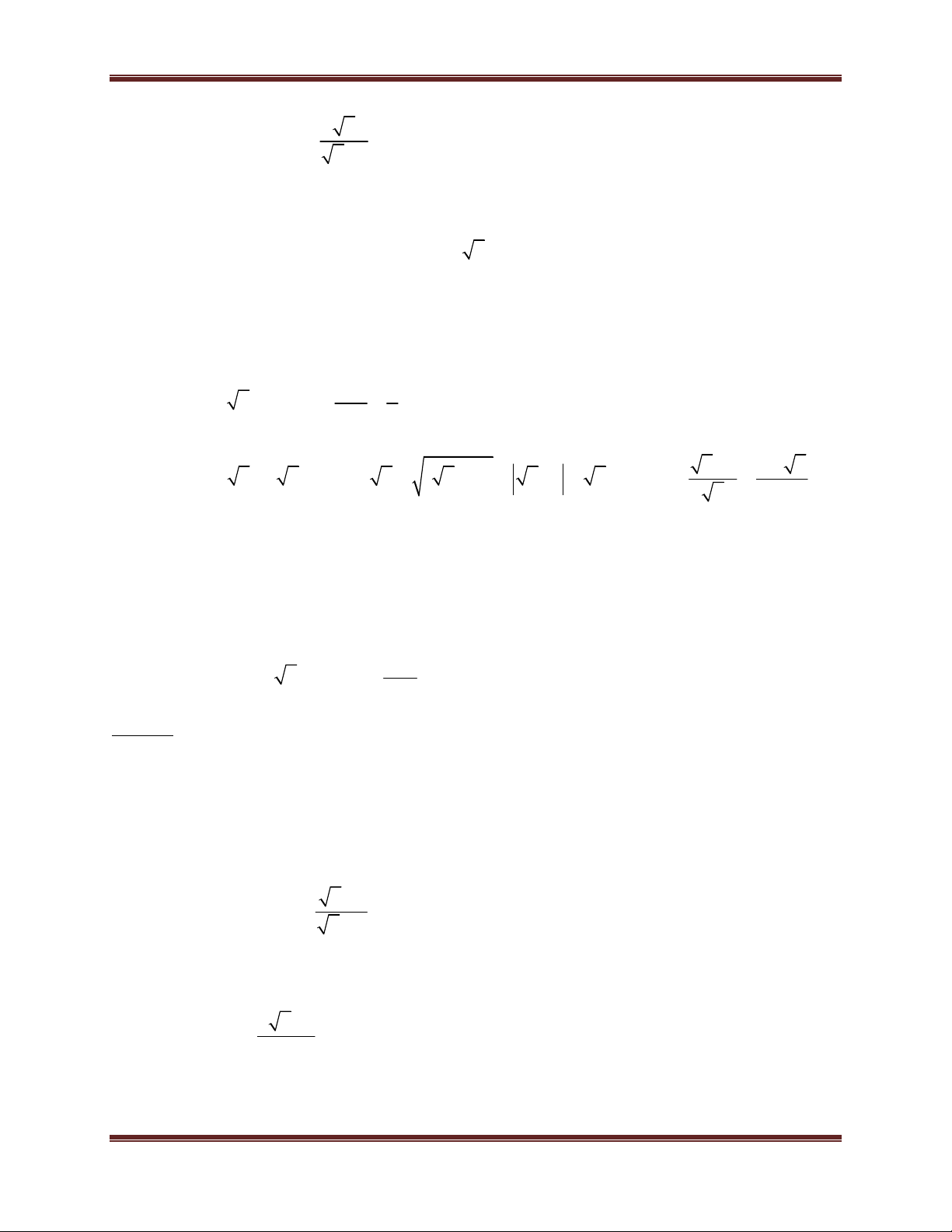
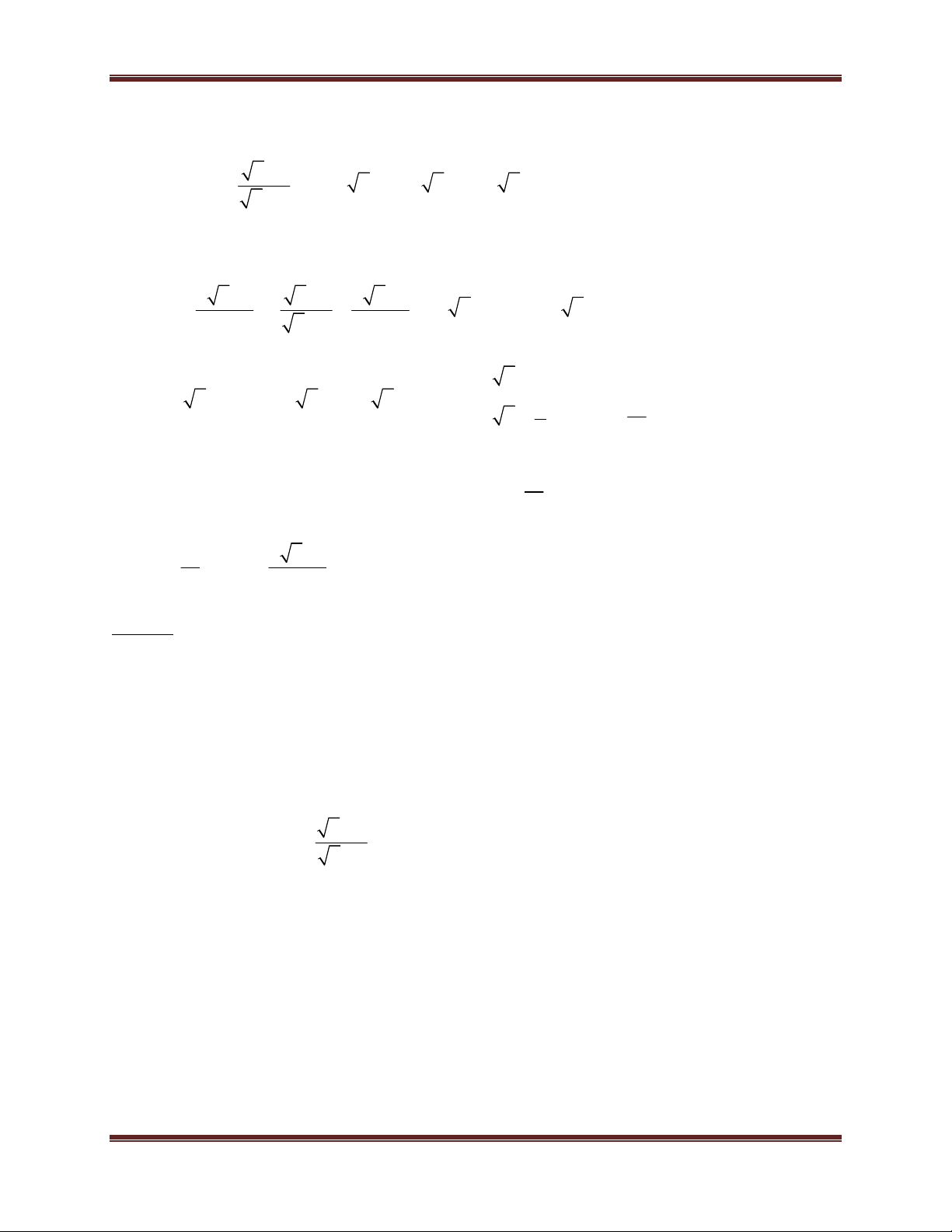
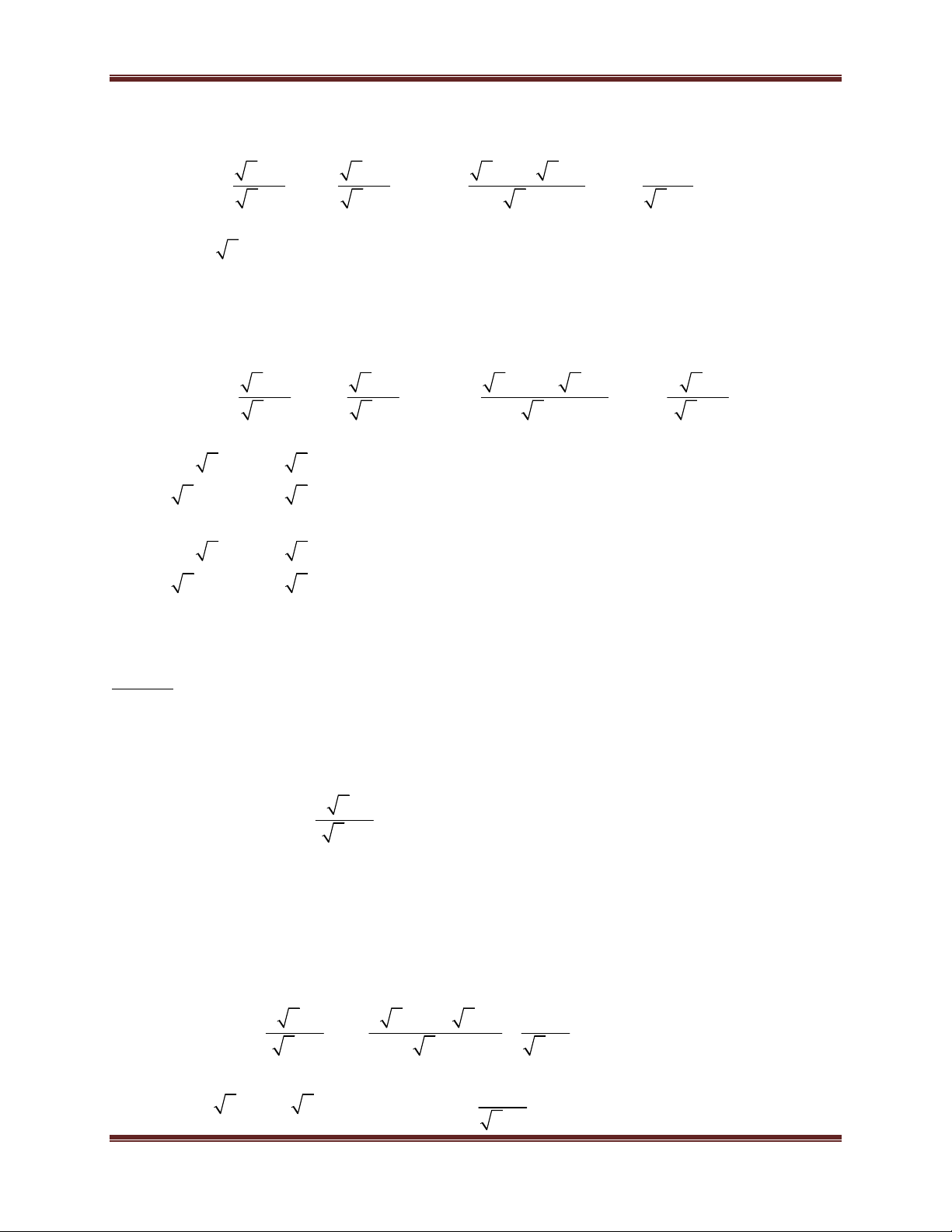
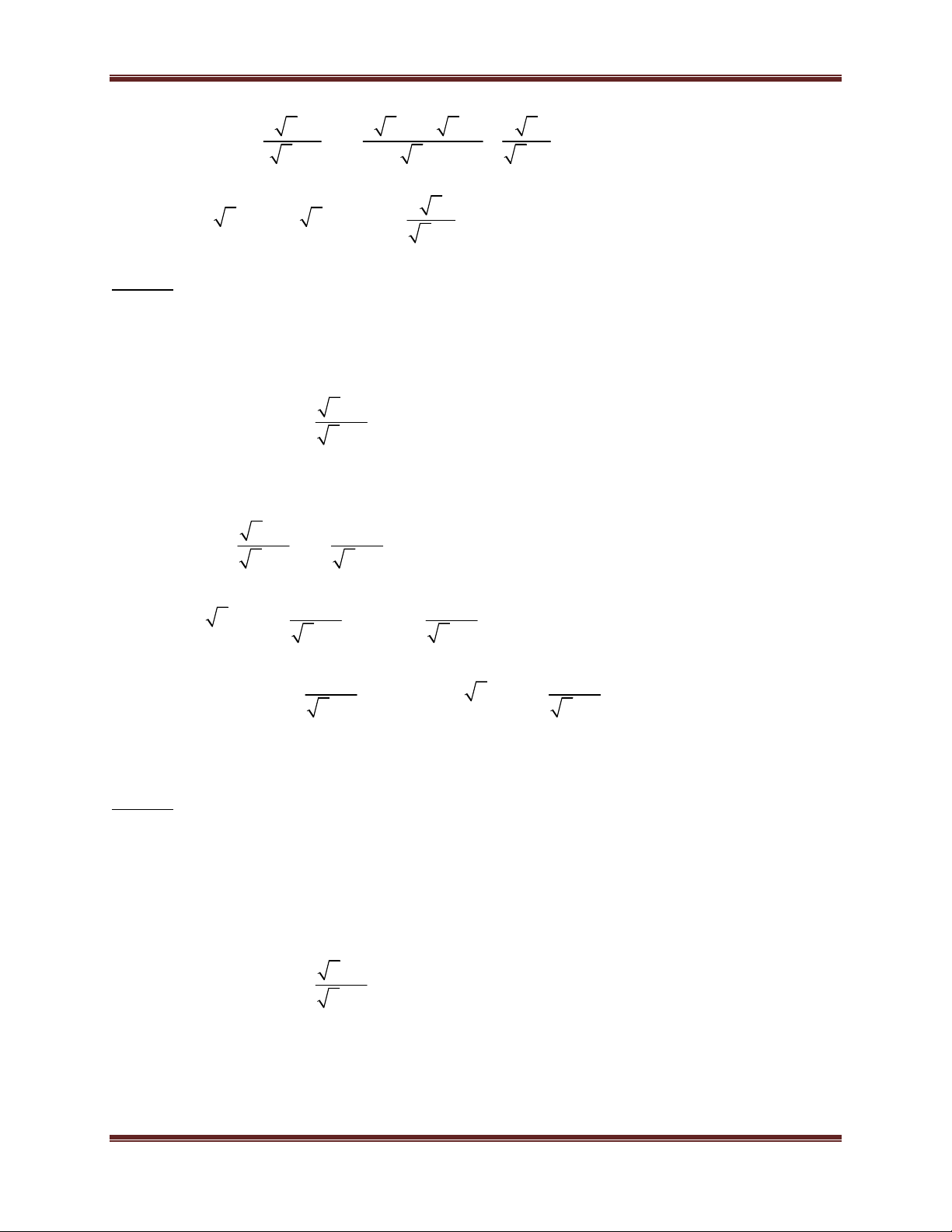
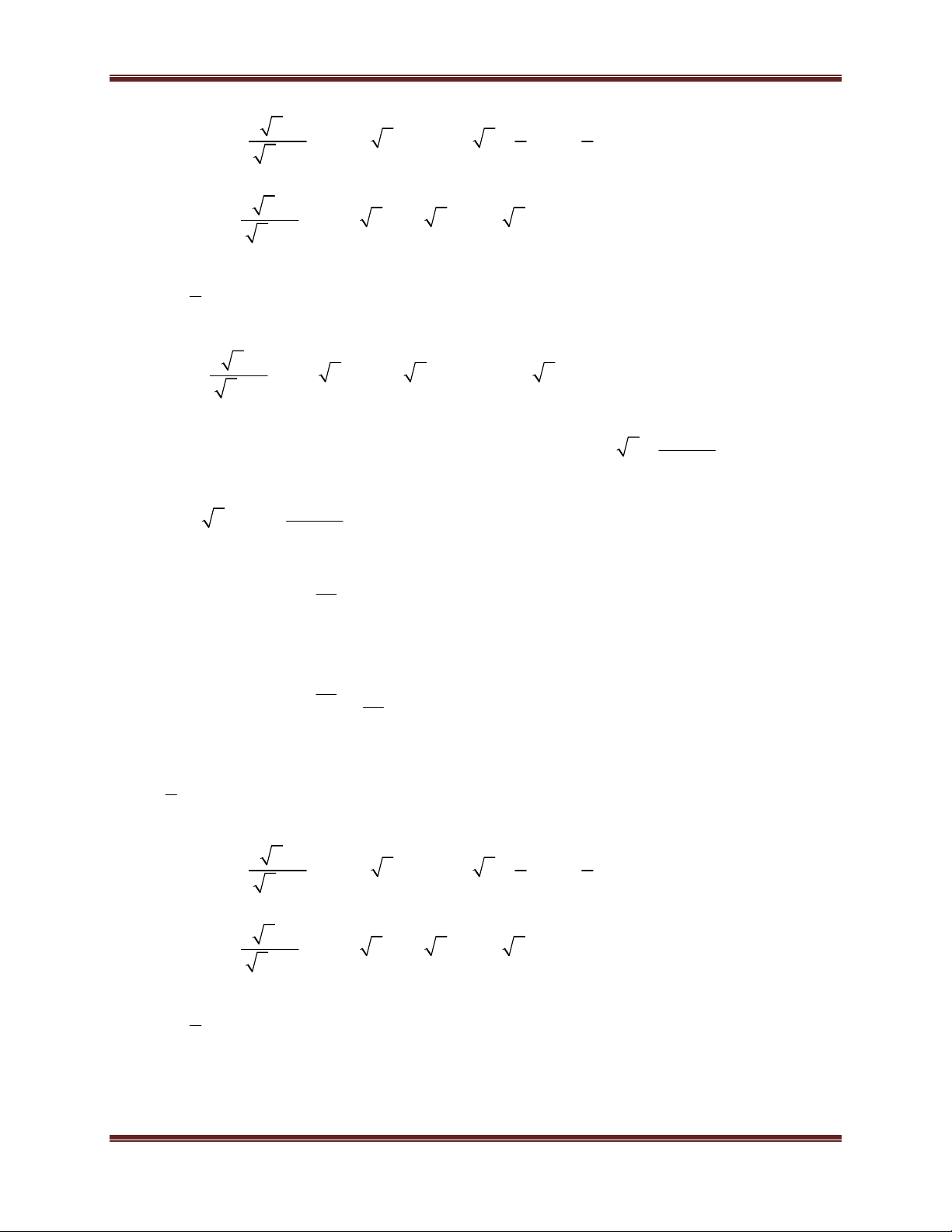
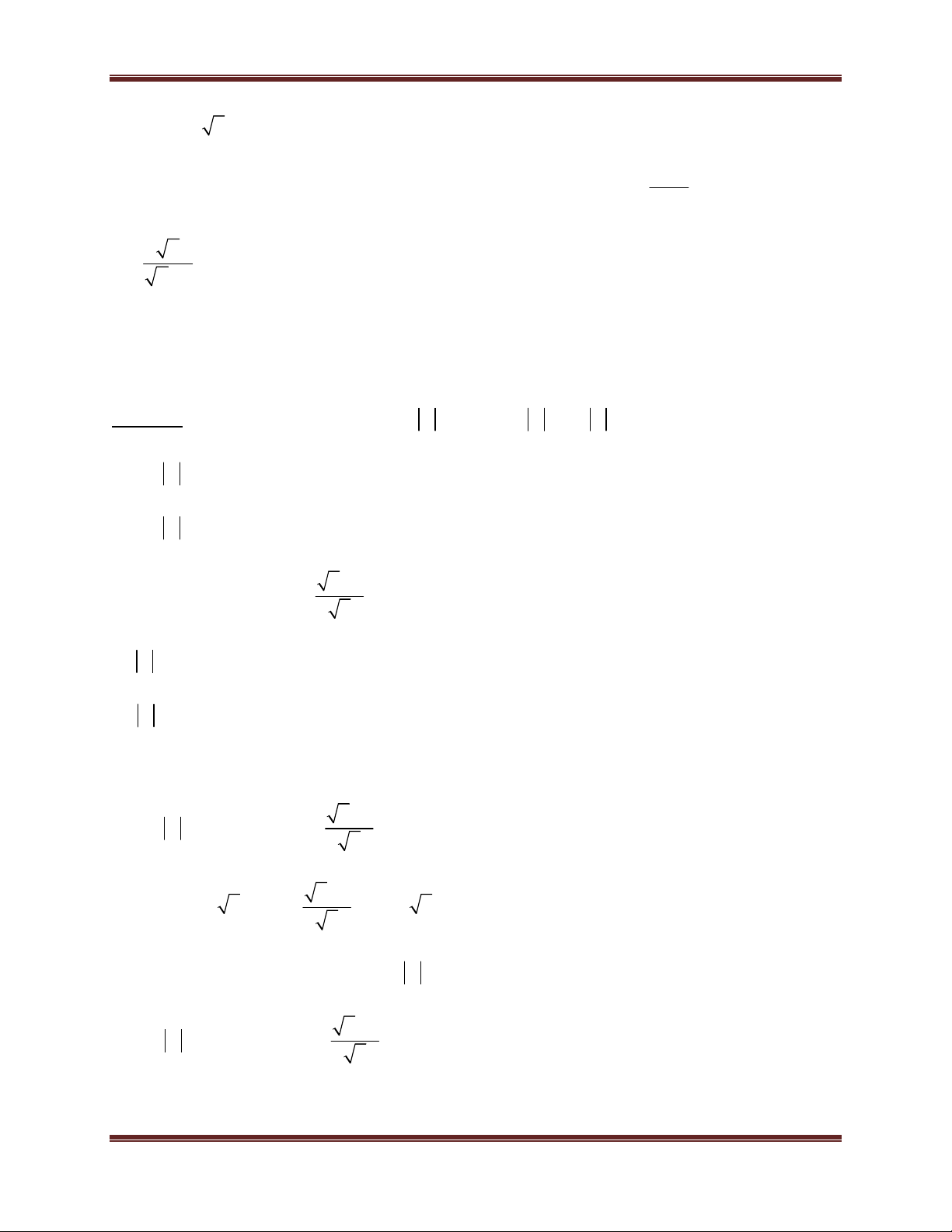
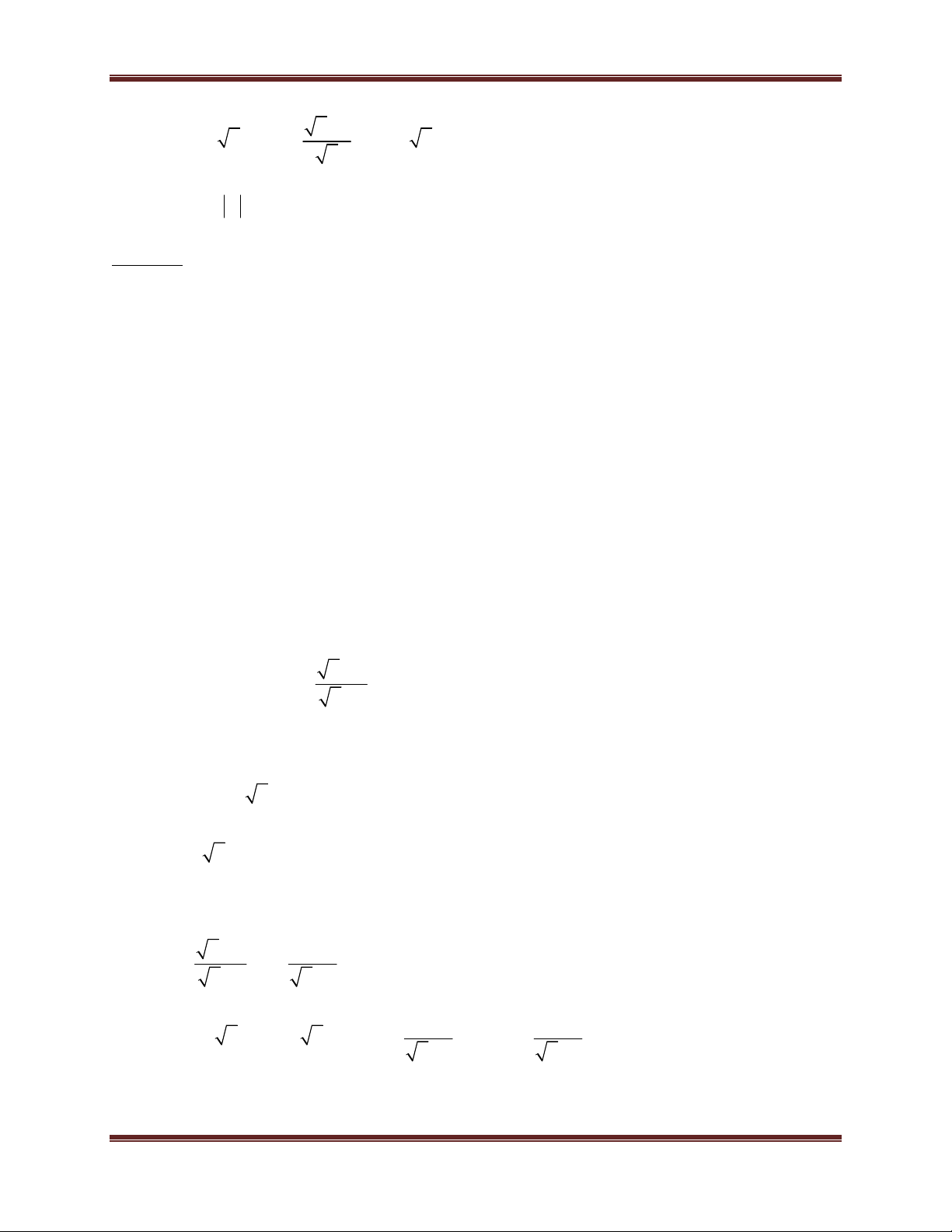
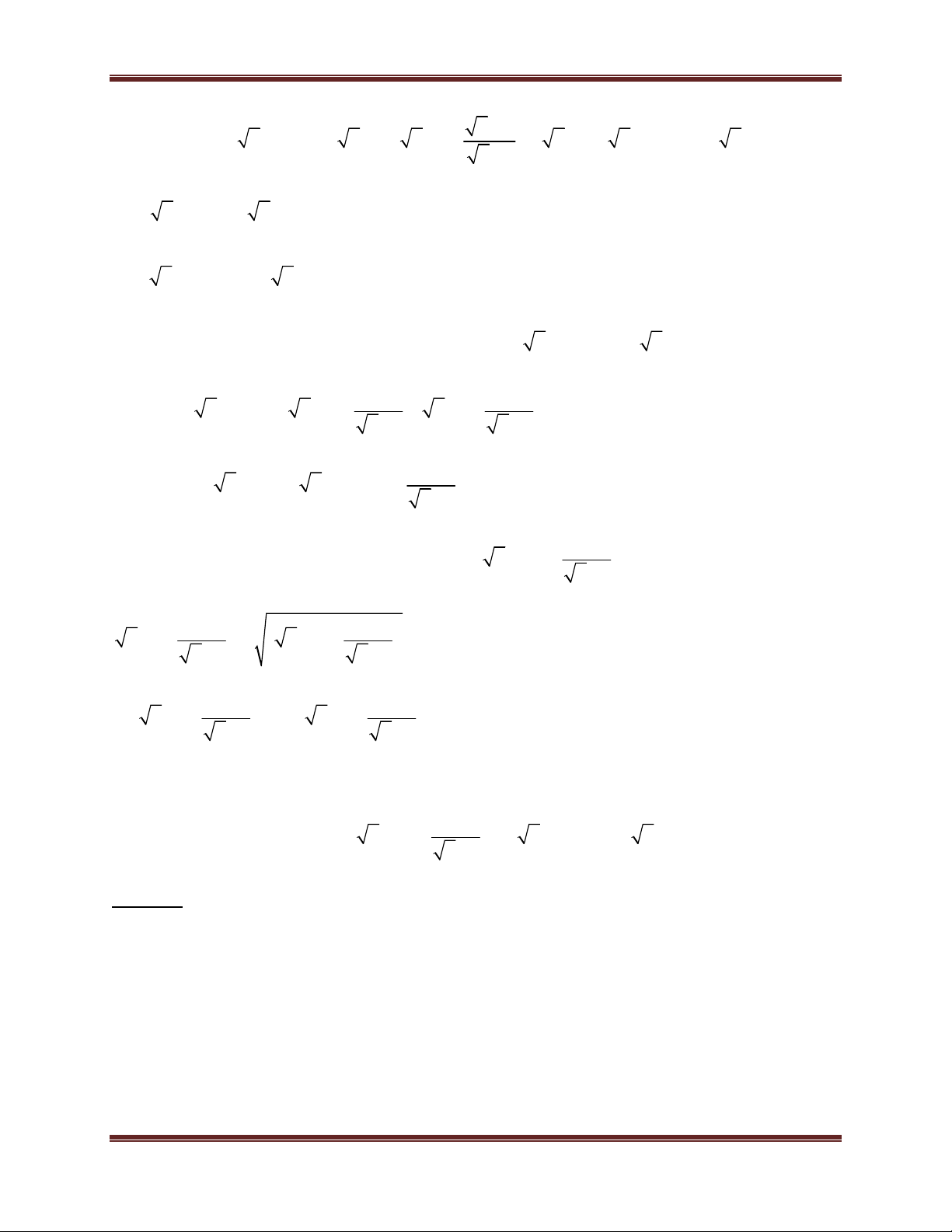
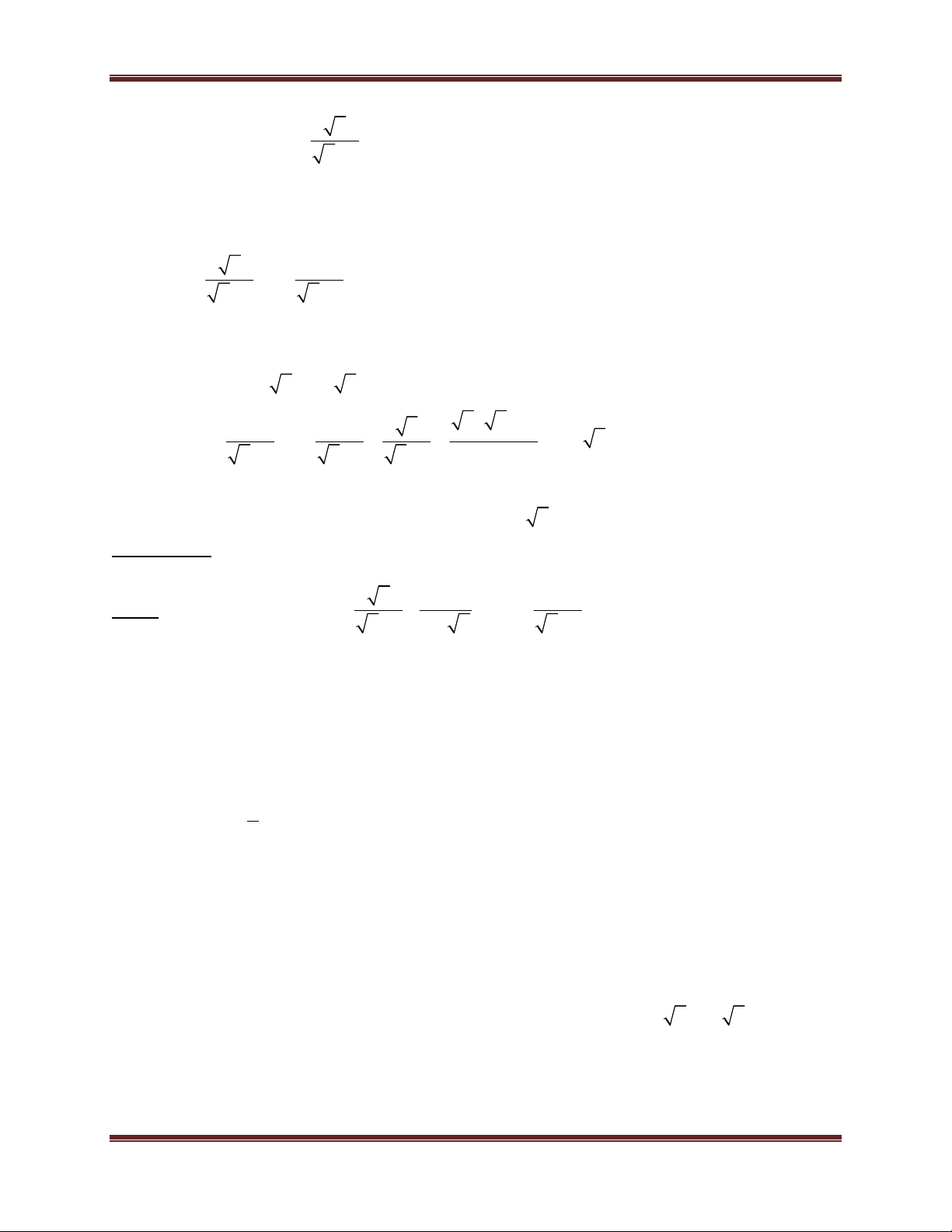
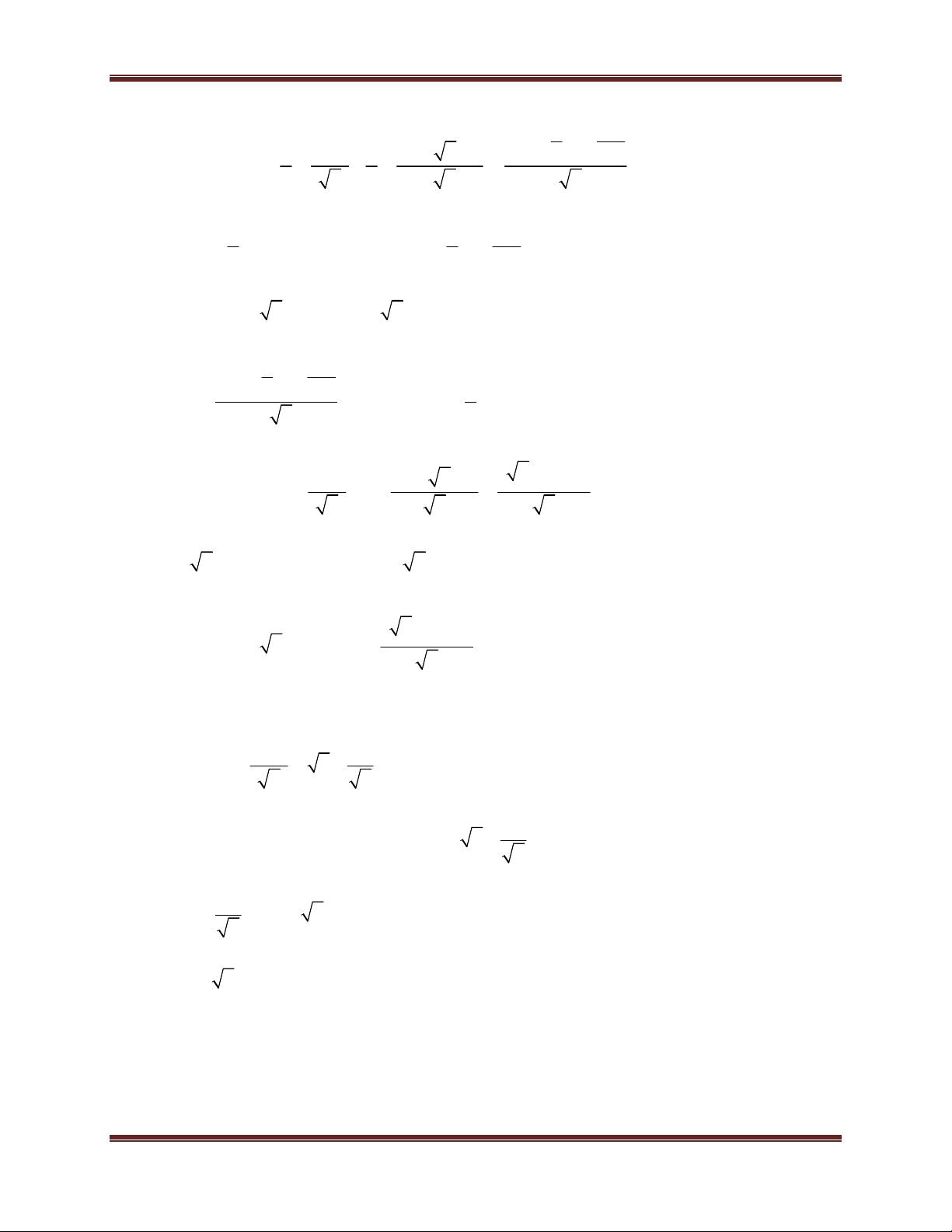
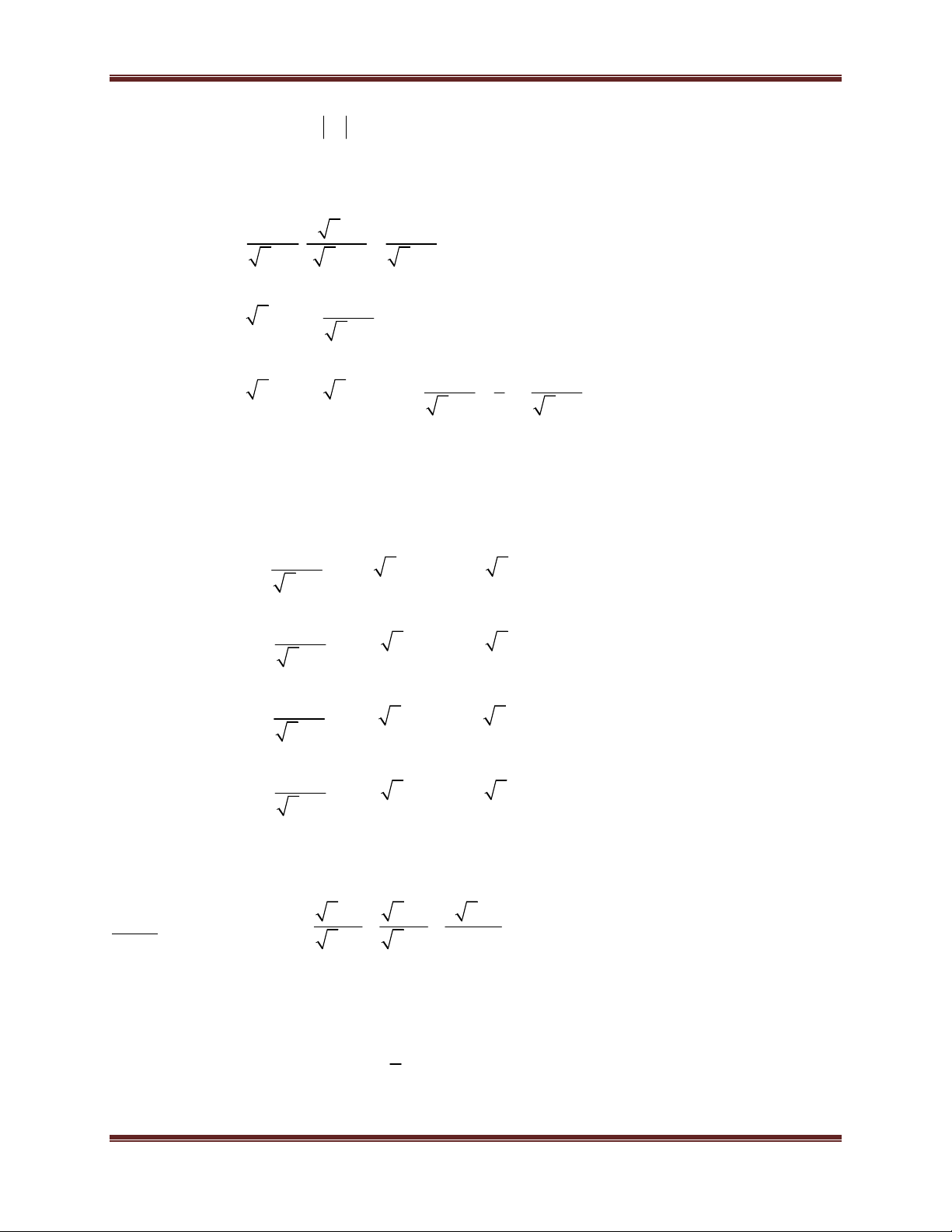
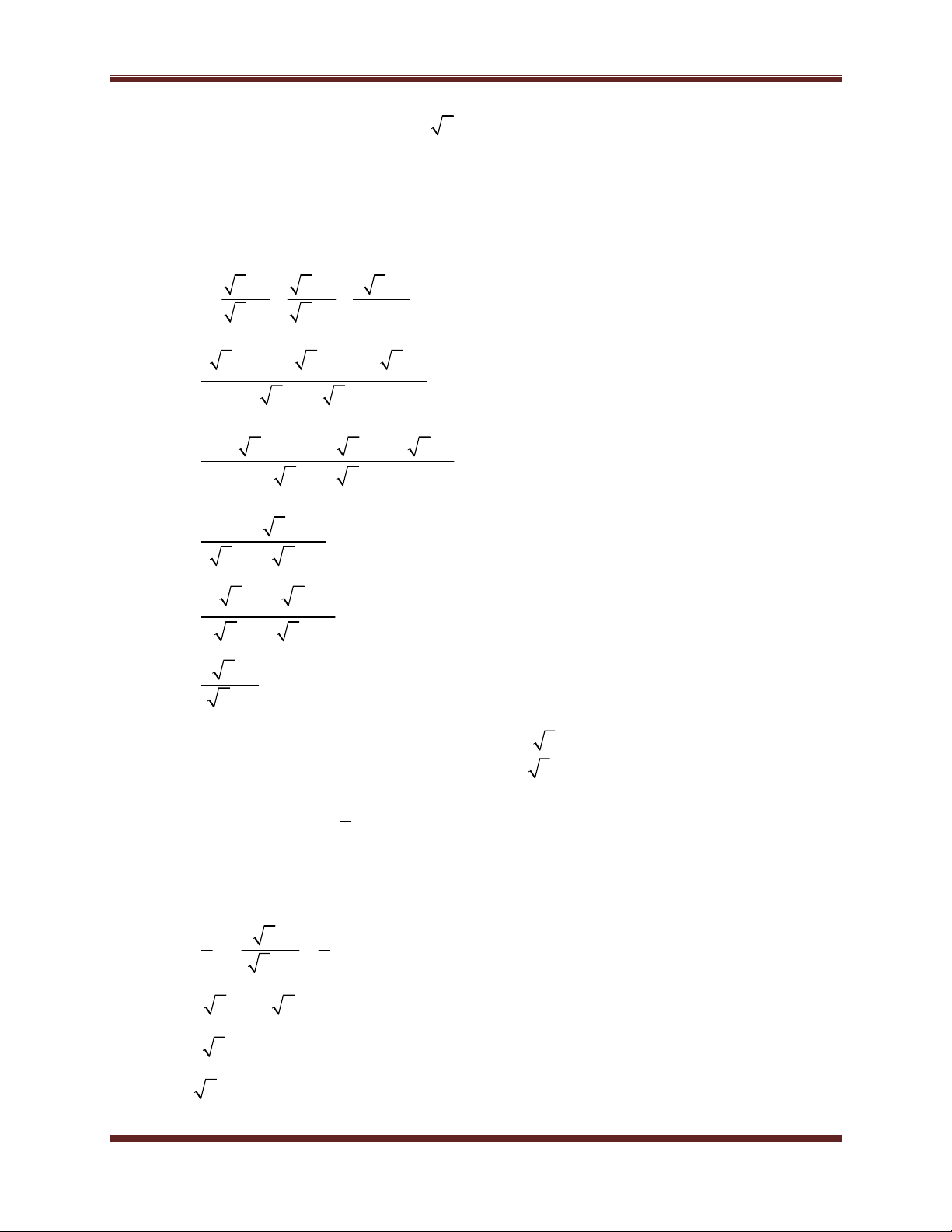
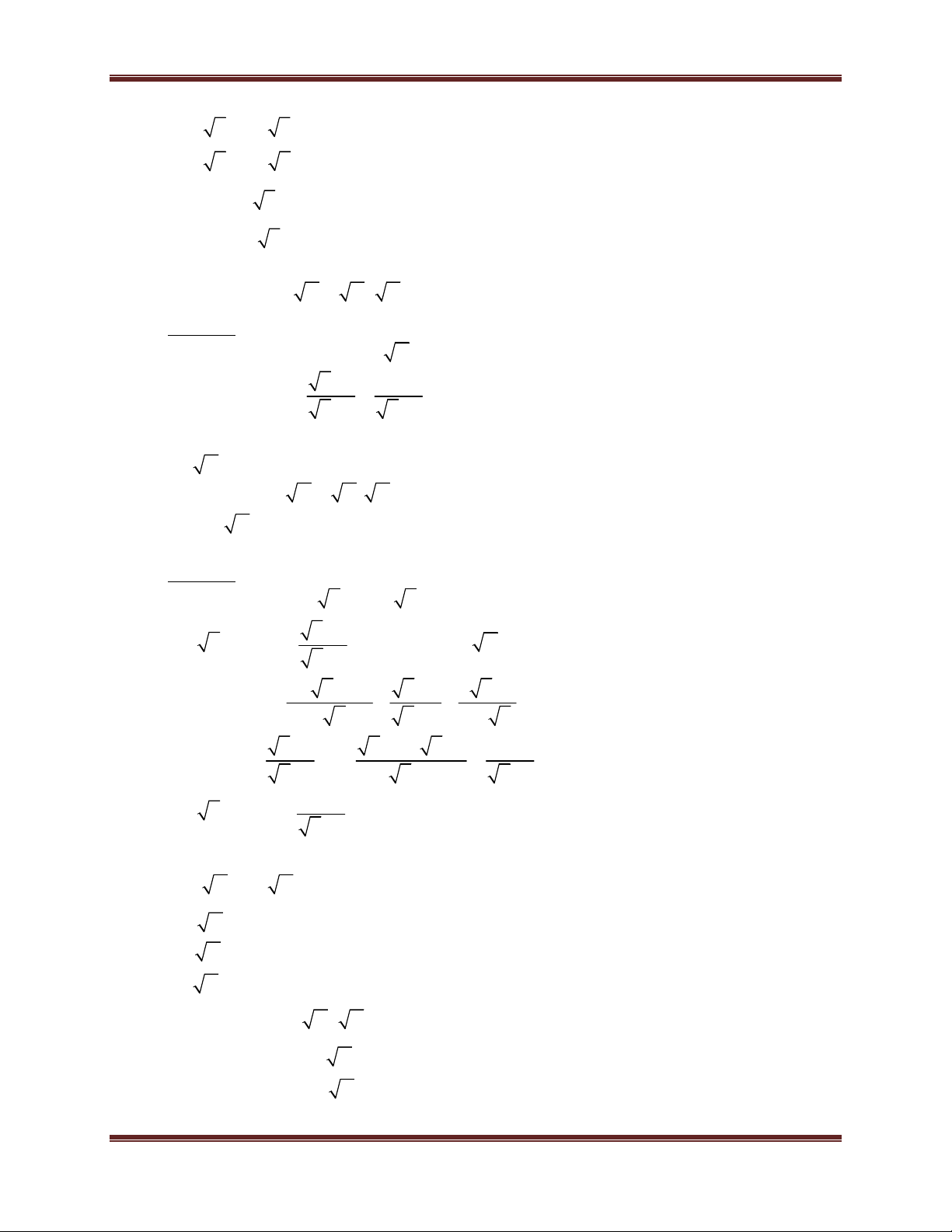
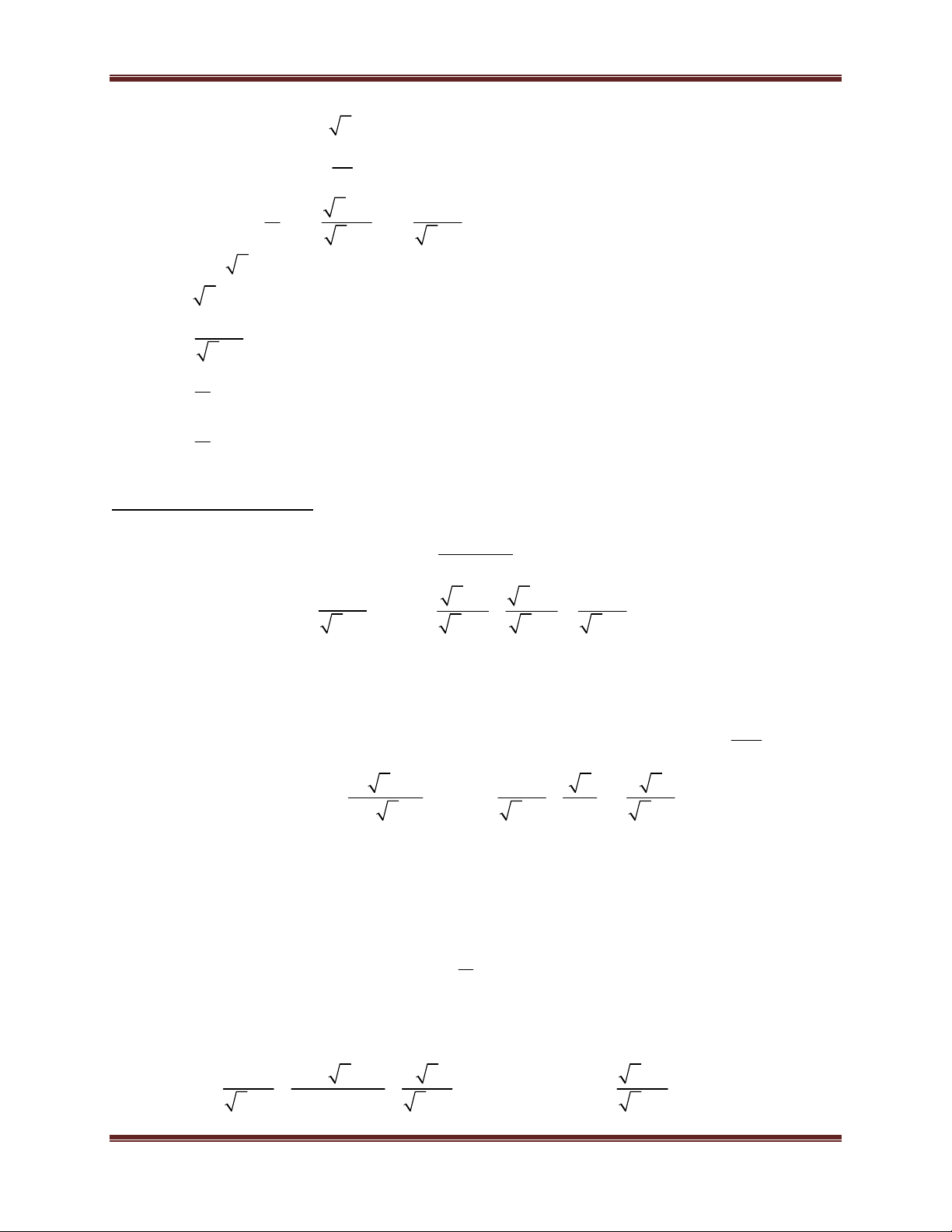
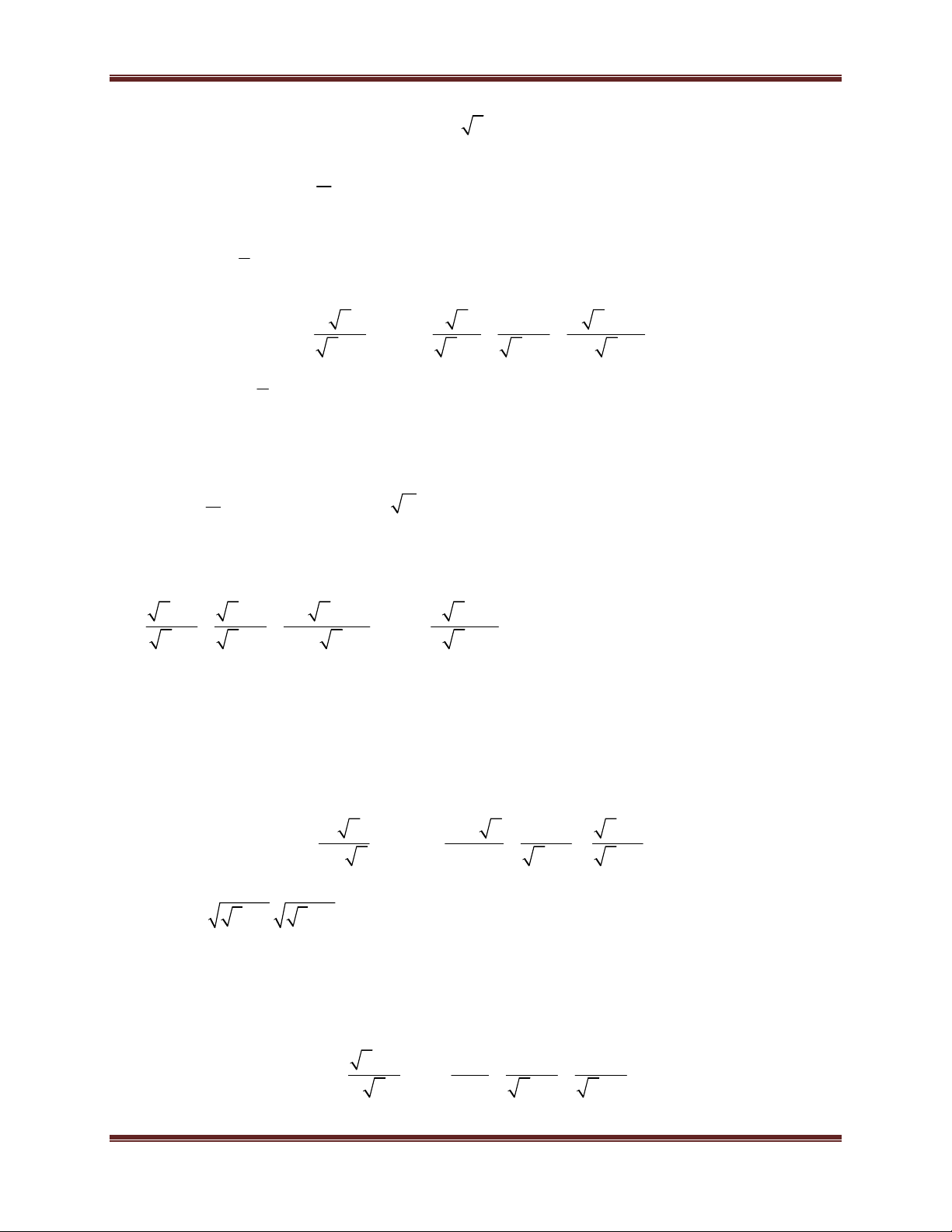
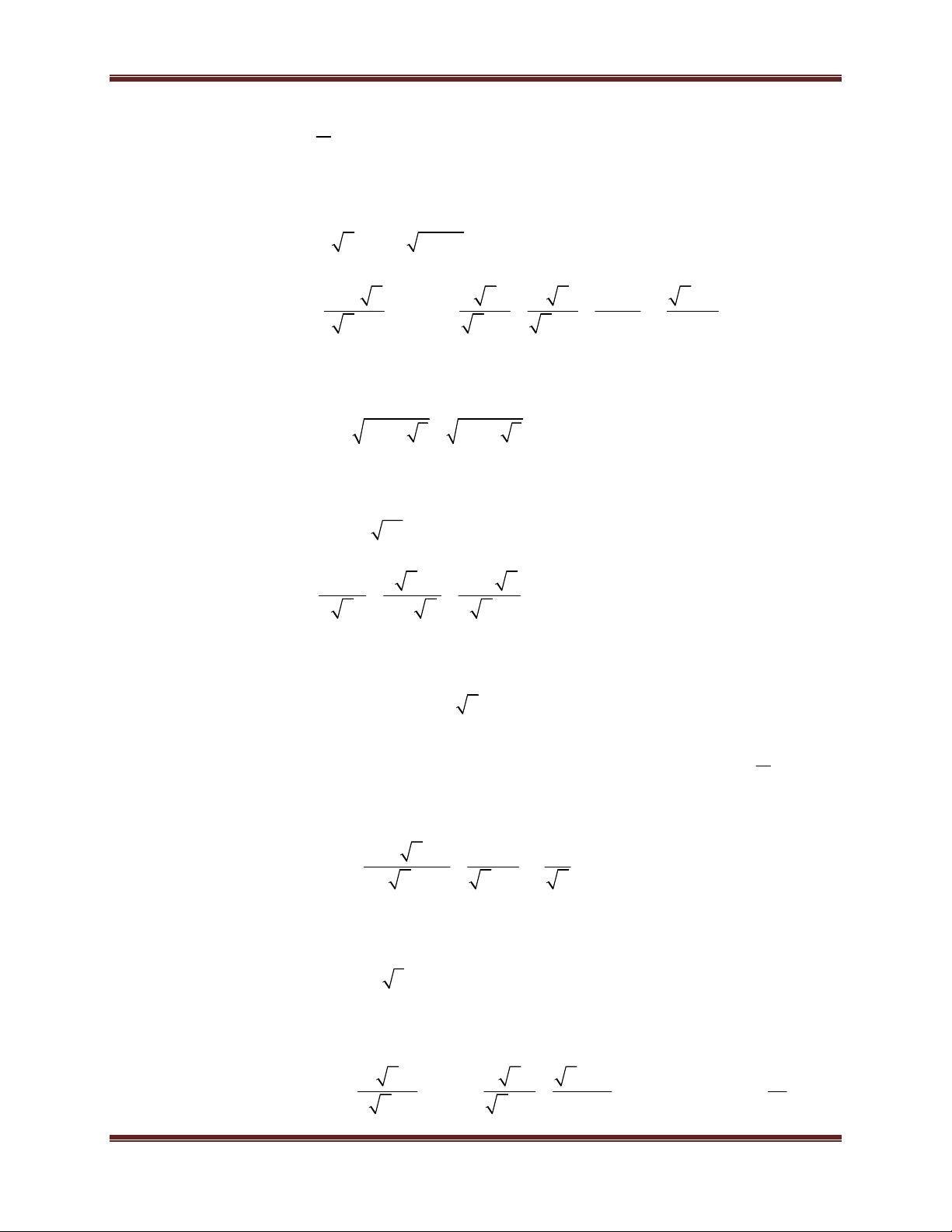
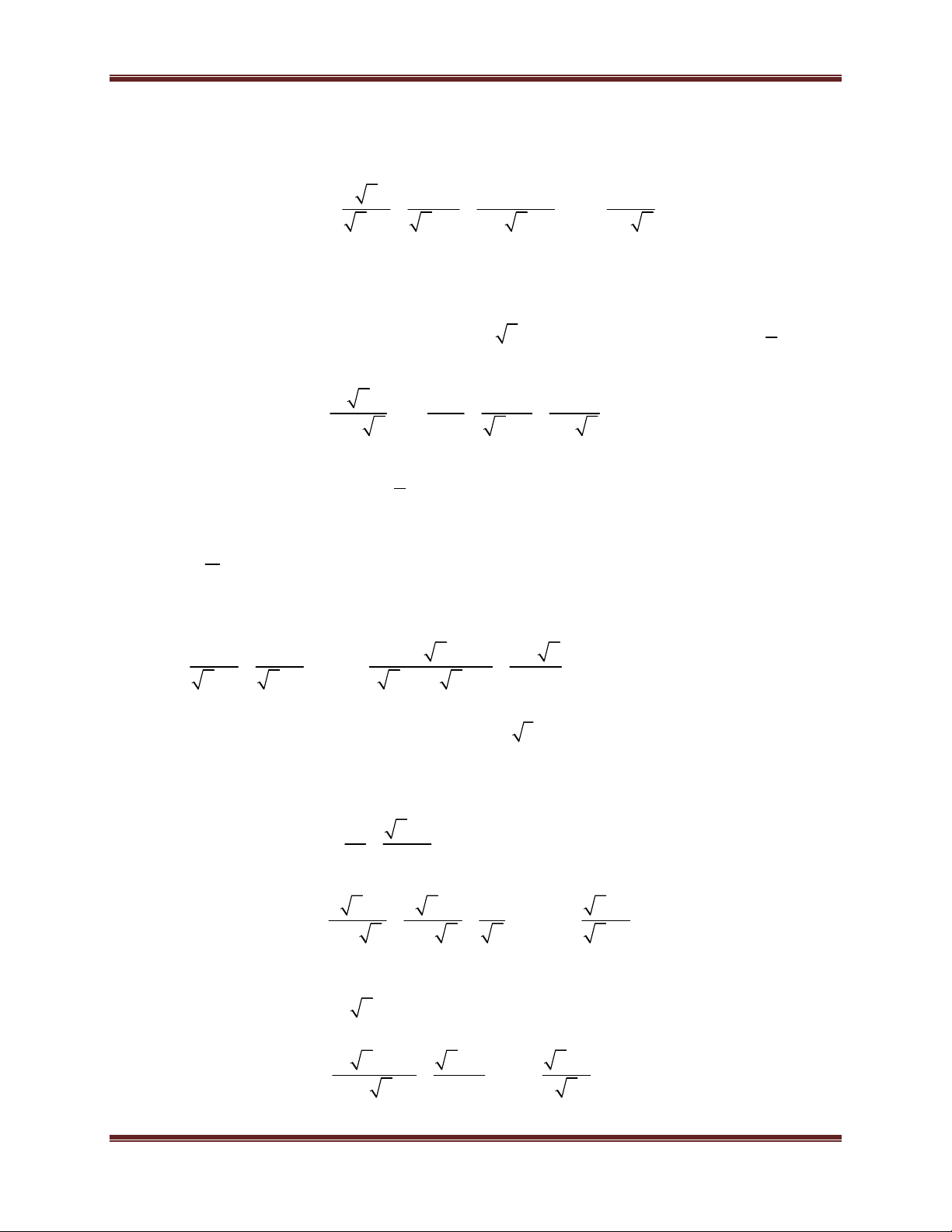
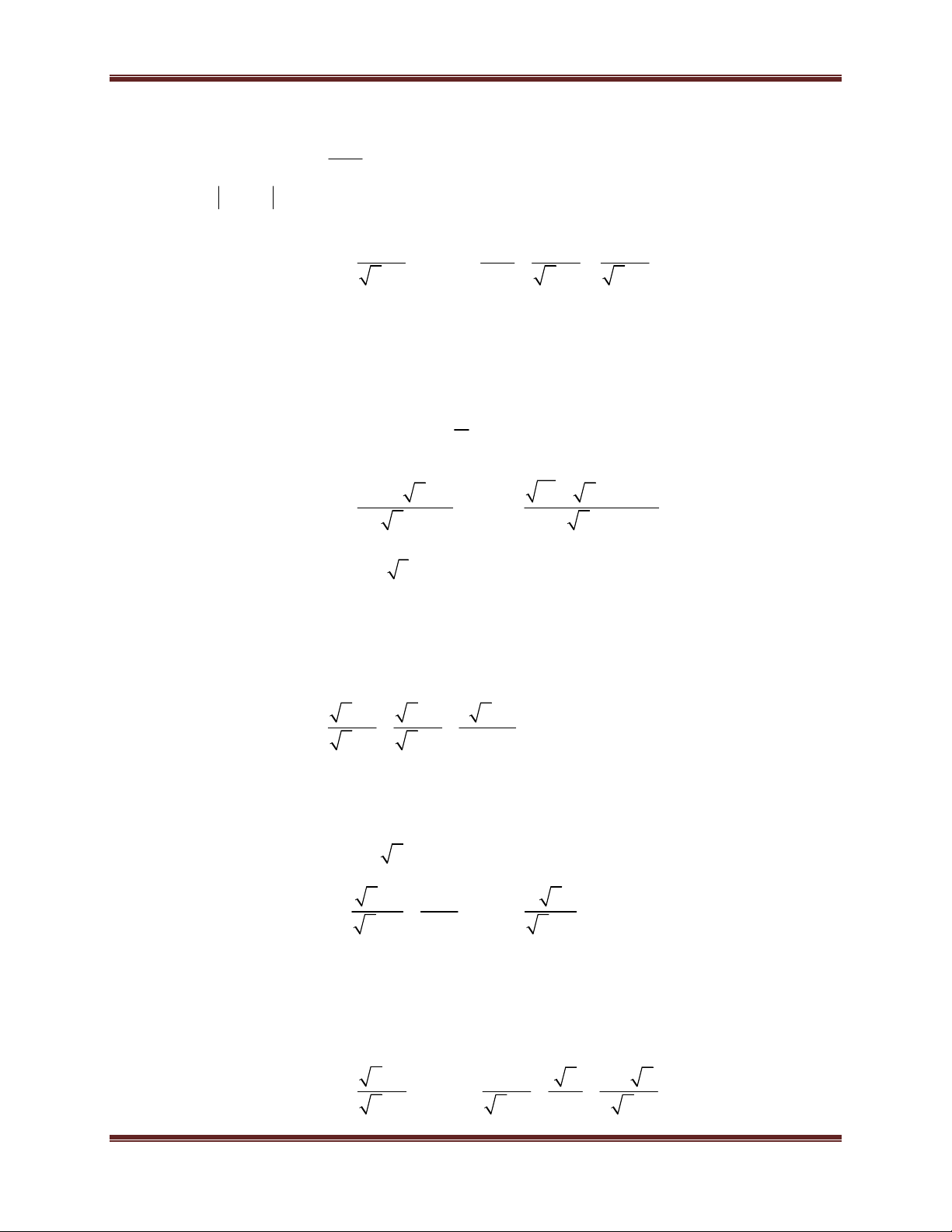
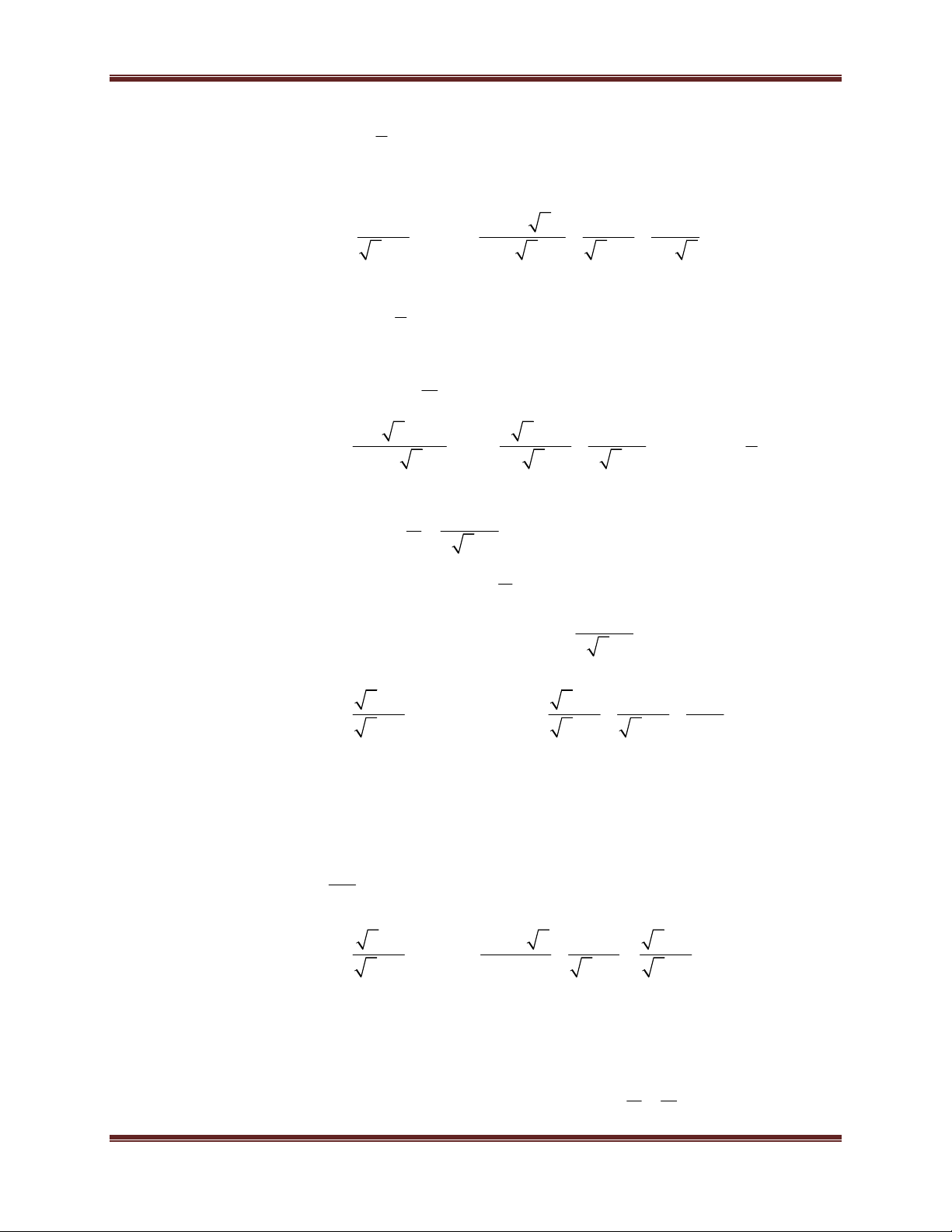
Preview text:

Lê Trung – Uyên Vi
Toán học là đam mê
RÚT GỌN BIỂU THỨC ĐẠI SỐ
VÀ CÁC BÀI TOÁN LIÊN QUAN A-LÝ THUYẾT
1. Kiến thức 6, 7, 8 quan trọng cần nhớ . A M A
a. Tính chất về phân số ( phân thức): 
(M  0, B  0) . B M B
b. Những hằng đẳng thức đáng nhớ  (A + B)2 = A2 + 2AB + B2  (A - B)2 = A2 - 2AB + B2  A2 - B2 = (A - B)(A + B) 
(A + B)3 = A3 + 3A2B + 3AB2 + B3 
A - B)3 = A3 - 3A2B + 3AB2 - B3 
A3 + B3 = (A + B)(A2 - AB + B2) 
A3 - B3 = (A - B)(A2 + AB + B2)
2. Các kiến thức về căn bậc hai  Nếu a ≥ 0, x ≥ 0, a = x  x2 = a  Để
A có nghĩa  A  0  2 A A AB
A. B ( với A  0; B  0) A A  
( với A  0; B  0) B B  2 A B A
B ( với B  0)
Tài liệu tự hoc- luyện thi vào 10 Page 1 Lê Trung – Uyên Vi
Toán học là đam mê  2 A B
A B ( với A  0; B  0)  2
A B   A B ( với A  0; B  0) A AB  
( với AB  0; B  0) B B A A B   ( với B  0) B B C
C( A B)   ( với 2 A  0; A  B ) 2 A B A B C
C( A B )  
( với A  0; B  0 và A B) A B A B
3. CÁC DẠNG BÀI TẬP VỀ RÚT GỌN BIỂU THỨC ĐẠI SỐ VÀ CÁC BÀI TOÁN CÓ LIÊN QUAN
Xét biểu thức A với biến số x
Dạng 1. Rút gọn biểu thức
- Ngoài việc rèn kỹ năng thực hiện các phép tính trong bài toán rút gọn. Học sinh hay quên
hoặc thiếu điều kiện xác định của biến x ( ĐKXĐ gồm điều kiện để các căn thức bậc hai có
nghĩa, các mẫu thức khác 0 và biểu thức chia (nếu có) khác 0)
Dạng 2. Tính giá trị của biểu thức A khi x = m ( với m là số hoặc biểu thức chứa x)
- Nếu m là biểu thức chứa căn x m ( bằng số), trước tiên phải rút gọn; nếu m là biểu thức
có dạng căn trong căn thường đưa về hằng đẳng thức để rút gọn; nếu m là biểu thức ta
phải đi giải phương trình tìm x.
- Trước khi tính giá trị của biểu thức A, học sinh thường quên xét xem m có thỏa mãn
ĐKXĐ hay không rồi mới được thay vào biểu thức dã rút gọn để tính.
Tài liệu tự hoc- luyện thi vào 10 Page 2 Lê Trung – Uyên Vi
Toán học là đam mê x
Ví dụ minh họa : Cho A
, điều kiện x  0, x  1. x 1
a) Tính giá trị của biểu thức A khi x  9.
b) Tính giá trị của biểu thức A khi x  3  2 2.
c) Tính giá trị của biểu thức A biết x thỏa mãn phương trình 2
x  5x  4  0 . Hướng dẫn giải 3 3 a) Có x  9 
x  3  A   3 1 2 2 1 2  2 b) Có x      2 3 2 2 2 1  x    2 2 1  2 1  2 1  A   2 2 x  1 c) Có 2
x  5x  4  0  
. Kết hợp điều kiên: x  0, x  1. x  4 
x  1 (loại) và x  4 (thỏa mãn) 2 Với x  4 
x  2  A   2 . 2 1
Dạng 3. Tìm giá trị của biến x để A k ( với k là hằng số hoặc là biểu thức chứa x)
- Thực chất đây là việc giải phương trình.
- Học sinh thường quên khi tìm được giá trị của x không xét xem giá trị x dó có thỏa mãn ĐKXĐ của A hay không. x 1
Ví dụ minh họa: Cho A
, điều kiện xác định x  0, x  4 . x  2
a) Tìm x biết A  2. 4 x 1 b) Tìm x biết A  . 4
Tài liệu tự hoc- luyện thi vào 10 Page 3 Lê Trung – Uyên Vi
Toán học là đam mê Hướng dẫn giải x 1 a) Có A  2   2 
x 1  2 x  4  x  3  (vô lí) x  2
 không tồn tại x để A  2. 4 x 1 x 1 4 x 1 b) Có A   
 4 x  4  4x  9 x  2 4 x  2 4  x  2 x  4
 4x  5 x  6  0   x  24 x  3  0    3   9  x   x   4  16 9
Kết hợp điều kiện x  0, x  4  x  4 ( loại) và x  ( thỏa mãn) 16 9 4 x 1 Vậy x  thì A  . 16 4
Dạng 4. Tìm giá trị của biến x để A k ( hoặc A k , A k , A k ,…) trong đó k là hằng số
hoặc là biểu thức chứa x.
- Thực chất đây là việc giải bất phương trình.
- Học sinh thường mắc sai lầm khi giải bất phương trình thường dùng tích chéo hoặc sử
dụng một số phép biến đổi sai. x  2
Ví dụ minh họa: Cho A
, điều kiện xác định x  0, x  9 . x  3
a) Tìm x để A  1.
b) Tìm x để A  2 .
Tài liệu tự hoc- luyện thi vào 10 Page 4 Lê Trung – Uyên Vi
Toán học là đam mê Hướng dẫn giải x  2 x  2
x  2  x  3 5 a) Để A  1   1  1  0   0   0 x  3 x  3 x  3 x  3
Mà 5  0  x  3  0  x  9.
Kết hợp điều kiện x  0, x  9  0  x  9
Vậy 0  x  9 thì A  1. x  2 x  2
x  2  2 x  6  x  8 b) Để A  2   2   2  0   0   0 x  3 x  3 x  3 x  3 8    x  0   x  8 x  64 TH1:       9  x  64 . x  9  x  3  0   x  3   8    x  0   x  8 x  64 TH2:      (vô lí)  loại x  9  x  3  0   x  3  
Vậy 9  x  64 thì A  2 .
Dạng 5. So sánh biểu thức A với một số hoặc một biểu thức.
- Thực chất đây là việc đi xét hiệu của biểu thức A với một số hoặc một biểu thức rồi so
sánh hiệu đó với số 0. 2 x 1
Ví dụ minh họa: Cho A
, điều kiện xác định x  0. x 1 a) So sánh A với 2. b) So sánh A với 1. Hướng dẫn giải 2 x 1
2 x 1 2 x  2 1
a) Xét hiệu A  2   2   x 1 x 1 x 1 1 
Có x  0  x  0 
x 1  0 và 1  0 
 0  A  2  0  A  2 . x 1
Tài liệu tự hoc- luyện thi vào 10 Page 5 Lê Trung – Uyên Vi
Toán học là đam mê 2 x 1
2 x 1 x 1 x
b) Xét hiệu A 1  1   x 1 x 1 x 1 x
Có x  0  x  0 và x 1  0 
 0  A 1  0  A  1. x 1
Dạng 6. Chứng minh biểu thức A k ( hoặc A k , A k , A k ) với k là một số.
- Thực chất đây là việc đưa về chứng minh đẳng thức hoặc bất đẳng thức. Ta xét hiệu
A k rồi xét dấu biểu thức. x  3
Ví dụ minh họa: Cho A
, điều kiện x  0. Chứng minh A  1 . x  2 Hướng dẫn giải x  3 1 Cách 1: Có A   1 . x  2 x  2 1 1 Có x  0  x  0   0  1  1 hay A  1 . x  2 x  2 1 1
Cách 2: Xét hiệu A 1  . Có x  0  x  0 
 0 với mọi x  0. x  2 x  2
A 1  0 hay A  1 .
Dạng 7. Tìm giá trị của biến x là số nguyên, số tự nhiên để biểu thức A có giá trị nguyên
- Cách làm: chia tử thức cho mẫu thức, rồi tìm giá trị của biến x để mẫu thức là ước của phần dư (một số)
- Học sinh thường quên kết hợp với điều kiên xác định của biểu thức. x  3
Ví dụ minh họa: Cho A
, điều kiện xác định x  0, x  4, x  9 .Tìm x nguyên để A x  2 có giá trị nguyên
Tài liệu tự hoc- luyện thi vào 10 Page 6 Lê Trung – Uyên Vi
Toán học là đam mê Hướng dẫn giải x  3 5 5 Có A   1
. Để A nhận giá trị nguyên  là số nguyên  x  2 x  2 x  2
x  2 là ước của 5  x  21; 1  ;5;   5 x  2 1 -1 5 -5 x 3 1 7 -3 x 9 (loại) 1 (thỏa mãn) 49(thỏa mãn) loại Vậy x 1; 
49 thì A có giá trị nguyên
Dạng 8. Tìm giá trị của biến x là số thực, số bất kì để biểu thức A có giá trị nguyên
- Học sinh thường nhầm lẫn cách làm của dạng này với dạng tìm giá trị của biến x là số
nguyên, số tự nhiên để biểu thức A có giá trị nguyên.
- Cách làm: sử dụng ĐKXĐ để xét xem biểu thức A nằm trong khoảng giá trị nào, rồi tính
giá trị của biểu thức A và từ đó tìm giá trị của biến x. 2 x 1
Ví dụ minh họa : Cho A
, điều kiện xác định x  0. Tìm x để A có giá trị nguyên. x  2 Hướng dẫn giải 2 x 1 5 Cách 1: Có A   2  x  2 x  2 5 5 Có x  0 
x  0  x  2  0   0  2   2  A  2 x  2 x  2 5 5 5 1 1 Lại có x  0  x  0 x  2  2    2     A   x  2 2 x  2 2 2 1 Vậy 
A  2 mà A   A0  ;1 2
Tài liệu tự hoc- luyện thi vào 10 Page 7 Lê Trung – Uyên Vi
Toán học là đam mê 2 x 1 1 1 +) Với A  0 
 0  2 x 1  0  x   x x  2 2 4 2 x 1 +)Với A  1   1  2 x 1  x  2 
x  3  x  9 x  2  1 
Vậy x   ;9 thì A có giá trị nguyên.  4  2 x 1 Cách 2: A
Ax  2  2 x 1   A  2 x  1   2A x  2 2  A 1
Dễ thấy A  2 không là nghiệm của phương trình  A  2  x A 2 2A 1 Vì x  0  x  0   0 A  2  1  2A 1  0  A  Th1:    2 (vô lí)  Loại A  2  0   A  2   1  2A 1  0  A  1  Th2:    2   A  2 A  2  0 2   A  2  1 Vậy 
A  2 mà A   A0  ;1 2 2 x 1 1 1 +) Với A  0 
 0  2 x 1  0  x   x x  2 2 4 2 x 1 +)Với A  1   1  2 x 1  x  2 
x  3  x  9 x  2  1 
Vậy x   ;9 thì A có giá trị nguyên.  4 
Tài liệu tự hoc- luyện thi vào 10 Page 8 Lê Trung – Uyên Vi
Toán học là đam mê
Dạng 9. Tìm giá trị của tham số để phương trình hoặc bất phương trình có nghiệm
- Học sinh cần biết cách tìm điều kiện để phương trình hoạc bất phương trình có nghiệm.
+ Học sinh đưa biểu thức chưa căn về dạng bậc hai sử dụng điều kiện để phương trình bậc hai có nghiệm
+Cô lập tham số m , tìm miền giá trị của vế chứa biến x rồi suy ra điều kiện để phương
trình có nghiệm thì biể thức chứa tham số m nằm trong miền giá trị của vế chứa biến x
Ví dụ minh họa 1: Cho A x
x , điều kiện xác định x  0; x  1. Tìm m để phương trình
A m có nghiệm x . Hướng dẫn giải 2 1 1  1  1
Có A m x
x m x x    m x    m   . 4 4  2  4 2 2  1  1  1  1 Do x  0  x      x    0  m  0    2  4  2  4
Vì x  0; x  1  x  1  x x  2  m  2
Vậy m  0; m  2 thì phương trình A m có nghiệm x . x x 1
Ví dụ minh họa 2: Cho A
, điều kiện xác định x  0; x  . Tìm m để phương 3 x 1 9
trình A m có nghiệm x . Hướng dẫn giải x x
Có A m
m x  (1 3m) x m  0 (1) 3 x 1 1 1 Đặt t
x , có x  0; x
t  0;t  9 3 2
(1)  t  (1 3m)t m  0 (2)
Vì a  1 khác 0  (2) luôn là phương trình bậc hai Ta có: 2 2
  (1 3m)  4m  9m 10m 1 1
(1) Có nghiệm khi (2) có ít nhất một nghiệm t  0 và t  3
TH1: Phương trình (2) có nghiệm khi t = 0  m = 0 1
TH2: Phương trình (2) có nghiệm kép t  0;t  3
Tài liệu tự hoc- luyện thi vào 10 Page 9 Lê Trung – Uyên Vi
Toán học là đam mê  1 m  0      9 m 1 
Với m  1  t  1 (thỏa mãn) 1 4  Với m   t  (không thỏa mãn) 9 3 1
TH3: Phương trình (2) có hai nghiệm trái dấu và t  3 ac  0 m  0   2   1  1  4  m  0
 (1 3m).  m  0  0      3   3 9
TH4: Phương trình (2) có hai nghiệm phân biệt cùng dương
(m 1)(9m 1)  0  1  1   3m  0  0  m  9 m  0  1
Kết hợp điều kiện lại 0  m  hoặc m = 1 9 x
Ví dụ minh họa 3: Cho A 
, điều kiện xác định x  0 . Tìm m để phương trình x 1 A  m có nghiệm. Hướng dẫn giải Ta có: A  m x   m x 1  m. x  m  x  1 m x  m (1)
+) TH1: Nếu m  1 thì phương trình (1) có 0. x  1 (vô lý) m
+) TH2: Nếu m  1 thì phương trình (1) có x  (2) 1 m
Tài liệu tự hoc- luyện thi vào 10 Page 10 Lê Trung – Uyên Vi
Toán học là đam mê Vì x  0  x  0 m
=> Để phương trình A  m có nghiệm thì phương trình (2) cần có  0 (3) 1 m x Vì  0  m  0 x 1
Từ (3) suy ra 1 m  0  m  1
Vậy với 0  m  1 thì phương trình A  m có nghiệm.
Dạng 10. Tìm giá trị của biến x để A A (hoặc A A ; A A ;...)
- Nếu A A  A < 0
- Nếu A A  A  0 x 1
Ví dụ minh họa: Cho A
, điều kiện xác định x  0 . Tìm x biết x a) A A b) A A Hướng dẫn giải x 1
a) Có A A  A < 0   0 x x 1
Mà x  0  x  0   0 
x 1  0  x  1. x
Kết hợp điều kiện ta có 0  x  1 thì A A x 1
b) Có A A  A  0   0 x
Tài liệu tự hoc- luyện thi vào 10 Page 11 Lê Trung – Uyên Vi
Toán học là đam mê x 1
Mà x  0  x  0   0 
x 1  0  x  1. x
Vậy x  1 thì A A
Dạng 11. Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức A.
- Học sinh cần biết cách tìm cực trị của phân thức ở một số dạng tổng quát.
- Học sinh cần đưa biểu thức rút gọn A về một trong những dạng sau để tìm cực trị:
+ Tử thức và mẫu thức là một số hoặc là một biểu thức có dấu xác định trong tập ĐKXĐ
+ Biến đổi biểu thức A thành một hằng đẳng thức có chứa biến x.
+ Biến đổi biểu thức A thành một tổng của hai (hoặc nhiều) số dương rồi áp dụng bất
đẳng thức Cô – si hoặc một vài bất đẳng thức phụ.
- Học sinh thường mắc sai lầm khi chỉ chứng minh biểu thức A k ( hoặc A k ) chưa chỉ
ra dấu bằng nhưng đã kết luận cực trị của biểu thức A. x  2
Ví dụ minh họa: Cho A
, điều kiện xác định x  0 . x 1
a) Tìm giá trị lớn nhất của A.
b) Đặt B   x  3 x  4.A. Tìm giá trị nhỏ nhất của B . c) Đặt C
x 1 A . Tìm giá trị nhỏ nhất của C . Hướng dẫn giải x  2 1 a) Có A   1 . x 1 x 1 1 1
Vì x  0  x  0  x 1  1   1  1  2  A  2 . x 1 x 1
Vậy giá trị lớn nhất của A bằng 2. Dấu “=” xẩy ra khi và chỉ khi x  0 .
Tài liệu tự hoc- luyện thi vào 10 Page 12 Lê Trung – Uyên Vi
Toán học là đam mê x  2
b) Có B   x  3 x  4.A   x   1  x  4.
  x  4 x  2  x  2 x  8 x 1 x
x     x  2 2 1 9 1  9 . 2 2 Có  x   1  0   x   1  9  9   B  9  .
Vậy giá trị nhỏ nhất của B là 9 . Dấu “=” xẩy ra  x  2 1  0 
x  1  x  1. 1 1 c) Có C x 1 A x  2   x 1 1 x 1 x 1 1
Có x  0  x  0  x 1  0 và  0 x 1 1
Áp dụng bât đẳng thức Cô – si với 2 số dương x 1 và ta có: x 1 1   x     x   1 1 2 1 .  x 1  x 1  1 1  x 1  2  x 1
1  3  C  3. x 1 x 1
Vậy giá trị nhỏ nhất của C bằng 3. 1
Dấu “=” xẩy ra khi và chỉ khi x 1 =   x  2 1  1 
x 1  1  x  0 . x 1
Dạng 12: Tìm giá trị lớn nhất, giá trị nhỏ nhất của A khi x N .
+ Học sinh chú ý bài toán thường cho dưới dạng điều kiện xác định x a, x b trong đó
a b . Ta phải tính giá trị với x là các số tự nhiện thuộc  ;
a b và trường hợp x là số tự nhiên lớn hơn b .
Tài liệu tự hoc- luyện thi vào 10 Page 13 Lê Trung – Uyên Vi
Toán học là đam mê x
Ví dụ minh họa: Cho A
, điều kiện xác định x  0; x  1.Với x   và x  1 x 1
Tìm giá trị lớn nhất của biểu thức . A Hướng dẫn giải x 1 Ta có: A   1 x 1 x 1
Với x   và x  1, ta xét các trường hợp:
TH1. x  0 thì A  0 .
TH2. Nếu x  2 thì x 1  2 1 2  2   1 1 1 2 Do đó: A  1  1    2  2 x 1 2 1 2 1 2 1
Dấu “=” xảy ra khi x  2 .
So sánh các trường hợp của P , ta thấy: max P  2  2 khi và chỉ khi x  2 . B. BÀI TẬP x 2 1
Bài 1. Cho các biểu thức : A   và B  ( với x > 0; x  1) x 1 x x x 1
1. Tính giá trị của biểu thức B khi x  9
2. Đặt C A : B , rút gọn biểu thức C
3. Tìm giá trị của x để C  3 1 4. So sánh C với 4 5. Chứng minh C  2
6. Tìm x nguyên để biểu thức C có giá trị nguyên
7. Tìm giá trị nhỏ nhất của biểu thức C
8. Tìm các giá trị của m để nghiệm x thoản mãn bất phương trình :  x.C x m  3
Tài liệu tự hoc- luyện thi vào 10 Page 14 Lê Trung – Uyên Vi
Toán học là đam mê Hướng dẫn giải 1 1
1. Với x  9 (thỏa mãn ĐKXĐ) thay vào biểu thức B, ta được : B   9 1 8 1
Vậy khi x  9 thì giá trị của biểu thức B  8
2. Đặt C A : B , rút gọn biểu thức C x 2 1 C  (  ) : x 1 x x x 1 x 2 1 C  (  ) : x 1 x ( x 1) x 1 2 ( x )  2 x 1 C  . x ( x 1) 1
(x  2)( x 1) C x ( x 1) x  2 C x 3. ĐKXĐ: x > 0; x  1 Để C  3 x  2   3 x x  2 3 x    0 x x
x  3 x  2  0 (*)
Giải phương trình (*) ta suy ra được : x  1 ( loại) và x  4 ( thỏa mãn ĐKXĐ)
Vậy để C  3 thì x  4
Tài liệu tự hoc- luyện thi vào 10 Page 15 Lê Trung – Uyên Vi
Toán học là đam mê 2  1  127 2x   1 x  2 1 4x x  8    4  16 4. Xét hiệu C      4 x 4 4 x 4 x 2 2  1   1  127 Vì 2x   0  
với mọi x nên 2x    0    4   4  16
Vì x  0 nên x  0 suy ra 4 x  0 2  1  127 2x      4  16 1 Suy ra  0 . Do đó C  4 x 4     x x x x  2 1 1 2 2 2
5. Xét hiệu C  2   2   x x x Vì  x  2 1
 0 với mọi x nên  x  2 1 1  0  x  2 1 1
Vì x  0 nên x  0 , suy ra  0 . Do đó C  2 x 6. ĐKXĐ: x > 0; x  1 x  2 2 Ta có : C   x x x 2
Để giá trị của biểu thức C nguyên thì x  nguyên x 2 Suy ra  Z x là ước của 2 x
Từ đó x nhận các giá trị 1 ; 2 nên x nhận các giá trị x  1 (loại) và x  4 ( TMĐK)
Khi đó với x  4 thì C có giá trị là 3
Vậy với x  4 thì biểu thức C có giá trị nguyên
Tài liệu tự hoc- luyện thi vào 10 Page 16 Lê Trung – Uyên Vi
Toán học là đam mê x  2 2 7. Ta có : C   x x x 2
Áp dụng bất đẳng thức Cô – si với hai số dương x và , ta được : x 2 x   2 2 xA  2 2 min 2 Dấu “ = ” xảy ra  x
x  2 ( thỏa mãn ĐKXĐ) x
Vậy giá trị nhỏ nhất A  2 2  x  2 min
8. Ta có :  x.C x m  3
Suy ra : x x 1 m  0  x
x 1 m  0 1 5  x x   m   0 4 4 2  1  5  x   m   0    2  4 2  1  5  x    m    2  4 2  1  1
Vì x  0 nên x  0 , suy ra x      2  4 2 1  1  5 1 5 Suy ra  x    m    
mm  1 4  2  4 4 4
Vậy với m  1 thì x thoản mãn bất phương trình :  x.C x m  3
Tài liệu tự hoc- luyện thi vào 10 Page 17 Lê Trung – Uyên Vi
Toán học là đam mê
Bài 2. Cho các biểu thức :  x  3 x   9  x x  3 x  2  4 x  8 M   1 :     và N   x 9   x x 6 2 x x 3           x  3
(với x  0; x  4; x  9) 1. Rút gọn biểu thức M
2. Tìm x để M M
3. Đặt Q M .N , tìm các giá trị của x để biểu thức Q có giá trị nguyên. Hướng dẫn giải 1. Rút gọn biểu thức M  x  3 x   9  x x  3 x  2  M   1 :      x 9   x x 6 2 x x 3           3   x  3
9  x   x  3 x  3   x  22 M  :
x 3 x 3
x  2 x 3 
x  2 x 3 3  M  . x  3   x  22 3 M x  2
2. ĐKXĐ : x  0; x  4; x  9
Để M M M  0 3   0 x  2  x  2  0  x  2  x  4
Kết hợp với ĐKXĐ: x  0 , suy ra 0  x  4
Tài liệu tự hoc- luyện thi vào 10 Page 18 Lê Trung – Uyên Vi
Toán học là đam mê
Vậy với 0  x  4 thì M M
3. ĐKXĐ : x  0; x  4; x  9 3 4 x  8 12
Q M .N  .  x  2 x  3 x  3 12 Vì x  0  x  0   0 x  3 1 1 12 Vì x  0  x  0  x  3  3     4 x  3 3 x  3 Do đó: 0  Q  4
Mà Q Z , suy ra Q 1; 2; 3;  4 12 TH1: Q  1   1  x  3  12 
x  9  x  81 ( thỏa mãn ĐKXĐ) x  3 12 TH2: Q  2   2  x  3  6 
x  3  x  9 ( loại) x  3 12 TH3: Q  3   3  x  3  4 
x  1  x  1 ( thỏa mãn ĐKXĐ) x  3 12 TH4: Q  4   4  x  3  3 
x  0  x  0 ( thỏa mãn ĐKXĐ) x  3
Vậy để biểu thức Q có giá trị nguyên thì x 0; 1;  81 x 1 x 1 3 x 1
Bài 3. Cho biểu thức A   
với x  0, x  1 x 1 x 1 x 1
1) Rút gọn biểu thức A .
2) Tính giá trị của A khi x  9 . 1
3) Tìm giá trị của x để A  . 2
4) Tìm các giá trị nguyên của x để A nhận giá trị nguyên.
Tài liệu tự hoc- luyện thi vào 10 Page 19 Lê Trung – Uyên Vi
Toán học là đam mê
5) Tìm m để phương trình mA
x  2 có hai nghiệm phân biệt.
6) Tính các giá trị của x để A  1.
7) Tính giá trị nhỏ nhất của biểu thức A . Hướng dẫn giải x 1 x 1 3 x 1 1) A   
x  0; x   1 x 1 x 1 x 1
x  2  x  2 1 1  3 x 1 A
x  1 x  1
x  2 x 1 x  2 x 1 3 x 1 A
x  1 x  1 2x  3 x 1
A   x  1 x  1
2 x  1 x  1
A   x  1 x  1 2 x 1 A x 1 2 9 1 5
2) Thay x  9 (TMĐK) vào A ta được: A   9 1 4 5
Vậy với x  9 thì A  4
3) ĐKXĐ: x  0, x  1 1 2 x 1 1 A    2 x 1 2  4 x  2  x 1  3 x  3  x  1
Tài liệu tự hoc- luyện thi vào 10 Page 20 Lê Trung – Uyên Vi
Toán học là đam mê
x  1 (Không thỏa mãn) 1
Vậy không có giá trị của x để A  2
4) ĐKXĐ: x  0, x  1 2   x x   1  3 2 1 3 Ta có: A    2  x 1 x 1 x 1 3
Để A nhận giá trị nguyên thì
nhận giá trị nguyên  3 x 1  x 1U x 1 3 U  3  ; 1;3;1 3     Ta có bảng sau: x 1 3 1 1 3 x 4 2 0 2 x   0 4 ĐK - - TM TM Vậy x 0; 
4 thì A nhận giá trị nguyên
5) ĐKXĐ: x  0, x  1 Để . m A x  2 2 x 1  . mx  2 x 1
 2m x m x x  2
x  2m   1
x m  2  0 (1) Đặt t
x t  0; t   1 ta có phương trình:   2
1  t  2m   1
x m  2  0   *
Phương trình (1) có hai nghiệm phân biệt khi phương trình (2) có hai nghiệm phân
biệt khác 1 và t t  0 2 1   0  P  0  S  0 
a b c  0 
Tài liệu tự hoc- luyện thi vào 10 Page 21 Lê Trung – Uyên Vi
Toán học là đam mê 2  m   m
 m   2 4 9 0 2
1   4.m  2  0     m  2 m  2  0         m  2 1  2m 1  0 m   2 1  (2m 1) m 2 0        m  2  
Vậy với m  2 thì pt (1) có 2 nghiệm phân biệt
6) ĐKXĐ: x  0, x  1 2 x 1 Để A  1   1 x 1
2 x 1 x 1   0 x 1 x  2   0 x 1 Ta có : x  0 x   ĐKXĐx 1  1 x   Đ ĐKX x  2   0 x 1  x  2  0  x  2  x  4
Kết hợp với điều kiện ta có 0  x  4; x  1
Vậy với 0  x  4; x  1 thì A  1
7) ĐKXĐ: x  0, x  1 3 A  2 
x  0; x   1 x 1 Ta có: x  0  x 1  1 3 3   3  2 
 2  3  A  1 x 1 x 1 Dấu “ = “ xảy ra 
x  0  x  0 (TMĐK)
Vậy GTNN của A là 1 khi x  0
Tài liệu tự hoc- luyện thi vào 10 Page 22 Lê Trung – Uyên Vi
Toán học là đam mê x 1  x 1
Bài 4. Cho biểu thức B     :
với x  0, x  1  x x 1 x 1    x x 1   1) Rút gọn B
2) Tính giá trị của B khi x  3  2 2  3  2 2 . 3) Tìm x để B x
4) Với x >1, hãy so sánh B với B Hướng dẫn giải   x 1 x 1 1) B     :   x  
1  x x   1
x 1  x x 1    
x x x 1 x x 1 B    .   x  
1  x x   1  x 1   x 1 B x 1 2 2
2) x  3  2 2  3  2 2   2   1   2   1  2 1 2 1  2
Thay x = 2 (TMĐK) vào B ta được    2 2 1 2 1 B    3  2 2 . 2 1 1
Vậy khi x  3  2 2  3  2 2 thì B  3  2 2
3) ĐKXĐ: x  0, x  1 B x x 1   x x 1 
x 1  x x
x  2 x 1  0   x  2 1  2  0
  x 1 2  x 1 2   0
Tài liệu tự hoc- luyện thi vào 10 Page 23 Lê Trung – Uyên Vi
Toán học là đam mê
x  1 2 L    x  1 2 
x  1 2 2  x  3  2 2
4) Xét hiệu B B B B   1 CÁCH 1
+) Ta có : x  1  B  0  B có nghĩa x 1 2  +) Xét 1 B  1   0 x 1 x 1  B  1  B  1
+) Ta có : B B
B ( B 1)  0  B B CÁCH 2 +) Ta có: x  1 x  1  x 1  0 x 1 Mà x 1  0   0  B  0  B  0   1 x 1 2 x  9 x  3 2 x 1 +) Lại có: B    x  5 x  6 x  2 3  x x 1 x 1 x 1 2 B 1  1   x 1 x 1 x 1 2 Mà x 1  0   0 x 1  B 1  0   B   1  B   1  0 Mà B  0  B 1  0  B 1  0 2 Từ (1) và (2)  B B   1  0
B B  0  B B
Tài liệu tự hoc- luyện thi vào 10 Page 24 Lê Trung – Uyên Vi
Toán học là đam mê 2 x  9 x  3 2 x 1
Bài 5. Cho biểu thức C   
với x  0, x  4, x  9 x  5 x  6 x  2 3  x 1) Rút gọn biểu thức C
2) Tính giá trị của x để C đạt giá trị lớn nhất 1 3) So sánh với 1 C Hướng dẫn giải 2 x  9 x  3 2 x 1 1) C   
x  2 x 3 x  2 x  3
2 x  9   x  3 x  3  2 x   1  x  2 C
x  2 x 3
2 x  9  x  9  2x  3 x  2 C
x  2 x 3 x x  2
C   x 2 x 3 x 1 C x  3
2) ĐKXĐ: x  0, x  4, x  9 1 Để C  min max C 1 x  3 x 1 4 4  Ta có:    1 C x 1 x 1 x 1 Ta có: x  0 x   ĐKXĐx 1  1 1   1 x 1 4   4  x 1 4   1  3  x 1 1   3  C 1   C x   ĐKXĐ 3
Tài liệu tự hoc- luyện thi vào 10 Page 25 Lê Trung – Uyên Vi
Toán học là đam mê Dấu “ = ” xảy ra 
x  0  x  0 (TMĐK) 1  Vậy GTLN của C là khi x = 0 3 1 x  3 4  3) Xét hiệu 1  1  C x 1 x 1 Ta có: x  0 x   ĐKXĐx 1  1  0 4   0 x 1 1  1  0 C 1   1 x   Đ ĐKX C C. BÀI TẬP TỰ LUYỆN A. Đề bài x  4  x 1 x  2  3
Bài 1 . Cho biểu thức A  và B     :
Với x  0, x  1, x  4 . x 1  x 2 x 1    x 1  
1) Tìm giá trị của x để A  4.
2) Rút gọn biểu thức B 18
3) Với các biểu thức A và B nói trên, hãy tìm giá trị nhỏ nhất của biểu thức . . A B 2 x 1  1 x   x
Bài 2. Cho hai biểu thức A  và P     : 
1 x  0; x   1 x x 1 
x 1 1 x   x 1      
1) Tính giá trị của biểu thức A với x  16
2) Rút gọn biểu thức P . A
3 ) Tìm giá trị lớn nhất của biểu thức M  . P Bài 3. Cho hai biểu thức 4 2x x 13 x x  5 A   
x  0; x  9 và B
x  0; x  9 x  3 x  9 x  3 x  3
Tài liệu tự hoc- luyện thi vào 10 Page 26 Lê Trung – Uyên Vi
Toán học là đam mê
1) Tính giá trị của biểu thức B với x  11 6 2 A
2) Rút gọn biểu thức P  . B 1 3) Tìm x để P  . 9 x x 5 x  4
Bài 4. Cho biểu thức A  và B   
x  0; x   1 x  2 x 1 x  2 x x  2 1 1) Tính A khi x  . 4 2) Rút gọn B. A 3) Biết P
. Hãy Chứng tỏ P P với  x    1 . B Bài 5. Cho hai biểu thức x  2 x  2 6 x  8 4 x 13 A    và B
x  0; x  1; x  4 x 1 x  2 x  3 x  2 x 1
1) Tính giá trị của biểu thức B với x  36 2) Rút gọn biểu thức A.
3) Tìm giá trị lớn nhất của biểu thức P  . A B 2 x  15  x 3  x  3
Bài 6. Cho biểu thức A  và B     :
, x  0, x  25. 3  xx 25 x 5    x  5   1) Khi 3 3 x  9 5  2.
5  2, Tính giá trị của A. 2) Rút gọn biểu thức B.
3) Tìm x để P A B nhận giá trị nguyên. x  2 x 1 1
Bài 7 . Cho hai biểu thức A  ; B   
(x  0; x  2) x x  4 x  2 x  2
Tài liệu tự hoc- luyện thi vào 10 Page 27 Lê Trung – Uyên Vi
Toán học là đam mê A
1) Rút gọn B và tính P B 2) Tìm x để B = |B|
3) Tìm x thỏa mãn: xP  10 x  29  x  25 2  5 xx 2 x 3x  9   x  2 
Bài 8. Cho biểu thức: A  và B     . 1 x 1  x  3 x  3 x 9   3      
(với x  0, x  9 )
1) Tính giá trị của A khi x  19  8 3  19  8 3 2) Rút gọn B 3) Gọi M  .
A B . So sánh M và M 2 2x  2 x x 1 x x
Bài 9. Cho biểu thức P   
với x  0, x  1. x x x x x x
1) Rút gọn biểu thức P .
2) Tìm giá trị của biểu thức P khi x  3  2 2 . 7
3) Chứng minh rằng với mọi giá trị của x đề biểu thức P có nghĩa thì biểu thức chỉ P
nhận một giá trị nguyên.
x  3 x  2 1  1
Bài 10. Cho hai biểu thức U     
với x  0 và x  4 .  x x 8 x 2    x  
1) Rút gọn biểu thức U.
2) Tìm giá trị của U tại x  14  6 5 .
3) Tìm tất cả các giá trị của x để biểu thức K  8U có giá trị là số nguyên x x x 10 9
Bài 11 . Cho hai biểu thức A  và B  
với x  0, x  4, x  . 4 x  3 x  2 x  4 16
Tài liệu tự hoc- luyện thi vào 10 Page 28 Lê Trung – Uyên Vi
Toán học là đam mê
1) Tính giá trị của biểu thức A khi x  25. 2) Rút gọn biểu thức . B
3) Tìm giá trị của x để B  2 . Ax 2 6   1 
Bài 12. : Cho biểu thức P      : 1     x 1 x  2 x x  2    1 x
với x  0 , x  1 , x  4 . 1 1) Rút gọn P .
2) Tính P biết x  3  2 2 .
3) Tìm x để P   . 2 x x  3 2 1
Bài 13. Cho biểu thức A  , B   
với x  0, x  9 . 1 3 x x  9 x  3 3  x 4
1) Tính giá trị biểu thức A khi x  . 9 2) Rút gọn B . B 3) Cho P
, tìm x để P  3 . A Bài 14 . Cho biểu thức : 1 1 x  3 x  2 x x A   và B  
( với x  0; x  1 ) x 1 x 1
( x  2)( x 1) x 1
1) Rút gọn và tính giá trị biểu thức A khi x  4  2 3 2) Rút gọn biểu thức B 1 x 1
3) Đặt M = B : A , tìm x để   1 M 8 x x 1 x x 1 4 x 1
Bài 15. Cho biểu thức: P    và Q
với x  0; x  1 x x x x x x 1
1) Tính giá trị của Q khi x  25 .
2) Rút gọn biểu thức A  . P Q .
3) Tìm các giá trị của x để . A x  8 .  x  2 x  2  x 1
Bài 16. Cho biểu thức A    ; B
với x  0, x  1
x  2 x 1 x 1     x
Tài liệu tự hoc- luyện thi vào 10 Page 29 Lê Trung – Uyên Vi
Toán học là đam mê
1) Tính giá trị của B khi x  36 2 2) Chứng minh rằng . A B x 1 3) Tìm x để . A B 1  . A B 1 x 12  3 1  1
Bài 17. Cho hai biểu thức A  và B   :  
với x  0, x  1 x 1  x 1 x 1  x 1
1) Tính giá trị của biểu thức A khi x  9 .
2) Rút gọn biểu thức B . A
3) Tìm giá trị nhỏ nhất của biểu thức M  . B 2x  3 x  2 3
x x  2x  2
Bài 18. Cho hai biểu thức A  và B
với x  0 và x  4 . x  2 x  2
1) Tính giá trị của A khi x  4  2 3 .
2) Tìm giá trị của x để B A 1.
3) Tìm giá trị nhỏ nhất của biểu thức C B A . x 1 x 1 3 x 1
Bài 19. Cho biểu thức A   
với x  0; x  1 x 1 x 1 x 1
1) Rút gọn biểu thức A .
2) Tìm giá trị nguyên của x để A  1.
3) Tìm m để phương trình mA
x  2 có hai nghiệm phân biệt x 1 2 x
Bài 20. Cho 2 biểu thức: A   và B
với x  0 và x  4 . x  2 x  4 x  2
1) Tính giá trị biểu thức B khi x  16 .
2) Rút gọn biểu thức M A : B .
3) Tìm các giá trị thực của x để M  1. x 1  1 x x x
Bài 21. Cho hai biểu thức A  và B    .
với x  0; x  1 x 1  x 1 x 1   2 x 1  
Tài liệu tự hoc- luyện thi vào 10 Page 30 Lê Trung – Uyên Vi
Toán học là đam mê 9
1) Tính giá trị của A khi x  4 2) Rút gọn B .
3) Với x   và x  1, hãy tìm giá trị lớn nhất của biểu thức P  . A B x 1 6  2 x 2 1
Bài 22. Cho hai biểu thức A  và B    x  2 x  3 x  2 x  2 1 x
với x  0; x  1; x  4 1
1) Tính giá trị của A khi x  4
2) Rút gọn biểu thức M = A.B m
3) Tìm m để phương trình M
(m là tham số) có nghiệm. 2 2 x 1  4 x  4x 1  1
Bài 23. Cho hai biểu thức A  ; B   
 ( x  0; x  ) 4x 2 x 1
 8x x 1 2 x 1     4  
1) Tính giá trị của A khi x 1 B 1
2) Chứng minh biểu thức T   . A 2 x 1 1
3)Với x  1 , tìm giá trị nhỏ nhất của L   4T. T 2x 1
4) Tìm các giá trị nguyên của x để biểu thức P T. nhận giá trị nguyên 2 x 1 dương. x  2 x  2 3 12
Bài 24. Cho hai biểu thức A
với x  0 và B    với x  2 x  2 x  2 x  4 x  0, x  4
1) Tính giá trị của biểu thức A khi x  9 2) Rút gọn biểu thức B 1
3) Cho biểu thức P
. Với x  , tìm giá trị lớn nhất của P. AB x 1  20  2 x 3  x  2
Bài 25. Cho hai biểu thức A  và B     :
với x  0, x  25 x  2  x 25 x 5    x  5  
1) Khi x  16 , tính giá trị của biểu thức A 2) Rút gọn biểu thức B B m
3) Tìm tất cả các giá trị nguyên của tham số m để phương trình  có nghiệm A 6
Tài liệu tự hoc- luyện thi vào 10 Page 31 Lê Trung – Uyên Vi
Toán học là đam mê x 1 1 x  2
Bài 26. Cho hai biểu thức P    và Q
với x  0; x  4; x  9 x  4 x  2 x  2 x  3
1. Tính giá trị của biểu thức Q khi x  64 x 2. Chứng minh P x  2
3. Với x Z , tìm GTLN của biểu thức K  . Q P   1
Tài liệu tự hoc- luyện thi vào 10 Page 32