Sáng kiến kinh nghiệm năm 2018-2019 - Công nghệ thông tin | Đại học Hoa Sen

Mã số đề tài 420 Sáng kiến kinh nghiệm năm học 2018 – 2019 MỤC LỤC
Mục lục :………………………………………………………… …... .…1
Danh mục viết tắt …………………………………………………………2 I.
Cơ sở đề xuất giải pháp……………………………………………….3
1. Sự cần thiết hình thành giải pháp………………………………….3
2. Mục tiêu của giải pháp ……………………………………………3
3. Phương pháp nguyên cứu…………………………………………4
4. Đối tượng và phạm vi áp dụng …………………………………..4 II.
Quá trình hình thành và nội dung giải pháp……………… ….……...5
1. Quá trình hình thành………………………………………………5
2. Đề xuất giải pháp …………………………………………………6
3. Nội dung giải pháp ……………………………………………….6 III.
Hiệu quả của giải pháp …………………………..………….. ……15
1. Thời gian áp dụng và hiệu quả ………………………………….15
2. Kinh nghiệm thực tiễn khi áp dụng giải pháp …………………..16
3. Khả năng triển khai và phạm vi áp dụng ………………………..16 IV.
Kết luận và đề xuất kiến nghị.………………………….……………17
1. Vấn đề cốt lõi của giải pháp ……………………………………..17
2. Đề xuất, kiến nghị ……………………………………………….17 V.
Tài liệu tham khảo …………………………………………………..18 -1-
Mã số đề tài 420 Sáng kiến kinh nghiệm năm học 2018 – 2019
Danh mục các chữ cái viết tắt
Giáo dục thường xuyên hướng nghiệp GDTX – HN Học sinh giỏi HSG Máy tính cầm tay MTCT Nhà xuất bản NXB
Sáng kiến kinh nghiệm: SKKN Trung học phổ thông THPT -2-
Mã số đề tài 420 Sáng kiến kinh nghiệm năm học 2018 – 2019 I.
CƠ SỞ ĐỀ XUẤT GIẢI PHÁP:
1. Sự cần thiết hình thành giải pháp
Hai năm vừa qua 2017, 2018 bộ GD-ĐT đã tổ chức kỳ thi THPT quốc gia với
hình thức thi trắc nghiệm và sẽ tiếp tục duy trì hình thức thi này vào những năm tiếp theo.
Như vậy, việc đổi mới trong việc dạy và học ở Trung tâm GDTX-HN Vũng Tàu là rất cần thiết.
Khi tham gia dạy học sinh lớp 12 vào hai năm học 2017-2018 và năm học
2018-2019, tôi thấy học sinh Trung tâm GDTX-HN Vũng Tàu rất khó khăn khi giải
quyết các bài toán dưới dạng trắc nghiệm, thường các em phải giải bài toán theo
hướng tự luận rồi mới chọn được đáp án. Chúng ta biết rằng học sinh có một công cụ
để hỗ trợ giải toán đó là MTCT, khi sử dụng MTCT học sinh chỉ biết thực hiện các
phép tính đơn giản như, cộng, trừ, nhân, chia, lũy thừa, logarit...
Trong khi đó đề thi học kỳ và đề thi THPT quốc gia luôn xuất hiện dạng bài
toán liên quan hàm số như tìm cực trị, tính đơn điệu, giá trị lớn nhất, nhỏ nhất và đồ
thị hàm số như nhận dạng đồ thị, tìm tiệm cận. Do đó tôi chọn đề tài này nhằm hỗ
trợ cho học sinh dễ dàng giải quyết một số bài toán trắc nghiệm trên dựa vào những
kiến thức lý thuyết đã học kết hợp sử dụng MTCT. Điều này rất có ích khi học sinh
tham gia làm bài kiểm tra, cũng như tham dự các kỳ thi học kỳ, thi THPT quốc gia.
Giúp các em định hướng và tự tin hơn khi làm bài.
2. Mục tiêu của giải pháp
Từ lý do chọn đề tài, từ cơ sở thực tiễn giảng dạy các lớp khối 12 ở Trung tâm
GDTX-HN Vũng Tàu, cùng với kinh nghiệm trong quá trình giảng dạy. Tôi đã tổng
hợp , khai thác và hệ thống hoá lại các kiến thức thành một chuyên đề: “ Sử dụng
máy tính cầm tay để giải nhanh một số dạng toán thường gặp liên quan đến hàm số ’’. -3-
Mã số đề tài 420 Sáng kiến kinh nghiệm năm học 2018 – 2019
Qua đề tài này tôi muốn nêu ra một số dạng bài tập liên quan hàm số như tìm
cực trị,tính đơn điệu, giá trị lớn nhất, nhỏ nhất và đồ thị hàm số như nhận dạng đồ
thị, tìm tiệm cận nhằm giúp các em hoàn thiện các kiến thức. Từ đó đạt kết quả cao
trong các kỳ thi học kỳ, thi THPT quốc gia .
3. Phương pháp nguyên cứu: Phương pháp
- Nghiên cứu lý luận chung.
- Khảo sát điều tra từ thực tế dạy và học .
- Tổng hợp so sánh, rút kinh nghiệm. Cách thực hiện:
- Trao đổi với đồng nghiệp, tham khảo ý kiến giáo viên cùng bộ môn
- Liên hệ thực tế trong nhà trường, áp dụng đúc rút kinh nghiệm qua quá trình giảng dạy.
- Thông qua việc giảng dạy trực tiếp ở các lớp khối 12 trong năm học từ 2017-2018 đến 2018-2019.
4. Đối tượng và phạm vi áp dụng
a. Về đối tượng nghiên cứu: Các bài toán liên quan hàm số với sự hỗ trợ của MTCT. b. Phạm vi nghiên cứu
- Nội dung phần Các bài toán liên quan hàm số trong chương trình Toán cơ bản khối 12.
- Một số bài giải các bài toán liên quan hàm số trong đề thi học kỳ, đề thi THPT Quốc gia.
Do khuôn khổ của bài viết, tôi xin đề xuất một số dạng toán thường gặp dùng
MTCT hỗ trợ giải mà những năm gần đây tôi đã áp dụng cho học sinh Trung Tâm GDTX- HN Vũng Tàu. -4-
Mã số đề tài 420 Sáng kiến kinh nghiệm năm học 2018 – 2019
Không trình bày cách sử dụng MTCT (phần này xem ở sách hướng dẫn sử dụng
máy tính kèm theo khi mua máy).
Những bài toán trình bày trong bài viết này được áp dụng minh họa cho máy
tính casio fx – 570ES plus , fx – 570VN plus, fx – 570MS , fx – 570ES ,. Vinacal .fx – 570ES plus…, .
Mỗi bài toán sẽ có rất nhiều cách giải, trong phạm vi của bài viết, tôi sẽ chỉ
trình bày những cách giải quyết những dạng toán học sinh hay gặp mà bản thân tôi cho là có hiệu quả cao. II.
QUÁ TRÌNH HÌNH THÀNH VÀ NỘI DUNG GIẢI PHÁP
1. Quá trình hình thành
Hiện nay, nếu lên google để tìm kiếm, bạn sẽ tìm được rất nhiều đề tài sáng kiến
kinh nghiệm liên quan đến các dạng toán trắc nghiệm về bài toán liên quan hàm số,
đồ thị hàm số, tuy vậy mỗi đề tài đều có những nét riêng độc đáo của nó, đề tài mà
tôi chia sẻ với quí đồng nghiệp cũng không ngoại lệ, cụ thể như sau:
 Phân loại các dạng và phương pháp giải các bài tập thường gặp trong kỳ thi
học kỳ và kỳ thi THPT quốc gia về bài toán liên quan hàm số, đồ thị hàm số.
 Tìm ra một số thủ thuật để giải nhanh, chính xác một số dạng toán trắc nghiệm
thường gặp về bài toán liên quan hàm số, đồ thị hàm số với sự hỗ trợ của MTCT .
 Từ đó giúp học sinh có thể đạt kết quả không thấp trong kỳ thi học kỳ và kỳ thi THPT quốc gia.
Thực tế, không chỉ học sinh yếu, trung bình mà cả học sinh khá khi gặp một
bài toán trắc nghiệm cần có kỹ năng tính toán và phải hoàn thành trong một khoảng
thời gian nhất định, chắc chắn các em căng thẳng và nhiều khi sẽ không chọn được
đáp án đúng. Vì vậy, để giúp học sinh có kỹ năng tính toán tốt và đỡ tốn nhiều thời
gian, tôi khuyên các em nên dùng MTCT để hỗ trợ kiểm tra đáp án, với cách này các
em thích thú và không ngần ngại làm toán, tạo nên sự đam mê học toán. -5-
Mã số đề tài 420 Sáng kiến kinh nghiệm năm học 2018 – 2019
2. Giải pháp đề xuất
Với thực trạng đã nêu như trên, để đạt được mục tiêu đề ra, tôi đưa ra các biện pháp thực hiện như sau:
Trước tiên, tôi chọn một số bài toán mà học sinh thường hay gặp .
- Nêu lên các dạng bài tập về các bài toán liên quan đến hàm số như tìm cực
trị,tính đơn điệu, giá trị lớn nhất, nhỏ nhất và đồ thị hàm số như nhận dạng đồ thị,
tìm tiệm cận. Định hướng, dẫn dắt cho học sinh tự tìm ra phương pháp giải từng
dạng toán đó. Để làm được điều này, tôi luôn hướng học sinh phải bắt nguồn từ nền
tảng kiến thức toán học mà các em đã được học tại lớp. Đây là khâu then chốt trong quá trình giảng dạy.
- Định hướng ôn tập cho học sinh: cung cấp cho học sinh một hệ thống các bài
tập thuộc các dạng toán theo thứ tự từ dễ đến khó và trích các bài toán liên quan
trong các đề thi học kỳ, đề thi THPT quốc gia. Yêu cầu học sinh mỗi bài giải đều
phải trình bày lời giải rõ ràng theo hướng tự luận, sau đó mỗi học sinh sẽ trình bày
bài giải của mình, những học sinh còn lại xem xét, so sánh với cách giải của bản
thân rồi nhận xét, và cuối cùng tôi hướng dẫn để học sinh tìm ra thủ thuật sử dụng
MTCT dựa trên bài giải của mình để tìm đáp án nhanh nhất và chính xác nhất.
Sau đây tôi trình bày cụ thể cách thực hiện giải pháp của mình khi dạy học sinh
Trung tâm GDTX-HN Vũng Tàu trong việc giải bài toán trắc nghiệm: 3. Nội dung giải pháp A. LÝ THUYẾT:
CÁC BÀI TOÁN LIÊN QUAN HÀM SỐ VÀ ĐỒ THỊ HÀM SỐ
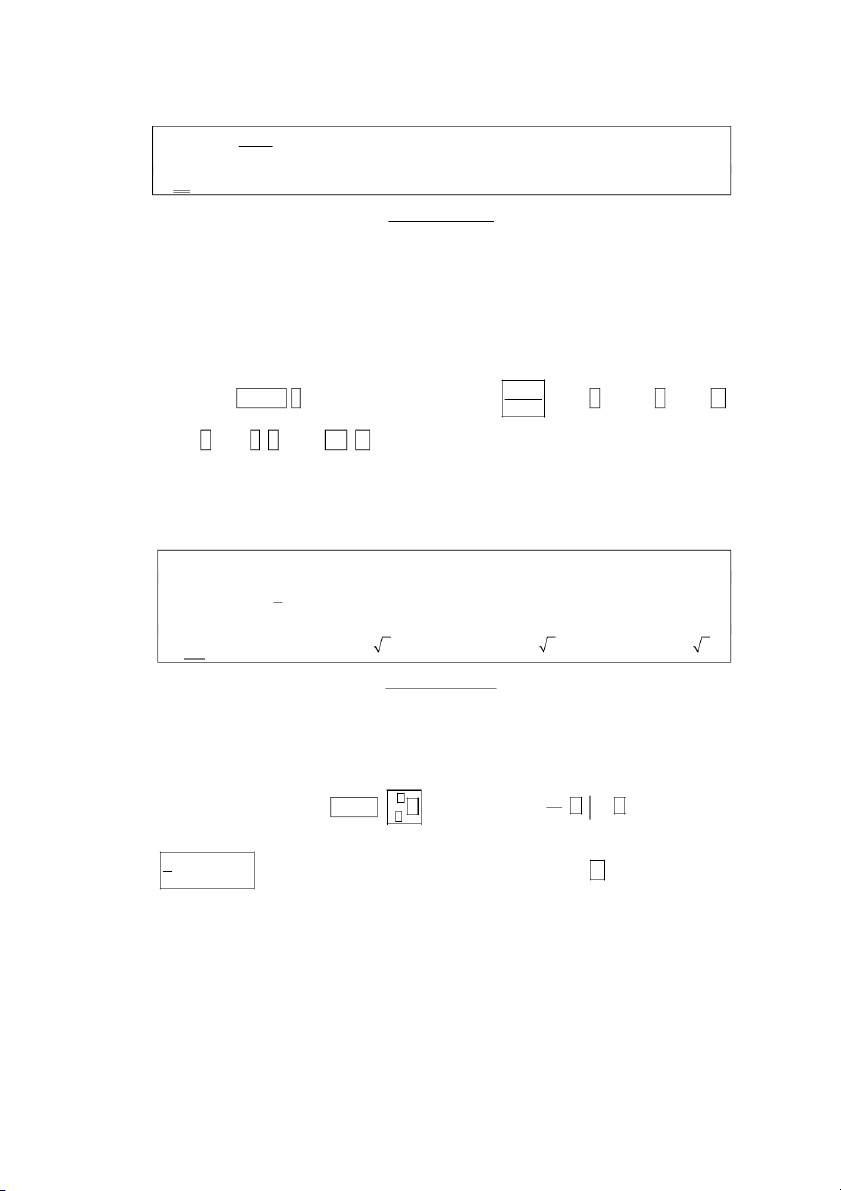
 TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ Định nghĩa:
Giả sử hàm số y = f(x) xác định trên K.
 y = f(x) đồng biến trên K   x1, x2  K: x1 < x2  f(x1) < f(x2) .
 y = f(x) nghịch biến trên K  x1, x2  K: x1 < x2  f(x1) > f(x2). -6-
Mã số đề tài 420 Sáng kiến kinh nghiệm năm học 2018 – 2019 Định lý:
Giả sử hàm số y  f (x) có đạo hàm trên khoảng D.
 Nếu f '(x) 0  , x
  D và f '(x) 0
 chỉ tại một số hữu hạn điểm thuộc D thì hàm số đồng biến trên D.
 Nếu f '(x) 0  , x
  D và f '(x) 0
 chỉ tại một số hữu hạn điểm thuộc D thì hàm số nghịch biến trên D.
 Nếu f '(x) 0  , x
  D thì hàm số không đổi trên D.
 CỰC TRỊ CỦA HÀM SỐ
1/ Điều kiện cần để hàm số có cực trị
Giả sử hàm số y  f (x) có cực trị tại x y  f x x f '(x ) 0  0 . Nếu
( ) có đạo hàm tại điểm 0 thì 0 .
2/ Điều kiện đủ để hàm số có cực trị Dấu hiệu 1:
Giả sử hàm số y  f (x) liên tục trên khoảng (a;b) chứa điểm x và có đạo hàm trên các 0 khoảng ( ;
a x ) và (x ;b) . Khi đó : 0 0 + Nếu f '( )
x đổi dấu từ âm sang dương khi x qua điểm x thì hàm số đạt cực tiểu tại x . 0 0 + Nếu f '( )
x đổi dấu từ dương sang âm khi x qua điểm x thì hàm số đạt cực đại tại x . 0 0 Dấu hiệu 2:
Giả sử hàm số y  f (x) có đạo hàm trên khoảng (a;b) chứa điểm x f '(x ) 0  f x 0, 0 và ( ) có
đạo hàm cấp hai khác 0 tại điểm x0 . Khi đó:
+ Nếu f '(x )  0 x 0
thì hàm số đạt cực đại tại điểm 0 .
+ Nếu f '(x )  0 x 0
thì hàm số đạt cực tiểu tại điểm 0 .
 GTLN, GTNN CỦA HÀM SỐ Định nghĩa:
Cho hàm số y = f(x) xác định trên D.  f x() M , x D
max f(x) M  x D: f( x)  D  0 0 M -7-
Mã số đề tài 420 Sáng kiến kinh nghiệm năm học 2018 – 2019  f x ( ) m,  x D min f(x) m   D x 0 D : f(x ) 0   m
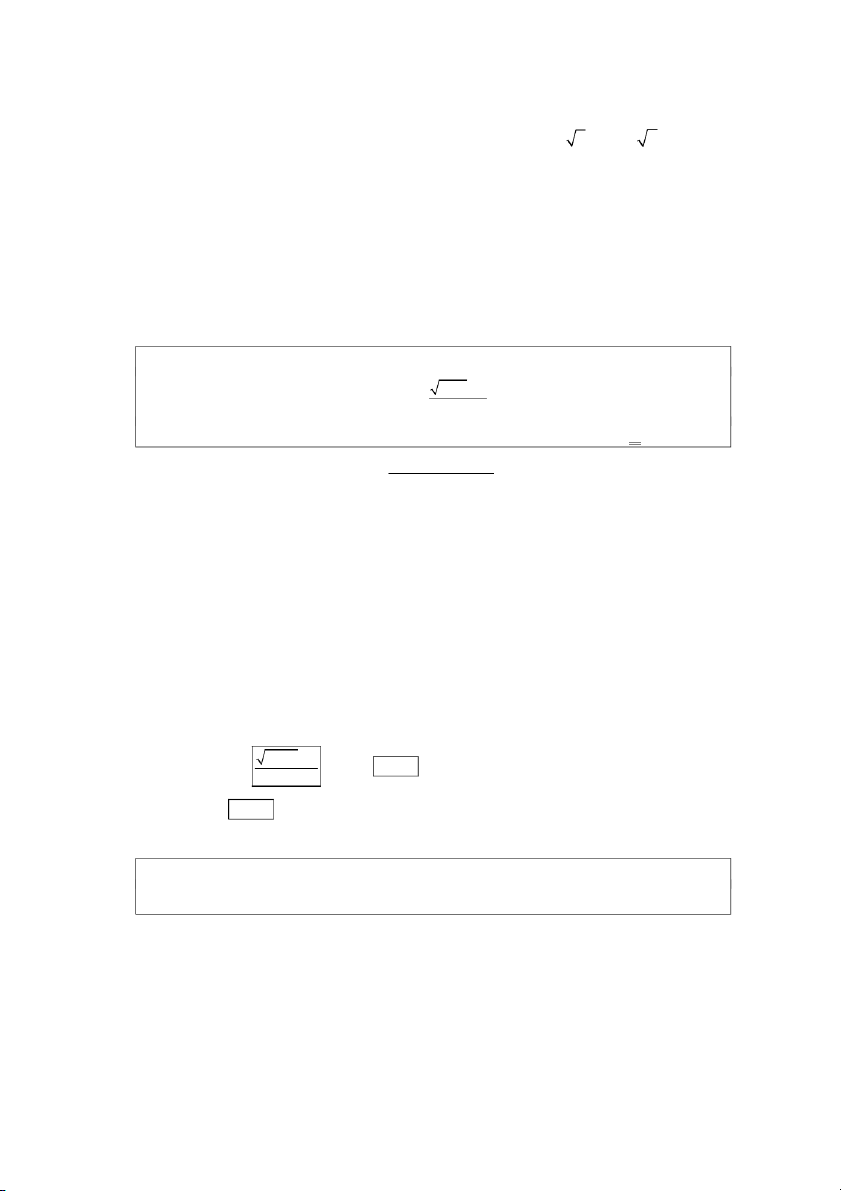
 ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
1. Đường tiệm cận ngang
Đường thẳng y y0 được gọi là đường tiệm cận ngang của đồ thị (C) của hàm số
y  f (x) nếu ít nhất một trong các điều kiện sau được thỏa lim f (x) y0 x  hoặc
lim f (x) y0 x   .
2. Đường tiệm cận đứng
Đường thẳng x  0
x được gọi là đường tiệm cận đứng của đồ thị (C) của hàm số
y  f (x) nếu ít nhất một trong các điều kiện sau được thỏa: lim f ( )
x  , lim f ( )x  x x  x x  0 0 lim f ( )
x   , lim f ( )x   . x x  x x 0 0
 ĐỒ THỊ HÀM SỐ
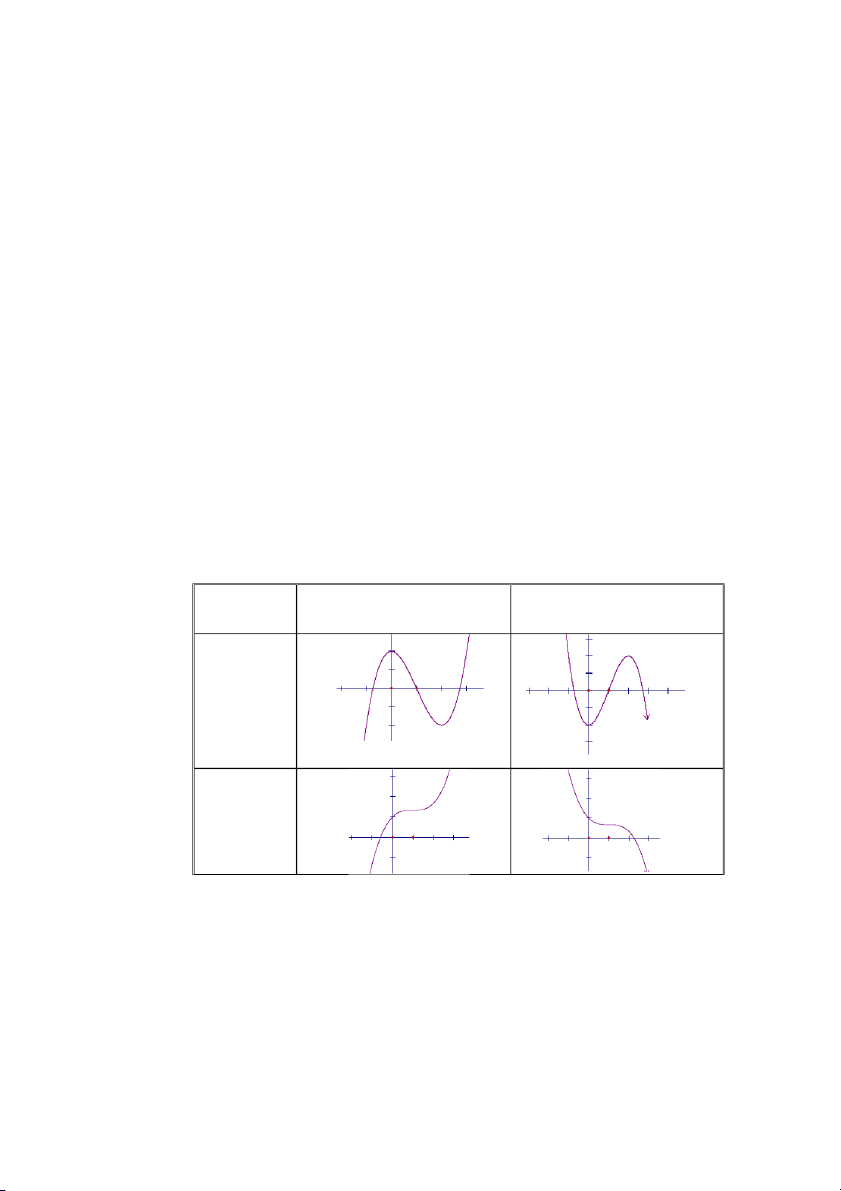
Các dạng đồ thị hàm số bậc 3: 3 2 y a
 x bx  cx  d (a 0  ) a > 0 a < 0 Phương trình 2 2 y’ = 0 O có hai nghiệm phân -2 -2 biệt. Phương trình 2 2 y’ = 0 có nghiệm kép -8-
Mã số đề tài 420 Sáng kiến kinh nghiệm năm học 2018 – 2019 4 Phương trình 2 y’ = 0 2 vô nghiệm
Các dạng đồ thị hàm số bậc 4 trùng phương: 4 2 y a
 x  bx  c (a 0  ) a > 0 a < 0 Phương 2 trình y’ = 0 có ba -2 nghiệm phân biệt Phương trình y’ = 0 2 có một nghiệm -2 ax  b
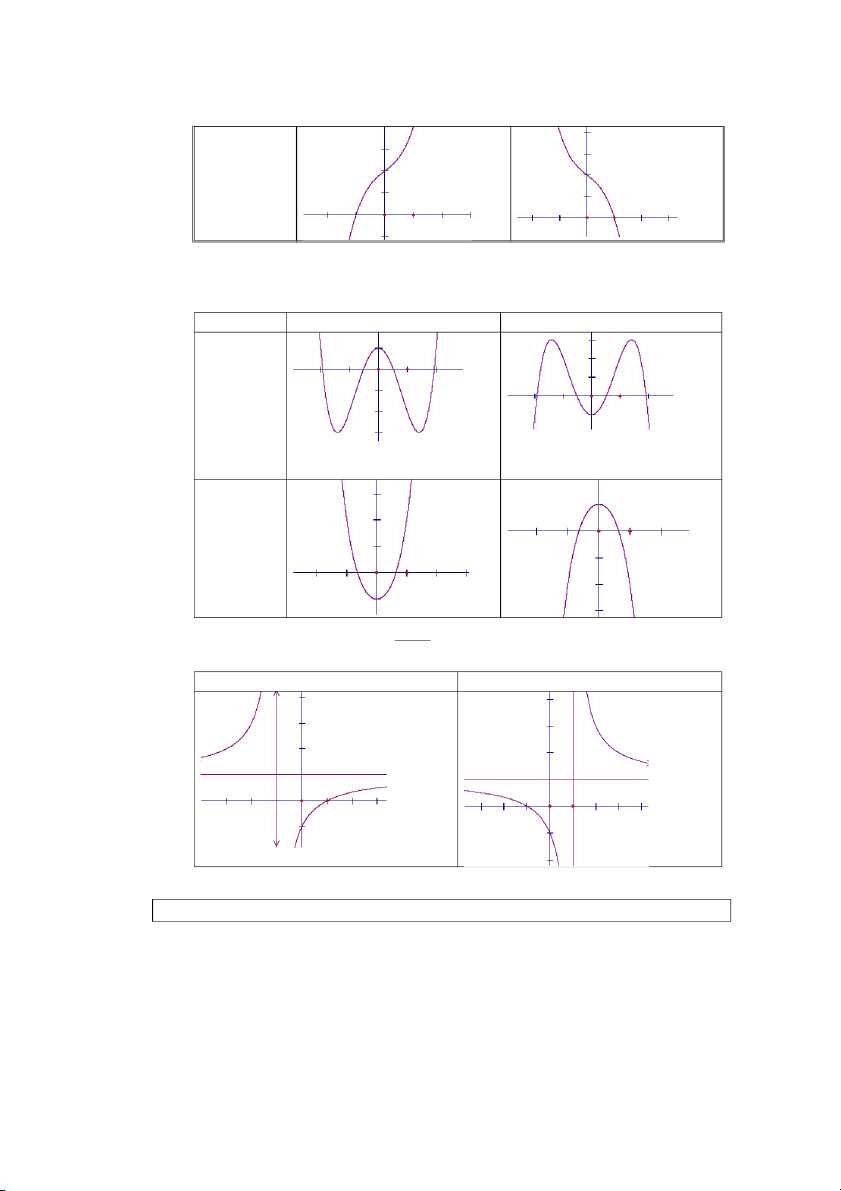
Các dạng đồ thị hàm số y 
(c 0, ad  bc 0) cx d ad – bc > 0
ad – bc < 0 4 4 2 2 -2
B. CÁC VÍ DỤ MINH HỌA
Ví dụ 1 : (Câu 13 đề thi THPT Quốc gia 2017-Mã đề 101) -9-
Mã số đề tài 420 Sáng kiến kinh nghiệm năm học 2018 – 2019 2 Hàm số y 
nghịch biến trên khoảng nào dưới đây ? 2 x 1 A. (0;). B. ( 1;1). C. ( ;   )  . D. ( ;  0). Hướng dẫn giải
 Nếu giải theo cách tự luận ta phải tính đạo hàm hàm số, tìm nghiệm đạo hàm ,
lập bảng biến thiên rồi mới chọn đáp án đúng. Cách giải này tốn nhiều thời
gian đối với một câu hỏi trắc nghiệm.
 Giải pháp 1: Hướng dẫn học sinh sử dụng MTCT với kiến thức đã học về định
nghĩa tính đơn điệu của hàm số. 2
Bấm MODE 7. Sau đó nhập hàm số f  X  
, bấm = g  X  = Start -1 2 X 1  = End 1 = Step 0.2 =
Ta dò bảng giá trị ta thấy giá trị hàm số tăng dần khi X nhận giá trị từ -1 đến 0,
giảm dần khi X nhận giá trị từ 0 đền 1 nên loại đáp án B; C; D.
Kết luận đáp án đúng là A.
Ví dụ 2: (Đề thi học kỳ I năm 2017-2018 TTGDTX-HNVT) 1 4 2
y  x  2x  3 Hàm số: 2
đạt cực đại tại x bằng A. 0. B.  2  . C. 2 . D. 2 . Hướng dẫn giải:
 Nếu giải theo hướng tự luận học sinh làm như sau: Tính đạo hàm hàm số, tìm
nghiệm đạo hàm, lập bảng biến thiên và kết luận  Giải pháp 2: d
Bước 1: Bấm máy tính: SHIFT  . Màn hình hiện
  x  .Nhập hàm số dx 1 4 2
X  2X  3 vào ô vuông thứ nhất, tại ô vuông thứ 2 nhập x  0 .Sau đó ấn dấu = 2
Ta được kết quả là 0. Có nghĩa ta đã tính đạo hàm của hàm số trên tại x 0  là 0. -10-
Mã số đề tài 420 Sáng kiến kinh nghiệm năm học 2018 – 2019
Tương tự ta bấm quy trình máy tính như trên và thay x  2, x  2 . Kết quả
cũng bằng 0 nên ta chưa chọn được đáp án.
Bước 2: Dựa vào dấu hiệu 2 tìm cực trị hàm số ta mới tính như sau: 3 y ' 2  x  4x +
+ Bấm quy trình tính đạo hàm như trên nhưng nhập hàm số là hàm số của y’. Tại x 0
 ta được kết quả bằng -4 nhỏ hơn 0.
Kết luận đáp án đúng là A.
Ví dụ 3. (Câu 18 đề thi THPT Quốc gia năm 2018-Mã đề 101).
Số tiệm cận đứng của đồ thị hàm số x 9  3 y  là 2 x  x A. 3. B. 2. C. 0. D.1. Hướng dẫn giải
 Nếu giải theo hướng tự luận học sinh làm như sau: tìm tập xác định hàm số,
tính giới hạn tại những giá trị x làm cho mẫu số bằng 0 và kết luận. Nhưng
bước tính giới hạn đối với học sinh TTGDTX-HN Vũng Tàu là một vấn đề rất
khó khăn. Vì vậy tôi đề xuất một giải pháp như sau.  Giải pháp 3:
Ta thấy hàm số có mẫu khác 0 khi x 0
 ; x  1. Vậy đồ thị hàm số nếu có tiệm
cận đứng thì chỉ có tối đa 2 tiệm cận đứng. Kiểm tra xem x 0
 ; x  1 có là tiệm cận
đứng không ta sẽ sử dụng MTCT để tính giới hạn hàm số này. Bấm máy tính như sau:  
Nhập hàm số X 9 3 ấn nút CALC X? 0.0000000001 KẾT QUẢ 0.1666. 2 X  X
Ấn lại nút CALC X? -1.0000000001 KẾT QUẢ -1715728753
Kết luận chỉ có 1 tiệm cận đứng x  1. Chọn đáp án D.
Ví dụ 4. ( Câu 23 đề thi THPT Quốc gia năm 20128-Mã đề 101).
Giá trị lớn nhất của hàm số 4 2
y x  4x  9 trên đoạn   2;  3 bằng -11-
Mã số đề tài 420 Sáng kiến kinh nghiệm năm học 2018 – 2019 A. 201. B. 2. C. 9. D. 54. Hướng dẫn giải
 Nếu giải tự luận học sinh sẽ làm theo các bước sau : tính đạo hàm hàm số, tìm
nghiệm đạo hàm, xét những giá trị nghiệm thuộc đoạn đang xét, tính giá trị
hàm số tại nghiệm thuộc đoạn đang xét , x=-2, x=-3. So sánh và kết luận. Ta
thấy cách giải như trên sẽ tốn nhiều thời gian và nhiều khi sự tính toán của học
sinh sẽ nhầm lẫn và khó để chọn được đáp án dúng. Do vậy tôi đề xuất giải
pháp đối với bài toán này như sau :  Giải pháp 4 :
Dựa vào kiến thức định nghĩa GTLN, GTNN của hàm số ta có cách sử dụng máy tính như sau :
Cài đặt lại máy tính : SHIFT MODE 5 1
Sau đó mới vào chương trình tính
MODE 7 . Nhập hàm số f  X  4 2
 X  4X  9 , bấm = Start -2 = End 3 = Step 0.2 =
Dò bảng giá trị của hàm số ta thấy giá trị lớn nhất của hàm số là 54. Kết luận đáp án là D.
Ví dụ 5. Câu 33 đề thi THPT Quốc gia năm 2017-Mã đề 101. x  m Cho hàm số y 
(m là tham số thực) thỏa mãn min y 3
 .Mệnh đề nào sau dưới x  1 [2;4] đây đúng ? A. m   1 .
B. 3  m 4 . C. m  4 . D. 1 m   3 . Hướng dẫn giải 
Đối với học sinh TTGDTX-HN Vũng Tàu bài toán trên là một bài toán khó,
khi gặp bài toán này học sinh sẽ bỏ qua. Nhưng với sự hỗ trợ của MTCT bài toán sẽ
trở nên dễ dàng hơn. Do vậy tôi đề xuất giải pháp như sau: -12-
Mã số đề tài 420 Sáng kiến kinh nghiệm năm học 2018 – 2019  Giải pháp 5:
Sử dụng chương trình MODE 7 để thử đáp án. X m
Nhập hàm số f  X  
( với m thay bằng một giá trị cụ thể trong mỗi đáp án) X  1
bấm = Start 2 = End 4 = Step 0.2 =
Dò bảng giá trị của hàm số ta thấy nếu xuất hiện giá trị nhỏ nhất của hàm số là 3 thì ta chọn đáp án đó.
Như đáp án C. m  4. Khi nhập hàm số ta thay m=5 và thực hiện quy trình bấm phím
như trên. Sau đó dò bảng giá trị hàm số ta thấy xuất hiện giá trị nhỏ nhất là 3.
Kết luận đáp án đúng là C.
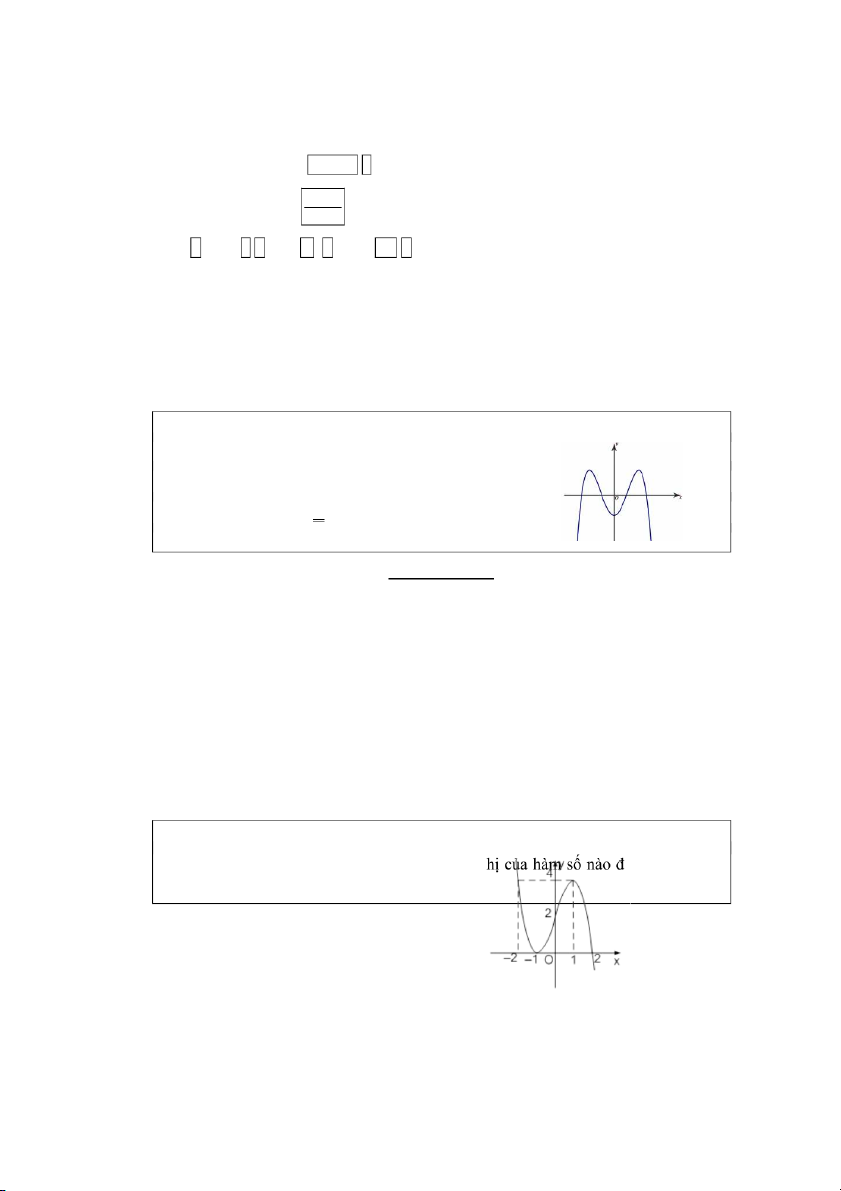
Ví dụ 6 ( Câu 11 đề thi THPT Quốc gia 2018-Mã đề 101).
Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây? A. 4 2
y x  3x  1 . B. 3 2
y x  3x  1. C. 3 2
y  x  3x  1. D. 4 2
y  x  3x  1 . Hướng dẫn giải 
Khi đọc câu hỏi này học sinh sẽ bối rối vì trên đồ thị không có số cụ thể và khi
đó không biết chọn lựa đáp án nào. Vì thế tôi định hướng học sinh làm như sau :  Giải pháp 6 :
Đối với câu hỏi này thì việc nhận dạng rất đơn giản.
Thứ nhất đây là dạng đồ thị hàm số bậc 4 nên ta loại đáp án C và B.
Thứ hai ta thấy nhánh cuối cùng của đồ thị bên tay phải đi xuống nên hệ số a  0 .
Kết luận đáp án đúng là D.
Ví dụ 7 ( Đề thi học kỳ I năm 2017-2018 TTGDTX-HN VT)
Đường cong trong hình bên là đồ thị bên là đồ t ược liệt kê sau đây: -13-
Mã số đề tài 420 Sáng kiến kinh nghiệm năm học 2018 – 2019 A. 3
y  x  3x  2 . B. 3
y x  3x  2 . C. 3
y x  3x  2 . D. 3
y  x 3x  2 . Hướng dẫn giải 
Nếu học sinh làm theo hướng tự luận khảo sát và vẽ đồ thị xong 4 hàm số trên
thì sẽ tốn rất nhiều thời gian để chọn được đáp án. Vì vậy tôi đề xuất giải pháp dựa
vào các yếu tố đồ thị hàm số như sau:  Giải pháp 7:
+ Ta thấy nhánh cuối cùng bên tay phải của đồ thị đi xuống nên hàm số có hệ số
a  0 nên ta loại đáp án B và C.
+ Giao điểm đồ thị với trục tung ta có x=0; y=2. Nhìn vào hàm số ở đáp án A và
D ta thấy cả hai đều đúng. Chưa chọn được đáp án.
+ Xác định toạ độ điểm cực đại và cực tiểu của đồ thị hàm số là
( xCĐ=1 ; yCĐ=4) ; (xCT=-1 ; yCT=0)
+ Dùng phím CALC nhập hàm số tính giá trị hàm số ở đáp án A lần lượt tại
x= 1 ta được y=-2 không trùng với giá trị yCĐ của đồ thị hàm số nên loại đáp án A.
Kết luận đáp án đúng là D.
C. MỘT SỐ BÀI TẬP 1 Câu 1. Cho hàm số 4 2
y  x  2x 1 . Tìm mệnh đề sai? 4
A. Hàm số nghịch biến trên khoảng (0; )  .
B. Hàm số nghịch biến trên khoảng ( ;   2).
C. Hàm số đồng biến trên khoảng ( -2; -1).
D. Hàm số đồng biến trên khoảng (2; + ).
Câu 2. Tọa độ điểm cực tiểu của hàm số y  3 x  3 x là A. (-1; -2) B. (0; 0) C. (1; 2) D. (-1; -4) -14-