Lý thuyết xác suất và thống kê
Giảng viên: TS. Nguyễn Như Lân Email: lan.nn@ou.edu.vn 1
 Định nghĩa xác suất bằng tần suất
Với n đủ lớn, giả sử khi thực hiện n lần phép thử τ
trong điều kiện giống nhau thì biến cố A xảy ra k lần. Ta có k P (A) ≈ n 2  Ví dụ 4.
Thống kê trên 10.000 người dân sống ở thành phố
cho thấy có 51 người bị bệnh cao huyết áp. Xác suất
người dân sống ở thành phố “bị bệnh cao huyết áp" là bao nhiêu? 3 BÀI TẬP
5. Một nhà máy gồm 3 phân xưởng A, B, C. Kiểm tra
một lô hàng của nhà máy gồm 1000 sản phẩm, người
ta thấy có 252 sản phẩm của phân xưởng A, 349 của
phân xưởng B và 399 của phân xưởng C. Lấy ngẫu
nhiên 01 sản phẩm của nhà máy. Tính xác suất nhận
được sản phẩm của các phân xưởng. 4
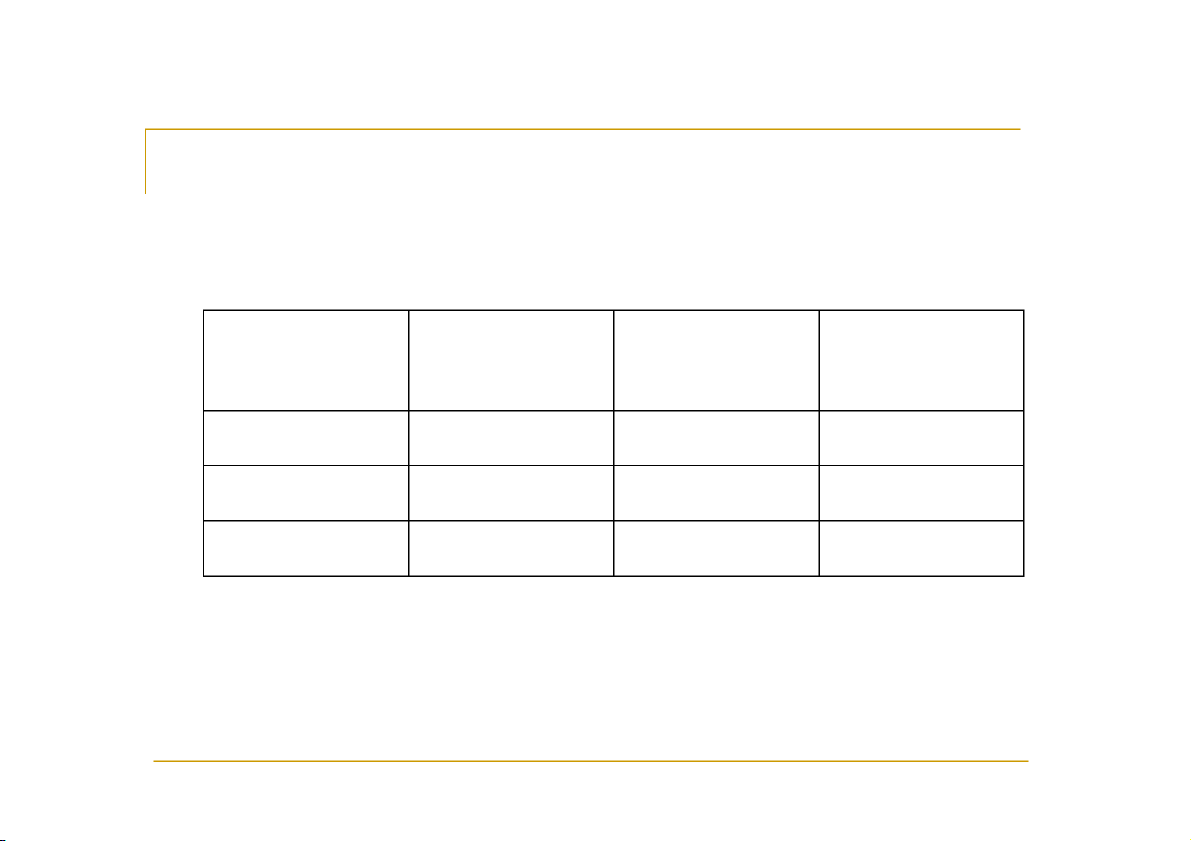
6. Buffon và Pearson thảy một đồng xu nhiều lần và
nhận được kết quả sau
Người thực Số lần thảy Số lần mặt Tần suất hiện số Buffon 4.040 2.048 ? Pearson 12.000 6.019 ? Pearson 24.000 12.012 ?
Xác suất nhận được mặt số là: ..?.. 5 Công thức cộng
 Cho A ⊂Ωvà B ⊂Ω. Khi đó A ∪ B ⊂Ω, A ∩ B ⊂ Ω và
P(A ∪ B) = P(A) + P(B) – P( A ∩ B) .
 Giả sử chúng ta có kết quả của phép thử là ω.
+/ ω ∈ A ∪ B ⇔ ω ∈ A hoặc ω ∈ B.
+/ ω ∈ A ∩ B ⇔ ω ∈ A và ω ∈ B. 6  Cho A ⊂Ω, ta có
0≤P(A)≤1và P(Ω\A) =1−P(A). 7
 Ví dụ 5. Hai người bán hàng trong một hiệu sách (gọi
là X và Y). Xác suất người X đi làm trể trong ngày là
0.2, xác suất người Y đi làm trể trong ngày là 0.15, và
xác suất cả hai cùng đi trể trong ngày là 0.09. Tìm các xác suất:
a) Tối thiểu một người đi làm trể.
b) Không có người nào đi làm trể. 8
 Ví dụ 6. Công ty quyết định tuyển dụng một nhân
viên trong số 3 người đến xin việc A, B và C. Cho
biết A và B có cùng xác suất để được tuyển dụng, C
có xác suất được tuyển dụng gấp đôi A. Tính xác suất a) C được tuyển dụng;
b) B không được tuyển dụng. 9
 Ví dụ 7. Qua điều tra về tình hình học thêm trong
sinh viên, ta biết 40% sinh viên học thêm ngoại ngữ,
55% học thêm tin học và 30% học thêm cả hai môn
này. Chọn ngẫu nhiên 1 sinh viên. Tính xác suất:
a) Chọn được sinh viên học thêm.
b) Chọn được sinh viên không học thêm. 10