Lý thuyết xác suất và thống kê
Giảng viên: TS. Nguyễn Như Lân Email: lan.nn@ou.edu.vn 1 Phân phối nhị thức
 Xét phép thử τ có không gian mẫu là  và A   với PA  p.
 Thực hiện n lần độc lập phép thử τ. Gọi X là số lần biến cố A xảy ra, ta có P X  k  C p  p n  n- 1 k k k .
Ta nói X có phân phối nhị thức, ký hiệu: X Bn; p. 
 Ví dụ 1. Trong một vùng dân cư có 65% gia đình có
máy giặt, chọn ngẫu nhiên 12 gia đình. Tính xác suất:
a) Chọn đúng 5 gia đình có máy giặt.
b) Có ít nhất hai gia đình có máy giặt.
 Hướng dẫn: Xét phép thử τ: Chọn ngẫu nhiên 1 gia đình.
A: “Chọn được gia đình có máy giặt”, thì P(A) = 0,65 (vùng dân
cư có 65% gia đình có máy giặt).
- Thực hiện phép thử τ lần thứ 2 thì P(A) = 0,65;
- Tiếp tục thực hiện phép thử τ lần thứ 3 thì P(A) = 0,65; ….
Chọn ngẫu nhiên 12 gia đình tức là chúng ta thực hiện 12 lần
phép thử τ và ở mỗi lần thực hiện phép thử τ thì xác suất của biến
cố A không thay đổi (P(A) = 0,65).
Như vậy, chúng ta có mô hình phân phối nhị thức với biến ngẫu
nhiên X là số lần chọn được gia đình có máy giặt, X B(12; 0,65). a) P(X = 5); b) P(X 2) = 1 – P(X < 2) = 1 – [P(X = 0) + P(X = 1)]. 4  Cho X  B(n; p), ta có i) EX  np; ii) VarX  np(1 p); iii) ModX  k thỏa 0 n  1p 1 ≤ k ≤ 0 n  1p.
 Ví dụ 2. Một nhân viên tiếp thị bán hàng ở 5 chỗ
khác nhau trong ngày. Xác suất bán được hàng ở mỗi nơi đều là 0.4.
a) Tìm xác suất để nhân viên này bán được hàng trong ngày.
b) Mỗi năm nhân viên này đi bán hàng 330 ngày. Gọi
Y là số ngày bán được hàng trong năm. Tìm giá trị tin
chắc nhất của Y, nghĩa là tìm số ngày bán được hàng
nhiều khả năng nhất trong một năm.
 X: Tổng số nơi bán được hàng trong ngày. a) P(X  1) = 0.92224.
b) Y B(330; 0,92224). Mod(Y) = 305. 7
 Ví dụ 3. Một lô thuốc gồm 10 lọ trong đó có 2 lọ
thuốc hỏng. Lấy ngẫu nhiên 5 lọ từ lô thuốc, có hoàn
lại. Gọi X là số lọ hỏng trong 5 lọ lấy ra. Tìm hàm mật độ của X.
 Ví dụ 4. Một nhà máy sản xuất với tỷ lệ phế phẩm là 7%.
a) Quan sát ngẫu nhiên 10 sản phẩm. Tính xác suất i) Có đúng 1 phế phẩm;
ii) Có ít nhất 1 phế phẩm;
iii) Có nhiều nhất 1 phế phẩm.
b) Hỏi phải quan sát ít nhất bao nhiêu sản phẩm để
xác suất nhận được ít nhất 1 phế phẩm ≥ 0,9.
Biến ngẫu nhiên liên tục
 Biến ngẫu nhiên có tập giá trị là một khoảng của tập
số thực hay cả tập số thực được gọi là biến ngẫu nhiên liên tục.
 Trong thực nghiệm, các biến ngẫu nhiên thường là rời
rạc. Tuy nhiên, khi biến ngẫu nhiên khảo sát lấy giá
trị tùy ý trên một khoảng của tập số thực hay cả tập số
thực, ta coi nó như biến ngẫu nhiên liên tục.
 Ví dụ: Nhiệt độ trong ngày ở TPHCM là biến ngẫu nhiên liên tục.
 Cho X là biến ngẫu nhiên liên tục có hàm mật độ là f(x), ta có b i) Pa  X  b  f  xd ;x a  ii) E X   xf   x d ;x   iii) Var  X   x  E   X  2 f xd .x    Phân phối chuẩn tắc
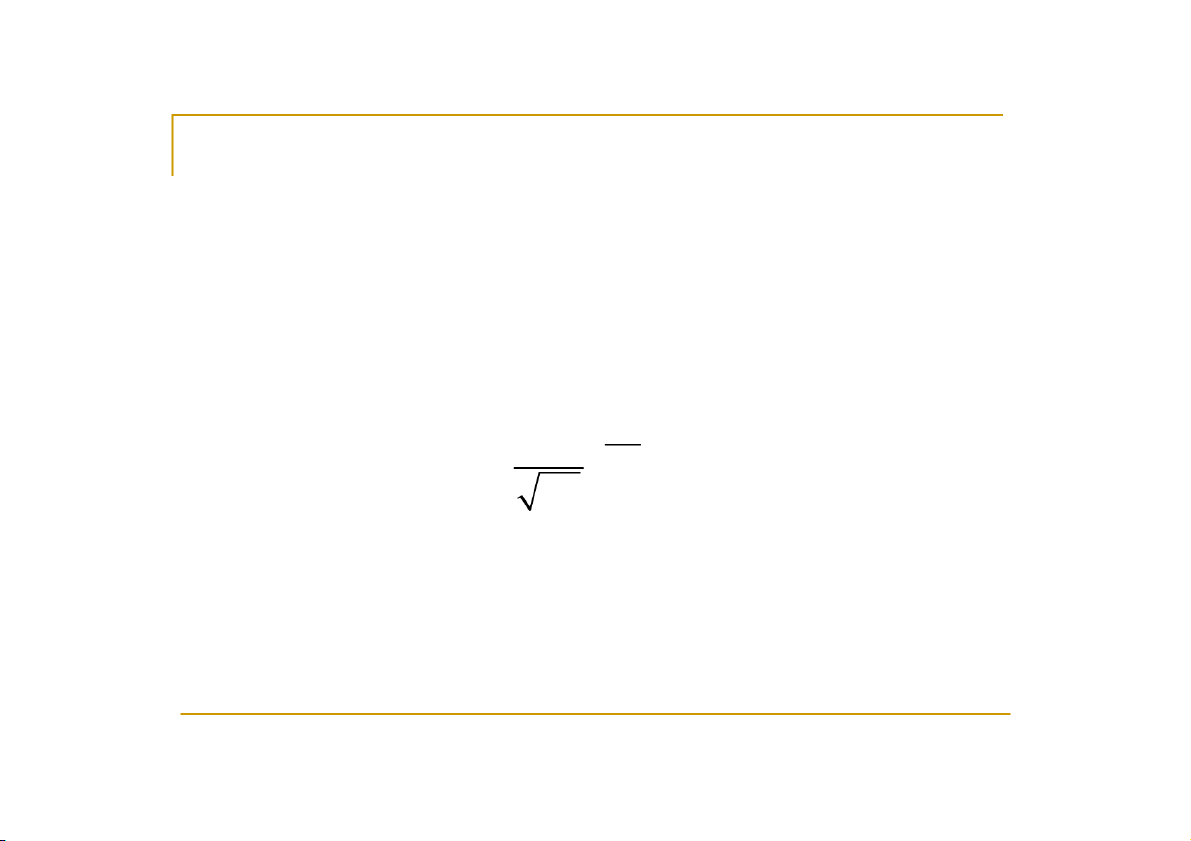
 Biến ngẫu nhiên liên tục Z có hàm mật độ được cho bởi 2  z f z 1 2  e ,   z   .  2π
được gọi là có phân phối chuẩn tắc và được ký hiệu là Z  N 0;  1 .  Cho Z  N  0 ; 1  , ta có i) E(Z) = 0 và σ = 1. Z
ii) P(Z ≥ 0) = P(Z ≤ 0) = 0,5.
iii) P(-a ≤ Z ≤ 0) = P(0 ≤ Z ≤ a) với mọi a > 0.
iv) P(Z ≤ -a) = P(Z ≥ a) = 0,5 - P(0 ≤ Z ≤ a) với a > 0.
v) P(Z ≥ -a) = P(Z ≤ a) = 0,5 + P(0 ≤ Z ≤ a) với a > 0. Ví dụ 5  Cho Z  N  0 ; 1  , tính: a) P(Z < -1,25); b) P(-0,5 < Z < 0,75); c) P(Z > 1). Ví dụ 6  Cho Z  N  0 ; 1  .
a) Tính P(Z > 1,7); P(Z > 0,96); P(Z < 1,44);
P(Z < -1,44); P(-1,01 < Z <0,33).
b) Tìm a sao cho P(Z > a) = 0,3333; P(Z < a) = 0,605;
P(Z > a) = 0,605; P(1 < Z < a) = 0,1. Phân phối chuẩn
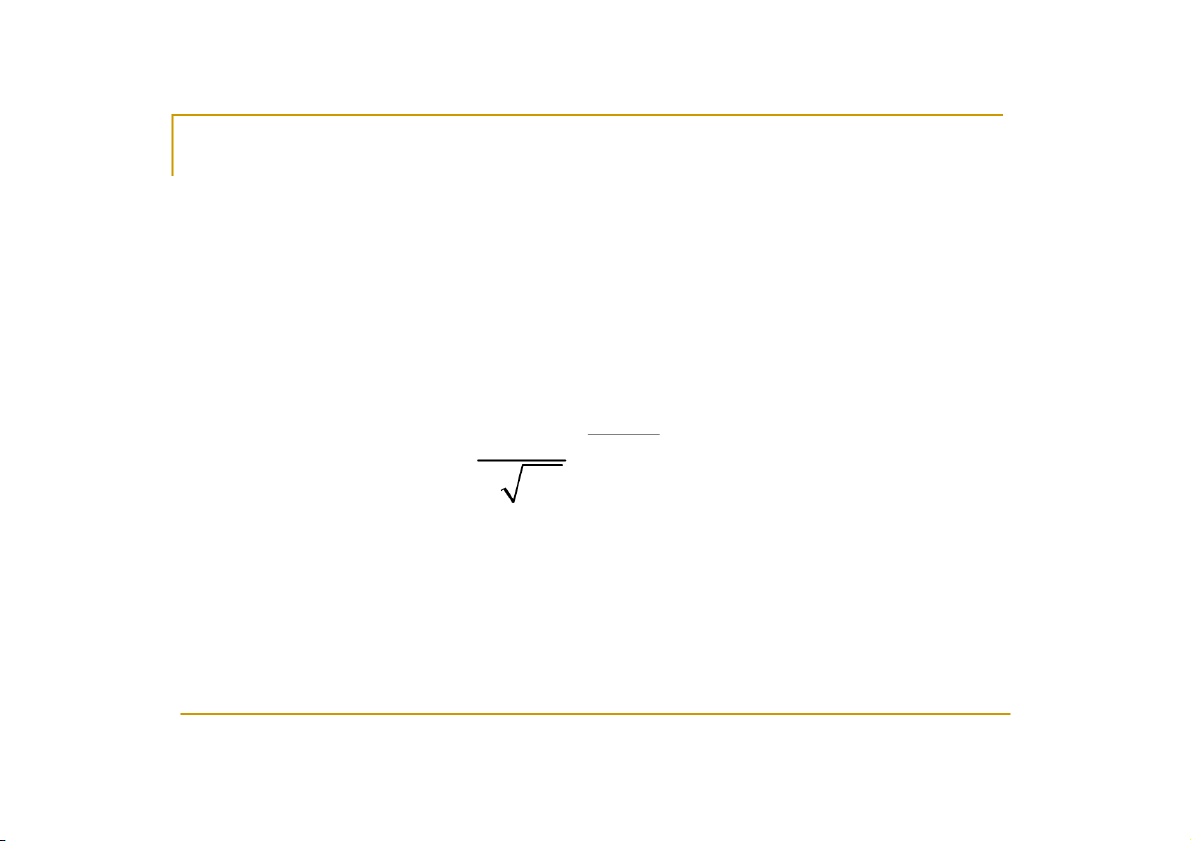
 Biến ngẫu nhiên liên tục X có hàm mật độ được cho bởi   x μ  2 f x 1 2 2σ  e ,    x   .  σ 2π
được gọi là có phân phối chuẩn, ký hiệu:   2 X N μ; σ . 2  Cho X  N  μ; σ , ta có i) E(X) = μ và σ = σ; X X μ ii) Z   N0; 1. σ Ví dụ 7
 Giả sử chiều cao người ta là đại lượng ngẫu
nhiên X có phân phối chuẩn với trung bình μ =
160 cm và phương sai σ2 = 100 cm2. Tính tỷ lệ
số người có chiều cao trong khoảng từ 150cm đến 170cm. Ví dụ 8  Gọi
X là thu nhập của công nhân (triệu
đồng/tháng) trong một xí nghiệp theo phân phối
chuẩn với trung bình μ = 2,74 và độ lệch chuẩn
σ = 0,32. Tìm giá trị của ẩn số a sao cho P(μ - a < X < μ + a) = 0,95. Ví dụ 9
 Trọng lượng của một loại sản phẩm do một nhà
máy sản xuất là biến ngẫu nhiên có phân phối
chuẩn với kỳ vọng là 250gr và độ lệch chuẩn là
5gr. Sản phẩm là loại I nếu trọng lượng của nó
từ 245gr trở lên. Tính tỷ lệ sản phẩm loại I của nhà máy này.