Lý thuyết xác suất và thống kê
Giảng viên: TS. Nguyễn Như Lân Email: lan.nn@ou.edu.vn 1 THỐNG KÊ
 Nghiên cứu trọng lượng người Việt Nam.
+ Tổng thể: Tất cả người Việt Nam;
+ Dấu hiệu quan sát: Trọng lượng.
 Kiểm tra hàm lượng chất béo trong một loại thực phẩm.
+ Tổng thể: Toàn bộ sản phẩm;
+ Dấu hiệu quan sát: Hàm lượng chất béo. Bài toán
 Chúng ta đưa ra kết luận về dấu hiệu ∗ của một tổng thể.
 Ví dụ: Cho biết chiều cao trung bình của thanh niên Việt nam. 3 Phương pháp thống kê
 Quan sát ngẫu nhiên một số trường hợp được gọi là
và trên cơ sở các số liệu quan sát
này, chúng ta suy rộng ra cho tổng thể.
 Muốn cho sự suy rộng ít bị sai lầm thì mẫu phải
đại diện cho tổng thể, và do đó, việc lấy mẫu
phải được thực hiện sao cho mọi cá thể có cơ
hội được quan sát đồng đều như nhau.
 Giả sử chúng ta quan sát
phần tử của tổng thể.
Gọi X là kết quả của lần quan sát thứ nhất; 1
X2 là kết quả của lần quan sát thứ 2; ……
Xn là kết quả của lần quan sát thứ n.
Khi đó X1, X2, …, Xn là các biến ngẫu nhiên được coi như và có .
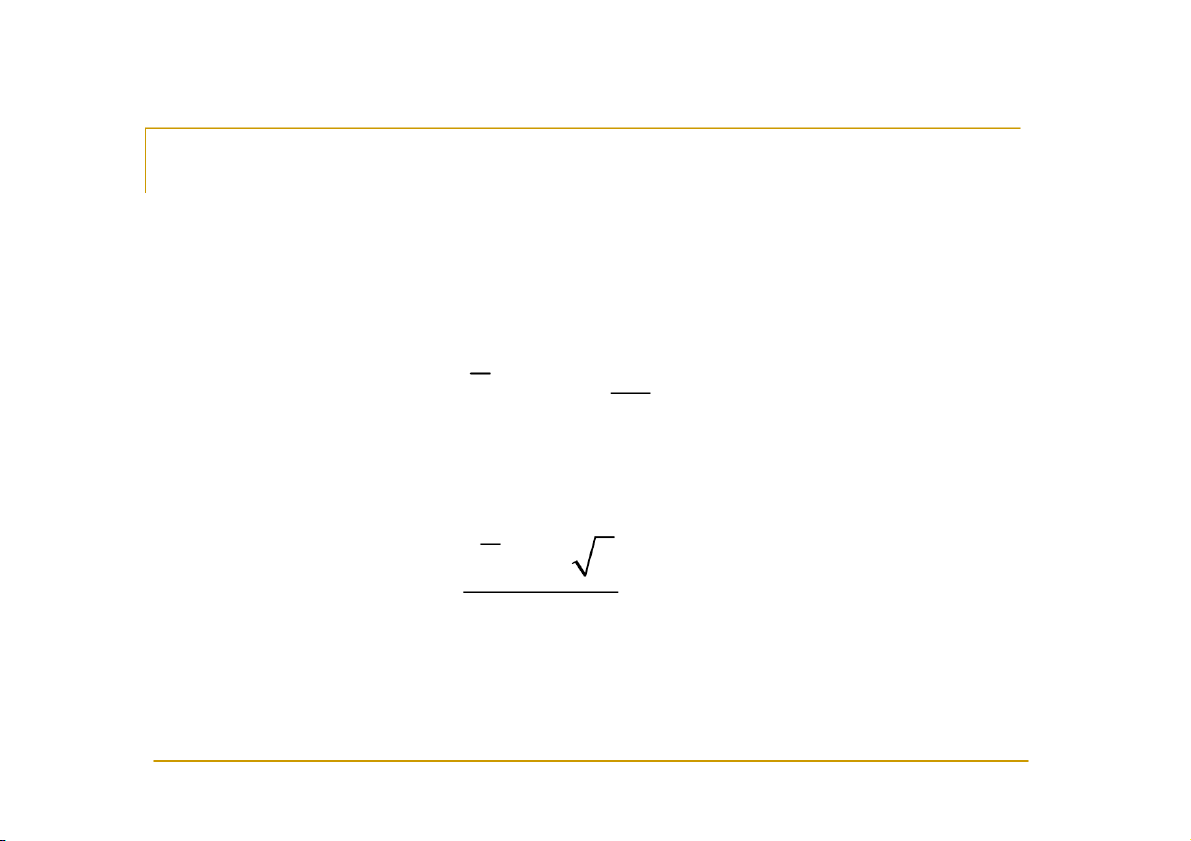
CÁC THỐNG KÊ THƯỜNG DÙNG X X ... X  Trung bình mẫu: 1 2 n X ; n  Phương sai mẫu: 2 2 2 X X X X ... X X 2 1 2 n S ; n 1
 Giá trị nhỏ nhất của mẫu: Y = min {X , …, X }; 1 1 n
 Giá trị lớn nhất của mẫu: Y = max {X , …, X }; n 1 n
 Tầm của mẫu: R = Yn – Y . 1 Mệnh đề
 Nếu tổng thể có phân phối chuẩn N(μ; σ2) thì 2 σ X N μ; n và X μ n T St n-1 . S
Tính giá trị trung bình, phương sai và độ lệch chuẩn của mẫu
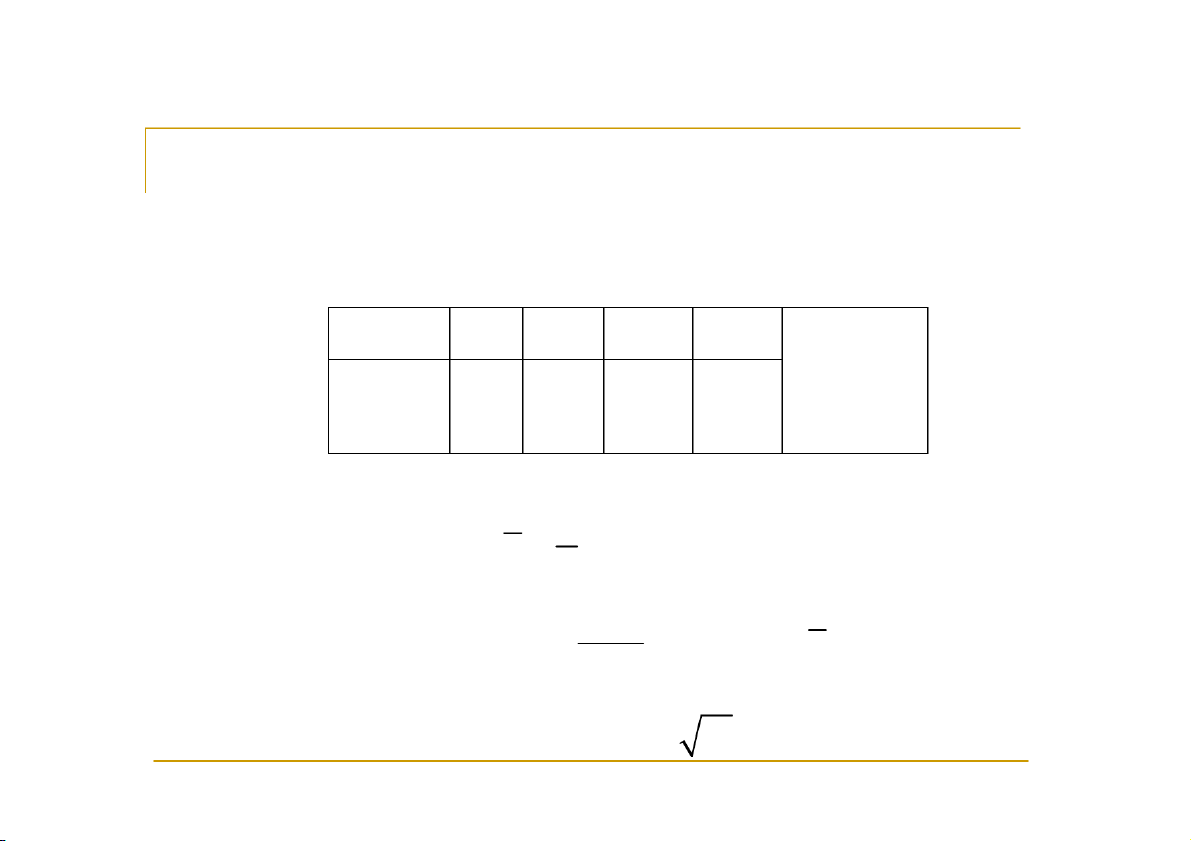
 Giả sử chúng ta có số liệu của mẫu như sau Giá trị x1 x2 … xk Tần n1 n2 … nk số 1 Khi đó: i) Trung bình mẫu: 1 ; 1 1 ii) Phương sai mẫu: 2 2 2 ; 1 1
iii) Độ lệch chuẩn của mẫu: 2 . Ví dụ 1
 Thu thập dữ liệu số trẻ em ở lứa tuổi đến trường
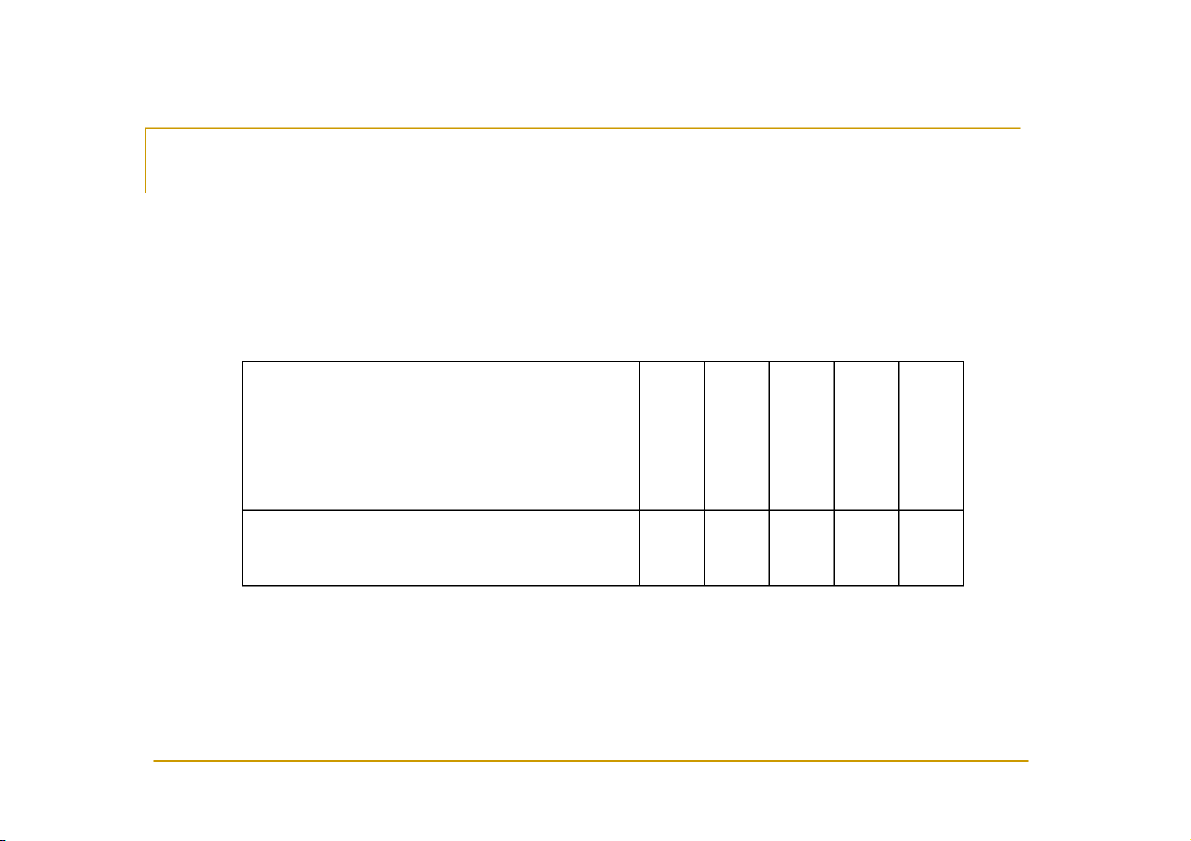
của 30 gia đình ta được bảng số liệu như sau: Số trẻ ở tuổi đến 0 1 2 3 4 trường Số hộ gia đình 12 6 7 3 2
Tính trung bình, phuơng sai và độ lệch chuẩn của mẫu. Ví dụ 2
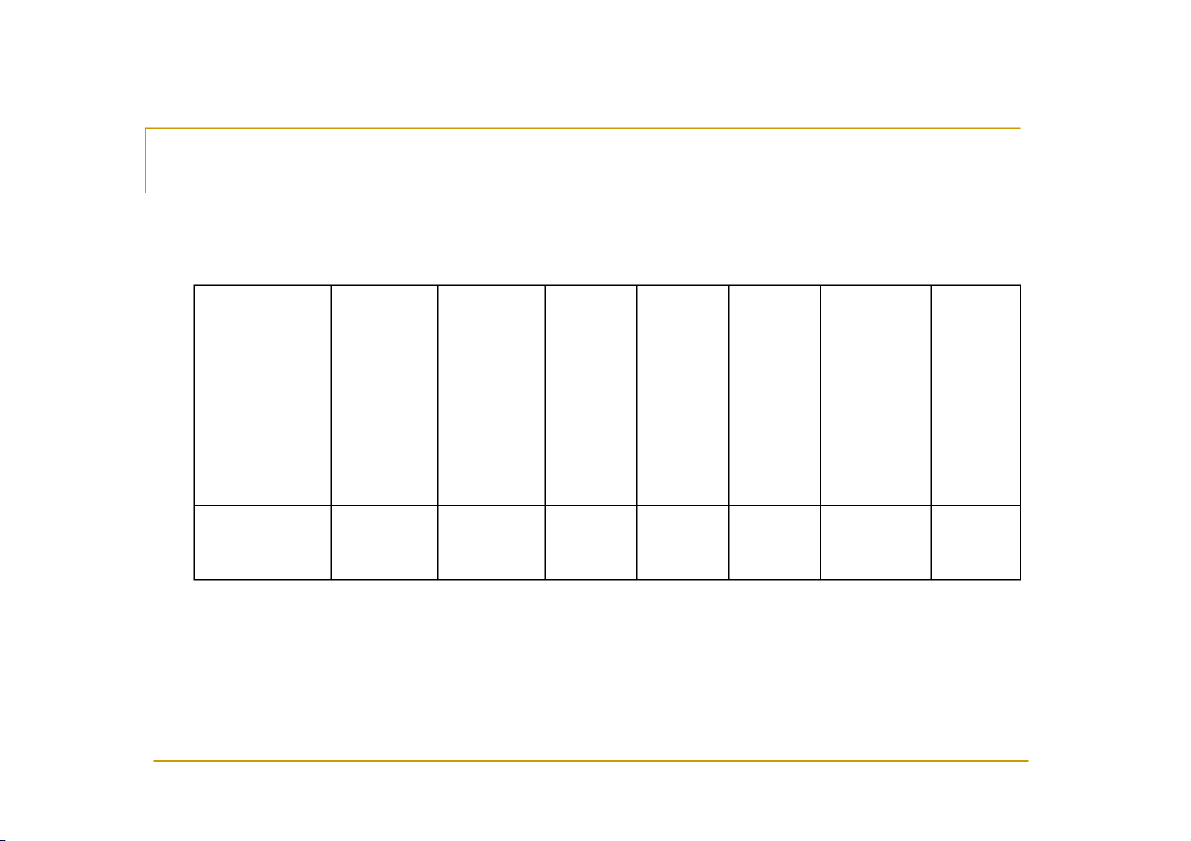
 Đo chiều cao của 100 SV ở một trường ĐH ta được
Chiều 154 - 158 - 162- 166- 170- 174- 178 cao 158 162 166 170 174 178 - 182 Số SV 9 25 27 20 13 5 1
Hãy tính trung bình, phuơng sai và độ lệch chuẩn của mẫu.