Số phức (dành cho học sinh Yếu – TB) – Đặng Việt Đông Toán 12

Số phức (dành cho học sinh Yếu – TB) – Đặng Việt Đông Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

26 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 4: Số phức

Môn: Toán 12

Thông tin:

31 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay
Bài 1: SỐ PHỨC VÀ CÁC PHÉP TOÁN SỐ PHỨC
A – LÝ THUYẾT CHUNG
1.1. Khái niệm số phức
Số phức (dạng đại số) : . Trong đó : là phần thực, là phần ảo, là đơn
vị ảo,
Tập hợp số phức kí hiệu: .
là số thực phần ảo của bằng .
là số ảo (hay còn gọi là thuần ảo) phần thực bằng .
Số vừa là số thực vừa là số ảo.
1.2. Hai số phức bằng nhau
Hai số phức và bằng nhau khi phần thực và phần
ảo của chúng tương đương bằng nhau.
Khi đó ta viết
1.4. Số phức liên hợp
Số phức liên hợp của là .
là số thực ; là số ảo .
1.5. Môđun của số phức
Độ dài của vectơ được gọi là môđun của số phức và kí hiệu là . Vậy hay
.
Một số tính chất:
;
.
; ;
.
2. Phép cộng trừ nhân chia số phức
2.1. Phép cộng và phép trừ số phức
Cho hai số phức và . Khi đó:
Số đối của số phức là .
z a bi a b; ,
a
b
i
i
2
1.
z
z
0
b
0
z
0
a
0
0
z a bi a b
1
,
z c di c d
2
,
a c
z z a bi c di
b d
1 2
z a bi a b,
z a bi
z z
z z z z z z z z z z z z a b
z z
2 2
1 1
2 2
; ' ' ; . ' . '; ; . .
z
z z
z
z z
OM
z
z
z OM
z a bi OM a b
2 2

z a b zz OM
2 2
z z
z z
0, ;
z z
0 0
z z z z
1 2 1 2
. .
z
z
z
z
1
1
2
2
z z z
z
z
1 1 2
2
2
2
.
z z z z z z
1 2 1 2 1 2
z a bi a b
1
,
z c di c d
2
,
z z a c b d i
1 2
z a bi
z a bi
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay
Tổng của một số phức với số phức liên hợp của nó bằng hai lần phần thực của số thực đó:
.
2.2. Phép nhân số phức
Cho hai số phức và .
Khi đó: .
Với mọi số thực và mọi số phức , ta có
Đặc biệt: với mọi số phức .
Lũy thừa của
:
.
2.3. Chia hai số phức
Số phức nghịch đảo của khác là số .
Phép chia hai số phức và là .
B – BÀI TẬP
Câu 1. Số phức
15 3
z i
có phần ảo bằng
A.
3
. B.
15
. C.
3
i
. D.
3
.
Câu 2. Số phức
1 2 2 3
z i i
bằng
A.
8.
B.
8 .
i
C.
4 .
i
D.
8 .
i
Câu 3. Cho số phức . Tìm phần thực của .
A. . B. . C. . D. không có.
Câu 4. Cho số phức
z
có điểm biểu diễn là điểm
A
trong hình vẽ bên. Tìm phần thực và phần ảo của số
phức
z
.
A. Phần thực bằng
3
, phần ảo bằng
2
. B. Phần thực bằng
3
, phần ảo bằng
2
.
C. Phần thực bằng
2
, phần ảo bằng
3
i
. D. Phần thực bằng
3
, phần ảo bằng
2
i
.
Câu 5. Cho số phức
1
1 2
z i
và
2
2 2
z i
. Tìm môđun của số phức
1 2
z z
.
A.
1 2
17
z z . B.
1 2
5
z z
. C.
1 2
2 2
z z . D.
1 2
1
z z
.
Câu 6. Cho số phức
3 2
z i
. Tìm phần ảo của số phức liên hợp của
z
.
A.
2
i
. B.
2
i
. C.
2
. D.
2
.
Câu 8. Tìm số phức
z
thỏa mãn
2 1 4 2
i i z i
.
A.
1 3
z i
. B.
1 3 .
z i
C.
1 3
z i
. D.
1 3
z i
.
Câu 9. Môđun của số phức
2 3
3
i
z i
i
là
z a bi z z a
, 2
z a bi a b
1
,
z c di c d
2
,
z z a bi c di ac bd ad bc i
1 2
–
k
z a bi a b,
k z k a bi ka kbi
. . .
z
0. 0
z
i
i i i i i i i i
0 1 2 3 2
1, , 1, .
n n n n
i i i i i i n
4 4 1 4 2 4 3
1, , 1, ,
z
0
z z
z
1
2
1
z
'
z
0
z z z z z
z z
z z z
z
1
2
' '. '.
'
.
3
z i
z
3
0
3
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay
A.
170
3
z . B.
170
7
z . C.
170
4
z . D.
170
5
z .
Câu 10. Tìm phần ảo của số phức
z
, biết
1 3
i z i
.
A.
1
B.
1
C.
2
D.
2
Câu 11. Cho số phức
1 2
z i
thì số phức liên hợp
z
có
A. phần thực bằng
1
và phần ảo bằng
2
. B. phần thực bằng
2
và phần ảo bằng
1
.
C. phần thực bằng
1
và phần ảo bằng
2
. D. phần thực bằng
2
và phần ảo bằng
1
.
Câu 13. Cho số phức
z a bi
,a b
. Khẳng định nào sau đây sai?
A.
2 2
z a b
. B.
z a bi
. C.
2
z
là số thực. D.
.
z z
là số thực.
Câu 14. Cho số phức
z a bi
,
,a b
. Tính môđun của số phức
z
.
A.
z a b
. B.
2 2
z a b
. C.
2 2
z a b
. D.
2 2
z a b
.
Câu 15. Trong mặt phẳng tọa độ
Oxy
, số phức liên hợp của số phức
1 2 1
z i i
có điểm biểu diễn là
điểm nào sau đây?
A.
3;1
Q . B.
3;1
N . C.
3; 1
M
. D.
1;3
P .
Câu 16. Cho số phức
z i
. Phần thực và phần ảo của số phức
z
là:
A. Phần thực bằng
5
và phần ảo bằng
2
. B. Phần thực bằng
2
và phần ảo bằng
5
.
C. Phần thực bằng
2
i
và phần ảo bằng
5
. D. Phần thực bằng
5
và phần ảo bằng
2
i
.
Câu 17. Cho số phức
1
z i
. Khi đó
3
z
bằng
A.
1
. B.
2
. C.
2 2
. D.
4
.
Câu 18. Tìm mô đun của số phức
z
thoả
3 (3 i)(1 i) 2
iz
.
A.
2 3
3
z
. B.
2 2
3
z
. C.
3 2
2
z
. D.
3 3
2
z
.
Câu 19. Số phức liên hợp của số phức
z i
là
A.
2
i
B.
1 2
i
C.
1 2
i
D.
1 2
i
Câu 20. Số nào trong các số phức sau là số thực?
A.
3 2 3 2
i i
. B.
3 2 3 2
i i
.
C.
5 2 5 2
i i
. D.
1 2 1 2
i i
.
Câu 21. Cho số phức
z
thỏa mãn:
2
(2 3 ) (4 ) (1 3 )
i z i z i
. Xác định phần thực và phần ảo của
.
z
A. Phần thực là
2
; phần ảo là
3.
B. Phần thực là
3
; phần ảo là
5 .
i
C. Phần thực là
2
; phần ảo là
5 .
i
D. Phần thực là
2
; phần ảo là
5.
Câu 22. Xét số phức
z
thỏa mãn
10
1 2 2 .
i z i
z
Mệnh đề nào dưới đây đúng?
A.
3
2.
2
z B.
2.
z C.
1
.
2
z D.
1 3
.
2 2
z
Câu 23. Cho hai số phức
1 3
z i
,
2
w i
. Tìm phần ảo của số phức
.
u z w
.
A.
7
. B.
5
i
. C.
5
. D.
7
i
.
Câu 24. Tìm số phức
z
thỏa mãn đẳng thức
2 1 2
iz z i
.
A.
1
z i
. B.
1
z
. C.
z i
. D.
1
z i
.
Câu 25. Cho số thực
x
,
y
thỏa
2 2 2 3 2 1
x y y x i x y y x i
. Khi đó giá trị của
2 2
4
M x xy y
là
A.
1
M
. B.
1
M
. C.
0
M
. D.
2
M
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay
Câu 26. Cho số phức
1 3
z i
, môđun của số phức
2
w z iz
là
A.
146
w . B.
146
w . C.
10
w . D.
0
w .
Câu 27. Cho số phức . Tìm phần thực của số phức .
A. . B. . C. . D. .
Câu 28. Rút gọn biểu thức
2018
1M i ta được
A.
1009
2
M
. B.
1009
2
M
. C.
1009
2
M i
. D.
1009
2
M i
.
Câu 29. Cho số phức
1 2
z i
. Tìm phần thực và phần ảo của số phức 2
w z z
.
A. Phần thực là
3
và phần ảo là
2
. B. Phần thực là
3
và phần ảo là
2
i
.
C. Phần thực là
2
i
và phần ảo là
3
. D. Phần thực là
2
và phần ảo là
3
.
Câu 32. Cho số phức
z
thỏa mãn:
2
(2 3 ) (4 ) (1 3 )
i z i z i
. Xác định phần thực và phần ảo của
.
z
A. Phần thực là
2
; phần ảo là
5 .
i
B. Phần thực là
2
; phần ảo là
5.
C. Phần thực là
2
; phần ảo là
3.
D. Phần thực là
3
; phần ảo là
5 .
i
Câu 33. Cho số phức
z
thỏa mãn điều kiện
2 4 3 2
i z i z i
. Số phức liên hợp của
z
là
A.
5 1
4 4
z i
. B.
5 1
4 4
z i
. C.
1 5
4 4
z i
. D.
1 5
4 4
z i
.
Câu 34. Cho số phức
z i
. Số phức
1
z
có phần thực là
A.
2
29
. B.
3
. C.
7
. D.
5
29
.
Câu 35. Cho số phức
z i
. Tìm phấn thực và phần ảo của số phức
2
z z
.
A. Phần thực
6
và phần ảo
5
. B. Phần thực
6
và phần ảo
5
i
.
C. Phần thực
6
và phần ảo
5
. D. Phần thực
6
và phần ảo
5 .
i
Câu 36. Tìm số thực
m
sao cho
2
1 1
m m i
là số ảo.
A.
1
m
. B.
0
m
. C.
1
m
. D.
1
m
.
Câu 37. Số phức
z
thỏa mãn
2 12 2
z z i
có:
A. Phần thực bằng
4
và phần ảo bằng
2
. B. Phần thực bằng
4
và phần ảo bằng
2
i
.
C. Phần thực bằng
4
và phần ảo bằng
2
i
. D. Phần thực bằng
4
và phần ảo bằng
2
.
Câu 38. Cho số phức
z
thỏa mãn
3
(1 3 )
1
i
z
i
. Môđun của số phức
bằng
A.
4 2.
B.
4 3.
C.
8 2.
D.
8 3.
Câu 40. Tổng phần thực và phần ảo của số phức
z
thoả mãn
1 2
iz i z i
bằng
A.
6
. B.
2
. C.
2
. D.
6
.
0, ,z a bi ab a b
2
1
w
z
2
2
2 2
b
a b
2 2
2
2 2
a b
a b
2
2 2
2
ab
a b
2 2
2
2 2
a b
a b
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay
Bài 2: PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC
A – LÝ THUYẾT CHUNG
1. Căn bậc hai của số thực âm
Cho số , nếu có số phức sao cho thì ta nói là một căn bậc hai của .
Mọi số phức đều có hai căn bậc hai.
Căn bậc hai của số thực âm là .
Tổng quát, các căn bậc hai của số thực âm là .
2. Phương trình bậc hai với hệ số thực
Cho phương trình bậc hai . Xét biệt số của phương trình.
Ta thấy:
Khi , phương trình có một nghiệm thực .
Khi , phương trình có hai nghiệm thực phân biệt .
Khi , phương trình có hai nghiệm phức .
B – BÀI TẬP
Câu 1:
G
ọi
1
z
và
2
z
là các nghiệm của phương trình
2
4 9 0
z z
. Gọi
,
M N
là các điểm biểu diễn của
1
z
và
2
z
trên mặt phẳng phức. Khi đó độ dài của
MN
là:
A.
2 5
MN . B.
5
MN
. C.
2 5
MN . D.
4
MN
.
Câu 2: Gọi
1 2 3
, ,
z z z
là ba nghiệm của phương trình
3
1 0
z
. Tính
1 2 3
S z z z
A.
4
S
B.
2
S
C.
3
S
D.
1
S
Câu 3: Gọi
1
z
,
2
z
là các nghiệm phức của phương trình
2
2 5 0
z z
. Giá trị của biểu thức
1 2
4 4
z z
bằng.
A.
7
B.
14
C.
7
D.
14
Câu 4: Phương trình bậc hai nào dưới đây nhận hai số phức
2 3
i
và
2 3
i
làm nghiệm?
A.
2
4 13 0
z z
B.
2
4 3 0
z z
C.
2
4 13 0
z z
D.
2
4 3 0
z z
Câu 5: Gọi
1
z
và
2
z
là 2 nghiệm của phương trình
2
2 6 5 0
z z
trong đó
2
z
có phần ảo âm. Phần thực và
phần ảo của số phức
1 2
3
z z
lần lượt là
A.
6;1
B.
6;1
C.
1; 6
D.
6; 1
Câu 6: Biết phương trình
2
2 0
z z m
m
có một nghiệm phức
1
1 3
z i
và
2
z
là nghiệm phức
còn lại. Số phức
1 2
2
z z
là ?
A.
3 9
i
. B.
3 3
i
. C.
3 9
i
. D.
3 3
i
.
Câu 7: Kí hiệu
1
z
,
2
z
,
3
z
,
4
z
là bốn nghiệm của phương trình
4 2
6 0
z z
. Tính
1 2 3 4
S z z z z
.
A.
2 2 3
S
B.
2 2 3
S
C.
2 2
S D.
2 3
S
Câu 8: Gọi
A
,
B
là hai điểm biểu diễn hai nghiệm phức của phương trình
2
2 5 0
z z
. Tính độ dài đoạn
thẳng
AB
:
A.
2
. B.
4
. C.
12
. D.
6
.
z
z
1
z z
2
1
z
1
z
z
0
z
i z
a
i a
ax bx c a b c a
2
0, , , , 0
b ac
2
4
0
b
x
a
2
0
b
x
a
1,2
2
0
b i
x
a
1,2
2
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay
Câu 9: Gọi
1
z
và
2
z
là hai nghiệm phức của phương trình
2
6 11 0
z z
. Giá trị của biểu thức
1 2
3
z z
bằng
A.
2 11
. B.
11
. C.
22
. D.
11
.
Câu 10: Trong tập các số phức, cho phương trình
2
6 0
z z m
, m
1
. Gọi
0
m
là một giá trị của
m
để phương trình
1
có hai nghiệm phân biệt
1
z
,
2
z
thỏa mãn
1 1 2 2
. .
z z z z
. Hỏi trong khoảng
0;20
có bao nhiêu giá trị
0
m
?
A.
13
. B.
11
. C.
12
. D.
10
.
Câu 11: Gọi
1
z
,
2
z
là hai nghiệm phức của phương trình
2
2 5 0
z z
, trong đó
1
z
có phần ảo dương. Tìm
số phức
2 2
1 2
2
w z z
.
A.
i
. B.
9 4
i
. C.
9 4
i
. D.
9 4
i
.
Câu 12: Phương trình
2
0
z az b
,( ,a b
) có nghiệm là
i
, tính
S a b
.
A.
19
S
. B.
19
S
. C.
7
S
. D.
7
S
.
Câu 13: Giải phương trình
2
4 5 0
z z
trên tập số phức ta được các nghiệm
A.
1 2
2 ; 2
z i z i
. B.
1 2
4 ; 4
z i z i
.
C.
1 2
4 ; 4
z i z i
. D.
1 2
2 ; 2
z i z i
.
Câu 14: Phương trình
2
3 9 0
z z
có hai nghiệm phức
1
z
,
2
z
. Tính
1 2 1 2
S z z z z
.
A.
12
S
. B.
6
S
. C.
6
S
. D.
12
S
.
Câu 15: Biết phương trình
2 2018
2017.2018 2 0
z z
có hai nghiệm
1
z
,
2
z
. Tính
1 2
S z z
.
A.
1009
2
S
. B.
1010
2
S
. C.
2018
2
S
. D.
2019
2
S
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay
Bài 3: TẬP HỢP ĐIỂM BIỂU DIỄN SỐ PHỨC
A – LÝ THUYẾT CHUNG
1. Biểu diễn hình học số phức
Số phức được biểu diễn bởi điểm hay
bởi trong mặt phẳng phức với hệ tọa độ .
2. Một số tập hợp điểm biểu diễn số phức z thường gặp:
tập hợp điểm là đường thẳng
tập hợp điểm là trục tung Oy
tập hợp điểm là trục hoành Ox
tập hợp điểm là hình tròn tâm bán kính
tập hợp điểm là đường tròn có tâm bán kính
tập hơp điểm là miền bên phải trục tung
tập hợp điểm là miền phía dưới trục hoành
tập hợp điểm là miền bên trái trục tung
tập hợp điểm là phía trên trục hoành
tập hợp điểm là đường Parabol
tập hợp điểm là đường Elip
tập hợp điểm là đường Hyperbol
B – BÀI TẬP
Câu 1: Trong hình vẽ bên, điểm
M
biểu diễn số phức
z
. Số phức
z
là
A.
2
i
. B.
2
i
. C.
1 2
i
. D.
1 2
i
.
Câu 2: Số phức
2 3
z i
có điểm biểu diễn trên mặt phẳng tọa độ là:
A.
2; 3
M
. B.
2;3
M
. C.
2;3
M
. D.
2; 3
M
.
Câu 3: Trong mặt phẳng phức, cho số phức
1 2
z i
. Điểm biểu diễn cho số phức
z
là điểm nào sau đây
A.
1; 2
M
B.
1;2
Q
C.
1;2
P
D.
2;1
N
Câu 4: Trong mặt phẳng
Oxy
, điểm
M
trong hình vẽ bên là điểm biểu diễn số phức
z
. Số phức
z
là
z a bi a b,
M a b
;
u a b
;
Oxy
ax by c
0
x
0
y
0
x a y b R
2 2
2
I a b
; ,
R
x a y b R
x y ax by c
2 2
2
2 2
2 2 0
I a b
; ,
R a b c
2 2
0
x
y
0
x
0
y
0
y ax bx c
2
x y
a b
2 2
2 2
1
x y
a b
2 2
2 2
1
x
y
O
M (a;b)
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay
A. 1 2i B. 2 i C. 1 2i D. 2 i
Câu 5: Trong mặt phẳng
Oxy
, cho các điểm
,A B
như hình vẽ bên. Trung điểm của đoạn thẳng
AB
biểu
diễn số phức.
A.
1
2
2
i . B.
1
2
2
i . C. 1 2i . D. 2 i .
Câu 6: Điểm nào trong hình vẽ dưới đây là điểm biểu diễn của số phức
1 2z i i ?
A. Q . B. M . C. N . D. P .
Câu 7: Hỏi điểm
3; 1M là điểm biểu diễn số phức nào sau đây?
A. 3z i B. 1 3z i C. 1 3z i D. 3z i
Câu 8: Điểm M trong hình vẽ bên là điểm biểu diễn của số phức z .
Tìm phần thực và phần ảo cú số phức z .
A. Phần thực bằng 3 và phần ảo bằng 4i. B. Phần thực bằng 4 và phần ảo bằng 3.
C. Phần thực bằng 4 và phần ảo bằng 3i . D. Phần thực bằng 3 và phần ảo bằng 4 .
Câu 9: Số phức 2 3z i có điểm biểu diễn là.
A.
2; 3A . B.
2; 3A . C.
2;3A . D.
2; 3A .
Câu 10: Trên mặt phẳng tọa độ
Oxy
cho điểm
M
trong hình vẽ bên là điểm biểu diễn của số phức z . Tìm
z ?
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 10
Facebook: https://www.facebook.com/dongpay
A.
3 4
z i
. B.
z i
. C.
z i
. D.
3 4
z i
.
Câu 11: Cho số phức
z
thỏa
1 2
z i
. Chọn phát biểu đúng:
A. Tập hợp điểm biểu diễn số phức
z
là một đường tròn có bán kính bằng
4
.
B. Tập hợp điểm biểu diễn số phức
z
là một đường thẳng.
C. Tập hợp điểm biểu diễn số phức
z
là một đường Parabol.
D. Tập hợp điểm biểu diễn số phức
z
là một đường tròn có bán kính bằng
2
.
Câu 12: Cho số phức
2 3
z i
. Điểm biểu diễn số phức liên hợp của
z
là
A.
2;3
. B.
2; 3
. C.
2; 3
. D.
2;3
.
Câu 13: Cho số phức
z i
. Biểu diễn hình học của
z
là điểm có tọa độ
A.
4;5
B.
4; 5
C.
4; 5
D.
4;5
Câu 14: Gọi
A
là điểm biểu diễn của số phức
2 5
z i
và
B
là 1điểm biểu diễn của số phức
z i
.
Tìm mệnh đề đúng trong các mệnh đề sau.
A. Hai điểm
A
và
B
đối xứng với nhau qua gốc toạ độ
O
.
B. Hai điểm
A
và
B
đối xứng với nhau qua đường thẳng
y x
.
C. Hai điểm
A
và
B
đối xứng với nhau qua trục hoành.
D. Hai điểm
A
và
B
đối xứng với nhau qua trục tung.
Câu 15: Cho hai số phức
3 5
z i
và
1 2
w i
. Điểm biểu diễn số phức
.
z z w z
trong mặt phẳng
Oxy
có tọa độ là
A.
6; 4
. B.
4; 6
. C.
4; 6
. D.
4; 6
.
Câu 16: Số phức
4 2
z i
có điểm biểu diễn trên mặt phẳng tọa độ là
M
. Tìm tọa độ điểm
M
A.
4; 2
M
. B.
4; 2
M
. C.
4;2
M
. D.
2;4
M .
Câu 17: Số phức liên hợp của số phức
1 2
z i i
có điểm biểu diễn là điểm nào dưới đây?
A.
1;2
A B.
2;1
F C.
2; 1
E
D.
1;2
B
Câu 18: Điểm
M
trong hình vẽ dưới đây biểu diễn số phức
z
.
x
y
2
3
M
O
1
y
x
O
M
3
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 11
Facebook: https://www.facebook.com/dongpay
Số phức
z
bằng
A.
i
. B.
2 3
i
. C.
2 3
i
. D.
i
.
Câu 19: Trên mặt phẳng tọa độ
Oxy
cho điểm
M
trong hình vẽ bên là điểm biểu diễn của số phức
z
.
Tìm
z
?
A.
z i
. B.
3 4
z i
. C.
3 4
z i
. D.
z i
.
Câu 20: Trong mặt phẳng toạ độ, điểm
1; 2
A
là điểm biểu diễn của số phức nào trong các số sau?
A.
1 2
z i
. B.
1 2
z i
. C.
2
z i
. D.
1 2
z i
.
Câu 21: Trong mặt phẳng tọa độ
Oxy
, Gọi
A
,
B
,
C
lần lượt là các điểm biểu diễn số phức
1 2
i
,
4 4
i
,
3
i
. Số phức biểu diễn trọng tâm tam giác
ABC
là
A.
1 3
i
. B.
3 9
i
. C.
i
. D.
1 3
i
.
Câu 22: Gọi
M
là điểm biểu diễn của số phức
z
trong mặt phẳng tọa độ,
N
là điểm đối xứng của
M
qua
Oy
(
M
,
N
không thuộc các trục tọa độ). Số phức
w
có điểm biểu diễn lên mặt phẳng tọa độ là
N
. Mệnh đề nào sau đây đúng ?
A.
w z
. B.
w z
. C.
w z
. D.
w z
.
Câu 23: Cho bốn điểm
A
,
B
,
C
,
D
trên hình vẽ biểu diễn 4 số phức khác nhau. Chọn mệnh đề sai.
A.
D
là biểu diễn số phức
1 2
z i
. B.
C
là biểu diễn số phức
1 2
z i
.
C.
A
là biểu diễn số phức
2
z i
. D.
B
là biểu diễn số phức
1 2
z i
.
Câu 24: Trong mặt phẳng tọa độ
Oxy
, gọi
M
là điểm biểu diễn số phức
3 4
z i
;
'
M
là điểm biểu diễn
cho số phức
1
'
2
i
z z
. Tính diện tích tam giác
'
OMM
.
A.
'
15
2
OMM
S
. B.
'
25
4
OMM
S
. C.
'
25
2
OMM
S
. D.
'
15
4
OMM
S
.
Câu 25: Điểm
M
trong hình vẽ bên là điểm biểu diễn số phức
z
tìm phần thực và phần ảo của số phức
z
.
x
y
3
-4
M
O 1
x
y
-2
-1
-2
1
-1
D
A
C
B
O
1
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 12
Facebook: https://www.facebook.com/dongpay
A. Phần thực là
2
và phần ảo là
1
. B. Phần thực là
2
và phần ảo là i .
C. Phần thực là
1
và phần ảo là
2
. D. Phần thực là
1
và phần ảo là 2i .
Câu 26: Trong mặt phẳng tọa độ Oxy , tập hợp điểm biểu diễn số phức z thỏa mãn 2 3z i i z là
A. đường tròn
2 2
2x y B. đường tròn
2 2
4x y
C. đường thẳng 2 3 0x y D. đường thẳng 2 1 0x y
Câu 27: Trong mặt phẳng tọa độ
Oxy
, gọi
M
là điểm biểu diễn số phức 3 4z i ;
'M
là điểm biểu diễn
cho số phức
1
'
2
i
z z
. Tính diện tích tam giác 'OMM .
A.
'
25
4
OMM
S
. B.
'
25
2
OMM
S
. C.
'
15
4
OMM
S
. D.
'
15
2
OMM
S
.
Câu 28: Cho
, ,A B C
lần lượt là các điểm biểu diễn các số phức 6 3i ;
1 2i i
;
1
i
. Tìm số phức có điểm
biểu diễn
D
sao cho ABCD là hình bình hành.
A. 8 4z i . B. 4 2z i . C. 8 5z i . D. 8 3z i .
Câu 29: Biết tập hợp các điểm biểu diễn số phức z thỏa mãn 1 2 4iz i là một đường tròn. Tìm tọa độ
tâm I của đường tròn đó.
A.
1;2I . B.
1; 2I . C.
2; 1I . D.
2;1I .
Câu 30: Điểm M trong hình bên là điểm biểu diễn cho số phức
A. 4 2z i . B. 2 4z i . C. 4 2z i . D. 2 4z i .
Câu 31: Cho số phức z thoả mãn 3 4 5z i . Biết rằng tập hợp điểm trong mặt phẳng toạ độ biểu diễn
các số phức z là một đường tròn. Tìm toạ độ tâm I và bán kính R của đường tròn đó.
A.
3; 4I , 5R . B.
3;4I , 5R .
C.
3; 4I , 5R . D.
3;4I , 5R .
Câu 32: Gọi M và N lần lượt là các điểm biểu diễn của
1
z ,
2
z trên mặt phẳng tọa độ, I là trung điểm MN
, O là gốc tọa độ (3 điểm O, M , N phân biệt và không thẳng hàng). Mệnh đề nào sau đây là
đúng?
A.
1 2
2z z OM ON . B.
1 2
2z z OI .
C.
1 2
z z OI . D.
1 2
z z OM ON .
Câu 33: Gọi
1
z là nghiệm phức có phần ảo âm của phương trình
2
2 3 0z z . Trên mặt phẳng tọa độ, điểm
nào sau đây là điểm biểu diễn của số phức
1
z ?
A.
1; 2Q i
. B.
1; 2N
. C.
1; 2M
. D.
1; 2P i
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 13
Facebook: https://www.facebook.com/dongpay
Câu 34: Cho
A
,
B
,
C
tương ứng là các điểm trong mặt phẳng phức biểu diễn các số phức
1
z i
,
2
2 5
z i
,
3
2 4
z i
. Số phức
z
biểu diễn bởi điểm
D
sao cho tứ giác
ABCD
là hình bình
hành là
A.
5
i
. B.
1 5
i
. C.
i
. D.
1 7
i
.
Câu 35: Điểm
M
trong hình vẽ dưới đây biểu diễn số phức
z
.
Số phức
1
z
bằng
A.
4 2
i
. B.
3 3
i
. C.
3 3
i
. D.
4 2
i
.
Câu 36: Cho số phức
z
thỏa mãn
2 0
iz i
. Khoảng cách từ điểm biểu diễn của
z
trên mặt phẳng tọa độ
Oxy
đến điểm
3; 4
M
là:
A.
2 2
. B.
2 5
. C.
13
. D.
2 10
.
Câu 37: Cho các số phức
z
thỏa mãn
1 1 2
z i z i
. Tập hợp các điểm biểu diễn các số phức
z
trên
mặt phẳng tọa độ là một đường thẳng. Phương trình đường thẳng đó là
A.
4 6 3 0
x y
B.
4 6 3 0
x y
C.
4 6 3 0
x y
D.
4 6 3 0
x y
Câu 38: Cho số phức . Trên mặt phẳng tọa độ , tìm điểm biểu diễn số phức .
A. . B. . C. . D. .
Câu 39: Tập hợp các điểm biểu diễn cho số phức
z
thỏa mãn
3 4 5
z i
là
A. Một đường Elip. B. Một đường tròn.
C. Một đường thẳng. D. Một đường parabol.
Câu 40: Cho số phức
z
thỏa mãn
1 2 5
z i
và
;
M x y
là điểm biểu diễn số phức
z
. Điểm
M
thuộc
đường tròn nào sau đây?
A.
2 2
1 2 5
x y
B.
2 2
1 2 25
x y
C.
2 2
1 2 25
x y
D.
2 2
1 2 5
x y
x
y
M
3
2
2
z i
Oxy
w iz
2; 1
M
2;1
M
1;2
M
1;2
M
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 14
Facebook: https://www.facebook.com/dongpay
HƯỚNG DẪN GIẢI
Bài 1: SỐ PHỨC VÀ CÁC PHÉP TOÁN SỐ PHỨC
Câu 1. Số phức
15 3
z i
có phần ảo bằng
A.
3
. B.
15
. C.
3
i
. D.
3
.
Hướng dẫn giải
Chọn D
Câu 2. Số phức
1 2 2 3
z i i
bằng
A.
8.
B.
8 .
i
C.
4 .
i
D.
8 .
i
Hướng dẫn giải
Chọn B
1 2 2 3 2 4 3 6 8
z i i i i i
Câu 3. Cho số phức . Tìm phần thực của .
A. . B. . C. . D. không có.
Hướng dẫn giải
Chọn B
Do là số thuần ảo nên có phần thực bằng .
Câu 4. Cho số phức
z
có điểm biểu diễn là điểm
A
trong hình vẽ bên. Tìm phần thực và phần ảo của số
phức
z
.
A. Phần thực bằng
3
, phần ảo bằng
2
. B. Phần thực bằng
3
, phần ảo bằng
2
.
C. Phần thực bằng
2
, phần ảo bằng
3
i
. D. Phần thực bằng
3
, phần ảo bằng
2
i
.
Hướng dẫn giải
Chọn A
Từ hình vẽ ta suy ra số phức
3 2 3 2
z i z i
.
Nên số phức
z
có phần thực bằng
3
, phần ảo bằng
2
.
Câu 5. Cho số phức
1
1 2
z i
và
2
2 2
z i
. Tìm môđun của số phức
1 2
z z
.
A.
1 2
17
z z . B.
1 2
5
z z
. C.
1 2
2 2
z z . D.
1 2
1
z z
.
Hướng dẫn giải
Chọn B
Ta có
2 2
1 2
1 2 2 2 3 4 3 4 5
z z i i i
Câu 6. Cho số phức
3 2
z i
. Tìm phần ảo của số phức liên hợp của
z
.
A.
2
i
. B.
2
i
. C.
2
. D.
2
.
Hướng dẫn giải
Chọn C
Ta có
3 2
z i
nên phần ảo của
z
là 2.
Câu 8. Tìm số phức
z
thỏa mãn
2 1 4 2
i i z i
.
A.
1 3
z i
. B.
1 3 .
z i
C.
1 3
z i
. D.
1 3
z i
.
Hướng dẫn giải
Chọn B
3
z i
z
3
0
3
3
z i
0
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 15
Facebook: https://www.facebook.com/dongpay
2 1 4 2 3 4 2 1 3 1 3
i i z i i z i z i z i
.
Câu 9. Môđun của số phức
2 3
3
i
z i
i
là
A.
170
3
z . B.
170
7
z . C.
170
4
z . D.
170
5
z .
Hướng dẫn giải
Chọn D
1 5 3
1 8 11 7
2 3 2 3
3 3 5 5 5 5
i i
z i i i i
i i
.
Suy ra
2 2
11 7 170
5 5 5
z
.
Câu 10. Tìm phần ảo của số phức
z
, biết
1 3
i z i
.
A.
1
B.
1
C.
2
D.
2
Hướng dẫn giải
Chọn D
Ta có:
1 3
i z i
3
1
i
z
i
3 1
1 1
i i
z
i i
1 2
z i
.
Vậy phần ảo của số phức
z
bằng
2
.
Câu 11. Cho số phức
1 2
z i
thì số phức liên hợp
z
có
A. phần thực bằng
1
và phần ảo bằng
2
. B. phần thực bằng
2
và phần ảo bằng
1
.
C. phần thực bằng
1
và phần ảo bằng
2
. D. phần thực bằng
2
và phần ảo bằng
1
.
Hướng dẫn giải
Chọn A
1 2
z i
. Do đó số phức liên hợp
z
có phần thực bằng
1
và phần ảo bằng
2
.
Câu 13. Cho số phức
z a bi
,a b
. Khẳng định nào sau đây sai?
A.
2 2
z a b
. B.
z a bi
. C.
2
z
là số thực. D.
.
z z
là số thực.
Hướng dẫn giải
Chọn C
Đáp án A và B đúng theo định nghĩa.
Đáp án C: Ta có
2
2 2 2
2
z a bi a bi b
là số phức có phần ảo khác
0
khi
0
b
Sai.
Đáp án D:
2
2 2 2
.
z z a bi a bi a bi a b
là một số thực
Đúng.
Câu 14. Cho số phức
z a bi
,
,a b
. Tính môđun của số phức
z
.
A.
z a b
. B.
2 2
z a b
. C.
2 2
z a b
. D.
2 2
z a b
.
Hướng dẫn giải
Chọn C
Do
2 2
z z a b
.
Câu 15. Trong mặt phẳng tọa độ
Oxy
, số phức liên hợp của số phức
1 2 1
z i i
có điểm biểu diễn là
điểm nào sau đây?
A.
3;1
Q . B.
3;1
N . C.
3; 1
M
. D.
1;3
P .
Hướng dẫn giải
Chọn C
Ta có
1 2 1
z i i
3
i
3
z i
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 16
Facebook: https://www.facebook.com/dongpay
Do đó điểm biểu diễn của
z
là
3; 1
M
.
Câu 16. Cho số phức
z i
. Phần thực và phần ảo của số phức
z
là:
A. Phần thực bằng
5
và phần ảo bằng
2
. B. Phần thực bằng
2
và phần ảo bằng
5
.
C. Phần thực bằng
2
i
và phần ảo bằng
5
. D. Phần thực bằng
5
và phần ảo bằng
2
i
.
Hướng dẫn giải
Chọn
C
5 2 5 2
z i z i
Phần thực là
5
và phần ảo là
2
.
Câu 17. Cho số phức
1
z i
. Khi đó
3
z
bằng
A.
1
. B.
2
. C.
2 2
. D.
4
.
Hướng dẫn giải
Chọn C
Ta có:
3 3
2 2 4 4 2 2
z i z .
Chú ý: Có thể sử dụng MTBT.
Câu 18. Tìm mô đun của số phức
z
thoả
3 (3 i)(1 i) 2
iz
.
A.
2 3
3
z
. B.
2 2
3
z
. C.
3 2
2
z
. D.
3 3
2
z
.
Hướng dẫn giải
Chọn B
Ta có:
2 2
3 (3 i)(1 i) 2
3 3
iz z i
2 2
3
z .
Câu 19. Số phức liên hợp của số phức
z i
là
A.
2
i
B.
1 2
i
C.
1 2
i
D.
1 2
i
Hướng dẫn giải
Chọn C
Số phức liên hợp của số phức
z i
là
1 2
z i
.
Câu 20. Số nào trong các số phức sau là số thực?
A.
3 2 3 2
i i
. B.
3 2 3 2
i i
.
C.
5 2 5 2
i i
. D.
1 2 1 2
i i
.
Hướng dẫn giải
Chọn B
3 2 3 2 6
i i
.
Câu 21. Cho số phức
z
thỏa mãn:
2
(2 3 ) (4 ) (1 3 )
i z i z i
. Xác định phần thực và phần ảo của
.
z
A. Phần thực là
2
; phần ảo là
3.
B. Phần thực là
3
; phần ảo là
5 .
i
C. Phần thực là
2
; phần ảo là
5 .
i
D. Phần thực là
2
; phần ảo là
5.
Hướng dẫn giải
Chọn D
Gọi
z a bi z a bi
, ta có:
2
(2 3 ) (4 ) (1 3 ) 2 3 4 8 6
3 2 4 3
3 2 4 2
3 5
i z i z i i a bi i a bi i
a b a b i i
a b a
a b b
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 17
Facebook: https://www.facebook.com/dongpay
2 5 .
z i
Câu 22. Xét số phức
z
thỏa mãn
10
1 2 2 .
i z i
z
Mệnh đề nào dưới đây đúng?
A.
3
2.
2
z B.
2.
z C.
1
.
2
z D.
1 3
.
2 2
z
Hướng dẫn giải
Chọn D
Ta có
1
2
1
.
z z
z
Vậy
10
1 2 2
i z i
z
2
10
2 2 1 .
z z i z
z
2 2
2
4 2
10 10
2 2 1 . .
z z z
z z
Đặt
2
0.
z a
2
2 2
4 2
2
2
1
10
2 2 1 2 0 1 1.
2
a
a a a a a z
a
a
Câu 23. Cho hai số phức
1 3
z i
,
2
w i
. Tìm phần ảo của số phức
.
u z w
.
A.
7
. B.
5
i
. C.
5
. D.
7
i
.
Hướng dẫn giải
Chọn A
1 3
z i
;
.w 1 3 2 1 7
u z i i i
.
Vậy phần ảo của số phức
u
bằng
7
.
Câu 24. Tìm số phức
z
thỏa mãn đẳng thức
2 1 2
iz z i
.
A.
1
z i
. B.
1
z
. C.
z i
. D.
1
z i
.
Câu 25. Cho số thực
x
,
y
thỏa
2 2 2 3 2 1
x y y x i x y y x i
. Khi đó giá trị của
2 2
4
M x xy y
là
A.
1
M
. B.
1
M
. C.
0
M
. D.
2
M
.
Hướng dẫn giải
Chọn A
Phương trình
2 2 3
2 2 1
x y x y
y x y x
3 3
3 1
x y
x y
0
1
x
y
Vậy
2
2
0 4.0.1 1 1
M
.
Câu 26. Cho số phức
1 3
z i
, môđun của số phức
2
w z iz
là
A.
146
w . B.
146
w . C.
10
w . D.
0
w .
Hướng dẫn giải
Chọn B
1 3 1 3
z i z i
2
2
w 1 3 1 3 6 8 3 5 11 w 146
z iz i i i i i i
.
Câu 27. Cho số phức . Tìm phần thực của số phức .
0, ,z a bi ab a b
2
1
w
z
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 18
Facebook: https://www.facebook.com/dongpay
A. . B. . C. . D. .
Hướng dẫn giải
Chọn B
.
Phần thực của là .
Câu 28. Rút gọn biểu thức
2018
1M i ta được
A.
1009
2
M
. B.
1009
2
M
. C.
1009
2
M i
. D.
1009
2
M i
.
Hướng dẫn giải
Chọn D
Ta có
1009
2018 2 1009 1009
1008 1009
1 1 2 2 2
M i i i i i i
.
Câu 29. Cho số phức
1 2
z i
. Tìm phần thực và phần ảo của số phức 2
w z z
.
A. Phần thực là
3
và phần ảo là
2
. B. Phần thực là
3
và phần ảo là
2
i
.
C. Phần thực là
2
i
và phần ảo là
3
. D. Phần thực là
2
và phần ảo là
3
.
Hướng dẫn giải
Chọn A
2 2 1 2 1 2 3 2
w z z i i i
. Phần thực là
3
và phần ảo là
2
.
Câu 32. Cho số phức
z
thỏa mãn:
2
(2 3 ) (4 ) (1 3 )
i z i z i
. Xác định phần thực và phần ảo của
.
z
A. Phần thực là
2
; phần ảo là
5 .
i
B. Phần thực là
2
; phần ảo là
5.
C. Phần thực là
2
; phần ảo là
3.
D. Phần thực là
3
; phần ảo là
5 .
i
Hướng dẫn giải
Chọn B
Giả sử số phức
,bz a bi a
.
Phương trình
2
(2 3 ) (4 ) (1 3 ) 2 3 4 8 6
3 2 4 2
3 5
i z i z i i a bi i a bi i
a b a
a b b
Câu 33. Cho số phức
z
thỏa mãn điều kiện
2 4 3 2
i z i z i
. Số phức liên hợp của
z
là
A.
5 1
4 4
z i
. B.
5 1
4 4
z i
. C.
1 5
4 4
z i
. D.
1 5
4 4
z i
.
Hướng dẫn giải
Chọn D
3 2 1 5 1 5
2 4 3 2 2 2 3 2
2 2 4 4 4 4
i
i z i z i i z i z i z i
i
Câu 34. Cho số phức
z i
. Số phức
1
z
có phần thực là
A.
2
29
. B.
3
. C.
7
. D.
5
29
.
Hướng dẫn giải
Chọn A
1
1 1 2 5 2 5 2 5
.
2 5 2 5 2 5 29 29 29
i i
z i
z i i i
2
2
2 2
b
a b
2 2
2
2 2
a b
a b
2
2 2
2
ab
a b
2 2
2
2 2
a b
a b
2 2
2 2 2 2 2
2 2 2 2
1 1 1 2
2
4
a b abi
w
z a b abi
a bi
a b a b
w
2 2 2 2
2 2
2 2 2 2 2 2
4
a b a b
a b a b a b
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 19
Facebook: https://www.facebook.com/dongpay
Số phức
1
z
có phần thực là
2
29
.
Câu 35. Cho số phức
z i
. Tìm phấn thực và phần ảo của số phức
2
z z
.
A. Phần thực
6
và phần ảo
5
. B. Phần thực
6
và phần ảo
5
i
.
C. Phần thực
6
và phần ảo
5
. D. Phần thực
6
và phần ảo
5 .
i
Hướng dẫn giải
Chọn C
Ta có
2 2 5 2 2 5 6 5
z z i i i
.
Câu 36. Tìm số thực
m
sao cho
2
1 1
m m i
là số ảo.
A.
1
m
. B.
0
m
. C.
1
m
. D.
1
m
.
Hướng dẫn giải
Chọn D
Số phức
2
1 1
m m i
là số ảo
2
1 0 1
m m
.
Câu 37. Số phức
z
thỏa mãn
2 12 2
z z i
có:
A. Phần thực bằng
4
và phần ảo bằng
2
. B. Phần thực bằng
4
và phần ảo bằng
2
i
.
C. Phần thực bằng
4
và phần ảo bằng
2
i
. D. Phần thực bằng
4
và phần ảo bằng
2
.
Hướng dẫn giải
Chọn D
Đặt
, ,z a bi a b
.
Ta có:
2 12 2
z z i
2 12 2
a bi a bi i
4
3 12 2
2
a
a bi i
b
.
Câu 38. Cho số phức
z
thỏa mãn
3
(1 3 )
1
i
z
i
. Môđun của số phức
bằng
A.
4 2.
B.
4 3.
C.
8 2.
D.
8 3.
Hướng dẫn giải
Chọn C
3
(1 3 )
4 4 4 4
1
i
z i z i
i
8 8 8 2
z iz i z iz
.
Câu 40. Tổng phần thực và phần ảo của số phức
z
thoả mãn
1 2
iz i z i
bằng
A.
6
. B.
2
. C.
2
. D.
6
.
Hướng dẫn giải
Chọn D
Đặt
z x yi
,x y
. Khi đó
1 2 1 2
iz i z i i x yi i x yi i
2 0 4
2 2
2 2
x y x
x y yi i
y y
, suy ra
6
x y
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 20
Facebook: https://www.facebook.com/dongpay
Bài 2: PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC
Câu 1:
G
ọi
1
z
và
2
z
là các nghiệm của phương trình
2
4 9 0
z z
. Gọi
,
M N
là các điểm biểu diễn của
1
z
và
2
z
trên mặt phẳng phức. Khi đó độ dài của
MN
là:
A.
2 5
MN . B.
5
MN
. C.
2 5
MN . D.
4
MN
.
Câu 2: Gọi
1 2 3
, ,
z z z
là ba nghiệm của phương trình
3
1 0
z
. Tính
1 2 3
S z z z
A.
4
S
B.
2
S
C.
3
S
D.
1
S
Hướng dẫn giải
Chọn C
Ta có:
3
1
1 3
1 0
2 2
1 3
2 2
z
z z i
z i
. Do đó:
1 3 1 3
1 3
2 2 2 2
S i i
.
Câu 3: Gọi
1
z
,
2
z
là các nghiệm phức của phương trình
2
2 5 0
z z
. Giá trị của biểu thức
1 2
4 4
z z
bằng.
A.
7
B.
14
C.
7
D.
14
Hướng dẫn giải
Chọn B
Ta có
2
2 5 0
z z
1
2
1 2
z i
z i
.
Nên
1 2
4 4
4 4
1 2 1 2 14
z z i i
.
Câu 4: Phương trình bậc hai nào dưới đây nhận hai số phức
2 3
i
và
2 3
i
làm nghiệm?
A.
2
4 13 0
z z
B.
2
4 3 0
z z
C.
2
4 13 0
z z
D.
2
4 3 0
z z
Hướng dẫn giải
Chọn C
Ta có:
2
4 13 0
z z
2 3
2 3
z i
z i
.
Câu 5: Gọi
1
z
và
2
z
là 2 nghiệm của phương trình
2
2 6 5 0
z z
trong đó
2
z
có phần ảo âm. Phần thực
và phần ảo của số phức
1 2
3
z z
lần lượt là
A.
6;1
B.
6;1
C.
1; 6
D.
6; 1
Hướng dẫn giải
Chọn D
Ta có
2
2 6 5 0
z z
1
2
3
3
2 2
i
z
i
z
. Suy ra
1 2
3 6
z z i
Vậy Phần thực và phần ảo của số phức
1 2
3
z z
lần lượt là
6; 1
.
Câu 6: Biết phương trình
2
2 0
z z m
m
có một nghiệm phức
1
1 3
z i
và
2
z
là nghiệm phức
còn lại. Số phức
1 2
2
z z
là ?
A.
3 9
i
. B.
3 3
i
. C.
3 9
i
. D.
3 3
i
.
Hướng dẫn giải
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 21
Facebook: https://www.facebook.com/dongpay
Chọn D
Ta có
1 2
2
z z
2 1
2 2 1 3 1 3
z z i i
1 2
2 1 3 2 1 3 3 3
z z i i i
.
Câu 7: Kí hiệu
1
z
,
2
z
,
3
z
,
4
z
là bốn nghiệm của phương trình
4 2
6 0
z z
. Tính
1 2 3 4
S z z z z
.
A.
2 2 3
S
B.
2 2 3
S
C.
2 2
S D.
2 3
S
Hướng dẫn giải
Chọn A
Ta có:
4 2
6 0
z z
2
2
2
3
z
z
2
3
z
z i
.
Kí hiệu
1
z
,
2
z
,
3
z
,
4
z
là bốn nghiệm của phương trình, ta có:
1 2 3 4
S z z z z
2 2 3
.
Câu 8: Gọi
A
,
B
là hai điểm biểu diễn hai nghiệm phức của phương trình
2
2 5 0
z z
. Tính độ dài đoạn
thẳng
AB
:
A.
2
. B.
4
. C.
12
. D.
6
.
Hướng dẫn giải
Chọn B
Ta có:
2
2 5 0
z z
1 2
1 2
z i
z i
suy ra
1;2
A và
1; 2
B
. Vậy
4
AB
.
Câu 9: Gọi
1
z
và
2
z
là hai nghiệm phức của phương trình
2
6 11 0
z z
. Giá trị của biểu thức
1 2
3
z z
bằng
A.
2 11
. B.
11
. C.
22
. D.
11
.
Hướng dẫn giải
Chọn A
Ta có
1
z
và
2
z
là hai số phức liên hợp của nhau nên
2 2
1 2 1 2
11
z z z z
1 2
11
z z
.
Do đó:
1 2 1
3 2 2 11
z z z
.
Câu 10: Trong tập các số phức, cho phương trình
2
6 0
z z m
, m
1
. Gọi
0
m
là một giá trị của
m
để phương trình
1
có hai nghiệm phân biệt
1
z
,
2
z
thỏa mãn
1 1 2 2
. .
z z z z
. Hỏi trong khoảng
0;20
có bao nhiêu giá trị
0
m
?
A.
13
. B.
11
. C.
12
. D.
10
.
Hướng dẫn giải
Chọn D
Điều kiện để phương trình
1
có hai nghiệm phân biệt là:
9 0 9
m m
.
Phương trình có hai nghiệm phân biệt
1
z
,
2
z
thỏa mãn
1 1 2 2
. .
z z z z
thì
1
phải có nghiệm phức.
Suy ra
0 9
m
.
Vậy trong khoảng
0;20
có
10
số
0
m
.
Câu 11: Gọi
1
z
,
2
z
là hai nghiệm phức của phương trình
2
2 5 0
z z
, trong đó
1
z
có phần ảo dương. Tìm
số phức
2 2
1 2
2
w z z
.
A.
i
. B.
9 4
i
. C.
9 4
i
. D.
9 4
i
.
Hướng dẫn giải
Chọn C
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 22
Facebook: https://www.facebook.com/dongpay
Ta có
1
2
2
1 2
2 5 0
1 2
z i
z z
z i
.
Suy ra
2 2
1 2 2 1 2
w i i
9 4
i
.
Câu 12: Phương trình
2
0
z az b
,( ,a b
) có nghiệm là
i
, tính
S a b
.
A.
19
S
. B.
19
S
. C.
7
S
. D.
7
S
.
Hướng dẫn giải
Chọn B
Phương trình
2
0
z az b
,( ,a b
) có nghiệm là
i
2
3 2 3 2 0
i a i b
9 4 3 0
12 2 0
a b
a
6
13
a
b
.
Vậy
6 13 19
S
.
Câu 13: Giải phương trình
2
4 5 0
z z
trên tập số phức ta được các nghiệm
A.
1 2
2 ; 2
z i z i
. B.
1 2
4 ; 4
z i z i
.
C.
1 2
4 ; 4
z i z i
. D.
1 2
2 ; 2
z i z i
.
Hướng dẫn giải
Chọn A
Ta có
2
4 5 0
z z
2
4 4 1
z z
2
2
2
z i
2
2
z i
z i
2
2
z i
z i
Suy ra
1
2
z i
và
2
2
z i
.
Câu 14: Phương trình
2
3 9 0
z z
có hai nghiệm phức
1
z
,
2
z
. Tính
1 2 1 2
S z z z z
.
A.
12
S
. B.
6
S
. C.
6
S
. D.
12
S
.
Hướng dẫn giải
Chọn C
Áp dụng định lý vietè, ta có:
1 1
3
S z z
;
1 2
9
P z z
.
Suy ra:
1 2 1 2
6
z z z z P S
.
Câu 15: Biết phương trình
2 2018
2017.2018 2 0
z z
có hai nghiệm
1
z
,
2
z
. Tính
1 2
S z z
.
A.
1009
2
S
. B.
1010
2
S
. C.
2018
2
S
. D.
2019
2
S
.
Hướng dẫn giải
Chọn B
Do các hệ số của phương trình
2 2018
2017.2018 2 0
z z
đều là số thực nên
1
z
,
2
z
là hai số phức
liên hợp.
Đặt
1
z a bi
;
2
,z a bi a b
. Ta có:
2 2 2018 1010
1 2 1 2
2 2 . 2 2 2
S z z a b z z .
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 23
Facebook: https://www.facebook.com/dongpay
Bài 3: TẬP HỢP ĐIỂM BIỂU DIỄN SỐ PHỨC
Câu 1: Trong hình vẽ bên, điểm M biểu diễn số phức z . Số phức z là
A. 2 i . B. 2 i . C. 1 2i . D. 1 2i .
Hướng dẫn giải
Chọn B
Dựa vào hình vẽ ta có 2z i , suy ra 2z i .
Câu 2: Số phức 2 3z i có điểm biểu diễn trên mặt phẳng tọa độ là:
A.
2; 3
M
. B.
2;3
M
. C.
2;3
M
. D.
2; 3
M
.
Câu 3: Trong mặt phẳng phức, cho số phức 1 2z i . Điểm biểu diễn cho số phức z là điểm nào sau đây
A.
1; 2M
B.
1;2Q
C.
1;2P
D.
2;1N
Hướng dẫn giải
Chọn B
Ta có: 1 2z i 1 2z i nên có điểm biểu diễn là
1;2
.
Câu 4: Trong mặt phẳng
Oxy
, điểm
M
trong hình vẽ bên là điểm biểu diễn số phức
z
. Số phức z là
A. 1 2i B. 2 i C. 1 2i D. 2 i
Hướng dẫn giải
Chọn D
Ta có 2 2z i z i .
Câu 5: Trong mặt phẳng
Oxy
, cho các điểm
,A B
như hình vẽ bên. Trung điểm của đoạn thẳng
AB
biểu
diễn số phức.
A.
1
2
2
i . B.
1
2
2
i . C. 1 2i . D. 2 i .
Hướng dẫn giải
Chọn B
Trung điểm
AB
là
1
;2
2
I
, biểu diễn số phức
1
2
2
i .
Câu 6: Điểm nào trong hình vẽ dưới đây là điểm biểu diễn của số phức
1 2z i i ?
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 24
Facebook: https://www.facebook.com/dongpay
A. Q . B. M . C. N . D. P .
Hướng dẫn giải
Chọn A
Ta có
1 2z i i 3z i . Điểm biểu diễn của số phức z là
3;1Q .
Câu 7: Hỏi điểm
3; 1M là điểm biểu diễn số phức nào sau đây?
A. 3z i B. 1 3z i C. 1 3z i D. 3z i
Hướng dẫn giải
Chọn D
Điểm
;M a b trong một hệ tọa độ vuông góc của mặt phẳng được gọi là điểm biểu diễn số phức
z a bi .
Do đó điểm
3; 1M là điểm biểu diễn số phức 3z i .
Câu 8: Điểm M trong hình vẽ bên là điểm biểu diễn của số phức z .
Tìm phần thực và phần ảo cú số phức z .
A. Phần thực bằng 3 và phần ảo bằng 4i. B. Phần thực bằng 4 và phần ảo bằng 3.
C. Phần thực bằng 4 và phần ảo bằng 3i . D. Phần thực bằng 3 và phần ảo bằng 4 .
Hướng dẫn giải
Từ hình vẽ ta có
3;4M nên 3 4z i . Vậy Phần thực bằng 3 và phần ảo bằng 4 .
Câu 9: Số phức 2 3z i có điểm biểu diễn là.
A.
2; 3A . B.
2; 3A . C.
2;3A . D.
2; 3A .
Câu 10: Trên mặt phẳng tọa độ
Oxy
cho điểm
M
trong hình vẽ bên là điểm biểu diễn của số phức z . Tìm
z ?
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 25
Facebook: https://www.facebook.com/dongpay
A.
3 4
z i
. B.
z i
. C.
z i
. D.
3 4
z i
.
Hướng dẫn giải
Chọn A
Ta có
3; 4
M
. Vậy điểm
M
biểu diễn cho số phức
3 4
z i
.
Câu 11: Cho số phức
z
thỏa
1 2
z i
. Chọn phát biểu đúng:
A. Tập hợp điểm biểu diễn số phức
z
là một đường tròn có bán kính bằng
4
.
B. Tập hợp điểm biểu diễn số phức
z
là một đường thẳng.
C. Tập hợp điểm biểu diễn số phức
z
là một đường Parabol.
D. Tập hợp điểm biểu diễn số phức
z
là một đường tròn có bán kính bằng
2
.
Câu 12: Cho số phức
2 3
z i
. Điểm biểu diễn số phức liên hợp của
z
là
A.
2;3
. B.
2; 3
. C.
2; 3
. D.
2;3
.
Hướng dẫn giải
Chọn D
Vì
2 3 2 3
z i z i
nên điểm biểu diễn của
z
có tọa độ
2;3
.
Câu 13: Cho số phức
z i
. Biểu diễn hình học của
z
là điểm có tọa độ
A.
4;5
B.
4; 5
C.
4; 5
D.
4;5
Hướng dẫn giải
Chọn A
Số phức
z i
có phần thực
4
a
; phần ảo
5
b
nên điểm biểu diễn hình học của số
phức
z
là
4;5
.
Câu 14: Gọi
A
là điểm biểu diễn của số phức
2 5
z i
và
B
là 1điểm biểu diễn của số phức
z i
.
Tìm mệnh đề đúng trong các mệnh đề sau.
A. Hai điểm
A
và
B
đối xứng với nhau qua gốc toạ độ
O
.
B. Hai điểm
A
và
B
đối xứng với nhau qua đường thẳng
y x
.
C. Hai điểm
A
và
B
đối xứng với nhau qua trục hoành.
D. Hai điểm
A
và
B
đối xứng với nhau qua trục tung.
Câu 15: Cho hai số phức
3 5
z i
và
1 2
w i
. Điểm biểu diễn số phức
.
z z w z
trong mặt phẳng
Oxy
có tọa độ là
A.
6; 4
. B.
4; 6
. C.
4; 6
. D.
4; 6
.
Hướng dẫn giải
y
x
O
M
3
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 26
Facebook: https://www.facebook.com/dongpay
Chọn D
Ta có
.
z z w z
3 5 1 2 3 5
i i i
3 5 7 11
i i
4 6
i
.
Câu 16: Số phức
4 2
z i
có điểm biểu diễn trên mặt phẳng tọa độ là
M
. Tìm tọa độ điểm
M
A.
4; 2
M
. B.
4; 2
M
. C.
4;2
M
. D.
2;4
M .
Hướng dẫn giải
Chọn C
Số phức
4 2
z i
có điểm biểu diễn trên mặt phẳng tọa độ là
4;2
M
.
Câu 17: Số phức liên hợp của số phức
1 2
z i i
có điểm biểu diễn là điểm nào dưới đây?
A.
1;2
A B.
2;1
F C.
2; 1
E
D.
1;2
B
Hướng dẫn giải
Chọn C
Ta có:
1 2 2 2
z i i i z i
nên điểm biểu diễn của số phức
z
là
2; 1
E
.
Câu 18: Điểm
M
trong hình vẽ dưới đây biểu diễn số phức
z
.
Số phức
z
bằng
A.
i
. B.
2 3
i
. C.
2 3
i
. D.
i
.
Hướng dẫn giải
Chọn B.
Theo hình vẽ thì
2 3
z i
2 3
z i
.
Câu 19: Trên mặt phẳng tọa độ
Oxy
cho điểm
M
trong hình vẽ bên là điểm biểu diễn của số phức
z
.
Tìm
z
?
A.
z i
. B.
3 4
z i
. C.
3 4
z i
. D.
z i
.
Hướng dẫn giải
Chọn B
Số phức
z
có phần thực
3
a
và phần ảo
4
b
nên
3 4
z i
.
Câu 20: Trong mặt phẳng toạ độ, điểm
1; 2
A
là điểm biểu diễn của số phức nào trong các số sau?
A.
1 2
z i
. B.
1 2
z i
. C.
2
z i
. D.
1 2
z i
.
Hướng dẫn giải
Chọn B
Số phức
z a bi
được biểu diễn bởi điểm
;
M a b
. Do đó điểm
1; 2
A
biểu diễn số phức
1 2
z i
.
x
y
2
3
M
O
1
x
y
3
-4
M
O 1
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 27
Facebook: https://www.facebook.com/dongpay
Câu 21: Trong mặt phẳng tọa độ
Oxy
, Gọi
A
,
B
,
C
lần lượt là các điểm biểu diễn số phức
1 2
i
,
4 4
i
,
3
i
. Số phức biểu diễn trọng tâm tam giác
ABC
là
A.
1 3
i
. B.
3 9
i
. C.
i
. D.
1 3
i
.
Hướng dẫn giải
Chọn A
Ta có
1; 2
A
,
4; 4
B
,
0; 3
C
nên trọng tâm
G
của tam giác ABC có tọa độ là
1; 3
G
.
Do đó, số phức biểu diễn điểm
G
là
1 3
i
.
Câu 22: Gọi
M
là điểm biểu diễn của số phức
z
trong mặt phẳng tọa độ,
N
là điểm đối xứng của
M
qua
Oy
(
M
,
N
không thuộc các trục tọa độ). Số phức
w
có điểm biểu diễn lên mặt phẳng tọa độ là
N
. Mệnh đề nào sau đây đúng ?
A.
w z
. B.
w z
. C.
w z
. D.
w z
.
Hướng dẫn giải
Chọn A
Gọi
z x yi
, ,x y
;
M x y
.
N
là điểm đối xứng của
M
qua
Oy
;
N x y
w x yi x yi z
.
Câu 23: Cho bốn điểm
A
,
B
,
C
,
D
trên hình vẽ biểu diễn 4 số phức khác nhau. Chọn mệnh đề sai.
A.
D
là biểu diễn số phức
1 2
z i
. B.
C
là biểu diễn số phức
1 2
z i
.
C.
A
là biểu diễn số phức
2
z i
. D.
B
là biểu diễn số phức
1 2
z i
.
Hướng dẫn giải
Chọn A
Theo hình vẽ thì điểm
D
là biểu diễn số phức
2
z i
. Suy ra B sai.
Câu 24: Trong mặt phẳng tọa độ
Oxy
, gọi
M
là điểm biểu diễn số phức
3 4
z i
;
'
M
là điểm biểu diễn
cho số phức
1
'
2
i
z z
. Tính diện tích tam giác
'
OMM
.
A.
'
15
2
OMM
S
. B.
'
25
4
OMM
S
. C.
'
25
2
OMM
S
. D.
'
15
4
OMM
S
.
Câu 25: Điểm
M
trong hình vẽ bên là điểm biểu diễn số phức
z
tìm phần thực và phần ảo của số phức
z
.
A. Phần thực là
2
và phần ảo là
1
. B. Phần thực là
2
và phần ảo là
i
.
C. Phần thực là
1
và phần ảo là
2
. D. Phần thực là
1
và phần ảo là
2
i
.
Hướng dẫn giải
x
y
-2
-1
-2
1
-1
D
A
C
B
O
1
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 28
Facebook: https://www.facebook.com/dongpay
Chọn C
Ta có số phức 1 2z i nên phần thực là
1
và phần ảo là
2
.
Câu 26: Trong mặt phẳng tọa độ Oxy , tập hợp điểm biểu diễn số phức z thỏa mãn 2 3z i i z là
A. đường tròn
2 2
2x y B. đường tròn
2 2
4x y
C. đường thẳng 2 3 0x y D. đường thẳng 2 1 0x y
Hướng dẫn giải
Chọn C
Gọi
; M x y là điểm biểu diễn số phức z x yi , với ,x y .
Ta có 2 3z i i z
1 2 3
x y i x y i
2 2 2
2
1 2 3x y x y 4 8 12 0x y 2 3 0x y
Câu 27: Trong mặt phẳng tọa độ
Oxy
, gọi
M
là điểm biểu diễn số phức 3 4z i ;
'M
là điểm biểu diễn
cho số phức
1
'
2
i
z z
. Tính diện tích tam giác 'OMM .
A.
'
25
4
OMM
S
. B.
'
25
2
OMM
S
. C.
'
15
4
OMM
S
. D.
'
15
2
OMM
S
.
Câu 28: Cho
, ,A B C
lần lượt là các điểm biểu diễn các số phức 6 3i ;
1 2i i
;
1
i
. Tìm số phức có điểm
biểu diễn
D
sao cho ABCD là hình bình hành.
A. 8 4z i . B. 4 2z i . C. 8 5z i . D. 8 3z i .
Câu 29: Biết tập hợp các điểm biểu diễn số phức z thỏa mãn 1 2 4iz i là một đường tròn. Tìm tọa độ
tâm I của đường tròn đó.
A.
1;2I . B.
1; 2I . C.
2; 1I . D.
2;1I .
Hướng dẫn giải
Chọn C
Gọi
;M x y là điểm biểu diễn số phức z x yi ,
,x y .
Ta có 1 2 4iz i . 2 4i z i 2 4z i 4IM , với
2; 1I .
tập hợp biểu diễn số phức z là đường tròn tâm
2; 1I bàn kính 4R .
Câu 30: Điểm M trong hình bên là điểm biểu diễn cho số phức
A. 4 2z i . B. 2 4z i . C. 4 2z i . D. 2 4z i .
Hướng dẫn giải
Chọn D
Điểm M biểu diễn cho số phức 2 4z i .
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 29
Facebook: https://www.facebook.com/dongpay
Câu 31: Cho số phức
z
thoả mãn
3 4 5
z i
. Biết rằng tập hợp điểm trong mặt phẳng toạ độ biểu diễn
các số phức
z
là một đường tròn. Tìm toạ độ tâm
I
và bán kính
R
của đường tròn đó.
A.
3; 4
I
,
5
R . B.
3;4
I ,
5
R .
C.
3; 4
I
,
5
R
. D.
3;4
I ,
5
R
.
Hướng dẫn giải
Chọn D
Đặt
z x yi
,x y
. Khi đó
2 2
3 4 5 3 4 25
z i x y
.
Vậy tập điểm biểu diễn số phức
z
là đường tròn tâm
3;4
I , bán kính
5
R
.
Câu 32: Gọi
M
và
N
lần lượt là các điểm biểu diễn của
1
z
,
2
z
trên mặt phẳng tọa độ,
I
là trung điểm
MN
,
O
là gốc tọa độ (
3
điểm
O
,
M
,
N
phân biệt và không thẳng hàng). Mệnh đề nào sau đây là
đúng?
A.
1 2
2
z z OM ON
. B.
1 2
2
z z OI
.
C.
1 2
z z OI
. D.
1 2
z z OM ON
.
Hướng dẫn giải
Chọn B
Gọi
1 1
;
M x y
là điểm biểu diễn của số phức
1 1 1
z x y i
.
2 2
;
N x y
là điểm biểu diễn của số phức
2 2 2
z x y i
.
Khi đó
1 2 1 2 1 2
z z x x y y i
2 2
1 2 1 2 1 2
z z x x y y
.
Vì
I
là trung điểm
MN
nên
1 2 1 2
;
2 2
x x y y
I
.
2 2
2 2
1 2 1 2
1 2 1 2 1 2
2 2
2 2
x x y y
OI x x y y z z
.
Câu 33: Gọi
1
z
là nghiệm phức có phần ảo âm của phương trình
2
2 3 0
z z
. Trên mặt phẳng tọa độ,
điểm nào sau đây là điểm biểu diễn của số phức
1
z
?
A.
1; 2
Q i
. B.
1; 2
N
. C.
1; 2
M
. D.
1; 2
P i
.
Hướng dẫn giải
Chọn C
2
1 2
2 3 0
1 2
z i
z z
z i
.
1
z
là nghiệm phức có phần ảo âm
1
1 2
z i
.
Vậy
1; 2
M
là điểm biểu diễn số phức
1
z
.
Câu 34: Cho
A
,
B
,
C
tương ứng là các điểm trong mặt phẳng phức biểu diễn các số phức
1
z i
,
2
2 5
z i
,
3
2 4
z i
. Số phức
z
biểu diễn bởi điểm
D
sao cho tứ giác
ABCD
là hình bình
hành là
A.
5
i
. B.
1 5
i
. C.
i
. D.
1 7
i
.
Hướng dẫn giải
Chọn A
Ta có
1;2
A ,
2;5
B ,
2;4
C .
Gọi
;
D x y
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 30
Facebook: https://www.facebook.com/dongpay
Ta có
3;3
AB
,
2 ;4
DC x y
Để
ABCD
là hình bình hành thì
AB DC
5
1
x
y
. Vậy
5
z i
.
Câu 35: Điểm
M
trong hình vẽ dưới đây biểu diễn số phức
z
.
Số phức
1
z
bằng
A.
4 2
i
. B.
3 3
i
. C.
3 3
i
. D.
4 2
i
.
Hướng dẫn giải
Chọn C
Điềm
2;3
M biểu diễn
2 3
z i
suy ra
1 2 3 1 3 3
z i i
.
Câu 36: Cho số phức
z
thỏa mãn
2 0
iz i
. Khoảng cách từ điểm biểu diễn của
z
trên mặt phẳng tọa độ
Oxy
đến điểm
3; 4
M
là:
A.
2 2
. B.
2 5
. C.
13
. D.
2 10
.
Hướng dẫn giải
Chọn D
Ta có:
2 ( 2)( )
2 1 0 2 1 2
1
i i i
iz iz i i
i
Điểm biểu diễn của số phức
z
là
(1;2)
A
2 2
(3 1) ( 4 2) 40 2 10
AM
Câu 37: Cho các số phức
z
thỏa mãn
1 1 2
z i z i
. Tập hợp các điểm biểu diễn các số phức
z
trên
mặt phẳng tọa độ là một đường thẳng. Phương trình đường thẳng đó là
A.
4 6 3 0
x y
B.
4 6 3 0
x y
C.
4 6 3 0
x y
D.
4 6 3 0
x y
Hướng dẫn giải
Chọn B
Gọi
z x yi
. Ta có
1 1 2
z i z i
2 2
1 1
x y
2 2
1 2
x y
4 6 3 0
x y
.
Câu 38: Cho số phức . Trên mặt phẳng tọa độ , tìm điểm biểu diễn số phức .
A. . B. . C. . D. .
Hướng dẫn giải
Chọn C
điểm biểu diễn cho là .
Câu 39: Tập hợp các điểm biểu diễn cho số phức
z
thỏa mãn
3 4 5
z i
là
A. Một đường Elip. B. Một đường tròn.
C. Một đường thẳng. D. Một đường parabol.
Hướng dẫn giải
x
y
M
3
2
2
z i
Oxy
w iz
2; 1
M
2;1
M
1;2
M
1;2
M
1 2
w iz i
1 2
w iz i
1;2
M
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 31
Facebook: https://www.facebook.com/dongpay
Chọn B
Tập hợp điểm biểu diễn cho số phức
z
là đường tròn tâm
I
, bán kính
5
R
.
Câu 40: Cho số phức
z
thỏa mãn
1 2 5
z i
và
;
M x y
là điểm biểu diễn số phức
z
. Điểm
M
thuộc
đường tròn nào sau đây?
A.
2 2
1 2 5
x y
B.
2 2
1 2 25
x y
C.
2 2
1 2 25
x y
D.
2 2
1 2 5
x y
Hướng dẫn giải
Chọn C
Ta có
1 2 5
z i
1 2 5
x y i
2 2
1 2 25
x y
.
Vậy điểm
M
thuộc đường tròn
2 2
1 2 25
x y
.
| 1/31
| | Tải xuống

Có thể bạn quan tâm:

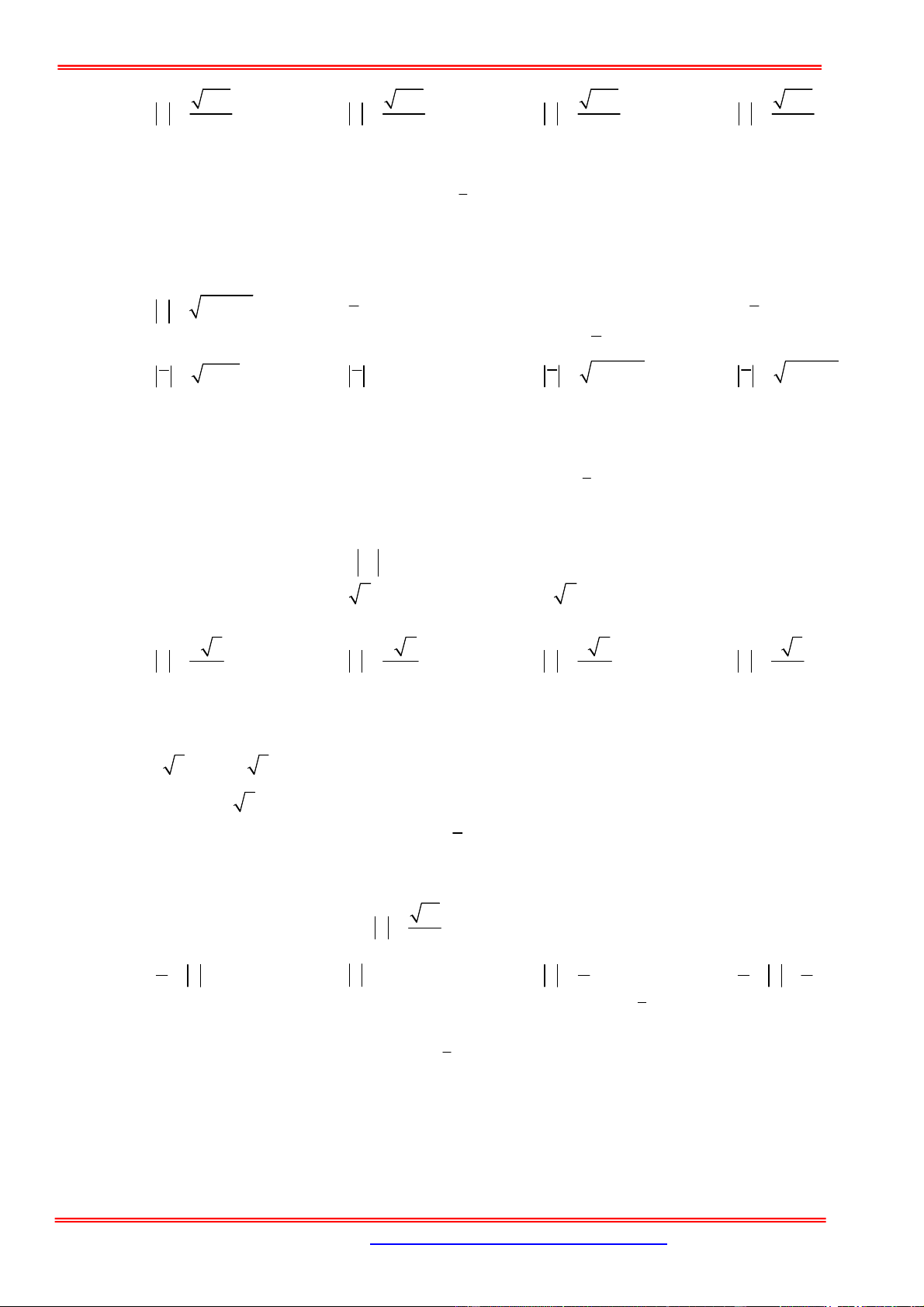
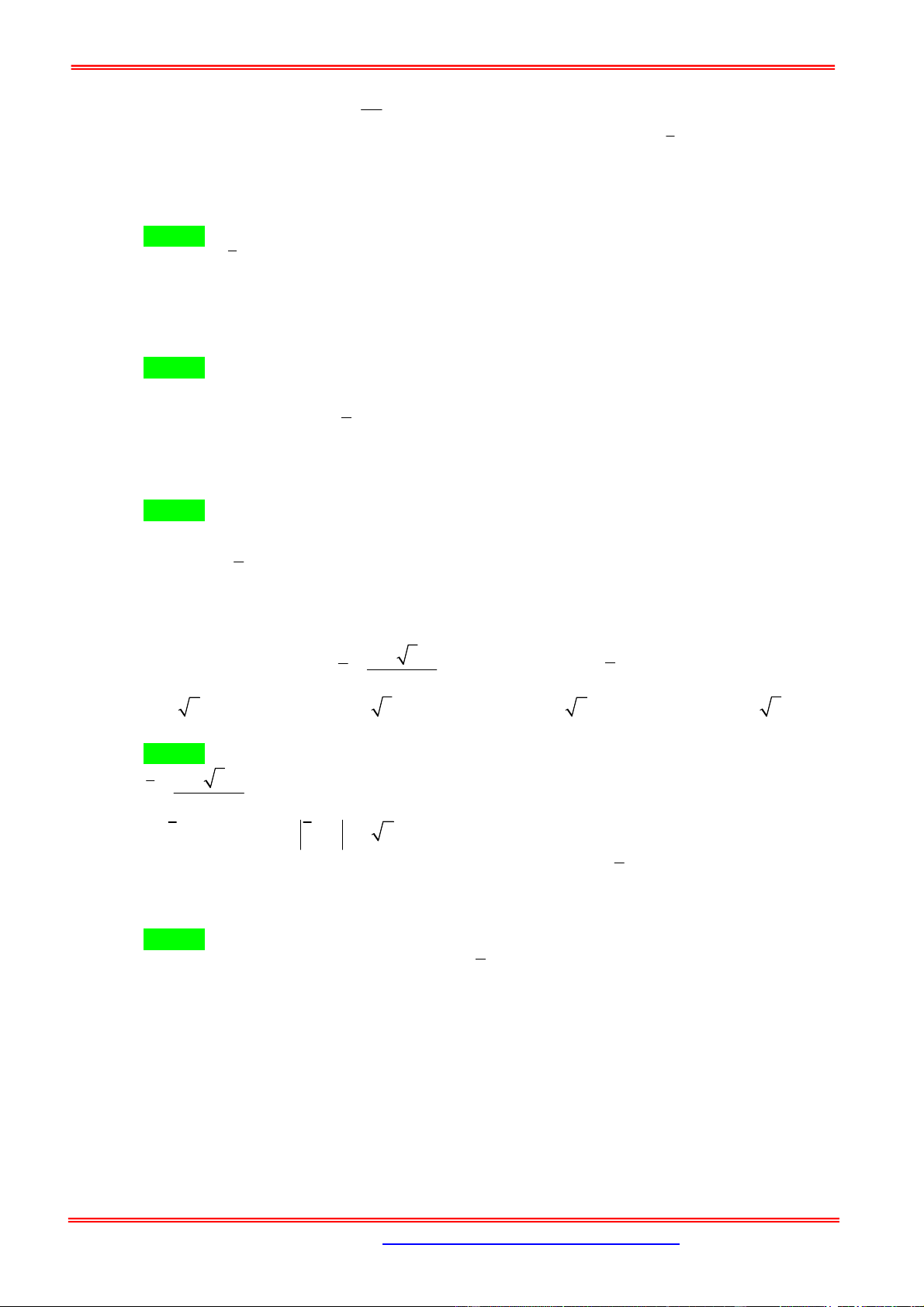
Preview text:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
Bài 1: SỐ PHỨC VÀ CÁC PHÉP TOÁN SỐ PHỨC A – LÝ THUYẾT CHUNG
1.1. Khái niệm số phức
 Số phức (dạng đại số) : z a bi; a,b   . Trong đó : a là phần thực, b là phần ảo, i là đơn  
vị ảo, i2  1.
 Tập hợp số phức kí hiệu:  .
z là số thực  phần ảo của z bằng 0 b  0 .  
z là số ảo (hay còn gọi là thuần ảo)  phần thực bằng 0 a  0 .  
 Số 0 vừa là số thực vừa là số ảo.
1.2. Hai số phức bằng nhau
 Hai số phức z a bi a, b   và z c di c, d   bằng nhau khi phần thực và phần 2   1  
ảo của chúng tương đương bằng nhau. a   c
 Khi đó ta viết z z a bi c di  1 2 b   d  
1.4. Số phức liên hợp
Số phức liên hợp của z a bi a, b   là z a bi .    z zz z ;
z z '  z z ' ; z z . '  z z 1 1 . ';    ; z z
.  a2  b2.  z z  2  2
z là số thực  z z ; z là số ảo z z  .
1.5. Môđun của số phức  
Độ dài của vectơ OM được gọi là môđun của số phức z và kí hiệu là z . Vậy z OM hay  z a bi OM a2 b2      . Một số tính chất:   z a2 b2   
zz OM ; z z
z  0, z  ;
z  0  z  0 . z z z z zz z .  z . z ; 1 1  ; 1 1 2  . 1 2 1 2 z z z 2 2 2 2 z2  z zz zz z . 1 2 1 2 1 2
2. Phép cộng trừ nhân chia số phức
2.1. Phép cộng và phép trừ số phức
Cho hai số phức z a bi a, b   và z c di c, d   . Khi đó: 2   1  
z z a c b d i 1 2    
 Số đối của số phức z a bi là z   a   bi .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
 Tổng của một số phức với số phức liên hợp của nó bằng hai lần phần thực của số thực đó:
z a bi,z z a 2 .
2.2. Phép nhân số phức
 Cho hai số phức z a bi a, b   và z c di c, d   . 2   1  
Khi đó: z z a bi c di ac – bd ad bc i . 1 2       
 Với mọi số thực k và mọi số phức z a bi a, b   , ta có   k z
.  k. a bi ka kbi. Đặc biệt: z
0.  0 với mọi số phức z .  
 Lũy thừa của i 0 1 2 3 2
: i  1, i i, i  1, i i i .  i  4n 4n 1 4n2 4n i i i i i 3 1, , 1, i, n           .
2.3. Chia hai số phức  1
Số phức nghịch đảo của z khác 0 là số z 1  z . 2 z z '  '. '. 1 z z z z
Phép chia hai số phức z ' và z  0 là  z ' z   . z 2 z z z . B – BÀI TẬP Câu 1.
Số phức z  15  3i có phần ảo bằng A. 3 . B. 15 . C. 3i . D. 3 . Câu 2.
Số phức z  1 2i 2  3i bằng A. 8. B. 8 . i C. 4   . i D. 8 . i Câu 3. Cho số phức z  3
i . Tìm phần thực của z . A. 3. B. 0 . C. 3  . D. không có. Câu 4.
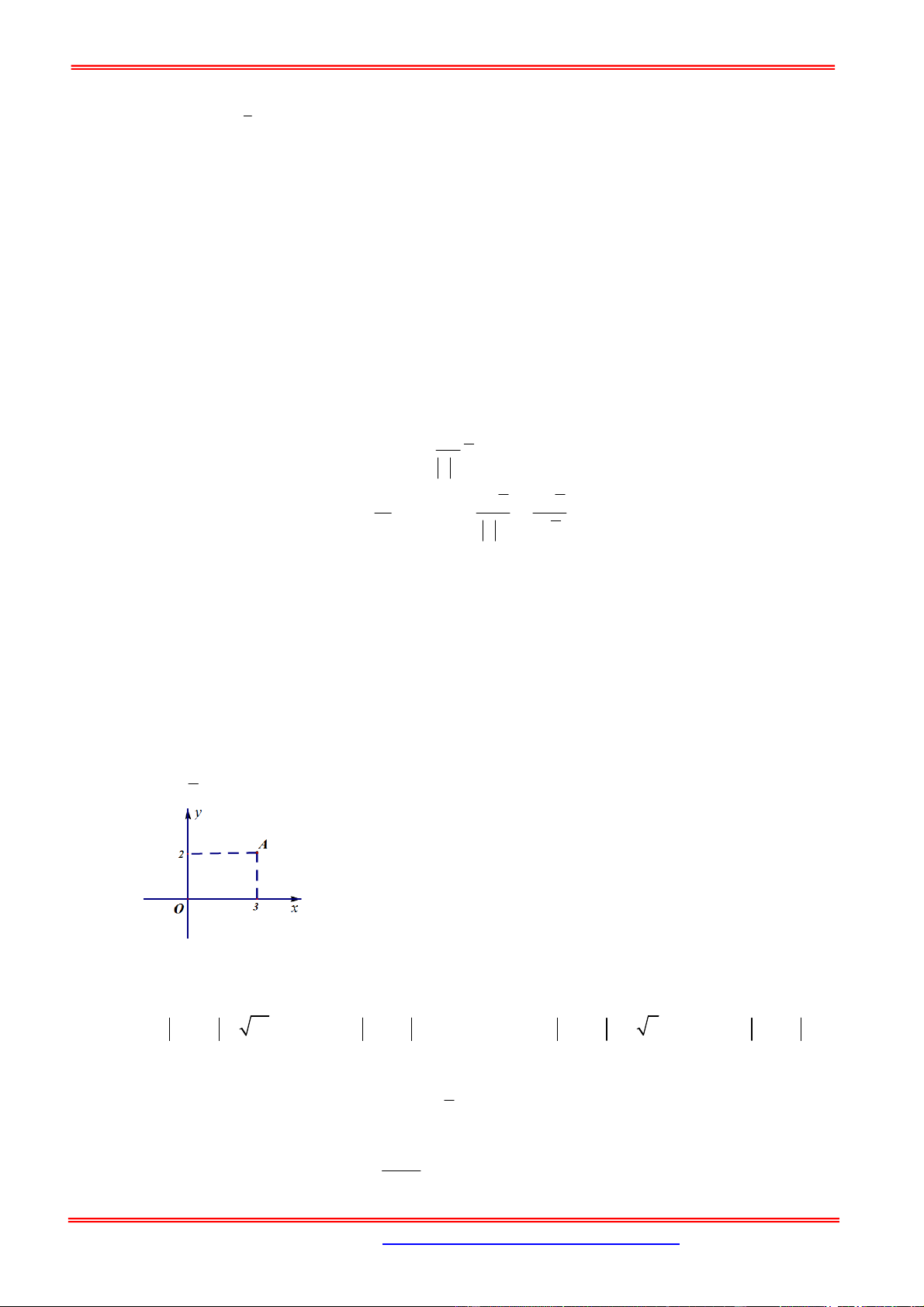
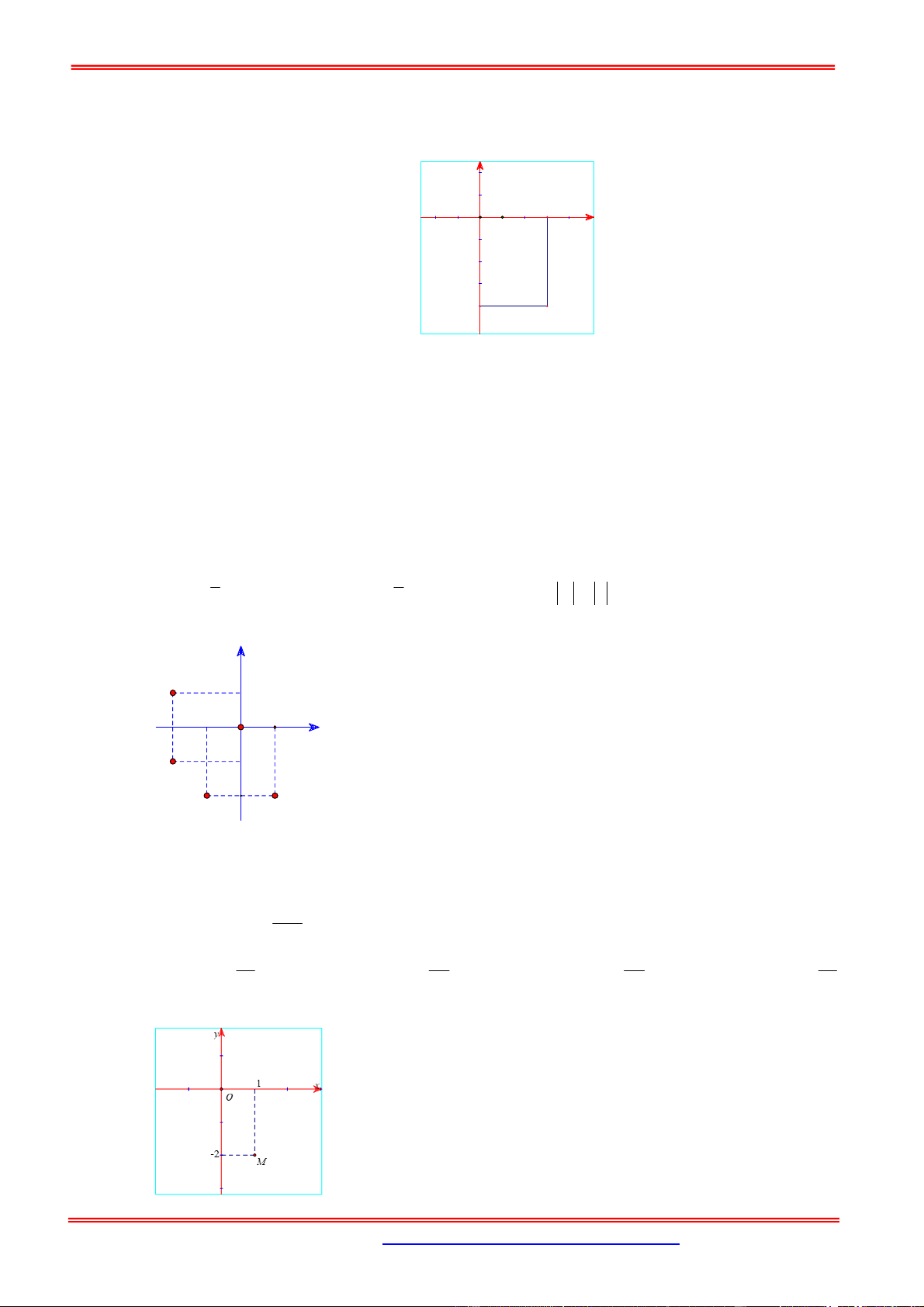
Cho số phức z có điểm biểu diễn là điểm A trong hình vẽ bên. Tìm phần thực và phần ảo của số phức z .
A. Phần thực bằng 3 , phần ảo bằng 2  .
B. Phần thực bằng 3 , phần ảo bằng 2 .
C. Phần thực bằng 2 , phần ảo bằng 3  i .
D. Phần thực bằng 3 , phần ảo bằng 2i . Câu 5.
Cho số phức z  1  2i và z  2
  2i . Tìm môđun của số phức z z . 1 2 1 2
A. z z  17 .
B. z z  5 .
C. z z  2 2 .
D. z z  1 . 1 2 1 2 1 2 1 2 Câu 6.
Cho số phức z  3  2i . Tìm phần ảo của số phức liên hợp của z . A. 2i . B. 2  i . C. 2 . D. 2  . Câu 8.
Tìm số phức z thỏa mãn 2  i 1 i  z  4  2i .
A. z 1 3i .
B. z  1 3 . i C. z  1   3i . D. z  1   3i . 1 5i Câu 9.
Môđun của số phức z  2  3i  là 3  i
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức 170 170 170 170 A. z  . B. z  . C. z  . D. z  . 3 7 4 5
Câu 10. Tìm phần ảo của số phức z , biết 1 iz  3  i . A. 1 B. 1 C. 2 D. 2
Câu 11. Cho số phức z  1 2i thì số phức liên hợp z có
A. phần thực bằng 1 và phần ảo bằng 2 .
B. phần thực bằng 2 và phần ảo bằng 1 .
C. phần thực bằng 1 và phần ảo bằng 2 .
D. phần thực bằng 2 và phần ảo bằng 1.
Câu 13. Cho số phức z a bi a,b   . Khẳng định nào sau đây sai? A. 2 2
z a b .
B. z a bi . C. 2
z là số thực. D. . z z là số thực.
Câu 14. Cho số phức z a bi , a, b  . Tính môđun của số phức z . A. z
a b . B. 2 2
z a b . C. 2 2 z
a b . D. 2 2 z
a b .
Câu 15. Trong mặt phẳng tọa độ Oxy , số phức liên hợp của số phức z  1 2i 1 i có điểm biểu diễn là
điểm nào sau đây? A. Q 3  ;1 . B. N 3  ;1 .
C. M 3;   1 . D. P  1  ;3 .
Câu 16. Cho số phức z  5
  2i . Phần thực và phần ảo của số phức z là:
A. Phần thực bằng 5  và phần ảo bằng 2  .
B. Phần thực bằng 2 và phần ảo bằng 5  .
C. Phần thực bằng 2i và phần ảo bằng 5  .
D. Phần thực bằng 5
 và phần ảo bằng 2i .
Câu 17. Cho số phức z  1 i . Khi đó 3 z bằng A. 1. B. 2 . C. 2 2 . D. 4 .
Câu 18. Tìm mô đun của số phức z thoả 3iz  (3  i)(1  i)  2 . 2 3 2 2 3 2 3 3 A. z  . B. z  . C. z  . D. z  . 3 3 2 2
Câu 19. Số phức liên hợp của số phức z  1  2i là
A. 2  i
B. 1  2i
C. 1  2i
D. 1  2i
Câu 20. Số nào trong các số phức sau là số thực?
A.  3  2i   3  2i .
B. 3  2i  3  2i .
C. 5  2i   5  2i .
D. 1 2i  1 2i .
Câu 21. Cho số phức z thỏa mãn: 2
(2  3i)z  (4  i)z  (1 3i) . Xác định phần thực và phần ảo của z. A. Phần thực là 2
 ; phần ảo là 3. B. Phần thực là 3  ; phần ảo là 5 . i C. Phần thực là 2  ; phần ảo là 5 . i D. Phần thực là 2
 ; phần ảo là 5. 10
Câu 22. Xét số phức z thỏa mãn 1 2iz
 2  i. Mệnh đề nào dưới đây đúng? z 3 1 1 3 A. z  2.
B. z  2. C. z  . D. z  . 2 2 2 2
Câu 23. Cho hai số phức z  1 3i , w  2  i . Tìm phần ảo của số phức u z.w . A. 7  . B. 5i . C. 5 . D. 7  i .
Câu 24. Tìm số phức z thỏa mãn đẳng thức iz  2z  1 2i .
A. z  1  i . B. z  1  .
C. z i  .
D. z  1  i .
Câu 25. Cho số thực x , y thỏa 2x y  2y xi x  2 y  3   y  2x  
1 i . Khi đó giá trị của 2 2
M x  4xy y là
A. M  1 .
B. M  1 .
C. M  0 . D. M  2 .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức 2
Câu 26. Cho số phức z  1  3i , môđun của số phức w z iz là
A. w  146 . B. w  146 .
C. w  10 .
D. w  0 . 1
Câu 27. Cho số phức z a bi ab  0, a,b   . Tìm phần thực của số phức w  . 2 z 2 b 2 2 a b 2ab 2 2 a b A. . B. . C.  . D. .  2 2 a b 2 2 2  2 2 a b  a b 2 2 2  2 2 a b
Câu 28. Rút gọn biểu thức M    i2018 1 ta được A. 1009 M  2 . B. 1009 M  2 . C. 1009 M  2 i . D. 1009 M  2  i .
Câu 29. Cho số phức z  1 2i . Tìm phần thực và phần ảo của số phức w  2z z .
A. Phần thực là 3 và phần ảo là 2 .
B. Phần thực là 3 và phần ảo là 2i .
C. Phần thực là 2i và phần ảo là 3 .
D. Phần thực là 2 và phần ảo là 3 .
Câu 32. Cho số phức z thỏa mãn: 2
(2  3i)z  (4  i)z  (1 3i) . Xác định phần thực và phần ảo của z. A. Phần thực là 2  ; phần ảo là 5 . i B. Phần thực là 2
 ; phần ảo là 5. C. Phần thực là 2
 ; phần ảo là 3. D. Phần thực là 3  ; phần ảo là 5 . i
Câu 33. Cho số phức z thỏa mãn điều kiện 2  iz  4  iz  3  2i . Số phức liên hợp của z là 5 1 5 1 1 5 1 5 A. z   i . B. z   i . C. z    i . D. z    i . 4 4 4 4 4 4 4 4
Câu 34. Cho số phức z  2  5i . Số phức 1 
z có phần thực là 2 5 A. . B. 3  . C. 7 . D.  . 29 29
Câu 35. Cho số phức z  2
  5i . Tìm phấn thực và phần ảo của số phức z  2z . A. Phần thực 6
 và phần ảo 5 . B. Phần thực 6
 và phần ảo 5i . C. Phần thực 6  và phần ảo 5  . D. Phần thực 6  và phần ảo 5  . i
Câu 36. Tìm số thực m sao cho  2 m   1  m  
1 i là số ảo.
A. m  1.
B. m  0 .
C. m  1.
D. m  1.
Câu 37. Số phức z thỏa mãn z  2z  12  2i có:
A. Phần thực bằng 4 và phần ảo bằng 2 .
B. Phần thực bằng 4 và phần ảo bằng 2  i .
C. Phần thực bằng 4 và phần ảo bằng 2i .
D. Phần thực bằng 4 và phần ảo bằng 2 . 3 (1 3i)
Câu 38. Cho số phức z thỏa mãn z
. Môđun của số phức z iz bằng 1 i A. 4 2. B. 4 3. C. 8 2. D. 8 3.
Câu 40. Tổng phần thực và phần ảo của số phức z thoả mãn iz  1 iz  2  i bằng A. 6  . B. 2 . C. 2 . D. 6 .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
Bài 2: PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC A – LÝ THUYẾT CHUNG
1. Căn bậc hai của số thực âm
 Cho số z , nếu có số phức z sao cho z 2  z thì ta nói z là một căn bậc hai của z . 1 1 1
 Mọi số phức z  0 đều có hai căn bậc hai.
 Căn bậc hai của số thực z âm là iz .
Tổng quát, các căn bậc hai của số thực a âm là ia .
2. Phương trình bậc hai với hệ số thực
Cho phương trình bậc hai ax 2  bx c  0, a  ,b,c  ,
a  0 . Xét biệt số   b2  a
4 c của phương trình. Ta thấy: b
 Khi   0 , phương trình có một nghiệm thực x   . a 2 b   
 Khi   0 , phương trình có hai nghiệm thực phân biệt x  . 1,2 a 2 b i
 Khi   0 , phương trình có hai nghiệm phức x  . 1,2 a 2 B – BÀI TẬP
Câu 1: Gọi z và z là các nghiệm của phương trình 2
z  4 z  9  0 . Gọi M , N là các điểm biểu diễn của z 1 2 1
và z trên mặt phẳng phức. Khi đó độ dài của MN là: 2
A. MN  2 5 .
B. MN  5 .
C. MN  2 5 .
D. MN  4 .
Câu 2: Gọi z , z , z là ba nghiệm của phương trình 3
z 1  0 . Tính S z z z 1 2 3 1 2 3
A. S  4
B. S  2
C. S  3
D. S  1
Câu 3: Gọi z , z là các nghiệm phức của phương trình 2
z  2z  5  0 . Giá trị của biểu thức 4 4
z z bằng. 1 2 1 2 A. 7  B. 14 C. 7 D. 14
Câu 4: Phương trình bậc hai nào dưới đây nhận hai số phức 2  3i và 2  3i làm nghiệm? A. 2
z  4z 13  0 B. 2
z  4z  3  0 C. 2
z  4z 13  0 D. 2
z  4z  3  0
Câu 5: Gọi z và z là 2 nghiệm của phương trình 2
2z  6z  5  0 trong đó z có phần ảo âm. Phần thực và 1 2 2
phần ảo của số phức z  3z lần lượt là 1 2 A. 6;1 B. 6  ;1 C. 1  ; 6 D. 6  ; 1
Câu 6: Biết phương trình 2
z  2z m  0 m   có một nghiệm phức z  1
  3i và z là nghiệm phức 1 2
còn lại. Số phức z  2z là ? 1 2 A. 3   9i . B. 3   3i . C. 3   9i . D. 3   3i .
Câu 7: Kí hiệu z , z , z , z là bốn nghiệm của phương trình 4 2
z z  6  0 . Tính S z z z z . 1 2 3 4 1 2 3 4
A. S  2  2  3
B. S  2  2  3
C. S  2 2
D. S  2 3
Câu 8: Gọi A , B là hai điểm biểu diễn hai nghiệm phức của phương trình 2
z  2z  5  0 . Tính độ dài đoạn thẳng AB : A. 2 . B. 4 . C. 12 . D. 6 .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
Câu 9: Gọi z và z là hai nghiệm phức của phương trình 2
z  6z 11  0 . Giá trị của biểu thức 3z z 1 2 1 2 bằng A. 2 11 . B. 11 . C. 22 . D. 11.
Câu 10: Trong tập các số phức, cho phương trình 2
z  6z m  0 , m    
1 . Gọi m là một giá trị của m 0 để phương trình  
1 có hai nghiệm phân biệt z , z thỏa mãn z .z z .z . Hỏi trong khoảng 1 2 1 1 2 2
0;20 có bao nhiêu giá trị m   ? 0 A. 13 . B. 11. C. 12 . D. 10 .
Câu 11: Gọi z , z là hai nghiệm phức của phương trình 2
z  2z  5  0 , trong đó z có phần ảo dương. Tìm 1 2 1 số phức 2 2
w z  2z . 1 2
A. 9  4i .
B. 9  4i .
C. 9  4i . D. 9   4i .
Câu 12: Phương trình 2
z az b  0 ,( a, b   ) có nghiệm là 3  2i , tính S a b .
A. S 19 . B. S  1  9 .
C. S  7 .
D. S  7 .
Câu 13: Giải phương trình 2
z  4z  5  0 trên tập số phức ta được các nghiệm
A. z  2  i; z  2  i .
B. z  4  i; z  4  i . 1 2 1 2 C. z  4
  i; z  4   i . D. z  2
  i; z  2   i . 1 2 1 2
Câu 14: Phương trình 2
z  3z  9  0 có hai nghiệm phức z , z . Tính S z z z z . 1 2 1 2 1 2 A. S  1  2 .
B. S  6 .
C. S  6 .
D. S  12 .
Câu 15: Biết phương trình 2 2018
z  2017.2018z  2
 0 có hai nghiệm z , z . Tính S z z . 1 2 1 2 A. 1009 S  2 . B. 1010 S  2 . C. 2018 S  2 . D. 2019 S  2 .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
Bài 3: TẬP HỢP ĐIỂM BIỂU DIỄN SỐ PHỨC A – LÝ THUYẾT CHUNG
1. Biểu diễn hình học số phức y
Số phức z a bi a, b   được biểu diễn bởi điểm M a;b hay     M (a;b)
bởi u a;b trong mặt phẳng phức với hệ tọa độ Oxy .   O x
2. Một số tập hợp điểm biểu diễn số phức z thường gặp:
ax by c  0  tập hợp điểm là đường thẳng
x  0  tập hợp điểm là trục tung Oy
y  0  tập hợp điểm là trục hoành Ox 2 2  x a  y bR2    
 tập hợp điểm là hình tròn tâm I a;b , bán kính R  2 2
x a   y b  R2  
 tập hợp điểm là đường tròn có tâm I a;b , bán kính   x 2   y2  a 2 x by 2  c  0  R a2 b2    c
x  0  tập hơp điểm là miền bên phải trục tung
y  0  tập hợp điểm là miền phía dưới trục hoành
x  0  tập hợp điểm là miền bên trái trục tung
y  0  tập hợp điểm là phía trên trục hoành  y ax 2 
bx c  tập hợp điểm là đường Parabol x 2 y2  
 1  tập hợp điểm là đường Elip a2 b2 x 2 y2  
 1  tập hợp điểm là đường Hyperbol a2 b2 B – BÀI TẬP
Câu 1: Trong hình vẽ bên, điểm M biểu diễn số phức z . Số phức z là
A. 2  i .
B. 2  i .
C. 1 2i .
D. 1 2i .
Câu 2: Số phức z  2  3i có điểm biểu diễn trên mặt phẳng tọa độ là:
A. M 2;  3 . B. M  2  ;  3 . C. M 2;  3 . D. M  2  ;  3 .
Câu 3: Trong mặt phẳng phức, cho số phức z  1 2i . Điểm biểu diễn cho số phức z là điểm nào sau đây
A. M 1; 2
B. Q 1; 2
C. P 1; 2
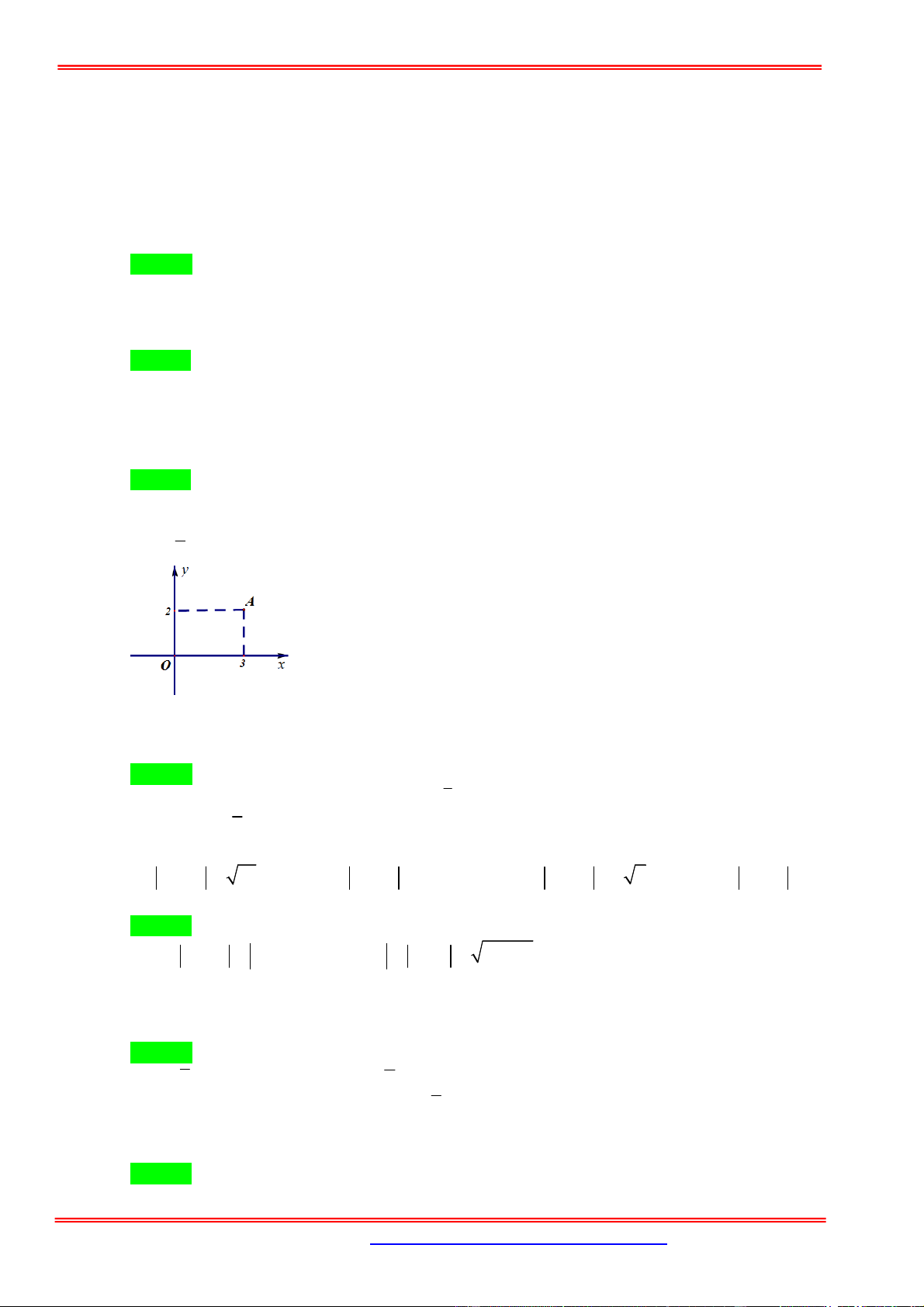
D. N 2;  1
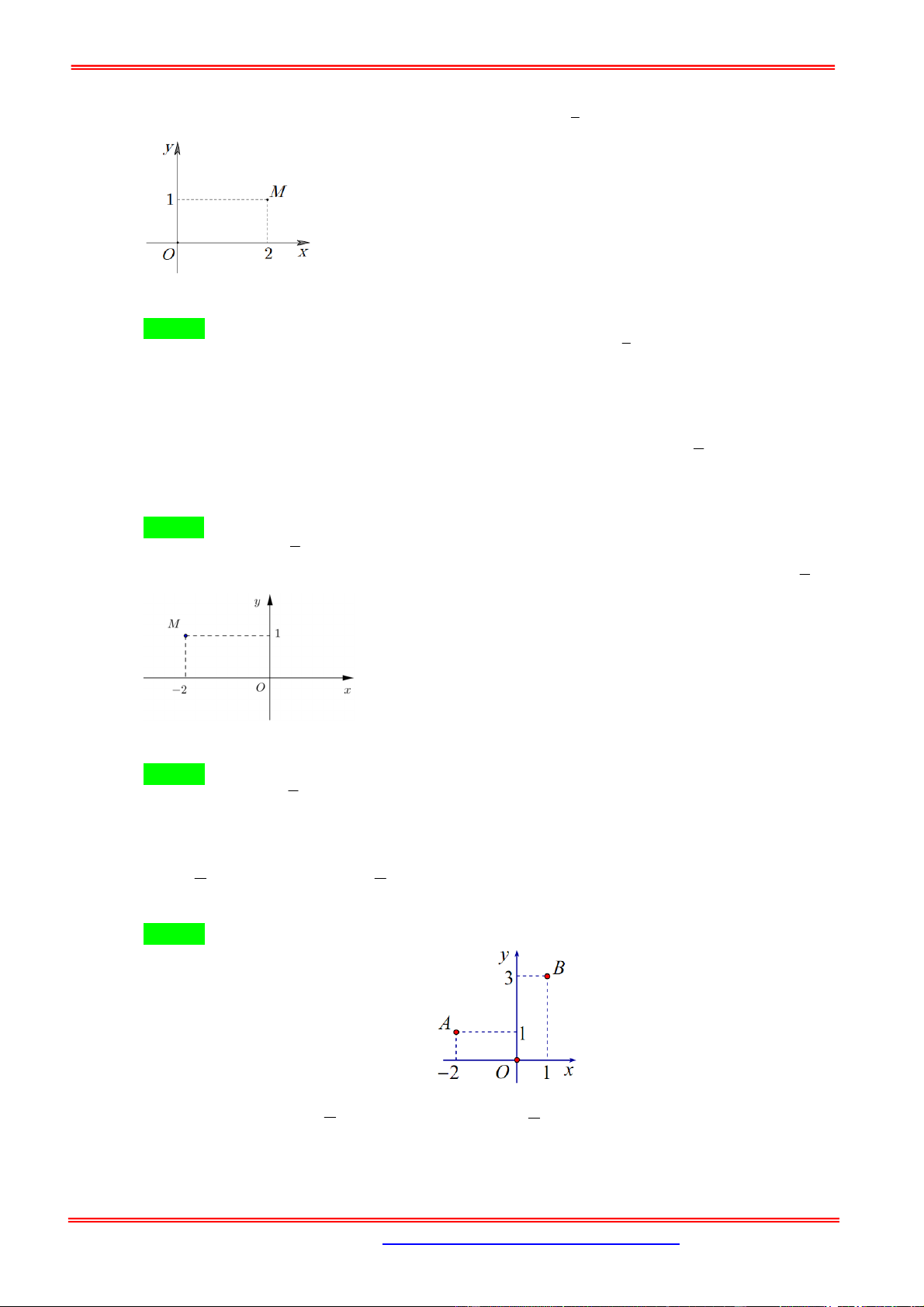
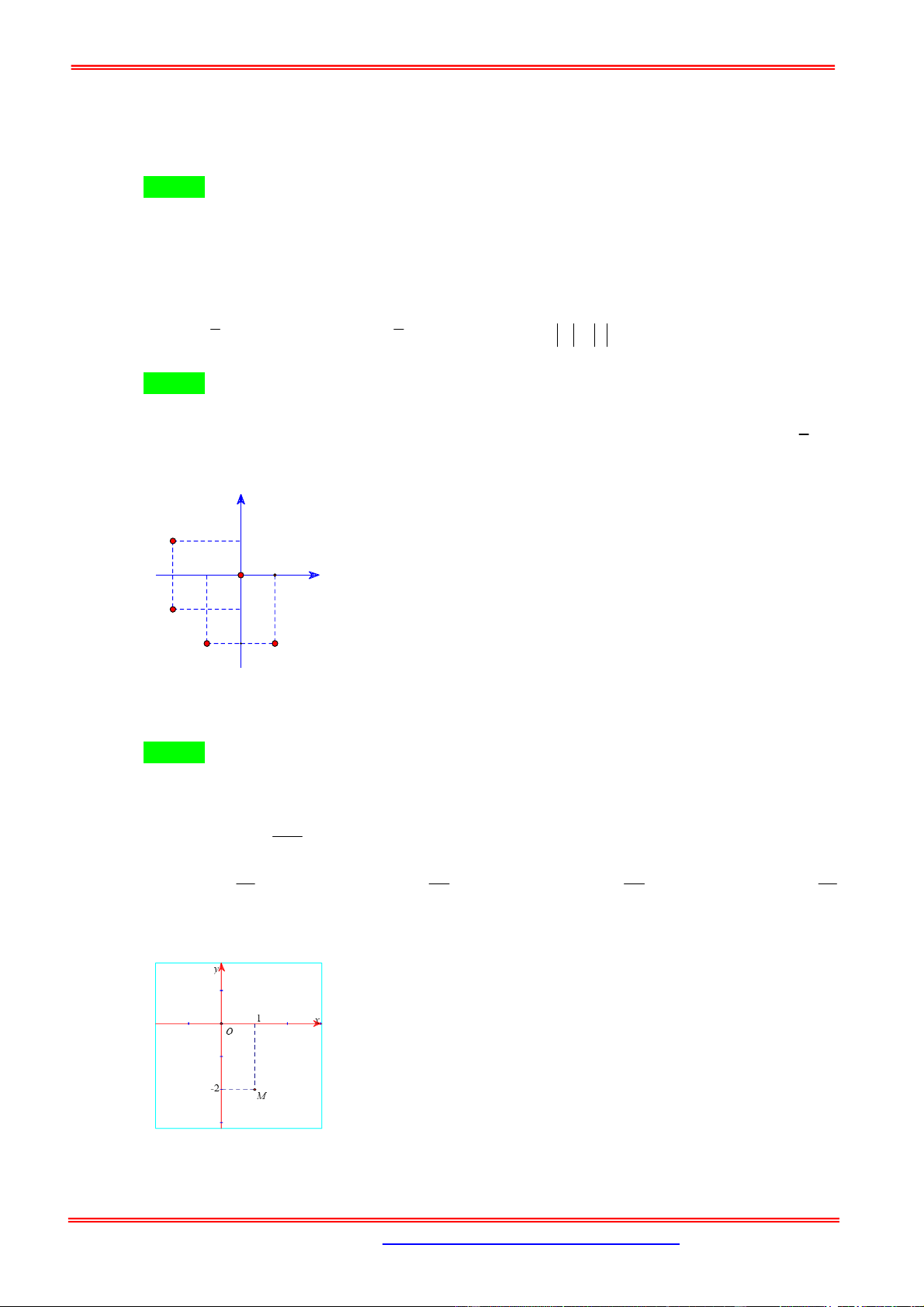
Câu 4: Trong mặt phẳng Oxy , điểm M trong hình vẽ bên là điểm biểu diễn số phức z . Số phức z là
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
A. 1 2i B. 2   i
C. 1 2i D. 2   i
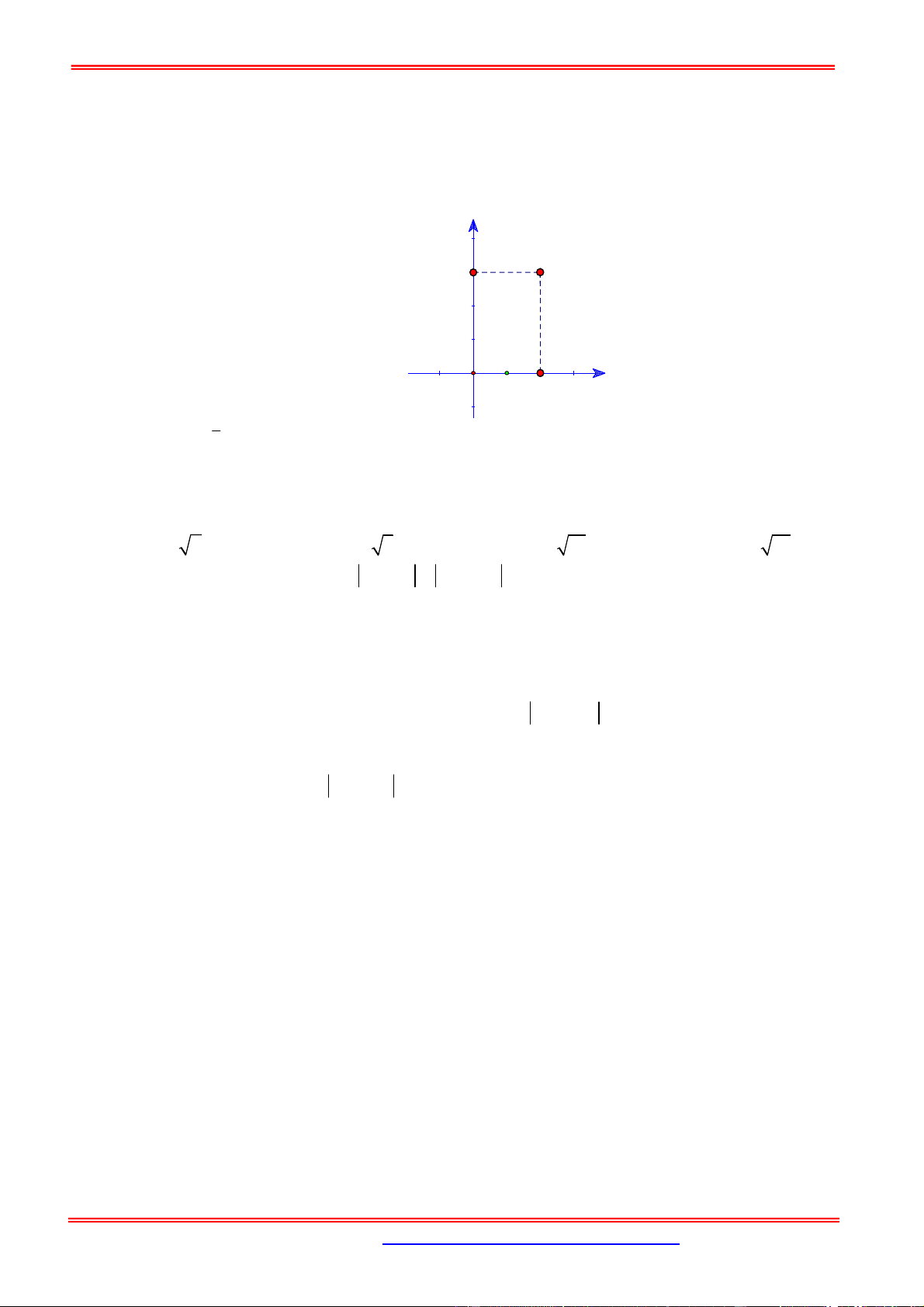
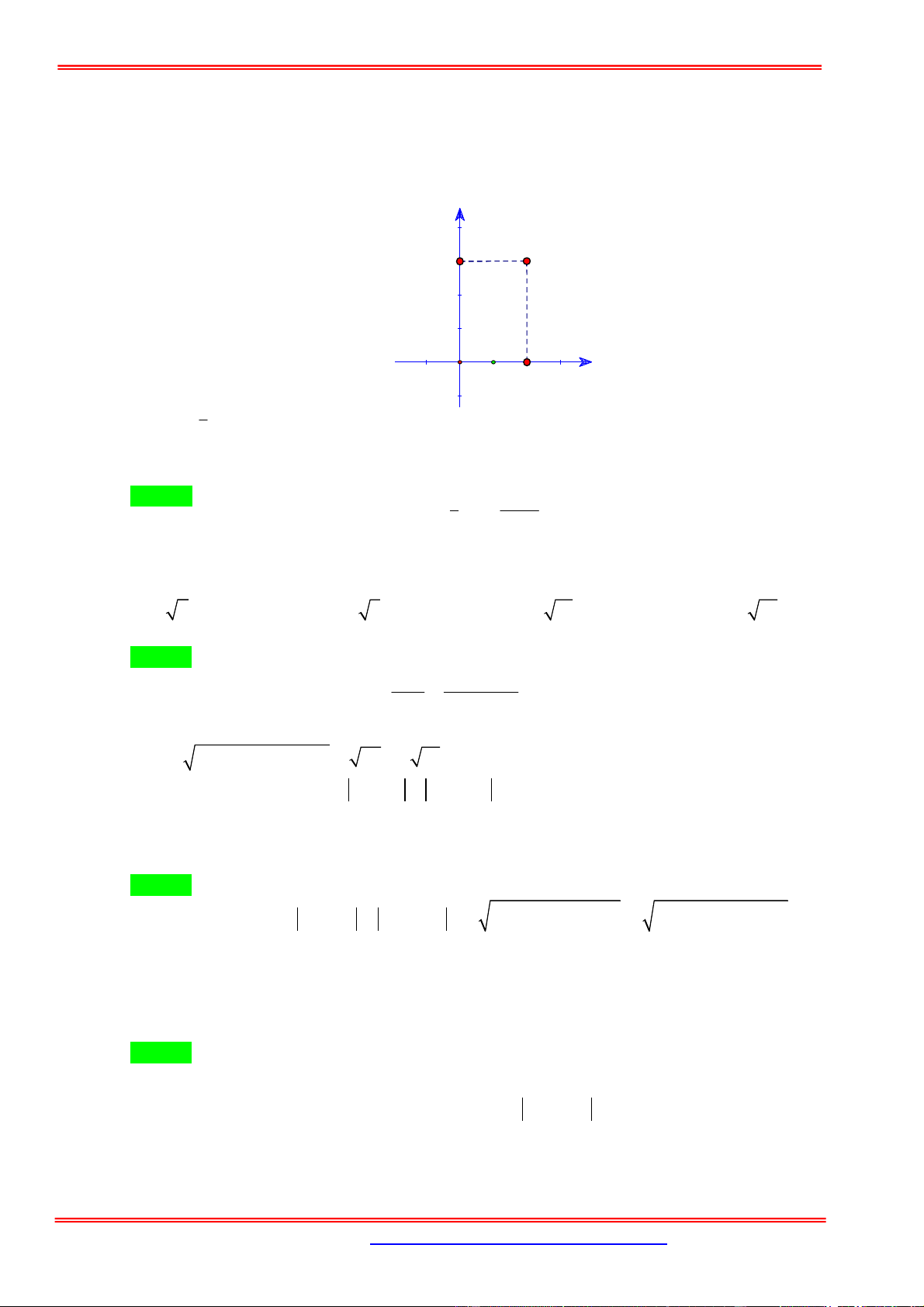
Câu 5: Trong mặt phẳng Oxy , cho các điểm ,
A B như hình vẽ bên. Trung điểm của đoạn thẳng AB biểu diễn số phức. 1 1 A. 2  i . B.   2i . C. 1   2i . D. 2  i . 2 2
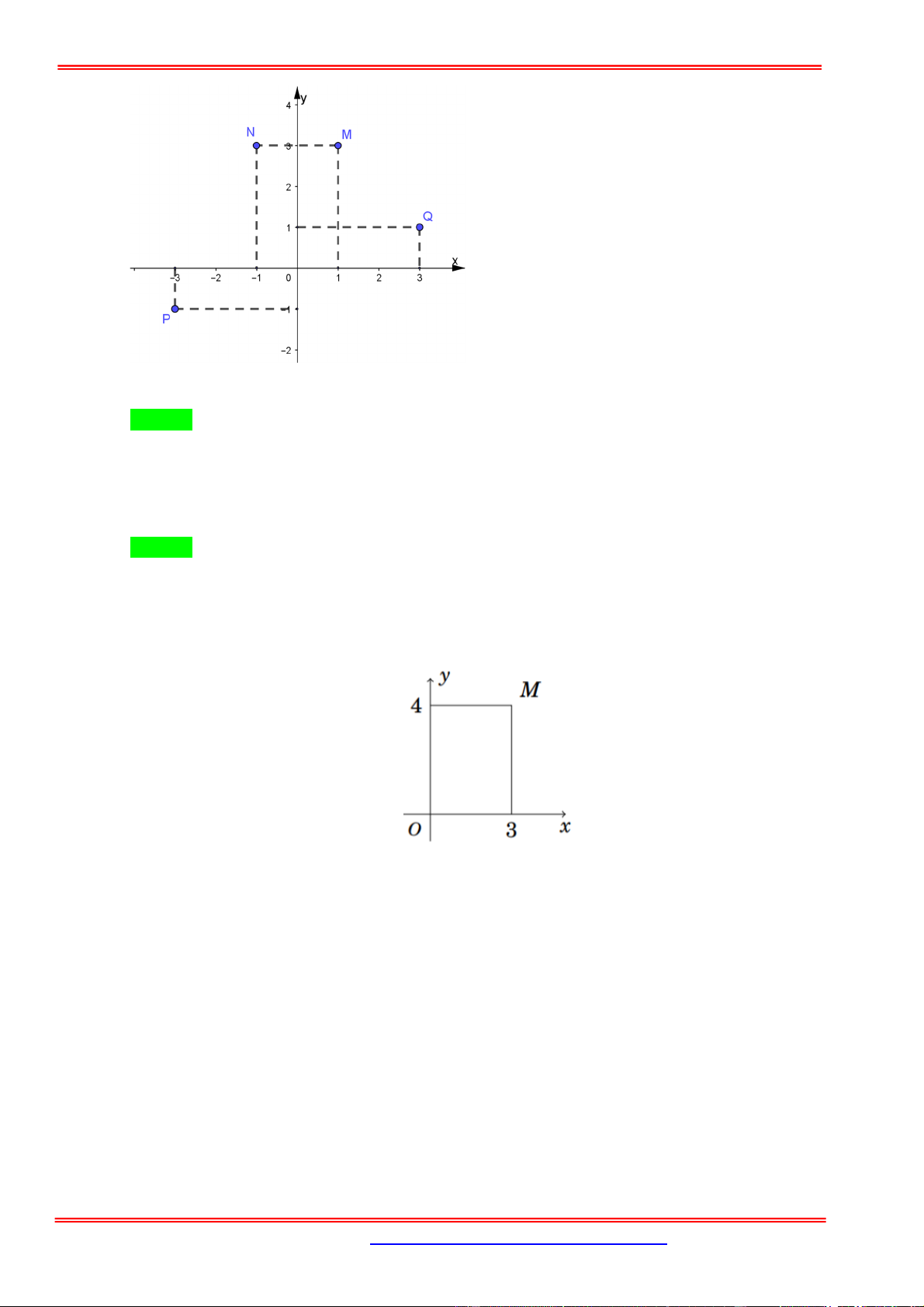
Câu 6: Điểm nào trong hình vẽ dưới đây là điểm biểu diễn của số phức z  1 i2  i ? A. Q . B. M . C. N . D. P .
Câu 7: Hỏi điểm M 3;  
1 là điểm biểu diễn số phức nào sau đây? A. z  3   i B. z  1   3i
C. z  1 3i
D. z  3  i
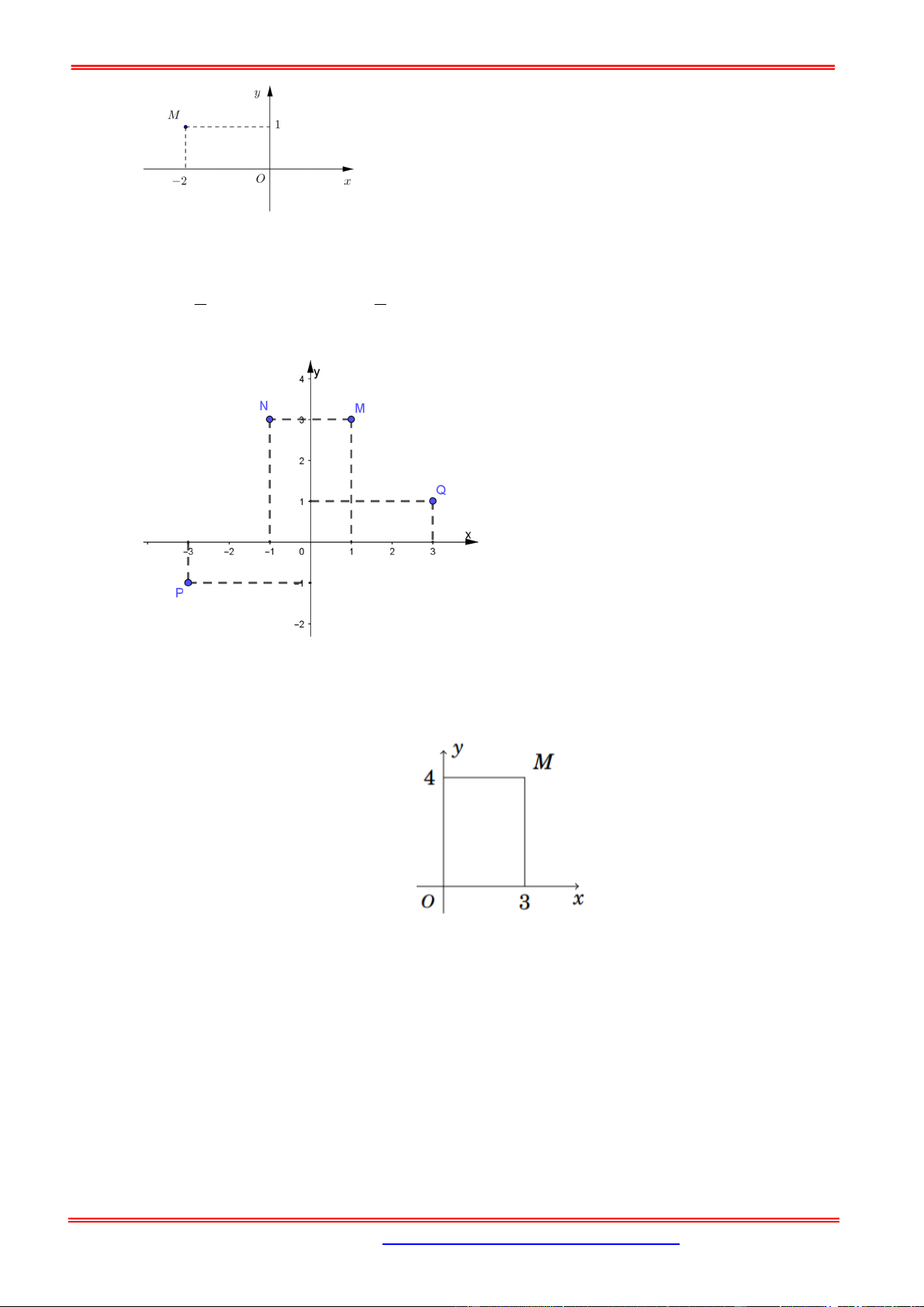
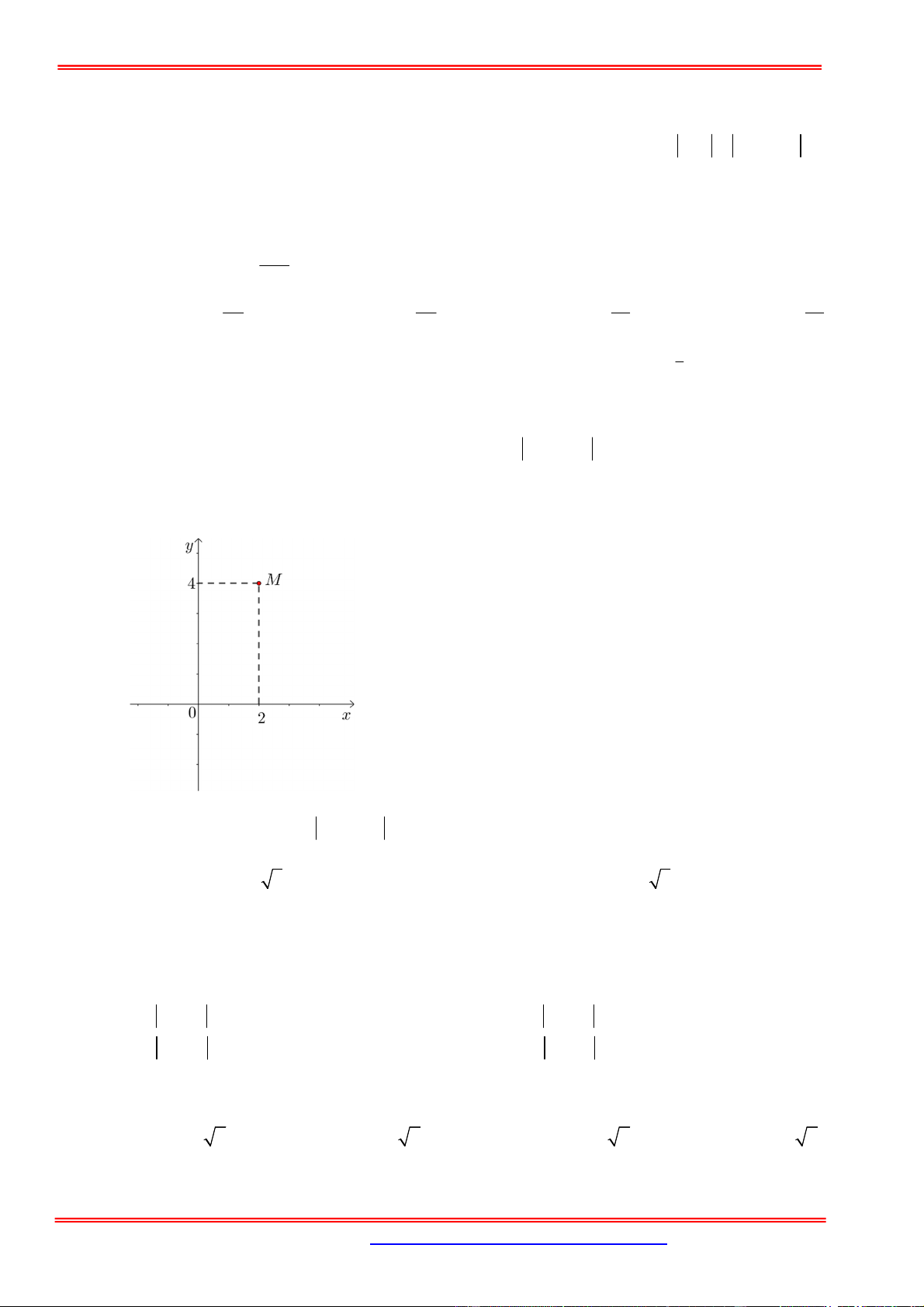
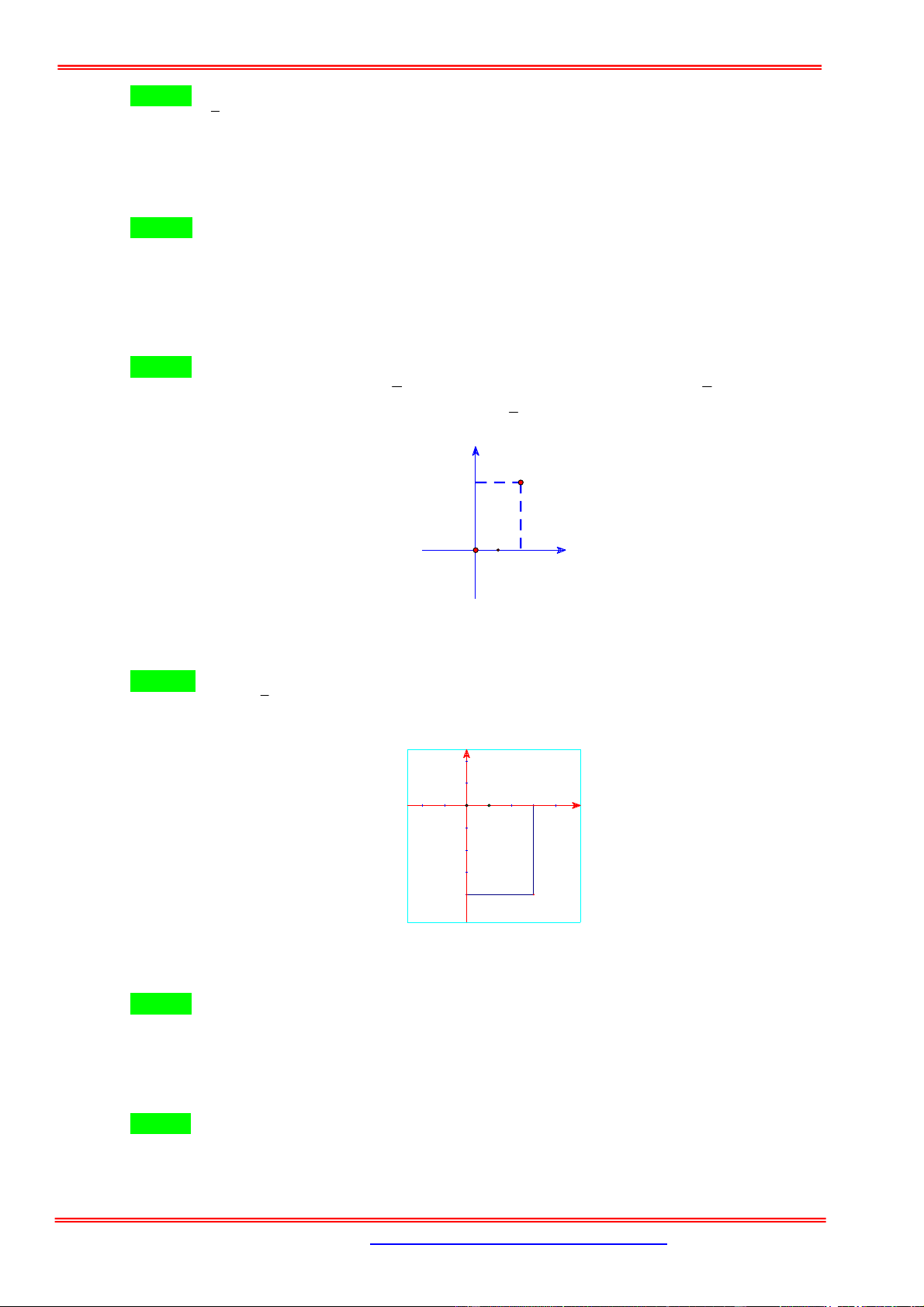
Câu 8: Điểm M trong hình vẽ bên là điểm biểu diễn của số phức z .
Tìm phần thực và phần ảo cú số phức z .
A. Phần thực bằng 3 và phần ảo bằng 4i .
B. Phần thực bằng 4 và phần ảo bằng 3.
C. Phần thực bằng 4 và phần ảo bằng 3i .
D. Phần thực bằng 3 và phần ảo bằng 4 .
Câu 9: Số phức z  2  3i có điểm biểu diễn là. A. A2; 3   .
B. A2;3 .
C. A2;3 .
D. A2;3 .
Câu 10: Trên mặt phẳng tọa độ O xy cho điểm M trong hình vẽ bên là điểm biểu diễn của số phức z . Tìm z ?
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức y 3 x O M
A. z  3 4i . B. z  3   4i . C. z  4   3i .
D. z  3 4i .
Câu 11: Cho số phức z thỏa z 1 i  2 . Chọn phát biểu đúng:
A. Tập hợp điểm biểu diễn số phức z là một đường tròn có bán kính bằng 4 .
B. Tập hợp điểm biểu diễn số phức z là một đường thẳng.
C. Tập hợp điểm biểu diễn số phức z là một đường Parabol.
D. Tập hợp điểm biểu diễn số phức z là một đường tròn có bán kính bằng 2 .
Câu 12: Cho số phức z  2  3i . Điểm biểu diễn số phức liên hợp của z là A.  2  ;3 . B.  2  ; 3   .
C. 2;3 . D. 2;3 .
Câu 13: Cho số phức z  4
  5i . Biểu diễn hình học của z là điểm có tọa độ A.  4  ;5 B.  4  ; 5  
C. 4; 5 D. 4;5
Câu 14: Gọi A là điểm biểu diễn của số phức z  2  5i và B là 1điểm biểu diễn của số phức z  2   5i .
Tìm mệnh đề đúng trong các mệnh đề sau.
A. Hai điểm A và B đối xứng với nhau qua gốc toạ độ O .
B. Hai điểm A và B đối xứng với nhau qua đường thẳng y x .
C. Hai điểm A và B đối xứng với nhau qua trục hoành.
D. Hai điểm A và B đối xứng với nhau qua trục tung.
Câu 15: Cho hai số phức z  3  5i và w  1
  2i . Điểm biểu diễn số phức z  z  .
w z trong mặt phẳng Oxy có tọa độ là
A. 6;  4 .
B. 4;  6 . C. 4; 6 .
D. 4;  6 .
Câu 16: Số phức z  4  2i có điểm biểu diễn trên mặt phẳng tọa độ là M . Tìm tọa độ điểm M A. M 4; 2   . B. M  4  ; 2 . C. M 4;  2 .
D. M 2;4 .
Câu 17: Số phức liên hợp của số phức z i 1 2i có điểm biểu diễn là điểm nào dưới đây?
A. A1;2 B. F  2   ;1
C. E 2;  1 D. B  1  ; 2
Câu 18: Điểm M trong hình vẽ dưới đây biểu diễn số phức z . y M 3 O 1 2 x
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 10
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
Số phức z bằng
A. 3  2i .
B. 2  3i .
C. 2  3i .
D. 3  2i .
Câu 19: Trên mặt phẳng tọa độ Oxy cho điểm M trong hình vẽ bên là điểm biểu diễn của số phức z . y 3 x O 1 -4 M Tìm z ? A. z  3   4i .
B. z  3  4i .
C. z  3  4i . D. z  4   3i .
Câu 20: Trong mặt phẳng toạ độ, điểm A1;  2 là điểm biểu diễn của số phức nào trong các số sau?
A. z  1 2i .
B. z  1 2i . C. z  2   i . D. z  1   2i .
Câu 21: Trong mặt phẳng tọa độ Oxy , Gọi A , B , C lần lượt là các điểm biểu diễn số phức 1
  2i , 4  4i , 3
i . Số phức biểu diễn trọng tâm tam giác ABC là
A. 1 3i . B. 3   9i .
C. 3  9i . D. 1   3i .
Câu 22: Gọi M là điểm biểu diễn của số phức z trong mặt phẳng tọa độ, N là điểm đối xứng của M qua
Oy ( M , N không thuộc các trục tọa độ). Số phức w có điểm biểu diễn lên mặt phẳng tọa độ là
N . Mệnh đề nào sau đây đúng ?
A. w  z .
B. w z .
C. w z .
D. w   z .
Câu 23: Cho bốn điểm A , B , C , D trên hình vẽ biểu diễn 4 số phức khác nhau. Chọn mệnh đề sai. y A 1 -2 -1 1 O x -1 D -2 C B
A. D là biểu diễn số phức z  1  2i .
B. C là biểu diễn số phức z  1  2i .
C. A là biểu diễn số phức z  2  i .
D. B là biểu diễn số phức z  1  2i .
Câu 24: Trong mặt phẳng tọa độ O xy , gọi M là điểm biểu diễn số phức z  3  4i ; M ' là điểm biểu diễn 1 i cho số phức z ' 
z . Tính diện tích tam giác OMM ' . 2 15 25 25 15 A. S  . B. S  . C. S  . D. S  . OMM ' 2 OMM ' 4 OMM ' 2 OMM ' 4
Câu 25: Điểm M trong hình vẽ bên là điểm biểu diễn số phức z tìm phần thực và phần ảo của số phức z .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 11
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức A. Phần thực là 2
 và phần ảo là 1. B. Phần thực là 2
 và phần ảo là i .
C. Phần thực là 1 và phần ảo là 2  .
D. Phần thực là 1 và phần ảo là 2  i .
Câu 26: Trong mặt phẳng tọa độ Oxy , tập hợp điểm biểu diễn số phức z thỏa mãn z i  2  3i z là A. đường tròn 2 2
x y  2 B. đường tròn 2 2
x y  4
C. đường thẳng x  2 y  3  0
D. đường thẳng x  2 y 1  0
Câu 27: Trong mặt phẳng tọa độ O xy , gọi M là điểm biểu diễn số phức z  3  4i ; M ' là điểm biểu diễn 1 i cho số phức z ' 
z . Tính diện tích tam giác OMM ' . 2 25 25 15 15 A. S  . B. S  . C. S  . D. S  . OMM ' 4 OMM ' 2 OMM ' 4 OMM ' 2 1
Câu 28: Cho A, B, C lần lượt là các điểm biểu diễn các số phức 6  3i ; 1 2ii ; . Tìm số phức có điểm i
biểu diễn D sao cho ABCD là hình bình hành. A. z  8   4i .
B. z  4  2i .
C. z  8  5i . D. z  8   3i .
Câu 29: Biết tập hợp các điểm biểu diễn số phức z thỏa mãn iz 1 2i  4 là một đường tròn. Tìm tọa độ
tâm I của đường tròn đó.
A. I 1; 2 . B. I  1  ;  2 . C. I  2  ;   1 . D. I 2  ;1 .
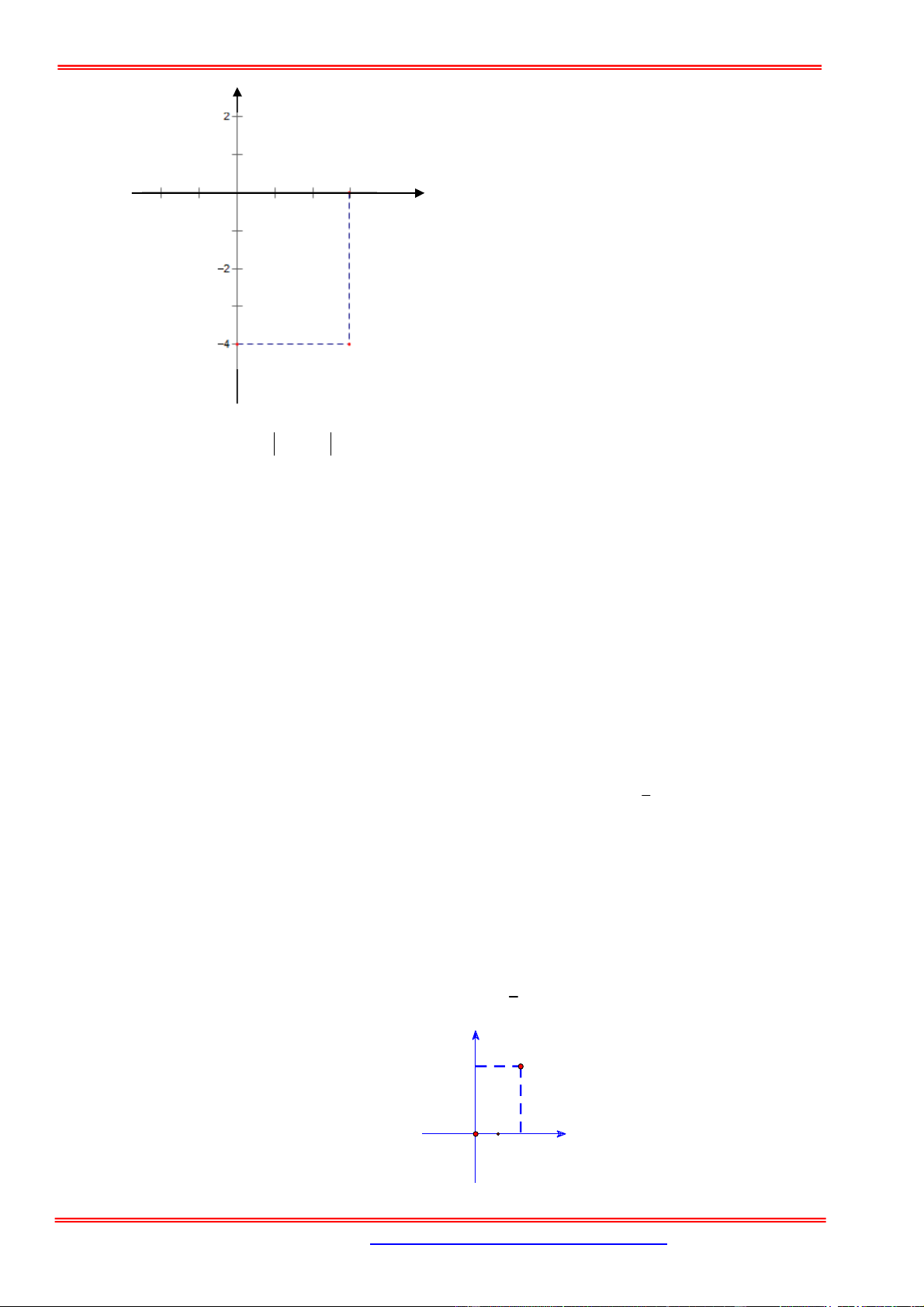
Câu 30: Điểm M trong hình bên là điểm biểu diễn cho số phức
A. z  4  2i .
B. z  2  4i .
C. z  4  2i .
D. z  2  4i .
Câu 31: Cho số phức z thoả mãn z  3  4i  5 . Biết rằng tập hợp điểm trong mặt phẳng toạ độ biểu diễn
các số phức z là một đường tròn. Tìm toạ độ tâm I và bán kính R của đường tròn đó. A. I 3; 4
  , R  5 . B. I  3
 ; 4 , R  5 . C. I 3; 4
  , R  5 . D. I  3
 ; 4 , R  5 .
Câu 32: Gọi M và N lần lượt là các điểm biểu diễn của z , z trên mặt phẳng tọa độ, I là trung điểm MN 1 2
, O là gốc tọa độ (3 điểm O , M , N phân biệt và không thẳng hàng). Mệnh đề nào sau đây là đúng?
A. z z  2 OM ON .
B. z z  2OI . 1 2   1 2
C. z z OI .
D. z z OM ON . 1 2 1 2
Câu 33: Gọi z là nghiệm phức có phần ảo âm của phương trình 2
z  2z  3  0 . Trên mặt phẳng tọa độ, điểm 1
nào sau đây là điểm biểu diễn của số phức z ? 1 A. Q  1  ; 2i . B. N  1  ; 2  .
C. M 1; 2 .
D. P 1; 2i .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 12
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
Câu 34: Cho A , B , C tương ứng là các điểm trong mặt phẳng phức biểu diễn các số phức z  1 2i , 1 z  2
  5i , z  2  4i . Số phức z biểu diễn bởi điểm D sao cho tứ giác ABCD là hình bình 2 3 hành là
A. 5  i .
B. 1 5i .
C. 3  5i . D. 1   7i .
Câu 35: Điểm M trong hình vẽ dưới đây biểu diễn số phức z . y 3 M 2 x
Số phức z 1 bằng
A. 4  2i .
B. 3  3i .
C. 3  3i .
D. 4  2i .
Câu 36: Cho số phức z thỏa mãn iz  2  i  0 . Khoảng cách từ điểm biểu diễn của z trên mặt phẳng tọa độ
Oxy đến điểm M 3; 4 là: A. 2 2 . B. 2 5 . C. 13 . D. 2 10 .
Câu 37: Cho các số phức z thỏa mãn z 1 i z 1 2i . Tập hợp các điểm biểu diễn các số phức z trên
mặt phẳng tọa độ là một đường thẳng. Phương trình đường thẳng đó là
A. 4x  6 y  3  0
B. 4x  6y  3  0
C. 4x  6 y  3  0
D. 4x  6y  3  0
Câu 38: Cho số phức z  2  i . Trên mặt phẳng tọa độ Oxy , tìm điểm biểu diễn số phức w iz .
A. M 2;  1 . B. M 2;  1 .
C. M 1;2 . D. M  1  ; 2 .
Câu 39: Tập hợp các điểm biểu diễn cho số phức z thỏa mãn z  3  4i  5 là
A. Một đường Elip.
B. Một đường tròn.
C. Một đường thẳng.
D. Một đường parabol.
Câu 40: Cho số phức z thỏa mãn z 1 2i  5 và M  ;
x y là điểm biểu diễn số phức z . Điểm M thuộc
đường tròn nào sau đây? 2 2 2 2 A. x  
1   y  2  5 B. x  
1   y  2  25 2 2 2 2 C. x  
1   y  2  25 D. x  
1   y  2  5
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 13
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức HƯỚNG DẪN GIẢI
Bài 1: SỐ PHỨC VÀ CÁC PHÉP TOÁN SỐ PHỨC Câu 1.
Số phức z  15  3i có phần ảo bằng A. 3 . B. 15 . C. 3i . D. 3 . Hướng dẫn giải Chọn D Câu 2.
Số phức z  1 2i 2  3i bằng A. 8. B. 8 . i C. 4   . i D. 8 . i Hướng dẫn giải Chọn B
z  1 2i2  3i   2  4i  3i  6  8  i Câu 3. Cho số phức z  3
i . Tìm phần thực của z . A. 3 . B. 0 . C. 3  . D. không có. Hướng dẫn giải Chọn B Do z  3
i là số thuần ảo nên có phần thực bằng 0 . Câu 4.
Cho số phức z có điểm biểu diễn là điểm A trong hình vẽ bên. Tìm phần thực và phần ảo của số phức z .
A. Phần thực bằng 3 , phần ảo bằng 2  .
B. Phần thực bằng 3 , phần ảo bằng 2 .
C. Phần thực bằng 2 , phần ảo bằng 3  i .
D. Phần thực bằng 3 , phần ảo bằng 2i . Hướng dẫn giải Chọn A
Từ hình vẽ ta suy ra số phức z  3  2i z  3  2i .
Nên số phức z có phần thực bằng 3 , phần ảo bằng 2  . Câu 5.
Cho số phức z  1  2i và z  2
  2i . Tìm môđun của số phức z z . 1 2 1 2
A. z z  17 .
B. z z  5 .
C. z z  2 2 .
D. z z  1 . 1 2 1 2 1 2 1 2 Hướng dẫn giải Chọn B
Ta có z z  1 2i   2   2i 2 2
 3  4i  3  4  5 1 2 Câu 6.
Cho số phức z  3  2i . Tìm phần ảo của số phức liên hợp của z . A. 2i . B. 2  i . C. 2 . D. 2  . Hướng dẫn giải Chọn C
Ta có z  3 2i nên phần ảo của z là 2. Câu 8.
Tìm số phức z thỏa mãn 2  i 1 i  z  4  2i .
A. z 1 3i .
B. z  1 3 . i C. z  1   3i . D. z  1   3i . Hướng dẫn giải Chọn B
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 14
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
2  i1 i  z  4  2i  3 i z  4  2i z  1 3i z  1 3i . 1 5i Câu 9.
Môđun của số phức z  2  3i  là 3  i 170 170 170 170 A. z  . B. z  . C. z  . D. z  . 3 7 4 5 Hướng dẫn giải Chọn D
1 5i3  i  1 8  11 7
z  2  3i   2  3i   i   i .   
3  i 3  i  5 5  5 5 2 2  11   7  170 Suy ra z        .  5   5  5
Câu 10. Tìm phần ảo của số phức z , biết 1 iz  3  i . A. 1 B. 1 C. 2 D. 2 Hướng dẫn giải Chọn D 3  i
3  i1 i
Ta có: 1 iz  3  i z   z
z  1 2i . 1 i
1 i1 i
Vậy phần ảo của số phức z bằng 2 .
Câu 11. Cho số phức z  1 2i thì số phức liên hợp z có
A. phần thực bằng 1 và phần ảo bằng 2 .
B. phần thực bằng 2 và phần ảo bằng 1 .
C. phần thực bằng 1 và phần ảo bằng 2 .
D. phần thực bằng 2 và phần ảo bằng 1. Hướng dẫn giải Chọn A
z  1 2i . Do đó số phức liên hợp z có phần thực bằng 1 và phần ảo bằng 2 .
Câu 13. Cho số phức z a bi a,b   . Khẳng định nào sau đây sai? A. 2 2
z a b .
B. z a bi . C. 2
z là số thực. D. . z z là số thực. Hướng dẫn giải Chọn C
Đáp án A và B đúng theo định nghĩa.
Đáp án C: Ta có z  a bi2 2 2 2
a  2bi b là số phức có phần ảo khác 0 khi b  0  Sai.
Đáp án D: z z  a bi a bi  a  bi2 2 2 2 .
a b là một số thực  Đúng.
Câu 14. Cho số phức z a bi , a, b  . Tính môđun của số phức z . A. z
a b . B. 2 2
z a b . C. 2 2 z
a b . D. 2 2 z
a b . Hướng dẫn giải Chọn C Do 2 2 z z
a b .
Câu 15. Trong mặt phẳng tọa độ Oxy , số phức liên hợp của số phức z  1 2i 1 i có điểm biểu diễn là
điểm nào sau đây? A. Q 3  ;1 . B. N 3  ;1 .
C. M 3;   1 . D. P  1  ;3 . Hướng dẫn giải Chọn C
Ta có z  1 2i 1 i  3  i z  3  i .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 15
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
Do đó điểm biểu diễn của z là M 3;   1 .
Câu 16. Cho số phức z  5
  2i . Phần thực và phần ảo của số phức z là:
A. Phần thực bằng 5  và phần ảo bằng 2  .
B. Phần thực bằng 2 và phần ảo bằng 5  .
C. Phần thực bằng 2i và phần ảo bằng 5  .
D. Phần thực bằng 5
 và phần ảo bằng 2i . Hướng dẫn giải Chọn C
z  5  2i z  5  2i  Phần thực là 5  và phần ảo là 2  .
Câu 17. Cho số phức z  1 i . Khi đó 3 z bằng A. 1. B. 2 . C. 2 2 . D. 4 . Hướng dẫn giải Chọn C Ta có: 3 3 z  2
  2i z  4  4  2 2 .
Chú ý: Có thể sử dụng MTBT.
Câu 18. Tìm mô đun của số phức z thoả 3iz  (3  i)(1  i)  2 . 2 3 2 2 3 2 3 3 A. z  . B. z  . C. z  . D. z  . 3 3 2 2 Hướng dẫn giải Chọn B 2 2
Ta có: 3iz  (3  i)(1 i)  2  z    i 3 3 2 2  z  . 3
Câu 19. Số phức liên hợp của số phức z  1  2i là
A. 2  i
B. 1  2i
C. 1  2i
D. 1  2i Hướng dẫn giải Chọn C
Số phức liên hợp của số phức z  1  2i là z  1  2i .
Câu 20. Số nào trong các số phức sau là số thực?
A.  3  2i   3  2i .
B. 3  2i  3  2i .
C. 5  2i   5  2i .
D. 1 2i  1 2i . Hướng dẫn giải Chọn B
3  2i  3 2i  6.
Câu 21. Cho số phức z thỏa mãn: 2
(2  3i)z  (4  i)z  (1 3i) . Xác định phần thực và phần ảo của z. A. Phần thực là 2
 ; phần ảo là 3. B. Phần thực là 3  ; phần ảo là 5 . i C. Phần thực là 2  ; phần ảo là 5 . i D. Phần thực là 2
 ; phần ảo là 5. Hướng dẫn giải Chọn D
Gọi z a bi z a bi , ta có: 2
(2  3i)z  (4  i)z  (1  3i)  2  3i a bi   4  i a bi  8  6i
 3a  2b  a bi  4  3i 3
a  2b  4 a  2      a b  3 b  5  
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 16
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức z  2   5i. 10
Câu 22. Xét số phức z thỏa mãn 1 2iz
 2  i. Mệnh đề nào dưới đây đúng? z 3 1 1 3 A. z  2.
B. z  2. C. z  . D. z  . 2 2 2 2 Hướng dẫn giải Chọn D  1 Ta có 1 z  . z 2 z 10  10 
Vậy 1 2iz
 2  i   z  2  2 z   1 i   .z z 2    z    2
  z  2   z  2 10 2 10 2 2 1   . z
. Đặt z a  0. 4 2    z z 2  10   a  1
 a  22  2a  2 4 2 1 
a a  2  0    
a  1  z  1. 2 2  a a  2  
Câu 23. Cho hai số phức z  1 3i , w  2  i . Tìm phần ảo của số phức u z.w . A. 7  . B. 5i . C. 5 . D. 7  i . Hướng dẫn giải Chọn A
z  1  3i ; u  .
z w  1 3i 2  i  1   7i .
Vậy phần ảo của số phức u bằng 7  .
Câu 24. Tìm số phức z thỏa mãn đẳng thức iz  2z  1 2i .
A. z  1  i . B. z  1  .
C. z i  .
D. z  1  i .
Câu 25. Cho số thực x , y thỏa 2x y  2y xi x  2 y  3   y  2x  
1 i . Khi đó giá trị của 2 2
M x  4xy y là
A. M  1 .
B. M  1 .
C. M  0 . D. M  2 . Hướng dẫn giải Chọn A
2x y x  2y  3
x  3y  3 x  0 Phương trình      
2y x y  2x 1  3
x y  1  y  1  Vậy M     2 2 0 4.0.1 1  1  . 2
Câu 26. Cho số phức z  1  3i , môđun của số phức w z iz là
A. w  146 . B. w  146 .
C. w  10 .
D. w  0 . Hướng dẫn giải Chọn B
z  1  3i z  1  3i 2 2
w  z iz  1  3i  i 1  3i  6i  8  i  3  5i  11  w  146 . 1
Câu 27. Cho số phức z a bi ab  0, a,b   . Tìm phần thực của số phức w  . 2 z
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 17
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức 2 b 2 2 a b 2ab 2 2 a b A. . B. . C.  . D. .  2 2 a b 2 2 2  2 2 a b  a b 2 2 2  2 2 a b Hướng dẫn giải Chọn B 2 2 1 1 1
a b  2abi w     . 2 za bi2 2 2
a b  2abia b 2 2 2 2 2  4a b 2 2 2 2 a b a b
Phần thực của w là  .
a b 2  a ba b 2 2 2 2 2 2 2 4
Câu 28. Rút gọn biểu thức M    i2018 1 ta được A. 1009 M  2 . B. 1009 M  2 . C. 1009 M  2 i . D. 1009 M  2  i . Hướng dẫn giải Chọn D 1009 2018 2 1009 1009 Ta có Mi   i        i     1008 i  1009 1 1 2 2 i  2 i .  
Câu 29. Cho số phức z  1 2i . Tìm phần thực và phần ảo của số phức w  2z z .
A. Phần thực là 3 và phần ảo là 2 .
B. Phần thực là 3 và phần ảo là 2i .
C. Phần thực là 2i và phần ảo là 3 .
D. Phần thực là 2 và phần ảo là 3 . Hướng dẫn giải Chọn A
w  2z z  2 1 2i  1 2i  3  2i . Phần thực là 3 và phần ảo là 2 .
Câu 32. Cho số phức z thỏa mãn: 2
(2  3i)z  (4  i)z  (1 3i) . Xác định phần thực và phần ảo của z. A. Phần thực là 2  ; phần ảo là 5 . i B. Phần thực là 2
 ; phần ảo là 5. C. Phần thực là 2
 ; phần ảo là 3. D. Phần thực là 3  ; phần ảo là 5 . i Hướng dẫn giải Chọn B
Giả sử số phức z a bi a, b   . 2
(2  3i)z  (4  i)z  (1 3i)  2  3ia bi   4  i a bi    8   6i Phương trình 3
a  2b  4 a  2     a b  3 b  5  
Câu 33. Cho số phức z thỏa mãn điều kiện 2  iz  4  iz  3  2i . Số phức liên hợp của z là 5 1 5 1 1 5 1 5 A. z   i . B. z   i . C. z    i . D. z    i . 4 4 4 4 4 4 4 4 Hướng dẫn giải Chọn D 3  2i 1 5 1 5
2  iz  4  iz  3 2i   2
  2iz  3  2i z     i z    i 2  2i 4 4 4 4
Câu 34. Cho số phức z  2  5i . Số phức 1 
z có phần thực là 2 5 A. . B. 3  . C. 7 . D.  . 29 29 Hướng dẫn giải Chọn A ii  1 1 2 5 2 5 2 5 1 z       . i z 2  5i
2  5i2  5i 29 29 29
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 18
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức 2 Số phức 1 
z có phần thực là . 29
Câu 35. Cho số phức z  2
  5i . Tìm phấn thực và phần ảo của số phức z  2z . A. Phần thực 6
 và phần ảo 5 . B. Phần thực 6
 và phần ảo 5i . C. Phần thực 6  và phần ảo 5  . D. Phần thực 6  và phần ảo 5  . i Hướng dẫn giải Chọn C
Ta có z  2z  2  5i  22  5i  6   5i .
Câu 36. Tìm số thực m sao cho  2 m   1  m  
1 i là số ảo.
A. m  1.
B. m  0 .
C. m  1.
D. m  1. Hướng dẫn giải Chọn D Số phức  2 m   1  m   1 i là số ảo 2
m 1  0  m  1  .
Câu 37. Số phức z thỏa mãn z  2z  12  2i có:
A. Phần thực bằng 4 và phần ảo bằng 2 .
B. Phần thực bằng 4 và phần ảo bằng 2  i .
C. Phần thực bằng 4 và phần ảo bằng 2i .
D. Phần thực bằng 4 và phần ảo bằng 2 . Hướng dẫn giải Chọn D
Đặt z a bi, a,b   .
Ta có: z  2z  12  2i a bi  2 a bi  12  2i a  4
 3a bi  12  2i   . b  2  3 (1 3i)
Câu 38. Cho số phức z thỏa mãn z
. Môđun của số phức z iz bằng 1 i A. 4 2. B. 4 3. C. 8 2. D. 8 3. Hướng dẫn giải Chọn C 3 (1 3i) z   4
  4i z  4  4i 1 i
z iz  8  8i z iz  8 2 .
Câu 40. Tổng phần thực và phần ảo của số phức z thoả mãn iz  1 iz  2  i bằng A. 6  . B. 2 . C. 2 . D. 6 . Hướng dẫn giải Chọn D
Đặt z x yi  ,
x y   . Khi đó iz  1 iz  2
i i x yi  1 i x yi  2  i
x  2 y  0 x  4
  x  2 y  yi  2  i    
, suy ra x y  6 . y  2 y  2  
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 19
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
Bài 2: PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC
Câu 1: Gọi z và z là các nghiệm của phương trình 2
z  4 z  9  0 . Gọi M , N là các điểm biểu diễn của 1 2
z và z trên mặt phẳng phức. Khi đó độ dài của MN là: 1 2
A. MN  2 5 .
B. MN  5 .
C. MN  2 5 .
D. MN  4 .
Câu 2: Gọi z , z , z là ba nghiệm của phương trình 3
z 1  0 . Tính S z z z 1 2 3 1 2 3
A. S  4
B. S  2
C. S  3
D. S  1 Hướng dẫn giải Chọn C  z  1   1 3 1 3 1 3 Ta có: 3
z 1  0  z  
i . Do đó: S  1   i   i  3 .  2 2 2 2 2 2   1 3 z   i  2 2
Câu 3: Gọi z , z là các nghiệm phức của phương trình 2
z  2z  5  0 . Giá trị của biểu thức 4 4
z z bằng. 1 2 1 2 A. 7  B. 14 C. 7 D. 14 Hướng dẫn giải Chọn B
z  1 2i Ta có 2
z  2z  5  0 1   . z  1 2i  2 4 4 Nên 4 4
z z  1 2i   1 2i  1  4 . 1 2
Câu 4: Phương trình bậc hai nào dưới đây nhận hai số phức 2  3i và 2  3i làm nghiệm? A. 2
z  4z 13  0 B. 2
z  4z  3  0 C. 2
z  4z 13  0 D. 2
z  4z  3  0 Hướng dẫn giải Chọn C
z  2  3i Ta có: 2
z  4z 13  0   . z  2  3i
Câu 5: Gọi z và z là 2 nghiệm của phương trình 2
2z  6z  5  0 trong đó z có phần ảo âm. Phần thực 1 2 2
và phần ảo của số phức z  3z lần lượt là 1 2 A. 6;1 B. 6  ;1 C. 1  ; 6 D. 6  ; 1 Hướng dẫn giải Chọn D  3 i z    1  2 2 Ta có 2
2z  6z  5  0  
. Suy ra z  3z  6   i 3 i 1 2  z    2  2 2
Vậy Phần thực và phần ảo của số phức z  3z lần lượt là 6  ; 1. 1 2
Câu 6: Biết phương trình 2
z  2z m  0 m   có một nghiệm phức z  1
  3i và z là nghiệm phức 1 2
còn lại. Số phức z  2z là ? 1 2 A. 3   9i . B. 3   3i . C. 3   9i . D. 3   3i . Hướng dẫn giải
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 20
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức Chọn D
Ta có z z  2
  z  2  z  2  1 3i  1 3i 2 1   1 2
z  2z  1  3i  2 1  3i  3  3i . 1 2    
Câu 7: Kí hiệu z , z , z , z là bốn nghiệm của phương trình 4 2
z z  6  0 . Tính S z z z z . 1 2 3 4 1 2 3 4
A. S  2  2  3
B. S  2  2  3
C. S  2 2
D. S  2 3 Hướng dẫn giải Chọn A 2  z  2  z   2 Ta có: 4 2
z z  6  0     . 2 z  3   z  i 3 
Kí hiệu z , z , z , z là bốn nghiệm của phương trình, ta có: 1 2 3 4
S z z z z  2 2  3 . 1 2 3 4
Câu 8: Gọi A , B là hai điểm biểu diễn hai nghiệm phức của phương trình 2
z  2z  5  0 . Tính độ dài đoạn thẳng AB : A. 2 . B. 4 . C. 12 . D. 6 . Hướng dẫn giải Chọn B
z  1 2i Ta có: 2
z  2z  5  0   suy ra A 1  ; 2 và B 1  ; 2
  . Vậy AB  4 . z  1 2i
Câu 9: Gọi z và z là hai nghiệm phức của phương trình 2
z  6z 11  0 . Giá trị của biểu thức 3z z 1 2 1 2 bằng A. 2 11 . B. 11 . C. 22 . D. 11. Hướng dẫn giải Chọn A 2 2
Ta có z và z là hai số phức liên hợp của nhau nên zz
z z  11  z z  11 . 1 2 1 2 1 2 1 2
Do đó: 3z z  2 z  2 11 . 1 2 1
Câu 10: Trong tập các số phức, cho phương trình 2
z  6z m  0 , m    
1 . Gọi m là một giá trị của m 0 để phương trình  
1 có hai nghiệm phân biệt z , z thỏa mãn z .z z .z . Hỏi trong khoảng 1 2 1 1 2 2
0;20 có bao nhiêu giá trị m   ? 0 A. 13 . B. 11. C. 12 . D. 10 . Hướng dẫn giải Chọn D
Điều kiện để phương trình  
1 có hai nghiệm phân biệt là:   9  m  0  m  9 .
Phương trình có hai nghiệm phân biệt z , z thỏa mãn z .z z .z thì   1 phải có nghiệm phức. 1 2 1 1 2 2
Suy ra   0  m  9 .
Vậy trong khoảng 0;20 có 10 số m . 0
Câu 11: Gọi z , z là hai nghiệm phức của phương trình 2
z  2z  5  0 , trong đó z có phần ảo dương. Tìm 1 2 1 số phức 2 2
w z  2z . 1 2
A. 9  4i .
B. 9  4i .
C. 9  4i . D. 9   4i . Hướng dẫn giải Chọn C
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 21
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
z  1 2i Ta có 2 1
z  2z  5  0   . z  1 2i  2 2 2
Suy ra w  1 2i  21 2i  9  4i .
Câu 12: Phương trình 2
z az b  0 ,( a, b   ) có nghiệm là 3  2i , tính S a b .
A. S 19 . B. S  1  9 .
C. S  7 .
D. S  7 . Hướng dẫn giải Chọn B 2 Phương trình 2
z az b  0 ,( a, b   ) có nghiệm là 3  2i  3  2i  a 3  2i  b  0 9
  4  3a b  0 a  6      . 1  2  2a  0  b  13  Vậy S  6  13  1  9 .
Câu 13: Giải phương trình 2
z  4z  5  0 trên tập số phức ta được các nghiệm
A. z  2  i; z  2  i .
B. z  4  i; z  4  i . 1 2 1 2 C. z  4
  i; z  4   i . D. z  2
  i; z  2   i . 1 2 1 2 Hướng dẫn giải Chọn A z  2  iz  2  i Ta có 2
z  4z  5  0  2
z  4z  4  1   z  2 2 2  i     z  2  i   z  2  i
Suy ra z  2  i và z  2  i . 1 2
Câu 14: Phương trình 2
z  3z  9  0 có hai nghiệm phức z , z . Tính S z z z z . 1 2 1 2 1 2 A. S  1  2 .
B. S  6 .
C. S  6 .
D. S  12 . Hướng dẫn giải Chọn C
Áp dụng định lý vietè, ta có: S z z  3 ; P z z  9 . 1 1 1 2
Suy ra: z z z z P S  6 . 1 2 1 2
Câu 15: Biết phương trình 2 2018
z  2017.2018z  2
 0 có hai nghiệm z , z . Tính S z z . 1 2 1 2 A. 1009 S  2 . B. 1010 S  2 . C. 2018 S  2 . D. 2019 S  2 . Hướng dẫn giải Chọn B
Do các hệ số của phương trình 2 2018
z  2017.2018z  2
 0 đều là số thực nên z , z là hai số phức 1 2 liên hợp.
Đặt z a bi ; z a bi , a b   . Ta có: 2   1 2 2 2018 1010
S z z  2 a b  2 z .z  2 2  2 . 1 2 1 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 22
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
Bài 3: TẬP HỢP ĐIỂM BIỂU DIỄN SỐ PHỨC
Câu 1: Trong hình vẽ bên, điểm M biểu diễn số phức z . Số phức z là
A. 2  i .
B. 2  i .
C. 1 2i .
D. 1 2i . Hướng dẫn giải Chọn B
Dựa vào hình vẽ ta có z  2  i , suy ra z  2  i .
Câu 2: Số phức z  2  3i có điểm biểu diễn trên mặt phẳng tọa độ là:
A. M 2;  3 . B. M  2  ;  3 . C. M 2;  3 . D. M  2  ;  3 .
Câu 3: Trong mặt phẳng phức, cho số phức z  1 2i . Điểm biểu diễn cho số phức z là điểm nào sau đây
A. M 1; 2
B. Q 1; 2
C. P 1; 2
D. N 2;  1 Hướng dẫn giải Chọn B
Ta có: z  1 2i z  1 2i nên có điểm biểu diễn là 1; 2 .
Câu 4: Trong mặt phẳng Oxy , điểm M trong hình vẽ bên là điểm biểu diễn số phức z . Số phức z là
A. 1 2i B. 2   i
C. 1 2i D. 2   i Hướng dẫn giải Chọn D Ta có z  2
  i z  2  i .
Câu 5: Trong mặt phẳng Oxy , cho các điểm ,
A B như hình vẽ bên. Trung điểm của đoạn thẳng AB biểu diễn số phức. 1 1 A. 2  i . B.   2i . C. 1   2i . D. 2  i . 2 2 Hướng dẫn giải Chọn B  1  1
Trung điểm AB là I  ; 2 
 , biểu diễn số phức   2i .  2  2
Câu 6: Điểm nào trong hình vẽ dưới đây là điểm biểu diễn của số phức z  1 i2  i ?
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 23
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức A. Q . B. M . C. N . D. P . Hướng dẫn giải Chọn A
Ta có z  1 i2  i  z  3  i . Điểm biểu diễn của số phức z là Q 3  ;1 .
Câu 7: Hỏi điểm M 3;  
1 là điểm biểu diễn số phức nào sau đây? A. z  3   i B. z  1   3i
C. z  1 3i
D. z  3  i Hướng dẫn giải Chọn D Điểm M  ;
a b trong một hệ tọa độ vuông góc của mặt phẳng được gọi là điểm biểu diễn số phức
z a bi .
Do đó điểm M 3;  
1 là điểm biểu diễn số phức z  3  i .
Câu 8: Điểm M trong hình vẽ bên là điểm biểu diễn của số phức z .
Tìm phần thực và phần ảo cú số phức z .
A. Phần thực bằng 3 và phần ảo bằng 4i .
B. Phần thực bằng 4 và phần ảo bằng 3.
C. Phần thực bằng 4 và phần ảo bằng 3i .
D. Phần thực bằng 3 và phần ảo bằng 4 . Hướng dẫn giải
Từ hình vẽ ta có M 3; 4 nên z  3  4i . Vậy Phần thực bằng 3 và phần ảo bằng 4 .
Câu 9: Số phức z  2  3i có điểm biểu diễn là. A. A2; 3   .
B. A2;3 .
C. A2;3 .
D. A2;3 .
Câu 10: Trên mặt phẳng tọa độ Oxy cho điểm M trong hình vẽ bên là điểm biểu diễn của số phức z . Tìm z ?
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 24
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức y 3 x O M
A. z  3 4i . B. z  3   4i . C. z  4   3i .
D. z  3 4i . Hướng dẫn giải Chọn A
Ta có M 3;  4 . Vậy điểm M biểu diễn cho số phức z  3 4i .
Câu 11: Cho số phức z thỏa z 1 i  2 . Chọn phát biểu đúng:
A. Tập hợp điểm biểu diễn số phức z là một đường tròn có bán kính bằng 4 .
B. Tập hợp điểm biểu diễn số phức z là một đường thẳng.
C. Tập hợp điểm biểu diễn số phức z là một đường Parabol.
D. Tập hợp điểm biểu diễn số phức z là một đường tròn có bán kính bằng 2 .
Câu 12: Cho số phức z  2  3i . Điểm biểu diễn số phức liên hợp của z là A.  2  ;3 . B.  2  ; 3   .
C. 2;3 . D. 2;3 . Hướng dẫn giải Chọn D
Vì z  2  3i z  2  3i nên điểm biểu diễn của z có tọa độ 2;3 .
Câu 13: Cho số phức z  4
  5i . Biểu diễn hình học của z là điểm có tọa độ A.  4  ;5 B.  4  ; 5  
C. 4; 5 D. 4;5 Hướng dẫn giải Chọn A Số phức z  4
  5i có phần thực a  4
 ; phần ảo b  5 nên điểm biểu diễn hình học của số phức z là  4  ;5 .
Câu 14: Gọi A là điểm biểu diễn của số phức z  2  5i và B là 1điểm biểu diễn của số phức z  2   5i .
Tìm mệnh đề đúng trong các mệnh đề sau.
A. Hai điểm A và B đối xứng với nhau qua gốc toạ độ O .
B. Hai điểm A và B đối xứng với nhau qua đường thẳng y x .
C. Hai điểm A và B đối xứng với nhau qua trục hoành.
D. Hai điểm A và B đối xứng với nhau qua trục tung.
Câu 15: Cho hai số phức z  3  5i và w  1
  2i . Điểm biểu diễn số phức z  z  .
w z trong mặt phẳng
Oxy có tọa độ là
A. 6;  4 .
B. 4;  6 . C. 4; 6 .
D. 4;  6 . Hướng dẫn giải
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 25
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức Chọn D
Ta có z  z  .
w z  3  5i  1 2i 3  5i   3  5i  7 11i  4  6i .
Câu 16: Số phức z  4  2i có điểm biểu diễn trên mặt phẳng tọa độ là M . Tìm tọa độ điểm M A. M 4; 2   . B. M  4  ; 2 . C. M 4;  2 .
D. M 2;4 . Hướng dẫn giải Chọn C
Số phức z  4  2i có điểm biểu diễn trên mặt phẳng tọa độ là M 4;  2 .
Câu 17: Số phức liên hợp của số phức z i 1 2i có điểm biểu diễn là điểm nào dưới đây?
A. A1;2 B. F  2   ;1
C. E 2;  1 D. B  1  ; 2 Hướng dẫn giải Chọn C
Ta có: z i 1 2i  2  i z  2  i nên điểm biểu diễn của số phức z là E 2;  1 .
Câu 18: Điểm M trong hình vẽ dưới đây biểu diễn số phức z . y M 3 O 1 2 x
Số phức z bằng
A. 3  2i .
B. 2  3i .
C. 2  3i .
D. 3  2i . Hướng dẫn giải Chọn B.
Theo hình vẽ thì z  2  3i z  2  3i .
Câu 19: Trên mặt phẳng tọa độ Oxy cho điểm M trong hình vẽ bên là điểm biểu diễn của số phức z . y 3 x O 1 -4 M Tìm z ? A. z  3   4i .
B. z  3  4i .
C. z  3  4i . D. z  4   3i . Hướng dẫn giải Chọn B
Số phức z có phần thực a  3 và phần ảo b  4 nên z  3  4i .
Câu 20: Trong mặt phẳng toạ độ, điểm A1;  2 là điểm biểu diễn của số phức nào trong các số sau?
A. z  1 2i .
B. z  1 2i . C. z  2   i . D. z  1   2i . Hướng dẫn giải Chọn B
Số phức z a bi được biểu diễn bởi điểm M  ;
a b . Do đó điểm A1;  2 biểu diễn số phức
z  1 2i .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 26
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
Câu 21: Trong mặt phẳng tọa độ Oxy , Gọi A , B , C lần lượt là các điểm biểu diễn số phức 1
  2i , 4  4i , 3
i . Số phức biểu diễn trọng tâm tam giác ABC là
A. 1 3i . B. 3   9i .
C. 3  9i . D. 1   3i . Hướng dẫn giải Chọn A
Ta có A 1; 2 , B 4; 4 , C 0; 3 nên trọng tâm G của tam giác ABC có tọa độ là G 1; 3 .
Do đó, số phức biểu diễn điểm G là 1 3i .
Câu 22: Gọi M là điểm biểu diễn của số phức z trong mặt phẳng tọa độ, N là điểm đối xứng của M qua
Oy ( M , N không thuộc các trục tọa độ). Số phức w có điểm biểu diễn lên mặt phẳng tọa độ là
N . Mệnh đề nào sau đây đúng ?
A. w  z .
B. w z .
C. w z .
D. w   z . Hướng dẫn giải Chọn A
Gọi z x yi , x, y    M  ; x y  .
N là điểm đối xứng của M qua Oy N  ;
x y   w  x yi   x yi  z .
Câu 23: Cho bốn điểm A , B , C , D trên hình vẽ biểu diễn 4 số phức khác nhau. Chọn mệnh đề sai. y A 1 -2 -1 1 O x -1 D -2 C B
A. D là biểu diễn số phức z  1  2i .
B. C là biểu diễn số phức z  1  2i .
C. A là biểu diễn số phức z  2  i .
D. B là biểu diễn số phức z  1  2i . Hướng dẫn giải Chọn A
Theo hình vẽ thì điểm D là biểu diễn số phức z  2  i . Suy ra B sai.
Câu 24: Trong mặt phẳng tọa độ Oxy , gọi M là điểm biểu diễn số phức z  3 4i ; M ' là điểm biểu diễn 1 i cho số phức z ' 
z . Tính diện tích tam giác OMM ' . 2 15 25 25 15 A. S  . B. S  . C. S  . D. S  . OMM ' 2 OMM ' 4 OMM ' 2 OMM ' 4
Câu 25: Điểm M trong hình vẽ bên là điểm biểu diễn số phức z tìm phần thực và phần ảo của số phức z . A. Phần thực là 2
 và phần ảo là 1. B. Phần thực là 2
 và phần ảo là i .
C. Phần thực là 1 và phần ảo là 2  .
D. Phần thực là 1 và phần ảo là 2  i . Hướng dẫn giải
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 27
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức Chọn C
Ta có số phức z  1  2i nên phần thực là 1 và phần ảo là 2  .
Câu 26: Trong mặt phẳng tọa độ Oxy , tập hợp điểm biểu diễn số phức z thỏa mãn z i  2  3i z là A. đường tròn 2 2
x y  2 B. đường tròn 2 2
x y  4
C. đường thẳng x  2 y  3  0
D. đường thẳng x  2 y 1  0 Hướng dẫn giải Chọn C Gọi M  ;
x y  là điểm biểu diễn số phức z x yi , với x, y   .
Ta có z i  2  3i z x   y  
1 i  2  x  3  yi
x   y  2    x2    y2 2 1 2 3
 4x  8 y 12  0  x  2 y  3  0
Câu 27: Trong mặt phẳng tọa độ Oxy , gọi M là điểm biểu diễn số phức z  3 4i ; M ' là điểm biểu diễn 1 i cho số phức z ' 
z . Tính diện tích tam giác OMM ' . 2 25 25 15 15 A. S  . B. S  . C. S  . D. S  . OMM ' 4 OMM ' 2 OMM ' 4 OMM ' 2 1
Câu 28: Cho A, B, C lần lượt là các điểm biểu diễn các số phức 6  3i ; 1 2ii ; . Tìm số phức có điểm i
biểu diễn D sao cho ABCD là hình bình hành. A. z  8   4i .
B. z  4  2i .
C. z  8  5i . D. z  8   3i .
Câu 29: Biết tập hợp các điểm biểu diễn số phức z thỏa mãn iz 1 2i  4 là một đường tròn. Tìm tọa độ
tâm I của đường tròn đó.
A. I 1; 2 . B. I  1  ;  2 . C. I  2  ;   1 . D. I 2  ;1 . Hướng dẫn giải Chọn C Gọi M  ;
x y  là điểm biểu diễn số phức z x yi ,  , x y   .
Ta có iz 1 2i  4  i . z  2  i  4  z  2  i  4  IM  4 , với I  2  ;   1 .
 tập hợp biểu diễn số phức z là đường tròn tâm I  2  ;  
1 bàn kính R  4 .
Câu 30: Điểm M trong hình bên là điểm biểu diễn cho số phức
A. z  4  2i .
B. z  2  4i .
C. z  4  2i .
D. z  2  4i . Hướng dẫn giải Chọn D
Điểm M biểu diễn cho số phức z  2  4i .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 28
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức
Câu 31: Cho số phức z thoả mãn z  3  4i  5 . Biết rằng tập hợp điểm trong mặt phẳng toạ độ biểu diễn
các số phức z là một đường tròn. Tìm toạ độ tâm I và bán kính R của đường tròn đó. A. I 3; 4
  , R  5 . B. I  3
 ; 4 , R  5 . C. I 3; 4
  , R  5 . D. I  3
 ; 4 , R  5 . Hướng dẫn giải Chọn D 2 2
Đặt z x yi  ,
x y   . Khi đó z  3  4i  5   x  3   y  4  25 .
Vậy tập điểm biểu diễn số phức z là đường tròn tâm I  3
 ; 4 , bán kính R  5 .
Câu 32: Gọi M và N lần lượt là các điểm biểu diễn của z , z trên mặt phẳng tọa độ, I là trung điểm MN 1 2
, O là gốc tọa độ (3 điểm O , M , N phân biệt và không thẳng hàng). Mệnh đề nào sau đây là đúng?
A. z z  2 OM ON .
B. z z  2OI . 1 2   1 2
C. z z OI .
D. z z OM ON . 1 2 1 2 Hướng dẫn giải Chọn B
Gọi M x ; y là điểm biểu diễn của số phức z x y i . 1 1  1 1 1
N x ; y là điểm biểu diễn của số phức z x y i . 2 2  2 2 2 2 2
Khi đó z z x x
y y i z z x xy y . 1 2  1 2   1 2  1 2  1 2   1 2   x x y y
Vì I là trung điểm MN nên 1 2 1 2 I ;   .  2 2  2 2  x x   y y   2OI  2      
x x 2   y y 2 1 2 1 2
z z . 1 2 1 2 1 2  2   2 
Câu 33: Gọi z là nghiệm phức có phần ảo âm của phương trình 2
z  2z  3  0 . Trên mặt phẳng tọa độ, 1
điểm nào sau đây là điểm biểu diễn của số phức z ? 1 A. Q  1  ; 2i . B. N  1  ; 2  .
C. M 1; 2 .
D. P 1; 2i . Hướng dẫn giải Chọn C z  1   2i 2
z  2z  3  0   .  z  1   2i
z là nghiệm phức có phần ảo âm  z  1   2i . 1 1
Vậy M 1; 2  là điểm biểu diễn số phức z . 1
Câu 34: Cho A , B , C tương ứng là các điểm trong mặt phẳng phức biểu diễn các số phức z  1 2i , 1 z  2
  5i , z  2  4i . Số phức z biểu diễn bởi điểm D sao cho tứ giác ABCD là hình bình 2 3 hành là
A. 5  i .
B. 1 5i .
C. 3  5i . D. 1   7i . Hướng dẫn giải Chọn A
Ta có A1;2 , B  2
 ;5 , C 2;4 . Gọi D  ; x y  .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 29
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức   Ta có AB   3
 ;3 , DC  2  ; x 4  y    x  5
Để ABCD là hình bình hành thì AB DC  
. Vậy z  5  i . y  1 
Câu 35: Điểm M trong hình vẽ dưới đây biểu diễn số phức z . y 3 M 2 x
Số phức z 1 bằng
A. 4  2i .
B. 3  3i .
C. 3  3i .
D. 4  2i . Hướng dẫn giải Chọn C
Điềm M 2;3 biểu diễn z  2  3i suy ra z 1  2  3i 1  3  3i .
Câu 36: Cho số phức z thỏa mãn iz  2  i  0 . Khoảng cách từ điểm biểu diễn của z trên mặt phẳng tọa độ
Oxy đến điểm M 3; 4 là: A. 2 2 . B. 2 5 . C. 13 . D. 2 10 . Hướng dẫn giải Chọn D i  2 (i  2)( i  )
Ta có: iz  2 1  0  iz i  2    1 2i i 1
Điểm biểu diễn của số phức z là A(1; 2) 2 2 AM  (3 1)  ( 4
  2)  40  2 10
Câu 37: Cho các số phức z thỏa mãn z 1 i z 1 2i . Tập hợp các điểm biểu diễn các số phức z trên
mặt phẳng tọa độ là một đường thẳng. Phương trình đường thẳng đó là
A. 4x  6 y  3  0
B. 4x  6y  3  0
C. 4x  6 y  3  0
D. 4x  6y  3  0 Hướng dẫn giải Chọn B 2 2 2 2
Gọi z x yi . Ta có z  1  i z 1  2i   x   1   y   1   x   1   y  2
 4x  6 y  3  0 .
Câu 38: Cho số phức z  2  i . Trên mặt phẳng tọa độ Oxy , tìm điểm biểu diễn số phức w iz .
A. M 2;   1 . B. M 2  ;1 .
C. M 1; 2 . D. M  1  ; 2 . Hướng dẫn giải Chọn C
w iz  1 2i  điểm biểu diễn cho w iz  1 2i là M 1; 2 .
Câu 39: Tập hợp các điểm biểu diễn cho số phức z thỏa mãn z  3  4i  5 là
A. Một đường Elip.
B. Một đường tròn.
C. Một đường thẳng.
D. Một đường parabol. Hướng dẫn giải
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 30
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Số Phức Chọn B
Tập hợp điểm biểu diễn cho số phức z là đường tròn tâm I 3;  
4 , bán kính R  5 .
Câu 40: Cho số phức z thỏa mãn z 1 2i  5 và M  ;
x y là điểm biểu diễn số phức z . Điểm M thuộc
đường tròn nào sau đây? 2 2 2 2 A. x  
1   y  2  5 B. x  
1   y  2  25 2 2 2 2 C. x  
1   y  2  25 D. x  
1   y  2  5 Hướng dẫn giải Chọn C 2 2
Ta có z 1 2i  5  x 1  y  2i  5   x   1
  y  2  25 . 2 2
Vậy điểm M thuộc đường tròn  x  
1   y  2  25 .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 31
Facebook: https://www.facebook.com/dongpay