



































Preview text:
1 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai MỤC LỤC 1
Số phức và một vài ứng dụng 1 A Lý thuyết 1 B Ví dụ giải toán 5 C Bài tập 14 1 Đề bài 14 2 Lời giải 16 D
Sử dụng số phức chứng minh bất đẳng thức 23 E
Sử dụng số phức giải phương trình, hệ phương trình 29 F
Hệ lặp sinh bởi các đa thức đối xứng ba biến 36 2
Sử dụng số phức để giải phương trình hàm đa thức 39
BÀI 1. SỐ PHỨC VÀ MỘT VÀI ỨNG DỤNG A. LÝ THUYẾT
1. Một số định nghĩa.
Một số phức z là một biểu thức dạng z = a + bi, trong đó a và b là những số thực
và i là số thỏa mãn i2 = −1. Số a gọi là phần thực, b gọi là phần ảo của số phức
z = a + bi, còn i gọi là đơn vị ảo.
Cho hai số phức z = a + bi và z0 = a0 + b0i. Khi đó: a = a0 z = z0 ⇔ b = b0.
Tập hợp tất cả các số phức thường được ký hiệu là C. Vậy:
C = {a + bi|a, b ∈ R}.
Số phức z = a + 0i có phần ảo bằng 0 được coi là số thực và viết là:
a + 0i = a ∈ R ⊂ C. MỤC LỤC
2 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai
Số phức z = 0 + bi có phần thực bằng 0 được gọi là số ảo (còn gọi là số thuần ảo) và viết là z = bi.
Số 0 = 0 + 0i = 0i vừa là số thực vừa là số ảo. √
2. Môđun của số phức. Cho số phức z = a + bi, khi đó
a2 + b2 được gọi là môđun (độ √
dài) của z, ký hiệu là |z|. Vậy |z| = a2 + b2.
3. Số phức liên hợp. Cho z = a + bi ∈ C, khi đó số phức liên hợp với z là z = a − bi.
4. Biểu diễn hình học của số phức. Trong mặt phẳng tọa độ Oxy, mỗi số phức z = a + bi
được biểu diễn bởi điểm M(a; b). Ngược lại mỗi điểm M(a; b) biểu diễn một số phức là
z = a + bi. Ta còn viết là M(a + bi) hay M(z).
5. Các phép toán trên số phức. Cho hai số phức z = a + bi và z0 = a0 + b0i. Khi đó:
Tổng của hai số phức z và z0 là: z + z0 = (a + a0) + (b + b0) i.
Số đối của số phức z = a + bi là số phức −z = −a − bi.
Hiệu của hai số phức z và z0 là: z − z0 = (a − a0) + (b − b0) i.
Tích của hai số phức z và z0 là: zz0 = (aa0 − bb0) + (ab0 + a0b) i.
Nghịch đảo của số phức z = a + bi 6= 0 là: ! 1 z z−1 = (a − bi) = . a2 + b2 |z|2
Thương của hai số phức z và z0 6= 0 là: z a0 b0 = z.z0−1 = (a + bi) − i z0 a02 + b02 a02 + b02 aa0 + bb0 ab0 − a0b = − i. a02 + b02 a02 + b02
Lũy thừa của số phức z được định nghĩa như sau:
z0 = 1, zn = z.z . . . z với n ∈ N∗. | {z } n chữ z 1 zn =
, với z 6= 0, n = −1, −2, −3, . . . z−n √
Căn bậc n (n ∈ N∗) của số phức z, kí hiệu n z, là số phức z1 sao cho zn = z. 1
Chú ý 1. Để chia hai số phức được nhanh chóng ta làm như sau: z z.z0 z.z0 = = . z0 z0.z0 |z0|2 z Tức là để tìm
ta chỉ cần nhân tử và mẫu cho số phức liên hợp của z0. z0
6. Tìm căn bậc hai của số phức z. MỤC LỤC
3 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai
Nếu z = 0 thì z có một căn bậc hai là 0. √ √
Nếu z = a > 0 thì z có hai căn bậc hai là a và − a. √ √
Nếu z = a < 0 thì z có hai căn bậc hai là −a i và − −a i.
Nếu z = a + bi (b 6= 0) thì ta tìm căn bậc hai của z như sau: Ta cần tìm số phức x + yi sao cho: x2 − y2 = a
(x + yi)2 = a + bi ⇔ x2 − y2 + 2xyi = a + bi ⇔ 2xy = b.
Giải hệ này ta tìm được x và y, tức là tìm được x + yi.
7. Dạng lượng giác của số phức. Cho số phức z = a + bi 6= 0. Trong mặt phẳng Oxy, số
phức z = a + bi được biểu diễn bởi một điểm duy nhất M(a; b). Ta có: p # » |z| = a2 + b2 = OM.
Số đo (radian) của mỗi góc lượng giác φ = (Ox, OM) gọi là acgumen của số phức z. Vậy
ta có: a = r cos φ, b = r sin φ, p # »
z = r(cos φ + i sin φ), với r = |z| = a2 + b2 = OM
và z = r(cos φ + i sin φ) được gọi là dạng lượng giác của số phức z = a + bi.
Lưu ý. Nếu φ là một acgumen của z thì mọi acgumen của z có dạng φ + k2π, k ∈ Z (người
ta thường nói acgumen của z 6= 0 sai khác k2π, k ∈ Z).
8. Các công thức thường dùng của dạng lượng giác. Cho hai số phức:
z = r(cos φ + i sin φ) 6= 0, z0 = r0(cos β + i sin β) 6= 0. Khi đó:
zz0 = rr0 [cos(φ + β) + i sin(φ + β)] z r =
[cos(φ − β) + i sin(φ − β)] z0 r0
zn = [r (cos φ + i sin φ)]n = rn (cos nφ + i sin nφ), ∀n = 0, 1, 2, . . .
Công thức sau cùng gọi là công thức Moa-vrơ.
9. Căn bậc n của số phức. Cho số phức z = r (cos ϕ + i sin ϕ) , r > 0.
Khi đó các căn bậc n của z là √ ϕ + 2kπ ϕ + 2kπ zk = n r cos + i sin
, k = 0, 1, 2, . . . , n − 1. n n
Các căn bậc hai của số phức z = r (cos ϕ + i sin ϕ) , r > 0 là √ ϕ ϕ √ ϕ ϕ z0 = r cos + i sin , z r cos + i sin . 2 2 1 = − 2 2 MỤC LỤC
4 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai
Các căn bậc ba của số phức z = r (cos ϕ + i sin ϕ) , r > 0 là √ ϕ ϕ z0 = 3 r cos + i sin , 3 3 √ ϕ + 2π ϕ + 2π z1 = 3 r cos + i sin , 3 3 √ ϕ + 4π ϕ + 4π z2 = 3 r cos + i sin . 3 3
Chú ý 2. Một phương trình nghiệm phức f (z) = 0, với z = x + iy, ta biến đổi thành h(x, y) = 0 h(x, y) + ig(x, y) = 0 ⇔ g(x, y) = 0.
Nghĩa là một phương trình nghiệm phức, bằng cách tách phần thực và phần ảo luôn có
thể đưa về hệ phương trình.
10. Đa thức với hệ số phức.
Định nghĩa 1. P(z) = a0zn + a1zn−1 + · · · + an−1z + an với các hệ số ai ∈ C và biến z ∈ C.
Ta cũng định nghĩa bậc, nghiệm... như đa thức với hệ số thực. Định lý Viet cũng được
Phát biểu thuận và đảo như đa thức hệ số thực.
Định lí 1 (D’ALEMBERT). Mọi đa thức bậc n hệ số phức:
P(z) = a0zn + a1zn−1 + · · · + an−1z + an (a0 6= 0)
đều có đủ n nghiệm phức phân biệt hay trùng nhau.
Hệ quả 1. Nếu z1, z2, . . . , zn là n nghiệm của
P(z) = a0zn + a1zn−1 + · · · + an−1z + an (a0 6= 0) thì ta có phân tích:
P(z) = a0(z − z1)(z − z2) . . . (z − zn).
11. Giải phương trình bậc hai trên C :
Az2 + Bz + C = 0 (với A 6= 0)
Phương pháp. Tính ∆ = B2 − 4AC. −B
Nếu ∆ = 0 thì phương trình có nghiệm kép z1 = z2 = . 2A
Nếu ∆ 6= 0 thì phương trình có hai nghiệm phân biệt −B + δ −B − δ z1 = , z 2A 2 = 2A
trong đó δ là một căn bậc hai của ∆. MỤC LỤC
5 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai
B. VÍ DỤ GIẢI TOÁN
BÀI 1 (ĐH 2013D). Cho số phức z thỏa mãn điều kiện (1 + i)(z − i) + 2z = 2i. z − 2z + 1
Tìm môđun của số phức: w = . z2 L Lời giải Ta có
(1 + i)(z − i) + 2z = 2i ⇔ z − i + iz − i2 + 2z = 2i −1 + 3i
⇔3z + iz = 3i − 1 ⇔ (3 + i)z = −1 + 3i ⇔ z = 3 + i (−1 + 3i)(3 − i) 10i ⇔z = ⇔ z = ⇔ z = i. 32 − i2 10 Do đó z − 2z + 1 −i − 2i + 1 1 − 3i √ w = = = = −1 + 3i ⇒ |w| = 10. z2 i2 −1 √ 1 3 BÀI 2. Cho ε = − + i. Hãy tính: 2 2 1 a + b 2 2 2 ε + cε a + bε + cε ;
2 (a + b) (a + bε) a + bε ; 3 a 2 2 ε + bε aε + bε . L Lời giải √ 1 3 Ta có: ε = − + i. Do đó: 2 2 √ √ √ !2 2 1 3 1 3 3 1 3 ε = − + i = − i + i2 = − − i, 2 2 4 2 4 2 2 √ √ ! ! 3 2 1 3 1 3 1 3 1 3
ε = ε.ε = − i + i = − i2 = + = 1, 2 2 2 2 4 4 4 4 4 3
ε = ε .ε = ε. 1 Theo trên ta có: a + b 2 2 ε + cε a + bε + cε =a2 + b2 3 3 2 2 2 4
ε + c2ε + abε + acε + baε + bcε + caε + cbε
=a2 + b2 + c2 + (ab + bc + ca) 2
ε + (ab + bc + ca)ε
=a2 + b2 + c2 + (ab + bc + ca)( 2 ε + ε )
=a2 + b2 + c2 − (ab + bc + ca) (do 2 ε + ε = −1). 2 Ta có: (a + b) (a + b 2 2 3 ε) a + bε
= (a + b) a2 + abε + baε + b2ε = (a + b) a2 + ab( 2
ε + ε) + b2 = (a + b) a2 − ab + b2 = a3 + b3. MỤC LỤC
6 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai 3 Ta có: a 2 2 3 4 2 3 ε + bε aε + bε
= a2ε + abε + abε + b2ε =a2 + ab 2 2
ε + abε + b2 = a2 + ab(ε + ε ) + b2 = a2 − ab + b2.
BÀI 3 (Kosovo National Mathematical Olympiad 2013, Grade 11). Cho z1 và z2 là hai
số phức thoả mãn |z1 + 2z2| = |2z1 + z2|. Chứng minh rằng với mọi số thực a, ta có: |z1 + az2| = |az1 + z2|. L Lời giải
Giả sử z1 = p + qi, z2 = r + si (với p, q, r, s ∈ R). Khi đó |z1 + 2z2| = |2z1 + z2|
⇔|(p + 2r) + i(q + 2s)| = |(2p + r) + i(2q + s)| q q ⇔ (p + 2r)2 + (q + 2s)2 = (2p + r)2 + (2q + s)2
⇔(p + 2r)2 + (q + 2s)2 = (2p + r)2 + (2q + s)2
⇔p2 + 4pr + 4r2 + q2 + 2qs + 4s2 = 4p2 + 4pr + r2 + 4q2 + 4qs + s2
⇔r2 + s2 = p2 + q2 ⇔ |z1| = |z2|. (1)
Ta có sự tương đương sau: |z1 + az2| = |az1 + z2|
⇔ |p + qi + a(r + si)| = |a(p + qi) + r + si|
⇔ |(p + ar) + (q + as)i| = |(ap + r) + (aq + s)i| q q ⇔ (p + ar)2 + (q + as)2 = (ap + r)2 + (aq + s)2
⇔(p2 + 2apr + a2r2) + (q2 + 2asq + a2s2)
=(a2 p2 + 2apr + r2) + (a2q2 + 2aqs + s2)
⇔p2 + a2r2 + q2 + a2s2 = a2 p2 + r2 + a2q2 + s2
⇔p2 + q2 − a2(p2 + q2) = r2 + s2 − a2(s2 + r2)
⇔(a2 − 1)(p2 + q2) = (a2 − 1)(r2 + s2) (đúng, do (1)).
Ta có điều phải chứng minh.
BÀI 4 (ĐH-2012D). Giải phương trình z2 + 3 (1 + i) z + 5i = 0 trên tập hợp các số phức. L Lời giải
Ta có ∆ = 9(1 + i)2 − 20i = 9(2i) − 20i = −2i = (1 − i)2. Vậy nghiệm là −3 − 3i + 1 − i z = z = −1 − 2i 2 ⇔ −3 − 3i − 1 + i z = −2 − i. z = 2 MỤC LỤC
7 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai
BÀI 5. Giải các phương trình sau trên tập số phức:
1 (z + 3i)(z2 − 2z + 5) = 0;
2 z3 + (2i − 3)z2 + 5z − 2i − 3 = 0. L Lời giải z = −3i z = −3i
1 Ta có (z + 3i)(z2 − 2z + 5) = 0 ⇔ ⇔ z2 − 2z + 5 = 0 z = −1 ± 2i.
Vậy phương trình có ba nghiệm: z = −3i, z = −1 − 2i, z = −1 + 2i.
2 Phương trình có một nghiệm đặc biệt z = 1 nên chia đa thức ta được
z3 + (2i − 3)z2 + 5z − 2i − 3 = 0
⇔(z − 1) z2 + (2i − 2)z + 2i + 3 = 0 z = 1 ⇔
z2 + (2i − 2)z + 2i + 3 = 0 (∗) Phương trình (*) có
∆0 = (i − 1)2 − (2i + 3) = i2 − 2i + 1 − 2i − 3 = −3 − 4i = (1 − 2i)2. z = i Do đó (∗) ⇔
Vậy phương trình đã cho có ba nghiệm là z = 2 − 3i. z = 1, z = i, z = 2 − 3i.
BÀI 6 (ĐH-2012B, phần riêng chương trình Nâng cao). Goi z1 và z2 là hai nghiệm của √
phương trình z2 − 2 3iz − 4 = 0. Viết dạng lượng giác của z1 và z2. L Lời giải √ √ 2
Phương trình z2 − 2 3iz − 4 = 0 có ∆0 = 3i
+ 4 = 3i2 + 4 = 1, có hai nghiệm là √ √ π π π π z1 = −1 + 3i = 2 − cos + sin i ; z 3i = 2 cos + sin i . 3 3 2 = 1 + 3 3
Vậy dạng lượng giác của z1, z2 là: 2π 2π π π z1 = 2(cos + i sin ); z cos + i sin . 3 3 2 = 2 3 3 2π 2π
BÀI 7. Tính (1 + ε)n, với ε = cos + i sin
, n là một số tự nhiên. 3 3 L Lời giải Ta có: 2π 2π π π 1 + ε = 1 + cos + i sin = 2cos2 π + 2 sin cos .i 3 3 3 3 3 π π π π π = 2 cos cos + i sin = cos + i sin . 3 3 3 3 3 MỤC LỤC
8 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai π π n nπ nπ Vậy: (1 + ε)n = cos + i sin = cos + i sin . 3 3 3 3
Lưu ý. Ta có các công thức lượng giác sau đây:
1 + cos x = 2cos2 x , 1 − cos x = 2sin2 x ; sin 2x = 2 sin x cos x. 2 2
BÀI 8. Sử dụng số phức, chứng minh rằng: cos 5x = 16cos5x − 20cos3x + 5 cos x. L Lời giải
Ta có (cos x + i sin x)5 = cos 5x + i sin 5x. (1) Mặt khác (cos x + i sin x)5
=cos5x + 5cos4x(i sin x) + 10cos3x(i sin x)2
+10cos2x(i sin x)3 + 5 cos x(i sin x)4 + (i sin x)5
=(cos5x − 10cos3xsin2x + 5 cos xsin4x)
+(5cos4x sin x − 10cos2xsin3x + sin5x)i. (2) Từ (1) và (2), suy ra
cos 5x = cos5x − 10cos3xsin2x + 5 cos xsin4x
= cos5x − 10cos3x(1 − cos2x) + 5 cos x(1 − 2cos2x + cos4x)
= 16cos5x − 20cos3x + 5 cos x.
Ta có điều phải chứng minh.
Lưu ý. Qua lời giải bài tập 8 này ta còn thu được kết quả:
sin 5x = 5cos4x sin x − 10cos2xsin3x + sin5x. √ √ 2 6 BÀI 9. Cho sin a + sin b = , cos a + cos b = . Tính: 2 2 cos(a + b), sin(a + b). L Lời giải
Đặt z1 = cos a + i sin a, z2 = cos b + i sin b. Khi đó 1 z1z1 = |z1|2 = 1 ⇒ z1 = . z1 1 1 1 z z Tương tự, z 1 + z2 1 + z2 2 = . Ta có z + = ⇒ z . Mà z 1 + z2 = 1z2 = 2 √ z1√ z2 z1z2 z1 + z2 6 2 √ π π z1 + z2 = + i = 2 cos + i sin , 2 2 6 6 √ √ 6 2 √ − π −π z1 + z2 = − i = 2 cos + i sin 2 2 6 6 MỤC LỤC
9 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai √ π π nên 2 cos + i sin π π z 6 6 1z2 = √ = cos + i sin . − π −π 3 3 2 cos + i sin 6 6
Lại có z1z2 = cos(a + b) + i sin(a + b). Vậy √ π 1 π 3 cos(a + b) = cos = , sin(a + b) = sin = . 3 2 3 2
BÀI 10. Cho a, b, c là các số thực thoả mãn điều kiện:
sin a + sin b + sin c = 0, cos a + cos b + cos c = 0.
Chứng minh rằng: sin 2a + sin 2b + sin 2c = 0, cos 2a + cos 2b + cos 2c = 0. L Lời giải
Đặt z1 = cos a + i sin a, z2 = cos b + i sin b, z3 = cos c + i sin c. Theo giả thiết, ta có 1 1 1
z1 + z2 + z3 = 0. Vì |z1| = |z2| = |z3| = 1 nên = z = z = z z 1, 2, 3. Vì thế 1 z2 z3
z21 + z22 + z23 = (z1 + z2 + z3)2 − 2 (z1z2 + z2z3 + z3z1) 1 1 1 = 02 − 2z1z2z3 + + = −2z z 1z2z3 (z1 + z2 + z3) 1 z2 z3
= −2z1z2z3 (z1 + z2 + z3) = −2z1z2z3.0 = 0.
Do đó cos 2a + cos 2b + cos 2c + i (sin 2a + sin 2b + sin 2c) = 0. Vậy
sin 2a + sin 2b + sin 2c = 0, cos 2a + cos 2b + cos 2c = 0.
BÀI 11. Rút gọn tổng S = sin x + sin 2x + · · · + sin nx. L Lời giải x Khi sin
= 0 ⇔ x = 2kπ, ta có S = 0. Tiếp theo giả sử x 6= 2kπ, k ∈ Z. Ta có 2
(1 + cos x + cos 2x + · · · + cos nx) + (sin x + sin 2x + · · · + sin nx) i
=1 + (cos x + i sin x) + (cos 2x + i sin 2x) + · · · + (cos nx + i sin nx)
=1 + (cos x + i sin x) + (cos x + i sin x)2 + · · · + (cos x + i sin x)n 1 − (cos x + i sin x)n+1
[1 − cos(n + 1)x] − i sin(n + 1)x = = 1 − (cos x + i sin x) (1 − cos x) − i sin x
[1 − cos(n + 1)x − i sin(n + 1)x] [(1 − cos x) + i sin x] = (1 − cos x)2 − i2sin2x
[1 − cos(n + 1)x − i sin(n + 1)x] [(1 − cos x) + i sin x] = 1 − 2 cos x + cos2x + sin2x
[1 − cos(n + 1)x − i sin(n + 1)x] [(1 − cos x) + i sin x] = 2 − 2 cos x
[1 − cos(n + 1)x] (1 − cos x) + sin(n + 1)x sin x = + 4sin2 x 2 MỤC LỤC
10 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai
[(1 − cos(n + 1)x) sin x − sin(n + 1)x (1 − cos x)] i + 4sin2 x 2
1 − cos x − cos(n + 1)x + cos nx sin nx + sin x − sin(n + 1)x = + i 4sin2 x 4sin2 x 2 2 (2n + 1)x x x x (2n + 1)x x 2sin2 x + 2 sin sin 2 sin cos − 2 cos sin = 2 2 2 + 2 2 2 2 i 4sin2 x 4sin2 x 2 2 x (2n + 1)x x (2n + 1)x sin + sin cos − cos = 2 2 2 2 x + x i 2 sin 2 sin 2 2 (n + 1)x nx (n + 1)x nx sin cos sin sin = 2 2 2 2 x + x i. sin sin 2 2 (n + 1)x nx sin sin
Vậy S = sin x + sin 2x + · · · + sin nx = 2 2 x . Tóm lại: sin 2 (n + 1)x nx sin sin 2 2
sin x + sin 2x + · · · + sin nx = x
khi x 6= 2kπ, k ∈ Z sin 2 0
khi x = 2kπ, k ∈ Z.
Lưu ý. Qua lời giải này, ta còn rút gọn được tổng
cos x + cos 2x + · · · + cos nx.
BÀI 12. Rút gọn tổng S = cos x + cos 3x + · · · + cos(2n − 1)x (x 6= kπ). L Lời giải Ta có
[cos x + cos 3x + · · · + cos(2n − 1)x] + [sin x + sin 3x + · · · + sin(2n − 1)x] i
= (cos x + i sin x) + (cos 3x + i sin 3x) + · · · + [cos(2n − 1)x + i sin(2n − 1)x]
= (cos x + i sin x) + (cos x + i sin x)3 + · · · + (cos x + i sin x)2n−1 1 − (cos x + i sin x)2n
= (cos x + i sin x) 1 − (cos x + isin x)2 1 − (cos x + i sin x)2n
= (cos x + i sin x) 2sin x (sin x − i cos x) 1 − (cos x + i sin x)2n
= (cos x + i sin x) (sin x + i cos x) 2sin x sin2x − i2cos2x 1 − (cos x + i sin x)2n 1 − (cos 2nx + i sin 2nx) =i. = i 2 sin x 2 sin x MỤC LỤC
11 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai i − i cos 2nx + i2 sin 2nx sin 2nx + i (1 − cos 2nx) = = 2 sin x 2 sin x sin 2nx sin2nx = + i. 2 sin x sin x sin 2nx
Suy ra S = cos x + cos 3x + · · · + cos(2n − 1)x = . 2 sin x
Lưu ý. Qua lời giải này ta còn thu được kết quả sin2nx
sin x + sin 3x + · · · + sin(2n − 1)x = . sin x
BÀI 13. Tìm đa thức dư khi chia đa thức x2000 + 3x19 − x + 1 cho đa thức x2 + 1. L Lời giải
Vì đa thức x2 + 1 có bậc là 2 nên đa thức dư có dạng ax + b, với a và b là các hằng số thực.
Đa thức x2 + 1 có hai nghiệm trong C là i và −i. Đặt P(x) = x2000 + 3x19 − x + 1. Khi đó
P(x) = x2000 + 3x19 − x + 1 = (x2 + 1)Q(x) + ax + b, ∀x ∈ R. (*)
Trong (*) lần lượt lấy x = i và x = −i, ta được
i2000 + 3i19 − i + 1 = ai + b
(−i)2000 + 3(−i)19 + i + 1 = a(−i) + b
i2000 + 3i19 − i + 1 = ai + b ⇔
i2000 − 3i19 + i + 1 = −ai + b
(i2)1000 + 3i.(i2)9 − i + 1 = ai + b ⇔
(i2)1000 − 3i.(i2)9 + i + 1 = −ai + b 1 − 3i − i + 1 = ai + b ⇔ 1 + 3i + i + 1 = −ai + b 2 − 4i = ai + b b = 2 a = −4 ⇔ ⇔ ⇔ 2 + 4i = −ai + b 2ai = −8i b = 2.
Vậy dư khi chia đa thức x2000 + 3x19 − x + 1 cho đa thức x2 + 1 là −4x + 2.
BÀI 14. Chứng minh rằng với mọi n ∈ N thì đa thức (x + 1)2n+1 + xn+2 chia hết cho đa thức x2 + x + 1. L Lời giải
Đa thức x2 + x + 1 có hai nghiệm là √ 1 3 2π 2π α = − + i = cos + i sin , 2 2 3 3 √ 1 3 2 π 2π β = − − i = cos − + i sin − . 2 2 3 3
Kí hiệu: P(x) = (x + 1)2n+1 + xn+2. Khi đó: 2π 2π π π α + 1 = 1 + cos + i sin = 2 cos2 π + 2i sin cos 3 3 3 3 3 MỤC LỤC
12 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai π π π = 2 cos cos + i sin . 3 3 3 Tương tự: 2 π 2π β + 1 = 1 + cos − + i sin − 3 3
= 2 cos2 − π + 2i sin − π cos − π 3 3 3 h i = 2 cos − π
cos − π + i sin − π . 3 3 3 Do đó: P( n+2
α) = (α + 1)2n+1 + α n+2 π 2n+1 π π 2n+1 2π 2π = 2 cos cos + i sin + cos + i sin 3 3 3 3 3 (2n + 1) π (2n + 1)π (2n + 4)π (2n + 4)π = cos + i sin + cos + i sin 3 3 3 3 (2n + 4) π (2n + 1)π (2n + 4)π (2n + 1)π = cos + cos + i sin + sin 3 3 3 3 (4n + 5)π π (4n + 5)π π = 2 cos cos + 2i sin cos = 0. 6 2 6 2
Vậy α là nghiệm của đa thức P(x). Tương tự ta cũng có P(β) = 0, hay β là nghiệm của
P(x). Vậy tất cả các nghiệm của đa thức x2 + x + 1 đều là nghiệm của đa thức P(x), ta có điều phải chứng minh.
BÀI 15. Cho đa thức f (x) ∈ R[x] và deg f (x) > 0 thoả mãn f (x) > 0, ∀x ∈ R. Chứng
minh rằng tồn tại A(x), B(x) ∈ R[x] sao cho f (x) = A2(x) + B2(x). L Lời giải
Ta có hằng đẳng thức:
(a2 + b2)(c2 + d2) = (ac + bd)2 + (ad − bc)2. (1)
Dễ thấy, nếu z là nghiệm của đa thức thì z cũng là nghiệm của đa thức. Do deg f (x) > 0
và f (x) > 0, ∀x ∈ R nên f (x) không có nghiêm thực, suy ra f (x) có phân tích
f (x) = c ∏(x − zi)(x − zi), zi ∈ C.
Đặt z = a + bi thì (x − z)(x − z) = x2 − 2ax + a2 + b2 = (x + a)2 + b2.
Áp dụng hằng đẳng thức (1) ta suy ra đpcm.
BÀI 16. Tìm tất cả các đa thức hệ số nguyên P(x), là monic bậc 2, sao cho tồn tại đa thức
Q(x) ∈ Z[x] mà các hệ số của đa thức R(x) = P(x)Q(x) đều thuộc tập {−1; 1}. L Lời giải
Theo giả thiết, P(x) có dạng P(x) = x2 + ax ± 1, với a là số nguyên. Giả sử n
R(x) = ∑ aixi; ai ∈ { − 1; 1}. i=0
Gọi z ∈ C là một nghiệm của R(x) sao cho |z| > 1. Khi đó ta có n−1 n−1 n−1 a |z|n − 1 |z|n = |zn| = i ∑ zi ≤ ∑ |zi| = ∑ |z|i = . a |z| − 1 i=0 n i=0 i=0 MỤC LỤC
13 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai Do đó ta có |z|n − 1 |z|n − 1 1 |z|n ≤ ⇒ |z| − 1 ≤ = 1 − < 1 ⇒ |z| < 2. |z| − 1 |z|n |z|n
Vậy mọi nghiệm của R(x), nếu có modul lớn hơn 1 thì sẽ có modul nhỏ hơn 2. Giả sử z1,
z2 là 2 nghiệm của P(x) ∈ Z[x], khi đó z1, z2 là 2 nghiệm của R(x). Theo Viet ta có |z1z2| = |z1| |z2| = 1. (1 ≤ |z1| < 2
Giả sử |z1| ≥ |z2|, khi đó 0 ≤ |z2| ≤ 1.
Ta lại có |a| = |z1 + z2| ≤ |z1| + |z2| < 3 ⇒ a ∈ {±2; ±1; 0}. (Q(x) = x + 1 (Q(x) = 1
Trường hợp 1: Với a = 0 ta được ∨ P(x) = x2 − 1 P(x) = x2 + 1.
Trường hợp 2: Với a = ±1 ta được P(x) = x2 ± x ± 1 ⇒ Q(x) = 1.
" P(x) = x2 ± 2x + 1 (⇒ Q(x) = ±1)
Trường hợp 3: Với a = ±2 ⇒ P(x) = x2 ± 2x − 1 (⇒ Q(x) = ±1).
Thử lại, ta được các đa thức thỏa mãn yêu cầu đề bài là:
P(x) = x2 − 1, P(x) = x2 + 1, P(x) = x2 ± x ± 1, P(x) = x2 ± 2x ± 1.
BÀI 17. Tìm tất cả các đa thức P(x) ∈ R[x] thỏa mãn
P (x) P x2 = P x3 + 2x , ∀x ∈ R. L Lời giải
Xét deg P (x) = 0 tức P (x) = C thay vào (1) ta được C = 0 hoặc C = 1, hay P (x) = 0,
P (x) = 1 là hai đa thức thỏa mãn yêu cầu đề bài. Giả sử deg P (x) > 0. Gọi x1 là nghiệm
(thực hoặc phức) của đa thức P (x) mà |x1| có giá trị lớn nhất. Nếu x1 = 0 thì
P (x) = xkQ (x) , Q (0) 6= 0, k ∈ N∗.
Suy ra x2kQ (x) Q x2 = x2 + 2k Q x3 + 2x, với mọi x. Thay x = 0 suy ra Q (0) = 0,
gặp mâu thuẫn, vậy x1 6= 0. Đặt x1 = t2 (chú ý t ∈ C ) từ giả thiết suy ra t6 + 2t2, t3 + 2t cũng là nghiệm, suy ra ( t2 ≥ t6 + 2t2 1 ≥ t4 + 2 ⇒ t2 ≥ t3 + 2t |t| ≥ t2 + 2 . √ √
Từ 1 ≥ t4 + 2 ≥ |t|4 − 2 suy ra |t| ≤ 4 3 < 2. MỤC LỤC
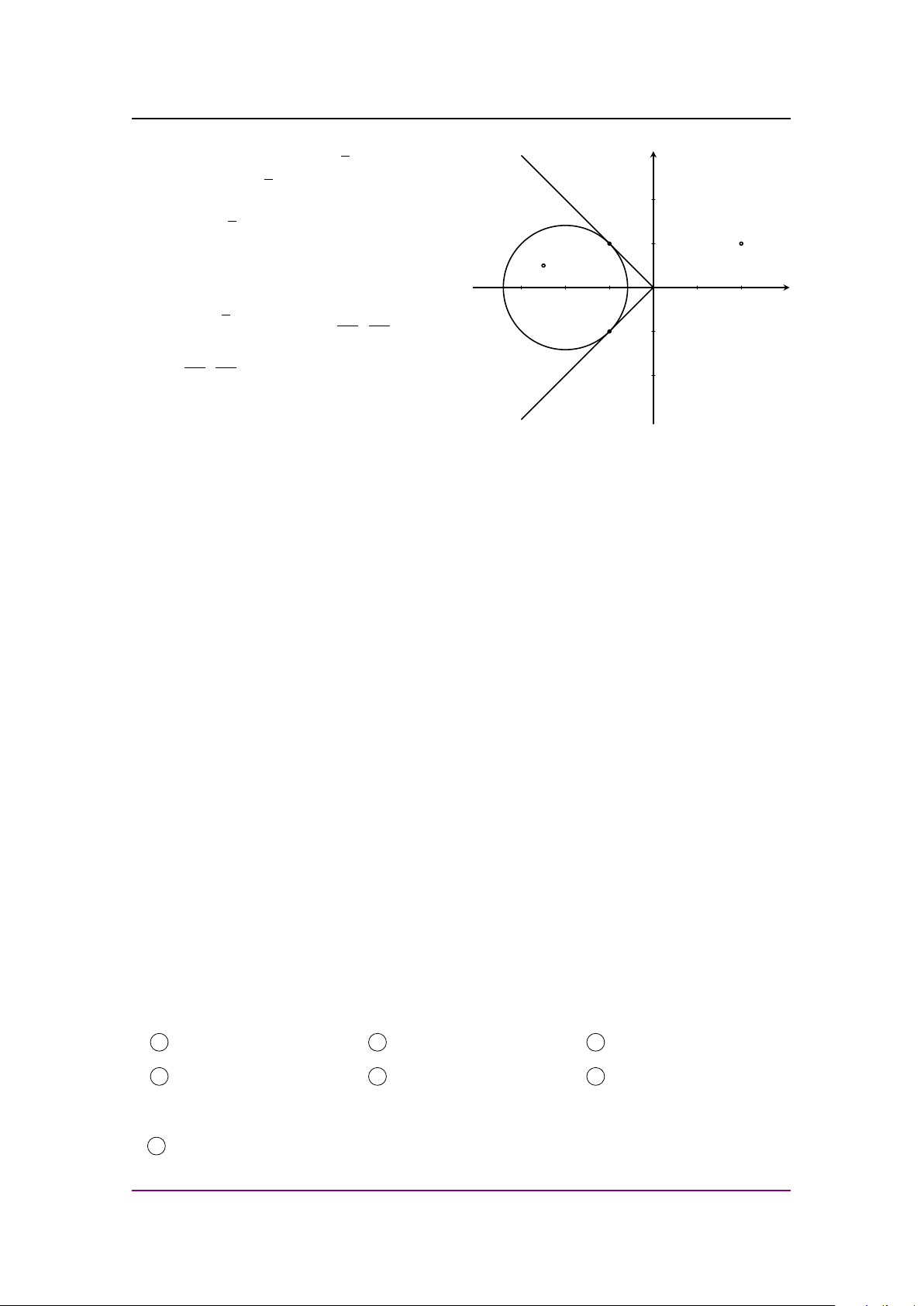
14 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai √ Vậy ta có y t2 + 2 ≤ |t| < 2. Đặt z = t2 ta √ được |z + 2| < 2 và |z2 + 2| ≤ 1 suy ra z 2
nằm trong đường tròn tâm (−2; 0) bán kính √ bằng R =
2 và z2 nằm trong đường tròn z2
tâm (−2; 0) bán kính R0 = 1. 1 z
Gọi ϕ ∈ [0; 2π] là một acgumen của z, do
z nằm trong đường tròn tâm (−2; 0) bán x −3 −2 −1 O √ 1 2 3 π 5π kính R = 2. suy ra ϕ ∈ ; suy ra 4 4 −1 3 π 5π 2ϕ ∈ ;
là acgumen của z2 điều này 2 2 −2
dẫn đến z2 không nằm trong đường tròn
tâm (−2; 0) bán kính R0 = 1 điều này vô
lý. Vậy P (x) = 0, P (x) = 1 là hai đa thức cần tìm.
Nhận xét 1. Bài toán trên còn có thể giải theo cách đơn giản như sau: Xét deg P (x) = 0
tức P (x) = C thay vào (1) ta được C = 0 hoặc C = 1, hay P (x) = 0, P (x) = 1 là hai đa
thức thỏa yêu cầu đề bài. Xét deg P (x) = n > 0. Đặt
P (x) = anxn + an−1xn−1 + · · · + a1x + a0.
So sánh hệ số tự do hai vế ta có a0 = 0 hoặc a0 = 1.
Nếu a0 = 0 đặt tiếp P (x) = xm · Q (x) với deg Q (x) = n − m và Q (0) 6= 0. Thay lại
vào phương trình ta được x2mQ (x) Q x2 = x2 + 2m Q x3 + 2x, cho x = 0 suy ra Q (0) = 0, vô lý.
Nếu a0 = 1 đặt tiếp P (x) = xm · Q (x) + 1 với deg Q (x) = n − m và Q (0) 6= 0.
Thay lại vào phương trình ta được
x2mQ (x) Q x2 + Q (x) + xmQ x2 = x2 + 2m Q x3 + 2x ,
từ đây cho x = 0 suy ra Q (0) = 2mQ (0) ⇔ Q (0) = 0, vô lý.
Chú ý 3. Sử dụng số phức để giải phương trình hàm đa thức sẽ được đề cập kĩ hơn ở bài 2 (ở trang 39). C. BÀI TẬP 1. Đề bài
BÀI 18. Phân tích ra thừa số phức: 1 a2 + 1; 2 a2 − a + 1; 3 2a4 − 5; 4 4a2 + 9b2; 5 3a2 + 5b2; 6 3a2 − 2ab + 7b2.
BÀI 19. Với x, y là hai số nguyên. Xét số phức z = x + yi.
1 Chứng minh rằng zn = xn + iyn, với xn, yn là những số nguyên (n ∈ N∗). MỤC LỤC
15 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai
2 Chứng minh rằng nếu A = x2 + y2 thì An = x2n + y2n (n ∈ Z, n ≥ 1).
3 Chứng minh rằng nếu A là tổng bình phương của hai số nguyên thì An cũng là tổng
bình phương của hai số nguyên (n ∈ Z, n ≥ 1).
BÀI 20. Giải phương trình sau trên tập số phức:
(z − 1)4 + (z + 3)4 + 128 = 0. (1) BÀI 21. Chứng minh rằng: nπ C0 − − · · · 2n C22n + C42n + C2k 2n(−1)k + · · · + C2n 2n (−1)n = 2n cos . 2 nπ C1 − − · · · 2n C32n + C52n
+ C2k−1(−1)k−1 + · · · + C2n−1(−1)n−1 = 2n sin . 2n 2n 2
BÀI 22. Thực hiện các yêu cầu sau: a) Tính tổng: C0 + C1 + C2 + · · · + C2010. 2010 2010 2010 2010 b) Chứng minh: C0 + C2 + C4 + · · · + C2010 = 22009. 2010 2010 2010 2010 c) Tính tổng: 3C1 + 33C3 + 35C5 + · · · + 32009C2009. 2010 2010 2010 2010 1 d) Chứng minh: C0 + C3 + · · · + C2007 + C2010 = (22010 + 2). 2010 2010 2010 2010 3
BÀI 23 (Chọn đội tuyển Romanian năm 1988). Cho các số thực x, y, z thoả mãn điều
kiện x + y + z = 0. Chứng minh rằng: |cos x| + |cos y| + |cos z| ≥ 1.
BÀI 24 (Đề nghị IMO năm 1989). Cho a, b, c là các số thực thoả mãn: cos a + cos b + cos c sin a + sin b + sin c = = m. cos(a + b + c) sin(a + b + c)
Chứng minh rằng: cos(a + b) + cos(b + c) + cos(c + a) = m.
BÀI 25. Với giá trị nào của số tự nhiên n thì đa thức P(x) = x2n + xn + 1 chia hết cho đa thức Q(x) = x2 + x + 1.
BÀI 26 (Mathematica Excalibur 5.1996). Tìm a ∈ Z sao cho đa thức x2 − x + a chia hết
đa thức x13 + x + 90 trong Z[x].
BÀI 27 (Việt Nam TST 2019). Với n là số nguyên dương, chứng minh rằng đa thức n Pn(x) = ∑ 2kC2k · 2n xk · (x − 1)n−k k=0
có đúng n nghiệm thực phân biệt. MỤC LỤC
16 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai 2. Lời giải 18.
1 Ta có a2 + 1 = a2 − i2 = (a − i)(a + i).
2 Ta có ∆ = 1 − 4 = −3 = 3i2. Phương trình a2 − a + 1 = 0 có hai nghiệm là √ √ 1 − 3i 1 + 3i a1 = , a 2 2 = 2 Do đó √ √ ! ! 1 − 3i 1 + 3i a2 − a + 1 = a − a − . 2 2 Cách khác. Ta có 1 1 3 1 2 3i2 a2 − a + 1 = a2 − 2.a. + + = a − − 2 4 4 2 4 √ √ √ !2 ! ! 1 2 3i 1 − 3i 1 + 3i = a − − = a − a − . 2 2 2 2 3 Ta có ! ! r r 5 5 5 2a4 − 5 = 2 a4 − = 2 a2 − a2 + 2 2 2 r ! r ! r ! 5 5 5 = 2 a − 4 a + 4 a2 − i2 2 2 2 r ! r ! r ! r ! 5 5 5 5 = 2 a − 4 a + 4 a − 4 i a + 4 i . 2 2 2 2
4 Nếu b = 0 thì 4a2 + 9b2 = 4a2. Nếu b 6= 0 thì " # a2 2a 2 4a2 + 9b2 = b2 4 + 9 = b2 − 9i2 b2 b 2a 2a = b.b − 3i + 3i = (2a − 3ib)(2a + 3ib). b b Cách khác. Ta có
4a2 + 9b2 = 4a2 − 9b2i2 = (2a)2 − (3bi)2 = (2a − 3bi)(2a + 3bi).
5 Tương tự câu (4).
6 Nếu b = 0 thì 3a2 − 2ab + 7b2 = 3a2. Nếu b 6= 0 thì a 2 a 1 7 3a2 − 2ab + 7b2 = 3b2 − 2. . + b b 3 3 MỤC LỤC
17 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai " # 2 a 2 a 1 1 7 1 = 3b2 − 2. . + + − b b 3 3 3 9 " # " # a 1 2 20 a 1 2 20 = 3b2 − + = 3b2 − − i2 b 3 9 b 3 9 r ! r ! a 1 20 a 1 20 = 3b2 − − i − + i b 3 9 b 3 9 √ √ ! ! b 20 b 20 = 3 a − − bi a − + bi 3 3 3 3 √ √ ! b 20 = 3a − b − 20bi a − + bi . 3 3 √ √ ! b 20
Kết luận: 3a2 − 2ab + 7b2 = 3a − b − 20bi a − + bi . 3 3 19.
1 Ta chứng minh bằng phương pháp quy nạp.
Mệnh đề đúng khi n = 1 vì z1 = z = x + iy, x, y là những số nguyên.
Giả sử zn = xn + iyn, với xn, yn là những số nguyên. Ta có
zn+1 = zn.z = (xn + iyn) (x + iy) = (x.xn − y.yn) + i (x.yn + xny).
Đặt x.xn − y.yn = xn+1, x.yn + xny = yn+1, khi đó xn+1, yn+1 là những số nguyên
và zn+1 = xn+1 + iyn+1. Theo nguyên lí quy nạp suy ra điều phải chứng minh.
2 Ta có A = x2 + y2 = (x + yi)(x − yi) = z.z (do z = x + yi). Suy ra
An = (z.z)n = zn (z)n = (xn + iyn) (xn − iyn) = x2n + y2n. 3 Suy ra từ câu (2).
Lưu ý. Sử dụng kết quả bài toán trên ta trả lời được một số câu hỏi hóc búa, chẳng hạn:
252011 có phải là tổng bình phương của hai số nguyên hay không? Câu trả lời là có, vì 25 = 32 + 42.
20. Đặt z = x − 1. Thay vào phương trình (1), ta được
(x − 2)4 + (x + 2)4 + 128 = 0 ⇔ x4 + 24x2 + 80 = 0 x2 = −4 x2 = 4i2 √ √ n o ⇔ ⇔
⇔ x ∈ −2i, 2i, 20i, − 20i . x2 = −20 x2 = 20i2 n √ √ o
Tập nghiệm của (1) là −1 − 2i, −1 + 2i, −1 + 20i, −1 − 20i . 21. Ta có (1 + i)2n MỤC LỤC
18 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai
=C02n + C12ni + C22ni2 + C32ni3 + C42ni4 + · · · + C2n−1i2n−1 + C2n 2n 2n i2n =C0 − 2n + C1 2ni − C2 2n
C32ni + C42n + · · · + C2n−1(−1)n−1i + C2n 2n 2n (−1)n h = C0 − 2n C22n + C42n + · · · + C2n 2n (−1)ni h + C1 − 2n
C32n + C52n + · · · + C2n−1(−1)n−1i i. 2n √ 1 1 √ π π Mặt khác: 1 + i = 2 √ + √ i = 2 cos + i sin . Suy ra: 2 2 4 4 √ 2n 2n π 2nπ nπ nπ (1 + i)2n = 2 cos + i sin = 2n cos + i sin . 4 4 2 2
Do đó đồng nhất phần thực và phần ảo ta được hai đẳng thức cần chứng minh. 22. Xét f (x) = (1 + x)2010 = C0 + 2010
C12010x + C22010x2 + · · · + C2010 2009 x2009 + C2010 2010 x2010, ∀x ∈ R. a) Ta có C0 + = 2010
C12010 + C22010 + · · · + C2010 2010 f (1) = 22010. b) Ta có f (1) = 22010 = C0 + + 2001
C12010 + C22010 + · · · + C2009 2010 C2010 2010 . f (−1) = 0 = C0 − + 2010
C12010 + C22010 + · · · − C2009 2010 C2010 2010 . Do đó
f (1) + f (−1) = 22010 = 2(C0 + ) 2010
C22010 + C42010 + · · · + C2010 2010 . Suy ra C0 + = 2010
C22010 + C42010 + · · · + C2010 2010 22009.
c) Tương tự câu b), xét f (3) − f (−3). √ 1 3 2π 2π d) Gọi z = − + i = cos + i sin
. Khi đó z2 + z + 1 = 0 và z3 = 1. Gọi 2 2 3 3 A = C0 + + · · · + + 2010 C32010 C2007 2010 C2010 2010
B = C12010 + C42010 + · · · + C2008 2010 C = C22010 + C5 + · · · + 2010 C2009 2010 . Ta có (1 + 1)2010 = A + B + C (1 + z)2010 = C0 + 2010
C12010z + C22010z2 + C32010z3 + · · · + C2010 2010 z2010 = A + zB + z2C (1 + z2)2010 = C0 + 2010
C12010z2 + C22010z4 + C32010z6 + · · · + C2010 2010 z2.2010 = A + z2B + zC. MỤC LỤC
19 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai Suy ra
3A = 22010 + (1 + z)2010 + (1 + z2)2010. (*)
Từ (*), dùng công thức Moivre ta tìm được 8040π 8040π (1 + z)2010 = z4020 = cos + i sin 3 3
= cos 2680π + i sin 2680π = 1. 4020π 4020π (1 + z2)2010 = z2010 = cos + i sin 3 3
= cos 1340π + i sin 1340π = 1. 1
Do đó (1 + z)2010 + (1 + z2)2010 = 2. Bởi vậy từ (*) suy ra A = (22010 + 2). 3
23. Vì z = −(x + y) nên cos z = cos(x + y). Xét số phức
a = cos 2x + i sin 2x, b = cos 2y + i sin 2y. Ta có
1 + a = (1 + cos 2x) + i sin 2x = 2 cos2 x + 2i sin x cos x = 2 cos x (cos x + i sin x).
Suy ra |1 + a| = 2 |cos x|. Tương tự: |1 + b| = 2 |cos y|. Ta có
1 + ab = 1 + cos(2x + 2y) + i sin(2x + 2y)
= 2 cos2(x + y) + 2i sin(x + y) cos(x + y)
= 2 cos(x + y) [cos(x + y) + i sin(x + y)].
Suy ra |1 + ab| = 2 |cos(x + y)| = 2 |cos z|. Vậy ta cần chứng minh:
|1 + a| + |1 + b| + |1 + ab| ≥ 2. (*) Ta có
|1 + a| + |1 + b| + |1 + ab| ≥ |1 + a| + |1 + ab − (1 + b)|
= |1 + a| + |b(1 − a)| = |1 + a| + |b| |1 − a|
= |1 + a| + |1 − a| ≥ |1 + a + 1 − a| = |2| = 2.
Vậy (*) đúng, ta có điều phải chứng minh.
24. Đặt x = cos a + i sin a, y = cos b + i sin b, z = cos c + i sin c.
Khi đó xyz = cos(a + b + c) + i sin(a + b + c). Mặt khác
x + y + z = (cos a + cos b + cos c) + i(sin a + sin b + sin c)
= m cos(a + b + c) + i.m sin(a + b + c)
= m[cos(a + b + c) + i sin(a + b + c)] = mxyz. MỤC LỤC
20 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai 1 1 1 Vậy: x + y + z = mxyz ⇒ + + = m. (1) xy yz zx
Ta có |x|2 = |y|2 = |z|2 = 1, suy ra 1 1 1 x.x = y.y = y.y = 1 ⇒ = x, = y, = z. (2) x y z
Thay (2) vào (1) ta được: x.y + y.z + z.x = m. (3) Mà ta lại có
x.y = (cos a − i sin a) (cos b − i sin b)
= (cos a cos b − sin a sin b) − i (sin a cos b + cos a sin b) = cos(a + b) − i sin(a + b).
Tương tự: y.z = cos(b + c) − i sin(b + c), z.x = cos(c + a) − i sin(c + a). Thay vào (3) ta được:
cos(a + b) + cos(b + c) + cos(c + a)
−i [sin(a + b) + sin(b + c) + sin(c + a)] = m.
Mà m = m + 0i nên cos(a + b) + cos(b + c) + cos(c + a) = m.
Lưu ý. Qua lời giải trên ta còn thu được:
sin(a + b) + sin(b + c) + sin(c + a) = 0.
25. Đa thức Q(x) có hai nghiệm là √ 1 3 2π 2π α = − + i = cos + i sin , 2 2 3 3 √ 1 3 2 π 2π β = − − i = cos − + i sin − . 2 2 3 3
Giả sử n = 3q + r, với r = 0, 1, 2. Khi n = 3k, ta có: P( 6k 3k α) = α + α + 1 2 6k 3k π 2π 2π 2π = cos + i sin + cos + i sin + 1 3 3 3 3
= cos 4kπ + i sin 4kπ + cos 2kπ + i sin 2kπ + 1 = 3 6= 0. Khi n = 3k + 1, ta có: P( 6k+2 3k+1 α) = α + α + 1 2 6k+2 3k+1 π 2π 2π 2π = cos + i sin + cos + i sin + 1 3 3 3 3 4π 4π 2π 2π = cos + i sin + cos + i sin + 1 = 0. 3 3 3 3
Tương tự, ta cũng có P(β) = 0. MỤC LỤC
21 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai Khi n = 3k + 2, ta có: P( 6k+4 3k+2 α) = α + α + 1 2 6k+4 3k+2 π 2π 2π 2π = cos + i sin + cos + i sin + 1 3 3 3 3 8π 8π 4π 4π = cos + i sin + cos + i sin + 1 = 0. 3 3 3 3
Tương tự, ta cũng có P(β) = 0.
Vậy P(x) chia hết cho Q(x) khi và chỉ khi n = 3k + 1 hoặc n = 3k + 2. √ 1 3 2π 2π
Cách khác. Ta có ε = − + i = cos + i sin
là một nghiệm của Q(x). Vậy 2 2 3 3 Q(ε) = 0.
Nhận xét 2. P(x) chia hết cho Q(x) khi và chỉ khi P(ε) = 0.
Chứng minh. Giả sử đa thức P(x) chia hết cho đa thức Q(x). Khi đó tồn tại đa thức
H(x) sao cho P(x) = Q(x).H(x). Suy ra: P(ε) = Q(ε).H(ε) = 0. Giả sử P(ε) = 0. Giả sử
P(x) = Q(x).H(x) + R(x), với R(x) là đa thức bậc nhất hoặc R(x) là đa thức hằng. Ta có
0 = P(ε) = Q(ε).H(ε) + R(ε) ⇒ R(ε) = 0.
Do ε là số phức và R(ε) = 0 nên R(x) ≡ 0. Suy ra P(x) chia hết cho Q(x).
Trở lại bài toán: Sử dụng nhận xét trên suy ra điều kiện để P(x) chia hết cho Q(x) là P(ε) = 0 hay 2 2n n π 2π 2π 2π cos + i sin + cos + i sin + 1 = 0 3 3 3 3 4n 4n 2n 2n ⇔ π π π π cos + i sin + cos + i sin + 1 = 0 3 3 3 3 4n 2n 4n 2n ⇔ π π π π cos + cos + 1 + i sin + sin = 0 3 3 3 3 2n π 4nπ 2nπ 2nπ cos + 1 + cos = 0 + = cos 2 cos2 0 ⇔ 3 3 ⇔ 3 3 4nπ 2nπ 4nπ −2nπ sin = sin sin + sin = 0 3 3 3 3 2n 1 n = 3k + 1 ⇔ π cos = − ⇔ 3 2 n = 3k + 2.
26. Giả sử đa thức x13 + x + 90 chia hết cho đa thức x2 − x + a trong Z[x]. Khi đó
x13 + x + 90 = (x2 − x + a)q(x), q(x) ∈ Z[x]. (*)
Thay lần lượt các giá trị x = −1; 0; 1 vào đẳng thức (∗) ta được:
88 = (2 + a)q(−1); 90 = aq(0); 92 = aq(1).
Bởi vì a chia hết 90 và 92 và a + 2 chia hết 88 vậy a chỉ nhận giá trị 2 hoặc −1. Nhưng đa
thức x2 − x − 1 có một nghiệm thực dương, còn đa thức x13 + x + 90 không có nghiệm MỤC LỤC
22 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai
thực dương, vậy nên a = 2 và ta cần chứng minh rằng x2 − x + 2 chia hết x13 + x + 90 .
Thật vậy gọi ω là một trong hai nghiệm phức của x2 − x + 2 ta có 2 4 8
ω = ω − 2, ω = −3ω + 2, ω = −3ω − 14, 12 13 ω
= 45ω − 46, ω + ω + 90 = 0.
Ta có điều phải chứng minh.
Lời bình. Lời giải trên là một sự kết hợp hài hòa Đa thức nguyên, phép chia hết và nghiệm số phức của đa thức.
27. Trước hết, ta thấy rằng nếu Pn(x0) = 0 thì 0 < x0 < 1. Thật vậy:
Nếu x0 > 1 thì x0 > 0, x0 − 1 > 0 nên Pn(x0) > 0, mâu thuẫn.
Nếu x0 < 0 thì đặt y0 = −x0 > 0, ta có Pn(x0) = (−1)nPn(y0), nhưng Pn(y0) > 0
nên Pn(x0) 6= 0, cũng không thỏa.
Tiếp theo, ta sẽ rút gọn Pn(x). Xét x0 ∈ (0; 1) và đặt 2x0 = a2, 1 − x0 = b2 thì
(x0 − 1)n−k = ((−1)(1 − x0))n−k = (ib)2n−2k, n
trong đó i2 = −1. Ta đưa về Tn = ∑ C2k · 2n
a2k · (ib)2n−2k. Xét khai triển k=0 2n 2n (a + ib)2n = ∑ Ck · 2n
ak · (ib)2n−k, (a − ib)2n = ∑ Ck2n(−1)kak · (ib)2n−k. k=0 k=0 (a + ib)2n + (a − ib)2n Suy ra Tn = . Ta thấy a2 + b2 = x 2 0 + 1 nên a 2 b 2 √ + √ = 1. x0 + 1 x0 + 1 a b π Đặt √ = cos ϕ, √
= sin ϕ với ϕ ∈ 0; . Khi đó x0 + 1 x0 + 1 2
(cos ϕ + i sin ϕ)2n + (cos ϕ − i sin ϕ)2n Tn = . 2
Theo công thức de Moive cho lũy thừa của số phức thì
cos(2nϕ) + i sin(2nϕ) + cos(2nϕ) − i sin(2nϕ) Tn = = cos(2nϕ). 2 Từ đó suy ra rằng π π
Pn(x0) = 0 ⇔ Tn(x0) = 0 ⇔ cos(2nϕ) = 0 ⇔ ϕ = + k , với 0 ≤ k ≤ n − 1. 4n 2n
Ứng với mỗi số ϕ, ta xác định được duy nhất số x0 ∈ (0; 1) nên có n số x0 sao cho
Pn(x) = 0, chứng tỏ rằng đa thức đã cho có n nghiệm thực phân biệt. Ta có điều phải chứng minh. MỤC LỤC
23 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai
Lưu ý. Biểu thức của bài toán có lẽ xuất phát từ việc rút gọn tổng nhị thức Newton dạng
“chẵn – lẻ” quen thuộc:
∑ C2knan−2kbk với việc xét khai triển (a + b)n và (a − b)n. Trở 0≤2k≤n
ngại lớn ở đây chính là mũ của các số hạng và hệ số nhị thức lại không khớp nhau. Dĩ
nhiên ta không thể chuyển C2k → Ck 2n
n được nên buộc phải nâng lũy thừa của mũ thành
bình phương. Tuy nhiên, nếu chỉ đặt đơn thuần 2x = a2, 1 − x = b2 thì ngay ở tổng chẵn
của đề cho cũng đan dấu. Chính dấu hiệu lạ đó đã gợi ý cho ta xét số phức i2 = −1 để
khắc phục điều này. Chú ý rằng số 2k trong đề bài có thể thay bằng ak với a > 0 bất kỳ
và bài toán vẫn đúng. Ngoài ra, nếu đổi việc xét các nhị thức ở vị trí chẵn có thể thay
bằng các vị trí chia hết cho 3, 5, . . . hay số nguyên tố p bất kỳ cũng sẽ tạo thành nhiều tình
huống thú vị khác. Cách tiếp cận bằng số phức ở đây có lẽ là duy nhất, vì việc chỉ ra các
khoảng chứa n nghiệm của Pn(x) là không khả thi; còn nếu quy nạp theo bậc n thì lại khó
tìm được công thức tường minh như ở bài toán đa thức Chebyshev.
D. SỬ DỤNG SỐ PHỨC CHỨNG MINH BẤT ĐẲNG THỨC
Tiếp theo ta sẽ xét một số ví dụ về dùng số phức để chứng minh bất đẳng thức. Đây
là phương pháp rất độc đáo, thú vị, dùng cái ảo để chứng minh cái thực. Ta thường sử dụng các kết quả sau:
|z1 + z2| ≤ |z1| + |z2|, ∀z1, z2 ∈ C.
|z1 + z2 + · · · + zn| ≤ |z1| + |z2| + · · · + |zn|, ∀z1, z2, . . . , zn ∈ C.
BÀI 28. Chứng minh rằng với các số thực ak, bk (k = 1, 2, . . . , n) thì: q
(a1 + a2 + · · · + an)2 + (b1 + b2 + · · · + bn)2 q q q ≤ a2 + b2 + a2 + b2 + · · · + a2 1 1 2 2 n + b2 n. (1) L Lời giải
Đặt ak + bki = zk (k = 1, 2, . . . , n). Khi đó
z1 + z2 + · · · + zn = (a1 + a2 + · · · + an) + (b1 + b2 + · · · + bn)i.
Bất đẳng thức (1) cần chứng minh có dạng
|z1 + z2 + · · · + zn| ≤ |z1| + |z2| + · · · + |zn|. (2)
Bất đẳng thức (2) đúng vì môđun của tổng các số phức thì không lớn hơn tổng của từng môđun.
BÀI 29. Cho ba số thực a, b, c thỏa mãn a + b + c = 6. Chứng minh rằng: √ p p p 1 + a2 + 4 + b2 + 9 + c2 ≥ 6 2. L Lời giải
Xét các số phức z1 = a + i, z2 = b + 2i, z3 = c + 3i. Khi đó p p p |z1| + |z2| + |z3| = a2 + 1 + b2 + 4 + c2 + 9. MỤC LỤC
24 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai Mặt khác
z1 + z2 + z3 = (a + b + c) + 6i = 6 + 6i √ √ p ⇒ |z1 + z2 + z3| = 62 + 62 = 72 = 6 2.
Mà |z1 + z2 + z3| ≤ |z1| + |z2| + |z3| nên √ p p p 1 + a2 + 4 + b2 + 9 + c2 ≥ 6 2.
Ta có điều phải chứng minh.
BÀI 30. Chứng minh rằng với mọi số thực a, b thì: q q 4cos2acos2b + sin2(a − b) +
4sin2asin2b + sin2(a − b) ≥ 2. (*) L Lời giải
Đặt z1 = 2 cos a cos b + sin(a − b)i, z2 = 2 sin a sin b + sin(a − b)i. Khi đó q q |z1| =
4cos2acos2b + sin2(a − b), |z2| = 4sin2asin2b + sin2(a − b). Mặt khác
z1 + z2 = 2 (cos a cos b + sin a sin b) + 2 sin(a − b)i
= 2 cos(a − b) + 2 sin(a − b)i. q Do đó |z1 + z2| =
4cos2(a − b) + 4sin2(a − b) = 2. Bởi vậy
(∗) ⇔ |z1| + |z2| ≥ |z1 + z2| (đúng).
BÀI 31. Chứng minh rằng với các số dương a, b, c thì: √ p p p a2 + ab + b2 + b2 + bc + c2 + c2 + ca + a2 ≥ 3(a + b + c). L Lời giải Xét các số phức √ √ √ b 3b c 3c a 3a z1 = (a + ) + i, z ) + i, z ) + i. 2 2 2 = (b + 2 2 3 = (c + 2 2 Khi đó |z1| + |z2| + |z3| s √ s s 2 √ 2 √ 2 b 2 3b c 2 3c a 2 3a = (a + ) + ( ) + (b + ) + ( ) + (c + ) + ( ) 2 2 2 2 2 2 p p p = a2 + ab + b2 + b2 + bc + c2 + c2 + ca + a2. MỤC LỤC
25 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai √ 3 3
Mặt khác: z1 + z2 + z3 = (a + b + c) + (a + b + c)i. Do đó 2 2 r 9 3 √ |z1 + z2 + z3| = (a + b + c)2 + (a + b + c)2 = 3(a + b + c). 4 4
Do |z1 + z2 + z3| ≤ |z1| + |z2| + |z3| nên ta có điều phải chứng minh.
BÀI 32. Chứng minh rằng nếu a, b, c là các số dương thỏa mãn: ab + bc + ca = abc √ √ √ a2 + 2b2 b2 + 2c2 c2 + 2a2 √ thì + + ≥ 3. ab bc ca L Lời giải
Bất đẳng thức cần chứng minh tương đương với r r r 1 2 1 2 1 2 √ + + + + + ≥ 3. b2 a2 c2 b2 a2 c2 1 1 1
Đặt x = , y = , z = . Ta cần chứng minh a b c q q √ p y2 + 2x2 + z2 + 2y2 + x2 + 2z2 ≥ 3. (*)
Từ giả thiết ab + bc + ca = abc, ta có 1 1 1 + + = 1 ⇒ x + y + z = 1. a b c Xét các số phức √ √ √ z1 = y + 2xi, z2 = z + 2yi, z3 = x + 2zi. Khi đó q q p |z1| + |z2| + |z3| = y2 + 2x2 + z2 + 2y2 + x2 + 2z2. Mặt khác √ z1 + z2 + z3 = (x + y + z) + 2(x + y + z)i q √ ⇒ |z1 + z2 + z3| = (x + y + z)2 + 2(x + y + z)2 = 3.
Mà |z1 + z2 + z3| ≤ |z1| + |z2| + |z3| nên ta có (∗), điều phải chứng minh.
BÀI 33. Chứng minh rằng với mọi số thực a, b, c và số dương k, ta có 2 k(a + b + c) − abc ≤ a2 + k b2 + k c2 + k . L Lời giải
Xét đa thức f bậc 3, nhận a, b, c làm nghiệm như sau:
f (t) = (t − a)(t − b)(t − c) = t3 − t2(a + b + c) + t(ab + bc + ca) − abc. MỤC LỤC
26 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai Bởi vì
|A + Bi|2 = (A + Bi)(A − Bi) = A2 + B2 ≥ A2 (với i2 = −1), nên ta có 2
| f (it)|2 = i3t3 − i2t2(a + b + c) + it(ab + bc + ca) − abc 2
= −it3 + t2(a + b + c) + it(ab + bc + ca) − abc ≥ t2(a + b + c) − abc2
| f (it)|2 = |(it − a)(it − b)(it − c)|2
= |it − a|2|it − b|2|it − c|2
= (it − a)(−it − a)(it − b)(−it − b)(it − c)(−it − c)
= a2 − i2t2 b2 − i2t2 c2 − i2t2 = (a2 + t2)(b2 + t2)(c2 + t2). Do đó
t2(a + b + c) − abc2 ≤ a2 + t2 b2 + t2 c2 + t2 , (*)
với t là số thực bất kì. Do đó, đặt k = t2, từ (∗) ta có điều phải chứng minh.
Lưu ý. Chọn k cụ thể ta sẽ được những bài toán mới, chẳng hạn chọn k = 3, ta được bài
toán: Cho a, b, c là các số thực dương thỏa mãn a2 + b2 + c2 ≤ 3. Chứng minh rằng abc + 8 ≥ 3(a + b + c).
BÀI 34. Chứng minh rằng với mọi số thực a, b, c, d và số dương k, ta có
k2 − k(ab + ac + ad + bc + bd + cd) + abcd2 ≤ a2 + k b2 + k c2 + k d2 + k . L Lời giải
Xét đa thức f bậc 4, nhận a, b, c, d làm nghiệm như sau:
f (t) = (t − a)(t − b)(t − c)(t − d)
= t4 − t3(a + b + c + d) + t2(ab + ac + ad + bc + bd + cd)
− t(abc + bcd + cda + dab) + abcd. Bởi vì
|A + Bi|2 = (A + Bi)(A − Bi) = A2 + B2 ≥ A2 (với i2 = −1),
nên với mọi số thực t, ta có
| f (it)|2 = |i4t4 − i3t3(a + b + c + d) + i2t2(ab + ac + ad + bc + bd + cd)
− it(abc + bcd + cda + dab) + abcd)|2
= |t4 + it3(a + b + c + d) − t2(ab + ac + ad + bc + bd + cd)
− it(abc + bcd + cda + dab) + abcd|2 2
≥ t4 − t2(ab + ac + ad + bc + bd + cd) + abcd . (1) MỤC LỤC
27 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai
| f (it)|2 = |(it − a)(it − b)(it − c)(it − d)|2
= |it − a|2|it − b|2|it − c|2|it − d|2
= (−a + it)(−a − it)(−b + it)(−b − it)(−c + it)(−c − it)(−d + it)(−d − it)
= a2 − i2t2 b2 − i2t2 c2 − i2t2 d2 − i2t2
= a2 + t2 b2 + t2 c2 + t2 d2 + t2 . (2)
Từ (1) và (2) ta có điều phải chứng minh.
BÀI 35 (Romanian Mathematical Olympiads 2003, Shortlist). Cho các số dương a, b,
c, d thỏa mãn a2 + b2 + c2 + d2 = 1. Chứng minh rằng 5
ab + ac + ad + bc + bd + cd ≤ + 4abcd. 4 L Lời giải
Trong kết quả bài toán 34, lấy k = 0, 25 ta được 1 1 2
− (ab + ac + ad + bc + bd + cd) + abcd 16 4 1 1 1 1 ≤ + a2 + b2 + c2 + d2 . 4 4 4 4
Theo bất đẳng thức Côsi, ta có !4 1 1 1 1 1 + a2 + b2 + c2 + d2 1 + a2 + b2 + c2 + d2 ≤ = . 4 4 4 4 4 16 Do đó 1 1 2 1
− (ab + ac + ad + bc + bd + cd) + abcd ≤ 16 4 16 1 1 1 ⇒
− (ab + ac + ad + bc + bd + cd) + abcd ≥ − 16 4 4 5
⇒ + 4abcd ≥ ab + ac + ad + bc + bd + cd. 4 1
Ta có điều phải chứng minh. Dấu "=" xảy ra khi a = b = c = d = . 2
BÀI 36 (Titu Andreescu, Gabriel Dospinescu). Cho các số thực a, b, c, d thỏa mãn
a2 + 1 b2 + 1 c2 + 1 d2 + 1 = 16. Chứng minh rằng
−3 ≤ ab + ac + ad + bc + bd + cd − abcd ≤ 5. L Lời giải MỤC LỤC
28 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai
Trong kết quả bài toán 34, lấy k = 1 ta được
(1 − (ab + ac + ad + bc + bd + cd) + abcd)2 ≤ a2 + 1 b2 + 1 c2 + 1 d2 + 1 = 16. Do đó
− 4 ≤ (ab + ac + ad + bc + bd + cd) − abcd − 1 ≤ 4
⇒ − 3 ≤ ab + ac + ad + bc + bd + cd − abcd ≤ 5.
Ta có điều phải chứng minh. Dấu "=" xảy ra chẳng hạn khi
a = b = c = d = 1; a = b = 1, c = d = −1.
BÀI 37 (USA Mathematical Olympiads 2014). Cho các số thực a, b, c, d thỏa mãn điều
kiện b − d ≥ 5 và tất cả các nghiệm x1, x2, x3, x4 của đa thức P(x) = x4 + ax3 + bx2 + cx + d
đều là nghiệm thực. Tìm giá trị nhỏ nhất của biểu thức
x21 + 1 x22 + 1 x23 + 1 x24 + 1 . L Lời giải
Theo định lí Viet, ta có d = x1x2x3x4 và
b = x1x2 + x1x3 + x1x4 + x2x3 + x2x4 + x3x4. Do b − d ≥ 5 nên
(x1x2 + x1x3 + x1x4 + x2x3 + x2x4 + x3x4) − x1x2x3x4 ≥ 5.
Trong kết quả bài toán 34, lấy k = 1 ta được
(1 − (x1x2 + x1x3 + x1x4 + x2x3 + x2x4 + x3x4) + x1x2x3x4)2 ≤ 1 + x2 1 1 + x22 1 + x23 1 + x24 . Do đó
16 ≤ (1 − (x1x2 + x1x3 + x1x4 + x2x3 + x2x4 + x3x4) − x1x2x3x4)2 ≤ 1 + x2 1 1 + x22 1 + x23 1 + x24 .
Xét đa thức P(x) = (x − 1)4 có 4 nghiệm x1 = x2 = x3 = x4 = 1, khi đó
x21 + 1 x22 + 1 x23 + 1 x24 + 1 = 16.
Vậy giá trị nhỏ nhất của biểu thức đã cho là 16. MỤC LỤC
29 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai
E. SỬ DỤNG SỐ PHỨC GIẢI PHƯƠNG TRÌNH, HỆ PHƯƠNG TRÌNH
Một phương trình nghiệm phức f (z) = 0, với z = x + iy, ta biến đổi thành h(x, y) = 0 h(x, y) + ig(x, y) = 0 ⇔ g(x, y) = 0.
Nghĩa là một phương trình nghiệm phức, bằng cách tách phần thực và phần ảo luôn có
thể đưa về hệ phương trình. 2x3 − 6xy2 = 5 (1)
BÀI 38. Giải hệ phương trình √ 6x2y − 2y3 = 5 3. (2) L Lời giải
Nhân hai vế của (2) với i rồi cộng với (1) ta được √
2x3 − 6xy2 + (6x2y − 2y3)i = 5 + 5 3i √ 5 5 3
⇔x3 − 3xy2 + (3x2y − y3)i = + i 2 2√ 5 5 3
⇔x3 + 3x2yi + 3xy2i2 + y3i3 = + i 2 2 √ ! 1 3 ⇔(x + yi)3 = 5 + i . 2 2 √ ! 1 3 π π
Vậy x + yi là căn bậc ba của số phức z = 5 + i = 5 cos + i sin . Mà z có 2 2 3 3 các căn bậc ba là √ π π z0 = 3 5 cos + i sin , 9 9 √ π + 2 π π + 2π √ 7π 7π z 3 3 1 = 3 5 cos + i sin = 3 5 cos + i sin , 3 3 9 9 √ π + 4 π π + 4π √ 13π 13π z 3 3 2 = 3 5 cos + i sin = 3 5 cos + i sin . 3 3 9 9
Vậy các nghiệm của hệ phương trình là √ √ √ π 7π 13π x = 3 5 cos x = 3 5 cos x = 3 5 cos 9 √ 9 9 π ; √ 7 ; π √ 13π y = 3 5 cos y = 3 9 5 cos y = 3 5 cos . 9 9
Lưu ý. Cách giải này rất độc đáo và nhanh hơn nhiều so với cách sử dụng tính đẳng cấp
của hệ, rồi đưa về phương trình đa thức bậc ba.
BÀI 39 (HSG Quốc gia năm học 2006-2007). Giải hệ phương trình 12 √ 1 − x = 2 y + 3x 12 √ 1 + y = 6. y + 3x MỤC LỤC
30 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai L Lời giải √ √
Điều kiện x ≥ 0, y ≥ 0, y + 3x 6= 0. Đặt u = 3x ≥ 0, v =
y ≥ 0. Thay vào hệ, ta được 12 u 12u √ √ 1 − = 2 u − = 2 3 (1) u2 + v2 3 ⇔ u2 + v2 12 12v v + = 6. (2) 1 + v = 6 u2 + v2 u2 + v2
Nhân phương trình (2) với i, sau đó cộng với phương trình (1) ta được 12(u − vi) √ u + vi − = 2 3 + 6i. (3) u2 + v2
Xét số phức z = u + vi, với u ≥ 0, v ≥ 0. Khi đó (3) viết lại 12z √ 12 √ z − = 2 3 + 6i ⇔ z − = 2( 3 + 3i) z.z z √
⇔ z2 − 2( 3 + 3i)z − 12 = 0. (4) Ta có √ √ √
∆0 = ( 3 + 3i)2 + 12 = −6 + 6 3i + 12 = 6 + 6 3i √ ! 1 3 π π = 12 + i = 12 cos + i sin . 2 2 3 3
Vậy ∆0 có hai căn bậc hai là √ √ √ ! √ 3 1 ± π π 12 cos + i sin = ± 12 + i = ± 3 + 3i . 6 6 2 2 Từ (4) ta có √ √ √ √ z = 3 + 3i + 3 + 3i = 3 + 3 + 3 + 3 i √ √ √ √ z = 3 + 3i − 3 − 3i = 3 − 3 + 3 − 3 i. Do u ≥ 0 và v ≥ 0 nên √ 2 √ √ 3 + 3 ( u = 3 + 3 x = 4 + 2 3 √ ⇒ x = ⇔ √ v = 3 + 3 3 y = 3 4 + 2 3 . √ 2 y = 3 + 3 √ ( x = 4 + 2 3
Hệ đã cho có nghiệm duy nhất √ y = 3 4 + 2 3 .
BÀI 40. Giải phương trình
x5 + 45x4 + 210x3 + 210x2 + 45x + 1 = 0. (1) MỤC LỤC
31 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai L Lời giải √
Xét x < 0. Ta có C2k i −x2k = C2k(− xk. Suy ra 20 20 1)k(−x)k = C2k 20 √ 10 √ 10 1 + i −x + 1 − i −x = 2 C0 + 10
C210x + C410x2 + · · · + C10 10 x5 . Do đó (1) ⇔2(C0 + 10
C210x + C410x2 + · · · + C10 10 x5) = 0 √ 10 √ 10 √ 10 1 + i −x ⇔ 1 + i −x + 1 − i −x = 0 ⇔ √ = −1. 1 − i −x √ 1 + i −x Nghĩa là √
là một căn bậc mười của −1 = cos π + i sin π. Do đó 1 − i −x √ 1 + i −x √ π + k2π π + k2π = cos + i sin , k = 0, 1, 2, . . . , 9. (2) 1 − i −x 10 10 Ta có √ π + k2π π + k2π 1 − i −x cos + i sin 10 10 π + k2π √ π + k2π π + k2π √ π + k2π = cos + −x sin + sin − −x cos i. 10 10 10 10
Từ (2) ta nhân chéo, sau đó đồng nhất phần thực với phần thực, phần ảo với phần ảo được kết quả √− π + k2π x = tan , k = 0, 1, 2, . . . , 9. (3) 20 √ Do
−x > 0 nên trong (3) ta chỉ cho k chạy từ 0 đến 4. Vậy phương trình (1) có 5 nghiệm là
x = −tan2 π + k2π , k = 0, 1, 2, 3, 4. (4) 20
Nhưng (1) là phương trình đa thức bậc 5 nên có không quá 5 nghiệm. Vậy (4) cho ta tất cả các nghiệm của (1).
Lưu ý. Sẽ là sai lầm nếu cho rằng √ √ 1 + x10 + 1 − x10 C0 + 10
C210x + C410x2 + · · · + C10 10 x5 = 2 √ √ và 1 + x10 + 1 −
x10 > 0 nên suy ra (1) vô nghiệm. Cần nhớ rằng giải phương
trình là tìm x thuộc tập xác định và thoả mãn phương trình (1). Bài toán 40 này còn được giải như sau :
(1) ⇔ (x + 1) x4 + 44x3 + 166x2 + 44x + 1 = 0.
Phương trình x4 + 44x3 + 166x2 + 44x + 1 = 0 gọi là phương trình với hệ số phản hồi,
trường hợp đặc biệt này, gọi là phương trình đối xứng. MỤC LỤC
32 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai
BÀI 41. Giải phương trình
64x6 − 2112x5 + 7920x4 − 7392x3 + 1980x2 − 132x + 1 = 0. L Lời giải
Đặt x = pt, thay vào phương trình, dẫn tới cần phải chọn p = 2. Một dấu hiệu khác cũng
khá rõ ràng, đó là hệ số tự do là 1, số hạng chứa luỹ thừa cao nhất là 64x6 = (−2x)6. √ √
BÀI 42. Chứng minh rằng 1 + x20 + 1 −
x20 = P10(x), trong đó P10(x) là một đa
thức bậc mười. Giải phương trình P10(x) = 0. L Lời giải
Ta có P10(x) = 2 C0 + C2 x + C4 x2 + · · · + C20x10 . Vậy P 20 20 20 20
10(x) là một đa thức bậc
mười. Dễ thấy rằng x ≥ 0 không thoả mãn phương trình P10(x) = 0. Tiếp theo xét x < 0. Khi đó √ 20 √ 20 P10(x) = 1 + i −x + 1 − i −x .
Phương trình P10(x) = 0 tương đương với √ 20 √ 20 √ 20 1 + i −x 1 + i −x = − 1 − i −x ⇔ √ = −1. 1 − i −x √ 1 + i −x Nghĩa là √
là một căn bậc hai mươi của −1 = cos π + i sin π. Do đó 1 − i −x √ 1 + i −x √ π + k2π π + k2π = cos + i sin , k = 0, 1, 2, . . . , 19. (1) 1 − i −x 20 20 Ta có √ π + k2π π + k2π 1 − i −x cos + i sin 20 20 π + k2π √ π + k2π π + k2π √ π + k2π = cos + −x sin + sin − −x cos i. 20 20 20 20
Từ (1) ta nhân chéo, sau đó đồng nhất phần thực với phần thực, phần ảo với phần ảo được kết quả √− π + k2π x = tan , k = 0, 1, 2, . . . , 19. (2) 40 √ Do
−x > 0 nên trong (2) ta chỉ cho k chạy từ 0 đến 9. Vậy phương trình P10(x) = 0 có
10 nghiệm là x = −tan2 π + k2π , k = 0, 1, . . . , 9. 40 √ x4 − 6x2y2 + y4 = 3 (1)
BÀI 43. Giải hệ phương trình 1 x3y − y3x = . (2) 4 L Lời giải
Xét số phức z = x + yi, với x, y ∈ R. Vì
z4 = (x + yi)4 = x4 + 4x3yi + 6x2y2i2 + 4xy3i3 + y4i4 MỤC LỤC
33 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai =
x4 − 6x2y2 + y4 + 4 x3y − y3x i. √ π π
nên từ hệ đã cho ta có z4 = 3 + i = 2 cos + i sin
. Vậy z = x + yi là một căn bậc 6 6 π π π π bốn của số phức 2 cos + i sin
. Các căn bậc bốn của số phức 2 cos + i sin là 6 6 6 6 √ √ 4 π π 13π 13π 2 cos + i sin , 4 2 cos + i sin , 24 24 24 24 √ √ 4 25π 25π 37π 37π 2 cos + i sin , 4 2 cos + i sin . 24 24 24 24 Hay √ π π x + yi = 4 2 cos + i sin 24 24 √ 13π 13π x + yi = 4 2 cos + i sin 24 24 √ 25π 25π x + yi = 4 2 cos + i sin 24 24 √ 37 37 π π x + yi = 4 2 cos + i sin . 24 24 Hệ đã cho có 4 nghiệm : √ √ π 13π x = 4 2 cos x = 4 2 cos 24 √ 24 π ; √ 13 ; π y = 4 2 sin 24 y = 4 2 sin 24 √ 25 π √ 37π x = 4 2 cos x = 4 2 cos 24 √ 24 25 ; π √ 37π y = 4 2 sin y = 4 2 sin . 24 24 3x − y x + = 3 x2 + y2
BÀI 44. Giải hệ phương trình x + 3y y − = 0. x2 + y2 L Lời giải
Điều kiện x2 + y2 6= 0. Xét số phức z = x + iy. Khi đó
iz = ix − y, x2 + y2 = |z|2 = z.z.
Hệ phương trình đã cho viết lại 3x − y x + = 3 (1) x2 + y2 x + 3y yi − i = 0. (2) x2 + y2
Lấy (1) trừ (2) theo vế ta được 3x − y x + 3y 3(x + yi) y − xi x − yi + + i = 3 ⇔ x − yi + − = 3 x2 + y2 x2 + y2 x2 + y2 x2 + y2 MỤC LỤC
34 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai Hay z iz 1 i z + 3 + = 3 ⇔ z + 3 +
= 3 ⇔ (z)2 − 3z + 3 + i = 0. z.z z.z z z
Ta có ∆ = 9 − 4(3 + i) = −3 − 4i. Xét số phức a + bi thoả mãn điều kiện ( a2 − b2 = −3 a2 − b2 = −3 −3 − 4i = (a + bi)2 ⇔ ⇔ 2 2ab = −4 b = − . a Khi đó 4 a2 −
= −3 ⇔ a4 + 3a2 − 4 = 0 ⇔ a2 = 1 ⇔ a = ±1. a2
Vậy (a; b) = (1; −2) ; (a; b) = (−1; 2) . Do đó ∆ = −3 − 4i có hai căn bậc hai là ± (1 − 2i). Suy ra 3 + (1 − 2i) z = = 2 − i 2 3 − (1 − 2i) z = = 1 + i. 2 Nghĩa là x − yi = 2 − i (x; y) = (2; 1) ⇔ x − yi = 1 + i (x; y) = (1; −1). x = 2 x = 1
Vậy hệ phương trình đã cho có hai nghiệm là và y = 1 y = −1.
BÀI 45 (HSG quốc gia-1996). Giải hệ phương trình: √ 1 3x 1 + = 2 x + y 1 √ p 7y 1 − = 4 2. x + y L Lời giải √ √
Điều kiện x > 0 và y > 0. Đặt u = x, v =
y. Hệ phương trình trở thành: 1 2 u 1 + = √ u2 + v2 3 √ 1 4 2 v 1 − = √ u2 + v2 7
Vì u2 + v2 là bình phương của môđun của số phức z = u + iv nên ta biến đổi hệ phương trình thành: u 2 u 2 u + = √ u + = √ (1) u2 + v2 3 √ u2 + v2 ⇔ 3 √ v 4 2 iv 4 2i v − = √ iv − = √ (2) u2 + v2 7 u2 + v2 7
Cộng (1) và (2) theo vế ta được: √ u − iv 2 4 2i u + iv + = √ + √ . (3) u2 + v2 3 7 MỤC LỤC
35 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai u − iv z z 1 Vì = = = nên (3) viết lại u2 + v2 |z|2 z.z z √ √ ! 1 2 4 2i 1 2 2i z + = √ + √ ⇔ z2 − 2 √ + √ z + 1 = 0. (4) z 3 7 3 7 Ta có √ √ √ !2 ∆0 1 2 2i 1 8 4 2i 38 4 2i = √ + √ − 1 = − + √ − 1 = − + √ . 3 7 3 7 21 21 21
Xét số phức a + bi thoả mãn điều kiện √ 38 a2 − b2 = − 38 4 2i − √ 21 + √ = (a + bi)2 ⇔ 21 21 4 2 2ab = √ 21 Khi đó 8 −38 −19 + 23 4 a2 − =
⇔ 21a4 + 38a2 − 8 = 0 ⇔ a2 = = . 21a2 21 21 21 2 √ 2 √ Vậy (a; b) = √ ; 2 ; (a; b) = − √ ; − 2 . Do đó 21 21 √ ! 1 2 2 2 √ z = u + iv = √ ± √ + √ ± 2 i. 3 21 7 1 2 u = √ + √ Vì 3 u > √ 21 0 và v > 0 nên Do đó 2 2 √ v = √ + 2. 7 1 2 2 11 4 √ √ √ x = + = + 3 21 21 3 7 √ !2 2 2 √ 22 8 y = √ + = + √ 2 . 7 7 7
Hệ phương trình đã cho có nghiệm duy nhất là 11 4 √ x = + 21 3 7 22 8 y = + √ . 7 7 MỤC LỤC
36 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai
F. HỆ LẶP SINH BỞI CÁC ĐA THỨC ĐỐI XỨNG BA BIẾN
BÀI 46. Tìm các số phức x, y, z khác nhau đôi một và thỏa mãn: x = y3 + z3 y = z3 + x3 z = x3 + y3. L Lời giải
Đặt σ1 = x + y + z, σ2 = xy + yz + zx, σ3 = xyz. Khi đó:
x3 + y3 + z3 = 3xyz + (x + y + z) x2 + y2 + z2 − xy − yz − zx = 3 2 3
σ3 + σ1 σ − − 1 3σ2 = σ1
3σ1σ2 + 3σ3. Hệ đã cho viết lại: x = 3
σ − 3σ1σ2 + 3σ3 − x3 1 y = 3 σ − 3 1
σ1σ2 + 3σ3 − y3 z = 3 σ − 3 1
σ1σ2 + 3σ3 − z3.
Hay x, y, z là nghiệm của phương trình: t = 3 3 σ − − = 1
3σ1σ2 + 3σ3 − t3 ⇔ t3 + t − σ1
3σ1σ2 + 3σ3 0. (1)
Mặt khác, theo định lí Viet thì x, y, z cũng là nghiệm của phương trình:
t3 − σ1t2 + σ2t − σ3 = 0. (2) Từ (1) và (2) suy ra: − σ1 = 0 σ1 = 0 σ2 = 1 ⇔ σ2 = 1 − 3 σ 3 = − σ − 3 1
σ1σ2 + 3σ3 σ3 = 0.
Như vậy x, y, z là nghiệm của phương trình: t = 0
t3 + t = 0 ⇔ t t2 + 1 = 0 ⇔ t = i t = −i.
Vậy nghiệm của hệ đã cho là (0; i; −i) và các hoán vị.
BÀI 47. Tìm các số phức a, b, c, d khác nhau đôi một và thỏa mãn: a4 = bcd + 1 b4 = cda + 1 c4 = dab + 1 d4 = abc + 1. L Lời giải MỤC LỤC
37 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai
Đặt σ4 = abcd. Lần lượt nhân phương trình thứ nhất, thứ hai, thứ ba, thứ tư với a, b, c, d ta được: a5 = abcd + a a5 = σ4 + a b5 = abcd + b b5 = ⇔ σ4 + b c5 = abcd + c c5 = σ 4 + c d5 = abcd + d d5 = σ4 + d.
Như vậy a, b, c, d là nghiệm của phương trình:
t5 = σ4 + t ⇔ t5 − t − σ4 = 0. (1)
Tuy nhiên phương trình (1) có đủ 5 nghiệm phức là a, b, c, d và r. Khi đó áp dụng định lí
Viet, ta được: σ4 = rσ4 ⇔ σ4 (r − 1) = 0. (2)
Nếu r = 1 thì do 1 là nghiệm của phương trình (1) nên
15 − 1 − σ4 = 0 ⇔ σ4 = 0.
Nếu r 6= 1 thì từ (2) suy ra σ4 = 0.
Như vậy, ta luôn có σ4 = 0. Vì thế nên (1) tương đương:
t5 − t = 0 ⇔ t t2 − 1 t2 + 1 = 0 ⇔ t ∈ {0; 1; −1; i; −i} .
Do σ4 = 0 nên trong 4 số a, b, c, d phải có một số bằng 0.
Hơn nữa bộ (a; b; c; d) = (0; 1; i; −i) không thỏa mãn hệ.
Với a, b, c, d ∈ {0; 1; −1; i; −i} thì a4, b4, c4, d4 ∈ {0; 1}, do đó từ hệ đã cho suy ra:
abc, bcd, cda, dab ∈ {0; −1}, dẫn tới trong 4 số a, b, c, d phải có đủ 3 số 0, i, −i.
Suy ra các nghiệm của hệ là (0; −1; i; i) và 23 hoán vị khác của nó.
BÀI 48. Tìm các số phức x, y, z khác nhau đôi một và thỏa mãn: y2 + z2 x3 + x2 = yz − 1 z2 + x2 y3 + y2 = zx − 1 x2 + y2 z3 + z2 = . xy − 1 L Lời giải
Điều kiện: xy 6= 1, yz 6= 1, zx 6= 1. Nếu x = 0 thì thay vào hệ ta được y2 + z2 = 0 y2 + z2 = 0 y = 0 y3 + y2 = −z2 ⇔ y3 = 0 ⇔ z = 0, z3 + z2 = −y2 z3 = 0
mâu thuẫn với giả thiết các số phức x, y, z khác nhau đôi một. Như vậy x 6= 0 và tương
tự, ta suy ra y 6= 0, z 6= 0. Đặt:
σ1 = x + y + z, σ2 = xy + yz + zx, σ3 = xyz. MỤC LỤC
38 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai
Khi đó: x2 + y2 + z2 = (x + y + z)2 − 2 (xy + yz + zx) = 2 σ − 2 1
σ2. Phương trình thứ nhất
của hệ đã cho trở thành: 2 σ − 2σ x3 + x2 = 1 2 − x2 σ3 − 1 x ⇔ 2
σ3x2 − x3 + σ3x − x2 = σ − 1 2σ2 − x2 ⇔x3 − 2
σ3x2 − σ3x + σ − 1 2σ2 = 0.
Điều này có nghĩa là x là nghiệm của phương trình: t3 − 2
σ3t2 − σ3t + σ − 1 2σ2 = 0. (1)
Tương tự, ta cũng suy ra được y, z là nghiệm của (1). Mặt khác, theo định lí Viet suy ra
x, y, z cũng là nghiệm của phương trình:
t3 − σ1t2 + σ2t − σ3 = 0. (2) Từ (1) và (2) suy ra: σ1 = σ3 σ3 = σ1 σ3 = σ1 σ2 = −σ3 ⇔ σ2 = −σ1 ⇔ σ2 = −σ1 2 2 2 σ 3 = −σ + 2 − 2 + 3 1 σ2 σ1 = −σ1 σ1 σ1 σ1 = 0 σ3 = σ1 ( ⇔
σ1; σ2; σ3) = (0; 0; 0) (loại) σ2 = −σ1 ⇔ (σ
1; σ2; σ3) = (−3; 3; −3) . σ1 ∈ {0; −3}
Như vậy x, y, z là nghiệm của phương trình: t + 1 3
t3 + 3t2 + 3t + 3 = 0 ⇔ (t + 1)3 = −2 ⇔ − √ = 1. (3) 3 2 t + 1
Phương trình (3) nghĩa là − √
là căn bậc 3 của 1 = cos 0 + i sin 0 hay: 3 2 √ t + 1 − √ t + 1 = − 3 2 = cos 0 + i sin 0 √ 3 ! √ 2 1 3 t + 1 2π 2π t + 1 = − 3 2 − + i − √ = cos + i sin ⇔ 2 2 3 2 3 3 √ ! √ t + 1 4 4 1 3 − √ π π = cos + i sin t + 1 = − 3 2 − − i . 3 2 3 3 2 2
Nghiệm (x; y; z) của hệ là √ √ √ √ ! ! ! 1 3 √ 1 3 − 3 2 − 1; − 3 2 − + i − 1; − 3 2 − − i − 1 2 2 2 2 và các hoán vị. MỤC LỤC
39 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai
BÀI 2. SỬ DỤNG SỐ PHỨC ĐỂ GIẢI PHƯƠNG TRÌNH HÀM ĐA THỨC
Nghiệm của đa thức đóng vai trò quan trọng trong việc xác định một đa thức. Cụ thể,
nếu đa thức P(x) bậc n (n ∈ N∗) có n nghiệm x1, x2, . . . , xn thì P(x) có dạng
P(x) = c (x − x1) (x − x2) . . . (x − xn).
Tuy nhiên nếu chỉ xét các nghiệm thực thì trong nhiều trường hợp sẽ không đủ số nghiệm.
Hơn nữa trong bài toán phương trình hàm đa thức, nếu chỉ xét các nghiệm thực thì lời
giải sẽ không hoàn chỉnh. Định lí cơ bản của đại số vì vậy đóng một vai trò hết sức quan
trọng trong dạng toán này.
Định lí cơ bản của đại số. Mọi đa thức bậc n hệ số phức (thực)
P(x) = anxn + an−1xn−1 + · · · + a1x + a0 (với an 6= 0)
đều có đủ n nghiệm phức (phân biệt hay trùng nhau).
Định lí Viet thuận: Nếu x1, x2, . . . , xn là n nghiệm (phân biệt hay trùng nhau) của
đa thức P(x) = anxn + an−1xn−1 + · · · + a1x + a0 (an 6= 0) thì: a S n−1
1 = x1 + x2 + · · · + xn = − an a S n−2
2 = x1 x2 + x1 x3 + · · · + xn−1 xn = an a S n−3
3 = x1 x2 x3 + x1 x2 x4 + · · · + xn−2 xn−1 xn = − an
. . . . . . . . . . . . . . . . . . . . . . . . a S 0 n = x1 x2 . . . xn = (−1)n. . an
Định lí Viet đảo: Nếu n số x1, x2, . . . , xn thỏa mãn x1 + x2 + · · · + xn = S1
x1x2 + x1x3 + · · · + xn−1xn = S2
x1x2x3 + x1x2x4 + · · · + xn−2xn−1xn = S3 . . . . . . . . . . . . x1x2 . . . xn = Sn
thì x1, x2, . . . , xn là nghiệm của phương trình
xn − S1xn−1 + S2xn−2 + · · · + (−1)n−1Sn−1x + (−1)nSn = 0.
Cho hai số phức z1 và z2. Khi đó: |z1z2| = |z1| |z2|
|z1 + z2| ≤ |z1| + |z2|, dấu bằng xảy ra khi và chỉ khi z1 = kz2, với k ≥ 0.
|z1 − z2| ≥ ||z1| − |z2||. MỤC LỤC
40 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai
BÀI 1 (Olympic Hồng Kông-1999). Cho k là số nguyên dương. Tìm các đa thức hệ số
thực thỏa mãn điều kiện P (P(x)) = [P(x)]k, ∀x ∈ R. (1) L Lời giải
Xét trường hợp P(x) ≡ C (C là hằng số). Từ (1) được C = Ck. Khi k = 1 thì C là hằng số bất kì. Khi k > 1 thì: C = 0
C = Ck ⇔ C Ck−1 − 1 = 0 ⇔ Ck−1 = 1.
Nếu k chẵn thì C = 1 hoặc C = 0, nếu k lẻ thì C = 0 hoặc C = 1 hoặc C = −1. Tiếp theo
ta xét trường hợp deg P ≥ 1. Vì đa thức P(x) − x luôn có nghiệm (xét cả nghiệm phức)
nên với mọi n ∈ N∗, tồn tại αn ∈ C sao cho P(αn) = αn. Từ đó theo (1) P( k
αn) = P (P(αn)) =
[P(αn)]k = αn, ∀n = 1, 2, . . . (2)
Từ (2) suy ra đa thức P(x) − xk có vô số nghiệm, hay P(x) − xk ≡ 0, nghĩa là P(x) ≡ xk.
Thử lại thấy thỏa mãn.
Kết luận: Nếu k = 0 thì P(x) ≡ C (C là hằng số bất kì). Nếu k > 1 thì các đa thức thỏa mãn đề bài là
P(x) ≡ 0, P(x) ≡ 1, P(x) ≡ xk.
BÀI 2. Tìm tất cả các đa thức hệ số thực P(x) thỏa mãn:
P(x)P(x + 1) = P(x2 + x + 1), ∀x ∈ R. (1) L Lời giải
Nếu P(x) ≡ a (a là hằng số) thì thay vào (1) ta được
a2 = a ⇔ a(a − 1) = 0 ⇔ a ∈ {0, 1} .
Bây giờ ta xét P(x) là đa thức có bậc lớn hơn hoặc bằng 1. Giả sử a là một nghiệm của
P(x). Khi đó a2 + a + 1 cũng là nghiệm. Trong (1) thay x bởi x − 1 ta được
P(x − 1)P(x) = P(x2 − x + 1), ∀x ∈ R.
Vì P(a) = 0 nên suy ra P(a2 − a + 1) = 0, vậy a2 − a + 1 cũng là nghiệm của P(x). Chọn
a là nghiệm có môđun lớn nhất (nếu có nhiều nghiệm như thế thì ta chọn một trong
chúng). Từ cách chọn suy ra a2 + a + 1 ≤ |a| , a2 − a + 1 ≤ |a| .
Theo bất đẳng thức về môđun ta có
|2a| = a2 + a + 1 + −a2 + a − 1 ≤ a2 + a + 1 + −a2 + a − 1
= a2 + a + 1 + a2 − a + 1 ≤ |a| + |a| = 2 |a| = |2a| .
Như vậy dấu bằng phải xảy ra ở các bất đẳng thức trên, suy ra
a2 + a + 1 + −a2 + a − 1 = a2 + a + 1 + −a2 + a − 1 , MỤC LỤC
41 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai
suy ra tồn tại số thực s ≥ 0 sao cho a2 + a + 1 = s −a2 + a − 1.
Nếu a2 + a + 1 < a2 − a + 1 thì:
2 a2 − a + 1 > a2 − a + 1 + a2 + a + 1 ≥ |2a| ⇒ a2 − a + 1 > |a| .
Tương tự nếu a2 + a + 1 > a2 − a + 1 thì a2 + a + 1 > |a|, mâu thuẫn với cách chọn
a. Vậy a2 − a + 1 = a2 + a + 1. Từ đó s = 1 và ta có
a2 + a + 1 = −a2 + a − 1 ⇔ a2 = −1 ⇔ a = ±i.
Vậy P(x) = (x2 + 1)mQ(x), trong đó Q(x) là đa thức không chia hết cho x2 + 1. Thay vào (1), ta có
(x2 + 1)mQ(x)(x2 + 2x + 2)mQ(x + 1) = [(x2 + x + 1)2 + 1]mQ(x2 + x + 1).
Hay Q(x)Q(x + 1) = Q(x2 + x + 1). Vậy Q(x) cũng thỏa (1). Nếu như Q(x) có nghiệm
thì ta làm tương tự như trên, nghiệm có môđun lớn nhất phải là i, −i. Nhưng điều này
không thể vì Q(x) không chia hết cho x2 + 1. Bởi vậy Q(x) là hằng số. Giả sử đó là c, thay
vào (1) ta được c = 1. Vậy P(x) = (x2 + 1)m. Thử lại ta kết luận: tất cả các đa thức thỏa mãn đề bài là
P(x) ≡ 0, P(x) ≡ 1, P(x) = (x2 + 1)m (với m = 1, 2, . . . )
BÀI 3. Tìm tất cả các đa thức P(x) với hệ số thực thỏa mãn:
P(x)P(2x2) = P(2x3 + x), ∀x ∈ R. (1) L Lời giải a = 0
Với đa thức hằng P(x) ≡ a, ta có a2 = a ⇔ a = 1.
Vậy P(x) ≡ 0 và P(x) ≡ 1 thỏa mãn bài ra. Tiếp theo xét trường hợp P(x) khác hằng số. Giả sử
P(x) = anxn + an−1xn−1 + · · · + a1x + a0 với an 6= 0
là đa thức thỏa mãn các yêu cầu bài toán. Từ (1) ta có (a
n xn + · · · + a1 x + a0) an(2x2)n + · · · + a1(2x2) + a0 ≡ a
n(2x3 + x)n + · · · + a1(2x3 + x) + a0 .
So sánh hệ số của x3n và hệ số tự do ở hai vế ta được 2na2 n = 2n an a2 do a a ⇒ n = an n 6=0 ⇒ n = 1 a2 = a a a 0 0 0 ∈ {0, 1} 0 ∈ {0, 1} .
Trường hợp 1. an = 1 và a0 = 0. Khi đó
P(x) = xn + an−1xn−1 + · · · + a1x = x`P1(x), với ` ∈ N∗, P1(0) 6= 0. MỤC LỤC
42 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai Thay vào (1) ta được
x`P1(x)(2x2)`P1(2x2) = (2x3 + x)`P1(2x3 + x), ∀x ∈ R
⇒P1(x)(2x2)`P1(2x2) = (2x2 + 1)`P1(2x3 + x), ∀x 6= 0. (2)
Do hàm đa thức liên tục trên R, nên từ (2), cho x → 0 ta được P1(0) = 0, đến đây ta gặp
mâu thuẫn. Vậy trường hợp 1 không xảy ra.
Trường hợp 2. an = 1 và a0 = 1. Giả sử α là một nghiệm thực của P(x). Khi đó do a0 = 1 nên 3 2 3
α 6= 0. Ta có P(2α + α) = P(α)P(2α ) = 0. Suy ra 2α + α cũng là một nghiệm của
P(x). Xét dãy số (αn) như sau: 3
α0 = α 6= 0 ; αn+1 = 2αn + αn, ∀n = 0, 1, 2, . . .
Nếu α > 0 thì (αn) là dãy tăng nghiêm ngặt, nếu α < 0 thì (αn) là dãy giảm nghiêm ngặt.
Từ đây suy ra nếu P(x) có một nghiệm thực khác không thì nó sẽ có vô số nghiệm thực.
Điều này không thể xảy ra. Kết hợp P(0) = 1 6= 0 suy ra P(x) 6= 0 với mọi x ∈ R. Suy ra
P(x) chỉ có nghiệm phức z1, z2, . . . , zn. Theo định lí Viet ta có
z1.z2 . . . zn = (−1)n ⇒ |z1| |z2| . . . |zn| = 1. (3)
Nếu tồn tại zk sao cho |zk| > 1. Điều này dẫn đến 2z2 + − (− k 1 = 2z2k
1) ≥ 2z2k − |−1| = 2 z2k − 1 > 1. Do đó 2z3 + z + 1 k k = |zk| 2z2k
> |zk |, suy ra P(x) có vô số nghiệm, điều này không thể
xảy ra. Vậy với mọi k = 1, 2, . . . n thì |zk| ≤ 1, từ đây và từ (3) suy ra |zk| = 1, ∀k = 1, n. Giả sử 3
α = cos φ + i sin φ là nghiệm phức của P(x), khi đó 2α + α cũng là nghiệm của P(x) và 1 = 3 2 2 2α
+ α = |α| . 2α + 1 = 2α + 1 = |2 cos 2φ + 2i sin 2φ + 1| q
= |(2 cos 2φ + 1) + (2 sin 2φ) i| =
(2 cos 2φ + 1)2 + (2 sin 2φ)2. Từ đó π
(2 cos 2φ + 1)2 + (2 sin 2φ)2 = 1 ⇔ cos 2φ = −1 ⇔ φ = + kπ. 2
Suy ra α = ±i. Do đó P(x) = (x2 + 1)k, k ∈ N. Thử lại thấy thỏa mãn.
Vậy tất cả các đa thức thỏa mãn yêu cầu đề bài là
P(x) ≡ 0 ; P(x) ≡ (x2 + 1)k, k ∈ N. Lưu ý.
Trong trường hợp 1, để suy ra P1(0) = 0 (để tạo ra mâu thuẫn) mà không cần dùng
giới hạn ta có thể làm như sau: Từ (2) suy ra đa thức
P1(x)(2x2)`P1(2x2) − (2x2 + 1)`P1(2x3 + x)
có vô số nghiệm nên nó là đa thức không, nghĩa là
P1(x)(2x2)`P1(2x2) = (2x2 + 1)`P1(2x3 + x), ∀x ∈ R.
Từ đây cho x = 0 ta được P1(0) = 0, mâu thuẫn. MỤC LỤC
43 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai
Bạn đọc hãy liên hệ bài toán 3 này với bài toán ?? ở trang ??.
BÀI 4. Tìm các đa thức P(x) có hệ số thực thỏa mãn điều kiện:
P(x).P(2x2) = P(x3 + x), ∀x ∈ R. (1) L Lời giải a = 0
Với đa thức hằng P(x) ≡ a, ta có a2 = a ⇔
Ta thấy P(x) ≡ 0 và P(x) ≡ 1 thỏa a = 1.
mãn bài ra. Tiếp theo xét trường hợp P(x) khác hằng số:
P(x) = anxn + an−1xn−1 + · · · + a1x + a0, an 6= 0, n ∈ N∗. (2)
Từ (1) ta có P(0) = 0 hoặc P(0) = 1. Do đó a0 = 0 hoặc a0 = 1.
Trường hợp 1. a0 = 0. Khi đó giả sử
P(x) = xmQ(x), Q(0) 6= 0, m ∈ N∗. Thay vào (1) ta được
xmQ(x).(2x2)m.Q(2x2) = (x3 + x)mQ(x3 + x), ∀x ∈ R
⇒Q(x).(2x2)mQ(2x2) = (x2 + 1)mQ(x3 + x), ∀x ∈ R. (3)
Từ (3), cho x = 0 ta được Q(0) = 0, đến đây ta gặp mâu thuẫn.
Trường hợp 2. a0 = 1. Đồng nhất hệ số bậc cao nhất ở (1) ta được 1 an.an.2n = an ⇔ an = . 2n
Từ (1) suy ra nếu P(x0) = 0 thì P(x3 + x 0
0) = 0, vậy nếu x0 là nghiệm thực của P(x) thì x3 + x 0
0 cũng là nghiệm của P(x). Xét dãy số (xn) như sau:
x0 6= 0 ; xn+1 = x3n + xn, ∀n = 0, 1, 2, . . .
Nếu x0 > 0 thì (xn) là dãy tăng nghiêm ngặt, nếu x0 < 0 thì (xn) là dãy giảm nghiêm
ngặt. Từ đây suy ra nếu P(x) có một nghiệm thực khác không thì nó sẽ có vô số nghiệm
thực. Điều này không thể xảy ra. Kết hợp P(0) = 1 6= 0 suy ra P(x) 6= 0 với mọi x ∈ R.
Suy ra P(x) chỉ có nghiệm phức z1, z2, . . . , zn. Theo định lí Viet ta có
z1.z2 . . . zn = (−1)n.2n ⇒ |z1| |z2| . . . |zn| = 2n.
Vì vậy tồn tại zk sao cho |zk| ≥ 2. Điều này dẫn đến z2 + − (− k 1 = z2k
1) ≥ z2k − |−1| = z2k − 1 ≥ 3. Do đó z3 + z + 1 k k = |zk| z2k
> |zk |, vậy P(x) có vô số nghiệm, điều này không thể xảy ra.
Vậy chỉ có hai đa thức thỏa mãn yêu cầu đề bài là P(x) ≡ 0 và P(x) ≡ 1.
Lưu ý. Bài toán 3 và bài toán 4 được tổng quát hoá thành bài toán 5 sau đây. MỤC LỤC
44 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai
BÀI 5. Cho số thực α ∈ [0; 2]. Tìm tất cả các đa thức khác không P(x) với hệ số thực thỏa mãn đồng nhất thức
P(x)P(2x2) = P(αx3 + x), ∀x ∈ R. L Lời giải
• Khi α = 0 thì P(x)P(2x2) = P(x), ∀x ∈ R, dẫn tới P(x) ≡ 0, P(x) ≡ 1.
• Khi α = 2, tiến hành tương tự như bài toán 3.
• Khi 0 < α < 2, tiến hành tương tự như bài toán 4.
BÀI 6 (Đề nghị thi Olympic 30/04/2011). Tìm tất cả các đa thức P(x) hệ số thực thỏa mãn phương trình hàm
P(x)P(3x2) = P(3x3 + x), ∀x ∈ R.
BÀI 7. Tìm tất cả các đa thức f (x) ∈ R[x] thỏa mãn
f (sin x + cos x) = f (sin x) + f (cos x), ∀x ∈ R. (1) L Lời giải
Dễ thấy đa thức f (x) ≡ c (c là hằng số) thỏa mãn các yêu cầu đề bài. Tiếp theo giả sử x
deg( f ) = n ≥ 1. Đặt t = tan , khi đó 2 2t 1 − t2 sin x = , cos x = . 1 + t2 1 + t2 Vậy (1) trở thành 1 + 2x − x2 2x 1 − x2 f = f + f . (2) 1 + x2 1 + x2 1 + x2 n
Giả sử f (x) = ∑ akxk + a0. Nhân cả hai vế của (2) với (1 + x2)n, rồi thay x bởi i (i là đơn k=1
vị ảo, i2 = −1) ta được a
n(2 + 2i)n = an (2i)n + 2n ⇔ (1 + i)n = 1 + in. (3) √ n
Số phức (1 + i)n có môđun là 2 . Ta có π π n nπ nπ 1 + in = 1 + cos + i sin = 1 + cos + i sin 2 2 2 2 r r r n 2 n n ⇒ π π π |1 + in| = 1 + cos + sin2 nπ = 2 + 2 cos = 4cos2 . 2 2 2 4 Do đó từ (3) suy ra
2n = 4cos2 nπ ⇔ 2n−2 = cos2 nπ . (4) 4 4 nπ
Khi n = 1 thì (4) đúng. Khi n = 2 thì (4) không đúng. Khi n > 2 thì 2n−2 > 2 > cos2 , 4
vậy (4) không đúng khi n > 2. Tóm lại (4) ⇔ n = 1. Do đó deg( f ) = 1 hay f (x) = ax + b.
Thay vào (1) được b = 0. Vậy f (x) ≡ ax. Các đa thức thỏa mãn yêu cầu đề bài là
f (x) ≡ c, f (x) ≡ ax (a, c là các hằng số, a 6= 0). MỤC LỤC
45 | Nguyễn Tài Chung - Giáo viên THPT Chuyên Hùng Vương - Gia Lai
BÀI 8. Tìm tất cả các đa thức hệ số thực f , g thỏa mãn:
f (g(x)) = f (x)g(x), ∀x ∈ R. (1) L Lời giải
Nếu g(x) ≡ 0 thì từ (1) suy ra f (x) là đa thức thỏa mãn f (0) = 0. Nếu f (x) ≡ 0 thì mọi
đa thức g(x) đều thỏa mãn yêu cầu đề bài. Tiếp theo giả sử f (x) 6≡ 0 và g(x) 6≡ 0. Từ (1) suy ra:
deg( f ). deg(g) = deg( f ) + deg(g). (2) deg( f ) = deg(g) = 0
Do deg( f ), deg(g) là những số tự nhiên nên (2) ⇔ deg( f ) = deg(g) = 2.
Khi deg( f ) = deg(g) = 0. Giả sử f (x) ≡ a, g(x) = b (a, b là những hằng số khác
0). Thay vào (1), ta được: a = ab ⇔ b = 1.
Giả sử deg( f ) = deg(g) = 2. Gọi x0 là một nghiệm của đa thức g(x) (x0 có thể là số phức). Từ (1) suy ra:
f (0) = f (g(x0)) = f (x0)g(x0) = 0 ⇒ f (x) = ax2 + bx (a 6= 0). Lúc này (1) trở thành:
a[g(x)]2 + bg(x) = ax2 + bx g(x), ∀x ∈ R
⇔ag(x) + b = ax2 + bx, ∀x ∈ R b b
⇔g(x) = ax2 + x − , ∀x ∈ R. a a
Kết luận: các cặp đa thức thỏa mãn yêu cầu đề bài là
f (x) ≡ anxn + · · · + a1x, g(x) ≡ 0
f (x) ≡ 0, g(x) là đa thức hệ số thực
f (x) ≡ a, g(x) ≡ 1 (a là hằng số khác 0) b b
f (x) ≡ ax2 + bx, g(x) ≡ ax2 + x −
(a, b là hằng số, a 6= 0). a a MỤC LỤC
Document Outline
- Số phức và một vài ứng dụng
- Lý thuyết
- Ví dụ giải toán
- Bài tập
- Đề bài
- Lời giải
- Sử dụng số phức chứng minh bất đẳng thức
- Sử dụng số phức giải phương trình, hệ phương trình
- Hệ lặp sinh bởi các đa thức đối xứng ba biến
- Sử dụng số phức để giải phương trình hàm đa thức




