Sử dụng phương pháp đại số, lượng giác giải bài toán tìm GTLN – GTNN môđun số phức Toán 12

Sử dụng phương pháp đại số, lượng giác giải bài toán tìm GTLN – GTNN môđun số phức Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

30 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 4: Số phức

Môn: Toán 12

Thông tin:

19 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
A. KIẾN THỨC CƠ BẢN
1. Định nghĩa
Lưu ý:
2. Bất đẳng thức tam giác
1 2 1 2
z z z z
dấubằngxảyrakhi
1 2
z kz
với
0
k
.
1 2 1 2
z z z z
dấubằngxảyrakhi
1 2
z kz
với
0
k
.
1 2 1 2
z z z z
dấubằngxảyrakhi
1 2
z kz
với
0
k
.
1 2 1 2
z z z z
dấubằngxảyrakhi
1 2
z kz
với
0
k
.
3. Bất đẳng thức AM-GM
Với
1 2
, ,...,
n
a a a
khôngâmtaluôncó
1 2 1 2
... . ....
n
n n
a a a n a a a
,
n
làsốtựnhiên
lớnhơn1.Dấubằngxảyrakhi
1 2
...
n
a a a
.
4. Bất đẳng thức Bunyakovsky
2
2 2 2 2 2 2
1 2 1 2 1 1 2 2
.... .... ...
n n n n
a a a b b b a b a b a b
Dấubằngxảyrakhi
1 2
1 2
...
a a
B. BÀI TẬP
Kĩ thuật 1: Đánh giá hai modun với nhau
Kĩthuậtnàychúngtatậndụngcácphépđánhgiá
a b a b
a b a b
Câu 1. Chosốphức
z
thỏamãn
2
1z i
.Giátrịlớnnhấtcủa
z
là
A.
5
. B.
2
. C.
2 2
. D.
2
.
Phân tích
Nhậnthấybêntrongmôđunchỉcó1vịtríchứa
z
bởivậytasẽnghĩđếnđánhgiáhai
modun
2
z i
,
z
vớinhau.
Côngcụchúngtahaydùngđểđánhgiácácmôđunvớinhau
a b a b
và
a b a b
.
Lời giải
Tacó:
2
2 2
1
z i z i z
.Dođó
2
1 1
z
2
2
z
0 2
z
.
Với
1z i
,tacó
2
1z i i
và
2
z
.
Dođó
max max
2
z z
.
Vậychọnđáp án D
CHUYÊN ĐỀ
SỬ DỤNG PHƯƠNG PHÁP ĐẠI SỐ, LƯỢNG GIÁC
GIẢI BÀI TOÁN TÌM GTLN - GTNN MÔĐUN SỐ PHỨC
Câu 2. Chosốphức
z
thỏamãn
z
khôngphảisốthựcvà
2
w
2
z
z
làsốthực.Tìmgiátrịlớnnhất
củabiểuthức
1P z i
.
A.
2 2
. B.
2
. C.
2
. D.
8
.
Phân tích
Đềbàicho
2
w
2
z
z
làsốthựcnêntatìmcáchbiểudiễnsốphức
z
theosốthựcđó.
Sauđótanhậnthấy
z
làẩncủaphươngtrìnhbậchai.Từđótasẽtìmđược
z
.
Nhậnthấybêntrongmôđunchỉcó1vịtríchứa
z
bởivậytasẽnghĩđếnđánhgiáhai
modun
1z i
,
z
vớinhau.
Côngcụchúngtahaydùngđểđánhgiácácmôdunvớinhau
a b a b
và
a b a b
.
Lời giải
Tacó
2 2
2
1
w w 2 2 0 *
2 w
z
z z z z
z
.
(*)làphươngtrìnhbậchaivớihệsốthực
1
w
.Vì
z
thỏa
*
nên
z
lànghiệmphương
trình
*
.Gọi
1 2
,z z
làhainghiệmcủa(*).
Suyra
1 2 1 2 1 2
2 2 2 2
z z z z z z z
.
Suyra
1 1 2 2 2 2
P z i z i
.Dấubằngxảyrakhi
1z i
.
Vậychọnđáp án A
Câu 3. Chosốphức
z
thỏa
2
z
.Tìmtíchgiátrịlớnnhấtvànhỏnhấtcủabiểuthức
z i
P
z
.
A.
3
.
4
B.
1
. C.
2
. D.
2
.
3
Phân tích
Nhậnthấy
z i
z
cóthểviếtlạithành
1
i
z
tứclàbêntrongcũngchỉ
cómộtvịtríchứa
z
.Nêntatìmcáchđánhgiá
z i
z
với
z
.
Côngcụchúngtahaydùngđểđánhgiácácmôdunvớinhau
a b a b
và
a b a b
.
Lời giải
Chọn A
Tacó
1 3
1 1 .
| | 2
i
P
z z
Mặtkhác:
1 1
1 1 .
| | 2
i
z z
Vậygiátrịnhỏnhấtcủa
P
là
1
2
,xảyrakhi
2 ;z i
giátrịlớnnhấtcủa
P
bằng
3
2
xảyrakhi
2 .z i
Câu 4. Xétsốphức
z
thỏamãn
2 1 3 2 2
z z i
.Mệnhđềnàodướiđâylàđúng?
A.
3
2
2
z
. B.
2
z
. C.
1 3
2 2
z
. D.
1
2
z
.
Lời giải
Cách 1
Sửdụngbấtđẳngthứcmodun,tacó
2 2 2 1 3 2 1 2 1 2 2
z z i z z i z z i
Dođódấubằngphảixảyra,tứclà
0
1
1 2
z i
z i z
z z i
Chọnđáp án C
Cách 2
Gọi
z x yi
,
;x y
đượcbiểudiễnbởiđiểm
;M x y
.
Suyra
2 2
2 2
2 1 3 2 1 3 1
z z i x y x y
2 3
MA MB
với
1;0 , 0;1
A B
.
Khiđó,điềukiệnbàitoántrởthành
2 3 2 2 2
MA MB AB
(1).
Mặtkhác,taluôncó:
2 3 2 2
MA MB MA MB MB AB MB
(2).
Từ(1)và(2),suyra:
2 2 3 2 2 2 0
AB MB MA MB AB AB MB AB MB
1 3
0 0;1 1 ;
2 2
MB M B Z
Câu 5. Chosốphức
z
thỏamãn
1
z
.Tìmgiátrịlớnnhất
max
M vàgiátrịnhỏnhất
min
M củabiểu
thức
2 3
1 1
M z z z
.
A.
max min
5; 1.
M M
B.
max min
5; 2.
M M
C.
max min
4; 1.
M M
D.
max min
4; 2.
M M
Phân tích
Tatìmcáchđánhgiá
2 3
1 1
z z z
với
z
.
Côngcụchúngtahaydùngđểđánhgiácácmôdunvớinhau
a b a b
và
a b a b
.
Lời giải
Chọn A
Tacó:
2 3
1 1 5
M z z z
,khi
max
1 5 5.
z M M
Mặtkhác:
3 3 3 3 3
3
1 1 1 1 1
1 1,
1 2 2 2
z z z z z
M z
z
khi
min
1 1 1.
z M M
Câu 6. Chosốphức
z
thỏamãn
1
3
z
z
.Tổngcủagiátrịlớnnhấtvàgiátrịnhỏnhấtcủa
z
là
A.
3
. B.
5
. C.
13
. D.
5
.
Phân tích
Tatìmcáchđánhgiá
1
z
z
với
z
.
Trướchếttacóbàitoántổngquát:Cho
, ,a b c
làcácsốthựcdươngvàsốphức
0
z
thỏamãn
b
az c
z
.Chứngminhrằng
2 2
4 4
2 2
c c ab c c ab
z
a a
.
Dấuđẳngthứcxảyrakhivàchỉkhi
z
làsốthuầnảo.
Dựavàodấuđẳngthứcxảyratachỉcầntiếnhànhgiảiphươngtrình
b
az c
z
rồilấy
trịtuyệtđốimỗinghiệm.Khiđósốdươngnhỏlà
min z
sốdươnglớnlà
max z
.
Lời giải
Tacó
2
1 1 3 13 3 13
3 3 1 0
2 2
z z z z z
z z
Dođó
3 13 3 13
min ;max
2 2
z z
.
Vậytổnggiátrịlớnnhấtvànhỏnhấtcủa
z
là
13
.
Kĩ thuật 2: Dùng các bất đẳng thức đại số
Kĩthuậtnàychúngtatậndụngcácphépđánhgiá
Với
1 2
, ,...
n
a a a
khôngâmtaluôncó
1 2 1 2
... . ....
n
n n
a a a n a a a
Dấubằngxảyrakhi
1 2
...
n
a a a
.
2
2 2 2 2 2 2
1 2 1 2 1 1 2 2
.... .... ...
n n n n
a a a b b b a b a b a b
Dấubằngxảyrakhi
1 2
1 2
...
a a
Câu 7. Chosốphức
z
thỏamãnđiềukiện
1 2
z .Tìmgiátrịlớnnhấtcủa
2
T z i z i
.
A.
max 8 2
T
. B.
max 4
T
. C.
max 4 2
T
. D.
max 8
T
.
Phân tích
Tatìmcáchbiểudiễn
z i
,
2z i
theo
1z
.Khiđó
2
T z i z i
biểudiễn
đượcdướidạng
và
1z
cũngbiểudiễnđượcdướidạng
Tatìmcáchđánhgiá
và
Lời giải
Chọn B
2 1 1 1 1
T z i z i z i z i
.
Đặt
1w z
.Tacó
1
w
và
1 1
T w i w i
.
Đặt
.w x y i
.Khiđó
2
2
.
2 2 2 2
2 2 2 2
2 2 2 2
1 1 1 1 1. 1 1 1. 1 1
1 1 1 1 1 1 2 2 2 4 4
T x y i x y i x y x y
x y x y x y
Vậy
max 4
T
.
Câu 8. Chosốphức
z
thỏamãn
3 3 8
z z
.Gọi
M
,
m
lầnlượtgiátrịlớnnhấtvànhỏnhất
của
.z
Khiđó
M m
bằng
A.
4 7.
B.
4 7.
C.
7.
D.
4 5.
Phân tích
Đềbàiyêucầutính
M m
dovậytasẽđitìmgiátrịlớnnhấtvàgiátrịnhỏnhấtcủa
z
Đềbàicho
3 3 8
z z
có2môđunmàmôđuncóthểbiểudiễnquacăn.Tứclàđề
bàichobiếttổnghaicăn.Dovậytasẽđánhgiátổnghaicănvớicănthứba.
CôngcụđểđánhtổnghaicănvớicănthứbacóthểdùngBunhiacopxki.
Lời giải
ChọnB
Gọi
z x yi
với
;x y
.
Tacó
8 3 3 3 3 2 4
z z z z z z
.
Dođó
4
M max z
khi
4z
.
Mà
2 2
2 2
3 3 8 3 3 8 3 3 8
z z x yi x yi x y x y
.
ÁpdụngbấtđẳngthứcBunhiacopxki,tacó
2 2 2 2
2 2 2 2 2 2
8 1. 3 1. 3 1 1 3 3
x y x y x y x y
2 2 2 2
8 2 2 2 18 2 2 2 18 64
x y x y
2 2 2 2
7 7 7
x y x y z
.
Dođó
M min z
.
Vậy
4 7
M m .
Câu 9. Tìmsốphức
z
saocho
3 4 5
z i
vàbiểuthức
2 2
2
P z z i
đạtgiátrịlớnnhất.
A.
2z i
. B.
5 5z i
. C.
2 2z i
. D.
4 3z i
.
Lời giải
Chọn B
Cách 1
Đặt
,z x yi x y
.
Khiđó
2 2
3 4 5 3 4 5
z i x y
.
Tacó
2 2
2 2
2 1 4 2 3 23 4 3 2 4
P x y x y x y P x y
Suyra
2 2
2 2
23 4 3 2 4 4 2 3 4 20.5 10
P x y x y
.
Suyra
13 33
P
.
Dođó:
max
33
P
khivàchikhi
3 4
5
4 2
5
4 3 2 4 10
x y
x
y
x y
.
Vậy
5 5z i
.
Cách 2
Đặt
,z x yi x y
.
Khiđó
2 2
3 4 5 3 4 5
z i x y
.
Đặt
3 5 sin 3 5 sin
4 5 cos 4 5 cos
x t x t
y t y t
.
2 2
2 4 2 3 4 3 5 sin 2 4 5 cos 3
P z z i x y t t
4 5 sin 2 5 cos 23
t t P
Theođiềukiệncónghiệmphươngtrìnhlượnggiác
2 2
2
2
4 5 2 5 23 46 429 0 13 33
P P P P
.
VậyGTLNcủa
P
là
33
5 5z i
.
Câu 10. Chosốphức
z
thỏamãn
1
z
vàsốphức
2
.
2
z i
w
iz
Khiđó,kếtluậnnàosauđâyđúng?
A.
w 2
. B.
w 1
. C.
w 2
. D.
1 w 2
.
Lời giải
Chọn B
Đặt
,z a bi a b
2 2
1
a b
do
1
z
.
2
2
z i
w
iz
2
2
2
2
2 2 1
2 2 1 4 2 1
2
2
2
a b i
a b i a b
b ai
b ai
b a
Tachứngminh
2
2
2
2
4 2 1
1
2
a b
b a
.
Thậtvậytacó:
2 2
2 2
4 2 1 2
a b b a
2 2
1
a b
.
Dấu
" "
xảyrakhivàchỉkhi
2 2
1
a b
.
Câu 11. Chobasốphức
1
z
,
2
z
,
3
z
thỏamãn
1 2 3
0
z z z
và
1 2 3
2
2
z z z
.Giátrịlớnnhấtcủa
biểuthứccủa
1 2 2 3 3 1
2 2
P z z z z z z
bằngbaonhiêu?
A.
max
7 2
3
P
. B.
max
3 6
2
P
. C.
max
4 5
5
P
. D.
max
10 2
3
P
.
Phân tích
Vớiphépbiếnđổi
2 2 2 2 2 2
1 2 2 3 3 1 1 2 3 1 2 3 1 2 3
z z z z z z z z z z z z z z z
giúpta
đánhgiá
1 2 2 3 3 1
z z z z z z
và
1 2 2
z z z
.
Lời giải
Chọn B
Ápdụngcôngthứcbiếnđổi
2 2 2 2 2 2
1 2 2 3 3 1 1 2 3
z z z z z z z z z
1 1 1 3
2 2 2 2
ÁpdụngbấtđẳngthứcBunhiacopxkitacó
2 2 2
2 2 2
1 2 2 3 3 1 1 2 2 3 3 1
3 3 6
2 2 1 2 2 3
2 2
P z z z z z z z z z z z z
Suyra
max
3 6
2
P
đápán
B
.
Câu 12. Vớihaisốphức
1 2
,z z
thỏamãn
1 2
8 6z z i
và
1 2
2
z z
.Tìmgiátrịlớnnhấtcủabiểuthức
1 2
P z z
.
A.
5 3 5
P . B.
2 26
P . C.
4 6
P . D.
34 3 2
P
.
Lời giải
Chọn B
Cách 1:Gọi
1 1 1
z a b i
và
2 2 2
z a b i
với
1 1 2 2
, , ,a b a b
.
Khiđó
1 2
1 2 1 2
1 2
1 2
1 2
1 2 1 2
2 2
1 2 1 2
8
8 6
8 6
6
2
2
4
a a
a a b b i i
z z i
b b
z z
a a b b i
a a b b
2 2 2 2
2 2 2 2
1 2 1 2 1 2 1 2 1 2 1 2
104 52
a a b b a a b b a a b b
*
.
Tacó
*
2 2 2 2 2 2 2 2 2 2
1 2 1 1 2 2 1 2 1 2
1 2 2.52 2 26
Bunh
P z z a b a b a a b b
max
2 26
P
đápán
B
.
Cách 2:Ápdụngcôngthứcbiếnđổi
2
.
z z z
và
1 2 1 2
z z z z
tacó:
2 2
1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2
z z z z z z z z z z z z z z z z z z z z
2 2
1 1 2 2 1 2
2 2 .
z z z z z z
Vậy
2 2 2 2
1 2 1 2 1 2
2
z z z z z z
.
Suyra
2 2
2 2 2
2 2
1 2 1 2
1 2
8 6 2
52
2 2
z z z z
z z
*
*
2 2
2 2
1 2 1 2 max
1 2 2.52 2 26 2 26
Bunh
P z z z z P
đápán
B
.
Câu 13. Xét các số phức
z a bi
,a b
thỏa mãn
4 3 5
z i . Tính
P a b
khi
1 3 1z i z i
đạtgiátrịlớnnhất.
A.
10
P
. B.
4P
. C.
6
P
. D.
8
P
.
Lời giải
Chọn A
Cách 1:
Tacó:
4 3 5
z i
2 2
4 3 5
a b
2 2
8 6 20
a b a b
Đặt
1 3 1A z i z i
tacó:
2 2 2 2
1 3 1 1
A a b a b
2 2 2 2
2 2 2
1 1 1 3 1 1
A a b a b
2 2
2 2 4 12
a b b
2 16 8 28
a b
8 4 2 7
a b
1
Mặtkháctacó:
4 2 7 4 4 2 3 15
a b a b
2 2
2 2
4 2 4 3 15 25
a b
2
Từ
1
và
2
tađược:
2
200
A
Để
max
10 2
A
4 2 7 25
4 3
4 2
a b
a b
6
4
a
b
Vậy
10
P a b
.
Cách 2:
Do
2 2
4 3 5 4 3 5
z i a b
Suyra
M C
cótâm
4;3
I
vàbánkính
5
R
Gọi
1;3
A
,
1; 1
B
,
0;1
I
Suyra
2 2
2
P MA MB MA MB
Mặtkháctacó
2
2 2 2
2
2
AB
MA MB MI
Suyra
Max Max
P MI I
làhìnhchiếuvuônggóccủa
M
trên
AB
, ,M I I
thẳnghàng.Vì
tathấy
IA IB MA MB
nênxảyradấu=.
Tacó
4; 3 , 4; 2
IM a a II
nên
AB
, ,M I I
thẳnghàng
2 4 4 3 2 2
a b a b
.
Tọađộ
M
lànghiệmcủahệ
2 2
2; 2
4 3 5
6; 4
2 2
a b
a b
a b
a b
Mặtkhác
2;2 2 10
6;4 10 2
M P MA MB
M P MA MB
Vậyđể
Max
P
thì
6;4
M
Suyra
10
a b
.
Cách 3
Tacó
2 2
4 3 5 4 3 5
z i a b
Đặt
5 sin 4
5 cos 3
a
b
.
Khiđó
2 2 2 2
1 3 1 1 3 1 1
M z i z i a b a b
10 5 sin 30 6 5 sin 8 5 cos 30
.
ÁpdụngBĐTBunhiacopski
2 16 5 sin 8 5 cos 60
M
2 8 5 2sin cos 60 10 2
.
Nên
max
10 2
M
khi
2
sin
5
1
cos
5
5 sin 4 6
5 cos 3 4
a
b
.
Vậy
10
P a b
.
Kĩ thuật 3: Dồn biến
Kĩthuậtnàychúngtađitheohướng
Vớisốphứcởdạngđạisốtừđềbàitađitìmmốiliênhệgiữaphầnthựcvàphầnảo.
Nếulàmđượcđiềunàytasẽdồnvề1biến.
Từđềbàichúngtađánhgiávềmộtmôđuncóthểlà
z
.
Câu 14. Trongcácsốphứcthỏamãnđiềukiện
3 2 .z i z i
Tìmsốphứccómôđunnhỏnhất?
A.
1 2z i
. B.
1 2
5 5
z i
. C.
1 2
5 5
z i
. D.
1 2z i
.
Phân tích
Đềbàicho
3 2z i z i
nêntasẽtìmđượcmốiliênhệgiữaphầnthựcvàphầnảo
củasốphứcz.Bởivậy
z
sẽdồnđượcmộtbiến.
Lời giải
Chọn C
Giảsử
,z x yi x y
.
2 2 2
2
3 2 3 2 1 3 2 1
z i z i x y i x y i x y x y
6 9 4 4 2 1 4 8 4 0 2 1 0 2 1y x y x y x y x y
.
2
2
2 2 2 2
2 1 5
2 1 5 4 1 5
5 5 5
z x y y y y y y
Suyra
min
5
5
z
khi
2 1
5 5
y x
Vậy
1 2
.
5 5
z i
Câu 15. Cho
z
thỏamãn
2 4 2z i z i
.TìmGTLNcủa
w
với
2 i
w
z
.
A.
2 2
w
. B.
10
8
w
. C.
10
4
w
. D.
10
w
.
Lời giải
Chọn C
Đặt
,z x yi x y
.Khiđó
2 4 2z i z i
2 4 2x yi i x yi i
2 2 2
2
2 4 2
x y x y
4 4 16 0
x y
4 0
x y
4
y x
.
Tacó
2 i
w
z
2
i
w
z
2 2 2
2
2
5 5
4
i
z
x y
x x
2
5
2 8 16
x x
2
5
2 2 8
x
.
Tacó
2
2 2 8 8
x
nên
2
5 5
2 2
2 8 16
w
x x
.Vậy
max
10
4
w
.
Câu 16. Chocácsốphức
1
1 3z i
,
2
5 3z i
.Tìmđiểm
;M x y
biểudiễnsốphức
3
z
,biếtrằng
trong mặt phẳng phức điểm
M
nằm trên đường thẳng
2 1 0
x y
và mô đun số phức
3 2 1
3 2w z z z
đạtgiátrịnhỏnhất.
A.
3 1
;
5 5
M
. B.
3 1
;
5 5
M
. C.
3 1
;
5 5
M
. D.
3 1
;
5 5
M
.
Lời giải
Chọn D
Tacóđiểm
; : 2 1 0
M x y d x y
nên
3
2 1; 2 1
M y y z y yi
Dođó
3 2 1
3 2 3 2 1 5 3 2 1 3 6 3 3w z z z y yi i i y y i
Suyra
2
2 2
2
1 4 4 6 5
6 3 3 3 5 2 1 3 5 3 ,
5 5 5 5
w y y y y y y
Vậy
6 5
min
5
w
,dấubằngxảyrakhi
1 3 1
;
5 5 5
y M
.
Câu 17. Cho
z
thỏamãn
2 4 2z i z i
.TìmGTLNcủa
w
với
2 i
w
z
.
A.
2 2
w
. B.
10
8
w
. C.
10
4
w
. D.
10
w
.
Lời giải
Chọn C
Đặt
,z x yi x y
.Khiđó
2 4 2z i z i
2 4 2x yi i x yi i
2 2 2
2
2 4 2
x y x y
4 4 16 0
x y
4 0
x y
4
y x
.
Tacó
2 i
w
z
2
i
w
z
2 2 2
2
2
5 5
4
i
z
x y
x x
2
5
2 8 16
x x
2
5
2 2 8
x
.
Tacó
2
2 2 8 8
x
nên
2
5 5
2 2
2 8 16
w
x x
.Vậy
max
10
4
w
.
Câu 18. Chosốphứczthoảmãn
1
z
.Tìmgiátrịlớnnhấtcủabiểuthức
1 2 1P z z
A.
max
2 5
P
. B.
max
2 10
P
. C.
max
3 5
P
. D.
max
3 2
P
.
Lời giải
Chọn A
Cách 1:
Đặt
; .
z x yi x y
Tacó
2 2
1 1.
z x y
Suyra
1;1
x
Tacó
2 2
2 2
1 2 1 1 2 1 2 2 2 2 2.
P z z x y x y x x
Xéthàm
2 2 2 2 2
f x x x
trênđoạn
1;1
,tađược
Tacó
1 2
2 2 2 2
f x
x x
,
3
0
5
f x x
Bảngbiếnthiên:
DựavàoBBT,tasuyra:
1;1
3
max 2 5
5
f x f
và
1;1
min 1 2
f x f
.
Cách 2: Bunhiacopxki
Theo BĐT Bunhiacopxki:
2 2 2
2 2
1 2 1 (1 2 ) 1 1 10 1 2 5
P z z z z z
.
Câu 19. Chosốphức
z
thỏamãn
1
z
.Tìmgiátrịlớnnhấtcủabiểuthức
1 3 1 .P z z
A.
3 15
B.
6 5
C.
20
D.
2 10.
Lời giải
Chọn D
Gọi
; ;z x yi x y
.Tacó:
2 2 2 2
1 1 1 1;1 .
z x y y x x
Tacó:
2 2
2 2
1 31 1 3 1 2 1 3 2 1
P z z x y x y x x
.
Xéthàmsố
2 1 3 2 1 ; 1;1 .
f x x x x
Hàmsốliêntụctrên
1;1
vàvới
1;1
x
tacó:
1 3 4
0 1;1 .
5
2 1 2 1
f x x
x x
Tacó:
max
4
1 2; 1 6; 2 10 2 10.
5
f f f P
Câu 20. Xétsốphức
z
thỏamãn
2 4 7 6 2
z i z i
.Gọi
m
,
M
lầnlượtlàgiátrịnhỏnhấtvàgiá
trịlớnnhấtcủa
1z i
.Tính
P m M
.
A.
13 73
P
. B.
5 2 2 73
2
P
. C.
5 2 2 73
P
. D.
5 2 73
2
P
.
Lời giải
Chọn B
Gọi
;M x y
làđiểmbiểudiễncủa
z
.Cácđiểm
2;1
A
,
4,7
B
,
1; 1
C
.
Tacó
2 4 7 6 2
z i z i
6 2
MA MB
,mà
6 2
AB
MA MB AB
.
Suyra
M
thuộcđoạnthẳng
AB
.
Phươngtrìnhđườngthẳng
: 3AB y x
,với
2;4
x
.
Tacó
2 2 2 2 2
2 2
1 1 1 1 1 4 2 6 17
z i MC z i MC x y x x x x
Đặt
2
2 6 17
f x x x
,
2;4
x
.
4 6
f x x
,
3
0
2
f x x
(nhận)
Tacó
2 13
f
,
3 25
2 2
f
,
4 73
f
.
Vậy
max
4 73
f x f
,
min
3 25
2 2
f x f
.
73
M
,
5 2
2
m
.
5 2 2 73
2
P
.
Câu 21. Chosốphức
z
thỏamãn
2 1 2 1 6
z i z i
.Tínhtổng
max minT z z
?
A.
5 5 2
2
T
. B.
0
T
. C.
6
T
. D.
3 5 2
2
T
.
Lời giải
Chọn A
Đặt
; ,z a bi a b
.
Tacó:
2 1 2 1 6
z i z i
2 1 2 2 1 6
a bi i a bi i
2 2 2 2
2 1 2 1 6
a b a b
2
2
2 2
45 9 1
5 9 9 1 0
5
b
a b a
1 5 1 5
b
Khiđó
2
2 2 2
45 9 1
5
b
z a b b
.
Khảosáthàmsố,tacó
2
2
1 5;1 5
45 9 1
min 1 5 5 1
5
b
b y
;
2
2
1 5;1 5
45 9 1
9 3 5
max
5 4 2
b
b y
.
Vậy
5 5 2
2
T
Câu 22. Chosốphứczthoảmãn
z 1
.GọiMvàmlầnlượtlàgiátrịlớnnhấtvàgiátrịnhỏnhấtcủa
biểuthức
2
1 1P z z z
.TínhgiátrịcủaM.n
A.
13 3
4
. B.
39
4
. C.
3 3
. D.
13
4
.
Lời giải
Chọn A
Cách 1:
Đặt
, ,z a bi a b
.Đặt
1t z
Tacó:
0 1 1 1 0 2
z z z t
.
2
2 2
2
2
1 1 1 1 1 2 2 2
2
t
t z z z zz z z z a a a
2 2 2 2
1 1 2 1 3 3
z z z z zz z z z z a t P t t
với
0;2
t
2
2
2
3, 3 2
3
3,0 3
t t t
P t t
t t t
Bảngbiếnthiên:
0;2 0;2
13 13 3
; 3 .
4 4
MaxP MinP M m
.
Cách 2:
(cos sinx)
z r x i a bi
Do
z 1
2
2 2
. 1
1
z z z
r a b
2 2cos 2cos 1
P x x
,dặt
cos 1;1 ( ) 2 2 2 1t x f t t t
TH1:
1
1;
2
t
max ( ) (1) 3
1
'( ) 2 0
1
min ( ) 3
2 2
2
f t f
f t
f t f
t
TH2:
1
;1
2
t
1 7 7 13
'( ) 2 0 max ( )
8 8 4
2 2
f t t f t f
t
13
( )
4
Maxf t
;
13 3
( ) 3 .
4
Minf t M n
.
Câu 23.
Chosốphức
z
thỏamãn
1
z
.Tìmtổnggiátrịlớnnhất,nhỏnhấtcủabiểuthức
P
với
2
1 1
P z z
?
A.
2 2
. B.
1 2 2
. C.
1 2 2
. D.
2 2
.
Lời giải
Tacó
2
2 2
1
1 1 2 ( 1) 2 2 2
z
P z z z z x x y x x
z
vì
2 2
1
x y
.
Khảosáthàmsố
( ) 2 2 2f x x x
với
1;1
x D
.
+ Với
0
x
tacó
( ) 2 2 2f x x x
tacó
1 2 2 2 1
'( ) 2
2 2 2 2
x
f x
x x
1 7
'( ) 0 2 2
4 8
f x x x
nêntacó
max (1) 0;min (0) 2
P P P P
.
+ Với
1 0
x
tađược
( ) 2 2 2f x x x
1
'( ) 2 0
2 2
f x
x
trêntậpđiềukiện.Hàmsốnghịchbiếntrên
1;0
.Từđótađược
max ( 1) 2;min (0) 2
P P P P
.
+Từtrêntađược
1;1
1;1
max ( 1) 2;min (0) 2
P P P P
.Vậykết.
Câu 24. Chosốphức
z
thỏamãn
. 1z z
.Tìmgiátrịnhỏnhấtcủabiểuthức:
3
3
P z z z z z
.
A.
15
4
. B.
3
4
. C.
13
4
. D.
3
.
Lời giải
Chọn B
Gọi
z a bi
,với
,a b
Tacó:
2z z a
;
2
. 1 1 1
z z z z
Khiđó
3 2
3 3
z
P z z z z z z z z z
z
2
2 2 2
2
. 3 2 1
z
P z z z z z zz z z z
z
2
2
2 2
1 3 3
1 4 1 2 4 1 2 2
2 4 4
P z z z z a a a a a
Vậy
min
3
4
P
.
Kĩ thuật 4: Lượng giác hóa
Câu 25. Chosốphức
z
thỏamãn
1 2 2
z i
.Tìmmôđunlớnnhấtcủasốphức
z
.
A.
9 4 5.
B.
11 4 5
. C.
6 4 5
. D.
5 6 5
.
Lời giải
Chọn A
Gọi
; ;z x yi x y
.Tacó:
2 2
1 2 2 1 2 4.
z i x y
Đặt
1 2sin ; 2 2cos ; 0;2
x t y t t
.
Lúcđó:
2 22
2 2
1 2sin 2 2cos 9 4sin 8cos 9 4 8 sin ;z t t t t t
2
9 4 5 sin 9 4 5; 9 4 5
z t z
max
9 4 5
z
đạtđượckhi
5 2 5 10 4 5
.
5 5
z i
Câu 26. Chosốphức
z
thỏamãn
1 6 2 10
i z i
.Tìmmôđunlớnnhấtcủasốphứcz.
A.
4 5
. B.
3 5.
C.
3.
D.
3 5
.
Lời giải
Chọn B
Gọi
; ;z x yi x y
.
Tacó:
2 2
6 2
1 6 2 10 1 . 10 2 4 5 2 4 5.
1
i
i z i i z z i x y
i
Đặt
2 5 sin ; 4 5 cos ; 0;2
x t y t t
.
Lúcđó:
2 2
2
2 2
2 5 sin 4 5 cos 25 4 5 sin 8 5 cos
25 4 5 8 5 sin ;
z t t t t
t
2
25 20sin 5;3 5
z t z
max
3 5
z
đạtđượckhi
3 6 .z i
Câu 27. Chosốphức
z
thỏamãn
1 2 3
z i
.Tìmmôđunlớnnhấtcủasốphức
2 .z i
A.
26 6 17.
B.
26 6 17 .
C.
26 8 17 .
D.
26 4 17.
Lời giải
Chọn A
Gọi
; ; 2 2z x yi x y z i x y i
.Tacó:
2 2
1 2 9 1 2 9
z i x y
.
Đặt
1 3sin ; 2 3cos ; 0;2 .
x t y t t
2 2
2
2 1 3sin 4 3cos 26 6 sin 4cos 26 6 17 sin ; .
z i t t t t t
max
26 6 17 2 26 6 17 2 26 6 17 .
z i z i
Câu 28. Chosốphức
z
thỏamãn
1
z
.Gọi
,M m
lầnlượtlàgiátrịlớnnhấtvàgiátrịnhỏnhấtcủa
tìm
1 3
1
2 2
Q z z i
.Tính
P M m
.
A.
4 2 3
. B.
2 2 3
. C.
2 6
. D.
2 6
.
Lời giải
Chọn C
Vì
1 cos sinz z x i x
và
1 3
cos sin 1 cos sin
2 2
Q x i x x i x i
2
2
2
2
1 3
cos 1 sin cos sin
2 2
x x x x
2 2cos 2 cos 3 sin 2 2 3;2 2 3
x x x
.
Dođó
2 2 3 2 2 3 2 6
P
.
Cách 2:Khibiết
1
z
,xétbađiểm
1 3
; , 1;0 , ;
2 2
M a b A B
tacó
Q MA MB
và
, ,M A B
cùngthuộcđườngtròn
,1
O
suyra
max
MA MB M
làđiểmchínhgiữacung
lớn
AB
.
min
MA MB M
làđiểmchínhgiữacungnhỏ
AB
.
Câu 29. Cho số phức
z
thay đổi thỏa mãn
1 5
z i
. Hỏi giá trị nhỏ nhất của biểu thức
7 9 2 1 8 8 P z i i z i
là?
A.
3 5
. B.
5 5
. C.
2 5
. D.
4 5
.
Lời giải
Chọn B
Với
1 5 cos sin
z i x i x
,tacó:
8 8
1 5 cos sin 7 9 2 1 5 cos sin
1
i
P i x i x i i x i x
i
8 8
5cos 6 5sin 8 2 5cos sin
1
i
x i x x i x
i
2 2 2 2
5cos 6 5sin 8 2 5cos 1 5sin 7
x x x x
25 60cos 80sin 100 2 25 10cos 70sin 50 5 5
x x x x
.
Câu 30. Chosốphức
z
thỏamãn
2
z i
.Gọi
,M m
lầnlượtlàgiátrịlớnnhấtvàgiátrịnhỏnhấtcủa
2 2 2 z z i
.Tính
P M m
A.
2 17
P
. B.
2 2 17
P
. C.
2 2 17
P
. D.
2 17
P
.
Hướngdẫngiải
Chọn B
Tacó:
2 cos sin
z i x i x
và
2 2 2 2 cos sin 2 2 cos sin 2 2 z z i x i x i x i x i i
2 2 2 2
2cos 2 2sin 1 2cos 2 2sin 1
x x x x
9 8cos 4sin 9 8cos 4sin
x x x x
2
2
18 16cos 2 9 8
1 in
cos 6s x x
x
2
18 16cos 2 80co 144cs
os 65
x xx
2;2 17
.
Câu 31. Gọi
,z x yi x y
là số phức thỏa mãn hai điều kiện
2 2
2 2 26
z z
và
3 3
2 2
z i
đạtgiátrịlớnnhất.Tínhtích
xy
.
A.
9
.
4
xy
B.
13
.
2
xy
C.
16
.
9
xy
D.
9
.
2
xy
Lời giải
Chọn D
Đặt
, .
z x iy x y
Thayvàođiềukiệnthứnhất,tađược
2 2
36.
x y
Đặt
3cos , 3sin .x t y t
Thayvàođiềukiệnthứhai,tacó
3 3
18 18sin 6.
4
2 2
P z i t
Dấubằngxảyrakhi
3 3 2 3 2
sin 1 .
4 4 2 2
t t z i
Kĩ thuật 5: Sử dụng biểu thức liên hợp
2
.
z z z
Câu 32. Chosốphức
z
thỏamãn
z
khôngphảilàsốthựcvà
2
2
z
w
z
làsốthựC.Giátrịlớnnhất
củabiểuthức
1M z i
là
A.
2 2
. B.
2
. C.
2
. D.
8
.
Lời giải
Chọn A
Do
w
làsốthực,suyra:
2
2
2
2 2 2 2
2
2 . 2 .
2 2 2 2
2
2
z z z z z z
w w z z z z z z
z z z z
z
z
2
2 . 0 . 2 2 2.
. 2
z
z z
z z z z z z z z
z z
Đặt
,z x yi x y
.Khiđó
2 2
2 2
z x y
(*).
Cách 1 (Theo đại số và kết hợp bất đẳng thức)
2 2
2 2
1 1 1 1 1 2 2 2
M z i x y i x y x y x y
(*)
2 2 4
x y
.
Suyra
2 2 2 2 2
max
2 2 4 2 2 4 8.2 4 8 2 2 2 2
M x y x y M M
Cách 2 (Theo hình học)
Gọiđiểm
;T x y
biểudiễnsốphức
z x yi
(*)
T
thuộcđườngtròn
C
cótâm
0;0
O
vàbánkính
2R
.
Tacó
2 2
1 1 1 1
M x y i x y TA
với
1;1
A
.
Do
1;1A
C
suyra
max max
2 2 2
M TA R
.
Chú ý:Nếu
max max
A C M TA OA R
.
Câu 33. Chosốphức
z
thỏamãn
2
4
z z
.Gọi
M
,
m
lầnlượtlàgiátrịlớnnhấtvàgiátrịnhỏnhất
của
z
.Tính
P M m
.
A.
2 17 1
2
P
. B.
17
P
. C.
17 1
2
P
. D.
2 17 1
2
P
.
Lời giải
Chọn B
Tacó
2
4
z z
2
4
1
z
z
4
1
z
z
4 4
1
z z
z z
4 4
1
z z
z
z
16
. 4 1
.
z z
z z
z
z z z
2
2
2
2 2
4
16
1
z z
z
z z
.
Vậyvới
0
a z
,tacó
2
2
16
1 8
a
a
17 1 17 1
2 2
a
.
Dođó
17 1 17 1
17
2 2
P
.
Câu 34. Chosốphức
z
thỏamãn
1
3
z
z
.Tính
max minP z z
.
A.
3
P
. B.
13
P
. C.
3 13
P
D.
3 13
P
.
Lời giải
Chọn B
Theogiảthiết,tacó
1 1 1 1
9 9
z z z z
z z z z
2
2
2 2
2 2
2 2 2 2
2
1 1
9 9
z z z
z z
z z
z z z z
2
2 2
2 2 2
2
1 1
9 11
z
z z
z z z
13 3 13 3
13
2 2
z P
Câu 35. Chosốphức
z
thỏamãn
1.
z
Gọi
M
và
m
lầnlượtlàgiátrịlớnnhấtvàgiátrịnhỏnhất
củabiểuthức
2
1 1 .
P z z z
Tínhgiátrịcủa
.M m
.
A.
13 3
.
4
B.
39
.
4
C.
3 3.
D.
13
.
4
Lời giải
Chọn A
Gọi
; ;z x yi x y
.Tacó:
1 . 1
z z z
Đặt
1t z
,tacó
0 1 1 1 2 0;2 .
z z z t
Tacó
2
2
2
1 1 1 . 2 2 .
2
t
t z z z z z z x x
Suyra
2
2 2 2
1 . 1 2 1 2 1 3
z z z z z z z z z x x t
.
Xéthàmsố
2
3 , 0;2 .
f t t t t
Bằngcáchdùngđạohàm,suyra
13 13 3
max ; min 3 . .
4 4
f t f t M n
Câu 36. Chosốphức
z
thỏamãn
3
1
4
z
z
.Tính
max minP z z
.
A.
4 2
P
. B.
2 2
P
. C.
4 2 2
P
. D.
2 2 2 1
P
.
Lời giải
Chọn D
Theogiảthiếttacó
3 3 3 3
1 1 1 1
16 116
z z z z
z z z z
2
4
2 2
4 4
6 6
2 2 2 2
2
1 1
16 16
z z z
z z
z z
z z z z
4
6
2 2
2
1 4 2 2 2 4 2 2 2
16 4 2 2
2 2
z
z z P
z z
.
_______________ TOANMATH.com _______________
| 1/19
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

CHUYÊN ĐỀ
SỬ DỤNG PHƯƠNG PHÁP ĐẠI SỐ, LƯỢNG GIÁC
GIẢI BÀI TOÁN TÌM GTLN - GTNN MÔĐUN SỐ PHỨC
A. KIẾN THỨC CƠ BẢN 1. Định nghĩa Lưu ý:
2. Bất đẳng thức tam giác
z z z z dấu bằng xảy ra khi z kz với k  0 . 1 2 1 2 1 2 
z z z z dấu bằng xảy ra khi z kz với k  0 . 1 2 1 2 1 2 
z z z z dấu bằng xảy ra khi z kz với k  0 . 1 2 1 2 1 2 
z z z z dấu bằng xảy ra khi z kz với k  0 . 1 2 1 2 1 2
3. Bất đẳng thức AM-GM
Với a , a ,..., a không âm ta luôn có a a  ... n
a n a .a ....a , n là số tự nhiên 1 2 n 1 2 n 1 2 n
lớn hơn 1.Dấu bằng xảy ra khi a a  ...a . 1 2 n
4. Bất đẳng thức Bunyakovsky
a a .... a b b ....b   a b a b ... a b n n n n 2 2 2 2 2 2 2 1 2 1 2 1 1 2 2 a a a Dấu bằng xảy ra khi 1 2   ... nb b b 1 2 n B. BÀI TẬP
Kĩ thuật 1: Đánh giá hai modun với nhau
Kĩ thuật này chúng ta tận dụng các phép đánh giá
a b a b
a b a b Câu 1.
Cho số phức z thỏa mãn 2
z i  1 . Giá trị lớn nhất của z là A. 5 . B. 2 . C. 2 2 . D. 2 . Phân tích
 Nhận thấy bên trong mô đun chỉ có 1 vị trí chứa z bởi vậy ta sẽ nghĩ đến đánh giá hai modun 2
z i , z với nhau.
 Công cụ chúng ta hay dùng để đánh giá các mô đun với nhau
a b a b và a b a b . Lời giải 2 2 2 Ta có: 2 2
z i z i z 1. Do đó z 1  1  z  2  0  z  2 .
Với z  1 i , ta có 2
z i i  1 và z  2 . Do đó zz  2 . max max
Vậy chọn đáp án D z Câu 2.
Cho số phức z thỏa mãn z không phải số thực và w 
là số thực. Tìm giá trị lớn nhất 2 2  z
của biểu thức P z 1 i . A. 2 2 . B. 2 . C. 2 . D. 8 . Phân tích z  Đề bài cho w 
là số thực nên ta tìm cách biểu diễn số phức z theo số thực đó. 2 2  z
Sau đó ta nhận thấy z là ẩn của phương trình bậc hai. Từ đó ta sẽ tìm được z .
 Nhận thấy bên trong mô đun chỉ có 1 vị trí chứa z bởi vậy ta sẽ nghĩ đến đánh giá hai
modun z  1 i , z với nhau.
 Công cụ chúng ta hay dùng để đánh giá các môdun với nhau
a b a b và a b a b . Lời giải z 1 Ta có w   w  2 2  z  2  z z z  2  0 * . 2   2  z w 1
(*) là phương trình bậc hai với hệ số thực
  . Vì z thỏa * nên z là nghiệm phương w
trình * . Gọi z , z là hai nghiệm của (*). 1 2
Suy ra z z  2  z z  2  z z  2  z  2 . 1 2 1 2 1 2
Suy ra P z 1 i z  1 i  2  2  2 2 . Dấu bằng xảy ra khi z  1  i .
Vậy chọn đáp án A z i Câu 3.
Cho số phức z thỏa z  2 . Tìm tích giá trị lớn nhất và nhỏ nhất của biểu thức P  . z 3 2 A. . B. 1. C. 2 . D. . 4 3 Phân tích z i i  Nhận thấy
có thể viết lại thành 1
tức là bên trong cũng chỉ z z z i
có một vị trí chứa z . Nên ta tìm cách đánh giá với z . z
 Công cụ chúng ta hay dùng để đánh giá các môdun với nhau
a b a b và a b a b . Lời giải Chọn A i 1 3 i 1 1 Ta có P  1  1  . Mặt khác: 1  1  . z | z | 2 z | z | 2 1 3
Vậy giá trị nhỏ nhất của P là
, xảy ra khi z  2i; giá trị lớn nhất của P bằng xảy ra khi 2 2 z  2 . i Câu 4.
Xét số phức z thỏa mãn 2 z 1  3 z i  2 2 . Mệnh đề nào dưới đây là đúng? 3 1 3 1 A.z  2 .
B. z  2 . C.z . D. z . 2 2 2 2 Lời giải Cách 1
Sử dụng bất đẳng thức modun, ta có
2 2  2 z 1  3 z i  2  z 1  z i   2 z 1  z i  2 2
Do đó dấu bằng phải xảy ra, tức là
z i  0  
z i z  1
z 1  z i  2   Chọn đáp án C Cách 2
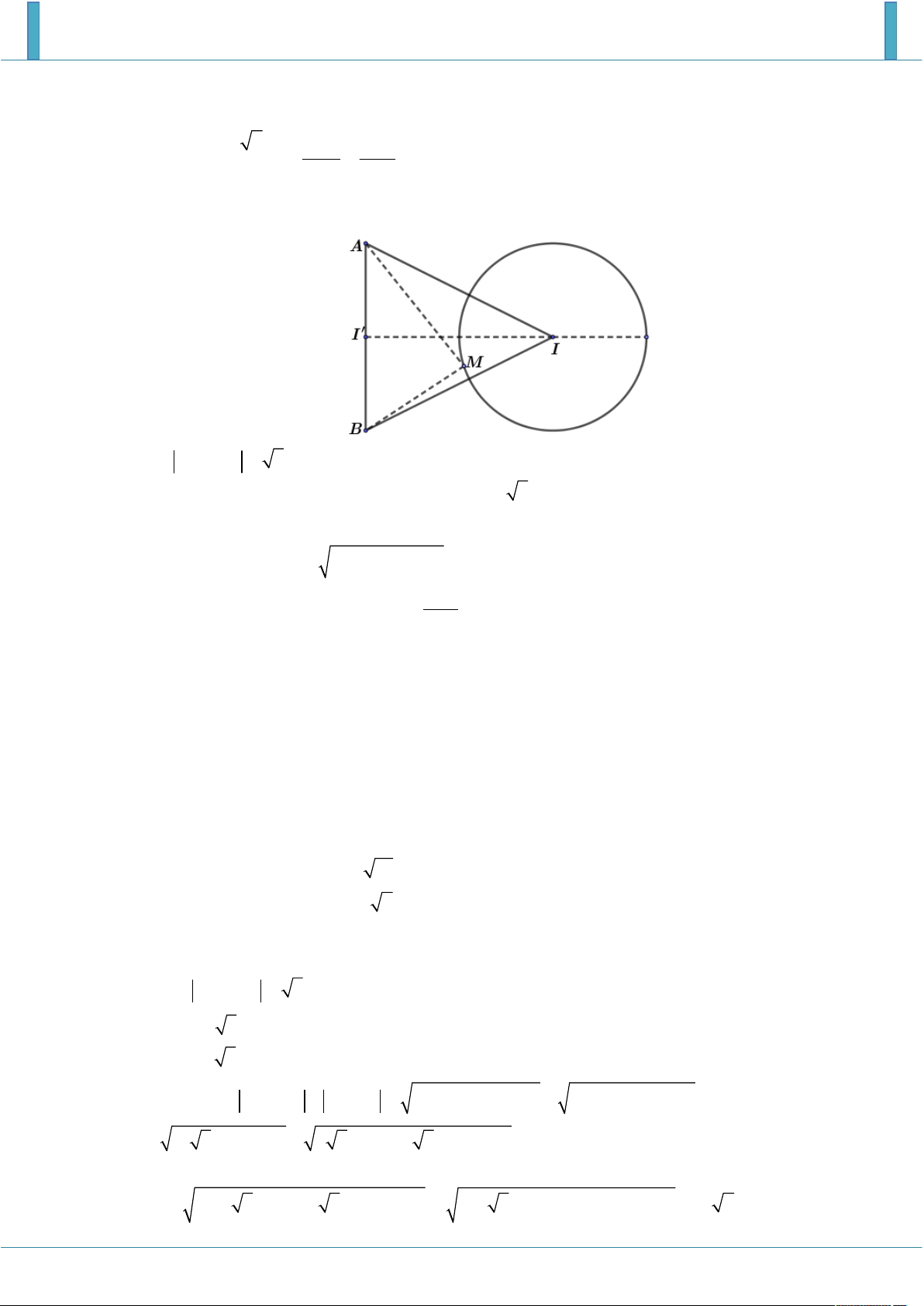
Gọi z x yi ,  x; y  được biểu diễn bởi điểm M x; y .
Suy ra z   z i
x  2  y
x   y  2 2 2 2 1 3 2 1 3 1
 2MA  3MB với A1;0, B 0  ;1 .
Khi đó, điều kiện bài toán trở thành 2MA  3MB  2 2  2AB (1).
Mặt khác, ta luôn có: 2MA  3MB  2 MA MB  MB  2 AB MB (2). Từ (1) và (2), suy ra:
2 AB MB  2MA  3MB  2AB  2AB MB  2AB MB  0  1 3 
MB  0  M B 0  ;1  Z  1 ;    2 2  Câu 5.
Cho số phức z thỏa mãn z  1. Tìm giá trị lớn nhất M
và giá trị nhỏ nhất M của biểu max min thức 2 3
M z z 1  z 1 . A. M  5; M  1. B. M  5; M  2. max min max min C. M  4; M  1. D. M  4; M  2. max min max min Phân tích  Ta tìm cách đánh giá 2 3
z z 1  z 1 với z .
 Công cụ chúng ta hay dùng để đánh giá các môdun với nhau
a b a b và a b a b . Lời giải Chọn A 2 3
Ta có: M z z 1 z 1  5 , khi z  1  M  5  M  5. max 3 3 3 3 3 1 z 1 z 1 z 1 z 1 z Mặt khác: 3 M   1 z     1, 1 z 2 2 2 khi z  1
  M  1  M  1. min 1 Câu 6.
Cho số phức z thỏa mãn z
 3 . Tổng của giá trị lớn nhất và giá trị nhỏ nhất của z là z A. 3 . B. 5 . C. 13 . D. 5 . Phân tích 1
 Ta tìm cách đánh giá z  với z . z
 Trước hết ta có bài toán tổng quát: Cho a, ,
b c là các số thực dương và số phức z  0 b 2 2
c c  4ab
c c  4ab thỏa mãn az
c . Chứng minh rằng  z  . z 2a 2a
Dấu đẳng thức xảy ra khi và chỉ khi z là số thuần ảo. b
 Dựa vào dấu đẳng thức xảy ra ta chỉ cần tiến hành giải phương trình az   c rồi lấy z
trị tuyệt đối mỗi nghiệm. Khi đó số dương nhỏ là min z số dương lớn là max z . Lời giải 1 1 2 3  13 3  13 Ta có z   z
 3  z  3 z 1  0   z z z 2 2 3   13 3  13 Do đó min z  ; max z  . 2 2
Vậy tổng giá trị lớn nhất và nhỏ nhất của z là 13 .
Kĩ thuật 2: Dùng các bất đẳng thức đại số
Kĩ thuật này chúng ta tận dụng các phép đánh giá
 Với a , a ,...a không âm ta luôn có a a  ... n
a n a .a ....a 1 2 n 1 2 n 1 2 n
Dấu bằng xảy ra khi a a  ...a . 1 2 n
 a a ....a b b ....b   a b a b ... a b n n n n 2 2 2 2 2 2 2 1 2 1 2 1 1 2 2 a a a Dấu bằng xảy ra khi 1 2   ... nb b b 1 2 n Câu 7.
Cho số phức z thỏa mãn điều kiện z 1 
2 . Tìm giá trị lớn nhất của T z i z  2  i .
A. max T  8 2 . B. max T  4 .
C. max T  4 2 . D. max T  8 . Phân tích
 Ta tìm cách biểu diễn z i , z  2  i theo z 1 . Khi đó T z i z  2  i biểu diễn được dưới dạng 
và z 1 cũng biểu diễn được dưới dạng  Ta tìm cách đánh giá  và Lời giải Chọn B
T z i z  2  i   z  
1  1 i   z   1  1 i .
Đặt w z 1 . Ta có w  1 và T w  1 i  w  1 i . 2
Đặt w x  . y i . Khi đó 2 2
w  2  x y .
T   x   1   y  
1 i   x   1   y  
1 i  1.  x  2 1   y  2 1 1.  x  2 1   y  2 1
 1 1  x  2 1   y  2 1   x  2 1   y  2 2 2 1   2 2 2
2x  2 y  4  4 Vậy max T  4 . Câu 8.
Cho số phức z thỏa mãn z  3  z  3  8 . Gọi M , m lần lượt giá trị lớn nhất và nhỏ nhất
của z . Khi đó M m bằng A. 4  7. B. 4  7. C. 7. D. 4  5. Phân tích
 Đề bài yêu cầu tính M m do vậy ta sẽ đi tìm giá trị lớn nhất và giá trị nhỏ nhất của z
 Đề bài cho z  3  z  3  8 có 2 môđun mà môđun có thể biểu diễn qua căn. Tức là đề
bài cho biết tổng hai căn. Do vậy ta sẽ đánh giá tổng hai căn với căn thứ ba.
 Công cụ để đánh tổng hai căn với căn thứ ba có thể dùng Bunhiacopxki. Lời giải Chọn B
Gọi z x yi với x; y   .
Ta có 8  z  3  z  3  z  3  z  3  2z z  4 .
Do đó M max z  4 khi z  4 . 2 2 Mà z   z  
x   yi x   yi    x   2
y   x   2 3 3 8 3 3 8 3 3  y  8 .
Áp dụng bất đẳng thức Bunhiacopxki, ta có  x 2 yx 2 y
x 2 y x 2 2 2 2 2 2 2 8 1. 3 1. 3 1 1 3 3 y                    2 2 x y     2 2 8 2 2 2 18
2 2x  2 y  18  64 2 2 2 2
x y  7 
x y  7  z  7 .
Do đó M min z  7 .
Vậy M m  4  7 . 2 2 Câu 9.
Tìm số phức z sao cho z  3  4i  5 và biểu thức P z  2  z i đạt giá trị lớn nhất.
A. z  2  i .
B. z  5  5i .
C. z  2  2i .
D. z  4  3i . Lời giải Chọn B Cách 1
Đặt z x yi x, y   . 2 2
Khi đó z  3  4i  5   x  3   y  4  5 . 2 2
Ta có P   x   2 2 2
y x   y   1
 4x  2 y  3  P  23  4  x  3  2  y  4 2 2 Suy ra P  
x     y     2 2 23 4 3 2 4
4  2  x 3   y  4   20.5 10 .
Suy ra 13  P  33 .  x  3 y  4   x  5 Do đó: P  33 khi và chi khi  4 2  . max    
x     y   y 5 4 3 2 4  10  
Vậy z  5  5i . Cách 2
Đặt z x yi x, y   . 2 2
Khi đó z  3  4i  5   x  3   y  4  5 . 
x  3  5 sin t x  3  5 sin t Đặt  .
y  4  5 cos t y  4  5 cos t  2 2
P z  2  z i  4x  2 y  3  4 3  5 sin t   24  5 cost  3
 4 5 sin t  2 5 cos t P  23
Theo điều kiện có nghiệm phương trình lượng giác   2  2  P  2 2 4 5 2 5 23
P  46P  429  0  13  P  33 .
Vậy GTLN của P là 33  z  5  5i . 2z i
Câu 10. Cho số phức z thỏa mãn z  1 và số phức w
. Khi đó, kết luận nào sau đây đúng? 2  iz A. w  2 . B. w  1 . C. w  2 . D. 1  w  2 . Lời giải Chọn B
Đặt z a bi a, b   2 2
a b  1 do z  1 . 2 2z i
2a  2b   1 i
2a  2b   2 1 i
4a  2b   1 w     2  iz
2  b  ai
2  b  ai 2  b2 2  a
4a  2b  2 2 1 Ta chứng minh  1. 2  b2 2  a 2 2 Thật vậy ta có: 2
a   b      b 2 4 2 1 2  a 2 2
a b  1 .
Dấu "  " xảy ra khi và chỉ khi 2 2 a b  1. 2
Câu 11. Cho ba số phức z , z , z thỏa mãn z z z  0 và z z z
. Giá trị lớn nhất của 1 2 3 1 2 3 1 2 3 2
biểu thức của P z z  2 z z  2 z z bằng bao nhiêu? 1 2 2 3 3 1 7 2 3 6 4 5 10 2 A. P  . B. P  . C. P  . D. P  . max 3 max 2 max 5 max 3 Phân tích  Với phép biến đổi 2 2 2 2 2 2 z zz zz zzzz
z z z
z z z giúp ta 1 2 2 3 3 1 1 2 3  1 2 3   1 2 3 
đánh giá z z z z z z và z z z . 1 2 2 3 3 1 1 2 2 Lời giải Chọn B 2 2 2 2 2 2 1 1 1 3
Áp dụng công thức biến đổi z zz zz zzzz     1 2 2 3 3 1 1 2 3 2 2 2 2
Áp dụng bất đẳng thức Bunhiacopxki ta có
P z z  2 z z  2 z z  1  2  2  2 2 2 3 3 6 2 2 2 z zz zz z  3  1 2 2 3 3 1 1 2 2 3 3 1  2 2 3 6 Suy ra P   đáp án B . max 2
Câu 12. Với hai số phức z , z thỏa mãn z z  8  6i và z z  2 .Tìm giá trị lớn nhất của biểu thức 1 2 1 2 1 2
P z z . 1 2
A. P  5  3 5 . B. P  2 26 . C. P  4 6 .
D. P  34  3 2 . Lời giải Chọn B
Cách 1: Gọi z a b i và z a b i với a , b , a , b   . 1 1 1 2 2 2 1 1 2 2 a a  8
z z  8  6i
a a   b b  1 2 i  8  6i   1 2  1 2 1 2  Khi đó     b   b  6 z z  2  
 a a   b b  1 2 i  2 1 2 1 2 1 2  a a
2  b b 2  4  1 2 1 2
 a a 2  b b 2  a a 2  b b 2 2 2 2 2
 104  a a b b  52 * . 1 2 1 2 1 2 1 2 1 2 1 2 Bunh * Ta có 2 2 2 2
P z z
a b a b   2 2 1  2  2 2 2 2
a a b b  2.52  2 26 1 2 1 1 2 2 1 2 1 2   P  2 26 max  đáp án B . 2
Cách 2: Áp dụng công thức biến đổi z.z z và z z z z ta có: 1 2 1 2 2 2 z zz zz z z zz z z zz z z zz z z z 1 2 1 2  1 2   1 2   1 2   1 2   1 2   1 2   1 2   1 2 
 2 z z z z   2 2 2 zz . 1 1 2 2 1 2  2 2 2 2 Vậy z zz z  2 zz . 1 2 1 2  1 2  2 2 2 2 2 2 2 z zz z 8  6  2 Suy ra 1 2 1 2 zz    52 * 1 2 2 2 Bunh   *
P z z  1  2  2 2 2 2 zz  2.52  2 26  P
 2 26  đáp án B . 1 2 1 2  max
Câu 13. Xét các số phức z a bi a,b   thỏa mãn
z  4  3i  5 . Tính P a b khi
z 1 3i z 1 i đạt giá trị lớn nhất. A. P  10 . B. P  4 . C. P  6 . D. P  8 . Lời giải Chọn A Cách 1: 2 2
Ta có: z  4  3i  5  a  4  b  3  5 2 2
a b  8a  6b  20
Đặt A z 1 3i z 1 i ta có:
A  a  2  b  2  a  2  b  2 1 3 1 1
A    a  2  b  2  a  2  b  2 2 2 2 1 1 1 3 1 1     2 2
2 2 a b   4b 12
 216a  8b  28  84a  2b  7   1 Mặt khác ta có: 2 2
4a  2b  7  4 a  4  2b  3 15   2 2
4  2 a  4  b  3  15  25 2 Từ   1 và 2 ta được: 2 A  200
4a  2b  7  25  a  6 Để A  10 2   max  a  4 b  3    b  4   4 2
Vậy P a b  10 . Cách 2: 2 2
Do z  4  3i  5  a  4  b  3  5
Suy ra M C  có tâm I 4;3 và bán kính R  5 Gọi A 1
 ;3 , B 1;   1 , I 0  ;1
Suy ra P MA MB   2 2 2 MA MB  2 AB Mặt khác ta có 2 2 2
MA MB  2MI   2 Suy ra PMI
I  là hình chiếu vuông góc của M trên AB M , I , I  thẳng hàng. Vì Max Max
ta thấy IA IB MA MB nên xảy ra dấu=.  
Ta có IM  a  4; a  3, II   4; 2 nên AB M , I , I  thẳng hàng  2  a  4  4
 b  3  a  2b  2 .
Tọa độ M là nghiệm của hệ  
a  42  b  32  5
a  2;b  2 
 a  6;b  4
a  2b  2   Mặt khác
M 2; 2  P MA MB  2 10
M 6; 4  P MA MB  10 2 Vậyđể P
thì M 6; 4 Suy ra a b  10 . Max Cách 3 2 2
Ta có z  4  3i  5  a  4  b  3  5 
a  5 sin   4 Đặt b .   5 cos  3  2 2 2 2
Khi đó M z 1 3i z 1 i  a  
1  b  3  a   1  b   1
 10 5 sin   30  6 5 sin   8 5 cos  30 . Áp dụng BĐT Bunhiacopski M
2 16 5 sin  8 5 cos  60  2 8 5 2sin  cos   60  10 2 .    2 sin     5 
a  5 sin   4  6 Nên M  10 2 khi  . max   1 cos  b   5 cos  3  4    5
Vậy P a b  10 .
Kĩ thuật 3: Dồn biến
Kĩ thuật này chúng ta đi theo hướng
 Với số phức ở dạng đại số từ đề bài ta đi tìm mối liên hệ giữa phần thực và phần ảo.
Nếu làm được điều này ta sẽ dồn về 1 biến.
 Từ đề bài chúng ta đánh giá về một môđun có thể là z .
Câu 14. Trong các số phức thỏa mãn điều kiện z  3i z  2  i . Tìm số phức có môđun nhỏ nhất? 1 2 1 2
A. z 1 2i . B. z    i . C. z   i . D. z  1   2i . 5 5 5 5 Phân tích
 Đề bài cho z  3i z  2  i nên ta sẽ tìm được mối liên hệ giữa phần thực và phần ảo
của số phức z. Bởi vậy z sẽ dồn được một biến. Lời giải Chọn C
Giả sử z x yi x, y   .
z i z   i x   y  i   x     y  i x   y  2   x  2   y  2 2 3 2 3 2 1 3 2 1
 6 y  9  4x  4  2 y  1  4x  8 y  4  0  x  2 y 1  0  x  2 y 1. 2  2  1 5 z
x y  2 y  2 2 2 2 2
1  y  5 y  4 y 1  5 y       5  5 5 5 2 1 1 2 Suy ra z  khi y    x  Vậy z   . i min 5 5 5 5 5 2  i
Câu 15. Cho z thỏa mãn z  2  4i z  2i . Tìm GTLN của w với w  . z 10 10 A. w  2 2 . B. w  . C. w  . D. w  10 . 8 4 Lời giải Chọn C
Đặt z x yi , x y   . Khi đó
z  2  4i z  2i x yi  2  4i x yi  2i   x  2   y  2  x   y  2 2 2 4 2
 4x  4 y  16  0  x y  4  0  y  4  x . Ta có 2  i 2  i 2  i 5 5 5 w   w      z z 2 2 z x y 2
x  4  x2 2 2x  8x 16 5  . 2  x  22  8 5 5 10 Ta có  x  2 2
2  8  8 nên w   . Vậy w  . 2 max 2x  8x 16 2 2 4
Câu 16. Cho các số phức z  1 3i , z  5
  3i . Tìm điểm M x; y biểu diễn số phức z , biết rằng 1 2 3
trong mặt phẳng phức điểm M nằm trên đường thẳng x  2 y 1  0 và mô đun số phức
w  3z z  2z đạt giá trị nhỏ nhất. 3 2 1  3 1   3 1   3 1   3 1  A. M  ;    . B. M ;    . C. M ;   . D. M  ;   .  5 5   5 5   5 5   5 5  Lời giải Chọn D
Ta có điểm M x; y  d : x  2 y 1  0 nên M 2 y 1; y  z  2 y 1 yi 3
Do đó w  3z z  2z  3 2 y 1 yi  5  3i  2 1 3i  6 y  3y  3 i 3 2 1         2 2 2  1  4 4 6 5
Suy ra w  6 y  3y  3 2
 3 5y  2 y 1  3 5 y    3  , y       5  5 5 5 6 5 1  3 1  Vậy min w
, dấu bằng xảy ra khi y   M  ;   . 5 5  5 5  2  i
Câu 17. Cho z thỏa mãn z  2  4i z  2i . Tìm GTLN của w với w  . z 10 10 A. w  2 2 . B. w  . C. w  . D. w  10 . 8 4 Lời giải Chọn C
Đặt z x yi , x y   . Khi đó
z  2  4i z  2i x yi  2  4i x yi  2i   x  2   y  2  x   y  2 2 2 4 2
 4x  4 y  16  0  x y  4  0  y  4  x . Ta có 2  i 2  i 2  i 5 5 5 w   w      z z 2 2 z x y 2
x  4  x2 2 2x  8x 16 5  . 2  x  22  8 5 5 10 Ta có  x  2 2
2  8  8 nên w   . Vậy w  . 2 max 2x  8x 16 2 2 4
Câu 18. Cho số phức z thoả mãn z  1. Tìm giá trị lớn nhất của biểu thức P z 1  2 z 1 A. P  2 5 . B. P  2 10 . C. P  3 5 . D. P  3 2 . max max max max Lời giải Chọn A Cách 1:
Đặt z x yi  ; x y  . Ta có 2 2
z  1  x y  1. Suy ra x 1;  1 2 2
Ta có P z  
z    x   2  y   x   2 1 2 1 1 2 1  y
2x  2  2 2x  2.
Xét hàm f x  2x  2  2 2
x  2 trên đoạn 1;  1 , ta được 1 2 3
Ta có f  x  
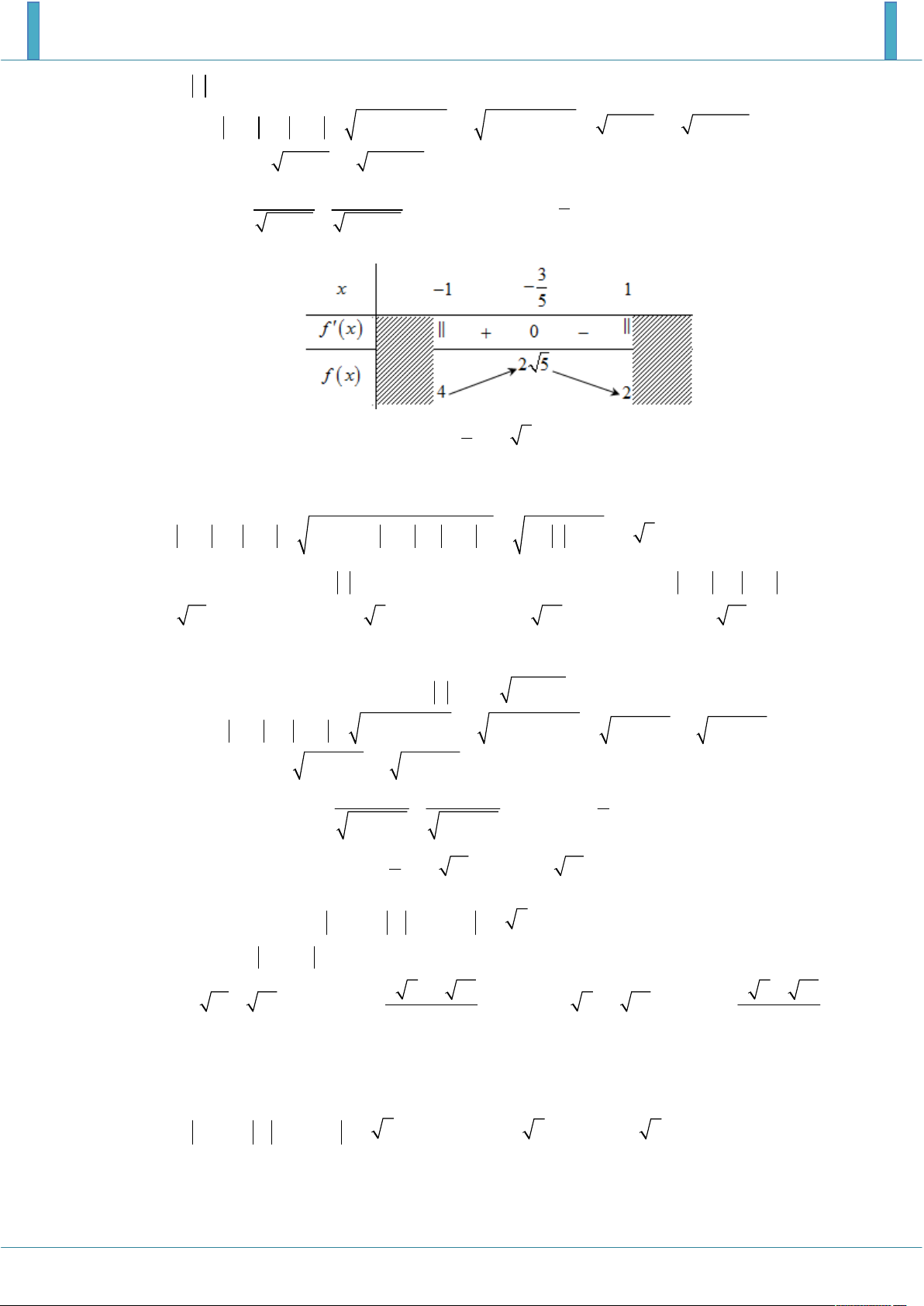
, f  x  0  x   2x  2 2x  2 5 Bảng biến thiên:  3 
Dựa vào BBT, ta suy ra: max f x  f   2 5  
và min f x  f   1  2 .  1  ;  1  5  1;  1 Cách 2: Bunhiacopxki
Theo BĐT Bunhiacopxki: P z   z     2 2 z   z     2 2 2 1 2 1 (1 2 ) 1 1 10 z   1  2 5 .
Câu 19. Cho số phức z thỏa mãn z  1. Tìm giá trị lớn nhất của biểu thức P  1 z  3 1 z . A. 3 15 B. 6 5 C. 20 D. 2 10. Lời giải Chọn D
Gọi z x yi;  x  ; y   . Ta có: 2 2 2 2 z  1 
x y  1  y  1 x x  1  ;  1 . 2 2
Ta có: P   z
z    x 2  y    x 2 1 3 1 1 3 1  y
2 1 x  3 21 x .
Xét hàm số f x  21 x  3 21 x; x  1  
;1 . Hàm số liên tục trên  1   ;1 và với 1 3 4 x   1  
;1 ta có: f  x  
 0  x     1   ;1 . 2 1 x 21 x 5  4  Ta có: f   1  2; f   1  6; f   2 10  P  2 10.   max  5 
Câu 20. Xét số phức z thỏa mãn z  2  i z  4  7i  6 2 . Gọi m , M lần lượt là giá trị nhỏ nhất và giá
trị lớn nhất của z 1  i . Tính P m M . 5 2  2 73 5 2  73
A. P  13  73 . B. P
. C. P  5 2  2 73 . D. P  . 2 2 Lời giải Chọn B
Gọi M x; y là điểm biểu diễn của z . Các điểm A2; 
1 , B 4, 7 , C 1;   1 .
Ta có z  2  i z  4  7i  6 2  MA MB  6 2 , mà AB  6 2  MA MB AB .
Suy ra M thuộc đoạn thẳng AB .
Phương trình đường thẳng AB : y x  3 , với x  2; 4 . 2 2 2 2 2 Ta có 2
z   i MC z   i MC   x     y     x     x   2 1 1 1 1 1 4
 2x  6x 17
Đặt f x 2
 2x  6x  17 , x  2; 4 . 3
f   x  4x  6 , f  x  0  x   ( nhận ) 2  3  25
Ta có f 2  13 , f     , f 4  73 .  2  2  3  25 Vậy f x
f 4  73 , f x  f   . max min    2  2 5 2 5 2  2 73
M  73 , m  .  P  . 2 2
Câu 21. Cho số phức z thỏa mãn z  2i 1  z  2i 1  6 . Tính tổng T  max z  min z ? 5 5  2 3 5  2 A. T  . B. T  0 . C. T  6 . D. T  . 2 2 Lời giải Chọn A
Đặt z a  ; bi , a b   .
Ta có: z  2i 1  z  2i 1  6
 a bi  2i 1  2 a bi  2i 1  6 2 2 2 2
 a  2  1 b  a  2  b   1  6 2 2 45  9 b 1 2 2   
 59  a   9b   1  a   0 5
 1  5  b  1 5 2 45  9 b 1 2 2    Khi đó z a b   2 b . 5 Khảo sát hàm số, ta có 2 45  9b   1 min  2
b y 1 5  5 1;      1 5;  1 5 5   2 45  9b   1  9  3 5 max  2 b y    .    1 5;  1 5 5 4 2     5 5  2 Vậy T  2
Câu 22. Cho số phức z thoả mãn z  1. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2
P z 1  z z 1 . Tính giá trị của M.n 13 3 39 13 A. . B. . C. 3 3 . D. . 4 4 4 Lời giải Chọn A Cách 1:
Đặt z a bi, a,b   . Đặt t z 1
Ta có : 0  z 1  z 1  z 1  0  t  2 . 2 2 t  2
t z 1   z   1  z   2 2
1  1 z z z z  1 z  2a  2  2a a  2 2 2 2 2
z z 1  z z z z z z 1 z z 2a 1  t  3  P t t  3 với t 0; 2 2 t  
t  3, 3  t  2 2
P t t  3   2  t
t  3, 0  t  3  Bảng biến thiên: 13 13 3  MaxP
; MinP  3  M .m  . 0;2 0;2 4 4  Cách 2:
z r(cos x i s inx)  a bi 2
z.z z  1  Do z  1   2 2 r a b  1 
P  2  2 cos x  2 cos x 1 , dặt t  cos x 1  ;1  f (t) 
2  2t  2t 1  1  TH1: t  1;  2   
max f (t)  f (1)  3 1  f '(t)   2  0    1  2  2t
min f (t)  f  3      2   1  TH2: t  ;1  2    1 7  7  13 f '(t) 
 2  0  t  
 max f (t)  f     2  2t 8  8  4 13 13 3  Maxf (t) 
; Minf (t)  3  M .n  . 4 4
Câu 23. Cho số phức z thỏa mãn z  1. Tìm tổng giá trị lớn nhất, nhỏ nhất của biểu thức P với 2
P  1 z  1 z ? A. 2  2 . B. 1 2 2 . C. 1   2 2 . D. 2  2 . Lời giải Ta có 2 1 z 2 2 P
 1 z z z  1 z  2 x  (x 1)  y  2 x  2  2x vì 2 2 x y  1. z
Khảo sát hàm số f (x)  2 x  2  2x với x D  1  ;1 . 1 2 2  2x 1
+ Với x  0 ta có f (x)  2x  2  2x ta có f '(x)  2   2  2x 2  2x 1 7 f '(x)  0  2  2x   x  
nên ta có max P P(1)  0; min P P(0)   2 . 4 8 + Với 1
  x  0 ta được f (x)  2
x  2  2x 1 f '(x)  2  
 0 trên tập điều kiện. Hàm số nghịch biến trên 1;0 . Từ đó ta được 2  2x
max P P(1)  2; min P P(0)   2 .
+ Từ trên ta được max P P(1)  2; min P P(0)   2 . Vậy kết. 1;  1 1;  1
Câu 24. Cho số phức z thỏa mãn .
z z  1. Tìm giá trị nhỏ nhất của biểu thức: 3
P z  3z z z z . 15 3 13 A. . B. . C. . D. 3 . 4 4 4 Lời giải Chọn B
Gọi z a bi , với a, b   2
Ta có: z z  2a ; .
z z  1  z  1  z  1  z  Khi đó 3 2
P z  3z z z z z z  3   z z    z  2 z 2 2 2
P z . z  3 
z z z  2zz z 1  z z 2 z 2  1  3 3
P   z z 2 2 2
1  z z  4a 1  2 a  4a 1 2 a  2 a       2  4 4 3 Vậy P  . min 4
Kĩ thuật 4: Lượng giác hóa
Câu 25. Cho số phức z thỏa mãn z 1 2i  2 . Tìm môđun lớn nhất của số phức z . A. 9  4 5 . B. 11 4 5 . C. 6  4 5 . D. 5  6 5 . Lời giải Chọn A 2 2
Gọi z x yi;  x  ; y   . Ta có: z 1 2i  2   x  
1   y  2  4.
Đặt x  1 2 sin t; y  2  2 cos t; t 0; 2  . Lúc đó: 2 z    t 2    t 2    t t  2 2 1 2sin 2 2 cos 9 4sin 8 cos
 9  4  8 sin t  ;    2 z 9 4 5 sin t   z  9 4 5 ; 9 4 5             5  2 5 10   4 5  z
 9  4 5 đạt được khi z   . i max 5 5
Câu 26. Cho số phức z thỏa mãn 1 iz  6  2i  10 . Tìm môđun lớn nhất của số phức z. A. 4 5 . B. 3 5. C. 3. D. 3  5 . Lời giải Chọn B
Gọi z x yi;  x  ; y   . Ta có: 6  2i
1 iz  6  2i  10  1 i . z
 10  z  2  4i  5   x  22   y  42  5. 1 i
Đặt x  2  5 sin t; y  4  5 cos t; t 0; 2  . Lúc đó:
z  2  5 sin t 2  4  5 cost 2 2
 25  4 5 sin t  8 5 cost
 25  4 52  8 5 2 sin t  ;    2
z  25  20sin t    z   5;3 5    z
 3 5 đạt được khi z  3  6 . i max
Câu 27. Cho số phức z thỏa mãn z 1 2i  3 . Tìm môđun lớn nhất của số phức z  2 . i A. 26  6 17 . B. 26  6 17 . C. 26  8 17 . D. 26  4 17 . Lời giải Chọn A
Gọi z x yi;  x  ; y    z  2i x   y  2i . Ta có: z   i
  x  2   y  2 1 2 9 1 2  9 .
Đặt x  1 3sin t; y  2  3cos t; t 0; 2 . 2
z  2i  1 3sin t 2   4
  3cos t 2  26  6sin t  4 cos t   26  6 17 sin t   ;   .
 26  6 17  z  2i  26  6 17  z  2i  26  6 17 . max
Câu 28. Cho số phức z thỏa mãn z  1. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của 1 3
tìm Q z 1  z  
i . Tính P M m . 2 2 A. 4  2 3 . B. 2  2 3 . C. 2 6 . D. 2  6 . Lời giải Chọn C 1 3
Vì z  1 z  cos x i sin x và Q  cos x i sin x 1  cos x i sin x   i 2 2 2 2  1   3   cos x  2 2 1  sin x  cos x      sin x   2  2      2 2 cos x 2 cos x 3 sin x 2 2 3 ; 2 2 3          .  
Do đó P  2 2  3  2 2  3  2 6 .  1 3 
Cách 2: Khi biết z  1, xét ba điểm M a;b, A1;0, B  ; 
 ta có Q MA MB và  2 2    M , ,
A B cùng thuộc đường tròn  , O
1 suy ra MAMB
M là điểm chính giữa cung max  
lớn AB . MA MB
M là điểm chính giữa cung nhỏ AB . min
Câu 29. Cho số phức z thay đổi thỏa mãn z 1 i  5 . Hỏi giá trị nhỏ nhất của biểu thức
P z  7  9i  2 1 iz  8  8i là? A. 3 5 . B. 5 5 . C. 2 5 . D. 4 5 . Lời giải Chọn B
Với z 1 i  5cos x i sin x , ta có: 8  8i
P  1 i  5cos x i sin x  7  9i  2 1 i  5cos x i sin x  1i 8  8i
 5cos x  6  i 5sin x  8  2 5cos x i sin x  1i   x  2   x  2   x  2   x  2 5 cos 6 5sin 8 2 5 cos 1 5sin 7
 25  60cos x  80sin x 100  2 25 10cos x  70sin x  50  5 5 .
Câu 30. Cho số phức z thỏa mãn z i  2 . Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
z  2  z  2  2i . Tính P M m
A. P  2  17 .
B. P  2  2 17 . C. P  2  2 17 . D. P  2  17 .
Hướng dẫn giải Chọn B
Ta có: z i  2 cos x i sin x và
z  2  z  2  2i  2cos x i sin x  i  2  2cos x i sin x  i  2  2i   x  2   x  2   x  2   x  2 2 cos 2 2 sin 1 2 cos 2 2 sin 1
 9  8cos x  4sin x  9  8cos x  4sin x   x    cos x2 2 18 16 cos 2 9 8 16 sin x 2
 18  16 cos x  2 80 cos x  144 cos x  65  2; 2 17  .   2 2
Câu 31. Gọi z x yi x, y   là số phức thỏa mãn hai điều kiện z  2  z  2  26 và 3 3 z  
i đạt giá trị lớn nhất. Tính tích xy . 2 2 9 13 16 9 A. xy  . B. xy  . C. xy  . D. xy  . 4 2 9 2 Lời giải Chọn D
Đặt z x iy x, y  . Thay vào điều kiện thứ nhất, ta được 2 2 x y  36.
Đặt x  3cos t, y  3sin t. Thay vào điều kiện thứ hai, ta có 3 3    P z  
i  18 18sin t   6.   2 2  4     3 3 2 3 2
Dấu bằng xảy ra khi sin t   1   t    z    . i    4  4 2 2 2
Kĩ thuật 5: Sử dụng biểu thức liên hợp . z z z z
Câu 32. Cho số phức z thỏa mãn z không phải là số thực và w
là số thựC. Giá trị lớn nhất 2 2  z
của biểu thức M z 1 i là A. 2 2 . B. 2 . C. 2 . D. 8 . Lời giải Chọn A
Do w là số thực, suy ra: zzz z z z 2 2 w w        2z  .
z z  2z z .z 2  2  2 2 2 2 2  z  2  z  2  z 2  z 2  z 2  zz  
z z   z zz z 2 2 .  0  
z.z  2  z  2  z  2. z.z  2 
Đặt z x yi x, y   . Khi đó 2 2 z
2  x y  2 (*).
Cách 1 (Theo đại số và kết hợp bất đẳng thức)
M z   i   x     y  i   x  2   y  2 2 2 1 1 1 1 1 
x y  2x  2 y  2 (*)
 2x  2 y  4 . Suy ra 2
M  2x  2 y  4   2 2 2  2  2 2
x y   4  8.2  4  8  M  2 2  M  2 2 max
Cách 2 (Theo hình học)
Gọi điểm T x ; y biểu diễn số phức z x yi (*)
T thuộc đường tròn C  có tâm O 0;0 và bán kính R  2 . 2 2
Ta có M   x   1   y  
1 i   x   1   y   1
TA với A1;  1 . Do A 
1;1  C  suy ra MTA  2R  2 2 . max max
Chú ý: Nếu A  C   MTAOA R . max max
Câu 33. Cho số phức z thỏa mãn 2
z  4  z . Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất
của z . Tính P M m . 2 17 1 17 1 2 17 1 A. P  . B. P  17 . C. P  . D. P  . 2 2 2 Lời giải Chọn B 2 z  4 4  4  4   4  4  Ta có 2
z  4  z   1  z   1  z z   1     z z   1     z zz  z   z  z  2 2 16  z z  4 z z 2 16    . z z
 4     1  z    1 . . z z z z 2 2   z z 16 17 1 17 1
Vậy với a z  0 , ta có 2 1  a   8   a  . 2 a 2 2 17 1 17 1 Do đó P    17 . 2 2 1
Câu 34. Cho số phức z thỏa mãn z
 3 . Tính P  max z  min z . z A. P  3 .
B. P  13 . C. P  3 13
D. P  3  13 . Lời giải Chọn B
Theo giả thiết, ta có  1  1   1   1  z z   9  z   z   9         z  z   z   z  1 z z 1  z z 2 2 2 2 2 2  2 zz    9  z    9 2 2 2 2 z z z z 2 2 1 2 z 2 1  9  z    z   11 2 2 2 z z z 13  3 13  3   z   P  13 2 2
Câu 35. Cho số phức z thỏa mãn z  1. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2
P z 1  z z 1 . Tính giá trị của M .m . 13 3 39 13 A. . B. . C. 3 3. D. . 4 4 4 Lời giải Chọn A
Gọi z x yi;  x  ; y   . Ta có: z  1  z.z  1
Đặt t z 1 , ta có 0  z 1  z 1  z 1  2  t 0; 2. 2 t  2 Ta có 2
t  1 z1 z   1 .
z z z z  2  2x x  . 2
Suy ra z z   z z z z z z   z   x  2 2 2 2 1 . 1 2 1
 2x 1  t  3 .
Xét hàm số f t  2
t t  3 , t 0; 2. Bằng cách dùng đạo hàm, suy ra 13 13 3
max f t  
; min f t   3  M .n  . 4 4 1
Câu 36. Cho số phức z thỏa mãn 3 z
 4 . Tính P  max z  min z . z A. P  4 2 . B. P  2 2 . C. P  4 2  2 .
D. P  2 2 2 1 . Lời giải Chọn D Theo giả thiết ta có  1  1   1  1 3 3 3 3  z z   16  z z   116         z  z   z  z  1 z z 1 z z 2 4 2 2 4 4  2 z 6 6  z    16  z    16 2 2 2 2 z z z z 4 6 1 2  z 4 2  2  2 4 2  2  2  16  z     z   P  4 2  2 . 2 2 z z 2 2
_______________ TOANMATH.com _______________