Sử dụng tính chất của đồ thị hàm số để tính diện tích hình phẳng Toán 12

Sử dụng tính chất của đồ thị hàm số để tính diện tích hình phẳng Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

17 9 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 1

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

Chuyên đề:

SỬ DỤNG TÍNH CHẤT CỦA ĐỒ THỊ HÀM SỐ ĐỂ TÍNH

DIỆN TÍCH HÌNH PHẲNG

I. MỘT SỐ DẠNG TOÁN

Nội dung các dạng toán xoay quanh bài toán ứng dụng tích phân tính diện tích hình phẳng với giả

thiết bài toán cho bởi đồ thị hàm liên quan.

Dạng 1. Sử dụng định nghĩa xác định công thức diện tích.

Dạng 2. Dựa vào các điểm đồ thị đi qua xác định hàm số đi đến công thức tính.

Dạng 3. Dựa vào tâm đối xứng, trục đối xứng của đồ thị xác định hàm số đi đến công thức tính.

Dạng 4. Dựa vào tiếp tuyến của đồ thị xác định hàm số đi đến công thức tính.

Dạng 5. Biến đổi đồ thị đưa về tính toán đơn giản.

Dạng 6. Tính diện tích dựa vào việc chia nhỏ hình.

Dạng 7. Toán thực tế với giả thiết có đồ thị hàm liên quan.

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 2

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

II. BÀI TẬP MINH HỌA

1) Dạng 1. Sử dụng định nghĩa xác định công thức diện tích.

Câu 1: (Đề THPT QG 2019) Cho hàm số





y f x



liên tục trên



Gọi

là diện tích hình phẳng giới hạn

bởi các đường





, 0, 1

y f x y x

   

và



(như hình vẽ bên).

f(x)

1-1

Mệnh đề nào sau đây đúng?

1 5

1 1

( )d ( )d

S f x x f x x



  

 

. B.

1 5

1 1

( )d ( )d

S f x x f x x



 

 

1 5

1 1

( )d ( )d

S f x x f x x



 

 

. D.

1 5

1 1

( )d ( )d

S f x x f x x



  

 

Lời giải

Chọn C

Ta có

     

1 5 1 5

1 1 1 1

( ) d d d d

S f x x f x x f x x f x x

 

   

   

Câu 2: Cho đồ thị hàm số

( )

y f x



trên

0; 8

 

 

 

như hình vẽ.

)

Biểu thức nào dưới đây có giá trị lớn nhất?

( )

f x dx



. B.

( )

f x dx



. C.

( )

f x dx



. D.

( )

f x dx



Lời giải

Chọn D

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 3

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

Dễ thấy

3 2

S S



. Mà

3 5 8

1 2 3

0 3 5

( ), ( ), ( )

S f x S f x S f x

   

  

, nên

1 2 3

( )

f x dx S S S

  



lớn

nhất.

Câu 3: Cho hàm số





y f x



liên tục trên



có đồ thị tạo với trục hoành các miền có diện tích

1 2 3 4

, , ,

S S S S

như hình vẽ. Biết

1 4 2 3

2 13

;

3 384

S S S S    , tích phân

 

2 2

x x

I f dx







bằng

f(x)

-1

3 ln 2

I  

I 

128 ln 2

I  

Lời giải

Chọn D

Đặt

2 2 ln 2

ln 2

x x

t dt dx dx

    

Đổi cận:

x t

   

;

1 2

x t

  

 

       

1 2 1 2

3 4

1 1/2 1/2 1

1 1 1 81

2 2

ln 2 ln 2 ln 2 128 ln 2

x x

I f dx f t dt f t dt f t dt S S



 









       













 

   

Câu 4: Diện tích phần hình phẳng gạch chéo trong hình vẽ bên dưới được tính theo công thức nào sau đây?

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 4

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

-1

4 2

1 3

4 d

2 2

x x x x



 







   











 



. B.

4 2

1 3

1 d

2 2

x x x x



 







   











 



4 2

1 3

1 d

2 2

x x x x



 







  











 



. D.

4 2

1 3

4 d

2 2

x x x x



 







   











 



Lời giải

Chọn B

Từ hình vẽ ta thấy phần diện tích hình phẳng cần tính là hình phẳng giới hạn bởi đồ thị hai hàm

số:

 

3 3

2 2

y f x x

  

;

 

4 2

1 5

2 2

y g x x x

   

và hai đường thẳng

1; 2

x x

  

Ngoài ra ta thấy đường





y f x



nằm trên đường





y g x



trên đoạn

1;2

 



 

 

nên ta có diện tích

phần gạch chéo trên hình vẽ là:

4 2

3 3 1 5

2 2 2 2

S x x x x



 

   

 

 

 

 

    

 

 

 

 

 

 

   

 

 



4 2

1 3

1 d

2 2

x x x x



 







    











 



Câu 5: Cho hình phẳng





giới hạn bởi đồ thị của hai hàm số





y f x



và





y f x



liên tục trên đoạn

;

a b

 

 

 

và hai đường thẳng

x a



x b



(tham khảo hình vẽ dưới). Công thức tính diện tích của hình





là

(x)

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 5

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

   

1 2

S f x f x x

 



. B.

   

 

1 2

S f x f x x

 



   

1 2

S f x f x x

 



. D.

   

2 1

d d

b b

a a

S f x x f x x

 

 

Lời giải

Chọn A

Theo định nghĩa ứng dụng tích phân tích diện tích hình phẳng.

Câu 6: Cho hàm số





y f x



xác định và liên tục trên đoạn

3; 3

 



 

 

và có đồ thị như hình vẽ. Biết rằng diện

tích hình phẳng

1 2

;

S S

giới hạn bởi đồ thị hàm số





y f x



và đường thẳng

lần lượt là

;

a b

. Tính tích

phân

 

f x dx





-1

y=f(x)

-4

-2

-3

3 3

a b

  

3 3

a b

 

3 3

a b

  

3 3

a b

 

Lời giải

Chọn A

Đặt

3 3

t x dt dx dx dt

    

     

1 3 3

1 1

3 3

f x dx f t dt f x dx

  

 

  

Gọi phương trình của đường thẳng

là





y g x



. Ta có

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 6

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

       

1 1 1

3 3 3

g x f x dx a g x dx f x dx a

  

 

    

 

 

  

   

1 1

3 3

1 1

2.2 2.2

2 2

f x dx a f x dx a

 

      

 

       

3 3 3

1 1 1

1 1

.4.4 .2.2 6

2 2

f x g x dx b f x dx b f x dx b

 





 



        





 



 





 

  

Do đó

         

1 3 1 3

1 3 3 1

1 1 1

3 6 2.

3 3 3 3 3

a b

f x dx f x dx f x dx f x dx a b

  

 

 

          

 

 

   

Câu 7: Cho hàm số

( )

y f x



liên tục trên



và có đồ thị





là đường cong như hình bên. Diện tích hình

phẳng giới hạn bởi đồ thị





, trục hoành và hai đường thẳng

0, 2

x x

 

(phần tô màu) là

1 2

0 1

( )d ( )d

S f x x f x x

  

 

. B.

1 2

0 1

( )d ( )d

S f x x f x x

 

 

( )d

S f x x





. D.

( )d

S f x x





Lời giải

Chọn B

Diện tích

của hình phẳng cần tìm là:

 

S f x x





Dựa vào đồ thị ta thấy phương trình





0, 0;2

f x x

 

 

 

 

có nghiệm duy nhất là



NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 7

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

Do đó

   

1 2

0 1

d d

S f x x f x x

 

 

Dựa vào đồ thị ta thấy





0, 0;1

f x x

 

  

 

 

và





0, 1;2

f x x

 

  

 

 

Vậy

   

1 2

0 1

d d

S f x x f x x

 

 

Câu 8: Cho hàm số





y f x



liên tục trên

;

a b

 

 

 

, có đồ thị như hình vẽ sau:

Mệnh đề nào dưới đây đúng?

 

f x x





là diện tích hình thang

ABMN

. B.

 

f x x





là dộ dài đoạn

 

f x x





là dộ dài đoạn

. D.

 

f x x





là dộ dài đoạn cong

Lời giải

Chọn B

       

f x x f x f b f a BM PM BP



     



Câu 9: Cho hàm số





y f x



liên tục trên



và hàm số









y g x x f x

 

có đồ thị trên đoạn

0;2

 

 

 

như hình vẽ bên. Biết diện tích miền được tô màu là



. Tính tích phân

 

I f x x







Lời giải

Chọn D

Quan sát đồ thị ta thấy





0, 1;2

g x x

 

  

 

 

y=g(x)

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 8

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

y=g(x)

Từ giả thiết ta có

 

S I g x x

  



 

2 2

1 1

d d

g x x x f x x

  

 

Đặt

x t



2 d d

x x t

 

. Khi

1 1

x t

  

, khi

2 4

x t

  

 

2 4

1 1

1 5

d d

2 2

x f x x f t t

  

 

 

d 5

f t t

 



 

d 5

f x x I

  



Câu 10: Cho hàm số





y f x



xác định và liên tục trên tập số thực. Miền hình phẳng trong hình vẽ được

giới hạn bởi đồ thị hàm số





y f x





và trục hoành đồng thời có diện tích

S a



. Biết rằng

   

2 1 2

x f x dx



 



và





f c



. Tính

 

f x dx



y=f'(x)

a b c

 

a b c

 

a b c

  

a b c

  

Lời giải

Chọn A

Đặt

2 2

t x dt dx

  

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 9

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

               

1 1 1

0 0 0 0

2 1 ' 2 1 1 1

2 2

x f x dx t f t dt t f t dt b x f x dx b

  

         

   

Đặt









u x du dx

dv f x dx v f x

 

 

  

 



 



 

 

 

 

               

1 1 1

0 0 0

1 1 2 1 0

x f x dx b x f x f x dx f x dx f f b



        

  

Ta lại có

               

1 3

0 1

1 0 1 3 2 1 0

a f x dx f x dx a f f f f f f a c

 

          

 

Do đó

     

2 1 0 .

f x dx f f b a b c

     



Câu 11: Cho hàm số





y f x



có đạo hàm liên tục trên



. Đồ thị hàm số





y f x



như hình bên dưới.

Biết diện tích hình phẳng





bằng

và

   

19 2

1 ; 2

12 3

f f

   

. Tính

 

' 2

I f x dx







I  B.

I  C.

I  D.

I 

(H)

(K)

-1

y=f'(x)

Lời giải

Chọn A

     

0 0 0

1 1 1

1 1

' 2 ' '

2 2

t x

dt dx

I f x dx I f t dt f x dx



 



   

  

Ta có

           

2 0 2 0

1 1 0 1

' ' ' 2 1 '

f x dx f x dx f x dx f f f x dx

  

      

   

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 10

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

 

2 19 8

3 12 3

f x dx



    



 

f x dx



 



Do đó

 

1 5

' .

2 24

I f x dx



 



Câu 12: Cho hàm số





y f x



xác định và liên tục trên



có đồ thị như hình vẽ bên. Biết diện tích các hình

phẳng













, ,

A B C

giới hạn bởi đồ thị hàm số





f x

và trục hoành lần lượt bằng

124 37 53

; ;

15 60 60

. Tích phân

 

  



15 2 4 3 5

f x x dx

bằng

y=f(x)

(C)

(B)

(A)

-2



. B.

437

. C.

293

. D.

158

Lời giải

Chọn A

Tính

 

       

  

3 3 3

2 2

1 1 1

15 2 4 3 5 (2 4) (2 4) (3 5)

f x x dx f x d x x dx

 



 



f x dx

Mà

 

 

 

 



 





        





 







 

 

 

   

2 0 1 2

2 2 0 1

15 15 15 124 37 53

( ) ( ) ( ) 64

2 2 2 15 60 60

f x dx f x dx f x dx f x dx

Vậy

 

       



15 2 4 3 5 64 36 28

f x x dx

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 11

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

Câu 13: (Đề thi thử THPT QG VTED năm 2019) Cho hàm số





y f x



xác định và liên tục trên đoạn

5; 3

 



 

 

có đồ thị như hình vẽ bên. Biết diện tích các hình phẳng

















, , ,

A B C D

giới hạn bởi đồ thị hàm số





f x

và trục hoành lần lượt bằng

6; 3;12;2

. Tích phân

 

2 2 1 1

f x dx



 



bằng

3-5

(D)

(C)

(B)

(A)

. B.

. C.

. D.

Lời giải

Chọn A

Tính

 

   





1 1 1 1

3 3 3 3

2 1

2 2 1 1 2 2 1 2 2 1 4

d x

f x dx f x dx dx f x

   



       

   

 

f x dx



 



Mà

 

f x dx





bằng diện tích hình phẳng giới hạn bởi đồ thị hàm số





f x

và trục hoành

Suy ra

 

6 3 12 2 23

f x dx



    



Vậy

 

2 2 1 1 23 4 27

f x dx



    



Câu 14: Cho đường cong





: 8 27

C y x x

 

và đường thẳng

y m



cắt





tại hai điểm phân biệt nằm

trong góc phần tư thứ nhất của hệ trục tọa độ

Oxy

và chia thành

miền phẳng có diện tích

1 2

S S

bằng nhau

(tham khảo hình vẽ). Mệnh đề nào dưới đây đúng?

 

. B.

 

. C.

 

. D.

 

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 12

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

y=m

Lời giải

Chọn C

Phương trình hoành độ giao điểm

8 27

x x m

 

. Giả sử như hình vẽ, hoành độ các giao điểm là

a b

 

. Ta có hệ

 

8 27

a a m

b b m





 







 





. Gọi





F x

là một nguyên hàm của hàm số





8 27

f x x x m

  

Khi đó các diện tích

           

1 2

0 0

( ) 0 ; ( )

a a b b

a a

S f x dx f x dx F F a S f x dx f x dx F b F a

        

   

Theo giả thiết thì

   

1 2

0 4 0

S S F b F b mb

      

Kết hợp với (1), ta được

4 32

9 27

b m  

Câu 15: Cho hàm số





y f x



xác định và liên tục trên đoạn

2;1

 



 

 

. Biết rằng diện tích hình phẳng

1 2

S S

giới hạn bởi đồ thị hàm số





f x

và đường thẳng





y g x ax b

  

lần lượt là

m n

. Tính tích phân

 

I f x dx







1-1-2

y=g(x)

y=f(x)

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 13

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

I m n   B.

I n m   C.

I m n   D.

I n m  

Lời giải

Chọn C

             

1 1 1 1 1 1

2 2 2 2 2 2

I f x dx f x dx g x dx g x dx f x g x dx g x dx

     

 

      

 

 

     

         

1 1 1

2 1 2

1 9

.3.3

2 2

f x g x dx f x g x dx g x dx m n m n



  

          

  

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 14

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

2) Dạng 2. Dựa vào các điểm đồ thị đi qua xác định hàm số đi đến công thức tính.

Câu 1: Cho các hàm số





f x ax bx c

  

và





g x mx n

 

có đồ thị lần lượt là đường cong





và

đường thẳng

(như hình vẽ). Biết



. Diện tích hình phẳng giới hạn bởi đồ thị





và đường thẳng

(phần tô màu) là



(trong đó

, ; ( ; ) 1

p q N p q

 

). Khẳng định nào sau đây đúng?

(C)

p q

 

. B.

p q



. C.



. D.

p q

 

Lời giải

Chọn D

Ta có

(0; ) ( ), (0; )

A c C B n d

 

và

5 5 ( )

AB c n c n

    

Phương trình hoành độ giao điểm của





và

2 2 2

( ) 0 ( ) 5 0(*)

ax bx c mx n ax b m x c n ax b m x

              

Lại có hoành độ giao điểm của





và

là



và



nên

(*)

có dạng

( 1)( 5) 0

a x x

  

Đồng nhất hệ số ta được



Diện tích hình phẳng giới hạn bởi





và

là

5 5

1 1

( 1)( 5) 6 5

S x x dx x x dx      

 

Suy ra

32, 3 35.

p q p q

    

Câu 2: Cho hai hàm số





3 2

f x ax bx cx d

   

và





g x mx n

 

(

, , , , ,

a b c d m n





). Biết rằng đồ

thị hàm số





y f x



và





y g x



cắt nhau tại ba điểm có hoành độ

1;2;3



(tham khảo hình vẽ phía bên

dưới); đồng thời diện tích



(phần hình phẳng tô màu xanh). Tính diện tích

(phần hình phẳng tô

màu đỏ).



. B.

S 

. C.

128

S 

. D.



NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 15

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

y=g(x)

y=f(x)

32-1

Lời giải

Chọn A

Ta có phương trình hoành độ giao điểm





















1 2 3 0

f x g x a x x x

     

Có

   

1 2 3 45 45 4.

S a x x x dx a a



        



Vậy

   

4 1 2 3 .

S x x x dx     



Câu 3: Hình phẳng được tô màu ở trong hình vẽ bên được giới hạn bởi một đồ thị hàm số bậc

với một

đường thẳng



cùng với trục hoành và trục tung. Diện tích hình phẳng đó bằng

. B.

. C.

. D.

1-2

Lời giải

Chọn A

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 16

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

Ta có đồ thị hàm số bậc ba

3 2

y ax bx cx d

   

có:

+ Giao với

tại điểm có tung độ bằng

2 2

 

+ Đi qua điểm





1; 0 2

a b c

    

+ Đi qua điểm





2; 0 8 4 2 2 4 2 1

a b c a b c

            

+ Có



là điểm cực trị của hàm số nên là nghiệm của phương trình

' 0 3 2 0

y a b c

    

Từ đó

1; b 0;c 3

   

Vậy hàm số bậc ba là:

3 2

y x x

  

Ta có đường thẳng đi qua hai điểm









2; 0 ; 0;2



là

y x

 

Giao điểm của hai đồ thị là

2; 0; 2

x x x

   

Vậy diện tích hình phẳng giới hạn với hai đồ thị trên như hình vẽ là:

 

4 4

S x x dx

  



Chọn đáp án A.

Câu 4: (Đề THPT QG 2018) Cho hai hàm số

 

3 2

f x ax bx cx

   

và





g x dx ex

  





, , , ,a b c d e





. Biết rằng đồ thị hàm số





y f x



và





y g x



cắt nhau tại 3 điểm có hoành độ lần lượt là



;



;

(tham khảo hình vẽ). Hình phẳng giới hạn bởi

đồ thị đã cho có diện tích bằng

-1

-3

Lời giải

Chọn D

Từ giao điểm hai đồ thị ta có





















3 1 1

f x g x a x x x

    

Suy ra

       

3 2

3 1 1

a x x x ax b d x c d x

        

Xét hệ số tự do suy ra

3 1

2 2

a a

    

Do đó

       

3 1 1

f x g x x x x

    

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 17

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

Diện tích bằng

       

1 1

3 1

1 1

3 1 1 d 3 1 1 d

2 2

S x x x x x x x x



 

       

 



Câu 5: Cho hai hàm số





3 2

f x x ax bx c

   

và









g x f dx e

 

với

, , ,

a b c d





có đồ thị như

hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số





y f x



. Diện tích hình phẳng giới hạn bởi

hai đường cong





y f x



và





y g x



gần nhất với kết quả nào dưới đây?

y=g(x)

y=f(x)

4,5

. B.

4,25

. C.

3,63

. D.

3,67

Lời giải

Chọn A

Từ đồ thị suy ra

( ) ( 3) .

f x a x x

 

và

(1) 4 1

f a

  

( ) ( 3)

f x x x

  

( )

g x

là hàm số bậc ba nên

( ) ( ) ( 3)

g x m x x

  

và

(1) 4 8

g m

   

( ) 8( ) ( 3)

g x x x

    

Vậy

   

. 4, 5

S f x g x dx   



Câu 6: Cho hai hàm số





3 2

f x ax bx cx

   

và





g x dx ex

  

với

; ; ; ;

a b c d e

là các số thực. Biết rằng đồ thị

của hàm số





y f x



và





y g x



cắt nhau tại ba điểm

, ,

A B C

có

hoành độ lần lượt là

1; 1; 2



(tham khảo hình vẽ). Hình phẳng giới

hạn bởi hai đồ thị đã cho có diện tích bằng

. B.

. D.

Lời giải

Chọn A

-1

-3

21-1

y=g(x)

y=f(x)

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 18

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

Ta có

























3 2 2 3 2

1 1 2

f x g x ax bx cx dx ex ax b d x c e x

             

Vì đồ thị của hàm số





y f x



và





y g x



cắt nhau tại ba điểm

, ,

A B C

có hoành độ lần lượt là

1; 1; 2



nên phương trình









f x g x



có ba nghiệm là

1; 1; 2



Kết hợp với điều kiện giả thiết suy ra





















1 1 2

f x g x a x x x

    

Đồng nhất hệ số tự do hai dạng biểu thức









f x g x



ta được

2 2 1

a a

  

Vậy





















3 2

1 1 2 2 2

f x g x x x x x x x

        

Diện tích hình phẳng giới hạn bởi hai đồ thị đã cho là:

3 2

2 2d

S x x x x



    



Câu 7: Hình phẳng





được giới hạn bởi đồ thị của hai hàm số đa thức bậc bốn

( )

y f x



và

( ).

y g x



Biết rằng đồ thị của hai hàm số này cắt nhau tại đúng ba điểm phân biệt có hoành độ lần lượt là −3;−1;2.

Diện tích của hình phẳng





(phần gạch sọc trên hình vẽ bên) gần nhất với kết quả nào dưới đây?

-3

-1

-3

3,11

. B.

2, 45

. C.

3,21

. D.

2,95

Lời giải

Chọn A

Tại điểm có hoành độ

 

hai đồ thị hàm số này tiếp xúc với nhau.

Có





( ) ( ) 3 ( 1)( 2).

f x g x a x x x    

Mà

3 3 9

(0) (0)

5 2 10

f g

 

 







   











 

9 1

.9.1.( 2)

10 20

a a



    

Vì vậy

 

2 2

( )

3 3

1 3733

( ) ( ) 3 ( 1)( 2) 3,11.

20 1200

S f x g x x x x dx

 

        

 

Câu 8: Cho hàm số bậc ba

( )

y f x



và hàm số bậc hai

( )

y g x



có đồ thị như hình vẽ. Biết rằng phần diện

tích

giới hạn bởi đồ thị của hai hàm số bằng

. Tính phần diện tích

giới hạn bởi hai đồ thị hàm số.

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 19

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

-1

y=g(x)

y=f(x)



. B.



. C.



. D.



Lời giải

Chọn A

Dựa vào đồ thị của hai hàm số ta thấy hai đồ thị cắt nhau tại các điểm có hoành độ lần lượt là

1, 1, 3



nên





















1 1 3

f x g x a x x x

    

và



Mặt khác diện tích

4 ( 1)( 1)( 3) 4 4

S a x x x dx a



       



Từ đó suy ra

 

3 3

1 1

( ) ( ) 4( 1)( 1)( 3) 4

S g x f x dx x x x dx

       

 

Vậy chọn đáp án A.

Câu 9: Cho hàm số

( )

y f x



xác định và liên tục trên đoạn

5; 3

 



 

 

. Biết rằng diện tích hình phẳng

1 2 3

, ,

S S S

giới hạn bởi đồ thị hàm số

( )

y f x



và đường thẳng





y g x ax bx c

   

lần lượt là

, ,

m n p

. Tích

phân

( )

f x dx





bằng

211

m n p  

. B.

208

m n p  

. C.

m n p  

. D.

m n p  

Lời giải

Chọn B

Đồ thị hàm





y g x



đi qua các điểm













0; 0 , 2;0 , 3;2

O A B



nên

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 20

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

4 2 0

9 3 2

a b









 





 





























 

2 4

15 15

g x x x

  .

           

2 0 3

5 2 0

m n p f x g x dx g x f x dx f x g x dx



 

     

       

     

     

  

   

3 3

5 5

f x dx g x dx

 

 

 



   

3 3

5 5

208

f x dx m n p g x dx m n p

 

       

 

y=g(x)

y=f(x)

-1

-2

-5

Câu 10: Cho hàm số

( )

y f x



là hàm số đa thức bậc bốn và có đồ thị như hình vẽ.

-1

Hình phẳng giới hạn bởi đồ thị hai hàm số

( ); '( )

y f x y f x

 

có diện tích gần bằng số nào sau

đây?

34, 8

. B.

. C.

63,5

72, 3

Lời giải

Chọn C

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 21

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

Hàm số đã cho có đồ thị đối xứng nhau qua trục tung nên nó là hàm số chẵn. Lại có hàm số

( )

y f x



là hàm đa thức bậc bốn nên hàm số đã cho là hàm trùng phương. Do đó

4 2

( ) , 0

f x ax bx c a

   

Từ hình vẽ ta thấy đồ thị hàm số đi qua các điểm

(1; 0)

(0;1)

và có điểm cực tiểu

(1; 0)

, điểm cực đại

(0;1)

nên ta có hệ

(1) 0

0 1

(0) 1

1 2

'(1) 0

4 2 0 1

'(0) 0

a b c a

c b

a b c









 

 



   

 



 





 



    

  

  



  

  

  

 







Với

1, 2, 1

a b c

   

ta có

4 2 3 2

( ) 2 1 ; '( ) 4 4 ; ''( ) 12 4

f x x x f x x x f x x

      

thỏa

''(0) 0, ''(1) 0

f f

 

nên các giá trị

1, 2, 1

a b c

   

thỏa mãn yêu cầu bài toán.

Phương trình hoành độ giao điểm của đồ thị hai hàm số

( ); '( )

y f x y f x

 

   

4 2 3 2 2

1 0

2 1 4 4 1 4 1

4 1 0

2 5

x x x x x x x

x x



 

 



         



  

 





Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số

( ); '( )

y f x y f x

 

là

   

 

2 5 2 5

4 3 2

1 1

2 5 1

4 3 2 4 3 2

2 5

4 3 2

( ) ( ) 4 2 4 1

4 2 4 1 4 2 4 1

4 2 4 1 63,52

S f x f x dx x x x x dx

x x x x dx x x x x dx

x x x x dx

 

 







      

          

     

 



NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 22

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

3) Dạng 3. Dựa vào tâm đối xứng, trục đối xứng của đồ thị xác định hàm số đi đến công thức tính.

Câu 1: Cho hàm số

4 3 2

( ) 16 21 20 3

y f x x x x x

     

và

hàm số









y g x a x b

   

có đồ thị như hình vẽ. Biết rằng

diện tích hình phẳng

1 2 3

, ,

S S S

giới hạn bởi đồ thị hàm số

( )

y f x



và đường cong





y g x



lần lượt là

, ,

m n p

. Tính

M a b m p n

    

2456

M  . B.

2531

M  .

2411

M 

. D.

2501

M 

Lời giải

Chọn B

Đồ thị hàm





y g x



đi qua các điểm









0; 0 , 2; 4

O A

 

nên

4 0

a b





 







 



















 















2 4 4

g x x x x

    

Nhận xét đồ thị hai hàm số nhận đường thẳng

 

là trục đối xứng nên

m p m p

   

Do đó,

   

 

1 1

4 3 2

3 3

2531

5 5 8 20 24 3

a b n f x g x dx x x x x dx

 

           

 

Câu 2: Cho hàm số

4 2

y x bx

  

(*) có đồ thị như hình vẽ. Gọi

1 2 3

, ,

S S S

lần lượt là diện tích của hình

phẳng













giới hạn bởi đồ thị hàm số (*) và trục hoành. Biết

1 3 2

S S S

 

. Giá trị của

là

. B.

. C.

. D.

Lời giải

y=f(x)

y=g(x)

-1

-3

-1

-2-4

-4

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 23

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

Chọn A

Đồ thị hàm số (*) cắt trục hoành tại

điểm phân biệt

 

Gọi

1 2 1 2

, ( )

t t t t



là nghiệm dương của phương trình

4 2

5 0

x bx

  

. Ta có

4 2

2 2

5 0 (1)

t bt

  

Vì đồ thị hàm số (*) nhận trục tung làm trục đối xứng nên

1 3 2 3

S S S S

   

Do đó

1 2 2

4 2 4 2 4 2

0 0

( 5) - ( 5) ( 5) 0

t t t

x bx dx x bx dx x bx dx

        

  

5 3 4 2

2 2 2 2 2

1 1 1 1

5 0 5 0(2)

5 3 5 3

t bt t t bt       

Từ (1) và (2) suy ra

36 6

b b

   

(vì b <0) và



Vậy

4 2

2 ( 6 5)

S x x dx   



suy ra Chọn A

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 24

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

4) Dạng 4. Dựa vào tiếp tuyến của đồ thị xác định hàm số đi đến công thức tính.

Câu 1: (Đề HSG Bắc Ninh 2019) Cho hàm số





y f x



là hàm đa thức bậc bốn và có đồ thị như hình vẽ.

Hình phẳng giới hạn bởi đồ thị hai hàm số









;

y f x y f x



 

có diện tích bằng

(x)

-1

-2

-1

127

. B.

107

. C.

. D.

127

Lời giải

Chọn B

Từ giả thiết đi đến













2 2

2 1

f x a x x   .

Vì đồ thị đi qua điểm





0;1

nên



     

2 2

2 1

f x x x   

           

2 2

1 1 1

2 1 1 2 2 1 2 1

2 2 2

f x x x x x x x x



          

Phương trình

      

 

2 1 2 4 2 0 2

f x f x x x x x x x



 





           









Vậy hình phẳng giới hạn bởi đồ thị của





f x

và





f x



là:

       

2 2

1 1 107

2 1 2 1 2 1

4 2 5

S x x x x x dx



        



Câu 2: Cho đồ thị hàm số

3 2

( )

f x x ax bx c

   

có đồ thị





. Đường thẳng

qua hai điểm

A B

trên

hình vẽ là tiếp tuyến của





tại

. Diện tích hình phẳng giới hạn bởi

và





bằng:

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 25

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

y=f(x)

-1

6,75

4,5

8,45

4,75

Lời giải

Chọn A

Đường thẳng

d y mx n

 

cắt đồ thị hàm số

3 2

( )

f x x ax bx c

   

tại điểm có hoành độ

1; 2

x x

  

trong đó tại điểm có hoành độ

 

là điểm tiếp xúc của hai đường.

Vì vậy





3 2 2

( ) ( 1) ( 2).

x ax bx c mx n x x       

Diện tích hình phẳng cần tính bằng:

2 2

3 2 2

1 1

( ) ( ) ( 1) ( 2) 6,75.

S x ax bx c mx n dx x x dx

 

         

 

Câu 3: Cho hàm số

3 2

y x ax bx c

   

có đồ thị





. Biết rằng tiếp

tuyến





của





tại điểm

có hoành độ bằng



cắt





tại

có

hoành độ bằng

(xem hình vẽ). Diện tích hình phẳng giới hạn bởi





và





(phần gạch chéo trong hình vẽ) bằng

. B.

. D.

Lời giải

Chọn C

Ta có





1; 1

A a b c

   

và

3 2

y x ax b



  





1 3 2

y a b



    

-1

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 26

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

Phương trình tiếp tuyến





của





tại









3 2 1 1

y a b x a b c

       

Phương trình hoành độ giao điểm của





và





là :









3 2

3 2 1 1

x ax bx c a b x a b c

          





Phương trình





có nghiệm

1; 2

x x

  





4 2 8 3 3 2 1

a b c a b a b c

          

9 0 0

a a

   

Suy ra





y x bx c

  

và









: 3 1 1

d y b x b c

     

Diện tích hình phẳng là :

  

 

3 1 1

S b x b c x bx c dx



 

        

 

 



 

3 2

x x dx



   



Câu 4: Cho hàm số





y f x



là hàm bậc ba có đồ thị





như hình vẽ bên dưới

y=f(x)

-1

Diện tích hình phẳng giới hạn bởi





và trục hoành bằng:

. B.

. C.

. D.

Lời giải

Chọn A

Phương trình của đồ thị





có dạng













1 1

y f x a x x

   





qua





0;1

nên



Suy ra

















: 1 1

C y f x x x

   

3 2

x x x

   

Diện tích hình phẳng cần tìm

 

3 2

1 d

S x x x x



   



4 3 2

x x x



 







   











 



Câu 5: Cho hàm số

4 2

y ax bx c

  

có đồ thị





, biết rằng





đi qua điểm





1;0



. Tiếp tuyến



tại

của đồ thị





cắt





tại hai điểm có hoành độ lần lượt là 0 và 2. Biết diện tích hình phẳng giới hạn

bởi



, đồ thị





và hai đường thẳng



;



có diện tích bằng

(đồ thị như hình vẽ).

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 27

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

-1

Tính diện tích hình phẳng giới hạn bởi



, đồ thị





và hai đường thẳng

 

;



. B.

. C.

. D.

Lời giải

Chọn A

Cách 1:

Hàm số

4 2

y ax bx c

  

. TXĐ:





Ta có:

' 4 2

y ax bx

 

Phương trình tiếp tuyến



của đồ thị





tại





1;0



có dạng









4 2 1

y a b x

   

Do tiếp tuyến



tại

của đồ thị





cắt





tại hai điểm có hoành độ lần lượt là 0 và 2 nên

phương trình









4 2

4 2 1

ax bx c a b x

     

nhận ba nghiệm là:

 

;



;



Suy ra:

c a b

b a





  







 





c a

b a















 





Vậy









4 2 4 2

3 2 3 2

y ax ax a a x x

     

và







2 1

y a x

 

Bài cho diện tích hình phẳng giới hạn bởi



, đồ thị





và hai đường thẳng



;



có diện

tích bằng

nên:

 

4 2

2 1 3 2 d

a x a x x x    



 

4 2

2 1 3 2 d

a x a x x x     



 

4 2

3 2 d

a x x x x    



3 2

5 5

a x x

 









   











 

28 56

5 5

a 

 

Diện tích hình phẳng giới hạn bởi



, đồ thị





và hai đường thẳng

 

;



là:

 

4 2

3 2 2 1 d

S a x x a x x



    



 

4 2 3 2

2 6 4 d 2.

5 5

x x x x x x



 







      











 



Cách 2:

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 28

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

Giả sử đường thẳng

d y kx m

 

là tiếp tuyến với





tại





0; 1



nên

 

và

 

Phương trình hoành độ giao điểm của

và





là









4 2

0 1 . . 2 0

ax bx kx a x x x

      

(do phương trình trên có 3 nghiệm như bài toán đã cho).

Theo bài ta có phương trình

   

1 . 2 d 2

a x x x x a

    



Từ đó ta được

 

4 2

2( 3 2) 4 1 d

S x x x x



 

    

 

 



 

4 2

2 6 4

x x x dx



   



Câu 6: Cho hàm số

4 2

y ax bx c

  

có đồ thị





, biết rằng





đi qua điểm





1;0



, tiếp tuyến

tại

của





cắt





tại hai điểm có hoành độ lần lượt là

và

và diện tích hình phẳng giới hạn bởi

, đồ

thị





và hai đường thẳng



;



có diện tích bằng

-1

Diện tích hình phẳng giới hạn bởi





và hai đường thẳng

 

;



có diện tích bằng

Lời giải

Chọn D

Ta có

4 2

y ax bx



 











: 4 2 1

d y a b x

   

Phương trình hoành độ giao điểm của

và





là:













4 2

4 2 1 1

a b x ax bx c

     

Phương trình





phải cho

nghiệm là





4 2

12 6 16 4

a b c

a b a b c





  







    













4 2 0 2

28 10 0 3

a b c





   









  





Mặt khác, diện tích phần tô màu là

  

4 2

4 2 1 d

a b x ax bx c x

 

      

 

 



 

28 32 8

4 4 2 2

5 5 3

a b a b c

      

 

112 32 28

2 4

5 3 5

a b c    

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 29

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

Giải hệ 3 phương trình









và





ta được



 



Khi đó,





4 2

: 3 2

C y x x

  





: 2 1

d y x

 

Diện tích cần tìm là

 

4 2

3 2 2 1 d

S x x x x



 

    

 

 



 

4 2

3 2

x x x dx



   



NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 30

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

5) Dạng 5. Biến đổi đồ thị đưa về tính toán đơn giản.

Câu 1: Cho parabol





: 2

P y x x

 





cắt trục hoành tại hai điểm

và đường thẳng

d y a







0 4

 

. Xét parabol





đi qua

và có đỉnh thuộc đường thẳng

y a



(đồ thị như hình vẽ). Gọi

là diện tích hình phẳng giới hạn bởi





và

là diện tích hình phẳng giới hạn bởi





và trục

hoành. Biết

1 2

S S



, tính

3 2

8 48

T a a a

  

y = a



. B.



. C.



. D.



Lời giải

Chọn B.

y = a

Để việc tính toán trở nên đơn giản, ta tịnh tiến hai parabol sang trái một đơn vị. Khi đó, phương

trình các parabol mới là





: 4

P y x

  

 

P y x a

  

Gọi

là các giao điểm của





và trục





2;0

 





2; 0

 

Gọi

là giao điểm của





và đường thẳng





4 ;

M a a

  





4 ;

N a a



Ta có

2 4 .d

S y y

 



 

 









  









 

 

4 4

a a

  

2 .d

S x a x

 







  











 



 







  











 

 .

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 31

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

Theo giả thiết

1 2

S S



 

4 8

4 4

3 3

a a   





4 4

a a

  

3 2

8 48 64

a a a

   

Vậy



Câu 2: Gọi

( )

là hình phẳng giới hạn bởi đồ thị hàm số

y x x

  

và trục hoành. Hai đường thẳng

y m



và

y n



chia

( )

thành 3 phần có diện tích bằng nhau. Giá trị của biểu thức

3 3

(4 ) (4 )

T m n

   

bằng

y = n

y = m

320

T 

. B.

512

T 

. C.

405



. D.

T 

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 32

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

6) Dạng 6. Tính diện tích dựa vào việc chia nhỏ hình

Câu 1: (Đề tham khảo THPT QG 2018) Cho





là hình phẳng giới hạn bởi parabol

y x



, cung tròn

có phương trình

y x

 

(với

0 2

 

) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của





bằng

4 3

 

. B.

4 3

 

. C.

4 2 3 3



 

. D.

5 3 2





Lời giải

Chọn B

Phương trình hoành độ giao điểm giữa parabol và cung tròn ta được

2 2

3 4 1

x x x

    

với

0 2

 

nên ta có



Ta có diện tích

1 2 2 2

2 2 3 2 2

0 1 1 1

3 3

3 4 4 4

3 3

S x dx x dx x x dx x dx

        

   

Đặt

2 sin 2 cos ; 1 ; 2

6 2

x t dx tdt x t x t

 

        

3 1 4 3

2 sin 2

3 2 6

S t t



 









    











 

Câu 2: Gọi

là diện tích hình phẳng giới hạn bởi các đường





y x 

3 1

y x

 

. Đường cong





chia

thành hai phần có diện tích là

1 2

S S

(trong đó

nằm trên trục hoành). Tính tỉ số

9 ln 4



. B.

9 ln 4

 

. C.

9 ln 2

 

. D.

9 ln 2



Lời giải

Chọn B

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 33

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

-1

y=(x 1)

y=3x 1

y=2

2 x

Phương trình hoành độ giao điểm của hai đường cong





y x  ,

3 1

y x

 

là:





1 3 1

x x

  

3 2

3 0

x x

  

















Do vậy

 

3 1 1

S x x dx

 

    

 

 



Phương trình hoành độ giao điểm của hai đường cong





y x 





là:





1 2



 





1 .

Dễ thấy



là nghiệm của





đồng thời hàm số





y x 

đồng biến trên



, hàm số





nghịch biến trên



nên





có nghiệm duy nhất



Phương trình hoành độ giao điểm của hai đường cong

3 1

y x

 





là:

3 1 2



 

(1).

Dễ thấy



là nghiệm của





đồng thời hàm số

3 1

y x

 

đồng biến trên



, hàm số





nghịch biến trên



nên (1) có nghiệm duy nhất



Ta có

 

2 3

0 2

3 1 2 3 1 1

S x dx x x dx



 

      

 

 

 

27 3

4 ln 4

 

2 1

ln 4

S S S  

Vậy

27 3

9 ln 4

4 ln 4

3 4

ln 4



  

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 34

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

Câu 3: Gọi tam giác cong





OAB

là hình phẳng giới hạn bởi đồ thị các hàm số

y x



y x

 



(tham khảo hình vẽ bên). Diện tích của





OAB

bằng

y=3-x

y=2x

. B.

. C.

. D.

Lời giải

Chọn A

y=3-x

y=2x

Gọi parabol





: 2

P y x



và đường thẳng





: 3

d y x

 

Ta có phương trình hoành độ giao điểm của





và





là:

2 2

2 3 2 3 0

x x x x







      



 





Suy ra tọa độ điểm

(1; 3)

và

( ) (3; 0)

d Ox B

 

Khi đó

1 3

( ) 1 2

0 1

2 8

2 d (3 )d 2

3 3

OAB

S S S x x x x

       

 

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 35

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

Câu 4: Diện tích miền phẳng giới hạn bởi các đường:

2 , 3

y y x

   

và



là:



1 1

ln 2 2



. B.

ln 2

 

. C.

S 

. D.

ln 2

 

Lời giải

Chọn A

y=1

y=3-x

y=2

Xét phương trình hoành độ giao điểm của các đường. Ta có:

2 3 1

x x

    

2 1 0

  

3 1 2

x x

    

Diện tích cần tìm là:

 

1 2

0 1

2 1 1

2 1 d 3 1 d 2

ln 2 2 ln 2 2

S x x x x x

   



 

 

 

           

 

 

 

 

 

   

 

Câu 5: Cho





là hình phẳng giới hạn bởi đường cong có phương trình

y x



, nửa đường tròn có

phương trình

y x

 

(với

0 2

 

) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của





bằng

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 36

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

3 1





. B.

3 2





. C.

4 1





. D.

4 2





Lời giải

Chọn B

Phương trình hoành độ giao điểm :

2 0

2 1

0 2

x x

x x x





  



    





 





Do đó

1 2

0 1

3 2

d 2 d

S x x x x





   

 

Câu 6: Cho





là hình phẳng giới hạn bởi parabol

y x

 

(với

0 2 2

 

), nửa đường tròn có

phương trình

y x

 

và trục hoành, trục tung (phần tô đậm trong hình vẽ). Diện tích của





bằng

3 14





. B.

2 2





. C.

3 4





. D.

3 2





Lời giải

Chọn D

Phương trình hoành độ giao điểm:

4 2

2 2

24 112 0

8 1 2

0 2 2

x x

x x x





  



     





 





NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 37

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

Do đó

2 2 2

2 2

0 2

1 3 2

1 d 8 d

4 3

S x x x x



 









    











 

 

Câu 7: Cho

( )

là hình phẳng giới hạn bởi parabol

y x



và đường Elip có phương trình

 

(phần tô đậm trong hình vẽ). Diện tích của

( )

bằng

-1

-2

2 3

 

. B.



. C.

 

. D.



Lời giải

Chọn A

Ta có

 

y    .

Phương trình hoành độ giao điểm của đường cong nửa trên của Elip và Parabol là

4 2

 

4 2

3 4 0

x x

   









 



 





 









Suy ra diện tích hình phẳng

( )

cần tính là

( )

1 d

4 2

S x x



 









  













 



1 3

4 d

2 3

x x



  



Xét

4 d

I x x



 



, đặt

2 sin

x t



ta được

4 4 sin 2 cos d

I t t t





 



2 cos d

t t









 

1 cos2 d

t t





 



sin 2





 







 











 

3 2



  .

Do đó

( )

3 3

3 2 3



  

2 3

 

 .

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 38

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

Vậy









 











P a b c

    

Câu 8: Tính diện tích

của hình phẳng (phần tô màu) trong hình sau



. B.

S 

. C.

S 

. D.



Lời giải

Chọn B

Dựa và hình vẽ, ta có hình phẳng được giới hạn bởi các đường:

y x









 











Suy ra





2 4

0 2

d 2 d

S x x x x x

   

 

Câu 9: Cho





là hình phẳng được tô đậm trong hình vẽ và được giới hạn bởi các đường có phương trình

y x x

 

khi

2 1

x x





 









 





. Diện tích của





bằng?

-1

1 32

. B.

. C.

. D.

Lời giải

Chọn B

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 39

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

Hoành độ giao điểm của hai đồ thị hàm số

y x

 

và

y x

 

là

2 1

x x x

    

Diện tích hình phẳng cần tính là

1 3

2 2

0 1

10 10

d 2 d

3 3

S x x x x x x x x

   

 

 

 

      

 

 

 

 

 

   

 

1 3

2 2

0 1

13 7

d 2 d

3 3

S x x x x x x

   

 

 

 

     

 

 

 

 

 

   

 

1 3

2 2

0 1

13 7

d 2 d

3 3

S x x x x x x

   

 

 

 

     

 

 

 

 

 

   

 

1 3

3 3

2 2

0 1

13 7 13

6 3 6 3 2

x x

S x x x

   

 

 

 

      

 

 

 

 

 

   

Câu 10: Diện tích hình phẳng giới hạn bởi các đồ thị hàm số

; ;

y x y y

  

bằng

27 ln 2

. B.

27 ln 3

. C.

28 ln 3

. D.

29 ln 3

Lời giải

Chọn B

Xét các pthđgđ

2 2

27 27

0; 3; 9

27 27

x x

x x x x x

x x

        

y=x

Suy ra

3 9

2 2

0 3

27 ln 3

27 27

x x

S x dx dx

   

 

 

 

    

 

 

 

 

 

   

 

Câu 11: Cho parabol

 

P y x



và đường tròn





có bán kính bằng

tiếp xúc với trục hoành đồng

thời có chung một điểm

duy nhất với





. Diện tích hình phẳng giới hạn bởi









và trục hoành

(phần tô đậm trong hình vẽ) bằng:

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 40

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

y=0.5x

27 3 8





. B.

9 3 9 4



 

. C.

29 3 9





. D.

3 3 2



 

Lời giải

Chọn A

Gọi





I b

là tậm của đường tròn









C b



;

A a a

 

















 

là tiếp điểm của





và











Phương trình tiếp tuyến chung của





và





2 2

1 1

: 0

2 2

y ax a ax y a

      

Tiếp tuyến



có véctơ chỉ phương





u a





; 1

IA a b a

 







  











 



Ta có

2 3

1 1

. 0 1 0

2 2

IA u IA a b a a b a

 







          











 





Hơn nữa

 





2 2 2

2 2 3 2

4 2

1 1 1

1 1 1 1 1

2 2 2

1 3 3

3 0 3 .

4 2

IA a b a a a a

a a a b

     

  

  

  

          

  

  

  

  

  

     

      

Phần tô đậm trong hình vẽ là hình giới hạn bởi nhánh bên phải parabol









P x



, nữa bên trái đường

tròn

 

3 3

C x

 























 

và trục hoành.

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 41

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

Ta có:

     

2 2

3 3 3 3

: 1 1 1 1

2 2

C x y x y

 









        













 

(vì

3 3

x 

)

 

: 2

P y x x y

  

(vì



Vậy diện tích phần tô đậm:

 

3 3 27 3 8

1 1 2 .

2 24

S y y dy



 

 







     













 



Câu 12: Cho parabol





P y x



và đường tròn





có bán kính

bằng

tiếp xúc với hai nhánh của





(như hình vẽ). Diện tích

hình phẳng giới hạn bởi





và





(phần tô đậm trong hình) gần

nhất với giá trị nào sau đây?

5,12

. B.

7, 06

8, 74

. D.

6, 03

Lời giải

Chọn D

Gọi





I b

là tậm của đường tròn









C b



;





;

A a a

là tiếp

điểm nhánh bên phải của





và











Phương trình tiếp tuyến chung của





và





2 2

: 2 2 0

y ax a ax y a

      

Tiếp tuyến



có véctơ chỉ phương





1;2

u a









;

IA a a b

 



Ta có





2 2

. 0 2 0

IA u IA a a a b b a

          





Hơn nữa





2 2 2 2

17 17 1 17 9

2 .

4 4 4 4 2

IA a a b a a b           

Phần tô đậm trong hình vẽ là hình giới hạn bởi parabol





và nữa bên dưới đường tròn

 

C y

 



















 

Ta có

 

2 2

9 17 9 17

2 4 2 4

C x y y x

 







      











 

(vì



)

4,5

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 42

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

Vậy diện tích phần tô đậm

2 2

9 17

2 6, 03.

2 4

S x x dx

 









    













 



Câu 13: Cho parabol





P y x



và đường tròn





có bán kính bằng

tiếp xúc với





tại gốc tọa độ

(như hình vẽ). Diện tích hình phẳng giới hạn bởi





và





(phần tô đậm trong hình) bằng:

y=x

2 3





. B.

3 3





. C.

5 3





. D.

3 3





Lời giải

Chọn D

Vì tính đối xứng, ta chỉ cần tính phần tô màu phía bên phải trục





Oy x



Qua hình vẽ, ta thấy:





có tâm

















2 2

0;2 : 2 4 4 2

I C x y x y       

Phương trình hoành độ giao điểm của





và





 

2 2 4 2

0 0

2 4 3 0 .

3 3

x y

x x x x

x y



  



      



  





Khi đó diện tích phần tô màu

 





2 4 2 8 9 3 .

S y y dy 

 





      











 



Câu 14: Cho hàm số





y f x



Đồ thị của hàm số





y f x





trên

5; 3

 



 

 

như hình vẽ (phần cong của đồ thị

là một phần của parabol

y ax bx c

  

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 43

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

-1

-4-5

Biết





0 0,



giá trị của









2 5 3 2

f f

 

bằng

109

. B.

. C.

. D.

Lời giải

Chọn C

Cách 1.

Parabol

y ax bx c

  

có đỉnh





1;4

và đi qua điểm





2; 3

nên ta có:

4 2 2 3.

4 2 3 3

a b c b y x x

a b c c







 



 



         

 

 

   

 











0 0



nên

































2 5 3 2 2 5 1 2 1 0 3 2 0

f f f f f f f f

     

          

     

     

 

   

1 0 2

2 2

5 1 0

2 d 2 2 3 d 3 2 3 d

x x x x x xf x



 

         



  

   

0 2

2 2

1 0

2.7 5 22 35

2 2 2 3 3 2 3 d 2. 3.

2 3 3 3

dS x x x x xx



             

 

Trong đó

là diện tích hình phẳng giới hạn bởi đồ thị hàm số





y f x





trục

và hai đường thẳng

5, 1

x x

   

và ta có:

1 11 1 1 7

.2. .1.

2 3 2 3 2

  

Cách 2.

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 44

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

Ta tính được:

 

3 14 , 5 4

2 2

, 4 1

3 3

2 3, 1

x x

f x x x

x x x





    





      





    





Ta có

           

4 4

5 5

1 1

4 5 3 14 4 5

2 2

f f f x dx x dx f f

 



           

 

.(1)

         

1 1

4 4

2 2

1 4 3 1 4 3

3 3

f f f x dx x dx f f

 

 









            











 

 

. (2)

Từ (1) và (2)

   

1 5

f f

    

. (3)

   

 

   

0 0

1 1

5 5

0 1 2 3 0 1

3 3

f f f x dx x x dx f f

 



           

 

. (4)

     

 

   

2 2

0 0

22 22

2 0 2 3 2 0

3 3

f f f x dx x x dx f f



         

 

.(5)

Mà





0 0.



(6)

Từ (3),(4),(5),(6)

     

5 22 31

1 , 2 , 5

3 3 6

f f f       

Do đó:

   

2 5 3 2

f f   .

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 45

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

7) Dạng 7. Toán thực tế với giả thiết có đồ thị hàm liên quan.

Câu 1: (Đề tham khảo THPT QG 2019) Một biển quảng cáo có dạng hình elip với bốn đỉnh

1 2 1 2

, , ,

A A B B

như hình vẽ bên. Biết chi phí để sơn phần tô đậm là đ

200.000 vn / m

và phần còn lại đ

100.000 vn / m

Hỏi số tiền để sơn theo cách trên gần nhất với số tiền nào dưới đây, biết

1 2

A A



1 2

B B



và tứ giác

MNPQ

là hình chữ nhật có



5.526.000

đồng. B.

5.782.000

đồng. C.

7.322.000

đồng. D.

7.213.000

đồng.

Lời giải

Chọn C

Gọi phương trình chính tắc của elip





có dạng:

2 2

x y

a b

 

Với

1 2

8 2 4

6 2 3

A A a a

B B b b

 

 

  

 



 

 

  

 

 

 

2 2

: 1 16

16 9 4

x y

E y x

       .

Suy ra diện tích của hình elip là

 





. 12 m

S a b  

Vì

MNPQ

là hình chữ nhật và

 

3 ;

MQ M x E

 







  











 

1 3 3

1 12 2 3; ; 2 3;

16 4 2 2

x M N

   

 

 

 

      

 

 

 

 

 

   

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 46

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

Gọi

1 2

;

S S

lần lượt là diện tích phần bị tô màu và không bị tô màu

Ta có

4 4

2 2

2 3 2 3

4. 16 d 3 16 d

S x x x x

   

 

Đặt

4 sin

x t



ta tính được





4 6 3 m

S  

Suy ra

 

1 2

8 6 3

S S S    

. Gọi

là tổng chi phí. Khi đó ta có









4 6 3 .100 8 6 3 .200 7.322.000

T      

(đồng).

Câu 2: Sàn của một viện bảo tàng mỹ thuật được lát bằng những viên gạch hình vuông cạnh

(cm) như

hình bên. Biết rằng người thiết kế đã sử dụng các đường cong có phương trình

y x



và





4 1

x y

 

để tạo hoa văn cho viên gạch. Diện tích được tô đậm gần nhất với giá trị nào dưới đây?

A. 506 (cm

)

747(cm

) C. 507(cm

) D. 746(cm

)

Lời giải

Chọn B

Gắn hệ trục tọa độ như hình vẽ.

Diện tích phần tô đậm là





 

   

1 2

2 2

0 1

112

4 2 0 2 2 1 747

S x dx x x dx dm cm

 

 

 





       



 









 

 

 

 

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 47

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

Câu 3: (Đề thi thử THPT QG Bắc Ninh lần 2 năm 2017) Một xưởng sản xuất gỗ muốn thiết kế những có

hình dạng là một phần của hình elip có kích thước giống hình bên. Biết miếng gỗ dày

2 .

Thể tích miếng

gỗ đã cho tính theo

nằm trong khoảng nào?





2340;2350

. B.





1170;1180

. C.





2240;2250

. D.





1200;1210

Lời giải

Chọn A

12,5

Chọn hệ tọa độ như hình vẽ, khi đó Elip đi qua các điểm









0;12, 5 , 25;10

B M

ta có

2 3

2 2

25 100 25

12,5

   

Ta được phương trình Elip:

2 2 2

3 2 3

1 12, 5 1

25 12, 5 25

9 9

x y x

y    

Diện tích bề mặt miếng là

4 12,5 1 23,406 2340,6

S dx V    



Câu 4: Một mặt bàn hình elip có chiều dài là

120

, chiều rộng là là

. Anh Phượng muốn gắn đá hoa

cương và dán gạch tranh trên mặt bàn theo hình (phần đá hoa cương bên ngoài và điểm nhấn bên trong là bộ

tranh gồm

miếng gạch với kích thước mỗi miếng là

25 40

cm cm



). Biết rằng đá hoa cương có giá và bộ

tranh gạch có giá

300.000

vnđ/bộ. Hỏi số tiền để gắn đá hoa cương và dán gạch tranh theo cách trên gần

nhất với số tiền nào dưới đây?

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 48

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

519.000

đồng. B.

610.000

đồng. C.

639.000

đồng. D.

279.000

đồng.

Lời giải

Chọn A

Gọi phương trình chính tắc của elip





có dạng:

2 2

x y

a b

 

Với

1 2

1,2 2 0,6

0,6 2 0, 3

A A a a

B B b b

 

 

  

 



 

 

  

 

 

 

2 2

: 1 0,36

0, 36 0,09 2

x y

E y x

      

Suy ra diên tích của hình elip là:

 

0,6 0,6

2 2 2

0 0

4 0,36 2 0, 36 0,18

S x dx x dx m

    

 

Gọi

1 2

;

S S

lần lượt là diện tích phần đá hoa cương và bộ tranh

Ta có





2x0,25x0, 4 0,2

S m

 

Suy ra

 





1 2

0,18 0,2

S S S m

    .

Gọi

là tổng chi phí. Khi đó ta có





0,18 0,2 .600000 300000 519.000



  

 (đồng).

Câu 5: Một mặt bàn hình elip có chiều dài là

120

, chiều rộng là

. Anh Hải muốn gắn đá hoa cương

cho mặt bàn theo hình (phần đá hoa cương trắng và phần đá hoa cương màu vàng), biết rằng phần màu vàng

cũng là elip có chiều dài

100

và chiều rộng là

. Biết rằng đá hoa cương màu trắng có giá

600.000 vn / m

và đá hoa cương màu trắng có giá

650.000 vn / m

. Hỏi số tiền để gắn đá hoa cương

theo cách trên gần nhất với số tiền nào dưới đây?

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 49

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

355.000

đồng. B.

339.000

đồng. C.

368.000

đồng. D.

353.000

đồng

Lời giải

Chọn A

Gọi phương trình chính tắc của elip





có dạng:

2 2

x y

a b

 

Với

1 2

1,2 2

0,6 2

A A a

B B b





 







 





0,6

0, 3





















 

2 2

: 1

0, 36 0, 09

x y

  

0, 36

y x

   

Suy ra diện tích của hình elip lớn là:

 

0,6 0,6

2 2 2

0 0

4 0, 36 2 0, 36 0,18

S x dx x dx m

    

 

Với

1 2

' ' 1 2 0,5

' ' 0, 4 2 0,2

A A a a

B B b b

 

 

  

 



 

 

  

 

 

 

2 2

: 1 0,25

0,25 0, 04 5

x y

E y x

      

Suy ra diện tích của hình elip nhỏ là:

 

0,5 0,5

2 2 2

0 0

2 8

4 0,25 0,25 0,1

5 5

S x dx x dx m

    

 

Gọi

1 2

;

S S

lần lượt là diện tích phần gắn đá hoa cương màu trắng và phần gắn đá hoa cương màu

vàng. Ta có

 





0,1 .

S S m 

Suy ra

   

0,18 0,1 0, 08

L N

E E

S S S

  

    

. Gọi

là tổng chi phí. Khi đó ta có

0, 08 .600000 0,1 .650000 355.000

 

 



(đồng).

Câu 6: Một biển quảng cáo có dạng hình elip với bốn đỉnh

1 2 1 2

, , ,

A A B B

như hình vẽ bên.

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 50

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

Người ta chia elip bởi Parabol có đỉnh

, trục đối xứng

1 2

B B

và đi qua các điểm

M N

. Sau đó

sơn phần tô đậm với giá

200.000

đồng/

và trang trí đèn led phần còn lại với giá

500.000

đồng/

. Hỏi kinh phí sử dụng gần nhất với giá trị nào dưới đây? Biết rằng

1 2

A A m



1 2

2 m

B B



2 m



2.431.000

đồng. B.

2.057.000

đồng. C.

2.760.000

đồng. D.

1.664.000

đồng.

Lời giải

Chọn A

-2 2

-1

+ Chọn hệ trục tọa độ

Oxy

sao cho

là trung điểm của

1 2

. Tọa độ các đỉnh





2; 0 ,







2;0 ,





0; 1







0;1

+ Phương trình đường Elip





2 2 2

1 1

4 1 4

x y x

y     

+ Ta có

 

3 3

1; , 1;

2 2

M N E

   

 

 

 

 

 

 

 

 

 

 

 

   

+ Parabol





có đỉnh





0; 1



và trục đối xứng là

nên





có phương trình





1, 0

y ax a

  





đi qua

M N

  







có phương trình

1 1

y x

 









  













 

+ Diện tích phần tô đậm

2. 1 1 1 d

4 2

S x x

 

 





 





    



 











 

 

 



2 3

4 d 1 2

3 2

x x

 









    













 



NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 51

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

Đặt

2 sin , ;

2 2

x t t

 

 

 

  

 

 

d 2 cos d

x t t

 

. Đổi cận:

0 0; 1

x t x t



     

2 3

4 4 sin .2 cos d 1 2

3 2

S t t t



 









     













 



3 4

4. cos d

3 3

t t



  



 

3 4

2. 1 cos2 d

3 3

t t



    



 

3 4 3 4

2 sin 2

3 3 3 6 3

t t



      

+ Diện tích hình Elip là

S ab

 

 



Diện tích phần còn lại

2 1

5 3 4

3 6 3

S S S



    

+ Kinh phí sử dụng là:

1 2

200000 500000 2431000

S S

 

(đồng).

Câu 7: Một người định xây một hòn non bộ bằng cách vẽ một đường tròn bán kính

trên mặt đất sau đó

lấy tâm đường tròn làm tâm của một hình vuông cạnh

như hình vẽ. Phần

(tất cả phần màu trắng) xây

thành bể để xếp hòn non bộ và thả cá, phần

2 3

S S

để trồng hoa. Tính diện tích trồng hoa.

3,65

3,56

4, 65

4, 56

Lời giải

Chọn A

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 52

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

-1

Chọn gốc tọa độ trùng với tâm đường tròn, khi đó phương trình đường tròn tâm

bán kính

là.

2 2 2

4 4

x y y x

     

Diện tích của hình tròn là







Diện tích hình vuông là





Các cạnh của hình vuông nằm trên các đường thẳng

1, 1

y x

   

Phương trình hoành độ giao điểm của đường tròn và đường thẳng



là.

4 1 3

x x

    

Diện tích phần bể ngoài hình vuông là





2 4 1

x dx



 







4 2 4 1

S x dx



    



Diện tích phần trồng hoa





2 3 1

4 3,65

S S S m

   

Câu 8: Nhà ông An có một khuôn viên dạng nửa hình tròn có đường kính bằng

4 5( )

. Ông An muốn thiết

kế khuôn viên một phần để lát gạch Ý (phần tô đậm) và hai phần còn lại để trồng hoa Nhật Bản ( phần không

tô màu). Phần tô đậm có dạng của một cánh hoa hình parabol có đỉnh trùng với tâm của nửa hình tròn và hai

đầu mút của cánh hoa nằm trên nửa đường tròn, cách nhau một khoảng bằng 4 (m). Biết các kích thước cho

như hình vẽ, kinh phí để trồng hoa Nhật Bản là

150.000

đồng / m

và kinh phí để lát gạch Ý là 250.000

đồng/ m

. Hỏi kinh phíông An để làm công trình đó gần nhất với kết quả nào sau đây?

5.916.400

đồng B.

5.906.400

đồng C.

5.609.400

đồng D.

5.906.500

đồng

Lời giải

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 53

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

Chọn B

(P)

Đặt hệ trục tọa độ như hình vẽ. Khi đó phương trình nửa đường tròn là:





2 2 2 2

2 5 20

y R x x x

     

Phương trình Parabol

( )

có đỉnh là gốc

sẽ có dạng

y ax



.Mặt khác

( )

đi qua điểm

(2; 4)

nên

4 .(2) 1

a a

  

Gọi

là phần diện tích của hình phẳng hạn bởi

( )

là nửa đường tròn ( phần tô màu).

Diện tích phần lát gạch Ý của khuôn viên là:

2 2

( 20 ). 11,940

S x x dx



   



Phần diện tích trồng cỏ Nhật Bản của khuôn viên là:

2 2 2

2 2

1 1

(2 5) ( 20 ) 19, 476

2 2

hinh tron

S S S x x dx



      



Vậy số tiền cần có là:

1 2

250.000.S 150.000.S 5.906.400

  

(đồng)

Câu 9: Một cái cổng hình parabol như hình vẽ. Chiều cao

GH m



, chiều rộng

AB m



0,9

AC BD m

 

. Chủ nhà làm hai cánh cổng khi đóng lại là hình chữ nhật CDEF tô đậm giá là

1200000

đồng/m

, còn các phần để trắng làm xiên hoa có giá là

900000

đồng/m

Hỏi tổng chi phí để là hai phần nói trên gần nhất với số tiền nào dưới đây?

11445000

(đồng). B.

7368000

(đồng). C.

4077000

(đồng). D.

11370000

(đồng)

Lời giải

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 54

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

Chọn A

Gắn hệ trục tọa độ Oxy sao cho

trùng

khi đó parabol có đỉnh





2; 4

và

đi qua gốc tọa độ.

y=-x

+4x

C B

3,10,9

Gọi phương trình của parabol là

y ax bx c

  

Do đó ta có

2 4

2 2 4

a b c











 







  

 

 



 

  

 







Nên phương trình parabol là

( )

y f x x x





 

Diện tích của cả cổng là

2 2 4 2

( 4x) 2 10, 67( )

3 3

S x dx x m

 







       











 



Do vậy chiều cao





0,9 2,79( )

CF DE f m

  





4 2.0,9 2,2

CD m

  

Diện tích hai cánh cổng là





. 6,138 6,14

CDEF

S CD CF m

  

Diện tích phần xiên hoa là

10,67 6,14 4,53( )

xh CDEF

S S S m

    

Nên tiền là hai cánh cổng là





6,14.1200000 7368000



và tiền làm phần xiên hoa là





4, 53.900000 4077000



Vậy tổng chi phí là 11445000 đồng.

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 55

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

Câu 10: Bồn hoa của một trường X có dạng hình tròn bán kính bằng

. Người ta chia bồn hoa thành các

phần như hình vẽ dưới đây và có ý định trồng hoa như sau: Phần bên trong hình vuông

ABCD

để trồng hoa.

Phần phần gạch xọc dùng để trồng cỏ. Ở

góc còn lại mỗi góc trồng một cây cọ. Biết

AB m



, giá trồng

hoa là

200.000

đ/m

, giá trồng cỏ là

100.000

đ/m

, mỗi cây cọ giá

150.000

đ. Hỏi cần bao nhiêu tiền để thực

hiện việc trang trí bồn hoa đó (làm tròn đến hàng nghìn).

13.265.000

đồng. B.

12.218.000

đồng. C.

14.465.000

đồng. D.

14.865.000

đồng.

Lời giải

Chọn A

Chọn hệ trục tọa độ sao cho gốc tọa độ trùng với tâm hình tròn, suy ra phương trình

đường tròn là:

2 2

x y

 

+ Diện tích hình vuông

ABCD

là:





4 4 16

ABCD

S m

  

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 56

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC



Số tiền để trồng hoa là:

16 200.000 3.200.000

  

(đồng).

+ Diện tích trồng cỏ là:





 

2 2

4 64 2 d 94,654

S x x m



   





Số tiền trồng cỏ là:

94,654 100.000 9.465.000

  

(đồng).

+ Số tiền trồng 4 cây cọ là:

150.000 4 600.000

  

(đồng).

Vậy tổng số tiền để thực hiện việc trang trí bồn hoa là:

1 2 3

13.265.000

T T T T

   

(đồng).

Câu 11: Người ta lát gạch trang trí một mảnh sân hình chữ nhật như hình dưới đây, trong đó









1 2

P P

là các

parabol giống nhau,





là đường tròn có tâm trùng với tâm của mảnh sân và lần lượt có duy nhất một điểm

chung với các parabol tại chính các đỉnh của các parabol ấy. Tính và làm tròn đến hai chữ số thập phân diện

tích phần lát gạch của mảnh sân trong trường hợp diện tích hình tròn bao bởi





lớn nhất.

8, 39

. B.

10,12

. C.

9,18

. D.

11,45

Lời giải

Chọn A

Đặt





và





vào mặt phẳng

Oxy

sao cho





có tâm là

và bán kính là





r r



như hình

dưới đây:

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 57

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

a-r

-r

Lúc này ta có









2 2 2 2

: , : ( 0)

C x y r P y ax r a

    





và





có duy nhất một điểm chung là đỉnh của





nên hệ phương trình

2 2 2

x y r

y ax r





 







 





có duy nhất một nghiệm là







(*)

 

2 2 2

2 2 4 2 2 2

2 1

x y r

x a x arx r r

y ax r





















 

   



 



  



 



  



  

 



  











 





nên (*)

  .

 

M P

 



















 

nên

2 7





. Tức

2 7























. Từ đây tìm được

2 7























Do hình tròn có diện tích lớn nhất nên



















. Lúc này





cắt tia

tại điểm có hoành độ

Diện tích cần tính là

1 1

4 4 .d 8, 39

2 4 2

S x x



 









    













 



Câu 12: Cho một mô hình



mô phỏng một đường hầm. Biết rằng đường hầm mô hình có chiều dài





5 cm

; khi cắt hình này bởi mặt phẳng vuông góc với đáy của nó, ta được thiết diện là một hình parabol có

độ dài đáy gấp đôi chiều cao parabol như hình vẽ. Chiều cao của mỗi thiết diện parobol cho bởi công thức

y x

 





, với





là khoảng cách tính từ lối vào lớn hơn của đường hầm mô hình. Tính thể tích

(theo đơn vị

) không gian bên trong đường hầm mô hình (làm tròn kết quả đến hàng đơn vị)

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng

https://www.facebook.com/groups/toanvd.vdc Trang 58

NHÓM TOÁN VD – VDC

NHÓM TOÁNVD – VDC

. B.

. C.

. D.

Lời giải

Chọn A

Xét một thiết diện parabol có chiều cao là

và độ dài đáy

và chọn hệ trục

Oxy

như hình vẽ

trên. Parabol





có phương trình





, 0

y ax h a

  

Ta có









B h P



ah h

  





a do h

   

Diện tích

của thiết diện:

1 4

S x h x



 







   











 



h x

 

 

4 2

3 5

S x x

 







  











 

Suy ra thể tích không gian bên trong của đường hầm mô hình:

 

5 5

0 0

4 2

d 3 d 28, 888

3 5

V S x x x x

 







    











 

 





29 cm

V 

Bấm Tải xuống để xem toàn bộ.

| 1/58

| | Tải xuống

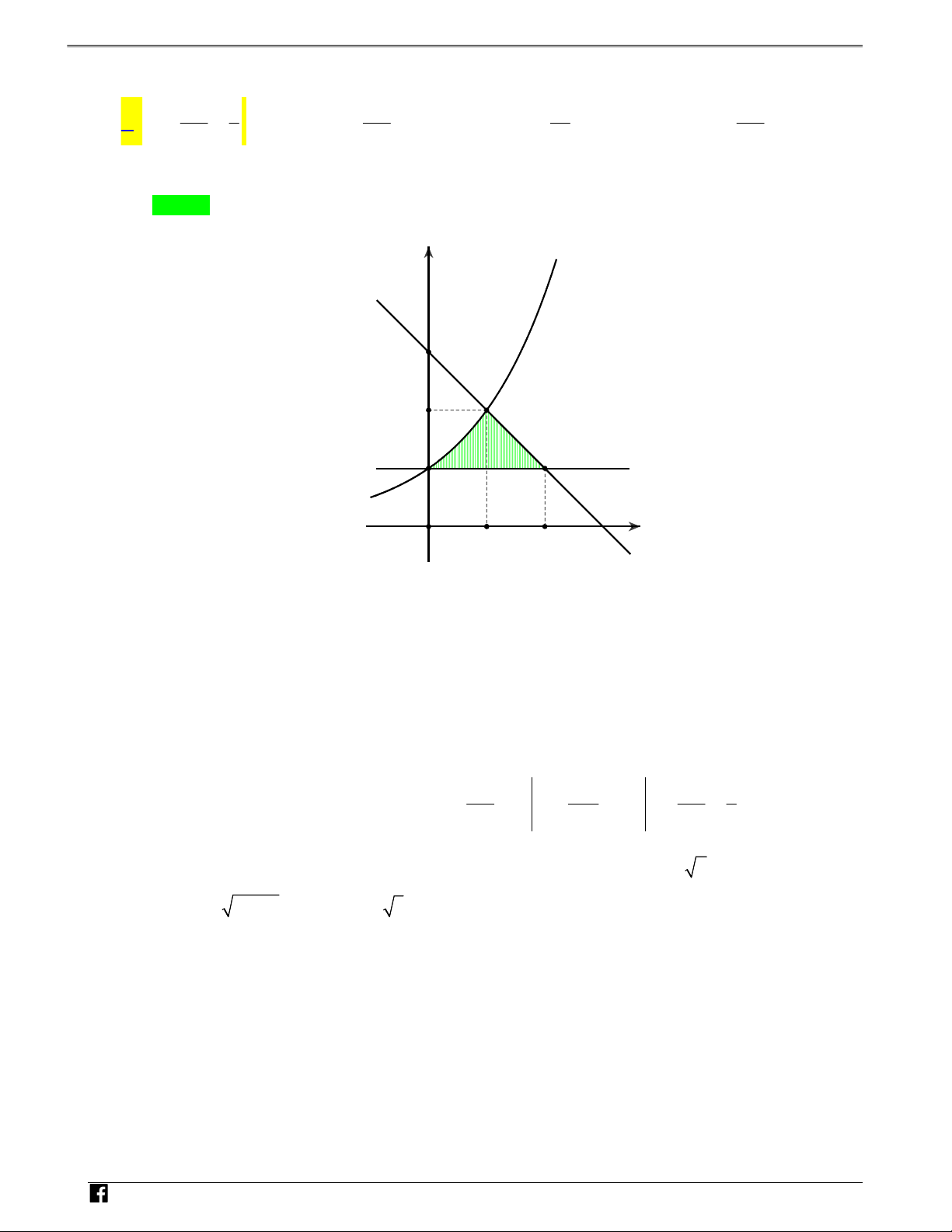
Preview text:

NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng Chuyên đề:
SỬ DỤNG TÍNH CHẤT CỦA ĐỒ THỊ HÀM SỐ ĐỂ TÍNH DIỆN TÍCH HÌNH PHẲNG N H Ó M T O Á N I. MỘT SỐ DẠNG TOÁN V
Nội dung các dạng toán xoay quanh bài toán ứng dụng tích phân tính diện tích hình phẳng với giả D –
thiết bài toán cho bởi đồ thị hàm liên quan. V D
Dạng 1. Sử dụng định nghĩa xác định công thức diện tích. C
Dạng 2. Dựa vào các điểm đồ thị đi qua xác định hàm số đi đến công thức tính.
Dạng 3. Dựa vào tâm đối xứng, trục đối xứng của đồ thị xác định hàm số đi đến công thức tính.
Dạng 4. Dựa vào tiếp tuyến của đồ thị xác định hàm số đi đến công thức tính.
Dạng 5. Biến đổi đồ thị đưa về tính toán đơn giản.
Dạng 6. Tính diện tích dựa vào việc chia nhỏ hình.
Dạng 7. Toán thực tế với giả thiết có đồ thị hàm liên quan. N H Ó M T O Á N V D – V D C
https://www.facebook.com/groups/toanvd.vdc Trang 1
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng II. BÀI TẬP MINH HỌA
1) Dạng 1. Sử dụng định nghĩa xác định công thức diện tích.
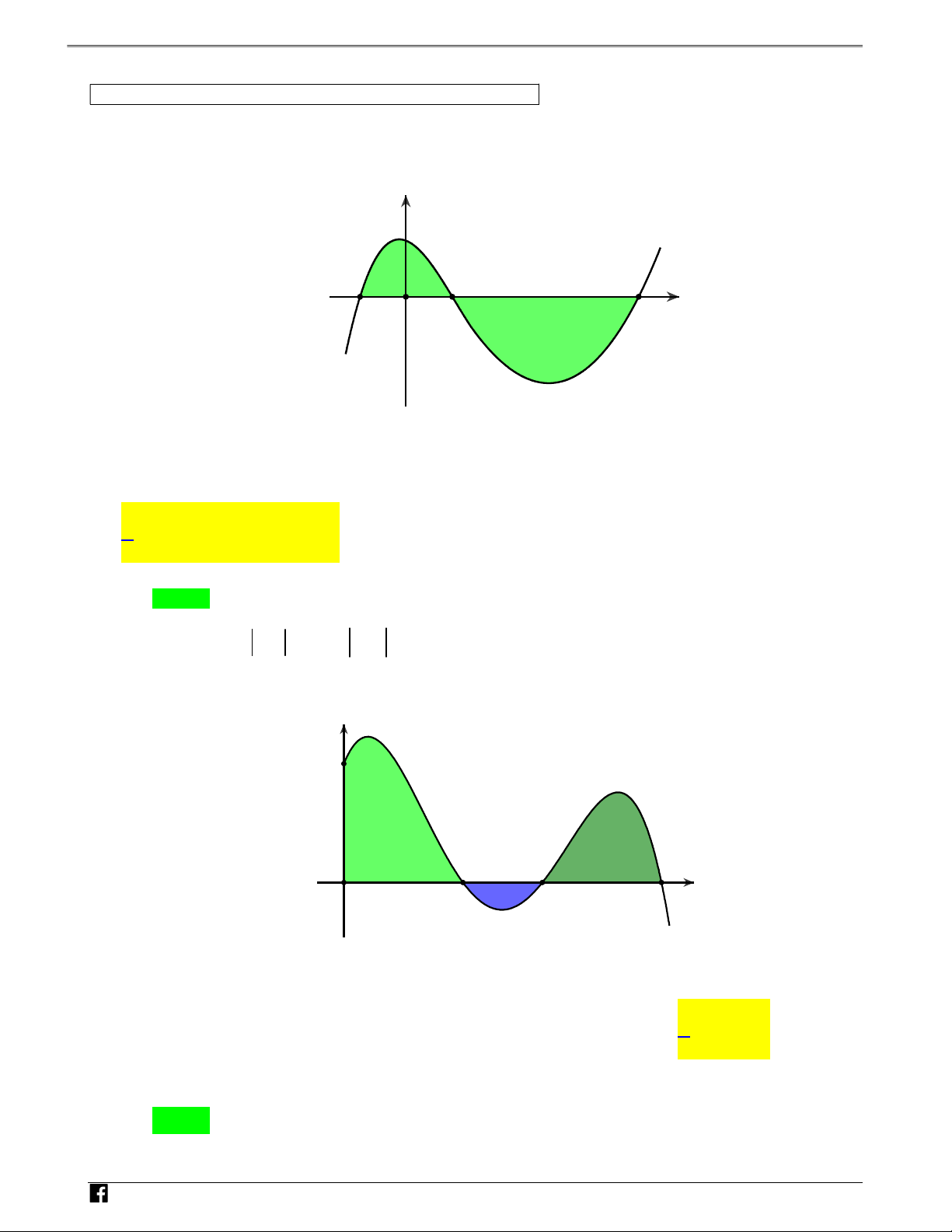
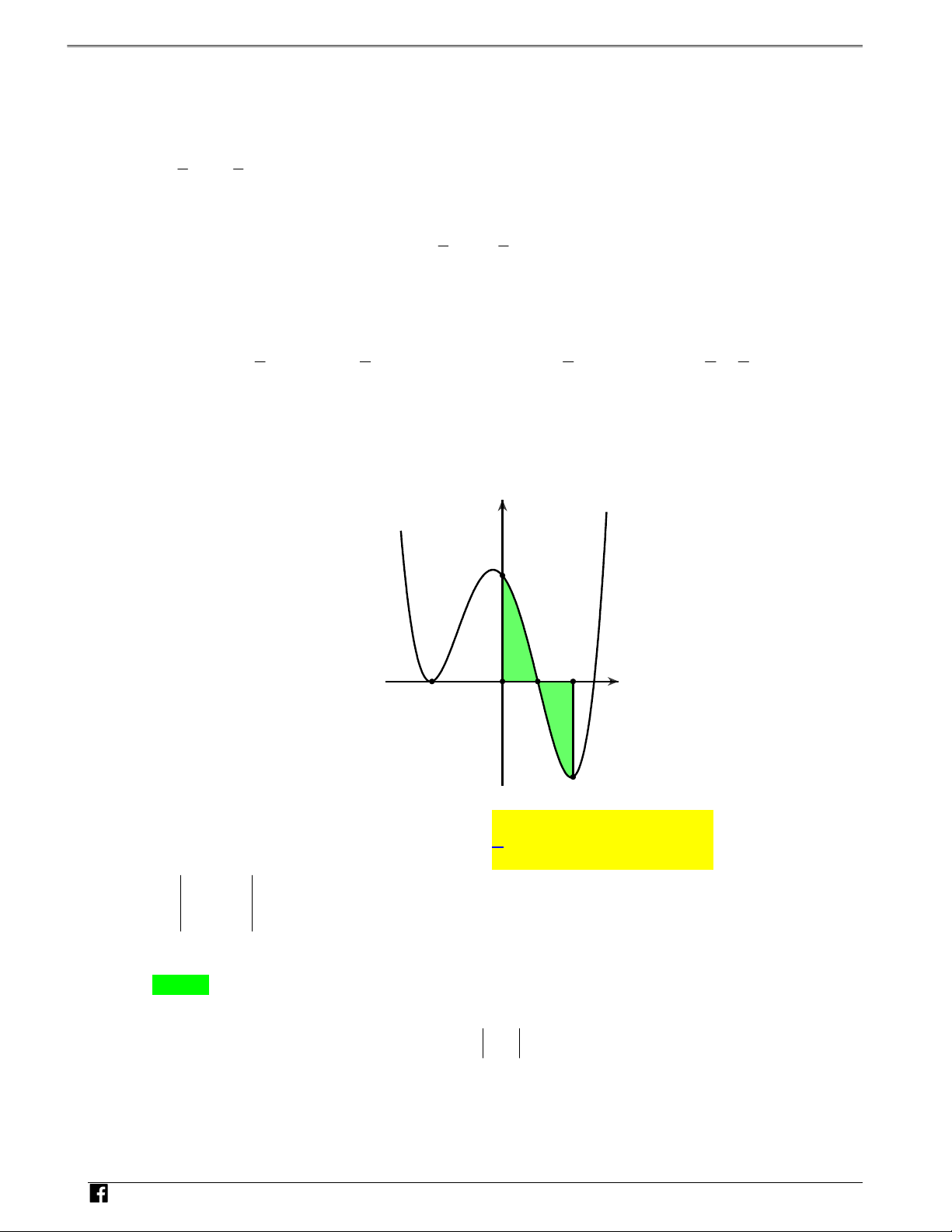
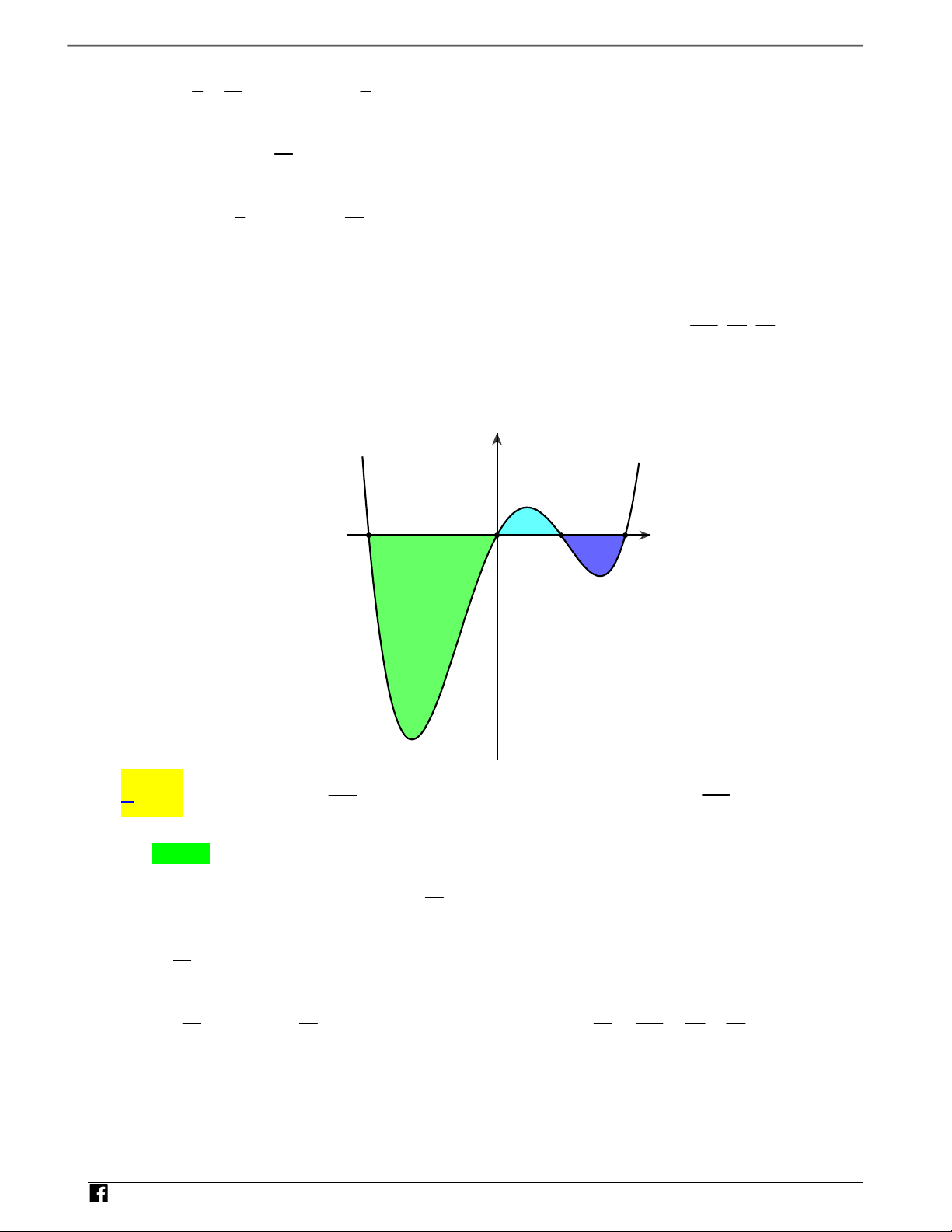
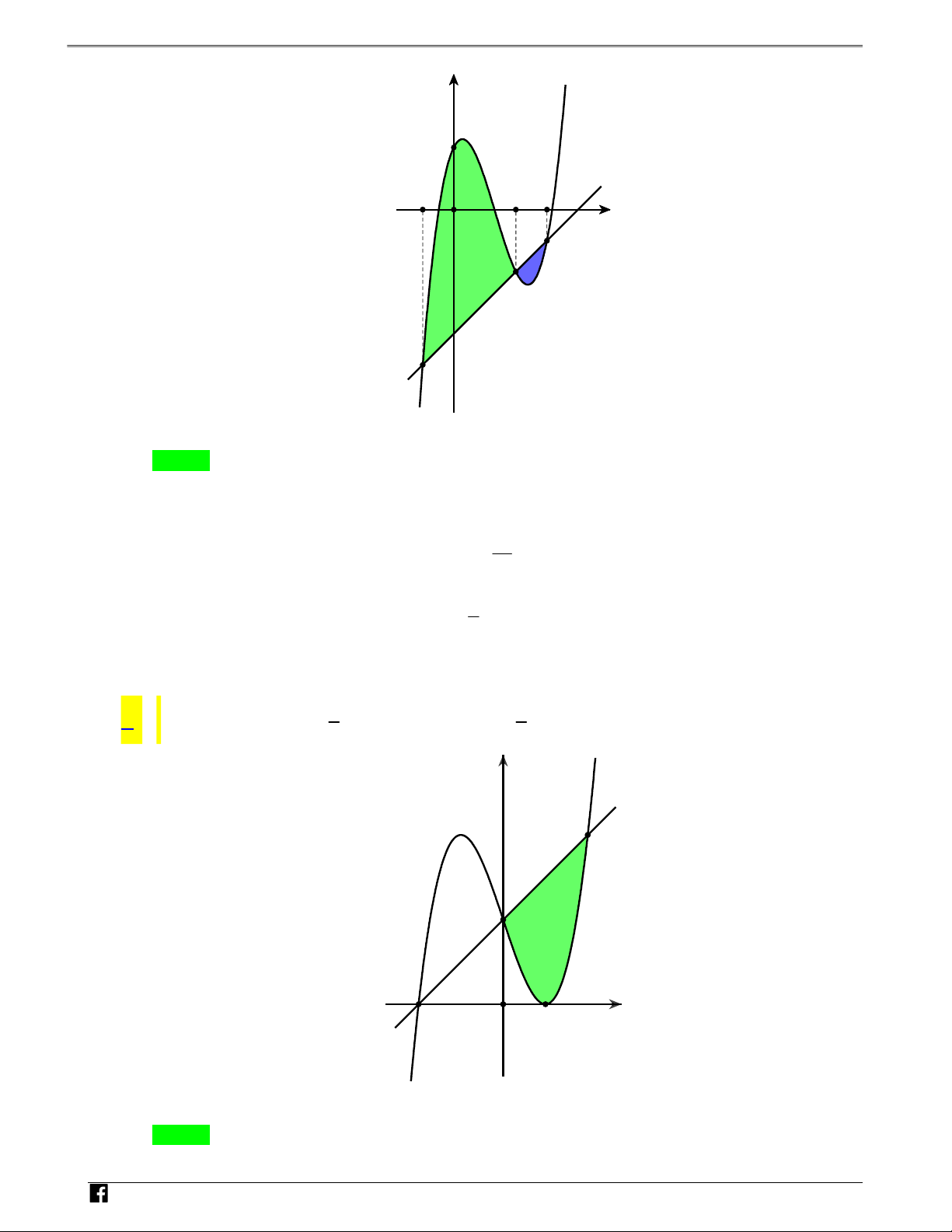
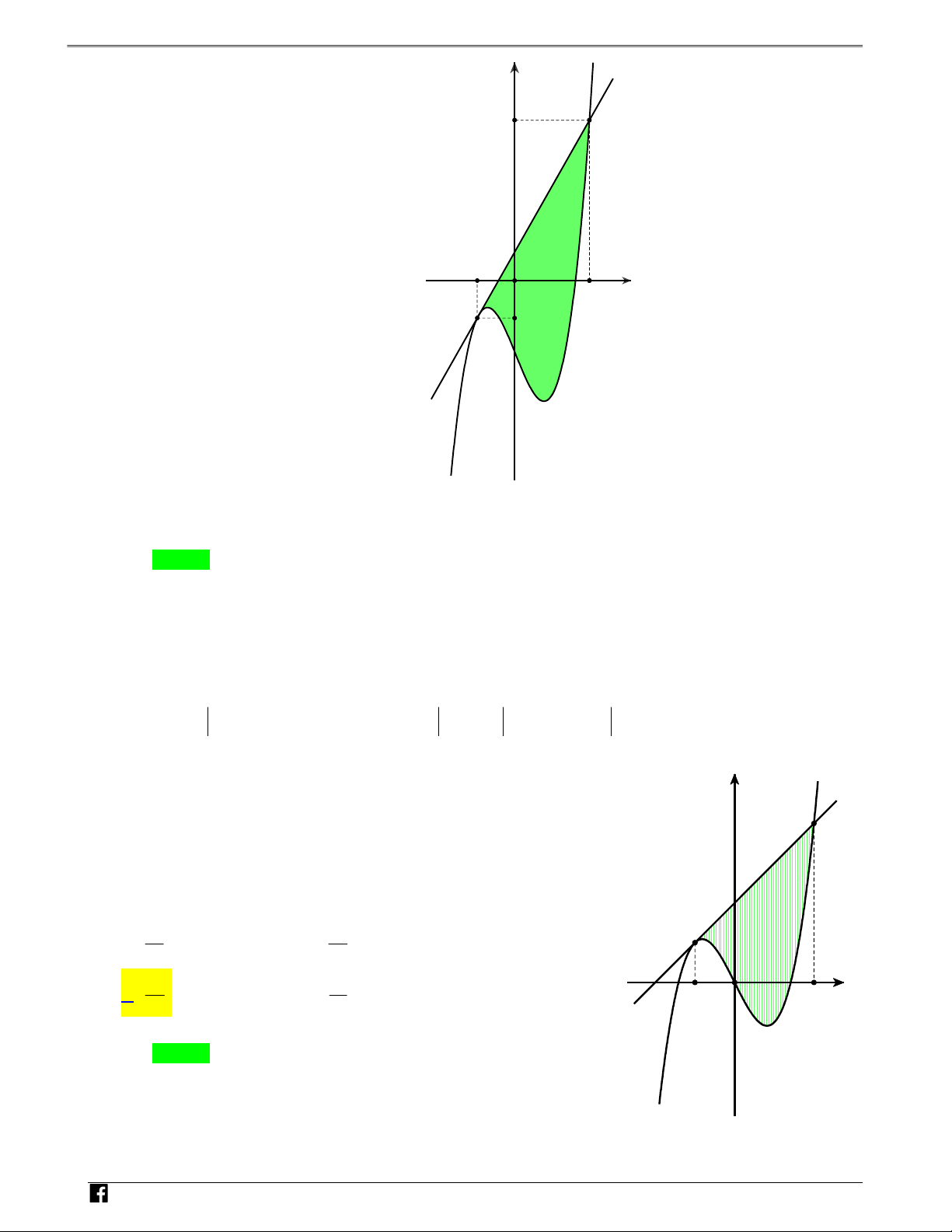
Câu 1: (Đề THPT QG 2019) Cho hàm số y  f  x liên tục trên .
 Gọi S là diện tích hình phẳng giới hạn N
bởi các đường y  f x,y  0,x  1 và x  5 (như hình vẽ bên). H Ó M y TOÁN y=f(x) V D -1 O 1 5 x – VDC
Mệnh đề nào sau đây đúng? 1 5 1 5
A. S   f (x)dx  f (x)dx   . B. S  f(x)dx  f(x)dx   . 1 1 1  1 1 5 1 5 C. S  f(x)dx  f(x)dx   . D. S   f(x)dx  f(x)dx   . 1  1 1 1 Lời giải Chọn C 1 5 1 5 Ta có S  f(x) dx  f   x dx  f  xdx  f  xdx . 1  1 1 1 N H
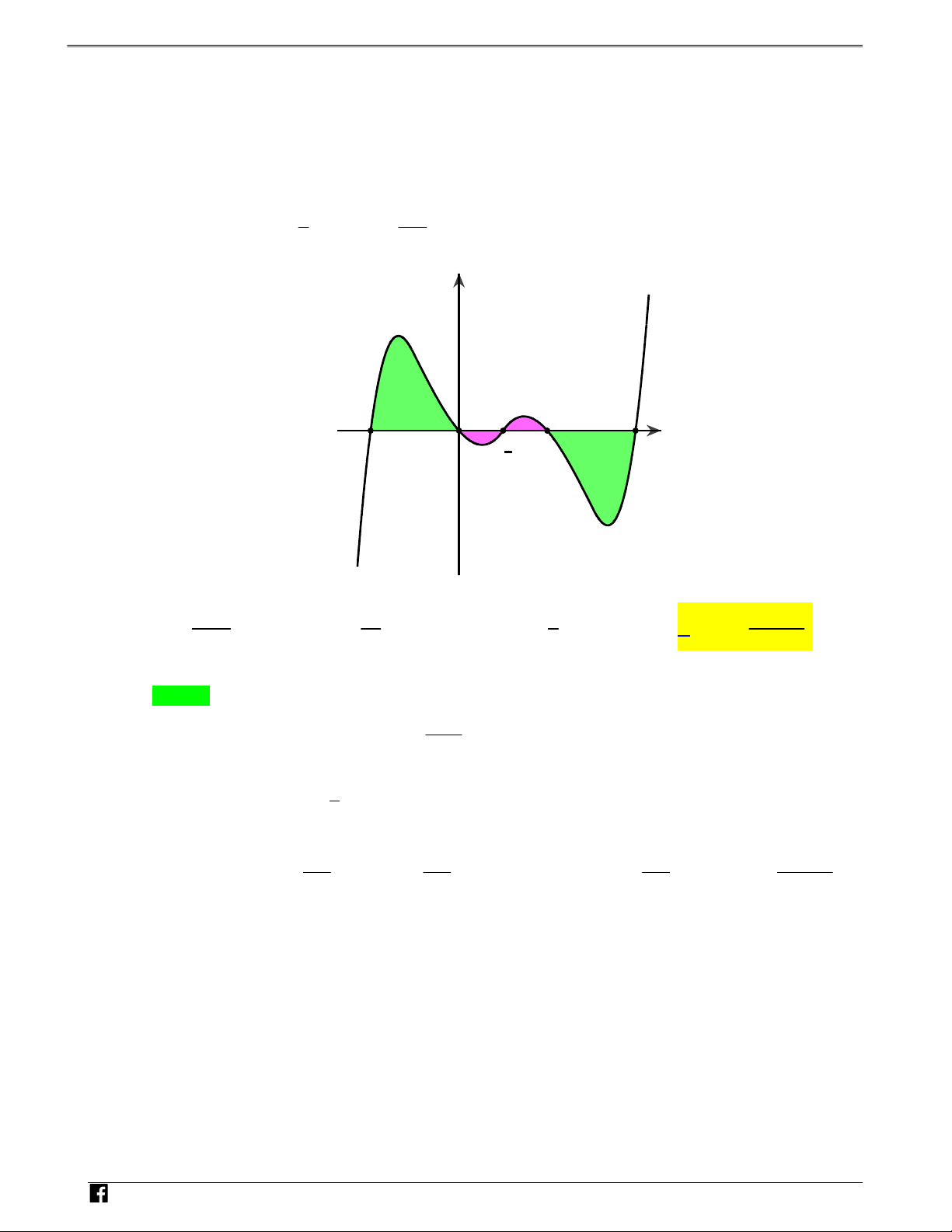
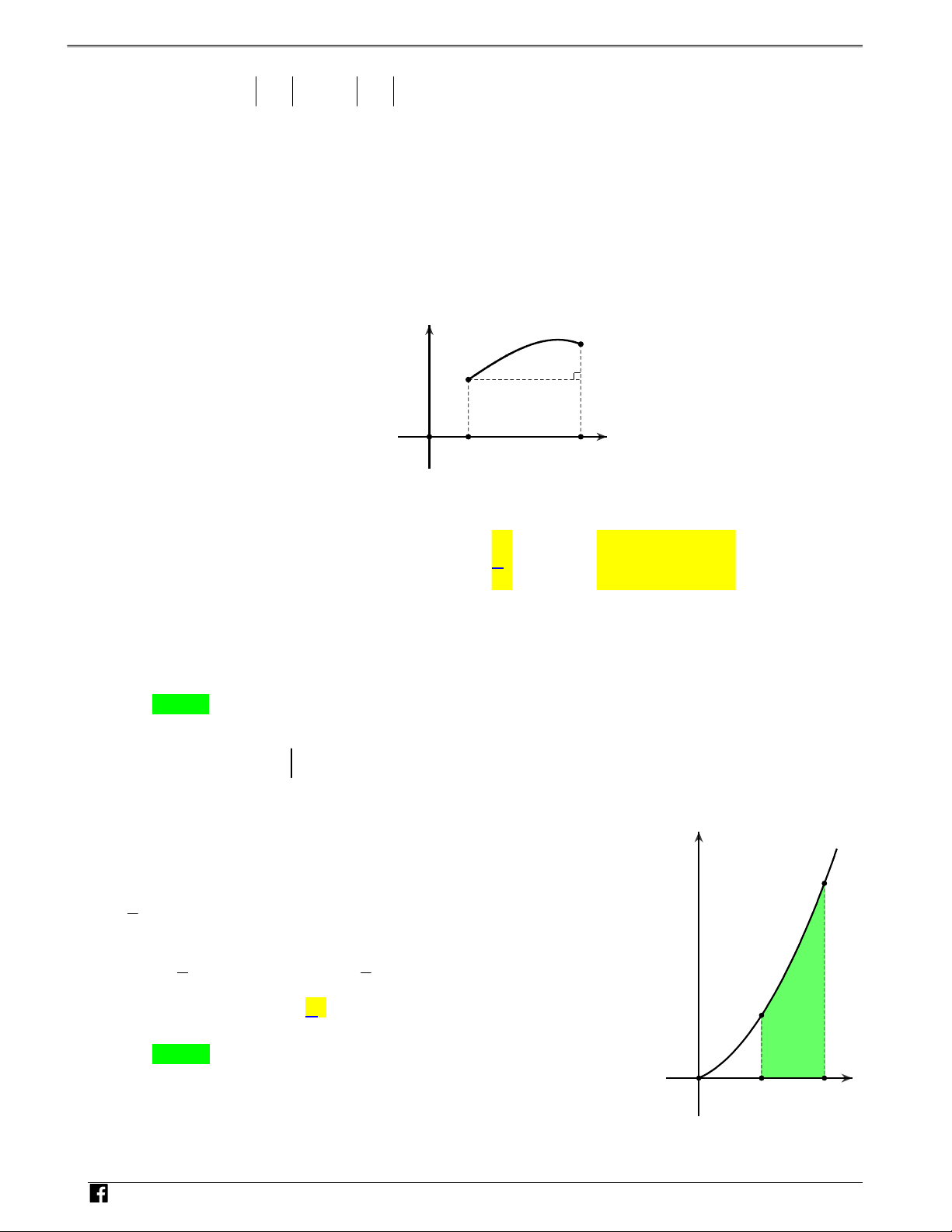
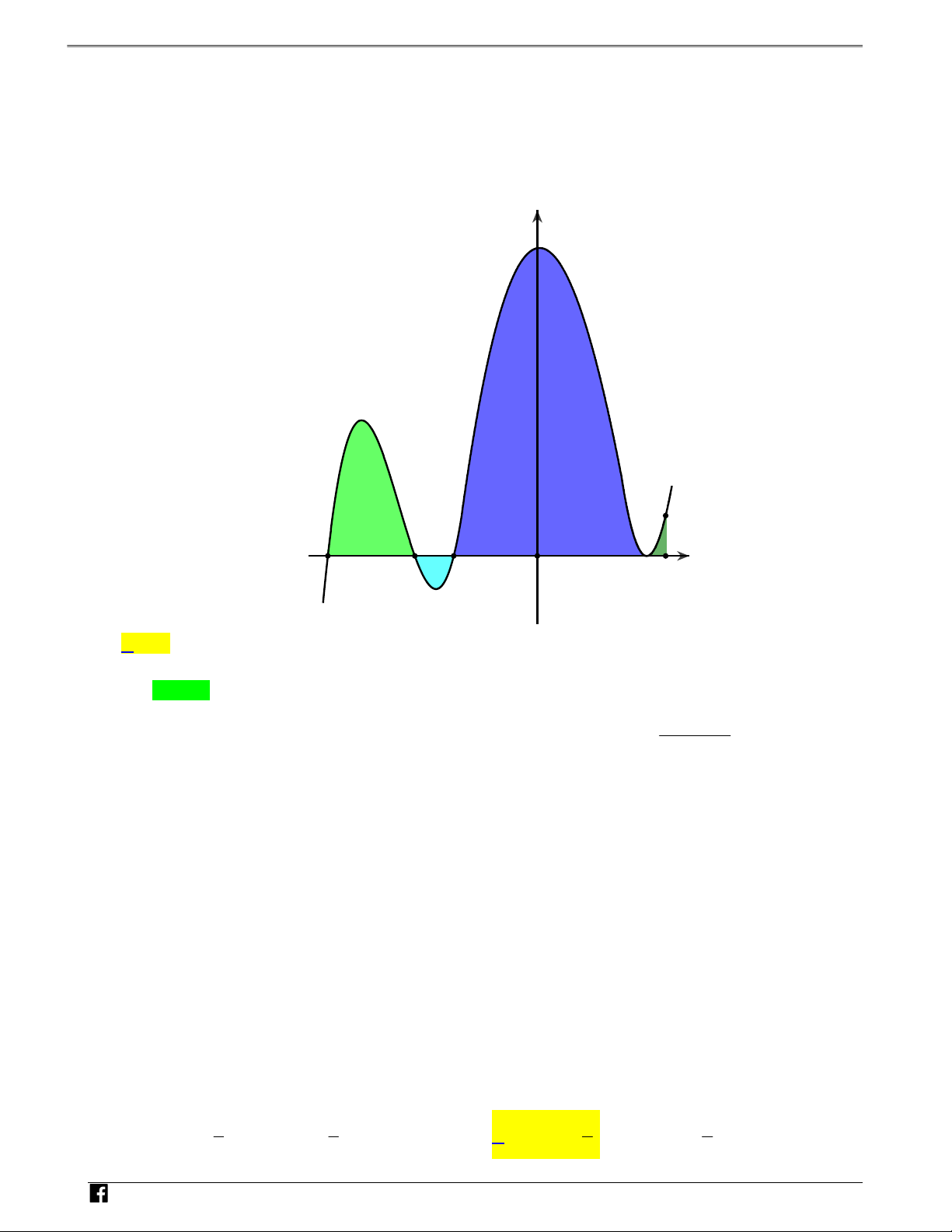
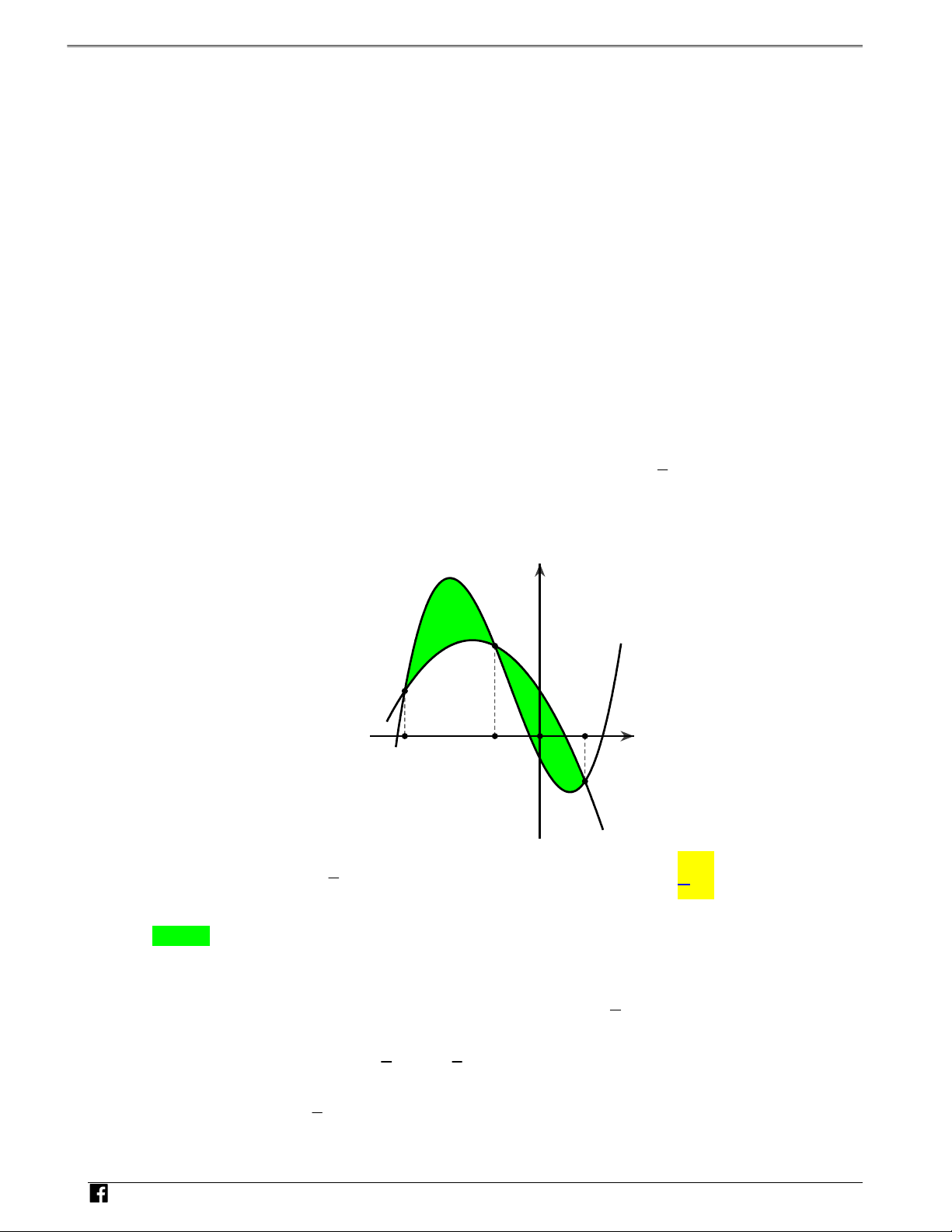
Câu 2: Cho đồ thị hàm số y  f(x) trên 0;8 Ó
  như hình vẽ. M T y O Á 3 N V D – V (S1) (S D 3) C O 3 (S )2 5 8 x
Biểu thức nào dưới đây có giá trị lớn nhất? 1 3 5 8 A. f(x)dx  . B. f(x)dx  . C. f(x)dx  . D. f(x)dx  . 0 0 0 0 Lời giải Chọn D
https://www.facebook.com/groups/toanvd.vdc Trang 2
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng 3 5 8 8
Dễ thấy S  S . Mà S  f(x),S   f(x),S  f(x) f(x)dx  S  S  S 3 2 1  2  3  , nên  lớn 1 2 3 0 3 5 0 nhất. N H
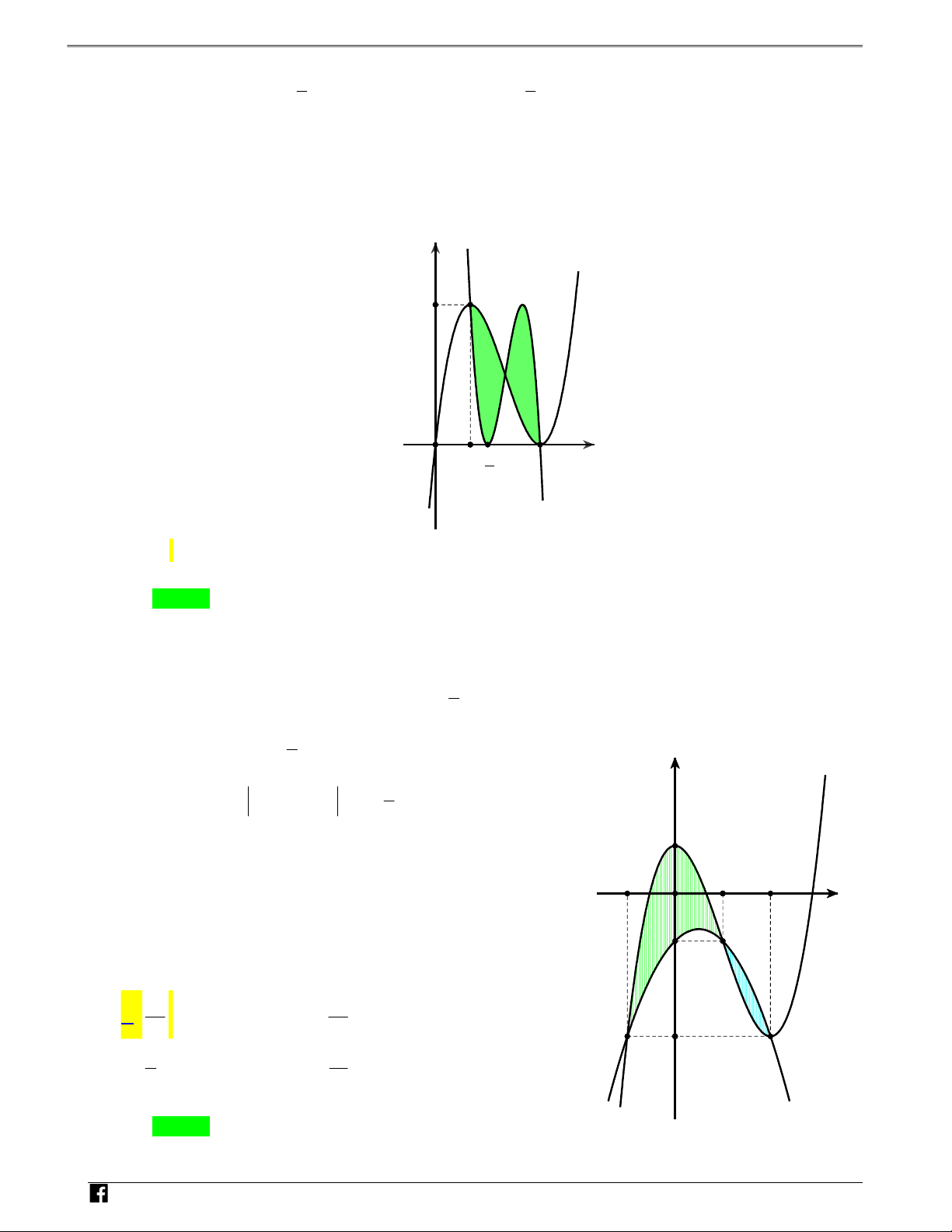
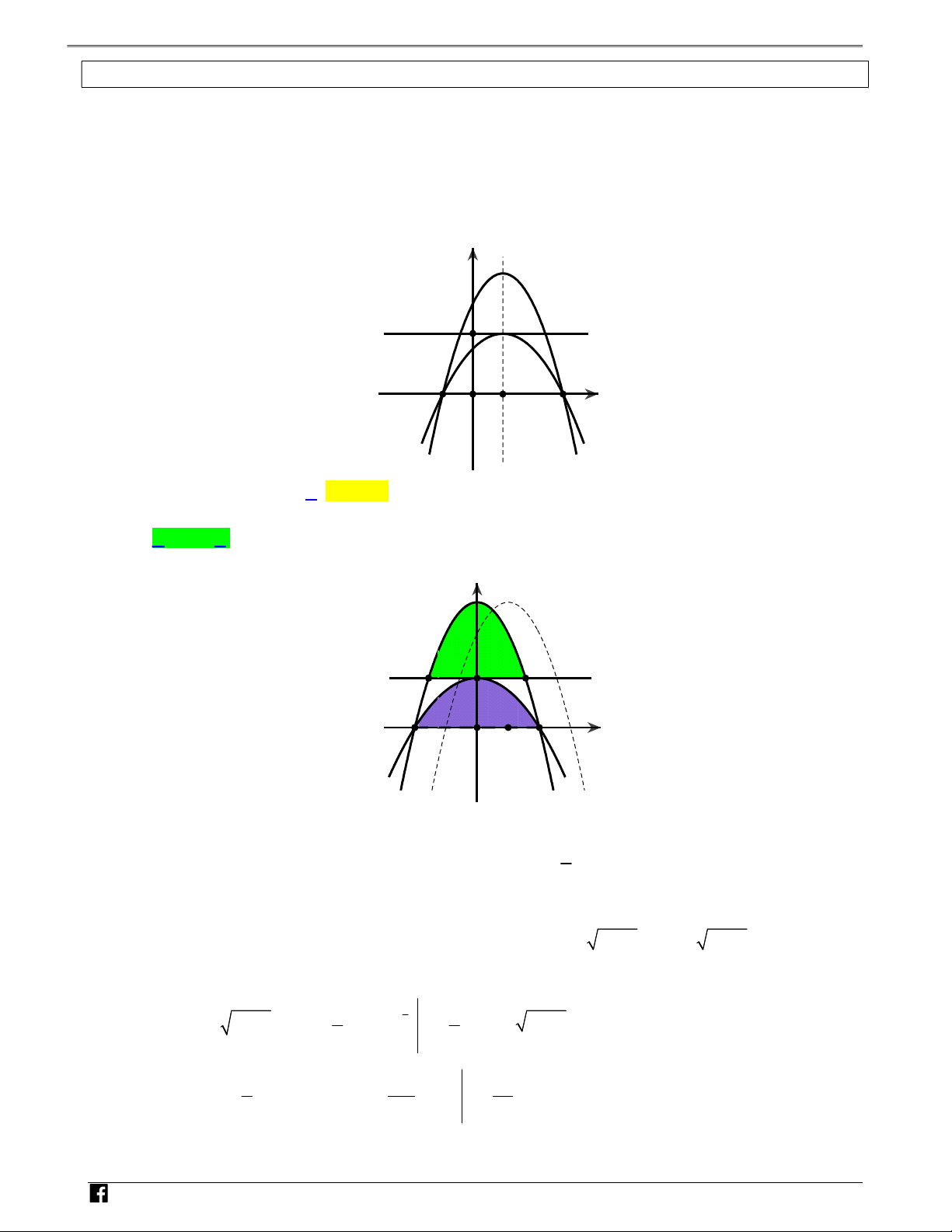
Câu 3: Cho hàm số y  f x liên tục trên  có đồ thị tạo với trục hoành các miền có diện tích S ,S ,S ,S Ó   1 2 3 4 M 1 2 13 T
như hình vẽ. Biết S  S  ;S  S  , tích phân  2x 2x I f dx bằng O    1 4 2 3 3 384 Á 1 N V y D – y=f(x) V D C S1 S S3 2 x 1 -1 O 1 2 2 S4 2 47 2 81 A. I   . B. I  . C. I  . D. I   . 3ln2 64 3 128 ln2 N Lời giải H Ó Chọn D M x x dt T
Đặt t  2  dt  2 ln 2dx  dx  O t ln2 Á N V 1 Đổi cận: x  1
  t  ; x  1  t  2 D 2 – V 1 2  1 2 D  x x 1 1   1 81 C I  2 f  2 dx  f  tdt   f  tdt  f  tdt   S S   . 3 4  ln2 ln2    ln2 128ln2 1 1/2 1/2 1 
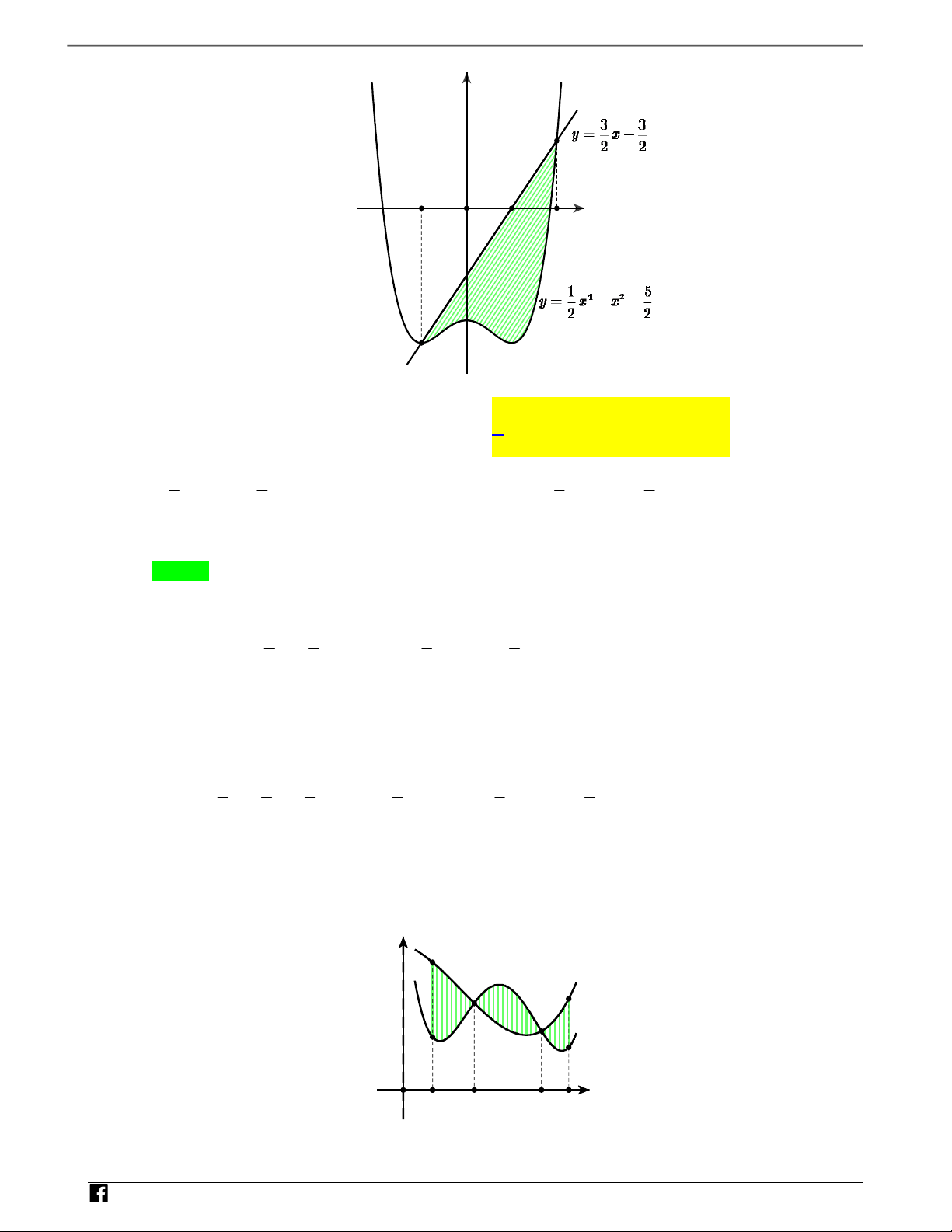
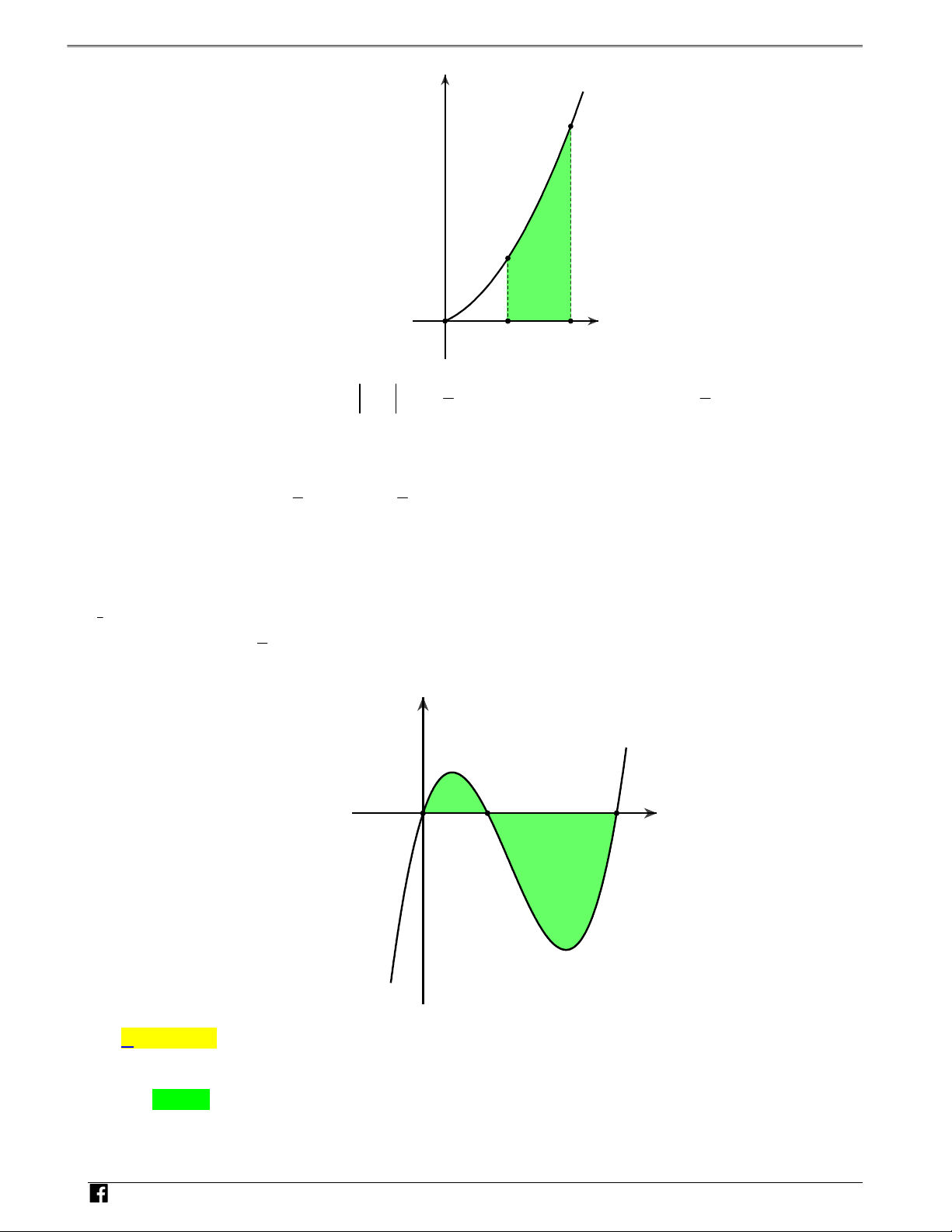
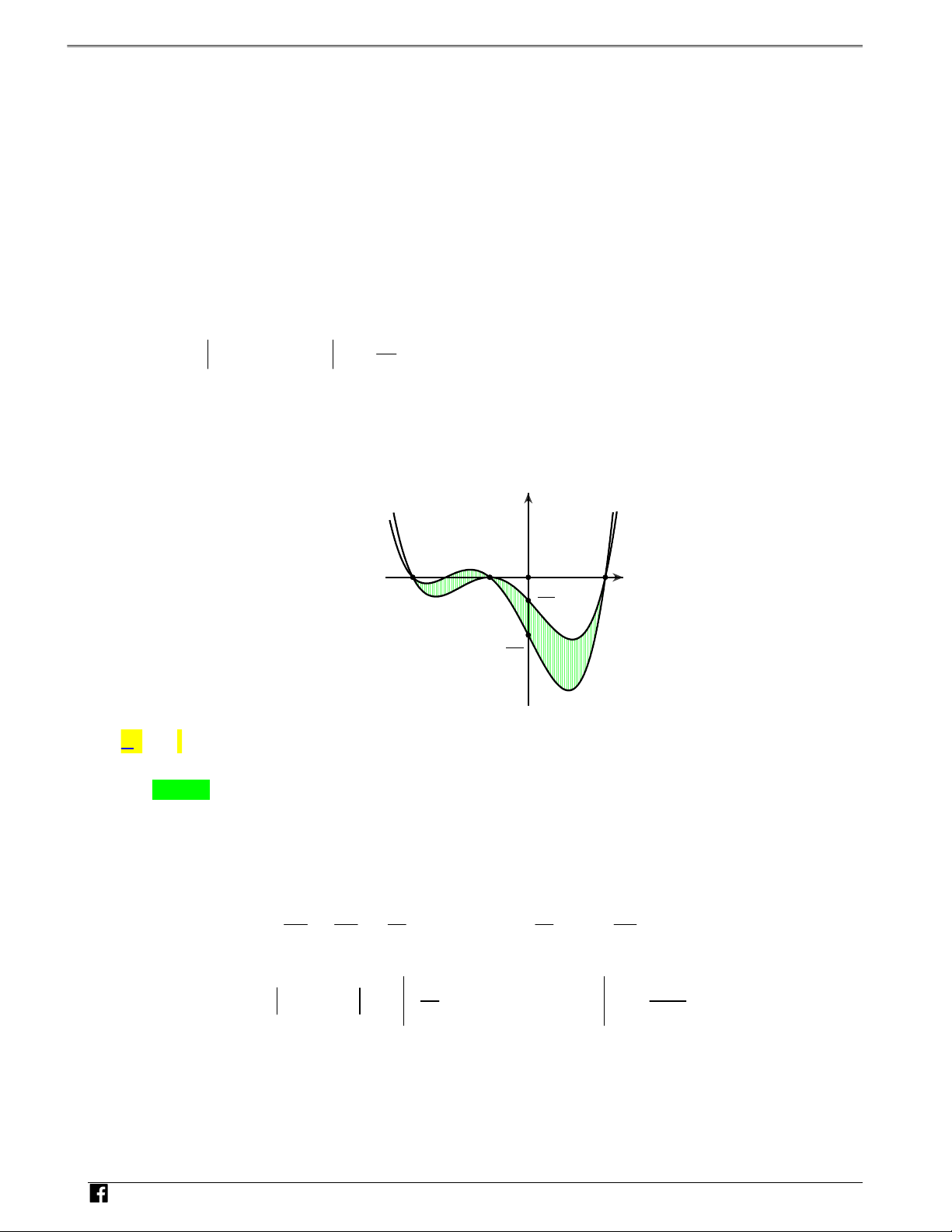
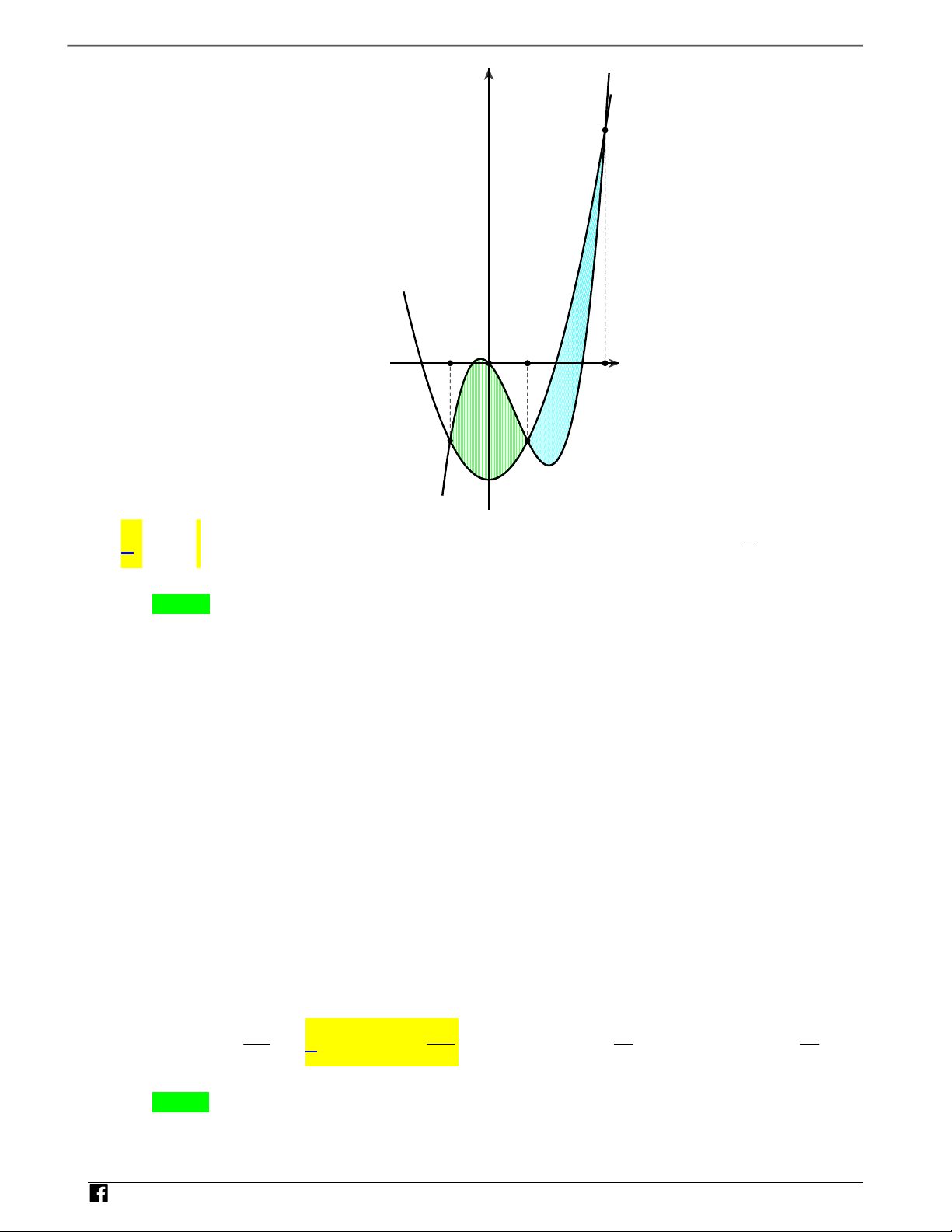
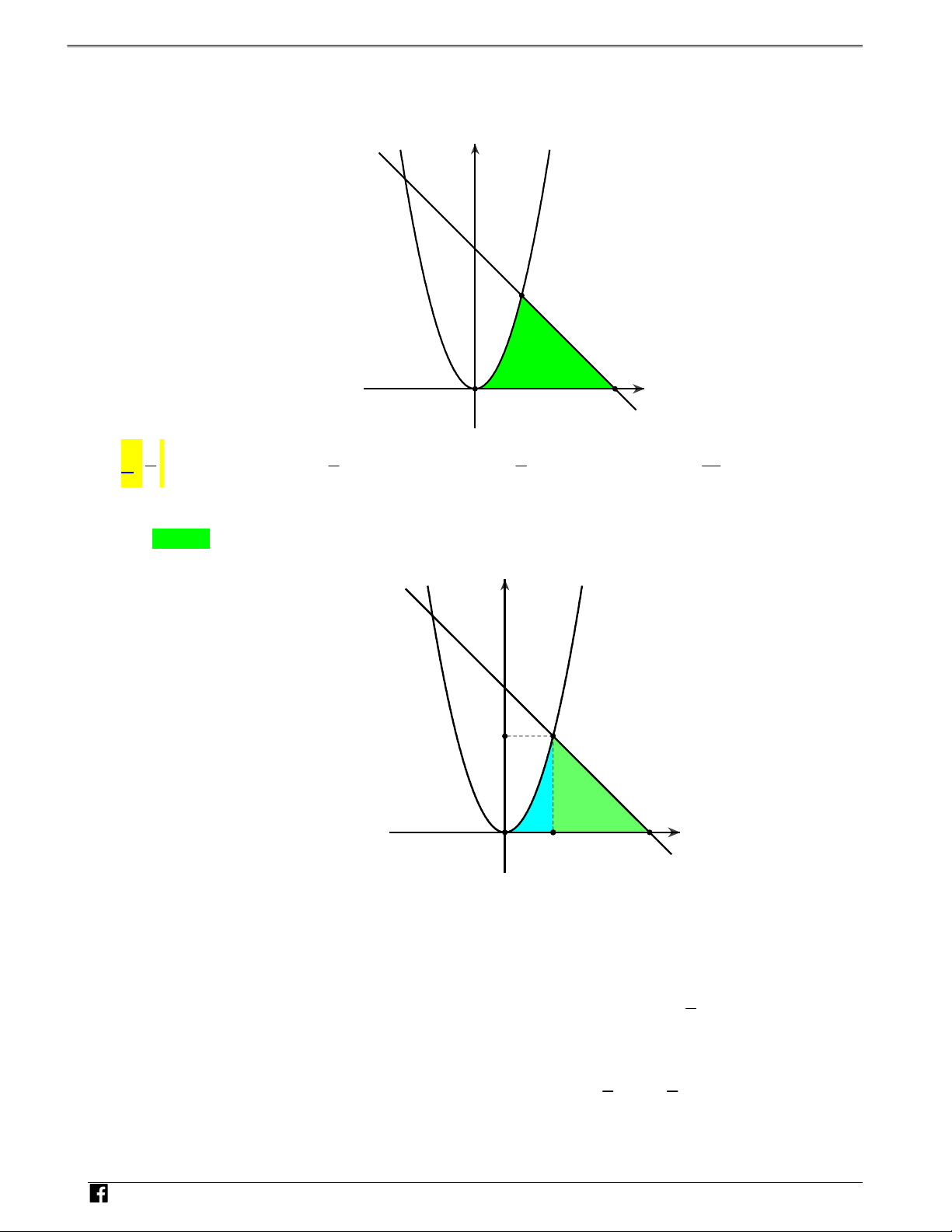
Câu 4: Diện tích phần hình phẳng gạch chéo trong hình vẽ bên dưới được tính theo công thức nào sau đây?
https://www.facebook.com/groups/toanvd.vdc Trang 3
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng y N H Ó M T -1 O 2 x O Á N V D – VDC 2  1 3  2  1 3  A.  4 2   x  x  x  4dx   4 2   . B.   x  x  x  1dx .  2 2    2 2  1  1  2 1 3  2  1 3  C.  4 2  x  x  x 1dx   4 2   . D.   x  x  x  4dx . 2 2    2 2  1  1  Lời giải Chọn B
Từ hình vẽ ta thấy phần diện tích hình phẳng cần tính là hình phẳng giới hạn bởi đồ thị hai hàm 1 5 số:y  f x 3 3  x  ; y  g x 4 2
 x  x  và hai đường thẳng x  1  ;x  2. 2 2 2 2 N H Ó
Ngoài ra ta thấy đường y  f x nằm trên đường y  g x trên đoạn  1;2  M     
 nên ta có diện tích T
phần gạch chéo trên hình vẽ là: O Á N 2 3 3  2       1 5  1 3 V     4 2 S x    4 2     x  x   dx    x  x  x  1dx D   .  2 2   2 2      2 2  1   1  – VD
Câu 5: Cho hình phẳng H  giới hạn bởi đồ thị của hai hàm số y  f x và y  f x liên tục trên đoạn 2   1   C a; b
  và hai đường thẳng x  a , x  b (tham khảo hình vẽ dưới). Công thức tính diện tích của hình H  là y y=f1(x) y=f (x) 2 O a c1 c x 2 b
https://www.facebook.com/groups/toanvd.vdc Trang 4
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng b b A. S  f x  f x dx  .
B. S   f x  f x dx . 1   2   1   2   a a b b b N C. S  f x  f x dx  . D. S  f x dx  f x dx  2   . 1   1   2   H a a a Ó M Lời giải TO Chọn A Á N
Theo định nghĩa ứng dụng tích phân tích diện tích hình phẳng. V D Câu 6: Cho hàm số
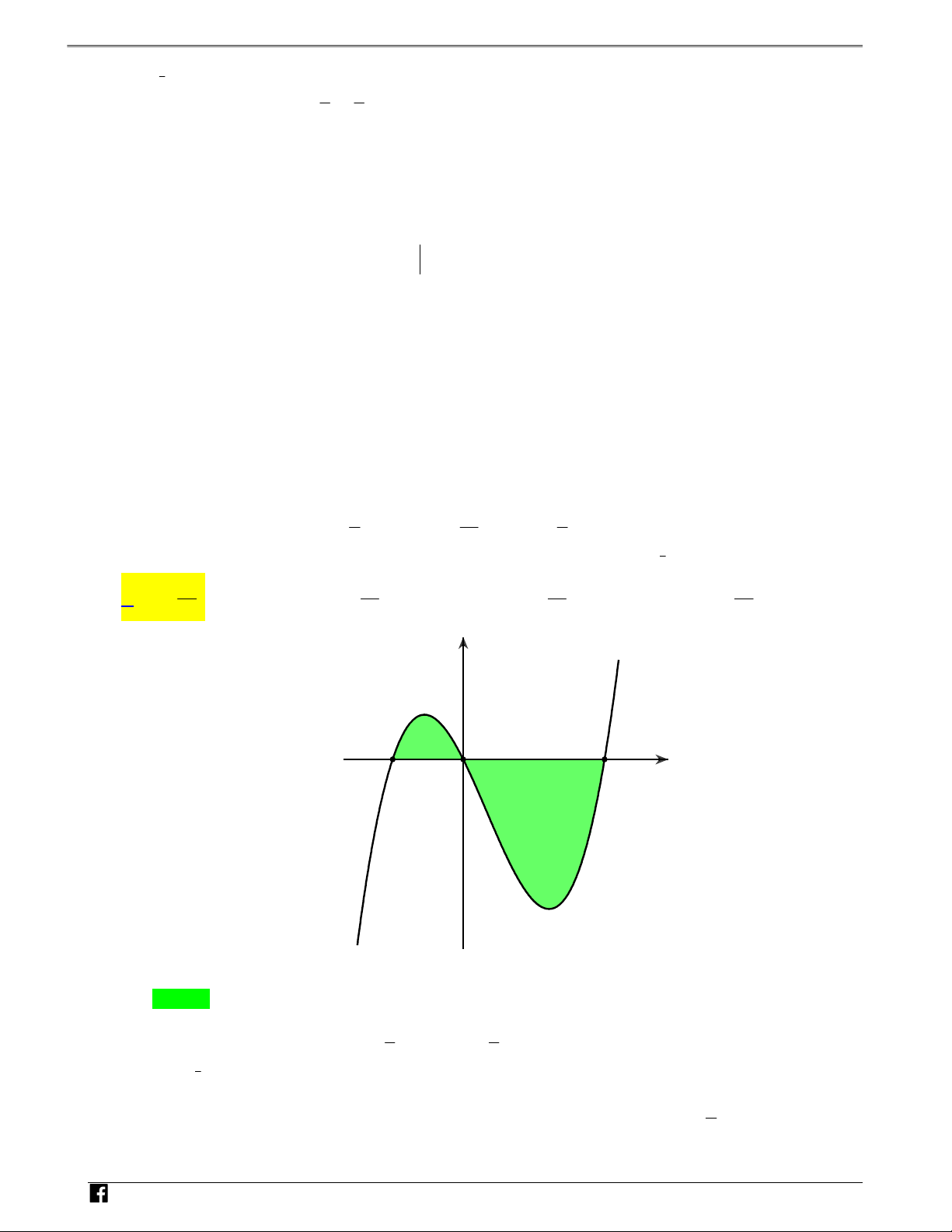
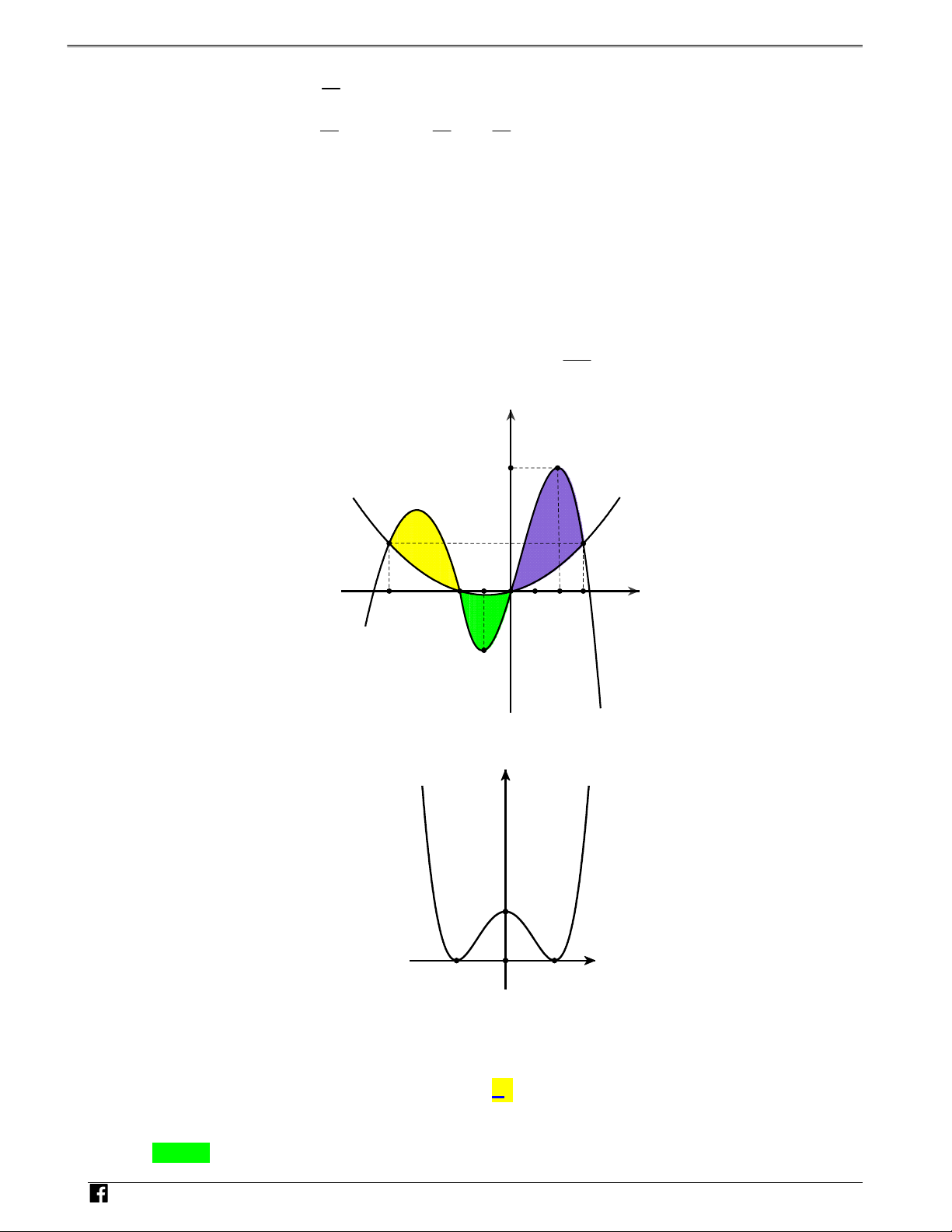
xác định và liên tục trên đoạn   – y  f x 3;3 
 và có đồ thị như hình vẽ. Biết rằng diện VD
tích hình phẳng S ;S giới hạn bởi đồ thị hàm số y  f x và đường thẳng d lần lượt là a;b . Tính tích 1 2 C 1 phân f  3xdx . 1  y=f(x) y 2 -3 -1 O 1 3 x S1 -2 S2 N H Ó M -4 T d O Á N V D – V a b a b a b a b A.    2. B.   2. C.    2. D.   2. D 3 3 3 3 3 3 3 3 C Lời giải Chọn A 1
Đặt t  3x  dt  3dx  dx  dt 3 1 f   x 3 1 dx  f  t 3 1 3 dt  f  xdx 3 3 1  3  3 
Gọi phương trình của đường thẳng d là y  g x. Ta có
https://www.facebook.com/groups/toanvd.vdc Trang 5
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng 1 g   x f x 1 d  x  a  g   x 1 dx  f  xdx a 3  3  3 1 1 N 1 1 H
 2.2  2.2  f xdx  a  f xdx  a    Ó 2 2 3 3  M T 3 3 3 O 1 1      Á f
  xgxdx b  f 
 xdx  .4.4 .2.2 b  f    xdx b 6   N 2 2  1 1 1 V D Do đó – V 1 3 1 3   D 1 1   1 a b C f  3xdx  f  xdx  f  xdx  f  xdx    a
 b  6    2. 3 3   3 3 3 1  3  3  1 
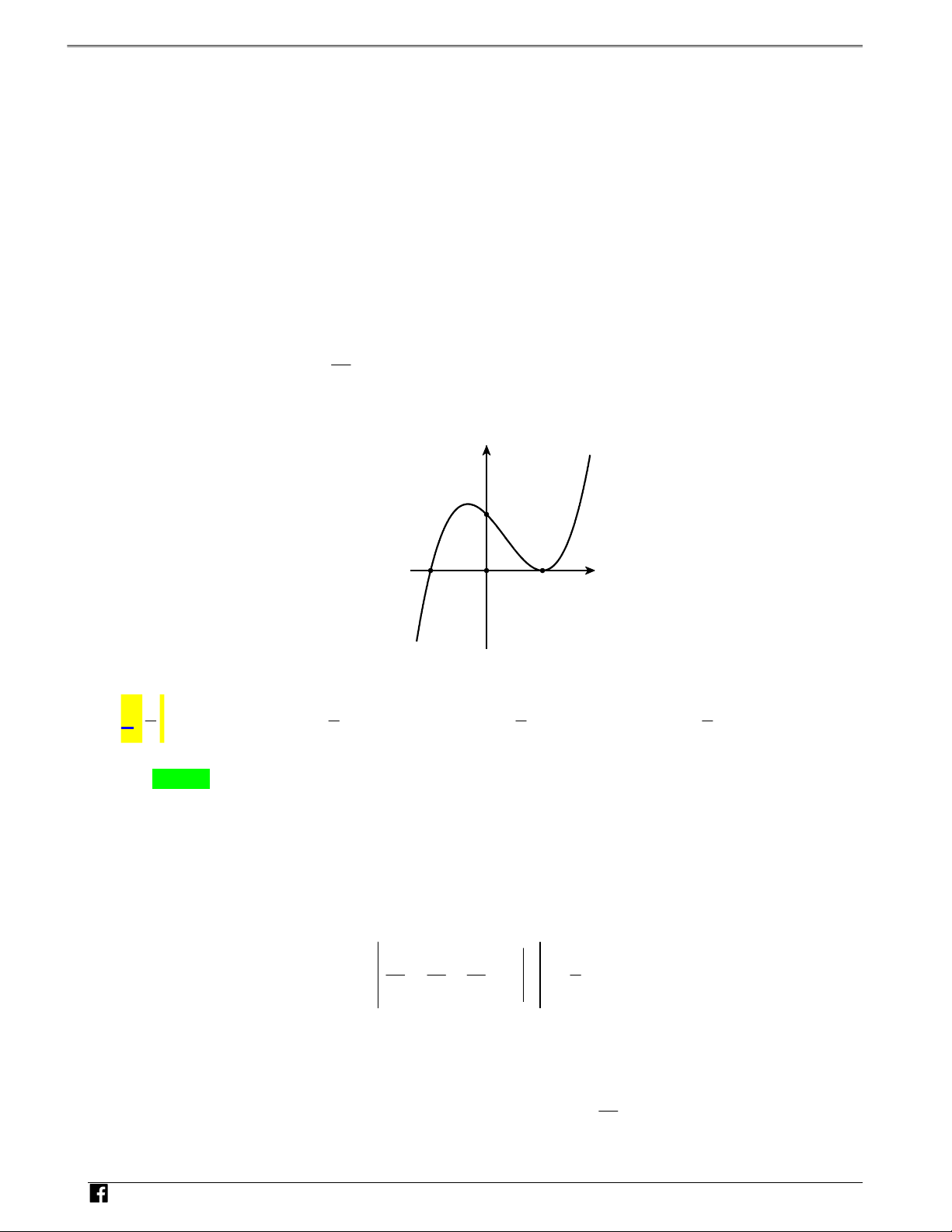
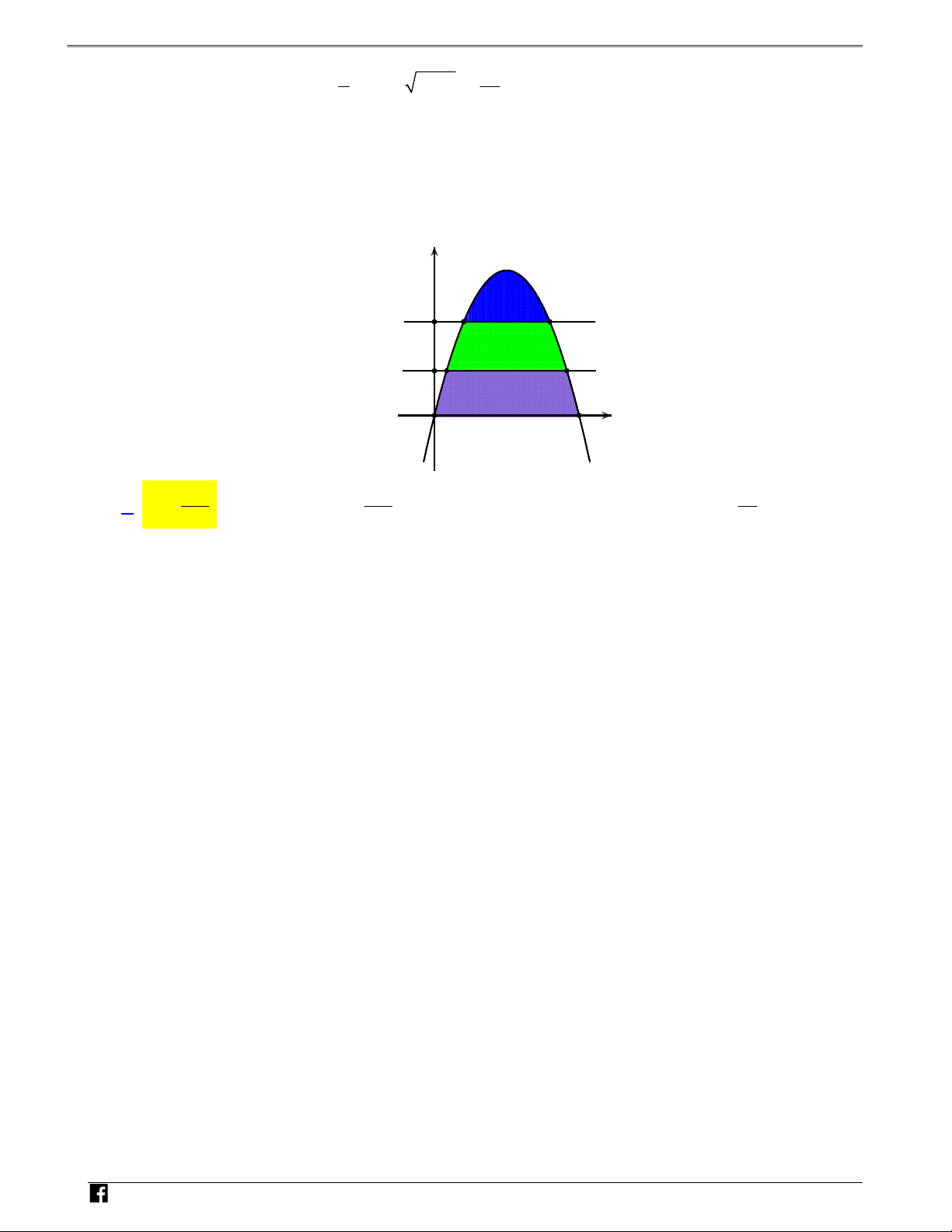
Câu 7: Cho hàm số y  f(x) liên tục trên  và có đồ thị C  là đường cong như hình bên. Diện tích hình
phẳng giới hạn bởi đồ thịC , trục hoành và hai đường thẳng x  0,x  2 (phần tô màu) là y 3 N H Ó O 1 2 x M TOÁN V D 1 2 1 2 – V A. S   f(x)dx  f(x)dx   . B. S  f(x)dx  f(x)dx   . D 0 1 0 1 C 2 2 C. S  f(x)dx  . D. S  f(x)dx  . 0 0 Lời giải Chọn B 2
Diện tích S của hình phẳng cần tìm là: S  f  xdx . 0
Dựa vào đồ thị ta thấy phương trình f x  0, x  0;2
  có nghiệm duy nhất là x  1.
https://www.facebook.com/groups/toanvd.vdc Trang 6
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng 1 2 Do đó S  f  x dx  f  x dx . 0 1          N
Dựa vào đồ thị ta thấy f x 0, x 0;1
  và f x 0, x 1;2   . H Ó M 1 2 Vậy . T S  f  xdx  f  xdx O 0 1 Á N   V
Câu 8: Cho hàm số y  f x liên tục trên a;b
  , có đồ thị như hình vẽ sau: D – V y B D C A P N M O a b x
Mệnh đề nào dưới đây đúng? b b A. f 
 xdx là diện tích hình thang ABMN . B. f
 xdx là dộ dài đoạn BP. a a b b C. f 
 xdx là dộ dài đoạn MN . D. f 
 xdx là dộ dài đoạn cong AB . a a N Lời giải H Ó Chọn B M T b O b Á f 
 xdx  f x  f b  f a  BM PM  BP . a     N a V D 2 –
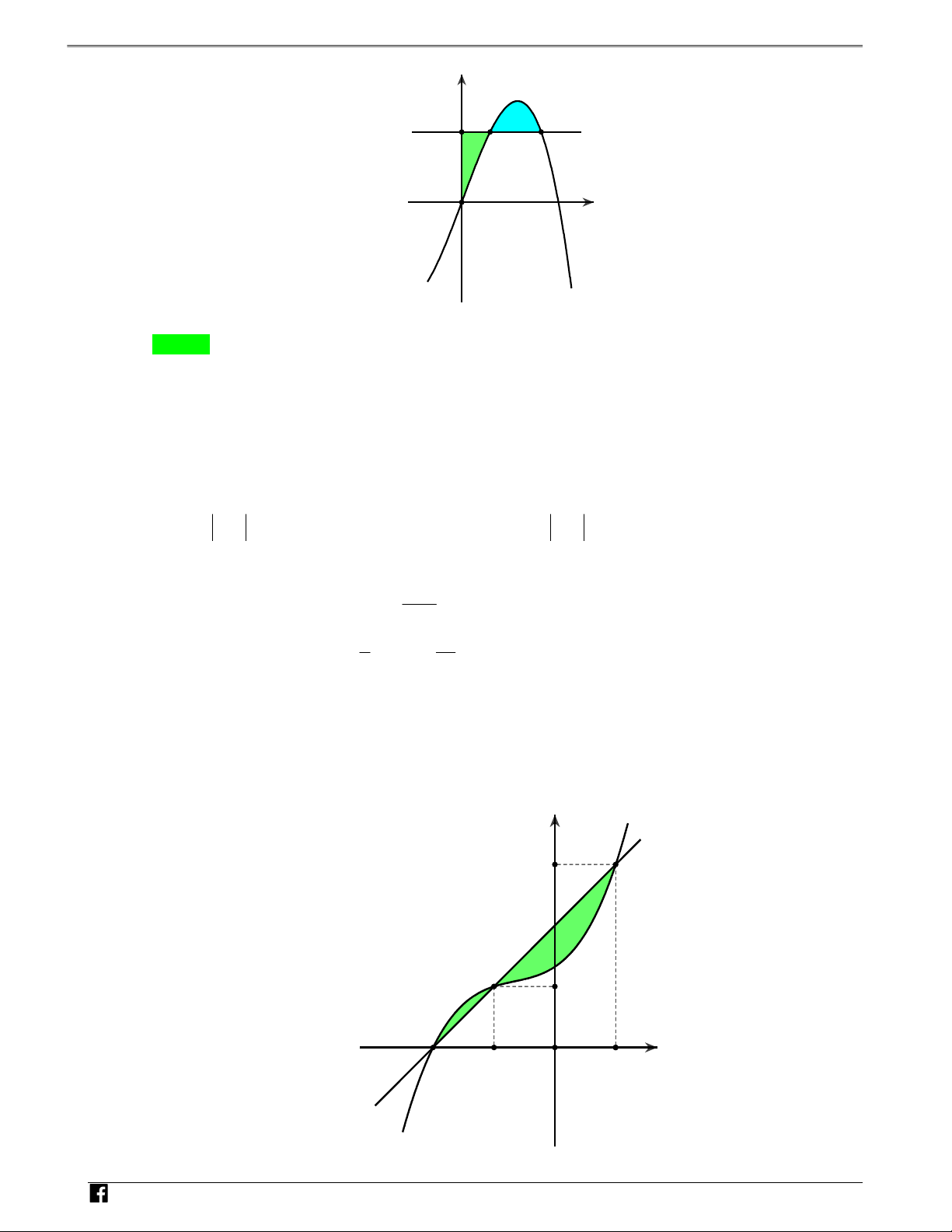
Câu 9: Cho hàm số y  f x liên tục trên  và hàm số y  gx  x f x  V y D
có đồ thị trên đoạn 0;2 C
  như hình vẽ bên. Biết diện tích miền được tô màu là 5 4
S  . Tính tích phân I  f  xdx 2 y=g(x) 1 5 5 A. I  B. I  4 2 C. I  10 D. I  5 Lời giải S Chọn D
Quan sát đồ thị ta thấy g x  0,x  1;2   . O 1 2 x
https://www.facebook.com/groups/toanvd.vdc Trang 7
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng y N H y=g(x) Ó M TOÁN S V D – V O 1 2 x D C 2 5 2 2 5
Từ giả thiết ta cóS  I  g x dx    g  xdx  x f   2xdx  2 2 1 1 1 Đặt 2
x  t  2x dx  dt . Khi x  1  t  1, khi x  2  t  4 2 4 4  x f x  4 2 1 x  f  t 5 d dt    f  tdt  5  f  xdx  5  I 2 2 1 1 1 1
Câu 10: Cho hàm số y  f x xác định và liên tục trên tập số thực. Miền hình phẳng trong hình vẽ được
giới hạn bởi đồ thị hàm số y  f x và trục hoành đồng thời có diện tích S  a . Biết rằng 1 2  1 2  1 2  b x f x dx   và f 3  c . Tính f  xdx. 2 N 0 0 H Ó y M TOÁ y=f'(x) N V D – O 1 3 x V D C A. a b  . c B. a  b  . c C. a   b  . c D. a  b  . c Lời giải Chọn A
Đặt t  2x  dt  2dx
https://www.facebook.com/groups/toanvd.vdc Trang 8
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng 1 2   x  f  x 1 b 1 2
1 ' 2 dx    t  1f t 1
dt   t  1f t 1
dt  b   x  1f xdx b 2 2 0 0 0 0 N     H u x 1 du  dx Đặt   Ó   d  v  f x dx v     f x M       TO 1 1 1 1 Á
x  1 f  x dx  b  x  1 f x  f x dx  f x dx  2f 1  f 0 b N            0         0 0 0 V D 1 3 – V Ta lại có a  f   xdx  f
 xdx  a  f  1 f 0 f  1 f  3  2f  1 f 0a c D 0 1 C 1 Do đó f
 xdx  2f  1 f 0b a b  .c 0
Câu 11: Cho hàm số y  f x có đạo hàm liên tục trên  . Đồ thị hàm số y  f 'x như hình bên dưới. 8 19 2 0
Biết diện tích hình phẳng H  bằng và f   1 
; f 2   . Tính I  f '  2xdx . 3 12 3 1 2 5 8 4 4 A. I  . B. I  . C. I  . D. I  . 24 13 13 26 y N y=f'(x) H Ó M T (K) O Á N -1 O 2 x V D (H) – VDC Lời giải Chọn A 0 I  f   x 0 t x 1 dx  I  f t dt  f x dx dt dx    0 2 1 ' 2 ' ' 2    2 2 1 1  1 2 2 0 2 0 8 Ta có
f 'xdx  f 'xdx  f 'xdx  f  
2  f  1  f 'xdx      3 1  1  0 1 
https://www.facebook.com/groups/toanvd.vdc Trang 9
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng 0 2 19     f  x 8 ' dx  3 12 3 1 0 5 N  f 'xdx   . H 12 1 Ó M 0 1 5 Do đó I  f ' x dx  . T    O 2 24 1 Á N
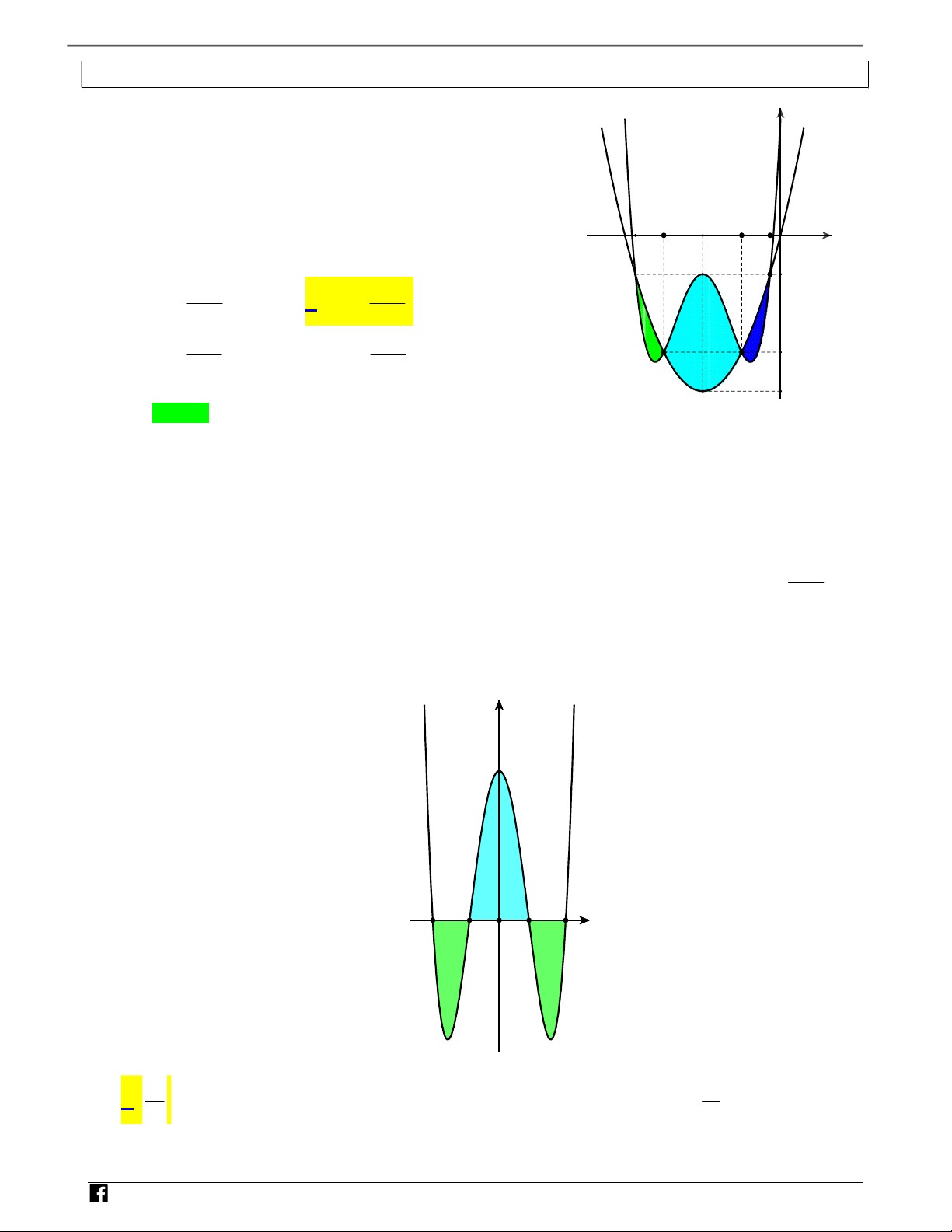
Câu 12: Cho hàm số y  f x xác định và liên tục trên  có đồ thị như hình vẽ bên. Biết diện tích các hình V   D 124 37 53 – phẳng
giới hạn bởi đồ thị hàm số
và trục hoành lần lượt bằng . Tích phân   A ,B,C f x ; ; V 15 60 60 D 3 C 2 15f 2x 43x   5dx bằng 1 y y=f(x) (B) -2 O 1 (C) 2 x (A) N H Ó M TOÁ N 437 158 V A. 28 . B. . C. 293 . D. D 4 15 – Lời giải V D Chọn A C 3 3 3 15 Tính 15f 2x 4 2 3x  5dx  f(2x  4)d(2x  4)  2 (3x     5)dx 2 1 1 1 2  15 f xdx   36 2 2 2  0 1 2  15 15 15  124 37 53 Mà  f x     dx 
f(x)dx  f (x)dx  f(x)dx                64 2 2 2 15 60 60 2  2 0 1       3 Vậy 15f 2x 4 2
3x  5dx  64  36    28 1
https://www.facebook.com/groups/toanvd.vdc Trang 10
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng
Câu 13: (Đề thi thử THPT QG VTED năm 2019) Cho hàm số y  f x xác định và liên tục trên đoạn 5;3 
 có đồ thị như hình vẽ bên. Biết diện tích các hình phẳng  
A ,B,C,D giới hạn bởi đồ thị hàm số 1 N
f x và trục hoành lần lượt bằng 6;3;12;2. Tích phân  2f 2x  11 dx bằng H  Ó 3  M y T O Á N V D – VDC (C) (A) (D) -5 (B) O 3 x A. 27 . B. 25 . C. 17 . D. 21 N Lời giải H Chọn A Ó M 1 1 1 1 d 2x  1 T Tính
2f 2x  1 1dx  2 f 2x  1dx  dx  2 f 2x     1 4      O 2 3  3  3  3  Á N 3 V  f  xdx 4  D 5  – V 3 D Mà f
 xdx bằng diện tích hình phẳng giới hạn bởi đồ thị hàm số f x và trục hoành C 5  3 Suy ra f
 xdx  6  3 122  23 5  1
Vậy  2f 2x  1 1dx  23  4  27 3 
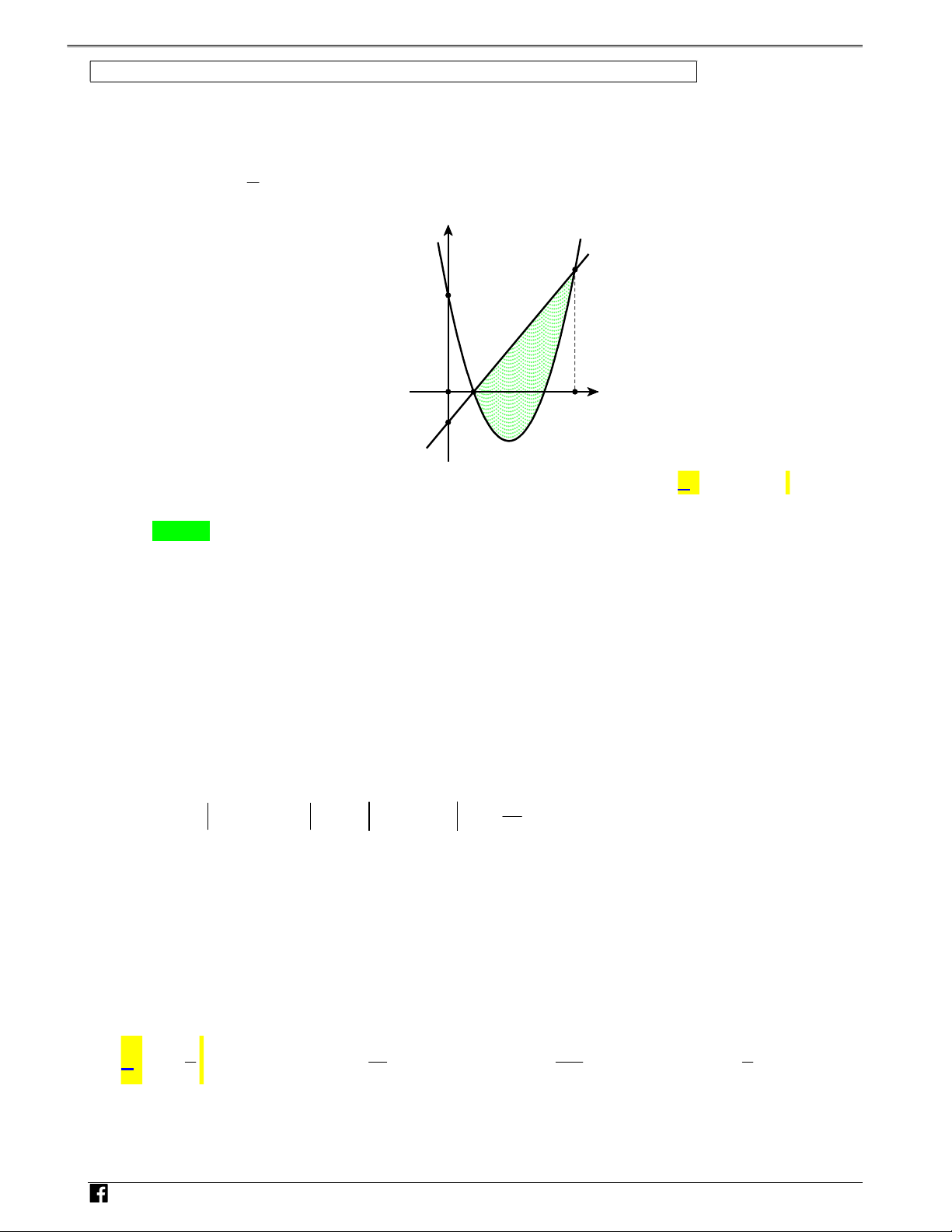
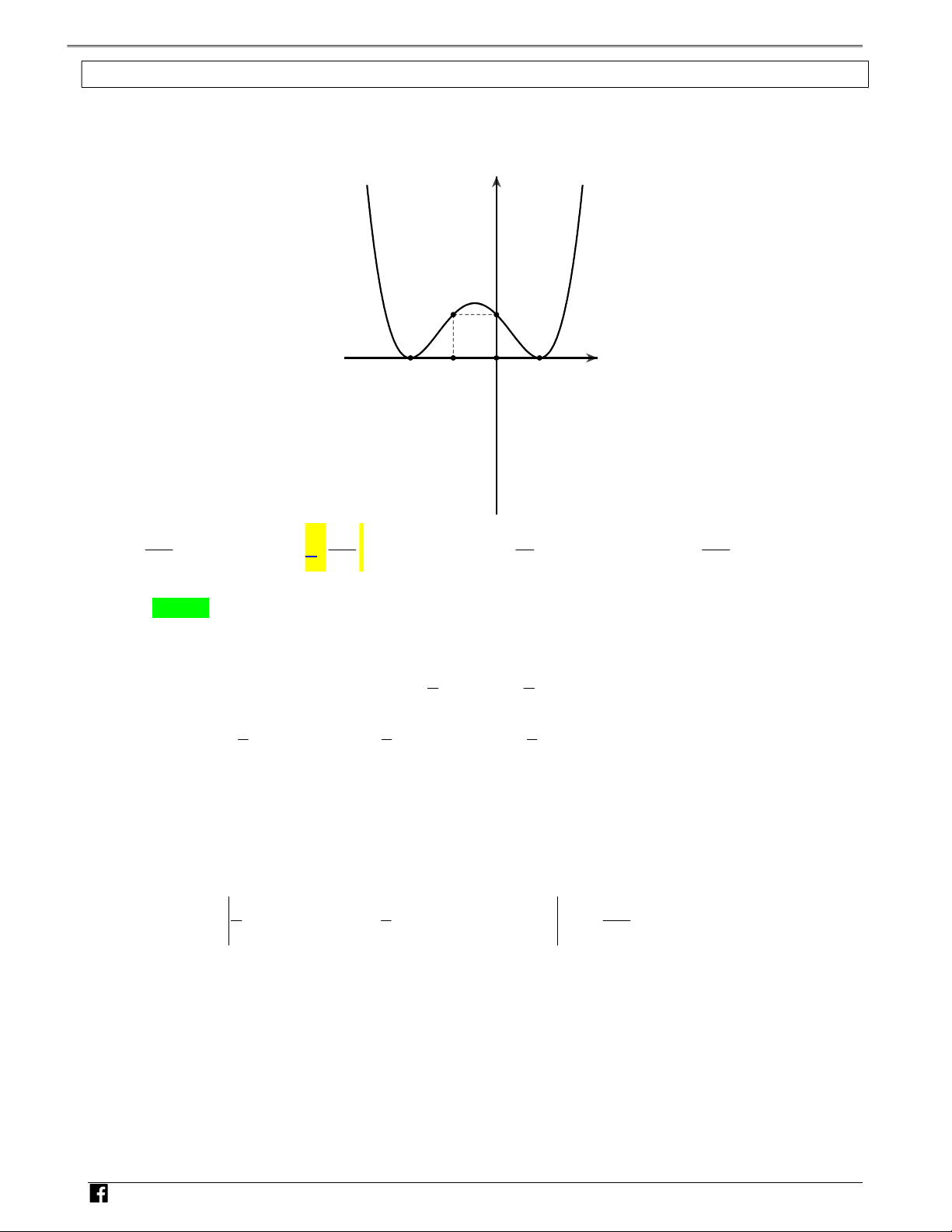
Câu 14: Cho đường cong C 3
: y  8x 27x và đường thẳng y  m cắt C tại hai điểm phân biệt nằm
trong góc phần tư thứ nhất của hệ trục tọa độ Oxy và chia thành 2 miền phẳng có diện tích S ,S bằng nhau 1 2
(tham khảo hình vẽ). Mệnh đề nào dưới đây đúng? 1 1 3 3 A. 0  m  . B.  m  1. C. 1  m  . D.  m  2 . 2 2 2 2
https://www.facebook.com/groups/toanvd.vdc Trang 11
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng y S2 S N 1 y=m H Ó M O x T O Á N V D – Lời giải V Chọn C D C
Phương trình hoành độ giao điểm 3
8x  27x  m . Giả sử như hình vẽ, hoành độ các giao điểm là 3 8  a 27a  m
0  a  b . Ta có hệ 
1 . Gọi F x là một nguyên hàm của hàm số 3   8  b 27b  m  f x 3  8x 27x m . Khi đó các diện tích a a b b S 
f(x)dx   f x dx  F 0  F a ;S 
f(x)dx  f x dx  F b  F a . 1         2         0 0 a a Theo giả thiết thì       4 2 27 0  4 b S S F b F b   mb  0 . 1 2 4 4 32
Kết hợp với (1), ta được b   m  . N 9 27 H
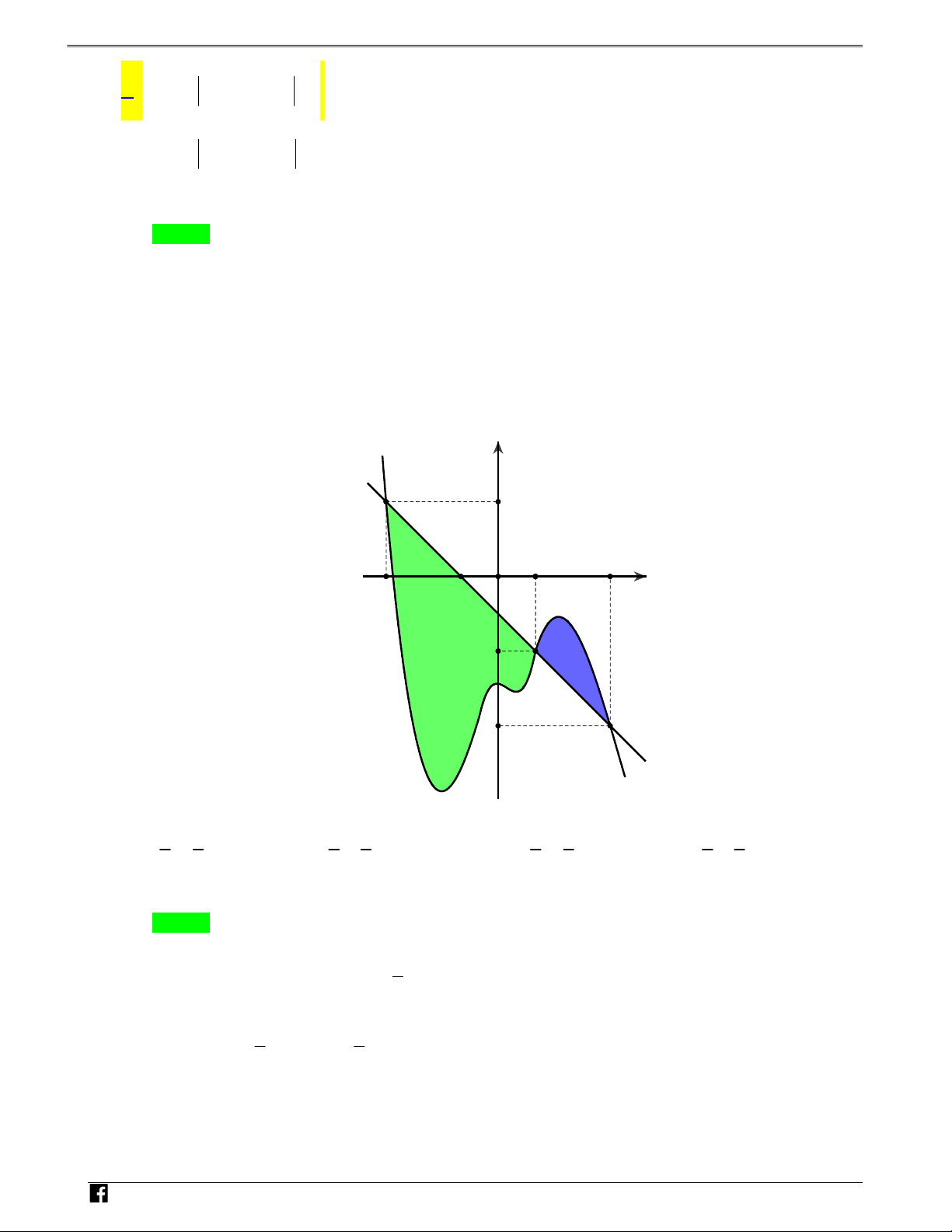
Câu 15: Cho hàm số y  f x xác định và liên tục trên đoạn 2;1 S ,S Ó   
 . Biết rằng diện tích hình phẳng 1 2 M
giới hạn bởi đồ thị hàm số f x và đường thẳng y  g x  ax b lần lượt là , m n . Tính tích phâ     Tn O 1 Á I  f  xdx. N V 2  D – y V D 3 C S2 S1 y=g(x) -2 -1 O 1 x y=f(x)
https://www.facebook.com/groups/toanvd.vdc Trang 12
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng 9 9 9 9 A. I  m  n  . B. I  n  m  . C. I  m  n  . D. I  n  m  . 2 2 2 2 Lời giải N Chọn C H Ó M 1 1 1 1 1 1   T I  f  xdx  f  xdx  g  xdx  g  xdx  f
  xgxdx  g   xdx O 2  2 2  2  2  2  Á N 1  1 1 V 1 9 D 
f xgxdx  f xgxdx  gxdx  m n  .3.3  m n     2 2 – 2  1  2  V D C N H Ó M TO Á N V D – V D C
https://www.facebook.com/groups/toanvd.vdc Trang 13
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng
2) Dạng 2. Dựa vào các điểm đồ thị đi qua xác định hàm số đi đến công thức tính.
Câu 1: Cho các hàm số   2
f x  ax bx  c và g x  mx  n có đồ thị lần lượt là đường cong Cvà
đường thẳng d (như hình vẽ). Biết AB  5 . Diện tích hình phẳng giới hạn bởi đồ thị C  và đường thẳng d NH p (phần tô màu) là
). Khẳng định nào sau đây đúng? Ó S  (trong đó * , p q  N ; (p;q)  1 M q TO y Á (C) N V A D – V d D C O 1 5 x B A. p q  20 . B. p  11q . C. pq  69. D. p  q  35 . Lời giải Chọn D Ta có (
A 0;c)  (C), B(0;n)  d và AB  5  c n  5 (c  n)
Phương trình hoành độ giao điểm của C  và d 2 2 2
ax bx c  mx  n  ax  (b  m)x  c n  0  ax  (b  m)x  5  0(*) N H
Lại có hoành độ giao điểm của và và nên Ó C d là x  1 x  5
(*)có dạng a(x 1)(x  5)  0 M
Đồng nhất hệ số ta được a  1 TO
Diện tích hình phẳng giới hạn bởi C  và d là Á N V 5 5 D 2 32
S  (x 1)(x  5) dx  x  6x  5 dx  –   3 1 1 V D C
Suy ra p  32, q  3  p  q  35.
Câu 2: Cho hai hàm số   3 2
f x  ax bx cx d và g x  mx  n (a, ,b ,cd,m,n   ). Biết rằng đồ
thị hàm số y  f x và y  g x cắt nhau tại ba điểm có hoành độ 1;2;3 (tham khảo hình vẽ phía bên
dưới); đồng thời diện tích S  45 (phần hình phẳng tô màu xanh). Tính diện tích S (phần hình phẳng tô 1 2 màu đỏ). 7 7 128 7 A. S  . B. S  . C. S  . D. S  . 2 3 2 12 2 3 2 6
https://www.facebook.com/groups/toanvd.vdc Trang 14
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng y y=f(x) N H Ó M -1 2 3 x T O O Á S1 N V S2 D – y=g(x) V D C Lời giải Chọn A
Ta có phương trình hoành độ giao điểm f x  g x  a x   1 x   2 x  3  0 2 45
Có S  a x  1 x  2 x  3 dx  45  a  45  a  4. 1      4 1  3 7
Vậy S   4 x  1 x  2 x  3 dx  . 2      3 2
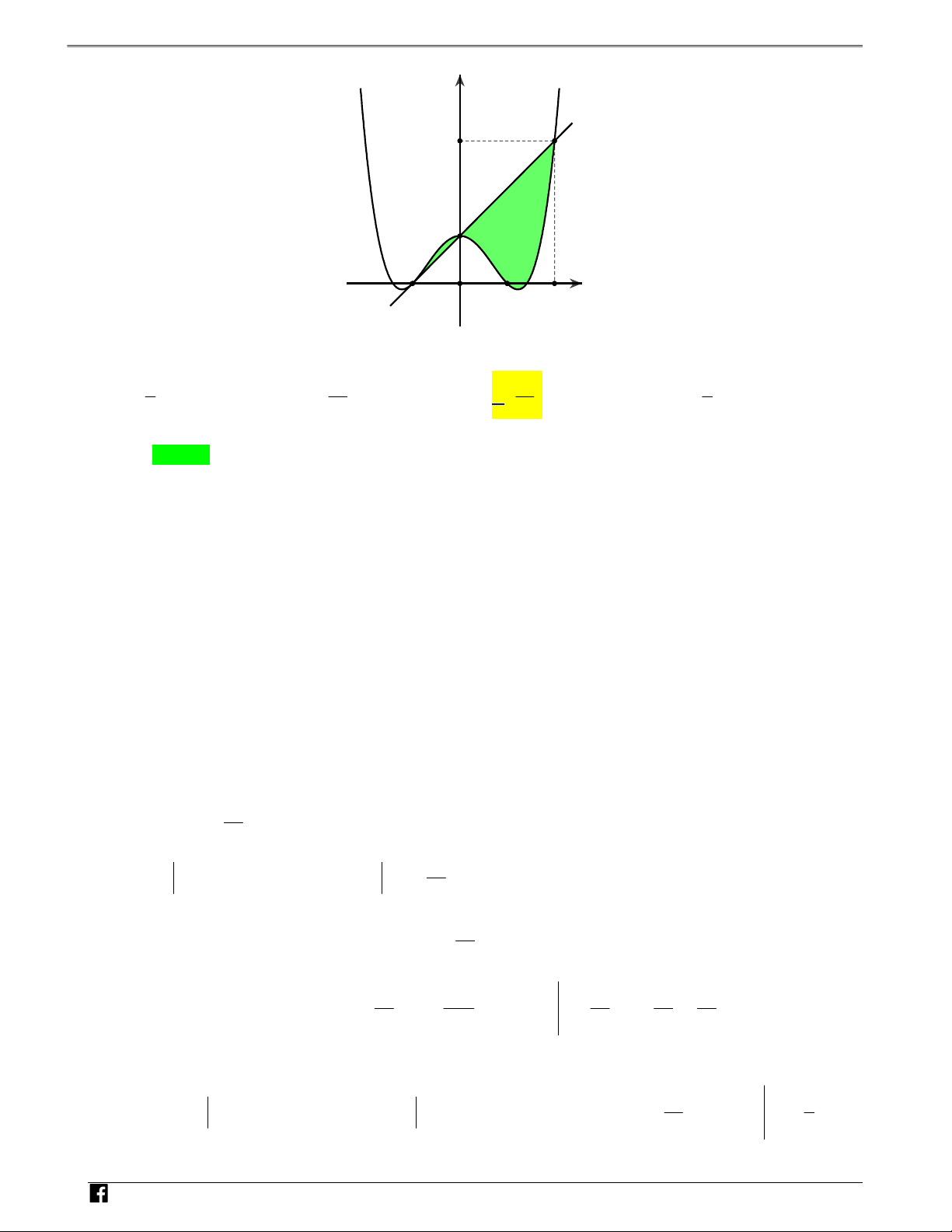
Câu 3: Hình phẳng được tô màu ở trong hình vẽ bên được giới hạn bởi một đồ thị hàm số bậc 3 với mộ Nt H
đường thẳng  cùng với trục hoành và trục tung. Diện tích hình phẳng đó bằng Ó M 4 1 A. 4 . B. . C. . D. 2 T 3 3 O Á y N V D – VDC 2 -2 O 1 x Lời giải Chọn A
https://www.facebook.com/groups/toanvd.vdc Trang 15
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng
Ta có đồ thị hàm số bậc ba 3 2
y  ax  bx cx  d có:
+ Giao với Oy tại điểm có tung độ bằng 2  d  2
+ Đi qua điểm 1;0  a b c  2 N H
+ Đi qua điểm 2;0  8a  4b  2c  2  4a  2b c  1 Ó M
+ Có x  1 là điểm cực trị của hàm số nên là nghiệm của phương trình T
y '  0  3a  2b  c  0 O Á
Từ đó a  1;b  0;c  3 N Vậy hàm số bậc ba là: 3 V y  x  3x  2 D
Ta có đường thẳng đi qua hai điểm là
2;0;0;2 y  x 2 – V
Giao điểm của hai đồ thị là x  2  ;x  0;x  2 D C 2
Vậy diện tích hình phẳng giới hạn với hai đồ thị trên như hình vẽ là: S    3 4x  x dx  4 0 Chọn đáp án A.
Câu 4: (Đề THPT QG 2018) Cho hai hàm số f x 3 2 1
 ax bx cx  và g x 2  dx  ex  1 2
a, ,b ,cd,e  . Biết rằng đồ thị hàm số y  f x và y  gx cắt nhau tại 3 điểm có hoành độ lần lượt là
3; 1; 1 (tham khảo hình vẽ). Hình phẳng giới hạn bởi 2 đồ thị đã cho có diện tích bằng y N H Ó M 1 TO x -3 -1 O Á N V D – V D 9 C A. 5 B. C. 8 D. 4 2 Lời giải Chọn D
Từ giao điểm hai đồ thị ta có f xg x  a x  3x   1 x  1. 3
Suy ra a x  3x   1 x   3
1  ax  b d 2x c dx  2 3 1
Xét hệ số tự do suy ra 3a    a  . 2 2 1
Do đó f xg x  x  3x   1 x  1. 2
https://www.facebook.com/groups/toanvd.vdc Trang 16
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng 1  1 1 1 Diện tích bằng S 
x  3x  1x  1dx  x  3x  1x    1dx  4. 2 2 3  1
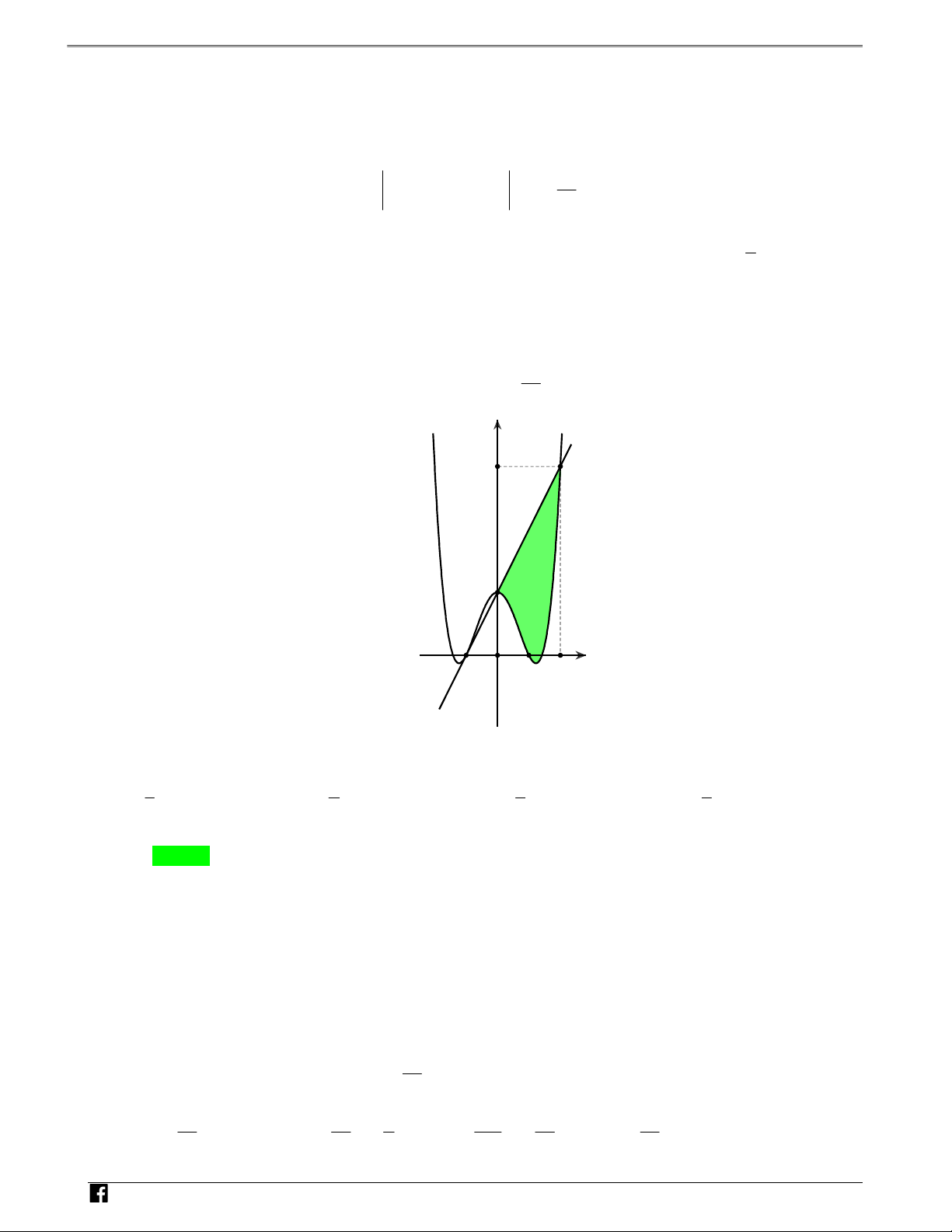
Câu 5: Cho hai hàm số   3 2
f x  x ax bx c và g x  f dx e với a, ,b ,cd   có đồ thị như NH
hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số y  f x. Diện tích hình phẳng giới hạn bởi ÓM
hai đường cong y  f x và y  g x gần nhất với kết quả nào dưới đây?     T O Á y N y=f(x) V D – VDC O 1 3 3 x 2 y=g(x) A. 4,5. B. 4,25 . C. 3,63 . D. 3,67 . Lời giải Chọn A Từ đồ thị suy ra 2
f(x)  a(x  3) .x và f(1)  4  a  1 2  f(x)  (x  3) x N H 3 Ó
g(x) là hàm số bậc ba nên 2
g(x)  m(x  ) (x  3) và g(1)  4  m  8  M 2 T 3 2 O
 g(x)  8(x  ) (x  3) Á 2 y N 3 V 9 Vậy S  f x  g x .dx   4,5 y=f(x) D  1     2 – 1 V Câu 6: Cho hai hàm số f x 3 2  ax bx  cx  1 và D C g x 2
 dx ex 1 với a; ;b c; d; e là các số thực. Biết rằng đồ thị
của hàm số y  f x và y  g x cắt nhau tại ba điểm , A , B C có -1 O 1 2 x
hoành độ lần lượt là 1; 1; 2 (tham khảo hình vẽ). Hình phẳng giới B -1
hạn bởi hai đồ thị đã cho có diện tích bằng 37 27 A. . B. . 12 12 A 8 5 -3 C C. . D. . 3 12 Lời giải y=g(x) Chọn A
https://www.facebook.com/groups/toanvd.vdc Trang 17
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng Ta có f xgx   3 2
ax bx  cx   2 dx ex   3  ax  b d 2 1 1 x  c ex  2
Vì đồ thị của hàm số y  f x và y  g x cắt nhau tại ba điểm ,
A B, C có hoành độ lần lượt là NH
1; 1; 2 nên phương trình f x  gx có ba nghiệm là 1; 1; 2 . Ó M
Kết hợp với điều kiện giả thiết suy ra f x  g x  a x  1 x 1 x  2 .         T O
Đồng nhất hệ số tự do hai dạng biểu thức ta được . Á f xgx 2a  2  a  1 N Vậy . V
f xgx  x  x  x   3 2 1 1 2  x  2x  x  2 D
Diện tích hình phẳng giới hạn bởi hai đồ thị đã cho là: – V 2 37 D 3 2 S  x  2x  x  2dx  C  . 12 1 
Câu 7: Hình phẳng H  được giới hạn bởi đồ thị của hai hàm số đa thức bậc bốn y  f(x) và y  g(x).
Biết rằng đồ thị của hai hàm số này cắt nhau tại đúng ba điểm phân biệt có hoành độ lần lượt là −3;−1;2.
Diện tích của hình phẳng H (phần gạch sọc trên hình vẽ bên) gần nhất với kết quả nào dưới đây? y O 2 -3 -1 - 3 x 5 - 32 N H Ó M T A. 3,11. B. 2, 45 . C. 3,21 . D. 2,95 O Á Lời giải N V Chọn A D
Tại điểm có hoành độ x  3 hai đồ thị hàm số này tiếp xúc với nhau. – VD
Có f x  g x  a x  2 ( ) ( ) 3 (x  1)(x  2). C 3   3     9 9 1 Mà f(0)  g(0)     a.9.1.( 2) a       . 5  2  10 10 20 2 2 2 1 3733 Vì vậy S  f(x) g(x)  
x  3 (x  1)(x  2) dx   3,11. (H )     20 1200 3  3 
Câu 8: Cho hàm số bậc ba y  f(x) và hàm số bậc hai y  g(x) có đồ thị như hình vẽ. Biết rằng phần diện
tích S giới hạn bởi đồ thị của hai hàm số bằng 4 . Tính phần diện tích S giới hạn bởi hai đồ thị hàm số. 1 2
https://www.facebook.com/groups/toanvd.vdc Trang 18
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng y N H Ó M TOÁN VD y=g(x) – VD -1 1 3 C O x S2 S1 y=f(x) 3 A. S  4 . B. S  2 . C. S  1 . D. S  2 2 2 2 2 Lời giải Chọn A
Dựa vào đồ thị của hai hàm số ta thấy hai đồ thị cắt nhau tại các điểm có hoành độ lần lượt là
1, 1, 3 nên f xgx  ax  1x  1x  3 và a  0. N H Ó 1 M
Mặt khác diện tích S  4  a(x  1)(x  1)(x  3)dx  4  a  4 1  T 1  O Á N 3 3 V Từ đó suy ra S 
g(x) f(x) dx   4(x  1)(x 1)(x  3)dx  4 D 2     1 1 – VD Vậy chọn đáp án A. C
Câu 9: Cho hàm số y  f(x) xác định và liên tục trên đoạn 5;3 
 . Biết rằng diện tích hình phẳng S ,S ,S 1 2 3
giới hạn bởi đồ thị hàm số y  f(x) và đường thẳng    2
y g x  ax bx  c lần lượt là m, , n p . Tích 3 phân f(x)dx  bằng 5  211 208 24 26 A. m  n  p  . B. m  n  p  . C. m  n  p  . D. m  n  p  . 45 45 5 5 Lời giải Chọn B
Đồ thị hàm y  g xđi qua các điểm O 0;0,A2;0,B3;2 nên
https://www.facebook.com/groups/toanvd.vdc Trang 19
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng  2 a   c   0  15   4   4 2 4  a  2b  0   b    g x 2  x  x .   15  15 15 N 9  a  3b  2  c   0 H   Ó  M 2 0 3 T       O m n  p  f
  xgx dx  g 
  x f x dx  f 
  xgx dx  Á 5 2  0 N 3 3 V D  f  xdx  g  xdx . – 5  5  V 3 3 D 208 C
 f xdx  m n  p  gxdx  m n  p    45 5  5  y 5 y=g(x) S3 2 S1 -1 -5 -2 x S O 2 3 2 N y=f(x) H Ó M T
Câu 10: Cho hàm số y  f(x) là hàm số đa thức bậc bốn và có đồ thị như hình vẽ. O Á N y V D – VDC 1 -1 O 1 x
Hình phẳng giới hạn bởi đồ thị hai hàm số y  f(x);y  f '(x)có diện tích gần bằng số nào sau đây? A. 34, 8 . B. 60. C. 63,5 D. 72,3 Lời giải Chọn C
https://www.facebook.com/groups/toanvd.vdc Trang 20
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng
Hàm số đã cho có đồ thị đối xứng nhau qua trục tung nên nó là hàm số chẵn. Lại có hàm số
y  f(x) là hàm đa thức bậc bốn nên hàm số đã cho là hàm trùng phương. Do đó 4 2
f(x)  ax bx  c, a  0. N H
Từ hình vẽ ta thấy đồ thị hàm số đi qua các điểm (1;0) ,(0;1) và có điểm cực tiểu (1;0) , điểm cực đại ÓM f(1)  0            T a b c 0 a   1 O f(0)  1      Á (0;1) nên ta có hệ   c   1  b   2 f '(1)  0   N  4  a 2b 0 c      1     V f '(0) 0   D – V
Với a  1,b  2,c  1 ta có 4 2 3 2
f(x)  x  2x  1 ; f '(x)  4x  4x ; f ' (x)  12x  4 thỏa DC
f ' (0)  0, f ' (1)  0 nên các giá trị a  1,b  2,c  1
thỏa mãn yêu cầu bài toán.
Phương trình hoành độ giao điểm của đồ thị hai hàm số y  f(x);y  f '(x) : x    x  
x  2x  1  4x  4x  x  1  4x x   2 2 1 0 1 4 2 3 2 2 1      2
x  4x 1  0 x  2  5  
Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số y  f(x);y  f '(x)là 2 5 2 5 4 3 2 S  f(x)  f (x) dx 
x  4x  2x  4x  1 dx   1  1  2 5
  x 4x 2x  4x   1 4 3 2 1 dx    4 3 2
x  4x  2x  4x  1dx  1  N 2 5 H 2 5 Ó    4 3 2
x  4x  2x  4x  1dx  63,52 M 1 TOÁ N V D – V D C
https://www.facebook.com/groups/toanvd.vdc Trang 21
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng
3) Dạng 3. Dựa vào tâm đối xứng, trục đối xứng của đồ thị xác định hàm số đi đến công thức tính. Câu 1: Cho hàm số 4 3 2
y  f(x)  x  16x  21x  20x  3 và y
hàm số y  g x  ax  2
2 b có đồ thị như hình vẽ. Biết rằng y=f(x) N H
diện tích hình phẳng S ,S ,S giới hạn bởi đồ thị hàm số y  f(x) y=g(x) 1 2 3 Ó M
và đường cong y  g x lần lượt là m, , n p . Tính TO
M  a b  m  p  n . Á -4 -3 -2 -1 O x N -1 V 2456 2531 D A. M  . B. M  . – 15 15 V 2411 2501 S D C. M  . D. M  . 1 S3 -3 C 15 15 S2 Lời giải -4 Chọn B
Đồ thị hàm y  g xđi qua các điểm O 0;0,A2;4 nên 4  a b  0  a   1  . b   4  
 g x  x  2 2 2  4  x  4x  b   4 
Nhận xét đồ thị hai hàm số nhận đường thẳng x  2 là trục đối xứng nên m  p  m  p  0 . 1 1  2531
Do đó, a b  n  5  f xgx dx  5   4 3 2
x  8x  20x  24x  3dx    . 15 3  3 Câu 2: Cho hàm số 4 2
y  x bx  5 (*) có đồ thị như hình vẽ. Gọi S ,S ,S lần lượt là diện tích của hình 1 2 3 phẳng ,
giới hạn bởi đồ thị hàm số (*) và trục hoành. Biết . Giá trị của N   A , B C S  S  S S là 1 3 2 2 H Ó y M TOÁNVD – VDC B O x A C 32 19 A. . B. 16 . C. 5. D. . 5 3 Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 22
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng Chọn A
Đồ thị hàm số (*) cắt trục hoành tại 4 điểm phân biệt  b  0 N
Gọi t ,t (t  t ) là nghiệm dương của phương trình 4 2
x  bx  5  0 . Ta có 4 2 t  bt  5  0 (1) 1 2 1 2 2 2 H Ó M S
Vì đồ thị hàm số (*) nhận trục tung làm trục đối xứng nên 2 S  S  S   S T 1 3 2 3 2 O Á N 1 t 2 t 2 t 4 2 4 2 4 2 V Do đó
(x bx  5)dx  - (x bx  5)dx  (x bx  5)dx  0    D 0 t 0 1 – VD 1 5 1 3 1 4 1 2 C
 t  bt  5t  0  t  bt  5  0(2) 2 2 2 2 2 5 3 5 3 Từ (1) và (2) suy ra 2
b  36  b  6 (vì b <0) và t  1 1 1 32 Vậy 4 2 S  2 (x  6x  5)dx  2  suy ra Chọn A 5 0 N H Ó M TO Á N V D – V D C
https://www.facebook.com/groups/toanvd.vdc Trang 23
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng
4) Dạng 4. Dựa vào tiếp tuyến của đồ thị xác định hàm số đi đến công thức tính.
Câu 1: (Đề HSG Bắc Ninh 2019) Cho hàm số y  f x là hàm đa thức bậc bốn và có đồ thị như hình vẽ.
Hình phẳng giới hạn bởi đồ thị hai hàm số y  f x;y  f x có diện tích bằng N H Ó y M y = f(x) TOÁN VD 1 – VDC -2 -1 O 1 x -1 127 107 13 127 A. . B. . C. . D. . 40 5 5 10 Lời giải Chọn B 2 2
Từ giả thiết đi đến f x  ax  2 x   1 . N 1 1 2 2 H
Vì đồ thị đi qua điểm A0; 
1 nên a   f x  x  2 x  1 Ó 4 4 M 1 2 1 2 1 T
 f x  x  2x  1  x  1x  
2  x  2x  12x  1. O 2 2 2 Á N x  1 V  2 D
Phương trình f x  f x  x  2x  
1 x  x 2  4x  2  0  x    2 –  x  4 V  D C
Vậy hình phẳng giới hạn bởi đồ thị của f x và f x là: 4 1 S           .  x 2x 2 1 107 2 1 x 2 x 1 2x 1 dx 2     4 2 5
Câu 2: Cho đồ thị hàm số 3 2
f(x)  x  ax  bx  c có đồ thị C. Đường thẳng d qua hai điểm , A B trên
hình vẽ là tiếp tuyến của Ctại A . Diện tích hình phẳng giới hạn bởi d và Cbằng:
https://www.facebook.com/groups/toanvd.vdc Trang 24
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng y N H Ó M TOÁN V -1 O 2 x D – -1 V D C d y=f(x) A. 6,75 B. 4,5 C. 8,45 D. 4,75 Lời giải Chọn A
Đường thẳng d : y  mx  n cắt đồ thị hàm số 3 2
f(x)  x  ax  bx  c tại điểm có hoành độ x  1
 ;x  2 trong đó tại điểm có hoành độ x  1 là điểm tiếp xúc của hai đường. Vì vậy  3 2 x ax bx c 2
(mx  n)  (x  1) (x  2). N
Diện tích hình phẳng cần tính bằng: H Ó 2 2 M 3 2 2
S  (x  ax bx c) (mx  n) dx  (x  1) (x  2) dx  6,75.   T 1  1 O Á Câu 3: Cho hàm số 3 2
y  x  ax bx c có đồ thị C. Biết rằng tiếp N y V D
tuyến d của C  tại điểm A có hoành độ bằng 1 cắt C  tại B có – B V
hoành độ bằng 2 (xem hình vẽ). Diện tích hình phẳng giới hạn bởi d D C
và C  (phần gạch chéo trong hình vẽ) bằng 13 25 A A. . B. . 2 4 27 11 C. . D. 4 2 -1 O 2 x Lời giải Chọn C
Ta có A1;a b c   1 và 2
y  3x  2ax b  y 1  3 2a b .
https://www.facebook.com/groups/toanvd.vdc Trang 25
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng
Phương trình tiếp tuyếnd của C  tại A : y  3 2a bx   1  a b c 1.
Phương trình hoành độ giao điểm của C  và d là : 3 2
x  ax bx  c  3 2a bx  1a b c 1  1. N H Phương trình Ó  1 có nghiệm x  1  ;x  2 M
 4a  2b  c  8  3 3  2a b a b  c 1  9a  0  a  0 . T   O Á Suy ra C  : 3
y  x bx  c và d : y  3 bx  1b c 1. N 2 V  3 D
Diện tích hình phẳng là : S  3 b  x 1 b c 1  x bx c          dx   – 1  V 2 D 3 27 C  3x x  2dx   . 4 1 
Câu 4: Cho hàm số y  f x là hàm bậc ba có đồ thị C  như hình vẽ bên dưới y y=f(x) 1 -1 O 1 x N
Diện tích hình phẳng giới hạn bởi C và trục hoành bằng: H   Ó M 4 3 5 3 A. . B. . C. . D. . T 3 4 3 5 O Lời giải Á N Chọn A V 2 D
Phương trình của đồ thị C có dạng y  f x  a x 1 x  1 .         – V C qua A 0;1 nên a  1. D     C 2
Suy ra C  : y  f x  x   1 x  1 3 2  x  x  x  1.
Diện tích hình phẳng cần tìm 1 1 4 3 2   S   3 2 x  x  x   1dx x x x      x 4   .  4 3 2  3 1  1 Câu 5: Cho hàm số 4 2
y  ax bx  c có đồ thị C, biết rằng C đi qua điểm A1;0. Tiếp tuyến 
tại A của đồ thị C  cắt C  tại hai điểm có hoành độ lần lượt là 0 và 2. Biết diện tích hình phẳng giới hạn 56
bởi  , đồ thị C  và hai đường thẳng x  0; x  2 có diện tích bằng (đồ thị như hình vẽ). 5
https://www.facebook.com/groups/toanvd.vdc Trang 26
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng y 3 N H Ó M T B O Á 1 N A V -1 O 2 x D – V D
Tính diện tích hình phẳng giới hạn bởi , đồ thị C  và hai đường thẳng x  1; x  0. C 2 1 1 1 A. . B. . C. . D. . 5 20 10 5 Lời giải Chọn A Cách 1: Hàm số 4 2
y  ax bx  c . TXĐ: D   Ta có: 3 y '  4ax  2bx .
Phương trình tiếp tuyến  của đồ thị C  tại A1;0 có dạng y   4  a  2bx  1.
Do tiếp tuyến  tại A của đồ thị C  cắt C  tại hai điểm có hoành độ lần lượt là 0 và 2 nên phương trình 4 2 ax bx  c   4
 a  2bx  1 nhận ba nghiệm là: x  1; x  0; x  2. N c   a  b c   2a H Suy ra:     . Ó b   3a b   3a M   T Vậy C : 4 2 4 2
y  ax  3ax  2a  a x  3x  2 và :y  2a x  1 . O       Á N
Bài cho diện tích hình phẳng giới hạn bởi  , đồ thị C  và hai đường thẳng x  0; x  2 có diện VD 56 tích bằng nên: – 5 V D 2 56 C 4 2
2a x  1 a x  3x  2 dx       5 0 2   ax  a 4 2 x  x   56 2 1 3 2 dx   5 0 2 2 5    a  4 2 x   x  x 56 3 2 dx    x  3 2  56  a.  x  x  28 56     a.   a  2 . 5  5  5 5 5 0 0
Diện tích hình phẳng giới hạn bởi  , đồ thị C  và hai đường thẳng x  1; x  0 là: 0 0 0 5   S  a  4 2 x  3x  22ax   1 dx    4 2 x  x  x x 3 2  2 2 6 4 dx 2  .  x  x     .  5  5 1  1  1 Cách 2:
https://www.facebook.com/groups/toanvd.vdc Trang 27
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng
Giả sử đường thẳng d : y  kx  m là tiếp tuyến với C  tại A0; 
1 nên c  1 và m  1. 2
Phương trình hoành độ giao điểm của d và C  là 4 2
ax bx  kx  0  a x  1 .x.x 2  0
(do phương trình trên có 3 nghiệm như bài toán đã cho). N H 2 2 56 Ó
Theo bài ta có phương trình a x  1 x.x 2 dx   a  2. M 5 0 TO 0 0 4 2 4 2 2 Á Từ đó ta được S 2(x 3x 2) 4   x 1    
 dx   2x 6x  4xdx  . N  5 1  1  V D Câu 6: Cho hàm số 4 2
y  ax bx c có đồ thị C, biết rằng C đi qua điểm A 1
 ;0, tiếp tuyến d tại – V
A của C cắt C tại hai điểm có hoành độ lần lượt là 0 và 2 và diện tích hình phẳng giới hạn bởi d , đồ DC 28
thị C và hai đường thẳng x  0; x  2 có diện tích bằng . 5 y 2 N -1 O 1 2 x H Ó M T O
Diện tích hình phẳng giới hạn bởi C và hai đường thẳng x  1; x  0 có diện tích bằng Á N 2 1 2 1 V A. B. C. D. D 5 4 9 5 – Lời giải V D Chọn D C Ta có 3
y  4ax  2bx  d : y  4a 2bx  1.
Phương trình hoành độ giao điểm của d và C là:  a  bx   4 2 4 2 1  ax bx c 1. Phương trình  
1 phải cho 2 nghiệm là x  0, x  2 . 4a  2b  c   4a  2b c  0  2
 12a 6b  16a  4b c   .  2  8a  10b c  0  3 2 28
Mặt khác, diện tích phần tô màu là   4a 2b  x  4 2 1 ax bx c        dx 5  0 28    a  b 32 8 4 4 2  a  b  2c 112 32 28 
a  b  2c   4. 5 5 3 5 3 5
https://www.facebook.com/groups/toanvd.vdc Trang 28
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng
Giải hệ 3 phương trình 2,  
3 và 4 ta được a  1, b  3, c  2. Khi đó, C  4 2
: y  x  3x  2 , d : y  2x  1. 0 0 N 1 Diện tích cần tìm là 4 2 S x 3x 2 2 x 1       dx 4 2  x  3x  2x dx  . H        5 Ó 1  1  M T O Á N V D – V D C N H Ó M T O Á N V D – V D C
https://www.facebook.com/groups/toanvd.vdc Trang 29
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng
5) Dạng 5. Biến đổi đồ thị đưa về tính toán đơn giản. Câu 1: Cho parabol P  2 : y  x
  2x  3 cắt trục hoành tại hai điểm A , B và đường thẳng d : y  a 1
0 a  4. Xét parabol P đi qua A, B và có đỉnh thuộc đường thẳng y a (đồ thị như hình vẽ). Gọi 2  N H
S là diện tích hình phẳng giới hạn bởi P và d . S là diện tích hình phẳng giới hạn bởi P và trục 2  1  1 2 Ó M
hoành. Biết S  S , tính 3 2 T  a  8a  48a . 1 2 T O Á y N V D – y = a V D C A B x O A. T  99 . B. T  64 . C. T  32 . D. T  72 . Lời giải Chọn B. y M N y = a N H Ó M A B T x O O Á N V D –
Để việc tính toán trở nên đơn giản, ta tịnh tiến hai parabol sang trái một đơn vị. Khi đó, phương V D a
trình các parabol mới là P : y  x
  4 , P : y   x a . 2  2 1  2 C 4
Gọi A , B là các giao điểm của P và trục Ox  A2;0, B2;0  AB  4 . 1 
Gọi M , N là giao điểm của P và đường thẳng d  M  4 a;a, N  4 a;a. 1  Ta có 4 4 3   S  2 4  y.dy 4  4 2
   4 y   4 a 4 a . 1    3     3 a a 2  2 a   3   2 S  2   x  a.dx  2 ax    ax 8a  . 2   4   12  3 0 0
https://www.facebook.com/groups/toanvd.vdc Trang 30
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng 4 8a
Theo giả thiết S  S  4 a 4 a    a3 2 4  4a 3 2  a  8a  48a  64. 1 2 3 3 Vậy T  64 . Câu 2: Gọi
là hình phẳng giới hạn bởi đồ thị hàm số 2
và trục hoành. Hai đường thẳng N (H) y  x   4x H Ó
y  m và y  n chia (H) thành 3 phần có diện tích bằng nhau. Giá trị của biểu thức M 3 3 bằng T T  (4  m)  (4  n) O Á y N V D y = m – VD y = n C O x 320 512 75 A. T  . B. T  . C. T  405 . D. T  . 9 15 2 N H Ó M T O Á N V D – V D C
https://www.facebook.com/groups/toanvd.vdc Trang 31
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng
6) Dạng 6. Tính diện tích dựa vào việc chia nhỏ hình
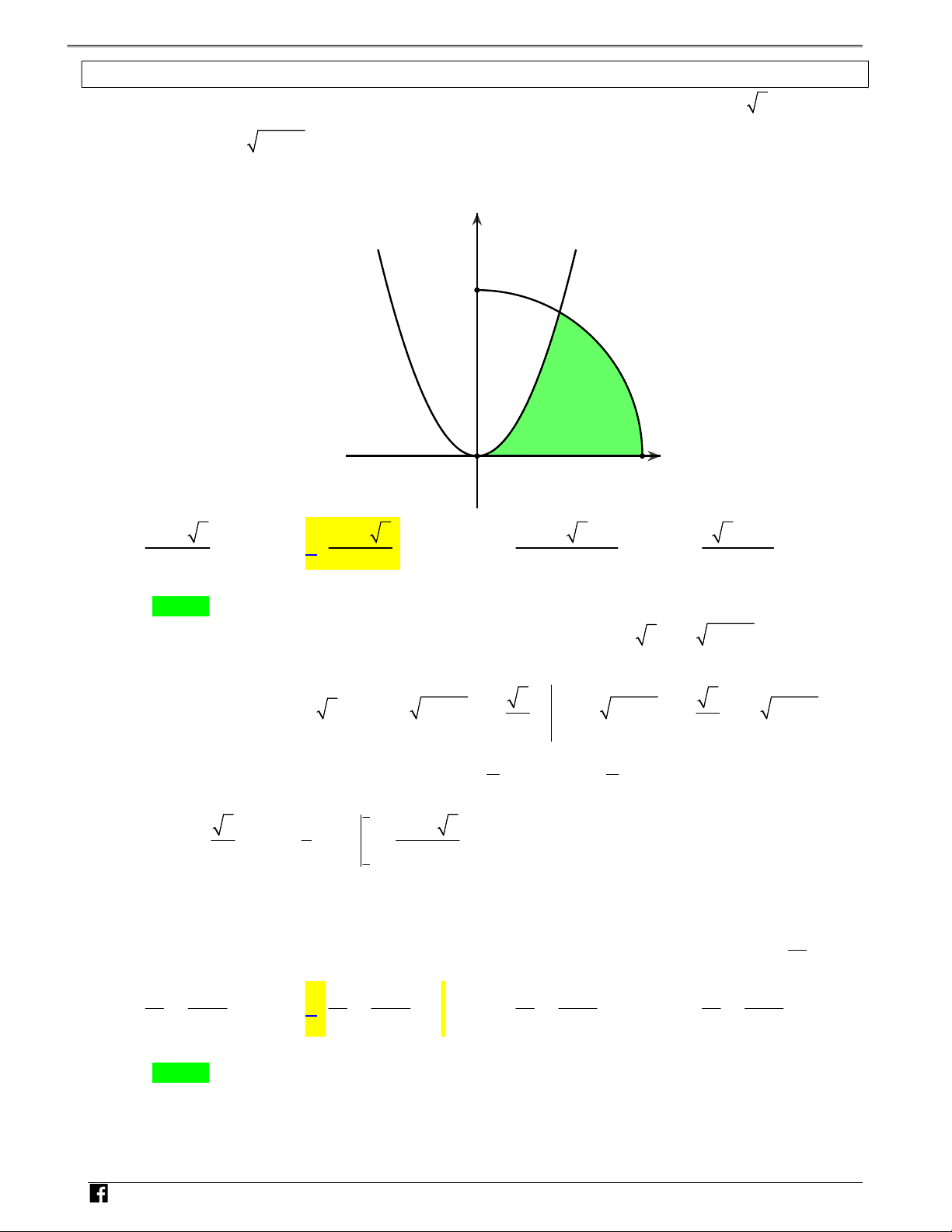
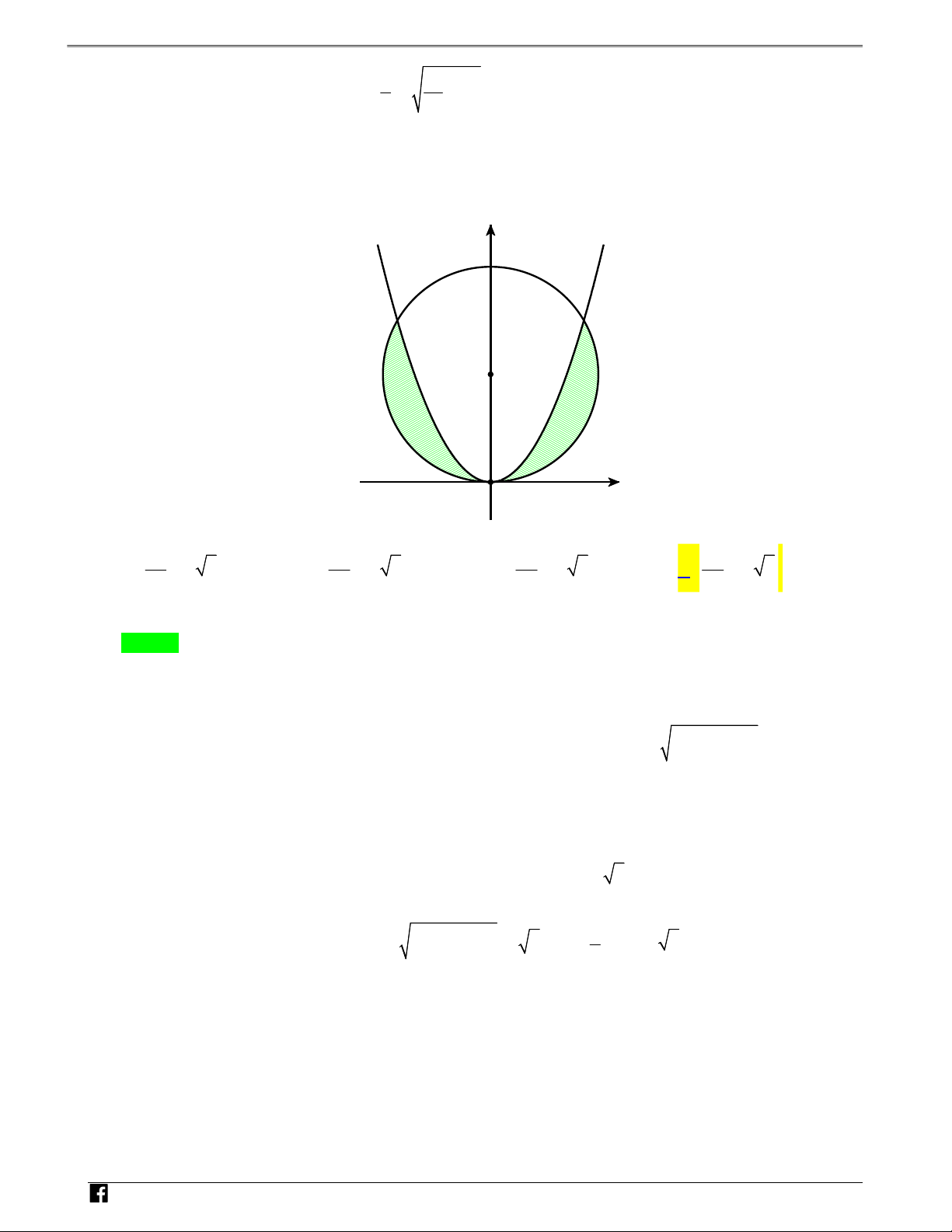
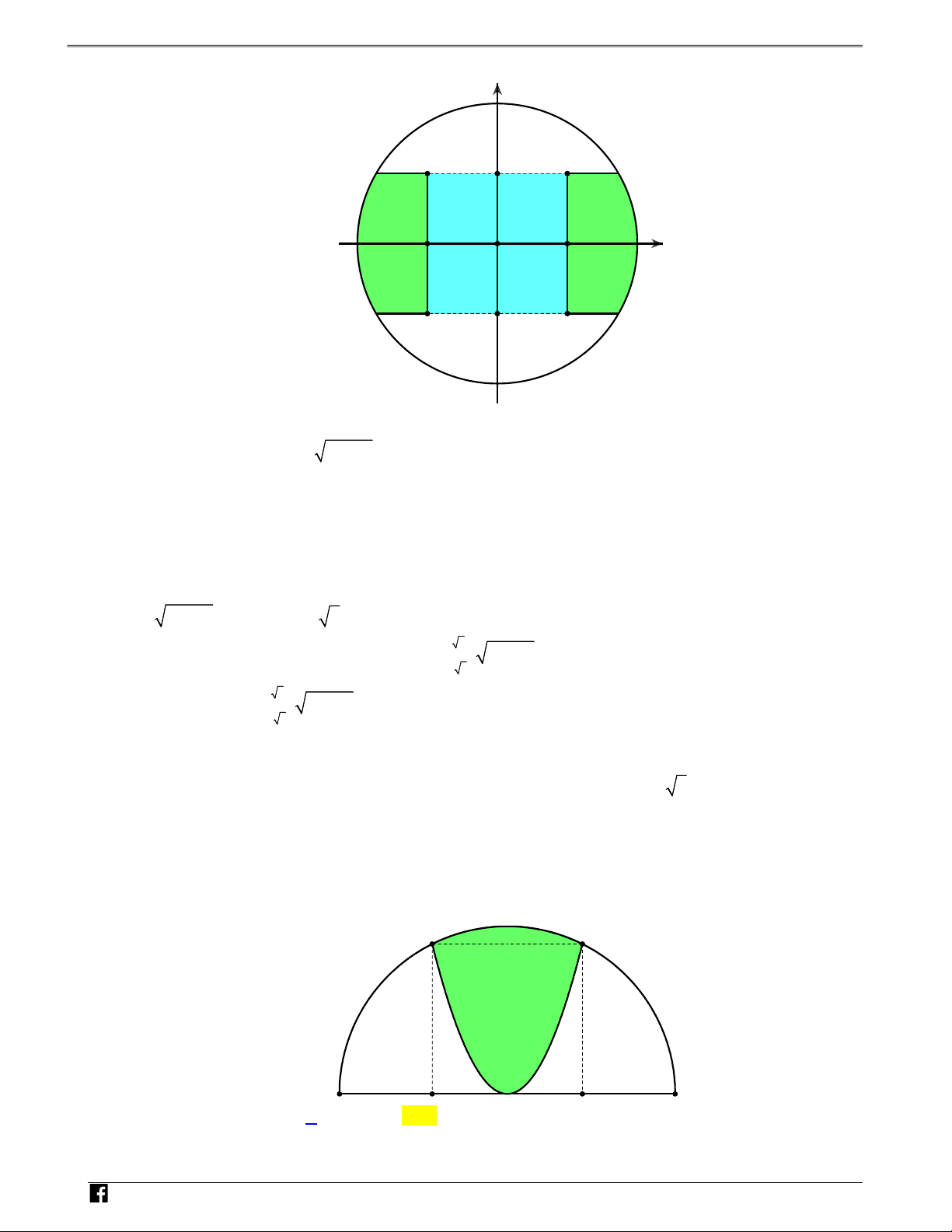
Câu 1: (Đề tham khảo THPT QG 2018) Cho H  là hình phẳng giới hạn bởi parabol 2 y  3x , cung tròn có phương trình 2
y  4  x (với 0  x  2 ) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của NH H bằng Ó   M T y O Á N V 2 D – VDC O 2 x 4  3 4  3 4  2 3  3 5 3  2 A. . B. . C. . D. . 12 6 6 3 Lời giải Chọn B
Phương trình hoành độ giao điểm giữa parabol và cung tròn ta được 2 2 3x  4  x  x  1  với nên ta có N 0  x  2 x  1 H 1 1 2 2 2 Ó 2 2 3 3 2 3 2 M Ta có diện tích S  3x dx  4  x dx  x  4  x dx   4  x dx     3 3 T 0 1 1 1 0 O Á   Đặt N
x  2sint  dx  2costdt;x  1  t  ;x  2  t  V 6 2 D  – 2 3  1    4  3 V  S   2 t  sin2t       D 3 2   6 C 6
Câu 2: Gọi S là diện tích hình phẳng giới hạn bởi các đường y  x  3
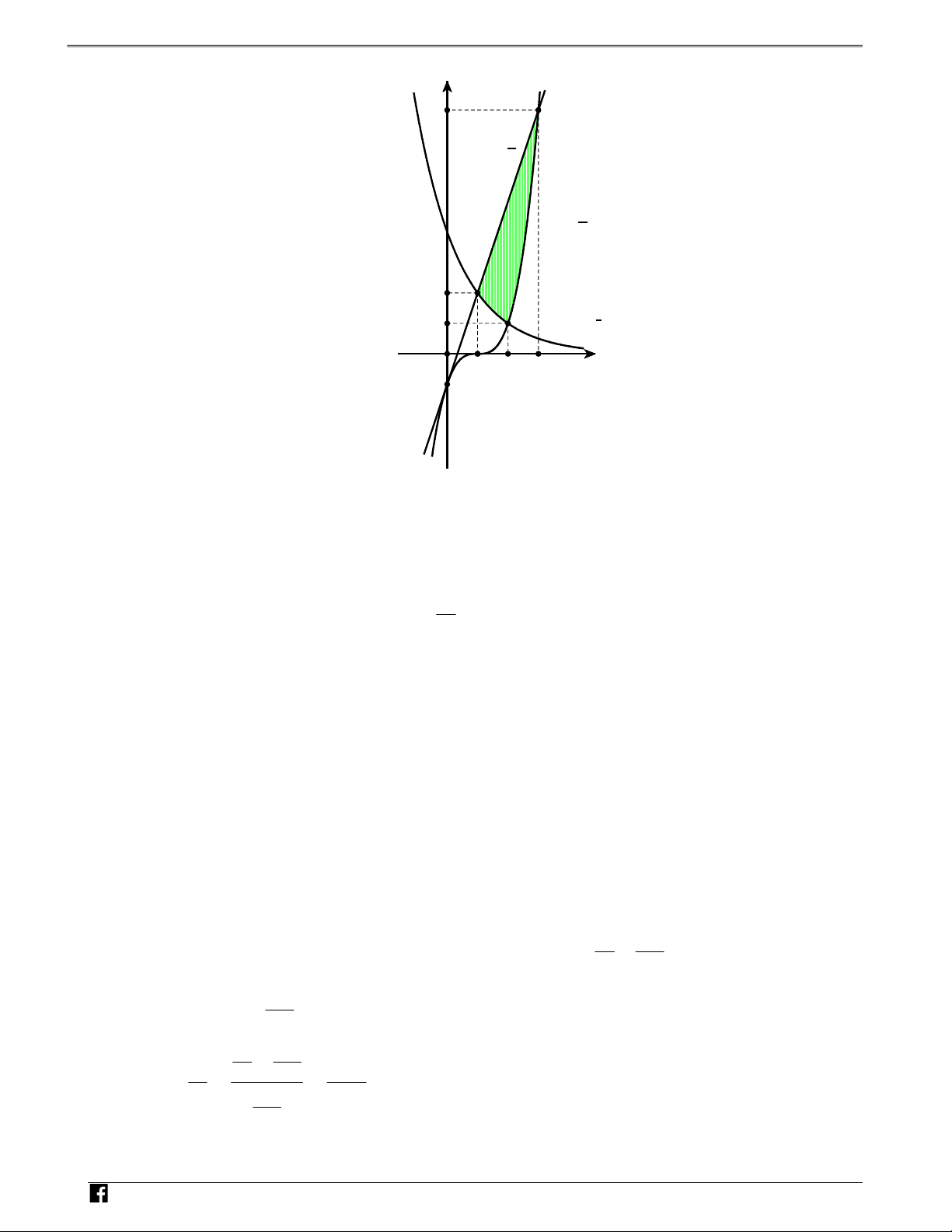
1 , y  3x 1. Đường cong S 2 2 x y  
chia S thành hai phần có diện tích là S ,S (trong đó S nằm trên trục hoành). Tính tỉ số 1 . 1 2 1 S2 S 9ln 4 S 9 ln 4 S 9ln2 S 9ln2 A. 1  . B. 1  1. C. 1  1. D. 1  S 4 S 4 S 4 S 4 2 2 2 2 Lời giải Chọn B
https://www.facebook.com/groups/toanvd.vdc Trang 32
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng y 8 y=3x 1 N H Ó M T y=(x 1)3 O Á N V 2 D – 1 y=22 x V D C O 1 2 3 x -1
Phương trình hoành độ giao điểm của hai đường cong y  x  3 1 , y  3x 1 là:  x  0 x  3 1  3x 1 3 2  x  3x  0    . x  3  3 3   27 Do vậy S  3x 1  x  1 dx   .   4 0 N
Phương trình hoành độ giao điểm của hai đường cong y  x  3 1 , 2 2 x y   là: H Ó M  3 2 1 2 x x      1 . TO
Dễ thấy x  2 là nghiệm của  
1 đồng thời hàm số y  x  3
1 đồng biến trên  , hàm sốÁ N 2 2 x y  
nghịch biến trên  nên x  . V
 1 có nghiệm duy nhất 2 D
Phương trình hoành độ giao điểm của hai đường cong y  3x  1, 2 2 x y   là: – V 2 3 1 2 x x    (1). D C
Dễ thấy x  1 là nghiệm của 2 đồng thời hàm số y  3x  1 đồng biến trên  , hàm số 2 2 x y    
nghịch biến trên  nên (1) có nghiệm duy nhất x  1 . 2 3 3   27 3 Ta có    2 3 1  2 x S x
 dx  3x 1 x 1 dx   . 1       4 ln 4 0 2 3 S  S  S  . 2 1 ln 4 27 3 S  4 ln 4 9ln 4 Vậy 1   1 . S 3 4 2 ln 4
https://www.facebook.com/groups/toanvd.vdc Trang 33
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng
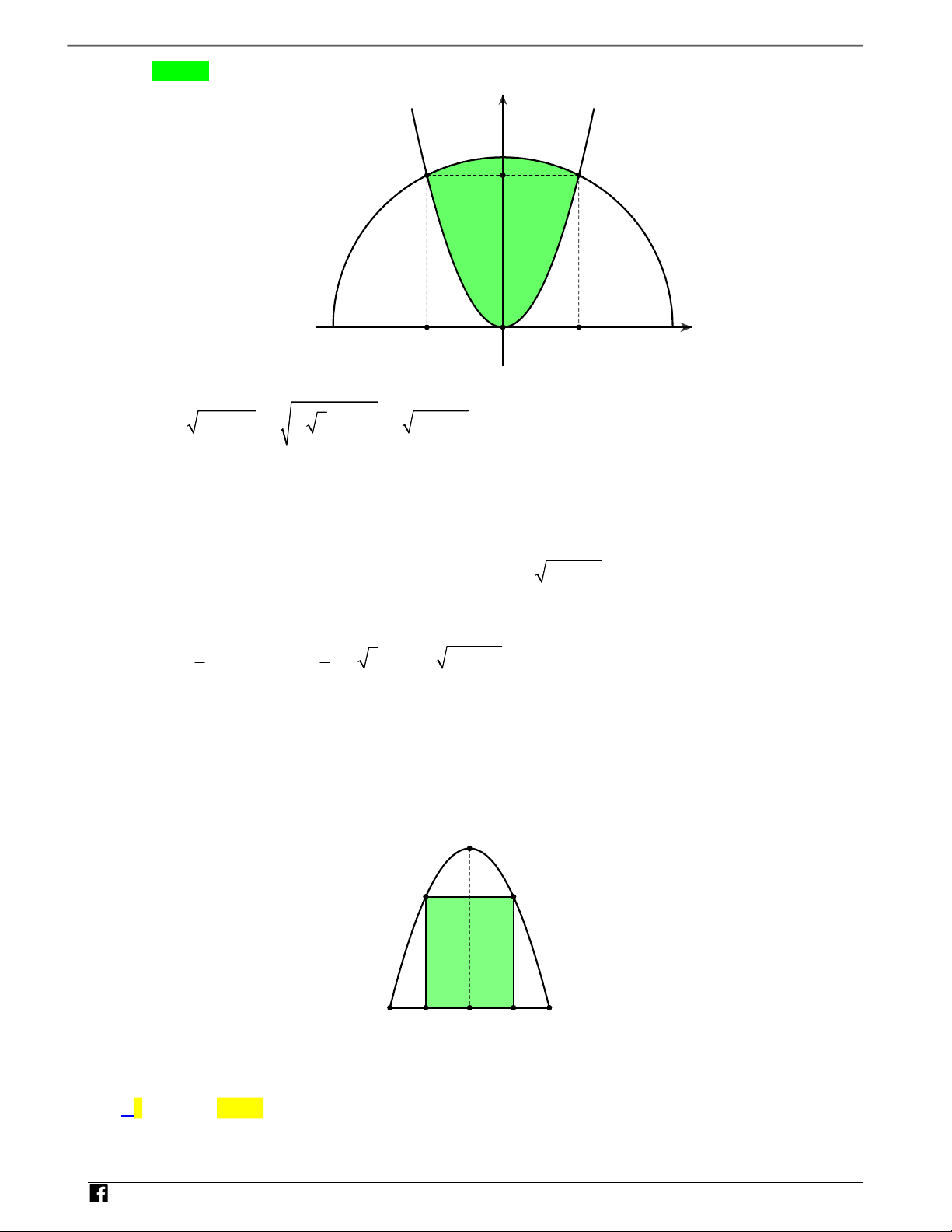
Câu 3: Gọi tam giác cong OAB là hình phẳng giới hạn bởi đồ thị các hàm số 2
y  2x , y  3  x , y  0
(tham khảo hình vẽ bên). Diện tích của OAB bằng N y H Ó M y=2x2 TOÁN V A D – VDC B x O y=3-x 8 5 4 10 A. . B. . C. . D. . 3 3 3 3 Lời giải Chọn A y y=2x2 N H Ó M T 2 O Á N V D S2 S 1 3 x – V O 1 D y=3-x C Gọi parabol P 2
: y  2x và đường thẳng d : y  3 x .
Ta có phương trình hoành độ giao điểm của P và d là: x  1  2 2
2x  3  x  2x  x  3  0   3  x    2 Suy ra tọa độ điểm (
A 1;3) và (d) Ox  B(3;0). 1 3 2 8 Khi đó 2 S
 S  S  2x dx  (3  x)dx   2  (OAB) 1 2   . 3 3 0 1
https://www.facebook.com/groups/toanvd.vdc Trang 34
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng
Câu 4: Diện tích miền phẳng giới hạn bởi các đường:  2x y , y  x   3 và y  1 là: 1 47 1 A. S  1 1  . B. S   1. C. S  . D. S   3. ln2 2 ln2 50 ln2 N H Lời giải Ó M Chọn A TOÁ y N V y=3-x D y=2x – VDC 2 y=1 1 O 1 2 x
Xét phương trình hoành độ giao điểm của các đường. Ta có: * 2x  x   3  x  1 N x H * 2  1  x  0 Ó M * x   3  1  x  2 TO Diện tích cần tìm là: Á N 1 2 1 2 x 2 V     x  2             x   1 1 D S
 2 1dx   x 3 1dx x      2x           ln2  2  ln2 2 – 0 1 0 1 V D C
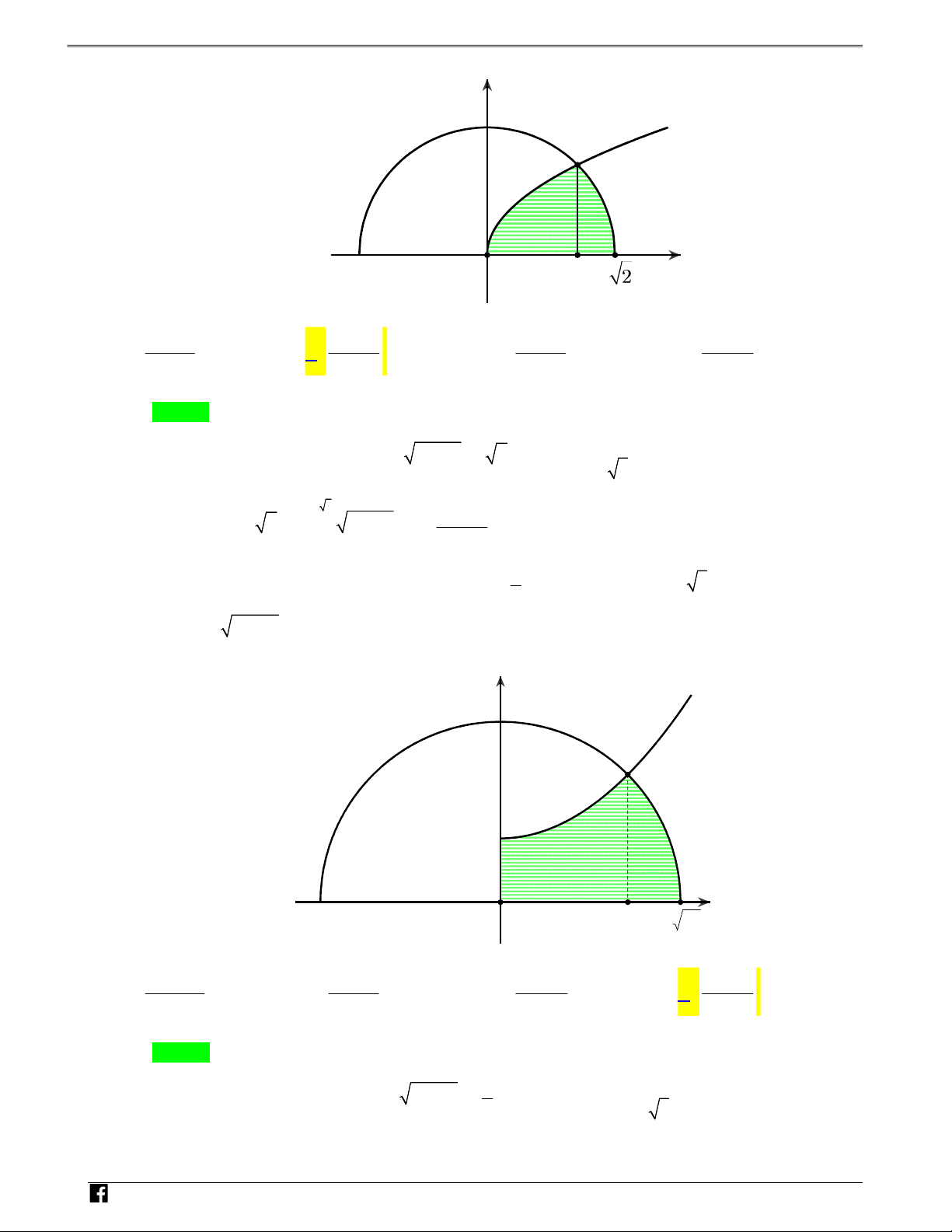
Câu 5: Cho H  là hình phẳng giới hạn bởi đường cong có phương trình y  x , nửa đường tròn có phương trình 2
y  2  x (với 0  x  2 ) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của H bằng
https://www.facebook.com/groups/toanvd.vdc Trang 35
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng y N H Ó M TOÁN O x 1 V D – V 3  1 3  2 4  1 4  2 D A. . B. . C. . D. . C 12 12 6 12 Lời giải Chọn B 2 x   x 2  0 
Phương trình hoành độ giao điểm : 2 2 x x      x  1 0   x  2  1 2 3 2 Do đó 2 S xdx 2 x dx         . 12 0 1 1
Câu 6: Cho H  là hình phẳng giới hạn bởi parabol 2
y  x  1 (với 0  x  2 2 ), nửa đường tròn có 4 phương trình 2
y  8  x và trục hoành, trục tung (phần tô đậm trong hình vẽ). Diện tích của H bằng NH y Ó M TOÁNVD – VDC x O 1 2 2 3  14 2  2 3  4 3  2 A. . B. . C. . D. . 6 3 6 3 Lời giải Chọn D 4 2 1 x   24x 112  0 
Phương trình hoành độ giao điểm: 2 2 8 x x 1       x  2 . 4 0   x  2 2 
https://www.facebook.com/groups/toanvd.vdc Trang 36
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng 2 2 2 1    3  2 Do đó 2 2 S   x  1dx  8  x dx    4   . 3 0 2 3 2 x 2 N
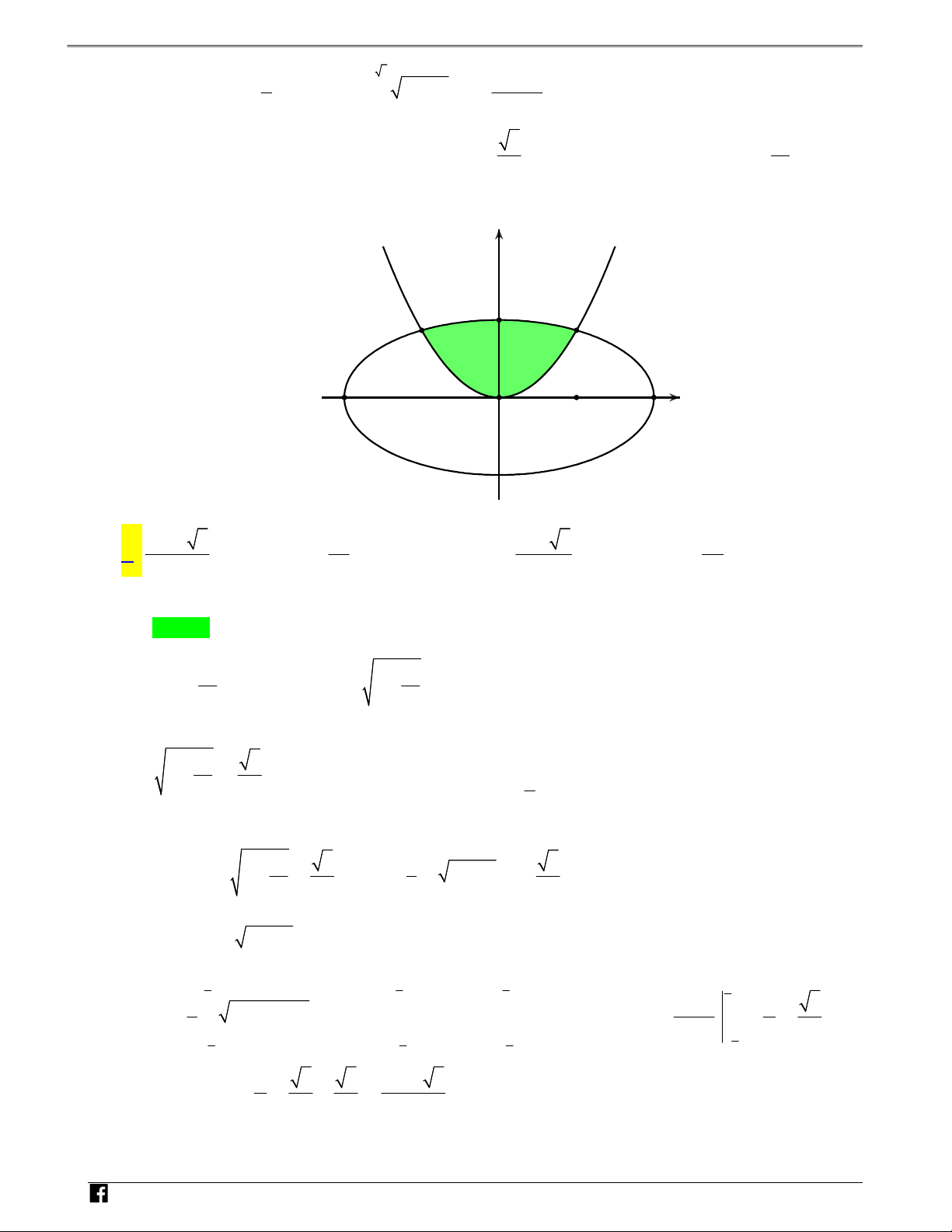
Câu 7: Cho (H ) là hình phẳng giới hạn bởi parabol 2 y 
x và đường Elip có phương trình  y  1 H 2 4 Ó
(phần tô đậm trong hình vẽ). Diện tích của (H ) bằng M TO y Á N V D – V 1 D C -2 O 1 2 x -1 2  3 2   3 3 A. . B. . C. . D. 6 3 4 4 Lời giải Chọn A N 2 x 2 2 x H Ta có  y  1  y   1 . Ó 4 4 M
Phương trình hoành độ giao điểm của đường cong nửa trên của Elip và Parabol là TO 2  2 x  1   Á x 3 x  1 2    N 1  x 4 2  3x  x  4  0  . 2 4   V 4 2 x   x  1   D  3 –
Suy ra diện tích hình phẳng (H ) cần tính là V D 1  2  x 3  1 1 3 C 2 S     1  x dx 2  4  x dx  (H )   .  4 2  2 3 1    1  1 Xét 2 I  4  x dx 
, đặt x  2 sint ta được 1     6 1 6 6 6   2 I  4  4 sin t2cos d t t 2  2 cos d t t  1  cos2t dt sin2t  t      3   . 2       2  3 2         6 6 6 6 3 3   Do đó S     2 3  . (H ) 3 2 3 6
https://www.facebook.com/groups/toanvd.vdc Trang 37
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng a   4  Vậy b   1 
 P  a  b  c  9 . c   6  N H Câu 8: Tính diện tích Ó
S của hình phẳng (phần tô màu) trong hình sau M y T O Á N V D – VDC O 2 4 x 8 10 11 7 A. S  . B. S  . C. S  . D. S  . 3 3 3 3 Lời giải Chọn B y   x 
Dựa và hình vẽ, ta có hình phẳng được giới hạn bởi các đường: y   x 2  . y   0  2 4 N H Suy ra S  xdx  
  x x 2dx π 2a 2 . Ó 0 2 M
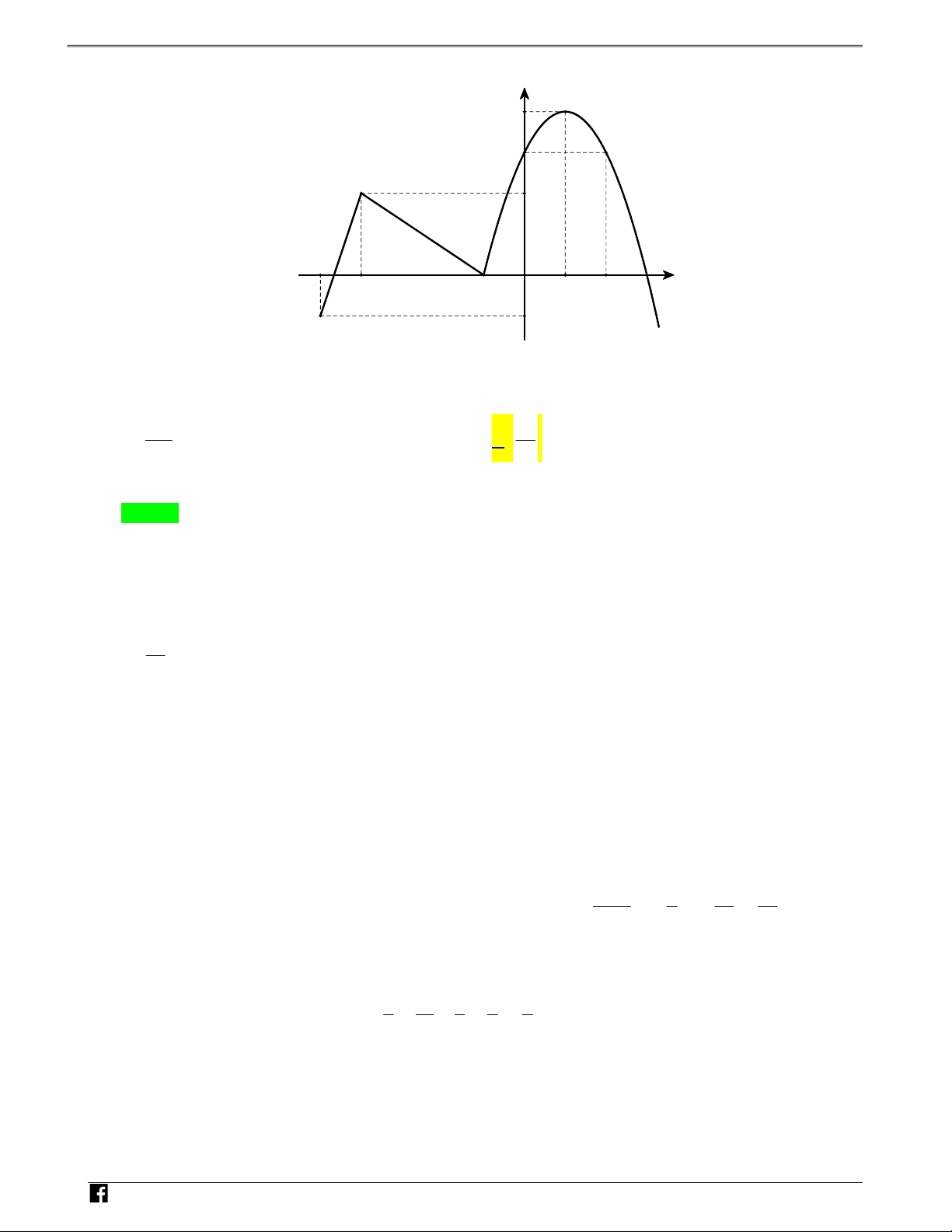
Câu 9: Cho H là hình phẳng được tô đậm trong hình vẽ và được giới hạn bởi các đường có phương trìnhT   O Á 10  x  khi x  1 2  N y  x  x , y  
. Diện tích của H  bằng? V 3 x   2 khi x  1  D  – y V D C O 1 2 3 x -1 11 13 11 14 A. . B. . C. . D. . 6 2 2 3 Lời giải Chọn B
https://www.facebook.com/groups/toanvd.vdc Trang 38
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng
Hoành độ giao điểm của hai đồ thị hàm số y  x  và y  x  2 là x   x  2 x  1.
Diện tích hình phẳng cần tính là 1 3 10     2  10       2 S x x x dx    
 x  x  x  2dx . N  3      3  H 0 1 Ó 1 3     M 13  2  7       2 S x x dx      x  x  2dx      T 3  3  0 1 O Á 1 3     N 13  2  7       2 S x x dx      x  x  2dx      V 3  3  0 1 D 1 3 – 3 3     13 x       7 x  13 V 2 2 S x     x   2x .      D  6 3  6 3  2 C 0 1 2 x
Câu 10: Diện tích hình phẳng giới hạn bởi các đồ thị hàm số 2 27 y  x ;y  ;y  bằng 27 x A. 27 ln 2 . B. 27 ln 3 . C. 28 ln 3 . D. 29 ln 3 . Lời giải Chọn B 2 2 x x Xét các pthđgđ 2 2 27 27 x   x  0;x   x  3;   x  9 . 27 x 27 x y y=x2 9 N H y= 2 7 Ó x M T 3 O 2 Á x N y= V 27 D O 3 9 x – V 3 2 9 2     D  x      27 x Suy ra 2         . C S x dx     dx  27 ln 3     27  x 27 0 3  1 Câu 11: Cho parabol P 2
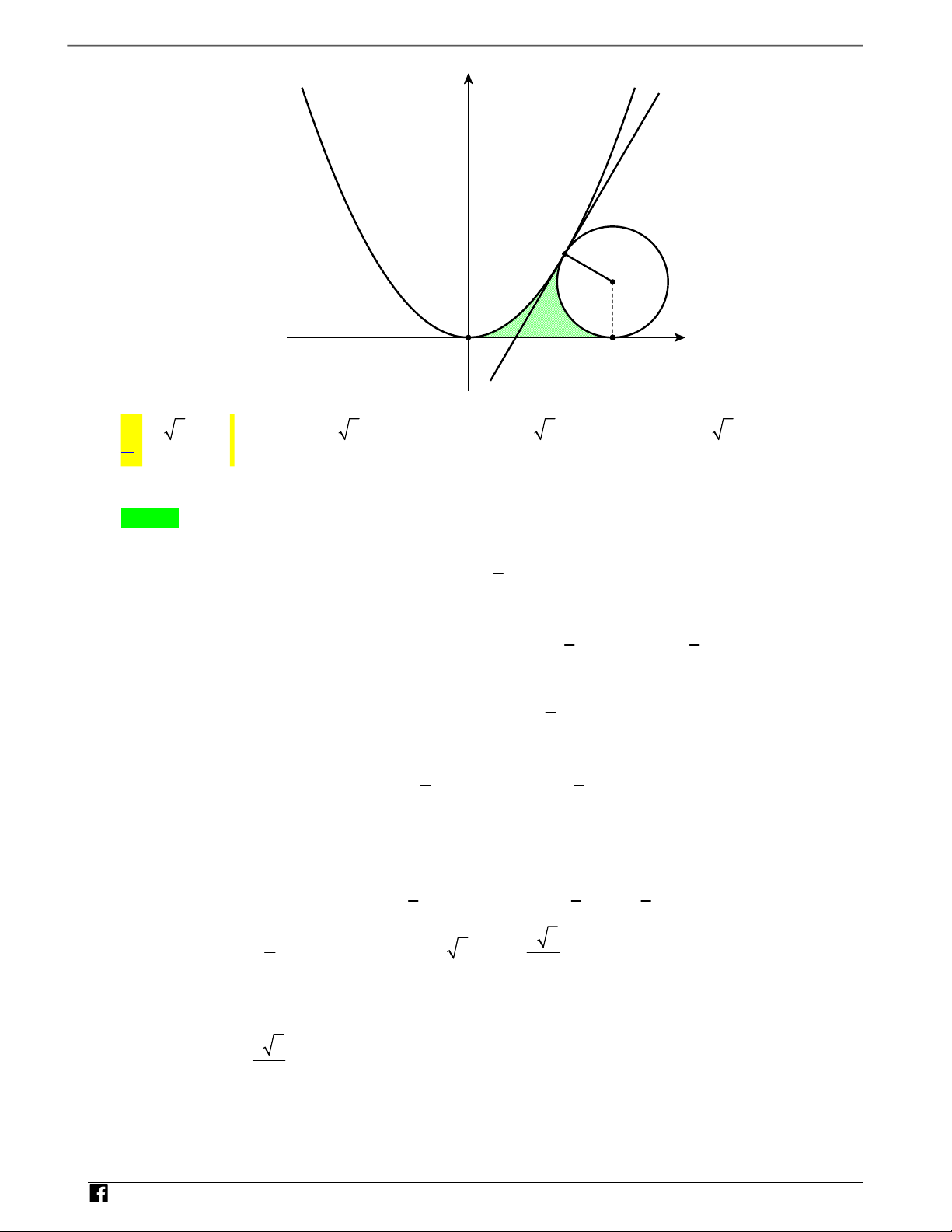
: y  x và đường tròn C có bán kính bằng 1 tiếp xúc với trục hoành đồng 2
thời có chung một điểm A duy nhất với P. Diện tích hình phẳng giới hạn bởi P, C  và trục hoành
(phần tô đậm trong hình vẽ) bằng:
https://www.facebook.com/groups/toanvd.vdc Trang 39
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng y y=0.5x2 N H Ó M TOÁ A N V I D – VD O B x C 27 3  8 9 3  9  4 29 3  9 3 3  2   A. . B. . C. . D. . 24 12 24 3 Lời giải Chọn A  1  Gọi I  ;b 
1 là tậm của đường tròn Cb  0;  2 A a  ; a  
là tiếp điểm của P và C  a  0.  2  1 1
Phương trình tiếp tuyến chung của P và C : 2 2
 : y  ax  a  ax  y  a  0. 2 2 N H Ó    1    M
Tiếp tuyến  có véctơ chỉ phương u  1;a. 2 IA  a   ;b a 1    .   2  T O Á     N 1   1 Ta có 2 3
IA    u.IA  0  a b  a  a 1  0  b  a . V 2  2 D – V Hơn nữa D C 2 2 2       IA  1  a b2 2 1  2  1      3  1         2 a 1 1 a a       a 1  1 2   2    2  1 4  a  2a   3 3 3  0  a  3  b  . 4 2
Phần tô đậm trong hình vẽ là hình giới hạn bởi nhánh bên phải parabol Px  0, nữa bên trái đường     tròn C  3 3 x     và trục hoành.  2   
https://www.facebook.com/groups/toanvd.vdc Trang 40
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng 2  3 3 2 3 3 2 3 3 Ta có: C  : x       y  1  1  x 
 1y  1 (vì x  )  2   2  2 N 1 H P 2
: y  x  x  2y (vì x  0). Ó 2 M T 3 O 2 3 3  2  27 3  8 Á
Vậy diện tích phần tô đậm: S  
   1y  1  2ydy   . N  2    24 0  V D – Câu 12: Cho parabol P 2
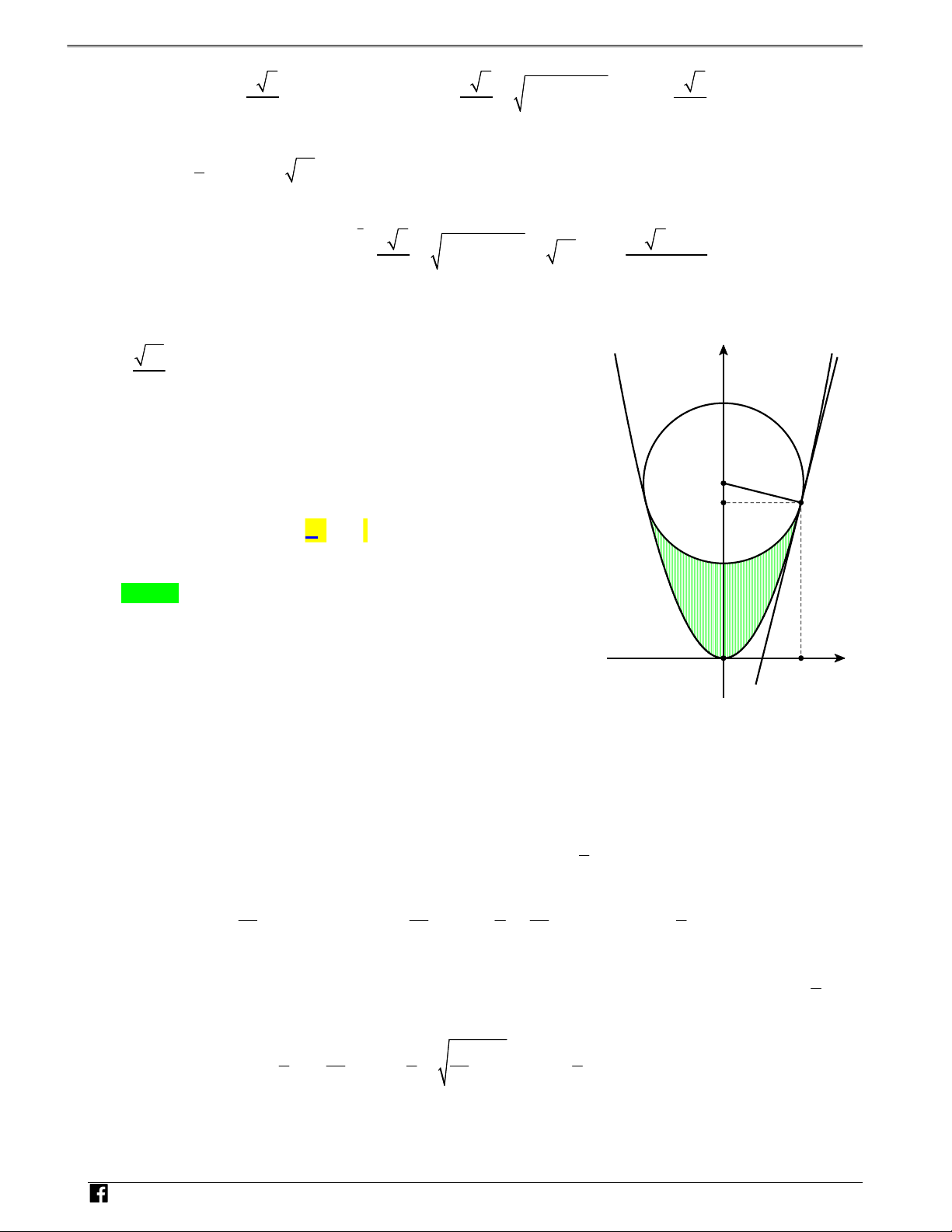
: y  x và đường tròn C có bán kính V D y C 17 bằng
tiếp xúc với hai nhánh của P (như hình vẽ). Diện tích   2
hình phẳng giới hạn bởi Pvà C  (phần tô đậm trong hình) gần
nhất với giá trị nào sau đây? 4,5 I A. 5,12 . B. 7, 06 . 4 A C. 8,74 . D. 6,03. Lời giải Chọn D
Gọi I 0;b là tậm của đường tròn C b  0; A 2 a;a  là tiếp N O 2 x H
điểm nhánh bên phải của P và C  a  0. Ó M T
Phương trình tiếp tuyến chung của P và C : 2 2
 : y  2ax a  2ax  y a  0. O Á N   2 V
Tiếp tuyến  có véctơ chỉ phương u  1;2a. IA  a;a b. D –  V  2 2 1 D
Ta có IA    u.IA  0  a  2a a b  0  b  a  . C 2 17 17 1 17 9 Hơn nữa IA   a  a b2 2 2 2 2   a    a  2  b  . 4 4 4 4 2  
Phần tô đậm trong hình vẽ là hình giới hạn bởi parabol P và nữa bên dưới đường tròn C  9 y       .  2 2  9   17 9 17 9 Ta có C  2 2 : x  y      y    x  (vì y  )  2 4 2 4 2
https://www.facebook.com/groups/toanvd.vdc Trang 41
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng 2 9 17 
Vậy diện tích phần tô đậm 2 2 S  2      x  x dx 6,03.  2 4    0  N Câu 13: Cho parabol P 2
: y  x và đường tròn C có bán kính bằng 2 tiếp xúc với P tại gốc tọa độ HÓ
(như hình vẽ). Diện tích hình phẳng giới hạn bởi P và C (phần tô đậm trong hình) bằng: M     TO y Á y=x2 N V D – VDC I 2 O x 5 4 8 8 A.  2 3 . B.  3 3 . C.  5 3 . D.  3 3 . 3 3 3 3 Lời giải Chọn D N H
Vì tính đối xứng, ta chỉ cần tính phần tô màu phía bên phải trục Oy x   0 . Ó M T 2 2 2 O
Qua hình vẽ, ta thấy: C  có tâm I 0;2  C  : x y  
2  4  x  4 y   2 . Á N V
Phương trình hoành độ giao điểm của P và C : D – V x  0  y  0 D x x 2 4 x 3x 0          . C  2 2 2 4 2 x  3  y  3  3  2     1
Khi đó diện tích phần tô màu S 2  4  y 2  ydy      89 3. 3 0
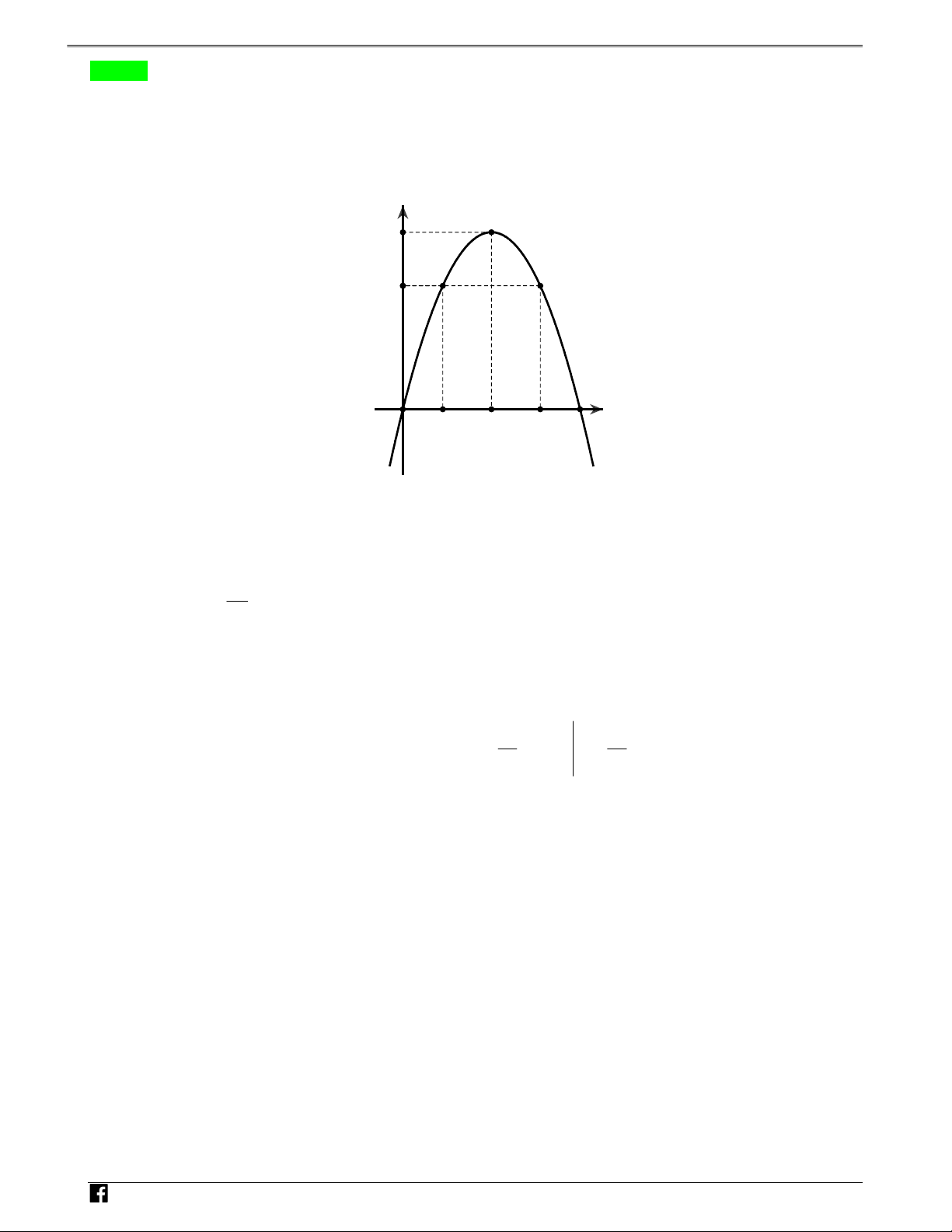
Câu 14: Cho hàm số y  f x. Đồ thị của hàm số y  f x trên 5;3 
 như hình vẽ (phần cong của đồ thị
là một phần của parabol 2 y  ax bx  c).
https://www.facebook.com/groups/toanvd.vdc Trang 42
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng y 4 N 3 H Ó M 2 TOÁN V -5 -4 -1 O 1 2 x D – -1 V D C
Biết f 0  0, giá trị của 2f  5   3f 2 bằng 109 35 A. . B. 33 . C. . D. 11. 3 3 Lời giải Chọn C Cách 1. Parabol 2
y  ax  bx  c có đỉnh I 1;4 và đi qua điểm 2;3 nên ta có:  b    1 a     1 N  2a  H   2 a  b c  4  b   2  y  x   2x  3. Ó     M 4  a  2b  c  3 c   3     T  O Á N
Do f 0  0 nên 2f  5 3f   2
2 f  5 f  1 2f     1 f 0 3f   2 f 0            V  D – 1  0 2 V  2 f   xdx 2  2x
  2x  3dx  3  2x   2x  3dx D 5  1  0 C 0   S    x   x   2 2 dx    2 2.7 5 22 35 2 2 2 3 3 x   2x  3 dx   2.  3.  . 1  2 3 3 3 1  0
Trong đó S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y  f x, trục Ox và hai đường thẳng 1 x  5  , x  1 1 11 1 1 7 và ta có: S  .2.  .1.  . 1 2 3 2 3 2 Cách 2.
https://www.facebook.com/groups/toanvd.vdc Trang 43
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng 3  x  14 ,  5  x  4   2 2
Ta tính được: f x    x  ,  4  x  1  . 3 3  2  x   2x  3, x  1  N  H Ó M 4  4 1 1 Ta có f 4  f 5   f  x dx 
3x  14 dx   f 4  f 5  .(1) T               O 2 2 5 5  Á N 1  1   V 2 2 f 1  f 4   f  x dx     x   dx  3  f 1   f 4  3 . (2) D                3 3  4 4 – VDC
Từ (1) và (2)  f   f   7 1 5  . (3) 2 f  f   0  f x 0 dx   2x   x   5
dx   f   f   5 0 1 2 3 0 1    . (4) 3 3 1  1  f   f   2  f x 2 dx   2x   x   22 dx   f   f   22 2 0 2 3 2 0    .(5) 3 3 0 0 Mà f 0  0. (6) 5 22 31
Từ (3),(4),(5),(6)  f  
1   , f 2  , f 5   3 3 6 N H Ó Do đó: f   f  . M     35 2 5 3 2 3 TO Á N V D – V D C
https://www.facebook.com/groups/toanvd.vdc Trang 44
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng
7) Dạng 7. Toán thực tế với giả thiết có đồ thị hàm liên quan.
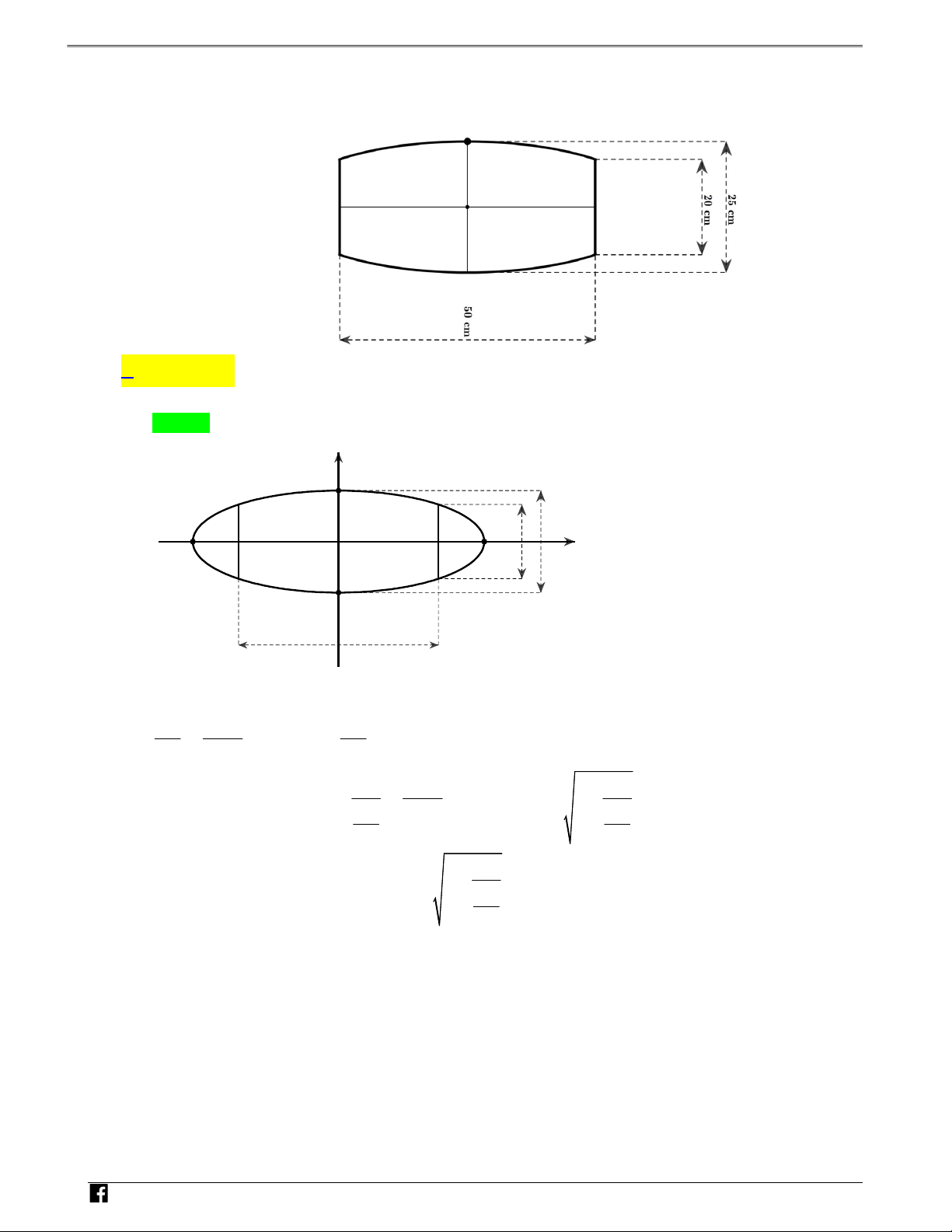
Câu 1: (Đề tham khảo THPT QG 2019) Một biển quảng cáo có dạng hình elip với bốn đỉnh A ,A ,B ,B 1 2 1 2
như hình vẽ bên. Biết chi phí để sơn phần tô đậm là đ 2
200.000 vn / m và phần còn lại đ 2 100.000 vn / m . NH
Hỏi số tiền để sơn theo cách trên gần nhất với số tiền nào dưới đây, biết AA  8m , B B  6m và tứ giác 1 2 1 2 Ó M
MNPQ là hình chữ nhật có MQ  3m ? TO B2 Á N V D M N – VDC A2 A1 Q P B1 A. 5.526.000 đồng. B. 5.782.000 đồng. C. 7.322.000 đồng. D. 7.213.000 đồng. Lời giải Chọn C y B2 3 N M H N Ó M x T 4 O A1 O A2 Á N V D Q P – VDC B1 2 2 x y
Gọi phương trình chính tắc của elip E có dạng:   1 2 2 a b A  A  8  2a a   4 x y 3 Với  1 2   E 2 2 2 B  B  6  2b  b    3 :   1  y   16  x .  1 2   16 9 4
Suy ra diện tích của hình elip là 2 S   a  .b  12 m . E   3
Vì MNPQ là hình chữ nhật và MQ  3  M x  ;     E   2 2 x 1     2 3   3 
  1  x  12  M   2 3; ;N 2     3;  16 4  2    2
https://www.facebook.com/groups/toanvd.vdc Trang 45
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng
Gọi S ;S lần lượt là diện tích phần bị tô màu và không bị tô màu 1 2 4 4 3 Ta có 2 2 S  4. 16  x dx  3 16  x dx 2 4   . 2 3 2 3 N H
Đặt x  4 sint ta tính được 2 S  4  6 3 m Ó 2   M
Suy ra S  S  S  8  6 3 . Gọi T là tổng chi phí. Khi đó ta có T 1 E 2 O Á (đồng). N
T  4 6 3.100 8 6 3.200  7.322.000 V
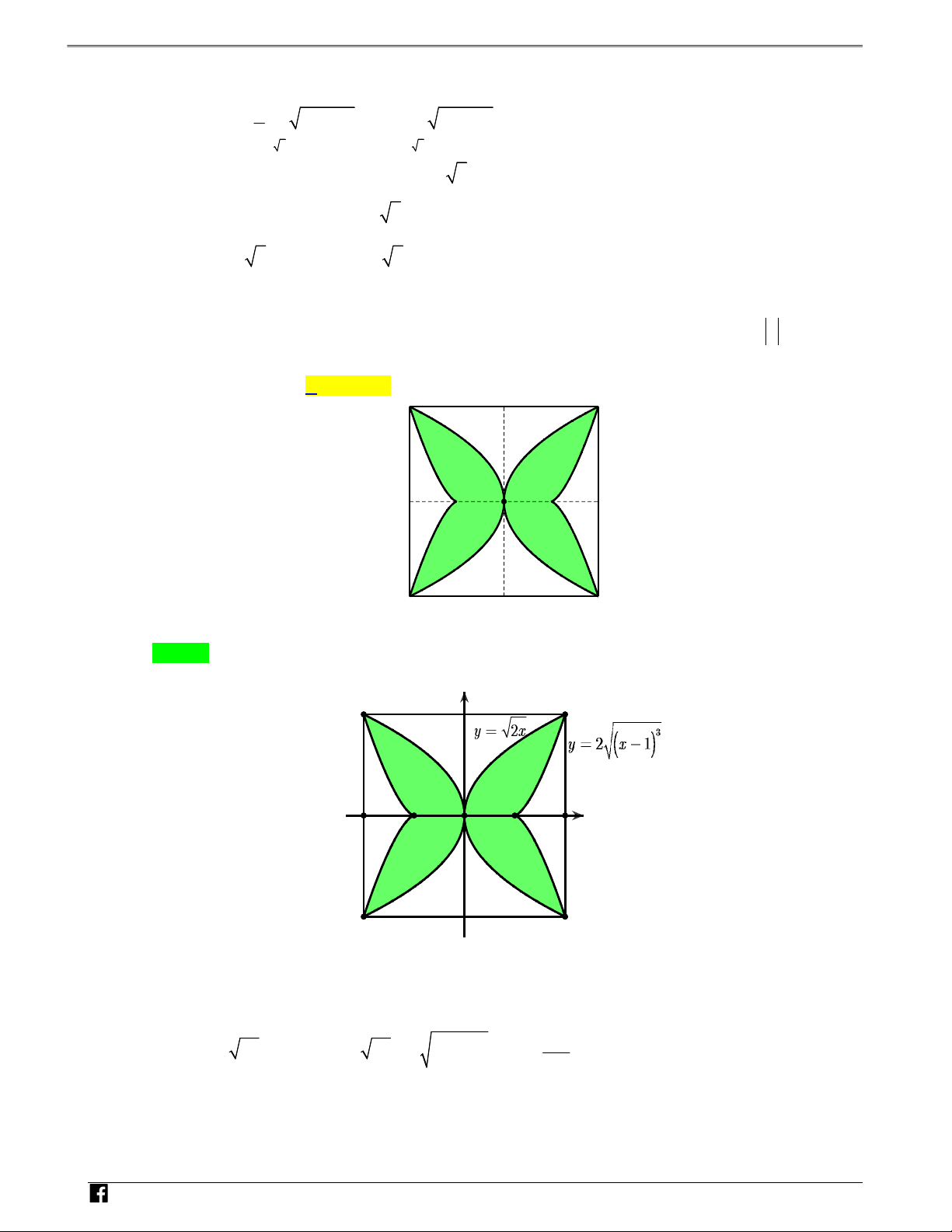
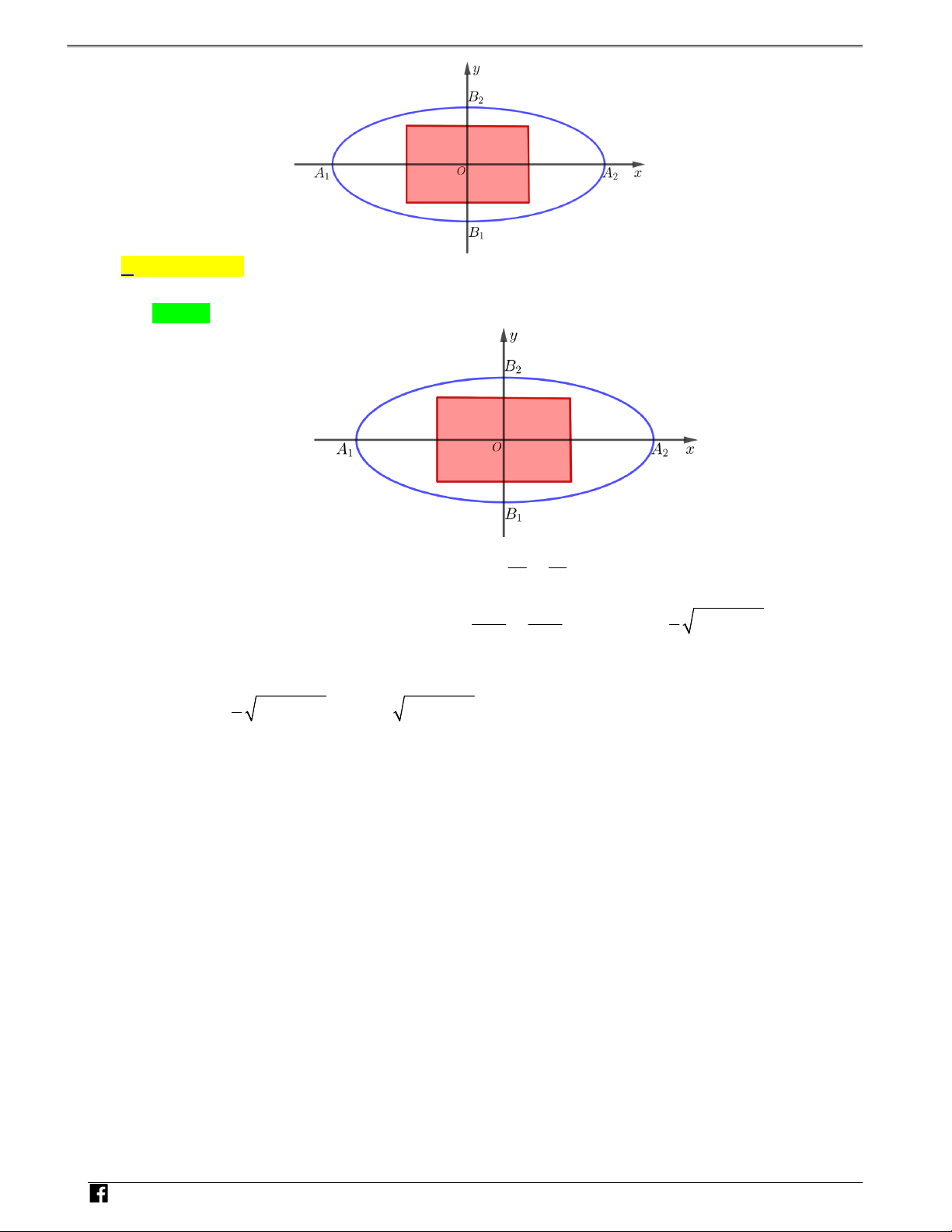
Câu 2: Sàn của một viện bảo tàng mỹ thuật được lát bằng những viên gạch hình vuông cạnh D 40 (cm) như –
hình bên. Biết rằng người thiết kế đã sử dụng các đường cong có phương trình 2 và V y  2x x  3 2 4 1  y DC
để tạo hoa văn cho viên gạch. Diện tích được tô đậm gần nhất với giá trị nào dưới đây? A. 506 (cm2) B. 747(cm2) C. 507(cm2) D. 746(cm2) Lời giải Chọn B N H Ó y M TOÁNVD – O 1 2 x V D C
Gắn hệ trục tọa độ như hình vẽ.
Diện tích phần tô đậm là 1     S     x   2 dx     x   x  3  112 4 2 0 2 2 1 dx         2 dm   747 2 cm     15 0 1 
https://www.facebook.com/groups/toanvd.vdc Trang 46
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng
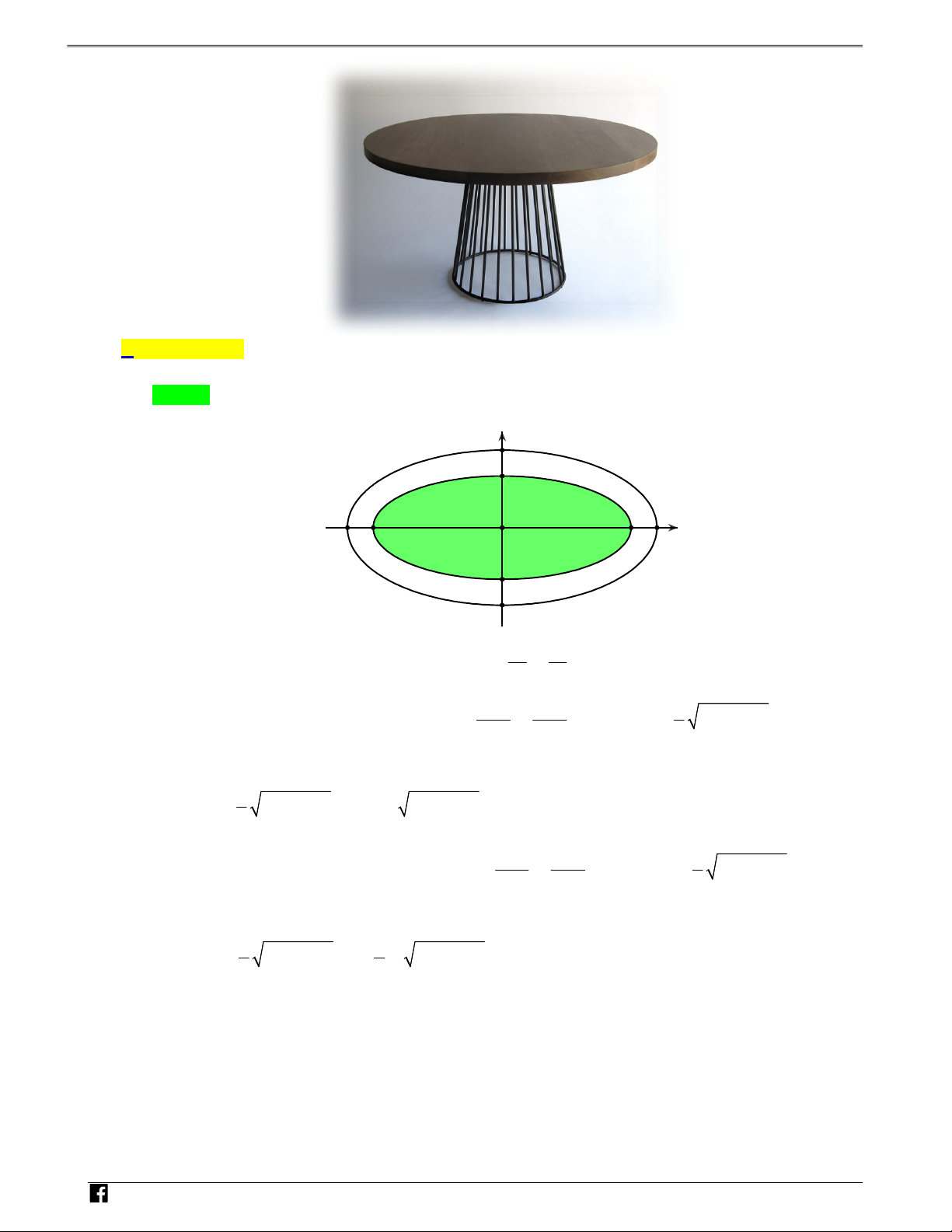
Câu 3: (Đề thi thử THPT QG Bắc Ninh lần 2 năm 2017) Một xưởng sản xuất gỗ muốn thiết kế những có
hình dạng là một phần của hình elip có kích thước giống hình bên. Biết miếng gỗ dày 2cm. Thể tích miếng gỗ đã cho tính theo 3 cm nằm trong khoảng nào? N H Ó M TOÁN VD – VD C A. 2340;2350 . B. 1170;1180 . C. 2240;2250 . D. 1200;1210 .         Lời giải Chọn A y B M 12,5 10 x O A 25 N H
Chọn hệ tọa độ như hình vẽ, khi đó Elip đi qua các điểm B 0;12,5 ,M 25;10 ta có Ó     M 2 3 25 100 2 25 T   1  a  O 2 2 a 12,5 9 Á N 2 2 2 V x y x
Ta được phương trình Elip:   1  y  12,5 1 D 3 2 3 25 12,5 25 – V 9 9 D 25 2 C x
Diện tích bề mặt miếng là S  4 12,5 1  dx  23,406 V  2340,6  3 25 0 9
Câu 4: Một mặt bàn hình elip có chiều dài là 120cm , chiều rộng là là 60cm . Anh Phượng muốn gắn đá hoa
cương và dán gạch tranh trên mặt bàn theo hình (phần đá hoa cương bên ngoài và điểm nhấn bên trong là bộ
tranh gồm 2 miếng gạch với kích thước mỗi miếng là 25cm  40cm ). Biết rằng đá hoa cương có giá và bộ
tranh gạch có giá 300.000 vnđ/bộ. Hỏi số tiền để gắn đá hoa cương và dán gạch tranh theo cách trên gần
nhất với số tiền nào dưới đây?
https://www.facebook.com/groups/toanvd.vdc Trang 47
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng N H Ó M TOÁ N A. 519.000 đồng. B. 610.000 đồng. C. 639.000 đồng. D. 279.000 đồng. V Lời giải D Chọn A – VDC 2 2 x y
Gọi phương trình chính tắc của elip E có dạng:   1 2 2 a b A  A  1,2  2a a   0,6 x y 1 Với  1 2   E 2 2 2 . B  B  0,6  2b  b    0,3 :   1  y   0,36  x  1 2   0,36 0,09 2 N
Suy ra diên tích của hình elip là: H 0,6 0,6 Ó 1 2 2 2 M S   x dx   x dx   m . E 4 0,36 2 0,36 0,18     2 T 0 0 O Gọi Á
S ;S lần lượt là diện tích phần đá hoa cương và bộ tranh 1 2 N 2 V
Ta có S  2x0,25x0, 4  0,2 m 2   D – Suy ra 2
S  S S  0,18  0,2 m . 1 E 2 V     D Gọi C
T là tổng chi phí. Khi đó ta có
T  0,18  0, 2.600000  300000  519.000 (đồng).
Câu 5: Một mặt bàn hình elip có chiều dài là 120cm , chiều rộng là 60cm . Anh Hải muốn gắn đá hoa cương
cho mặt bàn theo hình (phần đá hoa cương trắng và phần đá hoa cương màu vàng), biết rằng phần màu vàng
cũng là elip có chiều dài 100cm và chiều rộng là 40cm . Biết rằng đá hoa cương màu trắng có giá đ 2
600.000 vn / m và đá hoa cương màu trắng có giá đ 2
650.000 vn / m . Hỏi số tiền để gắn đá hoa cương
theo cách trên gần nhất với số tiền nào dưới đây?
https://www.facebook.com/groups/toanvd.vdc Trang 48
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng N H Ó M TOÁN VD – V D A. 355.000 đồng. B. 339.000 đồng. C. 368.000 đồng. D. 353.000 đồng C Lời giải Chọn A y B2 B'2 x A A' 1 1 O A'2 A2 B'1 B1 2 2 x y
Gọi phương trình chính tắc của elip E có dạng:   1 N   2 2 H a b Ó A  A  1,2  2a a   0,6 M x y 1 Với  1 2      E   2  y   0,36  x L  2 2 : 1 T B  B  0,6  2b  b   0,3 1 2   0,36 0,09 2 O Á
Suy ra diện tích của hình elip lớn là: N 0,6 0,6 V 1 2 2 2 D S   x dx   x dx   m E   . L  4 0,36 2 0,36 0,18   2 – 0 0 V     D A 'A ' 1 2a a   0,5   x y 2 C Với 1 2     E    y    x . N  2 2 2 : 1 0,25 B  'B '  0,4  2b b   0,2  1 2   0,25 0,04 5
Suy ra diện tích của hình elip nhỏ là: 0,5 0,5 2 2 8 2 2 S   x dx   x dx   m E   . N  4 0,25 0,25 0,1   5 5 0 0
Gọi S ;S lần lượt là diện tích phần gắn đá hoa cương màu trắng và phần gắn đá hoa cương màu 1 2 vàng. Ta có 2 S  S  0,1 m . 2  N E    Suy ra S  S S
 0,18  0,1  0,08 . Gọi T là tổng chi phí. Khi đó ta có 1 EL EN  T  0,08 .  600000  0,1 .
 650000  355.000 (đồng).
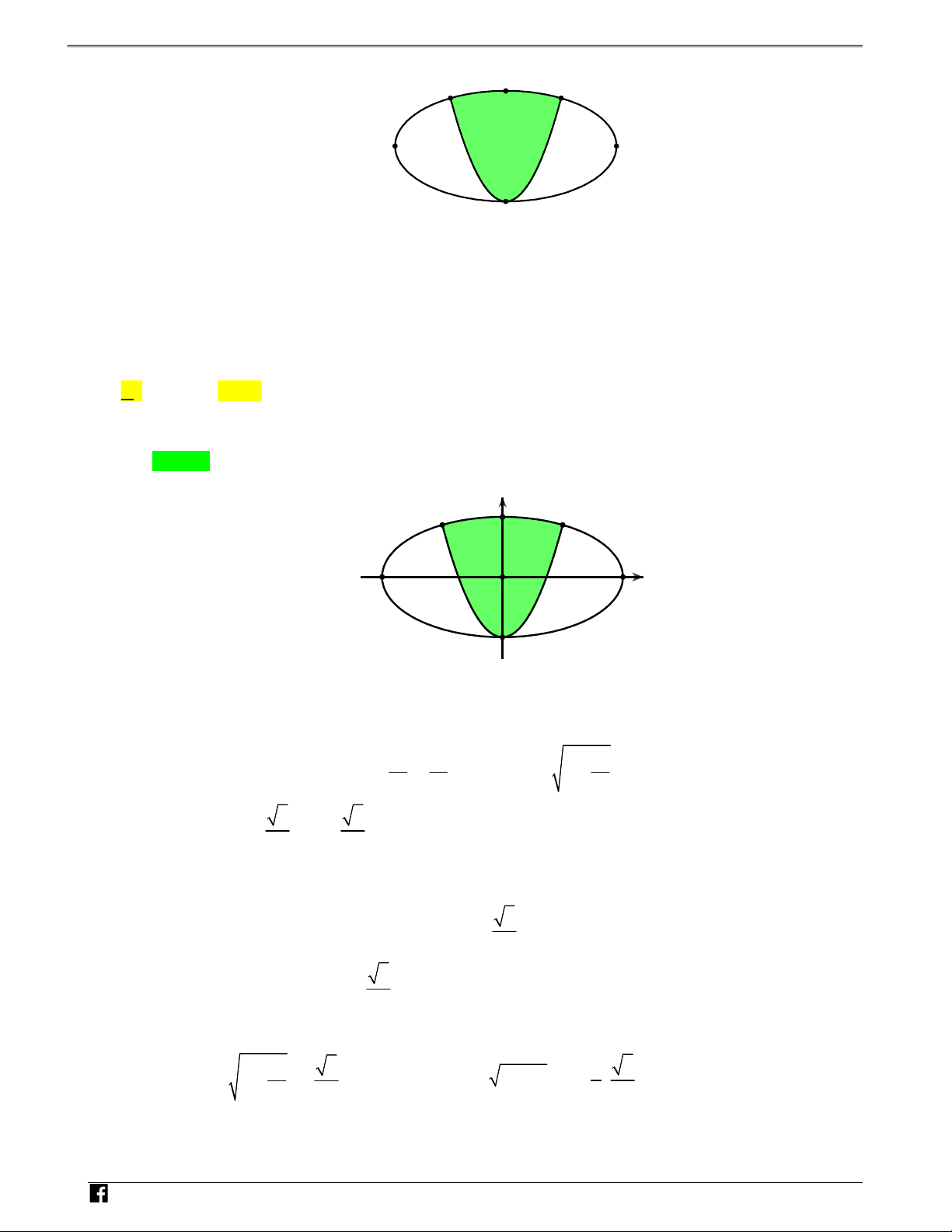
Câu 6: Một biển quảng cáo có dạng hình elip với bốn đỉnh A , A , B , B như hình vẽ bên. 1 2 1 2
https://www.facebook.com/groups/toanvd.vdc Trang 49
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng M B2 N N A A 1 2 H Ó M B 1 T O Á
Người ta chia elip bởi Parabol có đỉnh B , trục đối xứng B B và đi qua các điểm M, N . Sau đó 1 1 2 N V
sơn phần tô đậm với giá 200.000 đồng/ 2
m và trang trí đèn led phần còn lại với giá 500.000 D đồng/ 2
m . Hỏi kinh phí sử dụng gần nhất với giá trị nào dưới đây? Biết rằng A A  4m , – 1 2 V D B B  2m ,MN  2m . 1 2 C A. 2.431.000 đồng. B. 2.057.000 đồng. C. 2.760.000 đồng. D. 1.664.000 đồng. Lời giải Chọn A y M B2 N 1 x A -2 O 2 A 1 2 -1B1 N H
+ Chọn hệ trục tọa độ Oxy sao cho O là trung điểm của AA . Tọa độ các đỉnh A 2;0 , 1   Ó 1 2 M A 2;0 , B 0;1 , B 0;1 . 2   1   2   T O 2 2 2 Á x y x
+ Phương trình đường Elip E :   1  y   1 . N   4 1 4 V D      3     3 – + Ta có M  1; ,N 1     ;   E .       V 2   2   D C + Parabol có đỉnh và trục đối xứng là có phương trình P B 0;1 Ox nên P 1   2
y  ax 1,a  0. P đi qua M,N 3  a   1 2    P  3  có phương trình 2 y   1x 1  .  2   
+ Diện tích phần tô đậm 1  2  x  3    1   2 S  2. 2  3   1  1x 1 2  4  x dx      1  2     dx 1 4  2   3  2    0     0 
https://www.facebook.com/groups/toanvd.vdc Trang 50
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng   Đặt x  2 sin ,tt    ;  
 dx  2 cost dt . Đổi cận: x 0 t 0;x 1 t        . 2 2    6   6   6 N 2 2  3  S  4  4 sin t.2cost dt    3 4   1  2 2  4. cos t dt   H 1 3  2     3 3 Ó 0  0 M   T 6 3 4 3 4  3 4 O
 2. 1 cos2tdt     2t  sin2t6      . Á 3 3 0 3 3 3 6 3 0 N V
+ Diện tích hình Elip là S  a  b  2 . D 5 3 4 –
 Diện tích phần còn lại S S S       . V 2 1 3 6 3 D C
+ Kinh phí sử dụng là: 200000S  500000S  2431000 (đồng). 1 2
Câu 7: Một người định xây một hòn non bộ bằng cách vẽ một đường tròn bán kính 2m trên mặt đất sau đó
lấy tâm đường tròn làm tâm của một hình vuông cạnh 2m như hình vẽ. Phần S (tất cả phần màu trắng) xây 1
thành bể để xếp hòn non bộ và thả cá, phần S ,S để trồng hoa. Tính diện tích trồng hoa. 2 3 2 S1 S S 2 3 N H Ó 2 M TOÁ N A. 2 V 3,65m B. 2 3,56m C. 2 4,65m D. 2 4,56m D Lời giải – Chọn A V D C
https://www.facebook.com/groups/toanvd.vdc Trang 51
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng y N 1 H Ó M S1 S S 2 3 T O Á -1 O 1 2 x N V D – -1 V D C
Chọn gốc tọa độ trùng với tâm đường tròn, khi đó phương trình đường tròn tâm O bán kính 2 là. 2 2 2
x  y  4  y   4  x
Diện tích của hình tròn là  2 4 m 
Diện tích hình vuông là  2 4 m 
Các cạnh của hình vuông nằm trên các đường thẳng y  1,x  1
Phương trình hoành độ giao điểm của đường tròn và đường thẳng y  1 là. 2 4  x  1  x   3 3
Diện tích phần bể ngoài hình vuông là 2 2 4  x 1 dx N   3   H 3 Ó 2 M  S  4  2 4  x 1 dx 1   3   T 2 O
Diện tích phần trồng hoa S  S  4  S  3,65 m . 2 3 1   Á N V
Câu 8: Nhà ông An có một khuôn viên dạng nửa hình tròn có đường kính bằng 4 5(m). Ông An muốn thiế Dt
kế khuôn viên một phần để lát gạch Ý (phần tô đậm) và hai phần còn lại để trồng hoa Nhật Bản ( phần không –
tô màu). Phần tô đậm có dạng của một cánh hoa hình parabol có đỉnh trùng với tâm của nửa hình tròn và haiVD
đầu mút của cánh hoa nằm trên nửa đường tròn, cách nhau một khoảng bằng 4 (m). Biết các kích thước choC
như hình vẽ, kinh phí để trồng hoa Nhật Bản là 150.000 đồng / m2 và kinh phí để lát gạch Ý là 250.000
đồng/ m2. Hỏi kinh phíông An để làm công trình đó gần nhất với kết quả nào sau đây? 4m 4m 4m A. 5.916.400 đồng B. 5.906.400 đồng C. 5.609.400 đồng D. 5.906.500 đồng Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 52
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng Chọn B y (P) 4 N H M Ó M TOÁN VD – V O 2 x D C
Đặt hệ trục tọa độ như hình vẽ. Khi đó phương trình nửa đường tròn là: y  R  x   2 2 2 2 2 2 5  x  20  x
Phương trình Parabol (P) có đỉnh là gốc O sẽ có dạng 2
y  ax .Mặt khác (P) đi qua điểm M(2;4) nên 2 4  a.(2)  a  1
Gọi S là phần diện tích của hình phẳng hạn bởi (P)là nửa đường tròn ( phần tô màu). 1 2
Diện tích phần lát gạch Ý của khuôn viên là: 2 2
S  ( 20  x  x ).dx  11,940 1  2 
Phần diện tích trồng cỏ Nhật Bản của khuôn viên là: 2 1 1 2 2 2 S  S  S  (
 2 5)  ( 20  x  x )dx  19,476 N 2 hinh tron 2 2 2  H 2 Ó M
Vậy số tiền cần có là: T  250.000.S  150.000.S  5.906.400 (đồng) 1 2 TO
Câu 9: Một cái cổng hình parabol như hình vẽ. Chiều cao GH  4m , chiều rộng AB  4m Á, N
AC  BD  0,9m . Chủ nhà làm hai cánh cổng khi đóng lại là hình chữ nhật CDEF tô đậm giá làV D
1200000 đồng/m2, còn các phần để trắng làm xiên hoa có giá là 900000đồng/m2. – V G D C F E C H D B A
Hỏi tổng chi phí để là hai phần nói trên gần nhất với số tiền nào dưới đây? A. 11445000 (đồng). B. 7368000 (đồng). C. 4077000 (đồng). D. 11370000 (đồng) Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 53
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng Chọn A
Gắn hệ trục tọa độ Oxy sao cho AB trùng Ox , A trùng O khi đó parabol có đỉnh G 2;4 và N đi qua gốc tọa độ. H Ó M y T G O 4 Á N F E V D – VDC 0,9 2 3,1 4 O A C H D B x y=-x2+4x
Gọi phương trình của parabol là 2 y  ax bx  c c   0  a   1  b   Do đó ta có   2  b   4  . 2a    2  c   0 2  a  2b  c  4     N H
Nên phương trình parabol là 2 y  f(x)  x   4x Ó M 4 3 T   2  x 2  4 32 2 O
Diện tích của cả cổng là S  ( x   4x)dx     2x       10,67(m ) Á  3  0 3 0 N V D
Do vậy chiều cao CF  DE  f 0,9  2,79(m) – VD
CD  4  2.0,9  2,2m C
Diện tích hai cánh cổng là S  CDCF    2 . 6,138 6,14 m CDEF 
Diện tích phần xiên hoa là 2 S  S S
 10,67  6,14  4,53(m ) xh CDEF
Nên tiền là hai cánh cổng là 6,14.1200000  7368000đ
và tiền làm phần xiên hoa là 4,53.900000  4077000đ.
Vậy tổng chi phí là 11445000 đồng.
https://www.facebook.com/groups/toanvd.vdc Trang 54
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng
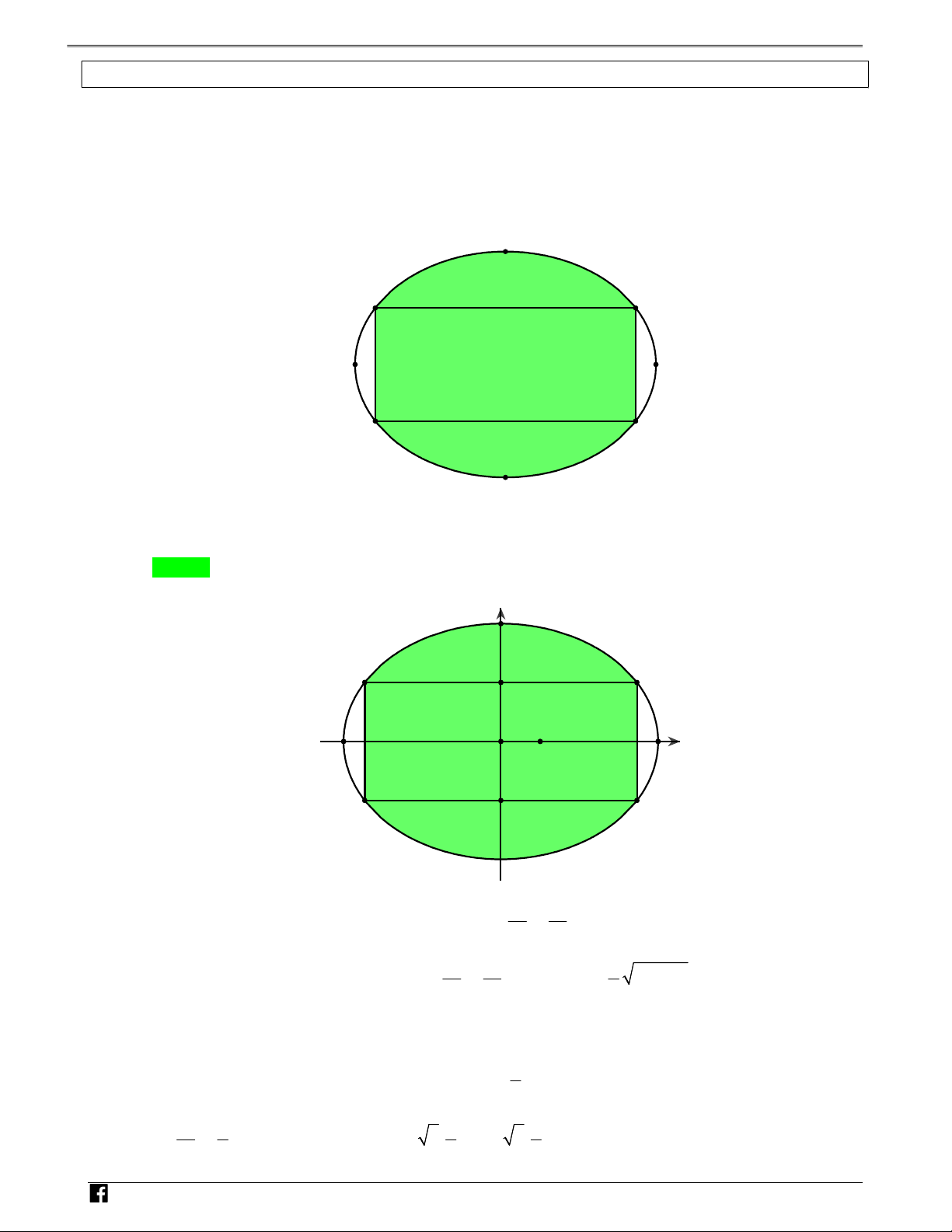
Câu 10: Bồn hoa của một trường X có dạng hình tròn bán kính bằng 8m . Người ta chia bồn hoa thành các
phần như hình vẽ dưới đây và có ý định trồng hoa như sau: Phần bên trong hình vuông ABCD để trồng hoa.
Phần phần gạch xọc dùng để trồng cỏ. Ở 4 góc còn lại mỗi góc trồng một cây cọ. Biết AB  4m , giá trồng
hoa là 200.000 đ/m2, giá trồng cỏ là 100.000 đ/m2, mỗi cây cọ giá 150.000 đ. Hỏi cần bao nhiêu tiền để thực N
hiện việc trang trí bồn hoa đó (làm tròn đến hàng nghìn). H Ó M TOÁN VD – VDC A. 13.265.000 đồng. B. 12.218.000 đồng. C. 14.465.000 đồng. D. 14.865.000 đồng. Lời giải Chọn A y N H Ó M TOÁNVD – V O 2 8 x D C
Chọn hệ trục tọa độ sao cho gốc tọa độ trùng với tâm hình tròn, suy ra phương trình đường tròn là: 2 2 x  y  64.
+ Diện tích hình vuông ABCD là: S     2 4 4 16 m . ABCD 
https://www.facebook.com/groups/toanvd.vdc Trang 55
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng
 Số tiền để trồng hoa là: T  16200.000  3.200.000 (đồng). 1 2
+ Diện tích trồng cỏ là: S  4  2
64  x  2dx  94,654  2 m . N 2  H Ó M
 Số tiền trồng cỏ là: T  94,654100.000  9.465.000 (đồng). 2 TO
+ Số tiền trồng 4 cây cọ là: (đồng). Á T  150.0004  600.000 3 N V
Vậy tổng số tiền để thực hiện việc trang trí bồn hoa là: D – (đồng). V
T  T T T  13.265.000 1 2 3 D C
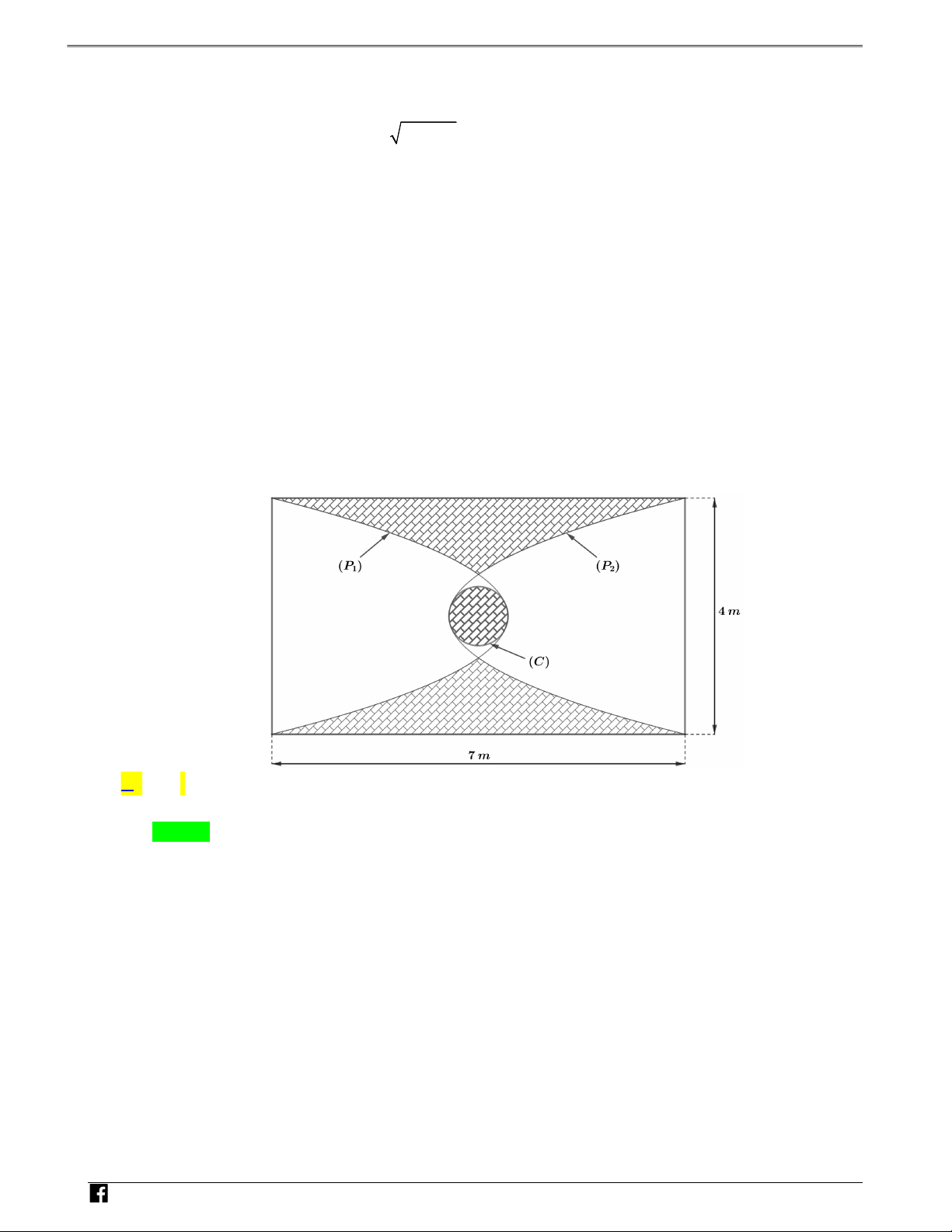
Câu 11: Người ta lát gạch trang trí một mảnh sân hình chữ nhật như hình dưới đây, trong đó P , P là các 1   2 
parabol giống nhau, C  là đường tròn có tâm trùng với tâm của mảnh sân và lần lượt có duy nhất một điểm
chung với các parabol tại chính các đỉnh của các parabol ấy. Tính và làm tròn đến hai chữ số thập phân diện
tích phần lát gạch của mảnh sân trong trường hợp diện tích hình tròn bao bởi C  lớn nhất. N H Ó M TOÁ N A. 8,39 . B. 10,12 . C. 9,18 . D. 11,45 . V D Lời giải – Chọn A V D
Đặt C  và P vào mặt phẳng Oxy sao cho C  có tâm là O và bán kính là r r  0 như hình 1  C dưới đây:
https://www.facebook.com/groups/toanvd.vdc Trang 56
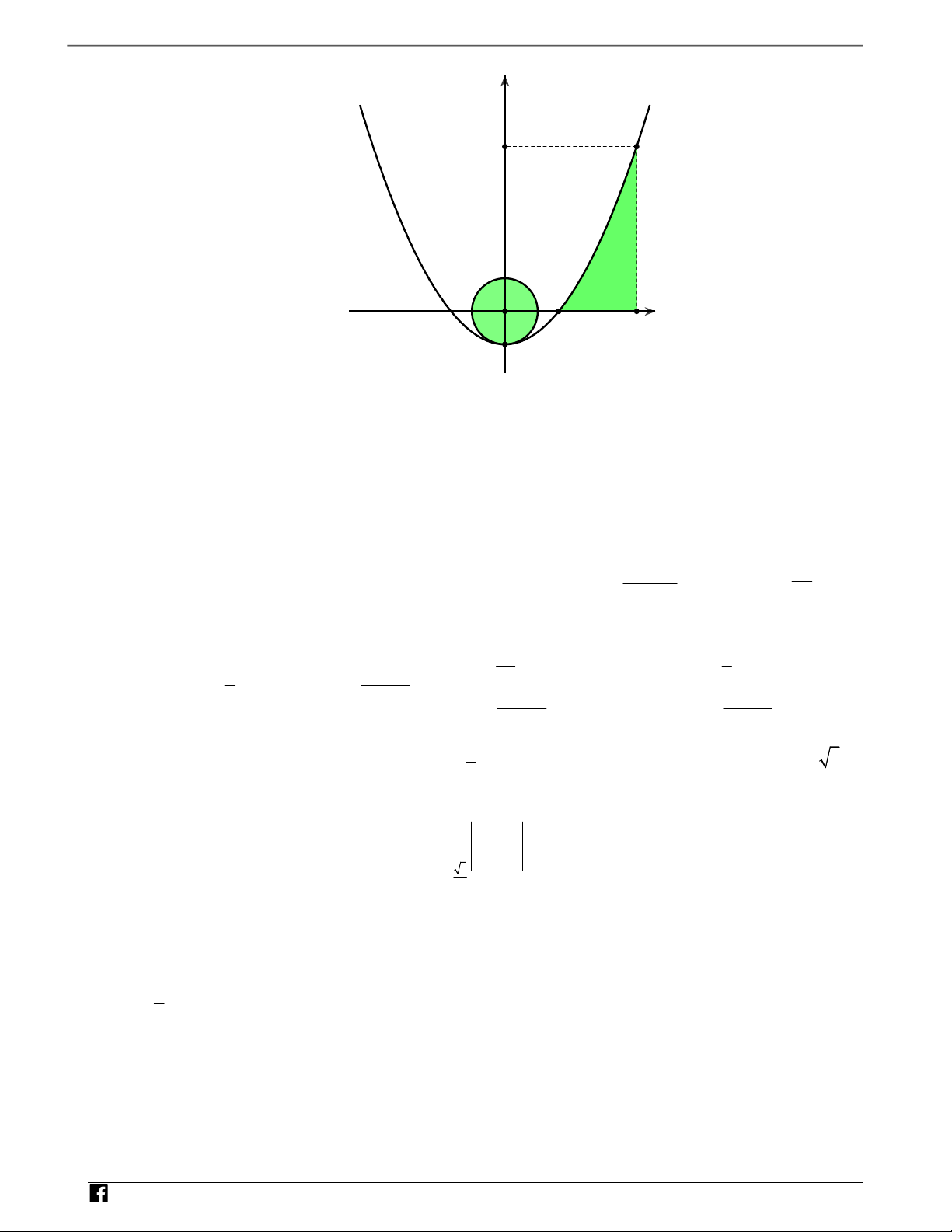
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng y 4a-r N M H Ó M TOÁN r V S D – O 2 x V D -r C Lúc này ta có C  2 2 2 x  y  r P 2 : , : y  ax r (a  0). 2 2 2 x  y  r
Do C  và P có duy nhất một điểm chung là đỉnh của P nên hệ phương trình  1  1   2 y   ax r 
có duy nhất một nghiệm là 0; r (*)  2 x  0    2 2 2 2 x  y  r  x       2 4 2 2 a x  2arx  r  2  r  1 Do  2 2ar 1      nên (*)  r  . 2 2  x           2 y ax r y ax r   a  2a  2 y   ax r   1   1  N  7 2r 7 r    r    H Do M 2  ;    2a  2   P nên a   . Tức . Từ đây tìm được . 1    Ó  2 8  2r  7   2r  7  M a    a    8  8 TO  1  Á r   2
Do hình tròn có diện tích lớn nhất nên . Lúc này . N  2 
P cắt tia Ox tại điểm có hoành độ 1  2 V a   1  D  – 2   2 1     2 1 V
Diện tích cần tính là    4S   4 x  .dx  8,39 D   . 2   4 2  C 2 2
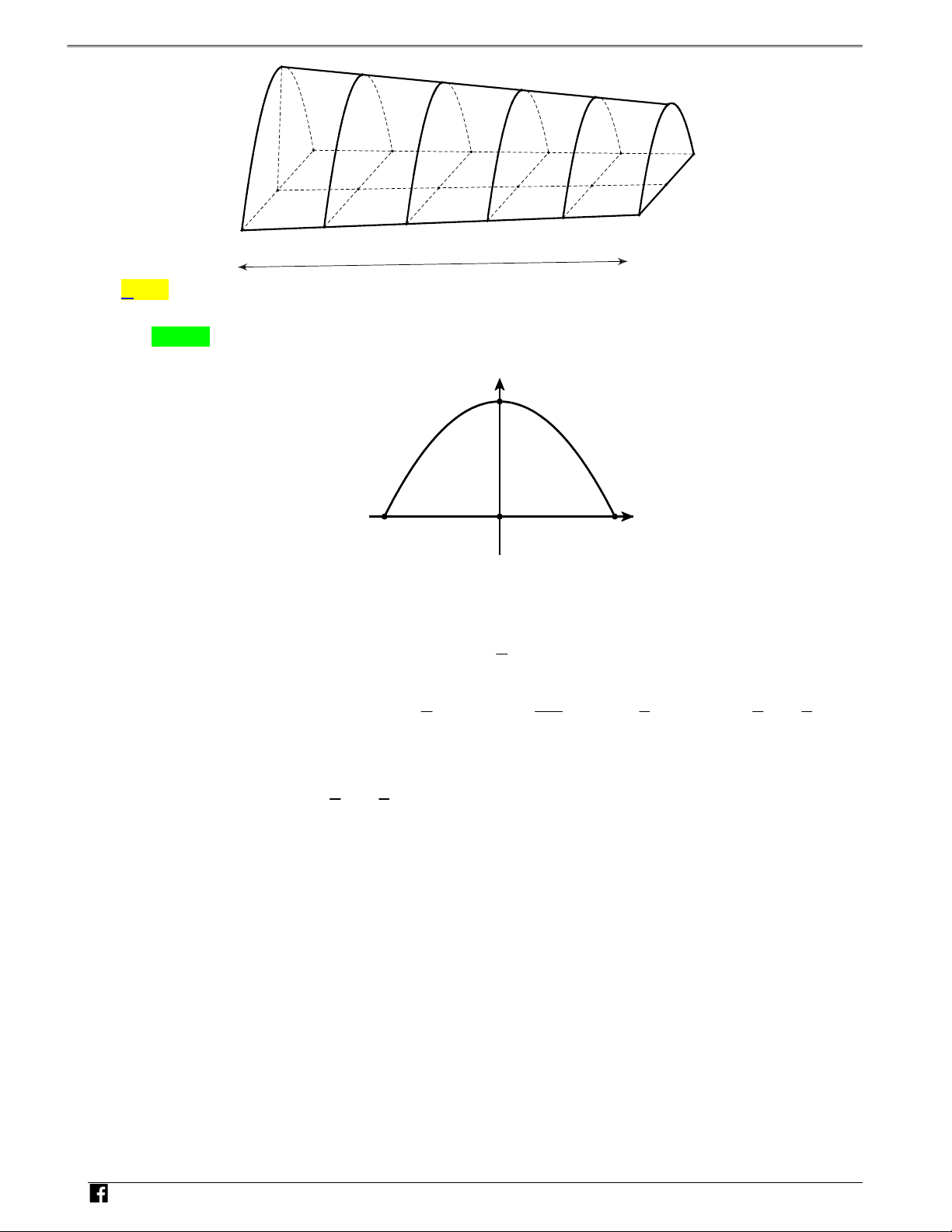
Câu 12: Cho một mô hình 3  D mô phỏng một đường hầm. Biết rằng đường hầm mô hình có chiều dài
5cm; khi cắt hình này bởi mặt phẳng vuông góc với đáy của nó, ta được thiết diện là một hình parabol có
độ dài đáy gấp đôi chiều cao parabol như hình vẽ. Chiều cao của mỗi thiết diện parobol cho bởi công thức 2
y  3  x cm, với x cm là khoảng cách tính từ lối vào lớn hơn của đường hầm mô hình. Tính thể tích 5 (theo đơn vị 3
cm ) không gian bên trong đường hầm mô hình (làm tròn kết quả đến hàng đơn vị)
https://www.facebook.com/groups/toanvd.vdc Trang 57
NHÓM TOÁN VD–VDC Sử dụng tính chất đồ thị hàm số để tính diện tích hình phẳng h N H h Ó M h TOÁ 5m N V A. 29 . B. 27 . C. 31. D. 33 . D Lời giải – V Chọn A D C y h O h x
Xét một thiết diện parabol có chiều cao là h và độ dài đáy 2h và chọn hệ trục Oxy như hình vẽ
trên. Parabol P có phương trình 2 y  ax  h, a  0 1 Ta có B h;  0  P 2
 0  ah  h  a   doh  0 N h H h 2 2 Ó  1     2  4h 2 4 2   M
Diện tích S của thiết diện: S    x  hdx          , h  3  x S x 3 x  h  3 5 3  5   T h  O
Suy ra thể tích không gian bên trong của đường hầm mô hình: Á N 5 5 2   V V  S  x 4 2 dx   3  x dx  28,888 3 V  29 cm D    3  5  0 0 – VDC
https://www.facebook.com/groups/toanvd.vdc Trang 58

Sử dụng tính chất của đồ thị hàm số để tính diện tích hình phẳng Toán 12

Thông tin :

Tài liệu liên quan:

Gắn hệ tọa độ Oxyz để giải các bài toán hình học không gian – Phương Nguyễn Toán 12

20 kĩ thuật chinh phục vận dụng cao số phức – Hoàng Xuân Nhàn Toán 12

Phân dạng bài tập và lời giải chi tiết chuyên đề Tích phân – Lưu Huy Thưởng Toán 12

Phương pháp giải các bài toán Tích phân – Trung tâm LTĐH Vĩnh Viễn Toán 12

Phương pháp giải các dạng Tích phân thường gặp Toán 12