Tài liệu chuyên đề đường tiệm cận của đồ thị hàm số

Tài liệu chuyên đề đường tiệm cận của đồ thị hàm số được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

Môn:

Toán 12 3.9 K tài liệu

Thông tin:
109 trang 1 năm trước
Tác giả:
Student
Mai Nguyệt
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Tài liệu chuyên đề đường tiệm cận của đồ thị hàm số

Tài liệu chuyên đề đường tiệm cận của đồ thị hàm số được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

60 30 lượt tải Tải xuống

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số 375 tài liệu

Môn: Toán 12 3.9 K tài liệu

Thông tin:

109 trang 1 năm trước

Tác giả:

Profile Mai Nguyệt
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 167
BÀI 4. ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
1. Nhánh vô cực của đường cong
( ) ( )
:C y fx=
Gọi
( ) ( )
;M xy C∈
.
Ta nói:
( )
C
có nhánh vô cực
⇔
x hay x
y hay y
→ +∞ → −∞
→ +∞ → −∞
VD1: Đồ thị
( )
C
của hàm số
2
yx=
có nhánh vô cực
VD2: Đồ thị
( )
C
của hàm số
2
4yx
= −
không có nhánh vô cực
vì
( ) ( )
;
M xy C∈
22x−≤ ≤
và
02y≤≤
.
2) Tiệm cận của đường cong
Cho đường cong
( ) ( )
:C y fx=
và
( ) ( )
;M xy C∈
,
H
là hình chiếu vuông góc của
M
lên
( )
∆
.
Đường thẳng
(
)
∆
được gọi là tiệm cận của
( )
C
khi và chỉ khi khoảng cách
MH
từ
M
đến
( )
∆
tiến về 0 khi
M
vẽ nên nhánh vô cực của
( )
C
.
Như vậy:
( )
∆
tiệm cận của
()C
lim 0
M
MH
→∞
⇔=
CHƯƠNG
I
ỨNG DỤNG ĐẠO HÀM
ĐỂ KHẢO SÁT HÀM SỐ
LÝ THUY
Ế
T.
I
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 168
3) Định nghĩa đường TCĐ và TCN của đồ thị hàm số
a) Tiệm cận đứng của đồ thị hàm số
Đường thẳng
0
xx=
được gọi là đường tiệm cận đúng
(TCĐ) của đồ thị hàm số
( )
y fx
=
nếu thỏa mãn ít nhất
một trong các điều kiện sau:
0
lim ( )
xx
fx
+
→
= +∞
;
0
lim ( )
xx
fx
+
→
= −∞
0
lim ( )
xx
fx
−
→
= +∞
;
0
lim ( )
xx
fx
−
→
= −∞
b) Tiệm cận ngang của đồ thị hàm số
Cho hàm số
( )
y fx=
có xác định trên một khoảng vô hạn
là khoảng có một trong các dạng
(, )a
+∞
;
( ,)a−∞
;
(,)−∞ +∞
.Đường thẳng
0
yy=
được gọi là đường TCN (hay TCN)
của đồ thị nếu thỏa mãn ít nhất một trong các điều kiện sau:
0
lim ( )
x
fx y
→−∞
=
;
0
lim ( )
x
fx y
→+∞
=
Lưu ý:
i) Hàm
ax b
y
cx d
+
=
+
với
0ac ≠
có tiệm cận đứng
d
x
c
= −
; tiệm cận ngang
a
y
c
=
.
ii) Hàm
( )
( )
fx
y
gx
=
với
( ) ( )
,f x gx
là những hàm đa thức
+) Nếu bậc tử nhỏ hơn bậc mẫu thì có tiệm cận ngang
0y =
.
+) Nếu bậc tử bằng bậc mẫu thì có tiệm cận ngang
n
n
a
y
b
=
với
,
nn
ab
là hệ số của lũy thừa
cao nhất trên tử và dưới mẫu.
+) Nếu bậc tử lớn hơn bậc mẫu thì không có tiệm cận ngang.
+)
0
xx=
là tiệm cận đứng
(
)
( )
( )
( )
(
)
( )
0
00
00
0; 0
0
lim
xx
gx f x
gx f x
fx
gx
→
= ≠
= =
⇔
= ±∞
.
iii) Ứng dụng máy tính CASIO để tìm tiệm cận đứng hoặc tiệm cận ngang
Để tìm tiệm cận đứng hoặc tiệm cận ngang của một hàm số thông qua máy tính CASIO, ta sử
dụng phím CALC trên máy.
Một số lưu ý về kết quả và cách bấm:
Giới hạn
Thao tác trên máy
tính
o
xx
+
→
CALC
10
10
o
x
−
+
o
xx
−
→
CALC
10
10
o
x
−
−
x → +∞
CALC
10
10
x → −∞
CALC
10
10−
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 169
DẠNG 1: TÌM TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ CHO BỞI CÔNG THỨC
Câu 1. Cho hàm số
23
()
2
x
y fx
x
−
= =
+
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm
số
()y fx=
.
Lời giải
Vì
lim 2; lim 2
xx
yy
→−∞ →+∞
= =
nên đồ thị hàm số có 1 tiệm cận ngang là
2y =
.
Vì
22
lim ; lim
xx
yy
+−
→− →−
= −∞ = +∞
nên đồ thị hàm số có 1 tiệm cận đứng
2x = −
.
Do đó đồ thị hàm số có tổng số 2 tiệm cận kể cả đứng và ngang.
Câu 2. Cho hàm số
2020 2021
()
1
x
y fx
x
−
= =
−
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ
thị hàm số
()y fx=
.
Câu 3. Cho hàm số
25
()
2
x
y fx
x
−
= =
−
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm
số
()y fx=
.
Câu 4. Cho hàm số
2
23
()
1
xx
y fx
x
++
= =
+
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ
thị hàm số
()y fx=
.
Câu 5. Cho hàm số
2
6
()
1
xx
y fx
x
−−
= =
−
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị
hàm số
()
y fx=
.
Câu 6. Cho hàm số
2
32
()
1
x
y fx
x
+−
= =
−
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị
hàm số
()
y fx=
.
Câu 7. Cho hàm số
2
2
6
()
32
xx
y fx
xx
−−
= =
++
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị
hàm số
()y fx=
.
Câu 8. Cho hàm số
2
2 33
()
24
xx x
y fx
x
+ +−
= =
−
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của
đồ thị hàm số
()y fx=
.
Câu 9. Cho hàm số
2
5 32
()
2
xx x
y fx
x
− ++
= =
−
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của
đồ thị hàm số
()y fx
=
.
HỆ THỐNG BÀI TẬP TỰ LUẬN.
II
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 170
DẠNG 2: TÌM TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ BIẾT BBT CỦA HÀM SỐ, ĐỒ THỊ CỦA HÀM
SỐ ĐÓ HOẶC HÀM SỐ LIÊN QUAN
Câu 1. Cho hàm số
()y fx=
có bảng biến thiên
Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
()y fx=
.
Lời giải
Vì
lim ; lim 3
xx
yy
→−∞ →+∞
= −∞ =
nên đồ thị hàm số có 1 tiệm cận ngang là
3y =
.
Vì
4
lim
xx
y
+
→
= +∞
nên đồ thị hàm số có 1 tiệm cận đứng
4
xx=
.
Do đó đồ thị hàm số có tổng số 2 tiệm cận kể cả đứng và ngang.
Câu 2. Cho hàm số
()fx
có bảng biến thiên
Tìm số tiệm cận của đồ thị hàm số
1
()
y
fx
=
?
Câu 3. Cho hàm số
( )
y fx=
xác định, liên tục trên
{ }
\1
và có bảng biến thiên như sau:
Tìm phương trình đường tiệm cận ngang của đồ thị hàm số đã cho?
Câu 4. Cho hàm số
()y fx
=
xác định trên
{
}
\0
, liên tục trên mỗi khoảng xác định và có bảng biến thiên
như sau:
Hỏi đồ thị hàm số trên có bao nhiêu đường tiệm cận đứng và ngang?
Câu 5. Cho hàm số
()y fx=
xác định trên
{ }
\1
, liên tục trên mỗi khoảng xác định và có bảng biến thiên
như sau:
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 171
Tìm các giá trị nguyên của
[
)
0;5m ∈
để đồ thị hàm số
( )
y fx=
có 3 đường tiệm cận đứng và
ngang?
Câu 6. Cho hàm số
()fx
có đồ thị như hình vẽ bên.
Tìm phương trình các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số trên.
Câu 7. Cho đồ thị hàm số
( )
y fx=
như hình bên. Đồ thị có bao nhiêu đường tiệm cận đứng và tiệm cận
ngang?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 172
DẠNG 3: TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ HÀM HỢP
Các dạng trong chủ đề: Cho hàm số
( )
y fx
=
biết bảng biến thiên hoặc đồ thị. Tìm các đường
tiệm cận đứng và tiệm cận ngang của đồ thị
( )
y gx=
thuộc một trong các dạng sau
1)
( )
()
y f ux=
,
2)
(
)
()
y g fx
=
,
3)
( )
(u( ))y gf x=
,
4)
(
)
, ()
y gxfx=
,
5)
( )
, (u(x))y gxf=
.
Phương pháp giải: Gọi
(
)
G
là đồ thị hàm số
( )
y gx=
.
1)Tìm tiệm cận ngang.
Xét hàm số dạng
( )
()
()
ux
gx
vx
=
.Một dấu hiệu thường dùng để nhận biết
( )
G
có tiệm cận ngang:
+ Hàm số
( )
y gx=
xác định trên
( )
;
a +∞
hoặc trên
( )
;a−∞
.
+ Bậc của
(x)
u
≤
Bậc của
(x)v
.
+
0
lim ( )
x
gx y
→+∞
=
hoặc
0
lim ( )
x
gx y
→−∞
=
⇒
Đường thẳng
0
yy=
là tiệm cận ngang của
(
)
G
.
2)Tìm tiệm cận đứng.
Xét dạng hàm số
( )
()
()
ux
gx
vx
=
. Một dấu hiệu thường dùng để nhận biết đường thẳng
0
xx=
là
tiệm cận đứng của
( )
G
:
+
0
()0vx =
và
0
()0ux
≠
,
( )
gx
xác định trên
(
)
0
;ax
hoặc
( )
0
;xb
.
+ Ít nhất một trong hai giới hạn
(
) ( )
00
lim , lim
xx xx
gx gx
+−
→→
là giới hạn vô cực.
Đường thẳng
0
xx=
là tiệm cận đứng của
( )
G
.
Trong chủ đề này, các dấu hiệu nhận biết ở trên dựa vào bảng biến thiên hoặc đồ thị của hàm số
( )
y fx=
.
Câu 1. Cho hàm số
( )
y fx=
có bảng biến thiên như hình dưới đây
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
( )
1
21
y
fx
=
−
.
Câu 2. Cho hàm số
( )
y fx=
liên tục trên
\1
và có bảng biến thiên như sau
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 173
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
( )
1
()
23
y gx
fx
= =
−
Câu 3. Cho hàm số
( ) ( )
32
,,,f x ax bx cx d a b c d R= + ++ ∈
có đồ thị như hình vẽ.
Đồ thị hàm số
( )
( )
( )
( )
( )
22
2
43
2
++ +
=
−
x x xx
gx
fx fx
có bao nhiêu đường tiệm cận đứng?
Câu 4. Cho đồ thị hàm đa thức bậc bốn
()y fx=
như hình vẽ bên dưới .
Hỏi đồ thị của hàm số
( )


62 2
2
(x +1)(x - 5x). x -2x
g(x) =
f (x)-2f(x) 2x -10
có bao nhiêu đường tiệm cận đứng và tiệm
cận ngang.
Câu 5. Cho hàm số
( )
32
f x ax bx cx d= + ++
là hàm số đa thức với hệ số thực, có đồ thị
()
C
như hình vẽ
bên.
Tìm số tiệm cận đứng của đồ thị hàm số
( )
( )
( ) ( ) ( )
2
2
32 1
1
xx x
gx
x f x fx
−+ −
=

+−

.
Câu 6. Cho hàm số bậc ba
()y fx=
có đồ thị như hình vẽ bên.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 174
Tìm số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
2
2
( 1)( 1)
()
() 2 ()
xx
y gx
f x fx
+−
= =
−
.
Câu 7. Cho hàm số
( )
32
y f x ax bx cx d= = + ++
,
( )
0a ≠
có đồ thị như hình dưới đây
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
( )
( )
( )
( )
( )
( )
2
2
2
23xx x
y gx
x x fx fx
+−
= =

−+

.
Câu 8. Cho hàm số bậc ba
()
y fx
=
có đồ thị như hình vẽ bên.
Tìm số đường tiệm cận đứng của đồ thị hàm số
2
()
() 1
x
y gx
fx
+
= =
+
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 175
Câu 9. Cho hàm số
( )
y fx
=
liên tục trên
\1
và có bảng biến thiên như sau
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
( )
( )
2
22
y gx f x x= = −−
.
Câu 10. Cho hàm số
(
)
y fx=
liên tục trên
và có đồ thị như hình
dưới đây
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
( )
2
1
x
y gx f
x
−

= =

+

Câu 11. Cho hàm số
( )
y fx=
là hàm đa thức liên tục trên
và có đồ thị như hình dưới đây
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
( )
(
)
( )
1
fx
y gx
fx
= =
−
.
Câu 12. Cho hàm số
( )
y fx=
xác định, liên tục trên
và có bảng biến thiên như sau :
Tìm số tiệm cận ngang và số tiệm cận đứng của đồ thị hàm số
( )
( )
3
3
11
=
++ −
gx
fx x
.
DẠNG 3: MỘT SỐ BÀI TOÁN VỀ TIỆM CẬN CHỨA THAM SỐ
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 176
Câu 1. Tìm các giá trị thực của tham số
m
để đồ thị hàm số
7
1
mx
y
mx
+
=
−
có tiệm cận đứng đi qua điểm
( )
1; 2A −
.
Câu 2. Tìm các giá trị thực của tham số
m
để đồ thị hàm số
( )
2
2x
fx
x xm
−
=
++
có ba đường tiệm cận.
Câu 3. Tìm tham số m để đồ thì hàm số
( 1) 5
2
m xm
y
xm
+−
=
−
có tiệm cận ngang là đường thẳng
1
y =
.
Câu 4. Tìm các tham số
m
để đồ thị hàm số
2
1
4
x
y
x mx
−
=
++
có đúng hai đường tiệm cận?
Câu 5. Cho hàm số
2
1
mx m
y
x
+
=
−
. Với giá trị nào của
m
thì đường tiệm cận đứng, tiệm cận ngang của đồ thị
hàm số cùng với hai trục tọa độ tạo thành một hình chữ nhật có diện tích là 8?
Câu 6. Biết đồ thị
( )
C
của hàm số
ax b
y
cx d
+
=
+
đi qua điểm
( )
1; 7A
−
và giao điểm hai tiệm cận của
(
)
C
là
điểm
(
)
2;3I −
. Biết
c
là số nguyên dương và
a, c
là các số nguyên tố cùng nhau. Tìm các số
,,,abcd
.
Câu 7. Cho hàm số
2
34
xm
y
xx
−
=
+−
. Giá trị nào của
m
để đồ thị hàm số đã cho có đúng 1 tiệm cận đứng?
Câu 8. Cho hàm số
2xm
y
xm
+
=
−
. Tìm tất cả các giá trị của
m
để đồ thị hàm số có 2 đường tiệm cận cùng
với hai trục tọa độ tạo thành một hình vuông
Lời giải
Ta có đường tiệm cận ngang của đồ thị hàm số là
2y =
Với
2. 1. 0 0mm m− ≠⇔ ≠
thì đường tiệm cận đứng của đồ thị hàm số là
xm=
Để 2 đường tiệm cận cùng với 2 trục tọa độ tạo thành một hình vuông thì
22mm=⇔=±
Câu 9. Cho hàm số
2
1
24
x
y
x mx
−
=
−+
. Tìm tất cả các giá trị thực của tham số
m
để đồ thị hàm số có đúng
ba đường tiệm cận.
Câu 10. Biết rằng đồ thị hàm số
1
2
ax
y
bx
có tiệm cận đứng là
2
x
và tiệm cận ngang là
3y
. Tìm
,ab
.
Câu 11. Tính tổng bình phương tất cả các giá trị của
m
để đồ thị hàm số
2
2 35 6y x x mx= − ++ −
có
tiệm cận ngang.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 1
BÀI 4. ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
1. Nhánh vô cực của đường cong
( ) ( )
:C y fx=
Gọi
( ) ( )
;M xy C∈
.
Ta nói:
( )
C
có nhánh vô cực
⇔
x hay x
y hay y
→ +∞ → −∞
→ +∞ → −∞
VD1: Đồ thị
( )
C
của hàm số
2
yx=
có nhánh vô cực
VD2: Đồ thị
( )
C
của hàm số
2
4yx
= −
không có nhánh vô cực
vì
( ) ( )
;
M xy C∈
22x−≤ ≤
và
02y≤≤
.
2) Tiệm cận của đường cong
Cho đường cong
( ) ( )
:C y fx=
và
( ) ( )
;M xy C∈
,
H
là hình chiếu vuông góc của
M
lên
( )
∆
.
Đường thẳng
(
)
∆
được gọi là tiệm cận của
( )
C
khi và chỉ khi khoảng cách
MH
từ
M
đến
( )
∆
tiến về 0 khi
M
vẽ nên nhánh vô cực của
( )
C
.
Như vậy:
( )
∆
tiệm cận của
()C
lim 0
M
MH
→∞
⇔=
CHƯƠNG
I
ỨNG DỤNG ĐẠO HÀM
ĐỂ KHẢO SÁT HÀM SỐ
LÝ THUY
Ế
T.
I
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 2
3) Định nghĩa đường TCĐ và TCN của đồ thị hàm số
a) Tiệm cận đứng của đồ thị hàm số
Đường thẳng
0
xx=
được gọi là đường tiệm cận đúng
(TCĐ) của đồ thị hàm số
( )
y fx
=
nếu thỏa mãn ít nhất
một trong các điều kiện sau:
0
lim ( )
xx
fx
+
→
= +∞
;
0
lim ( )
xx
fx
+
→
= −∞
0
lim ( )
xx
fx
−
→
= +∞
;
0
lim ( )
xx
fx
−
→
= −∞
b) Tiệm cận ngang của đồ thị hàm số
Cho hàm số
( )
y fx=
có xác định trên một khoảng vô hạn
là khoảng có một trong các dạng
(, )a
+∞
;
( ,)a−∞
;
(,)−∞ +∞
.Đường thẳng
0
yy=
được gọi là đường TCN (hay TCN)
của đồ thị nếu thỏa mãn ít nhất một trong các điều kiện sau:
0
lim ( )
x
fx y
→−∞
=
;
0
lim ( )
x
fx y
→+∞
=
Lưu ý:
i) Hàm
ax b
y
cx d
+
=
+
với
0ac ≠
có tiệm cận đứng
d
x
c
= −
; tiệm cận ngang
a
y
c
=
.
ii) Hàm
( )
( )
fx
y
gx
=
với
( ) ( )
,f x gx
là những hàm đa thức
+) Nếu bậc tử nhỏ hơn bậc mẫu thì có tiệm cận ngang
0y =
.
+) Nếu bậc tử bằng bậc mẫu thì có tiệm cận ngang
n
n
a
y
b
=
với
,
nn
ab
là hệ số của lũy thừa
cao nhất trên tử và dưới mẫu.
+) Nếu bậc tử lớn hơn bậc mẫu thì không có tiệm cận ngang.
+)
0
xx=
là tiệm cận đứng
(
)
( )
( )
( )
(
)
( )
0
00
00
0; 0
0
lim
xx
gx f x
gx f x
fx
gx
→
= ≠
= =
⇔
= ±∞
.
iii) Ứng dụng máy tính CASIO để tìm tiệm cận đứng hoặc tiệm cận ngang
Để tìm tiệm cận đứng hoặc tiệm cận ngang của một hàm số thông qua máy tính CASIO, ta sử
dụng phím CALC trên máy.
Một số lưu ý về kết quả và cách bấm:
Giới hạn
Thao tác trên máy
tính
o
xx
+
→
CALC
10
10
o
x
−
+
o
xx
−
→
CALC
10
10
o
x
−
−
x → +∞
CALC
10
10
x → −∞
CALC
10
10−
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 3
DẠNG 1: TÌM TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ CHO BỞI CÔNG THỨC
Câu 1. Cho hàm số
23
()
2
x
y fx
x
−
= =
+
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm
số
()y fx=
.
Lời giải
Vì
lim 2; lim 2
xx
yy
→−∞ →+∞
= =
nên đồ thị hàm số có 1 tiệm cận ngang là
2y =
.
Vì
22
lim ; lim
xx
yy
+−
→− →−
= −∞ = +∞
nên đồ thị hàm số có 1 tiệm cận đứng
2x = −
.
Do đó đồ thị hàm số có tổng số 2 tiệm cận kể cả đứng và ngang.
Câu 2. Cho hàm số
2020 2021
()
1
x
y fx
x
−
= =
−
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ
thị hàm số
()y fx=
.
Câu 3. Cho hàm số
25
()
2
x
y fx
x
−
= =
−
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm
số
()y fx=
.
Câu 4. Cho hàm số
2
23
()
1
xx
y fx
x
++
= =
+
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ
thị hàm số
()y fx=
.
Câu 5. Cho hàm số
2
6
()
1
xx
y fx
x
−−
= =
−
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị
hàm số
()
y fx=
.
Câu 6. Cho hàm số
2
32
()
1
x
y fx
x
+−
= =
−
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị
hàm số
()
y fx=
.
Câu 7. Cho hàm số
2
2
6
()
32
xx
y fx
xx
−−
= =
++
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị
hàm số
()y fx=
.
Câu 8. Cho hàm số
2
2 33
()
24
xx x
y fx
x
+ +−
= =
−
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của
đồ thị hàm số
()y fx=
.
Câu 9. Cho hàm số
2
5 32
()
2
xx x
y fx
x
− ++
= =
−
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của
đồ thị hàm số
()y fx
=
.
HỆ THỐNG BÀI TẬP TỰ LUẬN.
II
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 4
DẠNG 2: TÌM TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ BIẾT BBT CỦA HÀM SỐ, ĐỒ THỊ CỦA HÀM
SỐ ĐÓ HOẶC HÀM SỐ LIÊN QUAN
Câu 1. Cho hàm số
()y fx=
có bảng biến thiên
Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
()y fx=
.
Lời giải
Vì
lim ; lim 3
xx
yy
→−∞ →+∞
= −∞ =
nên đồ thị hàm số có 1 tiệm cận ngang là
3y =
.
Vì
4
lim
xx
y
+
→
= +∞
nên đồ thị hàm số có 1 tiệm cận đứng
4
xx=
.
Do đó đồ thị hàm số có tổng số 2 tiệm cận kể cả đứng và ngang.
Câu 2. Cho hàm số
()fx
có bảng biến thiên
Tìm số tiệm cận của đồ thị hàm số
1
()
y
fx
=
?
Lời giải
Vì
1
lim 0; lim
3
xx
yy
→−∞ →+∞
= =
nên đồ thị hàm số có 1 tiệm cận ngang
0y
=
và
1
3
y =
.
Từ bảng biến thiên, ta có
(x) 0f =
có hai nghiệm
2
xx=
và
( )
1
;xa x= ∈ −∞
.
Dễ thấy
lim
xa
y
+
→
= +∞
và
2
lim
xx
y
+
→
= +∞
nên đồ thị hàm số có 2 tiệm cận đứng là
2
xx=
và
xa=
Do đó đồ thị hàm số có tổng số 4 đường tiệm cận kể cả đứng và ngang.
Câu 3. Cho hàm số
(
)
y fx=
xác định, liên tục trên
{ }
\1
và có bảng biến thiên như sau:
Tìm phương trình đường tiệm cận ngang của đồ thị hàm số đã cho?
Lời giải
Tập xác định:
{ }
\1D =
.
Ta có
( ) ( )
lim 2; lim 2
xx
fx fx
→−∞ →+∞
= =
. Do đó
2y =
là đường tiệm cận ngang của đồ thị hàm số.
Câu 4. Cho hàm số
()y fx=
xác định trên
{ }
\0
, liên tục trên mỗi khoảng xác định và có bảng biến thiên
như sau:
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 5
Hỏi đồ thị hàm số trên có bao nhiêu đường tiệm cận đứng và ngang?
Lời giải
Tập xác định:
{ }
\0
D =
.
Ta có
( )
lim
x
fx
→−∞
= +∞
;
( )
lim
x
fx
→+∞
= −∞
do đó đồ thị hàm số không có tiệm cận ngang.
( )
0
lim 0
x
fx x
+
→
= −∞ ⇒ =
là đường tiệm cận đứng duy nhất của đồ thị hàm số.
Câu 5. Cho hàm số
()y fx=
xác định trên
{ }
\1
, liên tục trên mỗi khoảng xác định và có bảng biến thiên
như sau:
Tìm các giá trị nguyên của
[
)
0;5m ∈
để đồ thị hàm số
(
)
y fx=
có 3 đường tiệm cận đứng và
ngang?
Lời giải
Tập xác định
{ }
\1D =
. Ta có
( )
lim 2 2
x
fx y
→−∞
=⇒=
là đường tiệm cận ngang.
( )
1
lim 1
x
fx x
−
→
= −∞ ⇒ =
là tiệm cận đứng.
( )
lim
x
fx m y m
→+∞
=⇒=
là đường tiệm cận ngang.
Do đó, để đồ thị hàm số có 3 đường tiệm cận thì
2m ≠
, mà
[
)
0;5m∈
nên
{ }
0;1; 3; 4m ∈
.
Câu 6. Cho hàm số
()fx
có đồ thị như hình vẽ bên.
Tìm phương trình các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số trên.
Lời giải
Nhìn vào đồ thị, ta có:
( )
2
lim
x
fx
−
→
= −∞
và
( )
2
lim
x
fx
+
→
= +∞
. Do đó, đồ thị có một tiệm cận đứng
là đường thẳng
2.x =
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 6
Theo đồ thị, ta cũng có:
( )
lim 1
x
fx
→−∞
=
và
(
)
lim 1
x
fx
→+∞
=
. Do đó, đồ thị có tiệm cận ngang là
đường thẳng
1y =
.
Vậy đồ thị có tiệm cận đứng
2x
=
tiệm cận ngang
1y =
.
Câu 7. Cho đồ thị hàm số
( )
y fx=
như hình bên. Đồ thị có bao nhiêu đường tiệm cận đứng và tiệm cận
ngang?
Lời giải
Nhìn vào đồ thị, ta có:
( )
1
lim
x
fx
−
→−
= +∞
và
( )
1
lim
x
fx
+
→−
= −∞
. Do đó, đồ thị có một tiệm cận
đứng là đường thẳng
1
x = −
.
Theo đồ thị, ta cũng có:
( )
lim 2
x
fx
→−∞
=
và
( )
lim 2
x
fx
→+∞
=
. Do đó, đồ thị có tiệm cận ngang là
đường thẳng
2y =
.
Vậy đồ thị 2 đường tiệm cận là: tiệm cận đứng
1
x
= −
và tiệm cận ngang
2y =
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 7
DẠNG 3: TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ HÀM HỢP
Các dạng trong chủ đề: Cho hàm số
( )
y fx
=
biết bảng biến thiên hoặc đồ thị. Tìm các đường
tiệm cận đứng và tiệm cận ngang của đồ thị
( )
y gx=
thuộc một trong các dạng sau
1)
( )
()
y f ux=
,
2)
( )
()y g fx=
,
3)
( )
(u( ))y gf x=
,
4)
( )
, ()y gxfx=
,
5)
( )
, (u(x))y gxf=
.
Phương pháp giải: Gọi
( )
G
là đồ thị hàm số
( )
y gx=
.
1)Tìm tiệm cận ngang.
Xét hàm số dạng
( )
()
()
ux
gx
vx
=
.Một dấu hiệu thường dùng để nhận biết
( )
G
có tiệm cận ngang:
+ Hàm số
( )
y gx=
xác định trên
( )
;a +∞
hoặc trên
( )
;a−∞
.
+ Bậc của
(x)
u
≤
Bậc của
(x)v
.
+
0
lim ( )
x
gx y
→+∞
=
hoặc
0
lim ( )
x
gx y
→−∞
=
⇒
Đường thẳng
0
yy
=
là tiệm cận ngang của
( )
G
.
2)Tìm tiệm cận đứng.
Xét dạng hàm số
( )
()
()
ux
gx
vx
=
. Một dấu hiệu thường dùng để nhận biết đường thẳng
0
xx=
là
tiệm cận đứng của
( )
G
:
+
0
()0vx =
và
0
()0ux ≠
,
( )
gx
xác định trên
( )
0
;ax
hoặc
( )
0
;xb
.
+ Ít nhất một trong hai giới hạn
( ) ( )
00
lim , lim
xx xx
gx gx
+−
→→
là giới hạn vô cực.
⇒
Đường thẳng
0
xx=
là tiệm cận đứng của
( )
G
.
Trong chủ đề này, các dấu hiệu nhận biết ở trên dựa vào bảng biến thiên hoặc đồ thị của hàm số
( )
y fx=
.
Câu 1. Cho hàm số
( )
y fx=
có bảng biến thiên như hình dưới đây
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
( )
1
21
y
fx
=
−
.
Lời giải
Dựa vào bảng biến thiên ta có:
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 8
Phương trình
( )
2 10fx−=
(
)
1
2
1
;
2
1
2
1
;
2
xx
fx
xx

= ∈ −∞ −


⇔=⇔

= ∈ − +∞


.
Do
(
)
11
1
lim lim
21
xx xx
y
fx
++
→→
= = −∞
−
và
(
)
11
1
lim lim
21
xx xx
y
fx
−−
→→
= = +∞
−
nên
1
xx
=
là một tiệm cận đứng
của đồ thị hàm số
( )
1
21
y
fx
=
−
.
Do
( )
22
1
lim lim
21
xx xx
y
fx
++
→→
= = +∞
−
và
( )
22
1
lim lim
21
xx xx
y
fx
−−
→→
= = −∞
−
nên
2
xx
=
là một tiệm cận
đứng của đồ thị hàm số
( )
1
21
y
fx
=
−
.
Do
(
)
1
lim lim 1
21
xx
y
fx
→+∞ →+∞
= =
−
và
( )
1
lim lim 1
21
xx
y
fx
→−∞ →−∞
= =
−
nên
1y =
là một tiệm cận ngang của
đồ thị hàm số
( )
1
21
y
fx
=
−
.
Vậy đồ thị hàm số
( )
1
21
y
fx
=
−
có
2
đường tiệm cận đứng là
1
xx=
;
2
xx=
và
1
tiệm cận ngang
là
1y
=
.
Câu 2. Cho hàm số
( )
y fx=
liên tục trên
\1
và có bảng biến thiên như sau
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
( )
1
()
23
y gx
fx
= =
−
Lời giải
Dựa vào bảng biến thiên ta có:
Phương trình
( )
2 30fx−=
( )
( )
( )
1
2
1; 2
3
2;
2
xx
fx
xx
= ∈
⇔=⇔
= ∈ +∞
.
( )
11
1
lim ( ) lim
23
xx xx
gx
fx
++
→→
= = +∞
−
,
( )
11
1
lim ( ) lim
23
xx xx
gx
fx
−−
→→
= = −∞ ⇒
−
Đường thẳng
1
xx=
là một
tiệm cận đứng của đồ thị hàm số
( )
1
23
y
fx
=
−
.
( )
22
1
lim ( ) lim
23
xx xx
gx
fx
++
→→
= = −∞
−
,
( )
22
1
lim ( ) lim
23
xx xx
gx
fx
−−
→→
= = +∞ ⇒
−
Đường thẳng
2
xx=
là một
tiệm cận đứng của đồ thị hàm số
( )
1
23
y
fx
=
−
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 9
( )
1
lim ( ) lim 0
23
xx
gx
fx
→+∞ →+∞
= =
−
,
( )
1
lim ( ) lim 0
23
xx
gx
fx
→−∞ →−∞
= = ⇒
−
Đường thẳng
0
y =
là tiệm cận
ngang của đồ thị hàm số
( )
1
23
y
fx
=
−
.
Vậy đồ thị hàm số
( )
1
23
y
fx
=
−
có
2
đường tiệm cận đứng là
1
xx=
;
2
xx=
và
1
tiệm cận ngang
là
0
y =
.
Câu 3. Cho hàm số
( ) ( )
32
,,,f x ax bx cx d a b c d R= + ++ ∈
có đồ thị như hình vẽ.
Đồ thị hàm số
( )
( )
( )
( )
( )
22
2
43
2
++ +
=
−
x x xx
gx
fx fx
có bao nhiêu đường tiệm cận đứng?
Lời giải
Điều kiện
1
0
() 0
() 2
x
x
fx
fx
≤−
≥
≠
≠
Ta có
( )
(
)
( )
( )
( )
( )( )
( )
( )
( )
22
22
43
1 3 ( 1)
22
x x xx
x x xx
gx
fx fx fx fx
++ +
++ +
= =
−−
,
Xét phương trình
( )
( )
( )
( )
( )
2
0
20
2
fx
fx fx
fx
=
−=⇔
=
.
Với
( )
( )
1
3
0
1; 0 ( )
x
fx
xx l
= −
= ⇔
= ∈−
trong đó
3x = −
là nghiệm nghiệm kép, nên mẫu sẽ có nhân
tử
( )
2
3x +
do đó
3x = −
là một tiệm cận đứng.
Với
( ) ( )
( )
2
3
1
2 3; 1
;3
x
fx x x
xx
= −
= ⇔ = ∈− −
= ∈ −∞ −
, ba nghiệm này là nghiệm đơn, nên
( ) ( )( )( )
23
21fx kx xx xx−= + − −
, ta thấy trong
( )
gx
thì
( )
1x +
sẽ bị rút gọn nên có thêm
( )
2
3; 1xx= ∈− −
và
( )
3
;3xx= ∈ −∞ −
là tiệm cận đứng.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 10
Vậy tóm lại đồ thị có 3 tiệm cận đứng là
23
3; ;x xxxx=−= =
.
Câu 4. Cho đồ thị hàm đa thức bậc bốn
()
y fx
=
như hình vẽ bên dưới .
Hỏi đồ thị của hàm số
( )


62 2
2
(x +1)(x - 5x). x -2x
g(x) =
f (x)-2f(x) 2x -10
có bao nhiêu đường tiệm cận đứng và tiệm
cận ngang.
Lời giải
Điều kiện:
0
2
x
x
≤
≥
.
Giả sử
43 2
(x) ax
f bx cx dx e= + + ++
Vì
22
11
lim (x) ; lim (x)
22
xx
gg
aa
→−∞ →+∞
−
= =
nên đồ thị hàm số g(x) có 2 tiệm cận ngang
2
1
2
y
a
= ±
Dễ thấy
2
[ (x) 2 (x)](2 x 10) 0 ( )[ ( ) 2].2.( 5) 0f f fxfx x− − =⇔ − −=
có các nghiệm
12
0; 1; 2; x 5; ( 1;0); (2;3)x x x xx xx= = = = = ∈− = ∈
So sánh với điều kiện của căn và bội của nghiệm ta thấy đồ thị g(x) có các đường tiệm cận đứng là:
12
0; 2; ;x x xxxx= = = =
Vậy đồ thị hàm số g(x) có
6
đường tiệm cận kể cả ngang và đứng
Câu 5. Cho hàm số
( )
32
f x ax bx cx d= + ++
là hàm số đa thức với hệ số thực, có đồ thị
()C
như hình vẽ
bên.
Tìm số tiệm cận đứng của đồ thị hàm số
( )
( )
( ) ( ) ( )
2
2
32 1
1
xx x
gx
x f x fx
−+ −
=

+−

.
Lời giải
Điều kiện:
1
x
≥
( ) ( ) ( )
( ) ( )
( )
( )
( )
2
2
1
1
10 0
0
1
x loai
x
x f x fx fx
f x fx
fx
= −
= −

+ −=⇔ ⇔=

−=
=
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 11
Dựa vào đồ thị ta ta có
( )
(
)
1 12
2
1
( ) 1 1;2 ( ) 1 ( 1)( )( )
2;
x
fx x x fx ax x x x x
xx
=
=⇔ = ∈ ⇒ −= − − −
= ∈ +∞
.
( )
3
0;1
() 0
2
xx
fx
x
= ∈
= ⇔
=
và
2
3
( ) ( )( 2)f x ax x x=−−
.
Hàm số có tập xác định
( ) { }
12
1; \ ; ; 2
= +∞D xx
.
( )
( )( )
( )
2
12 3
12 1
1 ( 1)( )( ) ( )( 2)
xx x
gx
x ax xxxxaxx x
−− −
= =
+ −− − − −
( )
2
123
1
1 ( )( )( )( 2)
x
ax xxxx xx x
−
+− − − −
Tại các điểm
12
, 2, xxx xx= = =
mẫu của
( )
gx
nhận giá trị bằng
0
còn tử nhận các giá trị
dương. Và do hàm số xác định trên mỗi khoảng
( ) ( ) ( )
( )
11 2 2
1; , ;2 , 2; , ;+∞xx x x
nên giới hạn
một bên của hàm số
( )
y gx=
tại các điểm
12
, 2, xxx xx= = =
là các giới hạn vô cực.
Do đó, đồ thị hàm số
( )
y gx=
có 3 tiệm cận đứng, đó là các đường thẳng
12
, 2, xxx xx= = =
.
Vậy đồ thị hàm số
( )
y gx=
có 3 đường tiệm cận đứng.
Câu 6. Cho hàm số bậc ba
()y fx=
có đồ thị như hình vẽ bên.
Tìm số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
2
2
( 1)( 1)
()
() 2 ()
xx
y gx
f x fx
+−
= =
−
.
Lời giải
Ta có:
2
( ) 0 (1)
() 2 () 0 .
( ) 2 (2)
fx
f x fx
fx
=
−=⇔
=
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 12
Dựa vào đồ thị hàm số,ta thấy:
(1)
có nghiệm
1
1xa= <−
(nghiệm đơn) và
2
1
x
=
(nghiệm kép)
( )
2
( ) ( )( 1) 0⇒ =−− ≠f x kx a x k
(2)
có nghiệm ba nghiệm đơn
123
, ,
xxx
với
1 23
1 01xb x xc= <− < = < < =
(
)
() 2 ( )( ) 0.
⇒ −= − − ≠f x kx bxx c k
⇒
Hàm số
()y gx=
có tập xác định
{ }
\ ; ; 0;1;D ab c=
+) Tìm tiệm cận ngang:
Vì
[ ]
22
222
( 1)( 1) ( 1) ( 1)
( 1)( ) ( )
( 1)
()
() 2 () () () ()
2
+− +− +
−− − −
= = =
−−
xx xx
gx
f x fx f
x
x x bxx c
xk xf
ax
nên
( )
lim 0,
x
gx
→+∞
=
( )
lim 0
x
gx
→−∞
=
⇒
Đồ thị hàm số
()y gx=
nhận đường thẳng
0y
=
làm tiệm cận ngang.
+) Tìm tiệm cận đứng:
Tại các điểm
, , 0, 1, x ax bx x x c= = = = =
mẫu của
( )
gx
nhận giá trị bằng
0
còn tử nhận các
giá trị dương. Và do hàm số xác định trên
{
}
\ ; ; 0;1;D ab c=
nên giới hạn một bên của hàm số
( )
y gx=
tại các điểm
, , 0, 1, x ax bx x x c= = = = =
là các giới hạn vô cực. Do đó, đồ thị hàm số
( )
y gx
=
có 5 tiệm cận đứng, đó là các đường thẳng
, , 0, 1, x ax bx x x c
= = = = =
. Vậy đồ thị
hàm số
( )
y gx=
có 6 đường tiệm cận: 1 tiệm cận ngang
0y =
và 5 tiệm cận đứng
, , 0, 1, x ax bx x x c= = = = =
.
Câu 7. Cho hàm số
( )
32
y f x ax bx cx d= = + ++
,
( )
0
a ≠
có đồ thị như hình dưới đây
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
( )
( )
( )
( )
( )
( )
2
2
2
23xx x
y gx
x x fx fx
+−
= =

−+

.
Lời giải
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 13
Trước hết, ta cần tìm
0x ≥
để
(
)
( )
(
)
( )
2
2
0x x fx fx

− +=

.
Ta có:
(
)
(
)
( )
( )
( )
( )
2
2
0
1
0
0
1
x
x
x x fx fx
fx
fx
=
=

− +=⇔

=
= −
Từ đồ thị hàm số
( )
y fx=
ta thấy
( )
( )
2; 1
0
2
x
fx
x
α
= ∈− −
•=⇔
=
và
( ) ( )( )
2
2f x ax x
α
=−−
.
(
) ( )
( )
1
1 0; 2
2;
x
fx x
x
β
γ
= −
• =−⇔ = ∈
= ∈ +∞
⇒
( ) ( )( )( )
11f x ax x x
βγ
+= + − −
.
Vậy hàm số
( )
y gx=
có tập xác định là
( ) { }
0; \ ;1; 2; .D
βγ
= +∞
Khi đó ta có
( )
( )( )
( ) ( ) ( )
( )( ) ( )( )( )
2
13
3
11
21
xx x
x
y gx
xx fx fx
xax x ax x x
α βγ
−+
+
= = =
−+

− − +− −

( )( ) ( )( )(
)
2
2
3
12
x
a xx x x x x
αβγ
+
=
+− − − −
+) Tìm tiệm cận ngang: Ta có
( )
lim 0
x
gx
→+∞
=
(do bậc của tử nhỏ hơn bậc của mẫu)
0y⇒=
là
tiệm cận ngang của đồ thị hàm số
( )
y gx=
.
+) Tìm tiệm cận đứng:
( )
( )( )
( )( )( )
2
2
3
12
x
gx
a xx x x x x
αβγ
+
=
+− − − −
Mẫu thức của
( )
gx
có 6 nghiệm phân biệt là
; 1; 0; ; 2;
α βγ
−
.
* Tại
( )
2; 1x
α
= ∈− −
và
1x = −
các giới hạn một bên của
( )
gx
không tồn tại nên
;1xx
α
= = −
không phải tiệm cận đứng của đồ thị hàm số
( )
y gx=
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 14
* Tại
0x
=
ta có
(
)
(
)
(
) (
)(
)
( )
2
2
00
3
lim lim
12
xx
x
gx
a xx x x x x
αβγ
++
→→
+
= = +∞
+− − − −
nên
0x =
là
một tiệm cận đứng của đồ thị hàm số
( )
y gx=
.
* Tại
;2
xx
β
= =
và
x
γ
=
các giới hạn một bên của
( )
gx
đều là giới hạn vô cực (vì mẫu thức
bằng 0 còn tử thức khác 0 tại các điểm đó) nên
;2
xx
β
= =
và
x
γ
=
là các tiệm cận đứng của
đồ thị hàm số
( )
y gx
=
.
Vậy đồ thị hàm số
( )
y gx=
có
1
đường tiệm cận ngang là
0y =
và
4
đường tiệm cận đứng là
0; ; 2
xx x
β
= = =
và
x
γ
=
.
Câu 8. Cho hàm số bậc ba
()y fx=
có đồ thị như hình vẽ bên.
Tìm số đường tiệm cận đứng của đồ thị hàm số
2
()
() 1
x
y gx
fx
+
= =
+
.
Lời giải
Từ đồ thị ta thấy
( )
( )
(
)
2; 1
( ) 1 1; 0
1; 2
xa
fx x b
xc
= ∈− −
=−⇔ = ∈−
= ∈
lim (x)
xa
g
−
→
= +∞
nên
xa
=
là một tiệm cận đứng của đồ thị hàm số
()y gx=
.
lim (x)
xb
g
−
→
= −∞
nên
xb=
là một tiệm cận đứng của đồ thị hàm số
()y gx=
.
lim (x)
xc
g
−
→
= +∞
nên
xc=
là một tiệm cận đứng của đồ thị hàm số
()y gx=
.
Vậy đồ thị hàm số
()y gx=
có 3 tiệm cận đứng.
Câu 9. Cho hàm số
( )
y fx=
liên tục trên
\1
và có bảng biến thiên như sau
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 15
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
( )
( )
2
22y gx f x x= = −−
.
Lời giải
Ta có
2
1
2 21
3
x
xx
x
≠−
− −≠⇔
≠
. Vậy hàm số
( )
y gx=
có tập xác định là
{ }
\ 1; 3 .
D
= −
Dựa vào bảng biến thiên của hàm số
( )
y fx
=
ta có:
Do
( )
(
)
2
( 1) ( 1)
lim lim 2 2
xx
gx f x x
++
→− →−
= − − = +∞
và
(
)
( )
2
( 1) ( 1)
lim lim 2 2
xx
gx f x x
−−
→− →−
= − − = −∞
nên
1x
= −
là một tiệm cận đứng của đồ thị hàm số
( )
y gx=
.
Do
(
)
( )
2
33
lim lim 2 2
xx
gx f x x
++
→→
= − − = −∞
và
( )
(
)
2
33
lim lim 2 2
xx
gx f x x
−−
→→
= − − = +∞
nên
3x =
là một
tiệm cận đứng của đồ thị hàm số
( )
y gx=
.
Do
( )
( )
2
lim lim 2 2
xx
gx f x x
→+∞ →+∞
= − − = −∞
và
( )
( )
2
lim lim 2 2
xx
gx f x x
→−∞ →−∞
= − − = −∞
nên đồ thị hàm
số
( )
y gx=
không có tiệm cận ngang.
Vậy đồ thị hàm số
( )
( )
2
22
y gx f x x= = −−
có
2
đường tiệm cận đứng là
1x = −
;
3x =
và
không có tiệm cận ngang.
Câu 10. Cho hàm số
( )
y fx=
liên tục trên
và có đồ thị như hình
dưới đây
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
( )
2
1
x
y gx f
x
−

= =

+

Lời giải
Hàm số
( )
y gx=
có tập xác định là
{ }
\ 1.D = −
Dựa vào đồ thị của hàm số
( )
y fx=
ta có:
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 16
Do
(
)
( 1) ( 1)
2
lim lim
1
xx
x
gx f
x
++
→− →−
−

= = −∞

+

và
(
)
( 1) ( 1)
2
lim lim
1
xx
x
gx f
x
−−
→− →−
−

= = +∞

+

nên
1x = −
là một
tiệm cận đứng của đồ thị hàm số
( )
y gx=
.
Do
( )
2
lim lim 4
1
xx
x
gx f
x
→+∞ →+∞
−

= =

+

và
(
)
2
lim lim 4
1
xx
x
gx f
x
→−∞ →−∞
−

= =

+

nên
4y =
là một tiệm cận
ngang của đồ thị hàm số
( )
y gx=
.
Vậy đồ thị hàm số
( )
2
1
x
y gx f
x
−

= =

+

có
1
đường tiệm cận đứng là
1x = −
và có
1
tiệm cận
ngang là
4y =
.
Câu 11. Cho hàm số
( )
y fx=
là hàm đa thức liên tục trên
và có đồ thị như hình dưới đây
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
( )
( )
( )
1
fx
y gx
fx
= =
−
.
Lời giải
ĐKXĐ:
(
)
(
)
0
.
1
fx
fx
≥
≠
( )
41
0
2
x
fx
x
− ≤ ≤−
• ≥⇔
≥
( )
( )
( )
( )
4; 3
1 3; 1
2;
xa
fx x b
xc
≠ ∈− −
• ≠ ⇔ ≠ ∈− −
≠ ∈ +∞
.
Hàm số
( )
y gx=
có tập xác định là
[
) ( ) (
] [
) ( )
4; ; ; 1 2; ; .D a ab b c c= − ∪ ∪ − ∪ ∪ +∞
+) Tìm tiệm cận ngang: Ta có
( )
lim 0
x
gx
→+∞
=
(do bậc của tử nhỏ hơn bậc của mẫu)
0y⇒=
là
tiệm cận ngang của đồ thị hàm số
( )
y gx=
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 17
+) Tìm tiệm cận đứng:
Mẫu thức của
(
)
gx
có 3 nghiệm phân biệt là
;;abc
, và tại các điểm này các giới hạn một bên
của
( )
gx
đều là giới hạn vô cực (vì mẫu thức bằng 0 còn tử thức khác 0 tại các điểm đó) nên
;;x ax bx c= = =
là các tiệm cận đứng của đồ thị hàm số
( )
y gx=
.
Vậy đồ thị hàm số
( )
y gx=
có
1
đường tiệm cận ngang là
0y =
và
3
đường tiệm cận đứng là
;;x ax bx c= = =
.
Câu 12. Cho hàm số
( )
y fx=
xác định, liên tục trên
và có bảng biến thiên như sau :
Tìm số tiệm cận ngang và số tiệm cận đứng của đồ thị hàm số
(
)
( )
3
3
11
=
++ −
gx
fx x
.
Lời giải
Từ bảng biến thiên ta thấy
( ) ( )
3
33
3
11
1 10 1 1
1 , 1
xx
fx x fx x
x x aa
++=
++ −=⇔ ++ =⇔
+ + = <−
.
3
0
1 , 1 (2)
x
x x aa
=
⇔
+ + = <−
Lập bảng biến thiên của hàm số
3
() 1hx x x= ++
ta thấy với
1a <−
thì phương trình
3
1xx a+ +=
có nghiệm duy nhất
0
1x <−
Suy ra hàm số
( )
y gx
=
có tập xác định là
{ }
00
\ 0; , 1D xx= <−
.
+) Tìm tiệm cận ngang:
Đặt
3
1tx x= ++
. Khi
x → +∞
thì
t → +∞
và khi
x → −∞
thì
t → −∞
.
Do đó,
( )
( )
( )
3
3
3
lim 1 lim lim ( ) lim 0.
11
x t xx
f x x f t gx
fx x
→+∞ →+∞ →+∞ →+∞
+ + = = −∞ ⇒ = =
++ −
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 18
( )
(
)
(
)
3
3
3
lim 1 lim lim ( ) lim 0.
11
x t xx
f x x f t gx
fx x
→−∞ →−∞ →−∞ →−∞
+ + = = +∞ ⇒ = =
++ −
Suy ra đồ thị hàm số
( )
y gx=
có 1 tiệm cận ngang đó là đường thẳng
0y =
.
+) Tìm tiệm cận đứng:
(
)
(
)
3
3
11
gx
fx x
=
++ −
Tại xác điểm
0
0, x xx= =
mẫu của
( )
gx
nhận giá trị bằng
0
còn tử luôn nhận giá trị bằng 3.
Và do hàm số xác định trên mỗi khoảng
( ) ( ) ( )
00
; , ;0 , 0;xx−∞ +∞
nên giới hạn một bên của
hàm số
( )
y gx=
tại các điểm
0
0,
x xx= =
là các giới hạn vô cực.
Do đó, đồ thị hàm số
( )
y gx
=
có hai tiệm cận đứng, đó là các đường thẳng
0
0, x xx
= =
Vậy đồ thị hàm số
( )
y gx=
có 3 đường tiệm cận: 1 tiệm cận ngang
0y =
và 2 tiệm cận đứng
0
0, x xx
= =
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 19
DẠNG 3: MỘT SỐ BÀI TOÁN VỀ TIỆM CẬN CHỨA THAM SỐ
Câu 1. Tìm các giá trị thực của tham số
m
để đồ thị hàm số
7
1
mx
y
mx
+
=
−
có tiệm cận đứng đi qua điểm
( )
1; 2A −
.
Lời giải
Để đường tiệm cận đứng đi qua
( )
1; 2A −
thì đường tiệm cận đứng phải có phương trình
1x =
.
Khi đó
1x
=
là nghiệm của
10mx −=
. Suy ra
1m =
.
Thử lại: với
1m =
thì đồ thị hàm số
7
1
x
y
x
+
=
−
có đường tiệm cận đứng
1x =
đi qua
( )
1; 2A
−
.
Vậy
1m =
là giá trị cần tìm.
Câu 2. Tìm các giá trị thực của tham số
m
để đồ thị hàm số
( )
2
2x
fx
x xm
−
=
++
có ba đường tiệm cận.
Lời giải
Ta thấy
( )
lim 0
x
fx
→±∞
=
nên đồ thị hàm số có một tiệm cận ngang
0y
=
.
Đồ thị hàm số
( )
2
2x
fx
x xm
−
=
++
có ba đường tiệm cận
2
0x xm⇔ ++ =
có 2 nghiệm phân biệt
khác 2
2
14 0
22 0
m
m
−>
⇔
++ ≠
1
4
6
m
m
<
⇔
≠−
.
Câu 3. Tìm tham số m để đồ thì hàm số
( 1) 5
2
m xm
y
xm
+−
=
−
có tiệm cận ngang là đường thẳng
1y
=
.
Lời giải
Ta có:
Tiệm cận ngang của hàm số
( 1) 5
2
m xm
y
xm
+−
=
−
là:
y =
( 1) 5 1
lim 1
22
x
m x mm
xm
→±∞
+− +
= =
−
⇔
1m =
.
Vậy
1m =
.
Câu 4. Tìm các tham số
m
để đồ thị hàm số
2
1
4
x
y
x mx
−
=
++
có đúng hai đường tiệm cận?
Lời giải
Ta có
2
2
11
lim lim 0
4
1
xx
xx
y
m
xx
→±∞ →±∞
−
= =
++
.
Nên đồ thị hàm số luôn có một đường tiệm cận ngang là
0y =
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 20
Do đó để đồ thị hàm số có hai đường tiệm cận thì đồ thị hàm số cần có đúng một đường tiệm cận
đứng. Hay phương trình:
2
() 4 0
f x x mx= + +=
có nghiệm kép hoặc có hai nghiệm phân biệt
trong đó có 1 nghiệm bằng 1.
Ta có
22
4.1.4 16mm∆= − = −
Khi đó
2
2
16 0
16 0
(1) 0
m
m
f
−=
−>
=
2
4
4
16 0
5
m
m
m
m
=
⇔=−
−>
= −
4
4
5
m
m
m
=
⇔=−
= −
.
Vậy
{
}
4;4; 5m ∈− −
.
Câu 5. Cho hàm số
2
1
mx m
y
x
+
=
−
. Với giá trị nào của
m
thì đường tiệm cận đứng, tiệm cận ngang của đồ thị
hàm số cùng với hai trục tọa độ tạo thành một hình chữ nhật có diện tích là 8?
Lời giải
Để đồ thị hàm số tồn tại tiệm cận đứng thì
0 30 0
ad bc m m− ≠⇔− ≠⇔ ≠
.
Khi đó tiệm cận đứng, tiệm cận ngang của đồ thị lần lượt là các đường thẳng
1x =
và
2
ym=
.
Khi đó diện tích hình chữ nhật tạo thành là:
1.2 8 4 4mmm=⇔ =⇔=±
.
Câu 6. Biết đồ thị
( )
C
của hàm số
ax b
y
cx d
+
=
+
đi qua điểm
(
)
1; 7
A −
và giao điểm hai tiệm cận của
( )
C
là
điểm
(
)
2;3I −
. Biết
c
là số nguyên dương và
a, c
là các số nguyên tố cùng nhau. Tìm các số
,,,abcd
.
Lời giải
Đồ thị
( )
C
có tiệm cận đứng là
d
x
c
= −
và tiệm cận ngang là
a
y
c
=
với điều kiện
0ad bc
−≠
Khi đó ta có
( )
( )
*
,1
2
22
3
1:
33
2
3
ac
c
d
dc d
xb
c
c Cy
a ac a
x
c
=
∈
−=−
= =
+
⇔ → = ⇒ ⇒ =

= =
+
=
.
Do
( ) ( )
3
1; 7 7 10
12
b
AC b
−+
− ∈ ⇒= ⇔=
−+
.
Câu 7. Cho hàm số
2
34
xm
y
xx
−
=
+−
. Giá trị nào của
m
để đồ thị hàm số đã cho có đúng 1 tiệm cận đứng?
Lời giải
Ta có:
( )( )
2
34 1 4
xm xm
y
xx x x
−−
= =
+− − +
.
*) Với
1m =
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 21
Thì
(
)(
) ( )( )
11
11 11
lim ; lim
1 45 1 45
xx
xx
xx xx
+−
→→
−−
= =
−+ −+
và
(
)(
)
4
1
lim
14
x
x
xx
→− +
−
= +∞
−+
⇒
Đồ thị hàm số có 1 tiệm cận đứng là
4x = −
*) Với
4
m = −
Thì
( )( )
( )( )
44
41 41
lim ; lim
1 45 1 45
xx
xx
xx xx
++
→− →−
+− +−
= =
−+ −+
và
( )( )
1
4
lim
14
x
x
xx
+
→
+
= +∞
−+
⇒
Đồ thị hàm số có 1 tiệm cận đứng là
1x
=
*) Với
1, 4
m
≠−
thì đồ thị hàm số có 2 tiệm cận đứng là
1, 4xx= = −
Vậy
1, 4mm= = −
thì đồ thị hàm số đã cho có đúng
1
tiệm cận đứng.
Câu 8. Cho hàm số
2xm
y
xm
+
=
−
. Tìm tất cả các giá trị của
m
để đồ thị hàm số có 2 đường tiệm cận cùng
với hai trục tọa độ tạo thành một hình vuông
Lời giải
Ta có đường tiệm cận ngang của đồ thị hàm số là
2y =
Với
2. 1. 0 0mm m− ≠⇔ ≠
thì đường tiệm cận đứng của đồ thị hàm số là
xm=
Để 2 đường tiệm cận cùng với 2 trục tọa độ tạo thành một hình vuông thì
22mm=⇔=±
Câu 9. Cho hàm số
2
1
24
x
y
x mx
−
=
−+
. Tìm tất cả các giá trị thực của tham số
m
để đồ thị hàm số có đúng
ba đường tiệm cận.
Lời giải
Xét đồ thị hàm số
2
1
24
x
y
x mx
−
=
−+
( )
C
Ta có:
lim 0
x
y
→±∞
=
nên đồ thị hàm số có một đường tiệm cận ngang
0y =
.
Để đồ thị hàm số
( )
C
có ba đường tiệm cận thì đồ thị hàm số
( )
C
có hai đường tiệm cận đứng.
2
2 40x mx⇔ − +=
có hai nghiệm phân biệt
1x ≠
.
2
2
40
2
12 4 0
5
2
m
m
m
m
m
<−
−>
>
⇔⇔

− +≠
≠
.
Vậy với
2m <−
hoặc
5
2,
2
mm>≠
thì đồ thị hàm số có 3 đường tiệm cận
Câu 10. Biết rằng đồ thị hàm số
1
2
ax
y
bx
có tiệm cận đứng là
2x
và tiệm cận ngang là
3y
. Tìm
,ab
.
Lời giải
Để đồ thị hàm số có tiệm cận đứng thì
0b ≠
.
Đồ thị hàm số
1
2
ax
y
bx
+
=
−
có tiệm cận đứng là
2
x
b
=
và tiệm cận ngang là
a
y
b
=
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 22
Theo bài ra ta có:
2
2
3
1
3
a
b
ab
b
=
=
⇔

=
=
.
Vậy:
3; 1ab= =
.
Câu 11. Tính tổng bình phương tất cả các giá trị của
m
để đồ thị hàm số
2
2 35 6y x x mx= − ++ −
có
tiệm cận ngang.
Lời giải
Có
( )
2
lim lim 2 3 5 2 2 6
xx
y x x xm x
→+∞ →+∞

= − +− + + −

( )
2
35
lim 6 2
2 35 2
x
x
mx
xx x
→+∞

−+
= −+ +

− ++

Vậy đồ thị hàm số có tiệm cận ngang khi
20 2xm m→ +∞ ⇔ + = ⇔ = −
(do
2
35 3
lim 6 6
22
2 35 2
x
x
xx x
→+∞

−+ −
−= −

− ++

hữu hạn)
Có
( )
2
lim lim 2 3 5 2 2 6
xx
y x x xm x
→−∞ →−∞

= − ++ + − −

( )
2
35
lim 6 2
2 35 2
x
x
mx
xx x
→−∞

−+
= −+ −

− +−

Vậy đồ thị hàm số có tiệm cận ngang khi
20 2xm m→ −∞ ⇔ − = ⇔ =
(do
2
35 3
lim 6 6
22
2 35 2
x
x
xx x
→−∞

−+
−= −

− +−

hữu hạn)
Vậy tổng bình phương tất cả các giá trị của
m
thỏa mãn bằng
( )
( )
22
2 24−+ =
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 177
BÀI 4. ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
BÀI TẬP TRẮC NGHIỆM TRÍCH TỪ ĐỀ THAM KHẢO VÀ ĐỀ CHÍNH THỨC
CỦA BỘ GIÁO DỤC TỪ NĂM 2017 ĐẾN NAY
Câu 1: (MĐ 101-2022) Tiệm cân ngang của đồ thị hàm số
21
24
x
y
x
−
=
+
là đường thẳng có phương trình:
A.
2.x = −
B.
1.x =
C.
1.y =
D.
2.y = −
Câu 2: (MĐ 102-2022) Tiệm cận ngang của đồ thị hàm số
21
24
x
y
x
−
=
+
là đường thẳng có phương trình:
A.
2y = −
. B.
2x = −
. C.
1
x =
. D.
1y =
.
Câu 3: (MĐ 103-2022) Cho hàm số
( )
y fx
=
có bảng biến thiên như sau:
Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng có phương trình:
A.
1x = −
. B.
1y = −
. C.
2y = −
. D.
2x = −
.
Câu 4: (MĐ 104-2022) Cho hàm số
( )
y fx=
có bảng biến thiên như sau:
Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng có phương trình:
A.
1y = −
. B.
2y = −
. C.
2x = −
. D.
1x = −
.
Câu 5: (TK 2020-2021) Tiệm cận đứng của đồ thị hàm số
24
1
x
y
x
+
=
−
là đường thẳng:
A.
1.x =
B.
1.x = −
C.
2.x =
D.
2.x = −
Câu 6: (MĐ 101 2020-2021 – ĐỢT 1) Tiệm cận đứng của đồ thị hàm số
21
1
x
y
x
−
=
−
là đường thẳng có
phương trình
CHƯƠNG
I
ỨNG DỤNG ĐẠO HÀM
ĐỂ KHẢO SÁT HÀM SỐ
BÀI TẬP TRẮC NGHIỆM
III
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 178
A.
1x =
. B.
1x = −
. C.
2x =
. D.
1
2
x =
.
Câu 7: (MĐ 102 2020-2021 – ĐỢT 1) Tiệm cận đứng của đồ thị hàm số
1
2
x
y
x
+
=
−
là đường thẳng có
phương trình
A.
1.x
= −
B.
2.x
= −
C.
2.x =
D.
1.
x =
Câu 8: (MĐ 103 2020-2021 – ĐỢT 1) Tiệm cận đứng của đồ thị hàm số
21
1
x
y
x
+
=
−
là đường thẳng có
phương trình
A.
2x =
. B.
1
x =
. C.
1
2
x
−
=
. D.
1x = −
.
Câu 9: (MĐ 104 2020-2021 – ĐỢT 1) Tiệm cận đứng của đồ thị hàm số
1
2
x
y
x
−
=
+
là đường thẳng có
phương trình?
A.
2x
=
. B.
1
x = −
. C.
2x = −
. D.
1x =
.
Câu 10: (MĐ 101 2020-2021 – ĐỢT 2) Tiệm cận ngang của đồ thị hàm số
41
1
x
y
x
−
=
+
là đường thẳng có
phương trình:
A.
4
y = −
. B.
1y =
. C.
4
y
=
. D.
1
y = −
.
Câu 11: (MĐ 102 2020-2021 – ĐỢT 2) Tiệm cận ngang của đồ thị hàm số
51
1
x
y
x
−
=
+
là đường thẳng có
phương trình:
A.
5y =
. B.
1y =
. C.
5y = −
. D.
1y = −
.
Câu 12: (MĐ 103 2020-2021 – ĐỢT 2) Tiệm cận ngang của đồ thị hàm số
21
1
x
y
x
−
=
+
là đường thẳng có
phương trình:
A.
1
y =
. B.
1y = −
. C.
2y =
. D.
2y = −
.
Câu 13: (MĐ 104 2020-2021 – ĐỢT 2) Tiệm cận ngang của đồ thị hàm số
31
1
x
y
x
−
=
+
là đường thẳng có
phương trình:
A.
3y = −
. B.
1y = −
. C.
3y =
. D.
1y =
.
Câu 14: (Đề Minh Họa 2020 Lần 1) Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
2
5 41
1
xx
y
x

là
A.
0.
B.
1.
C.
2.
D.
3.
Câu 15: (Đề Tham Khảo 2020 Lần 2) Tiệm cận ngang của đồ thị hàm số
2
1
x
y
x
−
=
+
là
A.
2y = −
. B.
1y =
. C.
1x = −
. D.
2x =
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 179
Câu 16: (Mã 101 - 2020 Lần 1) Tiệm cận ngang của đồ thị hàm số
41
1
x
y
x
+
=
−
là
A.
1
4
y =
. B.
4y =
. C.
1y =
. D.
1y = −
.
Câu 17: (Mã 102 - 2020 Lần 1) Tiệm cận ngang của đồ thị hàm số là
A. . B. . C. . D. .
Câu 18: (Mã 103 - 2020 Lần 1) Tiệm cận ngang của đồ thị hàm số
21
1
x
y
x
+
=
−
là:
A.
1
2
y =
. B.
1y = −
. C.
1y =
. D.
2y =
.
Câu 19: (Mã 104 - 2020 Lần 1) Tiệm cận ngang của đồ thị hàm số
31
1
x
y
x
+
=
−
là:
A.
1
3
y =
. B.
3y =
. C.
1y = −
. D.
1y =
.
Câu 20: (Mã 101 – 2020 Lần 2) Tiệm cận đứng của đồ thị hàm số
22
1
x
y
x
+
=
−
là
A.
2x =
. B.
2= −x
. C.
1.x =
D.
1x = −
.
Câu 21: (Mã 102 - 2020 Lần 2) Tiệm cận đứng của đồ thị hàm số
1
3
x
y
x
−
=
−
là
A.
3x = −
. B.
1x = −
. C.
1x =
. D.
3x =
.
Câu 22: (Mã 103 - 2020 Lần 2) Tiệm cận đứng của đồ thị hàm số
22
1
x
y
x
−
=
+
là
A.
2x = −
. B.
1x =
. C.
1x = −
. D.
2x =
.
Câu 23: (Mã 104 - 2020 Lần 2) Tiệm cận đứng của đồ thị hàm số
1
3
x
y
x
+
=
+
là
A.
1x = −
. B.
1x =
. C.
3x = −
. D.
3x =
.
Câu 24: (Đề minh họa 1, Năm 2017) Cho hàm số
( )
y fx=
có
( )
lim 1
x
fx
→+∞
=
và
( )
lim 1
x
fx
→−∞
= −
. Khẳng
định nào sau đây là khẳng định đúng?
A. Đồ thị hàm số đã cho không có tiệm cận ngang.
B. Đồ t hị hàm số đã cho có đúng một tiệm cận ngang.
C. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng
1y =
và
1y = −
.
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng
1x =
và
1x = −
.
Câu 25: (Đề minh họa 1, Năm 2017) Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị của hàm
số
2
1
1
x
y
mx
+
=
+
có hai tiệm cận ngang.
A. Không có giá trị thực nào của
m
thỏa mãn yêu cầu đề bài.
B.
0m <
.
C.
0m =
.
D.
0m >
.
Câu 26: (Đề minh họa 2, Năm 2017) Đường thẳng nào dưới đây là tiệm cận đứng của đồ thị hàm số
21
1
+
=
+
x
y
x
?
51
1
x
y
x
+
=
−
1y =
1
5
y =
1y = −
5y =
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 180
A.
1=x
. B.
1= −
y
. C.
2=y
. D.
1= −x
.
Câu 27: (Đề minh họa 2, Năm 2017) Tìm tất cả các tiệm cận đứng của đồ thị hàm số
2
2
21 3
56
−− + +
=
−+
x xx
y
xx
.
A.
3= −x
và
2= −x
. B.
3= −x
. C.
3=x
và
2=x
. D.
3=x
.
Câu 28: (Đề minh họa 3, Năm 2017) Cho hàm số
()y fx=
có bảng biến thiên như hình vẽ bên. Hỏi đồ
thị hàm số đã cho có bao nhiêu đường tiệm cận?
A. 1. B. 3. C. 2. D. 4.
Câu 29: (Mã 101, Năm 2017) Số tiệm cận đứng của đồ thị hàm số
2
93
x
y
xx
+−
=
+
là:
A.
3
. B.
2
. C.
0
. D.
1
.
Câu 30: (Mã 102, Năm 2017) Số tiệm cận đứng của đồ thị hàm số
2
42x
y
xx
+−
=
+
là
A.
3
. B.
0
. C.
2
. D.
1
.
Câu 31: (Mã 103, Năm 2017) Đồ thị của hàm số nào trong các hàm số dưới đây có tiệm cận đứng?
A.
1
y
x
=
. B.
2
1
1
y
xx
=
++
. C.
4
1
1
y
x
=
+
. D.
2
1
1
y
x
=
+
.
Câu 32: (Mã 104, Năm 2017) Đồ thị hàm số
2
2
4
x
y
x
−
=
−
có mấy tiệm cận.
A.
0
. B.
3
. C.
1
. D.
2
.
Câu 33: (Đề minh họa, Năm 2018) Đồ thị của hàm số nào dưới đây có tiệm cận đứng?
A.
2
32
1
−+
=
−
xx
y
x
. B.
2
2
1
=
+
x
y
x
. C.
2
1= −yx
. D.
1
=
+
x
y
x
.
A.
3
. B.
2
. C.
0
. D.
1
.
Câu 34: (Mã 102, Năm 2018) Số tiệm cận đứng của đồ thị hàm số
2
42x
y
xx
+−
=
+
là
A.
3
. B.
0
. C.
2
. D.
1
.
Câu 35: (Mã 103, Năm 2018) Số tiệm cận đứng của đồ thị hàm số
2
25 5x
y
xx
+−
=
+
là
A.
2
. B.
0
. C.
1
. D.
3
.
Câu 36: (Mã 104, Năm 2018) Số tiệm cận đứng của đồ thị hàm số
2
16 4x
y
xx
+−
=
+
là
A.
0
. B.
3
. C.
2
. D.
1
.
Câu 37: (Đề minh họa, Năm 2019) Cho hàm số
( )
=y fx
có bảng biến thiên như sau
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 181
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
4
. B.
1
. C.
3
. D.
2
.
Câu 38: (Mã 101, Năm 2019) Cho hàm số
( )
=y fx
có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
4
. B.
1
. C.
3
. D.
2
.
Câu 39: (Mã 102, Năm 2019) Cho hàm số
( )
=y fx
có bảng biến thiên như sau
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A.
3
. B.
1
. C.
2
. D.
4
.
Câu 40: (Mã 103, Năm 2019) Cho hàm số
( )
=y fx
có bảng biến thiên như sau
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 41: (Mã 104, Năm 2019) Cho hàm số
( )
=y fx
có bảng biến thiên như sau
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A.
2
. B.
1
. C.
3
. D.
4
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 1
BÀI 4. ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
BÀI TẬP TRẮC NGHIỆM TRÍCH TỪ ĐỀ THAM KHẢO VÀ ĐỀ CHÍNH THỨC
CỦA BỘ GIÁO DỤC TỪ NĂM 2017 ĐẾN NAY
Câu 1: (MĐ 101-2022) Tiệm cân ngang của đồ thị hàm số
21
24
x
y
x
−
=
+
là đường thẳng có phương trình:
A.
2.x = −
B.
1.x =
C.
1.y
=
D.
2.y = −
Lời giải
Chọn C
Ta có
lim 1
x
y
→±∞
=
nên tiệm cận ngang của đồ thị hàm số
21
24
x
y
x
−
=
+
là đường thẳng có phương
trình
1.y =
Câu 2: (MĐ 102-2022) Tiệm cận ngang của đồ thị hàm số
21
24
x
y
x
−
=
+
là đường thẳng có phương trình:
A.
2y = −
. B.
2x = −
. C.
1x =
. D.
1y =
.
Lời giải
Chọn D
Có:
1
2
21
lim lim lim 1
4
24
2
xx x
x
x
y
x
x
→+∞ →+∞ →+∞
−
−
= = =
+
+
và:
1
2
21
lim lim lim 1
4
24
2
xx x
x
x
y
x
x
→−∞ →−∞ →−∞
−
−
= = =
+
+
Vậy đồ thị hàm số
21
24
x
y
x
−
=
+
có tiệm cận ngang là đường thẳng có phương trình:
1y =
.
Câu 3: (MĐ 103-2022) Cho hàm số
( )
y fx
=
có bảng biến thiên như sau:
CHƯƠNG
I
ỨNG DỤNG ĐẠO HÀM
ĐỂ KHẢO SÁT HÀM SỐ
BÀI TẬP TRẮC NGHIỆM
III
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 2
Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng có phương trình:
A.
1x
= −
. B.
1y = −
. C.
2
y
= −
. D.
2x = −
.
Lời giải
Chọn D
Ta có
( 2)
lim
x
y
+
→−
= +∞
,
( 2)
lim
x
y
−
→−
= −∞
.
Vậy tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng
2
x = −
.
Câu 4: (MĐ 104-2022) Cho hàm số
( )
y fx=
có bảng biến thiên như sau:
Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng có phương trình:
A.
1y = −
. B.
2
y = −
. C.
2x = −
. D.
1x = −
.
Lời giải
Chọn C
Ta có
( )
2
lim
x
fx
+
→−
= +∞
và
( )
2
lim
x
fx
−
→−
= −∞
nên tiệm cận đứng của đồ thị hàm số đã cho là
Câu 5: (TK 2020-2021) Tiệm cận đứng của đồ thị hàm số
24
1
x
y
x
+
=
−
là đường thẳng:
A.
1.x =
B.
1.
x
= −
C.
2.x =
D.
2.x = −
Lời giải
Ta có
1
24
lim
1
x
x
x

và
1
24
lim
1
x
x
x

nên
1x
là tiệm cận đứng.
Câu 6: (MĐ 101 2020-2021 – ĐỢT 1) Tiệm cận đứng của đồ thị hàm số
21
1
x
y
x
−
=
−
là đường thẳng có
phương trình
A.
1x =
. B.
1x = −
. C.
2x =
. D.
1
2
x =
.
Lời giải
Vì
1
21
lim
1
x
x
x
+
→
−
= +∞
−
nên đường thẳng
1x =
là tiệm cận đứng của đồ thị hàm số
21
1
x
y
x
−
=
−
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 3
Câu 7: (MĐ 102 2020-2021 – ĐỢT 1) Tiệm cận đứng của đồ thị hàm số
1
2
x
y
x
+
=
−
là đường thẳng có
phương trình
A.
1.x = −
B.
2.x = −
C.
2.x =
D.
1.x
=
Lời giải
Chọn C
Từ
22
1
lim lim
2
xx
x
y
x
++
→→
+
= = +∞
−
hoặc
22
1
lim lim
2
xx
x
y
x
−−
→→
+
= = −∞
−
nên suy ra đồ thị hàm số có tiệm cận
đứng là
2.x =
Câu 8: (MĐ 103 2020-2021 – ĐỢT 1) Tiệm cận đứng của đồ thị hàm số
21
1
x
y
x
+
=
−
là đường thẳng có
phương trình
A.
2x
=
. B.
1x
=
. C.
1
2
x
−
=
. D.
1x = −
.
Lời giải
Ta có
11
21 21
lim ;lim
11
xx
xx
xx
+−
→→
++
= +∞ = −∞
−−
.
Vậy tiệm cận đứng của đồ thị hàm số là đường thẳng
1x =
.
Câu 9: (MĐ 104 2020-2021 – ĐỢT 1) Tiệm cận đứng của đồ thị hàm số
1
2
x
y
x
−
=
+
là đường thẳng có
phương trình?
A.
2x
=
. B.
1x = −
. C.
2
x = −
. D.
1
x =
.
Lời giải
TXĐ:
{ }
\2D = −
.
Ta có
( )
2
lim
x
y
+
→−
= −∞
nên đồ thị hàm số nhận đường thẳng
2x = −
là tiệm cận đứng.
Câu 10: (MĐ 101 2020-2021 – ĐỢT 2) Tiệm cận ngang của đồ thị hàm số
41
1
x
y
x
−
=
+
là đường thẳng có
phương trình:
A.
4y = −
. B.
1y
=
. C.
4y
=
. D.
1
y = −
.
Lời giải
Ta có
1
4
41
lim lim lim 4
1
1
1
xx x
x
x
y
x
x
→±∞ →±∞ →±∞
−
−
= = =
+
+
.
Vậy tiệm cận ngang đồ thị hàm số đã cho là đường thẳng có phương trình:
4.y =
Câu 11: (MĐ 102 2020-2021 – ĐỢT 2) Tiệm cận ngang của đồ thị hàm số
51
1
x
y
x
−
=
+
là đường thẳng có
phương trình:
A.
5y =
. B.
1y
=
. C.
5y = −
. D.
1y = −
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 4
Lời giải
Tiệm cận ngang của đồ thị hàm số
51
1
x
y
x
−
=
+
là đường thẳng có phương trình
5
y
=
Câu 12: (MĐ 103 2020-2021 – ĐỢT 2) Tiệm cận ngang của đồ thị hàm số
21
1
x
y
x
−
=
+
là đường thẳng có
phương trình:
A.
1y =
. B.
1
y = −
. C.
2y =
. D.
2y = −
.
Lời giải
Tiệm cận ngang của đồ thị hàm số
21
1
x
y
x
−
=
+
là đường thẳng:
2y =
.
Câu 13: (MĐ 104 2020-2021 – ĐỢT 2) Tiệm cận ngang của đồ thị hàm số
31
1
x
y
x
−
=
+
là đường thẳng có
phương trình:
A.
3y = −
. B.
1y = −
. C.
3y =
. D.
1
y =
.
Lời giải
Ta có
31
lim lim 3
1
xx
x
y
x
→±∞ →±∞
−
= =
+
.
Vậy đồ thị hàm số
31
1
x
y
x
−
=
+
có tiệm cận ngang là đường thẳng
3y =
.
Câu 14: (Đề Minh Họa 2020 Lần 1) Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
2
5 41
1
xx
y
x

là
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải
Chọn C
Tiệm cận ngang:
Ta có:
2
2
2
2
2
2
2
2
41
41
5
5
5 41
lim lim lim lim 5
1
1
1
1
1
xx x x
x
xx
x
x
x
x
y
x
x
x
x
→+∞ →+∞ →+∞ →+∞

−−
−−

−−

= = = =

−
−
−


nên đồ thị
hàm số có một tiệm cận ngang
5y
=
.
Tiệm cận đứng:
Cho
2
1
1
1
x
x
x
=
= ⇔
= −
Ta có:
( )( )
( )( )
2
2
11 1 1
51 1
5 41 516
lim lim lim lim 3
1 1 12
1
xx x x
xx
xx x
y
xx x
x
→→ → →
+−
−− +
= = = = =
+− +
−
nên
1x =
không là tiệm
cận đứng.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 5
( ) ( )
( )
( )( )
( )
22 2
2
11 1 1
5 41 5 41 15 41
lim lim lim lim .
11 1 1
1
xx x x
xx xx xx
y
xx x x
x
++ + +
→− →− →− →−

−− −− −−
= = = = −∞


+− + −
−

vì
( )
( )
1
2
1
1
lim
1
5 41
lim 4
0
1
x
x
x
xx
x
+
+
→−
→−
= +∞
+
−−
=−<
−
.
Khi đó, đồ thị hàm số có một tiệm cận đứng
1x = −
.
Tổng cộng đồ thị hàm số có 2 tiệm cận.
Câu 15: (Đề Tham Khảo 2020 Lần 2) Tiệm cận ngang của đồ thị hàm số
2
1
x
y
x
−
=
+
là
A.
2y = −
. B.
1y =
. C.
1x = −
. D.
2x =
.
Lời giải
Chọn B
Ta có
2
lim 1
1
x
x
x
→+∞
−
=
+
và
2
lim 1
1
x
x
x
→−∞
−
=
+
Suy ra
1y =
là tiệm cận ngang của đồ thị hàm số.
Câu 16: (Mã 101 - 2020 Lần 1) Tiệm cận ngang của đồ thị hàm số
41
1
x
y
x
+
=
−
là
A.
1
4
y =
. B.
4y =
. C.
1y =
. D.
1y = −
.
Lời giải
Chọn B
Tiệm cận ngang
4
lim lim 4
1
xx
yy
→+∞ →−∞
= = =
Câu 17: (Mã 102 - 2020 Lần 1) Tiệm cận ngang của đồ thị hàm số là
A. . B. . C. . D. .
Lời giải
Chọn D
Ta có là tiệm cận ngang của đồ thị hàm số.
Câu 18: (Mã 103 - 2020 Lần 1) Tiệm cận ngang của đồ thị hàm số
21
1
x
y
x
+
=
−
là:
A.
1
2
y =
. B.
1y = −
. C.
1y =
. D.
2y =
.
51
1
x
y
x
+
=
−
1y =
1
5
y =
1y = −
5y =
51
lim lim 5
1
51
lim lim 5
1
xx
xx
x
y
x
x
y
x
→+∞ →+∞
→−∞ →−∞
+
= =
−
+
= =
−
⇒
5y =
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 6
Lời giải
Chọn D
Ta có
1
2
21
lim lim 2
1
1
1
xx
x
x
x
x
→±∞ →±∞
+
+
= =
−
−
. Suy ra đồ thị hàm số có tiệmcận ngang là
2y =
.
Câu 19: (Mã 104 - 2020 Lần 1) Tiệm cận ngang của đồ thị hàm số
31
1
x
y
x
+
=
−
là:
A.
1
3
y =
. B.
3y =
. C.
1y = −
. D.
1y =
.
Lời giải
Chọn B
Ta có :
31
lim lim 3
1
xx
x
y
x
→+∞ →+∞
+
= =
−
và
31
lim lim 3
1
xx
x
y
x
→−∞ →−∞
+
= =
−
nên
3y =
là tiệm cận ngang của đồ
thị hàm số.
Câu 20: (Mã 101 – 2020 Lần 2) Tiệm cận đứng của đồ thị hàm số
22
1
x
y
x
+
=
−
là
A.
2x =
. B.
2= −x
. C.
1.
x =
D.
1x = −
.
Lời giải
Chọn C
Tập xác định
{ }
\1D =
.
Ta có
11
lim ; lim
xx
yy
−+
→→
=−∞ =+∞
, suy ra đồ thị có tiệm cận đứng là
1x =
.
Câu 21: (Mã 102 - 2020 Lần 2) Tiệm cận đứng của đồ thị hàm số
1
3
x
y
x
−
=
−
là
A.
3x = −
. B.
1x
= −
. C.
1x
=
. D.
3x =
.
Lời giải.
Chọn D
3
1
lim
3
x
x
x
−
→
−
= −∞
−
. Suy ta tiệm cận đứng là đường thẳng
3x
=
.
Câu 22: (Mã 103 - 2020 Lần 2) Tiệm cận đứng của đồ thị hàm số
22
1
x
y
x
−
=
+
là
A.
2x = −
. B.
1x =
. C.
1x = −
. D.
2x =
.
Lời giải
Chọn C
Ta có
11
22
lim lim
1
xx
x
y
x
++
→− →−
−
= = −∞
+
và
11
22
lim lim
1
xx
x
y
x
−−
→− →−
−
= = +∞
+
nên đường thẳng
1x = −
là
tiệm cận đứng của đồ thị hàm số.
Câu 23: (Mã 104 - 2020 Lần 2) Tiệm cận đứng của đồ thị hàm số
1
3
x
y
x
+
=
+
là
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 7
A.
1x = −
. B.
1
x
=
. C.
3x = −
. D.
3x
=
.
Lời giải
Chọn C
Ta có
3
lim
x
y
+
→−
= −∞
và
3
lim
x
y
−
→−
= +∞
nên đồ thị hàm số nhận đường thẳng
3x = −
làm tiệm cận
đứng.
Câu 24: (Đề minh họa 1, Năm 2017) Cho hàm số
( )
y fx
=
có
( )
lim 1
x
fx
→+∞
=
và
( )
lim 1
x
fx
→−∞
= −
. Khẳng
định nào sau đây là khẳng định đúng?
A. Đồ thị hàm số đã cho không có tiệm cận ngang.
B. Đồ t hị hàm số đã cho có đúng một tiệm cận ngang.
C. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng
1y =
và
1
y = −
.
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng
1
x
=
và
1x = −
.
Lời giải
Chọn C
Câu 25: (Đề minh họa 1, Năm 2017) Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị của hàm
số
2
1
1
x
y
mx
+
=
+
có hai tiệm cận ngang.
A. Không có giá trị thực nào của
m
thỏa mãn yêu cầu đề bài.
B.
0m <
.
C.
0m =
.
D.
0m >
.
Lời giải
Chọn D
Ta có:
2
2
1
1
11
lim lim
1
1
xx
x
x
y
m
mx
m
x
→−∞ →−∞

−+

+

= = = −
+
+
và
2
2
1
1
11
lim lim lim
1
1
xx x
x
x
y
m
mx
m
x
→+∞ →+∞ →+∞
+
+
= = =
+
+
Vậy hàm số có hai tiệm cận ngang là :
11
;0yy m
mm
= =− ⇒>
Câu 26: (Đề minh họa 2, Năm 2017) Đường thẳng nào dưới đây là tiệm cận đứng của đồ thị hàm số
21
1
+
=
+
x
y
x
?
A.
1=
x
. B.
1= −y
. C.
2=y
. D.
1
= −x
.
Lời giải
Chọn D
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 8
Ta có suy ra đường thẳng là đường
tiệm cận đứng của đồ thị hàm số .
Câu 27: (Đề minh họa 2, Năm 2017) Tìm tất cả các tiệm cận đứng của đồ thị hàm số
2
2
21 3
56
−− + +
=
−+
x xx
y
xx
.
A.
3= −x
và
2= −x
. B.
3= −x
. C.
3=x
và
2=x
. D.
3=x
.
Lời giải
Chọn D
Tập xác định
Tương tự .Suy ra đường thẳng không là tiệm cận đứng của
đồ thị hàm số đã cho.
.
Suy ra đường thẳng là tiệm cận đứng của đồ thị hàm số đã cho.
Câu 28: (Đề minh họa 3, Năm 2017) Cho hàm số
()y fx=
có bảng biến thiên như hình vẽ bên. Hỏi đồ
thị hàm số đã cho có bao nhiêu đường tiệm cận?
A. 1. B. 3. C. 2. D. 4.
Lời giải
Chọn B
11 11
21 21
lim lim ; lim lim
11
++ −−
→− →− →− →−
++
= = −∞ = = +∞
++
xx xx
xx
yy
xx
1= −x
21
1
+
=
+
x
y
x
{ }
2;3\= D
( )
( )
( )
(
)
( )
( )
( )
(
)
( )
(
)
2
2
2
2
22
22
2
2
22
2
2
2
21 3
21 3
lim lim
56
5 62 1 3
21 3
lim
5 62
1 3
(3 1) 7
lim
6
32 1 3
++
+
+
→→
→
→
− − ++
−− + +
=
−+
− + −+ + +
− − ++
=
− + −+ + +
+
= = −
− −+ + +
xx
x
x
x xx
x xx
xx
x x x xx
x xx
x x x xx
x
x x xx
2
2
2
21 3 7
lim
56 6
−
→
−− + +
= −
−+
x
x xx
xx
2=x
22
22
33
21 3 21 3
lim ; lim
56 56
+−
→→
−− + + −− + +
= +∞ = −∞
−+ −+
xx
x xx x xx
xx xx
3=x
x2 x0
lim y TCD :x 2; lim y TCD :x 0;
+−
→→
= −∞ ⇒ = − = +∞ ⇒ =
x
limy0 TCN:y0.
→+∞
=⇒=
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 9
Câu 29: (Mã 101, Năm 2017) Số tiệm cận đứng của đồ thị hàm số
2
93x
y
xx
+−
=
+
là:
A.
3
. B.
2
. C.
0
. D.
1
.
Lời giải
Chọn D
Tập xác định của hàm số:
[
) { }
9; \ 0; 1D = − +∞ −
Ta có:
( )
1
lim
x
y
+
→−
=
(
)
2
1
93
lim
x
x
xx
+
→−
+−
+
= +∞
và
( )
1
lim
x
y
−
→−
( )
2
1
93
lim
x
x
xx
−
→−
+−
=
+
= −∞
.
⇒
TCĐ:
1x = −
.
0
lim
x
y
+
→
=
2
0
93
lim
x
x
xx
+
→
+−
+
( )
( )
2
0
lim
93
x
x
xx x
+
→
=
+ ++
( )
( )
0
1
lim
1 93
x
xx
+
→
=
+ ++
1
6
=
.
0
lim
x
y
−
→
=
2
0
93
lim
x
x
xx
−
→
+−
+
( )
( )
2
0
lim
93
x
x
xx x
−
→
=
+ ++
( )
( )
0
1
lim
1 93
x
xx
−
→
=
+ ++
1
6
=
.
⇒
0=x
không là đường tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có
1
tiệm cận đứng.
Câu 30: (Mã 102, Năm 2017) Số tiệm cận đứng của đồ thị hàm số
2
42x
y
xx
+−
=
+
là
A.
3
. B.
0
. C.
2
. D.
1
.
Lời giải
Chọn D
Tập xác định của hàm số:
[
) { }
4; \ 0; 1D = − +∞ −
Ta có:
0
1
lim
4
x
y
→
=
.
( ) ( )
2
11
42
lim lim
xx
x
y
xx
++
→− →−
+−
= = +∞
+
và
( ) ( )
2
11
42
lim lim
xx
x
y
xx
−−
→− →−
+−
= = −∞
+
⇒
TCĐ:
1x = −
.
Vậy đồ thị hàm số có
1
tiệm cận đứng.
Câu 31: (Mã 103, Năm 2017) Đồ thị của hàm số nào trong các hàm số dưới đây có tiệm cận đứng?
A.
1
y
x
=
. B.
2
1
1
y
xx
=
++
. C.
4
1
1
y
x
=
+
. D.
2
1
1
y
x
=
+
.
Lời giải
Chọn A
Đồ thị hàm số
1
y
x
=
có tiệm cận đứng là
0x =
.
Đồ thị các hàm số ở các đáp án
,,BCD
đều không có tiệm cận đứng do mẫu vô nghiệm.
Câu 32: (Mã 104, Năm 2017) Đồ thị hàm số
2
2
4
x
y
x
−
=
−
có mấy tiệm cận.
A.
0
. B.
3
. C.
1
. D.
2
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 10
Lời giải
Chọn D
Ta có
2
40 2xx−=⇔=±
2
2
21
lim
44
x
x
x
→
−

=

−

nên đường thẳng
2x =
không phải là tiệm cân đứng của đồ thị hàm số.
2
22
21
lim lim ,
42
xx
x
xx
++
→− →−
−

= = +∞

−+

( )
( )
2
22
21
lim lim ,
42
xx
x
xx
−−
→− →−
−

= = −∞

−+

nên đườngthẳng
2x = −
là
tiệm cân đứng của đồ thị hàm số.
2
2
lim 0
4
x
x
x
→±∞
−

=

−

nên đường thẳng
0y =
là tiệm cận ngang của đồ thị hàm số.
Vậy có đồ thị có hai đường tiệm cận.
Câu 33: (Đề minh họa, Năm 2018) Đồ thị của hàm số nào dưới đây có tiệm cận đứng?
A.
2
32
1
−+
=
−
xx
y
x
. B.
2
2
1
=
+
x
y
x
. C.
2
1= −yx
. D.
1
=
+
x
y
x
.
Lời giải
Chọn D
Ta có
11
lim , lim
11
−+
→− →−
= +∞ = −∞
++
xx
xx
xx
nên đường thẳng
1x
= −
là tiệm cận đứng của đồ thị hàm
số.
Câu 34: (Mã 101, Năm 2018) Số tiệm cận đứng của đồ thị hàm số
2
93x
y
xx
+−
=
+
là
A.
3
. B.
2
. C.
0
. D.
1
.
Lời giải
Chọn D
Tập xác định của hàm số:
[
) { }
9; \ 0; 1D = − +∞ −
Ta có:
( )
1
lim
x
y
+
→−
=
( )
2
1
93
lim
x
x
xx
+
→−
+−
+
= +∞
và
( )
1
lim
x
y
−
→−
( )
2
1
93
lim
x
x
xx
−
→−
+−
=
+
= −∞
.
⇒
TCĐ:
1x = −
.
0
lim
x
y
+
→
=
2
0
93
lim
x
x
xx
+
→
+−
+
( )
( )
2
0
lim
93
x
x
xx x
+
→
=
+ ++
( )
( )
0
1
lim
1 93
x
xx
+
→
=
+ ++
1
6
=
.
0
lim
x
y
−
→
=
2
0
93
lim
x
x
xx
−
→
+−
+
( )
( )
2
0
lim
93
x
x
xx x
−
→
=
+ ++
( )
( )
0
1
lim
1 93
x
xx
−
→
=
+ ++
1
6
=
.
⇒
0=x
không là đường tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có
1
tiệm cận đứng.
Câu 35: (Mã 102, Năm 2018) Số tiệm cận đứng của đồ thị hàm số
2
42x
y
xx
+−
=
+
là
A.
3
. B.
0
. C.
2
. D.
1
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 11
Lời giải
Chọn D
Tập xác định của hàm số:
[
) { }
4; \ 0; 1D = − +∞ −
Ta có:
0
1
lim
4
x
y
→
=
.
( )
(
)
2
11
42
lim lim
xx
x
y
xx
++
→− →−
+−
= = +∞
+
và
( ) ( )
2
11
42
lim lim
xx
x
y
xx
−−
→− →−
+−
= = −∞
+
⇒
TCĐ:
1x = −
.
Vậy đồ thị hàm số có
1
tiệm cận đứng.
Câu 36: (Mã 103, Năm 2018) Số tiệm cận đứng của đồ thị hàm số
2
25 5x
y
xx
+−
=
+
là
A.
2
. B.
0
. C.
1
. D.
3
.
Lời giải
Chọn C
Tập xác định
[
) { }
25; \ 1; 0D = − +∞ −
. Biến đổi
( )
( )
1
() .
1 25 5
fx
xx
=
+ ++
Vì
( ) ( )
( )
( )
11
1
lim lim
1 25 5
xx
y
xx
++
→− →−
= = +∞
+ ++
nên đồ thị hàm số đã cho có 1 tiệm cận đứng
1x = −
.
Câu 37: (Mã 104, Năm 2018) Số tiệm cận đứng của đồ thị hàm số
2
16 4x
y
xx
+−
=
+
là
A.
0
. B.
3
. C.
2
. D.
1
.
Lời giải
Chọn D
Tập xác định hàm số
[
) { }
16; \ 1; 0D = − +∞ −
.
Ta có
( )
( )
(
)
( )
( )
00 0 0
16 4 1 1
lim lim lim lim
18
1 16 4 1 16 4
xx x x
xx
y
xx
xxx xx
→→ → →
+−
= = = =
+
+ ++ + ++
.
( ) ( )
( )
( )
( )
( )
11 1
16 4 1
lim lim lim
1
1 16 4
xx x
x
y
xx
xx
++ +
→− →− →−
+−
= = = +∞
+
+ ++
.
vì
( )
( )
1
lim 16 4 15 4 0
x
x
+
→−
+ + = +>
,
( )
( )
1
lim 1 0
x
x
+
→−
+=
và
( )
1x
+
→−
thì
1 10xx>− ⇒ + >
.
Tương tự
( ) ( )
( )
( )
11
1
lim lim
1 16 4
xx
y
xx
−−
→− →−
= = −∞
+ ++
.
Vậy đồ thị hàm số đã cho có tiệm cận đứng là
1x = −
.
Câu 38: (Đề minh họa, Năm 2019) Cho hàm số
( )
=y fx
có bảng biến thiên như sau
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 12
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
4
. B.
1
. C.
3
. D.
2
.
Lời giải
Chọn C
Vì
( )
lim 5
→+∞
=
x
fx
⇒
đường thẳng
5=y
là tiệm cận ngang của đồ thị hàm số.
Vì
( )
lim 2
→−∞
=
x
fx
⇒
đường thẳng
2=y
là tiệm cận ngang của đồ thị hàm số.
Vì
(
)
1
lim
−
→
= +∞
x
fx
⇒
đường thẳng
1
=x
là tiệm cận đứng của đồ thị hàm số.
KL: Đồ thị hàm số có tổng số ba đường tiệm cận.
Câu 39: (Mã 101, Năm 2019) Cho hàm số
( )
=y fx
có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
4
. B.
1
. C.
3
. D.
2
.
Lời giải
Chọn D
Dựa vào bản biến thiên ta có
0
lim 0
x
yx
+
→
= +∞ ⇒ =
là tiệm cận đứng của đồ thị hàm số.
lim 2 2
x
yy
→−∞
=⇒=
là tiệm cận ngang của đồ thị hàm số.
Vậy tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là 2.
Câu 40: (Mã 102, Năm 2019) Cho hàm số
( )
=y fx
có bảng biến thiên như sau
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A.
3
. B.
1
. C.
2
. D.
4
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 13
Lời giải
Chọn C
Ta có:
( )
lim
x
fx
→+∞
= +∞
đồ thị hàm số không tồn tại tiệm cận ngang khi
.x → +∞
( )
lim 0
x
fx
→−∞
=
Vậy đồ thị hàm số
( )
y fx=
có tiệm cận ngang
0.y =
(
)
0
lim 2
x
fx
+
→
=
;
( )
0
lim .
x
fx
−
→
= −∞
Đồ thị hàm số
( )
y fx=
có tiệm cận đứng
0.x =
Vậy tổng số tiệm cận đứng và ngang là 2.
Câu 41: (Mã 103, Năm 2019) Cho hàm số
(
)
=y fx
có bảng biến thiên như sau
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn C
Dựa vào bảng biến thiên ta có
0
lim 0
x
yx
−
→
= −∞ ⇒ =
là tiệm cận đứng của đồ thị hàm số.
lim 1 1
x
yy
→−∞
=⇒=
là tiệm cận ngang của đồ thị hàm số.
lim 3 3
x
yy
→+∞
=⇒=
là tiệm cận ngang của đồ thị hàm số.
Vậy tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
3
.
Câu 42: (Mã 104, Năm 2019) Cho hàm số
( )
=y fx
có bảng biến thiên như sau
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A.
2
. B.
1
. C.
3
. D.
4
.
Lời giải
Chọn C
Dựa vào bảng biến thiên ta có
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 14
0
lim 0
x
yx
+
→
= +∞ ⇒ =
là tiệm cận đứng của đồ thị hàm số.
lim 0 0
x
yy
→−∞
=⇒=
là tiệm cận ngang của đồ thị hàm số.
lim 3 3
x
yy
→+∞
=⇒=
là tiệm cận ngang của đồ thị hàm số.
Vậy tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
3
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 182
BÀI 4. ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
DẠNG. XÁC ĐỊNH ĐƯỜNG TIỆM CẬN THÔNG QUA BẢNG BIẾN THIÊN, ĐỒ THỊ
1.1.1 Đường tiệm cận ngang
Cho hàm số
=
y fx()
xác định trên một khoảng vô hạn. Đường thẳng
yy
0
=
là đường tiệm
cận ngang của đồ thị hàm số
=
y fx
()
nếu ít nhất một trong các điều kiện sau được thỏa mãn:
xx
fx y fx y
00
lim ( ) , lim ( )
→+∞ →−∞
= =
1.1.2 Đường tiệm cận đứng
Đường thẳng
=xx
0
được gọi là đường tiệm cận đứng của đồ thị hàm số
()
y fx
=
nếu ít
nhất một trong các điều kiện sau được thỏa mãn:
+−
→→
= +∞ = −∞
xx xx
fx fx
00
lim ( ) , lim ( ) ,
00
lim ( ) , lim ( )
xx xx
fx fx
+−
→→
= −∞ = +∞
Lưu ý: Với đồ thị hàm phân thức dạng
( )
+
= ≠ −≠
+
ax b
y c ad bc
cx d
0; 0
luôn có tiệm cận ngang là
=
a
y
c
và tiệm cận đứng
= −
d
x
c
.
Câu 1: Cho hàm số có bảng biến thiên như hình sau
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
( )
y fx=
là
A.
3
. B.
2
. C.
4
. D.
1
.
CHƯƠNG
I
ỨNG DỤNG ĐẠO HÀM
ĐỂ KHẢO SÁT HÀM SỐ
BÀI TẬP TRẮC NGHIỆM
III
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 183
Câu 2: Cho hàm số
( )
fx
có bảng biến thiên như sau:
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là:
A.
4
. B.
3
. C.
1
. D.
2
.
Câu 3: Cho hàm số
()=y fx
có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
4
B.
2
C.
3
D.
1
Câu 4: Cho đồ thị hàm số
( )
y fx=
như hình bên. Khẳng định nào sau đây là đúng?
x
y
O
1
1
−
A. Đồ thị hàm số có tiệm cận đứng
0x =
, tiệm cận ngang
1y =
.
B. Hàm số có hai cực trị.
C. Đồ thị hàm số chỉ có một đường tiệm cận.
D. Hàm số đồng biến trong khoảng
( )
;0−∞
và
( )
0;+∞
.
Câu 5: Cho hàmsố
()fx
có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
4
. B.
1
. C.
3
. D.
2
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 184
Câu 6: Cho hàm số
()y fx
=
có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
4
. B.
1
. C.
3
. D.
2
.
Câu 7: Cho hàm số
( )
y fx=
có bảng biến thiên như sau
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho bằng
A.
2
. B.
1
. C.
0
. D.
3
.
Câu 8: Cho hàm số
(
)
y fx=
liên tục trên
{ }
\1
có bảng biến thiên như hình vẽ. Tổng số đường tiệm
cận đứng và đường tiệm cận ngang của đồ thị hàm số
( )
y fx=
A.
1
. B.
4
. C.
2
. D.
3.
Câu 9: Cho hàm số
y fx
có bảng biến như sau:
Số đường tiệm cận của đồ thị hàm số là:
A. 3 B. 1. C. 4. D. 2.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 185
Câu 10: Cho hàm số
( )
y fx=
có bảng biến thiên như sau
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A.
4
. B.
2
. C.
3
. D.
1
.
DẠNG 2. XÁC ĐỊNH ĐƯỜNG TIỆM CẬN ĐỒ THỊ HÀM SỐ THÔNG HÀM SỐ CHO TRƯỚC
1 Đường tiệm cận ngang
Cho hàm số
( )
y fx=
có TXD:
D
Điều kiện cần:
D
phải chứa
+∞
hoặc
−∞
Điều kiện đủ:
Dạng 1.
()
()
()
Px
y fx
Qx
= =
.
Nếu
( )
( )
:
degP x degQ x
>
thì không có tiệm cận ngang
Nếu
( ) (
)
:degP x degQ x
>
TCN
0y =
Nếu
( ) ( )
:degP x degQ x=
yk=
Dạng 2:
()y fx u v= = −
: Nhân liên hợp
2
()
uv
y fx
uv
−
⇒= =
+
2 Đường tiệm cận đứng
Cho hàm số
( )
( )
Px
y
Qx
=
có TXD:
D
Đkiện cần: giải
( )
0
0Qx x x
=⇔=
là TCĐ khi thỏa mãn đk đủ
Đkiện đủ:
Đkiện 1:
0
x
làm cho
()Px
và
()Qx
xác định.
Đkiện 2: -
0
x
không phải nghiêm
0
()Px x x⇒=
là TCĐ
-
0
x
là nghiêm
0
()Px x x⇒=
là TCĐ nếu
0
lim ( )
xx
fx
→
= ∞
Câu 11: Đồ thị hàm số
2
51 1
2
xx
y
xx

có tất cả bao nhiêu đường tiệm cận?
A.
3
B.
0
C.
2
D.
1
Câu 12: Tìm tất cả các tiệm cận đứng của đồ thị hàm số
2
2
21 3
56
−− + +
=
−+
x xx
y
xx
.
A.
3=x
và
2=x
. B.
3=x
. C.
3
= −x
và
2= −x
. D.
3= −
x
.
Câu 13: Số tiệm cận đứng của đồ thị hàm số
2
42x
y
xx
+−
=
+
là
A.
3
. B.
0
. C.
1
. D.
2
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 186
Câu 14: Đồ thị hàm số
( )
2
1
1
x
fx
x
+
=
−
có tất cả bao nhiêu tiệm cận đứng và tiệm cận ngang?
A.
4
. B.
3
. C.
1
. D.
2
.
Câu 15: Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
(
)
462
2
xx
y
x
+−
=
+
là?
A.
1
B.
3
C.
2
D.
4
Câu 16: Cho hàm số
2
42
23
32
xx
y
xx
++
=
−+
. Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?
A.
4
. B.
5
. C.
3
. D.
6
.
Câu 17: Hàm số
2
3
1x xx
y
xx
+ ++
=
+
có bao nhiêu đường tiệm cận?
A.
1
B.
3
C.
2
D.
4
Câu 18: Số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
21
32
−+
=
−+
x
y
xx
là
A.
4
B.
1
C.
3
D.
2
Câu 19: Cho hàm số
2
3
5 6 12
4 31
xx
y
xx
++−
=
−−
có đồ thị
( )
C
. Mệnh đề nào sau đây là đúng?
A. Đồ thị
( )
C
của hàm số không có tiệm cận.
B. Đồ thị
( )
C
của hàm số chỉ có một tiệm cận ngang
0y =
.
C. Đồ thị
(
)
C
của hàm số có một tiệm cận ngang
0y
=
và hai tiệm cận đứng
1
1;
2
xx= = −
.
D. Đồ thị
( )
C
của hàm số chỉ có một tiệm cận ngang
0y =
và một tiện cận đứng
1x =
Câu 20: Đồ thị hàm số
2
2
31
x xx
y
x
+−
=
+
có tất cả bao nhiêu đường tiệm cận?
A.
2
. B.
3
. C.
0
. D.
1
.
Câu 21: Đồ thị hàm số
2
2
14
23
x
y
xx


có số đường tiệm cận đứng là
m
và số đường tiệm cận ngang là
n
. Giá trị của
mn
là
A.
1
B.
2
C.
3
D.
0
Câu 22: Gọi
,nd
lần lượt là số đường tiệm cận ngang và số tiệm cận đứng của đồ thị hàm số
1
1
x
y
xx
. Khẳng định nào sau đây là đúng?
A.
0, 2nd

. B.
1nd
. C.
1, 2nd
. D.
0, 1nd
.
Câu 23: Đồ thị hàm số
2
51 1
2
xx
y
xx
+− +
=
−
có tất cả bao nhiêu đường tiệm cận?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 24: Tìm số đường tiệm cận của đồ thị hàm số
1
43 1 3 5
x
y
xx
−
=
+− −
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 187
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 25: Cho hàm số
2
42
23
32
xx
y
xx
++
=
−+
. Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?
A.
4
. B.
5
. C.
3
. D.
6
.
Câu 26: Đồ thị hàm số
2
58
3
x
y
xx
−
=
−
có bao nhiêu đường tiệm cận?
A. 2. B. 4. C. 1. D. 3.
Câu 27: Gọi
S
là tập hợp các giá trị nguyên
m
để đồ thị hàm số
2
2
62
+
=
−+
x
y
x xm
có hai đường tiệm
cận đứng. Số phần tử của
S
là
A. vô số. B.
12
. C.
14
. D.
13
.
Câu 28: Có bao nhiêu giá trị nguyên dương của tham số
m
để đồ thị hàm số
2
1
8
x
y
x xm
−
=
−+
có 3 đường
tiệm cận?
A.
14
. B.
8
. C.
15
. D.
16
.
Câu 29: Cho hàm số
( )
322
3
3 21
x
y
x mx m x m
−
=
− + +−
. Có bao nhiêu giá trị nguyên của tham số
m
thuộc
đoạn
[
]
2020;2020−
để đồ thị hàm số có 4 đường tiệm cận?
A. 4039. B. 4040. C. 4038. D. 4037.
Câu 30: Có bao nhiêu số nguyên của
m
thuộc đoạn
[ ]
100;100−
để đồ thị hàm số
(
)
2
1
2
y
xm xx
=
−−
có
đúng hai đường tiệm cân?
A.
200.
B.
2.
C.
199.
D.
0.
Câu 31: Tìm tất cả các giá trị của tham số thực
m
để đồ thị hàm số
2
2
32
xm
y
xx
+
=
−+
có đúng hai đường
tiệm cận.
A.
1m = −
B.
{1; 4}m ∈
C.
4m =
D.
{ 1; 4}m ∈− −
Câu 32: Có bao nhiêu giá trị nguyên của
m
để đồ thị hàm số
( )( )
22
63
6 39 6 1
x
y
mx x x mx
−
=
−+ + +
có đúng
một đường tiệm cận?
A.
0
. B.
2
. C.
1
. D. Vô số.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 188
Câu 33: Cho hàm số
(
)
2
1
24
x
x
yf
m
x
x
+
=
−+
=
. Tìm tất cả các giá trị của tham số
m
để đồ thị có ba đường
tiệm cận
A.
2m >
B.
2
5
2
m
m
<−
≠−
C.
2
2
5
2
m
m
m
>
<−
≠−
D.
2
2
m
m
<−
>
Câu 34: Biết rằng đồ thị của hàm số
( )
3 2017
3
n xn
y
xm
− +−
=
++
(
,
mn
là các số thực) nhận trục hoành làm
tiệm cận ngang và trục tung là tiệm cận đứng. Tính tổng
mn+
.
A.
0
B.
3−
C.
3
D.
6
Câu 35: Có bao nhiêu giá trị nguyên của tham số
m
để đồ thị hàm số
2
1
82
−
=
−+
x
y
mx x
có đúng bốn
đường tiệm cận?
A.
8
B.
6
C.
7
D. Vô số
Câu 36: Với giá trị nào của hàm số
m
để đồ thị hàm số
2
37
=− −+
y x mx x
có tiệm cạn ngang.
A.
1=m
B.
1= −m
C.
1= ±m
D. Không có
m
Câu 37: Cho hàm số
1
.
2
+
=
−
ax
y
bx
Tìm
,
ab
để đồ thị hàm số có
1=x
là tiệm cận đứng và
1
2
=y
là tiệm
cận ngang.
A.
1; 2=−=ab
. B.
4; 4= =ab
. C.
1; 2= =ab
. D.
1; 2=−=−
ab
.
Câu 38: Có bao nhiêu giá trị nguyên
[ ]
10;10m
∈−
sao cho đồ thị hàm số
2
1
26 3
x
y
x xm
−
=
+ −−
có hai
đường tiệm cận đứng?
A.
19
. B.
15
. C.
17
. D.
18
.
Câu 39: Có bao nhiêu giá trị nguyên của
m
để tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm
số
2
34
2
mx mx
y
x
++
=
+
bằng 3?
A.
4
. B.
2
. C. Vô số. D.
3
.
Câu 40: Tổng các giá trị của tham số
m
để đồ thị của hàm số
( )
22
1
21 2
x
y
x m xm
−
=
+ − +−
có đúng một
tiệm cận đứng.
A.
1
2
−
. B.
2
. C.
3
−
. D.
3
2
.
Câu 41: Cho hàm số
322
3
3 21
x
y
x mx m x m

. Có bao nhiêu giá trị nguyên thuộc đoạn
6;6
của tham số
m
để đồ thị hàm số có bốn đường tiệm cận?
A.
12
. B.
9
. C.
8
. D.
11
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 189
Câu 42: Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số
2
23++
=
−
x xm
y
xm
không có tiệm
cận đứng.
A.
1=m
. B.
1>m
. C.
1=m
và
0=m
. D.
0≠m
.
Câu 43: Có bao nhiêu giá trị nguyên của tham số thực
m
thuộc đoạn
2017;2017
để đồ thị hàm số
2
2
4
x
y
x xm

có hai tiệm cận đứng.
A.
2019
. B.
2021
. C.
2018
. D.
2020
.
Câu 44: Cho hàm số
()y fx
thỏa mãn
lim ( ) 2019
x
fx m

,
4
lim ( ) 2020
x
fx m

. Hỏi có tất cả bao
nhiêu giá trị của
m
để đồ thị của hàm số
()y fx
có duy nhất một tiệm cận ngang?
A. 4. B. 2. C. 3. D. 1.
Câu 45: Cho hàm số
(
)
2
1
21 2
y
x m x m xm
=

− ++ −

. Tìm tất cả các giá trị thực của tham số
m
để đồ
thị hàm số có 4 đường tiệm cận.
A.
01
1
2
m
m
<<
≠
. B.
1
1
2
m
m
<
≠
. C.
1m >
. D.
01
1
2
m
m
≤≤
≠
.
Câu 46: Có bao nhiêu giá trị nguyên của
m
để đồ thị hàm số
( )
(
)
22
63
6 39 6 1
x
y
mx x x mx
−
=
−+ + +
có đúng
1 đường tiệm cận?
A.
0.
B. 2. C.
1.
D. Vô số.
Câu 47: Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số:
2
1
y x mx
có tiệm cận ngang.
A.
0 1.
m
B.
1.m
C.
1.m

D.
1.m
Câu 48: Cho hàm số
2
2
24
x
y
mx x
−
=
−+
. Có tất cả bao nhiêu giá trị của tham số
m
để đồ thị hàm số có
đúng hai đường tiệm cận ?
A.
0
. B.
2
. C.
3
. D.
1
.
Câu 49: Gọi S là tập các giá trị nguyên của
m
sao cho đồ thị hàm số
2
2019
17 1
x
y
x mx
=
−−
có bốn đường
tiệm cận . Tính số phần tử của tập S.
A. Vô số B. 3 C. 5 D. 4
Câu 50: Gọi
S
là tập hợp tất cả các giá trị của tham số thực
m
sao cho đồ thị hàm số
3
3 42
()
11
x
fx
x mx x x m x
=
+ +− +++
nhận trục tung làm tiệm cận đứng. Khi đó tổng các phần
tử của
S
bằng
A.
1
2
. B.
1
2
−
. C.
1
3
. D.
1
3
−
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 190
Câu 51: Có bao nhiêu giá trị
m
nguyên thuộc khoảng
10;10
để đồ thị hàm số
( )1
2
xx m
y
x

có
đúng ba đường tiệm cận?
A.
12
. B.
11
. C.
0
. D.
10
.
Câu 52: Tìm số giá trị nguyên thuộc đoạn
[ ]
2019;2019−
của tham số
m
để đồ thị hàm số
2
3
x
y
x xm
−
=
+−
có đúng hai đường tiệm cận.
A.
2007
. B.
2010
. C.
2009
. D.
2008
.
Câu 53: Cho hàm số
2
1
23
x
y
mx x
−
=
−+
. Có tất cả bao nhiêu giá trị
m
để đồ thị hàm số có đúng hai đường
tiệm cận.
A. 2 B. 3 C. 0 D. 1
Câu 54: Cho hàm số
32
1
31
y
x xm
=
− +−
với
m
là tham số. Tìm tất cả các giá trị của
m
để đồ thị hàm
số đã cho có
4
đường thẳng tiệm cận.
A.
15m<<
. B.
12m−< <
. C.
1m <
hoặc
5
m >
. D.
2m >
hoặc
1m
<−
.
Câu 55: Hàm số
( )
2
31
1
x ax b
y
x
++ +
=
−
không có tiệm cận đứng. Khi đó hiệu
ab−
bằng:
A.
1
2
.
B.
3
4
−
. C.
5
4
−
.
D.
1
2
−
.
Câu 56: Có bao nhiêu giá trị nguyên của tham để
m
đồ thị hàm số
2
2016 2017 24 7xx
y
xm
−+ + −
=
−
có
tiệm cận đứng?
A. vô số.
B.
2
. C.
2017
D.
2019
.
Câu 57: Gọi
S
là tập hợp tất cả các giá trị của tham số thực
m
sao cho đồ thị hàm số
3
3 42
()
11
x
fx
x mx x x m x
=
+ +− +++
nhận trục tung làm tiệm cận đứng. Khi đó tổng các phần
tử của
S
bằng
A.
1
2
. B.
1
2
−
. C.
1
3
. D.
1
3
−
.
Câu 58: Có bao nhiêu giá trị
m
nguyên thuộc khoảng
10;10
để đồ thị hàm số
( )1
2
xx m
y
x

có
đúng ba đường tiệm cận?
A.
12
. B.
11
. C.
0
. D.
10
.
Câu 59: Tìm tất cả các giá trị thực của
m
sao cho đồ thị hàm số
1
1
2
+
+
=
x
mx
y
có đúng một đường tiệm
cận.
A.
01 <≤− m
. B.
01 ≤≤− m
. C.
1−<m
. D.
0>
m
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 137
BÀI 4. ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
DẠNG. XÁC ĐỊNH ĐƯỜNG TIỆM CẬN THÔNG QUA BẢNG BIẾN THIÊN, ĐỒ THỊ
1.1.1 Đường tiệm cận ngang
Cho hàm số
=
y fx()
xác định trên một khoảng vô hạn. Đường thẳng
yy
0
=
là đường tiệm
cận ngang của đồ thị hàm số
=
y fx
()
nếu ít nhất một trong các điều kiện sau được thỏa mãn:
xx
fx y fx y
00
lim ( ) , lim ( )
→+∞ →−∞
= =
1.1.2 Đường tiệm cận đứng
Đường thẳng
=xx
0
được gọi là đường tiệm cận đứng của đồ thị hàm số
()
y fx
=
nếu ít
nhất một trong các điều kiện sau được thỏa mãn:
+−
→→
= +∞ = −∞
xx xx
fx fx
00
lim ( ) , lim ( ) ,
00
lim ( ) , lim ( )
xx xx
fx fx
+−
→→
= −∞ = +∞
Lưu ý: Với đồ thị hàm phân thức dạng
( )
+
= ≠ −≠
+
ax b
y c ad bc
cx d
0; 0
luôn có tiệm cận ngang là
=
a
y
c
và tiệm cận đứng
= −
d
x
c
.
Câu 1: Cho hàm số có bảng biến thiên như hình sau
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
( )
y fx=
là
A.
3
. B.
2
. C.
4
. D.
1
.
Lời giải
Vì
lim 4, lim 1
xx
yy
→−∞ →+∞
= =−⇒
Đồ thị hàm số có hai tiệm cận ngang là
1y = −
và
4y =
.
11
lim , lim
xx
yy
−+
→− →−
= +∞ = −∞ ⇒
Đồ thị hàm số có tiệm cận đứng
1x = −
.
11
lim , lim
xx
yy
−+
→→
= −∞ = +∞ ⇒
Đồ thị hàm số có tiệm cận đứng
1x =
.
Nên đồ thị hàm số có 4 đường tiệm cận.
CHƯƠNG
I
ỨNG DỤNG ĐẠO HÀM
ĐỂ KHẢO SÁT HÀM SỐ
BÀI TẬP TRẮC NGHIỆM
III
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 138
Câu 2: Cho hàm số
( )
fx
có bảng biến thiên như sau:
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là:
A.
4
. B.
3
. C.
1
. D.
2
.
Lời giải
(
)
lim 3
→+∞
=
x
fx
ta được tiệm cận ngang
3=y
( )
( )
2
lim
−
→−
= +∞
x
fx
ta được tiệm cận đứng
2= −x
Câu 3: Cho hàm số
()
=y fx
có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
4
B.
2
C.
3
D.
1
Lời giải
Từ bảng biến thiên ta có:
+ Tiệm cận ngang
5y = −
+ Tiệm cận đứng
2.x =
Câu 4: Cho đồ thị hàm số
(
)
y fx=
như hình bên. Khẳng định nào sau đây là đúng?
x
y
O
1
1−
A. Đồ thị hàm số có tiệm cận đứng
0
x =
, tiệm cận ngang
1y =
.
B. Hàm số có hai cực trị.
C. Đồ thị hàm số chỉ có một đường tiệm cận.
D. Hàm số đồng biến trong khoảng
( )
;0−∞
và
( )
0;+∞
.
Câu 5: Cho hàmsố
()fx
có bảng biến thiên như sau
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 139
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
4
. B.
1
. C.
3
. D.
2
.
Lời giải
Dựa vào bảng biến thiên của hàm số ta có:
lim ( ) 0 0
x
fx y
→−∞
=⇒=
là một tiệm cận ngang
lim ( ) 5 5
x
fx y
→+∞
=⇒=
là một tiệm cận ngang
1
lim ( ) 1
x
fx x
−
→
= −∞ ⇒ =
là một tiệm cận đứng
Vậy đồ thị hàm số có tổng số đường tiệm cận là 3.
Câu 6: Cho hàm số
()y fx=
có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
4
. B.
1
. C.
3
. D.
2
.
Lời giải
Dựa vào bảng biến thiên của hàm số ta có:
lim ( ) 2 2
x
fx y
→±∞
=⇒=
là một tiệm cận ngang
1
lim ( ) 1
x
fx x
+
→
= −∞ ⇒ =
là một tiệm cận đứng
Vậy đồ thị hàm số có tổng số đường tiệm cận là
2
.
Câu 7: Cho hàm số
(
)
y fx=
có bảng biến thiên như sau
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho bằng
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 140
A.
2
. B.
1
. C.
0
. D.
3
.
Lời giải
Ta có
2
lim 2
x
yx
+
→−
= −∞ ⇒ = −
là tiệm cận đứng của đồ thị hàm số đã cho.
0
lim 0
x
yx
−
→
= +∞ ⇒ =
là tiệm cận đứng của đồ thị hàm số đã cho.
lim 0 0
x
yy
→+∞
=⇒=
là tiệm cận ngang của đồ thị hàm số đã cho.
Vậy đồ thị hàm số đã cho có tổng đường tiệm cận đứng và tiệm cận ngang là
3
.
Câu 8: Cho hàm số
( )
y fx=
liên tục trên
{ }
\1
có bảng biến thiên như hình vẽ. Tổng số đường tiệm
cận đứng và đường tiệm cận ngang của đồ thị hàm số
( )
y fx=
A.
1
. B.
4
. C.
2
. D.
3.
Lời giải
Chọn D
Do
11
lim ; lim
xx
y
+−
→→
= −∞ = +∞ ⇒
TCĐ:
1.x =
lim 1; lim 1
xx
yy
→+∞ →−∞
=−=⇒
đồ thị có 2 tiệm cận ngang là
1y = ±
Vậy, đồ thị hàm số đã cho có tổng số TCĐ và TCN là 3.
Câu 9: Cho hàm số
y fx
có bảng biến như sau:
Số đường tiệm cận của đồ thị hàm số là:
A. 3 B. 1. C. 4. D. 2.
Lời giải
Chọn A
Từ bảng biến thiên của hàm số ta có:
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 141
+
lim 0; lim 0
xx
yy
 

đồ thị hàm số nhận đường thẳng
0y
là tiệm cận ngang.
+
33
lim ; lim
xx
y

 
 
đồ thị hàm số nhận đường thẳng
3x 
là tiệm cận đứng.
+
33
lim ; lim
xx
y


 
đồ thị hàm số nhận đường thẳng
3
x
là tiệm cận đứng.
Vậy số đường tiệm cận của đồ thị hàm số là 3.
Câu 10: Cho hàm số
( )
y fx=
có bảng biến thiên như sau
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A.
4
. B.
2
. C.
3
. D.
1
.
Lời giải
Chọn C
Ta có:
lim ( ) 0
x
fx
→−∞
=
nên đường thẳng
0y =
là đường tiệm cận ngang của đồ thị hàm số
( )
y fx=
.
lim ( )
x
fx
→+∞
= −∞
nên đồ thị hàm số
( )
y fx=
không có tiệm cận ngang khi
x → +∞
.
2
lim ( )
x
fx
+
→−
= +∞
,
2
lim ( )
x
fx
−
→−
= −∞
nên đường thẳng
2x = −
là đường tiệm cận đứng của đồ
thị hàm số
( )
y fx=
.
2
lim ( )
x
fx
+
→
= +∞
,
2
lim ( )
x
fx
−
→
= −∞
nên đường thẳng
2x =
là đường tiệm cận đứng của đồ thị
hàm số
( )
y fx=
.
Vậy tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là 3 tiệm cận.
DẠNG 2. XÁC ĐỊNH ĐƯỜNG TIỆM CẬN ĐỒ THỊ HÀM SỐ THÔNG HÀM SỐ CHO TRƯỚC
1 Đường tiệm cận ngang
Cho hàm số
(
)
y fx=
có TXD:
D
Điều kiện cần:
D
phải chứa
+∞
hoặc
−∞
Điều kiện đủ:
Dạng 1.
()
()
()
Px
y fx
Qx
= =
.
Nếu
( ) ( )
:degP x degQ x>
thì không có tiệm cận ngang
Nếu
( ) (
)
:degP x degQ x>
TCN
0y =
Nếu
( ) ( )
:
degP x degQ x=
yk=
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 142
Dạng 2:
()y fx u v= = −
: Nhân liên hợp
2
()
uv
y fx
uv
−
⇒= =
+
2 Đường tiệm cận đứng
Cho hàm số
(
)
(
)
Px
y
Qx
=
có TXD:
D
Đkiện cần: giải
(
)
0
0Qx x x
=⇔=
là TCĐ khi thỏa mãn đk đủ
Đkiện đủ:
Đkiện 1:
0
x
làm cho
()Px
và
()Qx
xác định.
Đkiện 2: -
0
x
không phải nghiêm
0
()Px x x⇒=
là TCĐ
-
0
x
là nghiêm
0
()
Px x x
⇒=
là TCĐ nếu
0
lim ( )
xx
fx
→
= ∞
Câu 11: Đồ thị hàm số
2
51 1
2
xx
y
xx

có tất cả bao nhiêu đường tiệm cận?
A.
3
B.
0
C.
2
D.
1
Lời giải
Chọn D
Tập xác định:
1; \ 0D 
.
•
lim
x
y

2
51 1
lim
2
x
xx
xx


2 34
51 1 1
lim
2
1
x
x
x xx
x


0
0y
là đường tiệm cận ngang
của đồ thị hàm số.
•
0
lim
x
y
2
0
51 1
lim
2
x
xx
xx

2
2
0
51 1
lim
25 1 1
x
xx
x xx x


2
2
0
25 9
lim
25 1 1
x
xx
x xx x

0
25 9
lim
25 1 1
x
x
xx x

9
4
0x
không là đường tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có tất cả
1
đường tiệm cận.
Câu 12: Tìm tất cả các tiệm cận đứng của đồ thị hàm số
2
2
21 3
56
−− + +
=
−+
x xx
y
xx
.
A.
3=x
và
2=x
. B.
3=x
. C.
3= −x
và
2= −x
. D.
3= −x
.
Lời giải
Chọn B
Tập xác định
{
}
2;3\= D
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 143
( )
( )
( )
(
)
( )
( )
( )
(
)
2
2
2
2
22
22
2
2
22
2
21 3
21 3
lim lim
56
5 62 1 3
21 3
lim
5 62 1 3
xx
x
x xx
x xx
xx
x x x xx
x xx
x x x xx
++
+
→→
→
− − ++
−− + +
=
−+
− + −+ + +
− − ++
=
− + −+ + +
(
)
(
)
2
2
(3 1) 7
lim
6
32 1 3
+
→
+
= = −
− −+ + +
x
x
x x xx
Tương tự
2
2
2
21 3 7
lim
56 6
−
→
−− + +
= −
−+
x
x xx
xx
. Suy ra đường thẳng
2=x
không là tiệm cận đứng
của đồ thị hàm số đã cho.
22
22
33
21 3 21 3
lim ; lim
56 56
+−
→→
−− + + −− + +
= +∞ = −∞
−+ −+
xx
x xx x xx
xx xx
. Suy ra đường thẳng
3=x
là tiệm
cận đứng của đồ thị hàm số đã cho.
Câu 13: Số tiệm cận đứng của đồ thị hàm số
2
42x
y
xx
+−
=
+
là
A.
3
. B.
0
. C.
1
. D.
2
.
Lời giải
TXĐ:
[
) { }
4; \ 1; 0
D = − +∞ −
.
Ta có:
( ) ( )
2
11
42
lim lim
xx
x
y
xx
++
→− →−
+−
= = −∞
+
Nên đường thẳng
1x = −
là một đường tiệm cận đứng của đồ thị hàm số đã cho.
( )
( )
( )
( )
( )
( )
2
00 0 0
42 42
42 1 1
lim lim lim lim
4
1 42 1 42
xx x x
xx
x
y
xx
xxx xx
→→ → →
+− ++
+−
= = = =
+
+ ++ + ++
Nên đường thẳng
0x
=
không là tiệm cận đứng của đồ thị hàm số đã cho.
Vậy đồ thị hàm số đã cho có một tiệm cận đứng
1x = −
.
Câu 14: Đồ thị hàm số
( )
2
1
1
x
fx
x
+
=
−
có tất cả bao nhiêu tiệm cận đứng và tiệm cận ngang?
A.
4
. B.
3
. C.
1
. D.
2
.
Lờigiải
Tập xác định của hàm số
( ) ( )
; 1 1;D = −∞ − ∪ +∞
TH1:
1 10xx<− ⇒ + <
. Khi đó
( )
( )
( )( )
2
2
1
11
1
11
1
x
xx
fx
x
xx
x
−+
++
= = = −
−
−+
−
.
Suy ra hàm số TCN
1y = −
, không có TCĐ.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 144
TH2:
1 10xx>⇒ +>
. Khi đó
( )
( )
( )( )
2
2
1
11
1
11
1
x
xx
fx
x
xx
x
+
++
= = =
−
−+
−
.
Suy ra hàm số TCN
1y =
, TCĐ
1x
=
.
Vậy hàm số có 2 TCN và 1 TCN
Câu 15: Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
( )
462
2
xx
y
x
+−
=
+
là?
A.
1
B.
3
C.
2
D.
4
Lời giải
Chọn C
( )
62
4
462
lim lim 2
2
2
1
xx
xx
xx
x
x
→+∞ →+∞
+−
+−
= =
+
+
(
)
62
4
462
lim lim 2
2
2
1
xx
xx
xx
x
x
→−∞ →−∞
− +−
+−
= = −
+
+
( )
( )( )
( ) ( )
( )
( )
22 2
462
24 2
42 5
lim lim lim
22
462
2 462
xx x
xx
xx
x
x
xx
x xx
±± ±
→− →− →−
+−
+−
−−
= = =
+
++
+ ++
Vậy hàm số có hai tiệm cận ngang
2y = ±
.
Câu 16: Cho hàm số
2
42
23
32
xx
y
xx
++
=
−+
. Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?
A.
4
. B.
5
. C.
3
. D.
6
.
Lời giải
Điều kiện:
(
)
( )
( )
; 2 1;1 2 ;
x ∈ −∞ − ∪ − ∪ +∞
.
Do
lim lim
xx
yy
→+∞ →−∞
=
2
42
23
lim
32
x
xx
xx
→±∞
++
=
−+
2
24
23
1
lim 1
32
1
x
xx
xx
→±∞
++
= =
−+
1y⇒=
là đường tiệm cận
ngang của đồ thị hàm số.
Có
1
lim
x
y
−
→
= +∞
nên đường thẳng
1x =
là đường tiệm cận đứng.
Có
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
(
)
( )
( )
( )
11 1
12
12
lim lim lim 0
1 21 2 21 2
xx x
xx
xx
y
xx xx x xx
++ +
→− →− →−
++
++
= = =
++ −− + −−
nên
đường thẳng
1x = −
không là đường tiệm cận đứng.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 145
Có
(
)
2
lim
x
y
+
→
= +∞
nên đường thẳng
2
x
=
là đường tiệm cận đứng.
Có
(
)
2
lim
x
y
−
→−
= +∞
nên đường thẳng
2x = −
là đường tiệm cận đứng.
Vậy đồ thị hàm số có
4
đường tiệm cận (
1
tiệm cận ngang,
3
tiệm cận đứng).
Câu 17: Hàm số
2
3
1x xx
y
xx
+ ++
=
+
có bao nhiêu đường tiệm cận?
A.
1
B.
3
C.
2
D.
4
Lời giải
Chọn C
TXĐ:
{ }
\0D =
2
2
2
3
2
2
11
11
11
11
1
lim lim lim . 0
1
1
1
1
xx x
x
xx
xx
y
x
x
x
x
→−∞ →−∞ →−∞


− ++

− ++



= = =


+
+




2
2
2
3
2
2
11
11
11
11
1
lim lim lim . 0
1
1
1
1
xx x
x
xx
xx
y
x
x
x
x
→+∞ →+∞ →+∞


+ ++

+ ++



= = =


+
+




⇒
TCN:
0y =
0
lim
x
y
+
→
= +∞
⇒
TCĐ:
0x =
.
Câu 18: Số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
21
32
−+
=
−+
x
y
xx
là
A.
4
B.
1
C.
3
D.
2
Lời giải
Chọn D
Đkxđ:
2
20
2
2
2, 1
3 20
−≥
≥
⇔ ⇔>

≠≠
− +≠
x
x
x
xx
xx
Ta có:
2
2
21
lim
32
+
→

−+
= +∞


−+

x
x
xx
nên đường thẳng
2=x
là tiệm cận đứng của đồ thị hàm số.
2
21
lim 0
32
→+∞

−+
=


−+

x
x
xx
nên đường thẳng
0=y
là tiệm cận ngang của đồ thị hàm số.
Câu 19: Cho hàm số
2
3
5 6 12
4 31
xx
y
xx
++−
=
−−
có đồ thị
( )
C
. Mệnh đề nào sau đây là đúng?
A. Đồ thị
( )
C
của hàm số không có tiệm cận.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 146
B. Đồ thị
(
)
C
của hàm số chỉ có một tiệm cận ngang
0y =
.
C. Đồ thị
( )
C
của hàm số có một tiệm cận ngang
0y =
và hai tiệm cận đứng
1
1;
2
xx
= = −
.
D. Đồ thị
( )
C
của hàm số chỉ có một tiệm cận ngang
0y =
và một tiện cận đứng
1x =
Lời giải
Chọn D
TXĐ:
1
\ 1;
2
DR








Ta có:
11
lim ; lim
xx
yy


 
Đồ thị hàm số có một TCĐ là
1x
lim 0
x
y

Đồ thị hàm số có một TCN là
0y
Câu 20: Đồ thị hàm số
2
2
31
x xx
y
x
+−
=
+
có tất cả bao nhiêu đường tiệm cận?
A.
2
. B.
3
. C.
0
. D.
1
.
Lời giải
Chọn A
Xét hàm số
2
2
31
x xx
y
x
+−
=
+
có tập xác định
(
] [
)
1
; 0 1; \
3
D

= −∞ ∪ +∞ −


.
Ta có
2
1
3
2
lim
31
x
x xx
x
→−
+−
+
( )
(
)
2
1
2
3
3
lim
3 12
x
xx
x x xx
→−
+
=
+ −−
1
2
3
lim
2
x
x
x xx
→−
=
−−
1
4
=
;
2
0
2
lim 0
31
x
x xx
x
−
→
+−
=
+
và
2
1
21
lim
31 2
x
x xx
x
+
→
+−
=
+
nên đồ thị không có tiệm cận đứng.
2
11
33
11
2 1 21
21
lim lim lim
1
31 31 3
3
x
xx
xx
x xx
xx
xx
x
→−∞
→− →−
− − −−
+−
= = =
++
+
,
và
2
11
33
11
2 1 21
2
lim lim lim 1
1
31 31
3
x
xx
xx
x xx
xx
xx
x
→+∞
→− →−
+ − +−
+−
= = =
++
+
nên đồ thị có hai tiệm cận ngang
là
1
3
y =
và
1y =
.
Vậy đồ thị hàm số có tất cả hai đường tiệm cận.
Câu 21: Đồ thị hàm số
2
2
14
23
x
y
xx


có số đường tiệm cận đứng là
m
và số đường tiệm cận ngang là
n
. Giá trị của
mn
là
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 147
A.
1
B.
2
C.
3
D.
0
Lời giải
Chọn A
2; 2 \ 1D 
2
2
11
14
lim lim ;
23
xx
x
y
xx

 



2
2
11
14
lim lim
23
xx
x
y
xx

 



1x 
là tiệm cận đứng.
Đồ thị hàm số không có đường tiệm cận ngang.
Vậy
1mn
.
Câu 22: Gọi
,nd
lần lượt là số đường tiệm cận ngang và số tiệm cận đứng của đồ thị hàm số
1
1
x
y
xx
. Khẳng định nào sau đây là đúng?
A.
0, 2nd
. B.
1nd
. C.
1, 2nd
. D.
0, 1nd
.
Lời giải
Chọn A
Tập xác định:
0;1D
.
Từ tập xác định suy ra đồ thị hàm số không có tiệm cận ngang.
0n
.
+)
00 0
11
lim lim lim
11
xx x
x
y
x x xx





+)
11 1
11
lim lim lim
11
xx x
x
y
x x xx





Suy ra đồ thị hàm số có hai tiệm cận đứng,
2d
.
Câu 23: Đồ thị hàm số
2
51 1
2
xx
y
xx
+− +
=
−
có tất cả bao nhiêu đường tiệm cận?
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn C
Tập xác định của hàm số là
[
) ( )
1;0 2;D = − ∪ +∞
. Ta có
( )
( )
( )
( )
2
2
00 0
25 9 25 9 9
lim lim lim
4
251 1 251 1
xx x
xx x
y
xxxx xxx
→− →− →−
++
= = = −
− ++ + − ++ +
.
2
lim
x
y
→+
= +∞
.
2 34
51 1 1
lim lim 0
2
1
xx
xx x x
y
x
→+∞ →+∞
+− +
= =
−
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 148
Vậy đồ thị của hàm số có hai đường tiệm cận có phương trình
2x =
và
0y =
.
Câu 24: Tìm số đường tiệm cận của đồ thị hàm số
1
43 1 3 5
x
y
xx
−
=
+− −
.
A.
2
. B.
3
. C.
1
. D.
0
.
Lời giải
Chọn A
Tập xác định:
{ }
1
; \1
3
D

= − +∞

+ Ta có:
( )
( )
( )
( )
2
11 1
1 43 1 3 5
1 43 1 3 5
lim lim lim
91
43 1 3 5
91
xx x
x xx
x xx
x
xx
x
++ +
→→ →
− ++ +
− ++ +
= = = −∞
−−
+− −
−−
do đó đường thẳng
1x
=
là đường tiệm cận đứng của đồ thị hàm số.
+
2
1
1
11
lim lim
3
43 1 3 5 3 1 5
43
xx
x
x
xx
xx x
→+∞ →+∞
−
−
= = −
+− −
+ −−
do đó đường thẳng
1
3
y = −
là đường
tiệm cận ngang của đồ thị hàm số. Vậy đồ thị hàm số có 2 đường tiệm cận.
Câu 25: Cho hàm số
2
42
23
32
xx
y
xx
++
=
−+
. Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?
A.
4
. B.
5
. C.
3
. D.
6
.
Lời giải
Chọn B
□ Tập xác định
( )
(
)
(
)
; 2 1;1 2 ;D = −∞ − ∪ − ∪ +∞
.
□
( )
( )
( ) ( )
11
22
lim lim lim lim
xx
xx
y y yy
− + +−
→− →
→− →
= = = = +∞
.
⇒
Các đường tiệm cận đứng của đồ thị là
2x
= ±
,
1x = ±
.
□
lim lim 1
xx
yy
→−∞ →+∞
= =
⇒
đồ thị có một tiệm cận ngang
1y =
.
Câu 26: Đồ thị hàm số
2
58
3
x
y
xx
−
=
−
có bao nhiêu đường tiệm cận?
A. 2. B. 4. C. 1. D. 3.
Lời giải
Chọn B
Tập xác định
(
) ( )
; 0 3;D = −∞ ∪ +∞
2
8
5
58 58
lim lim lim lim 5
33
3
11
xx x x
xx
x
y
xx
x
xx
→+∞ →+∞ →+∞ →+∞
−
−−
= = = =
−
−−
⇒
Đường thẳng
5y =
là tiệm cận ngang của đồ thị hàm số.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 149
2
8
5
58 58
lim lim lim lim 5
33
3
11
xx x x
xx
x
y
xx
x
xx
→−∞ →−∞ →−∞ →−∞
−
−−
= = = = −
−
− − −−
⇒
Đường thẳng
5
y
= −
là tiệm cận ngang của đồ thị hàm số.
2
00
58
lim lim
3
xx
x
y
xx
−−
→→
−
= = −∞
−
Dạng 2:
()y fx u v= = −
: Nhân liên hợp
2
()
uv
y fx
uv
−
⇒= =
+
2 Đường tiệm cận đứng
Cho hàm số
(
)
( )
Px
y
Qx
=
có TXD:
D
Đkiện cần: giải
( )
0
0Qx x x=⇔=
là TCĐ khi thỏa mãn đk đủ
Đkiện đủ:
Đkiện 1:
0
x
làm cho
()Px
và
()Qx
xác định.
Đkiện 2: -
0
x
không phải nghiêm
0
()
Px x x⇒=
là TCĐ
-
0
x
là nghiêm
0
()Px x x⇒=
là TCĐ nếu
0
lim ( )
xx
fx
→
= ∞
Câu 27: Gọi
S
là tập hợp các giá trị nguyên
m
để đồ thị hàm số
2
2
62
+
=
−+
x
y
x xm
có hai đường tiệm
cận đứng. Số phần tử của
S
là
A. vô số. B.
12
. C.
14
. D.
13
.
Lời giải
Chọn B
Điều kiện xác định
2
20
62 0
+≥
−+ >
x
x xm
.
Để đồ thị hàm số có hai đường tiệm cận đứng thì phương trình
2
62 0−+ =x xm
có hai nghiệm
phân biệt
12
,xx
lớn hơn
2−
(
) (
)
12
2
9
92 0
9
2
2 32
2
8
4 12 2 0
2 622 0
<
′
∆= − >
<

⇔ + >− ⇔ >− ⇔


>−
++ >
− − ⋅− + >
m
m
m
xx
m
m
m
.
Do đó tập
{
}
7; 6; 5;...;4=−−−
S
có
12
giá trị.
Câu 28: Có bao nhiêu giá trị nguyên dương của tham số
m
để đồ thị hàm số
2
1
8
x
y
x xm
−
=
−+
có 3 đường
tiệm cận?
A.
14
. B.
8
. C.
15
. D.
16
.
Lời giải
Chọn A
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 150
Ta có
22
11
lim lim 0
88
xx
xx
x xm x xm
→−∞ →+∞
−−
= =
−+ −+
nên hàm số có một tiện cận ngang
0y
=
.
Hàm số có 3 đường tiệm cận khi và chỉ khi hàm số có hai đường tiệm cận đứng
⇔
phương
trình
2
80x xm−+=
có hai nghiệm phân biệt khác
1
Δ 16 0 16
70 7
mm
mm
′
= −> <

⇔⇔

−≠ ≠

.
Kết hợp với điều kiện
m
nguyên dương ta có
{ }
1;2;3;...;6;8;...;15m ∈
. Vậy có
14
giá trị của
m
thỏa mãn đề bài.
Câu 29: Cho hàm số
( )
322
3
3 21
x
y
x mx m x m
−
=
− + +−
. Có bao nhiêu giá trị nguyên của tham số
m
thuộc
đoạn
[ ]
2020;2020
−
để đồ thị hàm số có 4 đường tiệm cận?
A. 4039. B. 4040. C. 4038. D. 4037
.
Lời giải
Chọn D
Ta có
lim 0, lim 0
xx
yy
→+∞ →−∞
= =
⇒
đồ thị hàm số đã cho có 1 tiệm cận ngang.
Do đó đồ thị hàm số đã cho có 4 đường tiệm cận khi và chỉ khi nó có 3 tiệm cận đứng
( )
*
.
Có
( )
( )
( )
322 2
3 21 21x mx m x m x m x mx− + + −= − − +
( )
( )
322
2
3 21 0
2 10 2
xm
x mx m x m
x mx
=
− + + −=⇔
− +=
( )
*
⇔
( )
322
3 21 0x mx m x m− + + −=
có 3 nghiệm phân biệt khác
3
.
⇔
3m ≠
và
( )
2
có 2 nghiệm phân biệt khác
m
và khác 3.
2
2
2
2
3
5
3,
2. 1 0
3
1
3 2 .3 1 0
1
10
m
mm
m mm
m
m
m
m
≠
≠≠
− +≠

⇔⇔

>
− +≠


<−
′
∆= −>
Do đó tập tất cả giá trị nguyên của
m
thỏa ycbt là
{ }
2020; 2019;...; 2;2;4;5;...;2020−− −
.
Vậy có 4037 giá trị
m
thỏa ycbt.
Câu 30: Có bao nhiêu số nguyên của
m
thuộc đoạn
[ ]
100;100−
để đồ thị hàm số
( )
2
1
2
y
xm xx
=
−−
có đúng hai đường tiệm cân?
A.
200.
B.
2.
C.
199.
D.
0.
Lời giải
Chọn A
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 151
Ta có điều kiện xác định là
( )
0; 2
xm
x
≠
∈
, khi đó đồ thị hàm số sẽ không có tiệm cận ngang.
Ta có
02
lim , lim
xx
yy
+−
→→
=∞=∞
Suy ra
0, 2xx= =
là hai đường tiệm cận đứng
Vậy để đồ thị hàm số có đúng hai đường tiệm cận thì
0
2
m
m
≤
≥
, theo bài
m
thuộc đoạn
[ ]
100;100−
. Vậy có 200 số nguyên của
m
thỏa mãn đầu bài.
Câu 31: Tìm tất cả các giá trị của tham số thực
m
để đồ thị hàm số
2
2
32
xm
y
xx
+
=
−+
có đúng hai đường
tiệm cận.
A.
1m = −
B.
{1; 4}m ∈
C.
4m =
D.
{ 1; 4}m ∈− −
Lời giải
(
)( )
22
2
32 1 2
xm xm
y
xx x x
++
= =
−+ − −
.
lim 1
x
y
→±∞
= ⇒
1y =
là đường tiệm cận ngang.
Đồ thị hàm số
2
2
32
xm
y
xx
+
=
−+
có đúng hai đường tiệm cận
⇔
đồ thị hàm số có đúng một tiệm
cận đứng
⇔
pt
2
0xm+=
nhận nghiệm
1x
=
hoặc
2
x =
.
Khi đó:
1
4
m
m
= −
= −
.
Với
1m = −
có một tiệm cận đứng
2x =
.
Với
4m
= −
có một tiệm cận đứng
1x
=
.
Vậy
{ 1; 4}m ∈− −
.
Câu 32: Có bao nhiêu giá trị nguyên của
m
để đồ thị hàm số
( )
( )
22
63
6 39 6 1
x
y
mx x x mx
−
=
−+ + +
có đúng
một đường tiệm cận?
A.
0
. B.
2
. C.
1
. D. Vô số.
Lời giải
Kí hiệu
( )
C
là đồ thị hàm số
( )( )
22
63
6 39 6 1
x
y
mx x x mx
−
=
−+ + +
.
* Trường hợp 1:
0m =
.
Khi đó
( )
( )
2
63
6 39 1
x
y
xx
−
=
−+ +
. Đồ thị hàm số có đúng một đường tiệm cận ngang
0y =
.
Do đó chọn
0m =
.
* Trường hợp 2:
0m ≠
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 152
Xét phương trình
( )( )
(
)
22
6 3 9 6 1 01mx x x mx− + + +=
Nhận thấy:
(
)
C
luôn có một đường tiệm cận ngang
0y =
và phương trình
(
)
1
không thể có
duy nhất một nghiệm đơn với mọi
m
.
Do đó
( )
C
có đúng một đường tiệm cận khi và chỉ khi
( )
C
không có tiệm cận đứng
( )
1⇔
vô
nghiệm
2
93 0
9 90
m
m
−<
⇔
−<
3
11
m
m
>
⇔
−< <
, .
Kết hợp các trường hợp ta được
0m =
.
Câu 33: Cho hàm số
(
)
2
1
24
x
x
yf
m
x
x
+
=
−+
=
. Tìm tất cả các giá trị của tham số
m
để đồ thị có ba
đường tiệm cận
A.
2m >
B.
2
5
2
m
m
<−
≠−
C.
2
2
5
2
m
m
m
>
<−
≠−
D.
2
2
m
m
<−
>
Lời giải
Chọn C
Để đồ thị có ba đường tiệm cận thì
2
2 40x mx− +=
có hai nghiệm phân biệt
1≠−
( ) ( )
2
2
0
2
1 2 1 40
5
2
m
m
m
m
>
∆>

<−
⇔⇔

− − −+≠
≠− ⋅
Câu 34: Biết rằng đồ thị của hàm số
( )
3 2017
3
n xn
y
xm
− +−
=
++
(
,mn
là các số thực) nhận trục hoành làm
tiệm cận ngang và trục tung là tiệm cận đứng. Tính tổng
mn+
.
A.
0
B.
3−
C.
3
D.
6
Lờigiải
Chọn A
Theo công thức tìm nhanh tiệm cận của đồ thị hàm số
ax b
y
cx d
=
+
+
ta có
Đồ thị hàm số nhận
30
d
xm
c
=− =−−=
làm TCĐ
3m⇒=−
Đồ thị hàm số nhận
30
a
yn
c
= =−=
làm TCN
3n⇒=
.
Vậy
0mn+=
.
Câu 35: Có bao nhiêu giá trị nguyên của tham số
m
để đồ thị hàm số
2
1
82
−
=
−+
x
y
mx x
có đúng bốn
đường tiệm cận?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 153
A.
8
B.
6
C.
7
D. Vô số
Lời giải
TH1:
0<m
suy ra tập xác định của hàm số là
( )
12
;=D xx
, (
12
;xx
là nghiệm của phương trình
2
8 20− +=mx x
). Do đó
0<m
không thỏa yêu cầu của bài toán.
TH2:
1
0
82
−
==>=
−+
x
my
x
suy ra tập xác định của hàm số là
( )
;4= −∞
D
.
4
lim ; lim
−
→−∞
→
= −∞ = −∞
x
x
yy
. Khi đó ta có
4= −x
là đường tiệm cận đứng của đồ thị hàm số.
Do đó
0
=m
không thỏa yêu cầu của bài toán
TH3:
0>
m
suy ra tập xác định của hàm số là
( ) ( )
12
;;= −∞ ∪ +∞D xx
(
12
;xx
là nghiệm của
phương trình
2
8 20− +=mx x
). Do đó đồ thị hàm số có bốn đường tiệm cận khi phương trình
2
8 20− +=mx x
có hai nghiệm phân biệt khác
{ }
16 2 0 8
1 0; 0; 1; 2;3; 4;5;7
820 6
−> <


⇔> ∈⇔> ∈⇒=


−+≠ ≠


mm
mm mm m
mm
. Suy ra có tất cả
6
giá trị nguyên của
tham số
m
thỏa mãn yêu cầu của bài toán.
Câu 36: Với giá trị nào của hàm số
m
để đồ thị hàm số
2
37=− −+y x mx x
có tiệm cạn ngang.
A.
1=m
B.
1= −m
C.
1= ±
m
D. Không có
m
Lời giải
Chọn A
Đồ thị hàm số có tiệm cận ngang
⇒
Hàm số xác định trên một trong các miền
( ) (
]
(
)
;, ;,,−∞ −∞ +∞a aa
hoặc
[
)
;
+∞a
0≥m
TH1:
0 3 7, lim
→±∞
= ⇒ = − − + = ±∞
x
m yx x y
đồ thị không có tiệm cận ngang
TH2:
2
0, 3 7
> =− −+m y x mx x
Khi
2
37 3
lim lim
2
→+∞
→+∞

= − −+ =



x
x
y x xm
xx
đồ thị hàm số có tiệm cận ngang khi và chỉ khi
1=m
.
Vậy
1=m
Cách trắc nghiệm:
Thay
1=m
(
)
22
3
37 lim 37
2
→+∞
⇒=− −+⇒ − −+=
x
yxx x xx x
đồ thị hàm số có tiệm cận
ngang
(
)
2
lim 3 7
→−∞
⇒ − − + = −∞
x
xx x
không có tiệm cận ngang.
Thay
1= −m
(
)
22
37 lim 37
→+∞
⇒ =−− − +⇒ −− − +
x
yx xx x xx
không xác định.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 154
(
)
2
lim 3 7
→−∞
−− − +
x
x xx
không xác định.
Vậy
1
=m
Câu 37: Cho hàm số
1
.
2
+
=
−
ax
y
bx
Tìm
,ab
để đồ thị hàm số có
1=x
là tiệm cận đứng và
1
2
=y
là tiệm
cận ngang.
A.
1; 2=−=ab
. B.
4; 4= =ab
. C.
1; 2= =ab
. D.
1; 2
=−=−
ab
.
Lời giải
Chọn C
+
0= ⇒b
đồ thị hàm số
1
2
+
=
−
ax
y
không có tiệm cận.
+
0≠b
, tập xác định của hàm số
1
2
+
=
−
ax
y
bx
là
2
\

=


DR
b
.
1
1
lim lim lim
2
2
→±∞ →±∞ →±∞
+
+
= = =
−
−
xx x
a
ax a
x
y
bx b
b
x
.
⇒
đồ thị hàm số
1
2
+
=
−
ax
y
bx
có tiệm cận ngang là đường thẳng
1
2
2
= ⇒ = ⇔=
aa
y ba
bb
.
22
1
lim lim
2
++
→→
+∞
+
= =
−∞
−
xx
bb
ax
y
bx
.
⇒
đồ thị hàm số
1
2
+
=
−
ax
y
bx
có tiệm cận đứng là đường thẳng
22
121=⇒ =⇔=⇒=x ba
bb
.
Vậy
1; 2= =ab
.
Câu 38: Có bao nhiêu giá trị nguyên
[
]
10;10m ∈−
sao cho đồ thị hàm số
2
1
26 3
x
y
x xm
−
=
+ −−
có hai
đường tiệm cận đứng?
A.
19
. B.
15
. C.
17
. D.
18
.
Lời giải
Chọn C
Ta có đồ thị hàm số
2
1
26 3
x
y
x xm
−
=
+ −−
có hai đường tiệm cận đứng khi phương trình
2
2 6 30x xm+ − −=
có hai nghiệm phân biệt khác
1
( )
2
2
32 30
2.1 6.1 3 0
m
m
− −− >
⇔
+ − −≠
15
2
5
m
m
>−
⇔
≠
Từ đó ta suy ra tập các giá trị nguyên của
m
thỏa mãn là
{ }
7, 6, 5, 4, 3, 2, 1, 0,1, 2,3, 4, 6,7,8,9,10−−−−−−−
. Vậy có
17
giá trị nguyên của
m
thỏa mãn.
Câu 39: Có bao nhiêu giá trị nguyên của
m
để tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm
số
2
34
2
mx mx
y
x
++
=
+
bằng 3?
A.
4
. B.
2
. C. Vô số. D.
3
.
Lời giải
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 155
Chọn B
Đồ thị hàm số
2
34
2
mx mx
y
x
++
=
+
có nhiều nhất một tiệm cận đứng và hai tiệm cận ngang.
Điều kiện để đồ thị hàm số
2
34
2
mx mx
y
x
++
=
+
có 3 tiệm cận là nó có đúng 1 tiệm cận đứng
và 2 tiệm cận ngang.
* Xét điều kiện tồn tại
lim
x
y
→+∞
và
lim
x
y
→−∞
Trường hợp 1:
( )
2
3 40
g x mx mx= + +≥
với
x∀∈
2
0
16
0
0
9
9 16 0
m
m
m
mm
=
>
⇔ ⇔≤ ≤
∆= − ≤
Trường hợp 2:
( )
2
3 40g x mx mx= + +≥
với
( ) ( )
12
;;x xx∀ ∈ −∞ ∪ +∞
với
1
x
;
2
x
là nghiệm
của
(
)
gx
2
0
16
9
9 16 0
m
m
mm
>
⇔ ⇔>
∆= − >
Vậy
0m ≥
thì tồn tại
lim
x
y
→+∞
và
lim
x
y
→−∞
Khi đó:
2
2
34
34
lim lim lim
2
2
1
xx x
m
m
mx mx
xx
ym
x
x
→+∞ →+∞ →+∞
++
++
= = =
+
+
2
2
34
34
lim lim lim
2
2
1
xx x
m
m
mx mx
xx
ym
x
x
→−∞ →−∞ →−∞
−++
++
= = = −
+
+
Vậy điều kiện để đồ thị hàm số có hai đường tiệm cận ngang là
0m
>
* Xét trường hợp
2x = −
là nghiệm của tử số
2x⇒=−
là nghiệm của
( )
2
34g x mx mx=++
⇒
( )
20 2gm−=⇒=
Khi đó
2
2 64
2
xx
y
x
++
=
+
( )(
)
( )
22
21 2
21
lim lim
22
xx
xx
x
y
xx
−−
→− →−

++
+
⇒ = = − = −∞

++


⇒
Đồ thị hàm số có một tiệm cận đứng
2x = −
.
⇒
2
m =
thỏa mãn
* Xét trường hợp
2x = −
không là nghiệm của tử số, để
2x = −
là tiệm cận đứng của đồ thị
hàm số thì
( )
( )
(
)
20
2 0 42 0 2
20
g
g mm
g
−≠
⇔ − >⇔− >⇔ <
−≥
⇒
đồ thị hàm số có một đường tiệm cận đứng
2x = −
với
(
]
0; 2m∀∈
Vậy điều kiện để đồ thị hàm số
2
34
2
mx mx
y
x
++
=
+
có 3 tiệm cận là
(
]
0; 2m∀∈
Vậy có hai giá trị nguyên của
m
thỏa mãn đề bài là
1m =
;
2m =
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 156
Câu 40: Tổng các giá trị của tham số
m
để đồ thị của hàm số
( )
22
1
21 2
x
y
x m xm
−
=
+ − +−
có đúng một
tiệm cận đứng.
A.
1
2
−
. B.
2
. C.
3−
. D.
3
2
.
Lời giải
Chọn A
Đặt
( ) ( )
22
21 2xm mfx x+ − +−=
Đồ thị hàm số có đúng một tiệm cận đứng khi và chỉ khi
( )
0fx=
có 2 nghiệm phân biệt trong
đó có 1 nghiệm
1x =
hoặc
(
)
0
fx=
có nghiệm kép
( )
( )
( )
(
)
2
2
2
3
1 20
0
1
2
12 1 2 0
10 3
1; 3
3
3
3
0
2
2
2
mm
m
m
mm
fm
mm
m
m
m
− − −>
<

′
∆>
=

+ −+ −=

⇔ =⇔ ⇔ ⇔=−
= = −
′
∆=
=
=
=
.
Vậy tổng các giá trị
m
thỏa mãn là:
1
2
−
.
Câu 41: Cho hàm số
322
3
3 21
x
y
x mx m x m

. Có bao nhiêu giá trị nguyên thuộc đoạn
6;6
của tham số
m
để đồ thị hàm số có bốn đường tiệm cận?
A.
12
. B.
9
. C.
8
. D.
11
.
Lời giải
Chọn B
lim lim 0
xx
yy
 

nên đồ thị hàm số có tiệm cận ngang là đường thẳng
0y
.
Do đó, đồ thị hàm số có bốn đường tiệm cận khi phương trình
322
3 21 0x mx m x m 
có 3 nghiệm phân biệt
3x
.
Xét phương trình
322
3 21 0x mx m x m 
ta có
322
3 21 0x mx m x m 
2
2 10x m x mx 
2
2 10
xm
x mx

.
Phương trình có ba nghiệm phân biệt
3
x
khi và chỉ khi
3m
và phương trình
2
2 10x mx 
có hai nghiệm phân biệt
3x
2
2
3
3
1
10
1
3 2.3. 1 0
5
3
m
m
m
m
m
m
m







.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 157
Do
m
nguyên và
6;6m 
nên
6; 5; 4; 3; 2; 2; 4;5;6m

.
Vậy có
9
giá trị nguyên của
m
thỏa mãn đề bài.
Câu 42: Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số
2
23++
=
−
x xm
y
xm
không có tiệm
cận đứng.
A.
1=m
. B.
1>m
. C.
1=m
và
0=m
. D.
0≠m
.
Lời giải
Chọn C
TXĐ
{ }
\ m
.
Có
22
23 2 2
lim lim 2 2 3
→→

−+ −
= + −+

−−

xm xm
x xm m m
xm
xm xm
.
Để đồ thị hàm số không có tiệm cận đứng thì phải tồn tại
2
23
lim
→
−+
−
xm
x xm
xm
,
2
0
2 20
1
=
⇒ −=⇔
=
m
mm
m
Vậy đáp án C.
Câu 43: Có bao nhiêu giá trị nguyên của tham số thực
m
thuộc đoạn
2017;2017
để đồ thị hàm số
2
2
4
x
y
x xm

có hai tiệm cận đứng.
A.
2019
. B.
2021
. C.
2018
. D.
2020
.
Lời giải
Chọn D
Để đồ thị hàm số
2
2
4
x
y
x xm

có hai tiệm cận đứng thì phương trình
2
40x xm

có
hai nghiệm phân biệt khác
2
2017 4
40
12 2017; 2016;..;3 \ 12
12 0
m
m
mm
m
m







.
Do đó số giá trị nguyên của tham số
m
thỏa đề bài là:
3 ( 2017) 1 1 2020
giá trị.
Câu 44: Cho hàm số
()y fx
thỏa mãn
lim ( ) 2019
x
fx m

,
4
lim ( ) 2020
x
fx m

. Hỏi có tất cả bao
nhiêu giá trị của
m
để đồ thị của hàm số
()y fx
có duy nhất một tiệm cận ngang?
A. 4. B. 2. C. 3. D. 1.
Lời giải
Chọn B
Đồ thị hàm số
( )
y fx=
có duy nhất một tiệm cận ngang
4
3
0
2019 2020
2019
2020
m
mm
m
=
⇔= ⇔
=
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 158
Vậy có 2 giá trị của
m
thỏa bài toán
Câu 45: Cho hàm số
( )
2
1
21 2
y
x m x m xm
=

− ++ −

. Tìm tất cả các giá trị thực của tham số
m
để
đồ thị hàm số có 4 đường tiệm cận.
A.
01
1
2
m
m
<<
≠
. B.
1
1
2
m
m
<
≠
. C.
1m >
. D.
01
1
2
m
m
≤≤
≠
.
Lời giải
Chọn A
Điều kiện
.xm>
Ta có
lim 0 0
x
yy
→+∞
=⇒=
là tiệm cận ngang của đồ thị hàm số.
Xét phương trình
( )
( )
2
2
21 2 0
2 1 2 0(*)
xm
x m x m xm
x m xm
=

− + + −=⇔

− ++=
Để hàm số có 4 đường tiệm cận thì phương trình
(*)
có 2 nghiệm phân biệt
12
mx x<<
.
( )
( )( )
( )
2
22
1 2 12 1 2
12
11
21 0
22
1
0 00
2
01
10
2 2 12
mm
m
m
xmxm xxmxx m mm
m
xx m m m

≠≠

−>

≠

⇔ − − >⇔ − + − >⇔ − >⇔


<<
>
+ > +>



.
Câu 46: Có bao nhiêu giá trị nguyên của
m
để đồ thị hàm số
( )( )
22
63
6 39 6 1
x
y
mx x x mx
−
=
−+ + +
có đúng
1 đường tiệm cận?
A.
0.
B. 2. C.
1.
D. Vô số.
Lời giải
Chọn C
Đặt
( )
2
63f x mx x= −+
và
( )
2
961g x x mx
=++
. Ta xét các trường hợp:
+ Trường hợp 1:
0m =
khi đó ta có
( )
( )
2
63
6 39 1
x
y
xx
−
=
−+ +
đồ thị hàm số có 1 đường tiệm cận
ngang là đường thẳng
0y =
do đó
0m =
thỏa mãn yêu cầu bài toán.
+ Trường hợp 2:
0m ≠
và cả hai tam thức
( )
fx
và
( )
gx
đều vô nghiệm
2
'0
93 0
3
'0 1 1
9 90
f
g
m
m
m
m
m
∆<
−<
>

⇔ ⇔ ⇔ ⇔ ∈∅

∆ < −< <
−<
.
+ Trường hợp 3: Tam thức
( )
gx
nhận
1
2
x =
làm nghiệm
1 13
0
2 12
gm

=⇔=−


khi đó
( )
fx
luôn có 2 nghiệm phân biệt nên đồ thị hàm số đã cho có nhiều hơn 1 đường tiệm cận.
Vậy có 1 giá trị nguyên của
m
để đồ thị hàm số
( )( )
22
63
6 39 6 1
x
y
mx x x mx
−
=
−+ + +
có đúng 1
đường tiệm cận
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 159
Câu 47: Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số:
2
1y x mx
có tiệm cận ngang.
A.
0 1.m
B.
1.m
C.
1.
m

D.
1.m
Lời giải
Chọn B
Điều kiện cần và đủ để đồ thị hàm số:
2
1y x mx

có tiệm cận ngang là tồn tại số thực k
sao cho:
2
2
lim ( 1) k
lim ( 1) k
x
x
x
x mx
x mx





Hiển nhiên nếu
0m
thì giới
2
lim ( 1)
x
x mx


không hữu hạn
Nếu
0
m
ta có
+
2
lim ( 1) .
x
x mx


+
2
2
2
2
1
x(1 )
(1 ) 1
lim y lim ( 1) lim lim
1
1
1
xx x x
m
xm
x
x mx
x mx
m
x
   





Để giới hạn trên hữu hạn khi và chỉ khi m=1.
Câu 48: Cho hàm số
2
2
24
x
y
mx x
−
=
−+
. Có tất cả bao nhiêu giá trị của tham số
m
để đồ thị hàm số có
đúng hai đường tiệm cận ?
A.
0
. B.
2
. C.
3
. D.
1
.
Lời giải
Chọn D
Với
0m =
; ta có hàm số
2
2
24
x
y
x
−
= =−⇒
−+
Không thỏa mãn yêu cầu bài toán.
Với
0m ≠
, ta có:
2
2
lim 0
24
x
x
mx x
→±∞
−
= ⇒
−+
0y =
là tiệm cận ngang của đồ thị hàm số.
Đồ thị hàm số có đúng hai đường tiệm cận
⇔
đồ thị hàm số có đúng 1 tiệm cận đứng
⇔
2
2 40mx x− +=
có nghiệm duy nhất hoặc
2
2 40mx x− +=
có hai nghiệm phân biệt trong đó
có một nghiệm
2x =
.
2
2 40mx x− +=
có nghiệm duy nhất
1
0 14 0
4
mm
′
⇔∆ = ⇔ − = ⇔ =
.
2
2 40mx x− +=
có hai nghiệm phân biệt trong đó có một nghiệm
2x =
.
1
0
4
40
0
m
m
m
′
∆>
<
⇔⇔

=
=
⇒
0m =
không thỏa mãn điều kiện.
Vậy chỉ có một giá trị của
m
thỏa mãn yêu cầu bài toán.
Câu 49: Gọi S là tập các giá trị nguyên của
m
sao cho đồ thị hàm số
2
2019
17 1
x
y
x mx
=
−−
có bốn đường
tiệm cận . Tính số phần tử của tập S.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 160
A. Vô số B. 3 C. 5 D. 4
Lời giải
Chọn C
2019 2019
lim , lim
17 17
xx
yy
mm
→−∞ →+∞
= =
−−
.
Với
17m ≠
thì đồ thị hàm số có hai đường tiệm cận ngang là
2019 2019
,
17 17
yy
mm
= =
−−
.
Khi đó đồ thị hàm số đã cho có 4 đường tiệm cận khi và chỉ khi phương trình
( )
2
17 1 0 1x mx−− =
có hai nghiệm phân biệt khác 0.
Ta có:
( )
( )
( )
2
22
2 22
0
0
1 17 1
17 1 2
17 1
m
m
x mx
mx
x mx
≥
≥
⇔ −= ⇔ ⇔

−=
−=
Phương trình có 2 nghiệm phân biệt khác 0 khi và chỉ khi phương trình có hai nghiệm phân
biệt khác 0
2
0
0 17
17 0
m
m
m
≥
⇔ ⇔≤ <
−>
.
Suy ra
{ }
0,1, 2,3,4S =
.
Câu 50: Gọi
S
là tập hợp tất cả các giá trị của tham số thực
m
sao cho đồ thị hàm số
3
3 42
()
11
x
fx
x mx x x m x
=
+ +− +++
nhận trục tung làm tiệm cận đứng. Khi đó tổng các phần
tử của
S
bằng
A.
1
2
. B.
1
2
−
. C.
1
3
. D.
1
3
−
.
Lời giải
Chọn B
Ta có:
3
3 42
00
1
lim ( ) lim
11
xx
fx
x mx x x m x
x
→→
=
+ +− +++
.
Mà
3
3 42
0
11
lim
x
x mx x x m x
x
→
+ +− +++
3
3 42
0
34
2
3
3 4 24
0
3
11 11
lim
lim .
( 1 1) ( ( 1) 1 1)
x
x
x mx x x m x
x xx
x mx x x
m
xxmx xxx xx
→
→

+ +− ++−
= −+




++
=−+

+ ++ ++ + +++

Đồ thị hàm số
()
fx
nhận trục tung làm tiệm cận đứng
23
22
3
3 4 24
0
3
( ) ( 1) 1
lim( ) 0 0
23
( 1 1) ( 1) 1 1
x
xm x m
mm
xmx xx xx
→
++
⇔ − + =⇔ −+ =
+ ++ ++ + +++
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 161
2
6 3 20mm⇔ + −=
Vậy
12
1
.
2
mm+=−
Câu 51: Có bao nhiêu giá trị
m
nguyên thuộc khoảng
10;10
để đồ thị hàm số
( )1
2
xx m
y
x

có đúng ba đường tiệm cận?
A.
12
. B.
11
. C.
0
. D.
10
.
Lời giải
Chọn A
Xét
1gx xx m

.
Ta có
( )1
lim 1
2
x
xx m
x


và
( )1
lim 1
2
x
xx m
x



. Nên đồ thị hàm số luôn có hai
đường tiệm cận ngang
1
y
và
1y 
.
Trường hợp 1:
0
m
khi đó hàm số là
1
2
x
y
x
. Đồ thị hàm số có tiệm cận đứng là
2x 
.
Vậy
0m
thỏa mãn yêu cầu đề bài.
Trường hợp 2:
0m
. Hàm số
gx
có tập xác định là
;0 ;Dm 
.
2xD
.
( 2) 2 2 1 0gm 
nên
2x

là tiệm cận đứng của đồ thị hàm số
Vậy
1m
,
2m
,.
9m
thỏa mãn. Nên có
9
giá trị
m
.
Trường hợp 3:
0m
. Hàm số
gx
có tập xác định là
; 0;Dm 
.
Để
2x

là tiệm cận đứng của đồ thị hàm số thì trước hết
2xD
hay
2m 
. Nên chỉ
có
2m 
,
1
m 
thỏa mãn
Với
1m 
ta có
() 1 1gx xx 
,
( 2) 2 1 0g 
nên
2
x 
là tiệm cận đứng
của đồ thị hàm số.
Với
2m 
ta có
() 2 1gx xx 
,
( 2) 2 1 1 0g xx 
nên
2x 
là
tiệm cận đứng của đồ thị hàm số.
Vậy
12
giá trị
m
nguyên thỏa mãn yêu cầu.
Câu 52: Tìm số giá trị nguyên thuộc đoạn
[ ]
2019;2019−
của tham số
m
để đồ thị hàm số
2
3x
y
x xm
−
=
+−
có đúng hai đường tiệm cận.
A.
2007
. B.
2010
. C.
2009
. D.
2008
.
Lời giải
Chọn D.
Điều kiện xác định:
2
30x
x xm
−≥
+≠
.
Dựa vào điều kiện xác định ta suy ra hàm số đã cho không có giới hạn khi
x → −∞
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 162
2
3
lim 0,
x
x
m
x xm
→+∞
−
= ∀
+−
.
0y⇒=
là pt đường tiệm cận ngang.
Xét hàm số
( )
2
fx x x= +
.
( ) ( )
1
' 2 1; ' 0
2
fx x fx x= + =⇔=−
Dựa vào bảng biến thiên ta thấy:
Khi
12
m
<
thì đồ thị hàm số không có tiệm cận đứng.
Khi
12m
≥
thì đồ thị hàm số có 1 tiệm cận đứng.
Do đó để hàm số có đúng 2 đường tiệm cận thì
[ ]
12;2019m ∈
.
Vậy có
2008
giá trị nguyên của
m
.
Câu 53: Cho hàm số
2
1
23
x
y
mx x
−
=
−+
. Có tất cả bao nhiêu giá trị
m
để đồ thị hàm số có đúng hai đường
tiệm cận.
A. 2 B. 3 C. 0 D. 1
Lời giải
Chọn B
Nhận xét:
+
2
() 2 3f x mx x= −+
có bậc
1≥
nên đồ thị hàm số luôn có
1
tiệm cận ngang.
+ Do đó: Yêu cầu bài toán
9
đồ thị hàm số có đúng
1
tiệm cận đứng.
+
0m =
, đồ thị hàm số có 1 tiệm cận đứng là đường thẳng
3
0
2
xm=⇒=
thỏa bài toán.
+
0m ≠
, đồ thị hàm số có đúng 1 tiệm cận đứng khi và chỉ khi phương trình
2
2 30mx x− +=
có nghiệm kép hoặc nhận
1
x =
làm nghiệm
1
0
3
(1) 0
1
f
m
f
m
∆=
=
⇔⇔
=
= −
+ KL:
1
0; ; 1
3
m

∈−


.
Câu 54: Cho hàm số
32
1
31
y
x xm
=
− +−
với
m
là tham số. Tìm tất cả các giá trị của
m
để đồ thị hàm
số đã cho có
4
đường thẳng tiệm cận.
A.
15m<<
. B.
12m−< <
. C.
1m <
hoặc
5m >
. D.
2m >
hoặc
1m <−
.
Lời giải
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 163
Ta có
32
1
lim lim 0
31
xx
y
x xm
→+∞ →+∞
= =
− +−
,
32
1
lim lim
31
xx
y
x xm
→−∞ →−∞
=
− +−
không tồn tại. Suy ra
0
y
=
là đường tiệm cận ngang của đồ thị hàm số.
Do đó, để đồ thị hàm số đã cho có
4
đường thẳng tiệm cận thì phương trình
32
3 10
x xm
− + −=
có
3
nghiệm phân biệt.
Xét hàm số
( )
32
31gx x x m= − +−
. Tập xác định
D
=
.
( )
2
36gx x x
′
= −
;
( )
0
0
2
x
gx
x
=
′
= ⇔
=
.
Bảng biến thiên:
Từ bảng biến thiên, ta thấy phương trình
32
3 10x xm− + −=
có
3
nghiệm phân biệt khi và chỉ
khi
50 1 1 5mm m−< < −⇔< <
.
Câu 55: Hàm số
( )
2
31
1
x ax b
y
x
++ +
=
−
không có tiệm cận đứng. Khi đó hiệu
ab−
bằng:
A.
1
2
.
B.
3
4
−
. C.
5
4
−
.
D.
1
2
−
.
Lời giải
Chọn A
Do hàm số không có tiệm cận đứng nên
( ) ( ) ( )
2
31 1f x x ax b x g x= ++ + = −
.
Suy ra
( )
( )
3
20
10
1
4
3
5
2
0
'1 0
4
4
ab
a
f
ab
a
f
b
++=
= −
=

⇔ ⇔ ⇒−=

+=
=

= −
→
đáp án A.
Chú ý: Với
( ) ( ) ( )
0
n
f x x x gx= −
thì ta luôn có
( ) ( ) ( )
( )
( )
1
00 0 0
' '' ... 0
n
fxfxfx f x
−
= = = = =
.
Câu 56: Có bao nhiêu giá trị nguyên của tham để
m
đồ thị hàm số
2
2016 2017 24 7xx
y
xm
−+ + −
=
−
có
tiệm cận đứng?
A. vô số.
B.
2
. C.
2017
D.
2019
.
Lời giải
Chọn C
Biểu thức:
2
2016 2017xx−+ +
có nghĩa khi
2
2016 2017 0 1 2017xx x− + + ≥ ⇔− ≤ ≤
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 164
Đặt
( )
2
2016 2017
fx x x=−+ +
.
Xét
0xm x m− =⇔=
. Vậy đồ thị nếu có tiệm cận đứng chỉ có thể là
xm=
, khi đó điều kiện
là:
(
)
[
]
(
)
(
)
2
1;2017 1
1 2017
0
2016 2017
24 7 *
m
x
fm
mm
∈−
−≤ ≤

⇔

≠
−+ + ≠
Ta có
( ) ( )
2
1
* 2016 2015 0 2
2015
m
mm
m
≠
⇔ − + ≠⇔
≠
Từ
( )
( )
[
]
{ }
1 , 2 1;2017 \ 1;2015
m
m
∈
⇒ ∈ − →
có
2019 2 2017−=
số nguyên
m
thỏa mãn bài
toán
→
đáp án C.
Câu 57: Gọi
S
là tập hợp tất cả các giá trị của tham số thực
m
sao cho đồ thị hàm số
3
3 42
()
11
x
fx
x mx x x m x
=
+ +− +++
nhận trục tung làm tiệm cận đứng. Khi đó tổng các phần
tử của
S
bằng
A.
1
2
. B.
1
2
−
. C.
1
3
. D.
1
3
−
.
Lời giải
Chọn B
Ta có:
3
3 42
00
1
lim ( ) lim
11
xx
fx
x mx x x m x
x
→→
=
+ +− +++
.
Mà
3
3 42
0
11
lim
x
x mx x x m x
x
→
+ +− +++
3
3 42
0
34
2
3
3 4 24
0
3
11 11
lim
lim .
( 1 1) ( ( 1) 1 1)
x
x
x mx x x m x
x xx
x mx x x
m
xxmx xxx xx
→
→

+ +− ++−
= −+




++
=−+

+ ++ ++ + +++

Đồ thị hàm số
()fx
nhận trục tung làm tiệm cận đứng
23
22
3
3 4 24
0
3
( ) ( 1) 1
lim( ) 0 0
23
( 1 1) ( 1) 1 1
x
xm x m
mm
xmx xx xx
→
++
⇔ − + =⇔ −+ =
+ ++ ++ + +++
.
2
6 3 20mm
⇔ + −=
Vậy
12
1
.
2
mm+=−
Câu 58: Có bao nhiêu giá trị
m
nguyên thuộc khoảng
10;10
để đồ thị hàm số
( )1
2
xx m
y
x

có đúng ba đường tiệm cận?
A.
12
. B.
11
. C.
0
. D.
10
.
Lời giải
Chọn A
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 165
Xét
1gx xx m

.
Ta có
( )1
lim 1
2
x
xx m
x


và
( )1
lim 1
2
x
xx m
x



. Nên đồ thị hàm số luôn có hai
đường tiệm cận ngang
1
y
và
1y 
.
Trường hợp 1:
0m
khi đó hàm số là
1
2
x
y
x
. Đồ thị hàm số có tiệm cận đứng là
2
x 
.
Vậy
0m
thỏa mãn yêu cầu đề bài.
Trường hợp 2:
0m
. Hàm số
gx
có tập xác định là
;0 ;Dm 
.
2xD
.
( 2) 2 2 1 0gm 
nên
2x 
là tiệm cận đứng của đồ thị hàm số
Vậy
1m
,
2m
,.
9m
thỏa mãn. Nên có
9
giá trị
m
.
Trường hợp 3:
0
m
. Hàm số
gx
có tập xác định là
; 0;Dm 
.
Để
2
x 
là tiệm cận đứng của đồ thị hàm số thì trước hết
2xD
hay
2m 
. Nên chỉ
có
2m 
,
1m 
thỏa mãn
Với
1m 
ta có
() 1 1gx xx 
,
( 2) 2 1 0
g 
nên
2x 
là tiệm cận đứng
của đồ thị hàm số.
Với
2m 
ta có
() 2 1gx xx 
,
( 2) 2 1 1 0g xx 
nên
2x 
là
tiệm cận đứng của đồ thị hàm số.
Vậy
12
giá trị
m
nguyên thỏa mãn yêu cầu.
Câu 59: Tìm tất cả các giá trị thực của
m
sao cho đồ thị hàm số
1
1
2
+
+
=
x
mx
y
có đúng một đường tiệm
cận.
A.
01 <≤− m
. B.
01 ≤≤− m
. C.
1−<m
. D.
0>m
.
Lời giải
Chọn A
Nếu
0
m =
thì
1
1
y
x
=
+
. Hàm số này có tập xác định
{ }
\1D
= −
.
Ta có
1
lim 0
1
x
x
→+∞
=
+
nên đồ thị hàm số có tiệm cận ngang là
0y =
.
( )
1
1
lim
1
x
x
+
→−
= +∞
+
nên đồ thị hàm số có tiệm cận đứng
1x = −
.
Vậy với
0m =
thì đồ thị hàm số có hai đường tiệm cận .
Nếu
0m >
thì
2
10mx +>
với mọi
x
và tập xác định của hàm số là
{ }
\1D = −
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 166
2
1
lim
1
x
mx
x
→+∞
+
+
2
1
lim
1
1
x
m
x
m
x
→+∞
+
= =
+
,
2
1
lim
1
x
mx
x
→−∞
+
+
2
1
lim
1
1
x
m
x
m
x
→+∞
−+
= = −
+
. Suy ra đồ thị hàm
số có hai tiệm cận ngang là
ym
=
và
ym= −
.
( )
2
1
1
lim
1
x
mx
x
+
→−
+
= +∞
+
nên
1x = −
là đường tiệm cận đứng của đồ thị hàm số.
Vậy
0m >
không thỏa mãn.
Nếu
0
m
<
thì tập xác định của hàm số là
{ }
11
; \1D
mm

=−− − −


.
Trường hợp này đồ thị hàm số không có tiệm cận ngang. Để đồ thị hàm số có đúng một đường
tiệm cận thì đồ thị hàm số phải có một tiệm cận đứng. Điều này xảy ra khi
1
1
m
− − ≤−
1
1
m
⇔− ≥
1
1
m
⇔− ≥
1m⇔ ≥−
.
Vậy với
10m−≤ <
thì đồ thị hàm số có đúng một đường tiệm cận.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 191
BÀI 4. ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
DẠNG. XÁC ĐỊNH TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
( )
gx
KHI BIẾT BẢNG BIẾN THIÊN
HÀM SỐ
( )
fx
Câu 1: Cho đồ thị hàm số
( )
31
1
x
y fx
x
−
= =
−
. Khi đó đường thẳng nào sau đây là đường tiệm cận đứng
của đồ thị hàm số
( )
1
2
y
fx
=
−
?
A.
1x =
. B.
2
x = −
. C.
1x = −
. D.
2x =
.
Câu 2: Cho hàm số
( )
y fx=
có đồ thị như hình vẽ
Số tiệm cận đứng của đồ thị hàm số
( )
2019
1
y
fx
=
−
là
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 3: Cho hàm số
( )
fx
xác định và liên tục trên
{ }
\1−
có bảng biến thiên như sau:
CHƯƠNG
I
ỨNG DỤNG ĐẠO HÀM
ĐỂ KHẢO SÁT HÀM SỐ
BÀI TẬP TRẮC NGHIỆM. (MỨC 9 – 10)
III
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 192
Hỏi đồ thị hàm số
( )
1
y
fx
=
có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang?
A.
4
. B.
3
. C.
2
. D.
1
.
Câu 4: Cho hàm số
( )
y fx
=
thỏa mãn
(
)
lim 1
x
fx
→−∞
= −
và
( )
lim
x
fx m
→+∞
=
. Có bao nhiêu giá trị thực
của tham số
m
để hàm số
( )
1
2
y
fx
=
+
có duy nhất một tiệm cận ngang.
A.
1
. B.
0
. C.
2
. D. Vô số.
Câu 5: Cho hàm số
()y fx=
thỏa mãn
4
(tan ) cosfx x=
. Tìm tất cả các giá trị thực của
m
để đồ thị
hàm số
2019
()
()
gx
fx m
=
−
có hai tiệm cận đứng.
A.
0
m <
. B.
01m<<
. C.
0m >
. D.
1m <
.
Câu 6: Cho hàm số
( )
y fx=
xác định, liên tục trên
và có bảng biến thiên như hình bên dưới:
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
( )
1
21
y
fx
=
−
là:
A.
4
. B.
3
. C.
1
. D.
2
.
Câu 7: Cho hàm số
()y fx=
liên tục trên
{ }
\1
và có bảng biến thiên như sau:
Đồ thị
( )
1
23
y
fx
=
+
có bao nhiêu đường tiệm cận đứng?
A. 2. B. 0. C. 1. D. 3.
Câu 8: Cho hàm số
( )
y fx=
liên tục trên
{ }
\1
và có bảng biến thiên như sau:
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 193
Đồ thị hàm số
( )
1
25
y
fx
=
−
có bao nhiêu đường tiệm cận đứng?
A.
0
. B.
4
. C.
2
. D.
1
.
Câu 9: Cho hàm số
( )
y fx=
có bảng biến thiên như hình dưới đây.
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
(
)
1
21
y
fx
=
−
là
A.
0.
B.
1.
C.
2.
D.
3.
Câu 10: Cho hàm bậc ba
(
)
y fx
=
có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số
( )
(
)
( )
22
2
43
2
x x xx
y
xf x f x
++ +
=

−

có bao nhiêu đường tiệm cận đứng?
A.
2
. B.
3
. C.
4
. D.
6
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 194
Câu 11: Cho hàm số
(
)
32
f x ax bx cx d= + ++
có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số
( )
(
)
(
)
( )
2
2
32 1xx x
gx
xf x f x
−+ −
=

−

có bao nhiêu tiệm cận đứng?
A.
2
. B.
4
. C.
3
. D.
5
.
Câu 12: Cho hàm số bậc ba
( )
32
f x ax bx cx d= + ++
có đồ thị như hình vẽ sau.
Hỏi đồ thị hàm số
(
)
( )
(
) ( ) (
)
2
2
32 1
1
xx x
gx
x f x fx
−+ −
=

+−

có bao nhiêu tiệm cận đứng?
A.
5
. B.
4
. C.
6
. D.
3
.
Câu 13: Cho hàm số
()y fx=
là hàm số đa thức có đồ thì như hình vẽ dưới đây, đặt
( )
( ) ( )
2
2
2
−
=
−
xx
gx
f x fx
. Hỏi đồ thị hàm số
( )
=y gx
có bao nhiêu tiệm cận đứng?
A.
5
. B.
3
. C.
4
. D.
2
.
Câu 14: Cho hàm số
(
)
y fx
=
xác định, liên tục trên
và có bảng biến thiên như hình bên dưới.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 195
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
(
)
3
1
3
y
fx x
=
++
là
A. 2. B. 4. C. 3. D. 1.
Câu 15: Cho hàm số
(
)
32
y f x ax bx cx d= = + ++
có đồ thị như bên dưới.
Hỏi đồ thị hàm số
( )
( )
( ) ( )
2
2
22
3
xx x
y
x f x fx
−−
=

−−

có bao nhiêu đường tiệm cận đứng
A.
4
. B.
6
. C.
3
. D.
5
.
Câu 16: Cho hàm số
32
y ax bx cx d= + ++
,
( )
0a ≠
có đồ thị như hình dưới đây.
Hỏi đồ thị hàm số
( )
(
)
( )
( )
2
2
1 43
fx
gx
x xx
=
+ −+
có bao nhiêu đường tiệm cận đứng?
A.
2
. B.
1
. C.
3
. D.
4
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 196
Câu 17: Cho hàm số trùng phương
42
y ax bx c
có đồ thị như hình vẽ. Hỏi đồ thị hàm số
22
2
42
23




x xx
y
fx fx
có tổng cộng bao nhiêu tiệm cận đứng?
A. 5. B. 2. C. 3. D. 4.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 137
BÀI 4. ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
BÀI TẬP TRẮC NGHIỆM TRÍCH TỪ ĐỀ THAM KHẢO VÀ ĐỀ CHÍNH THỨC CỦA BỘ GIÁO
DỤC TỪ NĂM 2017 ĐẾN NAY
DẠNG. XÁC ĐỊNH TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
( )
gx
KHI BIẾT BẢNG BIẾN THIÊN
HÀM SỐ
( )
fx
Câu 1: Cho đồ thị hàm số
( )
31
1
x
y fx
x
−
= =
−
. Khi đó đường thẳng nào sau đây là đường tiệm cận đứng
của đồ thị hàm số
( )
1
2
y
fx
=
−
?
A.
1x
=
. B.
2
x = −
. C.
1x = −
. D.
2x =
.
Lời giải
( )
31
22
1
x
fx
x
−
=⇔=
−
3 12 2 1xx x⇒ −= − ⇔ =−
.
Với
(
)
1
2
y
fx
=
−
ta có
( )
( )
11
lim ; lim
xx
yy
+−
→− →−
= −∞ = +∞
Vậy đồ thị hàm số
( )
1
2
y
fx
=
−
có đường tiệm cận đứng
1x = −
.
Câu 2: Cho hàm số
( )
y fx=
có đồ thị như hình vẽ
Số tiệm cận đứng của đồ thị hàm số
( )
2019
1
y
fx
=
−
là
CHƯƠNG
I
ỨNG DỤNG ĐẠO HÀM
ĐỂ KHẢO SÁT HÀM SỐ
BÀI TẬP TRẮC NGHIỆM. (MỨC 9 – 10)
III
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 138
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn C
Từ đồ thị của hàm số
(
)
y fx
=
suy ra tập xác định của hàm số
( )
y fx=
là
D =
Do đó số đường tiệm cận đứng của đồ thị hàm số
( )
2019
1
y
fx
=
−
chính là số nghiệm của phương
trình
( )
1fx=
.
Qua đồ thị ta có: Đường thẳng
1
y =
cắt đồ thị hàm số
(
)
y fx=
tại 3 điểm phân biệt nên
phương trình
( )
1fx=
có 3 nghiệm phân biệt.
Vậy đồ thị hàm số
( )
2019
1
y
fx
=
−
có 3 đường tiệm cận đứng.
Câu 3: Cho hàm số
( )
fx
xác định và liên tục trên
{ }
\1−
có bảng biến thiên như sau:
Hỏi đồ thị hàm số
( )
1
y
fx
=
có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang?
A.
4
. B.
3
. C.
2
. D.
1
.
Lời giải
Chọn A
Ta có:
( )
( )
11
lim 2 lim
2
xx
fx
fx
→−∞ →−∞
=⇒=
;
( )
( )
11
lim 2 lim
2
xx
fx
fx
→+∞ →+∞
=−⇒ =−
.
Suy ra đồ thị hàm số
( )
1
y
fx
=
có hai đường tiệm cận ngang là
1
2
y =
và
1
2
y = −
.
Dựa vào bảng biến thiên của hàm số
( )
y fx=
ta thấy: phương trình
( )
0fx=
có hai nghiệm
phân biệt
12
1xx<− <
.
Khi đó:
( ) ( )
12
0fx fx= =
.
Ta có:
( )
( )
( )
1
1
1
lim 0
1
lim
0
xx
xx
fx
fx
f x khi x x
−
−
→
→
−
=
⇒ = +∞
>→
và
( )
( )
( )
2
2
2
lim 0
1
lim
0
xx
xx
fx
fx
f x khi x x
−
−
→
→
−
=
⇒ = +∞
>→
.
Vậy đồ thị hàm số
( )
1
y
fx
=
có hai tiệm cận đứng là đường thẳng
1
xx=
và
2
xx=
.
Do đó Chọn A
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 139
Câu 4: Cho hàm số
(
)
y fx=
thỏa mãn
( )
lim 1
x
fx
→−∞
= −
và
( )
lim
x
fx m
→+∞
=
. Có bao nhiêu giá trị thực
của tham số
m
để hàm số
(
)
1
2
y
fx
=
+
có duy nhất một tiệm cận ngang.
A.
1
. B.
0
. C.
2
. D. Vô số.
Lời giải
Chọn C
Ta có
( )
1
lim lim 1
2
xx
y
fx
→−∞ →−∞
= = ⇒
+
Đồ thị hàm số có tiệm cận ngang
1y =
.
TH 1: Nếu
1m = −
thì
( )
1
lim 1
2
x
fx
→−∞
=
+
và
( )
1
lim 1
2
x
fx
→+∞
=
+
thì đồ thị hàm số có một tiệm
cận.
TH 2: Nếu
1m
≠−
Để đồ thị hàm số có một tiệm cận ngang
( )
1
lim
2
x
fx
→+∞
⇔
+
không có giá trị hữu hạn
20 2mm⇔ +=⇔ =−
.
Vậy khi
{ }
2; 1m ∈− −
thì đồ thị hàm số có duy nhất một tiệm cận ngang.
Câu 5: Cho hàm số
()y fx=
thỏa mãn
4
(tan ) cosfx x=
. Tìm tất cả các giá trị thực của
m
để đồ thị
hàm số
2019
()
()
gx
fx m
=
−
có hai tiệm cận đứng.
A.
0m <
. B.
01m<<
. C.
0m >
. D.
1m <
.
Lời giải
Chọn B
( )
4
2
2
1
(tan ) cos (tan )
1 tan
fx xfx
x
=⇔=
+
22
1
()
(1 )
ft
t
⇒=
+
Hàm số
22
2019 2019
() ()
1
()
(1 )
gx gx
fx m
m
x
= ⇒=
−
−
+
Hàm số
()gx
có hai tiện cận đứng khi và chỉ khi phương trình
22
1
0
(1 )
m
x
−=
+
có hai nghiệm
phân biệt
22
1
(1 ) 1 0 1xm
m
⇔ + = >⇔ < <
.
Câu 6: Cho hàm số
( )
y fx=
xác định, liên tục trên
và có bảng biến thiên như hình bên dưới:
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
( )
1
21
y
fx
=
−
là:
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 140
A.
4
. B.
3
. C.
1
. D.
2
.
Lời giải
Đặt
( )
( )
1
21
hx
fx
=
−
.
*) Tiệm cận ngang:
Ta có:
(
)
(
)
1
lim lim 0
21
xx
hx
fx
→+∞ →+∞
= =
−
.
( )
( )
1
lim lim 0
21
xx
hx
fx
→−∞ →−∞
= =
−
.
Suy ra đồ thị hàm số có một đường tiệm cận ngang
0y =
.
*) Tiệm cận đứng:
Xét phương trình:
( )
2 10
fx−=
( )
1
2
fx⇔=
.
Dựa vào bảng biến thiên ta thấy phương trình
( )
1
2
fx=
có ba nghiệm phân biệt
,,abc
thỏa
mãn
12ab c
<< < <
.
Đồng thời
( ) ( ) ( )
lim lim lim
xa xb xc
hx hx hx
+−+
→→→
= = = +∞
nên đồ thị hàm số
( )
y hx=
có ba đường tiệm
cận đứng là
xa=
,
xb=
và
xc=
.
Vậy tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
( )
y hx=
là 4.
Câu 7: Cho hàm số
()y fx=
liên tục trên
{
}
\1
và có bảng biến thiên như sau:
Đồ thị
( )
1
23
y
fx
=
+
có bao nhiêu đường tiệm cận đứng?
A. 2. B. 0. C. 1. D. 3.
Lời giải
Chọn A
Đặt
( )
( )
1
23
= =
+
y gx
fx
có tử số là
1 0, x≠ ∀∈
Ta có
( ) (
)
3
2 30
2
fx fx+=⇔ =−
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 141
Từ bảng biến thiên có phương trình có 2 nghiệm phân biệt:
12
( ; 0) , (0 ;1)xx∈ −∞ ∈
.
Do đó đồ thị hàm số
( )
1
23
y
fx
=
+
có 2 đường tiệm cận đứng.
Câu 8: Cho hàm số
( )
y fx=
liên tục trên
{
}
\1
và có bảng biến thiên như sau:
Đồ thị hàm số
( )
1
25
y
fx
=
−
có bao nhiêu đường tiệm cận đứng?
A.
0
. B.
4
. C.
2
. D.
1
.
Lời giải
Ta có:
( ) ( )
( )
5
2 50 1
2
fx fx−=⇔ =
. Phương trình
( )
1
có
4
nghiệm phân biệt
1234
,,, 1xxxx≠
và giới hạn của hàm số
( )
1
25
y
fx
=
−
tại các điểm
1234
,,,xx xx
đều bằng
±∞
.
Mặt khác
( )
1
1
lim 0
25
x
fx
±
→
=
−
nên
1x =
không phải tiệm cận đứng.
Vậy đồ thị hàm số
( )
1
25
y
fx
=
−
có
4
đường tiệm cận đứng.
Câu 9: Cho hàm số
( )
y fx=
có bảng biến thiên như hình dưới đây.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 142
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
(
)
1
21
y
fx
=
−
là
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải
Số tiệm cận đứng của đồ thị hàm số
( )
1
21
y
fx
=
−
đúng bằng số nghiệm thực của phương trình
( ) (
)
1
2 10
2
fx fx−= ⇔ =
.
Mà số nghiệm thực của phương trình
( )
1
2
fx=
bằng số giao điểm của đồ thị hàm số
(
)
y fx
=
với đường thẳng
1
2
y =
.
Dựa vào bảng biến thiên ta thấy đường thẳng
1
2
y =
cắt đồ thị hàm số
()y fx=
tại 2 điểm phân
biệt. Vậy đồ thị hàm số
( )
1
21
y
fx
=
−
có 2 tiệm cận đứng.
Lại có
( )
1
lim 1
21
x
fx
→±∞
= ⇒
−
đồ thị hàm số có một tiệm cận ngang là
1y =
.
Vậy tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
( )
1
21
y
fx
=
−
là
3
.
Câu 10: Cho hàm bậc ba
( )
y fx=
có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số
(
)
( ) ( )
22
2
43
2
x x xx
y
xf x fx
++ +
=

−

có bao nhiêu đường tiệm cận đứng?
A.
2
. B.
3
. C.
4
. D.
6
.
Lời giải
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 143
( )
( ) ( )
( )( ) ( )
( ) ( )
22
2
43
13 1
.. 2
2
x x xx
x x xx
y
xfx fx
xf x fx
++ +
++ +
= =
−

−


Điều kiện tồn tại căn
2
xx+
:
0
1
x
x
≥
≤−
.
Xét phương trình
( ) ( ) ( )
( )
2
0
20 0
2
x
xf x fx fx
fx
=

− =⇔=

=
.
Với
0x =
ta có
( )( ) ( )
( ) ( )
(
)( )
( ) ( )
00
13 1
13 1
lim lim
.. 2
.. 2
xx
x x xx
xx x
xfx fx
xfx fx
++
→→
++ +
++ +
= = +∞
−

−



. Suy ra
0x =
là
tiệm cận đứng.
Với
( )
0fx=
3x⇒=−
hoặc
xa=
.
Ta có:
( )( ) ( )
( ) ( )
3
13 1
lim
.. 2
x
x x xx
xfx fx
+
→−
++ +
= −∞
−


nên
3x = −
là tiệm cận đứng.
Với
( )
2fx= ⇒
( )
( )
1
31
3
x
xb b
x cc
= −
= − < <−
= <−
. Ta có:
(
)( ) ( )
( ) ( )
13 1
lim 0
.. 2
xb
x x xx
xfx fx
+
→
++ +
=
−


( )( ) ( )
( ) ( )
( )( ) ( )
( ) ( )
1
1
13 1
lim 0
.. 2
13 1
lim 0
.. 2
x
x
x x xx
xfx fx
x x xx
xfx fx
+
−
→−
→−
++ +
=
−


++ +
=
−


nên
1x = −
không là tiệm
cận đứng.
( )( ) ( )
( ) ( )
13 1
lim
.. 2
xb
x x xx
xfx fx
+
→
++ +
= +∞
−


nên
xb=
là tiệm cận đứng.
( )( ) ( )
( ) ( )
13 1
lim
.. 2
xc
x x xx
xfx fx
+
→
++ +
= +∞
−


nên
xc=
là tiệm cận đứng.
Vậy đồ thị hàm số có 4 tiệm cận đứng.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 144
Câu 11: Cho hàm số
(
)
32
f x ax bx cx d= + ++
có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số
( )
(
)
(
)
( )
2
2
32 1xx x
gx
xf x fx
−+ −
=

−

có bao nhiêu tiệm cận đứng?
A.
2
. B.
4
. C.
3
. D.
5
.
Lời giải
Chọn C
Nhận xét 1: Với
0
1x ≥
và
(
)
0
lim
xx
gx
+
→
hoặc
(
)
0
lim
xx
gx
−
→
có kết quả là
+∞
hoặc
−∞
thì
0
xx=
là
tiệm cận đứng của của đồ thị hàm số
( )
gx
.
Nhận xét 2: Dựa vào đồ thị hàm số
( )
fx
ta có:
( )
( )
( )
2
1
2f x ax x x=−−
.
Ta có
(
) (
)
( )
(
)
2
0
00
1
x
xf x fx fx
fx
=

−=⇔=

=
.
( )
11
,0 1
0
2
xx x
fx
x
= <<
= ⇔
=
.
( )
22
33
1
1 ,1 2
,2
x
fx x x x
x xx
=
=⇔= <<
= >
suy ra
( ) ( )
( )( )
23
11fx ax xx xx−= − − −
.
Khi đó ta có
( )
( )
(
) ( )
(
)( )
( )
( )
2
2
32 1
12 1
.1
xx x
xx x
gx
xfx fx
xf x fx
−+ −
−− −
= =
−

−


.
( )
( )( )
( )
( ) ( )
( )(
)
( )
( )
( )( )
2
2
1 23
1 23
12 1
1
2
. 2. 1
xx x
x
gx
axxx x xx xx
xaxx x ax xx xx
−− −
−
= =
− −− −
− − −− −
.
1
0,
x xx= =
không phải tiệm cận đứng của đồ thị hàm số
( )
y gx=
không thỏa mãn điều kiện
0
1
x ≥
. Đồ thị hàm số
( )
gx
có
3
đường tiệm cận đứng là:
23
2, ,x xxxx= = =
.
Câu 12: Cho hàm số bậc ba
( )
32
f x ax bx cx d= + ++
có đồ thị như hình vẽ sau.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 145
Hỏi đồ thị hàm số
(
)
( )
( ) ( ) ( )
2
2
32 1
1
xx x
gx
x f x fx
−+ −
=

+−

có bao nhiêu tiệm cận đứng?
A.
5
. B.
4
. C.
6
. D.
3
.
Lời giải
Chọn D
Ta có
( )
( )( )
( ) ( ) ( )
12 1
11
xx x
gx
x fx fx
−− −
=
+−


Đkxđ:
( )
( )
1
0
1
x
fx
fx
≥
≠
≠
Dựa vào đồ thị hàm số
( )
y fx=
, ta có:
(
)
1
2
0
x
fx
xx
=
= ⇔
=
với
2x =
là nghiệm kép,
( )
1
0;1x ∈
.
( )
2
3
1
1
x
fx x x
xx
=
=⇔=
=
với
( )
23
1; 2 ; 2xx∈>
.
Vậy
( )
( )
( )
( )( ) ( )( )
( )( )
2
2
1 23
12 1
12 1
xx x
gx
ax x xx x xx xx
−− −
=
+− − −− −
( )( )( )( )(
)
2
123
1
12
x
ax x xx xx xx
−
=
+− − − −
Vậy đồ thị hàm số có 3 TCĐ
23
2; ;x xxxx= = =
.
Câu 13: Cho hàm số
()y fx=
là hàm số đa thức có đồ thì như hình vẽ dưới đây, đặt
(
)
( ) ( )
2
2
2
−
=
−
xx
gx
f x fx
. Hỏi đồ thị hàm số
( )
=y gx
có bao nhiêu tiệm cận đứng?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 146
A.
5
. B.
3
. C.
4
. D.
2
.
Lời giải
Chọn C
Ta xét phương trình
(
)
(
)
( )
( )
1
2
2
3 31
1
1
0
20
0
2
1
1,
x
xx
fx
f x fx
x
fx
xx
xx x x
=
= <−
=
−=⇔ ⇔
=
=
= >
= <− ≠
. Khi đó
( )
( ) ( )( )( )
( )( )( )( )
( )
2
2
123
123
1
; 0
1
1
−
= = ≠
−− − −
−−− −
xx
gx a
ax xx xx xx
axx xx xx xx
.
Vậy đồ thị hàm số
( )
=y gx
có
4
đường tiệm cận đứng.
Câu 14: Cho hàm số
( )
y fx
=
xác định, liên tục trên
và có bảng biến thiên như hình bên dưới.
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
( )
3
1
3
y
fx x
=
++
là
A. 2. B. 4. C. 3. D. 1.
Lời giải
Chọn A
Tính tiệm cận ngang.
Ta có
( )
3
3
1
lim 0
3
x
x
xx
fx x
→+∞
→+∞
+ → + ∞ ⇒ =
++
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 147
( )
3
3
1
lim 0
3
x
x
xx
fx x
→−∞
→−∞
+ → − ∞ ⇒ =
++
Vậy đồ thị hàm số có 1 tiệm cận ngang
0y
=
.
Tính tiệm cận đứng.
Số đường tiệm cận đứng của đồ thị hàm số là số nghiệm của phương trình
( )
3
30
fx x+ +=
.
Dựa vào bảng biến thiên ta có
( )
(
)
(
)
3 33
00
3 0 3 ; ;1
fxx fxx xxxx+ + = ⇔ + = − ⇔ + = ∈ −∞
Vì hàm số
3
yx x= +
đồng biến trên
do đó
( )
3
00
; ;1x x xx+ = ∈ −∞
có một nghiệm duy
nhất.
Vậy đồ thị hàm số
( )
3
1
3
y
fx x
=
++
có 1 tiệm cần đứng.
Câu 15: Cho hàm số
( )
32
y f x ax bx cx d= = + ++
có đồ thị như bên dưới.
Hỏi đồ thị hàm số
( )
( ) ( ) ( )
2
2
22
3
xx x
y
x f x fx
−−
=

−−

có bao nhiêu đường tiệm cận đứng
A.
4
. B.
6
. C.
3
. D.
5
.
Lời giải
Chọn C
Ta có
( )
2
32y x ax bx c
′
= ++
.
Dựa vào đồ thị hàm số, ta thấy hàm số đạt cực trị tại
0x =
,
2x =
. Do đó, ta có hệ
( )
( )
( )
( )
01
23
00
20
y
y
y
y
=
= −
′
=
′
=
1
0
12 4 0
84 4
d
c
ab
ab
=
=
⇒
+=
+=−
1
3
0
1
a
b
c
d
=
= −
⇒
=
=
.
Vậy
( )
32
31y fx x x= =−+
.
Khi đó
( )
( ) ( ) ( )
2
2
22
3
xx x
y
x f x fx
−−
=

−−

( )
( )
( )( )
2
32 32
22
3 31 3
xx x
x xx xx
−−
=
− −+ −
( )
( )
( )
2
2
2 32
22
3 31
xx x
xx x x
−−
=
− −+
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 148
Ta có
( )
( )
2
2 32
3 3 10xx x x− − +=
(
)
( )
(
)
1
2
3
0
3
1; 0
0;1
2;3
x
x
xx
xx
xx
=
=
⇔ = ∈−
= ∈
= ∈
.
Hàm số
(
)
(
)
(
)
2
2
2 32
22
3 31
xx x
y
xx x x
−−
=
− −+
có tập xác định
(
]
{ }
12
; 2 \ 0; ;D xx= −∞
.
(
)
(
)
(
)
2
2
2 32
0
22
lim
3 31
x
xx x
xx x x
+
→
−−
− −+
( )
( )
( )
2
2 32
0
22
lim
3 31
x
xx x
xx x x
+
→
−−
=
− −+
( )
( )
( )
2
32
0
22
lim
3 31
x
xx
xx x x
+
→
−−
= = −∞
− −+
.
Suy ra
0x =
là đường tiệm cận đứng.
(
)
( )
(
)
1
2
2
2 32
22
lim
3 31
xx
xx x
xx x x
+
→
−−
= +∞
− −+
,
(
)
( )
( )
2
2
2
2 32
22
lim
3 31
xx
xx x
xx x x
+
→
−−
= +∞
− −+
.
Suy ra
1
xx=
và
2
xx=
cũng là các đường tiệm cận đứng của đồ thị hàm số.
Câu 16: Cho hàm số
32
y ax bx cx d= + ++
,
( )
0a ≠
có đồ thị như hình dưới đây.
Hỏi đồ thị hàm số
( )
( )
( )
( )
2
2
1 43
fx
gx
x xx
=
+ −+
có bao nhiêu đường tiệm cận đứng?
A.
2
. B.
1
. C.
3
. D.
4
.
Lời giải
Điều kiện xác định:
( )
2
0
1
4 30
fx
x
xx
≥
≠−
− +≠
2
1
1
3
x
x
x
x
≥
≠−
⇔
≠
≠
2
3
x
x
≥
⇔
≠
.
Ta có
( )
3
lim
x
gx
+
→
( )
( )
(
)
2
2
3
lim
1 43
x
fx
x xx
+
→
=
+ −+
= +∞
và
( )
3
lim
x
gx
−
→
( )
( )
( )
2
2
3
lim
1 43
x
fx
x xx
−
→
=
+ −+
= −∞
.
Vậy đồ thị hàm số
( )
( )
(
)
( )
2
2
1 43
fx
gx
x xx
=
+ −+
có một đường tiệm cận đứng là:
3x =
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 149
Câu 17: Cho hàm số trùng phương
42
y ax bx c
có đồ thị như hình vẽ. Hỏi đồ thị hàm số
22
2
42
23




x xx
y
fx fx
có tổng cộng bao nhiêu tiệm cận đứng?
A. 5. B. 2. C. 3. D. 4.
Lời giải
Chọn D

22
2
42
23




x xx
y
fx fx
2
2
22
23




xx x
fx fx
Ta có:
2
2 30



fx fx
1
3

fx
fx
2
0
2
2
2



x mm
x
x nn
x
x
Dựa vào đồ thị ta thấy các nghiệm
0; 2xx 
là các nghiệm kép và đa thức
2
23fx fx



có bậc là 8 nên

2
22
22
22
22


xx x
y
axx x xmxn
Vậy hàm số có các tiệm cận đứng là
0; 2; ; x x xmxn
.
| 1/109

Tài liệu khác của Toán 12

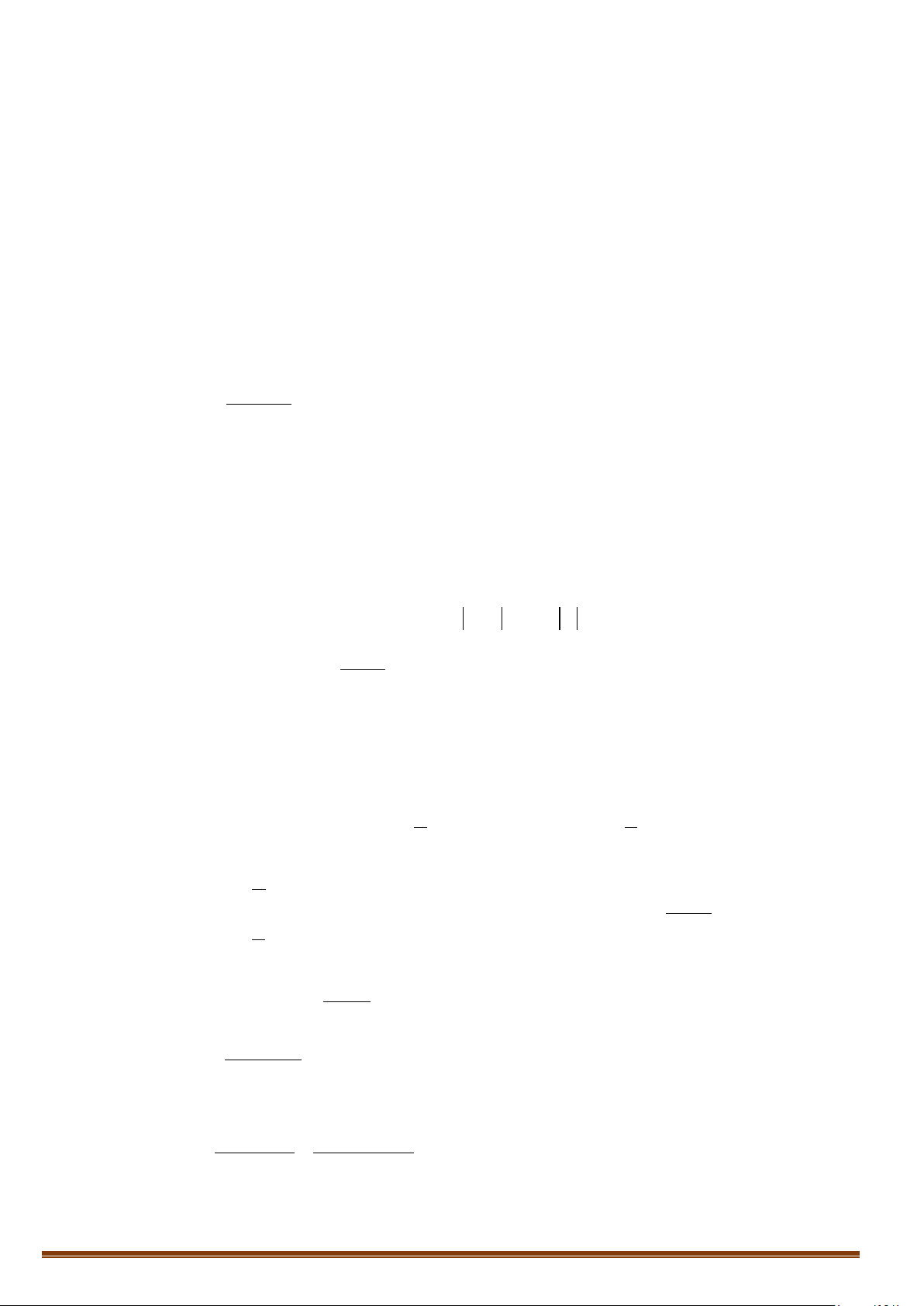
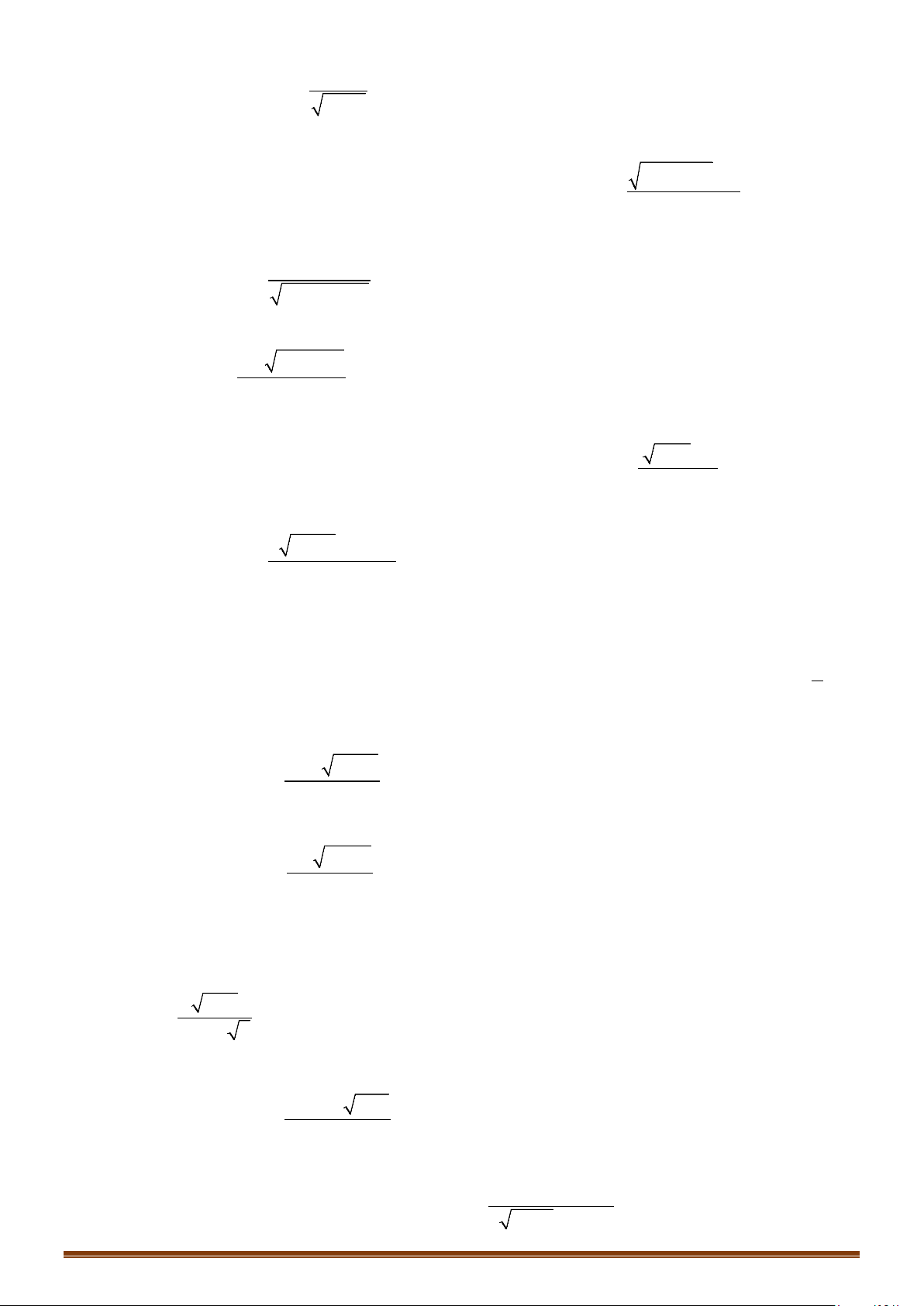
Preview text:

CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
NG I ỨNG DỤNG ĐẠO HÀM ƯƠ
ĐỂ KHẢO SÁT HÀM SỐ CH
BÀI 4. ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ I LÝ THUYẾT.
1. Nhánh vô cực của đường cong (C) : y = f (x) Gọi M ( ; x y)∈(C) .
x → +∞ hay x → −∞
Ta nói: (C) có nhánh vô cực ⇔ 
y → +∞ hay y → −∞
VD1: Đồ thị (C) của hàm số 2
y = x có nhánh vô cực
VD2: Đồ thị (C) của hàm số 2
y = 4 − x không có nhánh vô cực vì M ( ; x y)∈(C) ⇒ 2
− ≤ x ≤ 2 và 0 ≤ y ≤ 2 .
2) Tiệm cận của đường cong
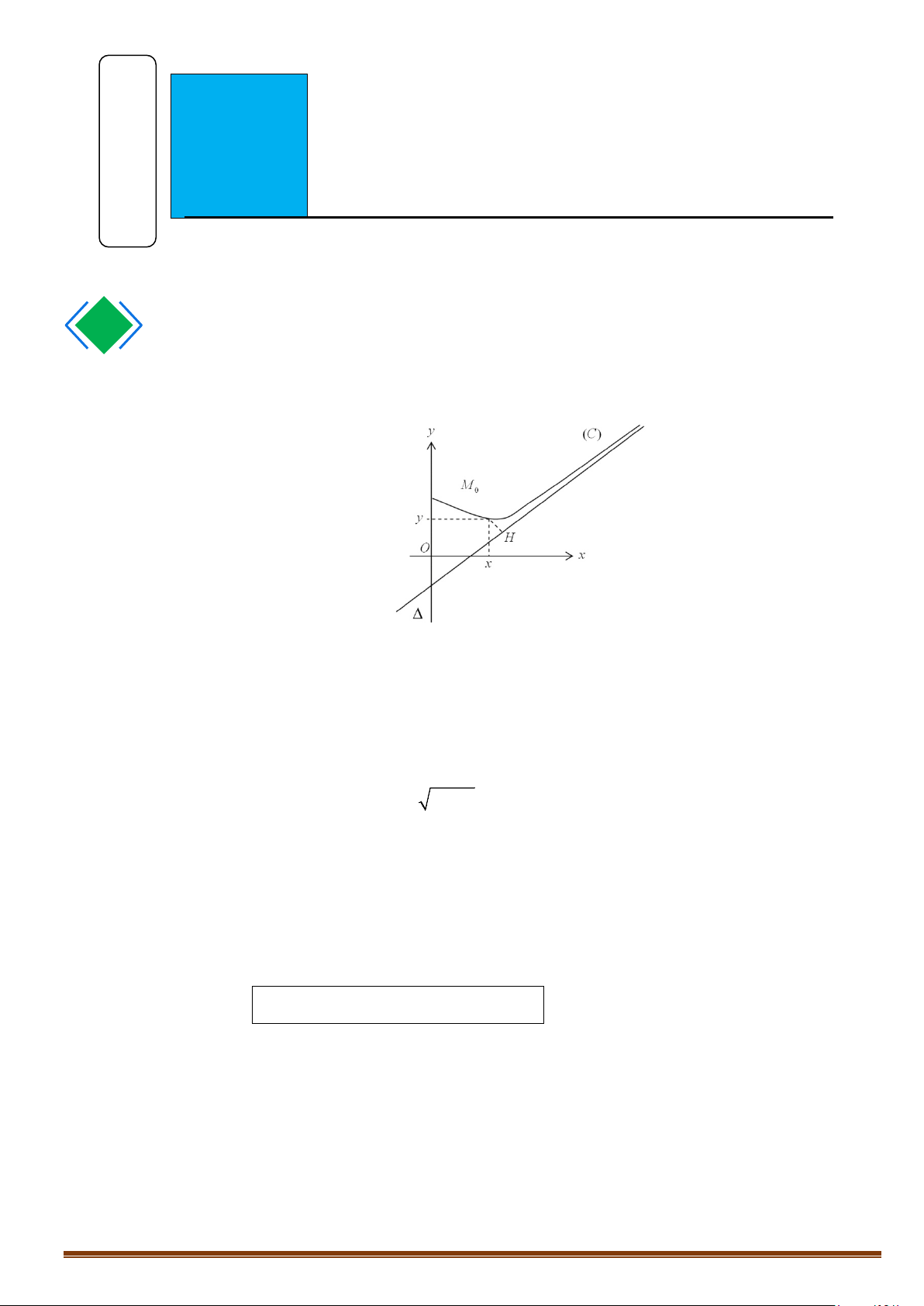
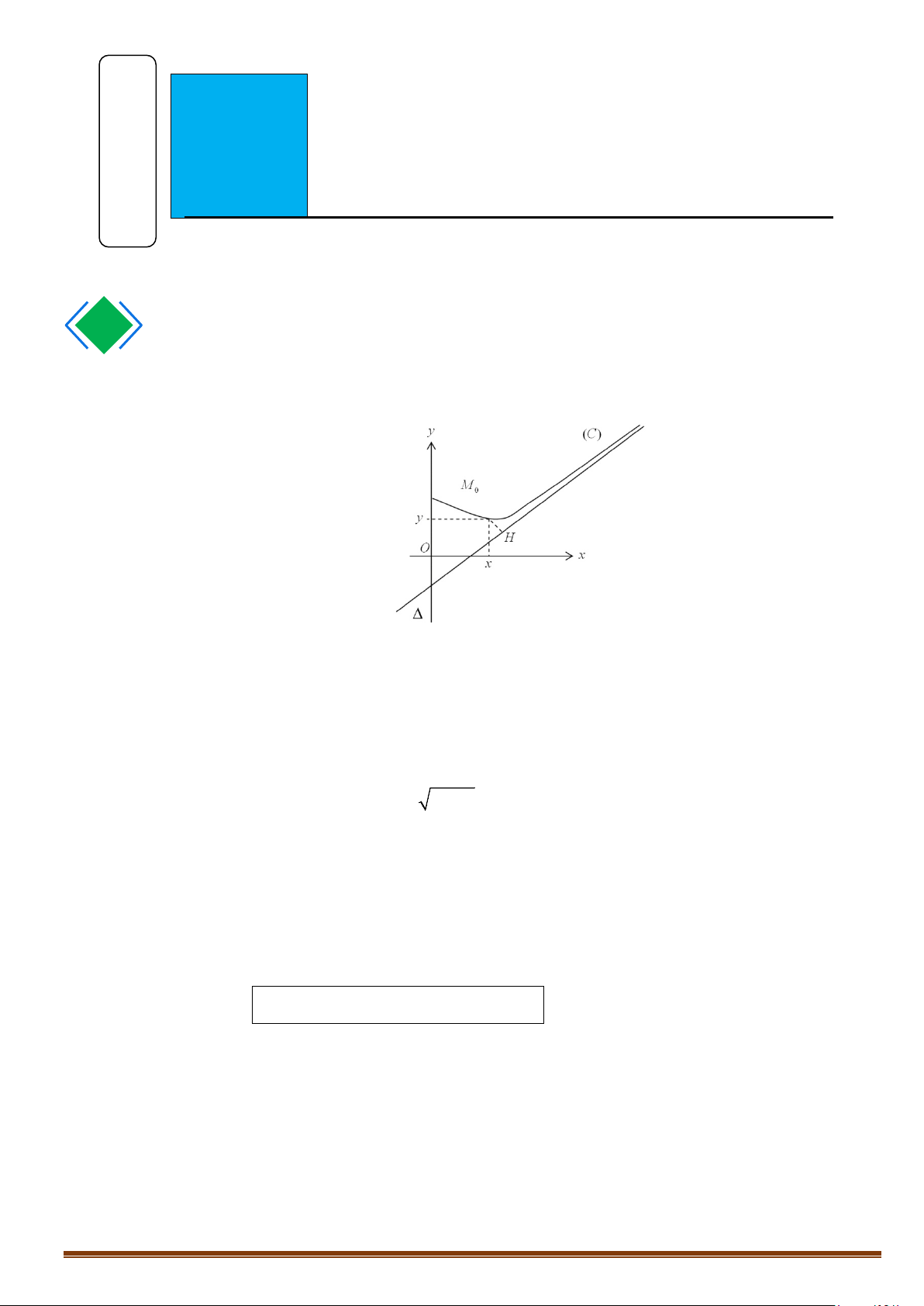
Cho đường cong (C) : y = f (x) và M ( ;
x y)∈(C) , H là hình chiếu vuông góc của M lên (∆) .
Đường thẳng (∆) được gọi là tiệm cận của (C) khi và chỉ khi khoảng cách MH từ M đến (∆)
tiến về 0 khi M vẽ nên nhánh vô cực của (C).
Như vậy: (∆) tiệm cận của (C) ⇔ lim MH = 0 M →∞ Page 167
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
3) Định nghĩa đường TCĐ và TCN của đồ thị hàm số
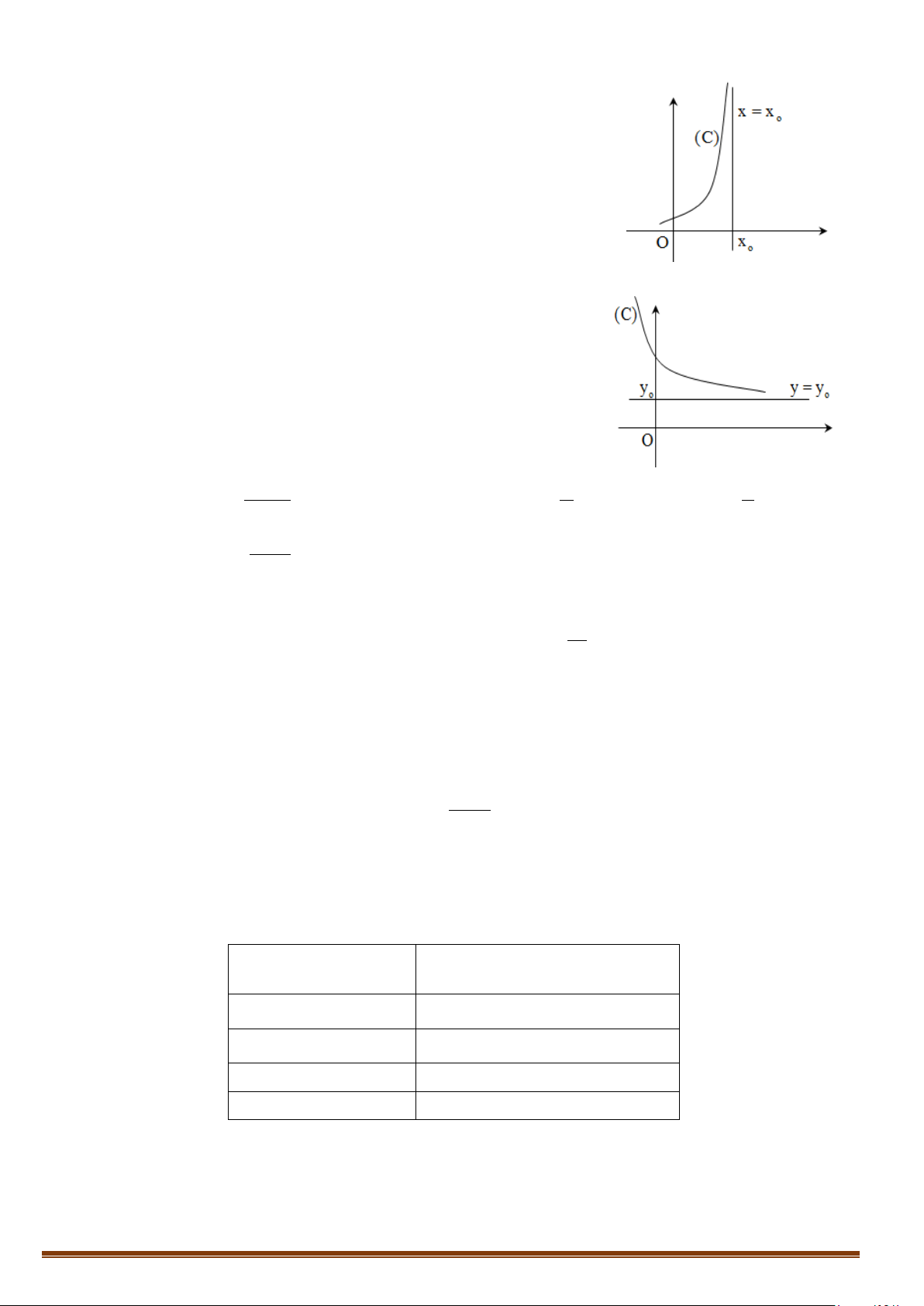
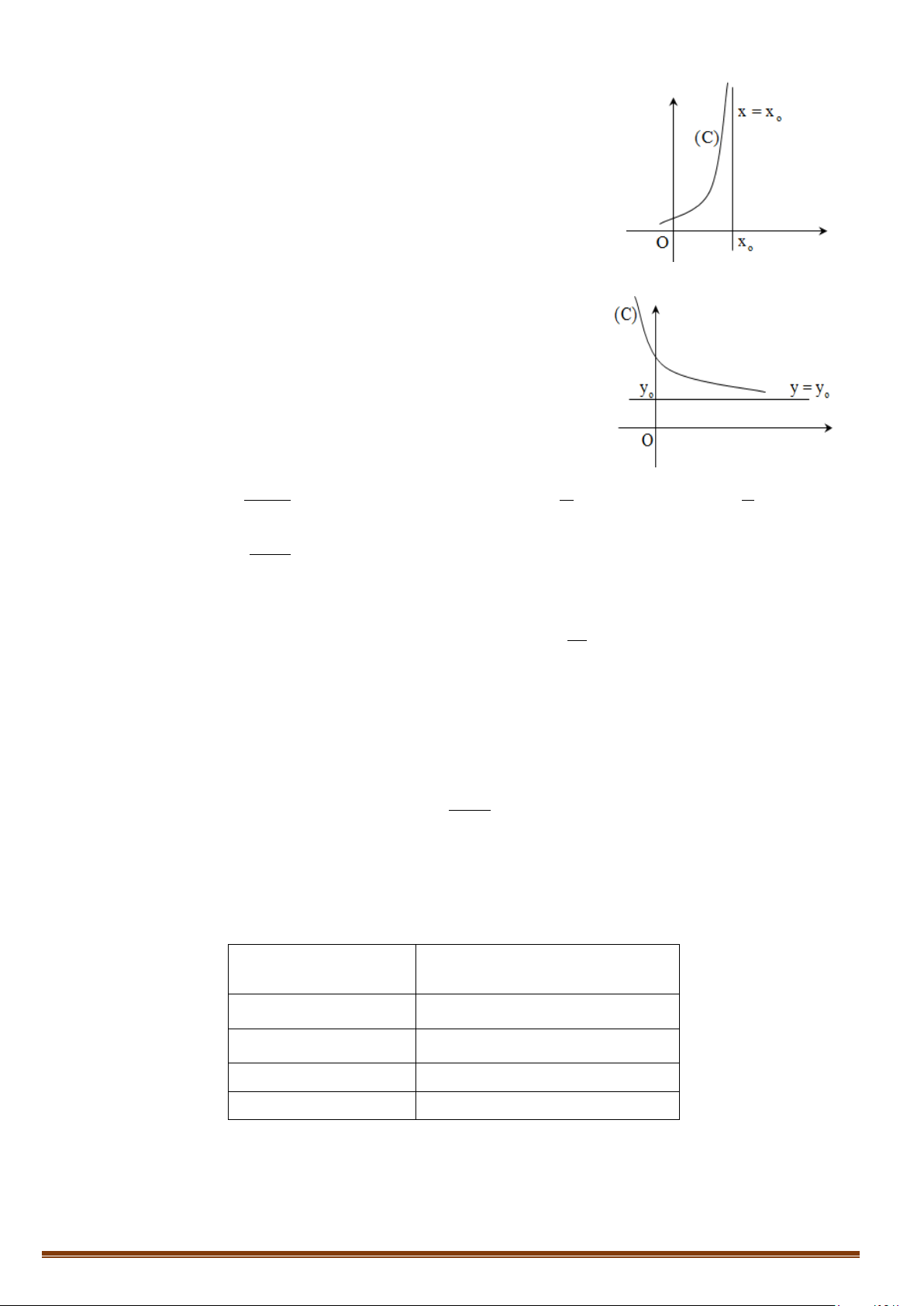
a) Tiệm cận đứng của đồ thị hàm số
Đường thẳng x = x được gọi là đường tiệm cận đúng 0
(TCĐ) của đồ thị hàm số y = f (x) nếu thỏa mãn ít nhất
một trong các điều kiện sau:
lim f (x) = +∞ ; lim f (x) = −∞ x + → + 0 x x→ 0 x
lim f (x) = +∞ ; lim f (x) = −∞ x − → − 0 x x→ 0 x
b) Tiệm cận ngang của đồ thị hàm số
Cho hàm số y = f (x) có xác định trên một khoảng vô hạn
là khoảng có một trong các dạng (a,+∞) ; (−∞,a) ; (−∞,+∞)
.Đường thẳng y = y được gọi là đường TCN (hay TCN) 0
của đồ thị nếu thỏa mãn ít nhất một trong các điều kiện sau:
lim f (x) = y ; lim f (x) = y 0 x→−∞ 0 x→+∞  Lưu ý: i) Hàm ax + b y =
với ac ≠ 0 có tiệm cận đứng d
x = − ; tiệm cận ngang a y = . cx + d c c f (x) ii) Hàm y =
với f (x), g (x) là những hàm đa thức g (x)
+) Nếu bậc tử nhỏ hơn bậc mẫu thì có tiệm cận ngang y = 0.
+) Nếu bậc tử bằng bậc mẫu thì có tiệm cận ngang an y =
với a b là hệ số của lũy thừa n , b n n
cao nhất trên tử và dưới mẫu.
+) Nếu bậc tử lớn hơn bậc mẫu thì không có tiệm cận ngang.
g (x = 0; f x ≠ 0 0 ) ( 0)  
g ( x = f x = 0 0 ) ( 0)
+) x = x là tiệm cận đứng ⇔ . 0    f (x)  lim = ±∞  x→  0 x g   (x)
iii) Ứng dụng máy tính CASIO để tìm tiệm cận đứng hoặc tiệm cận ngang
Để tìm tiệm cận đứng hoặc tiệm cận ngang của một hàm số thông qua máy tính CASIO, ta sử dụng phím CALC trên máy.
Một số lưu ý về kết quả và cách bấm: Giới hạn Thao tác trên máy tính x x+ → CALC 10 x − + o 10 o x x− → CALC 10 x − − o 10 o x → +∞ CALC 10 10 x → −∞ CALC 10 10 − Page 168
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
II HỆ THỐNG BÀI TẬP TỰ LUẬN.
DẠNG 1: TÌM TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ CHO BỞI CÔNG THỨC 2x − 3
Câu 1. Cho hàm số y = f (x) =
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm x + 2
số y = f (x) . Lời giải
Vì lim y = 2; lim y = 2 nên đồ thị hàm số có 1 tiệm cận ngang là y = 2 . x→−∞ x→+∞ Vì lim y = ;
−∞ lim y = +∞ nên đồ thị hàm số có 1 tiệm cận đứng x = 2 − . x 2+ x 2− →− →−
Do đó đồ thị hàm số có tổng số 2 tiệm cận kể cả đứng và ngang. 2020x − 2021
Câu 2. Cho hàm số y = f (x) =
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ 1− x
thị hàm số y = f (x) . 2x − 5
Câu 3. Cho hàm số y = f (x) =
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm x − 2
số y = f (x) . 2 x + 2x + 3
Câu 4. Cho hàm số y = f (x) =
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ x +1
thị hàm số y = f (x) . 2 x − x − 6
Câu 5. Cho hàm số y = f (x) =
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị x −1
hàm số y = f (x) . 2 x + 3 − 2
Câu 6. Cho hàm số y = f (x) =
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị x −1
hàm số y = f (x) . 2 x − x − 6
Câu 7. Cho hàm số y = f (x) =
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị 2 x + 3x + 2
hàm số y = f (x) . 2 + + − Câu 8. x 2x 3 3x
Cho hàm số y = f (x) =
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của 2x − 4
đồ thị hàm số y = f (x) . 2
5x − x + 3x + 2
Câu 9. Cho hàm số y = f (x) =
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của 2 − x
đồ thị hàm số y = f (x) . Page 169
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
DẠNG 2: TÌM TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ BIẾT BBT CỦA HÀM SỐ, ĐỒ THỊ CỦA HÀM
SỐ ĐÓ HOẶC HÀM SỐ LIÊN QUAN
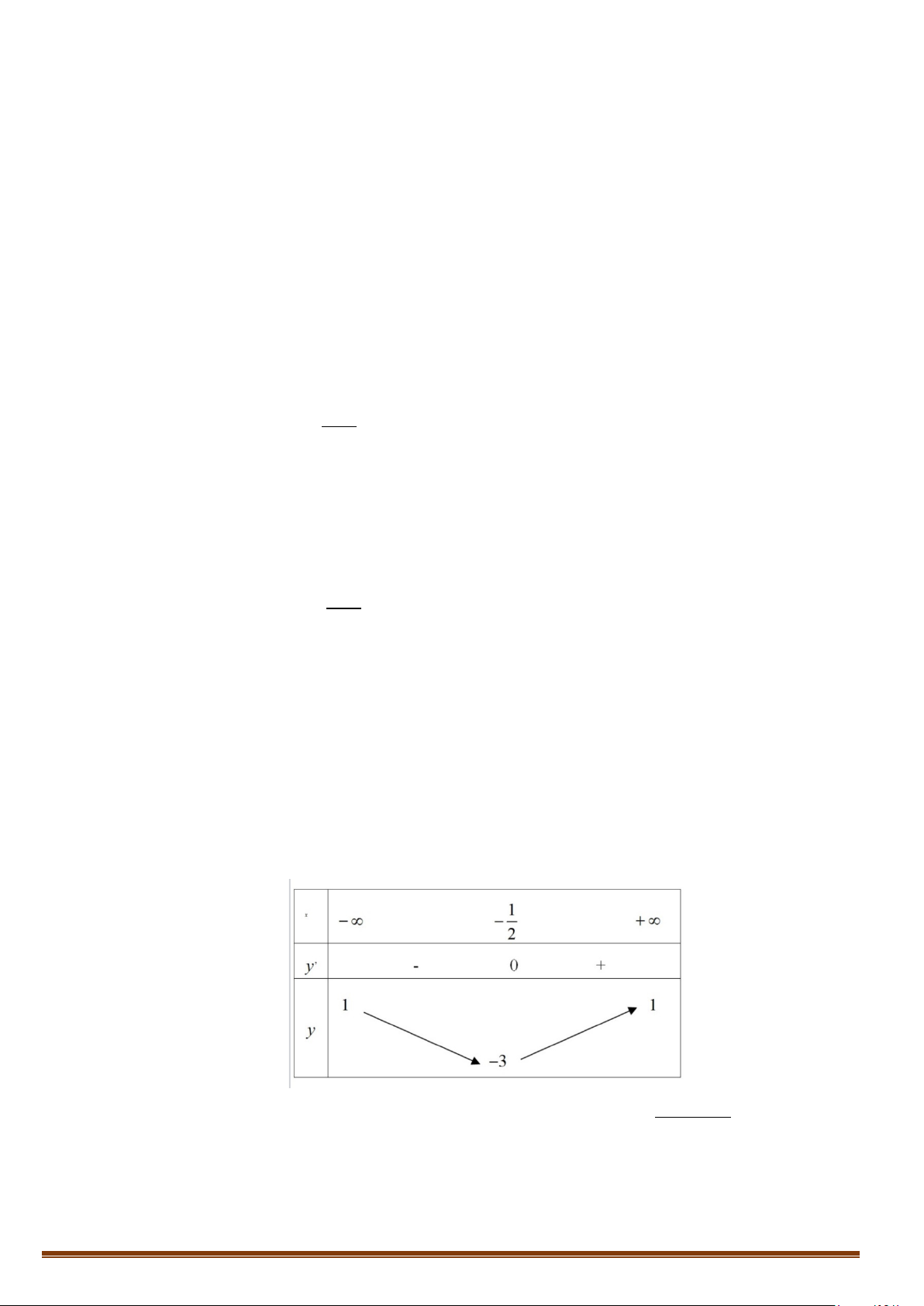
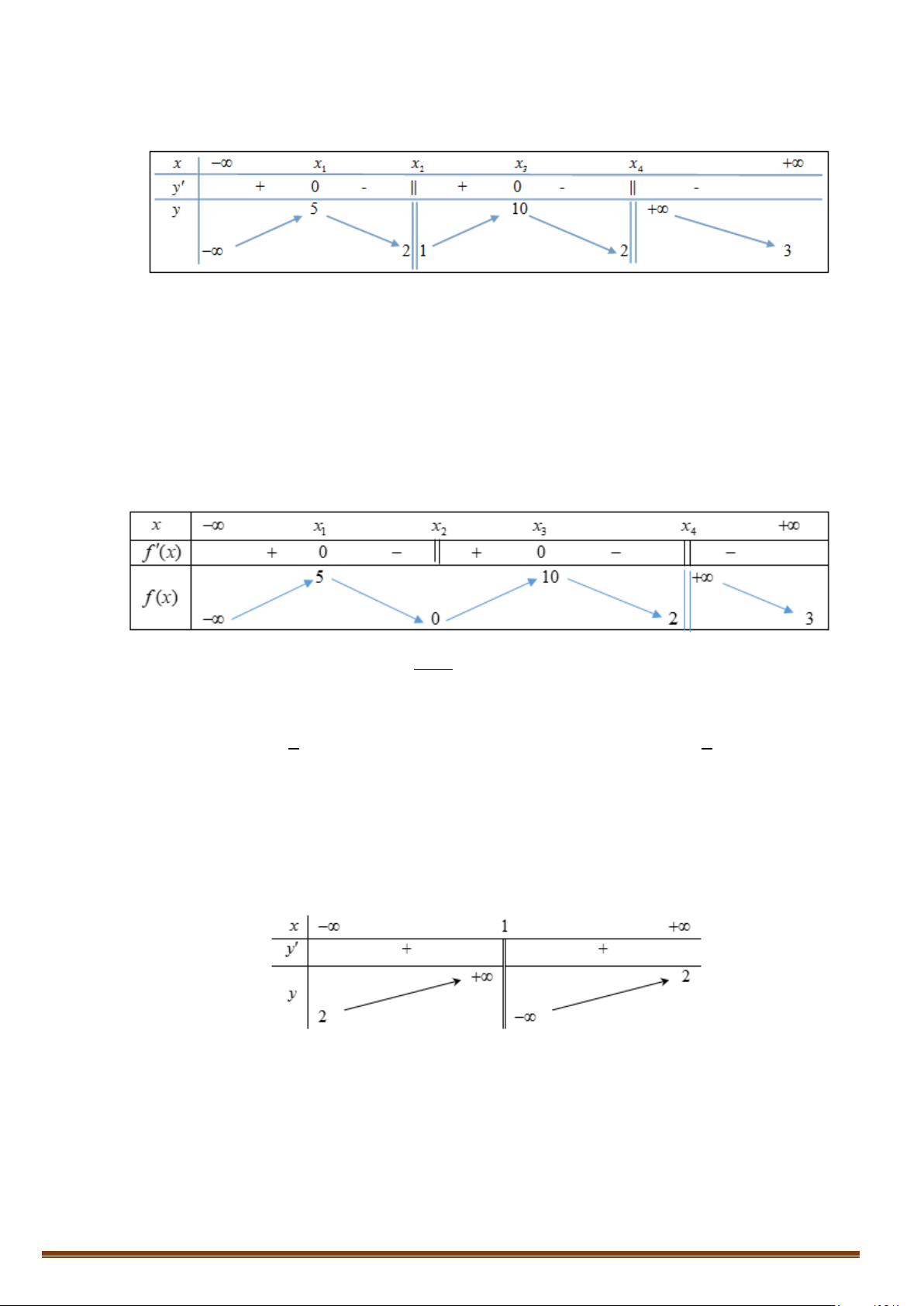
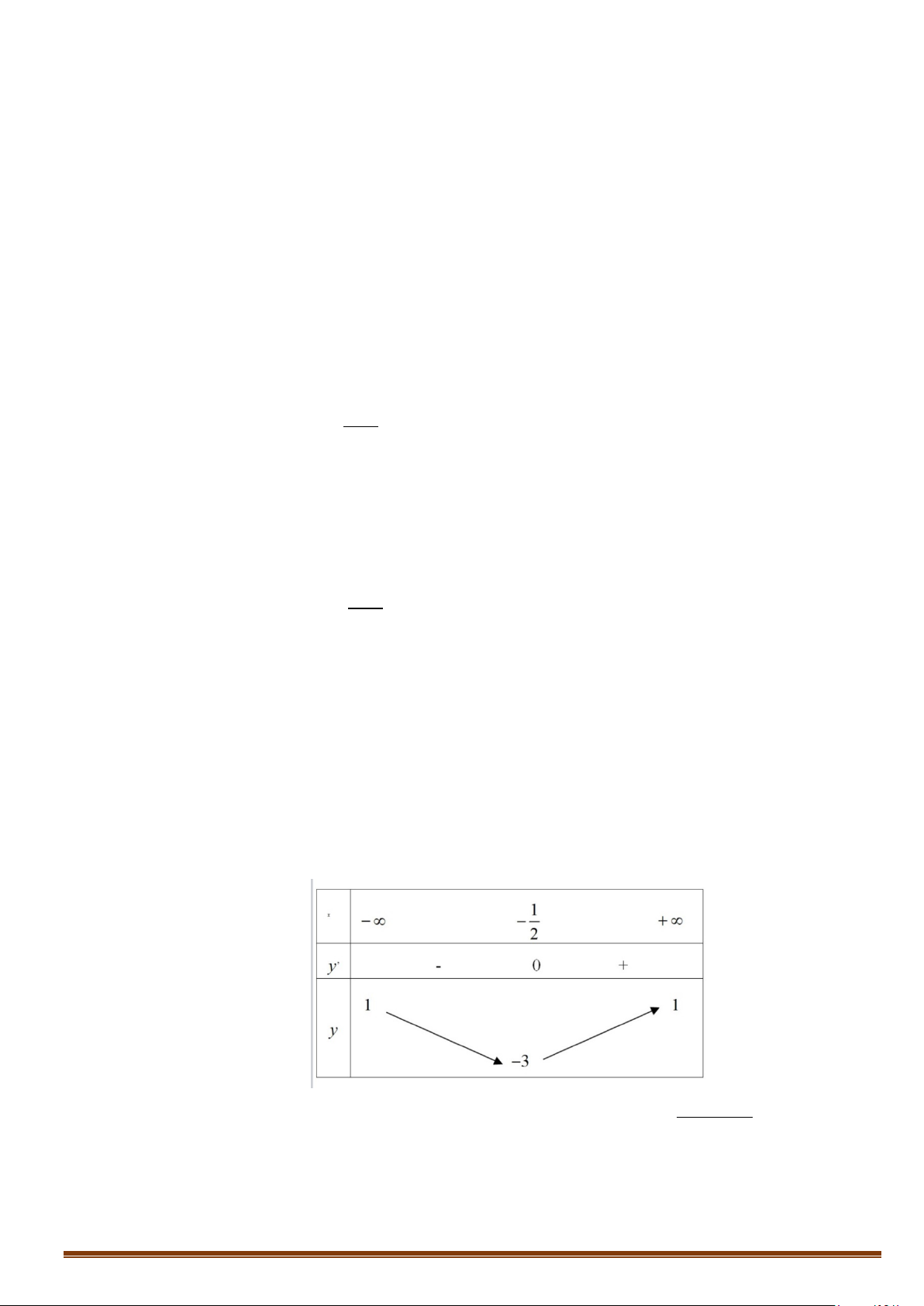
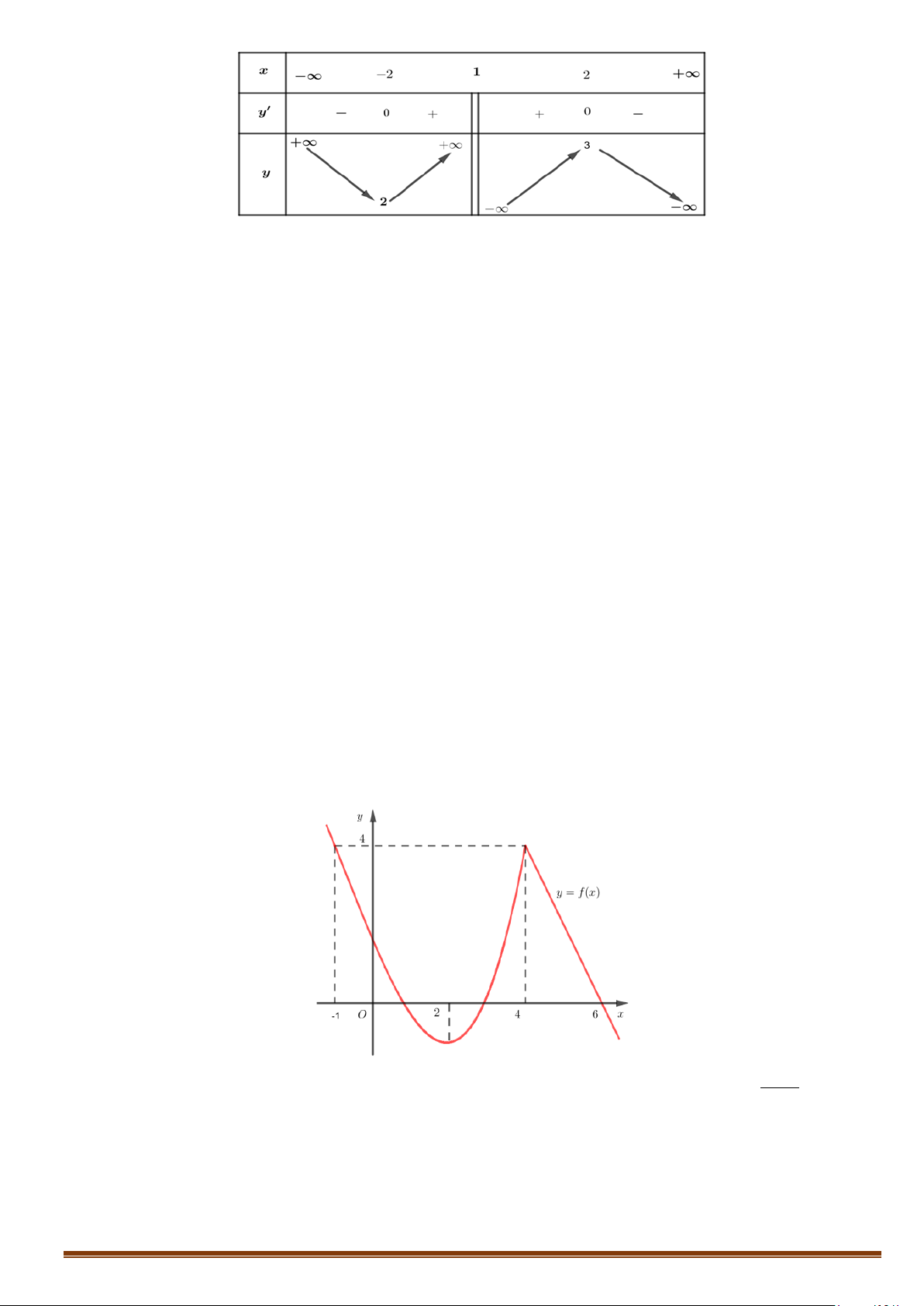
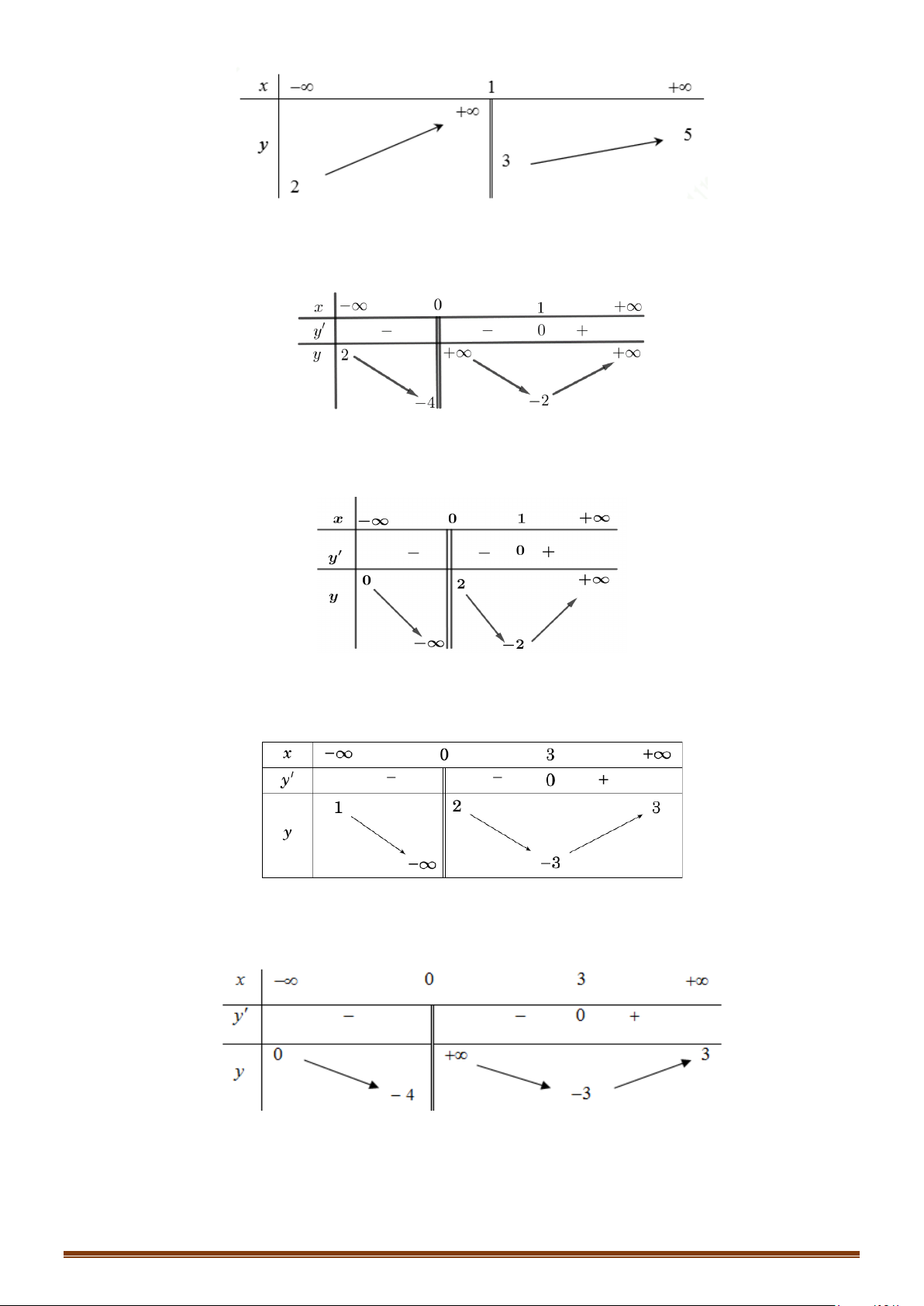
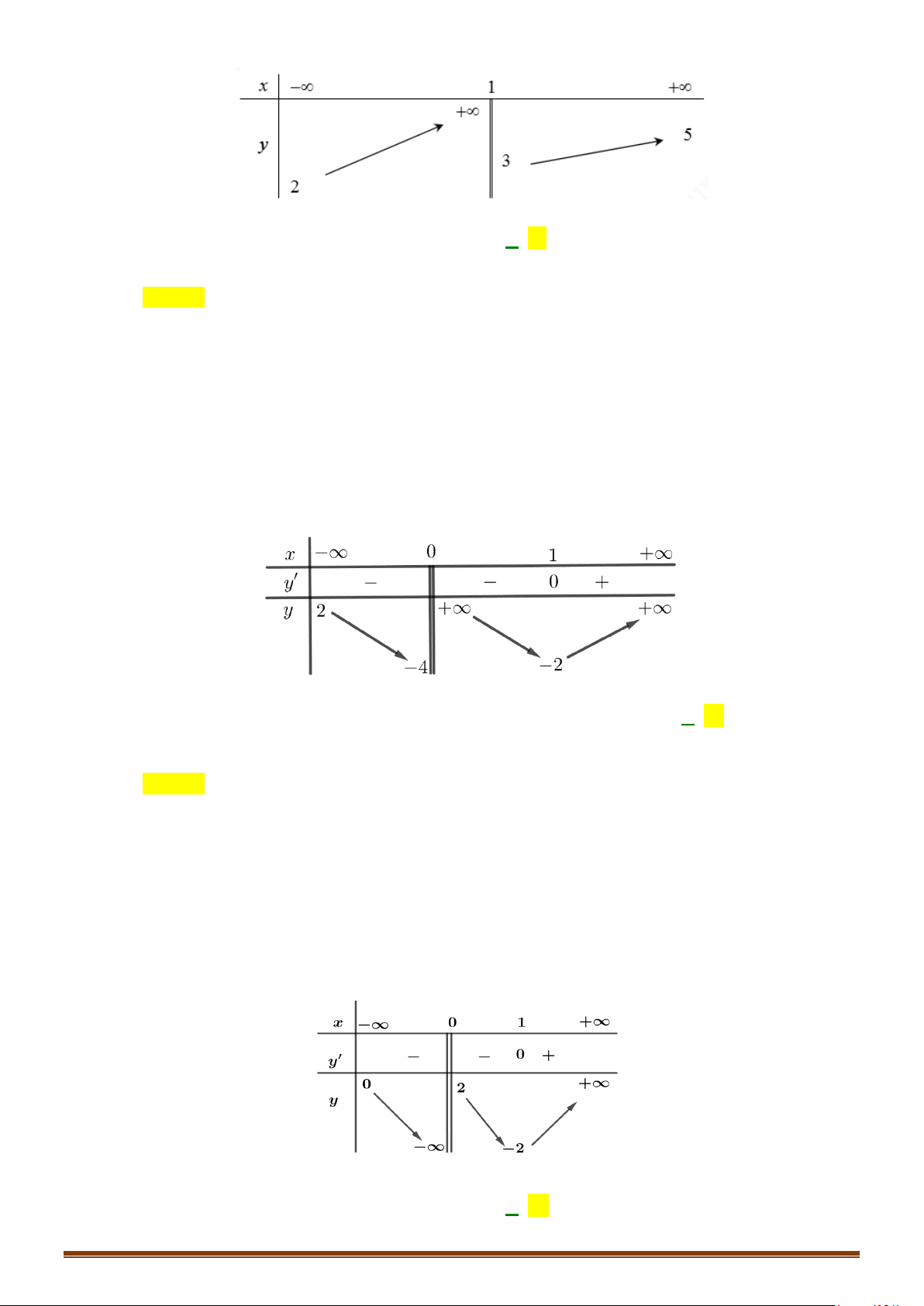
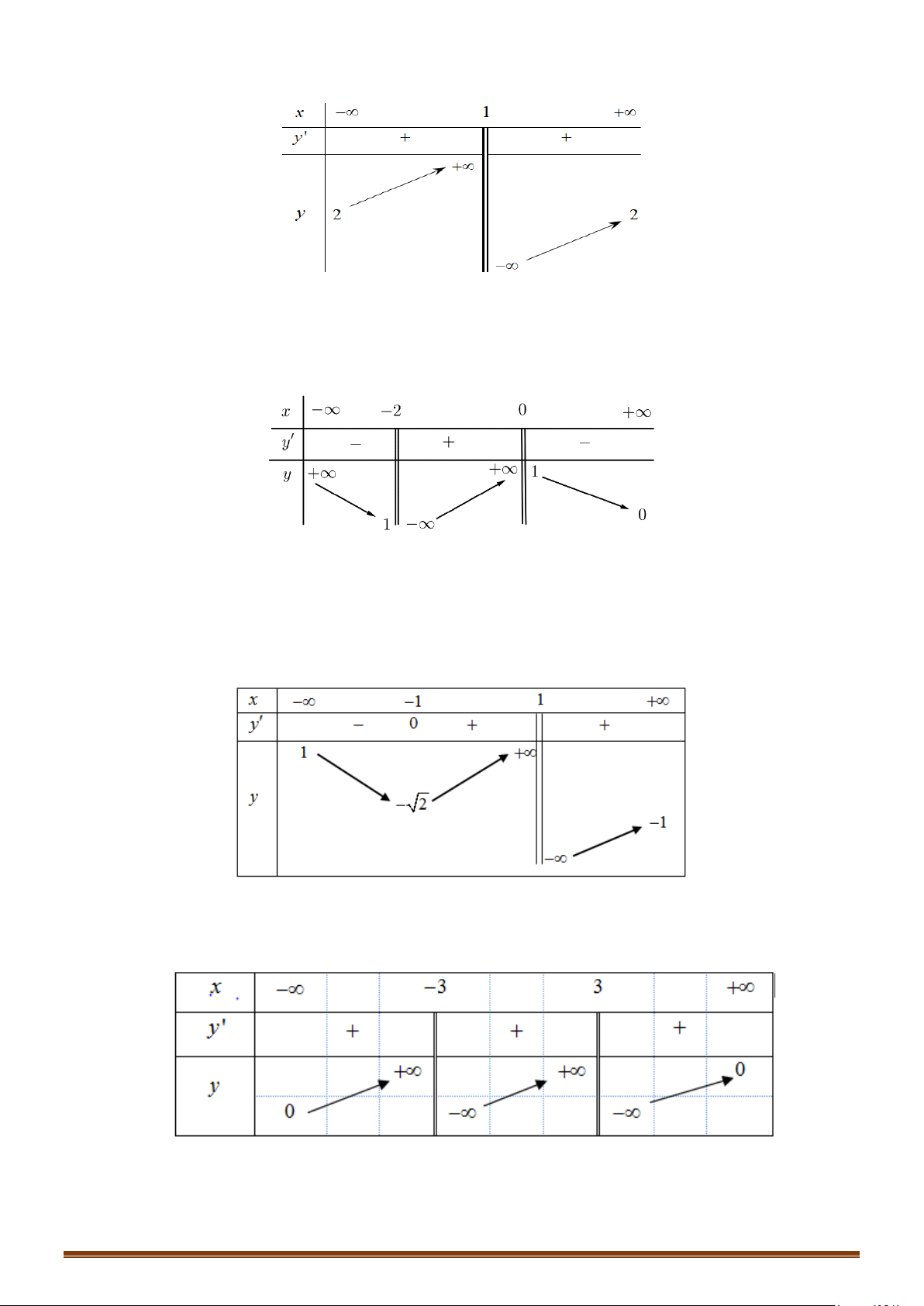
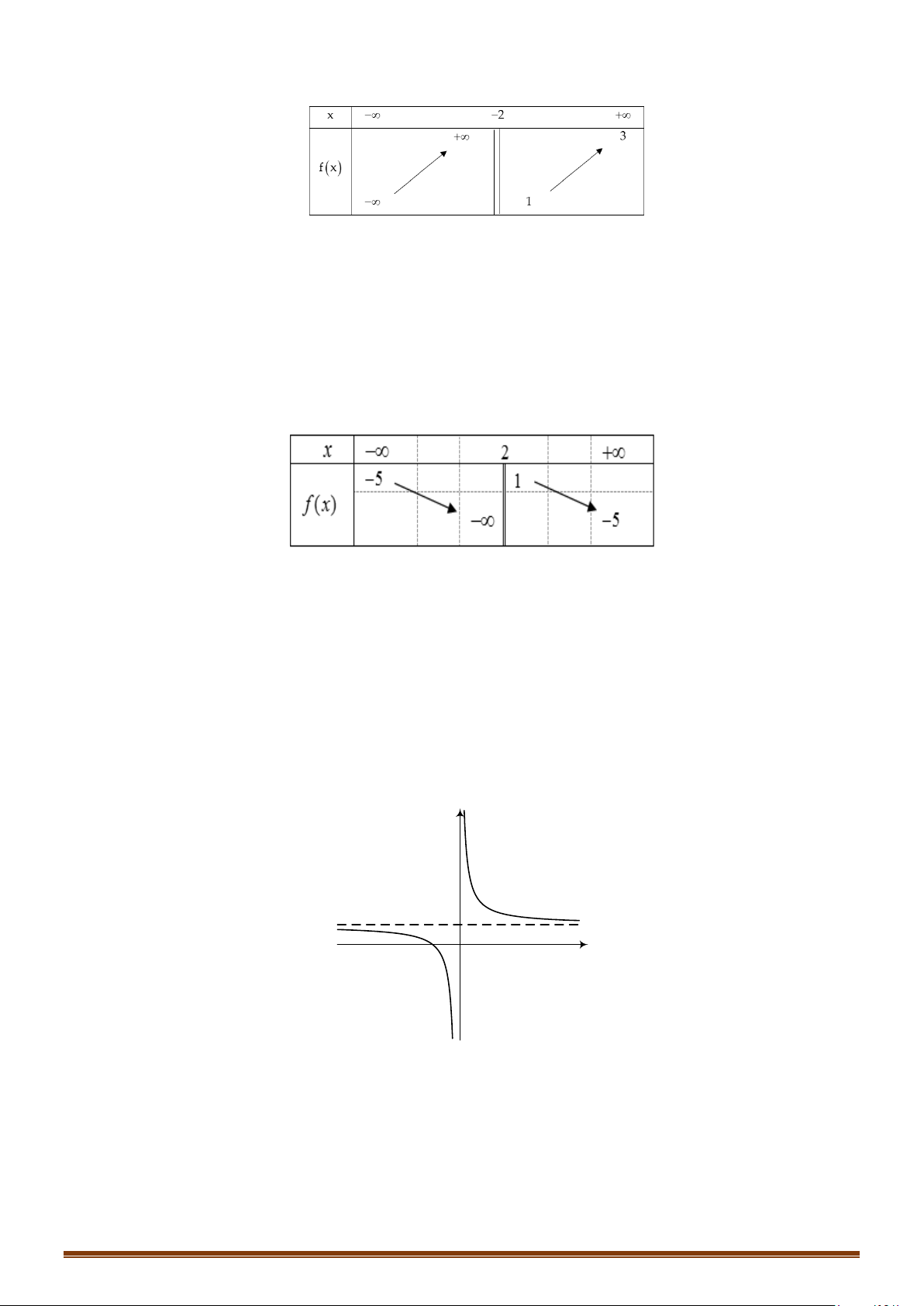
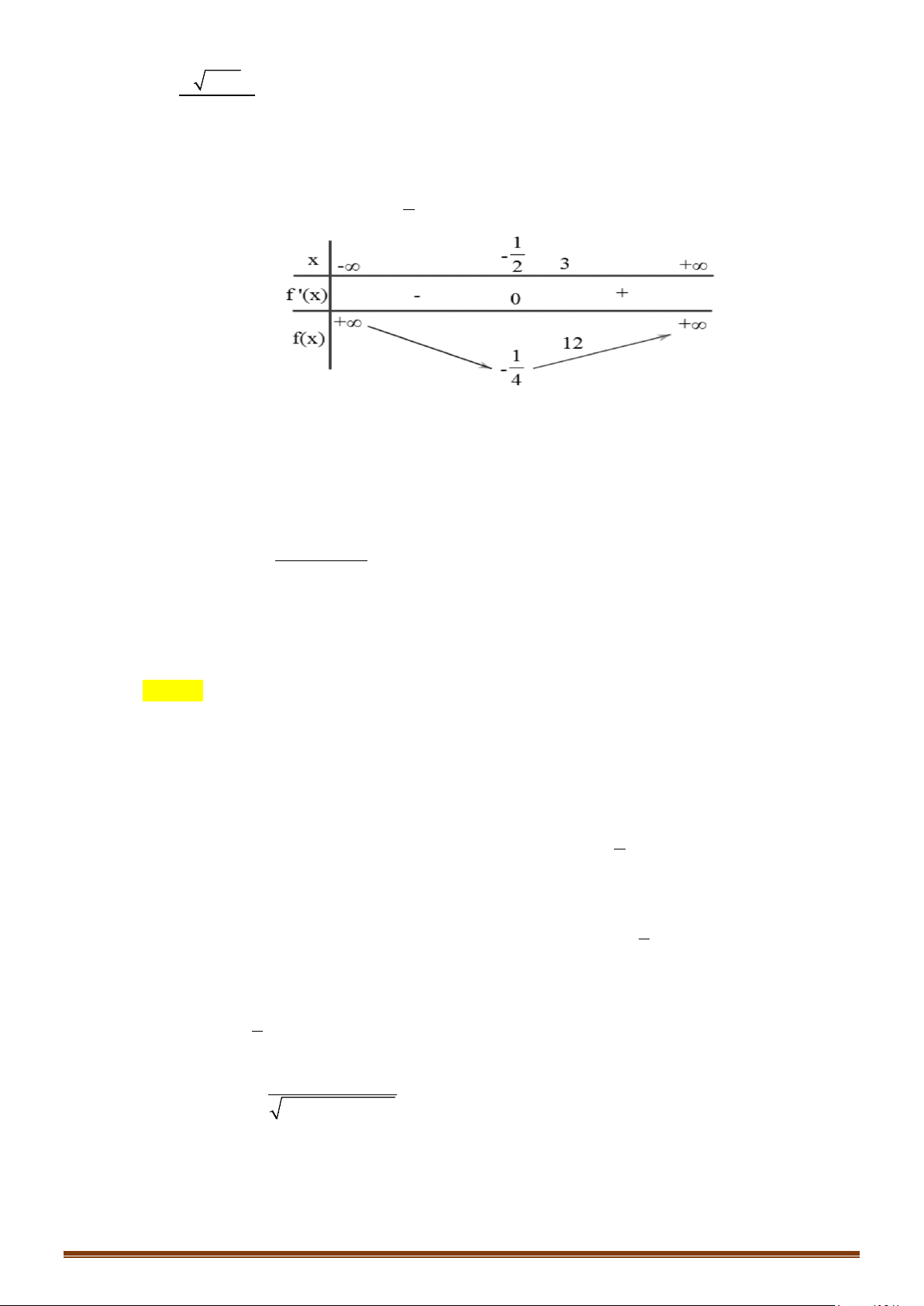
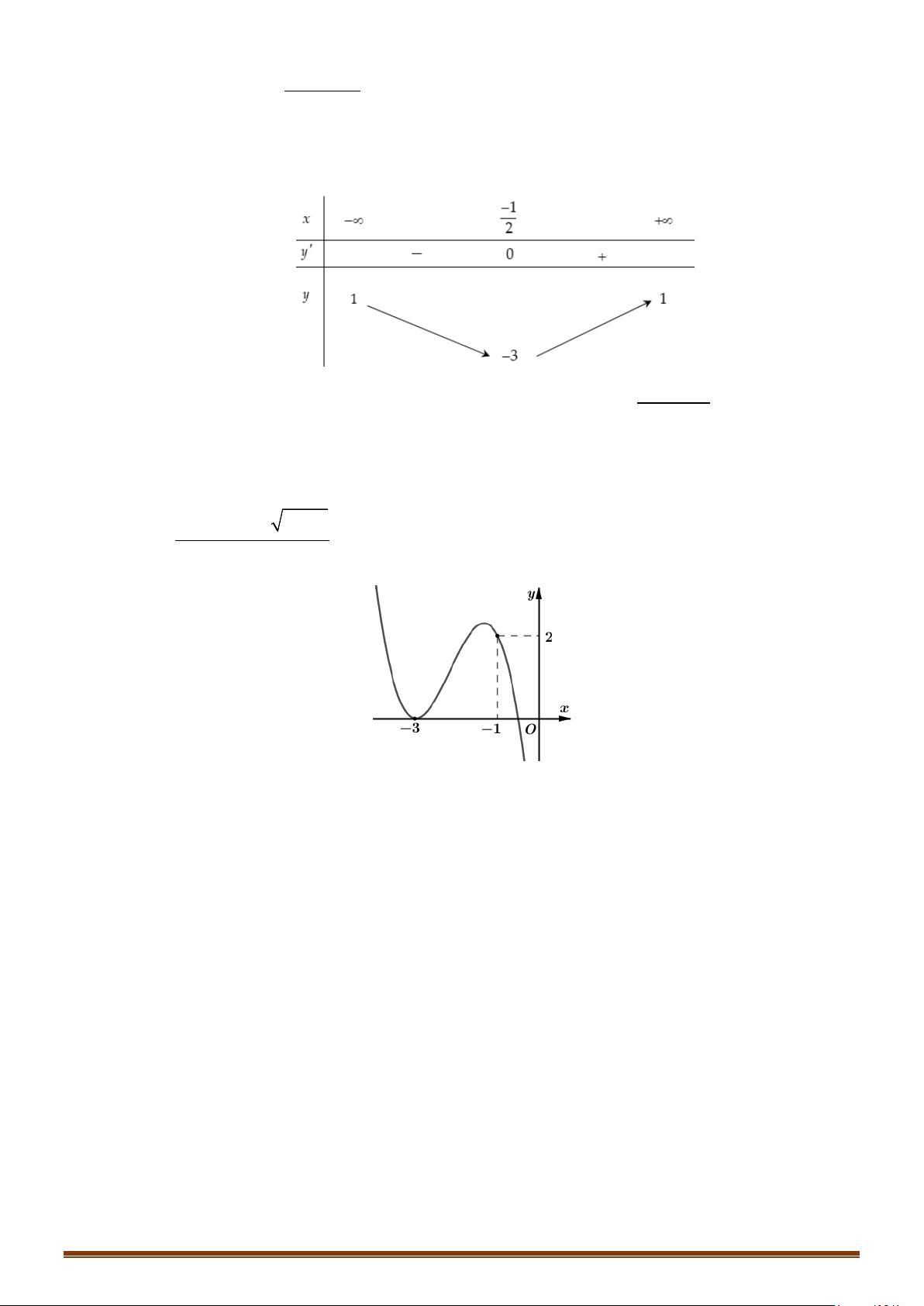
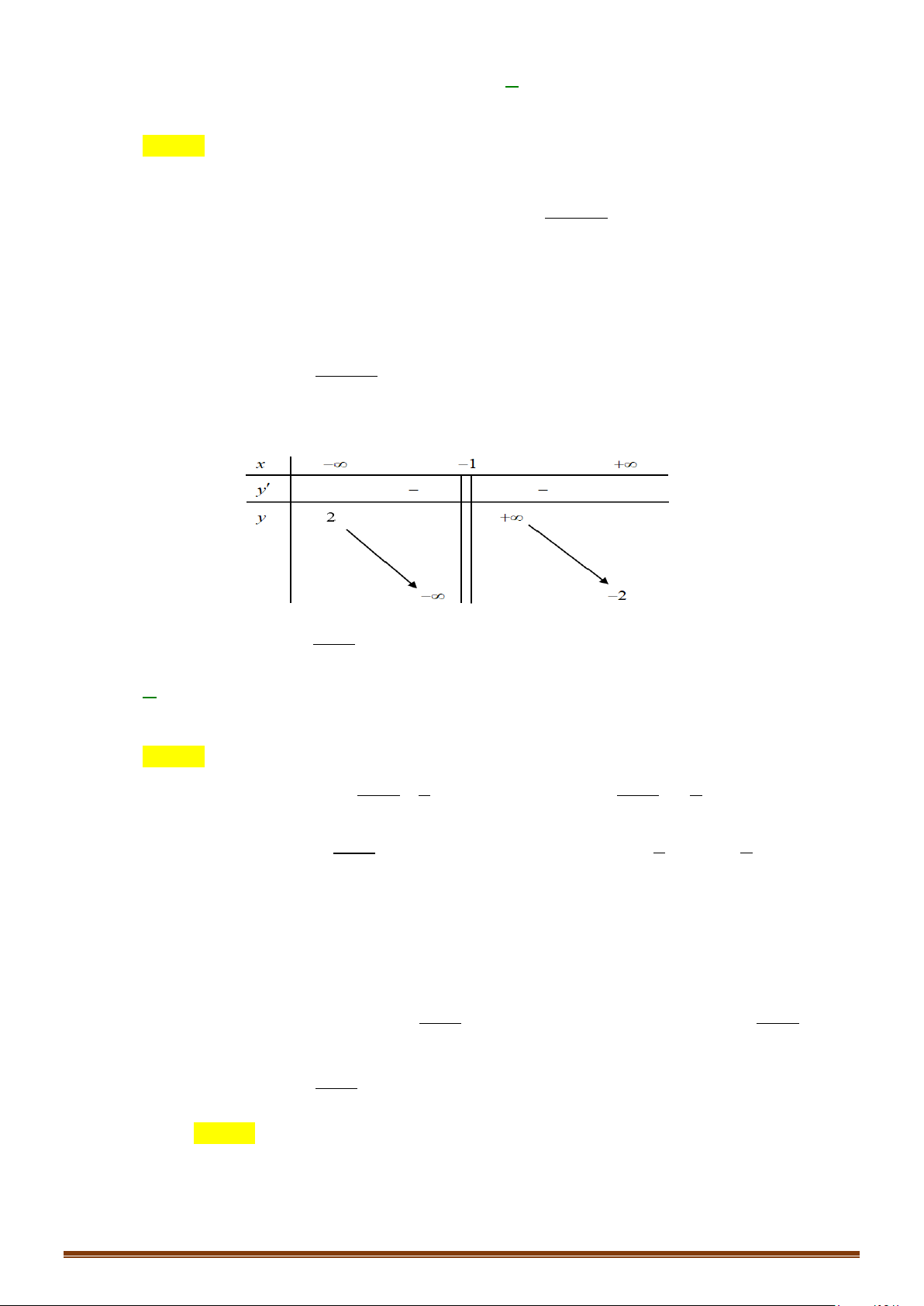
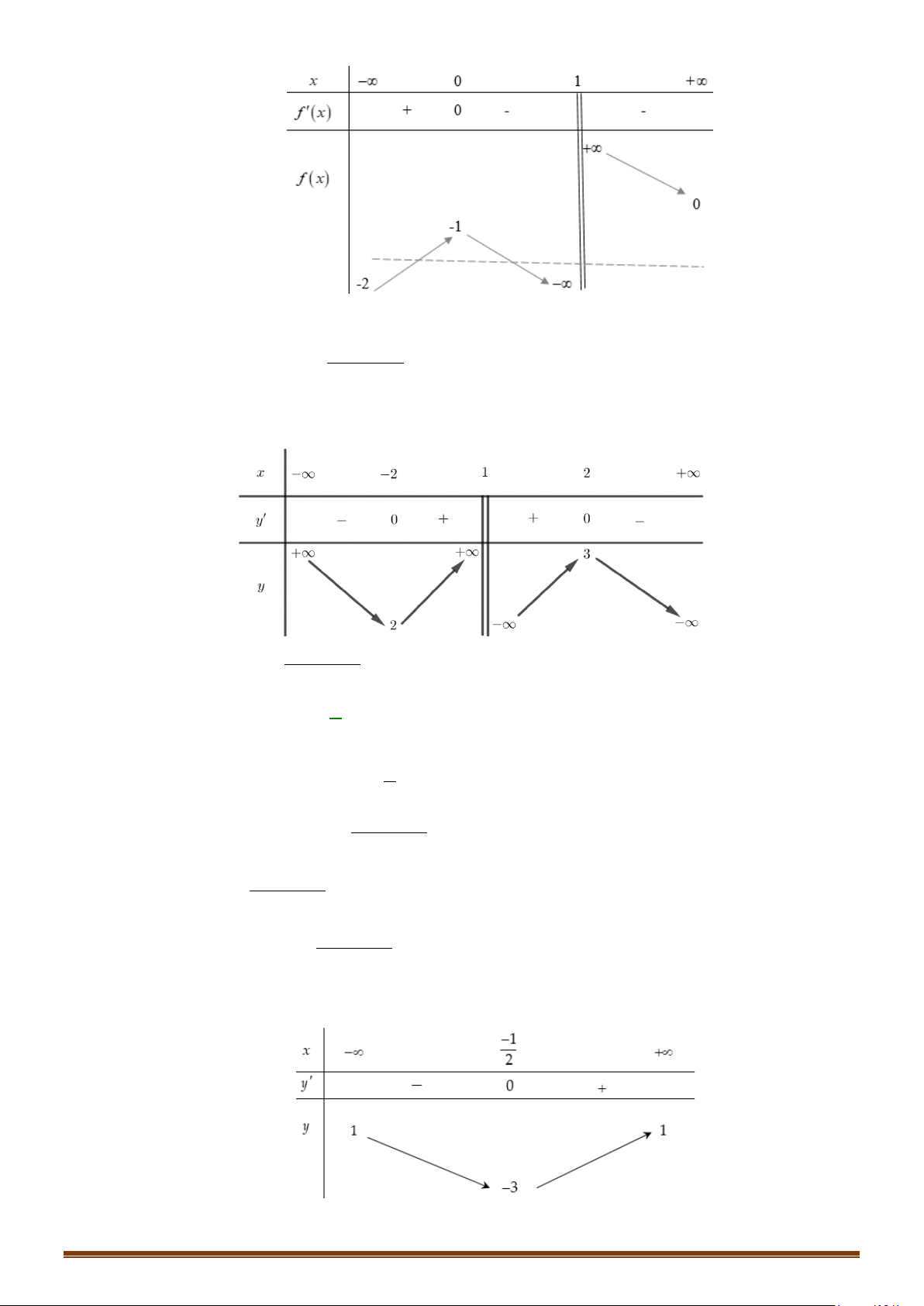
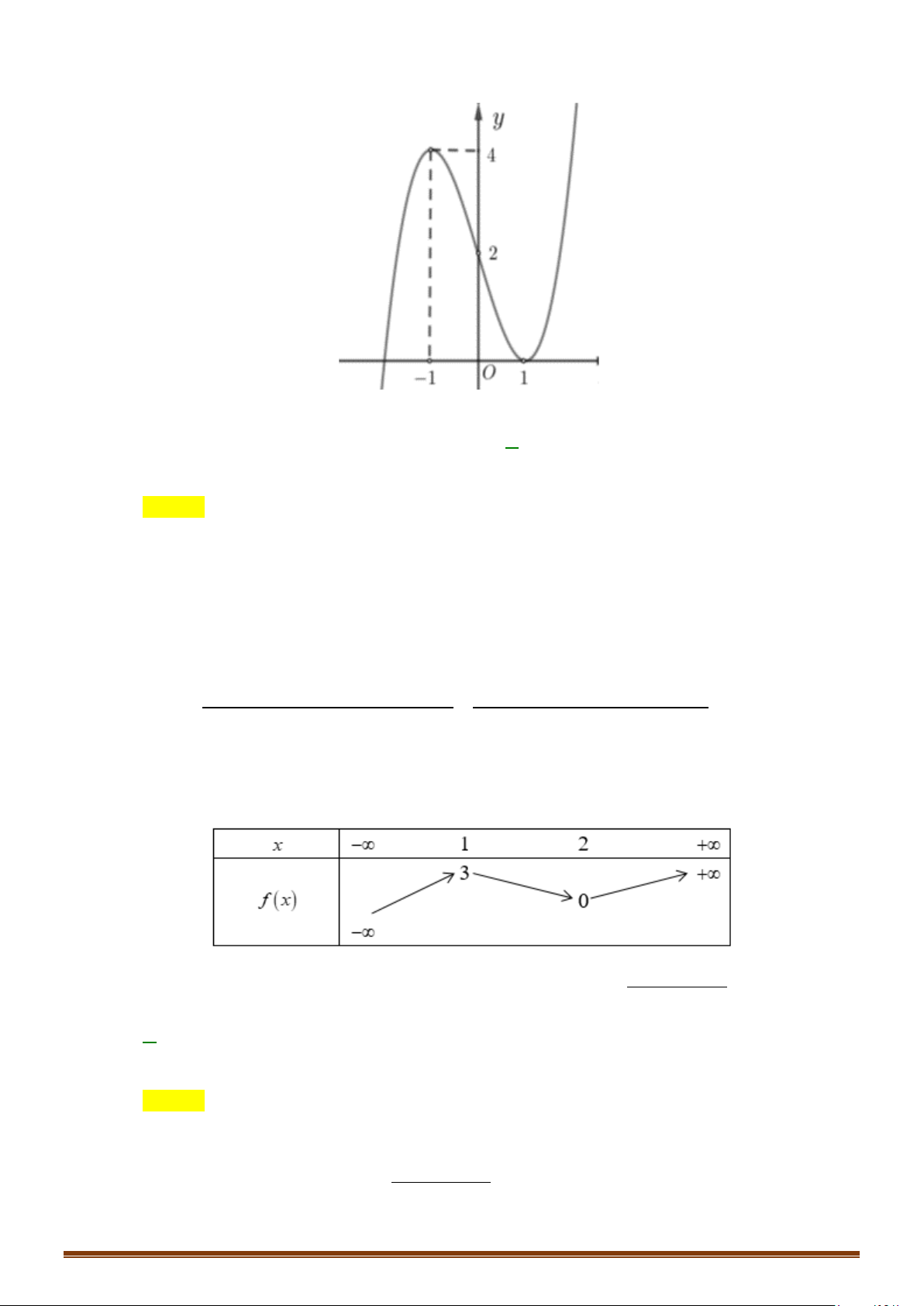
Câu 1. Cho hàm số y = f (x) có bảng biến thiên
Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = f (x) . Lời giải Vì lim y = ;
−∞ lim y = 3 nên đồ thị hàm số có 1 tiệm cận ngang là y = 3 . x→−∞ x→+∞
Vì lim y = +∞ nên đồ thị hàm số có 1 tiệm cận đứng x = x . x + 4 → 4 x
Do đó đồ thị hàm số có tổng số 2 tiệm cận kể cả đứng và ngang.
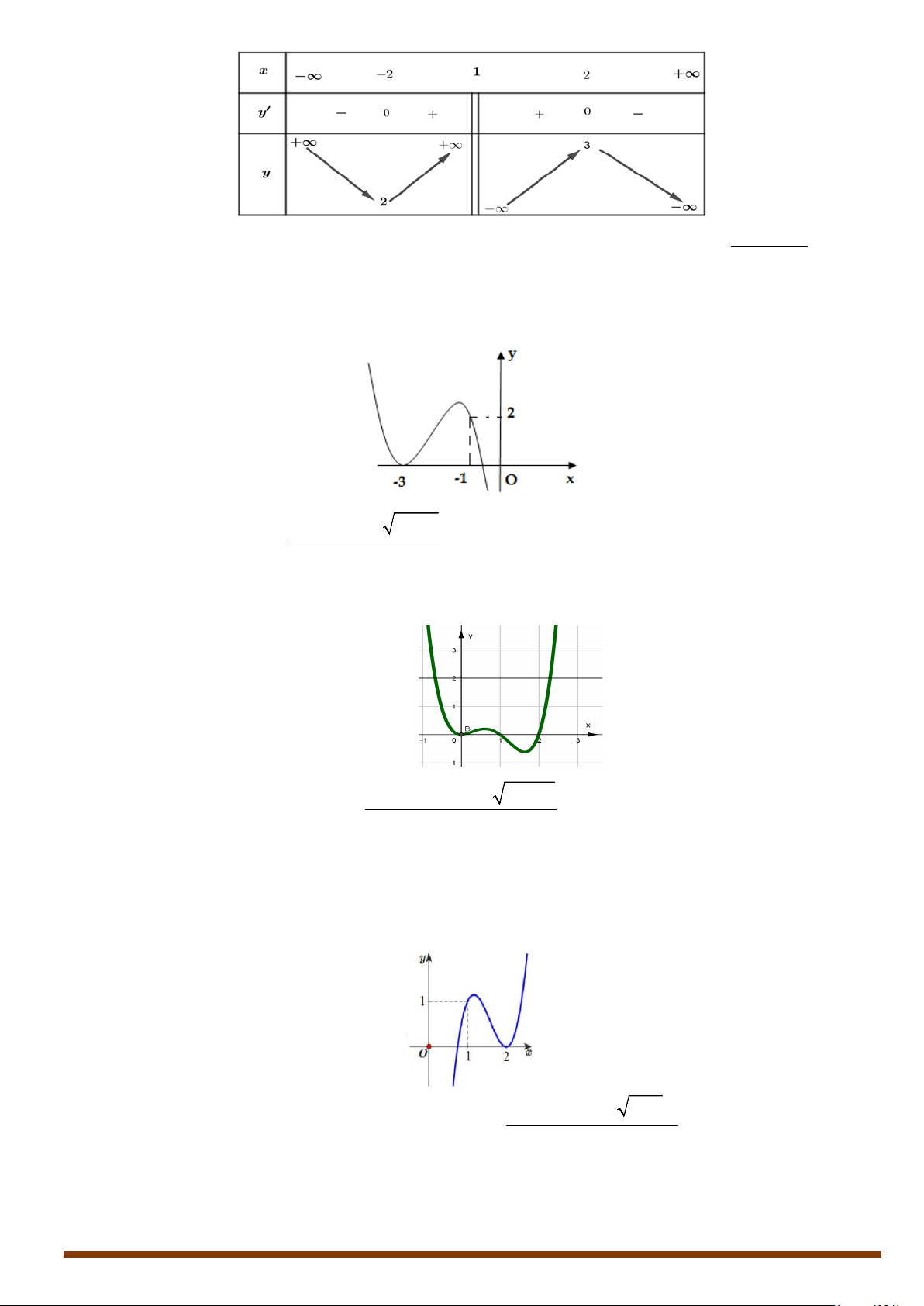
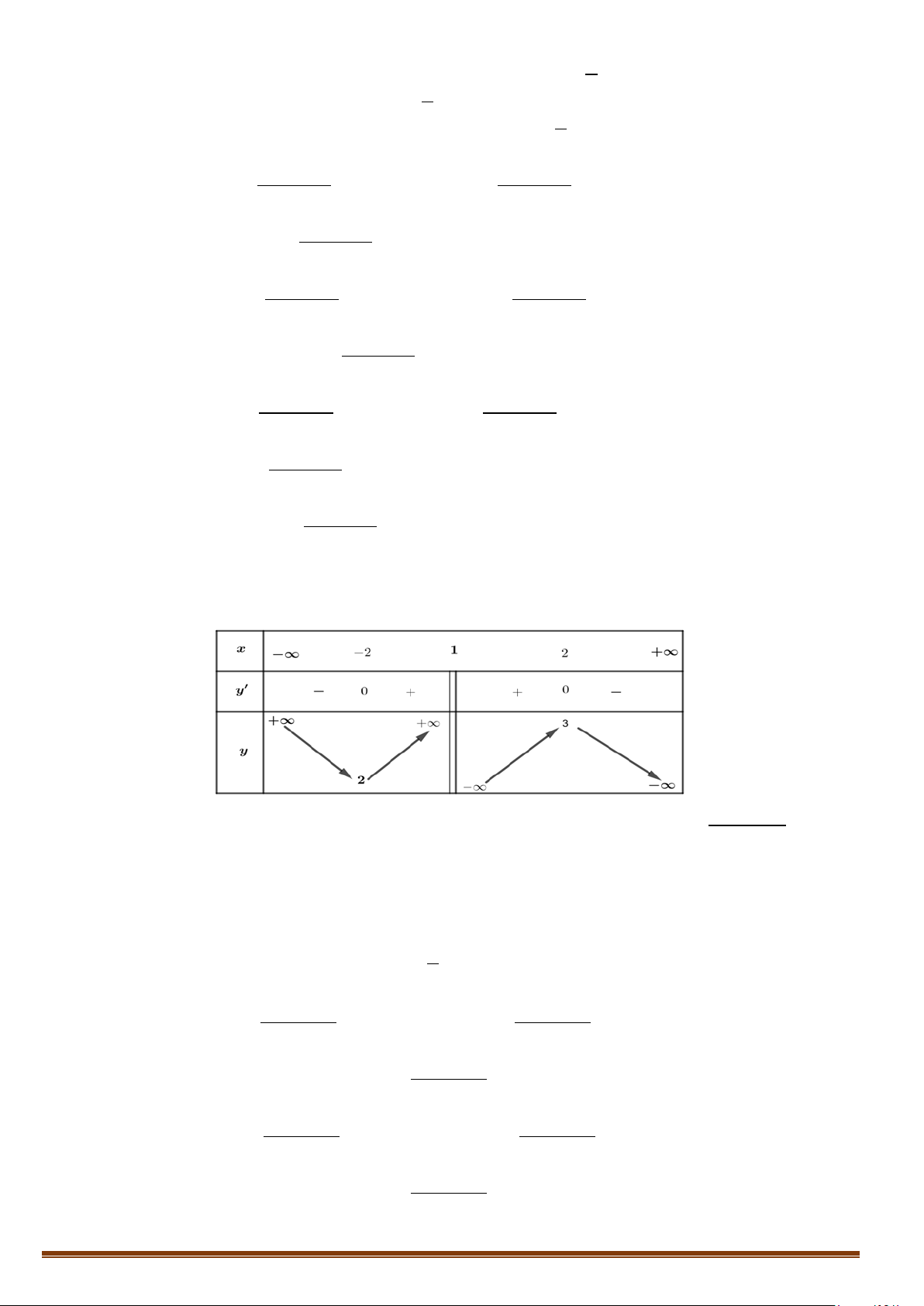
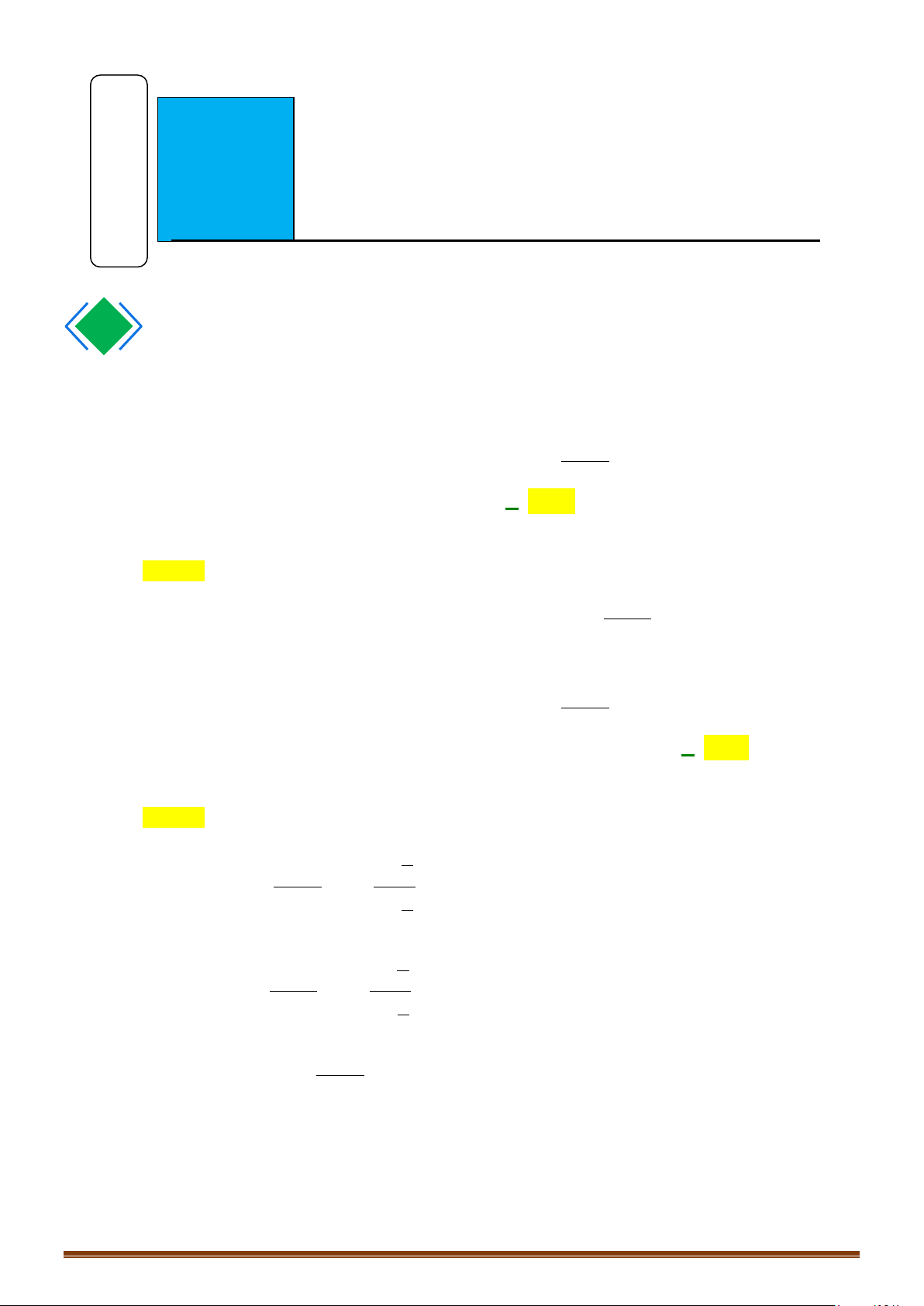
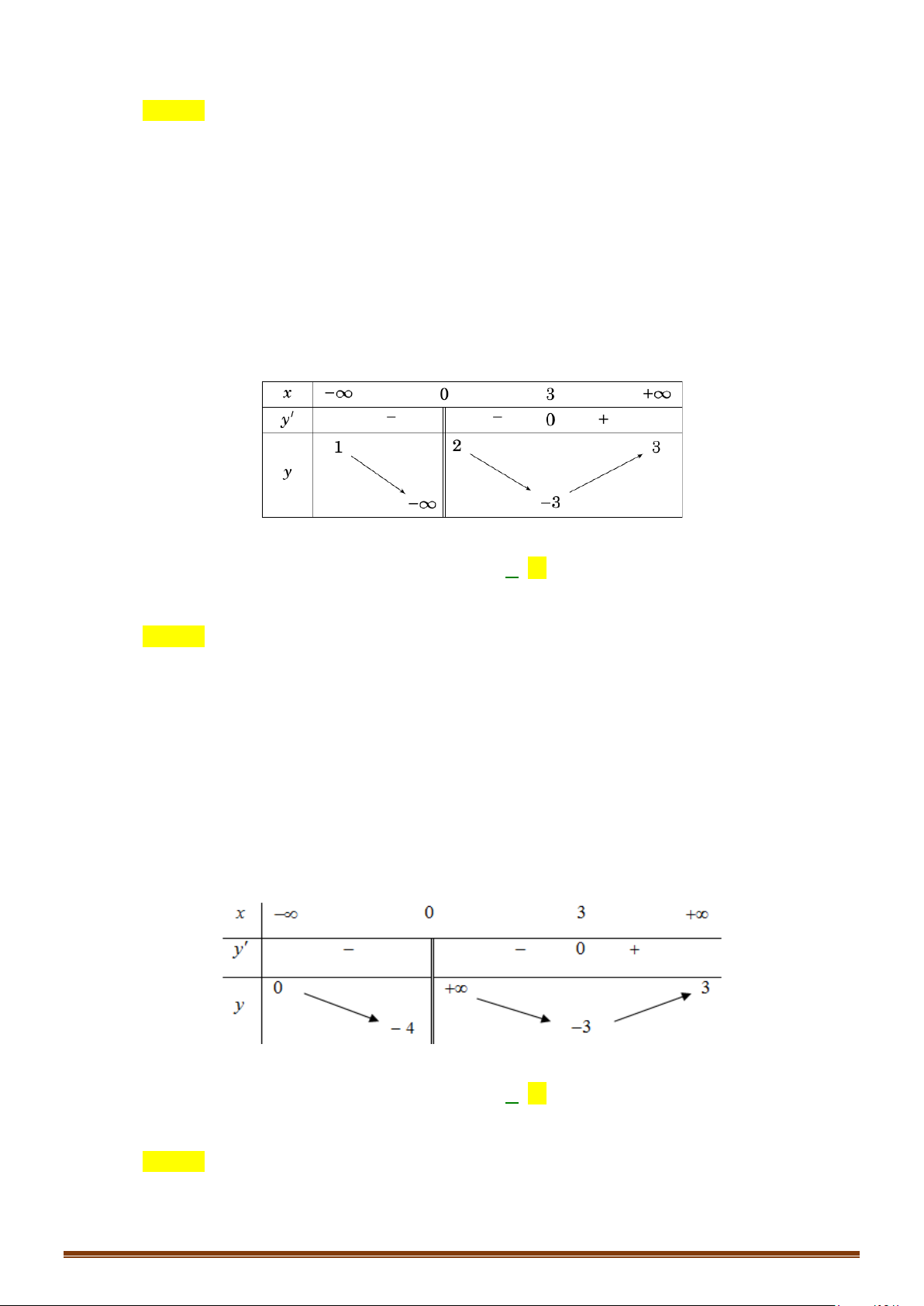
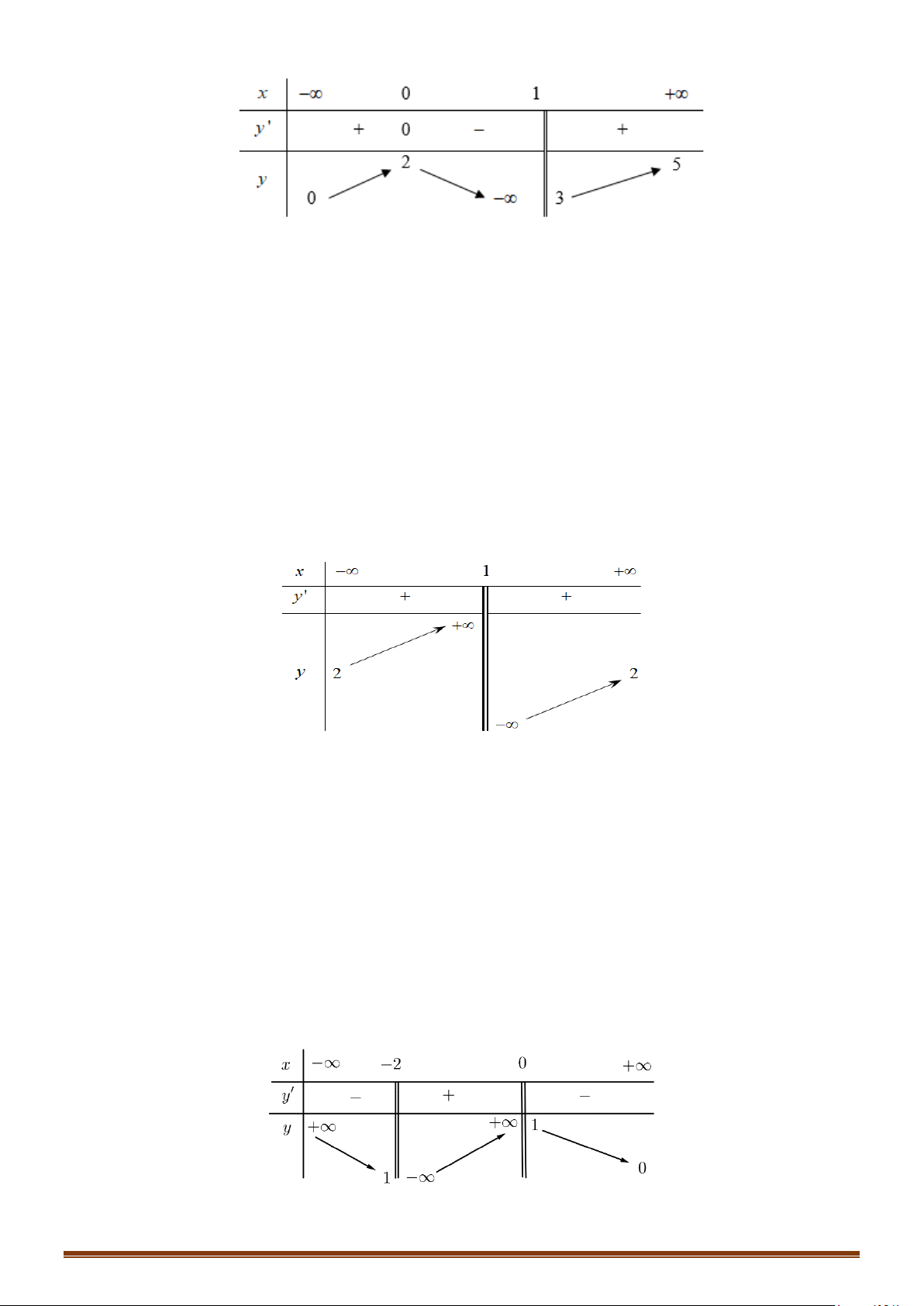
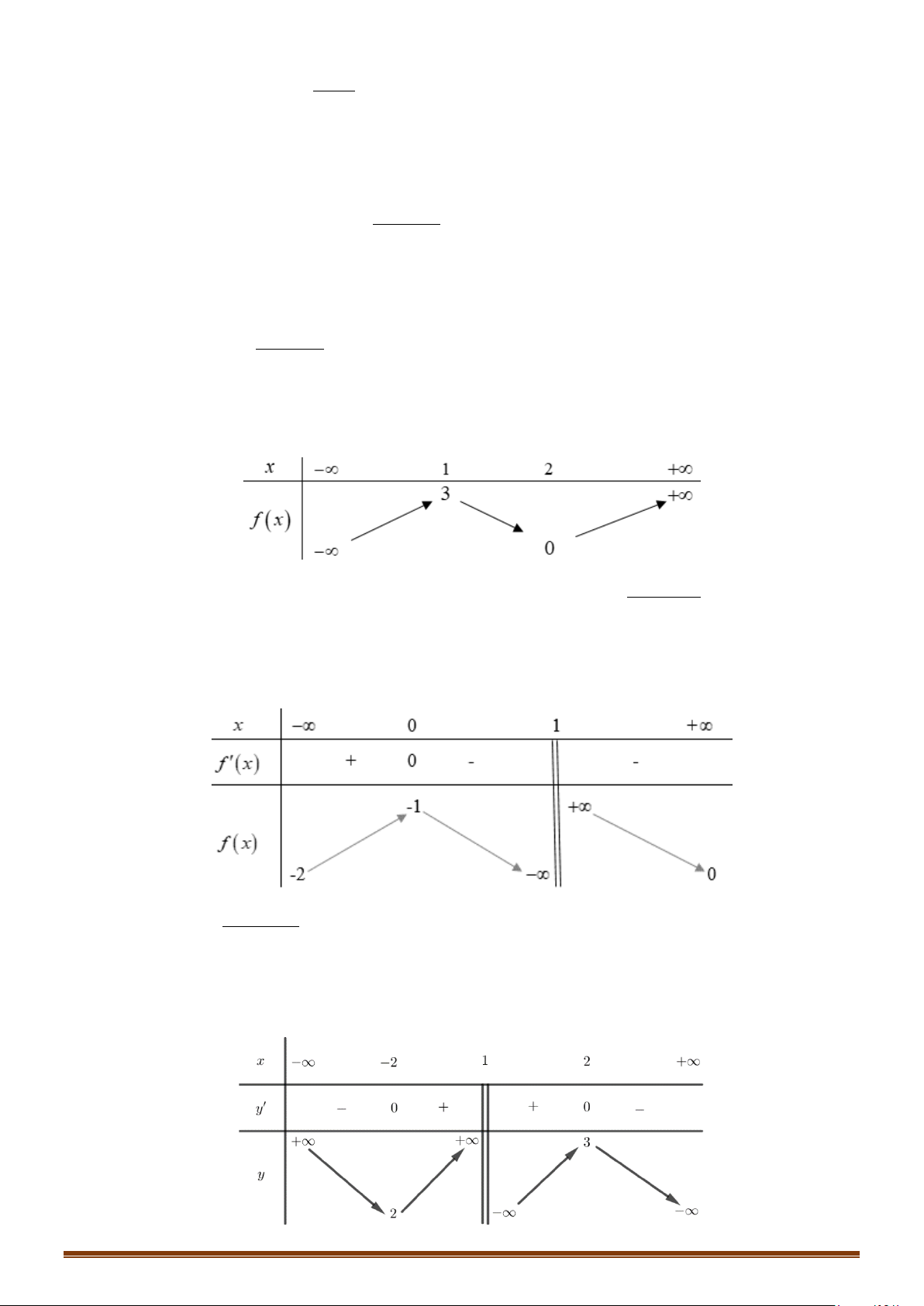
Câu 2. Cho hàm số f (x) có bảng biến thiên
Tìm số tiệm cận của đồ thị hàm số 1 y = ? f (x)
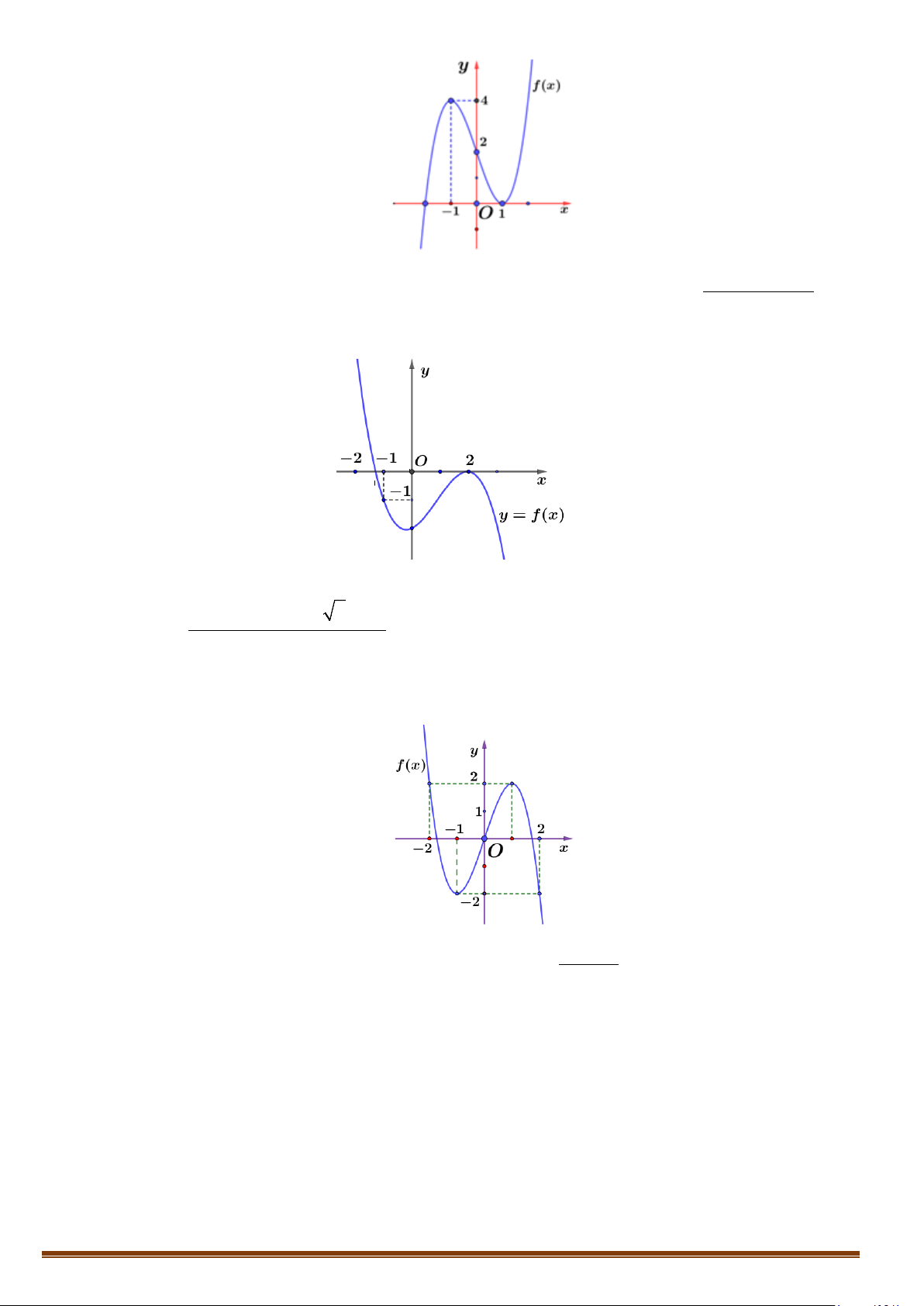
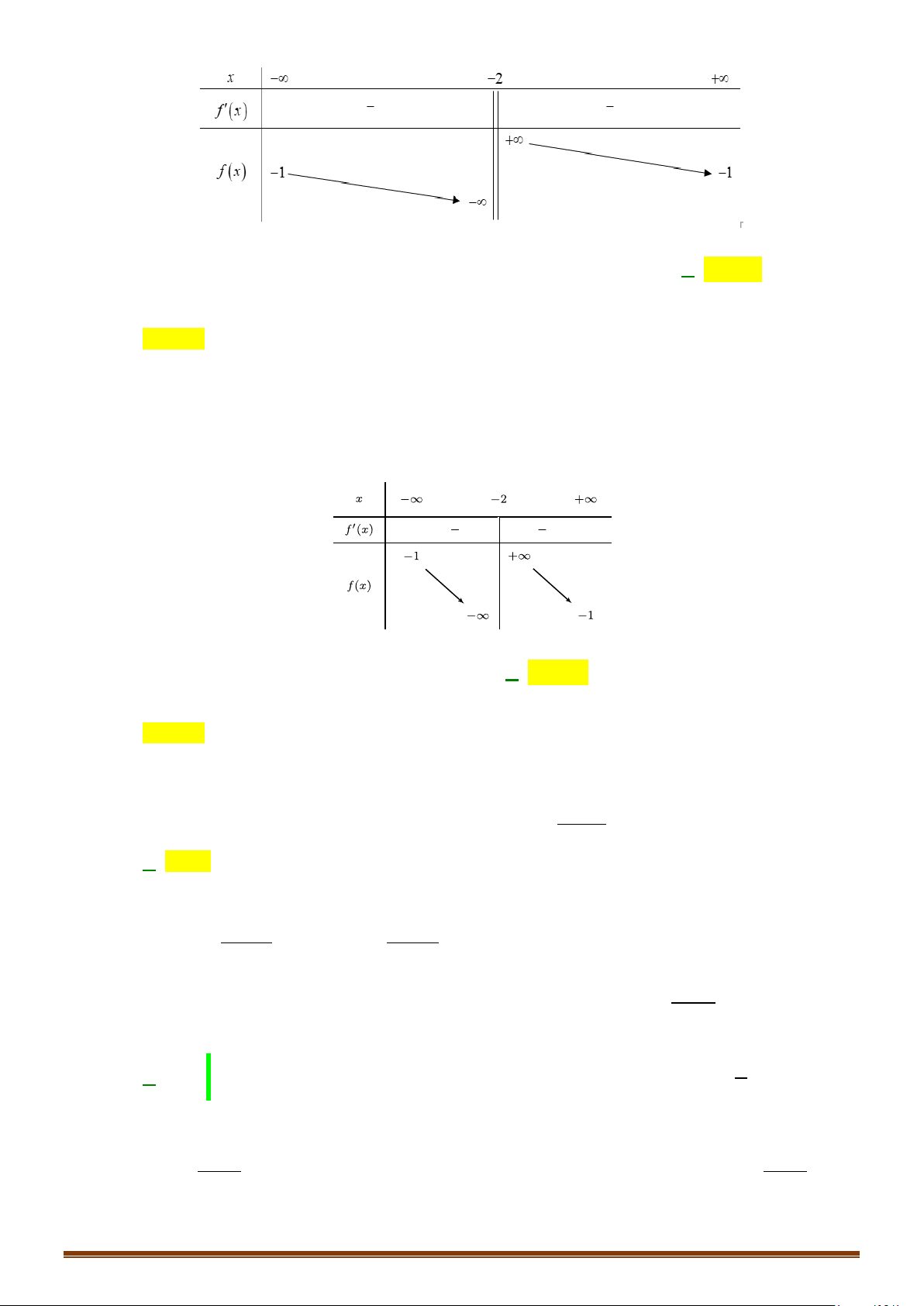
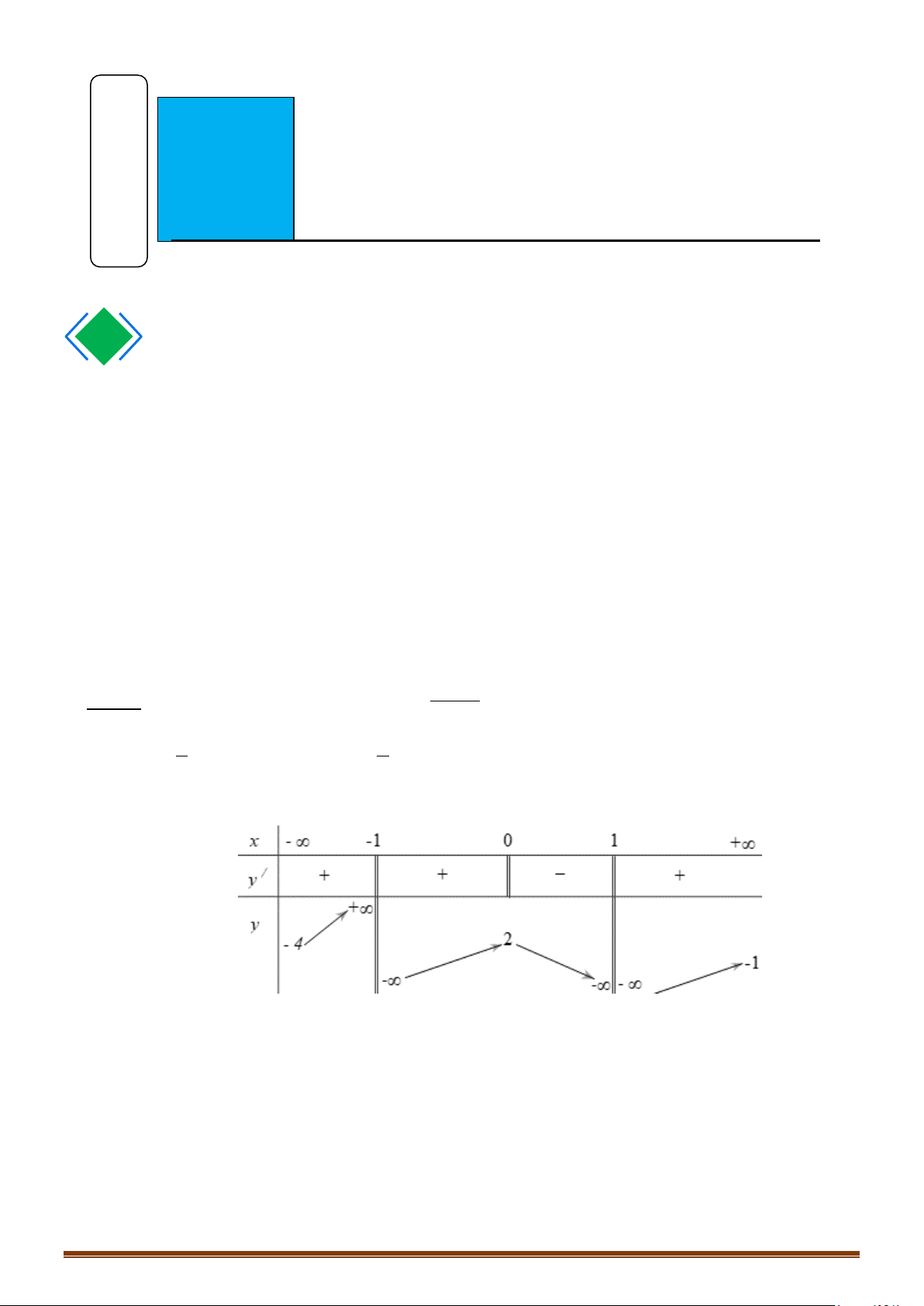
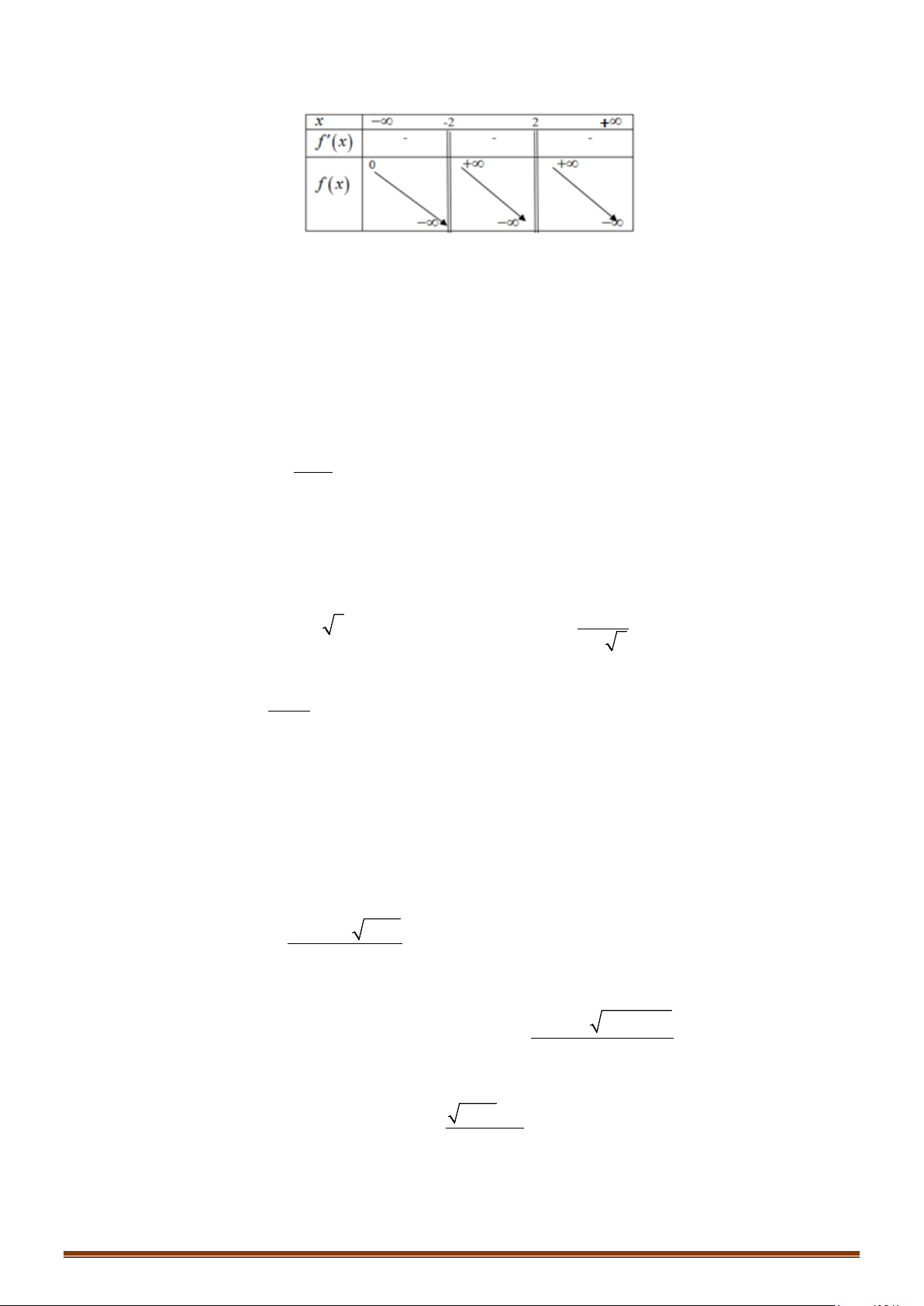
Câu 3. Cho hàm số y = f ( x) xác định, liên tục trên  \{ }
1 và có bảng biến thiên như sau:
Tìm phương trình đường tiệm cận ngang của đồ thị hàm số đã cho?
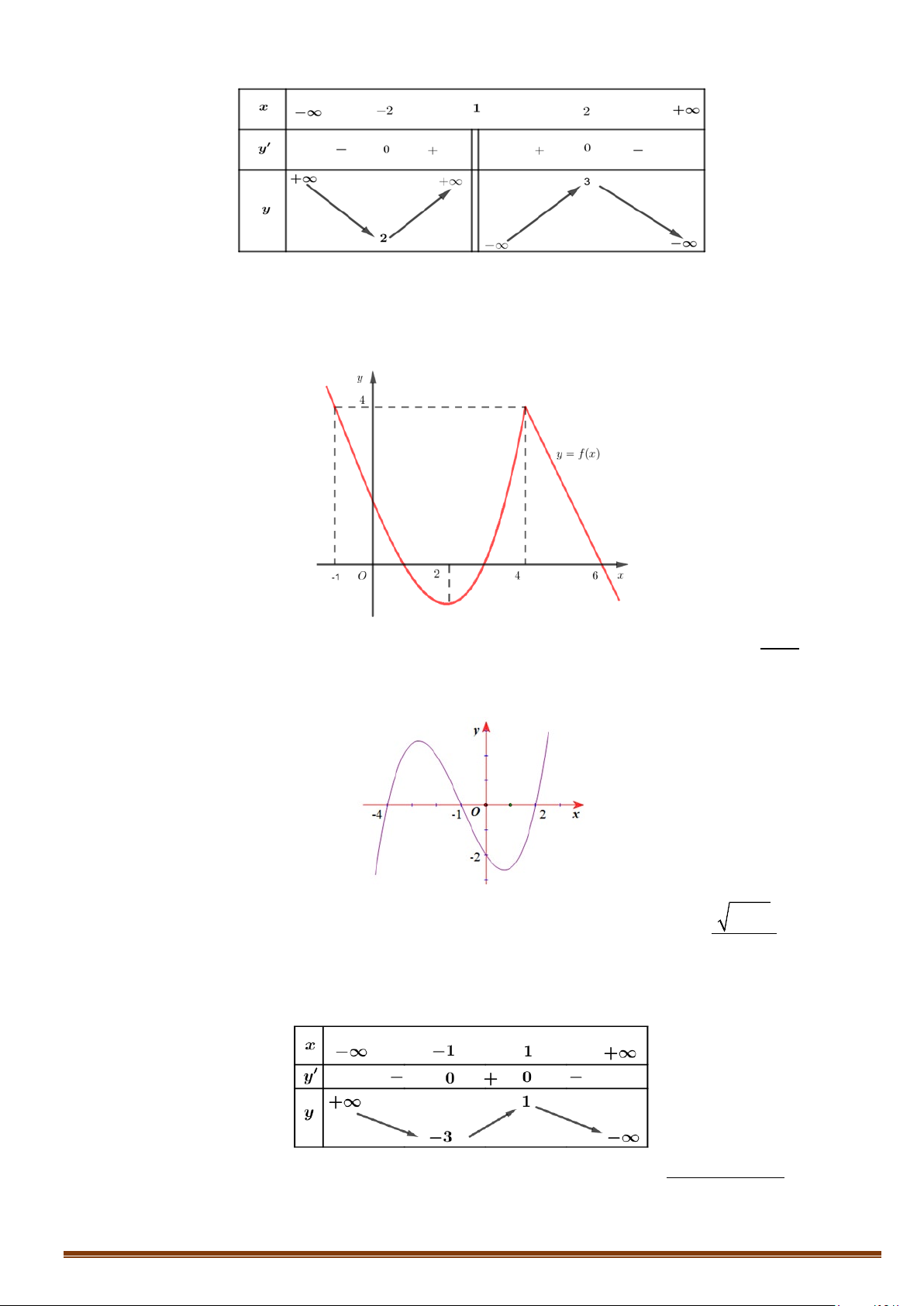
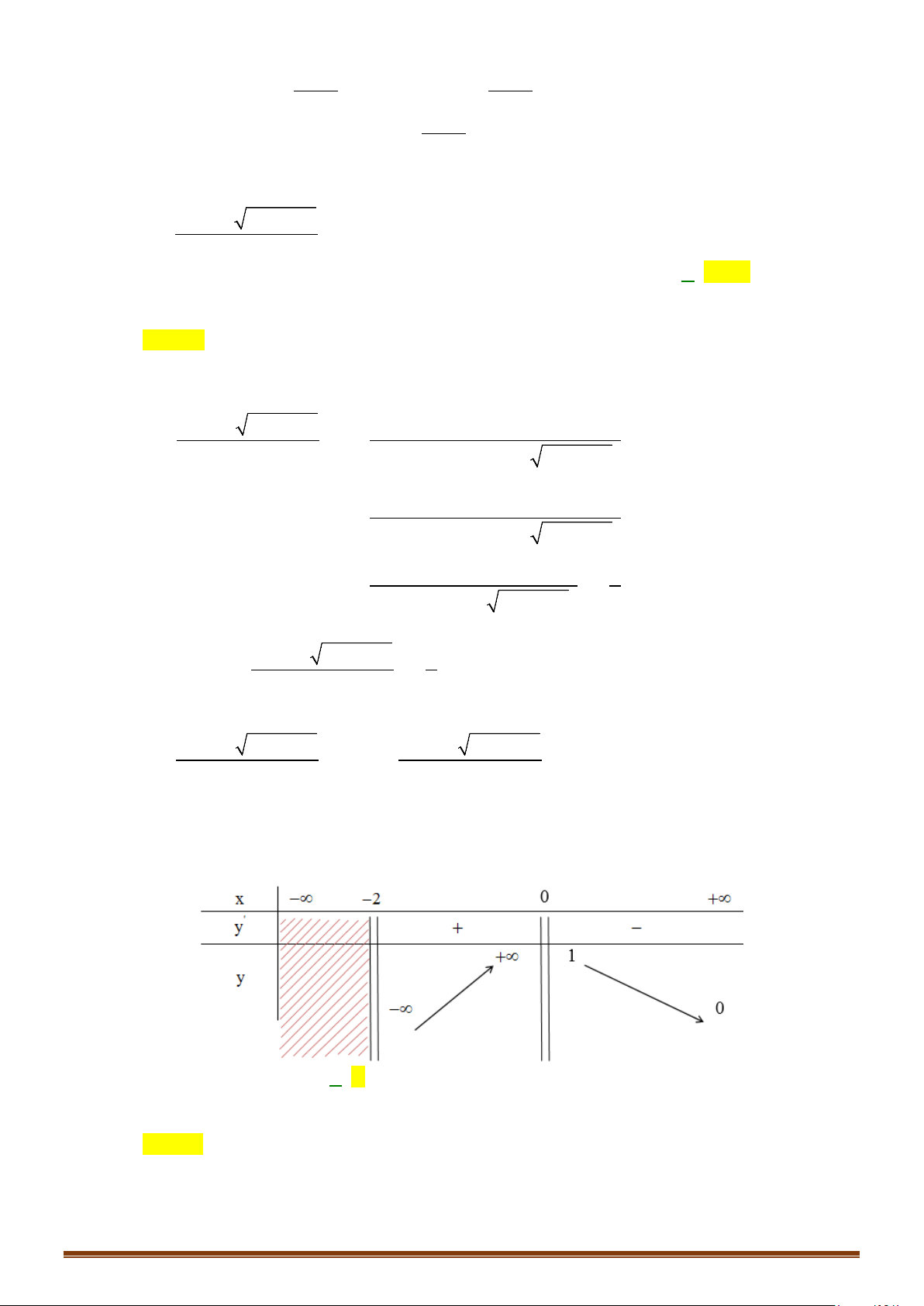
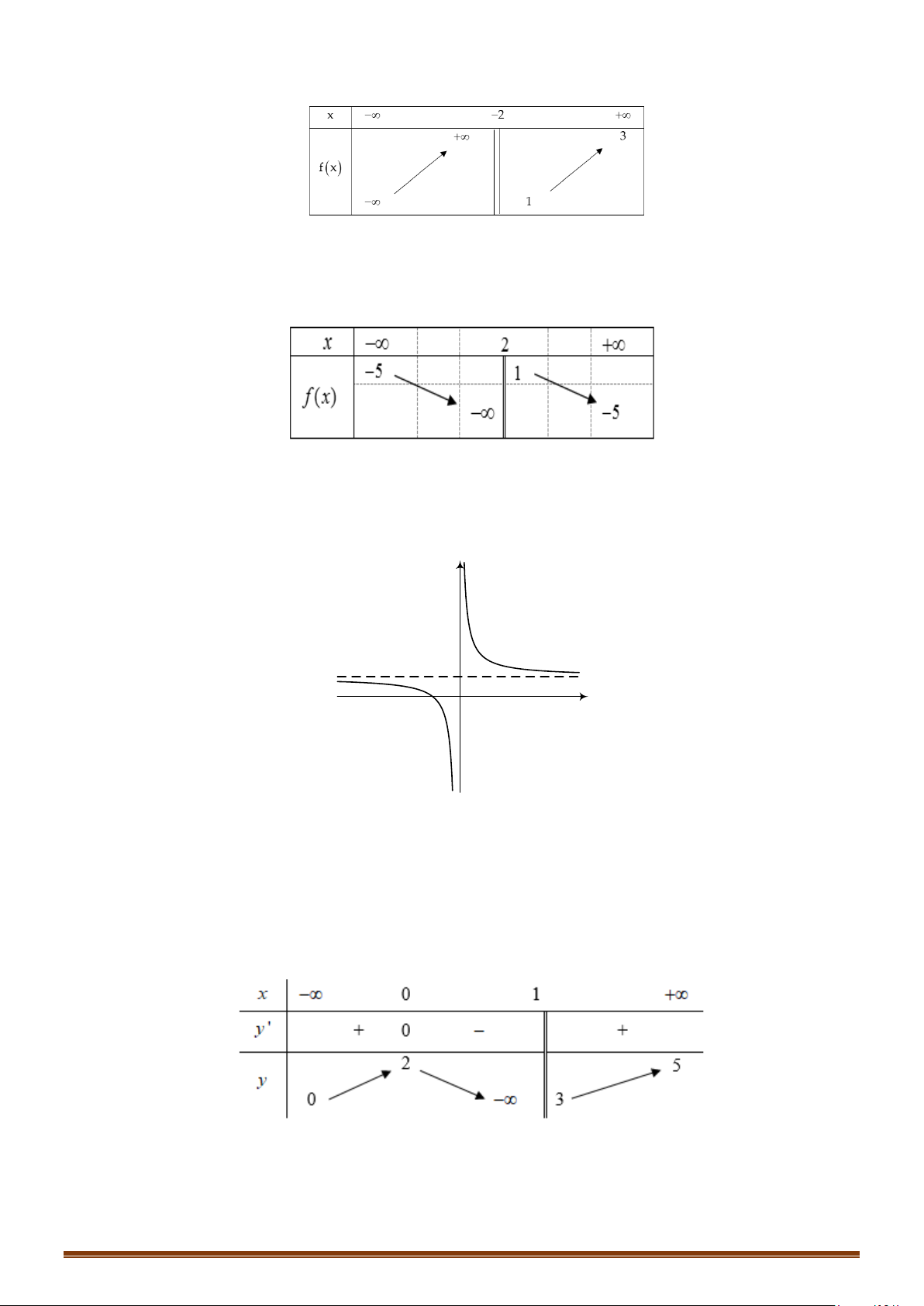
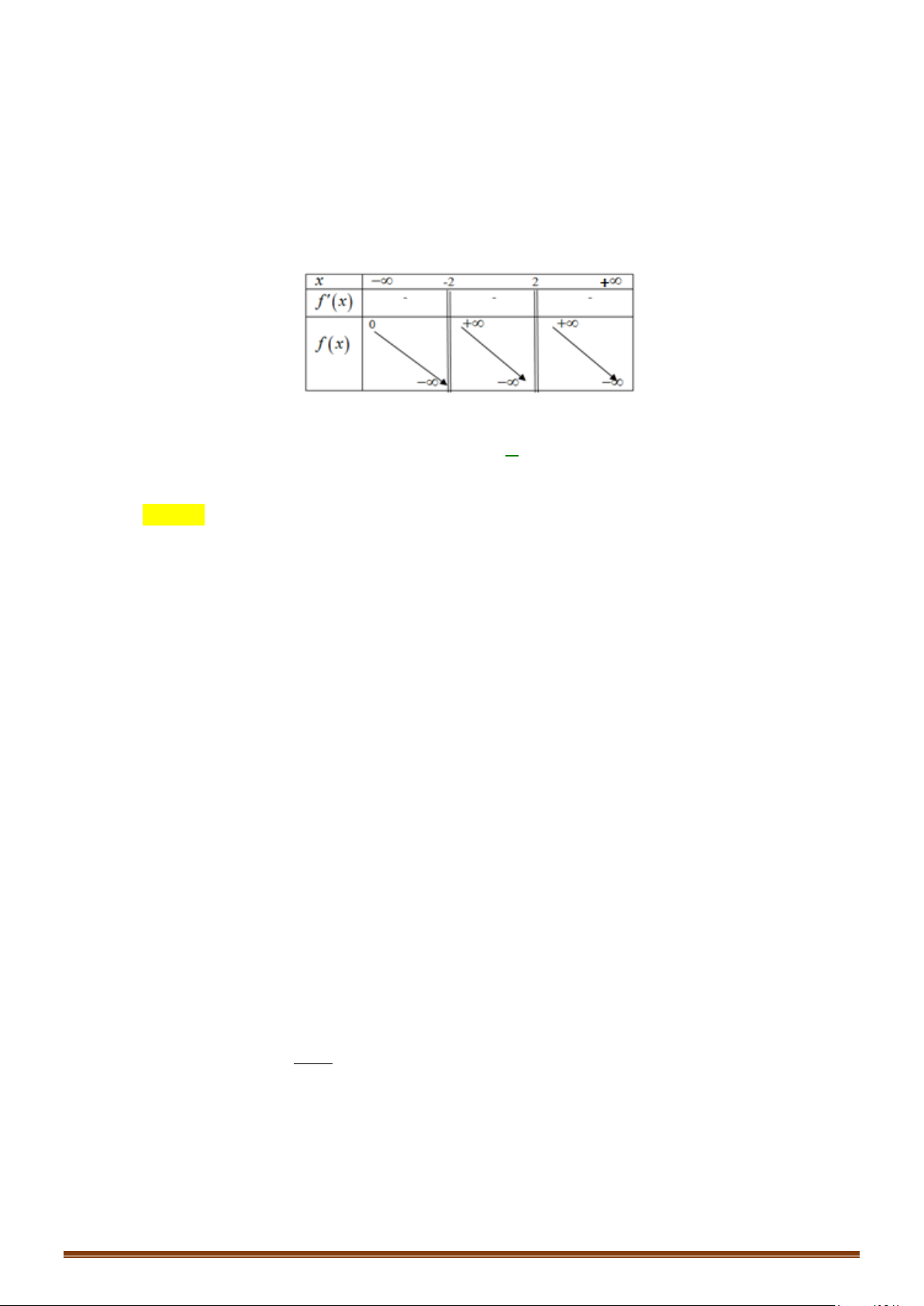
Câu 4. Cho hàm số y = f (x) xác định trên  \{ }
0 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
Hỏi đồ thị hàm số trên có bao nhiêu đường tiệm cận đứng và ngang?
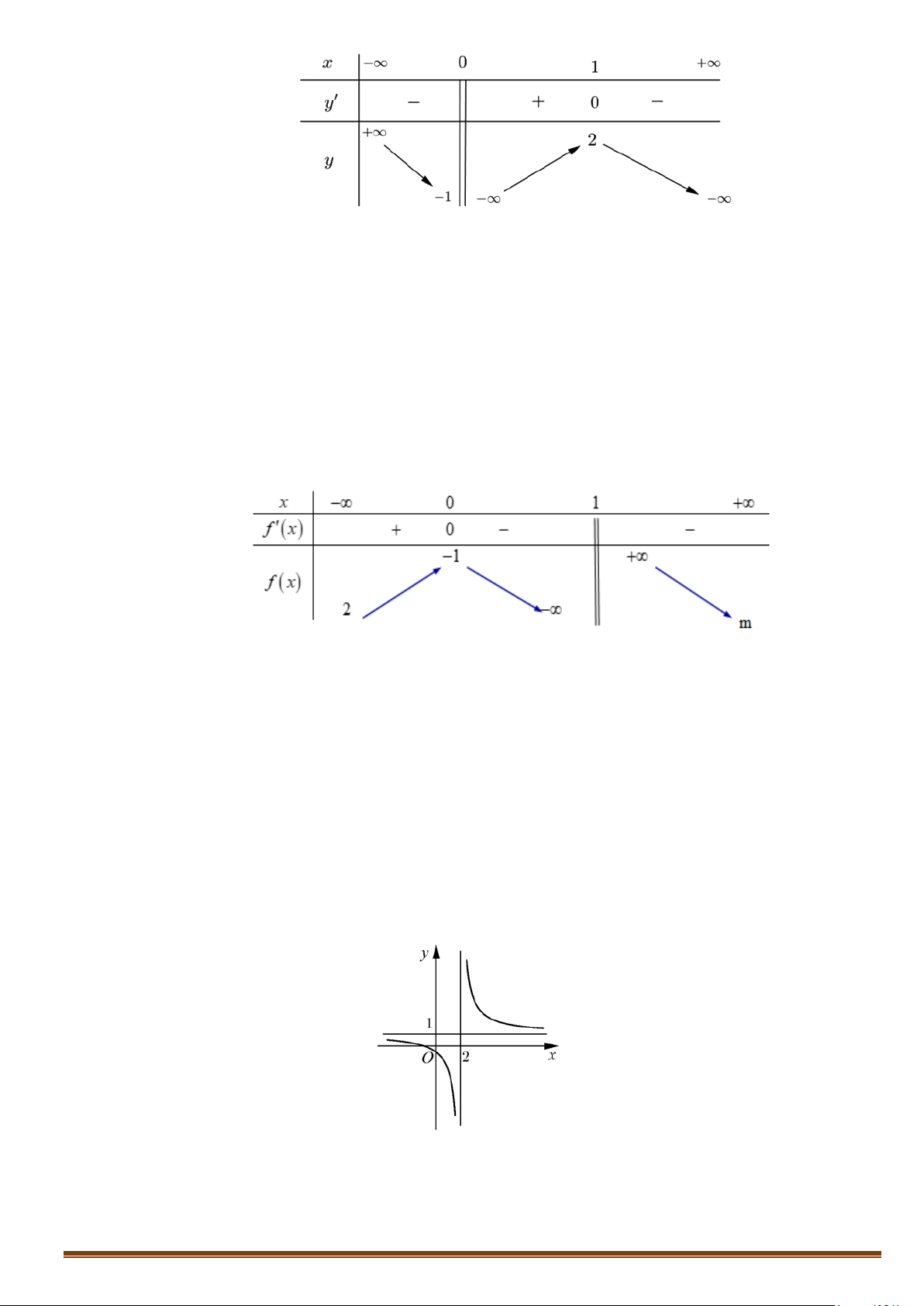
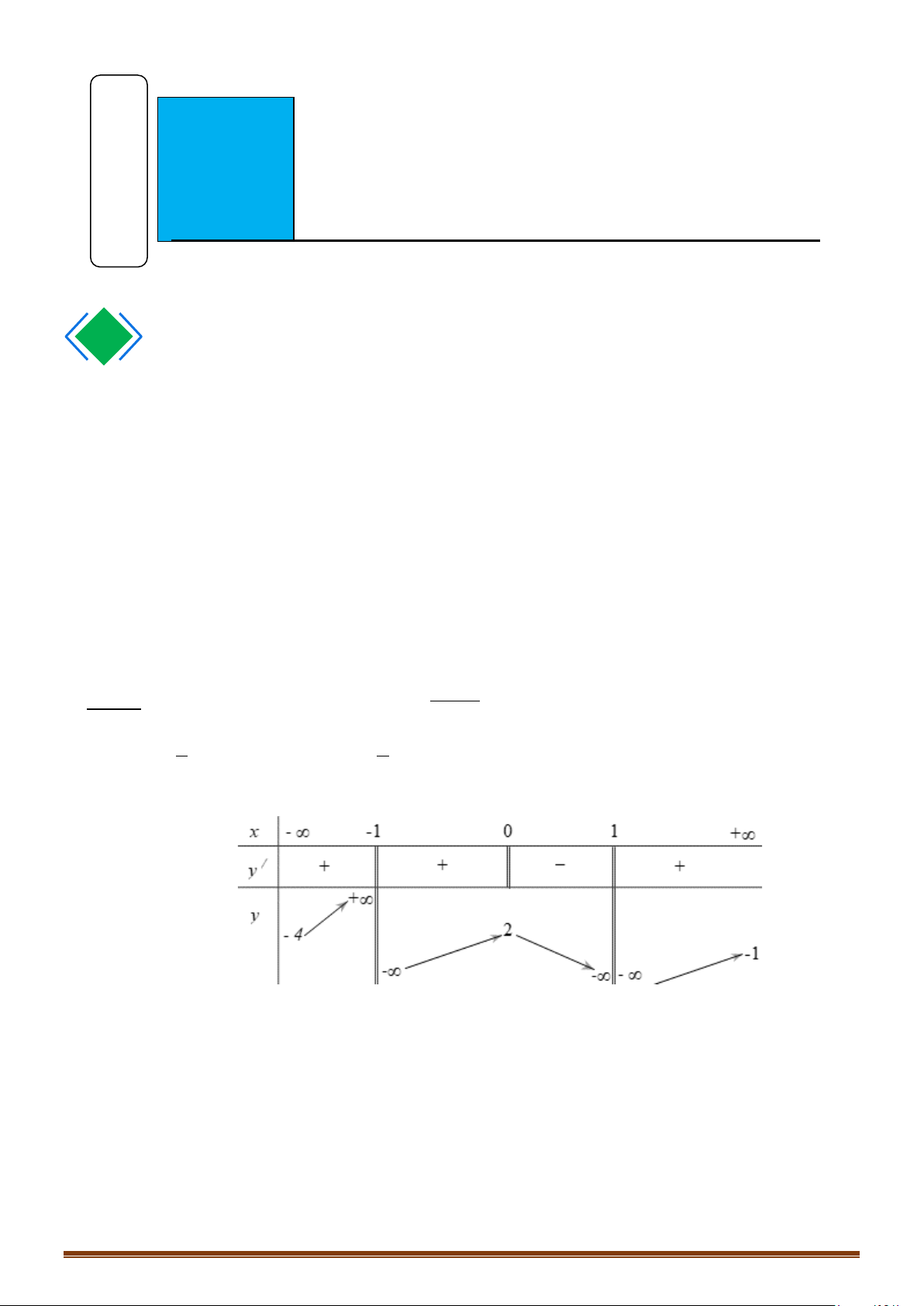
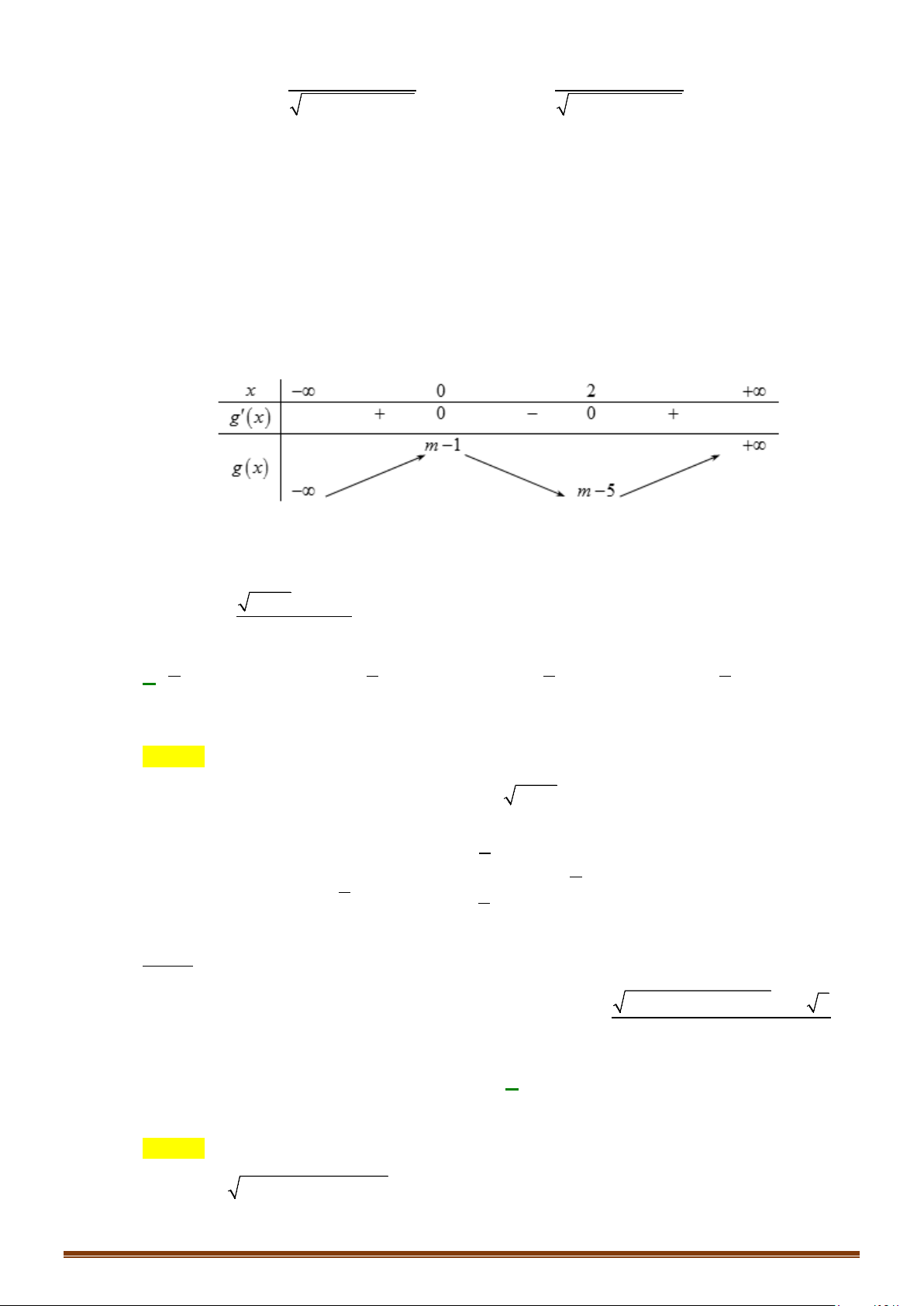
Câu 5. Cho hàm số y = f (x) xác định trên  \{ }
1 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau: Page 170
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Tìm các giá trị nguyên của m∈[0;5) để đồ thị hàm số y = f ( x) có 3 đường tiệm cận đứng và ngang?
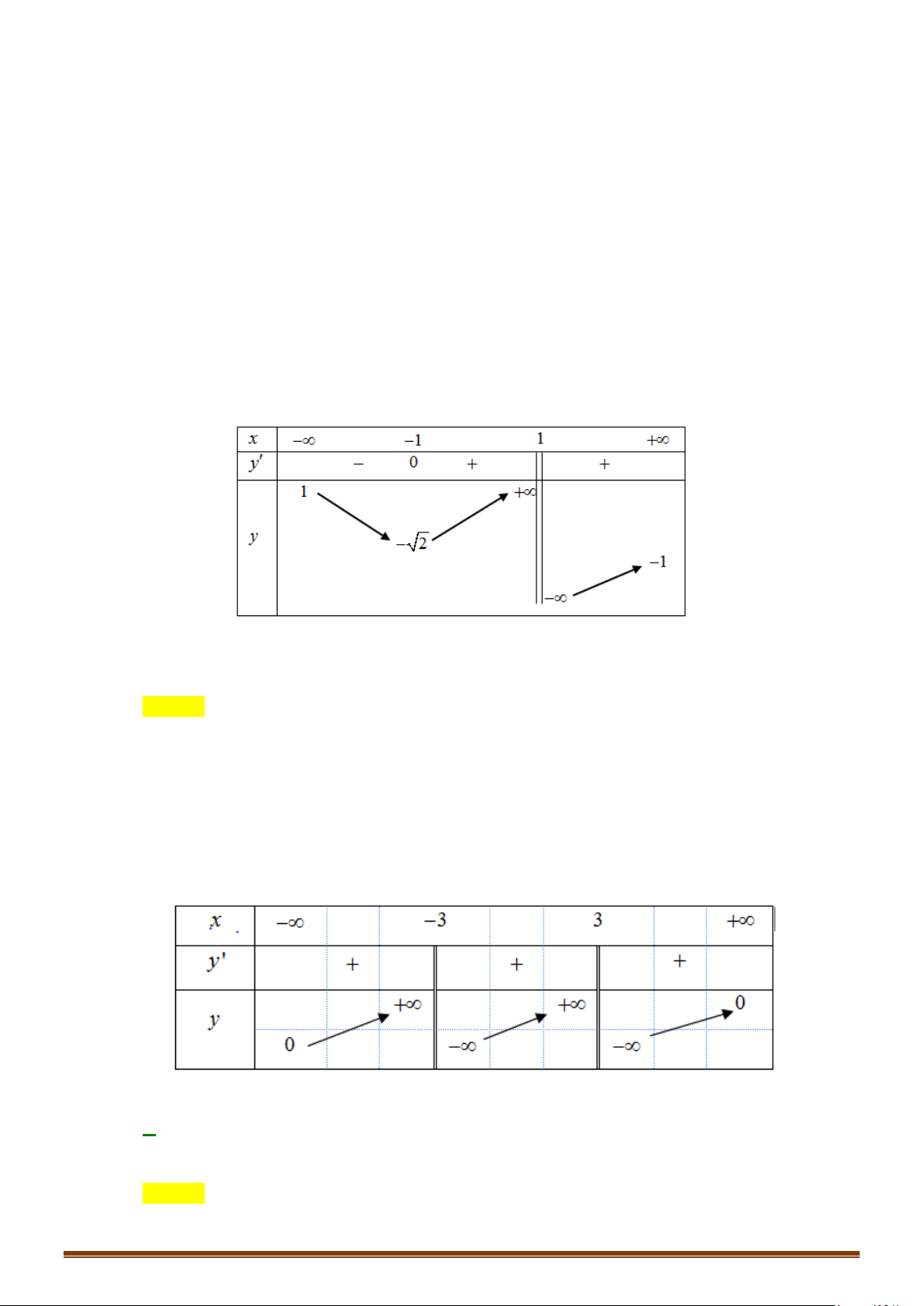
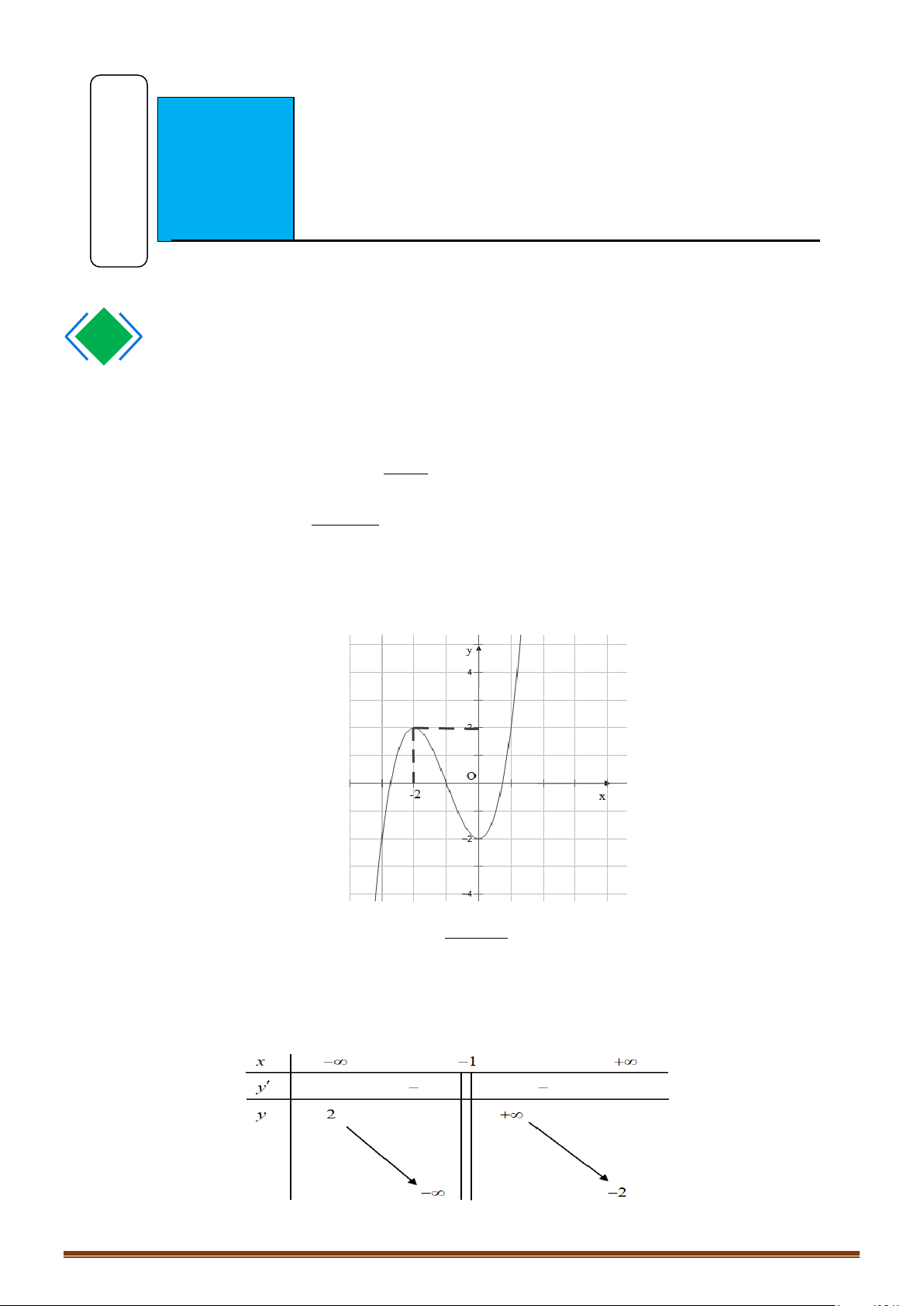
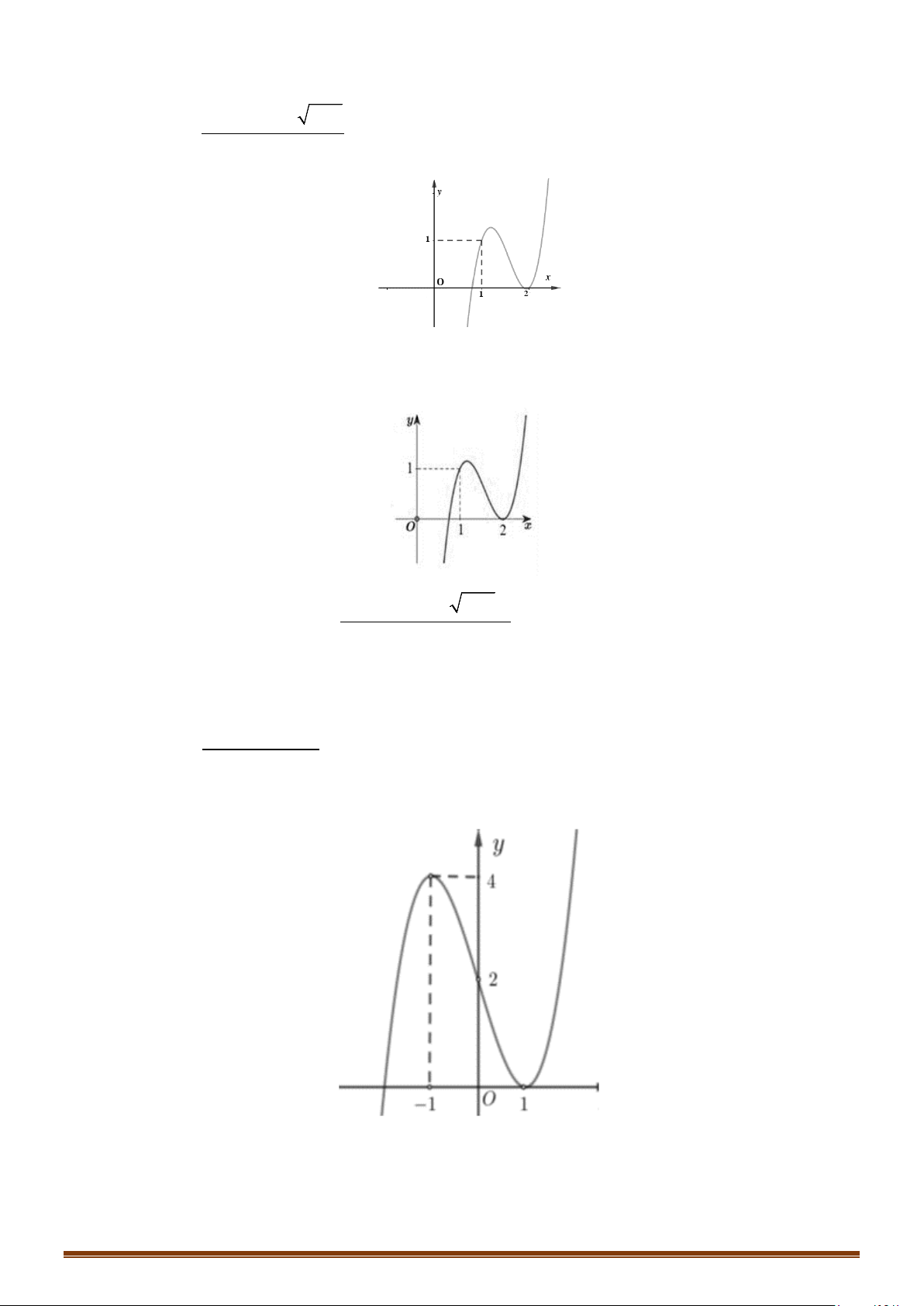
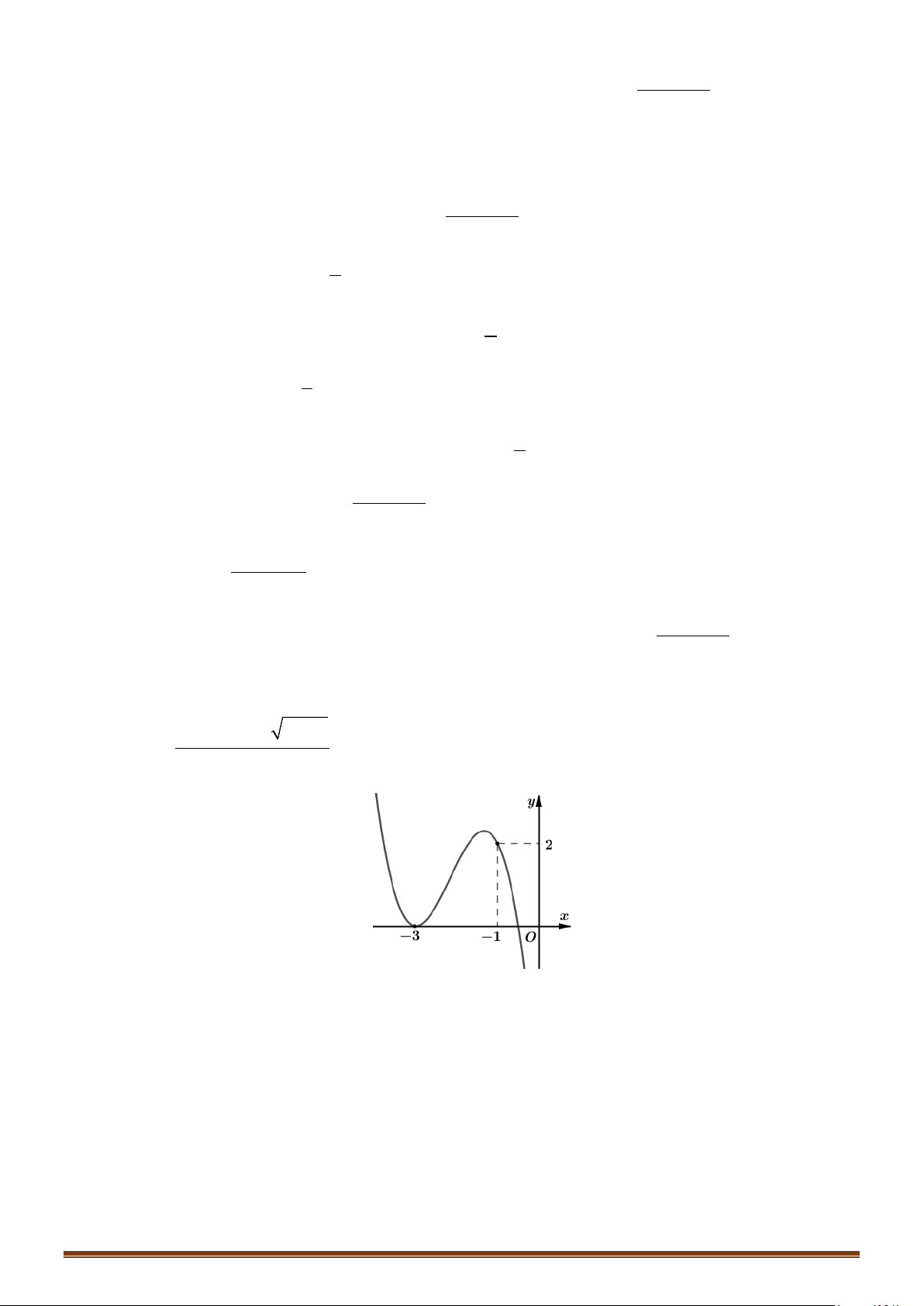
Câu 6. Cho hàm số f (x) có đồ thị như hình vẽ bên.
Tìm phương trình các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số trên.
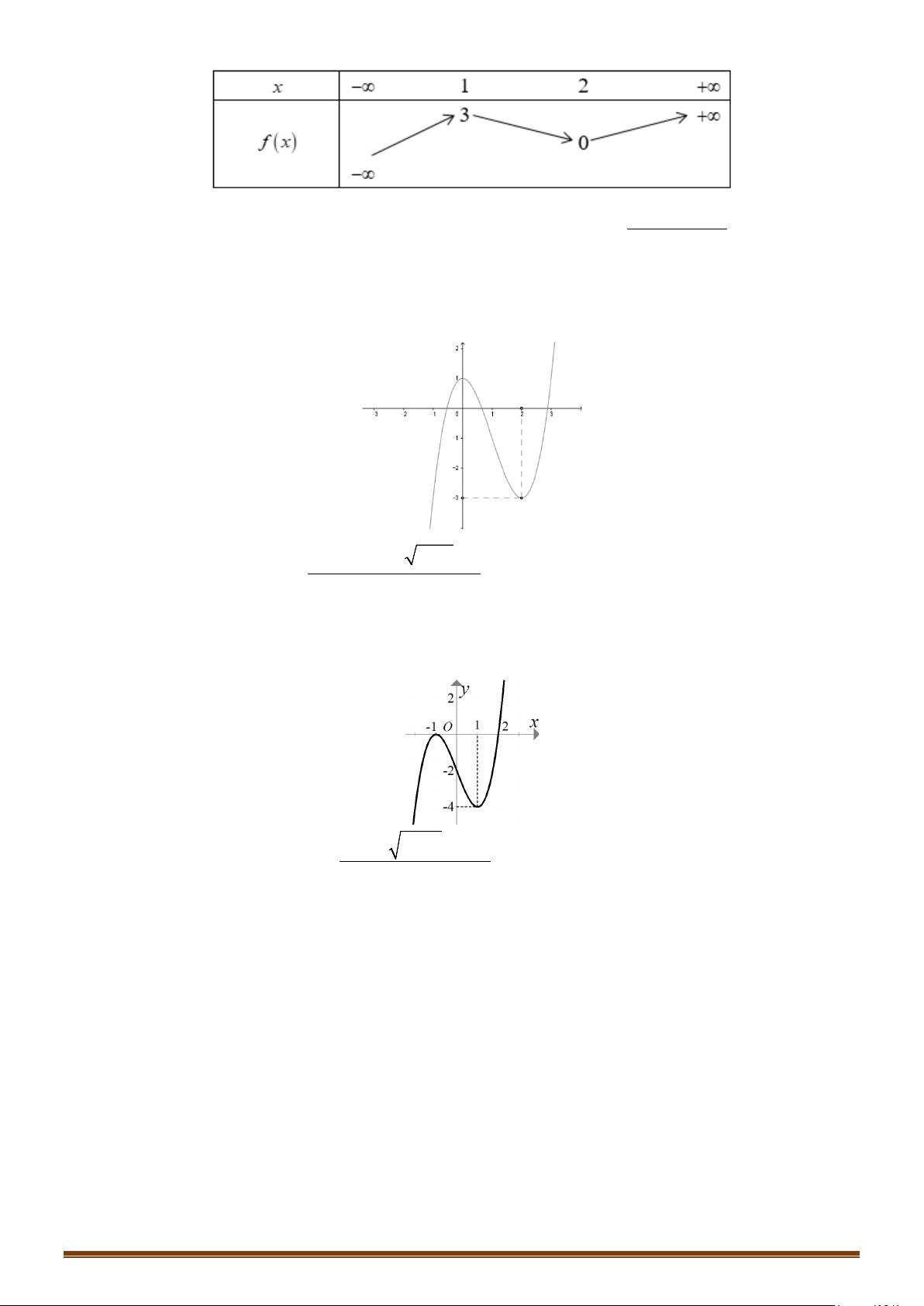
Câu 7. Cho đồ thị hàm số y = f (x) như hình bên. Đồ thị có bao nhiêu đường tiệm cận đứng và tiệm cận ngang? Page 171
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
DẠNG 3: TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ HÀM HỢP
Các dạng trong chủ đề: Cho hàm số y = f (x) biết bảng biến thiên hoặc đồ thị. Tìm các đường
tiệm cận đứng và tiệm cận ngang của đồ thị y = g (x) thuộc một trong các dạng sau
1) y = f (u(x)) ,
2) y = g ( f (x)) ,
3) y = g ( f (u(x))) ,
4) y = g (x, f (x)),
5) y = g (x, f (u(x))) .
Phương pháp giải: Gọi (G) là đồ thị hàm số y = g (x) .
1)Tìm tiệm cận ngang.
Xét hàm số dạng g (x) u(x) =
.Một dấu hiệu thường dùng để nhận biết (G) có tiệm cận ngang: v(x)
+ Hàm số y = g (x) xác định trên (a;+∞) hoặc trên ( ; −∞ a) .
+ Bậc của u(x) ≤ Bậc của v(x) .
+ lim g(x) = y hoặc lim g(x) = y ⇒ Đường thẳng y = y là tiệm cận ngang của(G) . 0 x→+∞ 0 x→−∞ 0
2)Tìm tiệm cận đứng.
Xét dạng hàm số g (x) u(x) =
. Một dấu hiệu thường dùng để nhận biết đường thẳng x = x v(x) 0 là
tiệm cận đứng của (G) :
+ v(x ) = 0 và u(x ) ≠ 0 , g (x) xác định trên ( ;
a x hoặc (x ;b . 0 ) 0 ) 0 0
+ Ít nhất một trong hai giới hạn lim g (x), lim g (x) là giới hạn vô cực. x + − → 0 x x→ 0 x
⇒ Đường thẳng x = x là tiệm cận đứng của (G) . 0
Trong chủ đề này, các dấu hiệu nhận biết ở trên dựa vào bảng biến thiên hoặc đồ thị của hàm số
y = f (x) .
Câu 1. Cho hàm số y = f ( x) có bảng biến thiên như hình dưới đây 1
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = . 2 f (x) −1
Câu 2. Cho hàm số y = f ( x) liên tục trên  \  
1 và có bảng biến thiên như sau Page 172
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ 1
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = g(x) = 2 f (x) −3
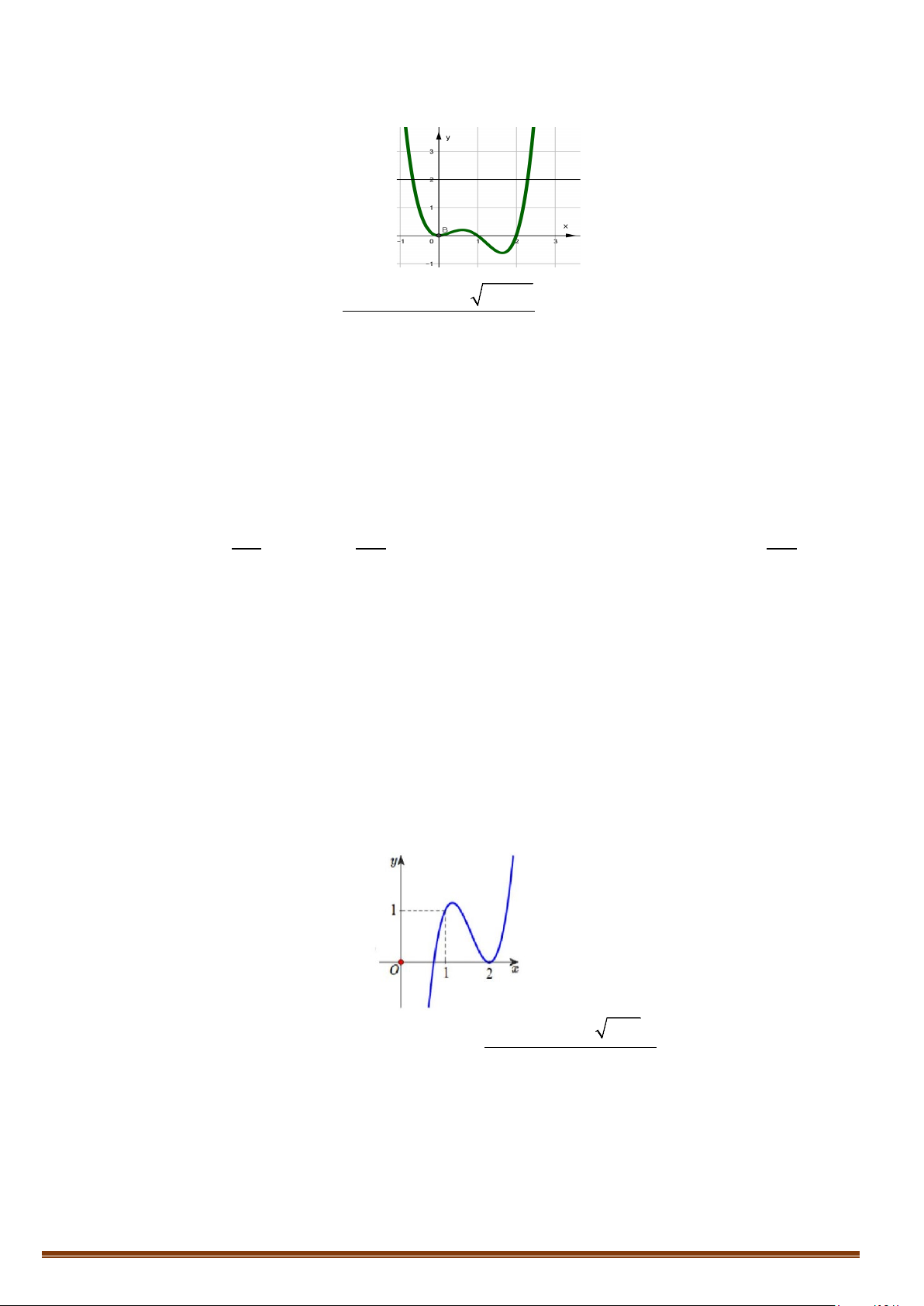
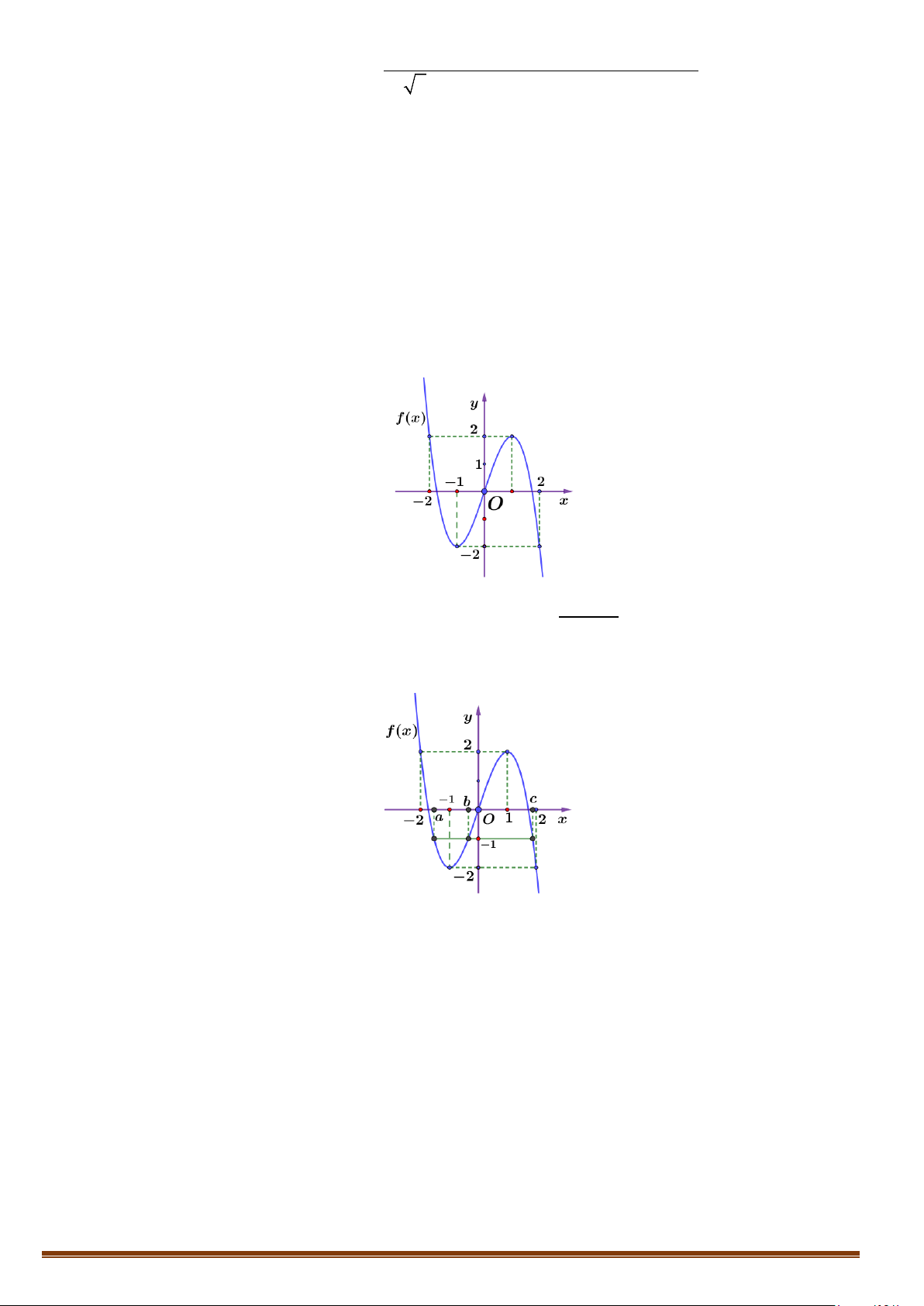
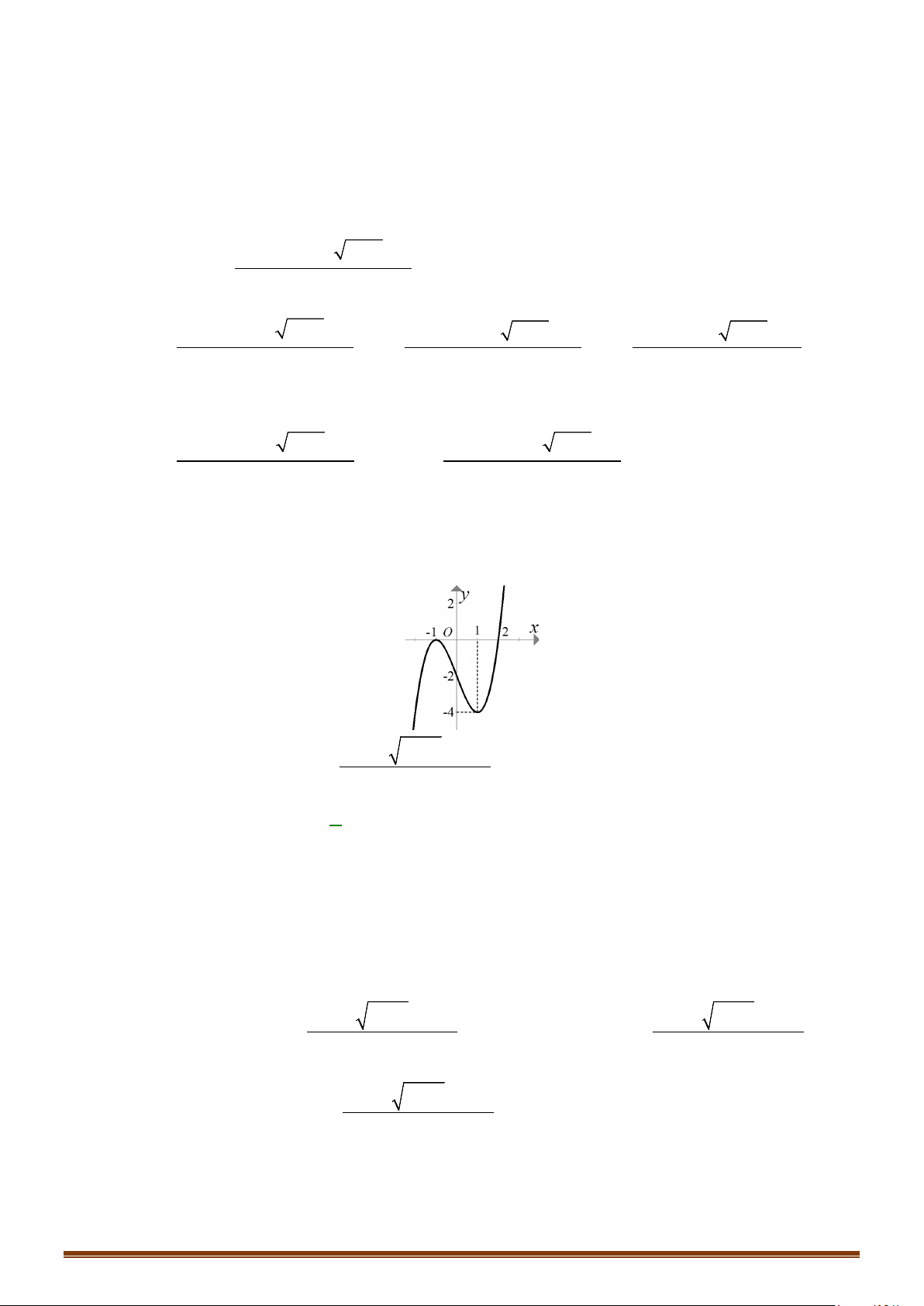
Câu 3. Cho hàm số f (x) 3 2
= ax + bx + cx + d (a, ,
b c,d ∈ R) có đồ thị như hình vẽ.
( 2x +4x+3) 2x + x
Đồ thị hàm số g (x) =
có bao nhiêu đường tiệm cận đứng?
( f (x))2 −2 f (x)
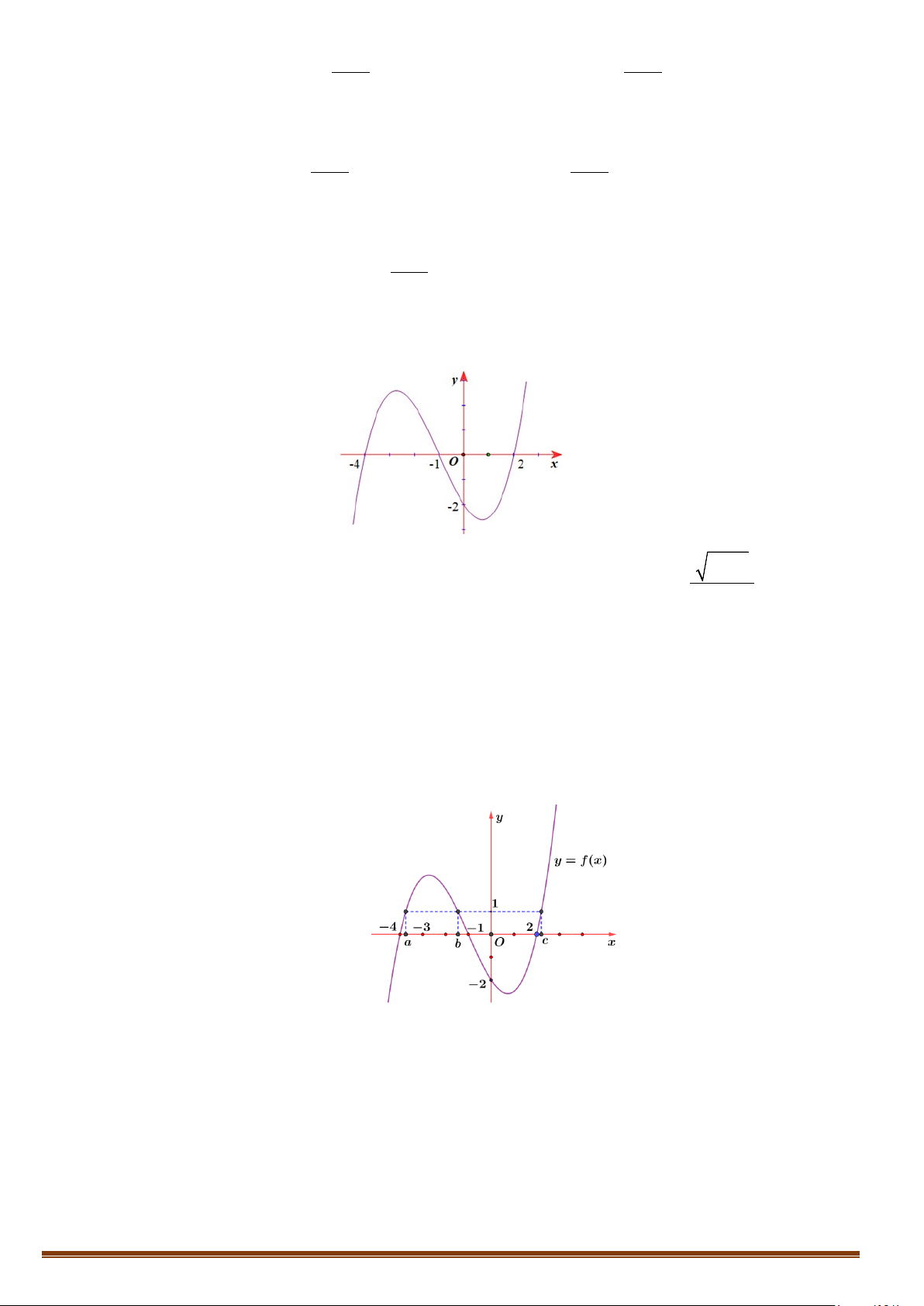
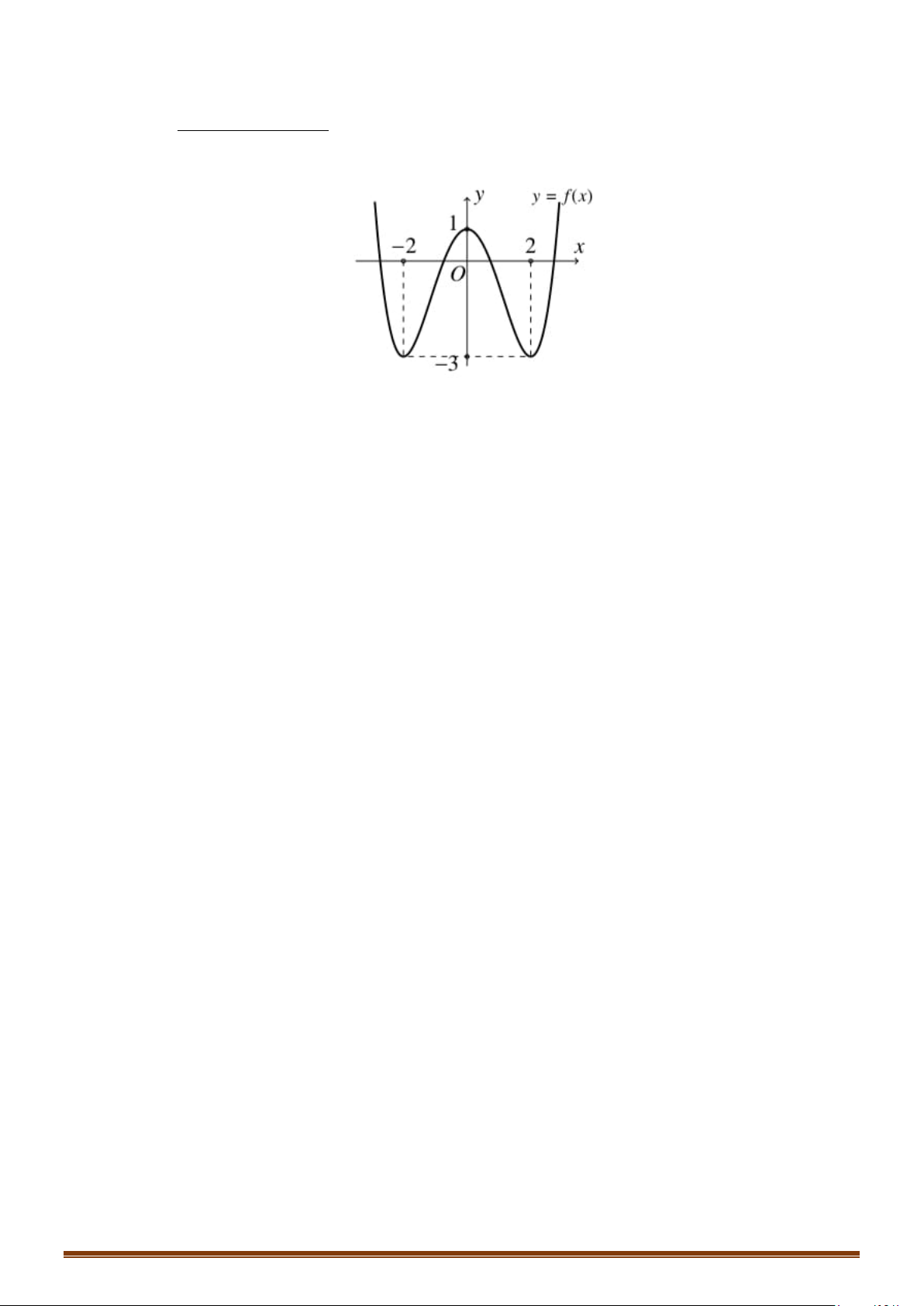
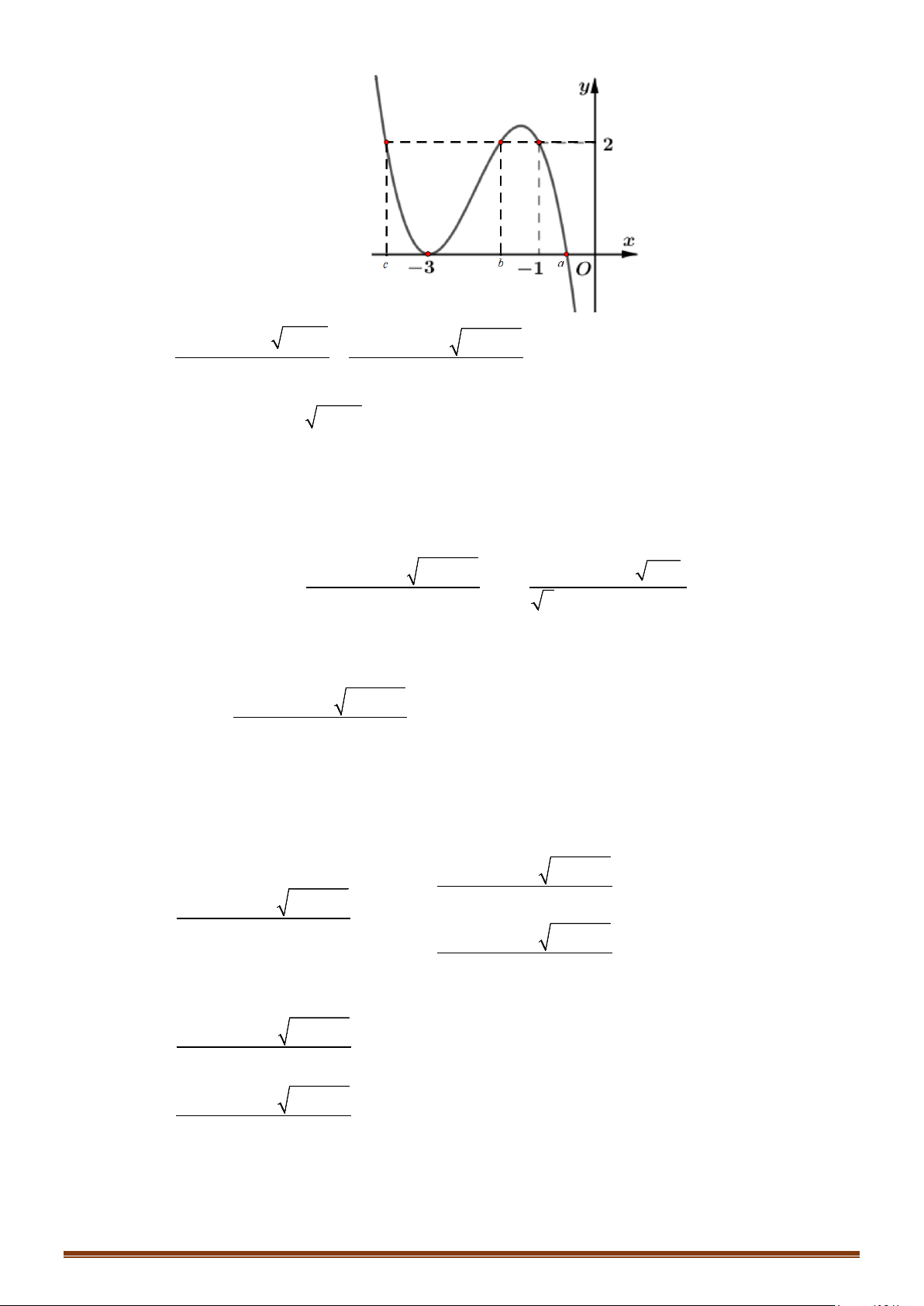
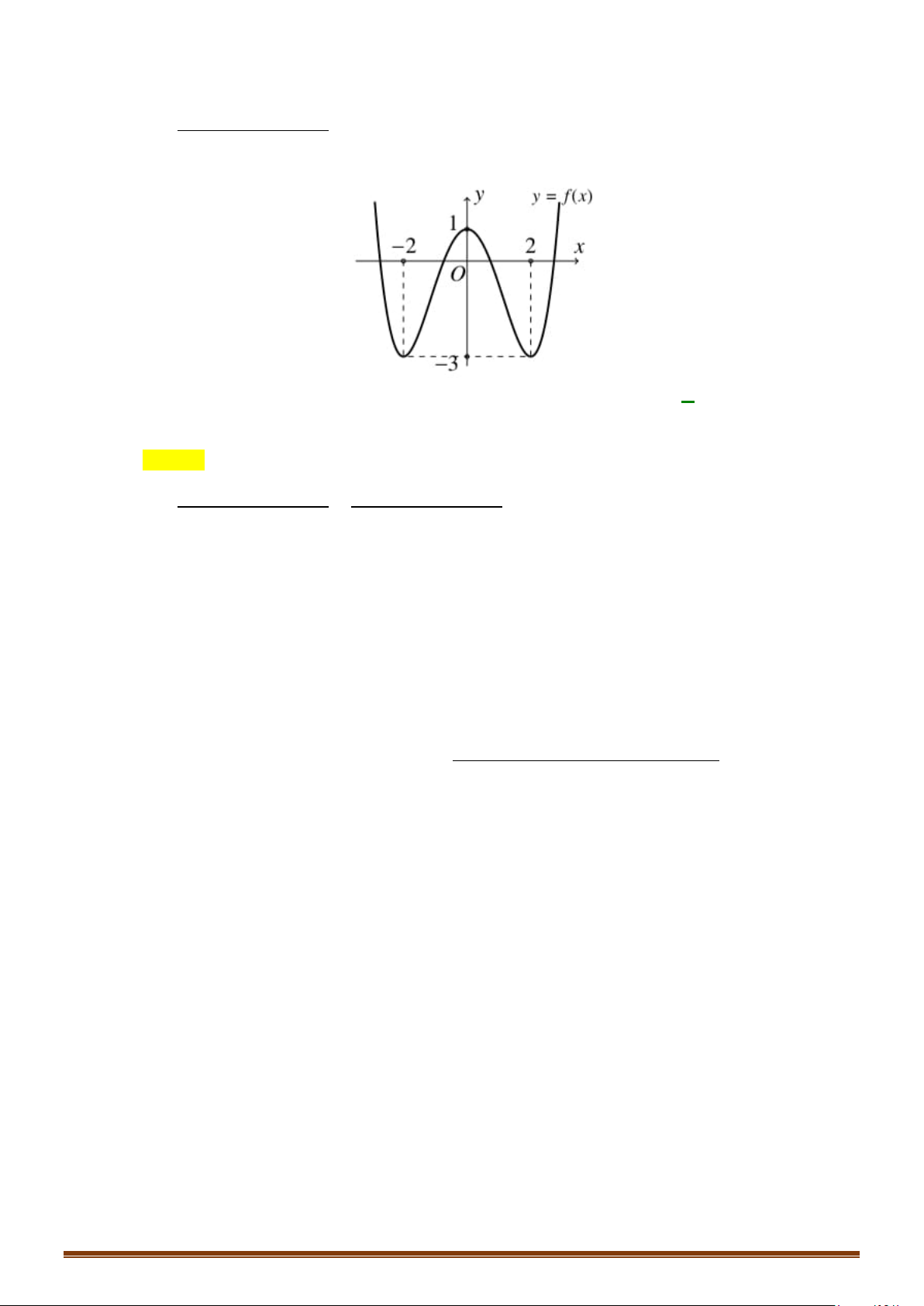
Câu 4. Cho đồ thị hàm đa thức bậc bốn y = f (x) như hình vẽ bên dưới . 6 2 2
Hỏi đồ thị của hàm số (x +1)(x - 5x). x -2x g(x) =
có bao nhiêu đường tiệm cận đứng và tiệm  2 f (x)-2f(x  ) (2x -10)   cận ngang.
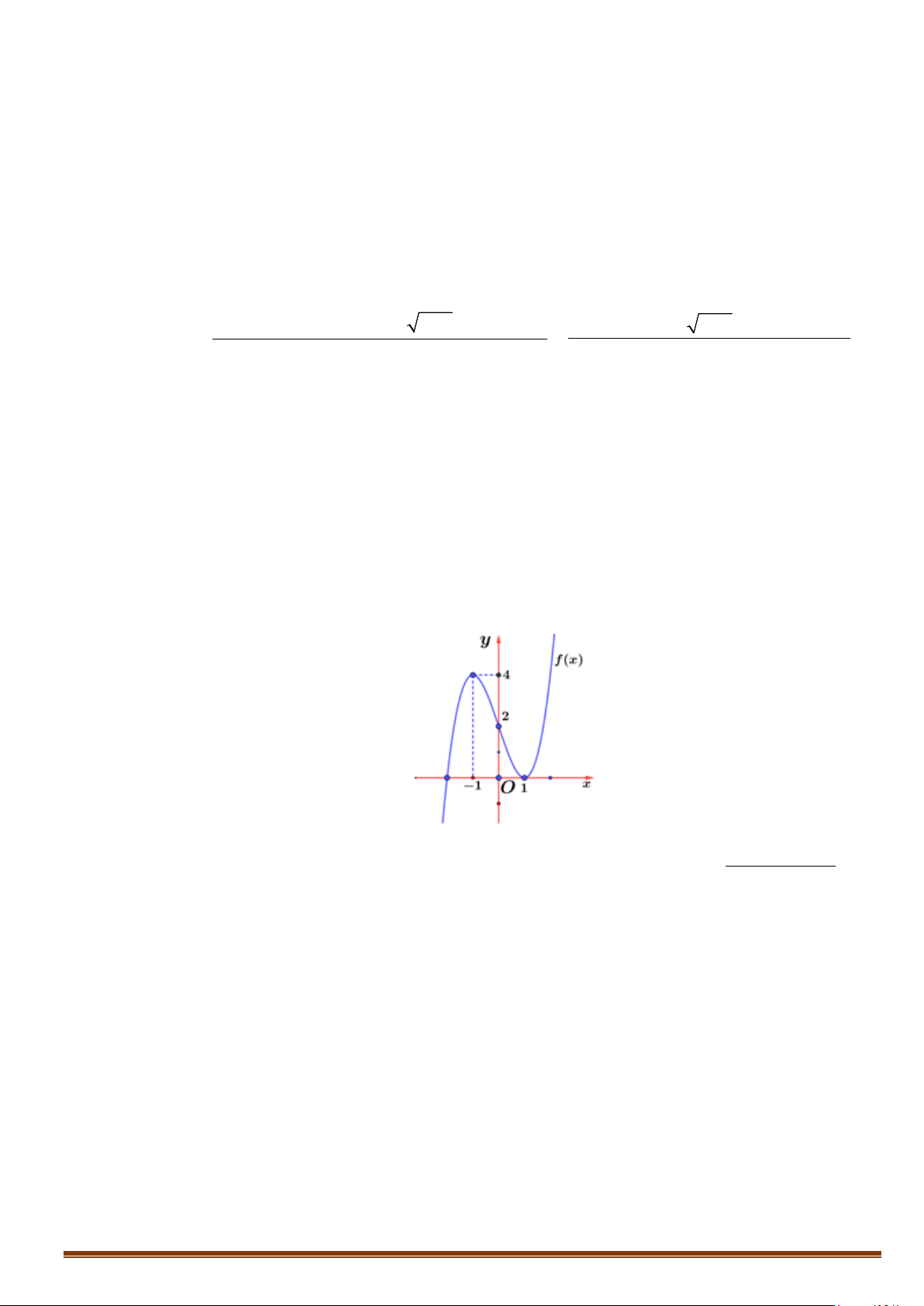
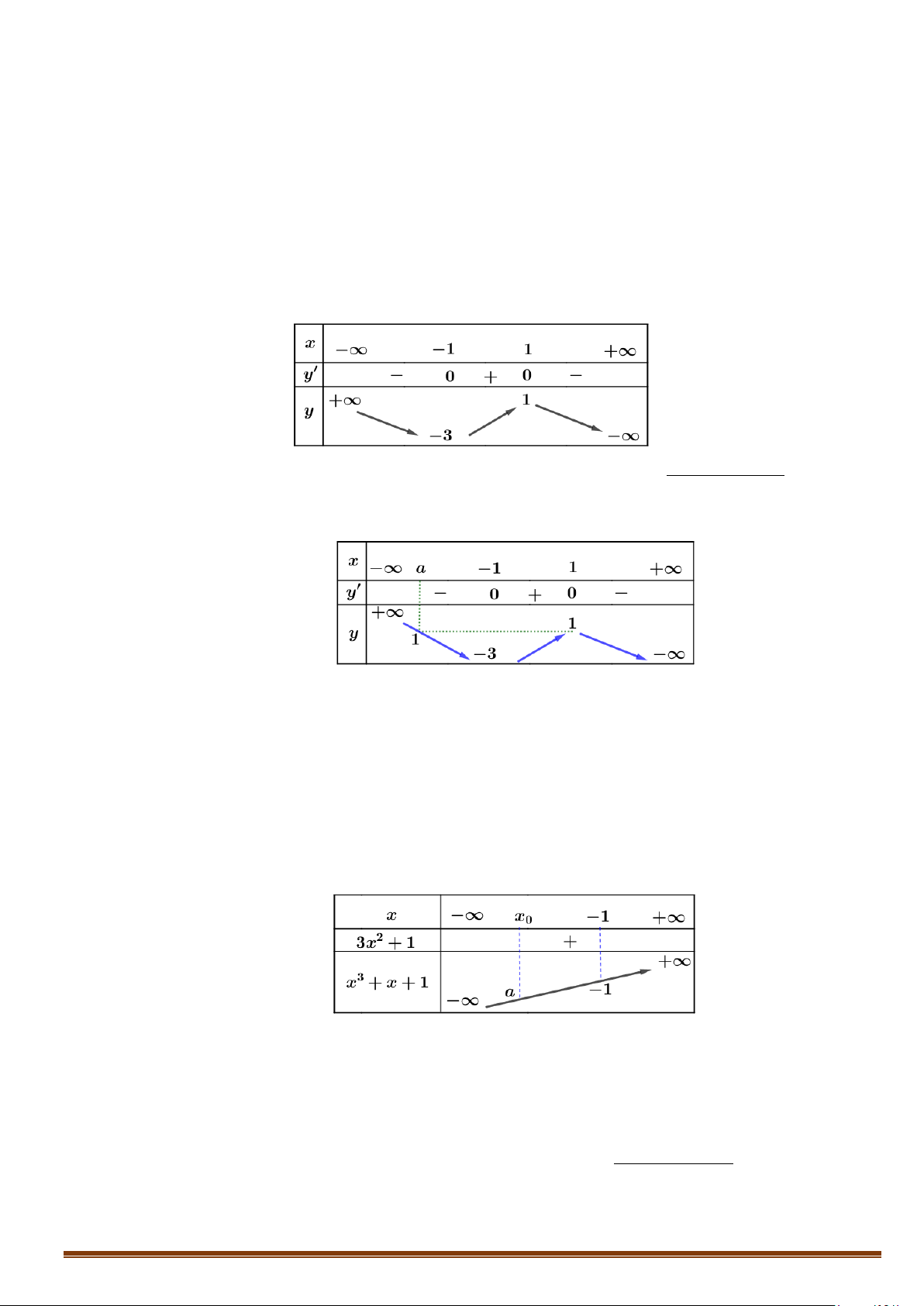
Câu 5. Cho hàm số ( ) 3 2
f x = ax + bx + cx + d là hàm số đa thức với hệ số thực, có đồ thị (C) như hình vẽ bên.
( 2x −3x+2) x−1
Tìm số tiệm cận đứng của đồ thị hàm số g (x) = ( . x + ) 2
1  f (x) − f (x)  
Câu 6. Cho hàm số bậc ba y = f (x) có đồ thị như hình vẽ bên. Page 173
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ 2 (x +1)(x −1)
Tìm số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = g(x) = . 2
f (x) − 2 f (x)
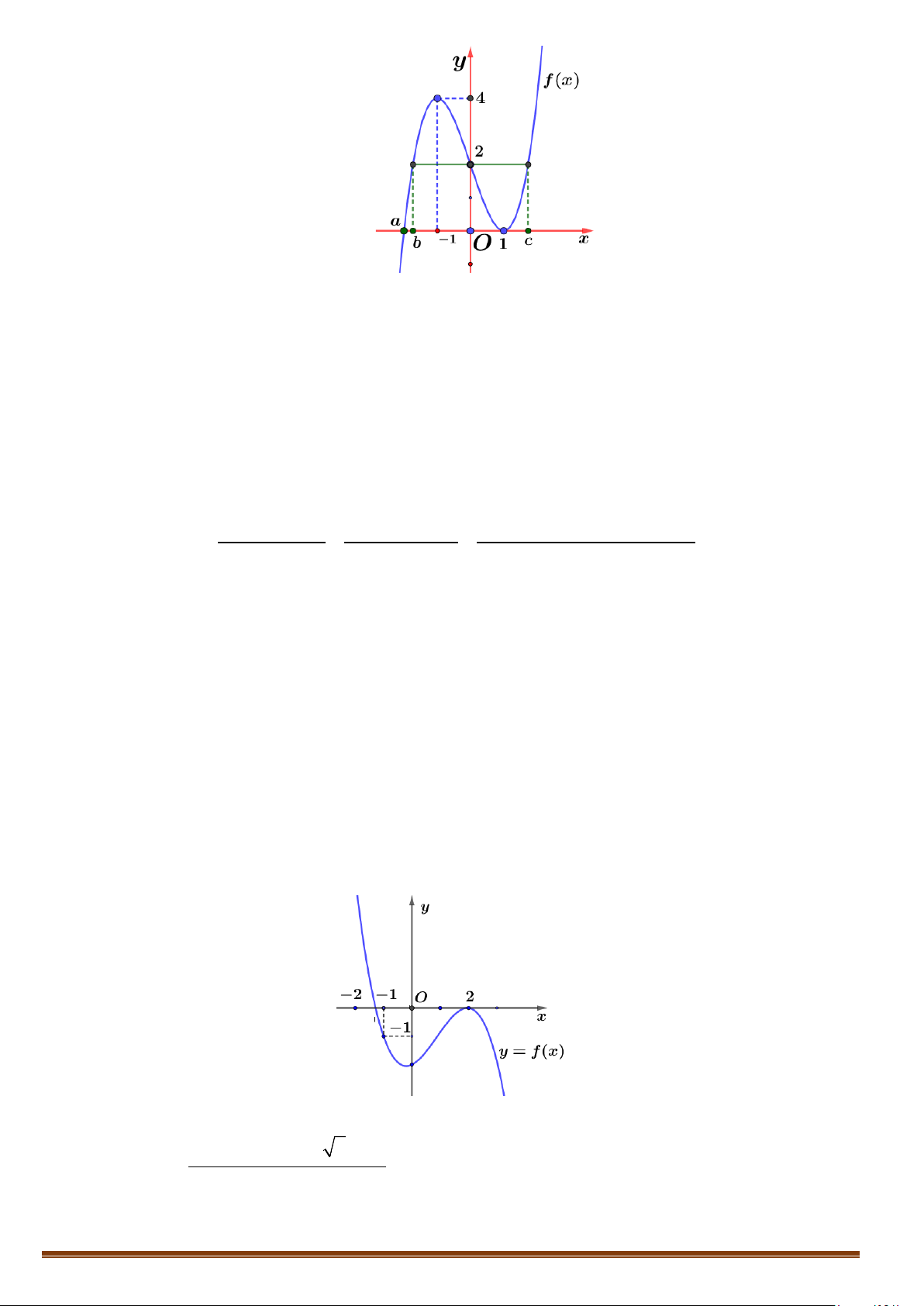
Câu 7. Cho hàm số = ( ) 3 2
y f x = ax + bx + cx + d , (a ≠ 0) có đồ thị như hình dưới đây
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số ( 2x +2x−3) = ( ) x y g x = ( .
x x)( f (x))2 2 f (x) − +  
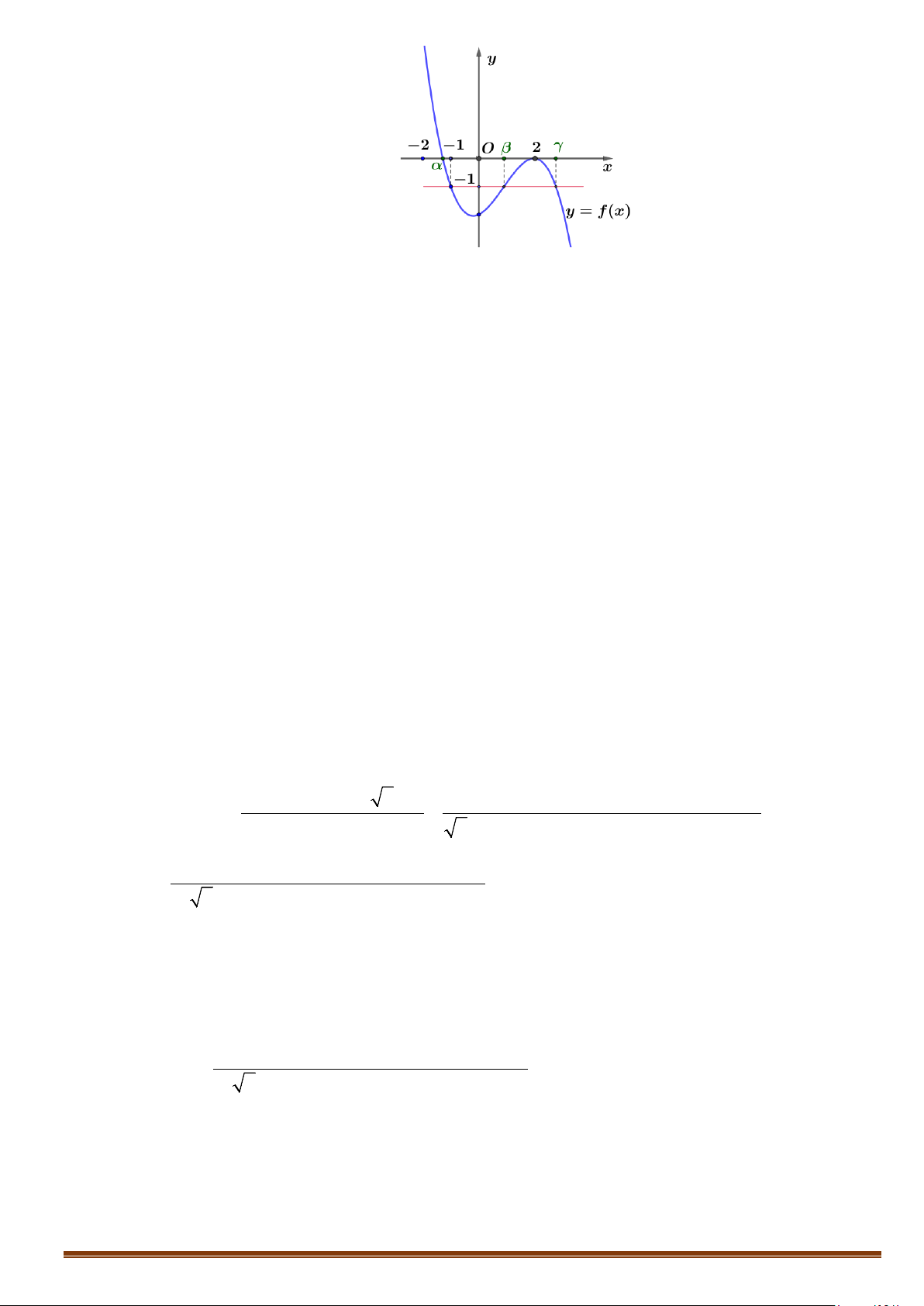
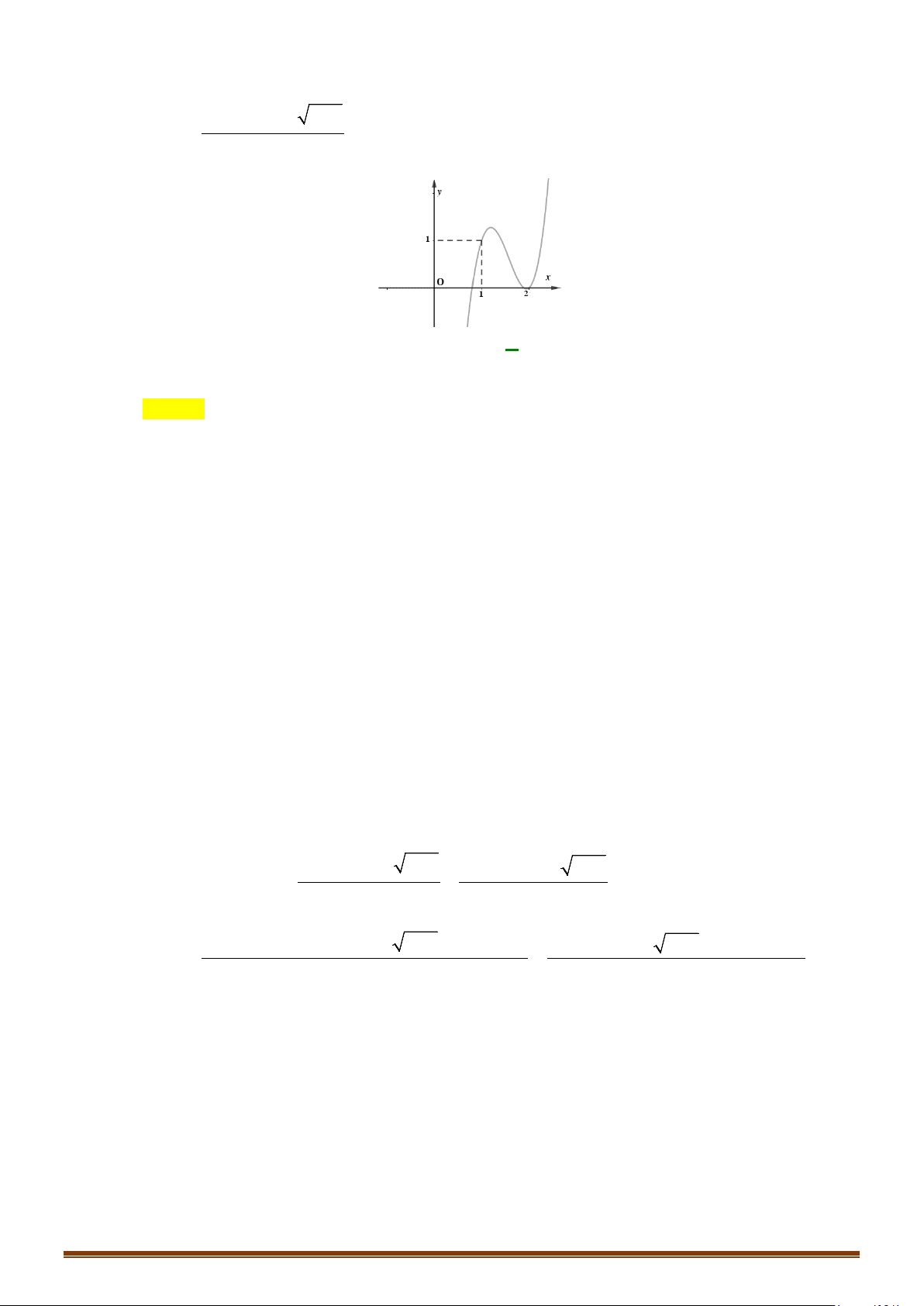
Câu 8. Cho hàm số bậc ba y = f (x) có đồ thị như hình vẽ bên. x + 2
Tìm số đường tiệm cận đứng của đồ thị hàm số y = g(x) = f (x)+1. Page 174
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 9. Cho hàm số y = f ( x) liên tục trên  \  
1 và có bảng biến thiên như sau
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = g (x) = f ( 2
x − 2x − 2) .
Câu 10. Cho hàm số y = f (x) liên tục trên  và có đồ thị như hình dưới đây  − x
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = g ( x) 2 = f   x 1  + 
Câu 11. Cho hàm số y = f (x) là hàm đa thức liên tục trên  và có đồ thị như hình dưới đây f x
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = g (x) ( ) = . f (x) −1
Câu 12. Cho hàm số y = f (x) xác định, liên tục trên  và có bảng biến thiên như sau :
Tìm số tiệm cận ngang và số tiệm cận đứng của đồ thị hàm số g (x) 3 = . f ( 3 x + x + ) 1 −1
DẠNG 3: MỘT SỐ BÀI TOÁN VỀ TIỆM CẬN CHỨA THAM SỐ Page 175
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 1. Tìm các giá trị thực của tham số m để đồ thị hàm số mx + 7 y =
có tiệm cận đứng đi qua điểm mx −1 A(1; 2 − ) .
Câu 2. Tìm các giá trị thực của tham số m để đồ thị hàm số f (x) x − 2 =
có ba đường tiệm cận. 2 x + x + m
Câu 3. Tìm tham số m để đồ thì hàm số
(m +1)x − 5m y =
có tiệm cận ngang là đường thẳng y =1. 2x − m
Câu 4. Tìm các tham số m để đồ thị hàm số x −1 y =
có đúng hai đường tiệm cận? 2 x + mx + 4 Câu 5. Cho hàm số 2mx + m y =
. Với giá trị nào của m thì đường tiệm cận đứng, tiệm cận ngang của đồ thị x −1
hàm số cùng với hai trục tọa độ tạo thành một hình chữ nhật có diện tích là 8?
Câu 6. Biết đồ thị (C) của hàm số ax + b y = đi qua điểm A( 1;
− 7) và giao điểm hai tiệm cận của (C) là cx + d điểm I ( 2;
− 3). Biết c là số nguyên dương và a,c là các số nguyên tố cùng nhau. Tìm các số
a,b,c, d . Câu 7. Cho hàm số x − m y =
. Giá trị nào của m để đồ thị hàm số đã cho có đúng 1 tiệm cận đứng? 2 x + 3x − 4 Câu 8. Cho hàm số 2x + m y =
. Tìm tất cả các giá trị của m để đồ thị hàm số có 2 đường tiệm cận cùng x − m
với hai trục tọa độ tạo thành một hình vuông
Lời giải
Ta có đường tiệm cận ngang của đồ thị hàm số là y = 2
Với 2.m −1.m ≠ 0 ⇔ m ≠ 0 thì đường tiệm cận đứng của đồ thị hàm số là x = m
Để 2 đường tiệm cận cùng với 2 trục tọa độ tạo thành một hình vuông thì m = 2 ⇔ m = 2 ± Câu 9. Cho hàm số 1− x y =
. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số có đúng 2 x − 2mx + 4
ba đường tiệm cận.
Câu 10. Biết rằng đồ thị hàm số ax 1 y
có tiệm cận đứng là x  2 và tiệm cận ngang là y  3 . Tìm a,b . bx 2
Câu 11. Tính tổng bình phương tất cả các giá trị của m để đồ thị hàm số 2
y = 2x −3x + 5 + mx − 6 có tiệm cận ngang. Page 176
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
NG I ỨNG DỤNG ĐẠO HÀM ƯƠ
ĐỂ KHẢO SÁT HÀM SỐ CH
BÀI 4. ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ I LÝ THUYẾT.
1. Nhánh vô cực của đường cong (C) : y = f (x) Gọi M ( ; x y)∈(C) .
x → +∞ hay x → −∞
Ta nói: (C) có nhánh vô cực ⇔ 
y → +∞ hay y → −∞
VD1: Đồ thị (C) của hàm số 2
y = x có nhánh vô cực
VD2: Đồ thị (C) của hàm số 2
y = 4 − x không có nhánh vô cực vì M ( ; x y)∈(C) ⇒ 2
− ≤ x ≤ 2 và 0 ≤ y ≤ 2 .
2) Tiệm cận của đường cong
Cho đường cong (C) : y = f (x) và M ( ;
x y)∈(C) , H là hình chiếu vuông góc của M lên (∆) .
Đường thẳng (∆) được gọi là tiệm cận của (C) khi và chỉ khi khoảng cách MH từ M đến (∆)
tiến về 0 khi M vẽ nên nhánh vô cực của (C).
Như vậy: (∆) tiệm cận của (C) ⇔ lim MH = 0 M →∞ Page 1
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
3) Định nghĩa đường TCĐ và TCN của đồ thị hàm số
a) Tiệm cận đứng của đồ thị hàm số
Đường thẳng x = x được gọi là đường tiệm cận đúng 0
(TCĐ) của đồ thị hàm số y = f (x) nếu thỏa mãn ít nhất
một trong các điều kiện sau:
lim f (x) = +∞ ; lim f (x) = −∞ x + → + 0 x x→ 0 x
lim f (x) = +∞ ; lim f (x) = −∞ x − → − 0 x x→ 0 x
b) Tiệm cận ngang của đồ thị hàm số
Cho hàm số y = f (x) có xác định trên một khoảng vô hạn
là khoảng có một trong các dạng (a,+∞) ; (−∞,a) ; (−∞,+∞)
.Đường thẳng y = y được gọi là đường TCN (hay TCN) 0
của đồ thị nếu thỏa mãn ít nhất một trong các điều kiện sau:
lim f (x) = y ; lim f (x) = y 0 x→−∞ 0 x→+∞  Lưu ý: i) Hàm ax + b y =
với ac ≠ 0 có tiệm cận đứng d
x = − ; tiệm cận ngang a y = . cx + d c c f (x) ii) Hàm y =
với f (x), g (x) là những hàm đa thức g (x)
+) Nếu bậc tử nhỏ hơn bậc mẫu thì có tiệm cận ngang y = 0.
+) Nếu bậc tử bằng bậc mẫu thì có tiệm cận ngang an y =
với a b là hệ số của lũy thừa n , b n n
cao nhất trên tử và dưới mẫu.
+) Nếu bậc tử lớn hơn bậc mẫu thì không có tiệm cận ngang.
g (x = 0; f x ≠ 0 0 ) ( 0)  
g ( x = f x = 0 0 ) ( 0)
+) x = x là tiệm cận đứng ⇔ . 0    f (x)  lim = ±∞  x→  0 x g   (x)
iii) Ứng dụng máy tính CASIO để tìm tiệm cận đứng hoặc tiệm cận ngang
Để tìm tiệm cận đứng hoặc tiệm cận ngang của một hàm số thông qua máy tính CASIO, ta sử dụng phím CALC trên máy.
Một số lưu ý về kết quả và cách bấm: Giới hạn Thao tác trên máy tính x x+ → CALC 10 x − + o 10 o x x− → CALC 10 x − − o 10 o x → +∞ CALC 10 10 x → −∞ CALC 10 10 − Page 2
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
II HỆ THỐNG BÀI TẬP TỰ LUẬN.
DẠNG 1: TÌM TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ CHO BỞI CÔNG THỨC 2x − 3
Câu 1. Cho hàm số y = f (x) =
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm x + 2
số y = f (x) . Lời giải
Vì lim y = 2; lim y = 2 nên đồ thị hàm số có 1 tiệm cận ngang là y = 2 . x→−∞ x→+∞ Vì lim y = ;
−∞ lim y = +∞ nên đồ thị hàm số có 1 tiệm cận đứng x = 2 − . x 2+ x 2− →− →−
Do đó đồ thị hàm số có tổng số 2 tiệm cận kể cả đứng và ngang. 2020x − 2021
Câu 2. Cho hàm số y = f (x) =
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ 1− x
thị hàm số y = f (x) . 2x − 5
Câu 3. Cho hàm số y = f (x) =
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm x − 2
số y = f (x) . 2 x + 2x + 3
Câu 4. Cho hàm số y = f (x) =
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ x +1
thị hàm số y = f (x) . 2 x − x − 6
Câu 5. Cho hàm số y = f (x) =
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị x −1
hàm số y = f (x) . 2 x + 3 − 2
Câu 6. Cho hàm số y = f (x) =
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị x −1
hàm số y = f (x) . 2 x − x − 6
Câu 7. Cho hàm số y = f (x) =
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị 2 x + 3x + 2
hàm số y = f (x) . 2 + + − Câu 8. x 2x 3 3x
Cho hàm số y = f (x) =
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của 2x − 4
đồ thị hàm số y = f (x) . 2
5x − x + 3x + 2
Câu 9. Cho hàm số y = f (x) =
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của 2 − x
đồ thị hàm số y = f (x) . Page 3
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
DẠNG 2: TÌM TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ BIẾT BBT CỦA HÀM SỐ, ĐỒ THỊ CỦA HÀM
SỐ ĐÓ HOẶC HÀM SỐ LIÊN QUAN
Câu 1. Cho hàm số y = f (x) có bảng biến thiên
Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = f (x) . Lời giải Vì lim y = ;
−∞ lim y = 3 nên đồ thị hàm số có 1 tiệm cận ngang là y = 3 . x→−∞ x→+∞
Vì lim y = +∞ nên đồ thị hàm số có 1 tiệm cận đứng x = x . x + 4 → 4 x
Do đó đồ thị hàm số có tổng số 2 tiệm cận kể cả đứng và ngang.
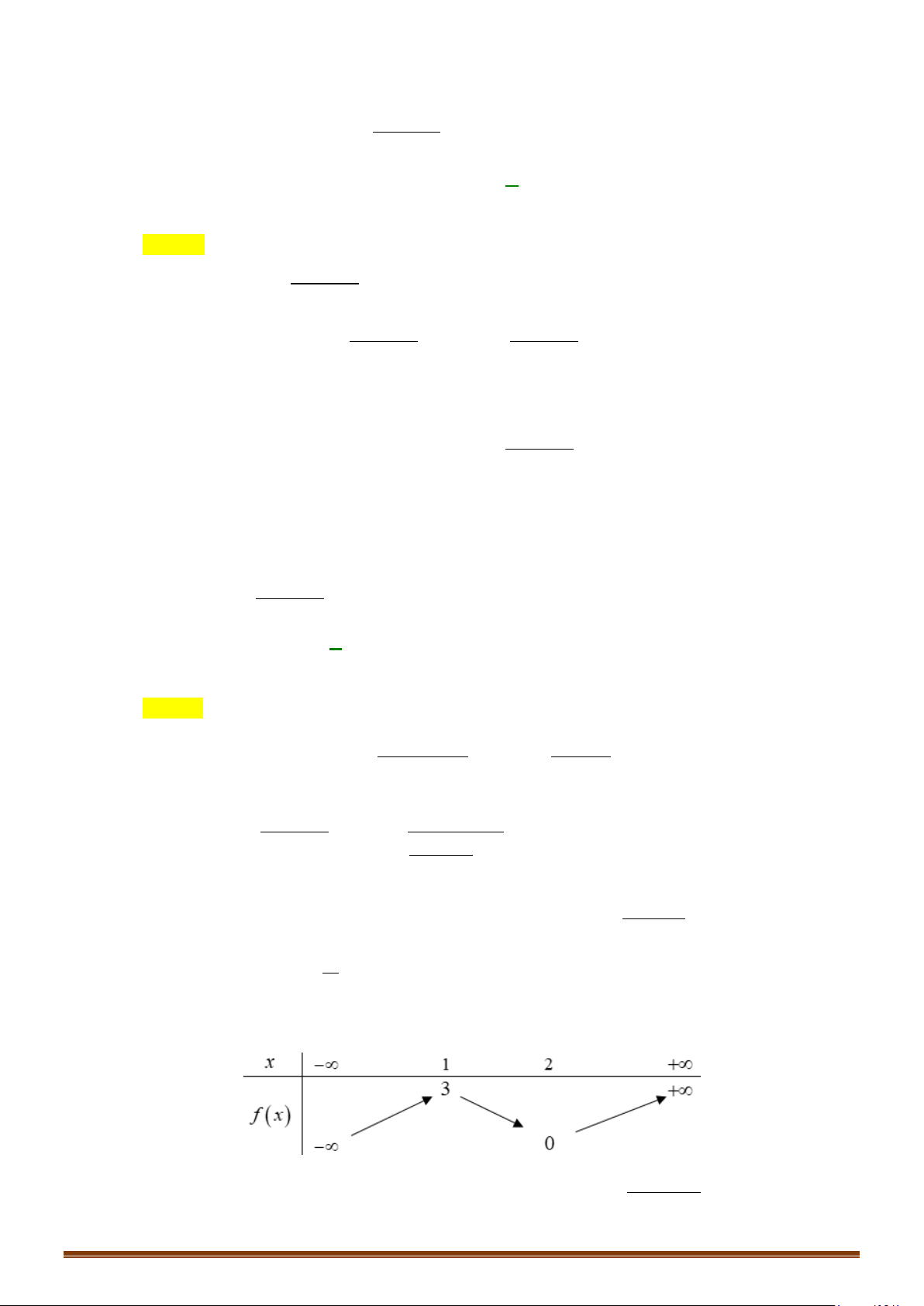
Câu 2. Cho hàm số f (x) có bảng biến thiên
Tìm số tiệm cận của đồ thị hàm số 1 y = ? f (x) Lời giải Vì 1
lim y = 0; lim y = nên đồ thị hàm số có 1 tiệm cận ngang y = 0 và 1 y = . x→−∞ x→+∞ 3 3
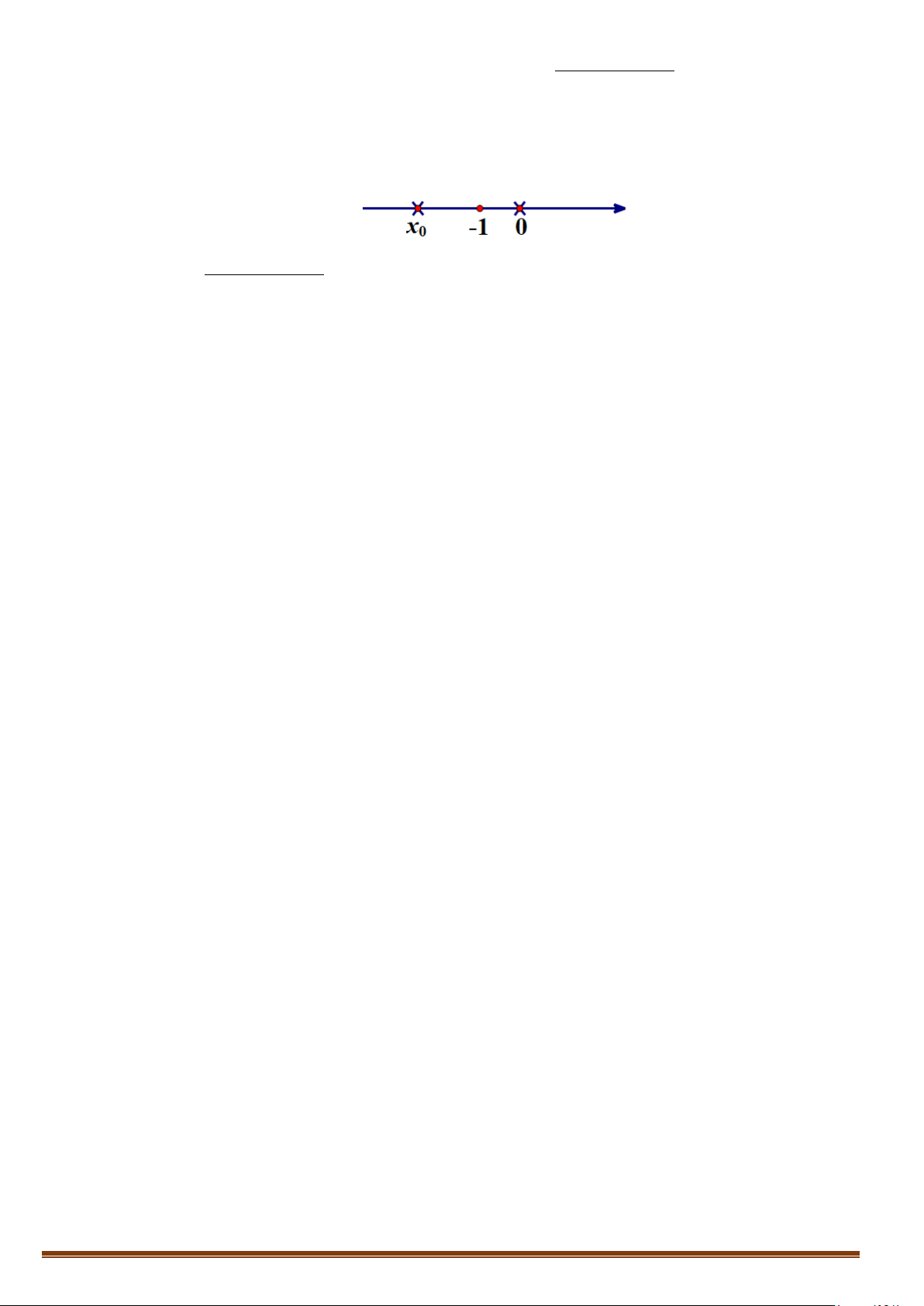
Từ bảng biến thiên, ta có f (x) = 0 có hai nghiệm x = x và x = a ∈( ; −∞ x . 1 ) 2
Dễ thấy lim y = +∞ và lim y = +∞ nên đồ thị hàm số có 2 tiệm cận đứng là x = x và x = a x a+ 2 → x + → 2 x
Do đó đồ thị hàm số có tổng số 4 đường tiệm cận kể cả đứng và ngang.
Câu 3. Cho hàm số y = f ( x) xác định, liên tục trên  \{ }
1 và có bảng biến thiên như sau:
Tìm phương trình đường tiệm cận ngang của đồ thị hàm số đã cho? Lời giải
Tập xác định: D =  \{ } 1 .
Ta có lim f (x) = 2; lim f (x) = 2 . Do đó y = 2 là đường tiệm cận ngang của đồ thị hàm số. x→−∞ x→+∞
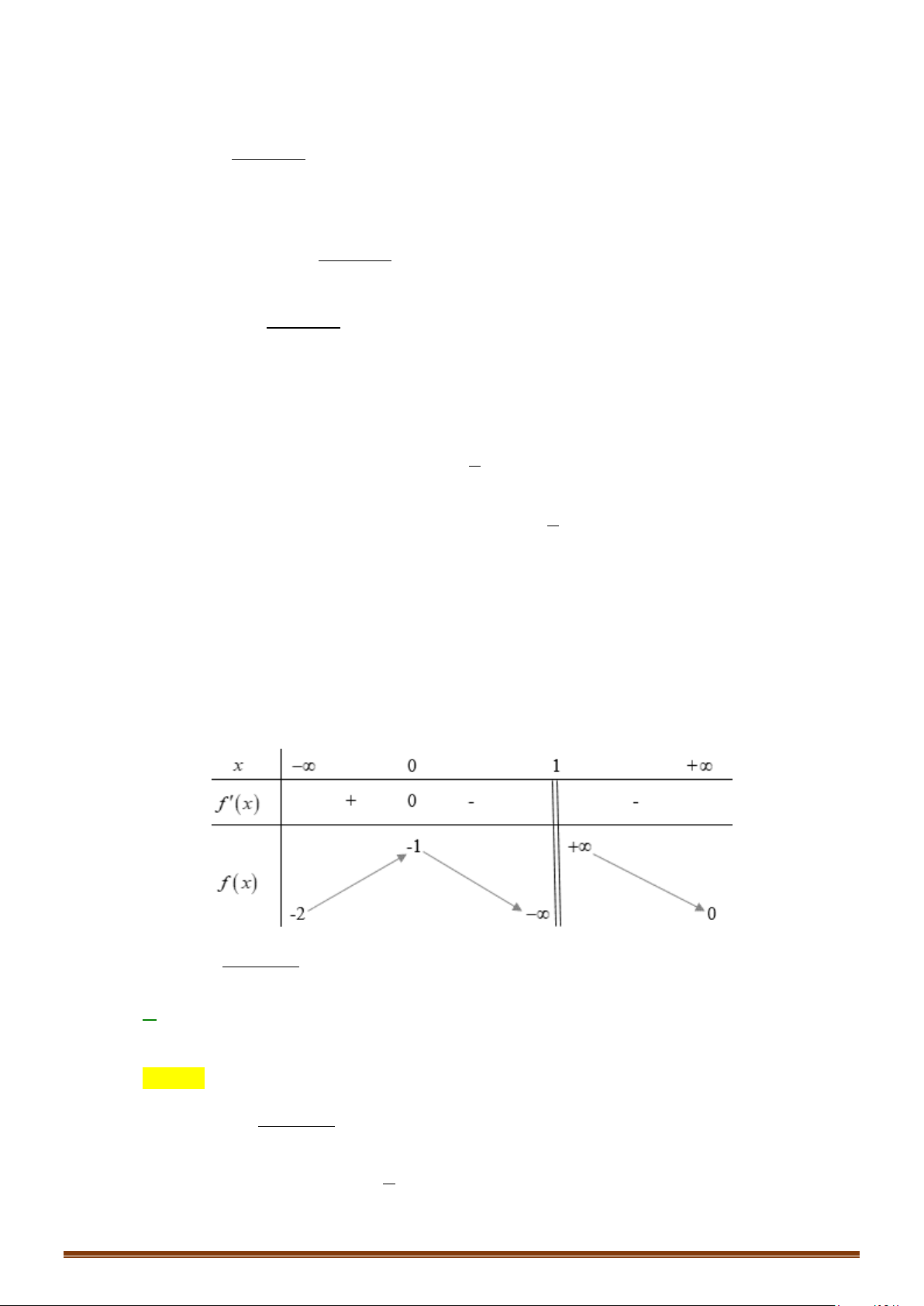
Câu 4. Cho hàm số y = f (x) xác định trên  \{ }
0 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau: Page 4
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Hỏi đồ thị hàm số trên có bao nhiêu đường tiệm cận đứng và ngang? Lời giải
Tập xác định: D =  \{ } 0 . Ta có
lim f (x) = +∞ ; lim f (x) = −∞ do đó đồ thị hàm số không có tiệm cận ngang. x→−∞ x→+∞
lim f (x) = −∞ ⇒ x = 0 là đường tiệm cận đứng duy nhất của đồ thị hàm số. x 0+ →
Câu 5. Cho hàm số y = f (x) xác định trên  \{ }
1 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
Tìm các giá trị nguyên của m∈[0;5) để đồ thị hàm số y = f ( x) có 3 đường tiệm cận đứng và ngang? Lời giải
Tập xác định D =  \{ } 1 . Ta có
lim f (x) = 2 ⇒ y = 2 là đường tiệm cận ngang. x→−∞
lim f (x) = −∞ ⇒ x =1 là tiệm cận đứng. x 1− →
lim f (x) = m ⇒ y = m là đường tiệm cận ngang. x→+∞
Do đó, để đồ thị hàm số có 3 đường tiệm cận thì m ≠ 2 , mà m∈[0;5) nên m∈{0;1;3; } 4 .
Câu 6. Cho hàm số f (x) có đồ thị như hình vẽ bên.
Tìm phương trình các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số trên. Lời giải
Nhìn vào đồ thị, ta có: lim f (x) = −∞ và lim f (x) = +∞ . Do đó, đồ thị có một tiệm cận đứng x 2− → x 2+ →
là đường thẳng x = 2. Page 5
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Theo đồ thị, ta cũng có: lim f (x) =1 và lim f (x) =1. Do đó, đồ thị có tiệm cận ngang là x→−∞ x→+∞
đường thẳng y =1.
Vậy đồ thị có tiệm cận đứng x = 2 tiệm cận ngang y =1.
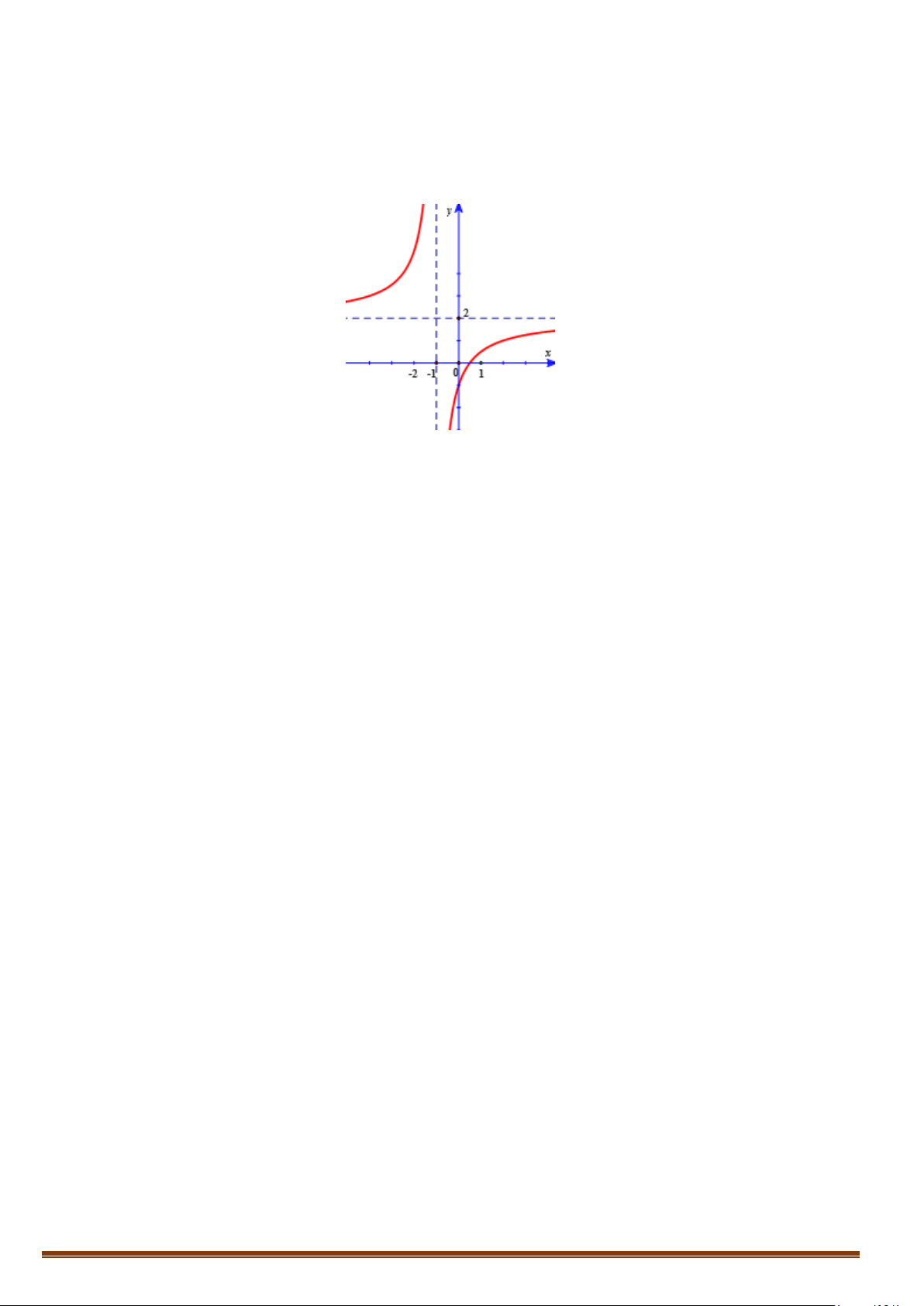
Câu 7. Cho đồ thị hàm số y = f (x) như hình bên. Đồ thị có bao nhiêu đường tiệm cận đứng và tiệm cận ngang? Lời giải
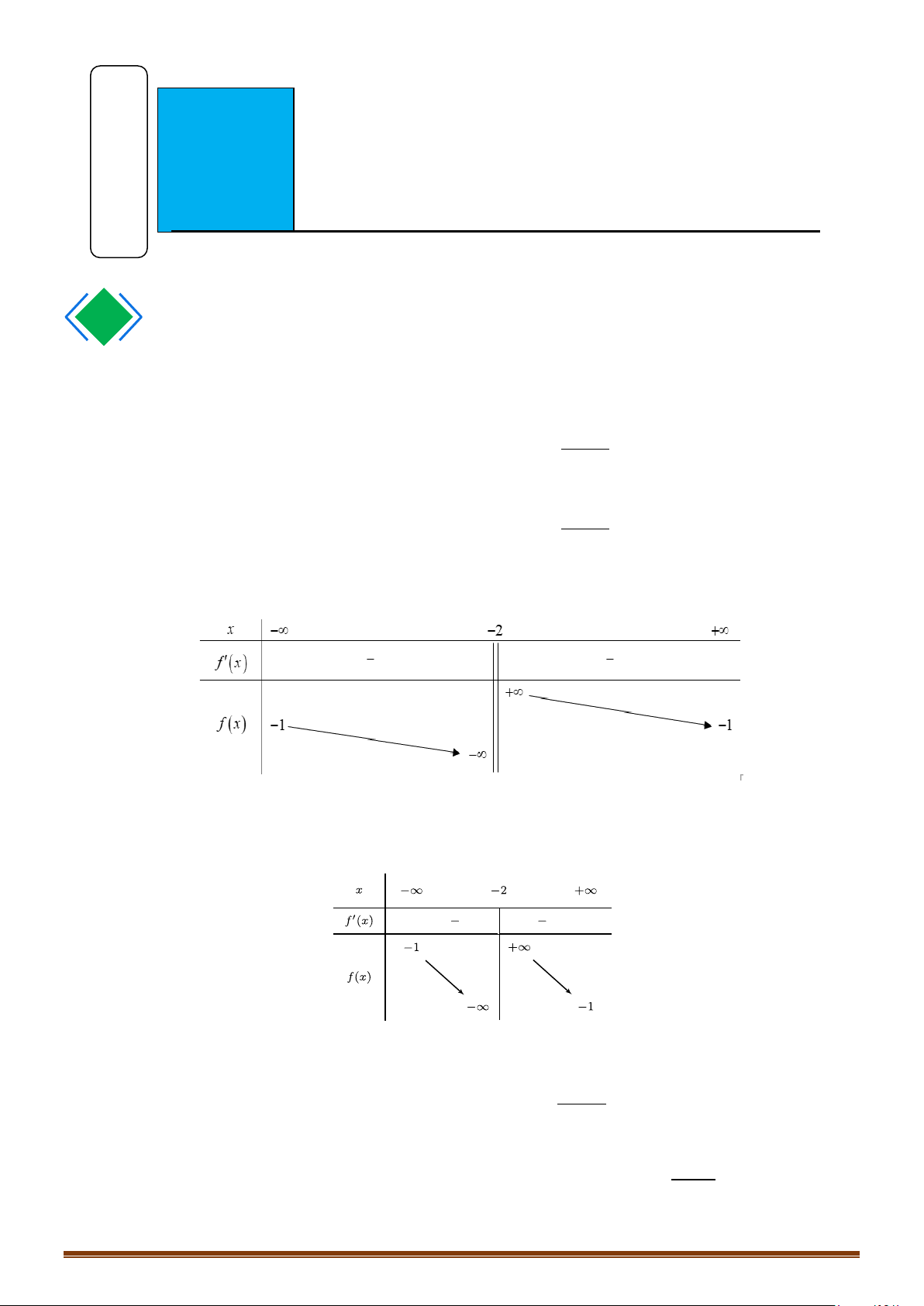
Nhìn vào đồ thị, ta có: lim f (x) = +∞ và lim f (x) = −∞ . Do đó, đồ thị có một tiệm cận x 1− →− x 1+ →−
đứng là đường thẳng x = 1 − .
Theo đồ thị, ta cũng có: lim f (x) = 2 và lim f (x) = 2 . Do đó, đồ thị có tiệm cận ngang là x→−∞ x→+∞
đường thẳng y = 2 .
Vậy đồ thị 2 đường tiệm cận là: tiệm cận đứng x = 1
− và tiệm cận ngang y = 2 . Page 6
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
DẠNG 3: TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ HÀM HỢP
Các dạng trong chủ đề: Cho hàm số y = f (x) biết bảng biến thiên hoặc đồ thị. Tìm các đường
tiệm cận đứng và tiệm cận ngang của đồ thị y = g (x) thuộc một trong các dạng sau
1) y = f (u(x)) ,
2) y = g ( f (x)) ,
3) y = g ( f (u(x))) ,
4) y = g (x, f (x)),
5) y = g (x, f (u(x))) .
Phương pháp giải: Gọi (G) là đồ thị hàm số y = g (x) .
1)Tìm tiệm cận ngang.
Xét hàm số dạng g (x) u(x) =
.Một dấu hiệu thường dùng để nhận biết (G) có tiệm cận ngang: v(x)
+ Hàm số y = g (x) xác định trên (a;+∞) hoặc trên ( ; −∞ a) .
+ Bậc của u(x) ≤ Bậc của v(x) .
+ lim g(x) = y hoặc lim g(x) = y ⇒ Đường thẳng y = y là tiệm cận ngang của(G) . 0 x→+∞ 0 x→−∞ 0
2)Tìm tiệm cận đứng.
Xét dạng hàm số g (x) u(x) =
. Một dấu hiệu thường dùng để nhận biết đường thẳng x = x v(x) 0 là
tiệm cận đứng của (G) :
+ v(x ) = 0 và u(x ) ≠ 0 , g (x) xác định trên ( ;
a x hoặc (x ;b . 0 ) 0 ) 0 0
+ Ít nhất một trong hai giới hạn lim g (x), lim g (x) là giới hạn vô cực. x + − → 0 x x→ 0 x
⇒ Đường thẳng x = x là tiệm cận đứng của (G) . 0
Trong chủ đề này, các dấu hiệu nhận biết ở trên dựa vào bảng biến thiên hoặc đồ thị của hàm số
y = f (x) .
Câu 1. Cho hàm số y = f ( x) có bảng biến thiên như hình dưới đây 1
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = . 2 f (x) −1 Lời giải
Dựa vào bảng biến thiên ta có: Page 7
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ   1  x x  ;  = ∈ −∞ − 1 1  2 
Phương trình 2 f (x) −1= 0 ⇔ f (x)  = ⇔  . 2   1 x x  ;  = ∈ − +∞  2  2    Do 1 lim y = lim = −∞ và 1 lim y = lim
= +∞ nên x = x là một tiệm cận đứng 1 x + + → x − − → 1x
x→ 1x 2 f ( x) 1 x
x→ 1x 2 f ( x) −1 −1 của đồ thị hàm số 1 y = . 2 f (x) −1 Do 1 lim y = lim = +∞ và 1 lim y = lim
= −∞ nên x = x là một tiệm cận 2 x + + → x − − → 2 x x→ 2
x 2 f ( x) 2 x x→ 2
x 2 f ( x) −1 −1
đứng của đồ thị hàm số 1 y = . 2 f (x) −1 Do 1 lim y = lim = và 1 lim y = lim
= 1nên y =1 là một tiệm cận ngang của x→+∞ x→+∞ f (x) 1 2 −1 x→−∞
x→−∞ 2 f ( x) −1 đồ thị hàm số 1 y = . 2 f (x) −1 Vậy đồ thị hàm số 1 y =
có 2 đường tiệm cận đứng là x = x ; x = x và 1 tiệm cận ngang 2 f (x) −1 1 2 là y =1.
Câu 2. Cho hàm số y = f ( x) liên tục trên  \  
1 và có bảng biến thiên như sau 1
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = g(x) = 2 f (x) −3 Lời giải
Dựa vào bảng biến thiên ta có: 3
x = x ∈ 1;2
Phương trình 2 f (x) −3 = 0 ⇔ f (x) 1 ( ) = ⇔ . 2
x = x ∈ 2;+∞  2 ( ) 1 1
 lim g(x) = lim
= +∞ , lim g(x) = lim
= −∞ ⇒ Đường thẳng x = x là một 1 x + + → x − − → 1x
x→ 1x 2 f ( x) 1 x
x→ 1x 2 f ( x) − 3 − 3
tiệm cận đứng của đồ thị hàm số 1 y = . 2 f (x) −3 1 1
 lim g(x) = lim
= −∞ , lim g(x) = lim
= +∞ ⇒ Đường thẳng x = x là một 2 x + + → x − − → 2 x x→ 2
x 2 f ( x) 2 x x→ 2
x 2 f ( x) − 3 − 3
tiệm cận đứng của đồ thị hàm số 1 y = . 2 f (x) −3 Page 8
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ 1 1
 lim g(x) = lim
= , lim g(x) = lim
= 0 ⇒ Đường thẳng y = 0 là tiệm cận x→+∞ x→+∞ f (x) 0 2 − 3 x→−∞
x→−∞ 2 f ( x) − 3
ngang của đồ thị hàm số 1 y = . 2 f (x) −3 Vậy đồ thị hàm số 1 y =
có 2 đường tiệm cận đứng là x = x ; x = x và 1 tiệm cận ngang 2 f (x) − 3 1 2 là y = 0.
Câu 3. Cho hàm số f (x) 3 2
= ax + bx + cx + d (a, ,
b c,d ∈ R) có đồ thị như hình vẽ.
( 2x +4x+3) 2x + x
Đồ thị hàm số g (x) =
có bao nhiêu đường tiệm cận đứng?
( f (x))2 −2 f (x) Lời giải  x ≤ 1 −     x ≥ 0
Điều kiện  f (x) ≠ 0  f (x) ≠ 2  
( 2x +4x+3) 2x + x (x+ )1(x+3) x(x+1) Ta có g (x) = = ( ,
f (x))2 − 2 f (x)
( f (x))2 −2 f (x) 2  f (x) = 0
Xét phương trình ( f (x)) − 2 f (x) = 0 ⇔  .  f  ( x) = 2 x = 3 −
Với f (x) = 0 ⇔  trong đó x = 3
− là nghiệm nghiệm kép, nên mẫu sẽ có nhân x = x ∈ 1; − 0 (l)  1 ( ) tử (x + )2 3 do đó x = 3
− là một tiệm cận đứng. x = 1 − 
Với f (x) = 2 ⇔ x = x ∈ 3 − ; 1
− , ba nghiệm này là nghiệm đơn, nên 2 ( ) x = x ∈ ; −∞ 3 −  3 ( )
f (x) − 2 = k (x + )
1 (x − x x − x , ta thấy trong g (x) thì (x + )
1 sẽ bị rút gọn nên có thêm 2 ) ( 3 ) x = x ∈ 3 − ; 1
− và x = x ∈ ; −∞ 3 − là tiệm cận đứng. 3 ( ) 2 ( ) Page 9
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Vậy tóm lại đồ thị có 3 tiệm cận đứng là x = 3
− ; x = x ; x = x . 2 3
Câu 4. Cho đồ thị hàm đa thức bậc bốn y = f (x) như hình vẽ bên dưới . 6 2 2
Hỏi đồ thị của hàm số (x +1)(x - 5x). x -2x g(x) =
có bao nhiêu đường tiệm cận đứng và tiệm  2 f (x)-2f(x  ) (2x -10)   cận ngang. Lời giải x ≤ 0 Điều kiện:  . x ≥ 2 Giả sử 4 3 2
f (x) = ax + bx + cx + dx + e Vì 1 − 1 lim g(x) = ; lim g(x) =
nên đồ thị hàm số g(x) có 2 tiệm cận ngang 1 y = ± 2 2 x→−∞ 2 x a →+∞ 2a 2 2a Dễ thấy 2
[f (x) − 2 f (x)](2 x−10) = 0 ⇔ f (x)[f (x) − 2].2.(x − 5) = 0 có các nghiệm
x = 0; x =1; x = 2;x = 5; x = x ∈( 1
− ;0); x = x ∈(2;3) 1 2
So sánh với điều kiện của căn và bội của nghiệm ta thấy đồ thị g(x) có các đường tiệm cận đứng là:
x = 0; x = 2; x = x ; x = x 1 2
Vậy đồ thị hàm số g(x) có 6 đường tiệm cận kể cả ngang và đứng
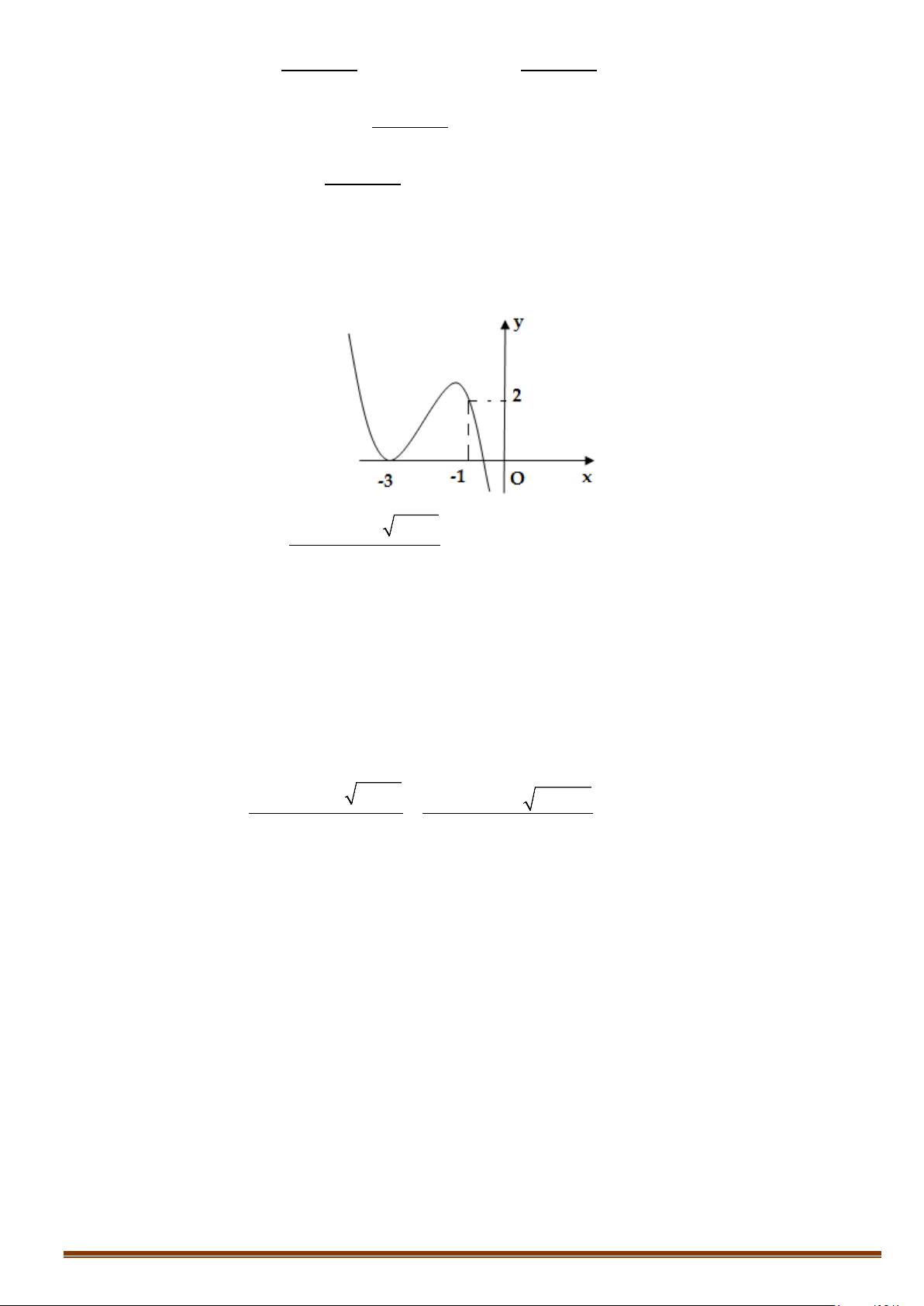
Câu 5. Cho hàm số ( ) 3 2
f x = ax + bx + cx + d là hàm số đa thức với hệ số thực, có đồ thị (C) như hình vẽ bên.
( 2x −3x+2) x−1
Tìm số tiệm cận đứng của đồ thị hàm số g (x) = ( . x + ) 2
1  f (x) − f (x)   Lời giải Điều kiện: x ≥1 x = 1 − (loai) (  = −  x + ) x 1 2
1  f (x) − f (x) = 0 ⇔    ⇔  f x = 0 . 2 f
(x)− f (x) ( ) = 0  f (x) =1 Page 10
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Dựa vào đồ thị ta ta có x =1 
f (x) =1 ⇔ x = x ∈ 1;2
⇒ f (x) −1 = a(x −1)(x − x )(x − x ) . 1 ( ) 1 2
x = x ∈ 2;+∞  2 ( ) x = x ∈ 0;1 3 ( )
f (x) = 0 ⇔  và 2
f (x) = a(x − x )(x − 2) 3 . x = 2
Hàm số có tập xác định D = (1;+∞) \{x ; x ;2 . 1 2 } − − − − g (x) (x ) 1 (x 2) x 1 x 1 = ( = x + ) 2
1 a(x −1)(x − x )(x − x )a(x − x )(x − 2) 2 a (x + )
1 (x − x )(x − x )(x − x )(x − 2) 1 2 3 1 2 3
Tại các điểm x = x , x = 2,
x = x mẫu của g ( x) nhận giá trị bằng 0 còn tử nhận các giá trị 1 2
dương. Và do hàm số xác định trên mỗi khoảng (1; x , x ;2 , 2; x , x ;+∞ nên giới hạn 1 ) ( 1 ) ( 2) ( 2 )
một bên của hàm số y = g (x) tại các điểm x = x , x = 2,
x = x là các giới hạn vô cực. 1 2
Do đó, đồ thị hàm số y = g (x) có 3 tiệm cận đứng, đó là các đường thẳng x = x , x = 2, x = x . 1 2
Vậy đồ thị hàm số y = g (x) có 3 đường tiệm cận đứng.
Câu 6. Cho hàm số bậc ba y = f (x) có đồ thị như hình vẽ bên. 2 (x +1)(x −1)
Tìm số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = g(x) = . 2
f (x) − 2 f (x) Lời giải
f (x) = 0 (1) Ta có: 2
f (x) − 2 f (x) = 0 ⇔  .
f (x) = 2 (2) Page 11
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Dựa vào đồ thị hàm số,ta thấy:
(1) có nghiệm x = a < 1
− (nghiệm đơn) và x =1 (nghiệm kép) 2
⇒ f (x) = k(x − a)(x −1) (k ≠ 0) 1 2
(2) có nghiệm ba nghiệm đơn x , x ,
x với x = b < 1
− < x = 0 <1 < x = c 1 2 3 1 2 3
⇒ f (x) − 2 = k(x − b)x(x − c) ( k ≠ 0).
⇒ Hàm số y = g(x) có tập xác định D =  \{a; ; b 0;1; } c
+) Tìm tiệm cận ngang: 2 2 2 Vì (x +1)(x −1) (x +1)(x −1) (x +1) g(x) = = =
nên lim g (x) = 0, 2
f (x) − 2 f (x)
f (x)[ f (x) − 2] 2
k (x −1)(x − b)x(x − c)(x − a) x→+∞
lim g (x) = 0 ⇒ Đồ thị hàm số y = g(x) nhận đường thẳng y = 0 làm tiệm cận ngang. x→−∞
+) Tìm tiệm cận đứng:
Tại các điểm x = a, x = b, x = 0, x =1,
x = c mẫu của g (x) nhận giá trị bằng 0 còn tử nhận các
giá trị dương. Và do hàm số xác định trên D =  \{ ; a ; b 0;1; }
c nên giới hạn một bên của hàm số
y = g (x) tại các điểm x = a, x = , b x = 0, x =1,
x = c là các giới hạn vô cực. Do đó, đồ thị hàm số
y = g (x) có 5 tiệm cận đứng, đó là các đường thẳng x = a, x = b, x = 0, x =1,
x = c . Vậy đồ thị
hàm số y = g (x) có 6 đường tiệm cận: 1 tiệm cận ngang y = 0 và 5 tiệm cận đứng x = a, x = b, x = 0, x =1, x = c .
Câu 7. Cho hàm số = ( ) 3 2
y f x = ax + bx + cx + d , (a ≠ 0) có đồ thị như hình dưới đây
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số ( 2x +2x−3) = ( ) x y g x = ( .
x x)( f (x))2 2 f (x) − +   Lời giải Page 12
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Trước hết, ta cần tìm x ≥ 0 để (x x)( f (x))2 2 f (x) − + = 0   . Ta có:  x = 0  ( = x
x)( f (x))2 x 1 2 f (x) − + = 0  ⇔    f (x) = 0  f (x) = 1 − 
Từ đồ thị hàm số y = f (x) ta thấy  = α ∈ − − • f (x) x ( 2; )1 0 = ⇔  và ( ) = ( −α )( − )2 2 f x a x x . x = 2 x = 1 −  • f (x) = 1
− ⇔ x = β ∈(0;2) ⇒ f (x) +1= a(x + )
1 (x − β )(x −γ ) . x = γ ∈(2;+∞  )
Vậy hàm số y = g (x) có tập xác định là D = (0;+∞) \{β;1;2;γ}. Khi đó ta có − + y = g (x)
(x )1(x 3) x x + 3 = = x(x − )
1 f (x)  f  ( x) +1
xa(x −α )(x − 2)2 a(x + )
1 (x − β )(x −γ ) x + 3 = 2 a x (x + )
1 (x − 2)2 (x −α )(x − β )(x −γ )
+) Tìm tiệm cận ngang: Ta có lim g (x) = 0 (do bậc của tử nhỏ hơn bậc của mẫu)⇒ y = 0 là x→+∞
tiệm cận ngang của đồ thị hàm số y = g (x) .
+) Tìm tiệm cận đứng: g (x) x + 3 = 2 2 a x (x + )
1 (x − 2) (x −α )(x − β )(x −γ )
Mẫu thức của g (x) có 6 nghiệm phân biệt là α; 1 − ;0; β;2;γ . * Tại x = α ∈( 2; − − ) 1 và x = 1
− các giới hạn một bên của g (x) không tồn tại nên x = α; x = 1 −
không phải tiệm cận đứng của đồ thị hàm số y = g (x) . Page 13
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ * Tại x = 0 x + 3
ta có lim g (x) = lim = +∞ nên x = 0 + + → → 2 x 0 x 0 a x (x + )
1 (x − 2)2 (x −α )(x − β )(x −γ ) là
một tiệm cận đứng của đồ thị hàm số y = g (x) .
* Tại x = β; x = 2 và x = γ các giới hạn một bên của g (x) đều là giới hạn vô cực (vì mẫu thức
bằng 0 còn tử thức khác 0 tại các điểm đó) nên x = β; x = 2 và x = γ là các tiệm cận đứng của
đồ thị hàm số y = g (x) .
Vậy đồ thị hàm số y = g (x) có 1 đường tiệm cận ngang là y = 0 và 4 đường tiệm cận đứng là
x = 0; x = β; x = 2 và x = γ .
Câu 8. Cho hàm số bậc ba y = f (x) có đồ thị như hình vẽ bên. x + 2
Tìm số đường tiệm cận đứng của đồ thị hàm số y = g(x) = f (x)+1. Lời giải Từ đồ thị ta thấy x = a ∈( 2; − − ) 1  f (x) = 1
− ⇔ x = b∈( 1; − 0) x = c∈  (1;2)
lim g(x) = +∞ nên x = a là một tiệm cận đứng của đồ thị hàm số y = g(x) . x a− →
lim g(x) = −∞ nên x = b là một tiệm cận đứng của đồ thị hàm số y = g(x) . x b− →
lim g(x) = +∞ nên x = c là một tiệm cận đứng của đồ thị hàm số y = g(x) . x c− →
Vậy đồ thị hàm số y = g(x) có 3 tiệm cận đứng.
Câu 9. Cho hàm số y = f ( x) liên tục trên  \  
1 và có bảng biến thiên như sau Page 14
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = g (x) = f ( 2
x − 2x − 2) . Lời giải x ≠ 1 − Ta có 2
x − 2x − 2 ≠ 1 ⇔ 
. Vậy hàm số y = g (x) có tập xác định là D =  \{ 1; − } 3 .  x ≠ 3
Dựa vào bảng biến thiên của hàm số y = f (x) ta có:
Do lim g (x) = lim f − −
= +∞ và lim g (x) = lim f − − = −∞ nên − − ( 2x 2x 2) + + ( 2x 2x 2) x→( 1) − x→( 1) − x→( 1) − x→( 1) − x = 1
− là một tiệm cận đứng của đồ thị hàm số y = g (x) .
Do lim g (x) = lim f − −
= −∞ và lim g (x) = lim f − −
= +∞ nên x = 3 là một − − ( 2x 2x 2) + + ( 2x 2x 2) x→3 x→3 x→3 x→3
tiệm cận đứng của đồ thị hàm số y = g (x) . Do g (x) = f ( 2 lim lim
x − 2x − 2) = −∞ và g (x) = f ( 2 lim lim
x − 2x − 2) = −∞ nên đồ thị hàm x→+∞ x→+∞ x→−∞ x→−∞
số y = g (x) không có tiệm cận ngang.
Vậy đồ thị hàm số y = g (x) = f ( 2
x − 2x − 2) có 2 đường tiệm cận đứng là x = 1 − ; x = 3 và
không có tiệm cận ngang.
Câu 10. Cho hàm số y = f (x) liên tục trên  và có đồ thị như hình dưới đây  − x
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = g ( x) 2 = f   x 1  +  Lời giải
Hàm số y = g (x) có tập xác định là D =  \{− } 1 .
Dựa vào đồ thị của hàm số y = f (x) ta có: Page 15
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Do ( )  2 lim lim − x g x f   − = = −∞ 2 x   
và lim g (x) = lim f = +∞   nên x = 1 − là một x ( 1)+ x ( 1)+ → − → −  x +1  − − x→( 1) − x→( 1) −  x +1 
tiệm cận đứng của đồ thị hàm số y = g (x) . Do ( )  2 lim lim − x g x f   − = = x    4 và g (x) 2 lim = lim f = 
 4 nên y = 4 là một tiệm cận x→+∞ x→+∞  x +1  x→−∞ x→−∞  x +1 
ngang của đồ thị hàm số y = g (x) . Vậy đồ thị hàm số ( )  2 − x y g x f  = = 
có 1 đường tiệm cận đứng là x = 1 −  x 1  +  và có 1 tiệm cận ngang là y = 4 .
Câu 11. Cho hàm số y = f (x) là hàm đa thức liên tục trên  và có đồ thị như hình dưới đây f x
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = g (x) ( ) = . f (x) −1 Lời giải
 f (x) ≥ 0
ĐKXĐ:  f (x) . ≠ 1 − ≤ ≤ − • f (x) 4 x 1 ≥ 0 ⇔   x ≥ 2
x ≠ a ∈( 4; − 3 − ) f (x) 1  •
≠ ⇔ x ≠ b∈( 3 − ;− ) 1  .
x ≠ c∈(2;+∞  )
Hàm số y = g (x) có tập xác định là D = [ 4;
− a) ∪(a;b) ∪( ; b − ]
1 ∪[2;c)∪( ;c+∞).
+) Tìm tiệm cận ngang: Ta có lim g (x) = 0 (do bậc của tử nhỏ hơn bậc của mẫu)⇒ y = 0 là x→+∞
tiệm cận ngang của đồ thị hàm số y = g (x) . Page 16
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
+) Tìm tiệm cận đứng:
Mẫu thức của g (x) có 3 nghiệm phân biệt là ; a ;
b c , và tại các điểm này các giới hạn một bên
của g (x) đều là giới hạn vô cực (vì mẫu thức bằng 0 còn tử thức khác 0 tại các điểm đó) nên
x = a; x = ;
b x = c là các tiệm cận đứng của đồ thị hàm số y = g (x) .
Vậy đồ thị hàm số y = g (x) có 1 đường tiệm cận ngang là y = 0 và 3 đường tiệm cận đứng là x = ; a x = ; b x = c .
Câu 12. Cho hàm số y = f (x) xác định, liên tục trên  và có bảng biến thiên như sau :
Tìm số tiệm cận ngang và số tiệm cận đứng của đồ thị hàm số g (x) 3 = . f ( 3 x + x + ) 1 −1 Lời giải
Từ bảng biến thiên ta thấy x + x +1 =1
f (x + x + )
1 −1 = 0 ⇔ f (x + x + ) 3 3 3 1 =1 ⇔  . 3
x + x +1 = a, a < 1 − x = 0 ⇔  3
x + x +1 = a, a < 1 ( − 2)
Lập bảng biến thiên của hàm số 3
h(x) = x + x +1 ta thấy với a < 1 − thì phương trình 3
x + x +1 = a có nghiệm duy nhất x < 1 − 0
Suy ra hàm số y = g (x) có tập xác định là D =  \{0; x , 1 x < − . 0} 0
+) Tìm tiệm cận ngang: Đặt 3
t = x + x +1. Khi x → +∞ thì t → +∞ và khi x → −∞ thì t → −∞ . Do đó, f ( 3 x + x + ) = f (t) 3 lim 1 lim
= −∞ ⇒ lim g(x) = lim = x→+∞ t→+∞ x→+∞ x→+∞ f ( 0. 3 x + x + ) 1 −1 Page 17
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ f ( 3 x + x + ) = f (t) 3 lim 1 lim
= +∞ ⇒ lim g(x) = lim = x→−∞ t→−∞ x→−∞ x→−∞ f ( 0. 3 x + x + ) 1 −1
Suy ra đồ thị hàm số y = g (x) có 1 tiệm cận ngang đó là đường thẳng y = 0.
+) Tìm tiệm cận đứng: g (x) 3 = f ( 3 x + x + ) 1 −1
Tại xác điểm x = 0, x = x mẫu của g (x) nhận giá trị bằng 0 còn tử luôn nhận giá trị bằng 3. 0
Và do hàm số xác định trên mỗi khoảng ( ;
−∞ x , x ;0 , 0;+∞ nên giới hạn một bên của 0 ) ( 0 ) ( )
hàm số y = g (x) tại các điểm x = 0, x = x là các giới hạn vô cực. 0
Do đó, đồ thị hàm số y = g (x) có hai tiệm cận đứng, đó là các đường thẳng x = 0, x = x0
Vậy đồ thị hàm số y = g (x) có 3 đường tiệm cận: 1 tiệm cận ngang y = 0và 2 tiệm cận đứng
x = 0, x = x . 0 Page 18
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
DẠNG 3: MỘT SỐ BÀI TOÁN VỀ TIỆM CẬN CHỨA THAM SỐ
Câu 1. Tìm các giá trị thực của tham số m để đồ thị hàm số mx + 7 y =
có tiệm cận đứng đi qua điểm mx −1 A(1; 2 − ) . Lời giải
Để đường tiệm cận đứng đi qua A(1; 2
− ) thì đường tiệm cận đứng phải có phương trình x =1.
Khi đó x =1 là nghiệm của mx −1 = 0 . Suy ra m =1.
Thử lại: với m =1 thì đồ thị hàm số x + 7 y =
có đường tiệm cận đứng x =1 đi qua A(1; 2 − ) . x −1
Vậy m =1 là giá trị cần tìm.
Câu 2. Tìm các giá trị thực của tham số m để đồ thị hàm số f (x) x − 2 =
có ba đường tiệm cận. 2 x + x + m Lời giải
Ta thấy lim  f (x) = 0 nên đồ thị hàm số có một tiệm cận ngang y = 0. x→±∞
Đồ thị hàm số f (x) x − 2 =
có ba đường tiệm cận 2
⇔ x + x + m = 0 có 2 nghiệm phân biệt 2 x + x + m 1  1  − 4m > 0 m < khác 2 ⇔  ⇔  4 . 2 2 + 2 + m ≠ 0 m ≠ 6 −
Câu 3. Tìm tham số m để đồ thì hàm số
(m +1)x − 5m y =
có tiệm cận ngang là đường thẳng y =1. 2x − m Lời giải Ta có:
Tiệm cận ngang của hàm số
(m +1)x − 5m y = là: 2x − m y =
(m +1)x − 5m m +1 lim = = 1 ⇔ m =1. x→±∞ 2x − m 2 Vậy m =1.
Câu 4. Tìm các tham số m để đồ thị hàm số x −1 y =
có đúng hai đường tiệm cận? 2 x + mx + 4 Lời giải 1 1 − Ta có 2 lim = lim x x y = 0 . x→±∞ x→±∞ m 4 1+ + 2 x x
Nên đồ thị hàm số luôn có một đường tiệm cận ngang là y = 0. Page 19
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Do đó để đồ thị hàm số có hai đường tiệm cận thì đồ thị hàm số cần có đúng một đường tiệm cận đứng. Hay phương trình: 2
f (x) = x + mx + 4 = 0 có nghiệm kép hoặc có hai nghiệm phân biệt
trong đó có 1 nghiệm bằng 1. Ta có 2 2
∆ = m − 4.1.4 = m −16  2   m −16 = 0 m = 4 m = 4 Khi đó  2  m −16 > 0  ⇔ m = 4 − ⇔ m = 4 − .      f (1) = 0 2 m −16 > 0 m = 5 −   m = 5 − Vậy m∈{ 4; − 4;− } 5 . Câu 5. Cho hàm số 2mx + m y =
. Với giá trị nào của m thì đường tiệm cận đứng, tiệm cận ngang của đồ thị x −1
hàm số cùng với hai trục tọa độ tạo thành một hình chữ nhật có diện tích là 8? Lời giải
Để đồ thị hàm số tồn tại tiệm cận đứng thì ad − bc ≠ 0 ⇔ 3
− m ≠ 0 ⇔ m ≠ 0 .
Khi đó tiệm cận đứng, tiệm cận ngang của đồ thị lần lượt là các đường thẳng x =1 và y = 2m .
Khi đó diện tích hình chữ nhật tạo thành là: 1.2m = 8 ⇔ m = 4 ⇔ m = 4 ± .
Câu 6. Biết đồ thị (C) của hàm số ax + b y = đi qua điểm A( 1;
− 7) và giao điểm hai tiệm cận của (C) là cx + d điểm I ( 2;
− 3). Biết c là số nguyên dương và a,c là các số nguyên tố cùng nhau. Tìm các số
a,b,c, d . Lời giải
Đồ thị (C) có tiệm cận đứng là d
x = − và tiệm cận ngang là a
y = với điều kiện ad − bc ≠ 0 c cd − = 2 −  cd = 2c  = a c = d 2 Khi đó ta có ( , ) 1 3  ⇔  →c =1⇒  ⇒ C : x + b y = . * ( ) a  a = 3 c c ∈ a = 3 x + 2 = 3  c Do (− )∈( ) 3 1;7 ⇒ 7 − + b A C = ⇔ b =10 . 1 − + 2 Câu 7. Cho hàm số x − m y =
. Giá trị nào của m để đồ thị hàm số đã cho có đúng 1 tiệm cận đứng? 2 x + 3x − 4
Lời giải − − Ta có: x m x m y = = . 2
x + 3x − 4 (x − ) 1 (x + 4) *) Với m =1 Page 20
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ − − − Thì x 1 1 x 1 1 lim = ; lim = và x 1 lim = +∞ x 1+ ( x − ) 1 (x + 4) x 1 5 − → →
(x − )1(x + 4) 5 x→ 4 − + ( x − ) 1 (x + 4)
⇒ Đồ thị hàm số có 1 tiệm cận đứng là x = 4 − *) Với m = 4 − + − + − + Thì x 4 1 x 4 1 lim = ; lim = và x 4 lim = +∞ x 4+ ( x − ) 1 (x + 4) x 4 5 + →− →−
(x − )1(x + 4) 5 x 1+ → (x − )1(x + 4)
⇒ Đồ thị hàm số có 1 tiệm cận đứng là x =1 *) Với m ≠ 1, 4
− thì đồ thị hàm số có 2 tiệm cận đứng là x =1, x = 4 − Vậy m =1,m = 4
− thì đồ thị hàm số đã cho có đúng 1 tiệm cận đứng. Câu 8. Cho hàm số 2x + m y =
. Tìm tất cả các giá trị của m để đồ thị hàm số có 2 đường tiệm cận cùng x − m
với hai trục tọa độ tạo thành một hình vuông
Lời giải
Ta có đường tiệm cận ngang của đồ thị hàm số là y = 2
Với 2.m −1.m ≠ 0 ⇔ m ≠ 0 thì đường tiệm cận đứng của đồ thị hàm số là x = m
Để 2 đường tiệm cận cùng với 2 trục tọa độ tạo thành một hình vuông thì m = 2 ⇔ m = 2 ± Câu 9. Cho hàm số 1− x y =
. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số có đúng 2 x − 2mx + 4
ba đường tiệm cận. Lời giải Xét đồ thị hàm số 1− x y = (C) 2 x − 2mx + 4
Ta có: lim y = 0 nên đồ thị hàm số có một đường tiệm cận ngang y = 0. x→±∞
Để đồ thị hàm số (C) có ba đường tiệm cận thì đồ thị hàm số (C) có hai đường tiệm cận đứng. 2
⇔ x − 2mx + 4 = 0 có hai nghiệm phân biệt x ≠ 1. m < 2 − 2 m 4 0   − > m > 2 ⇔  ⇔  . 1  − 2m + 4 ≠ 0  5 m ≠  2 Vậy với m < 2 − hoặc 5
m > 2,m ≠ thì đồ thị hàm số có 3 đường tiệm cận 2
Câu 10. Biết rằng đồ thị hàm số ax 1 y
có tiệm cận đứng là x  2 và tiệm cận ngang là y  3 . Tìm a,b . bx 2 Lời giải
Để đồ thị hàm số có tiệm cận đứng thì b ≠ 0 . Đồ thị hàm số ax +1 y = có tiệm cận đứng là 2
x = và tiệm cận ngang là a y = . bx − 2 b b Page 21
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ 2 = 2 ba = 3 Theo bài ra ta có:  ⇔ . a b    = 1 = 3 b
Vậy: a = 3;b =1.
Câu 11. Tính tổng bình phương tất cả các giá trị của m để đồ thị hàm số 2
y = 2x −3x + 5 + mx − 6 có tiệm cận ngang. Lời giải Có  2 lim y lim 2x 3x 5 2x  = − + − + + − →+∞ →+∞ (m 2)x 6 x x    3 − x + 5  = lim 
− 6 + m + 2 xx→+∞ 2 ( )
 2x − 3x + 5 + 2x
Vậy đồ thị hàm số có tiệm cận ngang khi x → +∞ ⇔ m + 2 = 0 ⇔ m = − 2  − +  (do 3x 5 3 lim  6 − −  = − 6 hữu hạn) x→+∞ 2
 2x − 3x + 5 + 2x  2 2 Có  2 lim y lim 2x 3x 5 2x  = − + + + − − →−∞ →−∞ (m 2)x 6 x x    3 − x + 5  = lim 
− 6 + m − 2 xx→−∞ 2 ( )
 2x − 3x + 5 − 2x
Vậy đồ thị hàm số có tiệm cận ngang khi x → −∞ ⇔ m − 2 = 0 ⇔ m = 2  − +  (do 3x 5 3 lim  − 6 = − 6 hữu hạn) x→−∞ 2
 2x − 3x + 5 − 2x  2 2 2 2
Vậy tổng bình phương tất cả các giá trị của m thỏa mãn bằng (− 2) +( 2) = 4 . Page 22
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
NG I ỨNG DỤNG ĐẠO HÀM ƯƠ
ĐỂ KHẢO SÁT HÀM SỐ CH
BÀI 4. ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
III BÀI TẬP TRẮC NGHIỆM
BÀI TẬP TRẮC NGHIỆM TRÍCH TỪ ĐỀ THAM KHẢO VÀ ĐỀ CHÍNH THỨC
CỦA BỘ GIÁO DỤC TỪ NĂM 2017 ĐẾN NAY
Câu 1: (MĐ 101-2022) Tiệm cân ngang của đồ thị hàm số 2x −1 y =
là đường thẳng có phương trình: 2x + 4 A. x = 2. − B. x =1. C. y =1. D. y = 2. −
Câu 2: (MĐ 102-2022) Tiệm cận ngang của đồ thị hàm số 2x −1 y =
là đường thẳng có phương trình: 2x + 4 A. y = 2 − . B. x = 2 − . C. x =1. D. y =1.
Câu 3: (MĐ 103-2022) Cho hàm số y = f (x) có bảng biến thiên như sau:
Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng có phương trình: A. x = 1 − . B. y = 1 − . C. y = 2 − . D. x = 2 − .
Câu 4: (MĐ 104-2022) Cho hàm số y = f (x) có bảng biến thiên như sau:
Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng có phương trình:
A. y = −1. B. y = −2 .
C. x = −2 .
D. x = −1.
Câu 5: (TK 2020-2021) Tiệm cận đứng của đồ thị hàm số 2x + 4 y =
là đường thẳng: x −1 A. x =1. B. x = 1. −
C. x = 2. D. x = 2. −
Câu 6: (MĐ 101 2020-2021 – ĐỢT 1) Tiệm cận đứng của đồ thị hàm số 2x −1 y = là đường thẳng có x −1 phương trình Page 177
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. x =1. B. x = 1 − . C. x = 2 . D. 1 x = . 2
Câu 7: (MĐ 102 2020-2021 – ĐỢT 1) Tiệm cận đứng của đồ thị hàm số x +1 y = là đường thẳng có x − 2 phương trình A. x = 1. − B. x = 2. − C. x = 2. D. x =1.
Câu 8: (MĐ 103 2020-2021 – ĐỢT 1) Tiệm cận đứng của đồ thị hàm số 2x +1 y = là đường thẳng có x −1 phương trình A. x = 2 . B. x =1. C. 1 x − = . D. x = 1 − . 2
Câu 9: (MĐ 104 2020-2021 – ĐỢT 1) Tiệm cận đứng của đồ thị hàm số x −1 y = là đường thẳng có x + 2 phương trình? A. x = 2 . B. x = 1 − . C. x = 2 − . D. x =1.
Câu 10: (MĐ 101 2020-2021 – ĐỢT 2) Tiệm cận ngang của đồ thị hàm số 4x −1 y = là đường thẳng có x +1 phương trình: A. y = 4 − . B. y =1. C. y = 4 . D. y = 1 − .
Câu 11: (MĐ 102 2020-2021 – ĐỢT 2) Tiệm cận ngang của đồ thị hàm số 5x −1 y = là đường thẳng có x +1 phương trình: A. y = 5. B. y =1. C. y = 5 − . D. y = 1 − .
Câu 12: (MĐ 103 2020-2021 – ĐỢT 2) Tiệm cận ngang của đồ thị hàm số 2x −1 y = là đường thẳng có x +1 phương trình: A. y =1. B. y = 1 − .
C. y = 2 . D. y = 2 − .
Câu 13: (MĐ 104 2020-2021 – ĐỢT 2) Tiệm cận ngang của đồ thị hàm số 3x −1 y = là đường thẳng có x +1 phương trình: A. y = 3 − . B. y = 1 − . C. y = 3 . D. y = 1.
Câu 14: (Đề Minh Họa 2020 Lần 1) Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số 2 5x 4x 1 y  là 2 x 1 A. 0. B. 1. C. 2. D. 3. x − 2
Câu 15: (Đề Tham Khảo 2020 Lần 2) Tiệm cận ngang của đồ thị hàm số y = là x +1 A. y = 2 − . B. y =1. C. x = 1 − .
D. x = 2 . Page 178
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 16: (Mã 101 - 2020 Lần 1) Tiệm cận ngang của đồ thị hàm số 4x +1 y = là x −1 A. 1 y = . B. y = 4 . C. y =1. D. y = 1 − . 4 +
Câu 17: (Mã 102 - 2020 Lần 1) Tiệm cận ngang của đồ thị hàm số 5x 1 y = là x −1 A. y =1. B. 1 y = . C. y = 1 − . D. y = 5. 5
Câu 18: (Mã 103 - 2020 Lần 1) Tiệm cận ngang của đồ thị hàm số 2x +1 y = là: x −1 A. 1 y = . B. y = 1 − . C. y =1. D. y = 2 . 2
Câu 19: (Mã 104 - 2020 Lần 1) Tiệm cận ngang của đồ thị hàm số 3x +1 y = là: x −1 A. 1 y = . B. y = 3. C. y = 1 − . D. y =1. 3
Câu 20: (Mã 101 – 2020 Lần 2) Tiệm cận đứng của đồ thị hàm số 2x + 2 y = là x −1 A. x = 2 . B. x = 2 − . C. x =1. D. x = 1 − .
Câu 21: (Mã 102 - 2020 Lần 2) Tiệm cận đứng của đồ thị hàm số x −1 y = là x − 3 A. x = 3 − . B. x = 1 − . C. x =1. D. x = 3.
Câu 22: (Mã 103 - 2020 Lần 2) Tiệm cận đứng của đồ thị hàm số 2x − 2 y = là x +1 A. x = 2 − . B. x =1. C. x = 1 − . D. x = 2 .
Câu 23: (Mã 104 - 2020 Lần 2) Tiệm cận đứng của đồ thị hàm số x +1 y = là x + 3 A. x = 1 − . B. x =1. C. x = 3 − . D. x = 3.
Câu 24: (Đề minh họa 1, Năm 2017) Cho hàm số y = f (x ) có lim f (x ) = 1 và lim f (x ) = 1 − . Khẳng x →+∞ x →−∞
định nào sau đây là khẳng định đúng?
A. Đồ thị hàm số đã cho không có tiệm cận ngang.
B. Đồ t hị hàm số đã cho có đúng một tiệm cận ngang.
C. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y = 1và y = 1 − .
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x = 1và x = 1 − .
Câu 25: (Đề minh họa 1, Năm 2017) Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số x + 1 y = có hai tiệm cận ngang. 2 mx + 1
A. Không có giá trị thực nào của m thỏa mãn yêu cầu đề bài. B. m < 0 .
C. m = 0 .
D. m > 0 .
Câu 26: (Đề minh họa 2, Năm 2017) Đường thẳng nào dưới đây là tiệm cận đứng của đồ thị hàm số 2x +1 y = ? x +1 Page 179
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. x =1. B. y = 1 − .
C. y = 2 . D. x = 1 − .
Câu 27: (Đề minh họa 2, Năm 2017) Tìm tất cả các tiệm cận đứng của đồ thị hàm số 2
2x −1− x + x + 3 y = . 2 x − 5x + 6 A. x = 3 − và x = 2 − . B. x = 3 − .
C. x = 3 và x = 2 . D. x = 3.
Câu 28: (Đề minh họa 3, Năm 2017) Cho hàm số y = f (x) có bảng biến thiên như hình vẽ bên. Hỏi đồ
thị hàm số đã cho có bao nhiêu đường tiệm cận? A. 1. B. 3. C. 2. D. 4.
Câu 29: (Mã 101, Năm 2017) Số tiệm cận đứng của đồ thị hàm số x + 9 − 3 y = là: 2 x + x A. 3. B. 2 . C. 0. D. 1.
Câu 30: (Mã 102, Năm 2017) Số tiệm cận đứng của đồ thị hàm số x + 4 − 2 y = là 2 x + x A. 3. B. 0. C. 2 . D. 1.
Câu 31: (Mã 103, Năm 2017) Đồ thị của hàm số nào trong các hàm số dưới đây có tiệm cận đứng? A. 1 y = . B. 1 y = . C. 1 y = . D. 1 y = . x 2 x + x +1 4 x +1 2 x +1
Câu 32: (Mã 104, Năm 2017) Đồ thị hàm số x − 2 y = có mấy tiệm cận. 2 x − 4 A. 0 . B. 3. C. 1. D. 2 .
Câu 33: (Đề minh họa, Năm 2018) Đồ thị của hàm số nào dưới đây có tiệm cận đứng? 2 2 A. x − 3x + 2 y = . B. = x y . C. 2
y = x −1 . D. = x y . x −1 2 x +1 x +1 A. 3. B. 2 . C. 0 . D. 1.
Câu 34: (Mã 102, Năm 2018) Số tiệm cận đứng của đồ thị hàm số x + 4 − 2 y = là 2 x + x A. 3. B. 0 . C. 2 . D. 1.
Câu 35: (Mã 103, Năm 2018) Số tiệm cận đứng của đồ thị hàm số x + 25 − 5 y = là 2 x + x A. 2 . B. 0. C. 1. D. 3. + −
Câu 36: (Mã 104, Năm 2018) Số tiệm cận đứng của đồ thị hàm số x 16 4 y = là 2 x + x A. 0 . B. 3. C. 2 . D. 1.
Câu 37: (Đề minh họa, Năm 2019) Cho hàm số y = f (x) có bảng biến thiên như sau Page 180
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là A. 4 . B. 1. C. 3. D. 2 .
Câu 38: (Mã 101, Năm 2019) Cho hàm số y = f (x) có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là A. 4 . B. 1. C. 3. D. 2 .
Câu 39: (Mã 102, Năm 2019) Cho hàm số y = f (x) có bảng biến thiên như sau
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là A. 3. B. 1. C. 2 . D. 4 .
Câu 40: (Mã 103, Năm 2019) Cho hàm số y = f (x) có bảng biến thiên như sau
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là A. 1. B. 2 . C. 3. D. 4 .
Câu 41: (Mã 104, Năm 2019) Cho hàm số y = f (x) có bảng biến thiên như sau
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là A. 2 . B. 1. C. 3. D. 4 . Page 181
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
NG I ỨNG DỤNG ĐẠO HÀM ƯƠ
ĐỂ KHẢO SÁT HÀM SỐ CH
BÀI 4. ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
III BÀI TẬP TRẮC NGHIỆM
BÀI TẬP TRẮC NGHIỆM TRÍCH TỪ ĐỀ THAM KHẢO VÀ ĐỀ CHÍNH THỨC
CỦA BỘ GIÁO DỤC TỪ NĂM 2017 ĐẾN NAY
Câu 1: (MĐ 101-2022) Tiệm cân ngang của đồ thị hàm số 2x −1 y =
là đường thẳng có phương trình: 2x + 4 A. x = 2. − B. x =1. C. y =1. D. y = 2. − Lời giải Chọn C Ta có lim y −
=1 nên tiệm cận ngang của đồ thị hàm số 2x 1 y =
là đường thẳng có phương x→±∞ 2x + 4 trình y =1.
Câu 2: (MĐ 102-2022) Tiệm cận ngang của đồ thị hàm số 2x −1 y =
là đường thẳng có phương trình: 2x + 4 A. y = 2 − . B. x = 2 − . C. x =1. D. y =1. Lời giải Chọn D 1 2 − Có: 2x −1 lim = lim = lim x y = 1 x→+∞ x→+∞ 2x + 4 x→+∞ 4 2 + x 1 2 − và: 2x −1 lim = lim = lim x y = 1 x→−∞
x→−∞ 2x + 4 x→−∞ 4 2 + x Vậy đồ thị hàm số 2x −1 y =
có tiệm cận ngang là đường thẳng có phương trình: y =1. 2x + 4
Câu 3: (MĐ 103-2022) Cho hàm số y = f (x) có bảng biến thiên như sau: Page 1
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng có phương trình: A. x = 1 − . B. y = 1 − . C. y = 2 − . D. x = 2 − . Lời giải Chọn D
Ta có lim y = +∞ , lim y = −∞ . x ( 2)+ → − x ( 2)− → −
Vậy tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng x = 2 − .
Câu 4: (MĐ 104-2022) Cho hàm số y = f (x) có bảng biến thiên như sau:
Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng có phương trình:
A. y = −1. B. y = −2 .
C. x = −2 .
D. x = −1. Lời giải Chọn C
Ta có lim f (x) = +∞ và lim f (x) = −∞ nên tiệm cận đứng của đồ thị hàm số đã cho là x 2+ →− x 2− →−
Câu 5: (TK 2020-2021) Tiệm cận đứng của đồ thị hàm số 2x + 4 y =
là đường thẳng: x −1 A. x =1. B. x = 1. −
C. x = 2. D. x = 2. − Lời giải Ta có 2x  4 lim 2x  4   và lim
  nên x  1 là tiệm cận đứng. x 1  x 1 x 1  x 1
Câu 6: (MĐ 101 2020-2021 – ĐỢT 1) Tiệm cận đứng của đồ thị hàm số 2x −1 y = là đường thẳng có x −1 phương trình A. x =1. B. x = 1 − . C. x = 2 . D. 1 x = . 2 Lời giải Vì 2x −1 lim −
= +∞ nên đường thẳng x =1 là tiệm cận đứng của đồ thị hàm số 2x 1 y = . x 1+ → x −1 x −1 Page 2
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 7: (MĐ 102 2020-2021 – ĐỢT 1) Tiệm cận đứng của đồ thị hàm số x +1 y = là đường thẳng có x − 2 phương trình A. x = 1. − B. x = 2. − C. x = 2. D. x =1. Lời giải Chọn C Từ x +1 lim y + = lim = +∞ hoặc x 1 lim y = lim
= −∞ nên suy ra đồ thị hàm số có tiệm cận x 2+ x 2+ → → x − 2 x 2− x 2− → → x − 2 đứng là x = 2.
Câu 8: (MĐ 103 2020-2021 – ĐỢT 1) Tiệm cận đứng của đồ thị hàm số 2x +1 y = là đường thẳng có x −1 phương trình A. x = 2 . B. x =1. C. 1 x − = . D. x = 1 − . 2 Lời giải Ta có 2x +1 2x +1 lim = +∞ ;lim = −∞ . x 1+ − x 1 x 1 − → → x −1
Vậy tiệm cận đứng của đồ thị hàm số là đường thẳng x =1.
Câu 9: (MĐ 104 2020-2021 – ĐỢT 1) Tiệm cận đứng của đồ thị hàm số x −1 y = là đường thẳng có x + 2 phương trình? A. x = 2 . B. x = 1 − . C. x = 2 − . D. x =1. Lời giải TXĐ: D =\{− } 2 .
Ta có lim y = −∞ nên đồ thị hàm số nhận đường thẳng x = 2
− là tiệm cận đứng. x ( 2)+ → −
Câu 10: (MĐ 101 2020-2021 – ĐỢT 2) Tiệm cận ngang của đồ thị hàm số 4x −1 y = là đường thẳng có x +1 phương trình: A. y = 4 − . B. y =1. C. y = 4 . D. y = 1 − . Lời giải 1 4 − Ta có 4x −1 lim = lim = lim x y = 4. x→±∞ x→±∞ x +1 x→±∞ 1 1+ x
Vậy tiệm cận ngang đồ thị hàm số đã cho là đường thẳng có phương trình: y = 4.
Câu 11: (MĐ 102 2020-2021 – ĐỢT 2) Tiệm cận ngang của đồ thị hàm số 5x −1 y = là đường thẳng có x +1 phương trình: A. y = 5. B. y =1. C. y = 5 − . D. y = 1 − . Page 3
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Lời giải
Tiệm cận ngang của đồ thị hàm số 5x −1 y =
là đường thẳng có phương trình y = 5 x +1
Câu 12: (MĐ 103 2020-2021 – ĐỢT 2) Tiệm cận ngang của đồ thị hàm số 2x −1 y = là đường thẳng có x +1 phương trình: A. y =1. B. y = 1 − .
C. y = 2 . D. y = 2 − . Lời giải
Tiệm cận ngang của đồ thị hàm số 2x −1 y =
là đường thẳng: y = 2 . x +1
Câu 13: (MĐ 104 2020-2021 – ĐỢT 2) Tiệm cận ngang của đồ thị hàm số 3x −1 y = là đường thẳng có x +1 phương trình: A. y = 3 − . B. y = 1 − . C. y = 3 . D. y = 1. Lời giải Ta có 3x −1 lim y = lim = 3. x→±∞ x→±∞ x + 1 Vậy đồ thị hàm số 3x −1 y =
có tiệm cận ngang là đường thẳng y = 3 . x +1
Câu 14: (Đề Minh Họa 2020 Lần 1) Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số 2 5x 4x 1 y  là 2 x 1 A. 0. B. 1. C. 2. D. 3. Lời giải Chọn C Tiệm cận ngang: 2  4 1  4 1 2 x 5− − 2  5 − − − − 2 Ta có: 5x 4x 1 lim lim lim  x x  = = = lim x x y = 5 nên đồ thị 2 x→+∞ x→+∞ x −1 x→+∞ 2  1  x→+∞ 1 x 1− 1− 2  2  x x
hàm số có một tiệm cận ngang y = 5. Tiệm cận đứng: Cho 2 x =1 x =1 ⇔  x = 1 − 2 5x − 4x −1 (5x + ) 1 (x − ) 1 Ta có: 5x +1 6 lim y = lim = lim = lim
= = 3 nên x =1không là tiệm 2 x 1 → x 1 → x −1 x 1 → ( x + ) 1 (x − ) 1 x 1 → x +1 2 cận đứng. Page 4
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ 2 2 2 5x − 4x −1 5x − 4x −1
 1 5x − 4x −1 lim y = lim = lim = lim  .  = −∞ x ( )+ x ( )+ 2 1 1 x −1 x ( ) 1 + ( x )1(x )1 x ( )1+ → − → − → − → −  x 1 x 1  + − + −    1 lim = +∞  x ( → − )+ x +1 vì 1  2 . 5x − 4x −1  lim = 4 − < 0 x ( → − ) 1 + x −1
Khi đó, đồ thị hàm số có một tiệm cận đứng x = 1 − .
Tổng cộng đồ thị hàm số có 2 tiệm cận. x − 2
Câu 15: (Đề Tham Khảo 2020 Lần 2) Tiệm cận ngang của đồ thị hàm số y = là x +1 A. y = 2 − . B. y =1. C. x = 1 − .
D. x = 2 . Lời giải Chọn B x − 2 x − 2 Ta có lim = 1 và lim = 1 x→+∞ x +1 x→−∞ x +1
Suy ra y = 1 là tiệm cận ngang của đồ thị hàm số.
Câu 16: (Mã 101 - 2020 Lần 1) Tiệm cận ngang của đồ thị hàm số 4x +1 y = là x −1 A. 1 y = . B. y = 4 . C. y =1. D. y = 1 − . 4 Lời giải Chọn B Tiệm cận ngang 4
lim y = lim y = = 4 x→+∞ x→−∞ 1 +
Câu 17: (Mã 102 - 2020 Lần 1) Tiệm cận ngang của đồ thị hàm số 5x 1 y = là x −1 A. y =1. B. 1 y = . C. y = 1 − . D. y = 5. 5 Lời giải Chọn D  5x +1 lim y = lim = 5  Ta có x→+∞ x→+∞ x −1 
⇒ y = 5 là tiệm cận ngang của đồ thị hàm số. 5x +1  lim y = lim = 5 x→−∞ x→−∞  x −1
Câu 18: (Mã 103 - 2020 Lần 1) Tiệm cận ngang của đồ thị hàm số 2x +1 y = là: x −1 A. 1 y = . B. y = 1 − . C. y =1. D. y = 2 . 2 Page 5
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Lời giải Chọn D 1 2 + Ta có 2x +1 lim = lim
x = 2. Suy ra đồ thị hàm số có tiệmcận ngang là y = 2. x→±∞ x −1 x→±∞ 1 1− x
Câu 19: (Mã 104 - 2020 Lần 1) Tiệm cận ngang của đồ thị hàm số 3x +1 y = là: x −1 A. 1 y = . B. y = 3. C. y = 1 − . D. y =1. 3 Lời giải Chọn B Ta có : 3x +1 lim y + = lim = 3 và 3x 1 lim y = lim
= 3 nên y = 3 là tiệm cận ngang của đồ x→+∞ x→+∞ x −1 x→−∞
x→−∞ x −1 thị hàm số.
Câu 20: (Mã 101 – 2020 Lần 2) Tiệm cận đứng của đồ thị hàm số 2x + 2 y = là x −1 A. x = 2 . B. x = 2 − . C. x =1. D. x = 1 − . Lời giải Chọn C
Tập xác định D =  \{ } 1 .
Ta có lim y = −∞; lim y = + ∞ , suy ra đồ thị có tiệm cận đứng là x =1. x 1− x 1+ → →
Câu 21: (Mã 102 - 2020 Lần 2) Tiệm cận đứng của đồ thị hàm số x −1 y = là x − 3 A. x = 3 − . B. x = 1 − . C. x =1. D. x = 3. Lời giải. Chọn D x −1 lim
= −∞ . Suy ta tiệm cận đứng là đường thẳng x = 3. x 3− → x − 3
Câu 22: (Mã 103 - 2020 Lần 2) Tiệm cận đứng của đồ thị hàm số 2x − 2 y = là x +1 A. x = 2 − . B. x =1. C. x = 1 − . D. x = 2 . Lời giải Chọn C Ta có 2x − 2 lim y − = lim = −∞ và 2x 2 lim y = lim
= +∞ nên đường thẳng x = 1 − là x 1+ x 1+ →− →− x +1 x 1− x 1− →− →− x +1
tiệm cận đứng của đồ thị hàm số.
Câu 23: (Mã 104 - 2020 Lần 2) Tiệm cận đứng của đồ thị hàm số x +1 y = là x + 3 Page 6
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. x = 1 − . B. x =1. C. x = 3 − . D. x = 3. Lời giải Chọn C
Ta có lim y = −∞ và lim y = +∞ nên đồ thị hàm số nhận đường thẳng x = 3 − làm tiệm cận x 3+ →− x 3− →− đứng.
Câu 24: (Đề minh họa 1, Năm 2017) Cho hàm số y = f (x ) có lim f (x ) = 1 và lim f (x ) = 1 − . Khẳng x →+∞ x →−∞
định nào sau đây là khẳng định đúng?
A. Đồ thị hàm số đã cho không có tiệm cận ngang.
B. Đồ t hị hàm số đã cho có đúng một tiệm cận ngang.
C. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y = 1và y = 1 − .
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x = 1và x = 1 − . Lời giải Chọn C
Câu 25: (Đề minh họa 1, Năm 2017) Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số x + 1 y = có hai tiệm cận ngang. 2 mx + 1
A. Không có giá trị thực nào của m thỏa mãn yêu cầu đề bài.
B. m < 0 .
C. m = 0 .
D. m > 0 . Lời giải Chọn D  1  − 1 +  x +  x Ta có: 1  1 lim y = lim = = − x →−∞ x →−∞ 2 mx + 1 1 m m + 2 x 1 1 + và x + 1 1 lim = lim = lim x y = x →+∞ x →+∞ 2 mx + 1 x →+∞ 1 m m + 2 x
Vậy hàm số có hai tiệm cận ngang là : 1 1 y = ;y = − ⇒ m > 0 m m
Câu 26: (Đề minh họa 2, Năm 2017) Đường thẳng nào dưới đây là tiệm cận đứng của đồ thị hàm số 2x +1 y = ? x +1 A. x =1. B. y = 1 − .
C. y = 2 . D. x = 1 − . Lời giải Chọn D Page 7
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ x + x + Ta có 2 1 2 1 lim y = lim = ; −∞ lim y = lim
= +∞ suy ra đường thẳng x = 1 − là đường x 1+ x 1+ x + x 1− x 1 1 − →− →− →− →− x +1 2x +1
tiệm cận đứng của đồ thị hàm số y = x + . 1
Câu 27: (Đề minh họa 2, Năm 2017) Tìm tất cả các tiệm cận đứng của đồ thị hàm số 2
2x −1− x + x + 3 y = . 2 x − 5x + 6 A. x = 3 − và x = 2 − . B. x = 3 − .
C. x = 3 và x = 2 . D. x = 3. Lời giải Chọn D
Tập xác định D = \{2; } 3
2x −1− x + x + 3 (2x − )2 1 − ( 2 2 x + x + 3) lim = lim + 2 x→2 x − x + x→2 5 6
+ ( 2x −5x + 6)( 2
2x −1+ x + x + 3) (2x − )2 1 − ( 2 x + x + 3) = lim x→2+ ( 2 x − 5x + 6)( 2
2x −1+ x + x + 3) (3x +1) 7 = lim = − x→2+ (x − )( 2
x − + x + x + ) 6 3 2 1 3 2 Tương tự
2x −1− x + x + 3 7 lim
= − .Suy ra đường thẳng x = 2 không là tiệm cận đứng của − 2 x→2 x − 5x + 6 6
đồ thị hàm số đã cho. 2 2
2x −1− x + x + 3
2x −1− x + x + 3 lim = ; +∞ lim = −∞ . + 2 − 2 x→3 x − x + x→3 5 6 x − 5x + 6
Suy ra đường thẳng x = 3 là tiệm cận đứng của đồ thị hàm số đã cho.
Câu 28: (Đề minh họa 3, Năm 2017) Cho hàm số y = f (x) có bảng biến thiên như hình vẽ bên. Hỏi đồ
thị hàm số đã cho có bao nhiêu đường tiệm cận? A. 1. B. 3. C. 2. D. 4. Lời giải Chọn B lim y = −∞ ⇒ TCD :x = 2;
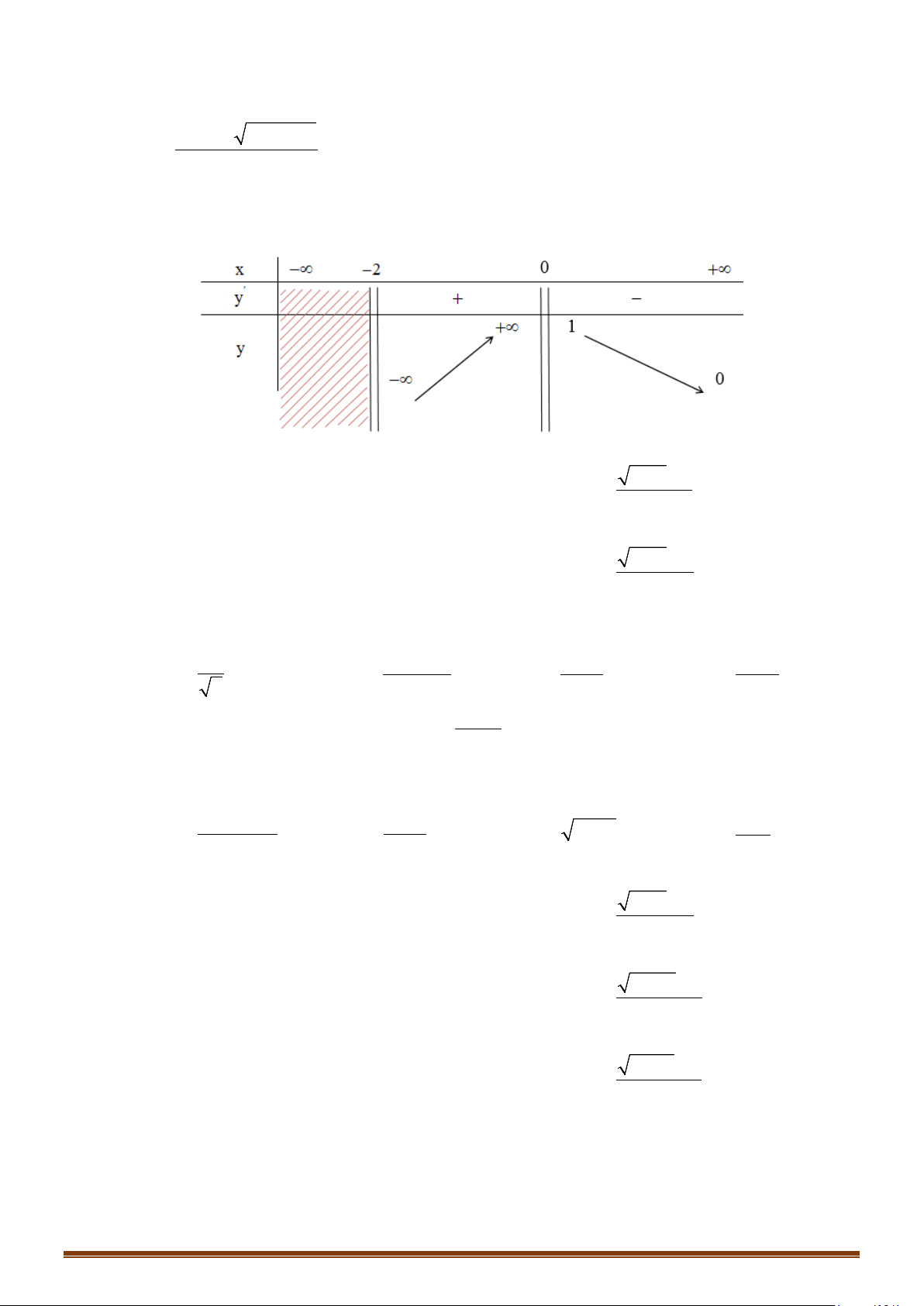
− lim y = +∞ ⇒ TCD :x = 0; lim y = 0 ⇒ TCN : y = 0. x 2+ x 0− → → x→+∞ Page 8
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 29: (Mã 101, Năm 2017) Số tiệm cận đứng của đồ thị hàm số x + 9 − 3 y = là: 2 x + x A. 3. B. 2 . C. 0. D. 1. Lời giải Chọn D
Tập xác định của hàm số: D = [ 9; − +∞) \{0;− } 1 Ta có: lim y = x + 9 − 3 lim x + 9 − 3 = +∞ và lim y = lim = −∞ . x ( ) 1 + → − x→(− )+ 2 1 x + x x ( ) 1 − → − x→(− )− 2 1 x + x ⇒ TCĐ: x = 1 − . lim + − y x 1 = x 9 3 lim = lim = lim 1 = . x 0+ → + 2 x→0 x + x x 0+ →
( 2x + x)( x+9 +3) x 0+ →
(x + )1( x+9 +3) 6 lim + − y x 1 = x 9 3 lim = lim = lim 1 = . x 0− → − 2 x→0 x + x x 0− →
( 2x + x)( x+9 +3) x 0− →
(x + )1( x+9 +3) 6
⇒ x = 0 không là đường tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có 1 tiệm cận đứng.
Câu 30: (Mã 102, Năm 2017) Số tiệm cận đứng của đồ thị hàm số x + 4 − 2 y = là 2 x + x A. 3. B. 0. C. 2 . D. 1. Lời giải Chọn D
Tập xác định của hàm số: D = [ 4; − +∞) \{0;− } 1 Ta có: 1 lim y = . x→0 4 x + 4 − 2 lim y + − = lim = +∞ và x 4 2 lim y = lim = −∞ x→(− )+ x→(− )+ 2 1 1 x + x x→(− )− x→(− )− 2 1 1 x + x ⇒ TCĐ: x = 1 − .
Vậy đồ thị hàm số có 1 tiệm cận đứng.
Câu 31: (Mã 103, Năm 2017) Đồ thị của hàm số nào trong các hàm số dưới đây có tiệm cận đứng? A. 1 y = . B. 1 y = . C. 1 y = . D. 1 y = . x 2 x + x +1 4 x +1 2 x +1 Lời giải Chọn A Đồ thị hàm số 1 y =
có tiệm cận đứng là x = 0 . x
Đồ thị các hàm số ở các đáp án B,C, D đều không có tiệm cận đứng do mẫu vô nghiệm.
Câu 32: (Mã 104, Năm 2017) Đồ thị hàm số x − 2 y = có mấy tiệm cận. 2 x − 4 A. 0 . B. 3. C. 1. D. 2 . Page 9
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Lời giải Chọn D Ta có 2
x − 4 = 0 ⇔ x = 2 ±  x − 2  1 lim = 
nên đường thẳng x = 2 không phải là tiệm cân đứng của đồ thị hàm số. 2 
x→2  x − 4  4  x − 2  1 lim  − = lim = +∞ x 2  1   , lim = lim = −∞  
, nên đườngthẳng x = 2 − là + 2 x 2  − x 2 x 4 + →− →−  x + 2 x ( )− 2
2  x − 4  x ( 2)− → − → − x + 2
tiệm cân đứng của đồ thị hàm số.  x − 2 lim  = 
 0 nên đường thẳng y = 0 là tiệm cận ngang của đồ thị hàm số. 2
x→±∞  x − 4 
Vậy có đồ thị có hai đường tiệm cận.
Câu 33: (Đề minh họa, Năm 2018) Đồ thị của hàm số nào dưới đây có tiệm cận đứng? 2 2 A. x − 3x + 2 y = . B. = x y . C. 2
y = x −1 . D. = x y . x −1 2 x +1 x +1 Lời giải Chọn D
Ta có lim x = +∞, lim x = −∞ nên đường thẳng x = 1
− là tiệm cận đứng của đồ thị hàm x 1− x + x 1 1 + →− →− x +1 số.
Câu 34: (Mã 101, Năm 2018) Số tiệm cận đứng của đồ thị hàm số x + 9 − 3 y = là 2 x + x A. 3. B. 2 . C. 0 . D. 1. Lời giải Chọn D
Tập xác định của hàm số: D = [ 9; − +∞) \{0;− } 1 Ta có: lim y = x + 9 − 3 lim x + 9 − 3 = +∞ và lim y = lim = −∞ . x ( ) 1 + → − x→(− )+ 2 1 x + x x ( ) 1 − → − x→(− )− 2 1 x + x ⇒ TCĐ: x = 1 − . lim + − y x 1 = x 9 3 lim = lim = lim 1 = . x 0+ → + 2 x→0 x + x x 0+ →
( 2x + x)( x+9 +3) x 0+ →
(x + )1( x+9 +3) 6 lim + − y x 1 = x 9 3 lim = lim = lim 1 = . x 0− → − 2 x→0 x + x x 0− →
( 2x + x)( x+9 +3) x 0− →
(x + )1( x+9 +3) 6
⇒ x = 0 không là đường tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có 1 tiệm cận đứng.
Câu 35: (Mã 102, Năm 2018) Số tiệm cận đứng của đồ thị hàm số x + 4 − 2 y = là 2 x + x A. 3. B. 0 . C. 2 . D. 1. Page 10
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Lời giải Chọn D
Tập xác định của hàm số: D = [ 4; − +∞) \{0;− } 1 Ta có: 1 lim y = . x→0 4 x + 4 − 2 lim y + − = lim = +∞ và x 4 2 lim y = lim = −∞ x→(− )+ x→(− )+ 2 1 1 x + x x→(− )− x→(− )− 2 1 1 x + x ⇒ TCĐ: x = 1 − .
Vậy đồ thị hàm số có 1 tiệm cận đứng.
Câu 36: (Mã 103, Năm 2018) Số tiệm cận đứng của đồ thị hàm số x + 25 − 5 y = là 2 x + x A. 2 . B. 0. C. 1. D. 3. Lời giải Chọn C 1
Tập xác định D = [ 2 − 5;+∞) \{ 1; − }
0 . Biến đổi f (x) = .
(x + )1( x+ 25 +5) 1 Vì lim y = lim
= +∞ nên đồ thị hàm số đã cho có 1 tiệm cận đứng x ( ) 1 + x ( ) 1 + → − → −
(x + )1( x+25 +5) x = 1 − . + −
Câu 37: (Mã 104, Năm 2018) Số tiệm cận đứng của đồ thị hàm số x 16 4 y = là 2 x + x A. 0 . B. 3. C. 2 . D. 1. Lời giải Chọn D
Tập xác định hàm số D = [ 1 − 6;+∞) \{ 1; − } 0 . Ta có x +16 − 4 x 1 1 lim y = lim = lim = lim = . x→0 x→0 (x + ) x→0 1 x x(x + )
1 ( x +16 + 4) x→0 (x + )1( x +16 + 4) 8 x +16 − 4 1 lim y = lim = lim = +∞ . x ( ) 1 + x ( ) 1 + (x + )1 x x ( ) 1 + → − → − → −
(x + )1( x+16 + 4) vì lim + + = + > , lim (x + ) 1 = 0 và x ( )1+ → − thì x > 1 − ⇒ x +1 > 0 . + ( x 16 4) 15 4 0 x→(− ) 1 x ( ) 1 + → − 1
Tương tự lim y = lim = −∞ . x ( ) 1 − x ( ) 1 − → − → −
(x + )1( x+16 +4)
Vậy đồ thị hàm số đã cho có tiệm cận đứng là x = 1 − .
Câu 38: (Đề minh họa, Năm 2019) Cho hàm số y = f (x) có bảng biến thiên như sau Page 11
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là A. 4 . B. 1. C. 3. D. 2 . Lời giải Chọn C
Vì lim f (x) = 5 ⇒đường thẳng y = 5 là tiệm cận ngang của đồ thị hàm số. x→+∞
Vì lim f (x) = 2 ⇒ đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số. x→−∞
Vì lim f (x) = +∞ ⇒đường thẳng x =1 là tiệm cận đứng của đồ thị hàm số. x 1− →
KL: Đồ thị hàm số có tổng số ba đường tiệm cận.
Câu 39: (Mã 101, Năm 2019) Cho hàm số y = f (x) có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là A. 4 . B. 1. C. 3. D. 2 . Lời giải Chọn D
Dựa vào bản biến thiên ta có
lim y = +∞ ⇒ x = 0 là tiệm cận đứng của đồ thị hàm số. x 0+ →
lim y = 2 ⇒ y = 2 là tiệm cận ngang của đồ thị hàm số. x→−∞
Vậy tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là 2.
Câu 40: (Mã 102, Năm 2019) Cho hàm số y = f (x) có bảng biến thiên như sau
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là A. 3. B. 1. C. 2 . D. 4 . Page 12
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Lời giải Chọn C Ta có:
lim f (x) = +∞ đồ thị hàm số không tồn tại tiệm cận ngang khi x → . +∞ x→+∞
lim f (x) = 0 Vậy đồ thị hàm số y = f (x) có tiệm cận ngang y = 0. x→−∞
lim f (x) = 2 ; lim f (x) = .
−∞ Đồ thị hàm số y = f (x) có tiệm cận đứng x = 0. x 0+ → x 0− →
Vậy tổng số tiệm cận đứng và ngang là 2.
Câu 41: (Mã 103, Năm 2019) Cho hàm số y = f (x) có bảng biến thiên như sau
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là A. 1. B. 2 . C. 3. D. 4 . Lời giải Chọn C
Dựa vào bảng biến thiên ta có
lim y = −∞ ⇒ x = 0 là tiệm cận đứng của đồ thị hàm số. x 0− →
lim y = 1 ⇒ y = 1 là tiệm cận ngang của đồ thị hàm số. x→−∞
lim y = 3 ⇒ y = 3 là tiệm cận ngang của đồ thị hàm số. x→+∞
Vậy tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là 3 .
Câu 42: (Mã 104, Năm 2019) Cho hàm số y = f (x) có bảng biến thiên như sau
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là A. 2 . B. 1. C. 3. D. 4 . Lời giải Chọn C
Dựa vào bảng biến thiên ta có Page 13
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
lim y = +∞ ⇒ x = 0 là tiệm cận đứng của đồ thị hàm số. x 0+ →
lim y = 0 ⇒ y = 0 là tiệm cận ngang của đồ thị hàm số. x→−∞
lim y = 3 ⇒ y = 3 là tiệm cận ngang của đồ thị hàm số. x→+∞
Vậy tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là 3 . Page 14
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
NG I ỨNG DỤNG ĐẠO HÀM ƯƠ
ĐỂ KHẢO SÁT HÀM SỐ CH
BÀI 4. ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
III BÀI TẬP TRẮC NGHIỆM
DẠNG. XÁC ĐỊNH ĐƯỜNG TIỆM CẬN THÔNG QUA BẢNG BIẾN THIÊN, ĐỒ THỊ
1.1.1 Đường tiệm cận ngang
Cho hàm số y = f x
( ) xác định trên một khoảng vô hạn. Đường thẳng y = y là đường tiệm 0
cận ngang của đồ thị hàm số y = f x
( ) nếu ít nhất một trong các điều kiện sau được thỏa mãn: lim f x
( ) = y , lim f x ( ) = y x 0 →+∞ x 0 →−∞
1.1.2 Đường tiệm cận đứng
Đường thẳng x = x được gọi là đường tiệm cận đứng của đồ thị hàm số y = f (x) nếu ít 0
nhất một trong các điều kiện sau được thỏa mãn: lim f x ( ) = +∞, lim f x
( ) = −∞, lim f (x) = −∞, lim f (x) = +∞ + − x →x x →x x x + x x − → → 0 0 0 0 ax +
Lưu ý: Với đồ thị hàm phân thức dạng = b y
(c ≠ 0; ad − bc ≠ 0) luôn có tiệm cận ngang là cx + d = a y
và tiệm cận đứng = − d x . c c
Câu 1: Cho hàm số có bảng biến thiên như hình sau
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = f (x) là A. 3. B. 2 . C. 4 . D. 1. Page 182
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 2: Cho hàm số f (x) có bảng biến thiên như sau:
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là: A. 4 . B. 3. C. 1. D. 2 .
Câu 3: Cho hàm số y = f (x) có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là A. 4 B. 2 C. 3 D. 1
Câu 4: Cho đồ thị hàm số y = f (x) như hình bên. Khẳng định nào sau đây là đúng? y 1 1 − O x
A. Đồ thị hàm số có tiệm cận đứng x = 0 , tiệm cận ngang y =1.
B. Hàm số có hai cực trị.
C. Đồ thị hàm số chỉ có một đường tiệm cận.
D. Hàm số đồng biến trong khoảng (−∞;0) và (0;+ ∞) .
Câu 5: Cho hàmsố f (x) có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là A. 4 . B. 1. C. 3. D. 2 . Page 183
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 6: Cho hàm số y = f (x) có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là A. 4 . B. 1. C. 3. D. 2 .
Câu 7: Cho hàm số y = f (x) có bảng biến thiên như sau
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho bằng A. 2 . B. 1. C. 0 . D. 3.
Câu 8: Cho hàm số y = f (x) liên tục trên  \{ }
1 có bảng biến thiên như hình vẽ. Tổng số đường tiệm
cận đứng và đường tiệm cận ngang của đồ thị hàm số y = f (x) A. 1. B. 4 . C. 2 . D. 3.
Câu 9: Cho hàm số yf x  có bảng biến như sau:
Số đường tiệm cận của đồ thị hàm số là: A. 3 B. 1. C. 4. D. 2. Page 184
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 10: Cho hàm số y = f (x) có bảng biến thiên như sau
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là A. 4 . B. 2 . C. 3 . D. 1.
DẠNG 2. XÁC ĐỊNH ĐƯỜNG TIỆM CẬN ĐỒ THỊ HÀM SỐ THÔNG HÀM SỐ CHO TRƯỚC
1 Đường tiệm cận ngang
Cho hàm số y = f (x) có TXD: D
Điều kiện cần: D phải chứa +∞ hoặc −∞ Điều kiện đủ: Dạng 1. P(x)
y = f (x) = . Q(x)
Nếu degP(x) > degQ(x) :thì không có tiệm cận ngang
Nếu degP(x) > degQ(x):TCN y = 0
Nếu degP(x) = degQ(x): y = k 2
Dạng 2: y = f (x) = u − v : Nhân liên hợp⇒ = ( ) u − v y f x = u + v
2 Đường tiệm cận đứng P(x) Cho hàm số y = có TXD: D Q(x)
Đkiện cần: giải Q(x) = 0 ⇔ x = x là TCĐ khi thỏa mãn đk đủ 0 Đkiện đủ:
Đkiện 1: x làm cho P(x) và Q(x) xác định. 0
Đkiện 2: - x không phải nghiêm P(x) ⇒ x = x là TCĐ 0 0
- x là nghiêm P(x) ⇒ x = x là TCĐ nếu 0 0 lim f (x) = ∞ x→ 0 x
Câu 11: Đồ thị hàm số
5x 1 x 1 y
có tất cả bao nhiêu đường tiệm cận? 2 x  2x A. 3 B. 0 C. 2 D. 1 2
Câu 12: Tìm tất cả các tiệm cận đứng của đồ thị hàm số
2x −1− x + x + 3 y = . 2 x − 5x + 6
A. x = 3 và x = 2 .
B. x = 3. C. x = 3 − và x = 2 − . D. x = 3 − .
Câu 13: Số tiệm cận đứng của đồ thị hàm số x + 4 − 2 y = là 2 x + x A. 3. B. 0 . C. 1. D. 2 . Page 185
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ +
Câu 14: Đồ thị hàm số f (x) x 1 =
có tất cả bao nhiêu tiệm cận đứng và tiệm cận ngang? 2 x −1 A. 4 . B. 3. C. 1. D. 2 . x(4x + 6) − 2
Câu 15: Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = là? x + 2 A. 1 B. 3 C. 2 D. 4 2 Câu 16: Cho hàm số x + 2x + 3 y =
. Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận? 4 2 x − 3x + 2 A. 4 . B. 5. C. 3. D. 6 . 2 Câu 17: Hàm số
x + x + x +1 y =
có bao nhiêu đường tiệm cận? 3 x + x A. 1 B. 3 C. 2 D. 4
Câu 18: Số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số x − 2 +1 y = là 2 x − 3x + 2 A. 4 B. 1 C. 3 D. 2 2 Câu 19: Cho hàm số
5 x + 6 + x −12 y =
có đồ thị (C). Mệnh đề nào sau đây là đúng? 3 4x − 3x −1
A. Đồ thị (C) của hàm số không có tiệm cận.
B. Đồ thị (C) của hàm số chỉ có một tiệm cận ngang y = 0.
C. Đồ thị (C) của hàm số có một tiệm cận ngang y = 0 và hai tiệm cận đứng 1
x =1; x = − . 2
D. Đồ thị (C) của hàm số chỉ có một tiệm cận ngang y = 0 và một tiện cận đứng x =1 2
Câu 20: Đồ thị hàm số
2x + x − x y =
có tất cả bao nhiêu đường tiệm cận? 3x +1 A. 2 . B. 3. C. 0 . D. 1. 2
Câu 21: Đồ thị hàm số 1 4 x y
có số đường tiệm cận đứng là m và số đường tiệm cận ngang là 2 x 2x3
n . Giá trị của mn là A. 1 B. 2 C. 3 D. 0
Câu 22: Gọi n,d lần lượt là số đường tiệm cận ngang và số tiệm cận đứng của đồ thị hàm số 1 x y
. Khẳng định nào sau đây là đúng? x  1 x
A. n  0,d  2 .
B. n d 1.
C. n 1,d  2 .
D. n  0,d 1. + − +
Câu 23: Đồ thị hàm số 5x 1 x 1 y =
có tất cả bao nhiêu đường tiệm cận? 2 x − 2x A. 0 . B. 1. C. 2 . D. 3. Câu 24: −
Tìm số đường tiệm cận của đồ thị hàm số x 1 y = .
4 3x +1 − 3x − 5 Page 186
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. 2 . B. 3. C. 1. D. 0 . 2 Câu 25: Cho hàm số x + 2x + 3 y =
. Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận? 4 2 x − 3x + 2 A. 4 . B. 5. C. 3. D. 6 . 5x −8
Câu 26: Đồ thị hàm số y =
có bao nhiêu đường tiệm cận? 2 x −3x A. 2. B. 4. C. 1. D. 3. Câu 27: Gọi x + 2
S là tập hợp các giá trị nguyên m để đồ thị hàm số y = có hai đường tiệm 2
x − 6x + 2m
cận đứng. Số phần tử của S là A. vô số. B. 12. C. 14. D. 13.
Câu 28: Có bao nhiêu giá trị nguyên dương của tham số m để đồ thị hàm số x −1 y = có 3 đường 2
x −8x + m tiệm cận? A. 14. B. 8 . C. 15. D. 16. Câu 29: Cho hàm số x − 3 y =
. Có bao nhiêu giá trị nguyên của tham số m thuộc 3 2 x − 3mx + ( 2 2m + ) 1 x − m đoạn [ 2020 −
;2020] để đồ thị hàm số có 4 đường tiệm cận? A. 4039. B. 4040. C. 4038. D. 4037.
Câu 30: Có bao nhiêu số nguyên của m thuộc đoạn [ 100 −
;100]để đồ thị hàm số 1 y = có (x − m) 2 2x − x
đúng hai đường tiệm cân? A. 200. B. 2. C. 199. D. 0. 2
Câu 31: Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số x + m y = có đúng hai đường 2 x − 3x + 2 tiệm cận. A. m = 1 − B. m∈{1;4} C. m = 4 D. m∈{−1; 4 − }
Câu 32: Có bao nhiêu giá trị nguyên của 6x − 3
m để đồ thị hàm số y = ( có đúng 2
mx − 6x + 3)( 2 9x + 6mx + ) 1 một đường tiệm cận? A. 0 . B. 2 . C. 1. D. Vô số. Page 187
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 33: Cho hàm số y = f (x) x +1 =
. Tìm tất cả các giá trị của tham số m để đồ thị có ba đường 2 x − 2mx + 4 tiệm cận  m > 2  m < 2 −  m < 2 − A. m  > 2 B.  m < 2 −  5 C. D. m ≠ −    m > 2  2  5 m ≠ −  2
(n −3) x + n − 2017
Câu 34: Biết rằng đồ thị của hàm số y = ( ,
m n là các số thực) nhận trục hoành làm x + m + 3
tiệm cận ngang và trục tung là tiệm cận đứng. Tính tổng m + n. A. 0 B. 3 − C. 3 D. 6
Câu 35: Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số x −1 y = có đúng bốn 2 mx −8x + 2
đường tiệm cận? A. 8 B. 6 C. 7 D. Vô số
Câu 36: Với giá trị nào của hàm số m để đồ thị hàm số 2
y = x − mx − 3x + 7 có tiệm cạn ngang. A. m =1 B. m = 1 − C. m = 1 ±
D. Không có m Câu 37: Cho hàm số ax +1 y =
. Tìm a,b để đồ thị hàm số có x =1 là tiệm cận đứng và 1 y = là tiệm bx − 2 2 cận ngang. A. a = 1; − b = 2 .
B. a = 4;b = 4.
C. a =1;b = 2 . D. a = 1; − b = 2 − .
Câu 38: Có bao nhiêu giá trị nguyên m∈[ 10
− ;10] sao cho đồ thị hàm số x −1 y = có hai 2
2x + 6x − m − 3
đường tiệm cận đứng? A. 19. B. 15. C. 17 . D. 18.
Câu 39: Có bao nhiêu giá trị nguyên của m để tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm 2 số mx + 3mx + 4 y = bằng 3? x + 2 A. 4 . B. 2 . C. Vô số. D. 3.
Câu 40: Tổng các giá trị của tham số m để đồ thị của hàm số x −1 y = có đúng một 2 x + 2(m − ) 2 1 x + m − 2 tiệm cận đứng. 1 3 A. − . B. 2 . C. 3 − . D. 2 2 . Câu 41: Cho hàm số x3 y
. Có bao nhiêu giá trị nguyên thuộc đoạn 6;6 3 2
x 3mx  2 2m   1 xm
của tham số m để đồ thị hàm số có bốn đường tiệm cận? A. 12. B. 9. C. 8 . D. 11. Page 188
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ 2
Câu 42: Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số 2x + 3x + = m y không có tiệm x − m cận đứng. A. m =1. B. m >1.
C. m =1và m = 0. D. m ≠ 0 .
Câu 43: Có bao nhiêu giá trị nguyên của tham số thực m thuộc đoạn  2017;2017 để đồ thị hàm số x  2 y
có hai tiệm cận đứng. 2
x 4x m A. 2019 . B. 2021. C. 2018 . D. 2020 .
Câu 44: Cho hàm số y f(x) thỏa mãn lim f(x)  2019m , 4
lim f (x)  2020m . Hỏi có tất cả bao x x
nhiêu giá trị của m để đồ thị của hàm số y f(x) có duy nhất một tiệm cận ngang? A. 4. B. 2. C. 3. D. 1. Câu 45: Cho hàm số 1 y =
. Tìm tất cả các giá trị thực của tham số m để đồ 2 x − (2m + )
1 x + 2mx − m  
thị hàm số có 4 đường tiệm cận. 0 < m <1 m <1 0 ≤ m ≤1 A.     1 . B.  . C. m >1. D.  . m ≠ 1 1  m ≠ m ≠  2  2  2
Câu 46: Có bao nhiêu giá trị nguyên của 6x − 3
m để đồ thị hàm số y = ( có đúng 2
mx − 6x + 3)( 2 9x + 6mx + ) 1 1 đường tiệm cận? A. 0. B. 2. C. 1. D. Vô số.
Câu 47: Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số: 2
y x mx 1 có tiệm cận ngang.
A. 0  m 1.
B. m 1.
C. m  1. D. m 1. Câu 48: Cho hàm số x − 2 y =
. Có tất cả bao nhiêu giá trị của tham số m để đồ thị hàm số có 2 mx − 2x + 4
đúng hai đường tiệm cận ? A. 0 . B. 2 . C. 3. D. 1.
Câu 49: Gọi S là tập các giá trị nguyên của m sao cho đồ thị hàm số 2019x y = có bốn đường 2 17x −1 − m x
tiệm cận . Tính số phần tử của tập S. A. Vô số B. 3 C. 5 D. 4
Câu 50: Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho đồ thị hàm số ( ) x f x =
nhận trục tung làm tiệm cận đứng. Khi đó tổng các phần 3 3 4 2
x + mx +1 − x + x +1 + m x tử của S bằng A. 1 . B. 1 − . C. 1 . D. 1 − . 2 2 3 3 Page 189
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
x(xm) 1
Câu 51: Có bao nhiêu giá trị m nguyên thuộc khoảng 10;10 để đồ thị hàm số y  có x  2
đúng ba đường tiệm cận? A. 12. B. 11. C. 0 . D. 10.
Câu 52: Tìm số giá trị nguyên thuộc đoạn [ 2019 −
;2019] của tham số m để đồ thị hàm số x − 3 y = 2
x + x − m
có đúng hai đường tiệm cận. A. 2007 . B. 2010 . C. 2009 . D. 2008 . Câu 53: Cho hàm số x −1 y =
. Có tất cả bao nhiêu giá trị m để đồ thị hàm số có đúng hai đường 2 mx − 2x + 3 tiệm cận. A. 2 B. 3 C. 0 D. 1 Câu 54: Cho hàm số 1 y =
với m là tham số. Tìm tất cả các giá trị của m để đồ thị hàm 3 2
x − 3x + m −1
số đã cho có 4 đường thẳng tiệm cận.
A. 1< m < 5. B. 1 − < m < 2 .
C. m <1 hoặc m > 5 . D. m > 2 hoặc m < 1 − . Câu 55: Hàm số
3x +1 + ax + b y =
không có tiệm cận đứng. Khi đó hiệu a −b bằng: (x − )2 1 A. 1 . − . C. 5 − . − . 2 B. 34 4 D. 12 2
Câu 56: Có bao nhiêu giá trị nguyên của tham để m đồ thị hàm số
−x + 2016x + 2017 − 24 7 y = có x − m tiệm cận đứng? A. vô số. B. 2 . C. 2017 D. 2019 .
Câu 57: Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho đồ thị hàm số ( ) x f x =
nhận trục tung làm tiệm cận đứng. Khi đó tổng các phần 3 3 4 2
x + mx +1 − x + x +1 + m x tử của S bằng A. 1 . B. 1 − . C. 1 . D. 1 − . 2 2 3 3
x(xm) 1
Câu 58: Có bao nhiêu giá trị m nguyên thuộc khoảng 10;10 để đồ thị hàm số y  có x  2
đúng ba đường tiệm cận? A. 12. B. 11. C. 0 . D. 10. 2
Câu 59: Tìm tất cả các giá trị thực của m sao cho đồ thị hàm số mx +1 y =
có đúng một đường tiệm x +1 cận.
A. −1 ≤ m < 0 .
B. −1 ≤ m ≤ 0 . C. m < 1 − . D. m > 0 . Page 190
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
NG I ỨNG DỤNG ĐẠO HÀM ƯƠ
ĐỂ KHẢO SÁT HÀM SỐ CH
BÀI 4. ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
III BÀI TẬP TRẮC NGHIỆM
DẠNG. XÁC ĐỊNH ĐƯỜNG TIỆM CẬN THÔNG QUA BẢNG BIẾN THIÊN, ĐỒ THỊ
1.1.1 Đường tiệm cận ngang
Cho hàm số y = f x
( ) xác định trên một khoảng vô hạn. Đường thẳng y = y là đường tiệm 0
cận ngang của đồ thị hàm số y = f x
( ) nếu ít nhất một trong các điều kiện sau được thỏa mãn: lim f x
( ) = y , lim f x ( ) = y x 0 →+∞ x 0 →−∞
1.1.2 Đường tiệm cận đứng
Đường thẳng x = x được gọi là đường tiệm cận đứng của đồ thị hàm số y = f (x) nếu ít 0
nhất một trong các điều kiện sau được thỏa mãn: lim f x ( ) = +∞, lim f x
( ) = −∞, lim f (x) = −∞, lim f (x) = +∞ + − x →x x →x x x + x x − → → 0 0 0 0 ax +
Lưu ý: Với đồ thị hàm phân thức dạng = b y
(c ≠ 0; ad − bc ≠ 0) luôn có tiệm cận ngang là cx + d = a y
và tiệm cận đứng = − d x . c c
Câu 1: Cho hàm số có bảng biến thiên như hình sau
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = f (x) là A. 3. B. 2 . C. 4 . D. 1. Lời giải
Vì lim y = 4, lim y = 1
− ⇒ Đồ thị hàm số có hai tiệm cận ngang là y = 1 − và y = 4 . x→−∞ x→+∞
lim y = +∞, lim y = −∞ ⇒ Đồ thị hàm số có tiệm cận đứng x = 1 − . x 1− x 1+ →− →−
lim y = −∞, lim y = +∞ ⇒ Đồ thị hàm số có tiệm cận đứng x =1. x 1− x 1+ → →
Nên đồ thị hàm số có 4 đường tiệm cận. Page 137
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 2: Cho hàm số f (x) có bảng biến thiên như sau:
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là: A. 4 . B. 3. C. 1. D. 2 . Lời giải
lim f (x) = 3 ta được tiệm cận ngang y = 3 x→+∞
lim f (x) = +∞ ta được tiệm cận đứng x = 2 − x ( 2)− → −
Câu 3: Cho hàm số y = f (x) có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là A. 4 B. 2 C. 3 D. 1 Lời giải
Từ bảng biến thiên ta có:
+ Tiệm cận ngang y = 5 −
+ Tiệm cận đứng x = 2.
Câu 4: Cho đồ thị hàm số y = f (x) như hình bên. Khẳng định nào sau đây là đúng? y 1 1 − O x
A. Đồ thị hàm số có tiệm cận đứng x = 0 , tiệm cận ngang y =1.
B. Hàm số có hai cực trị.
C. Đồ thị hàm số chỉ có một đường tiệm cận.
D. Hàm số đồng biến trong khoảng (−∞;0) và (0;+ ∞) .
Câu 5: Cho hàmsố f (x) có bảng biến thiên như sau Page 138
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là A. 4 . B. 1. C. 3. D. 2 . Lời giải
Dựa vào bảng biến thiên của hàm số ta có:
lim f (x) = 0 ⇒ y = 0 là một tiệm cận ngang x→−∞
lim f (x) = 5 ⇒ y = 5 là một tiệm cận ngang x→+∞
lim f (x) = −∞ ⇒ x =1là một tiệm cận đứng x 1− →
Vậy đồ thị hàm số có tổng số đường tiệm cận là 3.
Câu 6: Cho hàm số y = f (x) có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là A. 4 . B. 1. C. 3. D. 2 . Lời giải
Dựa vào bảng biến thiên của hàm số ta có:
lim f (x) = 2 ⇒ y = 2 là một tiệm cận ngang x→±∞
lim f (x) = −∞ ⇒ x =1là một tiệm cận đứng x 1+ →
Vậy đồ thị hàm số có tổng số đường tiệm cận là 2 .
Câu 7: Cho hàm số y = f (x) có bảng biến thiên như sau
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho bằng Page 139
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. 2 . B. 1. C. 0 . D. 3. Lời giải Ta có
lim y = −∞ ⇒ x = 2
− là tiệm cận đứng của đồ thị hàm số đã cho. x 2+ →−
lim y = +∞ ⇒ x = 0 là tiệm cận đứng của đồ thị hàm số đã cho. x 0− →
lim y = 0 ⇒ y = 0 là tiệm cận ngang của đồ thị hàm số đã cho. x→+∞
Vậy đồ thị hàm số đã cho có tổng đường tiệm cận đứng và tiệm cận ngang là 3.
Câu 8: Cho hàm số y = f (x) liên tục trên  \{ }
1 có bảng biến thiên như hình vẽ. Tổng số đường tiệm
cận đứng và đường tiệm cận ngang của đồ thị hàm số y = f (x) A. 1. B. 4 . C. 2 . D. 3. Lời giải Chọn D Do lim y = ;
−∞ lim = +∞ ⇒ TCĐ: x =1. x 1+ x 1− → → lim y = 1
− ; lim y =1⇒ đồ thị có 2 tiệm cận ngang là y = 1 ± x→+∞ x→−∞
Vậy, đồ thị hàm số đã cho có tổng số TCĐ và TCN là 3.
Câu 9: Cho hàm số yf x  có bảng biến như sau:
Số đường tiệm cận của đồ thị hàm số là: A. 3 B. 1. C. 4. D. 2. Lời giải Chọn A
Từ bảng biến thiên của hàm số ta có: Page 140
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
+ lim y  0; lim y  0  đồ thị hàm số nhận đường thẳng y  0 là tiệm cận ngang. x x + lim y  ;
 lim    đồ thị hàm số nhận đường thẳng x  3là tiệm cận đứng. x   3  x   3      + lim y  ;
 lim    đồ thị hàm số nhận đường thẳng x  3là tiệm cận đứng. x 3 x 3  
Vậy số đường tiệm cận của đồ thị hàm số là 3.
Câu 10: Cho hàm số y = f (x) có bảng biến thiên như sau
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là A. 4 . B. 2 . C. 3 . D. 1. Lời giải Chọn C Ta có:
 lim f (x) = 0 nên đường thẳng y = 0 là đường tiệm cận ngang của đồ thị hàm số y = f (x) x→−∞ .
 lim f (x) = −∞ nên đồ thị hàm số y = f (x) không có tiệm cận ngang khi x → +∞ . x→+∞
 lim f (x) = +∞ , lim f (x) = −∞ nên đường thẳng x = 2
− là đường tiệm cận đứng của đồ x 2+ →− x 2− →−
thị hàm số y = f (x) .
 lim f (x) = +∞ , lim f (x) = −∞ nên đường thẳng x = 2 là đường tiệm cận đứng của đồ thị x 2+ → x 2− →
hàm số y = f (x) .
Vậy tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là 3 tiệm cận.
DẠNG 2. XÁC ĐỊNH ĐƯỜNG TIỆM CẬN ĐỒ THỊ HÀM SỐ THÔNG HÀM SỐ CHO TRƯỚC
1 Đường tiệm cận ngang
Cho hàm số y = f (x) có TXD: D
Điều kiện cần: D phải chứa +∞ hoặc −∞ Điều kiện đủ: Dạng 1. P(x)
y = f (x) = . Q(x)
Nếu degP(x) > degQ(x) :thì không có tiệm cận ngang
Nếu degP(x) > degQ(x):TCN y = 0
Nếu degP(x) = degQ(x): y = k Page 141
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ 2
Dạng 2: y = f (x) = u − v : Nhân liên hợp⇒ = ( ) u − v y f x = u + v
2 Đường tiệm cận đứng P(x) Cho hàm số y = có TXD: D Q(x)
Đkiện cần: giải Q(x) = 0 ⇔ x = x là TCĐ khi thỏa mãn đk đủ 0 Đkiện đủ:
Đkiện 1: x làm cho P(x) và Q(x) xác định. 0
Đkiện 2: - x không phải nghiêm P(x) ⇒ x = x là TCĐ 0 0
- x là nghiêm P(x) ⇒ x = x là TCĐ nếu 0 0 lim f (x) = ∞ x→ 0 x
Câu 11: Đồ thị hàm số
5x 1 x 1 y
có tất cả bao nhiêu đường tiệm cận? 2 x  2x A. 3 B. 0 C. 2 D. 1 Lời giải Chọn D
Tập xác định: D 1;\ 0 . 5 1 1 1    2 3 4 • lim y
5x 1 x 1  lim  lim x x x
x  0  y  0 là đường tiệm cận ngang x 2 x x  2x x 2 1 x của đồ thị hàm số. 5x  2 1  x 1 2 • lim y
5x 1 x 1 25x  9x  lim  lim  lim x0 2 x0 x  2x x0  2
x  2x5x 1 x 1 x0 2
x  2x5x 1 x 1 25x  9 9  lim 
x0 x  25x 1 x 1 4
x  0 không là đường tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có tất cả 1 đường tiệm cận. 2
Câu 12: Tìm tất cả các tiệm cận đứng của đồ thị hàm số
2x −1− x + x + 3 y = . 2 x − 5x + 6
A. x = 3 và x = 2 .
B. x = 3. C. x = 3 − và x = 2 − . D. x = 3 − . Lời giải Chọn B
Tập xác định D = \{2; } 3 Page 142
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
2x −1− x + x + 3 (2x − )2 1 − ( 2 2 x + x + 3) lim = lim + 2 x→2 − + x→2 x 5x 6
+ ( 2x −5x + 6)( 2
2x −1+ x + x + 3) (2x − )2 1 − ( 2 x + x + 3) = lim x→2+ ( 2 x − 5x + 6)( 2
2x −1+ x + x + 3) (3x +1) 7 = lim = − x 2+ → (x − )( 2
x − + x + x + ) 6 3 2 1 3 2 Tương tự
2x −1− x + x + 3 7 lim
= − . Suy ra đường thẳng x = 2 không là tiệm cận đứng − 2 x→2 x − 5x + 6 6
của đồ thị hàm số đã cho. 2 2
2x −1− x + x + 3
2x −1− x + x + 3 lim = ; +∞ lim
= −∞ . Suy ra đường thẳng x = 3 là tiệm + 2 − 2 x→3 x − x + x→3 5 6 x − 5x + 6
cận đứng của đồ thị hàm số đã cho.
Câu 13: Số tiệm cận đứng của đồ thị hàm số x + 4 − 2 y = là 2 x + x A. 3. B. 0 . C. 1. D. 2 . Lời giải TXĐ: D = [ 4 − ;+∞) \{ 1; − } 0 . Ta có: x + 4 − 2 lim y = lim = −∞ x→(− )+ x→(− )+ 2 1 1 x + x
Nên đường thẳng x = 1
− là một đường tiệm cận đứng của đồ thị hàm số đã cho. x
( x+4 −2)( x+4 + + − 2 4 2 ) 1 1 lim y = lim = lim = lim = 2 x→0 x→0 x→0 x + x x(x + ) 1 ( x + 4 + 2) x→0 (x + ) 1 ( x + 4 + 2) 4
Nên đường thẳng x = 0 không là tiệm cận đứng của đồ thị hàm số đã cho.
Vậy đồ thị hàm số đã cho có một tiệm cận đứng x = 1 − . +
Câu 14: Đồ thị hàm số f (x) x 1 =
có tất cả bao nhiêu tiệm cận đứng và tiệm cận ngang? 2 x −1 A. 4 . B. 3. C. 1. D. 2 . Lờigiải
Tập xác định của hàm số D = (− ; ∞ − ) 1 ∪ (1;+∞) 2 x +1 − x +1 TH1: + x x 1
< −1 ⇒ x +1 < 0. Khi đó f (x) ( ) = = = − . 2 x −1 (x − ) 1 (x + ) 1 x −1
Suy ra hàm số TCN y = −1, không có TCĐ. Page 143
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ 2 x +1 x +1 TH2: + x x 1
> 1 ⇒ x +1 > 0 . Khi đó f (x) ( ) = = = . 2 x −1 (x − ) 1 (x + ) 1 x −1
Suy ra hàm số TCN y = 1, TCĐ x = 1.
Vậy hàm số có 2 TCN và 1 TCN x(4x + 6) − 2
Câu 15: Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = là? x + 2 A. 1 B. 3 C. 2 D. 4 Lời giải Chọn C 6 2 x( x ) 4 4 6 2 + − + − lim = lim x x = 2 x→+∞ x + 2 x→+∞ 2 1+ x 6 2 x( x ) − 4 4 6 2 + − + − lim = lim x x = 2 − x→−∞ x + 2 x→−∞ 2 1+ x x(4x + 6) − 2
(x + 2)(4x − 2) 4x − 2 5 lim lim lim − = = = x 2± x + 2 x
2± (x + 2)( x(4x + 6) + 2) x 2± →− →− →− x(4x + 6) + 2 2
Vậy hàm số có hai tiệm cận ngang y = 2 ± . 2 Câu 16: Cho hàm số x + 2x + 3 y =
. Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận? 4 2 x − 3x + 2 A. 4 . B. 5. C. 3. D. 6 . Lời giải Điều kiện: x∈( ; −∞ − 2 )∪( 1; − ) 1 ∪( 2;+∞). 2 3 2 1+ + 2 Do + + lim y x 2x 3 = lim y = lim = lim x x
= 1 ⇒ y =1 là đường tiệm cận x→+∞ x→−∞ x→±∞ 4 2
x − 3x + 2 x→±∞ 3 2 1− + 2 4 x x
ngang của đồ thị hàm số.
Có lim y = +∞ nên đường thẳng x =1 là đường tiệm cận đứng. x 1− → (x + ) 1 (x + 2) (x + ) 1 (x + 2) Có lim y = lim = lim = 0 nên x ( ) 1 + x ( ) 1 + (x + )
1 (x + 2)(x − )1(x − 2) x ( )1+ → − → − → −
(x+ 2)(x− )1(x− 2) đường thẳng x = 1
− không là đường tiệm cận đứng. Page 144
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Có lim y = +∞ nên đường thẳng x = 2 là đường tiệm cận đứng. + x→( 2)
Có lim y = +∞ nên đường thẳng x = − 2 là đường tiệm cận đứng. − x→(− 2)
Vậy đồ thị hàm số có 4 đường tiệm cận (1 tiệm cận ngang, 3 tiệm cận đứng). 2 Câu 17: Hàm số
x + x + x +1 y =
có bao nhiêu đường tiệm cận? 3 x + x A. 1 B. 3 C. 2 D. 4 Lời giải Chọn C TXĐ: D =  \{ } 0  1 1   1 1 x1 1  − + + 2   1− 1 x x + + 2   1  lim = lim = lim  . x x y  = 0 2 x→−∞ x→−∞  1 x→−∞   x 1 3 x 1+   1  + 2  2 x x       1 1   1 1 x1 1  + + + 2   1+ 1 x x + + 2   1  lim = lim = lim  . x x y  = 0 2 x→+∞ x→+∞  1 x→+∞   x 1 3 x 1+   1  + 2  2 x x      ⇒ TCN: y = 0
lim y = +∞ ⇒ TCĐ: x = 0 . x 0+ →
Câu 18: Số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số x − 2 +1 y = là 2 x − 3x + 2 A. 4 B. 1 C. 3 D. 2 Lời giải Chọn D x − 2 ≥ 0 x ≥ 2 Đkxđ:  ⇔  ⇔ x > 2 2
x − 3x + 2 ≠ 0
x ≠ 2, x ≠ 1  x − +  Ta có: 2 1 lim 
 = +∞ nên đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số. + x  2 →2 x 3x 2  − +    x − 2 +1  lim 
 = 0 nên đường thẳng y = 0 là tiệm cận ngang của đồ thị hàm số. x  2 →+∞ x 3x 2  − +   2 Câu 19: Cho hàm số
5 x + 6 + x −12 y =
có đồ thị (C). Mệnh đề nào sau đây là đúng? 3 4x − 3x −1
A. Đồ thị (C) của hàm số không có tiệm cận. Page 145
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
B. Đồ thị (C) của hàm số chỉ có một tiệm cận ngang y = 0.
C. Đồ thị (C) của hàm số có một tiệm cận ngang y = 0 và hai tiệm cận đứng 1
x =1; x = − . 2
D. Đồ thị (C) của hàm số chỉ có một tiệm cận ngang y = 0 và một tiện cận đứng x =1 Lời giải Chọn D   TXĐ: 1 D R\ 1;        2    
Ta có: lim y  ; lim y    Đồ thị hàm số có một TCĐ là x  1 x 1 x 1  
lim y  0  Đồ thị hàm số có một TCN là y  0 x 2
Câu 20: Đồ thị hàm số
2x + x − x y =
có tất cả bao nhiêu đường tiệm cận? 3x +1 A. 2 . B. 3. C. 0 . D. 1. Lời giải Chọn A 2 Xét hàm số
2x + x − x y   =
có tập xác định D = (−∞ ]∪[ +∞) 1 ;0 1; \ − . 3x +1  3 Ta có 2 2 2 +
lim x + x − x 3 = lim x x 1 = lim x = ; 1 x 1 →− 3x +1 x→− (3x + ) 1 ( 2
2x − x − x 1 2
x→− 2x − x − x 4 3 ) 3 3 2 2 2
lim x + x − x + − = 0 và 2x x x 1 lim
= nên đồ thị không có tiệm cận đứng. x 0− → 3x +1 x 1+ → 3x +1 2 1 1 2 2x − x 1− 2 − 1 2x x x − + − x x 1 lim = lim = lim = , x→−∞ 1 1 3x +1 x→− 3x +1 x→− 1 3 3 3 3+ x 1 1 2 2x + x 1− 2 + 1− và 2
lim x + x − x = lim x = lim
x =1 nên đồ thị có hai tiệm cận ngang x→+∞ 1 1 3x +1 x→− 3x +1 x→− 1 3 3 3+ x là 1 y = và y =1. 3
Vậy đồ thị hàm số có tất cả hai đường tiệm cận. 2
Câu 21: Đồ thị hàm số 1 4 x y
có số đường tiệm cận đứng là m và số đường tiệm cận ngang là 2 x 2x3
n . Giá trị của mn là Page 146
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. 1 B. 2 C. 3 D. 0 Lời giải Chọn A
D 2;2\   1 2 1 4 2 lim 1 4 x  lim  x y  ;  lim y  lim   x    2    x     2 1 1 x 2x3 x     1 x     1 x 2x3
x  1 là tiệm cận đứng.
Đồ thị hàm số không có đường tiệm cận ngang.
Vậy m n 1.
Câu 22: Gọi n,d lần lượt là số đường tiệm cận ngang và số tiệm cận đứng của đồ thị hàm số 1 x y
. Khẳng định nào sau đây là đúng? x  1 x
A. n  0,d  2 .
B. n d 1.
C. n 1,d  2 .
D. n  0,d 1. Lời giải Chọn A
Tập xác định: D 0;  1 .
Từ tập xác định suy ra đồ thị hàm số không có tiệm cận ngang. n  0 . +) 1 x 1 lim y  lim  lim   x 0
x 0 x   x 0 1 x     1 x x +) 1 x 1 lim y  lim  lim   x 1
x 1 x   x 1 1 x     1 x x
Suy ra đồ thị hàm số có hai tiệm cận đứng, d  2 . + − +
Câu 23: Đồ thị hàm số 5x 1 x 1 y =
có tất cả bao nhiêu đường tiệm cận? 2 x − 2x A. 0 . B. 1. C. 2 . D. 3. Lời giải Chọn C
Tập xác định của hàm số là D = [ 1 − ;0) ∪(2;+∞) . Ta có 2 25x + 9x 25x + 9 9 lim y = lim = lim = − . x→0− x→0− ( 2
x − 2x)(5x +1+ x +1) x→0− (x − 2)(5x +1+ x +1) 4 lim y = +∞ . x→2+ 5 1 1 1 + − + 2 3 4 lim = lim x x x x y = 0. x→+∞ x→+∞ 2 1− x Page 147
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Vậy đồ thị của hàm số có hai đường tiệm cận có phương trình x = 2 và y = 0. Câu 24: −
Tìm số đường tiệm cận của đồ thị hàm số x 1 y = .
4 3x +1 − 3x − 5 A. 2 . B. 3. C. 1. D. 0 . Lời giải Chọn A Tập xác định: 1 D  ;  = − +∞   \{ } 1  3  x (x − ) 1 (4 3x +1+3x + − 5 1 ) + Ta có: 4 3x +1 + 3x + 5 lim = lim = lim = −∞ x
+ 4 3x +1 − 3x − 5 x + 9 − (x − )2 1 1 x 1 1 + → → → 9 − (x − ) 1
do đó đường thẳng x =1 là đường tiệm cận đứng của đồ thị hàm số. 1 1− + x −1 x 1 lim = lim
= − do đó đường thẳng 1 y = − là đường
x→+∞ 4 3x +1 − 3x − 5 x→+∞ 3 1 5 3 3 4 + − 3− 2 x x x
tiệm cận ngang của đồ thị hàm số. Vậy đồ thị hàm số có 2 đường tiệm cận. 2 Câu 25: Cho hàm số x + 2x + 3 y =
. Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận? 4 2 x − 3x + 2 A. 4 . B. 5. C. 3. D. 6 . Lời giải Chọn B
□ Tập xác định D = ( ; −∞ − 2 )∪( 1; − ) 1 ∪( 2;+∞).
□ lim y = lim y = lim y = lim y = +∞ . − + + − x→(− 2) x→( 2) x→(− ) 1 x→( ) 1
⇒ Các đường tiệm cận đứng của đồ thị là x = ± 2 , x = 1 ± .
□ lim y = lim y =1 ⇒ đồ thị có một tiệm cận ngang y =1. x→−∞ x→+∞ 5x −8
Câu 26: Đồ thị hàm số y =
có bao nhiêu đường tiệm cận? 2 x −3x A. 2. B. 4. C. 1. D. 3. Lời giải Chọn B
Tập xác định D = ( ; −∞ 0)∪(3;+∞) 8 5 5x −8 5x −8 − lim = lim = lim = lim x y = 5 x→+∞ x→+∞ 2 x − 3 x x →+∞ 3 x→+∞ 3 x 1− 1− x x
⇒ Đường thẳng y = 5là tiệm cận ngang của đồ thị hàm số. Page 148
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ 8 5 5x −8 5x −8 − lim = lim = lim = lim x y = 5 − x→−∞ x→−∞ 2 x − 3 x x →−∞ 3 x→−∞ 3 −x 1− − 1− x x
⇒Đường thẳng y = 5
− là tiệm cận ngang của đồ thị hàm số. 5x −8 lim y = lim = −∞ x 0− x 0− → → 2 x −3x 2
Dạng 2: y = f (x) = u − v : Nhân liên hợp⇒ = ( ) u − v y f x = u + v
2 Đường tiệm cận đứng P(x) Cho hàm số y = có TXD: D Q(x)
Đkiện cần: giải Q(x) = 0 ⇔ x = x là TCĐ khi thỏa mãn đk đủ 0 Đkiện đủ:
Đkiện 1: x làm cho P(x) và Q(x) xác định. 0
Đkiện 2: - x không phải nghiêm P(x) ⇒ x = x là TCĐ 0 0
- x là nghiêm P(x) ⇒ x = x là TCĐ nếu 0 0 lim f (x) = ∞ x→ 0 x Câu 27: Gọi x + 2
S là tập hợp các giá trị nguyên m để đồ thị hàm số y = có hai đường tiệm 2
x − 6x + 2m
cận đứng. Số phần tử của S là A. vô số. B. 12. C. 14. D. 13. Lời giải Chọn B x + 2 ≥ 0
Điều kiện xác định  . 2
x − 6x + 2m > 0
Để đồ thị hàm số có hai đường tiệm cận đứng thì phương trình 2
x − 6x + 2m = 0 có hai nghiệm  9
∆′ = 9 − 2m > 0 m <   2  9   m <
phân biệt x , x lớn hơn 2
− ⇔ x + x > 2 − ⇔ 3  > 2 − ⇔ . 1 2 1 2  2 (     2 − m m  )2 −6⋅( 2 − ) + m > 4 +12 + 2 > 0  > 8 2 0 −   Do đó tập S = { 7 − ; 6 − ; 5 − ;...; } 4 có 12 giá trị.
Câu 28: Có bao nhiêu giá trị nguyên dương của tham số m để đồ thị hàm số x −1 y = có 3 đường 2
x −8x + m tiệm cận? A. 14. B. 8 . C. 15. D. 16. Lời giải Chọn A Page 149
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Ta có x −1 x −1 lim = lim
= 0 nên hàm số có một tiện cận ngang y = 0. 2 2
x→−∞ x − 8 + x x m
→+∞ x − 8x + m
Hàm số có 3 đường tiệm cận khi và chỉ khi hàm số có hai đường tiệm cận đứng ⇔ phương
Δ′ = 16 − m > 0 m < 16 trình 2
x −8x + m = 0 có hai nghiệm phân biệt khác 1 ⇔  ⇔ . m 7 0  − ≠ m ≠ 7
Kết hợp với điều kiện m nguyên dương ta có m∈{1;2;3;...;6;8;...; }
15 . Vậy có 14 giá trị của
m thỏa mãn đề bài. Câu 29: Cho hàm số x − 3 y =
. Có bao nhiêu giá trị nguyên của tham số m thuộc 3 2 x − 3mx + ( 2 2m + ) 1 x − m đoạn [ 2020 −
;2020] để đồ thị hàm số có 4 đường tiệm cận? A. 4039. B. 4040. C. 4038. D. 4037. Lời giải Chọn D
Ta có lim y = 0, lim y = 0 ⇒ đồ thị hàm số đã cho có 1 tiệm cận ngang. x→+∞ x→−∞
Do đó đồ thị hàm số đã cho có 4 đường tiệm cận khi và chỉ khi nó có 3 tiệm cận đứng (*) . Có 3 2 x − mx + ( 2
m + ) x − m = (x − m)( 2 3 2 1 x − 2mx + ) 1 x = m 3 2 x − 3mx + ( 2 2m + )
1 x − m = 0 ⇔  2 x − 2mx +1 = 0  (2) (*) ⇔ 3 2 x − mx + ( 2 3 2m + )
1 x − m = 0 có 3 nghiệm phân biệt khác 3.
⇔ m ≠ 3 và (2) có 2 nghiệm phân biệt khác m và khác 3. m ≠ 3  5  m ≠ 3,m ≠ 2 m 2 . m m 1 0  − + ≠  3 ⇔  ⇔ 2 3 − 2 .3  m +1 ≠  0 m > 1   2  ∆′ = − > m < 1  m 1 0 − 2
Do đó tập tất cả giá trị nguyên của m thỏa ycbt là { 2020 − ; 2019 − ;...; 2 − ;2;4;5;...; } 2020 .
Vậy có 4037 giá trị m thỏa ycbt.
Câu 30: Có bao nhiêu số nguyên của m thuộc đoạn [ 100 −
;100]để đồ thị hàm số 1
y = (x−m) 2 2x − x
có đúng hai đường tiệm cân? A. 200. B. 2. C. 199. D. 0. Lời giải Chọn A Page 150
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ x ≠ m
Ta có điều kiện xác định là 
, khi đó đồ thị hàm số sẽ không có tiệm cận ngang. x ∈  (0;2)
Ta có lim y = ∞, lim y = ∞ x 0+ x 2− → →
Suy ra x = 0, x = 2 là hai đường tiệm cận đứng m ≤ 0
Vậy để đồ thị hàm số có đúng hai đường tiệm cận thì 
, theo bài m thuộc đoạn [ 100 − ;100] m ≥ 2
. Vậy có 200 số nguyên của m thỏa mãn đầu bài. 2
Câu 31: Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số x + m y = có đúng hai đường 2 x − 3x + 2 tiệm cận. A. m = 1 − B. m∈{1;4} C. m = 4 D. m∈{−1; 4 − } Lời giải 2 2 x + m x + m y = = . 2
x − 3x + 2 (x − ) 1 (x − 2)
lim y =1⇒ y =1 là đường tiệm cận ngang. x→±∞ 2 Đồ thị hàm số x + m y =
có đúng hai đường tiệm cận ⇔ đồ thị hàm số có đúng một tiệm 2 x − 3x + 2 cận đứng ⇔ pt 2
x + m = 0 nhận nghiệm x =1 hoặc x = 2 . m = 1 − Khi đó:  . m = 4 − Với m = 1
− có một tiệm cận đứng x = 2 . Với m = 4
− có một tiệm cận đứng x =1. Vậy m∈{−1; 4 − } .
Câu 32: Có bao nhiêu giá trị nguyên của 6x − 3
m để đồ thị hàm số y = ( có đúng 2
mx − 6x + 3)( 2 9x + 6mx + ) 1 một đường tiệm cận? A. 0 . B. 2 . C. 1. D. Vô số. Lời giải Kí hiệu ( −
C) là đồ thị hàm số 6x 3 y = ( . 2
mx − 6x + 3)( 2 9x + 6mx + ) 1
* Trường hợp 1: m = 0. Khi đó 6x − 3 y = (
. Đồ thị hàm số có đúng một đường tiệm cận ngang y = 0. 6 − x + 3)( 2 9x + ) 1 Do đó chọn m = 0.
* Trường hợp 2: m ≠ 0 . Page 151
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Xét phương trình ( 2 mx − x + )( 2 6 3 9x + 6mx + ) 1 = 0 ( ) 1
Nhận thấy: (C) luôn có một đường tiệm cận ngang y = 0 và phương trình ( ) 1 không thể có
duy nhất một nghiệm đơn với mọi m .
Do đó (C) có đúng một đường tiệm cận khi và chỉ khi (C) không có tiệm cận đứng ⇔ ( ) 1 vô 9  − 3m < 0 m > 3 nghiệm ⇔  ⇔ , . 2  9  m − 9 < 0  1 − < m <1
Kết hợp các trường hợp ta được m = 0.
Câu 33: Cho hàm số y = f (x) x +1 =
. Tìm tất cả các giá trị của tham số m để đồ thị có ba 2 x − 2mx + 4 đường tiệm cận  m > 2  m < 2 −  m < 2 − A. m  > 2 B.  m < 2 −  5 C. D. m ≠ −    m > 2  2  5 m ≠ −  2 Lời giải Chọn C
Để đồ thị có ba đường tiệm cận thì 2
x − 2mx + 4 = 0 có hai nghiệm phân biệt ≠ 1 −   m > 2  ∆ > 0     m < 2 − ⇔ (  −  ) ⇔ 2  1 − 2m(− ) 1 + 4 ≠ 0  5 m ≠ − ⋅  2
(n −3) x + n − 2017
Câu 34: Biết rằng đồ thị của hàm số y = ( ,
m n là các số thực) nhận trục hoành làm x + m + 3
tiệm cận ngang và trục tung là tiệm cận đứng. Tính tổng m + n. A. 0 B. 3 − C. 3 D. 6 Lờigiải Chọn A
Theo công thức tìm nhanh tiệm cận của đồ thị hàm số ax + b y = ta có cx + d Đồ thị hàm số nhận d
x = − = −m − 3 = 0 làm TCĐ⇒ m = 3 − c Đồ thị hàm số nhận a
y = = n − 3 = 0 làm TCN⇒ n = 3. c
Vậy m + n = 0.
Câu 35: Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số x −1 y = có đúng bốn 2 mx −8x + 2
đường tiệm cận? Page 152
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. 8 B. 6 C. 7 D. Vô số Lời giải
TH1: m < 0 suy ra tập xác định của hàm số là D = (x ; x , ( x ; x là nghiệm của phương trình 1 2 ) 1 2 2
mx −8x + 2 = 0 ). Do đó m < 0 không thỏa yêu cầu của bài toán. TH2: x − 1 m = 0 => y =
suy ra tập xác định của hàm số là D = ( ;4 −∞ ) . 8 − x + 2 lim y = ;
−∞ lim y = −∞ . Khi đó ta có x = 4
− là đường tiệm cận đứng của đồ thị hàm số. x x 4− →−∞ →
Do đó m = 0 không thỏa yêu cầu của bài toán
TH3: m > 0 suy ra tập xác định của hàm số là D = ( ;
−∞ x ∪ x ;+∞ ( x ; x là nghiệm của 1 ) ( 2 ) 1 2 phương trình 2
mx −8x + 2 = 0 ). Do đó đồ thị hàm số có bốn đường tiệm cận khi phương trình 2
mx −8x + 2 = 0 có hai nghiệm phân biệt khác 16  − 2m > 0 m < 8 1  m 0;  ⇔
> m∈ ⇔ m > 0;m∈ ⇒ m = {1;2;3;4;5; }
7 . Suy ra có tất cả 6 giá trị nguyên của m 8 2 0  − + ≠ m ≠   6
tham số m thỏa mãn yêu cầu của bài toán.
Câu 36: Với giá trị nào của hàm số m để đồ thị hàm số 2
y = x − mx − 3x + 7 có tiệm cạn ngang. A. m =1 B. m = 1 − C. m = 1 ±
D. Không có m Lời giải Chọn A
Đồ thị hàm số có tiệm cận ngang
⇒ Hàm số xác định trên một trong các miền ( ; −∞ a),( ;
−∞ a],(a,+∞) hoặc [ ; a +∞) m ≥ 0
TH1: m = 0 ⇒ y = x − 3
− x + 7, lim y = ±∞ đồ thị không có tiệm cận ngang x→±∞ TH2: 2
m > 0, y = x − mx − 3x + 7   Khi 3 7 3
lim y = lim  x − x m − +
 = đồ thị hàm số có tiệm cận ngang khi và chỉ khi m = 1. x  2 →+∞  x→+∞ x x 2   Vậy m =1
Cách trắc nghiệm: Thay m =1 2
⇒ y = x − x − x + ⇒
x − x − x +
= đồ thị hàm số có tiệm cận x→+∞ ( 2 ) 3 3 7 lim 3 7 2 ngang ⇒ ( 2
lim x − x − 3x + 7 = −∞ không có tiệm cận ngang. x→−∞ ) Thay m = 1 − 2
⇒ y = x − −x − x + ⇒ x x x không xác định. x ( 2 3 7 lim − − − 3 + 7 →+∞ ) Page 153
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ x x x không xác định. x ( 2 lim − − − 3 + 7 →−∞ ) Vậy m =1 Câu 37: Cho hàm số ax +1 y =
. Tìm a,b để đồ thị hàm số có x =1 là tiệm cận đứng và 1 y = là tiệm bx − 2 2 cận ngang. A. a = 1; − b = 2 .
B. a = 4;b = 4.
C. a =1;b = 2 . D. a = 1; − b = 2 − . Lời giải Chọn C + ax +
b = 0 ⇒ đồ thị hàm số 1 y = không có tiệm cận. 2 − + ax +
b ≠ 0 , tập xác định của hàm số 1 y = là 2 D R \   = . bx − 2   b  1 ax +1 a + lim = lim = lim x y = a . x→±∞
x→±∞ bx − 2 x→±∞ 2 − b b x ax + ⇒ đồ thị hàm số 1 y =
có tiệm cận ngang là đường thẳng a a 1
y = ⇒ = ⇔ b = 2a . bx − 2 b b 2 ax +1 +∞ lim y = lim =  . 2+ 2+ bx − x x −∞ → → 2 b b ax + ⇒ đồ thị hàm số 1 y =
có tiệm cận đứng là đường thẳng 2 2
x = ⇒ =1 ⇔ b = 2 ⇒ a =1. bx − 2 b b
Vậy a =1;b = 2 .
Câu 38: Có bao nhiêu giá trị nguyên m∈[ 10
− ;10] sao cho đồ thị hàm số x −1 y = có hai 2
2x + 6x − m − 3
đường tiệm cận đứng? A. 19. B. 15. C. 17 . D. 18. Lời giải Chọn C Ta có đồ thị hàm số x −1 y =
có hai đường tiệm cận đứng khi phương trình 2
2x + 6x − m − 3 2 3   15
 − 2(−m − 3) > 0 m > − 2
2x + 6x − m − 3 = 0 có hai nghiệm phân biệt khác 1 ⇔  ⇔  2 2
2.1 + 6.1− m − 3 ≠ 0 m ≠ 5
Từ đó ta suy ra tập các giá trị nguyên của m thỏa mãn là { 7 − , 6, − 5 − , 4, − 3 − , 2, − 1 − ,0,1,2,3,4,6,7,8,9,1 }
0 . Vậy có 17 giá trị nguyên của m thỏa mãn.
Câu 39: Có bao nhiêu giá trị nguyên của m để tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm 2 số mx + 3mx + 4 y = bằng 3? x + 2 A. 4 . B. 2 . C. Vô số. D. 3. Lời giải Page 154
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Chọn B 2 mx + 3mx + 4
Đồ thị hàm số y =
có nhiều nhất một tiệm cận đứng và hai tiệm cận ngang. x + 2 2 mx + 3mx + 4
Điều kiện để đồ thị hàm số y = x + 2
có 3 tiệm cận là nó có đúng 1 tiệm cận đứng và 2 tiệm cận ngang.
* Xét điều kiện tồn tại lim y và lim y x→+∞ x→−∞ m = 0 Trường hợp 1:  16 g (x) 2
= mx + 3mx + 4 ≥ 0 với x
∀ ∈ ⇔ m > 0 ⇔ 0 ≤ m ≤   9  2
∆ = 9m −16m ≤ 0
Trường hợp 2: g (x) 2
= mx + 3mx + 4 ≥ 0 với x ∀ ∈( ;
−∞ x ∪ x ;+∞ với x ; x là nghiệm 1 ) ( 2 ) 1 2 m > 0 của g (x) 16 ⇔  ⇔ m > 2
∆ = 9m −16m > 0 9
Vậy m ≥ 0 thì tồn tại lim y và lim y x→+∞ x→−∞ Khi đó: 3m 4 2 m + + 2 mx + 3mx + 4 lim = lim = lim x x y = m x→+∞ x→+∞ x + 2 x→+∞ 2 1+ x 3m 4 2 − m + + 2 mx + 3mx + 4 lim = lim = lim x x y = − m x→−∞ x→−∞ x + 2 x→−∞ 2 1+ x
Vậy điều kiện để đồ thị hàm số có hai đường tiệm cận ngang là m > 0
* Xét trường hợp x = 2
− là nghiệm của tử số⇒ x = 2
− là nghiệm của g (x) 2 = mx + 3mx + 4 ⇒ g ( 2 − ) = 0 ⇒ m = 2 2 2(x + ) 1 (x + 2)  +  Khi đó 2x + 6x + 4 2(x ) y 1 = ⇒ lim y = = lim −  = −∞ x + 2 x 2− + x 2 x 2 − →− →−  x + 2   
⇒ Đồ thị hàm số có một tiệm cận đứng x = 2 − . ⇒ m = 2 thỏa mãn
* Xét trường hợp x = 2
− không là nghiệm của tử số, để x = 2
− là tiệm cận đứng của đồ thị g ( 2 − ) ≠ 0 hàm số thì  ⇔ g ( 2 − ) > ⇔ − > ⇔ < g  (− ) 0 4 2m 0 m 2 2 ≥ 0
⇒ đồ thị hàm số có một đường tiệm cận đứng x = 2 − với m ∀ ∈(0;2] 2 mx + 3mx + 4
Vậy điều kiện để đồ thị hàm số y = m ∀ ∈ 0;2 x + 2 có 3 tiệm cận là ( ]
Vậy có hai giá trị nguyên của m thỏa mãn đề bài là m =1; m = 2 . Page 155
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 40: Tổng các giá trị của tham số m để đồ thị của hàm số x −1 y = có đúng một 2 x + 2(m − ) 2 1 x + m − 2 tiệm cận đứng. 1 3 A. − . B. 2 . C. 3 − . D. 2 2 . Lời giải Chọn A Đặt f (x) 2 = x + (m − ) 2 2 1 x + m − 2
Đồ thị hàm số có đúng một tiệm cận đứng khi và chỉ khi f (x) = 0 có 2 nghiệm phân biệt trong
đó có 1 nghiệm x =1 hoặc f (x) = 0 có nghiệm kép
 (m− )2 −( 2 m − )  3 1 2 > 0  ∆′ >  0  m <   2 m =1     ⇔  f  ( ) = ⇔ 1  + 2  (m − ) 2 1 + m − 2 = 0 1 0 ⇔   m =1;m = 3 − ⇔ m = 3 − .   ∆′ = 3 0  3  3 m =  =  =  2 m m  2  2
Vậy tổng các giá trị m thỏa mãn là: 1 − . 2 Câu 41: Cho hàm số x3 y
. Có bao nhiêu giá trị nguyên thuộc đoạn 6;6 3 2
x 3mx  2 2m   1 xm
của tham số m để đồ thị hàm số có bốn đường tiệm cận? A. 12. B. 9. C. 8 . D. 11. Lời giải Chọn B
lim y  lim y  0 nên đồ thị hàm số có tiệm cận ngang là đường thẳng y  0. x x
Do đó, đồ thị hàm số có bốn đường tiệm cận khi phương trình 3 2
x mx  2 3 2m   1 xm  0
có 3 nghiệm phân biệt x  3. Xét phương trình 3 2
x mx  2 3 2m  
1 xm  0 ta có x m 3 2
x mx  2 3 2m  
1 xm  0  xm 2 x 2mx   1  0   . 2
x 2mx 1 0 
Phương trình có ba nghiệm phân biệt x  3 khi và chỉ khi m  3 và phương trình m3 m  3     m 1 2
x 2mx 1 0 có hai nghiệm phân biệt x  3  2  m 1 0    .  m 1  2 3  2.3.m 1 0     5 m   3 Page 156
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Do m nguyên và m 6;6 nên m 6;5;4;3;2;2;4;5;  6 .
Vậy có 9 giá trị nguyên của m thỏa mãn đề bài. 2
Câu 42: Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số 2x + 3x + = m y không có tiệm x − m cận đứng. A. m =1. B. m >1.
C. m =1và m = 0. D. m ≠ 0 . Lời giải Chọn C TXĐ \  { } m . 2 2 Có
2x − 3x + m  2m − 2m  lim
= lim 2x + 2m − 3+  . x→m x→ x − m mx − m  2
Để đồ thị hàm số không có tiệm cận đứng thì phải tồn tại 2x − 3 lim x + m , x→m x − mm = 0 2
⇒ 2m − 2m = 0 ⇔  m =1 Vậy đáp án C.
Câu 43: Có bao nhiêu giá trị nguyên của tham số thực m thuộc đoạn  2017;2017 để đồ thị hàm số x  2 y
có hai tiệm cận đứng. 2
x 4x m A. 2019 . B. 2021. C. 2018 . D. 2020 . Lời giải Chọn D
Để đồ thị hàm số x  2 y
có hai tiệm cận đứng thì phương trình 2
x 4x m  0 có 2
x 4x m
hai nghiệm phân biệt khác 2   2017  m  4 4m  0       m  12
m  2017;2016;..;  3 \   12 . 12   m   0   m   
Do đó số giá trị nguyên của tham số m thỏa đề bài là:3(2017) 11 2020 giá trị.
Câu 44: Cho hàm số y f(x) thỏa mãn lim f(x)  2019m , 4
lim f (x)  2020m . Hỏi có tất cả bao x x
nhiêu giá trị của m để đồ thị của hàm số y f(x) có duy nhất một tiệm cận ngang? A. 4. B. 2. C. 3. D. 1. Lời giải Chọn B
Đồ thị hàm số y = f (x) có duy nhất một tiệm cận ngang m = 0 4 2019m 2020m  ⇔ = ⇔  2019 . = 3 m  2020 Page 157
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Vậy có 2 giá trị của m thỏa bài toán Câu 45: Cho hàm số 1 y =
. Tìm tất cả các giá trị thực của tham số m để 2 x − (2m + )
1 x + 2mx − m  
đồ thị hàm số có 4 đường tiệm cận. 0 < m <1 m <1 0 ≤ m ≤1 A.     1 . B.  . C. m >1. D.  . m ≠ 1 1  m ≠ m ≠  2  2  2 Lời giải Chọn A Điều kiện x > . m
Ta có lim y = 0 ⇒ y = 0 là tiệm cận ngang của đồ thị hàm số. x→+∞ x = m Xét phương trình 2 x − (2m + )
1 x + 2mx − m = 0⇔    2 x − 
(2m + )1 x + 2m= 0(*)
Để hàm số có 4 đường tiệm cận thì phương trình (*)có 2 nghiệm phân biệt m < x < x 1 2 .  1  1 (2 − )2 1 > 0 m ≠ m m ≠   2  2  1  ⇔ (   − )( − )   m ≠
x m x m > 0 ⇔ x x − m(x + x ) 2 2
− m > 0 ⇔ m − m > 0 ⇔ . 1 2 1 2 1 2  2
x + x > 2m 2m+1> 2m 1  > 0 0 < m <1 1 2     
Câu 46: Có bao nhiêu giá trị nguyên của 6x − 3
m để đồ thị hàm số y = ( có đúng 2
mx − 6x + 3)( 2 9x + 6mx + ) 1 1 đường tiệm cận? A. 0. B. 2. C. 1. D. Vô số. Lời giải Chọn C Đặt f (x) 2
= mx − 6x + 3 và g (x) 2
= 9x + 6mx +1. Ta xét các trường hợp: 6x −3
+ Trường hợp 1: m = 0 khi đó ta có y = (
đồ thị hàm số có 1 đường tiệm cận 6 − x + 3)( 2 9x + )1
ngang là đường thẳng y = 0 do đó m = 0 thỏa mãn yêu cầu bài toán.
+ Trường hợp 2: m ≠ 0 và cả hai tam thức f (x) và g (x) đều vô nghiệm ∆  'f < 0 9  −  3m < 0 m > 3 ⇔  ⇔  ⇔  ⇔ m∈∅ . 2 ∆  '  g < 0 9  m − 9 < 0  1 − < m <1
+ Trường hợp 3: Tam thức g (x) nhận 1
x = làm nghiệm  1  13 g =   0 ⇔ m = − khi đó f (x) 2  2  12
luôn có 2 nghiệm phân biệt nên đồ thị hàm số đã cho có nhiều hơn 1 đường tiệm cận.
Vậy có 1 giá trị nguyên của 6x − 3
m để đồ thị hàm số y = ( có đúng 1 2
mx − 6x + 3)( 2 9x + 6mx + ) 1 đường tiệm cận Page 158
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 47: Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số: 2
y x mx 1 có tiệm cận ngang.
A. 0  m 1.
B. m 1.
C. m  1. D. m 1. Lời giải Chọn B
Điều kiện cần và đủ để đồ thị hàm số: 2
y x mx 1 có tiệm cận ngang là tồn tại số thực k   2
lim (x mx 1)  k  sao cho: x   2
lim (x mx 1)   k x  x
Hiển nhiên nếu m  0 thì giới 2
lim (x mx 1) không hữu hạn x Nếu m  0 ta có + 2
lim (x mx 1)  .  x 1 2 x(1m) + 2 x (1m)1 lim y  lim (  1)  lim  lim x x mx x x x 2
xmx 1 x 1 1 m  2 x
Để giới hạn trên hữu hạn khi và chỉ khi m=1. Câu 48: Cho hàm số x − 2 y =
. Có tất cả bao nhiêu giá trị của tham số m để đồ thị hàm số có 2 mx − 2x + 4
đúng hai đường tiệm cận ? A. 0 . B. 2 . C. 3. D. 1. Lời giải Chọn D
Với m = 0; ta có hàm số x − 2 y = = 2
− ⇒ Không thỏa mãn yêu cầu bài toán. 2 − x + 4
Với m ≠ 0 , ta có: x − 2 lim
= 0 ⇒ y = 0 là tiệm cận ngang của đồ thị hàm số. 2
x→±∞ mx − 2x + 4
Đồ thị hàm số có đúng hai đường tiệm cận ⇔ đồ thị hàm số có đúng 1 tiệm cận đứng ⇔ 2
mx − 2x + 4 = 0 có nghiệm duy nhất hoặc 2
mx − 2x + 4 = 0 có hai nghiệm phân biệt trong đó
có một nghiệm x = 2 . 2
mx − 2x + 4 = 0 có nghiệm duy nhất 1
⇔ ∆′ = 0 ⇔ 1− 4m = 0 ⇔ m = . 4 2
mx − 2x + 4 = 0 có hai nghiệm phân biệt trong đó có một nghiệm x = 2 .  1  ∆′ > 0 m < ⇔  ⇔ 
4 ⇒ m = 0 không thỏa mãn điều kiện. 4m = 0 m = 0
Vậy chỉ có một giá trị của m thỏa mãn yêu cầu bài toán.
Câu 49: Gọi S là tập các giá trị nguyên của m sao cho đồ thị hàm số 2019x y = có bốn đường 2 17x −1 − m x
tiệm cận . Tính số phần tử của tập S. Page 159
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. Vô số B. 3 C. 5 D. 4 Lời giải Chọn C 2019 2019 lim y = , lim y = . x→−∞
m − 17 x→+∞ 17 − m 2019 2019
Với m ≠ 17 thì đồ thị hàm số có hai đường tiệm cận ngang là y = , y = . m − 17 17 − m
Khi đó đồ thị hàm số đã cho có 4 đường tiệm cận khi và chỉ khi phương trình 2
17x −1 − m x = 0 ( )
1 có hai nghiệm phân biệt khác 0. m ≥ 0 m ≥ 0 Ta có: ( ) 2 1 17x 1 m x  ⇔ − = ⇔  ⇔ 2 2 2  17  x −1 = m x ( 2  17 − m  ) 2x =1 (2)
Phương trình có 2 nghiệm phân biệt khác 0 khi và chỉ khi phương trình có hai nghiệm phân m ≥ 0 biệt khác 0 ⇔  ⇔ 0 ≤ m < 17 . 2 17  − m > 0 Suy ra S = {0,1,2,3, } 4 .
Câu 50: Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho đồ thị hàm số ( ) x f x =
nhận trục tung làm tiệm cận đứng. Khi đó tổng các phần 3 3 4 2
x + mx +1 − x + x +1 + m x tử của S bằng A. 1 . B. 1 − . C. 1 . D. 1 − . 2 2 3 3 Lời giải Chọn B 1
Ta có: lim f (x) = lim . x→0 x→0 3 3 4 2
x + mx +1 − x + x +1 + m x x 3 3 4 2 Mà
x + mx +1 − x + x +1 lim + m x x→0 x  3 3 4 2 x + mx +1 −1 x + x +1 −1  = lim m x  − +  x→0  x x x    3 4 x mx x x  + + 2 = lim  − + m . x→0 3 3 4 2 3 4
x( x + mx +1 +1) x( (x + x +1) + x + x +1 +1)   
Đồ thị hàm số f (x) nhận trục tung làm tiệm cận đứng 2 3 (x + m) (x +1) 2 m 1 2 ⇔ lim( −
+ m ) = 0 ⇔ − + m = 0 . x→0 3 3 4 2 3 4 ( x + mx +1 +1)
(x + x +1) + x + x +1 +1 2 3 Page 160
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ 1 2
⇔ 6m + 3m − 2 = 0 Vậy m + m = − . 1 2 2
x(xm) 1
Câu 51: Có bao nhiêu giá trị m nguyên thuộc khoảng 10;10 để đồ thị hàm số y x  2
có đúng ba đường tiệm cận? A. 12. B. 11. C. 0 . D. 10. Lời giải Chọn A
Xét gx xxm1.
x(xm) 1
x(xm) 1 Ta có lim 1 và lim
 1. Nên đồ thị hàm số luôn có hai x x  2 x x  2
đường tiệm cận ngang y 1 và y  1. x 1
Trường hợp 1: m  0 khi đó hàm số là y
. Đồ thị hàm số có tiệm cận đứng là x  2 x  2.
Vậy m  0 thỏa mãn yêu cầu đề bài.
Trường hợp 2: m  0 . Hàm số gx có tập xác định là D ;0m;.
x  2  D . g(2)  2m 21 0 nên x  2 là tiệm cận đứng của đồ thị hàm số
Vậy m 1, m  2,. m  9 thỏa mãn. Nên có 9 giá trị m .
Trường hợp 3: m  0 . Hàm số gx có tập xác định là D ;m0;.
Để x  2 là tiệm cận đứng của đồ thị hàm số thì trước hết x  2  D hay m 2. Nên chỉ
có m  2 , m  1 thỏa mãn
Với m  1 ta có g(x)  xx  
1 1, g(2)  2 1 0nên x  2 là tiệm cận đứng của đồ thị hàm số.
Với m  2 ta có g(x)  xx  21, g(2)  xx  21 1 0 nên x  2 là
tiệm cận đứng của đồ thị hàm số.
Vậy 12 giá trị m nguyên thỏa mãn yêu cầu.
Câu 52: Tìm số giá trị nguyên thuộc đoạn [ 2019 −
;2019] của tham số m để đồ thị hàm số x − 3 y = 2
x + x − m
có đúng hai đường tiệm cận. A. 2007 . B. 2010 . C. 2009 . D. 2008 . Lời giải Chọn D. x − 3 ≥ 0
Điều kiện xác định:  . 2
x + x ≠ m
Dựa vào điều kiện xác định ta suy ra hàm số đã cho không có giới hạn khi x → −∞ . Page 161
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ x − 3 lim = 0, m ∀ . 2
x→+∞ x + x − m
⇒ y = 0 là pt đường tiệm cận ngang. Xét hàm số ( ) 2
f x = x + x .
f (x) = x + f (x) 1 ' 2 1; ' = 0 ⇔ x = − 2
Dựa vào bảng biến thiên ta thấy:
Khi m <12 thì đồ thị hàm số không có tiệm cận đứng.
Khi m ≥12 thì đồ thị hàm số có 1 tiệm cận đứng.
Do đó để hàm số có đúng 2 đường tiệm cận thì m∈[12;2019] .
Vậy có 2008 giá trị nguyên của m . Câu 53: Cho hàm số x −1 y =
. Có tất cả bao nhiêu giá trị m để đồ thị hàm số có đúng hai đường 2 mx − 2x + 3 tiệm cận. A. 2 B. 3 C. 0 D. 1 Lời giải Chọn B Nhận xét: + 2
f (x) = mx − 2x + 3có bậc ≥1 nên đồ thị hàm số luôn có 1 tiệm cận ngang.
+ Do đó: Yêu cầu bài toán 9 đồ thị hàm số có đúng 1 tiệm cận đứng.
+ m = 0, đồ thị hàm số có 1 tiệm cận đứng là đường thẳng 3
x = ⇒ m = 0 thỏa bài toán. 2
+ m ≠ 0 , đồ thị hàm số có đúng 1 tiệm cận đứng khi và chỉ khi phương trình 2
mx − 2x + 3 = 0  1 ∆ = f 0 =
có nghiệm kép hoặc nhận x m = 1 làm nghiệm  ⇔  ⇔ 3  f (1) = 0  m = 1 − + KL: 1 m 0; ; 1 ∈ − . 3    Câu 54: Cho hàm số 1 y =
với m là tham số. Tìm tất cả các giá trị của m để đồ thị hàm 3 2
x − 3x + m −1
số đã cho có 4 đường thẳng tiệm cận.
A. 1< m < 5. B. 1 − < m < 2 .
C. m <1 hoặc m > 5 . D. m > 2 hoặc m < 1 − . Lời giải Page 162
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Ta có 1 lim y = lim = 0, 1 lim y = lim không tồn tại. Suy ra x→+∞ x→+∞ 3 2
x − 3x + m −1 x→−∞ x→−∞ 3 2
x − 3x + m −1
y = 0 là đường tiệm cận ngang của đồ thị hàm số.
Do đó, để đồ thị hàm số đã cho có 4 đường thẳng tiệm cận thì phương trình 3 2
x − 3x + m −1 = 0 có 3 nghiệm phân biệt.
Xét hàm số g (x) 3 2
= x − 3x + m −1. Tập xác định D = . x = g′(x) 2
= 3x − 6x ; g′(x) 0 = 0 ⇔  . x = 2 Bảng biến thiên:
Từ bảng biến thiên, ta thấy phương trình 3 2
x − 3x + m −1 = 0 có 3 nghiệm phân biệt khi và chỉ
khi m − 5 < 0 < m −1 ⇔ 1< m < 5 . Câu 55: Hàm số
3x +1 + ax + b y =
không có tiệm cận đứng. Khi đó hiệu a −b bằng: (x − )2 1 A. 1 . − . C. 5 − . − . 2 B. 34 4 D. 12 Lời giải Chọn A
Do hàm số không có tiệm cận đứng nên f (x) = x + + ax + b = (x − )2 3 1
1 g (x) .  3  ( ) a + b + 2 = 0 1 = 0 a f = −  Suy ra   4 1  ⇔  ⇔ 
⇒ a − b = → đáp án A. f '  ( ) 3 1 = 0 a + = 0 5 2  4 b  = −  4 Chú ý: Với ( ) = ( n f x x − x
g x thì ta luôn có f (x ) = f '(x ) = f ' (x ) (n− )1 = ... = f x = 0 . 0 0 0 ( 0) 0 ) ( ) 2
Câu 56: Có bao nhiêu giá trị nguyên của tham để m đồ thị hàm số
−x + 2016x + 2017 − 24 7 y = có x − m tiệm cận đứng? A. vô số. B. 2 . C. 2017 D. 2019 . Lời giải Chọn C Biểu thức: 2
−x + 2016x + 2017 có nghĩa khi 2
−x + 2016x + 2017 ≥ 0 ⇔ 1 − ≤ x ≤ 2017 . Page 163
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Đặt f (x) 2
= −x + 2016x + 2017 .
Xét x − m = 0 ⇔ x = m . Vậy đồ thị nếu có tiệm cận đứng chỉ có thể là x = m , khi đó điều kiện  1 − ≤ x ≤ 2017 m∈  [ 1 − ;2017] ( ) 1 là:  ⇔  f  (m)  2 ≠ 0
 −m + 2016m + 2017 ≠ 24 7  (*) m ≠ 1 Ta có (*) 2
⇔ m − 2016m + 2015 ≠ 0 ⇔  (2) m ≠ 2015 Từ ( ) 1 ,(2) [ 1;2017]\{1; } 2015 m m ∈ ⇒ ∈ − 
→ có 2019 − 2 = 2017 số nguyên m thỏa mãn bài toán→ đáp án C.
Câu 57: Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho đồ thị hàm số ( ) x f x =
nhận trục tung làm tiệm cận đứng. Khi đó tổng các phần 3 3 4 2
x + mx +1 − x + x +1 + m x tử của S bằng A. 1 . B. 1 − . C. 1 . D. 1 − . 2 2 3 3 Lời giải Chọn B 1
Ta có: lim f (x) = lim . x→0 x→0 3 3 4 2
x + mx +1 − x + x +1 + m x x 3 3 4 2 Mà
x + mx +1 − x + x +1 lim + m x x→0 x  3 3 4 2 x + mx +1 −1 x + x +1 −1  = lim m x  − +  x→0  x x x    3 4 x mx x x  + + 2 = lim  − + m . x→0 3 3 4 2 3 4
x( x + mx +1 +1) x( (x + x +1) + x + x +1 +1)   
Đồ thị hàm số f (x) nhận trục tung làm tiệm cận đứng 2 3 (x + m) (x +1) 2 m 1 2 ⇔ lim( −
+ m ) = 0 ⇔ − + m = 0 . x→0 3 3 4 2 3 4 ( x + mx +1 +1)
(x + x +1) + x + x +1 +1 2 3 1 2
⇔ 6m + 3m − 2 = 0 Vậy m + m = − . 1 2 2
x(xm) 1
Câu 58: Có bao nhiêu giá trị m nguyên thuộc khoảng 10;10 để đồ thị hàm số y x  2
có đúng ba đường tiệm cận? A. 12. B. 11. C. 0 . D. 10. Lời giải Chọn A Page 164
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Xét gx xxm1.
x(xm) 1
x(xm) 1 Ta có lim 1 và lim
 1. Nên đồ thị hàm số luôn có hai x x  2 x x  2
đường tiệm cận ngang y 1 và y  1. x 1
Trường hợp 1: m  0 khi đó hàm số là y
. Đồ thị hàm số có tiệm cận đứng là x  2 x  2.
Vậy m  0 thỏa mãn yêu cầu đề bài.
Trường hợp 2: m  0 . Hàm số gx có tập xác định là D ;0m;.
x  2  D . g(2)  2m 21 0 nên x  2 là tiệm cận đứng của đồ thị hàm số
Vậy m 1, m  2,. m  9 thỏa mãn. Nên có 9 giá trị m .
Trường hợp 3: m  0 . Hàm số gx có tập xác định là D ;m0;.
Để x  2 là tiệm cận đứng của đồ thị hàm số thì trước hết x  2  D hay m 2. Nên chỉ
có m  2 , m  1 thỏa mãn
Với m  1 ta có g(x)  xx  
1 1, g(2)  2 1 0nên x  2 là tiệm cận đứng của đồ thị hàm số.
Với m  2 ta có g(x)  xx  21, g(2)  xx  21 1 0 nên x  2 là
tiệm cận đứng của đồ thị hàm số.
Vậy 12 giá trị m nguyên thỏa mãn yêu cầu. 2
Câu 59: Tìm tất cả các giá trị thực của m sao cho đồ thị hàm số mx +1 y =
có đúng một đường tiệm x +1 cận.
A. −1 ≤ m < 0 .
B. −1 ≤ m ≤ 0 . C. m < 1 − . D. m > 0 . Lời giải Chọn A Nếu m = 0 thì 1 y =
. Hàm số này có tập xác định D =  \{− } 1 . x +1 Ta có 1 lim
= 0 nên đồ thị hàm số có tiệm cận ngang là y = 0. x→+∞ x +1 1 lim
= +∞ nên đồ thị hàm số có tiệm cận đứng x = 1 − . x ( ) 1 + → − x +1
Vậy với m = 0 thì đồ thị hàm số có hai đường tiệm cận . Nếu m > 0 thì 2
mx +1 > 0 với mọi x và tập xác định của hàm số là D =  \{− } 1 . Page 165
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ 1 1 2 mx +1 m + − m + 2 2 2 lim mx +1 = lim x = m , lim = lim
x = − m . Suy ra đồ thị hàm x→+∞ x +1 x→+∞ 1 1+ x→−∞ x +1 x→+∞ 1 1+ x x
số có hai tiệm cận ngang là y = m và y = − m . 2 mx +1 lim = +∞ nên x = 1
− là đường tiệm cận đứng của đồ thị hàm số. x ( ) 1 + → − x +1
Vậy m > 0 không thỏa mãn.   Nếu m 1 1
< 0 thì tập xác định của hàm số là D = − − ; −  \{− } 1 . m m  
Trường hợp này đồ thị hàm số không có tiệm cận ngang. Để đồ thị hàm số có đúng một đường
tiệm cận thì đồ thị hàm số phải có một tiệm cận đứng. Điều này xảy ra khi 1 − − ≤ 1 − 1 ⇔ − ≥ 1 1 ⇔ − ≥ 1 ⇔ m ≥ 1 − . m m m Vậy với 1
− ≤ m < 0 thì đồ thị hàm số có đúng một đường tiệm cận. Page 166
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
NG I ỨNG DỤNG ĐẠO HÀM ƯƠ
ĐỂ KHẢO SÁT HÀM SỐ CH
BÀI 4. ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
III BÀI TẬP TRẮC NGHIỆM. (MỨC 9 – 10)
DẠNG. XÁC ĐỊNH TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ g (x) KHI BIẾT BẢNG BIẾN THIÊN
HÀM SỐ f (x)
Câu 1: Cho đồ thị hàm số y = f (x) 3x −1 =
. Khi đó đường thẳng nào sau đây là đường tiệm cận đứng x −1 của đồ thị hàm số 1 y = ? f (x) − 2 A. x = 1. B. x = 2 − . C. x = 1 − . D. x = 2 .
Câu 2: Cho hàm số y = f (x) có đồ thị như hình vẽ
Số tiệm cận đứng của đồ thị hàm số 2019 y = là f (x) −1 A. 1. B. 2 . C. 3. D. 4 .
Câu 3: Cho hàm số f (x) xác định và liên tục trên  \{ } 1
− có bảng biến thiên như sau: Page 191
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Hỏi đồ thị hàm số 1 y =
có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang? f (x) A. 4 . B. 3. C. 2 . D. 1.
Câu 4: Cho hàm số y = f (x) thỏa mãn lim f (x) = 1
− và lim f (x) = m . Có bao nhiêu giá trị thực x→−∞ x→+∞
của tham số m để hàm số 1 y =
có duy nhất một tiệm cận ngang. f (x) + 2 A. 1. B. 0 . C. 2 . D. Vô số.
Câu 5: Cho hàm số y = f (x) thỏa mãn 4
f (tan x) = cos x . Tìm tất cả các giá trị thực của m để đồ thị hàm số 2019 g(x) =
có hai tiệm cận đứng.
f (x) − m
A. m < 0 .
B. 0 < m <1.
C. m > 0.
D. m <1.
Câu 6: Cho hàm số y = f (x) xác định, liên tục trên  và có bảng biến thiên như hình bên dưới:
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số 1 y = là: 2 f (x) −1 A. 4 . B. 3. C. 1. D. 2 .
Câu 7: Cho hàm số y = f (x) liên tục trên  \{ }
1 và có bảng biến thiên như sau: Đồ thị 1 y =
có bao nhiêu đường tiệm cận đứng? 2 f (x)+3 A. 2. B. 0. C. 1. D. 3.
Câu 8: Cho hàm số y = f (x) liên tục trên  \{ }
1 và có bảng biến thiên như sau: Page 192
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Đồ thị hàm số 1 y =
có bao nhiêu đường tiệm cận đứng? 2 f (x) −5 A. 0 . B. 4 . C. 2 . D. 1.
Câu 9: Cho hàm số y = f (x) có bảng biến thiên như hình dưới đây.
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số 1 y = là 2 f (x) −1 A. 0. B. 1. C. 2. D. 3.
Câu 10: Cho hàm bậc ba y = f (x) có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số
( 2x +4x+3) 2x + x y =
có bao nhiêu đường tiệm cận đứng? 2
x f (x) − 2 f (x)   A. 2 . B. 3. C. 4 . D. 6 . Page 193
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 11: Cho hàm số ( ) 3 2
f x = ax + bx + cx + d có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số
( 2x −3x+2) − g (x) x 1 =
có bao nhiêu tiệm cận đứng? 2
x f (x) − f (x)   A. 2 . B. 4 . C. 3. D. 5.
Câu 12: Cho hàm số bậc ba ( ) 3 2
f x = ax + bx + cx + d có đồ thị như hình vẽ sau.
( 2x −3x+2) x−1
Hỏi đồ thị hàm số g (x) = (
có bao nhiêu tiệm cận đứng? x + ) 2
1  f (x) − f (x)   A. 5. B. 4 . C. 6 . D. 3.
Câu 13: Cho hàm số y = f (x) là hàm số đa thức có đồ thì như hình vẽ dưới đây, đặt 2 ( ) x − = x g x
. Hỏi đồ thị hàm số y = g (x) có bao nhiêu tiệm cận đứng? 2
f (x) − 2 f (x) A. 5. B. 3. C. 4 . D. 2 .
Câu 14: Cho hàm số y = f (x) xác định, liên tục trên  và có bảng biến thiên như hình bên dưới. Page 194
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số 1 y = là f ( 3 x + x) + 3 A. 2. B. 4. C. 3. D. 1.
Câu 15: Cho hàm số = ( ) 3 2
y f x = ax + bx + cx + d có đồ thị như bên dưới.
( 2x −2x) 2− x
Hỏi đồ thị hàm số y = (
có bao nhiêu đường tiệm cận đứng x − 3) 2
f (x) − f (x)   A. 4 . B. 6 . C. 3. D. 5. Câu 16: Cho hàm số 3 2
y = ax + bx + cx + d , (a ≠ 0) có đồ thị như hình dưới đây. f (x)
Hỏi đồ thị hàm số g (x) =
có bao nhiêu đường tiệm cận đứng? (x + )2 ( 2 1 x − 4x + 3) A. 2 . B. 1. C. 3. D. 4 . Page 195
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 17: Cho hàm số trùng phương 4 2
y ax bx c có đồ thị như hình vẽ. Hỏi đồ thị hàm số  2x   4  2 x  2xy
có tổng cộng bao nhiêu tiệm cận đứng?
f x 2 2 f x3   A. 5. B. 2. C. 3. D. 4. Page 196
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
NG I ỨNG DỤNG ĐẠO HÀM ƯƠ
ĐỂ KHẢO SÁT HÀM SỐ CH
BÀI 4. ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
III BÀI TẬP TRẮC NGHIỆM. (MỨC 9 – 10)
BÀI TẬP TRẮC NGHIỆM TRÍCH TỪ ĐỀ THAM KHẢO VÀ ĐỀ CHÍNH THỨC CỦA BỘ GIÁO
DỤC TỪ NĂM 2017 ĐẾN NAY
DẠNG. XÁC ĐỊNH TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ g (x) KHI BIẾT BẢNG BIẾN THIÊN
HÀM SỐ f (x)
Câu 1: Cho đồ thị hàm số y = f (x) 3x −1 =
. Khi đó đường thẳng nào sau đây là đường tiệm cận đứng x −1 của đồ thị hàm số 1 y = ? f (x) − 2 A. x = 1. B. x = 2 − . C. x = 1 − . D. x = 2 . Lời giải f (x) 3x −1 = 2 ⇔
= 2 ⇒ 3x −1 = 2x − 2 ⇔ x = 1 − . x −1 Với 1 y = ta có lim y = ; −∞ lim y = +∞ f (x) − 2 x ( ) 1 + x ( ) 1 − → − → − Vậy đồ thị hàm số 1 y =
có đường tiệm cận đứng x = 1 − . f (x) − 2
Câu 2: Cho hàm số y = f (x) có đồ thị như hình vẽ
Số tiệm cận đứng của đồ thị hàm số 2019 y = là f (x) −1 Page 137
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. 1. B. 2 . C. 3. D. 4 . Lời giải Chọn C
Từ đồ thị của hàm số y = f (x) suy ra tập xác định của hàm số y = f (x) là D = 
Do đó số đường tiệm cận đứng của đồ thị hàm số 2019 y =
chính là số nghiệm của phương f (x) −1
trình f (x) =1.
Qua đồ thị ta có: Đường thẳng y =1 cắt đồ thị hàm số y = f (x) tại 3 điểm phân biệt nên
phương trình f (x) =1 có 3 nghiệm phân biệt. Vậy đồ thị hàm số 2019 y =
có 3 đường tiệm cận đứng. f (x) −1
Câu 3: Cho hàm số f (x) xác định và liên tục trên  \{ } 1
− có bảng biến thiên như sau: Hỏi đồ thị hàm số 1 y =
có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang? f (x) A. 4 . B. 3. C. 2 . D. 1. Lời giải Chọn A Ta có: f (x) 1 1 lim = 2 ⇒ lim = ; f (x) 1 1 lim = 2 − ⇒ lim = − . x→−∞
x→−∞ f ( x) 2 x→+∞
x→+∞ f ( x) 2 Suy ra đồ thị hàm số 1 y =
có hai đường tiệm cận ngang là 1 y = và 1 y = − . f (x) 2 2
Dựa vào bảng biến thiên của hàm số y = f (x) ta thấy: phương trình f (x) = 0 có hai nghiệm phân biệt x < 1 − < x . 1 2
Khi đó: f (x = f x = 0 . 1 ) ( 2)
 lim f (x) = 0
 lim f (x) = 0
Ta có: x→x − 1 x→x − 1 1  ⇒ lim = +∞ và 2  ⇒ lim = +∞ .  − − →  > → f x  ( ) − x − → 1 > 0 x → f (x f x khi x x ) f  ( x) x 2 0 x khi x x ( ) 1 2 1
Vậy đồ thị hàm số y =
có hai tiệm cận đứng là đường thẳng x = x và x = x . f (x) 1 2 Do đó Chọn A Page 138
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 4: Cho hàm số y = f (x) thỏa mãn lim f (x) = 1
− và lim f (x) = m . Có bao nhiêu giá trị thực x→−∞ x→+∞
của tham số m để hàm số 1 y =
có duy nhất một tiệm cận ngang. f (x) + 2 A. 1. B. 0 . C. 2 . D. Vô số. Lời giải Chọn C Ta có 1 lim y = lim
= ⇒ Đồ thị hàm số có tiệm cận ngang y =1. x→−∞
x→−∞ f ( x) 1 + 2 TH 1: Nếu m = 1 − thì 1 lim = và 1 lim
= 1 thì đồ thị hàm số có một tiệm
x→−∞ f ( x) 1 + 2
x→+∞ f ( x) + 2 cận. TH 2: Nếu m ≠ 1 −
Để đồ thị hàm số có một tiệm cận ngang 1 ⇔ lim
không có giá trị hữu hạn
x→+∞ f ( x) + 2
⇔ m + 2 = 0 ⇔ m = 2 − . Vậy khi m∈{ 2; − − }
1 thì đồ thị hàm số có duy nhất một tiệm cận ngang.
Câu 5: Cho hàm số y = f (x) thỏa mãn 4
f (tan x) = cos x . Tìm tất cả các giá trị thực của m để đồ thị hàm số 2019 g(x) =
có hai tiệm cận đứng.
f (x) − m
A. m < 0 .
B. 0 < m <1.
C. m > 0.
D. m <1. Lời giải Chọn B 4 1
f (tan x) = cos x ⇔ f (tan x) = 1 ( ⇒ f (t) = 1+ tan x)2 2 2 2 (1+ t ) Hàm số 2019 2019 g(x) = ⇒ g(x) =
f (x) − m 1 − m 2 2 (1+ x ) Hàm số 1
g(x) có hai tiện cận đứng khi và chỉ khi phương trình
− m = 0 có hai nghiệm 2 2 (1+ x ) phân biệt 2 2 1 ⇔ (1+ x ) =
> 1 ⇔ 0 < m <1. m
Câu 6: Cho hàm số y = f (x) xác định, liên tục trên  và có bảng biến thiên như hình bên dưới:
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số 1 y = là: 2 f (x) −1 Page 139
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. 4 . B. 3. C. 1. D. 2 . Lời giải Đặt h(x) 1 = . 2 f (x) −1 *) Tiệm cận ngang: Ta có: h(x) 1 lim = lim = . x→+∞ x→+∞ f (x) 0 2 −1 h(x) 1 lim = lim = . x→−∞ x→−∞ f (x) 0 2 −1
Suy ra đồ thị hàm số có một đường tiệm cận ngang y = 0. *) Tiệm cận đứng:
Xét phương trình: 2 f (x) −1= 0 ⇔ f (x) 1 = . 2
Dựa vào bảng biến thiên ta thấy phương trình f (x) 1
= có ba nghiệm phân biệt a, , b c thỏa 2
mãn a <1< b < 2 < c .
Đồng thời lim h(x) = lim h(x) = lim h(x) = +∞ nên đồ thị hàm số y = h(x) có ba đường tiệm x a+ x b− x c+ → → →
cận đứng là x = a , x = b và x = c .
Vậy tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = h(x) là 4.
Câu 7: Cho hàm số y = f (x) liên tục trên  \{ }
1 và có bảng biến thiên như sau: Đồ thị 1 y =
có bao nhiêu đường tiệm cận đứng? 2 f (x)+3 A. 2. B. 0. C. 1. D. 3. Lời giải Chọn A
Đặt y = g (x) 1 =
có tử số là 1 ≠ 0, x ∀ ∈  2 f (x)+3
Ta có f (x)+ = ⇔ f (x) 3 2 3 0 = − . 2 Page 140
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Từ bảng biến thiên có phương trình có 2 nghiệm phân biệt: x ∈(−∞;0), x ∈(0;1) . 1 2 Do đó đồ thị hàm số 1 y =
có 2 đường tiệm cận đứng. 2 f (x)+3
Câu 8: Cho hàm số y = f (x) liên tục trên  \{ }
1 và có bảng biến thiên như sau: Đồ thị hàm số 1 y =
có bao nhiêu đường tiệm cận đứng? 2 f (x) −5 A. 0 . B. 4 . C. 2 . D. 1. Lời giải
Ta có: f (x) − = ⇔ f (x) 5 2 5 0 = ( ) 1 . Phương trình ( )
1 có 4 nghiệm phân biệt x , x , x , x ≠1 2 1 2 3 4
và giới hạn của hàm số 1 y =
tại các điểm x , x , x , x đều bằng ±∞ . 2 f (x) −5 1 2 3 4 Mặt khác 1 lim
= 0 nên x =1 không phải tiệm cận đứng. x 1± → 2 f (x) −5 Vậy đồ thị hàm số 1 y =
có 4 đường tiệm cận đứng. 2 f (x) −5
Câu 9: Cho hàm số y = f (x) có bảng biến thiên như hình dưới đây. Page 141
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số 1 y = là 2 f (x) −1 A. 0. B. 1. C. 2. D. 3. Lời giải 1
Số tiệm cận đứng của đồ thị hàm số y =
đúng bằng số nghiệm thực của phương trình 2 f (x) −1
f (x) − = ⇔ f (x) 1 2 1 0 = . 2
Mà số nghiệm thực của phương trình f (x) 1
= bằng số giao điểm của đồ thị hàm số y = f (x) 2 1
với đường thẳng y = . 2 1
Dựa vào bảng biến thiên ta thấy đường thẳng y = cắt đồ thị hàm số y = f (x) tại 2 điểm phân 2 1
biệt. Vậy đồ thị hàm số y = có 2 tiệm cận đứng. 2 f (x) −1 1 Lại có lim
= ⇒ đồ thị hàm số có một tiệm cận ngang là y =1. x→±∞ f (x) 1 2 −1
Vậy tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số 1 y = là 3. 2 f (x) −1
Câu 10: Cho hàm bậc ba y = f (x) có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số
( 2x +4x+3) 2x + x y =
có bao nhiêu đường tiệm cận đứng? 2
x f (x) − 2 f (x)   A. 2 . B. 3. C. 4 . D. 6 . Lời giải Page 142
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
( 2x +4x+3) 2x + x (x+ )1(x+3) x(x+ )1 y = = 2
x f (x) − 2 f (x)
.x f (x). f    ( x) − 2 x ≥ 0
Điều kiện tồn tại căn 2 x + x :  . x ≤ 1 − x = 0  Xét phương trình 2
x f (x) − 2 f (x) = 0 ⇔  
f ( x) = 0 .  f (x) = 2
(x + )1(x +3) x(x + )1
(x + )1(x +3) x +1 Với x = 0 ta có lim = lim
= +∞ . Suy ra x = 0 là x 0+
.x f (x). f (x) −  x 0 2 + → →
x. f (x). f (x) − 2     tiệm cận đứng.
Với f (x) = 0 ⇒ x = 3
− hoặc x = a .
(x + )1(x +3) x(x + )1 Ta có: lim = −∞ nên x = 3 − là tiệm cận đứng. x 3+ →−
.x f (x). f (x) − 2   x = 1 − 
Với f (x) = 2 ⇒ x = b( 3 − < b < − ) 1 . Ta có:
x = c(c < 3 −  )  (x + )
1 (x + 3) x(x + ) 1  lim = 0
(x + )1(x +3) x(x + )1 x→ 1+ −  .x f  (x). f  ( x) − 2 lim =   nên x = 1 − không là tiệm x b+ →
x f (x)  f (x) 0 . . − 2    (x + )
1 (x + 3) x(x + ) 1  lim = 0 x→ 1− −
.x f (x). f (x) − 2    cận đứng. (x + )
1 (x + 3) x(x + ) 1 lim
= +∞ nên x = b là tiệm cận đứng. x b+ →
.x f (x). f (x) − 2   (x + )
1 (x + 3) x(x + ) 1 lim
= +∞ nên x = c là tiệm cận đứng. x c+ →
.x f (x). f (x) − 2  
Vậy đồ thị hàm số có 4 tiệm cận đứng. Page 143
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 11: Cho hàm số ( ) 3 2
f x = ax + bx + cx + d có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số
( 2x −3x+2) − g (x) x 1 =
có bao nhiêu tiệm cận đứng? 2
x f (x) − f (x)   A. 2 . B. 4 . C. 3. D. 5. Lời giải Chọn C
Nhận xét 1: Với x ≥1 và lim g (x) hoặc lim g (x) có kết quả là +∞ hoặc −∞ thì x = x là 0 0 x + → − 0 x x→ 0 x
tiệm cận đứng của của đồ thị hàm số g (x) .
Nhận xét 2: Dựa vào đồ thị hàm số f (x) ta có: f (x) = a(x − x )(x − 2)2 . 1 x = 0  Ta có 2
x f (x) − f (x) = 0 ⇔  
f ( x) = 0 .  f (x) =1  = < < f (x) x x ,0 x 1 1 1 = 0 ⇔  . x = 2 x =1 f (x) 1 
= ⇔ x = x ,1< x < 2 
suy ra f (x) −1= a(x − )
1 (x − x x − x . 2 ) ( 3 ) 2 2
x = x , x >  2 3 3
( 2x −3x+2) x−1 (x− )1(x−2) x−1
Khi đó ta có g (x) = = . 2
x f (x) − f (x)
.x f (x)  f    ( x) −1 − − − g (x) (x ) 1 (x 2) x 1 x −1 = = .
.xa(x − x x − 2 .a x −1 x − x x − x a x x − x
x − 2 x − x x − x 1 ) ( )2 ( )( 2 ) ( 3 ) 2 ( 1 ) ( )( 2 ) ( 3 )
x = 0, x = x không phải tiệm cận đứng của đồ thị hàm số y = g (x) không thỏa mãn điều kiện 1
x ≥1. Đồ thị hàm số g (x) có 3 đường tiệm cận đứng là: x = 2, x = x , x = x . 0 2 3
Câu 12: Cho hàm số bậc ba ( ) 3 2
f x = ax + bx + cx + d có đồ thị như hình vẽ sau. Page 144
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
( 2x −3x+2) x−1
Hỏi đồ thị hàm số g (x) = (
có bao nhiêu tiệm cận đứng? x + ) 2
1  f (x) − f (x)   A. 5. B. 4 . C. 6 . D. 3. Lời giải Chọn D
x −1 x − 2 x −1 Ta có g (x) ( )( ) = ( x + )
1 f (x)  f (x) −1   x ≥1 
Đkxđ:  f (x) ≠ 0  f  ( x) ≠ 1
Dựa vào đồ thị hàm số y = f (x) , ta có:  = f (x) x 2 = 0 ⇔ 
với x = 2 là nghiệm kép, x ∈ 0;1 . 1 ( ) x =  x1 x =1 f (x) 1 
= ⇔ x = x với x ∈ 1;2 ; x > 2 . 2 ( ) 2  3 x =  x3
x −1 x − 2 x −1 Vậy g (x) ( )( ) = 2 a (x + )
1 (x − 2)2 (x − x x −1 x − x x − x 1 ) ( )( 2 ) ( 3 ) x −1 = 2 a (x + )
1 (x − 2)(x − x x − x x − x 1 ) ( 2 ) ( 3 )
Vậy đồ thị hàm số có 3 TCĐ x = 2; x = x ; x = x . 2 3
Câu 13: Cho hàm số y = f (x) là hàm số đa thức có đồ thì như hình vẽ dưới đây, đặt 2 ( ) x − = x g x
. Hỏi đồ thị hàm số y = g (x) có bao nhiêu tiệm cận đứng? 2
f (x) − 2 f (x) Page 145
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. 5. B. 3. C. 4 . D. 2 . Lời giải Chọn C x =1  = < −  f (x) x x 1 1 = 0 Ta xét phương trình 2
f (x) − 2 f (x) = 0 ⇔  ⇔  = . Khi đó  f  ( x) x 0 = 2
x = x >1 2 
x = x < 1, − x ≠  x 3 3 1 2 g (x) x − x 1 = = ; a ≠ 0 . ax(x − )2
1 (x − x x − x x − x
a x −1 x − x x − x x − x 1 ) ( 2 ) ( 3 ) ( )( 1 ) ( 2 ) ( 3 ) ( )
Vậy đồ thị hàm số y = g (x) có 4 đường tiệm cận đứng.
Câu 14: Cho hàm số y = f (x) xác định, liên tục trên  và có bảng biến thiên như hình bên dưới.
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số 1 y = là f ( 3 x + x) + 3 A. 2. B. 4. C. 3. D. 1. Lời giải Chọn A Tính tiệm cận ngang. Ta có 3 x→+∞ 1
x + x →+∞ ⇒ lim = x→+∞ f ( 0 3 x + x) + 3 Page 146
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ 3 x→−∞ 1
x + x →−∞ ⇒ lim = x→−∞ f ( 0 3 x + x) + 3
Vậy đồ thị hàm số có 1 tiệm cận ngang y = 0. Tính tiệm cận đứng.
Số đường tiệm cận đứng của đồ thị hàm số là số nghiệm của phương trình f ( 3 x + x) + 3 = 0.
Dựa vào bảng biến thiên ta có f ( 3
x + x) + 3 = 0 ⇔ f ( 3 x + x) 3 = 3
− ⇔ x + x = x ; x ∈ −∞;1 0 0 ( ) Vì hàm số 3
y = x + x đồng biến trên  do đó 3
x + x = x ; x ∈ −∞;1 có một nghiệm duy 0 0 ( ) nhất. Vậy đồ thị hàm số 1 y =
có 1 tiệm cần đứng. f ( 3 x + x) + 3
Câu 15: Cho hàm số = ( ) 3 2
y f x = ax + bx + cx + d có đồ thị như bên dưới.
( 2x −2x) 2− x
Hỏi đồ thị hàm số y = (
có bao nhiêu đường tiệm cận đứng x − 3) 2
f (x) − f (x)   A. 4 . B. 6 . C. 3. D. 5. Lời giải Chọn C
Ta có y′(x) 2
= 3ax + 2bx + c .
Dựa vào đồ thị hàm số, ta thấy hàm số đạt cực trị tại x = 0 , x = 2 . Do đó, ta có hệ y (0) =1 d = 1 a = 1    y (2) = 3 − c = 0 b  = 3 −  ⇒  ⇒  . y′(0) =  0 12a + 4b = 0  c = 0  y′    (2) = 0 8  a + 4b = 4 − d = 1
Vậy y = f (x) 3 2 = x − 3x +1.
( 2x −2x) 2− x
( 2x −2x) 2− x
( 2x −2x) 2− x Khi đó y = ( = = . x − 3) 2
f (x) − f (x) 3 2 3 2 2 2  
(x −3)(x −3x + )1(x −3x ) x (x −3) ( 3 2 x − 3x + ) 1 Page 147
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ x = 0  x = 3 Ta có 2 x (x − )2 ( 3 2 3 x − 3x + ) 1 = 0  ⇔ x = x ∈ 1; − 0 . 1 ( )  x = x ∈ 0;1 2 ( )  x = x ∈ 2;3  3 ( )
( 2x −2x) 2− x Hàm số y =
có tập xác định D = ( ;
−∞ 2]\{0; x ; x . 1 2} 2 x (x − 3)2 ( 3 2 x − 3x + ) 1
( 2x −2x) 2− x
x(x − 2) 2 − x (x − 2) 2− x lim = lim = lim = −∞ . + → 2 x x (x − 3)2 ( 3 2 0 x − 3x + ) 1 + → 2 x x (x −3)2 ( 3 2 0 x − 3x + ) 1 x + → x(x − 3)2 ( 3 2 0 x − 3x + ) 1
Suy ra x = 0 là đường tiệm cận đứng.
( 2x −2x) 2− x
( 2x −2x) 2− x lim = +∞ , lim = +∞ . + → 2 2 3 2 x + → 2 2 3 2 1
x x ( x − 3) (x − 3x + ) 1 x 2
x x ( x − 3) (x − 3x + ) 1 Suy ra x = x x = x 1 và
2 cũng là các đường tiệm cận đứng của đồ thị hàm số. Câu 16: Cho hàm số 3 2
y = ax + bx + cx + d , (a ≠ 0) có đồ thị như hình dưới đây. f (x)
Hỏi đồ thị hàm số g (x) =
có bao nhiêu đường tiệm cận đứng? (x + )2 ( 2 1 x − 4x + 3) A. 2 . B. 1. C. 3. D. 4 . Lời giải  ≥  f (x) ≥ 0 x 2   x ≠ 1 − x ≥ 2
Điều kiện xác định: x ≠ 1 − ⇔  ⇔  .  x ≠ 1 x ≠ 3 2
x − 4x + 3 ≠ 0   x ≠ 3 f (x) f (x)
Ta có lim g (x) = lim
= +∞ và lim g (x) = lim = −∞ . x 3+ → x + → (x + )2 1 ( 2 3 x − 4x + 3) x 3− → x − → (x + )2 1 ( 2 3 x − 4x + 3) f (x)
Vậy đồ thị hàm số g (x) =
có một đường tiệm cận đứng là: x = 3. (x + )2 ( 2 1 x − 4x + 3) Page 148
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 17: Cho hàm số trùng phương 4 2
y ax bx c có đồ thị như hình vẽ. Hỏi đồ thị hàm số  2x   4  2 x  2xy
có tổng cộng bao nhiêu tiệm cận đứng?
f x 2 2 f x3   A. 5. B. 2. C. 3. D. 4. Lời giải Chọn D  2x   4  2 x  2x
xx  22 x2 y  
f x 2 2 f x3 2  
f x 2 f x3  
x mm 2    x  0 f x1 
Ta có:  f x 2  2 f x3  0      
 x nn  2 f x   3   x  2  x  2 
Dựa vào đồ thị ta thấy các nghiệm x  0; x  2 là các nghiệm kép và đa thức 2 
xx  2 x2
f x 2  2 f x3  
có bậc là 8 nên y  2 2
a x x  22 x22 xmxn
Vậy hàm số có các tiệm cận đứng là x  0; x  2; x  ; m x n . Page 149
Document Outline

  • 001_01_10_GT12_BAI 4_TIEM CAN_TỰ LUẬN_DE
  • 001_01_10_GT12_BAI 4_TIEM CAN_TỰ LUẬN_HDG
  • 001_01_11_GT12_BAI 4_TIEM CAN_TRẮC NGHIỆM BỘ_DE
  • 001_01_11_GT12_BAI 4_TIEM CAN_TRẮC NGHIỆM BỘ_HDG
  • 001_01_12_GT12_BAI 4_TIEM CAN_BAI TẬP TRẮC NGHIỆM(MUC5-8)_DE
    • DẠNG. XÁC ĐỊNH ĐƯỜNG TIỆM CẬN THÔNG QUA BẢNG BIẾN THIÊN, ĐỒ THỊ
      • 1.1.1 Đường tiệm cận ngang
      • 1.1.2 Đường tiệm cận đứng
    • DẠNG 2. XÁC ĐỊNH ĐƯỜNG TIỆM CẬN ĐỒ THỊ HÀM SỐ THÔNG HÀM SỐ CHO TRƯỚC
      • 1 Đường tiệm cận ngang
      • 2 Đường tiệm cận đứng
  • 001_01_12_GT12_BAI 4_TIEM CAN_BAI TẬP TRẮC NGHIỆM(MUC5-8)_HDG_CHI TIẾT
    • DẠNG. XÁC ĐỊNH ĐƯỜNG TIỆM CẬN THÔNG QUA BẢNG BIẾN THIÊN, ĐỒ THỊ
      • 1.1.1 Đường tiệm cận ngang
      • 1.1.2 Đường tiệm cận đứng
    • DẠNG 2. XÁC ĐỊNH ĐƯỜNG TIỆM CẬN ĐỒ THỊ HÀM SỐ THÔNG HÀM SỐ CHO TRƯỚC
      • 1 Đường tiệm cận ngang
      • 2 Đường tiệm cận đứng
      • 2 Đường tiệm cận đứng
  • 001_01_12_GT12_BAI 4_TIEM CAN_BAI TẬP TRẮC NGHIỆM(MUC9-10)_DE
    • DẠNG. XÁC ĐỊNH TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ KHI BIẾT BẢNG BIẾN THIÊN HÀM SỐ
  • 001_01_12_GT12_BAI 4_TIEM CAN_BAI TẬP TRẮC NGHIỆM(MUC9-10)_HDG_CHI TIẾT
    • DẠNG. XÁC ĐỊNH TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ KHI BIẾT BẢNG BIẾN THIÊN HÀM SỐ